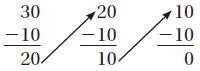Download Go Math Grade 7 Answer Key for Chapter 5 Percent Increase and Decrease pdf for free. Quick and easy learning is possible with Go Math 7th Grade Answer Key Chapter 5 Percent Increase and Decrease. So, we suggest the students of 7th standard to go through the HMH Go Math Grade 7 Key Chapter 5 Percent Increase and Decrease. Our team of Go Math Answer Key will help the Grade 7 students to score the highest marks.
Go Math Grade 7 Answer Key Chapter 5 Percent Increase and Decrease
Get a brief explanation for all the questions in Chapter 5 Percent Increase and Decrease Go Math Answer Key Grade 7. Tap on the links provided below and get the solutions according to the topics. So, utilize the time in the proper way and practice Go Math 7th Grade Solution Key Chapter 5 Percent Increase and Decrease.
Chapter 5 – Percent Increase and Decrease
- Percent Increase and Decrease – Guided Practice – Page No. 144
- Percent Increase and Decrease – Independent Practice – Page No. 145
- Percent Increase and Decrease – Page No. 146
Chapter 5 – Rewriting Percent Expressions
- Rewriting Percent Expressions – Guided Practice – Page No. 150
- Rewriting Percent Expressions – Independent Practice – Page No. 151
- Rewriting Percent Expressions – Page No. 152
Chapter 5 – Applications of Percent
- Applications of Percent – Guided Practice – Page No. 156
- Applications of Percent – Independent Practice – Page No. 157
- Applications of Percent – Page No. 158
Chapter 5
- MODULE QUIZ – 5.1 Percent Increase and Decrease – Page No. 159
- Selected Response – Page No. 160
- Module 5 – Page No. 162
- Unit 2 Performance Tasks – Page No. 163
- Unit 2 Performance Tasks (con’td) – Page No. 164
- Selected Response – Page No. 165
- Page No. 166
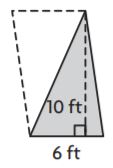
Percent Increase and Decrease – Guided Practice – Page No. 144
Find each percent increase. Round to the nearest percent.
Question 1.
From $5 to $8
______ %
Answer: 60%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 5
Final amount = 8
8 – 5 = 3
Percent change = 3/5 = 0.6 = 60%
Question 2.
From 20 students to 30 students
______ %
Answer: 50%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 20
Final amount = 30
We find the amount of change
30 – 20 = 10
We determine the percent of the increase
Percent change = 10/20 = 0.5 = 50%
Question 3.
From 86 books to 150 books
______ %
Answer: 74%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 86
Final amount = 150
We find the amount of change
150 – 86 = 64
We determine the percent of increase and round it to the nearest percent
Percent Change = 64/86 ≈ 0.74 = 74%
Question 4.
From $3.49 to $3.89
______ %
Answer: 11%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 3.49
Final amount = 3.89
We find the amount of change
3.89 – 3.49 = 0.40
We determine the percent of increase and round it to the nearest percent
Percent Change = 0.40/0.39 ≈ 0.11 = 11%
Question 5.
From 13 friends to 14 friends
______ %
Answer: 8%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 13
Final amount = 14
We find the amount of change
14 – 13 = 1
We determine the percent of increase and round it to the nearest percent
Percent Change = 1/13 ≈ 0.08 = 8%
Question 6.
From 5 miles to 16 miles
______ %
Answer: 220%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 5
Final amount = 16
We find the amount of change
16 – 5 = 11
We determine the percent of increase and round it to the nearest percent
Percent Change = 11/5 = 2.2 = 220%
Question 7.
Nathan usually drinks 36 ounces of water per day. He read that he should drink 64 ounces of water per day. If he starts drinking 64 ounces, what is the percent increase? Round to the nearest percent.
______ %
Answer: 78%
Explanation:
Given,
Nathan usually drinks 36 ounces of water per day. He read that he should drink 64 ounces of water per day.
Original Amount: 36
Final Amount: 64
Percent Charge = Amount of Change/Original Amount
We find the amount of change
64 – 36 = 28
We determine the percent of increase and round it to the nearest percent
Percent Change = 28/36 ≈ 0.78 = 78%
Thus the nearest percent is 78%
Find each percent decrease. Round to the nearest percent.
Question 8.
From $80 to $64
______ %
Answer: 20%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 80
Final amount = 64
We find the amount of change
Amount of change = Greater value – Lesser value
= 80 – 64 = 16
We determine the percent of increase and round it to the nearest percent
Percent Change = 16/80 = 0.20 = 20%
Thus the nearest percent is 20%
Question 9.
From 95 °F to 68 °F
______ %
Answer: 28%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 95
Final amount = 68
We find the amount of change
Amount of change = Greater value – Lesser value
= 95 – 68 = 27
We determine the percent of increase and round it to the nearest percent
Percent Change = 27/98 ≈ 0.28 = 28%
Thus the nearest percent is 28%
Question 10.
From 90 points to 45 points
______ %
Answer: 50%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 90
Final amount = 45
We find the amount of change
Amount of change = Greater value – Lesser value
90 – 45 = 45
We determine the percent of increase and round it to the nearest percent
Percent Change = 45/90 = 0.50 = 50%
Thus the nearest percent is 50%
Question 11.
From 145 pounds to 132 pounds
______ %
Answer: 9%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 145
Final amount = 132
We find the amount of change
Amount of change = Greater value – Lesser value
145 – 132 = 13
We determine the percent of increase and round it to the nearest percent
Percent Change = 13/145 ≈ 0.09 = 9%
The nearest percent is 9%
Question 12.
From 64 photos to 21 photos
______ %
Answer: 67%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 64
Final amount = 21
We find the amount of change
Amount of change = Greater value – Lesser value
64 – 21 = 43
We determine the percent of increase and round it to the nearest percent
Percent Change = 43/64 ≈ 0.67 = 67%
Therefore the nearest percent is 67%
Question 13.
From 16 bagels to 0 bagels
______ %
Answer: 100%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 16
Final amount = 0
We find the amount of change
Amount of change = Greater value – Lesser value
16 – 0 = 16
We determine the percent of increase and round it to the nearest percent
Percent Change = 16/16 = 1.0% = 100%
Question 14.
Over the summer, Jackie played video games 3 hours per day. When school began in the fall, she was only allowed to play video games for half an hour per day. What is the percent decrease? Round to the nearest percent.
______ %
Answer: 83%
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 3
Final amount = 0.5
We find the amount of change
Amount of change = Greater value – Lesser value
3 – 0.5 = 2.5
We determine the percent of increase and round it to the nearest percent
Percent Change = 2.5/3 ≈ 0.83 = 83%
The nearest percent is 83%
Find the new amount given the original amount and the percent of change.
Question 15.
$9; 10% increase
$ ______
Answer: $9.90
Explanation:
Percent Charge = Amount of Change/Original Amount
Original amount = 9
Increase = 10%
We find the amount of change
0.1 × 9 = 0.90
New Amount = Original Amount + Amount of Change
9 + 0.90 = 9.90
Question 16.
48 cookies; 25% decrease
______ cookies
Answer: 36 cookies
Explanation:
Original amount = 48
Decrease = 25%
We find the amount of change
0.25 × 48 = 12
New Amount = Original Amount – Amount of Change
48 – 12 = 36
Thus the answer is 36 cookies.
Question 17.
340 pages; 20% decrease
______ pages
Answer: 272 pages
Explanation:
Original Amount: 340 pages
Decrease: 20%
We find the amount of change
0.20 × 340 = 68
New Amount = Original Amount – Amount of Change
340 – 68 = 272
The answer is 272 pages.
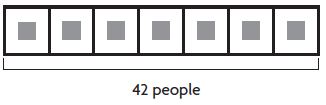
Question 18.
28 members; 50% increase
______ members
Answer: 42 members
Explanation:
Original Amount: 28
Increase: 50%
We find the amount of change
0.5 × 28 = 14
New amount = Original Amount + Amount of Change
28 + 14 = 42
The answer is 42 members
Question 19.
$29,000; 4% decrease
$ ______
Answer: $27,840
Explanation:
Original Amount: 29000
Decrease: 4%
We find the amount of change
0.04 × 29000 = 1160
New Amount = Original Amount – Amount of Change
29000 – 1160 = 27840
The answer is $27,840
Question 20.
810 songs; 130% increase
______ songs
Answer: 1863 songs
Explanation:
Original Amount: 810
Increase: 130%
We find the amount of change
1.3 × 810 = 1053
New amount = Original Amount + Amount of Change
810 + 1053 = 1863 songs
Question 21.
Adam currently runs about 20 miles per week, and he wants to increase his weekly mileage by 30%. How many miles will Adam run per week?
______ miles
Answer: 26 miles
Explanation:
Given,
Adam currently runs about 20 miles per week, and he wants to increase his weekly mileage by 30%.
Original Amount: 20
Increase: 30%
We find the amount of change
0.3 × 20 = 6
New amount = Original Amount + Amount of Change
= 20 + 6 = 26
Therefore Adam run 26 miles per week.
Essential Question Check-In
Question 22.
What process do you use to find the percent change of a quantity?
Type below:
_____________
Answer: In order to find the percent change of a quantity, we determine the amount of change in the quantity and divide it by the original amount.
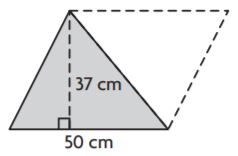
Percent Increase and Decrease – Independent Practice – Page No. 145
Question 23.
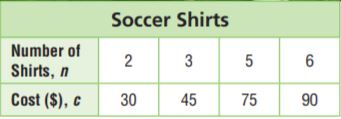
Complete the table.
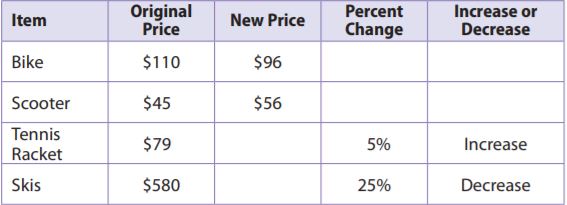
Type below:
_____________
Answer: bike: 13%, scooter 24%, increase, tennis racket: $83, skis: $435
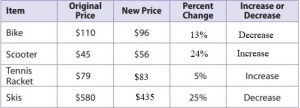
Explanation:
Since the new price is less than the original price, it is a percent decrease. percent decreases can be found using the equation percent decrease = (original – new)/original
Bike: 110 – 96/110 = 14/110 ≈ 13%
Scooter: 56 – 45/45 = 11/45 ≈ 24%
Use the equation percent increase = new – original/original
let x be the new price
skis: (580 – x)/580 = 0.25
580 – x = 0.25 × 580
580 – x = 145
x = 580 – 145 = 435
The new price is $435
Question 24.
Multiple Representations
The bar graph shows the number of hurricanes in the Atlantic Basin from 2006–2011.
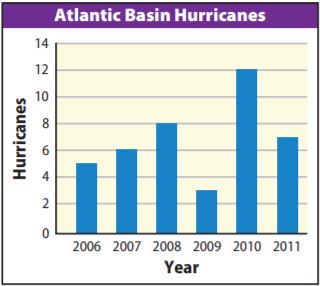
a. Find the amount of change and the percent of decrease in the number of hurricanes from 2008 to 2009 and from 2010 to 2011. Compare the amounts of change and percents of decrease.
Type below:
_____________
Answer: 2008 to 2009 has a smaller amount of change but a larger percent of decrease.
Explanation:
2008 to 2009:
amount of change: 8 – 3 = 5
percent decrease: 5/8 = 0.625 = 62.5%
2010 to 2011:
amount of change: 12 – 7 = 5
percent decrease: 5/12 ≈ 0.416 = 41.6%
The amount of change for 2010 to 2011 was greater than the amount of change for 2008 to 2009 but 2008 to 209 had a greater percent decrease than 2010 to 2011.
Question 24.
b. Between which two years was the percent of change the greatest? What was the percent of change during that period?
_______ %
Answer: 2009 and 2010, 300%
Explanation:
Use the percent change = amount of change/original amount.
The biggest change in heights is between 2009 and 2010.
The percent change is (12-3)/3 = 9/3 = 3 = 300%
Question 25.
Represent Real-World Problems
Cheese sticks that were previously priced at “5 for $1” are now “4 for $1”. Find each percent of change and show your work.
a. Find the percent decrease in the number of cheese sticks you can buy for $1.
_______ %
Answer: 20% decrease
Explanation:
Use the percent change = amount of change/original amount.
(5 – 4)/5 = 1/5 = 0.2 = 20% decrease
Question 25.
b. Find the percent increase in the price per cheese stick.
_______ %
Answer: 25% increase
Explanation:
First, find the price per cheese stick at each price.
Use the percent change = amount of change/original amount.
1.00/5 = 0.20
1/4 = 0.25
(0.25 – 0.20)/0.20 = 0.05/0.20 = 25% increase
Percent Increase and Decrease – Page No. 146
Question 26.
Percent error calculations are used to determine how close to the true values, or how accurate, experimental values really are. The formula is similar to finding percent of change.

chemistry class, Charlie records the volume of a liquid as 13.3 milliliters. The actual volume is 13.6 milliliters. What is his percent error? Round to the nearest percent.
_______ %
Answer: 2%
Explanation:
Use the formula

|13.3 – 13.6|/13.6 = |-0.3|/13.6 ≈ 0.02 = 2%
H.O.T.
Focus on Higher Order Thinking
Question 27.
Look for a Pattern
Leroi and Sylvia both put $100 in a savings account. Leroi decides he will put in an additional $10 each week. Sylvia decides to put in an additional 10% of the amount in the account each week.
a. Who has more money after the first additional deposit? Explain.
___________
Answer: the same
Explanation:
Since 10% of 100 is 100(0.10) = 10, they both make an additional deposit of 10, so they have the same amount of money after the first additional deposit.
Question 27.
b. Who has more money after the second additional deposit? Explain.
___________
Answer: Sylvia
Explanation:
Both Lerio and Sylvia have $110 in their account after their first deposits since they both started with $100 and both deposited $10 for their first deposit.
After the second deposit, Lerio has 110 + 10 = $120.
Sylvia has 110 + 0.10(110) = 110 + 11 = $121
So she has more money after the second deposit.
Question 27.
c. How do you think the amounts in the two accounts will compare after a month? A year?
Type below:
___________
Answer: Sylvia will continue to have more money after a month and a year since 10% of the balance is going to be greater than the 10 deposit that Leroi is making.
Question 28.
Critical Thinking
Suppose an amount increases by 100%, then decreases by 100%. Find the final amount. Would the situation change if the original increase was 150%? Explain your reasoning.
Type below:
___________
Answer: If an amount increases by 100%, then it will double. If it then decreases by 100%, it will become 0.
If you increase a number by 150% and then decrease it by 150%, you will not get to 0. 150% increase of 100 is 100 + 150 = 250.
A decrease of 150% is then 250 – 1.5(250) = 250 – 375 = -125
Question 29.
Look for a Pattern
Ariel deposited $100 into a bank account. Each Friday she will withdraw 10% of the money in the account to spend. Ariel thinks her account will be empty after 10 withdrawals. Do you agree? Explain.
___________
Answer: Ariel is incorrect. Her account balance will decrease as follows for the first 10 withdrawals:
1st withdrawal: 100 – 0.1(100) = 100 – 10 = 90
2nd withdrawal: 90 – 0.1(90) = 90 – 9 = 81
3rd withdrawal: 81 – 0.1(81) = 81 – 8.10 = 72.90
4th withdrawal: 72.90 – 0.1(72.90) = 72.90 – 7.29 = 65.61
5th withdrawal: 65.61 – 0.1(65.61) = 65.61 – 6.56 = 59.05
6th withdrawal: 59.05 – 0.1(59.05) = 59.05 – 5.91 = 53.14
7th withdrawal: 53.14 – 0.1(53.14) = 53.14 – 5.31 = 47.83
8th withdrawal: 47.83 – 0.1(47.83) = 47.83 – 4.78 = 43.05
9th withdrawal: 43.05 – 0.1(43.05) = 43.05 – 4.31 = 38.74
10th withdrawal: 38.74 – 0.1(38.74) = 38.74 – 3.87 = 34.87
Rewriting Percent Expressions – Guided Practice – Page No. 150
Question 1.
Dana buys dress shirts from a clothing manufacturer for s dollars each, and then sells the dress shirts in her retail clothing store at a 35% markup.
a. Write the markup as a decimal.
______
Answer: To convert a percent to a decimal, move the decimal place two places to the left. Therefore, 35% as a decimal is 0.35.
Question 1.
b. Write an expression for the retail price of the dress shirt.
Type below:
___________
Answer:
To write the expression, use the formula
retail price = original place + markup
Since s is the original place, if the markup is 35% = 0.35, then the markup is 0.35s.
Question 1.
c. What is the retail price of a dress shirt that Dana purchased for $32.00?
$ ______
Answer: Plugging in s = 32 into the expression gives a retail price of 1.35 = 1.35(32) = $43.20
Question 1.
d. How much was added to the original price of the dress shirt?
$ ______
Answer: The amount added to the original price is the amount of the markup. Since the amount of the markup is 0.35s and s = 32, then the amount of the markup was 0.35s = 0.35(32) = $11.20.
You can also find the amount of markup by subtracting the retail price and the original price. Since the retail price is $43.20 and the original price is $32, then the markup amount is $43.20 – $32 = $11.20
List the markup and retail price of each item. Round to two decimal places when necessary.
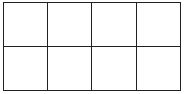
Question 2.

Markup: $ ______ Retail Price: $ ______
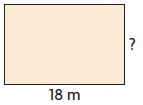
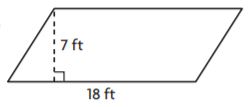
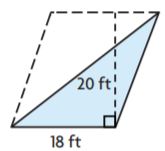
Answer: Markup: $ 2.70 Retail Price: $ 20.70
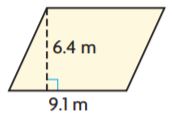
Explanation:
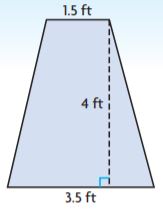
![]()
Use the formula markup = price(markup%)
18(0.15) = 2.70
Use the retail price formula = price + markup
18 + 2.70 = 20.70
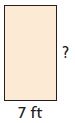
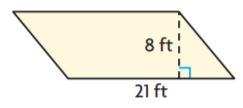
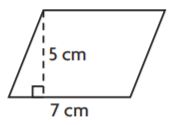
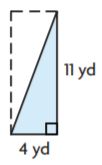
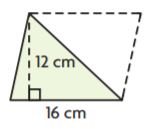
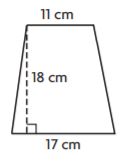
Question 3.
![]()
Markup: $ ______ Retail Price: $ ______
Answer:
![]()
Use the formula markup = (price)(markup %)
22.50(0.42) = 9.45
Use the retail price formula = price + markup
22.50 + 9.45 = 31.95
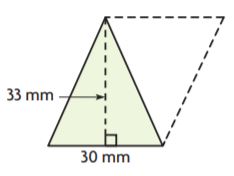
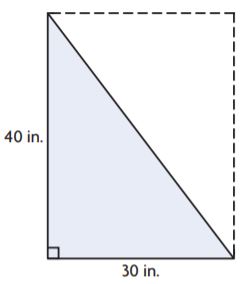
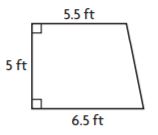
Question 4.
![]()
Markup: $ ______ Retail Price: $ ______
Answer:
![]()
Use the formula markup = (price)(markup %)
= 33.75(0.75) = 25.31
Use the formula retail price = price + markup
33.75 + 25.31 = 59.06
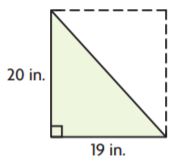
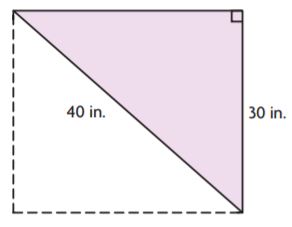
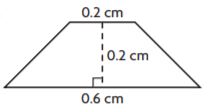
Question 5.
![]()
Markup: $ ______ Retail Price: $ ______
Answer:
![]()
Use the formula markup = (price)(markup %)
= 74.99(0.33) = 24.75
Use the formula retail price = price + markup
74.99 + 24.75 = 99.74
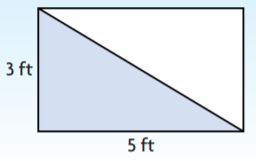
Question 6.

Markup: $ ______ Retail Price: $ ______
Answer:
![]()
Use the formula markup = (price)(markup %)
48.60(1.00) = 48.60
Use the formula retail price = price + markup
48.60 + 48.60 = 97.20
Question 7.

Markup: $ ______ Retail Price: $ ______
Answer:
![]()
Use the formula markup = (price)(markup %)
= 185 × 1.25 = 231.25
Use the formula retail price = price + markup
185 + 231.25 = 461.25
Find the sale price of each item. Round to two decimal places when necessary.
Question 8.
Original price: $45.00; Markdown: 22%
$ ______
Answer:
Use the formula markup = (price)(markup %)
45(0.22) = 9.90
Markdown is 9.90
Use the formula retail price = price + markup
45 – 9.90 = 35.10
Sale price is $35.10
Question 9.
Original price: $89.00; Markdown: 33%
$ ______
Answer:
Use the formula markup = (price)(markup %)
89 × 0.33 = 29.37
Use the formula retail price = price – markup
89 – 29.37 = 59.63
Question 10.
Original price: $23.99; Markdown: 44%
$ ______
Answer:
Use the formula markup = (price)(markup %)
23.99 × 0.44 = 10.56
Use the formula retail price = price – markup
23.99 – 10.56 = 13.43
Question 11.
Original price: $279.99, Markdown: 75%
$ ______
Answer:
Use the formula markup = (price)(markup %)
279.99 × 0.75 = 209.99
Use the formula retail price = price – markup
279.99 – 209.99 = 70
Essential Question Check-In
Question 12.
How can you determine the sale price if you are given the regular price and the percent of markdown?
Type below:
____________
Answer:
Use the formula
Sale price = Original Price – Markdown
If the Sale price is S, Original Price p, and x the average reduction, then the formula becomes:|
S = p – x . p
Rewriting Percent Expressions – Independent Practice – Page No. 151
Question 13.
A bookstore manager marks down the price of older hardcover books, which originally sell for b dollars, by 46%.
a. Write the markdown as a decimal.
______
Answer: 0.46
Explanation:
To convert a percent to decimal form, move the decimal point 2 places to the left and don’t write the percent symbol. Therefore, 46% as a decimal is 0.46.
Question 13.
b. Write an expression for the sale price of the hardcover book.
Type below:
____________
Answer: 0.54b
Explanation:
The sale price is the original price minus the discount amount. If the original price is discounted 46% and the original price is b dollars, the amount of the discount is 46% of b = 0.46b.
The sale price is then b – 0.46b = (1 – 0.46)b = 0.54b
Question 13.
c. What is the sale price of a hardcover book for which the original retail price was $29.00?
$ ______
Answer: $15.66
Explanation:
From part (b), the sale price of an item with an original price of b dollars is 0.54b. If the original price is then b = 29 dollars, the sale price is 0.54b = 0.54 × 29 = $15.66
Question 13.
d. If you buy the book in part c, how much do you save by paying the sale price?
$ ______
Answer: $13.34
Explanation:
The amount of savings is the difference between the original price and the sale price. If the original price is $29 and the sale price is $15.66, then the amount of savings is $29.00 – $15.66 = $13.34
Question 14.
Raquela’s coworker made price tags for several items that are to be marked down by 35%. Match each Regular Price to the correct Sale Price, if possible. Not all sales tags match an item.
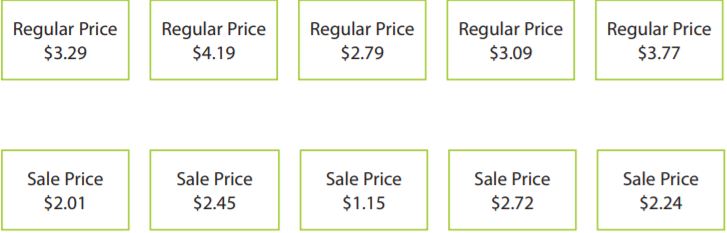
Type below:
_____________
Answer:
35% markdown means the expression for the sales price is p – 0.35p = 0.65p. Plug in the regular prices for p to find the sale prices. Remember the directions stated not all sales tags will match a regular price so you won’t be able to match every regular price ticket with a sale price ticket.
0.65(3.29) = 2.14
0.65(4.19) = 2.72
0.65(2.79) = 1.81
0.65(3.09) = 2.01
0.65(3.77) = 2.45
Question 15.
Communicate Mathematical Ideas
For each situation, give an example that includes the original price and final price after markup or markdown.
a. A markdown that is greater than 99% but less than 100%
Type below:
_____________
Answer:
A markdown that is greater than 99% but less than 100% could be 99.5%. If the original price is $100, then the final price is 100 – 100(0.995) = 100 – 99.50 = 0.50
Question 15.
b. A markdown that is less than 1%
Type below:
_____________
Answer:
A markdown that is less then 1% could be 0.5%. If the original price is $100, then the final price would be 100 – 0.005(100) = 100 – 0.50 = 99.50
Question 15.
c. A markup that is more than 200%
Type below:
_____________
Answer:
A markup that is more than 200% could be 300%. If the original price is $100, then the final price would be 100 + 100 (3.00) = 100 + 300 = 400
Rewriting Percent Expressions – Page No. 152
Question 16.
Represent Real-World Problems
Harold works at a men’s clothing store, which marks up its retail clothing by 27%. The store purchases pants for $74.00, suit jackets for $325.00, and dress shirts for $48.00. How much will Harold charge a customer for two pairs of pants, three dress shirts, and a suit jacket?
$ __________
Answer: $783.59
Explanation:
Given,
Harold works at a men’s clothing store, which marks up its retail clothing by 27%.
The store purchases pants for $74.00, suit jackets for $325.00, and dress shirts for $48.00.
If the markup is 27%, then the expression for the retail price is p + 0.27p = 1.27p
where p is the original price.
The retail price of the pants is then 1.27(74) = 93.98.
The retail price of the suit jackets is 1.27(325) = 412.75
The retail price of the dress shirts is 1.27(48) = 60.96
The total for two pants, three dress shirts, and one suit jacket would then be 2(93.98) + 3(60.96) + 412.75
= 187.96 + 182.88 + 412.75 = 783.59
Question 17.
Analyze Relationships
Your family needs a set of 4 tires. Which of the following deals would you prefer? Explain.
![]()
Type below:
____________
Answer: I and III
Explanation:
The percent discount for buying 3 tires and getting one free is 25% since you are getting 1/4 of the tires for free and 1/4 off = 25%.
This means deal (I) and deal (III) are the same. They are greater than a 20% discount so deals (I) and (III) are preferable.
H.O.T.
Focus on Higher Order Thinking
Question 18.
Critique Reasoning
Margo purchases bulk teas from a warehouse and marks up those prices by 20% for retail sale. When teas go unsold for more than two months, Margo marks down the retail price by 20%. She says that she is breaking even, that is, she is getting the same price for the tea that she paid for it. Is she correct? Explain.
_______
Answer:
She is not correct. If she originally purchases the teas for $100 and then marks the price up 20%, the retail price would then be 100 + 0.20(100) = 100 + 20 = 120.
The sales price would then be 120 – 0.2(120) = 120 – 24 = 96.
This less than the purchase price so she is losing money, not breaking even.
Question 19.
Problem Solving
Grady marks down some $2.49 pens to $1.99 for a week and then marks them back up to $2.49. Find the percent of increase and the percent of decrease to the nearest tenth. Are the percents of change the same for both price changes? If not, which is a greater change?
_______
Answer: The percent decrease is found by using the formula (original price – new price)/(original price). The percent decrease is then (2.49 – 1.99)/2.49 = 0.20 = 20%.
A percent increase is found by using the formula (new price – original price)/original price.
The percent increase is then (2.49 – 1.99)/1.99 = 0.25 = 25%
The percents of change are not the same. The percent increase is greater.
Question 20.
Persevere in Problem Solving
At Danielle’s clothing boutique, if an item does not sell for eight weeks, she marks it down by 15%. If it remains unsold after that, she marks it down an additional 5% each week until she can no longer make a profit. Then she donates it to charity.
Rafael wants to buy a coat originally priced $150, but he can’t afford more than $110. If Danielle paid $100 for the coat, during which week(s) could Rafael buy the coat within his budget? Justify your answer.
Type below:
_____________
Answer:
The expression for the markdown on the 8th week is p – 0.15p = 0.85p since it will get marked down 15% on the 8th week.
The expression for the additional markdowns is p – 0.05p = 0.95p since it will get marked down an additional 5% every week after the 8th week.
On the 8th week, it will be marked down to 0.85(150) = 127.50. This is more than Rafael can afford.
On the 9th week, it will be marked down to 0.95(127.50) = 121.13. This is still more than Rafael can afford.
On the 10th week, it will be marked down to 0.95(121.13) = 115.07. This is still more than Rafael can afford.
On the 11th week, it will be marked down to 0.95(115.07) = 109.32. Rafael can afford this price so he must wait until the 11th week.
Applications of Percent – Guided Practice – Page No. 156
Question 1.
5% of $30 =
$ _______
Answer: $1.5
Explanation:
We have to find:
5% of $30
0.50 × 30 = $1.5
Question 2.
15% of $70 =
$ _______
Answer: $10.5
Explanation:
We have to find:
15% of $70
0.15 × 70 = 10.5
Question 3.
0.4% of $100 =
$ _______
Answer: $0.40
Explanation:
We have to find:
0.4% of $100
0.004 × 100 = 0.40
Question 4.
150% of $22 =
$ _______
Answer: $33
Explanation:
We have to find:
150% of $22
1.5 × 22 = 33
Question 5.
1% of $80 =
$ _______
Answer: $0.8
Explanation:
We have to find:
1% of $80
0.01 × 80 = 0.8
Question 6.
200% of $5 =
$ _______
Answer: $10
Explanation:
We have to find:
200% of $5
2 × 5 = 10
Question 7.
Brandon buys a radio for $43.99 in a state where the sales tax is 7%.
a. How much does he pay in taxes?
$ _______
Answer: 3.08
Explanation:
We have to find the amount he pays in taxes by multiplying the cost by the sales tax percentage in decimal form remember to round to 2 decimal places.
43.99(0.07) = 3.08
Question 7.
b. What is the total Brandon pays for the radio?
$ _______
Answer: 47.07
Explanation:
To find the total Brandon pays for the radio we have to add the sales tax amount to the cost to find the total amount he pays.
43.99 + 3.08 = 47.07
Thus the total Brandon pays for the radio is $47.07.
Question 8.
Luisa’s restaurant bill comes to $75.50, and she leaves a 15% tip. What is Luisa’s total restaurant bill?
$ _______
Answer: $86.25
Explanation:
Given that,
Luisa’s restaurant bill comes to $75.50, and she leaves a 15% tip.
Use the formula for the total restaurant bill:
T = P + x. P
Where T represents the total bill, P represents Luisa’s bill and x represents percents for tip, then the total restaurant bill is:
T = 75 + 0.15 (75)
T = 75 + 11.25
T = $86.25
Therefore Lusia’s total restaurant bill is $86.25
Question 9.
Joe borrowed $2,000 from the bank at a rate of 7% simple interest per year. How much interest did he pay in 5 years?
$ _______
Answer: 700
Explanation:
Joe borrowed $2,000 from the bank at a rate of 7% simple interest per year.
We have to find the amount of interest per year
2000(0.07) = 140
Find the amount of interest for 5 years
140(5) = 700
Thus Joe pays $700 in 5 years.
Question 10.
You have $550 in a savings account that earns 3% simple interest each year. How much will be in your account in 10 years?
$ _______
Answer: $715
Explanation:
Given,
You have $550 in a savings account that earns 3% simple interest each year.
Use the formula for simple interest:
Bt = B0(1 + tr)
Where t is time interval, Bt is money after t years, B0 is deposit and r is interest for one year, then the formula becomes:
B10 = B0(1 + 10.r)
B10 = 550(1 + 10 (0.03))
B10 = $715
In your account after 10 years will be $715.
Question 11.
Martin finds a shirt on sale for 10% off at a department store. The original price was $20. Martin must also pay 8.5% sales tax.
a. How much is the shirt before taxes are applied?
$ _______
Answer: 18
Explanation:
We have to find the sales price of the shirt
20 – 0.1(20) = 20 – 2 = 18
The price of the shirt before taxes are applied is $18.
Question 11.
b. How much is the shirt after taxes are applied?
$ _______
Answer: 19.53
Explanation:
We have to find the price after sales tax
18 + 0.085(18) = 18 + 1.53 = 19.53
The price of the shirt after taxes are applied is $19.53
Question 12.
Teresa’s restaurant bill comes to $29.99 before tax. If the sales tax is 6.25% and she tips the waiter 20%, what is the total cost of the meal?
$ _______
Answer: 37.86
Explanation:
Given,
Teresa’s restaurant bill comes to $29.99 before tax. If the sales tax is 6.25% and she tips the waiter 20%.
Find the amount of sales tax
29.99(0.0625) = 1.87
Find the amount of the tip
29.99(0.20) = 6.00
The total cost by adding the bill account, sales tax, and tip amount.
29.99 + 1.87 + 6.00 = 37.86
Thus the total cost of the meal is $37.86
Essential Question Check-In
Question 13.
How can you determine the total cost of an item including tax if you know the price of the item and the tax rate?
Type below:
_____________
Answer: You can find the total cost of an item including tax by first multiplying the price of the item by the tax rate in decimal form to get the amount of sales tax. Then add the amount of sales tax to the price to get the total cost.
Applications of Percent – Independent Practice – Page No. 157
Question 14.
Emily’s meal costs $32.75 and Darren’s meal costs $39.88. Emily treats Darren by paying for both meals, and leaves a 14% tip. Find the total cost.
$ _______
Answer: 82.80
Explanation:
Emily’s meal costs $32.75 and Darren’s meal costs $39.88.
So, the total cost of the meals before tip is $32.75 + $39.88 = $72.63
Emily treats Darren by paying for both meals and leaves a 14% tip.
$72.63 = 0.14(72.63) ≈ $10.17
Round to two decimal places since dollar amounts must be rounded to the nearest cent.
The total cost that Dareen pays is then cost before tip + amount of tip = $72.63 + $10.17 = $82.80
Question 15.
The Jayden family eats at a restaurant that is having a 15% discount promotion. Their meal costs $78.65, and they leave a 20% tip. If the tip applies to the cost of the meal before the discount, what is the total cost of the meal?
$ _______
Answer: 82.58
Explanation:
The Jayden family eats at a restaurant that is having a 15% discount promotion.
The total cost of the meal = cost of meal + tip amount – discount amount
Their meal costs $78.65, and they leave a 20% tip.
We need to find the tip amount and the discount amount using the given cost of the meal, tip percent, and discount percent.
20% of 78.65 = 0.20 × 78.65 = $15.73
Since the cost of the meal before the discount is $78.65 and the discount percent is 15%, then the amount of the discount is
15% of 78365 = 0.15 × $78.65 ≈ $11.80
The total cost is then
78.65 + 15.73 – 11.80 = $82.58
Question 16.
A jeweler buys a ring from a jewelry maker for $125. He marks up the price by 135% for sale in his store. What is the selling price of the ring with 7.5% sales tax?
$ _______
Answer: 315.78
Explanation:
A jeweler buys a ring from a jewelry maker for $125. He marks up the price by 135% for sale in his store.
125 × 1.35 = 168.75
We can find the retail price by adding the markup to the purchase price
125 + 168.75 = 293.75
The amount of sales tax is 293.75 × 0.075 = 22.03
We can find the selling price by adding the tax amount to the retail price.
293.75 + 22.03 = 315.78
Therefore the selling price of the ring with 7.5% sales tax is $315.78
Question 17.
Luis wants to buy a skateboard that usually sells for $79.99. All merchandise is discounted by 12%. What is the total cost of the skateboard if Luis has to pay a state sales tax of 6.75%?
$ _______
Answer: 75.14
Explanation:
Given,
Luis wants to buy a skateboard that usually sells for $79.99. All merchandise is discounted by 12%.
79.99 × 0.12 = 9.60
79.99 – 9.60 = 70.39
First, we need to find the amount paid in taxes and then add that to the discount price to get the total cost.
70.39 × 0.0675 = 4.75
70.39 + 4.75 = 75.14
The total cost of the skateboard if Luis has to pay a state sales tax of 6.75% is $75.14
Question 18.
Kedar earns a monthly salary of $2,200 plus a 3.75% commission on the amount of his sales at a men’s clothing store. What would he earn this month if he sold $4,500 in clothing? Round to the nearest cent.
$ _______
Answer: 2368.75
Explanation:
Given,
Kedar earns a monthly salary of $2,200 plus a 3.75% commission on the amount of his sales at a men’s clothing store.
4500 × 0.0375 = 168.75
The total earnings can be known by adding his monthly salary and his commission.
2200 + 168.75 = 2368.75
Question 19.
Danielle earns a 7.25% commission on everything she sells at the electronics store where she works. She also earns a base salary of $750 per week. How much did she earn last week if she sold $4,500 in electronics merchandise? Round to the nearest cent.
$ _______
Answer: 1076.25
Explanation:
Danielle earns a 7.25% commission on everything she sells at the electronics store where she works.
She also earns a base salary of $750 per week.
The amount she made in the commission is 4500 × 0.0725 = 326.25
We can find the total earnings by adding her weekly pay and commission.
750 + 326.25 = 1076.25
Thus she earns $1076.25 last week if she sold $4,500 in electronics merchandise.
Question 20.
Francois earns a weekly salary of $475 plus a 5.5% commission on sales at a gift shop. How much would he earn in a week if he sold $700 in goods? Round to the nearest cent.
$ _______
Answer: 513.50
Explanation:
Given that, Francois earns a weekly salary of $475 plus a 5.5% commission on sales at a gift shop.
The amount he made in commission
700 × 0.055 = 38.50
We can find the total amount he earned by adding his weekly pay and commission
475 + 38.50 = $513.50
Question 21.
Sandra is 4 feet tall. Pablo is 10% taller than Sandra, and Michaela is 8% taller than Pablo
a. Explain how to find Michaela’s height with the given information.
Type below:
_____________
Answer:
First we have to find 10% of Sandra’s height: 0.10 × 4 = 0.4
This means that Pablo is then 4 + 0.4 = 4.4 feet tall.
Next find 8% of Pablo’s height: 4.4 × 0.08 = 0.352
This means that Michaela is 4.4 + 0.353 = 4.752 feet tall.
Question 21.
b. What is Michaela’s approximate height in feet and inches?
_______ feet _______ inches
Answer:
Convert from feet to inches.
1 feet = 12 inches
4.752 = 4 + 0.752
0.752 = 12 × 0.752 = 9 inches
4 feet = 12 × 4 = 48 inches
Thus the approximate height of Michaela is 4 feet 9 inches.
Question 22.
Eugene wants to buy jeans at a store that is giving $10 off everything. The tag on the jeans is marked 50% off. The original price is $49.98.
a. Find the total cost if the 50% discount is applied before the $10 discount.
$ _______
Answer: $14.99
Explanation:
Given that,
Eugene wants to buy jeans at a store that is giving $10 off everything.
The tag on the jeans is marked 50% off. The original price is $49.98.
0.5 × 49.98 = 24.99
Now subtract $10 discount.
24.99 – 10 = 14.99
The total cost if the 50% discount is applied before the $10 discount is $14.99
Question 22.
b. Find the total cost if the $10 discount is applied before the 50% discount.
$ _______
Answer: $19.99
Explanation:
We have to find the price after the $10 discount then find 50% of that price to find the discounted price.
49.98 – 10 = 39.98
0.5 × 39.98 = 19.99
Thus the total cost if the $10 discount is applied before the 50% discount is $19.99
Applications of Percent – Page No. 158
Question 23.
Multistep
Eric downloads the coupon shown and goes shopping at Gadgets Galore, where he buys a digital camera for $95 and an extra battery for $15.99.
a. What is the total cost if the coupon is applied to the digital camera?

$ _______
Answer: 101.49
Explanation:
Use the formula for the discount price:
DP = P – x.P
Price for the digital camera:
DP = 95 – 0.1(95)
DP = 95 – 9.5
DP = $85.5
Total cost = 85.5 + 15.99 = $101.49
Question 23.
b. What is the total cost if the coupon is applied to the extra battery?
$ _______
Answer: 109.391
Explanation:
Use the formula for the discount price:
DP = P – x.P
Price for the digital camera:
DP = 15.99 – 0.1(15.99)
DP = 15.99 – 1.599
DP = $14.399
Total cost = 95 + 14.399 = $109.391
Question 23.
c. To which item should Eric apply the discount? Explain.
____________
Answer: He should apply the discount to the digital camera because then the total cost is the lower.
Question 23.
d. Eric has to pay 8% sales tax after the coupon is applied. How much is his total bill?
$ _______
Answer:
Use formula for Discount price
If he uses coupon for the digital camera then his total cost will be
T = DP + 0.08 × DP
T = 101.49 + 8.1192
T = $109.6029
If he uses coupon for the extra battery his total cost will be
T = DP + 0.08 × DP
T = 109.391 + 0.08(109.391)
T = $118.14228
Question 24.
Two stores are having sales on the same shirts. The sale at Store 1 is “2 shirts for $22” and the sale at Store 2 is “Each $12.99 shirt is 10% off”.
a. Explain how much will you save by buying at Store 1.
$ _______
Answer:
For store 1, the shirts are 2 for $22. Ecah shirt then costs $22 ÷ 2 = $11
At store 2, each shirt is 10% off of $12.99 so each shirt costs:
$12.99 – 0.1(12.99) = $12.99 – $1.30 = $11.69
You will then save $11.69 – $11.00 = 0.69 per shirt if you buy them from Store 1.
Question 24.
b. If Store 3 has shirts originally priced at $20.98 on sale for 55% off, does it have a better deal than the other stores? Justify your answer.
_______
Answer:
If Store 3 sells shirts at 55% off of $20.98, then each shirt costs:
$20.98 – 0.55($20.98) = $20.98 – $11.54 = $9.44
This is lower than the costs per shirt of Store 1 and Store 2 so it has a better deal.
H.O.T.
Focus on Higher Order Thinking
Question 25.
Analyze Relationships
Marcus can choose between a monthly salary of $1,500 plus 5.5% of sales or $2,400 plus 3% of sales. He expects sales between $5,000 and $10,000 a month. Which salary option should he choose? Explain.
_______
Answer: Second Salary option is better
Explanation:
E = 1500 + 0.055(5000)
E = 1500 + 275
E = $1775
In the second case he will earn
E = 2400 + 0.03(5000)
E = 2400 + 150
E = $2550
Question 26.
Multistep
In chemistry class, Bob recorded the volume of a liquid as 13.2 mL. The actual volume was 13.7 mL. Use the formula to find percent error of Bob’s measurement to the nearest tenth of a percent.
_______ %
Answer: 3.6%
Explanation:

|13.2 – 13.7|/13.7 = |-0.5|/13.7
0.5/13.7 ≈ 0.036 = 3.6%
MODULE QUIZ – 5.1 Percent Increase and Decrease – Page No. 159
Find the percent change from the first value to the second.
Question 1.
36; 63
_______ %
Answer: 75%
Explanation:
Use the formula percent change = amount of change/first value
amount of change = 27
First value = 36
(63 – 36)/36 = 27/36 = 0.75 = 75%
Question 2.
50; 35
_______ %
Answer: 30%
Explanation:
Use the formula percent change = amount of change/first value
amount of change = 15
First value = 50
(50 – 35)/35 = 15/50 = 0.3 = 30%
Question 3.
40; 72
_______ %
Answer: 80%
Explanation:
Use the formula percent change = amount of change/first value
amount of change = 32
First value = 40
(72 – 40)/40 = 32/40 = 0.8 = 80%
5.2 Markup and Markdown
Use the original price and the markdown or markup to find the retail price.
Question 5.
Original price: $60; Markup: 15%
$ _______
Answer: $69
Explanation:
Use the formula retail price = original price + markup
60 + 60 × 0.15 = 60 + 9= 69
Question 6.
Original price: $32; Markup: 12.5%
$ _______
Answer: 36
Explanation:
Use the formula retail price = original price + markup
32 + 32 × 0.125 = 32 + 4 = $36
Question 7.
Original price: $50; Markdown: 22%
$ _______
Answer: 39
Explanation:
Use the formula retail price = original price + markup
50 – 50 × 0.22 = 50 – 11 = 39
Question 8.
Original price: $125; Markdown: 30%
$ _______
Answer: 87.50
Explanation:
Use the formula retail price = original price + markup
125 – 125 × 0.3 = 125 – 37.50 = 87.50
5.3 Applications of Percent
Question 9.
Mae Ling earns a weekly salary of $325 plus a 6.5% commission on sales at a gift shop. How much would she make in a work week if she sold $4,800 worth of merchandise?
$ _______
Answer: 637
Explanation:
Mae Ling weekly earnings is equal to her weekly salary plus her commission.
Since she earns 6.5 % commission on sales, if she sold $4800 worth of merchandise, her commission earnings would be 6.5 % of 4800 = 0.065 × 4800 = $312.
Since her weekly salary is 325, then her total weekly earnings is $325 + $312 = $637
Question 10.
Ramon earns $1,735 each month and pays $53.10 for electricity. To the nearest tenth of a percent, what percent of Ramon’s earnings are spent on electricity each month?
_______ %
Answer: 3.1%
Explanation:
Divide the electric payment by his monthly pay
53.10/1735 = 0.031 = 3.1%
Question 11.
James, Priya, and Siobhan work in a grocery store. James makes $7.00 per hour. Priya makes 20% more than James, and Siobhan makes 5% less than Priya. How much does Siobhan make per hour?
$ _______
Answer: 7.98 per hour
Explanation:
Since James makes $7 per hour and priya makes 20% more than this, find 20% of 7 and then add that to 7 to find the pay per hour for Priya.
7 + 0.2(7) = 7 + 1.40 = 8.40
Since Priya makes $8.40 per hour and Siobhan makes 5% less than this, find 5% of 8.40 and subtract that from 8.40 to find the pay per hour of Siobhan.
8.40 – 0.05(8.40) = 8.40 – 0.42 = 7.98
Question 12.
The Hu family goes out for lunch, and the price of the meal is $45. The sales tax on the meal is 6%, and the family also leaves a 20% tip on the pre-tax amount. What is the total cost of the meal?
$ _______
Answer: 56.70
Explanation:
Find the amount of tax
45 × 0.06 = 2.70
Find the amount of tip
45 × 0.20 = 9
Find the total cost by adding the cost of the meal, the tax, and the tip.
45 + 2.70 + 9 = $56.70
Essential Question
Question 13.
Give three examples of how percents are used in the real-world. Tell whether each situation represents a percent increase or a percent decrease.
Type below:
____________
Answer:
One example could be giving a tip when you eat at a restaurant. Since the cost increases, it represents a percent increase.
Second example is tax on purchase. Since the price increases it is a percent increase.
Third example is using a coupon when buying an item. Since the price decreases, it is a percent decrease.
Selected Response – Page No. 160
Question 1.
Zalmon walks \(\frac{3}{4}\) of a mile in \(\frac{3}{10}\) of an hour. What is his speed in miles per hour?
Options:
a. 0.225 miles per hour
b. 2.3 miles per hour
c. 2.5 miles per hour
d. 2.6 miles per hour
Answer: 2.5 miles per hour
Explanation:
Given that,
Zalmon walks \(\frac{3}{4}\) of a mile in \(\frac{3}{10}\) of an hour.
Divide the number of miles by the number of hours to get his speed in miles per hour.
\(\frac{3}{4}\) ÷ \(\frac{3}{10}\)
\(\frac{3}{4}\) ÷ \(\frac{10}{3}\) = \(\frac{5}{2}\)
Convert the fraction into the decimal form.
\(\frac{5}{2}\) = 2.5 miles per hour
Thus the correct answer is option C.
Question 2.
Find the percent change from 70 to 56.
Options:
a. 20% decrease
b. 20% increase
c. 25% decrease
d. 25% increase
Answer: 20% increase
Explanation:
Use the percent change = amount of change/original amount.
Since the number decreased from 70 to 56, it is a percent decrease.
= (70 – 56)/70 = \(\frac{14}{70}\) = 0.2 = 20%
Thus the correct answer is option A.
Question 3.
The rainfall total two years ago was 10.2 inches. Last year’s total was 20% greater. What was last year’s rainfall total?
Options:
a. 8.16 inches
b. 11.22 inches
c. 12.24 inches
d. 20.4 inches
Answer: 12.24 inches
Explanation:
Given,
The rainfall total two years ago was 10.2 inches. Last year’s total was 20% greater.
Find 20% of 10.2
10.2 × 0.20 = 2.04
Add the value to the original amount of 10.2
10.2 + 2.04 = 12.24
Therefore the correct answer is option C.
Question 4.
A pair of basketball shoes was originally priced at $80, but was marked up 37.5%. What was the retail price of the shoes?
Options:
a. $50
b. $83
c. $110
d. $130
Answer: $110
Explanation:
A pair of basketball shoes was originally priced at $80, but was marked up 37.5%.
Use the formula retail price = original price + markup
80 + 80 × 0.375 = 80 + 30 = 110
Thus the correct answer is option C.
Question 5.
The sales tax rate in Jan’s town is 7.5%. If she buys 3 lamps for $23.59 each and a sofa for $769.99, how much sales tax does she owe?
Options:
a. $58.85
b. $63.06
c. $67.26
d. $71.46
Answer: $63.06
Explanation:
The sales tax rate in Jan’s town is 7.5%.
If she buys 3 lamps for $23.59 each and a sofa for $769.99
Total cost before tax is 3 × 23.59 + 769.99
= 70.77 + 769.99 = 840.76
Find the amount of tax by multiplying the tax rate and total cost from the above solution and then round to 2 decimal place.
840.76 × 0.075 = 63.06
Thus the correct answer is option B.
Question 6.
The day after a national holiday, decorations were marked down 40%. Before the holiday, a patriotic banner cost $5.75. How much did the banner cost after the holiday?
Options:
a. $1.15
b. $2.30
c. $3.45
d. $8.05
Answer: $3.45
Explanation:
The day after a national holiday, decorations were marked down 40%. Before the holiday, a patriotic banner cost $5.75.
use the formula retail price = original price – markdown
5.75 – 5.75 × 0.4 = 5.75 – 2.30 = 3.45
Thus the correct answer is option C.
Question 7.
Dustin makes $2,330 each month and pays $840 for rent. To the nearest tenth of a percent, what percent of Dustin’s earnings are spent on rent?
Options:
a. 84%
b. 63.9%
c. 56.4%
d. 36.1%
Answer: 36.1%
Explanation:
Dustin makes $2,330 each month and pays $840 for rent.
Divide his rent by his monthly income. round to three decimal places and then convert to percent form.
840/2330 = 0.361 = 36.1%
Thus the correct answer is option D.
Question 8.
A scuba diver is positioned at -30 feet. How many feet will she have to rise to change her position to -12 feet?
Options:
a. -42 ft
b. -18 ft
c. 18 ft
d. 42 ft
Answer: 18 ft
Explanation:
Given,
A scuba diver is positioned at -30 feet.
-12 – (-30) = 12 + 30 = 18 feet
Thus the correct answer is option C.
Question 9.
A bank offers an annual simple interest rate of 8% on home improvement loans. Tobias borrowed $17,000 over a period of 2 years. How much did he repay altogether?
Options:
a. $1360
b. $2720
c. $18360
d. $19720
Answer: $19720
Explanation:
Given that,
A bank offers an annual simple interest rate of 8% on home improvement loans.
Tobias borrowed $17,000 over a period of 2 years
Find the amount of interest he paid using the formula
I = prt
where p is the amount borrowed
r is the interest rate
t is the number of years
17000 × 0.08 × 2 = 2720
Add the amount borrowed and amount of interest
17000 + 2720 = 19720.
Thus the correct answer is option D.
Mini-Task
Question 10.
The granola Summer buys used to cost $6.00 per pound, but it has been marked up 15%.
a. How much did it cost Summer to buy 2.6 pounds of granola at the old price?
$ ___________
Answer: $15.60
Explanation:
Multiply 2.6 by the old price of $6
2.6 × 6 = 15.60
It costs $15.60 to buy 2.6 pounds of granola at the old price.
Question 10.
b. How much does it cost her to buy 2.6 pounds of granola at the new price?
$ _______
Answer: $17.94
Explanation:
Find the new price using the formula retail price = original price + markup
Then find the total cost by buying 2.6 pounds at the new price.
6 + 6 × 0.15 = 6 + 0.9 = 6.90
2.6 × 6.90 = 17.94
The new price is $17.94
Question 10.
c. Suppose Summer buys 3.5 pounds of granola. How much more does it cost at the new price than at the old price?
$ _______
Answer: $3.15
Explanation:
3.5 × 6 = 21
3.5 × 6.90 = 24.15
24.15 – 21 = 3.15
Module 5 – Page No. 162
EXERCISES
Question 1.
Michelle purchased 25 audio files in January. In February she purchased 40 audio files. Find the percent increase.
_______ %
Answer: 60%
Explanation:
Given,
Michelle purchased 25 audio files in January. In February she purchased 40 audio files.
Use the percent change = amount of change/original amount.
(40 -25)/25 = 15/25 = 0.6 = 60%
Thus the percent increase is 60%
Question 2.
Sam’s dog weighs 72 pounds. The vet suggests that for the dog’s health, its weight should decrease by 12.5 percent. According to the vet, what is a healthy weight for the dog?
_______ pounds
Answer: 63 pounds
Explanation:
Given,
Sam’s dog weighs 72 pounds. The vet suggests that for the dog’s health, its weight should decrease by 12.5 percent.
72 × 0.125 = 9
Find a healthy weight by subtracting the change in weight from the original weight
72 – 9 = 63
The healthy weight of the dog is 63 pounds.
Question 3.
The original price of a barbecue grill is $79.50. The grill is marked down 15%. What is the sale price of the grill?
$ _______
Answer: 67.57
Explanation:
Given,
The original price of a barbecue grill is $79.50. The grill is marked down 15%.
Use the formula sale price = original price – markdown
= 79.50 – 79.50 × 0.15 = 79.50 – 11.93 = $67.57
Thus the sale price of the grill is $67.57
Question 4.
A sporting goods store marks up the cost s of soccer balls by 250%. Write an expression that represents the retail cost of the soccer balls. The store buys soccer balls for $5.00 each. What is the retail price of the soccer balls?
$ _______
Answer: $17.5
Explanation:
Use the formula retail price = original price + markup to find the expression for an original price of s and a markup percentage of 250%
s + 2.5s = 3.5s
substitute s = 5 into the expression to find the retail price
3.5 × 5 = 17.50
Thus the retail price of the soccer balls is $17.50
Unit 2 Performance Tasks – Page No. 163
Question 1.
Viktor is a bike tour operator and needs to replace two of his touring bikes. He orders two bikes from the sporting goods store for a total of $2,000 and pays using his credit card. When the bill arrives, he reads the following information:
Balance: $2000
Annual interest rate: 14.9%
Minimum payment due: $40
Late fee: $10 if payment not received by 3/1/2013
a. To keep his good credit, Viktor promptly sends in a minimum payment of $40. When the next bill arrives, it looks a lot like the previous bill.
Balance: $1,984.34
Annual interest rate: 14.9%
Minimum payment due: $40
Late fee: $10 if payment not received by 4/1/2013
Explain how the credit card company calculated the new balance. Notice that the given interest rate is annual, but the payment is monthly.
Type below:
_____________
Answer:
We have to find the balance after the first bill by subtracting the $40 payment from the original balance of $2000.
Balance after first bill: 2000 – 40 = 1960
Then find the amount of interest charged on the second bill by multiplying the balance of $1960 by the interest rate.
Remember since the interest rate is annually you have to divide it by 12 to get the monthly interest rate.
Interest on the second bill: 1960 × 0.149/12 = 24.34
And then add this interest amount to the balance of $1960 to get the balance on the second bill.
New balance: 1960 + 24.34 = 1984.34
Question 1.
b. Viktor was upset about the new bill, so he decided to send in $150 for his April payment. The minimum payment on his bill is calculated as 2% of the balance (rounded to the nearest dollar) or $20, whichever is greater. Fill out the details for Viktor’s new bill.
Type below:
_____________
Answer:
Find the balance after the $150 payment. The interest rate hasn’t changed so the annual interest rate on this new bill is the same as the previous bills.
balance after payment: 1984.34 – 150 = 1834.34
annual interest rate: 14/9%
Find the interest charged on the third bill. find the balance on the third bill by adding the interest charged to the balance of $1834.34.
interest on the third bill: 1834.34 × 0.149/12 = 22.78
balance: 1834.34 + 22.78 = 1857.12
To find what the minimum payment will be, first find 2% of the balance.
2% of balance: 0.02 × 1857.12 = 37.14
Minimum payment due: $37.00
Since this is greater than $20, the minimum payment is 2% of the balance rounded to the nearest dollar giving $37 as the payment.
The later fee date is one month after the late fee date of 04/01/2013 on the previous bill which gives 05/01/2013.
Question 1.
c. Viktor’s bank offers a credit card with an introductory annual interest rate of 9.9%. He can transfer his current balance for a fee of $40. After one year, the rate will return to the bank’s normal rate, which is 13.9%. The bank charges a late fee of $15. Give two reasons why Viktor should transfer the balance and two reasons why he should not
Type below:
_____________
Answer: Two reasons he should transfer is that the lower introductory rate would mean less interest charged in the first year and a lower normal rate would mean less interest charged after that first year as well. Two reasons he shouldn’t transfer the balance is that he would have to pay a transfer fee of $40 and that the late fee is $15 instead of $10 if he transfers the balance.
Unit 2 Performance Tasks (con’td) – Page No. 164
Question 2.
The table below shows how far several animals can travel at their maximum speeds in a given time.
a. Write each animal’s speed as a unit rate in feet per second.
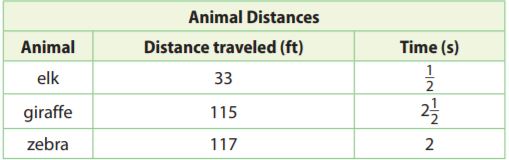
Elk: _________ feet per second
Giraffe: _________ feet per second
Zebra: _________ feet per second
Answer:
By seeing the above table we can find the unit rates by dividing the distance traveled by the time in second.
elk: 33 ÷ 1/2 = 33 × 2 = 66 feet per second
Giraffe: 115 ÷ 2 1/2 = 115 ÷ 5/2 = 115 2/5 = 46 feet per second
Zebra: 117 ÷ 2 = 58.5 feet per second
Question 2.
b. Which animal has the fastest speed?
_____________
Answer: The elk had the greatest unit rate so it has the fastest speed.
Question 2.
c. How many miles could the fastest animal travel in 2 hours if it maintained the speed you calculated in part a? Use the formula d = rt and round your answer to the nearest tenth of a mile. Show your work.
Elk: _________ miles
Giraffe: _________ miles
Zebra: _________ miles
Answer:
Elk: 90 miles
Giraffe: 62 miles
Zebra: 72 miles
Explanation:
There are 60 seconds in a minute and 60 minutes in an hour so there are 2 × 60 × 60 = 7200 seconds in 2 hours.
Multiply the unit rate of the elk by 7200 seconds to get the distance traveled in feet.
There are 5280 feet in 1 mile so divide the distance in feet by 5280 to get the distances in miles.
Elk:
66 × 7200 = 475200 feet
Now convert from feet to miles
475200 feet = 90 miles
Giraffe: 46 feet per second
62 × 7200 = 331200 feet
Now convert from feet to miles.
331200 = 62 miles
Zebra: 58.5 feet per second
58.5 × 7200 = 421200 feet
Now convert from feet to miles.
421200 feet = 72 miles
Question 3.
d. The data in the table represents how fast each animal can travel at its maximum speed. Is it reasonable to expect the animal from part b to travel that distance in 2 hours? Explain why or why not.
______
Answer: It is not reasonable. An animal can only travel at its maximum speed for a short amount of time which is usually only for a couple of minutes.
Selected Response – Page No. 165
Question 1.
If the relationship between distance y in feet and time x in seconds is proportional, which rate is represented by \(\frac{y}{x}\) = 0.6?
Options:
a. 3 feet in 5 s
b. 3 feet in 9 s
c. 10 feet in 6 s
d. 18 feet in 3 s
Answer: 3 feet in 5 s
Explanation:
\(\frac{y}{x}\) = 0.6
0.6 = \(\frac{6}{10}\)
Since \(\frac{6}{10}\) = \(\frac{3}{5}\), it represents a rate of 3 feet in 5 seconds,
Therefore the correct answer is option A.
Question 2.
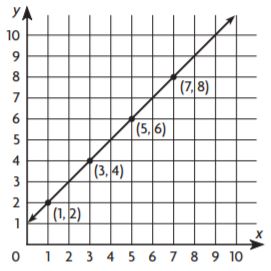
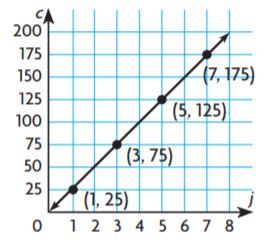
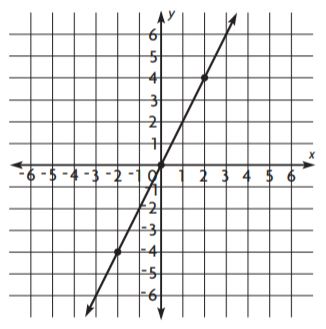
The Baghrams make regular monthly deposits in a savings account. The graph shows the relationship between the number x of months and the amount y in dollars in the account.
What is the equation for the deposit?

Options:
a. \(\frac{y}{x}\) = $25/month
b. \(\frac{y}{x}\) = $40/month
c. \(\frac{y}{x}\) = $50/month
d. \(\frac{y}{x}\) = $75/month
Answer: \(\frac{y}{x}\) = $50/month
Explanation:
By seeing the above graph we can say that the point is (2, 100). This means that \(\frac{y}{x}\) = \(\frac{100}{2}\) = 50.
Thus the correct answer is option C.
Question 3.
What is the decimal form of −4 \(\frac{7}{8}\)?
Options:
a. -4.9375
b. -4.875
c. -4.75
d. -4.625
Answer: -4.875
Explanation:
Given the fraction
−4 \(\frac{7}{8}\)
First divide \(\frac{7}{8}\) = 0.875
4 + 0.875 = 4.875
So, −4 \(\frac{7}{8}\) = -4.875
Therefore the answer is option B.
Question 4.
Find the percent change from 72 to 90.
Options:
a. 20% decrease
b. 20% increase
c. 25% decrease
d. 25% increase
Answer: 25% increase
Explanation:
Use the formula percent change = amount of change/original amount.
the value increased from 72 to 90 so it is a percent increase.
(90-72)/72 = 18/72 = 0.25 = 25%
Thus the correct answer is option D.
Question 5.
A store had a sale on art supplies. The price p of each item was marked down 60%. Which expression represents the new price?
Options:
a. 0.4p
b. 0.6p
c. 1.4p
d. 1.6p
Answer: 0.4p
Explanation:
Given that,
A store had a sale on art supplies.
The price p of each item was marked down 60%
Use the formula sale price = original price – markdown
p is the original price and the markdown percent is 40% then combine the like terms.
p – 0.6p = 0.4p
Therefore the correct answer is option A.
Question 6.
Clarke borrows $16,000 to buy a car. He pays simple interest at an annual rate of 6% over a period of 3.5 years. How much does he pay altogether?
Options:
a. $18800
b. $19360
c. $19920
d. $20480
Answer: $19360
Explanation:
Given,
Clarke borrows $16,000 to buy a car.
He pays simple interest at an annual rate of 6% over a period of 3.5 years.
Find the total amount of interest using the formula
I = prt
where p is the amount borrowed
r is the rate of interest
t is the number of years
16000 × 0.06 × 3.5 = 3360
Now add the amount of interest to the amount borrowed to find the total amount
16000 + 3360 = 19,360
Thus the correct answer is option B.
Question 7.
To which set or sets does the number 37 belong?
Options:
a. integers only
b. rational numbers only
c. integers and rational numbers only
d. whole numbers, integers, and rational numbers
Answer: whole numbers, integers, and rational numbers
Explanation:
37 can be written as 37/1 so it is a rational number. 37 doesn’t have a decimal or fraction so it is an integer. Since it is a positive integer, it is also a whole number.
Thus a suitable answer is option D.
Page No. 166
Question 8.
In which equation is the constant of proportionality 5?
Options:
a. x = 5y
b. y = 5x
c. y = x + 5
d. y = 5 – x
Answer: y = 5x
Explanation:
Directly proportional equations are of the form y = kx
where k is the constant of proportionality.
If k = 5, then the equation is y = 5x.
Thus the correct answer is option B.
Question 9.
Suri earns extra money by dog walking. She charges $6.25 to walk a dog once a day 5 days a week and $8.75 to walk a dog once a day 7 days a week. Which equation represents this relationship?
Options:
a. y = 7x
b. y = 5x
c. y = 2.50x
d. y = 1.25x
Answer: y = 1.25x
Explanation:
Given that,
Suri earns extra money by dog walking. She charges $6.25 to walk a dog once a day 5 days a week and $8.75 to walk a dog once a day 7 days a week.
Since 6.25/5 = 1.25
So, the equation is y = 1.25x
where x is the number of days and y is the total charge.
So, the correct answer is option D.
Question 10.
Randy walks \(\frac{1}{2}\) mile in each \(\frac{1}{5}\) hour. How far will Randy walk in one hour?
Options:
a. \(\frac{1}{2}\) miles
b. 2 miles
c. 2 \(\frac{1}{2}\) miles
d. 5 miles
Answer: 2 \(\frac{1}{2}\) miles
Explanation:
Given,
Randy walks \(\frac{1}{2}\) mile in each \(\frac{1}{5}\) hour.
\(\frac{1}{2}\) ÷ \(\frac{1}{5}\)
\(\frac{1}{2}\) × \(\frac{5}{1}\) = \(\frac{5}{2}\)
Convert the fraction to the improper fractions.
\(\frac{5}{2}\) = 2 \(\frac{1}{2}\) miles
Therefore the correct answer is option C.
Question 11.
On a trip to Spain, Sheila bought a piece of jewelry that cost $56.75. She paid for it with her credit card, which charges a foreign transaction fee of 3%. How much was the foreign transaction fee?
Options:
a. $0.17
b. $1.07
c. $1.70
d. $17.00
Answer: $1.70
Explanation:
On a trip to Spain, Sheila bought a piece of jewelry that cost $56.75.
She paid for it with her credit card, which charges a foreign transaction fee of 3%
Find the foreign transaction fee amount by multiplying the cost by the foreign transaction fee percentage.
56.75 × 0.03 = 1.70
Thus the correct answer is option C.
Question 12.
A baker is looking for a recipe that has the lowest unit rate for flour per batch of muffins. Which recipe should she use?
Options:
a. \(\frac{1}{2}\) cup flour for \(\frac{2}{3}\) batch
b. \(\frac{2}{3}\) cup flour for \(\frac{1}{2}\) batch
c. \(\frac{3}{4}\) cup flour for \(\frac{2}{3}\) batch
d. \(\frac{1}{3}\) cup flour for \(\frac{1}{4}\) batch
Answer: \(\frac{1}{2}\) cup flour for \(\frac{2}{3}\) batch
Explanation:
a. \(\frac{1}{2}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{2}\) × \(\frac{3}{2}\) = \(\frac{3}{4}\)
b. \(\frac{2}{3}\) ÷ \(\frac{1}{2}\) = \(\frac{2}{3}\) × \(\frac{2}{1}\) = \(\frac{4}{3}\) = 1 \(\frac{1}{3}\)
c. \(\frac{3}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{3}{4}\) × \(\frac{3}{2}\) = \(\frac{9}{8}\) = 1 \(\frac{1}{8}\)
d. \(\frac{1}{3}\) ÷ \(\frac{1}{4}\) = \(\frac{1}{3}\) ÷ \(\frac{4}{1}\) = 1 \(\frac{1}{3}\)
Thus the correct answer is option A.
Mini-Task
Question 13.
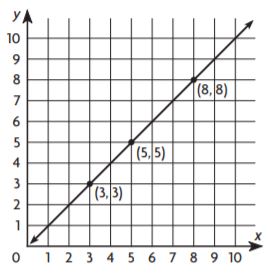
Kevin was able to type 2 pages in 5 minutes, 3 pages in 7.5 minutes, and 5 pages in 12.5 minutes.
a. Make a table of the data.
Type below:
___________
Answer:
| Number of Pages | 2 | 3 | 5 |
| Minutes | 5 | 7.5 | 12.5 |
Question 13.
b. Graph the relationship between the number of pages typed and the number of minutes.
Type below:
___________
Answer:
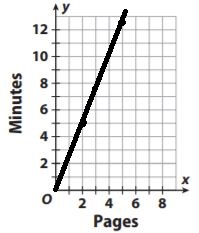
Question 13.
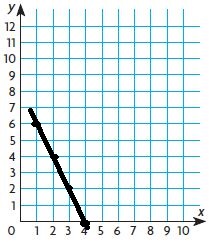
c. Explain how to use the graph to find the unit rate.
Type below:
___________
Answer: The unit rate is 2.5 pages per minute
Explanation:
By using the graph we need to find the slope of the line.
We can do this by using the formula of a slope:
m = (y2-y1)/(x2-x1) = (7.5-5)/(3-2) = 2.5
Thus the unit rate is 2.5 pages per minute.
Conclusion:
Hope the answers provided in Go Math Answer Key Grade 7 Chapter 5 Percent Increase and Decrease are quite satisfactory for all the students. Refer to our Go Math 7th Grade Chapter 5 Percent Increase and Decrease to get the solutions with best explanations. After your preparation test your math skills by solving the questions in the performance tasks.

































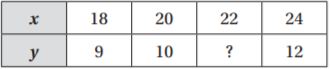
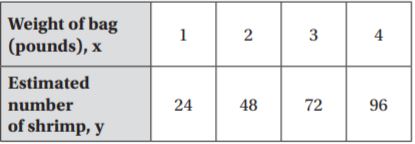
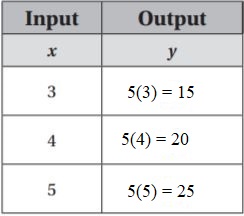
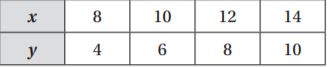





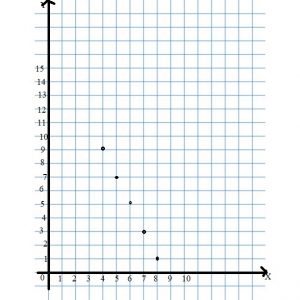
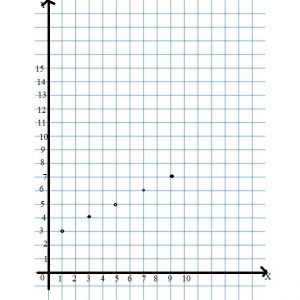






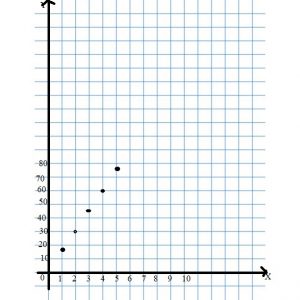

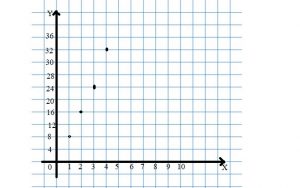


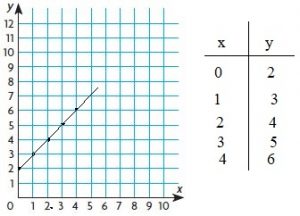
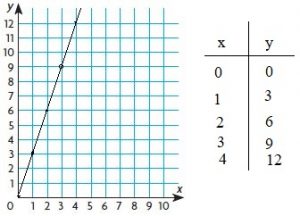


















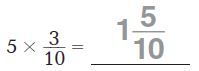



















 horses in each pen.
horses in each pen. horses in each pan
horses in each pan








 × 8 = 72 72 ÷
× 8 = 72 72 ÷  = 8
= 8 × 8 = 72; 72 ÷
× 8 = 72; 72 ÷  = 8
= 8


















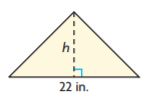
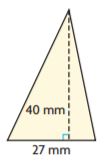
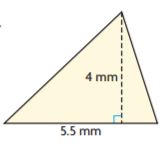
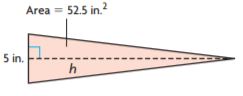

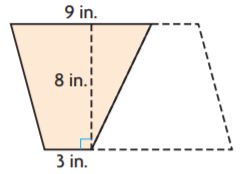
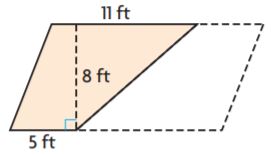
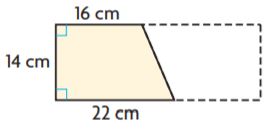
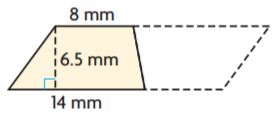





















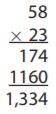




















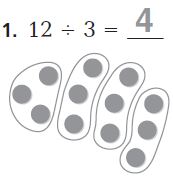


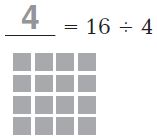









 = 28
= 28  = 28 ÷ 4
= 28 ÷ 4 = 28
= 28