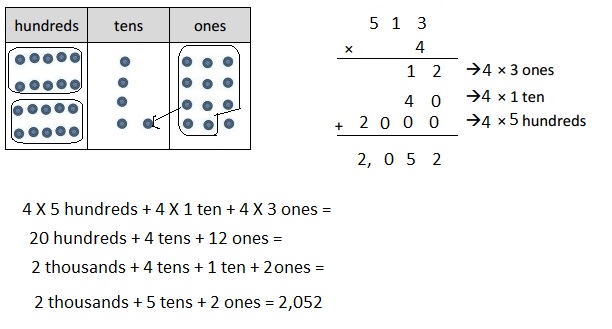
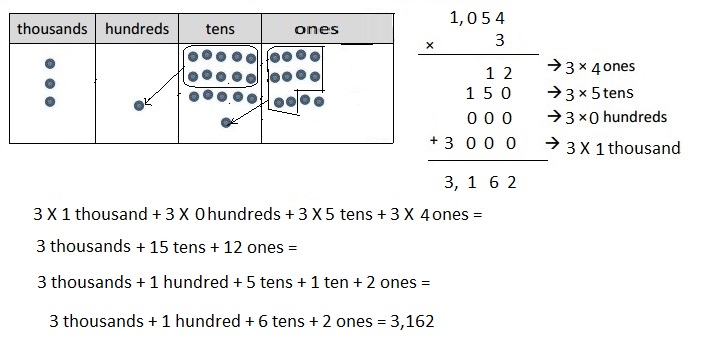
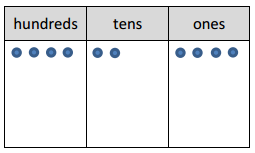
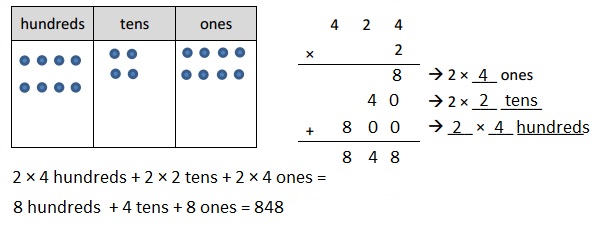
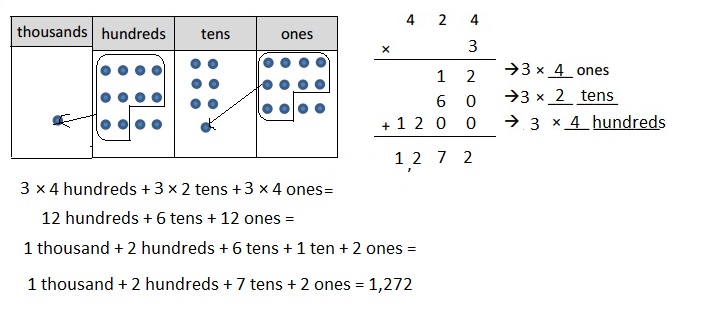
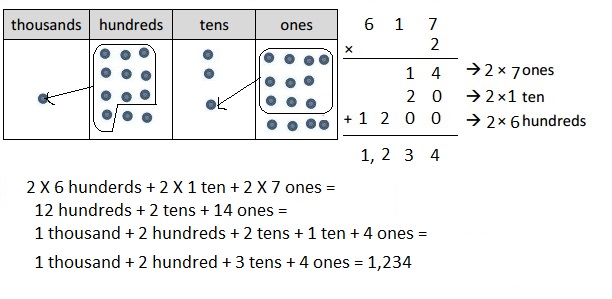
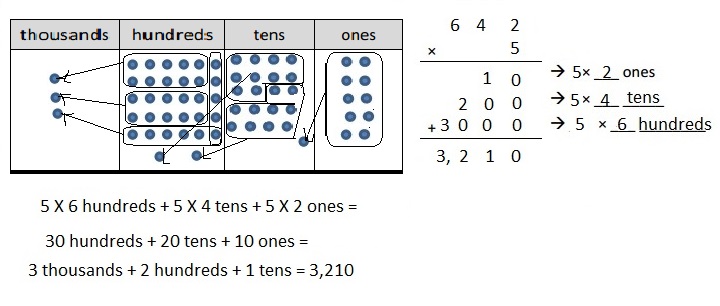
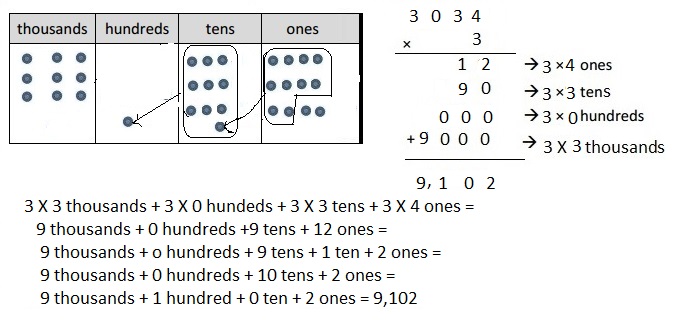
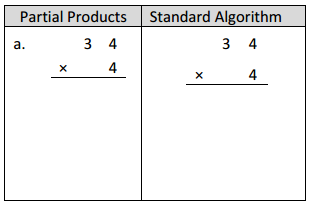
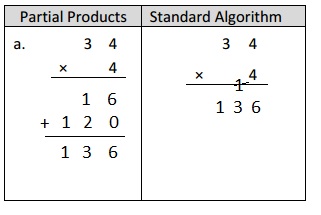
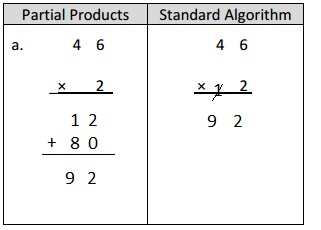
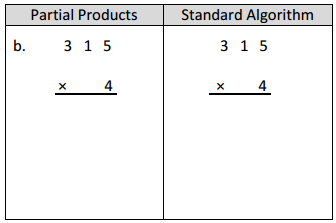
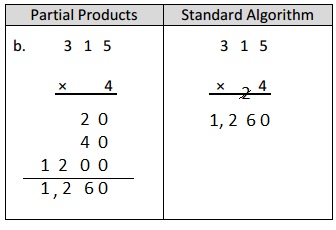
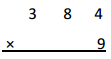
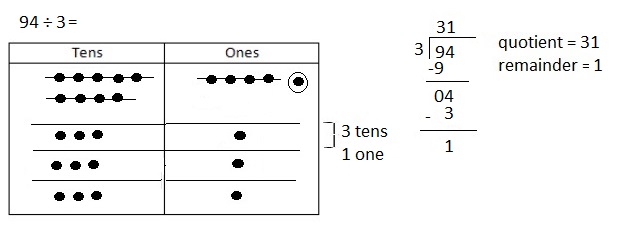
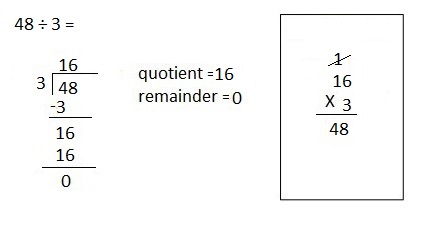
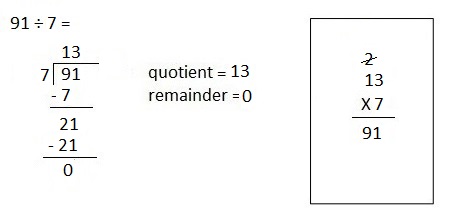
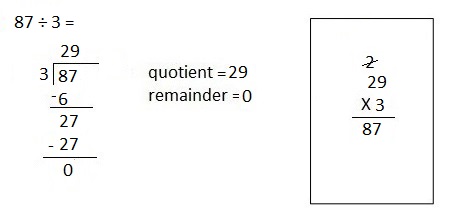
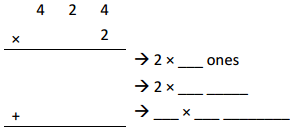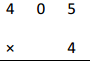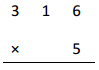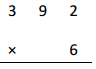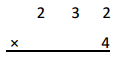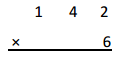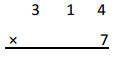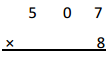Engage NY Eureka Math 4th Grade Module 3 Lesson 13 Answer Key
Eureka Math Grade 4 Module 3 Lesson 13 Sprint Answer Key
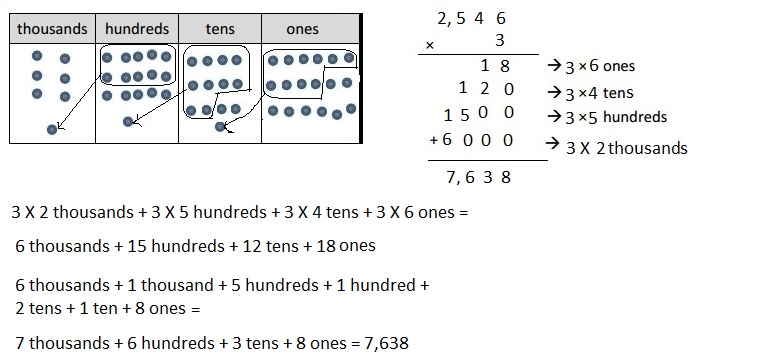
Mental Multiplication
Question 1.
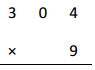
1 × 4 =
Answer:
1 X 4 = 4,
Explanation:
Given expression as 1 X 4, multiplying 1 with 4
we get 4, So 1 X 4 = 4.
Question 2.
10 × 4 =
Answer:
10 X 4 = 40,
Explanation:
Given expression as 10 X 4, multiplying 10 with 4
we get 40, So 10 X 4 = 40.
Question 3.
11 × 4 =
Answer:
11 X 4 = 44,
Explanation:
Given expression as 11 X 4, multiplying 11 with 4
we get 44, So 11 X 4 = 44.
Question 4.
1 × 2 =
Answer:
1 X 2 = 2,
Explanation:
Explanation:
Given expression as 1 X 2, multiplying 1 with 2
we get 2, So 1 X 2 = 2.
Question 5.
20 × 2 =
Answer:
20 X 2 = 100,
Explanation:
Given expression as 20 X 2, multiplying 20 with 2
we get 40, So 20 X 2 = 40.
Question 6.
21 × 2 =
Answer:
21 X 2 = 42,
Explanation:
Given expression as 21 X 2, multiplying 21 with 2
we get 42, So 21 X 2 = 42.
Question 7.
2 × 3 =
Answer:
2 X 3 = 6,
Explanation:
Given expression as 2 X 3, multiplying 2 with 3
we get 6, So 2 X 3 = 6.
Question 8.
30 × 3 =
Answer:
30 X 3 = 90,
Explanation:
Given expression as 30 X 3, multiplying 30 with 3
we get 90, So 30 X 3 = 90.
Question 9.
32 × 3 =
Answer:
32 X 3 = 96,
Explanation:
Given expression as 32 X 3, multiplying 32 with 3
we get 96, So 32 X 3 = 96.
Question 10.
3 × 5=
Answer:
3 X 5 = 15,
Explanation:
Given expression as 3 X 5, multiplying 3 with 5
we get 15, So 3 X 5 = 15.
Question 11.
20 × 5 =
Answer:
20 X 5 = 100,
Explanation:
Given expression as 20 X 5, multiplying 20 with 5
we get 100, So 20 X 5 = 100.
Question 12.
23 × 5 =
Answer:
23 X 5 = 115,
Explanation:
Given expression as 23 X 5, multiplying 23 with 5
we get 115, So 23 X 5 = 115.
Question 13.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given expression as 3 X 3, multiplying 3 with 3
we get 9, So 3 X 3 = 9.
Question 14.
40 × 3 =
Answer:
40 X 3 = 120,
Explanation:
Given expression as 40 X 3, multiplying 40 with 3
we get 120, So 40 X 3 = 120.
Question 15.
43 × 3 =
Answer:
43 X 3 = 129,
Explanation:
Given expression as 43 X 3, multiplying 43 with 3
we get 129, So 43 X 3 = 129.
Question 16.
4 × 2 =
Answer:
4 X 2 = 8,
Explanation:
Given expression as 4 X 2, multiplying 4 with 2
we get 8, So 4 X 2 = 8.
Question 17.
70 × 2 =
Answer:
70 X 2 = 140,
Explanation:
Given expression as 70 X 2, multiplying 70 with 2
we get 140, So 70 X 2 = 140.
Question 18.
74 × 2 =
Answer:
74 X 2 = 148,
Explanation:
Given expression as 74 X 2, multiplying 74 with 2
we get 148, So 74 X 2 = 148.
Question 19.
2 × 3 =
Answer:
2 X 3 = 6,
Explanation:
Given expression as 2 X 3, multiplying 2 with 3
we get 6, So 2 X 3 = 6.
Question 20.
60 × 3 =
Answer:
60 X 3 = 180,
Explanation:
Given expression as 60 X 3, multiplying 60 with 3
we get 180, So 60 X 3 = 180.
Question 21.
62 × 3 =
Answer:
62 X 3 = 186,
Explanation:
Given expression as 62 X 3 , multiplying 62 with 3
we get 186, So 62 X 3 = 186.
Question 22.
63 × 3 =
Answer:
63 X 3 = 189,
Explanation:
Given expression as 63 X 3, multiplying 63 with 3
we get 189, So 63 X 3 = 189.
Question 23.
21 × 3 =
Answer:
21 X 3 = 63,
Explanation:
Given expression as 21 X 3, multiplying 21 with 3
we get 63, So 21 X 3 = 63.
Question 24.
121 × 3 =
Answer:
121 X 3 = 363,
Explanation:
Given expression as 121 X 3, multiplying 121 with 3
we get 363, So 121 X 3 = 363.
Question 25.
42 × 2 =
Answer:
42 X 2 = 84,
Explanation:
Given expression as 42 X 2, multiplying 42 with 2
we get 84, So 42 X 2 = 84.
Question 26.
142 × 2 =
Answer:
142 X 2 = 284,
Explanation:
Given expression as 142 X 2, multiplying 142 with 2
we get 284, So 142 X 2 = 284.
Question 27.
242 × 2 =
Answer:
242 X 2 = 484,
Explanation:
Given expression as 242 X 2, multiplying 242 with 2
we get 484, So 242 X 2 = 484.
Question 28.
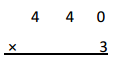
342 × 2 =
Answer:
342 X 2 = 684,
Explanation:
Given expression as 342 X 2, multiplying 342 with 2
we get 684, So 342 X 2 = 684.
Question 29.
442 × 2 =
Answer:
442 X 2 = 884,
Explanation:
Given expression as 442 X 2, multiplying 442 with 2
we get 884, So 442 X 2 = 884.
Question 30.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given expression as 3 X 3, multiplying 3 with 3
we get 9, So 3 X 3 = 9.
Question 31.
13 × 3 =
Answer:
13 X 3 = 39,
Explanation:
Given expression as 13 X 3, multiplying 13 with 3
we get 39, So 13 X 3 = 39.
Question 32.
213 × 3 =
Answer:
213 X 3 =639,
Explanation:
Given expression as 213 X 3, multiplying 213 with 3
we get 639, So 213 X 3 = 639.
Question 33.
1,213 × 3 =
Answer:
1,213 X 3 = 3,639,
Explanation:
Given expression as 1,213 X 3, multiplying 1,213 with 3
we get 1,213, So 1,213 X 3 = 3,639.
Question 34.
2,113 × 3 =
Answer:
2,113 X 3 = 6,339,
Explanation:
Given expression as 2,113 X 3, multiplying 2,113 with 3
we get 6,339, So 2,113 X 3 = 6,339.
Question 35.
2,131 × 3 =
Answer:
2,131 X 3 = 6,393,
Explanation:
Given expression as 2,131 X 3, multiplying 2,131 with 3
we get 6,393, So 2,131 X 3 = 6,393.
Question 36.
2,311 × 3 =
Answer:
2,311 X 3 = 6,933,
Explanation:
Given expression as 2,311 X 3, multiplying 2,311 with 3
we get 6,933, So 2,311 X 3 = 6,933.
Question 37.
24 × 4 =
Answer:
24 X 4 = 96,
Explanation:
Given expression as 24 X 4, multiplying 24 with 4
we get 96, So 24 X 4 = 96.
Question 38.
35 × 5 =
Answer:
35 X 5 = 175,
Explanation:
Given expression as 35 X 5, multiplying 35 with 5
we get 175, So 35 X 5 = 175.
Question 39.
54 × 3 =
Answer:
54 X 3 = 162,
Explanation:
Given expression as 54 X 3, multiplying 54 with 3
we get 162, So 54 X 3 = 162.
Question 40.
63 × 6 =
Answer:
63 X 6 = 378,
Explanation:
Given expression as 63 X 6, multiplying 63 with 6
we get 378, So 63 X 6 = 378.
Question 41.
125 × 4 =
Answer:
125 X 4 = 500,
Explanation:
Given expression as 125 X 4, multiplying 125 with 4
we get 500, So 125 X 4 = 500.
Question 42.
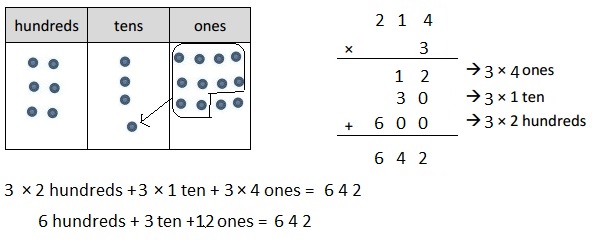
214 × 3 =
Answer:
214 X 3 = 642,
Explanation:
Given expression as 214 X 3, multiplying 214 with 3
we get 642, So 214 X 3 = 642.
Question 43.
5,213 × 2 =
Answer:
5,213 X 2 = 10,426,
Explanation:
Given expression as 5,213 X 2, multiplying 5,213 with 2
we get 10,426, So 5,213 X 2 = 10,426.
Question 44.
2,135 × 4 =
Answer:
2,135 X 4 = 8,540,
Explanation:
Given expression as 2,135 X 4, multiplying 2,135 with 4
we get 8,540, So 2,135 X 4 = 8,540.
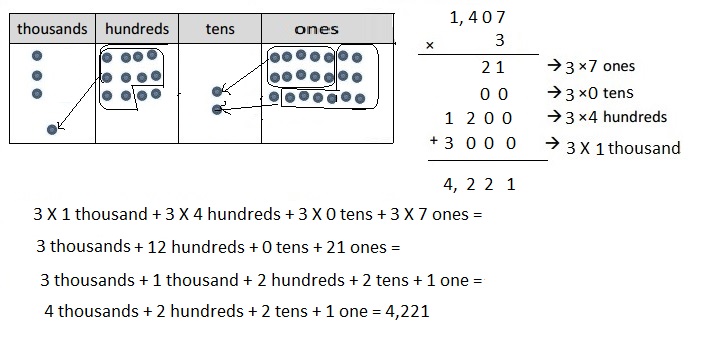
Mental Multiplication
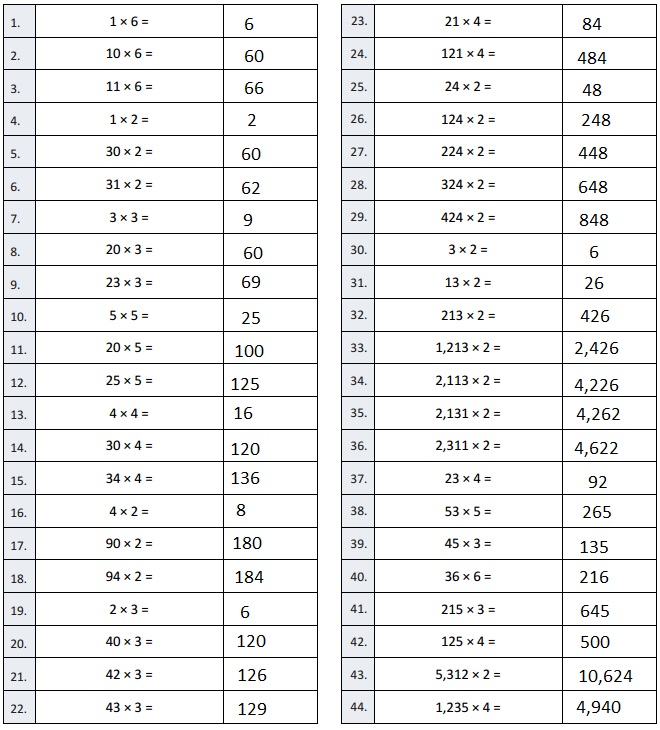
Question 1.
1 × 6 =
Answer:
1 X 6 = 6,
Explanation:
Given expression as 1 X 6, multiplying 1 with 6
we get 6, So 1 X 6 = 6.
Question 2.
10 × 6 =
Answer:
10 X 6 = 60,
Explanation:
Given expression as 10 X 6, multiplying 10 with 6
we get 60, So 10 X 6 = 60.
Question 3.
11 × 6 =
Answer:
11 X 6 = 66,
Explanation:
Given expression as 11 X 6, multiplying 11 with 6
we get 66, So 11 X 6 = 66.
Question 4.
1 × 2 =
Answer:
1 X 2 = 2,
Explanation:
Given expression as 1 X 2, multiplying 1 with 2
we get 2, So 1 X 2 = 2.
Question 5.
30 × 2 =
Answer:
30 X 2 = 60,
Explanation:
Given expression as 30 X 2, multiplying 30 with 2
we get 60, So 30 X 2 = 60.
Question 6.
31 × 2 =
Answer:
31 X 2 = 62,
Explanation:
Given expression as 31 X 2, multiplying 31 with 2
we get 62, So 31 X 2 = 62.
Question 7.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given expression as 3 X 3, multiplying 3 with 3
we get 9, So 3 X 3 = 9.
Question 8.
20 × 3 =
Answer:
20 X 3 = 60,
Explanation:
Given expression as 20 X 3, multiplying 20 with 3
we get 60, So 20 X 3 = 60.
Question 9.
23 × 3 =
Answer:
23 X 3 = 69,
Explanation:
Given expression as 23 X 3, multiplying 23 with 3
we get 69, So 23 X 3 = 69.
Question 10.
5 × 5 =
Answer:
5 X 5 = 25,
Explanation:
Given expression as 5 X 5, multiplying 5 with 5
we get 25, So 5 X 5 = 25.
Question 11.
20 × 5 =
Answer:
20 X 5 = 100,
Explanation:
Given expression as 20 X 5, multiplying 20 with 5
we get 100, So 20 X 5 = 100.
Question 12.
25 × 5 =
Answer:
25 X 5 = 125,
Explanation:
Given expression as 25 X 5, multiplying 25 with 5
we get 125, So 25 X 5 = 125.
Question 13.
4 × 4 =
Answer:
4 X 4 = 16,
Explanation:
Given expression as 4 X 4, multiplying 4 with 4
we get 16, So 4 X 4 = 16.
Question 14.
30 × 4 =
Answer:
30 X 4 = 120,
Explanation:
Given expression as 30 X 4, multiplying 30 with 4
we get 120, So 30 X 4 = 120.
Question 15.
34 × 4 =
Answer:
34 X 4 = 136,
Explanation:
Given expression as 34 X 4, multiplying 34 with 4
we get 136, So 34 X 4 = 136.
Question 16.
4 × 2 =
Answer:
4 X 2 = 8,
Explanation:
Given expression as 4 X 2, multiplying 4 with 2
we get 8, So 4 X 2 = 8.
Question 17.
90 × 2 =
Answer:
90 X 2 = 180,
Explanation:
Given expression as 90 X 2, multiplying 90 with 2
we get 180, So 90 X 2 = 180.
Question 18.
94 × 2 =
Answer:
94 X 2 = 188,
Explanation:
Given expression as 94 X 2, multiplying 94 with 2
we get 188, So 94 X 2 = 188.
Question 19.
2 × 3 =
Answer:
2 X 3 = 6,
Explanation:
Given expression as 2 X 3, multiplying 2 with 3
we get 6, So 2 X 3 = 6.
Question 20.
40 × 3 =
Answer:
40 X 3 = 120,
Explanation:
Given expression as 40 X 3, multiplying 40 with 3
we get 120, So 40 X 3 = 120.
Question 21.
42 × 3 =
Answer:
42 X 3 = 126,
Explanation:
Given expression as 42 X 3, multiplying 42 with 3
we get 126, So 42 X 3 = 126.
Question 22.
43 × 3 =
Answer:
43 X 3 = 129,
Explanation:
Given expression as 43 X 3, multiplying 43 with 3
we get 129, So 43 X 3 = 129.
Question 23.
21 × 4 =
Answer:
21 X 4 = 84,
Explanation:
Given expression as 21 X 4, multiplying 21 with 4
we get 84, So 21 X 4 = 84.
Question 24.
121 × 4 =
Answer:
121 X 4 = 484,
Explanation:
Given expression as 121 X 4, multiplying 121 with 4
we get 484, So 121 X 4 = 484.
Question 25.
24 × 2 =
Answer:
24 X 2 = 48,
Explanation:
Given expression as 24 X 2, multiplying 24 with 2
we get 48, So 24 X 2 = 48.
Question 26.
124 × 2 =
Answer:
124 X 2 = 248,
Explanation:
Given expression as 124 X 2, multiplying 124 with 2
we get 248, So 124 X 2 = 248.
Question 27.
224 × 2 =
Answer:
224 X 2 = 448,
Explanation:
Given expression as 224 X 2, multiplying 224 with 2
we get 448, So 224 X 2 = 448.
Question 28.
324 × 2 =
Answer:
324 X 2 = 648,
Explanation:
Given expression as 324 X 2, multiplying 324 with 2
we get 648, So 324 X 2 = 648.
Question 29.
424 × 2 =
Answer:
424 X 2 = 848,
Explanation:
Given expression as 424 X 2, multiplying 424 with 2
we get 848, So 424 X 2 = 848.
Question 30.
3 × 2 =
Answer:
3 X 2 = 6,
Explanation:
Given expression as 3 X 2, multiplying 3 with 2
we get 6, So 3 X 2 = 6.
Question 31.
13 × 2 =
Answer:
13 X 2 =
Explanation:
Given expression as 13 X 2, multiplying 13 with 2
we get 26, So 13 X 2 = 26.
Question 32.
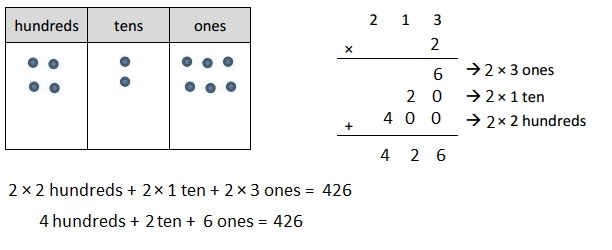
213 × 2 =
Answer:
213 X 2 = 426,
Explanation:
Given expression as 213 X 2, multiplying 213 with 2
we get 426, So 213 X 2 = 426.
Question 33.
1,213 × 2 =
Answer:
1,213 X 2 = 2,426,
Explanation:
Given expression as 1,213 X 2, multiplying 1,213 with 2
we get 2,426, So 1,213 X 2 = 2,426.
Question 34.
2,113 × 2 =
Answer:
2,113 X 2 = 4,226,
Explanation:
Given expression as 2,113 X 2, multiplying 2,113 with 2
we get 4,226, So 2,113 X 2 = 4,226.
Question 35.
2,131 × 2 =
Answer:
2,131 X 2 = 4,262,
Explanation:
Given expression as 2,131 X 2, multiplying 4,262 with 2
we get 4,262, So 2,131 X 2 = 4,262.
Question 36.
2,311 × 2 =
Answer:
2,311 X 2 = 4,262,
Explanation:
Given expression as 2,311 X 2, multiplying 2,311 with 2
we get 4,262, So 2,311 X 2 = 4,262.
Question 37.
23 × 4 =
Answer:
23 X 4 = 92,
Explanation:
Given expression as 23 X 4, multiplying 23 with 4
we get 92, So 23 X 4 = 92.
Question 38.
53 × 5 =
Answer:
53 X 5 = 265,
Explanation:
Given expression as 53 X 5, multiplying 53 with 5
we get 265, So 53 X 5 = 265.
Question 39.
45 × 3 =
Answer:
45 X 3 = 135,
Explanation:
Given expression as 45 X 3, multiplying 45 with 3
we get 135, So 45 X 3 = 135.
Question 40.
36 × 6 =
Answer:
36 X 6 = 216,
Explanation:
Given expression as 36 X 6, multiplying 36 with 6
we get 216, So 36 X 6 = 216.
Question 41.
215 × 3 =
Answer:
215 X 3 = 645,
Explanation:
Given expression as 215 X 3, multiplying 215 with 3
we get 645, So 215 X 3 = 645.
Question 42.
125 × 4 =
Answer:
125 X 4 = 500,
Explanation:
Given expression as 125 X 4, multiplying 125 with 4
we get 500, So 125 X 4 = 500.
Question 43.
5,312 × 2 =
Answer:
5,312 X 2 = 10,624,
Explanation:
Given expression as 5,312 X 2, multiplying 5,312 with 2
we get 10,624, So 5,312 X 2 = 10,624.
Explanation:
Given expression as 5,312 X 2, multiplying 5,312 with 2
we get 10,624, So 5,312 X 2 = 10,624.
Question 44.
1,235 × 4 =
Answer:
1,235 X 4 = 4,940,
Explanation:
Given expression as 1,235 X 4, multiplying 1,234 with 4
we get 4,940 So 1,235 X 4 = 4,940.
Eureka Math Grade 4 Module 3 Lesson 13 Problem Set Answer Key
Solve using the RDW process.
Question 1.
Over the summer, Kate earned $180 each week for 7 weeks.
Of that money, she spent $375 on a new computer and
$137 on new clothes. How much money did she have left?
Answer:
Kate is left with money of $748,
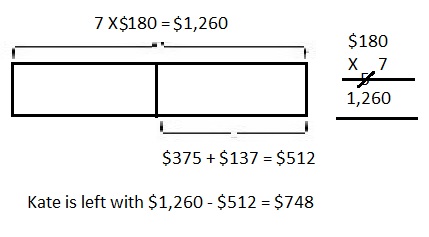
Explanation:
Given over the summer, Kate earned $180 each week for 7 weeks.
So Kate earned $180 X 7 =
5
$180
X 7
$1,260
Of that money, she spent $375 on a new computer and
$137 on new clothes. So Kate has spent $375 + $137 = $512,
Now money did Kate have left with is $1,260 – $512 = $748,
Solved using the RDW process as shown above.
Question 2.
Sylvia weighed 8 pounds when she was born.
By her first birthday, her weight had tripled.
By her second birthday, she had gained 12 more pounds.
At that time, Sylvia’s father weighed 5 times as much as she did.
What was Sylvia and her dad’s combined weight?
Answer:
Sylvia and her dad’s combined weight is 216 pounds,
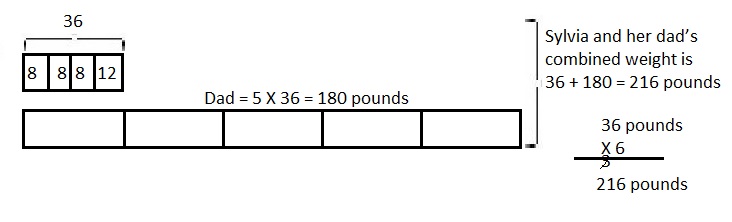
Explanation:
Given Sylvia weighed 8 pounds when she was born.
By her first birthday, her weight had tripled, So Sylvia
weighed on her first birthday is 8 pounds X 3 = 24 pounds,
By her second birthday, she had gained 12 more pounds means
24 pounds + 12 pounds = 36 pounds,
At that time, Sylvia’s father weighed 5 times as much as she did,
So 36 pounds X 5 =
3
36
X5
180 pounds
therefore, Sylvia and her dad’s combined weight is
180 ponds + 36 pounds = 216 pounds.
Solved using the RDW process as shown above.
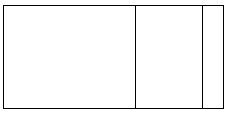
Question 3.
Three boxes weighing 128 pounds each and one
box weighing 254 pounds were loaded onto the back
of an empty truck. A crate of apples was then loaded onto
the same truck. If the total weight loaded onto the truck
was 2,000 pounds, how much did the crate of apples weigh?
Answer:
The crate of apples weigh 1,362 pounds,
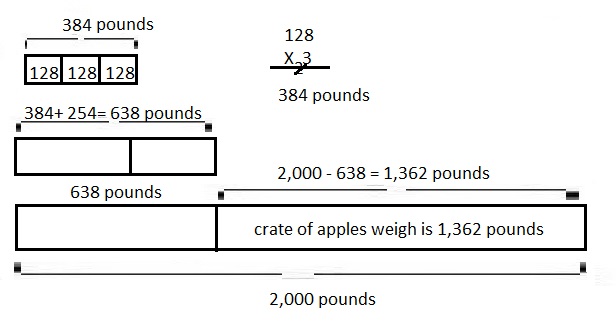
Explanation:
Given Three boxes weighing 128 pounds each so weight
of 3 boxes are 128 pounds X 3 =
2
128
X 3
384 pounds and one box weighing 254 pounds were
loaded onto the back of an empty truck. So now weight is
384 pounds + 254 pounds =
384 pounds
+254 pounds
638 pounds,
A crate of apples was then loaded onto the same truck.
If the total weight loaded onto the truck was 2,000 pounds,
therefore crate of apples weigh is
2,000 pounds
– 638 pounds
1,362 pounds.
Solved using the RDW process as shown above.
Question 4.
In one month, Charlie read 814 pages. In the same month,
his mom read 4 times as many pages as Charlie,
and that was 143 pages more than Charlie’s dad read.
What was the total number of pages read by Charlie and his parents?
Answer:
Total number of pages Charlie and his parents read are 7,183,

Explanation:
Given In one month, Charlie read 814 pages. In the same month,
his mom read 4 times as many pages as Charlie,
means Charlie’s mom read 814 X 4 =
1
814
X 4
3,256 pages, Charlie’s dad read 3,256 pages – 143 pages =
3,256
– 143
3,113 pages
Now total number of pages Charlie and his parents read are
814 + 3,256 + 3,113 =
814
3,256
+3,113
7,183 pages,Solved using the RDW process as shown above.
Eureka Math Grade 4 Module 3 Lesson 13 Exit Ticket Answer Key
Solve using the RDW process.
Question 1.
Michael earns $9 per hour. He works 28 hours each week.
How much does he earn in 6 weeks?
Answer:
Michael earns in 6 weeks is $1,512,

Explanation:
Given Michael earns $9 per hour. He works 28 hours each week,
means Michael earns in each week is 28 hours X $9 = $252,
Now in 6 weeks Michael earns $252 X 6 = $1,512.
Solved using the RDW process as shown above.
Question 2.
David earns $8 per hour. He works 40 hours each week.
How much does he earn in 6 weeks?
Answer:
David earns in 6 weeks is $1,920,

Explanation:
Given David earns $8 per hour. He works 40 hours each week,
means David earns in each week is 40 hours X $8 = $320,
Now in 6 weeks David earns $320 X 6 = $1,920.
Solved using the RDW process as shown above.
Question 3.
After 6 weeks, who earned more money?
How much more money?
Answer:
David earned more $408,

Explanation:
We got Michael earns in 6 weeks is $1,512 and
David earns in 6 weeks is $1,920 so more amount is earned
by David by $1,920 – $1,512 = $408 as shown above.
Eureka Math Grade 4 Module 3 Lesson 13 Homework Answer Key
Solve using the RDW process.
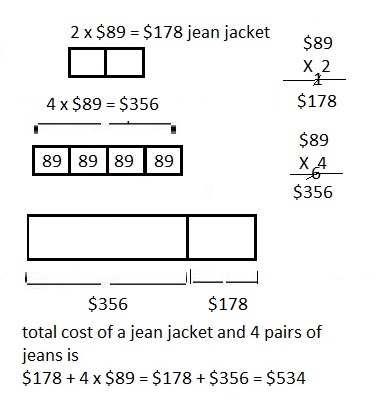
Question 1.
A pair of jeans costs $89. A jean jacket costs twice as much.
What is the total cost of a jean jacket and 4 pairs of jeans?
Answer:
The total cost of a Jean jacket and 4 pairs of jeans is $534,
Explanation:
Given a pair of jeans costs $89. A jean jacket costs twice as much,
So jean jcket costs 2 X $89 = $178,
The total cost of a jean jacket and 4 pairs of jeans is
$178 + 4 x $89 = $178 + $356 = $534.
Question 2.
Sarah bought a shirt on sale for $35. The original price
of the shirt was 3 times that amount. Sarah also bought a
pair of shoes on sale for $28. The original price of the
shoes was 5 times that amount. Together, how much money
did the shirt and shoes cost before they went on sale?
Answer:
Together,the shirt and shoes cost before they
went on sale is $245,

Explanation:
Given Sarah bought a shirt on sale for $35. The original price
of the shirt was 3 times that amount means the original price of
the shirt is 3 X $35 =
1
$35
X 3
$105
Sarah also bought a pair of shoes on sale for $28.
The original price of the shoes was 5 times that amount means
5 X $28 =
4
$28
X 5
$140,
Together,the shirt and shoes cost before they went on sale is
$105 + $140 = $245 as shown above.
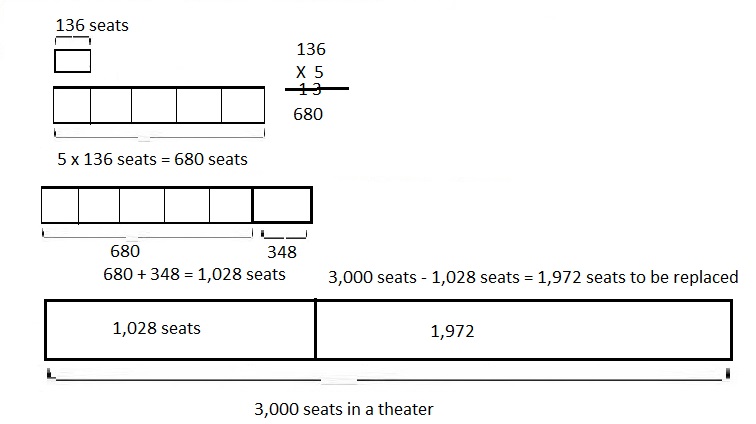
Question 3.
All 3,000 seats in a theater are being replaced.
So far, 5 sections of 136 seats and a sixth section
containing 348 seats have been replaced. How many more
seats do they still need to replace?
Answer:
Total more 1,972 seats needs to be still replaced,
Explanation:
Given all 3,000 seats in a theater are being replaced,
So far, 5 sections of 136 seats and a sixth section
containing 348 seats have been replaced means
5 X 136 seats + 348 seats are replaced = 680 + 348 = 1,028 seats
are replaced, So more seats needed to be still replaced are
3,000 seats – 1,028 seats = 1,972 seats as shown above.
Question 4.
Computer Depot sold 762 reams of paper. Paper Palace
sold 3 times as much paper as Computer Depot and
143 reams more than Office Supply Central.
How many reams of paper were sold by all three stores combined?
Answer:
Total 5,191 reams of paper were sold by all three stores combined,

Explanation:
Given Computer Depot sold 762 reams of paper. Paper Palace
sold 3 times as much paper as Computer Depot means
3 X 762 reams =
1
762
X 3
2,286 reams sold by Paper Palace,
Now 2,286 reams – 143 reams = 2,143 reams
by Office Supply Central, therefore all three stores combinedly
sold 762 + 2,286 + 2,143 = 5,191 reams of paper as shown above.
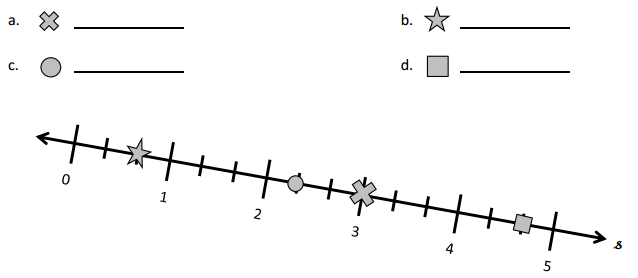
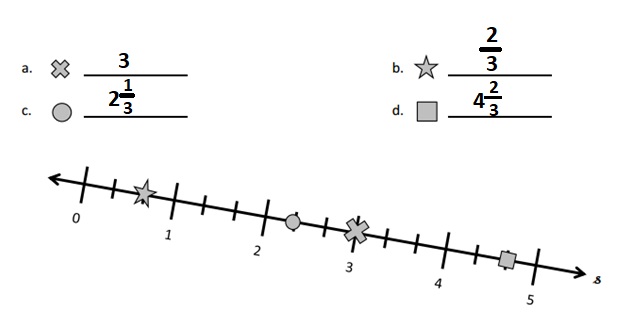



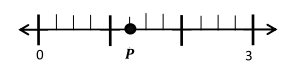
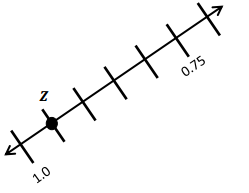
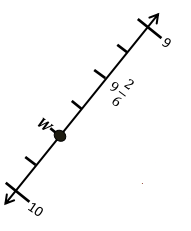
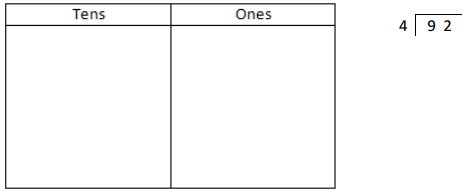
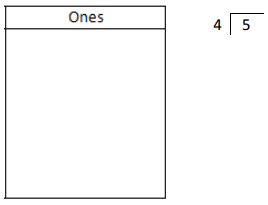
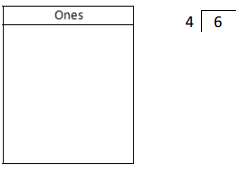
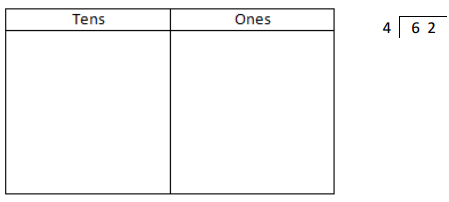
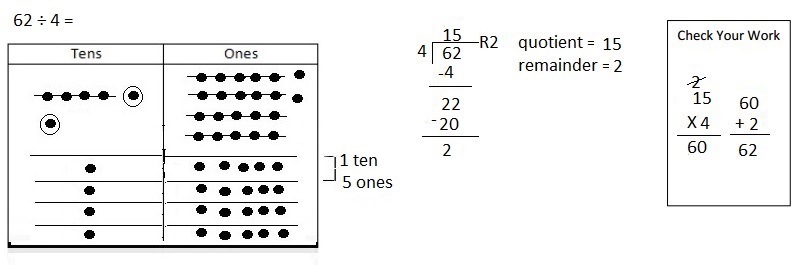
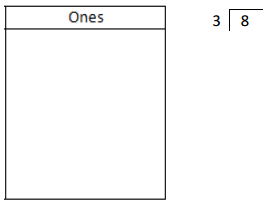
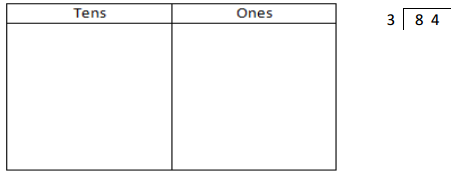
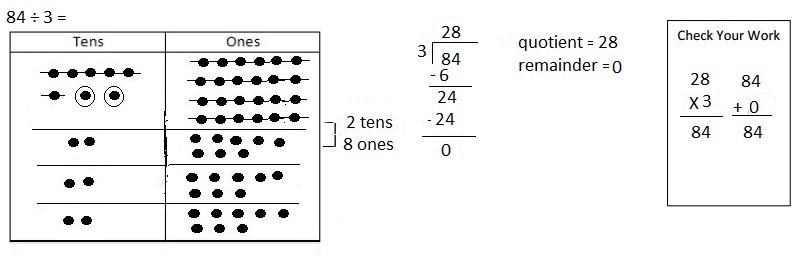
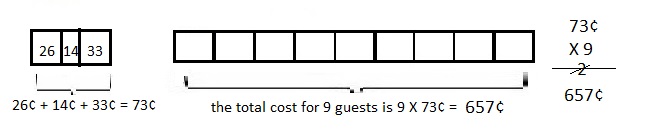
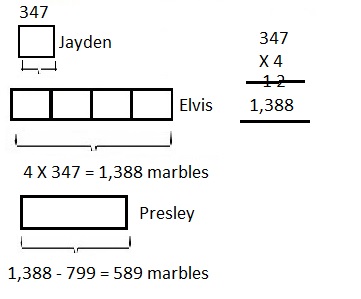
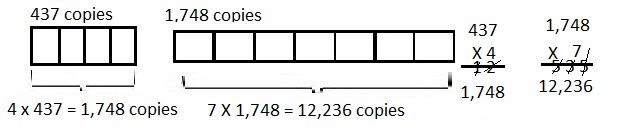
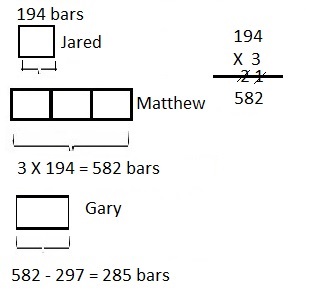
![]() ? ___________
? ___________![]() ? _________
? _________![]() ? __________
? __________![]() and the
and the ![]() ? __________
? __________
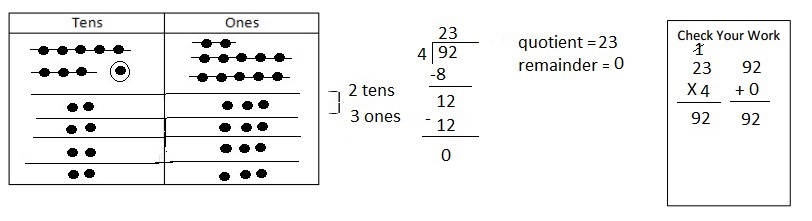
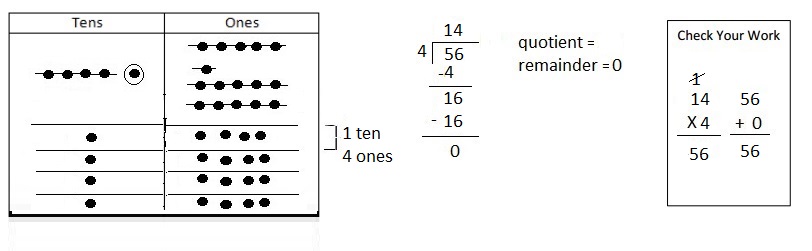
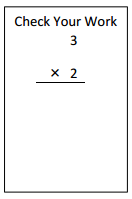
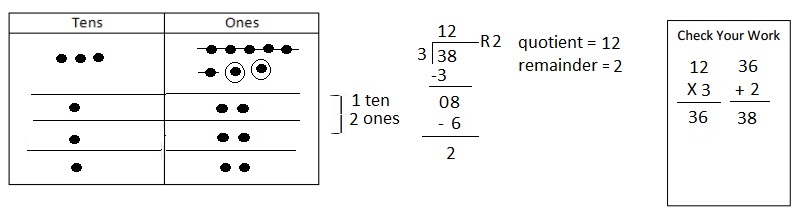
![]() is 3
is 3![]() is 8
is 8![]() is 14
is 14![]() and the
and the ![]() is (8 + 14)/2 = 11
is (8 + 14)/2 = 11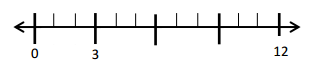
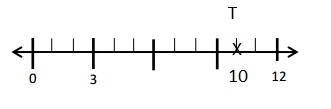
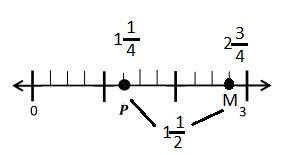
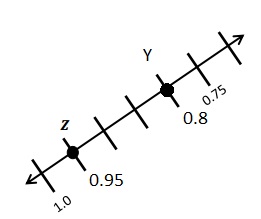
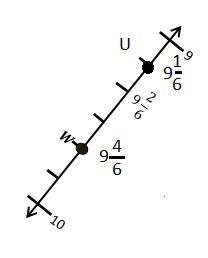


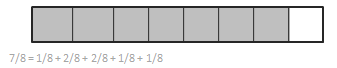
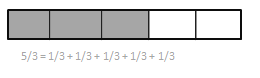
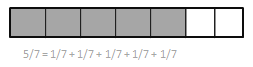
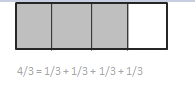
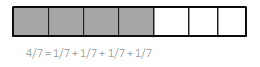
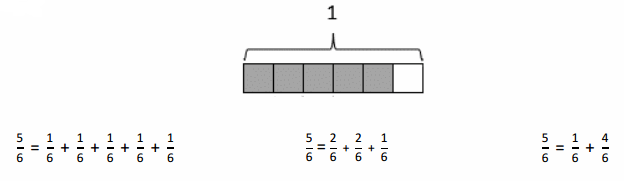
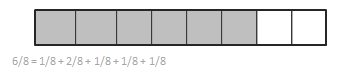
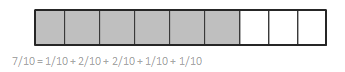






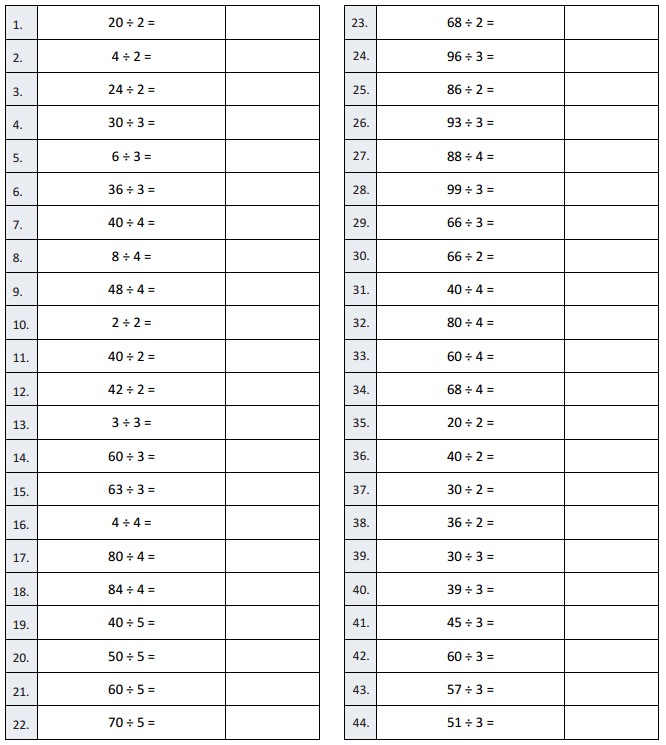
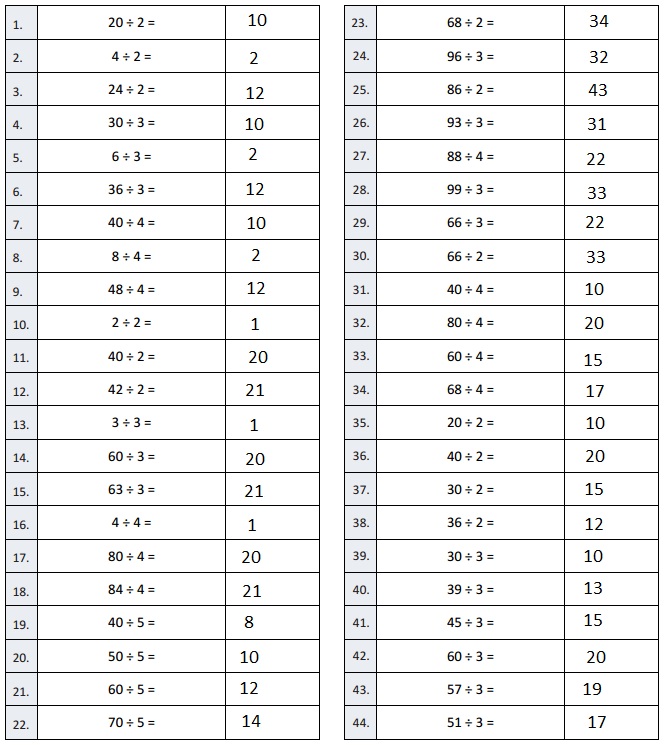
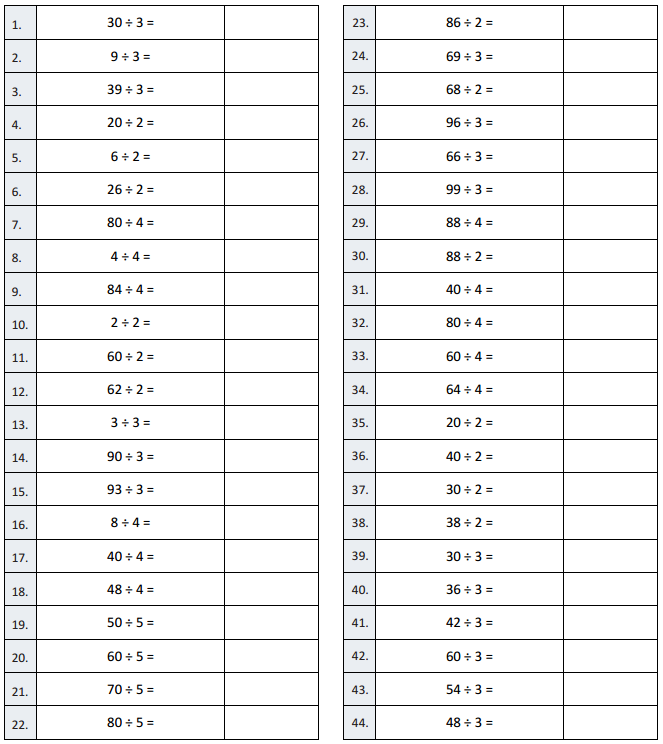
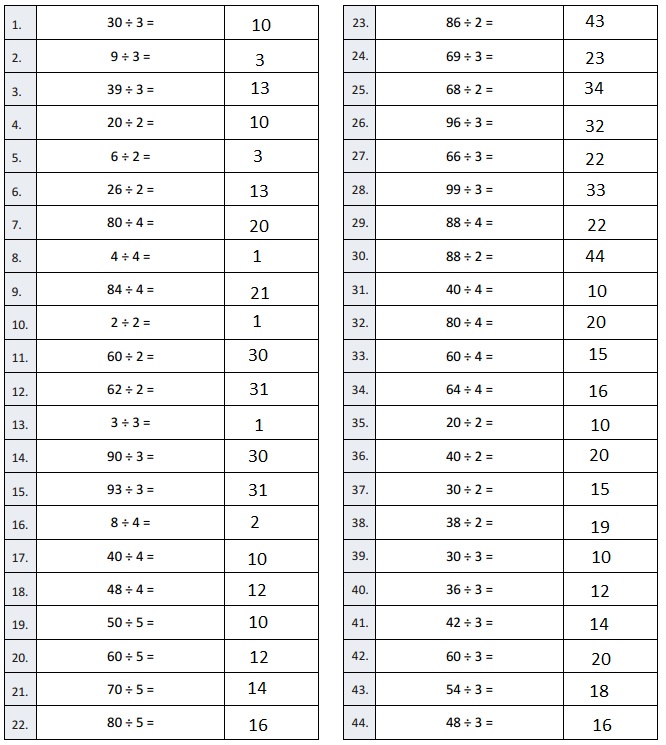
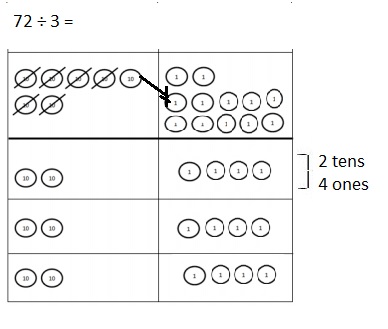
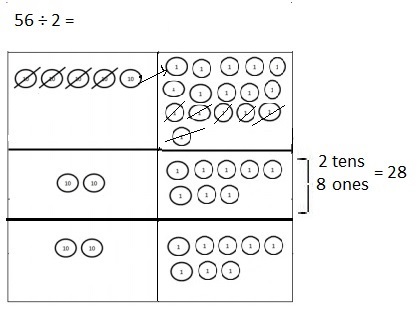
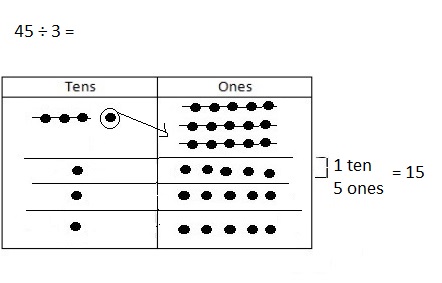
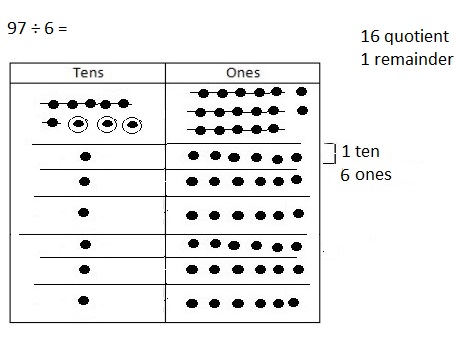
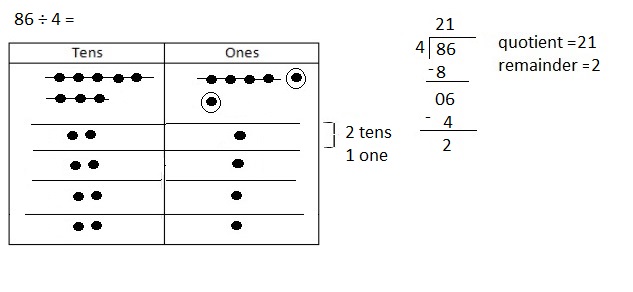
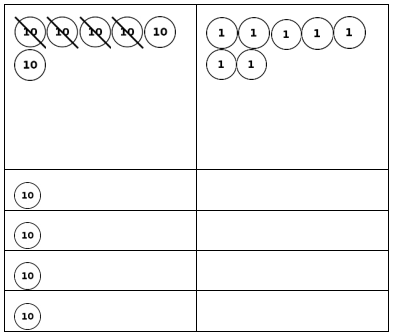
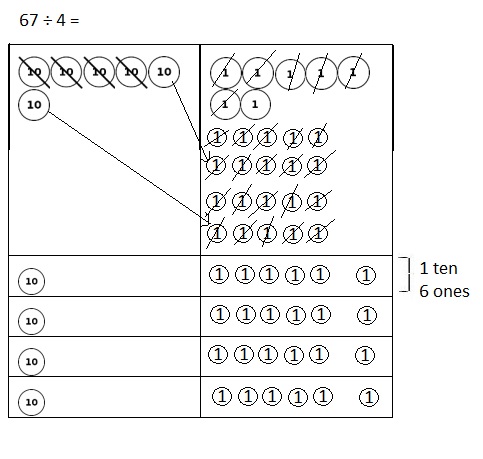
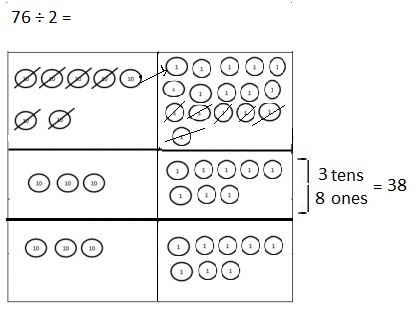
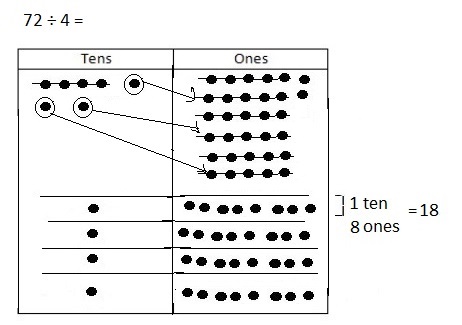
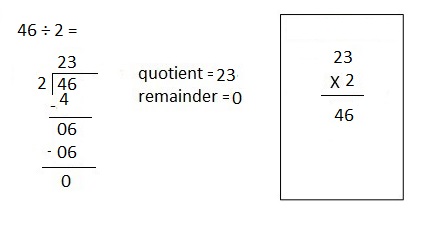
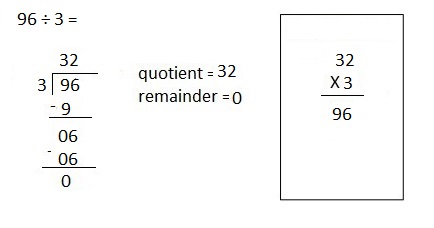
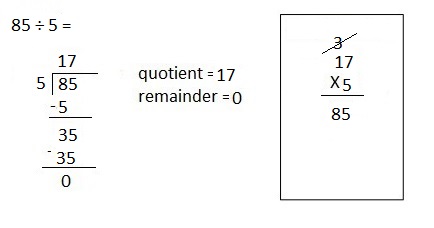
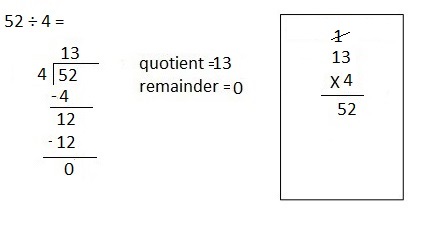



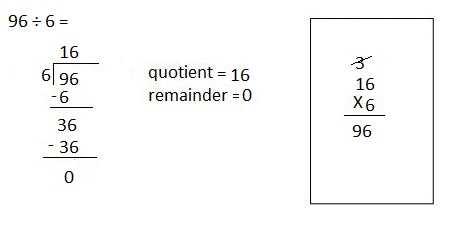
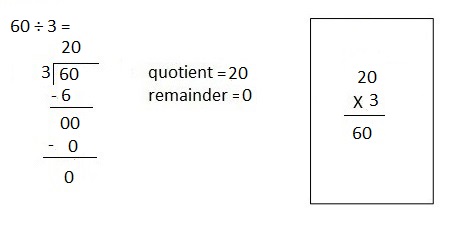
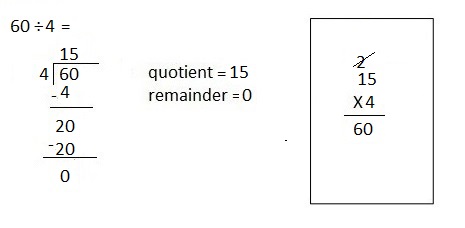
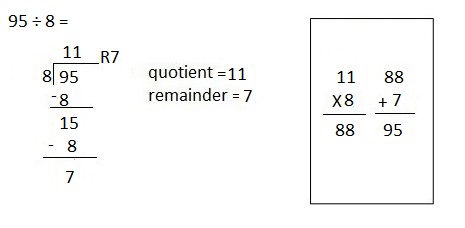



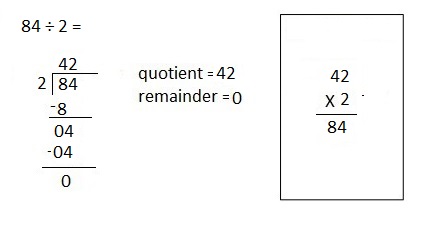








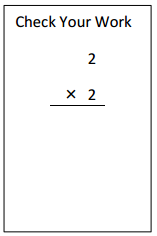

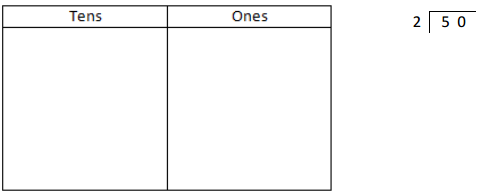

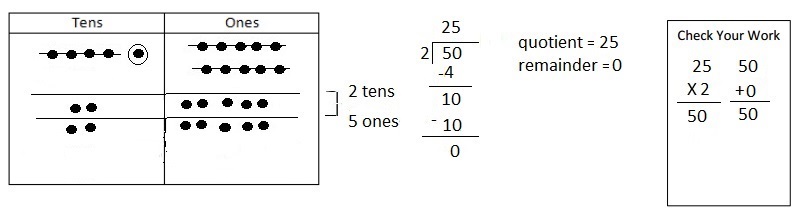
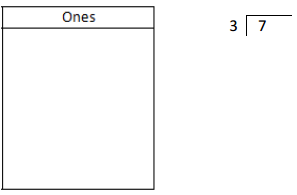
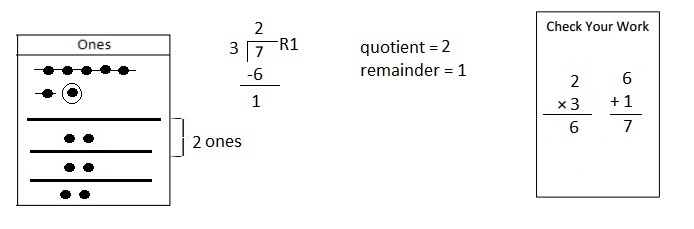

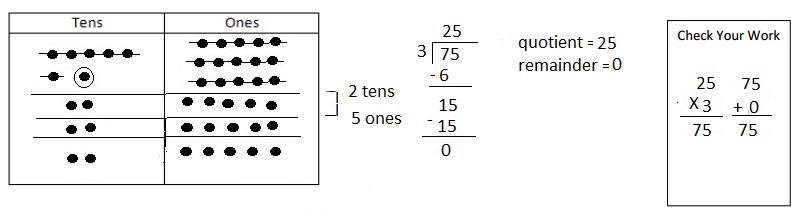
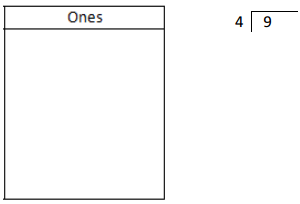
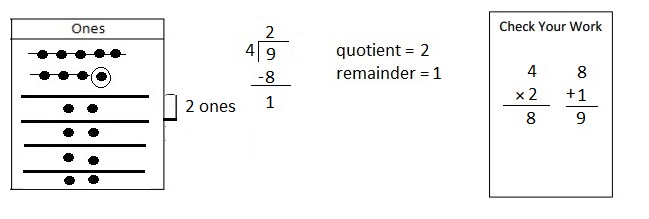




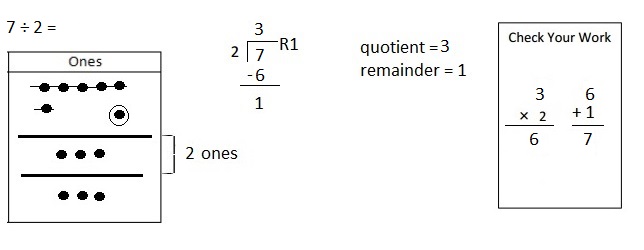
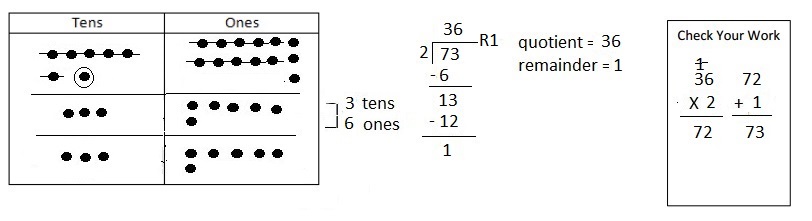

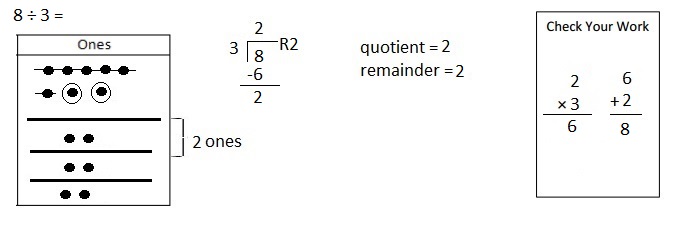



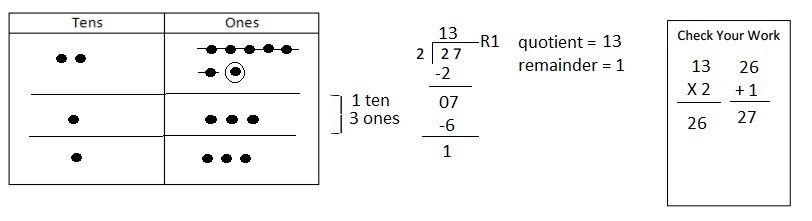

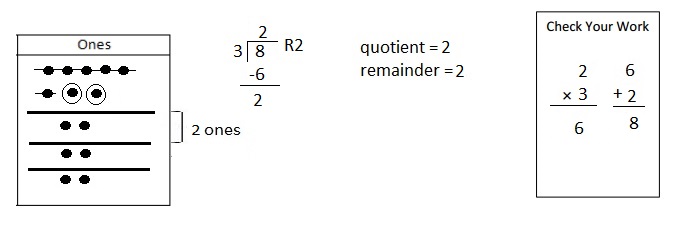

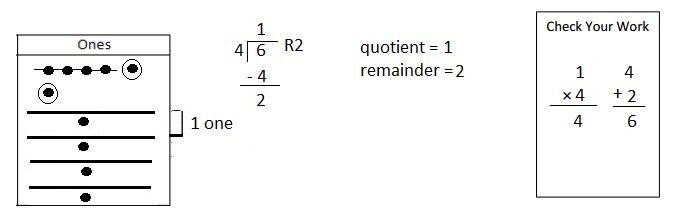
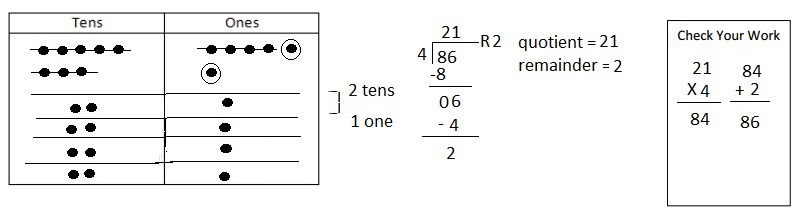

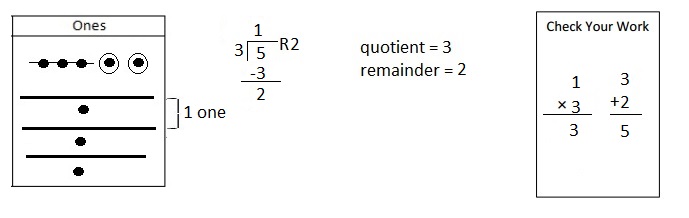

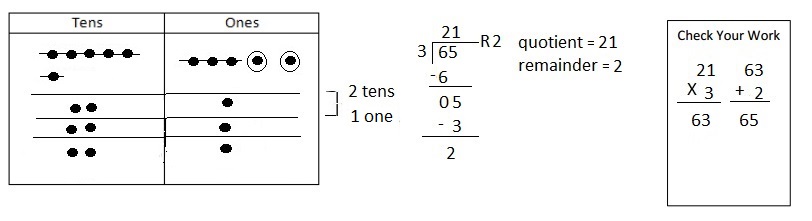



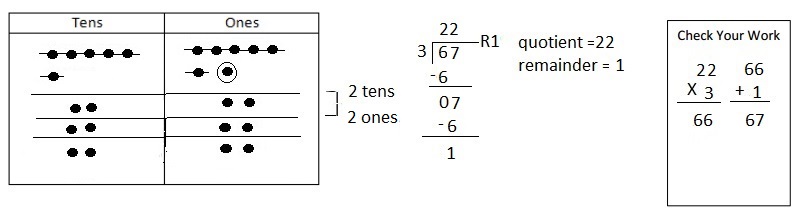
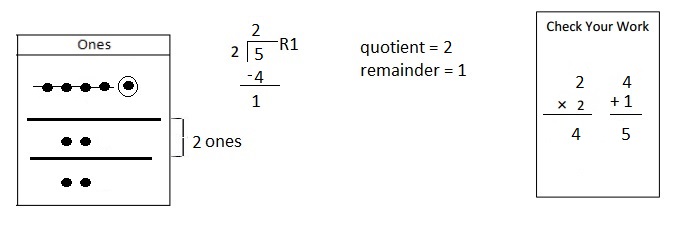
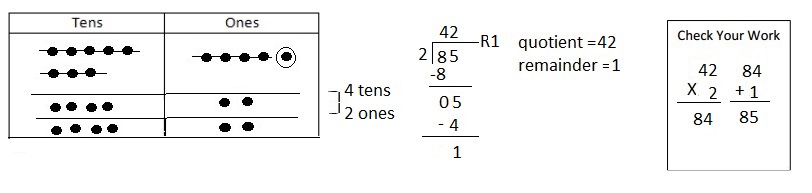

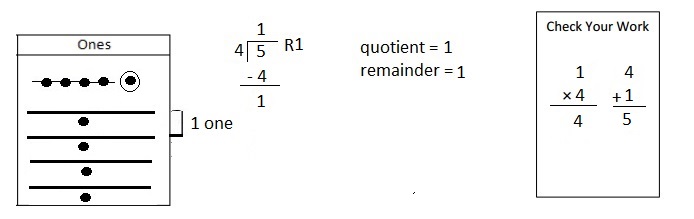

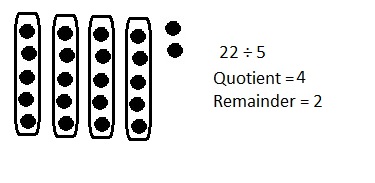
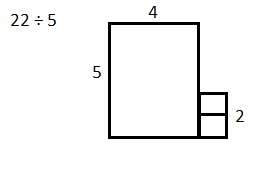

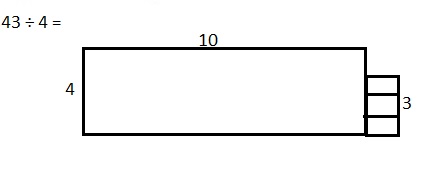
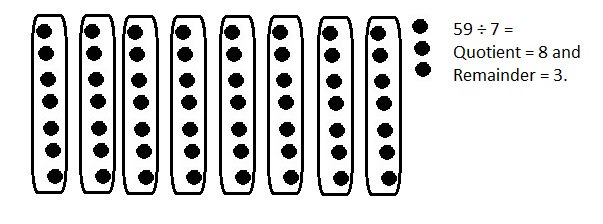
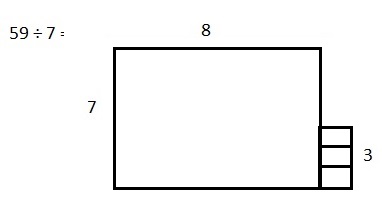
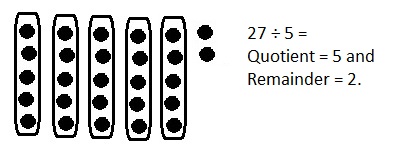
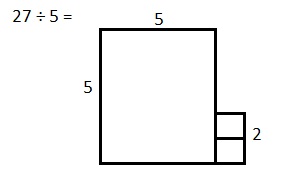
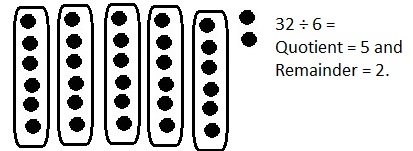
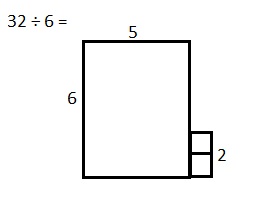

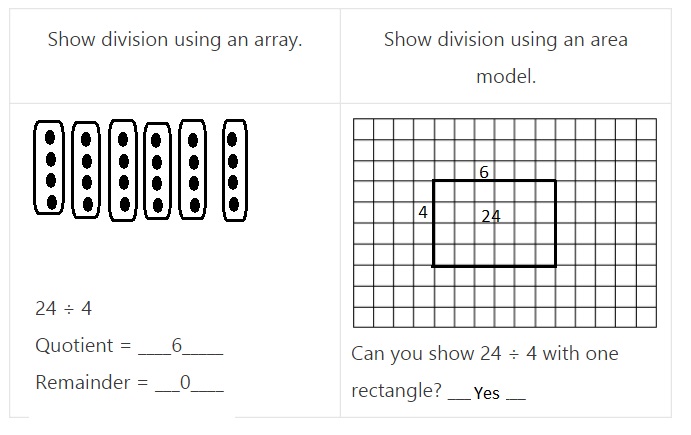

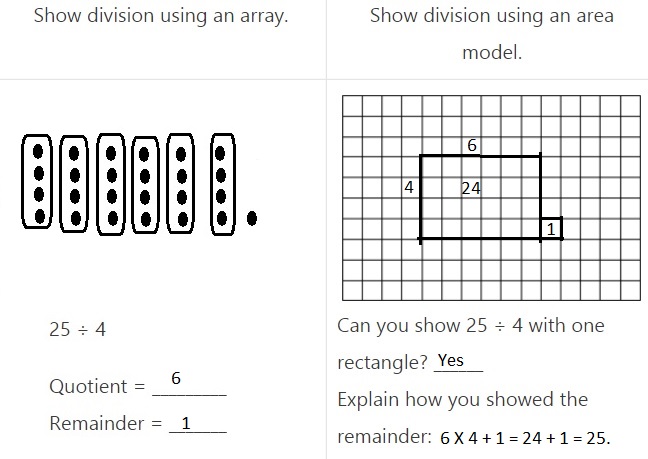
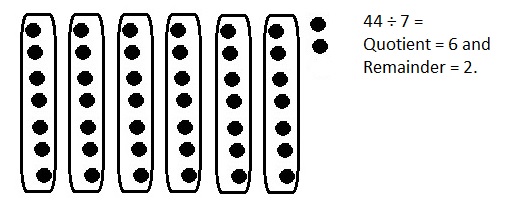
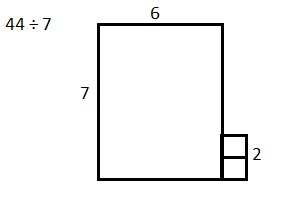
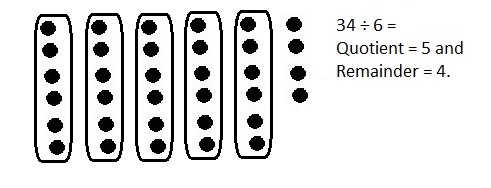
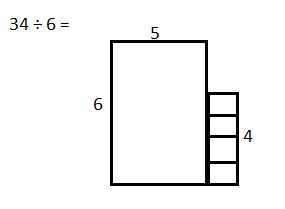

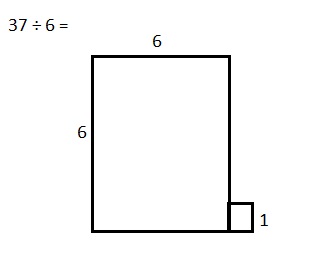






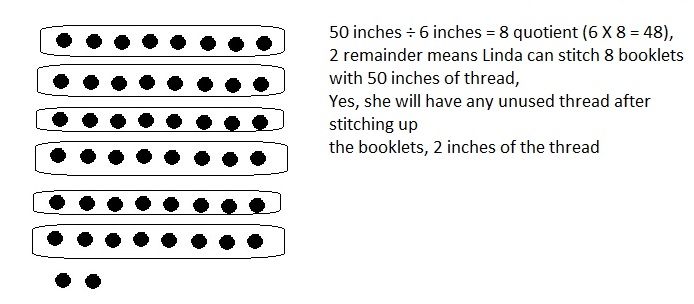
 Explanation:
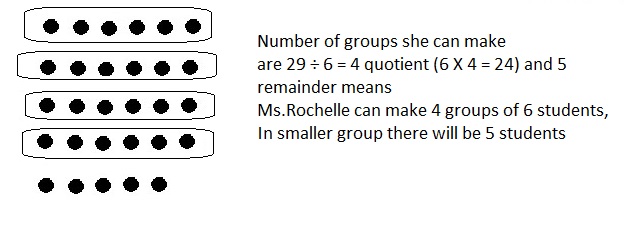
Explanation: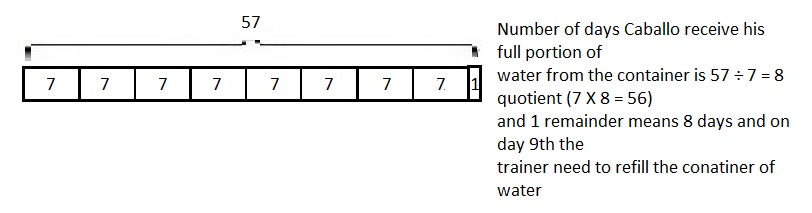



















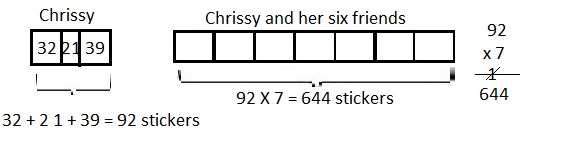










 Explanation:
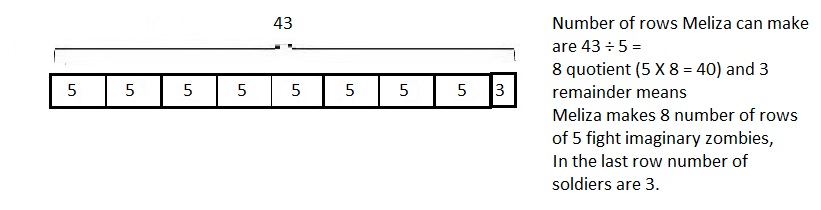
Explanation: