Download Big Ideas Math Answers Grade 6 Chapter 6 Equations Pdf for free of cost. If you are browsing for various questions of equations, then here is the one-stop solution. Know the benefit of referring to Big Ideas Math Book 6th Grade Answer Key Chapter 6 Equations. You can learn the tips and simple methods to solve all the problems. With the below-given material, it acts as a guide to get better marks in the exam. Get a free step-by-step solution from this ultimate guide ie., BIM 6th Grade Solutions Ch 6 Equations. Check the below sections to get various details and information.
Big Ideas Math Book 6th Grade Answer Key Chapter 6 Equations
It is necessary for the candidates to understand the concept in maths. Concept is important than scoring marks in the exam. Therefore relate the questions with real-time problems and understand the concept in depth. With all the factors into consideration, BIM 6th Grade Answer Key or Equations Pdf is prepared. Click on the links in the next sections and start practicing the problems. Follow the various topics, Steam videos and Solved problems available in BIM Equations book and pdf.
Performance Task
Lesson 1: Writing Equations in One Variable
- Lesson 6.1 Writing Equations in One Variable
- Writing Equations in One Variable Homework & Practice 6.1
Lesson: 2 Solving Equations Using Addition or Subtraction
- Lesson 6.2 Solving Equations Using Addition or Subtraction
- Solving Equations Using Addition or Subtraction Homework & Practice 6.2
Lesson: 3 Solving Equations Using Multiplication or Division
- Lesson 6.3 Solving Equations Using Multiplication or Division
- Solving Equations Using Multiplication or Division Homework & Practice 6.3
Lesson: 4 Writing Equations in Two Variables
- Lesson 6.4 Writing Equations in Two Variables
- Writing Equations in Two Variables Homework & Practice 6.4
Chapter 6 – Equations
- Equations Connecting Concepts
- Equations Chapter Review
- Equations Cumulative Practice
- Equations Practice Test
Equations STEAM Video/ Performance Task
STEAM Video
Rock Climbing
Equations can be used to solve many different kinds of problems in real life, such as estimating the amount of time it will take to climb a rock wall. Can you think of any other real-life situations where equations are useful?

In rock climbing, a pitch is a section of a climbing route between two anchor points. Watch the STEAM Video “Rock Climbing.”en answer the following questions.
1. How can you use pitches to estimate the amount of time it will take to climb a rock wall?
2. Are there any other methods you could use to estimate the amount of time it will take to climb a rock wall? Explain.
3. You know two of the three pieces of information below. Explain how you can find the missing piece of information.
Average climbing speed
Height of rock wall
Time to complete climb
Performance Task
Planning the Climb
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given information about two rock-climbing routes.

Route 1: 500 feet, 125 feet per pitch
Route 2: 1200 feet, 8 pitch
You will find the average speed of the climbers on Route 1 and the amount of time it takes to complete Route 2. Will the average speed of the climbers on Route 1 provide accurate predictions for the amount of time it takes to climb other routes? Explain why or why not.
Equations Getting Ready for Chapter 6
Chapter Exploration
Work with a partner. Every equation that has an unknown variable can be written as a question. Write a question that represents the equation. Then answer the question.

Answer:

Work with a partner. Write an equation that represents the question. Then answer the question.
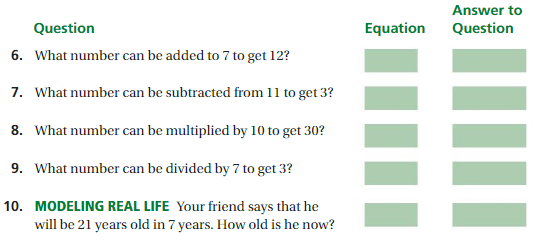
Answer:

Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
equation
independent variable
inverse operations
dependent variable
equation in two variables.
Lesson 6.1 Writing Equations in One Variable
EXPLORATION 1
Writing Equations
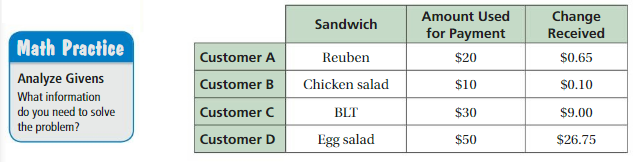
Work with a partner. Customers order sandwiches at a cafe from the menu board shown.

a. The equation 6.75x =20.25 represents the purchase of one customer from the menu board. What does the equation tell you about the purchase? What cannot be determined from the equation?
b. The four customers in the table buy multiple sandwiches of the same type. For each customer, write an equation that represents the situation. Then determine how many sandwiches each customer buys. Explain your reasoning.
Answer:

An equation
is a mathematical sentence that uses an equal sign, =, to show that two expressions are equal.
Expressions
4 + 8
x + 8
Equations
4 + 8 = 12
x + 8 = 12
To write a word sentence as an equation, look for key words or phrases such as is, the same as, or equals to determine where to place the equal sign.
Try It
Write the word sentence as an equation.
Question 1.
9 less than a number be equals 2.
Answer: 9-x=2
Explanation:
We have to write the equation for the word sentence
The phrase “less than” indicates -.
let the number be x.
9 – x = 2
Question 2.
The product of a number g and 5 is 30.
Answer: 5 × g=30
Explanation:
We have to write the equation for the word sentence
The phrase “product” indicates ‘×’
g × 5 = 30
Question 3.
A number k increased by 10 is the same as 24.
Answer: k + 10 = 24
Explanation:
We have to write the equation for the word sentence
The phrase “increased” indicates ‘+’
The equation is k + 10 = 24
Question 4.
The quotient of a number q and 4 is 12.
Answer: q ÷ 4 = 12
Explanation:
We have to write the equation for the word sentence
The phrase quotient indicates ‘÷’
The equation is q ÷ 4 = 12
Question 5.
2\(\frac{1}{2}\) is the same as the sum of a number w and \(\frac{1}{2}\).
Answer: 2 \(\frac{1}{2}\) = w + \(\frac{1}{2}\)
Explanation:
We have to write the equation for the word sentence
The phrase sum indicates ‘+’
The equation is 2 \(\frac{1}{2}\) = w + \(\frac{1}{2}\)
Question 6.
WHAT IF?
Each server decorates one table. Which equation can you use to find c?
Answer: We can use the multiplication equation to find c.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
VOCABULARY
How are expressions and equations different?
Answer: An expression is a number, a variable, or a combination of numbers and variables and operation symbols. An equation is made up of two expressions connected by an equal sign.
Question 8.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” equations.

Answer: n-4=8
4<8
Question 9.
OPEN-ENDED
Write a word sentence for the equation 28 −n= 5.
Answer: 28 less than a number n is equals to 5.
Question 10.
WRITING
You purchase x items for $4 each. Explain how the variable in the expression 4x and the variable in the equation 4x= 20 are similar. Explain how they are different.
Answer:
You purchase x items for $4 each
4x = 20
x = 20/4
x = 5
Question 11.
After four rounds, 74 teams are eliminated from a robotics competition. There are 18 teams remaining. Write and solve an equation to find the number of teams that started the competition.
Answer:
Given,
After four rounds, 74 teams are eliminated from a robotics competition. There are 18 teams remaining.
Let x be 74 teams
let y be 18 teams
The equation would be
x + y = 92
74 + 18 = 92
Thus the total number of teams are 92.
Question 12.
The mass of the blue copper sulfate crystal is two-thirds the mass of the red fluorite crystal. Write an equation you can use to find the mass (in grams) of the blue copper sulfate crystal.

Answer: blue copper sulfate crystal = 2/3 (red fluorite crystal)
Question 13.
DIG DEEPER!
You print photographs from a vacation. Find the number of photographs you can print for $3.60.

Answer: We can print 15 photographs for $3.60
Explanation:
Cost of each print = $0.24
The total cost for photographs is $3.60
3.60/0.24 = 15
Thus We can print 15 photographs for $3.60
Writing Equations in One Variable Homework & Practice 6.1
Review & Refresh
Factor the expression using the GCF.
Question 1.
6 + 27
Answer: 3 (2 + 9)
Explanation:
Given the expression 6 + 27
Take 3 as the common factor
3(2 + 9)
Question 2.
9w + 72
Answer: 9(w + 8)
Explanation:
Given the expression 9w + 72
Take 9 as the common factor
9w + 72 = 9(w + 8)
Question 3.
42 + 24n
Answer: 6(7 + 4n)
Explanation:
Given the expression 42 + 24n
Take 6 as the common factor
42 + 24n = 6(7 + 4n)
Question 4.
18h + 30k
Answer: 6(3h + 5k)
Explanation:
Given the expression 18h + 30k
Take 6 as the common factor
18h + 30k = 6(3h + 5k)
Question 5.
Which number is not equal to 225%?
A. 2\(\frac{1}{4}\)
B. \(\frac{9}{4}\)
C. \(\frac{50}{40}\)
D. \(\frac{45}{20}\)
Answer: C
225% is not equal to \(\frac{50}{40}\)
Evaluate the expression when a = 7.
Question 6.
6 + a
Answer: 13
Explanation:
Given the expression 6 + a
where a = 7
Substitute the value of a in the expression
6 + 7 = 13
Question 7.
a – 4
Answer: 3
Explanation:
Given the expression a – 4
where a = 7
Substitute the value of a in the expression
a – 4
7 – 4 = 3
Question 8.
4a
Answer: 28
Explanation:
Given the expression 4a
where a = 7
Substitute the value of a in the expression
4 × 7 = 28
Question 9.
\(\frac{35}{a}\)
Answer: 5
Explanation:
Given the expression \(\frac{35}{a}\)
where a = 7
Substitute the value of a in the expression
\(\frac{35}{7}\) = 5
Find the perimeter of the rectangle.
Question 10.
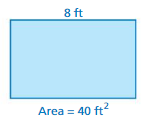
Answer:
l = 8 ft
Area = 40 sq ft
We know that,
Area of rectangle = l × w
40 sq. ft = 8 ft × w
w = 40/8 = 5 ft
Thus the width of the above rectangle is 5 ft.
Question 11.
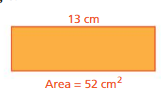
Answer:
l = 13 cm
w = ?
A = 52 sq. cm
We know that,
Area of rectangle = l × w
52 sq. cm = 13 cm × w
w = 52/13
w = 4 cm
Thus the width of the above rectangle is 4 cm.
Question 12.
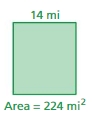
Answer:
A = 224 sq. miles
l = 14 miles
We know that,
Area of rectangle = l × w
224 sq. miles = 14 × w
w = 224/14
w = 16 miles
Thus the width of the above figure is 16 miles.
Concepts, Skills, & Problem Solving
WRITING EQUATIONS A roast beef sandwich costs $6.75. A customer buys multiple roast beef sandwiches. Write an equation that represents the situation. Then determine how many sandwiches the customer buys. (See Exploration 1, p. 245.)
Question 13.
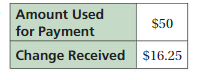
Answer:
Given,
A roast beef sandwich costs $6.75.
Amount used for payment = $50.
Change Received = $16.25
The total number of sandwich the customer buys = 5
Question 14.
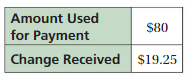
Answer:
Given,
A roast beef sandwich costs $6.75.
Amount used for payment = $80.
Change Received = $19.25
Amount used for payment – Change Received
= $ 80 – $19.25
= $60.75
1 sandwich = $6.75
The total number of sandwich the customer buys = 9
WRITING EQUATIONS Write the word sentence as an equation.
Question 15.
A number y decreased by 9 is 8.
Answer: y – 9 = 8
Explanation:
We have to write the word sentence in the equation form.
y – 9 = 8
Question 16.
The sum of a number x and 4 equals 12.
Answer: x + 4 = 12
Explanation:
We have to write the word sentence in the equation form.
x + 4 = 12
Question 17.
9 times a number b is 36.
Answer: 9b = 36
Explanation:
We have to write the word sentence in the equation form.
The phrase times indicates ‘×’
The equation would be 9b = 36
Question 18.
A number w divided by 5 equals 6.
Answer: w ÷ 5 = 6
Explanation:
We have to write the word sentence in the equation form.
The phrase divided by indicates ‘÷’
The equation would be w ÷ 5 = 6
Question 19.
54 equals 9 more than a number t.
Answer: 54 = 9 + t
Explanation:
We have to write the word sentence in the equation form.
The phrase more than indicates ‘+’
The equation would be 54 = 9 + t
Question 20.
5 is one-fourth of a number c.
Answer: 5 = 1/4 c
Explanation:
We have to write the word sentence in the equation form.
The phrase of indicates ‘×’
The equation would be 5 = 1/4 c
Question 21.
9.5 less than a number n equals 27.
Answer: 9.5 – n = 27
Explanation:
We have to write the word sentence in the equation form.
The phrase less than indicates ‘-‘
The equation would be 9.5 – n = 27
Question 22.
11\(\frac{3}{4}\) is the quotient of a number y and 6\(\frac{1}{4}\).
Answer: 11\(\frac{3}{4}\) = y ÷ 6\(\frac{1}{4}\)
Explanation:
We have to write the word sentence in the equation form.
The phrase quotient indicates ‘÷’
The equation would be 11\(\frac{3}{4}\) = y ÷ 6\(\frac{1}{4}\)
Question 23.
YOU BE THE TEACHER
Your friend writes the word sentence as an equation. Is your friend correct? Explain your reasoning.
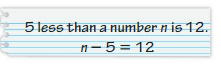
Answer:
Given the word sentence, 5 less than a number n is 12.
Question 24.
MODELING REAL LIFE
Students and faculty raise $6042 for band uniforms. The faculty raised $1780. Write an equation you can use to find the amount a (in dollars) the students raised.
Answer:
Given,
Students and faculty raise $6042 for band uniforms (x).
The faculty raised $1780 (y)
The students raised be z
z = x – y
z = 6042 – 1780
z = 4262
Question 25.
MODELING REAL LIFE
You hit a golf ball 90 yards. It travels three-fourths of the distance to the hole. Write an equation you can use to find the distance d (in yards) from the tee to the hole.
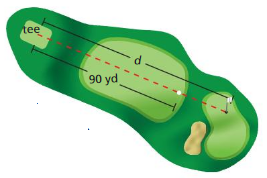
Answer:
Given,
You hit a golf ball 90 yards. It travels three-fourths of the distance to the hole.
3/4 × D = 90
D = 360/3
D = 120
GEOMETRY Write an equation you can use to find the value of x.
Question 26.
Perimeter of triangle: 16 in.
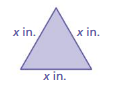
Answer:
side of the triangle = x
Perimeter of triangle 16 in
P = a + b + c
16 in = x + x + x
3x = 16
x = 16/3
x = 5.3
Thus the side of the triangle is 5.3 inches.
Question 27.
Perimeter of square: 30 mm
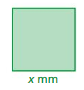
Answer:
4x = 30
x = 30/4
x = 7.5 mm
Question 28.
MODELING REAL LIFE
You sell instruments at a Caribbean music festival. You earn $326 by selling 12 sets of maracas,6 sets of claves, and x djembe drums. Find the number of djembe drums you sold.

Answer:
Let the price of maracas be m
Let the price of claves be c
Let the price of djembe drums be x
Number of maracas = 12 sets
Number of claves = 6 sets
Number of djembe drums = xx
Total earned amount = $326
The equation would be
12m + 6c + dxx = 326
The cost for 1 maracas is $14
For 12 sets = 12 × 14 = $168
The cost for 1 clave = $5
For 6 sets = 6 × 5 = $30
The cost for 1 djembe drums is $16
For x sets = 16x
12m + 6c + dxx = 326
168 + 30 + 16x = 326
16x = 128
x = 128 ÷ 16
x = 8
Question 29.
PROBLEM SOLVING
Neil Armstrong set foot on the Moon 109.4 hours after Apollo 11departed from the Kennedy Space Center. Apollo 11landed on the Moon about 6.6 hours before Armstrong’s first step. How many hours did it take for Apollo 11 to reach the Moon?
Answer:
Given,
Neil Armstrong set foot on the Moon 109.4 hours after Apollo 11 departed from the Kennedy Space Center.
Apollo 11landed on the Moon about 6.6 hours before Armstrong’s first step.
To find how many hours did it take for Apollo 11 to reach the Moon we have to subtract 6.6 hours from 109.4 hours
109.4 – 6.6 = 102.8 hours
Thus it took 102.8 hours for Apollo 11 to reach the Moon.
Question 30.
LOGIC
You buy a basket of 24 strawberries. You eat them as you walk to the beach. It takes the same amount of time to walk each block. When you are halfway there, half of the berries are gone. After walking 3 more blocks, you still have 5 blocks to go. You reach the beach 28 minutes after you began. One-sixth of your strawberries are left.
a. Is there enough information to find the time it takes to walk each block? Explain.
Answer:
Yes, you are given enough information to find the time to walk each block
To find the total number of block you, add
3 + 5 + 8 = 16
Also the time it takes to walk the 16 blocks is given 28 minutes.
b. Is there enough information to find how many strawberries you ate while walking the last block? Explain.

Answer:
No, there is not enough information to find how many strawberries ate while walking the last block.
You are only given the amount of strawberries you started with 24 and what you have left (1/6) with 5 blocks to go. Therefore you can only be given how many strawberries were eaten walking the last block.
Question 31.
DIG DEEPER!
Find a sales receipt from a store that shows the total price of the items and the total amount paid including sales tax.
a. Write an equation you can use to find the sales tax rate r.
b. Can you use r to find the percent for the sales tax? Explain.
Answer:
Total amount paid = total price + (total price × sales tax rate)
sample equation
14.20 = 13.27 + (13.27 × 0.07)
Yes, you can use r to find the percent for the sales tax.
Multiplying r by 100 gives the percent for the sales tax.
Question 32.
GEOMETRY
A square is cut from a rectangle. The side length of the square is half of the unknown width w. The area of the shaded region is 84 square inches. Write an equation you can use to find the width (in inches).
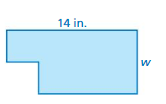
Answer:
Given,
A square is cut from a rectangle. The side length of the square is half of the unknown width w.
The area of the shaded region is 84 square inches.
84 square inches divided by 14 inches equals 6
84 divided by 14 = s
84 ÷ 14 = s
Lesson 6.2 Solving Equations Using Addition or Subtraction
EXPLORATION 1
Solving an Equation Using a Tape Diagram
Work with a partner. A student solves an equation using the tape diagrams below.
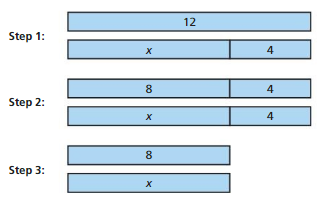
a. What equation did the student solve? What is the solution?
Answer: x + 4 = 12
Explanation:
By seeing step 1 we can say that the equation for the above tape diagram x + 4 = 12
b. Explain how the tape diagrams in Steps 2 and 3 relate to the equation and its solution.
Answer:
By seeing the steps 2 and 3 we can say
8 + 4 = 12
x + 4 = 12
x = 12 – 4
x = 8
EXPLORATION 2
Solving an Equation Using a Model
Work with a partner.
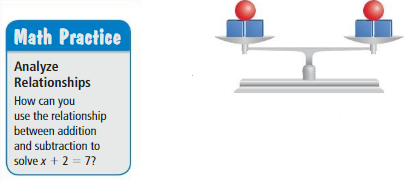
a. How are the two sides of an equation similar to a balanced scale?
b. When you add weight to one side of a balanced scale, what can you do to balance the scale? What if you subtract weight from one side of a balanced scale? How does this relate to solving an equation?
c. Use a model to solve x + 2 = 7. Describe how you can solve the equation algebraically.
Answer:
x + 2 = 7
x = 7 – 2
x = 5

Try It
Tell whether the given value is a solution of the equation.
Question 1.
a + 6 = 17; a = 9
Answer: not a solution
Explanation:
Given the equation a + 6 = 17
when a = 9
9 + 6 = 17
15 ≠ 17
Thus the equation is not a solution.
Question 2.
9 – g = 5; g = 3
Answer: not a solution
Explanation:
Given the equation 9 – g = 5
where g = 3
9 – 3 = 5
6 ≠ 5
Thus the equation is not a solution.
Question 3.
35 – 7n; n = 5
Answer: solution
Explanation:
Given the equation 35 – 7n
where n = 5
35 – 7(5)
35 – 35 = 0
Thus the equation is a solution.
Question 4.
\(\frac{q}{2}\) = 28; q = 14
Answer: not a solution
Explanation:
Given the equation \(\frac{q}{2}\) = 28
where q = 14
\(\frac{14}{2}\) = 28
7 ≠ 28
Thus the equation is not a solution.
You can use inverse operations to solve equations. Inverse operations “undo” each other. Addition and subtraction are inverse operations.
Solve the equation. Check your solution.
Question 5.
k – 3 = 1
Answer: k = 4
Explanation:
Given the equation k – 3 = 1
k = 1 + 3
k = 4
Question 6.
n – 10 = 4
Answer: n = 14
Explanation:
Given the equation n – 10 = 4
n = 4 + 10
n = 14
Question 7.
15 = r – 6
Answer: r = 21
Explanation:
Given the equation 15 = r – 6
15 + 6 = r
r = 21
Question 8.
s + 8 = 17
Answer: s = 9
Explanation:
Given the equation s + 8 = 17
s = 17 – 8
s = 9
Question 9.
9 = y + 6
Answer: y = 3
Explanation:
Given the equation 9 = y + 6
9 – 6 = y
y = 3
Question 10.
13 + m = 20
Answer: m = 7
Explanation:
Given the equation 13 + m = 20
m = 20 – 13
m = 7
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
CHECKING SOLUTIONS Tell whether the given value is a solution of the equation.
Question 11.
n + 8 = 42; n = 36
Answer: not a solution
Explanation:
Given the equation n + 8 = 42
where n = 36
36 + 8 = 44
44 ≠ 42
Thus the value is not a solution.
Question 12.
g – 9 = 24; g = 35
Answer: not a solution
Explanation:
Given the equation g – 9 = 24
where g = 35
35 – 9 = 24
26 ≠ 24
Thus the value is not a solution.
SOLVING EQUATIONS Solve the equation. Check your solution.
Question 13.
x – 8 = 12
Answer: 20
Explanation:
Given the equation x – 8 = 12
x = 12 + 8
x = 20
Question 14.
b + 14 = 33
Answer: 19
Explanation:
Given the equation b + 14 = 33
b = 33 – 14
b = 19
Question 15.
WRITING
When solving x + 5 =16, why do you subtract 5 from the left side of the equation? Why do you subtract 5 from the right side of the equation?
Answer:
To solve the equation we have to subtract 5.
x + 5 = 16
x = 16 – 5
x = 11
Question 16.
REASONING
Do the equations have the same solution? Explain your reasoning.
x – 8 = 6
x – 6 = 8
Answer:
i. x – 8 = 6
x = 6 + 8
x = 14
ii. x – 6 = 8
x = 8 + 6
x = 14
Yes both the equations has same solutions.
Question 17.
STRUCTURE
Just by looking at the equation x + 6 + 2x = 2x + 6 + 4, find the value of x. Explain your reasoning.
Answer:
x + 6 + 2x = 2x + 6 + 4
3x + 6 = 2x + 10
3x – 2x = 10 – 6
x = 4
Question 18.
An emperor penguin is 45 inches tall. It is 24 inches taller than a rockhopper penguin. Write and solve an equation to find the height (in inches) of a rockhopper penguin. Is your answer reasonable? Explain.

Answer:
Given,
An emperor penguin is 45 inches tall. It is 24 inches taller than a rockhopper penguin.
45 inches – 24 inches = 21 inches
Thus the height of the rockhopper penguin is 21 inches.
Question 19.
DIG DEEPER!
You get in an elevator and go up 2 floors and down8 floors before exiting. Then you get back in the elevator and go up 4 floors before exiting on the 12th floor. On what floors did you enter the elevator?
Answer: The answer to your question is 14 floor
Explanation:
To solve this problem start from the end changing the sense if it says up, then consider the action as down, etc.
Last floor = 12
Go down 4 floors = 12 – 4 = 8
Go up 8 floors = 8 + 8 = 16
Go down 2 floors = 16 – 2 = 14
Solving Equations Using Addition or Subtraction Homework & Practice 6.2
Review & Refresh
Write the word sentence as an equation.
Question 1.
Th sum of a number x and 9 is 15.
Answer: x + 9 = 15
Explanation:
We have to write the equation for the word sentence
The phrase sum indicates ‘+’
The equation would be x + 9 = 15
Question 2.
12 less than a number m equals 20.
Answer: 12 – m = 20
Explanation:
We have to write the equation for the word sentence
The phrase less than indicates ‘-‘
The equation would be 12 – m = 20
Question 3.
The product of a number d and 7 is 63.
Answer: d7 = 63
Explanation:
We have to write the equation for the word sentence
The phrase product indicates ‘×’
The equation would be d × 7 = 63
Question 4.
18 divided by a number s equals 3.
Answer: 18 ÷ s = 3
Explanation:
We have to write the equation for the word sentence
The phrase divided by indicates ‘÷’
The equation would be 18 ÷ s = 3
Divide. Write the answer in simplest form.
Question 5.
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
Answer: 2
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
\(\frac{1}{2}\) × \(\frac{4}{1}\) = 2
Question 6.
12 ÷ \(\frac{3}{8}\)
Answer: 32
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
12 × \(\frac{8}{3}\)
= 4 × 8
= 32
Question 7.
8 ÷ \(\frac{4}{5}\)
Answer: 10
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
8 × \(\frac{5}{4}\)
= 2 × 5
= 10
Question 8.
\(\frac{7}{9}\) ÷ \(\frac{3}{2}\)
Answer: \(\frac{14}{27}\)
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
\(\frac{7}{9}\) × \(\frac{2}{3}\) = \(\frac{14}{27}\)
Question 9.
Which ratio is not equivalent to 72 : 18?
A. 36 : 9
B. 18 : 6
C. 4 : 1
D. 288 : 72
Answer: B. 18 : 6
Explanation:
72 : 18 = 36:9, 4 : 1, 288 : 72
18 : 6 is not equivalent to 72 : 18
Thus the correct answer is option B.
Evaluate the expression.
Question 10.
(2 + 52) ÷ 3
Answer: 9
Explanation:
Given the expression (2 + 52) ÷ 3
(2 + 25) ÷ 3
27 ÷ 3 = 9
Question 11.
6 + 23 . 3 – 5
Answer: 25
Explanation:
Given the expression 6 + 23 . 3 – 5
6 + 8 . 3 – 5
6 + 24 – 5
6 + 19
25
Question 12.
4 . [3 + 3(20 – 42 – 2)]
Answer: 36
Explanation:
Given the expression 4 . [3 + 3(20 – 42 – 2)]
4(3 + 3(20 – 16 – 2))
4(3 + 3(2))
4 (3 + 6)
4(9)
36
Question 13.
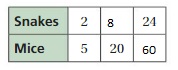
Find the missing values in the ratio table. Then write the equivalent ratios.
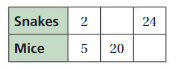
Answer:
Concepts, Skills, & Problem Solving
CHOOSE TOOLS Use a model to solve the equation. (See Explorations 1 and 2, p. 251.)
Question 14.
n + 7 = 9
Answer: n = 2
Explanation:
n + 7 = 9
n = 9 – 7
n = 2
Question 15.
t + 4 = 5
Answer: t = 1
Explanation:
t + 4 = 5
t = 5 – 4
t = 1
Question 16.
c + 2 = 8
Answer: c = 6
Explanation:
c + 2 = 8
c = 8 – 2
c = 6
CHECKING SOLUTIONS Tell whether the given value is a solution of the equation.
Question 17.
x + 42 = 85; x = 43
Answer: solution
Explanation:
x + 42 = 85
Substitute the value of x in the equation
x = 43
43 + 42 = 85
Question 18.
8b = 48; b = 6
Answer: solution
Explanation:
8b = 48
Substitute the value of b in the equation
b = 6
8(6) = 48
48 = 48
Question 19.
19 – g = 7; g = 15
Answer: not a solution
Explanation:
19 – g = 7
Substitute the value of g in the equation
g = 15
19 – 15 = 7
2 ≠ 7
This is not a solution
Question 20.
\(\frac{m}{4}\) = 16; m = 4
Answer: not a solution
Explanation:
\(\frac{m}{4}\) = 16
Substitute the value of m in the equation
\(\frac{4}{4}\) = 16
1 ≠ 16
This is not a solution
Question 21.
w + 23 = 41; w = 28
Answer: not a solution
Explanation:
w + 23 = 41
Substitute the value of w in the equation
28 + 23 = 41
51 ≠ 41
This is not a solution
Question 22.
s – 68 = 11; s = 79
Answer: solution
Explanation:
Given,
s – 68 = 11
Substitute the value of s in the equation
s = 79
79 – 68 = 11
11 = 11
This is a solution
SOLVING EQUATIONS Solve the equation. Check your solution.
Question 23.
y – 7 = 3
Answer:
Given the equation
y – 7 = 3
y = 3 + 7
y = 10
Question 24.
z – 3 = 13
Answer:
Given the equation
z – 3 = 13
z = 13 +3
z = 16
Question 25.
8 = r – 14
Answer:
Given the equation
8 = r – 14
r = 8 + 14
r = 22
Question 26.
p + 5 = 8
Answer:
Given the equation
p + 5 = 8
p = 8 – 5
p = 3
Question 27.
k + 6 = 18
Answer:
Given the equation
k + 6 = 18
k = 18 – 6
k = 12
Question 28.
64 = h + 30
Answer:
Given the equation
64 = h + 30
h = 64 – 30
h = 34
Question 29.
f – 27 = 19
Answer:
Given the equation
f – 27 = 19
f = 19 +27
f = 46
Question 30.
25 = q + 14
Answer:
Given the equation
25 = q + 14
q = 25 – 14
q = 11
Question 31.
\(\frac{3}{4}\) = j – \(\frac{1}{2}\)
Answer:
Given the equation
\(\frac{3}{4}\) = j – \(\frac{1}{2}\)
\(\frac{3}{4}\) + \(\frac{1}{2}\) = j
j = 1 \(\frac{1}{4}\)
Question 32.
x + \(\frac{2}{3}\) = \(\frac{9}{10}\)
Answer:
Given the equation
x + \(\frac{2}{3}\) = \(\frac{9}{10}\)
x = \(\frac{9}{10}\) – \(\frac{2}{3}\)
x = \(\frac{7}{30}\)
Question 33.
1.2 = m – 2.5
Answer:
Given the equation
1.2 = m – 2.5
m = 1.2 + 2.5
m = 3.7
Question 34.
a + 5.5 = 17.3
Answer:
Given the equation
a + 5.5 = 17.3
a = 17.3 – 5.5
a = 11.8
YOU BE THE TEACHER Your friend solves the equation. Is your friend correct? Explain your reasoning.
Question 35.
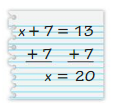
Answer:
x + 7 = 13
x = 13 – 7
x = 4
Your friend is incorrect
Question 36.
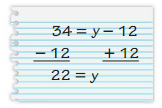
Answer:
34 = y – 12
y – 12 = 34
y = 34 + 12
y = 46
Question 37.
MODELING REAL LIFE
The main span of the Sunshine SkywayBridge is 366 meters long. The bridge’s main span is 30 meters shorter than the main span of the Dames Point Bridge. Write and solve an equation to find the length (in meters) of the main span of the Dames Point Bridge.

Answer:
Given,
The main span of the Sunshine SkywayBridge is 366 meters long.
The bridge’s main span is 30 meters shorter than the main span of the Dames Point Bridge.
336 – 30 = 306
Let the main span of the Sunshine SkywayBridge be x
Let the main span of the Dames Point Bridge be y
x – y = 306
Question 38.
PROBLEM SOLVING
A park has 22 elm trees. Elm leaf beetles have been attacking the trees. After removing several of the diseased trees, there are 13 healthy elm trees left. Write and solve an equation to find the number of elm trees that were removed.
Answer:
Given,
A park has 22 elm trees. Elm leaf beetles have been attacking the trees.
After removing several of the diseased trees, there are 13 healthy elm trees left.
x – y = 9
22 – 13 = 9
Thus the number of trees removed 9.
Question 39.
PROBLEM SOLVING
The area of Jamaica is 6460 square miles less than the area of Haiti. Find the area (in square miles) of Haiti.
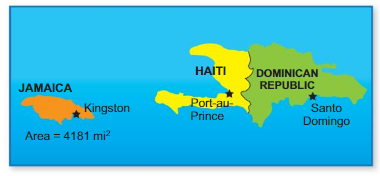
Answer:
Given,
The area of Jamaica is 6460 square miles less than the area of Haiti.
Y = X – 6460
Y = Haiti
X = area of Jamaica
Question 40.
REASONING
The solution of the equation x+ 3 = 12 is shown. Explain each step. Use a property, if possible.

Answer:
The sum of a number x and 3 is 12
x + 3 = 12
x = 12 – 3
x = 9
WRITING EQUATIONS Write the word sentence as an equation. Then solve the equation.
Question 41.
13 subtracted from a number w is 15.
Answer: w – 13 = 15
Explanation:
We have to write the equation for the word sentence
The phrase subtracted indicates ‘-‘
The equation would be w – 13 = 15
Question 42.
A number k increased by 7 is 34.
Answer: K + 7 = 34
Explanation:
We have to write the equation for the word sentence
The phrase increased indicates ‘+’
The equation would be K + 7 = 34
Question 43.
9 is the difference of a number n and 7.
Answer: n – 7 = 9
Explanation:
We have to write the equation for the word sentence
The phrase difference indicates ‘-‘
The equation would be n – 7 = 9
Question 44.
93 is the sum of a number g and 58.
Answer: g + 58 = 93
Explanation:
We have to write the equation for the word sentence
The phrase sum indicates ‘+’
The equation would be g + 58 = 93
Question 45.
11 more than a number k equals 29.
Answer: 11 + k = 29
Explanation:
We have to write the equation for the word sentence
The phrase more than indicates ‘+’
The equation would be 11 + k = 29
Question 46.
A number p decreased by 19 is 6.
Answer: p – 19 = 6
Explanation:
We have to write the equation for the word sentence
The phrase decreased indicates ‘-‘
The equation would be p – 19 = 6
Question 47.
46 is the total of 18 and a number d.
Answer: 18 + d = 46
Explanation:
We have to write the equation for the word sentence
The phrase total indicates ‘+’
The equation would be 18 + d = 46
Question 48.
84 is 99 fewer than a number c.
Answer: 84 = 99 – c
Explanation:
We have to write the equation for the word sentence
The phrase fewer than indicates ‘-‘
The equation would be 84 = 99 – c
SOLVING EQUATIONS Solve the equation. Check your solution.
Question 49.
b + 7 + 12 = 30
Answer:
Given the equation
b + 7 + 12 = 30
b = 30 – 19
b = 11
Question 50.
y + 4 − 1 = 18
Answer:
Given the equation
y + 4 − 1 = 18
y + 3 = 18
y = 18 – 3
y = 15
Question 51.
m + 18 + 23 = 71
Answer:
Given the equation
m + 18 + 23 = 71
m + 41 = 71
m = 71 – 41
m = 30
Question 52.
v − 7 = 9 + 12
Answer:
Given the equation
v − 7 = 9 + 12
v – 7 = 21
v = 21 + 7
v = 28
Question 53.
5 + 44 = 2 + r
Answer:
Given the equation
5 + 44 = 2 + r
49 = 2 + r
r = 49 – 2
r = 47
Question 54.
22 + 15 = d− 17
Answer:
Given the equation
22 + 15 = d− 17
37 = d – 17
d = 37 + 17
d = 54
GEOMETRY Solve for x.
Question 55.
Perimeter = 48 ft
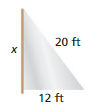
Answer:
P = a + b + c
48 ft = x + 20 + 12
x = 48 – 32
x = 16 ft
Question 56.
Perimeter = 132 in.
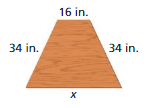
Answer:
P = a + b + c + d
132 = 34 + 16 + 34 + x
132 – 84 = x
x = 50 in
Question 57.
Perimeter = 93 ft
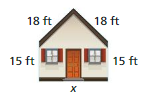
Answer:
P = 8(a + b + c + d + e)
93 ft = 8(18 + 18 + 15 + d + 15)
d = 93/528
d = 0.17
Question 58.
SIMPLIFYING AND SOLVING Compare and contrast the two problems.

Answer:
2(x + 3) – 4
= 2x + 6 – 4
= 2x + 2
Question 59.
PUZZLE
In a magic square, the sum of the numbers in each row, column, and diagonal is the same. Find the values of a, b, and c. Justify your answers.
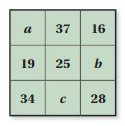
Answer:
The sum of rows and columns is 53.
a = 22
b = 0
c = 0
Question 60.
REASONING
On Saturday, you spend $33, give $15 to a friend, and receive $20 for mowing your neighbor’s lawn. You have $21 left. Use two methods to find how much money you started with that day.
Answer:
Given,
On Saturday, you spend $33, give $15 to a friend, and receive $20 for mowing your neighbor’s lawn.
You have $21 left.
x = a + b + c – d
x = 33 + 15 + 20 – 21
x = 68 – 21
x = 47
Question 61.
DIG DEEPER!
You have $15.

a. How much money do you have left if you ride each ride once?
b. Do you have enough money to ride each ride twice? Explain.
Answer:
a. bumper cost : $1.75
super pendulum : $1.25 + $1.50= $2.75
giant slide : $1.75-$0.50= $1.25
ferris wheels : $1.50+$0.50=$2
total money spent=$7.75
money left=$7.75-$15=$7.25
b. No,
money required to ride once =$7.75
total money required to ride twice=$7.75+$7.75=$15.5
Question 62.
CRITICAL THINKING
Consider the equation 15 − y = 8. Explain how you can solve the equation using the Addition and Subtraction Properties of Equality.
Answer:
15 − y = 8
15 = 8 + y
8 + y = 15
y = 15 – 8
y = 7
Lesson 6.3 Solving Equations Using Multiplication or Division
EXPLORATION 1
Solving an Equation Using a Tape Diagram
Work with a partner. A student solves an equation using the tape diagrams below.
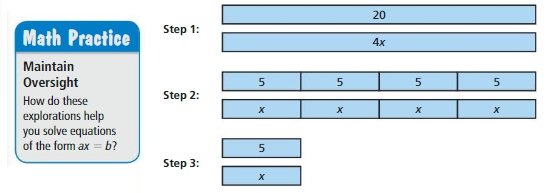
a. What equation did the student solve? What is the solution?
Answer:
ax = b
4x = 20
x = 20/4
x = 5
b. Explain how the tape diagrams in Steps 2 and 3 relate to the equation and its solution.
Answer:
Step 2 and step 3 shows that x = 5
EXPLORATION 2
Solving an Equation Using a Model
Work with a partner. Three robots go out to lunch. They decide to split the $12 bill evenly. The scale represents the number of robots and the price of the meal.
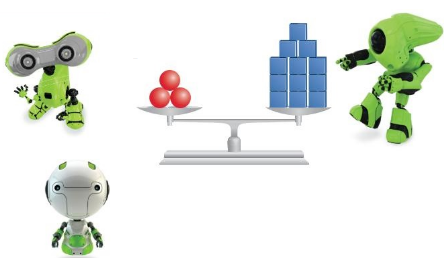
a. How much does each robot pay?
Answer:
Three robots go out to lunch.
They decide to split the $12 bill evenly.
12/3 = 4
Thus each robot pay $4.
b. When you triple the weight on one side of a balanced scale, what can you do to balance the scale? What if you divide the weight on one side of a balanced scale in half? How does this relate to solving an equation?
c. Use a model to solve 5x = 15. Describe how you can solve the equation algebraically.
Answer:
5x = 15
x = 15/5
x = 3
Try It
Solve the equation. Check your solution.
Question 1.
\(\frac{a}{8}\) = 6
Answer: a = 48
Explanation:
Given the equation
\(\frac{a}{8}\) = 6
a = 6 × 8
a = 48
Question 2.
14 = \(\frac{2y}{5}\)
Answer: y = 35
Explanation:
Given the equation
14 = \(\frac{2y}{5}\)
14 × 5 = 2y
2y = 70
y = 70/2
y = 35
Question 3.
3z ÷ 2 = 9
Answer: z = 6
Explanation:
Given the equation
3z ÷ 2 = 9
3z = 9 × 2
3z = 18
z = 18/3
z = 6
Question 4.
p . 3 = 18
Answer: p = 6
Explanation:
Given the equation
p . 3 = 18
p = 18/3
p = 6
Question 5.
12q = 60
Answer: q = 5
Explanation:
Given the equation
12q = 60
q = 60/12
q = 5
Question 6.
81 = 9r
Answer: r = 9
Explanation:
Given the equation
81 = 9r
r = 81/9
r = 9
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING EQUATIONS Solve the equation. Check your solution.
Question 7.
6 = \(\frac{2y}{3}\)
Answer: y = 9
Explanation:
Given the equation
6 = \(\frac{2y}{3}\)
6 × 3 = 2y
2y = 18
y = 18/2
y = 9
Question 8.
8s = 56
Answer: s = 7
Explanation:
Given the equation
8s = 56
s = 56/8
s = 7
Question 9.
WHICH ONE DOESN’T BELONG?
Which equation does not belong with the other three? Explain your reasoning.

Answer: \(\frac{1}{4}\)x = 27 does not belong with the other three.
Because
3x= 36
x = 36/3
x = 12
3/4 x = 9
3x = 36
x = 36/3
x = 12
4x = 48
x = 48/4
x = 12
STRUCTURE Just by looking at the equation, find the value of x. Explain your reasoning.
Question 10.
5x + 3x = 5x + 18
Answer:
Given the equation
x(5+3)=5x+18
8x=5x+18
8x-5x=18
3x=18
x=18/3
x=6
Question 11.
8x + \(\frac{x}{2}\) = 8x + 6
Answer:
Given the equation
8x + \(\frac{x}{2}\) = 8x + 6
x (8 + \(\frac{1}{2}\) ) = 8x + 6
8.5x = 8x + 6
8.5x – 8x = 6
0.5x = 6
x = 6/0.5
x = 12
Question 12.
The area of the screen of the smart watch is shown. What are possible dimensions for the length and the width of the screen? Justify your answer.

Answer:
Given,
Area = 1625 sq.mm
L = 65 mm
W = 25 mm
We know that,
Area of the rectangle = l × w
1625 = 65 × 25
Thus the length and width of the smart watch is 65 mm and 25 mm.
Question 13.
A rock climber climbs at a rate of 720 feet per hour. Write and solve an equation to find the number of minutes it takes for the rock climber to climb 288 feet.
Answer:
Given,
A rock climber climbs at a rate of 720 feet per hour.
The equation is y = 12x
It takes 24 minutes for the rock climber to get 288 feet
288 = 12x
288/12 = 12x/12
24 = x
Now we have time in minutes that it takes to get 288 feet.
Question 14.
DIG DEEPER!
A gift card stores data using a black, magnetic stripe on the back of the card. Find the width w of the stripe.
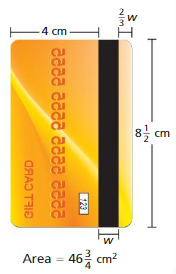
Answer:
Given,
Area = 46 \(\frac{3}{4}\) sq. cm
L = 8 \(\frac{1}{2}\) cm
w = 4 cm + x+ \(\frac{2}{3}\) cm
We know that,
Area of the rectangle = l × w
46 \(\frac{3}{4}\) = 4 cm + x+ \(\frac{2}{3}\) × 8 \(\frac{1}{2}\)
= (4 + 0.6 + x) × 8.5
46.75 = 34 + 5.4 + 8.5x
8.5x = 46.75 – 34 – 5.1
8.5x = 7.6
x = 7.6/8.5
x = 0.89
Thus the width is 0.89 cm
Solving Equations Using Multiplication or Division Homework & Practice 6.3
Review & Refresh
Solve the equation. Check your solution.
Question 1.
y – 5 = 6
Answer: y = 11
Explanation:
Given the equation
y – 5 = 6
y = 6 + 5
y = 11
Question 2.
m + 7 = 8
Answer: 1
Explanation:
Given the equation
m + 7 = 8
m = 8 – 7
m = 1
Question 3.
\(\frac{7}{8}\) = \(\frac{1}{4}\) + 9
Answer:
\(\frac{1}{4}\) + 9 = \(\frac{9}{4}\)
\(\frac{7}{8}\) ≠ \(\frac{9}{4}\)
not a solution
Question 4.
What is the value of a3 when a= 4?
A. 12
B. 43
C. 64
D. 81
Answer: 64
Explanation:
a3 when a= 4
4 × 4 × 4 = 64
Thus the correct answer is option C.
Multiply. Write the answer in simplest form.
Question 5.
\(\frac{1}{5}\) . \(\frac{2}{9}\)
Answer:
For fraction multiplication, multiply the numerators and then multiply the denominators to get
\(\frac{1}{5}\) . \(\frac{2}{9}\) = \(\frac{2}{45}\)
Question 6.
\(\frac{5}{12}\) × \(\frac{4}{7}\)
Answer:
For fraction multiplication, multiply the numerators and then multiply the denominators to get
\(\frac{5}{12}\) × \(\frac{4}{7}\) = \(\frac{5}{21}\)
Question 7.
2\(\frac{1}{3}\) . \(\frac{3}{10}\)
Answer:
For fraction multiplication, multiply the numerators and then multiply the denominators to get
2\(\frac{1}{3}\) = \(\frac{7}{3}\)
\(\frac{7}{3}\) × \(\frac{3}{10}\) = \(\frac{21}{30}\)
Question 8.
1\(\frac{3}{4}\) × 2\(\frac{2}{3}\)
Answer:
1\(\frac{3}{4}\) = \(\frac{7}{4}\)
2\(\frac{2}{3}\) = \(\frac{8}{4}\)
\(\frac{7}{4}\) × \(\frac{8}{4}\) = \(\frac{56}{16}\)
Multiply.
Question 9.
![]()
Answer: 0.36
Explanation:
Multiply the two decimals
0.4 × 0.9 = 0.36
Question 10.
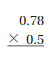
Answer: 0.39
Explanation:
Multiply the two decimals
0.78 × 0.5 = 0.39
Question 11.
2.63 × 4.31
Answer: 11.3353
Explanation:
Multiply the two decimals
2.63 × 4.31 = 11.3353
Question 12.
1.115 × 3.28
Answer: 69.2
Explanation:
Multiply the two decimals
1.115 × 3.28 = 69.2
Concepts, Skills, &Problem Solving
CHOOSE TOOLS Use a model to solve the equation. (See Explorations 1 and 2, p. 259.)
Question 13.
8x = 8
Answer: 1
Explanation:
Given the equation
8x = 8
x = 8/8
x = 1
Question 14.
9 = 3y
Answer: 3
Explanation:
Given the equation
9 = 3y
y = 9/3
y = 3
Question 15.
2z = 14
Answer: 7
Explanation:
Given the equation
2z = 14
z = 14/2
z = 7
SOLVING EQUATIONS Solve the equation. Check your solution.
Question 16.
\(\frac{s}{10}\) = 7
Answer: 70
Explanation:
Given the equation
\(\frac{s}{10}\) = 7
s = 7 × 10
s = 70
Question 17.
6 = \(\frac{t}{s}\)
Answer: 6s = t
Explanation:
Given the equation
6 = \(\frac{t}{s}\)
t = 6s
Question 18.
5x ÷ 6 = 20
Answer:
Given the equation
5x ÷ 6 = 20
5x = 20 × 6
5x = 120
x = 120/5
x = 24
Question 19.
24 = \(\frac{3}{4}\)r
Answer:
Given the equation
24 = \(\frac{3}{4}\)r
24 × 4 = 3r
96 = 3r
r = 32
Question 20.
3a = 12
Answer: 4
Explanation:
Given the equation
3a = 12
a = 12/3
a = 4
Question 21.
5 . z = 35
Answer: 7
Explanation:
Given the equation
5 . z = 35
z = 35/5
z = 7
Question 22.
40 = 4y
Answer: 10
Explanation:
Given the equation
40 = 4y
40/4 = y
y = 10
Question 23.
42 = 7k
Answer: 6
Explanation:
Given the equation
42 = 7k
7k = 42
k = 42/7
Question 24.
7x = 105
Answer: 15
Explanation:
Given the equation
7x = 105
x = 105/7
x = 15
Question 25.
75 = 6 . w
Answer: 12.5
Explanation:
Given the equation
75 = 6 . w
w = 75/6
w = 12.5
Question 26.
13 = d ÷ 6
Answer: 78
Explanation:
Given the equation
13 = d ÷ 6
d = 13 × 6
d = 78
Question 27.
9 = v ÷ 5
Answer: 45
Explanation:
Given the equation
9 = v ÷ 5
v = 9 × 5
v = 45
Question 28.
\(\frac{5d}{9}\) = 10
Answer: 18
Explanation:
Given the equation
\(\frac{5d}{9}\) = 10
5d = 10 × 9
5d = 90
d = 18
Question 29.
\(\frac{3}{5}\) = 4m
Answer: 0.15
Explanation:
Given the equation
\(\frac{3}{5}\) = 4m
3 = 4m × 5
20m = 3
m = 3/20
m = 0.15
Question 30.
136 = 17b
Answer: 19.4
Explanation:
Given the equation
136 = 17b
b = 136/17
b = 19.4
Question 31.
\(\frac{2}{3}\) = \(\frac{1}{4}\)k
Answer: 2.6
Explanation:
Given the equation
\(\frac{2}{3}\) = \(\frac{1}{4}\)k
k = \(\frac{8}{3}\)
k = 2.6
Question 32.
\(\frac{2c}{15}\) = 8.8
Answer: 66
Explanation:
Given the equation
\(\frac{2c}{15}\) = 8.8
2c = 8.8 × 15
2c = 132
c = 132/2
c = 66
Question 33.
7b ÷ 12 = 4.2
Answer: 7.2
Explanation:
Given the equation
7b ÷ 12 = 4.2
7b = 4.2 × 12
b = 7.2
Question 34.
12.5 . n = 32
Answer: 2.56
Explanation:
Given the equation
12.5 . n = 32
n = 32/12.5
n = 2.56
Question 35.
3.4 m = 20.4
Answer: m = 6
Explanation:
Given the equation
3.4 m = 20.4
m = 20.4/3.4
m = 6
Question 36.
YOU BE THE TEACHER
Your friend solves the equation x ÷ 4 =28. Is your friend correct? Explain your reasoning.
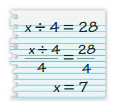
Answer: Your friend is correct
Explanation:
Your friend solves the equation x ÷ 4 =28.
x ÷ 4 = 28
x = 28/4
x = 7
Question 37.
ANOTHER WAY
Show how you can solve the equation 3x = 9 by multiplying each side by the reciprocal of 3.
Answer:
3x = 9
x = 9 × 1/3
x = 3
Question 38.
MODELING REAL LIFE
Forty-five basketball players participate in a three-on-three tournament. Write and solve an equation to find the number of three-person teams in the tournament.

Answer: 15
Explanation:
Let the number of teams be x
x × 3 = 45
x = 45/3
x = 15
Question 39.
MODELING REAL LIFE
A theater has 1200 seats. Each row has 20 seats. Write and solve an equation to find the number of rows in the theater.
Answer:
Given,
A theater has 1200 seats. Each row has 20 seats.
Let x be the number of rows.
1200 = 20 × x
x = 1200/20
x = 60
GEOMETRY Solve for x. Check your answer.
Question 40.
Area = 45 square units

Answer:
l = x
w = 5
Area = 45 square units
We know that,
Area of the Rectangle = l × w
45 = x × 5
x = 45/5
x = 9 units
Question 41.
Area = 176 square units
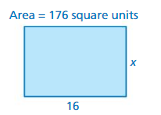
Answer:
a = 16
Area = 176 square units
We know that,
Area of the square = a × a
176 = 16 × x
x = 16
Question 42.
LOGIC
Ona test, you earn 92% of the possible points by correctly answering 6 five-point questions and 8 two-point questions. How many points p is the test worth?
Answer:
Given,
Ona test, you earn 92% of the possible points by correctly answering 6 five-point questions and 8 two-point questions.
(6 × 5) + (8 × 2) = 46
92 × 1/100 = 46
0.92x = 46
x = 46/0.92
x = 50
Question 43.
MODELING REAL LIFE
You use index cards to play a homemade game. The object is to be the first to get rid of all your cards. How many cards are in your friend’s stack?
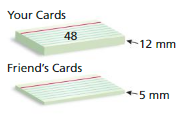
Answer:
The number of cards in your friend’s stack divided by the height of your’s friends stack equals the number of cards in your stack divided by the height of your stack.
x = the number of cards in your friend’s stack
x ÷ 5 = 48 ÷ 12
x ÷ 5 = 4
x = 4 × 5
x = 20
Question 44.
DIG DEEPER!
A slush drink machine fills 1440 cups in 24 hours.
a. Find the number c of cups each symbol represents.
b. To lower costs, you replace the cups with paper cones that hold 20% less. Find the number n of paper cones that the machine can fill in 24 hours.
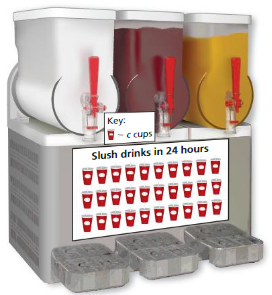
Answer:
The number of symbols times the number of cups per symbol equals the total number of cups filled.
C = The number of cups filled
30 × c = 1440
c = 1440/30
c = 48
Question 45.
NUMBER SENSE
The area of the picture is 100 square inches. The length is 4 times the width. Find the length and width of the picture.

Answer:
Given,
The area of the picture is 100 square inches.
The length is 4 times the width.
We know that,
Area of Rectangle = l × w
100 sq. in = 4w × w
100 = 4w²
w = √25 = 5
L = 4w
L = 4 × 5
L = 20
Lesson 6.4 Writing Equations in Two Variables
EXPLORATION 1
Writing Equations in Two Variables
Work with a partner. section 3.4 Exploration 1, you used a ratio table to create a graph for an airplane traveling 300 miles per hour. Below is one possible ratio table and graph.
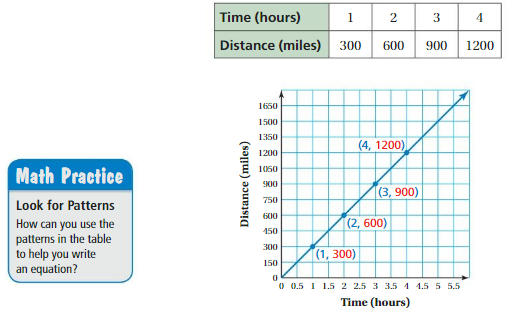
a. Describe the relationship between the two quantities. Which quantity depends on the other quantity?
Answer: By seeing the above graph we can say that miles depend on hours (time).
b. Use variables to write an equation that represents the relationship between the time and the distance. What can you do with this equation? Provide an example.
c. Suppose the airplane is 1500 miles away from its destination. Write an equation that represents the relationship between time and distance from the destination. How can you represent this relationship using a graph?
Answer: The relationship between distance and time is distance is inversely proportional to the time.
5x = 1500
An equation in two variables represents two quantities that change in relationship to one another. A solution of an equation in two variables is an ordered pair that makes the equation true.

Try It
Tell whether the ordered pair is a solution of the equation.
Question 1.
y = 7x, (2, 21)
Answer: No
Explanation:
Given the equation y = 7x
y = 7 × 2
y = 14
21 ≠ 14
The ordered pair is not the solution.
Question 2.
y = 5x + 1; (3, 16)
Answer: Yes
Explanation:
Given the equation y = 5x + 1
y = 5 × 3 + 1
y = 15 + 1
y = 16
The ordered pair is the solution.
Question 3.
The equation y = 10x + 25 represents the amount y(in dollars) in your savings account after x weeks. Identify the independent and dependent variables. How much is in your savings account after 8 weeks?
Answer:
Because the amount y remaining depends on the number x weeks.
Y is the dependent variable
X is the independent variable
y = 10x + 25
After 8 weeks x = 8
y = 10 (8) + 25
y = 80 + 25
y = 105
Graph the equation.
Question 4.
y = 3x
Answer:
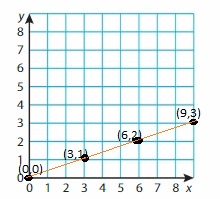
When x = 0
y = 3(0) = 0
A(x,y) = (0,0)
When x = 1
y = 3(1) = 3
B(x,y) = (3, 1)
When x = 2
y = 3(2) = 6
C(x,y) = (6, 2)
When x = 3
y = 3(3) = 9
D(x,y) = (9, 3)
Question 5.
y = 4x + 1
Answer:
y = 4x + 1
When x = 0
y = 4(0) + 1
y = 1
When x = 1
y = 4(1) + 1
y = 5
When x = 2
y = 4(2) + 1
y = 9
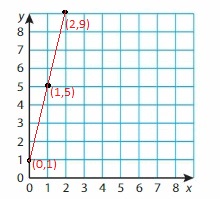
Question 6.
y = \(\frac{1}{2}\)x + 2
Answer:
Given,
y = \(\frac{1}{2}\)x + 2
when x = 0
y = \(\frac{1}{2}\)0 + 2
y = 2
when x = 1
y = \(\frac{1}{2}\)1 + 2
y = 2\(\frac{1}{2}\)
y = 2.5
when x = 2
y = \(\frac{1}{2}\)2 + 2
y = 1 + 2
y = 3
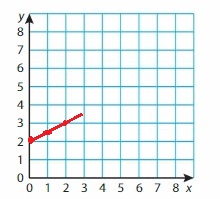
Question 7.
It costs $25 to rent a kayak plus $8 for each hour. Write and graph an equation that represents the total cost (in dollars) of renting the kayak.
Answer:
Given,
It costs $25 to rent a kayak plus $8 for each hour.
y = 8x + 25
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
WRITING
Describe the difference between independent variables and dependent variables.
Answer:
The independent variable is the cause. Its value is independent of other variables in your study. The dependent variable is the effect. Its value depends on changes in the independent variable.
IDENTIFYING SOLUTIONS Tell whether the ordered pair is a solution of the equation.
Question 9.
y = 3x + 8; (4, 20)
Answer:
Given the equation
y = 3x + 8
x = 4
y = 20
20 = 3(4) 8
20 = 12 + 8
20 = 20
The above equation is the solution.
Question 10.
y = 6x – 14; (7, 29)
Answer:
Given the equation
y = 6x – 14
29 = 6(7) – 14
29 = 42 – 14
29 ≠ 28
The above equation is not the solution.
Question 11.
PRECISION
Explain how to graph an equation in two variables.
Answer:
- Find three points whose coordinates are solutions to the equation. Organize them in a table.
- Plot the points in a rectangular coordinate system. Check that the points line up. …
- Draw the line through the three points. Extend the line to fill the grid and put arrows on both ends of the line.
Question 12.
WHICH ONE DOESN’T BELONG?
Which one does not belong with the other three? Explain your reasoning.
![]()
Answer: n = 4n – 6 does not belong to the other three equations because we can take n has common and we can solve the equation.
Remaining there is not possible to solve the equation.
Question 13.
A sky lantern rises at an average speed of 8 feet per second. Write and graph an equation that represents the relationship between the time and the distance risen. How long does it take the lantern to rise 100 feet?

Answer:
Given,
A sky lantern rises at an average speed of 8 feet per second.
the lantern to rise 100 feet = ?
8 feets = 1 sec
100 feets = 8 × x
x = 100/8
x = 12.5 sec
Question 14.
You and a friend start biking in opposite directions from the same point. You travel 108 feet every 8 seconds. Your friend travels 63 feet every 6 seconds. How far apart are you and your friend after 15 minutes?
Answer:
Given,
You and a friend start biking in opposite directions from the same point.
You travel 108 feet every 8 seconds. Your friend travels 63 feet every 6 seconds.
Your distance Y,
Y = 108ft/8 seconds × 60 sec/min × 15 min × 1mile/5280 ft
H is determined similarly
Total distance apart in miles = Y + H
You have only 36 minutes while he travels for all 40.
Writing Equations in Two Variables Homework & Practice 6.4
Review & Refresh
Solve the equation.
Question 1.
4x = 36
Answer: 9
Explanation:
Given the equation 4x = 36
x = 36/4
x = 9
Question 2.
\(\frac{x}{8}\) = 5
Answer: 40
Explanation:
Given the equation \(\frac{x}{8}\) = 5
x = 5 × 8
x = 40
Question 3.
\(\frac{4x}{3}\) = 8
Answer: 6
Explanation:
Given the equation \(\frac{4x}{3}\) = 8
4x = 8 × 3
4x = 24
x = 24/4
x = 6
Question 4.
\(\frac{2}{5}\)x = 6
Answer: 15
Explanation:
Given the equation \(\frac{2}{5}\)x = 6
2x = 5 × 6
2x = 30
x = 30/2
x = 15
Divide. Write the answer in simplest form.
Question 5.
3\(\frac{1}{2}\) ÷ \(\frac{4}{5}\)
Answer: 4 \(\frac{3}{8}\)
Explanation:
Convert any mixed numbers to fractions.
Then your initial equation becomes:
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
\(\frac{7}{2}\) × \(\frac{5}{4}\)
= \(\frac{35}{8}\)
Now convert the improper fraction to the mixed fraction.
\(\frac{35}{8}\) = 4 \(\frac{3}{8}\)
Question 6.
7 ÷ 5\(\frac{1}{4}\)
Answer: 1 \(\frac{1}{3}\)
Explanation:
Convert any mixed numbers to fractions.
Then your initial equation becomes:
7 ÷ 5\(\frac{1}{4}\)
5\(\frac{1}{4}\) = \(\frac{21}{4}\)
\(\frac{7}{1}\) ÷ \(\frac{21}{4}\) = 1 \(\frac{1}{3}\)
Question 7.
\(\frac{3}{11}\) ÷ 1\(\frac{1}{8}\)
Answer: \(\frac{8}{33}\)
Explanation:
Convert any mixed numbers to fractions.
Then your initial equation becomes:
\(\frac{3}{11}\) ÷ 1\(\frac{1}{8}\)
1\(\frac{1}{8}\) = \(\frac{9}{8}\)
\(\frac{3}{11}\) ÷ \(\frac{9}{8}\) = \(\frac{8}{33}\)
Question 8.
7\(\frac{1}{2}\) ÷ 1\(\frac{1}{3}\)
Answer: 5 \(\frac{5}{8}\)
Explanation:
Convert any mixed numbers to fractions.
Then your initial equation becomes:
7\(\frac{1}{2}\) = \(\frac{15}{2}\)
1\(\frac{1}{3}\) = \(\frac{4}{3}\)
\(\frac{15}{2}\) ÷ \(\frac{4}{3}\) = \(\frac{45}{8}\)
Now convert the improper fraction to the mixed fraction.
\(\frac{45}{8}\) = 5 \(\frac{5}{8}\)
Question 9.
Find the area of the carpet tile. Then find the area covered by120 carpet tiles.

Answer:
a = 16 in
Area of the square = a × a
A = 16 in × 16 in
A = 256 sq. in
Now we have to find the area covered by120 carpet tiles.
120 × 256 = 30720
Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 10.
![]()
Answer: 800
Explanation:
convert from meters to centimeters
1 m = 100 cm
8 m = 8 × 100 cm = 800 cm
Thus 8m = 800cm
Question 11.
![]()
Answer:
Explanation:
Convert from ounces to pounds
88 oz = 5.5 pounds
Question 12.
![]()
Answer: 709 mL
Explanation:
Convert from cups to milliliters
1 cup = 236.588 mL
3 cups = 709 mL
Question 13.
![]()
Answer: 9.321 mi
Explanation:
Convert from km to miles
1 km = 0.621 mi
15 km = 15 × 0.621 mi
15 km = 9.321 miles
Divide.
Question 14.
\(\sqrt [ 6 ]{ 34.8 } \)
Answer: 6th root of 34.8 is 1.806
Question 15.
\(\sqrt [ 4 ]{ 12.8 } \)
Answer: 4th root of 12.8 is 1.891
Question 16.
45.92 ÷ 2.8
Answer: 16.2
Explanation:
Multiplying two decimal numbers
45.92 ÷ 2.8 = 16.2
Question 17.
39.525 ÷ 4.25
Answer: 9.3
Explanation:
Multiplying two decimal numbers
39.525 ÷ 4.25 = 9.3
Concepts, Skills, &Problem Solving
WRITING EQUATIONS Use variables to write an equation that represents the relationship between the time and the distance. (See Exploration 1, p. 265.)
Question 18.
An eagle flies 40 miles per hour.
Answer:
y = distance, x = time, rate = 40 miles per minute
distance = rate . time
y = 40 . x
Question 19.
A person runs 175 yards per minute.
Answer:
y = distance, x = time, rate = 175 yards per minute
distance = rate . time
so y = 175 . x
IDENTIFYING SOLUTIONS Tell whether the ordered pair is a solution of the equation.
Question 20.
y = 4x; (0, 4)
Answer:
x = 0
y = 4
4 = 4(0)
4 ≠ 0
The ordered pair is not a solution of the equation.
Question 21.
y = 3x; (2, 6)
Answer:
x = 2
y = 6
y = 3x
6 = 3(2)
6 = 6
The ordered pair is a solution of the equation.
Question 22.
y = 5x – 10; (3, 5)
Answer:
x = 3
y = 5
y = 5x – 10
5 = 5(3) – 10
5 = 15 – 10
5 = 5
The ordered pair is a solution of the equation.
Question 23.
y = x + 7; (1, 6)
Answer:
x = 1
y = 6
y = x + 7
6 = 1 + 7
6 ≠ 8
The ordered pair is not a solution of the equation.
Question 24.
y = x + 4; (2, 4)
Answer:
x = 2
y = 4
4 = 2 + 4
4 ≠ 6
The ordered pair is not a solution of the equation.
Question 25.
y = x – 5; (6, 11)
Answer:
x = 6
y = 11
11 = 6 – 5
11 ≠ 1
The ordered pair is not a solution of the equation.
Question 26.
y = 6x + 1; (2, 13)
Answer:
x = 2
y = 13
13 = 6(2) + 1
13 = 12 + 1
13 = 13
The ordered pair is a solution of the equation.
Question 27.
y = 7x + 2; (2, 0)
Answer:
x = 2
y = 0
0 = 7(2) + 2
0 = 14 + 2
0 ≠ 16
The ordered pair is not a solution of the equation.
Question 28.
y = 2x – 3; (4, 5)
Answer:
x = 4
y = 5
y = 2x – 3
5 = 2(4) – 3
5 = 8 – 3
5 = 5
The ordered pair is a solution of the equation.
Question 29.
y = 3x – 3; (1, 0)
Answer:
x = 1
y = 0
y = 3x – 3
0 = 3(1) – 3
0 = 3 – 3
0 = 0
The ordered pair is a solution of the equation.
Question 30.
7 = y – 5x; (4, 28)
Answer:
x = 4
y = 28
7 = y – 5x
7 = 28 – 5(4)
7 = 28 – 20
7 ≠ 8
The ordered pair is not a solution of the equation.
Question 31.
y + 3 = 6x; (3, 15)
Answer:
x = 3
y = 15
y + 3 = 6x
15 + 3 = 6(3)
18 = 18
The ordered pair is a solution of the equation.
Question 32.
YOU BE THE TEACHER
Your friend determines whether (5, 1) is a solution of y = 3x + 2. Is your friend correct? Explain your reasoning.

Answer:
x = 5
y = 1
y = 3x + 2
1 = 3(5) + 2
1 = 15 + 2
1 ≠ 17
Your friend is correct.
IDENTIFYING VARIABLES Identify the independent and dependent variables.
Question 33.
The equation A = 25w represents the area A (in square feet) of a rectangular dance floor with a width of w feet.
Answer:
The area of the dance floor (A) depends on the dance floor
A is the dependent variable
and w is the independent variable
Question 34.
The equation c= 0.09s represents the amount c(in dollars) of commission a salesperson receives for making a sale of s dollars.
Answer:
The commissioner a salesperson receives (c) depends on the sales the salesperson makes
c is dependent variable
s is independent variable
Question 35.
The equation t = 12p+ 12 represents the total cost t (in dollars) of a meal with a tip of p percent (in decimal form).
Answer:
The total cost of a meal depends on the tip of percent
the dependent variable is t
the independent variable is p
Question 36.
The equation h = 60 − 4m represents the height h(in inches) of the water in a tank m minutes after it starts to drain.
Answer:
The height of the water (h) depends on the minutes the tank has been draining
the dependent variable is h
the independent variable is m
OPEN-ENDED Complete the table by describing possible independent or dependent variables.
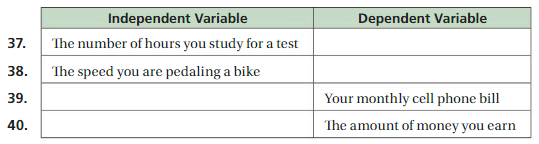
Answer:
37. Independent variable:
The grade you receive on the test dependent variable
38. Independent variable:
The time you reach your destination dependent variable.
39. Dependent variable:
The amount of minutes used to talk independent variable.
40. Dependent variable:
The number of hours you work independent variable.
GRAPHING EQUATIONS Graph the equation.
Question 41.
y = 2x
Answer:
Given,
y = 2x
when x = 0
y = 2(0)
y = 0
when x = 1
y = 2(1)
y = 2
when x = 2
y = 2(2)
y = 4
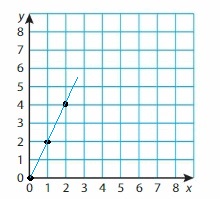
Question 42.
y = 5x
Answer:
Given,
y = 5x
when x = 0
y = 5(0)
y = 0
when x = 1
y = 5(1)
y = 5
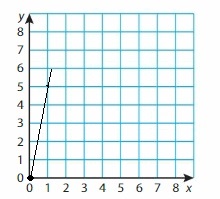
Question 43.
y = 6x
Answer:
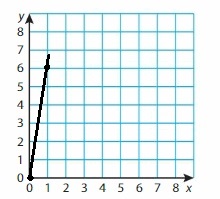
Question 44.
y = x + 2
Answer:
Given
y = x + 2
when x = 0
y = 0 + 2
y = 2
(x, y) = (0,2)
when x = 1
y = 1 + 2
y = 3
(x, y) = (1,3)
when x = 2
y = 2 + 2
y = 4
(x, y) = (2,4)
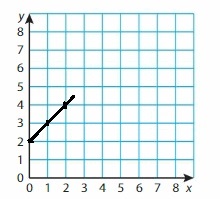
Question 45.
y = x + 0.5
Answer:
Given,
y = x + 0.5
when x = 0
y = 0 + 0.5
y = 0.5
when x = 1
y = 1 + 0.5
y = 1.5
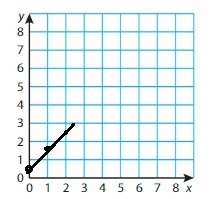
Question 46.
y = x + 4
Answer:
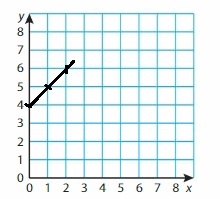
Question 47.
y = x + 10
Answer:
Question 48.
y = 3x + 2
Answer:
Given,
y = 3x + 2
when x = 0
y = 3(0) + 2
y = 0 + 2
y = 2
(x,y) = (0,2)
when x = 1
y = 3(1) + 2
y = 3 + 2
y = 5
(x,y) = (1,5)
when x = 2
y = 3(2) + 2
y = 6 + 2
y = 8
(x,y) = (2,8)
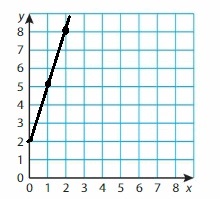
Question 49.
y = 2x + 4
Answer:
Given,
y = 2x + 4
when x = 0
y = 2x + 4
y = 2(0) + 4
y = 0 + 4
y = 4
when x = 1
y = 2x + 4
y = 2(1) + 4
y = 2 + 4
y = 6
when x = 2
y = 2x + 4
y = 2(2) + 4
y = 4 + 4
y = 8
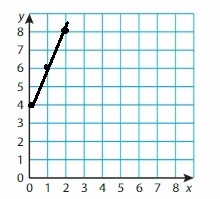
Question 50.
y = \(\frac{2}{3}\)x + 8
Answer:
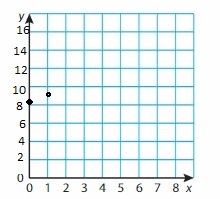
Question 51.
y = \(\frac{1}{4}\)x + 6
Answer:
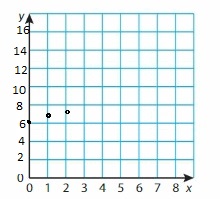
Question 52.
y = 2.5x + 12
Answer:
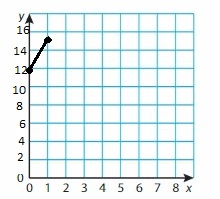
Question 53.
MODELING REAL LIFE
A cheese pizza costs $5. Additional toppings cost $1.50 each. Write and graph an equation that represents the total cost (in dollars) of a pizza.
Answer:
Let x be the total cost of pizza
let x be the number of toppings
Total cost equals the cost of cheese pizza plus the cost of additional toppings times the number of toppings
The equation would be x = 5 + 1.50t
Table & Graph:
Number of toppings Total cost, x = 5 + 1.50 t Ordered pairs (t, x)
1 6 (1, 6.50)
2 9 (2, 8)
3 9 (3, 9.50)
Question 54.
MODELING REAL LIFE
It costs $35 for a membership at a wholesale store. The monthly fee is $15. Write and graph an equation that represents the total cost (in dollars) of a membership.
Answer:
The equation is y = 35 + 25x
Table & Graph:
Number of months(x) Total cost, y = 35 + 25x Ordered pairs (t, x)
1 60 (1, 60)
2 85 (2, 85)
3 110 (3, 110)
Question 55.
PROBLEM SOLVING
The maximum size of a text message is 160 characters. A space counts as one character.
a. Write an equation that represents the number of remaining (unused) characters in a text message as you type.
b. Identify the independent and dependent variables.
c. How many characters remain in the message shown?

Answer:
x = the number of characters used
y = the number of characters unused
The equation would be y = 160 – x
The number of unused characters (y) depends on the number of used character (x)
The dependent variable is y
The Independent variable is x
Including space and punctuation, 15 characters were used
y = 160 – x
y = 160 – 15
y = 145
Question 56.
CHOOSE TOOLS
A car averages 60 miles per hour on a road trip. Use a graph to represent the relationship between the time and the distance traveled.
Answer:
PRECISION Write and graph an equation that represents the relationship between the time and the distance traveled.
Question 57.

Answer:
Question 58.

Answer:
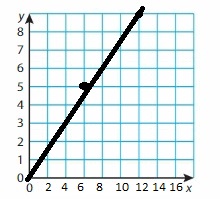
Question 59.

Answer:
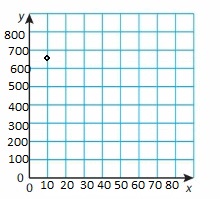
Question 60.

Answer:
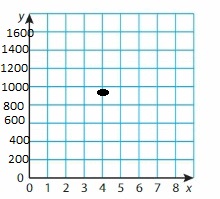
IDENTIFYING SOLUTIONS Fill in the blank so that the ordered pair is a solution of the equation.
Question 61.
![]()
Answer:
y = 8x + 3
x = 1
y = 8(1) + 3
y = 11
Thus the ordered pair (1, 11)
Question 62.
![]()
Answer:
y = 12x + 2
y = 14
14 = 12x + 2
14 – 2 = 12x
12 = 12x
x = 1
Thus the ordered pair (1, 14)
Question 63.
![]()
Answer:
y = 9x + 4
y = 22
22 = 9x + 4
22 – 4 = 9x
9x = 18
x = 2
Question 64.
DIG DEEPER!
Can the dependent variable cause a change in the independent variable? Explain.
Answer:
Just like an independent variable, a dependent variable is exactly what it sounds like. It is something that depends on other factors.
Question 65.
OPEN-ENDED
Write an equation that has (3, 4) as a solution.
Answer:
Standard form linear equation
ax + by = c
When a, b and c are constants
We want to make two equations that
i. have that form
ii. do not have all the same solutions and
iii. (3, 4) is a solution to both
a(3) + b(4) = c
3a + 4b = c
Question 66.
MODELING REAL LIFE
You walk 5 city blocks in 12 minutes. How many city blocks can you walk in 2 hours?
Answer:
Given,
You walk 5 city blocks in 12 minutes.
12 min = 5 city
2 hours = 120 minutes
120 minutes = 300 minutes
Question 67.
GEOMETRY
How fast should the ant walk to go around the rectangle in 4 minutes?
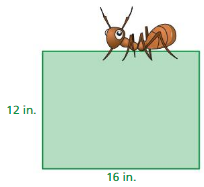
Answer:
First find the perimeter of the rectangle
P = 2L + 2W
P = 2(16) + 2(12)
P = 32 + 24 = 56 in
r = d/t
r = 56/4
r = 14 in/min
Question 68.
MODELING REAL LIFE
To estimate how far you are from lightning (in miles), count the number of seconds between a lightning flash and the thunder that follows. Then divide the number of seconds by 5. Use two different methods to find the number of seconds between a lightning flash and the thunder that follows when a storm is 2.4 miles away.
Answer:
If you count the number of seconds between the flash of lightning and the sound of thunder, and then divide by 5, you’ll get the distance in miles to the lightning: 5 seconds = 1 mile, 15 seconds = 3 miles, 0 seconds = very close.
Question 69.
REASONING
The graph represents the cost c (in dollars) of buying n tickets to a baseball game.
a. Should the points be connected with a line to show all the solutions? Explain your reasoning.
b. Write an equation that represents the graph.
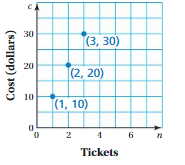
Answer: y = 5x + 0.5
Equations Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A tornado forms 12.25 miles from a weather station. It travels away from the station at an average speed of 440 yards per minute. How far from the station is the tornado after 30 minutes?

Understand the problem.
You know the initial distance between the tornado and the station, and the average speed the tornado is traveling away from the station. You are asked to determine how far the tornado is from the station after 30 minutes.
Make a plan.
First, convert the average speed to miles per minute. Then write an equation that represents the distance d (in miles) between the tornado and the station after t minutes. Use the equation to find the value of d when t = 30.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
440 × 30 = 13200
Question 2.
You buy 96 cans of soup to donate to a food bank. The store manager discounts the cost of each case for a total discount of $40. Use an equation in two variables to find the discount for each case of soup. What is the total cost when each can of soup originally costs $1.20?

Answer:
Given,
You buy 96 cans of soup to donate to a food bank.
The store manager discounts the cost of each case for a total discount of $40.
1 case = 12 cans
x = 96 cans
96 = 12 × x
x = 96/12
x = 8
8 cases
8 × $40 = $320
8 × $1.20 = $9.6
Question 3.
The diagram shows the initial amount raised by an organization for cancer research. A business agrees to donate $2 for every $5 donated by the community during an additional fundraising event. Write an equation that represents the total amount raised (in dollars). How much money does the community need to donate for the organization to reach its fundraising goal?

Answer: 13,000 – 8000 = 5,000
Performance Task
Planning the Climb
At the beginning of this chapter, you watched a STEAM video called “Rock Climbing.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Equations Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use an Example and Non-Example Chart to list examples and non-examples of a concept. Here is an Example and Non-Example Chart for the vocabulary term equation.

Choose and complete a graphic organizer to help you study the concept.

1. inverse operations
2. solving equations using addition or subtraction
3. solving equations using multiplication or division
4. equations in two variables
5. independent variables
6. dependent variables
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

6.1 Writing Equations in One Variable (pp. 245–250)
Learning Target: Write equations in one variable and write equations that represent real-life problems.
Write the word sentence as an equation.
Question 1.
The product of a number m and 2 is 8.
Answer: m × 2 = 8
Explanation:
We have to write the word sentence in the equation.
The phrase product indicates ‘×’
The equation would be m × 2 = 8
Question 2.
6 less than a number t is 7.
Answer: 6 – t = 7
Explanation:
We have to write the word sentence in the equation.
The phrase less than indicates ‘-‘
The equation would be 6 – t = 7
Question 3.
A number m increased by 5 is 7.
Answer: m + 5 = 7
Explanation:
We have to write the word sentence in the equation.
The phrase increased indicates ‘+’
The equation would be m + 5 = 7
Question 4.
8 is the quotient of a number g and 3.
Answer: g ÷ 3 = 8
Explanation:
We have to write the word sentence in the equation.
The phrase quotient indicates ‘÷’
The equation would be g ÷ 3 = 8
Question 5.
The height of the 50-milliliter beaker is one-third the height of the 2000-milliliter beaker. Write an equation you can use to find the height (in centimeters) of the 2000-milliliter beaker.
Answer: y = 3x
Explanation:
Given,
The height of the 50-milliliter beaker is one-third the height of the 2000-milliliter beaker.
Let the height of 2000 ml beaker = x
Given,
Height of 50 ml beaker, y = 1/3 of x
The equation to find the height of the 2000 ml beaker will be
y = 3x
which means the height of the 2000 ml beaker is three times the height of the 500 ml beaker.
Therefore, the equation is y = 3x.
Question 6.
There are 16 teams in a basketball tournament. After two rounds, 12 teams are eliminated. Write and solve an equation to find the number of teams remaining after two rounds.

Answer:
Given,
There are 16 teams in a basketball tournament. After two rounds, 12 teams are eliminated.
x = 16
y = 12
Number of teams remaining after two rounds = z
z = x – y
z = 16 – 12
z = 4
Question 7.
Write an equation that has a solution of x = 8.
Answer: 4x = 32
Question 8.
Write a word sentence for the equation y + 3 = 5.
Answer: The sum of the numbers y and 3 is 5.
6.2 Solving Equations Using Addition or Subtraction (pp. 251–258)
Learning Target: Write and solve equations using addition or subtraction.
Question 9.
Tell whether x = 7 is a solution of x + 9 = 16.
Answer: Yes
Explanation:
Given the equation
x + 9 = 16
x = 16 – 9
x = 7
Solve the equation. Check your solution.
Question 10.
x – 1 = 8
Answer: 9
Explanation:
Given the equation
x – 1 = 8
x = 8 + 1
x = 9
Question 11.
m + 7 = 11
Answer: 4
Explanation:
Given the equation
m + 7 = 11
m = 11 – 7
m = 4
Question 12.
21 = p – 12
Answer: 33
Explanation:
Given the equation
21 = p – 12
p – 12 = 21
p = 21 + 12
p = 33
Write the word sentence as an equation. Then solve the equation.
Question 13.
5 more than a number x is 9.
Answer: 5 + x = 9
Explanation:
We have to write the word sentence as an equation
The phrase more than indicates ‘+’
Thus the equation would be 5 + x = 9
Question 14.
82 is the difference of a number b and 24.
Answer: b – 24 = 82
Explanation:
We have to write the word sentence as an equation
The phrase difference indicates ‘-‘
Thus the equation would be b – 24 = 82
Question 15.
A stuntman is running on the roof of a train. His combined speed is the sum of the speed of the train and his running speed. The combined speed is 73 miles per hour, and his running speed is 15 miles per hour. Find the speed of the train.
Answer:
Given,
A stuntman is running on the roof of a train. His combined speed is the sum of the speed of the train and his running speed.
The combined speed is 73 miles per hour, and his running speed is 15 miles per hour.
Speed of the train = ?
Z = x – y
z = 73 – 15
z = 58
Question 16.
Before swallowing a large rodent, a python weighs 152 pounds. After swallowing the rodent, the python weighs 164 pounds. Find the weight of the rodent.

Answer:
Given that,
Before swallowing a large rodent, a python weighs 152 pounds.
After swallowing the rodent, the python weighs 164 pounds.
164 – 152 = 12 pounds
6.3 Solving Equations Using Multiplication or Division (pp. 259–264)
Learning Target: Write and solve equations using multiplication or division.
Solve the equation. Check your solution.
Question 17.
6 . q = 54
Answer: 9
Explanation:
Given the equation
6 . q = 54
q = 54/6
q = 9
Question 18.
k ÷ 3 = 21
Answer: 63
Explanation:
Given the equation
k ÷ 3 = 21
k = 21 × 3
k = 63
Question 19.
\(\frac{5}{7}\)a = 25
Answer: 35
Explanation:
Given the equation
\(\frac{5}{7}\)a = 25
5a = 7 × 25
a = 7 × 5
a = 35
Question 20.
The weight of an object on the Moon is about 16.5% of its weight on Earth. The weight of an astronaut on the Moon is 24.75 pounds. How much does the astronaut weigh on Earth?

Answer: 150 pounds
Explanation:
Given,
The weight of an object on the Moon is about 16.5% of its weight on Earth.
The weight of an astronaut on the Moon is 24.75 pounds.
Let the astronaut weight on Earth be represented by x.
Based on the information given in the question, thus can be formed into an equation as:
16.5% of x = 24.75
16.5% × x = 24.75
16.5/100 × x = 24.75
0.165x = 24.75
x = 24.75/0.165
x = 150 pounds
The astronaut weighs 150 pounds on Earth.
Question 21.
Write an equation that can be solved using multiplication and has a solution of x = 12.
Answer: 3x = 36
Question 22.
At a farmers’ market, you buy 4 pounds of tomatoes and 2 pounds of sweet potatoes. You spend 80% of the money in your wallet. How much money is in your wallet before you pay?

Answer: The money in your wallet before you pay is 20 dollars
Explanation:
Cost of 1 pound of tomato = 3 dollars
Therefore,
Cost of 4 pound of tomato = 4 x 3 = 12 dollars
Cost of 4 pound of tomato = 12 dollars
Cost of 1 pound of sweet potatoes = 2 dollars
Therefore,
Cost of 2 pound of sweet potatoes = 2 x 2 = 4 dollars
Cost of 2 pounds of sweet potatoes = 4 dollars
The combined cost spend at the market is:
cost spend at market = Cost of 4 pound of tomato + Cost of 2 pound of sweet potatoes
cost spend at market = 12 + 4 = 16 dollars
You spent 80% of the money in your wallet
Therefore, 80% of the money in your wallet is equal to 16 dollars
Let x be the money in your wallet
Then, we get
80 % of x = 16
80/100 × x = 16
0.8 x = 16
x = 16/0.8
x = 20
Thus money in your wallet before you pay is $20.
6.4 Writing Equations in Two Variables (pp. 265-272)
Learning Target: Write equations in two variables and analyze the relationship between the two quantities.
Tell whether the ordered pair is a solution of the equation.
Question 23.
y = 3x + 1; (2, 7)
Answer:
Given the equation
x = 2
y = 7
7 = 3(2) + 1
7 = 6 + 1
7 = 7
Yes, it is the solution of the equation.
Question 24.
y = 7x – 4; (4, 22)
Answer:
Given the equation
x = 4
y = 22
22 = 7(4) – 4
22 = 28 – 4
22 ≠ 24
No, it is not the solution of the equation.
Question 25.
The equation E = 360m represents the kinetic energy E (in joules) of a roller-coaster car with a mass of m kilograms. Identify the independent and dependent variables.

Answer: E is the dependent variable
m is the independent variable
Graph the equation.
Question 26.
y = x + 1
Answer:
Given,
y = x + 1
when x = 0
y = 0 + 1
y = 1
(x, y) = (0, 1)
when x = 1
y = 1 + 1
y = 2
(x, y) = (1, 2)
when x = 2
y = 2 + 1
y = 3
(x, y) = (2, 3)
Question 27.
y = 7x
Answer:
Question 28.
y = 4x + 3
Answer:
Question 29.
y = \(\frac{1}{2}\)x + 5
Answer:
Given,
y = \(\frac{1}{2}\)x + 5
when x = 0
y = \(\frac{1}{2}\)0+ 5
y = 5
when x = 0
y = \(\frac{1}{2}\)1+ 5
y = 5\(\frac{1}{2}\)
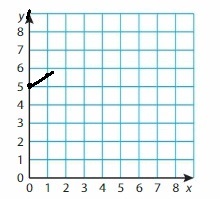
Question 30.
A taxi ride costs $3 plus $2.50 per mile. Write and graph an equation that represents the total cost (in dollars) of a taxi ride. What is the total cost of a five-mile taxi ride?

Answer:
Given,
A taxi ride costs $3 plus $2.50 per mile.
5 × 2.50 = $25.50
Question 31.
Write and graph an equation that represents the total cost (in dollars) of renting the bounce house. How much does it cost to rent the bounce house for 6 hours?

Answer:
C= $25 x 6 = $150
25×6=150+100=250
Question 32.
A car averages 50 miles per hour on a trip. Write and graph an equation that represents the relationship between the time and the distance traveled. How long does it take the car to travel 525 miles?
Answer:
Given,
A car averages 50 miles per hour on a trip.
50 miles – 1 hour
525 miles – x
50 × x = 525
x = 525/50
x = 10.50 hours
Thus it takes 10.5 hours to travel 525 miles.
Equations Practice Test
Question 1.
Write “7 times a number is 84” as an equation.
Answer: 7 × n = 84
Explanation:
We have to write the word sentence into the equation
The phrase times indicates ‘×’
Thus the equation would be 7 × n = 84
Solve the equation. Check your solution.
Question 2.
15 = 7 + b
Answer: b = 8
Explanation:
Given,
15 = 7 + b
b = 15 – 7
b = 8
Question 3.
v – 6 = 16
Answer: v = 22
Explanation:
Given,
v – 6 = 16
v = 16 + 6
v = 22
Question 4.
5x = 70
Answer: x = 14
Explanation:
Given,
5x = 70
x = 70/5
x = 14
Question 5.
\(\frac{6m}{7}\) = 30
Answer:
Given,
\(\frac{6m}{7}\) = 30
6m = 30 × 7
6m = 210
m = 210 ÷ 6
m = 35
Question 6.
Tell whether (3, 27) is a solution of y = 9x
Answer: solution
Explanation:
Given,
y = 9x
x = 3
y = 27
27 = 9(3)
27 = 27
Thus the ordered pair is a solution.
Question 7.
Tell whether (8, 36) is a solution of y = 4x + 2.
Answer: not a solution
Explanation:
Given,
y = 4x + 2.
x = 8
y = 36
36 = 4(8) + 2
36 = 32 + 2
36 ≠ 34
Question 8.
The drawbridge shown consists of two identical sections that open to allow boats to pass. Write s an equation you can use to find the length (in feet) of each section of the drawbridge.

Answer: 2s = 366ft
Question 9.
Each ticket to a school dance is $4. The total amount collected in ticket sales is $332. Find the number of students attending the dance.
Answer:
Given,
Each ticket to a school dance is $4.
The total amount collected in ticket sales is $332.
The equation would be
4s = 332
s = 83
Question 10.
A soccer team sells T-shirts for a fundraiser. The company that makes the T-shirts charges $10 per shirt plus a $20 shipping fee per order.
a. Write and graph an equation that represents the total cost (in dollars) of ordering the shirts.
Answer:
For this case, the first thing we must do is define variables:
c = total cost
x = x number of shirts.
The equation that adapts to the problem is:
c (x) = 10x + 20
b. Choose an ordered pair that lies on your graph in part(a). Interpret it in the context of the problem.

Answer:
Let’s choose the next ordered pair:
(x, c (x)) = (0, 20)
We verify that it is in the graph:
c (20) = 10 (0) + 20
c (20) = 20 (yes, it belongs to the graph).
In the context of the problem, this point means that the cost per shipment is $ 20
Question 11.
You hand in 2 homework pages to your teacher. Your teacher now has 32 homework pages to grade. Find the number of homework pages that your teacher originally had to grade.
Answer:
Given that,
You hand in 2 homework pages to your teacher.
Your teacher now has 32 homework pages to grade.
32 – 2 = 30
Question 12.
Write an equation that represents the total cost (in dollars) of the meal shown with a tip that is a percent of the check total. What is the total cost of the meal when the tip is 15%?

Answer: $41.40
Equations Cumulative Practice
Question 1.
You buy roses at a flower shop for $3 each. How many roses can you buy with $27?
A. 9
B. 10
C. 24
D. 81
Answer: 9
Explanation:
given,
You buy roses at a flower shop for $3 each.
27/3 = 9
Thus you can buy 9 roses with $27.
Thus the correct answer is option A.
Question 2.
You are making identical fruit baskets using 16 apples, 24 pears, and 32 bananas. What is the greatest number of baskets you can make using all of the fruit?
F. 2
G. 4
H. 8
I. 16
Answer: 8
Explanation:
Given,
You are making identical fruit baskets using 16 apples, 24 pears, and 32 bananas.
8 baskets
MULTIPLES OF 16, 24, and, 32
16: 1, 2, 4, 8, 16
24: 1, 2, 3, 4, 6, 8, 12, 24
32: 1, 2, 4, 8, 16, 32
Question 3.
Which equation represents the word sentence?
![]()
A. 18 – 5 = 9 – y
B. 18 + 5 = 9 – y
C. 18 + 5 = y – 9
D. 18 – 5 = y – 9
Answer: 18 + 5 = 9 – y
Explanation:
The suitable equation for the above word sentence is
18 + 5 = 9 – y
Thus the correct answer is option B.
Question 4.
The tape diagram shows the ratio of tickets sold by you and your friend. How many more tickets did you sell than your friend?

F. 6
G. 12
H. 18
I. 30
Answer: 6
Explanation:
Each rectangle = 6
6 × 5 = 30
6 × 2 = 12
30 + 12 = 42
Thus the correct answer is option A.
Question 5.
What is the value of x that makes the equation true?

59 + x = 112
Answer:
Given the equation
59 + x = 112
x = 112 – 59
x = 53
Thus the value of x that makes the equation true is 53
Question 6.
The steps your friend took to divide two mixed numbers are shown.
What should your friend change in order to divide the two mixed numbers correctly?
A. Find a common denominator of 5 and 2.
B. Multiply by the reciprocal of \(\frac{18}{5}\).
C. Multiply by the reciprocal of \(\frac{3}{2}\).
D. Rename 3\(\frac{3}{5}\) as 2\(\frac{8}{5}\).
Answer: Multiply by the reciprocal of \(\frac{3}{2}\).
Question 7.
A company ordering parts receives a charge of $25 for shipping and handling plus cp$20 per part. Which equation represents the cost (in dollars) of ordering parts?
F. c = 25 + 20p
G. c = 20 + 25p
H. p = 25 + 20c
I. p = 20 + 25c
Answer: c = 25 + 20p
Question 8.
Which property is illustrated by the statement?
5(a + 6) = 5(a) + 5(6)
A. Associative Property of Multiplication
B. Commutative Property of Multiplication
C. Commutative Property of Addition
D. Distributive Property
Answer: Distributive Property
Question 9.
What is the value of the expression?

46.8 ÷ 0.156
Answer:
Divide the two decimal numbers
we get the answer
300
Question 10.
In the mural below, the squares that are painted red are marked with the letter R.
What percent of the mural is painted red?
F. 24%
G. 25%
H. 48%
I. 50%
Answer: 48%
Question 11.
Which expression is equivalent to 28x + 70?
A. 14 (2x + 5)
B. 14 (5x + 2)
C. 2 (14x + 5)
D. 14 (7x)
Answer: 14 (2x + 5)
Explanation:
28x + 70
Taking 14 as the common factor
14(2x + 5)
Thus the correct answer is option A.
Question 12.
What is the first step in evaluating the expression?
3 . (5 + 2)2 ÷ 7
F. Multiply 3 and 5.
G. Add 5 and 2
H. Evaluate 52.
I. Evaluate 22.
Answer: G. Add 5 and 2
Question 13.
Jeff wants to save $4000 to buy a used car. He has already saved $850. He plans to save an additional $150 each week.

Part A Write and solve an equation to represent the number of weeks remaining until he can afford the car.
Jeff saves $150 per week by saving \(\frac{3}{4}\) of what he earns at his job each week.
He works 20 hours per week.
Part B Write an equation to represent the amount per hour that Jeff must earn to save $150 per week. Explain your reasoning.
Part C What is the amount per hour that Jeff must earn? Show your work and explain your reasoning.
Answer: 21 weeks
Explanation:
150 × 21 = 3150
3150 + 850 = 4000
Conclusion:
We put all our efforts and experience to prepare Big Ideas Math Book 6th Grade Answer Key Chapter 6 Equations pdf. Hope you are satisfied with the given data and information regarding Big Ideas Math Book 6th Grade Answer Key Chapter 6 Equations. If you have any kind of doubts, clarify with us here. We wish all the very best for all the aspirants preparing for the exam.