Students of Grade 8 can get a detailed explanation for all the questions in Go Math Answer Key Chapter 8 Solving Systems of Linear Equations. In addition to the exercise problems we also provide the solutions for the review test. So, go through all the answers and explanations provided by the math experts in Go Math Grade 8 Chapter 8 Solving Systems of Linear Equations Answer Key. Our aim is to provide easy and simple tricks to solve the problems in Go Math Grade 8 Answer Key Chapter 8 Solving Systems of Linear Equations.
Download Go Math Grade 8 Chapter 8 Solving Systems of Linear Equations Answer Key Pdf
Students who are interested to secure the highest marks in the exams are suggested to download the Go Math Grade 8 Answer Key Chapter 8 Solving Systems of Linear Equations pdf. All the solutions are provided in the pdf format as per the list of the chapters provided in the latest edition. Hence refer to Go Math 8th Grade Solution Key to learning the easy way of maths practice. Check the list of the topics covered in Chapter 8 Solving Systems of Linear Equations from the following section.
Lesson 1: Solving Systems of Linear Equations by Graphing
- Solving Systems of Linear Equations by Graphing – Page No. 232
- Solving Systems of Linear Equations by Graphing – Page No. 233
- Solving Systems of Linear Equations by Graphing Lesson Check – Page No. 234
Lesson 2: Solving Systems by Substitution
- Solving Systems by Substitution – Page No. 240
- Solving Systems by Substitution – Page No. 241
- Solving Systems by Substitution Lesson Check – Page No. 242
Lesson 3: Solving Systems by Elimination
- Solving Systems by Elimination – Page No. 248
- Solving Systems by Elimination – Page No. 249
- Solving Systems by Elimination Lesson Check – Page No. 250
Lesson 4: Solving Systems by Elimination with Multiplication
- Solving Systems by Elimination with Multiplication – Page No. 256
- Solving Systems by Elimination with Multiplication – Page No. 257
- Solving Systems by Elimination with Multiplication Lesson Check – Page No. 258
Lesson 5: Solving Solving Special Systems
- Solving Solving Special Systems – Page No. 262
- Solving Solving Special Systems – Page No. 263
- Solving Solving Special Systems Lesson Check – Page No. 264
Model Quiz
Review
Guided Practice – Solving Systems of Linear Equations by Graphing – Page No. 232
Solve each system by graphing.
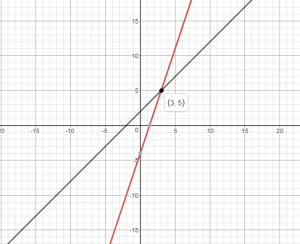
Question 1.
\(\left\{\begin{array}{l}y=3 x-4 \\y=x+2\end{array}\right.\)
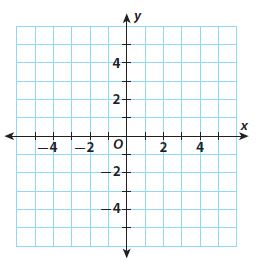
Type below:
______________
Answer:
Explanation:
y = 3x – 4
y = x + 2
The solution of thr linear system of equations is the intersection point of the two equations.
(3, 5) is the solution of the system of equations.
If x = 3, y = 3(3) – 4 = 9 – 4 = 5; y = 3 + 2 = 5
5 = 5; True
Question 2.
\(\left\{\begin{array}{l}x-3 y=2 \\-3x+9y=-6\end{array}\right.\)
Type below:
______________
Answer:
Infinitely many solutions
Explanation:
x – 3y = 2
-3x + 9y = -6
x – 3y – x = -x + 2
-3y = -x + 2
y = 1/3 . x – 2/3
-3x + 9y + 3x = 3x – 6
9y = 3x – 6
y = 3/9 . x – 6/9
y = 1/3 . x – 2/3
The solution of the linear system of equations is the intersection of the two equations.
Infinitely many solutions
Question 3.
Mrs. Morales wrote a test with 15 questions covering spelling and vocabulary. Spelling questions (x) are worth 5 points and vocabulary questions (y) are worth 10 points. The maximum number of points possible on the test is 100.
a. Write an equation in slope-intercept form to represent the number of questions on the test.
Type below:
______________
Answer:
y = -x + 15
Explanation:
Mrs. Morales wrote a test with 15 questions covering spelling and vocabulary. Spelling questions (x) are worth 5 points and vocabulary questions (y) are worth 10 points.
x + y = 15
x + y – x = -x + 15
y = -x + 15
Question 3.
b. Write an equation in slope-intercept form to represent the total number of points on the test.
Type below:
______________
Answer:
y = -1/2 . x + 10
Explanation:
The total number of points on test is 100
5x + 10y = 100
5x + 10y – 5x = -5x + 100
10y = -5x + 100
y = -5/10 . x + 100/10
y = -1/2 . x + 10
Question 3.
c. Graph the solutions of both equations.
Type below:
______________
Answer:
Question 3.
d. Use your graph to tell how many of each question type are on the test.
_________ spelling questions
_________ vocabulary questions
Answer:
10 spelling questions
5 vocabulary questions
ESSENTIAL QUESTION CHECK-IN
Question 4.
When you graph a system of linear equations, why does the intersection of the two lines represent the solution of the system?
Type below:
______________
Answer:
To solve a system of linear equations means finding the solutions that satisfy all the equations of that system. When we graph a system of linear equations, the intersection point lies on the line of each equation, which means that satisfies all the equations. Therefore, it is considered to be the solution to that system.
Solving Systems of Linear Equations by Graphing – Page No. 233
Question 5.
Vocabulary
A_________________ is a set of equations that have the same variables.
______________
Answer:
system of equations
Explanation:
A system of equations is a set of equations that have the same variables.
Question 6.
Eight friends started a business. They will wear either a baseball cap or a shirt imprinted with their logo while working. They want to spend exactly $36 on the shirts and caps. Shirts cost $6 each and caps cost $3 each.
a. Write a system of equations to describe the situation. Let x represent the number of shirts and let y represent the number of caps.
______________
Answer:
6x + 3y = 36
Explanation:
The sum of caps and shirts is 8. The total cost of caps and shirts is $36.
x + y = 8
6x + 3y = 36
Question 6.
b. Graph the system. What is the solution and what does it represent?
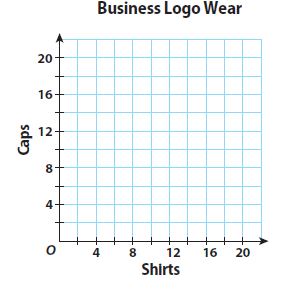
Type below:
______________
Answer:
The solution is (4, 4)
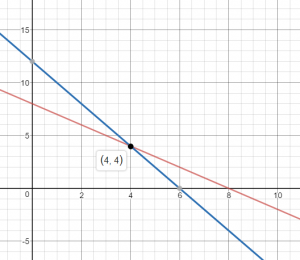
Explanation:
x + y – x = -x + 8
y = -x + 8
6x + 3y – 6x = -6x + 36
3y = -6x + 36
y = -6/2 . x + 36/3
y = -2x + 12
(4, 4). They should order 4 shirts and 4 caps.
Question 7.
Multistep The table shows the cost for bowling at two bowling alleys.
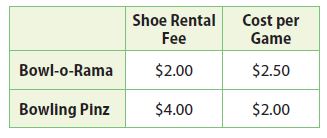
a. Write a system of equations, with one equation describing the cost to bowl at Bowl-o-Rama and the other describing the cost to bowl at Bowling Pinz. For each equation, let x represent the number of games played and let y represent the total cost.
Type below:
______________
Answer:
y = 2.5x + 2
y = 2x + 4
Explanation:
Cost at Bowl-o-Rama => y = 2.5x + 2
Cost at Bowling Pinz => y = 2x + 4
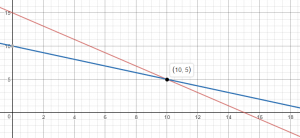
Question 7.
b. Graph the system. What is the solution and what does it represent?
Type below:
______________
Answer:
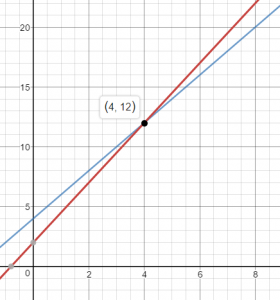
Explanation:
The solution of the linear system of equations is the intersection of the two equations.
(4, 12)
When 4 games are played, the total cost is $12.
Solving Systems of Linear Equations by Graphing – Page No. 234
Question 8.
Multi-Step Jeremy runs 7 miles per week and increases his distance by 1 mile each week. Tony runs 3 miles per week and increases his distance by 2 miles each week. In how many weeks will Jeremy and Tony be running the same distance? What will that distance be?
Type below:
______________
Answer:
After 4 weeks Jeremy and Tony will be running the same distance and that distance would be 11 miles.
Explanation:
Multi-Step Jeremy runs 7 miles per week and increases his distance by 1 mile each week.
y = x + 7
Tony runs 3 miles per week and increases his distance by 2 miles each week.
y = 2x + 3
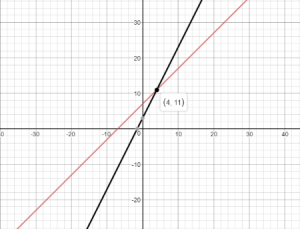
The solution of the system of linear equation is (4, 11) which means that after 4 weeks Jeremy and Tony will be running the same distance and that distance would be 11 miles.
Question 9.
Critical Thinking Write a real-world situation that could be represented by the system of equations shown below.
\(\left\{\begin{array}{l}y=4 x+10 \\y=3x+15\end{array}\right.\)
Type below:
______________
Answer:
The entry fee of the first gym is $10 and for every hour that you spend there, you pay an extra $4. If we denote with x the number of hours that somebody spends at the gym and with y the total cost is
y = 4x + 10
The entry fee of the second gym is $15 and for every hour that you spend there, you pay an extra $3. If we denote with x the number of hours that somebody spends at the gym and with y the total cost is
y = 3x + 15
y = 4x + 10
y = 3x + 15
FOCUS ON HIGHER ORDER THINKING
Question 10.
Multistep The table shows two options provided by a high-speed Internet provider.
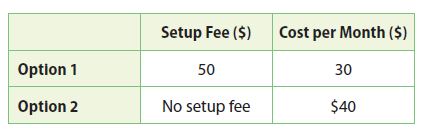
a. In how many months will the total cost of both options be the same? What will that cost be?
________ months
$ ________
Answer:
5 months
$ 200
Explanation:
Let y be the total cost after x month
y = 30x + 50
Let y be the total cost after x month
y = 40x
Substitute y = 40x in y = 30x + 50
40x = 30x + 50
40x – 30x = 50
10x = 50
x = 50/10
x = 5
The total cost of both options will be the same after 5 months. Total cost would be y = 40(5) = $200.
Question 10.
b. If you plan to cancel your Internet service after 9 months, which is the cheaper option? Explain.
______________
Answer:
When x = 9 months
y = 30(9) + 50 = $320
y = 40(9) = $360
$320 < $360
Option 1 is cheaper as the total cost is less for option 1
Question 11.
Draw Conclusions How many solutions does the system formed by x − y = 3 and ay − ax + 3a = 0 have for a nonzero number a? Explain.
Type below:
______________
Answer:
x – y = 3
ay – ax + 3a =0
ay – ax + 3a – 3a = 0 – 3a
ay – ax = – 3a
a(y – x) = -3a
y – x = -3
x – y = 3
Both equations are the same. The system of linear equations have infinitely many solutions.
Guided Practice – Solving Systems by Substitution – Page No. 240
Solve each system of linear equations by substitution.
Question 1.
\(\left\{\begin{array}{l}3x-2y=9 \\y=2x-7\end{array}\right.\)
x = ________
y = ________
Answer:
x = 5
y = 3
Explanation:
\(\left\{\begin{array}{l}3x-2y=9 \\y=2x-7\end{array}\right.\)
Substitute 2x – 7 in 3x – 2y = 9
3x – 2(2x – 7) = 9
3x – 4x + 14 = 9
-x + 14 = 9
-x + 14 – 14 = 9 – 14
-x = -5
x = -5/-1 = 5
y = 2(5) – 7 = 3
Solution is (5, 3)
Question 2.
\(\left\{\begin{array}{l}y=x-4 \\2x+y=5\end{array}\right.\)
x = ________
y = ________
Answer:
x = 3
y = -1
Explanation:
\(\left\{\begin{array}{l}y=x-4 \\2x+y=5\end{array}\right.\)
2x + x – 4 = 5
3x – 4 = 5
3x – 4 + 4 = 5 + 4
3x = 9
x = 9/3 = 3
y = 3 – 4 = -1
The solution is (3, -1)
Question 3.
\(\left\{\begin{array}{l}x+4y=6 \\y=-x+3\end{array}\right.\)
x = ________
y = ________
Answer:
x = 2
y = 1
Explanation:
\(\left\{\begin{array}{l}x+4y=6 \\y=-x+3\end{array}\right.\)
Substitute y = -x + 3 in x + 4y = 6
x + 4(-x + 3) = 6
x – 4x + 12 = 6
-3x + 12 = 6
-3x + 12 – 12 = 6 – 12
-3x = -6
x = -6/-3 = 2
y = -2 + 3 = 1
The solution is (2, 1)
Question 4.
\(\left\{\begin{array}{l}x+2y=6 \\x-y=3\end{array}\right.\)
x = ________
y = ________
Answer:
x = 4
y = 1
Explanation:
\(\left\{\begin{array}{l}x+2y=6 \\x-y=3\end{array}\right.\)
y = x – 3
Substitute y = x – 3 in x + 2y = 6
x + 2(x – 3) = 6
x + 2x – 6 = 6
3x = 12
x = 12/3
x = 4
4 – y = 3
-y = 3 – 4
-y = -1
y = 1
The solution is (4, 1)
Solve each system. Estimate the solution first.
Question 5.
\(\left\{\begin{array}{l}6x+y=4 \\x-4y=19\end{array}\right.\)
Estimate ______________
Solution ______________
Type below:
______________
Answer:
Estimate (2, -5)
Solution (1.4, -4.4)
Explanation:
\(\left\{\begin{array}{l}6x+y=4 \\x-4y=19\end{array}\right.\)
Let’s find the estimation by graphing the equations
Estimate: (2, -5)
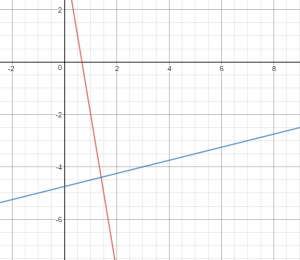
x = 4y + 19
6(4y + 19) + y = 4
24y + 114 + y = 4
25y + 114 = 4
25y = 4 – 114
25y = -110
y = -110/25
y = -4.4
x + 4(-4.4) = 19
x + 17.6 = 19
x = 19 – 17.6
x = 1.4
The solution is (1.4, -4.4)
Question 6.
\(\left\{\begin{array}{l}x+2y=8 \\3x+2y=6\end{array}\right.\)
Estimate ______________
Solution ______________
Type below:
______________
Answer:
Estimate (-1, 5)
Solution (-1, 4.5)
Explanation:
\(\left\{\begin{array}{l}x+2y=8 \\3x+2y=6\end{array}\right.\)
Let’s find the estimation by graphing the equations
Estimate: (-1, 5)
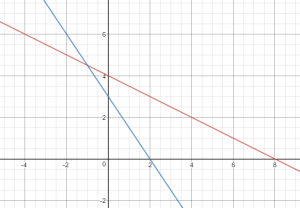
x = -2y + 8
Substitute the equation x = -2y + 8 in 3x + 2y = 6
3(-2y + 8) + 2y = 6
-6y + 24 + 2y = 6
-4y = 6 – 24
-4y = -18
y = -18/-4
y = 4.5
x + 2(4.5) = 8
x + 9 = 8
x = 8 – 9
x = -1
The solution is (-1, 4.5)
Question 7.
\(\left\{\begin{array}{l}3x+y=4 \\5x-y=22\end{array}\right.\)
Estimate ______________
Solution ______________
Type below:
______________
Answer:
Estimate (3, -6)
Solution (3.25, -5.75)
Explanation:
\(\left\{\begin{array}{l}3x+y=4 \\5x-y=22\end{array}\right.\)
Find the Estimation using graphing the equations.
Estimate: (3, -6)
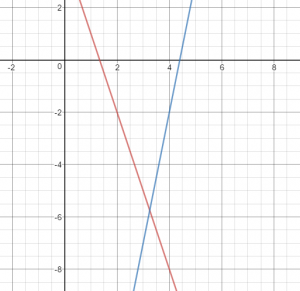
y = -3x + 4
Substitute y = -3x + 4 in 5x – y = 22
5x – (-3x + 4) = 22
5x + 3x -4 = 22
8x = 26
x = 26/8
x = 3.25
3(3.25) + y = 4
9.75 + y = 4
y = 4 – 9.75
y = -5.75
The solution is (3.25, -5.75)
Question 8.
\(\left\{\begin{array}{l}2x+7y=2 \\x+y=-1\end{array}\right.\)
Estimate ______________
Solution ______________
Type below:
______________
Answer:
Estimate (-2, 1)
Solution (-1.8, 0.8)
Explanation:
\(\left\{\begin{array}{l}2x+7y=2 \\x+y=-1\end{array}\right.\)
Find the Estimation using graphing the equations.
Estimate: (-2, 1)
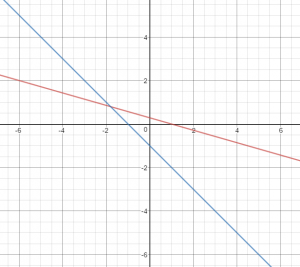
y = -x -1
Substitute y = -x – 1 in 2x + 7y = 2
2x + 7(-x – 1) = 2
2x – 7x -7 = 2
-5x = 2 + 7
-5x = 9
x = -9/5
x = -1.8
-1.8 + y = -1
y = -1 + 1.8
y = 0.8
The solution is (-1.8, 0.8)
Question 9.
Adult tickets to Space City amusement park cost x dollars. Children’s tickets cost y dollars. The Henson family bought 3 adult and 1 child tickets for $163. The Garcia family bought 2 adult and 3 child tickets for $174.
a. Write equations to represent the Hensons’ cost and the Garcias’ cost.
Hensons’ cost: ________________
Garcias’ cost:__________________
Type below:
______________
Answer:
Hensons’ cost: 3x + y = 163
Garcias’ cost: 2x + 3y = 174
Explanation:
Henson’s cost
3x + y = 163
Garcia’s cost
2x + 3y = 174
Question 9.
b. Solve the system.
adult ticket price: $ _________
Garcias’ cost: $ _________
Answer:
adult ticket price: $ 45
Garcias’ cost: $ 28
Explanation:
y = -3x + 163
Substitute y = -3x + 163 in 2x + 3y = 174
2x + 3(-3x + 163) = 174
2x -9x + 489 = 174
-7x = -315
x = -315/-7 = 45
3(45) + y = 163
135 + y = 163
y = 163 – 135
y = 28
adult ticket price: $ 45
Garcias’ cost: $ 28
ESSENTIAL QUESTION CHECK-IN
Question 10.
How can you decide which variable to solve for first when you are solving a linear system by substitution?
Type below:
______________
Answer:
The variable with the unit coefficient should be solved first when solving a linear system by substitution.
8.2 Independent Practice – Solving Systems by Substitution – Page No. 241
Question 11.
Check for Reasonableness Zach solves the system
\(\left\{\begin{array}{l}x+y=-3 \\x-y=1\end{array}\right.\)
and finds the solution (1, -2). Use a graph to explain whether Zach’s solution is reasonable.
Type below:
______________
Answer:
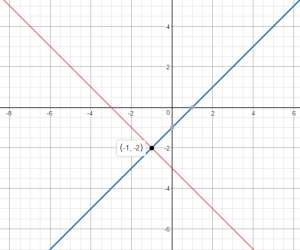
Explanation:
\(\left\{\begin{array}{l}x+y=-3 \\x-y=1\end{array}\right.\)
The x coordinate of the solution is negative, hence Zach’s solution is not reasonable.
Represent Real-World Problems Angelo bought apples and bananas at the fruit stand. He bought 20 pieces of fruit and spent $11.50. Apples cost $0.50 and bananas cost $0.75 each.
a. Write a system of equations to model the problem. (Hint: One equation will represent the number of pieces of fruit. A second equation will represent the money spent on the fruit.)

Type below:
______________
Answer:
x + y = 20
0.5x + 0.75y = 11.5
Explanation:
x + y = 20
0.5x + 0.75y = 11.5
where c is the number of Apples and y is the number of Bananas.
Question 12.
b. Solve the system algebraically. Tell how many apples and bananas Angelo bought.
________ apples
________ bananas
Answer:
14 apples
6 bananas
Explanation:
y = -x + 20
Substitute y = -x + 20 in 0.5x + 0.75y = 11.5
0.5x + 0.75(-x + 20) = 11.5
0.5x – 0.75x + 15 = 11.5
-0.25x + 15 = 11.5
-0.25x = 11.5 – 15
-0.25x = -3.5
x = -3.5/-0.25
x = 14
14 + y = 20
y = 6
Angelo bought 14 apples and 6 bananas.
Question 13.
Represent Real-World Problems A jar contains n nickels and d dimes. There is a total of 200 coins in the jar. The value of the coins is $14.00. How many nickels and how many dimes are in the jar?
________ nickels
________ dimes
Answer:
120 nickels
80 dimes
Explanation:
A jar contains n nickels and d dimes. There is a total of 200 coins in the jar. The value of the coins is $14.00.
$14 = 1400 cents
n + d = 200
5n + 10d = 1400
d = -n + 200
5n + 10(-n + 200) = 1400
5n – 10n + 2000 = 1400
-5n = -600
n = -600/-5
n = 120
120 + d = 200
d = 200 – 120
d = 80
There are 120 nickles and 80 dimes in the jar.
Question 14.
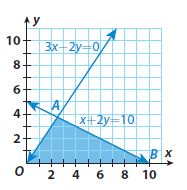
Multistep The graph shows a triangle formed by the x-axis, the line 3x−2y=0, and the line x+2y=10. Follow these steps to find the area of the triangle.
a. Find the coordinates of point A by solving the system
\(\left\{\begin{array}{l}3x-2y=0 \\x-2y=10\end{array}\right.\)
Point A: ____________________
Type below:
______________
Answer:
Point A: (2.5, 3.75)Coordinate of A is (2.5, 3.75)
Explanation:
\(\left\{\begin{array}{l}3x-2y=0 \\x-2y=10\end{array}\right.\)
x = -2y + 10
Substitute x = -2y + 10 in 3x – 2y = 0
3(-2y + 10) -2y = 0
-6y + 30 – 2y = 0
-8y = -30
y = -30/-8 = 3.75
x + 2(3.75) = 10
x + 7.5 = 10
x = 10 – 7.5
x = 2.5
Coordinate of A is (2.5, 3.75)
Question 14.
b. Use the coordinates of point A to find the height of the triangle.
height:__________________
height: \(\frac{□}{□}\) units
Answer:
height: 3.75
height: \(\frac{15}{4}\) units
Explanation:
Height of the triangle is the y coordinate of A
Height = 3.75
Question 14.
c. What is the length of the base of the triangle?
base:________________
base: ______ units
Answer:
base: 10 units
Explanation:
Length of the base = 10
Question 14.
d. What is the area of the triangle?
A = ______ \(\frac{□}{□}\) square units
Answer:
A = 18.75 square units
A = 18 \(\frac{3}{4}\) square units
Explanation:
Area of the triangle = 1/2 . Height . Base
Area = 1/2 . 3.75 . 10 = 18.75
Solving Systems by Substitution – Page No. 242
Question 15.
Jed is graphing the design for a kite on a coordinate grid. The four vertices of the kite are at A(−\(\frac{4}{3}\), \(\frac{2}{3}\)), B(\(\frac{14}{3}\), −\(\frac{4}{3}\)), C(\(\frac{14}{3}\), −\(\frac{16}{3}\)), and D(\(\frac{2}{3}\), −\(\frac{16}{3}\)). One kite strut will connect points A and C. The other will connect points B and D. Find the point where the struts cross.

Type below:
______________
Answer:
The struts cross as (8/3, 10/3)
Explanation:
1. From AC
Slope = (y2 – y1)/(x2 – x1) = [(-16/3)-(2/3)] ÷ [(14/3) – (-4/3)] = (-18/3) ÷ (18/3) = -1
y = mx + b
2/3 = -1(-4/3) + b
2/3 = 4/3 + b
1. From BD
Slope = (y2 – y1)/(x2 – x1) = [(-16/3)-(-4/3)] ÷ [(2/3) – (144/3)] = (-12/3) ÷ (-12/3) = 1
y = mx + b
-4/3 = 1(14/3) + b
-4/3 = 14/3 + b
-18/3 = b
-6 = b
y = mx + b
y = x -6
3. y = -x -2/3
y = x – 6
4. y = -x – 2/3
x – 6 = -x – 2/3
x = -x – 2/3 + 6
x = – x + 16/3
2x = 16/3
x = 16/6
x = 8/3
then y = x – 6
y = 8/3 – 18/3
y = -10/3
The struts cross as (8/3, 10/3)
FOCUS ON HIGHER ORDER THINKING
Question 16.
Analyze Relationships Consider the system
\(\left\{\begin{array}{l}6x-3y=15 \\x+3y=-8\end{array}\right.\)
Describe three different substitution methods that can be used to solve this system. Then solve the system.
Type below:
______________
Answer:
(1, -3) is the answer.
Explanation:
As there are three different substitution methods, we can write
Solve for y in the first equation, then substitute that value into the second equation.
Solve for x in the second equation, then substitute that value into the first equation.
Solve either equation for 3y, then substitute that value into the other equation.
From the Second method,
x + 3y = -8
x = -3y – 8
6x – 3y = 15
6 (-3y – 8) -3y = 15
-18y – 48 -3y = 15
-21y – 48 = 15
-21y = 63
y = -3
x + 3y = -8
x + 3(-3) = -8
x – 9 = -8
x = 1
(1, -3) is the answer.
Question 17.
Communicate Mathematical Ideas Explain the advantages, if any, that solving a system of linear equations by substitution has over solving the same system by graphing.
Type below:
______________
Answer:
The advantage of solving a system of linear equations by graphing is that it is relatively easy to do and requires very little algebra.
Question 18.
Persevere in Problem Solving Create a system of equations of the form
\(\left\{\begin{array}{l}Ax+By=C \\Dx+Ey=F\end{array}\right.\)
that has (7, −2) as its solution. Explain how you found the system.
Type below:
______________
Answer:
x + y = 5
x – y = 9
solves in :
x = (5+9)/2 = 7
y = 5-9)/2 = -2
A=1, B=2, C= 5
D=1, E= -1, F=9
x = 7
y = -2
IS a system (even if it is a trivial one) of equations so this answer would be acceptable.
The target for a system is to find it SOLUTION SET and not to conclude with x=a and y=b
Guided Practice – Solving Systems by Elimination – Page No. 248
Question 1.
Solve the system
\(\left\{\begin{array}{l}4x+3y=1 \\x-3y=-11\end{array}\right.\)
by adding.

Type below:
______________
Answer:
4x + 3y = 1
x – 3y = -11
Add the above two equations
4x + 3y = 1
+(x – 3y = -11)
Add to eliminate the variable y
5x + 0y = -10
Simplify and solve for x
5x = -10
Divide both sided by 5
x = -10/5 = -2
Substitute into one of the original equations and solve for y.
4(-2) + 3y = 1
-8 + 3y = 1
3y = 9
y = 9/3 = 3
So, (-2, 3) is the solution of the system.
Solve each system of equations by adding or subtracting.
Question 2.
\(\left\{\begin{array}{l}x+2y=-2 \\-3x+2y=-10\end{array}\right.\)
x = ________
y = ________
Answer:
x = 2
y = -2
Explanation:
\(\left\{\begin{array}{l}x+2y=-2 \\-3x+2y=-10\end{array}\right.\)
Subtract the equations
x + 2y = -2
-(-3x + 2y = -10)
y is eliminated as it has reversed coefficients. Solve for x
x + 2y + 3x – 2y = -2 + 10
4x = 8
x = 8/4 = 2
Substituting x in either of the equation to find y
2 + 2y = -2
2 + 2y -2 = -2 -2
2y = -4
y = -4/2 = -2
(2, -2) is the answer.
Question 3.
\(\left\{\begin{array}{l}3x+y=23 \\3x-2y=8\end{array}\right.\)
(________ , ________)
Answer:
(6, 5)
Explanation:
\(\left\{\begin{array}{l}3x+y=23 \\3x-2y=8\end{array}\right.\)
Subtract the equations
3x + y = 23
-(3x – 2y = 8)
x is eliminated as it has reversed coefficients. Solve for y
3x + y – 3x + 2y = 23 – 8
3y = 15
y = 15/3 = 5
Substituting y in either of the equation to find x
3x + 5 = 23
3x + 5 – 5 = 23 – 5
3x = 18
x = 18/3 = 6
Solution is (6, 5)
Question 4.
\(\left\{\begin{array}{l}-4x-5y=7 \\3x+5y=-14\end{array}\right.\)
(________ , ________)
Answer:
(7, -7)
Explanation:
\(\left\{\begin{array}{l}-4x-5y=7 \\3x+5y=-14\end{array}\right.\)
Add the equations
-4x – 5y = 7
+(3x + 5y = -14)
y is eliminated as it has reversed coefficients. Solve for x
-4x -5y +3x + 5y = 7 -14
-x = -7
x = -7/-1 = 7
Substituting x in either of the equation to find y
3(7) + 5y = -14
21 + 5y -21 = -14 -21
5y = -35
y = -35/5 = -7
The answer is (7, -7)
Question 5.
\(\left\{\begin{array}{l}x-2y=-19 \\5x+2y=1\end{array}\right.\)
(________ , ________)
Answer:
(-3, 8)
Explanation:
\(\left\{\begin{array}{l}x-2y=-19 \\5x+2y=1\end{array}\right.\)
Add the equations
x – 2y = -19
+(5x + 2y = 1)
y is eliminated as it has reversed coefficients. Solve for x
x – 2y + 5x + 2y = -19 + 1
6x = -18
x = -18/6 = -3
Substituting x in either of the equation to find y
-3 -2y = -19
-3 -2y + 3 = -19 + 3
-2y = -16
y = -16/-2 = 8
The answer is (-3, 8)
Question 6.
\(\left\{\begin{array}{l}3x+4y=18 \\-2x+4y=8\end{array}\right.\)
(________ , ________)
Answer:
(2, 3)
Explanation:
\(\left\{\begin{array}{l}3x+4y=18 \\-2x+4y=8\end{array}\right.\)
Subtract the equations
3x + 4y = 18
-(-2x + 4y = 8)
y is eliminated as it has reversed coefficients. Solve for x
3x + 4y + 2x – 4y = 18 – 8
5x = 10
x = 10/5 = 2
Substituting x in either of the equation to find y
3(2) + 4y = 18
6 + 4y – 6 = 18 – 6
4y = 12
y = 12/4 =3
Solution is (2, 3)
Question 7.
\(\left\{\begin{array}{l}-5x+7y=11 \\-5x+3y=19\end{array}\right.\)
(________ , ________)
Answer:
(-5, -2)
Explanation:
\(\left\{\begin{array}{l}-5x+7y=11 \\-5x+3y=19\end{array}\right.\)
Subtract the equations
-5x + 7y = 11
-(-5x + 3y = 19)
x is eliminated as it has reversed coefficients. Solve for y
-5x + 7y + 5x – 3y = 11 – 19
4y = -8
y = -8/4 = -2
Substituting y in either of the equation to find x
-5x + 7(-2) = 11
-5x -14 + 14 = 11 + 14
-5x = 25
x = 25/-5 = -5
Solution is (-5, -2)
Question 8.
The Green River Freeway has a minimum and a maximum speed limit. Tony drove for 2 hours at the minimum speed limit and 3.5 hours at the maximum limit, a distance of 355 miles. Rae drove 2 hours at the minimum speed limit and 3 hours at the maximum limit, a distance of 320 miles. What are the two speed limits?
a. Write equatios to represent Tony’s distance and Rae’s distance.
Type below:
______________
Answer:
Tony’s distance: 2x + 3.5y = 355
Rae’s distance: 2x + 3y = 320
where x is the minimum speed and y is the maximum speed.
Question 8.
b. Solve the system.
minimum speed limit:______________
maximum speed limit______________
minimum speed limit: ________ mi/h
maximum speed limit: ________ mi/h
Answer:
minimum speed limit:55
maximum speed limit70
minimum speed limit: 55mi/h
maximum speed limit: 70mi/h
Explanation:
Subtract the equations
2x + 3.5y = 355
-(2x + 3y = 320)
x is eliminated as it has reversed coefficients. Solve for y
2x + 3.5y – 2x – 3y = 355 – 320
0.5y = 35
y = 35/0.5 = 70
Substituting y in either of the equation to find x
2x + 3(70) = 320
2x + 210 – 210 = 320 – 210
2x = 110
x = 110/2 = 55
Minimum speed limit: 55 miles per hour
Maximum speed limit: 70 miles per hour
ESSENTIAL QUESTION CHECK-IN
Question 9.
Can you use addition or subtraction to solve any system? Explain.
________
Answer:
No. One of the variables should have the same coefficient in order to add or subtract the system.
8.3 Independent Practice – Solving Systems by Elimination – Page No. 249
Question 10.
Represent Real-World Problems Marta bought new fish for her home aquarium. She bought 3 guppies and 2 platies for a total of $13.95. Hank also bought guppies and platies for his aquarium. He bought 3 guppies and 4 platies for a total of $18.33. Find the price of a guppy and the price of a platy.

Guppy: $ ________
Platy: $ ________
Answer:
Guppy: $ 3.19
Platy: $ 2.19
Explanation:
3x + 2y = 13.95
3x + 4y = 18.33
where x is the unit price of guppy and y is the unit price of platy
Subtract the equations
3x + 2y = 13.95
-(3x + 4y = 18.33)
x is eliminated as it has reversed coefficients. Solve for y
3x + 2y – 3x – 4y = 13.95 – 18.33
-2y = -4.38
y = -4.38/-2 = 2.19
Substituting y in either of the equation to find x
3x + 2(2.19) = 13.95
3x + 4.38 – 4.38 = 13.95 – 4.38
3x = 9.57
x = 9.57/3 = 3.19
The price of a guppy is $3.19 and price of a platy is $2.19
Question 11.
Represent Real-World Problems The rule for the number of fish in a home aquarium is 1 gallon of water for each inch of fish length. Marta’s aquarium holds 13 gallons and Hank’s aquarium holds 17 gallons. Based on the number of fish they bought in Exercise 10, how long is a guppy and how long is a platy?
Length of a guppy = ________ inches
Length of a platy = ________ inches
Answer:
Length of a guppy = 3 inches
Length of a platy = 2 inches
Explanation:
3x + 2y = 13
3x + 4y = 17
where x is the length of guppy and y is the length of a platy
Subtract the equations
3x + 2y = 13
-(3x + 4y = 17)
x is eliminated as it has reversed coefficients. Solve for y
3x + 2y – 3x – 4y = 13 – 17
-2y = -4
y = -4/-2 = 2
Substituting y in either of the equation to find x
3x + 2(2) = 13
3x + 4 – 4 = 13 – 4
3x = 9
x = 9/3 = 3
The length of a guppy is 3 inches and price of a platy is 2 inches
Question 12.
Line m passes through the points (6, 1) and (2, -3). Line n passes through the points (2, 3) and (5, -6). Find the point of intersection of these lines.
Type below:
________________
Answer:
The intersection of these lines is (3.5, -1.5)
Explanation:
Find the slope of line m = (y2 – y1)/(x2 – x1) where (x2, y2) = (2, -3) and (x1, y1) = (6, 1)
Slope = (-3 -1)/(2 – 6) = -4/-4 = 1
Substitute the value of m and any of the given ordered pair (x, y) in point-slope form of equation: y – y1 = m(x – x1)
y – 1 = 1(x – 6)
y – 1 = x – 6
y = x – 6 + 1
x – y = 5
Find the slope of line n = (y2 – y1)/(x2 – x1) where (x2, y2) = (5, -6) and (x1, y1) = (2, 3)
Slope = (-6 -3)/(5 – 2) = -9/3 = -3
Substitute the value of m and any of the given ordered pair (x, y) in point-slope form of equation: y – y1 = m(x – x1)
y – 3 = -3(x – 2)
y – 3 = -3x + 6
y = -3x + 6 + 3
3x + y = 9
Add the equations
x – y = 5
+(3x + y = 9)
y is eliminated as it has reversed coefficients. Solve for x
x – y + 3x + y = 5 + 9
4x = 14
x = 14/4 = 3.5
Substituting x in either of the equation to find y
3.5 – y = 5
3.5 – y – 3.5 = 5 – 3.5
-y = 1.5
y = -1.5
The intersection of these lines is (3.5, -1.5)
Question 13.
Represent Real-World Problems Two cars got an oil change at the same auto shop. The shop charges customers for each quart of oil plus a flat fee for labor. The oil change for one car required 5 quarts of oil and cost $22.45. The oil change for the other car required 7 quarts of oil and cost $25.45. How much is the labor fee and how much is each quart of oil?
Labor fee: $ ________
Quart of oil: $ ________
Answer:
Labor fee: $ 14.95
Quart of oil: $ 1.5
Explanation:
5x + y = 22.45
7x + y = 25.45
where x is the unit cost of quarts of oil and y is the flat fee for labor
Subtract the equations
5x + y = 22.45
-(7x + y = 25.45)
y is eliminated as it has reversed coefficients. Solve for x
5x + y – 7x – y = 22.45 – 25.45
-2x = -3
x = -3/-2 = 1.5
Substituting x in either of the equation to find y
5(1.5) + y = 22.45
7.5 + y – 7.5 = 22.45 – 7.5
y = 14.95
Labor fee is $14.95 and unit cost of quart of oil is $1.5
Question 14.
Represent Real-World Problems A sales manager noticed that the number of units sold for two T-shirt styles, style A and style B, was the same during June and July. In June, total sales were $2779 for the two styles, with A selling for $15.95 per shirt and B selling for $22.95 per shirt. In July, total sales for the two styles were $2385.10, with A selling at the same price and B selling at a discount of 22% off the June price. How many T-shirts of each style were sold in June and July combined?
________ T-shirts of style A and style B were sold in June and July.
Answer:
15.95x + 22.95y = 2779
15.95x + 17.9y = 2385.10
where x is number of style A shirt and y is the number of style B shirt
In July, the price of style B shirt is 22% of the price of style B shirt in June, hence 0.78(22.95) = 17.90
Subtract the equations
15.95x + 22.95y = 2779
-(15.95x + 17.9y = 2385.10)
x is eliminated as it has reversed coefficients. Solve for y
15.95x + 22.95 – 15.95x – 17.9y = 2779 – 2385.10
5.05y = 393.9
y = 393.9/5.05 = 78
Substituting y in either of the equation to find x
15.95x +22.95(78) = 2779
15.95x + 1790.1 – 1790.1 = 2779 – 1790.1
15.95x = 988.9
x = 988.9/15.95 = 62
The number of style A T shirt sold in June is 62.
Since the number of T-shirts sold in both numbers is the same, the total number = 2. 62 = 124.
The number of style B T-shirts sold in June is 78.
Since the number of T-shirts sold in both numbers is the same, the total number = 2. 78 = 156.
Question 15.
Represent Real-World Problems Adult tickets to a basketball game cost $5. Student tickets cost $1. A total of $2,874 was collected on the sale of 1,246 tickets. How many of each type of ticket were sold?
 img 14
img 14
________ adult tickets
________ student tickets
Answer:
407 adult tickets
839 student tickets
Explanation:
x + y = 1246
5x + y = 2874
where x is the number of adult tickets sold and y is the number of student tickets sold.
Subtract the equations
x + y = 1246
-(5x + y = 2874)
y is eliminated as it has reversed coefficients. Solve for x
x + y – 5x – y = 1246 – 2874
-4x = -1628
x = -1628/-4 = 407
Substituting x in either of the equation to find y
407 + y = 1246
407 + y – 407 = 1246 – 407
y = 839
The number of adult tickets sold is 407 and student tickets sold is 839.
FOCUS ON HIGHER ORDER THINKING – Solving Systems by Elimination – Page No. 250
Question 16.
Communicate Mathematical Ideas Is it possible to solve the system
\(\left\{\begin{array}{l}3x-2y=10 \\x+2y=6\end{array}\right.\)
by using substitution? If so, explain how. Which method, substitution or elimination, is more efficient? Why?
________
Answer:
The system can be solved by substitution as x in equation 2 can be isolated.
3x – 2y = 10
x + 2y = 6
Solve the equation for x in the equation.
x = -2y + 6
Substitute the expression for x in the other equation and solve.
3(-2y + 6) -2y = 10
-6y + 18 – 2y = 10
-8y + 18 = 10
-8y = -8
y = -8/-8 = 1
Substitute the values of y into one of the equations and solve for the other variable x.
x + 2(1) = 6
x = 4
The solution is (4, 1)
As the cofficient if variable y is opposite, it will be eliminated and solved for x in less number of steps.
Elimination would be more efficient.
Question 17.
Jenny used substitution to solve the system
\(\left\{\begin{array}{l}2x+y=8 \\x-y=1\end{array}\right.\). Her solution is shown below.
Step 1: y = -2x + 8 Solve the first equation for y.
Step 2: 2x + (-2x + 8) = 8 Substitute the value of y in an original equation.
Step 3: 2x – 2x + 8 = 8 Use the Distributive Property.
Step 4: 8 = 8 Simplify.
a. Explain the Error Explain the error Jenny made. Describe how to correct it.
Type below:
______________
Answer:
2x + y = 8
x – y = 1
Rewritten equation should be substituted in the other original equation
Error is that Jenny solved for y in the first equation and substitute it in the original equation.
x – (-2x + 8) = 1
3x – 8 = 1
3x = 9
x = 9/3 = 3
x = 3
Question 17.
b. Communicate Mathematical Ideas Would adding the equations have been a better method for solving the system? If so, explain why.
________
Answer:
Yes
Explanation:
As the coefficient, if variable y is the opposite, it will be eliminated and solved for x in less number of steps.
Guided Practice – Solving Systems by Elimination with Multiplication – Page No. 256
Question 1.
Solve the system
\(\left\{\begin{array}{l}3x-y=8 \\-2x+4y=-12\end{array}\right.\)
by multiplying and adding.

Type below:
______________
Answer:
\(\left\{\begin{array}{l}3x-y=8 \\-2x+4y=-12\end{array}\right.\)
Multiply each term in the first equation by 4 to get opposite coefficients for the y-terms.
4(3x – y = 8)
12x – 4y = 32
Add the second equation to the new equation
12x – 4y = 32
+(-2x + 4y = -12)
Add to eliminate the variable y
10x = 20
Divide both sides by 10
x = 20/10 = 2
Substitue into one of the original equations and solve for y
y = 3(2) – 8 = -1
S0, (2, -2)is the solution of the system.
Solve each system of equations by multiplying first.
Question 2.
\(\left\{\begin{array}{l}x+4y=2 \\2x+5y=7\end{array}\right.\)
(________ , ________ )
Answer:
(6, -1)
Explanation:
x + 4y = 2
2x + 5y = 7
To eliminate x terms, multiply the 2nd equation by 2
2(x + 4y = 2)
2x + 8y = 4
Subtract the equations
2x + 8y = 4
-(2x + 5y = 7)
x is eliminated as it has reversed coefficients. Solve for y
2x + 8y – 2x – 5y = 4 – 7
3y = -3
y = -3/3 = -1
Substituting y in either of the equation to find x
x + 4(-1) = 2
x – 4 + 4 = 2 + 4
x = 6
Solution: (6, -1)
Question 3.
\(\left\{\begin{array}{l}3x+y=-1 \\2x+3y=18\end{array}\right.\)
(________ , ________ )
Answer:
(-3, 8)
Explanation:
\(\left\{\begin{array}{l}3x+y=-1 \\2x+3y=18\end{array}\right.\)
To eliminate y terms, multiply the 1st equation by 3
3(3x + y = -1)
9x + 3y = -3
Subtract the equations
9x + 3y = -3
-(2x + 3y = 18)
y is eliminated as it has reversed coefficients. Solve for x
9x + 3y – 2x – 3y = -3 -18
7x = -21
x = -21/7
x = -3
Substituting x in either of the equation to find y
3(-3) + y = -1
-9 + y + 9 = -1 + 9
y = 8
Solution: (-3, 8)
Question 4.
\(\left\{\begin{array}{l}2x+8y=21 \\6x-4y=14\end{array}\right.\)
Type below:
______________
Answer:
The soultion is (3.5, 1.75)
Explanation:
\(\left\{\begin{array}{l}2x+8y=21 \\6x-4y=14\end{array}\right.\)
To eliminate y terms, multiply the 2nd equation by 2
2(6x – 4y = 14)
2x + 8y = 21
Add the equations
2x + 8y = 21
+(12x – 8y = 28)
y is eliminated it has reversed coefficients. Solve for x
2x + 8y + 12x – 8y = 21 + 28
14x = 49
x = 49/14 = 3.5
Substituting x in either of the equation to find y
6(3.5) – 4y = 14
21 – 4y – 21 = 14 – 21
-4y = -7
y = -7/-4 = 1.75
The soultion is (3.5, 1.75)
Question 5.
\(\left\{\begin{array}{l}2x+y=3 \\-x+3y=-12\end{array}\right.\)
(________ , ________ )
Answer:
Explanation:
\(\left\{\begin{array}{l}2x+y=3 \\-x+3y=-12\end{array}\right.\)
To eliminate x terms, multiply the 2nd equation by 2
2(-x + 3y = -12)
-2x + 6y = -24
Add the equations
2x + y = 3
+(-2x + 6y = -24)
x is eliminated it has reversed coefficients. Solve for y
2x + y – 2x + 6y = 3 – 24
7y = -21
y = -21/7 = -3
Substituting y in either of the equation to find x
-x + 3(-3) = -12
-x -9 + 9 = -12 + 9
-x = -3
x = 3
The soultion is (3, -3)
Question 6.
\(\left\{\begin{array}{l}6x+5y=19 \\2x+3y=5\end{array}\right.\)
(________ , ________ )
Answer:
The soultion is (4, -1)
Explanation:
\(\left\{\begin{array}{l}6x+5y=19 \\2x+3y=5\end{array}\right.\)
To eliminate x terms, multiply the 2nd equation by 3
3(2x + 3y = 5)
6x + 9y = 15
Subtract the equations
6x + 5y = 19
-(6x + 9y = 15)
x is eliminated it has reversed coefficients. Solve for y
6x + 5y – 6x – 9y = 19 – 15
-4y = 4
y = 4/-4 = -1
Substituting y in either of the equation to find x
2x + 3(-1) = 5
2x – 3 + 3 = 5 + 3
2x = 8
x = 8/2 = 4
The soultion is (4, -1)
Question 7.
\(\left\{\begin{array}{l}2x+5y=16 \\-4x+3y=20\end{array}\right.\)
(________ , ________ )
Answer:
The soultion is (-2, 4)
Explanation:
\(\left\{\begin{array}{l}2x+5y=16 \\-4x+3y=20\end{array}\right.\)
To eliminate x terms, multiply the 1st equation by 2
2(2x + 5y = 16)
4x + 10y = 32
Add the equations
4x + 10y = 32
+(-4x + 3y = 20)
x is eliminated it has reversed coefficients. Solve for y
10y + 3y = 32 + 20
13y = 52
y = 52/13 = 4
Substituting y in either of the equation to find x
2x + 5(4) = 16
2x + 20 – 20 = 16 – 20
2x = -4
x = -4/2 = -2
The soultion is (-2, 4)
Question 8.
Bryce spent $5.26 on some apples priced at $0.64 each and some pears priced at $0.45 each. At another store he could have bought the same number of apples at $0.32 each and the same number of pears at $0.39 each, for a total cost of $3.62. How many apples and how many pears did Bryce buy?
a. Write equations to represent Bryce’s expenditures at each store
First store: _____________
Second store: _____________
Type below:
_____________
Answer:
First store: 0.64x + 0.45y = 5.26
Second store: 0.32x + 0.39y = 3.62
Explanation:
First store = 0.64x + 0.45y = 5.26
Second store = 0.32x + 0.39y = 3.62
where x is the number of apples and y is the number of pears.
Question 8.
b. Solve the system.
Number of apples: _______
Number of pears: _______
Answer:
Number of apples: 4
Number of pears: 6
Explanation:
First store = 0.64x + 0.45y = 5.26
Second store = 0.32x + 0.39y = 3.62
Multiply by 100
64x + 45y = 526
32x + 39y = 362
To eliminate x terms, multiply the 2nd equation by 2
2(32x + 39y = 362)
64x + 45y = 526
Subtract the equations
64x + 45y = 526
-(64x + 78y = 724)
x is eliminated it has reversed coefficients. Solve for y
64x + 45y – 64x – 78y = 526 – 724
-33y = -198
y = -198/-33 = 6
Substituting y in either of the equation to find x
32x + 39(6) = 362
32x + 234 – 234 = 362 – 234
32x = 128
x = 128/32 = 4
He bought 4 apples and 6 pears.
ESSENTIAL QUESTION CHECK-IN
Question 9.
When solving a system by multiplying and then adding or subtracting, how do you decide whether to add or subtract?
Type below:
_____________
Answer:
If the variable with the same coefficient but reversed sign, we add and if they have the same sign, we subtract.
Solving Systems by Elimination with Multiplication – Page No. 257
Question 10.
Explain the Error Gwen used elimination with multiplication to solve the system
\(\left\{\begin{array}{l}2x+6y=3 \\x-3y=-1\end{array}\right.\)
Her work to find x is shown. Explain her error. Then solve the system.
2(x − 3y) = -1
2x − 6y = -1
+2x + 6y = 3
_____________
4x + 0y = 2
x = \(\frac{1}{2}\)
Type below:
____________
Answer:
2x + 6y = 3
x – 3y = -1
To eliminate x terms, multiply the 2nd equation by 2
2(x – 3y = -1)
2x – 6y = -2
Error is the Gnew did not multiply the entire expression with 2.
Add the equations
2x + 6y = 3
+(2x – 6y = -2)
y is eliminated it has reversed coefficients. Solve for x
2x + 6y + 2x – 6y = 3 – 2
4x = 1
x = 1/4
Substituting x in either of the equation to find y
x – 3y = -1
1/4 – 3y – 1/4 = -1 -1/4
-3y = -5/4
y = -5/4(-3) = 5/12
Question 11.
Represent Real-World Problems At Raging River Sports, polyester-fill sleeping bags sell for $79. Down-fill sleeping bags sell for $149. In one week the store sold 14 sleeping bags for $1,456.
a. Let x represent the number of polyester-fill bags sold and let y represent the number of down-fill bags sold. Write a system of equations you can solve to find the number of each type sold.

Type below:
____________
Answer:
x + y = 14
79x + 149y = 1456
where x is the polyster-fill bags and y is the number of down-fill bags
Question 11.
b. Explain how you can solve the system for y by multiplying and subtracting.
Type below:
____________
Answer:
x + y = 14
79x + 149y = 1456
Multiply the second equation by 79. Subtract the new equation from the first equation and solve the resulting equation for y.
Question 11.
c. Explain how you can solve the system for y using substitution.
Type below:
____________
Answer:
Solve the second equation for x. Substitute the expression for x , in the first equation and solve the resulting equation for y.
Question 11.
d. How many of each type of bag were sold?
_______ polyester-fill
_______ down-fill
Answer:
9 polyester-fill
5 down-fill
Explanation:
x + y = 14
79x + 149y = 1456
To eliminate x terms, multiply the 2nd equation by 2
79(x + y = 14)
79x + 149y = 1456
Subtract the equations
79x + 79y = 1106
-(79x + 149y = 1456)
x is eliminated it has reversed coefficients. Solve for y
79x + 79y – 79x – 149y = 1106 – 1456
-70y = -350
y = -350/-70 = 5
Substituting y in either of the equation to find x
x + 5 = 14
x = 14 – 5
x = 9
There were 9 polyster-fill bags and 5 down-fill bags sold.
Question 12.
Twice a number plus twice a second number is 310. The difference between the numbers is 55. Find the numbers by writing and solving a system of equations. Explain how you solved the system.
x = _______
y = _______
Answer:
x = 105
y = 50
Explanation:
2x + 2y = 310
x – y = 55
To eliminate y terms, multiply the 2nd equation by 2
2(x – y = 55)
2x – 2y = 110
Add the equations
2x + 2y = 310
+ (2x – 2y = 110)
y is eliminated it has reversed coefficients. Solve for x
2x + 2y + 2x – 2y = 310 + 110
4x = 420
x = 420/4 = 105
Substituting x in either of the equation to find y
105 – y = 55
y = 105 – 55
y = 50
The solution is (105, 50)
Solving Systems by Elimination with Multiplication – Page No. 258
Question 13.
Represent Real-World Problems A farm stand sells apple pies and jars of applesauce. The table shows the number of apples needed to make a pie and a jar of applesauce. Yesterday, the farm picked 169 Granny Smith apples and 95 Red Delicious apples. How many pies and jars of applesauce can the farm make if every apple is used?
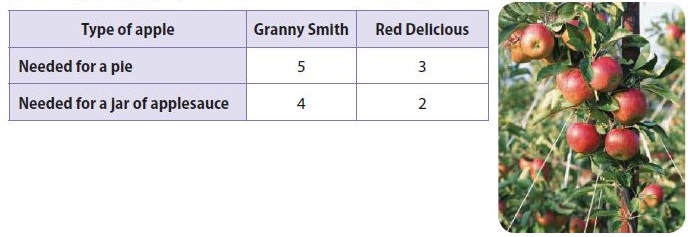
_______ pies
_______ jars of applesauce
Answer:
21 pies
16 jars of applesauce
Explanation:
5x + 4y = 169
3x + 2y = 95
where x is the number of apples needed for pie and y is the number of apples for jar of applesauce
To eliminate y terms, multiply the 2nd equation by 2
2(3x + 2y = 95)
6x + 4y = 190
Subtract the equations
5x + 4y = 169
– (6x + 4y = 190)
y is eliminated it has reversed coefficients. Solve for x
5x + 4y – 6x – 4y = 169 – 190
-x = -21
x = -21/-1 = 21
Substituting x in either of the equation to find y
5(21) + 4y = 169
105 + 4y – 105 = 169 – 105
4y = 64
y = 64/4 = 16
The number of apples needed for pie is 21 and the number of apples for jar of applesauce is 16.
FOCUS ON HIGHER ORDER THINKING
Question 14.
Make a Conjecture Lena tried to solve a system of linear equations algebraically and in the process found the equation 5 = 9. Lena thought something was wrong, so she graphed the equations and found that they were parallel lines. Explain what Lena’s graph and equation could mean.
Type below:
____________
Answer:
Lena’s graph is a parallel line which means the graph does not intersect each other, hence they have no solutions. Equation 5 = 9 means variables are eliminated and this statement is not true. This linear system has no solution.
Question 15.
Consider the system
\(\left\{\begin{array}{l}2x+3y=6 \\3x+7y=-1\end{array}\right.\)
a. Communicate Mathematical Ideas Describe how to solve the system by multiplying the first equation by a constant and subtracting. Why would this method be less than ideal?
Type below:
____________
Answer:
Multiplying the first equation by a constant and subtracting
2x + 3y = 6
3x + 7y = -1
Multiply the first equation by 1.5 and subtract. This would be less than ideal because you would introduce decimals into the solution process.
Question 15.
b. Draw Conclusions Is it possible to solve the system by multiplying both equations by integer constants? If so, explain how.
Type below:
____________
Answer:
Yes
Explanation:
Multiply the first equation by 3 and the second equation by 2. Both x-term coefficients would be 6. Solve by eliminating the x-terms using subtraction.
Question 15.
c. Use your answer from part b to solve the system.
(_______ , _______)
Answer:
(9, -4)
Explanation:
2x + 3y = 6
3x + 7y = -1
Multiply the first equation by 3 and the second equation by 2.
3(2x + 3y = 6)
2(3x + 7y = -1)
Subtract the equations
6x + 9y = 18
-(6x + 14y = -2)
x is eliminated it has reversed coefficients. Solve for y
6x + 9y – 6x – 14y = 18 + 2
-5y = 20
y = 20/-5 = -4
Substituting y in either of the equation to find x
2x + 3(-4) = 6
2x = 18
x = 18/2 = 9
The solution is (9, -4)
Guided Practice – Solving Solving Special Systems – Page No. 262
Use the graph to solve each system of linear equations
Question 1.
A. \(\left\{\begin{array}{l}4x-2y=-6 \\2x-y=4\end{array}\right.\)
B. \(\left\{\begin{array}{l}4x-2y=-6 \\x+y=6\end{array}\right.\)
C. \(\left\{\begin{array}{l}2x-y=4 \\6x-3y=-12\end{array}\right.\)
STEP 1 Decide if the graphs of the equations in each system intersect, are parallel, or are the same line.
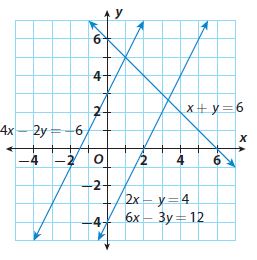
System A: The graphs __________
System B: The graphs __________
System C: The graphs __________
Answer:
System A: The graphs are parallel
System B: The graphs are intersecting
System C: The graphs are the same line
Explanation:
System A: 4x – 2y = -6
2x – y = 4
System B: 4x – 2y = -6
x + y = 6
System C: 2x – y = 4
6x – 3y = 12
Question 1.
STEP 2 Decide how many points the graphs have in common.
a. Intersecting lines have _______________ point(s) in common.
b. Parallel lines have _______________ point(s) in common.
c. The same lines have ___________ point(s) in common.
a. __________
b. __________
c. __________
Answer:
a. Intersecting lines have one point(s) in common.
b. Parallel lines have no point(s) in common.
c. The same lines have infinitely many points (s) in common.
Explanation:
From the graphs,
Intersecting lines have one point(s) in common
Parallel lines have no point(s) in common
The same lines have infinitely many points (s) in common
Question 1.
STEP 3 Solve each system.
System A has __________ points in common, so it has __________ solution.
System B has __________ point in common. That point is the solution, __________.
System C has __________ points in common. ________ ordered pairs on the line will make both equations true.
Type below:
___________
Answer:
System A has no points in common, so it has no solution. System B has one point in common. That point is the solution, (1,5). System C has an infinite number of points in common. All ordered pairs on the line will make both equations true.
Explanation:
Number of solutions for each system
System A has no points in common, so it has no solution. System B has one point in common. That point is the solution, (1,5). System C has an infinite number of points in common. All ordered pairs on the line will make both equations true.
Solve each system. Tell how many solutions each system has.
Question 2.
\(\left\{\begin{array}{l}x-3y=4 \\-5x+15y=-20\end{array}\right.\)
___________
Answer:
infinitely many solutions
Explanation:
x – 3y = 4
-5x + 15y = -20
To eliminate y terms, multiply the 1st equation by 5
5(x – 3y = 4)
5x – 15y = 20
Add the equations
5x – 15y = 20
+(-5x + 15y = -20)
x and y is eliminated as it has reversed coefficients.
5x – 15y – 5x + 15y = 20 – 20
0 = 0
The statement is true, hence the solution has infinitely many solutions.
Question 3.
\(\left\{\begin{array}{l}6x+2y=-4 \\3x+y=4\end{array}\right.\)
___________
Answer:
no solution
Explanation:
6x + 2y = -4
3x + y = 4
To eliminate y terms, multiply the 2nd equation by 5
2(3x + y = 4)
6x + 2y = 8
Subtract the equations
6x + 2y = -4
-(6x + 2y = 8)
x and y is eliminated as it has reversed coefficients.
6x + 2y – 6x – 2y = -4 -8
0 = -12
The statement is false, hence the solution has no solution.
Question 4.
\(\left\{\begin{array}{l}6x-2y=-10 \\3x+4y=-25\end{array}\right.\)
___________
Answer:
one solution
Explanation:
6x – 2y = -10
3x + 4y = -25
To eliminate y terms, multiply the 1st equation by 2
2(6x – 2y = -10)
12x – 4y = -20
Add the equations
12x – 4y = -20
+(3x + 4y = -25)
y is eliminated as it has reversed coefficients. Solve for x.
12x – 4y + 3x + 4y = -20 – 25
15x = -45
x = -45/15 = -3
Substitute x in any one of the original equations and solve for y
3(-3) + 4y = -25
-9 + 4y + 9 = -25 + 9
4y = -16
y = -16/4
y = -4
There is one solution, (-3, -4)
ESSENTIAL QUESTION CHECK-IN
Question 5.
When you solve a system of equations algebraically, how can you tell whether the system has zero, one, or an infinite number of solutions?
Type below:
___________
Answer:
When x and y are eliminated and the statement is true, the system has infinitely many solutions.
When x and y are eliminated and the statement is false, the system has no solutions.
When the system has one solution by solving, the system has one solution.
8.5 Independent Practice – Solving Solving Special Systems – Page No. 263
Solve each system by graphing. Check your answer algebraically.
Question 6.
\(\left\{\begin{array}{l}-2x+6y=12 \\x-3y=3\end{array}\right.\)
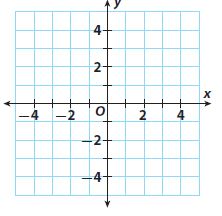
Solution: ______________
___________
Answer:
\(\left\{\begin{array}{l}-2x+6y=12 \\x-3y=3\end{array}\right.\)
Graph the equations on same coordinate plane
No solution as equations are parallel
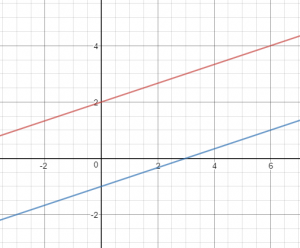
To eliminate y terms, multiply the 2nd equation by 2
2(x – 3y = 3)
2x – 6y = 6
Add the equations
-2x + 6y = 12
2x – 6y = 6
x and y is eliminated as it has reversed coefficients.
-2x + 6y + 2x – 6y = 12 + 6
0 = 18
The statement is false, hence the system has no solution.
Question 7.
\(\left\{\begin{array}{l}15x+5y=5 \\3x+y=1\end{array}\right.\)
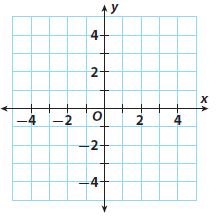
Solution: ______________
___________
Answer:
\(\left\{\begin{array}{l}15x+5y=5 \\3x+y=1\end{array}\right.\)
Graph the equations on same coordinate plane
Infinitely many solutions as equations are overlapping
To eliminate y terms, multiply the 2nd equation by 5
5(3x + y = 1)
15x + 5y = 5
Subtarct the equations
15x + 5y = 5
-(15x + 5y = 5)
x and y is eliminated as it has reversed coefficients.
15x + 5y -15x – 5y = 5 – 5
0 = 0
The statement is true, hence the system has infinitely many solutions.
For Exs. 8–
14, state the number of solutions for each system of linear equations
Question 8.
a system whose graphs have the same slope but different y-intercepts
___________
Answer:
No solutions
Explanation:
Equations are parallel
No solutions
Question 9.
a system whose graphs have the same y-intercepts but different slopes
___________
Answer:
One solution
Explanation:
Equations are intersecting
One solution
Question 10.
a system whose graphs have the same y-intercepts and the same slopes
___________
Answer:
Infinitely many solutions
Explanation:
Equations are overlapping
Infinitely many solutions
Question 11.
a system whose graphs have different y-intercepts and different slopes
___________
Answer:
One solution
Explanation:
Equations are intersecting
One solution
Question 12.
the system
\(\left\{\begin{array}{l}y=2 \\y=-3\end{array}\right.\)
___________
Answer:
No solutions
Explanation:
Equations are parallel
No solutions
Question 13.
the system
\(\left\{\begin{array}{l}y=2 \\y=-3\end{array}\right.\)
___________
Answer:
One solution
Explanation:
Equations are intersecting
One solution
Question 14.
the system whose graphs were drawn using these tables of values:

___________
Answer:
No solutions
Explanation:
Equations are parallel The slope is the same for both equations but the y-intercept is different.
No solutions
Question 15.
Draw Conclusions The graph of a linear system appears in a textbook. You can see that the lines do not intersect on the graph, but also they do not appear to be parallel. Can you conclude that the system has no solution? Explain.
___________
Answer:
No; although the lines do not intersect on the graph, they intersect at a point that is not on the graph. To prove that a system has no solution, you must do so algebraically
Solving Solving Special Systems – Page No. 264
Question 16.
Represent Real-World Problems Two school groups go to a roller skating rink. One group pays $243 for 36 admissions and 21 skate rentals. The other group pays $81 for 12 admissions and 7 skate rentals. Let x represent the cost of admission and let y represent the cost of a skate rental. Is there enough information to find values for x and y? Explain.

___________
Answer:
36x + 21y = 243
12x + 7y = 81
where x is the cost of admission and y is the cost of stake rentals.
Although the information can be used to develop a system of linear equation, where each equation has two variables when the system is solved, the number of solutions is infinite, Mee the values of x and y cannot be determined.
No
Question 17.
Represent Real-World Problems Juan and Tory are practicing for a track meet. They start their practice runs at the same point, but Tory starts 1 minute after Juan. Both run at a speed of 704 feet per minute. Does Tory catch up to Juan? Explain.
___________
Answer:
No; Both Juan and Tory-run at the same rate, so the lines representing the distances each has run are parallel. There is no solution to the system
FOCUS ON HIGHER ORDER THINKING
Question 18.
Justify Reasoning A linear system with no solution consists of the equation y = 4x − 3 and a second equation of the form y = mx + b. What can you say about the values of m and b? Explain your reasoning.
Type below:
___________
Answer:
y = 4x – 3
y = mx + b
Since the system has no solutions, the two equations are parallel. The value of the slope, m would be the same i.e. 4. The value of y-intercept, b can be any number except -3 as b is different for parallel lines.
Question 19.
Justify Reasoning A linear system with infinitely many solutions consists of the equation 3x + 5 = 8 and a second equation of the form Ax + By = C. What can you say about the values of A, B, and C? Explain your reasoning.
Type below:
___________
Answer:
3x + 5 = 8
Ax + By = C
Since the system has infinitely many solutions, the values of A, B, and C must all be the same multiple of 3, 5, and 8, respectively. The two equations represent a single line, so the coefficients and constants of one equation must be a multiple of the other.
Question 20.
Draw Conclusions Both the points (2, -2) and (4, -4) are solutions of a system of linear equations. What conclusions can you make about the equations and their graphs?
Type below:
___________
Answer:
If a system has more than one solution, the equations represent the same line and have infinitely many solutions.
Ready to Go On? – Model Quiz – Page No. 265
8.1 Solving Systems of Linear Equations by Graphing
Solve each system by graphing.
Question 1.
\(\left\{\begin{array}{l}y=x-1 \\y=2x-3\end{array}\right.\)
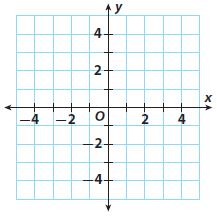
(________ , ________)
Answer:
(2, 1)
Explanation:
y = x – 1
y = 2x – 3
Graph the equations on the same coordinate plane
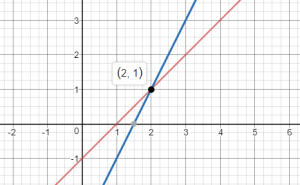
The solution of the system is the point of intersection
The solution is (2, 1)
Question 2.
\(\left\{\begin{array}{l}x+2y=1 \\-x+y=2\end{array}\right.\)
(________ , ________)
Answer:
(-1, 1)
Explanation:
x + 2y = 1
-x + y = 2
Graph the equations on same coordinate plane
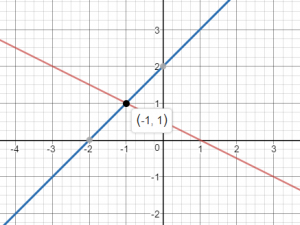
The solution of the system is the point of intersection
The solution is (-1, 1)
8.2 Solving Systems by Substitution
Solve each system of equations by substitution.
Question 3.
\(\left\{\begin{array}{l}y=2x \\x+y=-9\end{array}\right.\)
(________ , ________)
Answer:
(-3, -6)
Explanation:
y = 2x
x + y = -9
Substitute y from equation 1 in the other equation.
x + 2x = -9
3x = -9
x = -9/3
x = -3
Then, y = 2(-3) = -6
The Solution is (-3, -6)
Question 4.
\(\left\{\begin{array}{l}3x-2y=11 \\x+2y=9\end{array}\right.\)
(________ , ________)
Answer:
(5, 2)
Explanation:
3x – 2y = 11
x + 2y = 9
Solve for x in equation 2
x = – 2y + 9
Substitute x from equation 2 in the other equation
3(-2y + 9) – 2y = 11
-6y + 27 -2y = 11
-8y = -16
y = -16/-8 = 2
Substitute y in any of the equations to find x
x + 2(2) = 9
x + 4 – 4 = 9 – 4
x = 5
The solution is (5, 2)
8.3 Solving Systems by Elimination
Solve each system of equations by adding or subtracting.
Question 5.
\(\left\{\begin{array}{l}3x+y=9 \\2x+y=5\end{array}\right.\)
(________ , ________)
Answer:
(4, -3)
Explanation:
\(\left\{\begin{array}{l}3x+y=9 \\2x+y=5\end{array}\right.\)
Subtract the equations
3x + y = 9
-(2x + y = 5)
y is eliminated as it has reversed coefficients. Solve for x
3x + y – 2x – y = 9 – 5
x = 4
Substituting x in either of the equation to find y
2(4) + y = 5
8 + y – 8 = 5 – 8
y = -3
The solution is (4, -3)
Question 6.
\(\left\{\begin{array}{l}-x-2y=4 \\3x+2y=4\end{array}\right.\)
(________ , ________)
Answer:
(4, -4)
Explanation:
\(\left\{\begin{array}{l}-x-2y=4 \\3x+2y=4\end{array}\right.\)
Add the equations
-x – 2y = 4
+(3x + 2y = 4)
y is eliminated as it has reversed coefficients. Solve for x
-x – 2y + 3x + 2y = 4 + 4
2x = 8
x = 8/2 = 4
Substituting x in either of the equation to find y
3(4) + 2y = 4
12 + 2y – 12 = 4 – 12
2y = -8
y = -8/2 = -4
The solution is (4, -4)
8.4 Solving Systems by Elimination with Multiplication
Solve each system of equations by multiplying first.
Question 7.
\(\left\{\begin{array}{l}x+3y=-2 \\3x+4y=-1\end{array}\right.\)
(________ , ________)
Answer:
(1, -1)
Explanation:
\(\left\{\begin{array}{l}x+3y=-2 \\3x+4y=-1\end{array}\right.\)
Subtract the equations
3x + 9y = -6
-(3x + 4y = -1)
x is eliminated as it has reversed coefficients. Solve for y
3x + 9y – 3x – 4y = -6 + 1
5y = -5
y = -5/5
y = -1
Substituting y in either of the equation to find x
x + 3(-1) = -2
x – 3 = -2
x = -2 + 3
x = 1
The solution is (1, -1)
Question 8.
\(\left\{\begin{array}{l}2x+8y=22 \\3x-2y=5\end{array}\right.\)
(________ , ________)
Answer:
(3, 2)
Explanation:
\(\left\{\begin{array}{l}2x+8y=22 \\3x-2y=5\end{array}\right.\)
Multiply equation 2 by 4 so that y can be eliminated
4(3x – 2y = 5)
12x – 8y = 20
Add the equations
2x + 8y = 22
+(12x – 8y = 20)
y is eliminated as it has reversed coefficients. Solve for x
2x + 8y + 12x – 8y = 22 + 20
14x = 42
x = 42/14
x = 3
Substituting y in either of the equation to find x
2(3) + 8y = 22
6 + 8y = 22
8y = 22 – 6
8y = 16
y = 16/8
y = 2
The solution is (3, 2)
8.5 Solving Special Systems
Solve each system. Tell how many solutions each system has.
Question 9.
\(\left\{\begin{array}{l}-2x+8y=5 \\x-4y=-3\end{array}\right.\)
_____________
Answer:
no solution
Explanation:
\(\left\{\begin{array}{l}-2x+8y=5 \\x-4y=-3\end{array}\right.\)
Multiply equation 2 by 2 so that y can be eliminated
2(x – 4y = -3)
2x – 8y = -6
Add the equations
-2x + 8y = 5
+(2x – 8y = -6)
x and y is eliminated
-2x + 8y + 2x – 8y = 5 – 6
0 = -1
The statement is false. Hence, the system has no solution.
Question 10.
\(\left\{\begin{array}{l}6x+18y=-12 \\x+3y=-2\end{array}\right.\)
_____________
Answer:
infinitely many solutions
Explanation:
\(\left\{\begin{array}{l}6x+18y=-12 \\x+3y=-2\end{array}\right.\)
Multiply equation 2 by 6 so that x can be eliminated
6(x + 3y = -2)
6x + 18y = -12
Subtract the equations
6x + 18y = -12
-(6x + 18y = -12)
x and y is eliminated
6x + 18y -6x -18y = -12 + 12
0 = 0
The statement is true. Hence, the system has infinitely many solutions.
ESSENTIAL QUESTION
Question 11.
What are the possible solutions to a system of linear equations, and what do they represent graphically?
Type below:
___________
Answer:
System of linear equations can have no solution, which is represented by parallel lines; one solution, which is represented by intersecting lines; and infinitely many solutions, which is represented by overlapping lines.
Selected Response – Mixed Review – Page No. 266
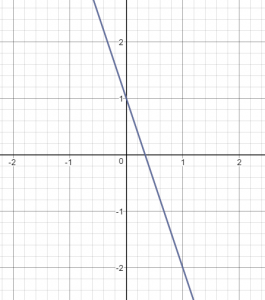
Question 1.
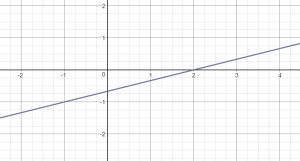
The graph of which equation is shown?
Options:
A. y = −2x + 2
B. y = −x + 2
C. y = 2x + 2
D. y = 2x + 1
Answer:
C. y = 2x + 2
Explanation:
Option A and B are eliminated as the slope of the graph is 2.
Option D is eliminated as the y-intercept from the graph should be 2.
Option C is the equation of the graph
Question 2.
Which best describes the solutions to the system
\(\left\{\begin{array}{l}x+y=-4 \\-2x-2y=0\end{array}\right.\)
Options:
A. one solution
B. no solution
C. infinitely many
D. (0, 0)
Answer:
B. no solution
Explanation:
\(\left\{\begin{array}{l}x+y=-4 \\-2x-2y=0\end{array}\right.\)
Multply equation 1 by 2 so that x can be eliminated
2(x + y = -4)
2x + 2y = -8
Add the equations
2x + 2y = -8
-2x – 2y = 0
x and y is eliminated
2x + 2y – 2x -2y = -8 + 0
0 = -8
The statement is false. Hence, the system has no solution.
Question 3.
Which of the following represents 0.000056023 written in scientific notation?
Options:
A. 5.6023 × 105
B. 5.6023 × 104
C. 5.6023 × 10-4
D. 5.6023 × 10-5
Answer:
D. 5.6023 × 10-5
Explanation:
Move the decimal 5 points right to get the equation.
D. 5.6023 × 10-5
Question 4.
Which is the solution to
\(\left\{\begin{array}{l}2x-y=1 \\4x+y=11\end{array}\right.\)
Options:
A. (2, 3)
B. (3, 2)
C. (-2, 3)
D. (3, -2)
Answer:
A. (2, 3)
Explanation:
\(\left\{\begin{array}{l}2x-y=1 \\4x+y=11\end{array}\right.\)
Add the equations
2x – y = 1
4x + y = 11
y is eliminated as it has reversed coefficients. Solve for x.
2x – y + 4x + y = 1 + 11
6x = 12
x = 12/6 = 2
Substituting x in either of the equation to find y
4(2) + y = 11
8 + y = 11
y = 11 – 8
y = 3
The solution is (2, 3)
Question 5.
Which expression can you substitute in the indicated equation to solve
\(\left\{\begin{array}{l}3x-y=5 \\x+2y=4\end{array}\right.\)
Options:
A. 2y – 4 for x in 3x – y = 5
B. 4 – x for y in 3x – y = 5
C. 3x – 5 for y in 3x – y = 5
D. 3x – 5 for y in x + 2y = 4
Answer:
D. 3x – 5 for y in x + 2y = 4
Explanation:
\(\left\{\begin{array}{l}3x-y=5 \\x+2y=4\end{array}\right.\)
Solve for y in equation 1
y = 3x – 5
Substitute in other equation x + 2y = 4
Question 6.
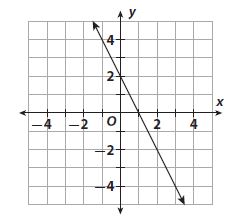
What is the solution to the system of linear equations shown on the graph?
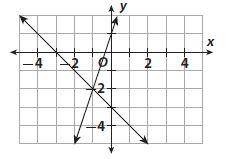
Options:
A. -1
B. -2
C. (-1, -2)
D. (-2, -1)
Answer:
C. (-1, -2)
Explanation:
The point of intersection is (-1, -2), which is the solution of the system
Question 7.
Which step could you use to start solving
\(\left\{\begin{array}{l}x-6y=8 \\2x-5y=3\end{array}\right.\)
Options:
A. Add 2x – 5y = 3 to x – 6y = 8.
B. Multiply x – 6y = 8 by 2 and add it to 2x – 5y = 3.
C. Multiply x – 6y = 8 by 2 and subtract it from 2x – 5y = 3.
D. Substitute x = 6y – 8 for x in 2x – 5y = 3.
Answer:
C. Multiply x – 6y = 8 by 2 and subtract it from 2x – 5y = 3.
Explanation:
x – 6y = 8
2x – 5y = 3
Multiply the 1st equation by 2 so that the coefficient of variable x is the same in both equations
Subtract the equations as x has the same sign.
Mini-Task
Question 8.
A hot-air balloon begins rising from the ground at 4 meters per second at the same time a parachutist’s chute opens at a height of 200 meters. The parachutist descends at 6 meters per second.
a. Define the variables and write a system that represents the situation.
Type below:
_____________
Answer:
y represents the distance from the ground and x represents the time in seconds
y = 4x
y = -6x + 200
Question 8.
b. Find the solution. What does it mean?
Type below:
_____________
Answer:
Substitute y from the equation 1 in the equation 2
4x = -6x + 200
4x + 6x = -6x + 200 + 6x
10x = 200
x = 200/10 = 20
Substitute x in any one of the equations and solve for x
y = 4(20) = 80
The solution is (20, 80)
The ballon and parachute meets after 20sec at 80m from the ground.
Final Words:
No Need to go to the tuitions or study hours if you follow our Go Math Grade 8 Answer Key Chapter 8 Solving Systems of Linear Equations PDF. I think the information seen in the Go Math 8th Grade Chapter 8 Solving Systems of Linear Equations is helpful for all the students. Get the step by step explanation for all the questions along with answers from the ccssmathanswers.com site. Bookmark our website to get the solutions for all the chapters in pdf format. All the Best Guys!!!