Redefine your true self with the Go Math Answer Key for Grade 5 curated by subject experts. Score higher grades in your exams and refer to Go Math Grade 5 Answer Key Chapter 9 Algebra: Patterns and Graphing to have strong command over fundamentals. Download the HMH Go Math 5th Grade Solution Key Chapter 9 free of cost and kick start your preparation immediately.
Go Math Grade 5 Answer Key Chapter 9 Algebra: Patterns and Graphing
You will get the necessary skillset needed to draw the line plots and graphs from 5th Grade Go Math Answer Key Ch 9. Access Detailed Solutions to all the problems and learn how to solve related problems when you encounter them during your exams. Seek Homework Help needed by accessing the Go Math Grade 5 Solution Key Chapter 9 Patterns and Graphing. Cross Check the Solutions from our Go Math Grade 5 Answer Key Algebra: Patterns and Graphing and understand the areas you are facing difficulty.
Lesson 1: Line Plot
Lesson 2: Ordered Pairs
Lesson 3: Investigate • Graph Data
Lesson 4: Line Graphs
Mid-Chapter Checkpoint
Lesson 5: Numerical Patterns
Lesson 6: Problem Solving • Find a Rule
Lesson 7: Graph and Analyze Relationships
Chapter 9 Review/Test
- Chapter Review/Test – Page No. 399
- Chapter Review/Test – Page No. 400
- Chapter Review/Test – Page No. 401
- Chapter Review/Test – Page No. 402
Share and Show – Page No. 371
Use the data to complete the line plot. Then answer the questions.
Lilly needs to buy beads for a necklace. The beads are sold by mass. She sketches a design to determine what beads are needed and then writes down their sizes. The sizes are shown below.

\(\frac{2}{5} g, \frac{2}{5} g, \frac{4}{5} g, \frac{2}{5} g, \frac{1}{5} g, \frac{1}{5} g, \frac{3}{5} g, \frac{4}{5} g, \frac{1}{5} g, \frac{2}{5} g, \frac{3}{5} g, \frac{3}{5} g, \frac{2}{5} g\)
Think: There are ___ Xs above \(\frac{1}{5}\) on the line plot, so the combined mass of the beads is _____ fifths, or _____ gram.
Question 1.
What is the combined mass of the beads with a mass of 1/5 gram?
\(\frac{□}{□}\) grams
Answer: \(\frac{3}{5}\) grams
Explanation:
For first we will count the number of \(\frac{1}{5}\) grams for each amount. Draw an x for the number of times each amount is recorded to complete the line plot.
There are 3 xs above \(\frac{1}{5}\) on the line plot, so the combined mass of the beads is 3 fifths
3 × \(\frac{1}{5}\) = 3/5 gram.
Question 2.
What is the combined mass of all the beads with a mass of \(\frac{2}{5}\) gram?
_____ grams
Answer: 2
Explanation:
For first we will count the number of \(\frac{2}{5}\) grams for each amount. Draw an x for the number of times each amount is recorded to complete the line plot.
There are 5 xs above \(\frac{2}{5}\) on the line plot, so the combined mass of the beads is 5 two fifths.
5 × \(\frac{2}{5}\) = 2 grams
Question 3.
What is the combined mass of all the beads on the necklace?
_____ grams
Answer: 6
Explanation:
Total mass of all the beads on the necklace is \(\frac{3}{5}\) + 2 + \(\frac{8}{5}\) + \(\frac{9}{5}\) = \(\frac{30}{5}\) = 6
Therefore the combined mass of all the beads on the necklace is 6.
Question 4.
What is the average weight of the beads on the necklace?
\(\frac{□}{□}\) grams
Answer: \(\frac{3}{7}\) grams
Explanation:
Divide the sum by the number of beads to find the average.
The number of beads = 3 + 5 + 3 + 2 = 14
Divide by 6.
6 ÷ 14 = 3/7
So, the average mass of the beads on the necklace is 3/7 gram.
On Your Own
Use the data to complete the line plot. Then answer the questions.
A breakfast chef used different amounts of milk when making pancakes, depending on the number of pancakes ordered. The results are shown below.
\(\frac{1}{2} c, \frac{1}{4} c, \frac{1}{2} c, \frac{3}{4} c, \frac{1}{2} c, \frac{3}{4} c, \frac{1}{2} c, \frac{1}{4} c, \frac{1}{2} c, \frac{1}{2} c\)
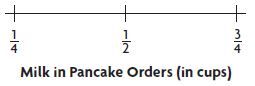
Question 5.
How much milk combined is used in \(\frac{1}{4}\)-cup amounts?
\(\frac{□}{□}\) cup
Answer: \(\frac{1}{2}\) cup
Explanation:
For first we will count the number of \(\frac{1}{4}\) cups for each amount.
2 × \(\frac{1}{4}\) = \(\frac{1}{2}\)
Question 6.
How much milk combined is used in \(\frac{1}{2}\)-cup amounts?
______ cups
Answer: 3 cups
Explanation:
For first we will count the number of \(\frac{1}{2}\) cups for each amount.
There are 6 \(\frac{1}{2}\) cups
6 × \(\frac{1}{2}\) = 3 cups
Question 7.
How much milk combined is used in \(\frac{3}{4}\)-cup amounts?
_____ \(\frac{□}{□}\) cups
Answer: 1 \(\frac{1}{2}\) cups
Explanation:
For first we will count the number of \(\frac{3}{4}\) cups for each amount.
There are 2 \(\frac{3}{4}\) cups of milk.
2 × \(\frac{3}{4}\) = \(\frac{3}{2}\)
Convert from improper fraction to the mixed fraction.
\(\frac{3}{2}\) = 1 \(\frac{1}{2}\) cups
Question 8.
How much milk is used in all the orders of pancakes?
_____ cups
Answer: 5 cups
Explanation:
\(\frac{1}{2} c\) + [/latex]\frac{1}{4} c[/latex] + [/latex]\frac{1}{2} c[/latex] + [/latex]\frac{3}{4} c[/latex] + [/latex]\frac{1}{2} c[/latex] + [/latex]\frac{3}{4} c[/latex] + [/latex]\frac{1}{2} c[/latex] +[/latex]\frac{1}{4} c[/latex] + [/latex]\frac{1}{2} c[/latex] + [/latex]\frac{1}{2} c[/latex]
= 3 + [/latex]\frac{1}{4} c[/latex] + [/latex]\frac{3}{4} c[/latex] + [/latex]\frac{3}{4} c[/latex] + [/latex]\frac{1}{4} c[/latex]
= 3 + 1 + 1 = 5cups
Therefore 5 cups of milk is used in all the orders of pancakes.
Question 9.
What is the average amount of milk used for an order of pancakes?
\(\frac{□}{□}\) cup of milk
Answer: \(\frac{1}{2}\) cup of milk
Explanation:
There are 6 \(\frac{1}{2}\) cups of milk.
The average amount of milk used for an order of pancakes is \(\frac{1}{2}\) cup.
Question 10.
Describe an amount you could add to the data that would make the average increase.
Type below:
_________
Answer: \(\frac{3}{4}\) cup
We can add \(\frac{3}{4}\) to the data to increase the average amount of milk.
UNLOCK the Problem – Page No. 372
Question 11.
For 10 straight days, Samantha measured the amount of food that her cat Dewey ate, recording the results, which are shown below. Graph the results on the line plot. What is the average amount of cat food that Dewey ate daily?

\(\frac{1}{2} c, \frac{3}{8} c, \frac{5}{8} c, \frac{1}{2} c, \frac{5}{8} c, \frac{1}{4} c, \frac{3}{4} c, \frac{1}{4} c, \frac{1}{2} c, \frac{5}{8} c\)
a. What do you need to know?
Type below:
_________
Answer: I need to know the average amount of cat food that Dewey ate daily.
Question 11.
b. How can you use a line plot to organize the information?

Type below:
_________
Answer:
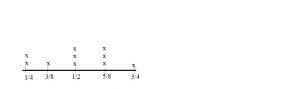
We can draw the line plot by using the given information.
Question 11.
c. What steps could you use to find the average amount of food that Dewey ate daily?
Type below:
_________
Answer: \(\frac{1}{2}\) cup
Explanation:
Number of days = 10
1/4 + 1/4 + 3/8 + 1/2 + 1/2 + 1/2 + 5/8 + 5/8 + 5/8 + 3/4 = 1 + 1 + 1/4 + 3/8 + 1/2 + 15/8
2 + 18/8 + 3/4 = 2 + 3 = 5
The average amount of food is 5 ÷ 10 = 5/10 = \(\frac{1}{2}\) cup
Question 11.
d. Fill in the blanks for the totals of each amount measured.
\(\frac{1}{4}\) cup: __________
\(\frac{3}{8}\) cup: __________
\(\frac{1}{2}\) cup: __________
\(\frac{5}{8}\) cup: __________
\(\frac{3}{4}\) cup: __________
Type below:
_________
Answer:
There are 2 xs above \(\frac{1}{4}\) cup: 2
There is 1 x above \(\frac{3}{8}\) cup: 1
There are 3 xs above \(\frac{1}{2}\) cup: 3
There are 3 xs above \(\frac{5}{8}\) cup: 3
There is 1 x above \(\frac{3}{4}\) cup: 1
Question 11.
e. Find the total amount of cat food eaten over 10 days.
_____ + _____ + _____ + _____ + _____ = _____
So, the average amount of food Dewey ate daily was ______.
Type below:
_________
Answer:
Number of days = 10
1/4 + 1/4 + 3/8 + 1/2 + 1/2 + 1/2 + 5/8 + 5/8 + 5/8 + 3/4 = 1 + 1 + 1/4 + 3/8 + 1/2 + 15/8
2 + 18/8 + 3/4 = 2 + 3 = 5 cups
Question 12.
Test Prep How many days did Dewey eat the least amount of cat food?
Options:
a. 1 day
b. 2 day
c. 3 day
d. 4 day
Answer: 1 day
By seeing the above line plot we can say that Dewey eats the least amount of cat food on day 1.
Thus the correct answer is option A.
Share and Show – Page No. 375
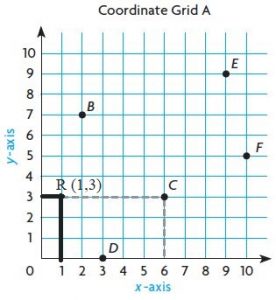
Use Coordinate Grid A to write an ordered pair for the given point.
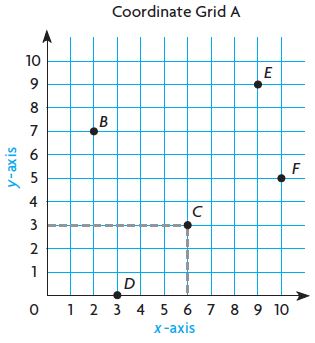
Question 1.
C( _____ , _____ )
Answer: 6, 3
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for C is (6, 3).
Question 2.
D( _____ , _____ )
Answer: 3, 0
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
Thus the ordered pair for D is (3, 0)
Question 3.
E( _____ , _____ )
Answer: 9, 9
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
Thus the ordered pair for E (9, 9)
Question 4.
F( _____ , _____ )
Answer: 10, 5
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
Thus the ordered pair for F is (10, 5)
Plot and label the points on Coordinate Grid A.
Question 5.
M (0, 9)
Type below:
_________
Answer:
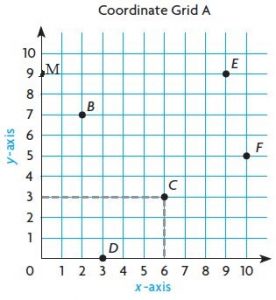
Question 6.
H (8, 6)
Type below:
_________
Answer:
Question 7.
K (10, 4)
Type below:
_________
Answer:
Question 8.
T (4, 5)
Type below:
_________
Answer:
Question 9.
W (5, 10)
Type below:
_________
Answer:
Question 10.
R (1, 3)
Type below:
_________
Answer:
On Your Own
Use Coordinate Grid B to write an ordered pair for the given point.
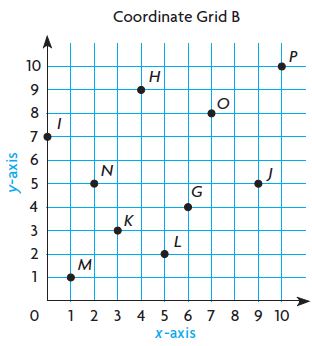
Question 11.
G( _____ , _____ )
Answer: 6, 4
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for G is (6, 4)
Question 12.
H( _____ , _____ )
Answer: 4, 9
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for H is (4, 9)
Question 13.
I( _____ , _____ )
Answer: 0, 7
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for I is (0, 7)
Question 14.
J( _____ , _____ )
Answer: 9, 5
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for J is (9, 5)
Question 15.
K( _____ , _____ )
Answer: 3, 3
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for K is (3, 3)
Question 16.
L( _____ , _____ )
Answer: 5, 2
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for L is (5, 2)
Question 17.
M( _____ , _____ )
Answer: 1, 1
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for M is (1, 1)
Question 18.
N( _____ , _____ )
Answer: 2, 5
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for N is (2, 5)
Question 19.
O( _____ , _____ )
Answer: 7, 8
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for O is (7, 8)
Question 20.
P( _____ , _____ )
Answer: 10, 10
Explanation:
Locate the point for which you want to write an ordered pair.
Look below at the x-axis to identify the points horizontal distance from 0, which is its x-coordinate.
Look to the left at the y-axis to identify the points vertical distance from 0, which is it’s y-coordinate.
So, the ordered pair for P is (10, 10)
Plot and label the points on Coordinate Grid B.
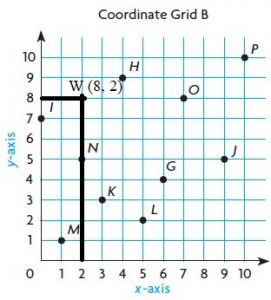
Question 21.
W (8, 2)
Answer:
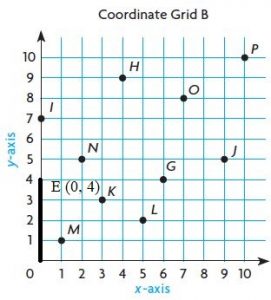
Question 22.
E (0, 4)
Answer:
Question 23.
X (2, 9)
Answer:
Question 24.
B (3, 4)
Answer:
Question 25.
R (4, 0)
Answer:
Question 26.
F (7, 6)
Answer:
Question 27.
T (5, 7)
Answer:
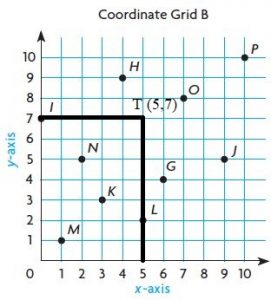
Question 28.
A (7, 1)
Answer:
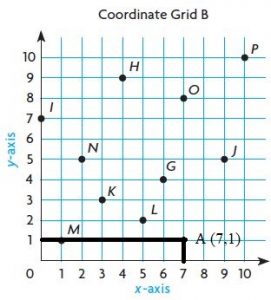
Question 29.
S (10, 8)
Answer:
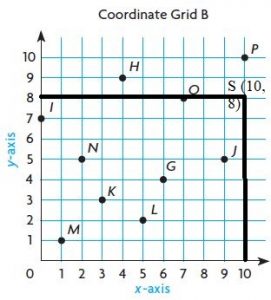
Question 30.
Y (1, 6)
Answer:
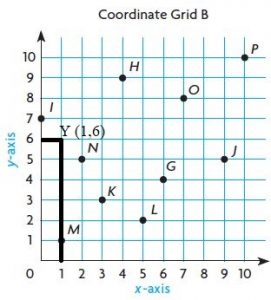
Question 31.
Q (3, 8)
Answer:
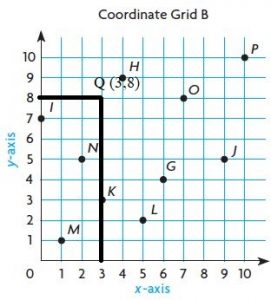
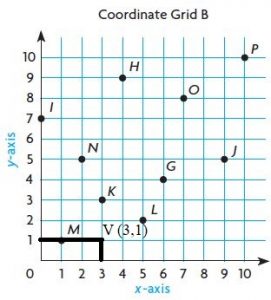
Question 32.
V (3, 1)
Answer:
Problem Solving – Page No. 376
Nathan and his friends are planning a trip to New York City. Use the map for 33–38. Each unit represents 1 city block.
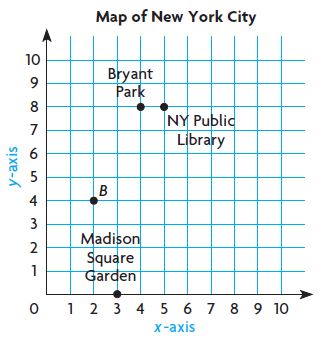
Question 33.
What ordered pair gives the location of Bryant Park?
( _____ , _____ )
Answer: 4, 8
Question 34.
What’s the Error? Nathan says that Madison Square Garden is located at (0, 3) on the map. Is his ordered pair correct? Explain.
Type below:
__________
Answer: He needs to put point 3 on Y-axis but he placed on X-Axis.
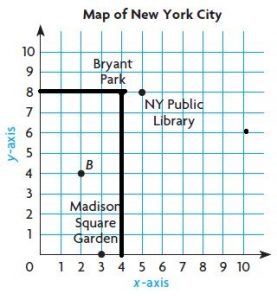
Question 35.
The Empire State Building is located 5 blocks right and 1 block up from (0, 0). Write the ordered pair for this location. Plot and label a point for the Empire State Building.
Type below:
__________
Answer: 5, 1
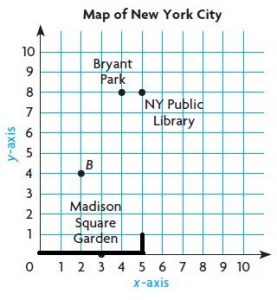
Question 36.
Paulo walks from point B to Bryant Park. Raul walks from point B to Madison Square Garden. If they only walk along the grid lines, who walks farther? Explain.
__________
Answer: Paulo
By seeing the above graph we can say that Paulo walks farther along the grid lines.
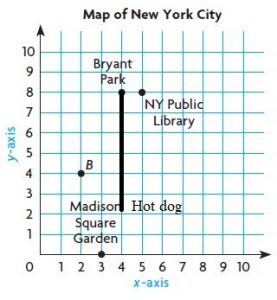
Question 37.
Explain how to find the distance between Bryant Park and a hot dog stand at the point (4, 2).
_____ city blocks
Answer: 6
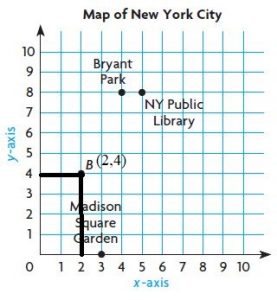
Question 38.
Test Prep Use the map above. Suppose a pizzeria is located at point B. What ordered pair describes this point?
Options:
a. (4,2)
b. (3,4)
c. (2,4)
d. (4,4)
Answer: (2,4)
Share and Show – Page No. 379
Graph the data on the coordinate grid.
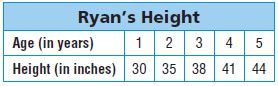
Question 1.
a. Write the ordered pairs for each point.
Type below:
__________
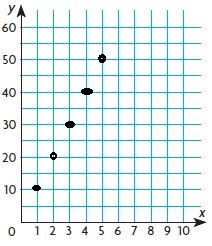
Answer: A(1, 30), B (2, 35), C (3, 38), D (4, 41), E (5, 44)
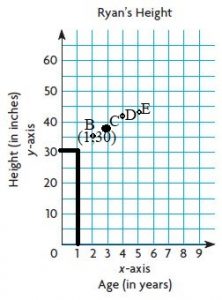
Question 1.
b. What does the ordered pair (3, 38) tell you about Ryan’s age and height?
Type below:
__________
Answer: The ordered pair tells that the age of Ryan is 3 and height is 38 inches.
Question 1.
c. Why would the point (6, 42) be nonsense?
Type below:
__________
Answer: The point (6, 42) be nonsense because the height will be increased. In the above-ordered pair the height is decreased. So, the statement is nonsense.
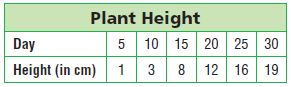
Question 2.
a. Write the ordered pairs for each point.
Type below:
__________
Answer: We can write the ordered pairs by using the above table Day is the x-axis and height is the y-axis. The coordinates are A (5,1), B (10,3), C (15, 8), D (20,12), E (25,16), F(30,19).
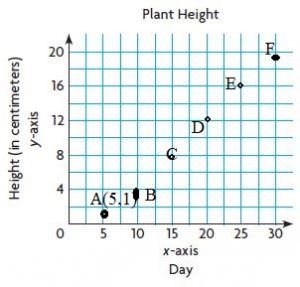
Question 2.
b. How would the ordered pairs be different if the heights of the plants were measured every 6 days for 30 days instead of every 5 days?
Answer:
If the heights of the plants were measured every 6 days for 30 days instead of every 5 days the coordinates will be A (6,1), B (12,3), C (18, 8), D (24,12), E (30,16)
Problem Solving – Page No. 380
What’s the Error?
Question 3.
Mary places a miniature car onto a track with launchers. The speed of the car is recorded every foot. Some of the data is shown in the table. Mary graphs the data on the coordinate grid below.

Look at Mary’s graphed data.
Find her error.
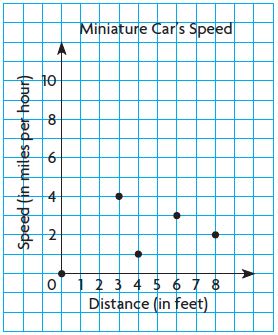
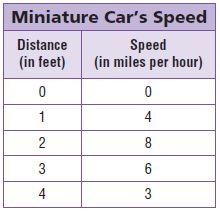
Graph the data and correct
the error.
• Describe the error Mary made.
Type below:
__________
Answer:
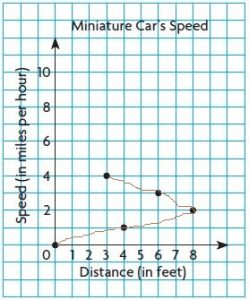
Graph the data and correct the error
Share and Show – Page No. 383
Use the table at the right for 1–3.
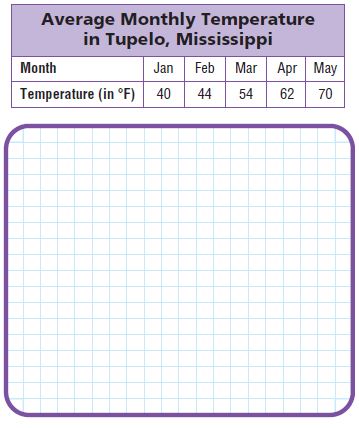
Question 1.
What scale and intervals would be appropriate to make a graph of the data?
Type below:
__________
Answer:
Scale is 1 cm = 10°F
Months will be on the x-axis.
The temperature will be on the y-axis.
Question 2.
Write the related pairs as ordered pairs.
Type below:
__________
Answer: The related pairs are A (Jan, 40), B (Feb, 44), C (Mar, 54), D (Apr, 62), E (May, 70)
Question 3.
Make a line graph of the data.
Type below:
__________
Question 4.
Use the graph to determine between which two months the least change in average temperature occurs.
Type below:
__________
Answer: By seeing the above graph we can say that Jan and Feb has the least change in the average temperature.
On Your Own
Use the table at the right for 5–7.
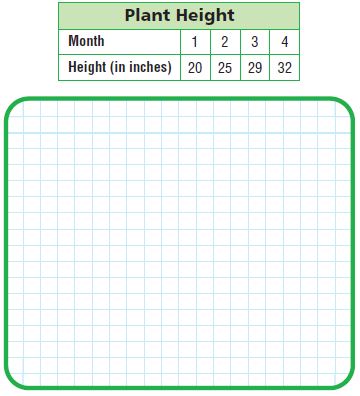
Question 5.
Write the related number pairs for the plant height as ordered pairs.
Type below:
__________
Answer: The related number pairs of the above table are A (1, 20), B(2, 25), C (3, 29), D (4, 32)
Question 6.
What scale and intervals would be appropriate to make a graph of the data?
Type below:
__________
Answer: The above table says that the X-Axis is Month and Y-Axis is Height in inches.
Scale is 1 cm = 5 inches.
Explanation:
The horizontal axis could represent months from 1 to 4. In this case, the scale interval is one month.
The vertical axis could represent height from 20 inches to 32 inches but we can show a break in the scale between 1 inch and 16 inches since there are no heights between 0 inches and 20 inches, the scale interval is 1 inch.
Question 7.
Make a line graph of the data.
Type below:
__________
Question 8.
Use the graph to find the difference in height between Month 1 and Month 2.
Type below:
__________
Answer: By observing the above graph we can say that the difference between months 1 and 2 is 5 inches.
25 – 20 = 5 inches
From the graph we can see that the plant grew the most between 1 and 2 months (about 5 inches), the least change is between 3 and 4 months (about 3 inches).
Question 9.
Use the graph to estimate the height at 1 \(\frac{1}{2}\) months.
_____ in.
Answer: The estimated height at 1 \(\frac{1}{2}\) months is 22.5 inches.
The average of month 1 and month 2 is (20 + 25) ÷ 2 = 45/2 = 22.5 inches.
Connect to science – Page No. 384
Evaporation changes water on Earth’s surface into water vapor. Water vapor condenses in the atmosphere and returns to the surface as precipitation. This process is called the water cycle. The ocean is an important part of this cycle. It influences the average temperature and precipitation of a place.

The overlay graph below uses two vertical scales to show monthly average precipitation and temperatures for Redding, California.
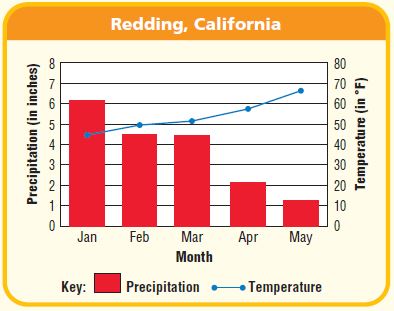
Use the graph for 10–13.
Question 10.
About how much precipitation falls in Redding, California, in February?
_____ inches
Answer: From the graph, we can see that the precipitation in February is 4.2 inches.
Question 11.
What is the average temperature for Redding, California, in February?
_____ °F
Answer: From the graph, we can see that the temperature in February is 50°F.
Question 12.
Explain how the overlay graph helps you relate precipitation and temperature for each month.
Type below:
__________
Answer: The average temperature for each month is plotted on the graph with the blue line and the red bar graph represents the precipitation. As the temperature increases the precipitation decreases.
Question 13.
Describe how the average temperature changes in the first 5 months of the year.
Type below:
__________
Answer: From the graph, we can see that the temperature in the first 5 months of the year but the amount of precipitation is decreasing. It’s logical because when the temperature is increasing the amount of precipitation is decreasing.
Question 14.
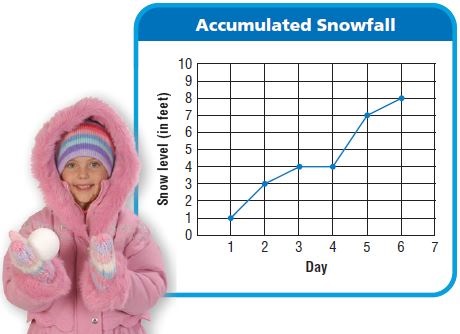
Test Prep Which day had an increase of 3 feet of snow from the previous day?
Options:
a. Day 2
b. Day 3
c. Day 5
d. Day 6
Answer: Day 5
Explanation:
By seeing the above graph we can say that the snow level has increased 3 feet from day 4 to Day 5.
Thus the correct answer is option C.
Mid-Chapter Checkpoint – Vocabulary – Page No. 385
Choose the best term from the box.

Question 1.
The ______ is the horizontal number line on the coordinate grid.
__________
Answer: X-Axis
The X-Axis is the horizontal number line on the coordinate grid.
Question 2.
A ______ is a graph that uses line segments to show how data changes over time.
__________
Answer: Line graph
A Line graph is a graph that uses line segments to show how data changes over time.
Concepts and Skills
Use the line plot at the right for 3–5.

Question 3.
How many kittens weigh at least \(\frac{3}{8}\) of a pound?
______ kittens
Answer: 9
Explanation:
The line plot shows that there are 4 xs above \(\frac{3}{8}\), 3 xs above \(\frac{1}{2}\) and 2 xs on \(\frac{5}{8}\).
To find the kittens weigh at least \(\frac{3}{8}\) we need to add all above \(\frac{3}{8}\)
= 4 + 3 + 2 = 9
Question 4.
What is the combined weight of all the kittens?
______ lb
Answer: 5
Explanation:
There are 3 xs above 1/4 on the line plot, so the combined weight of Kitten in the animal shelter is 3 fourths
3 × 1/4 = 3/4.
There are 4 xs above 3/8 on the line plot, so the combined weight of kittens in the animal shelter is 4 three eights or
4 × 3/8 = 12/8 = 3/2
There are 3 xs above 1/2 on the line plot, so the combined weight of kittens in the animal shelter is 3 halves = 3/2
There are 2 xs above 5/8 on the line plot, so the combined weight of kittens in the animal shelter is 10/8
3/4 + 1 4/8 + 1 1/2 + 1 2/8
= 3/4 + 12/8 + 3/2 + 10/8 = 6/8 + 12/8 + 12/8 + 10/8 = 40/8 = 5 lb
Question 5.
What is the average weight of the kittens in the shelter?
______ lb
Answer: 5/12
Explanation:
Divide the sum you found in example 4. 5 lb by the number of the kittens to find the average. The number of kittens is 12 so we will divide 5 lb by 12.
5 ÷ 12 = 5/12.
Thus the average weight of the kittens in the shelter as 5/12 lb.
Use the coordinate grid at the right for 6–13.
Write an ordered pair for the given point.
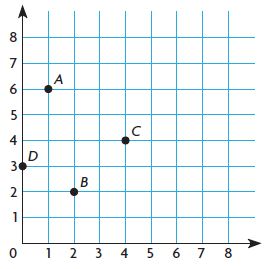
Question 6.
A( ______ , ______ )
Answer: 1, 6
The ordered pair for A is (1,6)
Question 7.
B( ______ , ______ )
Answer: 2, 2
The ordered pair for B is (2, 2)
Question 8.
C( ______ , ______ )
Answer: 4, 4
The ordered pair for C is (4, 4)
Question 9.
D( ______ , ______ )
Answer: 0, 3
The ordered pair for D is (0, 3)
Plot and label the point on the coordinate grid.
Question 10.
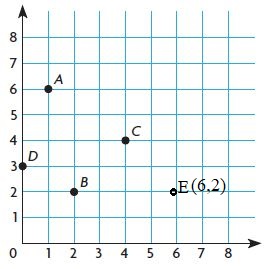
E(6, 2)
Type below:
__________
Answer:
Question 11.
F(5, 0)
Type below:
__________
Answer:
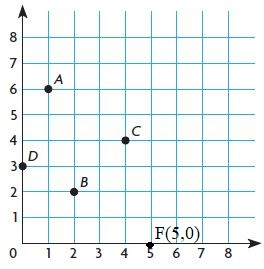
Question 12.
G(3, 4)
Type below:
__________
Answer:
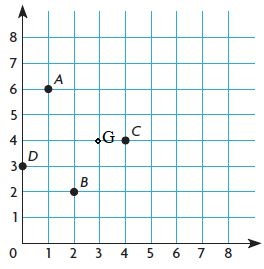
Question 13.
H(3, 1)
Type below:
__________
Answer:
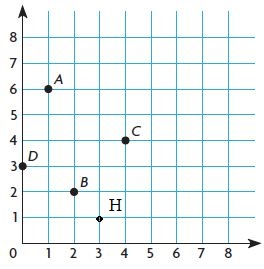
Mid-Chapter Checkpoint – Page No. 386
Question 14.
Jane drew a point that was 1 unit to the right of the y-axis and 7 units above the x-axis. What is the ordered pair for this location?
( ______ , ______ )
Answer: (1, 7)
The ordered pair for the location is (1, 7).
Question 15.
The graph below shows the amount of snowfall in a 6-hour period.
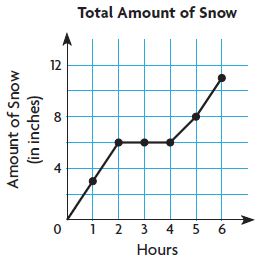
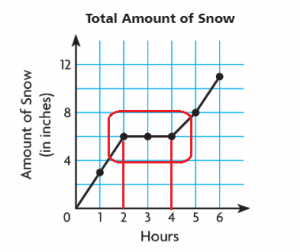
Between which hours did the least amount of snow fall?
between hour ______ and hour ______
Answer: From the graph, we can see that the least amount of snow fall between 2 hours and 4 hours, 0 inches.
Question 16.
Joy recorded the distances she walked each day for five days. How far did she walk in 5 days?
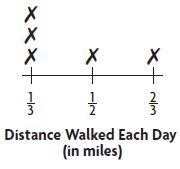
______ \(\frac{□}{□}\) miles
Answer: 2 \(\frac{1}{6}\) miles
Explanation:
There are 3 xs above \(\frac{1}{3}\) = 3 × \(\frac{1}{3}\) = 1
There are 1 x above \(\frac{1}{2}\) = 1 × \(\frac{1}{2}\) = \(\frac{1}{2}\)
There is 1 x above \(\frac{2}{3}\) = 1 × \(\frac{2}{3}\) = \(\frac{2}{3}\)
1 + \(\frac{2}{3}\) + \(\frac{1}{2}\) = (6 + 3 + 4)/6 = 13/6
The mixed fraction of 13/6 is 2 \(\frac{1}{6}\) miles
Thus she walked 2 \(\frac{1}{6}\) miles in 5 days.
Share and Show – Page No. 389
Use the given rules to complete each sequence. Then, complete the rule that describes how nickels are related to dimes.
Question 1.

Type below:
__________
Answer: The number of Dimes is 2 times the number of Nickels.
We need to add 5 to Nickels = 5 + 5 + 5 + 5 + 5 = 25
We need to add 10 to Dimes = 10 + 10 + 10 + 10 + 10 = 50
Complete the rule that describes how one sequence is related to the other. Use the rule to find the unknown term.
Question 2.
Multiply the number of books by ______ to find the amount spent.
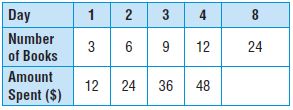
______
Explain:
__________
Answer: The amount spent is 4 times the number of books so we multiply the number of books by 4 to find the amount spent.
Multiply 4 to the amount spent = 24 × 4 = 96
Question 3.
Divide the weight of the bag by _____ to find the number of marbles.
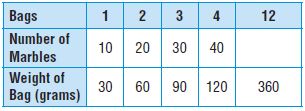
______
Explain:
__________
Answer: The weight of Bag is 3 times the number of marbles So, we divide the weight of Bag by 3 to find the number of marbles.
Divide 360 by 3
360/3 = 120
On Your Own
Complete the rule that describes how one sequence is related to the other. Use the rule to find the unknown term.
Question 4.
Multiply the number of eggs by _______ to find the number of muffins.
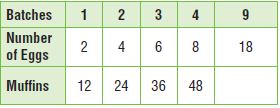
Type below:
__________
Answer: The muffins is 6 times the number of eggs so we multiply the number of eggs by 6 to find the muffins.
The unknown term in the table we will find when multiply 18 by 6.
18 × 6 = 108
The unknown term is 108.
Question 5.
Divide the number of meters by _______ to find the number of laps.
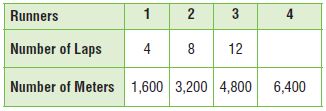
Type below:
__________
Answer: The number of meters is 400 times the number of laps so we divide the number of meters by 400 to find the number of laps.
The unknown term in the table we will find when divide 6400 by 400.
6400 ÷ 400 = 16
The unknown term is 16.
Question 6.
Suppose the number of eggs used in Exercise 4 is changed to 3 eggs for each batch of 12 muffins, and 48 eggs are used. How many batches and how many muffins will be made?
______ batches
______ muffins
Answer: 16 batches 192 muffins will be made.
Explanation:
If we change to 3 eggs for each batch of 12 muffins and 48 eggs are used we will have 16 batches.
16 × 3 = 48
The muffins are 4 times the number of eggs so we multiply the number of eggs by 4 to fins the number of muffins.
If the number of batches is 16 and there are 48 eggs to find the number of muffins we will multiply the number of eggs 48 with 4:
48 × 4 = 192
192 muffins will be made.
Problem Solving – Page No. 390
Question 7.
Emily has a road map with a key that shows an inch on the map equals 5 miles of actual distance. If a distance measured on the map is 12 inches, what is the actual distance? Write the rule you used to find the actual distance.
______ miles
Answer: 60 miles
Explanation:
For first the total length of roads is 5 inches + 7 inches = 12 inches
1 inch on the map represents 5 miles of actual distance so to find what actual distance corresponding to 12 inches we will find with using proportion.
1 inch : 5 inches = 12 inches: x inches
1 × x = 5 × 12
x = 60 miles
The actual distance which Emily will drive is 60 miles.
The rule which we used to find the actual distance is multiplied by 5 which is a mark in solution.
Question 8.
To make a shade of lavender paint, Jon mixes 4 ounces of red tint and 28 ounces of blue tint into one gallon of white paint. If 20 gallons of white paint and 80 ounces of red tint are used, how much blue tint should be added? Write a rule that you can use to find the amount of blue tint needed.
______ oz
Answer: 560 oz
Explanation:
For one gallon of white paint, Jon mixed 28 ounces of blue tint so to find how much tint corresponding to 20 gallons of white paint we will find with using proportion.
1 gallon of white paint:28 ounces of blue tint = 20 gallons of white paint:x ounces of the blue tint.
1 × x = 28 × 20
x = 560
560 ounces of blue tint should be added.
The rule which we used to find the amount of blue tint needed is to multiply by 28 which is the mark in solution.
Question 9.
In the cafeteria, tables are arranged in groups of 4, with each table seating 8 students. How many students can sit at 10 groups of tables? Write the rule you used to find the number of students.
______ students
Answer: 320 students
Explanation:
Tables are arranged in groups of 4, with each table seating 8 students, so in one group sit
4 × 8 = 32 students
To find how many students can sit at 10 groups of tables, we will find when multiplying 32 students with 10.
32 × 10 = 320
Finally, 320 students can sit at 10 groups of tables. The rule which we used to find the number of students is to multiply by 32 which is marked is a solution.
Question 10.
Test Prep What is the unknown number in Sequence 2 in the chart? What rule could you write that relates Sequence 1 to Sequence 2?
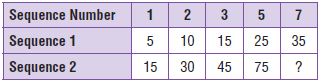
Options:
a. 70; Multiply by 2.
b. 100; Add 25.
c. 105; Multiply by 3.
d. 150; Add 150.
Answer: 105; Multiply by 3.
Explanation:
The unknown number in Sequence number 7 we will get when multiply 35 with 3 because the rule that releases the number of miles to the number of runners is multiplying by 3.
The unknown number is: 35 × 3 = 105
Thus the correct answer is option C.
Share and Show – Page No. 393
Question 1.
Max builds rail fences. For one style of fence, each section uses 3 vertical fence posts and 6 horizontal rails. How many posts and rails does he need for a fence that will be 9 sections long?

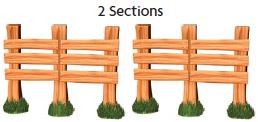

First, think about what the problem is asking and what you know. As each section of fence is added, how does the number of posts and the number of rails change?
Next, make a table and look for a pattern. Use what you know about 1, 2, and 3 sections. Write a rule for the number of posts and rails needed for 9 sections
of fence.
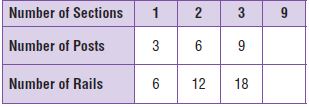
Possible rule for posts: _____________
Possible rule for rails: ______________
Finally, use the rule to solve the problem.
Type below:
__________
Answer:
Possible rule for posts: 27
Possible rule for rails: 54
Explanation:
The number of posts is 3 times the number of sections. So, we multiply the number of posts by 3.
With using the rule the unknown number is 9 × 3 = 27
Thus the possible rule for posts is 27.
Now multiply the number of rails by 2.
With using the rule the unknown number is 27 × 2 = 54
Thus the possible rule for rails is 54.
Question 2.
What if another style of rail fencing has 6 rails between each pair of posts? How many rails are needed for 9 sections of this fence?
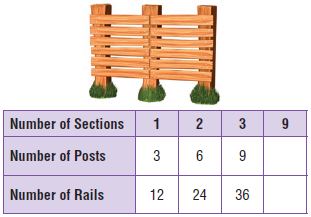
Possible rule for rails: ____________________
______ rails
Answer: 108 rails
Explanation:
The number of posts is 3 times the number of sections. So, we multiply the number of posts by 3.
With using the rule the unknown number is 9 × 3 = 27
Thus the possible rule for posts is 27.
Now multiply the number of rails by 4.
With using the rule the unknown number is 27 × 4 = 108
Thus the possible rule for rails is 108.
Question 3.
Leslie is buying a coat on layaway for $135. She will pay $15 each week until the coat is paid for. How much will she have left to pay after 8 weeks?
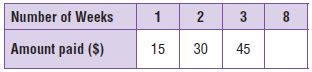
$ ______
Answer: $15
Explanation:
Leslie is buying a coat on layaway for $135. She will pay $15 each week until the coat is paid for.
Multiply the number of weeks by 15.
15 × 8 = $120
Now subtract $120 from $135
= $135 – $120 = $15
On Your Own – Page No. 394
Question 4.
Jane works as a limousine driver. She earns $50 for every 2 hours that she works. How much does Jane earn in one week if she works 40 hours per week? Write a rule and complete the table.
Possible rule: _____________
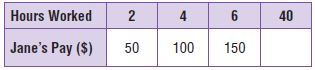
$ ______
Answer: 1000
Explanation:
The possible rule for Hour Worked: We can see that the difference between terms is 2.
So, the rule which describes this is Add 2.
The possible rule for Jane’s Pay: We can see that the difference between terms is 50.
So, the rule which describes this is Add 50.
Jane’s Pay is 25 times the hours worked so, we will multiply the hours worked by 25 to find Jane’s Pay.
The unknown number Jane’s Pay we will find when multiplying 40 with 25:
40 × 25 = 1000
She earns 1000 dollars.
Question 5.
Rosa joins a paperback book club. Members pay $8 to buy 2 tokens, and can trade 2 tokens for 4 paperback books. Rosa buys 30 tokens and trades them for 60 paperback books. How much money does she spend? Write a rule and complete the table.
Possible rule: _______________
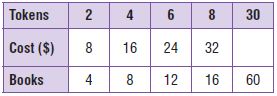
$ ______
Answer: 120
Explanation:
Possible rule for Tokens: We can see that the difference between terms is 8.
So, the rule which describes this is Add 8.
Possible rule for Games: We can see that the difference between terms is 4.
So, the rule which describes this is Add 4.
Tokens are 2 times the games so, we will divide the tokens by 2 to find how many games can she3 play.
The unknown number of games we will find when dividing 120 with 2:
120 ÷ 2 = 60
She can play 60 games for 120 tokens.
Question 6.
Paul is taking a taxicab to a museum. The taxi driver charges a $3 fee plus $2 for each mile traveled. How much does the ride to the museum cost if it is 8 miles away?
Answer: $40
Explanation:
Paul is taking a taxicab to a museum. The taxi driver charges a $3 fee plus $2 for each mile traveled.
That means the driver charged $5 per mile.
For 8 miles = 8 × $5 = $40.
Question 7.
Test Prep Which expression could describe the next figure in the pattern, Figure 4?
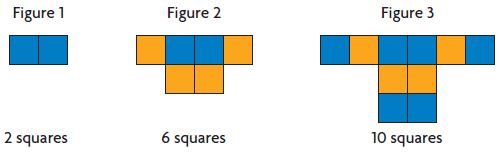
Options:
a. 2 × 5
b. 2 + 4 + 4
c. 2 + 4 + 4 + 4
d. 16
Answer: 2 + 4 + 4 + 4
Explanation:
We can see that the difference between two consecutive figures is 4 squares.
So, the rule which describes this is Add 4.
Thus figure 4 has 14 squares.
Thus the correct answer is option C.
Share and Show – Page No. 397
Graph and label the related number pairs as ordered pairs.
Then complete and use the rule to find the unknown term.
Question 1.
Multiply the number of tablespoons by ___ to find its weight in ounces.
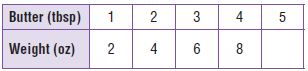
Type below:
_________
Answer: Multiply the number of tablespoons by 2 to find its weight in ounces.
5 × 2 = 10
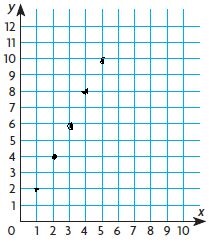
Question 2.
Multiply the number of hours by ____ to find the distance in miles.
Type below:
_________
Answer: Multiply the number of hours by 3 to find the distance in miles.
4 × 3 = 12 miles
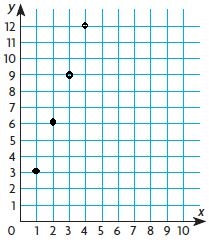
On Your Own
Graph and label the related number pairs as ordered pairs.
Then complete and use the rule to find the unknown term.
Question 3.
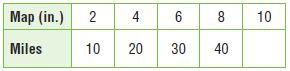
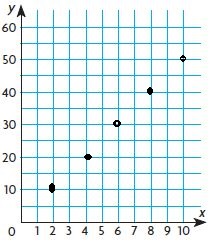
Multiply the number of inches by ____ to find the distance in miles.
Type below:
_________
Answer: Multiply the number of inches by 5 to find the distance in miles.
10 × 5 = 50
Question 4.
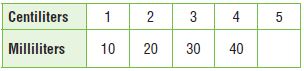
Multiply the number of centiliters by ____ to find the equivalent number of milliliters.
Answer:
Multiply the number of centiliters by 10 to find the equivalent number of milliliters.
5 × 10 = 50 milliliters
Problem Solving – Page No. 398
Sense or Nonsense?
Question 5.
Elsa solved the following problem.

Lou and George are making chili for the Annual Firefighter’s Ball. Lou uses 2 teaspoons of hot sauce for every 2 cups of chili that he makes, and George uses 3 teaspoons of the same hot sauce for every cup of chili in his recipe. Who has the hotter chili, George or Lou?
Write the related number pairs as ordered pairs and then graph them. Use the graph to compare who has the hotter chili, George or Lou.
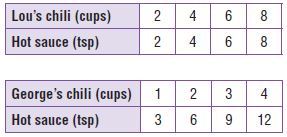
Lou’s chili: (2, 2), (4, 4), (6, 6), (8, 8)
George’s chili: (1, 3), (2, 6), (3, 9), (4, 12)
Elsa said that George’s chili was hotter than Lou’s because the graph showed that the amount of hot sauce in George’s chili was always 3 times as great as the amount of hot sauce in Lou’s chili.
Does Elsa’s answer make sense, or is it nonsense?
Explain.
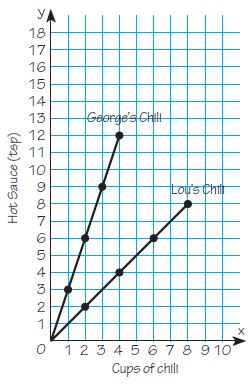
Answer: Elsa’s Answer makes sense.
Explanation:
Elsa’s answer makes sense because the amount of hot sauce in George’s chili was always 3 times as great as the amount of hot sauce in Lou’s chili. To prove this we will take two points from the graph which has an equal amount of cups of chili and compares the amount of hot sauce in George’s chili with the amount of hot sauce in Lou’s chili.
If we take 4 cups of George’s chili and Lou’s chili the amount of hot sauce in George’s chili is 12 teaspoons and the amount of hot sauce in Lou’s chili is 4 teaspoons.
12 is 3 times greater than 4 so Elsa’s answer makes sense.
Chapter Review/Test – Vocabulary – Page No. 399
Choose the best term from the box.

Question 1.
The __________ is the point where the x-axis and y-axis meet. Its __________ is 0, and its __________ is 0.
The ________ is the point where the x-axis and y-axis meet.
Its ________ is 0,
and its ________ is 0.
Answer:
The Origin is the point where the x-axis and y-axis meet.
Its x-coordinate is 0,
and its y-coordinate is 0.
Question 2.
A __________ uses line segments to show how data changes over time.
Answer: A line graph uses line segments to show how data changes over time.
Check Concepts
Use the table for 3–4.
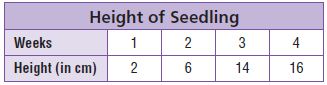
Question 3.
Write related number pairs of data as ordered pairs.
Type below:
__________
Answer:
The ordered pair for week 1 is (1, 2)
The ordered pair for week 2 is (2, 6)
The ordered pair for week 3 is (3, 14)
The ordered pair for week 4 is (4, 16)
Question 4.
Make a line graph of the data.
Type below:
__________
Answer:
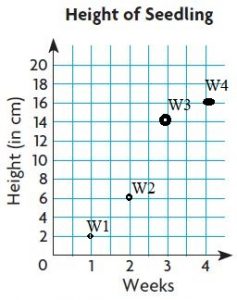
The ordered pair for week 1 is (1, 2)
The ordered pair for week 2 is (2, 6)
The ordered pair for week 3 is (3, 14)
The ordered pair for week 4 is (4, 16)
Complete the rule that describes how one sequence is related to the other. Use the rule to find the unknown term.
Question 5.
Multiply the number of eggs by ________ to find the number of cupcakes.
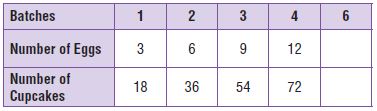
_______
Answer:
Multiply the number of eggs by 6 to find the number of cupcakes.
The unknown number in batches 6 we will get when multiply 18 with 6 because the rule that releases the number of eggs to the number of cupcakes is multiplying by 6.
The number of eggs is multiple of 3 and the number of cupcakes is multiple of 6.
Chapter Review/Test – Page No. 400
Fill in the bubble completely to show your answer.
Question 6.
The letters on the coordinate grid represent the locations of the first four holes on a golf course.
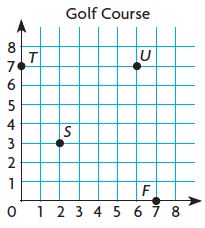
Which ordered pair describes the location of the hole labeled T?
Options:
a. (0, 7)
b. (1, 7)
c. (7, 0)
d. (7, 1)
Answer: (0, 7)
By seeing the above graph we can find the location of the hole label T i.e., (0, 7)
Use the line plot at the right for 7–8.
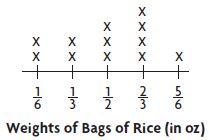
Question 7.
What is the average of the data in the line plot?
Options:
a. \(\frac{1}{2}\) pound
b. 1 pound
c. 6 pounds
d. 6 \(\frac{3}{4}\) pounds
Answer: 6 pounds
Explanation:
There are 3 xs above \(\frac{1}{2}\) pound = 3 × \(\frac{1}{2}\) = 3/2
There are 4 xs above \(\frac{2}{3}\) pound = 4 × \(\frac{2}{3}\) = 8/3
There is 1 x above \(\frac{5}{6}\) pound = 5/6
There are 2 xs above \(\frac{1}{6}\) = 2/6
There are 2 xs above \(\frac{1}{3}\) = 2/3
3/2 + 8/3 + 5/6 + 2/6 + 2/3 = 6 pounds
Thus the correct answer is option C.
Question 8.
How many bags of rice weigh at least \(\frac{1}{2}\) pound?
Options:
a. 2
b. 3
c. 5
d. 8
Answer: 8
Explanation:
By seeing the above line plot we can find the number of bags of rice weigh at least \(\frac{1}{2}\) pound
There are 3 xs above \(\frac{1}{2}\) pound = 3 × \(\frac{1}{2}\) = 3/2
There are 4 xs above \(\frac{2}{3}\) pound = 4 × \(\frac{2}{3}\) = 8/3
There is 1 x above \(\frac{5}{6}\) pound = 5/6
Total number of bags of rice weigh at least \(\frac{1}{2}\) pound = 3 + 4 + 1 = 8
Thus the correct answer is option D.
Chapter Review/Test – Page No. 401
Fill in the bubble completely to show your answer.
Use the table for 9–10.
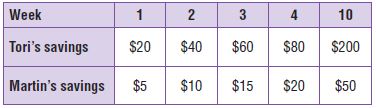
Question 9.
Compare Tori’s and Martin’s savings. Which of the following statements is true?
Options:
a. Tori saves 4 times as much per week as Martin.
b. Tori will always have exactly $15 more in savings than Martin has.
c. Tori will save 15 times as much as Martin will.
d. On week 5, Martin will have $30 and Tori will have $90.
Answer: Tori saves 4 times as much per week as Martin.
Explanation:
By seeing the above table we can say that Tori saves 4 times as much per week as Martin.
Thus the correct answer is option A.
Question 10.
What rule could you use to find Tori’s savings after 10 weeks?
Options:
a. Add 10 from one week to the next.
b. Multiply the week by 2.
c. Multiply Martin’s savings by 4.
d. Divide Martin’s savings by 4.
Answer: Multiply Martin’s savings by 4.
Explanation:
We can find the savings of Tori by multiplying the savings of Martins by 4.
Thus the suitable statement is Multiply Martin’s savings by 4.
Therefore the correct answer is option C.
Question 11.
In an ordered pair, the x-coordinate represents the number of hexagons and the y-coordinate represents the total number of sides. If the x-coordinate is 7, what is the y-coordinate?
Options:
a. 6
b. 7
c. 13
d. 42
Answer: 6
Explanation:
Given that x-coordinate represents the number of hexagons.
Thus x-coordinate is 6.
And also given that the y-coordinate represents the number of sides.
The figure hexagon contains 6 sides.
So, the y-coordinate is 6.
Thus the ordered pair is (7, 6)
Therefore the correct answer is option A.
Question 12.
Point A is 2 units to the right and 4 units up from the origin. What ordered pair describes point A?
Options:
a. (2, 0)
b. (2, 4)
c. (4, 2)
d. (0, 4)
Answer: (2, 4)
Explanation:
Point A is 2 units to the right and 4 units up from the origin.
2 units will be located on the x-axis and 4 units will be on the y-axis.
Thus the ordered pair for point A is (2, 4)
Therefore the correct answer is option B.
Chapter Review/Test – Page No. 402
Constructed Response
Question 13.
Mr. Stevens drives 110 miles in 2 hours, 165 miles in 3 hours, and 220 miles in 4 hours. How many miles will he drive in 5 hours?
Explain how the number of hours he drives is related to the number of miles he drives.
_____ miles
Answer: 275 miles
Explanation:
Given that, Mr. Stevens drives 110 miles in 2 hours, 165 miles in 3 hours, and 220 miles in 4 hours.
We have to divide the number of miles by number of hours
That means, 110/2, 165/3, 220/4
the distance gone in 5 hours can be found with this equation
110/2 x ?/5
multiply 110 by 5 then divide the product by 2
110 × 5= 550
550/2 =275
Thus the answer is Mr. Stevens goes 275 miles in 5 hr.
Performance Task
Question 14.
Tim opens the freezer door and measures the temperature of the air inside. He continues to measure the temperature every 2 minutes, as the door stays open, and records the data in the table.
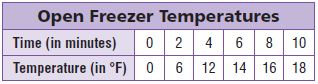
A). On the grid below, make a line graph showing the data in the table.
Type below:
__________
Question 14.
B). Use the graph to estimate the temperature at 7 minutes.
Estimate: _____ °F
Answer: By seeing the above graph we can say that the estimated temperature at 7 minutes is 15°F.
Question 14.
C). Write a question that can be answered by making a prediction. Then answer your question and explain how you made your prediction.
Type below:
__________
Question: Estimate the temperature at 5 minutes by using the graph.
Answer: By seeing the above table we can say that the estimated temperature at 5 minutes is 13°F
Conclusion
Fall in love with Maths by utilizing the Go Math 5th Standard 5 Answer Key. Make use of the Go Math Grade 5 Answer Key Chapter 9 Algebra: Patterns and Graphing as a reference for all your queries. Keep in touch with our site to avail updates on Class Specific Go Math Answer Key at your fingertips.
