Big Ideas Math Grade 8 Chapter 7 Functions is given by subject experts adhering to the latest syllabus guidelines. Become Proficient in the Concepts of Big Ideas Math Grade 8 Functions by consistently practicing from our BIM Book 8th Grade Ch 7 Functions Answer Key. To make it easy for you to understand the concepts we have provided step-by-step solutions in the Big Ideas Math Answers Grade 8 Chapter 7 Functions. You can download the quick resources without even paying a single penny.
Big Ideas Math Book 8th Grade Answer Key Chapter 7 Functions
Big Ideas Math Grade 8 Ch 7 Functions Solutions provided here cover the questions from Lessons 7.1 to 7.5, Practice Tests, Review Tests, Cumulative Practice, Assessment Tests, etc. You can have deeper insights into all the Topics of Functions such as the representation of functions, linear functions, analyzing and sketching graphs, etc. Use the below available quick links for Big Ideas Math 8th Grade Chapter 7 Functions Answer Key and clear all your ambiguities regarding the concerned topics.
STEAM Video/Performance Task
Getting Ready for Chapter 7
Lesson 1 Relations and Functions
Lesson 2 Representations of Functions
Lesson 3 Linear Functions
Lesson 4 Comparing Linear and Non Linear Functions
- Lesson 7.4 Comparing Linear and Non Linear Functions
- Comparing Linear and Non Linear Functions Homework & Practice 7.4
Lesson 5 Analyzing and Sketching Graphs
Functions Connecting Concepts
- Functions Connecting Concepts
- Functions Chapter Review
- Functions Practice Test
- Functions Cumulative Practice
Functions STEAM Video/Performance Task
STEAM Video
Apparent Temperature
Sometimes it feels hotter or colder outside than the actual apparent temperature. How hot or cold it feels is called the temperature. What weather factors might contribute to the apparent temperature?
Watch the STEAM Video “Apparent Temperature.” Then answer the following questions.

1. Robert says that the Wet-Bulb Globe Temperature (WBGT)index is used as a measure of apparent temperature.

In the formula, TW is the natural wet-bulb temperature, TG is the black-globe temperature, TD and is the dry-bulb temperature. Find WBGT when TW = 75ºF, TG = 100ºF, and TD = 84ºF.
2. Different categories of Wet-Bulb Globe Temperatures are shown in the chart. Each category can be represented by a different-colored flag. Which flag color is displayed when WGBT = 87.5ºF?
Performance Task
Heat Index
After completing this chapter, you will be able to use the STEAM concepts you learned to answer the questions in the Video Performance Task. You will be given information about heat index.

You will be asked to create a graph of the temperatures and heat indices. Why is it useful to know the heat index?
Functions Getting Ready for Chapter 7
Chapter Exploration
Work with a partner. Copy and complete the diagram.
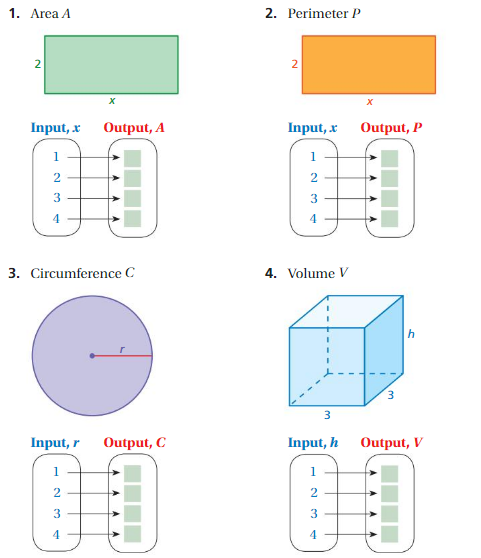
1. Answer: ( 1 , 2 ) , ( 2 , 4 ) , ( 3 , 6 ) , ( 4 , 8 ) .
Explanation: 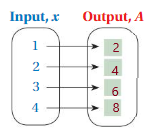
Given , Width w = 2 , Length l = x where x = 1 , 2 , 3 , 4 .
To find Area A of a rectangle we have , A = w × l
for x = 1 , A = 2 × 1 = 2 ,
for x = 2 , A = 2 × 2 = 4 ,
for x = 3 , A = 2 × 3 = 6 ,
for x = 4 , A = 2 × 4 = 8 ,
So, for every value of Input x = 1 , 2 , 3 , 4 we have Output A = 2 , 4 , 6 , 8 , respectively .
That is ( 1 , 2 ) , ( 2 , 4 ) , ( 3 , 6 ) , ( 4 , 8 ) .
2. Answer: ( 1 , 6 ) , ( 2 , 8 ) , ( 3 , 10 ) , ( 4 , 12 ).
Explanation: 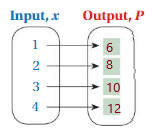
Given , Width w = 2 , Length l = x where x = 1 , 2 , 3 , 4 .
To find Perimeter of a rectangle we have , P = 2( l + w )
for x = 1 ,P = 2( 1 + 2 ) = 2 × 3 = 6 ,
for x = 2 , P = 2( 2 + 2 ) = 2 × 4 = 8 ,
for x = 3 , P = 2( 3 + 2 ) = 2 × 5 = 10 ,
for x = 4 , P = 2( 4 + 2 ) = 2 × 6 = 12 ,
So, for every value of Input x = 1 , 2 , 3 , 4 we have Output P = 6 , 8 , 10 , 12 , respectively .
That is ( 1 , 6 ) , ( 2 , 8 ) , ( 3 , 10 ) , ( 4 , 12 ) .
3. Answer : ( 1 , 6 ) , ( 2 , 12 ) , ( 3 , 18 ) , ( 4 , 24 ) .
Explanation: 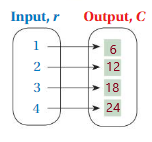
Given , Radius of a circle , where as r = 1 , 2 , 3 , 4
To find the circumference of a circle , we have C = 2Òr , Ò = 3.14 , or we can write it as 3 .
for r = 1 , C = 2 × 3 × 1 = 6 ,
for r = 2 , C = 2 × 3 × 2 = 12 ,
for r = 3 , C = 2 × 3 × 3 = 18 ,
for r = 4 , C = 2 × 3 × 4 = 24 ,
So, for every value of Input r = 1 , 2 , 3 , 4 we have Output C = 6 , 12 , 18 , 24 , respectively .
That is ( 1 , 6 ) , ( 2 , 12 ) , ( 3 , 18 ) , ( 4 , 24 ) .
4. Answer: ( 1 , 9 ) , ( 2 , 18 ) , ( 3 , 27 ) , ( 4 , 36 )
Explanation: 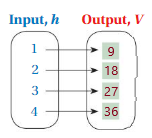
Given , Two Edges of a cube = 3 , h = 1 , 2 , 3 , 4
To find the Volume of the cube we have , V = a³
for h = 1 , V = 3 × 3 × 1 = 9 ,
for h = 2 , V = 3 × 3 × 2 = 12 ,
for h = 3 , V = 3 × 3 × 3 = 27 ,
for h = 4 , V = 3 × 3 × 4 = 36 ,
So, for every value of Input h = 1 , 2 , 3 , 4 we have Output V = 9 , 18 , 27 , 36 , respectively .
That is ( 1 , 9 ) , ( 2 , 18 ) , ( 3 , 27 ) , ( 4 , 36 ) .
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
input
mapping diagram
nonlinear function
output
linear function
Answer : Input : The ordered pairs can be used to show inputs and outputs of a function ,The input is the number you feed into the expression, and the output is what you get after the calculations are finished.
mapping diagram : A relation pairs inputs with outputs , A relation can be represented by ordered pairs or a mapping diagram .
nonlinear function : nonlinear functions are functions which are not linear. Quadratic functions are one type of nonlinear function. It is a relation between two variables , function that does not form a line when graphed.
output ; The ordered pairs can be used to show inputs and outputs of a function ,The input is the number you feed into the expression, and the output is what you get after the calculations are finished.
linear function : A linear function is a relation between two variables that produces a straight line when graphed. And it has one dependent variable and one independent variable .
Lesson 7.1 Relations and Functions
EXPLORATION 1
Interpreting Diagrams
Work with a partner. Describe the relationship between the inputs and outputs in each diagram. Then complete each diagram. Is there more than one possible answer? Explain your reasoning.
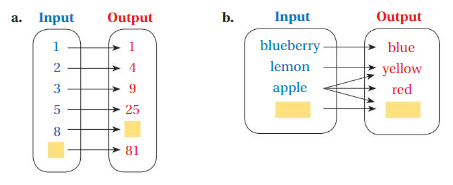
Answer: a. The relation between the inputs and outputs is outputs are the result of twice as many times the inputs.
b. The relation between the inputs and outputs is outputs are the result of colors of inputs . In this case we can notice that , for any one input we can have more than one output .
Explanation: 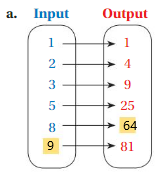
a. As shown in the diagrams , The relation between the inputs and outputs is outputs are the result of twice as many times the inputs , so for input 1 = 1 × 1 = 1 as output ,
for input 2 = 2 × 2 = 4 ,
for input 3 = 3 × 3 = 9 ,
for input 5 = 5 × 5 = 25 ,
for input 8 = 8 × 8 = 64 ,
for input 9 = 9 × 9 = 81 ,
So, for every value of Input = 1 , 2 , 3 , 5 , 8 , 9 , we have Output = 1 , 4 , 9 , 25 , 64 , 81 , respectively .
That is ( 1 , 1 ) , ( 2 , 4 ) , ( 3 , 9 ) , ( 5 , 25 ) , ( 8 , 64 ) , ( 9 , 81 ) .
b. The relation between the inputs and outputs is outputs are the result of colors of inputs . 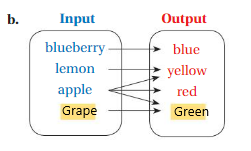
for input Blueberry = color is blue as output
for input lemon = color is yellow as output
for input Apple = color is yellow , red and green as output
for input Grape = color is green as output.
In this case we can notice that , for any one input we can have more than one output .
EXPLORATION 2
Describing Relationships Between Quantities
Work with a partner. The diagrams show the numbers of tickets bought by customers for two different plays and the total costs (in dollars).
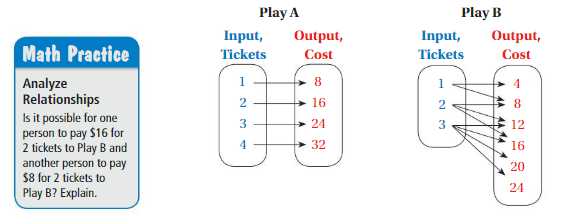
a. For each diagram, how many outputs does each input have?
b. Describe the prices of tickets for each play.
c. A person buys 4 tickets for each play. Can you determine the total cost of all 8 tickets? Explain.
Answer:
a. For Play A ,The number of inputs are equal to number of outputs ,
For Play B , The number of inputs are not equal to number of outputs .
So, input 1 = 2 outputs , input 2 = 3 outputs , input 3 = 4 outputs .
b. For Play A , The price of the each ticket is $8 .
For Play B , The price of each ticket is $4 or $8 .
c. For Play A , each ticket is $8 , Then for 4 tickets = 4 × $8 = $32 .
For Play B , each ticket is $4 or $8 , Then for 4 tickets = 4 × $8 = $32 . or 4 × $4 = $16 .
Explanation:
a. For Play A ,
The number of inputs are equal to number of outputs , 4 inputs = 4 outputs
That is ( 1 , 8 ) , ( 2 , 16 ) , ( 3 , 24 ) , ( 4 , 32 ) .
For Play B ,
The number of inputs are not equal to number of outputs , 3 inputs are not equal to 7 outputs
That is , for input 1 = 4 , 8 as outputs ,
for input 2 = 8 , 12 , 16 as outputs ,
for input 3 = 12 , 16 , 20 , 24 as outputs ,
So, input 1 = 2 outputs , input 2 = 3 outputs , input 3 = 4 outputs .
b. For Play A ,
The price of the each ticket is $8 .
For Play B ,
The price of each ticket is $4 or $8 .
c. Given , A person buys 4 tickets for each play.
For Play A , each ticket is $8 , Then for 4 tickets = 4 × $8 = $32 .
And for 8 tickets = 8 × $8 = $64 .
For Play B , each ticket is $4 or $8 , Then for 4 tickets = 4 × $8 = $32 . or 4 × $4 = $16 .
And for 8 tickets =8 × $4 =$32 or 8 × $8 = $64 .

Try It
List the ordered pairs shown in the mapping diagram.
Question 1.
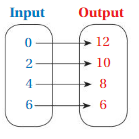
Answer: Ordered pairs are ( 0 , 12 ) , ( 2 , 10 ) , ( 4 , 8 ) , ( 6 , 6 ) .
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 0 , 12 ) , ( 2 , 10 ) , ( 4 , 8 ) , ( 6 , 6 ) .
Question 2.
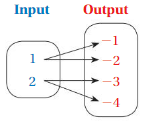
Answer: Ordered pairs are ( 1 , -1 ) , ( 1 , -2 ) , ( 2 , -3 ) , ( 2 , -4 ) .
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 1 , -1 ) , ( 1 , -2 ) , ( 2 , -3 ) , ( 2 , -4 ) .
Determine whether the relation is a function.
Question 3.
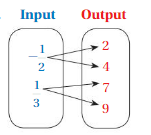
Answer: The relation is not a function
Explanation:
The each input has more than two outputs , Even one of those inputs are unclear of outputs
So , The relation is not a function .
Question 4.
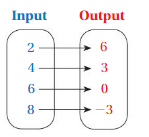
Answer: The relation is a function .
Explanation:
Each input has exactly one output ,
So , The relation is a function .
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
PRECISION
Describe how relations and functions are different.
Answer: Relations are nothing but the ordered pairs with Inputs and Outputs . On the other hand , Functions are The relation that pairs with one input with exactly one output are called Functions.
IDENTIFYING FUNCTIONS List the ordered pairs shown in the mapping diagram. Then determine whether the relation is a function.
Question 6.
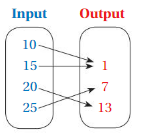
Answer: The ordered pairs are ( 10 , 1 ) , ( 15 , 1 ) , ( 20 , 13 ) , ( 25 , 7 ) and The relation is a function .
Explanation:
As shown , The ordered pairs are ( 10 , 1 ) , ( 15 , 1 ) , ( 20 , 13 ) , ( 25 , 7 ) .
Each input has exactly one output ,
So, The relation is a function .
Question 7.
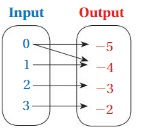
Answer: The ordered pairs are ( 0 , -5 ) , ( 0 , -4 ) , ( 1 , -4 ) , ( 2 , -3 ) , ( 3 , -2 ) and relation is not a function .
Explanation:
As shown , The ordered pairs are ( 0 , -5 ) , ( 0 , -4 ) , ( 1 , -4 ) , ( 2 , -3 ) , ( 3 , -2 ) .
The input 0 has more than one output ,
So, The relation is not a function .
Question 8.
OPEN-ENDED
Copy and complete the mapping diagram at the left to represent a relation that is a function. Then describe how you can not modify the mapping diagram so that the relation is a function.
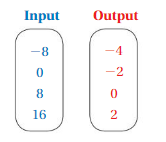
Answer: ordered pairs are ( -8 , -4 ) , ( 0 , -2 ) , ( 8 , 0 ) , ( 16 , 2 ) . To have the relation as a function we must have only one output for one input.
Explanation: 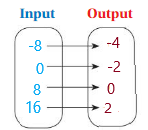
The ordered pairs of the diagram are ( -8 , -4 ) , ( 0 , -2 ) , ( 8 , 0 ) , ( 16 , 2 ) .
Each Input must have only one output in order to be the relation is a function ,
If ,The mapping diagram has the right to left representation or each input has more than one output , then the relation is not a function .
So , To have the relation as a function we must have only one output for one input.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
The mapping diagram represents the costs of reserving a hotel room for different numbers of nights.
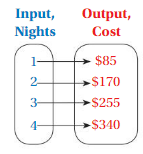
a. Is the cost a function of the number of nights reserved?
b. Describe the relationship between the cost and the number of nights reserved.
Answer: a. Yes , The cost is a function of the number of nights reserved .
b. The relationship between the cost and the number of nights reserved is , For every night reservation of the room is increasing by $85 with increase in the next reservation ,
Explanation:
a. From the diagram we have ,
Ordered pairs are ( 1 , -$85 ) , ( 2 , $170 ) , ( 3 , $255 ) , ( 4 , $340 ) . each input has exactly one output ,
So , the relation is a function and ,
Yes , The cost is a function of the number of nights reserved .
b. The relationship between the cost and the number of nights reserved is ,
For every night reservation of the room is increasing by $85 with increase in the next reservation,
that is , input 1 = $85 as output
Input 2 = $85 + $85 = $170 as output
Input 3 = $170 + $85 = $255 as output
Input 2 = $255 + $85 = $340 as output
So, The relationship between the cost and the number of nights reserved is ,
For every night reservation of the room is increasing by $85 with increase in the next reservation.
Question 10.
DIG DEEPER!
The graph represents the number of contestants in each round of a talent competition.
a. Is the number of contestants a function of the round number?
b. Predict the number of contestants in the talent competition during Round 7. Explain your reasoning.
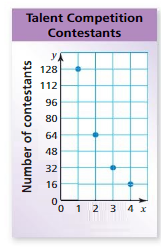
Answer: a. The number of contestants is a function of the round number.
b. The number of contestants in the talent competition during Round 7 are 2.
Explanation:
a. From the given graph , The ordered pairs are ( 1 , 128 ) , ( 2 , 64 ) , ( 3 , 32 ) , ( 4 , 16 ) .
Each input has only one output , The relation is a function .
So , the number of contestants is a function of the round number.
b. Firstly , The relation between the input and output is,
With every increase in the round number the number of contestants are decreasing by half the number of the previous round , That is, for input 1 = 128 as output
For input 2 = 128 – 64 = 64 as output
For input 3 = 64 – 32 = 32 as output
For input 4 = 32 – 16 = 16 as output
For input 5 = 16 – 8 = 8 as output
For input 6 = 8 – 4 = 4 as output
For input 7 = 4 – 2 = 2 as output,
So, The number of contestants in the talent competition during Round 7 are 2 .
Relations and Functions Homework & Practice 7.1
Review & Refresh
Choose an appropriate data display for the situation. Explain your reasoning.
Question 1.
the number of runners in each
age group at a marathon
Answer: In a marathon ,the people of all age group are participating for a promotion on healthy lifestyle, The number of runners in each group has kids, adults and old people to spread the awareness of leading a healthy life by running daily in the morning . Running or jogging in the morning can help us to maintain our body mass index at an optimal level which is good for heart. The Marathon is conducted by the government of health ministry to be example for the future generations.
Question 2.
the high temperature and the
attendance at a water park each day
Answer: Generally, The water park is normally crowded depending on the season and the temperature, In summer the attendance in the waterpark is at the utmost point because of the high temperature and the seasonal vacation. Going to the water park in summer is super fun due to the number of water slides , water rides will be a nice place to the whole family trip and as well as friends . In order to be there at a less crowded time spring is also a nice time to visit the water park .
Graph the linear equation.
Question 3.
y = 2x – 3
Answer: 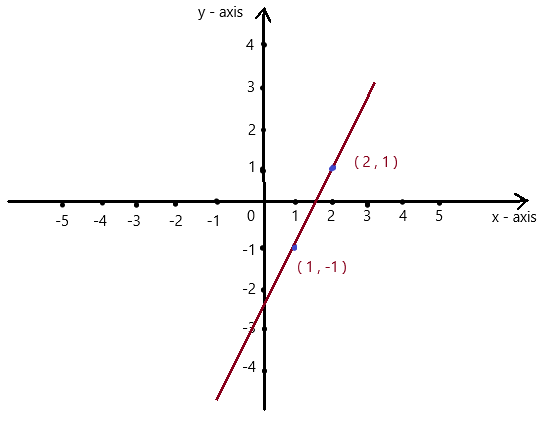
Explanation:
Given , y = 2x – 3 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 1 , then y = 2(1) – 3 = 2 – 3 = -1 . co-ordinates are (1 , -1)
if x = 2 , then y = 2(2) – 3 = 4 – 3 = 1 , co-ordinates are (2 , 1)
The co-ordinates (1 , -1) , (2 , 1) form a straight line .
So, y = 2x – 3 is a linear equation.
Question 4.
y = – 0.5x
Answer: 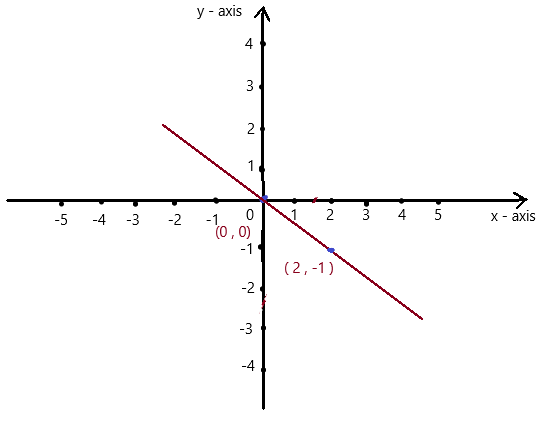
Explanation:
Given , y = -0.5x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = -0.5(0) = 0 . co-ordinates are (0 , 0)
if x = 2 , then y = -0.5(2) = -1 , co-ordinates are (2 , -1)
The co-ordinates (0 , 0) , (2 , -1) form a straight line .
So, y = -0.5x is a linear equation.
Question 5.
y = – 3x + 4
Answer: 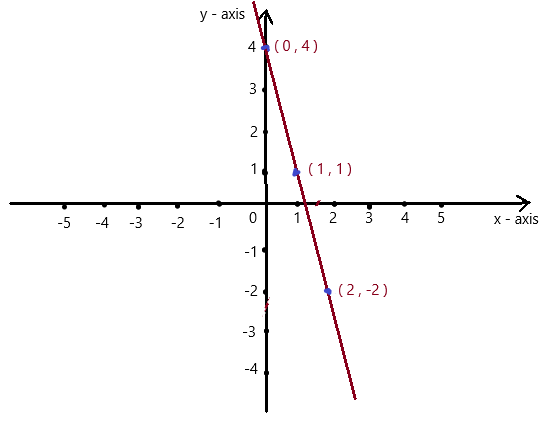
Explanation:
Given , y = – 3x + 4 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = – 3(0) + 4 = 4 . co-ordinates are (0 , 4)
if x = 1 , then y = – 3(1) + 4 = -3 + 4 = 1 , co-ordinates are (1 , 1)
if x = 2 , then y = – 3(2) + 4 = -6 + 4 = -2 , co-ordinates are (2 , -2)
The co-ordinates (0 , 4) , (1 , 1) , (2 , -2) form a straight line .
So, y = – 3x + 4 is a linear equation.
Question 6.
Which word best describes two figures that have the same size and the same shape?
A. congruent
B. adjacent
C. parallel
D. similar
Answer: A. congruent
Explanation:
Two figures which have the same size and shape are congruent.
Concepts, Skills, &Problem Solving
INTERPRETING DIAGRAMS Describe the relationship between the inputs and outputs in the diagram. Then complete the diagram. Is there more than one possible answer? Explain your reasoning. (See Exploration 1, p. 275.)
Question 7.
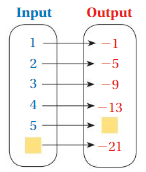
Answer: The relationship between the inputs and outputs in the diagram is ,
For every increase in number of input is having the output of adding -4 to the previous output.
Explanation: 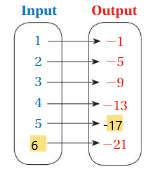
The relationship between the inputs and outputs in the diagram is ,
For every increase in number of input is having the output of adding -4 to the previous output ,
for input 1 = -1 as output
for input 2 = -1 + (-4) = -5 as output
for input 3 = -5 + (-4) = -9 as output
for input 4 = -9 + (-4) = -13 as output
for input 5 = -13 + (-4) = -17 as output
for input 6 = -17 + (-4) = -21 as output.
So, The relationship between the inputs and outputs in the diagram is ,
For every increase in number of input is having the output of adding -4 to the previous output .
In this case , we are witnessing only one output for one input.
Question 8.
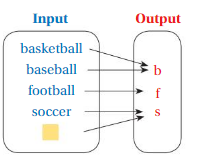
Answer: The relationship between the inputs and outputs in the diagram is,
Each input has the sports name and the output has the Starting letter of sports name.
Explanation: 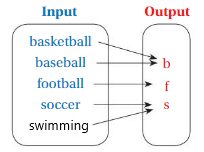
The relationship between the inputs and outputs in the diagram is,
Each input has the sports name and the output has the Starting letter of sports name.
For input basketball = b as output
For input baseball = b as output
For input football = f as output
For input soccer = s as output
For input swimming = s as output,
So, The relationship between the inputs and outputs in the diagram is,
Each input has the sports name and the output has the Starting letter of sports name.
In this case we have more than one output for input.
LISTING ORDERED PAIRS List the ordered pairs shown in the mapping diagram.
Question 9.
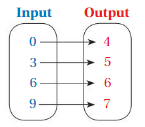
Answer: Ordered pairs are ( 0 , 4 ) , ( 3 , 5 ) , ( 6 , 6 ) , ( 9 , 7 ) .
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 0 , 4 ) , ( 3 , 5 ) , ( 6 , 6 ) , ( 9 , 7 ) .
Question 10.
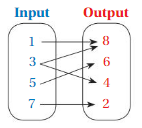
Answer: Ordered pairs are ( 1 , 8 ) , ( 3 , 8 ) , ( 3 , 4 ) , ( 5 , 6 ) , ( 7 , 2 ).
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 1 , 8 ) , ( 3 , 8 ) , ( 3 , 4 ) , ( 5 , 6 ) , ( 7 , 2 ).
Question 11.
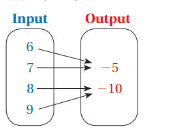
Answer: Ordered pairs are ( 6 , -5 ) , ( 7 , -5 ) , ( 8 , -10 ) , ( 9 , -10 ).
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 6 , -5 ) , ( 7 , -5 ) , ( 8 , -10 ) , ( 9 , -10 ).
IDENTIFYING FUNCTIONS Determine whether the relation is a function.
Question 12.
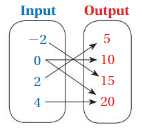
Answer: The relation is not a function .
Explanation:
The each input has more than two outputs , That is one input has multiple number of outputs.
Here , input 0 has two outputs which are 10 and 20 .
So , The relation is not a function .
Question 13.
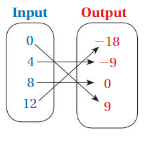
Answer: The relation is a function .
Explanation:
Each input has exactly one output ,
So , The relation is a function .
Question 14.
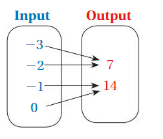
Answer: The relation is a function .
Explanation:
Each input has exactly one output ,
So , The relation is a function .
Question 15.
YOU BE THE TEACHER
Your friend determines whether the relation shown in the mapping diagram is a function. Is your friend correct? Explain your reasoning.
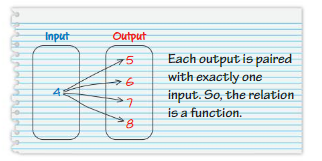
Answer: The relation is not a function .
Explanation:
The each input has more than two outputs , That is one input has multiple number of outputs.
Here , input 4 has four outputs which are 5, 6 , 7 and 8.
So , The relation is not a function .
REASONING Draw a mapping diagram that represents the relation. Then determine whether the relation is a function. Explain.
Question 16.
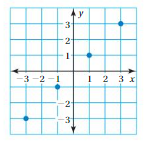
Answer: The mapping diagram representing the relation is 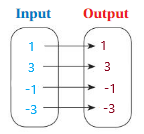
Explanation:
From the given graph , co-ordinates of the ordering pairs are( 1 , 1 ), ( 3 , 3 ), ( -1 , -1 ), ( -3 , -3 ).
Each input has exactly one output ,
So , The relation is a function .
Question 17.
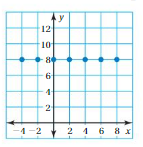
Answer: The mapping diagram representing the relation is 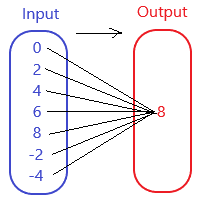
Explanation:
From the given graph , co-ordinates of the ordering pairs are( 0 , 8 ),( 2 , 8 ),( 4 , 8 ),( 6 , 8 ),( 8 , 8 ),( -2 , 8 ),( -4 , 8 ). Each input has exactly one output ,
So , The relation is a function.
Question 18.
Answer: The mapping diagram representing the relation is 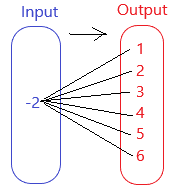
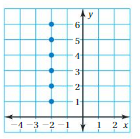
Explanation:
From the given graph , co-ordinates of the ordering pairs are( -2 , 1 ),( -2 , 2 ),( -2 , 3 ),( -2 , 4 ),( -2 , 5 ),( -2 , 6 ).
Each input has more than one output ,
So , The relation is not a function.
Question 19.
MODELING REAL LIFE
The normal pressure at sea level is 1 atmosphere of pressure(1 ATM). As you dive below sea level, the pressure changes. The mapping diagram represents the pressures at different depths.
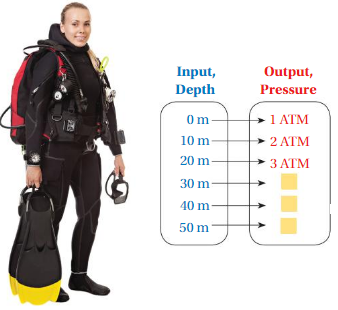
a. Complete the mapping diagram.
b. Is pressure a function of depth?
c. Describe the relationship between pressure and depth.
d. List the ordered pairs. Then plot the ordered pairs in a coordinate plane. What do you notice about the points?
e. RESEARCH What are common depths for beginner scuba divers? What are common depths for experienced scuba divers?
Answer: The detailed explanation of all the answers are given below .
Explanation:
a. The mapping diagram is 
b. Yes , the pressure is a function of depth, Because depth is related to pressure in the given mapping diagram.
c. The relationship between pressure and depth is,
for every 10m increase in Depth of input there is an increase in 1 ATM pressure .
d. The ordered pairs are ( 0 , 1 ) , ( 10 , 2 ) , (20 , 3 ) , ( 30 , 4 ) , ( 40 , 5 ), ( 50 , 6 ).
The plot of the ordered pairs in a coordinate plane is 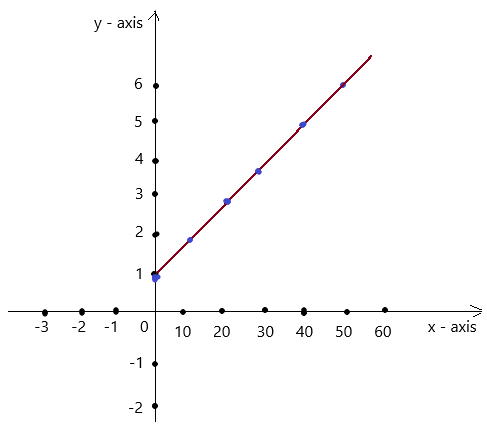
From the graph, we have seen that, if the depth of the diving of scuba drivers increases then the water pressure increases with increase in depth. So, the graph have straight line .
e. The common depths for beginner scuba divers is 30 feet to 60 feet or 9 to 18 meters ,
The common depths for experienced scuba divers is more than 60 feet or more than 18 meters .
Question 20.
DIG DEEPER!
The table shows the cost of purchasing 1, 2, 3, or 4 T-shirts from a souvenir shop.
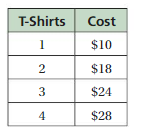
a. Is the cost a function of the number of T-shirts purchased?
b. Describe the relationship between the cost and the number cost per T-shirt of T-shirts purchased. How does the change as you purchase more T-shirts?
Answer: The detailed explanation of all the answers are given below .
Explanation:
a. Yes , The cost is a function of the number of T-shirts purchased, Because the cost of the purchased T-shirts is varying with the number of T-shirts purchased.
b. The relationship between the cost and the number cost per T-shirt of T-shirts purchased is,
Input is the cost of 1 T-shirt is $10 as output , Then for 2 T-shirts cost will be $20
If 2 T-shirts will be purchased at same time, cost will be decreased by $2 so it will be $10 + 8 = $18 for 2 T-shirts.
As per the single T-shirt cost , For 3 T-shirts will be $30,
So in the table given that 3 T-shirts will cost $24 , because it cost $18 + 6 = $24 for 3 T-shirts.
It goes same for 4 T-shirts , For 4 T-shirts will be $40, because it cost $24 + 4 = $28 for 4 T-shirts.
The change as you purchase more T-shirts is For every increase in purchase of the number of T-shirts is decrease in the cost of total T-shirts purchased.
Question 21.
REPEATED REASONING
The table shows the outputs for several inputs. Use two methods to predict the output for an input of 200.
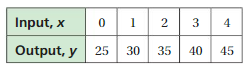
Answer: The output for an input of 200 is 1025.
Explanation:
Method 1. The relation between inputs and outputs is as follows,
y = 25 + 5x
As input increases by 1 , output increases by 5 units,
To find output of 200 as input ,
put x = 200 in the equation,
y = 25 + 5(200)
= 25 + 1000
= 1025.
So , y = 1025.
Method 2. As the table shown, for every increase in input there is an increase in 5 numbers in output,
So , For 1 input = 25 + 5 = 30 as output
For 2 input = 30 + 5 = 35 as out put
For 3 input = 35 + 5 = 40 as out put
For 4 input = 40 + 5 = 45 as out put
By doing this for number 200 as input we have , 1025 as output.
Lesson 7.2 Representations of Functions
EXPLORATION 1
Using a Table to Describe Relationships
Work with a partner. Make a table that shows the relationship between the figure number x and the area A of each figure. Then use an equation to find which figure has an area of 81 square units when the pattern continues.
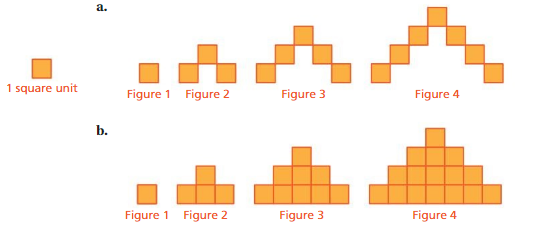
Answer: a. The equation is y = 2x – 1, For figure has an area of 81 square units is 41.
b. The equation is y = x², For figure has an area of 81 square units is 9.
Explanation:
a. figure shows the 1 square unit of each box for and it has a pattern of 2x – 1
figure 1 = 1 square unit
figure 2 =3 square units
figure 3 = 5 square unit and so on
So, the equation is y = 2x – 1 , it is in the form of y = mx + c,
Given to which figure has an area of 81 square units
substitute y = 81, we have
y = 2x – 1
81 = 2x – 1
2x = 82
x = 41
So, For figure has an area of 81 square units is 41.
b. As shown above , we know that ,
figure 1 = 1 square unit
figure 2 =4 square units
figure 3 = 9 square unit and so on
Here we have a pattern of power of its own number,
So, the Equation will be y = x²
Given to which figure has an area of 81 square units
substitute y = 81, we have
x = 9
So, For figure has an area of 81 square units is 9.
EXPLORATION 2
Using a Graph
Work with a partner. Use a graph to test the truth of each statement. If the statement is true, write an equation that shows how to obtain one measurement from the other.

a. “You can find the horsepower of a race-car car engine if you know its volume in cubic inches”

b. “You can find the volume of a race-car engine in cubic centimeters if you know its volume in cubic inches.”

Answer: a. Given ordered pairs are (200 , 375) , (350 , 650) , (350 , 250) , (500 , 600)
We can not find the horsepower of a race-car car engine if you know its volume in cubic inches
b. Given ordered pairs are (100 , 1640) , (200 , 3280) , (300 , 4920) ,
Yes, You can find the volume of a race-car engine in cubic centimeters if you know its volume in cubic inches
Explanation:
a. Given ordered pairs are (200 , 375) , (350 , 650) , (350 , 250) , (500 , 600)
We can not find the horsepower of a race-car car engine if you know its volume in cubic inches
b. Given ordered pairs are (100 , 1640) , (200 , 3280) , (300 , 4920) ,
Yes, You can find the volume of a race-car engine in cubic centimeters if you know its volume in cubic inches

Try It
Question 1.
Write a function rule for “The output is one-fourth of the input.”
Answer: y = \(\frac{x}{4}\)
Explanation:
Let us say x is input and y is output , then
The output is one-fourth of the input, will be ,
y = \(\frac{x}{4}\).
Find the value of y when x = 5.
Question 2.
y = 4x – 1
Answer: y = 19.
Explanation:
Given, y = 4x – 1
substitute x = 5 , we get
y = 4(5) – 1
y = 20 – 1 = 19
So, y = 19.
Question 3.
y = 10x
Answer: y = 50
Explanation:
Given, y =10x
substitute x = 5 , we get
y = 10(5)
y = 50
So, y = 50.
Question 4.
y = 7 – 3x
Answer: y = -8.
Explanation:
Given, y = 7 – 3x
substitute x = 5 , we get
y = 7 – 3(5)
y = 7 – 15 = -8
So, y = -8.
Graph the function.
Question 5.
y = x + 1
Answer: 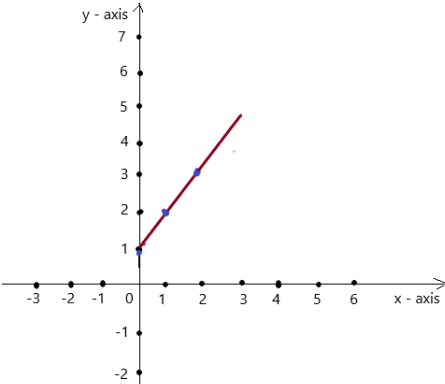
Explanation:
Given , y = x + 1 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 + 1 = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = 1 + 1 = 2 . co-ordinates are (1 , 2)
if x = 2 , then y = 2 + 1 = 3 , co-ordinates are (2 , 3)
The co-ordinates (0 , 1) , (1 , 2) , (2 , 3) form a straight line .
Question 6.
y = – 3x
Answer: 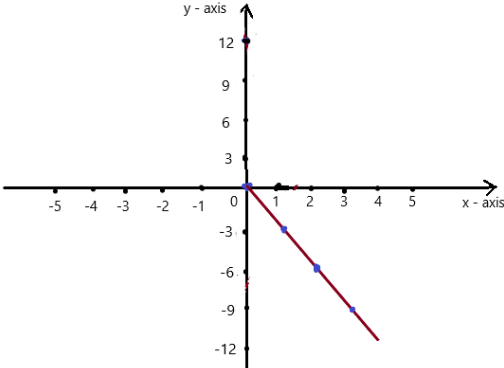
Explanation:
Given , y = – 3x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = -3(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = -3(1) = -3 . co-ordinates are (1 , -3)
if x = 2 , then y = -3(2) = -6 , co-ordinates are (2 , -6)
if x = 3 , then y = -3(3) = -9 , co-ordinates are (3 , -9)
The co-ordinates (0 , 0) , (1 , -3) , (2 , -6) ,(3 , -9) form a straight line .
Question 7.
y = 3x + 2
Answer: 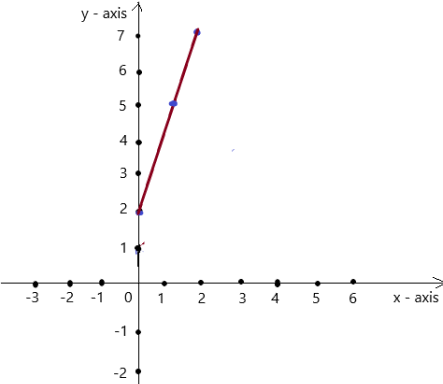
Explanation:
Given , y = 3x + 2 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =3(0) + 2 = 2 . co-ordinates are (0 , 2)
if x = 1 , then y = 3(1) + 2= 5 . co-ordinates are (1 , 5)
if x = 2 , then y =3(2) + 2 = 7 , co-ordinates are (2 , 7)
The co-ordinates (0 , 2) , (1 , 5) , (2 , 7) form a straight line .
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING FUNCTION RULES Write a function rule for the statement.
Question 8.
The output is three times the input.
Answer: y = 3x
Explanation:
Let us say x is input and y is output , then
The output is three times the input. will be ,
So , y = 3x .
Question 9.
The output is eight more than one-seventh of the input.
Answer: y = 8 + \(\frac{x}{7}\) .
Explanation:
Let us say x is input and y is output , then
The output is eight more than one-seventh of the input., will be ,
So, y = 8 + \(\frac{x}{7}\) .
EVALUATING A FUNCTION Find the value of y when x = 5.
Question 10.
y = 6x
Answer: y = 30
Explanation:
Given, y = 6x
substitute x = 5 , we get
y = 6(5) =30
So, y = 30
Question 11.
y = 11 – x
Answer: y = 6
Explanation:
Given, y = 11 – x
substitute x = 5 , we get
y = 11 – 5 = 6
So, y = 6.
Question 12.
y = \(\frac{1}{5}\)x + 1
Answer: y = 2.
Explanation:
Given, y = \(\frac{1}{5}\)x + 1
substitute x = 5 , we get
y = \(\frac{x}{5}\) + 1
y= \(\frac{5}{5}\) + 1
y = 1 + 1 = 2
So, y = 2 .
GRAPHING A FUNCTION Graph the function.
Question 13.
y = – 2x
Answer: 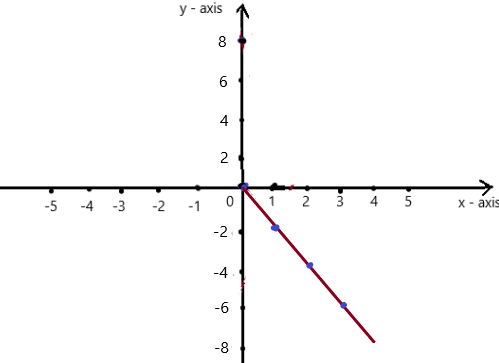
Explanation:
Given , y = – 2x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = – 2(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = – 2(1)= -2 . co-ordinates are (1 , -2)
if x = 2 , then y =- 2(2) = -4 , co-ordinates are (2 , -4)
if x = 3 , then y =- 2(3) = -6 , co-ordinates are (3 , -6)
The co-ordinates (0 , 0) , (1 , -2) , (2 , -4) , (3 , -6) form a straight line .
Question 14.
y = x – 3
Answer: 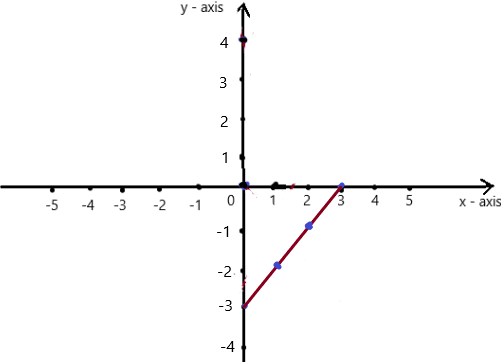
Explanation:
Given , y = x – 3 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 – 3 = -3 . co-ordinates are (0 , -3)
if x = 1 , then y = 1 – 3= -2 . co-ordinates are (1 , -2)
if x = 2 , then y = 2 – 3 = -1 , co-ordinates are (2 , -1)
if x = 3 , then y = 3 – 3 = 0 , co-ordinates are (3 , 0)
The co-ordinates (0 , -3) , (1 , -2) , (2 , -1) , (3 , 0) form a straight line .
Question 15.
y = 9 – 3x
Answer: 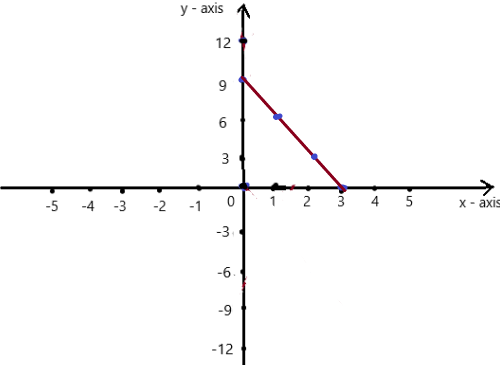
Explanation:
Given , y = 9 – 3x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 9 – 3(0) = 9 . co-ordinates are (0 , 9)
if x = 1 , then y = 9 – 3(1) = 6 . co-ordinates are (1 , 6)
if x = 2 , then y = 9 – 3(2) = 3 , co-ordinates are (2 , 3)
if x = 3 , then y = 9 – 3(3) = 0 , co-ordinates are (3 , 0)
The co-ordinates (0 , 9) , (1 , 6) , (2 , 3) , (3 , 0) form a straight line .
Question 16.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer: As mentioned in the explanation below a & d , b & c are different .
Explanation:
Given ,
a. what output is 4 more than twice the input 3?
Let us say that , y is output and x is input and given as 3 ,
then, we have y = 4 + 2(3) = 10.
b. What output is twice the sum of the input 3 and 4?
Let us say that , y is output and x is input and given as 3 ,
then, we have y = 2( 3 + 4 ) = 14.
c. what output is the sum of 2 times the input 3 and 4?
Let us say that , y is output and x is input and given as 3 ,
then, we have y = 2( 3 + 4 ) = 14.
d. what output is 4 increased by twice the input 3?
Let us say that , y is output and x is input and given as 3 ,
then, we have y = 4 + 2(3) = 10.
So, a & d , b & c are different .
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
The World Health Organization(WHO) suggests having 23 health-care workers for every 10,000 people. How many health-care workers are needed to meet the WHO suggestion for a population of 250,000 people? Justify your answer using a graph.

Answer: So, 575 health-care workers are needed to meet the WHO suggestion for a population of 250,000 people
Explanation:
Given, The World Health Organization(WHO) suggests having 23 health-care workers for every 10,000 people.
we need to find how many health-care workers are needed to meet the WHO suggestion for a population of 250,000 people,
For every 10,000 people we have 23 care takers
Then for 250,000 people we have
\(\frac{23 × 250,000}{10,000}\)
= 23 × 25
= 575
So, 575 health-care workers are needed to meet the WHO suggestion for a population of 250,000 people
Question 18.
DIG DEEPER!
A truck produces 22 pounds of carbon dioxide for every gallon of diesel fuel burned. The fuel economy of the truck is 18 miles per gallon. Write and graph a function that describes the relationship between carbon dioxide produced and distance traveled.
Answer: y = 22x + 18 is the linear equation
Explanation:
Given, A truck produces 22 pounds of carbon dioxide for every gallon of diesel fuel burned.
The fuel economy of the truck is 18 miles per gallon.
So, we have y = 22x + 18 is in the form of y = mx +c
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 22(0) + 18 = 18 . co-ordinates are (0 , 18)
if x = 1 , then y =22(1) + 18= 40 . co-ordinates are (1 , 40)
if x = 2 , then y =22(2) + 18 = 62 , co-ordinates are (2 , 62)
if x = 3 , then y =22(3) + 18 = 84 , co-ordinates are (3 , 84)
The co-ordinates (0 , 18) , (1 , 40) , (2 , 62) , (3 , 84) form a straight line .
The graph is 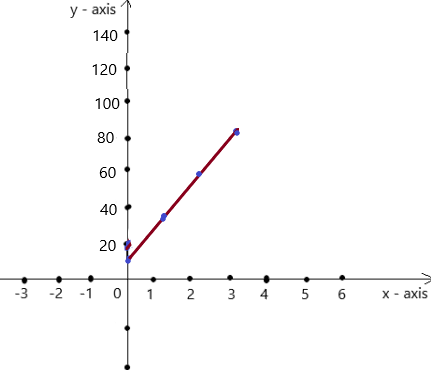
Representations of Functions Homework & Practice 7.2
Review & Refresh
Determine whether the relation is a function.
Question 1.
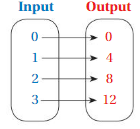
Answer: The relation is a function .
Explanation:
Each input has exactly one output ,
So , The relation is a function .
Question 2.
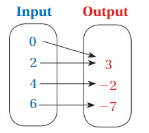
Answer: The relation is a function .
Explanation:
Each input has exactly one output ,
So , The relation is a function .
Question 3.
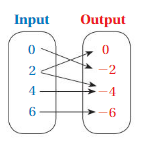
Answer: The relation is not a function .
Explanation:
The each input has more than two outputs , That is one input has multiple number of outputs.
Here , input 2 has two outputs which are 0 and -4 .
So , The relation is not a function .
Find the slope of the line.
Question 4.
Answer: slope = 1.
Explanation:
By using the slope equation , we know that
Slope = \(\frac{change in y}{change in x}\) or
slope = \(\frac{▲y}{▲x}\)
From the graph we know that change in y or ▲y is change from -2 to -4 =2
change in x or ▲x is change from 1 to 3 = 2 ,
So, slope = \(\frac{▲y}{▲x}\)
slope = \(\frac{2}{2}\)
slope = 1.
Question 5.
Answer: slope = \(\frac{5}{2}\) .
Explanation:
By using the slope equation , we know that
Slope = \(\frac{change in y}{change in x}\) or
slope = \(\frac{▲y}{▲x}\)
From the graph we know that change in y or ▲y is change from -4 to 1 = 5
change in x or ▲x is change from -1 to -3 = 2 ,
So, slope = \(\frac{▲y}{▲x}\)
slope = \(\frac{5}{2}\) .
Question 6.
Answer: slope = \(\frac{1}{3}\) .
Explanation:
By using the slope equation , we know that
Slope = \(\frac{change in y}{change in x}\) or
slope = \(\frac{▲y}{▲x}\)
From the graph we know that change in y or ▲y is change from -4 to -3 = 1
change in x or ▲x is change from 1 to 4 = 3 ,
So, slope = \(\frac{▲y}{▲x}\)
slope = \(\frac{1}{3}\) .
Concepts, Skills, & Problem Solving
USING A GRAPH Use a graph to test the truth of the statement. If the statement is true, write an equation that shows how to obtain one measurement from the other measurement. (See Exploration 2, p. 281.)
Question 7.
“You can find the weight of a cell phone in ounces if you know its screen size in inches.”

Answer: we can does not find the weight of a cell phone in ounces if you know its screen size in inches.
From the given table , Ordered pairs are (4 , 4) , (4.7 , 4.8) , (5 , 4.8) , (5.5 , 6.4)
First find the slope m of the line containing the two given points (4, 4) and (4.7, 4.8)
m = (y2-y1) / (x2-x1)
m= (4.8 – 4) / (4.7 – 4)
m = 0.8/0.7 .
So, we can does not find the weight of a cell phone in ounces if you know its screen size in inches.
Question 8.
“You can find the age of a child in years if you know the age of the child in months.”
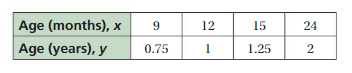
Answer: YES, y = 0.08x + 0.04 is a linear equations
Explanation:
From the given table , Ordered pairs are (9 , 0.75) , (12 , 1) , (15 , 1.25) , (24 , 2)
First find the slope m of the line containing the two given points (12 ,1) and (24, 2)
m = (y2-y1) / (x2-x1)
m= (2 – 1) / (24 – 12)
m = 1/12
m = 0.08.
substitute the slope in the (12 ,1) to get point slope to form a line.
y-y1 = m (x-x1)
y – 1 = 0.08(x – 12)
y –1 = 0.08x – 0.96
y = 0.08x –0.96 + 1
y =0.08 x + 0.04
So, y = 0.08x + 0.04 is a linear equation
WRITING FUNCTION RULES Write a function rule for the statement.
Question 9.
The output is half of the input.
Answer: y = \(\frac{x}{2}\).
Explanation:
Let us say x is input and y is output , then
The output is half of the input, will be ,
y = \(\frac{x}{2}\).
Question 10.
The output is eleven more than the input.
Answer: y = x + 11
Explanation:
Let us say x is input and y is output , then
The output is eleven more than the input, will be ,
y = x + 11
Question 11.
The output is three less than the input.
Answer: y = x – 3
Explanation:
Let us say x is input and y is output , then
The output is three less than the input, will be ,
y = x – 3
Question 12.
The output is the cube of the input.
Answer: y = x³
Explanation:
Let us say x is input and y is output , then
The output is the cube of the input, will be ,
y = x³
Question 13.
The output is six times the input.
Answer: y = 6x
Explanation:
Let us say x is input and y is output , then
The output is six times the input, will be ,
y = 6x
Question 14.
The output is one more than twice the input.
Answer: y = 2x + 1
Explanation:
Let us say x is input and y is output , then
The output is one more than twice the input, will be ,
y = 2x + 1
EVALUATING A FUNCTION Find the value of y for the given value of x.
Question 15.
y = x + 5; x = 3
Answer: y = 8
Explanation:
Given, y = x + 5
substitute x = 3 , we get
y = 3 + 5
So, y = 8.
Question 16.
y = 7x; x = – 5
Answer: y = -35.
Explanation:
Given, y = 7x
substitute x = -5 , we get
y = 7(-5)
So, y = -35.
Question 17.
y = 1 – 2x; x = 9
Answer: y = -17
Explanation:
Given, y = 1 – 2x
substitute x = 9 , we get
y = 1 – 2(9)
y = 1 – 18
So, y = -17.
Question 18.
y = 3x + 2; x = 0.5
Answer: y = 5.5
Explanation:
Given, y = 3x + 2
substitute x = 0.5 , we get
y = 3(0.5) + 2
y = 3.5 + 2
So, y = 5.5 .
Question 19.
y = 2x3; x = 3
Answer: y = 54
Explanation:
Given, y = 2x3
substitute x = 3 , we get
y = 2(3)³
y = 2 × 27 = 54
So, y = 54.
Question 20.
y = \(\frac{x}{2}\) + 9; x = – 12
Answer: y = 3
Explanation:
Given, y = \(\frac{x}{2}\) + 9
substitute x = -12 , we get
y = \(\frac{-12}{2}\) + 9
y = -6 + 9
So, y = 3 .
GRAPHING A FUNCTION Graph the function.
Question 21.
y = x + 4
Answer: 
Explanation:
Given , y = x + 4 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 + 4 = 4 . co-ordinates are (0 , 4)
if x = 1 , then y = 1 + 4 = 5 . co-ordinates are (1 , 5)
if x = 2 , then y = 2 + 4 = 6 , co-ordinates are (2 , 6)
if x = 3 , then y = 3 + 4 = 7 , co-ordinates are (3 , 7)
The co-ordinates (0 , 4) , (1 , 5) , (2 , 6) , (3 , 7) form a straight line .
Question 22.
y = 2x
Answer: 
Explanation:
Given , y = 2x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 2(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = 2(1) = 2 . co-ordinates are (1 , 2)
if x = 2 , then y = 2(2) = 4 , co-ordinates are (2 , 4)
if x = 3 , then y = 2(3) = 6 , co-ordinates are (3 , 6)
The co-ordinates (0 , 0) , (1 , 2) , (2 , 4) , (3 , 6) form a straight line .
Question 23.
y = – 5x + 3
Answer: 
Explanation:
Given , y = – 5x + 3 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =- 5(0) + 3 = 3 . co-ordinates are (0 , 3)
if x = 1 , then y = – 5(1) + 3 = -2 . co-ordinates are (1 , -2)
if x = 2 , then y = – 5(2) + 3 = -7 , co-ordinates are (2 , -7)
if x = 3 , then y = – 5(3) + 3 = -12 , co-ordinates are (3 , -12)
The co-ordinates (0 , 3) , (1 , -2) , (2 , -7) , (3 , -12) form a straight line .
Question 24.
y = \(\frac{x}{4}\)
Answer: 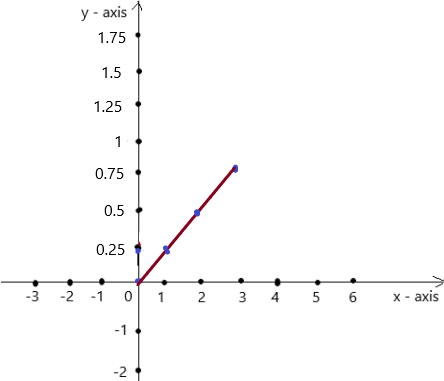
Explanation:
Given , y = \(\frac{x}{4}\) , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = \(\frac{0}{4}\) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = \(\frac{1}{4}\) = 0.25 . co-ordinates are (1 , 0.25)
if x = 2 , then y = \(\frac{2}{4}\) = 0.5 , co-ordinates are (2 , 0.5)
if x = 3 , then y = \(\frac{3}{4}\) = 0.75 , co-ordinates are (3 , 0.75)
The co-ordinates (0 , 0) , (1 , 0.25) , (2 , 0.5) , (3 , 0.75) form a straight line .
Question 25.
y = \(\frac{3}{2}\)x + 1
Answer: 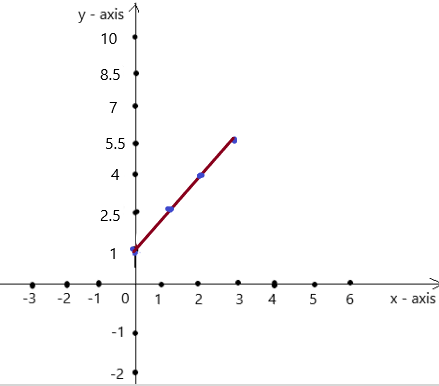
Explanation:
Given , y = \(\frac{3}{2}\)x + 1 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =\(\frac{3}{2}\)(0) + 1 = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = \(\frac{3}{2}\)(1) + 1= 2.5 . co-ordinates are (1 , 2.5)
if x = 2 , then y = \(\frac{3}{2}\)(2) + 1 = 4 , co-ordinates are (2 , 4)
if x = 3 , then y = \(\frac{3}{2}\)(3) + 1 = 5.5 , co-ordinates are (3 , 5.5)
The co-ordinates (0 , 1) , (1 , 2.5) , (2 , 4) , (3 , 5.5) form a straight line .
Question 26.
y = 1 + 0.5x
Answer: 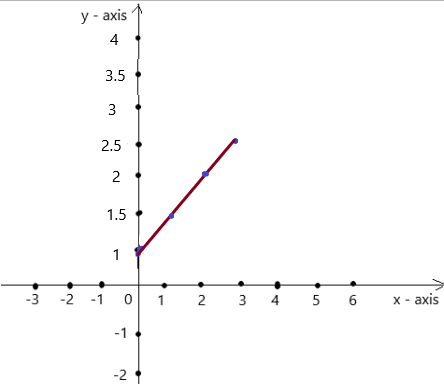
Explanation:
Given , y = 1 + 0.5x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =1 + 0.5(0) = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = 1 + 0.5(1) = 1.5 . co-ordinates are (1 , 1.5)
if x = 2 , then y = 1 + 0.5(2) = 2 , co-ordinates are (2 , 2)
if x = 3 , then y = 1 + 0.5(3) = 2.5 , co-ordinates are (3 , 2.5)
The co-ordinates (0 , 1) , (1 , 1.5) , (2 , 2) , (3 , 2.5) form a straight line .
MATCHING Match the graph with the function it represents.
A. y = \(\frac{x}{3}\)
B. y = x + 1
C. y = – 2x + 6
Question 27.
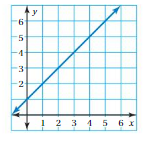
Answer: B. y = x + 1.
Explanation:
Given , y = x + 1 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 + 1 = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = 1 + 1 = 2 . co-ordinates are (1 , 2)
if x = 2 , then y = 2 + 1 = 3 , co-ordinates are (2 , 3)
The co-ordinates (0 , 1) , (1 , 2) , (2 , 3) form a straight line .
Question 28.
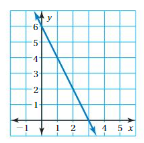
Answer: c. y = – 2x + 6
Explanation:
Given , y = – 2x + 6 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = – 2(0) + 6 = 6 . co-ordinates are (0 , 6)
if x = 1 , then y = – 2(1) + 6 = 4 . co-ordinates are (1 , 4)
if x = 2 , then y = – 2(2) + 6 = 2 , co-ordinates are (2 , 2)
if x = 3 , then y = – 2(3) + 6 = 0 , co-ordinates are (3 , 0)
The co-ordinates (0 , 6) , (1 , 4) , (2 , 2) , (3 , 0) form a straight line .
Question 29.
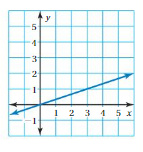
Answer: A. y = \(\frac{x}{3}\)
Explanation:
Given , y = \(\frac{x}{3}\) , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =\(\frac{0}{3}\) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = \(\frac{1}{3}\)= 0.3 . co-ordinates are (1 , 0.3)
if x = 2 , then y = \(\frac{2}{3}\)= 0.6 , co-ordinates are (2 , 0.6)
The co-ordinates (0 , 0) , (1 , 0.3) , (2 , 0.6) form a straight line .
Question 30.
YOU BE THE TEACHER
Your friend graphs the function represented by the input-output table. Is your friend correct? Explain your reasoning.
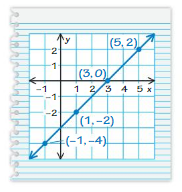
Answer: Yes , He is correct
Explanation:
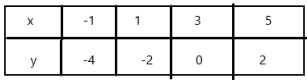
Ordered pairs are (-1 , -4) , (1 , -2) , (3 ,0) , (5 , 2)
these points form a straight line when graphed.
Yes , He is correct
Question 31.
MODELING REAL LIFE
A dolphin eats 30 pounds of fish per day.

a. Write and graph a function that relates the number p of pounds of fish that a dolphin eats in d days.
b. How many total pounds of fish does a dolphin eat in 30 days?
Answer:
Explanation:
a. Given , A dolphin eats 30 pounds of fish per day.
by each passing day eating fish is increased by the day passes .
So, y = 30x is the function,
The graph represents the function as
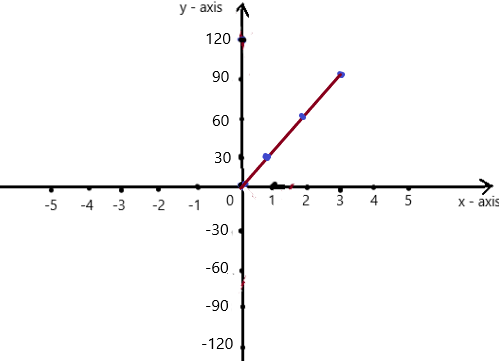
b. Given , A dolphin eats 30 pounds of fish per day.
then for 30 days ,
30 × 30 = 900 pounds
So, A dolphin eats 900 pounds of fish in 30 days
Question 32.
MODELING REAL LIFE
You fill a fish tank with 55 gallons of water on Saturday. The water evaporates at a rate of 1.5 gallons per day. You plan to add water when the tank reaches 49 gallons. When will you add water? Justify your answer.
Answer: As the action starts on Saturday , the tank will reach 49 gallons after 4 days , That is on Wednesday.
Explanation:
Given data ,, implies that slope of the function m = -1.5
The y intercept b= 55,
Then the equation will be y = 55 – 1.5x
Given , You plan to add water when the tank reaches 49 gallons.
determine x for y = 49 ,
So, 49 = 55 – 1.5x ,
1.5x = 55 – 49
1.5x = 6
x = \(\frac{6}{1.5}\)
x = 4.
As the action starts on Saturday , the tank will reach 49 gallons after 4 days , That is on Wednesday.
USING AN EQUATION Find the value of x for the given value of y.
Question 33.
y = 5x – 7; y = – 22
Answer: x = -3
Explanation:
Given, y = 5x – 7
x = \(\frac{y + 7}{5}\)
substitute y = -22 , we get
x = \(\frac{-22 + 7}{5}\)
x = \(\frac{- 15}{5}\)
x = -3
So, x = -3 .
Question 34.
y = 9 – 7x; y = 37
Answer: x = -4
Explanation:
Given, y = 9 – 7x
x = \(\frac{9 – y}{7}\)
substitute y = 37 , we get
x = \(\frac{9 – 37}{7}\)
x = \(\frac{- 28}{7}\)
x = -4
So, x = -4 .
Question 35.
y = \(\frac{x}{4}\) – 7; y = 2
Answer: x = 36
Explanation:
Given, y = \(\frac{x}{4}\) – 7
x = 4( y + 7)
substitute y = 2 , we get
x = 4( 2 + 7)
x = 4(9)
x = 36
So, x = 36 .
Question 36.
PROBLEM SOLVING
You decide to make and sell bracelets. The cost of your materials is $84.00. You charge $3.50 for each bracelet.

a. P Write a function that represents the profit for selling b bracelets.
b. Which variable is independent? dependent? Explain.
c. You will break even when the cost of your materials equals your income. How many bracelets must you sell to break even?
Answer: a. A function that represents the profit for selling b bracelets is p = 3.5b – 84.
b. Here , the profit depends on the number of bracelets sold , b is the independent variable and p is the dependent variable.
c. To break even you must sell 24 bracelets.
Explanation:
a. Given , The cost of your materials is $84.00. You charge $3.50 for each bracelet,
Let p be the profit , b be the number of bracelets sold,
So, profit = income – cost .
p = 3.5b – 84.
Thus , A function that represents the profit for selling b bracelets is p = 3.5b – 84.
b. Here , the profit depends on the number of bracelets sold , b is the independent variable and p is the dependent variable.
c. set the income expression from part a equal to the cost of 84 and solve for b ,
So, income = cost .
3.5b = 84 ,
b = \(\frac{84}{3.5}\)
b = 24.
To break even you must sell 24 bracelets.
Question 37.
MODELING REAL LIFE
A furniture store is having a sale where everything is 40% off.
a. Write and graph a function that represents the amount of discount on an item at regular price.
b. You buy a bookshelf that has a regular price of $85. What is the sale price of the bookshelf?
Answer: a. The function is y = 0.4x and the graph is given below.
b. The sale price of the bookshelf s $51.
Explanation:
a. A function that represents the amount of discount on an item at regular price is ,
Given , 40% = 0.4 ,
To find the percent of the number , we should multiply the number by the percent in the decimal form ,
so, the equation is d = 0.4p ,
let us convert it in to a function form , y = 0.4x
we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0.4(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = 0.4(1)= 0.4 . co-ordinates are (1 , 0.4)
if x = 2 , then y =0.4(2) = 0.8 , co-ordinates are (2 , 0.8)
if x = 3 , then y = 0.4(3) = 1.2 , co-ordinates are (3 , 1.2)
The co-ordinates (0 , 0) , (1 , 0.4) , (2 , 0.8) , (3 , 1.2) form a straight line .
The graph is 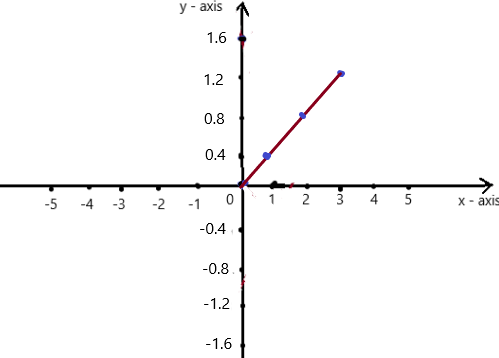
b. Given , You buy a bookshelf that has a regular price of $85.
The sale price of the bookshelf is ,
substituting the given price in p = 85 ,
it will be the discount d = 0.4 (85) = 34
Then the sale price is $85 – $34 = $51.
So, The sale price of the bookshelf s $51.
Question 38.
REASONING
You want to take a two-hour air boat tour. Which is a better deal, Snake Tours or Gator Tours? Use functions to justify your answer.

Answer: By using functions , $50 > $40 , So, Gator tours are cheaper than the snake tours .
Explanation:
Given , You want to take a two-hour air boat tour.
Let x be the hours of air boat tour and y be the cost of air boat tour ,
Snake tours , y = 25x
putt x = 2 ,
So , y = 25 (2) = 50 .
y = 50.
Gator tour , y = 35 + \(\frac{5}{2}\)x
Put x = 2 ,
So, y = 35 + \(\frac{5}{2}\) x
y = 35 + 2.5x
y = 35 + 2.5 (2)
y = 35 + 5
y = 40 .
Finally $50 > $40 , So, Gator tours are cheaper than the snake tours
Question 39.
REASONING
The graph of a function is a line that passes through the points (3, 2), (5, 8), and (8, y). What is the value of y?
Answer: The value of y is 17 , so, The third given point is (8, 17)
Explanation:
First find the slope m of the line containing the two given points (3,2) and (5,8)
m = (y2-y1) / (x2-x1)
m= (8 – 2) / (5 – 3)
m = 6 / 2
m = 3
Then use the slope and one of the given points (3,2) to find the y-intercept
y = mx +
2 = 3(3) + b
2 = 9 + b
-7 = b
The equation is y = 3x -7
Then find the third point (8, y) by replacing x by 8
y = 3x -7
y = 3(8) -7
y = 24 -7
y = 17
Question 40.
CRITICAL THINKING
Make a table where the independent variable is the side length of a square and the dependent variable is the perimeter. Make a second table where the independent variable is the side length of a square and the dependent variable is the area. Graph both functions in the same coordinate plane. Compare the functions.
Answer: The graph for the perimeter is linear , The graph for the Area is Quadratic .
Explanation:
Let us say , s be the side length of the square ,
Then the perimeter is P = 4s ,
The function will be y= 4x,
we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 4(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = 4(1) = 4 . co-ordinates are (1 , 4)
if x = 2 , then y = 4(2) =8 , co-ordinates are (2 , 8)
if x = 3 , then y = 4(3) = 0 , co-ordinates are (3 , 12)
The co-ordinates (0 , 0) , (1 , 4) , (2 ,8) , (3 , 12) form a straight line .
Table will be , 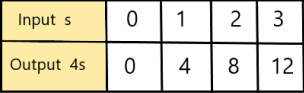
Let us say , s be the side length of the square ,
Then the Area is A = s² ,
The function will be y=x²,
we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0² = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = 1² = 1 . co-ordinates are (1 , 1)
if x = 2 , then y = 2² =4 , co-ordinates are (2 , 4)
if x = 3 , then y = 3² = 9 , co-ordinates are (3 , 9)
The co-ordinates (0 , 0) , (1 , 1) , (2 ,4) , (3 , 9) form a straight line .
Second table is 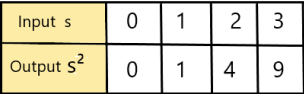
Then the graph is 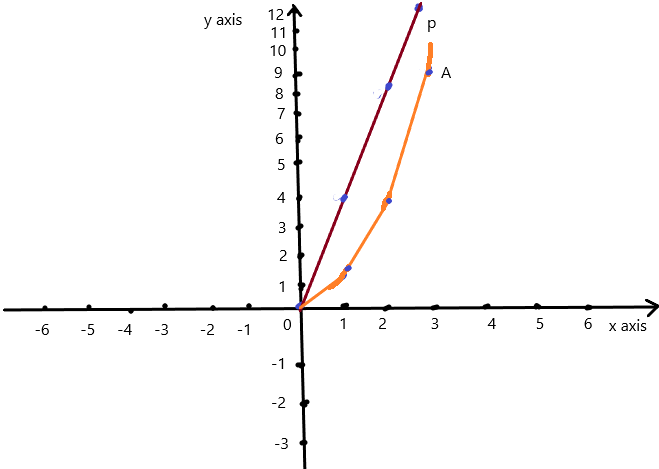
The graph for the perimeter is linear , The graph for the Area is Quadratic .
Question 41.
PUZZLE
The blocks that form the diagonals of each square are shaded. Each block has an area of one square unit. Find the “green area” of Square 20. Find the “green area” of Square 21. Explain your reasoning.
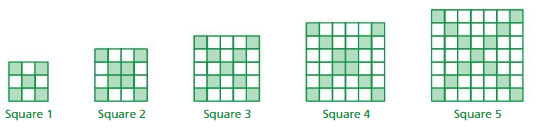
Answer: The green area of the Square 20 is 46 square units and The green area of the Square 21 is 48 square units.
Explanation:
Given , Each block has an area of one square unit,
Square 1 has the diagonals of each square are shaded. the “green area” is 3 + 3 = 6 square units ,
Square 2 has the diagonals of each square are shaded. the “green area” is 4 + 4 = 8 square units ,
Square 3 has the diagonals of each square are shaded. the “green area” is 5 + 5 = 10 square units ,
Square 4 has the diagonals of each square are shaded. the “green area” is 6 + 6 = 12 square units,
Square 5 has the diagonals of each square are shaded. the “green area” is 7 + 7 = 14 square units ,
Here , The number of squares are increasing by one block with the square numbers.
So for the , Square 20 has the diagonals of each square are shaded. the “green area” is 23 + 23 = 46 square units,
And Square 21 has the diagonals of each square are shaded. the “green area” is 24 + 24 = 48 square units.
Lesson 7.3 Linear Functions
EXPLORATION 1
Writing and Graphing Functions
Work with a partner. Each table shows a familiar pattern from geometry.
- Determine what the variables x and y represent. Then write a function rule that relates y to x.
- Is the function a linear function? Explain your reasoning.
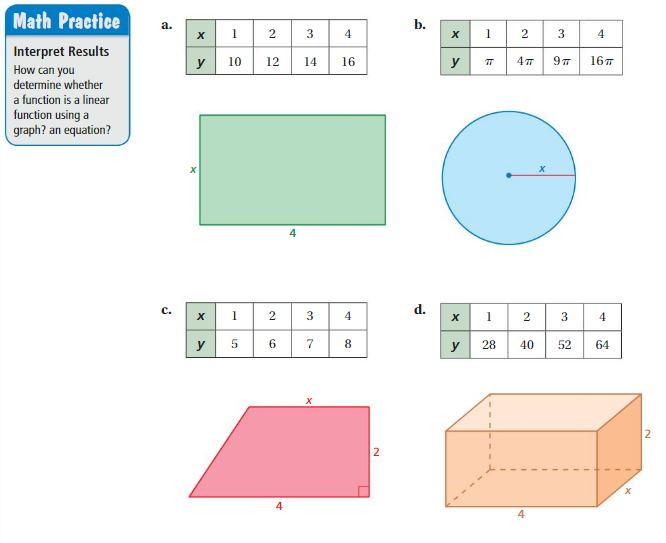
Answer: All of them are explained below
Explanation:
The variables x and y represents a rectangle
a. From the given table , Ordered pairs are (1 , 10) , (2 , 12) , (3 , 14) , (4 , 16)
First find the slope m of the line containing the two given points (1 ,-1) and (2, -2)
m = (y2-y1) / (x2-x1)
m= (-2 – (-1)) / (2 – 0)
m = -1 / 2 .
substitute the slope in the (1 , 10) to get point slope to form a line.
y-y1 = m (x-x1)
y – 10 = -1/2 ( x –1)
2(y – 10) = -x + 1
2y – 20 = -x+ 1
2y = -x + 21
y = \(\frac{-1}{2}\) (x – 21)
So , y = \(\frac{-1}{2}\) (x – 21) is linear function.
b. The variables x and y represent a circle
Ordered pairs are (1 , 3.14 ) , (2 , 6.28) , (3 , 9.42) , (4 , 12.5 )
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (1 , 3.14 ) , (2 , 6.28)
m = (y2-y1) / (x2-x1)
m= (6.28 –3.14) / (2– 1)
m = 3.14/1
m = 3.14
substitute the slope in the (8 , 4) to get point slope to form a line.
y-y1 = m (x-x1)
y – 3.14 =3.14 ( x –1)
y – 3.14 = 3.14x – 3.14
y = 3.14x – 3.14 + 3.14
y = 3.14x
So , y = 3.14x is linear function.
Where x is the diameter of the circle.
c. The variables x and y represents a trapezoid
a. From the given table , Ordered pairs are (1 , 5) , (2 , 6) , (3 , 7) , (4 , 8)
First find the slope m of the line containing the two given points (1 ,5) and (2, 6)
m = (y2-y1) / (x2-x1)
m= (6 – 5) / (2 – 1)
m = 1 .
substitute the slope in the (1 ,5) to get point slope to form a line.
y-y1 = m (x-x1)
y – 5 = 1(x – 1)
y – 5 = x – 1
y = x – 1 + 5
y = x + 4
So, y = x + 4 is a linear equation
d. The variables x and y represents a cube
a. From the given table , Ordered pairs are (1 , 28) , (2 , 40) , (3 , 52) , (4 , 64)
First find the slope m of the line containing the two given points (1 ,28) and (2, 40)
m = (y2-y1) / (x2-x1)
m= (40 – 28) / (2 – 1)
m = 12 .
substitute the slope in the (1 ,28) to get point slope to form a line.
y-y1 = m (x-x1)
y – 28 = 12(x – 1)
y – 28 = 12x – 12
y = 12x – 12 + 28
y = 12x + 16
So, y = 12x + 16 is a linear equation.

Try It
Question 1.
Use the graph to write a linear function that relates y to x.
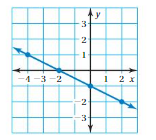
Answer: the linear function is y = \(\frac{-1}{2}\)x -1.
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-4 , 1) , (-2 , 0 ) , (0 , -1) , ( 2, -2 )
First find the slope m of the line containing the two given points (0 ,-1) and (2, -2)
m = (y2-y1) / (x2-x1)
m= (-2 – (-1)) / (2 – 0)
m = -1 / 2 .
Because the line crosses the y axis at ( 0, -1 ) , The y intercept is -1.
So , the linear function is y = \(\frac{-1}{2}\)x -1.
Question 2.
Use the table to write a linear function that relates y to x.
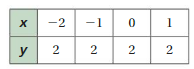
Answer: the linear function is y = (0)x + 2.
Explanation:
Ordered pairs are (-2 , 2) , (-1 , 2) , (0 , 2) , (1 , 2)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (0 ,2) and (1, 2)
m = (y2-y1) / (x2-x1)
m= (2 – 2) / (1 – 0)
m = 0
Because the line crosses the y axis at ( 0, 2 ) , The y intercept is 2.
So , the linear function is y = (0)x + 2.
Question 3.
WHAT IF?
The rate of descent doubles. Repeat parts (a) and (b).
Answer: a. the linear function is y = -1x + 65.
b. The slope indicates that the height decreases 1000 feet per minute.
The y intercept indicates that the descent begins at a cruising altitude of 65,000 feet.
Explanation:
a. From the Given table , The rate of descents is 5
If it doubles , then The rate of descents is 10.
The the ordered pairs will be (0 , 65) , (10 ,55) , (20 , 45) .
First find the slope m of the line containing the two given points (0 ,65) and (10, 55)
m = (y2-y1) / (x2-x1)
m= (55 – 65) / (10 – 0)
m = -10 / 10
m = -1
Because the line crosses the y axis at ( 0, 65 ) , The y intercept is 65.
So , the linear function is y = -1x + 65.
b. The slope indicates that the height decreases 1000 feet per minute.
The y intercept indicates that the descent begins at a cruising altitude of 65,000 feet.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
WRITING A LINEAR FUNCTION
Use the graph to write a linear function that relates y to x.
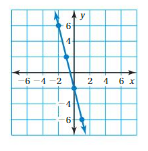
Answer: The linear function is y = -4x -2 .
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-2 , 6) , (-1 , 2 ) , (0 , -2) , ( 1, -6 )
First find the slope m of the line containing the two given points (0 ,-2) and (1, -6)
m = (y2-y1) / (x2-x1)
m= (-6 – (-2)) / (1 – 0)
m = -4 .
Because the line crosses the y axis at ( 0, -2) , The y intercept is -2.
So , the linear function is y = -4x -2 .
Question 5.
INTERPRETING A LINEAR FUNCTION
The table shows the revenue R (in millions of dollars) of a company when it spends A (in millions of dollars) on advertising.

a. Write and graph a linear function that relates R to A.
b. Interpret the slope and the y-intercept.
Answer: a. The linear function is y = 2x + 2. and the graph is shown below
b. The slope indicates that the increasing in the amount of spending on advertising by 2 million dollars
The y intercept indicates that the Revenue begins to increasing from the 2 million dollars.
Explanation:
a. From the given table ,
The the ordered pairs will be (0 , 2) , (2 ,6) , (4 , 10) , (6 , 14) , (8 ,18) .
The graph is 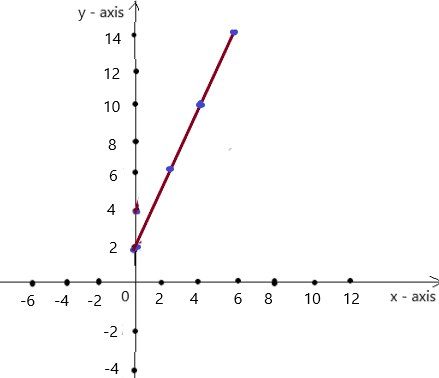
First find the slope m of the line containing the two given points (0 ,2) and (2, 6)
m = (y2-y1) / (x2-x1)
m= (6 – 2) / (2 – 0)
m = 4 / 2
m = 2
Because the line crosses the y axis at ( 0, 2 ) , The y intercept is 2.
So , the linear function is y = 2x + 2.
b. The slope indicates that the increasing in the amount of spending on advertising by 2 million dollars
The y intercept indicates that the Revenue begins to increasing from the 2 million dollars.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
Manager A earns $15 per hour and receives a $50 bonus. The graph shows the earnings of Manager B. (a) Which manager has a greater hourly wage? (b) After how many hours does Manager B earn more money than Manager A?
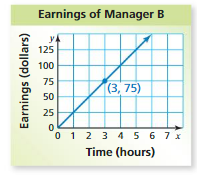
Answer: a. Manager B has the greater hourly wage than Manager A .
b. As manager A receives a $50 bonus , Manager B has to work an hour extra to earn more money than Manager A .
Explanation:
a. Manager A earns $15 per hour and receives a $50 bonus.
The ordered pairs will be (0 , 0) , (1 , 15) , (2 , 30) , (3 , 45)
The graph shows the earnings of Manager B.
Ordered pairs from the graph are (0 , 0) , (1 , 25) , (2 , 50) , (3 , 75)
So, Manager B has the greater hourly wage than Manager A .
b. As manager A receives a $50 bonus , Manager B has to work an hour extra to earn more money than Manager A .
Question 7.
Each month, you start with 2 gigabytes of data and use 0.08 gigabyte per day. The table shows the amount (in gigabytes) of data that your friend has left days after the start of each month. Who runs out of data first? Justify your answer.
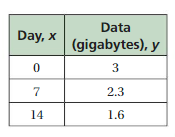
Answer: you will be run out of data first
Explanation:
a. Given , Each month, you start with 2 gigabytes of data and use 0.08 gigabyte per day.
Let x be the number of days and y be the total data in gigabytes.
So, y = -0.08x + 2 ,
You will be out of data if , -0.08x + 2 = 0 ,
-0.08x + 2 = 0
2 = 0.08x
x = \(\frac{2}{0.08}\)
x = 25.
Hence ,you will be run out of data in 25 days.
b. Daily data usage for the friend will be given by the slope of the graph.
The the ordered pairs will be (0 , 3) , (7 ,2.3) , (14 , 1.6) .
First find the slope m of the line containing the two given points (7 ,2.3) and (14, 1.6)
m = (y2-y1) / (x2-x1)
m= (1.6 – 2.3) / (14 – 7)
m = -0.7 / 7
m = -0.1
Because the line crosses the y axis at ( 0, 3 ) , The y intercept is 3.
So , the linear function is y = -0.1x + 3.
Your friend will be out of data if ,
-0.1x + 3 = 0
3 = 0.1x
x = \(\frac{3}{0.1}\)
x = 30 .
Hence ,Friend will be run out of data in 30 days
So , you will be run out of data first
Linear Functions Homework & Practice 7.3
Review & Refresh
Write a function rule for the statement. Then graph the function.
Question 1.
The output is ten less than the input.
Answer: y = x – 10.
Explanation:
Let us say x is input and y is output , then
The output is ten less than the input, will be ,
y = x – 10.
Question 2.
The output is one-third of the input.
Answer: y = \(\frac{x}{3}\)
Explanation:
Let us say x is input and y is output , then
The output is one-third of the input, will be ,
y = \(\frac{x}{3}\) .
Solve the system.
Question 3.
y = x + 5
y = – 3x + 1
Answer: X = 0 , Y = 5
Explanation:
Y=−3X+5 ——————-(1)
Y=X+5 ——————(2)
Substitute Y=X+5 in equation (1)
X+5=−3X+5
Solve it for X
X+3X=5−5
4X=0
X=0/4=0
X = 0
Substitute X=0 in equation (1)
Y=0+5
Y=5
Question 4.
x + y = – 4
6x + 2y = 4
Answer: X = 3 , Y= -7 .
Explanation:
2Y=−6X+4 ——————-(1)
Y= –X-4 ——————(2)
Substitute Y= –X-4 in equation (1)
2Y = −6X+4
2 ( –X – 4 ) = −6X + 4
-2X – 8 = -6X + 4
6X -2X = 8 + 4
4X = 12
X = 3
Substitute X=3 in equation (2)
Y=– 3 – 4
Y= -7 .
Question 5.
– 4x + 3y = 14
y = 2x + 8
Answer: X = -5 , Y = -2 .
Explanation:
3Y = 4X+14 ——————-(1)
Y = 2X + 8 ——————(2)
Substitute Y= 2X + 8 in equation (1)
3Y = 4X+14
3(2X + 8) = 4X+14
6X + 24 = 4X + 14
6X – 4X = 14 – 24
2X = -10
X = -5
Substitute X= -5 in equation (2)
Y= 2(-5) + 8
Y= -10 + 8
Y = -2.
Concepts, Skills, &Problem Solving
WRITING AND GRAPHING FUNCTIONS The table shows a familiar pattern from geometry. (a) Determine what the variables x and y represent. Then write a function rule that relates y to x. (b) Is the function a linear function? Explain your reasoning. (See Exploration 1, p. 289.)
Question 6.
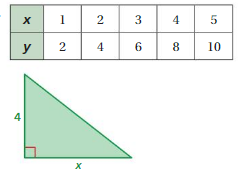
Answer: a. The variables x and y represent a right angle triangle
b. y = 2x is linear function.
Explanation:
In order to write the function we have to write the ordered pairs
Ordered pairs are (1 , 2) , (2 , 4) , (3 , 6 ) , (4 , 8), (5 , 10 ) .
a. the variables x and y represent a right angle triangle
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (1 , 2) , (2 , 4)
m = (y2-y1) / (x2-x1)
m= (4 – 2) / (2– 1)
m = 2/1
m = 2
b. substitute the slope in the (2 , 4) to get point slope to form a line.
y-y1 = m (x-x1)
y – 4 = 2 ( x – 2)
y – 4 = 2x – 4
y = 2x – 4 + 4
y = 2x
So , y = 2x is linear function.
Given side of triangle is 4 then x= 4/2 = 2
x = 2 and y = 4.
Question 7.
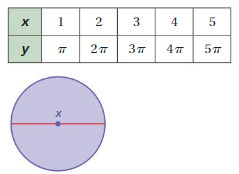
Answer: y = 3.14x is linear function. and The variables x and y represent a circle
Explanation:
Ordered pairs are (1 , 3.14 ) , (2 , 6.28) , (3 , 9.42) , (4 , 12.5 )
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (1 , 3.14 ) , (2 , 6.28)
m = (y2-y1) / (x2-x1)
m= (6.28 –3.14) / (2– 1)
m = 3.14/1
m = 3.14
substitute the slope in the (8 , 4) to get point slope to form a line.
y-y1 = m (x-x1)
y – 3.14 =3.14 ( x –1)
y – 3.14 = 3.14x – 3.14
y = 3.14x – 3.14 + 3.14
y = 3.14x
So , y = 3.14x is linear function.
Where x is the diameter of the circle.
WRITING LINEAR FUNCTIONS Use the graph or table to write a linear function that relates y to x.
Question 8.
Answer: The linear function is y = \(\frac{4}{3}\)x +2
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-3 , -2) , (0 , 2 ) , (3 , 6) , ( 6, 10 )
First find the slope m of the line containing the two given points (3 ,6) and (6, 10)
m = (y2-y1) / (x2-x1)
m= (10 – 6) / (6 – 3)
m = 4/3 .
Because the line crosses the y axis at ( 0, 2) , The y intercept is 2.
So , the linear function is y = \(\frac{4}{3}\)x +2 .
Question 9.
Answer: The linear function is y = (0)x +3 .
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-2 , 3) , (-1 , 3 ) , (0 , 3) , ( 1, 3 ) , (2 , 3)
First find the slope m of the line containing the two given points (1 ,3) and (2, 3)
m = (y2-y1) / (x2-x1)
m= (3 – 3) / (2 – 1)
m = 0 .
Because the line crosses the y axis at ( 0, 3) , The y intercept is 3.
So , the linear function is y = (0)x +3 .
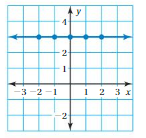
Question 10.
Answer: The linear function is y = \(\frac{-1}{4}\)x + 0.
Explanation:
Ordered pairs are (-8 , 2) , (-4 , 1) , (0 , 0) , (4 , -1)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (-8 ,2) and (-4, 1)
m = (y2-y1) / (x2-x1)
m= (1 – 2) / (-4 – (-8))
m = -1/4
Because the line crosses the y axis at ( 0, 0 ) , The y intercept is 0.
So , the linear function is y = \(\frac{-1}{4}\)x + 0.
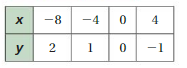
Question 11.
Answer: The linear function is y = \(\frac{2}{3}\)x + 5.
Explanation:
Ordered pairs are (-3 , 3) , (0 , 5) , (3 , 7) , (6 , 9)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (3 ,7) and (6, 9)
m = (y2-y1) / (x2-x1)
m= (9 – 7) / (6 – 3)
m = 2/3
Because the line crosses the y axis at ( 0, 5 ) , The y intercept is 5.
So , the linear function is y = \(\frac{2}{3}\)x + 5.
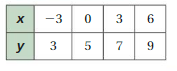
Question 12.
INTERPRETING A LINEAR FUNCTION
The table shows the length y (in inches) of a person’s hair after x months.
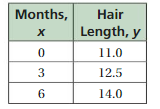
a. Write and graph a linear function that relates y to x.
b. Interpret the slope and the y-intercept.
Answer: a. The linear function is y = 0.5x + 11.
b. The slope indicates that the increasing in the hair length
The y intercept indicates that the increasing in hair length by time.
Explanation:
a. Given ,
The ordered pairs will be (0 , 11) , (3 ,12.5) , (6 , 14) .
The graph is 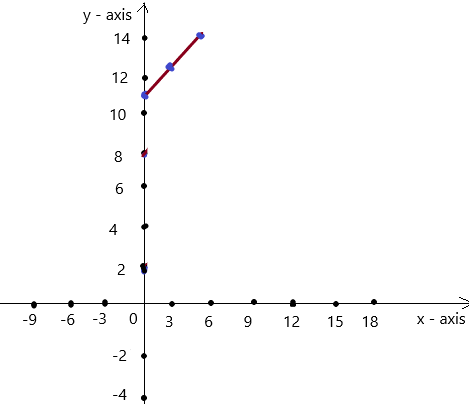
First find the slope m of the line containing the two given points (3 ,12.5) and (6 , 14)
m = (y2-y1) / (x2-x1)
m= (14 – 12.5) / (6 – 3)
m = 1.5 / 3
m = 0.5
Because the line crosses the y axis at ( 0, 11 ) , The y intercept is 11.
So , the linear function is y = 0.5x + 11.
b. The slope indicates that the increasing in the hair length
The y intercept indicates that the increasing in hair length by time.
Question 13.
INTERPRETING A LINEAR FUNCTION
The table shows the percent (in decimal form) of battery power remaining x hours after you turn on a laptop computer.
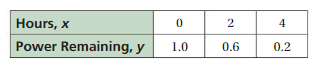
a. Write and graph a linear function that relates y to x.
b. Interpret the slope, the x-intercept, and the y-intercept.
c. After how many hours is the battery power at75%?
Answer: a. The linear function is y = -0.2x + 1.
b. given below the explanation.
c. Battery will be 75% after 1.25 hours.
Explanation:
a. Given ,
The ordered pairs will be (0 , 1) , (2 ,0.6) , (4 , 0.2) .
The graph is 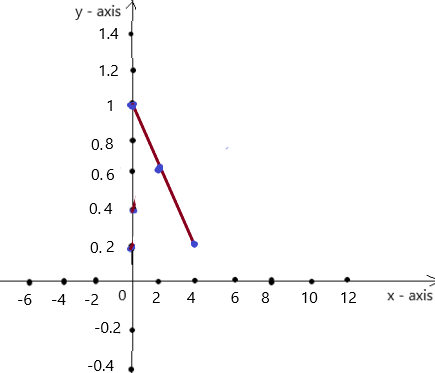
First find the slope m of the line containing the two given points (2 ,0.6) and (4 , 0.2)
m = (y2-y1) / (x2-x1)
m= (0.2 – 0.6) / (4 – 2)
m = -0.4 / 2
m = -0.2
Because the line crosses the y axis at ( 0, 1 ) , The y intercept is 1.
So , the linear function is y = -0.2x + 1.
b. Slope is -0.2 which means that as time increases by 1 hour, Battery power remaining decreases by 20% .
y intercept is 1, which means initially the battery power remaining before usage was 100%.
x intercept is 5 which means the battery remaining will be 0 after 5 hours.
c. battery percent will be 75% of 0.75 if ,
-0.2x + 1 = 0.75
0.2x = 1 – 0.75
x = 0.25/0.2
x = 1.25
Battery will be 75% after 1.25 hours.
Question 14.
MODELING REAL LIFE
The number y of calories burned after x minutes of kayaking is represented by the linear function y = 4.5x. The graph shows the number of calories burned by hiking.
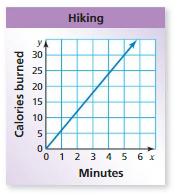
a. Which activity burns more calories per minute?
b. You perform each activity for 45 minutes. How many total calories do you burn? Justify your answer.
Answer: a. hiking burns more calories than kayaking .
b. In kayaking, 202.5 calories are burnt per minute. and In hiking , 225 calories are burnt per minute.
Explanation:
a. The number y of calories burned after x minutes of kayaking is represented by the linear function y = 4.5x.
So, The ordered pairs of the graph are (0 , 0) , (1 , 4.5) , (2 , 9) , (3, 13.5)
Here , In kayaking burns 4.5 calories per minute .
For hiking ,
The ordered pairs of the graph are (0 , 0) , (1 , 5) , (2 , 10) , (3, 15)
Here , In hiking burns 5 calories per minute.
Thus , hiking burns more calories than kayaking .
b. Given , perform each activity for 45 minutes.
Liner function of the kayaking is y = 4.5x
substitute x = 45 in equation
y = 4.5 (45)
y = 202.5
In kayaking, 202.5 calories are burnt per minute.
Linear function of the hiking is y = 5x
substitute x = 45 in equation
y = 5 (45)
y = 225
In hiking , 225 calories are burnt per minute.
Question 15.
DIG DEEPER!
You and a friend race each other. You give your friend a 50-foot head start. The distance y (in feet) your friend runs after x seconds is represented by the linear function y = 14x + 50. The table shows your distance at various times throughout the race. For what distances will you win the race? Explain.

Answer: you will win the race for distances greater than 190 feet
Explanation:
The distance y (in feet) your friend runs after x seconds is represented by the linear function y = 14x + 50.
The slope of the line is 14 so , your friend runs at the rate of 14 ft per second
To find your rate , the ordered pairs are (2 , 38) , (4 , 76) , (6 , 114) , (8 , 152)
First find the slope m of the line containing the two given points (2 ,38) and (4 , 76)
m = (y2-y1) / (x2-x1)
m= (76 – 38) / (4 – 2)
m = 38 / 2
m = 19
You are running at the rate of 19 ft per second.
To get the linear equation , substitute the slope in the (2 , 38) to get point slope to form a line.
Then we have , y = 19x
Now if x = 10 , to run faster then ,
y = 19(10)
y = 190 .
Your friend linear equation is y = 14x + 50 .
if x = 10 ,then
y = 14(10) + 50
y = 140 + 50
y = 190.
So , for x > 10 , means you will run farther than your friend which means you would win the race .
Therefore, you will win the race for distances greater than 190 feet.
Question 16.
REASONING
You and your friend are saving money to buy bicycles that cost $175 each. You have $45 to start and save an additional $5 each week. The graph shows the amount y(in dollars) that your friend has after x weeks. Who can buy a bicycle first? Justify your answer.
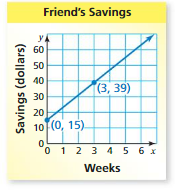
Answer: your friend will but the bicycle first.
Explanation:
Given , your friend savings are
the ordered pairs are (0,15) and (3,39)
First find the slope m of the line containing the two given points (0,15) and (3,39)
m = (y2-y1) / (x2-x1)
m= (39 – 15) / (3 – 0)
m = 24 / 3
m = 8
Because the line crosses the y axis at ( 0, 15 ) , The y intercept is 15.
So , the linear function is y = 8x + 15.
to buy bicycles that cost $175 each
if y = 175 , then
175 = 8x + 15
8x = 175 – 15
x = 160/8
x = 20
So, your friend need 20 weeks to buy the bicycle
Given, You have $45 to start and save an additional $5 each week
So , the linear function will be y = 5x + 45.
to buy bicycles that cost $175 each
if y = 175 , then
175 = 5x + 45
5x = 175 – 45
x = 130/5
x = 26
So, you need 26 weeks to buy the bicycle.
Hence, your friend will but the bicycle first.
Question 17.
CRITICAL THINKING
Is every linear equation a linear function? Explain your reasoning.
Answer: All linear equations produce straight lines when graphed, not all linear equations produce linear functions. In order to be a linear function, a graph must be both linear (a straight line) and a function (matching each x-value to only one y-value).
Question 18.
PROBLEM SOLVING
The heat index is calculated using the relative humidity and the temperature. For every 1 degree increase in the temperature from 94°F to 97°F at 75% relative humidity, the heat index rises 4°F. On a summer day, the relative humidity is 75%, the temperature is 94°F, and the heat index is 124°F. Estimate the heat index when the relative humidity is 75% and the temperature is 100°F. Use a function to justify your answer.

Answer: Heat index is 148°F
Explanation:
The form of linear equation is y = mx + c
and the slope of the function is given by m = (y2-y1) / (x2-x1)
Let y be the heat index and x be the temperature
Given , (94, 124)
For every 1 degree increase in the temperature from 94°F to 97°F at 75% relative humidity, the heat index rises 4°F
that is m = 4
Since the line passes through (94, 124) means
124 = 4x + c
124 = 4(94) + c
124 = 376 + c
c = 124 – 376
c = -252
Linear function for the heat index is y = 4x – 252
put x = 100
So, y = 4(100) – 252
y = 400 – 252
y = 148.
Finally, Heat index is 148°F.
Lesson 7.4 Comparing Linear and Non Linear Functions
EXPLORATION 1
Comparing Functions
Work with a partner. Each equation represents the height h (in feet) of a falling object after t seconds.
- Graph each equation. Explain your method.
- Decide whether each graph represents a or function.
- Compare the falling objects.
Answer: Explained below
Explanation:
a. Given, h = 300 – 15t can be written as y = 300 – 15x
h = 300 – 15t , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =300 – 15(0) = 300 . co-ordinates are (0 , 300)
if x = 1 , then y = 300 – 15(1) = 285 . co-ordinates are (1 , 285)
if x = 2 , then y = 300 – 15(2) = 270 , co-ordinates are (2 , 270)
if x = 3 , then y = 300 – 15(3) = 255 , co-ordinates are (3 , 255)
The co-ordinates (0 , 300) , (1 , 285) , (2 , 270) , (3 , 255) form a straight line .
The graph is 
Given , h = 300- 16t2 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =300- 16(0)2 = 300 . co-ordinates are (0 , 300)
if x = 1 , then y =300- 16(1)2 = 284 . co-ordinates are (1 , 284)
if x = 2 , then y = 300- 16(2)2 = 236 , co-ordinates are (2 , 236)
if x = 3 , then y = 300- 16(3)2 = 252 , co-ordinates are (3 , 252)
The co-ordinates (0 , 300) , (1 , 284) , (2 , 236) , (3 , 252) does not form a straight line .
The graph is 
b. For, h = 300 – 15t , The graph is linear so the so it is a function,
For h = 300- 16t2 , The graph is linear so the so it is a function.
c. Sky diver has the slow fall while compared to the bowling ball , because parachute can be controlled with the wind and can be divert the destination point, and bowling ball cannot be controlled while falling.

Try It
Does the table represent a linear or nonlinear function? Explain.
Question 1.
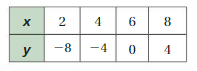
Answer: y = 2x – 12 is linear function.
Explanation:
Ordered pairs are (2 , -8) , (4 , -4) , (6 , 0) , (8 , 4)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (6 ,0) and (8, 4)
m = (y2-y1) / (x2-x1)
m= (4 – 0) / (8– 6)
m = 4/2
m = 2
substitute the slope in the (8 , 4) to get point slope to form a line.
y-y1 = m (x-x1)
y – 4 = 2 ( x – 8)
y – 4 = 2x – 16
y = 2x – 16 + 4
y = 2x – 12
So , y = 2x – 12 is linear function.
Question 2.
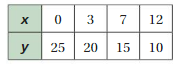
Answer: y = –\(\frac{5}{3}\)x + 25 is linear function.
Explanation:
Ordered pairs are (0 , 25) , (3 , 20) , (7 , 15) , (12 , 10)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (0 ,25) and (3, 20)
m = (y2-y1) / (x2-x1)
m= (20 – 25) / (3– 0)
m = -5/3
Because the line crosses the y axis at ( 0, 25 ) , The y intercept is 25.
So , the linear function is y = –\(\frac{5}{3}\)x + 25.
So , y = –\(\frac{5}{3}\)x + 25 is linear function.
Does the equation represent a linear or nonlinear function? Explain.
Question 3.
y = x + 5
Answer: y = x + 5 is a linear function
Explanation:
Given , y = x + 5 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 + 5 = 5 . co-ordinates are (0 , 5)
if x = 1 , then y = 1 + 5 = 6 . co-ordinates are (1 , 6)
if x = 2 , then y = 2 + 5 = 7 , co-ordinates are (2 , 7)
The co-ordinates (0 , 5) , (1 , 6) , (2 , 7) form a straight line .
Each x input has only one y output so it is a function .
And it forms a straight line when graphed .
So, y = x + 5 is a linear function.
Question 4.
y = \(\frac{4x}{3}\)
Answer: y = \(\frac{4x}{3}\) is a linear function.
Explanation:
Given , y = \(\frac{4x}{3}\) , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = \(\frac{4(0)}{3}\) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = \(\frac{4(1)}{3}\) = \(\frac{4}{3}\) = 1.3. co-ordinates are (1 , 1.3)
if x = 2 , then y = \(\frac{4(2)}{3}\) = \(\frac{8}{3}\) = 2.6 , co-ordinates are (2 , 2.6)
The co-ordinates (0 , 0) , (1 ,1.3 ) , (2 , 2.6) form a straight line .
Each x input has only one y output so it is a function .
And it forms a straight line when graphed .
So, y = \(\frac{4x}{3}\) is a linear function.
Question 5.
y = 1 – x2
Answer: y = 1 – x2 is not a linear function.
Explanation:
Given , y = 1 – x2 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 1 – 02 = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = 1 – 12 = 0 . co-ordinates are (1 , 0)
if x = 2 , then y = 1 – 22 = -3 , co-ordinates are (2 , -3)
The co-ordinates (0 , 5) , (1 , 6) , (2 , 7) form a straight line .
Each x input has only one y output so it is a function .
And it does not forms a straight line when graphed .
So, y = 1 – x2 is not a linear function.
Does the graph represent a linear or nonlinear function? Explain.
Question 6.
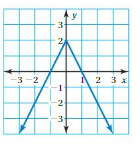
Answer: The graph represents a nonlinear function.
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , 2) , (-1 , 0) , (-2 , -2 ) , (-3 , -4), (0 , 1 ) , (2 , -2) , ( 3, -4 )
The inputs have more than one output ,
And points form a straight line
So , the graph is non linear function
Question 7.
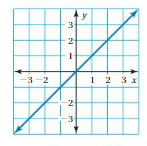
Answer: The graph is a linear function
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , 0) , (-1 , -1) , (-2 , -2 ) , (-3 , -3), (1 , 1 ) , (2 , 2) , ( 3, 3 )
The inputs have exactly one output ,
And points form a straight line
So , the graph is a linear function.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
IDENTIFYING FUNCTIONS Does the table or graph represent a linear or nonlinear function? Explain.
Question 8.
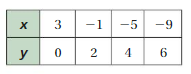
Answer: It is not a linear function
Explanation:
Ordered pairs are (3 , 0) , (-1 , 2) , (-5 , 4) , (-9 , 6)
Each input has exactly one output
and it does not form a straight line when graphed
So, it is not a linear function .
Question 9.
Answer: The graph is non linear function
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , -1) , (-1 , 0) , (-2 , 3 ) , (1 , 0 ) , (2 , 3) .
The inputs have exactly one output ,
And points does not form a straight line
So , the graph is non linear function
Question 10.
WHICH ONE DOESN’T BELONG?
Which equation does not belong with the other three? Explain your reasoning.

Answer: 5xy = -2 does not belong with the other three.
Explanation:
15y = 6x , y = \(\frac{2}{5}\)x , 10y = 4x .
These are evaluated as 5y = 2x
5xy = -2 , is different from 5y = 2x.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
The loudness of sound is measured in (dB). The graph shows the loudness y of a sound (in decibels) x meters from the source of the sound. Is the relationship between loudness and distance linear or nonlinear? Approximate the loudness of the sound 12 meters from the source.
Answer: The relationship between loudness and distance is nonlinear Function. And the loudness of the sound 12 meters from the source is approximately 85dB as shown in the graph.
Explanation:
As shown in the graph , the plot of the points does not form a straight line ,
Its a parabolic decay , The amount of loudness decreases with the increase in distance,
So, The relationship between loudness and distance is nonlinear Function.
And the loudness of the sound 12 meters from the source is approximately 85dB as shown in the graph.
Question 12.
A video blogger is someone who records a video diary. A new website currently hosts 90 video bloggers and projects a gain of 10 video bloggers per month. The table below shows the actual numbers of video bloggers. How does the projection differ from the actual change?

Answer: Projections are more than the actual values
Explanation:
So, Projections are more than the actual values
Comparing Linear and Non Linear Functions Homework & Practice 7.4
Review & Refresh
Write a linear function that relates y to x.
Question 1.
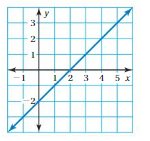
Answer: The linear function is y = x – 2
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , -2) , (1 , -1 ) , (-1 , -3) , ( 2, 0), (3 , 1) , (4 , 2) , ( 5, 3)
First find the slope m of the line containing the two given points (2 ,0) and (3, 1)
m = (y2-y1) / (x2-x1)
m= (1 – 0) / (3 – 2)
m = 1 .
Because the line crosses the y axis at ( 0, -2 ) , The y intercept is -2.
So , the linear function is y = x – 2 .
Question 2.
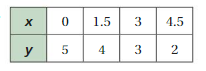
Answer: The linear function is y =\(\frac{-1}{1.5}\)x + 5.
Explanation:
Ordered pairs are (0 , 5) , (1.5 , 4) , (3 , 3) , (4.5 , 2)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (1.5 ,4) and (3, 3)
m = (y2-y1) / (x2-x1)
m= (3 – 4) / (3 – 1.5)
m = -1 /1.5
Because the line crosses the y axis at ( 0, 5 ) , The y intercept is 5.
So , the linear function is y =\(\frac{-1}{1.5}\)x + 5.
The vertices of a figure are given. Draw the figure and its image after a dilation with the given scale factor. Identify the type of dilation.
Question 3.
A (- 3, 1), B (- 1, 3), C (- 1, 1); k = 3
Answer: The New right angle triangle is larger than the original one So , its a increase .
Explanation:
Given , (- 3, 1), (- 1, 3), (- 1, 1) these pairs form a right angle triangle
K = 3 , For the dilation figure multiply the 3 with the given ordered pairs , then
(- 3, 1) × 3 = ( -9 , 3)
(- 1, 3) × 3 = ( -3 , 9)
(- 1, 1) × 3 = (-3 , 3)
From these new ordered pairs we form a new right angle triangle
The figure is 
The New right angle triangle is larger than the original one So , its a increase .
Question 4.
J (2, 4), K (6, 10), L (8, 10), M (8, 4); k = \(\frac{1}{4}\)
Answer: It is a reduction
Explanation:
Given , (2, 4), (6, 10), (8, 10) ,(8,4) these pairs forms a figure
K = 0.25 , For the dilation figure multiply the 3 with the given ordered pairs , then
(2, 4) × 0.25 = (0.5, 1)
(6, 10) × 0.25 = (1.5, 2.5)
(8, 10) × 0.25 = (2, 2.5)
(8, 4) × 0.25 = (2 , 1)
From these new ordered pairs we form a new figure
The figure is 
The New figure is smaller than the original , So, It is a reduction .
Concepts, Skills, & Problem Solving
COMPARING FUNCTIONS Graph each equation. Decide whether each graph represents a linear or nonlinear function. (See Exploration 1, p. 295.)
Question 5.
h = 5 + 6t Equation 1
h = 5 + 6t2 Equation 2
Answer: h = 5 + 6t Equation 1 is a linear function
h = 5 + 6t2 Equation 2 is a non linear function .
Explanation:
Given , h = 5 + 6t , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 5 + 6(0) = 5 . co-ordinates are (0 , 5)
if x = 1 , then y = 5 + 6(1) = 11 . co-ordinates are (1 , 11)
if x = 2 , then y = 5 + 6(2) = 17 , co-ordinates are (2 , 17)
if x = 3 , then y = 5 + 6(3) = 23 , co-ordinates are (3 , 23)
The co-ordinates (0 , 5) , (1 , 11) , (2 , 17) , (3 , 23) form a straight line .
Given , h = 5 + 6t2 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 5 + 6(0)² = 5 . co-ordinates are (0 , 5)
if x = 1 , then y = 5 + 6(1)² = 11 . co-ordinates are (1 , 11)
if x = 2 , then y = 5 + 6(2)² = 26 , co-ordinates are (2 , 26)
if x = 3 , then y = 5 + 6(3)² = 59 , co-ordinates are (3 , 59)
The co-ordinates (0 , 5) , (1 , 11) , (2 , 26) , (3 , 59) does not form a straight line .
The graph of both equations is 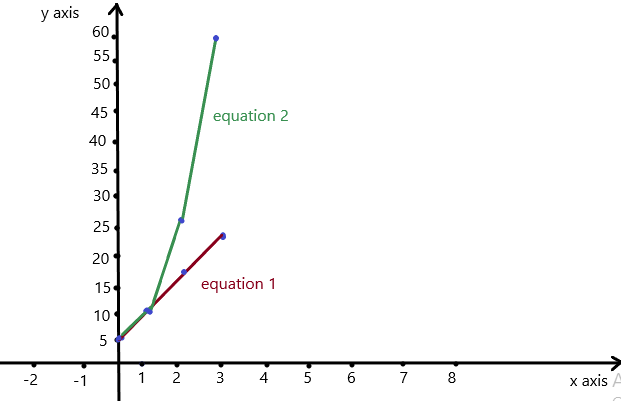
So, h = 5 + 6t Equation 1 is a linear function
h = 5 + 6t2 Equation 2 is a non linear function .
Question 6.
y = – \(\frac{x}{3}\) Equation 1
y = – \(\frac{3}{x}\) Equation 2
Answer: y = – \(\frac{x}{3}\) Equation 1 is a linear function
y = – \(\frac{3}{x}\) Equation 2 is a non linear function.
Given , y =- \(\frac{x}{3}\) , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =- \(\frac{0}{3}\) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = – \(\frac{1}{3}\) = – 0.3 . co-ordinates are (1 , – 0.3 )
if x = 2 , then y = – \(\frac{2}{3}\) = – 0.6 , co-ordinates are (2 ,-0.6)
if x = 3 , then y = – \(\frac{3}{3}\) = -1 , co-ordinates are (3 , -1)
The co-ordinates (0 , 0) , (1 , -0.3) , (2 , -0.6) , (3 , -1) form a straight line .
Given , y =- \(\frac{3}{x}\) , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =- \(\frac{3}{0}\) = no number
if x = 1 , then y = – \(\frac{3}{1}\) = – 3 . co-ordinates are (1 , – 1 )
if x = 2 , then y = – \(\frac{3}{2}\) = – 1.5 , co-ordinates are (2 ,-1.5)
if x = 3 , then y = – \(\frac{3}{3}\) = -1 , co-ordinates are (3 , -1)
The co-ordinates (1 , -1) , (2 , -1.5) , (3 , -1) form a straight line .
The graph of both the equations is 
So, y = – \(\frac{x}{3}\) Equation 1 is a linear function
y = – \(\frac{3}{x}\) Equation 2 is a non linear function.
IDENTIFYING FUNCTIONS FROM TABLES Does the table represent a linear or nonlinear function? Explain.
Question 7.
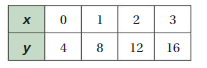
Answer: linear function is y = 4x + 4.
Explanation:
Ordered pairs are (0 , 4) , (1 , 8) , (2 , 12) , (3 , 16)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (2 , 12) and (3 , 16)
m = (y2-y1) / (x2-x1)
m= (16 – 12) / (3– 2)
m = 4/1
m = 4
Because the line crosses the y axis at ( 0, 4 ) , The y intercept is 4.
So , the linear equation is y = 4x + 4.
And it is a linear function.
The graph is 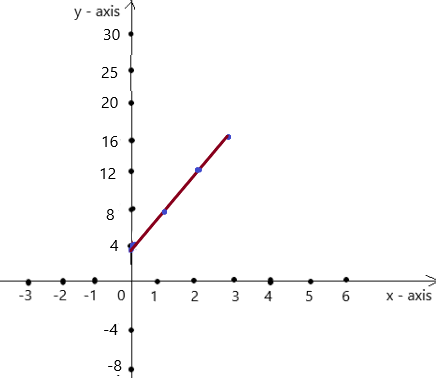
Question 8.
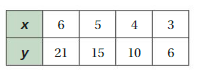
Answer: y = 4x – 6 is linear function.
Explanation:
Ordered pairs are (6 , 21) , (5 , 15) , (4 , 10) , (3 , 6)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (4 , 10) and (3 , 6)
m = (y2-y1) / (x2-x1)
m= (6 – 10) / (3– 4)
m = -4/-1
m = 4
substitute the slope in the(4 , 10) to get point slope to form a line.
y-y1 = m (x-x1)
y – 10 = 4 ( x – 4)
y – 10 = 4x – 16
y = 4x – 16 + 10
y = 4x – 6
So , y = 4x – 6 is linear function.
The graph is 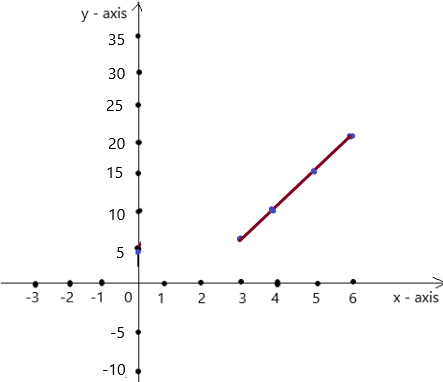
IDENTIFYING FUNCTIONS FROM EQUATIONS Does the equation represent a linear or nonlinear function? Explain.
Question 9.
2x + 3y = 7
Answer: The function is linear when m = \(\frac{-2}{3}\) and c = \(\frac{7}{3}\)
Explanation:
Given ,2x + 3y = 7
3y = 7 – 2x
y = \(\frac{-2}{3}\)x+ \(\frac{7}{3}\)
So, The function is linear when m = \(\frac{-2}{3}\) and c = \(\frac{7}{3}\)
Question 10.
y + x = 4x + 5
Answer: The function is linear when m = 3 and c = 5 .
Explanation:
Given , y + x = 4x + 5
y = 4x – x + 5
y = 3x + 5
So, The function is linear when m = 3 and c = 5 .
Question 11.
y = \(\frac{8}{x^{2}}\)
Answer: The function is linear when m = 8 and c = 0 .
Explanation:
Given , y = \(\frac{8}{x^{2}}\)
slope m = 8
c = 0
So, The function is linear when m = 8 and c = 0 .
IDENTIFYING FUNCTIONS FROM GRAPHS Does the graph represent a linear or nonlinear function? Explain.
Question 12.
Answer: The graph is linear function
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , 1) , (2 , 0) , (4 , -1 ) , (-2 , 2), ( -4, 3 )
The inputs have exactly one output ,
And points form a straight line
So , the graph is linear function
Question 13.
Answer: The graph is non linear function.
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , 0) , (-1 , -1) , (-4 , -2 ) , (1 , 1), ( 4, 2 )
The inputs have exactly one output ,
And points does not form a straight line
So , the graph is non linear function
Question 14.
IDENTIFYING A FUNCTION
The graph shows the volume V (in cubic feet) of a cube with an edge length of x feet. Does linear nonlinear the graph represent a linear or nonlinear function? Explain.
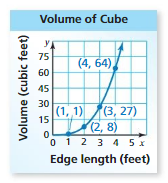
Answer: The graph is non linear function
n order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (1 , 1) , (2 , 8) , (3 , 27 ) , (4 , 64)
The inputs have exactly one output ,
And points does not form a straight line
So , the graph is non linear function
Question 15.
MODELING REAL LIFE
The frequency y (in terahertz) of a light wave is a function of its wavelength x (in nanometers). Is the function relating the wavelength of light to its frequency linear or nonlinear?
Answer: The function is a non linear function
Explanation:
table is as follows 
change in x is constant but change in y is not constant , it is increasing
So, the function is a non linear function .
Question 16.
DIG DEEPER!
The table shows the cost (in dollars) of pounds of sun flower seeds.
a. What is the missing -value that makes the table represent a linear function?
b. Write a linear function that represents the cost of x pounds of seeds. Interpret the slope.
c. Does the function have a maximum value? Explain your reasoning.
Answer: a. 3 pounds = $4.2
b. y = 1.4x is linear function.
c. If y has maximum value then the x also has maximum value.
Explanation:
a. As per the table 1 pound = $1.4
2 pounds = $2.8
3pounds = $4.2
4 pounds = $5.6
So, the price is increasing with weight of the seeds.
b. Ordered pairs are (2 , 2.8) , (3 , 4.2) , (4 , 5.6)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (3 , 4.2) and (4 , 5.6)
m = (y2-y1) / (x2-x1)
m= (5.6 – 4.2) / (4 – 3)
m = 1.4
substitute the slope in the (3 , 4.2) to get point slope to form a line.
y-y1 = m (x-x1)
y – 4.2 = 1.4 ( x – 3)
y – 4.2 = 1.4x – 4.2
y = 1.4x – 4.2 + 4.2
y = 1.4x
So , y = 1.4x is linear function.
c. As shown in the table , and the function if y increases then x also increases with respect to the y
So, if y has maximum value then the x also has maximum value.
Question 17.
MODELING REAL LIFE
A birch tree is 9 feet tall and grows at a rate of 2 feet per year. The table shows the height h (in feet) of a willow tree after x years.
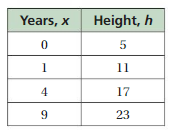
a. Does the table represent a linear or nonlinear function? Explain.
b. Which tree is taller after 10 years? Explain.
Answer: There is no linear relationship between x and y .
Explanation:
Table is as follows 
Change in y is constant but change in x is increasing , not a constant
Hence, there is no linear relationship between x and y .
Question 18.
CRITICAL THINKING
In their first year, Show A has 7 million viewers and Show B has 5 million viewers. Each year, Show A has 90% of the viewers it had in the previous year. Show B loses 200,000 viewers each year.
a. Determine whether the function relating the year to the number of viewers is linear or nonlinear for each show.
b. Which show has more viewers in its sixth year?
Answer: a. The function relating the year to the number of viewers is linear
b. Both shows has same number of viewers in the sixth year .
Explanation:
a. Given, In their first year, Show A has 7 million viewers and Show B has 5 million viewers. Each year, Show A has 90% of the viewers it had in the previous year. Show B loses 200,000 viewers each year.
For show A
So , In first year = 7
2 year = 90% of 7 = 6.3
3 year = 90% of 6.3 = 5.6
4 year = 90% of 5.6 = 5.04
5 year = 90% of 5 = 4.5
6 year = 90% of 4.5 = 4.05
So the ordered pairs are (1 , 7) , (2 , 6.3) , (3 , 5.6) , (4 , 5), (5 , 4.5) , (6 , 4)
For show B
In first year = 5 , As the viewers reduces by 2,00,000 in 5M
2 year = 5 – 0.2 = 4.8
3 year = 4.8 – 0.2 = 4.6
4 year = 4.6 – 0.2 = 4.4
5 year = 4.4 – 0.2 = 4.2
6 year = 54.2 – 0.2 = 4
So the ordered pairs are (1 , 5) , (2 , 4.8) , (3 , 4.6) , (4 , 4.4), (5 , 4.2) , (6 , 4)
As the year increases the viewers are also decreasing constantly as per the individual shows
So, The function relating the year to the number of viewers is linear .
b. As shown in part a , the ordered pairs having (6,4) represents the number of viewers to the year
So, Both shows has same number of viewers in the sixth year .
Question 19.
NUMBER SENSE
The ordered pairs represent a function. (0,- 1), (1, 0), (2, 3), (3, 8), and (4, 15)
a. Graph the ordered pairs and describe the pattern. Is the function linear or nonlinear?
b. Write an equation that represents the function.
Answer: a. The graph is shown below and function is linear
b. The linear equation is y = 7x – 1.
Explanation:
Given, ordered pairs represent a function. (0,- 1), (1, 0), (2, 3), (3, 8), and (4, 15)
a. the graph is 
Each input has exactly one output and it forms a straight line So, the graph is linear
b. First find the slope m of the line containing the two given points (3 ,8) and (4, 15)
m = (y2-y1) / (x2-x1)
m= (15 – 8) / (4– 3)
m = 7/1
m = 7
Because the line crosses the y axis at ( 0, -1 ) , The y intercept is -1.
So , the linear equation is y = 7x – 1.
Lesson 7.5 Analyzing and Sketching Graphs
EXPLORATION 1
Matching Situations to Graphs
Work with a partner. Each graph shows your speed during a bike ride. Match each situation with its graph. Explain your reasoning.
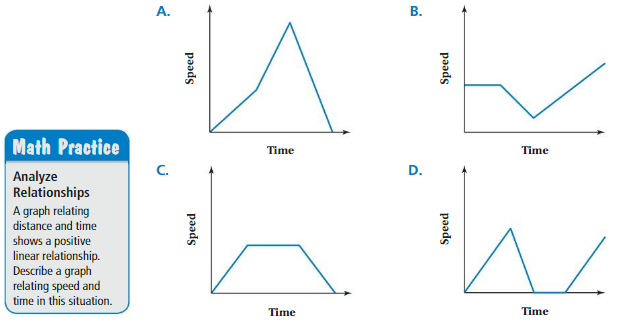
a. You increase your speed, then ride at a constant speed along a bike path. You then slow down until you reach your friend’s house. Analyze Relationships
b. You increase your speed, then go down a hill. You then quickly come to a stop at an intersection.
c. You increase your speed, then stop at a store for a couple of minutes. You then continue to ride, increasing your speed.
d. You ride at a constant speed, then go up a hill. Once on top of the hill, you increase your speed.
Answer: a – C ,
b – A ,
c – D ,
d – B ,
Explanation:
a. You increase your speed, then ride at a constant speed along a bike path. You then slow down until you reach your friend’s house. The graph C has the perfect graph representing the situation of given question.
b. You increase your speed, then go down a hill. You then quickly come to a stop at an intersection.
Because The graph A has the bike speed representing the situation for the time .
c. You increase your speed, then stop at a store for a couple of minutes. You then continue to ride, increasing your speed. Thus, The graph D is the final answer for the question
d. You ride at a constant speed, then go up a hill. Once on top of the hill, you increase your speed.
Because of the speed with respect to time the graph B is the correct answer for the question.
EXPLORATION 2
Interpreting a Graph
Work with a partner. Write a short paragraph that describe show the height changes over time in the graph shown. What situation can this graph represent?
Answer: The Graph can be representing a situation for low and high tides of the Ocean
Explanation:
As shown in the figure, The graph is plotted between the height and time,
We can take an example of an Ocean for its waves , As the time passes at the morning of a normal day, The waves of the ocean start rising higher at a period of time, and for the time being maintaining a peak height then drops to a lower height at a particular intervals of time , this process takes place for a while and vise versa.
Thus, the Graph can be representing a situation for low and high tides of the Ocean
Try It
Question 1.
The graph shows the location of a pelican relative to your location.
a. Describe the path of the pelican.
b. Write an explanation for the decrease in the vertical distance of the pelican.
Answer: Both of them are explained below.
Explanation:
a. The path of the pelican is flying in the air , As they always fly in line and the amazing thing is the deeper the prey the higher they dive.
The graph shows the relationship between the horizontal distance that is the height from the land, vertical distance is the point from where its destination point is located, so at the starting point of the flight it has more distance from the ground means flying at a higher level , as the time passes it reaches to the closer point of its destination point so the altitude of the flight decreases with the decrease in the vertical distance and at a particular distance reaches its point of destination.
b. The decrease in the vertical distance of the pelican. is due to its flight to the destination point as it requires to stop flying to reach it, so in order to have a smooth landing on the ground , the bird gradually decreases its speed by decreasing its altitude.
Question 2.
A fully-charged battery loses its charge at a constant rate until it has no charge left. You plug it in, and it fully recharges at a constant rate. Then it loses its charge at a constant rate until it has no charge left. Sketch a graph that represents this situation.
Answer: The graph is 
Explanation:
In the graph , let the x-axis be time and y-axis be the battery charge ,
A fully-charged battery loses its charge at a constant rate until it has no charge left. So, line segment starts from 100 and decreases until it touches the x-axis.
You plug it in, and it fully recharges at a constant rate. Thus, line segment increases at a constant rate until it reaches 100
Then it loses its charge at a constant rate until it has no charge left. line segment decreases again at a constant rate until it again touches the x-axis .
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
ANALYZING GRAPHS
The graph shows the growth rate of a plant over time.
a. Describe the change in growth rate.
b. Write an explanation for the decrease in growth rate and the increase in growth rate.
Answer: the answers are given below
Explanation:
a. the change in growth rate of a plant over the time is given by its size and height , So as the time passes the growth rate is constant from the the start and from a particular time the growth rate has been dropping slightly due to external or internal reasons of a plant and again at some time the growth rate is increasing at a constant rate until it reaches to its perfect growth of a plant.
b. The decrease in growth rate of the plant is due to some external causes like weather, rain, sunlight , watering, and the soil may effect its growth rate and the increase in growth rate is probably due to its soil fertility and sufficient sunlight providing sufficient chlorophyll.
Question 4.
SKETCHING GRAPHS
As you snowboard down a hill, you gain speed at a constant rate. You come to a steep section of the hill and gain speed at a greater constant rate. You then slow down at a constant rate until you come to a stop. Sketch a graph that represents this situation.
Answer: The graph is 
Explanation:
In the graph , let the x-axis be time and y-axis be the speed ,
As you snowboard down a hill, you gain speed at a constant rate, line segment decreases at a constant rate
You come to a steep section of the hill and gain speed at a greater constant rate, line segment becomes steeper i.e., the line segment decreases at a high constant rate.
You then slow down at a constant rate until you come to a stop, line segment becomes flatter i.e., the constant rate of decrease becomes less until it touches its x-axis
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
Two rowing teams are in a race. The graph shows their distances from the finish line over time. Describe the speed of each team throughout the race. Then determine which team finishes first.
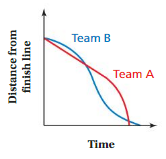
Answer: Team B will finishes race first.
Explanation:
Team A , The relationship between the time and distance from the finish line is given in the graph,
At starting point Team A has maintained a fair speed at the Beginning of the race and has been a little slow while reaching out to the destination point, and for a while they have been balancing the speed with the distance representing a curving point in the graph and directly dropping to the finish line drastically creating a slope, until it reaches in the x-axis line.
Team B , The relationship between the time and distance from the finish line is given in the graph,
As same as the Team A , Team B has a perfect start but it has been a way different them Team A because Team B has a game plan to win the race, as shown in the graph they have maintained a constant speed while reaching out to the destination and also having a smooth drift at a level of decreasing their distance from the finish line.
Team B will finishes the race first because they are having a constant and smooth decreasing speed which comes to an end gradually at the finishing line.
Question 6.
DIG DEEPER!
The graphs show the movements of two airplanes over time. Describe the movement of each airplane.
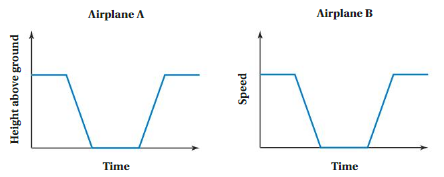
Answer: Detailed explanation is given below.
Explanation:
As shown in the graph , x-axis is time and y-axis be the height above ground
Airplane A, the line segment at a constant rate at the time of starting of the takeoff and then drops to a point while decreasing in the height to the ground for landing and for a constant time it is at the ground level until again it takes off having an increase in the height from the ground level , at last it maintains a constant speed.
Airplane B, the line segment at a constant rate at the time of starting of the takeoff and then drops to a point while decreasing in the height to the ground for landing and for a constant time it is at the ground level until again it takes off having an increase in the height from the ground level , at last it maintains a constant speed.
It is as same as the airplane A.
Analyzing and Sketching Graphs Homework & Practice 7.5
Review & Refresh
Does the table or equation represent a linear or nonlinear function? Explain.
Question 1.
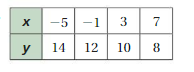
Answer: y = -0.5x + 11.5 is a linear function.
Explanation:
Ordered pairs are (-5 , 14) , (-1 , 12) , (3 , 10) , (7 , 8)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (3 , 10) and (7 , 8)
m = (y2-y1) / (x2-x1)
m= (8 – 10) / (7 – 3)
m = -2/4
m = -0.5
substitute the slope in the(3 , 10) to get point slope to form a line.
y-y1 = m (x-x1)
y – 10 = -0.5 ( x – 3)
y – 10 = -0.5x + 1.5
y = -0.5x + 1.5 + 10
y = -0.5x + 11.5
So , the linear equation is y = -0.5x + 11.5
And it is a linear function.
The graph is 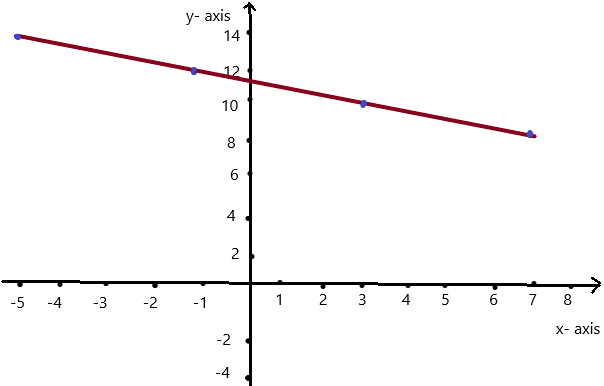
Question 2.
y = x2 + 8
Answer: The function is linear when m= 1 and c = 8.
Explanation:
Given , y = x2 + 8 ,
slope m = 1
c = 8
So, the function is linear when m = 1 and c= 8.
Graph the linear equation.
Question 3.
– 4x + y = – 1
Answer: The graph is 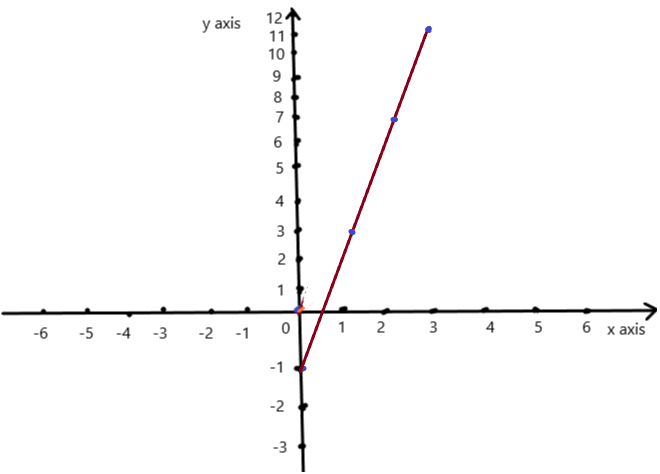
Explanation:
we can write – 4x + y = – 1 as y = 4x – 1
Given , y = 4x – 1 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 4(0) – 1 = -1 . co-ordinates are (0 , -1)
if x = 1 , then y = 4(1) – 1 = 3 . co-ordinates are (1 , 3)
if x = 2 , then y = 4(2) – 1 = 7 , co-ordinates are (2 , 7)
if x = 3 , then y = 4(3) – 1= 11 , co-ordinates are (3 , 11)
The co-ordinates (0 , -1) , (1 , 3) , (2 , 7) , (3 , 11) form a straight line .
Question 4.
2x – 3y = 12
Answer: The graph is 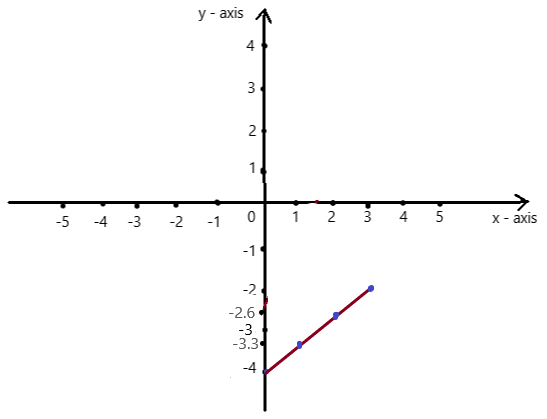
Explanation:
we can write 2x – 3y = 12 as y = \(\frac{2x-12}{3}\) or y = \(\frac{2}{3}\)x – 4
Given , y =\(\frac{2}{3}\)x – 4 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = \(\frac{2}{3}\)0 – 4= – 4 . co-ordinates are (0 , -4)
if x = 1 , then y = \(\frac{2}{3}\)1 – 4 = 0.66 – 4 = -3.3 . co-ordinates are (1 , -3.3)
if x = 2 , then y = \(\frac{2}{3}\)2 – 4 =0.66(2) – 4 =1.3 – 4 = -2.6, co-ordinates are (2 , -2.6)
if x = 3 , then y = \(\frac{2}{3}\)3 – 4 = 0.66(3) – 4 = 1.98 – 4 = -2.0 , co-ordinates are (3 , -2.0)
The co-ordinates (0 , -4) , (1 , -3.3) , (2 , -2.6) , (3 , -2) form a straight line .
Question 5.
5x + 10y = 30
Answer: The graph is 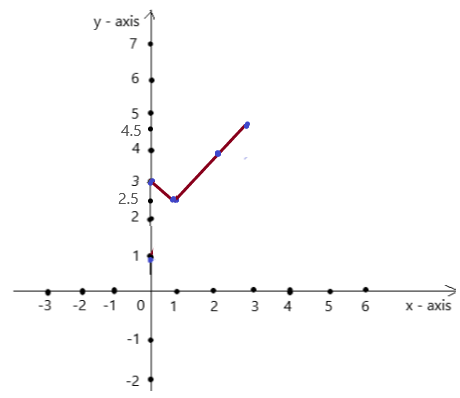
Explanation:
5x + 10y = 30 can be written as y = -0.5x + 3
take 5 common on both sides we get
x + 2y = 6
y = \(\frac{-x + 6}{2}\)
y = \(\frac{-x}{2}\) + 6
y = -0.5x + 3
Given , y =-0.5x + 3 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = -0.5(0) + 3 = 3 . co-ordinates are (0 , 3)
if x = 1 , then y = -0.5(1) + 3= 2.5 . co-ordinates are (1 , 2.5)
if x = 2 , then y = -0.5(2) + 3 = 4 , co-ordinates are (2 , 4)
if x = 3 , then y = -0.5(3) + 3 = 4.5 , co-ordinates are (3 , 4.5)
The co-ordinates (0 , 3) , (1 , 2.5) , (2 , 4) , (3 , 4.5)does not form a straight line .
Concepts, Skills, &Problem Solving
MATCHING DESCRIPTIONS WITH GRAPHS The graph shows your speed during a run. Match the verbal description with the part of the graph it describes. (See Exploration 1, p. 301.)
Question 6.
You run at a constant speed.
Answer: C
Explanation:
Because the line segment of the graph at point C show that the running speed is constant for a particular time ,
Thus forming a straight horizontal line.
Question 7.
You slow down at a constant rate.
Answer: D
Explanation:
Because the line segment of the graph at point D show that the running speed is decreasing at a constant rate for a particular time ,
Thus forming a straight steep line down the time axis.
Question 8.
You increase your speed at a constant rate.
Answer: A
Explanation:
Because the line segment of the graph at point A show that the running speed is increasing at a constant rate at a starting point of the race on time ,
Thus forming a slope in the graph.
Question 9.
You increase your speed at a faster and faster rate.
Answer: B
Explanation:
Because the line segment of the graph at point B show that the running speed is increasing at a faster rate after starting the race and maintaining a gradual growth of the speed and after reaching the next point speed is doubled from before ,
Thus forming a slope with a curve in the graph.
ANALYZING GRAPHS Describe the relationship between the two quantities.
Question 10.
Answer: As the Time passes there will be increase in the volume.
Explanation:
The graph shows the relation between the volume and time of a Balloon , To fill up the balloon with air, with the inlet of air increases in volume and the time taken to fill the balloon with air is shown ,
The line segment starts at initial point stating the balloon at a no air state, then gradually increases with constant halts having constant volume at a particular time and vice versa.
So, As the Time passes there will be increase in the volume.
Question 11.
Answer: As the times passes Dollars are maintaining imbalance.
Explanation:
The relationship between the time and dollars is given in the graph, As we all know money is never ever constant with time , As if it only increases or decreases or having both simultaneously , in this graph the line segment is having a steep and at some point of time it is maintaining a slight growth constantly with the time.
So, As the times passes Dollars are maintaining imbalance.
Question 12.
Answer: An engine power is directly proportional to the engine speed and its horse power
Explanation:
The relationship between the engine speed and horse power is given in the graph, Generally every automobile is is defined as the best for its horse power which is the heart of the engine and it highlights the speed of the vehicle, Here engine power is defined by the horse power and the engine speed the line segment is having a curve increment in the horse power due to the increase in engine speed.
So, An engine power is directly proportional to the engine speed and its horse power
Question 13.
Answer: As time increases the process of grams decaying will be faster.
Explanation:
The relationship between grams and time is given in the graph, its obvious that every product has its own expiry date, and if it crosses that its starts to decay, the graph implies that with the increase time the quality of the gram decreases or grams start to decay . The line segment in the graph shows that the gradually decrease indicating the spoiling rate of the grams with rate of change of time.
So, As time increases the process of grams decaying will be faster.
Question 14.
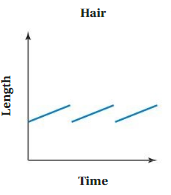
Answer: At the particular intervals of time hair growth has stopped and at regular intervals again starts growing with respect to the time.
Explanation:
The graph shows the relationship between the length of the hair and time taken to the growth of the hair, of course hair growth is not constant every time, here we have the graph with the line segment not constant and having breaks at the times of interval.
So, At the particular intervals of time hair growth has stopped and at regular intervals again starts growing with respect to the time.
Question 15.
Answer: In a period of time the balance will be reduced gradually at regular intervals maintaining a constant balance to clear the loan.
Explanation:
The relationship between the balance of the loan with the time period of the loan to be cleared, The loan should be cleared in the time limit and should maintain a neat balance, every increase in time period the balance is debited from the loan , there will be decrease in the balance and gaps are occurred in the graph.
so, In a period of time the balance will be reduced gradually at regular intervals maintaining a constant balance to clear the loan.
Question 16.
ANALYZING GRAPHS
Write an explanation for the relationship shown in the graph in Exercise 10.
Answer: The graph shows the relation between the volume and time of a Balloon , To fill up the balloon with air, with the inlet of air increases in volume and the time taken to fill the balloon with air is shown ,
The line segment starts at initial point stating the balloon at a no air state, then gradually increases with constant halts having constant volume at a particular time and vice versa.
Question 17.
MODELING REAL LIFE
The graph shows the natural gas usage for a house.
a. Describe the change in usage from January to March.
b. Describe the change in usage from March to May.
Answer: a. The change in usage from January to March, As shown in the graph the usage is at peaks in the month of January and started to decrease after that month and continuing to decrease in the month of March.
b. The change in usage from March to May, As shown in the graph the usage is continuing to decrease in the month of March and started to increase again in the month of May and maintaining to use highly from the month of May.
Explanation:
a. The change in usage from January to March, As shown in the graph the usage is at peaks in the month of January and started to decrease after that month and continuing to decrease in the month of March.
b. The change in usage from March to May, As shown in the graph the usage is continuing to decrease in the month of March and started to increase again in the month of May and maintaining to use highly from the month of May.
SKETCHING GRAPHS Sketch a graph that represents the situation.
Question 18.
The value of a television decreases at a constant rate, and then remains constant.
Answer: The graph is 
Explanation:
Draw the axis and label the x- axis as time and y- axis as value, then sketch the graph,
The value of the television decreases at a constant rate: line segment starts to decrease at a constant rate,
And then remains constant, after reaching a certain value : line segment becomes parallel to horizontal axis.
Question 19.
The distance from the ground changes as your friend swings on a swing.
Answer: The graph is 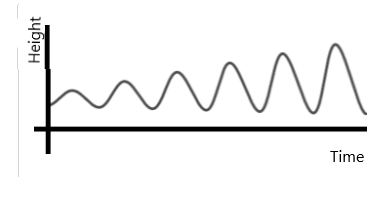
Explanation:
Your friend starts close to the ground and then swings up. Then she falls back down close to the ground again and swings back . When she swings back, she gets higher than when she was swinging forward, she then starts to swing forward again getting close to the ground and then going up even higher than when she was swinging backward, she continues to getting higher and higher every time she swings forwards and backwards,
Question 20.
The value of a rare coin increases at a faster and faster rate.
Answer: The graph is 
Explanation:
Draw the Axis and label them as x-axis as time and y – axis as distance,
The value of a rare coin increases at a faster and faster rate , so the curve moves upwards at an increasing rate.
Question 21.
You are typing at a constant rate. You pause to think about your next paragraph and then you resume typing at the same constant rate.
Answer: The graph is 
Explanation:
A constant rate means that portion of the graph is linear , pausing means the number of words stays constant, typing again at the same constant rate means the last piece of the graph is linear again with the same slope as the first portion of the graph.
Question 22.
CRITICAL THINKING
The graph shows the speed of an object over time.
a. Sketch a graph that shows the distance traveled by the object over time.
b. Describe a possible situation represented by the graphs.
Answer: a. The distance and time are directly proportional to each other.
b. As time passes the speed and time are relatively balancing each other in the graph.
Explanation:
a. The graph is 
In this graph the relationship between distance and time is shown, for example , let the object be a bike, the time taken to reach the destination for the bike is directly proportional to the distance travelled , So as time passes the distance is gradually increasing from the starting point.
So, the distance and time are directly proportional to each other.
b. Th graph shown , is the relationship between the speed and the time , let the object moving be Train,
it is running between the station so it has to be halted in the stations to be listed in the stoppings , So the line segment is started with a constant speed with the time and again at the time interval dropping the speed with respect to time it has maintaining the same speed .
So, As time passes the speed and time are relatively balancing each other in the graph.
Question 23.
MODELING REAL LIFE
The graph shows the average scores of two bowlers from the start of a season to the end of the season.
a. Describe each bowler’s performance.
b. Who had a greater average score most of the season? Who had a greater average score at the end of the season?
c. Write an explanation for the change in each bowler’s average score throughout the bowling season.
Answer: All the answers are explained below
Explanation:
a. Bowler A : As the graph represent the relationship between the score and the week, bowler A has started with the good take off and having able to grasp the same energy his performance on the goals are increasing rapidly over the week and had the good score than Bowler B.
Bowler B : As the graph represent the relationship between the score and the week, bowler B has started with the good take off but as the time passes the performance of the bowler is has been intended to decrease his scores gradually over the week.
b. Bowler A and Bowler B had a greater average score most of the season, but Bowler A had a greater average score at the end of the season
c. Bowler A has the same energy his performance on the goals are increasing rapidly over the week and had the good score than Bowler B. so it has a smaller change in average’s score in the bowling season .
While Bowler B has good take off but as the time passes the performance of the bowler is has been intended to decrease his scores gradually over the week. so he has a drastic change in average’s score in the bowling season .
Question 24.
DIG DEEPER!
You can use a supply and demand model to understand how the price of a product changes in a market. The supply curve of a particular product represents the quantity suppliers will produce at various prices. The demand curve for the product represents the quantity consumers are willing to buy at various prices.
a. Describe and interpret each curve.
b. Which part of the graph represents a surplus? Explain your reasoning.
c. The curves intersect at the equilibrium point, which is where the quantity produced equals the quantity demanded. Suppose that demand for a product suddenly increases, causing the entire demand curve to shift to the right. What happens to the equilibrium point?
Answer: All of them are explained below .
Explanation:
a. The supply curve of a particular product represents the quantity suppliers will produce at various prices, As shown in the graph, the relationship between the price and quantity is given , so if prices increases gradually Quantity increases .
The demand curve for the product represents the quantity consumers are willing to buy at various prices, As shown in the graph, the relationship between the price and quantity is given , so if prices decreases with increase in Quantity .
b. The graph does not implies any surplus because each demand and supply is given by their respective curve over the prices and quantity
c. As shown in the graph, The curves intersect at the equilibrium point, which is where the quantity produced equals the quantity demanded. Given, that demand for a product suddenly increases, causing the entire demand curve to shift to the right. Then the equilibrium point will be pointed where the two curves meet after the change in the demand graph so change in the supply graph is also possible.
Functions Connecting Concepts
Using the Problem-Solving Plan
Question 1.
The table shows the lengths x (in inches) and weights y(in pounds) of several infants born at a hospital. Determine whether weight is a function of length. Then estimate the weight of an infant that is 20 inches long.
Understand the problem.
You know the lengths and weights of several infants. You are asked to determine whether weight is a function of length and to estimate the weight of a 20-inch-long infant.
Make a plan.
Determine whether any of the lengths are paired with more than one weight. Then use a graphing calculator to find an equation that represents the data. Evaluate the equation when x = 20 to estimate the weight of a 20-inch-long infant.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer: Weight is the function of the length
Explanation:
From the table we have , Each length has only one weight , so weight is a function of length.
First find the slope m of the line containing the two given points (19.3 , 7.3) and (18.9 , 6.5)
m = (y2-y1) / (x2-x1)
m= (6.5 – 7.3) / (18.9 – 19.3)
m = 0.2
substitute the slope in the (19.3 , 7.3) to get point slope to form a line.
y-y1 = m (x-x1)
y – 7.3 = 0.2 ( x – 19.3)
y – 7.3 = 0.2x – 3.86
y = 0.2x – 3.86 + 7.3
y = 0.2x + 3.4
So , y = 0.2x + 3.4 is linear function.
For x = 20 ,
y = 0.2 (20) + 3.4
y = 4 + 3.4
y = 7.4
So, The weight of an infant that is 20 inches long. is 7.4.
Question 2.
Each mapping diagram represents a linear function. At what point do the graphs of the functions intersect? Justify your answer.
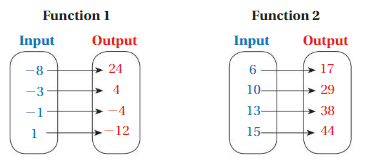
Answer: The point of intersection is (-1, -4)
Explanation:
Function 1 – Ordered pairs are ( -8 , 24 ) , ( -3 , 4 ) , ( -1 , -4 ) , ( 1 , -12) .
Function 2 – Ordered pairs are ( 6 , 17 ) , ( 10 , 29 ) , ( 13 , 38 ) , ( 15 , 44 ) .
Graph the points we get, 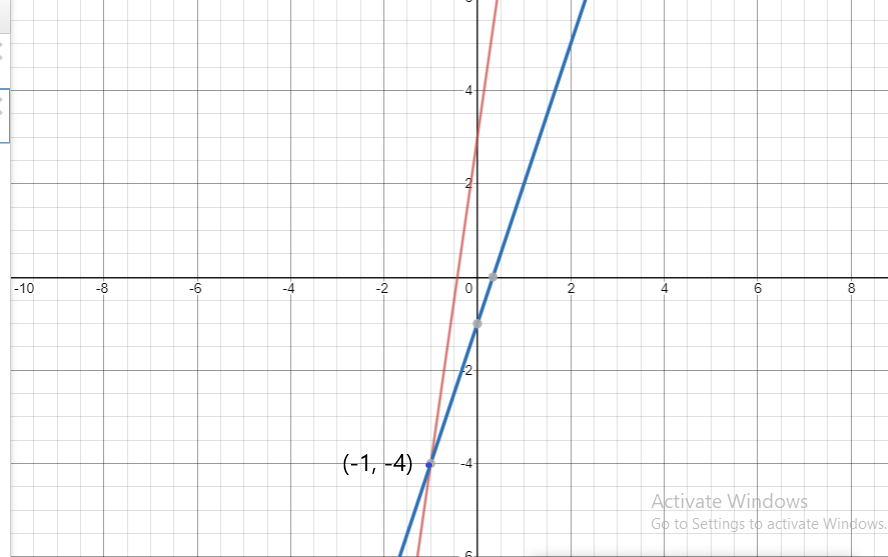 So, The point of intersection is (-1,-4).
So, The point of intersection is (-1,-4).
Performance Task
Heat Index
At the beginning of this chapter, you watched a STEAM Video called “Apparent Temperature.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Answer:
Functions Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Input: Ordered pairs can be used to show inputs and outputs , inputs are represented by x
Output: Ordered pairs can be used to show inputs and outputs , Outputs are represented by y
Relation: A relation pairs inputs with outputs
Mapping diagram: A relation can be represented by ordered pairs or mapping diagrams.
Function: The relation that pairs each input with exactly one output is a function.
Function rule: it is an equation, that describes the relationship between inputs(independent variables) and outputs(dependent variables).
Linear function: A linear function is a function whose graph is a straight line i.e., non vertical line . A linear can be written in the form y = mx + c , where m is the slope and c is the y intercept
Non linear function: The graph of a linear function shows a constant rate of change, A non linear function does not have a constant rate of change, So its graph is a not a line.
Graphic Organizers
You can use an Example and Non-Example Chart to list examples and non-examples of a concept. Here is an Example and Non-Example Chart for functions.
Choose and complete a graphic organizer to help you study the concept.

1. linear functions
2. nonlinear functions
3. linear functions with positive slope
4. linear functions with negative slope
Answer: 1. linear functions 
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

7.1 Relations and Functions (pp. 275–280)
Learning Target: Understand the concept of a function.
List the ordered pairs shown in the mapping diagram. Then determine whether the relation is a function.
Question 1.
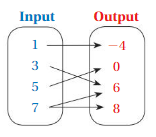
Answer: The ordered pairs are ( 1 , -4 ) , ( 3 , 6 ) , ( 5 , 0 ) , ( 7 , 6 ) , ( 7 , 8 ) and The relation is not a function .
Explanation:
As shown , The ordered pairs are ( 1 , -4 ) , ( 3 , 6 ) , ( 5 , 0 ) , ( 7 , 6 ) , ( 7 , 8 ) .
The input 7 has more than one output,
So, The relation is not a function .
Question 2.
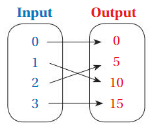
Answer: ordered pairs are ( 0 , 0 ) , ( 1 , 10 ) , ( 2 , 5 ) , ( 3 , 15 ) and The relation is a function .
Explanation:
As shown , The ordered pairs are ( 0 , 0 ) , ( 1 , 10 ) , ( 2 , 5 ) , ( 3 , 15 ).
Each input has exactly one output ,
So, The relation is a function .
Question 3.
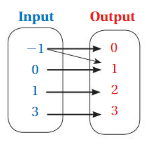
Answer: The ordered pairs are ( -1 , 0 ) , ( -1 , 1 ) , ( 0 , 1 ) , ( 1 , 2 ), ( 3 ,3 ) and The relation is not a function
Explanation:
As shown , The ordered pairs are ( -1 , 0 ) , ( -1 , 1 ) , ( 0 , 1 ) , ( 1 , 2 ), ( 3 ,3 ) .
The input -1 has more than one output ,
So, The relation is not a function .
Question 4.
For ordered pairs that represent relations, which coordinate represents the input? the output?
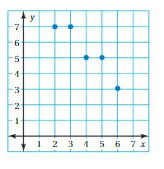
Answer: x coordinate is the input and y coordinate is the output
Explanation:
Ordered pairs from the given graph are ( 2 , 7 ) , ( 3 , 7 ) , ( 4 , 5 ) , ( 5 , 5 ) , ( 6 , 3 ) .
So , x coordinate is the input and y coordinate is the output
Question 5.
Draw a mapping diagram that represents the relation shown in the graph. Then determine whether the relation is a function. Explain.
Answer:
Explanation:
The mapping diagram is 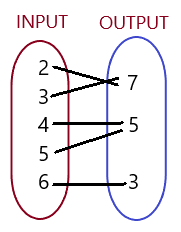
each input has more than one output
So, relation is not a function.
Question 6.
The mapping diagram represents the lengths (in centimeters) of a rubber band when different amounts of force (in Newtons) are applied.
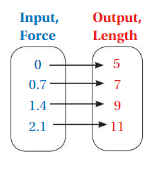
a. Is the length of a rubber band a function of the force applied to the rubber band?
b. Describe the relationship between the length of a rubber band and the force applied to the rubber band.
Answer: a. Yes
b. For every increase in 0.7 in input there is an increment of 2 in output.
Explanation:
a. The ordered pairs are ( 0 , 5 ) , ( 0.7 , 7 ) , ( 1.4 , 9 ) , ( 2.1 , 11 )
Each input has exactly one output
So, the length of a rubber band a function of the force applied to the rubber band.
b. For every increase in 0.7 in input there is an increment of 2 in output.
7.2 Representations of Functions (pp. 281–288)
Learning Target: Represent functions in a variety of ways.
Write a function rule for the statement.
Question 7.
The output is two less than the input.
Answer: y = x – 2
Explanation:
Let us say x is input and y is output , then
The output is two less than the input, will be
y = x – 2
Question 8.
The output is two more than one-fourth of the input.
Answer: y = \(\frac{x}{4}\) + 2
Explanation:
Let us say x is input and y is output , then
The output is two more than one-fourth of the input, will be
y = \(\frac{x}{4}\) + 2
Find the value of y for the given value of x.
Question 9.
y = 2x – 3; x = – 4
Answer: y = -8
Explanation:
Given, y = 2x
substitute x = -4 , we get
y = 2(-4)
y = -8.
Question 10.
y = 2 – 9x ; x = \(\frac{2}{3}\)
Answer: y = – 3.4
Explanation:
Given , y = 2 – 9x
substitute x = \(\frac{2}{3}\) , we get
y = 2 – 9 (0.6)
y = 2 – 5.4
y = – 3.4
Question 11.
y = \(\frac{x}{3}\) + 5; x = 6
Answer: y = 7.
Explanation:
Given, y = \(\frac{x}{3}\) + 5
substitute x = 6 , we get
y = \(\frac{6}{3}\) + 5
y = 2 + 5
y = 7.
Graph the function.
Question 12.
y = x + 3
Answer: The graph is 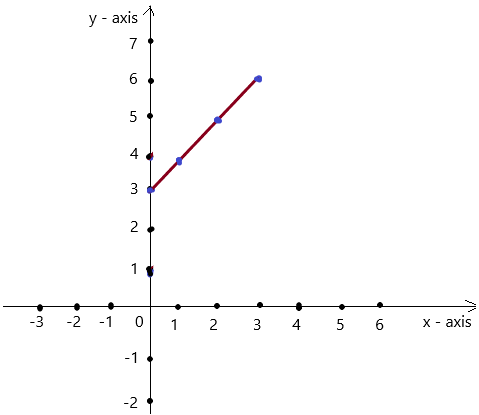
Explanation:
Given , y = x + 3 , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 0 + 3 = 3 . co-ordinates are (0 , 4)
if x = 1 , then y = 1 + 3 = 4 . co-ordinates are (1 , 5)
if x = 2 , then y = 2 + 3 = 5 , co-ordinates are (2 , 6)
if x = 3 , then y = 3 + 3 = 6 , co-ordinates are (3 , 7)
The co-ordinates (0 , 3) , (1 , 4) , (2 , 5) , (3 , 6) form a straight line .
Question 13.
y = – 5x
Answer: The graph is 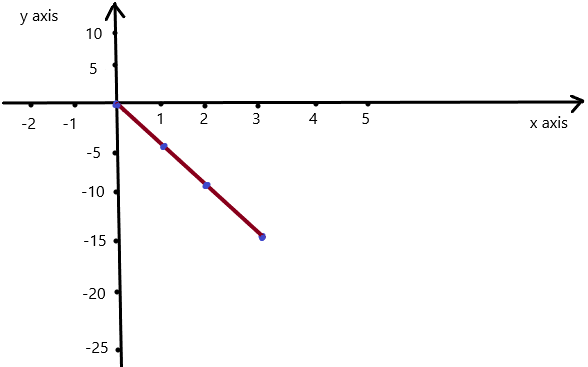
Explanation:
Given , y = – 5x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =- 5(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = – 5(1) = – 5 . co-ordinates are (1 , – 5)
if x = 2 , then y = – 5(2) = -10 , co-ordinates are (2 , -10)
if x = 3 , then y =- 5(3) = -15 , co-ordinates are (3 , -15)
The co-ordinates (0 , 0) , (1 , -5) , (2 , -10) , (3 , -15) form a straight line .
Question 14.
y = 3 – 3x
Answer: The graph is 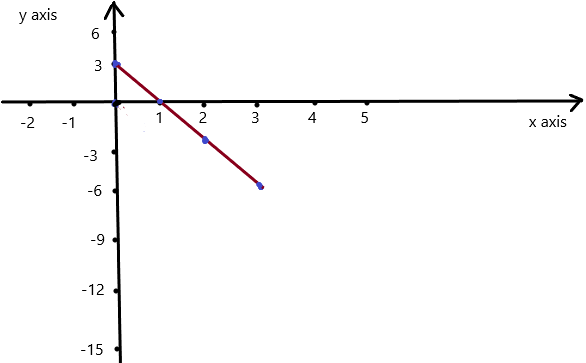
Explanation:
Given , y =3 – 3x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 3 – 3(0) = 3 . co-ordinates are (0 , 3)
if x = 1 , then y = 3 – 3(1) = 0 . co-ordinates are (1 , 0)
if x = 2 , then y = 3 – 3(2) = – 3 , co-ordinates are (2 , – 3)
if x = 3 , then y =3 – 3(3) = – 6 , co-ordinates are (3 , – 6)
The co-ordinates (0 , 3) , (1 , 0) , (2 , – 3) , (3 , – 6) form a straight line .
Question 15.
An online music store sells songs for $0.90 each.
a. Write a function that you can use to find the cost of buying songs.
b. What is the cost of buying 5 songs?
Answer: a. C = 0.90s
b. $4.5
Explanation:
a. The total cost is equal to the cost of each song times the number of songs, if each song is $0.90,
Then the total cost C of s songs is C = 0.90s.
b. Substituting s= 5 in C = 0.90s we get,
C = 0.90(5) = 4.5.
So, cost of 5 songs is $4.5.
7.3 Linear Functions (pp. 289–294)
Learning Target: Use functions to model linear relationships.
Use the graph or table to write a linear function that relates y to x.
Question 16.
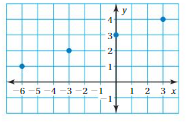
Answer: The linear function is y = \(\frac{1}{3}\)x + 3.
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (3 , 4) , (0 , 3 ) , (-3 , 2) , ( -6, 1 )
First find the slope m of the line containing the two given points (0 ,3) and (-3, 2)
m = (y2-y1) / (x2-x1)
m= (2 – 3) / (-3 – 0)
m = -1 / -3 .
m = 1/3 .
Because the line crosses the y axis at ( 0, 3 ) , The y intercept is 3.
So , the linear function is y = \(\frac{1}{3}\)x + 3.
Question 17.
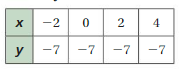
Answer: The linear function is y = −(0)x -7.
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-2 , -7) , (0 , -7 ) , (2 , -7) , ( 4 , -7 )
First find the slope m of the line containing the two given points (0 ,-7) and (2, -7)
m = (y2-y1) / (x2-x1)
m= (-7 – (-7)) / (2 – 0)
m = 0 .
Because the line crosses the y axis at ( 0, -7 ) , The y intercept is -7.
So , the linear function is y = −(0)x -7.
Question 18.
The table shows the age x (in weeks) of a puppy and its weight y (in pounds).
a. Write and graph a linear function that relates y to x.
b. Interpret the slope and the y-intercept.
c. After how many weeks will the puppy weigh 33 pounds?
Answer: a. y = \(\frac{3}{2}\)x + 3
b. 3 pounds
c. Age is 20 weeks
Explanation: 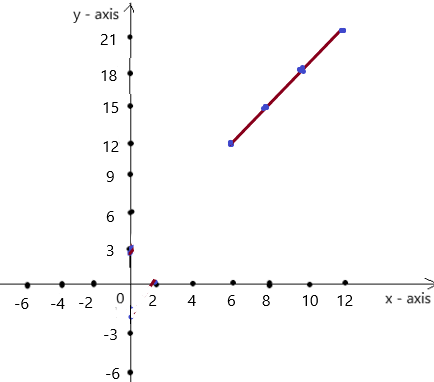
a. In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (6 , 12) , (8 , 15 ) , (10 , 18) , ( 12 , 21 )
First find the slope m of the line containing the two given points ((6 ,12) and (8 , 15)
m = (y2-y1) / (x2-x1)
m= (15 – 12) / (8 – 6)
m = 3/2 .
substitute the slope in the (6 ,12) to get point slope to form a line.
y-y1 = m (x-x1)
y – 12 = 3/2 ( x – 6)
2(y – 12) = 3(x – 6)
2y – 24 = 3x – 18
2y = 3x – 18 + 24
2y = 3x + 6
So , 2y = 3x + 6 or y = \(\frac{3}{2}\)x + 3 is linear function.
b. The slope measures the rate of change of weight due to change in weeks, Here the slope of 3/2 means that as one week passes, weight of the puppy increases by 3/2 pounds.
y intercept measures the weight of the puppy, when it was born which is 3 pounds in this case measured by c.
c. put y = 33,
33 = \(\frac3}{2}\)x + 3
30 = \(\frac{3}{2}\)x
30 × 2 = 3x
x = 60/3
x = 20.
So, Age is 20 weeks.
7.4 Comparing Linear and Nonlinear Functions (pp. 295–300)
Learning Target: Understand differences between linear and nonlinear functions.
Does the table represent a linear or nonlinear function? Explain.
Question 19.
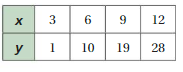
Answer: y = 3x – 8 is linear function.
Explanation:
Ordered pairs are (3 , 1 ) , (6 , 10) , (9 , 19) , (12 , 28)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (3 , 1 ) and (6 , 10)
m = (y2-y1) / (x2-x1)
m= (10 – 1) / (6– 3)
m = 9/3
m = 3
substitute the slope in the (3 , 1) to get point slope to form a line.
y-y1 = m (x-x1)
y – 1 = 3 ( x – 3)
y – 1 = 3x – 9
y = 3x – 9 + 1
y = 3x – 8
So , y = 3x – 8 is linear function.
Question 20.
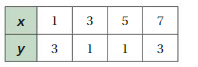
Answer: y = -x + 4 is linear function.
Explanation:
Ordered pairs are (1 , 3 ) , (3 , 1) , (5 , 1) , (7 , 3)
Plot the points in the table , Draw a line through the points
First find the slope m of the line containing the two given points (1 , 3 ) and (3 , 1)
m = (y2-y1) / (x2-x1)
m= (1 – 3) / (3– 1)
m = -2/2
m = -1
substitute the slope in the (1 , 3) to get point slope to form a line.
y-y1 = m (x-x1)
y – 3 = -1 ( x – 1)
y – 3 = -x + 1
y = -x + 1 + 3
y = -x + 4
So , y = -x + 4 is linear function.
Question 21.
Does the graph represent a linear or nonlinear function? Explain.
Answer: The graph represent a non linear function.
Explanation:
As shown in the graph linear function represents a straight line to which not happened here,
So , the graph is non linear function
Question 22.
Does the equation y = 2.3x represent a linear or nonlinear function? Explain.
Answer: y = 2.3x is a linear function.
Explanation:
Given , y = 2.3x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y = 2.3(0) = 0 . co-ordinates are (0 , 0)
if x = 1 , then y = 2.3(1) = 2.3 . co-ordinates are (1 , 2.3)
if x = 2 , then y = 2.3(2) = 4.6 , co-ordinates are (2 , 4.6)
The co-ordinates (0 , 0) , (1 , 2.3) , (2 , 4.6) form a straight line .
Each x input has only one y output so it is a function .
And it forms a straight line when graphed .
So, y = 2.3x is a linear function.
7.5 Analyzing and Sketching Graphs (pp. 301–306)
Learning Target: Use graphs of functions to describe relationships between quantities.
Question 23.
Describe the relationship between the two quantities in the graph.
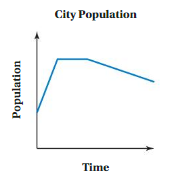
Answer: At certain point of time, line segment is increased with respect to time and maintained a constant change and again dropped gradually with the increase in time.
Explanation:
The relationship between the graph is population and time ,
At certain point of time, line segment is increased with respect to time and maintained a constant change and again dropped gradually with the increase in time.
So, the city population is not constant at all the time.
Sketch a graph that represents the situation.
Question 24.
You climb a climbing wall. You climb halfway up the wall at a constant rate, then stop and take a break. You then climb to the top of the wall at a greater constant rate.
Answer: The graph is 
Explanation:
You start climbing a wall at a constant rate so the first portion of the graph needs to be linear with a positive slope, you then take a break which means your height is constant so the second part of the graph needs to be a horizontal line, you then start climbing again at a constant rate, so the last part of the graph needs to be linear with a positive slope.
Question 25.
The price of a stock increases at a constant rate for several months before the stock market crashes. The price then quickly decreases at a constant rate.
Answer: The graph is 
Explanation:
The stock price is increasing at a constant rate so the first part of the graph needs to be linear with positive slope, Then price begins to drop quickly so the second part of the graph needs to be linear with a steep negative slope.
Question 26.
The graph shows the sales of two companies during a particular year.
a. Describe the sales of each company.
b. Which company has greater total sales for the year?
c. Give a possible explanation for the change in each company’s sales throughout the year.
Answer: All The explanation is given below
a. Company A – The sales of the company is increasing at a constant rate so the first part of the graph needs to be linear with positive slope, and decreasing with a slight negative steep and again increasing at a constant rate increasing the sales of the company
Company B – The sales of the company is increasing at a constant rate so the first part of the graph needs to be increase in curve with a slight decrease in the graph leading to decrease in sales and vise versa.
b. Company A has the greater total sales for the year compared to Company B, with maintaining the sales up to the mark without losses.
c. The change in each company’s sales throughout the year, Company A – The sales of the company is increasing at a constant rate so the first part of the graph needs to be linear with positive slope,
Company B – The sales of the company is increasing at a constant rate so the first part of the graph needs to be increase in curve with a slight decrease in the graph leading to decrease in sales
Functions Practice Test
Question 1.
List the ordered pairs shown in the mapping diagram. Then determine whether the relation is a function.
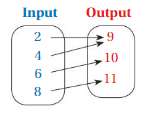
Answer: The relation is a function
Explanation:
As shown , Ordered pairs are the combinations of input and output
So , Ordered pairs are ( 2 , 9 ) , ( 4 , 9 ) , ( 6 , 10 ) , ( 8 , 11 ) .
Each input has exactly one output ,
So , The relation is a function .
Question 2.
Draw a mapping diagram that represents the relation. Then determine whether the relation is a function. Explain.
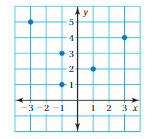
Answer: The mapping diagram is 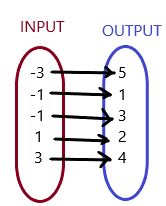
Explanation:
Ordered pairs from the given graph are ( -3 , 5 ) , ( -1 , 1 ) , ( -1 , 3 ) , ( 1 , 2 ) , ( 3 , 4 ) .
Each input has exactly one output ,
So , The relation is a function .
Question 3.
Write a function rule for “The output is twice the input.”
Answer: y = 2x
Explanation:
Let us say x is input and y is output , then
The output is twice the input. will be
y = 2x
Question 4.
Graph the function y = 1 – 3x.
Answer: The graph is 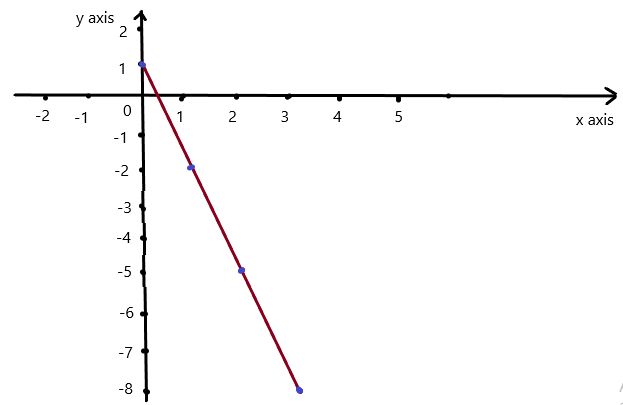
Explanation:
Given , y = 1 – 3x , we know y = mx + c , where m = slope , c = constant
To obtain the graph , we should have ordered pairs ,
So , if x = 0 , then y =1 – 3(0) = 1 . co-ordinates are (0 , 1)
if x = 1 , then y = 1 – 3(1) = -2 . co-ordinates are (1 , -2)
if x = 2 , then y = 1 – 3(2) = -5 , co-ordinates are (2 , -5)
if x = 3 , then y =1 – 3(3) = -8 , co-ordinates are (3 , -8)
The co-ordinates (0 , 1) , (1 , -2) , (2 , -5) , (3 , -8) form a straight line .
Question 5.
Use the graph to write a linear function that relates y to x.
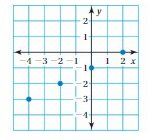
Answer: The linear function is y = 0.5x – 1
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (-4 , -3) , (-2 , -2 ) , (0 , -1) , ( 2 , 0 )
First find the slope m of the line containing the two given points (0 , -1) and ( 2 , 0 )
m = (y2-y1) / (x2-x1)
m= (0 – (-1)) / (2 – 0)
m = 1 / 2 .
m = 0.5 .
Because the line crosses the y axis at ( 0, -1 ) , The y intercept is -1.
So , the linear function is y = 0.5x – 1 .
Question 6.
Does the table represent a linear or nonlinear function? Explain.
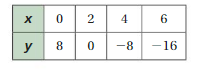
Answer: The linear function is y = −4x + 8
Explanation:
In order to write the function we have to write the ordered pairs of the graph ,
Ordered pairs are (0 , 8) , (2 , 0 ) , (4 , -8) , ( 6 , -16 )
First find the slope m of the line containing the two given points (0 , 8) and (2 , 0 )
m = (y2-y1) / (x2-x1)
m= (0 – 8) / (2 – 0)
m = -4
Because the line crosses the y axis at ( 0, 8 ) , The y intercept is 8.
So , the linear function is y = −4x + 8.
Question 7.
The table shows the number of y meters a water-skier travels in x minutes.
a. Write a function that relates y to x.
b. Graph the linear function.
c. At this rate, how many kilometers will the water-skier travel in 12 minutes?
d. Another water-skier travels at the same rate but starts a minute after the first water-skier. Will this water-skier catch up to the first water-skier? Explain.
Answer: All the answers are given below
Explanation:
Ordered pairs are (1 , 600) , (2 , 1200 ) , (3 , 1800) , ( 4 , 2400 ) , (5 , 3000)
First find the slope m of the line containing the two given points(1 , 600) and (2 , 1200 )
m = (y2-y1) / (x2-x1)
m= (1200 – 600) / (2 – 1)
m = 600
So, the line is of the form y = 600x + c
put x= 3 and y = 1800 in the above equation we get,
1800 = 600(3) + c
c = 1800 – 1800
c = 0.
So, The line is y = 600x.
b. The graph is 
c. put x = 12 in y = 600x
y = 600(12)
y = 7200
7200 meters, i.e., 7.2km
d. Another water skier travels at the same rate but starts a minute after the first water skier, Since both are travelling at the same rate , the water skier who was late will always be behind the first water skier.
Question 8.
The graph shows the prices of two stocks during one day.
a. Describe the changes in the price of each stock.
b. Which stock has a greater price at the end of the day?
c. Give a possible explanation for the change in the price of Stock B throughout the day.
Answer: Detailed Explanation is given below.
Explanation:
a. The changes in the price of each stock is Stock A has the constant increase in stock for a particular time and maintains a constant price forming a straight line in the graph, and again decreasing with a negative slope and vise versa, while Stock B is having steep negative slope that is decreasing in the prices with the time and having a constant horizontal line. and having a positive increase in the slope and same repeats again.
b. stock B has a greater price at the end of the day, having a positive increase in the slope
c. The change in the price of Stock B throughout the day, is having steep negative slope that is decreasing in the prices with the time and having a constant horizontal line. and having a positive increase in the slope and same repeats again, compared to stock A .
Question 9.
You are competing in a footrace. You begin the race by increasing your speed at a constant rate. You then run at a constant speed until you get a cramp and have to stop. You wait until your cramp goes away before you start increasing your speed again at a constant rate. Sketch a graph that represents the situation.
Answer: The graph is 
Explanation:
You begin the race by increasing your speed at a constant rate so the first portion of the graph needs to be linear with a positive slope , you then run at a constant speed so the next portion of the graph needs to be horizontal line , you then stop and take a break , so your speed is zero, which means the next portion of the line needs to be
horizontal line on the x axis , you then increase your speed again at a constant rate sop that the last portion of the graph needs to be linear with a positive slope
Functions Cumulative Practice

Question 1.
What is the slope of the line?
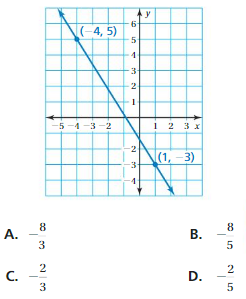
Answer: Not in the options but the answer is m = -4/3
Explanation:
Ordered pairs are (-4 , 5) , (1 , -3 ),
First find the slope m of the line containing the two given points
m = (y2-y1) / (x2-x1)
m= (-3 – 5) / (2 – (-4))
m = -8/6
m = -4/3.
Question 2.
Which value of a makes the equation 24 = \(\frac{a}{3}\) – 9 true?
F. 5
G. 11
H. 45
I. 99
Answer: I. 99
Explanation:
Substitute a = 99 , in the given equation we get,
24 = \(\frac{a}{3}\) – 9
24 = \(\frac{99}{3}\) – 9
24 = 33 – 9
24 = 24.
So, last option is the correct answer.
Question 3.
A mapping diagram is shown.
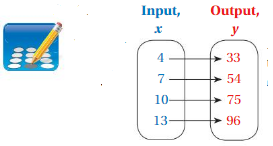
What number belongs in the box so that the equation describes the function represented by the mapping diagram?
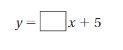
Answer: m = 7 , y = 7x + 5
Explanation:
Ordered pairs are (4 , 33) , (7 , 54 ), (10 , 75) , (13 , 96 ),
First find the slope m of the line containing the two given points (4 , 33) and (7 , 54 )
m = (y2-y1) / (x2-x1)
m= (54 – 33) / (7 – 4)
m = 21/3
m = 7.
So, y = 7x + 5
Question 4.
What is the solution of the system of linear equations?
3x + 2y = 5
x = y + 5
A. (3, – 2)
B. (- 2, 3)
C. (- 1, 4)
D. (1, – 4)
Answer: A. (3, – 2)
Explanation:
Given 3x + 2y = 5
Then substitute , x = y + 5 in the above equation
3( y + 5) + 2y = 5
3y + 15 + 2y = 5
5y + 15 = 5
5( y + 3) = 5
y + 3 = 1
y = 1 – 3
y = -2,
substitute y = -2 in x = y + 5 then
x = 3
So, (3 , -2)
Question 5.
The director of a research lab wants to present data to donors. The data show how the lab uses a large amount of donated money for research and only a small amount of money for other expenses. Which type of display best represents these data?
F. box-and-whisker plot
G. circle graph
H. line graph
I. scatter plot
Answer: I. scatter plot
Explanation:
Scatter plot is the best graph for this type of data where vertical axis will show the amount of money and Horizontal axis will show research and other expenses.
Question 6.
Which graph shows a nonlinear function?
Answer: option B
Explanation:
As all the other options are representing the linear function that is forming a straight line expect for option B , it is representing a non linear equation.
Question 7.
Which equation of a line passes through the point (—2, 3) and has a slope of \(\frac{3}{4}\)?
Answer: F. y – 3 = \(\frac{3}{4}\)(x + 2)
Explanation:
Given, y – 3 = \(\frac{3}{4}\)(x + 2)
it is in the form of y = mx + c
so, slope m = \(\frac{3}{4}\)
Substitute the given points in this equation that is x = -2 and y = 3
3 – 3 = \(\frac{3}{4}\)(-2 + 2)
0 = 0.
So, F is the correct option.
Question 8.
The tables show the sales (in millions of dollars) for two companies over a five-year period.
Part A Does the first table show a linear function? Explain your reasoning.
Part B Does the second table show a linear function? Explain your reasoning.
Answer: Part A, the first table shows a linear function,
Part B the second table shows a linear function.
Explanation:
Part A – ordered pairs are (1 , 2) , (2 , 4) , (3 , 6) , (4 , 8) , (5 , 10)
Each input has exactly one output and forms a straight line when graphed
So, it is a linear function.
Part B – ordered pairs are (1 , 1) , (2 , 1) , (3 , 2) , (4 , 3) , (5 , 5)
Each input has exactly one output and does not form a straight line when graphed
So, it is a linear function.
Question 9.
The equations y = – x + 4 and y = \(\frac{1}{2}\)x – 8 form a system of linear equations. The table shows the values of y for given values of x.
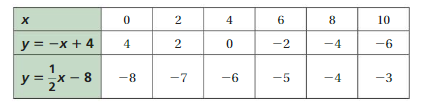
What can you conclude from the table?
A. The system has one solution, when x = 0.
B. The system has one solution, when x = 4.
C. The system has one solution, when x = 8.
D. The system has no solution.
Answer: C. The system has one solution, when x = 8.
Explanation:
Given , y = – x + 4 and y = \(\frac{1}{2}\)x – 8
for x = 8 we have
y = -8 + 4 = -4
y = 0.5(8) – 8 = 4 – 8 = -4
Both the equations have one solution for x = 8
So, The system has one solution, when x = 8.
Question 10.
The vertices of a triangle are A (- 1, 3), B (1, 2), and C (- 1, – 1). Dilate the triangle using a scale factor of 2. What is the y-coordinate of the image of B?

Answer: The New right angle triangle is larger than the original one So , its a increase .
Explanation:
Given , (- 1, 3), ( 1, 2 ), (- 1, -1) these pairs form a right angle triangle
K = 2 , For the dilation figure multiply the 3 with the given ordered pairs , then
(- 1, 3) × 2 = ( -2 , 6)
( 1, 2) × 2 = ( 2 , 4)
(- 1, -1) × 2 = (-2 , -2)
From these new ordered pairs we form a new right angle triangle
The New right angle triangle is larger than the original one So, it’s an increase.
Conclusion
Enhance your problem-solving skills and overall math proficiency using the Big Ideas Math Grade 8 Chapter 7 Functions. Give your best in exams by solving the Problems Over here aligned as per the Latest BIM Textbooks. In case of any suggestions do leave us your queries via the comment box so that we can get back to you.
Must Try:
