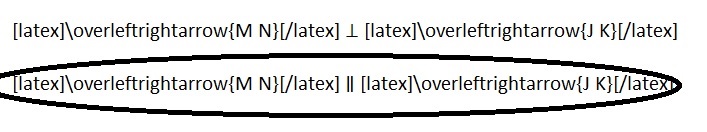Eureka Math

Engage NY Eureka Math 5th Grade Module 6 Lesson 27 Answer Key

Eureka Math Grade 5 Module 6 Lesson 27 Problem Set Answer Key

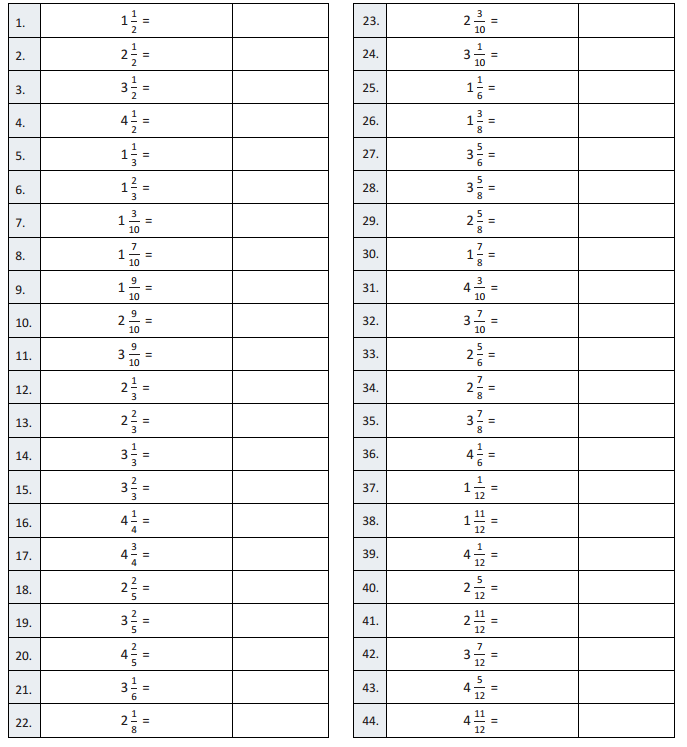
Question 1.
Use the RDW process to solve the word problems below.
a. Julia completes her homework in an hour. She spends \(\frac{7}{12}\) of the time doing her math homework and \(\frac{1}{6}\) of the time practicing her spelling words. The rest of the time she spends reading. How many minutes does Julia spend reading?
Answer :
Time taken by Julia to complete her home work = 1 hour .
Time spent in Doing Math Homework = \(\frac{7}{12}\)
Time spent in Practicing her spelling words = \(\frac{1}{6}\)
Time spent in Reading = x .
Time spent in Doing Math Homework + Time spent in Practicing spelling words + Time spent in Reading = 1hour
\(\frac{7}{12}\) + \(\frac{1}{6}\)  + x = 1
\(\frac{7 + 2 + 12x }{12}\) = 1
9 +12x = 12
12x = 12 – 9
12x = 3
x = \(\frac{3}{12}\)
x = \(\frac{1}{4}\)  .
Therefore Time spent in Reading = \(\frac{1}{4}\) hour .

b. Fred has 36 marbles. Elise has \(\frac{8}{9}\) as many marbles as Fred. Annika has \(\frac{3}{4}\) as many marbles as Elise. How many marbles does Annika have?
Answer:
Number of Marbles with Fred = 36
Number of Marbles with Elise =\(\frac{8}{9}\)  as many marbles as Fred =\(\frac{8}{9}\) (36)= 32
Number of Marbles with Annika = \(\frac{3}{4}\) as many marbles as Elise = \(\frac{3}{4}\) (32) = 24 .
Therefore Number of marbles with Annika = 24 .

Question 2.
Write and solve a word problem that might be solved using the expressions in the chart below.

Answer:

Eureka Math Grade 5 Module 6 Lesson 27 Reflection Answer Key

How did teaching other students how to solve a word problem strengthen your skills as a problem solver? What did you learn about your problem-solving skills? What are your strengths and weaknesses as a problem solver?
Answer:
Skills of a problem solver
Active listening.
Analysis.
Research.
Creativity.
Communication.
Dependability.
Decision making.
Team-building.

Problem-solving model
a. Define the problem. The system.
b. Think about it. “Let it simmer”.
c. Plan a solution. Consider possible strategies.
d. Carry out the plan. Be patient.
e. Look back. Encourage students to reflect.

Problem-Solving Strengths:
Divergent thinking
Challenges assumptions
Step-by-step approach
Seeks practical information
Builds off others’ ideas
Looks for how the solution impacts people
Looks at the big picture
Checks for connections between different problems

Problem – Solving Weakness :
Inaccurate information of question
Different approaches to solve problem
Explanation with diagrams
Clear explanation so that everyone should understand .

Eureka Math Grade 5 Module 6 Lesson 27 Homework Answer Key

Question 1.
Use the RDW process to solve the word problems below.
a. There are 36 students in Mr. Meyer’s class. Of those students, \(\frac{5}{12}\) played tag at recess, \(\frac{1}{3}\) played kickball, and the rest played basketball. How many students in Mr. Meyer’s class played basketball?
Answer :
Number of Students in Mr. Meyer’s class = 36 students.
Number of students played tag at recess = \(\frac{5}{12}\) (36 ) = 15 .
Number of students played kickball = \(\frac{1}{3}\) (36 ) = 12.
Number of students played basket ball = Total students – students who played ( recess + kickball )= 36 – (15 +12 )
= 36 – 27 = 9 students.
Therefore, Number of students played basket ball = 9 students.

b. Julie brought 24 apples to school to share with her classmates. Of those apples, \(\frac{2}{3}\) are red, and the rest are green. Julie’s classmates ate \(\frac{3}{4}\) of the red apples and \(\frac{1}{2}\) of the green apples. How many apples are left?
Answer:
Number of Apples Julie brought = 24
Number of red apples = \(\frac{2}{3}\) ( 24) = 16 .
Number of green apples = total – red apples = 24 – 16 = 8.
Number of red apples eaten = \(\frac{3}{4}\) ( 16 ) = 12 apples.
Number of green apples eaten = \(\frac{1}{2}\) ( 8 ) = 4 apples .
Number of red apples left = total red apples – number of red apples eaten = 16 – 12 = 4 apples.
Number of green apples left = total green apples – number of green apples eaten = 8 – 4 = 4 apples.
Total number of apples left = Number of left red apples left +Number of left green apples = 4 + 4 = 8 apples.

Question 2.
Write and solve a word problem for each expression in the chart below.

Answer:

Engage NY Eureka Math 5th Grade Module 6 Lesson 26 Answer Key

Eureka Math Grade 5 Module 6 Lesson 26 Problem Set Answer Key

Question 1.
For each written phrase, write a numerical expression, and then evaluate your expression.
a. Three fifths of the sum of thirteen and six
Numerical expression:
\(\frac{13}{5}\) (13 + 6 )
Solution:
\(\frac{13}{5}\) (13 + 6 ) = \(\frac{13}{5}\) (19) = \(\frac{247}{5}\)

b. Subtract four thirds from one seventh of sixty-three.
Numerical expression:
\(\frac{1}{7}\)(63) – \(\frac{4}{3}\)
Solution:
\(\frac{1}{7}\)(63) – \(\frac{4}{3}\) = 9 – \(\frac{4}{3}\) = \(\frac{27 – 4}{3}\) = \(\frac{23}{3}\) = 7\(\frac{2}{3}\)

c. Six copies of the sum of nine fifths and three
Numerical expression:
6(\(\frac{1}{5}\) + 3)
Solution:
6(\(\frac{1}{5}\) + 3) = 6(\(\frac{1 + 15 }{5}\))= 6(\(\frac{16}{5}\)) = \(\frac{96}{5}\)

d. Three fourths of the product of four fifths and fifteen
Numerical expression:
\(\frac{3}{4}\)(\(\frac{4}{5}\) (15)
Solution:
\(\frac{3}{4}\)(\(\frac{4}{5}\) (15)
= \(\frac{3}{4}\) 12
= 9

Question 2.
Write at least 2 numerical expressions for each phrase below. Then, solve.
a. Two thirds of eight
b. One sixth of the product of four and nine
Answer:
a. Numerical expression:
\(\frac{2}{3}\) (8 )or \(\frac{2}{3}\) × 8
Solution:
\(\frac{2}{3}\) × 8 = \(\frac{16}{3}\) = 5 \(\frac{1}{3}\) .
b. Numerical expression:
\(\frac{1}{6}\) (4 × 9 ) or \(\frac{1}{6}\) (9 × 4 )
Solution:
\(\frac{1}{6}\) (4 × 9 ) = \(\frac{1}{2}\) (4 × 3 ) = 2 × 3 = 6

Question 3.
Use <, >, or = to make true number sentences without calculating. Explain your thinking.
a. 217 × (42 + \(\frac{48}{5}\)) (217 × 42) + \(\frac{48}{5}\)
b. (687 × \(\frac{3}{16}\)) × \(\frac{7}{12}\) (687 × \(\frac{3}{16}\)) × \(\frac{3}{12}\)
c.  5 × 3.76 + 5 × 2.68 5 × 6.99

Answer:
a. 217 × (42 + \(\frac{48}{5}\)) > (217 × 42) + \(\frac{48}{5}\)
Explanation :
The left number is multiplied by greater number .
b. (687 × \(\frac{3}{16}\)) × \(\frac{7}{12}\) > (687 × \(\frac{3}{16}\)) × \(\frac{3}{12}\)
Explanation :
\(\frac{7}{2}\) is bigger than \(\frac{3}{12}\) . So, Multiplying the same factor by \(\frac{7}{2}\) will give you greater answer than multiplying by \(\frac{3}{2}\) or \(\frac{1}{4}\)
c. 5 × 3.76 + 5 × 2.68 < 5 × 6.99
Explanation :
If you add 3.76 and 2.68 its not as much as 6.99 and using the Distributive property , the first equation could be
5 ( 3.76 + 2.68 ) = 5 (6.44 ) .

Eureka Math Grade 5 Module 6 Lesson 26 Reflection Answer Key

How did the games we played today prepare you to practice writing, solving, and comparing expressions this summer? Why do you think these are important skills to work on over the summer? Will you teach someone at home how to play these games with you? What math skills will you need to teach in order for someone at home to be able to play with you?
Answer:
This Expressions help in comparing the costs of goods while doing shopping and critical thinking skills and ability to utilize math in everyday life.
It is Important to work on this skills on over summer helps in increasing the solving of problems in different approach and constantly Learning .
Yes , Teaching some one to play these games helps me to become perfect in that game .
Math skills that i need is to have patience and understanding in order to Explain clearly to all.

Eureka Math Grade 5 Module 6 Lesson 26 Homework Answer Key

Question 1.
For each written phrase, write a numerical expression, and then evaluate your expression.
a. Forty times the sum of forty-three and fifty-seven
Numerical expression:
Solution:
Answer:
Numerical expression:
40 ( 43 + 57 )
Solution:
40 ( 43 + 57 ) = 40 ( 100 ) = 4000 .

b. Divide the difference between one thousand three hundred and nine hundred fifty by four.
Numerical expression:
Solution:
Answer:
Numerical expression:
\(\frac{1300 – 950}{4}\)
Solution:
\(\frac{1300 – 950}{4}\) = \(\frac{350}{4}\) = \(\frac{175}{2}\) = 87\(\frac{1}{2}\) .

c. Seven times the quotient of five and seven
Numerical expression:
Solution:
Answer:
Numerical expression:
7×(5÷7)
Solution:
7×(5÷7) = 7 (\(\frac{5}{7}\) ) = 5

d. One fourth the difference of four sixths and three twelfths
Numerical expression:
Solution:
Answer:
Numerical expression:
\(\frac{1}{4}\)( \(\frac{4}{6}\) – \(\frac{3}{12}\))
Solution:
\(\frac{1}{4}\)( \(\frac{4}{6}\) – \(\frac{3}{12}\))
= \(\frac{1}{4}\)( \(\frac{2}{3}\) – \(\frac{1}{4}\))
= \(\frac{1}{4}\)( \(\frac{8- 3}{12}\))
= \(\frac{1}{4}\)( \(\frac{5}{12}\))
=\(\frac{5}{48}\)

Question 2.
Write at least 2 numerical expressions for each written phrase below. Then, solve.
a. Three fifths of seven
b. One sixth the product of four and eight
Answer a :
Numerical expression:
\(\frac{3}{5}\)( 7) or \(\frac{3}{5}\) × 7
Solution:
\(\frac{3}{5}\)( 7) = \(\frac{21}{5}\)

Question 3.
Use <, >, or = to make true number sentences without calculating. Explain your thinking.
a. 4 tenths + 3 tens + 1 thousandth 30.41
b. (5 × \(\frac{1}{10}\)) + (7 × \(\frac{1}{100}\)) 0.507
c. 8 × 7.20 8 × 4.36 + 8 × 3.59
Answer:
a. 4 tenths + 3 tens + 1 thousandth < 30.41
Explanation :
We have thousandth in the left  that means 0.001 (43) = 0.043
b. (5 × \(\frac{1}{10}\)) + (7 × \(\frac{1}{100}\))  = 0.507
Explanation :
(5 × \(\frac{1}{10}\)) + (7 × \(\frac{1}{100}\))
= 0.5 + 0.07 = 0.57
we have only \(\frac{1}{100}\) that means only 2 points of decimals
Where as the in 0.507 we have 3 decimal points .
c.
8 × 7.20 < 8 × 4.36 + 8 × 3.59
Explanation :
If you add 4.36 and 3.59 is greater than as 7.20 and using the Distributive property , the Second equation could be
8 ( 4.36 + 3.59 ) = 8 (7.95 ) .

Engage NY Eureka Math 5th Grade Module 6 Lesson 25 Answer Key

Eureka Math Grade 5 Module 6 Lesson 25 Homework Answer Key

Question 1.
Fred and Ethyl had 132 flowers altogether at first. After Fred sold \(\frac{1}{2}\) of his flowers and Ethyl sold 48 of her flowers, they had the same number of flowers left. How many flowers did each of them have at first?
Answer:
Total number of flowers = 132
Number of flowers with Fred = x
Number of flowers with Ethyl = 132 – x
Number of flowers sold by Fred = \(\frac{1}{2}\) x = \(\frac{x}{2}\)
Number of flowers sold by Ethyl = 48
Number of flowers remaining with Fred = x – \(\frac{x}{2}\) = \(\frac{x}{2}\)
Number of Flowers remaining with Ethyl = 132 – x – 48 = 84 – x
Number of flowers remaining with Fred = ethyl
\(\frac{x}{2}\) = 84 – x
x + \(\frac{x}{2}\) = 84
\(\frac{3x}{2}\) = 84
3x = 168
x = 56 .
Number of flowers with Fred = x = 56
Number of flowers with Ethyl = 132 – x = 132 – 56 = 79 .

The following problems are puzzles for your enjoyment. They are intended to encourage working together and family problem-solving fun. They are not a required element of this homework assignment.
Question 2.
Without removing any, move 2 matchsticks to make 4 identical squares. Which matchsticks did you move? Draw the new shape.

Answer:

Question 3.
Move 3 matchsticks to form exactly (and only) 3 identical squares. Which matchsticks did you move? Draw the new shape.

Answer:

Engage NY Eureka Math 5th Grade Module 6 Lesson 24 Answer Key

Eureka Math Grade 5 Module 6 Lesson 24 Homework Answer Key

Question 1.
Pat’s Potato Farm grew 490 pounds of potatoes. Pat delivered \(\frac{3}{7}\) of the potatoes to a vegetable stand. The owner of the vegetable stand delivered \(\frac{2}{3}\) of the potatoes he bought to a local grocery store, which packaged half of the potatoes that were delivered into 5-pound bags. How many 5-pound bags did the grocery store package?
Answer:
Weight of potatoes grown in pat farm = 490 pounds
Weight of potatoes pat delivered to vegetable stand = \(\frac{3}{7}\) × 490 = 210 pounds .
Weight of potatoes vegetable stand owner to local grocery store = \(\frac{2}{3}\)  × 210 = 140 pounds .
Weight of potatoes local grocery store packed in 5 – pound bags = half of the potatoes = 140 / 2 = 70 pounds .
Number of 5-pound bags did the grocery store packed = 70 / 5 = 14 bags .

The following problems are for your enjoyment. They are intended to encourage working together and family problem-solving fun. They are not a required element of this homework assignment.
Question 2.
Six matchsticks are arranged into an equilateral triangle. How can you arrange them into 4 equilateral triangles without breaking or overlapping any of them? Draw the new shape.

Answer:

By placing 3 match sticks in the middle of the triangle 4 equilateral triangles are formed is shown in the above figure .

Question 3.
Kenny’s dog, Charlie, is really smart! Last week, Charlie buried 7 bones in all. He buried them in 5 straight lines and put 3 bones in each line. How is this possible? Sketch how Charlie buried the bones.
Answer:

the possible way is shown in the above diagram

Engage NY Eureka Math 5th Grade Module 6 Lesson 23 Answer Key

Eureka Math Grade 5 Module 6 Lesson 23 Sprint Answer Key

A
Change Mixed Numbers into Improper Fractions

Question 1.
1\(\frac{1}{5}\) =
Answer:
1\(\frac{1}{5}\) = \(\frac{6}{5}\)

Question 2.
2\(\frac{1}{5}\) =
Answer:
2\(\frac{1}{5}\) = \(\frac{11}{5}\)

Question 3.
3\(\frac{1}{5}\) =
Answer:
3\(\frac{1}{5}\) = \(\frac{16}{5}\)

Question 4.
4\(\frac{1}{5}\) =
Answer:
4 \(\frac{1}{5}\) = \(\frac{21}{5}\)

Question 5.
1\(\frac{1}{4}\) =
Answer:
1\(\frac{1}{4}\) = \(\frac{5}{4}\)

Question 6.
1\(\frac{3}{4}\) =
Answer:
1\(\frac{3}{4}\) = \(\frac{7}{4}\)

Question 7.
1\(\frac{2}{5}\) =
Answer:
1\(\frac{2}{5}\) = \(\frac{7}{5}\)

Question 8.
1\(\frac{3}{5}\) =
Answer:
1\(\frac{3}{5}\) = \(\frac{8}{5}\)

Question 9.
1\(\frac{4}{5}\) =
Answer:
1\(\frac{4}{5}\) = \(\frac{9}{5}\)

Question 10.
2\(\frac{4}{5}\) =
Answer:
2\(\frac{4}{5}\) = \(\frac{14}{5}\)

Question 11.
3\(\frac{4}{5}\) =
Answer:
3\(\frac{4}{5}\) = \(\frac{19}{5}\)

Question 12.
2\(\frac{1}{4}\) =
Answer:
2\(\frac{1}{4}\)  = \(\frac{9}{4}\)

Question 13.
2\(\frac{3}{4}\) =
Answer:
2\(\frac{3}{4}\) = \(\frac{11}{4}\)

Question 14.
3\(\frac{1}{4}\) =
Answer:
3\(\frac{1}{4}\) = \(\frac{13}{4}\)

Question 15.
3\(\frac{3}{4}\) =
Answer:
3\(\frac{3}{4}\) = \(\frac{15}{4}\)

Question 16.
4\(\frac{1}{3}\) =
Answer:
4\(\frac{1}{3}\) = \(\frac{1}3{3}\)

Question 17.
4\(\frac{2}{3}\) =
Answer:
4\(\frac{2}{3}\) = \(\frac{14}{3}\)

Question 18.
2\(\frac{3}{5}\) =
Answer:
2\(\frac{3}{5}\) = \(\frac{13}{5}\)

Question 19.
3\(\frac{3}{5}\) =
Answer:
3\(\frac{3}{5}\) = \(\frac{18}{5}\)

Question 20.
4\(\frac{3}{5}\) =
Answer:
4\(\frac{3}{5}\) = \(\frac{23}{5}\)

Question 21.
2\(\frac{1}{6}\) =
Answer:
2\(\frac{1}{6}\) = \(\frac{1}{6}\)

Question 22.
3\(\frac{1}{8}\) =
Answer:
3\(\frac{1}{8}\) = \(\frac{25}{8}\)

Question 23.
2\(\frac{7}{10}\) =
Answer:
2\(\frac{7}{10}\) = \(\frac{27}{10}\)

Question 24.
4\(\frac{9}{10}\) =
Answer:
4\(\frac{9}{10}\) =\(\frac{49}{10}\)

Question 25.
1\(\frac{1}{8}\) =
Answer:
1\(\frac{1}{8}\)  = \(\frac{9}{8}\)

Question 26.
1\(\frac{5}{6}\) =
Answer:
1\(\frac{5}{6}\) = \(\frac{11}{6}\)

Question 27.
4\(\frac{5}{6}\) =
Answer:
4\(\frac{5}{6}\) = \(\frac{29}{6}\)

Question 28.
4\(\frac{5}{8}\) =
Answer:
4\(\frac{5}{8}\) = \(\frac{37}{8}\)

Question 29.
1\(\frac{5}{8}\) =
Answer:
1\(\frac{5}{8}\)  = \(\frac{13}{8}\)

Question 30.
2\(\frac{3}{8}\) =
Answer:
2\(\frac{3}{8}\) = \(\frac{19}{8}\)

Question 31.
3\(\frac{3}{10}\) =
Answer:
3\(\frac{3}{10}\) = \(\frac{33}{10}\)

Question 32.
4\(\frac{7}{10}\) =
Answer:
4\(\frac{7}{10}\) = \(\frac{47}{10}\)

Question 33.
4\(\frac{4}{5}\) =
Answer:
4\(\frac{4}{5}\)  = \(\frac{24}{5}\)

Question 34.
4\(\frac{1}{8}\) =
Answer:
4\(\frac{1}{8}\) = \(\frac{33}{8}\)

Question 35.
4\(\frac{3}{8}\) =
Answer:
4\(\frac{3}{8}\) = \(\frac{35}{8}\)

Question 36.
4\(\frac{7}{8}\) =
Answer:
4\(\frac{7}{8}\) = \(\frac{39}{8}\)

Question 37.
1\(\frac{5}{12}\) =
Answer:
1\(\frac{5}{12}\) = \(\frac{17}{12}\)

Question 38.
1\(\frac{7}{12}\) =
Answer:
1\(\frac{7}{12}\) = \(\frac{19}{12}\)

Question 39.
2\(\frac{1}{12}\) =
Answer:
2\(\frac{1}{12}\) = \(\frac{25}{12}\)

Question 40.
3\(\frac{1}{12}\) =
Answer:
3\(\frac{1}{12}\)= \(\frac{37}{12}\)

Question 41.
2\(\frac{7}{12}\) =
Answer:
2\(\frac{7}{12}\) = \(\frac{31}{12}\)

Question 42.
3\(\frac{5}{12}\) =
Answer:
3\(\frac{5}{12}\) = \(\frac{41}{12}\)

Question 43.
3\(\frac{11}{12}\) =
Answer:
3\(\frac{11}{12}\) = \(\frac{47}{12}\)

Question 44.
4\(\frac{7}{12}\) =
Answer:
4\(\frac{7}{12}\) = \(\frac{55}{12}\)

B
Change Mixed Numbers into Improper Fractions

Question 1.
1\(\frac{1}{2}\) =
Answer:
1\(\frac{1}{2}\)  = \(\frac{3}{2}\)

Question 2.
2\(\frac{1}{2}\) =
Answer:
2\(\frac{1}{2}\)  = \(\frac{5}{2}\)

Question 3.
3\(\frac{1}{2}\) =
Answer:
3\(\frac{1}{2}\)  = \(\frac{7}{2}\)

Question 4.
4\(\frac{1}{2}\) =
Answer:
4\(\frac{1}{2}\)  = \(\frac{9}{2}\)

Question 5.
1\(\frac{1}{3}\) =
Answer:
1\(\frac{1}{3}\)  = \(\frac{4}{3}\)

Question 6.
1\(\frac{2}{3}\) =
Answer:
1\(\frac{2}{3}\)  = \(\frac{5}{3}\)

Question 7.
1\(\frac{3}{10}\) =
Answer:
1\(\frac{3}{10}\)  = \(\frac{13}{10}\)

Question 8.
1\(\frac{7}{10}\) =
Answer:
1\(\frac{7}{10}\)  = \(\frac{17}{10}\)

Question 9.
1\(\frac{9}{10}\) =
Answer:
1\(\frac{9}{10}\)  = \(\frac{19}{10}\)

Question 10.
2\(\frac{9}{10}\) =
Answer:
2\(\frac{9}{10}[/latex = [latex]\frac{29}{10}[/latex

Question 11.
3[latex]\frac{9}{10}\) =
Answer:
3\(\frac{9}{10}[/latex = [latex]\frac{39}{10}[/latex

Question 12.
2[latex]\frac{1}{3}\) =
Answer:
2\(\frac{1}{3}\) = \(\frac{7}{3}\)

Question 13.
2\(\frac{2}{3}\) =
Answer:
2\(\frac{2}{3}\) =\(\frac{8}{3}\)

Question 14.
3\(\frac{1}{3}\) =
Answer:
3\(\frac{1}{3}\) = \(\frac{10}{3}\)

Question 15.
3\(\frac{2}{3}\) =
Answer:
3\(\frac{2}{3}\) = \(\frac{11}{3}\)

Question 16.
4\(\frac{1}{4}\) =
Answer:
4\(\frac{1}{4}\)  = \(\frac{17}{4}\)

Question 17.
4\(\frac{3}{4}\) =
Answer:
4\(\frac{3}{4}\) = \(\frac{19}{4}\)

Question 18.
2\(\frac{2}{5}\) =
Answer:
2\(\frac{2}{5}\) = \(\frac{12}{5}\)

Question 19.
3\(\frac{2}{5}\) =
Answer:
3\(\frac{2}{5}\) = \(\frac{17}{5}\)

Question 20.
4\(\frac{2}{5}\) =
Answer:
4\(\frac{2}{5}\) = \(\frac{22}{5}\)

Question 21.
3\(\frac{1}{6}\) =
Answer:
3\(\frac{1}{6}\) = \(\frac{19}{6}\)

Question 22.
2\(\frac{1}{8}\) =
Answer:
2\(\frac{1}{8}\) = \(\frac{17}{6}\)

Question 23.
2\(\frac{3}{10}\) =
Answer:
2\(\frac{3}{10}\) = \(\frac{23}{10}\)

Question 24.
3\(\frac{1}{10}\) =
Answer:
3\(\frac{1}{10}\) = \(\frac{31}{10}\)

Question 25.
1\(\frac{1}{6}\) =
Answer:
1\(\frac{1}{6}\) = \(\frac{7}{6}\)

Question 26.
1\(\frac{3}{8}\) =
Answer:
1\(\frac{3}{8}\) = \(\frac{11}{8}\)

Question 27.
3\(\frac{5}{6}\) =
Answer:
3\(\frac{5}{6}\)  = \(\frac{23}{6}\)

Question 28.
3\(\frac{5}{8}\) =
Answer:
3\(\frac{5}{8}\)  = \(\frac{29}{8}\)

Question 29.
2\(\frac{5}{8}\) =
Answer:
2\(\frac{5}{8}\) = \(\frac{21}{8}\)

Question 30.
1\(\frac{7}{8}\) =
Answer:
1\(\frac{7}{8}\)  = \(\frac{15}{8}\)

Question 31.
4\(\frac{3}{10}\) =
Answer:
4\(\frac{3}{10}\) = \(\frac{43}{10}\)

Question 32.
3\(\frac{7}{10}\) =
Answer:
3\(\frac{7}{10}\) =\(\frac{37}{10}\)

Question 33.
2\(\frac{5}{6}\) =
Answer:
2\(\frac{5}{6}\)  =\(\frac{17}{6}\)

Question 34.
2\(\frac{7}{8}\) =
Answer:
2\(\frac{7}{8}\)  = \(\frac{23}{8}\)

Question 35.
3\(\frac{7}{8}\) =
Answer:
3\(\frac{7}{8}\)  =\(\frac{31}{8}\)

Question 36.
4\(\frac{1}{6}\) =
Answer:
4\(\frac{1}{6}\) = \(\frac{25}{6}\)

Question 37.
1\(\frac{1}{12}\) =
Answer:
1\(\frac{1}{12}\)  =\(\frac{13}{12}\)

Question 38.
1\(\frac{11}{12}\) =
Answer:
1\(\frac{11}{12}\)  = \(\frac{23}{12}\)

Question 39.
4\(\frac{1}{12}\) =
Answer:
4\(\frac{1}{12}\)  = \(\frac{49}{12}\)

Question 40.
2\(\frac{5}{12}\) =
Answer:
2\(\frac{5}{12}\)  = \(\frac{29}{12}\)

Question 41.
2\(\frac{11}{12}\) =
Answer:
2\(\frac{11}{12}\)  = \(\frac{35}{12}\)

Question 42.
3\(\frac{7}{12}\) =
Answer:
3\(\frac{7}{12}\) = \(\frac{43}{12}\)

Question 43.
4\(\frac{5}{12}\) =
Answer:
4\(\frac{5}{12}\) = \(\frac{53}{12}\)

Question 44.
4\(\frac{11}{12}\) =
Answer:
4\(\frac{11}{12}\)  = \(\frac{59}{12}\)

Eureka Math Grade 5 Module 6 Lesson 23 Homework Answer Key

Question 1.
In the diagram, the length of Figure S is \(\frac{1}{2}\) the length of Figure T. If S has an area of 368 cm², find the perimeter of the figure.

Answer:
Length of Figure T = x
length of Figure S = \(\frac{1}{2}\) the length of Figure T = \(\frac{x}{2}\) .
Breadth = 16 cm
Area of Figure S = 368 cm²,
Area = Length × Breadth = \(\frac{x}{2}\) × 16 = 368
\(\frac{x}{2}\) = 23
x = 24 cms.
Length of figure S = \(\frac{x}{2}\) = 23 cms .
Length of figure T = x = 46 cms .
Total Length of Figure S and T = 23 + 46 = 69 cms
Perimeter of given Figure = S +T = 2 ( l + b) = 2 ( 69 + 16 ) = 2 ( 85 ) = 170 cms .

The following problems are puzzles for your enjoyment. They are intended to encourage working together and family problem-solving fun and are not a required element of this homework assignment.
Question 2.
Take 12 matchsticks arranged in a grid as shown below, and remove 2 matchsticks so 2 squares remain. How can you do this? Draw the new arrangement.

Answer:

If we remove any one vertical match sticks or one horizontal match sticks in the middle then 2 squares will be remained and is shown in below figure .

Question 3.
Moving only 3 matchsticks makes the fish turn around and swim the opposite way. Which matchsticks did you move? Draw the new shape.

Answer:

Engage NY Eureka Math 5th Grade Module 6 Lesson 21 Answer Key

Eureka Math Grade 5 Module 6 Lesson 21-23 Problem Set Answer Key

Question 1.
Pierre’s Paper
Pierre folded a square piece of paper vertically to make two rectangles. Each rectangle had a perimeter of
39 inches. How long is each side of the original square? What is the area of the original square? What is the area of one of the rectangles?
Answer:

ABCD is a square.
AEFD AND EBCF are two equal rectangles of perimeter 39 inches.
Length of the rectangle = 2x
Breadth of the rectangle = x
Perimeter of a rectangle = 2 (l + b) = 2 (2x +x ) = 6x = 39
x =\(\frac{39}{6}\) =6.5
2x = 13
Area of square ABCD = Side × Side = 2x × 2x = 13 × 13 = 169 sq. inches.
Area of Rectangle AEFD = Area of Rectangle EBCF = length ×  Breadth = 2x × x = 13 × 6.5 = 84.5 sq inches .

Question 2.
Shopping with Elise
Elise saved $184. She bought a scarf, a necklace, and a notebook. After her purchases, she still had $39.50. The scarf cost three-fifths the cost of the necklace, and the notebook was one-sixth as much as the scarf. What was the cost of each item? How much more did the necklace cost than the notebook?
Answer:
Money with Elisa = $184 .
Money left after shopping = $39.50
Money spent on shopping = $184 = 39.50 = 144.50$
Cost of scarf = \(\frac{3}{5}\) cost of the necklace.
Cost of Note book = \(\frac{1}{6}\) cost of the Scarf . = \(\frac{1}{6}\)\(\frac{3}{5}\) cost of the necklace = \(\frac{1}{10}\) cost of the necklace .
cost of necklace = x
Cost of scarf + notebook + necklace = money spent on shopping
\(\frac{3}{5}\) x + \(\frac{1}{10}\) x + x = 144.50$
\(\frac{6x + 1x +10x }{10}\) = 144.5
17x = 1445
x= \(\frac{1445}{17}\)
x = 85
Cost of Necklace = 85$
Cost of Scarf = \(\frac{3}{5}\) cost of the necklace = \(\frac{3}{5}\) 85 = 39$.
Cost of Notebook = \(\frac{1}{10}\) cost of the necklace = \(\frac{1}{10}\) 85 = 8.5$ .
Money more spent on necklace than the notebook = 85 – 8.5 = 76.5$ .

Question 3.
The Hewitt’s Carpet
The Hewitt family is buying carpet for two rooms. The dining room is a square that measures 12 feet on each side. The den is 9 yards by 5 yards. Mrs. Hewitt has budgeted $2,650 for carpeting both rooms. The green carpet she is considering costs $42.75 per square yard, and the brown carpet’s price is $4.95 per square foot. What are the ways she can carpet the rooms and stay within her budget?
Answer:
Side of dining room = 12 feet
Area of dining square room = Side ×  Side = 12 × 12 = 144 sq feets .
den is in the shape of rectangle .
Length by breadth = 9 yards by 5 yards
Area of rectangle den = length × Breadth = 9 × 5 = 45 sq yards .
Cost of green carpet = $42.75 per square yard
Cost of green carpet for 45 sqyards = 45 ×$42.75 per square yard = 1923.75 $.
Cost of Brown carpet = $4.95 per square foot
Cost of Brown carpet for 144 sq foot = 144 × $4.95 = 712.8$
Total Cost of Green carpet and Brown carpet = 1923.75 $ + 712.8$ = 2645.55$
Budget for carpeting both rooms = 2650$.
She carpet green carpet to den and Brown carpet to dining Room . Then she can stay within her budget .

Question 4.
AAA Taxi
AAA Taxi charges $1.75 for the first mile and $1.05 for each additional mile. How far could Mrs. Leslie travel for $20 if she tips the cab driver $2.50?
Answer:
Cost of First mile = $1.75
Cost of second mile = $1.75 + $1.05 =$2.8
Cost of Third mile = $1.75 + $1.05 =$2.8
Cost of fourth mile = $1.75 + $1.05 =$2.8 and so on that means cost of second mile is $2.8
Money spent for travel = $20
Tip given for driver = $2.5
Money given to driver for travel = $20 – $ 2.5 = $17.5
x = number of miles traveled after 1st mile
cost of first mile + x cost of second mile = $17.5
1.75 + x (2.8) = 17.5$
2.8x = 17.5 -1.75
2.8x = 15.75 $
x = 5.625 miles
She traveled 5.625 miles

Question 5.
Pumpkins and Squash
Three pumpkins and two squash weigh 27.5 pounds. Four pumpkins and three squash weigh 37.5 pounds. Each pumpkin weighs the same as the other pumpkins, and each squash weighs the same as the other squash. How much does each pumpkin weigh? How much does each squash weigh?
Answer:
all pumpkins weights are equal = p
all Squash weights equal = s
Three pumpkins and two squash weigh 27.5 pounds
3p +2s = 27.5
Four pumpkins and three squash weigh 37.5 pounds.
4p + 3s = 37.5
Taking lcm for 4 and 3 = 12
4(3p +2s = 27.5)
3(4p + 3s = 37.5)
=12p + 8s = 110
12p + 9s = 112.5
= 9s – 8s = 112.5 – 110
s = 2.5
= 3p +2s = 27.5
3p + 2(2.5) = 27.5
3p = 27.5 – 5
p = 22.5 / 3 = 7.5
Weight of Squash =2.5 pounds.
Weight of pumpkin = 7.5 pounds .

Question 6.
Toy Cars and Trucks
Henry had 20 convertibles and 5 trucks in his miniature car collection. After Henry’s aunt bought him some more miniature trucks, Henry found that one-fifth of his collection consisted of convertibles. How many trucks did his aunt buy?
Answer:
Number of convertibles = 20
Number of trucks = 5
Number of trucks bought by Henry’s aunt = One-fifth of his collection consisted of convertibles = \(\frac{1}{5}\) y =20 = y = 100 .
100 – 20 convertibles = 80 .
80 – 5 ( 5 trucks are already with henry ) = 75 trucks .

Question 7.
Pairs of Scouts
Some girls in a Girl Scout troop are pairing up with some boys in a Boy Scout troop to practice square dancing. Two-thirds of the girls are paired with three-fifths of the boys. What fraction of the scouts are square dancing?
(Each pair is one Girl Scout and one Boy Scout. The pairs are only from these two troops.)
Answer:
Two-thirds of the girls are paired with three-fifths of the boys
\(\frac{2}{3}\) girls = \(\frac{3}{5}\) boys
\(\frac{2}{3}\) girls = \(\frac{6}{9}\)
\(\frac{3}{5}\) boys = \(\frac{6}{10}\)
Fraction of the scouts are square dancing = \(\frac{6+ 6}{9 + 10}\) = \(\frac{12}{19}\)

Question 8.
Sandra’s Measuring Cups
Sandra is making cookies that require 5\(\frac{1}{2}\) cups of oatmeal. She has only two measuring cups: a one-half cup and a three-fourths cup. What is the smallest number of scoops that she could make in order to get 5\(\frac{1}{2}\) cups?
Answer:
Measuring cups : a one-half cup and a three-fourths cup.
To make 5\(\frac{1}{2}\) cups with \(\frac{11}{2}\) cups
To make \(\frac{11}{2}\) cups we require 11 scoops .
To make 5\(\frac{1}{2}\) cups with a three-fourths cup. we require 7 Scoops with one fourth left .
So take 6 scoops of \(\frac{3}{4}\) then 1 will left so take 2 \(\frac{1}{2}\) cups.
Then we require 6 \(\frac{3}{4}\) scoops and 2 \(\frac{1}{2}\) cups.
Total fewest scoops are 6 + 2 = 8 scoops .

Question 9.
Blue Squares
The dimensions of each successive blue square pictured to the right are half that of the previous blue square. The lower left blue square measures 6 inches by 6 inches.
a. Find the area of the shaded part.
b. Find the total area of the shaded and unshaded parts.
c. What fraction of the figure is shaded?

Answer:
There are 3 sets of squares . 1 out of 3 sets are shaded.
c. Fraction shaded = \(\frac{1}{3}\)
b. Total Area = (12 × 12 ) – ( \(\frac{3}{8}\) \(\frac{3}{8}\))
= 144 – \(\frac{9}{64}\)
= \(\frac{9216 – 9}{64}\)
= 143 \(\frac{55}{64}\) sq inches .
a. Area Shaded = \(\frac{1}{3}\) × 143 \(\frac{55}{64}\) sq inches .
= \(\frac{1}{3}\) \(\frac{9207}{64}\)
= 47 \(\frac{61}{64}\) inches .

Eureka Math Grade 5 Module 6 Lesson 21 Homework Answer Key

Question 1.
Sara travels twice as far as Eli when going to camp. Ashley travels as far as Sara and Eli together. Hazel travels 3 times as far as Sara. In total, all four travel 888 miles to camp. How far does each of them travel?
Answer:
Distance traveled by Eli = x
Distance traveled by Sara = twice as far as Eli = 2x
Distance traveled by Ashley = Sara and Eli together. = x + 2x = 3x
Distance traveled by Hazel = 3 times Sara = 3 ( 2x) = 6x
Total distance traveled by all four = 888 miles
x+ 2x+ 3x+ 6x = 888
12x = 888
3x = 222
x = 74 miles.
Distance traveled by Eli = x = 74 miles
Distance traveled by Sara = twice as far as Eli = 2x = 2(74) = 144 miles
Distance traveled by Ashley = Sara and Eli together. = x + 2x = 3x = 3(74) = 218 miles
Distance traveled by Hazel = 3 times Sara = 3 ( 2x) = 6x = 6(74) =  444 miles

The following problem is a brainteaser for your enjoyment. It is intended to encourage working together and family problem-solving fun. It is not a required element of this homework assignment.
Question 2.
A man wants to take a goat, a bag of cabbage, and a wolf over to an island. His boat will only hold him and one animal or item. If the goat is left with the cabbage, he’ll eat it. If the wolf is left with the goat, he’ll eat it. How can the man transport all three to the island without anything being eaten?

Answer:

The wolf does not eat cabbage, so the crossing can start with the goat.

The man leaves the goat and returns, puts the cabbage in the boat and takes it across. On the other bank, he leaves the cabbage but takes the goat.

He leaves the goat on the first bank and takes the wolf across. He leaves the cabbage with the wolf and rows back alone.

He takes the goat across.

Engage NY Eureka Math 5th Grade Module 6 Lesson 22 Answer Key

Eureka Math Grade 5 Module 6 Lesson 22 Homework Answer Key

Solve using any method. Show all your thinking.
Question 1.
Study this diagram showing all the squares. Fill in the table.

Answer:
all sides are written in the respective square and is shown in below figure .

Area of Square = Side × Side

The following problem is a brainteaser for your enjoyment. It is intended to encourage working together and family problem-solving fun. It is not a required element of this homework assignment.
Question 2.
Remove 3 matches to leave 3 triangles.

Answer:

If we remove middle 3 matches then 3 triangles are remained and is shown in above figure .

Engage NY Eureka Math 5th Grade Module 6 Lesson 20 Answer Key

Eureka Math Grade 5 Module 6 Lesson 20 Sprint Answer Key

A
Subtracting Fractions from a Whole Number

Question 1.
4 – \(\frac{1}{2}\) =
Answer:
4 – \(\frac{1}{2}\) = \(\frac{8 – 1 }{2}\) = \(\frac{7}{2}\)

Question 2.
3 – \(\frac{1}{2}\) =
Answer:
3 – \(\frac{1}{2}\) = \(\frac{6 – 1 }{2}\) = \(\frac{5}{2}\)

Question 3.
2 – \(\frac{1}{2}\) =
Answer:
2 – \(\frac{1}{2}\) = \(\frac{4-1}{2}\) = \(\frac{3}{2}\) = 1\(\frac{1}{2}\)

Question 4.
1 – \(\frac{1}{2}\) =
Answer:
1- \(\frac{1}{2}\) = \(\frac{2 – 1}{2}\) = \(\frac{1}{2}\)

Question 5.
1 – \(\frac{1}{3}\) =
Answer:
1 – \(\frac{1}{3}\) = \(\frac{3 – 1}{3}\) = \(\frac{2}{3}\)

Question 6.
2 – \(\frac{1}{3}\) =
Answer:
2 – \(\frac{1}{3}\) = \(\frac{6 – 1}{3}\) = \(\frac{5}{3}\) =  1\(\frac{2}{3}\)

Question 7.
4 – \(\frac{1}{3}\) =
Answer:
4 – \(\frac{1}{3}\) = \(\frac{12 – 1}{3}\) = \(\frac{11}{3}\)= 3\(\frac{2}{3}\)

Question 8.
4 – \(\frac{2}{3}\) =
Answer:
4 – \(\frac{2}{3}\) = \(\frac{12 – 2}{3}\) = \(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 9.
2 – \(\frac{2}{3}\) =
Answer:
2 – \(\frac{2}{3}\)= \(\frac{8 -2}{3}\)

Question 10.
2 – \(\frac{1}{4}\) =
Answer:
2 – \(\frac{1}{4}\) = \(\frac{8 -1}{4}\) = \(\frac{7}{4}\) = 1\(\frac{3}{4}\)

Question 11.
2 – \(\frac{3}{4}\) =
Answer:
2 – \(\frac{3}{4}\) = \(\frac{8 – 3}{4}\)= \(\frac{5}{4}\) = 1\(\frac{1}{4}\)

Question 12.
3 – \(\frac{3}{4}\) =
Answer:
3 – \(\frac{3}{4}\)= \(\frac{9 – 3}{4}\) = \(\frac{6}{4}\)= 1\(\frac{2}{4}\)

Question 13.
3 – \(\frac{1}{4}\) =
Answer:
3 – \(\frac{1}{4}\) = \(\frac{12 – 1}{4}\)= \(\frac{11}{4}\)= 2\(\frac{3}{4}\)

Question 14.
4 – \(\frac{3}{4}\) =
Answer:
4 – \(\frac{3}{4}\) = \(\frac{16 – 3}{4}\) = \(\frac{13}{4}\)= 3\(\frac{1}{4}\)

Question 15.
2 – \(\frac{1}{10}\) =
Answer:
2 – \(\frac{1}{10}\) = \(\frac{20 – 1}{10}\) = \(\frac{19}{10}\) = 1\(\frac{9}{10}\)

Question 16.
3 – \(\frac{9}{10}\) =
Answer:
3 – \(\frac{9}{10}\) = \(\frac{30 – 9}{10}\) = \(\frac{21}{10}\) = 2\(\frac{1}{10}\)

Question 17.
2 – \(\frac{7}{10}\) =
Answer:
2 – \(\frac{7}{10}\) = \(\frac{20- 7}{10}\)= \(\frac{13}{10}\)= 1 \(\frac{3}{10}\)

Question 18.
4 – \(\frac{3}{10}\) =
Answer:
4 – \(\frac{7}{10}\)= \(\frac{40 – 7}{10}\) = \(\frac{33}{10}\)= 3 \(\frac{3}{10}\)

Question 19.
3 – \(\frac{1}{5}\) =
Answer:
3 – \(\frac{1}{5}\) = \(\frac{15 – 1}{5}\) = \(\frac{14}{5}\)= 2 \(\frac{4}{5}\)

Question 20.
3 – \(\frac{2}{5}\) =
Answer:
3 – \(\frac{2}{5}\) = \(\frac{15 – 2}{5}\) = \(\frac{13}{5}\)=2\(\frac{3}{5}\)

Question 21.
3 – \(\frac{4}{5}\) =
Answer:
3 – \(\frac{4}{5}\) = \(\frac{15 – 4}{5}\) = \(\frac{11}{5}\)= 2\(\frac{1}{5}\)

Question 22.
3 – \(\frac{3}{5}\) =
Answer:
3 – \(\frac{3}{5}\) = \(\frac{15 – 3}{5}\) = \(\frac{12}{5}\)=2 \(\frac{2}{5}\)

Question 23.
3 – \(\frac{1}{8}\) =
Answer:
3 – \(\frac{1}{8}\)= \(\frac{24 – 1}{8}\)= \(\frac{23}{8}\) =2\(\frac{7}{8}\)

Question 24.
3 – \(\frac{3}{8}\) =
Answer:
3 – \(\frac{3}{8}\) = \(\frac{24 -3}{8}\) = \(\frac{21}{8}\) = 2\(\frac{5}{8}\)

Question 25.
3 – \(\frac{5}{8}\) =
Answer:
3 – \(\frac{5}{8}\) = \(\frac{24 – 5}{8}\) =\(\frac{19}{8}\) = 2\(\frac{3}{8}\)

Question 26.
3 – \(\frac{7}{8}\) =
Answer:
3 – \(\frac{7}{8}\) =\(\frac{24 – 7}{8}\) = \(\frac{23}{8}\) =2 \(\frac{7}{8}\)

Question 27.
2 – \(\frac{7}{8}\) =
Answer:
2 – \(\frac{7}{8}\) = \(\frac{16 – 7}{8}\) = \(\frac{9}{8}\) = 1\(\frac{1}{8}\)

Question 28.
4 – \(\frac{1}{7}\) =
Answer:
4 – \(\frac{1}{7}\) = \(\frac{32 -1}{7}\) = \(\frac{31}{7}\) = 4\(\frac{3}{7}\)

Question 29.
3 – \(\frac{6}{7}\) =
Answer:
3 – \(\frac{6}{7}\) =\(\frac{21 – 6}{7}\) =\(\frac{15}{7}\) = 2 \(\frac{1}{7}\)

Question 30.
2 – \(\frac{3}{7}\) =
Answer:
2 – \(\frac{6}{7}\) = \(\frac{14 – 6}{7}\) = \(\frac{8}{7}\) = 1\(\frac{1}{7}\)

Question 31.
4 – \(\frac{4}{7}\) =
Answer:
4 – \(\frac{4}{7}\) = \(\frac{28 – 4}{7}\) = \(\frac{24}{7}\) = 3\(\frac{3}{7}\)

Question 32.
3 – \(\frac{5}{7}\) =
Answer:
3 – \(\frac{5}{7}\) = \(\frac{21 – 5}{7}\) = \(\frac{16}{7}\) = 2\(\frac{2}{7}\)

Question 33.
4 – \(\frac{3}{4}\) =
Answer:
4 – \(\frac{3}{4}\) = \(\frac{16 – 3 }{4}\) = \(\frac{13}{4}\) = 3\(\frac{1}{4}\)

Question 34.
2 – \(\frac{5}{8}\) =
Answer:
2 – \(\frac{5}{8}\) = \(\frac{16 – 5 }{8}\) = \(\frac{11}{8}\) = 1\(\frac{3}{8}\)

Question 35.
3 – \(\frac{3}{10}\) =
Answer:
3 – \(\frac{3}{10}\) = \(\frac{30 – 3}{10}\) = \(\frac{27}{10}\)= 2 \(\frac{7}{10}\)

Question 36.
4 – \(\frac{2}{5}\) =
Answer:
4 – \(\frac{2}{5}\) = \(\frac{20 – 2}{5}\) = \(\frac{18}{5}\) = 3\(\frac{3}{5}\)

Question 37.
4 – \(\frac{3}{7}\) =
Answer:
4 – \(\frac{3}{7}\) = \(\frac{28 – 3}{7}\) = \(\frac{25}{7}\) = 3\(\frac{4}{7}\)

Question 38.
3 – \(\frac{7}{10}\) =
Answer:
3 – \(\frac{7}{10}\) = \(\frac{30 – 7}{10}\) = \(\frac{21}{10}\) = 2\(\frac{1}{10}\)

Question 39.
3 – \(\frac{5}{10}\) =
Answer:
3 – \(\frac{5}{10}\) = \(\frac{30 – 5}{10}\) = \(\frac{25}{10}\) = \(\frac{5}{2}\)

Question 40.
4 – \(\frac{2}{8}\) =
Answer:
4 – \(\frac{2}{8}\) = \(\frac{32 – 2}{8}\) = \(\frac{30}{8}\) = \(\frac{15}{4}\)

Question 41.
2 – \(\frac{9}{12}\) =
Answer:
2 – \(\frac{9}{12}\) = \(\frac{24 – 9}{12}\) = \(\frac{15}{12}\) = \(\frac{5}{4}\)

Question 42.
4 – \(\frac{2}{12}\) =
Answer:
4 – \(\frac{2}{12}\) = \(\frac{48 – 2}{12}\) = \(\frac{46}{12}\) = \(\frac{23}{6}\)

Question 43.
3 – \(\frac{2}{6}\) =
Answer:
3 – \(\frac{2}{6}\) = \(\frac{18 – 2}{6}\) = \(\frac{16}{6}\) = \(\frac{8}{3}\)

Question 44.
2 – \(\frac{8}{12}\) =
Answer:
2 – \(\frac{8}{12}\) = 2 – \(\frac{2}{3}\) = \(\frac{6 – 2}{3}\) = \(\frac{4}{3}\)

B
Subtracting Fractions from a Whole Number

Question 1.
1 – \(\frac{1}{2}\) =
Answer:
1 – \(\frac{1}{2}\) = \(\frac{2 – 1}{2}\) = \(\frac{1}{2}\)

Question 2.
2 – \(\frac{1}{2}\) =
Answer:
2 – \(\frac{1}{2}\)  = \(\frac{4 -1}{2}\) = \(\frac{3}{2}\) =1\(\frac{1}{2}\)

Question 3.
3 – \(\frac{1}{2}\) =
Answer:
3 – \(\frac{1}{2}\) = \(\frac{6 – 1}{2}\) = \(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 4.
4 – \(\frac{1}{2}\) =
Answer:
4 – \(\frac{1}{2}\)  = \(\frac{8 -1}{2}\) = \(\frac{7}{2}\) =3\(\frac{1}{2}\)

Question 5.
1 – \(\frac{1}{4}\) =
Answer:
1 – \(\frac{1}{4}\) = \(\frac{4 – 1}{4}\) = \(\frac{3}{4}\)

Question 6.
2 – \(\frac{1}{4}\) =
Answer:
2 – \(\frac{1}{4}\) = \(\frac{8 – 1}{4}\) = \(\frac{1}{4}\)

Question 7.
4 – \(\frac{1}{4}\) =
Answer:
4 – \(\frac{1}{4}\)  = \(\frac{16 – 1}{4}\) = \(\frac{15}{4}\) = 3\(\frac{3}{4}\)

Question 8.
4 – \(\frac{3}{4}\) =
Answer:
4 – \(\frac{1}{4}\)  = \(\frac{16 – 3}{4}\) = \(\frac{13}{4}\) =3\(\frac{1}{4}\)

Question 9.
2 – \(\frac{3}{4}\) =
Answer:
2 – \(\frac{3}{4}\) = \(\frac{8 – 3}{4}\)= \(\frac{5}{4}\)= 1\(\frac{1}{4}\)

Question 10.
2 – \(\frac{1}{3}\) =
Answer:
2 – \(\frac{1}{3}\)  = \(\frac{6 – 1}{3}\) = \(\frac{5}{3}\) = 1\(\frac{2}{3}\)

Question 11.
2 – \(\frac{2}{3}\) =
Answer:
2 – \(\frac{2}{3}\) = \(\frac{6 – 2}{3}\) = \(\frac{4}{3}\)= 1\(\frac{1}{3}\)

Question 12.
3 – \(\frac{2}{3}\) =
Answer:
3 – \(\frac{2}{3}\) = \(\frac{9 -2}{3}\) =\(\frac{7}{3}\) = 2\(\frac{1}{3}\)

Question 13.
3 – \(\frac{1}{3}\) =
Answer:
3 – \(\frac{1}{3}\) = \(\frac{9 – 1}{3}\)= \(\frac{8}{3}\)= 2\(\frac{2}{3}\)

Question 14.
4 – \(\frac{2}{3}\) =
Answer:
4 – \(\frac{2}{3}\) = \(\frac{12 – 2}{3}\)= \(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 15.
3 – \(\frac{1}{10}\) =
Answer:
3 – \(\frac{1}{10}\) = \(\frac{30 – 1}{10}\) = \(\frac{29}{10}\)

Question 16.
2 – \(\frac{9}{10}\) =
Answer:
2 – \(\frac{9}{10}\)  = \(\frac{20 – 9}{10}\) = \(\frac{11}{10}\) = 1\(\frac{1}{10}\)

Question 17.
4 – \(\frac{7}{10}\) =
Answer:
4 – \(\frac{7}{10}\) = \(\frac{40 – 7}{10}\) = \(\frac{33}{10}\) = 3\(\frac{3}{10}\)

Question 18.
3 – \(\frac{3}{10}\) =
Answer:
3 – \(\frac{3}{10}\) = \(\frac{30 – 3}{10}\)= \(\frac{27}{10}\)= 2\(\frac{7}{10}\)

Question 19.
2 – \(\frac{1}{5}\) =
Answer:
2 – \(\frac{1}{5}\) = \(\frac{10 – 1}{5}\) = \(\frac{9}{5}\) = 1\(\frac{4}{5}\)

Question 20.
2 – \(\frac{2}{5}\) =
Answer:
2 – \(\frac{2}{5}\) = \(\frac{10 – 2}{5}\) = \(\frac{8}{5}\) = 1\(\frac{3}{5}\)

Question 21.
2 – \(\frac{4}{5}\) =
Answer:
2 – \(\frac{4}{5}\) = \(\frac{10 – 2}{5}\) = \(\frac{8}{5}\) = 1\(\frac{3}{5}\)

Question 22.
3 – \(\frac{3}{5}\) =
Answer:
3 – \(\frac{3}{5}\) = \(\frac{15 – 3}{5}\) = \(\frac{12}{5}\) = 2\(\frac{2}{5}\)

Question 23.
2 – \(\frac{1}{8}\) =
Answer:
2 – \(\frac{1}{8}\)  = \(\frac{16 – 1}{8}\) = \(\frac{15}{8}\) = 1 \(\frac{7}{8}\)

Question 24.
2 – \(\frac{3}{8}\) =
Answer:
2 – \(\frac{3}{8}\)  = \(\frac{16 – 3}{8}\) = \(\frac{13}{8}\) = 1\(\frac{5}{8}\)

Question 25.
2 – \(\frac{5}{8}\) =
Answer:
2 – \(\frac{5}{8}\)  = \(\frac{16 -5}{8}\) = \(\frac{11}{8}\) = 1\(\frac{3}{8}\)

Question 26.
2 – \(\frac{7}{8}\) =
Answer:
2 – \(\frac{7}{8}\) = \(\frac{16 – 7}{8}\) = \(\frac{9}{8}\) =1\(\frac{1}{8}\)

Question 27.
4 – \(\frac{7}{8}\) =
Answer:
4 – \(\frac{7}{8}\) = \(\frac{28 – 7}{8}\) = \(\frac{21}{8}\) = 2\(\frac{5}{8}\)

Question 28.
3 – \(\frac{1}{7}\) =
Answer:
3 – \(\frac{1}{7}\) = \(\frac{21 – 1}{7}\) = \(\frac{20}{7}\) = 2\(\frac{6}{7}\)

Question 29.
2 – \(\frac{6}{7}\) =
Answer:
2 – \(\frac{6}{7}\) = \(\frac{14 – 6}{7}\) = \(\frac{8}{7}\) =1\(\frac{1}{7}\)

Question 30.
4 – \(\frac{3}{7}\) =
Answer:
4 – \(\frac{3}{7}\) = \(\frac{28 -3}{7}\) = \(\frac{25}{7}\) =3\(\frac{4}{7}\)

Question 31.
3 – \(\frac{4}{7}\) =
Answer:
3 – \(\frac{4}{7}\)  = \(\frac{21 – 4}{7}\) = \(\frac{17}{7}\) =2\(\frac{3}{7}\)

Question 32.
2 – \(\frac{5}{7}\) =
Answer:
2 – \(\frac{5}{7}\)  = \(\frac{14 – 5}{7}\) = \(\frac{9}{7}\) =1\(\frac{2}{7}\)

Question 33.
3 – \(\frac{3}{4}\) =
Answer:
3 – \(\frac{3}{4}\) = \(\frac{12 – 3}{4}\) = \(\frac{9}{4}\)= 2\(\frac{1}{4}\)

Question 34.
4 – \(\frac{5}{8}\) =
Answer:
4 – \(\frac{5}{8}\) = \(\frac{32 – 5}{8}\) = \(\frac{27}{8}\) = 3\(\frac{3}{8}\)

Question 35.
2 – \(\frac{3}{10}\) =
Answer:
2 – \(\frac{3}{10}\)  = \(\frac{20 -3}{10}\) = \(\frac{17}{10}\) = 1\(\frac{7}{10}\)

Question 36.
3 – \(\frac{2}{5}\) =
Answer:
3 – \(\frac{2}{5}\)  = \(\frac{15 – 2}{5}\) = \(\frac{13}{5}\) = 2\(\frac{3}{5}\)

Question 37.
3 – \(\frac{3}{7}\) =
Answer:
3 – \(\frac{3}{7}\) = \(\frac{21 – 3}{7}\) = \(\frac{18}{7}\) = 2\(\frac{4}{7}\).

Question 38.
2 – \(\frac{7}{10}\) =
Answer:
2 – \(\frac{7}{10}\)  = \(\frac{20 – 7}{10}\) = \(\frac{14}{10}\) = \(\frac{7}{5}\) =1\(\frac{2}{5}\)

Question 39.
2 – \(\frac{5}{10}\) =
Answer:
2 – \(\frac{5}{10}\) = \(\frac{20 – 5}{10}\) = \(\frac{15}{10}\)= \(\frac{3}{2}\) = 1\(\frac{1}{2}\)

Question 40.
4 – \(\frac{6}{8}\) =
Answer:
4 – \(\frac{6}{8}\) = \(\frac{32 – 6}{8}\) = \(\frac{28}{8}\) = \(\frac{7}{2}\)=3\(\frac{1}{2}\)

Question 41.
4 – \(\frac{3}{12}\) =
Answer:
4 – \(\frac{3}{12}\) = \(\frac{48 – 3}{12}\) = \(\frac{45}{12}\) = \(\frac{15}{4}\) = 3\(\frac{3}{4}\)

Question 42.
3 – \(\frac{10}{12}\) =
Answer:
3 – \(\frac{10}{12}\)  = \(\frac{36 -10}{12}\) = \(\frac{26}{12}\) = \(\frac{13}{6}\) = 2\(\frac{1}{6}\)

Question 43.
2 – \(\frac{4}{6}\) =
Answer:
2 – \(\frac{4}{6}\)  = \(\frac{12 -4}{6}\) = \(\frac{8}{6}\) = \(\frac{2}{3}\)

Question 44.
4 – \(\frac{4}{12}\) =
Answer:
4 – \(\frac{4}{12}\)  = \(\frac{48 -4}{12}\) = \(\frac{42}{12}\) = \(\frac{7}{2}\) =3\(\frac{1}{2}\)

Eureka Math Grade 5 Module 6 Lesson 20 Problem Set Answer Key

Question 1.
The line graph below tracks the total tomato production for one tomato plant. The total tomato production is plotted at the end of each of 8 weeks. Use the information in the graph to answer the questions that follow.

a. How many pounds of tomatoes did this plant produce at the end of 13 weeks?
b. How many pounds of tomatoes did this plant produce from Week 7 to Week 11? Explain how you know.
c. Which one-week period showed the greatest change in tomato production? The least? Explain how you know.
d. During Weeks 6–8, Jason fed the tomato plant just water. During Weeks 8–10, he used a mixture of water and Fertilizer A, and in Weeks 10–13, he used water and Fertilizer B on the tomato plant. Compare the tomato production for these periods of time.
Answer:
a. 10 pounds of Tomatoes were produced at the end of 13 week .
b. Number of pounds of tomatoes produced from Week 7 to Week 11 = week 11 production – week 7 production = 9 – 3 = 6 pounds.
c. Week 9 to 10 the line is steeper that means the greatest change in tomato production. In week 11- 12 the line is flat that means no        production taken place . so, least production .
d. The Water helped make tomatoes , But the fertilizer A seemed to make more tomatoes than just water. Fertilizer B didnot seem to help at all because the production in week 10-13 plant hardly increased production .

Question 2.
Use the story context below to sketch a line graph. Then, answer the questions that follow.
The number of fifth-grade students attending Magnolia School has changed over time. The school opened in 2006 with 156 students in the fifth grade. The student population grew the same amount each year before reaching its largest class of 210 students in 2008. The following year, Magnolia lost one-seventh of its fifth graders. In 2010, the enrollment dropped to 154 students and remained constant in 2011. For the next two years, the enrollment grew by 7 students each year.

a. How many more fifth-grade students attended Magnolia in 2009 than in 2013?
b. Between which two consecutive years was there the greatest change in student population?
c. If the fifth-grade population continues to grow in the same pattern as in 2012 and 2013, in what year will the number of students match 2008’s enrollment?
Answer:

a.  Number of students attended in 2009 = 180
Number of students attended in 2013 = 168 .
Number of more students attended in 2009 than 2013 = 180 -168 = 12
12 more students attended in 2009 than 2013 .
b. Between 2008 – 2009 there is greatest change in student population that is from 210 to 180 = 30 students.
c. The number students in 2008 = 210 ,
In 2012 and 2013 the number of students increased =  7 students
For one year there is a increase in 7 students
At 2013 the number of students = 168
Number of more students required = 210 – 168 = 42
Number of years required = 42  ÷  7 = 6 years
It requires more 6 years from 2013 that means by 2019 .

Eureka Math Grade 5 Module 6 Lesson 20 Exit Ticket Answer Key

Use the following information to complete the line graph below. Then, answer the questions that follow.
Harry runs a hot dog stand at the county fair. When he arrived on Wednesday, he had 38 dozen hot dogs for his stand. The graph shows the number of hot dogs (in dozens) that remained unsold at the end of each day of sales.

a. How many dozen hot dogs did Harry sell on Wednesday? How do you know?
b. Between which two-day period did the number of hot dogs sold change the most? Explain how you determined your answer.
c. During which three days did Harry sell the most hot dogs?
d. How many dozen hot dogs were sold on these three days?
Answer:
a. The number of hot dogs = 38 dozens .
On Wednesday number of hot dogs left = 30 that means 38 – 30 = 8 dozens are sold .
b. Saturday and Sunday because on Saturday he started 22 and ended at 14  = 8 dozens are sold and On Sunday he started at 14 and        ended at 4 that means 10 dozens are sold .
c. Friday, Saturday and Sunday .
Friday he started at 27 and ended at 22 that means 5 dozens .
Saturday he started 22 and ended at 14  = 8 dozens are sold .
On Sunday he started at 14 and ended at 4 that means 10 dozens are sold .
d. Friday = 5
Saturday = 8
Sunday = 10
Total = 5 + 8 + 10 = 23 dozens .

Eureka Math Grade 5 Module 6 Lesson 20 Homework Answer Key

Use the graph to answer the questions.
Johnny left his home at 6 a.m. and kept track of the number of kilometers he traveled at the end of each hour of his trip. He recorded the data in a line graph.

a. How far did Johnny travel in all? How long did it take?
b. Johnny took a one-hour break to have a snack and take some pictures. What time did he stop? How do you know?
c. Did Johnny cover more distance before his break or after? Explain.
d. Between which two hours did Johnny ride 4 kilometers?
e. During which hour did Johnny ride the fastest? Explain how you know.
Answer:
a. The distance traveled by Johnny = he ends at 20 – he started at 4 = 16kms
The Time taken = ends at 12 p.m  –  starts at 7 a.m = 5 hours.
b.  At 9 a.m to 10 a.m   the line is flat that means no journey has taken place so, he might have taken one hour break during this time .
c.  He took break from 9 to 10 a.m
Distance covered before break = 7 to 9 a.m= 14 – 4 = 10 kms.
Distance covered after break = 10 to 12 p.m = 20 – 14 = 6 kms .
Before break the distance covered is more .
d.  Between 7 – 8 a.m and 10 – 11 a.m John ride 4 kilometers. .
e. 8 am to 9 am because in one hour he covered 6 kilometers.

Engage NY Eureka Math 5th Grade Module 6 Lesson 19 Answer Key

Eureka Math Grade 5 Module 6 Lesson 19 Sprint Answer Key

A
Make Larger Units

Question 1.
\(\frac{2}{4}\) =
Answer:
\(\frac{2}{4}\) =\(\frac{1}{2}\)

Question 2.
\(\frac{2}{6}\) =
Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 3.
\(\frac{2}{8}\) =
Answer:
\(\frac{2}{8}\) = \(\frac{1}{4}\)

Question 4.
\(\frac{5}{10}\) =
Answer:
\(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 5.
\(\frac{5}{15}\) =
Answer:
\(\frac{5}{15}\) = \(\frac{1}{3}\)

Question 6.
\(\frac{5}{20}\) =
Answer:
\(\frac{5}{20}\) = \(\frac{1}{4}\)

Question 7.
\(\frac{4}{8}\) =
Answer:
\(\frac{4}{8}\) = \(\frac{1}{2}\)

Question 8.
\(\frac{4}{12}\) =
Answer:
\(\frac{4}{12}\) = \(\frac{1}{3}\)

Question 9.
\(\frac{4}{16}\) =
Answer:
\(\frac{4}{16}\) = \(\frac{1}{4}\)

Question 10.
\(\frac{3}{6}\) =
Answer:
\(\frac{3}{6}\) = \(\frac{1}{2}\) 

Question 11.
\(\frac{3}{9}\) =
Answer:
\(\frac{3}{9}\) = \(\frac{1}{3}\)

Question 12.
\(\frac{3}{12}\) =
Answer:
\(\frac{3}{12}\) = \(\frac{1}{4}\)

Question 13.
\(\frac{4}{6}\) =
Answer:
\(\frac{4}{6}\) = \(\frac{2}{3}\)

Question 14.
\(\frac{6}{12}\) =
Answer:
\(\frac{6}{12}\) = \(\frac{1}{2}\)

Question 15.
\(\frac{6}{18}\) =
Answer:
\(\frac{6}{18}\) = \(\frac{1}{3}\)

Question 16.
\(\frac{6}{30}\) =
Answer:
\(\frac{6}{30}\) = \(\frac{1}{5}\)

Question 17.
\(\frac{6}{9}\) =
Answer:
\(\frac{6}{9}\) = \(\frac{2}{3}\)

Question 18.
\(\frac{7}{14}\) =
Answer:
\(\frac{7}{14}\) = \(\frac{1}{2}\)

Question 19.
\(\frac{7}{21}\) =
Answer:
latex]\frac{7}{21}[/latex] = latex]\frac{1}{3}[/latex]

Question 20.
\(\frac{7}{42}\) =
Answer:
\(\frac{7}{42}\) = \(\frac{1}{6}\)

Question 21.
\(\frac{8}{12}\) =
Answer:
\(\frac{8}{12}\) = \(\frac{2}{3}\)

Question 22.
\(\frac{9}{18}\) =
Answer:
\(\frac{9}{18}\) = \(\frac{1}{2}\)

Question 23.
\(\frac{9}{27}\) =
Answer:
\(\frac{9}{27}\) = \(\frac{1}{3}\)

Question 24.
\(\frac{9}{63}\) =
Answer:
\(\frac{9}{63}\) = \(\frac{1}{7}\)

Question 25.
\(\frac{8}{12}\) =
Answer:
\(\frac{8}{12}\) = \(\frac{2}{3}\)

Question 26.
\(\frac{8}{16}\) =
Answer:
\(\frac{8}{16}\) = \(\frac{1}{2}\)

Question 27.
\(\frac{8}{24}\) =
Answer:
\(\frac{8}{24}\) = \(\frac{1}{3}\)

Question 28.
\(\frac{8}{64}\) =
Answer:
\(\frac{8}{64}\) = \(\frac{1}{8}\)

Question 29.
\(\frac{12}{18}\) =
Answer:
\(\frac{12}{18}\) = \(\frac{2}{3}\)

Question 30.
\(\frac{12}{16}\) =
Answer:
\(\frac{12}{16}\) = \(\frac{3}{4}\)

Question 31.
\(\frac{9}{12}\) =
Answer:
\(\frac{9}{12}\) = \(\frac{3}{4}\)

Question 32.
\(\frac{6}{8}\) =
Answer:
\(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 33.
\(\frac{10}{12}\) =
Answer:
\(\frac{10}{12}\) = \(\frac{5}{6}\)

Question 34.
\(\frac{15}{18}\) =
Answer:
\(\frac{15}{18}\) = \(\frac{5}{6}\)

Question 35.
\(\frac{8}{10}\) =
Answer:
\(\frac{8}{10}\) = \(\frac{4}{5}\)

Question 36.
\(\frac{16}{20}\) =
Answer
\(\frac{16}{20}\) = \(\frac{4}{5}\)

Question 37.
\(\frac{12}{15}\) =
Answer:
\(\frac{12}{15}\) = \(\frac{4}{5}\)

Question 38.
\(\frac{18}{27}\) =
Answer:
\(\frac{18}{27}\) = \(\frac{6}{9}\)

Question 39.
\(\frac{27}{36}\) =
Answer:
\(\frac{27}{36}\) = \(\frac{3}{4}\)

Question 40.
\(\frac{32}{40}\) =
Answer:
\(\frac{32}{40}\) = \(\frac{4}{5}\)

Question 41.
\(\frac{45}{54}\) =
Answer:
\(\frac{45}{54}\) = \(\frac{5}{6}\)

Question 42.
\(\frac{24}{36}\) =
Answer:
\(\frac{24}{36}\) = \(\frac{6}{9}\)

Question 43.
\(\frac{60}{72}\) =
Answer:
\(\frac{60}{72}\) = \(\frac{5}{6}\)

Question 44.
\(\frac{48}{60}\) =
Answer:
\(\frac{48}{60}\) = \(\frac{4}{5}\)

B
Make Larger Units

Question 1.
\(\frac{5}{10}\) =
Answer:
\(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 2.
\(\frac{5}{15}\) =
Answer:
\(\frac{5}{15}\) = \(\frac{1}{3}\)

Question 3.
\(\frac{5}{20}\) =
Answer:
\(\frac{5}{20}\) = \(\frac{1}{4}\)

Question 4.
\(\frac{2}{4}\) =
Answer:
\(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 5.
\(\frac{2}{6}\) =
Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 6.
\(\frac{2}{8}\) =
Answer:
\(\frac{2}{8}\) = \(\frac{1}{4}\)

Question 7.
\(\frac{3}{6}\) =
Answer:
\(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 8.
\(\frac{3}{9}\) =
Answer:
\(\frac{3}{9}\) = \(\frac{1}{3}\)

Question 9.
\(\frac{3}{12}\) =
Answer:
\(\frac{3}{12}\) = \(\frac{1}{4}\)

Question 10.
\(\frac{4}{8}\) =
Answer:
\(\frac{4}{8}\) = \(\frac{1}{2}\)

Question 11.
\(\frac{4}{12}\) =
Answer:
\(\frac{4}{12}\) = \(\frac{1}{3}\)

Question 12.
\(\frac{4}{16}\) =
Answer:
\(\frac{4}{16}\) = \(\frac{1}{4}\)

Question 13.
\(\frac{4}{6}\) =
Answer:
\(\frac{4}{6}\) = \(\frac{2}{3}\)

Question 14.
\(\frac{7}{14}\) =
Answer:
\(\frac{7}{14}\) = \(\frac{1}{2}\)

Question 15.
\(\frac{7}{21}\) =
Answer:
\(\frac{7}{21}\) = \(\frac{1}{3}\)

Question 16.
\(\frac{7}{35}\) =
Answer:
\(\frac{7}{35}\) = \(\frac{1}{5}\)

Question 17.
\(\frac{6}{9}\) =
Answer:
\(\frac{6}{9}\) = \(\frac{2}{3}\)

Question 18.
\(\frac{6}{12}\) =
Answer:
\(\frac{6}{12}\) = \(\frac{1}{2}\)

Question 19.
\(\frac{6}{18}\) =
Answer:
\(\frac{6}{18}\) = \(\frac{1}{3}\)

Question 20.
\(\frac{6}{36}\) =
Answer:
\(\frac{6}{36}\) = \(\frac{1}{6}\)

Question 21.
\(\frac{8}{12}\) =
Answer:
\(\frac{8}{12}\) = \(\frac{2}{3}\)

Question 22.
\(\frac{8}{16}\) =
Answer:
\(\frac{8}{16}\) = \(\frac{1}{2}\)

Question 23.
\(\frac{8}{24}\) =
Answer:
\(\frac{8}{24}\) = \(\frac{1}{3}\)

Question 24.
\(\frac{8}{56}\) =
Answer:
\(\frac{8}{56}\) = \(\frac{1}{7}\)

Question 25.
\(\frac{8}{12}\) =
Answer:
\(\frac{8}{12}\) = \(\frac{2}{3}\)

Question 26.
\(\frac{9}{18}\) =
Answer:
\(\frac{9}{18}\) = \(\frac{1}{2}\)

Question 27.
\(\frac{9}{27}\) =
Answer:
\(\frac{9}{27}\) = \(\frac{1}{3}\) =

Question 28.
\(\frac{9}{72}\) =
Answer:
\(\frac{9}{72}\) = \(\frac{1}{8}\)

Question 29.
\(\frac{12}{18}\) =
Answer:
\(\frac{12}{18}\) = \(\frac{4}{6}\)

Question 30.
\(\frac{6}{8}\) =
Answer:
\(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 31.
\(\frac{9}{12}\) =
Answer:
\(\frac{9}{12}\) = \(\frac{3}{4}\)

Question 32.
\(\frac{12}{16}\) =
Answer:
\(\frac{12}{16}\) = \(\frac{3}{4}\)

Question 33.
\(\frac{8}{10}\) =
Answer:
\(\frac{8}{10}\) = \(\frac{4}{5}\)

Question 34.
\(\frac{16}{20}\) =
Answer:
\(\frac{16}{20}\) = \(\frac{4}{5}\)

Question 35.
\(\frac{12}{15}\) =
Answer:
\(\frac{12}{15}\) = \(\frac{4}{5}\)

Question 36.
\(\frac{10}{12}\) =
Answer:
\(\frac{10}{12}\) = \(\frac{5}{6}\)

Question 37.
\(\frac{15}{18}\) =
Answer:
\(\frac{15}{18}\) = \(\frac{5}{6}\)

Question 38.
\(\frac{16}{24}\) =
Answer:
\(\frac{16}{24}\) = \(\frac{2}{3}\)

Question 39.
\(\frac{24}{32}\) =
Answer:
\(\frac{24}{32}\) = \(\frac{3}{4}\)

Question 40.
\(\frac{36}{45}\) =
Answer:
\(\frac{36}{45}\) = \(\frac{4}{5}\)

Question 41.
\(\frac{40}{48}\) =
Answer:
\(\frac{40}{48}\) = \(\frac{5}{6}\)

Question 42.
\(\frac{24}{36}\) =
Answer:
\(\frac{24}{36}\) = \(\frac{2}{3}\)

Question 43.
\(\frac{48}{60}\) =
Answer:
\(\frac{48}{60}\) = \(\frac{4}{5}\)

Question 44.
\(\frac{60}{72}\) =
Answer:
\(\frac{60}{72}\) = \(\frac{5}{6}\)

Eureka Math Grade 5 Module 6 Lesson 19 Problem Set Answer Key

Question 1.
The line graph below tracks the rain accumulation, measured every half hour, during a rainstorm that began at 2:00 p.m. and ended at 7:00 p.m. Use the information in the graph to answer the questions that follow.

a. How many inches of rain fell during this five-hour period?
b. During which half-hour period did \(\frac{1}{2}\) inch of rain fall? Explain how you know.
c. During which half-hour period did rain fall most rapidly? Explain how you know.
d. Why do you think the line is horizontal between 3:30 p.m. and 4:30 p.m.?
e. For every inch of rain that fell here, a nearby community in the mountains received a foot and a half of snow. How many inches of snow fell in the mountain community between 5:00 p.m. and 7:00 p.m.?
Answer:
a.  The Rain fell During this Five-hour period is 1\(\frac{3}{4}\) inches .
b. The \(\frac{1}{2}\) inch of rain fall during 2:30 to 3:00 p.m
Explanation :
The line went up \(\frac{1}{2}\) inch as time went 2:30 to 3:00 p.m
c. The rain fall most rapidly took place during 4:30 to 5:00 p.m because the line steepest .
d. The line is horizontal between 3:30 p.m. and 4:30 p.m because they is a constant rainfall .
e. The rainfall from 5:00 p.m. to 7:00 p.m is \(\frac{1}{2}\). That means The community got a foot and a half of snow.
12 inches = 1 foot .
For 1 inch we receive foot and a half of snow = 1\(\frac{1}{2}\).
For \(\frac{1}{2}\) we receive \(\frac{3}{4}\) foot of snow .( \(\frac{1}{2}\) of foot and a half of snow ) .
=\(\frac{3}{4}\)  (12 inches)  = 9 inches .

Question 2.
Mr. Boyd checks the gauge on his home’s fuel tank on the first day of every month. The line graph to the right was created using the data he collected.

a. According to the graph, during which month(s) does the amount of fuel decrease most rapidly?
b. The Boyds took a month-long vacation. During which month did this most likely occur? Explain how you know using the data in the graph.
c. Mr. Boyd’s fuel company filled his tank once this year. During which month did this most likely occur? Explain how you know.
d. The Boyd family’s fuel tank holds 284 gallons of fuel when full. How many gallons of fuel did the Boyds use in February?
e. Mr. Boyd pays $3.54 per gallon of fuel. What is the cost of the fuel used in February and March?
Answer:
a. The amount of fuel decrease most rapidly From January .
b. In the Month of july no fuel is used .because the line is flat .
c. In the may month the tank is filled because the line went up that means the fuel is filled .
d. Amount of fuel used to fill = 284 gallons .
Total Number of lines = 16
Each line represent how much of fuel = 284 /16 = 17.75 gallons.
In febuary 2 units went down that means 17.75 × 2 = 35.5 gallons .
that means 35.5 gallons of fuel is used .
e. In febuary 2 units went down that means 17.75 × 2 = 35.5 gallons that means 35.5 gallons of fuel is used .
In March 1 unit went down that means 17.75 × 1 = 17.75 gallons .
Total Fuel used in febuary and march = 35.5 +17.75 = 53.25.
Cost of Each galloon of fuel = $3.54 per gallons.
Cost of 53.25 gallon of fuel = $3.54 × 53.25 per gallons. = 188.505$ .

Eureka Math Grade 5 Module 6 Lesson 19 Exit Ticket Answer Key

The line graph below tracks the water level of Plainsview Creek, measured each Sunday, for 8 weeks. Use the information in the graph to answer the questions that follow.

a. About how many feet deep was the creek in Week 1? ________
b. According to the graph, which week had the greatest change in water depth? __________
c. It rained hard throughout the sixth week. During what other weeks might it have rained? Explain why you think so.
d. What might have been another cause leading to an increase in the depth of the creek?
Answer:
a. The depth of the creek in Week 1 was 4 feet.
b. The greatest change in water depth Occurred in Week 2 that is 1\(\frac{1}{2}\).
c. In week 6 the water level is increased t 1 unit that means it have rained . In week 1 and week 2 the water level is increased     \(\frac{1}{2}\) and 1\(\frac{1}{2}\) units respectively .
d. Riffles and glides leading to an increase in the depth of the creek .

Eureka Math Grade 5 Module 6 Lesson 19 Homework Answer Key

Question 1.
The line graph below tracks the balance of Howard’s checking account, at the end of each day, between May 12 and May 26. Use the information in the graph to answer the questions that follow.

a. About how much money does Howard have in his checking account on May 21?
b. If Howard spends $250 from his checking account on May 26, about how much money will he have left in his account?
c. Explain what happened with Howard’s money between May 21 and May 23
d. Howard received a payment from his job that went directly into his checking account. On which day did this most likely occur? Explain how you know.
e. Howard bought a new television during the time shown in the graph. On which day did this most likely occur? Explain how you know.
Answer:
a. The Money in the account on 21st may = it is marked on 1\(\frac{1}{4}\) . It represents in1000$.
So, 1\(\frac{1}{2}\) = 1.25$ in thousands =1.25 × 1000 =1250$ .
b. The point is marked between 1 and 1\(\frac{1}{4}\) so take 1.1$ approximately .
So, 1.1$= 1.1$ in thousands =1.1 × 1000 =1100$ .
Amount spent = $250 .
Remaining amount = $1100 – 250 = 850$ approximately .
c. The Money in the Howard’s account between May 21 and May 23 is same ,No transaction have taken place .
d. On 16 may we can see the line went up that means account is credited with the money . so, On 16th may the salary has been                 credited to his account .
e. On 18th may we see a decline in the account balance  that means how much has been debited from the account . so, on 18 th may       he might have bought new tv .

Question 2.
The line graph below tracks Santino’s time at the beginning and end of each part of a triathlon. Use the information in the graph to answer the questions that follow.

a. How long does it take Santino to finish the triathlon?
b. To complete the triathlon, Santino first swims across a lake, then bikes through the city, and finishes by running around the lake. According to the graph, what was the distance of the running portion of the race?
c. During the race, Santino pauses to put on his biking shoes and helmet and then later to change into his running shoes. At what times did this most likely occur? Explain how you know.
d. Which part of the race does Santino finish most quickly? How do you know?
e. During which part of the triathlon is Santino racing most quickly? Explain how you know.
Answer:
a. Santino started his work at 1:00 and he finished at 2:50 p.m that means he took 1:50 mins to complete .
b. The distance of the running portion of the race is in the ending that means in the graph we notice a point at 2:20 he starts running         so it is marked at 5kms .
c. We notice at between 1:10 and 1:20 a straight line that means he might put his his helmet and biking shoes at 1:15 to 1:18                      approximately because after swimming he started biking the race.
Later at in between 2:10 to 2:20 we see a straight line that means in the finishing he runs around the lake. so, that means he might        have put in running shoes around 2:13 to 2:20 p.m  .
d. The swimming is started at 1:00 and ends at 1:15 p.m = 15 mins
The racing of bike started at 1:19 and ends at 2:13 = 54 mins around .
The Running is started at 2:20 and ends at 2:50p,m = 30mins .
That means swimming is completed faster .
e. Biking because it has the steepest line as per graph .

Engage NY Eureka Math 5th Grade Module 6 Lesson 18 Answer Key

Eureka Math Grade 5 Module 6 Lesson 18 Problem Set Answer Key

Question 1.
Use the plane to the right to complete the following tasks.

a. Draw a line t whose rule is y is always 0.7.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points.

c. Complete the drawing to create a figure that is symmetric about line t. For each point in Table A, record the corresponding point on the other side of the line of symmetry in Table B.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
C. The Table B is written below

d . The differences in the Table A is same as the difference in the Table B .
e. The X-coordinates in the table A is same as the in the Table B.

Question 2.
This figure has a second line of symmetry. Draw the line on the plane, and write the rule for this line.
Answer:
The X is always the 0.7 is the rule used for second symmetry of line .

Question 3.
Use the plane below to complete the following tasks.

a. Draw a line u whose rule is y is equal to x + \(\frac{1}{4}\).
b. Construct a figure with a total of 6 points, all on the same side of the line.
c. Record the coordinates of each point, in the order in which they were drawn, in Table A.
d. Swap your paper with a neighbor, and have her complete parts (e–f), below.

e. Complete the drawing to create a figure that is symmetric about u. For each point in Table A, record the corresponding point on the other side of the line of symmetry in Table B.
f. Explain how you found the points symmetric to your partner’s about u.
Answer:
a. Line u is drawn
c. Points of Table A .

d. Points of Table B

f. Using the line of symmetry i counted the units . The units should be equal distance from the line of u . Points are marked carefully because rule used here is y is equal to x + \(\frac{1}{4}\) .

Eureka Math Grade 5 Module 6 Lesson 18 Exit Ticket Answer Key

Kenny plotted the following pairs of points and said they made a symmetric figure about a line with the rule:
y is always 4.
(3, 2) and (3, 6)
(4, 3) and (5, 5)
(5, \(\frac{3}{4}\)) and (5, 7\(\frac{1}{4}\))
(7, 1\(\frac{1}{2}\)) and (7, 6\(\frac{1}{2}\))
Is his figure symmetrical about the line? How do you know?
Answer:

No,
Explanation :
The units should be equal distance from the line of . But the point (4, 3) and (5,5) have different lengths from the line .
so, the image formed is not symmetric figure .

Eureka Math Grade 5 Module 6 Lesson 18 Homework Answer Key

Question 1.
Use the plane to the right to complete the following tasks.

a. Draw a line s whose rule is x is always 5.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points in order.

c. Complete the drawing to create a figure that is symmetric about line s. For each point in Table A, record the symmetric point on the other side of s.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
c. The points of Table B are

d. The Y-coordinates in Table A and Table B are equal .
e.  The x-coordinates in Table A with those in Table B are in reverse order like 1-9 , 2-8,3-7, 4-6 and 5-5 numbers are interchanged with respective number .

Question 2.
Use the plane to the right to complete the following tasks.

a. Draw a line p whose rule is, y is equal to x.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points.

c. Complete the drawing to create a figure that is symmetric about line p. For each point in Table A, record the symmetric point on the other side of the line p in Table B.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
c. The points of Table B.

Engage NY Eureka Math 5th Grade Module 6 Lesson 17 Answer Key

Eureka Math Grade 5 Module 6 Lesson 17 Problem Set Answer Key

Question 1.
Draw to create a figure that is symmetric about \(\overleftrightarrow{A D}\).

Answer:

Explanation :
Symmetric means – An exact matching of form and arrangement of parts on opposite sides of a boundary, such as a plane or line, or around a central point or axis.
Here the axis is \(\overleftrightarrow{A D}\) . and opposite image is formed opposite to \(\overleftrightarrow{A D}\) as shown in above figure .

Question 2.
Draw precisely to create a figure that is symmetric about \(\overleftrightarrow{H I}\)

Answer:

Explanation :
Symmetric means – An exact matching of form and arrangement of parts on opposite sides of a boundary, such as a plane or line, or around a central point or axis.
Here the axis is \(\overleftrightarrow{H I}\) . and opposite image is formed opposite to \(\overleftrightarrow{H I}\) as shown in above figure

Question 3.
Complete the following construction in the space below.
a. Plot 3 non-collinear points, D, E, and F.
b. Draw \(\overline{D E}\), \(\overline{E F}\), and \(\overleftrightarrow{D F}\).
c. Plot point G, and draw the remaining sides, such that quadrilateral DEFG is symmetric about \(\overleftrightarrow{D F}\).
Answer:

Question 4.
Stu says that quadrilateral HIJK is symmetric about \(\overleftrightarrow{H J}\) because IL = LK. Use your tools to determine Stu’s mistake. Explain your thinking.

Answer:

Explanation :
Even though the IL=IK, the adjacent angles from the line of symmetric \(\overleftrightarrow{H J}\) should be of same size . ∠LJK should be equal to ∠LJI. ∠LHK should be equal to ∠LHI.

Eureka Math Grade 5 Module 6 Lesson 17 Exit Ticket Answer Key

Question 1.
Draw 2 points on one side of the line below, and label them T and U.
Answer:

Explanation :
Given Points T and U are marked on the given line .

Question 2.
Use your set square and ruler to draw symmetrical points about your line that correspond to T and U, and label them V and W.

Answer:

Explanation :
Using set square two parallel lines are represented in the above figure . TU ll VW .

Eureka Math Grade 5 Module 6 Lesson 17 Homework Answer Key

Question 1.
Draw to create a figure that is symmetric about \(\overleftrightarrow{D E}\).

Answer:

Explanation :
Symmetric means – An exact matching of form and arrangement of parts on opposite sides of a boundary, such as a plane or line, or around a central point or axis.
Here the axis is \(\overleftrightarrow{E D}\) . and opposite image is formed opposite to \(\overleftrightarrow{E D}\) as shown in above figure .

Question 2.
Draw to create a figure that is symmetric about \(\overleftrightarrow{L M}\).

Answer:

Explanation :
Symmetric means – An exact matching of form and arrangement of parts on opposite sides of a boundary, such as a plane or line, or around a central point or axis.
Here the axis is \(\overleftrightarrow{L M}\) . and opposite image is formed opposite to \(\overleftrightarrow{L M}\) as shown in above figure .

Question 3.
Complete the following construction in the space below.
a. Plot 3 non-collinear points, G, H, and I.
b. Draw \(\overline{G H}\), \(\overline{H I}\), and \(\overleftrightarrow{I G}\).
c. Plot point J, and draw the remaining sides, such that quadrilateral GHIJ is symmetric about \(\overleftrightarrow{I G}\).
Answer:

Question 4.
In the space below, use your tools to draw a symmetric figure about a line.
Answer:

Explanation :
Symmetric means – An exact matching of form and arrangement of parts on opposite sides of a boundary, such as a plane or line, or around a central point or axis.
Here the axis is \(\overleftrightarrow{A D}\) . and opposite image is formed opposite to \(\overleftrightarrow{A D}\) as shown in above figure .

Engage NY Eureka Math 5th Grade Module 6 Lesson 16 Answer Key

Eureka Math Grade 5 Module 6 Lesson 16 Problem Set Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Draw \(\overline{A B}\).
b. Plot point C (0, 8).
c. Draw \(\overline{A C}\).
d. Explain how you know ∠CAB is a right angle without measuring it.
e. Sean drew the picture below to find a segment perpendicular to (AB) ̅. Explain why Sean is correct.

Answer:

d.
Explanation :
∠CAB is a right angle because I can Draw a triangle that has \(\overline{A B}\) has its long side. The length is 5 units and the Height is 2 units . When I slide the triangle to the left and rotated, I know 2 acute angles will form a 90 degrees or right angle .
e.
Sean is correct because I notice that he slid and rotated the triangle and the 2 acute angles form the right angle .

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Draw \(\overline{Q T}\).
b. Plot point R (2, 6\(\frac{1}{2}\)).
c. Draw \(\overline{Q R}\).
d. Explain how you know ∠RQT is a right angle without measuring it.
e. Compare the coordinates of points Q and T. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points Q and R. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

d.
Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠RQT will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points Q and T are ( 3\(\frac{1}{2}\) , 4 ) and (6, 5\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 6 – 3\(\frac{1}{2}\)= 2\(\frac{1}{2}\) .
The difference of y-coordinate = 5\(\frac{1}{2}\) – 4 = 1\(\frac{1}{2}\).
f. The coordinates of points Q and R are ( 3\(\frac{1}{2}\) , 4 ) and (2, 6\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 3\(\frac{1}{2}\) – 2 = 1\(\frac{1}{2}\) .
The difference of y-coordinate = 6\(\frac{1}{2}\) – 4 = 2\(\frac{1}{2}\).
g. The differences in the X-coordinate of the points Q and T is same as the differences in the Y-coordinate of the points Q and R .
The differences in the Y-coordinate of the points Q and T is same as the differences in the X-coordinate of the points Q and R. Just        the Numbers flipped.

Question 3.
\(\overline{E F}\) contains the following points. E: (4, 1) F: (8, 7)
Give the coordinates of a pair of points G and H, such that \(\overline{E F}\) ⊥ \(\overline{G H}\).
G: (_____, _____) H: (_____, _____)
Answer:
As the above rule is applied of Question -2-g and the Coordinate of Points are written .
G: (1, 8) H: ( 7, 4)

Eureka Math Grade 5 Module 6 Lesson 16 Exit Ticket Answer Key

Use the coordinate plane below to complete the following tasks.
a. Draw \(\overline{U V}\).
b. Plot point W (4\(\frac{1}{2}\),6).
c. Draw \(\overline{V W}\).
d. Explain how you know that ∠UVW is a right angle without measuring it.

Answer:

d.
Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠UVW will be 90 degrees Since the 3 angles form a straight line .

Eureka Math Grade 5 Module 6 Lesson 16 Homework Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Draw \(\overline{P Q}\).
b. Plot point R (3, 8).
c. Draw \(\overline{P R}\).
d. Explain how you know ∠RPQ is a right angle without measuring it.
e. Compare the coordinates of points P and Q. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points P and R. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

d. Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠RPQ will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points P and Q are ( 2, 4 ) and (6, 3) Respectively .
The differences of x- coordinate = 6 – 2= 4 .
The difference of y-coordinate = 4- 3 = 1.
f. The coordinates of points P and R are ( 2, 4 ) and ( 3, 8 ) Respectively .
The differences of x- coordinate = 3 – 2 = 1
The difference of y-coordinate = 8 – 4 = 4
g. The differences in the X-coordinate of the points P and Q  is same as the differences in the Y-coordinate of the points P and R .
The differences in the Y-coordinate of the points P and Q is same as the differences in the X-coordinate of the points P and R . Just        the Numbers flipped.

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Draw \(\overline{C B}\).
b. Plot point D(\(\frac{1}{2}\), 5\(\frac{1}{2}\)).
c. Draw \(\overline{C D}\).
d. Explain how you know ∠DCB is a right angle without measuring it.
e. Compare the coordinates of points C and B. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points C and D. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

d. Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠DCB will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points C and B. are (1\(\frac{3}{4}\), 4 ) and (3\(\frac{1}{4}\), 5) Respectively .
The differences of x- coordinate = 3\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = \(\frac{13}{4}\) –\(\frac{7}{4}\) = 1\(\frac{6}{4}\)=\(\frac{2}{3}\)
The difference of y-coordinate = 5 – 4 =1
f. The coordinates of points C and D are (1\(\frac{3}{4}\), 4 ) and (\(\frac{1}{2}\), 5\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 1\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{7}{4}\)– \(\frac{2}{4}\)= \(\frac{5}{4}\)= 1\(\frac{1}{4}\)
The difference of y-coordinate =5\(\frac{1}{2}\) – 4 = 1\(\frac{1}{2}\)
g. All the differences are different .No Relationship is formed .

Question 3.
\(\overline{S T}\) contains the following points. S: (2, 3) T: (9, 6)
Give the coordinates of a pair of points, U and V, such that \(\overline{S T}\) ⊥ \(\overline{S T}\).
U: (_____, _____) V: (_____, _____)
Answer:

the coordinates of a pair of points, U and V, such that \(\overline{S T}\) ⊥ \(\overline{S T}\).
U: (, ) V: (_____, _____)
The coordinates of points S and T are(2, 3) and (9, 6) Respectively .
The differences of x- coordinate = 9 – 2= 7 .
The difference of y-coordinate = 6- 3 = 3.

The coordinates of points T and (6, 13) are (9, 6) and (6, 13)
The differences of x- coordinate = 9 – 6 = 3
The difference of y-coordinate = 13 – 6 = 7

The differences in the X-coordinate of the points S and T  is same as the differences in the Y-coordinate of the points T and (6, 13) .
The differences in the Y-coordinate of the points S and T is same as the differences in the X-coordinate of the points T and (6, 13) .        Just the Numbers flipped.
U: (3, 9) V: (6, 2)

Engage NY Eureka Math 5th Grade Module 6 Lesson 15 Answer Key

Eureka Math Grade 5 Module 6 Lesson 15 Problem Set Answer Key

Question 1.
Circle the pairs of segments that are perpendicular.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 2.
In the space below, use your right triangle templates to draw at least 3 different sets of perpendicular lines.
Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 3.
Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 4.
Draw 2 different lines perpendicular to line e.

Explanation :

Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.
Answer:

Eureka Math Grade 5 Module 6 Lesson 15 Exit Ticket Answer Key

Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Eureka Math Grade 5 Module 6 Lesson 15 Homework Answer Key

Question 1.
Circle the pairs of segments that are perpendicular.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 2.
In the space below, use your right triangle templates to draw at least 3 different sets of perpendicular lines.
Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 3.
Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 4.
Draw 2 different lines perpendicular to line b.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Engage NY Eureka Math 5th Grade Module 6 Lesson 14 Answer Key

Eureka Math Grade 5 Module 6 Lesson 14 Problem Set Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of P and R. P: (_____, _____) R: (_____, _____)
b. Draw \(\overleftrightarrow{P R}\).
c. Plot the following coordinate pairs on the plane.
S: (6, 7) T: (11, 9)
d. Draw \(\overleftrightarrow{S T}\).
e. Circle the relationship between \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{S T}\).
\(\overleftrightarrow{P R}\) ⊥ \(\overleftrightarrow{S T}\)
\(\overleftrightarrow{P R}\) ∥ \(\overleftrightarrow{S T}\)
f. Give the coordinates of a pair of points, U and V, such that \(\overleftrightarrow{U V}\) ∥ \(\overleftrightarrow{P R}\).
U: (_____, _____) V: (_____, _____)
g. Draw \(\overleftrightarrow{U V}\).
Answer:
a. The locations of P and R. P: (6, 4) R: (11, 6) .
b.

c.

e.

Explanation :
Both the lines are equidistant from each other so, the \(\overleftrightarrow{P R}\) is parallel to  \(\overleftrightarrow{S T}\) .
f. The coordinate points of u and v are U ( 6, 1) and V (11, 3)
g.

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
e. Explain the pattern you made use of when generating coordinate pairs for L and M.
f. Give the coordinates of a point, H, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{G H}\).
G: (1\(\frac{1}{2}\), 4) H: (____, ____)
g. Explain how you chose the coordinates for H.
Answer:
a. The locations of E and F. E: (1,3\(\frac{1}{2}\) ) F: (3, 1\(\frac{1}{2}\))
b.

c. The L and M points are L ( 3, 3\(\frac{1}{2}\)) and M ( 4\(\frac{1}{2}\), 2)
d.

e. The pattern made when generating coordinate pairs for L and M are parallel lines .
f. G: (1\(\frac{1}{2}\), 4) H: (3, 2\(\frac{1}{2}\))
g. The the coordinates for H is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{G H}\).
Explanation :
Plot the point G and then draw a parallel line from Point G such a way that it should be parallel to latex]\overleftrightarrow{E F}[/latex] .
After that take a point H on that parallel line .

Eureka Math Grade 5 Module 6 Lesson 14 Exit Ticket Answer Key

Use the coordinate plane below to complete the following tasks.

a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
Answer:
a. The locations of E and F. E: (2, 4) F: (5, 3) .
b.

c. The coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\) are
L: (3, 5) M: (6, 4)
d.

Eureka Math Grade 5 Module 6 Lesson 14 Homework Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of M and N. M: (_____, _____) N: (_____, _____)
b. Draw \(\overleftrightarrow{M N}\).
c. Plot the following coordinate pairs on the plane.
J: (5, 7) K: (8, 5)
d. Draw \(\overleftrightarrow{J K}\).
e. Circle the relationship between \(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\).
\(\overleftrightarrow{M N}\) ⊥ \(\overleftrightarrow{J K}\)
\(\overleftrightarrow{M N}\) ∥ \(\overleftrightarrow{J K}\)
f. Give the coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (_____, _____) G: (_____, _____)
g. Draw \(\overleftrightarrow{F G}\).
Answer:
a. The locations of M and N. M: (6, 4) N: (3, 6)
b.
c. The J and K are plotted on the graph .
d.

e.

Explanation :
\(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\) are Equidistant from each other so, parallel lines .

f. The coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (2, 4) G: (5, 2)
g.

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of A and B. A: (____, ____) B: (____, ____)
b. Draw \(\overleftrightarrow{A B}\).
c. Generate coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (____, ____) D: (____, ____)
d. Draw \(\overleftrightarrow{C D}\).
e. Explain the pattern you used when generating coordinate pairs for C and D.
f. Give the coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (____, ____)
g. Explain how you chose the coordinates for F.
Answer:
a. The locations of A and B. A: (4, 3\(\frac{1}{2}\)) B: (2 , 3)
b.

c. The coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (3\(\frac{1}{2}\), 2\(\frac{1}{2}\)) D: (5\(\frac{1}{2}\), 3)
d.

e. The pattern you used when generating coordinate pairs for C and D are \(\overleftrightarrow{A B}\) ∥     \(\overleftrightarrow{C D}\).
f. The coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (4\(\frac{1}{2}\) , 3)
g.

The the coordinates for F is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{A B}\).
Explanation :
Plot the point E and then draw a parallel line from Point E such a way that it should be parallel to latex]\overleftrightarrow{A B}[/latex] .
After that take a point F on that parallel line .

Engage NY Eureka Math 5th Grade Module 6 Lesson 11 Answer Key

Eureka Math Grade 5 Module 6 Lesson 11 Sprint Answer Key

A
Round to the Nearest One

Question 1.
3.1 ≈
Answer:
3.1 ≈ 3

Question 2.
3.2 ≈
Answer:
3.2 ≈ 3

Question 3.
3.3 ≈
Answer:
3.3 ≈ 3

Question 4.
3.4 ≈
Answer:
3.4 ≈ 3

Question 5.
3.5 ≈
Answer:
3.5 ≈ 4

Question 6.
3.6 ≈
Answer:
3.6 ≈ 4

Question 7.
3.9 ≈
Answer:
3.9 ≈ 4

Question 8.
13.9 ≈
Answer:
13.9 ≈ 14

Question 9.
13.1 ≈
Answer:
13.1 ≈ 13

Question 10.
13.5 ≈
Answer:
13.5 ≈ 14

Question 11.
7.5 ≈
Answer:
7.5 ≈ 8

Question 12.
8.5 ≈
Answer:
8.5 ≈ 9

Question 13.
9.5 ≈
Answer:
9.5 ≈ 10

Question 14.
19.5 ≈
Answer:
19.5 ≈ 20

Question 15.
29.5 ≈
Answer:
29.5 ≈ 30

Question 16.
89.5 ≈
Answer:
89.5 ≈ 90

Question 17.
2.4 ≈
Answer:
2.4 ≈ 2

Question 18.
2.41 ≈
Answer:
2.41 ≈ 2

Question 19.
2.42 ≈
Answer:
2.42 ≈ 2

Question 20.
2.45 ≈
Answer:
2.45 ≈ 2

Question 21.
2.49 ≈
Answer:
2.49 ≈ 2

Question 22.
2.51 ≈
Answer:
2.51 ≈ 3

Question 23.
12.51 ≈
Answer:
12.51 ≈ 13

Question 24.
16.61 ≈
Answer:
16.61 ≈ 17

Question 25.
17.41 ≈
Answer:
17.41 ≈ 17

Question 26.
11.51 ≈
Answer:
11.51 ≈ 12

Question 27.
11.49 ≈
Answer:
11.49 ≈ 11

Question 28.
13.49 ≈
Answer:
13.49 ≈ 13

Question 29.
13.51 ≈
Answer:
13.51 ≈ 14

Question 30.
15.51 ≈
Answer:
15.51 ≈ 16

Question 31.
15.49 ≈
Answer:
15.49 ≈ 16

Question 32.
6.3 ≈
Answer:
6.3 ≈ 6

Question 33.
7.6 ≈
Answer:
7.6 ≈ 8

Question 34.
49.5 ≈
Answer:
49.5 ≈ 50

Question 35.
3.45 ≈
Answer:
3.45 ≈ 3

Question 36.
17.46 ≈
Answer:
17.46 ≈ 17

Question 37.
11.76 ≈
Answer:
11.76 ≈ 12

Question 38.
5.2 ≈
Answer:
5.2 ≈ 5

Question 39.
12.8 ≈
Answer:
12.8 ≈ 13

Question 40.
59.5 ≈
Answer:
59.5 ≈ 60

Question 41.
5.45 ≈
Answer:
5.45 ≈ 5

Question 42.
19.47 ≈
Answer:
19.47 ≈ 19

Question 43.
19.87 ≈
Answer:
19.87 ≈ 20

Question 44.
69.51 ≈
Answer:
69.51 ≈ 70

B
Round to the Nearest One

Question 1.
4.1 ≈
Answer:
4.1 ≈ 4

Question 2.
4.2 ≈
Answer:
4.2 ≈ 4

Question 3.
4.3 ≈
Answer:
4.3 ≈ 4

Question 4.
4.4 ≈
Answer:
4.4 ≈ 4

Question 5.
4.5 ≈
Answer:
4.5 ≈ 5

Question 6.
4.6 ≈
Answer:
4.6 ≈ 5

Question 7.
4.9 ≈
Answer:
4.9 ≈ 5

Question 8.
14.9 ≈
Answer:
14.9 ≈ 15

Question 9.
14.1 ≈
Answer:
14.1 ≈ 14

Question 10.
14.5 ≈
Answer:
14.5 ≈ 15

Question 11.
7.5 ≈
Answer:
7.5 ≈ 8

Question 12.
8.5 ≈
Answer:
8.5 ≈ 9

Question 13.
9.5 ≈
Answer:
9.5 ≈ 10

Question 14.
19.5 ≈
Answer:
19.5 ≈ 20

Question 15.
29.5 ≈
Answer:
29.5 ≈ 30

Question 16.
79.5 ≈
Answer:
79.5 ≈ 80

Question 17.
3.4 ≈
Answer:
3.4 ≈ 3

Question 18.
3.41 ≈
Answer:
3.41 ≈ 3

Question 19.
3.42 ≈
Answer:
3.42 ≈ 3

Question 20.
3.45 ≈
Answer:
3.45 ≈ 3

Question 21.
3.49 ≈
Answer:
3.49 ≈ 3

Question 22.
3.51 ≈
Answer:
3.51 ≈ 4

Question 23.
13.51 ≈
Answer:
13.51 ≈ 14

Question 24.
17.61 ≈
Answer:
17.61 ≈ 18

Question 25.
18.41 ≈
Answer:
18.41 ≈ 18

Question 26.
12.51 ≈
Answer:
12.51 ≈ 13

Question 27.
12.49 ≈
Answer:
12.49 ≈ 12

Question 28.
14.49 ≈
Answer:
14.49 ≈ 14

Question 29.
14.51 ≈
Answer:
14.51 ≈ 15

Question 30.
16.51 ≈
Answer:
16.51 ≈ 17

Question 31.
16.49 ≈
Answer:
16.49 ≈ 16

Question 32.
7.3 ≈
Answer:
7.3 ≈ 7

Question 33.
8.6 ≈
Answer:
8.6 ≈ 9

Question 34.
39.5 ≈
Answer:
39.5 ≈ 40

Question 35.
4.45 ≈
Answer:
4.45 ≈ 4

Question 36.
18.46 ≈
Answer:
18.46 ≈ 18

Question 37.
12.76 ≈
Answer:
12.76 ≈ 13

Question 38.
6.2 ≈
Answer:
6.2 ≈ 6

Question 39.
13.8 ≈
Answer:
13.8 ≈ 14

Question 40.
49.5 ≈
Answer:
49.5 ≈ 50

Question 41.
6.45 ≈
Answer:
6.45 ≈ 6

Question 42.
19.48 ≈
Answer:
19.48 ≈ 19

Question 43.
19.78 ≈
Answer:
19.78 ≈ 20

Question 44.
59.51 ≈
Answer:
59.51 ≈ 60

Eureka Math Grade 5 Module 6 Lesson 11 Problem Set Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Double x

Line m
Rule: Double x, and then add 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Double x
y= 2x

Line m
Rule: Double x, and then add 1
y= 2x + 1

The given points are plotted on the graph .

b. The Line l and Line m are parallel to each other.
c.
Line n
Rule: double x, and then subtract 1
y= 2x – 1

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(1\(\frac{1}{2}\), 1\(\frac{1}{2}\))
(2\(\frac{1}{4}\), 2\(\frac{1}{4}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.
Rule: multiply x by \(\frac{1}{3}\),
y= x \(\frac{1}{3}\) + 1

b. Two points that fall on this line are
x = \(\frac{1}{2}\)
y = 1\(\frac{1}{6}\)
Point ( \(\frac{1}{2}\) , 1\(\frac{1}{6}\) )
x = 1
y =1\(\frac{1}{3}\)
Point (1, 1\(\frac{1}{3}\)) .

Question 3.
Complete the tables for the given rules.

Line l
Rule: Halve x

Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Halve x

Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)
y = \(\frac{x}{2}\) + \(\frac{3}{2}\) = \(\frac{x+3}{2}\)

a.

b. Both the lines l and m are parallel to each other.
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1

Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{2}{3}\), and then subtract 1 would contain.
(1\(\frac{1}{3}\), \(\frac{1}{9}\))
(2, \(\frac{1}{3}\))
(1\(\frac{3}{2}\), 1\(\frac{1}{2}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:

Explanation :
Line n
Rule: multiply x by \(\frac{2}{3}\), and then subtract 1
y = \(\frac{2x}{3}\) – 1 = \(\frac{2x – 3 }{3}\)

b. The other two points that fall on this line are (6 , 3 ) and (9, 5 ) .

Eureka Math Grade 5 Module 6 Lesson 11 Exit Ticket Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Triple x

Line m
Rule: Triple x, and then add 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
Answer:
a.
Line l
Rule: Triple x
y = 3x

Line m
Rule: Triple x, and then add 1
y = 3x + 1

b. Line m is parallel to line m and is shown in above graph .

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(3, 2\(\frac{1}{2}\))
Answer:

Explanation :
Line n
Rule: x by \(\frac{1}{3}\), and then add 1
y = \(\frac{x}{3}\) + 1 = \(\frac{ x + 3 }{3}\)

Eureka Math Grade 5 Module 6 Lesson 11 Homework Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Double x

Line m
Rule: Double x, and then subtract 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then add 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Double x
y = 2x

Line m
Rule: Double x, and then subtract 1
y = 2x – 1

b. The l and m are parallel lines . both lines are parallel to each other .
c.
Line n
Rule: Double x, and then add 1
y = 2x +1

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{2}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{4}\))
(2, 2)
(3, \(\frac{1}{2}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.

Explanation :
Rule: x by \(\frac{1}{2}\), and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)

b. The other two points are (4, 3) and ( 6, 4)

Question 3.
Complete the tables for the given rules.

Line l
Rule: Halve x, and then add 1

Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Halve x, and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)

Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)
y = \(\frac{x}{2}\) + \(\frac{5}{4}\) = \(\frac{ 2x + 5 }{4}\)

b. Line l and line m are parallel to each other and is shown in above graph .
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1 = \(\frac{ x – 2 }{2}\) .

Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\) would contain.
(1, \(\frac{1}{4}\))
(2, \(\frac{1}{4}\))
(3, 1\(\frac{3}{4}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.

Explanation :
Rule: multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\)
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .

b. The other 2 points that fall on this line are (6, 4) and ( 8, 5\(\frac{ 1 }{2}\))
Explanation :
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .
x= 6
y = \(\frac{ 3 x 6 – 2 }{4}\) = 4
and
x = 8
y= \(\frac{ 3 x 8 – 2 }{4}\) = \(\frac{ 22 }{4}\) = \(\frac{ 11 }{2}\) = 5\(\frac{ 1 }{2}\)