Engage NY Eureka Math 5th Grade Module 6 Lesson 14 Answer Key
Eureka Math Grade 5 Module 6 Lesson 14 Problem Set Answer Key
Question 1.
Use the coordinate plane below to complete the following tasks.
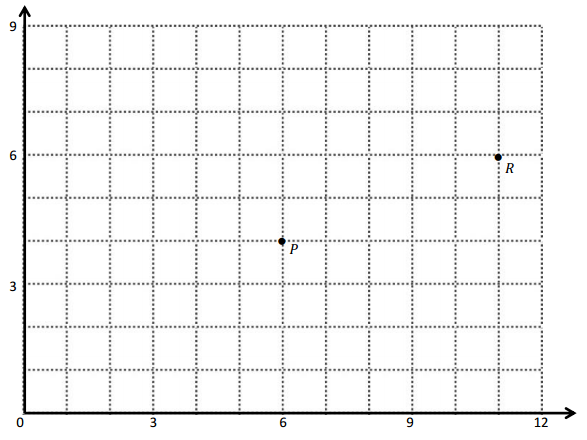
a. Identify the locations of P and R. P: (_____, _____) R: (_____, _____)
b. Draw \(\overleftrightarrow{P R}\).
c. Plot the following coordinate pairs on the plane.
S: (6, 7) T: (11, 9)
d. Draw \(\overleftrightarrow{S T}\).
e. Circle the relationship between \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{S T}\).
\(\overleftrightarrow{P R}\) ⊥ \(\overleftrightarrow{S T}\)
\(\overleftrightarrow{P R}\) ∥ \(\overleftrightarrow{S T}\)
f. Give the coordinates of a pair of points, U and V, such that \(\overleftrightarrow{U V}\) ∥ \(\overleftrightarrow{P R}\).
U: (_____, _____) V: (_____, _____)
g. Draw \(\overleftrightarrow{U V}\).
Answer:
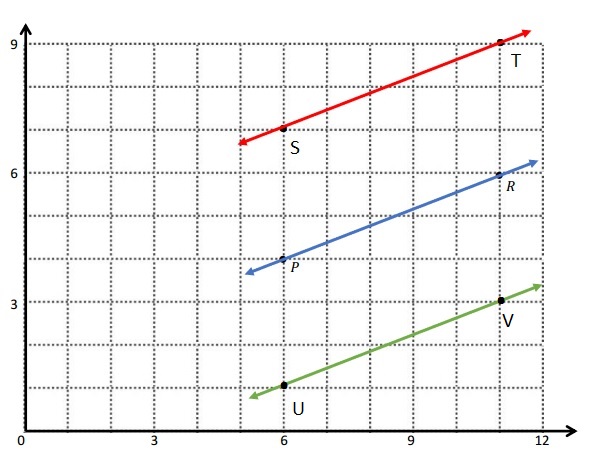
a. The locations of P and R. P: (6, 4) R: (11, 6) .
b.
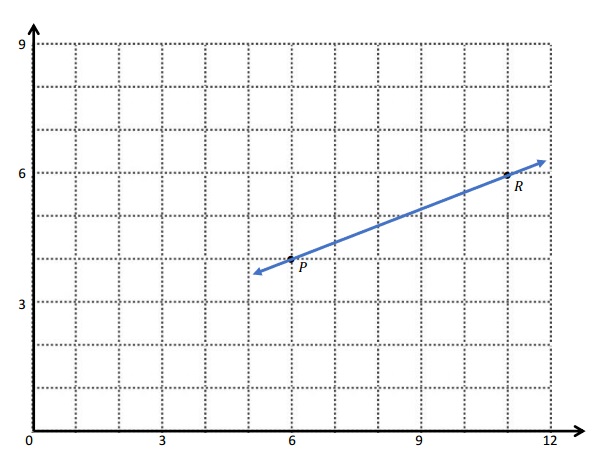
c.
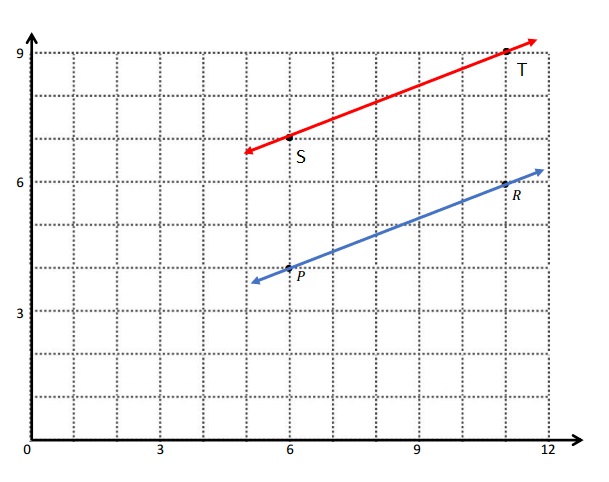
e.
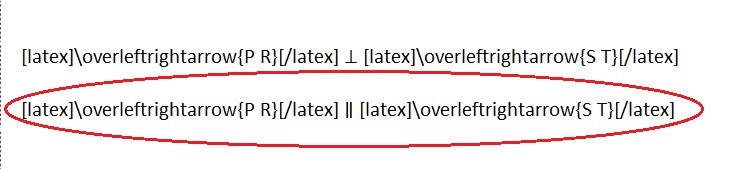
Explanation :
Both the lines are equidistant from each other so, the \(\overleftrightarrow{P R}\) is parallel to \(\overleftrightarrow{S T}\) .
f. The coordinate points of u and v are U ( 6, 1) and V (11, 3)
g.
Question 2.
Use the coordinate plane below to complete the following tasks.
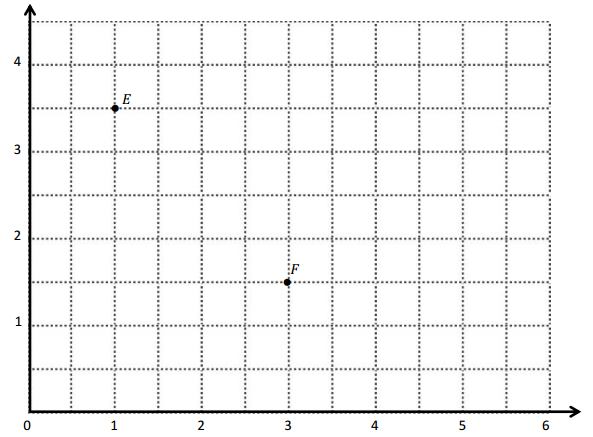
a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
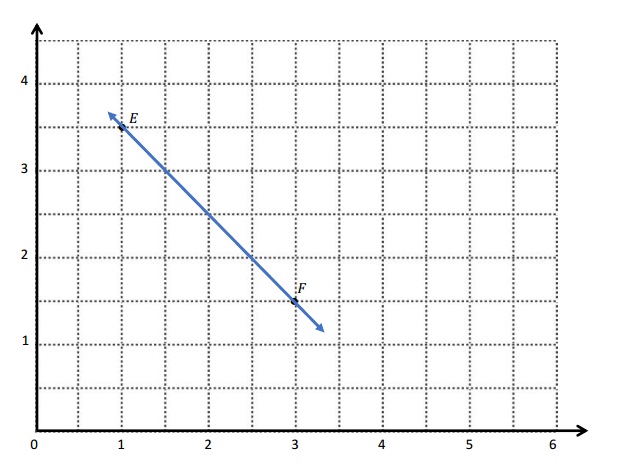
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
e. Explain the pattern you made use of when generating coordinate pairs for L and M.
f. Give the coordinates of a point, H, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{G H}\).
G: (1\(\frac{1}{2}\), 4) H: (____, ____)
g. Explain how you chose the coordinates for H.
Answer:
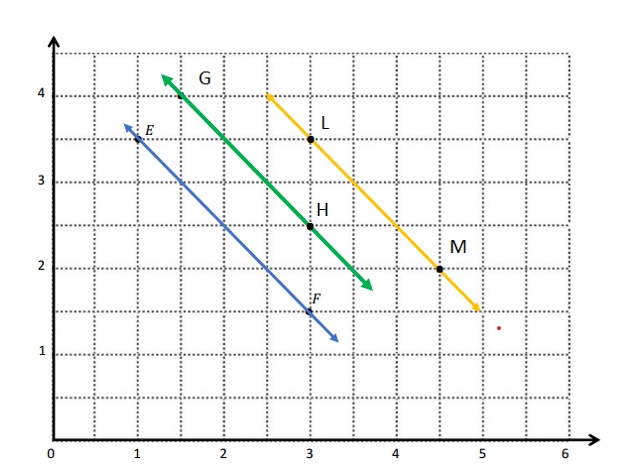
a. The locations of E and F. E: (1,3\(\frac{1}{2}\) ) F: (3, 1\(\frac{1}{2}\))
b.
c. The L and M points are L ( 3, 3\(\frac{1}{2}\)) and M ( 4\(\frac{1}{2}\), 2)
d.
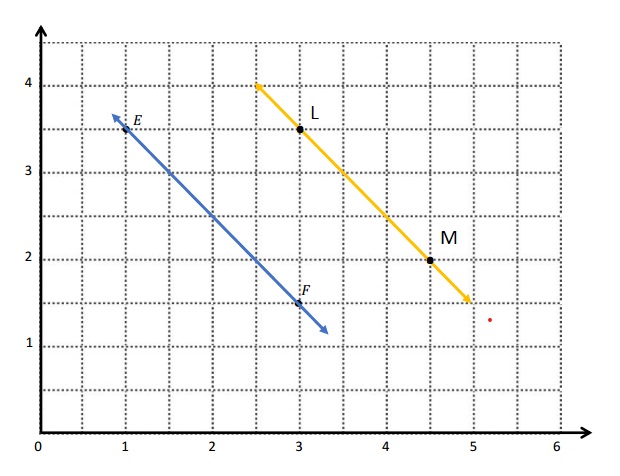
e. The pattern made when generating coordinate pairs for L and M are parallel lines .
f. G: (1\(\frac{1}{2}\), 4) H: (3, 2\(\frac{1}{2}\))
g. The the coordinates for H is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{G H}\).
Explanation :
Plot the point G and then draw a parallel line from Point G such a way that it should be parallel to latex]\overleftrightarrow{E F}[/latex] .
After that take a point H on that parallel line .
Eureka Math Grade 5 Module 6 Lesson 14 Exit Ticket Answer Key
Use the coordinate plane below to complete the following tasks.
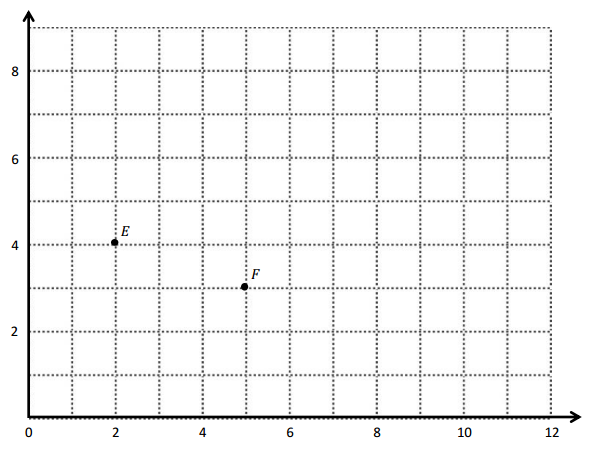
a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
Answer:
a. The locations of E and F. E: (2, 4) F: (5, 3) .
b.
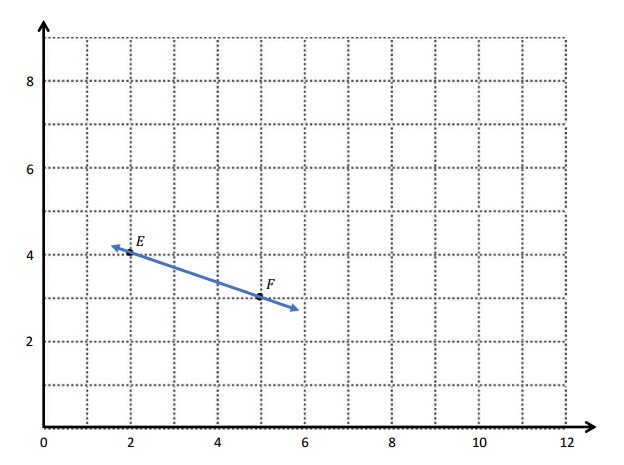
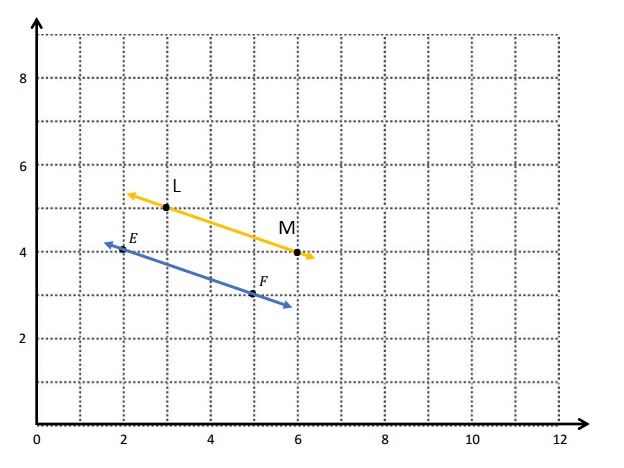
c. The coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\) are
L: (3, 5) M: (6, 4)
d.
Eureka Math Grade 5 Module 6 Lesson 14 Homework Answer Key
Question 1.
Use the coordinate plane below to complete the following tasks.
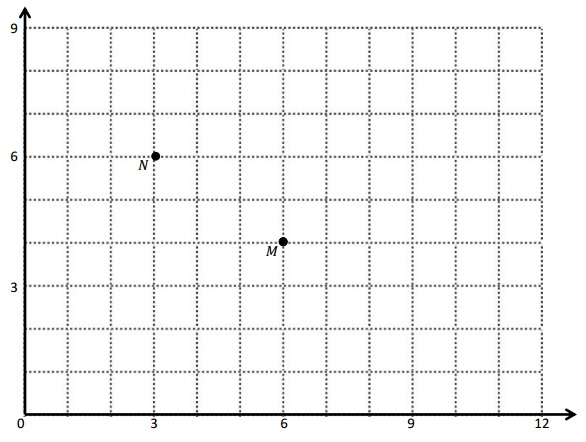
a. Identify the locations of M and N. M: (_____, _____) N: (_____, _____)
b. Draw \(\overleftrightarrow{M N}\).
c. Plot the following coordinate pairs on the plane.
J: (5, 7) K: (8, 5)
d. Draw \(\overleftrightarrow{J K}\).
e. Circle the relationship between \(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\).
\(\overleftrightarrow{M N}\) ⊥ \(\overleftrightarrow{J K}\)
\(\overleftrightarrow{M N}\) ∥ \(\overleftrightarrow{J K}\)
f. Give the coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (_____, _____) G: (_____, _____)
g. Draw \(\overleftrightarrow{F G}\).
Answer:
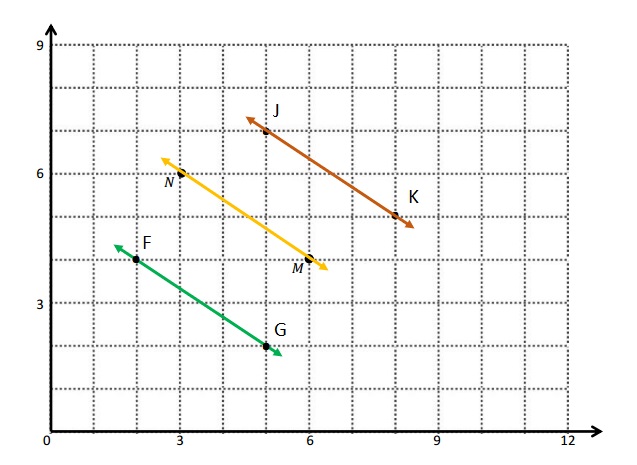
a. The locations of M and N. M: (6, 4) N: (3, 6)
b. 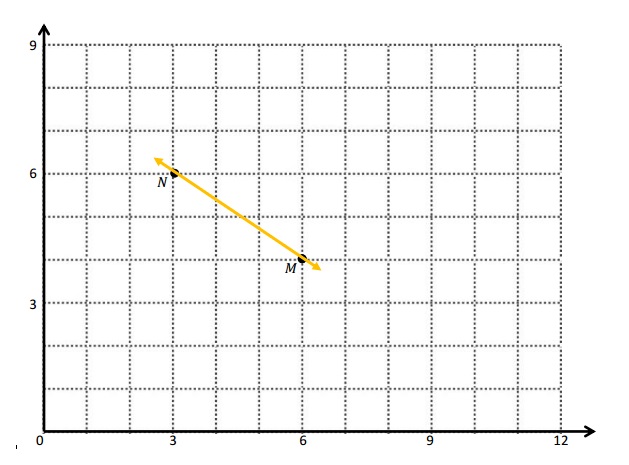
c. The J and K are plotted on the graph .
d.
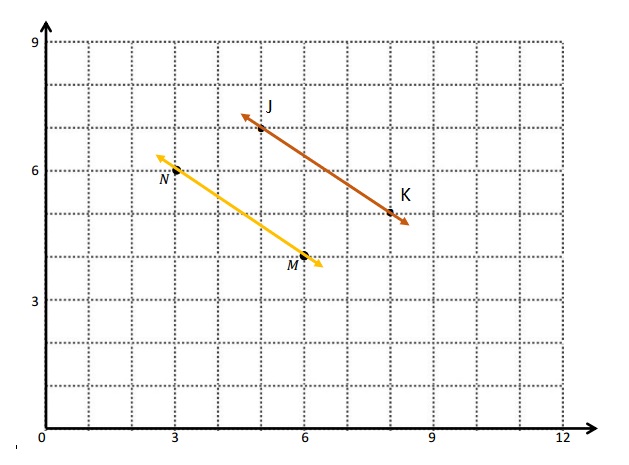
e.
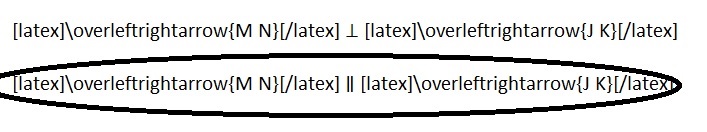
Explanation :
\(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\) are Equidistant from each other so, parallel lines .
f. The coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (2, 4) G: (5, 2)
g.
Question 2.
Use the coordinate plane below to complete the following tasks.
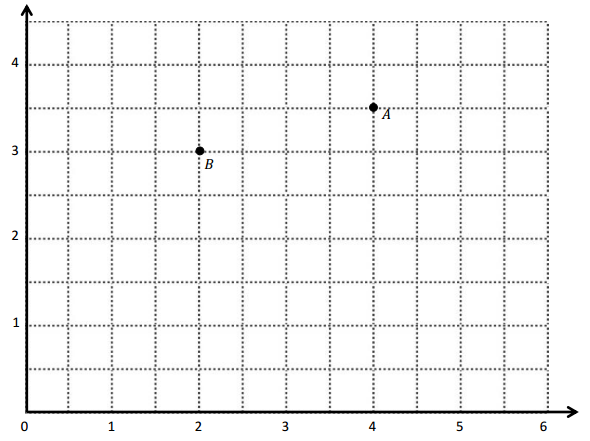
a. Identify the locations of A and B. A: (____, ____) B: (____, ____)
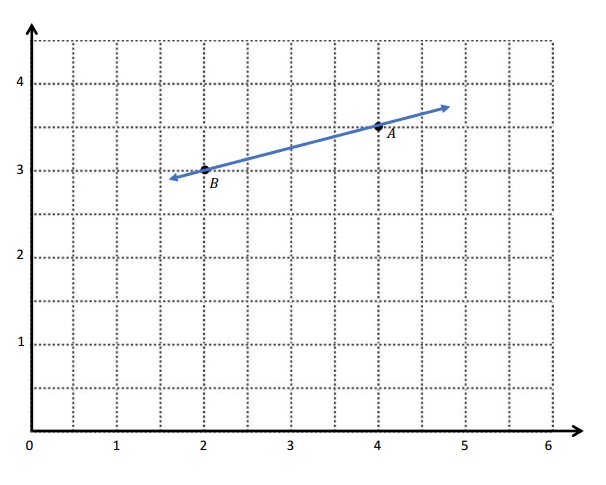
b. Draw \(\overleftrightarrow{A B}\).
c. Generate coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (____, ____) D: (____, ____)
d. Draw \(\overleftrightarrow{C D}\).
e. Explain the pattern you used when generating coordinate pairs for C and D.
f. Give the coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (____, ____)
g. Explain how you chose the coordinates for F.
Answer:
a. The locations of A and B. A: (4, 3\(\frac{1}{2}\)) B: (2 , 3)
b.
c. The coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (3\(\frac{1}{2}\), 2\(\frac{1}{2}\)) D: (5\(\frac{1}{2}\), 3)
d.
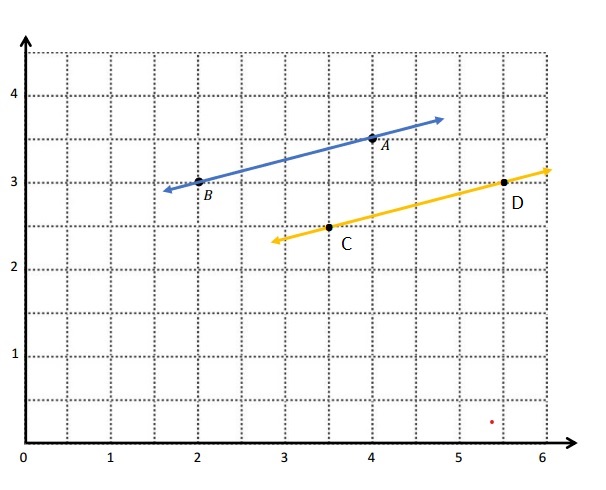
e. The pattern you used when generating coordinate pairs for C and D are \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
f. The coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (4\(\frac{1}{2}\) , 3)
g.
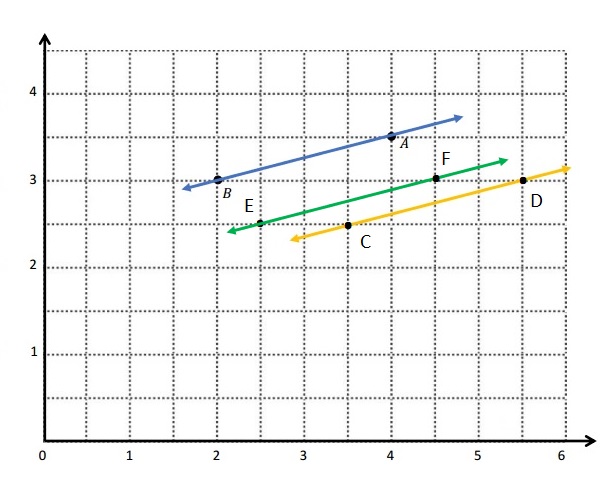
The the coordinates for F is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{A B}\).
Explanation :
Plot the point E and then draw a parallel line from Point E such a way that it should be parallel to latex]\overleftrightarrow{A B}[/latex] .
After that take a point F on that parallel line .