Eureka Math

Engage NY Eureka Math 5th Grade Module 6 Lesson 13 Answer Key

Eureka Math Grade 5 Module 6 Lesson 13 Problem Set Answer Key

Question 1.
Use a right angle template and straightedge to draw at least four sets of parallel lines in the space below.
Answer:

Explanation :
4 set of parallel lines are drawn and is shown in above figure .

Question 2.
Circle the segments that are parallel.

Answer:

Explanation :
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 3.
Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 4.
Draw 2 different lines parallel to line b.

Answer:

Explanation :
Parallel lines m and n are drawn parallel to b and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Eureka Math Grade 5 Module 6 Lesson 13 Exit Ticket Answer Key

Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Eureka Math Grade 5 Module 6 Lesson 13 Homework Answer Key

Question 1.
Use your right angle template and straightedge to draw at least three sets of parallel lines in the space below.
Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 2.
Circle the segments that are parallel.

Answer:
Explanation :
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.
All the parallel lines are circled in the given figure .

Question 3.
Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 4.
Draw 2 different lines parallel to line b.

Answer:

Explanation :
Parallel lines m and n are drawn parallel to b and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Engage NY Eureka Math 5th Grade Module 6 Lesson 12 Answer Key

Eureka Math Grade 5 Module 6 Lesson 12 Sprint Answer Key

A
Subtract Decimals

Question 1.
5 – 1 =
Answer:
5 – 1 = 4

Question 2.
5.9 – 1 =
Answer:
5.9 – 1 = 4.9
Explanation :

Question 3.
5.93 – 1 =
Answer:
5.93 – 1 = 4.93
Explanation :

Question 4.
5.932 – 1 =
Answer:
5.932 -1 = 4.932

Explanation :

Question 5.
5.932 – 2 =
Answer:
5.932 – 2 = 3.932

Explanation :

Question 6.
5.932 – 4 =
Answer:
5.932 – 4 = 1.932

Explanation :

Question 7.
0.5 – 0.1 =
Answer:
0.5 – 0.1 = 0.4

Explanation :

Question 8.
0.53 – 0.1 =
Answer:
0.53 – 0.1 = 0.43
Explanation :

Question 9.
0.539 – 0.1 =
Answer:
0.539 – 0.1 = 0.439
Explanation :

Question 10.
8.539 – 0.1 =
Answer:
8.539 – 0.1 = 8.439

Explanation :

Question 11.
8.539 – 0.2 =
Answer:

Explanation :

Question 12.
8.539 – 0.4 =
Answer:
8.539 – 0.4 = 8.139

Explanation :

Question 13.
0.05 – 0.01 =
Answer:
0.05 – 0.01 = 0.04

Explanation :

Question 14.
0.057 – 0.01 =
Answer:
0.057 – 0.01 =0.047

Explanation :

Question 15.
1.057 – 0.01 =
Answer:
1.057 – 0.01 = 1.047
Explanation :

Question 16.
1.857 – 0.01 =
Answer:
1.857 – 0.01 = 1.847
Explanation :

Question 17.
1.857 – 0.02 =
Answer:
1.857 – 0.02 = 1.837

Question 18.
1.857 – 0.04 =
Answer:
1.857 – 0.04 = 1.817

Question 19.
0.005 – 0.001 =
Answer:
0.005 – 0.001 = 0.004
Explanation :

Question 20.
7.005 – 0.001 =
Answer:
7.005 – 0.001 = 7.004
Explanation :

Question 21.
7.905 – 0.001 =
Answer:
7.905 – 0.001 = 7.904

Question 22.
7.985 – 0.001 =
Answer:
7.985 – 0.001 = 7.984

Question 23.
7.985 – 0.002 =
Answer:
7.985 – 0.002 = 7.983

Question 24.
7.985 – 0.004 =
Answer:
7.985 – 0.004 =7.981

Question 25.
2.7 – 0.1 =
Answer:
2.7 – 0.1 = 2.6

Question 26.
2.785 – 0.1 =
Answer:
2.785 – 0.1 = 2.775
Explanation :

Question 27.
2.785 – 0.5 =
Answer:
2.785 – 0.5 = 2.285

Question 28.
4.913 – 0.4 =
Answer:
4.913 – 0.4 = 4.513

Question 29.
3.58 – 0.01 =
Answer:
3.58 – 0.01 = 3.47

Explanation :

Question 30.
3.586 – 0.01 =
Answer:
3.586 – 0.01 = 3.576

Question 31.
3.586 – 0.05 =
Answer:
3.586 – 0.05 = 3.536

Question 32.
7.982 – 0.04 =
Answer:
7.982 – 0.04 = 7.942

Question 33.
6.126 – 0.001 =
Answer:
6.126 – 0.001 = 6.125

Question 34.
6.126 – 0.004 =
Answer:
6.126 – 0.004 = 6.122

Question 35.
9.348 – 0.006 =
Answer:
9.348 – 0.006 = 9.342

Question 36.
8.347 – 0.3 =
Answer:
8.347 – 0.3 = 8.047

Question 37.
9.157 – 0.05 =
Answer:
9.157 – 0.05 = 9.107

Question 38.
6.879 – 0.009 =
Answer:
6.879 – 0.009 = 6.870

Question 39.
6.548 – 2 =
Answer:
6.548 – 2 = 6.348

Question 40.
6.548 – 0.2 =
Answer:
6.548 – 0.2 = 6.348

Question 41.
6.548 – 0.02 =
Answer:
6.548 – 0.02 = 6.528

Question 42.
6.548 – 0.002 =
Answer:
6.548 – 0.002 = 6.546

Question 43.
6.196 – 0.06 =
Answer:
6.196 – 0.06 = 6.136

Question 44.
9.517 – 0.004 =
Answer:
9.517 – 0.004 = 9.513

B
Subtract Decimals

Question 1.
6 – 1 =
Answer:
6 – 1 = 5

Question 2.
6.9 – 1 =
Answer:
6.9 – 1 = 5.9

Question 3.
6.93 – 1 =
Answer:
6.93 – 1 = 5.93

Question 4.
6.932 – 1 =
Answer:
6.932 – 1 = 5.932

Question 5.
6.932 – 2 =
Answer:
6.932 – 2 = 4.932

Question 6.
6.932 – 4 =
Answer:
6.932 – 4 = 2.932

Question 7.
0.6 – 0.1 =
Answer:
0.6 – 0.1 = 0.5

Question 8.
0.63 – 0.1 =
Answer:
0.63 – 0.1 = 0.53

Question 9.
0.639 – 0.1 =
Answer:
0.639 – 0.1 = 0.539

Question 10.
8.639 – 0.1 =
Answer:
8.639 – 0.1 = 8.539

Question 11.
8.639 – 0.2 =
Answer:
8.639 – 0.2 = 8.439

Question 12.
8.639 – 0.4 =
Answer:
8.639 – 0.4 = 8.239

Question 13.
0.06 – 0.01 =
Answer:
0.06 – 0.01 = 0.05

Question 14.
0.067 – 0.01 =
Answer:
0.067 – 0.01 = 0.057

Question 15.
1.067 – 0.01 =
Answer:
1.067 – 0.01 = 1.057

Question 16.
1.867 – 0.01 =
Answer:
1.867 – 0.01 = 1.857

Question 17.
1.867 – 0.02 =
Answer:
1.867 – 0.02 = 1.847

Question 18.
1.867 – 0.04 =
Answer:
1.867 – 0.04 = 1.827

Question 19.
0.006 – 0.001 =
Answer:
0.006 – 0.001 = 0.005

Question 20.
7.006 – 0.001 =
Answer:
7.006 – 0.001 = 7.005

Question 21.
7.906 – 0.001 =
Answer:
7.906 – 0.001 = 7.905

Question 22.
7.986 – 0.001 =
Answer:
7.986 – 0.001 = 7.985

Question 23.
7.986 – 0.002 =
Answer:
7.986 – 0.002 = 7.984

Question 24.
7.986 – 0.004 =
Answer:
7.986 – 0.004 = 7.982

Question 25.
3.7 – 0.1 =
Answer:
3.7 – 0.1 = 3.6

Question 26.
3.785 – 0.1 =
Answer:
3.785 – 0.1 = 3.685

Question 27.
3.785 – 0.5 =
Answer:
3.785 – 0.5 = 3.285

Question 28.
5.924 – 0.4 =
Answer:
5.924 – 0.4 = 5.524

Question 29.
4.58 – 0.01 =
Answer:
4.58 – 0.01 = 4.57

Question 30.
4.586 – 0.01 =
Answer:
4.586 – 0.01 = 4.576

Question 31.
4.586 – 0.05 =
Answer:
4.586 – 0.05 = 4.536

Question 32.
6.183 – 0.04 =
Answer:
6.183 – 0.04 =6.143

Question 33.
7.127 – 0.001 =
Answer:
7.127 – 0.001 = 7.126

Question 34.
7.127 – 0.004 =
Answer:
7.127 – 0.004 = 7.123

Question 35.
1.459 – 0.006 =
Answer:
1.459 – 0.006 = 1.453

Question 36.
8.457 – 0.4 =
Answer:
8.457 – 0.4 = 8.057

Question 37.
1.267 – 0.06 =
Answer:
1.267 – 0.06 = 1.207

Question 38.
7.981 – 0.001 =
Answer:
7.981 – 0.001 = 7.980

Question 39.
7.548 – 2 =
Answer:
7.548 – 2 = 5.548

Question 40.
7.548 – 0.2 =
Answer:
7.548 – 0.2 = 7.348

Question 41.
7.548 – 0.02 =
Answer:
7.548 – 0.02 = 7.528

Question 42.
7.548 – 0.002 =
Answer:
7.548 – 0.002 = 7.546

Question 43.
7.197 – 0.06 =
Answer:
7.197 – 0.06 = 7.191

Question 44.
1.627 – 0.004 =
Answer:
1.627 – 0.004 =1.623

Eureka Math Grade 5 Module 6 Lesson 12 Problem Set Answer Key

Question 1.
Write a rule for the line that contains the points (0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).

a. Identify 2 more points on this line. Draw the line on the grid below.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Answer:
a.
(0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).
Rule : add \(\frac{3}{4}\) to x .
y = x + add \(\frac{3}{4}\)

b. A rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Rule : subtract \(\frac{3}{4}\) from x .
D = (1, \(\frac{1}{4}\)).

Question 2.
Create a rule for the line that contains the points (1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\)).
a. Identify 2 more points on this line. Draw the line on the grid on the right.

b. Write a rule for a line that passes through the origin and lies between \(\overleftrightarrow{B C}\) and \(\overleftrightarrow{G H}\).
Answer:
a. Rule :Multiply x by \(\frac{1}{4}\)
(1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\))

b. Rule :Multiply x by \(\frac{3}{4}\) .

Question 3.
Create a rule for a line that contains the point (\(\frac{1}{4}\), 1\(\frac{1}{4}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: _________

b. A line parallel to the x-axis: _________

c. Multiplication: _________

d. A line parallel to the y-axis: _________

e. Multiplication with addition: _________

Answer:

a. Addition:  add 1 to x

b. A line parallel to the x-axis: y is always 1\(\frac{1}{4}\).

c. Multiplication: multiply x by 5 .

d. A line parallel to the y-axis: x coordinate is always 4

e. Multiplication with addition: multiply x and add \(\frac{1}{4}\)

Question 4.
Mrs. Boyd asked her students to give a rule that could describe a line that contains the point (0.6, 1.8). Avi said the rule could be multiply x by 3. Ezra claims this could be a vertical line, and the rule could be x is always 0.6. Erik thinks the rule could be add 1.2 to x. Mrs. Boyd says that all the lines they are describing could describe a line that contains the point she gave. Explain how that is possible, and draw the lines on the coordinate plane to support your response.

Answer:

Explanation :
Mrs. Boyd’s gave only one point (0.6, 1.8) on the line .Many lines can be drawn from one point . With 2 points we can say the rule but without 2 points we cannot say the rule.

Question 5.
Create a mixed operation rule for the line that contains the points (0, 1) and (1, 3).

a. Identify 2 more points, O and P, on this line. Draw the line on the grid.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{O P}\) and goes through point (1, 2\(\frac{1}{2}\)).
Answer:
Rule : Multiply x by 2 and add 1 .
a.

b. Rule : Multiply by x and add 2.

Eureka Math Grade 5 Module 6 Lesson 12 Exit Ticket Answer Key

Write the rule for the line that contains the points (0, 1\(\frac{1}{2}\)) and (1\(\frac{1}{2}\), 3).

a. Identify 2 more points on this line. Draw the line on the grid.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)).
Answer:
Rule : add \(\frac{1}{2}\) to x .

b.
The Rule that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)) is  Subtract \(\frac{1}{2}\) from x .

Eureka Math Grade 5 Module 6 Lesson 12 Homework Answer Key

Question 1.
Write a rule for the line that contains the points (0, \(\frac{1}{4}\)) and (2\(\frac{1}{2}\), 2\(\frac{3}{4}\)).

a. Identify 2 more points on this line. Draw the line on the grid below.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\).
Answer:
Rule : Add \(\frac{1}{4}\) to x .

b.
Rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\) is add 1\(\frac{1}{4}\) to x .

Question 2.
Give the rule for the line that contains the points (1, 2\(\frac{1}{2}\)) and (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)).
a. Identify 2 more points on this line. Draw the line on the grid above.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{G H}\).
Answer:
a.
Rule : For all x-coordinates the y- coordinate is 2\(\frac{1}{2}\)

b. A rule for a line that is parallel to \(\overleftrightarrow{G H}\) is
For all x-coordinates the y- coordinate is 1\(\frac{3}{4}\) .

Question 3.
Give the rule for a line that contains the point (\(\frac{3}{4}\), 1\(\frac{1}{2}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: ________________

b. A line parallel to the x-axis: ________________

c. Multiplication: ________________

d. A line parallel to the y-axis: ________________

e. Multiplication with addition: _____________

Answer:

a. Addition: add \(\frac{3}{4}\) to x

b. A line parallel to the x-axis: all x coordinate have y coordinate as 2

c. Multiplication: multiply by 2

d. A line parallel to the y-axis: All y coordinates have the same x coordinate 2

e. Multiplication with addition: multiply by 2 and add 1

Question 4.
On the grid, two lines intersect at (1.2, 1.2). If line a passes through the origin and line b contains the point (1.2, 0), write a rule for line a and line b.

Answer:

For line a the Rule is x coordinate . The y coordinate is same the x coordinate .
For line b the Rule is All y coordinates have the same x coordinate 1.2 .

Engage NY Eureka Math 5th Grade Module 6 Lesson 10 Answer Key

Eureka Math Grade 5 Module 6 Lesson 10 Problem Set Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
a. Yes, Line p represents the rule x and y are equal because all x and y coordinates are equal .
Some of the coordinate points on line p are ( 1, 1) , (2, 2) .
b. A  line, d, that is parallel to line p and contains point D is shown in below graph with coordinate points (1, 3)          and (3, 5)

c. The 3 coordinate pairs on line d are (1, 3) , (1\(\frac{1}{2}\), 3\(\frac{1}{2}\)) and                           (3\(\frac{1}{2}\), 5\(\frac{1}{2}\)) .
d. A rule for line d, is y is 2 more than x .
e. A line, e, that is parallel to line p and contains point E .

f . 3 points that are on line e are (2, 1) , ( 3, 2) and (5, 4).
g. A rule for line e, is y is 1 less than x .
h. Line p is parallel to line d and line p is parallel to line e .

Question 2.
Write a rule for a fourth line that would be parallel to those above and would contain the point (3\(\frac{1}{2}\), 6). Explain how you know.
Answer:
First plot the point F (3\(\frac{1}{2}\), 6) and draw a line that is parallel to line p , d and e.

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
a. Yes , Line p represents the rule x and y are equal because the coordinates of x and y are equal .
two coordinate points on line p are (1, 1) and (8, 8)
b.

c. The 3 points on line v are ( 2, 4) , (3,6) and ( 4, 8).
d. The rule to describe line v is the y coordinate is double the x coordinate .
e.

f. The 3 points on line w are (2, 1), (4, 2) and ( 10, 5)
g. The rule to describe line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a      greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .

Question 4.
Circle the rules that generate lines that are parallel to each other.
add 5 to x
multiply x by \(\frac{2}{3}\)
x plus \(\frac{1}{2}\)
x times 1\(\frac{1}{2}\)
Answer:

Eureka Math Grade 5 Module 6 Lesson 10 Exit Ticket Answer Key

Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, a, that is parallel to line p and contains point A.
c. Name 3 points on line a.
d. Identify a rule to describe line a.
Answer:
b.

c. The 3 points on line a are (4, 1) , ( 5, 2) and (6, 3)
d. The rule to describe line a is the y coordinate is 3 less than x coordinate .

Eureka Math Grade 5 Module 6 Lesson 10 Homework Answer Key

Question 1.
Use the coordinate plane to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
b.

c. The 3 coordinates pairs of line d are (1, 3) , (2, 4) and (3, 5).
d. The rule to describe line d is the y coordinate is 2 more than the x coordinate .
e.

f. The 3 points on line e are (2, 1) , (3, 2) and (5, 4) .
g. The rule to describe line e is the y coordinate is 1 less than the x coordinate .
h. Line d and Line e are both parallel to line p .

Question 2.
Write a rule for a fourth line that would be parallel to those above and that would contain the point (5\(\frac{1}{2}\), 2). Explain how you know.
Answer:

Explanation :
First mark the point F ((5\(\frac{1}{2}\), 2)) and then draw a line that is parallel to line p .
The 3 coordinate points on line f are (4, \(\frac{1}{2}\)) , (4 \(\frac{1}{2}\), 1 ) and (6 , 2\(\frac{1}{2}\)).
The rule for line f is the y coordinate is 3\(\frac{1}{2}\) less than the x coordinate .

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
b.

c. The 3 points on line v are (1, 2) , ( 2, 4) and (5, 10) .
d. The rule to describe the line v is the y coordinate is double the x coordinate .
e.

f. The 3 coordinate points on line w are ( 2, 1), (4, 2) and (6, 3) .
g. The rule to describe the line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a      greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .

Engage NY Eureka Math 5th Grade Module 6 Lesson 9 Answer Key

Eureka Math Grade 5 Module 6 Lesson 9 Problem Set Answer Key

Question 1.
Complete the table for the given rules.

Line a
Rule: y is 1 more than x

Line b
Rule: y is 4 more than x

a. Construct each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line c, whose rule is y is 7 more than x, would look like. Draw your prediction on the plane above.
Answer:
a.
Line a
Rule: y is 1 more than x
y = x + 1

Line b
Rule: y is 4 more than x
y = x + 4

b. Lines a and b are parallel lines .
c. The line c
rule: y is 7 more than x
y = x + 7

Even line c is parallel to line a and line b .

Question 2.
Complete the table for the given rules.

Line e
Rule: y is twice as much as x

Line f
Rule: y is half as much as x

a. Construct each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line g, whose rule is y is 4 times as much as x, would look like. Draw your prediction in the plane above.
Answer:
a.
Line e
Rule: y is twice as much as x
y = 2x

Line f
Rule: y is half as much as x
y = x/2

b. Both the lines e and f intersect at (0, 0)
c. line g
rule: y is 4 times as much as x
y = 4x

All 3 lines intersect at (0, 0)

Eureka Math Grade 5 Module 6 Lesson 9 Exit Ticket Answer Key

Complete the table for the given rules. Then, construct lines l and m on the coordinate plane.

Line l
Rule: y is 5 more than x

Line m
Rule: y is 5 times as much as x

Answer:
Line l
Rule: y is 5 more than x
y = x + 5

Line m
Rule: y is 5 times as much as x
y = 5x

Lines l and m are shown in the above graph .

Eureka Math Grade 5 Module 6 Lesson 9 Homework Answer Key

Question 1.
Complete the table for the given rules.

Line a
Rule: y is 1 less than x

Line b
Rule: y is 5 less than x

a. Construct each line on the coordinate plane.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line c, whose rule is y is 7 less than x, would look like. Draw your prediction on the plane above.
Answer:
a.
Line a
Rule: y is 1 less than x
y = x – 1

Line b
Rule: y is 5 less than x
y = x – 5

b. Both the lines are a and b are parallel lines.
c.
Line c
Rule: y is 7 less than x
y = x – 7

All the 3 lines are parallel lines  and are shown in above graph .

Question 2.
Complete the table for the given rules.

Line e
Rule: y is 3 times as much as x

Line f
Rule: y is a third as much as x

a. Construct each line on the coordinate plane.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line g, whose rule is y is 4 times as much as x, and line h, whose rule is y is one-fourth as much as x, would look like. Draw your prediction in the plane above.
Answer:
a.
Line e
Rule: y is 3 times as much as x
y = 3x

Line f
Rule: y is a third as much as x

b. Both the lines e and f intersect at (0, 0)
c.
Line g
Rule: y is 4 times as much as x
y = 4x

Line h
Rule: y is one-fourth as much as x
y = x/4

All the 4 lines intersect at (0, 0 ) and is shown in the above graph .

Engage NY Eureka Math 5th Grade Module 6 Lesson 8 Answer Key

Eureka Math Grade 5 Module 6 Lesson 8 Sprint Answer Key

A
Multiply Decimals by 10, 100, and 1,000

Question 1.
62.3 × 10 =
Answer:
62.3 × 10 = 623

Question 2.
62.3 × 100 =
Answer:
62.3 × 100 = 6230

Question 3.
62.3 × 1,000 =
Answer:
62.3 × 1,000 = 62300

Question 4.
73.6 × 10 =
Answer:
73.6 × 10 = 736

Question 5.
73.6 × 100 =
Answer:
73.6 × 100 = 7360

Question 6.
73.6 × 1,000 =
Answer:
73.6 × 1,000 = 73600

Question 7.
0.6 × 10 =
Answer:
0.6 × 10 = 6

Question 8.
0.06 × 10 =
Answer:
0.06 × 10 = 0.6

Question 9.
0.006 × 10 =
Answer:
0.006 × 10 = 0.06

Question 10.
0.3 × 10 =
Answer:
0.3 × 10 = 3

Question 11.
0.3 × 100 =
Answer:
0.3 × 100 = 30

Question 12.
0.3 × 1,000 =
Answer:
0.3 × 1,000 = 300

Question 13.
0.02 × 10 =
Answer:
0.02 × 10 = 0.2

Question 14.
0.02 × 100 =
Answer:
0.02 × 100 = 2

Question 15.
0.02 × 1,000 =
Answer:
0.02 × 1,000 = 20

Question 16.
0.008 × 10 =
Answer:
0.008 × 10 = 0.08

Question 17.
0.008 × 100 =
Answer:
0.008 × 100 = 0.8

Question 18.
0.008 × 1,000 =
Answer:
0.008 × 1,000 = 8

Question 19.
0.32 × 10 =
Answer:
0.32 × 10 = 3.2

Question 20.
0.67 × 10 =
Answer:
0.67 × 10 = 6.7

Question 21.
0.91 × 100 =
Answer:
0.91 × 100 = 91

Question 22.
0.74 × 100 =
Answer:
0.74 × 100 = 74

Question 23.
4.1 × 1,000 =
Answer:
4.1 × 1,000 = 4100

Question 24.
7.6 × 1,000 =
Answer:
7.6 × 1,000 = 7600

Question 25.
0.01 × 1,000 =
Answer:
0.01 × 1,000 = 10

Question 26.
0.07 × 1,000 =
Answer:
0.07 × 1,000 = 70

Question 27.
0.072 × 100 =
Answer:
0.072 × 100 = 7.2

Question 28.
0.802 × 10 =
Answer:
0.802 × 10 = 8.02

Question 29.
0.019 × 1,000 =
Answer:
0.019 × 1,000 = 19

Question 30.
7.412 × 1,000 =
Answer:
7.412 × 1,000 = 7412

Question 31.
6.8 × 100 =
Answer:
6.8 × 100 = 680

Question 32.
4.901 × 10 =
Answer:
4.901 × 10 = 49.01

Question 33.
16.07 × 100 =
Answer:
16.07 × 100 = 1607

Question 34.
9.19 × 10 =
Answer:
9.19 × 10 = 91.9

Question 35.
18.2 × 100 =
Answer:
18.2 × 100 = 1820

Question 36.
14.7 × 1,000 =
Answer:
14.7 × 1,000 = 14700

Question 37.
2.021 × 100 =
Answer:
2.021 × 100 = 202.1

Question 38.
172.1 × 10 =
Answer:
172.1 × 10 = 1721

Question 39.
3.2 × 20 =
Answer:
3.2 × 20 = 64

Question 40.
4.1 × 20 =
Answer:
4.1 × 20 = 82

Question 41.
3.2 × 30 =
Answer:
3.2 × 30 = 96

Question 42.
1.3 × 30 =
Answer:
1.3 × 30 = 39

Question 43.
3.12 × 40 =
Answer:
3.12 × 40 = 124.8

Question 44.
14.12 × 40 =
Answer:
14.12 × 40 = 564.8

B
Multiply Decimals by 10, 100, and 1,000

Question 1.
46.1 × 10 =
Answer:
46.1 × 10 = 461

Question 2.
46.1 × 100 =
Answer:
46.1 × 100 = 4610

Question 3.
46.1 × 1,000 =
Answer:
46.1 × 1,000 = 46100

Question 4.
89.2 × 10 =
Answer:
89.2 × 10 = 892

Question 5.
89.2 × 100 =
Answer:
89.2 × 100 = 8920

Question 6.
89.2 × 1,000 =
Answer:
89.2 × 1,000 = 89200

Question 7.
0.3 × 10 =
Answer:
0.3 × 10 = 3

Question 8.
0.03 × 10 =
Answer:
0.03 × 10 = 0.3

Question 9.
0.003 × 10 =
Answer:
0.003 × 10 = 0.03

Question 10.
0.9 × 10 =
Answer:
0.9 × 10 = 9

Question 11.
0.9 × 100 =
Answer:
0.9 × 100 =90

Question 12.
0.9 × 1,000 =
Answer:
0.9 × 1,000 = 900

Question 13.
0.04 × 10 =
Answer:
0.04 × 10 = 0.4

Question 14.
0.04 × 100 =
Answer:
0.04 × 100 = 4

Question 15.
0.04 × 1,000 =
Answer:
0.04 × 1,000 = 40

Question 16.
0.007 × 10 =
Answer:
0.007 × 10 = 0.07

Question 17.
0.007 × 100 =
Answer:
0.007 × 100 = 0.7

Question 18.
0.007 × 1,000 =
Answer:
0.007 × 1,000 = 7

Question 19.
0.45 × 10 =
Answer:
0.45 × 10 = 4.5

Question 20.
0.78 × 10 =
Answer:
0.78 × 10 = 7.8

Question 21.
0.28 × 100 =
Answer:
0.28 × 100 = 28

Question 22.
0.19 × 100 =
Answer:
0.19 × 100 = 19

Question 23.
5.2 × 1,000 =
Answer:
5.2 × 1,000 = 5200

Question 24.
8.7 × 1,000 =
Answer:
8.7 × 1,000 = 8700

Question 25.
0.01 × 1,000 =
Answer:
0.01 × 1,000 = 10

Question 26.
0.08 × 1,000 =
Answer:
0.08 × 1,000 = 80

Question 27.
0.083 × 10 =
Answer:
0.083 × 10 = 0.83

Question 28.
0.903 × 10 =
Answer:
0.903 × 10 =9.03

Question 29.
0.017 × 1,000 =
Answer:
0.017 × 1,000 = 17

Question 30.
8.523 × 1,000 =
Answer:
8.523 × 1,000 =8523

Question 31.
7.9 × 100 =
Answer:
7.9 × 100 = 790

Question 32.
5.802 × 10 =
Answer:
5.802 × 10 = 58.02

Question 33.
27.08 × 100 =
Answer:
27.08 × 100 = 2708

Question 34.
8.18 × 10 =
Answer:
8.18 × 10 = 81.8

Question 35.
29.3 × 100 =
Answer:
29.3 × 100 = 2930

Question 36.
25.8 × 1,000 =
Answer:
25.8 × 1,000 = 25800

Question 37.
3.032 × 100 =
Answer:
3.032 × 100 = 303.2

Question 38.
283.1 × 10 =
Answer:
283.1 × 10 = 2831

Question 39.
2.1 × 20 =
Answer:
2.1 × 20 = 42

Question 40.
3.3 × 20 =
Answer:
3.3 × 20 = 6.6

Question 41.
3.1 × 30 =
Answer:
3.1 × 30 = 93

Question 42.
1.2 × 30 =
Answer:
1.2 × 30 = 36

Question 43.
2.11 × 40 =
Answer:
2.11 × 40 = 84.4

Question 44.
13.11 × 40 =
Answer:
13.11 × 40 = 524.4

Eureka Math Grade 5 Module 6 Lesson 8 Problem Set Answer Key

Question 1.
Create a table of 3 values for x and y such that each y-coordinate is 3 more than the corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with x-coordinates greater than 12. (______ , ______) and (______ , ______)
Answer:
a. 3 points are plotted on the graph where each y-coordinate is 3 more than the corresponding x-coordinate.

b. 3 points are connected with a straight line .
c. The coordinates of 2 other points that fall on this line with x-coordinates greater than 12 and each y-coordinate is 3 more than the corresponding x-coordinate are (13 , 16) and ( 15 , 18)

Question 2.
Create a table of 3 values for x and y such that each y-coordinate is 3 times as much as its corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with y-coordinates greater than 25. (______ , ______) and (______ , ______)
Answer:
a. 3 Points are plotted on the graph where each y-coordinate is 3 times as much as its corresponding x

b. All the points are connected with a straight line .
c. The coordinates of 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 3 times as much as its corresponding x – coordinate are (9, 27 ) and (10 , 30 )

Question 3.
Create a table of 5 values for x and y such that each y-coordinate is 1 more than 3 times as much as its corresponding x value.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that would fall on this line whose x-coordinates are greater than 12. (______ , ______) and (______ , ______)
Answer:
a. y = 3x + 1

b. A  straightedge line is drawn to connect these points is shown in above graph .
c. The coordinates of 2 other points that would fall on this line whose x-coordinates are greater than 12 and each      y-coordinate is 1 more than 3 times as much as its corresponding x value are (14 , 44 ) and (15 , 46 ) .

Question 4.
Use the coordinate plane below to complete the following tasks.

a. Graph the lines on the plane.
line l: x is equal to y

line m: y is 1 more than x

line n: y is 1 more than twice x

b. Which two lines intersect? Give the coordinates of their intersection.
c. Which two lines are parallel?
d. Give the rule for another line that would be parallel to the lines you listed in Problem 4(c).
Answer:
a.

line l: x is equal to y

line m: y is 1 more than x
y=x+1

line n: y is 1 more than twice x
y = 2x + 1

b. The two lines intersect are m and n lines .The coordinates of their intersection are ( 0, 1)
c. The two parallel lines are n and m lines.
d. The rule for another line that would be parallel to the lines you listed in Problem 4(c) is y is 2 more than x

Eureka Math Grade 5 Module 6 Lesson 8 Exit Ticket Answer Key

Complete this table with values for y such that each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Name 2 other points that fall on this line with y-coordinates greater than 25.
Answer:
a.
Each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate
y = 2x + 5
All the points are plotted in the graph .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate are (11, 27) and ( 12, 29)

Eureka Math Grade 5 Module 6 Lesson 8 Homework Answer Key

Question 1.
Complete this table such that each y-coordinate is 4 more than the corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to construct a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with x-coordinates greater than 18. (______ , ______) and (______ , ______)
Answer:
a.
Each y-coordinate is 4 more than the corresponding x-coordinate.
y = 4x
The points are plotted on the the coordinate plane .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The coordinates of 2 other points that fall on this line with x-coordinates greater than 18 and each y-coordinate is 4 more than the corresponding x-coordinate  (19 , 76 ) and (20 , 80)

Question 2.
Complete this table such that each y-coordinate is 2 times as much as its corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with y-coordinates greater than 25. (______ , ______) and (______ , ______)
Answer:
a.
Each y-coordinate is 2 times as much as its corresponding x-coordinate.
y = 2x
The points are plotted on the the coordinate plane .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The coordinates of 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 2 times as much as its corresponding x-coordinate. (13, 26 ) and ( 15, 30) .

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Graph these lines on the plane.
line l: x is equal to y

line m: y is 1 less than x

line n: y is 1 less than twice x

b. Do any of these lines intersect? If yes, identify which ones, and give the coordinates of their intersection.
c. Are any of these lines parallel? If yes, identify which ones.
d. Give the rule for another line that would be parallel to the lines you listed in Problem 3(c).
Answer:
a.
line l: x is equal to y
y = x

line m: y is 1 less than x
y = x – 1

line n: y is 1 less than twice x
y = 2x – 1

b.
Yes, The Two lines which intersect are line l and n.
They intersect at coordinate (1, 1).
c. Yes, We have parallel lines.
The parallel lines are line l and m.
d. The rule for another line that would be parallel to the lines you listed in Problem 3(c) is y is 2 less than x .

Engage NY Eureka Math 5th Grade Module 6 Lesson 7 Answer Key

Eureka Math Grade 5 Module 6 Lesson 7 Problem Set Answer Key

Question 1.
Complete the chart. Then, plot the points on the coordinate plane below.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates of points on the line.
c. Name 2 other points that are on this line.
Answer:

a.

Points are plotted and all points are connected with a straight line .
b. A rule showing the relationship between the x- and y-coordinates of points on the line is the difference between x and y coordinates of all points is 1 .
The x-coordinate and y-coordinate both are increased by 2 with respective to the x and y coordinates .
c. The other 2 points that are on the line are ( 3, 4) ( 5, 6)

Question 2.
Complete the chart. Then, plot the points on the coordinate plane below.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates.
c. Name 2 other points that are on this line.
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates of points on the line is Double the x coordinate is the y coordinates .
c. The 2 other points that are on this line are (\(\frac{3}{4}\), 1 \(\frac{3}{4}\)) and (1\(\frac{1}{4}\), 2\(\frac{1}{2}\))

Question 3.
Use the coordinate plane below to answer the following questions.

a. Give the coordinates for 3 points that are on line a. ________ ________ ________
b. Write a rule that describes the relationship between the x- and y-coordinates for the points on line a.
c. What do you notice about the y-coordinates of every point on line b?
d. Fill in the missing coordinates for points on line d.
(12, _____) (6, _____) (_____, 24) (28, _____) (_____, 28)
e. For any point on line c, the x-coordinate is _______.
f. Each of the points lies on at least 1 of the lines shown in the plane on the previous page. Identify a line that contains each of the following points.
i. (7, 7) a
ii. (14, 8) ______
iii. (5, 10) ______
iv. (0, 17) ______
v. (15.3, 9.3) ______
vi. (20, 40) ______
Answer:
a. The coordinates for 3 points that are on line a. (4, 4) ( 6, 6) and (8 , 8 )
b. A rule that describes the relationship between the x- and y-coordinates for the points on line a is Both the x          and y coordinates are equal.
c. The y-coordinates of every point on line b are equal that means the y – coordinate for all x-coordinates is 17 .
d. The missing coordinates for points on line d.
(12, 6 ) (6, 0 ) (30 , 24) (28, 30 ) (36 , 28)
e. For any point on line c, the x-coordinate is 5 .
f.
i. (7, 7)- a
ii. (14, 8) – d
iii. (5, 10) – c or e
iv. (0, 17) – b
v. (15.3, 9.3) – d
vi. (20, 40) – e

Eureka Math Grade 5 Module 6 Lesson 7 Exit Ticket Answer Key

Complete the chart. Then, plot the points on the coordinate plane.

Question 1.
Use a straightedge to draw a line connecting these points.
Answer:

Question 2.
Write a rule to show the relationship between the x- and y-coordinates for points on the line.
Answer:
A rule to show the relationship between the x- and y-coordinates for points on the line is the difference between x and y coordinate is 4

Question 3.
Name two other points that are also on this line. __________ __________
Answer:
The two other points that are also on this line are (1, 5) and (4, 8)

Eureka Math Grade 5 Module 6 Lesson 7 Homework Answer Key

Question 1.
Complete the chart. Then, plot the points on the coordinate plane.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates of points on this line.
c. Name two other points that are also on this line.
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates of points on this line is The difference                between x coordinate and y coordinate is 2
c . The two other points that are also on this line are (3, 1) and ( 4, 2) .

Question 2.
Complete the chart. Then, plot the points on the coordinate plane.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates for points on the line.
c. Name two other points that are also on this line. _____________ _____________
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates for points on the line is Increasing from 0 to (\(\frac{1}{2}\) , (\(\frac{1}{2}\) to 1 and 1 to 2 increasing by double the x coordinate .
c. The two other points that are also on this line are

Question 3.
Use the coordinate plane to answer the following questions.

a. For any point on line m, the x-coordinate is _______.
b. Give the coordinates for 3 points that are on line n.
c. Write a rule that describes the relationship between the x- and y-coordinates on line n.
d. Give the coordinates for 3 points that are on line q.
e. Write a rule that describes the relationship between the x- and y-coordinates on line q.
f. Identify a line on which each of these points lie.
i. (10, 3.2) ______
ii. (12.4, 18.4) ______
iii. (6.45, 12) ______
iv. (14, 7) ______
Answer:
a. For any point on line m, the x-coordinate is 10 .
b. The coordinates for 3 points that are on line n are ( 2, 8) , ( 4, 10) and (6, 12)
c. A rule that describes the relationship between the x- and y-coordinates on line n is the difference between the       all the x-coordinates and respective y – coordinates is 6 .
d. The coordinates for 3 points that are on line q are ( 4, 2) , (8, 4 ) and ( 12, 6).
e. A rule that describes the relationship between the x- and y-coordinates on line q is the differences is 2 multiple      2, 4, 6 . . . . . .
f. A line on which each of these points lie.
i. (10, 3.2) is m line
ii. (12.4, 18.4) is n line
iii. (6.45, 12) is l line
iv. (14, 7) is q line .

Engage NY Eureka Math 5th Grade Module 6 Lesson 3 Answer Key

Eureka Math Grade 5 Module 6 Lesson 3 Problem Set Answer Key

Question 1.
Use the grid below to complete the following tasks.
a. Construct an x-axis that passes through points A and B.
b. Construct a perpendicular y-axis that passes through points C and F.
c. Label the origin as 0.
d. The x-coordinate of B is 5\(\frac{2}{3}\). Label the whole numbers along the x-axis.
e. The y-coordinate of C is 5\(\frac{1}{3}\). Label the whole numbers along the y-axis.

Answer:

Question 2.
For all of the following problems, consider the points A through N on the previous page.
a. Identify all of the points that have an x-coordinate of 3\(\frac{1}{3}\).
Answer :
The points that have an x-coordinate of 3\(\frac{1}{3}\) are J, I, H and D .

b. Identify all of the points that have a y-coordinate of 2\(\frac{2}{3}\).
Answer :
The points that have a y-coordinate of 2\(\frac{2}{3}\) are E, F, H and K .

c. Which point is 3\(\frac{1}{3}\) units above the x-axis and 2\(\frac{2}{3}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point H and its coordinate pair is ( 3\(\frac{1}{3}\) , 2\(\frac{2}{3}\) )

d. Which point is located 5\(\frac{1}{3}\) units from the y-axis?
Answer :
Point C .

e. Which point is located 1\(\frac{2}{3}\) units along the x-axis?
Answer :
Point M .

f. Give the coordinate pair for each of the following points.
K: __
I: ______
B: ______
C: ______
Answer :
The coordinate pair of K is (5\(\frac{1}{3}\), 2\(\frac{2}{3}\))
The coordinate pair of I is (3\(\frac{1}{3}\), 1\(\frac{2}{3}\))
The coordinate pair of B is (5\(\frac{2}{3}\), 0)
The coordinate pair of C is (0, 5\(\frac{1}{3}\) )

g. Name the points located at the following coordinates.
(1\(\frac{2}{3}\), \(\frac{2}{3}\)) ______
(0, 2\(\frac{2}{3}\)) ______
(1, 0) ______
(2, 5\(\frac{2}{3}\)) ______
h. Which point has an equal x- and y-coordinate? ________
i. Give the coordinates for the intersection of the two axes. (____ , ____) Another name for this point on the plane is the ___________.
j. Plot the following points.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))
k. What is the distance between E and H, or EH?
l. What is the length of HD?
m. Would the length of ED be greater or less than EH+HD?
n. Jack was absent when the teacher explained how to describe the location of a point on the coordinate plane. Explain it to him using point J.
Answer:
(1\(\frac{2}{3}\), \(\frac{2}{3}\))  is Point M
(0, 2\(\frac{2}{3}\)) is Point F
(1, 0) is Point  A
(2, 5\(\frac{2}{3}\)) is Point N
h. The point L has an equal x- and y-coordinate
i. (0,0) Origin.
j.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))

Eureka Math Grade 5 Module 6 Lesson 3 Exit Ticket Answer Key

Question 1.
Use a ruler on the grid below to construct the axes for a coordinate plane. The x-axis should intersect points L and M. Construct the y-axis so that it contains points K and L. Label each axis.

a. Place a hash mark on each grid line on the x- and y-axis.
b. Label each hash mark so that A is located at (1, 1).
c. Plot the following points:

Answer:

Eureka Math Grade 5 Module 6 Lesson 3 Homework Answer Key

Question 1.
Use the grid below to complete the following tasks.
a. Construct a y-axis that passes through points Y and Z.
b. Construct a perpendicular x-axis that passes through points Z and X.
c. Label the origin as 0.
d. The y-coordinate of W is 2\(\frac{3}{5}\). Label the whole numbers along the y-axis.
e. The x-coordinate of V is 2\(\frac{2}{5}\). Label the whole numbers along the x-axis.

Answer:

Question 2.
For all of the following problems, consider the points K through X on the previous page.
a. Identify all of the points that have a y-coordinate of 1\(\frac{3}{5}\).
Answer :
The points that have a y-coordinate of 1\(\frac{3}{5}\) are R, M and Q.

b. Identify all of the points that have an x-coordinate of 2\(\frac{1}{5}\).
Answer :
The points that have an x-coordinate of 2\(\frac{1}{5}\) are O, M and L .

c. Which point is 1\(\frac{3}{5}\) units above the x-axis and 3\(\frac{1}{5}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point P and its coordinate pair is ( 1\(\frac{3}{5}\) , 3\(\frac{1}{5}\) )

d. Which point is located 1\(\frac{1}{5}\) units from the y-axis?
Answer :
Point K .

e. Which point is located \(\frac{2}{5}\) unit along the x-axis?
Answer :
Point R .

f. Give the coordinate pair for each of the following points.
T: ________
U: ________
S: ________
K: ________
Answer :
The coordinate pair of T is (2\(\frac{3}{5}\), 2\(\frac{4}{5}\))
The coordinate pair of U is ( \(\frac{3}{5}\), \(\frac{3}{5}\))
The coordinate pair of S is ( 1, \(\frac{2}{5}\))
The coordinate pair of K is (1\(\frac{1}{5}\), 3\(\frac{2}{5}\))

g. Name the points located at the following coordinates.
(\(\frac{3}{5}\), \(\frac{3}{5}\)) ______
(3\(\frac{2}{5}\), 0) ______
(2\(\frac{1}{5}\), 3) ______
(0, 2\(\frac{3}{5}\)) ______
Answer :
(\(\frac{3}{5}\), \(\frac{3}{5}\)) is Point U
(3\(\frac{2}{5}\), 0) is Point X
(2\(\frac{1}{5}\), 3) is Point L
(0, 2\(\frac{3}{5}\)) is Point W

h. Plot a point whose x- and y-coordinates are equal. Label your point E.
Answer :
Point is plotted at (1,1) where x and y coordinates are 1

i. What is the name for the point on the plane where the two axes intersect? ___________ Give the coordinates for this point. ( ____ , ____ )
Answer :
(0,0) ,Origin .

j. Plot the following points.
A: (1\(\frac{1}{5}\), 1)
B: (\(\frac{1}{5}\), 3)
C: (2\(\frac{4}{5}\), 2\(\frac{2}{5}\))
D: (1\(\frac{1}{5}\), 0)
Answer :

k. What is the distance between L and N, or LN?
Answer :
Point L is at 2\(\frac{1}{5}\)
Point N is at 3
Distance of LN = 3 – 2\(\frac{1}{5}\) = \(\frac{15}{5}\) – \(\frac{11}{5}\)= \(\frac{4}{5}\)

l. What is the distance of MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point Q is at  3\(\frac{1}{5}\)
Distance of MQ = 3 \(\frac{1}{5}\) – 2\(\frac{1}{5}\) = \(\frac{16}{5}\) – \(\frac{11}{5}[/latex = [latex]\frac{5}{5}\) =1

m. Would RM be greater than, less than, or equal to LN+MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point R is at  \(\frac{2}{5}\)
Distance of RM = 2 \(\frac{1}{5}\) – \(\frac{2}{5}\) = \(\frac{11}{5}\) – \(\frac{2}{5}\) = \(\frac{9}{5}\)
Distance of LN = \(\frac{4}{5}\)
Distance of MQ = 1
LN +MQ = 1 + \(\frac{4}{5}\) = \(\frac{9}{5}\)
RM is Equal to LN +MQ

n. Leslie was explaining how to plot points on the coordinate plane to a new student, but she left off some important information. Correct her explanation so that it is complete.
“All you have to do is read the coordinates; for example, if it says (4, 7), count four, then seven, and put a point where the two grid lines intersect.”
Answer:
Leslie should say how to specify which is x and y coordinates and how to plot the points .

Engage NY Eureka Math 5th Grade Module 6 Lesson 5 Answer Key

Eureka Math Grade 5 Module 6 Lesson 5 Problem Set Answer Key

Question 1.
Use the coordinate plane to the right to answer the following questions.

a. Use a straightedge to construct a line that goes through points A and B. Label the line e.
b. Line e is parallel to the ______-axis and is perpendicular to the ______-axis.
c. Plot two more points on line e. Name them C and D.
d. Give the coordinates of each point below.
A: ________
B: ________
C: ________
D: ________
e. What do all of the points of line e have in common?
f. Give the coordinates of another point that would fall on line e with an x-coordinate greater than 15.
Answer:

b. Line e is parallel to the X-axis and is perpendicular to the Y-axis.
d. The coordinates of each point below.
A: (3, 4)
B: (11, 4)
C: (5, 4)
D: (8, 4)
e. All of the points of line e have in common Y-Coordinate.
f. The coordinates of another point that would fall on line e with an x-coordinate greater than 15 is ( 16, 4 )

Question 2.
Plot the following points on the coordinate plane to the right.

P: (1\(\frac{1}{2}\), \(\frac{1}{2}\))
Q: (1\(\frac{1}{2}\), 2\(\frac{1}{2}\))
R: (1\(\frac{1}{2}\), 1\(\frac{1}{2}\))
S: (1\(\frac{1}{2}\), \(\frac{3}{4}\))
a. Use a straightedge to draw a line to connect these points. Label the line h.
b. In line h, x = _____ for all values of y.
c. Circle the correct word.
Line h is parallel perpendicular to the x-axis.
Line h is parallel perpendicular to the y-axis.
d. What pattern occurs in the coordinate pairs that let you know that line h is vertical?
Answer:

b. In line h, x =1\(\frac{1}{2}\)  for all values of y.
c.
d . All the coordinate pairs form a straight line .

Question 3.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the x-axis? Circle your answer(s). Without plotting them, explain how you know.
a. (1.4, 2.2) and (4.1, 2.4)
b. (3, 9) and (8, 9)
c. (1\(\frac{1}{4}\), 2) and (1\(\frac{1}{4}\), 8)
Answer:
Option b
Explanation :
To form a parallel line to x -axis, the y-coordinates should be same for all x-coordinates. so in option c we have same y -coordinates b. (3, 9) and (8, 9).

Question 4.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the y-axis? Circle your answer(s). Then, give 2 other coordinate pairs that would also fall on this line.
a. (4, 12) and (6, 12)
b. (\(\frac{3}{5}\), 2\(\frac{3}{5}\)) and (\(\frac{1}{5}\), 3 \(\frac{1}{5}\))
c. (0.8, 1.9) and (0.8, 2.3)
Answer:
Option c
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates. so in option a we have same y -coordinates (0.8, 1.9) and (0.8, 2.3)
The 2 Other coordinate pairs that would also fall on this line are (0.8, 2) and (0.8, 2.1)

Question 5.
Write the coordinate pairs of 3 points that can be connected to construct a line that is 5\(\frac{1}{2}\) units to the right of and parallel to the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A (5\(\frac{1}{2}\) ,\(\frac{1}{2}\))
B (5\(\frac{1}{2}\), 2\(\frac{1}{2}\))
C (5\(\frac{1}{2}\), 3)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.

Question 6.
Write the coordinate pairs of 3 points that lie on the x-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 3, 0 )
B ( 5, 0)
C ( 7, 0)
Explanation :
To lie 3 points on x – axis y coordinates should be 0 . then any point with different x-coordinates lie on x-axis.

Question 7.
Adam and Janice are playing Battleship. Presented in the table is a record of Adam’s guesses so far.
He has hit Janice’s battleship using these coordinate pairs. What should he guess next? How do you know? Explain using words and pictures.
(3, 11) hit
(2, 11) miss
(3, 10) hit
(4, 11) miss
(3, 9) miss
Answer:
Next Coordinate will be (3, 8)

Explanation :
By plotting the 5 coordinate points above the shape formed is T . So, The next coordinate can be (3, 8) it completes the letter T.

Eureka Math Grade 5 Module 6 Lesson 5 Exit Ticket Answer Key

Question 1.
Use a straightedge to construct a line that goes through points A and B. Label the line l.

Answer:

Explanation :
A and B points are joined and labeled as line l

Question 2.
Which axis is parallel to line l?
Which axis is perpendicular to line l?
Answer:
y – axis is parallel to line l
x – axis is perpendicular to line l

Question 3.
Plot two more points on line l. Name them C and D.
Answer:

Explanation :
Two points are plotted on line l and named as C and D .
C is marked at ( 4, 5 )
D is marked at ( 4, 4)

Question 4.
Give the coordinates of each point below.
A: ___________
B: ___________
C: ___________
D: ___________
Answer:
A : ( 4, 6 )
B: ( 4, 3 )
C: ( 4, 5 )
D: ( 4, 4 )

Question 5.
Give the coordinates of another point that falls on line l with a y-coordinate greater than 20.
Answer:
( 4, 22 )
Explanation :
All the x- coordinates are the same it is parallel line to y – axis and given y – coordinate should be greater than 20 so, (4, 22) .

Eureka Math Grade 5 Module 6 Lesson 5 Homework Answer Key

Question 1.
Use the coordinate plane to answer the questions.

a. Use a straightedge to construct a line that goes through points A and B. Label the line g.
b. Line g is parallel to the ______-axis and is perpendicular to the ______-axis.
c. Draw two more points on line g. Name them C and D.
d. Give the coordinates of each point below.
A: ___________
B: ___________
C: ___________
D: ___________
e. What do all of the points on line g have in common?
f. Give the coordinates of another point that falls on line g with an x-coordinate greater than 25.
Answer:

b. Line g is parallel to the x-axis and is perpendicular to the y-axis.
c.

d. The Coordinates are written below
A: (4, 8)
B: (9, 8)
C: (5, 8)
D: (7, 8)
e. All of the points on line g have in common is y-coordinate .
f. The coordinates of another point that falls on line g with an x-coordinate greater than 25 is  ( 28 , 8) .
All of the points on line g have in common is y-coordinate .

Question 2.
Plot the following points on the coordinate plane to the right.

H: (\(\frac{3}{4}\), 3)
I: (\(\frac{3}{4}\), 2\(\frac{1}{4}\))
J: (\(\frac{3}{4}\), \(\frac{1}{2}\))
K: (\(\frac{3}{4}\), 1\(\frac{3}{4}\))
a. Use a straightedge to draw a line to connect these points. Label the line f.
b. In line f, x = ______ for all values of y.
c. Circle the correct word:
Line f is parallel perpendicular to the x-axis.
Line f is parallel perpendicular to the y-axis.
d. What pattern occurs in the coordinate pairs that make line f vertical?
Answer:
a.

b. In line f, x = \(\frac{3}{4}\) for all values of y.
c.
d. all the points form a straight line .

Question 3.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the x-axis? Circle your answer(s). Without plotting them, explain how you know.
a. (3.2, 7) and (5, 7)
b. (8, 8.4) and (8, 8.8)
c. (6\(\frac{1}{2}\), 12) and (6.2, 11)
Answer:
a. (3.2, 7) and (5, 7)
Explanation :
To form a parallel line to x -axis, the y-coordinates should be same for all x-coordinates.
In  option a. (3.2, 7) and (5, 7) we have same x – coordinate .

Question 4.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the y-axis? Circle your answer(s). Then, give 2 other coordinate pairs that would also fall on this line.
a. (3.2, 8.5) and (3.2, 24)
b. (13\(\frac{1}{2}\), 4\(\frac{2}{3}\)) and (13\(\frac{1}{3}\), 7)
c. (2.9, 5.4) and (7.2, 5.4)
Answer:
a. (3.2, 8.5) and (3.2, 24)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.
In Option a. (3.2, 8.5) and (3.2, 24) we have same x-coordinates .

Question 5.
Write the coordinate pairs of 3 points that can be connected to construct a line that is 5\(\frac{1}{2}\) units to the right of and parallel to the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 5\(\frac{1}{2}\), 2\(\frac{1}{2}\) )
B ( 5\(\frac{1}{2}\), 5\(\frac{1}{2}\))
C ( 5\(\frac{1}{2}\), 4)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.

Question 6.
Write the coordinate pairs of 3 points that lie on the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 0, 2 )
B ( 0, 4)
C ( 0, 6)
Explanation :
The 3 points that lie on the y-axis means x-coordinate should be 0 then all the points lie on y-axis .

Question 7.
Leslie and Peggy are playing Battleship on axes labeled in halves. Presented in the table is a record of Peggy’s guesses so far. What should she guess next? How do you know? Explain using words and pictures.
(5, 5) miss
(4, 5) hit
(3\(\frac{1}{2}\), 5) miss
(4\(\frac{1}{2}\), 5) miss
Answer:

Explanation :
All the above points form a straight line so, the next point should also form a straight line so, the next point is (3, 5 )

Engage NY Eureka Math 5th Grade Module 6 Lesson 6 Answer Key

Eureka Math Grade 5 Module 6 Lesson 6 Problem Set Answer Key

Question 1.
Plot the following points, and label them on the coordinate plane.

A: (0.3, 0.1)
B: (0.3, 0.7)
C: (0.2, 0.9)
D: (0.4, 0.9)
a. Use a straightedge to construct line segments \(\overline{A B}\) and \(\overline{C D}\).
b. Line segment _________ is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment _________ is parallel to the y-axis and is perpendicular to the x-axis.
d. Plot a point on line segment \(\overline{A B}\) that is not at the endpoints, and name it U. Write the coordinates. U ( _____ , _____ )
e. Plot a point on line segment \(\overline{C D}\) and name it V. Write the coordinates. V ( _____ , _____ )
Answer:
a.

b. Line segment \(\overline{C D}\) is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment \(\overline{A B}\) is parallel to the y-axis and is perpendicular to the x-axis.
d. The coordinates. U ( 0.3 , 0.5 )

e. The coordinates. V ( 0.3 , 0.9 )

Question 2.
Construct line f such that the y-coordinate of every point is 3\(\frac{1}{2}\), and construct line g such that the x-coordinate of every point is 4\(\frac{1}{2}\).

a. Line f is ________ units from the x-axis.
b. Give the coordinates of the point on line f that is \(\frac{1}{2}\) unit from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 3\(\frac{1}{2}\) units from the x-axis.
d. Line g is _________ units from the y-axis.
e. Give the coordinates of the point on line g that is 5 units from the x-axis. ________
f. With a red pencil, shade the portion of the grid that is more than 4\(\frac{1}{2}\) units from the y-axis.
Answer:
Line f is drawn with points A and B with the y-coordinate of every point is 3\(\frac{1}{2}\) .
A : (1, 3\(\frac{1}{2}\))
B : (3,  3\(\frac{1}{2}\))
Line g is drawn with points C and D with the x-coordinate of every point is 4\(\frac{1}{2}\) .
C : (4\(\frac{1}{2}\) , 3 )
D : ( 4\(\frac{1}{2}\) , 1)

a. Line f is 4\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between f and x-axis is the y-coordinate .

b. The coordinate of the point is ( \(\frac{1}{2}\) , 3\(\frac{1}{2}\) )
c.

d. Line g is 4\(\frac{1}{2}\) units from the y-axis.
Explanation :
Distance between g and y-axis is the x-coordinate .
e. The coordinates of the point on line g that is 5 units from the x-axis is ( 4\(\frac{1}{2}\) , 5 )
f.

Question 3.
Complete the following tasks on the plane below.
a. Construct a line m that is perpendicular to the x-axis and 3.2 units from the y-axis.
b. Construct a line a that is 0.8 unit from the x-axis.
c. Construct a line t that is parallel to line m and is halfway between line m and the y-axis.
d. Construct a line h that is perpendicular to line t and passes through the point (1.2, 2.4).
e. Using a blue pencil, shade the region that contains points that are more than 1.6 units and less than 3.2 units from the y-axis.
f. Using a red pencil, shade the region that contains points that are more than 0.8 unit and less than 2.4 units from the x-axis.
g. Give the coordinates of a point that lies in the double-shaded region.

Answer:


g. The coordinates of a point that lies in the double-shaded region is (1, 2)

Eureka Math Grade 5 Module 6 Lesson 6 Exit Ticket Answer Key

Question 1.
Plot the point H (2\(\frac{1}{2}\), 1\(\frac{1}{2}\)).
Answer:

Question 2.
Line l passes through point H and is parallel to the y-axis. Construct line l.
Answer:

Question 3.
Construct line m such that the y-coordinate of every point is \(\frac{3}{4}\).
Answer:

Explanation :
For same y -coordinate of every point is \(\frac{3}{4}\) then draw a line from \(\frac{3}{4}\) from x-axis .

Question 4.
Line m is ________ units from the x-axis.
Answer:
Line m is \(\frac{3}{4}\) units from the x-axis.
Explanation :
It is represented by y-coordinate of line m .

Question 5.
Give the coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis.
Answer:
The coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis is (\(\frac{1}{2}\) , \(\frac{3}{4}\) ).

Question 6.
With a blue pencil, shade the portion of the plane that is less than \(\frac{3}{4}\) unit from the x-axis.
Answer:

Question 7.
With a red pencil, shade the portion of the plane that is less than 2\(\frac{1}{2}\) units from the y-axis.
Answer:

Question 8.
Plot a point that lies in the double-shaded region. Give the coordinates of the point.
Answer:
The point that lies in the double-shaded region is W ( 2 , \(\frac{1}{2}\) )

Eureka Math Grade 5 Module 6 Lesson 6 Homework Answer Key

Question 1.
Plot and label the following points on the coordinate plane.

C: (0.4, 0.4)
A: (1.1, 0.4)
S: (0.9, 0.5)
T: (0.9, 1.1)
a. Use a straightedge to construct line segments \(\overline{C A}\) and \(\overline{S T}\).
b. Name the line segment that is perpendicular to the x-axis and parallel to the y-axis. _________
c. Name the line segment that is parallel to the x-axis and perpendicular to the y-axis. _________
d. Plot a point on \(\overline{C A}\), and name it E. Plot a point on line segment \(\overline{S T}\), and name it R.
e. Write the coordinates of points E and R.
E ( ____ , ____ ) R ( ____ , ____ )
Answer:

a.

c. The line segment that is perpendicular to the x-axis and parallel to the y-axis is \(\overline{S T}\)
d. The line segment that is parallel to the x-axis and perpendicular to the y-axis is \(\overline{C A}\)
e.

f. The coordinates of points E and R.
E ( 0.8 , 0.4 ) R ( 0.9 , 0.8 )

Question 2.
Construct line m such that the y-coordinate of every point is 1\(\frac{1}{2}\), and construct line n such that the x-coordinate of every point is 5\(\frac{1}{2}\).

a. Line m is ________ units from the x-axis.
b. Give the coordinates of the point on line m that is 2 units from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 1\(\frac{1}{2}\) units from the x-axis.
d. Line n is _________ units from the y-axis.
e. Give the coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis.
f. With a red pencil, shade the portion of the grid that is less than 5\(\frac{1}{2}\) units from the y-axis.
Answer:
Line m is drawn with points A and B with the y-coordinate of every point is 1\(\frac{1}{2}\) .
A : (1, 1\(\frac{1}{2}\))
B : (3,  1\(\frac{1}{2}\))
Line n is drawn with points C and D with the x-coordinate of every point is 5\(\frac{1}{2}\) .
C : (5\(\frac{1}{2}\) , 3 )
D : ( 5\(\frac{1}{2}\) , 6)

a. a. Line m is 1\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between x-axis and line m is the y coordinate .

b. The coordinates of the point on line m that is 2 units from the y-axis is ( 2, 1\(\frac{1}{2}\) )
c.

d. Line n is 5\(\frac{1}{2}\) units from the y-axis.
Explanation :
Explanation :
Distance between y-axis and line n is the x – coordinate .

e. The coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis is (5\(\frac{1}{2}\) , 3\(\frac{1}{2}\))
f.

Question 3.
Construct and label lines e, r, s, and o on the plane below.
a. Line e is 3.75 units above the x-axis.
b. Line r is 2.5 units from the y-axis.
c. Line s is parallel to line e but 0.75 farther from the x-axis.
d. Line o is perpendicular to lines s and e and passes through the point (3\(\frac{1}{4}\), 3\(\frac{1}{4}\)).
Answer:

Question 4.
Complete the following tasks on the plane.
a. Using a blue pencil, shade the region that contains points that are more than 2\(\frac{1}{2}\) units and less than 3\(\frac{1}{4}\) units from the y-axis.
b. Using a red pencil, shade the region that contains points that are more than 3\(\frac{3}{4}\) units and less than 4\(\frac{1}{2}\) units from the x-axis.
c. Plot a point that lies in the double-shaded region, and label its coordinates.

Answer:

Explanation :
In double shaded (3,4 ) is a point that is marked as shown in above figure .

Engage NY Eureka Math 5th Grade Module 6 Lesson 4 Answer Key

Eureka Math Grade 5 Module 6 Lesson 4 Problem Set Answer Key

Battleship Rules

Goal: To sink all of your opponent’s ships by correctly guessing their coordinates.
Materials

• 1 grid sheet (per person/per game)
• Red crayon/marker for hits
• Black crayon/marker for misses
• Folder to place between players

Ships

• Each player must mark 5 ships on the grid.
  • Aircraft carrier—plot 5 points.
  • Battleship—plot 4 points.
  • Cruiser—plot 3 points.
  • Submarine—plot 3 points.
  • Patrol boat—plot 2 points

Setup

• • With your opponent, choose a unit length and fractional unit for the coordinate plane.
  • Label the chosen units on both grid sheets.
  • Secretly select locations for each of the 5 ships on your My Ships grid.
  • All ships must be placed horizontally or vertically on the coordinate plane.
  • Ships can touch each other, but they may not occupy the same coordinate.

Play

• • Players take turns firing one shot to attack enemy ships.
  • On your turn, call out the coordinates of your attacking shot. Record the coordinates of each attack shot.
  • Your opponent checks his/her My Ships grid. If that coordinate is unoccupied, your opponent says, “Miss.” If you named a coordinate occupied by a ship, your opponent says, “Hit.”
  • Mark each attempted shot on your Enemy Ships grid. Mark a black ✖ on the coordinate if your opponent says, “Miss.” Mark a red ✓ on the coordinate if your opponent says, “Hit.”
  • On your opponent’s turn, if he/she hits one of your ships, mark a red ✓on that coordinate of your My Ships grid. When one of your ships has every coordinate marked with a ✓, say, “You’ve sunk my [name of ship].”

Victory

• • The first player to sink all (or the most) opposing ships, wins.
    
    Aircraft carrier—5 points
    Battleship—4 points
    Cruiser—3 points
    Submarine—3 points
    Patrol boat—2 points

Draw a red ✓over any coordinate your opponent hits.
Once all of the coordinates of any ship have been hit, say, “You’ve sunk my [name of ship].”

Attack Shots
Record the coordinates of each shot below and whether it was a ✓(hit) or an ✖ (miss).
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
Enemy Ships

• Draw a black ✖ on the coordinate if your opponent says, “Miss.”
• Draw a red ✓ on the coordinate if your opponent says, “Hit.”
• Draw a circle around the coordinates of a sunken ship.
  

Eureka Math Grade 5 Module 6 Lesson 4 Exit Ticket Answer Key

Fatima and Rihana are playing Battleship. They labeled their axes using just whole numbers.
a. Fatima’s first guess is (2, 2). Rihana says, “Hit!” Give the coordinates of four points that Fatima might guess next.
b. Rihana says, “Hit!” for the points directly above and below (2, 2). What are the coordinates that Fatima guessed?
Answer:

Eureka Math Grade 5 Module 6 Lesson 4 Homework Answer Key

Your homework is to play at least one game of Battleship with a friend or family member. You can use the directions from class to teach your opponent. You and your opponent should record your guesses, hits, and misses on the sheet as you did in class.
When you have finished your game, answer these questions.
Question 1.
When you guess a point that is a hit, how do you decide which points to guess next?
Answer:

Question 2.
How could you change the coordinate plane to make the game easier or more challenging?
Answer:

Question 3.
Which strategies worked best for you when playing this game?
Answer:

Engage NY Eureka Math 5th Grade Module 6 Lesson 2 Answer Key

Eureka Math Grade 5 Module 6 Lesson 2 Problem Set Answer Key

Question 1.
a. Use a set square to draw a line perpendicular to the x-axes through points P, Q, and R. Label the new line as the y-axis.

Answer :

Explanation :
A line is said to be perpendicular to another line if the two lines intersect at a right angle.

b. Choose one of the sets of perpendicular lines above, and create a coordinate plane. Mark 7 units on each axis, and label them as whole numbers.
Answer:

Explanation :
7 units are marked on the first figure on both the axes .

Question 2.
Use the coordinate plane to answer the following.

a. Name the shape at each location.

Answer :

b. Which shape is 2 units from the y-axis?
Answer :
Circle is 2 units from y – axis .
c. Which shape is 1 units from the y-axis?
Answer :
Parallelogram is 1 units from the y-axis

d. Which shape is 4 units from the y-axis and 3 units from the x-axis?
Answer:
Diamond is 4 units from the y-axis and 3 units from the x-axis

Question 3.
Use the coordinate plane to answer the following.

a. Fill in the blanks.

b. Name the shape whose x-coordinate is \(\frac{1}{2}\) more than the value of the heart’s x-coordinate.
Answer :
Star shape

c. Plot a triangle at (3, 4).
Answer :

Explanation :
X- coordinate = 3
Y-coordinate = 4 .

d. Plot a square at (4 \(\frac{3}{4}\), 5).
Answer :

Explanation :
X- coordinate = 4 \(\frac{3}{4}\)
Y- coordinate = 5

e. Plot an X at (\(\frac{1}{2}\), \(\frac{3}{4}\)).
Answer:

Explanation :
X – Coordinate  = (\(\frac{1}{2}\)
Y- Coordinate  = \(\frac{3}{4}\)).

Question 4.
The pirate’s treasure is buried at the X on the map. How could a coordinate plane make describing its location easier?

Answer:
It would give you the exact location when you describe the position with x and y axis .
It would you draw x- axis along the island and y axis along the left side and mark the point for  x then the location would be exactly clear to find easier .

Eureka Math Grade 5 Module 6 Lesson 2 Exit Ticket Answer Key

Question 1.
Name the coordinates of the shapes below.

Answer:

Question 2.
Plot a square at (3, 3\(\frac{1}{2}\)).
Answer:

Question 3.
Plot a triangle at (4\(\frac{1}{2}\), 1).
Answer:

Eureka Math Grade 5 Module 6 Lesson 2 Homework Answer Key

Question 1.
a. Use a set square to draw a line perpendicular to the x-axis through point P. Label the new line as the y-axis.

Answer a :

b. Choose one of the sets of perpendicular lines above, and create a coordinate plane. Mark 5 units on each axis, and label them as whole numbers.
Answer:

Explanation :
In First figure the x-axis and y-axis is divided into 5 parts as shown in above figure .

Question 2.
Use the coordinate plane to answer the following.

a. Name the shape at each location.

Answer :

b. Which shape is 2 units from the x-axis?
Answer :
Star

c. Which shape has the same x- and y-coordinate?
Answer:
Square it is located at (3,3)

Question 3.
Use the coordinate plane to answer the following.

a. Name the coordinates of each shape.

Answer :

shape.

b. Which 2 shapes have the same y-coordinate?
Answer :
Heart and star have same y – coordinate as 2

c. Plot an X at (2, 3).
Answer :

d. Plot a square at (3, 2\(\frac{1}{2}\)).
Answer :

e. Plot a triangle at (6, 3\(\frac{1}{2}\)).
Answer:

Question 3.
Mr. Palmer plans to bury a time capsule 10 yards behind the school. What else should he do to make naming the location of the time capsule more accurate?

Answer:
If Palmer drew an x-axis and y-axis and a scale he would have the exact location of the time capsule .

Engage NY Eureka Math 5th Grade Module 6 Lesson 1 Answer Key

Eureka Math Grade 5 Module 6 Lesson 1 Problem Set Answer Key

Question 1.
Each shape was placed at a point on the number line s. Give the coordinate of each point below.

Answer:

Explanation :
The given number line is divided into 3 equals parts from 0-1,1-2 and so on.
Fraction of each part is \(\frac{1}{3}\).
So, the coordinates of each point located is written in above figure .

Question 2.
Plot the points on the number lines.
a.

Plot A so that its distance from the origin is 2.
Answer :

Explanation :
The given Number line is divided into 3 parts from 0 -3 that means each unit is 1 .
Point A is marked at 2 and is shown in above figure .

b.

Plot R so that its distance from the origin is \(\frac{5}{2}\).
Answer :

Explanation :
The Each part of the above number line is \(\frac{1}{2}\).
R is plotted at \(\frac{5}{2}\). and is shown in above figure .

c.

Plot L so that its distance from the origin is 20.
Answer :

Explanation :
The Each part of the above number line is 5 .
The representation of number line is in decreasing order of 5 . so L is plotted below 35
L is plotted at 20 and is shown in above figure .

d.

Plot a point T so that its distance from the origin is \(\frac{2}{3}\) more than that of S.
Answer:

Explanation :
The given Number line is divided into 6 Equal parts from 4 – 5 that means each unit is \(\frac{1}{6}\).
Point S is marked at  4\(\frac{1}{6}\) and is shown in above figure .
point T so that its distance from the origin is \(\frac{2}{3}\) more than that of S.
Point T = 4\(\frac{1}{6}\) + \(\frac{2}{3}\) = \(\frac{25}{6}\) + \(\frac{4}{6}\)
= \(\frac{29}{6}\) = 4 \(\frac{5}{6}\)
Point T = 4 \(\frac{5}{6}\)  . is marked and is shown in above figure .

Question 3.
Number line g is labeled from 0 to 6. Use number line g below to answer the questions.

a. Plot point A at \(\frac{3}{4}\).
b. Label a point that lies at 4\(\frac{1}{2}\) as B.
c. Label a point, C, whose distance from zero is 5 more than that of A.
The coordinate of C is _______.
d. Plot a point, D, whose distance from zero is 1\(\frac{1}{2}\) less than that of B.
The coordinate of D is ________.
e. The distance of E from zero is 1\(\frac{3}{4}\) more than that of D. Plot point E.
f. What is the coordinate of the point that lies halfway between A and D? _______ Label this point F.

Answer c :
Point A = \(\frac{3}{4}\)
Point C = 5 + \(\frac{3}{4}\)=5 \(\frac{3}{4}\)
Answer d :
Point B = 4\(\frac{1}{2}\)
Point D = 1\(\frac{1}{2}\) less than that of B = 4\(\frac{1}{2}\)  – 1\(\frac{1}{2}\) = 3 .
Answer e :
Point D = 3
Point E = 1\(\frac{3}{4}\) more than that of D = 3 + 1\(\frac{3}{4}\) = 4\(\frac{3}{4}\).
Answer f :
The Coordinate of the point that lies halfway between A and D = Point F = 1.875

Question 4.
Mrs. Fan asked her fifth-grade class to create a number line. Lenox created the number line below:

Parks said Lenox’s number line is wrong because numbers should always increase from left to right. Who is correct? Explain your thinking.
Answer:
Lenox is right .
Explanation :
Any Orientation is acceptable .

Question 5.
A pirate marked the palm tree on his treasure map and buried his treasure 30 feet away. Do you think he will be able to easily find his treasure when he returns? Why or why not? What might he do to make it easier to find?

Answer:
No,
Explanation :
Because point or location will help to find the treasure easily .

Eureka Math Grade 5 Module 6 Lesson 1 Exit Ticket Answer Key

Question 1.
Use number line l to answer the questions.

a. Plot point C so that its distance from the origin is 1.
b. Plot point E \(\frac{4}{5}\) closer to the origin than C. What is its coordinate? _________
c. Plot a point at the midpoint of C and E. Label it H.
Answer:
a .Point C is plotted .
b .Point E = \(\frac{4}{5}\)closer to the origin than C. = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\) .
c. Point H = the midpoint of C and E = 1 + \(\frac{1}{5}\) = \(\frac{6}{5}\)/2 =\(\frac{6}{10}\) = \(\frac{2}{3}\) .

Eureka Math Grade 5 Module 6 Lesson 1 Homework Answer Key

Question 1.
Answer the following questions using number line q below.
a. What is the coordinate, or the distance from the origin, of the ? ___________
b. What is the coordinate of the ? _________
c. What is the coordinate of the ? __________
d. What is the coordinate at the midpoint of the and the ? __________

Answer:
a the coordinate, or the distance from the origin, of the is 3
b the coordinate of the is  8
c the coordinate of the is 14
d the coordinate at the midpoint of the and the is (8 + 14)/2 = 11
Explanation :
The number line is divided into 3 parts from 0-3,3-6 and so on . . . .
So Each unit is 1 .

Question 2.
Use the number lines to answer the questions.

a Plot T so that its distance from the origin is 10.

b Plot M so that its distance is \(\frac{11}{4}\) from the origin. What is the distance from P to M?

c Plot a point that is 0.15 closer to the origin than Z.

d Plot U so that its distance from the origin is \(\frac{3}{6}\) less than that of W.
Answer a :

Explanation :
The each part of the above number line is 1 unit .
T is plotted at 11 and is shown in above figure .

Answer b :

Explanation :
The each part of the above number line is \(\frac{1}{4}\) unit .
Point P = 1\(\frac{1}{4}\) = \(\frac{5}{4}\)
Point M= \(\frac{11}{4}\)
Distance between P and M =\(\frac{11}{4}\) – \(\frac{5}{4}\) = \(\frac{6}{4}\)

Answer c :

Explanation :
Point Z = 0.95
Point Y = point that is 0.15 closer to the origin than Z. = 0.95- 0.15 = 0.8
Point Y is plotted .

Answer d :

Explanation :
Point W = 9 \(\frac{4}{6}\)
Plot U so that its distance from the origin is \(\frac{3}{6}\) less than that of W
Point U = 9\(\frac{4}{6}\) – \(\frac{3}{6}\) = 9 \(\frac{1}{6}\).
Point U is plotted .

Question 3.
Number line k shows 12 units. Use number line k below to answer the questions.

a. Plot a point at 1. Label it A.
b. Label a point that lies at 3\(\frac{1}{2}\) as B.
c. Label a point, C, whose distance from zero is 8 units farther than that of B.
The coordinate of C is __________.
d. Plot a point, D, whose distance from zero is \(\frac{6}{2}\) less than that of B.
The coordinate of D is __________.
e. What is the coordinate of the point that lies \(\frac{17}{2}\) farther from the origin than D? Label this point E.
f. What is the coordinate of the point that lies halfway between F and D? Label this point G.
Answer:
All the points are plotted and shown in the below figure .

Explanation :
a Point A = 1
b Point B = 3\(\frac{1}{2}\)
c Point C = 8 units farther than that of B = 8 + 3\(\frac{1}{2}\) = 11 \(\frac{1}{2}\)
The coordinate of C is 11 \(\frac{1}{2}\)
d Point D = \(\frac{6}{2}\) less than that of B = 3\(\frac{1}{2}\) – \(\frac{6}{2}\)
= \(\frac{7}{2}\) – \(\frac{6}{2}\)  = \(\frac{1}{2}\)
The coordinate of D is \(\frac{1}{2}\)
e Point E = \(\frac{17}{2}\) farther from the origin than D = \(\frac{1}{2}\)  + \(\frac{17}{2}       \)  = \(\frac{18}{2}\) = 9
f  Point F = 9 \(\frac{1}{2}\)
Point G = halfway between F and D =( 9 \(\frac{1}{2}\) + \(\frac{1}{2}\) )/2 = 10/2 = 5

Question 4.
Mr. Baker’s fifth-grade class buried a time capsule in the field behind the school. They drew a map and marked the location of the capsule with an X so that his class can dig it up in ten years. What could Mr. Baker’s class have done to make the capsule easier to find?

Answer:
The Location of the capsule is marked with x in the map. but to find easier he could add the number of feet’s from the school or a land mark or depth of the time capsule buried etc if given will help to find the time capsule easier even after ten years .

Students of Grade 4 can get a strong foundation on mathematics concepts by referring to the Eureka Math Book. It was developed by highly professional mathematics educators and the solutions prepared by them are in a concise manner for easy grasping. To achieve high scores in Grade 4, students need to solve all questions and exercises included in Eureka’s Math Grade 4 Book.

Engage NY Eureka Math 4th Grade Module 5 Lesson 2 Answer Key

Eureka Math Answer Key for Grade 4 aids teachers to differentiate instruction, building, and reinforcing foundational mathematics skills that alter from the classroom to real life.
With the help of the Eureka Primary School Grade 4 Answer Key, You can think deeply regarding what you are learning, and you will really learn math easily just like that. So teachers and students can find this Eureka Answer Key for Grade 4 more helpful in raising students’ scores and supporting teachers to educate the students.

Eureka Math Grade 4 Module 5 Lesson 2 Problem Set Answer Key

Question 1.
Step 1: Draw and shade a tape diagram of the given fraction.
Step 2: Record the decomposition as a sum of unit fractions.
Step 3: Record the decomposition of the fraction two more ways.
(The first one has been done for you.)
a. \(\frac{5}{8}\)

b. \(\frac{9}{10}\)

Answer:
9/10 = 1/10 + 2/10 + 2/10 + 3/10 + 1/10.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
9/10 = 1/10 + 2/10 + 2/10 + 3/10 + 1/10.
9/10 = 5 /10 + 4 /10 + 1/10.
9/10 = 3/10 + 2/10 + 3/10 + 1/10.

c. \(\frac{3}{2}\)

Answer:
3/2 = 1/2 + 2/2.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
3/2 = 1/2 + 2/2.
3/2 = 1/2 + 1/2 + 1/2.

Question 2.
Step 1: Draw and shade a tape diagram of the given fraction.
Step 2: Record the decomposition of the fraction in three different ways using number sentences.
a. \(\frac{7}{8}\)

Answer:
7/8 = 1/8 + 2/8 + 2/8 + 1/8 + 1/8.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
7/8 = 1/8 + 2/8 + 2/8 + 1/8 + 1/8.
7/8 = 1 /8 + 4 /10 + 2/8.
7/8 = 1/8 + 2/8 + 3/8 + 1/8.

b. \(\frac{5}{3}\)

Answer:
5/3 = 1/3 + 1/3 + 1/3 + 1/3 + 1/3.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
5/3 = 1/3 + 1/3 + 1/3 + 1/3 + 1/3.
5/3 = 1 /3 + 2/3 + 2/3.
5/3 = 1/3 + 2/3 + 1/3 + 1/3.

c. \(\frac{7}{5}\)

Answer:
5/7 = 1/7 + 1/7 + 1/7 + 1/7 + 1/7.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
5/7 = 1/7 + 1/7 + 1/7 + 1/7 + 1/7.
5/7 = 1 /7 + 2/7 + 2/7.
5/7 = 1/7 + 1/7 + 2/7 + 1/7.

d. 1\(\frac{1}{3}\)

Answer:
4/3 = 1/3 + 1/3 + 1/3 + 1/3.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
4/3 = 1/3 + 1/3 + 1/3 + 1/3.
4/3 = 1 /3 + 2/3 + 1/3.
4/3 = 1/3 + 1/3 + 2/3.

Eureka Math Grade 4 Module 5 Lesson 2 Exit Ticket Answer Key

Step 1: Draw and shade a tape diagram of the given fraction.
Step 2: Record the decomposition of the fraction in three different ways using number sentences.
\(\frac{4}{7}\)

Answer:
4/7 = 1/7 + 1/7 + 1/7 + 1/7.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
4/7 = 1/7 + 1/7 + 1/7 + 1/7.
4/7 = 1 /7 + 2/7 + 1/7.
4/7 = 1/7 + 1/7 + 2/7.

Eureka Math Grade 4 Module 5 Lesson 2 Homework Answer Key

Question 1.
Step 1: Draw and shade a tape diagram of the given fraction.
Step 2: Record the decomposition as a sum of unit fractions.
Step 3: Record the decomposition of the fraction two more ways.
(The first one has been done for you.)
a. \(\frac{5}{6}\)

b. \(\frac{6}{8}\)

Answer:
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
6/8 = 1 /8 + 2/8 + 2/8 + 1/8.
6/8 = 1/8 + 2/8 + 3/8.

c. \(\frac{7}{10}\)

Answer:
7/10 = 1/10 + 2/10 + 2/10 + 1/10 + 2/10 + 2/10.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
7/10 = 1/10 + 2/10 + 2/10 + 1/10 + 2/10 + 2/10.
7/10 = 1 /10 + 2/10 + 4/10 + 3/10.
7/10 = 1/10 + 2/10 + 7/10.

Question 2.
Step 1: Draw and shade a tape diagram of the given fraction.
Step 2: Record the decomposition of the fraction in three different ways using number sentences.
a. \(\frac{10}{12}\)

Answer:
10/12 = 1/12 + 2/12 + 3/12 + 1/12 + 2/12 + 1/12.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
10/12 = 1/12 + 2/12 + 3/12 + 1/12 + 2/12 + 1/12.
10/12 = 1 /12 + 2/12 + 4/12 + 3/12.
10/12 = 1/12 + 2/12 + 7/12.

b. \(\frac{5}{4}\)

Answer:
5/4 = 1/4 + 2/4 + 1/4 + 1/4.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
5/4 = 1/4 + 2/4 + 1/4 + 1/4.
5/4 = 1 /4 + 24 + 1/4 + 1/4.
5/4 = 1/4 + 2/4 + 1/4.

c. \(\frac{6}{5}\)

Answer:
5/6 = 1/6 + 2/6 + 1/6 + 1/6.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
5/6 = 1/6 + 2/6 + 1/6 + 1/6.
5/6 = 1 /6 + 2/6+ 1/6 + 1/6.
5/6 = 1/6 + 2/6 + 2/6.

d. 1\(\frac{1}{4}\)

Answer:
5/4 = 1/4 + 1/4 + 1/4 + 1/4 + 1/4.

Explanation:
In the above-given question,
given that,
draw and shade a tape diagram.
5/4 = 1/4 + 1/4 + 1/4 + 1/4 + 1/4.
5/4 = 1 /4 + 2/4 + 1/4 + 1/4.
5/4 = 1/4 + 2/4 + 2/4.

Students of Grade 4 can get a strong foundation on mathematics concepts by referring to the Eureka Math Book. It was developed by highly professional mathematics educators and the solutions prepared by them are in a concise manner for easy grasping. To achieve high scores in Grade 4, students need to solve all questions and exercises included in Eureka’s Math Grade 4 Book.

Engage NY Eureka Math 4th Grade Module 6 Lesson 15 Answer Key

Eureka Math Answer Key for Grade 4 aids teachers to differentiate instruction, building, and reinforcing foundational mathematics skills that alter from the classroom to real life.
With the help of the Eureka Primary School Grade 4 Answer Key, You can think deeply regarding what you are learning, and you will really learn math easily just like that. So teachers and students can find this Eureka Answer Key for Grade 4 more helpful in raising students’ scores.

Eureka Math Grade 4 Module 6 Lesson 15 Problem Set Answer Key

Question 1.
100 pennies = $___.______ 100₵ = \(\frac{}{100}\) dollar
Answer:

Question 2.
1 penny = $___.______ 1₵ = \(\frac{}{100}\) dollar
Answer:

Question 3.
6 pennies = $___.______ 6₵ = \(\frac{}{100}\) dollar
Answer:

Question 4.
10 pennies = $___.______ 10₵ = \(\frac{}{100}\) dollar
Answer:

Question 5.
26 pennies = $___.______ 26₵ = \(\frac{}{100}\) dollar
Answer:

Question 6.
10 dimes = $___.______ 100₵ = \(\frac{}{10}\) dollar
Answer:

Question 7.
1 dime = $___.______ 10₵ = \(\frac{}{10}\) dollar
Answer:

Question 8.
3 dimes = $___.______ 30₵ = \(\frac{}{10}\) dollar
Answer:

Question 9.
5 dimes = $___.______ 50₵ = \(\frac{}{10}\) dollar
Answer:

Question 10.
6 dimes = $___.______ 60₵ = \(\frac{}{10}\) dollar
Answer:

Question 11.
4 quarters = $___.______ 100₵ = \(\frac{}{100}\) dollar
Answer:

Question 12.
1 quarter = $___.______ 25₵ = \(\frac{}{100}\) dollar
Answer:

Question 13.
2 quarters = $___.______ 50₵ = \(\frac{}{100}\) dollar
Answer:

Question 14.
3 quarters = $___.______ 75₵ = \(\frac{}{100}\) dollar
Answer:

Solve. Give the total amount of money in fraction and decimal form.
Question 15.
3 dimes and 8 pennies
Answer:

Question 16.
8 dimes and 23 pennies
Answer:

Question 17.
3 quarters 3 dimes and 5 pennies
Answer:

Question 18.
236 cents is what fraction of a dollar?
Answer:

Solve. Express the answer as a decimal.
Question 19.
2 dollars 17 pennies + 4 dollars 2 quarters
Answer:

Question 20.
3 dollars 8 dimes + 1 dollar 2 quarters 5 pennies
Answer:

Question 21.
9 dollars 9 dimes + 4 dollars 3 quarters 16 pennies
Answer:

Eureka Math Grade 4 Module 6 Lesson 15 Exit Ticket Answer Key

Solve. Give the total amount of money in fraction and decimal form.
Question 1.
2 quarters and 3 dimes
Answer:

Question 2.
1 quarter 7 dimes and 23 pennies
Answer:

Solve. Express the answer as a decimal.
Question 3.
2 dollars 1 quarter 14 pennies + 3 dollars 2 quarters 3 dimes
Answer:

Eureka Math Grade 4 Module 6 Lesson 15 Homework Answer Key

Question 1.
100 pennies = $___.______ 100₵ = \(\frac{}{100}\) dollar
Answer:

Question 2.
100 pennies = $___.______ 100₵ = \(\frac{}{100}\) dollar
Answer:

Question 3.
3 pennies = $___.______ 3₵ = \(\frac{}{100}\) dollar
Answer:

Question 4.
20 pennies = $___.______ 20₵ = \(\frac{}{100}\) dollar
Answer:

Question 5.
37 pennies = $___.______ 37₵ = \(\frac{}{100}\) dollar
Answer:

Question 6.
10 dimes = $___.______ 100₵ = \(\frac{}{10}\) dollar
Answer:

Question 7.
2 dimes = $___.______ 20₵ = \(\frac{}{10}\) dollar
Answer:

Question 8.
4 dimes = $___.______ 40₵ = \(\frac{}{10}\) dollar
Answer:

Question 9.
6 dimes = $___.______ 60₵ = \(\frac{}{10}\) dollar
Answer:

Question 10.
9 dimes = $___.______ 90₵ = \(\frac{}{10}\) dollar
Answer:

Question 11.
3 quarters = $___.______ 75₵ = \(\frac{}{100}\) dollar
Answer:

Question 12.
2 quarters = $___.______ 50₵ = \(\frac{}{100}\) dollar
Answer:

Question 13.
4 quarters = $___.______ 100₵ = \(\frac{}{100}\) dollar
Answer:

Question 14.
1 quarter = $___.______ 25₵ = \(\frac{}{100}\) dollar
Answer:

Solve. Give the total amount of money in fraction and decimal form.
Question 15.
5 dimes and 8 pennies
Answer:

Question 16.
3 quarters and 13 pennies
Answer:

Question 17.
3 quarters 7 dimes and 16 pennies
Answer:

Question 18.
187 cents is what fraction of a dollar?
Answer:

Solve. Express the answer in decimal form.
Question 19.
1 dollar 2 dimes 13 pennies + 2 dollars 3 quarters
Answer:

Question 20.
2 dollars 6 dimes + 2 dollars 2 quarters 16 pennies
Answer:

Question 21.
8 dollars 8 dimes + 7 dollars 1 quarter 8 dimes
Answer:

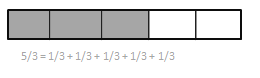
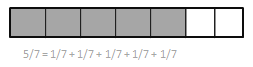
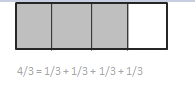
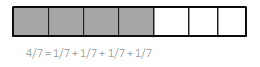
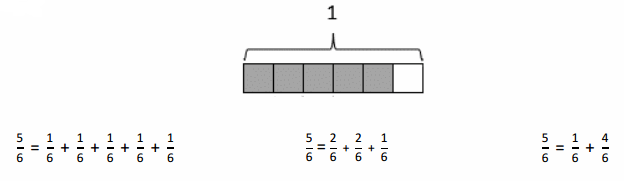
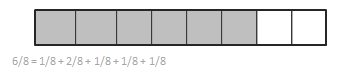
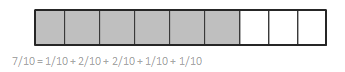
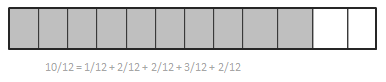
Engage NY Eureka Math 4th Grade Module 3 Lesson 19 Answer Key

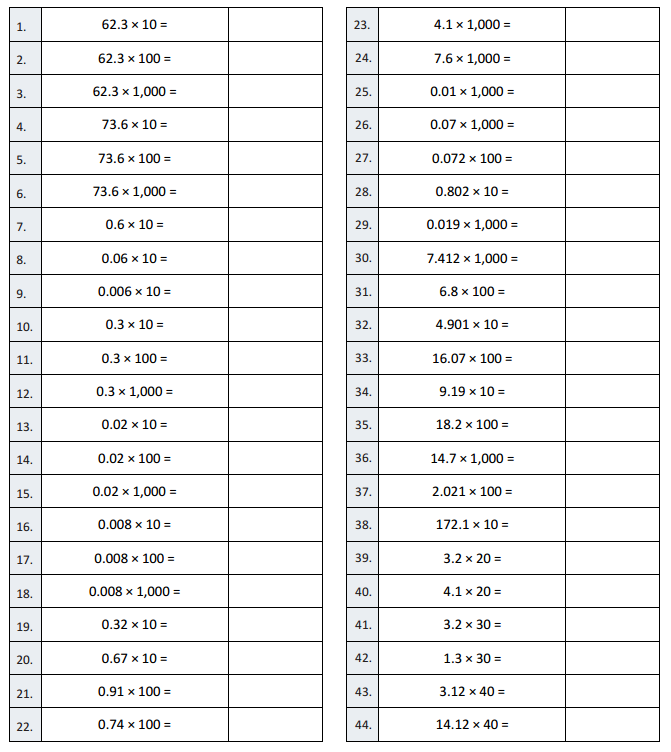
Eureka Math Grade 4 Module 3 Lesson 19 Sprint Answer Key

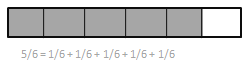
Mental Division

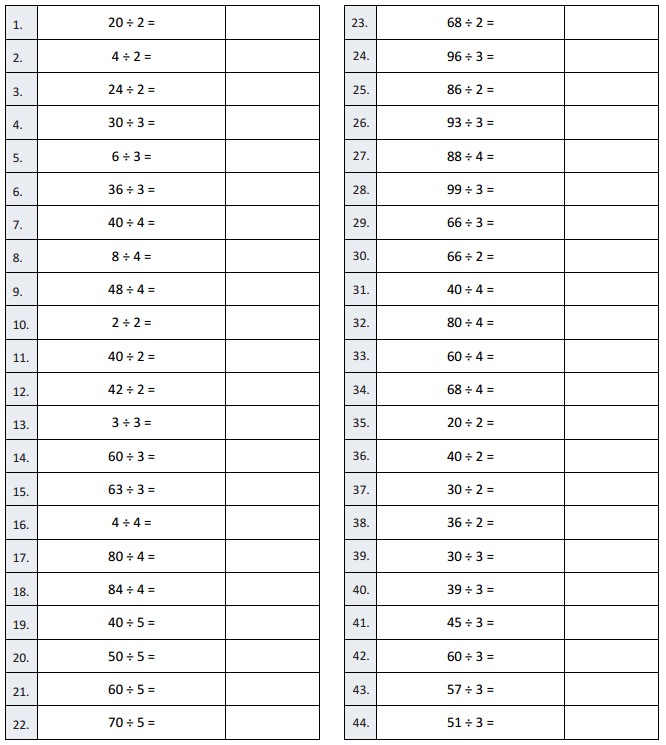
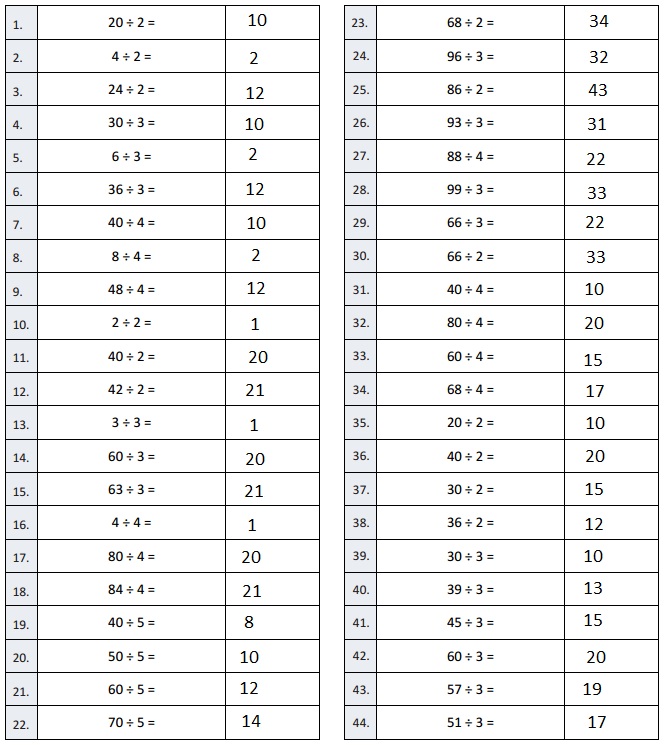
Question 1.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10,

Explanation :
Given expression 20 ÷ 2  when 20 is divided by 2
we get 10, So quotient is 10 and remainder is 0 and
(2 X 10 = 20).

Question 2.
4 ÷ 2 =
Answer:
4 ÷ 2 = 2,

Explanation :
Given expression 4 ÷ 2  when 4 is divided by 2
we get 2, So quotient is 2 and remainder is 0 and
(2 X 2 = 4).

Question 3.
24 ÷ 2 =
Answer:
24 ÷ 2 = 12,

Explanation :
Given expression 24 ÷ 2  when 24 is divided by 2
we get 12, So quotient is 12 and remainder is 0 and
(2 X 12 = 24).

Question 4.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10,

Explanation :
Given expression 30 ÷ 3  when 30 is divided by 3
we get 10, So quotient is 10 and remainder is 0 and
(3 X 10 = 30).

Question 5.
6 ÷ 3 =
Answer:
6 ÷ 3 = 2,

Explanation :
Given expression 6 ÷ 3  when 6 is divided by 3
we get 2, So quotient is 2 and remainder is 0 and
(3 X 2 = 6).

Question 6.
36 ÷ 3 =
Answer:
36 ÷ 3 = 12,

Explanation :
Given expression 36 ÷ 3  when 6 is divided by 3
we get 12, So quotient is 12 and remainder is 0 and
(3 X 12 = 36).

Question 7.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10,

Explanation :
Given expression 40 ÷ 4  when 40 is divided by 4
we get 10, So quotient is 10 and remainder is 0 and
(4 X 10 = 40).

Question 8.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2,

Explanation :
Given expression 40 ÷ 4  when 40 is divided by 4
we get 10, So quotient is 10 and remainder is 0 and
(4 X 10 = 40).

Question 9.
48 ÷ 4 =
Answer:
48 ÷ 4 = 12,

Explanation :
Given expression 48 ÷ 4  when 48 is divided by 4
we get 12, So quotient is 12 and remainder is 0 and
(4 X 12 = 46).

Question 10.
2 ÷ 2 =
Answer:
2 ÷ 2 = 1,

Explanation :
Given expression 2 ÷ 2  when 2 is divided by 2
we get 1, So quotient is 1 and remainder is 0 and
(2 X 1 = 2).

Question 11.
40 ÷ 2 =
Answer:
40 ÷ 2 = 20,

Explanation :
Given expression 40 ÷ 2  when 40 is divided by 2
we get 20, So quotient is 20 and remainder is 0 and
(2 X 20 = 40).

Question 12.
42 ÷ 2 =
Answer:
42 ÷ 2 = 21,

Explanation :
Given expression 42 ÷ 2  when 42 is divided by 2
we get 21, So quotient is 21 and remainder is 0 and
(2 X 21 = 42).

Question 13.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1,

Explanation :
Given expression 3 ÷ 3 when 1 is divided by 3
we get 3, So quotient is 1 and remainder is 0 and
(3 X 1 = 3).

Question 14.
60 ÷ 3 =
Answer:
60 ÷ 3 =20,

Explanation :
Given expression 60 ÷ 3 when 60 is divided by 3
we get 20, So quotient is 20 and remainder is 0 and
(3 X 20 = 60).

Question 15.
63 ÷ 3 =
Answer:
63 ÷ 3 = 21,

Explanation :
Given expression 63 ÷ 3 when 63 is divided by 3
we get 21, So quotient is 21 and remainder is 0 and
(3 X 21 = 63).

Question 16.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1,

Explanation :
Given expression 4 ÷ 4 when 4 is divided by 4
we get 1, So quotient is 1 and remainder is 0 and
(4 X 1 = 4).

Question 17.
80 ÷ 4 =
Answer:
80 ÷ 4 = 20,

Explanation :
Given expression 80 ÷ 4 when 80 is divided by 4
we get 20, So quotient is 20 and remainder is 0 and
(4 X 20 = 80).

Question 18.
84 ÷ 4 =
Answer:
84 ÷ 4 = 21,

Explanation :
Given expression 84 ÷ 4 when 84 is divided by 4
we get 21, So quotient is 21 and remainder is 0 and
(4 X 21 = 84).

Question 19.
40 ÷ 5 =
Answer:
40 ÷ 5 = 8,

Explanation :
Given expression 40 ÷ 5 when 40 is divided by 5
we get 8, So quotient is 8 and remainder is 0 and
(5 X 8 = 40).

Question 20.
50 ÷ 5 =
Answer:
50 ÷ 5 = 10,

Explanation :
Given expression 50 ÷ 5 when 50 is divided by 5
we get 10, So quotient is 10 and remainder is 0 and
(5 X 10 = 50).

Question 21.
60 ÷ 5 =
Answer:
60 ÷ 5 = 12,

Explanation :
Given expression 60 ÷ 5 when 60 is divided by 5
we get 12, So quotient is 12 and remainder is 0 and
(5 X 12 = 60).

Question 22.
70 ÷ 5 =
Answer:
70 ÷ 5 = 14,

Explanation :
Given expression 70 ÷ 5 when 70 is divided by 5
we get 14, So quotient is 14 and remainder is 0 and
(5 X 14 = 70).

Question 23.
68 ÷ 2 =
Answer:
68 ÷ 2 = 34,

Explanation :
Given expression 68 ÷ 2 when 68 is divided by 2
we get 34, So quotient is 34 and remainder is 0 and
(2 X 34 = 68).

Question 24.
96 ÷ 3 =
Answer:
96 ÷ 3 = 32,

Explanation :
Given expression 96 ÷ 3 when 96 is divided by 3
we get 32, So quotient is 32 and remainder is 0 and
(3 X 32 = 96).

Question 25.
86 ÷ 2 =
Answer:
86 ÷ 2 = 43,

Explanation :
Given expression 86 ÷ 2 when 86 is divided by 2
we get 43, So quotient is 43 and remainder is 0 and
(2 X 43 = 86).

Question 26.
93 ÷ 3 =
Answer:
93 ÷ 3 = 31,

Explanation :
Given expression 93 ÷ 3 when 93 is divided by 3
we get 31, So quotient is 31 and remainder is 0 and
(3 X 31 = 93).

Question 27.
88 ÷ 4 =
Answer:
88 ÷ 4 = 22,

Explanation :
Given expression 88 ÷ 4 when 88 is divided by 4
we get 22, So quotient is 22 and remainder is 0 and
(4 X 22 = 88).

Question 28.
99 ÷ 3 =
Answer:
99 ÷ 3 = 33,

Explanation :
Given expression 99 ÷ 3 when 99 is divided by 3
we get 33, So quotient is 33 and remainder is 0 and
(3 X 33 = 99).

Question 29.
66 ÷ 3 =
Answer:
66 ÷ 3 = 22,

Explanation :
Given expression 66 ÷ 3 when 66 is divided by 3
we get 22, So quotient is 22 and remainder is 0 and
(22 X 3 = 66).

Question 30.
66 ÷ 2 =
Answer:
66 ÷ 2 = 33,

Explanation :
Given expression 66 ÷ 2 when 66 is divided by 2
we get 33, So quotient is 33 and remainder is 0 and
(33 X 2 = 66).

Question 31.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10,

Explanation :
Given expression 40 ÷ 4 when 40 is divided by 4
we get 10, So quotient is 10 and remainder is 0 and
(4 X 10 = 40).

Question 32.
80 ÷ 4 =
Answer:
80 ÷ 4 = 20,

Explanation :
Given expression 80 ÷ 4 when 80 is divided by 4
we get 20, So quotient is 20 and remainder is 0 and
(4 X 20 = 80).

Question 33.
60 ÷ 4 =
Answer:
60 ÷ 4 = 15,

Explanation :
Given expression 60 ÷ 4 when 60 is divided by 4
we get 15, So quotient is 15 and remainder is 0 and
(4 X 15 = 60).

Question 34.
68 ÷ 4 =
Answer:
68 ÷ 4 = 17,

Explanation :
Given expression 68 ÷ 4 when 68 is divided by 4
we get 17, So quotient is 17 and remainder is 0 and
(4 X 17 = 68).

Question 35.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10,

Explanation :
Given expression 20 ÷ 2 when 20 is divided by 2
we get 10, So quotient is 10 and remainder is 0 and
(2 X 10 = 20).

Question 36.
40 ÷ 2 =
Answer:
40 ÷ 2 = 20,

Explanation :
Given expression 40 ÷ 2 when 40 is divided by 2
we get 20, So quotient is 20 and remainder is 0 and
(2 X 20 = 40).

Question 37.
30 ÷ 2 =
Answer:
30 ÷ 2 = 15,

Explanation :
Given expression 30 ÷ 2 when 30 is divided by 2
we get 15, So quotient is 15 and remainder is 0 and
(2 X 15 = 30).

Question 38.
36 ÷ 2 =
Answer:
36 ÷ 2 = 18,

Explanation :
Given expression 36 ÷ 2 when 36 is divided by 2
we get 18, So quotient is 18 and remainder is 0 and
(2 X 18 = 36).

Question 39.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10,

Explanation :
Given expression 30 ÷ 3 when 30 is divided by 3
we get 10, So quotient is 10 and remainder is 0 and
(3 X 10 = 30).

Question 40.
39 ÷ 3 =
Answer:
39 ÷ 3 = 13,

Explanation :
Given expression 39 ÷ 3 when 39 is divided by 3
we get 13, So quotient is 13 and remainder is 0 and
(3 X 13 = 39).

Question 41.
45 ÷ 3 =
Answer:
45 ÷ 3 = 15,

Explanation :
Given expression 45 ÷ 3 when 45 is divided by 3
we get 15, So quotient is 15 and remainder is 0 and
(3 X 15 = 45).

Question 42.
60 ÷ 3 =
Answer:
60 ÷ 3 = 20,

Explanation :
Given expression 60 ÷ 3 when 60 is divided by 3
we get 20, So quotient is 20 and remainder is 0 and
(3 X 20 = 60).

Question 43.
57 ÷ 3 =
Answer:
57 ÷ 3 = 19,

Explanation :
Given expression 57 ÷ 3 when 57 is divided by 3
we get 19, So quotient is 19 and remainder is 0 and
(3 X 19 = 57).

Question 44.
51 ÷ 3 =
Answer:
51 ÷ 3 = 17,

Explanation :
Given expression 51 ÷ 3 when 51 is divided by 3
we get 17, So quotient is 17 and remainder is 0 and
(3 X 17 = 51).

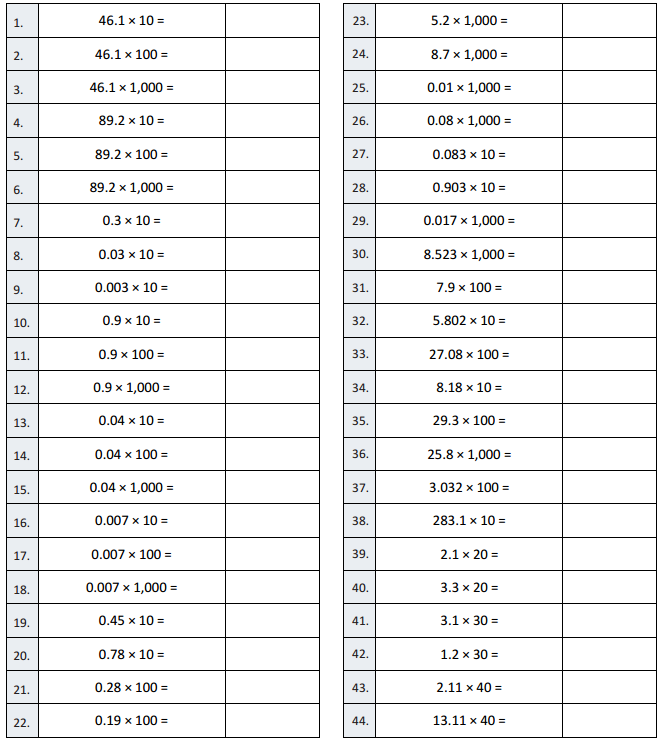
Mental Division

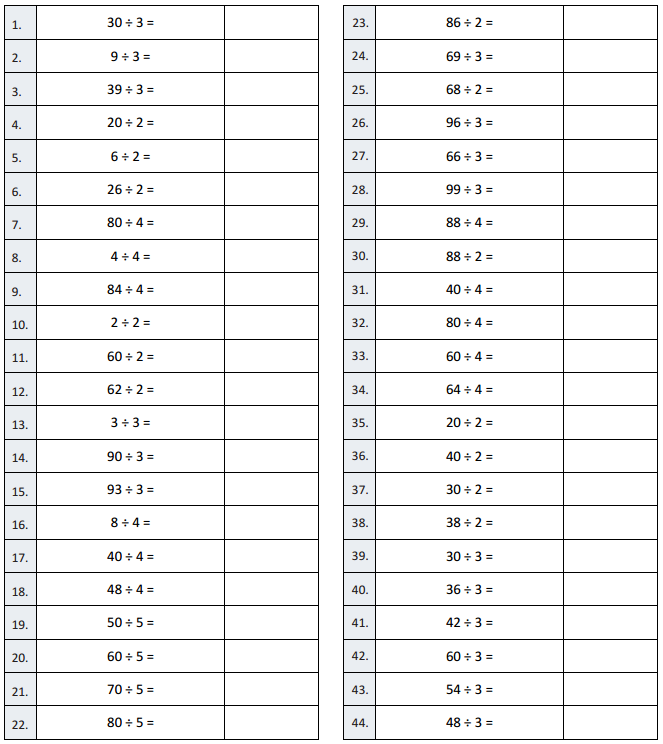
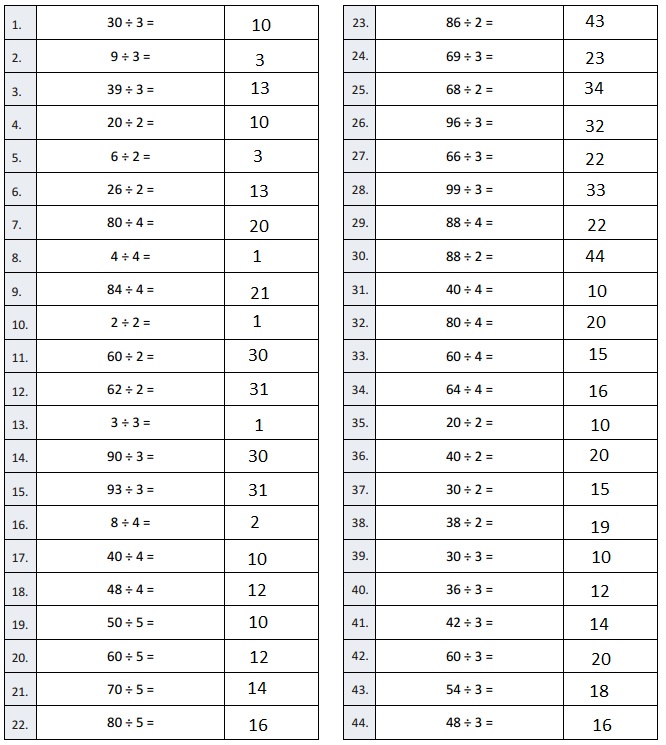
Question 1.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10,

Explanation :
Given expression 30 ÷ 3 when 30 is divided by 3
we get 10, So quotient is 10 and remainder is 0 and
(3 X 10 = 30).

Question 2.
9 ÷ 3 =
Answer:
9 ÷ 3 = 3,

Explanation :
Given expression 9 ÷ 3 when 9 is divided by 3
we get 3, So quotient is 3 and remainder is 0 and
(3 X 3 = 9).

Question 3.
39 ÷ 3 =
Answer:
39 ÷ 3 = 13,

Explanation :
Given expression 39 ÷ 3 when 39 is divided by 3
we get 13, So quotient is 13 and remainder is 0 and
(3 X 13 = 39).

Question 4.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10,

Explanation :
Given expression 20 ÷ 2 when 20 is divided by 2
we get 10, So quotient is 10 and remainder is 0 and
(2 X 10 = 20).

Question 5.
6 ÷ 2 =
Answer:
6 ÷ 2 = 3,

Explanation :
Given expression 6 ÷ 2 when 6 is divided by 2
we get 3, So quotient is 3 and remainder is 0 and
(2 X 3 = 6).

Question 6.
26 ÷ 2 =
Answer:
26 ÷ 2 = 13,

Explanation :
Given expression 26 ÷ 2 when 26 is divided by 2
we get 13, So quotient is 13 and remainder is 0 and
(2 X 13 = 26).

Question 7.
80 ÷ 4 =
Answer:
80 ÷ 4 = 20,

Explanation :
Given expression 80 ÷ 4 when 80 is divided by 4
we get 20, So quotient is 20 and remainder is 0 and
(4 X 20 = 80).

Question 8.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1,

Explanation :
Given expression 4 ÷ 4 when 4 is divided by 4
we get 1, So quotient is 4 and remainder is 0 and
(4 X 1 = 4).

Question 9.
84 ÷ 4 =
Answer:
84 ÷ 4 = 21,

Explanation :
Given expression 84 ÷ 4 when 84 is divided by 4
we get 21, So quotient is 21 and remainder is 0 and
(4 X 21 = 84).

Question 10.
2 ÷ 2 =
Answer:
2 ÷ 2 = 1,

Explanation :
Given expression 2 ÷ 2 when 2 is divided by 2
we get 1, So quotient is 1 and remainder is 0 and
(2 X 1 = 2).

Question 11.
60 ÷ 2 =
Answer:
60 ÷ 2 = 30,

Explanation :
Given expression 60 ÷ 2 when 60 is divided by 2
we get 30, So quotient is 30 and remainder is 0 and
(2 X 30 = 60).

Question 12.
62 ÷ 2 =
Answer:
62 ÷ 2 = 31,

Explanation :
Given expression 62 ÷ 2 when 62 is divided by 2
we get 31, So quotient is 31 and remainder is 0 and
(2 X 31 = 62).

Question 13.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1,

Explanation :
Given expression 3 ÷ 3 when 3 is divided by 3
we get 1, So quotient is 1 and remainder is 0 and
(3 X 1 = 3).

Question 14.
90 ÷ 3 =
Answer:
90 ÷ 3 = 30,

Explanation :
Given expression 90 ÷ 3 when 90 is divided by 3
we get 30, So quotient is 30 and remainder is 0 and
(3 X 30 = 90).

Question 15.
93 ÷ 3 =
Answer:
93 ÷ 3 = 31,

Explanation :
Given expression 93 ÷ 3 when 93 is divided by 3
we get 31, So quotient is 31 and remainder is 0 and
(3 X 31 = 93).

Question 16.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2,

Explanation :
Given expression 8 ÷ 4 when 8 is divided by 4
we get 2, So quotient is 2 and remainder is 0 and
(4 X 2 = 8).

Question 17.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10,

Explanation :
Given expression 40 ÷ 4 when 40 is divided by 4
we get 10, So quotient is 10 and remainder is 0 and
(4 X 10 = 40).

Question 18.
48 ÷ 4 =
Answer:
48 ÷ 4 = 12,

Explanation :
Given expression 48 ÷ 4 when 48 is divided by 4
we get 12, So quotient is 12 and remainder is 0 and
(4 X 12 = 48).

Question 19.
50 ÷ 5 =
Answer:
50 ÷ 5 = 10,

Explanation :
Given expression 50 ÷ 5 when 50 is divided by 5
we get 10, So quotient is 10 and remainder is 0 and
(5 X 10 = 50).

Question 20.
60 ÷ 5 =
Answer:
60 ÷ 5 = 12,

Explanation :
Given expression 60 ÷ 5 when 60 is divided by 5
we get 12, So quotient is  and remainder is 0 and
(5 X 12 = 60).

Question 21.
70 ÷ 5 =
Answer:
70 ÷ 5 = 14,

Explanation :
Given expression 70 ÷ 5 when 70 is divided by 5
we get 14, So quotient is 14 and remainder is 0 and
(5 X 14 = 70).

Question 22.
80 ÷ 5 =
Answer:
80 ÷ 5 = 16,

Explanation :
Given expression 80 ÷ 5 when 80 is divided by 5
we get 16, So quotient is 16 and remainder is 0 and
(5 X 16 = 80).

Question 23.
86 ÷ 2 =
Answer:
86 ÷ 2 = 43,

Explanation :
Given expression 86 ÷ 2 when 86 is divided by 2
we get 43, So quotient is 43 and remainder is 0 and
(2 X 43 = 86).

Question 24.
69 ÷ 3 =
Answer:
69 ÷ 3 = 23,

Explanation :
Given expression 69 ÷ 3 when 69 is divided by 3
we get 23, So quotient is 23 and remainder is 0 and
(3 X 23 = 69).

Question 25.
68 ÷ 2 =
Answer:
68 ÷ 2 = 34,

Explanation :
Given expression 68 ÷ 2 when 68 is divided by 2
we get 34, So quotient is 34 and remainder is 0 and
(2 X 34 = 68).

Question 26.
96 ÷ 3 =
Answer:
96 ÷ 3 = 32,

Explanation :
Given expression 96 ÷ 3 when 96 is divided by 3
we get 32, So quotient is 32 and remainder is 0 and
(3 X 32 = 96).

Question 27.
66 ÷ 3 =
Answer:
66 ÷ 3 = 22,

Explanation :
Given expression 66 ÷ 3 when 66 is divided by 3
we get 22, So quotient is 22 and remainder is 0 and
(3 X 22 = 66).

Question 28.
99 ÷ 3 =
Answer:
99 ÷ 3 = 33,

Explanation :
Given expression 99 ÷ 3 when 99 is divided by 3
we get 33, So quotient is 33 and remainder is 0 and
(3 X 33 = 99).

Question 29.
88 ÷ 4 =
Answer:
88 ÷ 4 = 22,

Explanation :
Given expression 88 ÷ 4 when 88 is divided by 4
we get 22, So quotient is 22 and remainder is 0 and
(4 X 22 = 88).

Question 30.
88 ÷ 2 =
Answer:
88 ÷ 2 = 44,

Explanation :
Given expression 88 ÷ 2 when 88 is divided by 2
we get 44, So quotient is 44 and remainder is 0 and
(2 X 44 = 88).

Question 31.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10,

Explanation :
Given expression 40 ÷ 10 when 40 is divided by 4
we get 10, So quotient is 10 and remainder is 0 and
(4 X 10 = 40).

Question 32.
80 ÷ 4 =
Answer:
80 ÷ 4 = 20,

Explanation :
Given expression 80 ÷ 4 when 80 is divided by 4
we get 20, So quotient is 20 and remainder is 0 and
(4 X 20 = 80).

Question 33.
60 ÷ 4 =
Answer:
60 ÷ 4 = 15,

Explanation :
Given expression 60 ÷ 4 when 60 is divided by 4
we get 15, So quotient is 15 and remainder is 0 and
(4 X 15 = 60).

Question 34.
64 ÷ 4 =
Answer:
64 ÷ 4 = 16,

Explanation :
Given expression 64 ÷ 4 when 64 is divided by 4
we get 16, So quotient is 16 and remainder is 0 and
(4 X 16 = 64).

Question 35.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10,

Explanation :
Given expression 20 ÷ 2 when 20 is divided by 2
we get 10, So quotient is 10 and remainder is 0 and
(2 X 10 = 20).

Question 36.
40 ÷ 2 =
Answer:
40 ÷ 2 = 20,

Explanation :
Given expression 40 ÷ 2 when 40 is divided by 2
we get 20, So quotient is 20 and remainder is 0 and
(2 X 20 = 40).

Question 37.
30 ÷ 2 =
Answer:
30 ÷ 2 = 15,

Explanation :
Given expression 30 ÷ 2 when 30 is divided by 2
we get 15, So quotient is 15 and remainder is 0 and
(2 X 15 = 30).

Question 38.
38 ÷ 2 =
Answer:
38 ÷ 2 = 19,

Explanation :
Given expression 38 ÷ 2 when 38 is divided by 2
we get 19, So quotient is 19 and remainder is 0 and
(2 X 19 = 38).

Question 39.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10,

Explanation :
Given expression 30 ÷ 3 when 30 is divided by 3
we get 10, So quotient is 10 and remainder is 0 and
(3 X 10 = 30).

Question 40.
36 ÷ 3 =
Answer:
36 ÷ 3 = 12,

Explanation :
Given expression 36 ÷ 3 when 36 is divided by 3
we get 12, So quotient is 12 and remainder is 0 and
(3 X 12 = 36).

Question 41.
42 ÷ 3 =
Answer:
42 ÷ 3 = 14,

Explanation :
Given expression 42 ÷ 3 when 42 is divided by 3
we get 14, So quotient is 14 and remainder is 0 and
(3 X 14 = 42).

Question 42.
60 ÷ 3 =
Answer:
60 ÷ 3 = 20,

Explanation :
Given expression 60 ÷ 3 when 60 is divided by 3
we get 20, So quotient is 20 and remainder is 0 and
(3 X 20 = 60).

Question 43.
54 ÷ 3 =
Answer:
54 ÷ 3 = 18,

Explanation :
Given expression 54 ÷ 3 when 54 is divided by 3
we get 18, So quotient is 18 and remainder is 0 and
(3 X 18 = 54).

Question 44.
48 ÷ 3 =
Answer:
48 ÷ 3 = 16,

Explanation :
Given expression 48 ÷ 3 when 48 is divided by 3
we get 16, So quotient is 16 and remainder is 0 and
(3 X 16 = 48).

Eureka Math Grade 4 Module 3 Lesson 19 Problem Set Answer Key

Question 1.
When you divide 94 by 3, there is a remainder of 1.
Model this problem with place value disks. In the place
value disk model, how did you show the remainder?
Answer:

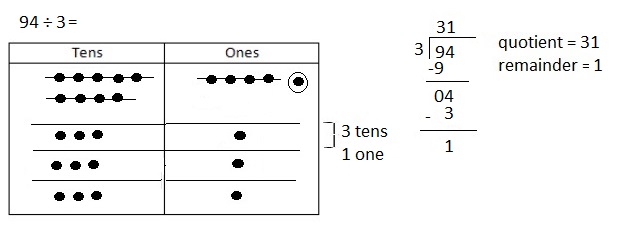
I showed my remainder by circling the remaining one
in the ones place.

Explanation:
When we divide 94 by 3, there is a remainder of 1.
Modeled the problem with place value disks. In the place
value disk model, showed the remainder by circling the
remaining one in the ones place.

Question 2.
Cayman says that 94 ÷ 3 is 30 with a remainder of 4.
He reasons this is correct because (3 × 30) + 4 = 94.
What mistake has Cayman made? Explain how he can
correct his work.
Answer:
Cayman mistake is that his remainder is greater than
his divisor means he can divide more.
Instead of 30 groups he can make 31 groups.

Explanation:
Given Cayman says that 94 ÷ 3 is 30 with a remainder of 4.
He reasons this is correct because (3 × 30) + 4 = 94.
Instead of 30 groups he can make 31 groups,
94 ÷ 3 when 94 is divided by 3
we get 31 as quotient and remainder is 1.

Question 3.
The place value disk model is showing 72 ÷ 3.
Complete the model. Explain what happens to the
1 ten that is remaining in the tens column.

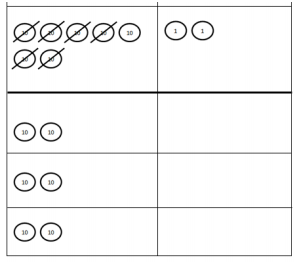
Answer:
The 1 ten remaining gets decomposed into
10 ones column,

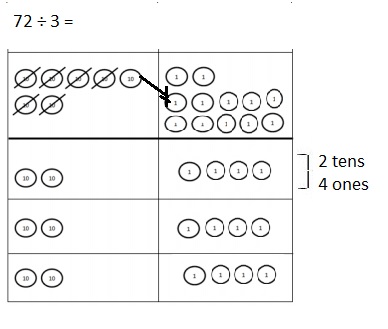
Explanation:
Given the place value disk model is showing 72 ÷ 3.
Completed the model. Explained what happens to the
1 ten that is remaining in the tens column gets decomposed
into10 ones column as shown above.

Question 4.
Two friends evenly share 56 dollars.
a. They have 5 ten-dollar bills and 6 one-dollar bills.
Draw a picture to show how the bills will be shared.
Will they have to make change at any stage?
Answer:
Yes, they will have to make change for 1 dollar bill.

Explanation:
In order to share its the ten dollar bill needs to be decomposed
into one dollar bills.
Drawn a picture to show how the bills will be shared
and have to make changes as shown above.

b. Explain how they share the money evenly.
Answer:
Each friend gets 2 ten dollar bills and 8 one dollar bills,

Explanation:
Given two friends evenly share 56 dollars,
they have 5 ten-dollar bills and 6 one-dollar bills,
they shared the money evenly as 2 ten dollar bills and
8 one dollar bills.

Question 5.
Imagine you are filming a video explaining the
blem 45 ÷ 3 to new fourth graders. Create a script to
explain how you can keep dividing after getting a
remainder of 1 ten in the first step.
Answer:

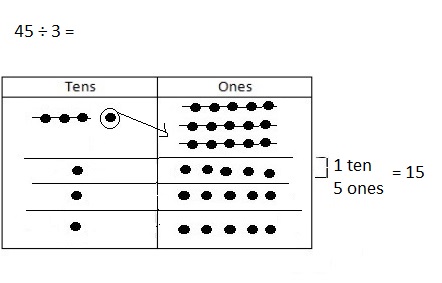
Explanation:
Watch as I solve 45 ÷ 3 using a place value chart.
First I divide my tens, Each of the 3 groups can equally
have 1 ten. There is 1 ten remaining, We can continue
dividing by decomposing the 1 ten into 10 ones. Watch as
I show this on my chart. Now I have 15 ones that can be
equally distributed into our 3 groups. Each group will get
5 ones. Now we can see that 45 ÷ 3 is 1 ten 5 ones or 15.

Eureka Math Grade 4 Module 3 Lesson 19 Exit Ticket Answer Key

Question 1.
Molly’s photo album has a total of 97 pictures.
Each page of the album holds 6 pictures.
How many pages can Molly fill? Will there be any
pictures left? If so, how many? Use place value disks to solve.
Answer:
Molly can fill 16 pages,
Yes, there will be 1 picture left,

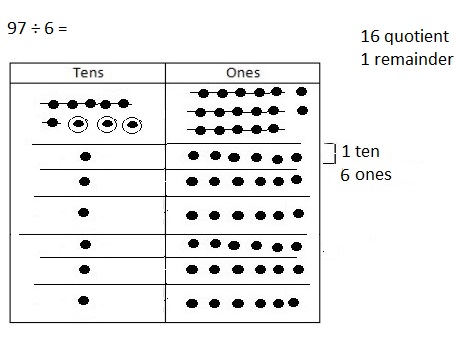
Explanation:
Given Molly’s photo album has a total of 97 pictures.
Each page of the album holds 6 pictures, So number of
pages can Molly fill are 97 ÷ 6 = 16 quotient and 1 remainder
means Molly can fill 16 pages and there will be 1 picture left
as shown above using place value disks.

Question 2.
Marti’s photo album has a total of 45 pictures.
Each page holds 4 pictures. She said she can only
fill 10 pages completely. Do you agree? Explain why or why not.
Answer:
No, I don’t agree, why because she can fill 11 pages completly
with 1 picture left,

Explanation:
Marti’s photo album has a total of 45 pictures.
Each page holds 4 pictures. She said she can only
fill 10 pages completely, I don’t agree because
if we divide 45 pictures by 4 we get 11 pages but she
said she can only fill 10 pages completely so disagree.

Eureka Math Grade 4 Module 3 Lesson 19 Homework Answer Key

Question 1.
When you divide 86 by 4, there is a remainder of 2.
Model this problem with place value disks. In the
place value disk model, how can you see that there is a remainder?
Answer:
I showed my remainder by circling the remaining two
in the ones place,

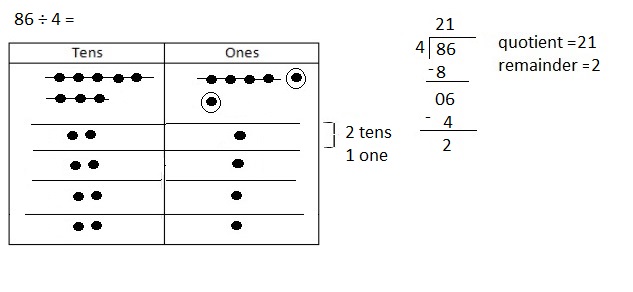
Explanation:
When we divide 86 by 4, there is a remainder of 2.
Modeled the problem with place value disks. In the place
value disk model, showed the remainder by circling the
remaining two in the ones place.

Question 2.
Francine says that 86 ÷ 4 is 20 with a remainder of 6.
She reasons this is correct because (4 × 20) + 6 = 86.
What mistake has Francine made? Explain how she can
correct her work.
Answer:
Francine mistake is that her remainder is greater than
his divisor means he can divide more.
Instead of 20 groups he can make 21 groups,

Explanation:
Given Francine says that 86 ÷ 4 is 20 with a remainder of 6.
Her reasons this is correct because (4 X 20) + 6 = 86.
Instead of 20 groups he can make 21 groups,
86 ÷ 4 when 86 is divided by 4
we get 21 as quotient and remainder is 2.

Question 3.
The place value disk model is showing 67 ÷ 4.
Complete the model. Explain what happens to
the 2 tens that are remaining in the tens column.

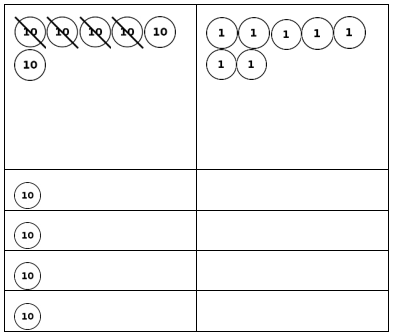
Answer:
The 2 tens remaining gets decomposed into
20 ones column,

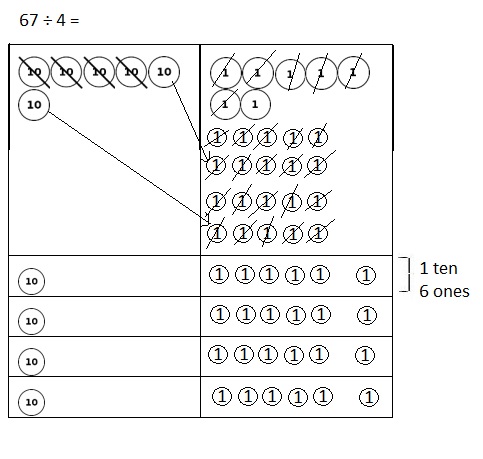
Explanation:
Given the place value disk model is showing 67 ÷ 4.
Completed the model. Explained what happens to the
2 tens that is remaining in the tens column gets decomposed
into 20 ones column as shown above.

Question 4.
Two friends share 76 blueberries.
a. To count the blueberries, they put them into small
bowls of 10 blueberries. Draw a picture to show how the
blueberries can be shared equally. Will they have to split
apart any of the bowls of 10 blueberries when they share them?
Answer:
Yes, they will have to make change for 1 bowl,

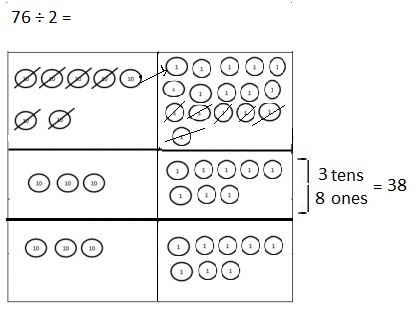
Explanation:
In order to share it the 10 blueberries needs to be decomposed
into ones blueberries.
Drawn a picture to show how the blueberries will be shared
and have to make changes as shown above.

b. Explain how the friends can share the blueberries fairly.
Answer:
Each friend gets 3 ten blueberries and 8 blueberries,

Explanation:
Given two friends can share 76 blueberries,
they have 3 ten-blueberries and 8 one-blueberries,
Each friend shared 3 ten blueberries and 8 blueberries.

Question 5.
Imagine you are drawing a comic strip showing how to
solve the problem 72 ÷ 4 to new fourth graders. Create a
script to explain how you can keep dividing after getting a
remainder of 3 tens in the first step.
Answer:

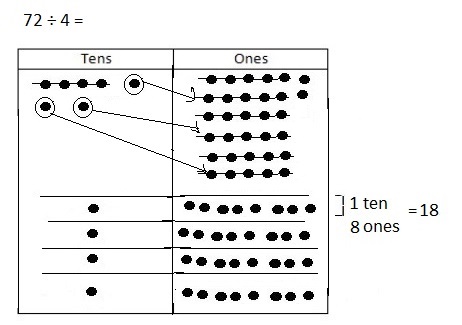
Explanation:
Created a script as I solve 72 ÷ 4 using a place value chart.
First I divide my tens into 4 groups I get 4 tens into 1 group,
There are 3 tens remaining, We can continue
dividing by decomposing the tens into 30 ones. Watch as
I show this on my chart. Now I have 32 ones that can be
equally distributed into our 4 groups. Each group will get
8 ones. Now we can see that 72 ÷ 4 is 1 ten 8 ones or 18.