Engage NY Eureka Math 5th Grade Module 6 Lesson 3 Answer Key
Eureka Math Grade 5 Module 6 Lesson 3 Problem Set Answer Key
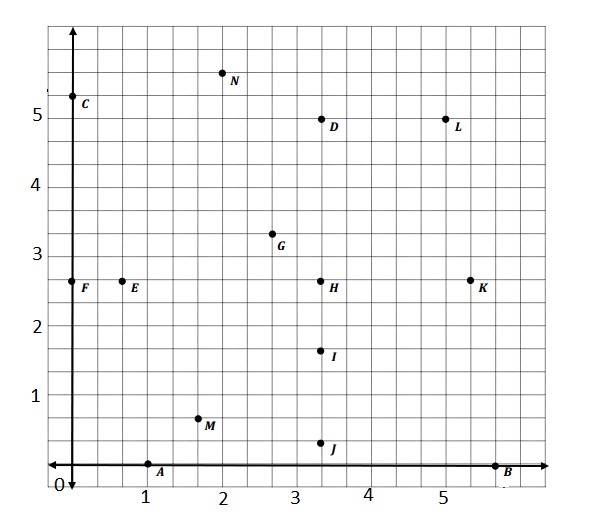
Question 1.
Use the grid below to complete the following tasks.
a. Construct an x-axis that passes through points A and B.
b. Construct a perpendicular y-axis that passes through points C and F.
c. Label the origin as 0.
d. The x-coordinate of B is 5\(\frac{2}{3}\). Label the whole numbers along the x-axis.
e. The y-coordinate of C is 5\(\frac{1}{3}\). Label the whole numbers along the y-axis.

Answer:
Question 2.
For all of the following problems, consider the points A through N on the previous page.
a. Identify all of the points that have an x-coordinate of 3\(\frac{1}{3}\).
Answer :
The points that have an x-coordinate of 3\(\frac{1}{3}\) are J, I, H and D .
b. Identify all of the points that have a y-coordinate of 2\(\frac{2}{3}\).
Answer :
The points that have a y-coordinate of 2\(\frac{2}{3}\) are E, F, H and K .
c. Which point is 3\(\frac{1}{3}\) units above the x-axis and 2\(\frac{2}{3}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point H and its coordinate pair is ( 3\(\frac{1}{3}\) , 2\(\frac{2}{3}\) )
d. Which point is located 5\(\frac{1}{3}\) units from the y-axis?
Answer :
Point C .
e. Which point is located 1\(\frac{2}{3}\) units along the x-axis?
Answer :
Point M .
f. Give the coordinate pair for each of the following points.
K: __
I: ______
B: ______
C: ______
Answer :
The coordinate pair of K is (5\(\frac{1}{3}\), 2\(\frac{2}{3}\))
The coordinate pair of I is (3\(\frac{1}{3}\), 1\(\frac{2}{3}\))
The coordinate pair of B is (5\(\frac{2}{3}\), 0)
The coordinate pair of C is (0, 5\(\frac{1}{3}\) )
g. Name the points located at the following coordinates.
(1\(\frac{2}{3}\), \(\frac{2}{3}\)) ______
(0, 2\(\frac{2}{3}\)) ______
(1, 0) ______
(2, 5\(\frac{2}{3}\)) ______
h. Which point has an equal x- and y-coordinate? ________
i. Give the coordinates for the intersection of the two axes. (____ , ____) Another name for this point on the plane is the ___________.
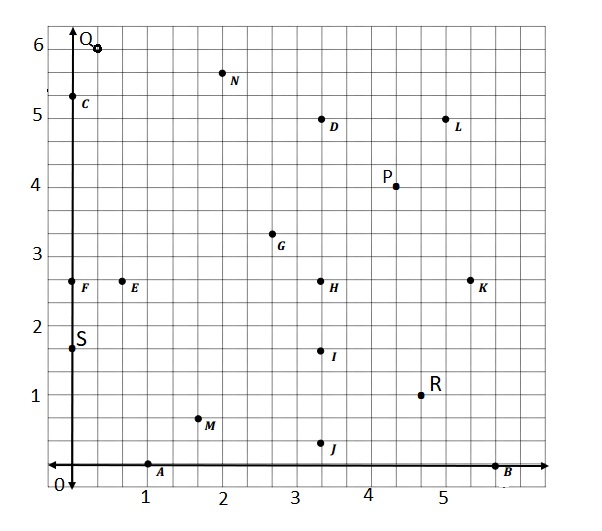
j. Plot the following points.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))
k. What is the distance between E and H, or EH?
l. What is the length of HD?
m. Would the length of ED be greater or less than EH+HD?
n. Jack was absent when the teacher explained how to describe the location of a point on the coordinate plane. Explain it to him using point J.
Answer:
(1\(\frac{2}{3}\), \(\frac{2}{3}\)) is Point M
(0, 2\(\frac{2}{3}\)) is Point F
(1, 0) is Point A
(2, 5\(\frac{2}{3}\)) is Point N
h. The point L has an equal x- and y-coordinate
i. (0,0) Origin.
j.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))
Eureka Math Grade 5 Module 6 Lesson 3 Exit Ticket Answer Key
Question 1.
Use a ruler on the grid below to construct the axes for a coordinate plane. The x-axis should intersect points L and M. Construct the y-axis so that it contains points K and L. Label each axis.
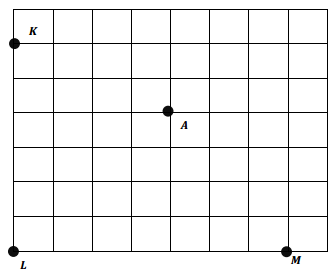
a. Place a hash mark on each grid line on the x- and y-axis.
b. Label each hash mark so that A is located at (1, 1).
c. Plot the following points:
| Point | X -coordinate |
Y -coordinate |
| B | \(\frac{1}{4}\) | 0 |
| C | 1 | \(\frac{3}{4}\) |
Answer:
Eureka Math Grade 5 Module 6 Lesson 3 Homework Answer Key
Question 1.
Use the grid below to complete the following tasks.
a. Construct a y-axis that passes through points Y and Z.
b. Construct a perpendicular x-axis that passes through points Z and X.
c. Label the origin as 0.
d. The y-coordinate of W is 2\(\frac{3}{5}\). Label the whole numbers along the y-axis.
e. The x-coordinate of V is 2\(\frac{2}{5}\). Label the whole numbers along the x-axis.
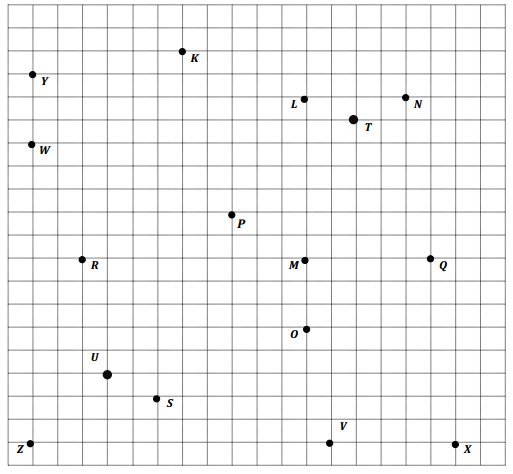
Answer:
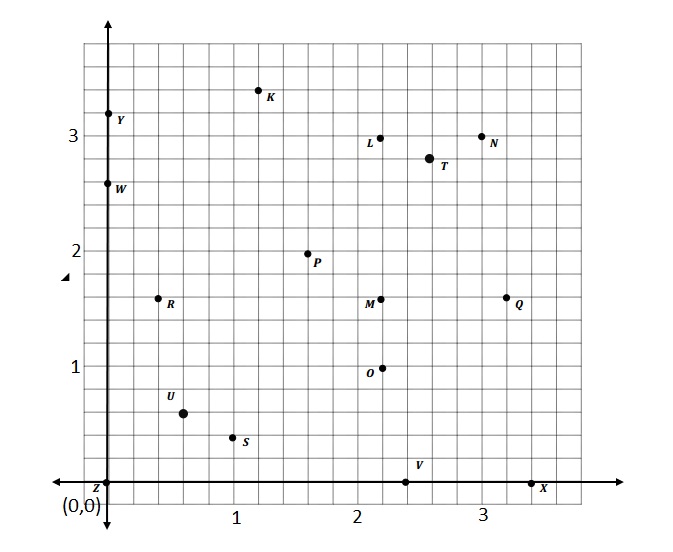
Question 2.
For all of the following problems, consider the points K through X on the previous page.
a. Identify all of the points that have a y-coordinate of 1\(\frac{3}{5}\).
Answer :
The points that have a y-coordinate of 1\(\frac{3}{5}\) are R, M and Q.
b. Identify all of the points that have an x-coordinate of 2\(\frac{1}{5}\).
Answer :
The points that have an x-coordinate of 2\(\frac{1}{5}\) are O, M and L .
c. Which point is 1\(\frac{3}{5}\) units above the x-axis and 3\(\frac{1}{5}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point P and its coordinate pair is ( 1\(\frac{3}{5}\) , 3\(\frac{1}{5}\) )
d. Which point is located 1\(\frac{1}{5}\) units from the y-axis?
Answer :
Point K .
e. Which point is located \(\frac{2}{5}\) unit along the x-axis?
Answer :
Point R .
f. Give the coordinate pair for each of the following points.
T: ________
U: ________
S: ________
K: ________
Answer :
The coordinate pair of T is (2\(\frac{3}{5}\), 2\(\frac{4}{5}\))
The coordinate pair of U is ( \(\frac{3}{5}\), \(\frac{3}{5}\))
The coordinate pair of S is ( 1, \(\frac{2}{5}\))
The coordinate pair of K is (1\(\frac{1}{5}\), 3\(\frac{2}{5}\))
g. Name the points located at the following coordinates.
(\(\frac{3}{5}\), \(\frac{3}{5}\)) ______
(3\(\frac{2}{5}\), 0) ______
(2\(\frac{1}{5}\), 3) ______
(0, 2\(\frac{3}{5}\)) ______
Answer :
(\(\frac{3}{5}\), \(\frac{3}{5}\)) is Point U
(3\(\frac{2}{5}\), 0) is Point X
(2\(\frac{1}{5}\), 3) is Point L
(0, 2\(\frac{3}{5}\)) is Point W
h. Plot a point whose x- and y-coordinates are equal. Label your point E.
Answer :
Point is plotted at (1,1) where x and y coordinates are 1
i. What is the name for the point on the plane where the two axes intersect? ___________ Give the coordinates for this point. ( ____ , ____ )
Answer :
(0,0) ,Origin .
j. Plot the following points.
A: (1\(\frac{1}{5}\), 1)
B: (\(\frac{1}{5}\), 3)
C: (2\(\frac{4}{5}\), 2\(\frac{2}{5}\))
D: (1\(\frac{1}{5}\), 0)
Answer :
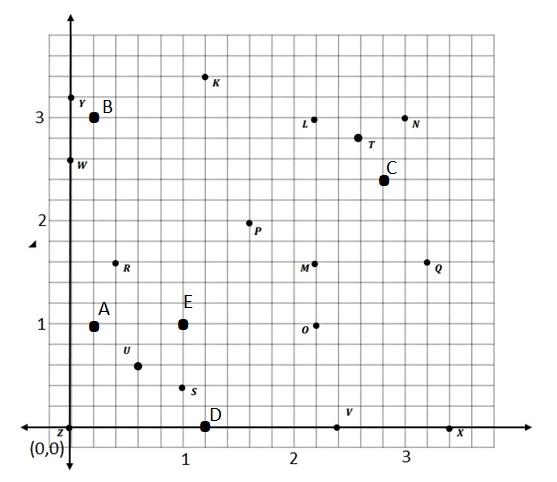
k. What is the distance between L and N, or LN?
Answer :
Point L is at 2\(\frac{1}{5}\)
Point N is at 3
Distance of LN = 3 – 2\(\frac{1}{5}\) = \(\frac{15}{5}\) – \(\frac{11}{5}\)= \(\frac{4}{5}\)
l. What is the distance of MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point Q is at 3\(\frac{1}{5}\)
Distance of MQ = 3 \(\frac{1}{5}\) – 2\(\frac{1}{5}\) = \(\frac{16}{5}\) – \(\frac{11}{5}[/latex = [latex]\frac{5}{5}\) =1
m. Would RM be greater than, less than, or equal to LN+MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point R is at \(\frac{2}{5}\)
Distance of RM = 2 \(\frac{1}{5}\) – \(\frac{2}{5}\) = \(\frac{11}{5}\) – \(\frac{2}{5}\) = \(\frac{9}{5}\)
Distance of LN = \(\frac{4}{5}\)
Distance of MQ = 1
LN +MQ = 1 + \(\frac{4}{5}\) = \(\frac{9}{5}\)
RM is Equal to LN +MQ
n. Leslie was explaining how to plot points on the coordinate plane to a new student, but she left off some important information. Correct her explanation so that it is complete.
“All you have to do is read the coordinates; for example, if it says (4, 7), count four, then seven, and put a point where the two grid lines intersect.”
Answer:
Leslie should say how to specify which is x and y coordinates and how to plot the points .