Prasanna

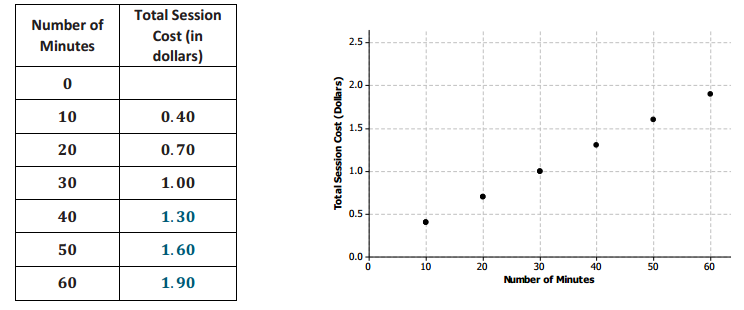
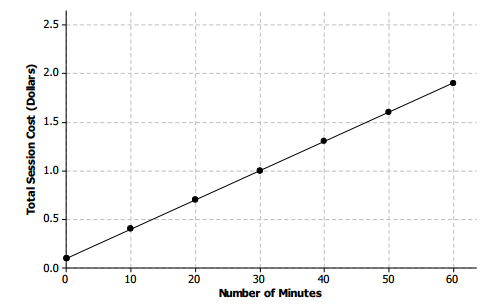
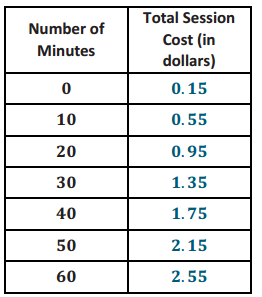
Engage NY Eureka Math 8th Grade Module 6 Lesson 4 Answer Key

Eureka Math Grade 8 Module 6 Lesson 4 Exercise Answer Key

Exercise 1.
Read through each of the scenarios, and choose the graph of the function that best matches the situation. Explain the reason behind each choice.
a. A bathtub is filled at a constant rate of 1.75 gallons per minute.
b. A bathtub is drained at a constant rate of 2.5 gallons per minute.
c. A bathtub contains 2.5 gallons of water.
d. A bathtub is filled at a constant rate of 2.5 gallons per minute.

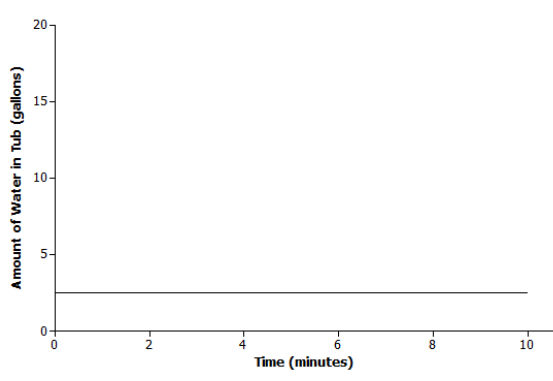
Scenario:
Explanation:
Answer:
Scenario: c

Explanation: The amount of water in the tub does not change over time; it remains constant at 2.5 gallons.

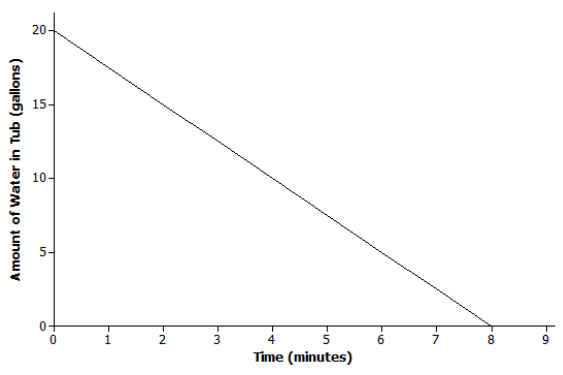
Scenario:
Explanation:
Answer:
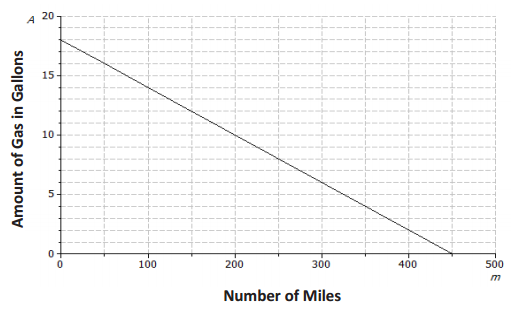
Scenario: b

Explanation: The bathtub is being drained at a constant rate of 2.5 gallons per minute. So, the amount of water is decreasing, which means that the slope of the line is negative. The graph of the function also shows that there are initially 20 gallons of water in the tub.

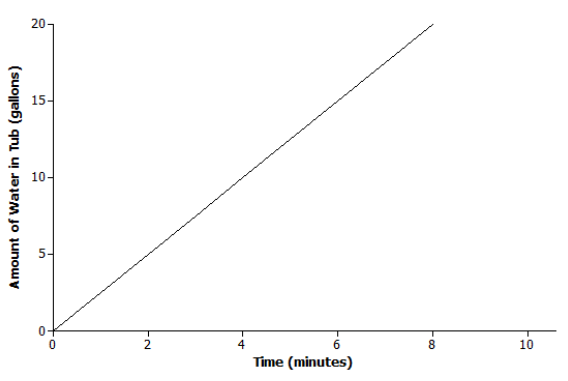
Scenario:
Explanation:
Answer:
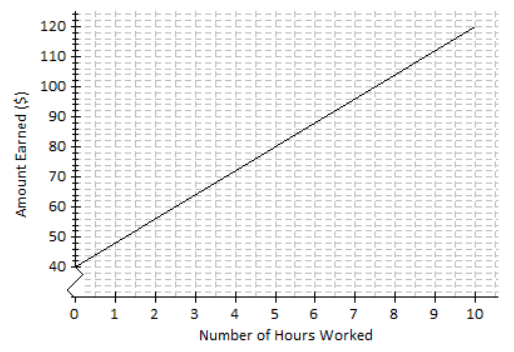
Scenario: d

Explanation: The tub is being filled at a constant rate of 2.5 gallons per minute, which implies that the amount of water in the tub is increasing, so the line has a positive slope. Based on the graph, the amount of water is also increasing at a faster rate than in choice (a).

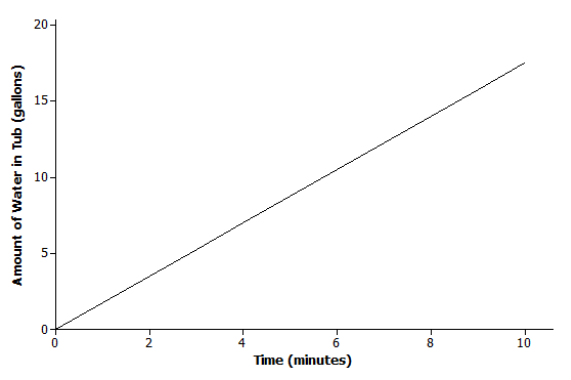
Scenario:
Explanation:
Answer:
Scenario: d

Explanation: The tub is being filled at a constant rate of 2.5 gallons per minute, which implies that the amount of water in the tub is increasing, so the line has a positive slope. Based on the graph, the amount of water is also increasing at a faster rate than in choice (a).

Exercise 2.
Read through each of the scenarios, and sketch a graph of a function that models the situation.
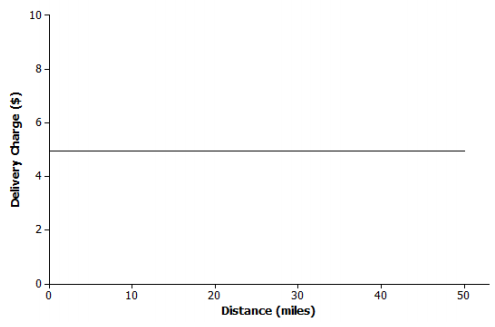
a. A messenger service charges a flat rate of $4.95 to deliver a package regardless of the distance to the destination.
Answer:

Answer:
The delivery charge remains constant regardless of the distance to the destination.

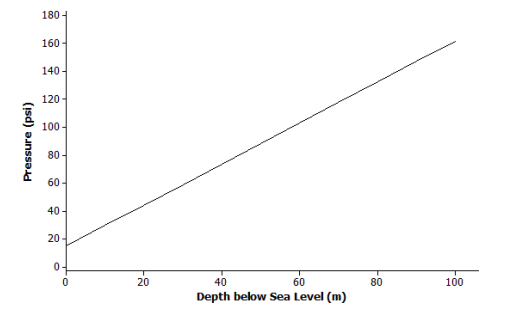
b. At sea level, the air that surrounds us presses down on our bodies at 14.7 pounds per square inch (psi). For every 10 meters that you dive under water, the pressure increases by 14.7 psi.

Answer:
The initial value is 14.7 psi. The function increases at a rate of 14.7 psi for every 10 meters, or 1.47 psi per meter.

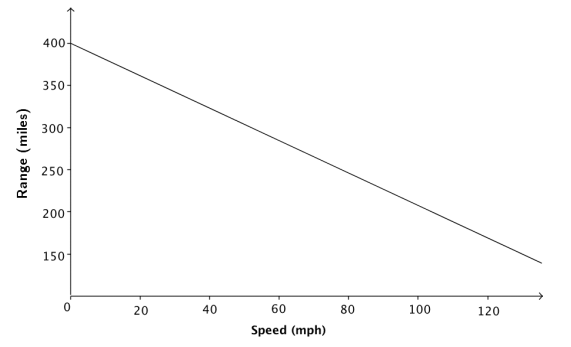
c. The range (driving distance per charge) of an electric car varies based on the average speed the car is driven. The initial range of the electric car after a full charge is 400 miles. However, the range is reduced by 20 miles for every 10 mph increase in average speed the car is driven.

Answer:
The initial value of the function is 400. The function is decreasing by 20 miles for every 10 mph increase in speed. In other words, the function decreases by 2 miles for every 1 mph increase in speed.

Exercise 3.
The graph below represents the total number of smartphones that are shipped to a retail store over the course of 50 days.

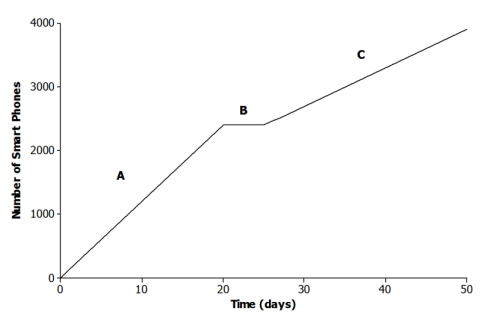
Match each part of the graph (A, B, and C) to its verbal description. Explain the reasoning behind your choice.
i. Half of the factory workers went on strike, and not enough smartphones were produced for normal shipments.
Answer:
C; if half of the workers went on strike, then the number of smartphones produced would be less than normal. The rate of change for C is less than the rate of change for A.

ii. The production schedule was normal, and smartphones were shipped to the retail store at a constant rate.
Answer:
A; if the production schedule is normal, the rate of change of interval A is greater than the rate of change of interval C.

iii. A defective electronic chip was found, and the factory had to shut down, so no smartphones were shipped.
Answer:
B; if no smartphones are shipped to the store, the total number remains constant during that time.

Exercise 4.
The relationship between Jameson’s account balance and time is modeled by the graph below.

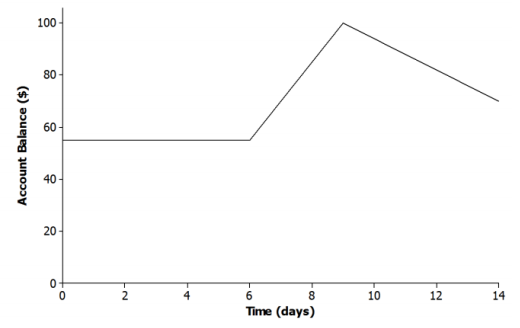
a. Write a story that models the situation represented by the graph.
Answer:
Answers will vary.
Jameson was sick and did not work for almost a whole week. Then, he mowed several lawns over the next few days and deposited the money into his account after each job. It rained several days, so instead of working, Jameson withdrew money from his account each day to go to the movies and out to lunch with friends.

b. When is the function represented by the graph increasing? How does this relate to your story?
Answer:
It is increasing between 6 and 9 days. Jameson earned money mowing lawns and made a deposit to his account each day. The money earned for each day was constant for these days. This is represented by a straight line.

c. When is the function represented by the graph decreasing? How does this relate to your story?
Answer:
It is decreasing between 9 and 14 days. Since Days 9–14 are represented by a straight line, this means that Jameson spent the money constantly over these days. Jameson cannot work because it is raining. Perhaps he withdraws money from his account to spend on different activities each day because he cannot work.

Eureka Math Grade 8 Module 6 Lesson 4 Problem Set Answer Key

Question 1.
Read through each of the scenarios, and choose the graph of the function that best matches the situation. Explain the reason behind each choice.
a. The tire pressure on Regina’s car remains at 30 psi.
b. Carlita inflates her tire at a constant rate for 4 minutes.
c. Air is leaking from Courtney’s tire at a constant rate.

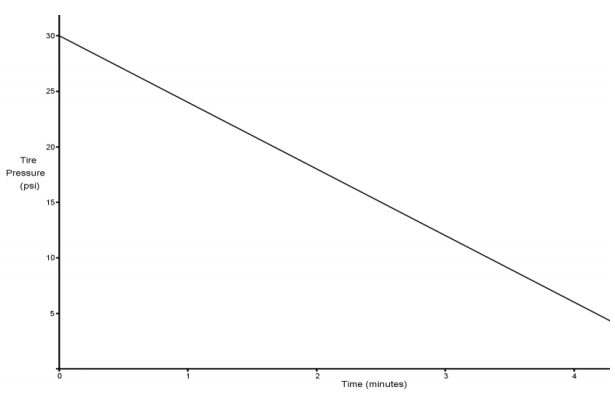
Scenario:
Explanation:
Answer:
Scenario: c

Explanation: The tire pressure decreases each minute at a constant rate.

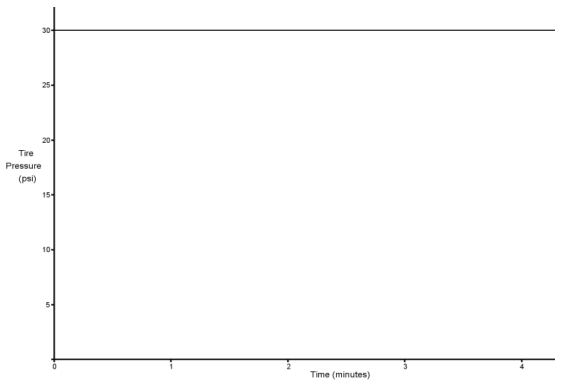
Scenario:
Explanation:
Answer:
Scenario: a

Explanation: The tire pressure remains at 30 psi.

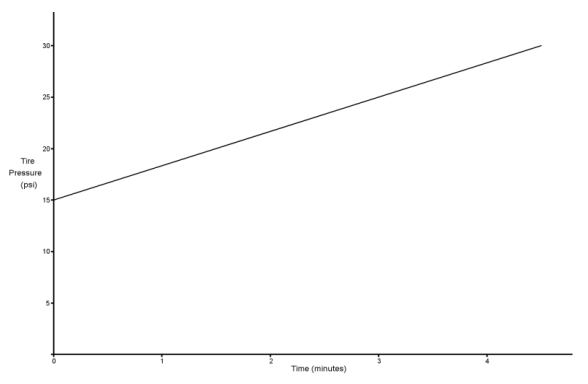
Scenario:
Explanation:
Answer:
Scenario: b

Explanation: The tire pressure is increasing each minute at a constant rate for 4 minutes.

Question 2.
A home was purchased for $275,000. Due to a recession, the value of the home fell at a constant rate over the next 5 years.
a. Sketch a graph of a function that models the situation.

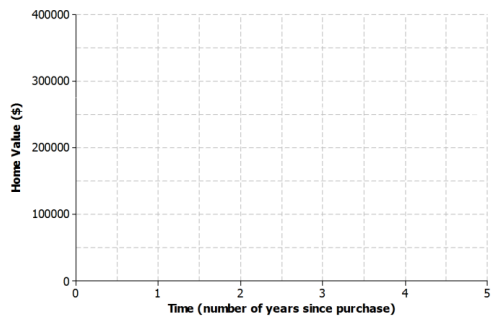
Answer:
Graphs will vary; a sample graph is provided.

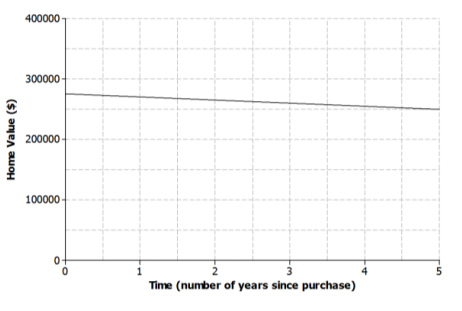
b. Based on your graph, how is the home value changing with respect to time?
Answer:
Answers will vary; a sample answer is provided.
The value is decreasing by $25,000 over 5 years or at a constant rate of $5,000 per year.

Question 3.
The graph below displays the first hour of Sam’s bike ride.

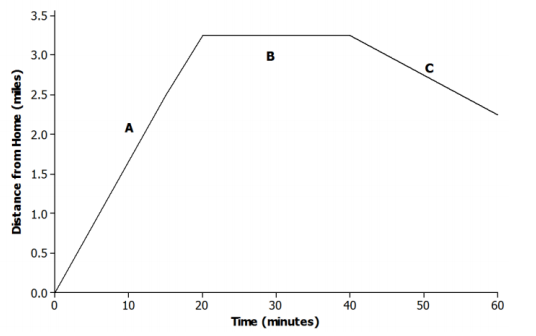
Match each part of the graph (A, B, and C) to its verbal description. Explain the reasoning behind your choice.
i. Sam rides his bike to his friend’s house at a constant rate.
Answer:
A; the distance from home should be increasing as Sam is riding toward his friend’s house.

ii. Sam and his friend bike together to an ice cream shop that is between their houses.
Answer:
C; Sam was at his friend’s house, but as they start biking to the ice cream shop, the distance from Sam’s home begins to decrease.

iii. Sam plays at his friend’s house.
Answer:
B; Sam remains at the same distance from home while he is at his friend’s house.

Question 4.
Using the axes below, create a story about the relationship between two quantities.
a. Write a story about the relationship between two quantities. Any quantities can be used (e.g., distance and time, money and hours, age and growth). Be creative. Include keywords in your story such as increase and decrease to describe the relationship.
Answer:
Answers will vary. Give students the freedom to write a basic linear story or a piecewise story.
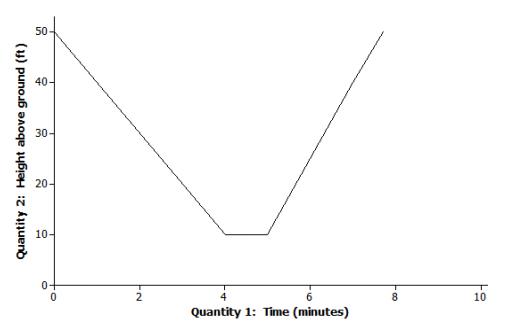
A rock climber begins her descent from a height of 50 feet. She slowly descends at a constant rate for 4 minutes. She takes a break for 1 minute; she then realizes she left some of her gear on top of the rock and climbs more quickly back to the top at a constant rate.

b. Label each axis with the quantities of your choice, and sketch a graph of the function that models the relationship described in the story.

Answer:
Answers will vary based on the story from part (a).

Eureka Math Grade 8 Module 6 Lesson 4 Exit Ticket Answer Key

Question 1.
The graph below shows the relationship between a car’s value and time.

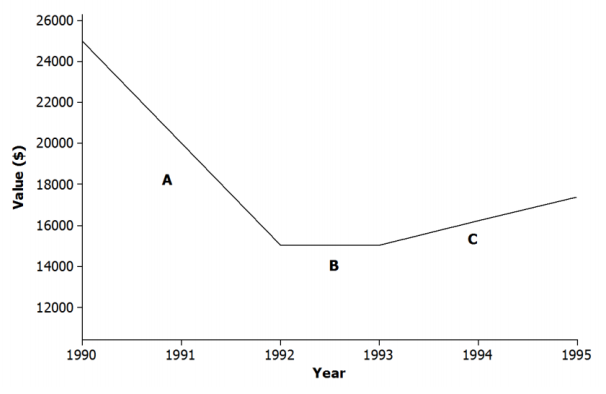
Match each part of the graph (A, B, and C) to its verbal description. Explain the reasoning behind your choice.
i. The value of the car holds steady due to a positive consumer report on the same model.
Answer:
B; if the value is holding steady, there is no change in the car’s value between years.

ii. There is a shortage of used cars on the market, and the value of the car rises at a constant rate.
Answer:
C; if the value of the car is rising, it represents an increasing function.

iii. The value of the car depreciates at a constant rate.
Answer:
A; if the value depreciates, it represents a decreasing function.

Question 2.
Henry and Roxy both drive electric cars that need to be recharged before use. Henry uses a standard charger at his home to recharge his car. The graph below represents the relationship between the battery charge and the amount of time it has been connected to the power source for Henry’s car.

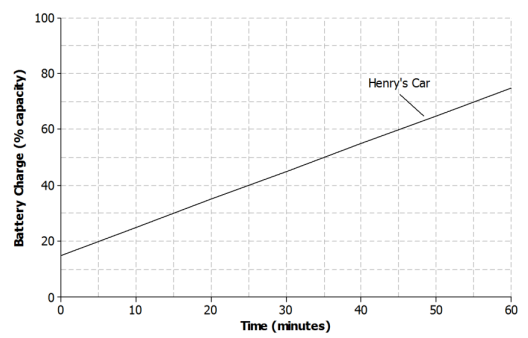
Answer:

a. Describe how Henry’s car battery is being recharged with respect to time.
Answer:
The battery charge is increasing at a constant rate of 10% every 10 minutes.

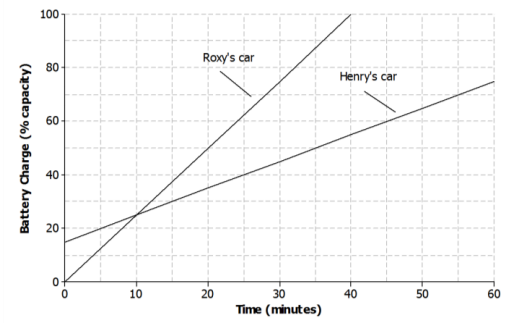
b. Roxy has a supercharger at her home that can charge about half of the battery in 20 minutes. There is no remaining charge left when she begins recharging the battery. Sketch a graph that represents the relationship between the battery charge and the amount of time on the axes above. Assume the relationship is linear.
Answer:
See the above graph.

c. Which person’s car will be recharged to full capacity first? Explain.
Answer:
Roxy’s car will be completely recharged first. Her supercharger has a greater rate of change compared to Henry’s charger.

Engage NY Eureka Math 8th Grade Module 7 Lesson 1 Answer Key

Eureka Math Grade 8 Module 7 Lesson 1 Example Answer Key

Example 1.
Write an equation that allows you to determine the length of the unknown side of the right triangle.

Answer:
Write an equation that allows you to determine the length of the unknown side of the right triangle.
Note: Students may use a different symbol to represent the unknown side length.
Let b cm represent the unknown side length. Then, 5² + b² = 13².
Verify that students wrote the correct equation; then, allow them to solve it. Ask them how they knew the correct answer was 12. They should respond that 13²-5² = 144, and since 144 is a perfect square, they knew that the unknown side length must be 12 cm.

Example 2.
Write an equation that allows you to determine the length of the unknown side of the right triangle.

Answer:
→ Write an equation that allows you to determine the length of the unknown side of the right triangle.
Let c cm represent the length of the hypotenuse. Then, 4² + 9² = c².

→ There is something different about this triangle. What is the length of the missing side? If you cannot find the length of the missing side exactly, then find a good approximation.
Provide students time to find an approximation for the length of the unknown side. Select students to share their answers and explain their reasoning. Use the points below to guide their thinking as needed.

→ How is this problem different from the last one?
The answer is c² = 97. Since 97 is not a perfect square, the exact length cannot be represented as an integer.

→ Since 97 is not a perfect square, we cannot determine the exact length of the hypotenuse as an integer; however, we can make an estimate. Think about all of the perfect squares we have seen and calculated in past discussions. The number 97 is between which two perfect squares?
The number 97 is between 81 and 100.
If c² were 81, what would be the length of the hypotenuse?
The length would be 9 cm.
If c² were 100, what would be the length of the hypotenuse?
The length would be 10 cm.

→ At this point, we know that the length of the hypotenuse is somewhere between 9 cm and 10 cm. Think about the length to which it is closest. The actual length of the hypotenuse is determined by the equation c² = 97. To which perfect square number, 100 or 81, is 97 closer?
The number 97 is closer to the perfect square 100 than to the perfect square 81.

→ Now that we know that the length of the hypotenuse of this right triangle is between 9 cm and 10 cm, but closer to 10 cm, let’s try to get an even better estimate of the length. Choose a number between 9 and 10 but closer to 10. Square that number. Do this a few times to see how close you can get to the number 97.

Provide students time to check a few numbers between 9 and 10. Students should see that the length is somewhere between 9.8 cm and 9.9 cm because 9.8² = 96.04 and 9.9² = 98.01. Some students may even check 9.85; 9.85² = 97.0225. This activity shows students that an estimation of the length being between 9 cm and 10 cm is indeed accurate, and it helps students develop an intuitive sense of how to estimate square roots.

Example 3.
Write an equation to determine the length of the unknown side of the right triangle.

Answer:
→ Write an equation to determine the length of the unknown side of the right triangle.
Let c cm represent the length of the hypotenuse. Then, 3² + 8² = c².
Verify that students wrote the correct equation, and then allow them to solve it. Instruct them to estimate the length, if necessary. Then, let them continue to work. When most students have finished, ask the questions below.

→ Could you determine an answer for the length of the hypotenuse as an integer?
No. Since c² = 73, the length of the hypotenuse is not a perfect square.
Optionally, you can ask, “Can anyone find the exact length of the hypotenuse as a rational number?” It is important that students recognize that no one can determine the exact length of the hypotenuse as a rational number at this point.

→ Since 73 is not a perfect square, we cannot determine the exact length of the hypotenuse as a whole number. Let’s estimate the length. Between which two whole numbers is the length of the hypotenuse? Explain.
Since 73 is between the two perfect squares 64 and 81, we know the length of the hypotenuse must be between 8 cm and 9 cm.
→ Is the length closer to 8 cm or 9 cm? Explain.
The length is closer to 9 cm because 73 is closer to 81 than it is to 64.
→ The length of the hypotenuse is between 8 cm and 9 cm but closer to 9 cm.

Example 4.
In the figure below, we have an equilateral triangle with a height of 10 Inches. What do we know about an equilateral triangle?

Answer:
→ In the figure below, we have an equilateral triangle with a height of 10 inches. What do we know about an equilateral triangle?
Equilateral triangles have sides that are all of the same length and angles that are all of the same degree, namely 60°.
Let’s say the length of the sides is x inches. Determine the approximate length of the sides of the triangle.

→ What we actually have here are two congruent right triangles.
Trace one of the right triangles on a transparency, and reflect it across the line representing the height of the triangle to convince students that an equilateral triangle is composed of two congruent right triangles.

With this knowledge, we need to determine the length of the base of one of the right triangles. If we know that the length of the base of the equilateral triangle is x inches, then what is the length of the base of one of the right triangles? Explain.

Eureka Math Grade 8 Module 7 Lesson 1 Exercise Answer Key

Exercise 1.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x cm be the length of the unknown side.
6² + x² = 11²
36 + x² = 121
x² = 85
The length of the unknown side of the triangle is approximately 9 cm. The number 85 is between the perfect squares 81 and 100. Since 85 is closer to 81 than 100, then the length of the unknown side of the triangle is closer to 9 cm than it is to 10 cm.

Exercise 2.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let c in. be the length of the hypotenuse.
6² + 10² = c²
36 + 100 = c²
136 = c²
The length of the hypotenuse is approximately 12 in. The number 136 is between the perfect squares 121 and 144. Since 136 is closer to 144 than 121, the length of the unknown side of the triangle is closer to 12 in. than it is to 11 in.

Exercise 3.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x mm be the length of the unknown side.
9² + x² = 11²
81 + x² = 121
x² = 40
The length of the hypotenuse is approximately 6 mm. The number 40 is between the perfect squares 36 and 49. Since 40 is closer to 36 than 49, then the length of the unknown side of the triangle is closer to 6 mm than it is to 7 mm.

Eureka Math Grade 8 Module 7 Lesson 1 Problem Set Answer Key

Question 1.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x in. be the length of the unknown side.
13² + x² = 15²
169 + x² = 225
x² = 56
The number 56 is between the perfect squares 49 and 64. Since 56 is closer to 49 than it is to 64, the length of the unknown side of the triangle is closer to 7 in. than it is to 8 in.

Question 2.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x cm be the length of the unknown side.
x² + 12² = 13²
x² + 144 = 169
x² = 25
x = 5
The length of the unknown side is 5 cm. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 25. Since 25 is a perfect square, 25 is equal to 5²; therefore, x = 5, and the unknown length of the triangle is 5 cm.

Question 3.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let c in. be the length of the hypotenuse.
4² + 12² = c²
16 + 144 = c²
160 = c²
The number 160 is between the perfect squares 144 and 169. Since 160 is closer to 169 than it is to 144, the length of the hypotenuse of the triangle is closer to 13 in. than it is to 12 in.

Question 4.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x cm be the length of the unknown side.
x² + 11² = 13²
x² + 121 = 169
x² = 48
The number 48 is between the perfect squares 36 and 49. Since 48 is closer to 49 than it is to 36, the length of the unknown side of the triangle is closer to 7 cm than it is to 6 cm.

Question 5.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let c in. be the length of the hypotenuse.
6² + 8² = c²
36 + 64 = c²
100 = c²
10 = c
The length of the hypotenuse is 10 in. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 100. We know 100 is a perfect square, and 100 is equal to 10²; therefore, c = 10, and the length of the hypotenuse of the triangle is 10 in.

Question 6.
Determine the length of the unknown side of the right triangle. Explain how you know your answer is correct.

Answer:
Let c cm be the length of the hypotenuse.
7² + 4² = c²
49 + 16 = c²
65 = c²
The number 65 is between the perfect squares 64 and 81. Since 65 is closer to 64 than it is to 81, the length of the hypotenuse of the triangle is closer to 8 cm than it is to 9 cm.

Question 7.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.

Answer:
Let x mm be the length of the unknown side.
3² + x² = 12²
9 + x² = 144
x² = 135
The number 135 is between the perfect squares 121 and 144. Since 135 is closer to 144 than it is to 121, the length of the unknown side of the triangle is closer to 12 mm than it is to 11 mm.

Question 8.
The triangle below is an isosceles triangle. Use what you know about the Pythagorean theorem to determine the approximate length of the base of the isosceles triangle.

Answer:
Let x ft. represent the length of the base of one of the right triangles of the isosceles triangle.
x² + 7² = 9²
x² + 49 = 81
x² = 32
Since 32 is between the perfect squares 25 and 36 but closer to 36, the approximate length of the base of the right triangle is 6 ft. Since there are two right triangles, the length of the base of the isosceles triangle is approximately 12 ft.

Question 9.
Give an estimate for the area of the triangle shown below. Explain why it is a good estimate.

Answer:
Let x cm represent the length of the base of the right triangle.
x² + 3² = 7²
x² + 9 = 49
x² = 40
Since 40 is between the perfect squares 36 and 49 but closer to 36, the approximate length of the base is 6 cm.
A = \(\frac{1}{2}\)(6)(3) = 9
So, the approximate area of the triangle is 9 cm². This is a good estimate because of the approximation of the length of the base. Further, since the hypotenuse is the longest side of the right triangle, approximating the length of the base as 6 cm makes mathematical sense because it has to be shorter than the hypotenuse.

Eureka Math Grade 8 Module 7 Lesson 1 Exit Ticket Answer Key

Question 1.
Determine the length of the unknown side of the right triangle. If you cannot determine the length exactly, then determine which two integers the length is between and the integer to which it is closest.

Answer:
Let x in. be the length of the unknown side.
9² + x² = 15²
81 + x² = 225
x² = 144
x = 12
The length of the unknown side is 12 in. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 144. We know 144 is a perfect square, and 144 is equal to 12²; therefore, x = 12, and the unknown length of the triangle is 12 in.

Question 2.
Determine the length of the unknown side of the right triangle. If you cannot determine the length exactly, then determine which two integers the length is between and the integer to which it is closest.

Answer:
Let x mm be the length of the unknown side.
2² + 7² = x²
4 + 49 = x²
53 = x²
The number 53 is between the perfect squares 49 and 64. Since 53 is closer to 49 than 64, the length of the unknown side of the triangle is closer to 7 mm than 8 mm.

Engage NY Eureka Math 8th Grade Module 5 Lesson 8 Answer Key

Eureka Math Grade 8 Module 5 Lesson 8 Exploratory Challenge/Exercise Answer Key

Exercise 1.
Consider the function that assigns to each number x the value x².
a. Do you think the function is linear or nonlinear? Explain.
Answer:
I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

b. Develop a list of inputs and outputs for this function. Organize your work using the table below. Then, answer the questions that follow.

Answer:

c. Plot the inputs and outputs as ordered pairs defining points on the coordinate plane.

Answer:

d. What shape does the graph of the points appear to take?
Answer:
It appears to take the shape of a curve.

e. Find the rate of change using rows 1 and 2 from the table above.
Answer:
\(\frac{25 – 16}{ – 5 – ( – 4)}\) = \(\frac{9}{ – 1}\) = – 9

f. Find the rate of change using rows 2 and 3 from the table above.
Answer:
\(\frac{16 – 9}{ – 4 – ( – 3)} = \) = \(\frac{7}{ – 1}\) = – 7

g. Find the rate of change using any two other rows from the table above.
Answer:
Student work will vary.
\(\frac{16 – 25}{4 – 5}\) = \(\frac{ – 9}{ – 1}\) = 9

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible.
Answer:
This is definitely a nonlinear function because the rate of change is not a constant for different intervals of inputs. Also, we would expect the graph of a linear function to be a set of points in a line, and this graph is not a line. As was stated before, the expression x² is nonlinear.

Exercise 2.
Consider the function that assigns to each number x the value x³.
a. Do you think the function is linear or nonlinear? Explain.
Answer:
I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

b. Develop a list of inputs and outputs for this function. Organize your work using the table below. Then, answer the questions that follow.

Answer:

c. Plot the inputs and outputs as ordered pairs defining points on the coordinate plane.

Answer:

d. What shape does the graph of the points appear to take?
Answer:
It appears to take the shape of a curve.

e. Find the rate of change using rows 2 and 3 from the table above.
Answer:
\(\frac{ – 8 – ( – 3.375)}{ – 2 – ( – 1.5)}\) = \(\frac{ – 4.625}{ – 0.5}\) = 9.25

f. Find the rate of change using rows 3 and 4 from the table above.
Answer:
\(\frac{ – 3.375 – ( – 1)}{ – 1.5 – ( – 1)}\) = \(\frac{ – 2.375}{ – 0.5}\) = 4.75

g. Find the rate of change using rows 8 and 9 from the table above.
Answer:
\(\frac{1 – 3.375}{1 – 1.5}\) = \(\frac{ – 2.375}{ – 0.5}\) = 4.75

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible.
Answer:
This is definitely a nonlinear function because the rate of change is not a constant for any interval of inputs. Also, we would expect the graph of a linear function to be a line, and this graph is not a line. As was stated before, the expression x³ is nonlinear.

Exercise 3.
Consider the function that assigns to each positive number x the value \(\frac{1}{x}\).
a. Do you think the function is linear or nonlinear? Explain.
Answer:
I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

b. Develop a list of inputs and outputs for this function. Organize your work using the table below. Then, answer the questions that follow.

Answer:

c. Plot the inputs and outputs as ordered pairs defining points on the coordinate plane.

Answer:

d. What shape does the graph of the points appear to take?
Answer:
It appears to take the shape of a curve.

e. Find the rate of change using rows 1 and 2 from the table above.
Answer:
\(\frac{10 – 5}{0.1 – 0.2}\) = \(\frac{5}{ – 0.1}\) = – 50

f. Find the rate of change using rows 2 and 3 from the table above.
Answer:
\(\frac{5 – 2.5}{0.2 – 0.4}\) = \(\frac{2.5}{ – 0.2}\) = – 12.5

g. Find the rate of change using any two other rows from the table above.
Answer:
Student work will vary.
\(\frac{1 – 0.625}{1 – 1.6}\) = \(\frac{0.375}{ – 0.6}\) = – 0.625

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible.
Answer:
This is definitely a nonlinear function because the rate of change is not a constant for any interval of inputs. Also, we would expect the graph of a linear function to be a line, and this graph is not a line. As was stated before, the expression \(\frac{1}{x}\) is nonlinear.

Exercises 4–10
In each of Exercises 4–10, an equation describing a rule for a function is given, and a question is asked about it. If necessary, use a table to organize pairs of inputs and outputs, and then plot each on a coordinate plane to help answer the question.

Exercise 4.
What shape do you expect the graph of the function described by y = x to take? Is it a linear or nonlinear function?
Answer:

I expect the shape of the graph to be a line. This function is a linear function described by the linear equation y = x. The graph of this function is a line.

Exercise 5.
What shape do you expect the graph of the function described by y = 2x² – x to take? Is it a linear or nonlinear function?
Answer:

I expect the shape of the graph to be something other than a line. This function is nonlinear because its graph is not a line. Also the equation describing the function is not of the form y = mx + b. It is not linear.

Exercise 6.
What shape do you expect the graph of the function described by 3x + 7y = 8 to take? Is it a linear or nonlinear function?
Answer:

I expect the shape of the graph to be a line. This function is a linear function described by the linear equation 3x + 7y = 8. The graph of this function is a line. (We have y = – \(\frac{3}{7}\) x + \(\frac{8}{7}\).)

Exercise 7.
What shape do you expect the graph of the function described by y = 4x³ to take? Is it a linear or nonlinear function?
Answer:

I expect the shape of the graph to be something other than a line. This function is nonlinear because its graph is not a line. Also the equation describing the function is not of the form y = mx + b. It is not linear.

Exercise 8.
What shape do you expect the graph of the function described by \(\frac{3}{x}\) = y to take? Is it a linear or nonlinear function? (Assume that an input of x = 0 is disallowed.)
Answer:

I expect the shape of the graph to be something other than a line. This function is nonlinear because its graph is not a line. Also the equation describing the function is not of the form y = mx + b. It is not linear.

Exercise 9.
What shape do you expect the graph of the function described by \(\frac{4}{x^{2}}\) = y to take? Is it a linear or nonlinear function? (Assume that an input of x = 0 is disallowed.)
Answer:

I expect the shape of the graph to be something other than a line. This function is nonlinear because its graph is not a line. Also the equation describing the function is not of the form y = mx + b. It is not linear.

Exercise 10.
What shape do you expect the graph of the equation x² + y² = 36 to take? Is it a linear or nonlinear function? Is it a function? Explain.
Answer:

I expect the shape of the graph to be something other than a line. It is nonlinear because its graph is not a line. It is not a function because there is more than one output for any given value of x in the interval ( – 6, 6). For example, at x = 0 the y – value is both 6 and – 6. This does not fit the definition of function because functions assign to each input exactly one output. Since there is at least one instance where an input has two outputs, it is not a function.

Eureka Math Grade 8 Module 5 Lesson 8 Problem Set Answer Key

Question 1.
Consider the function that assigns to each number x the value x² – 4.
a. Do you think the function is linear or nonlinear? Explain.
Answer:
The equation describing the function is not of the form y = mx + b. It is not linear.

b. Do you expect the graph of this function to be a straight line?
Answer:
No

c. Develop a list of inputs and matching outputs for this function. Use them to begin a graph of the function.

Answer:

Question 2.
Consider the function that assigns to each number x greater than – 3 the value \(\frac{1}{x + 3}\).
a. Is the function linear or nonlinear? Explain.
Answer:
The equation describing the function is not of the form y = mx + b. It is not linear.

b. Do you expect the graph of this function to be a straight line?
Answer:
No

c. Develop a list of inputs and matching outputs for this function. Use them to begin a graph of the function.

Answer:

d. Was your prediction to (b) correct?
Answer:
Yes, the graph appears to be taking the shape of some type of curve.

Question 3.
a. Is the function represented by this graph linear or nonlinear? Briefly justify your answer.

Answer:
The graph is clearly not a straight line, so the function is not linear.

b. What is the average rate of change for this function from an input of x = – 2 to an input of x = – 1?
Answer:
\(\frac{ – 2 – 1}{ – 2 – ( – 1)}\) = \(\frac{ – 3}{ – 1}\) = 3

c. What is the average rate of change for this function from an input of x = – 1 to an input of x = 0?
Answer:
\(\frac{1 – 2}{ – 1 – 0}\) = \(\frac{ – 1}{ – 1}\) = 1
As expected, the average rate of change of this function is not constant.

Eureka Math Grade 8 Module 5 Lesson 8 Exit Ticket Answer Key

Question 1.
The graph below is the graph of a function. Do you think the function is linear or nonlinear? Briefly justify your answer.

Answer:
Student work may vary. The plot of this graph appears to be a straight line, and so the function is linear.

Question 2.
Consider the function that assigns to each number x the value \(\frac{1}{2}\) x². Do you expect the graph of this function to be a straight line? Briefly justify your answer.
Answer:
The equation is nonlinear (not of the form y = mx + b), so the function is nonlinear. Its graph will not be a straight line.

Engage NY Eureka Math 8th Grade Module 6 Lesson 2 Answer Key

Eureka Math Grade 8 Module 6 Lesson 2 Example Answer Key

Example 1: Rate of Change and Initial Value
The equation of a line can be interpreted as defining a linear function. The graphs and the equations of lines are important in understanding the relationship between two types of quantities (represented in the following examples by x and y).
In a previous lesson, you encountered an MP3 download site that offers downloads of individual songs with the following price structure: a $3 fixed fee for a monthly subscription plus a fee of $0.25 per song. The linear function that models the relationship between the number of songs downloaded and the total monthly cost of downloading songs can be written as
y = 0.25x + 3,
where x represents the number of songs downloaded and y represents the total monthly cost (in dollars) for
MP3 downloads.
a. In your own words, explain the meaning of 0.25 within the context of the problem.
Answer:
In the example on the previous page, the value 0.25 means there is a cost increase of $0.25 for every 1 song downloaded.

b. In your own words, explain the meaning of 3 within the context of the problem.
Answer:
In the example on the previous page, the value of 3 represents an initial cost of $3 for downloading 0 songs. In other words, there is a fixed cost of $3 to subscribe to the site.

The values represented in the function can be interpreted in the following way:

Eureka Math Grade 8 Module 6 Lesson 2 Exercise Answer Key

Exercises 1–6: Is It a Better Deal?
Another site offers MP3 downloads with a different price structure: a $2 fixed fee for a monthly subscription plus a fee of $0.40 per song.
Exercise 1.
Write a linear function to model the relationship between the number of songs downloaded and the total monthly cost. As before, let x represent the number of songs downloaded and y represent the total monthly cost (in dollars) of downloading songs.
Answer:
y = 0.4x + 2

Exercise 2.
Determine the cost of downloading 0 songs and 10 songs from this site.
Answer:
y = 0.4(0) + 2 = 2.00. For 0 songs, the cost is $2.00.
y = 0.4(10) + 2 = 6.00. For 10 songs, the cost is $6.00.

Exercise 3.
The graph below already shows the linear model for the first subscription site (Company 1): y = 0.25x + 3. Graph the equation of the line for the second subscription site (Company 2) by marking the two points from your work in Exercise 2 (for 0 songs and 10 songs) and drawing a line through those two points.

Answer:

Exercise 4.
Which line has a steeper slope? Which company’s model has the more expensive cost per song?
Answer:
The line modeled by the second subscription site (Company 2) is steeper. It has the larger slope value and the greater cost per song.

Exercise 5.
Which function has the greater initial value?
Answer:
The first subscription site (Company 1) has the greater initial value. Its monthly subscription fee is $3 compared to only $2 for the second site.

Exercise 6.
Which subscription site would you choose if you only wanted to download 5 songs per month? Which company would you choose if you wanted to download 10 songs? Explain your reasoning.
Answer:
For 5 songs: Company 1’s cost is $4.25 (y = 25(5) + 3); Company 2’s cost is $4.00 (y = 0.4(5) + 2). So, Company 2 would be the better choice. Graphically, Company 2’s model also has the smaller y – value when x = 5.
For 10 songs: Company 1’s cost is $5.50 (y = 0.25(10) + 3); Company 2’s cost is $6.00 (y = 0.4(10) + 2). So, Company 1 would be the better choice. Graphically, Company 1’s model also has the smaller y – value at x = 10.

Exercises 7–9: Aging Autos

Exercise 7.
When someone purchases a new car and begins to drive it, the mileage (meaning the number of miles the car has traveled) immediately increases. Let x represent the number of years since the car was purchased and y represent the total miles traveled. The linear function that models the relationship between the number of years since purchase and the total miles traveled is y = 15000x.
a. Identify and interpret the rate of change.
Answer:
The rate of change is 15,000. It means that the mileage is increasing by 15,000 miles per year.

b. Identify and interpret the initial value.
Answer:
The initial value is 0. This means that there were no miles on the car when it was purchased.

c. Is the mileage increasing or decreasing each year according to the model? Explain your reasoning.
Answer:
Since the rate of change is positive, it means the mileage is increasing each year.

Exercise 8.
When someone purchases a new car and begins to drive it, generally speaking, the resale value of the car (in dollars) goes down each year. Let x represent the number of years since purchase and y represent the resale value of the car (in dollars). The linear function that models the resale value based on the number of years since purchase is
y = 20000 – 1200x.
a. Identify and interpret the rate of change.
Answer:
The rate of change is – 1,200. The resale value of the car is decreasing $1,200 every year since purchase.

b. Identify and interpret the initial value.
Answer:
The initial value is $20,000. The car’s value at the time of purchase was $20,000.

c. Is the resale value increasing or decreasing each year according to the model? Explain.
Answer:
The slope is negative. This means that the resale value decreases each year.

Exercise 9.
Suppose you are given the linear function y = 2.5x + 10.
a. Write a story that can be modeled by the given linear function.
Answer:
Answers will vary. I am ordering cupcakes for a birthday party. The bakery is going to charge $2.50 per cupcake in addition to a $10 decorating fee.

b. What is the rate of change? Explain its meaning with respect to your story.
Answer:
The rate of change is 2.5, which means that the cost increases $2.50 for every additional cupcake ordered.

c. What is the initial value? Explain its meaning with respect to your story.
Answer:
The initial value is 10, which in this story means that there is a flat fee of $10 to decorate the cupcakes.

Eureka Math Grade 8 Module 6 Lesson 2 Problem Set Answer Key

Question 1.
A rental car company offers the following two pricing methods for its customers to choose from for a
one – month rental:
Method 1: Pay $400 for the month, or
Method 2: Pay $0.30 per mile plus a standard maintenance fee of $35.
a. Construct a linear function that models the relationship between the miles driven and the total rental cost for Method 2. Let x represent the number of miles driven and y represent the rental cost (in dollars).
Answer:
y = 35 + 0.30x

b. If you plan to drive 1,100 miles for the month, which method would you choose? Explain your reasoning.
Answer:
Method 1 has a flat rate of $400 regardless of miles. Using Method 2, the cost would be $365
(y = 35 + 0.3(1100)). So, Method 2 would be preferred.

Question 2.
Recall from a previous lesson that Kelly wants to add new music to her MP3 player. She was interested in a monthly subscription site that offered its MP3 downloading service for a monthly subscription fee plus a fee per song. The linear function that modeled the total monthly cost in dollars (y) based on the number of songs downloaded (x) is
y = 5.25 + 0.30x.
The site has suddenly changed its monthly price structure. The linear function that models the new total monthly cost in dollars (y) based on the number of songs downloaded (x) is y = 0.35x + 4.50.
a. Explain the meaning of the value 4.50 in the new equation. Is this a better situation for Kelly than before?
Answer:
The initial value is 4.50 and means that the monthly subscription cost is now $4.50. This is lower than before, which is good for Kelly.

b. Explain the meaning of the value 0.35 in the new equation. Is this a better situation for Kelly than before?
Answer:
The rate of change is 0.35. This means that the cost is increasing by $0.35 for every song downloaded. This is more than the download cost for the original plan.

c. If you were to graph the two equations (old versus new), which line would have the steeper slope? What does this mean in the context of the problem?
Answer:
The slope of the new line is steeper because the new linear function has a greater rate of change. It means that the total monthly cost of the new plan is increasing at a faster rate per song compared to the cost of the old plan.

d. Which subscription plan provides the better value if Kelly downloads fewer than 15 songs per month?
Answer:
If Kelly were to download 15 songs, both plans will cost the same ($9.75). Therefore, the new plan is cheaper if Kelly downloads fewer than 15 songs.

Eureka Math Grade 8 Module 6 Lesson 2 Exit Ticket Answer Key

In 2008, a collector of sports memorabilia purchased 5 specific baseball cards as an investment. Let y represent each card’s resale value (in dollars) and x represent the number of years since purchase. Each card’s resale value after 0, 1, 2, 3, and 4 years could be modeled by linear equations as follows:
Card A: y = 5 – 0.7x
Card B: y = 4 + 2.6x
Card C: y = 10 + 0.9x
Card D: y = 10 – 1.1x
Card E: y = 8 + 0.25x

Question 1.
Which card(s) are decreasing in value each year? How can you tell?
Answer:
Cards A and D are decreasing in value, as shown by the negative values for rate of change in each equation.

Question 2.
Which card(s) had the greatest initial value at purchase (at 0 years)?
Answer:
Since all of the models are in slope – intercept form, Cards C and D have the greatest initial values at $10 each.

Question 3.
Which card(s) is increasing in value the fastest from year to year? How can you tell?
Answer:
Card B is increasing in value the fastest from year to year. Its model has the greatest rate of change.

Question 4.
If you were to graph the equations of the resale values of Card B and Card C, which card’s graph line would be steeper? Explain.
Answer:
The Card B line would be steeper because the function for Card B has the greatest rate of change; the card’s value is increasing at a faster rate than the other values of other cards.

Question 5.
Write a sentence explaining the 0.9 value in Card C’s equation.
Answer:
The 0.9 value means that Card C’s value increases by 90 cents per year.

Engage NY Eureka Math 8th Grade Module 6 Lesson 3 Answer Key

Eureka Math Grade 8 Module 6 Lesson 3 Example Answer Key

Example 1: Rate of Change and Initial Value Given in the Context of the Problem
A truck rental company charges a $150 rental fee in addition to a charge of $0.50 per mile driven. Graph the linear function relating the total cost of the rental in dollars, C, to the number of miles driven, m, on the axes below.

Answer:

a. If the truck is driven 0 miles, what is the cost to the customer? How is this shown on the graph?
Answer:
$150, shown as the point (0, 150). This is the initial value. Some students might say “b.” Help them to use the term initial value.

b. What is the rate of change that relates cost to number of miles driven? Explain what it means within the context of the problem.
Answer:
The rate of change is 0.5. It means that the cost increases by $0.50 for every mile driven.

c. On the axes given, sketch the graph of the linear function that relates C to m.
Answer:
Students can plot the initial value (0, 150) and then use the rate of change to identify additional points as needed. A 1, 000-unit increase in m results in a 500-unit increase for C, so another point on the line is (1000, 650).

d. Write the equation of the linear function that models the relationship between number of miles driven and total rental cost.
Answer:
C = 0.5m + 150

Eureka Math Grade 8 Module 6 Lesson 3 Exercise Answer Key

Exercises
Jenna bought a used car for $18, 000. She has been told that the value of the car is likely to decrease by $2, 500 for each year that she owns the car. Let the value of the car in dollars be V and the number of years Jenna has owned the car be t.

Answer:

Exercise 1.
What is the value of the car when t = 0? Show this point on the graph.
Answer:
$18, 000. Shown by the point (0, 18000)

Exercise 2.
What is the rate of change that relates V to t? (Hint: Is it positive or negative? How can you tell?)
Answer:
-2, 500. The rate of change is negative because the value of the car is decreasing.

Exercise 3.
Find the value of the car when:
a. t = 1
Answer:
$18000 – $2500 = $15500

b. t = 2
Answer:
$18000 – 2($2500) = $13000

c. t = 7
Answer:
$18000 – 7($2500) = $500

Exercise 4.
Plot the points for the values you found in Exercise 3, and draw the line (using a straightedge) that passes through those points.
Answer:
See the graph above.

Exercise 5.
Write the linear function that models the relationship between the number of years Jenna has owned the car and the value of the car.
Answer:
V = 18000 – 2500t or V = -2500t + 18000

An online bookseller has a new book in print. The company estimates that if the book is priced at $15, then 800 copies of the book will be sold per day, and if the book is priced at $20, then 550 copies of the book will be sold per day.

Answer:

Exercise 6.
Identify the ordered pairs given in the problem. Then, plot both on the graph.
Answer:
The ordered pairs are (15, 800) and (20, 550). See the graph above.

Exercise 7.
Assume that the relationship between the number of books sold and the price is linear. (In other words, assume that the graph is a straight line.) Using a straightedge, draw the line that passes through the two points.
Answer:
See the graph above.

Exercise 8.
What is the rate of change relating number of copies sold to price?
Answer:
Between the points (15, 800) and (20, 550), the run is 5, and the rise is -(800-550) = -250. So, the rate of change is \(\frac{-250}{5}\) = -50.

Exercise 9.
Based on the graph, if the company prices the book at $18, about how many copies of the book can they expect to sell per day?
Answer:
650

Exercise 10.
Based on the graph, approximately what price should the company charge in order to sell 700 copies of the book per day?
Answer:
$17

Eureka Math Grade 8 Module 6 Lesson 3 Problem Set Answer Key

Question 1.
A plumbing company charges a service fee of $120, plus $40 for each hour worked. Sketch the graph of the linear function relating the cost to the customer (in dollars), C, to the time worked by the plumber (in hours), t, on the axes below.

Answer:

a. If the plumber works for 0 hours, what is the cost to the customer? How is this shown on the graph?
Answer:
$120 This is shown on the graph by the point (0, 120).

b. What is the rate of change that relates cost to time?
Answer:
40

c. Write a linear function that models the relationship between the hours worked and the cost to the customer.
Answer:
C = 40t + 120

d. Find the cost to the customer if the plumber works for each of the following number of hours.
i) 1 hour
Answer:
$160

ii) 2 hours
Answer:
$200

iii) 6 hours
Answer:
$360

e. Plot the points for these times on the coordinate plane, and use a straightedge to draw the line through the points.
Answer:
See the graph on the previous page.

Question 2.
An author has been paid a writer’s fee of $1, 000 plus $1.50 for every copy of the book that is sold.
a. Sketch the graph of the linear function that relates the total amount of money earned in dollars, A, to the number of books sold, n, on the axes below.

Answer:

b. What is the rate of change that relates the total amount of money earned to the number of books sold?
Answer:
1.5

c. What is the initial value of the linear function based on the graph?
Answer:
1, 000

d. Let the number of books sold be n and the total amount earned be A. Construct a linear function that models the relationship between the number of books sold and the total amount earned.
Answer:
A = 1.5n + 1000

Question 3.
Suppose that the price of gasoline has been falling. At the beginning of last month (t = 0), the price was $4.60 per gallon. Twenty days later (t = 20), the price was $4.20 per gallon. Assume that the price per gallon, P, fell at a constant rate over the twenty days.

Answer:

a. Identify the ordered pairs given in the problem. Plot both points on the coordinate plane above.
Answer:
(0, 4.60) and (20, 4.20); see the graph above.

b. Using a straightedge, draw the line that contains the two points.
Answer:
See the graph above.

c. What is the rate of change? What does it mean within the context of the problem?
Answer:
Using points (0, 4.60) and (20, 4.20), the rate of change is -0.02 because \(\frac{4.20-4.60}{20-0}\) = \(\frac{-0.4}{20}\) = -0.02. The price of gas is decreasing $0.02 each day.

d. What is the function that models the relationship between the number of days and the price per gallon?
Answer:
P = -0.02t + 4.6

e. What was the price of gasoline after 9 days?
Answer:
$4.42; see the graph above.

f. After how many days was the price $4.32?
Answer:
14 days; see the graph above.

Eureka Math Grade 8 Module 6 Lesson 3 Exit Ticket Answer Key

Question 1.
A car starts a journey with 18 gallons of fuel. Assuming a constant rate, the car consumes 0.04 gallon for every mile driven. Let A represent the amount of gas in the tank (in gallons) and m represent the number of miles driven.

Answer:

a. How much gas is in the tank if 0 miles have been driven? How would this be represented on the axes above?
Answer:
There are 18 gallons in the tank. This would be represented as (0, 18), the initial value, on the graph above.

b. What is the rate of change that relates the amount of gas in the tank to the number of miles driven? Explain what it means within the context of the problem.
Answer:
-0.04; the car consumes 0.04 gallon for every mile driven. It relates the amount of fuel to the miles driven.

c. On the axes above, draw the line that represents the graph of the linear function that relates A to m.
Answer:
See the graph above. Students can plot the initial value (0, 18) and then use the rate of change to identify additional points as needed. A 50-unit increase in m results in a 2-unit decrease for A, so another point on the line is (50, 16).

d. Write the linear function that models the relationship between the number of miles driven and the amount of gas in the tank.
Answer:
A = 18 – 0.04m or A = -0.04m + 18

Question 2.
Andrew works in a restaurant. The graph below shows the relationship between the amount Andrew earns in dollars and the number of hours he works.

a. If Andrew works for 7 hours, approximately how much does he earn in dollars?
Answer:
$96

b. Estimate how long Andrew has to work in order to earn $64.
Answer:
3 hours

c. What is the rate of change of the function given by the graph? Interpret the value within the context of the problem.
Answer:
Using the ordered pairs (7, 96) and (3, 64), the slope is 8. It means that the amount Andrew earns increases by $8 for every hour worked.

Engage NY Eureka Math 8th Grade Module 6 Lesson 1 Answer Key

Eureka Math Grade 8 Module 6 Lesson 1 Example Answer Key

Example 2: Another Rate Plan
A second wireless access company has a similar method for computing its costs. Unlike the first company that Lenore was considering, this second company explicitly states its access fee is $0.15, and its usage rate is $0.04 per minute.
Total Session Cost = $0.15 + $0.04 (number of minutes)
Answer:
→ How is this plan presented differently?
In this case, we are given the access fee and usage rate with an equation. In the first example, just data points were given.

→ Based on the work with the first set of problems, how do you think the two plans are different?
The values for the access fee and usage charge per minute are different, or the initial value and the rate of change are different.

Eureka Math Grade 8 Module 6 Lesson 1 Exercise Answer Key

Exercises 1–6

Exercise 1.
Lenore makes a table of this information and a graph where number of minutes is represented by the horizontal axis and total session cost is represented by the vertical axis. Plot the three given points on the graph. These three points appear to lie on a line. What information about the access plan suggests that the correct model is indeed a linear relationship?

Answer:
The amount charged for the minutes connected is based upon a constant usage rate in dollars per minute.

Exercise 2.
The rate of change describes how the total cost changes with respect to time.
a. When the number of minutes increases by 10 (e.g., from 10 minutes to 20 minutes or from 20 minutes to 30 minutes), how much does the charge increase?
Answer:
When the number of minutes increases by 10 (e.g., from 10 minutes to 20 minutes or from 20 minutes to 30 minutes), the cost increases by $0.30 (30 cents).

b. Another way to say this would be the usage charge per 10 minutes of use. Use that information to determine the increase in cost based on only 1 minute of additional usage. In other words, find the usage charge per minute of use.
Answer:
If $0.30 is the usage charge per 10 minutes of use, then $0.03 is the usage charge per 1 minute of use (i.e., the usage rate). Since the usage rate is constant, students should use what they have learned in Module 4.

Exercise 3.
The company’s pricing plan states that the usage rate is constant for any number of minutes connected to the Internet. In other words, the increase in cost for 10 more minutes of use (the value that you calculated in Exercise 2) is the same whether you increase from 20 to 30 minutes, 30 to 40 minutes, etc. Using this information, determine the total cost for 40 minutes, 50 minutes, and 60 minutes of use. Record those values in the table, and plot the corresponding points on the graph in Exercise 1.
Answer:
Consider the following table and graphs.

Exercise 4.
Using the table and the graph in Exercise 1, compute the hypothetical cost for 0 minutes of use. What does that value represent in the context of the values that Lenore is trying to figure out?
Answer:
Since there is a $0.30 decrease in cost for each decrease of 10 minutes of use, one could subtract $0.30 from the cost value for 10 minutes and arrive at the hypothetical cost value for 0 minutes. That cost would be $0.10. Students may notice that such a value follows the regular pattern in the table and would represent the fixed access fee for connecting. (This value could also be found from the graph after completing Exercise 6.)

Exercise 5.
On the graph in Exercise 1, draw a line through the points representing 0 to 60 minutes of use under this company’s plan. The slope of this line is equal to the constant rate of change, which in this case is the usage rate.
Answer:

Exercise 6.
Using x for the number of minutes and y for the total cost in dollars, write a function to model the linear relationship between minutes of use and total cost.
Answer:
y = 0.03x + 0.10

Exercises 7–16

Exercise 7.
Let x represent the number of minutes used and y represent the total session cost in dollars. Construct a linear function that models the total session cost based on the number of minutes used.
Answer:
y = 0.04x + 0.15

Exercise 8.
Using the linear function constructed in Exercise 7, determine the total session cost for sessions of 0, 10, 20, 30, 40, 50, and 60 minutes, and fill in these values in the table below.

Answer:

Exercise 9.
Plot these points on the original graph in Exercise 1, and draw a line through these points. In what ways does the line that represents this second company’s access plan differ from the line that represents the first company’s access plan?
Answer:
The second company’s plan line begins at a greater initial value. The same plan also increases in total cost more quickly over time; in other words, the slope of the line for the second company’s plan is steeper.

Exercises 10–12

MP3 download sites are a popular forum for selling music. Different sites offer pricing that depends on whether or not you want to purchase an entire album or individual songs à la carte. One site offers MP3 downloads of individual songs with the following price structure: a $3 fixed fee for a monthly subscription plus a charge of $0.25 per song.
Exercise 10.
Using x for the number of songs downloaded and y for the total monthly cost in dollars, construct a linear function to model the relationship between the number of songs downloaded and the total monthly cost.
Answer:
Since $3 is the initial cost and there is a 25 cent increase per song, the function would be
y = 3 + 0.25x or y = 0.25x + 3.

Exercise 11.
Using the linear function you wrote in Exercise 10, construct a table to record the total monthly cost (in dollars) for MP3 downloads of 10 songs, 20 songs, and so on up to 100 songs.

Answer:

Exercise 12.
Plot the 10 data points in the table on a coordinate plane. Let the x-axis represent the number of songs downloaded and the y-axis represent the total monthly cost (in dollars) for MP3 downloads.
Answer:

A band will be paid a flat fee for playing a concert. Additionally, the band will receive a fixed amount for every ticket sold. If 40 tickets are sold, the band will be paid $200. If 70 tickets are sold, the band will be paid $260.
Exercise 13.
Determine the rate of change.
Answer:
The points (40,200) and (70,260) have been given.
So, the rate of change is 2 because \(\frac{260-200}{70-40}\) = 2.

Exercise 14.
Let x represent the number of tickets sold and y represent the amount the band will be paid in dollars. Construct a linear function to represent the relationship between the number of tickets sold and the amount the band will be paid.
Answer:
Using the rate of change and (40,200):
200 = 2(40) + b
200 = 80 + b
120 = b
Therefore, the function is y = 2x + 120.

Exercise 15.
What flat fee will the band be paid for playing the concert regardless of the number of tickets sold?
Answer:
The band will be paid a flat fee of $120 for playing the concert.

Exercise 16.
How much will the band receive for each ticket sold?
Answer:
The band receives $2 per ticket.

Eureka Math Grade 8 Module 6 Lesson 1 Problem Set Answer Key

Question 1.
Recall that Lenore was investigating two wireless access plans. Her friend in Europe says that he uses a plan in which he pays a monthly fee of 30 euro plus 0.02 euro per minute of use.
a. Construct a table of values for his plan’s monthly cost based on 100 minutes of use for the month, 200 minutes of use, and so on up to 1,000 minutes of use. (The charge of 0.02 euro per minute of use is equivalent to 2 euro per 100 minutes of use.)
Answer:

b. Plot these 10 points on a carefully labeled graph, and draw the line that contains these points.

Answer:

c. Let x represent minutes of use and y represent the total monthly cost in euro. Construct a linear function that determines the monthly cost based on minutes of use.
Answer:
y = 30 + 0.02x

d. Use the function to calculate the cost under this plan for 750 minutes of use. If this point were added to the graph, would it be above the line, below the line, or on the line?
Answer:
The cost for 750 minutes would be €45. The point (750,45) would be on the line.

Question 2.
A shipping company charges a $4.45 handling fee in addition to $0.27 per pound to ship a package.
a. Using x for the weight in pounds and y for the cost of shipping in dollars, write a linear function that determines the cost of shipping based on weight.
Answer:
y = 4.45 + 0.27x

b. Which line (solid, dotted, or dashed) on the following graph represents the shipping company’s pricing method? Explain.

Answer:
The solid line would be the correct line. Its initial value is 4.45, and its slope is 0.27. The dashed line shows the cost decreasing as the weight increases, so that is not correct. The dotted line starts at an initial value that is too low.

Question 3.
Kelly wants to add new music to her MP3 player. Another subscription site offers its downloading service using the following: Total Monthly Cost = 5.25 + 0.30(number of songs).
a. Write a sentence (all words, no math symbols) that the company could use on its website to explain how it determines the price for MP3 downloads for the month.
Answer:
“We charge a $5.25 subscription fee plus 30 cents per song downloaded.”

b. Let x represent the number of songs downloaded and y represent the total monthly cost in dollars. Construct a function to model the relationship between the number of songs downloaded and the total monthly cost.
Answer:
y = 5.25 + 0.30x

c. Determine the cost of downloading 10 songs.
Answer:
5.25 + 0.30(10) = 8.25
The cost of downloading 10 songs is $8.25.

Question 4.
Li Na is saving money. Her parents gave her an amount to start, and since then she has been putting aside a fixed amount each week. After six weeks, Li Na has a total of $82 of her own savings in addition to the amount her parents gave her. Fourteen weeks from the start of the process, Li Na has $118.
a. Using x for the number of weeks and y for the amount in savings (in dollars), construct a linear function that describes the relationship between the number of weeks and the amount in savings.
Answer:
The points (6, 82) and (14, 118) have been given.
So, the rate of change is 4.5 because \(\frac{118-82}{14-6}\) = \(\frac{36}{8}\) = 4.5.
Using the rate of change and (6, 82):
82 = 4.5(6) + b
82 = 27 + b
55 = b
The function is y = 4.5x + 55.

b. How much did Li Na’s parents give her to start?
Answer:
Li Na’s parents gave her $55 to start.

c. How much does Li Na set aside each week?
Answer:
Li Na is setting aside $4.50 every week for savings.

d. Draw the graph of the linear function below (start by plotting the points for x = 0 and x = 20).

Answer:

Eureka Math Grade 8 Module 6 Lesson 1 Exit Ticket Answer Key

A rental car company offers a rental package for a midsize car. The cost comprises a fixed $30 administrative fee for the cleaning and maintenance of the car plus a rental cost of $35 per day.
Question 1.
Using x for the number of days and y for the total cost in dollars, construct a function to model the relationship between the number of days and the total cost of renting a midsize car.
Answer:
y = 35x + 30

Question 2.
The same company is advertising a deal on compact car rentals. The linear function y = 30x + 15 can be used to model the relationship between the number of days, x, and the total cost in dollars, y, of renting a compact car.
a. What is the fixed administrative fee?
Answer:
The administrative fee is $15.

b. What is the rental cost per day?
Answer:
It costs $30 per day to rent the compact car.

Engage NY Eureka Math 8th Grade Module 5 End of Module Assessment Answer Key

Eureka Math Grade 8 Module 5 End of Module Assessment Task Answer Key

Question 1.
a. We define x as a year between 2008 and 2013 and y as the total number of smartphones sold that year, in millions. The table shows values of x and corresponding y values.

i) How many smartphones were sold in 2009?
Answer:
17.3 Million Smartphones were sold in 2009

ii) In which year were 90 million smartphones sold?
Answer:
90 Million Smartphones were sold in 2011

iii) Is y a function of x? Explain why or why not.
Answer:
Yes, It is a function because for each input there is exactly one output. Specifically only one number will be assigned to represent the number of smartphones sold in the given year.

b. Randy began completing the table below to represent a particular linear function. Write an equation to represent the function he was using and complete the table for him.

Answer:

y = 3x + 4

c. Create the graph of the function in part (b).

Answer:

d. At NYU in 2013, the cost of the weekly meal plan options could be described as a function of the number of meals. Is the cost of the meal plan a linear or nonlinear function? Explain.

8 meals: $125/week
10 meals: $135/week
12 meals: $155/week
21 meals: $220/week
Answer:
\(\frac{125}{8}\) = 15.625
\(\frac{135}{10}\) = 13.5
\(\frac{155}{12}\) = 12.917
\(\frac{220}{21}\) = 10.476
The cost of the meal plan is a nonlinear function. The cost per meal is different based on the plan. Chosen for example, one plan charges almost $16 per meal while another is about $10. Also, when the data is graphed, The points do not fall on a line.

Question 2.
The cost to enter and go on rides at a local water park, Wally’s Water World, is shown in the graph below.

A new water park, Tony’s Tidal Takeover, just opened. You have not heard anything specific about how much it costs to go to this park, but some of your friends have told you what they spent. The information is organized in the table below.

Each park charges a different admission fee and a different fee per ride, but the cost of each ride remains the same.
a. If you only have $14 to spend, which park would you attend (assume the rides are the same quality)? Explain.
Answer:
Let x represent the number of rides
Let w represent the total cost at wally’s water world
W = 2x + 8
Wally’s
W = 2x + 8
14 = 2x + 8
6 = 2x
3 = x

Tony’s
T = 0.75x + 12
14 = 0.75x + 12
2 = 0.75x
2.67 ≈ x
At wally’s you can go in 3 rides with $14, At tony’s just 2 rides. I would go to wally’s because i could go on more rides.

b. Another water park, Splash, opens, and they charge an admission fee of $30 with no additional fee for rides. At what number of rides does it become more expensive to go to Wally’s Water World than Splash? At what number of rides does it become more expensive to go to Tony’s Tidal Takeover than Splash?
Answer:
Let S represent total cost at splash, S = 30
Wally’s
30 = 2x + 8
22 = 2x
11 = x

Tony’s
30 = 0.75x + 12
18 = 0.75x
24 = x
At Wally’s you can go on 11 rides with $30. The 12th ride makes wally’s more expensive than splash.
At Tony’s you can go on 24 rides with $30. The 25th ride makes tony’s more expensive than splash.

c. For all three water parks, the cost is a function of the number of rides. Compare the functions for all three water parks in terms of their rate of change. Describe the impact it has on the total cost of attending each park.
Answer:
Wally’s rate of change is 2, $2 per ride.
Tony’s rate of change is 0.75, $0.75 per ride.
Splash’s rate of change is 0, $0 extra per ride.
Wally’s has the greatest rate of change that means that the total cost at wally’s will increase the fastest as we go on more rides. At tony’s the rate of change is just 0.75 so the total cost increases with the number of rides we go on, but not as quickly as wally’s. Splash has a rate of change of zero, The number of rides we go on does not impact the total cost at all.

Question 3.
For each part below, leave your answers in terms of π.
a. Determine the volume for each three-dimensional figure shown below.

Answer:
V = \(\frac{1}{3}\) π (16)(9)
= (16)(3)π
= 48 π
The volume is 48 π mm²

V = π (4)(5.3)
= π (21.2)
= 21.2 π
The volume is 21.2 π cm³.

V = \(\frac{4}{3}\) π (3²)
= 4(9) π
= 36 π
The volume is 36 πin³

b. You want to fill the cylinder shown below with water. All you have is a container shaped like a cone with a radius of 3 inches and a height of 5 inches; you can use this cone-shaped container to take water from a faucet and fill the cylinder. How many cones will it take to fill the cylinder?

Answer:
Volume of cylinder = π (64) (3)
= 192 π
Volume of cone = \(\frac{1}{3}\) π (9) (5)
= \(\frac{45}{3}\) π
= 15 π
The volume of cylinder is 192 π in³
The volume of cone is 15 π in³
\(\frac{192 \pi}{15 \pi}\) = \(\frac{192}{15}\) = 12.8
It takes 12.8 cone of the given size to fill the cylinder.

c. You have a cylinder with a diameter of 15 inches and height of 12 inches. What is the volume of the largest sphere that will fit inside of it?

Answer:
The cylinder has radius of 7.5 cm, but the height is just 12 cm. That means the maximum radius for the sphere is 6 cm. Anything larger would not fit in the cylinder. Then the volume of the largest sphere that will fit in the cylinder is 288 in³.
V= \(\frac{4}{3}\) π (6³)
= \(\frac{4}{3}\) π (216)
= 288 π

Engage NY Eureka Math 8th Grade Module 5 Lesson 6 Answer Key

Eureka Math Grade 8 Module 5 Lesson 6 Exercise Answer Key

Exercise
A function assigns to the inputs shown the corresponding outputs given in the table below.

a. Do you suspect the function is linear? Compute the rate of change of this data for at least three pairs of inputs and their corresponding outputs.
Answer:
\(\frac{2 – ( – 1)}{1 – 2}\) = \(\frac{3}{ – 1}\)
= – 3

\(\frac{ – 7 – ( – 13)}{4 – 6}\) = \(\frac{6}{ – 2}\)
= – 3

\(\frac{2 – ( – 7)}{1 – 4}\) = \(\frac{9}{ – 3}\)
= – 3
Yes, the rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to – 3. Since the rate of change is the same, then I know it is a linear function.

b. What equation seems to describe the function?
Answer:
Using the assignment of 2 to 1:
2 = – 3(1) + b
2 = – 3 + b
5 = b
The equation that seems to describe the function is y = – 3x + 5.

c. As you did not verify that the rate of change is constant across all input/output pairs, check that the equation you found in part (a) does indeed produce the correct output for each of the four inputs 1, 2, 4, and 6.
Answer:
For x = 1 we have y = – 3(1) + 5 = 2.
For x = 2 we have y = – 3(2) + 5 = – 1.
For x = 4 we have y = – 3(4) + 5 = – 7.
For x = 6 we have y = – 3(6) + 5 = – 13.
These are correct.

d. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be a plot of four points lying on a common line. As we were not told about any other inputs for this function, we must assume for now that there are only these four input values for the function.
The four points lie on the line with equation y = – 3x + 5.

Eureka Math Grade 8 Module 5 Lesson 6 Problem Set Answer Key

Question 1.
A function assigns to the inputs given the corresponding outputs shown in the table below.

a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs.
\(\frac{9 – 17}{3 – 9}\) = \(\frac{ – 8}{ – 6}\)
= \(\frac{4}{3}\)

\(\frac{17 – 21}{9 – 12}\) = \(\frac{ – 4}{ – 3}\)
= \(\frac{4}{3}\)

\(\frac{21 – 25}{12 – 15}\) = \(\frac{ – 4}{ – 3}\)
= \(\frac{4}{3}\)
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to \(\frac{4}{3}\). Since the rate of change is the same, the function does appear to be linear.

b. Find a linear equation that describes the function.
Answer:
Using the assignment of 9 to 3
9 = \(\frac{4}{3}\) (3) + b
9 = 4 + b
5 = b
The equation that describes the function is y = \(\frac{4}{3}\) x + 5. (We check that for each of the four inputs given, this equation does indeed produce the correct matching output.)

c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four points in a row. They all lie on the line given by the equation
y = \(\frac{4}{3}\) x + 5.

Question 2.
A function assigns to the inputs given the corresponding outputs shown in the table below.

a. Is the function a linear function?
Answer:
\(\frac{2 – 0}{ – 1 – 0}\) = \(\frac{2}{ – 1}\)
= – 2

\(\frac{0 – 2}{0 – 1}\) = \(\frac{ – 2}{ – 1}\)
= 2
No. The rate of change is not the same when I check the first two pairs of inputs and corresponding outputs. All rates of change must be the same for all inputs and outputs for the function to be linear.

b. What equation describes the function?
Answer:
I am not sure what equation describes the function. It is not a linear function.

Question 3.
A function assigns the inputs and corresponding outputs shown in the table below.

a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs..
Answer:
\(\frac{2 – 6}{0.2 – 0.6}\) = \(\frac{ – 4}{ – 0.4}\)
= 10

\(\frac{6 – 15}{0.6 – 1.5}\) = \(\frac{ – 9}{ – 0.9}\)
= 10

\(\frac{15 – 21}{1.5 – 2.1}\) = \(\frac{ – 6}{ – 0.6}\)
= 10
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to 10. The function appears to be linear.

b. Find a linear equation that describes the function.
Answer:
Using the assignment of 2 to 0.2:
2 = 10(0.2) + b
2 = 2 + b
0 = b
The equation that describes the function is y = 10x . It clearly fits the data presented in the table.

c. What will the graph of the function look like? Explain.
Answer:
The graph will be four distinct points in a row. They all sit on the line given by the equation y = 10x.

Question 4.
Martin says that you only need to check the first and last input and output values to determine if the function is linear. Is he correct? Explain.
Answer:
No, he is not correct. For example, consider the function with input and output values in this table.

Using the first and last input and output, the rate of change is
\(\frac{9 – 12}{1 – 3}\) = \(\frac{ – 3}{ – 2}\)
= \(\frac{3}{2}\)
But when you use the first two inputs and outputs, the rate of change is
\(\frac{9 – 10}{1 – 2}\) = \(\frac{ – 1}{ – 1}\)
= 1
Note to teacher: Accept any example where the rate of change is different for any two inputs and outputs.

Question 5.
Is the following graph a graph of a linear function? How would you determine if it is a linear function?

Answer:
It appears to be a linear function. To check, I would organize the coordinates in an input and output table. Next, I would check to see that all the rates of change are the same. If they are the same rates of change, I would use the equation y = mx + b and one of the assignments to write an equation to solve for b. That information would allow me to determine the equation that represents the function.

Question 6.
A function assigns to the inputs given the corresponding outputs shown in the table below.

a. Does the function appear to be a linear function?
Answer:
\(\frac{ – 6 – ( – 5)}{ – 6 – ( – 5)}\) = \(\frac{1}{1}\)
= 1

\(\frac{ – 5 – ( – 5)}{ – 5 – ( – 5)}\) = \(\frac{1}{1}\)
= 1

\(\frac{ – 4 – ( – 2)}{ – 4 – ( – 2)}\) = \(\frac{2}{2}\)
= 1
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to 1. Since the rate of change is constant so far, it could be a linear function.

b. What equation describes the function?
Answer:
Clearly the equation y = x fits the data. It is a linear function.

c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four distinct points in a row. These four points lie on the line given by the equation y = x.

Eureka Math Grade 8 Module 5 Lesson 6 Exit Ticket Answer Key

Question 1.
Sylvie claims that a function with the table of inputs and outputs below is a linear function. Is she correct? Explain.

Answer:
\(\frac{ – 25 – (10)}{ – 3 – 2}\) = \(\frac{ – 35}{ – 5}\)
= 7

\(\frac{10 – 31}{2 – 5}\) = \(\frac{ – 21}{ – 3}\)
= 7

\(\frac{31 – 54}{5 – 8}\) = \(\frac{ – 23}{ – 3}\)
= \(\frac{23}{3}\)
No, this is not a linear function. The rate of change was not the same for each pair of inputs and outputs inspected, which means that it is not a linear function.

Question 2.
A function assigns the inputs and corresponding outputs shown in the table to the right.
a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs.

Answer:
\(\frac{3 – ( – 2)}{ – 2 – 8}\) = \(\frac{5}{ – 10}\) = – \(\frac{1}{2}\)
\(\frac{ – 2 – ( – 3)}{8 – 10}\) = \(\frac{1}{ – 2}\) = – \(\frac{1}{2}\)
\(\frac{ – 3 – ( – 8)}{10 – 20}\) = \(\frac{5}{ – 10}\) = – \(\frac{1}{2}\)
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to – \(\frac{1}{2}\) . Since the rate of change is the same for at least these three examples, the function could well be linear.

b. Can you write a linear equation that describes the function?
Answer:
We suspect we have an equation of the form y = – \(\frac{1}{2}\) x + b. Using the assignment of 3 to – 2:
3 = – \(\frac{1}{2}\) ( – 2) + b
3 = 1 + b
2 = b
The equation that describes the function might be y = – \(\frac{1}{2}\) x + 2.
Checking: When x = – 2, we get y = – \(\frac{1}{2}\) ( – 2) + 2 = 3. When x = 8, we get y = – \(\frac{1}{2}\) (8) + 2 = – 2. When x = 10, we get y = – \(\frac{1}{2}\) (10) + 2 = – 3. When x = 20, we get y = – \(\frac{1}{2}\) (20) + 2 = – 8.
It works.

c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four distinct points all lying in a line. (They all lie on the line with equation y = – \(\frac{1}{2}\) x + 2 ).

Eureka Math Grade 8 Module 5 Lesson 6 Multi – Step Equations I Answer Key

Set 1:
3x + 2 = 5x + 6
4(5x + 6) = 4(3x + 2)
\(\frac{3x + 2}{6}\) = \(\frac{5x + 6}{6}\)
Answer:
Answer for each problem in this set is x = – 2.

Set 2:
6 – 4x = 10x + 9
– 2( – 4x + 6) = – 2(10x + 9)
\(\frac{10x + 9}{5}\) = \(\frac{6 – 4x}{5}\)
Answer:
Answer for each problem in this set is x = – \(\frac{3}{14}\).

Set 3:
5x + 2 = 9x – 18
8x + 2 – 3x = 7x – 18 + 2x
\(\frac{2 + 5x}{3}\) = \(\frac{7x – 18 + 2x}{3}\)
Answer:
Answer for each problem in this set is x = 5.

Engage NY Eureka Math 8th Grade Module 5 Lesson 11 Answer Key

Eureka Math Grade 8 Module 5 Lesson 11 Example Answer Key

Example 1.
Compute the exact volume for the sphere shown below.

Answer:
Provide students time to work; then, have them share their solutions.
Sample student work:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(4³ )
= \(\frac{4}{3}\) π(64)
= \(\frac{256}{3}\) π
= 85 \(\frac{1}{3}\) π
The volume of the sphere is 85 \(\frac{1}{3}\) π cm³.

Example 2.
A cylinder has a diameter of 16 inches and a height of 14 inches. What is the volume of the largest sphere that will fit into the cylinder?

Answer:
→ What is the radius of the base of the cylinder?
The radius of the base of the cylinder is 8 inches.

→ Could the sphere have a radius of 8 inches? Explain.
No. If the sphere had a radius of 8 inches, then it would not fit into the cylinder because the height is only 14 inches. With a radius of 8 inches, the sphere would have a height of 2r, or 16 inches. Since the cylinder is only 14 inches high, the radius of the sphere cannot be 8 inches.

→ What size radius for the sphere would fit into the cylinder? Explain.
A radius of 7 inches would fit into the cylinder because 2r is 14, which means the sphere would touch the top and bottom of the cylinder. A radius of 7 means the radius of the sphere would not touch the sides of the cylinder, but would fit into it.

→ Now that we know the radius of the largest sphere is 7 inches, what is the volume of the sphere?
Sample student work:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(7³ )
= \(\frac{4}{3}\) π(343)
= \(\frac{1372}{3}\) π
= 457 \(\frac{1}{3}\) π
The volume of the sphere is 457 \(\frac{1}{3}\) π cm³.

Eureka Math Grade 8 Module 5 Lesson 11 Exercise Answer Key

Exercises 1–3

Exercise 1.
What is the volume of a cylinder?
Answer:
V = πr² h

Exercise 2.
What is the height of the cylinder?
Answer:
The height of the cylinder is the same as the diameter of the sphere. The diameter is 2r.

Exercise 3.
If volume(sphere) = 2/3 volume(cylinder with same diameter and height), what is the formula for the volume of a sphere?
Answer:
Volume(sphere) = \(\frac{2}{3}\) (πr²h)
Volume(sphere) = \(\frac{2}{3}\) (πr²2r)
Volume(sphere) = \(\frac{4}{3}\) (πr³)

Exercises 4–8

Exercise 4.
Use the diagram and the general formula to find the volume of the sphere.

Answer:
V = \(\frac{4}{3}\) πr³
V = \(\frac{4}{3}\) π(6³ )
V ≈ 288π
The volume of the sphere is about 288π in³.

Exercise 5.
The average basketball has a diameter of 9.5 inches. What is the volume of an average basketball? Round your answer to the tenths place.
Answer:
V = \(\frac{4}{3}\) πr³
V = \(\frac{4}{3}\) π(4.75³ )
V = \(\frac{4}{3}\) π(107.17)
V ≈ 142.9π
The volume of an average basketball is about 142.9π in³.

Exercise 6.
A spherical fish tank has a radius of 8 inches. Assuming the entire tank could be filled with water, what would the volume of the tank be? Round your answer to the tenths place.
Answer:
V = \(\frac{4}{3}\) πr³
V = \(\frac{4}{3}\) π(8³ )
V = \(\frac{4}{3}\) π(512)
V ≈ 682.7π
The volume of the fish tank is about 682.7π in³.

Exercise 7.
Use the diagram to answer the questions.

a. Predict which of the figures shown above has the greater volume. Explain.
Answer:
Student answers will vary. Students will probably say the cone has more volume because it looks larger.

b. Use the diagram to find the volume of each, and determine which has the greater volume.
Answer:
V = \(\frac{1}{3}\) πr² h
V = \(\frac{1}{3}\) π(2.5²)(12.6)
V = 26.25π
The volume of the cone is 26.25π mm³.
V = \(\frac{4}{3}\) πr³
V = \(\frac{4}{3}\) π(2.8³)
V = 29.269333…π
The volume of the sphere is about 29.27π mm³. The volume of the sphere is greater than the volume of the cone.

Exercise 8.
One of two half spheres formed by a plane through the sphere’s center is called a hemisphere. What is the formula for the volume of a hemisphere?

Answer:
Since a hemisphere is half a sphere, the volume(hemisphere) = \(\frac{1}{2}\) (volume of sphere).
V = \(\frac{1}{2}\) (\(\frac{4}{3}\) πr³ )
V = \(\frac{2}{3}\) πr³

Eureka Math Grade 8 Module 5 Lesson 11 Problem Set Answer Key

Question 1.
Use the diagram to find the volume of the sphere.

Answer:
V = \(\frac{4}{3}\) πr³
V = \(\frac{4}{3}\) π(9³)
V = 972π
The volume of the sphere is 972π cm³.

Question 2.
Determine the volume of a sphere with diameter 9 mm, shown below.

Answer:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(4.5³ )
= \(\frac{364.5}{3}\) π
= 121.5π
The volume of the sphere is 121.5π mm³.

Question 3.
Determine the volume of a sphere with diameter 22 in., shown below.

Answer:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(11³ )
= \(\frac{5324}{3}\) π
= 1774 \(\frac{2}{3}\) π
The volume of the sphere is 1774 \(\frac{2}{3}\) π in³.

Question 4.
Which of the two figures below has the lesser volume?

Answer:
The volume of the cone:
V = \(\frac{1}{3}\) πr² h
= \(\frac{1}{3}\) π(16)(7)
= \(\frac{112}{3}\) π
= 37 \(\frac{1}{3}\) π

The volume of the sphere:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(2³ )
= \(\frac{32}{3}\) π
= 10 \(\frac{2}{3}\) π
The cone has volume 37 \(\frac{1}{3}\) π in³ and the sphere has volume 10 \(\frac{2}{3}\) π in³. The sphere has the lesser volume.

Question 5.
Which of the two figures below has the greater volume?

Answer:
The volume of the cylinder:
V = πr² h
= π(3²)(6.2)
= 55.8π

The volume of the sphere:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(5³)
= \(\frac{500}{3}\) π
= 166 \(\frac{2}{3}\) π
The cylinder has volume 55.8π mm³ and the sphere has volume 166 \(\frac{2}{3}\) π mm³. The sphere has the greater volume.

Question 6.
Bridget wants to determine which ice cream option is the best choice. The chart below gives the description and prices for her options. Use the space below each item to record your findings.

A scoop of ice cream is considered a perfect sphere and has a 2-inch diameter. A cone has a 2-inch diameter and a height of 4.5 inches. A cup, considered a right circular cylinder, has a 3-inch diameter and a height of 2 inches.
Answer:

a. Determine the volume of each choice. Use 3.14 to approximate π.
Answer:
First, find the volume of one scoop of ice cream.
Volume of one scoop = \(\frac{4}{3}\) π(1³)
The volume of one scoop of ice cream is \(\frac{4}{3}\) π in³, or approximately 4.19 in³.
The volume of two scoops of ice cream is \(\frac{8}{3}\) π in³, or approximately 8.37 in³.
The volume of three scoops of ice cream is \(\frac{12}{3}\) π in³, or approximately 12.56 in³.
Volume of half scoop = \(\frac{2}{3}\) π(1³)
The volume of half a scoop of ice cream is \(\frac{2}{3}\) π in³, or approximately 2.09 in³.
Volume of cone = \(\frac{1}{3}\) (πr²)h
V = \(\frac{1}{3}\) π(1²)4.5
V = 1.5π
The volume of the cone is 1.5π in³, or approximately 4.71 in³. Then, the cone with half a scoop of ice cream on top is approximately 6.8 in³.
V = πr² h
V = π1.5²(2)
V = 4.5π
The volume of the cup is 4.5π in³, or approximately 14.13 in³.

b. Determine which choice is the best value for her money. Explain your reasoning.
Answer:
Student answers may vary.
Checking the cost for every in³ of each choice:
\(\frac{2}{4.19}\) ≈ 0.47723…
\(\frac{2}{6.8}\) ≈ 0.29411…
\(\frac{3}{8.37}\) ≈ 0.35842…
\(\frac{4}{12.56}\) ≈ 0.31847…
\(\frac{4}{14.13}\) ≈ 0.28308…
The best value for her money is the cup filled with ice cream since it costs about 28 cents for every in³.

Eureka Math Grade 8 Module 5 Lesson 11 Exit Ticket Answer Key

Question 1.
What is the volume of the sphere shown below?

Answer:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(3³ )
= \(\frac{108}{3}\) π
= 36π
The volume of the sphere is 36π in³.

Question 2.
Which of the two figures below has the greater volume?

Answer:
V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(4³)
= \(\frac{256}{3}\) π
= 85 \(\frac{1}{3}\) π
The volume of the sphere is 85 \(\frac{1}{3}\) π mm³.
V = \(\frac{1}{3}\) πr² h
= \(\frac{1}{3}\) π(3²)(6.5)
= \(\frac{58.5}{3}\) π
= 19.5π
The volume of the cone is 19.5π mm³. The sphere has the greater volume.

Engage NY Eureka Math 8th Grade Module 5 Lesson 10 Answer Key

Eureka Math Grade 8 Module 5 Lesson 10 Exercise Answer Key

Opening Exercise
a.
i. Write an equation to determine the volume of the rectangular prism shown below.

Answer:
V = 8(6)(h)
= 48h
The volume is 48h mm³.

ii. Write an equation to determine the volume of the rectangular prism shown below.

Answer:
V = 10(8)(h)
= 80h
The volume is 80h in³.

iii. Write an equation to determine the volume of the rectangular prism shown below.

Answer:
V = 6(4)(h)
= 24h
The volume is 24h cm³.

iv. Write an equation for volume, V, in terms of the area of the base, B.
V = Bh

b. Using what you learned in part (a), write an equation to determine the volume of the cylinder shown below.

Answer:
V = Bh
= 4² πh
= 16πh
The volume is 16πh cm³.

Exercises 1–3

Exercise 1.
Use the diagram to the right to answer the questions.

a. What is the area of the base?
Answer:
The area of the base is (4.5)(8.2) in² or 36.9 in².

b. What is the height?
Answer:
The height of the rectangular prism is 11.7 in.

c. What is the volume of the rectangular prism?
Answer:
The volume of the rectangular prism is 431.73 in³.

Exercise 2.
Use the diagram to the right to answer the questions.

a. What is the area of the base?
Answer:
A = π2²
A = 4π
The area of the base is 4π cm².

b. What is the height?
Answer:
The height of the right circular cylinder is 5.3 cm.

c. What is the volume of the right circular cylinder?
Answer:
V = (πr²)h
V = (4π)5.3
V = 21.2π
The volume of the right circular cylinder is 21.2π cm³.

Exercise 3.
Use the diagram to the right to answer the questions.

a. What is the area of the base?
Answer:
A = π6²
A = 36π
The area of the base is 36π in².

b. What is the height?
Answer:
The height of the right circular cylinder is 25 in.

c. What is the volume of the right circular cylinder?
Answer:
V = (36π)25
V = 900π
The volume of the right circular cylinder is 900π in³.

Exercises 4–6

Exercise 4.
Use the diagram to find the volume of the right circular cone.

Answer:
V = \(\frac{1}{3}\) (πr²)h
V = \(\frac{1}{3}\) (π4²)9
V = 48π
The volume of the right circular cone is 48π mm³.

Exercise 5.
Use the diagram to find the volume of the right circular cone.

Answer:
V = \(\frac{1}{3}\) (πr²)h
V = \(\frac{1}{3}\) (π2.3²)15
V = 26.45π
The volume of the right circular cone is 26.45π m³.

Exercise 6.
Challenge: A container in the shape of a right circular cone has height h, and base of radius r, as shown. It is filled with water (in its upright position) to half the height. Assume that the surface of the water is parallel to the base of the inverted cone. Use the diagram to answer the following questions:

a. What do we know about the lengths of AB and AO?
Answer:
Then we know that |AB| = r, and |AO| = h.

b. What do we know about the measure of ∠OAB and ∠OCD?
Answer:
∠OAB and ∠OCD are both right angles.

c. What can you say about △OAB and △OCD?
Answer:
We have two similar triangles, △OAB and △OCD by AA criterion.

d. What is the ratio of the volume of water to the volume of the container itself?
Answer:
Since \(\frac{|A B|}{|C D|}\) = \(\frac{|A O|}{|C O|}\), and |AO| = 2|OC|, we have \(\frac{|A B|}{|C D|}\) = 2\(\frac{2|O C|}{|C O|}\).
Then |AB| = 2|CD|.
Using the volume formula to determine the volume of the container, we have V = \(\frac{1}{3}\) π|AB|² |AO|.
By substituting |AB| with 2|CD| and |AO| with 2|OC| we get:
V = \(\frac{1}{3}\) π(2|CD|)² (2|OC|)
V = 8(\(\frac{1}{3}\) π|CD|² |OC|), where \(\frac{1}{3}\) π|CD|² |OC| gives the volume of the portion of the container that is filled with water.
Therefore, the volume of the water to the volume of the container is 1:8.

Eureka Math Grade 8 Module 5 Lesson 10 Problem Set Answer Key

Question 1.
Use the diagram to help you find the volume of the right circular cylinder.

Answer:
V = πr² h
V = π(1)² (1)
V = π
The volume of the right circular cylinder is π ft³.

Question 2.
Use the diagram to help you find the volume of the right circular cone.

Answer:
V = \(\frac{1}{3}\) πr² h
V = \(\frac{1}{3}\) π(2.8)² (4.3)
V = 11.237333…π
The volume of the right circular cone is about 11.2π cm³.

Question 3.
Use the diagram to help you find the volume of the right circular cylinder.

Answer:
If the diameter is 12 mm, then the radius is 6 mm.
V = πr² h
V = π(6)² (17)
V = 612π
The volume of the right circular cylinder is 612π mm³.

Question 4.
Use the diagram to help you find the volume of the right circular cone.

Answer:
If the diameter is 14 in., then the radius is 7 in.
V = \(\frac{1}{3}\) πr² h
V = \(\frac{1}{3}\) π(7)² (18.2)
V = 297.26666…π
V ≈ 297.3π
The volume of the right cone is about 297.3π in³.

Question 5.
Oscar wants to fill with water a bucket that is the shape of a right circular cylinder. It has a 6-inch radius and 12-inch height. He uses a shovel that has the shape of a right circular cone with a 3-inch radius and 4-inch height. How many shovelfuls will it take Oscar to fill the bucket up level with the top?
Answer:
V = πr² h
V = π(6)² (12)
V = 432π
The volume of the bucket is 432π in³.
V = \(\frac{1}{3}\) πr² h
V = \(\frac{1}{3}\) π(3)² (4)
V = 12π
The volume of shovel is 12π in³.
\(\frac{432 \pi}{12 \pi}\) = 36
It would take 36 shovelfuls of water to fill up the bucket.

Question 6.
A cylindrical tank (with dimensions shown below) contains water that is 1-foot deep. If water is poured into the tank at a constant rate of 20 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\) for 20 min., will the tank overflow? Use 3.14 to estimate π.

Answer:
V = πr² h
V = π(3)² (12)
V = 108π
The volume of the tank is about 339.12 ft³.
V = πr² h
V = π(3)² (1)
V = 9π
There is about 28.26 ft³ of water already in the tank. There is about 310.86 ft³ of space left in the tank. If the water is poured at a constant rate for 20 min., 400 ft³ will be poured into the tank, and the tank will overflow.

Eureka Math Grade 8 Module 5 Lesson 10 Exit Ticket Answer Key

Question 1.
Use the diagram to find the total volume of the three cones shown below.

Answer:
Since all three cones have the same base and height, the volume of the three cones will be the same as finding the volume of a cylinder with the same base radius and same height.
V = πr² h
V = π(2)²3
V = 12π
The volume of all three cones is 12π ft³.

Question 2.
Use the diagram below to determine which has the greater volume, the cone or the cylinder.

Answer:
V = πr² h
V = π4² (6)
V = 96π
The volume of the cylinder is 96π cm³.
V = \(\frac{1}{3}\) πr² h
V = \(\frac{1}{3}\) π6² (8)
V = 96π
The volume of the cone is 96π cm³.
The volume of the cylinder and the volume of the cone are the same, 96π cm³.