Prasanna

Greater than and Less than Symbols are used to compare any numbers. If a number is bigger than another symbol greater than symbol is used and when a number is less than the other number less than symbol is used. Refer to the entire article to learn about Greater than and Less than Symbols, Notations, and Tricks to remember them easily. Using Symbols will help you save time and space and users can understand them easily.

Greater than and Less than Symbols – Definition

Greater than and Less than Symbols denotes the inequality between two values. The symbol used to represent greater than is “>” and less than is “<“.

Greater than Sign

Greater than Symbol is placed between two values if the first value is greater than the second value. In Inequality, greater than symbol will always be pointed towards the greater value, and the symbol consisting of two equal length strokes connecting in an acute angle at the right.

For Example 8>5, here 8 is greater than 5

Less than Sign

Less than symbol is placed between two values when the first value is less than the second value. In Inequality, less than symbol will always be pointed towards the lesser value, and the symbol consisting of two equal length strokes connecting in an acute angle at the left.

For Example 10<15, here 10 is less than 15.

Greater than and Less than Symbols makes it easy for the readers to understand.

All Symbols – Summary

Below is the list of Inequality Symbols and their Notations. They are along the lines

Tricks to Remember Greater than and Less than Symbols

To remember Greater than and Less than Symbols two methods are used. They are as follows

• Alligator Method
• L Method

Alligator Method: We know an Alligator or Crocodile always wants to eat a larger number of fishes. Alligator Mouth Opens always opens towards the largest number. Consider the numbers on both sides represent the number of fishes.

For Example: 10>6

Alligator mouth opens towards 10 since it wants to et 10 fishes rather than 6 fishes. It means 6 <10

L Method: Letter L appears similar to the Less than Symbol “<“.

Example: 20<40

Also, Read: Greater or Less than and Equal to

Applications of Greater than and Less than Symbols

In Mathematics we always don’t end with equality. At times, you can even have greater than and less than symbols. The Statements can be expressed using a Mathematical Expression.

Example: Consider there are x number of students in a class and they are more than 50 students if 10 more joined the class then they are 50 students in the class. Expressing this statement in mathematical expression we get

x+10>50

Solving Inequalities is similar to solving equations. While dealing with Inequalities Problems you should pay attention to the inequality sign direction. Some of the tricks that don’t affect the direction of inequalities are as listed below

• Multiply or Divide the Inequalities on both the sides with the same Positive Number.
• Add or Subtract the same number on both sides of the Inequality Expression.

Worked out Examples on Greater than and Less than Symbols

Question 1.

Diya has thirteen bananas and Manvi has twenty bananas. Find out who has more bananas?

Solution:

No. of Bananas Diya has = 13

No. of Bananas Manvi has = 20

Since 20>13

Thus, Manvi has more Bananas.

2. Dheeraj sleeps for thirty minutes and Manav sleeps for forty-five minutes every day in the afternoon. Find out who sleeps for less time?

Solution:

No. of Minutes Deeraj Sleeps = 30 min

No. of Minutes Manav Sleeps = 45 min

since 30<45

Dheeraj Sleeps for Less time compared to Manav.

FAQs on Greater than and Less than Symbols

1. What are the Different Inequality Symbols?

The different Inequality Symbols are

Greater than (>)
Less than (<)
Not equal to (≠)
Greater than or equal to (≥)
Less than or equal to (≤)

2. How to Remember Greater than and Less than Symbols?

You can use different methods like Alligator Method and L Method to remember the Greater than and Less than Symbols easily.

3. When can we use Greater than and Less than Symbols?

We can use Greater than and Less than Symbols to represent the Inequality Expressions. The Symbols used to denote greater than and less than are >, <.

Are you searching everywhere to find Word Problems on Division? If so, you have come the right way where you can find the complete list of Division Word Problems here. Practice using the Division Word Problems available here and test your level of understanding. For the sake of your convenience, we even listed Step by Step Solutions to all the Division Questions available. Have a glance at them and learn how to solve Word Problems on Division easily and quickly.

Examples of Word Problems Involving Division

1. There are 150 grade 4 students, in a school. The students are to be equally divided into 6 classes. How many students do we have in each class?

Solution:

No. of Grade 4 Students = 150

Since 150 Students are to be divided equally among 6 Classes we have the equation as such

= \(\frac { 150 }{ 6 } \)

= 25

Therefore, 6 Classes will have 25 Students each if 150 students divided equally.

2. Mary made 323 cupcakes. She packed 5 cupcakes into each box. How many boxes of cupcakes did she pack? How many cupcakes were left unpacked?

Solution:

No. of Cupcakes mary made = 323

She packed 5 Cupcakes into each box = 5

No. of boxes of cupcakes she packed =\(\frac { 323}{ 5 } \)

= 64 remainder 3

Therefore, 3 cupcakes are left unpacked.

3. If 9000 kg of wheat is packed in 85 bags, how much wheat will each bag contain?

Solution:

Since 85 bags contain wheat of 9000kg

Therefore, 1 bag contains wheat (9000 ÷ 85) kg

= 105kg

Each bag contains 105kg.

4. 85 people have been invited to a banquet. The caterer is arranging tables. Each table can seat 10 people. How many tables are needed?

Solution:

Since 85 people have been invited to a banquet and 10 people can be seated in  1 table

No. of Tables needed = 85 ÷ 10

Quotient = 8

Remainder = 5

80 People can be organized in 8 Tables and 5 People will be left. So the Caterer has to arrange one more table so that the 5 People can sit.

Thus, the total number of tables needed = 8+1

= 9

5. How many hours are there in 1800 minutes? 

Solution:

We know 1 hr = 60 minutes

To know how many hours are there in 1800 minutes we have to divide by 60 minutes

= 1800 ÷ 60

= 30 hours

Therefore, there are 30 hours in 1800 minutes.

6. A bus can hold 96 passengers. If there are 8 rows of seats on the bus, how many seats are in each row?

Solution:

The capacity of the bus that it can hold = 96 Passengers

No. of Rows in the Bus = 8

No. of Seats in each row = Capacity of Bus ÷ No. of Rows

= 96 ÷ 8

= 12

Therefore, there are 12 seats in each row.

7. $5,800 is distributed equally among 20 men. How much money will each person get?

Solution:

From the given data

Money received by 20 men = $5,800

Money received by 1 man = $5,800 ÷ 20

=

Thus $290 is received by each man when a sum of $5800 is distributed equally among 20 men.

8. Tarun had 56 apples. He divides all apples evenly among 7 friends. How many apples did Tarun give to each of his friends?

Solution:

Tarun had 56 apples

He divided all apples evenly among 7 friends

No. of Apples Tarun gave to each friend = Total Apples Tarun had ÷ No. of Friends he equally distributed the Apples among

= 56 ÷ 7

= 8

Therefore, Tarun gave 8 Apples each to his 7 friends on distributing 56 apples equally.

9. Nandy needs 6 lemons to make a glass of orange juice. If Nandy has 252 oranges, how many glasses of orange juice can she make?

Solution:

No. of Lemons Nandy need to make an Orange Juice = 6

Total No. of Oranges Nandy has = 252

To find out how many glasses of orange juice Nandy can make simply divide the total number of oranges she has with the. of lemons needed to make an orange juice.

= 252÷6

= 42

Therefore, Nandy can make 42 glasses of Orange Juice.

10. In your classes you counted 130 hands. How many students were in the class?

Solution:

No. of Hands Counted = 130

Each student has 2 hands

To find how many students were in the class simply divide the total no. of hands counted by the no. of hands each student has i.e. 130÷2 = 65

Therefore, there were 65 students in the Class.

The most important part of elementary education is learning multiplication tables. Check the 20 Times Table Multiplication Chart here and master the table at an early age to build a foundation in mathematics. With the help of the multiplication table of 20, you can get perfect in various topics like algebra, fractions, divisions, etc. Know the tips to memorize 20 Tables and become perfect with all the multiplication tables.

20 Times Table Multiplication Chart

For all the complex calculations, we use calculators. But for simple calculations, using the calculator is not the correct way. Memorizing the tables will help you to improve your problem-solving skills. It is always recommended for the students to memorize the tables from at least 2 to 20. If you memorize the multiplication tables, then you can quickly solve all the problems and it can be used as a building block in maths. Check how each integer gives the solution when multiplied by 20. Follow the tips and tricks to know the multiplication table of 20.

Tips to Memorise Multiplication Tables

1. To memorize the multiplication table, you have to know how many numbers are increased to get each resultant.
2. Add the same number to which you are finding the multiple.
3. To find the first number, you have to double it, and then again to find the second number, you have to add the multiplication number.
4. Break up the numbers into manageable chunks.
5. Practice each table until you get perfect for it.
6. Practice the number of multiplication facts.

Do Check:

• 14 Times Table
• 15 Times Table Multiplication Chart

20 Times Table Multiplication Chart

20 Times Table Multiplication Chart shows that the multiplication of 20 with various whole numbers present. Here is the table of 20.

To obtain the multiplication table of 20, we need to multiply each natural number by 20. The multiplication chart of 20 is nothing but the repetition of addition. As we know that 20 * 1 = 20, adding 20 to that number will give the next multiple numbers. Similarly, if we add 20 to the next multiples, we get the Table of 20. The multiples of 20 till 10 are

20 * 1 = 20

20 * 2 = 40

20 * 3 = 60

20 * 4 = 80

20 * 5 = 100

20 * 6 = 120

20 * 7 = 140

20 * 8 = 160

20 * 9 = 180

20 * 10 = 200

Easy ways to learn Multiplication Chart of 20

We will mention the easy ways to learn and remember the multiplication table.

Tip 1: The order does not Matter

When two numbers are multiplied, the order in which the numbers are multiplied does not matter. You can multiply the first number with the second or the second number with the first.

So, you don’t have to memorize both 4*3 and 3*4, just you have to remember that 4 and 3 make 12. Memorizing the numbers in such a way will cut the job in half.

Tip 2: Divide the table into “Chunks”

It is really hard to remember the whole table at once. So, divide the table into chunks and memorize it.

1. Start learning the multiplication tables with 5
2. Now, learn the multiplication numbers up to 9 times 5.
3. Learn the multiplications which you use them more and also learn simple tables like 2,3,4 etc.
4. Also, learn the numbers which multiply with the repeated numbers like 5 * 5, 7 * 7, 8 * 8 etc.

Some Patterns   

There are a few patterns that help you to remember some patterns.

2x is nothing but doubling the number. It is nothing but adding the number to itself.

Therefore, the pattern is 2,4,6,8,10…

5x comes with the pattern of ending with 0 or 5.

Therefore, the pattern is 5,10,15,20,25,30

9x comes with the pattern of “ones” place going down and “tens” place going up.

Therefore, the pattern is 9, 18, 27, 36, 45, 54, 63…

10x is the easiest way to remember. You just need to add zero to the number before it.

Therefore, the pattern is 10,20,30,40,50,60…

The Hard Ones

The hard ones are 6 * 7 = 42, 6 * 8 = 48, 7 * 8 = 56

Better you often say it in your mind and remember them.

Importance of Multiplication Tables

Being reliant on one’s memory is much brighter than something else. If you remember the multiplication chart, you will get the feeling of self-confidence. With the help of the multiplication table, you can keep the information at the fingertips to use it whenever required. It increases the memory power and stimulates the calculation speed. Students who master the multiplication tables from 2 to 20 can know the method of holding and observing things.

Tables from 2 to 10 are basic and fundamental, it helps in the calculation of simple arithmetic operations. Quick computation and a great deal of time are the major advantages of mastering multiplication charts.

Solved Examples involving Multiplication Table of 20

Problem 1:

There are 3 monkeys. Each monkey has 20 bananas. How many bananas are there in total?

Solution:

As given in the question,

No of monkeys = 3

No of bananas each monkey has = 20

To find the total number of bananas, we have to apply the law of multiplication.

Therefore, the total number of bananas = 3 * 20 = 60

Thus, all the monkeys have 60 bananas in total.

Hence, the final solution is 60 bananas.

Problem 2:

The first squirrel has 134 nuts. The second squirrel has 20 times as many nuts as the first squirrel. How many nuts does a second squirrel have?

Solution:

As given in the question,

No of nuts, the first squirrel has = 134

No of times the second squirrel has = 20

To find the no of nuts the second squirrel has, we have to apply the law of multiplication

Therefore, the nuts that the second squirrel has = 134 * 20

= 2680

Thus, the second squirrel has 2680 nuts

Hence, the final solution is 2680 nuts

Problem 3:

To find out the cost of the stolen diamonds, multiply the cost of one diamond with the total number of diamonds stolen.

Solution:

As given in the question,

Cost of one diamond = Rs. 16000

Total number of diamonds stolen: 20

Total worth of stolen diamonds = 20 * Rs 16000 = Rs. 3,20,000

Thus, the final solution is 3,20,000 Rupees

Worried about where to find instant help regarding the Capacity and Volume Conversions Chart in both Metric and Customary units? Then, halt your search as you have reached the right place and we will provide you with the necessary Capacity and Volume Units Conversion Chart. You can use them during your calculations in day-to-day life and make your problem-solving easy.

For the sake of your convenience, we have prepared the Capacity and Volume Conversion Table. In addition to the Metric and Customary Units of Capacity and Volume, we explained the concept much better by considering few examples. Check out the Solved Problems on Capacity and Volume Conversions and learn to apply the logic when you need them during your math calculations.

Capacity and Volume Conversion Charts

When it comes to Capacity and Volume the standard unit is the liter. The other standard units in the Capacity and Volume Conversion are explained below. Make the most out of them whenever you need to change between one unit of capacity or volume to the other. Having Units of Capacity or Volume in similar units makes it easy for you to solve problems. They are as follows

Customary Units for Capacity and Volume Conversion Table are explained as follows

Also, Read:

• Units of Length Conversion Charts
• Units of Mass and Weight Conversion Chart
• Math Conversion Chart

Solved Examples on Capacity and Volume Conversions

1. Convert 45 ml into l?

Solution:

We know 1 ml = \(\frac { 1 }{ 1000 } \) l

Substituting the value of 1 ml we get the equation as

= 45*\(\frac { 1 }{ 1000 } \) l

= \(\frac { 45 }{ 1000 } \) l

= 0.045 l

Therefore, 45 ml converted to l is 0.045l

2. Convert 8 hl into l?

Solution:

We know 1 hl = 100 l

Substituting the value of 1 hl we have the equation as follows

= 8*100 l

= 800 l

Therefore 8hl converted to l is 800 l

3. Convert 0.025l into ml?

Solution:

We know 1 l = 1000 ml

0.025 l = 0.025*1000 ml

= \(\frac { 25 }{ 1000 } \)*1000 ml

= 25 ml

Therefore, 0.025l converted to ml is 25ml

FAQs on Units of Capacity and Volume Conversion Chart

1. What are all the Units of Capacity?

There are five basic units in the customary system of measurement and units are as follows

• Ounce
• Cup
• Pint
• Quart
• Gallon

2. What is th Biggest Unit of Capacity?

The Biggest Unit of Capacity is Liter(L).

3. What’s the difference between capacity and volume?

Volume and capacity both are properties of three-dimensional objects. Volume is the space that a three-dimensional object occupies, whereas capacity, on the other hand, describes how much a container can hold.

Variation can be clearly understood if you know about Variables. In Mathematics, we generally deal with two types of quantities namely variables and constants. If the value of a quantity remains unchanged during different scenarios then it is said to be constant. On the other hand, if the value of a quantity changes under varying conditions then it is said to be a variable. Refer to the complete article to know about the Definition of Variation, Types of Variation, and Solved Examples on Variation, etc.

What is Variation?

In Mathematical Equations when a relationship is established there exist two types of quantities one is constant and the other is variable. Constant will not alter with the change in other parameters of the equation and the other is a variable that changes with different situations. The Changing of variable parameters is called a Variation.

You can understand the concept of variation with a simple equation y = mx

Here m is the constant and if we consider m = 2 then y becomes 2x

If x = 1, then y becomes y = 2*1 = 2

If x = 2, then y becomes y = 2*2 = 4

By changing the value of y, x gets different values. This is the variation of y with different values of x and similarly, you can get different values of y if the value of x changes.

Types of Variation

Variations can be of different types according to the pattern of changing or relationships of variables. We have explained the most common types of variation here and they are as follows

Direct Variation: If variables change proportionately i.e. either decrease or increase then it is said to be a direct variation. If A is in direct variation with B then it can be symbolically written as A α B.

Indirect Variation: In the case of Indirect or Inverse Variation variables change disproportionately i.e. when one variable increases the other one decreases. The behavior of Variables is exactly the opposite of direct variation. Thus, it is called an Indirect or Inverse Variation. If A is in indirect variation with B then it is symbolically written as A α \(\frac { 1 }{ B } \)

Joint Variation: If Two or more variables are related directly or one variable change with change product of two or more variables then it is said to be a Joint Variation. If A is in joint variation with B and C then it is symbolically represented as such A α BC

Combined Variation: Combined Variation is a combination of direct, indirect, or joint variation. In this kind of variation, three or more variables exist. If A is in combination with B, C then it can be symbolically represented as A α \(\frac { B }{ C } \) or A α \(\frac { C }{ B } \)

Partial Variation: If two variables are related using a formula or a variable is related by the sum of two or more variables then it is said to be a Partial Variation. y = mx+c is a straight line equation and is an example of Partial Variation.

FAQs on Variation

1. How do you define Variation?

Changing of Variable Parameters is called a Variation.

2. What are the Types of Variation?

There are different types of variation and they are as follows

• Direct Variation
• Indirect Variation
• Joint Variation
• Combined Variation
• Partial Variation

3. What is a direct variation proportion?

A Relations is said to be in direct variation when one variable changes and the second variable changes proportionally.

Subsets fall under the mathematics concept Sets. A Set is a collection of objects or elements enclosed within curly braces {}. If Set A is a Collection of Odd Numbers and Set B includes { 1, 3, 5} then B is said to be a subset of A and is denoted by B⊆A whereas A is the Superset of B.

Elements of Set can be anything such as variables, constants, real numbers, whole numbers, etc. It can include a null set too at times. Learn about Subsets Definition, Symbol, Formula, Types, and Examples in the later modules.

What is a Subset?

Set A is said to be a subset of Set B if all the elements present in Set A are also present in Set B. In other words, we can say Set A is contained within Set B.

Example:  If Set A has {a, b} and set B has {a, b, c}, then A is the subset of B because elements of A are also present in set B.

Subset Symbol

In Set theory, the Subset is denoted by the symbol ⊆ and is usually read as the Subset of. Using the symbol let us denote the subsets as follows

A ⊆ B; which denotes Set A is a subset of Set B.

Remember a Subset may include all the elements that are present in the Set.

Also, Read:

• Intersection of Sets

All Subsets of a Set

Subsets of any set consist of all possible sets including its elements and even null set. Let us provide you an example and provide the possible combinations of a set so that you can better understand.

Example:

What are the Subsets of Set A = {5, 6, 7, 8}?

Solution:

Given Set A = {5, 6, 7, 8}

Subsets include

{}

{5}, {6}, {7}, {8},

{5,6}, {5, 7}, {5,8}, {6,7},{6,8}, {7,8},

{5,6,7}, {6,7,8}, {5,7,8}, {5,6,8}

{5,6,7,8}

Types of Subsets

Subsets are Classified into two types namely

• Proper subsets
• Improper subsets

Proper Subsets: Proper Set includes only a few elements of the original set.

Improper Subsets: Improper Set includes all the elements of the original set along with the null set.

Example:

If set A = { 4, 6, 8}, then,

Number of subsets: {4}, {6}, {8}, {4,6}, {6,8}, {4,8}, {4,6,8} and Φ or {}.

Proper Subsets: {}, {4}, {6}, {8}, {4,6}, {6,8}, {4,8}

Improper Subset: {4,6,8}

There is no proper formula to find how many subsets are there. You just need to write each one of them and distinguish whether it is a proper subset or improper subset.

What are Proper Subsets?

Set A is said to be a Proper Subset of Set B if Set B has at least one element that doesn’t exist in Set A.

Example: If Set A has elements as {4, 6} and set B has elements as {4, 6, 16}, then Set A is the Proper Subset of B because 16 is not present in the set A.

Proper Subset Symbol

A Proper Subset is represented by the symbol ⊂ and is read as “Proper Subset of”. Using this symbol we can denote the Proper Subset for Set A and Set B as A ⊂ B.

Proper Subset Formula

If we have to pick the “n” number of elements from a set containing the “N” number of elements you can do so in ^NC_n number of ways.

How many Subsets and Proper Subsets does a Set have?

If a Set has “n” elements then there are 2ⁿ subsets for the given set and there are 2ⁿ -1 proper subsets for the given set.

Consider an example, If set X has the elements, X = {x, y}, then the proper subset of the given subset are { }, {x}, and {y}.

Here, the number of elements in the set is 2.

We know that the formula to calculate the number of proper subsets is 2ⁿ – 1.

= 2² – 1

= 4 – 1

= 3

Thus, the number of proper subset for the given set is 3 ({ }, {x}, {y}).

What are Improper Subsets?

A Subset that contains all the elements of the original set are called Improper Sets. It is represented using the symbol ⊆.

Set A ={1,2,3} Then, the subsets of A are;

{}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3} and {1,2,3}.

Where, {}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3} are the proper subsets and {1,2,3} is the improper subsets. Therefore, we can write {1,2,3} ⊆ A.

Note: Empty Set is an Improper Subset of itself and is a Proper Subset of any other set.

Power Set

Power Set is said to be a collection of all subsets. It is denoted by P(A).

If Set A has elements {a, b} then the Power Set of A is

P(A) = {∅, {a}, {b}, {a, b}}

Properties of Subsets

Below is the list of Some of the Important Properties of Subsets and they are as such

• Every Set is a subset of the given set itself. It means A ⊂ A or B ⊂ B, etc.
• Empty Set is a Subset of Every Set.
• If A is a Subset of B it means A is contained within B.
• If Set A is a subset of Set B then we can infer that B is a superset of A.

Subsets Example Problems

1. How many subsets containing three elements can be formed from the set?

S = { 1, 2, 3, 4, 5, 6, 7 }

Solution:

No. of Elements in the Set = 7

No. of Elements in the Subset = 3

No. of Possible Elements containing the 3 Elements is 7C₃

=\(\frac { 7! }{ (7-3)!*3! } \)

= \(\frac { 7*6*5*4! }{ 4!*3! } \)

= 35

2. Find the number of subsets and the number of proper subsets for the given set A = {4, 5, 6, 7,8}?

Solution:

Given: A = {4, 5, 6, 7,8}

The number of elements in the set is 4

We know that,

The formula to calculate the number of subsets of a given set is 2ⁿ

= 2⁵ = 32

The number of subsets is 32

The formula to calculate the number of proper subsets of a given set is 2ⁿ – 1

= 2⁵ – 1

= 32 – 1 = 31

The number of proper subsets is 31.

FAQs on Subsets

1. What are Types of Subsets?

Subsets are classified into two types and they are as follows

• Proper Subsets
• Improper Subsets

2. What is the formula to calculate the number of proper subsets and subsets for a given set?

If a set has “n” number of elements then the number of subsets and proper subsets is given by the formulas

The formula to calculate the number of proper subsets for a given set is 2ⁿ-1

The formula to find the number of subsets is 2ⁿ

3. What is the symbol to denote Subset?

The subset is denoted by the symbol ⊆.

In Set theory, there are various types of set operations like Subsets, Difference of sets, Union of sets, Complement of sets, and Intersections of sets. Students can easily understand and learn the set theory concepts by referring to our articles. So, today we have come up with the Intersection of Sets topic. Let’s go through this page and learn about the intersection of sets definition, symbol, properties, and examples.

Intersection of Sets Definition

If the Intersection of two sets A and B, then it is denoted by A∩B, where it contains all the elements which are common to both A and B. The symbol to denote the intersection of sets is ‘∩’. All those elements that relate to both A and B denote the intersection of A and B. Hence, we can say that,
A ∩ B = {x : x ∈ A and x ∈ B}

For n sets A₁, A₂, A₃,……A _n where all these sets are the subset of Universal set (set U). The definition of the intersection is the set of all elements which are common to all these n sets.

What is the Intersection of Two Sets?

If there are two sets, Set A and Set B, then the intersection of sets is given by:

A∩B = n(A) + n(B) – n(A∪B), where

n(A) is the cardinal number of set A,
n(B) is the cardinal number of set B,
n(A∪B) is the cardinal number of a union of two sets ie., A and B.

For Example: The intersection of two sets ie., A = {1, 2, 3} and B = {2, 3, 4} then find A∩B?

We know, A∩B = n(A) + n(B) – n(A∪B)

After calculating the process of the intersection of two sets, the result is like this A∩B = {2, 3}.

Properties of Intersection of a Set

i) Commutative Law: The union of two sets A and B follow the commutative law i.e., A ∩ B = B ∩ A

ii) Associative Law: The intersection operation follows the associative law i.e., If we have three sets A, B, and C then, (A ∩ B) ∩ C = A ∩ (B ∩ C)

iii) Identity Law: The intersection of an empty set with any set A gives the empty set itself i.e., A ∩ ∅ = ∅

iv) Idempotent Law: The intersection of any set A with itself gives the set A i.e., A ∩ A = A

v) Law of U: The intersection of a universal set U with its subset A gives the set A itself. A ∩ U = A

vi) Distributive Law: According to this law: A ∩ (B ∪ C) = ( A ∩ B ) ∪ (A ∩ C)

Solved Examples on Intersection of Sets

1. Let U be the universal set consisting of all the n – sided regular polygons where 5 ≤ n ≤ 9. If set A, B, and C are defined as:

A = {pentagon, hexagon, octagon}

B = {pentagon, hexagon, nonagon, heptagon}

C = {nonagon}

Find the intersection of the sets A and B

Solution:

Given Universal Set U = {pentagon , hexagon , heptagon , octagon , nonagon}, A = {pentagon, hexagon, octagon}, B = {pentagon, hexagon, nonagon, heptagon}, C = {nonagon}

Now, calculate the intersection of sets A and B

Here, the intersection of sets means the common elements consist in both A and B:

The elements of A = {pentagon, hexagon, octagon}, and B = {pentagon, hexagon, nonagon, heptagon}

Then, A ∩ B = {pentagon, hexagon}.

2. If A = {1,3,5,7,9} and B = {2,3,5,6,8}. Find intersection of two set A and B.

Solution:

Given Set A = {1,3,5,7,9} and Set B = {2,3,5,6,8}

Here 3, 5 are the common elements in both A and B sets.

So, the intersection of two sets A and B are, A ∩ B = {3, 5}.

3. If P = {x, y, z} and Q = {ф}. Find the intersection of two given sets P and Q.

Solution:

Given sets are P = {x, y, z} and Q = {ф}

The Intersection of given sets P ∩ Q = { }.

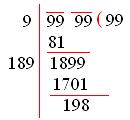
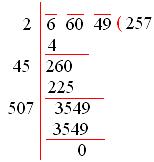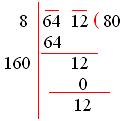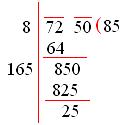A number composed of the sum of the place-values of its digits is called an expanded form of a number. Learn how a number can be expanded using the place values of its digits. We have given the process to expand a number and with different examples. All the examples are given along with the explanation. Practice all the problems available here and get a grip on the expanded form a number concept.

How to Expand a Number?

Check out the below steps to learn how to expand the number. Following these simple steps, you can expand a number easily. They are as follows

1. Firstly, take the unit place of a number and multiply it with 1.
2. Take the next number left to it and multiply it by 10.
3. Repeat the same process by increasing the 0 in the multiplicand.

Example: Write the expanded form for the number 2385?

Solution:
The given number is 2385.
Firstly, multiply the number 5 with 1. 5 × 1 = 5.
Multiply 8 with 10. 8 × 10 = 80.
Next, Multiply 3 with 100. 3 × 100 = 300.
Multiply 2 with 1,000. 2 × 1,000 = 2,000.
Add all the numbers to get the number.
2,000 + 300 + 80 + 5 = 2385.

Here, 2385 is the standard form and 2,000 + 300 + 80 + 5 is the expanded form.

Expanded Form of Numbers Examples

1. Write the expanded form for the number 70,34,51,395?

Solution:
The given number is 70,34,51,395.
Firstly, multiply the number 5 with 1. 5 × 1 = 5.
Multiply 9 with 10. 9 × 10 = 90.
Next, Multiply 3 with 100. 3 × 100 = 300.
Multiply 1 with 1000. 1 × 1000 = 1000.
Multiply 5 with 10000. 5 × 10000 = 50000.
Also, Multiply 4 with 100000. 4 × 100000 = 400000.
Multiply 3 with 1000000. 3 × 1000000 = 3000000.
Multiply 0 with 10000000. 0 × 10000000 = 0.
Next, Multiply 7 with 100000000. 7 × 100000000 = 700000000.
Add all the numbers to get the number.
700000000 + 0 + 3000000 + 400000 + 50000 + 1000 + 300 + 90 + 5 = 70,34,51,395.

Here, 70,34,51,395 is the standard form and 700000000 + 0 + 3000000 + 400000 + 50000 + 1000 + 300 + 90 + 5 is the expanded form.

2. Write the number in figures and then in words for the following expanded form
(i) 70000 + 6000 + 400 + 40 + 6

Solution:
Given expanded form is 70000 + 6000 + 400 + 40 + 6
Add the values to get a expanded form.
76446 (in figures)
Seventy-six thousand four hundred forty-six (in words)

(ii) 200000 + 40000 + 3000 + 20 + 7

Solution:
Given expanded form is 200000 + 40000 + 3000 + 20 + 7
Add the values to get an expanded form.
24327 (in figures)
Twenty-four thousand three hundred twenty-seven (in words)

3. Write in expanded form
(i) 39369

Solution:
The given number is 39369.
Firstly, multiply the number 9 with 1. 9 × 1 = 9.
Multiply 6 with 10. 6 × 10 = 60.
Next, Multiply 3 with 100. 3 × 100 = 300.
Multiply 9 with 1000. 9 × 1000 = 9000.
Multiply 3 with 10000. 3 × 10000 = 30000.
Add all the numbers to get the number.
30000 + 9000 + 300 + 60 + 9 = 39369.

Here, 39369 is the standard form and 30000 + 9000 + 300 + 60 + 9 is the expanded form.

(ii) 528,358

Solution:
The given number is 528,358.
Firstly, multiply the number 8 with 1. 8 × 1 = 8.
Multiply 5 with 10. 5 × 10 = 50.
Next, Multiply 3 with 100. 3 × 100 = 300.
Multiply 8 with 1000. 8 × 1000 = 8000.
Multiply 2 with 10000. 2 × 10000 = 20000.
Also, Multiply 5 with 100000. 5 × 100000 = 500000.
Add all the numbers to get the number.
500000 + 20000 + 8000 + 300 + 50 + 5 = 528,358.

Here, 528,358 is the standard form and 500000 + 20000 + 8000 + 300 + 50 + 5 is the expanded form.

Examples on Writing a Number in Expanded Form

I. Write the expanded form for the given numbers
(i) 6,01,217
(ii) 7,06,283
(iii) 5,33,786
(iv) 4,84,848
(v) 8,33,004

Solution

(i) The given number is 6,01,217.
Firstly, multiply the number 7 with 1. 7 × 1 = 7.
Multiply 1 with 10. 1 × 10 = 10.
Next, Multiply 2 with 100. 2 × 100 = 200.
Multiply 1 with 1000. 1 × 1000 = 1000.
Multiply 0 with 10000. 0 × 10000 = 0.
Also, Multiply 6 with 100000. 6 × 100000 = 600000.
Add all the numbers to get the number.
600000 + 0+ 1000 + 200 + 10 + 7 = 6,01,217.

Here, 6,01,217 is the standard form and 600000 + 0+ 1000 + 200 + 10 + 7 is the expanded form.

(ii) The given number is 7,06,283.
Firstly, multiply the number 3 with 1. 3 × 1 = 3.
Multiply 8 with 10. 8 × 10 = 80.
Next, Multiply 2 with 100. 2 × 100 = 200.
Multiply 6 with 1000. 6 × 1000 = 6000.
Multiply 0 with 10000. 0 × 10000 = 0.
Also, Multiply 7 with 100000. 7 × 100000 = 700000.
Add all the numbers to get the number.
700000 + 0 + 6000 + 200 + 80 + 3 = 7,06,283.

Here, 7,06,283 is the standard form and 700000 + 0 + 6000 + 200 + 80 + 3 is the expanded form.

(iii) The given number is 5,33,786.
Firstly, multiply the number 6 with 1. 6 × 1 = 6.
Multiply 8 with 10. 8 × 10 = 80.
Next, Multiply 7 with 100. 7 × 100 = 700.
Multiply 3 with 1000. 3 × 1000 = 3000.
Multiply 3 with 10000. 3 × 10000 = 30000.
Also, Multiply 5 with 100000. 5 × 100000 = 500000.
Add all the numbers to get the number.
500000 + 30000 + 3000 + 700 + 80 + 6 = 5,33,786.

Here, 5,33,786 is the standard form and 500000 + 30000 + 3000 + 700 + 80 + 6 is the expanded form.

(iv) The given number is 4,84,848.
Firstly, multiply the number 8 with 1. 8 × 1 = 8.
Multiply 4 with 10. 4 × 10 = 40.
Next, Multiply 8 with 100. 8 × 100 = 800.
Multiply 4 with 1000. 4 × 1000 = 4000.
Multiply 8 with 10000. 8 × 10000 = 80000.
Also, Multiply 4 with 100000. 4 × 100000 = 400000.
Add all the numbers to get the number.
400000 + 80000 + 4000 + 800 + 40 + 8 = 4,84,848.

Here, 4,84,848 is the standard form and 400000 + 80000 + 4000 + 800 + 40 + 8 is the expanded form.

(v) The given number is 8,33,004.
Firstly, multiply the number 4 with 1. 4 × 1 = 4.
Multiply 0 with 10. 0 × 10 = 0.
Next, Multiply 0 with 100. 0 × 100 = 0.
Multiply 3 with 1000. 3 × 1000 = 3000.
Multiply 3 with 10000. 3 × 10000 = 30000.
Also, Multiply 8 with 100000. 8 × 100000 = 800000.
Add all the numbers to get the number.
800000 + 30000 + 3000 + 0 + 0 + 4 = 8,33,004.

Here, 8,33,004 is the standard form and 800000 + 30000 + 3000 + 0 + 0 + 4 is the expanded form.

II. Write the given number in standard form
(i) 40,000 + 3,000 + 600 + 3
(ii) 3,00,000 + 70,000 + 5,000 + 600 + 40
(iii) 7,00,000 + 50,000 + 3,000 + 200 + 80 + 4
(iv) 6,00,000 + 20,000 + 7,000 + 300 + 40 + 6
(v) 2,00,000 + 30,000 + 4,000 + 300 + 20 + 3
(vi) 8,00,000 + 3

Solution:
(i) Given expanded form is 40,000 + 3,000 + 600 + 3
Add the values to get an expanded form.
43603 (in figures)
Forty-three thousand six hundred three (in words)

(ii) Given expanded form is 3,00,000 + 70,000 + 5,000 + 600 + 40
Add the values to get a expanded form.
375640 (in figures)
Three hundred seventy-five thousand six hundred forty (in words)

(iii) Given expanded form is 7,00,000 + 50,000 + 3,000 + 200 + 80 + 4
Add the values to get an expanded form.
753284 (in figures)
Seven hundred fifty-three thousand two hundred eighty-four (in words)

(iv) Given expanded form is 6,00,000 + 20,000 + 7,000 + 300 + 40 + 6
Add the values to get a expanded form.
627346 (in figures)
Six hundred twenty-seven thousand three hundred forty-six (in words)

(iv) Given expanded form is 2,00,000 + 30,000 + 4,000 + 300 + 20 + 3
Add the values to get a expanded form.
234323 (in figures)
Two hundred thirty-four thousand three hundred twenty-three (in words)

(v) Given expanded form is 8,00,000 + 3
Add the values to get an expanded form.
8,00,003 (in figures)
Eight hundred thousand three (in words)

Do you want to easily learn the multiplication table of 15? Then, refer to the 15 Times Table Multiplication Chart and the explanation we have given below. By referring to the 15 multiplication table chart, students can easily gain confidence and also get better results in the exam. It is also easy to remember any number that is multiplied by 15. Also, the multiplication of any number with 15 is easy using a 15 Times Table Multiplication Chart. Check out the below explanation for a better understanding.

15 Times Table Multiplication Chart

See the below 15 Times Table which will helps you to learn all the multiplications with 15.

15 × 0 = 0
15 × 1 = 15
15 × 2 = 30
15 × 3 = 45
15 × 4 = 60
15 × 5 = 75
15 × 6 = 90
15 × 7 = 105
15 × 8 = 120
15 × 9 = 135
15 × 10 = 150
15 × 11 = 165
15 × 12 = 180

Tips to Learn 15 Times Table

It is really easy to remember 15 Times Table with the simple tricks. All you have to do is remember one’s place digits, ten’s place digits, odd numbers, and even numbers. Look at the below explanation to learn the trick to find the resultant values of the 15 Times Table.

The one’s place always follows the pattern of 5-0.

• 15 × 1 = 15
• 15 × 2 = 30

For ten’s place digit in resultants, follow two consecutive even numbers and next two consecutive odd numbers.

• 15 × 1 = 15 (odd number at ten’s place)
• 15 × 2 = 30 (odd number at ten’s place)
• 15 × 3 = 45 (even number at ten’s place)
• 15 × 4 = 60 (even number at ten’s place)

Solved Problems on Table of 15

1. Using 15 times table, Evaluate: a) 15 times 7, b) 15 times 6 minus 5, and c) 5 times 5 plus 15 times 6?

Solution:
a) First, we will write 15 times 7 mathematically.
Using 15 times table, we have 15 times 7 = 15 × 7 = 105.
Hence, 15 times 7 is 105.
b) First, we will write 15 times 6 minus 5 mathematically.
Using table of 15, we have 15 times 6 minus 5 = 15 × 6 – 5 = 90 – 5 = 85
Hence, 15 times 6 minus 5 is 95.
c) First, we will write 5 times 5 plus 15 times 6 mathematically.
Using table of 15, we have: 5 times 5 plus 15 times 6 = 5 × 5 + 15 × 6 = 25+ 90 = 115
Hence, 5 times 5 plus 15 times 6 is 115.

2. Using the 15 times table, find: a) What is the 18th multiple of 15? and b) What is the 16th multiple of 15?

Solution:
a) To find the 18th multiple of 15, we need to call out 15 times table till 18 or multiply 15 by 18. We get 15 × 18 = 270
Thus, the 18th multiple of 15 is 270.
b) Similarly, to find the 16th multiple of 15 we need to call out the table of 15 till 16 or multiply 16 by 15 i.e. 15 × 16 = 240
Thus, the 16th multiple of 15 is 240.

3. Sam wants to give 30 chocolates to each of her 15 friends. This means 1 friend will get 2 chocolates. Using the table of 15 find how many chocolates should Sam purchase?

Solution:
Total number of friends = 15 and 1 friend will get chocolate = 2
Therefore, the total number of chocolates = 15 × 2 = 30.

Everything cannot be explained with sentences. There are some rotations to represent some words. In maths, there are some notations given for sets of numbers. Learn the Different Notations in Sets and know how to use them while solving problems. We have given Notations of sets of numbers and also their explanation. Also, get a complete grip on notations of numbers. Refer to the entire article to improve your preparation level.

What are Different Notations in Sets?

Check out the different notations insets below.

∈ – Belongs to
∉ – Does not belong to
: or | – Such that
∅ – Null set or empty set
n(A) – Cardinal number of the set A
∪ – Union of two sets
∩ – The intersection of two sets
N – Set of natural numbers = {1, 2, 3, ……}
W – Set of whole numbers = {0, 1, 2, 3, ………}
I or Z – Set of integers = {………, -2, -1, 0, 1, 2, ………}
Z+ – Set of all positive integers
Q – Set of all rational numbers
Q+ – Set of all positive rational numbers
R – Set of all real numbers
R+ – Set of all positive real numbers
C – Set of all complex numbers

The above notations are the various types of problems on sets.

Note:
(i) The pair of curly braces { } denotes a set. All the elements of a set are placed inside the pair of curly braces. Those elements are separated using commas.
(ii) The set always represents a capital letter such as; A, B, C, ………
(iii) The elements of the sets are represented with small letters.
(iv) There is no particular order for elements of a set.
(v) Also, the elements of a set are not repeated.
(vi) The Greek letter Epsilon ‘∈’ is used for the words ‘belongs to’, ‘is an element of’, etc. Therefore, p ∈ S will be read as ‘p belongs to set S’ or ‘p is an element of the set S’.
(vii) The symbol ‘∉’ stands for ‘does not belong to’ also for ‘is not an element of’. Therefore, p ∉ S will read as ‘p does not belong to set S’ or ‘p is not an element of the set S’.

Read Related Articles:

• Intersection of Sets
• Subset

Union

Let A and B be two sets.
Now, we can define the following new set.
A ∪ B = {c | c ∈ A or c ∈ B}
(That is, c may be in A or in B or in both A and B)
A ∪ B is read as “A union B”
Now that A u B contains all the elements of A and all the elements of B and the figure given below illustrates this.
It is clear that A ⊆ A ∪ B and also B ⊆ A ∪ B.

Intersection

Let A and B be two sets.
Now, we can define the following new set.
A ∩ B = {c | c ∈ A and c ∈ B}
(That is c must be in both A and B)
A ∩ B is read as “A intersection B”
Now that A n B contains only those elements which belong to both A and B and the figure given below illustrates this.
It is trivial that A ∩ B ⊆ A and also A ∩ B ⊆ B.

Set Difference

Let A and B be two sets.
Now, we can define the following new set.
A \ B = {c | c ∈ A but c ∉ B}
(That is c must be in A and must not be in B)
A \ B is read as “A difference B”
Now that A \ B contains only elements of A that are not in B and the figure given below illustrates this. A \ B can also write as A – B

Symmetric Difference

Let A and B be two sets.
Now, we can define the following new set.
A Δ B = (A \ B) u (B \ A)
A Δ B is read as “A symmetric difference B”
Now that A Δ B contains all elements in A u B which are not in A n B and the figure given below illustrates this.

Complement

If A ⊆ U, where U is a universal set, then U \ A is called the complement of A with respect to U. If the underlying universal set is fixed, then we denote U \ A by A’ and it is called the complement of A.
A’ = U \ A
The difference set A \ B can also be viewed as the complement of B with respect to A.

Disjoint Sets

Two sets A and B are said to be disjoint if they do not have any common element. That is, A and B are disjoint if A n B = ᵩ
It is clear that n(A u B) = n(A) + n(B), if A and B are disjoint finite set.

Subset of a Set

A set M is a subset of set N if every element of M is also an element of N.
In symbol, we write m ⊆ n. We can read it as “M is a subset of N” or “M is contained in N”.
Read ⊈ as “M is a not subset of N” or “M is not contained in N”

Proper Subset

A set M is said to be a proper subset of set N if M ⊆ N and M ≠ N.
In symbol, we write M ⊂ N. We can read it as “M is a proper subset of N”

Power Set

The set of all subsets of X is said to be the power set of the set X.
The power set of X is denoted by P(X)

Superset

A set M is said to be a proper subset of set N if M ⊆ N and M ≠ N.
In symbol, we write M ⊂ N. We can read it as N is called superset of M.

Formula to Find Number of Subsets

If M is denoted as the given set and it has n number of elements, then we can find the formula of subsets as
Number of subsets = 2ⁿ
Formula to find the number of proper subsets
Number of proper subsets = 2^n-1

Null set or Empty set

A set that contains no element is called a null set or an empty set. And it is denoted by { } or ∅. Hence, the cardinal number of a null set is zero.

Multiplication of Fractions steps and methods are here. Check rules, tricks, and tips to solve fraction multiplication problems. Refer to the important formulae and also types involved in it. Know the fraction multiplication solved examples, types, and parts of fractions, variables, etc. Go through the below sections to get the complete details regarding multiplication methods, formulae, rules, etc.

Multiplication of Fractions – Introduction

Fractions multiplication starts with numerators multiplication followed by denominators multiplication. The resultant fraction of the multiplication fraction can be simplified further and can be reduced to its lowest terms. Fraction Multiplication is not the same as adding or subtracting the fraction values.

Any two or more fractions with different denominators can easily be multiplied. The main thing to be considered is the fractions should not be mixed fractions, they should be either proper or improper fractions. There are various steps involved in multiplying the fractions. They are:

1. In the fractions multiplication, we multiply the numerator with the numerator term to get the desired result of the numerator.
2.  In the fractions multiplication, we multiply the denominator with the denominator term to get the desired result of the denominator.
3. After finding the resultant numerator and denominator values, check for simplification if possible
4. Once the simplification is done, we get the final resultant value.

How to Multiply Mixed Fractions?

Consider a mixed fraction which is the form of a \(\frac { b }{ c } \).

In the above-mixed fraction, convert the fraction value into an improper fraction. After converting it into an improper fraction, apply all the above steps we do in the multiplication of fractions. To convert mixed fractions into improper fractions, we apply the following steps:

• Multiply the whole number (a) with the denominator (c). We get the result value (a * c)
• To the above result value (a * c), add the numerator value (b). After the addition of the numerator, we find the numerator of the improper fraction.
• The denominator value of the improper fraction will be the denominator of the same mixed fraction.
• Generally, we can write it as a \(\frac { b }{ c } \) = \(\frac { c*a + b}{ c } \)

Also Read:

• Addition and Subtraction of Fractions

Multiplication of Proper Fractions

Multiplication of proper fractions is the easiest form of all the fractions multiplication.

Example:

Solve the equation \(\frac { 2 }{ 3 } \) × \(\frac { 4 }{ 6 } \)?

Solution:

As given in the question,

The equation is \(\frac { 2 }{ 3 } \) × \(\frac { 4 }{ 6 } \)

Here, \(\frac { 2 }{ 3 } \), \(\frac { 4 }{ 6 } \) are the proper fractions. To multiply the proper fractions, we have to follow the steps.

Step 1: First of all, multiply the numerators together i.e., 2 and 4. The solution is 2 * 4 = 8

Step 2: Next, multiply the denominators together ie., 3 and 6. The solution is 3 * 6 = 18. The fraction value can be written as \(\frac { 2*4 }{ 3*6 } \) = \(\frac { 8 }{ 18 } \)

Step 3: Check if you can simplify the resultant equation. On simplification, we can write it as \(\frac { 4 }{ 9 } \)

Multiplication of Improper Fractions

An improper fraction is the one that has a greater denominator than the numerator. If we multiply an improper fraction, we result in an improper fraction.

Example: 

Solve the equation \(\frac { 3 }{ 2 } \) × \(\frac { 7 }{ 5 } \) of the improper fractions?

Solution:

As given in the question,

The equation is \(\frac { 3 }{ 2 } \) × \(\frac { 7 }{ 5 } \)

Here, \(\frac { 3 }{ 2 } \), \(\frac { 7 }{ 5 } \) are improper fractions. To multiply the improper fractions, we have to follow the steps.

Step 1: First of all, multiply the numerators together i.e., 3 and 7. The solution is 3 * 7 = 21

Step 2: Next, multiply the denominators together i.e., 2 and 5. The solution is 2 * 5 = 10. The fraction value can be written as \(\frac { 3*7 }{ 2*5 } \) = \(\frac { 21 }{ 10 } \)

Step 3: Check if you can simplify the resultant equation. In the above equation, simplification is not possible.

Step 4: Now, convert the fraction into an improper fraction. Hence, the result is 2[/latex] = \(\frac { 1 }{ 10 } \)

Multiplication of Mixed Fractions

Mixed Fractions are those fractions which have a whole number and a fraction like 2 [/latex] = \(\frac { 1 }{ 2 } \). When multiplying both the mixed fractions, we have to convert the mixed fractions into improper fractions.

Example:

Multiply the fractions 2\(\frac { 2 }{ 3 } \) and 3\(\frac { 1 }{ 4 } \)

Solution:

The given equation is 2\(\frac { 2 }{ 3 } \) x 3\(\frac { 1 }{ 4 } \)

Here, 2\(\frac { 2 }{ 3 } \) and 3\(\frac { 1 }{ 4 } \) are mixed fractions. To multiply the mixed fractions, we have to follow the following steps.

Step 1: First of all, convert the mixed fractions to improper fractions. To convert the mixed fraction of 2\(\frac { 2 }{ 3 } \), we write it as \(\frac { (3×2+2) }{ 3 } \). The result is 8/3. To convert the mixed fraction of 3\(\frac { 1 }{ 4 } \), we write it as \(\frac { (4×3+1) }{ 4 } \). The result is 13/4

Step 2: Multiply the numerators together i.e., 8 and 13. The solution is 8 * 13 = 104

Step 3: Next, multiply the denominators together i.e., 3 and 4. The solution is 3 * 4 = 12. The fraction value can be written as \(\frac { 8*13 }{ 3*4 } \) = \(\frac { 104 }{ 12 } \)

Step 4: Check if you can simplify the resultant equation. In the above equation, the simplification can be done as \(\frac { 26 }{3 } \).

Step 5: Now, convert the fraction into an improper fraction. Hence the result is 8\(\frac { 2 }{ 3 } \)

Multiplying Fractions Examples

Problem 1: 

A recipe calls for \(\frac { 3 }{ 4 } \) cups of sugar. Amari is tripling the recipe. How much amount of sugar will be needed?

Solution:

As given in the question,

Amount of sugar for recipe = \(\frac { 3 }{ 4 } \)

No of times Amari multiplied the recipe = 3

Therefore, to find the amount of sugar we apply the multiplication of fractions

Hence, \(\frac { 3 }{ 4 } \) * \(\frac { 3 }{ 1 } \) = \(\frac { 9 }{ 4 } \)

Now, convert the proper fraction into an improper fraction i.e., 2\(\frac { 1 }{ 4 } \)

Thus, the final solution is 2\(\frac { 1 }{ 4 } \)

Problem 2:

\(\frac { 4 }{ 5 } \) of all students at Riverwood High School are involved in an extracurricular activities. Of those students, \(\frac { 2 }{ 3 } \) are involved in a fall activity. What fraction of students at Riverwood are involved in a fall activity?

Solution:

As given in the question,

No of students involved in extracurricular activities = \(\frac { 4 }{ 5 } \)

No of students involved in fall activity = \(\frac { 2 }{ 3 } \)

To find the fraction of students involved in a fall activity, we have to apply the multiplication of fractions

Hence \(\frac { 2 }{ 3 } \) x \(\frac { 4 }{ 5 } \) = \(\frac { 8 }{ 15 } \)

Thus, \(\frac { 8 }{ 15 } \) fraction of students are involved in a fall activity.

Therefore, the final solution is \(\frac { 8 }{ 15 } \)

Problem 3:

Jimmy has a collection of 18 video games. Of the 18 video games. \(\frac { 1 }{ 3 } \) are sports games. How many of his games are sports games?

Solution:

As given in the question,

No of video games = 18

Part of sports games = \(\frac { 1 }{ 3 } \)

To find the no of sports games, we apply multiplication of fractions

Hence \(\frac { 1 }{ 3 } \) x \(\frac { 18 }{ 1 } \)

=\(\frac { 18 }{ 3 } \)

On further simplications, we get the result as 6.

Therefore, Jimmy has a collection of 6 sports games.

In practice tests on square and square roots, we are providing different methods of problems with solutions. We are providing four options for every question. Practice the test paper on square roots and find the correct answer for the given questions. Improve your preparation level for every problem. Different methods included for every problem. Therefore, choose the best and easy method and learn the problems.

Get clarity on every concept of Square root by the provided links on our website.

Objective Questions on Square and Square Roots

1 . Which of the following numbers is a perfect square?
(a) 131
(b) 144
(c) 165
(d) 251

2. A perfect square number can never have the digit …… at the unit’s place.
(a) 6
(b) 4
(c) 8
(d) 5

3. Which of the following is a Pythagorean triplet?
(a) (2, 4, 6)
(b) (5, 8, 2)
(c) (2, 9, 5)
(d) (3, 4, 5)

4. Sum of the first n natural numbers is
(a) n^2
(b) n(n + 1) / 2
(c) n² + 1
(d) (2n² – 1) / 2

5. √625 = ?
(a) 45
(b) 35
(c) 25
(d) 55

6. What least number must be added to 720 to make it a perfect square?
(a) 5
(b) 2
(c) 7
(d) 9

7. √0.81 = ?
(a) 0.9
(b) 0.09
(c) 0.99
(d) 0.96

8. √0.00065536 is equal to
(a) 0.256
(b) 0.0256
(c) 0.00256
(d) 0.000256

9. √1.0219 = ?
(a) 1.0109
(b) 1.03
(c) 0.505
(d) 1.056

10. √0.25 × √1.6 = ?
(a) 0.15
(b) 0.2
(c) 0.25
(d) 20

11. √289/√256 = ?
(a) 3 / 25
(b) 30 √32
(c) 17 / 16
(d) 1.25

12. √6084/144 = ?
(a) 22 / 17
(b) 25 / 12
(c) 32 / 4
(d) 39 / 6

13. Find the square root of 3844
(a) 56
(b) 52
(c) 62
(d) 65

14. Evaluate √4562496
(a) 2256
(b) 2136
(c) 2563
(d) 2222

15. Find the value of 49^2 X 25^2 = ?
(a) 1501621
(b) 1500625
(c ) 1502624
(d)1500725

16. 15^2 + √0.81 + 25 = ?
(a) 250.9
(b) 252.9
(c) 251.9
(d) 255.9

17. 25% of 125 + ? = 250
(a) 218
(b) 220.75
(c) 225.75
(d) 218.75

It is really easy to find Square root of numbers that are perfect squares when it comes to Square Root of Numbers that are Not Perfect Squares, it is difficult to find them. If you need to find the square root of a number m places of decimals, then the number of digits in the decimal part must be 2m. If the decimals are less than 2m, then add the required zeros at the right to the decimal part. Check out the complete concepts of Square Root on our website.

Square Root of Decimal Numbers using Long Division Method

Have a look at the procedure on how to solve square roots that aren’t perfect squares. They are as follows

• If we have to find a square root of number correct up to ‘n’ places of decimal, then we need to find the square root of number up to (n + 1) places of decimal.
• Also, if the digit place is (n + 1) decimal place is equal to 5 or greater than 5, then the digit at ‘n’ place increases by 1.
• Furthermore, if the digit place is (n + 1) decimal place is less than 5, then the digit at ‘n’ place remains the same and deletes the digit at (n + 1) place.

Square Root of Numbers that are not Perfect Squares Examples

1. Evaluate √2 correct up to two places of decimal?

Solution:
The given number is √2.
The square root of 1 is 1. Also, the square root of 2.25 is 1.5.
The 2 is in between 1 and 2.25.
Therefore, to find the square root of a 2, add 6 zeros after the decimal point.
√2.000000 = √(1.414 × 1.414)
Grouping the factors into the pairs of equal factors.
(1.414 × 1.414)
1.414 is the square root of 2.

The two places of decimal after the number is 1.41.

2. Evaluate √3 correct up to 3 places of decimal?

Solution:
The given number is √3.
The square root of 2.25 is 1.5. Also, the square root of 3.0625 is 1.75.
The 3 is in between 2.25 and 3.0625.
Therefore, to find the square root of a 3, add 10 zeros after the decimal point.
√3.0000000000 = √(1.7324 × 1.7324)
Grouping the factors into the pairs of equal factors.
(1.7324 × 1.7324)
1.7324 is the square root of 3.

The three places of decimal after the number is 1.732.

3. Evaluate √0.8 correct up to two places of decimal?

Solution:
The given number is √0.8.
The square root of 0.49 is 0.7. Also, the square root of 0.81 is 0.9.
The 0.8 is in between 0.7 and 0.9.
Therefore, to find the square root of 0.8, add 5zeros after the decimal point.
√0.800000 = √(0.894 × 0.894)
Grouping the factors into the pairs of equal factors.
(0.894 × 0.894)
0.894 is the square root of 0.8.

The two places of decimal after the number is 0.89.

Square Root of Number in the Fraction Form is explained clearly in this article. Finding natural numbers is easy but when it comes to fractions it is a little bit difficult to find the Square Root of Numbers. So, to make the process easy, we have given the step by step procedure on How do you find the Square Root of a Fraction. Check all the sample problems on finding the square root of numbers in fraction form and get to know the concept involved.

How to Find the Square Root of a Fraction?

If m and n are squares of some numbers then, √(m ÷ n) = √m ÷ √n. If you find any problem in mixed form, then convert it into fractions.

1. Find the square root of √(144 ÷ 81)?

Solution:
Given the number is √(144 ÷ 81).
Firstly, separate the numerator and denominator.
√(144) ÷ √(81)
Find the separate Square Roots of the numerator and denominator.
Find the prime factors of √(144)
√(144) = 12 × 12
Grouping the factors into the pairs of equal factors.
(12 × 12)
Take one number from each group and multiply them to find the number whose square is 144.
12
The square root of 144 is 12.
Find the prime factors of √(81)
√(81) = 9 × 9
Grouping the factors into the pairs of equal factors.
(9 × 9)
Take one number from each group and multiply them to find the number whose square is 81.
9.
The square root of 81 is 9.
The final answer is 12 ÷ 9 = 4/3

Therefore, the square root of √(144 ÷ 81) = 4/3.

2. Evaluate √(256 ÷ 64)?

Solution:
Given the number is √(256 ÷ 64).
Firstly, separate the numerator and denominator.
√(256) ÷ √(64)
Find the separate Square Roots of the numerator and denominator.
Find the prime factors of √(256)
√(256) = 16 × 16
Grouping the factors into the pairs of equal factors.
(16 × 16)
Take one number from each group and multiply them to find the number whose square is 256.
16
The square root of 256 is 16.
Find the prime factors of √(64)
√(64) = 8 × 8
Grouping the factors into the pairs of equal factors.
(8 × 8)
Take one number from each group and multiply them to find the number whose square is 64.
8.
The square root of 64 is 8.
The final answer is 256 ÷ 64 = 16/8

Therefore, the square root of √(256 ÷ 64) = 16/8.

3. Evaluate √(49 ÷ 121)?

Solution:
Given the number is √(49 ÷ 121).
Firstly, separate the numerator and denominator.
√(49) ÷ √(121)
Find the separate Square Roots of the numerator and denominator.
Find the prime factors of √(49)
√(49) = 7 × 7
Grouping the factors into the pairs of equal factors.
(7 × 7)
Take one number from each group and multiply them to find the number whose square is 49.
7
The square root of 49 is 7.
Find the prime factors of √(121)
√(121) = 11 × 11
Grouping the factors into the pairs of equal factors.
(11 × 11)
Take one number from each group and multiply them to find the number whose square is 121.
11.
The square root of 121 is 11.
The final answer is 49 ÷ 121 = 7/11

Therefore, the square root of √(49 ÷ 121) = 7/11.

4. Evaluate √(25 ÷ 169)?

Solution:
Given the number is √(25 ÷ 169).
Firstly, separate the numerator and denominator.
√(25) ÷ √(169)
Find the separate Square Roots of the numerator and denominator.
Find the prime factors of √(25)
√(25) = 5 × 5
Grouping the factors into the pairs of equal factors.
(5 × 5)
Take one number from each group and multiply them to find the number whose square is 25.
5
The square root of 25 is 5.
Find the prime factors of √(169)
√(169) = 13 × 13
Grouping the factors into the pairs of equal factors.
(13 × 13)
Take one number from each group and multiply them to find the number whose square is 169.
13.
The square root of 169 is 13.
The final answer is 25 ÷ 169 = 5/13

Therefore, the square root of √(25 ÷ 169) = 5/13.

5. Find the value of √(196 ÷ 9)?

Solution:
Given the number is √(196 ÷ 9).
Firstly, separate the numerator and denominator.
√(196) ÷ √(9)
Find the separate Square Roots of the numerator and denominator.
Find the prime factors of √(196)
√(196) = 13 × 13
Grouping the factors into the pairs of equal factors.
(13 × 13)
Take one number from each group and multiply them to find the number whose square is 196.
13
The square root of 196 is 13.
Find the prime factors of √(9)
√(9) = 3 × 3
Grouping the factors into the pairs of equal factors.
(3 × 3)
Take one number from each group and multiply them to find the number whose square is 9.
3.
The square root of 9 is 3.
The final answer is 196 ÷ 9 = 13/3

Therefore, the square root of √(196 ÷ 9) = 13/3.

6. Find out the value of √25 × √16?

Solution:
Given that √25 × √16.
Find the separate Square Roots of the two numbers.
Find the prime factors of √(25)
√(25) = 5 × 5
Grouping the factors into the pairs of equal factors.
(5  × 5)
Take one number from each group and multiply them to find the number whose square is 25.
5
The square root of 25 is 5.
Find the prime factors of √(16)
√(16) = 4 × 4
Grouping the factors into the pairs of equal factors.
(4 × 4)
Take one number from each group and multiply them to find the number whose square is 16.
4.
The square root of 16 is 4.
The final answer is √25 × √16 = 5 × 4 = 20

Therefore, √25 × √16 = 20.

Square Root of Numbers in the Decimal Form is finding the Square Root of given Decimal numbers. We can use the prime factorization method or long division method to find out the Square Root of a Decimal. Choose the best method and know the procedure, then find the Square Root of a Decimal number. We have given all concepts of Square root on our website along with examples.

How to find the Square Root of a Decimal?

Let us have a look at the procedure to find out the Square Root of a Decimal. Following the simple steps listed below, you can find the square root of a decimal easily. They are along the lines

1. Make the number of decimal places even by placing a zero on the extreme right of the decimal part.
2. Coming to an integral part, keep the periods as done while finding the square root of a perfect square of some natural number.
3. In the given decimal part, keep the periods on every pair of digits those starts with the first decimal place.
4. Now, find the square root of a given number.
5. Put the decimal point in the square root as soon as the integral part is exhausted.

Finding Square Root of a Decimal Number Examples

1. Evaluate √42.25?

Solution:

Solution:
Given the number is √42.25,
To find the square root of a perfect square by the prime factorization method, we have to find the factors of 42.25.
42.25 = 6.5 × 6.5
Grouping the factors into the pairs of equal factors.
(6.5 × 6.5)
Take one number from each group and multiply them to find the number whose square is 42.25.
6.5.

The square root of 42.25 is 6.5.

2. Evaluate √1.96?

Solution:
Given the number is √1.96,
To find the square root of a perfect square by the prime factorization method, we have to find the factors of 1.96.
1.96 = 1.4 × 1.4
Grouping the factors into the pairs of equal factors.
(1.4 × 1.4)
Take one number from each group and multiply them to find the number whose square is 1.96.
1.4.

The square root of 1.96 is 1.4.

3. Evaluate √39.69?

Solution:
Given the number is √39.69,
To find the square root of a perfect square by the prime factorization method, we have to find the factors of 39.69.
39.69 = 6.3 × 6.3
Grouping the factors into the pairs of equal factors.
(6.3 × 6.3)
Take one number from each group and multiply them to find the number whose square is 39.69.
6.3.

The square root of 39.69 is 6.3.

4. Evaluate √547.56?

Solution:
Given the number is √547.56,
To find the square root of a perfect square by the prime factorization method, we have to find the factors of 547.56.
547.56 = 23.4 × 23.4
Grouping the factors into the pairs of equal factors.
(23.4 × 23.4)
Take one number from each group and multiply them to find the number whose square is 547.56.
23.4.

The square root of 547.56 is 23.4.

5. Evaluate √0.064516?

Solution:
Given the number is √0.064516,
To find the square root of a perfect square by the prime factorization method, we have to find the factors of 0.064516.
0.064516 = 0.254 × 0.254
Grouping the factors into the pairs of equal factors.
(0.254 × 0.254)
Take one number from each group and multiply them to find the number whose square is 0.064516.
0.254.

The square root of 0.064516 is 0.254.