Prasanna

An Irregular Figure is a figure that is not a standard geometric shape and you can’t calculate the area of them using the standard area formulas. However, some irregular shapes are formed using two or more standard geometric figures. Thus, to find the area of the irregular shapes we split them according to shapes whose formulas we know and then add the area of those figures.

Irregular Shapes Definition

Irregular shapes are polygons that have five or more sides of varying lengths. These shapes or figures can be decomposed further into squares, triangles, and quadrilaterals to evaluate the area.

How to Calculate Area of Irregular Figures?

There are various methods to calculate the Area of Irregular Shapes and we have outlined few popular ones in the below modules. They are as under

• Evaluating Area using Unit Squares
• Divide the Irregular Shapes into two or more regular shapes
• Divide the Irregular Shapes with Curves into two or more regular shapes

Evaluating Area using Unit Squares

Use this Technique if you are dealing with shapes that are curves apart from a perfect circle, semicircle, and are irregular quadrilaterals. In this technique, you need to divide the shape into unit squares. The total number of unit squares that fall within the shape determines the total area. Count the squares as 1 if the shaded region covers more than half to have an accurate estimation.

Divide the Irregular Shapes into two or more regular shapes

You can use this technique for irregular shapes that are a combination of known shapes such as triangles, polygons. Use the predefined formulas to find the area of such shapes and then add them up to know the total area.

Example:

The above figure has two regular shapes square, semi circle

We can find the areas of them individually and then team up to know the Area of Irregular Shape

Given Side of a Square = 4

Area of Square = S²

Substituting the side value in the area of square formula we get

Area of Square = 4²

= 16

Area of a Semi-Circle = \(\frac { 1 }{ 2 } \) π*r²

Diameter = 4

Radius = d/2 = 4/2 = 2

Area of a Semi-Circle = \(\frac { 1 }{ 2 } \)(3.14*2²)

= \(\frac { 1 }{ 2 } \)(3.14*4)

= \(\frac { 1 }{ 2 } \)12.56

= 6.28

Area of Irregular Shape = Area of Square + Area of Semi Circle

= 16+6.28

= 22.28

Divide the Irregular Shapes with Curves into two or more regular shapes

In this technique decompose the given irregular shape into multiple squares, triangles, or other quadrilaterals. Based on the Curve and Shapes, part of the figure can be a circle, semi-circle, or quadrant.

Given Irregular Shape can be divided into multiple squares, rectangles, semi-circle, etc.

We can split the above figure into two rectangles, half circle

Let us find the area of rectangle 1

Area of Rectangle 1 = Base * Height = 4 * 10 = 40

Later find the area of rectangle 2:

Area of Rectangle 2 = Base * Height = 3 * (8 – 4) = 12

Let us find the Area of Semi Circle

A = \(\frac { 1 }{ 2 } \) π*r²

Area of Semi Circle =  (1/2)(3.14)1² = 1.57

Sum up all the individual areas to get the Area of the Irregular Shape

Total Area = 40 + 12 + 1.57 = 53.57

Examples on Area of Irregular Shapes

1. Work out the Area for the following Shape?

Solution:

Given Irregular Shape can be further divided into two rectangles

Area of 1st rectangle = 10*5

= 50 cm²

Area of 2nd Rectangle = (9-5)*(10-6)

= 4*4

= 16 cm²

Therefore, the Area of Irregular Shape can be obtained by combining the areas of two rectangles

Area of Irregular Shape = Area of 1st rectangle + Area of 2nd Rectangle

= 50 cm² +16 cm²

= 66 cm²

2. Find the Area of Irregular Figure provided below?

Solution:

We can split the above Irregular Figure into known shapes like Rectangle, Squares.

Firstly, find the area of the rectangle = Length* Breadth

= 5*14

= 70 cm²

Area of Square = Side²

= 4²

= 16 cm²

Area of Irregular Figure = Area of Rectangle + Area of Square

= 70 cm²+ 16 cm²
= 86 cm²

One of the major roles played in the Probability concept in mathematics is a deck of 52 playing cards. The concept of Playing cards probability problems is solved on the basis of a well-shuffled pack of 52 cards. Whenever we face the probability topic in statistics, most of the problems with a well-shuffled pack of 52 playing cards. So, this article will make you learn what is the basic concept of cards, the formula, how to find the probability of playing cards, and worked-out problems on Playing Cards Probability.

Basic Stuff About Playing Cards Probability

In a deck or pack of playing cards, you will find the 52 playing cards which are divided into 4 suits of 13 cards. The shapes of those 4 suits are i.e. spades ♠ hearts ♥, diamonds ♦, clubs ♣. Also, these 4 suits are colored in two colors ie., red and black. Spades and clubs are black in color and the remaining Diamonds and hearts are Red in color.

The four different types of cards are shown in the picture given below.

How are 52 Cards Divided?

In each suit of playing cards includes an Ace, King, Queen, Jack or Knaves, 10, 9, 8, 7, 6, 5, 4, 3, and 2. In the pack of 52 cards, there are 12 face cards which are King, Queen, and Jack (or Knaves). Check out the below image and get full clarity about the 13 cards of each suit in the 52 playing cards.

Also, have a look at the below points to memorize easily about the pack of 52 playing cards:

1. Club – 13 cards
2. Heart – 13 cards
3. Spade – 13 cards
4. Diamond – 13 cards
5. No. of black cards – 26
6. No. of red cards – 26
7. No. of Ace cards (named as “A”) – 4
8. No. of Jack cards (named as “J” – 4
9. No. of Queen cards (named as “Q”) – 4
10. No. of King cards (named as “K”) – 4
11. No. of face cards (named as “J”, “Q” and “K”) – 12

Formula

Based on the classic definition of the probability the formula to find the probability with playing cards is as follows:

Probability = No. of favorable comes/ No.of all possible outcomes
          or
P(A) = n(A)/n(S)

In the case of 52 playing cards, n(S) = 52.

How to Find the Probability of Playing Cards?

In the following steps, we have explained how to find the probability of playing cards. So, follow the below steps to calculate the probability:

1. In the first step, you have to find the number of favorable events.
2. Next, identify the whole number of possible outcomes that can occur.
3. At last, divide the number of favorable events by the complete number of possible outcomes.

To help you in solving the playing cards probability, we have given some solved examples of probability below. Let’s get into the practice problems of playing cards probability.

Probability Cards Questions

Example 1:

A card is drawn at random from a well-shuffled deck of 52 cards. What is the probability that the drawn card is Queen?

Solution:

Assume E be the event of drawing a Queen Card.

In total there are 4 Queen cards in 52 playing cards

Then,

n(E) = 4

And, we know that

n(S) = 52

Now, apply the formula to find the playing cards probability for the drawn card,

P(E) = n(E) / n(S)

P(E) = 4/52 = 1/13

So, the probability of getting a Queen card is 1/13.

Example 2:

A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting a card of Heart.

Solution:

Let A represents the event of getting a Heart cart.

No.of Heart cards are 13

Therefore, n(A) = 13

Here, the total no. of possible outcomes of A is 52

P(A) = No.of favourable comes/ a total no. of possible outcomes of A

= n(A)/n(S)

=13/52

=1/4

Hence, the required probability of getting a card of Heart is 1/4.

In Mathematics there are four basic operations namely Addition, Subtraction, Multiplication, Division. Division Operation is one of the basic arithmetic operations. In Division Process there are two major parts namely Divisor and Dividend. Get to know the definition of each of the parts of the division explained in detail below. Know the Formula to find Dividend When Divisor, Quotient, and Remainer are given.

Dividend Divisor Quotient and Remainder Definitions

Dividend: The number or value that we divide is known as a dividend.

Divisor: The number that divides the dividend is known as a divisor

Quotient: The result obtained from the division process is known as a quotient

Remainder: The number left over after the division process is known as the remainder.

How to find the Dividend? | Dividend Formula

The Formula to Calculate Dividend is given as under

Dividend = Divisor x Quotient + Remainder

Whenever you divide a number with another number you will get the result.

a/b = c

Here “a” is the dividend and “b” is the divisor whereas “c” is the quotient. Thus, we can write it as follows

Dividend = Divisor*Quotient

Rearranging the Terms we can find the other terms if any two are known.

However, if you have a remainder after the division process then the formula is as follows

Dividend = Divisor*Quotient+Remainder

You can verify the same by applying the formula of dividend

We know Dividend = Divisor*Quotient+Remainder

487 = 32*15+7

487 = 480+7

487 = 487

So the answer is correct.

Check out Examples on Division of Integers to learn about the Terms Dividend, Divisor, Quotient, and Remainder in detail. Let us consider few examples to verify the answer of division.

Properties of Division

Below we have listed few division properties explained by considering few examples. Keep these below points in mind you will find the division problems much simple to solve.

Property 1: If you divide zero by a number the quotient is always zero.

Examples:

(i) 0 ÷ 2 = 0

(ii) 0 ÷ 10 = 0

(iii) 0 ÷ 15 = 0

(iv) 0 ÷ 214 = 0

(v) 0 ÷ 320 = 0

(vi) 0 ÷ 6132 = 0

Property 2: The division of a number by zero is not defined.

Example:

34 divided by 0 is not defined

Property 3: If we divide any number with 1 the quotient is always the number itself.

Examples

(i) 22 ÷ 1 = 22

(ii) 658 ÷ 1 = 658

(iii) 3250 ÷ 1 = 3250

(iv) 5483 ÷ 1 = 5483

Property 4: If we divide a non-zero number by itself the quotient is always one.

(i) 40 ÷ 40 = 1

(ii) 92 ÷ 92 = 1

(iii) 2137 ÷ 2137 = 1

(iv) 4130 ÷ 4130 = 1

You can refer to our Properties of Division of Integers to have an idea of more such properties.

Worried about How to Read and Write Large Numbers during your math calculations? Then you have come the right way where you will get complete details on Reading & Writing Large Numbers.  Know-How to Read and Write Large Numbers in Words, Numerals by referring to the later modules. Check out the Place Value Chart available below to know about different groups.

How to Read and Write Large Numbers?

Numbers are separated into groups or periods such as ones, tens, hundreds, thousands, millions, and so on. However, in each group, there exists three subgroups namely ones, tens, hundreds. Refer to the below examples provided so that you will have an idea of periods or groups. Thus, you can answer the questions on reading or writing large numbers into words, numerals, or vice versa.

Also, keep in mind that while reading or writing large numbers you need to begin from the left side with the largest group and then move towards the right side.

Reading and Writing Large Numbers in Hundreds and Thousands

(i) 4,017 – Four thousand seventeen

(ii) 6,129 -Six thousand twenty-nine

(iii) 9,780 – Nine thousand seven hundred eighty

(iv) 61,015 – Sixty-one thousand fifteen

(v) 82, 535 – Eighty two thousand five hundred thirty-five

(vi) 611,010 – Six hundred eleven thousand ten

(vii) 431,002 – Four hundred thirty one thousand two

Examples on Writing the Number Names in Words

(i) 528 – Five Hundred and Twenty-Eight

(ii) 3904 – Three Thousand Nine Hundred and Four

(iii) 49,103 – Forty-Nine Thousand One Hundred and Three

(iv) 713,084 – Seven Hundred Thirteen Thousand and Eighty-Four

(v) 3,183,012 –  Three million one hundred eighty-three thousand twelve

(vi) 75,868,501 – Seventy-five million eight hundred sixty-eight thousand five hundred and one

(vii) 427,215,640 – Four hundred twenty-seven million two hundred fifteen thousand six hundred forty

Writing the Numbers in Numerals Examples

(i) Eighty-four – 84

(ii) Five hundred twelve – 512

(iii) Seven thousand three – 7003

(iv) Fifty-two thousand three hundred and four – 52,304

(v) Seven hundred fifty-one thousand three hundred fifty-one – 751,351

(vi) Five million seven hundred five thousand five hundred eighty-three – 5,705,583

(vii) Nineteen million six hundred forty-nine thousand three hundred twenty-two – 19,649,322

Conversion Of Hours Into Seconds: Looking for a perfect guide to make you understand how to convert hrs to sec? then, this is the right page for you. Both Hours and seconds are units used to measure time. Here, we have explained completely about hours to seconds conversion with solved examples. Also, you can have a look at the Math Conversion Chart on our site to get a deeper idea of length, mass, capacity conversions along with the time conversions. Check the below modules and know what are the definitions for Hour and Second, simple conversion formula, and worked-out examples on how to convert hrs to sec.

Definitions for Hours & Seconds

Hour(hr): Hour is defined as a unit of time equal to 1/24 of a day or 60 minutes or 3,600 seconds. An hour is an SI unit of time for use with the metric system. The abbreviation of Hours is ‘hr’. For instance, 1 hour can be addressed as 1 hr. According to the conversion base 1 hour = 3600 seconds.

Seconds(sec):

First, the second was predicated on the length of the day but since 1967, the definition of a Seconds is exactly “the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom” (at a temperature of 0 K). Also, the second is a base unit of time. One second is equal to 0.00027777777777778 hr.

Formula to Hours to Seconds Conversion

The simple formula to convert hours into seconds is as follows:

Hours to Seconds Conversion Scale

In order to help you more understandable below, we have compiled a detailed explanation on how to convert Hrs to Sec easily. So, continue your read and learn the simple process of conversion of Hours into Seconds.

How to Convert Hours(hrs) to Seconds(sec)?

To Convert an Hours time measurement to a Seconds time measurement, multiply the time value by the conversion ratio and change the units to time. Let’s speak on the conversion of hr to sec even more deeply by following the lines and know how to convert hours to seconds easily.

As we discussed in the above definitions, One hour is equal to 3600 seconds, so the time in seconds is equal to the hours multiplied by 3,600.

Thus, the formula for Time conversion of Hr into Sec is Seconds = Hours × 3,600.

Once, you know the formula of conversion then substitute the given hours into the hrs to sec formula and calculate the hours to seconds conversion.

Seek help from the below-provided solved examples on Conversion of Hours into Seconds and understand the calculation process involved in converting from hr to sec.

Worked-out Examples on Hours into Seconds Conversion

Example 1:

Convert 3 hours into seconds?

Solution:

First, consider the given hours in the question ie., Hours = 3hrs

Now, apply the direct formula of hours to seconds conversion:

Seconds = Hours X 3600 sec

Seconds = 3 X 3600 sec

Seconds = 10,800 sec

Therefore, the conversion of hours into seconds for given 3hr = 10,800 sec.

Example 2:

Convert 4 hours 20 minutes into seconds.

Solution:

First, we have to convert 4hrs into seconds by multiply with the conversion ratio,

ie., Sec = hr x 3600 = 4 x 3600 = 14,400 sec

Next, we have to convert 20 minutes into seconds. As per the definition, 1 minute is equal to 60 seconds.

So, multiple by 60 minutes,

20 x 60 = 1200

Finally, to convert 4 hours 20 minutes into seconds, add them together:

ie., 14,400 + 1200 = 15600

Therefore, the conversion of 4 hours 20 minutes into seconds is 15600 sec. 

Common Conversions Facts About Hrs to Sec

Below are a few easy & quick Hours to Seconds Conversion Facts:

1 minute = 60 seconds
1 hour = 60 minutes
1 hour = 3600 seconds
12 hours = 720 minutes
12 hours = 43,200 seconds
1 day = 24 hours = 1440 minutes
1 day = 24 hours = 86,400 seconds

Hour to Second Conversion Table

Here is the conversion table of Hours(hrs) to Seconds(sec):

FAQs on Conversion Of Hours Into Seconds

1. What is the rule for converting hours to seconds?

The time in seconds is equal to the hours multiplied by 3600.

2. How many seconds has 1 hour?

As per the definition, one minute is equal to 60 seconds and 60 minutes in one hour implies that 1 hour = 60 * 60. Now, product it and you’ll get 1 hour has 3,600 seconds.

3. How do you convert Hr to Sec?

As there are 3600 seconds in an hour, to convert hours to seconds, multiply by 3600.

Wondering where to find Metric Conversions Chart and Customary Units Conversion of Length? Don’t worry as you will get all of them here. We know the Standard Unit of Length is Meter and is expressed in short as “m”. 1 m is usually divided into 100 equal parts and each part is named as Centimeter and written in short as “cm”.

Long distances are measured in Kilometers and 1 Km is equal to 1000 m and is written as “km”. Different Units of Length and their Equivalents are expressed in the further modules. Check out our Math Conversion Chart to learn about length, mass, capacity, conversions etc. In Most Cases, we use Kilometre (km), Metre (m), and Centimetre (cm) as units of length measurement. You can also check Customary Units of Length, its Chart in the below sections.

Length Conversion Charts

Different Units of Length Conversions are explained here which you can use as a part of your calculations. Make the most out of them whenever you need unit conversions.

Customary Units of Length are expressed here in the below table so that you can use the conversions of length.

Solved Examples on Unit Conversions

1. Convert 0.7 m to cm?

Solution:

We know 1 m = 100 cm

0.7m = 0.7*100

= 70 Cm

Therfore, 0.7m converted to cm is 70 cm.

2. Convert 5 m 16 cm to m?

Solution:

We know 1 cm = \(\frac { 1 }{ 100 } \) m

5m 16 cm = 5m +\(\frac { 16 }{ 100 } \)m

= 5m+0.16m

= 5.16m

Therefore, 5m 16 cm converted to m is 5.16m

3. Convert 14 km 350 m into km?

Solution:

We know 1 km = 1000m

1m = \(\frac { 1 }{ 1000 } \) km

14km 350m = 14 km+\(\frac { 350 }{ 1000 } \) km

= 14km+0.35km

= 14.35 km

14 km 350 m converted to m is 14.35km

4. The length of a square tile is 120 cm. What will be the length of the tile strip in millimeters if 12 tiles are kept in a line?

Solution:

Length of Square Tile = 120 cm

Length of 12 Tile Strips in mm = 120*12

= 1440 mm

Therefore, the Length of the Tile Strip in mm is 1440mm.

Three-Dimensional Figures are shapes that consist of 3 dimensions such as length, breadth, and height. Three-Dimensional shapes also called solids. The length, breadth, and height are the three important measurements of 3-dimensional figures. There are different 3-dimensional shapes used in real-time. They are cuboids, cubes, Prisms, Pyramids, cylinders and cones, etc.

Solid Shapes

Solid shapes are the fixed objects they have fixed size, shape, and space. Let us check different examples of Solid Shapes to deeply understand the Solid Geometrical Figures.

Surface Area and Volume of Three-Dimensional shapes

Surface Area is defined as the complete area of the surface of the three-dimensional object. It is measured in square units. The surface area can be calculated using three different classifications.

• Curved Surface Area (CSA) is the area present in all the curved regions.
• Lateral Surface Area (LSA) is the area of all the flat surfaces and all the curved regions excluding base areas.
• Total Surface Area (TSA) is the area of all the surfaces including the base of a Three-Dimensional object.

The volume of the 3D shape is explained as the total space occupied by the three-dimensional object. It is measured in terms of cubic units and denoted by V.

Faces, Vertices, and Edges of a 3-Dimensional Shape

Have a look at the Faces, Vertices, and Edges of a 3-dimensional object.

• A solid consists of a flat part on it. Each flat part of a solid is known as the Face of a solid.
• The corner or Vertex is an end where three faces of a solid join together. Vertices are the plural form of the vertex.
• When two faces of a solid meet in a line called an Edge.

Types of Three Dimensional Shapes(3D Shapes)

Here we are going to discuss the list of three-dimensional shapes, their properties, and formulas. We even took examples for a better understanding of the concept.

1. Cuboid

A cuboid is also known as a rectangular prism consists of rectangle faces. The cuboid has 90 degrees angles each. Also, it has 8 vertices, 12 edges, 6 faces.
The formula of surface area and volume of a cuboid is given below.
Surface Area of a Cuboid = 2(lb + bh + lh) Square units
The volume of a Cuboid = lbh Cubic units
Examples of Cuboid are a box, a book, a matchbox, a brick, a tile, etc.,

Example:
Let us consider the below figure to completely understand a Cuboid

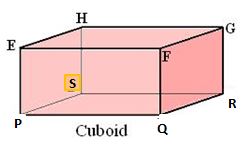
(i) Faces of a Cuboid: A cuboid consists of 6 faces. From the given figure, the 6 faces of the cuboid are PQRS, EFGH, PSHE, QRGF, PQFE, and SRGH.
(ii) Vertices of a Cuboid: A cuboid has 8 vertices. From the given figure, the 8 vertices of the cuboid are P, Q, R, S, E, F, G, H.
(iii) Edges of a Cuboid: A cuboid has 12 edges. From the given figure, the 12 edges of the cuboid are PQ, QR, RS, SP, EF, FG, GH, HE, PE, SH, QF, RG.

2. Cube

A Cube is of solid shape and consists of 6 square faces. The Cube all edges are equal. Also, it has 8 vertices, 12 edges, 6 faces.
The formula of surface area and volume of a Cube is given below.
Surface Area of a Cube = 6a² Square units
The volume of a Cube = a³ Cubic units

Example:
Let us consider the below figure to completely understand a Cube.

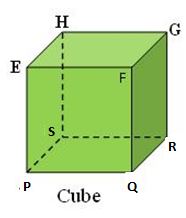
(i) Faces of a Cube: A cube consists of 6 faces. From the given figure, the 6 faces of the cube are PQRS, EFGH, PSHE, QRGF, PQFE, and SRGH.
(ii) Vertices of a Cube: A cube consists of 8 vertices. From the given figure, the 8 vertices of the cube are P, Q, R, S, E, F, G, H.
(iii) Edges of a Cube: A cube consists of 12 edges. From the given figure, the 12 edges of the cube are PQ, QR, RS, SP, EF, FG, GH, HE, PE, SH, QF, RG.

3. Prism

A prism has two equal ends, flat faces or surfaces, and also it has an identical cross-section across its length. If the cross-section of a prism looks like a triangle, then the prism is called a triangular prism. The prism will not have any curve. Also, it has 6 vertices, 9 edges, 5 faces (2 triangles and 3 rectangles).
The formula of surface area and volume of a Prism is given below.
Surface Area of a prism = 2(Base Area) + (Base perimeter × length) square units
The volume of a prism = Base Area × Height Cubic units

Example:
Let us consider the below figure to completely understand a triangular prism.

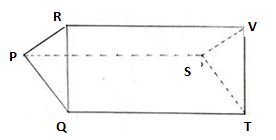
(i) Faces of a Triangular Prism: A triangular prism consists of 2 triangular faces and 3 rectangular faces. From the given figure, 2 triangular faces are ∆PQR and ∆STV, 3 rectangular faces are PQTS, PSVR, and RSTV.
(ii) Vertices of a Triangular Prism: A triangular prism consists of 6 vertices. From the given figure, the 6 vertices of the triangular prism are P, Q, R, S, T, V.
(iii) Edges of a Triangular Prism: A triangular prism consists of 9 edges. From the given figure, the 9 edges of the triangular prism are PQ, QR, RP, ST, TV, VS, PS, QT, RV.

4. Pyramid

A pyramid has a triangular face on the outside and its base is square, triangular, quadrilateral, or in the shape of any polygon. Also, it has 5 vertices, 8 edges, 5 faces.
The formula of surface area and volume of a Prism is given below.
Surface Area of a Pyramid = (Base area) + (1/2) × (Perimeter) × (Slant height) square units
The volume of a Pyramid = 1/ 3 × (Base Area) × height Cubic units

Example:
1. Let us consider the below figure to completely understand a Square Pyramid.

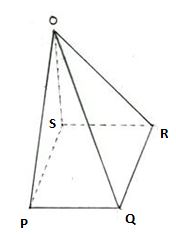
(i) Vertices of a Square Pyramid: A square pyramid consists of 5 vertices. From the given figure, OPQRS is a square pyramid having O, P, Q, R, S as its vertices.
(ii) Faces of a Square Pyramid: A square pyramid consists of faces one of which is a square face and the rest four are triangular faces. From the given figure, OPQRS is a square pyramid having PQRS as its square face and OPS, ORS, OQR, and OPQ as its triangular faces.
(iii) Edges of a Square Pyramid: A square pyramid consists of 8 edges. From the given figure, the square pyramid OPQRS has 8 edges, namely, PQ, QR, RS, SP, OP, OQ, OR, and OS.

2. Let us consider the below figure to completely understand a Rectangular Pyramid.

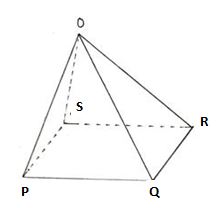
(i) Vertices of a Rectangular Pyramid: A Rectangular pyramid consists of 5 vertices. From the given figure, OPQRS is a Rectangular pyramid having O, P, Q, R, S as its vertices.
(ii) Faces of a Rectangular Pyramid: A Rectangular pyramid consists of 1 rectangular face and 4 triangular faces. From the given figure, OPQRS is a rectangular pyramid having PQRS as its rectangular face and OPS, OSR, OPQ, OQR as its triangular faces.
(iii) Edges of a Rectangular Pyramid: A rectangular pyramid consists of 8 edges. From the given figure, the rectangular pyramid OPQRS has 8 edges, namely, PQ, QR, RS, SP, OP, OQ, OR, and OS.

3. Let us consider the below figure to completely understand a triangular Pyramid.

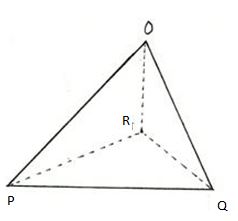
(i) Vertices of a triangular Pyramid: A triangular pyramid consists of 4 vertices. From the given figure, PQRS is a Rectangular pyramid having P, Q, R, S as its vertices.
(ii) Faces of a triangular Pyramid: A triangular pyramid consists of 4 triangular faces. From the given figure, PQRS is a rectangular pyramid having PQR, OPQ, OPR, and OQR triangular faces.
(iii) Edges of a triangular Pyramid: A triangular pyramid consists of 6 edges. From the given figure, the triangular pyramid PQRS has 6 edges, namely, OP, OQ, OR, PQ, PR, QR.

Cylinder

A cylinder is explained as a figure that has two circular bases connected by a curved surface. The cylinder will not consist of any vertices. Also, it has 1 curved face, 2 edges, 2 flat faces.
The formula of surface area and volume of a cylinder is given below.
Surface Area of a cylinder = 2πr(h +r) Square units
The curved surface of a cylinder = 2πrh Square units
The volume of a Cylinder = πr2 h Cubic units

Cone

A cone is defined as a three-dimensional figure, which has a circular base and has a single vertex. The cone decreases smoothly from the circular flat base to the top point. Also, it has 1 vertex, 1 edge, 1 flat face – circle, 1 curved face.
The formula of surface area and volume of a cylinder is given below.
Surface Area of a cone = πr(r +√(r²+h²)  Square units
The curved surface of the area of a cone = πrl Square units
Slant height of a cone = √(r²+h²) Cubic units
The volume of a cone = ⅓ πr²h Cubic units

Sphere

A sphere appears round in shapes and every point on its surface is equidistant from the center point. The distance from the center to any point of the sphere is called the radius of the sphere. Also, it has No vertex, No edges, 1 curved face.
The formula of surface area and volume of a cylinder is given below.
The Curved Surface Area of a Sphere = 2πr² Square units
The Total Surface Area of a Sphere = 4πr² Square units
The volume of a Sphere = 4/3(πr³) cubic units

Types of Fractions and their rules, methods, and formulae are defined here. Know the various types of fractions along with their usage in various situations. Refer to the terminology involved in fractions and also know the problems involved in it. Follow fraction rules and real-life scenarios of fractions. Check the below sections to find examples, rules, methods, etc.

Types of Fractions | What are Fractions?

Before going to know about types of fractions, first know what are fractions and how they work in real life. Fractions are derived from the Latin word “fractus” which means the number or quantity that represents the part or portion of the whole. In the language of layman, a fraction means a number that describes the size of the parts of a whole. Fractions are generally declared with the numerator displaying above the line and below the line, the denominator will be displayed. The terms numerators and denominators are also used in other fractions like mixed, complex, and compound.

Fractions can be written as the equal or same number of parts being counted which is called the numerator over the number or quantity of parts in whole which is called the denominator. There are three major types of fractions which are proper fractions, improper fractions, and mixed fractions. These fractions are divided based on numerator and denominator. Apart from these major fractions, there are also other fractions such as like fractions, unlike fractions, equivalent fractions, etc.

Proper, Improper, and Mixed fractions are defined as single fractions and the remaining fractions determine the comparison of fractions.

Fraction Definition and Terminology

The fraction is considered as the ratio between two numbers. Fractions are defined by a/b. a is called the numerator which means the equal number of parts that are counted. b is called the denominator which means a number of parts in the whole. The numerator and denominator are divided with a line. The line denoted the separation between the numerator and the denominator.

Fraction Types

There are various types of fractions available. We have listed a few of them and explained their definitions, examples in detail. They are as such

1. Proper Fraction:

A proper fraction is that where the value of the numerator is less than the value of the denominator

If you include a numerator, a denominator and a line in between, then it is called a fraction. Proper Fraction is defined as Numerator < Denominator. The value of the proper fraction is always less than 1.

Example:

1/2, 9/15,30/45 are the proper fractions

2. Improper Fraction:

An improper fraction is that where the value of the denominator is less than the value of the numerator. Improper fractions are defined as Numerator > Denominator. Each natural number can be written in fractions in which the denominator is always 1. For example: 20/1,40/1,35/1. The value of the improper fraction is always greater than 1.

Examples: 

3/2, 16/10,45/15 are the improper fractions

3. Mixed Fraction:

A mixed fraction is the combination of a natural number and a fraction. These fractions are improper fractions. Mixed fractions can easily be converted into improper fractions and also mixed fractions can also be converted to improper fractions. The mixed fraction is always greater than 1.

Examples:

3 4/3, 4 5/4, 6 2/3

4. Like Fraction:

If the fractions have the same denominator, then they are called like fractions. For additional simplifications, we can easily make with the like fractions. Addition, Subtraction, Division and multiplication operations can be made easily on like factors.

Examples:

1/2,3/2.5/2,7/2,9/2 are like fractions.

5. Unlike Fractions:

If the factors have different or unique denominators, then they are called, unlike fractions. Simplification of fractions is a lengthy process, therefore we factorize the denominators and then simplify the numerators.

Suppose that we have to add two fractions 1/2 and 1/3.

As the denominators are different, take the LCM of 2 and 3 is equal to 6.

Now, we multiply 1/2 and 1/3 by 2. Multiply it both in numerator and denominator.

Therefore, the fraction becomes 3/6 and 2/6

Now if add 3/6 and 2/6, we get 5/6

Examples:

1/3,1/5,1/7 are unlike fractions

6. Equivalent Fractions:

When more fractions have a similar or same result even after simplification, they represent a similar portion of the whole. Those fractions are equal or similar to each other which are called equivalent fractions.

Examples:

1/2 and 2/4 are equivalent to each other.

1/3 and 3/9 are also equivalent to each other.

How to Convert Improper Fractions into Mixed Fractions?

To convert an improper fraction into mixed fractions, the numerator is divided by the denominator, and the quotient is written as the whole number and the remainder as the numerator.

Example:

Convert the fraction 17/4 into a mixed fraction?

Solution:

To solve the above problem, the steps undertaken are

• Divide the numerator of the given fraction 17 by the denominator of the fraction 4.
• After solving, the quotient is 4 and the remainder is 1.
• Now, combine the whole number 4 with the fraction of 1/4.
• Therefore, the mixed fraction is 4 1/4.

How to Convert Mixed Fraction to Proper Fraction?

The mixed fraction is converted to a proper fraction by multiplying the denominator of the fraction with the whole number and the product is added to the numerator.

The steps that are to be followed to convert mixed fraction as a proper fraction are:

• Multiply the denominator with the whole number.
• Suppose that 2 1/3 is an improper fraction.
• In the above equation, 2 is the whole number and 3 is the denominator.
• 2 * 3 = 6
• Add the product of the numerator
• 6 + 1 = 7
• Now, after adding the product, numerator changes to 7 and denominator changes to 3.
• Now, write the result as an improper fraction as 7/3

How to add Unlike Fractions?

To add the unlike fractions, first, we have to convert them to like fractions. The steps that are involved in adding the unlike fractions are:

1. First, calculate the LCM of both the denominators.
2. The result of LCM will be the denominator of fractions.
3.  Now, we have to calculate the equivalent value of the 1st fraction. To calculate the equivalent, first, divide the LCM calculated in the previous step with the denominator of the 1st fraction. Now, multiply the numerator with the denominator value.
4. In the same way, calculate the equivalent value of the second fraction. To find the equivalent value of the 2nd fraction, divide that LCM that is calculated in the first step by the denominator of the second fraction. Now multiply it with the numerator, therefore both the fractions have the same numerator.
5. Finally, add both the values of the numerator as shown in the previous section.

In geometry, you will various math concepts like Angles, Lines, Shapes, Area and Perimeter, etc. Today, we will discuss completely the concept named Angles and its types. Based on measurements, there are various types of angles. Usually, an angle is measured in degrees and it is one of the core concepts of geometry in Maths. Are you excited to learn deeply about the topic called Angle? Then, refer to the below modules thoroughly and know what is an angle, what are the Types of Angles, definitions, figures, and some solved examples.

What is an Angle?

An Angle is a geometrical shape formed when two rays join with a common end-point. “side and vertex’ are the two components of an angle. Angles are classified based on their measures.

Parts of Angle

• Vertex – Point where the arms meet.
• Arms – Two straight line segments form a vertex.
• Angle – When a ray turn about its endpoint, the measure of its rotation between its initial and final position is called Angle.

If these two ray joins in various fashions to form a various type of angles in maths. Let’s, start learning what are the different types of angles and their definitions and figures.

Classification of Angles

In nature, there are several types of angles that exist. Each and every angle of them hold great value in our everyday living standards.

Basically, Angles are classified on the basis of:

• Magnitude
• Rotation

Types of Angles Based on Magnitude

In maths, mainly, there are 6 types of angles on the basis of direction. And also, all these six angle types are commonly used in geometry. The names of different angles types are as follows:

• Acute Angle
• Obtuse Angle
• Right Angle
• Straight Angle
• Reflex Angle
• Complete Angle

The below image illustrates specific types of angles based on magnitude:

1. Acute Angle:

An acute angle is an angle that lies between 0 degrees to 90 degrees. In other words, an angle is less than 90° is called an acute angle.

Illustration:

∠XYZ is greater than 0° but less than 90° so, this is an acute angle type.

2. Obtuse Angle:

Opposite of the Acute angle is called Obtuse Angle. In other words, the angle that lies between 90 degrees and 180 degrees is known as the obtuse angle.

Illustration:

3. Right Angle:

An angle that measures at exactly 90 degrees is called a right angle. Basically, it forms when two lines are perpendicular to each other. See the below-illustrated figure of a right angle.

4. Straight Angle:

An angle that measures 180° is known as Straight angle. The following figure illustrated the straight angle.

5. Reflex Angle:

The angle that lies between 180 degrees and 360 degrees is called a reflex angle. If you want to calculate the reflex angle then you must require an acute angle. The below figure illustrates the reflex angle.

6. Complete Angle:

An angle measured 360 degrees is called a Complete Angle. 1 Revolution is equal to 360° and the illustration of the complete angle is as shown in the below figure:

Solved Examples on Types of Angles

1. The sum of three angles is (x+6), (x -4), and (x + 8) forms a right angle. Find the value of x.

Solution:

⇒ (x+6) + (x-4) + (x+8) = 90

⇒ 3x + 10 = 90

⇒ 3x = 80

x = 26

Therefore, the value of x is 26 degrees.

2. A certain angle is such that, two times the sum of its size and 70° is 90°. What is the name of this angle?

Solution:

The angle be x°

⇒ 2(x + 70°) = 90°

⇒ 2x + 140° = 90°

⇒ 2x = 50°

x = 25°

The angle is 25°

Since 25° is less than 90°, so the type of the angle is an Acute angle.

Are you looking for help on how to convert a decimal fraction to a fraction number? Don’t Fret as you will find easy methods to convert from decimal to fraction here. Before, diving let’s learn about Decimals, Fractions Definitions. To Convert a Decimal to a Fraction place the decimal number over its place value. For better understanding, we even listed Solved Problems on Decimal Fraction to Fraction Number Conversions here. You can easily convert from decimals to fractions and no calculators are needed.

Decimal Definition

Decimal Numbers are the Numbers that have base 10 in Computer Science. However, in Mathematics Decimal Number is a number that has a decimal point in between digits. In Other Words, we can say that decimals are fractions that have denominator 10 or multiples of 10.

Example: 2.35, 6.78, 8.79 are decimals

Fraction Definition

A fraction is a part of a whole number and is represented as a ratio of two numbers a/b in which a, b are integers and b≠0. The two numbers are namely numerator and denominator. There are different types of fractions namely proper, improper, mixed fractions. we can perform all basic operations on the fractions.

Example: \(\frac { 1 }{ 3 } \), \(\frac { 3 }{ 4 } \) are fractions

How to Convert a Decimal to Fraction?

Learn the Steps to Convert Decimal to Fraction here. Follow the below-listed procedure to change between Decimals to Fractions easily. They are in the following fashion

• Firstly, write the fraction with the decimal number as the numerator and with 1 in the denominator.
• Remove the decimal places by multiplication. Firstly, count how many places are there right to the decimal. Let Suppose there are x places then you need to multiply both the numerator and denominator with 10^x
• Reduce the fraction to the lowest form by dividing both the numerator and denominator of the fraction with GCF.

Steps to Convert a Repeating Decimal to Fraction

Converting a regular Decimal to Fraction is an easy method. But, converting a recurring or repeating decimal fraction is a bit tedious and can be confusing. Let us learn how to convert a repeating decimal to a fraction by considering few examples.

Step 1: Let us assume the decimal number as X

Step 2: Count the number of trailing or repeating digits. If there are x digits multiply with 10^x and consider it as the 2nd equation.

Step 3: Subtract Equation (1) from (2) and Solve for X

Step 4: Reduce the obtained fraction to the lowest form by dividing both the numerator and denominator with their GCF. The obtained fraction is the converted value of the repeating decimal given.

Decimal to Fraction Table

Below is the list of decimal values converted to fractions that you might find useful during your calculations. They are in the following fashion

Decimal to Fraction Conversion Examples

1. Convert 2.25 to fraction?

Solution:

Step 1: To change 2.25 to fraction firstly write the numerator part with a decimal number leaving the denominator part with 1.

Step 2: Count the number of decimal places to the right of the decimal point. Since give decimal value has 2 digits next to the decimal point multiply with 10² both the numerator and denominator.

= \(\frac { (2.25*100) }{ (1*100) } \)

= \(\frac { 225 }{ 100 } \)

Step 3: Reduce the obtained fraction in the earlier step to its lowest form by dividing them with GCF. GCF(225, 100) = 25

i.e. \(\frac { 225÷25 }{ 100÷25 } \)

= \(\frac { 9 }{ 4 } \)

Therefore, 2.25 converted to fraction form is \(\frac { 9 }{ 4 } \)

2. Convert 101.1 to fraction?

Solution:

Given Decimal value is 101.1

Step 1: Place the given decimal value in the numerator of the fraction and place 1 in the denominator.

Step 2: Count the number of digits after the decimal point. Since the given decimal value has only 1 digit multiply both the numerator and denominator with 10. i.e. \(\frac { 101.1*10 }{ 1*10 } \) = \(\frac { 1011 }{ 10 } \)

Step 3:  The above fraction can’t be reduced further since the GCF is 1.

Therefore, 2.25 converted to fraction form is \(\frac {1011 }{ 10 } \)

FAQs on Decimal to Fraction

1. What is a Decimal?

Decima Number is defined as a number whose whole number part and fraction part is separated by a decimal point(dot).

2. What are the types of Decimals?

There are two different types of Decimals

• Terminating Decimals or Non-Recurring Decimals
• Non-Terminating or Recurring Decimals

3. What is a Fraction?

A fraction is a numerical value that is a part of a whole. It is evaluated by dividing a whole into a number of parts.

4. How do I Convert a Decimal to a Fraction?

To Convert a Decimal to a Fraction, place the decimal number over its place value.

Conversion Of Minutes Into Seconds:  Wondering how to calculate the conversion of minutes into seconds in a simple way? Then, you have stepped on the correct page. Here, we have curated the definitions, formula, process of converting min to sec with solved problems. Students can easily convert minutes into seconds within no time by referring to this article. Also, have a glance at the Math Conversion Chart for getting knowledge about length, mass, capacity, conversions, etc. Let’s get into this article and ace up your preparation about conversion between min and sec.

What is Minute?

The definition of a minute is a unit of time equal to 1/60 of an hour or 60 seconds. A Minute is separated into seconds and multiplied into hours. The short form of Minutes is ‘min’. For instance, 1 Minute can be written as 1 min.

What is Second?

The second is called the base unit of time. Seconds are classified into milliseconds and multiplied into minutes. Scientists defined one minute to be 60 seconds. The second is the SI base unit for a time in the metric system. The shortened of the is ‘sec’. For example, 1 Second can be written as 1 sec.

Minutes to Seconds Conversion Formula

In terms of math, the conversion formula below is the correct way to calculate minutes to seconds conversion. The simple formula to convert min to sec is as follows:

How to Convert Minutes(min) to Seconds(sec)

To convert minutes unit of time into seconds unit of time, all you need to perform is multiple the time value by 60. Hence, one minute is equal to 60 seconds. Use the simple Minute to Second conversion formula and substitute the given values in the formula and find out the conversion of minutes into seconds easily.

[number of ] mins x 60 = [number of ] secs

To understand the process of converting minute to second, we have listed out some worked-out examples on minutes to seconds conversion in the below module. Have a look at them and practice well to grasp the concept of conversion of min to sec.

Solved Examples of Min to Sec Conversion

1. Convert 7 minutes to seconds using the conversion formula?

Solution:

Given Minutes = 7

Now, convert them into seconds by using the conversion formula,

The conversion formula for minutes to seconds is Seconds = Minutes x 60 s/min

Substitute the minutes into the formula and calculate the seconds,

Seconds = 7 x 60 = 420 sec

Therefore, 7 minutes = 420 seconds. 

2. How many seconds are there in 4 minutes?

Solution:

Since we know that, 1 minute = 60 seconds, we can make use of this information to solve:

4 minutes x 60 seconds / 1 minute = 4 x 60 sec = 240 sec. 

3. Convert 25 minutes 15 seconds into seconds?

Solution:

As we know, 1 minute = 60 seconds

25 minutes 15 seconds = (25 × 60) seconds + 15 seconds

= 1500 seconds + 15 seconds

= 1515 seconds.

For better learnings about time conversions like Conversion Of Hours Into Seconds visit our website thoroughly.

Minute to Second Conversion Table

FAQs on Conversion Of Minutes Into Seconds

1. How many seconds does 1 minute have?

In one minute, there are 60 seconds. In short, a second is 1/60 of a minute.

2. What is 75 minutes as seconds?

75 minutes = 4500 seconds.

3. Why we use minutes and seconds units?

Minutes and Seconds units are used to measure the time.

The Perimeter of a Square is the length that the boundary covers. You can obtain the Perimeter of a Square by adding all the sides together. Refer to the entire article and learn about Perimeter of a Square Definition, Formula, Derivation, Solved Examples, etc.

A Square is a type of rectangle in which the adjacent sides are equal. In other words, we can frame the Definition as Square has all sides of equal length. Refer to the Properties of Square here along with Solved Example Questions in the later sections.

(i) All the angles in a square are the same and equal 90º.

(ii) All the sides of a square are equal.

What is the Perimeter of a Square?

The Perimeter of any closed geometrical shape is defined as the distance around the object. Usually, the Perimeter of a Square is found by summing all four sides together. Since the square has equal sides thus perimeter will be 4 times the side i.e., 4*Side

The Formula for Perimeter of a Square(P) = 4 × Side

Derivation of Perimeter of a Square

The Perimeter of a Square is defined as the length of the boundary of the object.

The Formula to Calculate the Perimeter of a Square = Sum of Lengths of all 4 Sides

Here Length of Each Side = a units

Perimeter = Side +Side + Side+Side

= a+a+a+a

= 4a units

where a, is the length of a side of square.

Solved Perimeter of Square Questions

Question 1.

Find the Perimeter of a Square whose side is 4 cm?

Solution:

We know the formula to calculate Perimeter of a Square = 4*Side

Given Length of the Side = 4 cm

Substitute the Side Length in the formula of Perimeter

Perimeter of a Square = 4*4

= 16 cm

Therefore, the Perimeter of a Square is 16 cm.

Question 2.

Calculate the Perimeter of a Square if its Side is 12cm?

Solution:

The formula for Perimeter of a Square = 4*Side

Given Length of the Side = 12 cm

Substitute the Side Length in the Formula of Perimeter we have

Perimeter of a Square = 4*12 cm

= 48 cm

Therefore, the Perimeter of a Square is 48 cm.

Question 3.

If the Perimeter of a Square is 84 cm find its Side?

Solution:

Perimeter of a Square = 84 cm

The Formula for Perimeter of a Square =4*Side

4*Side = 84 cm

Side = 84/4

= 21 cm

Therefore, the Length of the Side is 21 cm.

FAQs on Perimeter of a Square

1. What is the Perimeter of a Square?

Perimeter of a Square is the total length of the boundary of squares.

2. How to find the Perimeter of a Square?

To find the Perimeter of a Square add all the sides. There are 4 Sides in a Square and Sum of all 4 Sides gives the Perimeter.

3. What is the Formula for Perimeter of a Square?

The Formula for Perimeter of a Square is P = Side+Side+Side+Side i.e. 4*Side

Have a look at the Properties of Perfect Squares and know how to solve problems on Perfect Square concepts. You can easily learn to solve problems on your own once you get a complete grip on the Perfect Square Concept. We have clearly mentioned every property of a perfect square along with examples. Check out the examples for a better understanding. All concepts available on Square are given on our website for free of cost and you can prepare anytime and anywhere.

Different Properties of Perfect Squares

See different properties of perfect squares given below.

Property 1:
Numbers those end with 2, 3, 7, or 8 will never a perfect square. Also, all the numbers ending in 1, 4, 5, 6, 9, 0 are not square numbers.
Examples:
The numbers 20, 32, 73, 167, 298 end in 0, 2, 3, 7, 8 respectively.
So, none of them is a perfect square.

Property 2:
A number that ends with an odd number of zeros is never a perfect square.
Examples:
The numbers 150, 3000, 700000 end in one zero, three zeros, and five zeros respectively.
So, none of them is a perfect square.

Property 3:
The square of an even number is always even.
Examples:
12² = 144, 14² = 196, 16² = 256, 18² = 324, etc.

Property 4:
The square of an odd number is always odd.
Examples:
11² = 121, 13² = 169, 15² = 225, 17² = 289, 19² = 361, etc. All the numbers are odd.

Property 5:
The square of a proper fraction is smaller than the fraction.
Examples:
(3/4)² = (3/4 × 3/4) = 9/16 and 9/16 < 3/4, since (16 × 3) < (9 × 4).

Property 6:
For every natural number n, we have
(n + 1)² – n² = (n + 1 + n)(n + 1 – n) = {(n + 1) + n}.
Therefore, {(n + 1)² – n²} = {(n + 1) + n}.
Examples:
(i) {1 + 3 + 5 + 7 + 9} = sum of first 5 odd numbers = 5²
(ii) {1 + 3 + 5 + 7 + 9 + 11 + 13 + 15} = sum of first 8 odd numbers = 8²

Property 7:
For every natural number n, we can write as the sum of the first n odd numbers = n²
Examples:
(i) {1 + 3 + 5 + 7 + 9} = sum of first 5 odd numbers = 5²
(ii) {1 + 3 + 5 + 7 + 9 + 11 + 13 + 15} = sum of first 8 odd numbers = 8²

Property 8 (Pythagorean Triplets):
Three natural numbers m, n, p is said to form a Pythagorean triplet (m, n, p) if (m² + n²) = p².
Note:
For every natural number m > 1, we have (2m, m² – 1, m² + 1) as a Pythagorean triplet.
Examples:
(i) Putting m = 6 in (2m, m² – 1, m² + 1) we get (12, 35, 37) as a Pythagorean triplet.
(ii) Putting m = 7 in (2m, m² – 1, m² + 1) we get (14, 48, 50) as a Pythagorean triplet.

Solved Examples on Properties of Perfect Squares

1. Without adding, find the sum (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19).

Solution:
(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19) = sum of first 10 odd numbers
Find the square of the 10 to get the answer.
= (10)² = 100

100 is the sum of the given numbers 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19.

2. Express 81 as the sum of nine odd numbers.

Solution:
81 = 9² = sum of first nine odd numbers
Let us write the first nine odd numbers and add them naturally.
= (1 + 3 + 5 + 7 + 9 + 11 + 13) = 81.

3. Find the Pythagorean triplet whose smallest member is 4.

Solution:
For every natural number m > 1. (2m, m² – 1, m² + 1) is a Pythagorean triplet.
Putting 2m = 8, i.e., m = 4, we get the triplet (8, 15, 17).

The final answer is (8, 15, 17).

A Perfect Square is formed by squaring a whole number. For example 1² = 1; 2² = 4; 3² = 9; 4² = 16; 5² = 25 and so on. Thus 1, 4, 9, 16, 25, etc., are perfect squares. Learn complete information regarding the perfect square and how to find it in this article. We have given examples and also their explanations to understand it easily. Therefore, it is now your part to begin practice and get a complete grip on the concept.

Examples:
1 = 1²; 4 = 2²; 9 = 3²; 16 = 4²; 25 = 5² and so on. Here 1, 4, 9, 16, 25, etc., are perfect squares.

How to Find a Perfect Square or Square Number?

A perfect square number is defined as the product of pairs of equal factors. Or it can also express as grouped in pairs of equal factors.

1. Find out if the following numbers are perfect squares?
(i) 169
(ii) 512
(iii) 64

Solution:
(i) Given number is 169
Find the prime factors of the given number 169.
The prime factors of 169 are 13 and 13.
Grouping the factors into the pairs of equal factors.
(13 × 13)
Factors of the 169 are 13 × 13.

Therefore, 169 is a perfect square.

(ii) Given number is 512
Find the prime factors of the given number 512.
The prime factors of 169 are 8, 8, and 8.
Grouping the factors into the pairs of equal factors.
(8 × 8) × 8
Factors of the 169 are 8 × 8 × 8.
8 is not grouped in pairs of equal factors.

Therefore, 512 is not a perfect square.

(iii) Given number is 64
Find the prime factors of the given number 64.
The prime factors of 64 are 8, and 8.
Grouping the factors into the pairs of equal factors.
(8 × 8)
Factors of the 169 are 8 × 8.

Therefore, 64 is a perfect square.

2. Is 16 a perfect square? If so, find the number whose square is 16.

Solution:
Given number is 16
Find the prime factors of the given number 16.
The prime factors of 16 are 2, 2, 2, and 2.
Grouping the factors into the pairs of equal factors.
(2 × 2) ×(2 × 2)
Therefore, 16 is a perfect square.
Take one number from each group and multiply them to find the number whose square is 16.
2 × 2 = 4.

4 is the number whose square is 16.

3. Is 576 a perfect square? If so, find the number whose square is 576.

Solution:
Given number is 576
Find the prime factors of the given number 16.
The prime factors of 16 are 2, 2, 3, 3, 4, and 4.
Grouping the factors into the pairs of equal factors.
(2 × 2) × (3 × 3) × (4 × 4)
Therefore, 576 is a perfect square.
Take one number from each group and multiply them to find the number whose square is 576.
2 × 3 × 4 = 24.

24 is the number whose square is 576.

4. Show that 288 is not a perfect square.

Solution:
Given number is 288
Find the prime factors of the given number 288.
The prime factors of 16 are 2, 3, 3, 4, and 4.
Grouping the factors into the pairs of equal factors.
2 × (3 × 3) × (4 × 4)
2 is not grouped in pairs of equal factors.

Therefore, 288 is not a perfect square.

5. Find the smallest number by which 100 must be multiplied to make it a perfect square?

Solution:
The given number is 100.
Find the prime factors of the given number 100.
The prime factors of 100 are 5, 5, and 4.
Grouping the factors into the pairs of equal factors.
4 × (5 × 5)
4 is not grouped in pairs of equal factors.
Therefore, by multiplying 4 to 100, we make 100 as a perfect square.

4 is the smallest number by which 100 must be multiplied to make it a perfect square

6. Find the smallest number by which 180 must be divided so as to get a perfect square.

Solution:
The given number is 180.
Find the prime factors of the given number 180.
The prime factors of 180 are 2, 2, 3, 3, and 5.
Grouping the factors into the pairs of equal factors.
5 × (3 × 3) × (2 × 2)
5 is not grouped in pairs of equal factors.
Therefore, by dividing 5 by 180, we make 180 a perfect square.

5 is the smallest number by which 180 must be divided so as to get a perfect square.