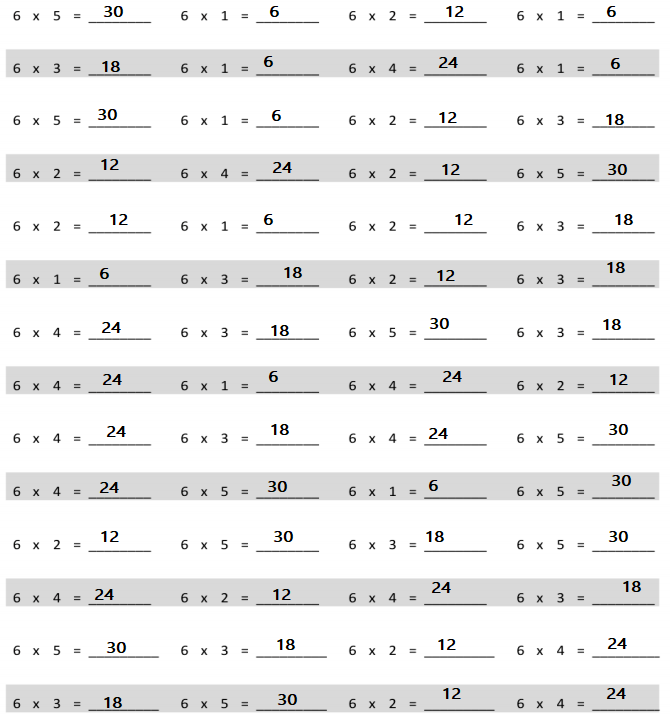
7Engage NY Eureka Math 4th Grade Module 2 Lesson 5 Answer Key
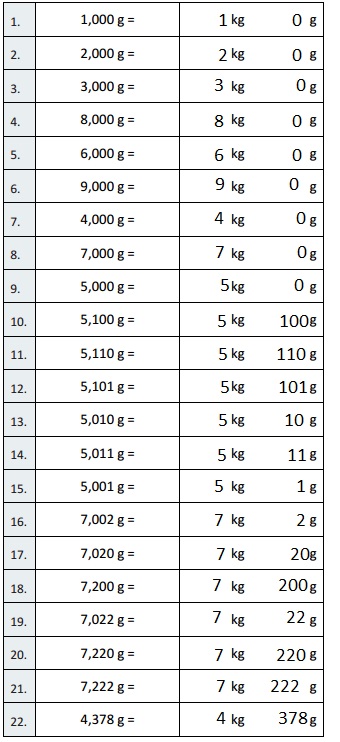
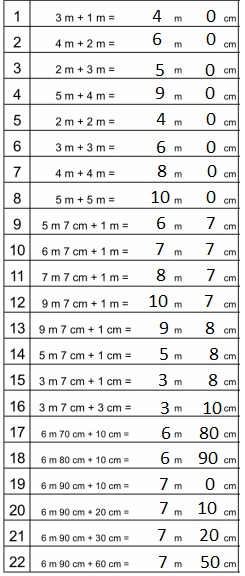
Eureka Math Grade 4 Module 2 Lesson 5 Sprint Answer Key
A
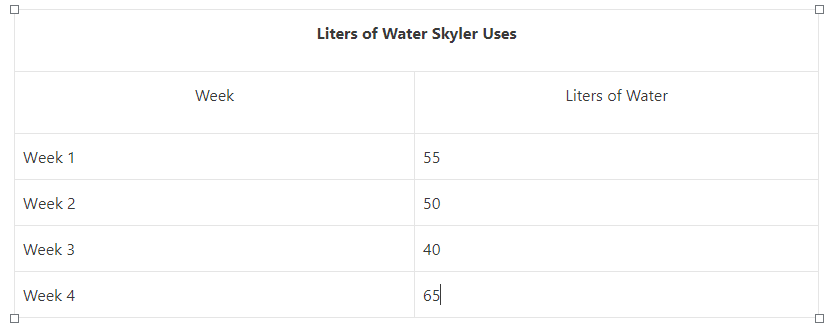
Convert to Kilograms and Grams
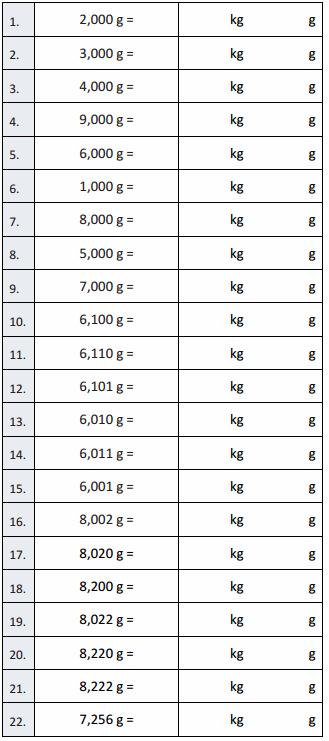
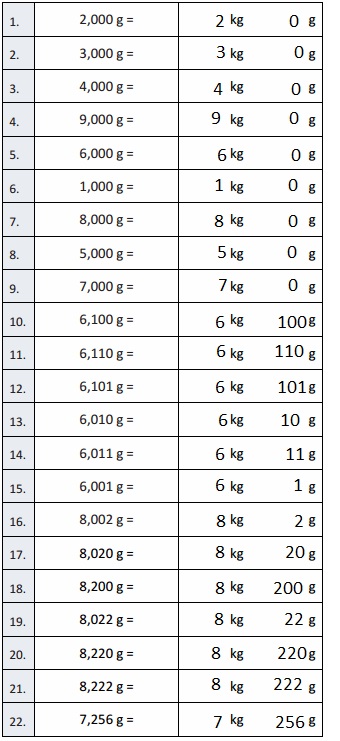
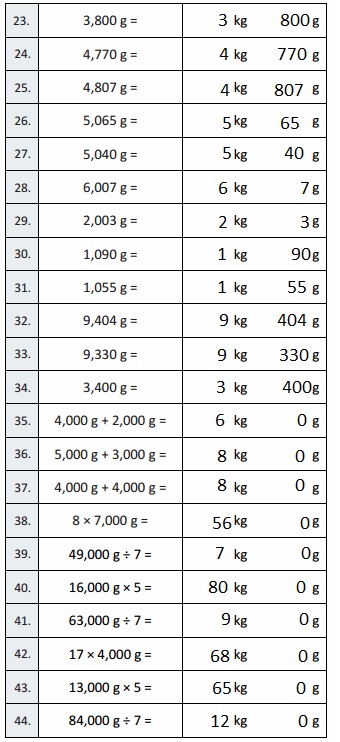
Question 1.
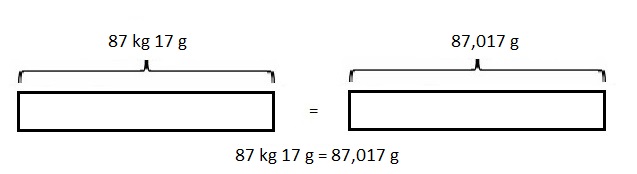
2,000 g = 2 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,000 g = 2 X 1000 g ÷ 1000 = 2 kg 0 g.
Question 2.
3,000 g = 3 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,000 g = 3 X 1000 g ÷ 1000 = 3 kg 0 g.
Question 3.
4,000 g = 4 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,000 g = 4 X 1000 g ÷ 1000 = 4 kg 0 g.
Question 4.
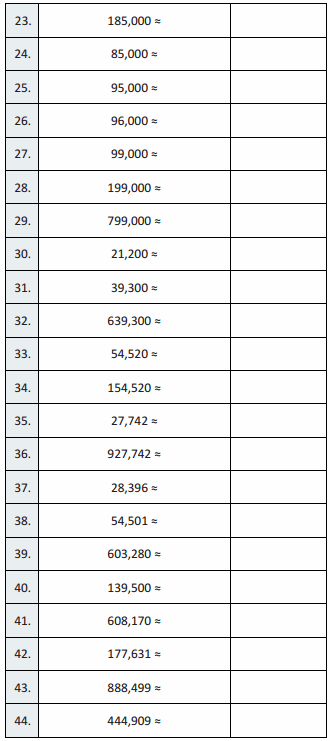
9,000 g = 9 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 9,000 g = 9 X 1000 g ÷ 1000 = 9 kg 0 g.
Question 5.
6,000 g = 6 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,000 g = 6 X 1000 g ÷ 1000 = 6 kg 0 g.
Question 6.
1,000 g = 1 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,000 g = 1 X 1000 g ÷ 1000 = 1 kg 0 g.
Question 7.
8,000 g = 8 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,000 g = 8 X 1000 g ÷ 1000 = 8 kg 0 g.
Question 8.
5,000 g = 5 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,000 g = 5 X 1000 g ÷ 1000 = 5 kg 0 g.
Question 9.
7,000 g = 7 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,000 g = 7 X 1000 g ÷ 1000 = 7 kg 0 g.
Question 10.
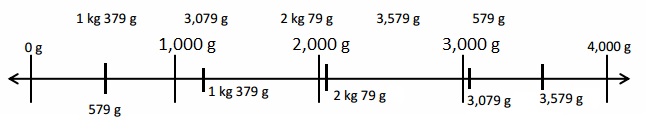
6,100 g = 6 kg 100 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,100 g = 6,100 g ÷ 1000 = 6 kg 100 g.
Question 11.
6,110 g = 6 kg 110 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,110 g = 6 ,110 g ÷ 1000 = 6 kg 110 g.
Question 12.
6,101 g = 6 kg 101 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,101 g = 6,101 g ÷ 1000 = 6 kg 101 g.
Question 13.
6,010 g = 6 kg 10 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,010 g = 6,010 g ÷ 1000 = 6 kg 10 g.
Question 14.
6,011 g = 6 kg 11 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,011 g = 6,011 g ÷ 1000 = 6 kg 11 g.
Question 15.
6,001 g = 6 kg 1 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,001 g = 6,001 g ÷ 1000 = 6 kg 1 g.
Question 16.
8,002 g = 8 kg 2 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,002 g = 8,002 g ÷ 1000 = 8 kg 2 g.
Question 17.
8,020 g = 8 kg 20 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,002 g = 8,002 g ÷ 1000 = 8 kg 2 g.
Question 18.
8,200 g = 8 kg 200 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,200 g = 8,200 g ÷ 1000 = 8 kg 200 g.
Question 19.
8,022 g = 8 kg 22 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,022 g = 8,022 g ÷ 1000 = 8 kg 22 g.
Question 20.
8,220 g = 8 kg 220 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,220 g = 8,220 g ÷ 1000 = 8 kg 220 g.
Question 21.
8,222 g = 8 kg 222 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,222 g = 8,222 g ÷ 1000 = 8 kg 222 g.
Question 22.
7,256 g = 7 kg 256 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,256 g = 7,256 g ÷ 1000 = 7 kg 256 g.
Question 23.
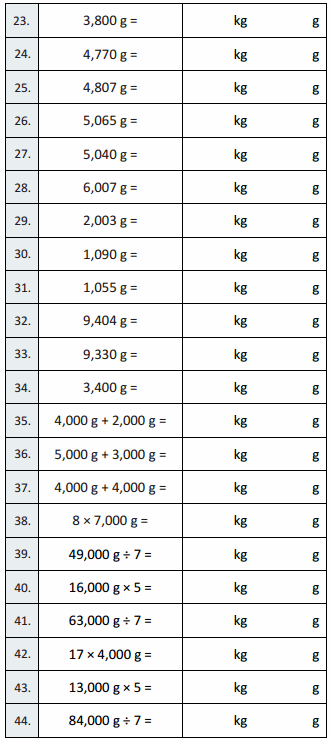
3,800 g = 3 kg 800 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,800 g = 3,800 g ÷ 1000 = 3 kg 800 g.
Question 24.
4,770 g = 4 kg 770 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,770 g = 4,770 g ÷ 1000 = 4 kg 770 g.
Question 25.
4,807 g = 4 kg 807 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,807 g = 4,807 g ÷ 1000 = 4 kg 807 g.
Question 26.
5,065 g = 5 kg 065 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,065 g = 5,065 g ÷ 1000 = 5 kg 065 g.
Question 27.
5,040 g = 5 kg 40 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,040 g = 5,040 g ÷ 1000 = 5 kg 40 g.
Question 28.
6,007 g = 6 kg 7 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,007 g = 6,007 g ÷ 1000 = 6 kg 7 g.
Question 29.
2,003 g = 2 kg 3 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,003 g = 2,003 g ÷ 1000 = 2 kg 3 g.
Question 30.
1,090 g = 1 kg 90 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,090 g = 1,090 g ÷ 1000 = 1 kg 90 g.
Question 31.
1,055 g = 1 kg 55 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,055 g = 1,055 g ÷ 1000 = 1 kg 55 g.
Question 32.
9,404 g = 9 kg 404 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 9,404 g = 9,404 g ÷ 1000 = 9 kg 404 g.
Question 33.
9,330 g = 9 kg 330 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 9,330 g = 9,330 g ÷ 1000 = 9 kg 330 g.
Question 34.
3,400 g = 3 kg 400 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,400 g = 3,400 g ÷ 1000 = 3 kg 400 g.
Question 35.
4,000 g + 2,000 g = 6 kg 0 g,
Explanation:
Given 4,000 g + 2,000 g = 6,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,000 g + 2,000 g = 6,000 g = 6,000 g ÷ 1000 = 6 kg 0 g.
Question 36.
5,000 g + 3,000 g = 8 kg 0 g,
Explanation:
Given 5,000 g + 3,000 g = 8,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,000 g + 3,000 g = 8,000 g = 8,000 g ÷ 1000 = 8 kg 0 g.
Question 37.
4,000 g + 4,000 g = 8 kg 0 g,
Explanation:
Given 4,000 g + 4,000 g = 8,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,000 g + 4,000 g = 8,000 g = 8,000 g ÷ 1000 = 8 kg 0 g.
Question 38.
8 × 7,000 g = 56 kg 0 g,
Explanation:
Given 8 X 7,000 g = 56,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8 × 7,000 g = 56,000 g = 56,000 g ÷ 1000 = 56 kg 0 g.
Question 39.
49,000 g ÷ 7 = 7 kg 0 g,
Explanation:
Given 49,000 g ÷ 7 = 7,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 49,000 g ÷ 7 = 7,000 g = 7,000 g ÷ 1000 = 7 kg 0 g.
Question 40.
16,000 g × 5 = 80 kg 0 g,
Explanation:
Given 16,000 g X 5 = 80,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 16,000 g X 5 = 80,000 g = 80,000 g ÷ 1000 = 80 kg 0 g.
Question 41.
63,000 g ÷ 7 = 9 kg 0 g,
Explanation:
Given 63,000 g ÷ 7 = 9,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 63,000 g ÷ 7 = 9,000 g = 9,000 g ÷ 1000 = 9 kg 0 g.
Question 42.
17 × 4,000 g = 68 kg 0 g,
Explanation:
Given 17 X 4,000 g = 68,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 17 X 4,000 g = 68,000 g = 68,000 g ÷ 1000 = 68 kg 0 g.
Question 43.
13,000 g × 5 = 65 kg 0 g,
Explanation:
Given 13,000 g X 5 = 65,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 13,000 g X 5 = 65,000 g = 65,000 g ÷ 1000 = 65 kg 0 g.
Question 44.
84,000 g ÷ 7 = 12 kg 0 g,
Explanation:
Given 84,000 g ÷ 7 = 12,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 84,000 g ÷ 7 = 12,000 g = 12,000 g ÷ 1000 = 12 kg 0 g.
B
Convert to Kilograms and Grams
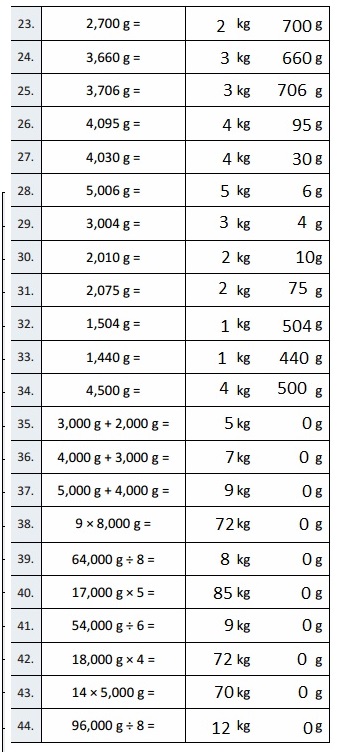
Question 1.
1,000 g = 1 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,000 g = 1 X 1000 g ÷ 1000 = 1 kg 0 g.
Question 2.
2,000 g = 2 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,000 g = 2 X 1000 g ÷ 1000 = 2 kg 0 g.
Question 3.
3,000 g = 3 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,000 g = 3 X 1000 g ÷ 1000 = 3 kg 0 g.
Question 4.
8,000 g = 8 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 8,000 g = 8 X 1000 g ÷ 1000 = 8 kg 0 g.
Question 5.
6,000 g = 6 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 6,000 g = 6 X 1000 g ÷ 1000 = 6 kg 0 g.
Question 6.
9,000 g = 9 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 9,000 g = 9 X 1000 g ÷ 1000 = 9 kg 0 g.
Question 7.
4,000 g = 4 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,000 g = 4 X 1000 g ÷ 1000 = 4 kg 0 g.
Question 8.
7,000 g = 7 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,000 g = 7 X 1000 g ÷ 1000 = 7 kg 0 g.
Question 9.
5,000 g = 5 kg 0 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,000 g = 5 X 1000 g ÷ 1000 = 5 kg 0 g.
Question 10.
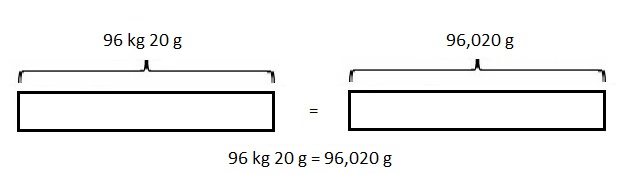
5,100 g = 5 kg 100 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,100 g = 5,100 g ÷ 1000 = 5 kg 100 g.
Question 11.
5,110 g = 5 kg 110 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,110 g = 5 ,110 g ÷ 1000 = 5 kg 110 g.
Question 12.
5,101 g = 5 kg 101 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,101 g = 5,101 g ÷ 1000 = 5 kg 101 g.
Question 13.
5,010 g = 5 kg 10 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,010 g = 5,010 g ÷ 1000 = 5 kg 10 g.
Question 14.
5,011 g = 5 kg 11 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,011 g = 5,011 g ÷ 1000 = 5 kg 11 g.
Question 15.
5,001 g = 5 kg 1 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,001 g = 5,001 g ÷ 1000 = 5 kg 1 g.
Question 16.
7,002 g = 7 kg 2 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,002 g = 7,002 g ÷ 1000 = 7 kg 2 g.
Question 17.
7,020 g = 7kg 20 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,020 g = 7,020 g ÷ 1000 = 7 kg 20 g.
Question 18.
7,200 g = 7 kg 200 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,200 g = 7,200 g ÷ 1000 = 7 kg 200 g.
Question 19.
7,022 g = 7 kg 22 g,
7,022 g = 7 kg 22 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,022 g = 7,022 g ÷ 1000 = 7 kg 22 g.
Question 20.
7,220 g = 7 kg 220 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,220 g = 7,220 g ÷ 1000 = 7 kg 220 g.
Question 21.
7,222 g = 7 kg 222 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 7,222 g = 7,222 g ÷ 1000 = 7 kg 222 g.
Question 22.
4,378 g = 4 kg 378 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,378 g = 4,378 g ÷ 1000 = 4 kg 378 g.
Question 23.
2,700 g = 2 kg 700 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,700 g = 2,700 g ÷ 1000 = 2 kg 700 g.
Question 24.
3,660 g = 3 kg 660 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,660 g = 3,660 g ÷ 1000 = 3 kg 660 g.
Question 25.
3,706 g = 3 kg 706 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,706 g = 3,706 g ÷ 1000 = 3 kg 706 g.
Question 26.
4,095 g = 4 kg 95 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,095 g = 4,095 g ÷ 1000 = 4 kg 95 g.
Question 27.
4,030 g = 4 kg 30 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,030 g = 4,030 g ÷ 1000 = 4 kg 30 g.
Question 28.
5,006 g = 5 kg 6 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,006 g = 5,006 g ÷ 1000 = 5 kg 6 g.
Question 29.
3,004 g = 3 kg 4 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,004 g = 3,004 g ÷ 1000 = 3 kg 4 g.
Question 30.
2,010 g = 2 kg 10 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,010 g = 2,010 g ÷ 1000 = 2 kg 10 g.
Question 31.
2,075 g = 2 kg 75 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 2,075 g = 2,075 g ÷ 1000 = 2 kg 75 g.
Question 32.
1,504 g = 1 kg 504 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,504 g = 1,504 g ÷ 1000 = 1 kg 504 g.
Question 33.
1,440 g = 1 kg 440 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 1,440 g = 1,440 g ÷ 1000 = 1 kg 440 g.
Question 34.
4,500 g = 4 kg 500 g,
Explanation:
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,500 g = 4,500 g ÷ 1000 = 4 kg 500 g.
Question 35.
3,000 g + 2,000 g = 5 kg 0 g,
Explanation:
Given 3,000 g + 2,000 g = 5,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 3,000 g + 2,000 g = 5,000 g = 5,000 g ÷ 1000 = 5 kg 0 g.
Question 36.
4,000 g + 3,000 g = 7 kg 0 g,
Explanation:
Given 4,000 g + 3,000 g = 7,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 4,000 g + 3,000 g = 7,000 g = 7,000 g ÷ 1000 = 7 kg 0 g.
Question 37.
5,000 g + 4,000 g = 9 kg 0 g,
Explanation:
Given 5,000 g + 4,000 g = 9,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 5,000 g + 4,000 g = 9,000 g = 9,000 g ÷ 1000 = 9 kg 0 g.
Question 38.
9 × 8,000 g = 72 kg 0 g,
Explanation:
Given 9 X 8,000 g = 72,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 9 × 8,000 g = 72,000 g = 72,000 g ÷ 1000 = 72 kg 0 g.
Question 39.
64,000 g ÷ 8 = 8 kg 0 g,
Explanation:
Given 64,000 g ÷ 8 = 8,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 64,000 g ÷ 8 = 8,000 g = 8,000 g ÷ 1000 = 8 kg 0 g.
Question 40.
17,000 g × 5 = 85 kg 0 g,
Explanation:
Given 17,000 g X 5 = 85,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 17,000 g X 5 = 85,000 g = 85,000 g ÷ 1000 = 85 kg 0 g.
Question 41.
54,000 g ÷ 6 = 9 kg 0 g,
Explanation:
Given 54,000 g ÷ 6 = 9,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 54,000 g ÷ 6 = 9,000 g = 9,000 g ÷ 1000 = 9 kg 0 g.
Question 42.
18,000 g × 4 = 72 kg 0 g,
Explanation:
Given 18,000 g X 4 = 72,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 18,000 g X 4 = 72,000 g = 72,000 g ÷ 1000 = 72 kg 0 g.
Question 43.
14 × 5,000 g = 70 kg 0 g,
Explanation:
Given 14 X 5,000 g = 70,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 14 X 5,000 g = 70,000 g = 70,000 g ÷ 1000 = 70 kg 0 g.
Question 44.
96,000 g ÷ 8 = 12 kg 0 g,
Explanation:
Given 96,000 g ÷ 8 = 12,000 g
Converted the conversion table as shown above as
We know 1000 g or 103 = 1 kg,
So 96,000 g ÷ 8 = 12,000 g = 12,000 g ÷ 1000 = 12 kg 0 g.
Eureka Math Grade 4 Module 2 Lesson 5 Problem Set Answer Key
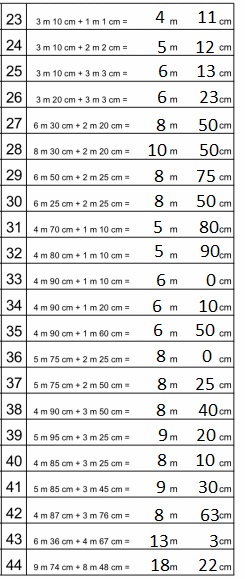
Model each problem with a tape diagram.
Solve and answer with a statement.
Question 1.
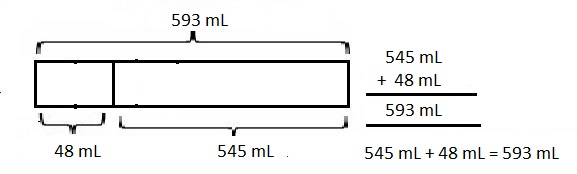
The potatoes Beth bought weighed 3 kilograms 420 grams.
Her onions weighed 1,050 grams less than the potatoes.
How much did the potatoes and onions weigh together?

The potatoes and onions wiegh together 5,790 g or 5 kg 790 g,
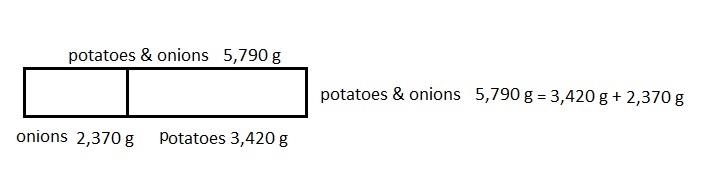
Statement: Both the potatoes and onions wiegh together are
five thousand seven hundred ninety grams or five kilograms and
seven hundred ninety grams,
Explanation:
Given the potatoes Beth bought weighed 3 kilograms 420 grams.
Her onions weighed 1,050 grams less than the potatoes.
So onions wiegh is 3 kg 420 g – 1,050 g =
3 X 1000 g + 420 g = 3,420 g,
now 3,420 g – 1,050 g = 2,370 g,
So the potatoes and onions weigh together are
3,420 g + 2,370 g = 5,790 g or 5,790 ÷ 1,000 = 5 kg 790 g,
Therefore, the potatoes and onions weigh together
5,790 g or 5 kg 790 g,
Modeled problem with a tape diagram as shown above and
statement is both the potatoes and onions wiegh together are
five thousand seven hundred ninety grams or five kilograms and
seven hundred ninety grams.
Question 2.
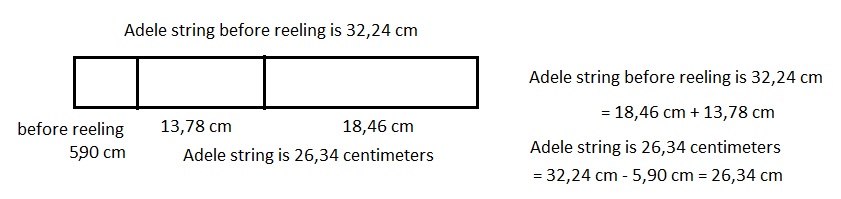
Adele let out 18 meters 46 centimeters of string to fly her kite.
She then let out 13 meters 78 centimeters more before
reeling back in 590 centimeters. How long was her string
after reeling it in?
Adele string is 26,34 centimeters or 26 meters 34 centimeters long
after reeling it in.
Statement: Adele string is twenty six thousand thirty centimeters or
twenty six meters and thirty centimeters long after reeling it in,
Explanation:
Given Adele let out 18 meters 46 centimeters of string to fly her kite.
She then let out 13 meters 78 centimeters more before
reeling back in 590 centimeters. So Adele string length after
reeling it in is 18 m 46 cm + 13 m 78 cm – 590 cm =
as 18 m 46 cm = 18 x 100 cm + 46 cm = 18,00 cm + 46 cm =
18,46 cm and 13 m 78 cm = 13 X 100 cm + 78 cm =
13,00 cm + 78 cm = 13,78 cm.
Now (18,46 cm + 13,78 cm) – 590 cm = 32,24 cm – 590 cm =
26,34 cm or 26,34 cm ÷ 100 = 26 m 34 cm,
Therefore, Adele string is 26,34 centimeters or
26 meters 34 centimeters long after reeling it in.
Modeled problem with a tape diagram as shown above and
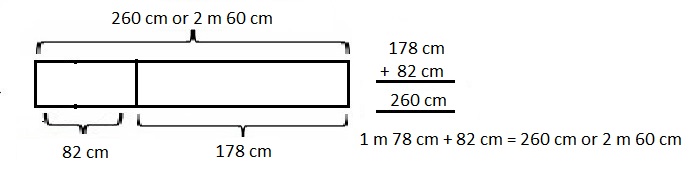
statement is Adele string is twenty six thousand thirty centimeters or
twenty six meters and thirty centimeters long after reeling it in.
Question 3.
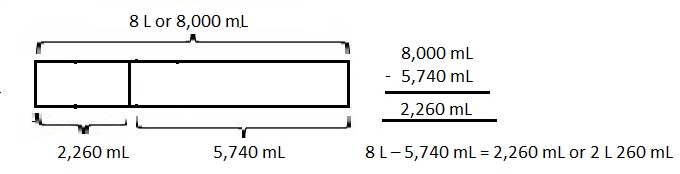
Shyan’s barrel contained 6 liters 775 milliliters of paint.
She poured in 1 liter 118 milliliters more.
The first day, Shyan used 2 liters 125 milliliters of the paint.
At the end of the second day, there were 1,769 milliliters of paint remaining in the barrel.
How much paint did Shyan use on the second day?
On the second day Shyan uses 3,999 milliliters or
3 liters 999 milliliters of the paint,

Statement : Shyan on the second day uses three thousand
nine hundred ninety nine milliliters or 3 liters and nine
hundred ninety nine milliliters of the paint,
Explanation:
Given Shyan’s barrel contained 6 liters 775 milliliters of paint.
She poured in 1 liter 118 milliliters more.
The first day, Shyan used 2 liters 125 milliliters of the paint.
At the end of the second day, there were 1,769 milliliters of paint remaining in the barrel. Total amount of the paint is
6 L 775 mL + 1 L 118 mL = 7 L 893 mL,
Paint left after first day is 7 L 893 mL – 2 L 125 mL =
7 L 893 mL = 7 X 1000 mL + 893 mL = 7,893 mL,
2 L 125 mL = 2 X 1000 mL + 125 mL = 2,125 mL,
So 7,893 mL – 2,125 mL = 5,768 mL paint is left after first day,
Now Second day paint used is 5,768 mL – 1,769 mL = 3,999 mL
or 3,999 mL ÷ 1000 = 3 L 999 mL paint has been
used on the second day by Shyan.
Modeled problem with a tape diagram as shown above and
statement Shyan on the second day uses three thousand
nine hundred ninety nine milliliters or 3 liters and nine
hundred ninety nine milliliters of the paint.
Question 4.
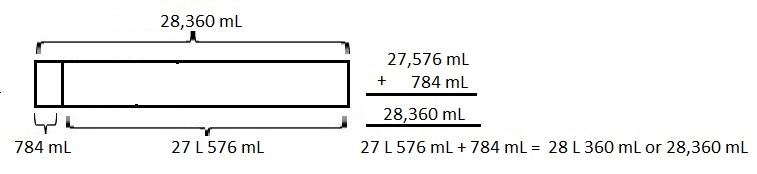
On Thursday, the pizzeria used 2 kilograms 180 grams
less flour than they used on Friday. On Friday, they used
12 kilograms 240 grams. On Saturday, they used 1,888 grams
more than on Friday. What was the total amount of flour used
over the three days?
The total amount of flour used over three days is
36,428 grams or 36 kilograms 428 grams,
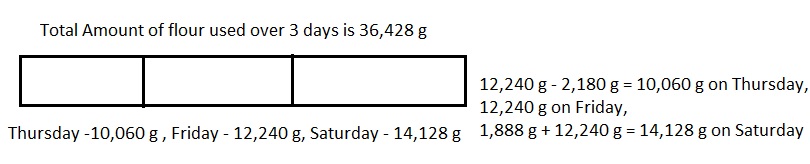
Statement : The total amount of flour used over three days is
thirty six thousand four hundred twenty eight grams or thirty six
kilograms and four hundred twenty eight grams,
Explanation:
Given On Thursday, the pizzeria used less 2 kilograms 180 grams
less flour than they used on Friday. On Friday, they used
12 kilograms 240 grams. On Saturday, they used 1,888 grams
more than on Friday. So on Thursday they used
12 kg 240 g – 2 kg 180 g =
12 X 1000 g + 240 g = 12,240 g,
2 X 1000 + 180 g = 2,180g,
12,240 g – 2,180 g = 10,060 g on Thursday,
On Saturday they used 1,888 g + 12,240 g = 14,128 g,
Now the total amount of flour used over the three days is
10,060 g + 12,240 g + 14,128 g = 36,428 g or 36,428 g ÷ 1000 =
36 kg 428 g. Therefore the total amount of flour used over three days is
36,428 grams or 36 kilograms 428 grams,
Modeled problem with a tape diagram as shown above and
statement is the total amount of flour used over three days is
thirty six thousand four hundred twenty eight grams or thirty six
kilograms and four hundred twenty eight grams.
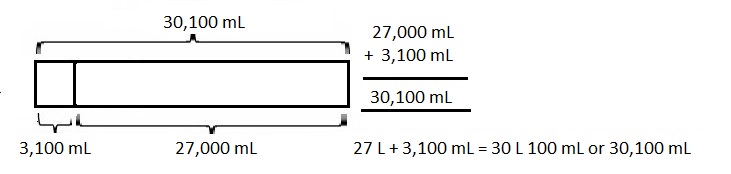
Question 5.
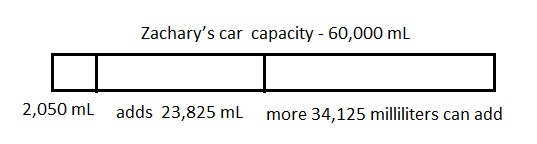
The gas tank in Zachary’s car has a capacity of 60 liters.
He adds 23 liters 825 milliliters of gas to the tank,
which already has 2,050 milliliters of gas.
How much more gas can Zachary add to the gas tank?
More 34,125 milliliters or 34 L 125 mL gas can Zachary
add to the gas tank,
Statement : More thirty four thousand one hundred twenty five milliliters or thirty four liters and one hundred twenty five milliliters gas can
Zachary add to the gas tank,
Explanation:
Given the gas tank in Zachary’s car has a capacity of 60 liters.
He adds 23 liters 825 milliliters of gas to the tank,
which already has 2,050 milliliters of gas.
So the gas tank has 23 L 825 mL + 2,050 mL =
as 23 L 825 mL = 23 X 1000 mL + 825 mL =
23,000 mL + 825 mL = 23,825 mL gas,
Now 23,825 mL + 2,050 mL = 25,875 mL
More gas can Zachary add to the gas tank is 60 L – 25,875 mL =
as 60 L = 60 X 1,000 mL = 60,000 mL,
So 60,000 – 25,875 mL = 34,125 mL or 34,125 mL ÷ 1000 =
34 L 125 mL, therefore, more 34,125 milliliters or
34 L 125 mL gas can Zachary add to the gas tank.
Modeled problem with a tape diagram as shown above and
statement is more thirty four thousand one hundred
twenty five milliliters or thirty four liters and one hundred
twenty five milliliters gas can Zachary add to the gas tank.
Question 6.
A giraffe is 5 meters 20 centimeters tall. An elephant is
1 meter 77 centimeters shorter than the giraffe.
A rhinoceros is 1 meter 58 centimeters shorter than
the elephant. How tall is the rhinoceros?
The rhinoceros is 185 centimeters tall or 1 meter 85 centimeters tall,
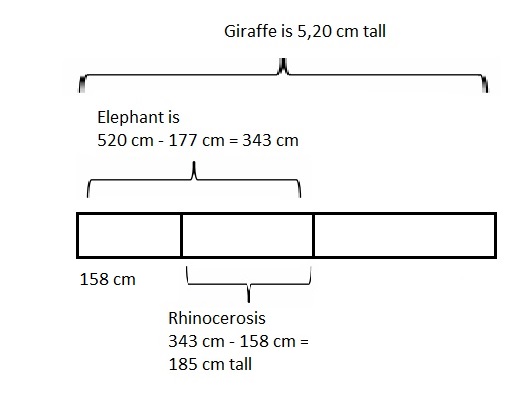
Statement: The rhinoceros is one hundred eighty five
centimeters tall or one meter eighty five centimeters tall,
Explanation:
Given A giraffe is 5 meters 20 centimeters tall. An elephant is
1 meter 77 centimeters shorter than the giraffe and
A rhinoceros is 1 meter 58 centimeters shorter than
the elephant. So height of rhinoceros is first we see
height of elephant as 5 m 20 cm – 1 m 77 cm =
as 5 X 100 cm + 20 cm = 5,20 cm and
1 m 77 cm = 1 X 100 cm +77 cm = 1,77 cm,
so 520 cm – 177 cm = 343 cm, Now rhinoceros is
343 cm – 1 m 58 cm =
as 1 m 58 cm = 1 X 100 cm + 58 cm = 158 cm
so 343 cm – 158 cm = 185 cm or 185 cm ÷ 100 = 1 m 85 cm,
therefore the rhinoceros is 185 centimeters tall or
1 meter 85 centimeters tall, modeled problem with a
tape diagram as shown above and statement is the
rhinoceros is one hundred eighty five centimeters tall or
one meter eighty five centimeters tall.
Eureka Math Grade 4 Module 2 Lesson 5 Exit Ticket Answer Key
Model each problem with a tape diagram.
Solve and answer with a statement.
Question 1.
Jeff places a pineapple with a mass of 890 grams on a
balance scale. He balances the scale by placing two oranges,
an apple, and a lemon on the other side. Each orange weighs
280 grams. The lemon weighs 195 grams less than each orange.
What is the mass of the apple?
The mass of the apple is 245 grams,

Statement : The mass of the apple is two hundred forty five grams,
Explanation:
Given Jeff places a pineapple with a mass of 890 grams on a
balance scale. He balances the scale by placing two oranges,
an apple, and a lemon on the other side. Each orange weighs
280 grams. The lemon weighs 195 grams less than each orange.
So the lemon weighs 280 g – 195 g = 85 grams,
Now weigh of two oranges is 280 g + 280 g = 560 grams,
given 2 oranges + lemon + apple = 890 grams, therefore weigh of
apple = 890 g – (560g + 85 g) = 890 g – 645 g = 245 g,
therefore, the mass of the apple is 245 g, modeled problem
with a tape diagram as shown above and statement is mass
of apple is two hundred fortyy five grams.
Question 2.
Brian is 1 meter 87 centimeters tall. Bonnie is 58 centimeters
shorter than Brian. Betina is 26 centimeters taller than Bonnie.
How tall is Betina?
Betina is 155 cm or 1 m 55 cm tall,
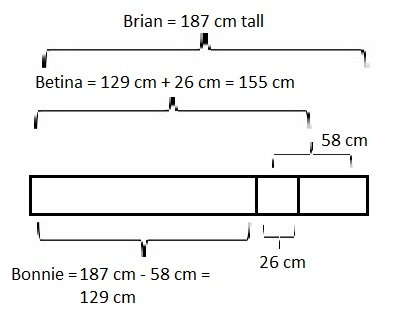
Statement: Betina is one hundred fifty five centimeters or
one meter fifty five centimeters tall,
Explanation:
Given Brian is 1 meter 87 centimeters tall.
Bonnie is 58 centimeters shorter than Brian means
Bonnie is 1 m 87 cm – 58 = as 1 m 87 cm =
1 X 100 cm + 87 cm = 187 cm, 187 cm – 58 cm = 129 cm,
Bonnie is 129 cm and Betina is 26 centimeters taller than
Bonnie means Betina is 129 cm + 26 cm = 155 cm or
155 cm ÷ 100 = 1 m 55 cm,
So Betina is 155 cm or 1 m 55 cm tall, modeled problem
with a tape diagram as shown above and statement is
Betina is one hundred fifty five centimeters or
one meter fifty five centimeters tall.
Eureka Math Grade 4 Module 2 Lesson 5 Homework Answer Key
Model each problem with a tape diagram. Solve and answer with a statement.
Question 1.
The capacity of Jose’s vase is 2,419 milliliters of water.
He poured 1 liter 299 milliliters of water into the empty vase.
Then, he added 398 milliliters. How much more water will
the vase hold?
Jose’s vase can hold more 722 milliliters of water,
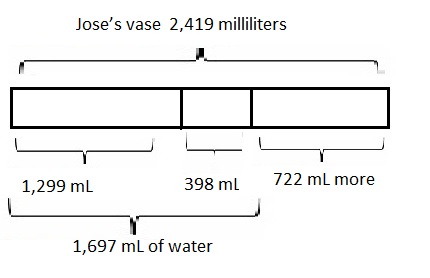
Statement : Jose’s vase can hold more seven hundred twenty
two milliliters of water,
Explanation:
Given the capacity of Jose’s vase is 2,419 milliliters of water.
He poured 1 liter 299 milliliters of water into the empty vase.
Then, he added 398 milliliters. So now water in the vase is
1 L 299 mL + 398 mL as 1 L 299 mL = 1 X 1000 mL + 299 mL =
1,299 mL + 398 mL = 1,697 mL of water,
Now we can pour more is 2,419 mL – 1,697 mL = 722 mL more,
therefore, Jose’s vase can hold more 722 milliliters of water,
modeled problem with a tape diagram as shown above and
statement is Jose’s vase can hold more seven hundred
twenty two milliliters of water.
Question 2.
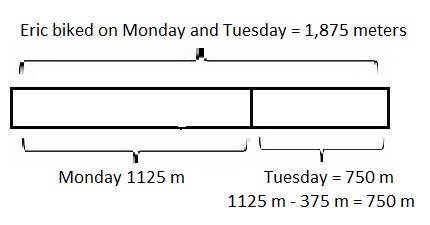
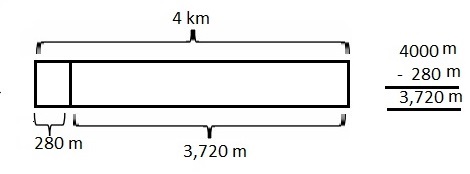
Eric biked 1 kilometer 125 meters on Monday.
On Tuesday, he biked 375 meters less than on Monday.
How far did he bike both days?
Eric biked both days as 1,875 meters or 1 kilometer 875 meters,
Statement : Eric biked both days as one thousand eight
hundred seventy five meters or one kilometer eight
hundred seventy five meters,
Explanation:
Given Eric biked 1 kilometer 125 meters on Monday.
On Tuesday, he biked 375 meters less than on Monday.
So on Tuesday he biked 1 k 125 m – 375 m =
as 1 X 1000 m + 125 m = 1,125 m ,
1125 m – 375 m = 750 m,
therefore Eric biked on Monday and Tuesday is
1,125 m + 750 m = 1,875 m or 1,875 m ÷ 1,000 = 1 k 875 m,
therefore, Eric biked both days as 1,875 meters or
1 kilometer 875 meters, modeled problem with a tape diagram
as shown above and statement is Eric biked both days as one thousand eight hundred seventy five meters or one kilometer eight
hundred seventy five meters.
Question 3.
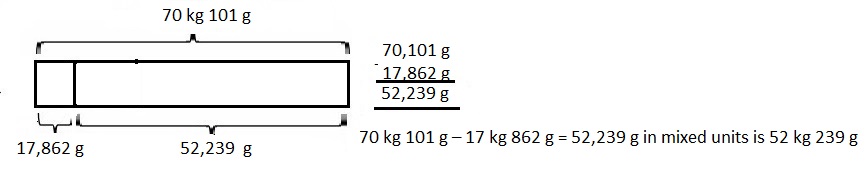
Zachary weighs 37 kilograms 95 grams. Gabe weighs
4,650 grams less than Zachary. Harry weighs
2,905 grams less than Gabe. How much does Harry weigh?
Harry weigh 29,540 grams or 29 kilogram 540 grams,

Statement : Harry weigh’s twenty nine thousand five hundred
forty grams or twenty nine kilograms five hundred
forty grams,
Explanation:
Given Zachary weighs 37 kilograms 95 grams. Gabe weighs
4,650 grams less than Zachary and Harry weighs
2,905 grams less than Gabe. So Gabe weigh’s
37 kg 95 g – 4,650 g as 37 kg 95 g =
37 X 1000 g + 95 g = 37,095 g so Gabe is
37,095 g – 4,650 g = 32,445 g,
Now Harry weigh’s 32,445 g – 2,905 g = 29,540 grams or
29,540 g ÷ 1,000 = 29 kilograms 540 grams,
therefore, Harry weigh 29,540 grams or 29 kilogram 540 grams,
modeled problem with a tape diagram as shown above and
statement is Harry weigh’s twenty nine thousand five hundred
forty grams or twenty nine kilograms five hundred
forty grams.
Question 4.
A Springer Spaniel weighs 20 kilograms 490 grams.
A Cocker Spaniel weighs 7,590 grams less than a
Springer Spaniel. A Newfoundland weighs
52 kilograms 656 grams more than a Cocker Spaniel.
What is the difference, in grams, between the weights of the Newfoundland and the Springer Spaniel?
The difference in grams, between the weights of the
Newfoundland and the Springer Spaniel is 45,066 grams,
 Statement: The difference in grams, between the weights of the
Statement: The difference in grams, between the weights of the
Newfoundland and the Springer Spaniel is forty five thousand
sixty six grams,
Explanation:
Given a Springer Spaniel weighs 20 kilograms 490 grams.
A Cocker Spaniel weighs 7,590 grams less than a
Springer Spaniel. A Newfoundland weighs
52 kilograms 656 grams more than a Cocker Spaniel.
So Cocker spaniel weigh’s 20 kg 490 g – 7,590 g
as 20 kg 490 g = 20 X 1000 g + 490 g = 20,490 g,
So 20,490 g – 7,590 g = 12,900 g,
Now Newfoundland weighs 52 kg 656 g +12,900 g as
52 kg 656 g = 52 X 1000 g + 656 g = 52,656 g,
52,656 g + 12,900 g = 65,556 g,
Now the difference in grams, between the weights of the
Newfoundland and the Springer Spaniel is
65,556 g – 20,490 g = 45,066 grams,
modeled problem with a tape diagram as shown above and
statement is the difference in grams, between the weights of the
Newfoundland and the Springer Spaniel is forty five thousand
sixty six grams.
Question 5.
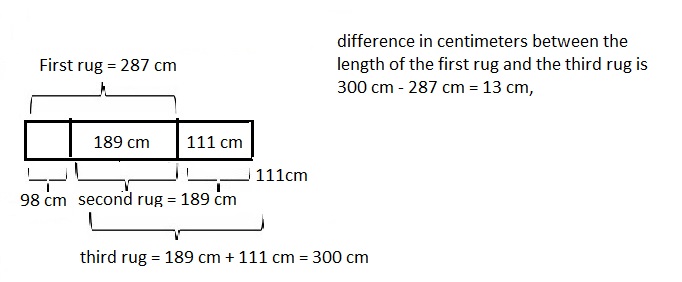
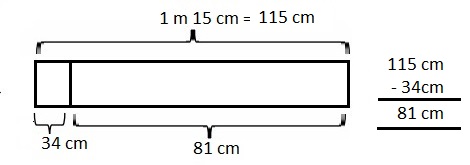
Marsha has three rugs. The first rug is 2 meters 87 centimeters long.
The second rug has a length 98 centimeters
less than the first. The third rug is 111 centimeters
longer than the second rug. What is the difference in
centimeters between the length of the first rug and the third rug?
The difference in centimeters between the length of
the first rug and the third rug is 13 cm,
Statement : The difference in centimeters between the length of
the first rug and the third rug is thirteen centimeters,
Explanation:
Given Marsha has three rugs. The first rug is
2 meters 87 centimeters long.
The second rug has a length 98 centimeters
less than the first. The third rug is 111 centimeters
longer than the second rug so the second rug is
2 m 87 cm – 98 cm as 2 m 87 cm = 2 X 100 cm + 87 cm = 287 cm,
Now 287 cm – 98 cm = 189 cm and the third rug is
189 cm + 111 cm = 300 cm,
first rug is 287 cm, second rug is 189 cm and third rug is 300 cm,
Now the difference in centimeters between the length of
the first rug and the third rug is 300 cm – 287 cm = 13 cm,
modeled problem with a tape diagram as shown above and
statement is the difference in centimeters between the length of
the first rug and the third rug is thirteen centimeters.
Question 6.
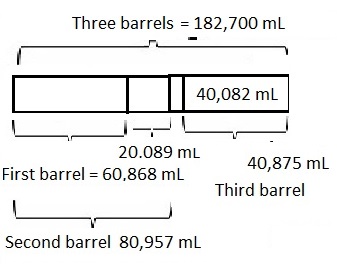
One barrel held 60 liters 868 milliliters of sap.
A second barrel held 20,089 milliliters more sap than the first.
A third barrel held 40 liters 82 milliliters less sap than the second.
If the sap from the three barrels was poured into a
larger container, how much sap would there be in all ?
182,700 milliliters or 182 liters 700 milliliters of sap
would be there in all,
Statement: one lakh eighty two thousand seven hundred
milliliters or one hundred eighty two liters and
seven hundred milliliters of sap would be there in all,
Explanation:
Given one barrel held 60 liters 868 milliliters of sap.
A second barrel held 20,089 milliliters more sap than the first.
A third barrel held 40 liters 82 milliliters less sap than the second.
Second barrel holds 60 L 868 mL + 20,089 mL as
60 L 868 mL = 60 X 1000 mL + 868 mL = 60,868 mL,
60,868 mL + 20,089 mL = 80,957 mL,
Third barrel holds 80,957 mL – 40 L 82 mL as
40 L 82 mL = 40 X 1000 mL + 82 mL = 40,082 mL,
so 80,957 mL – 40,082 mL = 40,875 mL,
First barrel holds 60,868 mL,
Second barrel holds 80,957 mL,
Third barrel holds 40,875 mL,
Now if the sap from the three barrels was poured into a
larger container it will contain
60,868 mL + 80,957 mL + 40,875 mL = 182,700 mL,
modeled problem with a tape diagram as shown above and
statement is one lakh eighty two thousand seven hundred
milliliters or one hundred eighty two liters and
seven hundred milliliters of sap would be there in all.




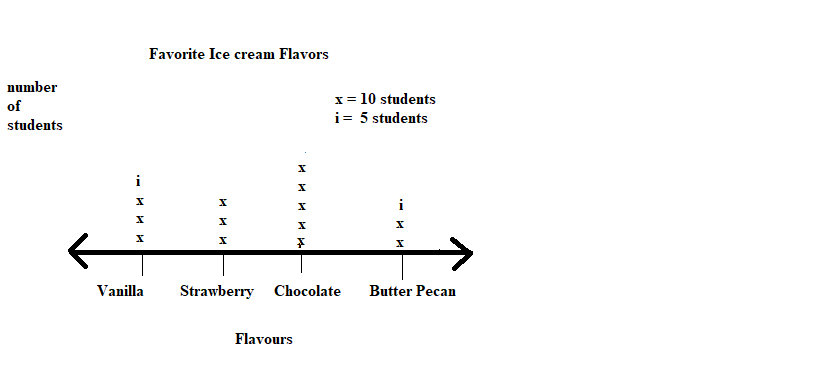






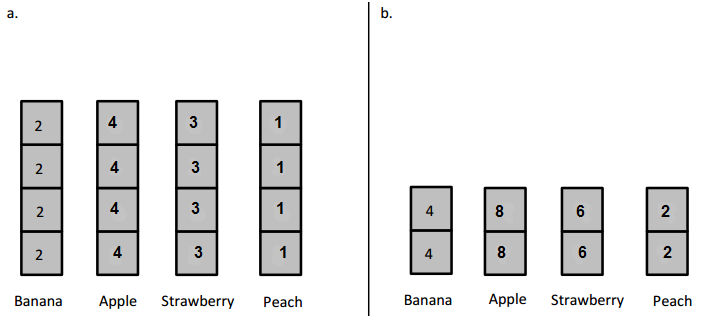


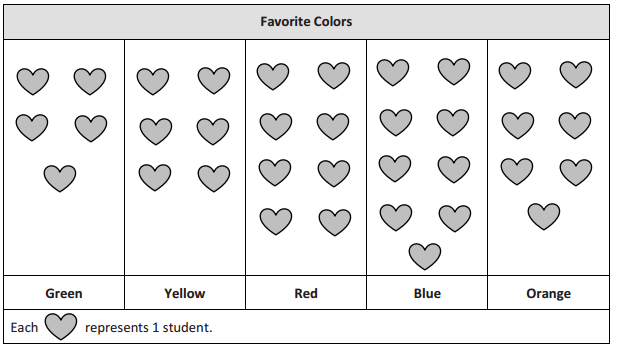
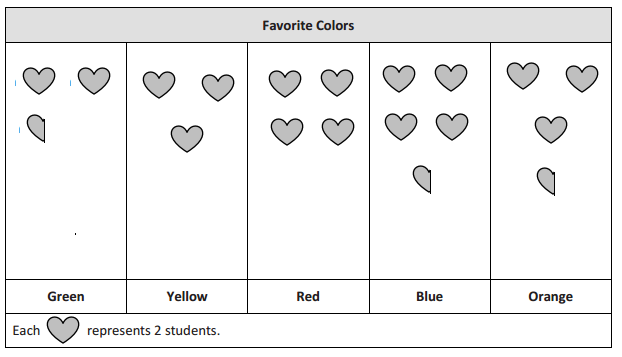

 represents 1 student.
represents 1 student.

















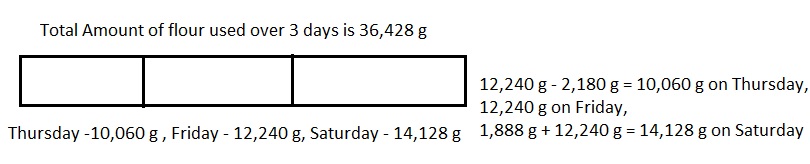








 Statement: The difference in grams, between the weights of the
Statement: The difference in grams, between the weights of the







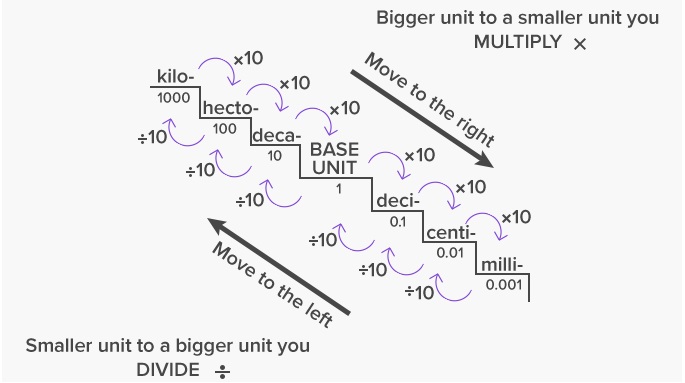
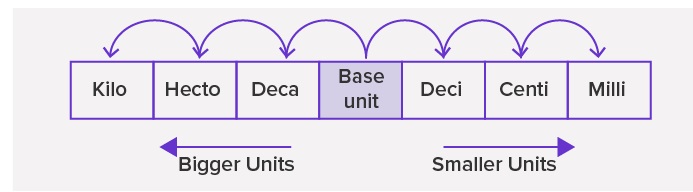 The given figure shows the arrangement of the metric units, which are smaller or bigger than the base unit.The units to the right of the base unit are smaller than the base unit. As we move to the right, each unit is 10 times smaller or one-tenth of the unit to its left. So, a ‘deci’ means one-tenth of the base unit, ‘centi’ is one-tenth of ‘deci’ or one-hundredth of the base unit and ‘milli’ is one-tenth of ‘centi’ or one-thousandth of the base unit.The units to the left of the base unit are bigger than the base unit. As we move to the left, each unit is 10 times greater than the unit to its right. So, a ‘deca’ means ten times of the base unit, ‘hecto’ is ten times of ‘deca’ or hundred times of the base unit and ‘killo’ is ten times of ‘hecto’ or thousand times of the base unit.
The given figure shows the arrangement of the metric units, which are smaller or bigger than the base unit.The units to the right of the base unit are smaller than the base unit. As we move to the right, each unit is 10 times smaller or one-tenth of the unit to its left. So, a ‘deci’ means one-tenth of the base unit, ‘centi’ is one-tenth of ‘deci’ or one-hundredth of the base unit and ‘milli’ is one-tenth of ‘centi’ or one-thousandth of the base unit.The units to the left of the base unit are bigger than the base unit. As we move to the left, each unit is 10 times greater than the unit to its right. So, a ‘deca’ means ten times of the base unit, ‘hecto’ is ten times of ‘deca’ or hundred times of the base unit and ‘killo’ is ten times of ‘hecto’ or thousand times of the base unit.
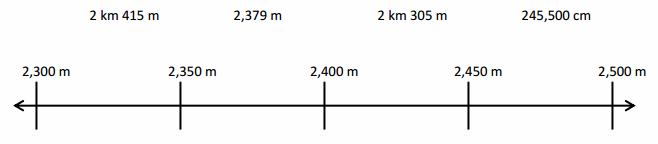
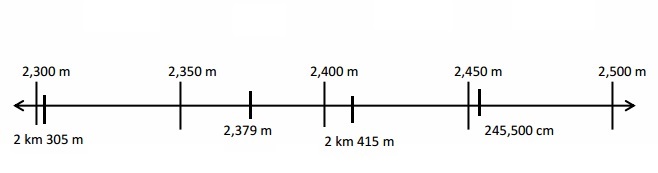
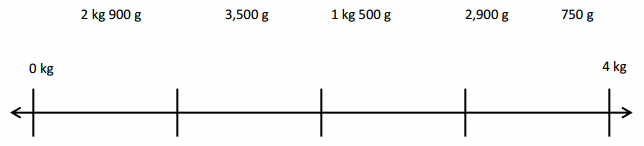
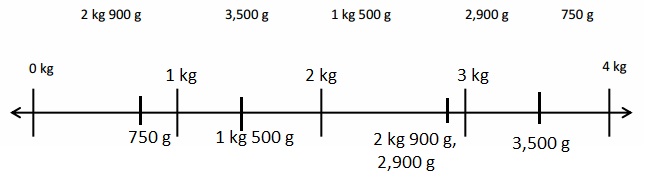
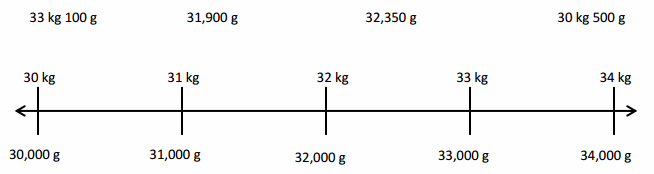
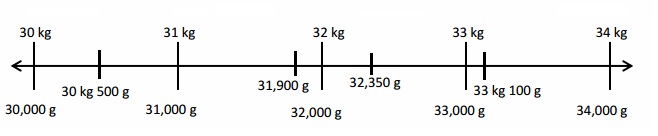
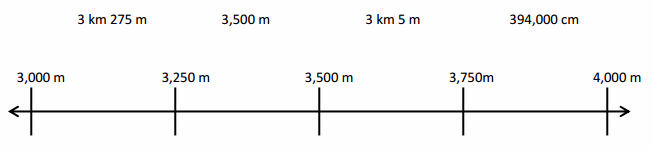
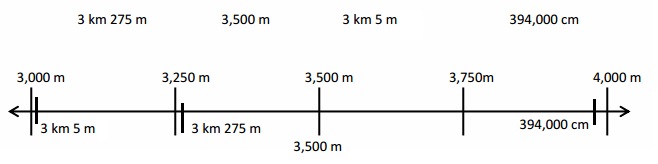
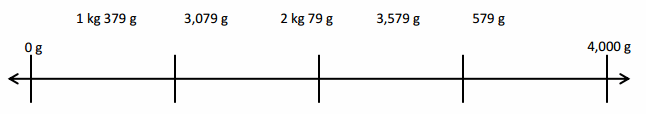

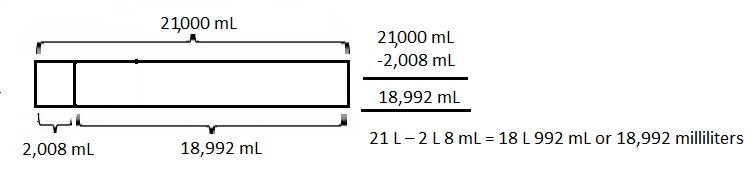
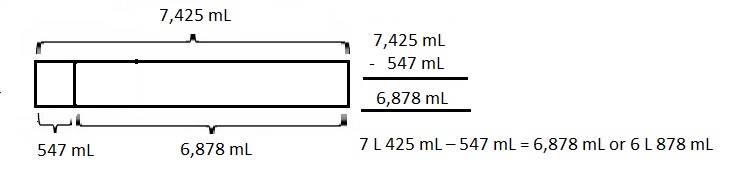
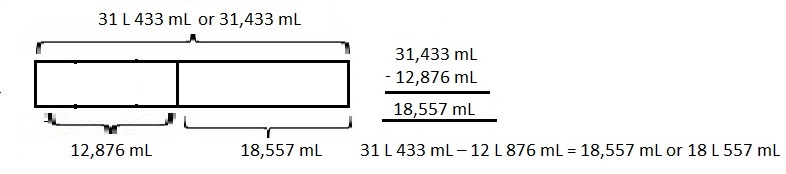

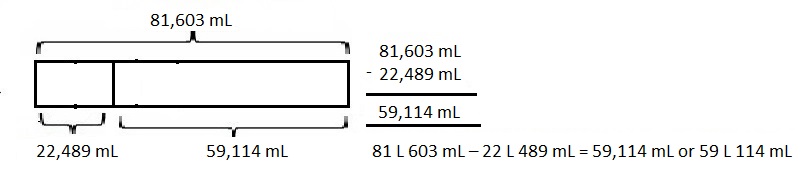
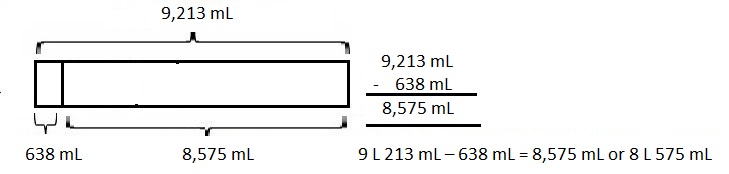
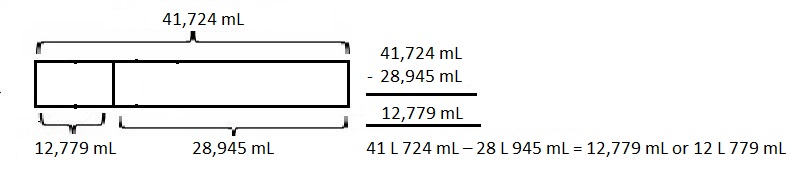
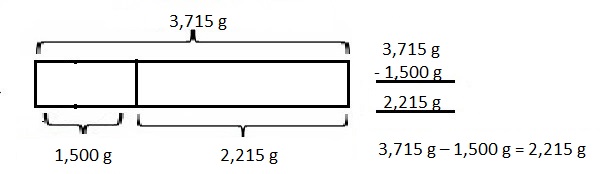
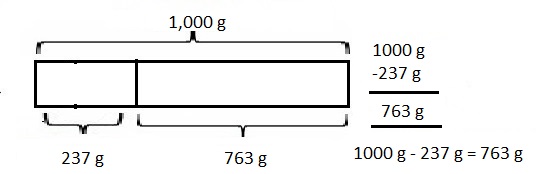
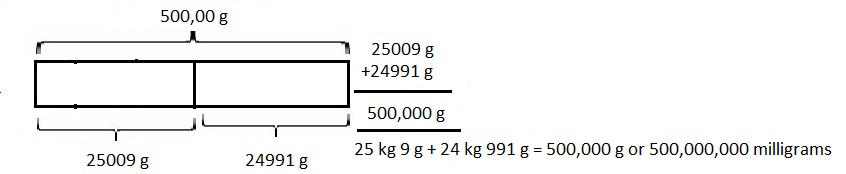


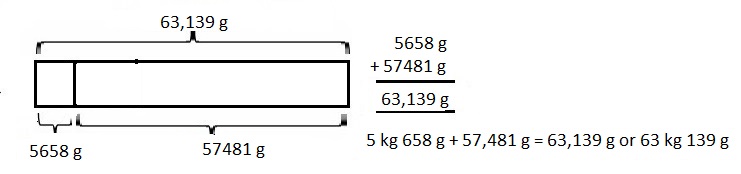

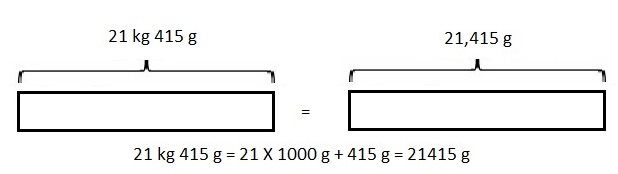
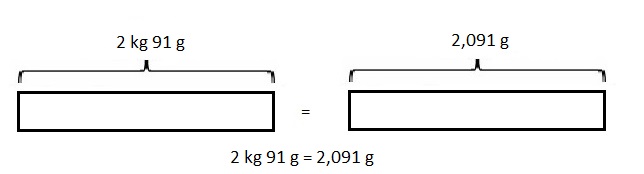
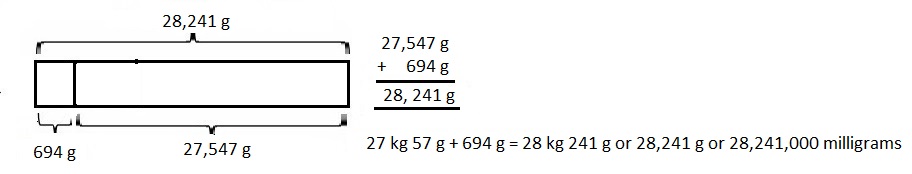


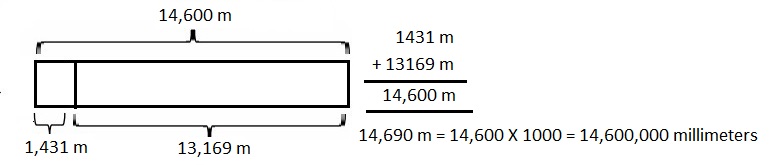

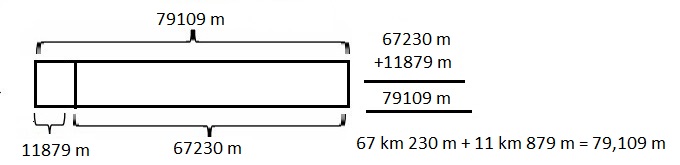
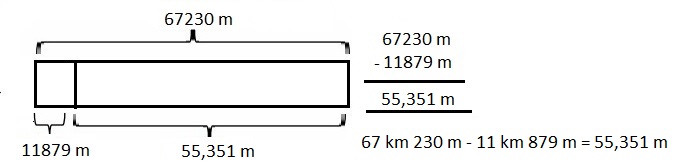 67 kilometer and 230 meters minus 11 kilometers and
67 kilometer and 230 meters minus 11 kilometers and