Prasanna

Fraction as a part of a whole definition, rules, facts, and examples here. Get various problems and solutions involved in whole fractions. Know the tips to solve various problems and find the definition here. Follow the step-by-step procedure to solve part-whole fraction problems. Refer to the models that are present in whole fractions. Check the below sections to know the various concepts involved in fraction whole parts.

What is a Fraction of a Whole?

In the interpretation of part-whole, the denominator value shows equal parts number in whole and the numerator represents the number of parts that are included in a particular fraction. The construct of the whole-part is often represented with the model area like dividing the shape into equal parts. The fraction represents the part of the object. Therefore, the fraction is the whole object part. It is a collection of objects or part of the collection. If the number is not a whole number, then it is a fraction number.

The fraction is a whole number part like 1, 2, 3, 4, 5, 6, ………. 200 …….. etc.

Example of fraction numbers: \(\frac { 1 }{ 3 } \), \(\frac { 1 }{ 5 } \), \(\frac { 1 }{ 7 } \), \(\frac { 1 }{ 9 } \), \(\frac { 1 }{ 11 } \), \(\frac { 1 }{ 13 } \), etc.

How do you write a Fraction as a Whole?

The way to represent whole parts is a fraction. If the fraction is represented with a/b, then the numerator “a” represents the equal number of parts where the whole number is divided into parts. The denominator “b” represents the way that represents the whole number. The denominator value cannot be zero, as division by zero is the undefined value.

Important Concepts of Whole Parts

Property of one

The number which is divided by itself and which is not divided by zero is called the property of one.

Example: 3/3 = 1 where 3 ≠ 0

Mixed Numbers

The mixed number is nothing but the whole number (a) along with the fraction value (b/c) where c ≠ 0 and it ca be written as a b/c where c ≠ 0

Example: 4¾ is the mixed fraction

Proper and Improper Fractions

If the proper fraction is ab, then a<b and if the improper fraction is ab, then a≥b

Conversion of an improper fraction into a mixed fraction

1. The numerator has to be divided with denominator
2. Check remainder, quotient, divisor
3. Note down the mixed number as the quotient i.e., remainder/divisor

Conversion of a mixed fraction into an improper fraction

1. The denominator has to be multiplied by the whole number
2. The product we get in Step 1 has to be added to the numerator
3. In the last step, add the final product and put the denominator as it is

Fractions of equivalent property

If the numbers are a, b and c where c ≠ 0, b ≠ 0 then a/b = a-c/b-c

Also, Check:

• Fractions
• Types of Fractions
• Dividing Fractions

Problems on Fraction as a Part of a Whole

Problem 1:

Mary had some stamps. She gave 7 stamps to her younger brothers. Mary then had 14 stamps. How many stamps did Mary have at first?

Solution:

As given in the question,

No of stamps she gave to her younger brother = 7

No of stamps she had = 14

To find the number of stamps at first, we have to add the values

Therefore 7 + 14 = 21

Thus, Mary had 21 stamps at first

Problem 2:

Rahul spent \(\frac { 3 }{ 4 } \) of an hour for 2 days working on his science project. Kite spent \(\frac { 1 }{ 4 } \)of an hour for 6 days working on his science project. Find the one who spent most f his time working on the science project?

Solution:

As given in the question,

Amount of time Rahul spent for an hour = \(\frac { 3 }{ 4 } \)

No of working days = 2

Amount of time Kite spent for an hour = \(\frac { 1 }{ 4 } \)

No of working days = 6

To find the total time they spent on the science project, we apply the law of multiplication here

Therefore, amount of time Rahul spent = \(\frac { 3 }{ 4 } \) * 2

It can be written as \(\frac { 3 }{ 4 } \) + \(\frac { 3 }{ 4 } \) = \(\frac { 6 }{ 4 } \) hours

Hence, Rahul takes \(\frac { 6 }{ 4 } \) hours to complete the science project

The amount of time Kite spent on his project = \(\frac { 1 }{ 4 } \) * 6

It can be written as \(\frac { 1 }{ 4 } \) + \(\frac { 1 }{ 4 } \) +\(\frac { 1 }{ 4 } \) +\(\frac { 1 }{ 4 } \) +\(\frac { 1 }{ 4 } \) +\(\frac { 1 }{ 4 } \) = \(\frac { 6 }{ 4 } \)

Hence, Kite takes \(\frac { 6 }{ 4 } \) hours to complete the science project

From, the above simplification, we came to know that both of them completes the project in some time.

Therefore, they both complete the science project in \(\frac { 6 }{ 4 } \) hours

Problem 3:

Baine worked 3\(\frac { 1 }{ 5 } \) hrs before work and 2\(\frac { 2 }{ 3 } \) hrs after lunch. How many hours did she work altogether? How many hours did she leave in her 8 days of work?

Solution:

As given in the question,

Baine worked before work = 3\(\frac { 1 }{ 5 } \) hrs

Baine worked after lunch = 2\(\frac { 2 }{ 3 } \)

Therefore, the total amount of time he worked = 3\(\frac { 1 }{ 5 } \) hrs + 2\(\frac { 2 }{ 3 } \)

We have to find the common denominator for 3 and 5

To find the no of hours she worked altogether, we have to add both the fraction values

3\(\frac { 1 }{ 5 } \) hrs + 2\(\frac { 2 }{ 3 } \)

The result is 5\(\frac { 13 }{ 15 } \) hours

To find the number of hours left in her day, we have to subtract the fraction values

Now, we just can’t drop 5\(\frac { 13 }{ 15 } \) as it is \(\frac { 0 }{ 15 } \)

The way we can write 8 is 7 plus 1 and \(\frac { 0 }{ 15 } \)

Thus, \(\frac { 0 }{ 15 } \) is 1 times 15 is 15, plus 0 is just 15

So, I have 7 and \(\frac { 15 }{ 15 } \) minus 5 and \(\frac { 13 }{ 15 } \)

Now, I am ready to subtract 15 minus 13 is 2, and 7 minus 5 is 2

She has two hours and \(\frac { 2 }{ 15 } \)

That is what she has left

Hence, she has worked so far is \(\frac { 2 }{ 15 } \)

Therefore, 5\(\frac { 13 }{ 15 } \) hours they work altogether

\(\frac { 2 }{ 15 } \) hours she left in her 8 days of work

Joint Variation definition, rules, methods and formulae are here. Check the joint variation problems and solutions to prepare for the exam. Refer to problems of direct and inverse variations and the relationship between the variables. Know the different type of variations like inverse, direct, combined and joint variation. Go through the below sections to check definition, various properties, example problems, value tables, concepts etc.

Joint Variation – Introduction

Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for which constant “X”. The joint variation will be useful to represent interactions of multiple variables at one time.

Most of the situations are complicated than the basic inverse or direct variation model. One or the other variables depends on the multiple other variables. Joint Variation is nothing but the variable depending on 2 or more variables quotient or product. To understand clearly with an example, The amount of busing candidates for each of the school trip varies with the no of candidates attending the distance from the school. The variable c (cost) varies jointly with n (number of students) and d (distance).

Joint Variation problems are very easy once you get the perfection of the lingo. These problems involve simple formulae or relationships which involves one variable which is equal to the “one” term which may be linear (with just an “x” axis), a quadratic equation (like “x²) where more than one variable (like “hr²”), and square root (like “\sqrt{4 – r^2\,}4−r2​”) etc.

Functions of 2 or More Variables

It is very uncommon for the output variable to depend on 2 or more inputs. Most of the familiar formulas describe the several variables functions. For suppose, if the rectangle perimeter depends on the length and width. The cylinder volume depends on its height and radius. The travelled distance depends on the time and speed while travelling. The function notation of the formulas can be written as

P = f(l,w) = 2l + 2w where P is the perimeter and is a function of width and length

V = f(r,h) = Πr²h where V is the volume and is a function of radius and height

d = f(r,t) = rt where d is the distance and is a function of time and rate.

Tables of Values

Just for the single variable functions, we use the tables to describe two-variable functions. The heading of the table shows row and column and it shows the value if two input variables and the complete table shows the values of the output variable.

Graphs

You can easily make graphs in three dimensions for two-variable functions. Instead of representing graphs, we represent functions by holding two or one variable constants.

Also, Read:

• What is Variation
• Practice Test on Ratio and Proportion

How to Solve Joint Variation Problems?

Follow the step by step procedure provided below to solve problems involving Joint Variation and arrive at the solution easily. They are along the lines

Step 1: Write the exact equation. The problems of joint variation can be solved using the equation y =kxz. While dealing with the word problems. you should also consider using variables other than x,y and z. Use the variables which are relevant to the problem being solved. Read the problem carefully and determine the changes in the equation of joint variation such as cubes, squares or square roots.

Step 2: With the help of the information in the problem, you have to find the value of k which is called the constant of proportionality and variation.

Step 3: Rewrite the equation starting with 1 substituting the value of k and found in step 2.

Step 4: Use the equation in step 3 and the information in the problem to answer the question. While solving the word problems, remember including the units in the final answer.

Joint Variation Problems with Solutions

Problem 1:

The area of a triangle varies jointly as the base and the height. Area = 12m² when base = 6m and height = 4m. Find base when Area = 36m² and height = 8m?

Solution:

The area of the triangle is represented with A

The base is represented with b

Height is represented with h

As given in the question,

A = 12m² when B = 6m and H = 4m

We know the equation,

A = kbh where k is the constant value

12 = k(6)(4)

12 = k(24)

Divide by 24 on both sides, we get

12/24 = k(24)/24

1/2 = k

The value of k = 1/2

As the equation is

A = kbh

A = 1/2bh

To find the base of the triangle of A = 36m² and H = 8m

A = 1/2bh

36 = 1/2(b)(8)

36 = 4b

Dividing both sides by 4, we get

36/4 = 4b/4

9 = b

The value of base = 9m

Hence, the base of the triangle when A = 36m² and H = 8m is 9m

Problem 2:

Wind resistance varies jointly as an object’s surface velocity and area. If the object travels at 80 miles per hour and has a surface area of 30 square feet which experiences 540 newtons wind resistance. How much fast will the car move with 40 square feet of the surface area in order to experience a wind resistance of 495 newtons?

Solution:

Let w be the wind resistance

Let s be the object’s surface area

Let v be the object velocity

The object’s surface area = 80 newtons

The wind resistance = 540 newtons

The object velocity = 30

We know the equation,

w = ksv where k is the constant

(540) = k (80) (30)

540 = k (2400)

540/2400 = k

9/40 = k

The value of k is 9/40

To find the velocity of the car with s = 40, w = 495 newtons and k = 9/40

Substitute the values in the equation

w = ksv

495 = (9/40) (40) v

495 = 9v

495/9 = v

v = 55 mph

The velocity of a car is 55mph for which the object’s surface area is 40 and wind resistance is 495 newtons

Hence, the final solution is 55mph

Problem 3:

For the given interest, SI (simple interest) varies jointly as principal and time. If 2,500 Rs left in an account for 5 years, then the interest of 625 Rs. How much interest would be earned, if you deposit 7,000 Rs for 9 years?

Solution:

Let i be the interest

Let p be the principal

Let t be the time

The interest is 625 Rs

The principal is 2500

The time is 5 hours

We know the equation,

i = kpt where k is the constant

Substituting the values in the equation,

(625) = k(2500)(5)

625 = k(12,500)

Dividing 12,500 on both the sides

625/12,500 = k (12,500)/12,500

1/20 = k

The value of k = 1/20

To find the interest where the deposit is 7000Rs for 9 years, use the equation

i = kpt

i = (1/20) (7000) (9)

i = (350) (9)

i = 3,150

Therefore, the interest is 3,150 Rs, if you deposit 7,000 Rs for 9 years

Thus, the final solution is Rs. 3,150

Problem 4:

The volume of a pyramid varies jointly as its height and the area of the base. A pyramid with a height of 21 feet and a base with an area of 24 square feet has a volume of 168 cubic feet. Find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet?

Solution:

Let v be the volume of a pyramid

Let h be the height of a pyramid

Let a be the area of a pyramid

The volume v = 168 cubic feet

The height h = 21 feet

The area a = 24 square feet

We know the equation,

V = Kha where K is the constant,

Substitute the values in the equation

168 = k(21)(24)

168 = k(504)

Divide 504 on both sides

168/504 = k(504)/504

1/3 = k

The value of k = 1/3

To find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet

Therefore,

h = 18 feet

a = 42 square feet

V = kha

V = (1/3) (18) (42)

V = (6) (42)

V = 252 ft³

The volume of the pyramid = 252 ft³ which has a height of 18 feet and a base with an area of 42 square feet

Therefore, the final solution is 252 ft³

Problem 5:

The amount of oil used by a ship travelling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in travelling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour?

Solution:

As given in the question,

No of barrels of oil = 200

The distance at which the oil is travelling = 200 miles

The distance at which the ship is travelling = 36 miles per hour

We know the equation,

A = kds² where k is constant

200 = k.200.(36)²

Dividing both sides by 200

200/200 = k.200.(36)²/200

1 = k.(36)²

k = 1/1296

The value of k is 1/1296

To find the no of barrels when the ship travels 360 miles at 18 miles per hour

Substitute the values in the equation

A = kds²

A = 1/1296 * 360 * 18²

A = 90

Therefore, 90 barrels of oil is used when the ship travels 360 miles at 18 miles per hour

Thus, the final solution is 90 barrels

Check Word Problems On Pythagorean Theorem in the below sections. Refer Pythagorean Theorem Study Material along with the solutions and steps to solve them. Get various model questions on Pythagoreans theorem and improve your mathematical knowledge along with other math skills. Know the shortcuts, tips, and tricks to solve Pythagorean Theorem Problems. Assess your preparation standard taking the help of the Pythagorean Theorem Questions available and cross-check your solutions here.

How to Solve Problems on Pythagorean Theorem?

Follow the simple steps listed here to solve problems related to the Pythagorean Theorem. They are along the lines

Step 1: Look at all the terms in the final equation

Step 2: Find out which right triangles contain those terms

Step 3: Start with those right triangles and apply the Pythagorean Theorem

Pythagorean Theorem Word Problems

Problem 1:

A 35-foot ladder is leaning against the side of a building and its positioned such that the base of the ladder is 21 feet from the base of the building. Find the distance above the ground where the point of the ladder touches the building?

Solution:

Let the point above the ground = x

As given in the question,

Length of the foot ladder = 35

Base of the ladder = 21 feet

Let the equation be a² + b² = c²

(21)² + (x)² = (35)²

441 + x = 1225

Subtracting by 441 on both sides

x = 784

Squaring and both sides

x = √784

x = 28

28 feet far above the ground is the point where the ladder touches the building.

Problem 2:

Lainey runs a string of lights from the ground straight up a door frame that is 2.5 meters tall. Then they run the rest of the string in a straight line to a point on the ground that is 6 meters from the base of the door frame. There are 10 lights per meter of a string. How many total lights are on the string?

Solution:

As given in the question,

The length of the lights = 2.5 meters

The base of the door frame = 6 meters

No of lights per meter = 10

To find the total number of lights on a string, we write the equation

h² = (2.5)² + (6)²

h²= 6.25 + 36

h²= 42.25

h = √42.25

String Length = 2.5 + √42.25

Therefore, no of lights = 9m * 10 lights = 90 lights

Thus, the total lights on the string = 90 lights

Problem 3:

Fencing at a hardware store costs $16.97 per yard. How much would it cost to fence in a triangular-shaped yard that has a leg of 11 feet and another leg of 60 feet?

Note: The yard is in the shape of a right triangle.

Solution:

Amount of fencing at hardware store = $16.97 per yard

Length of one leg = 11 feet

Length of another leg = 60 feet

As given the yard is in the shape of right triangle

We know the equation,

a² + b² = c²

(11)² + (60)² = c²

121 + 3600 = c²

3721 = c²

Squaring on both sides

√3721 = √c²

61 = c

The amount for a fence in a triangular-shaped yard = $61

Thus, the final solution is $61

Problem 4:

If a 34-foot ladder is placed against the top of a 30-foot building. How many feet will be at the bottom of the ladder from the bottom of the building?

Solution:

As given in the question,

Length of the ladder = 34 foot

Length of the building = 30 foot

Let the length of bottom of the ladder = x

a² + b² = c²

(30)² + x² = (34)²

900 + x² = 1156

x² = 256

Add square root on both sides

√x² = √256

x = 16 feets

Therefore, the bottom of the ladder from the bottom of the building will be 16 feets

Thus, the final solution is 16 feet

Problem 5:

A certain television is advertised as a 34-inch TV. If the width of the TV is 30 inches, how many inches tall is the TV?

Solution:

As given in the question,

Size of the TV = 34 inch

Width of the TV = 30 inch

Length of TV = x

To know the length of TV, we have to find the equation

a² + b² = c²

(30)² + x² = (34)²

900 + x² = 1156

Add square root on both sides

√x² = √1156

x = 34

TV is 34 inches tall.

Thus, the final solution is 34 inches

Problem 6:

Ramu starts driving north for 9 miles, then takes a right turn, and then he drives east for another 40 miles. At the end of driving, what is the distance of a straight line from the starting point?

Solution:

As given in the question,

Driving for north = 9 miles

Driving for east =40 miles

Let the straight line distance = x

The equation will be

a² + b² = c²

(9)² + (40)² = c²

81 + 1600 = c²

1681 = c²

Add square roots on both sides

√1681 = √c²

41 = c

Therefore, the straight line distance from the starting point is 41 miles

Thus, the final solution is 41 miles

Problem 7:

In a right-angled triangle, the hypotenuse square is equal to the sum of the squares of other two sides?

Solution:

Given: A right-angle triangle in which one of the sides is 90°

To prove: AC² = AB² + BC²

Construction: Draw BD ⊥ AC

In Δ’s ADB and ABC

∠ADB = ∠ABC (Each 90°)

∠A = ∠A (Common)

ΔADB ∼ ΔABC (By A-A Criteria)

AD/AB = AB/AC

AB² = AD * AC is the first equation

In Δ’s BDC and ABC

∠CDB = ∠ABC (Each 90°)

∠C = ∠C (Common)

ΔBDC ∼ ΔABC (By A-A Criteria)

DC/BC = BC/AC

BC² = AC * DC is the (2) equation

AB² = AD * AC is the (3) equation

Adding the equations (1) and (2)

AB² + BC² = AD * AC + AC * AD

AB² + BC² = AC (AD + DC)

AB² + BC² = AC (AC)

AB² + BC² = AC²

∴ Hence proved

Problem 8:

In the triangle, if the square of one side of the triangle is equal to the sum of the squares of another two sides of the triangle, then the angle that is opposite to the first side is a right angle triangle?

Solution:

 Given: ΔABC such that AB² + BC² = AC²

To prove: ∠B = 90°

Construction: Draw ΔDEF such that DE = AB, EF = BC and ∠E = 90°

Since ΔDEF is right-angled,

By Pythagoras theorem

DE² + EF² = DF²

AB² + BC² = DF² (By const DE = AB and EF = BC)

AC² = DF² (Given AB² + BC² = AC²)

AC = DF

To prove: ∠B = 90°

In Δs ABC and DEF

AB = DE (By const)

BC = EF (By const)

AC = DF (Proved)

ΔABC ≅ ΔDEF (SSS)

∠B = ∠E = 90°

ΔABC is a right triangle

Problem 9:

Mary wants to cut across a rectangular lot rather than walk around it. Of the lot is 120 feet long and 50 feet wide. Mary walks diagonally across the lot, how many feet is the short cut?

Solution:

As given in the question,

Length of the lot = 120 feet

Width of the lot = 50 feet

Let the shortcut distance be x

As per the Pythagorean theorem,

a² + b² = c²

(50)² + (120)² = x²

2500 + 14,400 = x²

16,900 = x²

130 = x

Therefore, Mary walks 130 feet shortcut

Thus, the final solution is 130 feet

Problem 10:

The length of a living room is 2 feet less than twice its width. If the diagonal is 2 feet more than twice the width, find the dimensions of the room?

Solution:

Let the width of the living room = x

Given that

Length of the living room = 2 feet less than twice its width

Diagonal = 2 feet more than twice the width

From the given equations,

Width represents x² + (2x – 2)² = (2x + 2)²

Length represents x² = (2x + 2)² – (2x-2)²

From both the equations,

x² = (4x + 8x + 4) – (4x – 8x + 4)

x² = 16x

(x²-16x) = 0

x(x-16) = 0

x = 0, x=16

Therefore, the width = 16

Length = (2x – 2) = 2(16) – 2 = 30

Thus, the length of the living room = 30 feet

Width = 16 feet

Hence, the final solution is l = 30 feet and w = 16 feet

Problem 11:

A man goes 12m east and 9m north. Find the distance from the initial point?

Solution:

As given in the question,

The distance man goes to east = 12m

i.e., BC = 12m

The distance man goes to north = 9m

i.e., AB = 9m

To find the initial point (AC), apply the Pythagorean theorem

AC² = AB² + BC²

AC² = (9)² + (12)²

AC² = 81 + 144

AC² = 225

AC = √225

AC = 15

Therefore, he is 15m far from his initial point

Thus, the final solution is 15m

Problem 12:

Hari wants to hang a 7m long banner from the roof of her shop. The hooks for the strings are 10m apart. Hari wants the top of the banner to hang 1m below the roof. How long should each of the strings be?

Solution:

As per the question,

Length of the long banner = 7m

Hooks for strings = 10m apart

Length where the banner to hang below the roof = 1m

Let the length of the string = x

Hence, the equation will be

7 + 2x = 10

2x = 3

x = 1.5

Now, apply the Pythagorean theorem,

C² = (1)² + (1.5)²

C² = 1 + 2.25

C² = 3.25

C = √3.25

C = 1.80

Hence, each string should be 1.80m

Thus, the final solution is 1.80m

Problem 13:

Two kids are flying a kite with a string of 50 meters long. If the kids are 35 meters apart, how high is the kite off the ground?

Solution:

As given in the question,

Length of the string = 50 meters

The distance of kids apart = 35 meters

The height of the kite off the ground = b

Applying the Pythagorean theorem, we get

a² + b² = c²

(35)² + b² = (50)²

1225 + b² = 2500

b² = 1275

b = √1275

b = 35.70

Therefore, 35.70m is the kite off the ground

Thus, the final solution is 35.70 m

Problem 14:

A carpenter needs to add 2 braces to a barn door. If the door measures 12 * 16 feet, how much wood will he need for both braces?

Solution:

As given in the question,

No of braces = 2

Length of the door = 12 feet

The breadth of the door = 16 feet

To find the amount of wood for braces, we apply Pythagorean theorem

a² + b² = c²

(12)² + (16)² = c²

144 + 256 = c²

400 = c²

c = √400

c = 20

Amount of wood for both the braces = 2 * 20 = 40ft

Therefore, the carpenter requires 40 ft of wood for both the braces.

Thus, the final solution is 40 ft

Problem 15:

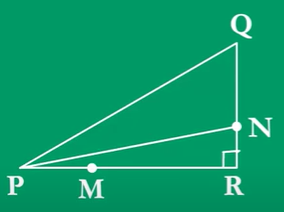
M and N are points on the sides RP and RQ respectively of triangle PQR right-angled at R. Prove that PN² + QM² = PQ² + MN²?

Solution:

PN² = PR² + RN² is the (1) equation

QM² = MR² + RQ² is the (2) equation

Adding the equation (1) and (2)

PN² + QM² = MR² + RQ² + PR² + RN²

PN² + QM² = (MR² + RN²) + (RQ² + PR²)

PN² + QM² = MN² + PQ²

∴ Hence, it is proved

The modulus of a Complex Number is here. Know the example problems of modules and various forms involved in them. Follow cartesian form, trigonometric or polar form, exponential form, modulus properties, the principal value of the argument of LPA. Refer to the important topics and terminology used in complex values. Check the below sections to know the absolute value and the modulus of the complex number.

Modulus of a Complex Number – Definition

The modulus of a complex number gives you the distance of the complex numbers from the origin point in the argand plane. the conjugate of the complex number gives the reflection of that number about the real axis in the same argand plane. The modulus of the complex number is always positive which is |z| > 0. Also, the complex values have a similar module that lies on a circle.

Cartesian Form

z¡ = x + iy is the complex number that is in the cartesian form. The modulus can be represented as |z|. The value of |z| = √x² + y²

Trigonometric or Polar Form

The complex number in the polar form is represented with z. The equation of z = r cisθ or z = r∠θ, r(cosθ + isinθ) where r represents the distance of the point z from the origin or the modulus. θ is the subtended angle by z from the positive x-axis.

Here, r = √x² + y² & θ represents its argument.

Exponential Form

The complex number “z” in the form of exponential can be expressed as z = re^i∅ or |z|e^iarg(z) represents the complex number modulus and ∅ is the argument value.

Properties of Modulus

• If |z| = 0, then z = 0 + i0
• |z| = |-z| = |\(\overline{z}\)| = |iz|
• -|z| ≤ Re(z) ≤ |z|
• -|z| ≤ Im(z) ≤ |z|
• \(\overline{z}\)z = |z|², if |\(\overline{z}\)| = 1

These type of modulus are called as unimodulars

then \(\overline{z}\) = 1/z

• • |z₁z₂| = |z₁||z₂|, is true for n complex numbers
  • |zⁿ|= |z|ⁿ
  • |z₁/z₂| = |z₁|/|z₂|
  • |z₁ + z₂|² + |z₁ – z₂|² = 2(|z₁|² + |z₂|²)

Definition and Meaning of Arg

Argument or Arg in complex numbers resembles the angle which is subtended by any of the complex points on the argand plane from the +(positive) x-axis. For the complex number z, the argument is represented with arg(z) which gives us the measurement of the angle between the + (positive) x-axis and also the

For any complex number z, its argument is represented by arg(z). It gives us the measurement of the angle between the positive x-axis and the line joining origin and the point. There are three ways to express an argument of a complex number. The three ways are as follows.

General Argument

For all the complex numbers z, the general argument is z = x + iy or r(cosθ + isinθ)

Im(z) = r sinØ and Re(z) = r cosØ which shows the real and imaginary parts of the complex numbers and also are the functions of sin and cosine. Hence, they are periodic with the period 2Π which means that there exist infinite complex numbers which have the same argument or angle. The same case follows for modulus too.

Assume the complex numbers in the first quadrant (z) = x + iy (x,y >0)

The general argument will be defined as Ø = 2nΠ + tan^-1y/x where n ∈l.

Here, tan^-1y/x is known as the argument principle value and hence its value depends upon the quadrant in that point lies.

Also, Read: Properties of Complex Numbers

Prinicipal Value of Argument (PA) or Amplitude (amp)

A general argument or a well-defined complex number cannot be expressed. We used the principle value or amplitude instead of the general argument in the case where the well-defined complex function is required.

In the principle argument, Φ value is restricted to be in interval ( -Π < Φ ≤ Π) or (-Π, Π]. The range of principle argument represents the half-circled range from the +(positive) x-axis in either direction.

LPA (Least Positive Argument)

LPA is another type of argument, where the angle range Ø is kept as (0< Ø ≤ 2Π) or (0,2Π]. This type of argument has only anticlockwise rotation is considered. To find the complex number in any of the quadrants, the angle has to be calculated from the positive x-axis in the counterclockwise or anticlockwise direction only.

The native way of calculating the angle to the point (a,b) can be done by using arctan (b/a) but arctan takes the value in the range of [-Π/2, Π/2], which gives the wrong result for the negative x component coordinates. We can fix it by adding or subtracting Π and it depends on the quadrant of the Argand diagram in which the point lies in

• 1st quadrant (Θ) = arctan (b/a)
• 2nd quadrant (Θ) = arctan (b/a) + Π
• 3rd quadrant (Θ) = arctan (b/a) – Π
• 4th quadrant (Θ) = arctan (b/a)

Modulus of a Complex Number Examples

Problem 1:

If |z-(4/z)| = 2. Find the maximum value of |z|?

Solution:

As given in the question,

|z-(4/z)|

The equation is

|z-(4/z)| ≥ |z| -|4/z|

2 ≥ |z| – 4/|z|

2|z| ≥ |z|² – 4

|z|² – 2|z| – 4 ≤ 0

|z| ≤ √5 + 1

The maximum value of z,

|z| ≤ √5 + 1

Problem 2:

If z + |z| = 1 + 4i. Find the value of |z|?

Solution:

The given equation is

z= x + iy

z + |z| = 1 + 4i

x + iy + √(x² + y²) = 1 + 4i

y=4 and x + √(x² + y²) = 1

x + √(x² + 4²) = 1

√(x² + 4²) = 1-x

Squaring on both the sides, we get

x² + 4² = 1 + x² – 2x

2x = -15

or x = -15/2

|z| = √x² + y²

|z| = √(-15/2)² + 4²

|z| = √(225/4 + 16)

|z| = √(225 + 64/4

|z| = √(289/4)

|z| = 17/2

The value of |z| = 17/2

Problem 3:

For the equation, z = (3-2i)/2i. Find the complex number modulus?

Solution:

As given in the question,

z = (3-2i)/2i

z = (3)/2i – 2i/2i

z= 3/2i – 1

z= 3i/(2i)² – 1

z = -3i/2 – 1

|z| = √(-3/2)² + (-1)²

|z| = √(9/4 + 1)

|z| = √(9+4)/4

|z| = √13/4

|z| = √13/2

Therefore, the complex modules is |z| = √13/2

Subsets of a Given Set mean the subset having the elements present in a set. In other words, Subsets are a part of the set. A set is nothing but a collection of elements placed within curly braces. The example of a set is {a, b, c}. If we take a set of even numbers and name it as A and set B has {2, 4, 6}, then B is the subset of set A. It is represented as B⊆A. The elements of sets may be variables, groups of real numbers, constants, or whole numbers, etc.

What is Subset of a Set?

The subset is said to be a part of the set. Subset must have the elements that present in a set. If set A is said to be a subset of Set B, then all the elements of Set A are must present in Set B. Set A is contained inside Set B.
Example: If Set A has {C, D} and set B has {C, D, E}, then A is the subset of B because all the elements of A are also present in set B. The subset is denoted by the symbol ⊆ we read as ‘subset of’. A ⊆ B; which means Set A is a subset of Set B.

All Subsets of a Set

The subset of any given set must consist of all possible sets along with the elements and also having a null set. Check out the below example to understand the subset of a set.
Example: A = {7, 6, 8, 9}
Solution: Given that A = {6, 7, 8, 9}.
Subsets = {}, {6}, {7}, {8}, {9},
{6,7}, {6,8}, {6,9}, {7,8},{7,9}, {8,9},
{6,7,8}, {7,8,9}, {6,8,9}, {6,7,9}
{6, 7, 8, 9}

Types of Subsets

Mainly, there are two different types of subsets available. they are classified as

• Proper Subset
• Improper Subsets

Proper Subset

The proper subset contains some elements of an original set along with a null set. Set A is treated to be a proper subset of Set B if Set B has at least one element that is not present in Set A. A proper subset is denoted by ⊂ and it is read as ‘is a proper subset of’. We can show a proper subset for set A and set B as A ⊂ B.

Proper Subset Formula

If we take n number of elements from a set having N number of elements, then it shows as  ^NC_n number of ways. The number of possible subsets having n number of elements from a set containing N number of elements is equal to  ^NC_n.

Also, Read:

• Different Notations in Sets
• Intersection of Sets

Improper Subset

A subset that has all elements of the original set is called an improper subset. It is denoted by ⊆. The Improper Subset consists of all elements of a set that doesn’t miss any element.

Example: Set P = {3, 5, 7}
The subsets of P are {}, {3}, {5}, {7}, {3,5}, {5,7}, {3,7} and {3,5,7}.
Where, {}, {3}, {5}, {7}, {3,5}, {5,7}, {3,7} are the proper subsets and {3,5,7} is the improper subsets. Therefore, we can write {3,5,7} ⊆ P.

Note: The empty set is an improper subset of itself but it is a proper subset of any other set.

Power Set

The power set is defined as the collection of all the subsets. It is represented by P(A).
If A is set having elements {a, b}. Then the power set of A will be
P(A) =  {∅, {a}, {b}, {a, b}}

How many Subsets and Proper Subsets does a Set have?

Let us consider a set that consists of n elements, then the number of a subset of the given set is 2ⁿ and the number of proper subsets of the given subset is given by 2ⁿ-1.

Example: If set A consists the elements, A = {c, d}, then the proper subset of the given subset are {}, {c}, {d}.
The number of elements in the set is 2.
The formula to find the number of proper subsets is 2ⁿ – 1.
= 2² – 1
= 4 – 1
= 3
Thus, the number of proper subset for the given set is 3 ({ }, {c}, {d}).

Properties of Subsets

The below are some of the important properties of subsets.

• Every set is considered as a subset of the given set itself. It means that X ⊂ X or Y ⊂ Y, etc
• Also, we can say, an empty set is considered as a subset of every set.
• A is a subset of B. It means that A is contained in B
• If a set A is a subset of set B, we can say that B is a superset of A

Solved Examples on Subsets of a Given Set

1. If A {2, 3, 7}, then write all the possible subsets of A. Find their numbers?

Solution:
Given that set A {2, 3, 7}.
Let us write all the possible subsets of a given set.
The subset of A containing no elements – {  }
The subset of A containing one element each – {2} {3} {7}
The subset of A containing two elements each – {2, 3} {2, 7} {3, 7}
The subset of A containing three elements – {2, 3, 7}
Therefore, all possible subsets of A are { }, {2}, {3}, {7}, {2, 3}, {2, 7}, {3, 7}, {2, 3, 7}
Therefore, the number of all possible subsets of A is 8 which is equal to 2³.
Proper subsets are = {  }, {2}, {3}, {7}, {2, 3}, {3, 7}

Number of proper subsets are 7 = 8 – 1 = 2³ – 1.

2. If the number of elements in a set is 4, find the number of subsets and proper subsets.

Solution:
Number of elements in a set = 4
Then, number of subsets = 2⁴ = 16
Also, the number of proper subsets = 2⁴ – 1
= 16 – 1 = 15

3. If A = {5, 6, 7, 8, 9}

The formula to calculate the number of proper subsets of a given set is 2ⁿ – 1
then the number of proper subsets = 2⁵ – 1
= 32 – 1 = 31   {Take [ 2ⁿ – 1]}
and the formula to calculate the number of subsets of a given set is 2ⁿ
power set of A = 2⁵ = 32 {Take [2ⁿ]}

The transverse and conjugate axis of the hyperbola is here. Check the definition of the transverse and conjugate axis. Refer to Standard forms of the hyperbola with the center, vertices, and foci. Learn How to find the Length of Transverse and Conjugate Axes of a Hyperbola. Know the procedure to solve hyperbola problems along with solutions.

Hyperbola – Definition

The hyperbola is a set of all the points in such a way that the difference of distance between any of the points on the hyperbola to the fixed points is always constant. The fixed points of the hyperbola are called the “foci of hyperbola”. The hyperbola graph is not continuous i.e., every hyperbola has two distinct points or branches. The transverse axis is nothing but the line segment where both endpoints of the hyperbola are on it.

The transverse axis endpoints are known as vertices of the hyperbola. “Center” is the point halfway between the foci which is the midpoint of the traverse axis. The transverse axis of hyperbola x² / a² – y² / b² = 1 is along the x-axis and the length of a hyperbola is 2a.

Important Formulae and Terms of Hyperbola

There are a few terms related to hyperbola which has to be understood to get perfection in this concept. The important terms used in hyperbola are:

• Eccentricity: 1 + [(transverse axis)² + (conjugate axis)²]
• Directrix: x = (-a/e), x = (a/e)
• Focii: S’ = (-ae,0), S = (ae,0)
• Conjugate Axis: The line segment of length 2b, between 2 points B’ = (0,-b) & B = (0,b) is called hyperbola conjugate axis.
• Transverse Axis: The line segment of the length 2a in which focii ” S’ ” and “S” lie is called the hyperbola transverse axis.
• Principle Axis: The conjugate and transverse axis both combinedly called a principle axis.
• Vertices: A’ = (-a, 0) & A = (a, 0)
• Double Ordinate: The chord that is perpendicular to the transverse axis is known as double ordinate.
• Focal Chord: A chord that passes through a focus is known as a focal chord.
• Latus Rectum: The focal chord which is perpendicular to the transverse axis is called the latus rectum.

The length of latus rectum = [(conjugate)² / transverse] = (2b² / a) = 2a (e² – 1)

The difference of the focal distances is the constant value

i.e., |PS-PS’| = 2a

Length of latus rectum = 2e * (the distance of the focus from the corresponding directrix)

Endpoints of Latus Rectum: (± ae, ± b2 / a)

Centre: The point at which bisects every chord of the conic which is drawn through it and is called the center of the conic.

C: (0, 0) is the centre of [(x²/a²) – (y²/b²)] = 1

Key Points about Transverse and Conjugate Axis of the Hyperbola

• • Any point present on the conjugate hyperbola will be in the form (a tan θ, b sec θ).
  • The equation of the hyperbola conjugate to xy = c² is xy = -c²
  • Conjugate Hyperbola + Hyperbola = 2 (Pair of Asymptotes).
  • The point where a pair of the diameter of conjugates meets a hyperbola and the form of the conjugates of a parallelogram, where vertices lie on asymptotes and the area is constant.
  • The equation of asymptotes and hyperbola differ by the similar constant by which the asymptotes equations and conjugate hyperbola differ.
  • If a pair of diameters of hyperbola conjugate meet the hyperbola and its conjugate in T, T’ and R, R’ respectively. Then the asymptotes bisect TR and TR’.
  • If e1 and e2 are the hyperbola eccentricities and its conjugate then the equation is e₁^-2 + e₂^-2 = 1
  •  Two hyperbolas with similar eccentricity are said to be similar.
  • The focus of conjugate and hyperbola are concyclic and they form the square vertices.

Standard Forms of Hyperbola Equation with Center (0,0)

The standard form of hyperbola equation with center (0,0) and the transverse axis on x-axis is x² / a² – y² / b² = 1

where,

• the transverse axis length is 2a
• the vertices coordinates are (±a,0)
• the conjugate axis length is 2b
• the co-vertices coordinates are (0, ±b)
• the distance between foci is 2c, where c²=a² + b²
• the foci coordinates are (±c,0)
• the asymptotes equation is y = ±b/a x

The standard form of hyperbola equation with center (0,0) and the transverse axis on y-axis is y² / a² – x² / b² = 1

where,

• the transverse axis length is 2a
• the vertices coordinates are (0,±a)
• the conjugate axis length is 2b
• the co-vertices coordinates are (±b,0)
• the distance between foci is 2c, where c²=a² + b²
• the foci coordinates are (0,±c)
• the asymptotes equation is y = ±a/b x

Standard Forms of Hyperbola Equation with Vertices and Foci

• • First of all, determine if the transverse axis lies on the x-axis or y-axis. Check that a² is under the variable with +(positive) coefficient. Therefore, if you set another variable equal to zero (0), you can find the intercepts easily. The point at which the intercepts of hyperbola coincide with vertices, it is centered as an origin.
  • If the equation is of the form x² / a² – y² / b² = 1, then the axis of the transverse line lies on the x-axis. The vertices are pointed at (±a,0) and foci are pointed at (±c,0).
  • If the equation is of the form y² / a² – x² / b² = 1, then the axis of the transverse line lies on the y-axis. The vertices are pointed at (0,±a) and the foci are pointed at (0,±c)
  • Solve the value for a, by using the equation a = √a²
  • Solve the value for c, using the equation c = √a² + b²

Transverse and Conjugate Axes of Hyperbola Examples

Problem 1:

Find the lengths of conjugate and transverse axis of the hyperbola 16x² – 9y² = 144?

Solution:

The given equation of the hyperbola is 16x² – 9y² = 144

x²/9 – y²/16 = 1 is the (1) equation

The above equation (1) is of the form x² / a² – y² / b² = 1, where a² = 9 and b²=16

Therefore, the length of the transverse axis is 2a, which can be written as 2*3 = 6 and the length of the conjugate axis is 2b, which can be written as 2*4 = 8

Problem 2:

Find the lengths of conjugate and transverse axis of the hyperbola 3x² – 6y² = -18?

Solution:

The given equation of the hyperbola is 3x² – 6y² = -18

The hyperbola equation can be written as x²/6 – y²/3 = 1 is the (1) equation

The above equation (1) is of the form x² / a² – y² / b² = -1, where a² = 6 and b²=3

Hence, the length of the transverse axis is equal to 2b which is 2 * √3 = 2√3 and the length of the conjugate axis is equal to 2a which is 2 * √6 = 2√6

Problem 3:

Find the hyperbola eccentricity whose latus rectum is half of the transverse axis?

Solution:

Let the equation of the hyperbola be x² / a² – y² / b² = 1

Transverse axis = 2a and lactus-rectum = (2b²/a)

According to the question, (2b²/a) = (1/2) * 2a

2b²=a (Since, b²=a²(e²-1))

2a²(e²-1) = a²

2e²-2 = 1

e²=(3/2)

e = √(3/2)

Therefore, hyperbola eccentricity is √(3/2).

Thus, the final solution is √(3/2).

The interesting topic of mathematics is Time. Measurement of the time requires some specifications and units. Know the different units of time and various circumstances it is used in. Follow the terminology used in time and know the solved examples involving time. Check the below sections to know the details like units of time conversion chart, mathematical conversions, terminology, formulae, etc.

How to Convert Units of Time?

To convert a unit of time, we can use the factor of conversions. The conversion for a unit of time can be done by using division or multiplication. With the help of the conversion factor, simplification will be easier. The most used equation while converting units of time is

S * C = E

where S is considered as the starting value, C is considered as the conversion factor and E is desired as the converted solution.

Time – Definition

Time is considered as the continuous existence progress in the past, present, and also future. With the help of the unit of time, one can easily measure the existence of the event present. The most commonly used time units are:

• Hour
• Minute
• Second

Popular Time Measurement Units

The most commonly used units of time include hour, minute, week, day, year, and month. In consideration of long durations of time, year multiples are also used for a certain time frame. A decade is equal to 10 years, the century is equal to 100 years, the millennium is equal to 1,000 years and a mega-annum is equal to 1,000,000 years.

Units of Time

How to Convert Units of Time?

Follow the simple steps to change between one unit of time to another. They are in the following fashion

Step 1: In the first step, identify the units that are used in the problem.

Step 2: Find and determine the relationship between the given units.

Step 3: Check and determine the fraction form (the conversion factor). The denominator value must have the same unit as the given original measurement.

Step 4: Multiply the given original measurement with the conversion factor.

Time Unit Conversion Table

Relationship Between Units of Time

Also, Check:

• Units of Length Conversion Charts
• Units of Mass and Weight Conversion Chart
• Math Conversion Chart

How to Solve Unit Conversion Problems?

Step 1: Read the problem carefully and write down any key points

Step 2: Highlight or underline the main question

Step 3: Make a plan, write out exactly what needs to be done in order to obtain the solution.

Step 4: Proceed by using the mathematical operations necessary as described in Step 3

Step 5: Check your answer

Time Measurement Examples

Problem 1:

Convert 4 hours into seconds?

Solution:

As we have to convert 4 hours into seconds, first convert 4 hours into minutes and then to seconds

“Hours into Minutes”

To convert hours into minutes, multiply with 60

Therefore 4 hours = 4 * 60 = 240 minutes

“Minutes into Seconds”

To convert minutes into seconds, multiply with 60

Therefore, 240 minutes = 240 * 60 = 14400 seconds

Thus, 4 hours in seconds = 14400 seconds

Problem 2:

Convert 3 hours 10 minutes into seconds?

Solution:

As we have to convert 3 hours 10 minutes into seconds, first convert 3 hours into minutes and then add that to 10 minutes and later convert that to seconds

“Hours to Minutes”

To convert hours into minutes, multiply with 60

Therefore 3 hours = 3 * 60 = 180 minutes

Now, add 180 minutes to 10 minutes

Thus, minutes = 190 minutes

“Minutes into Seconds”

1 min = 60 seconds

Therefore, 190 * 60 = 11,400 seconds

Thus, 3 hours 10 mins = 11,400 seconds

Problem 3:

Calgrand’s juice can produce 500 gallons of apple juice in quart-sized containers for $750. If they can sell the apple juice for $3.25 per quart, how much will they earn by selling all 500 gallons?

Solution:

As given in the question,

Amount of apple juice = 500 gallons

Amount of quart-sized containers = $750

Amount of juice per quart = $3.25

Let x be the no of quarts sold

Profits = Revenue – Cost

$3.25 * x

500 gallons * (4 quarts/ 1 gallon) = 2000 quarts

2000 * 3.25 = 650000

$6500 – $750 = $5750

Amount of money they earn by selling all 500 gallons = $5750

Therefore, the final amount of money they earn = $5750

Problem 4:

John went on vacation and left her dog at a kennel. The kennel charges $13 per hour. If John left his dog there for $9.25 days, how much was his bill?

Solution:

As given in the question,

Amount of kennel per hour = $13

No of days = $9.25

To convert the days into hours, multiply it with 24

9.25 * 24hours/1day = 22200

To find the amount of bill = x * cost per hour

222 * 13 = 2886

Therefore, John bill was $2886

Problem 5:

A top drug company has just invented a new colon drug. They can produce 1 millimeter for $7.35. How much will it cost them to produce 2 kilolitres of this colon drug?

Solution:

As given in the question,

Amount to invent a new colon drug = $7.35

To produce 2 kilolitres of the colon drug

2 kilolitres = 2,000,000 millilitres

For 1 millimeter = 7.35 * 2,000,000 = 1470000000

Therefore, it will cost $14.7 to produce 2 kilolitres of the colon drug.

Thus, the final solution is $14.7

Division of a decimal by a whole number examples are here. Know the steps to divide all the decimal values to whole numbers. Also, know the formulae and tricks to solve division problems. Check solved examples of decimals division by a whole number. In the below sections, we have mentioned the complete details regarding formulae, step-by-step procedure, tricks, and examples.

Division of a Decimal by a Whole Number

Before going to check how to divide a decimal by a whole number, know how to convert the decimal value into a whole number. If you convert the decimal value into a whole number, then the division rule can be easily applied to it. The division is the most challenging part of all the operations present in mathematics.

It is challenging because, to divide the values, you also have to use operations like multiplication, subtraction, addition etc. With the help of the divisions, you get perfect in estimations and rounding the values. Dividing the decimal values is almost the same as dividing the whole numbers. Here, you just have to use the decimal point value in the dividend to determine the decimal value places in the final solution.

How to Divide Decimal Numbers?

Rules for Division of a Decimal Value by a Whole Number

• We have to use the long division or division of decimals by the whole number, ignoring the decimal points. We have to treat the decimal values as whole numbers and then divide the values.
• In the final answer (quotient), we have to place the decimal value point in the same place where the number that is divided exactly has. Hence, we get the appropriate solution when decimal values are divided by whole numbers.

How to Divide a Decimal Value by a Whole Number?

1. Write the division equation in the standard form. Divide the part of the whole number of the decimal value by the divisor.
2. Now, place the decimal value point in the quotient above the decimal point which is present in the dividend. You have to bring the tenths digits down.
3. In the case that tenths digits are not divisible by the divisor, you have to add 0 in the quotient also in front of the digit in the tenths place.
4. Now, the divisor has to be divided by the dividend.
5. Add zeros in the dividend until you get the remainder as 0.

Dividing a Decimal by One Digit Whole Number

To divide a decimal by a one-digit whole number, you have to follow a few steps:

• Divide the value as you normally do. You can do it normally as there is no decimal value in the number.
• While bringing the digit down which comes after the decimal point, you have to place the decimal value in the quotient.

Dividing a Decimal by Two Digit Whole Number

To divide a decimal by a two-digit whole number, you have to follow a few steps:

• As there is no decimal point in the given number you have to divide the number normally.
• While bringing the first digit on the right side of the decimal value point down, you have to place the decimal value in the quotient.

Also, Read:

• Division of Integers
• Properties of Division of Integers
• Examples on Division of Integers

How to do Long Division with Decimal Values?

1. First of all, check if the number has a decimal value, if it has the decimal value, move that decimal value point to the right by counting the number of place values you have moved it to.
2. Once, you have done with the decimal value, move that point in the number you are dividing with the same place number to the right.
3. Insert the decimal value point in the quotient space, present exactly above the decimal value point in the number below the division bar.
4. Divide the value until you get the remainder as zero or till you have enough decimal places in the solution or quotient. There is also another case where the remainder repeats indicating the answer is the repeating decimal.

Dividing Decimals by Whole Numbers Examples

Question 1:

Divide the decimal value 360.57 by 51?

Solution:

To divide the decimal value 360.57, first divide 360 by 51

When dividing 360/51, we get the quotient as 7

Now, multiply 51 with 7, which results in 357

Then, subtract the result 357 from 360, the remainder is 3

As, 3 is the remainder, now go for the division of decimal value by 51

Now, bring down the value 5, as it follows the decimal point, place the decimal point in the quotient.

We continue it and divide 35 by 51. As 35 is less than 51, add 0 in the quotient and bring down the succeeding number “7”

Now, divide 357/51 which results as 7

35-357 = 0

Hence, the division is done and the solution is 7.07

Therefore, the final solution of dividing 360.57 by 51 is 7.07

Question 2:

Divide the decimal value 47.5 by 5?

Solution:

To divide the decimal value 47.5, first divide 47 by 5

When dividing 47/51, we get the quotient as 9

Now, multiply 9 with 5, which results in 45

Then, subtract the result 47 from 45, the remainder is 2

As, 2 is the remainder, now go for the division of decimal value by 47

Now, bring down the value 2, as it follows the decimal point, place the decimal point in the quotient.

We continue it and divide 25 by 5, the result will be 5

Subtract the value 25 from 25 then the final remainder will be 0.

Hence, the division is done and the solution is 9.5

Therefore, the final solution of dividing 47.5 by 5 is 9.5

Follow the table of sines and cosines here. Check the calculators and tables for trigonometric functions like sines and cosines. Refer to trigonometry ratio tables and also tricks to remember the trigonometry table. Know the various steps involved in preparing the trigonometry table and the determination of values to it. Check the below sections to know the various details regarding sine and cosine tables and calculations.

Table of Sines and Cosines

Trigonometry is the most important concept in mathematics which involves the lengths and areas of a triangle. These are mostly associated with right-angle triangles where one of those angles is 90 degrees. Trigonometry has a huge number of applications in various fields of Mathematics. Geometric Calculations can easily be figured out using trigonometric values, formulas, and functions as well. In the below sections, we are providing the trigonometric ratios table which helps to find the trigonometric standard angle values like 0°, 30°, 45°, 60°, and 90°, etc.

Various trigonometric ratios like sine, cosine, tan, secant, cotangent are present. In short, these ratios can be defined as cosec, sec, sin, cos, tan, cot. With the help of these ratios, trigonometric problems can easily be solved and you can calculate various mathematical derivations. Hence, it is necessary for you to learn and remember the trigonometric values of the standard angles.

The trigonometric ratio tables are mostly used to calculate the number of areas. In today’s world, trigonometry is used for science, navigation, and engineering. The ratio tables were effectively used in the era of pre-digital, where the pocket calculators were not available. The most essential application of trigonometric ratio tables is FFT(Fast Fourier Transform) algorithms.

Trigonometric Ratios Table

Tips and Tricks to Remember Trigonometric Table

Remembering the trigonometric table is a tough task for the students. But, if you follow a few tips and tricks, you can easily remember it. If you remember the table, you can easily solve many questions. The first step you have to do to remember the table is to get perfection in trigonometric formulae. The ratio table completely depends on the trigonometric formulae. We are providing a few steps to remember the trigonometric table.

Before, knowing the tricks to remember a table, look at the important formulae which helps you to prepare a table.

• cot x = tan (90° – x)
• cosec x = sec (90° – x)
• sin x = cos (90° – x)
• 1/cos x = sec x
• tan x = cot (90° – x)
• cos x = sin (90° – x)
• sec x = cosec (90° – x)
• 1/sin x = cosec x
• 1/tan x = cot x

Also, read:

• Worksheet on Trigonometric Identities
• Trigonometrical Ratios Table
• Trigonometrical Ratios of 90 Degree Minus Theta

How to Create a Trigonometry Table

Step 1:

Starting creating a table with angles on the top row listing. The angles must be 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°. Once you include all the angles as columns, now include all the trigonometric functions as rows. Include functions like sin, cos, tan, cosec, sec, cot, etc.

Step 2: 

In this step, we have to determine the values of sin, we have to divide the values of 0,1,2,3,4 by 4, and next we have to take the square root. For suppose, if you have to find the value of 0°, we have to write √(0/4) which results as 0. Now, find the value of 30°, we have to write √(1/4) which results as 1/2. Now, find the value of 45°, we have to write √(2/4) which results in 1/√2. In the same way, we have to find the values of the remaining angles. Hence the final table values of sin will be as follows.

Step 3:

In the next step, we have to determine the values of cos for all the required angles. The cos values are the opposite of the sin values which means that the value of sin(0-x) is similar to the value of cos(90-x). To find the value of cosine divide the values with 4 in the opposite order of sin i.e., 4, 3, 2, 1, 0 by 4 and take the square root.

For suppose, to find the value of 0°, we have to write √(4/4) results as 1. To find the value of 30°, we have to write it as (√3/4) results as √3/2. To find the value of 45°, we have to write as (√2/4) results as 1/√2. In the same way, we have to find the values of the remaining angles. Hence the final table values of cos will be as follows.

Step 4:

Now, determine the values of a tangent for all the required angles. The formula to find the tangent values is tan x = sin x/cos x. To find the value of tan, use the formulae mentioned above. To find the value of tan 0°, use the values of sin and cos, i.e., we have to use the formula tan 0° = sin 0°/cos 0° which is 0/1 and results in 0. To find the value of 30°, tan 30° = sin 30°/cos 30° which is (1/2) / (√3/2), results in 1/√3. In the same way, find the values of the remaining angles. Hence the final values will of tan will be as follows.

Step 5:

In Step 5, we have to determine the value of the cot. The cot values are the opposite of the tan values which means that the value of tan(0-x) is similar to the value of cot(90-x). To find the value of cot, we have to take the value as 1/tan. To find the value of 0°, use the value of 1/tan 0° which is 1/0 = ∞. To find the value of tan 30°, use the value as 1/tan 30° which is 1/(1/√3) = √3. In the same way, find the values of the remaining angles. Hence the final values will of the cot will be as follows.

 Step 6:

In the next step, we have to determine the value of cosecant. The cos values are the inverse of the sin values. To find the value of cos, we have to take the value as 1/sin. To find the value of 0°, use the value of 1/sin 0° which is 1/0 = ∞. To find the value of cos 30°, use the value as 1/sin 30° which is 1/(1/2) = 2. In the same way, find the values of the remaining angles. Hence the final values will of cos will be as follows.

Step 7:

In the last step, we determine the value of the secant. The sec values are the inverse of the cos values. To find the value of sec, we have to take the value as 1/cos. To find the value of 0°, use the value of cos 0°, 1/cos 0° which is 1/1 = 1. To find the value of cos 30°, use the value as 1/cos 30° which is 1/1/√3 = √2. In the same way, find the values of the remaining angles. Hence the final values will of sec will be as follows.

FAQs on Table of Sines and Cosines

1. What is Trigonometry?

Trigonometry is the mathematics branch which deals with angles and sides of the triangle.

2. What are the Trigonometric Functions and their Types?

Trigonometric functions are defined for the functions of the right-angled triangle. There are 6 basic trigonometric function types. They are:

1. Sin function
2. Cos function
3. Tan function
4. Cot function
5. Sec function
6. Cosec function

3. Find out the Values of the Trigonometric Functions?

There are various values of all the trigonometric functions

• Cosec = 1/Sin = Hypotenuse/Opposite
• Sec = 1/Cos = Hypotenuse/Adjacent
• Sin = Opposite/Hypotenuse
• Cos = Adjacent/Hypotenuse
• Tan = Opposite/Adjacent
• Cot = 1/Tan = Adjacent/Opposite

Multiplication Table of 25 helps students to learn the multiples of 25 with 1 to 20 whole numbers. Math Tables can make your confidence to the next level in solving long math calculations. So, try learning and remembering the 25 times table with the help of this article and do math problems quicker. In this guide of 25 times table, we will learn & understand how to read and write multiplication table of 25. Also, you can observe some tips and hints to remember the table of twenty-five along with worked-out examples.

25 Times Table Multiplication Chart | Table of 25 Chart

The 25 Times Table Chart is provided below in an image format for quick reference. Students who feel hard to learn and memorize the twenty-five times table can refer to the picture over here and do calculations at a faster pace. Also, you can download this Multiplication chart of 25 for free of cost and paste the printout on your walls and try to recite the table of 25 for better memorization.

Learn Writing Multiplication Table of Twenty-Five | 25 Times Up to 20

Reading the multiplication table of 25 is an important skill that students should have for solving the long divisions and multiplications problems. The table of 25 is easily understandable by the students as it is an equal group of 25. It will make problem-solving faster. Also, by recognizing the patterns of the multiples of 25 aids to use them in daily life situations. So, check out the given below table of 25 times multiplication and memorize it for a long run.

How to Read Twenty-five Times Multiplication in Words?

One time twenty-five is 25

Two times twenty-five is 50

Three times twenty-five is 75

Four times twenty-five is 100

Five times twenty-five is 125

Six times twenty-five is 150

Seven times twenty-five is 175

Eight times twenty-five is 200

Nine times twenty-five is 225

Ten times twenty-five is 250

Tips & Tricks to Memorize 25 Times Table

Below listed tips & tricks helps students to learn the Twenty-five Multiplication Table easily and do fast calculations mentally. They are as follows

• 25 table is very easy to remember by seeing the multiples of 25 because the digit at the unit’s place is always 0 or 5. Check the image below and try to memorize the table of 25.

• Add 25 to the first multiple and get the next multiple of 25. Repeat the process until you reach the required whole number.

Get More Math Tables:

Worked-out Examples on Multiplication Table of Twenty-Five

1. Apply 25 times table and solve 25 times 3 minus 8 plus 15?

Solution:

First, express the given statement in mathematical form ie., 25 times 3 minus 8 plus 15 = 25 x 3 – 8 + 9

Use the table of 25, and get the value for 25 x 3 – 8 + 9

= 75 – 8 + 9

= 67 + 9

= 76

Therefore, 25 times 3 minus 8 plus 15 is 76.

2. Rohan prepares 25 cookies per day. Using 25 times table explain how many has he made in the first week of May month?

Solution:

May has 31 days. First week of may means 7 days

Per day rohan makes 25 cookies

So, per week rohan makes 25 x 7 = 175

Hence, Rohan has made 175 cookies.

Students do you know that the number 22 is a palindrome number? Also, learn more about the 22 Times Table from this guide. In this article, you guys will find various options to learn and memorize the table of 22. So, refer to this page and collect all the information that you look for. Remembering the Math Tables from 0 to 25 are very necessary at the time of primary classes. So, we have curated the tips and tricks to memorize the Twenty-Two Times Table here along with worked-out examples.

22 Times Table Multiplication Chart

Here, we will find the multiplication chart of 22 in an image format to download and memorize daily. This 22 times table image can be helpful for further reference. So, download the Printable Table of 22 Image and paste it on your walls to remember regularly and solve the mathematical problems easily and quickly.

How to Learn Writing Multiplication Table of 22 | Twenty-Two Times Table Up to 20

Learning and memorizing the Math Multiplication Table of 22 is a crucial skill for long multiplication and division because:

• It aids in working the mental math calculations.
• You can solve all math problems with speed and accuracy.
• Also, this table of 22 times multiplication helps in grasping the pattern of multiples.

So, check out the below-tabulated Multiplication Table of Twenty-Two and enhance your problem-solving skills for fast calculations.

How to Read Twenty-Two Times Multiplication?

One time twenty-two is 22

Two times twenty-two are 44

Three times twenty-two are 66

Four times twenty-two are 88

Five times twenty-two are 110

Six times twenty-two are 132

Seven times twenty-two are 154

Eight times twenty-two are 176

Nine times twenty-two are 198

Ten times twenty-two are 220

Get More Math Tables:

Tips & Tricks for Multiplication Table of Twenty-Two

Here, we have shared some of the tips & tricks that help students to learn and memorize the twenty-two times table easily and solve the math problems quickly.

• Firstly, students have to remember the 2 times table. Take the first ten multiples of 2 ie., 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20.
• Always the digits we multiply with are whole numbers. The digit in one’s place is an even number gained by multiplying 2 with the whole number and then do a summation of both.
• Now, we can find the multiples of 22 with the desired whole number by multiplying the number by 2 at first. After 5 whole numbers, we have to add up the products. For instance, 22 times 7 = (2 times 7) + (2 times 7) = 14 + 14 = (14+1)4 = 154, and so on.

Worked-Out Examples Involving 22 Multiplication Table

1. Using the table of 22, Find the result for the following expression 22 times 5 minus 3 times 22?

Solution:

First, consider the given statement 22 times 5 minus 3 times 22 mathematically,

22 times 5 minus 3 times 22 = 22 x 5 – 3 x 22

Use the table of 22 and solve this expression ie., 22 = 22 x 5 – 3 x 22

= 110 – 66  = 44

Therefore, 22 times 5 minus 3 times 22 is 44.

2. Use the 22 times table, and evaluate the value of 6 plus 22 times 5 minus 9.

Solution:

First, we will write 6 plus 22 times 5 minus 9 mathematically.

ie., 6 plus 22 times 5 minus 9 = 6 + 22 x 5 – 9

By using the 22 times table, solve the result for the expression ie., 6 + 22 x 5 – 9

= 6 + 110 – 9

= 116 – 9

= 107

Hence, 6 plus 22 times 5 minus 9 is 107.

Math Tables are very important for students to solve all complex multiplication and division mathematical problems. 20 Times Table is one of the easiest tables to learn and memorize for a lifetime. Here, we have curated complete details about the Multiplication Table of Twenty. Go through this page and read the Tips & Tricks of Multiplication Table of 20 for memorizing, and also know How to Read and Write Twenty Times Table from this article. However, practice with the given worksheets of 20 Multiplication Table & get a good grip on understanding of the concept.

20 Times Table Multiplication Chart

In the table of 20 multiplication chart, you will see the multiplication of 20 with the first ten whole numbers. Let’s check out the image format of the multiplication chart of twenty below and solve all complex calculations so easily and accurately. Students can learn the table of 20 quickly by using this chart. So, download the Table of 20  Chart in pdf form and make use of it for better remembrance.

Multiplication Table of Twenty

It is very easy to learn the multiplication table of 20. Just we need to add 20 to the first multiple and get the next multiples of 20. Twenty multiplication table is a repeated addition where 20 x 1 = 20 then add 20 for getting the next multiple. So, go through the given table and learn the writing the 20 times table up to 20 whole numbers. Also, you will find the section to learn how to read twenty times table on this page. Stay tuned to this article.

How to Read First 10 Multiples of 20?

One time twenty is 20

Two times twenty are 40

Three times twenty are 60

Four times twenty are 80

Five times twenty are 100

Six times twenty are 120

Seven times twenty are 140

Eight times twenty are 160

Nine times twenty are 180

Ten times twenty are 200

Get More Math Tables:

Tips to Learn & Memorize Twenty Times Table

To memorize the 20 times table for a lifetime, follow the below-listed tips and tricks of the Multiplication table of twenty:

• First and foremost, memorizing the 2 times table is necessary to obtain the multiples of 20. 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20 are the first ten multiples of 2, now add 0 to the unit’s place in the multiplies of 2. For instance: 20 x 1 = 20, 20 × 2 = 40, 20 × 3 = 60, and so on.
• Another trick to remember the 20 times table is to add 20 to the first multiple of 20 and get the next multiples of 20.

Worksheets on Table of 20 | Solved Examples on Multiplication Chart of 20

Practicing & Answering the worksheets of the multiplication tables of twenty will guide you to apply all multiplication facts of the 20 times tables in complex calculations. The provided Solved Examples on Table of 20 aid you to understand how to solve problems using the 20 multiplication table:

1. Hari wishes to buy 20 pens. The cost of each pen is 7 rupees and find the cost of 20 pens in dollars using 20 times table?

Solution:

Given, Cost of 1 pen = 7 rupees

Now, estimate the cost of 20 pens = 20 × 7 =140 Rupees

Next, Convert 140 rupees into dollars

Hence, the cost of 20 pens in dollars is $1.90

2. John is playing a Ludo game in which after finishing every level, he receives 20 credit points. Using 20 times table, find the total points he scored after winning the 6th level?

Solution:

Credit gained after every level = 20 points

Now, calculate the credits scored at the 6th level using the 20 times table

ie., 20 x 6 = 120 points.

Therefore, Jhon would have scored 120 credit points on completing the 6th level.

3. Evaluate the value of 20 times 9 minus 11, with the help of 20 Multiplication Table?

Solution:

First, write down 20 times 9 minus 11 mathematically.

Using 20 times table, estimate the value of 20 times 9 minus 11

= 20 × 9 – 11 = 180 – 11 = 169

Hence, 20 times 9 minus 11 is 169.

Mathematics is the basic & standard subject that shows the impact on our daily life tasks. Since childhood parents and teachers help students to understand the basic concepts of maths thoroughly. One of the fundamentals of Mathematics is Math Tables. If students at primary school read and memorize the multiplication tables from 0 to 25 can aid in solving the long mathematical calculations.

Here, we have covered 23 Times Table necessary information such as tips to memorize the table of 23, how to read and write multiplication table of twenty-three, etc. View this article thoroughly and do calculations quickly by using the 23 times multiplication chart.

Multiplication Chart of 23

Table of Twenty-Three Chart is given in image format in order to help the students in remembering the math tables quickly. Reading & Remembering the 23x Times Table is quite tricky and necessary to answer the long multiplication and division mathematical sums with speed and accuracy. So, make use of this multiplication chart of 23 available here and do mental calculations for saving time in annual or competitive exams. Download the printable 23 times table multiplication chart for free of cost and learn well.

How to Write Multiplication Table of 23?

Learning how to read and write the multiplication table of 23 not only help primary school students or college students but also helpful for the aspirants appearing various private and government competitive exams. All math multiplication and division calculations are solved with the help of multiplication tables. So, check out the given table of 23 up to 20 whole numbers and learn reading and writing of 23 times multiplication table.

Learn Reading 23 Times Multiplication in Words

Twenty-three times one is equal to twenty-three.
Twenty-three times two is equal to fourty-six.
Twenty-three times three is equal to sixty-nine.
Twenty-three times four is equal to ninety-two.
Twenty-three times five is equal to one hundred and fifteen.
Twenty-three times six is equal to one hundred and thirty-eight.
Twenty-three times seven is equal to one hundred and sixty-one.
Twenty-three times eight is equal to one hundred and eighty-four.
Twenty-three times nine is equal to two hundred and seven.
Twenty-three times ten is equal to two hundred and thirty.
Twenty-three times eleven is equal to two hundred and fifty-three.
Twenty-three times twelve is equal to two hundred and seventy-six.
Twenty-three times thirteen is equal to two hundred and ninety-nine.
Twenty-three times fourteen is equal to three hundred and twenty-two.
Twenty-three times fifteen is equal to three hundred and fourty-five.
Twenty-three times sixteen is equal to three hundred and sixty-eight.
Twenty-three times seventeen is equal to three hundred and ninety-one.
Twenty-three times eighteen is equal to four hundred and fourteen.
Twenty-three times nineteen is equal to four hundred and thirty-seven.
Twenty-three times twenty is equal to four hundred and sixty.
Twenty-three times twenty-one is equal to four hundred and eighty-three.
Twenty-three times twenty-two is equal to five hundred and six.
Twenty-three times twenty-three is equal to five hundred and twenty-nine.

Tips to Remember Table of 23

The simplest trick that helps students to learn the 23 times table is given below. Check out the points listed here and solve long math problems quickly by following the tips & tricks of the 23 multiplication table.

• First, draw a 3×3 grid and follow the two points that are discussed below.
• Now, take digits from 1 to 9 and place them in the grid as shown in the image.
• Next, go for blue digits. These digits can be placed by following the pattern ie., put the first 3 even number in the first row and skip the fourth one and then put next 3 odd numbers in the second row. Again skip the fourth odd number and write the 3 even numbers in the third row, until you reach 23.
• For better clarification, check out the below-given image and understand the trick to memorize the twenty-three times table.

Get More Math Tables:

Solved Examples involving Twenty-Three Times Table

1. Using the 23 Times Table, Calculate the value of 5 plus 23 times 9 minus 3.

Solution:

First, we have to write down the given statement 5 plus 23 times 9 minus 3 mathematically.

Now, by using the table of 23, solve the expression 5 plus 23 times 9 minus 3 = 5 + 23 x 9 – 3

= 5 + 207 – 3 = 212 – 3 = 209

Hence, 5 plus 23 times 9 minus 3 is 209.

2. Evaluate 23 times 6 minus 23 times 8 applying 23 times table?

Solution:

First, write 23 times 6 minus 23 times 8 mathematically.

ie., 23 x 6 – 23 x 8

Then, use the table of 23 and solve the expression

23 x 6 – 23 x 8 = 138 -184 = -46

Therefore, 23 times 6 minus 23 times 8 is -46. 

3. Misthi has 8 cards with numbers 46, 21, 56, 102, 92, 68, 136, 207 written on them. Take help from the table of 23,  and assist maria in identifying the cards which are 23 times any number?

Solution:

Given 8 cards are 46, 21, 56, 102, 92, 68, 138, 207

From the table of 23, the first 10 multiples of 23 are 23, 46, 69, 92, 115, 138, 161, 184, 207, 230.

Among the 8 cards that Maria has, there are four cards with the numbers 46, 92, 138, and 207. These 4 card numbers are the only multiples of 23.

Table of 18 is the most complicated math tables below 20. The values of the Multiplication Table of 18 are a bit difficult to remember and calculate. Thus, we have presented the 18 Times Table both in the image and tabular format for your reference. In fact, our article guides on how to read and write the 18 Times Multiplication Table. Furthermore, we even added the Tips and Tricks to Memorize the 18 Table quickly and efficiently.

Multiplication Chart of 18

Utilize the 18 Times Table provided below to remember the table more effectively. You can use it as a flashcard to do your mental math calculations much simply and quickly. You can download the Multiplication Table of 18 Chart for quick guidance and try to memorize it to do math problems easily.

How to Read 18 Times Table?

One time eighteen is 18

Two times eighteen are 36

Three times eighteen are 54

Four times eighteen are 72

Five times eighteen are 90

Six times eighteen are 108

Seven times eighteen are 126

Eight times eighteen are 144

Nine times eighteen are 162

Ten times eighteen are 180

Eleven times eighteen are 198

Twelve times eighteen are 216

Multiplication Table of 18 up to 20

Below is the complete 18 Multiplication Table for natural numbers 1 to 20. Use the Table of 18 for fast calculations. Make the most out of the Multiplication Table of Eighteen and solve your math problems involving multiplication or division in no time.

Get More Math Tables:

Tips to Remember Multiplication Table of Eighteen

To Memorize the 18 Times Table there are certain tips and tricks to be followed and they are as such

• You can get the 18 Times Table taking the help of the 19 Times Table by simply subtracting the 1-10 natural numbers from the multiples of 19. Subtract the same number from the multiple with which you are multiplying 19. For Example 19×1 -1 =18, 19×2-2 =36,……
• You can also memorize the 8 Times Table to obtain the 18 Table. We know the first 10 multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 . . . . To obtain the multiples of 18, simply add natural numbers to the ten’s digit of the multiples of 8. Thus Multiplication Table of 18 is obtained as such (1+0)8, (2+1)6, (3+2)4, (4+3)2, (5+4)0, (6+4)8, (7+5)6, (8+6)4, (9+7)2, (10+8)0 = 18, 36, 54, 72, 90, 108, 126, 144, 162, 180.
• The other way is you can fix the numbers at units place i.e. 8, 4, 6, 2, 0 as these are the numbers and patterns followed by 18 Table by adding the first 5 consecutive odd numbers at ten’s digit place and next 5 consecutive even numbers in ten’s digit place.

Worked out Examples Involving 18 Table

1. With help of an 18 times table, Find a) What is 18 times 5? and b) What is 18 times 6 minus 4?

Solution:

a) 18 times 5

Expressing the given statement in math expression we have

18*5

= 90

b) 18 times 6 minus 4

Expressing the given statement in math expression we have

= 18*6-4

= 104

2. If a dog eats 4 bones in a day. Evaluate using the table of 18, how many bones will the dog eat in 18 days?

Solution:

No. of bones dog eat in a day = 4

No. of bones it will eat in 18 days = 18*no. of bones, it eats in one day

= 18*4

= 72

Therefore, the dog eats 72 bones in 18 days

3. Ram distributes 7 candies in one day? Using the 18 Table find how many candies will ram distribute in 18 days?

Solution:

No. of Candies Ram distribute in one day = 7

No. of Candies Ram distribute in 18 days = 18*7

= 126

Therefore, Ram distributes 126 candies in 18 days.