Introduction to Basic Geometrical Ideas
The term ‘Geometry’ is derived from the Greek word ‘Geometron’. This has 2 equivalents. ‘Geo’ means Earth and ‘metron’ means Measurement.

Points
It is a position or location on a plane surface, which are denoted by a single capital letter.

Lines and Angles

Line Segment

It is a part of a line with the finite length and 2 endpoints.

The points A and B are called the endpoints of the segment.

It is named as:

Line

It is made up of infinitely many points with infinite length and no endpoint.

It extends indefinitely in both directions.

Named as:

Or sometimes

Intersecting Lines

The two lines that share one common point are called Intersecting Lines.

This shared point is called the point of intersection.

Here, line l and m are intersecting at point C.

Real life example of intersecting lines:

Parallel Lines

Two or more lines that never intersect (Never cross each other) are called Parallel Lines.

Real life examples of parallel lines:

Ray

It is a part of a line with one starting point whereas extends endlessly in one direction.

Real life examples of the ray are:

Curves

Anything which is not straight is called a curve.

1. Simple Curve – A curve that does not cross itself.

2. Open Curve – Curve in which its endpoints do not meet.

3. Closed Curve – Curve that does not have an endpoint and is an enclosed figure.

A closed curve has 3 parts which are as follows

1. Interior of the curve

It refers to the inside/inner area of the curve.

The blue coloured area is the interior of the figure.

2. The exterior of the curve.

It refers to the outside / outer area of the curve.

The point marked A depicts the exterior of the curve.

3. The boundary of the curve

It refers to the dividing line thus it divides the interior and exterior of the curve.

The black line which is dividing the interior and exterior of the curve is the boundary.

The interior and boundary of the curve together are called the curves “region”.

Polygons

It is a 2d closed shape made of line segments / straight lines only.

• Sides –It refers to the line segments which form the polygon, as in the above figure AB, BC, CD, DA are its sides.
• Vertex – Point where 2 line segments meet, as in the above figure A, B, C and D are its vertices.
• Adjacent Sides – If any 2 sides share a common endpoint they are said to be adjacent to each other thus called adjacent sides, as in the above figure AB and BC, BC and CD, CD and DA, DA and AB are adjacent sides.
• Adjacent Vertices – It refers to the endpoints of the same side of the polygon. As in the above figure A and B, B and C, C and D, D and A are adjacent vertices.
• Diagonals – It refers to the joins of the vertices which are not adjacent to each other. As in the above figure, AC and BD are diagonals of the polygon.

Angles

A figure formed from 2 rays which share a common endpoint is called Angle.

The rays forming the angle are known as its arms or sides.

The common endpoint is known as its vertex.

An angle is also associated with 3 parts

1. Interior – It refers to the inside/inner area.

The green coloured area is the interior of the angle.

2. Angle/boundary – It refers to the arms of the angle.

The red point is on the arm of the angle.

3. Exterior – It refers to the outside / outer area.

The blue point depicts the exterior of the figure.

Naming an Angle

While naming an angle the letter depicting the vertex appears in the middle.

Example

The above angle can also be named as ∠CBA.

An angle can also be named just by its vertex.

Example

Triangle

It is a 3 sided polygon. It is also the polygon with the least number of the sides.

Vertices: A, B and C

Sides: AB, BC and CA

Angles: ∠A, ∠B and ∠C

• Here, the light blue coloured area is the interior of the angle.
• The black line is the boundary.
• Whereas, the dark blue area is the exterior of the angle.

Quadrilaterals

It is a 4 sided polygon

Vertices: A, B, C, D

Sides: AB, BC, CD, DA

Angle: ∠A, ∠B, ∠C, ∠D

Opposite Sides: AB and DC, BC and AD

Opposite Angles: ∠B and ∠D, ∠A and ∠C

Adjacent Angles: ∠A and ∠B, ∠B and ∠C, ∠C and ∠D, ∠D and ∠A.

Circles

It is a simple closed curve and is not considered as a polygon.

Parts of Circles

1. Radius – It is a straight line connecting the centre of the circle to the boundary of the same. Radii is the plural of ‘radius’.

2. Diameter –It is a straight line from one side of the circle to the other side passing through the centre.

3. Circumference – It refers to the boundary of the circle.

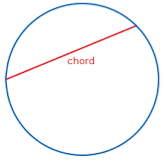
4. Chord – Any line that connects two points on the boundary of the circle is called Chord. Diameter is the longest chord.

5. Arc – It is the portion of the boundary of the circle.

6. Interior of the Circle – Area inside the boundary of the circle is called the Interior of the Circle.

7. The Exterior of the Circle – Area outside the boundary of the circle is called the Exterior of the Circle.

8. Sector– It is the region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides.

9. Segment – It is the region in the interior of the circle enclosed by an arc and a chord.

Semi-circle

A diameter divides the circle into two semi-circles. Hence the semicircle is the half of the circle, which has the diameter as the part of the boundary of the semicircle.

Students can get various questions related to simultaneous linear equations word problems on this page. Practice all the questions to get a clear idea of the topic. You can also find a detailed solution for each problem on the Practice Test on Word Problems Involving Simultaneous Linear Equations page. Solve the questions and verify your answers to get good marks in the exam.

Steps to Solve Linear Equations Word Problems

Follow these steps and instructions while solving the system of linear equations and get the answers easily.

• Take the unknown parameters as the variables x and y.
• According to the information provided in the question, make those variables as the linear equations.
• Solve those simultaneous linear equations by using substitution or elimination or comparison method.
• And get the value of one variable.
• Substitute the obtained variable value in any one of the equations to find other variable values.

Simultaneous Linear Equations Word Problems

Example 1.

In a rectangle, if the length is increased and the width is reduced each by 2 cm then the area is reduced by 26 sq.cm . If the length is reduced by 1 cm and the width increased by 2 cm , then the area increases by 30 sq.cm . Find the area of the rectangle?

Solution:

Let the length and width of the rectangle is x and y.

Then, the rectangle area = xy

According to the question,

If the length and width of the rectangle is reduced by 2 cm, then the area is reduced by 26 cm.

(x + 2)(y – 2) = x . y – 26

xy – 2x + 2y – 4 = xy – 26

xy – 2x + 2y – xy = -26 + 4

2y – 2x = -22

2(y – x) = -22

y – x = -22/2

y – x = -11 —– (i)

If the length is reduced by 1 cm and the width increased by 2 cm , then the area increases by 30 sq.cm

(x – 1) . (y + 2) = x . y + 30

xy + 2x – y – 2 = xy + 30

xy + 2x – y – xy = 30 + 2

2x – y = 32 —– (ii)

Add equation (i) and equation (ii)

y – x + (2x – y) = -11 + 32

y – x + 2x – y = 21

x = 21

Substitute x = 21 in equation (i)

y – 21 = -11

y = -11 + 21

y = 10

So, Area of the rectnagle = x . y

= 21 x 10

= 210 sq. cm.

Hence, the rectangle area is 210 sq. cm.

Example 2.

One number is five times the other number. The difference between the two numbers is 32. Find the two numbers?

Solution:

Let the two numbers be x and y.

Given that, one number is five times the other number.

x = 5y ——- (i)

The difference between the two numbers is 32.

x – y = 32 ——- (ii)

Substitute x = 5y in equation (ii)

5y – y = 32

4y = 32

y = 32/4

y = 8

Putting y = 8 in equation (i)

x = 5 x 8

x = 40

Hence, the two numbers are 40, 8.

Example 3.

I am four times old as my grand-daughter. After five years, I will be 2½ times as old as my grand-daughter. Find my present age and the present age of my grand-daughter?

Solution:

Let my present age of is x, the present age of my grand-daughter is y.

According to the question,

I am four times old as my grand-daughter

x = 4y —– (i)

After five years, I will be 2½ times as old as my grand-daughter.

(x + 5) = 2½(y + 5)

x + 5 = 5/2(y + 5)

2(x + 5) = 5(y + 5)

2x + 10 = 5y + 25

2x – 5y = 25 – 10

2x – 5y = 15 —– (ii)

Put x = 4y in equation (ii)

2(4y) – 5y = 15

8y – 5y = 15

3y = 15

y = 5

Put y = 5 in equation (i)

x = 4(5)

x = 20

Therefore, my present age is 20 years, my grand daughter’s present age is 5 years.

Example 4.

The difference between the two numbers is 15. Two times the smaller number added to the larger number gives 30. Find the two numbers?

Solution:

Let the smaller number is x, largest number is y.

Given that, the difference between numbers is 15.

y – x = 15 —– (i)

Two times the smaller number added to the larger number gives 30

2x + y = 30 —— (ii)

Subtract equation (ii) from equation (i)

2x + y – (y – x) = 30 – 15

2x + x = 15

3x = 15

x = 15/3

x = 5

Put x = 5 in equation (i)

y – 5 = 15

y = 15 + 5

y = 20

Therefore, the two numbers are 5, 20.

Example 5.

If I double a number and add three times a second number, the answer is 1. If I multiply the first number by 3 and take away twice the second number, the answer is 8. Find the numbers?

Solution:

Let the two numbers be x, y.

As per the first condition in the question,

Double a number and add three times the second number, the answer is 1.

2x + 3y = 1 —- (i)

Second condition is multiply the first number by 3 and take away twice the second number, the answer is 8.

3x – 2y = 8 —– (ii)

x = (8 + 2y)/3

Substituting x = (8 + 2y)/3 in equation (i)

2(8 + 2y)/3 + 3y = 1

(16 + 4y)/3 + 3y = 1

(16 + 4y + 9y)/3 = 1

16 + 13y = 3

13y = 3 – 16

13y = -13

y = -13/13

y = -1

Substitute y = -1 in equation (ii)

3x – 2(-1) = 8

3x + 2 = 8

3x = 8 – 2

3x = 6

x = 6/3

x = 2

So the numbers are 2, -1.

Example 6.

The numerator of a fraction is 4 smaller than its denominator. If both the numerator and denominator are increased by 1, the fraction is 5/8. Find the original fraction?

Solution:

Let the fraction be x/y.

Given that, the numerator of a fraction is 4 smaller than its denominator.

x – 4 = y

x – y – 4 = 0 —- (i)

If both the numerator and denominator are increased by 1, the fraction is 5/8

(x + 1) / (y + 1) = 5/8

8(x + 1) = 5 (y + 1)

8x + 8 = 5y + 5

8x – 5y + 8 – 5 = 0

8x – 5y + 3 = 0 —- (ii)

Multiply the equation (i) by 5.

5(x – y – 4) = 0

5x – 5y – 20 = 0 —– (iii)

Subtract equation (iii) from the equation (ii)

8x – 5y + 3 – (5x – 5y – 20) = 0

8x – 5y + 3 – 5x + 5y + 20 = 0

3x + 23 = 0

x = -23/3

Put x = -23/3 in equation (i)

-23/3 – y – 4 = 0

y = -23/3 – 4

y = (-23 – 12)/3

y = -35/3

So, the fraction is (-23/3) / (-35/3) = 23/35.

Example 7.

The sum of ages of a mother and her son two years ago was 40. In two years’ time from now, the age of the mother will be three times that of her son by then. Find their ages after 7 years’ time?

Solution:

The present ages of a mother and her son is x and y respectively.

The sum of ages of a mother and her son two years ago was 40

(x – 2) + (y – 2) = 40

x + y – 4 = 40

x + y = 44 ——- (i)

In two years time from now, the age of the mother will be three times that of her son by then

(x + 2) = 3(y + 2)

x + 2 = 3y + 6

x – 3y + 2 – 6 = 0

x – 3y – 4 = 0 —— (ii)

Subtract equation (ii) from equation (i)

x – 3y – 4 – (x + y) = 0 – 44

x – 3y – 4 – x – y = -44

-4y = -44 + 4

-4y = -40

y = 40/4

y = 10

Put y = 10 in equation (i)

x + 10 = 44

x = 44 – 10

x = 34

So, the present ages of mother and son are 34 years, 10 years.

The mother age after 7 years is 34 + 7 = 41 years, son age after 7 years is 10 + 7 = 17 years.

Example 8.

The Sum of the cost price of the two products is $50. The Sum of the selling price of the same two products is $52. If one is sold at 20% profit and another one is sold at 20% loss, find the cost price of each product.

Solution:

Let x, y are the cost prices of two products.

Given that, the sum of the cost prices of the two products is $50.

x + y = 50 —— (i)

One product is sold at 20% profit and another one is sold at 20% loss.

Assume that x is sold at 20% profit. Then its selling price is = 120% of x = 1.2x

Then another product y is sold at 20% loss. Then its selling price = 80% of y = 0.8y

The sum of the selling price of the two products is $52.

1.2x + 0.8y = 52

Multiply both sides by 10.

12x + 8y = 520

3x + 2y = 130 —- (ii)

Multiply the equation (i) by 2 and subtract it from equation (iii).

2x + 2y = 100

3x + 2y – (2x + 2y) = 130 – 100

3x + 2y – 2x – 2y = 30

x = 30

Put x = 30 in equation (i)

30 + y = 50

y = 50 – 30

y = 20

So, the cost prices of the two products are $30 and $20.

Example 9.

Points A and B are 50 km part on a highway. A car starts from A and another car starts from B at the same time. If they traveled in the same direction, they meet in 5 hours but if they move towards each other they meet in 1 hour. Find their speeds?

Solution:

Given that,

The distance between two points = 50 km

Speed = distance / time

When they travel in the same direction,

Suppose take B travels for x km, then A will traveled for 50 + x

Speed of car A = (50 + x) / 5

Speed of car B = x / 5

When they travel in the opposite direction,

Suppose they meet when A travels for y km, then B will have traveled 50−y km in the same time.

Speed of car A = y/1

Speed of car B = (50 – y) / 1

Equating the speeds of the cars in both cases,

Speed of car A,

(50 + x) / 5 = y

50 + x = 5y

x – 5y + 50 = 0 —— (i)

Speed of car B,

x/5 = (50 – y)

x = 5(50 – y)

x = 250 – 5y

x + 5y – 250 = 0 —- (ii)

Subtracting equation (ii) from equation (i)

x + 5y – 250 – (x – 5y + 50) = 0

x + 5y – 250 – x + 5y – 50 = 0

10y – 300 = 0

10y = 300

y = 300/10

y = 30

Substitute y = 30 in equation (i)

x – 5(30) + 50 = 0

x – 150 + 50 = 0

x – 100 = 0

x = 100

Therefore, the speed of car A is 100 km/hr and car B is 30 km/hr.

Example 10.

In the triangle, the sum of two angles is 90° which is the measure of the third angle. Also, the difference between these 2 angles is 10°, find the measure of these two unknown angles?

Solution:

Let the measures of two angles of a triangle are x, y.

The sum of two angles is 90°.

x + y = 90°  —– (i)

The difference between these 2 angles is 10°

x – y = 10° —– (ii)

Add equation (i) and equation (ii)

x + y + x – y = 90 – 10

2x = 80

x = 40°

Put x = 40° in equation (ii)

40° – y = 10°

40° – 10° = y

30° = y

Therefore, the unknown two angles of the triangle are 40°, 30°.

By solving the system of linear equations in two variables, you will get an ordered pair having x coordinate and y coordinate values (x, y) that satisfies both equations. Here those simultaneous linear equations are in the form of word problems. So, you can solve different word problems with the help of linear equations.

We have already learned some steps and methods to solve the simultaneous linear equations in two variables. Assume the unknown quantities in the question as x, y variables and represent them in the form of a linear equation according to the condition mentioned in the question. And follow the methods to solve the formed system of linear equations to get the values of unknown quantities. We have also provided simultaneous equations problems with solutions that help you to grasp the concept.

Simultaneous Equations Word Problems

Example 1.

One number is greater than thrice the other number by 6. If 4 times the smaller number exceeds the greater by 7, find the numbers?

Solution:

Let x, y be the two numbers

So that x > y

Given that, one number is greater than thrice the other number by 6.

Then, we can write it as

x = 3y + 6 ——— (i)

According to the question,

4 times the smaller number exceeds the greater by 7.

4y – x = 7 ——— (ii)

Substitute (3y + 6) in equation (ii).

4y – (3y + 6) = 7

4y – 3y – 6 = 7

y – 6 = 7

y = 7 + 6

y = 13

Substitute y = 13 in equation (i)

x = 3(13) + 6

x = 39 + 6

x = 45

So, the two numbers are 45, 13.

Example 2.

The sum of two numbers is 25 and their difference is 5. Find those two numbers?

Solution:

Let the two numbers be x and y.

According to the question,

The sum of two numbers is 25

x + y = 25 —— (i)

The difference of numbers is 5.

x – y = 5 —– (ii)

Add both the equations (i) & (ii)

x + y + x – y = 25 + 5

2x = 30

x = 30/2

x = 15

Putting x = 15 in equation (i)

15 + y = 25

y = 25 – 15

y = 10

So, the two numbers are 15, 10.

Example 3.

The sum of two numbers is 50. If the larger is doubled and the smaller is tripled, the difference is 25. Find the two numbers.

Solution:

Let the two numbers be x and y

According to the given question,

The sum of two numbers is 50.

x + y = 50 —— (i)

The larger number is doubled and the smaller number is tripled, the difference is 25.

2x – 3y = 25 —— (ii)

Multiply the first equation by 3.

3(x + y) = 3 x 50

3x + 3y = 150 —— (iii)

Add equation (ii) and equation (iii)

2x – 3y + 3x + 3y = 25 + 150

5x = 175

x = 175/5

x = 35

Substituting the value of x in equation (i)

35 + y = 50

y = 50 – 35

y = 15

Hence the two numbers are 35, 15.

Example 4.

The class IX students of a certain public school wanted to give a farewell party to the outgoing students of class X. They decided to purchase two kinds of sweets, one costing Rs. 70 per kg and the other costing Rs. 85 per kg. They estimated that 34 kg of sweets were needed. If the total money spent on sweets was Rs. 2500, find how much sweets of each kind they purchased?

Solution:

Let the quantity of sweets purchased be x kg which cost Rs. 70 per kg and sweets purchased y kg which cost Rs. 85 per kg.

According to the question,

x + y = 34 ——- (i)

70x + 85y = 2500 ——– (ii)

Multiplying the equation (i) by 70, we get

70(x + y) = 34 x 70

70x + 70y = 2380 —– (iii)

Subtracting equation (iii) from equation (ii), we get

70x + 70y – (70x + 85y) = 2380 – 2500

70x + 70y – 70x – 85y = -120

-15y = -120

y = 120/75

y = 1.6

Substitute y = 1.6 in equation (i)

x + 1.6 = 34

x = 34 – 1.6

x = 32.4

Hence, the sweets purchased 1 kg 600 grams which cost Rs. 85 per kg and 32 kg 400 grams which cost Rs. 70 per Kg.

Example 5.

A two-digit number is eight times the sum of its digits. The number formed by reversing the digits is 18 less than the given number. Find the given number?

Solution:

Let the two-digit number be xy.

Given that, the two digit number is eight times the sum of its digits.

xy = 8(x + y) —– (i)

In the two digit number xy, x is in the tens position and y is in ones position.

Then,

xy = 10 . x + 1 . y

xy = 10x + y ——- (ii)

Substitute equation (ii) in equation (i)

10x + y = 8(x + y)

10x + y = 8x + 8y

10x – 8x = 8y – y

2x = 7y

2x – 7y = 0 —– (iii)

According to the question,

The number formed by reversing the digits 18 less than the given number.

xy – yx = 18

(10 . x + 1 . y) – (10 . y + 1 . x) = 18

(10x + y) – (10y + x) = 18

10x + y – 10y – x = 18

9x – 9y = 18

9(x – y) = 18

(x – y) = 18/9

x – y = 2 —— (iv)

Multiply equation (iv) by 2.

2(x – y) = 2 x 2

2x – 2y = 4 —— (v)

Subtract equation (v) from equation (iii)

(2x – 2y) – (2x – 7y) = 4 – 0

2x – 2y – 2x + 7y = 4

5y = 4

y = 4/5

Substitute y = 4/5 in equation (iv)

x – 4/5 = 2

x = 2 + 4/5

x = (10 + 4)/5

x = 14/5

So, the required two digit number is 144/5.

Example 6.

If the numerator of a certain fraction is increased by 2 and the denominator by 1, the fraction becomes equal to ⅗ and if the numerator and denominator are each diminished by 1, the fraction becomes equal to ⅔, find the fraction.

Solution:

Let the fraction be x/y.

According the given question,

(x + 2) / (y + 1) = ⅗

5(x + 2) = 3(y + 1)

5x + 10 = 3y + 3

5x – 3y = 3 – 10

5x – 3y = -7 —— (i)

(x – 1) / (y – 1) = ⅔

3(x – 1) = 2(y – 1)

3x – 3 = 2y – 2

3x – 2y = -2 + 3

3x – 2y = 1 —— (ii)

Multiply the equation (i) by 2, equation (ii) by 3.

2(5x – 3y) = 2 x -7 ⇒ 10x – 6y = -14

3(3x – 2y) = 3 x 1 ⇒ 9x – 6y = 3

(10x – 6y) – (9x – 6y) = -14 – 3

10x – 6y – 9x + 6y = -17

x = -17

Substitute x = -17 in equation (i)

5(-17) – 3y = -7

-85 – 3y = -7

-3y = -7 + 85

-3y = 78

y = -78 / 3

y = -26

Therefore, the fraction is 17/26.

Example 7.

If four times the age of the son is added to the age of the father, the sum is 64. But if twice the age of the father is added to the age of the son, the sum is 82. Find the ages of father and son?

Solution:

Let the father’s age be x years, the son’s age be y years.

According to the question,

4y + x = 64 —– (i)

2x + y = 82 —— (ii)

Multiply the equation (i) by 2

2(x + 4y) = 64 x 2

2x + 8y = 128

Subtract 2x + 8y = 128 from equation (ii)

(2x + 8y) – (2x + y) = 128 – 82

2x + 8y – 2x – y = 46

7y = 46

y = 46/7

y = 6 years 7 months

Substituting y = 46/7 in equation (ii)

2x + 46/7 = 82

2x = 82 – 46/7

2x = (574 – 64)/7

2x = 510/7

x = 510/14

x = 36 years 4 months

Therefore, the father’s age is 36 years 4 months, the son’s age is 6 years 7 months.

Solving a pair of equations indicate that those pairs are simultaneous linear equations. By solving the equations, you can say that those equations are the system of linear equations and consistent or not. Get the solved example questions along with solutions in the below-mentioned sections of this page.

Pair of Equations Problems

Example 1.

If solvable, solve the following pairs of equations:

(i) 3x + 2y = 5, x + 4y = 7

(ii) 3x – 2y = 4, 18x – 12y – 24 = 0

Solution:

(i) 3x + 2y = 5, x + 4y = 7

Here, comparing the co-efficient of x, y we get;

3/1 ≠ 2/4

Therefore, subtracting the two equations, we get the general solution.

6x – 10 = x – 7

5x = -7 + 10

5x = 3

x = 3/5

Substitute x = 3/5 in x + 4y = 7

3/5 + 4y = 7

4y = 7 – 3/5 = 32/5

y = 32/20

Therefore, the required solution is x = 3/5, y = 32/20.

(ii) 3x – 2y = 4, 18x – 12y – 24 = 0

Here, comparing the co-efficient of x, y we get;

3/18 = -2/-12 = -4/-24

Therefore, two equations are, in fact, same.

Assuming x = c in 3x – 2y = 4 we get;

y = (3c – 4)/2

Therefore, required solution: x = c

y = (3c – 4)/2 for any real value of c.

Example 2.

From the following pairs of equations find the pair or pairs representing simultaneous equations:

(i) 5x + 2y – 6 = 0, 2x + y – 7 = 0

(ii) 6x + 4y + 9 = 0, 3x + 2y +7 = 0

Solution:

(i) 5x + 2y – 6 = 0, 2x + y – 7 = 0

5/2 ≠ 2/1 ≠ -6/-7

So the two equations represent simultaneous equations; in this case they have only one solution.

(ii) 6x + 4y + 9 = 0, 3x + 2y +7 = 0

6/3 = 4/2 ≠9/7

So, the given equations are not simultaneous equations.

Example 3.

For which value of k, kx + y = 5 and x + ky = 1 are inconsistent?

Solution:

The two equations will be inconsistent if k/1 = 1/k ≠ 5/1 that means, k² = 1 or k = ±1

Therefore, the two given equations will be inconsistent if k = ±1.

Example 4.

From the following pairs of equations find the pair or pairs representing simultaneous equations:

(i) x + y = 5, x – 2y = 11

(ii) 3x – 4y + 2 = 0, 12x – 16y + 8 = 0

Solution:

(i) x + y = 5, x – 2y = 11

1/1 ≠ 1/-2 ≠ -5/-11

So the two equations represent simultaneous equations; in this case they have only one solution.

(ii) 3x – 4y + 2 = 0, 12x – 16y + 8 = 0

3/12 = -2/-16 = 2/8

So, these are simultaneous equations and have infinite solutions.

Example 5.

If solvable, solve the following pairs of equations:

(i) 5x + 7y = 9, x – 2y = 3

(ii) 3x – 2y = 2, 9x – 6y = 6

Solution:

(i) 5x + 7y = 9, x – 2y = 3

Here, comparing co-efficient of x and y, we get;

5/1 ≠ 7/-2

Therefeore, solve the value of x,

x = 39/17

Put x = 39/17 in x – 2y = 3

39/17 – 3 = 2y

(39 – 51)/17 = 2y

2y = -12/17

y = -12/34

Therefore, the required solution is x = 39/17, y = -12/34

(ii) 3x – 2y = 2, 9x – 6y = 6

Here, comparing co-efficient of x and y, we get;

3/9 = -2/-6 = 2/6

Therefore, two equations are, in fact, same.

Assuming x = c in 3x – 2y = 2

3c – 2y = 2

(3c – 2) = 2y

y = (3c – 2)/2

y = (3c – 2)/2 for any real value of c.

Learn the conditions for the solvability of a system of linear equations in two variables in the following sections. If the simultaneous equations have no solution, then they are called inconsistent and if they have a solution, then they are called consistent. To help you understand the fundamentals of the concept we have given the Solved Examples with Answers explaining everything in detail.

Conditions for Solvability of Simultaneous Linear Equations in Two Variables

Let the pair of linear equations in two variables are

a₁x + b₁y + c₁ = 0 ——- (1)

a₂x + b₂y + c₂= 0 ——- (2)

By using the cross-multiplication method, we get

x/(b₁c₂ – b₂c₁) = y/(a₂c₁ – a₁c₂) = 1/(a₁b₂ – a₂b₁)

So, x = (b₁c₂ – b₂c₁) / (a₁b₂ – a₂b₁)

y = (a₂c₁ – a₁c₂) / (a₁b₂ – a₂b₁)

Now see when the solvability of simultaneous linear equations in two variables (i), (ii) are solavble.

(I) If (a₁b₂ – a₂b₁) ≠ 0 for any values of (b₁c₂ – b₂c₁), (a₂c₁ – a₁c₂) we will get the unique solutions for the x and y variables.

Example:

x – 2y – 8 = 0 ——- (1)

x + y – 5 = 0 ——— (2)

Here, a₁ = 1, b₁ = -2, c₁ = -8, a₂ = 1, b₂ = 1, c₂ = -5

Substitute these values in (a₁b₂ – a₂b₁), we get

(a₁b₂ – a₂b₁) = (1 x 1 – 1 x -2) = 1 + 2 = 3 ≠ 0

So, x = (b₁c₂ – b₂c₁) / (a₁b₂ – a₂b₁)

= (-2 x -5 – 1 x -8) / 3 = (-10 + 8)/3 = 18/3 = 6

y = (a₂c₁ – a₁c₂) / (a₁b₂ – a₂b₁)

= (1 x -8 – 1 x -5)/3 = (-8 + 5)/3 = -3/3 = -1

Therefore, when (a₁b₂ – a₂b₁) ≠ 0, then the system of linear equations are always consistent.

(II) If (a₁b₂ – a₂b₁) = 0 and any one of (b₁c₂ – b₂c₁) and (a₂c₁ – a₁c₂) is zero, then

Let us take a₁/a₂ = b₁/b₂ = c₁/c₂ = k, where k ≠ 0

Then, a₁ = ka₂, b₁ = kb₂, c₁ = kc₂

And system of linear equations are changed to

ka₂x + kb₂y + kc₂ = 0

a₂x + b₂y + c₂ = 0

From this equation, we can write

x = (-b₂y – c₂) / a₂

This indicates for each value of y, there is a definite value of x or there are infinite number of solutions of the simultaneous equations in this case.

Example:

x + 2y + 5 = 0

3x + 6y + 15 = 0

Here, a₁/a₂ = b₁/b₂ = c₁/c₂ = 1/3

Actually, we get the second equation by multiplying the first equation by 3. Express one equation x interms of y

x = -2y -5

Some of the solutions are

(III) If (a₁b₂ – a₂b₁) = 0 and any one from (b₁c₂ – b₂c₁) and (a₂c₁ – a₁c₂) is non zero, (then other one is also non-zero)

Let us take k = a₁/a₂ = b₁/b₂ ≠ c₁/c₂ = k

So, a₁ = ka₂, b₁ = kb₂

In this case, the chnaged linear equations are

ka₂x + kb₂y + c₂ = 0

a₂x + b₂y + c₂= 0

These equations do not have solution for x and y.

So the equations are inconsistent.

While drawing graphs, we can see that the linear equations in two variables always represent a straight line and the equations of the above form represent two parallel straight lines. This is why these lines do not intersect each other and not have a common point.

Example:

7x + y + 3 = 0

14x + 2y – 1 = 0

Here, a₁ = 7, b₁ = 1, c₁ = 3, a₂ = 14, b₂ = 2, c₂ = -1

And, a₁/a₂ = b₁/b₂ ≠ c₁/c₂

So, the given system of linear equations is inconsistent.

From the above discussions, we can write that

a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂= 0 will be

(i) Consistent if a₁/a₂ ≠ b₁/b₂, we will get a unique solution

(ii) Inconsistent, there will be no solution if a₁/a₂ = b₁/b₂ ≠ c₁/c₂ where c₁ ≠ 0, c₂ ≠ 0

(iii) Consistent and have infinite solutions if a₁/a₂ = b₁/b₂ = c₁/c₂ where c₁ ≠ 0, c₂ ≠ 0

Solvability of Linear Equations Examples

Example 1.

Check whether the linear equations x + 2y + 4 = 0, 3x – 5y + 1 = 0 are consistent or inconsistent?

Solution:

Given system of linear equations are

x + 2y + 4 = 0

3x – 5y + 1 = 0

Here, a₁ = 1, b₁ = 2, c₁ = 4, a₂ = 3, b₂ = -5, c₂ = 1

(a₁b₂ – a₂b₁) = (1 x -5 – 3 x 2) = (-5 – 6) = -11

x = (b₁c₂ – b₂c₁) / (a₁b₂ – a₂b₁)

= (2 x 1 – (-5) x 4) / -11 = (2 + 20)/-11

= -22/11 = -2

y = (a₂c₁ – a₁c₂) / (a₁b₂ – a₂b₁)

= (3 x 4 – 1 x 1) / -11 = (12 – 1)/-11 = -11/11

= -1

Here, (a₁b₂ – a₂b₁) ≠ 0

Therefore, the given simultaneous linear equations are consistent and have a unique solution.

Example 2.

Check whether the linear simultaneous equations 3x – y – 2 = 0, 6x – 2y – 4 = 0 are consistent or inconsistent?

Solution:

Given Linear Simultaneous Equations are

3x – y – 2 = 0, 6x – 2y – 4 = 0

Here, a₁ = 3, b₁ = -1, c₁ = -2, a₂ = 6, b₂ = -2, c₂ = -4

(a₁b₂ – a₂b₁) = (3 x -2 – 6 x -1) = (-6 + 6) = 0

and (b₁c₂ – b₂c₁) = (-1 x -4 – (-2) x -2) = (4 – 4) = 0

(a₂c₁ – a₁c₂) = (6 x -2 – 3 x (-4)) = (-12 + 12) = 0

a₁/a₂ = b₁/b₂ = c₁/c₂ = 1/2

Actually, we get the second equation by multiplying the first equation by 2. Express one equation x in terms of y

x = (y + 2) / 3

Some of the solutions are

Therefore, the given linear equations are consistent and have an infinite number of solutions.

Example 3.

State whether the linear equations -2x + 3y – 2 = 0, 2x – 3y – 5 = 0 are consistent or not?

Solution:

Given linear equations are -2x + 3y – 2 = 0, 2x – 3y – 5 = 0

Here, a₁ = -2, b₁ = 3, c₁ = -2, a₂ = 2, b₂ = -3, c₂ = -5

(a₁b₂ – a₂b₁) = (-2 x -3 – 2 x 3) = (6 – 6) = 0

(b₁c₂ – b₂c₁) = (3 x -5 – (-3) x (-2)) = (-15 – 6) = -21

a₁/a₂ = b₁/b₂ = -1

The equations are inconsistent and has no solution.

Cross multiplication method is used to solve a pair of simultaneous linear equations in two variables. This method helps you to find the accurate values of variables easily. It is applicable only when we have two linear equations in two variables. Get the steps to solve the system of linear equations with the cross multiplication method in the following sections. Also, check out the solved examples for a better understanding of the concept.

Cross Multiplication Method for Solving Pair of Linear Equations

Follow the easy and simple guidelines listed below while solving Pair of Linear Equations. They are in the following fashion

• Observe the given pair of linear equations and transpose them in the form of ax + by + c = 0
• And represent them as the coefficient constant of term x, the coefficient constant of term y, coefficient of x, and coefficient of y.
• Cross multiply those constants.
• Express the cross multiplicands of x, y, and constants under x, y, and 1.
• Equate them to find the values of x, y.

Check out the derivation to get more details about the Cross-Multiplication Method.

General Solution Using the Method of Cross-Multiplication

Let the pair of linear equations in two variables are

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

For solving these linear equations follow the below included steps

Given simultaneous linear equations in two variables are

a₁x + b₁y + c₁ = 0 ——- (i)

a₂x + b₂y + c₂ = 0 ——– (ii)

Multiply equation (i) by b₂ and equation (ii) by b₁.

b₂ (a₁x + b₁y + c₁ = 0)

b₂ (a₁x + b₁y + c₁) = b₂ x 0

a₁b₂x + b₁b₂y + b₂c₁ = 0 ——- (iii)

b₁ (a₂x + b₂y + c₂ = 0)

b₁ (a₂x + b₂y + c₂) = b₁ x 0

a₂b₁x + b₂b₁y + c₂b₁ = 0 —- (iv)

Subtract equation (iv) from equation (iii)

[a₁b₂x + b₁b₂y + b₂c₁ = 0] – [a₂b₁x + b₂b₁y + c₂b₁ = 0]

[a₁b₂x + b₁b₂y + b₂c₁] – [a₂b₁x + b₂b₁y + c₂b₁] = 0

a₁b₂x + b₁b₂y + b₂c₁ – a₂b₁x – b₂b₁y – c₂b₁ = 0

x(a₁b₂ – a₂b₁) + b₂c₁ – c₂b₁ = 0

x(a₁b₂ – a₂b₁) = c₂b₁ – b₂c₁

x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁)

Substitute x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) in equation (i)

a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) + b₁y + c₁ = 0

b₁y = -a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁

y = (-a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁) / b₁

y = (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂)

The solution of the equations is

x / (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) = y / (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂) = 1/(b₂a₁ – b₁a₂)

The above method is called Cross-Multiplication Methos as it uses cross-multiplication technique.

You can also represent the cross-multiplication as the following diagram.

Cross Multiplication Method Examples

Example 1.

Solve the linear equations x + y = 5, x – y = 3 by using the cross multiplication method?

Solution:

Given system of linear equations are

x + y = 5

x – y = 3

On transposition, we get

x + y – 5 = 0

x – y – 3 = 0

Writing the co-efficient in the following way, we get:

By cross-multiplication method:

x/[(1(-3) – (-1)(-5)] = y/[(-5)1 – 1(-3)] = 1//[1(-1) – 1(1)]

x/(-3 – 5) = y/(-5 + 3) = 1/(-1 – 1)

x/(-8) = y/(-2) = 1/(-2)

x/(-8) = 1/(-2), y/(-2) = 1/(-2)

x/8 = 1/2, y/2 = 1/2

x = 8/2, y = 2/2

x = 4, y = 1

Therefore, required solution is x = 4, y = 1.

Example 2.

Solve the simultaneous linear equations 3x – 4y = 0, 9x – 8y = 12 by the method of cross-multiplication?

Solution:

Given simultaneous equations are,

3x – 4y = 0

9x – 8y = 12

On transposition, we get

3x – 4y = 0 ——– (i)

9x – 8y – 12 = 0 ———- (ii)

Multiply equation (i) by -8 and equation (ii) by -4.

-8(3x – 4y) = 0 x -8

-24x + 32y = 0 —— (iii)

-4(9x – 8y – 12) = 0 x -4

-36x + 32y + 48 = 0 ——- (iv)

Subtract equation (iv) from equation (iii)

[-24x + 32y = 0] – [-36x + 32y + 48 = 0]

-24x + 32y – (-36x + 32y + 48) = 0

-24x + 32y + 36x – 32y – 48 = 0

12x – 48 = 0

12x = 48

x = 48/12

x = 4

Substitute x = 4 in equation (ii)

9(4) – 8y – 12 = 0

36 – 8y – 12 = 0

-8y + 24 = 0

-8y = -24

y = 24/8

y = 3

Therefore, required solution is x = 4, y = 3.

Example 3.

Solve the linear equations 2x + 3y = 5, x – 4y = 8 by using the cross multiplication method?

Solution:

Given linear equations are 2x + 3y = 5, x – 4y = 8

On transposing, we get

2x + 3y – 5 = 0 ——- (i)

x – 4y – 8 = 0 ——- (ii)

Multiply equation (ii) by 2, equation (i) by 1.

From equation (i), we get

2x + 3y – 5 = 0 —– (iii)

From equation (ii), we get

2(x – 4y – 8) = 0

2x – 8y – 16 = 0 —— (iv)

Subtract equation (iii) from equation (iv).

[2x – 8y – 16] – [2x + 3y – 5] = 0

2x – 8y – 16 – 2x – 3y + 5 = 0

-11y – 11 = 0

-11y = 11

y = -11/11

y = -1

Substitute y = -1 in equation (i)

2x + 3(-1) – 5 = 0

2x – 3 – 5 = 0

2x – 8 = 0

2x = 8

x = 8/2

x = 4

Therefore, the required solution is x = 4, y = -1.

Example 4.

Solve the system of linear equations 2x + 5y = 20, x + 2y = 4?

Solution:

Given simultaneous linear equations are 2x + 5y = 20, x + 2y = 4

On transposing, we get

2x + 5y – 20 = 0 —— (i)

x + 2y – 4 = 0 —— (ii)

Multiply equation (i) by 2.

2(2x + 5y – 20) = 2 x 0

4x + 10y – 40 = 0 ——- (iii)

Multiply equation (ii) by 5.

5(x + 2y – 4) = 0 x 5

5x + 10y – 20 = 0 —– (iv)

Subtract equation (iii) from equation (iv)

[5x + 10y – 20] – [4x + 10y – 40] = 0

5x + 10y – 20 – 4x – 10y + 40 = 0

x + 20 = 0

x = -20

Put x = -20 in equation (iii)

4(-20) + 10y – 40 = 0

-80 + 10y – 40 = 0

10y – 120 = 0

10y = 120

y = 120/10

y = 12

Therefore the required solution is x = -20, y = 12.

The solution to the simultaneous linear equations can be obtained by using the substitution method. It is one of the categories of the algebraic methods that give solution for system of linear equations. In this page, you will learn about substitution method definition, and how to solve equations using substitution method with example questions.

What is meant by Substitution Method?

The substitution method is one among the algebraic methods that help you to solve the simultaneous equations. As the word substitution says that, the value of one variable from one equation is substituted in the other equation. So, a pair of linear equations gets transformed into one linear equation in one variable. Later, solve the obtained equation to get the solution.

Substitution Method for Solving System of Linear Equations

For instance, the simultaneous equations with two variables can be solved using the below mentioned detailed steps. Follow them and find the solution of a system of linear equations easily.

• Simplify the given equations by expanding the paranthesis.
• Find the value of one variable in terms of the second variable from any of the given equations.
• Substitute this variable value in other equations.
• Solve the equation and get the value of one of the variables.
• Substitute that value in any one of the equations to find the value of another variable.

General Solution using the Substitution Method

Let us take two linear equations

ax + by = c —— (i)

dx + ey = f ——- (ii)

Express y in terms of x

From equation (i), we get

by = c – ax

y = (c – ax) / b

Substitute the obtained value of y in equation (ii), we get

dx + [e(c – ax)] / b = f

On simplifying this equation,

dx + (ec – aex)/b = f

dx + ec/b – aex/b = f

dx – aex/b = f – ec/b

x(d – ae/b) = (bf – ec)/b

x = [(bf – ec)/b] / [(db – ae)/b]

x = (bf – ec) / (bd – ae)

Putting the value of x in equation (i)

a[(bf – ec) / (bd – ae)] + by = c

[(abf – ace)/(bd – ae)] + by = c

by = c – [(abf – ace)/(bd – ae)]

y = {c – [(abf – ace)/(bd – ae)]} / b

y = [bc(bd – ae) – (abf – ace)] / b

Therefore, solution set is x = (bf – ec) / (bd – ae), y = [bc(bd – ae) – (abf – ace)] / b.

Substitution Method Examples with Answers

Example 1.

Solve the equations 3x + 2y = 7, 5x – 3y = 37 by substitution method?

Solution:

Given simultaneous equations are

3x + 2y = 7 ——- (i)

5x – 3y = 37 ——- (ii)

From equation (i) 3x + 2y = 7, express y in terms of x

From equation (i) 3x + 2y = 7, we get;

2y = 7 – 3x

Therefore, y = (7 – 3x) / 2

Substitute the obtained value of y in equation (ii),

By putting y = (7 – 3x) / 2 in equation (ii) 5x – 3y = 37, we get

5x – 3[(7 – 3x) / 2] = 37

5x – (21 – 9x)/2 = 37

5x – 21/2 + 9x/2 = 37

5x + 9x/2 = 37 + 21/2

(10x + 9x)/2 = (74 + 21)/2

19x = 95

x = 95/19

x = 5

Therefore, x = 5

Putting the value of x in equation (ii),

Subsutitute x = 5 in 5x – 3y = 37

5(5) – 3y = 37

25 – 3y = 37

25 – 37 = 3y

-12 = 3y

y = -12/3

y = -4

Therefore, x= 5 and y = -4 is the solution for the system of linear equations 3x + 2y = 7, 5x – 3y = 37.

Example 2.

Solve the simultaneous equations 3x + y = 9, 5x + 4y = 22 using the substitution method?

Solution:

Given system of linear equations are,

3x + y = 9 —— (i)

5x + 4y = 22 —— (ii)

Express y in terms of x

From equation (i), we get

y = 9 – 3x

Substituting y = 9 – 3x in equation (ii), we get

5x + 4(9 – 3x) = 22

5x + 36 – 12x = 22

36 – 7x = 22

36 – 22 = 7x

7x = 14

x = 14/7

x = 2

Putting x = 2 in equation (i), we get

3(2) + y = 9

6 + y = 9

y = 9 – 6

y = 3

Therefore, x = 2, y = 3 is the solution for the linear equations 3x + y = 9, 5x + 4y = 22.

Example 3.

Solve the system of linear equations x – 2y = 8, x + y = 5 by the method of substitution?

Solution:

Given simultaneous linear equations are

x – 2y = 8 —— (i)

x + y = 5 ——- (ii)

Express x in terms of y

From equation (i) we get

x = 8 + 2y

Substitute x = 8 + 2y in equation (ii)

8 + 2y + y = 5

8 + 3y = 5

3y = 5 – 8

3y = -3

y = -3/3

y = -1

Putting y = -1 in equation (i) we get

x – 2(-1) = 8

x + 2 = 8

x = 8 – 2

x = 6

Therefore, x = 6, y = -1 is the solution for the linear equations x – 2y = 8, x + y = 5.

Example 4.

Solve the pair of equations 2x + 3y = 9, x = 3 + y using the substitution method?

Solution:

Given system of linear equations are

2x + 3y = 9 —- (i)

x = 3 + y —— (ii)

Substitute x = 3 + y in the equation (i)

2(3 + y) + 3y = 9

6 + 2y + 3y = 9

6 + 5y = 9

5y = 9 – 6

5y = 3

y = 3/5

Put y = 3/5 in equation (ii)

x = 3 + 3/5

x = (15 + 3)/5

x = 18/5

Therefore, x = 18/5, y = 3/5 is the solution for the equations 2x + 3y = 9, x = 3 + y.

SEO Title: Substitution Method for Solving System of Linear Equations Examples

Meta Description: Use the Substitution Method for Solving the Simultaneous Linear Equations easily. Get Substitution Method Steps explained in detail with Example Problems.

Cross-Multiplication Method to Solve System of Linear Equations | Cross Multiplication Method Examples

Cross multiplication method is used to solve a pair of simultaneous linear equations in two variables. This method helps you to find the accurate values of variables easily. It is applicable only when we have two linear equations in two variables. Get the steps to solve the system of linear equations with the cross multiplication method in the following sections. Also, check out the solved examples for a better understanding of the concept.

Cross Multiplication Method for Solving Pair of Linear Equations

Follow the easy and simple guidelines listed below while solving Pair of Linear Equations. They are in the following fashion

• Observe the given pair of linear equations and transpose them in the form of ax + by + c = 0
• And represent them as the coefficient constant of term x, the coefficient constant of term y, coefficient of x, and coefficient of y.
• Cross multiply those constants.
• Express the cross multiplicands of x, y, and constants under x, y, and 1.
• Equate them to find the values of x, y.

Check out the derivation to get more details about the Cross-Multiplication Method.

General Solution Using the Method of Cross-Multiplication

Let the pair of linear equations in two variables are

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

For solving these linear equations follow the below included steps

Given simultaneous linear equations in two variables are

a₁x + b₁y + c₁ = 0 ——- (i)

a₂x + b₂y + c₂ = 0 ——– (ii)

Multiply equation (i) by b₂ and equation (ii) by b₁.

b₂ (a₁x + b₁y + c₁ = 0)

b₂ (a₁x + b₁y + c₁) = b₂ x 0

a₁b₂x + b₁b₂y + b₂c₁ = 0 ——- (iii)

b₁ (a₂x + b₂y + c₂ = 0)

b₁ (a₂x + b₂y + c₂) = b₁ x 0

a₂b₁x + b₂b₁y + c₂b₁ = 0 —- (iv)

Subtract equation (iv) from equation (iii)

[a₁b₂x + b₁b₂y + b₂c₁ = 0] – [a₂b₁x + b₂b₁y + c₂b₁ = 0]

[a₁b₂x + b₁b₂y + b₂c₁] – [a₂b₁x + b₂b₁y + c₂b₁] = 0

a₁b₂x + b₁b₂y + b₂c₁ – a₂b₁x – b₂b₁y – c₂b₁ = 0

x(a₁b₂ – a₂b₁) + b₂c₁ – c₂b₁ = 0

x(a₁b₂ – a₂b₁) = c₂b₁ – b₂c₁

x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁)

Substitute x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) in equation (i)

a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) + b₁y + c₁ = 0

b₁y = -a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁

y = (-a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁) / b₁

y = (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂)

The solution of the equations is

x / (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) = y / (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂) = 1/(b₂a₁ – b₁a₂)

The above method is called Cross-Multiplication Methos as it uses cross-multiplication technique.

You can also represent the cross-multiplication as the following diagram.

Cross Multiplication Method Examples

Example 1.

Solve the linear equations x + y = 5, x – y = 3 by using the cross multiplication method?

Solution:

Given system of linear equations are

x + y = 5

x – y = 3

On transposition, we get

x + y – 5 = 0

x – y – 3 = 0

Writing the co-efficient in the following way, we get:

By cross-multiplication method:

x/[(1(-3) – (-1)(-5)] = y/[(-5)1 – 1(-3)] = 1//[1(-1) – 1(1)]

x/(-3 – 5) = y/(-5 + 3) = 1/(-1 – 1)

x/(-8) = y/(-2) = 1/(-2)

x/(-8) = 1/(-2), y/(-2) = 1/(-2)

x/8 = 1/2, y/2 = 1/2

x = 8/2, y = 2/2

x = 4, y = 1

Therefore, required solution is x = 4, y = 1.

Example 2.

Solve the simultaneous linear equations 3x – 4y = 0, 9x – 8y = 12 by the method of cross-multiplication?

Solution:

Given simultaneous equations are,

3x – 4y = 0

9x – 8y = 12

On transposition, we get

3x – 4y = 0 ——– (i)

9x – 8y – 12 = 0 ———- (ii)

Multiply equation (i) by -8 and equation (ii) by -4.

-8(3x – 4y) = 0 x -8

-24x + 32y = 0 —— (iii)

-4(9x – 8y – 12) = 0 x -4

-36x + 32y + 48 = 0 ——- (iv)

Subtract equation (iv) from equation (iii)

[-24x + 32y = 0] – [-36x + 32y + 48 = 0]

-24x + 32y – (-36x + 32y + 48) = 0

-24x + 32y + 36x – 32y – 48 = 0

12x – 48 = 0

12x = 48

x = 48/12

x = 4

Substitute x = 4 in equation (ii)

9(4) – 8y – 12 = 0

36 – 8y – 12 = 0

-8y + 24 = 0

-8y = -24

y = 24/8

y = 3

Therefore, required solution is x = 4, y = 3.

Example 3.

Solve the linear equations 2x + 3y = 5, x – 4y = 8 by using the cross multiplication method?

Solution:

Given linear equations are 2x + 3y = 5, x – 4y = 8

On transposing, we get

2x + 3y – 5 = 0 ——- (i)

x – 4y – 8 = 0 ——- (ii)

Multiply equation (ii) by 2, equation (i) by 1.

From equation (i), we get

2x + 3y – 5 = 0 —– (iii)

From equation (ii), we get

2(x – 4y – 8) = 0

2x – 8y – 16 = 0 —— (iv)

Subtract equation (iii) from equation (iv).

[2x – 8y – 16] – [2x + 3y – 5] = 0

2x – 8y – 16 – 2x – 3y + 5 = 0

-11y – 11 = 0

-11y = 11

y = -11/11

y = -1

Substitute y = -1 in equation (i)

2x + 3(-1) – 5 = 0

2x – 3 – 5 = 0

2x – 8 = 0

2x = 8

x = 8/2

x = 4

Therefore, the required solution is x = 4, y = -1.

Example 4.

Solve the system of linear equations 2x + 5y = 20, x + 2y = 4?

Solution:

Given simultaneous linear equations are 2x + 5y = 20, x + 2y = 4

On transposing, we get

2x + 5y – 20 = 0 —— (i)

x + 2y – 4 = 0 —— (ii)

Multiply equation (i) by 2.

2(2x + 5y – 20) = 2 x 0

4x + 10y – 40 = 0 ——- (iii)

Multiply equation (ii) by 5.

5(x + 2y – 4) = 0 x 5

5x + 10y – 20 = 0 —– (iv)

Subtract equation (iii) from equation (iv)

[5x + 10y – 20] – [4x + 10y – 40] = 0

5x + 10y – 20 – 4x – 10y + 40 = 0

x + 20 = 0

x = -20

Put x = -20 in equation (iii)

4(-20) + 10y – 40 = 0

-80 + 10y – 40 = 0

10y – 120 = 0

10y = 120

y = 120/10

y = 12

Therefore the required solution is x = -20, y = 12.

The elimination method is one of the process to solve the linear equations having two variables. Here variables are removed to find the solution set. It is more comfortable and easy when compared with the substitution method. Get the simple steps to solve two simultaneous linear equations with two variables in the below sections.

How to Solve System of Equations by Elimination Method?

Elimination methods mean multiplying the variable coefficients with a constant and eliminate one particular variable. Get the detailed steps to solve the system of linear equations in the following sections.

• Multiply the given two linear equations by some suitable non-zero integer to make the coefficients of either x or y numerically equal.
• After that, either add or subtract one equation from the second equation such that one variable gets removed. Now, solve that to get an equation in one variable.
• Here, if you get a statement including no variable, then the given linear equations have infinite solutions.
• If you get a false statement including no variable, then the given linear equation has no solution.
• Solve the equation in one variable to get its value.
• Place the obtained value in any of the linear equations to find the value of another variable.

General Solution:

Let us take two linear equations

ax + by = c — (i)

dx + ey = f —– (ii)

Multiply equation (i) with d

d(ax + by) = d x c

adx + bdy = cd —– (iii)

Similarly, multiply equation (ii) with a

a(dx + ey) = f x a

adx + aey = af —– (iv)

Subtract equation (iii) from equation (iv) as per the elimination method rule

[adx + bdy = cd] – [adx + aey = af]

adx + bdy – adx – aey = cd – af

bdy – aey = cd – af

y(bd – ae) = cd – af

y = (cd – af) / (bd – ae)

Substitute y = (cd – af) / (bd – ae) in equation (i)

ax + b(cd – af) / (bd – ae) = c

ax = c – (bcd – abf) / (bd – ae)

x = [c – (bcd – abf) / (bd – ae)] / a

= [c(bd – ae) – (bcd – abf)] / a(bcd – abf)

= (bcd – ace – bcd + abf) / a(bcd – abf)

= (abf – ace) / a(bcd – abf)

= a(bf – ce) / a(bcd – abf)

= (bf – ce) / (bcd – abf)

Therefore, the solution set is x = (bf – ce) / (bcd – abf), y = (cd – af) / (bd – ae).

Workedout Examples on Elimination Method

Example 1.

Solve the simultaneous linear equations 2x + 2y = 7, 4x + 3y = 12 by the method of elimination?

Solution:

Given system of linear equations are

2x + 2y = 7 —— (i)

4x + 3y = 12 ——- (ii)

Multiply the equation (i) by 2.

(2x + 2y = 7) —– (x 2)

4x + 4y = 14 —— (iii)

Subtract (iii) from (ii), we get

[4x + 4y = 14] – [4x + 3y = 12]

(4x + 4y) – (4x + 3y) = 14 – 12

4x + 4y – 4x – 3y = 2

y = 2

Substituting the value of y = 2 in equation (ii), we get

4x + 3(2) = 12

4x + 6 = 12

4x = 12 – 6

4x = 6

x = 6/4

x = 3/2

Therefore, x = 3/2 and y = 2 is the solution of the system of equations 2x + 2y = 7, 4x + 3y = 12.

Example 2.

Solve the following linear equations by using elimination method?

y = 2x – 6, y = ½x + 6

Solution:

Given simultaneous linear equations are,

y = 2x – 6 —— (i)

y = ½x + 6 ——- (ii)

Subtract equation (i) from equation (ii) to eliminate the variable y.

[y = 2x – 6] – [y = ½x + 6]

y – y = (2x – 6) – (½x + 6)

0 = 2x – 6 – ½x – 6

3x/2 – 12 = 0

3x/2 = 12

3x = 24

x = 24/3

x = 8

Substitute x = 8 in equation (i) to get the value of y.

y = 2(8) – 6

y = 16 – 6

y = 10

Therefore, x = 8 and y = 10 is the solution of the system of equations y = 2x – 6, y = ½x + 6.

Example 3.

Solve the system of linear equations x + 7y = 10, 3x – 2y = 7 by the elimination method?

Solution:

Given linear equations are,

x + 7y = 10 —– (i)

3x – 2y = 7 ——- (ii)

Multiply the equation (i) by 3

(x + 7y = 10) —– (x 3)

3(x + 7y) = 10 x 3

3x + 21y = 30 ——- (iii)

Subtract equation (iii) from equation (ii) to find the value of one variable.

[3x + 21y = 30] – [3x – 2y = 7]

(3x + 21y) – (3x – 2y) = 30 – 7

3x + 21y – 3x + 2y = 23

23y = 23

y = 23/23

y = 1

Place y = 1 in the equation (i) to get the value of another variable.

x + 7(1) = 10

x + 7 = 10

x = 10 – 7

x = 3

Therefore, x = 3, y = 1 is the solution of the linear equations x + 7y = 10, 3x – 2y = 7.

Example 4.

Use elimination method to solve the below included simultaneous equations?

x + 3y = 10, 8x + y = 11

Solution:

Given system of linear equations are

x + 3y = 10 —— (i)

8x + y = 11 ——- (ii)

Multiply the equation (i) by 8

(x + 3y = 10) —— (x 8)

8(x + 3y) = 8 x 10

8x + 24y = 80 —– (iii)

Subtract equation (iii) from equation (ii) to get the value of one variable.

[8x + 24y = 80] – [8x + y = 11]

(8x + 24y) – (8x + y) = 80 – 11

8x + 24y – 8x – y = 69

23y = 69

y = 69/23

y = 3

Put y = 3 in equation (i) and solve to find the value of another variable.

x + 3(3) = 10

x + 9 = 10

x = 10 – 9

x = 1

Therefore, x = 1, y = 3 is the solution for the simultaneous linear equations x + 3y = 10, 8x + y = 11.

Before you start practicing the Difference of Two Squares Concept know the step-by-step process to solve the Factoring Difference of Two Squares. Therefore, students can easily learn all types of factoring problems here. Without any late, begin your practice and finish solving every problem included. Refer to Solved Examples on Difference of Two Squares with Answers Provided.

Difference of Two Squares Questions

1. m⁴ – (n + r)⁴

Solution:
Given expression is m⁴ – (n + r)⁴
Rewrite the given expression in the form of a² – b².
(m²)² – ( (n + r)²)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = m² and b = (n + r)²
[m² + (n + r)²] [m² – (n + r)²]
[m² + n² + r² + 2nr] [(m)² – (n + r)²]
From the above equation, [(m)² – (n + r)²] is in the form of a² – b².
[(m)² – (n + r)²]
Now, apply the formula of a² – b² = (a + b) (a – b), where a = m and b = (n + r)
[m + (n + r)] [m – (n + r)]
Now, [m² + n² + r² + 2nr] [(m)² – (n + r)²]
[m² + n² + r² + 2nr] [m + (n + r)] [m – (n + r)]
[m² + n² + r² + 2nr] [m + n + r] [m – n – r]

The final answer is [m² + n² + r² + 2nr] [m + n + r] [m – n – r]

2. 4a² – b² + 6b – 9.

Solution:
Given expression is 4a² – b² + 6b – 9.
Rewrite the given expression.
4a² – (b² – 6b + 9)
b² – 6b + 9 is in the form of a² – b² + 2ab where a = b, b = 3
We know that a² – b² + 2ab = (a – b)²
Therefore, b² – 6b + 9 = (b – 3)²
So, 4a² – (b – 3)²
The above equation 4a² – (b – 3)² is in the form of a² – b².
[(2a)² – (b – 3)²]
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 2a and b = (b – 3)
(2a + b – 3) {2a – (b – 3)},
(2a + b – 3) (2a – b – 3)

The final answer is (2a + b – 3) (2a – b – 3)

3. 25x² – (4m² – 12mn + 9n²)

Solution:
Given expression is 25x² – (4m² – 12mn + 9n²)
(4m² – 12mn + 9n²) is in the form of a² – b² + 2ab where a = 2m, b = 3n
We know that a² – b² + 2ab = (a – b)²
Therefore, (4m² – 12mn + 9n²) = (2m – 3n)²
So, 25x² – (2m – 3n)²
The above equation 25x² – (2m – 3n)² is in the form of a² – b².
[(5x)² – (2m – 3n)²]
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 5x and b = (2m – 3n)
[5x + (2m – 3n)] [5x – (2m – 3n)]
(5x + 2m – 3n) (5x – 2m + 3n)

The final answer is (5x + 2m – 3n) (5x – 2m + 3n)

Know the process to find Factorization by using identities. Based on the identities, we can simply factorize an algebraic equation. That means, depending on the identities or identity values, we can easily reduce the number of expressions into n number of terms. Generally, for the simplest factorization process, we have to follow some basic expressions. They are

(i) (x + y)^2 = (x)^2 + 2xy + (y)^2.
(ii) (x – y)^2 = (x)^2 – 2xy + (y)^2.
(iii) x^2 – y^2 = (x + y) (x – y).

Factoring Polynomials Identities Steps

Go through the below-listed guidelines on how to factor polynomials using algebraic identities. They are in the following fashion

• Note down the given expression and compare the expression with the basic expressions.
• If there are three terms and all are identified with the positive sign, then that is related to (x + y)^2.
• If the first and last terms are with the positive sign and the middle term is identified with the negative sign, then that is related to (x – y)^2.
• If there are only two terms with one positive sign and one negative sign, then that is related to x^2 – y^2.
• Now, compare the co-efficient values with the basic expressions.
• Find the values of coefficients.
• Based on the values, reduce the given expression into simple terms.

Factorization Using Identities Examples with Answers

1. Factorize using the formula of a square of the sum of two terms

(i) a² + 6a + 9

Solution: Given expression is a² + 6a + 9
There are three terms are identified with the positive sign. Then it is related to the expression (x)^2 + 2xy + (y)^2 = (x + y)^2.
Now, compare the co-efficient values of a² + 6a + 9 with the expression (x)^2 + 2xy + (y)^2.
Here, x = a, 2y = 6 then y = 3.
So, (x + y)^2 = (a + 3)^2.

Finally, our expression a^2 + 6a + 9 is reduced to (a + 3)^2.

(ii) a^2 + 20a + 100

Solution:
Given expression is a^2 + 20a + 100.
There are three terms that are identified with a positive sign. Then it is related to the expression (x)^2 + 2xy + (y)^2 = (x + y)^2.
Now, compare the co-efficient values of a^2 + 20a + 100 with the expression(x)^2 + 2xy + (y)^2.
Here, x = a, 2y = 20 then y = 10.
So, (x + y)^2 = (a + 10)^2.

Finally, our expression a^2 + 20a + 100 is reduced to (a + 10)^2.

2. Factorize using the formula of the square of the difference of two terms

(i) 4p^2 – 12pq + 9q^2

Solution:
Given expression is 4p^2 – 12pq + 9q^2.
There are three terms that are identified with the positive sign of the first and last terms and the negative sign of the middle term.
Then it is related to the expression (x)^2 – 2xy + (y)^2 = (x – y)^2.
Now, compare the co-efficient values of 4p^2 – 12pq + 9q^2with the expression (x)^2 – 2xy + (y)^2.
Here, x^2 = 4p^2 then x =2p, y^2 = 9q^2 then y = 3q.
So, (x – y)^2 = (2p – 3q)^2.

Finally, our expression 4p^2 – 12pq + 9q^2is reduced to (2p – 3q)^2.

(ii) a^2 – 10a + 25

Solution:
Given expression is a^2 – 10a + 25.
There are three terms that are identified with the positive sign of the first and last terms and the negative sign of the middle term.
Then it is related to the expression (x)^2 – 2xy + (y)^2 = (x – y)^2.
Now, compare the co-efficient values of a^2 – 10a + 25 with the expression (x)^2 – 2xy + (y)^2.
Here, x^2 = a^2 then x =a, y^2 = 25 then y = 5.
So, (x – y)^2 = (a – 5)^2.

Finally, our expression a^2 – 10a + 25 is reduced to (a – 5)^2.

3. Factorize using the formula of a difference of two squares:

(i) 49a^2 – 64

Solution:
Given expression is 49a^2 – 64
There are two terms identified with the positive sign of the first term and the negative sign of the last term.
Now, compare the co-efficient values of 49a^2 – 64 with the expression (x)^2 – (y)^2.
Here, x^2 = 49a^2 = (7a)^2 then x =7a, y^2 = 64 = (8)^2 then y = 8.
So, (x)^2 – (y)^2 = (7a)^2 – (8)^2.
(x + y) (x – y) = (7a + 8) (7a – 8)

Finally, our expression 49a^2 – 64is reduced to (7a + 8) (7a – 8).

(ii) 16a^2 – 36b^2

Solution:
Given expression is 16a^2 – 36b^2
There are two terms identified with the positive sign of the first term and the negative sign of the last term.
Now, compare the co-efficient values of 16a^2 – 36b^2 with the (x)^2 – (y)^2.
Here, x^2 = 16a^2 = (4a)^2 then x =4a, y^2 = 36b^2 = (6b)^2 then y = 6b.
So, (x)^2 – (y)^2 = (4a)^2 – (6b)^2.
(x + y) (x – y) = (4a + 6b) (4a – 6b)

Finally, our expression 16a^2 – 36b^2 is reduced to (4a + 6b) (4a – 6b).

(iii) 1 – [5(2p – 5q)]^2

Solution:
Given expression is 1 – [5(2p – 5q)]^2
We can write it as (1)^2 – [5(2p – 5q)]^2
There are two terms identified with the positive sign of the first term and the negative sign of the last term.
Now, compare the co-efficient values of (1)^2 – [5(2p – 5q)]^2 with the (x)^2 – (y)^2.
Here, x^2 = (1)^2 then x =1,
y^2 = [5(2p – 5q)]^2then y = 5(2p – 5q).
So, (x)^2 – (y)^2 = (1)^2 – [5(2p – 5q)]^2.
(x + y) (x – y) = [1 + 5(2p – 5q)] [1 – 5(2p – 5q)].

Finally, our expression 1 – 25(2p – 5q)^2 is reduced to [1 + 5(2p – 5q)] [1 – 5(2p – 5q)].

4. Factor completely using the formula of a difference of two squares

(i) p^4 –q^4

Solution:
Given expression is p^4 –q^4
We can write it as (p^2)^2 – (q^2)^2
There are two terms identified with the positive sign of the first term and the negative sign of the last term.
Now, compare the co-efficient values of (p^2)^2 – (q^2)^2with the (x)^2 – (y)^2.
Here, x^2 = (p^2)^2 then x =p^2,
y^2 = (q^2)^2 then y = q^2.
So, (x)^2 – (y)^2 = (p^2)^2 – (q^2)^2.
(x + y) (x – y) = (p^2 + q^2) (p^2 –q^2).

Finally, our expression p^4 – q^4 is reduced to (p^2 + q^2) (p^2 – q^2).

Factorization of Quadratic Trinomials is the process of finding factors of given Quadratic Trinomials. If ax^2 + bx + c is an expression where a, b, c are constants, then the expression is called a quadratic trinomial in x. The expression ax^2 + bx + c has an x^2 term, x term, and an independent term. Find Factoring Quadratics Problems with Solutions in this article.

Factorization of Quadratic Trinomials Forms

The Factorization of Quadratic Trinomials is in two forms.

(i) First form: x^2 + px + q
(ii) Second form: ax^2 + bx + c

How to find Factorization of Trinomial of the Form x^2 + px + q?

If x^2 + px + q is an Quadratic Trinomial, then x² + (m + n) × + mn = (x + m)(x + n) is the identity.

Solved Examples on Factorization of Quadratic Trinomial of the Form x^2 + px + q 

1. Factorize the algebraic expression of the form x^2 + px + q

(i) a² – 7a + 12

Solution:
The Given expression is a² – 7a + 12.
By comparing the given expression a² – 7a + 12 with the basic expression x^2 + px + q.
Here, a = 1, b = – 7, and c = 12.
The sum of two numbers is m + n = b = – 7 = – 4 – 3.
The product of two number is m * n = a * c = -4 * (- 3) = 12
From the above two instructions, we can write the values of two numbers m and n as – 4 and -3.
Then, a² – 7a + 12 = a² – 4a -3a + 12.
= a (a – 4) – 3(a – 4).
Factor out the common terms.

Then, a² – 7a + 12 = (a – 4) (a – 3).

(ii) a² + 2a – 15

Solution:
The Given expression is a² + 2a – 15.
By comparing the given expression a² + 2a – 15 with the basic expression x^2 + px + q.
Here, a = 1, b = 2, and c = -15.
The sum of two numbers is m + n = b = 2 = 5 – 3.
The product of two number is m * n = a * c = 5 * (- 3) = -15
From the above two instructions, we can write the values of two numbers m and n as 5 and -3.
Then, a² + 2a – 15 = a² + 5a – 3a – 15.
= a (a + 5) – 3(a + 5).
Factor out the common terms.

Then, a² + 2a – 15 = (a + 5) (a – 3).

How to find Factorization of trinomial of the form ax^2 + bx + c?

To factorize the expression ax^2 + bx + c we have to find the two numbers p and q, such that p + q = b and p × q = ac

Solved Examples on Factorization of trinomial of the form ax^2 + bx + c 

2. Factorize the algebraic expression of the form ax2 + bx + c

(i) 15b² – 26b + 8

Solution:
The Given expression is 15b² – 26b + 8.
By comparing the given expression 15b² – 26b + 8 with the basic expression ax² + bx + c.
Here, a = 15, b = -26, and c = 8.
The sum of two numbers is p + q = b = -26 = 5 – 3.
The product of two number is p * q = a * c = 15 * (8) = 120
From the above two instructions, we can write the values of two numbers p and q as -20 and -6.
Then, 15b² – 26b + 8 = 15b² – 20 – 6b + 8.
= 5b (3b – 4) – 2(3b – 4).
Factor out the common terms.

Then, 15b² – 26b + 8 = (3b – 4) (5b – 2).

(ii) 3a² – a – 4

Solution:
The Given expression is 3a² – a – 4.
By comparing the given expression 3a² – a – 4 with the basic expression ax² + bx + c.
Here, a = 3, b = -1, and c = -4.
The sum of two numbers is p + q = b = -1 = 5 – 3.
The product of two number is p * q = a * c = 3 * (-4) = -12
From the above two instructions, we can write the values of two numbers p and q as -4 and 3.
Then, 3a² – a – 4 = 3a² – 4a -3a – 4.
= a (3a – 4) – 1(3a – 4).
Factor out the common terms.

Then, 3a² – a – 4 = (3a – 4) (a – 1).

Learn the process to Factorize the Trinomial ax Square Plus bx Plus c. One of the basic expressions for trinomial is ax² + bx + c. To find the ax² + bx + c factors, firstly, we need to find the two numbers and that is p and q. Here, the second term ‘b’ is the sum of the two numbers that is p + q = b. The product of the first and last terms is equal to the product of two numbers that is p * q = ac. Based on these two instructions, we need to find the values of p and q.

Steps to Factorize the Trinomial of Form ax² + bx + c?

1. Note down the given expression and compare it with the basic expression ax² + bx + c.
2. Note down the product and sum terms and find the two numbers.
3. Depends on the values of two numbers, expand the given expression.
4. Factor out the common terms.
5. Finally, we will get the product of two terms which is equal to the trinomial expression.

Solved Examples on Factoring Trinomials of the Form ax² + bx + c

1. Resolve into factors.

(i) 2s² + 9s + 10.

Solution:
The Given expression is 2s² + 9s + 10.
By comparing the given expression 2s² + 9s + 10 with the basic expression ax² + bx + c.
Here, a = 2, b = 9, and c = 10.
The sum of two numbers is p + q = b = 9 = 5 + 4.
The product of two number is p * q = a * c = 2 * 10 = 20 = 5 * 4.
From the above two instructions, we can write the values of two numbers p and q as 5 and 4.
Then, 2s² + 9s + 10 = 2s² + 5s + 4s + 20.
= 2s (s + 5) + 4 (s + 5).
Factor out the common terms.

Then, 2s² + 9s + 10 = (2s + 4) (s + 5).

(ii) 6s² + 7s –3

Solution:
The Given expression is 6s² + 7s – 3.
By comparing the given expression 6s² + 7s – 3 with the basic expression ax² + bx + c.
Here, a = 6, b = 7, and c = 3.
The sum of two numbers is p + q = b = 7 = 9 – 2.
The product of two number is p * q = a * c = 6 * 3 = 18 = 9 * 2.
From the above two instructions, we can write the values of two numbers p and q as 9 and 2.
Then, 6s² + 7s -3 = 6s² + 9s – 2s – 3.
= 6s² – 2s + 9s – 3.
= 2s (3s – 1) + 3(3s – 1).
Factor out the common terms.

Then, 6s² + 7s – 3 = (3s – 1) (2s + 3).

2. Factorize the trinomial.

(i) 2x² + 7x + 3.

Solution:
The Given expression is 2x² + 7x + 3.
By comparing the given expression 2x² + 7x + 3 with the basic expression ax² + bx + c.
Here, a = 2, b = 7, and c = 3.
The sum of two numbers is p + q = b = 7 = 6 + 1.
The product of two number is p * q = a * c = 2 * 3 = 6 = 6 * 1.
From the above two instructions, we can write the values of two numbers p and q as 6 and 1.
Then,2x² + 7x + 3 = 2x² + 6x + x + 3.
= 2x (x + 3) + (x + 3).
Factor out the common terms.

Then, 2x² + 7x + 3 = (x + 3) (2x + 1).

(ii) 3s² – 4s – 4.

Solution:
The Given expression is 3s² – 4s – 4.
By comparing the given expression 3s² – 4s – 4 with the basic expression ax² + bx + c.
Here, a = 3, b = – 4, and c = – 4.
The sum of two numbers is p + q = b = – 4 = – 6 + 2.
The product of two number is p * q = a * c = 3 * (- 4) = – 12 = (- 6) * 2.
From the above two instructions, we can write the values of two numbers p and q as – 6 and 2.
Then, 3s² – 4s – 4 = 3s² – 6s + 2s – 4.
= 3s (s – 2) + 2(s – 2).
Factor out the common terms.

Then, 3s² – 4s – 4 = (s – 2) (3s + 2).

Learn How to Factorize the Trinomial x² + px +q? A Trinomial is a three-term algebraic expression. By Factoring the trinomial expression, we will get the product of two binomial terms. Here, the trinomial expression contains three terms which are combined with the operations like addition or subtraction. Here, we need to find the coefficient values, and based on the coefficient values, we can find out the binomial terms as products of trinomial expression.

How to Factorize the Trinomial x² + px + q?

To find x^2 + px + q, we have to find the two terms (m + n) = p and mn = q.
Substitute (m + n) = p and mn = q in x^2 + px + q.
x^2 + px + q = x^2 + (m + n)x + mn.
By expanding the above expression, we will get
x^2 + px + q = x^2 + mx + nx + mn.
separate the common terms from the above expression.
that is, x(x + m) + n(x + m).
factor out the common term.
that is, (x + m) (x + n).
So, x^2 + px + q = (x + m)(x + n).

Factorization of Trinomial Steps

• Note down the given trinomial expression and compare the expression with the basic expression.
• Find out the product and sum of co-efficient values that is (m + n) and mn.
• Based on the above step, find out the two co-efficient values m and n.
• Finally, we will get the product of two terms which are equal to the trinomial expression.

Examples on Factoring Trinomials of Form x² + px + q

1. Resolve into factors

(i) a² + 3a -28

Solution:
Given Expression is a² + 3a -28.
Compare the a² + 3a -28 with the x^2 + px +q
Here, p = m + n = 3 and q = mn = -28
q is the product of two co-efficient. That is, 7 *(- 4) = -28
p is the sum of two co-efficient. That is 7 + ( – 4) = 3.
So, a² + 3a -28 = a² + [7 + (-4)]a – 28.
= a² + 7a – 4a – 28.
=a (a + 7) – 4(a + 7)
Factor out the common term.
That is, (a + 7) (a – 4).

Finally, the expression a² + 3a -28 = (a + 7) (a – 4).

(ii) a² + 8a + 15

Solution:
Given Expression is a² + 8a + 15.
Compare the a² + 8a + 15 with the x^2 + px +q.
Here, p = m + n = 8 and q = mn = 15.
q is the product of two co-efficient. That is, 5 * 3 = 15.
p is the sum of two co-efficient. That is 5 + 3 = 8.
So, a² + 8a + 15 = a² + (5 + 3)a + 15.
= a² + 5a + 3a + 15.
=a (a + 5) + 3(a + 5).
Factor out the common term.
That is, (a + 5) (a + 3).

Finally, the expression a² + 8a + 15= (a + 5) (a + 3).

2. Factorize the Trinomial

(i) a² + 15a + 56

Solution:
Given Expression is a² + 15a + 56.
Compare the a² + 15a + 56 with the x^2 + px +q.
Here, p = m + n = 15 and q = mn = 56.
q is the product of two co-efficient. That is, 7 * 8 = 56.
p is the sum of two co-efficient. That is 7 + 8 = 15.
So, a² + 15a + 56= a² + (7 + 8) a + 56.
= a² + 7a + 8a + 56.
=a (a + 7) + 8(a + 7).
Factor out the common term.
That is, (a + 7) (a + 8).

Finally, the expression a² + 15a + 56= (a + 7) (a + 8).

(ii) a² + a – 56

Solution:
Given Expression is a² + a – 56.
Compare the a² + a – 56 with the x^2 + px +q.
Here, p = m + n = 1 and q = mn = – 56.
q is the product of two co-efficient. That is, – 7 * 8 = – 56.
p is the sum of two co-efficient. That is – 7 + 8 = 1.
So, a² + a – 56 = a² + ( – 7 + 8)a – 56.
= a² – 7a + 8a – 56.
=a (a – 7) + 8(a – 7).
Factor out the common term.
That is, (a – 7) (a + 8).

Finally, the expression a^2 + a – 56 = (a – 7) (a + 8).

Are you looking for How to Evaluate the Difference of Two Squares Problems? We have given all Difference of Two Squares problems along with the evaluation of Difference of Two Squares with detailed explanation. Students can refer to all factorization problems on our website and begin their practice to score good marks in the exam.

Solved Problems to Evaluate the Difference of Two Squares

Use the formula of the difference of two squares to evaluate the following algebraic expressions:

(i) (202)² – (123)²

Solution:
Given expression is (202)² – (123)²
The above equation (202)² – (123)² is in the form of a² – b².
(202)² – (123)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 202 and b = 123
(202 + 123) (202 – 123)
(325) (79)
25675

The final answer is 25675.

(ii) (600)² – (598)²

Solution:
Given expression is (600)² – (598)²
The above equation (600)² – (598)² is in the form of a² – b².
(600)² – (598)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 600 and b = 598
(600 + 598) (600 – 598)
(1198) (2)
2396

The final answer is 2396.

(iii) (4.2)² – (2.1)²

Solution:
Given expression is (4.2)² – (2.1)²
The above equation (4.2)² – (2.1)² is in the form of a² – b².
(4.2)² – (2.1)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 4.2 and b = 2.1
(4.2 + 2.1) (4.2 – 2.1)
(6.3) (2.1)
13.23

The final answer is 13.23.

(iv) (97.8)² – (0.4)²

Solution:
Given expression is (97.8)² – (0.4)²
The above equation (97.8)² – (0.4)² is in the form of a² – b².
(97.8)² – (0.4)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 97.8 and b = 0.4
(97.8 + 0.4) (97.8 – 0.4)
(98.2) (97.4)
9564.68

The final answer is 9564.68.

(v) (8.4)² – (1.8)²

Solution:
Given expression is (8.4)² – (1.8)²
The above equation (8.4)² – (1.8)² is in the form of a² – b².
(8.4)² – (1.8)²
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 8.4 and b = 1.8
(8.4 + 1.8) (8.4 – 1.8)
(10.2) (6.6)
67.32

The final answer is 67.32.

Factoring a polynomial is the product of the two or more polynomials. Learn How to Factorize the Difference of Two Squares in this article. Break down all the huge algebraic expressions into small factors with the help of factorization. Solved Problems on Factoring the Difference of Two Squares are explained clearly along with the solutions. Visit all factorization problems and get complete knowledge of the factorization concept.

Solved Problems on How to Factorize the Difference of Two Squares

1. Factorize the following algebraic expressions

(i) m² – 121

Solution:
Given expression is m² – 121
Rewrite the above expression.
m² – (11)² 
The above equation m² – (11)² is in the form of a² – b².
m² – (11)² 
Now, apply the formula of a² – b² = (a + b) (a – b), where a = m and b = 11
(m + 11) (m – 11)

The final answer is (m + 11) (m – 11)

(ii) 49a² – 16b²

Solution:
Given expression is 49a² – 16b²
Rewrite the above expression.
(7a)² – (4b)² 
The above equation (7a)² – (4b)²  is in the form of a² – b².
(7a)² – (4b)² 
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 7a and b = 4b
(7a + 4b) (7a – 4b)

The final answer is (7a + 4b) (7a – 4b)

2. Factor the following

(i) 48m² – 243n²

Solution:
Given expression is 48m² – 243n²
Take 3 common
3{16m² – 81n²}
Rewrite the above expression.
3{(4m)² – (9n)²} 
The above equation {(4m)² – (9n)²}   is in the form of a² – b².
{(4m)² – (9n)²} 
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 4m and b = 9n
(4m + 9n) (4m – 9n)
3{(4m + 9n) (4m – 9n)}

The final answer is 3{(4m + 9n) (4m – 9n)}

(ii) 3a³ – 48a

Solution:
Given expression is 3a³ – 48a
Take 3 common
3a{a² – 16}
Rewrite the above expression.
3a{(a)² – (4)²} 
The above equation {(a)² – (4)²}    is in the form of a² – b².
{(a)² – (4)²} 
Now, apply the formula of a² – b² = (a + b) (a – b), where a = a and b = 4
(a + 4) (a – 4)
3a{(a + 4) (a – 4)}

The final answer is 3a{(a + 4) (a – 4)}

3. Factor the expressions

(i) 25(a + 3b)² – 16 (a – 3b)²

Solution:
Given expression is 25(a + 3b)² – 16 (a – 3b)²
Rewrite the above expression.
{[5(a + 3b)]² – [4 (a – 3b)]²} 
The above equation {[5(a + 3b)]² – [4 (a – 3b)]²} is in the form of a² – b².
{[5(a + 3b)]² – [4 (a – 3b)]²}
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 5(a + 3b) and b = 4 (a – 3b)
(5(a + 3b) + 4 (a – 3b)) (5(a + 3b) – [4 (a – 3b)])
(5a + 15b + 4a – 12b) (5a + 15b – 4a + 12b)
(9a + 3b) (a + 27b)
3(3a + b) (a + 27b)

The final answer is 3(3a + b) (a + 27b)

(ii) 4x² – 16/(25x²)

Solution:
Given expression is 4x² – 16/(25x²)
Rewrite the above expression.
{[2x]² – [4/5x]²}
The above equation {[2x]² – [4/5x]²} is in the form of a² – b².
{[2x]² – [4/5x]²}
Now, apply the formula of a² – b² = (a + b) (a – b), where a = 2x and b = 4/5x
(2x + 4/5x) (2x – 4/5x)

The final answer is (2x + 4/5x) (2x – 4/5x)