Big Ideas Math Algebra 1 Answers Chapter 9 Solving Quadratic Equations

If you are seeking homework help to complete the chapter 9 Solving Quadratic Equations Questions then stay connected with us. Here we have shared the best solution for your concerns ie., Big Ideas Math Algebra 1 Answers Chapter 9 Solving Quadratic Equations Pdf Exercise-wise. This guide will aid students in enhancing their problem-solving and subject knowledge skills. You can easily understand the concepts of Ch 9 Solving Quadratic Equations with the help of the BIM Algebra 1 Textbook Solution Key and perform well in various tests. Utilize this Ch 9 Algebra 1 Big Ideas Math Book Answers for exam revision guide and score high in all examinations.

Lesson-wise Chapter 9 Solving Quadratic Equations Big Ideas Math Algebra 1 Textbook Solutions

Big Ideas math book Algebra 1 ch 9 Answer key cover all required preparation materials such as Questions from Exercises 9.1 to 9.6, Chapter Tests, Practice Tests, Cumulative Assessment, Review Tests, etc. By solving all these resources of the BIM Answer Key, you can easily understand each and every concept of Algebra 1 chapter 9 Solving Quadratic Equations. Access and download the needed exercise of the Big Ideas Math Algebra 1 Answers Ch 9 Solving Quadratic Equations from the below links and ace up your preparation to become a pro at mathematics.

• Solving Quadratic Equations Maintaining Mathematical Proficiency – Page 477
• Solving Quadratic Equations Mathematical Practices – Page 478
• Lesson 9.1 Properties of Radicals – Page(480-488)
• Properties of Radicals 9.1 Exercises – Page(485-488)
• Lesson 9.2 Solving Quadratic Equations by Graphing – Page(490-496)
• Solving Quadratic Equations by Graphing 9.2 Exercises – Page(494-496)
• Lesson 9.3 Solving Quadratic Equations Using Square Roots – Page(498-502)
• Solving Quadratic Equations Using Square Roots 9.3 Exercises – Page(501-502)
• Solving Quadratic Equations Study Skills: Keeping a Positive Attitude – Page 503
• Solving Quadratic Equations 9.1 – 9.3 Quiz – Page 504
• Lesson 9.4 Solving Quadratic Equations by Completing the Square – Page(506-514)
• Solving Quadratic Equations by Completing the Square 9.4 Exercises – Page(511-514)
• Lesson 9.5 Solving Quadratic Equations Using the Quadratic Formula – Page(516-524)
• Solving Quadratic Equations Using the Quadratic Formula 9.5 Exercises – Page(521-524)
• Lesson 9.6 Solving Nonlinear Systems of Equations – Page(526-532)
• Solving Nonlinear Systems of Equations 9.6 Exercises – Page(530-532)
• Solving Quadratic Equations Performance Task: Form Matters – Page 533
• Solving Quadratic Equations Chapter Review – Page(534-536)
• Solving Quadratic Equations Chapter Test – Page 537
• Solving Quadratic Equations Cumulative Assessment – Page(538-539)

Solving Quadratic Equations Maintaining Mathematical Proficiency

Factor the trinomial.
Question 1.
x² + 10x + 25
Answer:

Question 2.
x² – 20x + 100
Answer:

Question 3.
x² + 12x + 36
Answer:

Question 4.
x² – 18x + 81
Answer:

Question 5.
x² + 16x + 64
Answer:

Question 6.
x² – 30x + 225
Answer:

Solve the system of linear equations by graphing.
Question 7.
y = -5x + 3
y = 2x – 4
Answer:

Question 8.
y = \(\frac{3}{2}\)x – 2
y = –\(\frac{1}{2}\)x + 5
Answer:

Question 9.
y = \(\frac{1}{2}\)x + 4
y = -3x – 3
Answer:

Question 10.
ABSTRACT REASONING
What value of c makes x² + bx + c a perfect square trinomial?
Answer:

Solving Quadratic Equations Mathematical Practices

Mathematically proficient students monitor their work and change course as needed.

Monitoring Progress

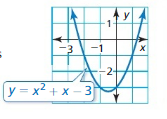
Question 1.
Use the graph in Example 1 to approximate the negative solution of the equation x² + x – 1 = 0 to the nearest thousandth.
Answer:

Question 2.
The graph of y = x² + x – 3 is shown. Approximate both solutions of the equation x² + x – 3 = 0 to the nearest thousandth.
Answer:

Lesson 9.1 Properties of Radicals

Essential Question How can you multiply and divide square roots?

EXPLORATION 1

Operations with Square Roots
Work with a partner. For each operation with square roots, compare the results obtained using the two indicated orders of operations. What can you conclude?
a. Square Roots and Addition
Is \(\sqrt{36}\) + \(\sqrt{64}\) equal to \(\sqrt{36+64}\)?
In general, is \(\sqrt{a}\) + \(\sqrt{b}\) equal to \(\sqrt{a+b}\)? Explain your reasoning.

b. Square Roots and MultiplicationIs \(\sqrt{4}\) • \(\sqrt{9}\) equal to \(\sqrt{{4} \cdot 9}\)?
In general, is \(\sqrt{a}\) • \(\sqrt{b}\) equal to \(\sqrt{{a} \cdot b}\)? Explain your reasoning.

c. Is \(\sqrt{36}\) – \(\sqrt{64}\) equal to \(\sqrt{36+64}\)?
In general, is \(\sqrt{a}\) – \(\sqrt{b}\) equal to \(\sqrt{a-b}\)? Explain your reasoning.

d. Square Roots and Division
Is \(\frac{\sqrt{100}}{\sqrt{4}}\) equal to \(\sqrt{\frac{100}{4}}\)?
In general, is \(\frac{\sqrt{a}}{\sqrt{b}}\) equal to \(\sqrt{\frac{a}{b}}\)? Explain your reasoning.

EXPLORATION 2

Writing Counter examples
Work with a partner. A counterexample is an example that proves that a general statement is not true. For each general statement in Exploration 1 that is not true, write a counterexample different from the example given.

Communicate Your Answer

Question 3.
How can you multiply and divide square roots?
Answer:

Question 4.
Give an example of multiplying square roots and an example of dividing square roots that are different from the examples in Exploration 1.
Answer:

Question 5.
Write an algebraic rule for each operation.
a. the product of square roots
b. the quotient of square roots
Answer:

Monitoring Progress

Simplify the expression.
Question 1.
\(\sqrt{24}\)
Answer:

Question 2.
–\(\sqrt{80}\)
Answer:

Question 3.
\(\sqrt{49 x^{3}}\)
Answer:

Question 4.
\(\sqrt{49 n^{5}}\)
Answer:

Simplify the expression.
Question 5.
\(\sqrt{\frac{23}{9}}\)
Answer:

Question 6.
–\(\sqrt{\frac{17}{100}}\)
Answer:

Question 7.
\(\sqrt{\frac{36}{z^{2}}}\)
Answer:

Question 8.
\(\sqrt{\frac{4 x^{2}}{64}}\)
Answer:

Question 9.
\(\sqrt[3]{54}\)
Answer:

Question 10.
\(\sqrt[3]{16 x^{4}}\)
Answer:

Question 11.
\(\sqrt[3]{\frac{a}{-27}}\)
Answer:

Question 12.
\(\sqrt[3]{\frac{25 c^{7} d^{3}}{64}}\)
Answer:

Simplify the expression.
Question 13.
\(\frac{1}{\sqrt{5}}\)
Answer:

Question 14.
\(\frac{\sqrt{10}}{\sqrt{3}}\)
Answer:

Question 15.
\(\frac{7}{\sqrt{2 x}}\)
Answer:

Question 16.
\(\sqrt{\frac{2 y^{2}}{3}}\)
Answer:

Question 17.
\(\frac{5}{\sqrt[3]{32}}\)
Answer:

Question 18.
\(\frac{8}{1+\sqrt{3}}\)
Answer:

Question 19.
\(\frac{\sqrt{13}}{\sqrt{5}-2}\)
Answer:

Question 20.
\(\frac{12}{\sqrt{2}+\sqrt{7}}\)
Answer:

Question 21.
WHAT IF?
In Example 6, how far can you see when your eye level is 35 feet above the water?
Answer:

Question 22.
The dimensions of a dance floor form a golden rectangle. The shorter side of the dance floor is 50 feet. What is the length of the longer side of the dance floor?
Answer:

Simplify the expression.
Question 23.
3\(\sqrt{2}\) – \(\sqrt{6}\) + 10\(\sqrt{2}\)
Answer:

Question 24.
4\(\sqrt{7}\) – 6\(\sqrt{63}\)
Answer:

Question 25.
4\(\sqrt [3]{ 5x }\) – 11\(\sqrt [3]{ 5x }\)
Answer:

Question 26.
\(\sqrt{3}\)(8\(\sqrt{2}\) + 7\(\sqrt{32}\))
Answer:

Question 27.
(2\(\sqrt{5}\) – 4)²
Answer:

Question 28.
\(\sqrt [3]{ -4 }\)(\(\sqrt [3]{ 2 }\) – \(\sqrt [3]{ 16 }\))
Answer:

Properties of Radicals 9.1 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
The process of eliminating a radical from the denominator of a radical expression is called _______________.
Answer:

Question 2.
VOCABULARY
What is the conjugate of the binomial \(\sqrt{x}\) + 4?
Answer:

Question 3.
WRITING
Are the expressions \(\frac{1}{3} \sqrt{2 x}\) and \(\sqrt{\frac{2 x}{9}}\) equivalent? Explain your reasoning.
Answer:

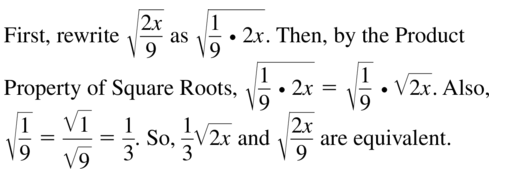
Question 4.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 5–12, determine whether the expression is in simplest form. If the expression is not in simplest form, explain why.
Question 5.
\(\sqrt{19}\)
Answer:

Question 6.
\(\sqrt{\frac{1}{7}}\)
Answer:

Question 7.
\(\sqrt{48}\)
Answer:

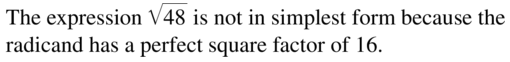
Question 8.
\(\sqrt{34}\)
Answer:

Question 9.
\(\frac{5}{\sqrt{2}}\)
Answer:

Question 10.
\(\frac{3 \sqrt{10}}{4}\)
Answer:

Question 11.
\(\frac{1}{2+\sqrt[3]{2}}\)
Answer:

Question 12.
\(6-\sqrt[3]{54}\)
Answer:

In Exercises 13–20, simplify the expression.
Question 13.
\(\sqrt{20}\)
Answer:

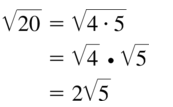
Question 14.
\(\sqrt{32}\)
Answer:

Question 15.
\(\sqrt{128}\)
Answer:

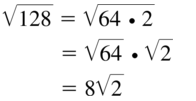
Question 16.
–\(\sqrt{72}\)
Answer:

Question 17.
\(\sqrt{125b}\)
Answer:

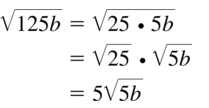
Question 18.
\(\sqrt{4 x^{2}}\)
Answer:

Question 19.
\(-\sqrt{81 m^{3}}\)
Answer:

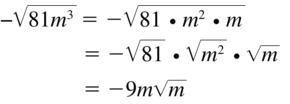
Question 20.
\(\sqrt{48 n^{5}}\)
Answer:

In Exercises 21–28, simplify the expression.
Question 21.
\(\sqrt{\frac{4}{49}}\)
Answer:

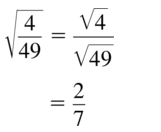
Question 22.
\(-\sqrt{\frac{7}{81}}\)
Answer:

Question 23.
\(-\sqrt{\frac{23}{64}}\)
Answer:

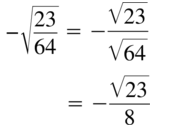
Question 24.
\(\sqrt{\frac{65}{121}}\)
Answer:

Question 25.
\(\sqrt{\frac{a^{3}}{49}}\)
Answer:

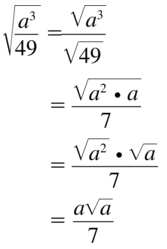
Question 26.
\(\sqrt{\frac{144}{k^{2}}}\)
Answer:

Question 27.
\(\sqrt{\frac{100}{4x^{2}}}\)
Answer:

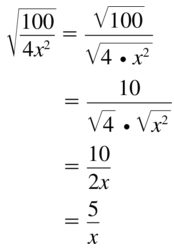
Question 28.
\(\sqrt{\frac{25 v^{2}}{36}}\)
Answer:

In Exercises 29–36, simplify the expression.
Question 29.
\(\sqrt [3]{ 16 }\)
Answer:

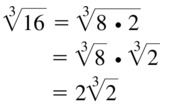
Question 30.
\(\sqrt [3]{ -108 }\)
Answer:

Question 31.
\(\sqrt[3]{-64 x^{5}}\)
Answer:

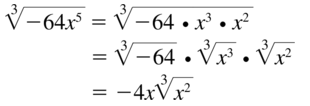
Question 32.
–\(\sqrt[3]{343 n^{2}}\)
Answer:

Question 33.
\(\sqrt[3]{\frac{6 c}{-125}}\)
Answer:

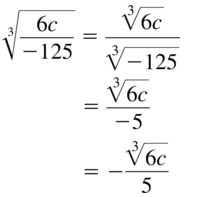
Question 34.
\(\sqrt[3]{\frac{8 h^{4}}{27}}\)
Answer:

Question 35.
\(-\sqrt[3]{\frac{81 y^{2}}{1000 x^{3}}}\)
Answer:

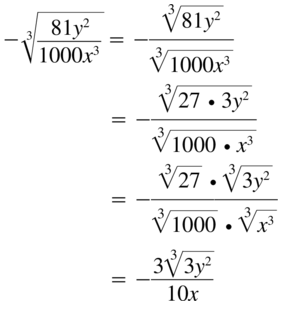
Question 36.
\(\sqrt[3]{\frac{21}{-64 a^{3} b^{6}}}\)
Answer:

ERROR ANALYSIS In Exercises 37 and 38, describe and correct the error in simplifying the expression.
Question 37.

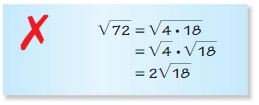
Answer:

Question 38.

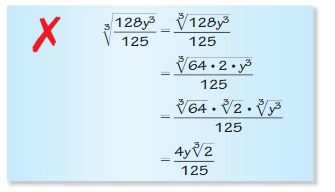
Answer:

In Exercises 39–44, write a factor that you can use to rationalize the denominator of the expression.
Question 39.
\(\frac{4}{\sqrt{6}}\)
Answer:

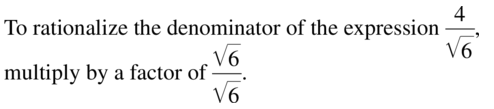
Question 40.
\(\frac{1}{\sqrt{13 z}}\)
Answer:

Question 41.
\(\frac{2}{\sqrt[3]{x^{2}}}\)
Answer:

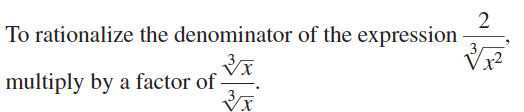
Question 42.
\(\frac{3 m}{\sqrt[3]{4}}\)
Answer:

Question 43.
\(\frac{\sqrt{2}}{\sqrt{5}-8}\)
Answer:

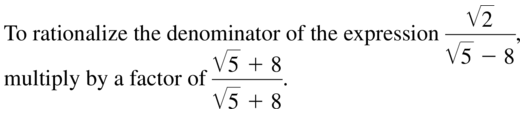
Question 44.
\(\frac{5}{\sqrt{3}+\sqrt{7}}\)
Answer:

In Exercises 45–54, simplify the expression.
Question 45.
\(\frac{2}{\sqrt{2}}\)
Answer:

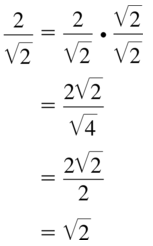
Question 46.
\(\frac{4}{\sqrt{3}}\)
Answer:

Question 47.
\(\frac{\sqrt{5}}{\sqrt{48}}\)
Answer:

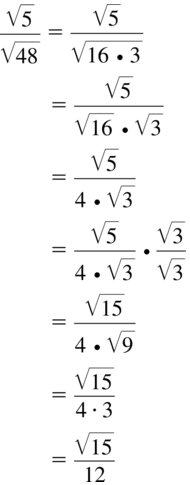
Question 48.
\(\sqrt{\frac{4}{52}}\)
Answer:

Question 49.
\(\frac{3}{\sqrt{a}}\)
Answer:

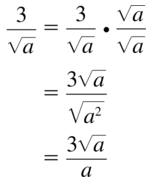
Question 50.
\(\frac{1}{\sqrt{2 x}}\)
Answer:

Question 51.
\(\sqrt{\frac{3 d^{2}}{5}}\)
Answer:

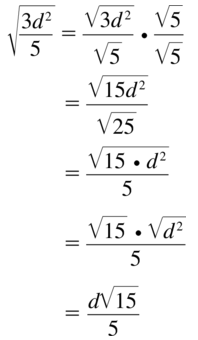
Question 52.
\(\frac{\sqrt{8}}{\sqrt{3 n^{3}}}\)
Answer:

Question 53.
\(\frac{4}{\sqrt[3]{25}}\)
Answer:

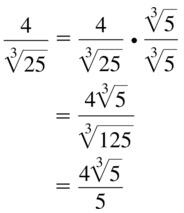
Question 54.
\(\sqrt[3]{\frac{1}{108 y^{2}}}\)
Answer:

In Exercises 55–60, simplify the expression.
Question 55.
\(\frac{1}{\sqrt{7}+1}\)
Answer:

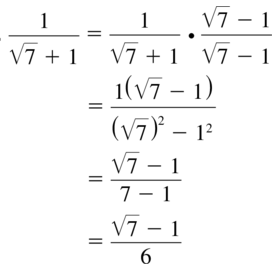
Question 56.
\(\frac{2}{5-\sqrt{3}}\)
Answer:

Question 57.
\(\frac{\sqrt{10}}{7-\sqrt{2}}\)
Answer:

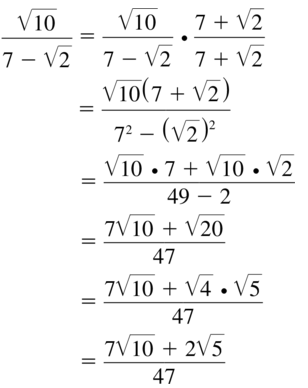
Question 58.
\(\frac{\sqrt{5}}{6+\sqrt{5}}\)
Answer:

Question 59.
\(\frac{3}{\sqrt{5}-\sqrt{2}}\)
Answer:

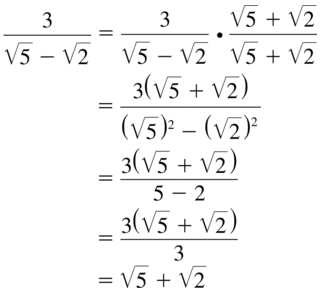
Question 60.
\(\frac{\sqrt{3}}{\sqrt{7}+\sqrt{3}}\)
Answer:

Question 61.
MODELING WITH MATHEMATICS
The time t (in seconds) it takes an object to hit the ground is given by t = \(\sqrt{\frac{h}{16}}\), where his the height (in feet) from which the object was dropped.

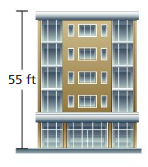
a. How long does it take an earring to hit the ground when it falls from the roof of the building?
b. How much sooner does the earring hit the ground when it is dropped from two stories (22 feet) below the roof?
Answer:

Question 62.
MODELING WITH MATHEMATICS
The orbital period of a planet is the time it takes the planet to travel around the Sun. You can find the orbital period P (in Earth years) using the formula P = \(\sqrt{d^{3}}\), where d is the average distance (in astronomical units, abbreviated AU) of the planet from the Sun.

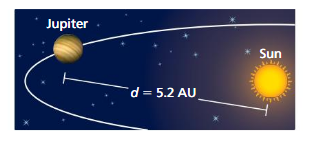
a. Simplify the formula.
b. What is Jupiter’s orbital period?
Answer:

Question 63.
MODELING WITH MATHEMATICS
The electric current I (in amperes) an appliance uses is given by the formula I = \(\sqrt{\frac{P}{R}}\), where P is the power (in watts) and R is the resistance (in ohms). Find the current an appliance uses when the power is 147 watts and the resistance is 5 ohms.

Answer:

Question 64.
MODELING WITH MATHEMATICS
You can find the average annual interest rate r (in decimal form) of a savings account using the formula r = \(\sqrt{\frac{V_{2}}{V_{0}}}\) – 1, where V₀ is the initial investment and V₂ is the balance of the account after 2 years. Use the formula to compare the savings accounts. In which account would you invest money? Explain.

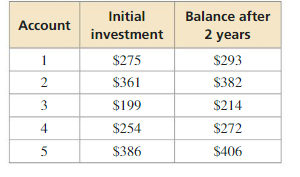
Answer:

In Exercises 65–68, evaluate the function for the given value of x. Write your answer in simplest form and in decimal form rounded to the nearest hundredth.
Question 65.
h(x) = \(\sqrt{5x}\); x = 10
Answer:

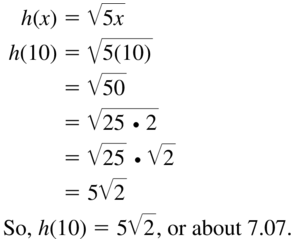
Question 66.
g(x) = \(\sqrt{3x}\); x = 60
Answer:

Question 67.
r(x) = \(\sqrt{\frac{3 x}{3 x^{2}+6}}\); x = 4
Answer:

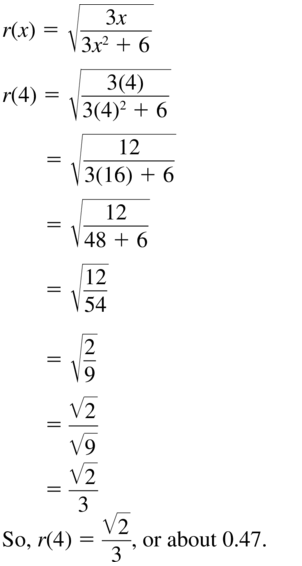
Question 68.
p(x) = \(\sqrt{\frac{x-1}{5 x}}\); x = 8
Answer:

In Exercises 69–72, evaluate the expression when a = −2, b = 8, and c = \(\frac{1}{2}\). Write your answer in simplest form and in decimal form rounded to the nearest hundredth.
Question 69.
\(\sqrt{a^{2}+b c}\)
Answer:

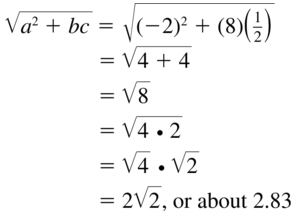
Question 70.
\(-\sqrt{4 c-6 a b}\)
Answer:

Question 71.
\(-\sqrt{2 a^{2}+b^{2}}\)
Answer:

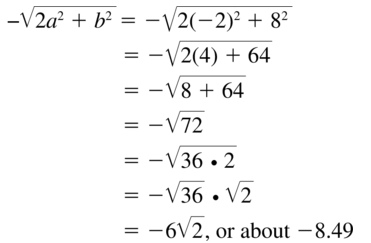
Question 72.
\(\sqrt{b^{2}-4 a c}\)
Answer:

Question 73.
MODELING WITH MATHEMATICS
The text in the book shown forms a golden rectangle. What is the width w of the text?

Answer:

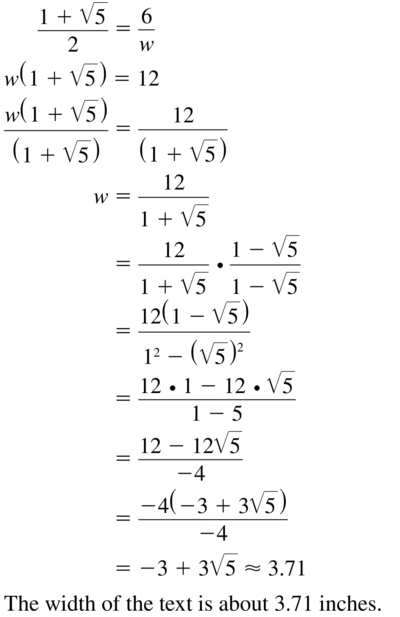
Question 74.
MODELING WITH MATHEMATICS
The flag of Togo is approximately the shape of a golden rectangle. What is the width w of the flag?

Answer:

In Exercises 75–82, simplify the expression.
Question 75.
\(\sqrt{2}\) – 2\(\sqrt{2}\) + 6\(\sqrt{2}\)
Answer:

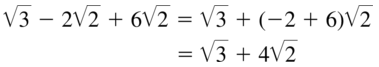
Question 76.
\(\sqrt{5}\) – 5\(\sqrt{13}\) – 8\(\sqrt{5}\)
Answer:

Question 77.
2\(\sqrt{6}\) – 5\(\sqrt{54}\)
Answer:

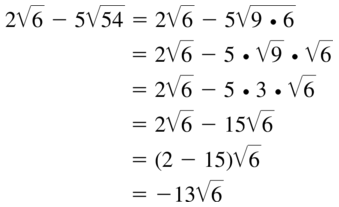
Question 78.
9\(\sqrt{32}\) + \(\sqrt{2}\)
Answer:

Question 79.
\(\sqrt{12}\) + 6\(\sqrt{3}\) + 2\(\sqrt{6}\)
Answer:

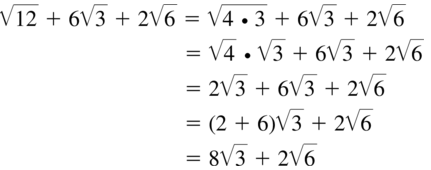
Question 80.
3\(\sqrt{7}\) – 5\(\sqrt{14}\) + 2\(\sqrt{28}\)
Answer:

Question 81.
\(\sqrt[3]{-81}\) + 4\(\sqrt[3]{3}\)
Answer:

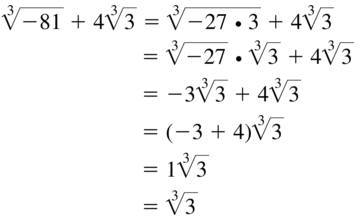
Question 82.
6\(\sqrt[3]{128 t}\) – 2\(\sqrt[3]{2 t}\)
Answer:

In Exercises 83–90, simplify the expression.
Question 83.
\(\sqrt{2}\)(\(\sqrt{45}\) + \(\sqrt{5}\))
Answer:

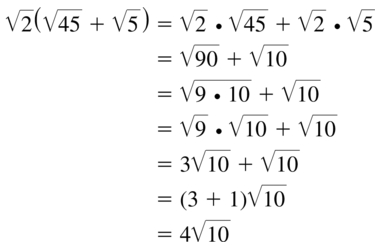
Question 84.
\(\sqrt{3}\)(\(\sqrt{72}\) – 3\(\sqrt{2}\))
Answer:

Question 85.
\(\sqrt{5}\)(2\(\sqrt{6x}\) – \(\sqrt{96x}\))
Answer:

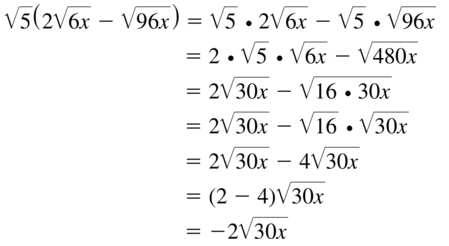
Question 86.
\(\sqrt{7y}\)(\(\sqrt{27y}\) + 5\(\sqrt{12y}\))
Answer:

Question 87.
(4\(\sqrt{2}\) – \(\sqrt{98}\))²
Answer:

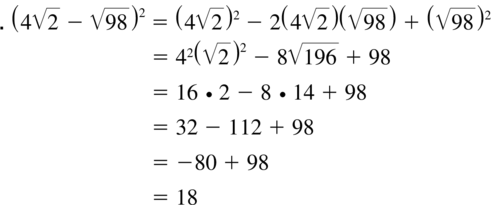
Question 88.
(\(\sqrt{3}\) + \(\sqrt{48}\)) (\(\sqrt{20}\) – \(\sqrt{5}\))
Answer:

Question 89.
\(\sqrt[3]{3}(\sqrt[3]{4}+\sqrt[3]{32})\)
Answer:

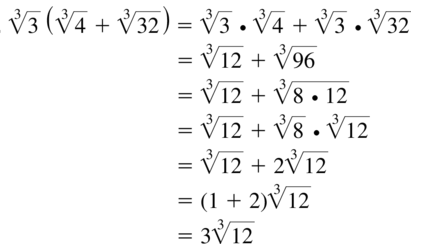
Question 90.
\(\sqrt[3]{2}(\sqrt[3]{135}-4 \sqrt[3]{5})\)
Answer:

Question 91.
MODELING WITH MATHEMATICS
The circumference C of the art room in a mansion is approximated by the formula C ≈ \(\sqrt\frac{a^{2}+b^{2}}{2}\). Approximate the circumference of the room.

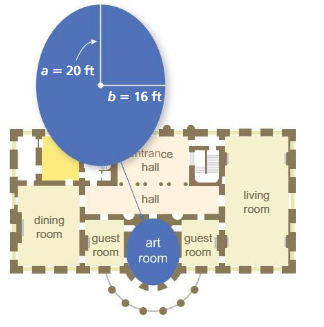
Answer:

Question 92.
CRITICAL THINKING
Determine whether each expression represents a rational or an irrational number. Justify your answer.

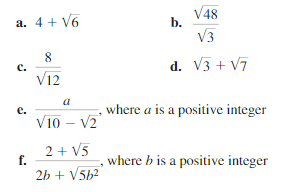
Answer:

In Exercises 93–98, simplify the expression.
Question 93.
\(\sqrt[5]{\frac{13}{5 x^{5}}}\)
Answer:

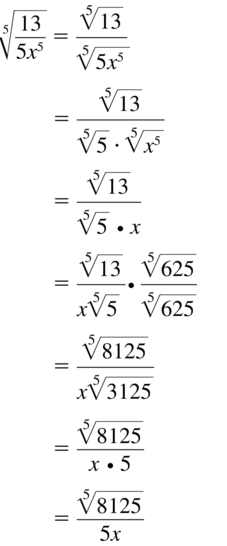
Question 94.
\(\sqrt[4]{\frac{10}{81}}\)
Answer:

Question 95.
\(\sqrt[4]{256 y}\)
Answer:

Question 96.
\(\sqrt[5]{160 x^{6}}\)
Answer:

Question 97.
\(6 \sqrt[4]{9}-\sqrt[5]{9}+3 \sqrt[4]{9}\)
Answer:

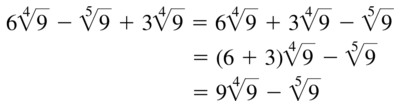
Question 98.
\(\sqrt[5]{2}(\sqrt[4]{7}+\sqrt[5]{16})\)
Answer:

REASONING In Exercises 99 and 100, use the table shown.

Question 99.
Copy and complete the table by (a) finding each sum ( 2 + 2, 2 + \(\frac{1}{4}\), etc. ) and (b) finding each product ( 2 • 2, 2 • \(\frac{1}{4}\), etc. )
Answer:

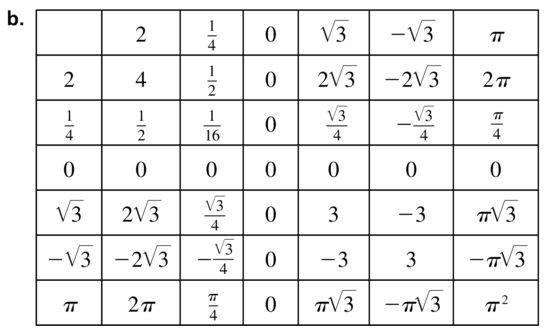
Question 100.
Use your answers in Exercise 99 to determine whether each statement is always, sometimes, or never true. Justify your answer.
a. The sum of a rational number and a rational number is rational.
b. The sum of a rational number and an irrational number is irrational.
c. The sum of an irrational number and an irrational number is irrational.
d. The product of a rational number and a rational number is rational.
e. The product of a nonzero rational number and an irrational number is irrational.
f. The product of an irrational number and an irrational number is irrational.
Answer:

Question 101.
REASONING
Let m be a positive integer. For what values of m will the simplified form of the expression \(\sqrt{2^{m}}\) contain a radical? For what values will it not contain a radical? Explain.
Answer:

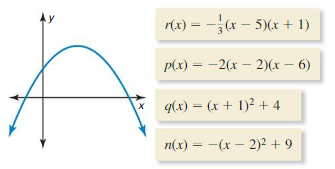
Question 102.
HOW DO YOU SEE IT?
The edge length s of a cube is an irrational number, the surface area is an irrational number, and the volume is a rational number. Give a possible value of s.

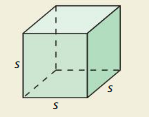
Answer:

Question 103.
REASONING
Let a and b be positive numbers. Explain why \(\sqrt{ab}\) lies between a and b on a number line. (Hint: Let a< b and multiply each side of a < b by a. Then let a < b and multiply each side by b.)
Answer:

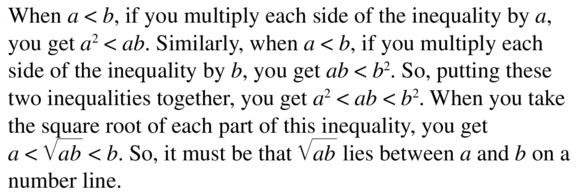
Question 104.
MAKING AN ARGUMENT
Your friend says that you can rationalize the denominator of the expression \(\frac{2}{4+\sqrt[3]{5}}\) by multiplying the numerator and denominator by 4 – \(\sqrt[3]{5}\). Is your friend correct? Explain.
Answer:

Question 105.
PROBLEM SOLVING
The ratio of consecutive terms \(\frac{a_{n}}{a_{n}-1}\) in the Fibonacci sequence gets closer and closer to the golden ratio \(\frac{1+\sqrt{5}}{2}\) as n increases. Find the term that precedes 610 in the sequence.
Answer:

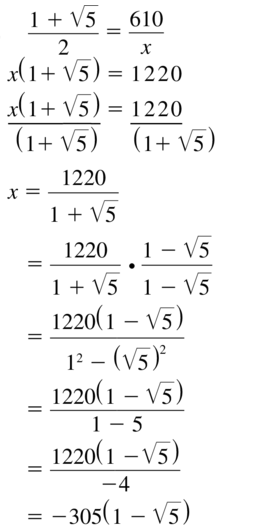
Question 106.
THOUGHT PROVOKING
Use the golden ratio \(\frac{1+\sqrt{5}}{2}\) and the golden ratio conjugate \(\frac{1-\sqrt{5}}{2}\) for each of the following.
a. Show that the golden ratio and golden ratio conjugate are both solutions of x² – x – 1 = 0.
b. Construct a geometric diagram that has the golden ratio as the length of a part of the diagram.
Answer:

Question 107.
CRITICAL THINKING
Use the special product pattern (a + b)(a² – ab + b²) = a³ + b³ to simplify the expression \(\frac{2}{\sqrt[3]{x}+1}\). Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency

Graph the linear equation. Identify the x-intercept.
Question 108.
y = x – 4
Answer:

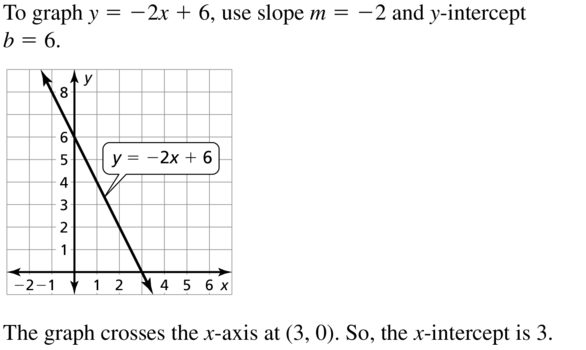
Question 109.
y = -2x + 6
Answer:

Question 110.
y = –\(\frac{1}{3}\)x – 1
Answer:

Question 111.
y = \(\frac{3}{2}\)x + 6
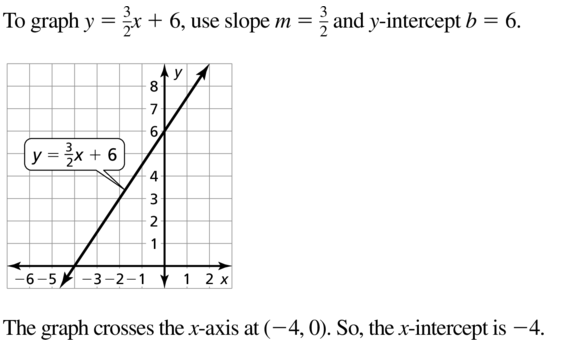
Answer:

Solve the equation. Check your solution.
Question 112.
32 = 2^x
Answer:

Question 113.
27^x = 3^{x – 6}
Answer:

Question 114.
(\(\frac{1}{6}\))^2x = 216^{1 – x}
Answer:

Question 115.
625^x = (\(\frac{1}{25}\))^{x + 2}
Answer:

Lesson 9.2 Solving Quadratic Equations by Graphing

Essential Question How can you use a graph to solve a quadratic equation in one variable?

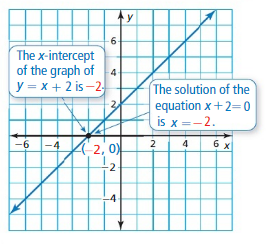
Based on what you learned about the x-intercepts of a graph in Section 3.4, it follows that the x-intercept of the graph of the linear equation
y = ax + b 2 variables
is the same value as the solution of
ax + b = 0. 1 variable
You can use similar reasoning to solve quadratic equations.

EXPLORATION 1

Solving a Quadratic Equation by Graphing
Work with a partner.
a. Sketch the graph of y = x² – 2x.

b. What is the definition of an x-intercept of a graph? How many x-intercepts does this graph have? What are they?
c. What is the definition of a solution of an equation in x? How many solutions does the equation x² – 2x = 0 have? What are they?
d. Explain how you can verify the solutions you found in part (c).

EXPLORATION 2

Solving Quadratic Equations by Graphing
Work with a partner. Solve each equation by graphing.
a. x² – 4 = 0
b. x² + 3x = 0
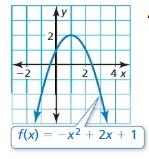
c. -x² + 2x + 1 = 0
d. x² – 2x + 1
e. x² – 3x + 5 = 0
f. -x² + 3x – 6 = 0

Communicate Your Answer

Question 3.
How can you use a graph to solve a quadratic equation in one variable?

Answer:

Question 4.
After you find a solution graphically, how can you check your result algebraically? Check your solutions for parts (a)-(d) in Exploration 2 algebraically.
Answer:

Question 5.
How can you determine graphically that a quadratic equation has no solution?
Answer:

Monitoring Progress

Solve the equation by graphing. Check your solutions.
Question 1.
x² – x – 2 = 0
Answer:

Question 2.
x² + 7x = -10
Answer:

Question 3.
x² + x = 12
Answer:

Solve the equation by graphing.
Question 4.
x² + 36 = 12x
Answer:

Question 5.
x² + 4x = 0
Answer:

Question 6.
x² + 10x = -25
Answer:

Question 7.
x² = 3x – 3
Answer:

Question 8.
x² + 7x = -6
Answer:

Question 9.
2x + 5 = -x²
Answer:

Question 10.
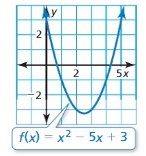
Graph f(x) = x² + x – 6. Find the zeros of f.
Answer:

Question 11.
Graph f(x) = -x² + 2x + 2. Approximate the zeros of f to the nearest tenth.
Answer:

Question 12.
WHAT IF?
After how many seconds is the football 65 feet above the ground?
Answer:

Solving Quadratic Equations by Graphing 9.2 Exercises

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
What is a quadratic equation?
Answer:

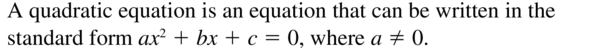
Question 2.
WHICH ONE DOESN’T BELONG?
Which equation does not belong with the other three? Explain your reasoning.

Answer:

Question 3.
WRITING
How can you use a graph to find the number of solutions of a quadratic equation?
Answer:

Question 4.
WRITING
How are solutions, roots, x-intercepts, and zeros related?
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 5–8, use the graph to solve the equation.
Question 5.
-x² + 2x + 3 = 0

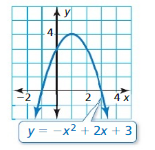
Answer:

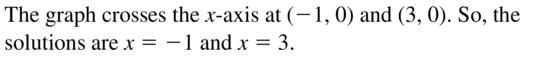
Question 6.
x² – 6x + 8 = 0

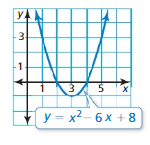
Answer:

Question 7.
x² + 8x + 16 = 0

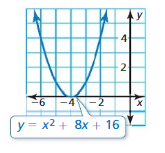
Answer:

Question 8.
-x² – 4x – 6 = 0

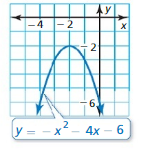
Answer:

In Exercises 9–12, write the equation in standard form.
Question 9.
4x² = 12
Answer:

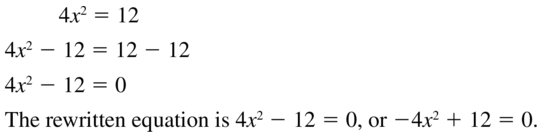
Question 10.
-x² = 15
Answer:

Question 11.
2x – x² = 1
Answer:

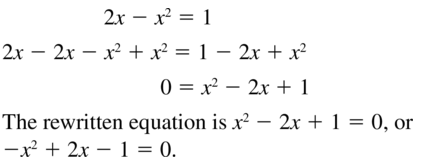
Question 12.
5 + x = 3x²
Answer:

In Exercises 13–24, solve the equation by graphing.
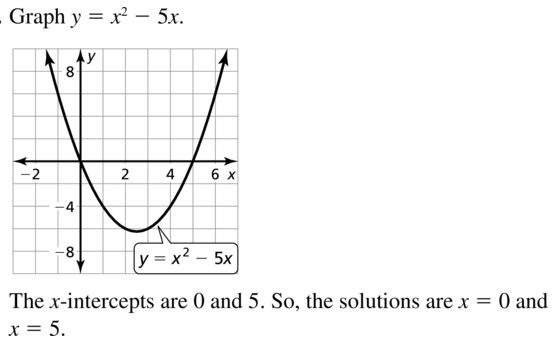
Question 13.
x² – 5x = 0
Answer:

Question 14.
x² – 4x + 4 = 0
Answer:

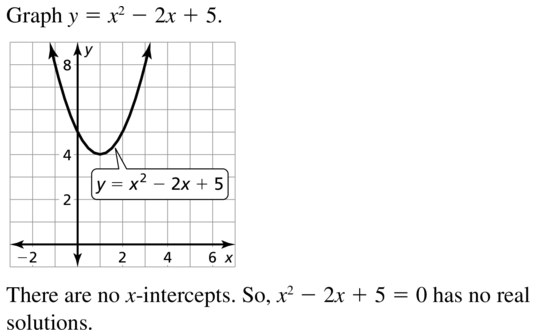
Question 15.
x² – 2x + 5 = 0
Answer:

Question 16.
x² – 6x – 7 = 0
Answer:

Question 17.
x² – 6x = 9
Answer:

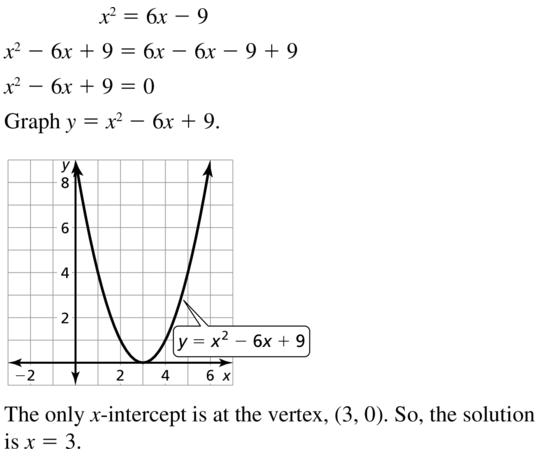
Question 18.
-x² = 8x + 20
Answer:

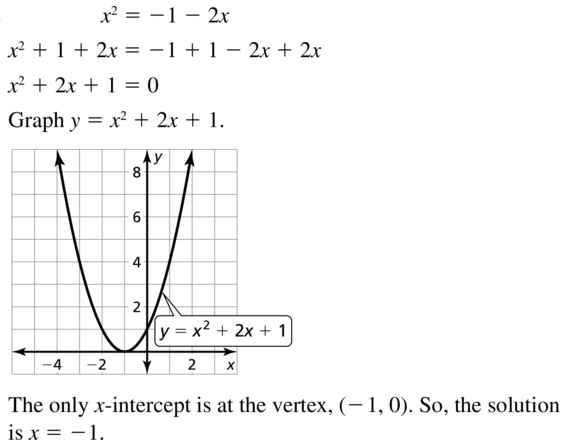
Question 19.
x² = -1 – 2x
Answer:

Question 20.
x² = -x – 3
Answer:

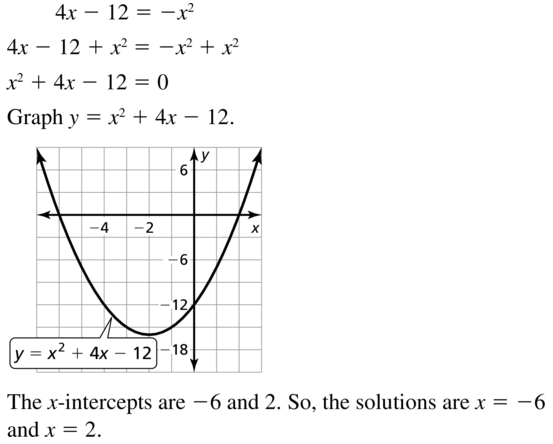
Question 21.
4x – 12 = -x²
Answer:

Question 22.
5x – 6 = x²
Answer:

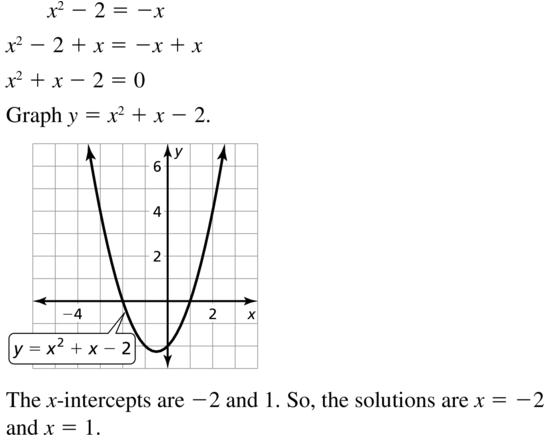
Question 23.
x² – 2 = -x
Answer:

Question 24.
16 + x² = -8x
Answer:

Question 25.
ERROR ANALYSIS
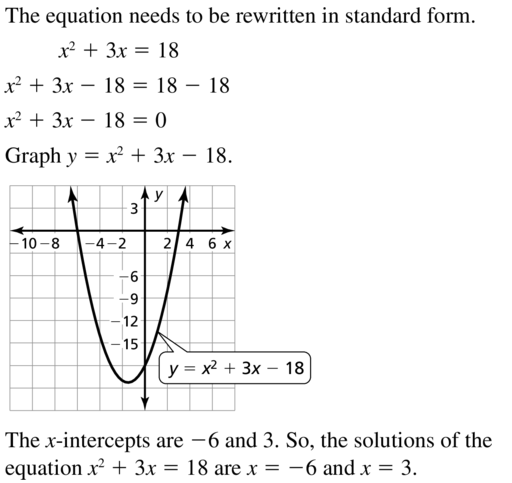
Describe and correct the error in solving x² + 3x = 18 by graphing.

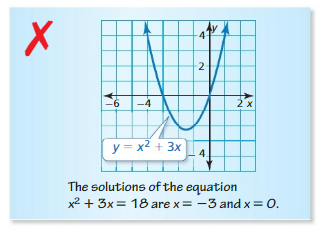
Answer:

Question 26.
ERROR ANALYSIS
Describe and correct the error in solving x² + 6x + 9 = 0 by graphing.

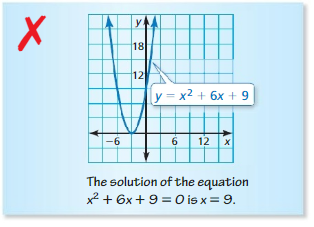
Answer:

Question 27.
MODELING WITH MATHEMATICS
The height y (in yards) of a flop shot in golf can be modeled by y = -x² + 5x, where x is the horizontal distance (in yards).

a. Interpret the x-intercepts of the graph of the equation.
b. How far away does the golf ball land?
Answer:

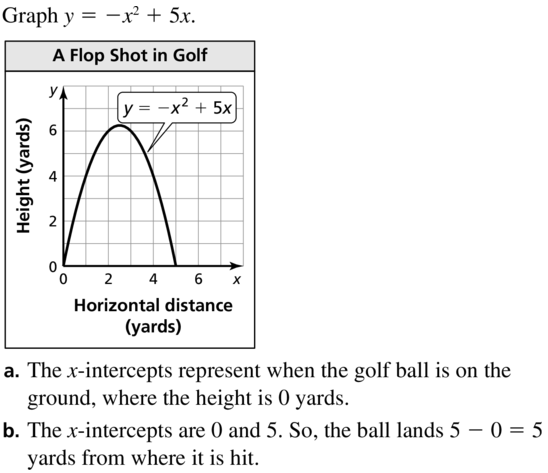
Question 28.
MODELING WITH MATHEMATICS
The height h (in feet) of an underhand volleyball serve can be modeled by h = -16t² + 30t + 4, where t is the time (in seconds).
a. Do both t-intercepts of the graph of the function have meaning in this situation? Explain.
b. No one receives the serve. After how many seconds does the volleyball hit the ground?
Answer:

In Exercises 29–36, solve the equation by using Method 2 from Example 3.
Question 29.
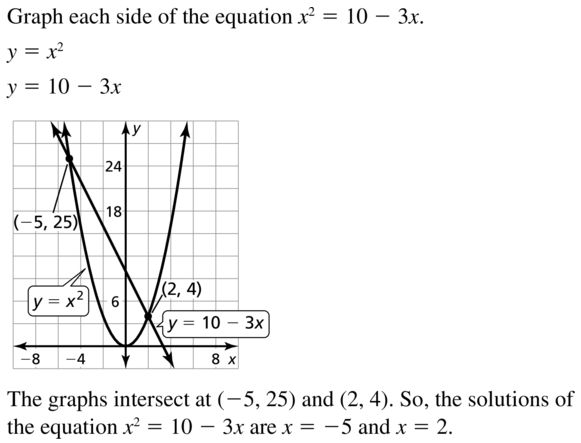
x² = 10 – 3x
Answer:

Question 30.
2x – 3 = x²
Answer:

Question 31.
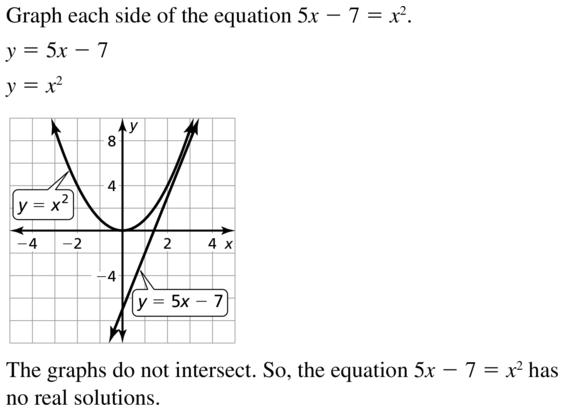
5x – 7 = x²
Answer:

Question 32.
x² = 6x – 5
Answer:

Question 33.
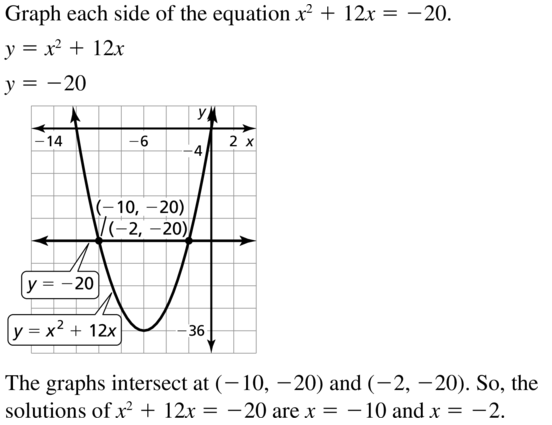
x² + 12x = -20
Answer:

Question 34.
x² + 8x = 9
Answer:

Question 35.
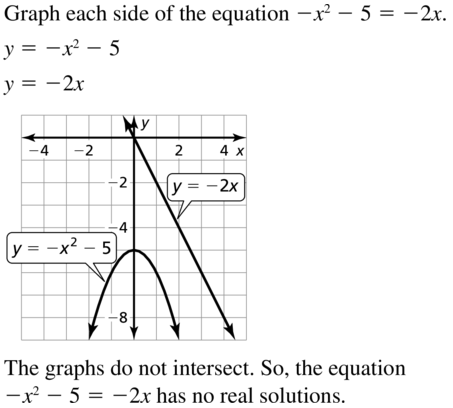
-x² – 5 = -2x
Answer:

Question 36.
-x² – 4 = -4x
Answer:

In Exercises 37–42, find the zero(s) of f.
Question 37.

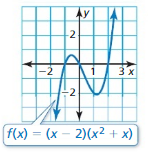
Answer:

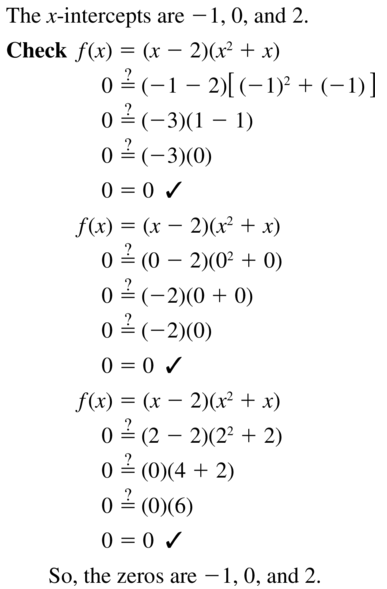
Question 38.

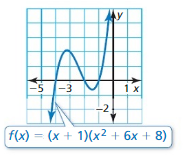
Answer:

Question 39.

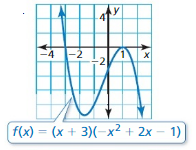
Answer:

Question 40.

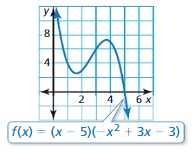
Answer:

Question 41.

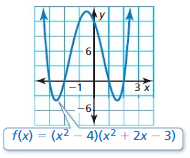
Answer:

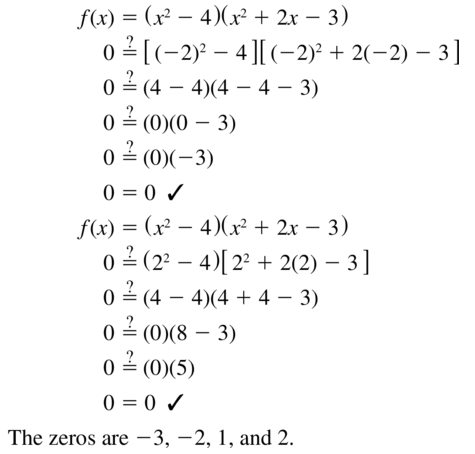
Question 42

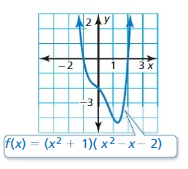
Answer:

In Exercises 43–46, approximate the zeros of f to the nearest tenth.
Question 43.

Answer:

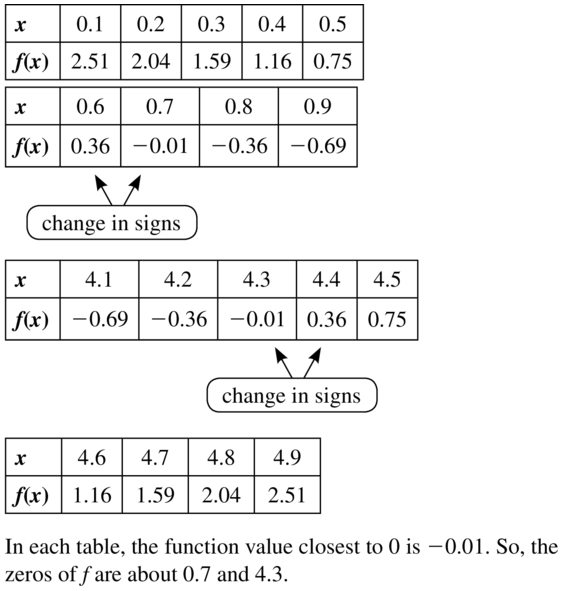
Question 44.

Answer:

Question 45.

Answer:

Question 46.

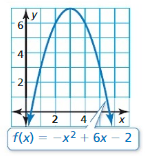
Answer:

In Exercises 47–52, graph the function. Approximate the zeros of the function to the nearest tenth, if necessary.
Question 47.
f(x) = x² + 6x + 1
Answer:

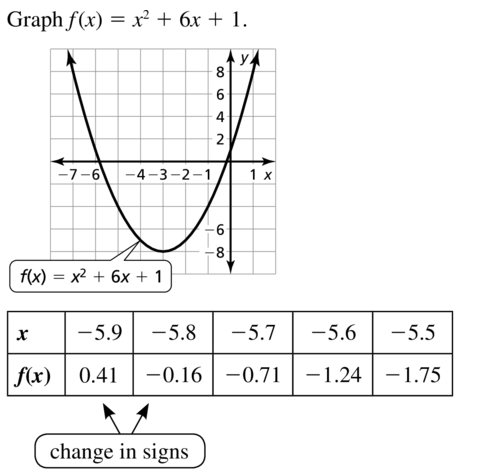
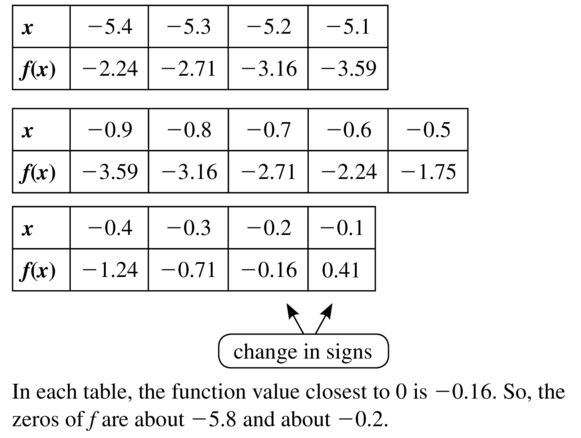
Question 48.
f(x) = x² – 3x + 2
Answer:

Question 49.
y = -x² + 4x – 2
Answer:

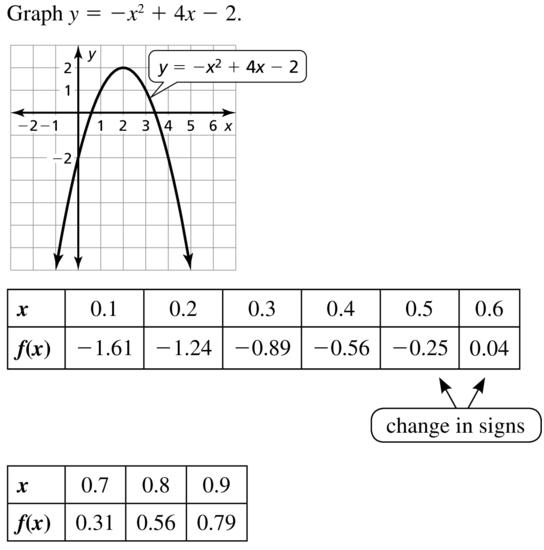
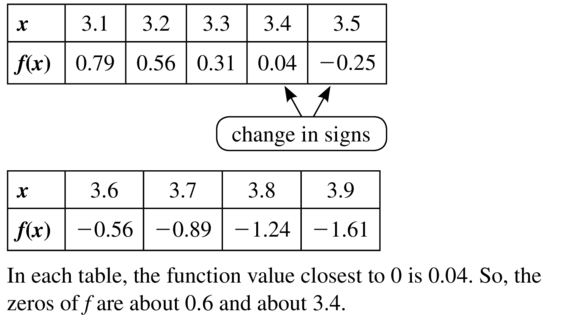
Question 50.
y = -x² + 9x – 6
Answer:

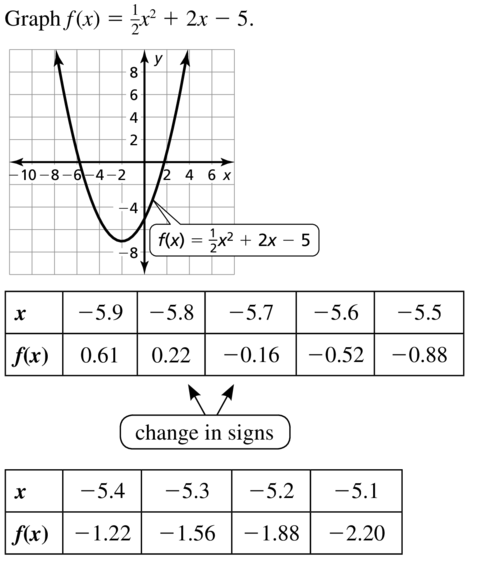
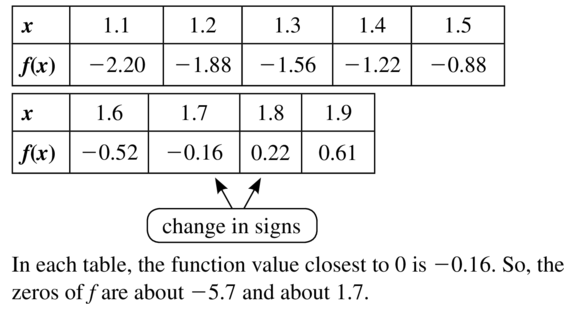
Question 51.
f(x) = \(\frac{1}{2}\)x² + 2x – 5
Answer:

Question 52.
f(x) = -3x² + 4x + 3
Answer:

Question 53.
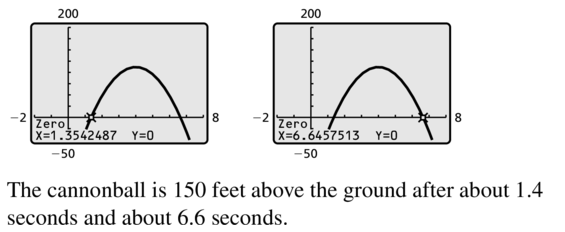
MODELING WITH MATHEMATICS
At a Civil War reenactment, a cannonball is fired into the air with an initial vertical velocity of 128 feet per second. The release point is 6 feet above the ground. The function h = -16t² + 128t + 6 represents the height h (in feet) of the cannonball after t seconds.
a. Find the height of the cannonball each second after it is fired.
b. Use the results of part (a) to estimate when the height of the cannonball is 150 feet.
c. Using a graph, after how many seconds is the cannonball 150 feet above the ground?

Answer:

Question 54.
MODELING WITH MATHEMATICS
You throw a softball straight up into the air with an initial vertical velocity of 40 feet per second. The release point is 5 feet above the ground. The function h = -16t² + 40t + 5 represents the height h (in feet) of the softball after t seconds.

a. Find the height of the softball each second after it is released.
b. Use the results of part (a) to estimate when the height of the softball is 15 feet.
c. Using a graph, after how many seconds is the softball 15 feet above the ground?
Answer:

MATHEMATICAL CONNECTIONS In Exercises 55 and 56, use the given surface area S of the cylinder to find the radius r to the nearest tenth.
Question 55.
S = 225 ft²

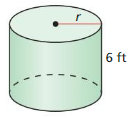
Answer:

Question 56.
S = 750 m²

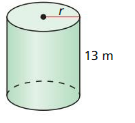
Answer:

Question 57.
WRITING
Explain how to approximate zeros of a function when the zeros are not integers.
Answer:

Question 58.
HOW DO YOU SEE IT?
Consider the graph shown.

a. How many solutions does the quadratic equation x² = -3x + 4 have? Explain.
b. Without graphing, describe what you know about the graph of y = x² + 3x – 4.
Answer:

Question 59.
COMPARING METHODS
Example 3 shows two methods for solving a quadratic equation. Which method do you prefer? Explain your reasoning.
Answer:

Question 60.
THOUGHT PROVOKING
How many different parabolas have -2 and 2 as x-intercepts? Sketch examples of parabolas that have these two x-intercepts.
Answer:

Question 61.
MODELING WITH MATHEMATICS
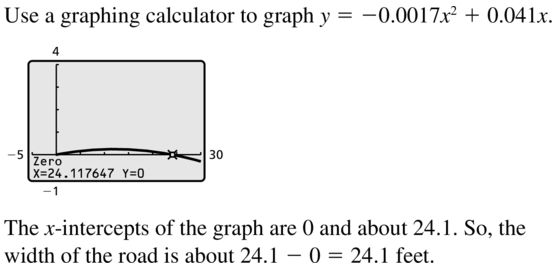
To keep water off a road, the surface of the road is shaped like a parabola. A cross section of the road is shown in the diagram. The surface of the road can be modeled by y = -0.0017x² + 0.041x, where x and y are measured in feet. Find the width of the road to the nearest tenth of a foot.

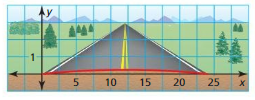
Answer:

Question 62.
MAKING AN ARGUMENT
A stream of water from a fire hose can be modeled by y = -0.003x² + 0.58x + 3,where x and y are measured in feet. A firefighter is standing 57 feet from a building and is holding the hose 3 feet above the ground. The bottom of a window of the building is 26 feet above the ground. Your friend claims the stream of water will pass through the window. Is your friend correct? Explain.
Answer:

REASONING In Exercises 63–65, determine whether the statement is always, sometimes, or never true. Justify your answer.
Question 63.
The graph of y = ax² + c has two x-intercepts when a is negative.
Answer:

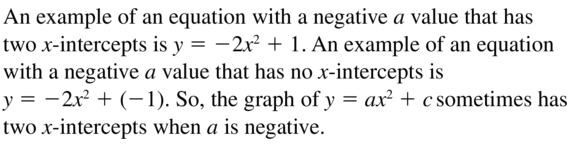
Question 64.
The graph of y = ax² + c has no x-intercepts when a and c have the same sign.
Answer:

Question 65.
The graph of y = ax² + bx + c has more than two x-intercepts when a ≠ 0.
Answer:

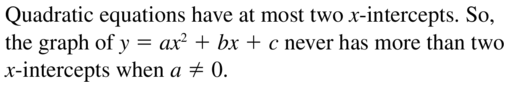
Maintaining Mathematical Proficiency

Determine whether the table represents an exponential growth function, an exponential decay function, or neither. Explain.
Question 66.

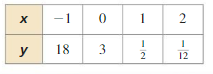
Answer:

Question 67.

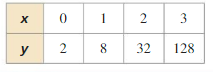
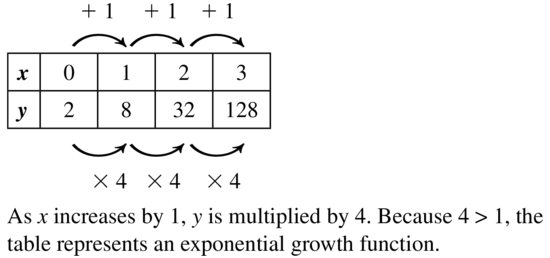
Answer:

Lesson 9.3 Solving Quadratic Equations Using Square Roots

Essential Question How can you determine the number of solutions of a quadratic equation of the form ax² + c = 0?

EXPLORATION 1

The Number of Solutions of ax² + c = 0
Work with a partner. Solve each equation by graphing. Explain how the number of solutions of ax² + c = 0 relates to the graph of y = ax² + c.
a. x² – 4 = 0
b. 2x² + 5 = 0
c. x² = 0
d. x² – 5 = 0

EXPLORATION 2

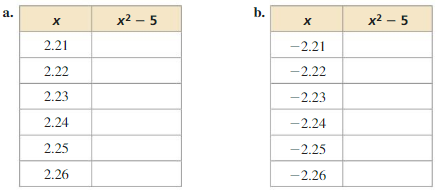
Estimating Solutions
Work with a partner. Complete each table. Use the completed tables to estimate the solutions of x² – 5 = 0. Explain your reasoning.

EXPLORATION 3

Using Technology to Estimate Solutions
Work with a partner. Two equations are equivalent when they have the same solutions.

a. Are the equations x² – 5 = 0 and x² = 5 equivalent? Explain your reasoning.
b. Use the square root key on a calculator to estimate the solutions of x² – 5 = 0. Describe the accuracy of your estimates in Exploration 2.
c. Write the exact solutions of x² – 5 = 0.

Communicate Your Answer

Question 4.
How can you determine the number of solutions of a quadratic equation of the form ax² + c = 0?
Answer:

Question 5.
Write the exact solutions of each equation. Then use a calculator to estimate the solutions.
a. x² – 2 = 0
b. 3x² – 18 = 0
c. x² – 8
Answer:

Monitoring Progress

Solve the equation using square roots.
Question 1.
-3x² = -75
Answer:

Question 2.
x² + 12 = 10
Answer:

Question 3.
4x² – 15 = -15
Answer:

Question 4.
(x + 7)² = 0
Answer:

Question 5.
4(x – 3)² = 9
Answer:

Question 6.
(2x + 1)² = 36
Answer:

Solve the equation using square roots. Round your solutions to the nearest hundredth.
Question 7.
x² + 8 = 19
Answer:

Question 8.
5x² – 2 = 0
Answer:

Question 9.
3x² – 30 = 4
Answer:

Question 10.
WHAT IF?
In Example 4, the volume of the tank is 315 cubic feet. Find the length and width of the tank.
Answer:

Question 11.
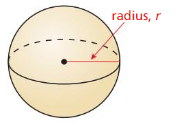
The surface area S of a sphere with radius r is given by the formula S = 4πr². Solve the formula for r. Then find the radius of a globe with a surface area of 804 square inches.
Answer:

Solving Quadratic Equations Using Square Roots 9.3 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
The equation x² = d has ____ real solutions when d > 0.
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers

Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, determine the number of real solutions of the equation. Then solve the equation using square roots.
Question 3.
x² = 25
Answer:

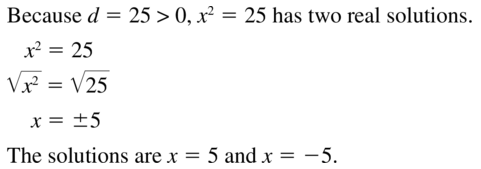
Question 4.
x² = -36
Answer:

Question 5.
x² = -21
Answer:

Question 6.
x² = 400
Answer:

Question 7.
x² = 0
Answer:

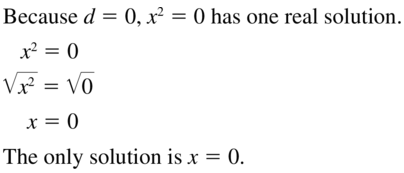
Question 8.
x² = 169
Answer:

In Exercises 9–18, solve the equation using square roots.
Question 9.
x² – 16 = 0
Answer:

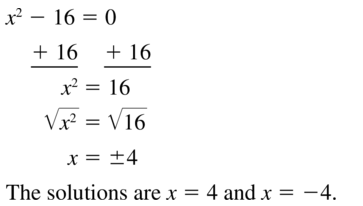
Question 10.
x² + 6 = 0
Answer:

Question 11.
3x² + 12 = 0
Answer:

Question 12.
x² – 55 = 26
Answer:

Question 13.
2x² – 98 = 0
Answer:

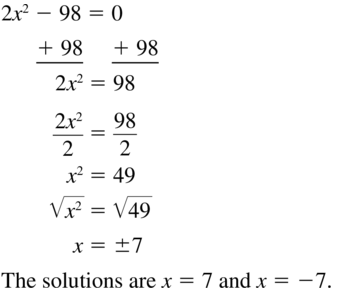
Question 14.
-x² + 9 = 9
Answer:

Question 15.
-3x² – 5 = -5
Answer:

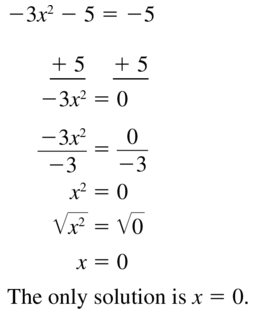
Question 16.
4x² – 371 = 29
Answer:

Question 17.
4x² + 10 = 11
Answer:

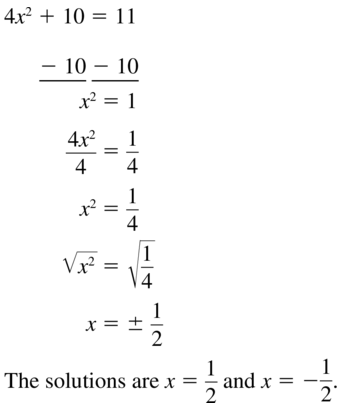
Question 18.
9x² – 35 = 14
Answer:

In Exercises 19–24, solve the equation using square roots.
Question 19.
(x + 3)² = 0
Answer:

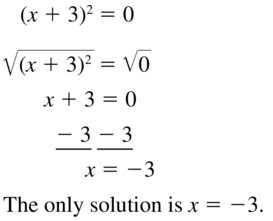
Question 20.
(x – 1)² = 4
Answer:

Question 21.
(2x – 1)² = 81
Answer:

Question 22.
(4x + 5)² = 9
Answer:

Question 23.
9(x + 1)² = 16
Answer:

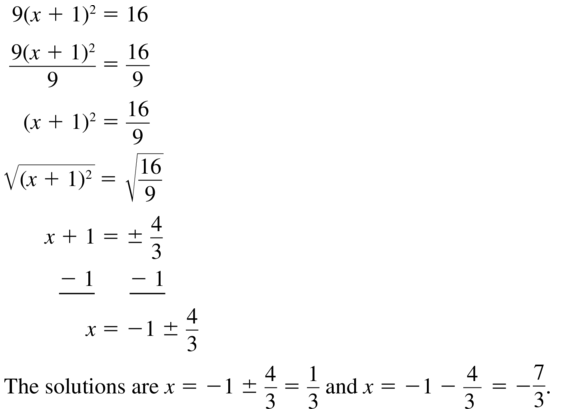
Question 24.
4(x – 2)² = 25
Answer:

In Exercises 25–30, solve the equation using square roots. Round your solutions to the nearest hundredth.
Question 25.
x² + 6 = 13
Answer:

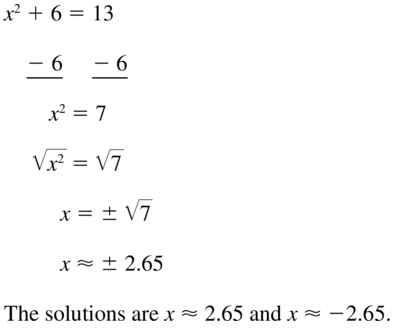
Question 26.
x² + 11 = 24
Answer:

Question 27.
2x² – 9 = 11
Answer:

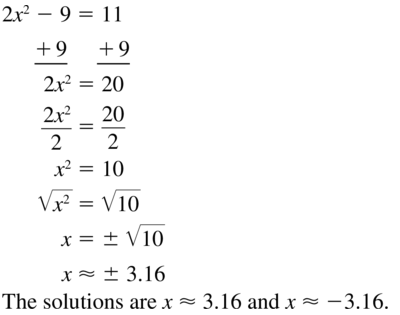
Question 28.
5x² + 2 = 6
Answer:

Question 29.
-21 = 15 – 2x²
Answer:

Question 30.
2 = 4x² – 5
Answer:

Question 31.
ERROR ANALYSIS
Describe and correct the error in solving the equation 2x² – 33 = 39 using square roots.

Answer:

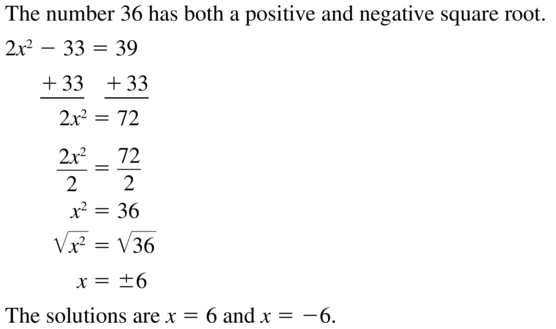
Question 32.
MODELING WITH MATHEMATICS
An in-ground pond has the shape of a rectangular prism. The pond has a depth of 24 inches and a volume of 72,000 cubic inches. The length of the pond is two times its width. Find the length and width of the pond.

Answer:

Question 33.
MODELING WITH MATHEMATICS
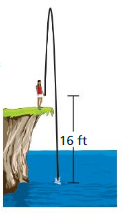
A person sitting in the top row of the bleachers at a sporting event drops a pair of sunglasses from a height of 24 feet. The function h = -16x² + 24 represents the height h (in feet) of the sunglasses after x seconds. How long does it take the sunglasses to hit the ground?
Answer:

Question 34.
MAKING AN ARGUMENT
Your friend says that the solution of the equation x² + 4 = 0 is x = 0. Your cousin says that the equation has no real solutions. Who is correct? Explain your reasoning.
Answer:

Question 35.
MODELING WITH MATHEMATICS
The design of a square rug for your living room is shown. You want the area of the inner square to be 25% of the total area of the rug. Find the side length x of the inner square.

Answer:

Question 36.
MATHEMATICAL CONNECTIONS
The area A of a circle with radius r is given by the formula A = πr².
a. Solve the formula for r.
b. Use the formula from part (a) to find the radius of each circle.

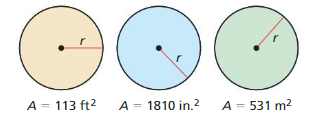
c. Explain why it is beneficial to solve the formula for r before finding the radius.
Answer:

Question 37.
WRITING
How can you approximate the roots of a quadratic equation when the roots are not integers?
Answer:

Question 38.
WRITING
Given the equation ax² + c = 0, describe the values of a and c so the equation has the following number of solutions.
a. two real solutions
b. one real solution
c. no real solutions
Answer:

Question 39.
REASONING
Without graphing, where do the graphs of y = x² and y = 9 intersect? Explain.
Answer:

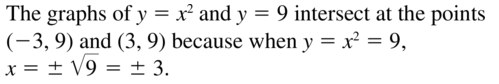
Question 40.
HOW DO YOU SEE IT?
The graph represents the function f(x) = (x – 1)². How many solutions does the equation (x – 1)² = 0 have? Explain.

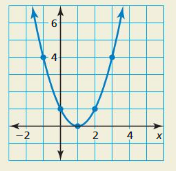
Answer:

Question 41.
REASONING
Solve x² = 1.44 without using a calculator. Explain your reasoning.
Answer:

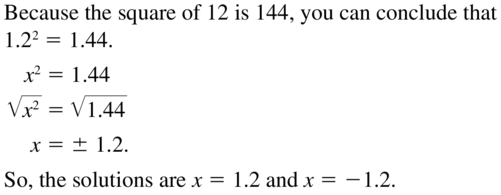
Question 42.
THOUGHT PROVOKING
The quadratic equation ax² + bx + c = 0can be rewritten in the following form. \(\left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}\) Use this form to write the solutions of the equation.
Answer:

Question 43.
REASONING
An equation of the graph shown is y = \(\frac{1}{2}\)(x – 2)² + 1. Two points on the parabola have y-coordinates of 9. Find the x-coordinates of these points.

Answer:

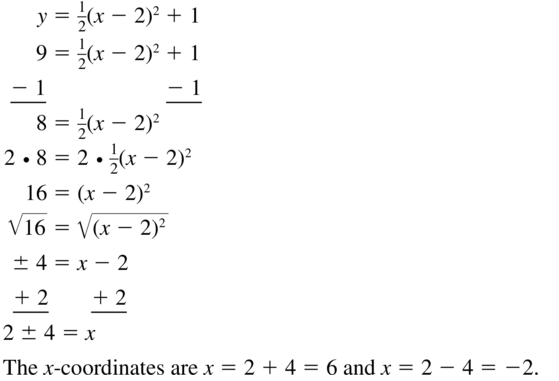
Question 44.
CRITICAL THINKING
Solve each equation without graphing.
a. x² – 12x + 36 = 64
b. x² + 14x + 49 = 16
Answer:

Maintaining Mathematical Proficiency

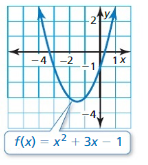
Factor the polynomial.
Question 45.
x² + 8x + 16
Answer:

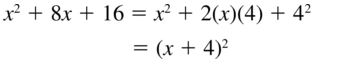
Question 46.
x² – 4x + 4
Answer:

Question 47.
x² – 14x + 49
Answer:

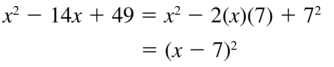
Question 48.
x² + 18x + 81
Answer:

Question 49.
x² + 12x + 36
Answer:

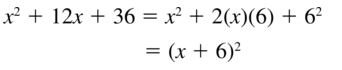
Question 50.
x² – 22x + 121
Answer:

Solving Quadratic Equations Study Skills: Keeping a Positive Attitude

9.1–9.3 What Did You Learn?

Core Vocabulary

Core Concepts

Mathematical Practices

Question 1.
For each part of Exercise 100 on page 488 that is sometimes true, list all examples and counterexamples from the table that represent the sum or product being described.
Answer:

Question 2.
Which Examples can you use to help you solve Exercise 54 on page 496?
Answer:

Question 3.
Describe how solving a simpler equation can help you solve the equation in Exercise 41 on page 502.
Answer:

Study Skills: Keeping a Positive Attitude

Do you ever feel frustrated or overwhelmed by math? You’re not alone. Just take a deep breath and assess the situation. Try to find a productive study environment, review your notes and the examples in the textbook, and ask your teacher or friends for help.

Solving Quadratic Equations 9.1 – 9.3 Quiz

Simplify the expression.
Question 1.
\(\sqrt{112 x^{3}}\)
Answer:

Question 2.
\(\sqrt{\frac{18}{81}}\)
Answer:

Question 3.
\(\sqrt[3]{-625}\)
Answer:

Question 4.
\(\frac{12}{\sqrt{32}}\)
Answer:

Question 5.
\(\frac{4}{\sqrt{11}}\)
Answer:

Question 6.
\(\sqrt{\frac{144}{13}}\)
Answer:

Question 7.
\(\sqrt[3]{\frac{54 x^{4}}{343 y^{6}}}\)
Answer:

Question 8.
\(\sqrt{\frac{4 x^{2}}{28 y^{4} z^{5}}}\)
Answer:

Question 9.
\(\frac{6}{5+\sqrt{3}}\)
Answer:

Question 10.
2\(\sqrt{5}\) + 7\(\sqrt{10}\) – 3\(\sqrt{20}\)
Answer:

Question 11.
\(\frac{10}{\sqrt{8}-\sqrt{10}}\)
Answer:

Question 12.
\(\sqrt{6}\)(7\(\sqrt{12}\) – 4\(\sqrt{3}\))
Answer:

Use the graph to solve the equation.
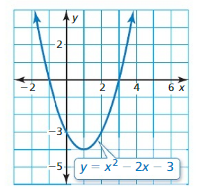
Question 13.
x² – 2x – 3 = 0

Answer:

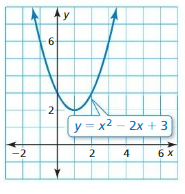
Question 14.
x² – 2x + 3 = 0

Answer:

Question 15.
x² + 10x + 25 = 0

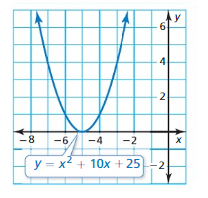
Answer:

Solve the equation by graphing.
Question 16.
x² + 9x + 14 = 0
Answer:

Question 17.
x² – 7x = 8
Answer:

Question 18.
x + 4 = -x²
Answer:

Solve the equation using square roots.
Question 19.
4x² = 64
Answer:

Question 20.
-3x² + 6 = 10
Answer:

Question 21.
(x – 8)² = 1
Answer:

Question 22.
Explain how to determine the number of real solutions of x² = 100 without solving.
Answer:

Question 23.
The length of a rectangular prism is four times its width. The volume of the prism is 380 cubic meters. Find the length and width of the prism.

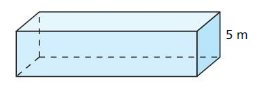
Answer:

Question 24.
You cast a fishing lure into the water from a height of 4 feet above the water. The height h (in feet) of the fishing lure after t seconds can be modeled by the equation h = -16t² + 24t + 4.

a. After how many seconds does the fishing lure reach a height of 12 feet?
b. After how many seconds does the fishing lure hit the water?
Answer:

Lesson 9.4 Solving Quadratic Equations by Completing the Square

Essential Question How can you use “completing the square” to solve a quadratic equation?

EXPLORATION 1

Solving by Completing the Square
Work with a partner.

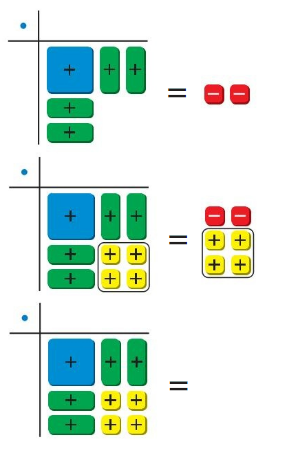
a. Write the equation modeled by the algebra tiles. This is the equation to be solved.
b. Four algebra tiles are added to the left side to “complete the square.” Why are four algebra tiles also added to the right side?
c. Use algebra tiles to label the dimensions of the square on the left side and simplify on the right side.
d. Write the equation modeled by the algebra tiles so that the left side is the square of a binomial. Solve the equation using square roots.

EXPLORATION 2

Solving by Completing the Square
Work with a partner.
a. Write the equation modeled by the algebra tiles.

b. Use algebra tiles to “complete the square.”
c. Write the solutions of the equation.
d. Check each solution in the original equation.

Communicate Your Answer

Question 3.
How can you use “completing the square” to solve a quadratic equation?
Answer:

Question 4.
Solve each quadratic equation by completing the square.
a. x² – 2x = 1
b. x² – 4x = -1
c. x² + 4x = -3
Answer:

Monitoring Progress

Complete the square for the expression. Then factor the trinomial.
Question 1.
x² + 10x
Answer:

Question 2.
x² – 4x
Answer:

Question 3.
x² + 7x
Answer:

Solve the equation by completing the square. Round your solutions to the nearest hundredth, if necessary.
Question 4.
x² – 2x = 3
Answer:

Question 5.
m² + 12m = -8
Answer:

Question 6.
3g² – 24g + 27 = 0
Answer:

Determine whether the quadratic function has a maximum or minimum value. Then find the value.
Question 7.
y = -x² – 4x + 4
Answer:

Question 8.
y = x² + 12x + 40
Answer:

Question 9.
y = x² – 2x – 2
Answer:

Determine whether the function could be represented by the graph in Example 6. Explain.
Question 10.
h(x) = (x – 8)² + 10
Answer:

Question 11.
n(x) = -2(x – 5)(x – 20)
Answer:

Question 12.
WHAT IF?
Repeat Example 7 when the function is y = -16x² + 128x.
Answer:

Question 13.
WHAT IF?
You want the chalkboard to cover 4 square feet. Find the width of the border to the nearest inch.
Answer:

Solving Quadratic Equations by Completing the Square 9.4 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
The process of adding a constant c to the expression x² + bx so that x² + bx + c is a perfect square trinomial is called ________________.
Answer:

Question 2.
VOCABULARY
Explain how to complete the square for an expression of the form x² + bx.
Answer:

Question 3.
WRITING
Is it more convenient to complete the square for x² + bx when b is odd or when b is even? Explain.
Answer:

Question 4.
WRITING
Describe how you can use the process of completing the square to find the maximum or minimum value of a quadratic function.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 5–10, find the value of c that completes the square.
Question 5.
x² – 8x + c
Answer:

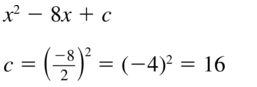
Question 6.
x² – 2x + c
Answer:

Question 7.
x² + 4x + c
Answer:

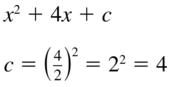
Question 8.
x² + 12x + c
Answer:

Question 9.
x² – 15x + c
Answer:

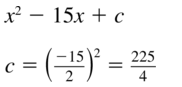
Question 10.
x² + 9x + c
Answer:

In Exercises 11–16, complete the square for the expression. Then factor the trinomial.
Question 11.
x² – 10x
Answer:

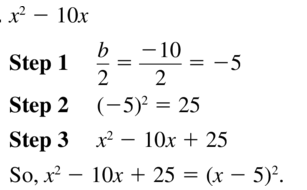
Question 12.
x² – 40x
Answer:

Question 13.
x² + 16x
Answer:

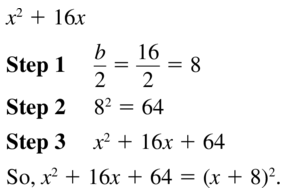
Question 14.
x² + 22x
Answer:

Question 15.
x² + 5x
Answer:

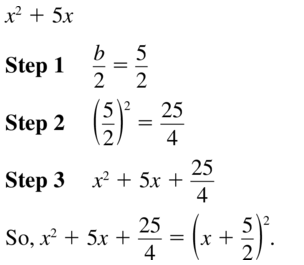
Question 16.
x² – 3x
Answer:

In Exercises 17–22, solve the equation by completing the square. Round your solutions to the nearest hundredth, if necessary.
Question 17.
x² + 14x = 15
Answer:

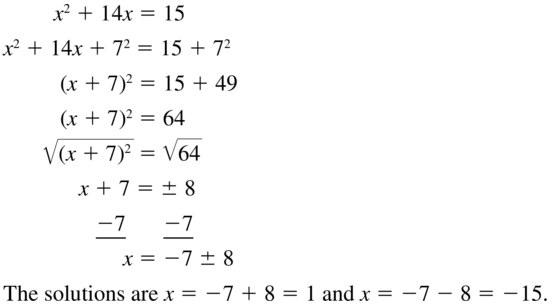
Question 18.
x² – 6x = 16
Answer:

Question 19.
x² – 4x = -2
Answer:

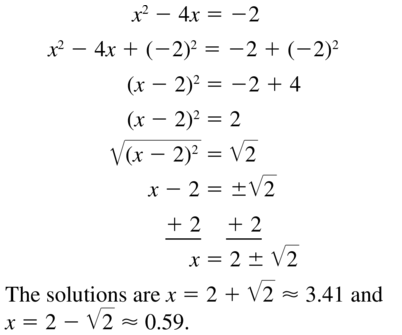
Question 20.
x² + 2x = 5
Answer:

Question 21.
x² – 5x = 8
Answer:

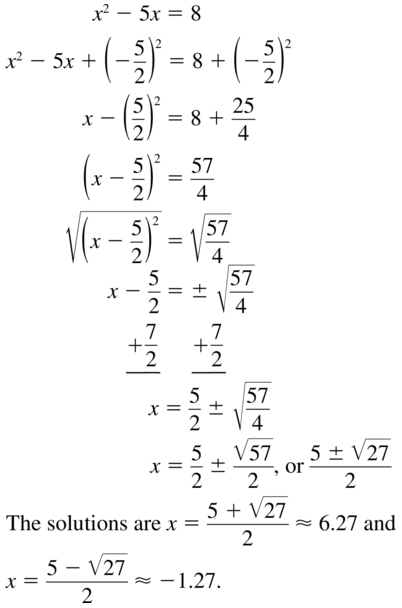
Question 22.
x² + 11x = -10
Answer:

Question 23.
MODELING WITH MATHEMATICS
The area of the patio is 216 square feet.

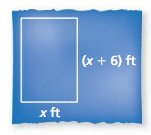
a. Write an equation that represents the area of the patio.
b. Find the dimensions of the patio by completing the square.
Answer:

Question 24.
MODELING WITH MATHEMATICS
Some sand art contains sand and water sealed in a glass case, similar to the one shown. When the art is turned upside down, the sand and water fall to create a new picture. The glass case has a depth of 1 centimeter and a volume of 768 cubic centimeters.

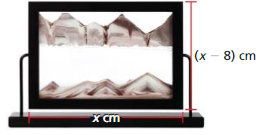
a. Write an equation that represents the volume of the glass case.
b. Find the dimensions of the glass case by completing the square.
Answer:

In Exercises 25–32, solve the equation by completing the square. Round your solutions to the nearest hundredth, if necessary.
Question 25.
x² – 8x + 15 = 0
Answer:

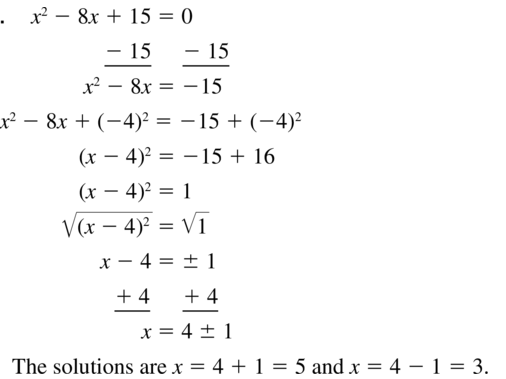
Question 26.
x² + 4x – 21 = 0
Answer:

Question 27.
2x² + 20x + 44 = 0
Answer:

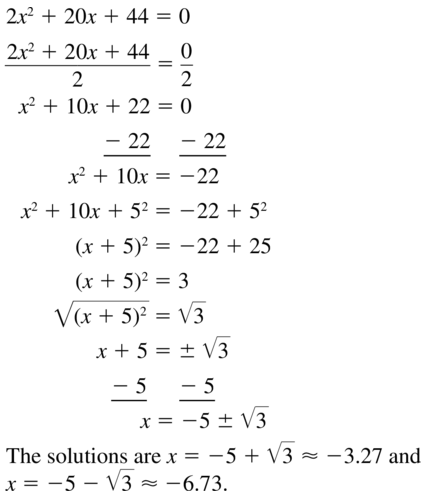
Question 28.
3x² – 18x + 12 = 0
Answer:

Question 29.
-3x² – 24x + 17 = -40
Answer:

Question 30.
-5x² – 20x + 35 = 30
Answer:

Question 31.
2x² – 14x + 10 = 26
Answer:

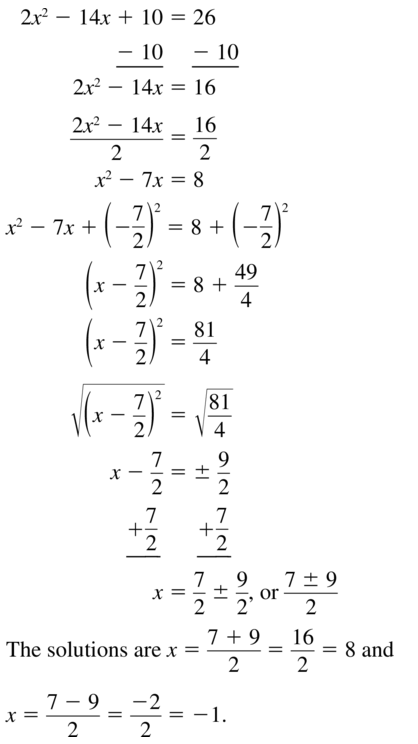
Question 32.
4x² + 12x – 15 = 5
Answer:

Question 33.
ERROR ANALYSIS
Describe and correct the error in solving x² + 8x = 10 by completing the square.

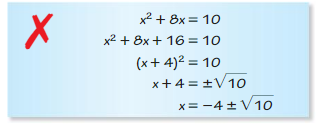
Answer:

Question 34.
ERROR ANALYSIS
Describe and correct the error in the first two steps of solving 2x² – 2x – 4 = 0 by completing the square.

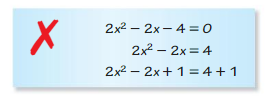
Answer:

Question 35.
NUMBER SENSE
Find all values of b for which x² + bx + 25 is a perfect square trinomial. Explain how you found your answer.
Answer:

Question 36.
REASONING
You are completing the square to solve 3x² + 6x = 12. What is the first step?
Answer:

In Exercises 37–40, write the function in vertex form bycompleting the square. Then match the function with its graph.
Question 37.
y = x² + 6x + 3
Answer:

Question 38.
y = -x² + 8x – 12
Answer:

Question 39.
y = -x² – 4x – 2
Answer:

Question 40.
y = x² – 2x + 4
Answer:

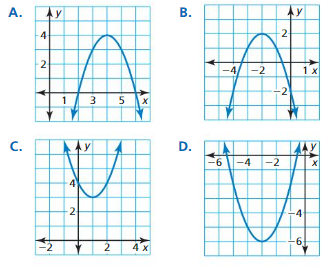
In Exercises 41–46, determine whether the quadratic function has a maximum or minimum value. Then find the value.
Question 41.
y = x² – 4x – 2
Answer:

Question 42.
y = x² + 6x + 10
Answer:

Question 43.
y = -x² – 10x – 30
Answer:

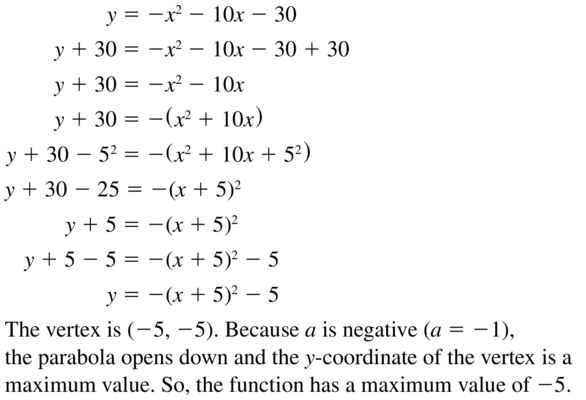
Question 44.
y = -x² + 14x – 34
Answer:

Question 45.
f(x) = -3x² – 6x – 9
Answer:

Question 46.
f(x) = 4x² – 28x + 32
Answer:

In Exercises 47–50, determine whether the graph could represent the function. Explain.
Question 47.
y = -(x + 8)(x + 3)

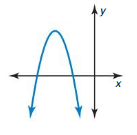
Answer:

Question 48.
y = (x – 5)²

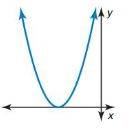
Answer:

Question 49.
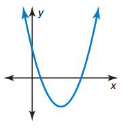
y = \(\frac{1}{4}\)(x + 2)² – 4

Answer:

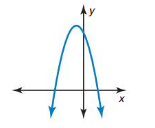
Question 50.
y = -2(x – 1)(x + 2)

Answer:

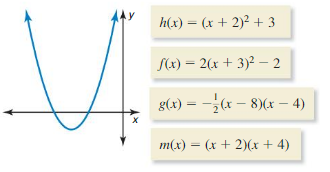
In Exercises 51 and 52, determine which of the functions could be represented by the graph. Explain.
Question 51.

Answer:

Question 52.

Answer:

Question 53.
MODELING WITH MATHEMATICS
The function h = -16t² + 48t represents the height h (in feet) of a kickball t seconds after it is kicked from the ground.
a. Find the maximum height of the kickball.
b. Find and interpret the axis of symmetry.
Answer:

Question 54.
MODELING WITH MATHEMATICS
You throw a stone from a height of 16 feet with an initial vertical velocity of 32 feet per second. The function h = -16t² + 32t + 16 represents the height h (in feet) of the stone after t seconds.

a. Find the maximum height of the stone.
b. Find and interpret the axis of symmetry.
Answer:

Question 55.
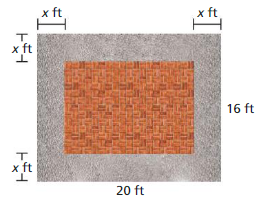
MODELING WITH MATHEMATICS
You are building a rectangular brick patio surrounded by a crushed stone border with a uniform width, as shown. You purchase patio bricks to cover 140 square feet. Find the width of the border.

Answer:

Question 56.
MODELING WITH MATHEMATICS
You are making a poster that will have a uniform border, as shown. The total area of the poster is 722 square inches. Find the width of the border to the nearest inch.

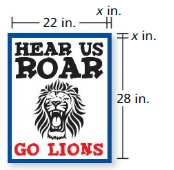
Answer:

MATHEMATICAL CONNECTIONS In Exercises 57 and 58, find the value of x. Round your answer to the nearest hundredth, if necessary.
Question 57.
A = 108 m²

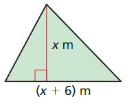
Answer:

Question 58.
A = 288 in.²

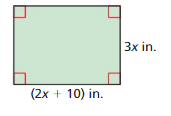
Answer:

In Exercises 59–62, solve the equation by completing the square. Round your solutions to the nearest hundredth, if necessary.
Question 59.
0.5x² + x – 2 = 0
Answer:

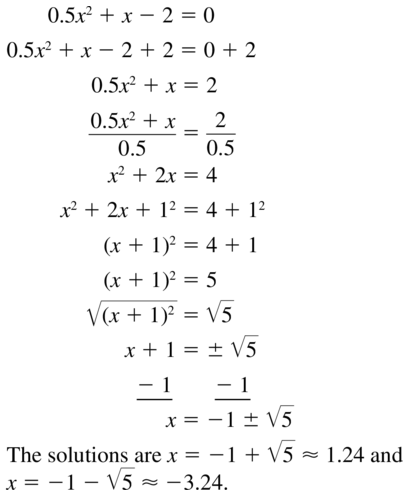
Question 60.
0.75x² + 1.5x = 4
Answer:

Question 61.
\(\frac{8}{3}\) x – \(\frac{2}{3}\)x² = –\(\frac{5}{6}\)
Answer:

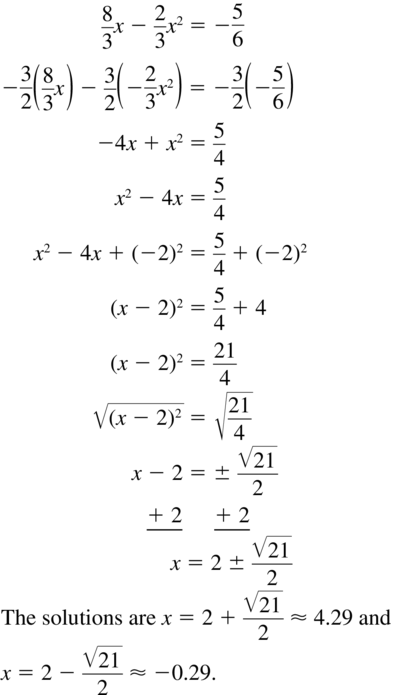
Question 62.
\(\frac{1}{4}\)x² + \(\frac{1}{2}\)x – \(\frac{5}{4}\) = 0
Answer:

Question 63.
PROBLEM SOLVING
The distance d (in feet) that it takes a car to come to a complete stop can be modeled by d = 0.05s² + 2.2s, where s is the speed of the car (in miles per hour). A car has 168 feet to come to a complete stop. Find the maximum speed at which the car can travel.
Answer:

Question 64.
PROBLEM SOLVING
During a “big air” competition, snowboarders launch themselves from a half-pipe, perform tricks in the air, and land back in the half-pipe. The height h (in feet) of a snowboarder above the bottom of the half-pipe can be modeled by h = -16t² + 24t + 16.4, where t is the time (in seconds) after the snowboarder launches into the air. The snowboarder lands 3.2 feet lower than the height of the launch. How long is the snowboarder in the air? Round your answer to the nearest tenth of a second.

Answer:

Question 65.
PROBLEM SOLVING
You have 80 feet of fencing to make a rectangular horse pasture that covers 750 square feet. A barn will be used as one side of the pasture, as shown.

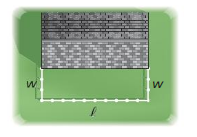
a. Write equations for the amount of fencing to be used and the area enclosed by the fencing.
b. Use substitution to solve the system of equations from part (a). What are the possible dimensions of the pasture?
Answer:

Question 66.
HOW DO YOU SEE IT?
The graph represents the quadratic function y = x² – 4x + 6.

a. Use the graph to estimate the x-values for which y = 3.
b. Explain how you can use the method of completing the square to check your estimates in part (a).
Answer:

Question 67.
COMPARING METHODS
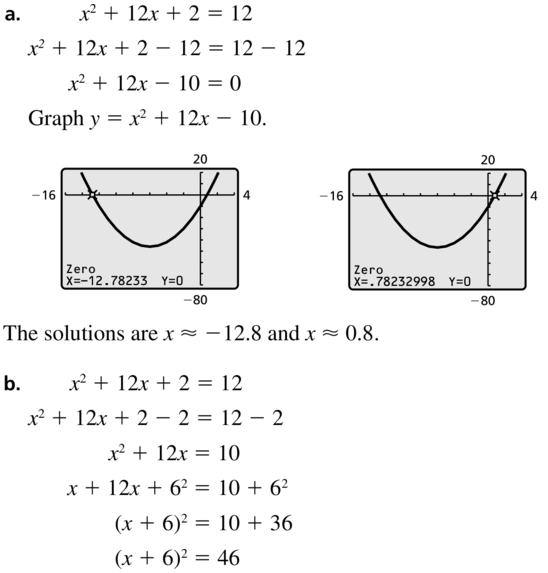
Consider the quadratic equation x² + 12x + 2 = 12.
a. Solve the equation by graphing.
b. Solve the equation by completing the square.
c. Compare the two methods. Which do you prefer? Explain.
Answer:

Question 68.
THOUGHT PROVOKING
Sketch the graph of the equation x² – 2xy + y² – x – y = 0. Identify the graph.
Answer:

Question 69.
REASONING
The product of two consecutive even integers that are positive is 48. Write and solve an equation to find the integers.
Answer:

Question 70.
REASONING
The product of two consecutive odd integers that are negative is 195. Write and solve an equation to find the integers.
Answer:

Question 71.
MAKING AN ARGUMENT
You purchase stock for $16 per share. You sell the stock 30 days later for $23.50 per share. The price y (in dollars) of a share during the 30-day period can be modeled by y = -0.025x² + x + 16, where x is the number of days after the stock is purchased. Your friend says you could have sold the stock earlier for $23.50 per share. Is your friend correct? Explain.

Answer:

Question 72.
REASONING
You are solving the equation x² + 9x = 18. What are the advantages of solving the equation by completing the square instead of using other methods you have learned?
Answer:

Question 73.
PROBLEM SOLVING
You are knitting a rectangular scarf. The pattern results in a scarf that is 60 inches long and 4 inches wide. However, you have enough yarn to knit 396 square inches. You decide to increase the dimensions of the scarf so that you will use all your yarn. The increase in the length is three times the increase in the width. What are the dimensions of your scarf?

Answer:

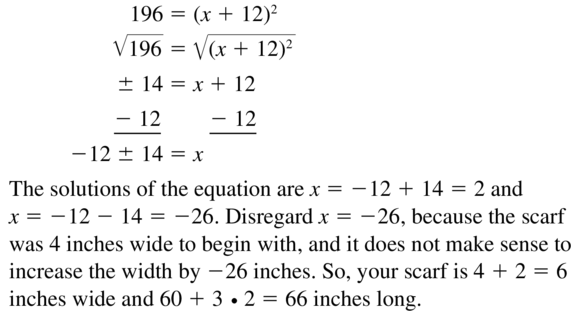
Question 74.
WRITING
How many solutions does x² + bx = c have when c < -(\(\frac{b}{2}\))² ? Explain.
Answer:

Maintaining Mathematical Proficiency

Write a recursive rule for the sequence.
Question 75.

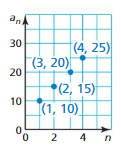
Answer:

Question 76.

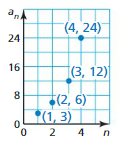
Answer:

Question 77.

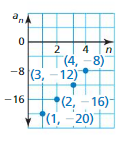
Answer:

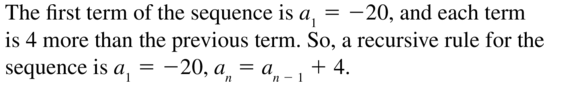
Simplify the expression \(\sqrt{b^{2}-4 a c}\) for the given values.
Question 78.
a = 3, b = -6, c = 2
Answer:

Question 79.
a = -2, b = 4, c = 7
Answer:

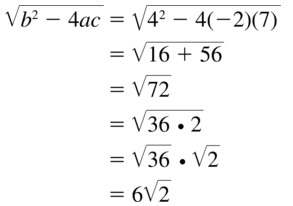
Question 80.
a = 1, b = 6, c = 4
Answer:

Lesson 9.5 Solving Quadratic Equations Using the Quadratic Formula

Essential Question How can you derive a formula that can be used to write the solutions of any quadratic equation in standard form?

EXPLORATION 1

Deriving the Quadratic Formula
Work with a partner. The following steps show a method of solving ax² + bx + c = 0. Explain what was done in each step.

EXPLORATION 2

Deriving the Quadratic Formula by Completing the Square
Work with a partner.
a. Solve ax² + bx + c = 0 by completing the square. (Hint: Subtract c from each side, divide each side by a, and then proceed by completing the square.)
b. Compare this method with the method in Exploration 1. Explain why you think 4a and b² were chosen in Steps 2 and 3 of Exploration 1.

Communicate Your Answer

Question 3.
How can you derive a formula that can be used to write the solutions of any quadratic equation in standard form?
Answer:

Question 4.
Use the Quadratic Formula to solve each quadratic equation.
a. x² + 2x – 3 = 0
b. x² – 4x + 4 = 0
c. x² + 4x + 5 = 0
Answer:

Question 5.
Use the Internet to research imaginary numbers. How are they related to quadratic equations?

Answer:

Monitoring Progress

Solve the equation using the Quadratic Formula. Round your solutions to the nearest tenth, if necessary.
Question 1.
x² – 6x + 5 = 0
Answer:

Question 2.
\(\frac{1}{2}\)x² + x – 10 = 0
Answer:

Question 3.
-3x² + 2x + 7 = 0
Answer:

Question 4.
4x² – 4x = -1
Answer:

Question 5.
WHAT IF?
When were there about 60 wolf breeding pairs?
Answer:

Question 6.
The number y of bald eagle nesting pairs in a state x years since 2000 can be modeled by the function y = 0.34x² + 13.1x + 51.
a. When were there about 160 bald eagle nesting pairs?
b. How many bald eagle nesting pairs were there in 2000?
Answer:

Determine the number of real solutions of the equation.
Question 7.
-x² + 4x – 4 = 0
Answer:

Question 8.
6x² + 2x = -1
Answer:

Question 9.
\(\frac{1}{2}\)x² = 7x – 1
Answer:

Find the number of x-intercepts of the graph of the function.
Question 10.
y = -x² + x – 6
Answer:

Question 11.
y = x² – x
Answer:

Question 12.
f(x) = x² + 12x + 36
Answer:

Solve the equation using any method. Explain your choice of method.
Question 13.
x² + 11x – 12 = 0
Answer:

Question 14.
9x² – 5 = 4
Answer:

Question 15.
5x² – x – 1 = 0
Answer:

Question 16.
x² = 2x – 5
Answer:

Solving Quadratic Equations Using the Quadratic Formula 9.5 Exercises

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
What formula can you use to solve any quadratic equation? Write the formula.
Answer:

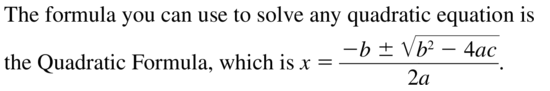
Question 2.
VOCABULARY
In the Quadratic Formula, what is the discriminant? What does the value of the discriminant determine?
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, write the equation in standard form. Then identify the values of a, b, and c that you would use to solve the equation using the Quadratic Formula.
Question 3.
x² = 7x
Answer:

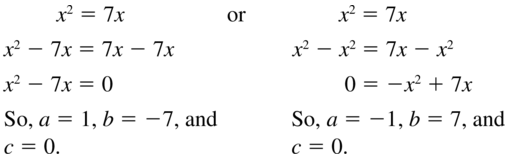
Question 4.
x² – 4x = -12
Answer:

Question 5.
-2x² + 1 = 5x
Answer:

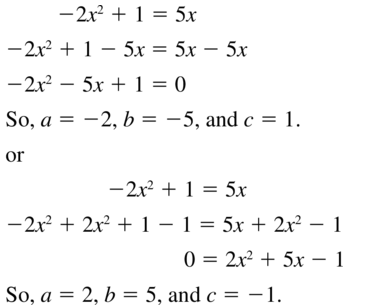
Question 6.
3x + 2 = 4x²
Answer:

Question 7.
4 – 3x = -x² + 3x
Answer:

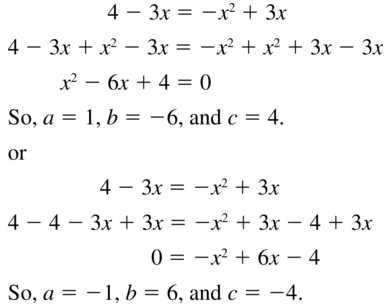
Question 8.
-8x – 1 = 3x² + 2
Answer:

In Exercises 9–22, solve the equation using the Quadratic Formula. Round your solutions to the nearest tenth, if necessary.
Question 9.
x² – 12x + 36 = 0
Answer:

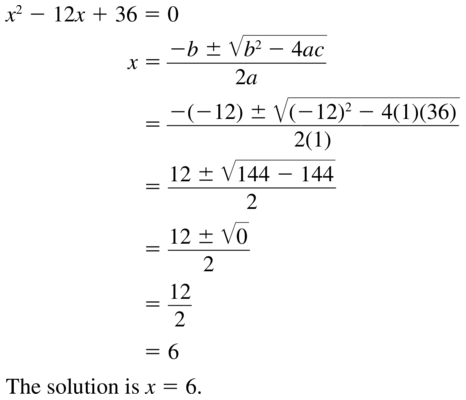
Question 10.
x² + 7x + 16 = 0
Answer:

Question 11.
x² – 10x – 11 = 0
Answer:

Question 12.
2x² – x – 1 = 0
Answer:

Question 13.
2x² – 6x + 5 = 0
Answer:

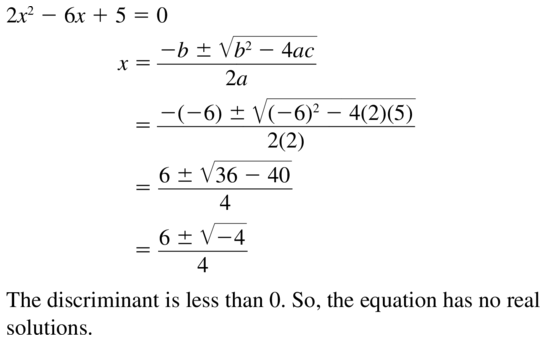
Question 14.
9x² – 6x + 1 = 0
Answer:

Question 15.
6x² – 13x = -6
Answer:

Question 16.
-3x² + 6x = 4
Answer:

Question 17.
1 – 8x = -16x²
Answer:

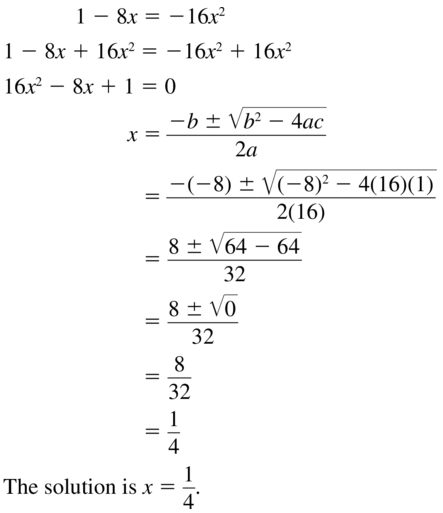
Question 18.
x² – 5x + 3 = 0
Answer:

Question 19.
x² + 2x = 9
Answer:

Question 20.
5x² – 2 = 4x
Answer:

Question 21.
2x² + 9x + 7 = 3
Answer:

Question 22.
8x² + 8 = 6 – 9x
Answer:

Question 23.
MODELING WITH MATHEMATICS
A dolphin jumps out of the water, as shown in the diagram. The function h = -16t² + 26t models the height h (in feet) of the dolphin after t seconds. After how many seconds is the dolphin at a height of 5 feet?

Answer:

Question 24.
MODELING WITH MATHEMATICS
The amount of trout y (in tons) caught in a lake from 1995 to 2014 can be modeled by the equation y = -0.08x² + 1.6x + 10, where x is the number of years since 1995.
a. When were about 15 tons of trout caught in the lake?
b. Do you think this model can be used to determine the amounts of trout caught in future years? Explain your reasoning.
Answer:

In Exercises 25–30, determine the number of real solutions of the equation.
Question 25.
x² – 6x + 10 = 0
Answer:

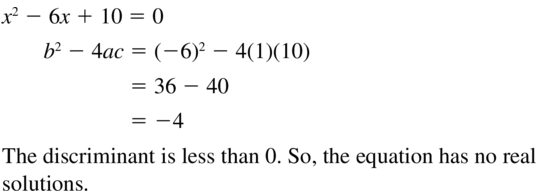
Question 26.
x² – 5x – 3 = 0
Answer:

Question 27.
2x² – 12x = -18
Answer:

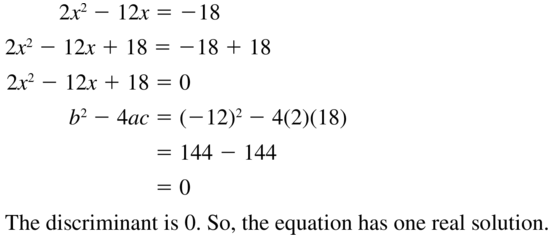
Question 28.
4x² = 4x – 1
Answer:

Question 29.
–\(\frac{1}{4}\)x² + 4x = -2
Answer:

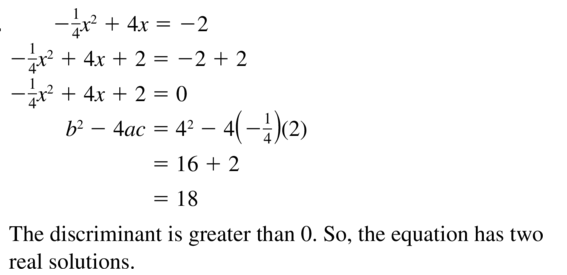
Question 30.
-5x² + 8x = 9
Answer:

In Exercises 31–36, find the number of x-intercepts of the graph of the function.
Question 31.
y = x² + 5x – 1
Answer:

Question 32.
y = 4x² + 4x + 1
Answer:

Question 33.
y = -6x² + 3x – 4
Answer:

Question 34.
y = -x² + 5x + 13
Answer:

Question 35.
f(x) = 4x² + 3x – 6
Answer:

Question 36.
f(x) = 2x² + 8x + 8
Answer:

In Exercises 37–44, solve the equation using any method. Explain your choice of method.
Question 37.
-10x² + 13x = 4
Answer:

Question 38.
x² – 3x – 40 = 0
Answer:

Question 39.
x² + 6x = 5
Answer:

Question 40.
-5x² = -25
Answer:

Question 41.
x² + x – 12 = 0
Answer:

Question 42.
x² – 4x + 1 = 0
Answer:

Question 43.
4x² – x = 17
Answer:

Question 44.
x² + 6x + 9 = 16
Answer:

Question 45.
ERROR ANALYSIS
Describe and correct the error in solving the equation 3x² – 7x – 6 = 0 using the Quadratic Formul

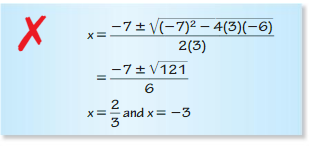
Answer:

Question 46.
ERROR ANALYSIS
Describe and correct the error in solving the equation -2x² + 9x = 4 using the Quadratic Formula.

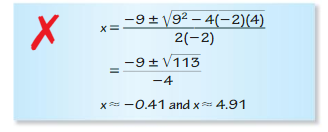
Answer:

Question 47.
MODELING WITH MATHEMATICS
A fountain shoots a water arc that can be modeled by the graph of the equation y = -0.006x² + 1.2x + 10, where x is the horizontal distance (in feet) from the river’s north shore and y is the height (in feet) above the river. Does the water arc reach a height of 50 feet? If so, about how far from the north shore is the water arc 50 feet above the water?

Answer:

Question 48.
MODELING WITH MATHEMATICS
Between the months of April and September, the number y of hours of daylight per day in Seattle, Washington, can be modeled by y = -0.00046x² + 0.076x + 13, where x is the number of days since April 1.
a. Do any of the days between April and September in Seattle have 17 hours of daylight? If so, how many?
b. Do any of the days between April and September in Seattle have 14 hours of daylight? If so, how many?
Answer:

Question 49.
MAKING AN ARGUMENT
Your friend uses the discriminant of the equation 2x² – 5x – 2 = -11 and determines that the equation has two real solutions. Is your friend correct? Explain your reasoning.
Answer:

Question 50.
MODELING WITH MATHEMATICS
The frame of the tent shown is defined by a rectangular base and two parabolic arches that connect the opposite corners of the base. The graph of y = -0.18x² + 1.6x models the height y (in feet) of one of the arches x feet along the diagonal of the base. Can a child who is 4 feet tall walk under one of the arches without having to bend over? Explain.

Answer:

MATHEMATICAL CONNECTIONS In Exercises 51 and 52, use the given area A of the rectangle to find the value of x. Then give the dimensions of the rectangle.
Question 51.
A = 91 m²

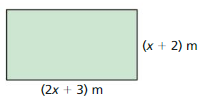
Answer:

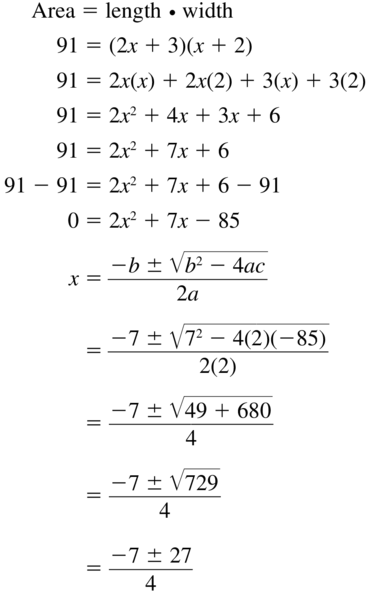
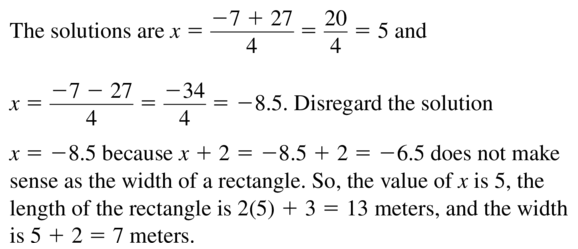
Question 52.
A = 209 ft²

Answer:

COMPARING METHODS In Exercises 53 and 54, solve the equation by (a) graphing, (b) factoring, and (c) using the Quadratic Formula. Which method do you prefer? Explain your reasoning.
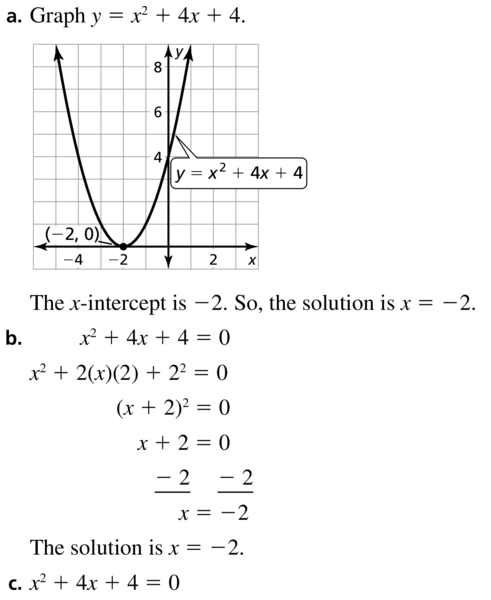
Question 53.
x² + 4x + 4 = 0
Answer:

Question 54.
3x² + 11x + 6 = 0
Answer:

Question 55.
REASONING
How many solutions does the equation ax² + bx + c = 0 have when a and c have different signs? Explain your reasoning.
Answer:

Question 56.
REASONING
When the discriminant is a perfect square, are the solutions of ax² + bx + c = 0 rational or irrational? (Assume a, b, and c are integers.) Explain your reasoning.
Answer:

REASONING In Exercises 57–59, give a value of c for which the equation has (a) two solutions, (b) one solution, and (c) no solutions.
Question 57.
x² – 2x + c = 0
Answer:

Question 58.
x² – 8x + c = 0
Answer:

Question 59.
4x² + 12x + c = 0
Answer:

Question 60.
REPEATED REASONING
You use the Quadratic Formula to solve an equation.
a. You obtain solutions that are integers. Could you have used factoring to solve the equation? Explain your reasoning.
b. You obtain solutions that are fractions. Could you have used factoring to solve the equation? Explain your reasoning.
c. Make a generalization about quadratic equations with rational solutions.
Answer:

Question 61.
MODELING WITH MATHEMATICS
The fuel economy y(in miles per gallon) of a car can be modeled by the equation y = -0.013x² + 1.25x + 5.6, where 5 ≤ x ≤ 75 and x is the speed (in miles per hour) of the car. Find the speed(s) at which you can travel and have a fuel economy of 32 miles per gallon.
Answer:

Question 62.
MODELING WITH MATHEMATICS
The depth d (in feet) of a river can be modeled by the equation d = -0.25t² + 1.7t + 3.5, where 0 ≤ t ≤ 7 and t is the time (in hours) after a heavy rain begins. When is the river 6 feet deep?
Answer:

ANALYZING EQUATIONS In Exercises 63–68, tell whether the vertex of the graph of the function lies above, below, or on the x-axis. Explain your reasoning without using a graph.
Question 63.
y = x² – 3x + 2
Answer:

Question 64.
y = 3x² – 6x + 3
Answer:

Question 65.
y = 6x² – 2x + 4
Answer:

Question 66.
y = -15x² + 10x – 25
Answer:

Question 67.
f(x) = -3x² – 4x + 8
Answer:

Question 68.
f(x) = 9x² – 24x + 16
Answer:

Question 69.
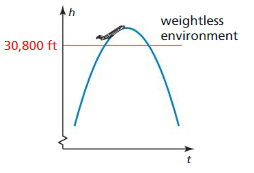
REASONING
NASA creates a weightless environment by flying a plane in a series of parabolic paths. The height h (in feet) of a plane after t seconds in a parabolic flight path can be modeled by h = -11t² + 700t + 21,000. The passengers experience a weightless environment when the height of the plane is greater than or equal to 30,800 feet. For approximately how many seconds do passengers experience weightlessness on such a flight? Explain.

Answer:

Question 70.
WRITING EQUATIONS
Use the numbers to create a quadratic equation with the solutions x = -1 and x = –\(\frac{1}{4}\)

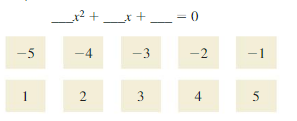
Answer:

Question 71.
PROBLEM SOLVING
A rancher constructs two rectangular horse pastures that share a side, as shown. The pastures are enclosed by 1050 feet of fencing. Each pasture has an area of 15,000 square feet.

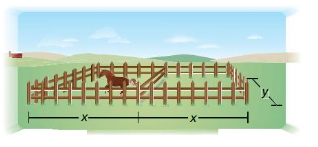
a. Show that y = 350 – \(\frac{4}{3}\)x.
b. Find the possible lengths and widths of each pasture.
Answer:

Question 72.
PROBLEM SOLVING
A kicker punts a football from a height of 2.5 feet above the ground with an initial vertical velocity of 45 feet per second.

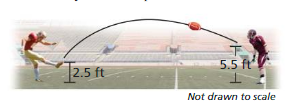
a. Write an equation that models this situation using the function h = -16t² + v⁰t + s⁰, where h is the height (in feet) of the football, t is the time (in seconds) after the football is punted, v0 is the initial vertical velocity (in feet per second), and s0 is the initial height (in feet).
b. The football is caught 5.5 feet above the ground, as shown in the diagram. Find the amount of time that the football is in the air.
Answer:

Question 73.
CRITICAL THINKING
The solutions of the quadratic equation ax² + bx + c = 0 are x = \(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\) and x = \(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\). Find the mean of the solutions. How is the mean of the solutions related to the graph of y = ax² + bx + c? Explain.
Answer:

Question 74.
HOW DO YOU SEE IT?
Match each graph with its discriminant. Explain your reasoning.

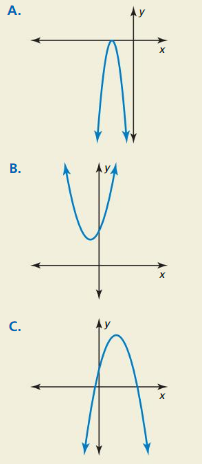
a. b² – 4ac > 0
b. b² – 4ac = 0
c. b² – 4ac < 0
Answer:

Question 75.
CRITICAL THINKING
You are trying to hang a tire swing. To get the rope over a tree branch that is 15 feet high, you tie the rope to a weight and throw it over the branch. You release the weight at a height s₀ of 5.5 feet. What is the minimum initial vertical velocity v₀ needed to reach the branch? (Hint: Use the equation h = -16t² + v₀ t + s₀)
Answer:

Question 76.
THOUGHT PROVOKING
Consider the graph of the standard form of a quadratic function y = ax² + bx + c. Then consider the Quadratic Formula as given by
x = \(-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a}\)
Write a graphical interpretation of the two parts of this formula.
Answer:

Question 77.
ANALYZING RELATIONSHIPS
Find the sum and product of \(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\) and \(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\). Then write a quadratic equation whose solutions have a sum of 2 and a product of \(\frac{1}{2}\).
Answer:

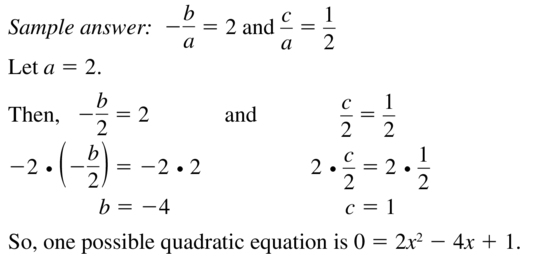
Question 78.
WRITING A FORMULA
Derive a formula that can be used to find solutions of equations that have the form ax² + x + c = 0. Use your formula to solve -2x² + x + 8 = 0.
Answer:

Question 79.
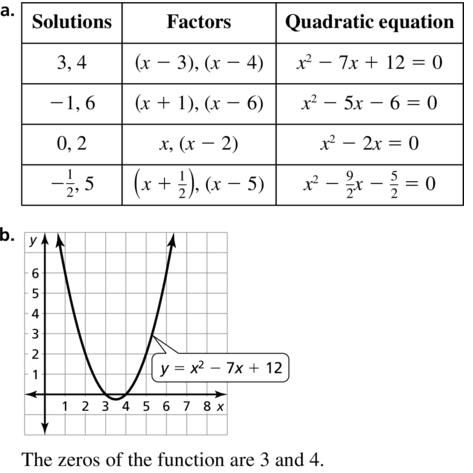
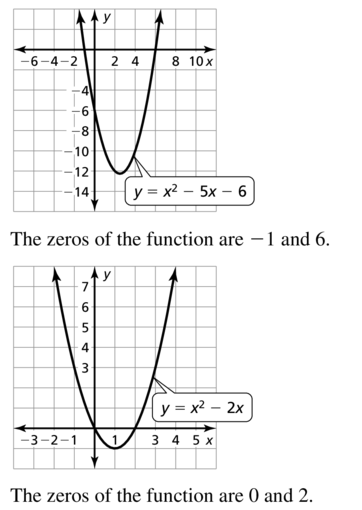
MULTIPLE REPRESENTATIONS
If p is a solution of a quadratic equation ax² + bx + c = 0, then (x – p) is a factor of ax2 + bx + c.
a. Copy and complete the table for each pair of solutions.

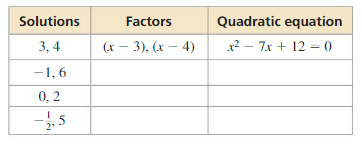
b. Graph the related function for each equation. Identify the zeros of the function.
Answer:

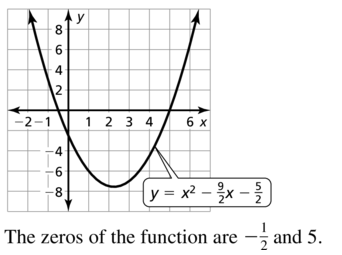
CRITICAL THINKING In Exercises 80–82, find all values of k for which the equation has (a) two solutions, (b) one solution, and (c) no solutions.
Question 80.
2x² + x + 3k = 0
Answer:

Question 81.
x² = 4kx + 36 = 0
Answer:

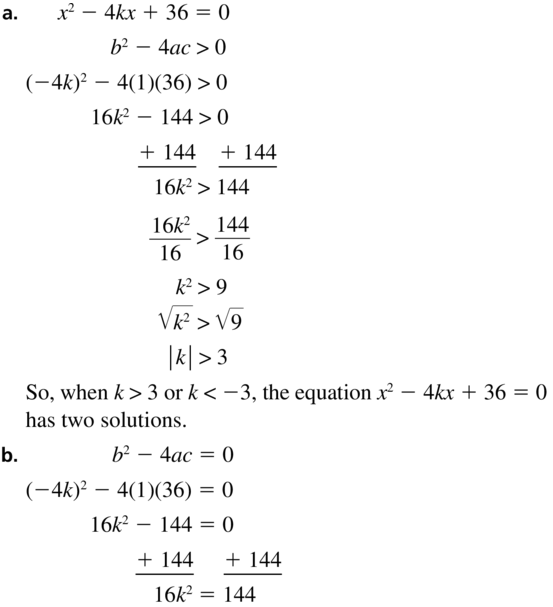
Question 82.
kx² + 5x – 16 = 0
Answer:

Maintaining Mathematical Proficiency

Solve the system of linear equations using any method. Explain why you chose the method.
Question 83.
y = -x + 4
y = 2x – 8
Answer:

Question 84.
x = 16 – 4y
3x – 4y = 8
Answer:

Question 85.
2x – y = 7
2x + 7y = 31
Answer:

Question 86.
3x – 2y = -20
x + 1.2y = 6.4
Answer:

Lesson 9.6 Solving Nonlinear Systems of Equations

Essential Question How can you solve a system of two equations when one is linear and the other is quadratic?

EXPLORATION 1
Solving a System of Equations
Work with a partner. Solve the system of equations by graphing each equation and finding the points of intersection.

System of Equations
y = x + 2 Linear
y = x² + 2x

EXPLORATION 2

Analyzing Systems of Equations
Work with a partner. Match each system of equations with its graph. Then solve the system of equations.

Communicate Your Answer

Question 3.
How can you solve a system of two equations when one is linear and the other is quadratic?
Answer:

Question 4.
Write a system of equations (one linear and one quadratic) that has (a) no solutions, (b) one solution, and (c) two solutions. Your systems should be different from those in Explorations 1 and 2.

Answer:

Monitoring Progress

Solve the system by graphing.
Question 1.
y = x² + 4x – 4
y = 2x – 5
Answer:

Question 2.
y = -x + 6
y = -2x² – x + 3
Answer:

Question 3.
y = 3x – 15
y = \(\frac{1}{2}\)x² – 2x – 7
Answer:

Solve the system by substitution.
Question 4.
y = x² + 9 5.
y = 9
Answer:

Question 5.
y = -5x
y = x² – 3x – 3
Answer:

Question 6.
y = -3x² + 2x + 1
y = 5 – 3x
Answer:

Solve the system by elimination.
Question 7.
y = x² + x
y = x + 5
Answer:

Question 8.
y = 9x² + 8x – 6
y = 5x – 4
Answer:

Question 9.
y = 2x + 5
y = -3x² + x – 4
Answer:

Use the method in Example 4 to approximate the solution(s) of the system to the nearest thousandth.
Question 10.
y = 4^x
y = x² + x + 3
Answer:

Question 11.
y = 4x² – 1
y = -2(3)^x + 4
Answer:

Question 12.
y = x² + 3x
y = -x² + x + 10
Answer:

Solve the equation. Round your solution(s) to the nearest hundredth.
Question 13.
3^x – 1 = x² – 2x + 5
Answer:

Question 14.
4x² + x = -2 (\(\frac{1}{2}\))^x + 5
Answer:

Solving Nonlinear Systems of Equations 9.6 Exercises

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
Describe how to use substitution to solve a system of nonlinear equations.
Answer:

Question 2.
WRITING
How is solving a system of nonlinear equations similar to solving a system of linear equations? How is it different?
Answer:

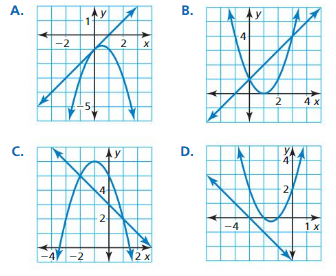
In Exercises 3–6, match the system of equations with its graph. Then solve the system.
Question 3.
y = x² – 2x + 1
y = x + 1
Answer:

Question 4.
y = x² + 3x + 2
y = -x – 3
Answer:

Question 5.
y = x – 1
y = -x² + x – 1
Answer:

Question 6.
y = -x + 3
y = -x² – 2x + 5
Answer:

In Exercises 7–12, solve the system by graphing.
Question 7.
y = 3x² – 2x + 1
y = x + 7
Answer:

Question 8.
y = x² + 2x + 5
y = -2x – 5
Answer:

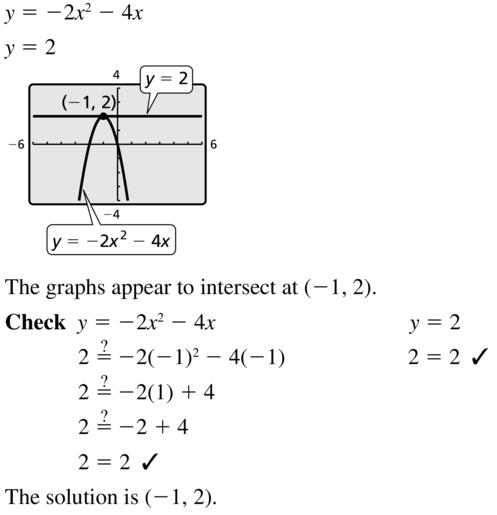
Question 9.
y = -2x² – 4x
y = 2
Answer:

Question 10.
y = \(\frac{1}{2}\)x² – 3x + 4
y = x – 2
Answer:

Question 11.
y = \(\frac{1}{3}\) x² + 2x – 3
y = 2x
Answer:

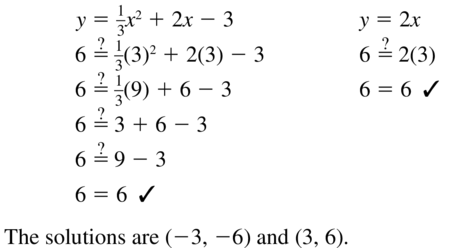
Question 12.
y = 4x² + 5x – 7
y = -3x + 5
Answer:

In Exercises 13–18, solve the system by substitution.
Question 13.
y = x – 5
y = x² + 4x – 5
Answer:

Question 14.
y = -3x²
y = 6x + 3
Answer:

Question 15.
y = -x + 7
y = -x² – 2x – 1
Answer:

Question 16.
y = -x² + 7
y = 2x + 4
Answer:

Question 17.
y – 5 = -x²
y = 5
Answer:

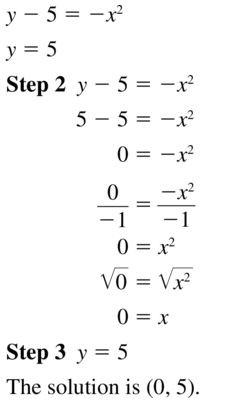
Question 18.
y = 2x² + 3x – 4
y – 4x = 2
Answer:

In Exercises 19–26, solve the system by elimination.
Question 19.
y = x² – 5x – 7
y = -5x + 9
Answer:

Question 20.
y = -3x² + x + 2
y = x + 4
Answer:

Question 21.
y = -x² – 2x + 2
y = 4x + 2
Answer:

Question 22.
y = -2x² + x – 3
y = 2x – 2
Answer:

Question 23.
y = 2x – 1
y = x²
Answer:

Question 24.
y = x² + x + 1
y = -x – 2
Answer:

Question 25.
y + 2x = 0
y = x² + 4x – 6
Answer:

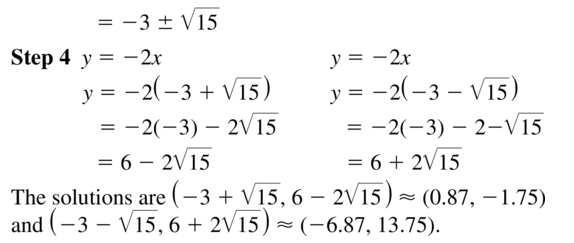
Question 26.
y = 2x – 7
y + 5x = x² – 2
Answer:

Question 27.
ERROR ANALYSIS
Describe and correct the error in solving the system of equations by graphing.

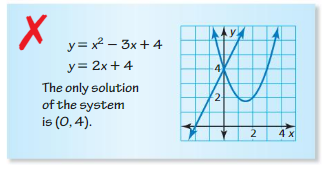
Answer:

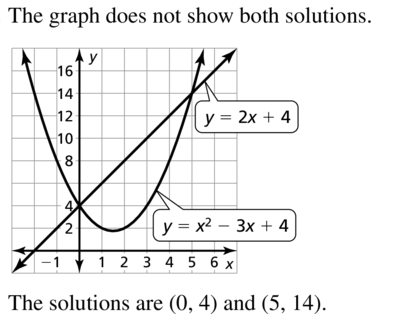
Question 28.
ERROR ANALYSIS
Describe and correct the error in solving for one of the variables in the system.

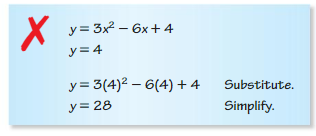
Answer:

In Exercises 29–32, use the table to describe the locations of the zeros of the quadratic function f.
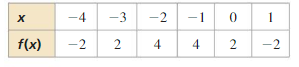
Question 29.

Answer:

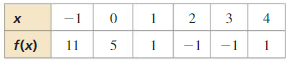
Question 30.

Answer:

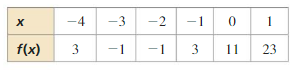
Question 31.

Answer:

Question 32.

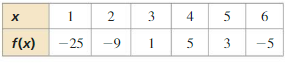
Answer:

In Exercises 33–38, use the method in Example 4 to approximate the solution(s) of the system to the nearest thousandth.
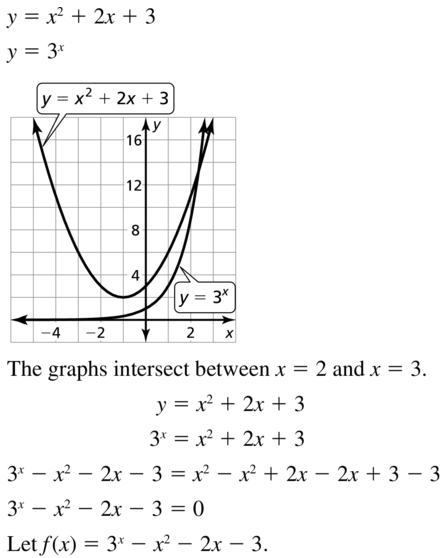
Question 33.
y = x² + 2x + 3
y = 3^x
Answer:

Question 34.
y = 2^x + 5
y = x² – 3x + 1
Answer:

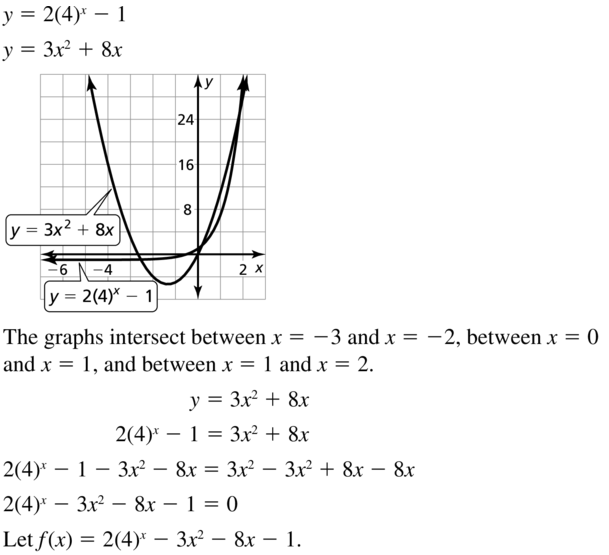
Question 35.
y = 2(4)^x – 1
y = 3x² + 8x
Answer:

Question 36.
y = -x² – 4x – 4
y = -5^x – 2
Answer:

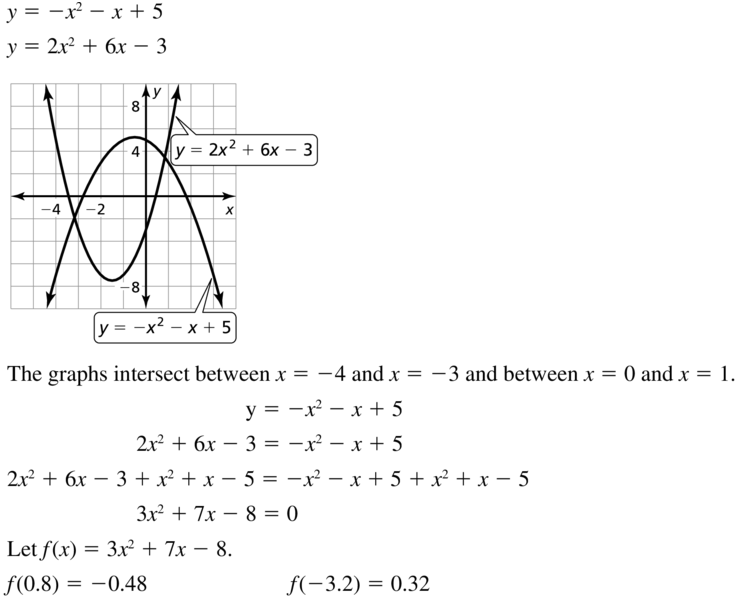
Question 37.
y = -x² – x + 5
y = 2x² + 6x – 3
Answer:

Question 38.
y = 2x² + x – 8
y = x² – 5
Answer:

In Exercises 39–46, solve the equation. Round your solution(s) to the nearest hundredth.
Question 39.
3x + 1 = x² + 7x – 1
Answer:

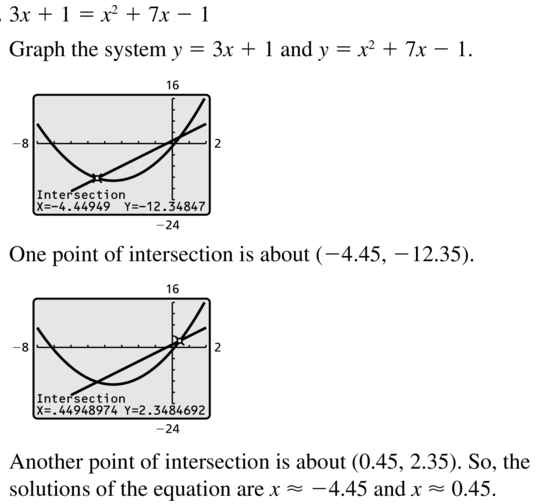
Question 40.
-x² + 2x = -2x + 5
Answer:

Question 41.
x² – 6x + 4 = -x² – 2x
Answer:

Question 42.
2x² + 8x + 10 = -x² – 2x + 5
Answer:

Question 43.
-4 (\(\frac{1}{2}\))^x = -x² – 5
Answer:

Question 44.
1.5(2)^x – 3 = -x² + 4x
Answer:

Question 45.
8^x-2 + 3 = 2 (\(\frac{3}{2}\))^x
Answer:

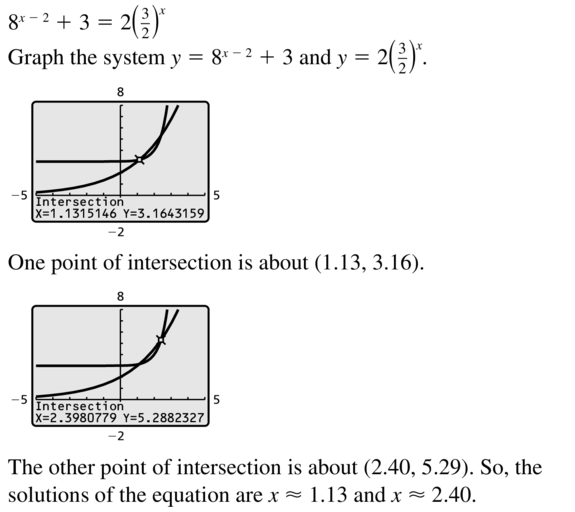
Question 46.
-0.5(4)^x = 5^x – 6
Answer:

Question 47.
COMPARING METHODS
Solve the system in Exercise 37 using substitution. Compare the exact solutions to the approximated solutions.
Answer:

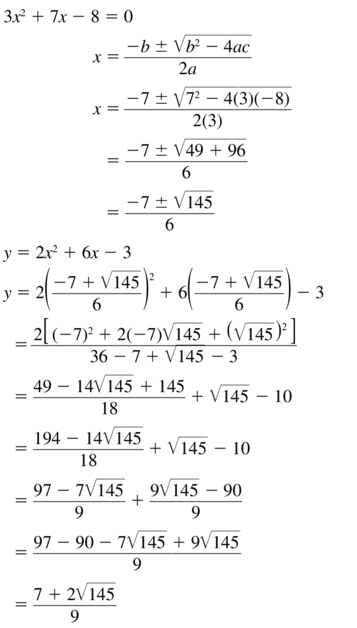
Question 48.
COMPARING METHODS
Solve the system in Exercise 38 using elimination. Compare the exact solutions to the approximated solutions.
Answer:

Question 49.
MODELING WITH MATHEMATICS
The attendances y for two movies can be modeled by the following equations, where x is the number of days since the movies opened.
y = -x² + 35x + 100 Movie A
y = -5x + 275 Movie B
When is the attendance for each movie the same?
Answer:

Question 50.
MODELING WITH MATHEMATICS
You and a friend are driving boats on the same lake. Your path can be modeled by the equation y = -x² – 4x – 1, and your friend’s path can be modeled by the equation y = -2x + 8. Do your paths cross each other? If so, what are the coordinates of the point(s) where the paths meet?

Answer:

Question 51.
MODELING WITH MATHEMATICS
The arch of a bridge can be modeled by y = -0.002x² + 1.06x, where x is the distance (in meters) from the left pylons and y is the height (in meters) of the arch above the water. The road can be modeled by the equation y = 52. To the nearest meter, how far from the left pylons are the two points where the road intersects the arch of the bridge?

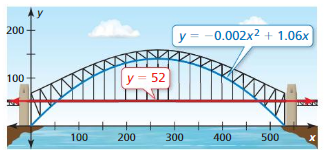
Answer:

Question 52.
MAKING AN ARGUMENT
Your friend says that a system of equations consisting of a linear equation and a quadratic equation can have zero, one, two, or infinitely many solutions. Is your friend correct? Explain.
Answer:

COMPARING METHODS In Exercises 53 and 54, solve the system of equations by (a) graphing, (b) substitution, and (c) elimination. Which method do you prefer? Explain your reasoning.
Question 53.
y = 4x + 3
y = x² + 4x – 1
Answer:

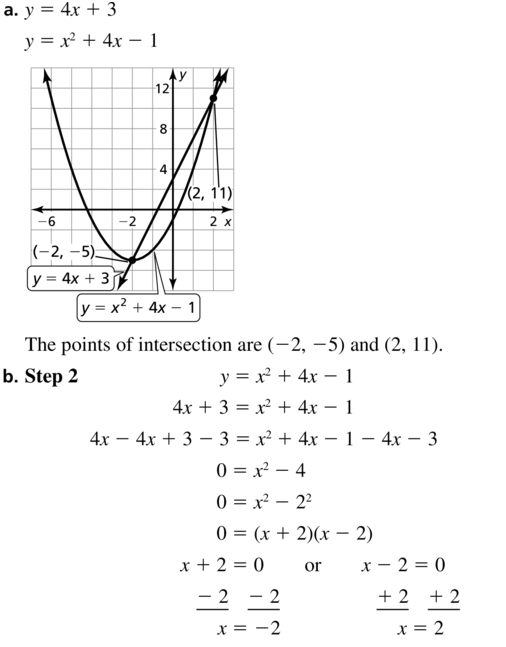
Question 54.
y = x² – 5
y = -x + 7
Answer:

Question 55.
MODELING WITH MATHEMATICS
The function y = -x² + 65x + 256 models the number y of subscribers to a website, where x is the number of days since the website launched. The number of subscribers to a competitor’s website can be modeled by a linear function. The websites have the same number of subscribers on Days 1 and 34.
a. Write a linear function that models the number of subscribers to the competitor’s website.
b. Solve the system to verify the function from part (a).
Answer:

Question 56.
HOW DO YOU SEE IT?
The diagram shows the graphs of two equations in a system that has one solution.

a. How many solutions will the system have when you change the linear equation to y = c + 2?
b. How many solutions will the system have when you change the linear equation to y = c – 2?
Answer:

Question 57.
WRITING
A system of equations consists of a quadratic equation whose graph opens up and a quadratic equation whose graph opens down. Describe the possible numbers of solutions of the system. Sketch examples to justify your answer.
Answer:

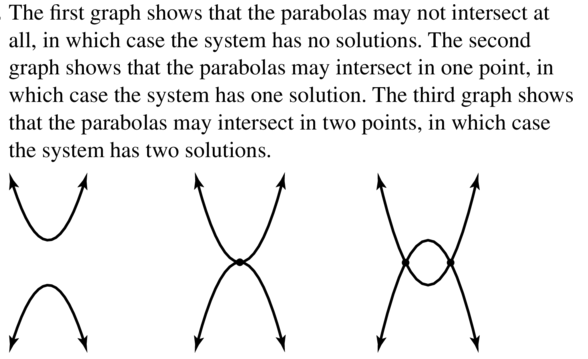
Question 58.
PROBLEM SOLVING
The population of a country is 2 million people and increases by 3% each year. The country’s food supply is sufficient to feed 3 million people and increases at a constant rate that feeds 0.25 million additional people each year.
a. When will the country first experience a food shortage?
b. The country doubles the rate at which its food supply increases. Will food shortages still occur? If so, in what year?
Answer:

Question 59.
ANALYZING GRAPHS
Use the graphs of the linear and quadratic functions.

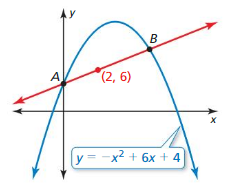
a. Find the coordinates of point A.
b. Find the coordinates of point B.
Answer:

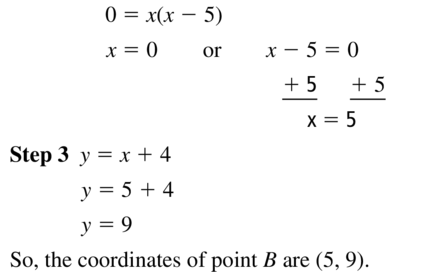
Question 60.
THOUGHT PROVOKING
Is it possible for a system of two quadratic equations to have exactly three solutions? exactly four solutions? Explain your reasoning. (Hint: Rotations of the graphs of quadratic equations still represent quadratic equations.)
Answer:

Question 61.
PROBLEM SOLVING
Solve the system of three equations shown.
y = 2x – 8
y = x² – 4x – 3
y = -3(2)^x
Answer:

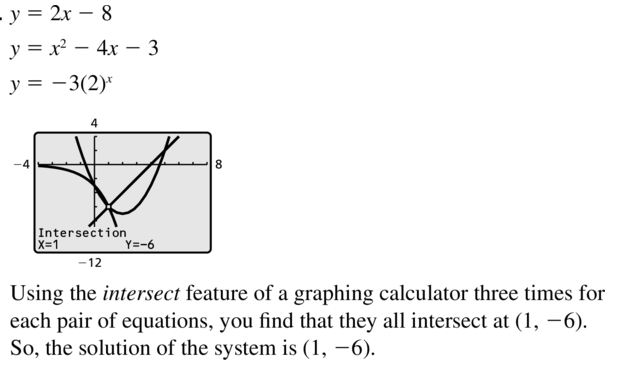
Question 62.
PROBLEM SOLVING
Find the point(s) of intersection, if any, of the line y = -x – 1 and the circle x² + y² = 41.
Answer:

Maintaining Mathematical Proficiency

Graph the system of linear inequalities.
Question 63.
y > 2x
y > -x + 4
Answer:

Question 64.
y ≥ 4x + 1
y ≤ 7
Answer:

Question 65.
y – 3 ≤ -2x
y + 5 < 3x Answer: Question 66. x + y > -6
2y ≤ 3x + 4
Answer:

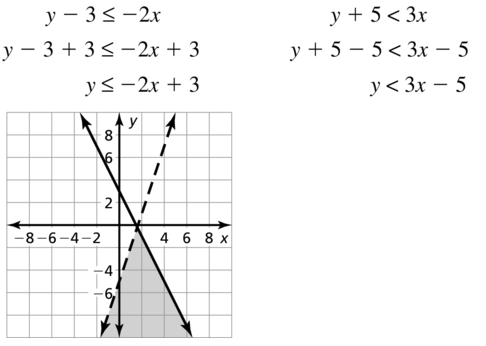
Graph the function. Describe the domain and range.
Question 67.
y = 3x² + 2
Answer:

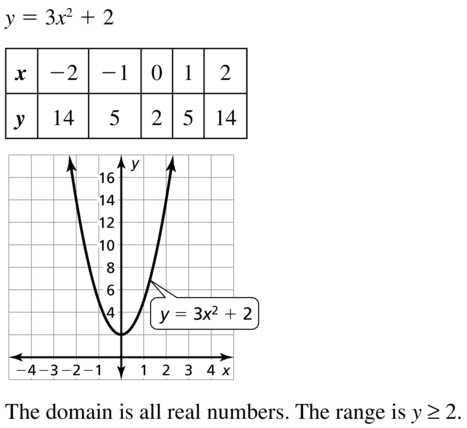
Question 68.
y = -x² – 6x
Answer:

Question 69.
y = -2x² + 12x – 7
Answer:

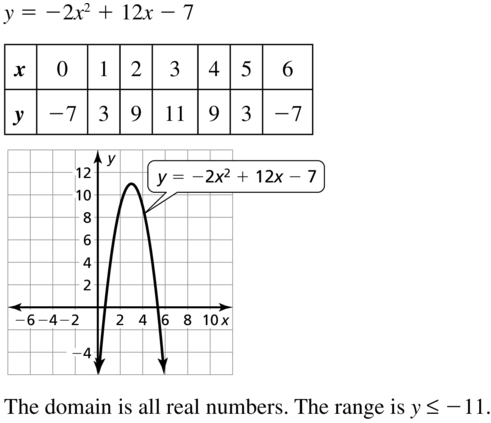
Question 70.
y = 5x² + 10x – 3
Answer:

Solving Quadratic Equations Performance Task: Form Matters

9.4–9.6 What Did You Learn?

Core Vocabulary

Core Concepts
Section 9.4
Completing the Square, p. 506

Section 9.5
Quadratic Formula, p. 516
Interpreting the Discriminant, p. 518

Section 9.6
Solving Systems of Nonlinear Equations, p. 526

Mathematical Practices
Question 1.
How does your answer to Exercise 74 on page 514 help create a shortcut when solving some quadratic equations by completing the square?
Answer:

Question 2.
What logical progression led you to your answer in Exercise 55 on page 522?
Answer:

Question 3.
Compare the methods used to solve Exercise 53 on page 532. Discuss the similarities and differences among the methods.
Answer:

Performance Task Form Matters

Each form of a quadratic function has its pros and cons. Using one form, you can easily find the vertex, but the zeros are more difficult to find. Using another form, you can easily find the y-intercept, but the vertex is more difficult to find. Which form would you use in different situations? How can you convert one form into another? To explore the answers to these questions and more, go to.

Solving Quadratic Equations Chapter Review

9.1 Properties of Radicals (pp. 479–488)

Simplify the expression.
Question 1.
\(\sqrt{72 p^{7}}\)
Answer:

Question 2.
\(\sqrt{\frac{45}{7 y}}\)
Answer:

Question 3.
\(\sqrt[3]{\frac{125 x^{11}}{4}}\)
Answer:

Question 4.
\(\frac{8}{\sqrt{6}+2}\)
Answer:

Question 5.
4\(\sqrt{3}\) + 5\(\sqrt{12}\)
Answer:

Question 6.
15\(\sqrt [ 3 ]{ 2 }\) – 2\(\sqrt [ 3 ]{ 54 }\)
Answer:

Question 7.
(3\(\sqrt{7}\) + 5)²
Answer:

Question 8.
\(\sqrt{6}\)(\(\sqrt{18}\) + \(\sqrt{8}\))
Answer:

9.2 Solving Quadratic Equations by Graphing (pp. 489–496)

Solve the equation by graphing

Question 9.
x² – 9x + 18 = 0
Answer:

Question 10.
x² – 2x = -4
Answer:

Question 11.
-8x – 16 = x²
Answer:

Question 12.
The graph of f(x) = (x + 1)(x² + 2x – 3) is shown. Find the zeros of f.
Answer:

Question 13.
Graph f(x) = x² + 2x – 5. Approximate the zeros of f to the nearest tenth.
Answer:

9.3 Solving Quadratic Equations Using Square Roots (pp. 497–502)

Solve the equation using square roots. Round your solutions to the nearest hundredth, if necessary.
Question 14.
x² + 5 = 17
Answer:

Question 15.
x² – 14 = -14
Answer:

Question 16.
(x + 2)² = 64
Answer:

Question 17.
4x² + 25 = -75
Answer:

Question 18.
(x – 1)² = 0
Answer:

Question 19.
19 = 30 – 5x²
Answer:

9.4 Solving Quadratic Equations by Completing the Square (pp. 505–514)

Solve the equation by completing the square. Round your solutions to the nearest hundredth, if necessary.
Question 20.
x² + 6x – 40 = 0
Answer:

Question 21.
x² + 2x + 5 = 4
Answer:

Question 22.
2x² – 4x = 10
Answer:

Determine whether the quadratic function has a maximum or minimum value. Then find the value.
Question 23.
y = -x² + 6x – 1
Answer:

Question 24.
f(x) = x² + 4x + 11
Answer:

Question 25.
y = 3x² – 24x + 15
Answer:

Question 26.
The width w of a credit card is 3 centimeters shorter than the length ℓ. The area is 46.75 square centimeters. Find the perimeter.
Answer:

9.5 Solving Quadratic Equations Using the Quadratic Formula (pp. 515–524)

Solve the equation using the Quadratic Formula. Round your solutions to the nearest tenth, if necessary.
Question 27.
x²+ 2x – 15 = 0
ans;

Question 28.
2x² – x + 8 = 16
Answer:

Question 29.
-5x² + 10x = 5
ans;

Find the number of x-intercepts of the graph of the function.
Question 30.
y = -x² + 6x – 9
Answer:

Question 31.
y = 2x² + 4x + 8
Answer:

Question 32.
y = – \(\frac{1}{2}\)x² + 2x
Answer:

9.6 Solving Nonlinear Systems of Equations (pp. 525–532)

Solve the system using any method.
Question 33.
y = x² – 2x – 4
y = -5
Answer:

Question 34.
y = x² – 9
y = 2x + 5
Answer:

Question 35.
y = 2(\(\frac{1}{2}\))^x – 5
y = -x² – x + 4
Answer:

Solving Quadratic Equations Chapter Test

Solve the equation using any method. Explain your choice of method.
Question 1.
x² – 121 = 0
Answer:

Question 2.
x² – 6x = 10
Answer:

Question 3.
-2x² + 3x + 7 = 0
Answer:

Question 4.
x² – 7x + 12 = 0
Answer:

Question 5.
5x² + x – 4 = 0
Answer:

Question 6.
(4x + 3)² = 16
Answer:

Question 7.
Describe how you can use the method of completing the square to determine whether the function f(x) = 2x² + 4x – 6 can be represented by the graph shown.

Answer:

Question 8.
Write an expression involving radicals in which a conjugate can be used to simplify the expression.
Answer:

Solve the system using any method.
Question 9.
y = x² – 4x – 2
y = -4x + 2
Answer:

Question 10.
y = -5x² + x – 1
y = -7
Answer:

Question 11.
y = \(\frac{1}{2}\)(4)^x + 1
y = x² – 2x + 4
Answer:

Question 12.
A skier leaves an 8-foot-tall ramp with an initial vertical velocity of 28 feet per second. The function h = -16t² + 28t + 8 represents the height h (in feet) of the skier after t seconds. The skier has a perfect landing. How many points does the skier earn?

Answer:

Question 13.
An amusement park ride lifts seated riders 265 feet above the ground. The riders are then dropped and experience free fall until the brakes are activated 105 feet above the ground. The function h = -16t² + 265 represents the height h (in feet) of the riders t seconds after they are dropped. How long do the riders experience free fall? Round your solution to the nearest hundredth.
Answer:

Question 14.
Write an expression in simplest form that represents the area of the painting shown.

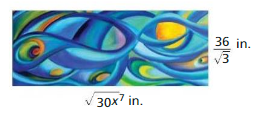
Answer:

Question 15.
Explain how you can determine the number of times the graph of y = 5x² – 10x + 5 intersects the x-axis without graphing or solving an equation.
Answer:

Question 16.
Consider the quadratic equation ax² + bx + c = 0 Find values of a, b, and c so that the graph of its related function has (a) two x x-intercepts, (b) one x-intercepts.and (c) no x-intercepts.
Answer:

Question 17.
The numbers y of two types of bacteria after x hours are represented by the models below.
y = 3x² + 8x + 20 Type A
y = 27x + 60 Type B
a. When are there 400 Type A bacteria?
b. When are the number of Type A and Type B bacteria the same?
c. When are there more Type A bacteria than Type B? When are there more Type B bacteria than Type A? Use a graph to support your answer.
Answer:

Solving Quadratic Equations Cumulative Assessment

Question 1.
The graphs of four quadratic functions are shown. Determine whether the discriminants of the equations formed by setting each function equal to zero are positive, negative, or zero.f(x) = 0, g(x) = 0, h(x) = 0, and j(x) = 0

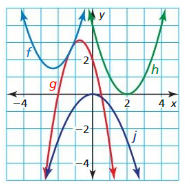
Answer:

Question 2.
The function f(x) = a(1.08)^x represents the total amount of money (in dollars) in Account A after x years. The function g(x) = 600(b)^x represents the total amount of money (in dollars) in Account B after x years. Fill in values for a and b so that each statement is true.
a. When a = ____ and b = ____, Account B has a greater initial amount and increases at a faster rate than Account A.
b. When a = ____ and b = ____, Account B has a lesser initial amount than Account A but increases at a faster rate than Account A.
c. When a = ____ and b = ____, Account B and Account A have the same initial amount, and Account B increases at a slower rate than Account A.
Answer:

Question 3.
Your friend claims to be able to find the radius r of each figure, given the surface area S. Do you support your friend’s claim? Justify your answer.

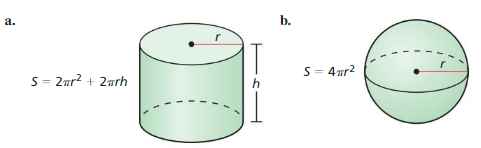
Answer:

Question 4.
The tables represent the numbers of items sold at a concession stand on days with different average temperatures. Determine whether the data represented by each table show a positive, a negative, or no correlation.

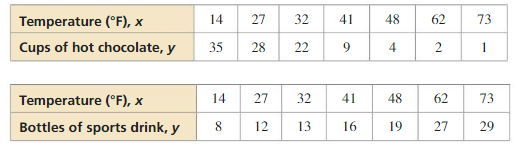
Answer:

Question 5.
Which graph shows exponential growth?

Answer:

Question 6.
Which statement best describes the solution(s) of the system of equations?
y = x² + 2x – 8
y = 5x + 2
A. The graphs intersect at one point, (-2, -8). So, there is one solution.
B. The graphs intersect at two points, (-2, -8) and (5, 27). So, there are two solutions.
C. The graphs do not intersect. So, there is no solution.
D. The graph of y = x² + 2x – 8 has two x-intercepts. So, there are two solutions.
Answer:

Question 7.
Which expressions are in simplest form?

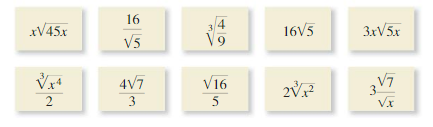
Answer:

Question 8.
The domain of the function shown is all integers in the interval -3 < x ≤ 3. Find all the ordered pairs that are solutions of the equation y = f(x).
f(x) = 4x – 5
Answer: