The basics must be strong to grow with perfect knowledge. Students need to learn the math basics strongly to become a master in maths. Big Ideas Math Answers Grade 4 Chapter 2 Add and Subtract Multi-Digit Numbers is the best reference to make your student’s basics strong. The Big Ideas Grade 4 Chapter 2 Add and Subtract Multi-Digit Numbers Math Answers will help your students to achieve their dreams of learning maths with simple methods. From the fundamentals of Add and Subtract Multi-Digit Numbers to difficult problems, all are given on this page.
Big Ideas 4th Grade Chapter 2 Add and Subtract Multi-Digit Numbers Math Book Answer Key
Check out the Big Ideas Math Answers Grade 4 Chapter 2 Add and Subtract Multi-Digit Numbers links provided in the below section to begin your preparation. We have given a detailed explanation for each and every problem for your better understanding. So, make use of every given link and try to score the best marks in the exams. The basics mentioned here will not only help you in the exam but also in real life. Be the first to learn the best of math topics by referring to bigideasmathanswers.com
Lesson: 1 Estimate Sum and Differences
Lesson 2.1 Estimate Sum and Differences
Estimate Sum and Differences Homework & Practice 2.1
Lesson: 2 Add Multi-Digit Numbers
Lesson 2.2 Add Multi-Digit Numbers
Add Multi-Digit Numbers Homework & Practice 2.2
Lesson: 3 Subtract Multi-Digit Numbers
Lesson 2.3 Subtract Multi-Digit Numbers
Subtract Multi-Digit Numbers Homework & Practice 2.3
Lesson: 4 Use Strategies to Add and Subtract
Lesson 2.4 Use Strategies to Add and Subtract
Use Strategies to Add and Subtract Homework & Practice 2.4
Lesson: 5 Problem Solving: Addition and Subtraction
Lesson 2.5 Problem Solving: Addition and Subtraction
Problem Solving: Addition and Subtraction Homework & Practice 2.5
Performance Task
Add and Subtract Multi-Digit Numbers Performance Task
Add and Subtract Multi-Digit Numbers Activity
Add and Subtract Multi-Digit Numbers Chapter Practice
Lesson 2.1 Estimate Sum and Differences
Explore and Grow
Estimate to find each sum by rounding to the nearest thousand, hundred, or ten. Explain why you chose to round to that place value.
A football team had 917 spectators at their first game and 872 at their second game. About how many spectators did the team have at both games?
Answer: The answer is 1789.
Explanation:
Number of spectators in First game: 917
Number of spectators in First game: 872
To get the number of spectators in both the games, we have to add the number of spectators in first game and second game.
That means, 917 + 872 = 1789.
A company budgets $1,800 for a company picnic. They spend $917 on the location and $872 on food. Did they stay within their budget?
Answer: Yes, they can stay within their budget.
Explanation:
Total budget: $1,800
Spend for location: $917
Spend for food: $872
Total spend = spend for location + spend for food.
That means, total spend = $917 + $872 = $1789.
Balance budget = Total budget – Total spend
That means, Balance budget: $1800 – $1789 = $11
As, the total spend for the company picnic is lesser than the company budget, they can stay within the budget.
Reasoning
Explain why you may choose to round to different place values in different situations.
Answer: “Round to” are the approximate values we give that are the nearest possible values to the exact values. Sometimes, we may be sufficient with the estimate or nearest values. We may not require the exact values. In such situations, we can go ahead with the round to values. For example, you organized a lunch at your home. The caterer asks you for the number of guests for whom the lunch has to be served. You cannot give him the exact number of guests. You give him the round of value of the number of guests attend based on your past experience and present situation. In such cases, round to is very helpful.
Think and Grow: Estimate Sum and Differences
An estimate is a number that is close to an exact number. You can use rounding to estimate sums and differences.
Example
Estimate 8,675 + 3,214.
One Way: Round each addend to the nearest hundred. Then find the sum.
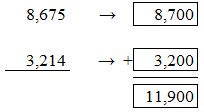
So, 8,675 + 3,214 is about rounding the two numbers to the nearest hundreds. 8,700 is the nearest hundreds value for 8,675. 3200 is the nearest hundreds value for 3214.
Then, we will add 8,700 and 3,200.
8,700 + 3,200 = 11, 900
Another Way: Round each addend to the nearest thousand. Then find the sum.
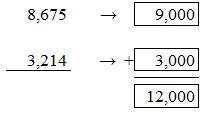
So, 8,675 + 3,214 is about rounding the two numbers to the nearest thousands. 9,000 is the nearest thousands value for 8,675. 3,000 is the nearest thousands value for 3214.
Then, we will add 9,000 and 3,000.
9,000 + 3,000 = 12, 000
.
Example
Estimate 827,615 – 54,3006.
One Way: Round each addend to the nearest thousand. Then find the difference.
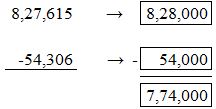
So, 827,615 – 54,306 is about rounding the two numbers to the nearest thousands. 8,28,000 is the nearest thousands value for 8,27,615. 54,000 is the nearest thousands value for 54,306.
Then, we will subtract 54,000 from 8,28,000.
8,28,000 – 54,000 = 7,74,000.
Another Way: Round each addend to the nearest ten thousand. Then find the difference.

So, 827,615 – 54,306 is about rounding the two numbers to the nearest ten thousands. 8,30,000 is the nearest thousands value for 8,27,615. 50,000 is the nearest thousands value for 54,306.
Then, we will subtract 50,000 from 8,30,000.
8,28,000 – 54,000 = 7,80,000.
Show and Grow
Estimate the sum or difference.
Question 1.
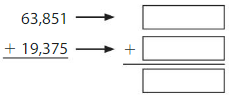
Answer: We will here round of the values to the nearest hundreds. 63,900 is the nearest hundred for 63,851. For, 19,375 the nearest hundred value is 19,400.
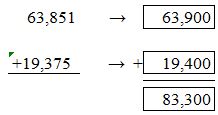
Now we will add 63,900 to 19,400.
63,900 + 19,400 = 83,300.
Question 2.
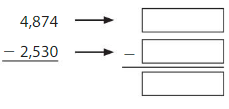
Answer: We will here round of the values to the nearest hundreds. 4,900 is the nearest hundred for 4,874. For, 2,530 the nearest hundred value is 2,500.
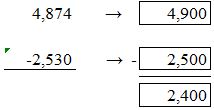
Now we will subtract 2,500 from 4,900.
4,900 – 2,500 = 2,400.
Apply and Grow: Practice
Estimate the sum or difference.
Question 3.
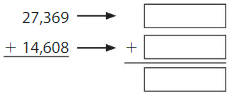
Answer:
We here round the values to the nearest hundreds value.
For 27,369 the nearest hundreds value is 27,400. For 14,608 the nearest hundred value is 14,600.
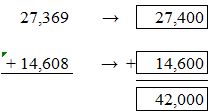
27,400 + 14,600 = 42,000.
So, the estimate of the sum of 27,369 and 14,608 by rounding to the nearest hundreds value is 42,000.
Question 4.
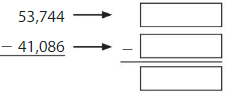
Answer:
We here round the values to the nearest hundreds value.
For 53,744 the nearest hundreds value is 53,700. For 41,086 the nearest hundred value is 41,100.
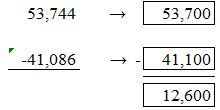
53,700 – 41,100 = 12,600.
So, the estimate of the difference of 53,744 and 41,086 by rounding to the nearest hundreds value is 12,600.
Question 5.
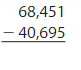
Answer:
We here round the values to the nearest thousands value.
For 68,451 the nearest thousands value is 68,000. For 40,695 the nearest thousands value is 41,000.
68,000 – 41,000 = 27,000.
So, the estimate of the difference of 68,451 and 40,695 by rounding to the nearest thousands value is 27,000.
Question 6.
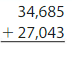
Answer:
We here round the values to the nearest thousands value.
For 34,685 the nearest thousands value is 35,000. For 27,043 the nearest thousands value is 27,000.
35,000 + 27,000 = 62,000.
So, the estimate of the sum of 34,685 and 27,043 by rounding to the nearest thousands value is 62,000.
Question 7.
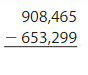
Answer:
We here round the values to the nearest ten thousands value.
For 908,465 the nearest ten thousands value is 910,000. For 653,629 the nearest ten thousands value is 650,000.
910,000 – 650,000 = 260,000.
So, the estimate of the difference of 908,465 and 653,299 by rounding to the nearest ten thousands value is 260,000.
Question 8.
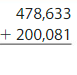
Answer:
We here round the values to the nearest ten thousands value.
For 478,633 the nearest ten thousands value is 480,000. For 200,081 the nearest ten thousands value is 200,000.
480,000 + 200,000 = 680,000.
So, the estimate of the sum of 478,633 and 200,081 by rounding to the nearest ten thousands value is 680,000.
Question 9.
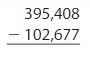
Answer:
We here round the values to the nearest thousands value.
For 395,408 the nearest thousands value is 395,000. For 102,677 the nearest thousands value is 103,000.
395,000 – 103,000 = 292,000.
So, the estimate of the difference of 395,408 and 102,677 by rounding to the nearest thousands value is 292,000.
Question 10.
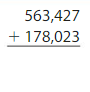
Answer:
For 563,427 the nearest ten thousands value is 560,000. For 178,023 the nearest ten thousands value is 180,000.
560,000 + 180,000 = 740,000.
So, the estimate of the sum of 563,427 and 178,023 by rounding to the nearest ten thousands value is 740,000.
Question 11.
888,056 – 423,985 = _______
Answer:
We here round the values to the nearest ten thousands value.
For 888,056 the nearest ten thousands value is 890,000. For 423,985 the nearest ten thousands value is 420,000.
890,000 – 420,000 = 472,000.
So, the estimate of the difference of 888,056 and 423,985 by rounding to the nearest ten thousands value is 470,000.
Question 12.
713,642 + 49,018 = ______
Answer:
We here round the values to the nearest thousands value.
For 713,642 the nearest thousands value is 714,000. For 49,018 the nearest thousands value is 49,000.
714,000 + 49,000 = 763,000.
So, the estimate of the sum of 713,642 and 49,018 by rounding to the nearest thousands value is 763,000.
Question 13.
DIG DEEPER!
Is 20,549 + 9,562 greater than or less than 30,000? Explain how you know without finding the exact sum.
Answer:
We will solve this using round to estimates.
For 20,549 the nearest hundreds value is 20,500. For 9,562 the nearby smaller hundreds value is 9,500.
20,500 + 9,500 = 30,000.
The estimate sum is 30,000. We still have the values of 49 and 62 in both the values. So, the value of the sum of 20,549 and 9,562 is greater than 30,000.
Question 14.
Writing
Describe a real-life situation in which estimation would not be appropriate to use.
Answer:
Think and Grow: Modeling Real Life
Example
About how many more pounds does the whale shark weigh than the orca?

Round the weight of each animal to the nearest thousand because you do not need a precise answer.
Orca: 8,000 Whale shark: 40,000.
Subtract the estimated weight of the orca from the estimated weight of the whale shark.
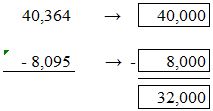
The whale shark weighs about 32,000 more pounds than the orca.
Show and Grow
Question 15.
About how many more votes did Candidate A receive than Candidate B?
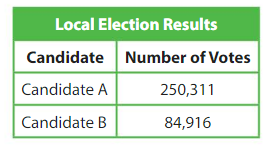
Answer:
Round the number of votes to the nearest thousands value.
Candidate A: 250,000. Candidate B: 85,000

Candidate A scored about 165,000 votes more than Candidate B.
Question 16.
Mount Saint Helens is a volcano that is 8,363 feet tall. Mount Fuji is a volcano that is 4,025 feet taller than Mount Saint Helens. About howtall is Mount Fuji?

Answer:
Round the heights of the volcanoes to the nearest hundreds value.
Mount Saint Helens: 8,400. Mount Fuji: 4,000.
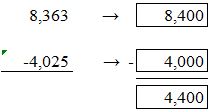
So, Mount Helens is about 4,400 feet taller than Mount Fuji.
Question 17.
An educational video has 6,129 fewer views than a gaming video. The educational video has 483,056 views. About how many views does the gaming video have?
Answer:
Here, it is given that the educational video has 6,129 fewer views than the gaming video.
That means, Gaming Video views – 6,129 = Educational video views.
Or Gaming video views = Educational video views + 6,129.
Given educational video views = 483,056
Therefore, Gaming video views = 483,056 + 6,129 = 489,185.
So, the number of gaming video views = 489,185.
Estimate Sum and Differences Homework & Practice 2.1
Estimate the sum or difference.
Question 1.
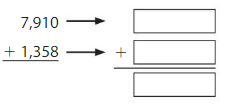
Answer:
Round the values to the nearest hundreds values.
For 7,910 the nearest hundreds value is 7,900. For 1,358, the nearest hundreds value is 1,400.
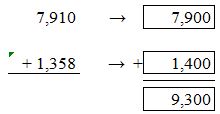
7,900 + 1,400 = 9,300.
Question 2.
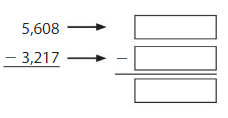
Answer:
Round the values to the nearest hundreds values.
For 5,608 the nearest hundreds value is 5,600. For 3,217, the nearest hundreds value is 3,200.
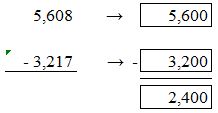
5,600 – 3,200 = 2,400
Question 3.
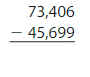
Answer:
Round the values to the nearest thousands values.
For 73,406 the nearest thousands value is 73,000. For 45,699 the nearest thousands value is 46,000.
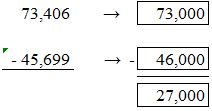
73,000 – 46,000 = 27,000
Question 4.
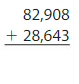
Answer:
Round the values to the nearest thousands values.
For 82,908 the nearest thousands value is 83,000. For 28,643 the nearest thousands value is 29,000.
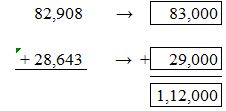
83,000 + 29,000 = 1,12,000
Question 5.
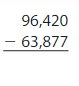
Answer:
Round the values to the nearest thousands values.
For 96,420 the nearest thousands value is 96,000. For 63,877 the nearest thousands value is 64,000.

96,000 – 64,000 = 32,000
Question 6.
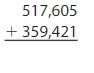
Answer:
Round the values to the nearest ten thousands values.
For 517,605 the nearest ten thousands value is 520,000. For 359,421 the nearest ten thousands value is 360,000.

520,000 + 360,000 = 880,000
Question 7.
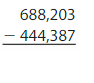
Answer:
Round the values to the nearest ten thousands values.
For 688,203 the nearest ten thousands value is 690,000. For 444,387 the nearest ten thousands value is 440,000.

690,000 – 440,000 = 250,000
Question 8.
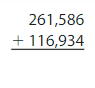
Answer:
Round the values to the nearest ten thousands values.
For 261,586 the nearest ten thousands value is 260,000. For 116,934 the nearest ten thousands value is 120,000.
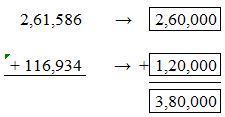
260,000 + 120,000 = 380,000
Estimate the sum or difference.
Question 9.
864,733 – 399,608 = ______
Answer:
Round the values to the nearest ten thousands values.
864,733: 860,000
399,608: 400,000
860,000 – 400,000 = 460,000
Question 10.
134,034 + 26,987 = ______
Answer:
Round the values to the nearest thousands values.
134,034: 134,000
26,987: 27,000
134,000 + 27,000 = 161,000
Question 11.
Number Sense
Descartes estimates a difference by rounding each number to the nearest ten thousand. His estimate is 620,000. Which problems could he have estimated?

Answer:
Round off all the given values to their nearest ten thousand value.
690,000 – 70,000 = 620,000
890,000 – 270,000 = 620,000
680,000 – 50,000 = 630,000
700,000 – 80,000 = 620,000.
So, Descartes could have estimated problems 1,2 and 4 and all the three give the estimated difference of 620,000.
Question 12.
Reasoning
When might you estimate the difference of 603,476 and 335,291 to the nearest hundred? to the nearest hundred thousand?
Answer:
When the precision of the difference value should be in hundreds, then round the values to hundred and calculate the difference.
603,476: 603,500 & 335,291: 335,300
603,500 – 335,300 = 268,200.
When the precision of the difference value should be in thousands, then round the values to thousands and calculate the difference.
603,476: 603,000 & 335,291: 335,000
603,000 – 335,000 = 268,000
Question 13.
Modeling Real Life
A storm causes causes 23,890 homes to be without power on the east side of a city and 18,370 homes to be without power on the west side. About how many homes altogether are without power?

Answer:
Homes without power on east side: 23,890
Homes without power on west side: 18,370
Round the values to the nearest thousands value.
So, homes without power on east side = 24,000 and homes without power on west side = 18,000.
Total homes without power = 24,000 + 18,000 = 42,000
Therefore, total estimate of homes without power due to storm are 42,000.
Question 14.
Modeling Real Life
You walk 5,682 steps. Your teacher walks 4,219 steps more than you. About how many steps does your teacher walk?

Answer:
Round the number of steps to the nearest hundreds value.
Number of steps I walked, 5,682 rounding it to the nearest hundreds value = 5,700
Number of steps teacher walked additional more than me, 4,219 rounding it to the nearest hundreds value = 4,200
Total number of steps teacher walked = Number of steps I walked + additional number of steps teacher walked.
Therefore total number of steps teacher walked = 5,700 + 4,200 = 9,900.
Review & Refresh
Find the product.
Question 15.
3 × 3 × 2 = ______
Answer:
Break the multiplication into steps as follows:
(3 X 3) x 2
= 9 x 2
=18
Question 16.
2 × 4 × 7 = ______
Answer:
Break the multiplication into steps as follows:
2 X (4 X 7)
= 2 X 28
= 56
Question 17.
3 × 3 × 5 = ______
Answer:
Break the multiplication into steps as follows:
(3 X 3) X 5
= 9 X 5
= 45.
Question 18.
6 × 2 × 3 = ______
Answer:
Break the multiplication into steps as follows:
6 X (2 X 3)
=6 X 6
= 36.
Question 19.
4 × 9 × 2 = ______
Answer:
Break the multiplication into steps as follows:
4 X (9 X 2)
= 4 X 18
= 72
Question 20.
4 × 10 × 2 = ______
Answer:
Break the multiplication into steps as follows:
4 X (10 X 2)
= 4 X 20
= 80.
Lesson 2.2 Add Multi-Digit Numbers
Explore and Grow
Which addition problem shows a correct way to find 38 +7? Why?

Answer:
The second option shows the correct way.
Explanation: As per place value rule, 7 is the units position value. A units digit always should be added to the units digit of the other number. In the first option, 7 is under 3, which is actually in tens digit position. The second option displays it correctly pointing 7 under the units digit value, 8.
Which addition problem shows a correct way to find 403 + 1,248? Why?

Answer:
The first option shows the correct way.
Explanation: As per place value rule, a units digit always should be added to the units digit of the other number. Similarly, tens digit value to the other number’s tens digit value and the hundreds digit value. First option maintains the rule correctly pointing 8 under 3, both which are units values. Similarly, 4 under 0 and 2 under 8. The second option started the sum from the left, which means, adding thousands digit value of 1,248 to the hundreds digit value of 403.
Reasoning
Why do you need to use place value when adding? Explain.
Answer:
While adding, we use place value i.e., we go from right hand side to the left hand side. In other words, we add the digits as per the place value. The digit of every number holds the place value. That means, a digit in tens place has the value of multiple of ten. Similarly, a digit in hundreds place has the value of multiple of hundred.
For example, In the number 23, 2 digit holds the value of multiple of ten. That means, 2 X 10.
To continue the parity of the sum, we follow the place value rule by adding digits as per the place values.
Think and Grow: Add Multi-Digit Numbers
Example
Add: 307,478 + 95,061.
Estimate: 307,000 + 95,000 = _______
Use place value to line up the addends.

Add the ones, then the tens, and then the hundreds. Regroup if necessary.

Add the thousands, then the ten thousands, and then the hundred thousands. Regroup if necessary.

Show and Grow
Find the sum. Check whether your answer is reasonable.
Question 1.
Estimate: _______
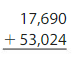
Answer:
Estimate: Round the values to the nearest hundreds.
17,700 + 53,000 = 70,700.
Add the tens, then hundreds, thousands and then the ten thousands. Regroup if necessary.
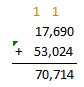
Check: Because 70,714 is close to the estimate, 70,700, the answer is reasonable.
Question 2.
Estimate: ______
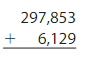
Answer:
Round the values to the nearest hundreds.
297,900 + 6,100 = 304,000
Add the ones, tens, then hundreds and thousands. Regroup if necessary.
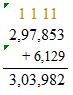
Check: Because 303,982 is close to the estimate, 304,000, the answer is reasonable.
Apply and Grow: Practice
Find the sum. Check whether your answer is reasonable.
Question 3.
Estimate: ______
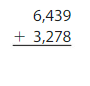
Answer:
Round the values to the nearest hundreds.
Estimate: 6,400 + 3,300 = 9,700
Add the ones, tens, then hundreds and thousands. Regroup if necessary.
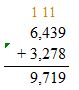
Check: Because 9,719 is close to the estimate, 9,700, the answer is reasonable.
Question 4.
Estimate: ______
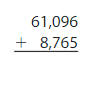
Answer:
Round the values to the nearest hundreds.
Estimate: 61,100 + 8,800 = 69,900
Add the ones, tens, then hundreds, then thousands and ten thousands. Regroup if necessary.
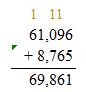
Check: Because 69,861 is close to the estimate, 69,900, the answer is reasonable.
Question 5.
Estimate: ______

Answer:
Round the values to the nearest hundreds.
Estimate: 82,200 + 4,700 = 86,900
Add the ones, tens, then hundreds, then thousands and ten thousands. Regroup if necessary.
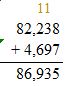
Check: Because 86,935 is close to the estimate, 86,900, the answer is reasonable.
Question 6.
Estimate: ______
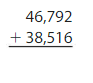
Answer:
Round the values to the nearest hundreds.
Estimate: 46,800 + 38,500 = 85,300
Add the ones, tens, then hundreds, then thousands and ten thousands. Regroup if necessary.

Check: Because 85,308 is close to the estimate, 85,300, the answer is reasonable.
Question 7.
Estimate: ______
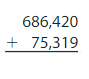
Answer:
Round the values to the nearest hundreds.
Estimate: 686,400 + 75,300 = 761,700
Add the ones, tens, then hundreds, then thousands and ten thousands. Regroup if necessary.
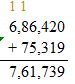
Check: Because 761,739 is close to the estimate, 761,700, the answer is reasonable.
Question 8.
Estimate: ______
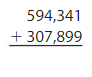
Answer:
Round the values to the nearest thousands.
Estimate: 594,000 + 308,000 = 902,000
Add the ones, tens, then hundreds, then thousands, ten thousands and then hundred thousands. Regroup if necessary.

Check: Because 902,240 is close to the estimate, 902,000, the answer is reasonable.
Question 9.
Estimate: ______
246,890 + 13,579 = ______
Answer:
Round the values to the nearest thousands.
Estimate: 247,000 + 14,000 = 261,000
Add the ones, tens, then hundreds, then thousands and then ten thousands. Regroup if necessary.
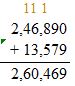
Check: Because 260,469 is close to the estimate, 261,000, the answer is reasonable.
Question 10.
Estimate: ______
822,450 + 8,651 = _______
Answer:
Round the values to the nearest thousands.
Estimate: 822,000 + 9,000 = 831,000
Add the ones, tens, then hundreds, then thousands and then ten thousands. Regroup if necessary.
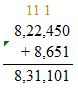
Check: Because 831,101 is close to the estimate, 831,000, the answer is reasonable.
Question 11.
A video receives 10,678 views the first day. It receives 25,932 views the second day. How many views does the video receive in two days?
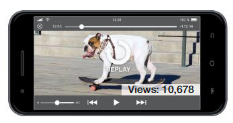
Answer:
Number of views on first day = 10,678
Number of views on second day = 25,932.
Total number of views = number of views on first day + number of views on second day.
Total number of views = 10,678 + 25,932
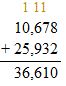
Therefore, total number of views = 36,610 views.
Question 12.
YOU BE THE TEACHER
Is Newton correct? Explain.

Answer:
No, Newton is not correct.
Explanation: Newton is doing the sum without following the place values. He is adding the units place digit of the second number to the hundreds value of the first number. Similarly, he is also adding tens, hundreds and thousands place value digits of the first number to the thousands, ten thousands and hundred thousands place value digits of the first number respectively.
The correct method is as follows:
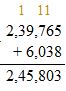
Question 13.
DIG DEEPER!
Find the missing digits.

Answer:
The digit missing in the first number is 5.
The digit missing in the second number is 4.
Explanation: Add the tens value digits 7 and 9. 7+9 = 16. Regroup 1 onto the hundreds place numbers.
1+ missing digit + 1 = 7. Therefore, the missing digit in first number becomes 5, as 1+5+1=7.
In the thousands place, 9+missing digit gives the value of 3 in the sum. the highest possible sum of 9 with a missing digit is 9+9=18. To get 3 in the units place of the sum, 9 has to be added with 4 because 9+4 gives a value of 13. Therefore the missing digit of second number is 4.
Think and Grow: Modeling Real Life
Example
A family is traveling in a car from Seattle to Atlanta. They travel 1,099 miles the first two days and 1,082 miles the next two days. Has the family arrived in Atlanta?
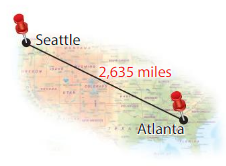
Add the distances traveled.
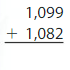
Compare the distance traveled to the distance from Seattle to Atlanta.
The family ______ arrived in Atlanta.
Show and Grow
Question 14.
One World Trade Center has 2,226 steps. A visitor enters the building and climbs 1,387 steps, takes a break, and climbs839 more steps. Did the visitor reach the top of the building?

Answer:
Add the total number of steps:
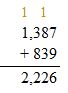
Number of steps climbed: 2,226 and the number of steps of the world trade center, 2,226 are equal.
Therefore, the visitor has reached the top of the World Trade Center.
Question 15.
There were 51,787 more people who rode the city buses on Saturday than on Sunday. On Sunday, 174,057 people rode the buses. How many people rode the buses on Saturday?
Answer:
Given: People rode on city bus on Saturday = 51,787 + People rode on city bus on Sunday.
Therefore, People rode on city bus on Saturday = 51,787 + 174,057
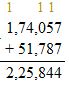
Therefore, People rode on city bus on Saturday = 225,844.
Question 16.
The deepest part of the Atlantic Ocean is 8,577 feet shallower than the deepest part of the Pacific Ocean. The deepest part of the Atlantic Ocean is 27,493 feet deep. How deep is the deepest part of the Pacific Ocean?
Answer:
Given: Depth of Atlantic Ocean = Depth of Pacific Ocean – 8,577.
So, Depth of Atlantic Ocean = 27,493 – 8,577
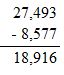
Therefore, depth of Atlantic ocean = 18,916 feet.
Add Multi-Digit Numbers Homework & Practice 2.2
Find the sum. Check whether your answer is reasonable
Question 1.
Estimate: ______
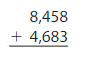
Answer:
Round the values to the nearest hundreds.
Estimate: 8,500 + 4,700 = 13,200
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
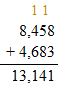
Check: Because 13,141 is close to the estimate, 13,200, the answer is reasonable.
Question 2.
Estimate: ______
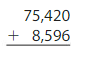
Answer:
Round the values to the nearest hundreds.
Estimate: 75,400 + 8,600 = 84,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
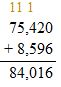
Check: Because 84,016 is close to the estimate, 86,000, the answer is reasonable.
Question 3.
Estimate: ______
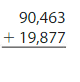
Answer:
Round the values to the nearest thousands.
Estimate: 90,000 + 20,000 = 110,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
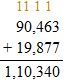
Check: Because 110,340 is close to the estimate, 110,000, the answer is reasonable.
Question 4.
Estimate: ______
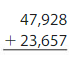
Answer:
Round the values to the nearest thousands.
Estimate: 48,000 + 24,000 = 72,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
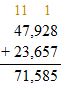
Check: Because 71,585 is close to the estimate, 72,000, the answer is reasonable.
Question 5.
Estimate: ______
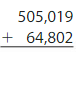
Answer:
Round the values to the nearest thousands.
Estimate: 505,000 + 65,000 = 570,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
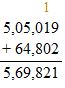
Check: Because 569,821 is close to the estimate, 570,000, the answer is reasonable.
Question 6.
Estimate: ______
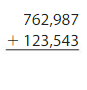
Answer:
Round the values to the nearest thousands.
Estimate: 505,000 + 65,000 = 570,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
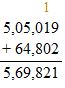
Check: Because 569,821 is close to the estimate, 570,000, the answer is reasonable.
Find the sum. Check whether your answer is reasonable.
Question 7.
Estimate: ______
547,795 + 9,418 = ______
Answer:
Round the values to the nearest thousands.
Estimate: 548,000 + 9,000 = 557,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
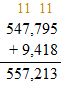
Check: Because 557,213 is close to the estimate, 557,000, the answer is reasonable.
Question 8.
Estimate: ______
401,269 + 58,135 = ______
Answer:
Round the values to the nearest thousands.
Estimate: 401,000 + 58,000 = 459,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
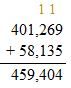
Check: Because 459,404 is close to the estimate, 459,000, the answer is reasonable.
Question 9.
Number Sense
Find and explain the error. What is the correct sum?
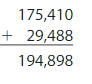
Answer:
Round the values to the nearest thousands.
Estimate: 175,000 + 29,000 = 204,000
Add the ones, tens, then hundreds and then thousands. Regroup if necessary.
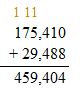
Check: Because 459,404 is close to the estimate, 459,000, the answer is reasonable.
Question 10.
Writing
Write a word problem that can be solved by finding the sum of 75,629 and 23,548.
Answer:
A purchases a house worth $23,548 more than the house purchased by B. House purchased by B is worth $75,629. Find the worth of the house purchased by A.
Worth of house purchased by A = Worth of house purchased by B + $23,548
Worth of house purchased by A = $75,629 + $23,548
Therefore, worth of house purchased by A = $ 99,177.
Question 11.
Modeling Real Life
Two chefs need to make 2,500 food samples for the opening day of their restaurant. Chef A makes 1,346 samples. Chef B makes 1,084 samples. Did the chefs make enough samples?

Answer:
Food samples made by Chef A = 1,346.
Food samples made by Chef B = 1,084.
Total food samples made = Food samples made by Chef A + Chef B.
So, total food samples made = 1,346+1,084 = 2,430.
Total food samples required = 2,500.
The total food samples made are lesser than the required number of food samples. So, the chefs A & B didn’t make enough food samples.
Question 12.
Modeling Real Life
House A costs $24,450 less than House B. How much does House B cost?

Answer:
Given, Cost of House A = Cost of House B – $24,450.
So, Cost of House B = Cost of House A + $24,450.
Therefore, Cost of House B = $175,500 + $ 24,450 = $ 199,950.
Review & Refresh
Find the quotient.
Question 13.
6 ÷ 2 = ______
Answer:
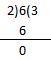
Therefore, the quotient is 3.
Question 14.
24 ÷ 4 = ______
Answer:

Quotient = 6.
Question 15.
32 ÷ 8 = ______
Answer:
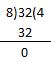
Quotient = 4.
Question 16.
14 ÷ 7 = ______
Answer:
![]()
Quotient = 2.
Question 17.

Answer:
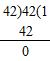
Quotient = 1
Question 18.

Answer:

Quotient = 7.
Question 19.

Answer:
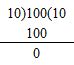
Quotient = 10
Question 20.

Answer:
![]()
Quotient = 9.
Lesson 2.3 Subtract Multi-Digit Numbers
Explore and Grow
Which subtraction problem shows a correct way to find 94 – 8? Why?

Answer:
First one shows the correct way to find the subtraction because it follows the place value rule by subtracting the units digit value of second number from the units digit value of the first number.
Which subtraction problem shows a correct way to find 3,710 – 251? Why?

Answer:
Second one shows the correct way to find the subtraction because it follows the place value rule by subtracting the units, tens and hundreds digit values of second number from the units, tens and hundreds digit values of the first number respectively.
Reasoning
Why do you need to use place value when subtracting? Explain.
Answer:
While subtracting, we use place value rule i.e., we go from right hand side to the left hand side. In other words, we add the digits as per the place value. The digit of every number holds the place value. That means, a digit in tens place has the value of multiple of ten. Similarly, a digit in hundreds place has the value of multiple of hundred.
For example, In the number 23, 2 digit holds the value of multiple of ten. That means, 2 X 10.
To continue the parity of the sum, we follow the place value rule by subtracting digits as per the place values.
Think and Grow: Subtract Multi-Digit Numbers

Show and Grow
Find the difference. Then check your answer.
Question 1.
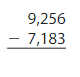
Answer: 2073

Check: Use addition to check your answer. 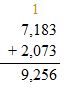
Question 2.
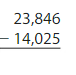
Answer: 9,821
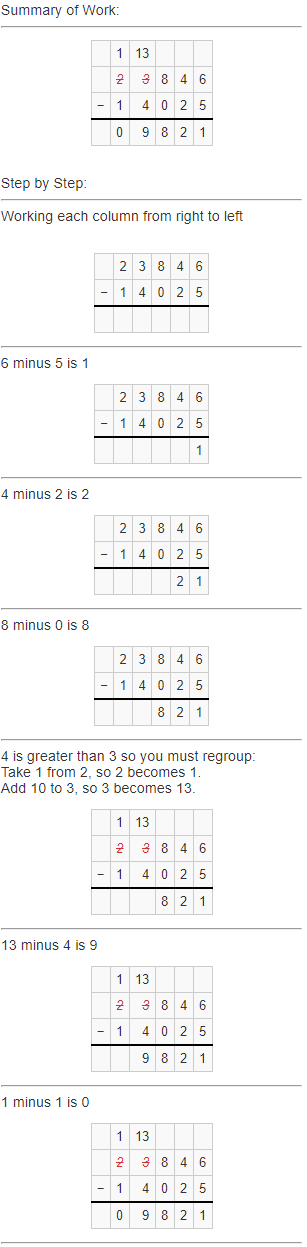
Check: Use addition to check your answer. 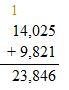
Question 3.
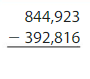
Answer: 452,107

Check: Use addition to check the solution. 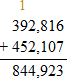
Question 4.
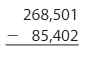
Answer: 183099

Check: Use addition to check the solution. 
Apply and Grow: Practice
Find the difference. Then check your answer.
Question 5.
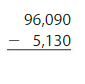
Answer: 90,960

Check: Use addition to check the solution. 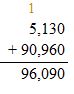
Question 6.
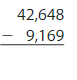
Answer: 33,479

Check: Use addition to check the solution. 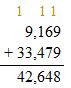
Question 7.
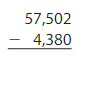
Answer: 53,122
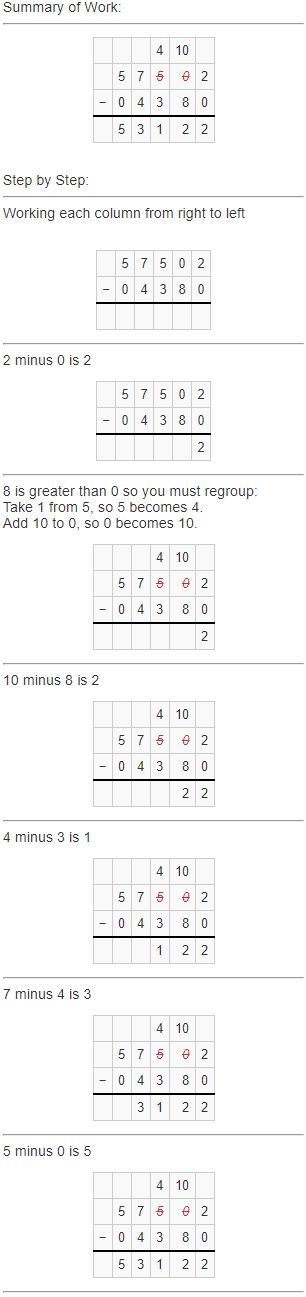
Check: Use addition to check the solution. 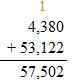
Question 8.
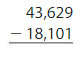
Answer: 25,528.
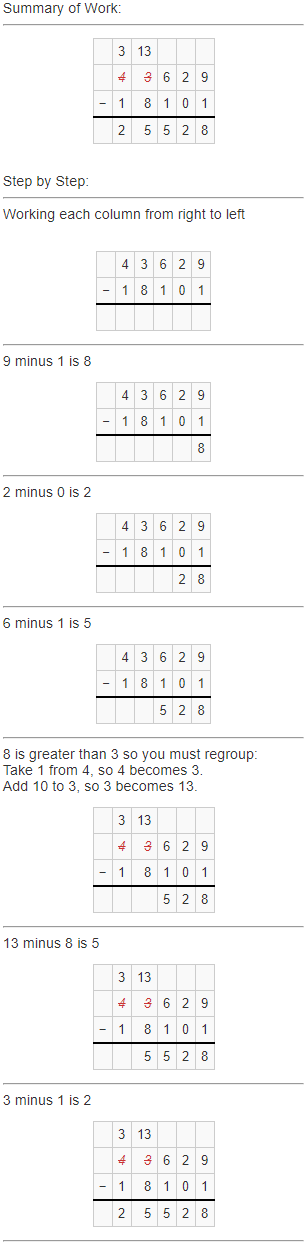
Check: Use addition to check the solution. 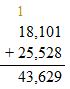
Question 9.

Answer: 338,681

Check: Use addition to check the solution. 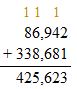
Question 10.
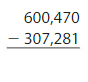
Answer: 293,189

Check: Use addition to check the solution. 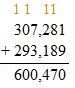
Question 11.
281,660 – 44,521 = ______
Answer: 237,139

Check: Use addition to check the solution. 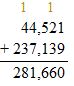
Question 12.
798,400 – 5,603 = ______
Answer: 792,379.

Check: Use addition to check the solution. 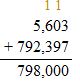
Question 13.
103,219 people attended a championship football game last year. 71,088 people attend the game this year. How many more people attended the game last year than this year?

Answer: 32,131
People attended last year = 103,219
People attended this year = 71,088
People attended more last year than this year = People attended last year – People attended this year
People attended more last year than this year = 103,219 – 71,088

Therefore, People attended more last year than this year = 32,131.
Question 14.
Number Sense
Find and explain the error. What is the correct difference?
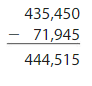
Answer: The error in the solution is the regrouping is not applied correctly. The correct regrouping process is as follows:

Therefore, the correct difference = 363,505
Question 15.
Number Sense
Which statements describe the difference of 32,064 and 14,950?
The difference is about 17,000.
The difference is less than 17,000.
The difference is greater than 17,000.
The difference is 17,000.
Answer: The first and third statements describe the difference.
Explanation: Find the difference of 32,064 and 14,950 by rounding them to the nearest hundreds values and then to the nearest thousands values.
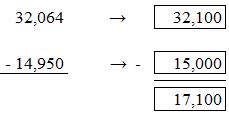
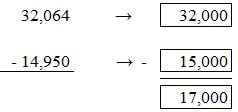
When you round the values to the nearest hundreds values, the statement 3 is satisfied. While rounding the values to the nearest thousands values, statement 1 is satisfied.
Think and Grow: Modeling Real Life
Example
The shoreline of Lake Michigan is 1,090 miles shorter than the shoreline of Lake Superior. How long is the shoreline of Lake Michigan?
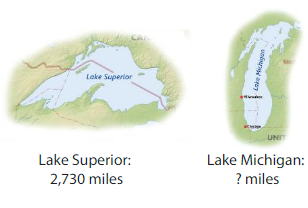
Subtract 1,090 from the length of the shoreline of Lake Superior.
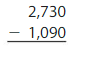
The shoreline of Lake Michigan is 1640 miles long.
Show and Grow
Question 16.
The new car is $15,760 less than the new truck. How much does the new car cost?

Answer: $ 16,755
Explanation:
Cost of truck = $ 32,535.
Cost of car = Cost of truck – $ 15,760
Therefore Cost of car = $ 32,535 – $ 15,760

Therefore, Cost of car = $ 16,775.
Question 17.
Last year, an amusement park had 770,495 more guests than a water park. The attendance at the amusement park was 875,562 guests. What was the attendance at the water park?
Answer: 105,067
Number of guests in at Amusement park = 875,562
Number of guests at water park = number of guests at amusement park – 770,495 guests.
Number of guests at water park = 875,562 – 770,495

Therefore, the number of guests at water park = 105,067.
Question 18.
How many fewer miles did the pilot fly in Years 1 and 2 combined than in Year 3?
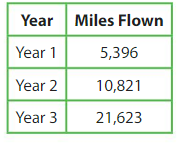
Answer: 5,406
Number of miles the pilot fly in years 1 and 2 combined = number of miles fly in year 1 + number of miles fly in year 2.
So, total number of miles fly in years 1 and 2 = 5,396 + 10,821 = 16,217. 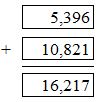
Fewer miles pilot flew in years 1 and 2 combined than year 3 = Number of miles flew in year 3 Number of miles pilot flew in years 1 & 2 combined.

Therefore, the pilot flew a combined of 5,406 miles fewer in years 1 and 2 compared to year 3.
Subtract Multi-Digit Numbers Homework & Practice 2.3
Find the difference. Then check your answer.
Question 1.
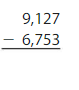
Answer: 2,374
Explanation:
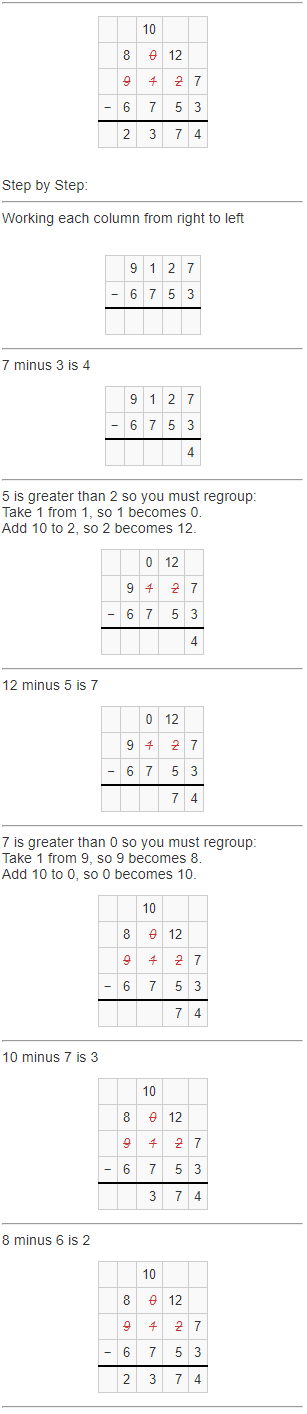
Question 2.
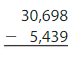
Answer: 25259.
Explanation:
Question 3.
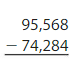
Answer: 21,284
Explanation:
Question 4.
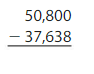
Answer: 13,162
Explanation:

Question 5.
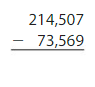
Answer: 140,938
Explanation:

Question 6.
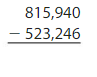
Answer: 292,694
Explanation:

Find the difference. Then check your answer.
Question 7.
319,120 – 278,188 = _______
Answer: 40,932
Explanation:

Check: Add 278,188 to 40,932 to verify.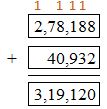
Question 8.
312,396 – 23,891 = ______
Answer: 288,505
Explanation:

Check: Add 23,891 to 288,505 to verify. 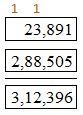
Question 9.
Writing
Write and solve a subtraction word problem using the numbers 34,508 and 8,529.
Answer:
The bike racing 8,529 more curators than the Formula 1 racing. The attendance at the bike racing park was 34,508 guests. What was the attendance at the Formula 1 racing?
Attendance at Bike racing = 34,508.
Attendance at Formula 1 racing = Attendance at Bike racing – 8,529.
So, Attendance at Formula 1 racing = 34,508 – 8,529

Therefore, attendance at Formula 1 racing = 25,979.
Use the time line to answer the questions.
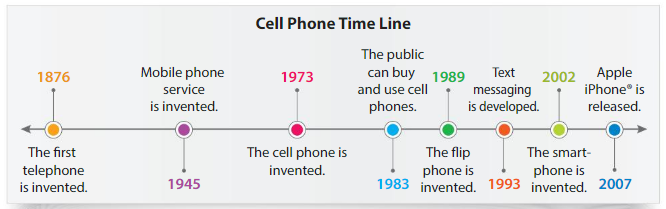
Question 10.
Modeling Real Life
How many years after the first cell phone was invented was the smartphone invented?
Answer: 29 years.
Year of first cell phone invented = 1973.
Year of first smart phone invented = 2002.
Number of years after smart phone invented = 2002 – 1973

Therefore, the years after smart phone invented from first cell phone is 29 years.
Question 11.
Modeling Real Life
How many years passed from the invention of the first telephone to the release of the iPhone?

Answer: 131 years.
Explanation:
Year when first telephone invented = 1876.
Year of the launch of first iPhone = 2007.
Years passed from invention of first telephone to the invention of first iPhone = Launch year of iPhone – invention year of first telephone.
So, years passed = 2007 – 1876
Therefore, years passed after the invention of first telephone to the launch of first iPhone are 131 years.
Review & Refresh
Find the area of the shape.
Question 12.
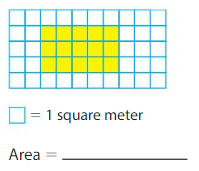
Answer: 15 square meter.
Explanation:
Given, one block = 1 square meter.
Total number of blocks highlighted = 15.
Therefore, total area = 15 square meters.
Question 13.
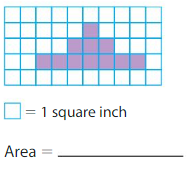
Answer: 11 square inch
Explanation:
Given, one block = 1 square inch.
Total number of blocks highlighted = 11.
Therefore, total area = 11 square inch.
Lesson 2.4 Use Strategies to Add and Subtract
Explore and Grow
Choose any strategy to find 8,005 + 1,350.

For the given numbers, 8,005 and 1,350 the normal addition can be done using grouping using the place value rule. There is no need for the regrouping as well. However, we here will use the partial sums strategy to find the sum.
8000 + 005 = 8005
1000 + 350 = 1350
9000 + 355 = 9355
Choose any strategy to find 54,000 – 10,996.
Answer: 64996
For the given numbers, 54,000 and 10,996 we have to apply compensation strategy.
Add 4 to 10,996 to round it to the nearest thousands value.
10,996 + 4 = 11,000.
54,000 – 11,000 = 43,000.
Now subtract 4 from the result.
43,4000 – 4 = 42,996.
Therefore,54,000 – 10,996 = 42,996.
Reasoning
Explain why you chose your strategies. Compare your strategies to your partner’s strategies. How are they the same or different?
Answer:
Think and Grow: Use Strategies to Add or Subtract

Show and Grow
Find the sum or difference. Then check your answer.
Question 1.
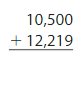
Answer: 22,719.
We will use partial sums to add.
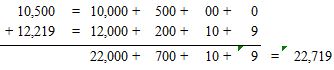
Therefore, 10,500 + 12,219 = 22,7199.
Question 2.
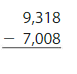
Answer:
We will use compensation strategy to find the difference.
7,008 – 8 = 7,000.
9,318 – 7,000 = 2,318.
2,318 – 8 = 2,310.
Therefore, 9,318 – 7,008 = 2,310.
Apply and Grow: Practice
Find the sum or difference. Then check your answer.
Question 3.
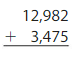
Answer: 16,457.
We here use regrouping strategy to solve this.
Question 4.
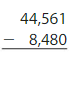
Answer: 36,081
Subtract the given numbers using regrouping model.
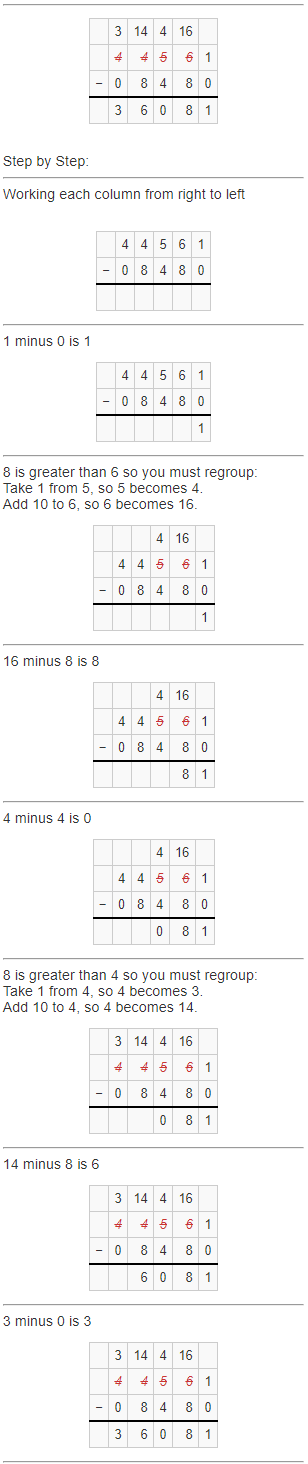
Therefore, the difference of 44,561 and 8480is 36,081
Question 5.
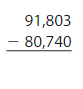
Answer: 11,063
Use compensation strategy to solve this:
Add 40 to 91,803.
91,803 + 40 = 91,843
91,843 – 80,740 = 11,103.
Now subtract 60 from the result.
11,103 – 40 = 11,063.
Question 6.
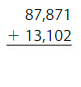
Answer: 100,973
Use regrouping to add the numbers.
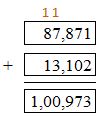
Question 7.
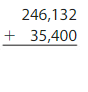
Answer: 281,712
Use partial sum method to calculate this.
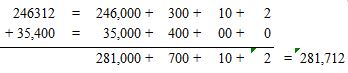
Question 8.
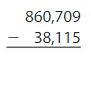
Answer: 822,594
Use regrouping method to find the difference:

Question 9.
780,649 – 13,754 = ______
Answer: 766,895
Use regrouping method:

Question 10.
417,890 + 90,284 = ______
Answer: 508,172
Use regrouping method to sum.
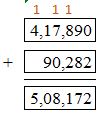
Question 11.
614,008 + 283,192 = ______
Answer: 897,200
Use regrouping method to find the sum.
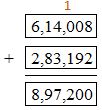
Question 12.
801,640 – 206,427 = ______
Answer: 595,213
Use regrouping:

Question 13.
Structure
Write an equation shown by the number line.
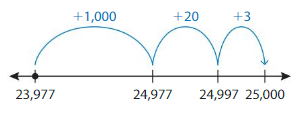
Answer:
23,977 + 1000 = 24,977 + 20 = 24,997 + 3 = 25,000.
Think and Grow: Modeling Real Life
Example
Inner Core Earth’s mantle is 1,802 miles thick. Earth’s outer core is 1,367 miles thick. How many miles thinner is Earth’s outer core than its mantle?
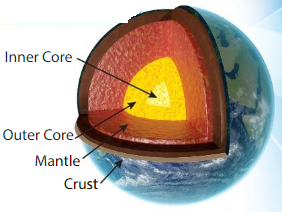
Subtract the thickness of the outer core from the thickness of the mantle. Use compensation to subtract.
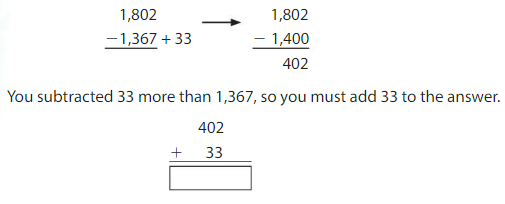
Earth’s outer core is 435 miles thinner than its mantle.
Show and Grow
Question 14.
Your friend’s heart beats 144,000 times in one day. Your heart beats 115,200 times in one day. How many fewer times does your heart beat than your friend’s?
Answer: 28,800
Number of times heart beats of my friend = 144,000
Number of times heart beats of me = 115,200
The fewer times my heart beats than my friend = 144,000 – 115,200

Question 15.
You, your friend, and your cousin are playing a video game. You score 2,118 more points than your friend. Your friend scores 1,503 fewer points than your cousin. What is each player’s score? Who wins?PlayerScoreYou?Friend6,010Cousin?
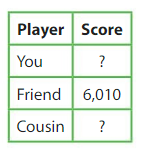
Answer:
Given, friend’s score = 6,010.
My score = My friend’s score + 2,118 = 6,010 + 2,118 = 8,128.
My cousin’s score = My friend’s score – 1,503 = 6,010 – 1,503 = 4,507.
Question 16.
Students at a school want tore cycle a total of 50,000 cans and bottles. So far, the students recycled 40,118 cans and 9,863 bottles. Did the students reach their goal? If not, how many more cans and bottles need recycled?

Answer: No, the students fell short by 19.
Number of cans recycled = 40,118.
Number of bottles recycled = 9,863
Total recycled = 40,118 + 9,863 = 49,981.
Students planned number for recycling = 50,000.
Shortage = 50,000 – 49,981 = 19.
The students fell short by 19 cans or bottles to recycle.
Use Strategies to Add and Subtract Homework & Practice 2.4
Find the sum or difference. Then check your answer.
Question 1.
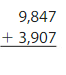
Answer: 13,754
Use regrouping method to add the numbers.
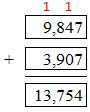
Question 2.
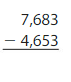
Answer: 3,030
Use compensation method to subtract.
Subtract 30 from the first number to make it’s hundreds tens and units digits same those of the second number..
7,683 – 30 = 7,653.
Now subtract the second number from the result.
7,653 – 4,683 = 3,000
Now add 30 which was subtracted in the beginning to the result again to compensate.
3,000 + 20 = 3,030.
Question 3.
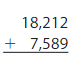
Answer: 25,801
Use compensation method to add the numbers.
We, here can see both the numbers are near to their nearest hundreds. The first number is 12 greater than its nearest hundreds value and the second is 11 lesser than its nearest hundreds value.
Subtract 11 from the first number and add 11 to the second number. Adding and subtracting compensates the net value.
18,212 – 11 = 18,201.
7,589 + 11 = 7,600.
Now add both the results.
18,201 + 7,600 = 25,801.
Question 4.
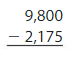
Answer: 7,625
Use compensation method to do the subtraction.
Subtract 25 from the first number to make the tens and units digits same those of the second number.
9,800 – 25 = 9,775.
Now subtract the second number from the result.
9,775 – 2,175 = 7,600.
Now add 25 to the result which was subtracted initially to compensate.
7,600 + 25 = 7,625.
Question 5.
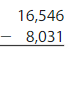
Answer: 8,515
Use regrouping to subtract.
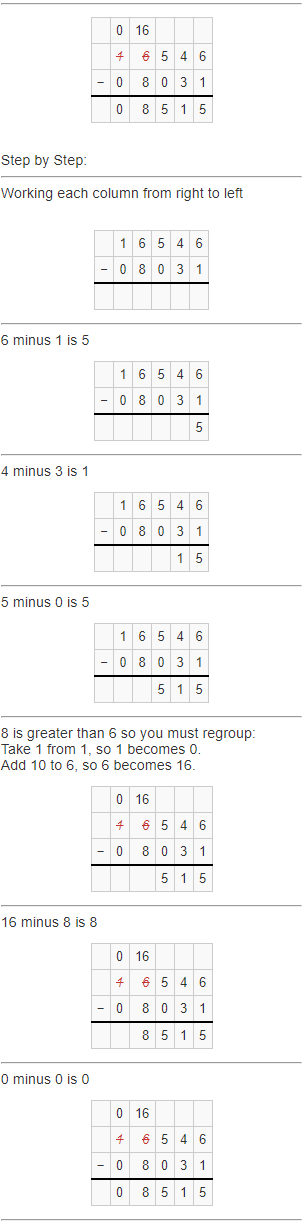
Question 6.
Answer: 161,935
Use regrouping to sum.

Question 7.
814,327 – 32,475 = ______
Answer: 781,852.
Use regrouping method to subtract.

Question 8.
294,801 + 46,030 = ______
Answer:
Use regrouping to sum.

Question 9.
512,006 + 318,071 = ______
Answer: 830,085.
Use compensation method.
Subtract 6 from the first number.
512,006 – 6 = 512,000.
Add the second number to the result.
512,000 + 318,071 = 830,071.
Now add 6 again to the result to compensate.
830,071 + 6 = 830,085.
Question 10.
746,620 – 529,706 = _______
Answer: 216,914
Use grouping to subtract.

Question 11.
YOU BE THE TEACHER
Your friend uses compensation to add. Is your friend correct? Explain.
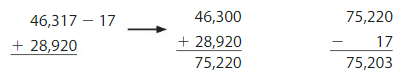
Answer: No, the addition is incorrect.
Explanation:
In step 1, 17 was subtracted to round it to the nearest hundreds. To compensate the subtraction, 17 should be added to the result in the final step. But, 17 was subtracted instead.
Correct answer = 75,220 + 17 = 75,237.
Question 12.
Writing
Which strategy would you use to subtract 9,618 from 58,007? Explain.
Answer: 48,389
We here use regrouping strategy.

Question 13.
Modeling Real Life
There are about 500,000 detectable earthquakes each year. About 99,500 of the detectable earthquakes are felt. How many earthquakes are detectable, but are not felt each year?

Answer:
Given, number of detectable earthquakes = 500,000.
Number of detectable earthquakes that are felt = 99,500.
Number of earthquakes that cannot be felt = 500,000 – 99,500 = 405,000.
Question 14.
DIG DEEPER!
A committee wants to purchase a playground for $52,499. They put a donation of $8,025 towards the purchase of the playground. Then they make 2 payments of $4,275. How much money does the committee have left to pay for the playground?
Answer:
Cost of playground = $52,499.
Donation towards purchase = $8,025.
Next payments made = $4,275.
Amount left to pay = Total cost pf playground – donation – payment.
So, amount left = $52,499 – $8,025 – $4,275 = ($52,499 – $8,025) – $4,275
= $44,474 – $4,275 = $40,199.
So, the money left to pay by the committee to purchase the playground is $40,199
Review & Refresh
Write an equation to solve. Use a letter to represent the unknown number. Check whether your answer is reasonable.
Question 15.
There are 4 boxes. Each box has 6 granola bars. Your soccer team eats 18 granola bars. How many granola bars are left?
Answer: 6.
Let the total number of granola bars = X.
Given X = 4 Boxes of 6 granola bars each.
So, X = 6 * 4 = 24.
Number of Granola bars ate by Soccer team = 18.
Number of granola bars left = total granola bars – granola bars ate = 24 – 18 = 6.
Therefore, number of granola bars left = 6.
Question 16.
Newton has 35 blocks. Descartes has 28 blocks. Newton divides his blocks into7 equal groups and gives Descartes one group. How many blocks does Descartes have now?
Answer: 33.
Total blocks Newton has = 35.
Dividing 35 into 7 equal groups = 35/7.
So, number of blocks in each group = 35/7 = 5.
Number of blocks with Descartes = 28.
Number of blocks with Descartes after Newton giving one group of blocks = 28 + 5 = 33.
Lesson 2.5 Problem Solving: Addition and Subtraction
Explore and Grow
Use addition or subtraction to make a conclusion about the table.
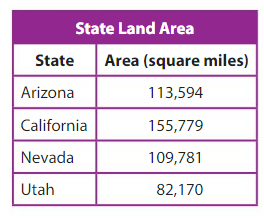
Answer:
We use addition and also subtraction.
Let’s solve this problem. How much is the combined area of Arizona and California is bigger than the combined area of Nevada and Utah.
Combined area (1) of Arizona and California = 113,594 + 155,779 = 269,373.
Combined area (2) of Nevada and Utah = 109,781 + 82,170 = 191,951.
Difference in combined areas = Combined area 1 – Combined area 2 = 269,373 – 191,951.

Therefore, the combined area of Arizona and California is 77,422 square miles bigger than the combined area of Nevada and Utah.
Think and Grow: Problem Solving: Addition and Subtraction
Example
You have3,914 songs in your music library. You download 1,326 more songs. Then you delete 587 songs. How many songs do you have now?
Understand the Problem
What do you know?
• You have 3,914 songs.
• You download 1,326 more
• You delete 587 songs.
What do you need to find?
• You need to find how many songs you have now.
Make a Plan
How will you solve?
• Add 3,914 and 1,326 to find how many songs you have after downloading some songs.
• Then subtract 587 from the sum to find how many songs you have now.
Solve
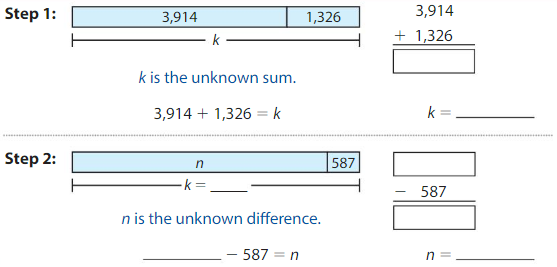
k = 4,240
n = k – 587 = 5,240 – 587 = 3,653
You have 4,653 songs now.
Show and Grow
Question 1.
Explain how you can check whether your answer above is reasonable.
Answer:
You can check the answer by doing the subtraction first and the addition later.
First, subtract 587 songs that were deleted.
Therefore, 3,914 – 587 = 3,327.
Now add the downloaded songs, 1,326 to the result.
So, 3,327 + 1,326 = 4,653.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
There are about 12,762 known ant species. There are about 10,997 known grasshopper species. The total number of known ant, grasshopper, and spider species is 67,437. How many known spider species are there?

Answer: 43,678.
Given, number of ant species: 12,762.
Number of grasshopper species: 10,997.
Total number of ant, grasshopper and spider species: 67,437.
So, Number of (ant species + grasshopper species + spider species) = 67,437.
That means, 12,762 + 10,997 + number of spider species = 67,437.
Now, initially add the number of ant and grasshopper species using compensation strategy.
Add 3 to the number of grasshopper species: 10,997 + 3 = 11,000.
Now add the result to the number of ant species: 12,762 + 11,000 = 23,762.
Now subtract 3 to compensate: 23,762 – 3 = 23,759.
So, Number of spider species = 67,437 – 23,759.
Do the subtraction using regrouping.

Therefore, the known number of spider species = 43,678.
Question 3.
A quarterback threw for 66,111 yards between 2001 and 2016. His all-time high was 5,476 yards in 1 year. In his second highest year, he threw for 5,208 yards. How many passing yards did he throw in the remaining years?
Answer: 55,427
Total number of yards = 66,111 yards.
His first and second all-time high were 5,476 yards and 5,208 yards respectively.
Total yards in first and second year all-time high = 5,476 + 5,208 = 10,684.
The number of yards he threw in the remaining years = 66,111 – 10684
Find the difference using regrouping.

Therefore, number of yards he threw in the remaining years = 55,427 yards
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
There are 86,400 seconds in 1 day. On most days, a student spends 28,800 seconds sleeping and 28,500 seconds in school. How many seconds are students not awake, but in school?
Answer:
Given, Number of seconds student sleeps = 28,800.
Number of seconds student spends at school = 28,500.
The
Question asked was the number of seconds the student spend not awake (sleeping), but in school.
In the given data, it’s not mentioned that the student spends time sleeping at school separately. So, with the given information, we cannot calculate the number of seconds student was not awake, but at school.
Question 5.
A pair of rhinoceroses weigh 14,860 pounds together. The female weighs 7,206 pounds. How much more does the male weigh than the female?

Answer: 258 pounds.
Given,
Weight of female rhino =7,206 pounds.
Weight of the rhino pair = 14,860.
Weight of male rhino = 14,860 – 7,206
Solve this using compensation strategy.
Add 6 to the first number = 14,860 + 6 = 14,866.
Now subtract the second number from the result.
That means, 14,866 – 7,206 = 7,460.
Now, subtract 6 from the result to compensate = 7,460 – 6 = 7,454.
So, weight of male rhino = 7,464.
Weight of male rhino more than female rhino = male rhino weight – female rhino weight. = 7,464 – 7,206 = 258 pounds.
Question 6.
Earth is 24,873 miles around. If a person’s blood vessels were laid out in a line, they would be able to circle Earth two times, plus 10,254 more miles. How many miles long are a person’s blood vessels when laid out in a line?
Answer: 60,000 miles.
Given circumference of earth = 24,873 miles.
So, length of person’s blood vessels = 2 times the earth’s circumference + 10,254 miles.
That means, length of person’s blood vessels = (2 X 24,873) + 10,254 = 49,746 + 10,254.
Add the two numbers using grouping technique.
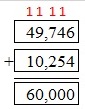
Therefore,, the length of human blood vessels = 60,000 miles.
Question 7.
Alaska has 22,041 more miles of shoreline than Florida and California combined. Alaska has 33,904 miles of shoreline. Florida has 8,436 miles of shoreline. How many miles of shoreline does California have?
Answer: 3,427 miles
Give, Shoreline of Alaska = 33,904.
Shoreline of Florida = 8,436 miles.
Shore lines of Florida + California = Shoreline of Alaska – 22,041 miles.
That means, 8,436 miles + Shoreline of California = 33,904 miles – 22,041 miles.
Subtract the right hand side using regrouping.
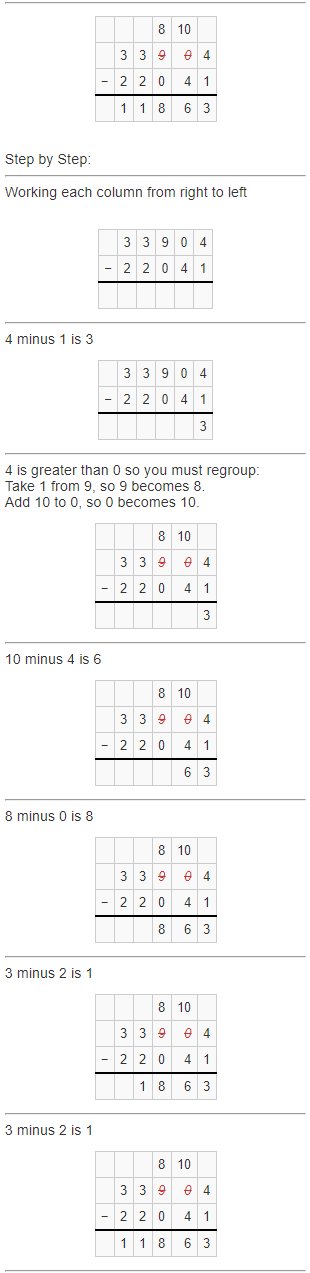
So, Shoreline of California + 8436 miles = 11,863 miles.
That means, Shoreline of California = 11,863 miles – 8436 miles
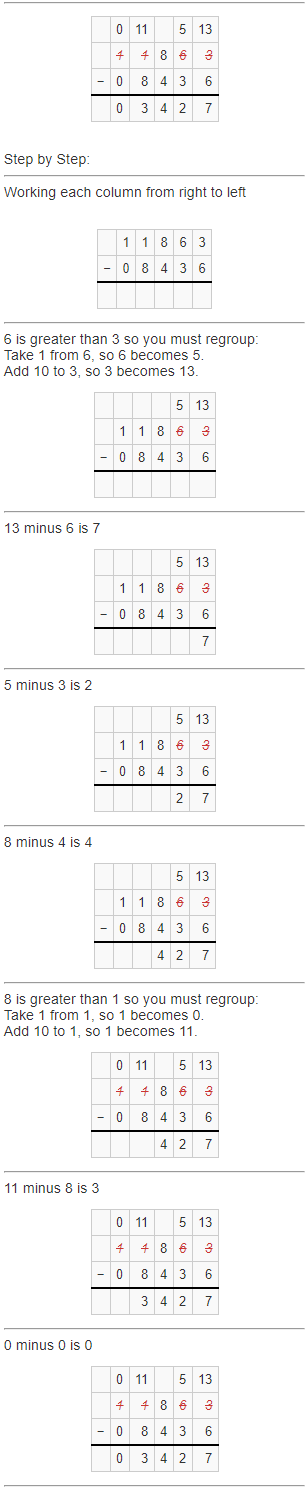
Therefore, shoreline of California = 3,427 miles.
Think and Grow: Modeling Real Life
Example
The attendance on the second day of a music festival is 10,013 fewer people than on the third day.How many total people attend the three-day music festival?
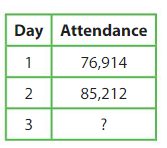
Think: What do you know? What do you need to find? How will you solve?3?

_______ total people attend the music festival.
Show and Grow
Question 8.
A construction company uses 3,239 more bricks to construct Building 1 than Building 2. How many bricks does the company use to construct all three buildings?
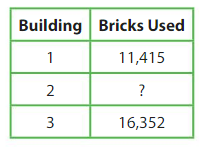
Answer:
Given,
Number of bricks used for Building 1 = 11,415.
Number of bricks used for Building 3 = 16,352.
Number of bricks used for building 2 = Number of bricks used for Building 1 – 3,239.
So, Number of bricks used for Building 2 = 11,415 – 3,239.
Use regrouping to subtract.

So, number of bricks used for constructing Building 2 = 8,176.
So, bricks used to construct all three buildings = Bricks used for (Building 1 + Building 2 + Building 3)
So, total bricks used in construction = 11,415 + 8,176 + 16,352.
Use grouping to add the three numbers.
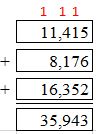
Therefore, the number of bricks used to construct all the three buildings = 35,943.
Problem Solving: Addition and Subtraction Homework & Practice 2.5
Understand the problem. Then make a plan. How will you solve? Explain.
Question 1.
A cargo plane weighs 400,000 pounds. After a load of cargo is removed, the plane weighs 336,985 pounds. Then a 12,395-pound load is removed. How many pounds of cargo are removed in all?
Answer: 75,410
Given,
Weight of plane with cargo = 400,000 pounds.
Weight of plane after removing first load of cargo = 336,985.
So, Weight of first cargo load = 400,000 – 336,985.
Use Count on to strategy to find the difference.
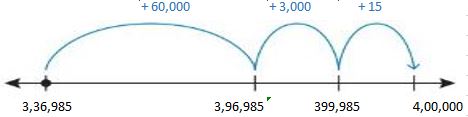
So, the difference is 60,000 + 3,000 + 15 = 63,015.
So, the weight of the first cargo = 63,015.
Given, weight of the second cargo = 12,395.
Total weight of the cargo = 63,015 + 12,395

So, the total weight of the cargo unloaded = 75,410 pounds.
Question 2.
A ski resort uses 5,200 gallons of water per minute to make snow. A family uses 361 gallons of water each day. How many more gallons of water does the ski resort use to make snow in 2 minutes than a family uses in 1 day?
Answer: 10,039 Gallons
Given,
Water required to make snow for 1 minute = 5,200 gallons.
Water required for household usage per day = 361 gallons.
Water required for ski resort to prepare snow per two minutes = 2 X 5,200 = 10,400 gallons.
The more water required than the water consumed by the household one day usage = 10,400 – 361.
Subtract using compensation.
Add 39 to the second number.
361 + 39 = 400.
Now subtract the result from the second number.
10,400 – 400 = 10,000.
Now, add 39 to the result to compensate.
10,000 + 39 = 10,039.
So, the additional water used for ski resort to make snow for 2 minutes than the water used by household per one day is 10,039 gallons.
Question 3.
In July, a website receives 379,162 fewer orders than in May and June combined. The website receives 542,369 orders in May and 453,708 orders in June. How many orders does the website receive in July?
Answer: 542,369
Given,
Orders received in May = 542,369.
Orders received in June = 453,708.
Total orders in May and June = 542,369 + 453,708.

So, orders received in July = 996,077 – 379,162.
Subtract using regrouping.

So, the number of orders received in the month of July = 542,369.
Question 4.
Writing
Write and solve a two-step word problem that can be solved using addition or subtraction.
Answer:
A father wants to buy a laptop to his son worth $3,495. He makes 2 payments of $1,500. How much money does the he have left to pay for the laptop?
Cost of laptop = $3,495.
Number of payments of $1,500 done = 2.
That means $1,500 X 2 = 3,000
Money left to pay by the father for the laptop = Cost of laptop – Amount paid
= $3,495 – $3,000.
$3,495 – $3,000 = $495.
So, money left to buy laptop = $495
Question 5.
Modeling Real Life
World War I lasted from 1914 to1918. World War II lasted from 1939 to 1945. How much longer did World War II last than World War I?
Answer: 2 years
Duration of World war 1 = 1918 – 1914 = 4 years.
Duration of World war 2 = 1945 – 1939 = 6 years.
The longer did World war 2 last = Duration of World war 2 – Duration of World war 1 = 6 years – 4 years
Therefore, World war 2 lasted 2 years longer than World war 1.
Question 6.
Modeling Real Life
Twenty people each donate $9 to a charity. Sixty people each donate $8. The charity organizer wants to raise a total of $1,500. How much more money does the organizer need to raise?
Answer:
Twenty people each donate $9 to a charity = 20 X $9 = $180
Sixty people each donate $8 = 60 X $8 = $480.
Total fund collected = $180 + $480 = $660
The charity organizer wants to raise a total of $1,500.
So, money left by the charity organizer to collect = $1500 – $660 = $740.
Question 7.
DIG DEEPER!
The blackpoll warbler migrates 2,376 miles, stops, and then flies another 3,289 miles to reach its destination. The arctic tern migrates 11,013 miles, stops, and then flies another 10,997 miles to reach its destination. How much farther is the arctic tern’s migration than the blackpoll warbler’s migration?

Answer: 16,345 miles
Total migration of Blackpoll Warbler = 2,376 + 3,289
Total migration of arctic tern = 11,013 + 10,997
Total migration of Blackpoll:  Total migration of arctic tern:
Total migration of arctic tern: 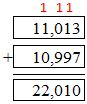
Farther the arctic tern’s migration than the blackpoll warbler’s migration = 22,010 – 5,665.
Use grouping to subtract.

So, farther the arctic tern’s migration than the blackpoll warbler’s migration is 16,345 miles.
Review & Refresh
Write the time. Write another way to say the time.
Question 8.
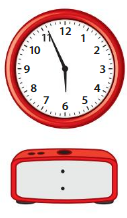
Answer: 5 hours 56 minutes (05:56)
Other way: 4 minutes to 6’O Clock.
Question 9.
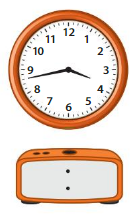
Answer: 3 hours 43 minutes (03:43)
Other way: 17 minutes to 4’O Clock.
Question 10.
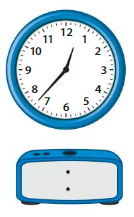
Answer: 12 hours 37 minutes (12:37)
Add and Subtract Multi-Digit Numbers Performance Task
Question 1.
The time line shows the population of Austin, Texas from 1995 to 2015.
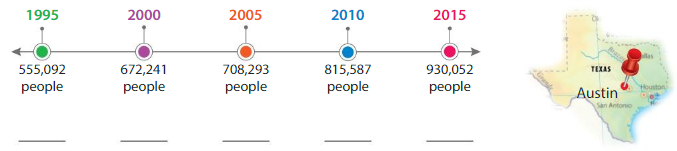
a. Which place would you round to when estimating population? Explain.
b. Estimate Austin’s population each year on the time line.
c. Use your estimates to complete the bar graph.
d. Between the years 1995 and 2015, did Austin’s population increase, decrease, or stay the same? Explain.
e. During which five-year period did the population increase the most? Explain.
f. About how many more people lived in Austin in the year 2015 than in the year 1995?
g. Do you think the population will be more than 1,000,000 in the year 2020? Explain.
Answer:
a) Round the values to the nearest ten thousands because the values are in lakhs.
b) ![]()
c)
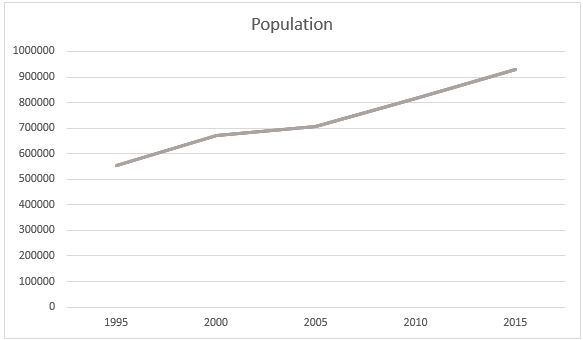
d) Between the years, 1995 and 2015, Austin’s population was increased. The population was constantly increasing as per the given table and the chart.
e) During the five year period between 1995 and 2000, the population increased more. The graph was more steeper than the other time lines. That indicates more population growth during that period.
f) Population in 2015 = 930,052
Population in 1995 = 555,092.
Round the values to the nearest ten thousands values.

So, the population increase between 1995 and 2015 was estimated to be 370,000.
g) Yes, the population grown more than 100,000 in 5 years time except between 2000 and 2005. So, if that is the case, the population will be more than 1,000,000 by 2020.
Add and Subtract Multi-Digit Numbers Activity
Race to the Moon
Directions:
1. Players take turns.
2. On your turn, flip a Race for the Moon Card and find the sum or difference.
3. Move your piece to the next number on the board that is highlighted in your answer.

Add and Subtract Multi-Digit Numbers Chapter Practice
2.1 Estimate Sum and Differences
Estimate the sum or difference.
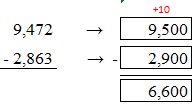
Question 1.
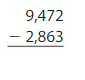
Answer: 6,600
Round the numbers to the nearest hundreds values.
Question 2.
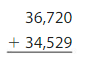
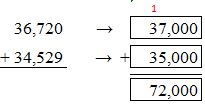
Answer: 72,000
Round the numbers to their nearest thousands
Question 3.
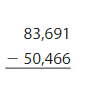
Answer: 34,000.
Round the numbers to the nearest thousand values.

Question 4.
742,086 – 486,629 = ______
Answer: 250,000
Round the numbers to the nearest ten thousands value.
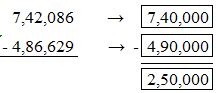
Question 5.
216,987 + 72,429 = ______
Answer: 289,000
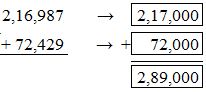
2.2 Add Multi-Digit Numbers
Find the sum. Check whether your answer is reasonable.
Question 6.
Estimate: ______
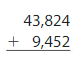
Answer: 53,300
Round the numbers to their nearest hundreds value:
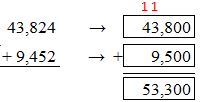
Check: Use grouping to find the exact Sum:

As, 53,276 is nearest to the estimate value 53,300, the estimate is correct.
Question 7.
Estimate: ______
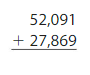
Answer: 80,000
Round the numbers to the nearest thousands value:
Check: Use grouping to find the exact Sum:

As, 79,960 is nearest to the estimate value 80,000, the estimate is correct.
Question 8.
Estimate: ______
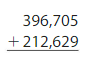
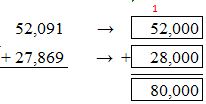
Answer: 610,000
Round the numbers to the nearest ten thousands values.

Check: Use grouping to find the exact Sum:

As, 609,334 is nearest to the estimate value 610,000, the estimate is correct.
Question 9.
Logic
Find the missing digits

Answer:

In this given problem, look at the units place. The result is 1 and as the units digit of the first number is 6, then the should be nothing else but 11. So, 11 – 6 = 5. So, the missing units digit of the second number is 5. The tens position also gets satisfied with the result being 11 as the regrouping gives the tens digit of the result 11 again.
If that’s the case, the regrouping again takes another addition of 1 to the hundreds place. It gives the result as follows:
1 + __ + 9 = Units digit of 5.
1+9 = 10. So, the 1 has to go for the thousands place as per regrouping. So, 0 + __ = 5.
So, the hundreds place of the first number is 5.

In this given problem, look at the tens place. The result is 2 and as the tens digit of the second number is 8, There is also a carrying of 1 from the units place to add in the sum.
So, 1 + __ + 8 = 12 (before regrouping of tens place). So, the missing units digit of the first number is 3. The hundreds position also gets satisfied with the result being 12 as the regrouping gives the hundreds digit of the result 15.
The regrouping again takes another addition of 1 to the ten thousands place. It gives the result as follows:
1 + 6 + __ = Units digit of 5. It clearly shows that there will be another regrouping.
7 + __ = 15.
7 + 8 = 15.
So, the ten thousands place of the second number is 8.
2.3 Subtract Multi-Digit Numbers
Find the difference. Then check your answer.
Question 10.
Answer: 4757.
Use grouping to subtract.

Question 11.
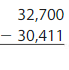
Answer: 2,289.
Use compensation method.
Add 11 to the first number.
32,700 + 11 = 32,711
Now subtract the second number from result.
So, 32,711 – 30,411 = 2,300.
Now subtract 11 from the result to compensate.
2,300 – 11 = 2,289.
Question 12.
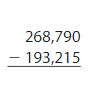
Answer: 75,575
Use grouping to subtract.

Question 13.
973,287 – 8,345 = ______
Answer: 964,942
Use grouping to subtract.

Question 14.
762,179 – 21,280 = ______
Answer: 740,899
Use grouping to subtract.

2.4 Use Strategies to Add or Subtract
Find the sum or difference. Then check your answer.
Question 15.
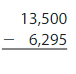
Answer: 7,205
Use compensation method.
Subtract 5 from the first number.
13,500 – 5 = 13,495.
Now subtract second number from the result.
13,495 – 6,295 = 7,200.
Now add 5 to the result to compensate.
7,200 + 5 = 7,205.
Question 16.
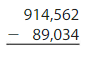
Answer: 825,528.
Use regrouping.

Check: Add the result to the second number to check.
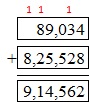
Question 17.
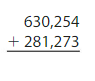
Answer: 911,527.
Use regrouping to solve this.
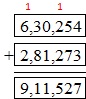
2.5 Problem Solving: Addition and Subtraction
Question 18.
Modeling Real Life
A library has 12,850 books. There are 1,932 poetry books, 5,047 nonfiction books, and 2,891 graphic novels. The rest are fiction. How many fiction books does the library have?
Answer:
Number of books in the library = 12,850.
Given, Number of (poetry books + notification books + graphic novels + fiction books) = Total books.
So, 1,932 + 5,047 + 2,891 + fiction books = 12,850.
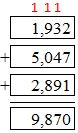
So, 9,870 + Fiction books = 12,850.
So, Fiction books = 12,850 – 9,870.
Use compensation to do this subtraction.
Add 20 to the first number.
12,850 + 20 = 12,870.
12,870 – 9,870 = 3,000.
Now subtract 20 from the result to compensate.
3,000 – 20 = 2,980.
Therefore, the number of fiction books in the library are 2,980.
Question 19.
Modeling Real Life
A technology teacher wants to buy a 3-D printer for $3,495. He makes 3 payments of $999. How much money does the teacher have left to pay for the 3-D printer?
Answer: $498.
Cost of 3-D printer = $3,495.
Number of payments of $999 done = 3.
That means $999 + $999 + $999.
Use compensation technique to add the three numbers.
Add $1 to each payment of $999.
$999 + $1 = $1,000.
So, the addition has to be done for $1,000 + $1,000 + $1,000 = $3,000.
Now, subtract $3 from the result to compensate.
$3,000 – $3 = $2,997.
Money left to pay by the technology teacher for the 3-D printer = Cost of 3-D printer – Amount paid
= $3,495 – $2,997.
Use compensation method to do the subtraction. Add $3 to the second number.
$2,997 + $3 = $3,000.
Now subtract the result from the first number.
$3,495 – $3,000 = $495.
Add $3 to compensate.
$495 + $3 = $498.
So, the money left to pay by the technology teacher for the 3-D printer = $498.
Conclusion:
Come and fall in love with Maths by utilizing the Big Ideas Math Answers Grade 4 Chapter 2 Add and Subtract Multi-Digit Numbers. Make use of the Big Ideas Math Answers Grade 4 Chapter 2 Add and Subtract Multi-Digit Numbers as a reference for all your queries. Keep in touch with our site to avail updates on Class Specific Big Ideas Math Book 4th Grade Answer Key Chapter 2 Add and Subtract Multi-Digit Numbers at your fingertips.
