A perfect preparation will come to your hand when you have the best source with you. Finding the best source will help you to save your time while preparing and also get a grip on the concept. The only best source to learn all the Grade 5 Chapter 13 Understand Volume is our Big Ideas Math Answers Grade 5 Chapter 13 Understand Volume. Why every student love to use our Big Ideas Math Answers 5th Grade Answer Key Chapter 13 Understand Volume? Do you want to know why? Because we have provided from basic concepts to difficult concepts.
Big Ideas Math Book 5th Grade Chapter 13 Understand Volume Answer Key
We are providing different methods to solve problems, practice tests, quiz, objective question and answers, ad a detailed explanation for problems, etc. Get a free pdf of Big Ideas Math Answer Key Grade 5th. Good practice will help you to score the best marks in the exam. Therefore, without wasting your time, quickly start your preparation now. We have given quick links along with various problems. Try to practice all problems and become a pro in your math subject.
Lesson: 1 Understand the Concept of Volume
- Lesson 13.1 Understand the Concept of Volume
- Understand the Concept of Volume Homework & Practice 13.1
Lesson: 2 Find Volumes of Right Rectangular Prisms
- Lesson 13.2 Find Volumes of Right Rectangular Prisms
- Find Volumes of Right Rectangular Prisms Homework & Practice 13.2
Lesson: 3 Apply the Volume Formula
Lesson: 4 Find Unknown Dimensions
Lesson: 5 Find Volumes of Composite Figures
- Lesson 13.5 Find Volumes of Composite Figures
- Find Volumes of Composite Figures Homework & Practice 13.5
Chapter: 13 – Understand Volume
Lesson 13.1 Understand the Concept of Volume
Explore and Grow
Use centimeter cubes to make each figure.
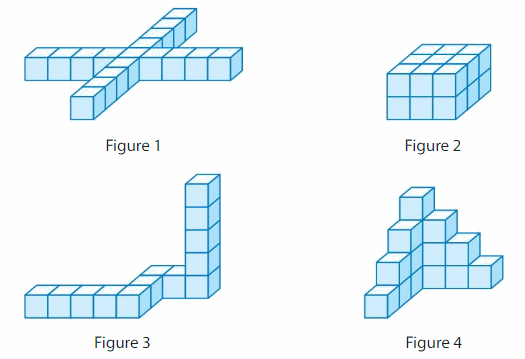
Which figure takes up the most space? Which figure takes up the least space? How do you know?
Answer:
Figure-3 occupies more space.
Explanation:
figure-1
volume = length x width x height
where l = length, w = width and h = height
volume = 9 x 9 x 1
In the above-given figure l=9 ft, w =9 ft and h = 1ft
volume = 9 x 9 x 1
volume = 81x 1
volume = 81 cubic ft
figure-2
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 3 x 2
In the above-given figure l=3 ft, w =3 ft and h = 2 ft
volume = 3 x 3 x 2
volume = 9 x 2
volume = 18 cubic ft
figure-3
volume = length x width x height
where l = length, w = width and h = height
volume = 7 x 3 x 5
In the above-given figure l=7 ft, w =3 ft and h = 5 ft
volume = 7 x 3 x 5
volume = 21 x 5
volume = 105 cubic ft
figure-4
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 3 x 1
In the above-given figure l=3 ft, w =3 ft and h = 1 ft
volume = 3 x 3 x 1
volume = 9 x 1
volume = 9 cubic ft
Structure
Can two different figures take up the same amount of space? Explain.
Answer:
Yes.
Explanation:
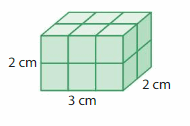
In example 1 :if we consider l= 3 cm and w = 2 cm and h = 2cm
v = l x w x h
volume = length x width x height
v = 3 x 2 x 2
v = 6 x 2
v = 12 cubic cm
In example 2 : if we consider l= 2 cm and w = 3 cm and h = 2cm.
v = l x w x h
volume = length x width x height
v = 2 x 3 x 2
v = 6 x 2
v = 12 cubic cm.
both the volumes are same.
Think and Grow: Use Unit Cubes to Find Volume
Key Idea
Volume is a measure of the amount of space that a solid figure occupies. The volume of a unit cube is 1 cubic unit. You can count unit cubes to find the volume of a solid figure.
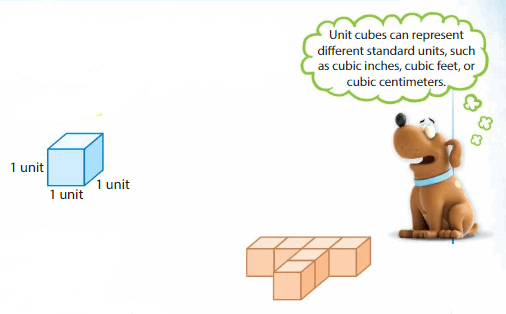
Example
Find the volume of the figure.
The figure is made of __ unit cubes.
So, the volume of the figure is _1_ cubic units.
Answer:
The volume of the figure = 12 cubic feet.
The figure is made up of 7 unit cubes.
So, the volume of the figure is 1 cubic units.
Explanation:
The volume of the figure = l x w x h
where l = length, w = width and h = height.
given that l = 4 , w= 3 and h = 1
v = 4 x 3 x 1
v = 12 x 1
v = 12 cubic feet.
The figure is made up of 7 unit cubes.
So, the volume of the figure is 1 cubic units.
Example
Find the volume of the figure.
Each unit cube has an edge length of ___

So, each unit cube has a volume of ___.
The figure is made of ___ unit cubes.
So, the volume of the figure is ___.
Answer:
Each cube has an edge length of 1 unit
So, each cube has a volume of 1 cubic unit.
The figure is made of 12 unit cubes.
So, the volume of the figure is 12 cubic cm
Explanation:
Each cube has an edge length of 1 unit
So, each cube has a volume of 1 cubic unit.
v = l x w x h
v = 1 x 1 x 1
v = 1 cubic unit
volume of figure = l x w x h
v = 3 x 2 x 2
where l = 3 cm , w = 2 cm and h = 2 cm given.
v = 3 x 2 x 2
v = 6 x 2
v = 12 cubic cm.
Show and Grow
Find the volume of the figure.
Question 1.
Volume = 6 cubic units
Answer:
The volume of the cube = 16 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 1 x 4
In the above-given figure l=4 ft, w =1 ft and h = 4ft
volume = 4 x 1 x 4
volume = 4 x 4
volume = 16 cubic ft
Question 2.
Volume = ___
Answer :- 16
Explanation:- width*length*height(w*l*h)
= 2*4*2
=16
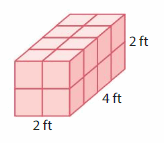
Answer:
The volume of cube = 16 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 2 x 2
In the above-given figure l=4 ft, w = 2 ft and h = 2ft
volume = 4 x 2 x 2
volume = 8 x 12
volume = 16 cubic ft
Apply and Grow: Practice
Find the volume of the figure.
Question 3.
Volume = ___
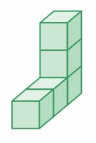
Answer:
The volume of the figure = 9 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 1 x 3
In the above-given figure l=3 ft, w = 1 ft and h = 3ft
volume = 3 x 3
volume = 9 cubic ft
Question 4.
Volume = ___
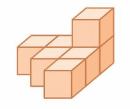
Answer:
The volume of the figure = 18 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 3 x 2
In the above-given figure l=3 ft, w = 3 ft and h = 2ft
volume = 3 x 3 x 2
volume = 9 x 2
volume = 18 cubic feet
Question 5.
Volume = ____
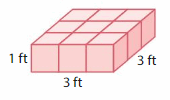
Answer:
The volume of the figure = 9 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 1 x 3
In the above-given figure l=3 ft, w = 1 ft and h = 3 ft
volume = 3 x 1 x 3
volume = 3 x 3
volume = 9 cubic feet
Question 6.
Volume = ____
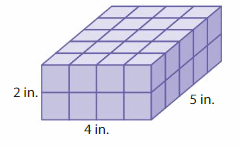
Answer:
The volume of the figure = 40 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 2 x 5
In the above-given figure l=4 ft, w = 2 ft and h = 5 ft
volume = 4 x 2 x 5
volume = 8 x 5
volume = 40 cubic feet
Question 7.
Cube-shaped shipping boxes, like the one shown, are packed into a van. They form a solid without any gaps or overlaps that is 3 feet long, 2 feet wide, and 3 feet tall. What is the volume of the solid formed?
Answer:
The volume of the solid formed = 40 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 2 x 3
In the above-given figure l=3 ft, w = 2 ft and h = 3 ft
volume = 3 x 2 x 3
volume = 6 x 3
volume = 18 cubic feet
Question 8.
YOU BE THE TEACHER
Your friend says the volume of the figure is 12 cubic centimeters. Is your friend correct? Explain.
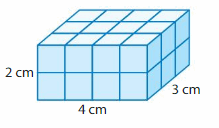
Answer:
No my friend is not correct.
The volume of the figure = 24 cubic cm.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 2 x 3
In the above-given figure l=4 ft, w = 2 ft and h = 3 ft
volume = 4 x 2 x 3
volume = 8 x 3
volume = 24 cubic feet
Question 9.
DIG DEEPER!
What is the volume of the figure formed by the missing cubes?
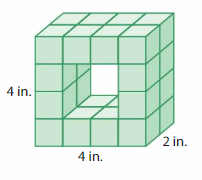
Answer:
The volume of the figure formed by the missing cubes = 32 cubic inches.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 4 x 2
In the above-given figure l=4 ft, w = 4 ft and h = 2 ft
volume = 4 x 4 x 2
volume = 16 x 2
volume = 32 cubic feet
Think and Grow: Modeling Real Life
Example
The puzzle is made of unit cubes. A box can hold 20 of the puzzles without any gaps or overlaps. What is the volume of the box?
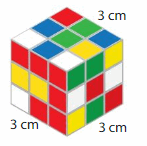
Find the volume of one puzzle.
The puzzle is made of unit cubes that each have an edge length of ___.
So, each unit cube has a volume of ___.
One puzzle is made of ___ unit cubes.
So, the volume of one puzzle is ___.
Answer:
The puzzle is made of unit cubes that each have an edge length of 3cm.
so, each unit cube has a volume of 1 cm.
one puzzle is made up of 3 cm
so, the volume of one puzzle is 27 cubic cm.
Explanation:
In the above-given figure,
length = 3 cm, width = 3 cm, height = 3cm
volume of the cube = l x w x h
where l = length, w = width and h = height
volume = 3 x 3 x 3
volume = 9 x 3
volume = 27 cubic cm

Multiply the volume of one puzzle by the number of puzzles
___ × ___ = ____
So, the volume of the box is ___.
Answer:
The volume of the box =
Show and Grow
Question 10.
A container holds 8 of the snowglobe boxes shown, without any gaps or overlaps. What is the volume of the container?
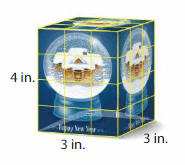
Answer:
The volume of the container = 36 cubic in.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 3 x 3
In the above-given figure l=4 in, w = 3 in and h = 3 in
volume = 4 x 3 x 3
volume = 13 x 3
volume = 36 cubic in
Question 11.
The shelving unit is made of six small compartments, one medium compartment, and one large compartment. Each small compartment has a length, a width, and a height of 1 foot. What is the volume of the shelving unit?

Answer:
The volume of the shelving unit = 4 cubic feet.
Explanation:
In the above-given question the shelving unit is made of six small compartments, one medium compartment, and one large compartment.
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 1 x 1
In the above-given figure l=4 ft, w = 1 ft and h = 1 ft
volume = 4 x 1 x 1
volume = 4 x 1
volume = 4 cubic feet.
Understand the Concept of Volume Homework & Practice 13.1
Find the volume of the figure.
Question 1.
Volume = ___
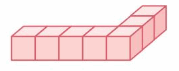
Answer:
The volume of the figure = 15 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 5 x 1 x 3
In the above-given figure l=5 ft, w = 1 ft and h = 3 ft
volume = 5 x 1 x 3
volume = 5 x 3
volume = 15 cubic feet.
Question 2.
Volume = ___
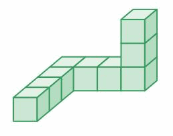
Answer:
The volume of the figure = 27 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 3 x 3
In the above-given figure l=3 ft, w = 3 ft and h = 3 ft
volume = 3 x 3 x 3
volume = 9 x 3
volume = 27 cubic feet.
Question 3.
Volume = ___
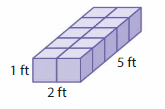
Answer:
The volume of the figure = 10 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 2 x 1 x 5
In the above-given figure l=2 ft, w = 1 ft and h = 5 ft
volume = 2 x 1 x 5
volume = 2 x 5
volume = 10 cubic feet.
Question 4.
Volume = ___
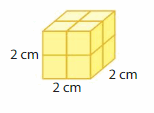
Answer:
The volume of the figure = 8 cubic cm.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 2 x 2 x 2
In the above-given figure l=2 cm, w = 2 cm and h = 2 cm
volume = 2 x 2 x 2
volume = 4 x 2
volume = 8 cubic cm.
Question 5.
Cube-shaped boxes, like the one shown, are placed together for a display at a store. They form a solid without any gaps or overlaps that is 5 feet long, 4 feet wide, and 1 foot tall. What is the volume of the solid formed?
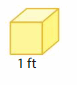
Answer:
The volume of the solid formed = 20 cubic ft.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 5 x 4 x 1
In the above-given figure l= 5 ft , w = 4 ft and h = 1 ft
volume = 5 x 4 x 1
volume = 20 x 1
volume = 20 cubic ft.
Question 6.
YOU BE THE TEACHER
Your friend says the figures have the same volume. Is your friend correct? Explain.
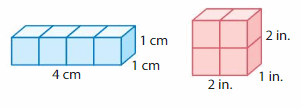
Answer:
Yes, my friend is correct.
Explanation:
In the 1st given figure l= 4 cm, w = 1cm h = 1 cm.
volume = l x w x h
volume = 4 x 1 x 1
volume = 4 x 1
volume = 4 cubic cm
In the 2nd given figure l= 2 in , w = 1 in h = 2 in .
volume = l x w x h
volume = 2 x 1 x 2
volume = 2 x 2
volume = 4 cubic in
Question 7.
DIG DEEPER!
Newton uses 32 centimeter cubes to build a solid. The base of the solid is shown. What is the height of the solid?
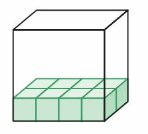
Answer:
The height of the solid = 24 cm
Explanation:
In the above-given figure, Newton uses 32-centimeter cubes to build a solid.
The number of cubes filled in the solid = 8 cm cubes.
The remaining cubes used to fill the solid is
32 – 8
24
The height of the solid = 24 cm
Question 8.
Modeling Real Life
A container holds 27 of the spring toy boxes shown, without any gaps or overlaps. What is the volume of the container?
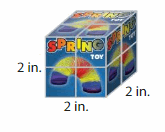
Answer:
The volume of the container = 8 cubic in.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 2 x 2 x 2
In the above-given figure l= 2 in , w = 2 in and h = 2 in.
volume = 2 x 2 x 2
volume = 4 x 2
volume = 8 cubic in.
Question 9.
Modeling Real Life
A store stacks boxes in an organized display. Each shaded box has a length, a width, and a height of 1 foot. What is the volume of the display?
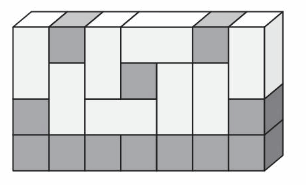
Answer:
The volume of the display = 28 cubic ft.
Explanation:
In the above-given figure,
the shaded box has a length, width, and height of 1 foot.
volume = length x width x height
where l = length, w = width and h = height
volume = 7 x 2 x 2
In the above-given figure l= 7 ft , w = 2 ft and h = 2 ft.
volume = 7 x 2 x 2
volume = 14 x 2
volume = 28 cubic ft.
Review & Refresh
Divide.
Question 10.
3 ÷ 5 = ___
Answer:
Divisor = 3
dividend = 5
Quotient = 1.6
Explanation:
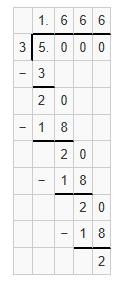
Question 11.
1 ÷ 4 = ___
Answer:
Divisor = 1
dividend = 4
Quotient = 4
Explanation:
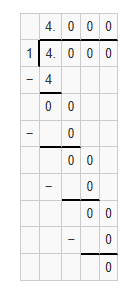
Question 12.
7 ÷ 8 = ___
Answer:
Divisor = 7
dividend = 8
Quotient = 4
Explanation:
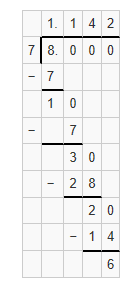
Lesson 13.2 Find Volumes of Right Rectangular Prisms
Explore and Grow
You can stack identical layers of unit cubes to build a rectangular prism.
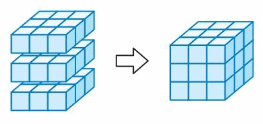
Use centimeter cubes to make one layer of a rectangular prism. Then stack identical layers and complete the table.
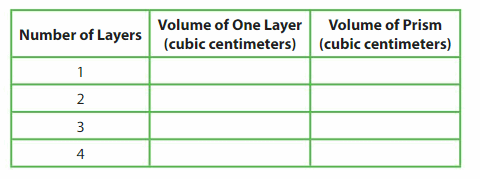
Answer:
The volume of one layer = 9 cubic cm
volume of 2 layers = 216 cubic cm
volume of 3 layers = 729 cubic cm
volume of 4 layers = 1,728 cubic cm
the volume of prism for 1 layer = 9 cubic cm
the volume of prism for 2 layers = 72 cubic cm
the volume of prism for 3 layers = 729 cubic cm
volume of prism for 4 layers = 1,728 cubic cm
Explanation:
Given that,
the number of layers are 1, 2, 3, 4.
volume of 1 layer = l x w x h
l = 3, w = 1 , h = 3
volume = 3 x 1 x 3
v = 9 cubic cm
volume of 2nd layer = l x w x h
l = 6, w = 6 , h = 6
volume = 6 x 6 x 6
v = 9 cubic cm
volume of 3rd layer = l x w x h
l = 9, w = 9 , h = 9
volume = 9 x 9 x 9
v = 729 cubic cm
volume of 4th layer = l x w x h
l = 12, w = 12 , h = 12
volume = 12 x 12 x 12
v = 1,728 cubic cm
volume of rectangular prism = l x w x h
where l= length, w = width and h= height
volume of 1 layer = l x w x h
l = 3, w = 1 , h = 3
volume = 3 x 1 x 3
v = 9 cubic cm
volume of 2nd layer = l x w x h
l = 6, w = 6 , h = 6
volume = 6 x 6 x 6
v = 9 cubic cm
volume of 3rd layer = l x w x h
l = 9, w = 9 , h = 9
volume = 9 x 9 x 9
v = 729 cubic cm
volume of 4th layer = l x w x h
l = 12, w = 12 , h = 12
volume = 12 x 12 x 12
volume = 1,728 cubic cm
Precision
Explain the relationship among the values in each row of the table.
Think and Grow: Find Volumes of Right Rectangular Prisms
Key Idea
A right rectangular prism is a solid figure with six rectangular faces.
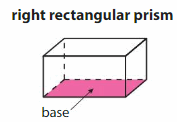
To find the volume of a right rectangular prism, multiply the number of unit cubes that cover the base by the number of layers of unit cubes.
Example
Find the volume of the rectangular prism.
Each unit cube has an edge length of ___
So, each unit cube has a volume of ___.
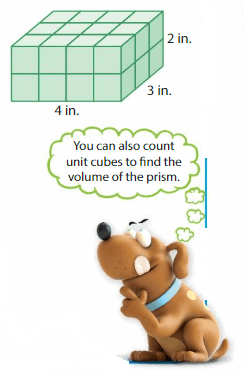
Answer:
The volume of the rectangular prism = 24 cubic in.
Each unit cube has an edge length = 1 cm
so, each unit cube has a volume = 1 cubic cm
Explanation:
The volume of the rectangular prism = l x w x h
where l = length, w = width and h = height
In the above figure, given that l = 4 in, w = 3 in, and h = 2 in.
v= 4 x 3 x 2
v = 12 x 2
v = 24 cubic in.
each cube has an edge length of 1 cm
in the above-figure shown that each cube has a length of 1 cm.
each cube has a volume of 1 cubic cm.
v = 1 x 1 x 1
v = 1 x 1
v = 1 cubic cm
Find the number of unit cubes in a base layer. Then multiply by the number of layers to find the volume.
A base layer is made of ___ × ___ = ___ unit cubes.
The prism is made of _____ layers of unit cubes.
So, the prism is made of ___ × ___ = ___ unit cubes.
The volume of the prism is ___.
Answer:
A base layer is made up of 4 x 1 = 4 cm cubes.
The prism is made up of 2 layers of unit cubes.
So, the prism is made up of 8 x 1 = 8 unit cubes.
The volume of the prism = 24 cubic in
Explanation:
In the above-given figure,
the base layer is made up of 4 cubes and it has 1 unit
4 x 1 = 4 unit cubes.
In the above-given figure,
the prism is made up of 2 layers of unit cubes.
so the prism is made up of 8 unit cubes.
8 x 1 = 8 unit cubes.
volume of the prism = length x width x height
v = l x w x h
v = 4 x 3 x 2
v = 24 cubic in
Show and Grow
Find the volume of the rectangular prism.
Question 1.
Volume = ___
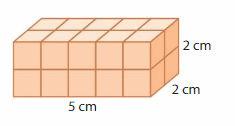
Answer:
The volume of rectangular prism = 20 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 5 cm , w = 2 cm , h = 2 cm.
volume = l x w x h
v = 5 x 2 x 2
v = 10 x 2
v = 20 cubic cm.
Question 2.
Volume = ___
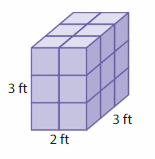
Answer:
The volume of rectangular prism = 18 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 2 ft , w = 3 ft , h = 3 ft .
volume = l x w x h
v = 2 x 3 x 3
v = 6 x 3
v = 18 cubic ft .
Apply and Grow: Practice
Find the volume of the rectangular prism.
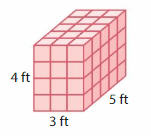
Question 3.
Volume = ___
Answer:
The volume of rectangular prism = 60 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 4 ft , w = 3 ft , h = 5 ft .
volume = l x w x h
v = 4 x 3 x 5
v = 12 x 5
v = 60 cubic ft .
Question 4.
Volume = ___
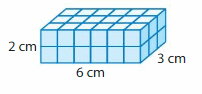
Answer:
The volume of rectangular prism = 36 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 6cm , w = 2 cm , h = 3 cm.
volume = l x w x h
v = 6 x 2 x 3
v = 12 x 3
v = 36 cubic cm .
Question 5.
Volume = ___
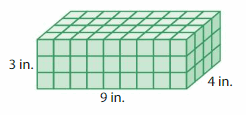
Answer:
The volume of rectangular prism = 108 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 9 in , w = 3 in , h = 4 in.
volume = l x w x h
v = 9 x 3 x 4
v = 27 x 4
v = 108 cubic in .
Question 6.
Volume = ___
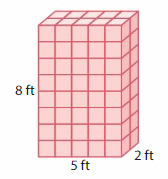
Answer:
The volume of rectangular prism = 80 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 5 ft , w = 8 ft , h = 2 ft.
volume = l x w x h
v = 5 x 8 x 2
v = 40 x 2
v = 80 cubic ft .
Question 7.
A rectangular prism is made of unit cubes, like the one shown. The prism is 6 centimeters long, 3 centimeters wide, and 4 centimeters tall. What is the volume of the prism?
![]()
Answer:
The volume of rectangular prism = 72 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given question, l= 6 cm , w = 3 cm , h = 4 cm.
volume = l x w x h
v = 6 x 3 x 4
v = 18 x 4
v = 72 cubic cm .
Question 8.
Structure
What happens to the volume of a rectangular prism when you double its height? Justify your answer by giving an example.
Answer:
The volume of the rectangular prism is increased.
Explanation:
For example, we are assuming l = 3 in , w = 2 in and h = 2 in.
volume of the rectangular prism = l x w x h
v = 3 x 2 x 2
In the above given question height is doubled.
h = 4
v = 3 x 2 x 4
v = 6 x 4
v = 24 cubic in
Question 9.
DIG DEEPER!
How many unit cubes can fit inside the rectangular prism? Explain.
Answer:
80 unit cubes can fit inside the rectangular prism.
Explanation:
For example, we are assuming l = 5 , w = 8 and h = 2 ft .
v = l x w x h
v = 5 x 8 x 2
v = 40 x 2
v = 80 cubiic feets.
Think and Grow: Modeling Real Life
Example
A package containing video games has a volume of 150 cubic inches. The diagram shows the number of packages that can fit in a shipping box. Estimate the volume of the shipping box.
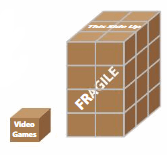
Find the number of packages in a base layer of the shipping box. Then multiply by the number of layers to find the total number of packages.
A base layer of the shipping box can hold 2 × 3 = 6 packages. There are 4 layers. So, the shipping box holds 4 × 6 = 24 packages.
Multiply the volume of 1 package by the number of packages that fit in the shipping box.
24 × __ = __ cubic inches
So, the volume of the shipping box is about __ cubic inches.
Answer:
a. The number of packages in a base layer of the shipping box = 6 packages.
number of layers = 4 and total number of packages = 6
6 x 4 = 24
The number of packages that fit in the shipping box = 6 boxes
1 x 6 = 6
volume of 1 package = 1 cube.
Explanation:
a. The number of packages in a base layer of the shipping box = 6 packages.
6 x 4 = 24
number of layers = 4 and total number of packages = 6
6 x 4 = 24
The number of packages that fit in the shipping box = 6 boxes
1 x 6 = 6
volume of 1 package = 1 cube.
Show and Grow
Question 10.
A book has a volume of 91 cubic inches. The diagram shows the number of books that can fit in a container.
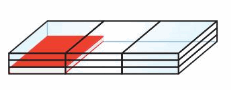
Estimate the volume of the container.
Answer:
The volume of the container = 819 in
Explanation:
In the above-given figure,
A book has a volume of 91 cubic inches.
9 books can fit in the container .
91 x 9 = 819 in.
Question 11.
DIG DEEPER!
Your teacher stores 12 of the crates in a supply closet. The closet is 3 feet long, 2 feet wide, and 7 feet tall. How much extra space is in the closet?

Answer:
The extra space in the closet = 43 cubic ft.
Explanation:
volume of closet = l x w x h
where l = length, w = width and h = height.
l = 3 ft , w = 2 ft and h = 7 ft.
v = 3 x 2 x 7
v = 6 x 7
v = 42 cubic feet
In the above given figure,
l = 1 ft , w = 1 ft, and h = 1 ft
v = 1 x 1 x 1
v = 1 cubic cm
The extra space = 42 + 1
43 cubic ft
Find Volumes of Right Rectangular Prisms Homework & Practice 13.2
Find the volume of the rectangular prism.
Question 1.
Volume = ___
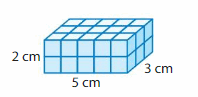
Answer:
The volume of the right rectangular prism = 30 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 5 cm , w = 2 cm , h = 3 cm.
volume = l x w x h
v = 5 x 2 x 3
v = 10 x 3
v = 30 cubic cm.
Question 2.
Volume = ___
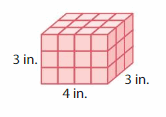
Answer:
The volume of the right rectangular prism = 120 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 4 in , w = 3 in , h = 3 in.
volume = l x w x h
v = 4 x 3 x 3
v = 40 x 3
v = 120 cubic in
Question 3.
Volume = ___
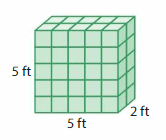
Answer:
The volume of the right rectangular prism = 50 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l= 5 ft , w = 5 ft , h = 2 ft.
volume = l x w x h
v = 5 x 5 x 2
v = 25 x 2
v = 50 cubic ft.
Question 4.
Volume = ___
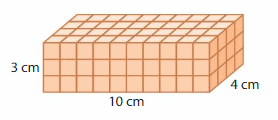
Answer:
The volume of the right rectangular prism = 120 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given figure, l=10 cm , w = 3 cm , h = 4cm.
volume = l x w x h
v = 10 x 3 x 4
v = 30 x 4
v = 120 cubic cm.
Question 5.
A rectangular prism is made of unit cubes, like the one shown. The prism is 7 inches long, 2 inches wide, and 4 inches tall. What is the volume of the prism?

Answer:
The volume of the right rectangular prism = 120 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
In the above-given question , l=7 in , w = 2 in , h = 4 in.
volume = l x w x h
v = 7 x 2 x 4
v = 14 x 4
v = 176 cubic in.
Question 6.
Reasoning
A cube has a volume of 27 cubic inches. What is the edge length of the cube?
Answer:
The edge length of the cube = 3 in
Explanation:
In the above-given question,
the volume of cube = 27 cubic inches.
v = l x w x h
v = 3 x 3 x 3
The edge length of the cube = 3 in
Question 7.
Reasoning
You, Newton, and Descartes each build the rectangular prism shown. You stack all three prisms on top of each other. What is the volume of the new prism? How many times greater is the volume of the new prism than the volume of your original prism?
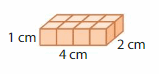
Answer:
The volume of the new prism = 24 cubic cm
Explanation:
In the above-given figure,
l = 4 cm , w = 1 cm and h = 2 cm given.
v = l x w x h
v = 4 x 1 x 2
v = 4 x 2
v = 8 cubic cm
I stack all 3 prisms on top of each other.
The volume of the new prism = 12 x 1 x 2
v = 12 x 2
v = 24 cubic cm.
Question 8.
Modeling Real Life
A shoe box has a volume of 336 cubic inches. The diagram shows the number of shoe boxes that can fit in a shipping box. Estimate the volume of the shipping box.
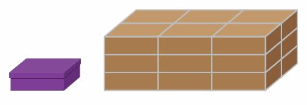
Answer:
The volume of the shipping box = 3,024 cubic in.
Explanation:
Given that a shoebox has a volume of 336 cubic inches.
In the shipping box, we can fit 9 shoe boxes.
volume of the shipping box = 336 x 9
volume = 3,024 cubic in
Question 9.
Modeling Real Life
The wooden pallet can hold a maximum of 5 layers of boxes.A worker places 48 boxes, like the one shown, on to the pallet with no gaps. How many more boxes can fit?
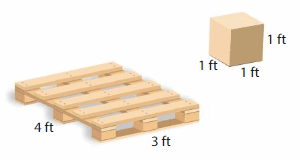
Answer:
The more boxes can fit = 3 boxes.
Explanation:
Given that the wooden pallet can hold a maximum of 5 layers of boxes.
A worker places 48 boxes
The more boxes can fit = 5 x 9
5 x 9 = 45 cubic ft
48 – 45 = 3 boxes.
Review & Refresh
Use a common denominator to write an equivalent fraction for each fraction.
Question 10.
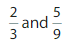
Answer:
(18/27) , (15/27)
Explanation:
Factors of 3 = 1, 3
factrs of 9 = 1, 3 , 9
from those the common are 1, 3.
1 x 3 = 3
3 x 3 = 9
2 x 9 = 18
5 x 3 = 15
(18/27) , (15/27)
Question 11.
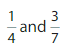
Answer:
(7/28) , (12/28)
Explanation:
Factors of 4 = 1, 4 and 2.
factrs of 7 = 1, 7
from those the common are 1
7 x 4 = 28
7 x 1 = 7
3 x 4 = 12
(7/28) , (12/28)
Lesson 13.3 Apply the Volume Formula
Explore and Grow
Work with a partner. Use centimeter cubes to create several different rectangular prisms, each with a volume of 12 cubic centimeters. Record your results in the table.
What do you notice about the dimensions of each prism?
Answer:
The dimensions of each prism = 2cm, 3 cm ,2cm.
length = 2 width = 3 and height = 2.
Base length, base width, and height
2, 3, 2.
3, 2, 2.
2, 2, 3.
4, 3, 1.
Explanation:
In the above-given question,
volume of each cube = 12 cubic cm.
we can assume length = 2cm width = 3cm and height = 2cm.
otherwise we can assume length = 3 cm width = 2 cm and height = 2cm.
length = 2 cm width = 2 cm and height = 3 cm.
length = 4 cm width = 3 cm and height = 1 cm.
Structure
How can you find the volume of a rectangular prism without using unit cubes?
Answer:
we can find the volume of a rectangular prism by using cm cubes.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 in , w = 3 in , h = 3 in.
volume = l x w x h
v = 4 x 3 x 3
v = 40 x 3
v = 120 cubic in
Think and Grow: Use a Formula to Find Volume
Key Idea
You can use the length, width, and height of a rectangular prism to find its volume.
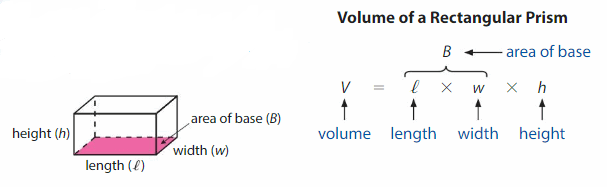
Volume of a Rectangular Prism
Example
Find the volume of the rectangular prism.
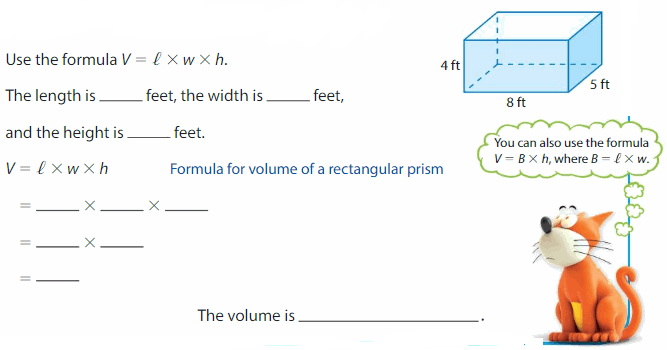
Answer:
The volume of rectangular prism = 160 cubic feet.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 in , w = 3 in , h = 3 in.
volume = l x w x h
v = 4 x 3 x 3
v = 40 x 3
v = 120 cubic in
Show and Grow
Find the volume of the rectangular prism.
Question 1.
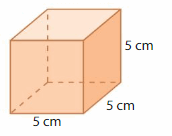
Answer:
The Volume of rectangular prism = 125 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 5 cm , w = 5 cm , h = 5 cm.
volume = l x w x h
v = 5 x 5 x 5
v = 25 x 5
v = 125 cubic cm.
Question 2.
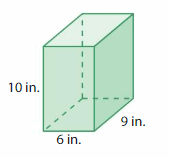
Answer:
The Volume of rectangular prism = 540 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 6 in , w = 9 in , h = 10 in.
volume = l x w x h
v = 6 x 9 x 10
v = 54 x 10
v = 540 cubic in.
Apply and Grow: Practice
Find the volume of the rectangular prism.
Question 3.
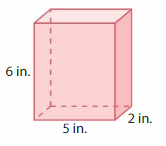
Answer:
The Volume of rectangular prism = 60 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 5 in , w = 2 in , h = 5 in.
volume = l x w x h
v = 5 x 2 x 6
v = 10 x 6
v = 60 cubic in.
Question 4.
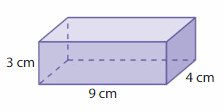
Answer:
The Volume of rectangular prism = 108 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 9 cm , w = 4 cm , h = 3 cm .
volume = l x w x h
v = 9 x 4 x 3
v = 36 x 3
v = 108 cubic cm.
Question 5.
Newton’s dog house is a rectangular prism. The house is 5 feet long, 4 feet wide, and 5 feet tall. What is the volume of the house?
Answer:
The Volume of house = 100 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 5 ft , w = 4 ft , h = 5 ft .
volume = l x w x h
v = 5 x 4 x 5
v = 20 x 5
v = 100 cubic ft.
Question 6.
A hole dug for an in-ground swimming pool is a rectangular prism. The hole is 20 feet long, 10 feet wide, and 6 feet tall. What is the volume of the hole?
Answer:
The Volume of the hole = 1200 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 20 ft , w = 10 ft , h = 6 ft .
volume = l x w x h
v = 20 x 10 x 6
v = 200 x 6
v = 1200 cubic ft.
Question 7.
Structure
Compare the dimensions and volumes of the three rectangular prisms. What do you notice?
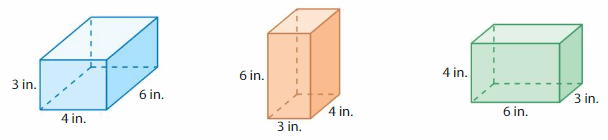
Answer:
The dimensions and volumes of the 3 rectangular prisms are equal volumes.
Explanation:
volume of the 1st rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 in , w = 6 in , h = 3 in .
volume = l x w x h
v = 4 x 6 x 3
v = 24 x 3
v = 72 cubic in.
volume of the 3rd rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 6 in , w = 3 in , h = 4 in .
volume = l x w x h
v = 6 x 3 x 4
v = 18 x 4
v = 72 cubic in.
volume of the 2nd rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 3 in , w = 4 in , h = 6 in .
volume = l x w x h
v = 3 x 4 x 6
v = 12 x 6
v = 72 cubic in.
Question 8.
DIG DEEPER!
What is the volume of Newton’s rectangular prism?

Answer:
volume of the Newtons rectangular prism = 400 cubic cm
Explanation:
volume of the Newtons rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 2 cm , w = 6 in , h = 3 in .
height = 5times of length = 5 x 2 = 10 cm
width = 2 times of height = 10 x 2 = 20 cm
volume = l x w x h
v = 2 x 20 x 10
v = 40 x 10
v = 400 cubic cm.
Think and Grow: Modeling Real Life
Example
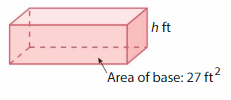
The dump truck bed is a rectangular prism. The area of the base is 8 square yards.The height is 2 yards. The driver needs to transport 18 cubic yards of gravel. Can he transport all of the gravel at once?

Use a formula to find the volume of the dump truck bed.

The volume of the dump truck bed is ___.
Compare the volume of the bed to the amount of gravel.
![]()
So, the driver __ transport all of the gravel at once.
Answer:
The volume of dump truck bed = 16 sq yards.
the volume of bed to the amount of gravel = 16: 18
so, the driver cannot transport all of the gravel at once.
Explanation:
The volume of dump truck bed = base x height
v = b x h
where base = 8 yds and height = 2 yards.
v = 8 x 2
v = 16 sq yds.
volume of bed to the amount of gravel is 18 yards given.
16: 18
so, the driver cannot transport all of the gravel at once.
Show and Grow
Question 9.
The aquarium is a rectangular prism. The area of the base is 288 square inches. Can the aquarium hold 4,500 cubic inches of water? Explain.

Answer:
Yes, the aquarium can hold 4,500 cubic inches of water.
Explanation:
the volume of rectangular prism = base x height
area = 288 sq inches given . height = 16 in
volume = 288 x 16
v = 4608 cubic in.
The aquarium can hold 4,500 cubic in of water.
Question 10.
DIG DEEPER!
A principal orders two types of lockers for the school. Which locker has a greater volume? How much greater?
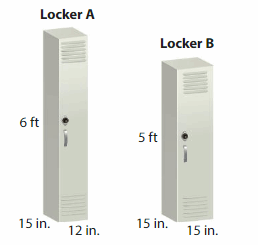
Answer:
Locker B has greater volume than Locker A.
Explanation:
volume of the Locker A = length x width x height
where l = length, w= width and h = height
Assume, l= 12 in , w = 15 in , h = 6 in .
volume = l x w x h
v = 12 x 15 x 6
v = 180 x 6
v = 1080 cubic in.
volume of the Locker B = length x width x height
where l = length, w= width and h = height
Assume, l= 15 in , w = 15 in , h = 5 in .
volume = l x w x h
v = 15 x 15 x 5
v = 225 x 5
v = 1125 cubic in.
Apply the Volume Formula Homework & Practice 13.3
Find the volume of the rectangular prism.
Question 1.
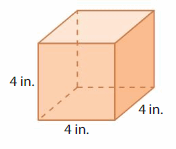
Answer:
The Volume of the rectangular prism = 64 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 in , w = 4 in , h = 4 in .
volume = l x w x h
v = 4 x 4 x 4
v = 16 x 4
v = 64 cubic in.
Question 2.
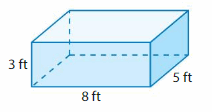
Answer:
The Volume of the rectangular prism = 120 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 8 ft , w = 5 ft , h = 3 ft .
volume = l x w x h
v = 8 x 5 x 3
v = 40 x 3
v = 120 cubic ft.
Question 3.
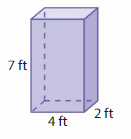
Answer:
The Volume of the rectangular prism = 56 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 ft , w = 2ft , h = 7 ft .
volume = l x w x h
v = 4 x 2 x 7
v = 8 x 7
v = 56 cubic ft.
Question 4.
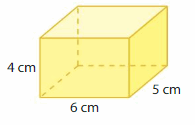
Answer:
The Volume of the rectangular prism = 120 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 6 cm , w = 5 cm , h = 4 cm .
volume = l x w x h
v = 6 x 5 x 4
v = 30 x 4
v = 120 cubic cm.
Question 5.
A toy chest is a rectangular prism. The chest is 4 feet long, 2 feet wide, and 2 feet tall. What is the volume of the chest?
Answer:
The Volume of the chest = 16 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 ft , w = 2 ft , h = 2 ft .
volume = l x w x h
v = 4 x 2 x 2
v = 8 x 2
v = 16 cubic ft.
Question 6.
YOU BE THE TEACHER
Your friend uses the formula V = B × h and finds V = 10 × 9 = 90 cubic inches. Is your friend correct? Explain.
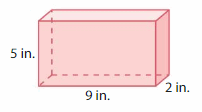
Answer:
No, my friend is not correct.
Explanation:
volume = base x height
v = 9 x 5
where base = 9 in, height = 5 in given.
v = 45 cubic in.
Question 7.
Number Sense
Find the volume of the rectangular prism. Then double the dimensions of the prism and find the new volume. How does the new volume compare to the original volume?
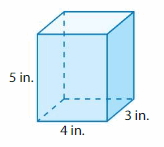
Answer:
The new Volume of the prism= 3600 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 4 in , w = 3 in , h = 5 in .
volume = l x w x h
v = 4 x 3 x 5
v = 12 x 5
v = 60 cubic in.
Given that the dimensions are doubled.
4 x 4 = 16 , 3 x 3 = 9, 5 x 5 = 25
volume of the new rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l= 16 in , w = 9 in , h = 25 in .
volume = l x w x h
v = 16 x 9 x 25
v = 144 x 25
v = 3600 cubic in.
Question 8.
Modeling Real Life
A sandbox is a rectangular prism. The area of the base is 3,600 square inches. The height is 11 inches. You add 38,000 cubic inches of sand to the box. Do you fill the sandbox to the top? Explain.
Answer:
Yes, we can fill the sandbox to the top.
Explanation:
volume = base x height
v = 3600 x 11
v = 39,600 cubic in.
if we add 38,000 cubic inches of sand to the box
39,600 + 38,000
77,600 inches.
Question 9.
DIG DEEPER!
Each piece of Descartes’s clubhouse is a cube. What is the volume of the clubhouse? Explain.
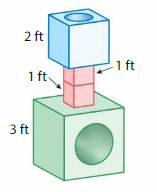
Answer:
The volume of the clubhouse = 6 cubic feet.
Explanation:
volume of the cube = length x width x height
where l = length, w= width and h = height
Assume, l= 3 ft , w = 2 ft , h = 1 ft .
volume = l x w x h
v = 3 x 2 x 1
v = 6 x 1
v = 6 cubic ft.
Review & Refresh
Find the quotient. Then check your answer.
Question 10.
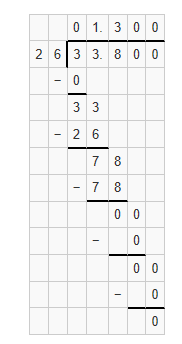
3.38 ÷ 2.6 = ___
Answer:
Quotient = 1.3
Explanation:
Question 11.
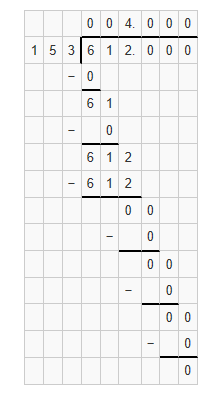
6.12 ÷ 1.53 = __
Answer:
Quotient = 4.0
Explanation:
Question 12.
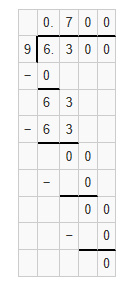
0.63 ÷ 0.9 = ___
Answer:
Quotient = 0.7
Explanation:
Lesson 13.4 Find Unknown Dimensions
Explore and Grow
For each row of the table, use centimeter cubes to create the rectangular prism described. Then complete the table.
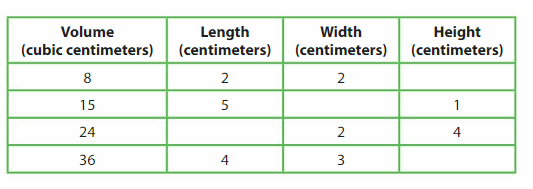
Construct Arguments
Explain how you determined the unknown dimension for each rectangular prism.
Answer:
volume = 8, length = 2cm, width = 2 cm, height = 2 cm.
volume = 15, length = 5cm, width = 3 cm, height = 1 cm.
volume = 24, length = 8cm, width = 2 cm, height = 4 cm.
volume = 36, length = 4cm, width = 3 cm, height = 3 cm.
Explanation:
Volume of rectangular prism = l x w x h
length = 2cm, width = 2cm given.
volume = 2 x 2 x 2
v = 8 cubic cm, h = 2 cm
Volume of rectangular prism = l x w x h
length = 5cm, height= 1cm given.
volume = 2 x 3 x 1
v = 15 cubic cm, w = 3 cm
Volume of rectangular prism = l x w x h
width = 2cm, height= 4cm given.
volume =3 x 2 x 4
v = 24 cubic cm, l = 3 cm
Volume of rectangular prism = l x w x h
length = 4cm, width= 3cm given.
volume =4 x 3 x 3
v = 36 cubic cm, h = 3 cm
Think and Grow: Find Unknown Dimensions
Example
The volume of the rectangular prism is 56 cubic feet. Find the height.

Answer:
The height of the rectangular prism = cm
Explanation:
Given that volume of rectangular prism = 56 cubic feet.
volume = base x height
v = 56 given base = 8
56 = 8 x h
h = (56/8)
h = 7 cm
Example
The volume of the rectangular prism is 180 cubic centimeters. Find the length.

Answer:
The length of prism = 9 cm
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given , w = 5 cm , h = 4 cm .
volume = l x w x h
180 = l x 5 x 4
180 = l x 20
180 = 20 l
l = (180/20)
l = 9 cm.
Show and Grow
Find the unknown dimension of the rectangular prism.
Question 1.
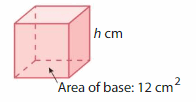
Answer:
The height of prism = 1 cm
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given , l = 3 cm , w = 4 cm .
volume = l x w x h
12 = 3 x 4 x h
12 = l2 x h
12 = 12h
h= (20/20)
h = 1 cm.
Question 2.
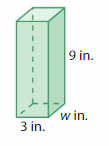
Answer:
The width of prism = 1 cm
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given , l = 3 cm , h = 9 cm .
volume = l x w x h
27 = 3 x w x 9
27 = 27 w
w= (27/27)
w = 1 cm.
Apply and Grow: Practice
Find the unknown dimension of the rectangular prism.
Question 3.
Volume = 400 cubic inches
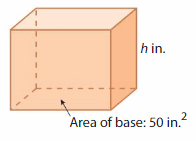
Answer:
The height of the rectangular prism = 8 in
Explanation:
Given that volume of rectangular prism = 56 cubic feet.
volume = base x height
v = 400 given base = 50
400 = 50 x h
h = (400/50)
h = 8 in
Question 4.
Volume = 343 cubic centimeters
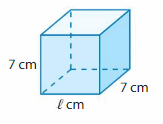
Answer:
The length of the rectangular prism = 8 in
Explanation:
Given that volume of rectangular prism = 56 cubic feet.
volume = base x height
v = 343 given base = 49 sq cm
343 = 49 x l
l = (343/49)
l = 8 in
Question 5.
Volume = 132 cubic feet
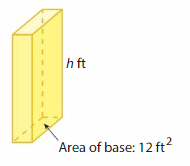
Answer:
The height of the rectangular prism = 11 ft
Explanation:
Given that volume of rectangular prism = 132cubic feet.
volume = base x height
v = 132 given base = 12 sq ft
132 = 12 x h
h = (132/12)
h = 11 ft
Question 6.
Volume = 512 cubic inches
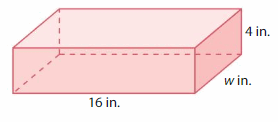
Answer:
The Width of the rectangular prism = 8 in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l=16 in , v = 512 cubicin , h = 4 in.
volume = l x w x h
512 = 16 x w x 4
512 = w x 64
512 = 64 w
w = (512/64)
w = 8 in
Question 7.
Writing
Explain how to find an unknown dimension of a rectangular prism given its volume and the other two dimensions.
Answer:
The Width of the rectangular prism = 8 in.
Explanation:
We have to assume v = 512 cubic in, l= 16 and h= 4 in
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
Assume, l=16 in , v = 512 cubicin , h = 4 in.
volume = l x w x h
512 = 16 x w x 4
512 = w x 64
512 = 64 w
w = (512/64)
w = 8 in
Question 8.
DIG DEEPER!
A rectangular prism has a volume of 720 cubic centimeters. The height of the prism is 10 centimeters. The length is twice the width. What are the dimensions of the base?
Answer:
The dimensions of the base = 72 cm
Explanation:
Given that volume of rectangular prism = 720 cubic cm.
volume = base x height
v = 720 given h = 10
720 = b x 10
720 =10 b
b = (720/10)
b = 72 cm
Think and Grow: Modeling Real Life
Example
A traveler buys the painting shown. The volume of the suitcase is 1,820 cubic inches. Can the painting lie flat inside the suitcase?
Use a formula to find the length of the suitcase.

Answer:
Yes, the painting lies flat inside the suitcase.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height.
given , v = 1,820 , h = 7 in, w = 13 in .
volume = l x w x h
1820 = l x 13x 7
1820 = l x 91
l = (1820/91)
l = 20 in
The area of the painting = l x w
painting is in the shape of a rectangle
area of rectangle = l x w
area = 14 x 11
area = 154
Show and Grow
Question 9.
The volume of the candle is 576 cubic centimeters. Will the candle fit completely inside the glass jar? Explain.
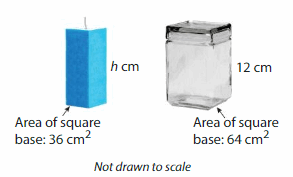
Answer:
Yes, the candle will fit completely inside the glass jar.
Explanation:
Given that volume of candle = 576 cubic cm.
volume = base x height
v = 576 given b = 36 sq cm
576 = 36 x h
576= 36 h
h = (576/36)
h = 16 cm
Given that volume of glass jar = 576 cubic cm.
volume = base x height
given b = 64 sq cm h = 12 cm
v = 64 x 12
v= 768 cubic cm
Question 10.
DIG DEEPER!
The popcorn boxes have the same volume, but different dimensions. What is the width of Box B?
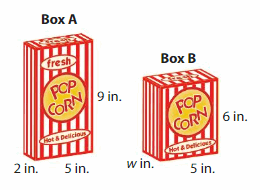
Answer:
The Width of the Box B = 3 in.
Explanation:
volume of the Box A = length x width x height
where l = length, w= width and h = height
given, l=5 in , w = 2 in , h = 9 in.
volume = l x w x h
v = 5 x 2 x 9
v = 10 x 9
v = 90 cubic in
volume of the Box B = length x width x height
where l = length, w= width and h = height
given, l=5 in , v = 90 cubic in , h = 6 in.
volume = l x w x h
90 = 5 x w x 6
90 = 30 x w
90 = 30 w
w = (90/30)
w = 3 in
Find Unknown Dimensions Homework & Practice 13.4
Question 1.
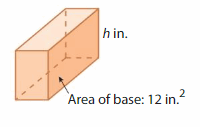
Answer:
The unknown dimensions are l= 6in, w= 2 in,and h = 1 in.
Explanation:
given that area of the base = 12 sq in
area = l x w
12 = 6 x 2
v = l x w x h
12 = 6 x 2h
12 = 12 h
h = (12/12)
h = 1 in
Question 2.
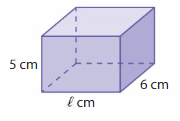
Answer:
length of the prism = 1 cm
Explanation:
Given that volume of prism = 30 cubic cm.
volume = length x base x height
given b = 6 cm h = 5 cm
30 = l x 6 x 5
30= 30 l
l = (30/30)
l = 1 cm
Find the unknown dimension of the rectangular prism.
Question 3.
Volume = 480 cubic feet
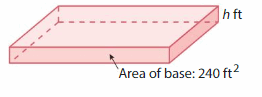
Answer:
The height of the rectangular prism = 2 ft
Explanation:
Given that volume of rectangular prism = 56 cubic feet.
volume = base x height
v = 480 cubic feet given base = 240 sq ft
480 = 240 x h
480 = 240 h
h = (480/240)
h = (48/24)
h = 2 ft
Question 4.
Volume = 351 cubic inches
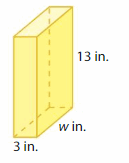
Answer:
The Width of the prism =7.3125 in
Explanation:
volume of the Box B = length x width x height
where l = length, w= width and h = height
given, l=3 in , v = 351 cubic in , h = 13 in.
volume = l x w x h
351 = 3 x w x 16
351 = 48 x w
351 = 48 w
w = (351/48)
w = 7.3125 in
Question 5.
Open-Ended
A rectangular prism has a volume of 144 cubic feet. The height of the prism is 6 feet. Give one possible pair of dimensions for the base.
Answer:
The base of the rectangular prism = 24 ft
Explanation:
Given that volume of rectangular prism = 144 cubic feet.
volume = base x height
v = 144 cubic feet given height = 6 ft
144 = b x 6
144 = 6b
b = (144/6)
b = 24 feet
Question 6.
DIG DEEPER!
The volume of the rectangular prism is 64 cubic centimeters. What is the value of y?
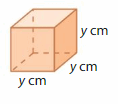
Answer:
The value of y = 4 cm
Explanation:
Given that the volume of rectangular prism = 64 cubic in.
v = l x w x h
64 = lwh
64 = 4 x 4 x 4
64 = 16 x 4
64 = 64
Question 7.
Modeling Real Life
The volume of the gift is 900 cubic inches. Can the gift fit inside the shipping box? Explain.
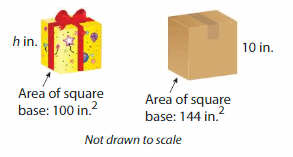
Answer:
Yes, the gift will fit inside the shipping box.
Explanation:
Given that volume of gift = 900 cubic in.
volume = base x height
v = 900 given b = 100 sq in
900 = 100 x h
900= 100h
h = (900/100)
h = 9 in
Given that base of shipping box = 576 cubic cm.
volume = base x height
given b = 144 sq in h = 10 in
v = 144 x 10
v= 1440 cubic in.
Question 8.
DIG DEEPER!
You fill the entire fish tank with water. Then you dump out some of the water.The volume of the water in the tank decreases by 96 cubic inches. How deep is the water now?
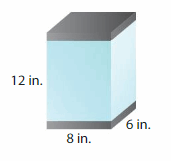
Answer:
The water in the tank = 480 cubic in.
Explanation:
volume of the Box A = length x width x height
where l = length, w= width and h = height
given, l=8 in , w = 6 in , h = 12 in.
volume = l x w x h
v = 8 x 6 x 12
v = 48 x 12
v = 576 cubic in
given that volume of water in the tank is decreased by 96 cubic in.
v = 576 – 96
v = 480 cubic in.
Review & Refresh
Divide.
Question 9.
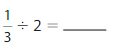
Answer:
Divisor = 0.3
Dividend = 2
Remainder = 2
Quotient = 6.6
Explanation:
(1/3) = 0.33
Question 10.
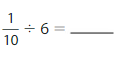
Answer:
Divisor = 0.1
Dividend = 6
Remainder = 0
Quotient = 60
Explanation:
(1/10) = 0.1

Question 11.
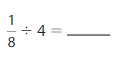
Answer:
Divisor = 0.125
Dividend = 4
Remainder = 0
Quotient = 32
Explanation:
(1/10) = 0.125
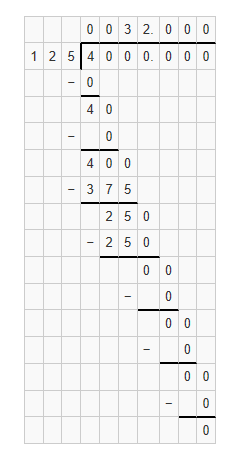
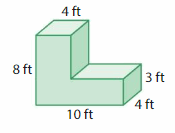
Lesson 13.5 Find Volumes of Composite Figures
Explore and Grow
Use centimeter cubes to find the volume of the figure. Explain your method.
Answer:
volume of figure 1 = 60 cubic cm.
volume of figure 2 = 36 cubic cm.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=6 cm , w = 2 cm , h = 5 cm.
volume = l x w x h
v = 6 x 2 x 5
v = 12 x 5
v = 60 cubic cm
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=6 cm , v = 3 cm , h = 2 cm.
volume = l x w x h
v = 6 x 3 x 2
v = 18 x 2
v = 36 cubic cm.
Structure
Describe another way to find the volume of the figure
Think and Grow: Find the Volume of a Composite Figure
Key Idea
A composite figure is made of two or more composite figure solid figures. You can break apart a composite figure to find its volume.
Example
Find the volume of the composite figure.
Break apart the figure into rectangular prisms. Find the dimensions of each prism.
Answer:
volume of figure 1 = 320 cubic ft.
volume of figure 2 = 1200 cubic ft.
Explanation:
volume of the figure 2( right side) = length x width x height
where l = length, w= width and h = height
given, l=10 ft , w = 4 ft , h = 3 ft.
volume = l x w x h
v = 10 x 4 x 3
v = 40 x 3
v = 1200 cubic ft.
volume of the figure 1 (left side) = length x width x height
where l = length, w= width and h = height
given, l=10 ft , w = 4 ft , h = 8 ft.
volume = l x w x h
v = 10 x 4 x 8
v = 40 x 8
v = 320 cubic feet.
Show and Grow
Question 1.
Find the volume of the composite figure.
Answer:
volume of figure 1 = 60 cubic cm.
volume of figure 2 = 990 cubic cm.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=10 cm , w = 2 cm , h = 3 cm.
volume = l x w x h
v = 10 x 2 x 3
v = 20 x 3
v = 60 cubic cm.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=10 cm , w = 11 cm , h = 9 cm.
volume = l x w x h
v = 10 x 11 x 9
v = 110 x 9
v = 990 cubic cm
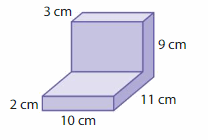
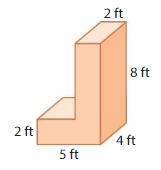
Apply and Grow: Practice
Find the volume of the composite figure.
Question 2.
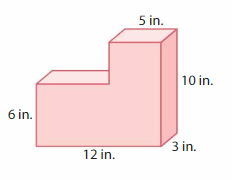
Answer:
volume of figure 1 = 360 cubic in.
volume of figure 2 = 360 cubic in.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=12 in , w = 3 in , h = 10 in.
volume = l x w x h
v = 12 x 3 x 10
v = 36 x 10
v = 360 cubic in.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=12 in , w = 5 in , h = 6 in.
volume = l x w x h
v = 12 x 5 x 6
v = 60 x 6
v = 360 cubic in .
Question 3.
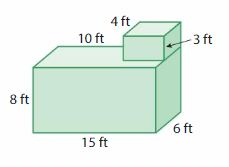
Answer:
volume of figure 1 = 720 cubic ft.
volume of figure 2 = 120 cubic ft.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=15 ft , w = 6 ft , h = 8 ft.
volume = l x w x h
v = 15 x 6 x 8
v = 90 x 8
v = 720 cubic ft.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=10 ft , w = 4 ft , h = 3 ft.
volume = l x w x h
v = 10 x 4 x 3
v = 40 x 3
v = 120 cubic ft
Question 4.
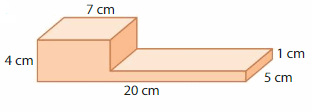
Answer:
volume of figure 1 = 720 cubic ft.
volume of figure 2 = 120 cubic ft.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=20 cm , w = 5 cm , h = 1 cm.
volume = l x w x h
v = 20 x 5 x 1
v = 100 x 8
v = 720 cubic ft.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=10 ft , w = 4 ft , h = 3 ft.
volume = l x w x h
v = 10 x 4 x 3
v = 40 x 3
v = 120 cubic ft
Question 5.
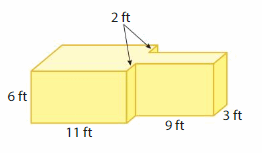
Answer:
volume of figure 1 = 132 cubic ft.
volume of figure 2 = 52 cubic ft.
Explanation:
volume of the figure 2( right side) = length x width x height
where l = length, w= width and h = height
given, l=9 ft , w = 3 ft , h = 2 ft.
volume = l x w x h
v = 9 x 3 x 2
v = 27 x 2
v = 52 cubic ft.
volume of the figure 1 (left side) = length x width x height
where l = length, w= width and h = height
given, l=11ft , w = 6 ft , h = 2 ft.
volume = l x w x h
v = 11 x 6 x 2
v = 66 x 2
v = 132 cubic ft.
Question 6.
Number Sense
Write one possible equation for the volume of the composite figure.
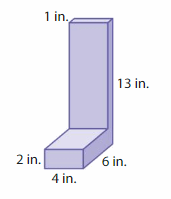
Answer:
4 x + 6 y = 13
4 x + 2 y = 1
Question 7.
YOU BE THE TEACHER
Your friend finds the volume of the composite figure. Is your friend correct? Explain.
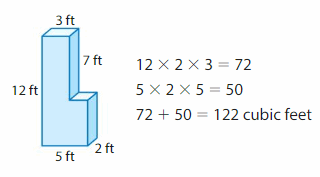
Answer:
yes, my friend is correct.
Explanation:
volume = l x w x h
v = 12 x 2 x 3
v = 72 cubic ft
v = l x w x h
v = 5 x 2 x 5
v = 10 x 5
v = 50 cubic ft.
v = 72 + 50
v = 122 cubic ft.
Think and Grow: Modeling Real Life
Example
The depth of the swimming pool is 5 feet. How many cubic feet of water can the pool hold?
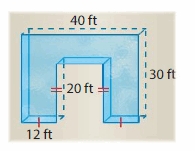
Break apart the pool into rectangular prisms. Find the dimensions of each prism.
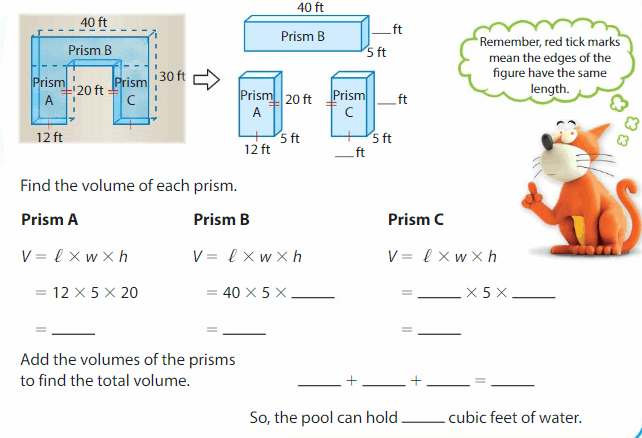
Answer:
so, the cube can hold 1200 cubic feet of water.
Explanation:
volume of prism A = l x w x h
l = 12 , w = 5 , h = 20
v = 12 x 5 x 20
v = 60 x 20
v = 1200 cubic feet.
volume of prism B = l x w x h
l = 40 , w = 5 v = 1200
1200 = 40 x 5 x h
1200 = 200 x h
1200 = 200h
h = (1200/200)
h = 6 ft
volume of prism C = l x w x h
h = 6, w = 5 , v = 1200
1200 = l x 5 x 6
1200 = l x 30
1200 = 30 l
l = (1200/30)
l = 40 ft
Show and Grow
Question 8.
How many cubic centimeters of wood are needed to make the game piece?
Answer:
The game needed to make the game piece = 90 cubic cm.
Explanation:
volume of prism A= l x w x h
v = 9 x 2 x 3
v = 18 x 3
v = 54 cubic cm
volume of pridm B= l x w x h
v = 6 x 2 x 3
v = 12 x 3
v = 36 cubic cm.
Question 9.
DIG DEEPER!
What is the volume of the building surrounding the outdoor courtyard? Explain your method.
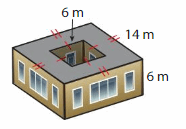
Answer:
The building surrounding the outdoor courtyard = 1,008 cubic m
Explanation:
volume of building surrounding inside = l x w x h
h = 6, w = 6 m , h = 14
v = 6 x 6 x 14
v = 36 x 14
v = 504 cubic m.
The outdoor courtyard is 2 times the inside courtyard.
v = 504 x 2
v = 1,008 cubic m
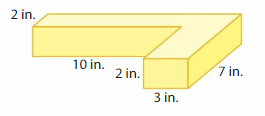
Find Volumes of Composite Figures Homework & Practice 13.5
Question 1.
Find the volume of the composite figure.
Answer:
volume of figure 1 = 160 cubic ft.
volume of figure 2 = 12 cubic ft.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=5 ft , w = 4 ft , h = 8 ft.
volume = l x w x h
v = 5 x 4 x 8
v = 20 x 8
v = 160 cubic ft.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l= 3ft , w = 2 ft , h = 2 ft.
volume = l x w x h
v = 3 x 2 x 2
v = 6 x 2
v = 12 cubic ft.
Find the volume of the composite figure.
Question 2.
Answer:
volume of figure 1 = 40 cubic in.
volume of figure 2 = 42 cubic in.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=10 ft , w = 2 in , h = 2 in.
volume = l x w x h
v = 10 x 2 x 2
v = 20 x 2
v = 40 cubic in.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l= 3in , w = 7 in , h = 2 in.
volume = l x w x h
v = 3 x 7 x 2
v = 21 x 2
v = 42 cubic in.
Question 3.
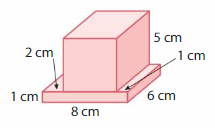 \
\
Answer:
volume of figure 1 = 25 cubic cm.
volume of figure 2 = 48 cubic cm.
Explanation:
volume of the figure 1( top ) = length x width x height
where l = length, w= width and h = height
given, l=5 cm , w = 1 cm , h = 5 cm.
volume = l x w x h
v = 5 x 1 x 5
v = 5 x 5
v = 25 cubic cm.
volume of the figure 2 (bottom ) = length x width x height
where l = length, w= width and h = height
given, l= 8 cm , w = 6 cm , h = 1 cm.
volume = l x w x h
v = 8 x 6 x 1
v = 48 x 1
v = 48 cubic cm.
Question 4.
Structure
Find the volume of the composite figure two different ways.
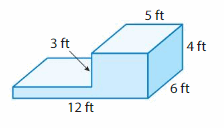
Answer:
volume of figure 1 = 288 cubic ft.
volume of figure 2 = 60 cubic ft.
Explanation:
volume of the figure 1( bottom) = length x width x height
where l = length, w= width and h = height
given, l= 12 ft , w = 6 ft , h = 4 ft.
volume = l x w x h
v = 12 x 6 x 4
v = 72 x 4
v = 288 cubic ft.
volume of the figure 2 (top) = length x width x height
where l = length, w= width and h = height
given, l= 5 ft , w = 4 ft , h = 3 ft.
volume = l x w x h
v = 5 x 4 x 3
v = 20 x 3
v = 60 cubic ft.
Question 5.
Modeling Real Life
The height of the garden bed is 2 feet. How many cubic feet of soil are in the garden bed?
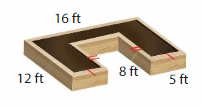
Answer:
The soil in the garden bed= 48 cubic feet.
Explanation:
v = l x w x h
where l = 16 – 2 (5)
l = 16 -10 = 6 ft
w = 12 – 8
w = 4 ft
h = 2 ft given
v = 6 x 4 x 2
v = 24 x 2
v = 48 cubic ft
Question 6.
DIG DEEPER!
The dimensions of each step are the same. How many cubic inches of concrete does a worker need to make the staircase?
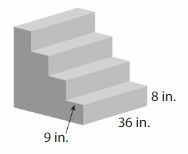
Answer:
The concrete does a worker need to make the staircase = 10,368 cubic in.
Explanation:
volume of the figure = length x width x height
where l = length, w= width and h = height
given, l= 36 in , w = 9 in , h = 8 in.
volume = l x w x h
v = 36 x 9 x 8
v = 324 x 8
v = 2,592 cubic in.
In the above-given figure there are 4 steps.
v = 2592 x 4
v = 10,368 cubic in
Review & Refresh
Question 7.
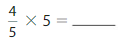
Answer: 4
Question 8.
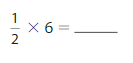
Answer: 3
Question 9.
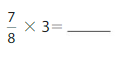
Answer: 21/8
Understand Volume Performance Task 13
Mechanical engineers follow guidelines when designing and installing elevators to make sure passengers are safe and the elevators are wheelchair accessible. Many elevators have heating and air conditioning units attached to them, so it is important to know the volume inside the elevator to keep the air a comfortable temperature.

Question 1.
The inside of the elevator shown is in the shape of a rectangular prism.
a. What is the volume of the inside of the elevator?
b. Another elevator has the same height and width. The length of the inside is doubled. How does this affect the volume?
c. Five people ride with their luggage on the elevator. Each person weighs about 200 pounds. The total combined weight of their luggage is about 425 pounds. About how many more pounds can the elevator hold?
Answer:
a. The volume of the inside elevator = 240 cubic ft
b. The volume increases.
c.The more pounds the elevator can hold = 1,875 pounds.
Explanation:
a. The volume of the inside elevator = l x w x h
given that elevator is in the shape of a rectangular prism.
v = 5 x 6 x 8
where l = 5 , w = 6 and h = 8
v = 5 x 6 x 8
v = 30 x 8
v = 240 cubic ft.
b. given that if the length is doubled = 2 x 5
l = 10
v = 10 x 6 x 8
v = 60 x 8
v = 480 cubic ft
c. Five people ride with their luggage on the elevator. Each person weighs about 200 pounds. The total combined weight of their luggage is about 425 pounds.
425 + 200
625 pounds.
Maximum capacity = 2500 pounds
2500 – 625 = 1,875 pounds
Question 2.
The inside of all new elevators must be wheelchair accessible. The minimum requirements are shown. The inside volume of an older elevator is 144 cubic feet. The base is a square and the height is 9 feet.
a. Explain why the older elevator does not meet the wheelchair requirements.
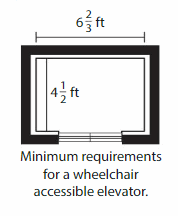
b. A new wheelchair-accessible elevator is added to the building. Its height is 9 feet. Find the minimum volume of the new elevator. How does this compare to the volume of the old elevator?
Answer:
a. The older elevator does not meet the wheelchair requirements because the elevator is added to the building.
b. The minimum volume of the new elevator = 30 cubic ft
Explanation:
a. The older elevator does not meet the wheelchair requirements because the elevator is added to the building.
b. The minimum volume of the new elevator = base x height
h = 6 x 2/3 = 20/3 = 6.66
6.66/2 = 3.33
v = 3.33 x 9
v = 30 cubic ft.
Understand Volume Activity
Directions:
- Players take turns rolling a die.
- On your turn, move your piece the number of spaces shown on the die.
- Find the volume of the rectangular prism.
- Cover the volume with a counter. Your turn is over.
- The first player to get three in a row, horizontally, vertically, or diagonally, wins!
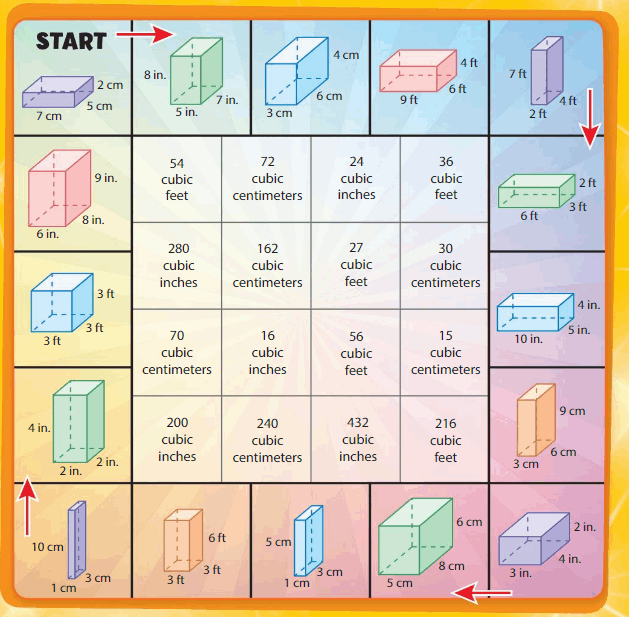
Understand Volume Chapter Practice
13.1 Understand the Concept of Volume
Find the volume of the figure.
Question 1.
Volume = ____
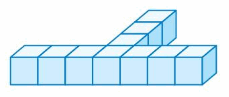
Answer:
The volume of the cube = 28 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 7 x 4 x 1
In the above-given figure l=7 ft, w =4 ft and h = 1ft
volume = 7 x 4 x 1
volume = 28 x 1
volume = 28 cubic ft
Question 2.
Volume = ____
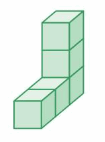
Answer:
The volume of the cube = 9 cubic feet.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 1 x 3
In the above-given figure l=3 ft, w =1 ft and h = 3ft
volume = 3 x 1 x 3
volume = 3 x 3
volume = 9 cubic ft
Question 3.
Volume = ____
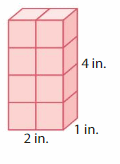
Answer:
The volume of the cube = 8 cubic in.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 2 x 1 x 4
In the above-given figure l=2 in, w =1 in and h = 4 in.
volume = 2 x 1 x 4
volume = 2 x 4
volume = 8 cubic in.
Question 4.
Volume = ____
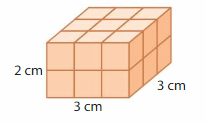
Answer:
The volume of the cube = 18 cubic cm.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 3 x 3 x 2
In the above-given figure l= 3 cm, w =3cm and h = 2 cm.
volume = 3 x 3 x 2
volume = 9 x 2
volume = 18 cubic cm.
Question 5.
Volume = ____
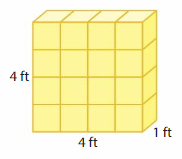
Answer:
The volume of the cube = 16 cubic ft.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 1 x 4
In the above-given figure l= 4 ft, w = 1 ft and h = 4ft.
volume = 4 x 1 x 4
volume = 4 x 4
volume = 16 cubic ft.
Question 6.
Volume = ____
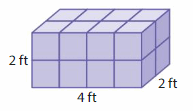
Answer:
The volume of the cube = 16 cubic ft.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 4 x 2 x 2
In the above-given figure l= 4 ft, w = 2 ft and h = 2ft.
volume = 4 x 2 x 2
volume = 8 x 2
volume = 16 cubic ft.
Question 7.
Modeling Real Life
A container holds 30 of the phone boxes shown, without any gaps or overlaps. What is the volume of the container?
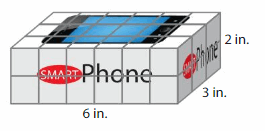
Answer:
The volume of the container = 36 cubic in.
Explanation:
volume = length x width x height
where l = length, w = width and h = height
volume = 6 x 3 x 2
In the above-given figure l= 6 in, w = 3 in and h = 2 in.
volume = 6 x 3 x 2
volume = 18 x 2
volume = 36 cubic in.
13.2 Find Volumes of Right Rectangular Prisms
Question 8.
Volume =
Question 9.
Volume =___
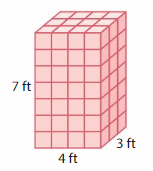
Answer:
The Volume of the rectangular prism = 84 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 4 ft , w = 3 ft, h = 7 ft .
volume = l x w x h
v = 4 x 3 x 7
v = 12 x 7
v = 84 cubic ft.
Question 10.
A rectangular prism is made of unit cubes, like the one shown. The prism is 9 centimeters long, 3 centimeters wide, and 5 centimeters tall. What is the volume of the prism?
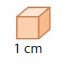
Answer:
The Volume of the rectangular prism = 135 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 9 cm , w = 3 cm, h = 5 cm.
volume = l x w x h
v = 9 x 3 x 5
v = 27 x 5
v = 135 cubic cm.
13.3 Apply the Volume Formula
Find the volume of the rectangular prism.
Question 11.
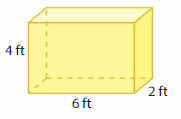
Answer:
The Volume of the rectangular prism = 48 cubic ft.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 6 ft , w = 2 ft, h = 4 ft .
volume = l x w x h
v = 6 x 2 x 4
v = 12 x 4
v = 48 cubic ft.
Question 12.
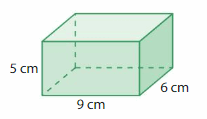
Answer:
The Volume of the rectangular prism = 270 cubic cm.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 9 cm , w = 6 cm, h = 5 cm .
volume = l x w x h
v = 9 x 6 x 5
v = 54 x 5
v = 270 cubic cm.
Question 13.
Descartes’s cat cave is a rectangular prism. The cave is 14 inches long, 13 inches wide, and 12 inches tall. What is the volume of the cave?

Answer:
The Volume of the cave = 2,184 cubic in.
Explanation:
volume of the rectangular prism = length x width x height
where l = length, w= width and h = height
given, l= 14 in , w = 13 in, h = 12 in .
volume = l x w x h
v = 14 x 13 x 12
v = 182 x 12
v = 2,184 cubic in.
13.4 Find Unknown Dimensions
Find the unknown dimension of the rectangular prism.
Question 14.
Answer:
The unknown dimensions are l= 9 ft, w= 3 ft,and h = 1 ft.
Explanation:
given that area of the base = 27 sq ft
area = l x w
27 = 9 x 3
v = l x w x h
27 = 9 x 3 x h
27 = 27 h
h = (27/27)
h = 1 ft
Question 15.
Answer:
The unknown dimensions are l= 6 cm, w= 1 cm,and h = 8 cm.
Explanation:
given that area of the base = 48 sq cm.
area = l x w x h
48 = 6 x w x 8
v = l x w x 8
48 = 48 x w
48 = 48 w
w = (48/48)
w = 1 cm
Question 16.
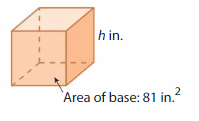
Answer:
The unknown dimensions are l=9 in , w= 9 in,and h = 1 in.
Explanation:
given that area of the base = 81 sq in.
area = l x w x h
81 = 9 x 9 x h
v = l x w x h
81 = 81 x h
81 = 81 h
h = (81/81)
h = 1 in
Question 17.
Answer:
The unknown dimensions are l=1 ft , w= 6 ft ,and h = 3 ft.
Explanation:
given that area of the base = 18 sq ft.
area = l x w x h
18 = l x 6 x 3
v = l x w x h
18 = l x 6 x 3
18 = 18 l
l = (18/18)
h = 1 ft
Question 18.
Open-Ended
A rectangular prism has a volume of 128 cubic feet. The height of the prism is 8 feet. Give one possible set of dimensions for the base.
Answer:
The dimensions of the base = 16 sq ft.
Explanation:
Given that volume of rectangular prism = 128 cubic feet.
volume = base x height
v = 128 given height = 8 ft
128 = b x 8
b = (128/8)
b = 16 sq ft.
Question 19.
Modeling Real Life
You buy the drawing pad shown. The volume of the drawer is 800 cubic inches. Can the drawing pad lie flat inside the drawer?
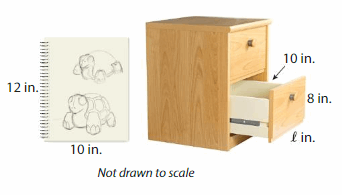
Answer:
Yes, the drawing pad will fit inside the drawer.
Explanation:
Given that volume of drawer = 800 cubic in.
volume =length x width x height
v = 800 given w = 10 inand h = 8in
800 = l x w x h
800= l x 10 x 8
800 = 80 l
l = (800/80)
l = 10 in
Given that base of drawig pad = 10 in.
volume = base x height
given b = 10 in h = 12 in
v = 10 x 12
v= 120 cubic in.
13.5 Find Volumes of Composite Figures
Find the volume of the composite figure
Question 20.
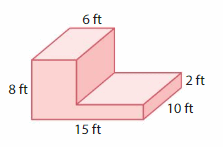
Answer:
volume of figure 1 = 300 cubic ft.
volume of figure 2 = 480 cubic ft.
Explanation:
volume of the figure 1( left side) = length x width x height
where l = length, w= width and h = height
given, l=15 ft , w = 10 ft , h = 2 ft.
volume = l x w x h
v = 15 x 10 x 2
v = 150 x 2
v = 300 cubic ft.
volume of the figure 2 (right side) = length x width x height
where l = length, w= width and h = height
given, l=6 ft , w = 10 ft , h = 8 ft.
volume = l x w x h
v = 6 x 10 x 8
v = 60 x 8
v = 480 cubic ft.
Question 21.
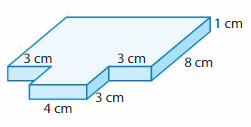
Answer:
volume of figure 1 = 88 cubic cm.
volume of figure 2 = 12 cubic cm.
Explanation:
volume of the figure 1( top) = length x width x height
where l = length, w= width and h = height
given, l=11 cm , w = 8 cm , h = 1 cm.
volume = l x w x h
v = 11 x 8 x 1
v = 88 x 1
v = 88 cubic cm.
volume of the figure 2 (bottom) = length x width x height
where l = length, w= width and h = height
given, l=4 cm , w = 3 cm , h = 1 cm.
volume = l x w x h
v = 4 x 3 x 1
v = 12 x 1
v = 12 cubic cm.
Conclusion:
The question and answers seen in the above article are prepared as per the latest syllabus. So, the students of the 5th Class can make use of the links and kickstart your preparation. Clarify your doubts by posting the comments in the below comment box. Keep in touch with us to get the Answer Key for all Big Ideas Math Grade 5 Chapters.
