Download Big Ideas Math Answers Grade 5 Chapter 7 Divide Decimals PDF for free. Learn every topic of BIM Grade 5 Chapter 7 Divide Decimals Answers. Make use of our material and check out the step-by-step explanation to learn all the concepts easily. Enjoy the learning of maths with the help of our BIM Grade 5 Answer Key for Chapter 7 Divide Decimals. Our complete guide will help you to score the best marks in the exam and also in your preparation. Therefore, without any second thought prepare with Big Ideas Math Book 5th class Answer Key Chapter 7 Divide Decimals and get a good score in the exam.
Big Ideas Chapter 7 Divide Decimals 5th Grade Math Book Answer Key
Find the best tips that make your students love to practice maths and encourage them to use them for easy practicing. We have also provided different tricks to solve all the math problems. Big Ideas math 5th grade Chapter 7 Divide Decimals textbook Answer Key is the best source for the students. All the relevant links of Divide Decimals are given below. Check the links and begin your practice now.
Lesson: 1 Division Pattern with Decimals
Lesson: 2 Estimate Decimals Quotients
Lesson: 3 Use Models to Divide Decimals by Whole Numbers
- Lesson 7.3 Use Models to Divide Decimals by Whole Numbers
- Use Models to Divide Decimals by Whole Numbers Homework & Practice 7.3
Lesson: 4 Divide Decimals by One-Digit Numbers
- Lesson 7.4 Divide Decimals by One-Digit Numbers
- Divide Decimals by One-Digit Numbers Homework & Practice 7.4
Lesson: 5 Divide Decimals by Two-Digit Numbers
- Lesson 7.5 Divide Decimals by Two-Digit Numbers
- Divide Decimals by Two-Digit Numbers Homework & Practice 7.5
Lesson: 6 Use Models to Divide Decimals
Lesson: 7 Divide Decimals
Lesson: 8 Insert Zeros in the Dividend
Lesson: 9 Problem Solving: Decimal Operations
- Lesson 7.9 Problem Solving: Decimal Operations
- Problem Solving: Decimal Operations Homework & Practice 7.9
Chapter: 7 – Divide Decimals
Lesson 7.1 Division Pattern with Decimals
Explore and Grow
Use the relationship between positions in a place value chart to find each quotient.
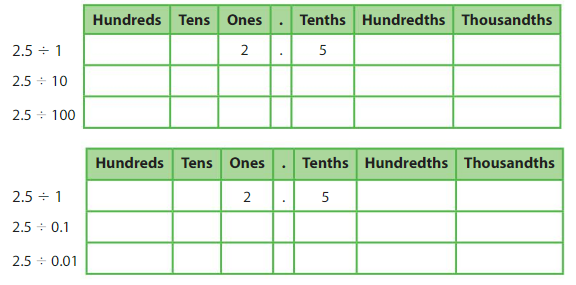
What patterns do you notice?
Answer:
Structure
Describe the placement of the decimal point when dividing a decimal by 10, 100, 0.1, and 0.01.
Answer:
Think and Grow: Division Pattern with Decimals
Example
Find 74 ÷ 103.
Use place value concepts. Every time you multiply a number by \(\frac{1}{10}\) or divide a number by 10, each digit in the number shifts one position to the right in a place value chart.
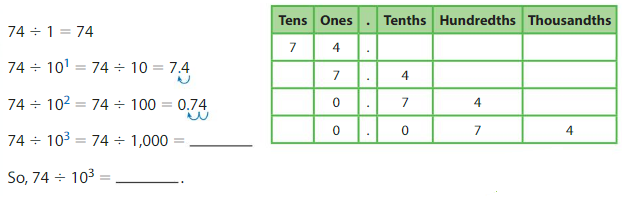
Notice the pattern: In each quotient, the number of places the decimal point moves to the left is the same as the exponent.

Example
Find 5.8 ÷ 0.01.
Use place value concepts. Every time you multiply a number by 10 or divide a number by 0.1, each digit in the number shifts one position to the left in a place value chart.

Notice the pattern: When you divide by 0.1, the decimal point moves one place to the right. When you divide by 0.01, the decimal point moves two places to the right.
Show and Grow
Find the quotient.
Question 1.
62.5 ÷ 102 = ______
Answer: 0.625
Explanation: First Simplify the 102 which means 10X10 =100 then we need to calculate the fraction to a decimal just divide the numerator(62.5) by the denominator (100): 62.5 ÷ 100 =0.625 so, 62.5/100 =0.625
Question 2.
1.84 ÷ 0.1 = ______
Answer: 18.4
Explanation: To convert this simple fraction to a decimal just divide the numerator (1.84) by the denominator (0.1): 1.84 ÷ 0.1 = 18.4 so, 1.84/0.1 = 18.4
Apply and Grow: Practice
Find the quotient.
Question 3.
76 ÷ 10 = ______
Answer: 7.6
Explanation: To convert this simple fraction to a decimal just divide the numerator (76) by the denominator (10): 76 ÷ 10 = 7.6 so, 76/10 = 7.6
Question 4.
3.65 ÷ 0.1 = _______
Answer: 36.5
Explanation: To convert this simple fraction to a decimal just divide the numerator (3.65) by the denominator (0.1): 3.65 ÷ 0.1 = 36.5. so, 3.65/0.1 = 36.5
Question 5.
2.9 ÷ 0.01 = ______
Answer: 290
Explanation: To convert this simple fraction to a decimal just divide the numerator (2.9) by the denominator (0.01): 2.9 ÷ 0.01 = 290. so, 2.9/0.01 = 290
Question 6.
18.7 ÷ 102 = ______
Answer: 0.187
Explanation: First Simplify the 102 which means 10X10 =100 then we need to calculate the fraction to a decimal just divide the numerator(18.7) by the denominator (100): 18.7 ÷ 100 =0.187 so, 18.7/100 =0.187
Find the value of k.
Question 7.
95.8 ÷ k = 958
Answer: K = 0.1
Explanation: Lets solve your equation step by step 95.8/k = 958
Multiply both side by side K.
95.8 = 958K
958k = 95.8 (Flip the equation)
958k/958 = 95.8/958(Divide both sides by 958)
K=0.1
Question 8.
k ÷ 103 = 0.35
Answer: K =350
Explanation: K÷103 =0.35
Step 1: calculate the value of the power which means 103 = 10x10x10=1000
k/1000=0.35
step 2: multiply both side by 1000
1000X K/1000 = 1000X0.35
Step 3: simplify
1000 X K/1000 = 1000X0.35
K = 350
Question 9.
245 ÷ k = 24,500
Answer: K =0.01
Explanation: variable K cannot be equal to 0 since division by zero is not defined. Multiply both side of equation by K
245 = 24500K
swap sides so that all variables terms are on the left hand side
24500K = 245
Divide both sides by 24500.
K =245/24500
Reduces the fraction 245/24500 to lowest terms by extracting and cancelling out 245
K = 1/100 ,Therefore K = 0.01
Question 10.
Newton goes on a 10-day road trip. He takes $435 with him. He spends all of his money and spends the same amount each day. How much money does he spend each day?

Answer: $43.5/per day
Explanation: Newton takes $435 for 10 days road trip.
435/10 = 43.5
Newton Spend the money per day is = $43.5/day
Question 11.
Number Sense
For which equations does b = 100?
49 ÷ b = 0.49
247 ÷ b = 0.247
1.3 ÷ b = 0.013
0.5 ÷ b = 0.05
Answer:
49 ÷ b = 0.49
1.3 ÷ b = 0.013
For these two equations b value should be 100.
Question 12.
YOU BE THE TEACHER
Your friend says 8,705 ÷ 103 is equivalent 8,705 × 0.001. Is your friend correct? Explain.
Answer:
First simplify the 103 which means 10 10
10 = 1000
8,705 ÷ 103
= 8,705 ÷ 1000
= 8,705
= 8,705 0.001
8,705 ÷ 103 is equivalent 8,705 × 0.001
So, my friend answer is correct.
Think and Grow: Modeling Real Life
Example
A contractor buys 2 adjacent lots of land. One lot is 0.55 acre and the other is 1.65 acres. The contractor divides the land equally for 10 new homes. How much land does each home have?

To find how much land each home has, divide the sum of the lot sizes by 10.
Add the sizes of the lots.
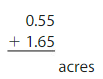
Divide the total number of acres by 10. Dividing 2.20 by 10, or 101, shifts the digits ______ position to the right in a place value chart. So, the decimal point moves ______ place to the left.
2.20 ÷ 10 = 2.20 ÷ 101 = ______
Each home has ________ acre.
Show and Grow
Question 13.
An art teacher has 68.5 pounds of clay and orders 56.5 more pounds. The teacher equally divides the clay among 100 students. How much clay does each student get?
Answer:
To find how much clay each student get, divide the sum of the clay by 100.
Add the quantities of the clay.
68.5 + 56.5 = 125
Divide the total clay by 100. Dividing 125 by 100, or 102
125 ÷ 100 = 125 ÷ 102 = 1.25
Each student gets 1.25 pounds clay.
Question 14.
A museum has a replica of the Space Needle that is 6.05 feet tall. It is one-hundredth of the height of the actual Space Needle. How tall is the actual Space Needle?

Answer:
Replica of the Space Needle height = 6.05 feet
Let actual Space Needle height = h
(h) = 6.05
h = 6.05 100 = 605
So actual Space Needle height is 605 feet.
Question 15.
DIG DEEPER!
A pile of 102 loonies weighs 627 grams and a pile of 102 toonies weighs 730 grams. How much more does a toonie weigh than a loonie? Is there more than one way to solve the problem? Explain.

Answer:
A pile of 102 loonies weight = 627 grams
A pile of 102 toonies weight = 730 grams
730 – 627 = 103
Toonie weighs 103 grams more than a loonie.
Method – 2
1 loonie weight = = 6.27
1 toonie weight = = 7.30
7.30 – 6.27 = 1.03
For 102 toonies and loonies = 1.03 x 102 = 103
Toonie weighs 103 grams more than a loonie.
Division Pattern with Decimals Homework & Practice 7.1
Find the quotient.
Question 1.
810 ÷ 10 = ______
Answer: 81
Explanation:
To convert this simple fraction to a decimal just divide the numerator (810) by the denominator (10):
When we divide by 10, the decimal point moves one place to the left.
810 ÷ 10 = 81.
Question 2.
7.4 ÷ 0.01 = ______
Answer: 740
Explanation: To convert this simple fraction to a decimal just divide the numerator (7.4) by the denominator (0.01). When we divide by 0.01, the decimal point moves two places to the right. : 7.4 ÷ 0.01 = 740.
Question 3.
903 ÷ 103 = ______
Answer: 0.903
First Simplify the 103 which means 10 x 10 x 10 =1000, then we need to calculate the fraction to a decimal just divide the numerator (903) by the denominator (1000).
When we divide by 1000, the decimal point moves three places to the left.
Question 4.
267.1 ÷ 0.01 = ______
Answer: 26710
Explanation: To convert this simple fraction to a decimal just divide the numerator (267.1) by the denominator (0.01).
When we divide by 0.01, the decimal point moves two places to the right :
267.1 ÷ 0.01 = 26710
Question 5.
5.6 ÷ 0.1 = ______
Answer: 56
Explanation: To convert this simple fraction to a decimal just divide the numerator (5.6) by the denominator (0.1).
When we divide by 0.1, the decimal point moves one place to the right :
5.6 ÷ 0.1 = 56
Question 6.
0.4 ÷ 102 = ______
Answer: 0.004
First Simplify the 102 which means 10 x 10 = 100, then we need to calculate the fraction to a decimal just divide the numerator (0.4) by the denominator (100).
When we divide by 100, the decimal point moves two places to the left :
0.4 ÷ 100 = 0.004
Find the value of k.
Question 7.
89 ÷ k = 8.9
Answer: k = 10
Explanation: Lets solve your equation step by step 89 ÷ k = 8.9
Multiply both sides by K.
89 = 8.9 K
8.9 K = 89 (Flip the equation)
=
(Divide both sides by 8.9)
k = 10
Question 8.
k ÷ 0.01 = 36
Answer: k = 0.36
= 36
Multiply both sides by 0.01
x 0.01 = 36 x 0.01
k = 0.36
Question 9.
72.4 ÷ 0.724
Answer: 100
To convert this simple fraction to a decimal just divide the numerator (72.4) by the denominator (0.724).
Question 10.
A box of 100 sanitizing wipes costs $12. How much does one wipe cost?
Answer:
100 sanitizing wipes = $12
one wipe cost = = $0.12
When we divide by 100, the decimal point moves two places to the left.
Question 11.
Patterns
How does the value of a number change when you divide by 10? 100? 1,000?
Answer:
When we divide by 10, the decimal point moves one place to the left.
When we divide by 100, the decimal point moves two places to the left.
When we divide by 1000, the decimal point moves three places to the left.
Question 12.
Writing
How can you determine where to place the decimal point when dividing 61 by 1,000?
Answer:
When we divide by 1000, the decimal point moves three places to the left.
so, = 0.061
Question 13.
DIG DEEPER!
What is Newton’s number?

Answer:
3.4 is the number.
57 – 23 = 34
34 x 0.1 = 3.4
Question 14.
Modeling Real Life
A family buys 2 personal watercrafts for $3,495 each. The family makes 10 equal payments for the watercrafts. What is the amount of each payment?
Answer:
To find amount of each payment, divide the sum of the personal watercrafts by 10.
Add 2 personal watercrafts.
3,495 + 3,495 = 6990
Divide the total sum by 10. Dividing 6990 by 10, or 101
6990 ÷ 10 = 6990 ÷ 101 = 699
So, the amount of each payment = $699.
Question 15.
Modeling Real Life
A group of people attempts to bake the largest vegan cake. They use 17 kilograms of cocoa powder, which is one-tenth the amount of kilograms of dates they use. How many kilograms of cocoa power and dates do they use altogether?
Answer:
Cocoa powder = 17 kilograms
Let dates amount = d
(1/10)d = 17
dates(d) = 17 x 10 = 170 kilograms
Sum of cocoa power and dates = 17 + 170 = 187 kilograms
Review & Refresh
Find the sum or difference.
Question 16.
0.75 – 0.23 = ______
Answer: 0.52
Question 17.
1.46 + 1.97 = ______
Answer: 3.43
Lesson 7.2 Estimate Decimals Quotients
Explore and Grow
Choose an expression to estimate each quotient. Write the expression. You may use an expression more than once.

Compare your answers with a partner. Did you choose the same expressions?
Answer:
Construct Arguments
Which estimated quotient do you think will be closer to the quotient 8.3 ÷ 2.1? Explain your reasoning.

Answer:
Think and Grow: Estimate Decimals Quotients
Key Idea
You can use compatible numbers to estimate quotients involving decimals. When the divisor is greater than the dividend, rename the dividend as tenths or hundredths, then divide.
Example
Estimate 146.26 ÷ 41.2.
Round the divisor 41.2 to 40.
Think: What numbers close to 146.26 are easily divided by 40?

Choose 160 because 146.26 is closer to 160. So, 146.26 ÷ 41.2 is about _____.
Example
Estimate 4.2 ÷ 8.
Rename 4.2 as tenths.
4.2 is 42 tenths. 42 tenths is close to40 tenths. 40 and 8 are compatible numbers.
40 tenths ÷ 8 = _______ tenths, or ______
So, 4.2 ÷ 8 is about ______.
Show and Grow
Estimate the quotient.
Question 1.
17.4 ÷ 3.1
Answer:
Round the divisor 3.1 to 3.
Think: What numbers close to 17.4 are easily divided by 3?
Use 18.
18 ÷ 3 = 6
So, 17.4 ÷ 3.1 is about 6.
Question 2.
57.5 ÷ 6.89
Answer:
Round the divisor 6.89 to 7.
Think: What numbers close to 57.5 are easily divided by 7?
Use 56.
56 ÷ 7 = 8
So, 57.5 ÷ 6.89 is about 8.
Question 3.
3.7 ÷ 5
Answer:
Rename 3.7 as tenths
3.7 is 37 tenths. 37 is close to 35.
35 tenths ÷ 5 = 7 tenths or 0.7
So, 3.7 ÷ 5 is about 0.7
Question 4.
25.8 ÷ 30
Answer:
Rename 25.8 as tenths
25.8 is 258 tenths. 258 is close to 270.
270 tenths ÷ 30 = 9 tenths or 0.9
So, 25.8 ÷ 30 is about 0.9
Apply and Grow: Practice
Estimate the quotient.
Question 5.
3.5 ÷ 6
Answer:
Rename 3.5 as tenths
3.5 is 35 tenths. 35 is close to 36.
36 tenths ÷ 6 = 6 tenths or 0.6
So, 3.5 ÷ 6 is about 0.6
Question 6.
1.87 ÷ 9
Answer:
Rename 1.87 as tenths
1.87 is 18.7 tenths. 18.7 is close to 18.
18 tenths ÷ 9 = 2 tenths or 0.2
So, 1.87 ÷ 9 is about 0.2
Question 7.
46 ÷ 2.3
Answer:
Round the divisor 2.3 to 2.
46 ÷ 2 = 23
Question 8.
31.1 ÷ 6.5
Answer:
Round the divisor 6.5 to 6.
31.1 is closer to 30.
30 ÷ 6 = 5
So, 31.1 ÷ 6.5 is about 5.
Question 9.
91.08 ÷ 5.2
Answer:
Round the divisor 5.2 to 5.
91.08 is closer to 90.
90 ÷ 5 = 18
So, 91.08 ÷ 5.2 is about 18.
Question 10.
137.14 ÷ 12.2
Answer:
Round the divisor 12.2 to 12.
137.14 is closer to 144.
12 and 144 are compatible numbers.
144 ÷ 12 = 12
So, 137.14 ÷ 12.2 is about 12.
Question 11.
A group of 6 friends goes ice skating. They pay $43.50 altogether for admission and skate rental. The friends share the cost equally. How much does each friend pay?

Answer:
Total amount paid = $43.50
6 friends goes ice skating.
43.5 is closer to 42.
42 ÷ 6 = 7
So, each friend pay about $7.
Question 12.
Reasoning
Descartes estimates 43.2 ÷ 7.3 using mental math. Do you think he uses 43 ÷ 7 or 42 ÷ 7? Explain.
Answer:
Round the divisor 7.3 to 7
Think: What numbers close to 43.2 are easily divided by 7?
Use 42.
42 and 7 are compatible numbers.
42 ÷ 7 = 6
So, 42 ÷ 7 is correct.
Question 13.
DIG DEEPER!
Describe a division situation in which an estimate of two decimals is appropriate.
Answer:
Think and Grow: Modeling Real Life
Example
Your friend types 25 words each minute. About how many more words can your friend type each minute than you?

To find how many words you can type each minute, divide the number of words you type in 15 minutes by 15.
Think: What numbers close to 307.5 are easily divided by 15?

Choose 300 because 307.5 is closer to 300. So, 307.5 ÷ 15 is about _______.
So, you type about _______ words each minute.
Subtract the words you type each minute from the words your friend types each minute.
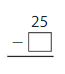
Your friend can type about ______ more words each minute than you.
Show and Grow
Question 14.
Newton subscribes to a television streaming service and buys a gym membership. He spends $143.99 on the streaming service for 12 months. About how much more does it cost each month for the gym membership than the streaming service?

Answer:
To find much more does it cost each month, divide how much he spends for 12 months by 12.
Think: What numbers close to $143.99 are easily divided by 12?
Use 144
144 ÷ 12 = 12
Gym Membership each month = $19.99 = $20
20 – 12 = $8
The gym membership costs $8 more than the streaming service.
Question 15.
A fish tank pump filters 158.5 gallons of water each hour. About how many gallons of water does the pump filter each minute?
Answer:
Fish tank pump filters 158.5 gallons of water
1 hour = 60 minutes
Think: What numbers close to 158.5 are easily divided by 60?
Use 180
180 ÷ 60 = 3
Pump filters about 3 gallons of water each minute.
Question 16.
DIG DEEPER!
A group of 32 students goes to a museum and a play. The total cost for the museum is $358.98 and the total cost for the play is $256.48. About how much does it cost for each student to go to the museum and the play?
Answer:
Cost for museum = $358.98
Cost for the play = $256.48
358.98 + 256.48 = $615.46
Think: What numbers close to 615.46 are easily divided by 32?
Use 608. It is closer to 615.46
608 ÷ 32 = $19
Each student go to the museum and the play costs about $19.
Estimate Decimals Quotients Homework & Practice 7.2
Estimate the quotient.
Question 1.
2.3 ÷ 6
Answer:
Rename 2.3 as tenths
2.3 is 23 tenths. 23 is close to 24.
24 tenths ÷ 6 = 4 tenths or 0.4
So, 2.3 ÷ 6 is about 0.4
Question 2.
1.67 ÷ 8
Answer:
Rename 1.67 as hundredths
1.67 is 167 hundredths. 167 is close to 168.
168 hundredths ÷ 8 = 21 hundredths or 0.21
So, 1.67 ÷ 8 is about 0.21
Question 3.
28 ÷ 4.7
Answer:
Round the divisor 4.7 to 5
28 is closer to 30
30 ÷ 5 = 6
So, 28 ÷ 4.7 is about 6.
Question 4.
13.8 ÷ 4.9
Answer:
Round the divisor 4.9 to 5
Think: What numbers close to 13.8 are easily divided by 5?
Use 15.
15 ÷ 5 = 3
So, 13.8 ÷ 4.9 is about 3.
Question 5.
42.1 ÷ 7.3
Answer:
Round the divisor 7.3 to 7
Think: What numbers close to 42.1 are easily divided by 7?
Use 42.
42 ÷ 7 = 6
So, 42.1 ÷ 7.3 is about 6.
Question 6.
201.94 ÷ 18.1
Answer:
Round the divisor 18.1 to 18
Think: What numbers close to 201.94 are easily divided by 18?
Use 198.
198 ÷ 18 = 11
So, 201.94 ÷ 18.1 is about 11.
Question 7.
A carpenter has a plank of wood that is 121.92 centimeters long. He cuts the plank into 4 equal pieces. About how long is each piece?

Answer:
Given that,
Plank of wood = 121.92 cm long
121.92 is closer to 120.
120 ÷ 4 = 30
So, each piece is 30 cm long.
Question 8.
Reasoning
A family used 9.8 gallons of gasoline to drive 275.5 miles. To determine how far they drove using one gallon of gasoline, can they use an estimate, or is an exact answer required? Explain.
Answer:
Given that,
9.8 gallons of gasoline drives = 275.5 miles
1 gallon = 275.5 ÷ 9.8
Divisor 9.8 is rounded to 10.
275.5 is closer to 276.
276 ÷ 10 is about 27.6
Question 9.
YOU BE THE TEACHER
Your friend says 9 ÷ 2.5 is about 3. Is your friend’s estimate reasonable? Explain.
Answer:
Round the divisor 2.5 to 3.
9 ÷ 3 =3
So, my friend’s estimate is reasonable.
Number Sense
Without calculating, tell whether the quotient is greater than or less than 1. Explain.
Question 10.
4.58 ÷ 0.3
Answer:
When the dividend is greater than the divisor, the quotient is greater than 1.
Question 11.
0.6 ÷ 12
Answer:
When the divisor is greater than the dividend, the quotient is less than 1.
Question 12.
Modeling Real Life
The maximum allowed flow rate for a shower head in California is 42.5 gallons of water in 17 minutes. About how much greater is this than the maximum allowed flow rate for a kitchen faucet in California?

Answer:
To find much much greater it is, divide how much gallons of water in 17 minutes by 17.
Think: What numbers close to 42.5 are easily divided by 17?
Use 34. 34 is closer to 42.5.
34 ÷ 17 =2
Kitchen faucet = 2.2 gallons
2.2 – 2 = 0.2
Shower head in California is about 0.2 gallons greater than the maximum allowed flow rate for a kitchen faucet in California.
Question 13.
Modeling Real Life
To compare the amounts in the table, you assume the same amount of snow fell each hour for 24 hours. About how many more inches of snow fell in Colorado each hour than in Utah?
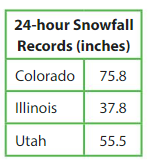
Answer:
Time t = 24 hours
Colorado snowfall = 75.8 is closer to 72
Illinois snowfall = 37.8
Utah snowfall = 55.5 is closer to 48
(72 – 48)/24 = 1
Snow fall in Colorado each hour is about 1 inch more than in Utah.
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 14.
56 × 78 = _____
Answer: 4368
Question 15.
902 × 27 = ______
Answer: 24,354
Question 16.
4,602 × 35 = _______
Answer: 1,61,070
Lesson 7.3 Use Models to Divide Decimals by Whole Numbers
Explore and Grow
Complete the table.

Answer:
Reasoning
When you divide a decimal by a whole number, what does the quotient represent?
Answer:
Think and Grow: Use Models to Divide Decimals
Example
Use a model to find 2.16 ÷ 3.
Think: 2.16 is 2 ones, 1 tenth, and 6 hundredths.
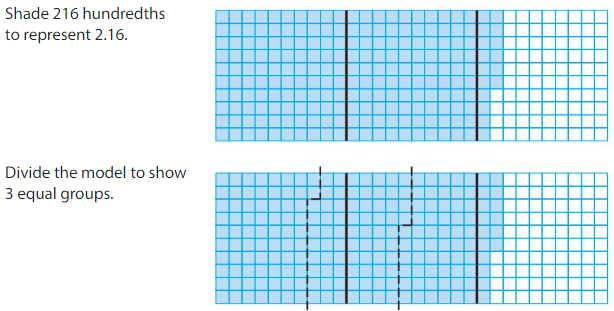
• 21 tenths can be divided equally as 3 groups of _______ tenths.
• 6 hundredths can be divided equally as 3 groups of _______ hundredths.
So, 216 hundredths can be divided equally as 3 groups of _______ hundredths.
So, 2.16 ÷ 3 = _______
Show and Grow
Question 1.
Use the model to find 3.25 ÷ 5.
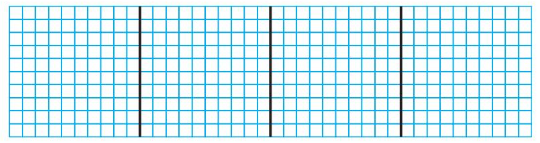
3.25 ÷ 5 = ______
Answer:
Think: 3.25 is 3 ones, 2 tenths and 5 hundredths.
32 tenths can be divided equally as 5 groups
So, 325 hundredths can be divided equally as 5 groups
So, 3.25 ÷ 5 = 0.65
Apply and Grow: Practice
Use the model to find the quotient.
Question 2.
2.4 ÷ 4
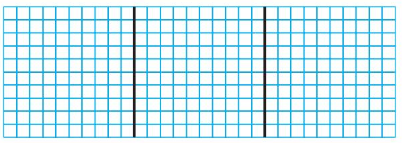
Answer:
Think: 2.4 is 2 ones and 4 tenths
24 tenths can be divided equally as 4 groups of 6 tenths.
So, 2.4 ÷ 4 = 6 tenths = 0.6
Question 3.
1.36 ÷ 2
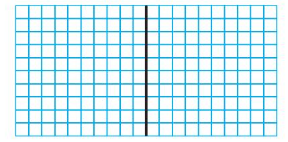
Answer:
Think: 1.36 is 1 ones, 3 tenth and 6 hundredths.
13 tenths can be divided equally as 2 groups
So, 136 hundredths can be divided equally as 2 groups
So, 1.36 ÷ 2 = 0.68
Use a model to find the quotient.
Question 4.
1.5 ÷ 3
Answer:
Think: 1.5 is 1 ones and 5 tenths
15 tenths can be divided equally as 3 groups of 5 tenths.
So, 1.5 ÷ 3 = 5 tenths = 0.5
Question 5.
2.7 ÷ 9
Answer:
Think: 2.7 is 2 ones and 7 tenths
27 tenths can be divided equally as 9 groups of 3 tenths.
So, 2.7 ÷ 9 = 3 tenths = 0.3
Question 6.
1.44 ÷ 8
Answer:
Think: 1.44 is 1 ones, 4 tenth and 4 hundredths.
14 tenths can be divided equally as 8 groups
So, 144 hundredths can be divided equally as 8 groups
So, 1.44 ÷ 8 = 0.18
Question 7.
3.12 ÷ 6
Answer:
Think: 3.12 is 3 ones, 1 tenth and 2 hundredths.
31 tenths can be divided equally as 6 groups
So, 312 hundredths can be divided equally as 6 groups
So, 3.12 ÷ 6 = 0.52
Question 8.
Reasoning
Do you start dividing the ones first when finding 5.95 ÷ 7? Explain.
Answer:
Think: 5.95 is 5 ones, 9 tenth and 5 hundredths.
We have to start dividing the tenths first because 5 ones is less than 7.
59 tenths can be divided equally as 7 groups
So, 595 hundredths can be divided equally as 7 groups
So, 5.95 ÷ 7 = 0.85
Question 9.
Number Sense
Without dividing, determine whether the quotient of 9.85 and 5 is greater than or less than 2. Explain.
Answer: Quotient of 9.85 and 5 is less than 2, because 5 x 2 =10 and 9.85 is less than 10.
Think and Grow: Modeling Real Life
Example
A bag of 3 racquetballs weighs 4.2 ounces. What is the weight of each racquetball?

Divide the weight of the bag by 3 to find the weight of each racquetball.
Think: 4.2 is 4 ones and 2 tenths.
Shade 42 tenths to represent 4.2. Divide the model to show 3 equal groups.
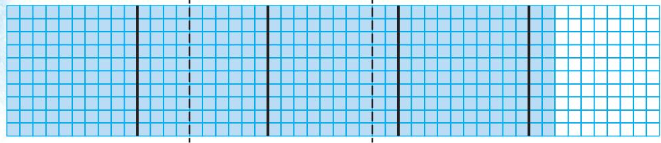
42 tenths can be divided equally as 3 groups of ______ tenths.
4.2 ÷ 3 = ______
So, each racquetball weighs ______ ounces.
Show and Grow
Question 10.
You cut a 3.75-foot-long string into 5 pieces of equal length to make a beaded wind chime. What is the length of each piece of string?

Answer:
Divide the length of the string by 5 to find the length of each piece of string.
Think: 3.75 is 3 ones, 7 tenths and 5 hundredths.
37 tenths can be divided equally as 5 groups of 7 tenths with remainder 2. Remainder has to place before 5 hundredths.
25 hundredths can be divided equally as 5 groups of 5 hundredths.
So, 375 hundredths can be divided equally as 5 groups of 75 hundredths.
3.75 ÷ 5 = 0.75
Question 11.
DIG DEEPER!
You pay $5.49 for 3 pounds of plums and $6.36 for 4 pounds of peaches. Which fruit costs more per pound? How much more?
Answer:
Think: 5.49 is 5 ones, 4 tenths and 9 hundredths.
5 ones can be divided equally as 3 groups of 1 ones with remainder 2. Remainder has to place before 4 tenths.
24 tenths can be divided equally as 3 groups of 8 tenths
9 hundredths can be divided equally as 3 groups of 3 hundredths
So, 549 hundredths can be divided equally as 3 groups of 183 hundredths.
Plums = 5.49 ÷ 3 = 1.83
Think: 6.36 is 6 ones, 3 tenths and 6 hundredths.
6 ones can be divided equally as 4 groups of 1 ones with remainder 2. Remainder has to place before 3 tenths.
23 tenths can be divided equally as 4 groups of 5 tenths with remainder 3. Remainder has to place before 6 hundredths.
36 hundredths can be divided equally as 4 groups of 9 hundredths
So, 636 hundredths can be divided equally as 4 groups of 159 hundredths.
Peaches = 6.36 ÷ 4 = 1.59
1.83 – 1.59 = 0.24
So, plums costs 0.24 more per pound than peaches.
Use Models to Divide Decimals by Whole Numbers Homework & Practice 7.3
Use the model to find the quotient.
Question 1.
1.5 ÷ 5
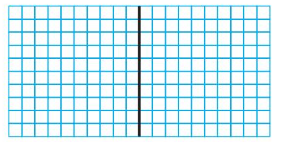
Answer:
Think: 1.5 is 1 ones and 5 tenths
15 tenths can be divided equally as 5 groups of 3 tenths.
So, 1.5 ÷ 5 = 3 tenths = 0.3
Question 2.
2.55 ÷ 3
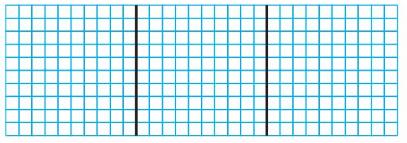
Answer:
Think: 2.55 is 2 ones, 5 tenths and 5 hundredths.
25 tenths can be divided equally as 3 groups of 8 tenths with remainder 1. Remainder has to place before 5 hundredths.
15 hundredths can be divided equally as 3 groups of 5 hundredths.
So, 255 hundredths can be divided equally as 3 groups of 85 hundredths.
2.55 ÷ 3 = 0.85
Use a model to find the quotient.
Question 3.
1.6 ÷ 8
Answer:
Think: 1.6 is 1 ones and 6 tenths
16 tenths can be divided equally as 8 groups of 2 tenths.
So, 1.6 ÷ 8 = 2 tenths = 0.2
Question 4.
2.1 ÷ 7
Answer:
Think: 2.1 is 2 ones and 1 tenths
21 tenths can be divided equally as 7 groups of 3 tenths.
So, 2.1 ÷ 7 = 3tenths = 0.3
Question 5.
1.56 ÷ 2
Answer:
Think: 1.56 is 1 ones, 5 tenths and 6 hundredths.
15 tenths can be divided equally as 2 groups of 7 tenths with remainder 1. Remainder has to place before 6 hundredths.
16 hundredths can be divided equally as 2 groups of 8 hundredths.
So, 156 hundredths can be divided equally as 2 groups of 78 hundredths.
1.56 ÷ 2 = 0.78
Question 6.
2.84 ÷ 4
Answer:
Think: 2.84 is 2 ones, 8 tenths and 4 hundredths.
28 tenths can be divided equally as 4 groups of 7 tenths.
4 hundredths can be divided equally as 4 groups of 1 hundredths.
So, 284 hundredths can be divided equally as 4 groups of 71 hundredths.
2.84 ÷ 4 = 0.71
Question 7.
Structure
Write a decimal division equation represented by the model.
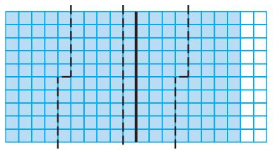
Answer:
1.8 ÷ 3
Question 8.
Writing
Explain how dividing a decimal by a whole number is similar to dividing a whole number by a whole number.
Answer:
When dividing a decimal by a whole number, first we will divide the decimal by the whole number ignoring decimal point. Now put the decimal point in the quotient same as the decimal places in the dividend.
So , dividing a decimal by a whole number is similar to dividing a whole number by a whole number.
Question 9.
Modeling Real Life
A designer learns there are 5.08 centimeters in 2 inches. How many centimeters are in 1 inch?
Answer:
5.08 ÷ 2
Think: 5.08 is 5 ones, 0 tenths and 8 hundredths.
50 tenths can be divided equally as 2 groups of 25 tenths.
8 hundredths can be divided equally as 2 groups of 4 hundredths.
So, 508 hundredths can be divided equally as 2 groups of 254 hundredths.
So, 2.54 cm are in 1 inch.
Question 10.
Modeling Real Life
Newton buys 4 gallons of gasoline. He pays $8.64. How much does 1 gallon of gasoline cost?
Answer:
8.64 ÷ 4
Think: 8.64 is 8 ones, 6 tenths and 4 hundredths.
8 ones can be divided equally as 4 groups of 2 ones.
6 tenths can be divided equally as 4 groups of 1 tenths with remainder 2. Remainder has to place before 4 hundredths.
24 hundredths can be divided equally as 4 groups of 6 hundredths.
So, 864 hundredths can be divided equally as 4 groups of 216 hundredths.
1 gallon of gasoline cost is 216 hundredths = $2.16
Review & Refresh
Find the product. Explain the strategy you used.
Question 11.
0.9 × 1.1 = ______
Answer:
First multiply 9 x 11 = 99, then put the decimal point in the answer as sum of the decimal places in the both numbers.
decimal places = 1 + 1 = 2
99 after putting decimal places = 0.99
Question 12.
1.2 × 2.7 = ______
Answer:
First multiply 12 x 27 = 324 then put the decimal point in the answer as sum of the decimal places in the both numbers.
decimal places = 1 + 1 = 2
324 after putting decimal places = 3.24
Question 13.
1.4 × 0.8 = ______
Answer: 1.12
Lesson 7.4 Divide Decimals by One-Digit Numbers
Explore and Grow
Complete the table.
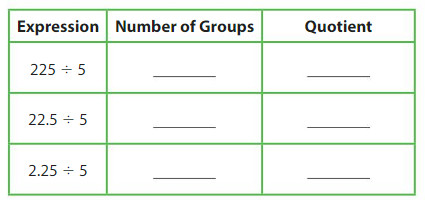
What pattern do you notice in the placement of the decimal point?
Answer:
Reasoning
How is dividing decimals by one-digit whole numbers similar to dividing whole numbers?
Answer:
Think and Grow: Divide Decimals by One-Digit Numbers
Example
Find
Find 7.38 ÷ 6. Estimate ________

Show and Grow
Find the quotient. Then check your answer.
Question 1.
\(\sqrt [ 2 ]{ 9.16 } \)
Answer:
Divide the ones
9 ÷ 2
4 ones x 2 = 8
9 ones – 8 ones
There are 1 ones left over.
Divide the tenths
116 ÷ 2
58 tenths x 2
116 – 116 = 0
There are 0 tenths left over.
So, 9.16 ÷ 2 = 4.58
Question 2.
\(\sqrt [ 5 ]{ 23.5 } \)
Answer:
Divide the ones
23 ÷ 5
4 ones x 5 = 20
23 ones – 20 ones
There are 3 ones left over.
Divide the tenths
35 ÷ 5
7 tenths x 5
35 – 35 = 0
There are 0 tenths left over.
So, 23.5 ÷ 5 = 4.7
Question 3.
\(\sqrt [ 3 ]{ 6.27 } \)
Answer:
Divide the ones
6 ÷ 3
2 ones x 3 = 6
6 ones – 6 ones
There are 0 ones left over.
Divide the tenths
27 ÷ 3
9 tenths x 3
27 – 27 = 0
There are 0 tenths left over.
So, 6.27 ÷ 3 = 2.09
Apply and Grow: Practice
Find the quotient. Then check your answer.
Question 4.
\(\sqrt [ 4 ]{ 16.8 } \)
Answer:
Divide the ones
16 ÷ 4
4 ones x 4 = 16
16 ones – 16 ones
There are 0 ones left over.
Divide the tenths
8 ÷ 4
2 tenths x 4
8 – 8 = 0
There are 0 tenths left over.
So, 16.8 ÷ 4 = 4.2
Question 5.
\(\sqrt [ 9 ]{ 1.53 } \)
Answer:
Divide the tenths
15 ÷ 9
1 tenths x 9
15 – 9 = 6
There are 6 tenths left over.
Divide the hundredths
63 ÷ 9 = 7 hundredths
So, 1.53 ÷ 9 = 0.17
Question 6.
\(\sqrt [ 5 ]{ 82.5 } \)
Answer:
Divide the ones
82 ÷ 5
16 ones x 5 = 80
82 ones – 80 ones
There are 2 ones left over.
Divide the tenths
25 ÷ 5
5 tenths x 5
25 – 25 = 0
There are 0 tenths left over.
So, 82.5 ÷ 5 = 16.5
Question 7.
77.4 ÷ 3 = ______
Answer:
Divide the ones
77 ÷ 3
25 ones x 3 = 75
77 ones – 75 ones
There are 2 ones left over.
Divide the tenths
24 ÷ 3
8 tenths x 3
24 – 24 = 0
There are 0 tenths left over.
So, 77.4 ÷ 3 = 25.8
Question 8.
113.6 ÷ 8 = ______
Answer:
Divide the ones
113 ÷ 8
14 ones x 8 = 112
113 ones – 112 ones
There are 1 ones left over.
Divide the tenths
16 ÷ 8
2 tenths x 8
16 – 16 = 0
There are 0 tenths left over.
So, 113.6 ÷ 8 = 14.2
Question 9.
129.43 ÷ 7 = ______
Answer:
Divide the ones
129 ÷ 7
18 ones x 7 = 126
129 ones – 126 ones
There are 3 ones left over.
Divide the tenths
34 ÷ 7
4 tenths x 7
34 – 28 = 6
There are 6 tenths left over.
Divide the hundredths
63 ÷ 7 = 9 hundredths
So, 129.43 ÷ 7 = 18.49
Find the value of y.
Question 10.
y ÷ 2 = 4.8
Answer:
y = 4.8 x 2
y = 9.6
Question 11.
6.05 ÷ 5 = y
Answer:
6.05 ÷ 5
Divide the ones
1 ones x 5 = 5
6 ones – 5 ones
There are 1 ones left over.
Divide the tenths
105 ÷ 5
21 tenths x 5
105 – 105 = 0
There are 0 tenths left over.
So, 6.05 ÷ 5 = 1.21
y = 1.21
Question 12.
y ÷ 8 = 4.29
Answer:
y = 4.29 x 8
y = 34.32
Question 13.
Reasoning
Newton finds 75.15 ÷ 9. In what place is the first digit of the quotient? Explain.
Answer:
75.15 ÷ 9
Divide the ones
75 ÷ 9
8 ones x 9 = 72
75 ones – 72 ones
There are 3 ones left over.
Divide the tenths
31 ÷ 9
3 tenths x 9
31 – 27= 4
There are 4 tenths left over.
Divide the hundredths
45 ÷ 9 = 5 hundredths
75.15 ÷ 9 = 8.35, here quotient is in ones place.
Question 14.
DIG DEEPER!
Find the missing digits.

Answer:
Divide the ones
47 ÷ 6
7 ones x 6 = 42
47 ones – 42 ones = 3 ones
So, first digit of the quotient is 7.
We know that divisor x quotient = dividend
6 x 7.89 = 47.34
So, missing digits are 7 and 4.
Think and Grow: Modeling Real Life
Example
A group of 5 gold miners finds the amounts of gold shown. They divide the gold equally. How many ounces does each miner get?
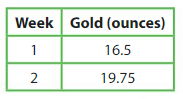
To find how many ounces each miner gets, divide the total amount of gold by 5.
Add the amounts of gold.

Each miner gets _______ ounces of gold.
Show and Grow
Question 15.
A pharmacist combines the medicine from both vials and divides it equally into 7 doses. How much medicine is in each dose?
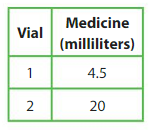
Answer:
To find how much medicine is in each dose, divide the total amount of medicine by 7.
Add the amounts of medicine.
4.5 + 20 = 24.5
24.5 ÷ 7
Divide the ones
24 ÷ 7
3 ones x 7 = 21
24 ones – 21 ones
There are 3 ones left over.
Divide the tenths
35 ÷ 7
5 tenths x 7
35 – 35 = 0
There are 0 tenths left over.
24.5 ÷ 7 = 3.5
So, 3.5 milliliters medicine is in each dose.
Question 16.
Identical rectangular stepping stones form a path in a garden. What are the dimensions of each stone?
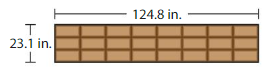
Answer:
Question 17.
DIG DEEPER!
A customer saves $9.24 by buying the set rather than buying them individually. What is one flying disc priced individually?
Answer:
Divide Decimals by One-Digit Numbers Homework & Practice 7.4
Find the quotient. Then check your answer.
Question 1.
\(\sqrt [ 3 ]{ 9.6 } \)
Answer:
Divide the ones
9 ÷ 3
3 ones x 3 = 9
9 ones – 9 ones
There are 0 ones left over.
Divide the tenths
6 ÷ 3
2 tenths x 3
6 – 6 = 0
There are 0 tenths left over.
So, 9.6 ÷ 3 = 3.2.
Question 2.
\(\sqrt [ 6 ]{ 7.56 } \)
Answer:
Divide the ones
7 ÷ 6
1 ones x 6 = 6
7 ones – 6 ones
There are 1 ones left over.
Divide the tenths
15 ÷ 6
2 tenths x 6
15 – 12 = 3
There are 3 tenths left over.
Divide the hundredths
36 ÷ 6 = 6 hundredths.
So, 7.56 ÷ 6 = 1.26.
Question 3.
\(\sqrt [ 8 ]{ 42.4 } \)
Answer:
Divide the ones
42 ÷ 8
5 ones x 8 = 40
42 ones – 40 ones
There are 2 ones left over.
Divide the tenths
24 ÷ 8
3 tenths x 8
24 – 24 = 0
There are 0 tenths left over.
So, 42.4 ÷ 8 = 5.3.
Question 4.
63.6 ÷ 4 = ______
Answer:
Divide the ones
63 ÷ 4
15 ones x 4 = 60
63 ones – 60 ones
There are 3 ones left over.
Divide the tenths
36 ÷ 4
9 tenths x 4
36 – 36 = 0
There are 0 tenths left over.
63.6 ÷ 4 = 15.9
Question 5.
15.68 ÷ 7 = ______
Answer:
Divide the ones
15 ÷ 7
2 ones x 7 = 14
15 ones – 14 ones
There are 1 ones left over.
Divide the tenths
16 ÷ 7
2 tenths x 7
16 – 14 = 2
There are 2 tenths left over.
Divide the hundredths
28 ÷ 7 = 4 hundredths
15.68 ÷ 7 = 2.24
Question 6.
143.82 ÷ 9 = _______
Answer:
Divide the ones
143 ÷ 9
15 ones x 9 = 135
143 ones – 135 ones
There are 8 ones left over.
Divide the tenths
88 ÷ 9
9 tenths x 9
88 – 81 = 7
There are 7 tenths left over.
Divide the hundredths
72 ÷ 9 = 8 hundredths
143.82 ÷ 9 = 15.98
Find the value of y.
Question 7.
y ÷ 6 = 7.8
Answer:
y = 7.8 x 6
y= 46.8
Question 8.
14.9 ÷ 5 = y
Answer:
Divide the ones
14 ÷ 5
2 ones x 5 = 10
14 ones – 10 ones
There are 4 ones left over.
Divide the tenths
49 ÷ 5
9 tenths x 5
49 – 45 = 4
There are 4 tenths left over.
Divide the hundredths
40 ÷ 5 = 8 hundredths
14.9 ÷ 5 = 2.98
y = 2.98
Question 9.
y ÷ 2 = 4.7
Answer:
y = 4.7 x 2
y = 9.4
Question 10.
Number Sense
Evaluate the expression.
(213.3 – 95.7) ÷ 8
Answer:
(213.3 – 95.7) ÷ 8 = 117.6 ÷ 8
Divide the ones
117 ÷ 8
14 ones x 8 = 112
117 ones – 112 ones
There are 5 ones left over.
Divide the tenths
56 ÷ 8
7 tenths x 8
56 – 56 = 0
There are 0 tenths left over.
(213.3 – 95.7) ÷ 8 = 117.6 ÷ 8 = 14.7
Question 11.
Writing
Write and solve a real-life problem that involves dividing a decimal by a whole number.
Answer:
In 5 minutes John eats 7.5 chocolates. how many chocolates can he eat in one minute?
7.5 ÷ 5
Divide the ones
7 ÷ 5
1 ones x 5 = 5
7 ones – 5 ones
There are 2 ones left over.
Divide the tenths
25 ÷ 5 = 5 tenths
7.5 ÷ 5 = 1.5
In 1 minute, he can eat 1.5 chocolates.
Question 12.
YOU BE THE TEACHER
Your friend finds 197.2 ÷ 4. Is your friend correct? Explain.
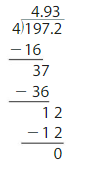
Answer:
Divide the ones
197 ÷ 4
49 ones x 4 = 196
197 ones – 196 ones
There are 1 ones left over.
Divide the tenths
12 ÷ 4
3 tenths x 4 = 12
12 – 12 = 0
There are 0 tenths left over.
197.2 ÷ 4 = 49.3
So, my friend answer is not correct.
Question 13.
Modeling Real Life
You buy 2 packages of ground beef. One package contains 4.5 pounds and the other contains 2.25 pounds. You put equal amounts of meat into 9 freezer bags. How many pounds of meat are in each bag?
Answer:
To find many pounds of meat are in each bag, divide the total meat by 9.
Add the two packages of meat.
4.5 + 2.25 = 6.75
6.75 ÷ 9
Divide the tenths
67 ÷ 9
7 tenths x 9 = 63
67 tenths – 63 tenths
There are 4 tenths left over.
Divide the hundredths
45 ÷ 9 = 5 hundredths
6.75 ÷ 9 = 0.75
Question 14.
DIG DEEPER!
A homeowner hangs wallpaper on the walls of her bathroom. What is the width of the bathroom?
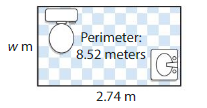
Answer:
We know that perimeter of a rectangle = 2(l + w)
8.52 = 2(2.74 + w)
2.74 + w = 8.52 ÷ 2
8.52 ÷ 2
Divide the ones
8 ÷ 2 = 4 ones
Divide the tenths
52 ÷ 2 = 26 tenths
8.52 ÷ 2 = 4.26
2.74 + w = 4.26
Width w = 4.26 – 2.74 = 1.52
So, width of the bathroom = 1.52 m
Review & Refresh
Use partial quotients to divide.
Question 15.
607 ÷ 15 = ______
Answer:
15 x 40 = 600 with remainder 7.
Question 16.
4,591 ÷ 33 = ______
Answer:
Question 17.
6,699 ÷ 87 = ______
Answer:
87 x 50 = 4350
6,699 – 4350 = 2349
87 x 20 = 1740
2349 – 1740 = 609
87 x 5 = 435
609 – 435 = 174
87 x 2 = 174
6,699 ÷ 87 = 50 + 20 + 5 + 2 = 77.
Lesson 7.5 Divide Decimals by Two-Digit Numbers
Explore and Grow
Write a division problem you can use to find the width of each rectangle. Then find the width of each rectangle.
Answer:
Precision
Explain how you can use estimation to check your answers.
Answer:
Think and Grow: Divide Decimals by Two-Digit Numbers
Example
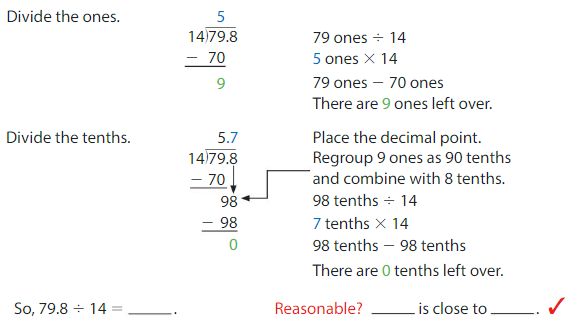
Find 79.8 ÷ 14. Estimate _________
Regroup 7 tens as 70 ones and combine with 9 ones.
Example
Find 20.54 ÷ 26.
Step 1: Estimate the quotient.
2,000 hundredths ÷ 25 = _______ hundredths
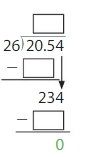
Step 2: Divide as you do with whole numbers.
Step 3: Use the estimate to place the decimal point.
So, 20.54 ÷ 26 = _______.
Show and Grow
Find the quotient. Then check your answer.
Question 1.
\(\sqrt [ 12 ]{ 51.6 } \)
Answer:
Divide the ones
51 ÷ 12
4 ones x 12 = 48
51 ones – 48 ones
There are 3 ones left over.
Divide the tenths
36 ÷ 12
3 tenths x 12 = 36
36 – 36 = 0
There are 0 tenths left over.
So, 51.6 ÷ 12 = 4.3
Question 2.
\(\sqrt [ 17 ]{ 140.25 } \)
Answer:
Divide the ones
140 ÷ 17
8 ones x 17 = 136
140 ones – 136 ones
There are 4 ones left over.
Divide the tenths
42 ÷ 17
2 tenths x 17 = 34
42 – 34 = 8
There are 8 tenths left over.
Divide the hundredths
85 ÷ 17 = 5 hundredths.
So, 140.25 ÷ 17 = 8.25
Question 3.
\(\sqrt [ 61 ]{ 32.33 } \)
Answer:
Divide the tenths
323 ÷ 61
5 ones x 61 = 305
323 tenths – 305 tenths
There are 18 tenths left over.
Divide the hundredths
183 ÷ 61 = 3 hundredths
So, 32.33 ÷ 61 = 0.53
Apply and Grow: Practice
Place a decimal point where it belongs in the quotient.
Question 4.
251.75 ÷ 19 = 1 3 . 2 5
Answer:
When dividing a decimal by a whole number, first we will divide the decimal by the whole number ignoring decimal point. Now put the decimal point in the quotient same as the decimal places in the dividend.
Question 5.
88.04 ÷ 62 = 1 . 4 2
Answer:
Question 6.
3.22 ÷ 23 = 0 .1 4
Answer:
Find the quotient. Then check your answer.
Question 7.
\(\sqrt [ 54 ]{ 97.2 } \)
Answer:
Divide the ones
97 ÷ 54
1 ones x 54 = 54
97 ones – 54 ones
There are 43 ones left over.
Divide the tenths
432 ÷ 54 = 8 tenths
So, 97.2 ÷ 54 = 1.8
Question 8.
\(\sqrt [ 91 ]{ 200.2 } \)
Answer:
Divide the ones
200 ÷ 91
2 ones x 91 = 182
200 ones – 182 ones
There are 18 ones left over.
Divide the tenths
182 ÷ 91 = 2 tenths
So, 200.2 ÷ 91 = 2.2
Question 9.
\(\sqrt [ 2 ]{ 56.2 } \)
Answer:
Divide the ones
56 ÷ 2
28 ones x 2 = 56
56 ones – 56 ones
There are 0 ones left over.
Divide the tenths
2 ÷ 2 = 1 tenths
So, 56.2 ÷ 2 = 28.1
Question 10.
6.08 ÷ 16 = _____
Answer:
Divide the tenths
60 ÷ 16
3 tenths x 16 = 48
60 tenths – 48 tenths
There are 12 tenths left over.
Divide the hundredths
128 ÷ 16
8 hundredths x 16
128 – 128 = 0
There are 0 hundredths left over.
So, 6.08 ÷ 16 = 0.38
Question 11.
7.45 ÷ 5 = _______
Answer:
Divide the tenths
74 ÷ 5
14 tenths x 5 = 70
74 tenths – 70 tenths
There are 4 tenths left over.
Divide the hundredths
45 ÷ 5
9 hundredths x 5 = 45
45 – 45 = 0
There are 0 hundredths left over.
So, 7.45 ÷ 5 = 1.49
Question 12.
147.63 ÷ 37 = _______
Answer:
Divide the ones
147 ÷ 37
3 ones x 37 = 111
147 ones – 111 ones
There are 36 ones left over.
Divide the tenths
366 ÷ 37
9 tenths x 37 = 333
366 – 333 = 33
Divide the hundredths
333 ÷ 37 = 9 hundredths
So, 147.63 ÷ 37 = 3.99
Find the value of y.
Question 13.
y ÷ 44 = 1.82
Answer:
y = 44 x 1.82
y = 80.08
Question 14.
106.6 ÷ 82 = y
Answer:
Divide the ones
106 ÷ 82
1 ones x 82 = 82
106 ones – 82 ones
There are 24 ones left over.
Divide the tenths
246 ÷ 82
3 tenths x 82 = 246
246 – 246 = 0
106.6 ÷ 82 = 1.3, y = 1.3
Question 15.
y ÷ 13 = 2.6
Answer:
y = 13 x 2.6
y = 33.8
Question 16.
Logic
Newton and Descartes find 44.82 ÷ 18. Only one of them is correct. Without solving, who is correct? Explain.

Answer:
Descartes answer is correct, 44.82 ÷ 18 = 2.49
When dividing a decimal by a whole number, first we will divide the decimal by the whole number ignoring decimal point. Now put the decimal point in the quotient same as the decimal places in the dividend.
Question 17.
DIG DEEPER!
Find a decimal that you can divide by a two-digit whole number to get the quotient shown. Fill in the boxes with your dividend and divisor.
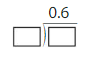
Dividend is 20 and divisor is 12.
Think and Grow: Modeling Real Life
Example
You practice paddle boarding for 3 weeks. You paddle the same amount each day for 5 days each week. You paddle 22.5 miles altogether. How many miles do you paddle each day?

To find the total number of days you paddle in 3 weeks, multiply the days you paddle each week by 3.
5 × 3 = 15 So, you paddle board _______ days in 3 weeks.
To find the number of miles you paddle each day, divide the total number of miles by the number of days you paddle in 3 weeks.
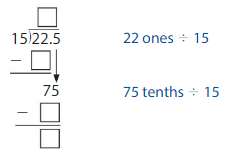
You paddle _______ miles each day.
Show and Grow
Question 18.
Descartes borrows $6,314.76 for an all-terrain vehicle. He pays back the money in equal amounts each month for 3 years. What is his monthly payment?
Answer:
Time t = 3 years = 3 x 12 = 36 months
Descartes borrowed amount = $6,314.76
6,314.76 ÷ 36
63 ÷ 36 = 1 and 27 is left over
271 ÷ 36 = 7 and 19 is left over
194 ÷ 36 = 5 and 14 is left over
147 ÷ 36 = 4 and 3 is left over
36 ÷ 36 = 1 and 0 left over.
6,314.76 ÷ 36 = 175.41
Descartes monthly payment is $175.41
Question 19.
A blue car travels 297.6 miles using 12 gallons of gasoline and a red car travels 358.8 miles using 13 gallons of gasoline. Which car travels farther using 1 gallon of gasoline? How much farther?
Answer:
297 ones ÷ 12 = 24 ones x 12 = 288
297 ones – 288 ones
There are 9 ones left over.
96 ÷ 12 = 8 tenths x 12 = 96
96 – 96 = 0
There are 0 hundredths left over.
So, 297.6 ÷ 12 = 24.8
358 ones ÷ 13 = 27 ones x 13 = 351
358 ones – 351 ones
There are 7 ones left over.
78 ÷ 13 = 6 tenths x 13 = 78
78 – 78 = 0
There are 0 hundredths left over.
So, 358.8 ÷ 13 = 27.6
Red car – blue car = 27.6 – 24.8 = 2.8
Red car travels 2.8 miles farther than blue car using 1 gallon of gasoline.
Question 20.
DIG DEEPER!
The rectangular dog park has an area of 2,616.25 square feet. How much fencing does an employee need to enclose the dog park?

Answer:
Divide Decimals by Two-Digit Numbers Homework & Practice 7.5
Place a decimal point where it belongs in the quotient.
Question 1.
127.2 ÷ 24 = 5 . 3
Answer:
Question 2.
48.64 ÷ 32 = 1 . 5 2
Answer:
Question 3.
514.18 ÷ 47 = 1 0 . 9 4
Answer:
Find the quotient. Then check your answer.
Question 4.
\(\sqrt [ 72 ]{ 93.6 } \)
Answer:
Divide the ones
93 ÷ 72
1 ones x 72 = 72
93 ones – 72 ones
There are 21 ones left over.
Divide the tenths
216 ÷ 72 = 3 tenths.
So, 93.6 ÷ 72 = 1.3
Question 5.
\(\sqrt [ 7 ]{ 3.92 } \)
Answer:
Divide the tenths
39 ÷ 7
5 ones x 7 = 35
39 ones – 35 ones
There are 4 ones left over.
Divide the hundredths
42 ÷ 7 = 6 tenths.
So, 3.92 ÷ 7 = 0.56
Question 6.
\(\sqrt [ 29 ]{ 1.74 } \)
Answer:
Divide the hundredths
174 ÷ 29
6 ones x 29 = 174
174 hundredths – 174 hundredths
There are 0 hundredths left over.
So, 1.74 ÷ 29 = 0.06
Question 7.
24.3 ÷ 9 = _______
Answer:
Divide the ones
24 ÷ 9
2 ones x 9 = 18
24 ones – 18 ones
There are 6 ones left over.
Divide the tenths
63 ÷ 9
7 tenths x 9 = 63
63 – 63 = 0
There are 0 tenths left over.
So, 24.3 ÷ 9 = 2.7
Question 8.
244.9 ÷ 31 = ______
Answer:
Divide the ones
244 ÷ 31
7 ones x 31 = 217
244 ones – 217 ones
There are 27 ones left over.
Divide the tenths
279 ÷ 31
9 tenths x 31
279 – 279 = 0
There are 0 tenths left over.
So, 244.9 ÷ 31 = 7.9
Question 9.
55.62 ÷ 27 = ______
Answer:
Divide the ones
55 ÷ 27
2 ones x 27 = 54
55 ones – 54 ones
There is 1 ones left over.
Divide the tenths
162 ÷ 27
6 tenths x 27
162 – 162 = 0
There are 0 tenths left over.
So, 55.62 ÷ 27 = 2.06
Find the value of y.
Question 10.
y ÷ 16 = 0.23
Answer:
y = 16 x 0.23
y = 3.68
Question 11.
44.1 ÷ 21 = y
Answer:
Divide the ones
44 ÷ 21
2 ones x 21 = 42
44 ones – 42 ones
There are 2 ones left over.
Divide the tenths
21 ÷ 21
1 tenths x 21
21 – 21 = 0
There are 0 tenths left over.
So, 44.1 ÷ 21 = 2.1
Question 12.
y ÷ 28 = 11.04
Answer:
y = 28 x 11.04
y = 309.12
Question 13.
YOU BE THE TEACHER
Your friend finds 21.44 ÷ 16. Is your friend correct? Explain.
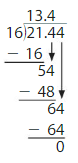
Answer:
My friend answer is not correct.
When dividing a decimal by a whole number, first we will divide the decimal by the whole number ignoring decimal point. Now put the decimal point in the quotient same as the decimal places in the dividend.
Divide the ones
21 ÷ 16
1 ones x 16 = 16
21 ones – 16 ones
There are 5 ones left over.
Divide the tenths
54 ÷ 16
3 tenths x 16
54 tenths – 48 tenths
There are 6 tenths left over.
Divide the hundredths
64 ÷ 16
4 hundredths x 16
64 hundredths- 64 hundredths
There are 0 hundredths left over.
So, 21.44 ÷ 16 = 1.34
Question 14.
DIG DEEPER!
A banker divides the amount shown among 12 people. How can she regroup the money? How much money does each person get?

Answer:
Question 15.
Modeling Real Life
You have hip-hop dance practice for 5 weeks. You attend practice 5 days each week. Each practice is the same length of time. You practice for 37.5 hours altogether. How many hours do you practice each day?
Answer:
To find the total number of days you practice in 5 weeks, multiply the days you practice each week by 5.
5 × 5 = 25 So, you practice 25 days in 5 weeks.
To find the number of hours you practice each day, divide the total number of hours by the number of days you practice in 5 weeks.
37.5 ÷ 25
Divide the ones
37 ÷ 25
1 ones x 25 = 25
37 ones – 25 ones
There are 12 ones left over.
Divide the tenths
125 ÷ 25
5 tenths x 25
125 tenths – 125 tenths
There are 0 tenths left over.
So, 37.5 ÷ 25 = 1.5
So, I practice dance 1.5 hours each day.
Question 16.
DIG DEEPER!
Your rectangular classroom rug has an area of 110.5 square feet. What is the perimeter of the rug?
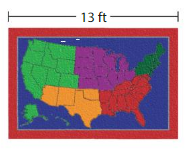
Answer:
Review & Refresh
Find the product.
Question 17.
0.52 × 0.4 = _______
Answer: 0.208
Question 18.
0.7 × 21.3 = _______
Answer: 14.91
Question 19.
1.52 × 8.6 = ______
Answer: 13.072
Lesson 7.6 Use Models to Divide Decimals
Explore and Grow
Use the model to find each quotient.
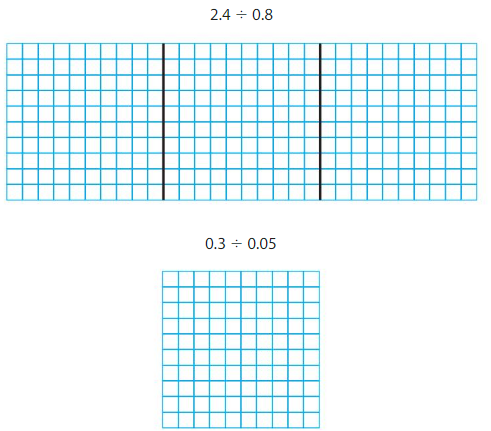
Answer:
Structure
When using a model to divide decimals, how do you determine the number of rows and columns to shade? How do you divide the shaded region?
Answer:
Think and Grow: Use Models to Divide Decimals
Example
Use a model to find 1.2 ÷ 0.3.
Shade 12 columns to represent 1.2.
Divide the model to show groups of 0.3.
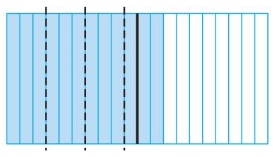
There are ______ groups of ______ tenths.
So, 1.2 ÷ 0.3 = ________.
Example
Use a model to find 0.7 ÷ 0.14.

Shade 7 columns to represent 0.7.
Divide the model to show groups of 0.14.
There are ______ groups of _______ hundredths.
So, 0.7 ÷ 0.14 = ______.
Show and Grow
Use the model to find the quotient.
Question 1.
1.5 ÷ 0.5 = _____
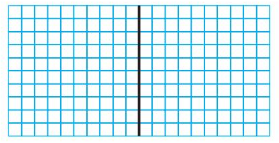
Answer:
Shade 15 columns to represent 1.5.
Divide the model to show groups of 0.5.
There are 3 groups of 5 tenths.
So, 1.5 ÷ 0.5 = 3
Question 2.
1.72 ÷ 0.86 = ______
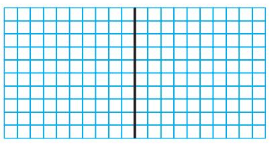
Answer:
Shade 17.2 columns to represent 1.72.
Divide the model to show groups of 0.86.
There are 2 groups of 86 hundredths.
So, 1.72 ÷ 0.86 = 2
Apply and Grow: Practice
Use the model to find the quotient.
Question 3.
0.32 ÷ 0.04 = ______

Answer:
Shade 3.2 columns to represent 0.32.
Divide the model to show groups of 0.04.
There are 8 groups of 4 hundredths.
So, 0.32 ÷ 0.04 = 8
Question 4.
0.9 ÷ 0.15 = ______

Answer:
Shade 9 columns to represent 0.9.
Divide the model to show groups of 0.15.
There are 6 groups of 15 hundredths.
So, 0.9 ÷ 0.15 = 6
Question 5.
1.4 ÷ 0.07 = _____
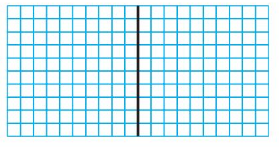
Answer:
Shade 14 columns to represent 1.4.
Divide the model to show groups of 0.07.
There are 20 groups of 7 hundredths.
So, 1.4 ÷ 0.07 = 20
Question 6.
1.08 ÷ 0.09 = _____
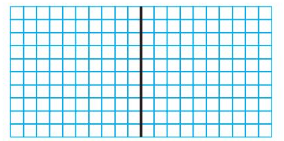
Answer:
Shade 10.8 columns to represent 1.08.
Divide the model to show groups of 0.09.
There are 12 groups of 9 hundredths.
So, 1.08 ÷ 0.09 = 12
Question 7.
You have$1.50 in dimes. You exchange all of your dimes for quarters. How many quarters do you get?
Answer:
Quarter = 0.25
1.50 ÷ 0.25
Shade 15 columns to represent 1.50.
Divide the model to show groups of 0.25.
There are 6 groups of 25 hundredths.
So, 1.50 ÷ 0.25 = 6 quarters.
Question 8.
YOU BE THE TEACHER
Your friend uses the model below and says 1.6 ÷ 0.08 = 2. Is your friend correct? Explain.
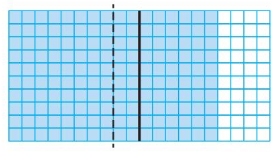
Answer:
1.6 ÷ 0.08
Shade 16 columns to represent 1.6.
Divide the model to show groups of 0.08.
There are 20 groups of 8 hundredths.
So, 1.6 ÷ 0.08 = 20
So, my friend answer is wrong.
Question 9.
Structure
Use the model to find the missing number.
0.72 ÷ ____ = 8

Answer:
Shade 7.2 columns to represent 0.72.
Divide the model to show groups of 8.
There are 0.09 groups of 800 hundredths.
So, 0.72 ÷ 0.09 = 8
Missing number is 0.09.
Think and Grow: Modeling Real Life
Example
Is aluminum more than 5 times as dense as neon?
Divide the density of aluminum by the density of neon to find how many times as dense it is.
Use a model. Shade 27 columns to represent 2.7.
Divide the model to show groups of 0.9.
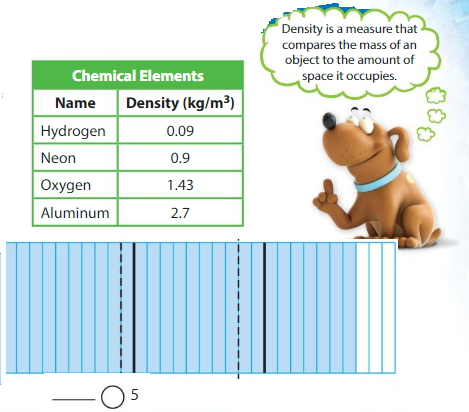
There are ______ groups of ______ tenths.
So, 2.7 ÷ 0.9 = _______.
Compare the quotient to 5.
So, aluminum ________ more than 5 times as dense as neon.
Show and Grow
Question 10.
Use the table above. Is neon more than 9 times as dense as hydrogen?
Answer:
Divide the density of neon by the density of hydrogen to find how many times as dense it is.
Use a model. Shade 9 columns to represent 0.9.
Divide the model to show groups of 0.09.
There are 10 groups of 9 hundredths.
So, 0.9 ÷ 0.09 = 10
Compare the quotient to 9.
So, neon is more than 9 times as dense as hydrogen.
Question 11.
You fill a bag with peanuts, give the cashier $5, and receive $3.16 in change. How many pounds of peanuts do you buy?

Answer:
Amount to buy peanuts = 5 – 3.16 = 1.84
peanuts per pound = $0.23
1.84 ÷ 0.23
Shade 18.4 columns to represent 1.84.
Divide the model to show groups of 0.23.
There are 8 groups of 23 hundredths.
So, 1.84 ÷ 0.23 = 8
I can buy 8 pounds of peanuts.
Question 12.
DIG DEEPER!
You have 2.88 meters of copper wire and 5.85 meters of aluminum wire. You need 0.24 meter of copper wire to make one bracelet and 0.65 meter of aluminum wire to make one necklace. Can you make more bracelets or more necklaces? Explain.
Answer:
Copper wire = 2.88 ÷ 0.24
Shade 28.8 columns to represent 2.88.
Divide the model to show groups of 0.24.
There are 12 groups of 24 hundredths.
So, 2.88 ÷ 0.24 = 12
Aluminum wire = 5.85 ÷ 0.65
Shade 58.5 columns to represent 5.85.
Divide the model to show groups of 0.65.
There are 9 groups of 65 hundredths.
So, 5.85 ÷ 0.65 = 9
So, we can make more bracelets.
Use Models to Divide Decimals Homework & Practice 7.6
Use the model to find the quotient.
Question 1.
0.08 ÷ 0.02 = _____

Answer:
Shade 8 columns to represent 0.08.
Divide the model to show groups of 0.02.
There are 4 groups of 2 hundredths.
So, 0.08 ÷ 0.02 = 4
Question 2.
0.4 ÷ 0.05 = ______

Answer:
Shade 5 columns to represent 0.4.
Divide the model to show groups of 0.05.
There are 8 groups of 5 hundredths.
So, 0.4 ÷ 0.05 = 8
Question 3.
1.7 ÷ 0.85 = ______
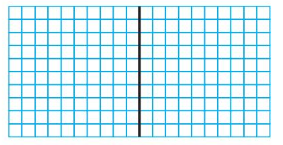
Answer:
Shade 17 columns to represent 1.7.
Divide the model to show groups of 0.85.
There are 2 groups of 85 hundredths.
So, 1.7 ÷ 0.85 = 2
Question 4.
1.5 ÷ 0.3 = _______
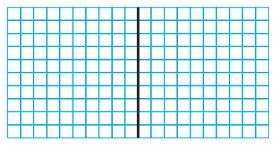
Answer:
Shade 15 columns to represent 1.5.
Divide the model to show groups of 0.3.
There are 5 groups of 3 tenths.
So, 1.5 ÷ 0.3 = 5
Question 5.
You have a piece of scrapbook paper that is 1.5 feet long. You cut it into pieces that are each 0.5 foot long. How many pieces of scrap book paper do you have now?
Answer:
1.5 ÷ 0.5
Shade 15 columns to represent 1.5.
Divide the model to show groups of 0.5.
There are 3 groups of 5 tenths.
So, 1.5 ÷ 0.5 = 3
So, I have 3 pieces of scrap book paper.
Question 6.
YOU BE THE TEACHER
Your friend uses the model below and says 0.12 ÷ 0.04 = 0.03. Is your friend correct? Explain.

Answer:
0.12 ÷ 0.04
Shade 1.2 columns to represent 0.12.
Divide the model to show groups of 0.04.
There are 3 groups of 4 hundredths.
So, 0.12 ÷ 0.04 = 3
My friend is not correct.
Question 7.
Writing
Write a real-life problem that involves dividing a decimal by another decimal.
Answer:
Question 8.
Modeling Real Life
Does the watercolor paint cost more than 3 times as much as the paintbrush? Explain.
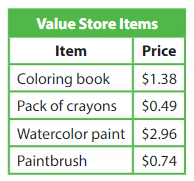
Answer:
Divide the price of watercolor paint by the price of paintbrush to find how many times as cost it is.
Use a model. Shade 29.6 columns to represent 2.96.
Divide the model to show groups of 0.74.
There are 4 groups of 74 hundredths.
So, 2.96 ÷ 0.74
Compare the quotient to 3.
So, watercolor paint costs more than 3 times as much as the paintbrush.
Question 9.
DIG DEEPER!
You have 3.75 cups of popcorn kernels. You fill a machine with 0.25 cup of kernels 3 times each hour. How many hours pass before you run out of kernels?

Answer:
Filling kernels each hour = 0.25 x 3 = 0.75
Total cups of popcorn kernels = 3.75
3.75 ÷ 0.75
Shade 37.5 columns to represent 3.75.
Divide the model to show groups of 0.75.
There are 5 groups of 75 hundredths.
So, 3.75 ÷ 0.75 = 5 hours
Review & Refresh
Complete the equation. Identify the property shown.
Question 10.
3 × 14 = 14 × 3
Answer: Commutative Property of Multiplication
Question 11.
8 × (3 + 10) = (8 × 3) + (8 × 10)
Answer: Distributive Property
Lesson 7.7 Divide Decimals
Explore and Grow
Use the model to find 0.96 ÷ 0.32.

Find 96 ÷ 32.
Answer:
Structure
How can multiplying by a power of 10 help you divide decimals?
Answer:
Think and Grow: Divide Decimals by Decimals
Key Idea
To divide by a decimal, multiply the divisor by a power of 10 to make it a whole number. Multiply the dividend by the same power of 10. Then divide as you would with whole numbers.
Example
Find 6.12 ÷ 1.8. Estimate _______

Example
Find 2.43 ÷ 0.09.

So, 2.43 ÷ 0.09 = ______.
Show and Grow
Multiply the divisor by a power of 10 to make it a whole number. Then write the equivalent expression.
Question 1.
3.5 ÷ 0.5
Answer:
Step 1: Multiply 0.5 by a power of 10 to make it a whole number. Then multiply 3.5 by the same power of 10.
0.5 x 10 = 5
3.5 x 10 = 35
35 ÷ 5 = 7
So, 3.5 ÷ 0.5 = 7
Question 2.
9.84 ÷ 2.4
Answer:
Step 1: Multiply 2.4 by a power of 10 to make it a whole number. Then multiply 9.84 by the same power of 10.
2.4 x 10 = 24
9.84 x 10 = 98.4
Step 2: Divide 98.4 ÷ 24
98 ÷ 24 = 4 with remainder 2.
24 ÷ 24 = 1 with remainder 0.
So, 9.84 ÷ 2.4 = 4.1
Question 3.
4.68 ÷ 0.78
Answer:
Step 1: Multiply 0.78 by a power of 10 to make it a whole number. Then multiply 4.68 by the same power of 10.
0.78 x 100 = 78
4.68 x 100 = 468
Step 2: Divide 468 ÷ 78 = 6
So, 4.68 ÷ 0.78 = 6
Apply and Grow: Practice
Place a decimal point where it belongs in the quotient.
Question 4.
28.47 ÷ 0.39 = 7 3 . 0
Answer:
Question 5.
75.85 ÷ 3.7 = 2 0 . 5
Answer:
Question 6.
4.51 ÷ 4.1 = 1 . 1
Answer:
Find the quotient. Then check your answer.
Question 7.
\(\sqrt [ 1.5 ]{ 7.5 } \)
Answer:
Step 1: Multiply 7.5 by a power of 10 to make it a whole number. Then multiply 1.5 by the same power of 10.
7.5 x 10 = 75
1.5 x 10 = 15
75 ÷ 15 = 5
So, 7.5 ÷ 1.5 = 5
Question 8.
\(\sqrt [ 0.13 ]{ 0.91 } \)
Answer:
Step 1: Multiply 0.91 by a power of 100 to make it a whole number. Then multiply 0.13 by the same power of 100.
0.91 x 100 = 91
0.13 x 100 = 13
91 ÷ 13 = 7
So, 0.91 ÷ 0.13 = 7
Question 9.
\(\sqrt [ 2.4 ]{ 2.88 } \)
Answer:
Step 1: Multiply 2.88 by a power of 10 to make it a whole number. Then multiply 2.4 by the same power of 10.
2.88 x 10 = 28.8
2.4 x 10 = 24
Step 2: Divide 28.8 ÷ 24
28 ÷ 24 = 1 with remainder 4.
48 ÷ 24 = 2 with remainder 0.
So, 2.88 ÷ 2.4 = 1.2
Question 10.
\(\sqrt [ 0.6 ]{ 7.8 } \)
Answer:
Step 1: Multiply 7.8 by a power of 10 to make it a whole number. Then multiply 0.6 by the same power of 10.
7.8 x 10 = 78
0.6 x 10 = 6
78 ÷ 6 = 13
So, 7.8 ÷ 0.6 = 13
Question 11.
\(\sqrt [ 3.6 ]{ 4.32 } \)
Answer:
Step 1: Multiply 4.32 by a power of 10 to make it a whole number. Then multiply 3.6 by the same power of 10.
4.32 x 10 = 43.2
3.6 x 10 = 36
Step 2: Divide 43.2 ÷ 36
43 ÷ 36 = 1 with remainder 7.
72 ÷ 36 = 2 with remainder 0.
So, 4.32 ÷ 3.6 = 1.2
Question 12.
\(\sqrt [ 0.1 ]{ 11.2 } \)
Answer:
Step 1: Multiply 11.2 by a power of 10 to make it a whole number. Then multiply 0.1 by the same power of 10.
11.2 x 10 = 112
0.1 x 10 = 1
112 ÷ 1 = 112
So, 11.2 ÷ 0.1 = 112
Question 13.
40.42 ÷ 8.6 = ______
Answer:
Step 1: Multiply 8.6 by a power of 10 to make it a whole number. Then multiply 40.42 by the same power of 10.
8.6 x 10 = 86
40.42 x 10 = 404.2
Step 2: Divide 404.2 ÷ 86
404 ÷ 86 = 4 with remainder 60.
602 ÷ 86 = 7 with remainder 0.
So, 40.42 ÷ 8.6 = 4.7
Question 14.
7.2 ÷ 2.4 = _______
Answer:
Step 1: Multiply 2.4 by a power of 10 to make it a whole number. Then multiply 7.2 by the same power of 10.
2.4 x 10 = 24
7.2 x 10 = 72
Step 2: Divide 72 ÷ 24 = 3
So, 7.2 ÷ 2.4 = 3
Question 15.
5.76 ÷ 1.8 = _______
Answer:
Step 1: Multiply 1.8 by a power of 10 to make it a whole number. Then multiply 5.76 by the same power of 10.
1.8 x 10 = 18
5.76 x 10 = 57.6
Step 2: Divide 57.6 ÷ 18
57 ÷ 18 = 3 with remainder 3.
36 ÷ 18 = 2 with remainder 0.
So, 5.76 ÷ 1.8 = 3.2
Question 16.
YOU BE THE TEACHER
Descartes says 4.14 ÷ 2.3 = 1.8. Is he correct? Explain.
Answer:
Step 1: Multiply 2.3 by a power of 10 to make it a whole number. Then multiply 4.14 by the same power of 10.
2.3 x 10 = 23
4.14 x 10 = 41.4
Step 2: Divide 41.4 ÷ 23
41 ÷ 23 = 1 with remainder 18.
184 ÷ 23 = 8 with remainder 0.
So, 4.14 ÷ 2.3 = 1.8.
Descartes answer is correct.
Question 17.
Logic
What can you conclude about Newton’s quotient?

Answer:
The quotient will be above 5.72.
Because if the divisor is less than 1 then the quotient must be greater than the dividend.
Think and Grow: Modeling Real Life
Example
A farmer sells a bag of papayas for $5.46. How much does the bag of papayas weigh?
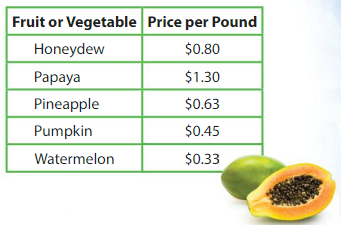
Divide the price of the papayas by the price per pound to find how much the bag of papayas weighs.
5.46 ÷ 1.3 = ? Estimate _______

So, the bag of papayas weighs _______ pounds.
Show and Grow
Use the table above.
Question 18.
You buy a honeydew for $6.08. What is the weight of the honeydew?
Answer:
Honeydew price = $0.8
6.08 ÷ 0.8
Step 1: Multiply 0.8 by a power of 10 to make it a whole number. Then multiply 6.08 by the same power of 10.
0.8 x 10 = 8
6.08 x 10 = 60.8
Step 2: Divide 60.8 ÷ 8
60 ÷ 8 = 7 with remainder 4.
48 ÷ 8 = 6 with remainder 0.
So, 6.08 ÷ 0.8 = 7.6
Weight of the honeydew = 7.6 pounds
Question 19.
You buy a pumpkin for $7.20 and a watermelon for $5.94. Does the watermelon or the pumpkin weigh more? How much more?
Answer:
Pumpkin = 7.20 ÷ 0.45
Watermelon = 5.94 ÷ 0.33
7.20 ÷ 0.45
Step 1: Multiply 0.45 by a power of 10 to make it a whole number. Then multiply 7.20 by the same power of 10.
0.45 x 100 = 45
7.20 x 100 = 720
Step 2: Divide 720 ÷ 45 = 16
Pumpkin weight = 16 pounds
5.94 ÷ 0.33
Step 1: Multiply 0.33 by a power of 10 to make it a whole number. Then multiply 5.94 by the same power of 10.
0.33 x 100 = 33
5.94 x 100 = 594
Step 2: Divide 594 ÷ 33 = 18
Watermelon weight = 18 pounds
Watermelon weighs 2 pounds more than the pumpkin.
Question 20.
DIG DEEPER!
You pay $5 for a pineapple and receive $2.48 in change. The inedible parts of the pineapple weigh 1.75 pounds. How many pounds of edible pineapple do you have? Explain.

Answer:
Amount paid = 5 – 2.48 = $2.52
pineapple price per pound = $0.63
2.52 ÷ 0.63
Step 1: Multiply 0.63 by a power of 10 to make it a whole number. Then multiply 2.52 by the same power of 10.
0.63 x 100 = 63
2.52 x 100 = 252
Step 2: Divide 252 ÷ 63 = 4
Total weight = 4 pounds
Edible pineapple = total weight – inedible pineapple weight
= 4 – 1.75
= 2.25
Edible pineapple weight = 2.25 pounds.
Divide Decimals Homework & Practice 7.7
Multiply the divisor by a power of 10 to make it a whole number. Then write the equivalent expression.
Question 1.
16.15 ÷ 1.9
Answer:
Step 1: Multiply 1.9 by a power of 10 to make it a whole number. Then multiply 16.15 by the same power of 10.
1.9 x 10 = 19
16.15 x 10 = 161.5
Step 2: Divide 161.5 ÷ 19
161 ÷ 19 = 8 with remainder 9.
95 ÷ 19 = 5 with remainder 0.
So, 16.15 ÷ 1.9 = 8.5
Question 2.
0.36 ÷ 0.09
Answer:
Step 1: Multiply 0.09 by a power of 10 to make it a whole number. Then multiply 0.36 by the same power of 10.
0.09 x 100 = 9
0.36 x 100 = 36
Step 2: Divide 36 ÷ 9 = 4
So, 0.36 ÷ 0.09 = 4
Question 3.
2.04 ÷ 1.7
Answer:
Step 1: Multiply 1.7 by a power of 10 to make it a whole number. Then multiply 2.04 by the same power of 10.
1.7 x 10 = 17
2.04 x 10 = 20.4
Step 2: Divide 20.4 ÷ 17
20 ÷ 17 = 1 with remainder 3.
34 ÷ 17 = 2 with remainder 0.
So, 2.04 ÷ 1.7 = 1.2
Place a decimal point where it belongs in the quotient.
Question 4.
81.27 ÷ 13.5 = 6 . 0 2
Answer:
Question 5.
5.76 ÷ 3.2 = 1 . 8
Answer:
Question 6.
47.15 ÷ 2.3 = 2 0 . 5
Answer:
Find the quotient. Then check your answer.
Question 7.
\(\sqrt [ 5.3 ]{ 21.2 } \)
Answer:
Step 1: Multiply 5.3 by a power of 10 to make it a whole number. Then multiply 21.2 by the same power of 10.
5.3 x 10 = 53
21.2 x 10 = 212
212 ÷ 53 = 4
So, 21.2 ÷ 5.3 = 4
Question 8.
\(\sqrt [ 0.03 ]{ 76.38 } \)
Answer:
Step 1: Multiply 0.03 by a power of 10 to make it a whole number. Then multiply 76.38 by the same power of 10.
0.03 x 100 = 3
76.38 x 100 = 7,638
Step 2: Divide 7638 ÷ 3
76 ÷ 3 = 25 with remainder 1.
138 ÷ 3 = 46 with remainder 0.
So, 76.38 ÷ 0.03 = 25.46
Question 9.
\(\sqrt [ 6.2 ]{ 33.48 } \)
Answer:
Step 1: Multiply 6.2 by a power of 10 to make it a whole number. Then multiply 33.48 by the same power of 10.
6.2 x 10 = 62
33.48 x 10 = 334.8
Step 2: Divide 334.8 ÷ 62
334 ÷ 62 = 5 with remainder 24.
248 ÷ 62 = 4 with remainder 0.
So, 33.48 ÷ 6.2 = 5.4
Find the quotient. Then check your answer.
Question 10.
0.63 ÷ 0.09 = ______
Answer:
Step 1: Multiply 0.09 by a power of 10 to make it a whole number. Then multiply 0.63 by the same power of 10.
0.09 x 100 = 9
0.63 x 100 = 63
Step 2: Divide 63 ÷ 9 = 7
So, 0.63 ÷ 0.09 = 7
Question 11.
10.53 ÷ 3.9 = ______
Answer:
Step 1: Multiply 3.9 by a power of 10 to make it a whole number. Then multiply 10.53 by the same power of 10.
3.9 x 10 = 39
10.53 x 10 = 105.3
Step 2: Divide 105.3 ÷ 39
105 ÷ 39 = 2 with remainder 27.
273 ÷ 39 = 7 with remainder 0.
So, 10.53 ÷ 3.9 = 2.7
Question 12.
33.8 ÷ 2.6 = ______
Answer:
Step 1: Multiply 2.6 by a power of 10 to make it a whole number. Then multiply 33.8 by the same power of 10.
2.6 x 10 = 26
33.8 x 10 = 338
Step 2: Divide 338 ÷ 26 = 13
So, 33.8 ÷ 2.6 = 13
Question 13.
Logic
Without calculating, determine whether 5.4 ÷ 0.9 is greater than or less than 5.4. Explain.
Answer:
5.4 ÷ 0.9 is greater than 5.4
If the divisor is less than 1 then the quotient must be greater than the dividend.
Question 14.
Structure
Explain how 35.64 ÷ 2.97 compares to 3,564 ÷ 297.
Answer:
Both 35.64 ÷ 2.97 and 3,564 ÷ 297 are same.
Both dividend and divisor are multiplied by same power of 10.
35.64 x 100 = 3564
2.97 x 100 = 297.
Question 15.
Modeling Real Life
A farmer sells a bag of grapes for $5.88. How much do the grapes weigh?
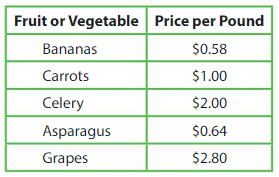
Answer:
Bag of grapes price = $5.88
Grapes price per pound = $2.80
5.88 ÷ 2.8
Step 1: Multiply 2.8 by a power of 10 to make it a whole number. Then multiply 5.88 by the same power of 10.
2.8 x 10 = 28
5.88 x 10 = 58.8
Step 2: Divide 58.8 ÷ 28
58 ÷ 28 = 2 with remainder 2.
28 ÷ 28 = 1 with remainder 0.
So, 5.88 ÷ 2.8 = 2.1
Grapes weight = 2.1 pounds
Question 16.
DIG DEEPER!
Descartes makes 2.5 times as many ounces of applesauce as Newton. Newton eats 8 ounces of his applesauce, and then divides the rest equally into 3 containers. How much applesauce is in each of Newton’s containers?

Answer:
From the given information, Newton makes applesauce = 72.5 ÷ 2.5
Step 1: Multiply 2.5 by a power of 10 to make it a whole number. Then multiply 72.5 by the same power of 10.
2.5 x 10 = 25
72.5 x 10 = 725
Step 2: Divide 725 ÷ 25 = 29
So, newton makes 29 ounces of applesauce
He eats 8 ounces = 29 – 8 = 21
21 ÷ 3 = 7 ounces.
7 ounces of applesauce is in each of Newton’s containers.
Review & Refresh
Question 17.
Write the number in two other forms.
Standard form:
Word form: two hundred thirty thousand, eighty-two
Expanded form:
Answer:
Standard form is 230,082
Expanded form is 200000 + 30000 + 80 + 2.
Lesson 7.8 Insert Zeros in the Dividend
Explore and Grow
Use the model to find each quotient.
Answer:
Reasoning
Why is the number of digits in the quotients you found above different than the number of digits in the dividends?
Answer:
Think and Grow: Inserting Zeros in the Dividend
Example
Find 52.6 ÷ 4. Estimate ________
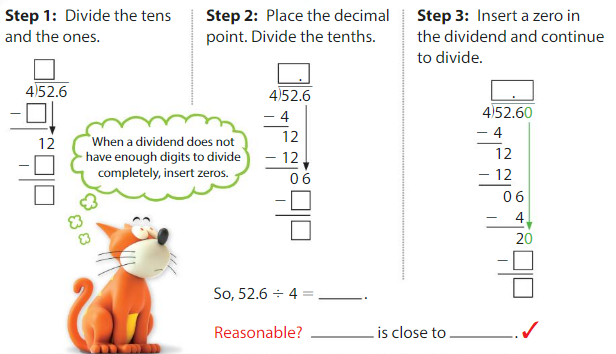
Example
Find 1 ÷ 0.08.

Show and Grow
Find the quotient. Then check your answer.
Question 1.
\(\sqrt [ 0.5 ]{ 85 } \)
Answer:
Multiply 0.5 by a power of 10 to make it a whole number. Then multiply 85 by the same power of 10.
0.5 x 10 = 5
85 x 10 = 850
850 ÷ 5 = 170
So, 85 ÷ 0.5 = 170.
Question 2.
\(\sqrt [ 15 ]{ 9.6 } \)
Answer:
Insert a zero in the dividend and continue to divide.
96 ÷ 15 = 6 with remainder 6.
60 ÷ 15 = 4 with remainder 0.
So, 9.6 ÷ 15 = 0.64
Question 3.
\(\sqrt [ 0.24 ]{ 2.52 } \)
Answer:
Multiply 0.24 by a power of 10 to make it a whole number. Then multiply 2.52 by the same power of 10.
0.24 x 100 = 24
2.52 x 100 = 252
252 ÷ 24
252 ÷ 24 = 10 with remainder 12.
Insert a zero in the dividend and continue to divide.
120 ÷ 24 = 5 with remainder 0.
So, 2.52 ÷ 0.24 = 10.5.
Apply and Grow: Practice
Place a decimal point where it belongs in the quotient.
Question 4.
3.24 ÷ 0.48 = 6 . 7 5
Answer:
Question 5.
35 ÷ 0.5 = 7 0.
Answer:
Question 6.
12.8 ÷ 2.5 = 5 .1 2
Answer:
Find the quotient. Then check your answer.
Question 7.
\(\sqrt [ 2.4 ]{ 0.84 } \)
Answer:
Multiply 2.4 by a power of 10 to make it a whole number. Then multiply 0.84 by the same power of 10.
2.4 x 10 = 24
0.84 x 10 = 8.4
Insert a zero in the dividend and continue to divide.
84 ÷ 24 = 3 with remainder 12.
120 ÷ 24 = 5 with remainder 0.
So, 0.84 ÷ 2.4 = 0.35
Question 8.
\(\sqrt [ 0.32 ]{ 2.08 } \)
Answer:
Multiply 0.32 by a power of 10 to make it a whole number. Then multiply 2.08 by the same power of 10.
0.32 x 100 = 32
2.08 x 100 = 208
208 ÷ 32 = 6 with remainder 16.
Insert a zero in the dividend and continue to divide.
160 ÷ 32 = 5 with remainder 0.
So, 2.08 ÷ 0.32 = 6.5
Question 9.
\(\sqrt [ 4 ]{ 45.8 } \)
Answer:
45.8 ÷ 4
45 ÷ 4 = 11 with remainder 1.
18 ÷ 4 = 4 with remainder 2.
Insert a zero in the dividend and continue to divide.
20 ÷ 4 = 5 with remainder 0.
So, 45.8 ÷ 4 = 11.45.
Question 10.
9 ÷ 1.2 = ______
Answer:
Multiply 1.2 by a power of 10 to make it a whole number. Then multiply 9 by the same power of 10.
1.2 x 10 = 12
9 x 10 = 90
90 ÷ 12
Insert a zero in the dividend and continue to divide.
12 ) 90 ( 7.5
84
——-
60
– 60
——-
0
So, 9 ÷ 1.2 = 7.5
Question 11.
3.5 ÷ 2.5 = ______
Answer:
Multiply 2.5 by a power of 10 to make it a whole number. Then multiply 3.5 by the same power of 10.
2.5 x 10 = 25
3.5 x 10 = 35
35 ÷ 25
Insert a zero in the dividend and continue to divide.
25 ) 35 ( 1.4
25
——-
100
-100
——-
0
So, 3.5 ÷ 2.5 = 1.4
Question 12.
1.8 ÷ 12 = ______
Answer:
Insert a zero in the dividend and continue to divide.
12 ) 18 ( 1.5
12
——-
60
– 60
——-
0
So, 1.8 ÷ 12 = 0.15
Question 13.
You read 2.5 chapters of the book each night. How many nights does it take you to finish the book?

Answer:
Total chapters in the book = 15
15 ÷ 2.5
Multiply 2.5 by a power of 10 to make it a whole number. Then multiply 15 by the same power of 10.
2.5 x 10 = 25
15 x 10 = 150
150 ÷ 25 = 6 nights to finish the book.
Question 14.
Precision
Why does Newton place zeros to the right of the dividend but Descartes does not?
Answer:
Newton’s dividend does not have enough digits to divide completely, so he placed zeros to the right of the dividend.
Descartes dividend is a multiple of divisor and it is divided completely, so no need of placing zeros.
Think and Grow: Modeling Real Life
Example
The John Muir Trail in Yosemite National Park is 210 miles long. A hiker completes the trail in 20 days by hiking the same distance each day. How many miles does the hiker travel each day?

Divide 210 miles by 20 to find how many miles the hiker travels each day.
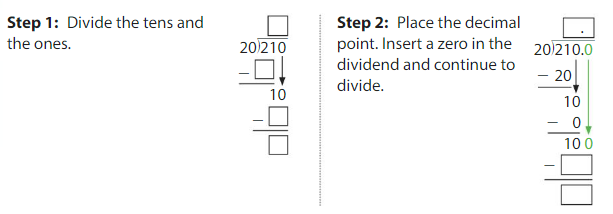
So, the hiker travels _______ miles each day.
Show and Grow
Question 15.
A box of 15 tablets weighs 288 ounces. Each tablet weighs the same number of ounces. What is the weight of each tablet?
Answer:
Divide 288 ounces by 15 to find the weight of each tablet.
288 ÷ 15
15 ) 288 ( 19.2
15
——-
138
-135
——-
30
– 30
——-
0
288 ÷ 15 = 19.2
The weight of each tablet = 19.2 ounces.
Question 16.
Which bag of dog food costs less per pound? Explain why it makes sense to write each quotient as a decimal in this situation.

Answer:
Question 17.
DIG DEEPER!
A farmer sells a pound of rice for $0.12 and a pound of oats for $0.08. Can you buy more pounds of rice or oats with $3? How much more? Explain.
Answer:
Rice = 3 ÷ 0.12
Multiply 0.12 by a power of 10 to make it a whole number. Then multiply 3 by the same power of 10.
0.12 x 100 = 12
3 x 100 = 300
300 ÷ 12 = 25
Oats = 3 ÷ 0.08
Multiply 0.08 by a power of 10 to make it a whole number. Then multiply 3 by the same power of 10.
0.08 x 100 = 8
3 x 100 = 300
300 ÷ 8 = 37.5
I can buy 12.5 pounds oats more than the rice.
Insert Zeros in the Dividend Homework & Practice 7.8
Place a decimal point where it belongs in the quotient.
Question 1.
9.3 ÷ 0.31 = 3 0.
Answer:
Question 2.
10 ÷ 0.8 = 1 2 . 5
Answer:
Question 3.
0.76 ÷ 0.25 = 3 . 0 4
Answer:
Find the quotient. Then check your answer.
Question 4.
\(\sqrt [ 0.8 ]{ 30 } \)
Answer:
Multiply 0.8 by a power of 10 to make it a whole number. Then multiply 30 by the same power of 10.
0.8 x 10 = 8
30 x 10 = 300
300 ÷ 8
30 ÷ 8 = 3 with remainder 6.
60 ÷ 8 = 7 with remainder 4.
Insert a zero in the dividend and continue to divide.
40 ÷ 8 = 5 with remainder 0.
So, 30 ÷ 0.8 = 37.5.
Question 5.
\(\sqrt [ 15 ]{ 91.2 } \)
Answer:
91.2 ÷ 15
91 ÷ 15 = 6 with remainder 1.
Insert a zero in the dividend and continue to divide.
120 ÷ 15 = 8 with remainder 0.
So, 91.2 ÷ 15 = 6.08
Question 6.
\(\sqrt [ 35 ]{ 97.3 } \)
Answer:
97.3 ÷ 35
97 ÷ 35 = 2 with remainder 27.
273 ÷ 35 = 7 with remainder 28.
Insert a zero in the dividend and continue to divide.
280 ÷ 35 = 8 with remainder 0.
So, 97.3 ÷ 35 = 2.78.
Question 7.
3.57 ÷ 0.84 = ______
Answer:
Multiply 0.84 by a power of 10 to make it a whole number. Then multiply 3.57 by the same power of 10.
0.84 x 100 = 84
3.57 x 100 = 357
357 ÷ 84
Insert a zero in the dividend and continue to divide.
84 ) 357 ( 4.25
336
——-
210
-168
——-
420
– 420
——-
0
3.57 ÷ 0.84 = 4.25
Question 8.
20.2 ÷ 4 = _____
Answer:
Insert a zero in the dividend and continue to divide.
4 ) 20.2 ( 5.05
20
——
20
20
——
0
20.2 ÷ 4 = 5.05
Question 9.
1.74 ÷ 0.25 = _______
Answer:
Multiply 0.25 by a power of 10 to make it a whole number. Then multiply 1.74 by the same power of 10.
0.25 x 100 = 25
1.74 x 100 = 174
174 ÷ 25
Insert a zero in the dividend and continue to divide.
25 ) 174 ( 6.96
150
——-
240
-225
——-
150
-150
——-
0
1.74 ÷ 0.25 = 6.96
Question 10.
A painter has 5 gallons of paint to use in a room. He uses 2.5 gallons of paint for 1 coat. How many coats can he paint?

Answer:
Multiply 2.5 by a power of 10 to make it a whole number. Then multiply 5 by the same power of 10.
2.5 x 10 = 25
5 x 10 = 50
50 ÷ 25 = 2
He can paint 2 coats.
Question 11.
YOU BE THE TEACHER
Your friend say she can find 5.44 ÷ 0.64 by dividing both the divisor and dividend by 0.01 to make an equivalent problem with a whole-number divisor. Is he correct? Explain.
Answer:
To divide this 5.44 ÷ 0.64, multiply 0.64 by a power of 10 to make it a whole number. Then multiply 5.44 by the same power of 10.
Multiplying by 100 and dividing by 0.01 both are same.
So, my friend is correct.
Question 12.
Writing
Explain when you need to insert a zero in the dividend when dividing.
Answer:
When dividend does not have enough digits to divide completely, then we need to insert a zero in the dividend.
For example, 35 ÷ 25
Here 35 is not a multiple of 25, so we have to add a zero to 35.
Question 13.
Modeling Real Life
You cut a 12-foot-long streamer into 8 pieces of equal length. How long is each piece?
Answer:
Length of each piece = 12 ÷ 8
8 ) 12 ( 1.5
8
—–
40
40
—–
0
So, length of each piece = 1.5
Question 14.
DIG DEEPER!
How many days longer does the bag of dog food last for the 20-pound dog than the 40-pound dog? Explain.

Answer:
Total cups of dog food = 200
20-pound dog eats per day = 1.25 cups
40-pound dog eats per day = 1.25 x 2 = 2.5 cups
200 ÷ 1.25
Multiply 1.25 by a power of 10 to make it a whole number. Then multiply 200 by the same power of 10.
1.25 x 100 = 125
200 x 100 = 20,000
20,000 ÷ 125
200 ÷ 125 = 1 with remainder 75
7500 ÷ 125 = 60 with remainder 0.
So, 200 ÷ 1.25 = 160
Food lasts for the 20-pound dog = 160 days
40-pound dog = 200 ÷ 2.5
Multiply 2.5 by a power of 10 to make it a whole number. Then multiply 200 by the same power of 10.
2.5 x 10 = 25
200 x 10 = 2000
2000 ÷ 25 = 80
Food lasts for the 40-pound dog = 80 days
Review & Refresh
Find the sum. Check whether your answer is reasonable.
Question 15.
1.7 + 6.8 = ________
Answer: 8.5
Question 16.
150.23 + 401.79 = _______
Answer: 552.02
Lesson 7.9 Problem Solving: Decimal Operations
Explore and Grow
Make a plan to solve the problem.
Three friends take a taxi ride that costs $4.75 per mile. They travel 10.2 miles and tip the driver $8. They share the total cost equally. How much does each friend pay?

Answer:
Reasoning
Explain how you can work backward to check your answer.
Answer:
Think and Grow: Problem Solving: Decimal Operations
Example
You spend $67.45 on the video game controller, the gaming headset, and 3 video games. The video games each cos the same amount. How much does each video game cost?

Understand the Problem
What do you know?
• You spend a total of $67.45.
• The controller costs $15.49 and the headset costs $21.99.
• You buy 3 video games that each cost the same amount.
What do you need to find?
• You need to find the cost of each video game.
Make a Plan
How will you solve?
Write and solve an equation to find the cost of each video game.
Solve
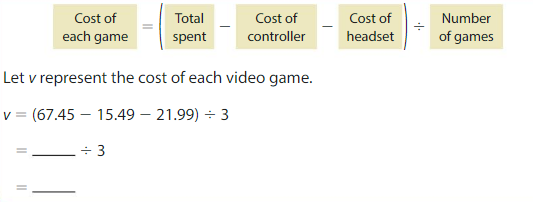
So, each video game costs ______.
Show and Grow
Question 1.
Explain how you can check whether your answer above is reasonable.
Answer:
v = (67.45 – 15.49 – 21.99) ÷ 3
= 29.97 ÷ 3
v = 9.99
So, each video game costs $9.99.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
Your friend pays $84.29 for a sewing machine and 6 yards of fabric. The sewing machine costs $59.99. How much does each yard of fabric cost?
Answer:
What do you know?
• You spend a total of $84.29 for a sewing machine and 6 yards of fabric.
• The sewing machine costs $59.99 and the 6 yards of fabric costs $24.3.
What do you need to find?
We have to find each yard of fabric cost.
1 yard of fabric cost = 24.3 ÷ 6
So, each yard of fabric costs = $4.05
Question 3.
There are 25.8 grams of fiber in 3 cups of cooked peas. There are 52.5 grams of fiber in 5 cups of avocados. Which contains more fiber in 1 cup, cooked peas or avocados?
Answer:
Cooked peas = 25.8 ÷ 3 = 8.6 grams
Avocados = 52.5 ÷ 3 = 10.5 grams
So, avocados contains more fiber in 1 cup.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
Your friend makes a hexagonal frame with a perimeter of 7.5 feet. You make a triangular frame with a perimeter of 5.25 feet. Whose frame has longer side lengths? How much longer?
Answer:
Hexagonal perimeter = 6a = 7.5 feet
Triangular perimeter = 3sides(3a) = 5.25 feet
So, 6a ÷ 2 = 3a
7.5 ÷ 2 = 3.75 feet
5.25 – 3.75 = 1.5 feet
So, triangular frame has 1.5 feet longer side lengths.
Question 5.
You spend $119.92 on the wet suit, the snorkeling equipment, and 2 research books. The books each cost the same amount. How much does each book cost?

Answer:
Write and solve an equation to find the cost of each book.
cost of each book = (Amount spend – wet suit cost – snorkeling equipment cost) ÷ 2
= (119.92 – 64.95 – 14.99) ÷ 2
= 39.98 ÷ 2
= 19.99
So, each book costs $19.99.
Question 6.
DIG DEEPER!
You pour goop into molds and bake them to make plastic lizards. You run out of goop and go shopping for more. Which package costs less per ounce of goop? Explain.


Answer:
Fluorescent package = 40.5 ÷ 2.25 = $18
Color-Changing package = 16.2 ÷ 1.8 = $9
So, Color-Changing package costs less per ounce of goop.
Think and Grow: Modeling Real Life
Example
Descartes spends $16.40 on the game app, an e-book, and 5 songs. The e-book costs 4 times as much as the game app. The songs each cost the same amount. How much does each song cost?
Think: What do you know? What do you need to find? How will you solve?
Step 1: Multiply the cost of the app by4 to find the cost of the e-book.
1.99 × 4 = 7.96 The e-book costs _______.
Step 2: Write and solve an equation to find the cost of each song.

Let c represent the cost of each song.
c = (16.40 – 1.99 – 7.96) ÷ 5c
= _____ ÷ 5
= _____
So, each song costs $ ______.
Show and Grow
Question 7.
You spend $2.24 on a key chain, a bookmark, and 2 pencils. The key chain costs 3 times as much as the bookmark. The pencils each cost the same amount. How much does each pencil cost?

Answer:
Given that,
Bookmark cost = $0.45
Key chain cost = 3 x 0.45 = $1.35
Write and solve an equation to find the cost of each pencil.
cost of each pencil = (Amount spend – keychain cost – bookmark cost) ÷ 2
= (2.24 – 1.35 – 0.45) ÷ 2
= 0.44 ÷ 2
= $0.22
So, cost of each pencil = $0.22.
Question 8.
Newton buys an instant-print camera, a camera bag, and 2 packs of film. He pays $113.96 after using a $5 coupon. The camera costs $69.40, which is 5 times as much as the camera case. How much does each pack of film cost?
Answer:
Total cost = 113.96 + 5 = $118.96
Camera cost = $69.40
Camera case cost = 69.40 ÷ 5 = $13.88
Write and solve an equation to find the cost of each pack of film cost.
cost of each pack of film = (amount spend – camera cost – camera case cost) ÷ 2
= (118.96 – 69.40 – 13.88) ÷ 2
= 35.68 ÷ 2
= 17.84
So, cost of each pack of film = $17.84
Problem Solving: Decimal Operations Homework & Practice 7.9
Understand the problem. What do you know? What do you need to find? Explain.
Question 1.
A 20-ounce bottle of ketchup costs $2.80. A 14-ounce bottle of mustard costs $2.38. Which item costs less per ounce? How much less?
Answer:
20-ounce bottle of ketchup costs = $2.80
14-ounce bottle of mustard costs = $2.38
1 ounce ketchup = 2.8 ÷ 20 = $0.14
1 ounce mustard = 2.38 ÷ 14 = $0.17
Ketchup costs $0.03 less per ounce than mustard.
Question 2.
Gymnast A scores the same amount in each of his 4 events. Gymnast B scores the same amount in each of his 3 events. Which gymnast scores more in each of his events? How much more?
Answer:
Gymnast A in each of his events = 33.56 ÷ 4 = 8.39 points
Gymnast B in each of his events = 25.05 ÷ 3 = 8.35 points
Gymnast A scores 0.04 points more in each of his events than gymnast B.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 3.
Three children’s tickets to the circus cost $53.85. Two adult tickets to the circus cost $63.90. How much more does 1 adult ticket cost than 1 children’s ticket? Which item costs more per ounce? How much more?
Answer:
3 children’s tickets cost = $53.85
2 adult tickets cost = $63.90
1 adult ticket cost = 63.90 ÷ 2 = $31.95
1 children’s ticket cost = 53.85 ÷ 3 = $17.95
One adult ticket cost is $14 more than 1 children’s ticket.
Question 4.
A chef at a restaurant buys 50 pounds of red potatoes for $27.50 and 30 pounds of sweet potatoes for $22.50. Which kind of potato costs more per pound? How much more?
Answer:
Red potatoes per pound = 27.5 ÷ 50 = $0.55
Sweet potatoes per pound = 22.5 ÷ 30 = $0.75
Sweet potatoes costs $0.2 more per pound than red potatoes.
Question 5.
Modeling Real Life
You download 2 music videos, a TV series, and a movie for $42.95 total. The TV series costs 2 times as much as the movie. How much does each music video cost?
Answer:
Total cost = $42.95
Movie cost = $12.99
TV series cost = $25.98
Write and solve an equation to find the cost of each music video cost.
cost of each music video = (total cost – movie cost – TV series cost) ÷ 2
= (42.95 – 12.99 – 25.98) ÷ 2
= 3.98 ÷ 2
= 1.99
So, cost of each music video = $1.99.
Question 6.
DIG DEEPER!
Which item costs more per ounce? How much more?

Answer:
Glue cost = 23.04 ÷ 1 = 23.04
Paste cost = 4.00 ÷ 2 = 2
Glue costs $21.04 more than paste.
Review & Refresh
Find the quotient.
Question 7.
4,000 ÷ 20 = ______
Answer: 200
Question 8.
900 ÷ 300 = _______
Answer: 3
Question 9.
5,600 ÷ 800 = _______
Answer: 7
Divide Decimals Performance Task
Question 1.
Multiple teams adopt different sections of a state highway to clean. The teams must clean both sides of their adopted section of the highway.

a. The teams clean their section of the highway over 4 days. They clean the same distance each day.How many miles of the highway does each team clean each day?
b. Each team divides their daily distance equally among each team member. Which team’s members clean the greatest distance each day?
c. The team that collects the greatest amount of litter per team member wins a prize.Which team wins the prize?
Answer:
Question 2.
In a community, 25 people volunteer to clean the rectangular park shown. The park is divided into sections of equal area. One section is assigned to each volunteer. What is the area of the section that each volunteer cleans? What is one possible set of dimensions for 24.5 m each section?
Answer:
Divide Decimals Activity
Race Around the World: Division
Directions:
1. Players take turns.
2. On your turn, flip a Race Around the World: Division Card and find the quotient.
3. Move your piece to the next number on the board that is highlighted in the quotient.
4. The first player to make it back to North America wins!

Answer:
Divide Decimals Chapter Practice
7.1 Division Patterns with Decimals
Find the quotient.
Question 1.
25 ÷ 102 = ______
Answer:
First Simplify the 102 which means 10 x 10 =100, then we need to calculate the fraction to a decimal just divide the numerator (25) by the denominator (100).
When we divide by 100, the decimal point moves two places to the left.
25 ÷ 102 = 0.25.
Question 2.
1.69 ÷ 0.01 = ______
Answer: To convert this simple fraction to a decimal just divide the numerator (1.69) by the denominator (0.01). When we divide by 0.01, the decimal point moves two places to the right.
1.69 ÷ 0.01 = 169.
Question 3.
681 ÷ 103 = ______
Answer:
First Simplify the 103 which means 10 x 10 x 10 =1000, then we need to calculate the fraction to a decimal just divide the numerator (681) by the denominator (1000).
When we divide by 1000, the decimal point moves three places to the left.
681 ÷ 103 = 0.681.
Question 4.
5.7 ÷ 0.1 = _____
Answer:
To convert this simple fraction to a decimal just divide the numerator (5.7) by the denominator (0.1). When we divide by 0.1, the decimal point moves one places to the right.
5.7 ÷ 0.1 = 57
Question 5.
200 ÷ 0.01 = _____
Answer:
To convert this simple fraction to a decimal just divide the numerator 200 by the denominator (0.01). When we divide by 0.01, the decimal point moves one places to the right.
Question 6.
41.3 ÷ 10 = _____
Answer: To convert this simple fraction to a decimal just divide the numerator (41.3) by the denominator (10). When we divide by 10, the decimal point moves one places to the left.
41.3 ÷ 10 = 4.13
Find the value of k.
Question 7.
74 ÷ k = 7,400
Answer:
74 ÷ 7400 = k
Explanation: To convert this simple fraction to a decimal just divide the numerator (74) by the denominator (7400). When we divide by 100, the decimal point moves two places to the left.
74 ÷ 7400 = 0.01
k = 0.01.
Question 8.
k ÷ 0.1 = 8.1
Answer:
k = 8.1 x 0.1
k = 0.81.
Question 9.
0.35 ÷ k = 0.035
Answer:
0.35 ÷ 0.035 = k
Explanation: To convert this simple fraction to a decimal just divide the numerator (0.35) by the denominator (0.035). When we divide by 0.01, the decimal point moves two places to the right.
0.35 ÷ 0.035 = 10
k = 10.
7.2 Estimate Decimal Quotients
Estimate the quotient.
Question 10.
9.6 ÷ 2
Answer:
9.6 is closer to 10.
10 ÷ 2 = 5
9.6 ÷ 2 is about 5.
Question 11.
37.2 ÷ 6.4
Answer:
Round the divisor 6.4 to 6.
Think: What numbers close to 37.2 are easily divided by 6?
Use 36.
36 ÷ 6 = 6
So, 37.2 ÷ 6.4 is about 6.
Question 12.
44.8 ÷ 4.7
Answer:
Round the divisor 4.7 to 5.
Think: What numbers close to 44.8 are easily divided by 5?
Use 45.
45 ÷ 5 = 9
So, 44.8 ÷ 4.7 is about 9.
Question 13.
78.2 ÷ 10.8
Answer:
Round the divisor 10.8 to 11.
Think: What numbers close to 78.2 are easily divided by 11?
Use 77.
77 ÷ 11 = 7
So, 78.2 ÷ 10.8 is about 7.
7.3 Use Models to Divide Decimals by Whole Numbers
Use the model to find the quotient.
Question 14.
1.4 ÷ 2
Answer:
Think: 1.4 is 1 ones and 4 tenths.
14 tenths can be divided equally as 2 groups of 7 tenths.
1.4 ÷ 2 = 0.7
Question 15.
2.85 ÷ 3
Answer:
Think: 2.85 is 2 ones, 8 tenths and 5 hundredths.
28 tenths can be divided equally as 3 groups of 9 tenths with remainder 1. Remainder has to place before 5 hundredths.
15 hundredths can be divided equally as 3 groups of 5 hundredths.
So, 285 hundredths can be divided equally as 3 groups of 95 hundredths.
2.85 ÷ 3 = 0.95
Use a model to find the quotient.
Question 16.
1.28 ÷ 4
Answer:
Think: 1.28 is 1 ones, 2 tenths and 8 hundredths.
12 tenths can be divided equally as 4 groups of 3 tenths
8 hundredths can be divided equally as 4 groups of 2 hundredths.
So, 128 hundredths can be divided equally as 4 groups of 32 hundredths.
1.28 ÷ 4 = 0.32
Question 17.
3.5 ÷ 5
Answer:
Think: 3.5 is 3 ones and 5 tenths.
35 tenths can be divided equally as 5 groups of 7 tenths.
3.5 ÷ 5 = 0.7
7.4 Divide Decimals by One-Digit Numbers
Find the quotient. Then check your answer.
Question 18.
\(\sqrt [ 3 ]{ 14.1 } \)
Answer:
Divide the ones
14 ÷ 3
4 ones x 3 = 12
14 ones – 12 ones
There are 2 ones left over.
Divide the tenths
21 ÷ 3 = 7 tenths.
So, 14.1 ÷ 3 = 4.7
Question 19.
\(\sqrt [ 6 ]{ 67.68 } \)
Answer:
Divide the ones
67 ÷ 6
11 ones x 6 = 66
67 ones – 66 ones
There are 1 ones left over.
Divide the tenths
16 ÷ 6
2 tenths x 6 = 12
16 – 12 = 4
There are 4 tenths left over.
Divide the hundredths
48 ÷ 6 = 8 hundredths.
So, 67.68 ÷ 6 = 11.28
Question 20.
\(\sqrt [ 8 ]{ 105.6 } \)
Answer:
Divide the ones
105 ÷ 8
13 ones x 8 = 104
105 ones – 104 ones
There are 1 ones left over.
Divide the tenths
16 ÷ 8 = 2 tenths.
So, 105.6 ÷ 8 = 13.2
Question 21.
Number Sense
Evaluate (84.7 + 79.8) ÷ 7.
Answer:
(84.7 + 79.8) ÷ 7 = 164.5 ÷ 7
Divide the ones
164 ÷ 7
23 ones x 7 = 161
164 ones – 161 ones
There are 3 ones left over.
Divide the tenths
35 ÷ 7
5 tenths x 7
35 – 35 = 0
There are 0 tenths left over.
So, 164.5 ÷ 7 = 23.5
7.5 Divide Decimals by Two-Digit Numbers
Find the quotient. Then check your answer.
Question 22.
\(\sqrt [ 32 ]{ 45.12 } \)
Answer:
Divide the ones
45 ÷ 32
1 ones x 32 = 32
45 ones – 32 ones
There are 13 ones left over.
Divide the tenths
131 ÷ 32
4 tenths x 32 = 128
131 – 128 = 3
There are 3 tenths left over.
Divide the hundredths
32 ÷ 32 = 1 hundredths.
So, 45.12 ÷ 32 = 1.41
Question 23.
\(\sqrt [ 15 ]{ 9.15 } \)
Answer:
Divide the tenths
91 ÷ 15
6 tenths x 15 = 90
91 – 90 = 1
There are 1 tenths left over.
Divide the hundredths
15 ÷ 15 = 1 hundredths.
So, 9.15 ÷ 15 = 0.61
Question 24.
\(\sqrt [ 73 ]{ 102.2 } \)
Answer:
Divide the ones
102 ÷ 73
1 ones x 73 = 73
102 ones – 73 ones
There are 29 ones left over.
Divide the tenths
292 ÷ 73 = 4 tenths.
So, 102.2 ÷ 73 = 1.4
Question 25.
17.4 ÷ 87 = ______
Answer:
Divide the tenths
174 ÷ 87
2 tenths x 87
174 – 174 = 0
There are 0 tenths left over.
17.4 ÷ 87 = 0.2
Question 26.
245.82 ÷ 51 = _______
Answer:
Divide the ones
245 ÷ 51
4 ones x 51 = 204
245 ones – 204 ones
There are 41 ones left over.
Divide the tenths
418 ÷ 51
8 tenths x 51
418 – 408 = 10
There are 10 tenths left over.
Divide the hundredths
102 ÷ 51 = 2 hundredths
So, 245.82 ÷ 51 = 4.82
Question 27.
5.88 ÷ 42 = ______
Answer:
Divide the tenths
58 ÷ 42
1 tenths x 42 = 42
58 tenths – 42 tenths
There are 16 tenths left over.
Divide the hundredths
168 ÷ 42
4 hundredths x 42
168 – 168 = 0
There are 0 hundredths left over.
So, 5.88 ÷ 42 = 0.14
7.6 Use Models to Divide Decimals
Use the model to find the quotient.
Question 28.
0.9 ÷ 0.45 = ______

Answer:
Shade 9 columns to represent 0.9.
Divide the model to show groups of 0.45.
There are 2 groups of 45 hundredths.
So, 0.9 ÷ 0.45 = 2
Question 29.
0.1 ÷ 0.05 = ______

Answer:
Shade 1 column to represent 0.1.
Divide the model to show groups of 0.05.
There are 2 groups of 5 hundredths.
So, 0.1 ÷ 0.05 = 2
Question 30.
1.6 ÷ 0.4 = ______
Answer:
Shade 16 columns to represent 1.6.
Divide the model to show groups of 0.4.
There are 4 groups of 4 tenths.
So, 1.6 ÷ 0.4 = 4
Question 31.
1.9 ÷ 0.38 = ______
Answer:
Shade 19 columns to represent 1.9.
Divide the model to show groups of 0.38.
There are 5 groups of 38 hundredths.
So, 1.9 ÷ 0.38 = 5
7.7 Divide Decimals
Find the quotient. Then check your answer.
Question 32.
\(\sqrt [ 2.57 ]{ 20.56 } \)
Answer:
Multiply 2.57 by a power of 10 to make it a whole number. Then multiply 20.56 by the same power of 10.
2.57 x 100 = 257
20.56 x 100 = 2056
2056 ÷ 257 = 8
So, 20.56 ÷ 2.57 = 8.
Question 33.
\(\sqrt [ 4.7 ]{ 16.92 } \)
Answer:
Multiply 4.7 by a power of 10 to make it a whole number. Then multiply 16.92 by the same power of 10.
4.7 x 10 = 47
16.92 x 10 = 169.2
Step 2 : Divide 169.2 ÷ 47
169 ÷ 47 = 3 with remainder 28.
282 ÷ 47 = 6 with remainder 0.
So, 16.92 ÷ 4.7 = 3.6.
Question 34.
\(\sqrt [ 5.3 ]{ 63.6 } \)
Answer:
Multiply 5.3 by a power of 10 to make it a whole number. Then multiply 63.6 by the same power of 10.
5.3 x 10 = 53
63.6 x 10 = 636
636 ÷ 53 = 12
So, 63.6 ÷ 5.3 = 12.
7.8 Insert Zeros in the Dividend
Question 35.
\(\sqrt [ 4 ]{ 36.2 } \)
Answer:
36.2 ÷ 4
36 ÷ 4 = 9
Insert a zero in the dividend and continue to divide.
20 ÷ 4 = 5
So, 36.2 ÷ 4 = 9.05.
Question 36.
\(\sqrt [ 4.8 ]{ 85.2 } \)
Answer:
Multiply 4.8 by a power of 10 to make it a whole number. Then multiply 85.2 by the same power of 10.
4.8 x 10 = 48
85.2 x 10 = 852
852 ÷ 48
85 ÷ 48 = 1 with remainder 37.
372 ÷ 48 = 7 with remainder 36.
Insert a zero in the dividend and continue to divide.
360 ÷ 48 = 7 with remainder 24.
240 ÷ 48 = 5 with remainder 0.
So, 85.2 ÷ 4.8 = 17.75.
Question 37.
\(\sqrt [ 12 ]{ 52.2 } \)
Answer:
52.2 ÷ 12
52 ÷ 12 = 4 with remainder 4.
42 ÷ 12 = 3 with remainder 6.
Insert a zero in the dividend and continue to divide.
60 ÷ 12 = 5 with remainder 0.
So, 52.2 ÷ 12 = 4.35.
Question 38.
5 ÷ 0.8 = ______
Answer:
Multiply 0.8 by a power of 10 to make it a whole number. Then multiply 5 by the same power of 10.
0.8 x 10 = 8
5 x 10 = 50
50 ÷ 8
Insert a zero in the dividend and continue to divide.
8 ) 50 ( 6.25
48
——-
20
-16
——-
40
40
——–
0
So, 5 ÷ 0.8 = 6.25
Question 39.
23.7 ÷ 6 = ______
Answer:
Insert a zero in the dividend and continue to divide.
6 ) 23.7 ( 3.95
18
——-
57
– 54
——-
30
30
——–
0
23.7 ÷ 6 = 3.95
Question 40.
138.4 ÷ 16 = ______
Answer:
Insert a zero in the dividend and continue to divide.
16 ) 138.4 ( 8.65
128
——-
104
– 96
——–
80
80
7.9 Problem Solving: Decimal Operations
Question 41.
You spend $28.08 on the fabric scissors, buttons, and two craft kits. The kits each cost the same amount. How much does ASSORTED $6.13 each kit cost?

Answer:
Given that,
Total amount spent = $28.08
Fabric scissors cost = $6.13
Buttons cost = $3.97
Write and solve an equation to find the cost of each kit.
cost of each kit = (amount spend – fabric scissors cost – buttons cost) ÷ 2
= (28.08 – 6.13 – 3.97) ÷ 2
= 17.98 ÷ 2
= 8.99
So, cost of each craft kit = $8.99
Divide Decimals Cumulative Practice
Question 1.
Which statement is true?

Answer:
According to BODMAS rule,
Statement c is correct.
Question 2.
You round 23 × 84 and get an underestimate. How did you estimate?
A. 20 × 80
B. 30 × 90
C. 25 × 90
D. 25 × 90
Answer:
23 × 84 round to 20 × 80 because it is closer to given equation.
84 is close to 80 and all the others options having number 90.
Difference between the numbers in remaining options is greater than the option A numbers.
Question 3.
Which expressions have a product that is shown?
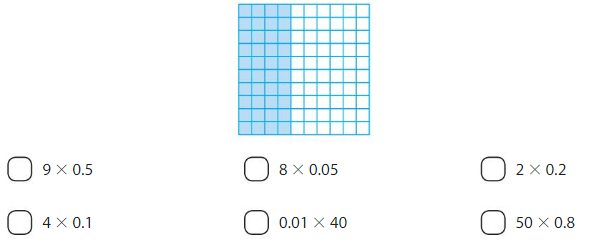
Answer:
Except option 1, remaining all the other options have the product(0.4) shown in the image.
Question 4.
What number is \(\frac{1}{10}\) of 800?
A. 0.8
B. 8
C. 80
D. 8,000
Answer:
(800) = 80
Question 5.
Which number divided by 0.01 is 14 more than 37?
A. 0.51
B. 5.1
C. 51
D. 5,100
Answer:
14 more than 37 = 37 + 14 = 51
51 x 0.01 = 0.51
So, the answer is 0.51.
Question 6.
Which expressions have a quotient of 40?
Answer:
2800 ÷ 70, 160 ÷ 4, 3600 ÷ 900 and 8000 ÷ 200 have a quotient of 40.
Question 7.
Which equation is shown by the quick sketch?
Answer:
Question 8.
What is the value of k?
0.036 × k = 36
A. 10
B. 103
C. 100
D. 36
Answer:
k = 36 ÷ 0.036
k = 1000 = 103(option B).
Question 9.
What is the quotient of 11.76 and 8?
A. 1.47
B. 1.97
C. 14.7
D. 94.08
Answer:
11.76 ÷ 8
11 ÷ 8 = 1 with remainder 3.
37 ÷ 8 = 4 with remainder 5.
56 ÷ 8 = 7 with remainder 0.
So, quotient of 11.76 and 8 = 1.47(option A).
Question 10.
Newton wins a race by seven thousandths of a second. What is this number in standard form?
A. 0.007
B. 0.07
C. 0.7
D. 7,00
Answer:
0.007 is in standard form.
Question 11.
Evaluate 30 – (9 + 6) ÷ 3.
A. 5
B. 19
C. 9
D. 25
Answer:
According to BODMAS rule.
30 – (9 + 6) ÷ 3
= 30 – (15 ÷ 3)
= 30 – 5
= 25
Question 12.
A food truck owner sells 237 gyros in 1 day. Each gyro costs $7.How much money does the owner collect in 1 day?

A. $659
B. $1,419
C. $1,659
D. $11,249
Answer:
Each gyro costs $7
237 gyros in 1 day cost = 237 x 7 = $1659
So, the owner collects $1659 in 1 day.
Question 13.
What is the quotient of 4,521 and 3?

Answer:
4521 ÷ 3 = 1507
So, quotient of 4,521 and 3 is 1507.
Question 14.
What is the value of b?
104 = 10b × 10
A. 3
B. 4
C. 5
D. 10
Answer:
104 = 10b × 10
If b= 3,
10b × 10 = 103 × 10
= 103+1
= 104
So, b= 3.
Question 15.
Part A What is the area of the sandbox?

Part B The playground committee wants to make the area of the sandbox 2 times the original area. What is the new area? Explain.
Answer:
Question 16.
Which expressions have a product of 1,200?
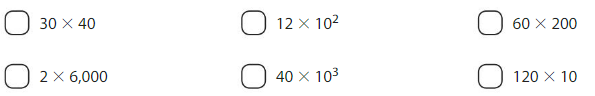
Answer:
30 x 40, 12 x 102 and 120 x 10 have a product of 1,200.
Question 17.
A 5-day pass to a theme park costs $72.50. A 2-day pass to the same park costs $99.50. How much more does the 2-day pass cost each day than the 5-day pass each day?
A. $14.50
B. $35.25
C. $49.75
D. $64.25
Answer:
5-day pass costs each day = 72.5 ÷ 5 = $14.5
2-day pass costs each day = 99.5 ÷ 2 = $49.75
2-day pass cost each day $35.25 more than the 5-day pass each day.
Question 18.
Which expressions have a quotient with the first digit in the tens place?

Answer:
4,536 ÷ 56 = 81
6,750 ÷ 45 = 150
2,403 ÷ 89 = 27
1,496 ÷ 17 = 88
Except option 2, all the other options have a quotient with the first digit in the tens place.
Divide Decimals STEAM Performance Task
You experiment with levers for your school’s science fair.

Question 1.
You balance the seesaw lever by placing different weights on either side at different distances from the middle. You find the formula for balancing the seesaw lever is (left weight) × (left distance) = (right weight) × (right distance). You test the formula using various combinations of weights.
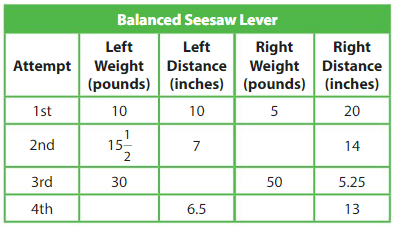
a. Use the formula to complete the table for the 2nd and 3rd attempts.
b. For your 4th attempt, you have up to 25 pounds in weights to place on each side of the lever. Choose a whole pound weight for the left side and balance the lever to complete the table.
c. The total length of your seesaw lever is 40 inches. Can you balance a 50-pound weight with a 1-pound weight? Explain.
d. For your science fair display, you balance the lever by placing another gram weight on the right side. Which gram weight should you use?
e. How can you apply what you learn from the science fair project to a playground?
Answer:
You help set up tables for the science fair. There are 93 science fair displays. You use the display boards to determine how many tables to use.
Question 2.
Each display board opens up to form three sides of a trapezoid as shown.
a. How much room do you think each display board needs to open up? Explain.
b. You place the display boards next to each other on 12-foot long tables. How many display boards can you fit on one table?
c. You use one table for snacks and one table for award ribbons. What is the least number of tables you can use? Explain.
d. The diagram shows the room where the science fair is held. Each table for the science fair is 3 feet wide. Your teacher says the ends of the tables can touch to save space. Complete the diagram to arrange the tables so that visitors and judges can see each display board.
Answer:
Question 3.
Use the Internet or some other resource to learn about other types of science fair projects. Describe one interesting science fair project you want to complete.

Answer: One of the interesting science fair project is :-
How To Make A Bottle Rocket
-> Did you know you can make and launch a water bottle rocket using a plastic bottle, water, cork, needle adaptor and pump ?
How do water bottle rockets work?
As you pump air into the bottle the pressure inside the bottle builds up until the force of the air pushing on the water is enough to force the cork out of the end of the bottle. The water rushes out of the bottle in one direction whilst the bottle pushes back in the other. This results in the bottle shooting upwards.
What you need to make a bottle rocket
-> An empty plastic bottle
-> Cardboard made into a cone and 4 fins
-> A cork
-> A pump with a needle adaptor
-> Water
You can buy a kit with the parts apart from the pump and the bottle-please check the contents before buying.
Instructions – How to make a bottle rocket
Push the needle adaptor of the pump through the cork, it needs to go all the way through so you might have to trim the cork a little bit.
-> Decorate the bottle with the cone and fins.
-> Fill the bottle one quarter full of water and push the cork in tightly.
-> Take the bottle outside and connect the pump to the needle adaptor. Ours wouldn’t stand up on the fins so we rested it on a box, but if you make some strong fins it should stand up by itself.
-> Pump air into the bottle, making sure all spectators stand back, the bottle will lift off with force after a few seconds.
Why does the water bottle rocket launch?
As you pump air into the bottle pressure builds up inside. If you keep pumping, the force of the air pushing on the water eventually becomes strong enough to force the cork out of the bottle allowing water to rush out in one direction while the bottle pushes back in the other direction. This forces the rocket upwards.
Space
Conclusion:
I wish the information provided in the above article regarding Big Ideas Math Book 5th Grade Answer Key Chapter 7 Divide Decimals is helpful for you. For any queries, you can post the comments in the below section.
