Big Ideas Math Answers Grade 8 Chapter 5 include questions on System of Linear Equations by Graphing, Substitution, Elimination, Connecting Concepts, etc. All the Problems in the Big Ideas Grade 8 Ch 5 System of Linear Equations are provided in a simple and easy-to-understand language. Learn the problem-solving methods used by referring to our Big Ideas Math Grade 8 Answers Chapter 5 System of Linear Equations and apply them to similar kinds of problems. Download the BIM Chapter 5 System of Linear Equations Answer Key and understand the related concepts in no time.
Big Ideas Math Book 8th Grade Answer Key Chapter 5 Systems of Linear Equations
Big Ideas Math Answers Grade 8 Ch 5 is curated by subject experts adhering to the latest syllabus guidelines. Practice as many times as possible and attempt the exams with utmost confidence and score well. Enhance your subject knowledge and gain a deeper understanding of concepts at the surface level. Simply click on the direct links available and begin preparing the respective topics in no time.
Performance
- Systems of Linear Equations STEAM Video/Performance
- Systems of Linear Equations Getting Ready for Chapter 5
Lesson: 1 Solving Systems of Linear Equations by Graphing
- Lesson 5.1 Solving Systems of Linear Equations by Graphing
- Solving Systems of Linear Equations by Graphing Homework & Practice 5.1
Lesson: 2 Solving Systems of Linear Equations by Substitution
- Lesson 5.2 Solving Systems of Linear Equations by Substitution
- Solving Systems of Linear Equations by Substitution Homework & Practice 5.2
Lesson: 3 Solving Systems of Linear Equations by Elimination
- Lesson 5.3 Solving Systems of Linear Equations by Elimination
- Solving Systems of Linear Equations by Elimination Homework & Practice 5.3
Lesson: 4 Solving Special Systems of Linear Equations
- Lesson 5.4 Solving Special Systems of Linear Equations
- Solving Special Systems of Linear Equations Homework & Practice 5.4
Chapter: 5 – Systems of Linear Equations
- Systems of Linear Equations Connecting Concepts
- Systems of Linear Equations Chapter Review
- Systems of Linear Equations Practice Test
- Systems of Linear Equations Cumulative Practice
Systems of Linear Equations STEAM Video/Performance
STEAM Video
Gold Alloys
An alloy is a mixture of different metals melted together at high temperatures. A dental filling is created using a gold alloy. What are other uses of alloys?
Watch the STEAM Video “Gold Alloys.” Then answer the following questions.
Question 1.
Enid says that the proportion of gold in an alloy can be measured in karats. For example, 24 karats represent 100% gold and 18 karats represent 75% gold.
a. A dental filling is 9 karats. What percent of the filling is gold?
b. A watch is 60% gold. How many karats is the watch?
Answer:
a. 37.5% of the filling is gold.
b. 14.4 karats are the watch
Explanation:
a. A dental filling is 9 karats.
24 karats represent 100% gold
So, 9 karats = (100 * 9)/24
= 900/24
= 37.5%
37.5% of the filling is gold.
b. A watch is 60% gold
24 karats represent 100% gold
So, watch = (60 * 24)/100
= 1440/100
= 14.4
14.4 karats are the watch
Question 2.
What percent gold is each described alloy?
a. A mixture of 2 grams 10-karat gold and 2 grams 14-karat gold
b. A mixture of 6 grams 24-karat gold and 4 grams 9-karat gold
Answer:
a. 200%
b. 750%
Explanation:
a. 24 karats represents 100% gold
10 karat gold is 125/3 %
14 -karat gold gold is 175/3 %
2 grams 10-karat gold = 2(125/3) = 250/3
2 grams 14-karat gold = 2(175/3) = 350/3
The alloy mixture = (250 + 350)/3
= 600/3 = 200
b. 6 grams 24-karat gold
6 grams = 600%
9-karat gold = 75/2
4 grams 9-karat gold = 4(75)/2 = 150%
The alloy mixture = 600% + 150% = 750%
Performance Task
Mixing Alloys
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given a list of gold alloys available at a jewelry store.
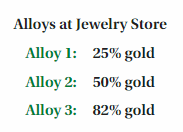

You will use a system of equations to determine the amounts of the given alloys that a jeweler needs to create a new alloy. Why might a jeweler need to create a mixture with a specific proportion of gold?
Systems of Linear Equations Getting Ready for Chapter 5
Getting Ready for Chapter 5
Chapter Exploration
Question 1.
Work with a partner. Your family starts a bed-and-breakfast. You spend $500 fixing up a bedroom to rent. The cost for food and utilities is $10 per night. Your family charges $60 per night to rent the bedroom.
a. Write an equation that represents the costs.

b. Write an equation that represents the revenue (income).

c. A set of two (or more) linear equations is called a system of linear equations. Write the system of linear equations for this problem.
Answer:
a. C = 10x + 500
b. R = 60x
c. The system of linear equations are
C = 10x + 500
R = 60x
Explanation:
a. Cost, C = $10 per night . Number of nights, x + $500
C = 10x + 500
b.
Revenue, R = $60 per night . Number of nights x
R = 60x
c. The system of linear equations are
C = 10x + 500
R = 60x
Question 2.
Work with a partner. Use a graphing calculator to solve the system.
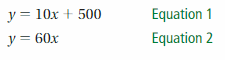
a. Enter the equations into your calculator. Then graph the equations. What is an appropriate window?
b. On your graph, how can you determine which line is the graph of which equation? Label the equations on the graph shown.
c. Visually estimate the point of intersection of the graphs.
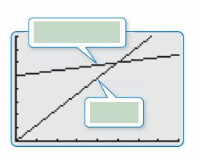
d. To find the solution, use the intersect feature to find the point of intersection. The solution is ![]()
Answer:
The solution is (10, 600)
Explanation:
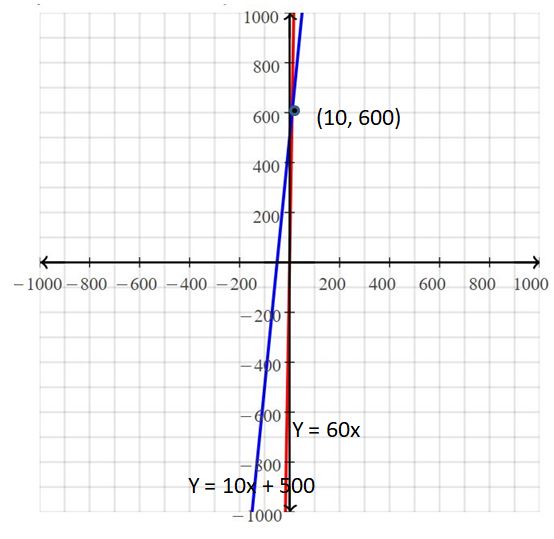
The solution is (10, 600)
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
![]()
Lesson 5.1 Solving Systems of Linear Equations by Graphing
EXPLORATION 1
Work with a partner. You charge your headphones and your phone. The equations below represent the battery powers p% of the devices after x minutes of charging.

a. You check the battery power of each device every 10 minutes. Copy and complete the table. How do the devices’ battery powers compare?
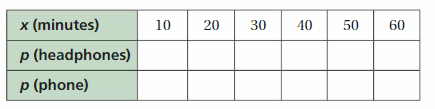
b. After how much time do the devices have the same battery power? What is the battery power at that time? Justify your answer.

c. The solutions of a linear equation are all the points on its graph. How many solutions can two linear equations share? Explain your reasoning.
d. Graph the battery power equations in the same coordinate plane. What do you notice?
e. Use a graphing calculator to check your answers in part(b). Explain your method.

Answer:
a. 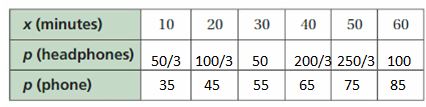
d. The solution is (75/2, 125/2)
Explanation:
a. Headphones equation is p = 5/3 x
p1 = 5/3 (10) = 50/3, p2 = 5/3 (20) = 100/3, p3 = 5/3 (30) = 50, p4 = 5/3 (40) = 200/3, p5 = 5/3 (50) = 250/3
p6 = 5/3 (60) = 100
Phone equation is p = x + 25
p1 = 10 + 25 = 35, p2 = 20 + 25 = 45, p3 = 30 + 25 = 55, p4 = 40 + 25 = 65
p5 = 50 + 25 = 75, p6 = 60 + 25 = 85
b. 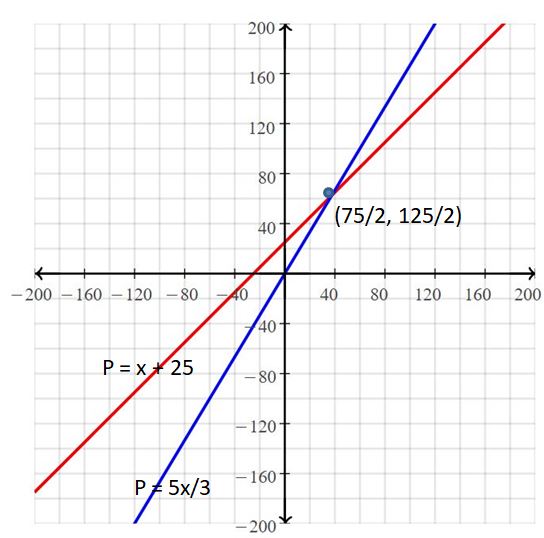
The solution is (75/2, 125/2)
p = 5/3 x, p = x + 25
Put x = 75/2
p = 5/3 (75/2)
= 125/2
p = 75/2 + 25
= 125/2
5.1 Lesson
Try It
Solve the system by graphing.
Question 1.
y = x – 1
y = -x + 3
Answer:
The solution is (1, 2).
Explanation:
The given systems of linear equations are y = x – 1, y = -x + 3
Graph the equations
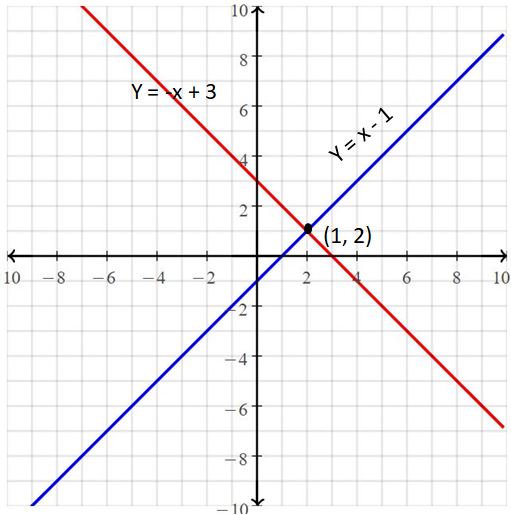
The graphs appear to intersect at (1, 2)
So, the solution is (1, 2)
Question 2.
y = -5x + 14
y = x – 10
Answer:
The solution is (4, -6)
Explanation:
The given systems of linear equations are y = -5x + 14, y = x – 10
Graph the equations
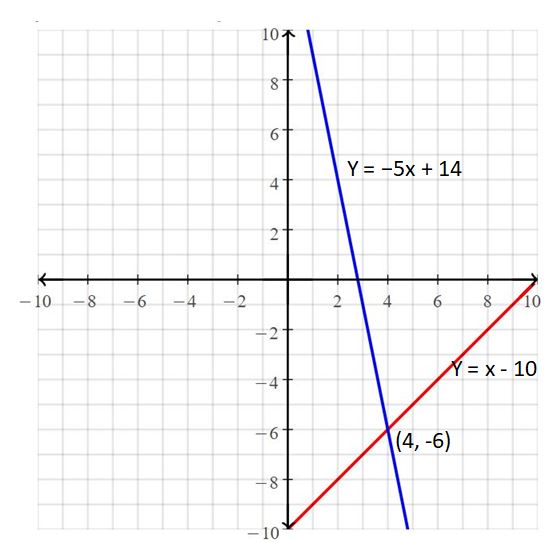
The lines intersect at (4, -6)
So, the solution is (4, -6)
Question 3.
y = x
y = 2x + 1
Answer:
The solution is (-1, -1)
Explanation:
The given systems of linear equations are y = x, y = 2x + 1
Graph the equations
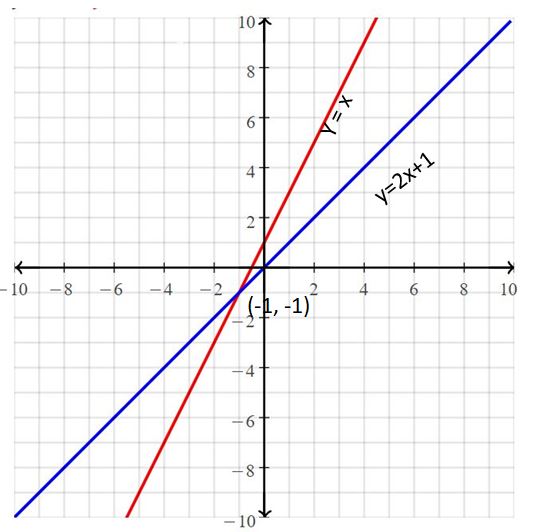
The lines intersect at (-1, -1)
So, the solution is (-1, -1)
Question 4.
y = -4x – 7
x + y = 2
Answer:
The solution is (-3, 5)
Explanation:
The given systems of linear equations are y = -4x – 7, x + y = 2
Graph the equations
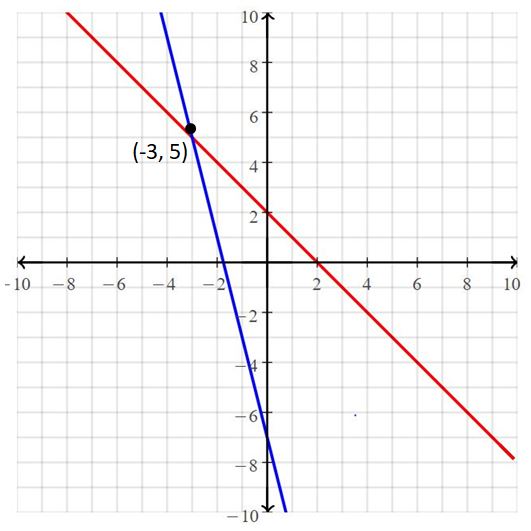
The lines intersect at (-3, 5)
So, the solution is (-3, 5)
Question 5.
x – y = 5
-3x + y = -1
Answer:
The solution is (-2, -7)
Explanation:
The given systems of linear equations are x – y = 5, -3x + y = -1
Graph the equations
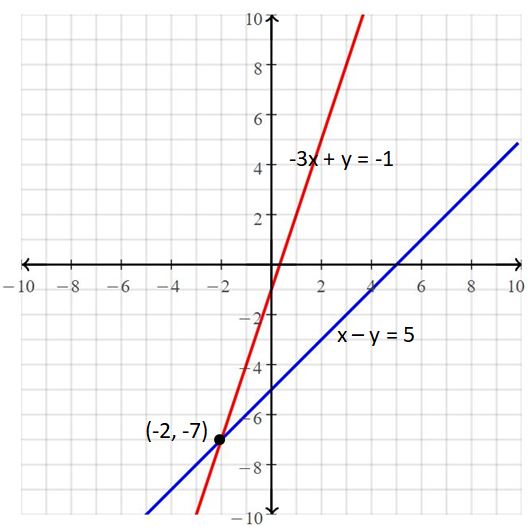
The lines intersect at (-2, -7)
So, the solution is (-2, -7)
Question 6.
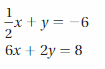
Answer:
The solution is (4, -8)
Explanation:
The given systems of linear equations are 1/2 x + y = -6, 6x + 2y = 8
Graph the equations
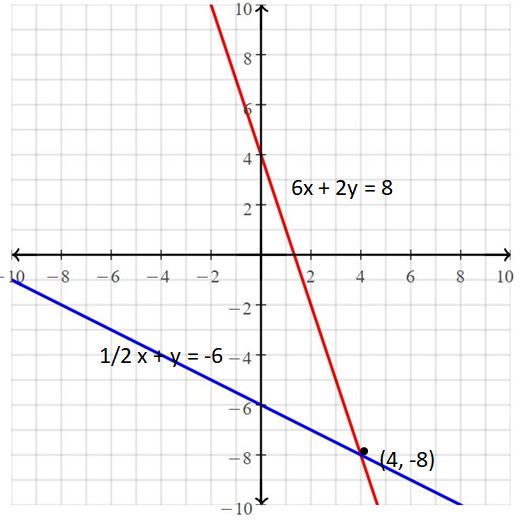
The lines intersect at (4, -8)
So, the solution is (4, -8)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by graphing.
Question 7.
y = x + 1
y = 4x +1
Answer:
The solution is (0, 1).
Explanation:
The given systems of linear equations are y = x + 1, y = 4x +1
Graph the equations
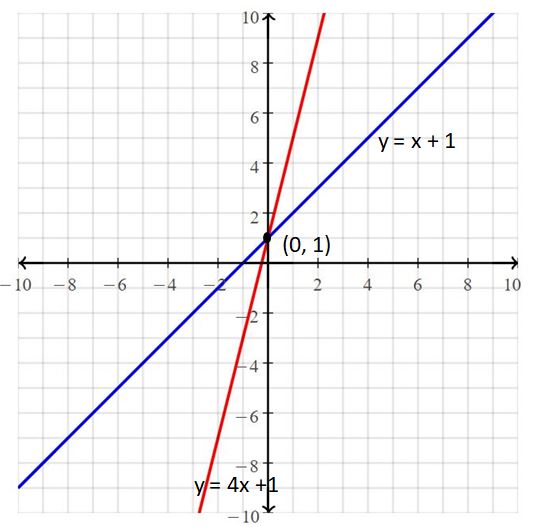
The lines intersect at (0, 1)
So, the solution is (0, 1)
Question 8.
3x – y = -1
y = -x + 5
Answer:
The solution is (1, 4).
Explanation:
The given systems of linear equations are 3x – y = -1, y = -x + 5
Graph the equations
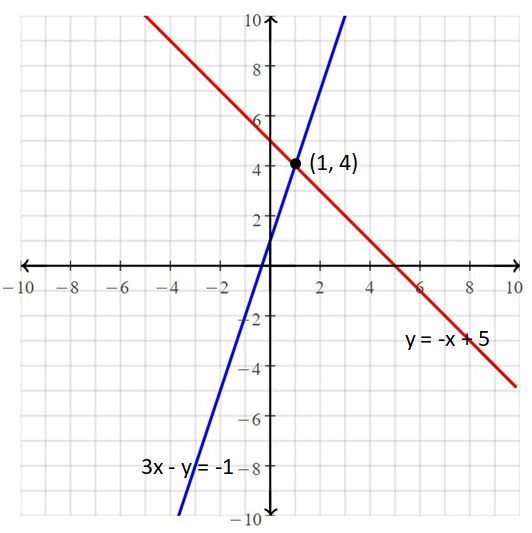
The lines intersect at (1, 4)
So, the solution is (1, 4).
Question 9.
x + 2y = 3
-x + 3y = 7
Answer:
The solution is (-1, 2).
Explanation:
The given systems of linear equations are x + 2y = 3, -x + 3y = 7
Graph the equations
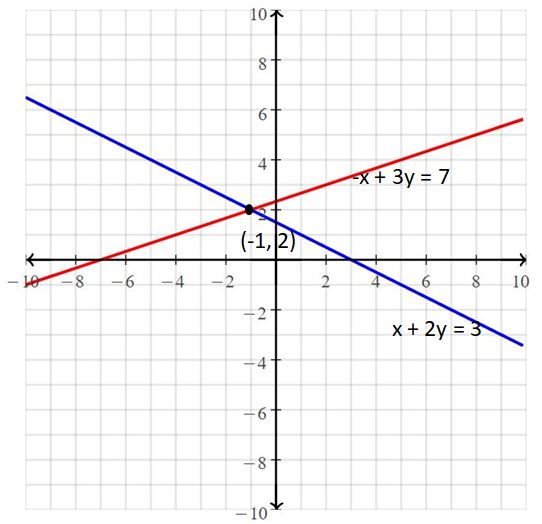
The lines intersect at (-1, 2)
So, the solution is (-1, 2).
Question 10.
WRITING
Explain why the solution of a system of linear equations is the point of intersection of their graphs.
Answer:
The solution of a system of linear equations in two variables is an ordered pair that is a solution of each equation in the system. The ordered pair is obtained by drawing a graph for two equations and the point of intersection.
Question 11.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
The solution of the system is (1, 6)
The graphs of the equations intersect at (1, 6)
Ordered pair (1, 6) makes both equations true
Explanation:
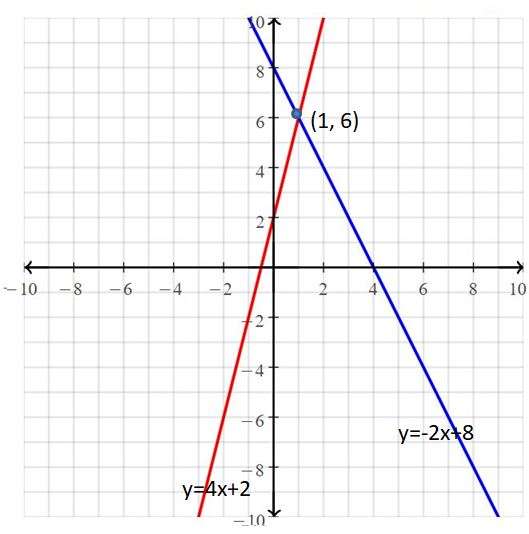
The point of intersection is the solution.
The solution is (1, 6).
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
Your family attends a comic convention. Each autograph costs $20 and each photograph costs $50. Your family buys a total of 5 autographs and photographs for $160. How many photographs does your family buy?

Answer:
The number of photographs the family buys will be 2.
Explanation:
Each autograph costs $20 and photograph costs $50
According to the question, the family buys a total of 5 items including both autographs and photographs for $160.
Let’s assume the number of autographs bought be x, while the number of photographs is 5 – x
Thus, cost to buy autographs will be 20* x = 20x and photographs will be 50(5 – x) = 250 – 50x
now, total cost becomes 20x + 250 – 50x, which will be equal to 160. lets find number of each items x
20x + 250 – 50x = 160
-30x = 160 – 250
-30x = -90
x = 3
Hence, the cost of buying autographs will be $20 * 3 = $60 and the cost to buy photographs will be (250 – 50) * 3 = 250 – 150 = $100
The number of photographs the family buys will be 5 – 3 = 2
Question 13.
DIG DEEPER!
Two apps on your phone take away points for using your phone at school. You have 140 points on the first app and 80 points on the second app when a school day begins. Each time you check your phone, you lose 10 points on your first app and p points on your second app. After you check your phone ten times, you have the same number of points on each app. Find the value of p.
Answer:
p = 4
Explanation:
App one has 140 points and 80 points on the second app
As per the question, app one loses 10 points for each check while app second loses p points. We check the phone 10 times
So, total points lost by app 1 will be 10 * 10 = 100, and points lost by app 2 will be p * 10 = 10p
After 10 times both apps are left with the same points.
So let’s find the value of p
Thus, points left in the first app will be 140 – 100 = 40 while in the second app will be 80 – 10p
40 = 80 – 10p
10p = 80 – 40
10p = 40
p = 40/10
p = 4
Solving Systems of Linear Equations by Graphing Homework & Practice 5.1
Review & Refresh
Write an equation in point-slope form of the line that passes through the given point and has the given slope.
Question 1.
(3, -4); m = 1
Answer:
y = x – 7
Explanation:
Given that,
(3, -4); m = 1
x₁ = 3, y₁ = -4
Slope intercept form of a line is (y – y₁) = m(x – x₁)
Therefore, (y – (-4)) = 1(x – 3)
(y + 4) = (x – 3)
y = x – 3 – 4
y = x – 7
Question 2.
(5, 6); m = \(\frac{3}{5}\)
Answer:
5y = 3x + 15
Explanation:
Given that,
(5, 6); m = \(\frac{3}{5}\)
x₁ = 5, y₁ = 6
Slope intercept form of a line is (y – y₁) = m(x – x₁)
Therefore, (y – 6) = 3/5(x – 5)
5(y – 6) = 3(x – 5)
5y – 30 = 3x – 15
5y = 3x – 15 + 30
5y = 3x + 15
Question 3.
(1, 10); m = –\(\frac{1}{4}\)
Answer:
4y = 41 – x
Explanation:
Given that,
(1, 10); m = –\(\frac{1}{4}\)
x₁ = 1, y₁ = 10
Slope intercept form of a line is (y – y₁) = m(x – x₁)
Therefore, (y – 10) = -1/4(x – 1)
4(y – 10) = -1(x – 1)
4y – 40 = -x + 1
4y = -x + 1 + 40
4y = 41 – x
Solve the equation. Check your solution
Question 4.
![]()
Answer:
c = 8
Explanation:
Given equation is 3/4 c – 1/4 c + 3 = 7
2/4 c + 3 = 7
1/2 c = 7 – 3
1/2 c = 4
c = 4 * 2
c = 8
Substituting c = 8 in 3/4 c – 1/4 c + 3 = 7
3/4 (8) – 1/4 (8) + 3 = 6 – 2 + 3
= 9 – 2 = 7
Question 5.
5(2 – y) + y = -6
Answer:
y = 4
Explanation:
Given equation is 5(2 – y) + y = -6
10 – 5y + y = -6
10 – 4y = -6
10 + 6 = 4y
4y = 16
y = 16/4
y = 4
Substituting y = 4 in 5(2 – y) + y = -6
5(2 – 4) + 4 = 5(-2) + 4
= -10 + 4 = -6
Question 6.
6x – 3(x + 8) = 9
Answer:
x = 11
Explanation:
Given equation is 6x – 3(x + 8) = 9
6x – 3x – 24 = 9
3x – 24 = 9
3x = 9 + 24
3x = 33
x = 33/3
x = 11
Substituting x = 11 in 6x – 3(x + 8) = 9
6(11) – 3(11 + 8) = 66 – 3(19)
= 66 – 57 = 9
Concepts, Skills, &Problem Solving
USING A GRAPH TO SOLVE A PROBLEM
The equations below represent the numbers y of tickets sold after x weeks for two different local music festivals. (See Exploration 1, p. 199.)

Question 7.
You check the ticket sales for both festivals each week for 10 weeks. Create a table for the ticket sales each week. How do the festivals’ ticket sales compare?
Answer:
We can say that tickets for the country Music Festival sold more by mid the 4th week. After the mid of 4th-week tickets for the Pop Music Festival sold more than the country music festival.
Explanation:
Ticket sales for a country music festival and pop music festival are calculated in the tables below for 10 weeks

From the above tables, we can say that tickets for the country Music Festival sold more by mid of the 4th week. After the mid of 4th-week tickets for the Pop Music Festival sold more than the country music festival.
Question 8.
After how much time have the same number of tickets been sold for both festivals? What is the number of tickets sold at that time?
Answer:
The number of tickets sold for both festivals each is 185.
Explanation:
Country music festival y = 10x + 150
Pop musuic festival y = 20x + 115
As per the question, we will equate both the equation to get x value
10x + 150 = 20x + 115
10x – 20x = 115 – 150
-10x = -35
x = 35/10
x = 3.5
Thus, we get 3.5 weeks after which both festivals would sold equal number of tickets.
Let us find the number of tickets at that time
Put x = 3.5 in y = 10x + 150
y = 10(3.5) + 150
= 35 + 150 = 185
Hence, the number of tickets sold for both festivals each are 185.
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by graphing.
Question 9.
y = 2x + 9
y = 6 – x
Answer:
The solution is (-1, 7)
Explanation:
The given systems of linear equations are y = 2x + 9, y = 6 – x
Graph the equations
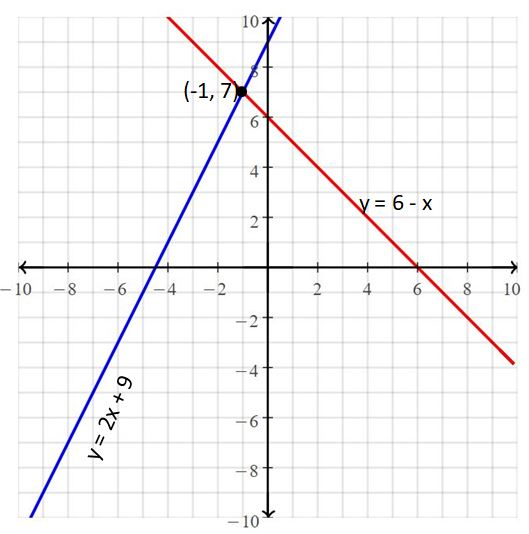
The lines intersect at (-1, 7)
So, the solution is (-1, 7)
Question 10.
y = -x – 4
y = \(\frac{3}{5}\)x + 4
Answer:
The solution is (-5, 1).
Explanation:
The given systems of linear equations are y = -x – 4, y = \(\frac{3}{5}\)x + 4
Graph the equations
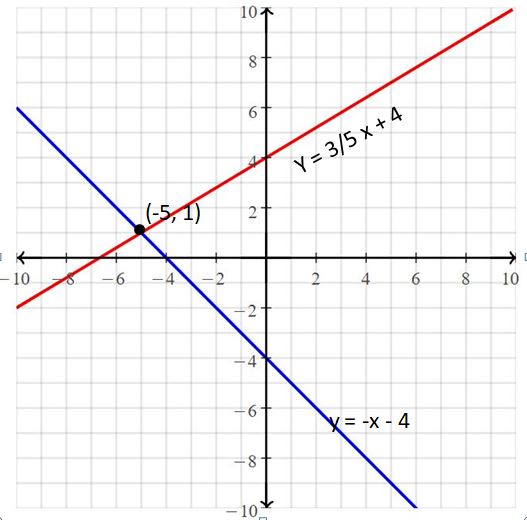
The lines intersect at
So, the solution is (-5, 1)
Question 11.
y = 2x + 5
y = \(\frac{1}{2}\)x – 1
Answer:
The solution is (-4, -3).
Explanation:
The given systems of linear equations are y = 2x + 5, y = \(\frac{1}{2}\)x – 1
Graph the equations
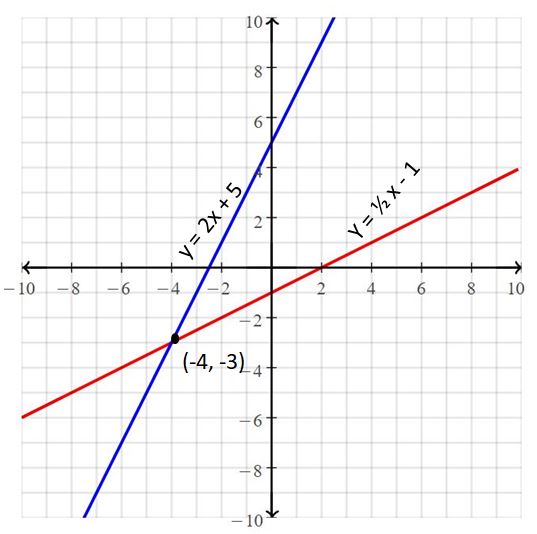
The lines intersect at (-4, -3)
So, the solution is (-4, -3).
Question 12.
x + y = 27
y = x + 3
Answer:
The solution is (12, 15).
Explanation:
The given systems of linear equations are x + y = 27, y = x + 3
Graph the equations
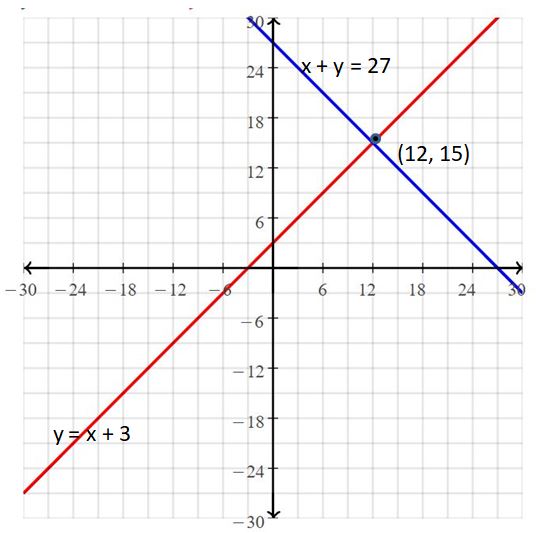
The lines intersect at (12, 15)
So, the solution is (12, 15).
Question 13.
y – x = 17
y = 4x + 2
Answer:
The solution is (5, 22)
Explanation:
The given systems of linear equations are y – x = 17, y = 4x + 2
Graph the equations
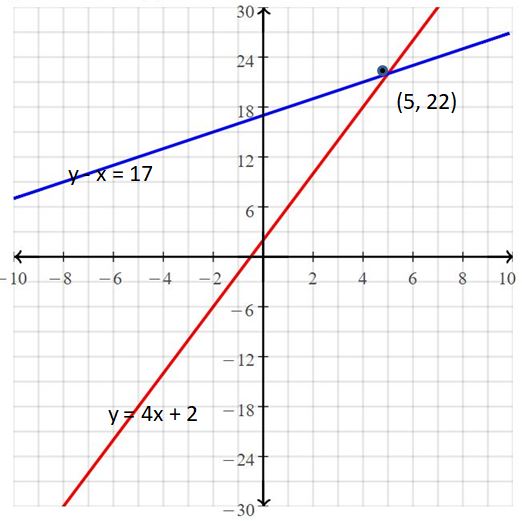
The lines intersect at (5, 22)
So, the solution is (5, 22)
Question 14.
x – y = 7
0.5x + y =5
Answer:
The solution is (8, 1).
Explanation:
The given systems of linear equations are x – y = 7, 0.5x + y =5
Graph the equations
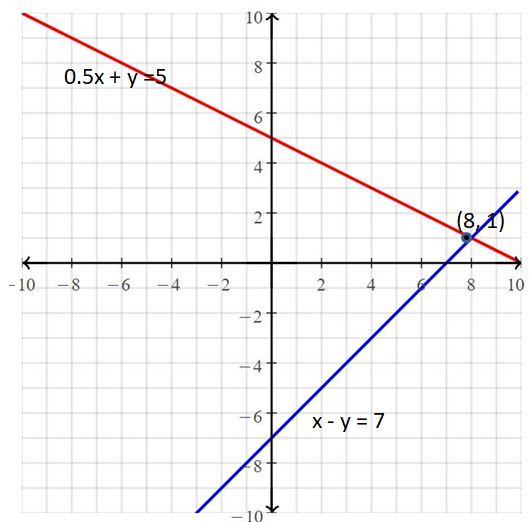
The lines intersect at (8, 1)
So, the solution is (8, 1)
USING A GRAPHING CALCULATOR
Use a graphing calculator to solve the system.
Question 15.
2.2x + y = 12.5
1.4x – 4y =1
Answer:
The solution is (5, 1.5).
Explanation:
The given systems of linear equations are 2.2x + y = 12.5, 1.4x – 4y = 1
Graph the equations
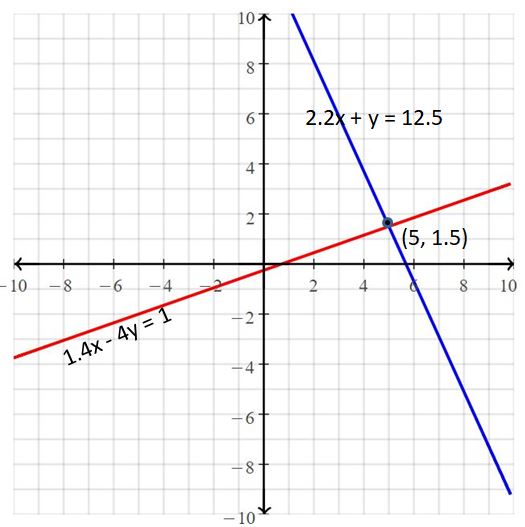
The lines intersect at (5, 1.5)
So, the solution is (5, 1.5)
Question 16.
2.1x + 4.2y = 14.7
-5.7x – 1.9y = -11.4
Answer:
The solution is (1, 3)
Explanation:
The given systems of linear equations are 2.1x + 4.2y = 14.7, -5.7x – 1.9y = -11.4
Graph the equations
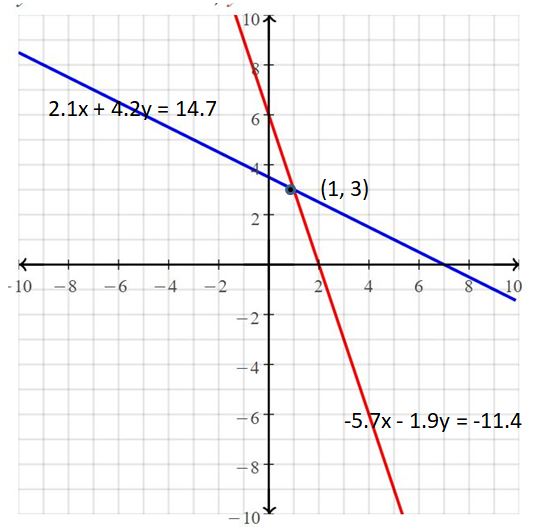
The lines intersect at (1, 3)
So, the solution is (1, 3)
Question 17.
-1.1x – 5.5y = -4.4
0.8x – 3.2y = -11.2
Answer:
The solution is (-6, 2)
Explanation:
The given systems of linear equations are -1.1x – 5.5y = -4.4, 0.8x – 3.2y = -11.2
Graph the equations
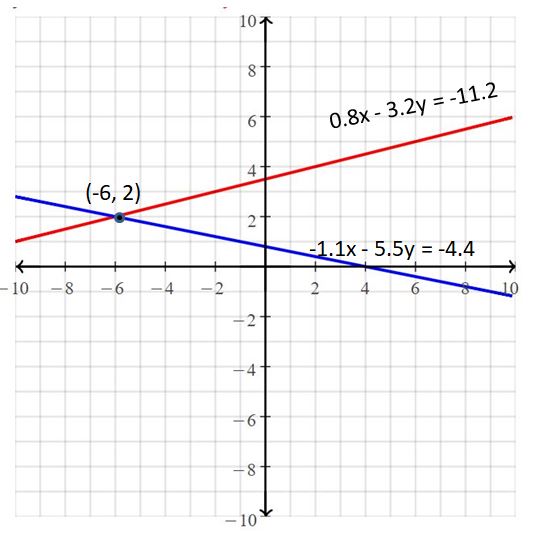
The lines intersect at (-6, 2)
So, the solution is (-6, 2)
Question 18.
YOU BE THE TEACHER
Your friend solves the system of linear equations below. Is your friend correct? Explain your reasoning.
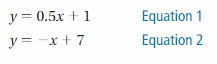
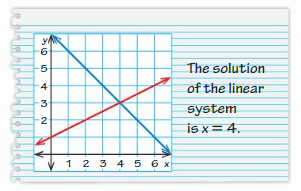
Answer:
Correct.
Explanation:
The given system of equations are y = 0.5x + 1, y = – + 7
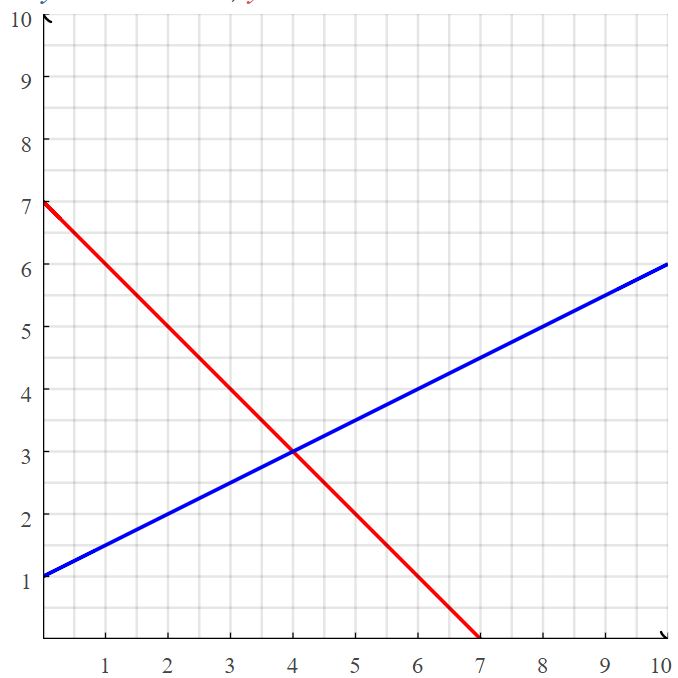
The point of intersection is (4, 3)
So, the solution is (4, 3)
Question 19.
MODELING REAL LIFE
You have a total of 42 math and science problems for homework. You have 10 more math problems than science problems. How many problems do you have in each subject? Use a system of linear equations to justify your answer.
Answer:
26 math and 16 science problems.
Explanation:
Write the system of equations where m and s are the number of math and science problems
m + s = 42 —- (1)
m = 10 + s —- (2)
Substitute equation (2) in equation (1)
10 + s + s = 42
10 + 2s = 42
2s = 42 – 10
2s = 32
s = 32/2
s = 16
Put s = 16 in equation (2)
m = 10 + 16
m = 26
So, 26 math and 16 science problems.
Question 20.
PROBLEM SOLVING
A generator contains 60 gallons of fuel and uses 2.5 gallons per hour. A more efficient power generator contains 40 gallons of fuel and uses 1.5 gallons per hour. After how many hours do the generators have the same amount of fuel? Which generator runs longer? Justify your answers.
Answer:
After 20 hours both generators will be having an equal amount of fuel. The generator has 40 gallons of fuel that will run for a longer time.
Explanation:
A generator contains 60 gallons of fuel and uses 2.5 gallons per hour. A more efficient power generator contains 40 gallons of fuel and uses 1.5 gallons per hour
Let’s assume that after x hours, both generate will have an equal amount of fuel
Thus, fuel consumed by the first generator will be 2.5x gallons and for the more efficient generator will be 1.5x gallons
Fuel left in the less efficient generator will be (60 – 2.5x) gallons. Fuel left in a more efficient generator will be (40 – 1.5x) gallons.
60 – 2.5x = 40 – 1.5x
-2.5x + 1.5x = 40 – 60
-x = -20
x = 20
Thus, fuel left in each generator will be 60 – 2.5 * 20 = 10 gallons
Now lets find which generator will run longer.
The number of hours less efficient generator would run is equal to 60/2.5 = 24 hours
The number of hours more efficient generator would run is equal to 40/1.5 = 26.66 hours
Hence, After 20 hours both generators will be having an equal amount of fuel.
The generator has 40 gallons of fuel that will run for a longer time.
Question 21.
PROBLEM SOLVING
You and your friend are in a canoe race. Your friend is a half-mile in front of you and paddling 3 miles per hour. You are paddling 3.4 miles per hour.
a. You are 8.5 miles from the finish line. How long will it take you to catch up with your friend? your friend
b. You both maintain your paddling rates for the remainder of the race. How far ahead of your friend will you be when you cross the finish line?
Answer:
a. It takes 1 hour 25 minutes for you to catch up to your friend.
b. You 0.5 miles ahead of your friend when you finish the race.
Explanation:
a. Let d be the distance traveled by your friend, h=then you have to travel d + 0.5 to catch up since you are currently 0.5 miles behind your friends.
distance = rate * time
you is d + 0.5 = 3.4t
a friend is d = 3t
Substitute the equation for your friend into the equation for y to solve d
3t + 0.5 = 3.4t
0.5 = 3.4t – 3t
0.4t = 0.5
t = 0.5/0.4
t = 1.25
b. Time it takes you to complete the race
8.5 = 3.4t
t = 8.5/3.4
t = 2.5
Distance traveled by a friend in that time 3(2.5) = 7.5
Your friend started 8 miles from the finishing line so you will be 8 – 7.5 = 0.5 miles ahead of your friend when you finish the race.
OPEN-ENDED
Write a system of linear equations that fits the description. Use a graph to justify your answer.
Question 22.
The solution of the system is a point on the line y = -9x + 1.
Answer:
The equations have infinitely many solutions.
Explanation:
The given equation is y = -9x + 1
Multiply both sides by 2
2y = 2(-9x + 1)
2y = -18x + 2
Draw a graph for the system of equations y = -9x + 1, 2y = -18x + 2
The equations have infinitely many solutions.
Question 23.
The solution of the system is (3, -1).
Answer:
m = -1/3
Explanation:
The slope intercept form is y = mx + c
-1 = 3m
m = -1/3
Question 24.
DIG DEEPER!
A graph of a system of two linear equations is shown. Write the system of linear equations represented by the graph. What is the solution to the system?
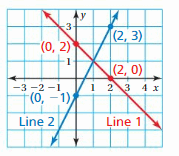
Answer:
The systems of linear equations are y = -x + 2, y = 2x – 1
The solution is (1, 1)
Explanation:
for line 1,
x₁ = 0, y₁ = 2, x₂ = 2, y₂ = 0
Slope m = (y₂ – y₁)/(x₂ – x₁)
= (0 – 2)/(2 – 0)
= -2/2 = -1
Slope intercept form of a line is y = mx + b
The line passes through (0, 2)
2 = 0(x) + b
b = 2
y = -1(x) + 2
y = -x + 2
For line 2
x₁ = 2, y₁ = 3, x₂ = 0, y₂ = -1
Slope m = (-1 – 3)/(0 – 2)
= -4/-2
= 2
y = 2x + b
The line passes through (0, -1)
-1 = 2(0) + b
n = -1
The slope intercept form of a line is y = 2x – 1
So, the systems of linear equations are y = -x + 2, y = 2x – 1
The point of intersection in the graph is (1, 1)
Question 25.
CRITICAL THINKING
Your friend is trying to grow her hair as long as her cousin’s hair. The table shows their hair lengths (in inches) in different months.
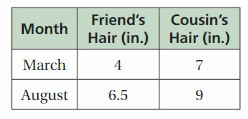
a. Write a system of linear equations that represents this situation. Let x = 1 represent January.
b. Will your friend’s hair ever be as long as her cousin’s hair? If so, in what month?
Answer:
a. The equation of the line for a friend’s hair is y = 1/2 x + 5/2, the equation of the line for a friend’s cousin hair is y =2/5x + 29/5
b. After 33 months length of hair of both girls would be the same.
Explanation:
a. The length of hair is represented by y coordinate and month is represented as x coordinate
The slope formula when we know two points is m = (y₂ – y₁)/(x₂ – x₁)
x₁ = 3, y₁ = 4, x₂ = 8, y₂ = 6.5
m = (6.5 – 4)/(8 -3)
= 2.5/5
m = 1/2
The slope form of a line is (y – y₁) = m(x – x₁)
y – 4 = 1/2 (x – 3)
2(y – 4) = (x – 3)
2y – 8 = x – 3
2y = x – 3 + 8
2y = x + 5
y = 1/2 x + 5/2
Hence, the equation of line for friend’s hair is y = 1/2 x + 5/2
Equations of line for friend’s cousin hair
x₁ = 3, y₁ = 7, x₂ = 8, y₂ = 9
m = (y₂ – y₁)/(x₂ – x₁)
= (9 – 7)/(8 – 3)
= 2/5
Now to find the equation of line for friends cousin hair
(y – y₁) = m(x – x₁)
(y – 7) = 2/5 (x – 3)
5(y – 7) = 2(x – 3)
5y – 35 = 2x – 6
5y = 2x – 6 + 35
5y = 2x + 29
y = 2/5x + 29/5
Hence, the equation of line for friend’s cousin hair is y =2/5x + 29/5
b.
2/5x x + 29/5 = 1/2 x + 5/2
2/5 x – 1/2x =5/1 – 29/5
(4x – 5x)/10 = (25 – 58)/10
-x/10 = -33/10
x = 33
Hence, after 33 months length of hair of both girls would be same.
Question 26.
REASONING
Is it possible for a system of two linear equations to have multiple solutions? Explain your reasoning.
Answer:
No, it is not possible for a system of two linear equations to have multiple solutions. Because the system of linear equations is the straight lines and those lines intersect at only one point.
Question 27.
GEOMETRY
The length of a rectangle is 8 feet more than its width. The perimeter of the rectangle is 72 feet. Find the width of the rectangle.
Answer:
The width of the rectangle is 14 ft.
Explanation:
Let us say rectangle length is l, its width is l – 8
Rectangle perimeter = 2(l + b)
72 = 2(l + l – 8)
72/2 = 2l – 8
36 = 2l – 8
2l = 36 + 8
2l = 44
l = 44/2
l = 22
rectangle width is 22 – 8 = 14 ft
Lesson 5.2 Solving Systems of Linear Equations by Substitution
EXPLORATION 1
Work with a partner.
a. Find the value of each symbol in the systems below. Compare your solution methods with other pairs of students.
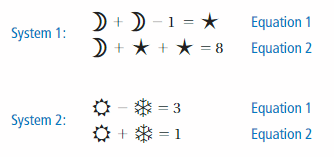
b. Use a method similar to your method in part(a) to solve the system below. Then explain how to solve a system of linear equations in two variables algebraically.

EXPLORATION 2
Writing and Solving Systems of Equations
Work with a partner. Roll two number cubes that are different colors. Then write the ordered pair shown by the number cubes.
a. Write a system of linear equations that has your ordered pair as its solution. Explain how you found your system.
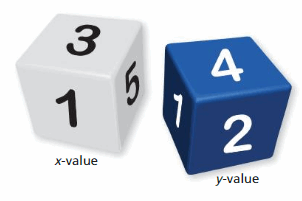
b. Exchange systems with another pair of students. Use a method from Exploration 1 to solve the system.
5.2 Lesson
Try It
Solve the system by substitution. Check your solution.
Question 1.
y = 2x + 3
y = 5x
Answer:
The solution is (1, 1)
Explanation:
The given systems of linear equations are
y = 2x + 3 —- (i)
y = 5x —– (ii)
Substitute equation (ii) in equation (i)
5x = 2x + 3
5x – 2x = 3
3x = 3
x = 3/3
x = 1
Substitute x = 1 in equation (ii)
y = 5(1)
y = 1
So, the solution is (1, 1)
Question 2.
4x + 2y = 0
y = \(\frac{1}{2}\)x – 5
Answer:
The solution is (0, -5)
Explanation:
The given systems of linear equations are
4x + 2y = 0 —– (i)
y = \(\frac{1}{2}\)x – 5 —– (ii)
Substitute equation (ii) in equation (i)
4x + 2(1/2 x) = 0
4x + x = 0
5x = 0
x = 0
putting x = 0 in equation (ii)
y = 1/2 (0) – 5
y = -5
So, the solution is (0, -5)
Question 3.
x = 5y + 3
2x + 4y = -1
Answer:
The solution is (1/2, -1/2)
Explanation:
The given systems of linear equations are
x = 5y + 3 —- (i)
2x + 4y = -1 —- (ii)
Substitute equation (i) in equation (ii)
2(5y + 3) + 4y = -1
10y + 6 + 4y = -1
14y = -1 – 6
14y = -7
y = -7/14
y = -1/2
Put y = -1/2 in equation (i)
x = 5(-1/2) + 3
= -5/2 + 3
= 1/2
So, the solution is (1/2, -1/2)
Try It
Solve the system. Explain your choice of method.
Question 4.
y = -3x + 2
y = 2
Answer:
The solution set is (0, 2)
Explanation:
The given systems of linear equations are
y = -3x + 2 —- (1)
y = 2 —- (2)
substitute equation (2) in (1)
2 = -3x + 2
2 – 2 = -3x
-3x = 0
x = 0
So, the solution set is (0, 2)
Question 5.
4y = x
x + 4y = -8
Answer:
T4y = x
x + 4y = -8
Explanation:
The given systems of linear equations are
4y = x —– (i)
x + 4y = -8 —– (ii)
Substitute x = 4y in equation (ii)
4y + 4y = 8
8y = 8
y = 1
Put y = 1 in equation (i)
4(1) = x
x = 4
So, the solution set is (4, 1)
Question 6.
2x + 2y = 1
-x + 2y = -3
Answer:
The solution set is (4/3, -5/6)
Explanation:
The given systems of linear equations are
2x + 2y = 1 —- (i)
-x + 2y = -3
2y + 3 = x —- (ii)
Substitute equation (ii) in equation (i)
2(2y + 3) + 2y = 1
4y + 6 + 2y = 1
6y + 6 = 1
6y = 1 – 6
6y = -5
y = -5/6
Put y = -5/6 in equation (ii)
2(-5/6) + 3 = x
x = -5/3 +3
x = 4/3
So, the solution set is (4/3, -5/6)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
REASONING
Does solving a system of linear equations by graphing give the same solution as solving by substitution? Explain.
Answer:
Yes.
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by substitution. Check your solution.
Question 8.
y = x – 8
y = 2x – 14
Answer:
The solution set is (6, -2)
Explanation:
The given systems of linear equations are
y = x – 8 —- (i)
y = 2x – 14 —- (ii)
Substitute equation (i) in (ii)
x – 8 = 2x – 14
-8 + 14 = 2x – x
x = 6
Putting x = 6 in equation (i)
y = 6 – 8
y = -2
Substitute x = 6, y = -2 in equation (i)
-2 = 6 – 8
So, the solution set is (6, -2)
Question 9.
x = 2y + 2
2x – 5y = 1
Answer:
The solution set is (8, 3)
Explanation:
The given systems of linear equations are
x = 2y + 2 —- (i)
2x – 5y = 1 —- (ii)
Substituting equation (i) in (ii)
2(2y + 2) – 5y = 1
4y + 4 – 5y = 1
4 – 1 = y
y = 3
Put y = 3 in equation (i)
x = 2(3) + 2
x = 8
Substitute x = 8, y = 3 in 2x – 5y = 1
2(8) – 5(3) = 16 – 15 = 1
So, the solution set is (8, 3)
Question 10.
x – 5y = 1
-2x + 9y = -1
Answer:
The solution is (-4, -1)
Explanation:
The given systems of linear equations are
x – 5y = 1
x = 1 + 5y —– (i)
-2x + 9y = -1 —- (ii)
Substitute equation (i) in (ii)
-2(1 + 5y) + 9y = -1
-2 – 10y + 9y = -1
-2 – y = -1
y = -2 + 1
y = -1
Put y = -1 in (i)
x = 1 + 5(-1)
x = 1 – 5
x = -4
Put x = -4, y = -1 in (ii)
-2(-4) + 9(-1) = 8 – 9 = -1
So, the solution is (-4, -1)
CHOOSING A SOLUTION METHOD
Solve the system. Explain your choice of method.
Question 11.
y = -x + 3
y = 2x
Answer:
The solution set is (1, 2).
Explanation:
The given systems of linear equations are
y = -x + 3
y = 2x
Equating both equations
-x + 3 = 2x
3 = 2x + x
3x = 3
x = 1
Substitute x = 1 in y = 2x
y = 2(1)
y = 2
So, the solution set is (1, 2).
Question 12.
0.5x + y = 2
0.5x = 1 + y
Answer:
The solution set is (3, 1/2).
Explanation:
The given systems of linear equations are
0.5x + y = 2 —— (i)
0.5x = 1 + y
x = 1/0.5 + y/0.5
x = 2 + 2y —- (ii)
Substitute equation (ii) in (i)
0.5(2 + 2y) + y = 2
1 + y + y = 2
2y + 1 = 2
2y = 2 – 1
2y = 1
y = 1/2
Put y = 1/2 in equation (i)
0.5x + 1/2 = 2
0.5x = 2 – 0.5
0.5x = 1.5
x = 1.5/0.5
x = 3
So the solution set is (3, 1/2).
Question 13.
x = 5y
y = 22 – 2x
Answer:
The solution set is (10, 2)
Explanation:
The given systems of linear equations are
x = 5y —- (i)
y = 22 – 2x —– (ii)
Substitute x = 5y in equation (ii)
y = 22 – 2(5y)
y = 22 – 10y
y + 10y = 22
11y = 22
y = 2
Put y = 2 in x = 5y
x = 5(2)
x = 10
So, the solution set is (10, 2)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 14.
To stock your school store, you buy a total of 25 sweatshirts and hats for $172.50. You pay $8.00 per sweatshirt and $2.50 per hat. How many of each item do you buy?
Answer:
The number of sweatshirts you buy would be 20 and the hat you buy would be 5.
Explanation:
Let’s assume the number of sweatshirts bought be x, while the number of hats will be 25 – x
Thus, cost to buy sweatshirts is 8 * x = 8x, and for hats will be 2.5 * (25 – x) = 62.50 – 2.50x
Therefore, total cost is 8x + 62.50 – 2.5x which is equal to 172.50
8x + 62.50 – 2.5x = 172.50
5.5x = 172.50 – 62.50
5.5x = 110
x = 110/5.5
x = 20
Hence, the cost of buying sweatshirts will be $20 * 8 = $160 and the cost to buy hats will be (25 – 20)2.50 = 12.5
The number of sweatshirts you buy would be 20 and the hat you buy would be (25 – 20) = 5
Question 15.
DIG DEEPER!
The length of a volleyball court is twice its width. The perimeter of the court is 180 feet. Find the area of the volleyball court. Justify your answer.
Answer:
The area of the rectangle will be 1800 sq ft.
Explanation:
The perimeter of the volleyball court is 180 feet. The length of the court is twice its width
Let us take the length and width of the court be 2x, x
Perimeter = 2(l + b)
As per the question
2(l + b) = 180
2x + x = 90
3x = 90
x = 90/3
x = 30
Thus, the length of court is 2 . 30 = 60 and width is 30 ft
Area = length * width
= 60 * 30
= 1800
Hence, the area of the rectangle will be 1800 sq ft.
Solving Systems of Linear Equations by Substitution Homework & Practice 5.2
Review & Refresh
Solve the system by graphing.
Question 1.
y = 2x – 3
y = -x + 9
Answer:
The solution is (4, 5)
Explanation:
The given systems of linear equations are y = 2x – 3, y = -x + 9
Graph the equations
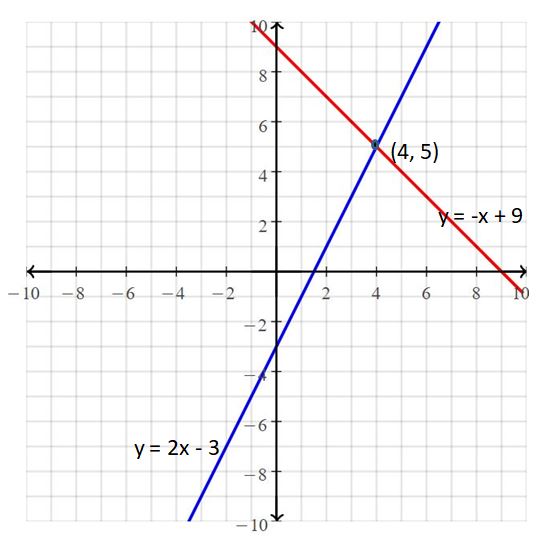
The lines intersect at (4, 5)
So, the solution is (4, 5)
Question 2.
6x + y = -2
y = -3x + 1
Answer:
The solution is (-1, 4)
Explanation:
The given systems of linear equations are 6x + y = -2, y = -3x + 1
Graph the equations
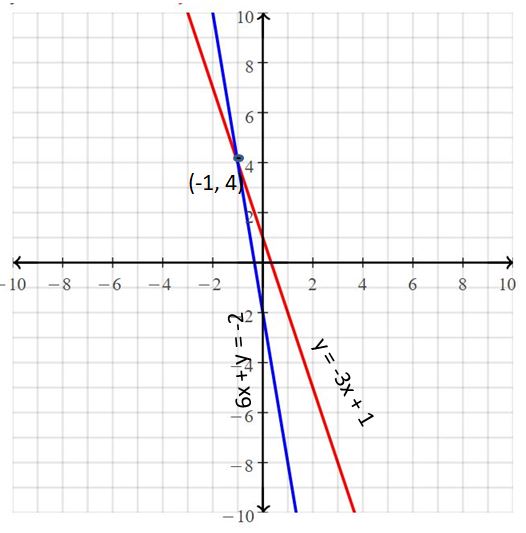
The lines intersect at (-1, 4)
So, the solution is (-1, 4)
Question 3.
4x + 2y = 2
3x = 4 – y
Answer:
The solution is (3, -5).
Explanation:
The given systems of linear equations are 4x + 2y = 2, 3x = 4 – y
Graph the equations
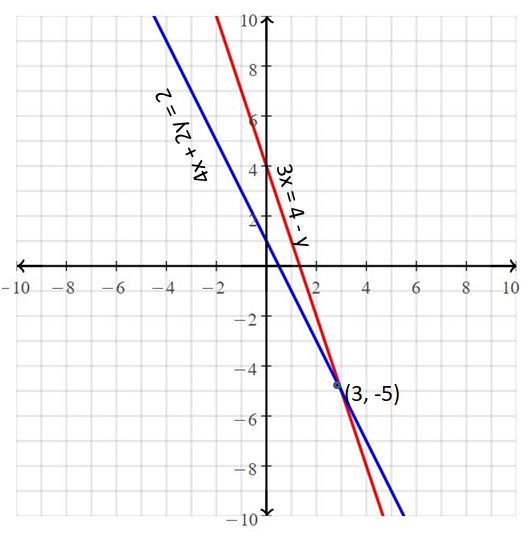
The lines intersect at (3, -5)
So, the solution is (3, -5)
Question 4.
Use the figure to find the measure of ∠2
A. 17°
B. 73°
C. 83°
D. 107°
Answer:
B. 73°
Explanation:
Given that,
∠1 = 107 degrees
∠1 + ∠2 = 180
107 + ∠2 = 180
∠2 = 180 – 107
= 73 degrees
Concepts, Skills, &Problem Solving
SOLVING A SYSTEM ALGEBRAICALLY
Find the value of each symbol in the system. (See Exploration 1, p. 205.)
Question 5.

Question 6.
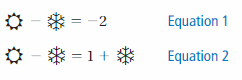
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by substitution. Check your solution.
Question 7.
y = x – 4
y = 4x – 10
Answer:
The solution set is (2, -2).
Explanation:
The given systems of linear equations are
y = x – 4 —- (i)
y = 4x – 10 —– (ii)
Substitute (ii) in (i)
4x – 10 = x – 4
4x – x = -4 + 10
3x = 6
x = 2
Put x = 2 in (i)
y = 2 – 4
y = -2
Substitute x = 2, y = -2 in equation (ii)
-2 = 4(2) – 10
= 8 – 10
So, the solution set is (2, -2).
Question 8.
y = 2x + 5
y = 3x – 1
Answer:
The solution set is (6, 17).
Explanation:
The given systems of linear equations are
y = 2x + 5 —– (i)
y = 3x – 1 —— (ii)
Substitute (ii) in (i)
3x – 1 = 2x + 5
3x – 2x = 5 + 1
x = 6
Substitute x = 6 in (i)
y = 2(6) + 5
y = 12 + 5
y = 17
Put x = 6, y = 17 in (ii)
17 = 3(6) – 1
= 18 – 1
So, the solution set is (6, 17)
Question 9.
x = 2y + 7
3x – 2y = 3
Answer:
The solution set is (-2, -9/2).
Explanation:
The given systems of linear equations are
x = 2y + 7 —– (i)
3x – 2y = 3 —– (ii)
Substitute (i) in (ii)
3(2y + 7) – 2y = 3
6y + 21 – 2y = 3
4y = 3 – 21
4y = -18
y = -9/2
Substitute y = -9/2 in (i)
x = 2(-9/2) + 7
x = -9 + 7
x = -2
Put x = -2, y = -9/2 in (ii)
3(-2) – 2(-9/2) = -6 + 9 = 3
So, the solution set is (-2, -9/2)
Question 10.
4x – 2y =14
y = \(\frac{1}{2}\)x – 1
Answer:
The solution set is (4, 1)
Explanation:
The given systems of linear equations are
4x – 2y =14 —– (i)
y = \(\frac{1}{2}\)x – 1 —– (ii)
Substitute equation (i) in (ii)
4x – 2(0.5x – 1) = 14
4x – x + 2 = 14
3x = 14 – 2
3x = 12
x = 4
Substitute x = 4 in (i)
4(4) – 2y = 14
16 – 14 = 2y
2 = 2y
y = 1
Put x = 4, y = 1 in (ii)
1 = 1/2 (4) – 1
= 2 – 1
So, the solution set is (4, 1)
Question 11.
2x = y – 10
2x + 7 = 2y
Answer:
The solution set is (-13/2, -3)
Explanation:
The given systems of linear equations are
2x = y – 10
y = 2x + 10 —- (i)
2x + 7 = 2y —— (ii)
Substitute (i) in (ii)
2x + 7 = 2(2x + 10)
2x + 7 = 4x + 20
4x – 2x = 7 – 20
2x = -13
x = -13/2
Substitute x = -13/2 in (i)
y = 2(-13/2) + 10
= -13 + 10
= -3
Put x = -13/2, y = -3 in (ii)
2(-13/2) + 7 = 2(-3)
-13 + 7 = -6
So, the solution set is (-13/2, -3)
Question 12.
8x – \(\frac{1}{3}\)y = 0
12x + 3 =y
Answer:
The solution set is (1/4, 6).
Explanation:
The given systems of linear equations are
8x – \(\frac{1}{3}\)y = 0 —– (i)
12x + 3 =y —— (ii)
Substitute (ii) in (i)
8x – 1/3(12x + 3) = 0
8x – 4x – 1 = 0
4x – 1 = 0
4x = 1
x = 1/4
Substitute x = 1/4 in (ii)
12(1/4) + 3 = y
3 + 3 = y
y = 6
Put x = 1/4, y = 6 in (ii)
12(1/4) + 3 = 3 + 3 = 6
So, the solution set is (1/4, 6).
Question 16.
MODELING REAL LIFE
There are a total of 64 students in a film making club and a yearbook club. The filmmaking club has 14 more students than the yearbook club.
a. Write a system of linear equations that represents this situation.
b. How many students are in the film making club? the yearbook club?

Answer:
a. x + y = 64, x = y + 14
b. The number of students in the filmmaking club and yearbook club are 39 and 25 respectively.
Explanation:
a. Let us take the number of students in film making club to be x and the number of students in the yearbook club be y
x + y = 64 —- (i)
It is given that the number of students in the filmmaking club is greater than students in the yearbook club by 14
So, x = y + 14 —- (ii)
b. Put equation (ii) in (i)
y + 14 + y = 64
2y + 14 = 64
2y = 64 – 14
2y = 50
y = 25
Substitute y = 25 in (i)
x + 25 = 64
x = 64 – 25
x = 39
Hence, the number of students in filmmaking club and yearbook club are 39 and 25 respectively.
Question 17.
MODELING REAL LIFE
A drama club earns $1040 from production by selling 64 adult tickets and 132 student tickets. An adult ticket costs twice as much as a student ticket.
a. Write a system of linear equations that represents this situation.
b. What is the cost of each ticket?
Answer:
a. 64a + 132s = 1040, a = 2s
b. The price of a student ticket is $4, adult ticket is $8.
Explanation:
Write the system of equations that models the problem where a is the price of an adult ticket and s is the price of a student ticket
64a + 132s = 1040
a = 2s
b. Substitute a = 2s in 64a + 132s = 1040
64(2s) + 132s = 1040
128s + 132s = 1040
260s = 1040
s = 1040/260
s = $4 per student ticket
a = 2(4) = $8 per adult ticket.
Question 18.
OPEN-ENDED
Write a system of linear equations that has the ordered pair (1, 6) as its solution.
Answer:
The system of linear equations that pass through (1, 6) is y – 6 = m(x – 1)
Explanation:
We know that the equation of a line that passes through a point is (y – y₁) = m(x – x₁)
The line pass through (1,6 )
So, y – 6 = m(x – 1)
We can get system of linear equations by inserting different values of m in above equation
If we put m = 1, then equation is y – 6 = 1(x – 1)
y – 6 = x – 1
y = x – 1 + 6
y = x + 5
Hence, the system of linear equation is y – 6 = m(x – 1) that pass through (1, 6).
CHOOSING A SOLUTION METHOD
Solve the system. Explain your choice of method.
Question 19.
y – x = 4
x + y = 6
Answer:
The solution set is (1, 5)
Explanation:
The given system of linear equations are
y – x = 4
y = 4 + x —– (i)
x + y = 6 —– (ii)
Substitute (i) in (ii)
x + 4 + x = 6
2x + 4 = 6
2x = 6 – 4
2x = 2
x = 1
Substitute x = 1 in (i)
y = 4 + 1
y = 5
So, the solution set is (1, 5)
Question 20.
0.5x + y = 4
0.5x – y =-1
Answer:
The solution set is (3, 2.5)
Explanation:
The given system of linear equations are
0.5x + y = 4 —- (i)
0.5x – y =-1
0.5x + 1 = y —- (ii)
Substitute (ii) in (i)
0.5x + 0.5x + 1 = 4
x + 1 = 4
x = 4 – 1
x = 3
Substitute x = 3 in (ii)
y = 0.5(3) + 1
= 2.5
So, the solution set is (3, 2.5)
Question 21.
y = 2x + 5
y = -3x
Answer:
The solution set is (-1, 3)
Explanation:
The given system of linear equations are
y = 2x + 5 —- (i)
y = -3x —– (ii)
Substitute (i) in (ii)
-3x = 2x + 5
-3x – 2x = 5
-5x = 5
x = -1
Substitute x = -1 in (i)
y = 2(-1) + 5
y = -2 + 5
y = 3
So, the solution set is (-1, 3)
Question 22.
CRITICAL THINKING
A system consists of two different proportional relationships. What is the solution to the system? Justify your answer.
Answer:
The solution is (0, 0).
Explanation:
The proportional relationships in the system of linear equations mean that there is no constant available in the equation.
Therefore, the lines will always pass through the origin (0, 0)
Hence, the solution is (0, 0).
Question 23.
GEOMETRY
The measure of the obtuse angle in the isosceles triangle is two and a half times the measure of one of the acute angles. Write and solve a system of linear equations to find the measure of each angle.
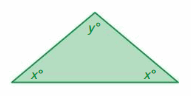
Answer:
The systems of linear equations are x + 2y = 180°, x = 2.5y
x = 100°, y = 40°
Explanation:
In an isosceles triangle, there are two angles that are the same and one that is different. We know there is one angle that is more than 90° because that is the definition of an obtuse angle. We also know that the sum of all the angles of a triangle equals 180°.
Let’s put all this together and find the measures of the angles.
x + 2y = 180°
x = 2.5y
Put x = 2.5 y in x + 2y = 180°
2.5y + 2y = 180°
4.5y = 180
y = 180/4.5
y = 40
Put y = 40 in x = 2.5y
x = 2.5(40)
x = 100
Question 24.
NUMBER SENSE
The sum of the digits of a two-digit number is 8. When the digits are reversed, the number increases by 36. Find the original number.
Answer:
The original number is 26.
Explanation:
Let the two-digit number be xy
The sum of the digits of a two-digit number is 8
x + y = 8
y = 8 – x —- (i)
So, the number is 10x + y
When the digits are reversed, the number increases by 36
10y + x = 36 + 10x + y
10y – y = 36 + 10x – x
9y = 36 + 9x
Put y = 8 – x
9(8 – x) = 36 + 9x
72 – 9x = 36 + 9x
72 – 36 = 18x
18x = 36
x = 36/18
x = 2
Put x = 2 in equation (i)
y = 8 – 2
y = 6
So, the original number is 26.
Question 25.
DIG DEEPER!
A hospital employs a total of 77 nurses and doctors. The ratio of nurses to doctors is 9 : 2. How many nurses are employed at the hospital? How many doctors are employed at the hospital?
Answer:
There are 63 nurses, 14 doctors are employed at the hospital.
Explanation:
Let x be the number of nurses and y be the number of doctors
A hospital employs a total of 77 nurses and doctors
x + y = 77 —- (i)
The ratio of nurses to doctors is 9:2.
x/y = 9/2
x = 9/2y
Put x = 9/2y in (i)
9/2 y + y = 77
11/2 y = 77
11y = 77 * 2
y = 14
x = 9/2 (14)
y = 63
So, there are 63 nurses, 14 doctors are employed at the hospital.
Question 26.
REPEATED REASONING
A DJ has a total of 1075 dance, rock, and country songs on her system. The dance selection is three times the rock selection. The country selection has 105 more songs than the rock selection. How many songs on the system is dance? rock? country?

Answer:
582 dance, 299 countries, and 194 ock songs on the system.
Explanation:
Let d, r, c be the number of dance, rock and country songs
A DJ has a total of 1075 dance, rock, and country songs on her system
d + r + c = 1075 —- (i)
The dance selection is three times the size of the rock selection
d = 3r —- (ii)
The country selection has 105 more songs than the rock selection
c = 105 + r —– (iii)
Put (ii), (iii) in (i)
3r + r + 105 + r = 1075
5r = 1075 – 105
5r = 970
r = 194
d = 3(194) = 582
c = 105 + 194 = 299
So, 582 dance, 299 country, and 194 ock songs on the system.
Lesson 5.3 Solving Systems of Linear Equations by Elimination
EXPLORATION 1
Work with a partner. A student found the value of in the system using substitution as shown.

a. Find another way to obtain the equation 4x = -4 from the original system. Does your method produce an equation in one variable for any system? Explain.
b. Can you use your method in part(a) to solve each system below? If so, solve the system. If not, replace one of the equations with an equivalent equation that allows you to use your method in part(a). Then solve the system.

c. Compare your solution methods in part(b) with other pairs of students.
5.3 Lesson
Try It
Solve the system by elimination. Check your solution.
Question 1.
2x – y = 9
4x + y =21
Answer:
The solution set is (5, 1).
Explanation:
The given system of linear equations are
2x – y = 9 —- (i)
4x + y =21 —– (ii)
Add both equations
2x – y + 4x + y = 9 + 21
6x = 30
x = 30/6
x = 5
Put x = 5 in (i)
2(5) – y = 9
10 – y = 9
10 – 9 = y
y = 1
Substitute x = 5, y = 1 in (ii)
4(5) + 1 = 20 + 1 = 21
So, the solution set is (5, 1).
Question 2.
-5x + 2y = 13
5x + y = -1
Answer:
The solution set is (-1, 4).
Explanation:
The given system of linear equations are
-5x + 2y = 13 —– (i)
5x + y = -1 —— (ii)
Add both equations
-5x + 2y + 5x + y = 13 – 1
3y = 12
y = 4
Substitute y = 4 in (ii)
5x + 4 = -1
5x = -1 – 4
5x = -5
x = -1
Substitute x = -1, y = 4 in (i)
-5(-1) + 2(4) = 5 + 8 = 13
So, the solution set is (-1, 4).
Question 3.
3x + 4y = -6
7x + 4y = -14
Answer:
The solution set is (-2, 0).
Explanation:
The given system of linear equations are
3x + 4y = -6 —- (i)
7x + 4y = -14 —– (ii)
Subtract (ii) from (i)
3x + 4y – (7x + 4y) = -6 + 14
3x + 4y – 7x – 4y = 8
-4x = 8
x = -8/4
x = -2
Substitute x = -2 in (i)
3(-2) + 4y = -6
-6 + 4y = -6
4y = -6 + 6
y = 0
Substitute x = -2, y = 0 in (ii)
7(-2) + 4(0) = -14
So, the solution set is (-2, 0).
Try It
Solve the system by elimination. Check your solution.
Question 4.
3x + y = 11
6x + 3y = 24
Answer:
The solution set is (3, 2)
Explanation:
The given system of linear equations are
3x + y = 11 —— (i)
6x + 3y = 24 ——- (ii)
Divide equation (ii) by 1/3
1/3(6x + 3y = 24)
2x + y = 8 —- (iii)
Subtract (iii) from (i)
3x + y – (2x + y) = 11 – 8
3x + y – 2x – y = 3
x = 3
Put x = 3 in (i)
3(3) + y = 11
9 + y = 11
y = 11 – 9
y = 2
Substitute x = 3, y = 2 in (iii)
2(3) + 2 = 6 + 2 = 8
So, the solution set is (3, 2)
Question 5.
4x – 5y = -19
-x – 2y = 8
Answer:
The solution set is (-6, -1)
Explanation:
The given system of linear equations are
4x – 5y = -19 —– (i)
-x – 2y = 8 —— (ii)
Multiply both sides of equation (ii) by 4
4(-x – 2y = 8)
-4x – 8y = 32 —- (iii)
Add (i) & (iii)
4x – 5y – 4x – 8y = -19 + 32
-13y = 13
y = -1
Substitute y = -1 in (ii)
-x – 2(-1) = 8
-x + 2 = 8
-x = 8 – 2
x = -6
Substitute x = -6, y = -1 in (ii)
-(-6) – 2(-1) = 6 + 2 = 8
So, the solution set is (-6, -1)
Question 6.
5y = 15 – 5x
y = -2x + 3
Answer:
The solution set is (0, 3)
Explanation:
The given system of linear equations are
5y = 15 – 5x —– (i)
y = -2x + 3 —– (ii)
Divide equation (i) by 1/5
1/5(5y = 15 – 5x)
y = 3 – x —– (iii)
Subtract (iii) from (ii)
y – y = -2x + 3 – (3 – x)
0 = -2x + 3 – 3 + x
-x = 0
x = 0
Substitute x = 0 in (iii)
y = 3 – 0
y = 3
Substitute x = 0, y = 3 in (ii)
3 = -2(0) + 3
So, the solution set is (0, 3)
Try It
Question 7.
Change one word in Choice B so that it represents an efficient approach to solving the system.
Answer:
Multiply equation (i) by -1 and subtract the equations.
Explanation:
The given system of linear equations are
x – 2y = 6 —- (i)
-x + 4y = 6 —- (ii)
multiply equation (i) by -1 and subtract the equations.
-1(x – 2y = 6)
-x + 2y = -6
-x + 2y – (-x + 4y) = -6 – 6
-x + 2y + x – 4y = -12
-2y = -12
y = 6
Put y = 6 in (i)
x – 2(6) = 6
x – 12 = 6
x = 6 + 12
x = 18
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by elimination. Check your solution.
Question 8.
2x + y = 4
-2x + 2y = 5
Answer:
The solution set is (1/2, 3)
Explanation:
The given system of linear equations are
2x + y = 4 —— (i)
-2x + 2y = 5 —– (ii)
Add equations
2x + y – 2x + 2y = 4 + 5
3y = 9
y = 3
Substitute y = 3 in (i)
2x + 3 = 4
2x = 4 – 3
2x = 1
x = 1/2
Substitute x = 1/2, y = 3 in (ii)
-2(1/2) + 2(3) = -1 + 6 = 5
So, the solution set is (1/2, 3)
Question 9.
-x + y = 1
-3x + y =7
Answer:
The solution set is (-3, -2).
Explanation:
The given system of linear equations are
-x + y = 1 —- (i)
-3x + y =7 —– (ii)
Subtract equations
-x + y – (-3x + y) = 1 – 7
-x + y + 3x – y = -6
2x = -6
x = -3
Substitute x = -3 in (ii)
-3(-3) + y = 7
9 + y = 7
y = 7 – 9
y = -2
Substitute x = -3, y = -2 in (i)
-(-3) – 2 = 3 – 2 = 1
So, the solution set is (-3, -2).
Question 10.
y = -2x + 3
4x – 5y = 13
Answer:
The solution set is (2, -1).
Explanation:
The given system of linear equations are
y = -2x + 3
2x + y = 3 —– (i)
4x – 5y = 13 —– (ii)
Multiply equation (i) by 2 and subtract
2(2x + y = 3)
4x + 2y = 6
4x + 2y – (4x – 5y) = 6 – 13
4x + 2y – 4x + 5y = -7
7y = -7
y = -1
Substitute y = -1 in (i)
2x – 1 = 3
2x = 4
x = 2
Substitute x = 2, y = -1 in (ii)
4(2) – 5(-1) = 8 + 5 = 13
So, the solution set is (2, -1).
CHOOSING A SOLUTION METHOD
Solve the system. Explain your choice of method.
Question 11.
y = 6x – 1
y = 3x – 4
Answer:
The solution set is (-1, -7)
Explanation:
The given system of linear equations are
y = 6x – 1 —- (i)
y = 3x – 4 —– (ii)
Equating both the equations
6x – 1 = 3x – 4
6x – 3x = -4 + 1
3x = -3
x = -3/3
x = -1
Substitute x = -1 in equation (i)
y = 6(-1) – 1
y = -7
So, the solution set is (-1, -7)
Question 12.
3x = y + 2
3x + 2y = 5
Answer:
The solution set is (1, 1).
Explanation:
The given system of linear equations are
3x = y + 2 —- (i)
3x + 2y = 5 —– (ii)
Substitute equation (i) in (ii)
y + 2 + 2y = 5
3y = 5 – 2
3y = 3
y = 1
Substitute y = 1 in (i)
3x = 1 + 2
3x = 3
x = 1
So, the solution set is (1, 1).
Question 13.
2x – y = 7
x + y = 5
Answer:
The solution set is (4, 1).
Explanation:
The given system of linear equations are
2x – y = 7 —- (i)
x + y = 5 —- (ii)
Add equations
2x – y + x + y = 7 + 5
3x = 12
x = 4
Substitute x = 4 in (ii)
4 + y = 5
y = 5 – 4
y = 1
So, the solution set is (4, 1).
Question 14.
WHICH ONE DOESN’T BELONG?
Which system does not belong with the other three? Explain your reasoning.

Answer:
2x + 3y = 11, 3x – 2y = 10 is does not belong to other three.
Explanation:
1. 3x + 3y = 3 —- (i)
2x – 3y = 7 —- (ii)
Add equations
3x + 3y + 2x – 3y = 3 + 7
5x = 10
x = 2
Substitute x = 2 in (ii)
2(2) – 3y = 7
4 – 3y = 7
-3y = 7 – 4
-3y = 3
y = -1
The solution set is (2, -1).
2. -2x + y = 6 — (i)
2x – 3y = -10 — (ii)
Add equations
-2x + y + 2x – 3y = 6 – 10
-2y = -4
y = 2
Substitute y = 2 in (i)
-2x + 2 = 6
-2x = 4
x = -2
The solution set is (-2, 2)
3. 2x + 3y = 11 —- (i)
3x – 2y = 10
3x = 10 + 2y
x = (10 + 2y)/3
Substitute x = (10 + 2y)/3 in (i)
2(10 + 2y)/3 + 3y = 11
20 + 4y + 9y = 33
20 + 13y = 33
13y = 33 – 20
y = 1
Put y = 1 in (i)
2x + 3 = 11
2x = 11 – 3
2x = 8
x = 4
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 15.
A fitness instructor purchases exercise bikes and treadmills for two gyms. For the first gym, 2 exercise bikes and 3 treadmills cost $2200. For the second gym, 3 exercise bikes and 4 treadmills cost $3000. How much does a treadmill cost?
Answer:
The cost of a treadmill is $600.
Explanation:
Let x and y be the price of exercise bikes and treadmills, respectively
Using the fact that
Total cost = cost of exercise bike . Number of bikes in a gym + Cost of treadmill . Number of treadmills in a gym
2x + 3y = 2200 —- (i)
3x + 4y = 3000 —– (ii)
Multiply (i) by 3 and (ii) by 2
3(2x + 3y = 2200)
6x + 9y = 6600 —- (iii)
2(3x + 4y = 3000)
6x + 8y = 6000 —– (iv)
Subtract equations
6x + 9y – 6x – 8y = 6600 – 6000
y = 600
The cost of treadmill is $600.
Question 16.
DIG DEEPER!
At your school, cooking club members raise $5 per member for a charity, and woodshop club members raise $10 per member for a different charity. The cooking club has three times as many members as the woodshop club. The difference in the number of members in the two clubs is 12 members. How much does each club raise?

Answer:
Money raised for charity by the cooking club is $90, Money raised for charity by the woodshop club $60.
Explanation:
Let x and y be the number of members of the cooking club and woodshop club
The cooking club has three times as many members as the woodshop club.
x = 3y
The difference in the number of members in the two clubs is 12 members.
x – y = 12
3y – y = 12
2y = 12
y = 6
So, x = 3(6) = 18
Money raised for charity by cooking club = Number of members in a cooking club. Charity per member of cooking club
= x . 5
= 18 . 5
= $90
Money raised for charity by woodshop club = Number of members in woodshop club. Charity per member of woodshop club
= y . 10
= 6 . 10
= $60
Solving Systems of Linear Equations by Elimination Homework & Practice 5.3
Review & Refresh
Solve the system by substitution. Check your solution.
Question 1.
x = 5 – y
x – y = 3
Answer:
The solution set is (4, 1).
Explanation:
The given system of linear equations are
x = 5 – y —- (i)
x – y = 3 —- (ii)
Substitute equation (i) in (ii)
5 – y – y = 3
5 – 2y = 3
5 – 3 = 2y
2 = 2y
y = 1
Substitute y = 1 in (i)
x = 5 – 1
x = 4
Substitute x = 4, y = 1 in (ii)
4 – 1 = 3
So, the solution set is (4, 1).
Question 2.
x – 5y = 1
-x + y = 7
Answer:
The solution set is (-9, -2)
Explanation:
The given system of linear equations are
x – 5y = 1
x = 1 + 5y —- (i)
-x + y = 7 —- (ii)
Substitute (i) in (ii)
-1 – 5y + y = 7
-1 – 4y = 7
-4y = 7 + 1
-4y = 8
y = -2
Substitute y = -2 in (i)
x = 1 + 5(-2)
x = 1 – 10
x = -9
Substitute x = -9, y = -2
-(-9) – 2 = 9 – 2 = 7
So, the solution set is (-9, -2)
Question 3.
x + 6y = -2
-x = 3y – 10
Answer:
The solution set is (22, -4).
Explanation:
The given system of linear equations are
x + 6y = -2 —- (i)
-x = 3y – 10 —- (ii)
Substitute (ii) in (i)
-3y + 10 + 6y = -2
3y + 10 = -2
3y = -2 – 10
3y = -12
y = -4
Substitute y = -4 in (ii)
-x = 3(-4) – 10
-x = -12 – 10
-x = -22
x = 22
Substitute x = 22, y = -4 in (i)
22 + 6(-4) = 22 – 24 = -2
So, the solution set is (22, -4).
The vertices of a triangle are given. Draw the triangle and its image after a dilation with the given scale factor. Identify the type of dilation.
Question 4.
A(1, 1), B(1, 3), C(3, 1); k = 2
Answer:
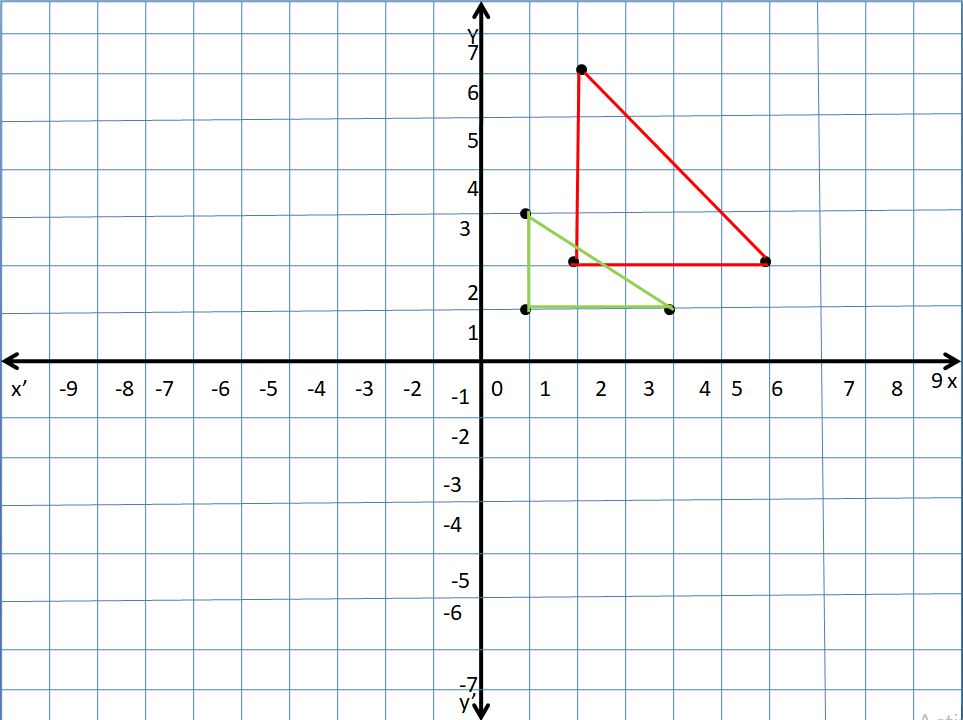
The new triangle is larger than the original triangle so it’s an increase.
Explanation:
The vertices of a triangle are A(1, 1), B(1, 3), C(3, 1)
Multiply the coordinates by 2 and then graph the original and new coordinates.
New coordinates are D(2, 2), E(2, 6), F(6, 2)
The new triangle is larger than the original triangle so it’s an increase.
Question 5.
D(-8, -4), E(-4, 8), F(0, 0); k = 0.5
Answer:
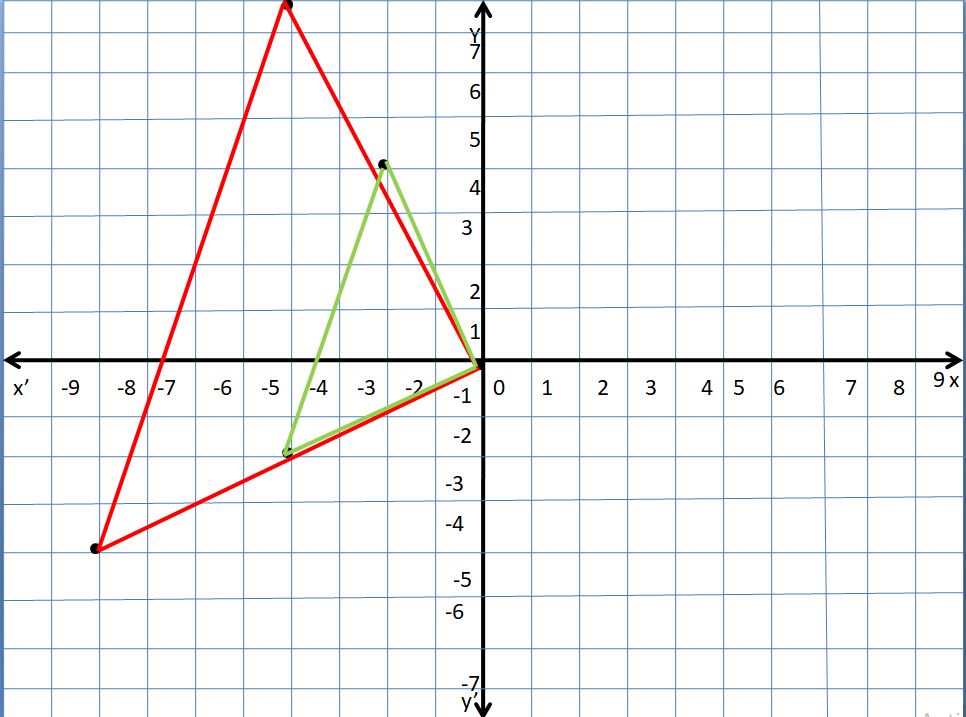
The new triangle is smaller than the original triangle so it’s a reduction.
Explanation:
The vertices of a triangle are D(-8, -4), E(-4, 8), F(0, 0)
Multiply the coordinates by 0.5 and then graph the original and new coordinates
The new coordinates are A(-4, -2), B(-2, 4), C(0, 0)
The new triangle is smaller than the original triangle so it’s a reduction.
Concepts, Skills, &Problem Solving
SOLVING A SYSTEM ALGEBRAICALLY
Explain how to obtain the equation 3x = 6 from the given system. (See Exploration 1, p. 211.)
Question 6.
2x + y = 5
x – y = 1
Answer:
Add both equations
Explanation:
The given system of linear equations are
2x + y = 5 —– (i)
x – y = 1 —– (ii)
Add both equations
2x + y + x – y = 5 + 1
3x = 6
Question 7.
5x + 2y = 2
x + y = -2
Answer:
Multiply the equation 2 by 2 and Subtract equation obtained equation from (i)
Explanation:
The given system of linear equations are
5x + 2y = 2 —– (i)
x + y = -2 —— (ii)
Multiply the equation 2 by 2
2(x + y) = 2(-2)
2x + 2y = -4
Subtract equation obtained equation from (i)
5x + 2y – 2x – 2y = 2 + 4
3x = 6
Question 8.
-x + y = -3
6x – 3y =15
Answer:
Multiply the equation (i) by 3, Add equations (i) & (iii)
Explanation:
The given system of linear equations are
-x + y = -3 —- (i)
6x – 3y =15 —- (ii)
Multiply the equation (i) by 3
3(-x + y = -3)
-3x + 3y = -9 —- (ii)
Add equation (i) & (iii)
6x – 3y – 3x + 3y = 15 – 9
3x = 6
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by elimination. Check your solution.
Question 9.
x + 3y = 5
-x – y = -3
Answer:
The solution set is (2, 1).
Explanation:
The given system of linear equations are
x + 3y = 5 —- (i)
-x – y = -3 —– (ii)
Add equations (i) & (ii)
x + 3y – x – y = 5 – 3
2y = 2
y = 1
Substitute y = 1 in (ii)
-x – 1 = -3
-x = -3 + 1
-x = -2
x = 2
Substitute x = 2, y = 1 in (i)
2 + 3(1) = 2 + 3 = 5
So, the solution set is (2, 1).
Question 10.
x – 2y = -7
3x + 2y = 3
Answer:
The solution set is (-1, 3).
Explanation:
The given system of linear equations are
x – 2y = -7 —- (i)
3x + 2y = 3 —- (ii)
Add equations (i), (ii)
x – 2y + 3x + 2y = -7 + 3
4x = -4
x = -1
Substitute x = -1 in (i)
-1 – 2y = -7
-2y = -7 + 1
-2y = -6
y = 3
Substitute x = -1, y = 3 in (i)
-1 – 2(3) = -1 – 6 = -7
So, the solution set is (-1, 3).
Question 11.
4x + 3y = -5
-x + 3y = -10
Answer:
The solution set is(1, -3).
Explanation:
The given system of linear equations are
4x + 3y = -5 —- (i)
-x + 3y = -10 —- (ii)
Subtract equations (i), (ii)
4x + 3y – (-x + 3y) = -5 – (-10)
4x + 3y + x – 3y = -5 + 10
5x = 5
x = 1
Substitute x = 1 in (ii)
-1 + 3y = -10
3y = -10 + 1
3y = -9
y = -3
Substitute x = 1, y = -3 in (i)
4(1) + 3(-3) = 4 – 9 = -5
So, the solution set is(1, -3).
Question 12.
2x + 7y = 1
2x – 4y = 12
Answer:
The solution set is (4, -1).
Explanation:
The given system of linear equations are
2x + 7y = 1 —- (i)
2x – 4y = 12 —– (ii)
Subtract equations (i), (ii)
2x – 4y – (2x + 7y) = 12 – 1
2x – 4y – 2x – 7y = 11
-11y = 11
y = -1
Substitute y = -1 in (ii)
2x – 4(-1) = 12
2x + 4 = 12
2x = 12 – 4
2x = 8
x = 4
Substitute x = 4, y = -1 in (i)
2(4) + 7(-1) = 8 – 7 = 1
So, the solution set is (4, -1).
Question 13.
2x + 5y = 16
3x – 5y = -1
Answer:
The solution set is (3, 2).
Explanation:
The given system of linear equations are
2x + 5y = 16 —- (i)
3x – 5y = -1 —– (ii)
Add both equations
2x + 5y + 3x – 5y = 16 – 1
5x = 15
x = 3
Substitute x = 3 in (i)
2(3) + 5y = 16
5y = 16 – 6
5y = 10
y = 2
Substitute x = 3, y = 2 in (ii)
3(3) – 5(2) = 9 – 10 = -1
So, the solution set is (3, 2).
Question 14.
3x – 2y = 4
6x – 2y = -2
Answer:
The solution set is (-2, -5).
Explanation:
The given system of linear equations are
3x – 2y = 4 —– (i)
6x – 2y = -2 —– (ii)
Subtract equations
3x – 2y – (6x – 2y) = 4 – (-2)
3x – 2y – 6x + 2y = 4 + 2
-3x = 6
x = -2
Substitute x = -2 in (i)
3(-2) – 2y = 4
-6 – 2y = 4
-2y = 4 + 6
-2y = 10
y = -5
Substitute x = -2, y = -5 in (ii)
6(-2) – 2(-5) = -12 + 10 = -2
So, the solution set is (-2, -5).
Question 15.
YOU BE THE TEACHER
Your friend solves the system. Is your friend correct? Explain your reasoning.
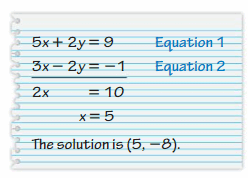
Answer:
Wrong.
Explanation:
The given equations are 5x + 2y = 9 —- (i)
3x – 2y = -1 —- (ii)
Add both equations
5x + 2y + 3x – 2y = 9 – 1
8x = 8
x = 1
Put x = 1 in (ii)
3(1) – 2y = -1
3 – 2y = -1
-2y = -1 – 3
-2y = -4
y = 2
So, the solution set is (1, 2).
Question 16.
MODELING REAL LIFE
You and your friend are selling raffle tickets for a new laptop. You sell 14 more tickets than your friend sells. Together, you and your friend sell 58 tickets.
a. Write a system of linear equations that represents this situation.
b. How many tickets do each of you sell?
Answer:
a. x = 14 + y, x + y = 58
b. The number of tickers you sell is 36, the number of tickets your friend sells is 22.
Explanation:
a. Let x be the number of tickets you sell and let y be the number of tickets your friend sells.
You sell 14 more tickets than your friend sells
x = 14 + y —- (i)
Together, you and your friend sell 58 tickets.
x + y = 58 —- (ii)
b. Substitute equation (i) in (ii)
14 + y + y = 58
14 + 2y = 58
2y = 58 – 14
2y = 44
y = 44/2
y = 22
Substitute y = 22 in (i)
x = 14 + 22
x = 36
So, The number of tickers you sell is 36, the number of tickets your friend sells is 22.
Question 17.
MODELING REAL LIFE
You can jog around your block twice and the park once in 10 minutes. You can jog around your block twice and the park 3 times in 22 minutes. Write a system of linear equations that represents this situation. How long does it take you to jog around the park?

Answer:
The system of linear equations are 2x + y = 10, 2x + 3y = 22
It takes 6 minutes to jog around the park.
Explanation:
Let x be the number of minutes it takes to jog around the block and y be the number of minutes it takes to jog around the park
You can jog around your block twice and the park once in 10 minutes
2x + y = 10 —- (i)
You can jog around your block twice and the park 3 times in 22 minutes
2x + 3y = 22 —- (ii)
Subtract equations
2x + y – 2x – 3y = 10 – 22
-2y = -12
y = 6
Substitute y = 6 in (i)
2x + 6 = 10
2x = 10 – 6
2x = 4
x = 2
So, it takes 6 minutes to jog around the park.
SOLVING A SYSTEM OF LINEAR EQUATIONS
Solve the system by elimination. Check your solution.
Question 18.
2x – y = 0
3x – 2y = -3
Answer:
The solution set is (3, 6).
Explanation:
The systems of linear equations are
2x – y = 0 —- (i)
3x – 2y = -3 —– (ii)
Multiply equation (i) by 2
2(2x – y = 0)
4x – 2y = 0 —- (iii)
Subtract equation (ii) from (iii)
4x – 2y – (3x – 2y) = 0 – (-3)
4x – 2y – 3x + 2y = 3
x = 3
Substitute x = 3 in (i)
2(3) – y = 0
6 – y = 0
y = 6
Substitute x = 3, y = 6 in (i)
2(3) – 6 = 6 – 6 = 0
So, the solution set is (3, 6).
Question 19.
x + 4y = 1
3x + 5y = 10
Answer:
The solution set is (5, -1).
Explanation:
The systems of linear equations are
x + 4y = 1 —- (i)
3x + 5y = 10 —- (ii)
Multiply equation (i) by 3
3(x + 4y = 1)
3x + 12y = 3 —- (iii)
Subtract equation (iii) from (ii)
3x + 5y – (3x + 12y) = 10 – 3
3x + 5y – 3x – 12y = 7
-7y = 7
y = -1
Substitute y = -1 in (i)
x + 4(-1) = 1
x – 4 = 1
x = 1 + 4
x = 5
Substitute x = 5, y = -1 in (i)
5 + 4(-1) = 5 – 4 = 1
So, the solution set is (5, -1).
Question 20.
-2x + 3y = 7
5x + 8y = -2
Answer:
The solution set is (-2, 1).
Explanation:
The systems of linear equations are
-2x + 3y = 7 —- (i)
5x + 8y = -2 —– (ii)
Multiply equation (i) by 5 and equation (ii) by 2
5(-2x + 3y = 7)
-10x + 15y = 35 —- (iii)
2(5x + 8y = -2)
10x + 16y = -4 —- (iv)
Add equations (iii) & (iv)
-10x + 15y + 10x + 16y = 35 – 4
31y = 31
y = 1
Substitute y = 1 in (i)
-2x + 3(1) = 7
-2x = 7 – 3
-2x = 4
x = -2
Substitute x = -2, y = 1 in (ii)
5(-2) + 8(1) = -10 + 8 = -2
So, the solution set is (-2, 1).
Question 21.
3x + 3 = 3y
2x – 6y = 2
Answer:
The solution set is (-2, -1).
Explanation:
The systems of linear equations are
3x + 3 = 3y —- (i)
2x – 6y = 2 —- (ii)
Multiply equation (i) by 2
2(3x + 3 = 3y)
6x + 6 = 6y
6x – 6y = -6 —- (iii)
Subtract equations (ii) & (iii)
2x – 6y – 6x + 6y = 2 + 6
-4x = 8
x = -2
Substitute x = -2 in (i)
3(-2) + 3 = 3y
-6 + 3 = 3y
-3 = 3y
y = -1
Substitute x = -2, y = -1 in (i)
3(-2) + 3 = 3(-1)
-6 + 3 = -3
So, the solution set is (-2, -1).
Question 22.
2x – 6 = 4y
7y =-3x + 9
Answer:
The solution set is (3, 0).
Explanation:
The systems of linear equations are
2x – 6 = 4y
2x – 4y = 6 —- (i)
7y = -3x + 9
3x + 7y = 9 —- (ii)
Multiply (i) by 7 and (ii) by 4
7(2x – 4y = 6)
14x – 28y = 42 —- (iii)
4(3x + 7y = 9)
12x + 28y = 36 —- (iv)
Add equations (iii) & (iv)
14x – 28y + 12x + 28y = 42 + 36
26x = 78
x = 78/26
x = 3
Substitute x = 3 in (i)
2(3) – 4y = 6
6 – 4y = 6
6 – 6 = 4y
y = 0
Substitute x = 3, y = 0 in (i)
2(3) – 4(0) = 6 – 0 = 6
So, the solution set is (3, 0).
Question 23.
5x = 4y + 8
3y = 3x – 3
Answer:
The solution set is (4, 3).
Explanation:
The systems of linear equations are
5x = 4y + 8
5x – 4y = 8 — (i)
3y = 3x – 3
3x – 3y = 3 —- (ii)
Multiply (i) by 3 and (ii) by 4
3(5x – 4y = 8)
15x – 12y = 24 — (iii)
4(3x – 3y = 3)
12x – 12y = 12 —- (iv)
Subtract obtained equations
15x – 12y – 12x + 12y = 24 – 12
3x = 12
x = 4
Substitute x = 4 in (ii)
3(4) – 3y = 3
12 – 3y = 3
-3y = 3 – 12
-3y = -9
y = 3
Substitute x = 4, y = 3 in (ii)
3(4) – 3(3) = 12 – 9 = 3
So, the solution set is (4, 3).
Question 24.
YOU BE THE TEACHER
Your friend solves the system. Is your friend correct? Explain your reasoning.

Answer:
Wrong.
Explanation:
Given equations are
x + y = 1 — (i)
5x + 3y = -3 (ii)
Multiply equation (i) by -5
-5(x + y = 1)
-5x – 5y = -5 — (iii)
Add equations (iii) & (ii)
-5x – 5y + 5x + 3y = -3 – 5
-2y = -8
y = 4
Put y = 4 in (i)
x + 4 = 1
x = 1 – 4 = -3
So, the solution set is (-3, 4).
CHOOSING A SOLUTION METHOD
Solve the system. Explain your choice of method.
Question 25.
x + y = 4
x – y = 4
Answer:
The solution set is (4, 0).
Explanation:
The systems of linear equations are
x + y = 4 — (i)
x – y = 4 — (ii)
Add equations
x + y + x – y = 4 + 4
2x = 8
x = 4
Substitute x = 4 in (i)
4 + y = 4
y = 4 – 4
y = 0
So, the solution set is (4, 0).
Question 26.
y = x – 3
y = -2x + 3
Answer:
The solution set is (2, -1).
Explanation:
The systems of linear equations are
y = x – 3 — (i)
y = -2x + 3 — (ii)
Equate both equations
x – 3 = -2x + 3
x + 2x = 3 + 3
3x = 6
x = 2
Substitute x = 2 in (i)
y = 2 – 3
y = -1
So, the solution set is (2, -1).
Question 27.
x + 2y = 0
2x – y = 4
Answer:
The solution set is (8/5, -4/5)
Explanation:
The systems of linear equations are
x + 2y = 0 —- (i)
2x – y = 4 —- (ii)
y = 2x – 4
Substitute y = 2x – 4 in (i)
x + 2(2x – 4) = 0
x + 4x – 8 = 0
5x = 8
x = 8/5
Substitute x = 8/5 in (i)
8/5 + 2y = 0
2y = -8/5
y = -4/5
So, the solution set is (8/5, -4/5)
Question 28.
y + 5x = 1
5y – x = 5
Answer:
The solution set is (0, 1).
Explanation:
The systems of linear equations are
y + 5x = 1 —- (i)
5y – x = 5 —- (ii)
5y – 5 = x
Substitute x = 5y – 5 in (i)
y + 5(5y – 5) = 1
y + 25y – 25= 1
26y = 1 + 25
26y = 26
y = 1
Substitute y = 1 in (i)
1 + 5x = 1
5x = 0
x = 0
So, the solution set is (0, 1).
Question 29.
2 = x – 3y
-2x + y = 4
Answer:
The solution set is (-14/5, -8/5)
Explanation:
The systems of linear equations are
2 = x – 3y
x = 2 + 3y — (i)
-2x + y = 4 —- (ii)
Substitute (i) in (ii)
-2(2 + 3y) + y = 4
-4 – 6y + y = 4
-5y = 4 + 4
y = -8/5
Substitute y = -8/5 in (i)
x = 2 + 3(-8/5)
x = 2 – 24/5
x = -14/5
So, the solution set is (-14/5, -8/5)
Question 30.
8x + 5y = 6
8x = 3 – 2y
Answer:
The solution set is (1/8, 1).
Explanation:
The systems of linear equations are
8x + 5y = 6 —- (i)
8x = 3 – 2y —- (ii)
Substitute (ii) in (i)
3 – 2y + 5y = 6
3y = 6 – 3
3y = 3
y = 1
Substitute y = 1 in (ii)
8x = 3 – 2(1)
8x = 1
x = 1/8
So, the solution set is (1/8, 1).
NUMBER SENSE
For what value of a might you choose to solve the system by elimination? Explain.
Question 31.
4x – y = 3
ax + 10y = 6
Answer:
If a is 4 or -4 it is easy to solve the systems of linear equations using the elimination method as by just subtracting or adding the equations, we can eliminate x.
Explanation:
The systems of linear equations are
4x – y = 3
ax + 10y = 6
If a is 4 or -4 it is easy to solve the systems of linear equations using the elimination method as by just subtracting or adding the equations, we can eliminate x.
Question 32.
x – 7y = 6
-6x + ay = 9
Answer:
If a is 7 or -7 it is easy to solve the systems of linear equations using the elimination method as by just adding or subtracting the equations, we can eliminate x.
Explanation:
The systems of linear equations are
x – 7y = 6
-6x + ay = 9
If a is 7 or -7 it is easy to solve the systems of linear equations using the elimination method as by just adding or subtracting the equations, we can eliminate x.
CRITICAL THINKING
Determine whether the line through the first pair of points intersects the line through the second pair of points. Explain.
Question 33.
Line 1: (-2, 1), (2, 7)
Line 2: (-4, -1), (0, 5)
Answer:
No
Explanation:
Equation of a line passing through points (x₁, y₁) and (x₂, y₂) is y – y₁ = (y₂ – y₁)/(x₂ – x₁) (x – x₁)
So, equation of line 1 is
y – 1 = (7 – 1)/(2 + 2)(x + 2)
y – 1 = 6/4 (x + 2)
y – 1 = 3/2 (x + 2)
2(y – 1) = 3(x + 2)
2y – 2 = 3x + 6
3x – 2y = -2 – 6
3x – 2y = -8
Equation of line 2 is
y + 1 = (5 + 1)/(0 + 4) (x + 4)
y + 1 = 6/4 (x + 4)
y + 1 = 3/2 (x + 4)
2(y + 1) = 3(x + 4)
2y + 2 = 3x + 12
3x – 2y = 2 – 12
3x – 2y = -10
As the slope of the lines are same, but the consant is different, the lines are parallek to each other and there is no point of intersection.
Question 34.
Line 1: (-2, 8), (0, 2)
Line 2: (3, -2), (6, 4)
Answer:
Yes
Explanation:
Equation of a line passing through points (x₁, y₁) and (x₂, y₂) is y – y₁ = (y₂ – y₁)/(x₂ – x₁) (x – x₁)
So, line 1 is
y – 8 = (2 – 8)/(0 + 2) (x + 2)
y – 8 = -6/2 (x + 2)
y – 8 = -3(x + 2)
y – 8 = -3x – 6
3x + y = -6 + 8
3x + y = 2
Line 2 is
y + 2 = (4 + 2)/(6 – 3) (x – 3)
y + 2 = 6/3 (x – 3)
y + 2 = 2(x – 3)
y + 2 = 2x – 6
2x – y = 8
As the slopes are different, so the lines intesect each other.
Question 35.
REASONING
Two airplanes are flying to the same airport. Their positions are shown in the graph. Write a system of linear equations that represents this situation. Solve the system by elimination to justify your answer.
Answer:
x = 6, y = 12.
Explanation:
To write the system we need the slope of each line and at least one point on the line. The two lines to consider will be the lines connecting the location of each plane to the airport they are flying to. It is also worth noting that the coordinates of the airport represent the point of intersection of the two lines and thus the solution to the system.
Airport (6, 12), Airplane 1 (2, 4), Airplane 2 (15, 9)
the slope of the line connecting airplane 1 and the airport = (4 – 12)/(2- 6)
= -8/-4 = 2
The line equation is y – 4 = 2(x -4)
2x – y = 0
slope of the line connecting airplane 2 and the airport = (4 – 9)/(2 – 15)
= -5/-13 = 5/13
The line equation is y – 9 = 5/13 (x – 15)
x + 3y = 42
So, the system of linear equations are
2x – y = 0 —- (i)
x + 3y = 42 —– (ii)
Multiply (ii) by 2
2(x + 3y = 42)
2x + 6y = 84 — (iii)
Subtract (iii) & (i)
2x – y – 2x – 6y = 0 – 84
-7y = -84
y = 12
Put y = 12 in (i)
2x – 12 = 0
x = 6
We have proven that the location of the airport is in fact the solution to our system.
Question 36.
MODELING REAL LIFE
A laboratory uses liquid nitrogen tanks of two different sizes. The combined volume of 3 large tanks and 2 small tanks is 24 liters. The combined volume of 2 large tanks and 3 small tanks is 21 liters. What is the volume of each size of tank? Justify your answer.
Answer:
The volume of the large tank is 6 lit, the volume of the small tank is 3 lit.
Explanation:
Let x and y be the volume of the large and small tank
The combined volume of 3 large tanks and 2 small tanks is 24 liters. The combined volume of 2 large tanks and 3 small tanks is 21 liters
Combined volume = No of large tanks x volume of large tank + No of small tanks x volume of small tank
3x + 2y = 24 — (i)
2x + 3y = 21 —- (ii)
Multiply (i) by -2 and (ii) by 3
-2(3x + 2y = 24)
-6x – 4y = -48
3(2x + 3y = 21)
6x + 9y = 63
Add obtained equations
-6x – 4y + 6x + 9y = -48 + 63
5y = 15
y = 3
Put y = 3 in (i)
3x + 6 = 24
3x = 24 – 6
3x = 18
x = 6
So, the volume of the large tank is 6 lit, volume of the small tank is 3 lit.
Question 37.
PROBLEM SOLVING
The table shows the numbers of correct answers on a practice standardized test. You score 86 points on the test and your friend scores 76 points. How many points is each type of question worth?
Answer:
The marks for correct multiple choice questions, short response questions are 2 and 4.
Explanation:
Let x, y be the marks of multiple choice & short response questions
Total marks = no of correct MCQs x marks for correct MCQs + no of short response questions x marks for short response questions
23x + 10y = 86 — (i)
28x + 5y = 76 —- (ii)
Multiply (ii) by 2
2(28x + 5y = 76)
56x + 10y = 152 —- (iii)
Subtract (i) & (iii)
23x + 10y – 56x – 10y = 86 – 152
-33x = -66
x = 2
Put x = 2 in (i)
23(2) + 10y = 86
10y = 86 – 46
10y = 40
y = 4
So, the marks for correct multiple choice questions, short response questions are 2 and 4.
Question 38.
LOGIC
You solve a system of equations in which x represents the number of adult memberships sold and y represents the number of student memberships sold. Can (-6, 24) be the solution to the system? Explain your reasoning.
Answer:
If x represents the number of adult tickets sold, then x must be a non-negative number since there can’t be a negative number of tickets sold.
Therefore (-6, 24) can’t be a solution since that would give x = 6.
Explanation:
If x represents the number of adult tickets sold, then x must be a non-negative number since there can’t be a negative number of tickets sold.
Therefore (-6, 24) can’t be a solution since that would give x = 6.
Question 39.
PROBLEM SOLVING
The table shows the activities of two tourists at a vacation resort. You want to go parasailing for 1 hour and horseback riding for 2 hours. How much do you expect to pay?

Answer:
The cost of parasailing for 1 hour and horseback riding for hours is $90.
Explanation:
Let x and y represent per hour price for parasailing and horseback riding
Total cost = no of hours of parasailing x per hour price for parasailing + no of hours of horseback riding x per hour price for horseback riding
2x + 5y = 205 —- (i)
3x + 3y = 240 — (ii)
Multiply (i) by 3 and (ii) by 2
3(2x + 5y = 205)
6x + 15y = 615 — (iii)
2(3x + 3y = 240)
6x + 6y = 480 —- (iv)
Subtract (iii) & (iv)
6x + 15y – 6x – 6y = 615 – 480
9y = 135
y = 15
Put y = 15 in (i)
2x + 15(5) = 205
2x = 205 – 75
2x = 130
x = 65
So, the Cost of parasailing for 1 hour and harseback riding for hours is x + 2y
= 65 + 2(15)
= $95.
Question 40.
REASONING
Write a system of linear equations containing 2x + y = 0 and that has the solution (2, -4).
Answer:
The system of linear equations are 2x + y = 0, x – y = 6.
Explanation:
The equation of a line that passes through (2, -4) is y = mx + b
-4 = 2m + b
Let us take m slope as 1
-4 = 2 + b
b = -4 – 2
b = -6
So, line is y = x – 6
So, the system of linear equations are 2x + y = 0, x – y = 6.
Question 41.
REASONING
A metal alloy is a mixture of two or more metals. A jeweler wants to make 8 grams of 18-karat gold, which is 75% gold. The jeweler has an alloy that is 90% gold and an alloy that is 50% gold. old. How much of each alloy should the jeweler use?

Answer:
The jeweler should use 5, 3 grams of first and second alloy.
Explanation:
Let x, y be the amount of first & second alloy
Amount of gold = percentage of gold in first alloy x amount of first alloy + percentage of gold in second alloy x amount of the second alloy
x + y = 8
0.9x + 0.5y = 6
y = 8 – x
0.9x + 0.5(8 – x) = 6
0.4x + 4 = 6
0.4x = 2
x = 5
y = 8 – 5
y = 3
The jeweler should use 5, 3 grams of first and second alloy.
Question 42.
PROBLEM SOLVING
It takes a powerboat traveling with the current 30 minutes to go 10 miles. The return trip takes 50 minutes traveling against the current. What is the speed of the current?
Answer:
The current speed is 4 miles per hour.
Explanation:
Let r be the speed of the boat and w be the speed of water current
downstream 10 = (r + w)30
1 = 3(r + w)
3r + 3w = 1 — (i)
Upstream 10 = (r – w)50
1 = 5(r – w)
5r – 5w = 1 —- (ii)
Multiply (i) by 5 and (ii) by 3 and add them
15r + 15w + 15r – 15w = 5 + 3
30r = 8
r = 4/15
substitute r = 4/15 in (ii)
5(4/15) – 5w = 1
4/3 – 5w = 1
-5w = -1/3
w = 1/15 miles per inute
= 1/15 (60) = 4 miles per hour
The current speed is 4 miles per hour.
Question 43.
DIG DEEPER!
Solve the system of equations by elimination.
2x – y + 3z = -1
x + 2y – 4z = -1
y – 2z = 0
Answer:
The solution set is (-1, 2, 1).
Explanation:
The given systems of linear equations are
2x – y + 3z = -1 —– (i)
x + 2y – 4z = -1 —- (ii)
y – 2z = 0 —– (iii)
Substitute y = 2z in (i) & (ii)
2x – 2z + 3z = -1
2x+ z = -1 —- (iv)
x + 4z – 4z = -1
x = -1
Substitute x = -1 in (iv)
2(-1) + z = -1
z = -1 + 2
z = 1
Substitute z = 1 in (iii)
y – 2 = 0
y = 2
So, the solution set is (-1, 2, 1).
Lesson 5.4 Solving Special Systems of Linear Equations
EXPLORATION 1
Exploring Solutions of Systems
Work with a partner. You spend $50 on a sewing machine to makedog backpacks. Each backpack costs you $15 for materials.
a. Represent the cost (in dollars) to make backpacks in the coordinate plane.

b. You charge $25 per backpack. How many backpacks do you have to break even sell to ? Use a graph to justify your answer.
c. Can you break even when you sell each backpack for $20? $15? Use graphs to justify your answers.

d. Explain whether it is possible for a system of linear equations to have the numbers of solutions below.
- no solution
- exactly one solution
- exactly two solutions
- infinitely many solutions

5.4 Lesson
Try It
Solve the system. Explain your choice of method.
Question 1.
y = -x + 3
y = -x + 5
Answer:
There is no solution.
Explanation:
The given systems of linear equations are
y = -x + 3
y = -x + 5
The two lines are parallel to each other.
So, there is no solution.
Question 2.
y = -5x – 2
5x + y = 0
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are y = -5x – 2, 5x + y = 0
The two lines are parallel to each other.
So, the system has no solution.
Question 3.
x = 2y + 10
2x + 3y = -1
Answer:
The solution set is (4, -3)
Explanation:
The given systems of linear equations are x = 2y + 10, 2x + 3y = -1
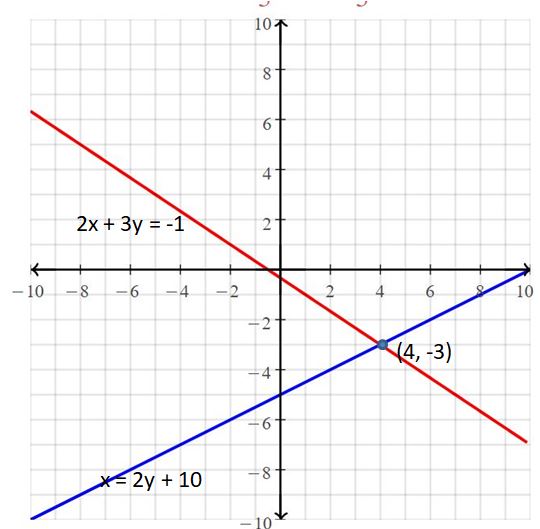
The point of intersection of two lines is (4, -3)
So, the solution set is (4, -3)
Try It
Solve the system. Explain your choice of method.
Question 4
x + y = 3
x = y – 3
Answer:
The solution set is (0, 3).
Explanation:
The given systems of linear equations are
x + y = 3 — (i)
x = y – 3 —- (ii)
Substitute (ii) in (i)
y – 3 + y = 3
2y = 6
y = 3
Substitute y = 3 in (ii)
x = 3 – 3
x = 0
So, the solution set is (0, 3).
Question 5.
2x + y = 5
4x + 2y = 0
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are
2x + y = 5 —- (i)
4x + 2y = 0 —- (ii)
Solve by graphing
The lines are parallel so the system has no solution.
Question 6.
2x – 4y = 10
-12x + 24y = -60
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
2x – 4y = 10 —- (i)
-12x + 24y = -60 — (ii)
Multiply (i) by 6
6(2x – 4y = 10)
12x – 24y = 60 — (iii)
Add (ii) & (iii)
-12x + 24y + 12x – 24y = -60 + 60
0 = 0
So, the system has infinitely many solutions.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
STRUCTURE
Without graphing or solving, determine the number of solutions of the system. Explain your reasoning.
Question 7.
y = 5x – 9
y = 5x + 9
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
y = 5x – 9
y = 5x + 9
the slope of the two lines are the same i.e 5
So, the system has infinitely many solutions.
Question 8.
y = 6x + 2
y = 3x + 1
Answer:
The system has one solution.
Explanation:
The given systems of linear equations are
y = 6x + 2
slope1 = 6
y = 3x + 1
slope2 = 3
Slopes are different
So, the system has one solution.
Question 9.
y = 8x – 2
y – 8x = -2
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
y = 8x – 2
slope 1 = 8
y – 8x = -2
y = -2 + 8x
slope 2 = 8
the slope of the two lines are the same i.e 8
So, the system has infinitely many solutions.
CHOOSING A METHOD
Solve the system. Explain your choice of method.
Question 10.
2x + y = 6
x – y = 3
Answer:
The solution set is (3, 0).
Explanation:
The given systems of linear equations are
2x + y = 6 —- (i)
x – y = 3 — (ii)
Add equations
2x + y + x – y = 3 + 6
3x = 9
x = 3
Substitute x = 3 in (ii)
3 – y = 3
y = 0
So, the solution set is (3, 0).
Question 11.
4y – 4x = 8
y = x + 2
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
4y – 4x = 8 — (i)
y = x + 2 —- (ii)
Substitute 2 in 1
4(x + 2) – 4x = 8
4x + 8 – 4x = 8
8 = 8
So, the system has infinitely many solutions.
Question 12.
5x – 4y = 12
7.5x = 6(y – 1)
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are
5x – 4y = 12
7.5x = 6(y – 1)
By graphing
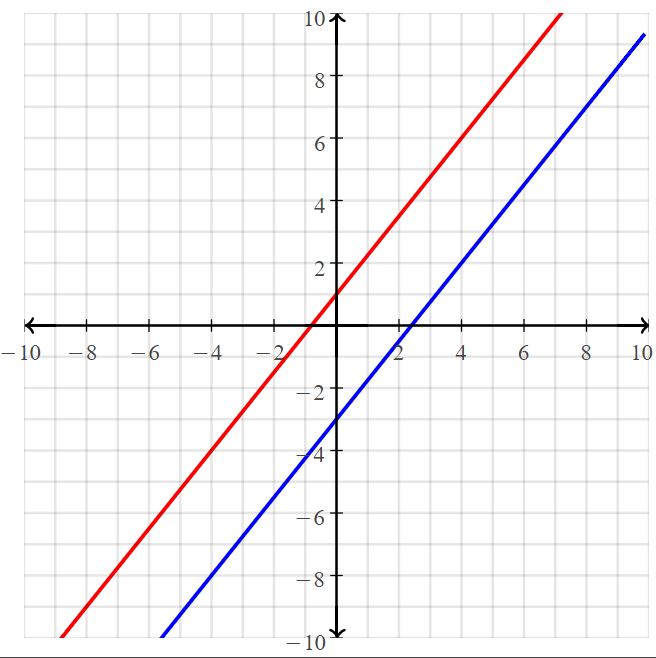
The lines are parrel
So, the system has no solution.
Question 13.
-6x = 9
6x – y = 3
Answer:
The solution set is (-3/2, -12)
Explanation:
The given systems of linear equations are
-6x = 9
6x – y = 3
-6x = 9
x = -9/6
x = -3/2
Substitute x = -3/2 in 6x – y = 3
6(-3/2) – y = 3
-18/2 – 3 = y
y = -24/2
y = -12
So, the solution set is (-3/2, -12)
Question 14.
0.5x + 4y = -11
-1.5x – 12y = 33
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
0.5x + 4y = -11
-1.5x – 12y = 33
By graphing
Two equations are on the same line.
So, the system has infinitely many solutions.
Question 15.
x = y + 2
3x = 6(y + 2)
Answer:
The solution set is (0, -2).
Explanation:
The given systems of linear equations are
x = y + 2
3x = 6(y + 2)
By graphing
The point of intersection of two equations is (0, -2)
so, the solution set is (0, -2).
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
Your friend wants to sell painted rocks. He spends $10.00 on startup costs, and each painted rock costs him $0.75 to make. A store offers to pay your friend’s startup costs and buy his painted rocks for $0.75 each. How many painted rocks does your friend need to sell to make a profit?
Answer:
No profit.
Explanation:
The cost on startup is $10 and each painted rock costs around $0.75 to make
A store pays startup cost and buys his painted rocks for $0.75 each
There will be no profit because the cost price and selling price is the same. He buys for $0.75 and sells the same for $0.75.
Question 17.
DIG DEEPER!
The difference in age of two orangutans is 6 years. In 4 years, is it possible for the older orangutan to be twice as old as the younger orangutan? three times as old? Justify your answers.

Answer:
Both are possible
Explanation:
Let us take the age of two orangutans as x and y
The difference in age of two orangutans is 6 years
x – y = 6
So, x is the older one
x = 6 + y
If the older orangutan to be twice as old as the younger orangutan
x = 2y
2y – y = 6
y = 6
If the older orangutan to be three times as old as the younger orangutan
x = 3y
3y – y = 6
2y = 6
y = 3
Both are possible, the older orangutan to be twice as old as the younger orangutan when younger age is 6 years and the older orangutan to be three times as old as the younger orangutan when the younger age is 3 years.
Solving Special Systems of Linear Equations Homework & Practice 5.4
Review & Refresh
Solve the system by elimination. Check your solution.
Question 1.
x + 2y = 4
-x – y = 2
Answer:
The solution set is (-8, 6)
Explanation:
The given systems of linear equations are
x + 2y = 4 — 1
-x – y = 2 — 2
Add both equations
x + 2y – x – y = 4 + 2
y = 6
Substitute y = 6 in 2
-x – 6 = 2
-x = 2 + 6
x = -8
Substitute x = -8, y = 6 in 2
8 – 6 = 2
So, the solution set is (-8, 6)
Question 2.
2x – y = 1
x + 3y – 4 = 0
Answer:
The solution set is (1, 1).
Explanation:
The given systems of linear equations are
2x – y = 1 —- (i)
x + 3y – 4 = 0 —- (ii)
Multiply (i) by 3
3(2x – y = 1)
6x – 3y = 3 —- (iii)
Add (iii) & (ii)
6x – 3y + x + 3y – 4 = 3
7x = 3 + 4
7x = 7
x = 1
Substitute x = 1 in (i)
2(1) – y = 1
2 – y = 1
2 – 1 = y
y = 1
Substitute x = 1, y = 1 in (i)
2(1) – 1 = 2 – 1 = 1
So, the solution set is (1, 1).
Question 3.
3x = -4y + 10
4x + 3y = 11
Answer:
The solution set is (2, 1).
Explanation:
The given systems of linear equations are
3x = -4y + 10
3x + 4y = 10 —- (i)
4x + 3y = 11—- (ii)
Multiply (i) by 4 and (ii) by 3
4(3x + 4y = 10)
12x + 16y = 40 —- (iii)
3(4x + 3y = 11)
12x + 9y = 33 —- (iv)
Subtract (iii) from (iv)
12x + 16y – 12x – 9y = 40 – 33
7y = 7
y = 1
Substitute y = 1 in (i)
3x + 4 = 10
3x = 6
x = 2
Substitute x = 2, y = 1 in (i)
3(2) + 4 = 6 + 4 = 10
So, the solution set is (2, 1).
Write an equation of the line that passes through the given points.
Question 4.
(0, 0), (2, 6)
Answer:
y = 3x
Explanation:
The equation of a line when two points given is
(y – y₁) = [(y₂ – y₁)/(x₂ – x₁)](x – x₁)
x₁ = 0, y₁ = 0, x₂ = 2, y₂ = 6
So, (y – 0) = [(6 – 0)/(2 – 0)] (x – 0)
y = 3x
Question 5.
(0, -3), (3, 3)
Answer:
y = 2x – 3
Explanation:
The equation of a line when two points given is
(y – y₁) = [(y₂ – y₁)/(x₂ – x₁)](x – x₁)
x₁ = 0, y₁ = -3, x₂ = 3, y₂ = 3
So, (y + 3) = [(3 + 3)/(3 – 0)](x – 0)
(y + 3) = 2x
y = 2x – 3
Question 6.
(-6, 5), (0, 2)
Answer:
x + 2y = 6
Explanation:
The equation of a line when two points are given is
(y – y₁) = [(y₂ – y₁)/(x₂ – x₁)](x – x₁)
x₁ = -6, y₁ = 5, x₂ = 0, y₂ = 2
So, (y – 5) = [(2 – 5)/(0 + 6)](x + 6)
y – 6 = -3/6 (x + 6)
y – 6 = -1/2 (x + 6)
2(y – 6) = -1(x + 6)
2y – 12 = -x – 6
2y = -x – 6 + 12
x + 2y = 6
Concepts, Skills, &Problem Solving
EXPLORING SOLUTIONS OF SYSTEMS
Use a graph to determine the number of solutions of the system. (See Exploration 1, p. 219.)
Question 7.
y = 2x + 1
y = 2x + 5
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are y = 2x + 1, y = 2x + 5
Graph the equations
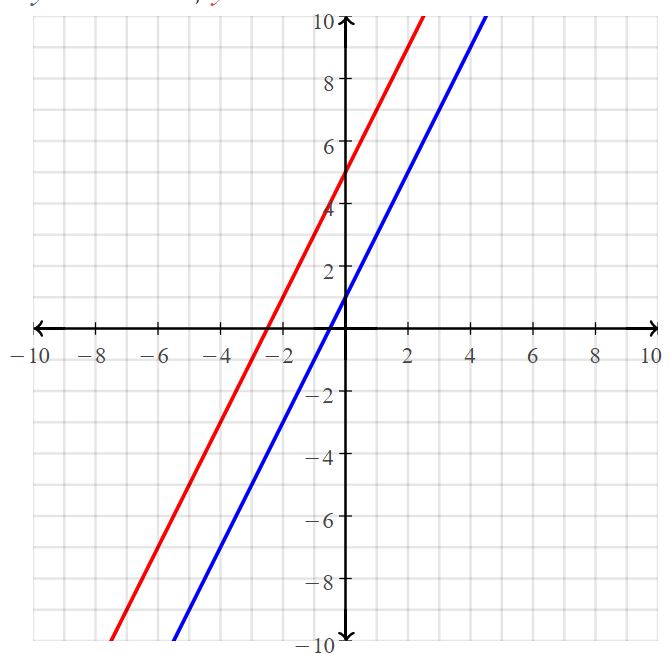
The lines are parallel
So, the system has no solution.
Question 8.
y + 8 = 0
y = 8
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are y + 8 = 0, y = 8
Graph the equations
The lines are parallel
So, the system has no solution.
Question 9.
x + y = 2
5x + y = 9
Answer:
The solution is (7/4, 1/4)
Explanation:
The given systems of linear equations are x + y = 2, 5x + y = 9
Graph the equations
The lines intersect at (7/4, 1/4)
So, the solution is (7/4, 1/4)
SOLVING A SYSTEM
Solve the system. Explain your choice of method.
Question 10.
y = 2x – 2
y = 2x + 9
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are
y = 2x – 2 — (i)
y = 2x + 9 — (ii)
Equate equations
2x – 2 = 2x + 9
So, the system has no solution.
Question 11.
y = 3x + 1
-x + 2y = -3
Answer:
The solution is (-1, -2).
Explanation:
The given systems of linear equations are y = 3x + 1, -x + 2y = -3
Graph the equations
The lines intersect at (-1, -2)
So, the solution is (-1, -2).
Question 12.
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are
y = π/3 x + π —- (i)
-πx + 3y = -6π —- (ii)
Substitute (i) in (ii)
-πx + 3(π/3 x + π) = -6π
-πx + πx + 3π = -6π
So, the system has no solution.
Question 13.
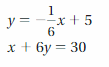
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
y = -1/6 x + 5 —-(i)
x + 6y = 30 —- (ii)
Substitute (i) in (ii)
x + 6(-1/6 x + 5) = 30
x – x + 30 = 30
So, the system has infinitely many solutions.
Question 14.
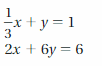
Answer:
The system has infinitely many solutions.
Explanation:
The given systems of linear equations are
1/3 x + y = 1 —- (i)
2x + 6y = 6 —- (ii)
Divide (ii) by 1/6
1/6(2x + 6y = 6)
1/3 x + y = 1 —- (iii)
equation (i) & (iii) are same
So, the system has infinitely many solutions.
Question 15.
-2x + y = 1.3
2(0.5x – y) = 4.6
Answer:
The solution is (-2.4, -3.5)
Explanation:
The given systems of linear equations are -2x + y = 1.3, 2(0.5x – y) = 4.6
Graph the equations
The lines intersect at (-2.4, -3.5)
So, the solution is (-2.4, -3.5)
Question 16.
2(x + y) = 9
1 = -4(x + y)
Answer:
The system has no solution.
Explanation:
The given systems of linear equations are 2(x + y) = 9, 1 = -4(x + y)
Graph the equations
The lines are parallel
So, the system has no solution.
Question 17.
y = 9x
x + y = 1
Answer:
The solution is (1/10, 9/10)
Explanation:
The given systems of linear equations are y = 9x, x + y = 1
Graph the equations
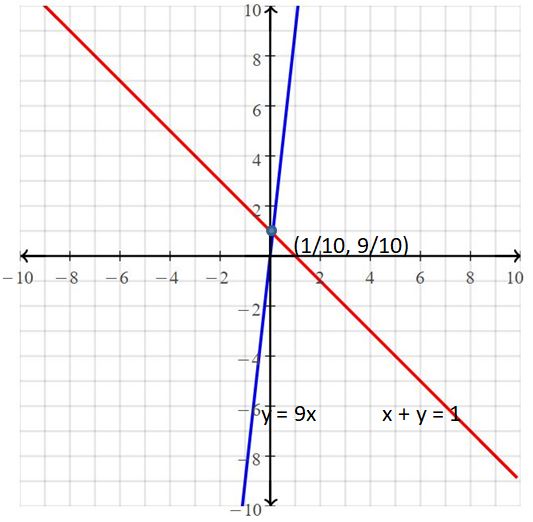
The lines intersect at (1/10, 9/10)
So, the solution is (1/10, 9/10)
Question 18.
0.2y = 4.6x + 1.2
-2.3x = -0.1y + 0.6
Answer:
The system has infinitely many solutions
Explanation:
The given systems of linear equations are 0.2y = 4.6x + 1.2, -2.3x = -0.1y + 0.6
Graph the equations
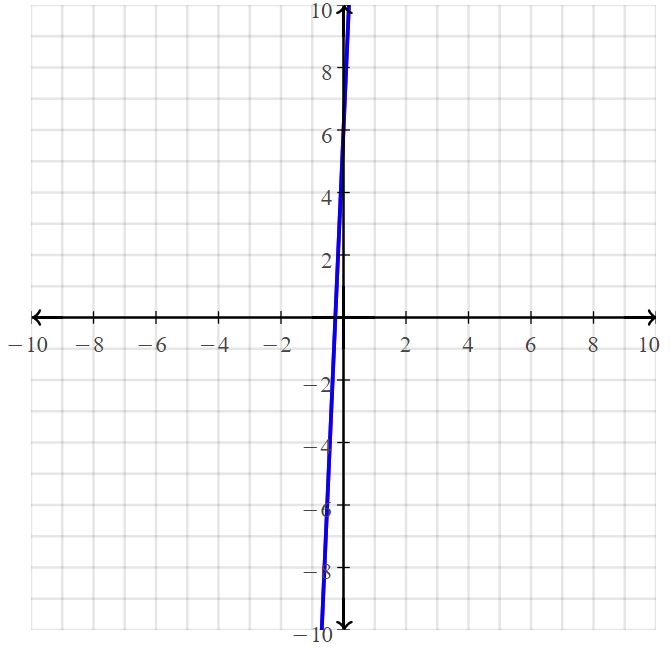
Two equations lies on the same line
So, the system has infinitely many solutions
Question 19.
YOU BE THE TEACHER
Your friend finds the number of solutions of the system. Is your friend correct? Explain your reasoning.
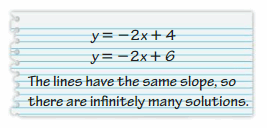
Answer:
Correct.
Explanation:
The given systems of linear equations are
y = -2x + 4
y = -2x + 6
Two equations have the same slope
So, the system has infinitely many solutions.
Question 20.
REASONING
In a pig race, your pig has a head start of 3 feet and runs at a rate of 2 feet per second. Your friend’s pig also runs at a rate of 2 feet per second. A system of linear equations that represents this situation is y = 2x + 3 and y = 2x. Does your friend’s pig catch up to your pig? Explain.

Answer:
No.
Explanation:
y = 2x + 3 and y = 2x
Substitute y = 2x in y = 2x + 3
2x = 2x + 3
2x – 2x = 3
0 = 3
The system has no solution
Your friend’s pig never catch up to your pig
Question 21.
REASONING
One equation in a system of linear equations has a slope of 3. The other equation has a slope of 4. How many solutions does the system have? Explain.
Answer:
The system has one solution.
Explanation:
One equation in a system of linear equations has a slope of 3. The other equation has a slope of 4
As the slopes are different. The system has one solution.
Question 22.
LOGIC
How can you use the slopes and the y-intercepts of equations in a system one solution, infinitely many solutions, or no solution?
Answer:
The slope-intercept form of a line is y = mx + c
If the slope is the same, different y-intercept for the two equations, then the system has no solution.
If the slope is different for two equations, then the system has one solution.
If the slope is the same, the same y-intercept for two equations, then the system has infinitely many solutions.
Question 23.
PROBLEM SOLVING
You and a friend both work two different jobs. The system of linear equations represents the total earnings (in dollars) for x hours worked at the first job and y hours worked at the second job. Your friend earns twice as much as you.

a. One week, both of you work 4 hours at the first job. How many hours do you and your friend work at the second job?
b. Both of you work the same number of hours at the second job. Compare the number of hours you and your friend work at the first job.
Answer:
a. 16 hours you and your friend work at the second job
b. If both work the same y hours at a second job, then both will same x hours at the first job.
Explanation:
Let x represent the first job and y represents the second job
The system of linear equations for the total number of hours for the first job & second job for you & your friend is
4x + 8y = 64
8x + 16y = 128
a. If x = 4
8(4) + 16y = 128
32 + 16y = 128
16y = 128 – 32
16y = 96
y = 16 hours
b. If both work the same y hours at the second job, then both will same x hours at the first job.
Question 24.
MODELING REAL LIFE
You download a digital album for $10.00. Then you and your friend each download the same number of individual songs for $0.99 each. Write a system of linear equations that represents this situation. Will you and your friend spend the same amount of money? Explain.
Answer:
No
Explanation:
Write the equations for you and your friends’ total cost y where x is the number of songs
you y = 10 + 0.99x
your friend y = 0.99x
The two equations have the same slope but different y-intercepts so the system has no solution.
Question 25.
MODELING REAL LIFE
The table shows the research activities of two students at an observatory. How much does a student pay to use the telescope for one hour?
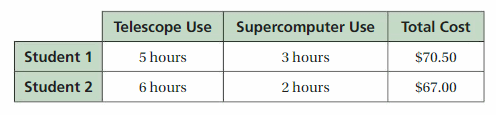
Answer:
A student must pay $7.5 for using a telephone per hour and $11 for using a supercomputer per hour.
Explanation:
Let the cost of telephonic use be x, supercomputer use be y. The system of equations are
5x + 3y = 70.50 — (i)
6x + 2y = 67 —- (ii)
Multiply (i) by 2 and (ii) by 3 and subtract them
10x + 6y = 141
18x + 6y = 201
10x + 6y – 18x – 6y = 141 – 201
-8x = -60
x = 7.5
Substitute x = 7.5 in (ii)
6(7.5) + 2y = 67
45 + 2y = 67
2y = 67 – 45
2y = 22
y = 11
So, a student must pay $7.5 for using telephone per hour and $11 for using supercomputer per hour.
Question 26.
REASONING
Does the system shown always, sometimes, or never have a solution when a = b? a ≥ b? a < b? Explain your reasoning.
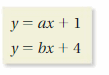
Answer:
If a = b, the system will always have no solution
If a ≥ b, the system will sometimes have no solution.
If a < b, the system will never have no solution.
Explanation:
If a = b, then two linear equations will have the same slope but different y-intercepts. So, they will always have no solution
If a ≥ b, then the slopes may be different or the same so they may intersect once or not at all. Therefore, they will sometimes have no solution.
If a < b, then the equations have a different slope so they will intersect once. so, they will never have no solution.
Question 27.
LOGIC
The table shows the numbers of lift tickets and ski rentals sold to different groups. Is it possible to determine how much each lift ticket costs using the information for Groups 1 and 2? Groups 1 and 3? Justify your answers.
Answer:
a. It is not possible to find out the cost of lift tickets using the given information.
b. The cost of a lift ticket is $14, cost of ski rental is $10.
Explanation:
Let the cost for lift tickets and cost for sky rentals be y. The system of equations are
36x + 18y = 684 — (i)
24x + 12y = 456 —- (ii)
18x + 18y = 432 —-(iii)
3(12x + 6y) = 684
12x + 6y = 228
2(12x + 6y) = 456
12x + 6y = 228
Both the equations are same. So, they have infinately many solutions.
Hence, it is not possible to find out the cost of lift tickets using the given information.
b. Subtract 1 from 2
36x + 18y – 18x – 18y = 684 – 432
18x = 252
x = 14
Put x = 14
36(14) + 18y = 684
504 + 18y = 684
18y = 180
y = 10
The cost of lift ticket is $14, cost of ski rentaks is $10.
Question 28.
DIG DEEPER!
Find the values of a and b so the system is shown has the solution (2, 3). Does the system have any other solutions for these values of a and b? Explain.
Answer:
(a, b) = (2, 2)
Explanation:
Given that,
12x – 2by = 12
3ax – by = 6
The value of a, b if (x, y) = (2, 3)
12(2) – 2b(3) = 12
24 – 6b = 12
6b = 24 – 12
6b = 12
b = 2
3a(2) – 3b = 6
6a – 3(2) = 6
6a – 6 = 6
6a = 12
a = 2
The system of equations are
12x – 4y = 12
2(6x – 2y) = 12
6x – 2y = 6 — (i)
6x – 2y = 6 — (ii)
As both the equations are same, they have infinately many solutions
(a, b) = (2, 2)
Systems of Linear Equations Connecting Concepts
Connecting Concepts
Using the Problem-Solving Plan
Question 1.
An animal shelter has a total of 65 cats and dogs. The ratio of cats to dogs is 6:7. Find the number of cats and the number of dogs in the shelter.

Understand the problem.
You know the total number of cats and dogs in an animal shelter, and the ratio of cats to dogs. You are asked to find the number of cats and the number of dogs in the shelter.
Make a plan.
Write a system of equations. Use the total number of cats and dogs to write an equation relating the number of cats and the number of dogs. Use the ratio of cats to dogs to write a second equation. Then solve the system.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
The number of cats in the shelter is 30, the number of dogs are 35.
Explanation:
Let us take the number of dogs as x, cats as y
An animal shelter has a total of 65 cats and dogs.
x + y = 65 — (i)
The ratio of cats to dogs is 6:7
x : y = 6 : 7
6x = 7y
x = 7y/6
Substitute x = 7y/6 in (i)
7y/6 + y = 65
7y + 6y = 65(6)
13y = 390
y = 30
Substitute y = 30 in (i)
x + 30 = 65
x = 65 – 30
x = 35
So, the number of cats in the shelter are 30, number of dogs are 35.
Question 2.
The measure of ∠1 is 15 degrees less than two times the measure of ∠2. Find the measure of each of the four angles formed by the intersecting lines. Justify your answer.
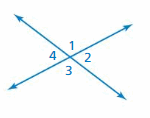
Answer:
The angles are ∠1 = 125, ∠2 = 55, ∠3 = 125, ∠4 = 55.
Explanation:
The measure of ∠1 is 15 degrees less than two times the measure of ∠2.
∠1 – 15 = 2(∠2) — (i)
∠1 + ∠2 = 180 degrees — (ii)
∠1 = 180 – ∠2
180 – ∠2 – 15 = 2(∠2)
165 = 2∠2 + ∠2
165 = 3∠2
∠2 = 55 degrees
Substitute ∠2 = 55 in (i)
∠1 – 15 = 2(55)
∠1 = 110 + 15
∠1 = 125 degrees
So, the angles are ∠1 = 125, ∠2 = 55, ∠3 = 125, ∠4 = 55.
Question 3.
A landscaper plants grass seed over the entire area of two parks that are similar in shape. The ratio of the perimeter of Park A to the perimeter of Park B is 2 : 1. The parks have a combined area of 9000 square feet. How many square feet does the landscaper cover with grass seed at ParkA? Park B? Justify your answer.

Answer:
The landscaper cover with grass seed at ParkA is 60√2 at park B is 30√2.
Explanation:
let the side of park A is x, park b is y.
The ratio of the perimeter of Park A to the perimeter of Park B is 2 : 1
x : y = 2 : 1
x = 2y — (i)
The parks have a combined area of 9000 square feet
x² + y² = 9000 —- (ii)
Substitute x = 2y in (ii)
(2y)² + y² = 9000
4y² + y² = 9000
5y² = 9000
y² = 1800
y = 30√2
Substitute y = 30√2 in (i)
x = 2(30√2)
= 60√2
The landscaper cover with grass seed at ParkA is 60√2 at park B is 30√2.
Performance Task
Mixing Alloys
At the beginning of this chapter, you watched a STEAM Video called “Gold Alloys.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Systems of Linear Equations Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
![]()
Graphic Organizers
You can use a Four Square to organize information about a concept. Each of the four squares can be a category, such as definition, vocabulary, example, non-example, words, algebra, table, numbers, visual, graph, or equation. Here is an example of a Four Square for solving systems of linear equations by graphing.
Choose and complete a graphic organizer to help you study the concept.
- solving systems of linear equations by substitution
- solving systems of linear equations by elimination
- systems of linear equations with no solution
- systems of linear equations with infinitely many solutions

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

5.1 Solving Systems of Linear Equations by Graphing (pp. 199-204)
Solve the system by graphing.
Question 1.
y = 2x – 3
y = x + 2
Answer:
The solution is (5, 7)
Explanation:
The given systems of linear equations are y = 2x – 3, y = x + 2
Graph the equations
The lines intersect at (5, 7)
So, the solution is (5, 7)
Question 2.
y = -x + 4
x + 2y = 0
Answer:
The solution is (8, -4)
Explanation:
The given systems of linear equations are y = -x + 4, x + 2y = 0
Graph the equations
The lines intersect at (8, -4)
So, the solution is (8, -4)
Question 3.
x – y = -2
2x – 3y = -2
Answer:
The solution is (-4, -2).
Explanation:
The given systems of linear equations are x – y = -2, 2x – 3y = -2
Graph the equations
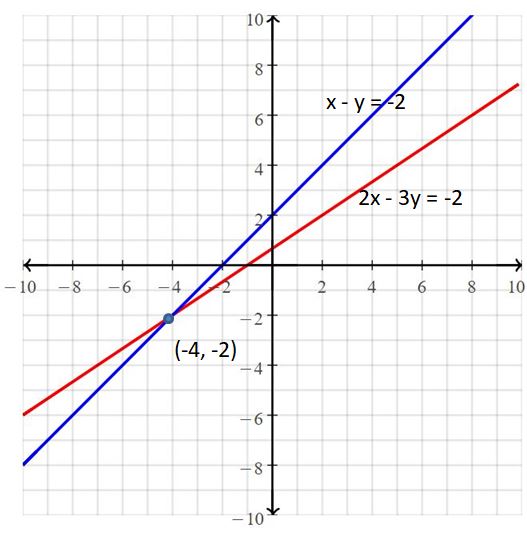
The lines intersect at (-4, -2)
So, the solution is (-4, -2)
Use a graphing calculator to solve the system.
Question 4.
y = -0.5x
y = 0.75x + 1.25
Answer:
The solution is (-1, 0.5)
Explanation:
The given systems of linear equations are y = -0.5x, y = 0.75x + 1.25
Graph the equations
The lines intersect at (-1, 0.5)
So, the solution is (-1, 0.5)
Question 5.
y = 0.2x – 3
10x + 3y = 5
Answer:
The solution is (1.3, -2.7)
Explanation:
The given systems of linear equations are y = 0.2x – 3, 10x + 3y = 5
Graph the equations
The lines intersect at (1.3, -2.7)
So, the solution is (1.3, -2.7)
Question 6.
2.6x + 1.3y = 7.8
1.2x – 3.6y = 12
Answer:
The solution is (4, -2)
Explanation:
The given systems of linear equations are 2.6x + 1.3y = 7.8, 1.2x – 3.6y = 12
Graph the equations
The lines intersect at (4, -2)
So, the solution is (4, -2)
Question 7.
The sum of the two numbers is 38. Find each number when one number is 8 more than the other number. Use a system of linear equations to justify your answer.
Answer:
The numbers are 15, 28.
Explanation:
Let the two numbers be x, y
The sum of two numbers is 38
x + y = 38 — (i)
One number is 8 more than the other number
x + 8 = y — (ii)
Substitute y = x + 8 in (i)
x + x + 8 = 38
2x + 8 = 38
2x = 38 – 8
2x = 30
x = 15
Substitute x = 15 in (ii)
y = 15 + 8
y = 23
So, the numbers are 15, 28.
Question 8.
You observe the heights of two plants for an experiment. Plant A has a height of 8 centimeters and grows 1 centimeter each week. Plant B has a height of 4 centimeters and grows 2 centimeters each week.
a. Write a system of linear equations that represents this situation.

b. Will the plants ever have the same height? If so, what is the height?
Answer:
a. y = x + 8, y = 2x + 4
b. The same height will be 12 cm after4 weeks.
Explanation:
Let the total height be y, growth of the plant each week be x.
Plant A has a height of 8 centimeters and grows 1 centimeter each week. Plant B has a height of 4 centimeters and grows 2 centimeters each week.
a. y = x + 8 — (i)
y = 2x + 4 —- (ii)
b. If plants ever have the same height
x + 8 = 2x + 4
2x – x = 8 – 4
x = 4
y = 4 + 8
y = 12
The same height will be 12 cm after4 weeks.
Question 9.
Write a system of linear equations containing the equation y = -3x + 2 and that has a solution of (-1, 5). Use a graph to justify your answer.
Answer:
The equation is y = x + 6
Explanation:
Equation is y = -3x + 2
The point is (-1, 5)
The slope intercept form is y = mx + c
5 = -m + c
If m = 1
then c = 5 = -1 + c
c = 6
Then the equation is y = x + 6
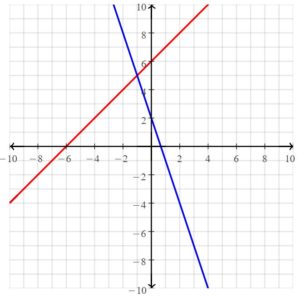
5.2 Solving Systems of Linear Equations by Substitution (pp. 205–210)
Solve the system by substitution. Check your solution.
Question 10.
y = -3x – 7
y = x + 9
Answer:
The solution set is (-4, 5).
Explanation:
The given system of linear equations are
y = -3x – 7 —- (i)
y = x + 9 —- (ii)
Substitute (i) in (ii)
-3x – 7 = x + 9
-3x – x = 9 + 7
-4x = 16
x = -4
Substitute x = -4 in (i)
y = -3(-4) – 7
y = 12 – 7
y = 5
Substitute x = -4, y = 5 in (i)
5 = -3(-4) – 7 = 12 – 7
So, the solution set is (-4, 5).
Question 11.
Answer:
The solution set is (-8, 0)
Explanation:
The given system of linear equations are
1/2 x + y = -4 —- (i)
y = 2x + 16 —-(ii)
Substitute (ii) in (i)
1/2 x + 2x + 16 = -4
2.5x = -4 – 16
2.5x = -20
x = -8
Substitute x = -8 in (ii)
y = 2(-8) + 16
y = -16 + 16
y = 0
Substitute x = -8, y = 0 in (ii)
0 = 2(-8) + 16 = -16 + 16
So, the solution set is (-8, 0)
Question 12.
-x + 5y = 28
x + 3y = 20
Answer:
The solution set is (2, 6)
Explanation:
The given system of linear equations are
-x + 5y = 28
x + 3y = 20 —- (ii)
x = 5y – 28 —- (i)
Substitute (i) in (ii)
5y – 28 + 3y = 20
8y – 28 = 20
8y = 48
y = 6
Substitute y = 6 in (i)
x = 5(6) – 28
= 30 – 28
x = 2
Substitute y = 6, x = 2 in (ii)
2 + 3(6) = 2 + 18 = 20
So, the solution set is (2, 6)
Question 13.
Zoo admission costs $6 for children and $9 for adults. On Monday, 2200 people visit the zoo and the zoo collects $14,850 in admissions.
a. Write a system of linear equations that represents this situation.
b. How many zoo visitors are children? adults?

Answer:
a. 6x + 9y = 14850, x + y = 2200
b. There are 1650 child visitors and 550 adult visitors.
Explanation:
The cost for the zoo is $6 for children & $9 for adults. On Monday, 2200 people visit the zoo and the zoo collects $14,850 in admissions.
a. The system of equations are
6x + 9y = 14850 — (i)
x + y = 2200 — (ii)
b. Multiply (ii) by 6
6x + 6y = 13200
6x + 6y – 6x – 9y = 13200 – 14850
-3y = -1650
y = 550
Substitute y = 550 in (ii)
x + 550 = 2200
x = 2200 – 550
x = 1650
There are 1650 child visitors and 550 adult visitors.
Solve the system. Explain your choice of method.
Question 14.
y = x – 2
y = -2x + 1
Answer:
The solution set is (1, -1).
Explanation:
The given system of linear equations are
y = x – 2 — (i)
y = -2x + 1 — (ii)
x – 2 = -2x + 1
x + 2x = 1 + 2
3x = 3
x = 1
Substitute x = 1 in (i)
y = 1 – 2
y = -1
So, the solution set is (1, -1).
Question 15.
3y + 9 = 3x
y = –\(\frac{1}{3}\)x + 1
Answer:
The solution set is (3, 0).
Explanation:
The given system of linear equations are
3y + 9 = 3x — (i)
y = –\(\frac{1}{3}\)x + 1 —- (ii)
Substitute (ii) in (i)
3(-1/3 x + 1) + 9 = 3x
-x + 3 + 9 = 3x
4x = 12
x = 3
Substitute x = 3 in (i)
9 = 9 + 3y
y = 0
So, the solution set is (3, 0).
Question 16.
-x + 2y = -4
4y = x
Answer:
The solution set is (8, 2).
Explanation:
The given system of linear equations are
-x + 2y = -4 —- (i)
4y = x —- (ii)
Substitute (ii) in (i)
-4y + 2y = -4
-2y = -4
y = 2
Substitute y = 2 in (ii)
x = 4(2)
x = 8
So, the solution set is (8, 2).
Question 17.
The measure of an acute angle in a right triangle is one-fourth the measure of the other acute angle. Write a system of linear equations that represents this situation and use it to find the measures of the acute angles of the triangle.
Answer:
x = 72 degrees, y = 18 degrees
Explanation:
Let two acute angles be x, y
The measure of an acute angle in a right triangle is one-fourth the measure of the other acute angle
x + y = 90 — (i)
y = 1/4 x — (ii)
Substitute (ii) in (i)
x + 1/4 = 90
5/4 x = 90
x = 90 . (4/5)
x = 72 degrees
So, y = 1/4 (72)
y = 18 degrees
5.3 Solving Systems of Linear Equations by Elimination (pp. 211–218)
Solve the system by elimination. Check your solution.
Question 18.
2x + 5y = 60
2x – 5y = -20
Answer:
The solution set is (10, 8).
Explanation:
The given system of linear equations are
2x + 5y = 60 — (i)
2x – 5y = -20 — (ii)
Add both equations
2x + 5y + 2x – 5y = 60 – 20
4x = 40
x = 10
Substitute x = 10 in (i)
2(10) + 5y = 60
20 + 5y = 60
5y = 60 – 20
5y = 40
y = 8
Substitute x = 10, y = 8 in (i)
2(10) + 5(8) = 20 + 40 = 60
So, the solution set is (10, 8).
Question 19.
4x – 3y = 15
2x + y = -5
Answer:
The solution set is (3/2, -3).
Explanation:
The given system of linear equations are
4x – 3y = 15 —- (i)
2x + y = -5 —- (ii)
Multiply (ii) by 3
6x + 3y = -15 —- (iii)
Add (ii) & (i)
4x – 3y + 6 + 3y = 15 – 15
4x – 6 = 0
4x = 6
x = 3/2
Substitute x = 3/2 in (i)
4(3/2) – 3y = 15
6 – 3y = 15
-3y = 15 – 6
-3y = 9
y = -3
Substitute x = 3/2, y = -3 in (i)
4(3/2) – 3(-3) = 6 + 9 = 15
So, the solution set is (3/2, -3).
Question 20.
A gift basket that contains jars of jam and packages of bread mix costs $45. There are 8 items in the basket. Jars of jam cost $6 each, and packages of bread mix cost $5 each. Write and solve a system of linear equations to find the number of each item in the gift basket.
Answer:
5 jars of jam and 3 packages of bread mix.
Explanation:
Let j be the no of jars of jam, b bethe no of packages of bread mix
j + b = 8
6j + 5b = 45
5j + 5b = 40
6j + 5b – 5j – 5b = 45 – 40
j = 5
5 + b = 8
b = 3
So, 5 jars of jam and 3 packages of bread mix.
Question 21.
When might it be easier to solve a system by elimination instead of graphing?
Answer:
Substitution is easier to solve a system by elimination instead of graphing.
Question 22.
You have a total of 10 coins consisting of nickels and dimes in your pocket. The value of the coins is $0.70. Write and solve a system of linear equations to find the numbers of nickels and dimes in your pocket.
Answer:
There are 6 nickels and 4 dimes.
Explanation:
The no of coins of nickles and dimes 10.
x + y = 10 — (i)
0.05x + 0.1y = 0.70 — (ii)
Multiply (i) by 0.05
0.05x + 0.05y = 0.5
0.05x + 0.1y – 0.05x – 0.05y = 0.70 – 0.50
0.05y = 0.2
y = 4
x + 4 = 10
x = 6
There are 6 nickles and 4 dimes.
5.4 Solving Special Systems of Linear Equations (pp. 219–224)
Solve the system. Explain your choice of method.
Question 23.
x + 2y = -5
x – 2y = -5
Answer:
The solution set is (-5, 0)
Explanation:
The given system of linear equations are
x + 2y = -5
x – 2y = -5
add both equations
x + 2y + x – 2y = -5 – 5
2x = -10
x = -5
Substitute x = -5 in x – 2y = -5
-5 – 2y = -5
-2y = 0
y = 0
So, the solution set is (-5, 0)
Question 24.
3x – 2y = 1
9x – 6y = 3
Answer:
The system has infinitely many solutions.
Explanation:
The given system of linear equations are
3x – 2y = 1 —- (i)
9x – 6y = 3 —- (ii)
Multiply (ii) by 1/3
3x – 2y = 1 —- (iii)
Both (iii) & (ii) are samem so the system has infinitely many solutions.
Question 25.
8x – 2y = 16
-4x + y = 8
Answer:
The system has no solution.
Explanation:
The given system of linear equations are
8x – 2y = 16 — (i)
-4x + y = 8 — (ii)
Multiply (i) by 1/2
4x – y = 8 — (iii)
Add (iii) & (ii)
-4x + y – 4x + y = 8 + 8
So, the system has no solution.
Question 26.
4y = x – 8
–\(\frac{1}{4}\)x + y = -1
Answer:
The system has no solution.
Explanation:
The given system of linear equations are
4y = x – 8
–\(\frac{1}{4}\)x + y = -1
Graph the equations
Lines are parallel
So, the system has no solution.
Question 27.
-2x + y = -2
3x + y = 3
Answer:
The solution set is (1, 0).
Explanation:
The given system of linear equations are
-2x + y = -2 —(i)
3x + y = 3 — (ii)
Subtract equations
-2x + y – 3x – y = -2 – 3
-5x = -5
x = 1
Substitute x = 1 in (i)
-2(1) + y = -2
-2 + y = -2
y = 0
Substitute x = 1, y = 0 in (i)
-2(1) + 0 = -2
So, the solution set is (1, 0).
Question 28.
3x = \(\frac{1}{3}\)y + 2
9x – y =-6
Answer:
The system has no solution.
Explanation:
The given system of linear equations are
3x = \(\frac{1}{3}\)y + 2
9x – y =-6
The lines are parallel
So, the system has no solution.
Question 29.
You have $50 in your savings account and plan to deposit $10 each week. Your friend has $25 in her savings account and plans to also deposit $10 each week.
a. Write a system of linear equations that represents this situation.
b. Will your friend’s account ever have the same amount of money as your account? Explain.

Answer:
a. y = 10x + 50, y = 10x + 25
b. No, the amount will never be equal.
Explanation:
Let the total amount be y and the number of weeks is x
a. You have $50 in your savings account and plan to deposit $10 each week.
y = 10x + 50
Your friend has $25 in her savings account and plans to also deposit $10 each week.
y = 10x + 25
b. No, the account will never have the same amounts. By inspection, the lines are parallel and have the same slopes but different y-intercepts. So, the amount will always be $25 greater than the friend account but will not be the same.
Write a system of linear equations that fits the description. Use a graph to justify your answer.
Question 30.
The system has no solution.
Answer:
The possible systems of linear equations can be y = -5x – 2, 5x + y = 0.
Explanation:
The conditions where two equations have no solution are The lines should be parallel having the same slopes but different y-intercepts.
So, let us consider the slope as -5 and different y-intercepts.
Then, the possible systems of linear equations can be y = -5x – 2, 5x + y = 0.
Question 31.
The system has infinitely many solutions.
Answer:
The system of linear equations can be 0.5x + 4y = -11, -1.5x – 12y = 33.
Explanation:
The condition is lines are the same and have the same slope, y-intercepts.
So, the system of linear equations can be 0.5x + 4y = -11, -1.5x – 12y = 33

Question 32.
The system has one solution.
Answer:
The system of linear equations can be -2x + y = 1.3, 2(0.5x – y) = 4.6
Explanation:
The system has only one solution means the lines intersect and have different slopes.
So, the system of linear equations can be -2x + y = 1.3, 2(0.5x – y) = 4.6

Question 33.
Solve the system by graphing, by substitution, and by elimination. Which method do you prefer? Explain your reasoning.
5x + y = 8
2y = -10x + 8
Answer:
The system has no solution.
Out of all methods, I feel graphing is easier.
Explanation:
The given system of linear equations are
5x + y = 8 —- (i)
2y = -10x + 8 —- (ii)
Graph the above equations
The lines are parallel. So, the system has no solution.
Using substitution method
Multiply equation (ii) by 1/2
2y = -10x + 8
y = -5x + 4
Substitute y = -5x + 4 in (i)
5x + -5x + 4 = 8
4 = 8
So, the system has no solution
Using elimination method
y = -5x + 4
5x + y = 4 — (iii)
Subtract (i) & (iii)
5x + y – -5x – y = 8 – 4
0 = 4
So, the system has no solution.
Question 34.
Your friend chooses to solve the system of equations by graphing. Would you choose the same method? Why or why not?
5x + 2y = 12
y = x – 8
Answer:
The solution set is (4, -4).
Explanation:
The given system of linear equations are
5x + 2y = 12, y = x – 8
Yes, I will also choose graphing to solve the equations.
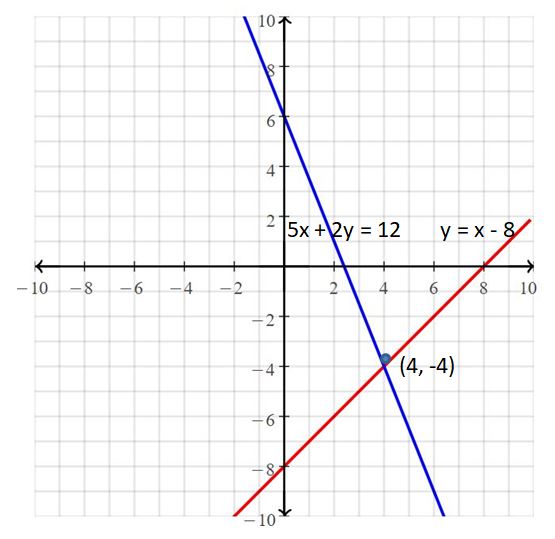
The solution set is (4, -4).
Systems of Linear Equations Practice Test
5 Practice Test
Question 1.
Solve the system by graphing.
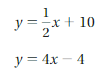
Answer:
The solution is (4, 12).
Explanation:
The given systems of linear equations are y = 1/2 x + 10, y = 4x – 4
Graph the equations
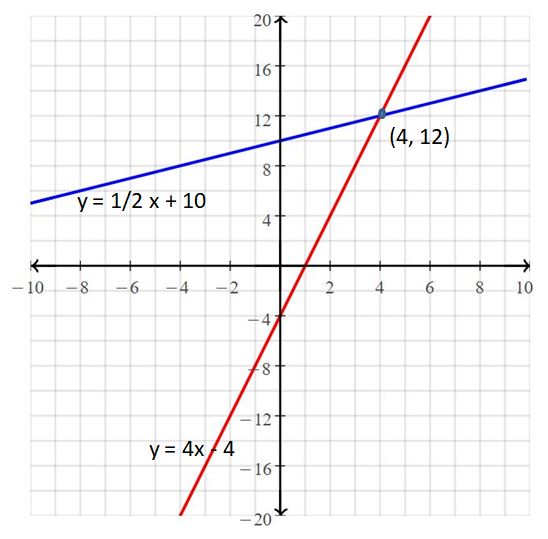
The lines intersect at (4, 12)
So, the solution is (4, 12)
Question 2.
Solve the system by substitution.
-3x + y = 2
-x + y – 4 = 0
Answer:
The solution set is (1, 5)
Explanation:
The given system of linear equations are
-3x + y = 2
y = 2 + 3x —- (i)
-x + y – 4 = 0 —- (ii)
Substitute (i) in (ii)
-x + 2 + 3x – 4 = 0
2x – 2 = 0
2x = 2
x = 1
Substitute x = 1 in (i)
y = 2 + 3(1)
y = 2 + 3
y = 5
So, the solution set is (1, 5)
Question 3.
Solve the system by elimination. Solve the system. Check your solution.
x + y = 12
3x = 2y + 6
Answer:
The solution set is (-18, 30)
Explanation:
The given system of linear equations are
x + y = 12 —- (i)
3x = 2y + 6
3x – 2y = 6 —- (ii)
Multiply equation (i) by 2
2(x + y = 12)
2x + 2y = 24 —- (iii)
Subtract (ii) from (iii)
3x – 2y – 2x – 2y = 6 – 24
x = -18
Substitute x = -18 in (i)
-18 + y = 12
y = 12 + 18
y = 30
So, the solution set is (-18, 30)
Question 4.
Solve the system. Explain your choice of method.
-2x + y + 3 = 0
3x + 4y = -1
Answer:
The solution set is (1, -1).
Explanation:
The given system of linear equations are
-2x + y + 3 = 0
3x + 4y = -1
By graphing
The solution set is (1, -1).
Without graphing or solving, determine whether the system of linear equations has one solution, infinitely many solutions, or no solution. Explain your reasoning.
Question 5.
y = 4x + 8
y = 5x + 1
Answer:
The system has one solution.
Explanation:
The given system of linear equations are
y = 4x + 8 — (i)
y = 5x + 1 —- (ii)
Equate both equations
4x + 8 = 5x + 1
5x – 4x = 8 – 1
x = 7
Substitute x = 7 in (i)
y = 4(7) + 8
y = 28 + 8
y = 36
So, the system has one solution.
Question 6.
2y = 16x – 2
y = 8x – 1
Answer:
The system has infinitely many solutions
Explanation:
The given system of linear equations are
2y = 16x – 2 — (i)
y = 8x – 1 — (ii)
Substitute (ii) in (i)
2(8x – 1) = 16x – 2
16x – 2 = 16x – 2
So, the system has infinitely many solutions.
Question 7.
y = -3x + 2
6x + 2y = 10
Answer:
The system has no solution.
Explanation:
The given system of linear equations are
y = -3x + 2 — (i)
6x + 2y = 10 — (ii)
Substitute (i) in (ii)
6x + 2(-3x + 2) = 10
6x – 6x + 4 = 10
4 = 10
So, the system has no solution.
Question 8.
In the diagram, the measure of ∠1 is three times the measure of ∠2. Find the measure of each angle.
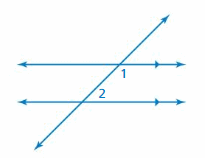
Answer:
∠1 = 3(∠2) = ∠6
∠3 = 180 – ∠2 = ∠5 = ∠7
∠4 = ∠2
Explanation:
The measure of ∠1 is three times the measure of ∠2
∠1 = 3(∠2)
∠5 + ∠2 = 180
∠5 = 180 – ∠2
∠6 + ∠1 = 180
∠6 + 3(∠2) = 180
∠6 = 180 – 3(∠2)
∠2 + ∠3 = 180
∠3 = 180 – ∠2 = ∠5
So, ∠4 = ∠2
Question 9.
The price of 2 pears and 6 apples is $14. The price of 3 pears and 9 apples is $21. Can you determine the unit prices for pears and apples? Explain.
Answer:
They have infinitely many solutions.
Explanation:
Let the price of 1 pears be x, price of 1 apple be y
The price of 2 pears and 6 apples is $14
2x + 6y = 14 — (i)
x + 3y = 7
The price of 3 pears and 9 apples is $21
3x + 9y = 21 —- (ii)
x + 3y = 7
Both the equations are the same. So they have infinitely many solutions.
Question 10.
A bouquet of lilies and tulips has 12 flowers. Lilies cost $3 each, and tulips cost $2 each. The bouquet costs $32. Write and solve a system of linear equations to find the numbers of lilies and tulips in the bouquet.

Answer:
8 lilies and 4 tulips.
Explanation:
Let l be the no of lilies, t be the no of tulips
A bouquet of lilies and tulips has 12 flowers
l + t = 12 —- (i)
Lilies cost $3 each, and tulips cost $2 each. The bouquet costs $32.
3l + 2t = 32 — (ii)
Multiply (i) by 3
3(l + t = 12)
3l + 3t = 36 — (iii)
Subtract (iii) from (ii)
3l + 3t – (3l + 2t) = 36 – 32
3l + 3t – 3l – 2t = 4
t = 4
Substitute t = 4 in (i)
l + 4 = 12
l = 12 – 4
l = 8
8 lilies and 4 tulips.
Question 11.
How much does it cost for 2 specials and 2 glasses of milk?
Answer:
The cost of 2 specials & 2 glasses of milk is $16.1.
Explanation:
Let specials be x and glasses of milk be y
4x + 2y = 28 — (i)
3x + 4y = 26.25 — (ii)
2(4x + 2y = 28)
8x + 4y = 56
subtract equations
8x + 4y – (3x + 4y) = 56 – 26.25
8x + 4y – 3x – 4y = 29.75
5x = 29.75
x = 5.95
Substitute x = 5.95 in (i)
4(5.95) + 2y = 28
23.8 + 2y = 28
2y = 28 – 23.8
2y = 4.2
y = 2.1
The cost of 2 specials & 2 glasses of milk is 2x + 2y
= 2(5.95) + 2(2.1)
= 11.9 + 4.2
= 16.1
The cost of 2 specials & 2 glasses of milk is $16.1.
Systems of Linear Equations Cumulative Practice
Question 1.
What is the solution of the system of equations?
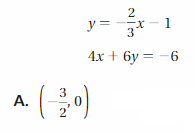
B. (0, -1)
C. no solution
D. infinitely many solutions

Answer:
B. (0, -1)
Explanation:
The given system of linear equations are
y = 2/3 x – 1
4x + 6y = -6
By graphing
so, the solution set is (-1, 0)
Question 2.
What is the value of x?
Answer:
x = 40 degrees
Explanation:
x + 140 = 180
x = 180 – 140
x = 40 degrees
Question 3.
Which of the following shows Rectangle E’F’G’H’, the image of Rectangle EFGH after it is translated 4 units down?
Answer:
F.
Explanation:
By observing all the images we can say that F is the answer.
Question 4.
Which point is a solution of the system of equations?
x + 3y = 10
x = 2y – 5
A. (1, 3)
B. (3, 1)
C. (55, -15)
D. (-35, -15)
Answer:
The solution set is (1, 3).
Explanation:
The given system of linear equations are
x + 3y = 10
x = 2y – 5
Substitute x = 2y – 5 in x + 3y = 10
2y – 5 + 3y = 10
5y = 10 + 5
5y = 15
y = 3
Substitute y = 3 in x = 2y – 5
x = 2(3) – 5
x = 6 – 5
x = 1
So, the solution set is (1, 3).
Question 5.
The graph of a system of two linear equations is shown. Which point is the solution of the system?
F. (-1, 2)
G. (0, 4)
H. (2, -1)
I. (0, 0)
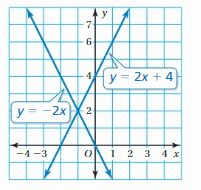
Answer:
F. (-1, 2)
Explanation:
From the graph, the point of intersection of two equations is (-1, 2)
So, the solution set is (-1, 2).
Question 6.
A scenic train ride has one price for adults and one price for children. One family of two adults and two children pays $62 for the train ride. Another family of one adult and four children pays $70. Which system of linear equations can you use to find the price x for an adult and the price y for a child?
A. 2x + 2y = 70
x + 4y = 62
B. x + y = 62
x + y = 70
C. 2x + 2y = 62
4x + y = 70
D. 2x + 2y = 62
x + 4y = 70
Answer:
D. 2x + 2y = 62
x + 4y = 70
Explanation:
If x is the cost of an adult ticket, y is the cost of a child ticket, then
One family of two adults and two children pays $62 for the train ride.
2x + 2y = 62
Another family of one adult and four children pays $70.
x + 4y = 70.
Question 7.
Which of the following is true about the graph of the linear equation y =-7x + 5?
F. The slope is 5, and the y-intercept is -7.
G. The slope is -5, and the y-intercept is -7.
H. The slope is -7, and the y-intercept is -5.
I. The slope is -7, and the y-intercept is 5.
Answer:
H. The slope is -7, and the y-intercept is -5.
Explanation:
The given equation is y =-7x + 5
The equation in the form of y = mx + c
So, slope m = -7, y-intercept c = 5
Question 8.
What is the measure (in degrees) of the exterior angle of the triangle?
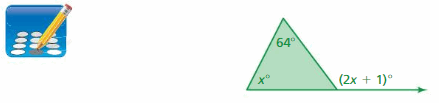
Answer:
The exterior angle of the triangle is 127 degrees
Explanation:
The Sum of angles of a triangle is 180
x + 64 + y = 180
x + y = 180 – 64
x + y = 116
y = 116 – x — (i)
Sum of unknown angle and exterior angle is 180
y + 2x + 1 = 180
y + 2x = 180 – 1
2x + y = 179 —(ii)
Substitute (i) in (ii)
2x + 116 – x = 179
x + 116 = 179
x = 179 – 116
x = 63
So, the exterior angle is (2x + 1) = 2(63) + 1
= 126 + 1 = 127 degrees
Question 9.
The graph of which equation is parallel to the line that passes through the points (-1, 5) and (4, 7)?

Answer:
c.
Explanation:
The equation of a line pass through two points is (y – y₁) = [ =(y₂ – y₁)/(x₂ – x₁)](x – x₁)
x₁ = -1, y₁ = 5, x₂ = 4, y₂ = 7
So, (y – 5) = (7 – 5)/(4 + 1)(x + 1)
y – 5 = 2/5(x + 1)
5(y – 5) = 2(x + 1)
5y – 25 = 2x + 2
5y = 2x + 2 + 25
5y = 2x + 27
y = 2/5 x + 27/5
Question 10.
You buy 3 T-shirts and 2 pairs of shorts for $42.50. Your friend buys 5 T-shirts and 3 pairs of shorts for $67.50. Use a system of linear equations to find the cost of each T-shirt. Show your work and explain your reasoning.

Answer:
The cost of each T-shirt is $7.5.
Explanation:
Let t be the price of a t-shirt, s be the price of a pair of shorts
You buy 3 T-shirts and 2 pairs of shorts for $42.50.
3t + 2s = 42.50
Your friend buys 5 T-shirts and 3 pairs of shorts for $67.50
5t + 3s = 67.50
Multiply the first equation by 3 and second by 2 and then subtract two equations
3(3t + 2s = 42.50) ➝ 9t + 6s = 127.50
2(5t + 3s = 67.50) ➝ 10t + 6s = 135
10t + 6s – 9t – 6s = 135 – 127.50
t = 7.5
The cost of each T-shirt is $7.5.
Question 11.
The red figure is congruent to the blue figure. Which of the following is a sequence of rigid motions between the figures?
F.Translate the red triangle 6 units left and then 4 units down.
G. Reflect the red triangle in the x-axis, and then translate 4 units down.
H. Reflect the red triangle in the y-axis, and then translate 4 units down.
I. Rotate the red triangle 180° clockwise about the origin.
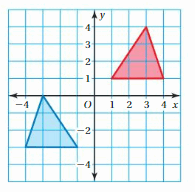
Answer:
I. Rotate the red triangle 180° clockwise about the origin.
Explanation:
The vertices of the red triangle is (1, 1), (4, 1), (3, 4)
The vertices of the blue triangle are (-1, -3), (-4, -3), (-3, 0)
Question 12.
Which of the following is true about the graph of the linear equation y = 2?
A. The graph is a vertical line that passes through (2, 0).
B. The graph is a vertical line that passes through (0, 2).
C. The graph is a horizontal line that passes through (2, 0).
D. The graph is a horizontal line that passes through (0, 2).
Answer:
C. The graph is a horizontal line that passes through (2, 0).
Explanation:
The graph for the linear equation y = 2 is
Question 13.
The sum of one-third of a number and 10 is equal to 13. What is the number?
F. \(\frac{8}{3}\)
G. 9
H. 29
I. 69
Answer:
G. 9
Explanation:
Let the number be n
The sum of one-third of a number and 10 is equal to 13
1/3 n + 10 = 13
1/3 n = 13 – 10
1/3 n = 3
n = 3 x 3
n = 9
Question 14.
Solve the equation 4x + 7y = 16 for x.
A. x = 4 + \(\frac{7}{4}\)y
B. x = 4 – \(\frac{7}{4}\)y
C. x = 4 + \(\frac{4}{7}\)y
D. x = 16 – 7y
Answer:
B. x = 4 – \(\frac{7}{4}\)y
Explanation:
The given equation is 4x + 7y = 16
4x = 16 – 7y
x = (16 – 7y)/4
x = 4 – 7y/4
Conclusion:
The solutions given in this Big Ideas Math Grade 8 Chapter 5 are prepared by the subject experts. So, don’t worry about the answers just go through the answers and try to solve the problems. Test your knowledge by practicing the questions in the practice test section. After solving them cross check the answers. Follow our ccssmathanswers.com to get the latest updates regarding all Grade 8 Chapters.
