Searching for the best material for Integers, Number Lines, and Coordinate Plane? If yes, then there is a one-stop solution for your search. We are providing the Big Ideas Math Book 6th Grade Answers Ch 8 Integers, Number Lines, and the Coordinate Plane pdf in the next sections. Follow our material and make your preparation as expected. You can easily score marks if you practice all the problems of BIM 6th Grade Answer Key which gives the step by step solution to all the problems. Scroll to the next sections to find various details like tasks, examples, answer keys, free pdf’s and so on.
Big Ideas Math Book 6th Grade Answer Key Chapter 8 Integers, Number Lines, and the Coordinate Plane
Big Ideas Math Book 6th Grade Answer Key Chapter 8 Integers, Number Lines, and the Coordinate Plane free pdf is here. Download BIM 6th Grade Chapter 8 Solution Key pdf from the below given links. If you are really worried about your preparation, then definitely you have to check this article. Because we are providing all the tips and tricks to solve the problems. Before starting your practice, understand all the concepts and learn each and every small topic, so that you can overcome all your weakess and score better marks. Follow all the concepts involving Integers, Comparing and Ordering Integers, Rational Numbers etc.
Performance Task
- Integers, Number Lines, and the Coordinate Plane STEAM Video/Performance Task
- Integers, Number Lines, and the Coordinate Plane Getting Ready for Chapter
Lesson: 1 Integers
- Lesson 8.1 Integers
- Integers Homework & Practice 8.1
Lesson: 2 Comparing and Ordering Integers
- Lesson 8.2 Comparing and Ordering Integers
- Comparing and Ordering Integers Homework & Practice 8.2
Lesson: 3 Rational Numbers
- Lesson 8.3 Rational Numbers
- Rational Numbers Homework & Practice 8.3
Lesson: 4 Absolute Value
- Lesson 8.4 Absolute Value
- Absolute Value Homework & Practice 8.4
Lesson: 5 The Coordinate Plane
- Lesson 8.5 The Coordinate Plane
- The Coordinate Plane Homework & Practice 8.5
Lesson: 6 Polygons in the Coordinate Plane
- Lesson 8.6 Polygons in the Coordinate Plane
- Polygons in the Coordinate Plane Homework & Practice 8.6
Lesson: 7 Writing and Graphing Inequalities
- Lesson 8.7 Writing and Graphing Inequalities
- Writing and Graphing Inequalities Homework & Practice 8.7
Lesson: 8 Solving Inequalities
- Lesson 8.8 Solving Inequalities
- Solving Inequalities Homework & Practice 8.8
Chapter: 8 – Integers, Number Lines, and the Coordinate Plane
- Integers, Number Lines, and the Coordinate Plane Connecting Concepts
- Integers, Number Lines, and the Coordinate Plane Chapter Review
- Integers, Number Lines, and the Coordinate Plane Practice Test
- Integers, Number Lines, and the Coordinate Plane Cumulative Practice
Integers, Number Lines, and the Coordinate Plane STEAM Video/Performance Task
STEAM Video
Designing a CubeSat
A CubeSat is a type of miniature satellite that is used for space research. Each CubeSat has the dimensions shown and a mass of no more than 1.33 kilograms.

Watch the STEAM Video “Designing a CubeSat.” Then answer the following questions.
1. For what fields of study do you think CubeSats can be used?
2. Tony says g-forces are a measure of how heavy you feel. e table shows the g-forces on a CubeSat at three points in time. Why can g-forces be as high as 6 during a rocket launch and as low as 0 in space?
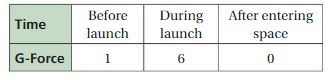
3. What would happen to a CubeSatthatcannot withstand a g-force of 6? a g-force of 0?
Performance Task
Launching a CubeSat
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given information about three different types of Cubesats that you can purchase.

You will determine which of the three CubeSats is the best option for a mission. Why might g-force, pressure, and temperature be important considerations for making your decision?
Integers, Number Lines, and the Coordinate Plane Getting Ready for Chapter
Chapter Exploration
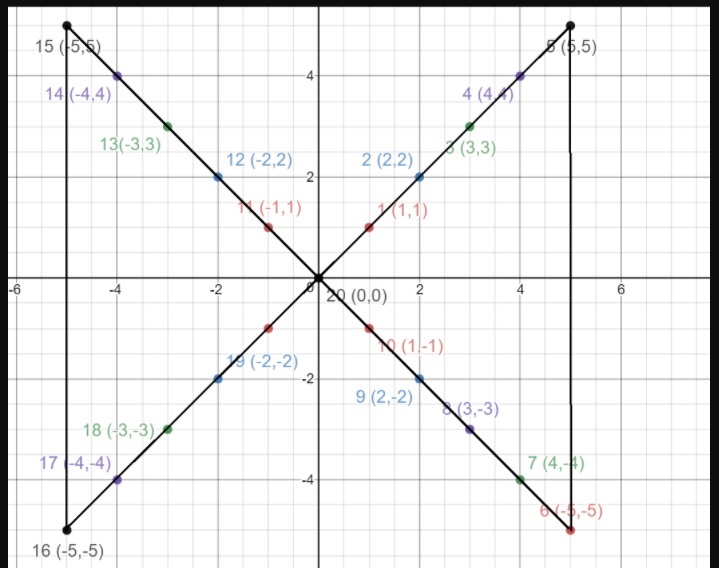
Question 1.
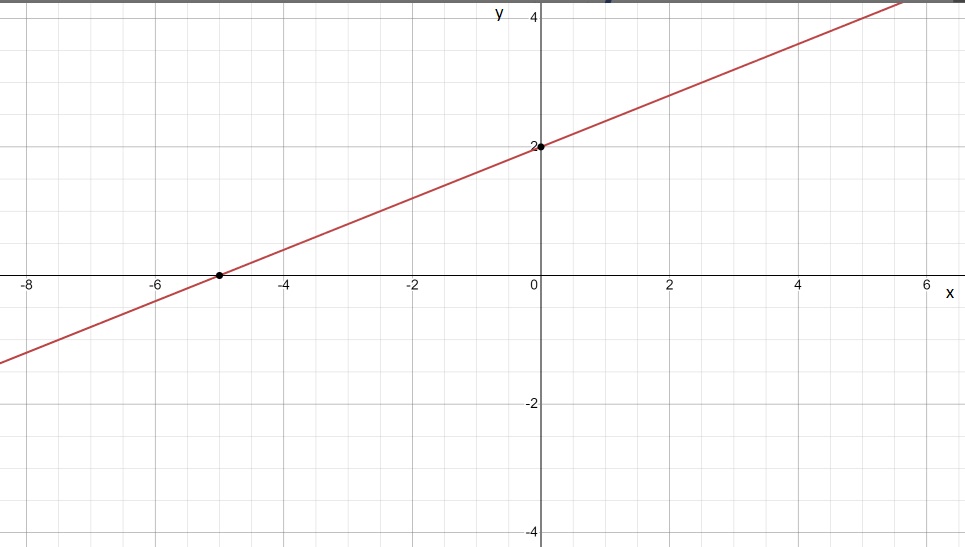
Work with a partner. Plot and connect the points to make a picture.
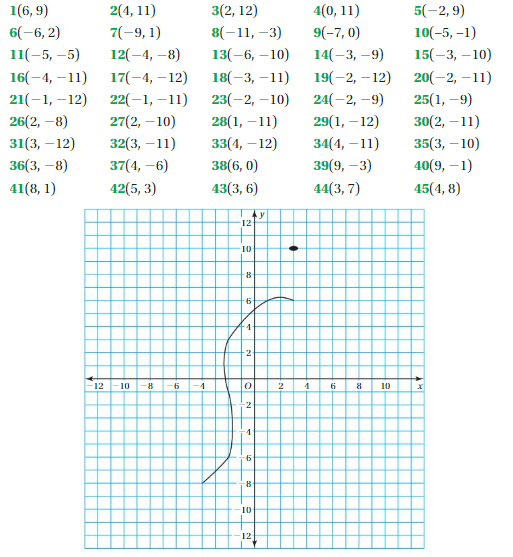
Answer:
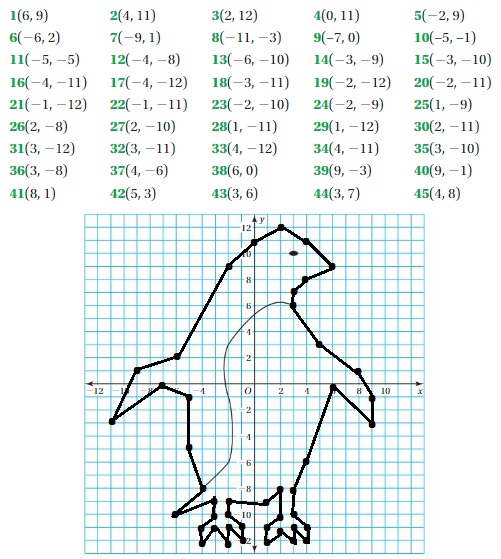
Question 2.
Create your own “dot-to-dot” picture. Use at least 20 points.
Answer:
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
negative numbers
opposites
inequality
quadrants
Lesson 8.1 Integers
Exploration 1
Reading and Describing Temperatures
Work with a partner. The thermometers show the temperatures in four cities.
Honolulu, Hawaii
Anchorage, Alaska
Death Valley, California
Seattle, Washington
a. Match each temperature with its most appropriate location.
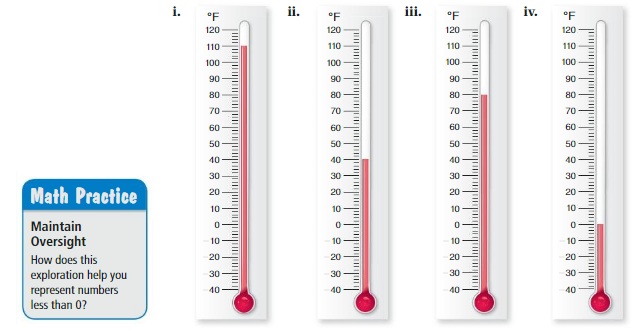
Answer:
Honolulu, Hawaii – 110 degrees Fahrenheit
Anchorage, Alaska – 0 degrees Fahrenheit
Death Valley, California – 80 degrees Fahrenheit
Seattle, Washington – 40 degrees Fahrenheit
b. What do all of the temperatures have in common?
Answer :
Measuring in degrees fahrenheit and Readings
c. What does it mean for a temperature to be below zero? Provide an example. Can you think of any other situations in which numbers may be less than zero? Maintain OversightHow does this exploration help you represent numbers less than 0?
Answer:
Temperature to be below zero means cold weather starts .
Example:
When used by weather forecasters in the U.S., it means “below 0°F”. ( It essentially means, “It’s gonna be cold; bring your mittens and a warm hat.”
d. The thermometers show temperatures on a vertical number line. How else can you represent numbers less than zero? Provide an example.
Answer:
Positive numbers are greater than 0. They can be written with or without a positive sign (+).
1 5 20 10,000
Negative numbers are less than 0. They are written with a negative sign (−).
-1 -5 -20 -10,000
Two numbers that are the same distance from 0 on a number line, but on opposite sides of 0, are called opposites. The opposite of 0 is 0.
Try It
Write a positive or negative integer that represents the situation.
Question 1.
A hiker climbs 900 feet up a mountain.
Answer:
+900, 900 feet
Explaination :
Positive numbers are greater than 0. They can be written with or without a positive sign (+).
Question 2.
You have a debt of $24.
Answer:
-24
Explaination :
Debt is an amount of money borrowed by one party from another.
Debt of $24 is represented as -24.
Question 3.
A student loses 5 points for not showing work on a quiz.
Answer:
-5
Explaination :
lose is a another meaning of negative.
Student loses 5 points is indicated as -5.
Question 4.
A savings account earns $10.
Answer:
+10
Explaination :
Earns is another vocabulary to positive.
earns $10 is represented as +10 or 10.
Graph the integer and its opposite.
Question 5.
6
Answer:
(6, -6)
Explanation:
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 6.
-4
Answer:
(4, -4)
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 7.
-12
Answer:
(12, -12)
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 8.
1
Answer:
(1, -1)
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING INTEGERS Write a positive or negative integer that represents the situation.
Question 9.
A baseball is thrown at a speed of 78 miles per hour.
Answer:
+78
Explanation :
A baseball is thrown at a speed of 78 miles per hour. So, thrown indicated +ve
+78 or 78.
Question 10.
A submarine is 3750 feet below sea level.
Answer:
-3750
Explanation :
submarine is 3750 feet below sea level. so, below indicates -ve
-3750
GRAPHING INTEGERS Graph the integer and its opposite.
Question 11.
8
Answer:
(8, -8)
Explaination :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 12.
– 7
Answer:
(7 -7)
Explaination :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 13.
11
Answer:
(11, -11)
Explaination :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 14.
VOCABULARY
Which of the following numbers are integers?
18, 4.1, -9, \(\frac{1}{6}\) , 1.75, 22
Answer:
An integer is defined as a number that can be written without a fractional component.
18, -9, 22
Question 15.
VOCABULARY
List three words or phrases used in real life that indicate negative integers.
Answer:
minus , below , down , debt, low.
Question 16.
WRITING
Describe the opposite of a positive integer, the opposite of a negative integer, and the opposite of zero.
Answer:
Opposite of positive integer is negative integer.
A negative integer is a whole number that has value less than zero. Negative integer are normally whole numbers, for example, -3, -5, -8, -10 etc
Opposite of negative integer is positive integer.
The positive integer are the numbers 1, 2, 3, … , sometimes called the counting numbers or natural numbers, for example , +1, 2 , +3 ……..
Opposite of zero
We do not consider zero to be a positive or negative number. So, zero (0) opposite is zero(0).
Question 17.
The world record for scuba diving is 332 meters below sea level. Write an integer that represents a new world record. Explain.
Answer:
1090 ft is represented as the new world record in scuba diving.
Explanation:
converting m to ft
1 m – 3.2808 ft
332 m – 1090 ft.
Question 18.
The indoor and outdoor temperatures are shown. The freezing point of water is 32°F. Write integers that represent how each temperature must change to reach the freezing point of water. Explain.

Answer:
Given:
Freezing point of water = 32°F
From the pic the outdoor temperature = 25°F
To reach the freezing point of water outdoor we need to increase the temperature outdoor temperature.
32°F -25°F = 7°F
Outdoor temperature should be increased by 7°F.
From the pic indoor temperature= 68°F
Similarly, to reach the freezing point of water indoor we need to decrease the indoor temperature.
68°F -32°F = 36°F
Indoor temperature should be reduced by 36°F.
Question 19.
An ion is an atom that has a positive or negative electric charge. When an ion has more protons than electrons, it has a positive charge. When an ion has fewer protons than electrons, it has a negative charge. Explain what it means for an atom to have an electric charge of zero.
Answer:
When an atom has an equal number of electrons and protons, it has an equal number of negative electric charges (the electrons) and positive electric charges (the protons). The total electric charge of the atom is therefore zero and the atom is said to be neutral.
Integers Homework & Practice 8.1
Review & Refresh
Find the volume of the prism.
Question 1.
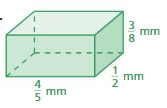
Answer:
Given:
Length of cuboid : 4/5 mm
Width of the cuboid: 1/2 mm
Height of the cuboid: 3/8 mm
Volume of the cuboid = l*w*h
\(\frac{4}{5}\)*\(\frac{1}{2}\)*\(\frac{3}{8}\)= (4x1x3)/(5x2x8)=3/20
\(\frac{3}{20}\) cubic mm.
Question 2.
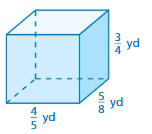
Answer:
Given:
Length of cuboid : 4/5 yd
Width of the cuboid: 5/8 yd
Height of the cuboid: 3/4 yd
Volume of the cuboid = l*w*h
\(\frac{4}{5}\)*\(\frac{5}{8}\)*\(\frac{3}{4}\)= (4x5x3)/(5x8x4)=3/8
\(\frac{3}{8}\) cubic yd.
Question 3.
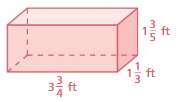
Answer:
Given:
Length of cuboid : 15/4 ft
Width of the cuboid: 4/3 ft
Height of the cuboid: 8/5 ft
Volume of the cuboid = l*w*h
\(\frac{15}{4}\)*\(\frac{4}{3}\)*\(\frac{8}{5}\)= (15x4x8)/(4x3x5)=8
\(\frac{8}{1}\) cubic ft.
Factor the expression using the GCF.
Question 4.
4m + 32
Answer:
When we find all the factors of two or more numbers, and some factors are the same (“common”), then the largest of those common factors is the Greatest Common Factor. Abbreviated “GCF”.
4m + 32
divide the equation by 4
\(\frac{4m}{4}\) + \(\frac{32}{4}\)
\(\frac{4(m + 8)}{1}\)
4 is the greatest common factor.
Question 5.
18z – 22
Answer:
18z – 22
Take 2 common we get,
2 ( 9z – 11)
2 is the greatest common factor.
Explanation:
When we find all the factors of two or more numbers, and some factors are the same (“common”), then the largest of those common factors is the Greatest Common Factor. Abbreviated “GCF”.
Question 6.
38x + 80
Answer:
38x + 80
Take 2 common we get,
2 ( 19z + 40)
no more possible to simplify so
2 is the greatest common factor.
Explanation:
When we find all the factors of two or more numbers, and some factors are the same (“common”), then the largest of those common factors is the Greatest Common Factor. Abbreviated “GCF”.
Question 7.
42n – 27s
Answer:
42n – 27s
Take 3 common we get,
3 (14n – 9s)
no more possible to simplify so
3 is the greatest common factor.
Explanation:
When we find all the factors of two or more numbers, and some factors are the same (“common”), then the largest of those common factors is the Greatest Common Factor. Abbreviated “GCF”.
Question 8.
The height of a statue is 276 inches. What is the height of the statue in meters? Round your answer to the nearest hundredth.
A. 1.09 m
B. 7.01 m
C. 108.66 m
D. 701.04 m
Answer:
1 inch = 0.025 m
Height of a statue = 276 inches
convert it into meters =276 inch x 0.025 = 7.01 m
So,
B is the answer.
Concepts, Skills, & Problem Solving
OPEN-ENDED Describe a situation that can be represented by the integer. (See Exploration 1, p. 345.)
Question 9.
– 6
Answer:
The Temperature is decreased by 6 °F
Question 10.
12
Answer:
Earned bonus of 12 points
Question 11.
– 45
Answer:
Had lose of 45 coins .
WRITING INTEGERS Write a positive or negative integer that represents the situation.
Question 12.
A football team loses 3 yards.
Answer:
-3
As loses represents negative
Question 13.
The temperature is 6 degrees below zero.
Answer:
below zero indicates negative
-6 degrees
Question 14.
You earn $15 raking leaves.
Answer:
Earn represents positive
+15$
Question 15.
A person climbs 600 feet up a mountain.
Answer:
+600 feet as its up a mountain.
Question 16.
You withdraw$42 from an account.
Answer:
-42$ withdraw from my account.
Question 17.
An airplane climbs to 37,500 feet.
Answer:
An airplane climbs to +37,500 feet
Question 18.
The temperature rises 17 degrees.
Answer:
Temperature rises indicates increase +17 degrees
Question 19.
You lose 56 points in a video game.
Answer:
I lose -56 points from my video game.
Question 20.
A ball falls 350 centimeters.
Answer:
A ball falls -350 centimeters
Question 21.
You receive 5 bonus points in class.
Answer:
I receive +5 points in class.
Question 22.
MODELING REAL LIFE
On December 17, 1903, the Wright brothers accomplished the first powered flight. The plane traveled a distance of 120 feet. Write this distance as an integer.

Answer:
Distance Traveled by the plane = 120 feet.
It means +120 .
Question 23.
MODELING REAL LIFE
A stock market gains 83 points. The next day, the stock market loses 47 points. Write each amount as an integer.
Answer:
+83 = Stock Market gains 83 points.
– 47 = The next day the stock market loses 47 points.
GRAPHING INTEGERS
Graph the integer and its opposite.
Question 24.
– 5
Answer:
The opposite of -5 = +5

Question 25.
– 8
Answer:
The opposite of -8 = +8

Question 26.
14
Answer:
The opposite of 14 = -14
![]()
Question 27.
9
Answer:
The opposite of 9 = -9

Question 28.
– 14
Answer:
The opposite of -14 = +14
![]()
Question 29.
20
Answer:
The opposite of +20 = -20

Question 30.
– 26
Answer:

Question 31.
18
Answer:
The opposite of 18 is -18

Question 32.
30
Answer:
The opposite of 30 is – 30

Question 33.
– 150
Answer:
The opposite of -150 is 150

Question 34.
– 32
Answer:
The opposite of – 32 is 32

Question 35.
400
Answer:
The opposite of 400 is -400

Question 36.
YOU BE THE TEACHER
Your friend describes the positive integers. Is your friend correct? Explain your reasoning.
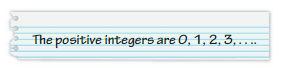
Answer:
No
Explanation:
The natural numbers 1, 2, 3, 4, 5, ……… are called positive integers.
Positive numbers are represented to the right of zero on the number line. Positive numbers are greater than negative numbers as well a zero.
Because zero is neither positive nor negative . Zero is a neutral number.
USING A NUMBER LINE Identify the integer represented by the point on the number line.
Question 37.
A
Answer:
The point A is marked at 5
Question 38.
B
Answer:
The point B is marked at -8
Question 39.
C
Answer:
The point C is marked at -15
Question 40.
D
Answer:
The point D is marked at 18

Question 41.
DIG DEEPER!
Low tide, represented by the integer −1, is 1 foot below the average water level. High tide is 5 feet higher than low tide.
a. What does 0 represent in this situation?
b. Write an integer that represents the average water level relative to high tide.

Answer a :
The Low Tide = -1
Average water level = 0
Explanation:
As the low tide is just below average water level . When average water level =0
Then low tide can be – 1
Answer b :
High Tide = 4
Explanation:
High tide is 5 feet higher than low tide so we get
High Tide = -1 + 5 = 4
An integer that represents the average water level relative to high tide = 4
Question 42.
REPEATED REASONING
Consider an integer n.
a. Is the opposite of n always less than 0? Explain your reasoning.
b. What can you conclude about the opposite of the opposite of n? Justify your answer.
c. Describe the meaning of −[−(−n)]. What is it equal to?
Answer a:
Only if n is a positive integer
Explanation:
The integer n is a positive integer then only the negative integer of n is always less than 0 Positive numbers are represented to the right of zero on the number line and Negative numbers are represented to the left of zero on the number line.
Answer b :
n is a integer . opposite of n is -n and opposite of (opposite of n) = opposite of (-n)= +n
Answer c :
– x – = +
– x + = –
−[−(−n)]= means minus of minus of minus n
−[−(−n)]= – (+ n)= -n
Question 43.
In a game of tug-of-war, a team wins by pulling the flag over its goal line. The flag begins at0. During a game, the flag moves 8 feet to the right,12 feet to the left, and 13 feet back to the right.Did a team win? Explain. If not, what does each team need to do in order to win?
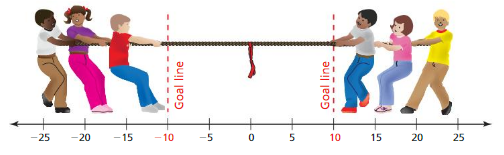
Answer:
Flag begins at 0
After First pull:
The flag moves 8 feet to the right means = 0 + 8 =8
After Second pull:
The flag is at 8 now then it moves 12 feet to the left .
Now the flag is at = 8 – 12 = -4
After Third pull:
Now the flag is at -4 now then it moves to 13 feet to the right
Then the flag is at = -4 + 13 = 9
Now the flag is at 9 that means to win the flag should cross goal line that means + 10
No team wins
To win the right side team the flag should move 1 or more to the right
To win the left side team the flag should move 11 or more to the left.
Lesson 8.2 Comparing and Ordering Integers
EXPLORATION 1
Seconds to Liftoff
Work with a partner. You are listening to a command center before the liftoff of a rocket. You hear the following:
“T minus 10 seconds . . . go for main engine start . . . T minus 9 . . . 8 . . . 7 . . . 6 . . . 5 . . . 4 . . . 3 . . . 2 . . . 1 . . . we have liftoff.”


a. Represent these events on a number line.
Answer:
Rocket clears launchpad tower = +6 = A Event
Launch Verification = -16 = B Event
Main Engine Start = -3 = C Event
Rocket Topping sequence complete = -110 = D Event
Launch control system enabled = -90 = E Event
Boosters ignite = 0 = F Event

b. List the events in the order they occurred. Explain your reasoning.
Answer:
1 – Rocket Topping sequence complete = -110 = D Event
2 – Launch control system enabled = -90 = E Event
3 – Launch Verification = -16 = B Event
4 – Main Engine Start = -3 = C Event
5 – Boosters ignite = 0 = F Event
6 – Rocket clears launchpad tower = +16 = A Event
As per the above number line the events which take place are ordered from left side to right side
c. Extend the number line in part(a) to show events in an astronaut’s day. Include at least five events before liftoff and at least five events after liftoff. Use the Internet or another reference source to gather information.
Answer:
1 – Rocket Topping sequence complete = -110 = D Event
2 – Launch control system enabled = -90 = E Event
3 – Launch Verification = -16 = B Event
4 – Main Engine Start = -3 = C Event
5 – Boosters ignite = 0 = F Event
6 – Rocket clears launchpad tower = +6 = A Event
7- Stage 1 Burnout = +16 = G Event
8 – Fairing Jettison = +25 = H Event
9 – Stage 1 Separation = + 30 = I Event
10 – Stage 2 Ignition = +35 = J Event
11 – Transfer to the launch pad = – 120 = K Event

Recall that on a horizontal number line, numbers to the left are less than numbers to the right. Numbers to the right are greater than numbers to the left. On a vertical number line, numbers below are less than numbers above. Numbers above are greater than numbers below.
Try It
Copy and Complete the statement using < or >.
Question 1.
![]()
Answer:
0 > -4
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller. Think what the number represents. Think what the value is.
Question 2.
![]()
Answer:
-5 < 5
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 3.
![]()
Answer:
-8 < -7
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller. Think what the number represents. Think what the value is.
Order the integers from least to greatest.
Question 4.
-2, -3, 3, 1, -1
Answer:
-3, -2, -1, 1, 3
Question 5.
4, -7, -8, 6, 1
Answer:
-8, -7, 1, 4, 6
Question 6.
In Example 3, what is the least possible integer value of the number?
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
ORDERING INTEGERS Order the integers from least to greatest.
Question 7.
6, – 4, – 1, 3, 5
Answer:
-4, -1, 3, 5, 6
Question 8.
– 7, – 9, 0, 8, – 2
Answer:
-9, -7, -2, 0, 8
Question 9.
WRITING
Explain how to determine which of two integers is greater.
Answer:
We are used to big positive numbers meaning a big value – the bigger the number, the more, or higher, or longer, or expensive, or whatever the number represents.
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller. Think what the number represents and what the value is.
Question 10.
REASONING
The positions of four fish are shown.
a. Use red, blue, yellow, and green dots to graph the positions of the fish on a horizontal number line and a vertical number line.
b. Explain how to use the number lines from part(a) to order the positions from least to greatest.
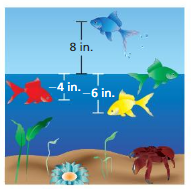
Answer a :
The position of red fish = -4
The position of Yellow fish = -6
The position of green fish = 0
The position of Blue fish = 8


Answer b:
Least to greatest numbers are
-6, -4, 0, 8
Explanation:
From the above horizontal number line we notice that the numbers from left to right of number line represent least to greatest numbers.
Question 11.
NUMBER SENSE
a and bare negative integers. Compare a and b. Explain your reasoning.
![]()
Answer:
b > a
Explanation:
we notice that the numbers from left to right of number line represent least to greatest numbers.The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller. Think what the number represents. Think what the value is..
Question 12.
The freezing temperature of nitrogen is −210°C, and the freezing temperature of oxygen is −219°C. A container of nitrogen and a container of oxygen are both cooled to −215°C. Do the contents of each container freeze? Explain.
Answer:
The temperature of liquid nitrogen can readily be reduced to its freezing point 63 K (−210 °C; −346 °F) by placing it in a vacuum chamber pumped by a vacuum pump
The temperature at which a substance freezes is called the freezing point. The freezing point of oxygen is -219°C . This means that they need to be cooled to lower temperatures to make them freeze.
Question 13.
DIG DEEPER!
The diagram shows the daily high temperatures during a school week. Was a positive Celsius temperature recorded on Tuesday? on Friday? Explain.

Answer:
No
Explanation:
The natural numbers 1, 2, 3, 4, 5, ……… are called positive integers.
Positive numbers are represented to the right of zero on the number line. Positive numbers are greater than negative numbers as well a zero.
Because zero is neither positive nor negative . Zero is a neutral number.
Therefore positive Celsius temperature recorded on Monday and Friday .
Comparing and Ordering Integers Homework & Practice 8.2
 .2
.2
Review & Refresh
Write a positive or negative integer that represents the situation.
Question 1.
You walk up 83 stairs.
Answer:
up indicates + .so it is + 83
Question 2.
A whale is 17 yards below sea level.
Answer:
Below indicates – . So it is -17
Question 3.
An organization receives a $75 donation.
Answer:
Receives indicates +. So it is +$75
Question 4.
A rock falls 250 feet off a cliff.
Answer:
Falls indicates – . So it is -250
Question 5.
What is the area of the trapezoid?
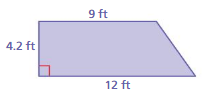
A. 6.3 ft2
B. 44.1 ft2
C. 50.4 ft2
D. 88.2 ft2
Answer:
Height of Trapezoid = 4.2ft
Base 1 of Trapezoid = 12ft
Base 2 of Trapezoid = 9 ft
Area of Trapezoid = half-height × (base1 + base2) = \(\frac{4.2}{2}\) (12 + 9)
=2.1 × 21 = 44.1 ft2
Divide. Write the answer in simplest form.
Question 6.
\(\frac{1}{5} \div \frac{1}{9}\)
Answer:
\(\frac{1}{5}\)÷latex]\frac{9}{1}[/latex]= 9/5=1.8
Question 7.
\(\frac{2}{5} \div \frac{1}{3}\)
Answer:
(2/5) /(1/3) = (2×3) /5 = 6/5=1.2
Question 8.
\(\frac{1}{4}\) ÷ 3
Answer:
\(\frac{1}{4}\)× \(\frac{1}{3}\)=\(\frac{1}{12}\) = 0.083
Question 9.
\(\frac{4}{7}\) ÷ 8
Answer:
\(\frac{4}{7}\) × \(\frac{1}{8}\)=\(\frac{1}{14}\) =0.071
Concepts, Skills, &Problem Solving
OPEN-ENDED Name an event that could occur at the given time (in seconds) in Exploration 1. Describe when the event occurs in the order of events from the exploration. (See Exploration 1, p. 351.)
Question 10.
– 300
Answer:
Question 11.
– 150
Answer:
Question 12.
10
Answer:
COMPARING INTEGERS Copy and complete the statement using < or >.
Question 13.
![]()
Answer:
3 > 0
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 14.
![]()
Answer:
-2 < 0
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 15.
![]()
Answer:
6 > -6
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 16.
![]()
Answer:
3 > -4
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 17.
![]()
Answer:
-1 < 4
Explanation:
All Positive Numbers are greater than the Negative numbers .
Question 18.
![]()
Answer:
-7 > -8
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 19.
![]()
Answer:
-3 < -2
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 20.
![]()
Answer:
-5 > – 10
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
YOU BE THE TEACHER
Your friend compares two integers. Is your friend correct? Explain your reasoning.
Question 21.

Answer:
No My friend is wrong.
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
-1 is nearer to 0 than -3 so -1 is greater
-3 < – 1
Question 22.

Answer:
Yes it is True .
– 7 < -3
ORDERING INTEGERS Order the integers from least to greatest.
Question 23.
0, – 1, 2, 3, – 3
Answer:
-3, -1, 0, 2, 3
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 24.
– 4, – 2, – 3, 2, 1
Answer:
-4, -3, -2, 1, 2
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 25.
– 2, 3, – 3, – 4, 4
Answer:
-4, -3, -2, 3, 4
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 26.
5, – 11, – 9, 3, – 4
Answer:
-11, -9, -4. 3, 5
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 27.
– 3, 8, 4, 0, – 13
Answer:
-13, -3, 0, 4, 8
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 28.
– 7, 2, 6, – 4, 3
Answer:
-7, -4, 2, 3, 6
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 29.
12, – 8, – 16, 7, 1
Answer:
-16, -8, 1, 7, 12
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 30.
10, – 10, 30, – 30, – 50
Answer:
-50, -30, -10, 10, 30
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 31.
– 5, 15, – 10, – 20, 25
Answer:
-20, -10, -5, 15, 25
Explanation:
With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.All Positive Numbers are greater than the Negative numbers .
Question 32.
MODELING REAL LIFE
An archaeologist discovers the two artifacts shown.
a. What integer represents ground level?
b. A dinosaur bone is 42 centimeters below ground level. Is it deeper than both of the artifacts? Explain.

Answer a :
An integer represents ground level = 0 (as it is neutral)
Answer b :
Dinosaur bone is at = – 42cms
First artifact is at =-38 cms
Second artifact is at = – 44 cms
No it not depper than both the artifacts.
Explanation:
It is in between the artifacts. as -42 lies in between -38 and -44
Question 33.
REASONING
A number is between −2 and −10. What is the least possible integer value of this number? What is the greatest possible integer value of this number?
Answer:
The numbers between -2 and -10 = -3, -4, -5, -6, -7, -8, -9
Greatest value = -3
Least Value = – 9
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 34.
NUMBER SENSE
Describe the locations of the integers m and n on a number line for each situation.
a. m < n
b. m > n
c. n > m
Answer a :
m < n where m = 1 and n = 3

Answer b :
m > n where n = -1 and m = 1
Answer c :
n > m where n = 5 and m = -5
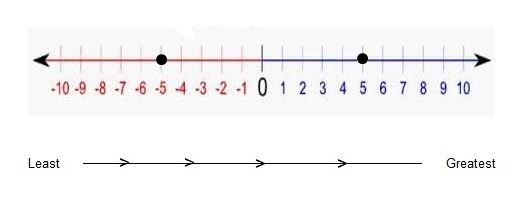
CRITICAL THINKING Tell whether the statement is always, sometimes, or never true. Explain.

Question 35.
A positive integer is greater than its opposite.
Answer:
YES,
Explanation:
The opposite number of a positive number is negative numbers. Negative are always lesser than positive numbers.
Question 36.
An integer is less than its opposite and greater than 0.
Answer:
No
Explanation:
integer = 5
The opposite of 5 is -5
Here integer is not less than its oppositeand greater than 0 it is -5 < 5 .
Question 37.
MODELING REAL LIFE
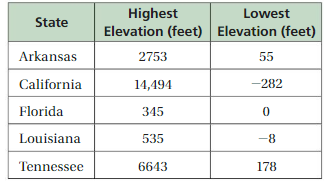
The table shows the highest and lowest elevations for five states.
a. Order the states by their highest elevations, from least to greatest.
b. Order the states by their lowest elevations, from least to greatest.
c. What does the lowest elevation for Florida represent?
Answer a :
Florida < Louisiana <Arkansas < Tennessee < California
345< 535 < 2753 < 6643 < 14494
Answer b :
California < Louisiana < Florida < Arkansas < Tennessee
-282 < -8 < 0 < 55 < 178
Question 38.
NUMBER SENSE
Point A is on a number line halfway between −17 and 5. Point Bis halfway between Point A and 0. What integer does Point B represent?
Answer:
Point A = half way between -17 and 5 = (- 17 + 5) ÷ 2 = – 12÷2 = -6
Point B = halfway between Point A and 0 = (-6 + 0) ÷ 2= -6 ÷ 2 = – 3
Therefore Point B represent -3 integer
Question 39.
REASONING
Eleven Fahrenheit temperatures are shown on a map during a weather report. When the temperatures are ordered from least to greatest, the middle temperature is below off. Do you know exactly how many of the temperatures are represented by negative numbers? Explain.
Answer:
Question 40.
PUZZLE
Nine students each choose one integer. Here are seven of them:
5, − 8, 10, − 1, − 12, − 20, and 1.
a. When all nine integers are ordered from least to greatest, the middle integer is 1. Describe the integers chosen by the other two students.
b. When all nine integers are ordered from least to greatest, the middle integer is −3. Describe the integers chosen by the other two students.
Answer a :
Order the numbers so that 1 is in the middle:
-20, -12, -8, -1, 1, 5, 10, x, x -> The other 2 numbers must be greater than 1, as the range can be 2 < x, x being the number chosen
Answer b .
Order the numbers so that -3 is in the middle:
x, -20, -12, -8, (-3), -1, 1, 5, 10 -> The other number must be less than -3, as the range is x < – 3, x being the number chosen
Lesson 8.3 Rational Numbers
EXPLORATION 1
Locating Fractions on a Number Line
Work with a partner. Represent the events on a number line using a fraction or a mixed number.

Answer:

Integers, fractions, and decimals make up the set of rational numbers. A rational number is a number that can be written as a – b, where a and b are integers and b ≠ 0.
Try It
Graph the number and its opposite.
Question 1.
2\(\frac{1}{2}\)
Answer:
2 × \(\frac{1}{2}\) = \(\frac{2}{2}\) = 1
The opposite of 1 is -1
Question 2.
–\(\frac{4}{5}\)
Answer:
–\(\frac{4}{5}\)= – ( 4 ÷ 5) = – 0.8
The opposite of – 0.8 is 0.8
Question 3.
– 3.5
Answer:
The opposite of – 3.5 is 3.5
Question 4.
5.25
Answer:
The opposite of 5.25 is -5.25
Copy and complete the statement using < or >.
Question 5.
![]()
Answer:
–\(\frac{4}{7}\) = -0.57
–\(\frac{1}{7}\)= -0.14
– 0.57 < -0.14
Question 6.
![]()
Answer:
–\(\frac{5}{3}\) = -1.66
–\(\frac{11}{6}\) = -1.83
-1.66 > – 1.83
Question 7.
![]()
Answer:
– 0.5 < 0.3
Question 8.
![]()
Answer:
-6.5 > – 6.75
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
COMPARING RATIONAL NUMBERS Copy and complete the statement using < or >.
Question 9.
![]()
Answer:
–\(\frac{2}{3}\) = -0.66
–\(\frac{5}{9}\) = -0.55
-0.66 < -0.55
Question 10.
![]()
Answer:
–\(\frac{9}{4}\)= – 2.25
–\(\frac{19}{8}\)= -2.375
-2.25 > -2.375
Question 11.
![]()
Answer:
-1.7 > -2.4
Question 12.
NUMBER SENSE
Which statement is not true?
A. On a number line, −2\(\frac{1}{6}\) is to the left of −2\(\frac{2}{3}\).
B. −2 \(\frac{2}{3}\) is less than −2\(\frac{1}{6}\).
C. On a number line, −2\(\frac{2}{3}\) is to the left of −2\(\frac{1}{6}\).
Answer A :
−2\(\frac{1}{6}\) = −\(\frac{1}{3}\) = – 0.33
−2\(\frac{2}{3}\) = −\(\frac{4}{3}\) = -1.33
Explanation:

Answer B :
−2 \(\frac{2}{3}\) = − \(\frac{4}{3}\) = -1.33
−2\(\frac{1}{6}\) = −\(\frac{1}{3}\) = – 0.33
-1.33 < – 0.33
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Answer C :
−2 \(\frac{2}{3}\) = − \(\frac{4}{3}\) = -1.33
−2\(\frac{1}{6}\) = −\(\frac{1}{3}\) = – 0.33
From the above number line we notice that -1.33 is left of -0.33
Question 13.
WRITING
Explain how to determine whether a number is a rational number.
Answer:
The rational number which is represented in the \(\frac{p}{q}\)form and where q is not equal to zero.
Examples :
\(\frac{2}{3}\), \(\frac{7}{3}\)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 14.
You and your friend rappel down a cliff. Your friend descends 0.11 mile and then waits for you to catch up. You descend and your current change in elevation is −0.12 mile. Have you reached your friend? Explain.

Answer:
Distance traveled by my friend = 0.11
Question 15.
The table shows the changes in the value of a stock over a period of three days. On which day does the value of the stock change the most? Explain your reasoning.
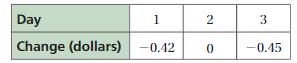
Answer:
Change in stock is most in day 3 that is – 0.45
Explanation:
On day 1 the stock change is -0.42
On day 2 there is no stock change that is 0
On day 3 the stock change is -0.45
From 0 to -0.45 change is more
Rational Numbers Homework & Practice 8.3
Review & Refresh
Copy and complete the statement using < or >.
Question 1.
![]()
Answer:
5 < 8
Question 2.
![]()
Answer:
-4 > -7
Question 3.
![]()
Answer:
2 > -5
Question 4.
![]()
Answer:
0 > -3
Question 5.
You pay $48 for 8 pounds of chicken. Which is an equivalent rate?
A. $44 for 4 pounds
B. $28 for 4 pounds
C. $15 for 3 pounds
D. $30 for 5 pounds
Answer:
$30 for 5 pounds
Explanation:
You pay $48 for 8 pounds of chicken.
$48 = 8 Pounds
$__ = 5 Ponds.
Do Cross Multiplication
(48 × 5)÷8 = 6 × 5 = $30
Find the whole.
Question 6.
40% of what number is 24?
Answer:
40 % = 24
100 % = ?
The answer is 60.
Explanation:
Do cross multiplication we get :
100 % × 24 = 40% × ?
2400 ÷ 40 = 60.
Therefore answer is 60.
Question 7.
12% of what number is 9?
Answer:
12 % = 9
100 % = ?
The answer is 75.
Explanation:
Do cross multiplication we get :
100 % × 9 = 12% × ?
900 ÷ 12 = 75.
Therefore answer is 75.
Question 8.
48% of what number is 84?
Answer:
48 % = 84
100 % = ?
The answer is 175.
Explanation:
Do cross multiplication we get :
100 % × 84 = 48% × ?
8400 ÷ 48 = 175.
Therefore answer is 175.
Question 9.
140% of what number is 98?
Answer:
140 % = 98
100 % = ?
The answer is 70.
Explanation:
Do cross multiplication we get :
100 % × 98 = 140% × ?
9800 ÷ 140 = 70.
Therefore answer is 70.
Multiply.
Question 10
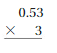
Answer:
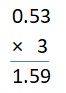
Question 11.
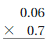
Answer:
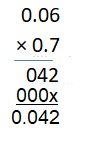
Question 12.
3.7 × 4.854
Answer:
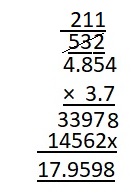
Question 13.
2.9 × 8.8609
Answer:
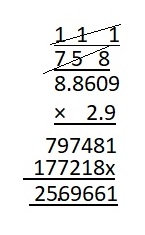
Concepts, Skills, &Problem Solving
USING TOOLS Use a fraction or a mixed number to represent the time on a number line. Let 0 represent noon. (See Exploration 1, p. 357.)
Question 14.
8:30 A.M.
Answer:
Question 15.
12:15 P.M.
Answer:
Question 16.
3:12 P.M.
Answer:
GRAPHING RATIONAL NUMBERS
Graph the number and its opposite.
Question 17.
\(\frac{2}{3}\)
Answer:
\(\frac{2}{3}\) = 0.6
The opposite of 0.6 = – 0.6
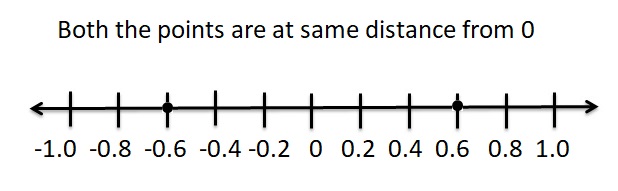
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘0.6’, is ‘-0.6’ on the number line, but on the other side of 0.
Question 18.
– 4.3
Answer:
The opposite of -4.3 = 4.3

Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘4.3’, is ‘-4.3’ on the number line, but on the other side of 0.
Question 19.
2.15
Answer:
The opposite of 2.15 = -2.15
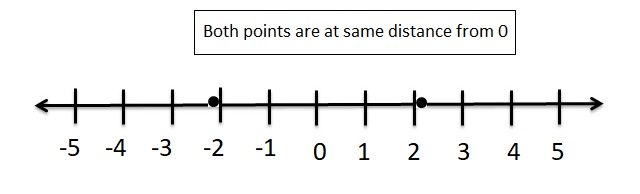
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 20.
– \(\frac{3}{7}\)
Answer:
–\(\frac{3}{7}\) = -0.4
The opposite of -0.4 = 0.4
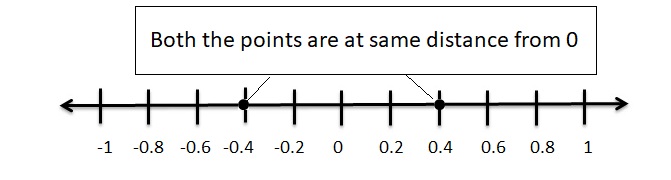
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘0.4’, is ‘-0.4’ on the number line, but on the other side of 0.
Question 21.
– 0.4
Answer:
The opposite of -0.4 = 0.4
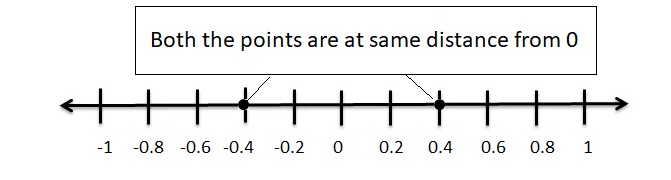
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 22.
5\(\frac{1}{3}\)
Answer:
5\(\frac{1}{3}\) = \(\frac{16}{3}\)=5.3
The opposite of 5.3 = -5.3
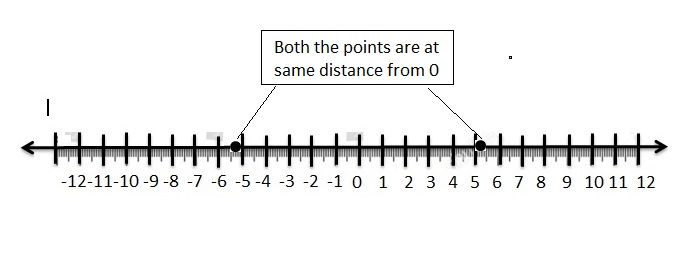
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘5.3’, is ‘-5.3’ on the number line, but on the other side of 0.
Question 23.
– 2\(\frac{1}{4}\)
Answer:
– 2\(\frac{1}{4}\)=- \(\frac{9}{4}\)=-2.25
The opposite of -2.25 = 2.25
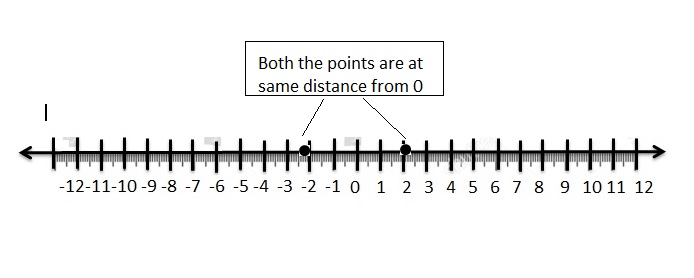
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 24.
-5 \(\frac{3}{10}\)
Answer:
-5 \(\frac{3}{10}\) =- \(\frac{3}{2}\) = -1.5
The opposite of -1.5 = 1.5
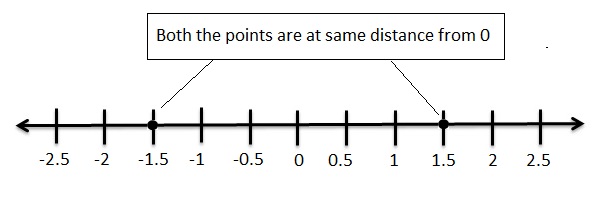
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
COMPARING RATIONAL NUMBERS Copy and complete the statement using < or >.
Question 25.
![]()
Answer:
-3\(\frac{1}{3}\) > -3\(\frac{2}{3}\)
Question 26.
![]()
Answer:
–\(\frac{1}{2}\) < –\(\frac{1}{6}\)
Question 27.
![]()
Answer:
–\(\frac{3}{4}\) < \(\frac{5}{8}\)
Question 28.
![]()
Answer:
-2\(\frac{2}{3}\) < -2\(\frac{1}{2}\)
Question 29.
![]()
Answer:
-1\(\frac{5}{6}\) < -1\(\frac{3}{4}\)
Question 30.
![]()
Answer:
-4.6 > – 4.8
Question 31.
![]()
Answer:
-0.12 < -0.05
Question 32.
![]()
Answer:
2.41 > -3.16
Question 33.
![]()
Answer:
-3.524 > -3.542
ORDERING RATIONAL NUMBERS Order the numbers from least to greatest.
Question 34.
1.3, – 2, – 1.8, 0, – 1.75
Answer:
-2, -1.8, -1.75, 0, 1.3
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 35.
– 4, – 4.35, – 4.9, – 5, – 4.3
Answer:
-5, -4.9, -4.35, – 4.3 , -4
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 36.
1.6, 1.2, 0, 0.8, – 0.1
Answer:
-0.1, 0, 0.8, 1.2, 1.6
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 37.
\(-\frac{1}{2}, \frac{1}{8}, \frac{3}{4},-1,-\frac{1}{4}\)
Answer:
-0.5, 0.125, 0.75, -1, -0.25 above fractions in decimals points
-1, -0.5, -0.25, 0.125, 0.75
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 38.
\(-2 \frac{3}{10},-2 \frac{2}{5},-2,-2 \frac{1}{2},-3\)
Answer:
-2.3, -0.8, -2, -2.5, -3
-3, -2.5, -2.3, -2, -0.8
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 39.
\(-\frac{1}{20},-\frac{5}{8}, 0,-1,-\frac{3}{4}\)
Answer:
-0.05, -0.625, 0, -1, -0.75
-0.75, -0.625, -0.05, -1, 0
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 40.
MODELING REAL LIFE
In rough water, a small sand dollar burrows v centimeter into the sand. A larger sand dollar burrows -1 \(\frac{1}{4}\) centimeters into the sand. Which sand dollar burrowed deeper?

Answer:
small sand dollar burrows = – \(\frac{1}{2}\) = -0.5
Larger sand dollar burrows = -1 \(\frac{1}{4}\) =- \(\frac{5}{4}\) = -1.25cms
The Larger sand dollar burrows deeper .
Explanation:
Here don’t consider the negative signs from ground level that is 0 it is Large sand dollar that is burrowed deeper.
Question 41.
MODELING REAL LIFE
Two golfers calculate their average scores relative to par over several rounds of golf. Golfer A has an average score of −1\(\frac{1}{4}\). Golfer B has an average score of −1\(\frac{3}{8}\). Who has the lesser average score?
Answer:
Average score of Golfer A = −1\(\frac{1}{4}\)=−\(\frac{5}{4}\)=−1.25
Average score of Golfer B = −1\(\frac{3}{8}\)= −\(\frac{11}{8}\)=−1.375
The golfer B has lesser average score.
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 42.
MODELING REAL LIFE
The apparent magnitude of a star measures how bright the star appears as seen from Earth. The brighter the star, the lesser the number. Which star is the brightest?

Answer:
The Deneb is the brightest star = 1.25 (positive number greatest number than all others )
Sirius < Canopus < Alpha Centauri < Antares < Deneb
-1.46 < -0.72 < -0.27 < 0.96 < 1.25
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 43.
REPEATED REASONING
The daily water level relative to the pier is recorded for seven straight days at a tide station on the Big Marco River in Florida. On which days is the water level higher than on the previous day? On which days is it lower? Explain.
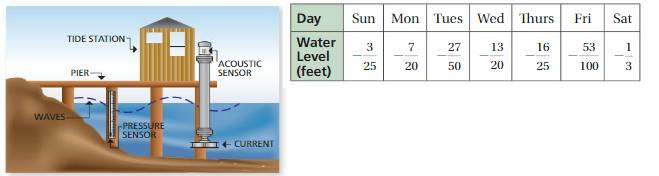
Answer:
The water level on Sun =−\(\frac{3}{25}\) =−0.12
The water level on Mon=−\(\frac{7}{20}\)= −0.35
The water level on Tue= −\(\frac{27}{50}\) =−0.54
The water level on Wed=−\(\frac{13}{20}\)=−0.65
The water level on Thrus=−\(\frac{16}{25}\)=−0.64
The water level on Fri=−\(\frac{53}{100}\)=−0.53
The water level on Sat =−\(\frac{1}{3}\)=−0.33
Explanation:
On Monday The water level is compared to previous day= – 0.12 – ( – 0.35 ) = 0.23
On Tuesday The water level is compared to previous day=-0.35 – ( -0.54) = 0.19
On Wednesday The water level is compared to previous day= -0.54 – ( – 0.65) =0.11
On Thrusday The water level is compared to previous day= – 0.65 – ( – 0.64)=0.01
On Friday The water level is compared to previous day= – 0.64 – ( – 0.53)=0.11
On Saturday The water level is compared to previous day = – 0.53 – ( -0.33 )=0.20
On Monday the water level is more compared to the previous day .
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 44.
DIG DEEPER!
A guitar tuner allows you to tune a guitar string to its correct pitch. The units on a tuner are measured in cents. The units tell you how far the string tone is above or below the correct pitch.
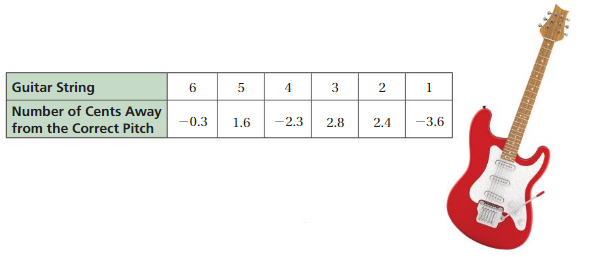
a. What number on the tuner represents a correctly tuned guitar string?
b. Which strings have a pitch below the correct pitch?
c. Which string has a pitch closest to its correct pitch?
d. Which string has a pitch farthest from its correct pitch?
e. The tuner is rated to be accurate to within 0.5 cent of the true pitch. Which string could possibly be correct? Explain your reasoning.
Answer a :
The Number on the tuner represents a correctly tuned guitar string = 0
Answer b :
The string below the correct pitch = 6
Explanation:
As The string 6 is only -0.3 distance away from the correctly tuned guitar string other than strings.
Answer c :
A pitch closest to its correct pitch = 6
Explanation:
As The string 6 is only -0.3 distance away from the correctly tuned guitar string other than strings. which is the least distance between them.
Answer d :
String which is pitch farthest from its correct pitch is 1.
Explanation:
As The string 1 is only -3.6 distance away from the correctly tuned guitar string other than strings. which is the Farthest distance between them.
Answer e :
No string tuner is rated to be accurate to within 0.5 cent of the true pitch
Explanation:
Correct tuner is at 0
0.5 cent of the true pitch = 0
Which is not possible
Question 45.
NUMBER SENSE
What integer values of x make the statement − \(\frac{3}{x}\) < − \(\frac{x}{3}\) true?
Answer:
− \(\frac{3}{x}\) < − \(\frac{x}{3}\)
X should be more than 3 .
if x is in the numerator in the fraction form it resultant will be more when divided by 3
If x is in the denominator in the fraction form it resultant will be less when 3 is divided by x
Explanation:
For example: take x = 4
− \(\frac{3}{4}\) =−0.75
− \(\frac{4}{3}\) = −1.33
−0.75 < −1.33
Lesson 8.4 Absolute Value
EXPLORATION 1
Comparing Positions of Objects
Work with a partner. The diagram shows the positions of several objects.
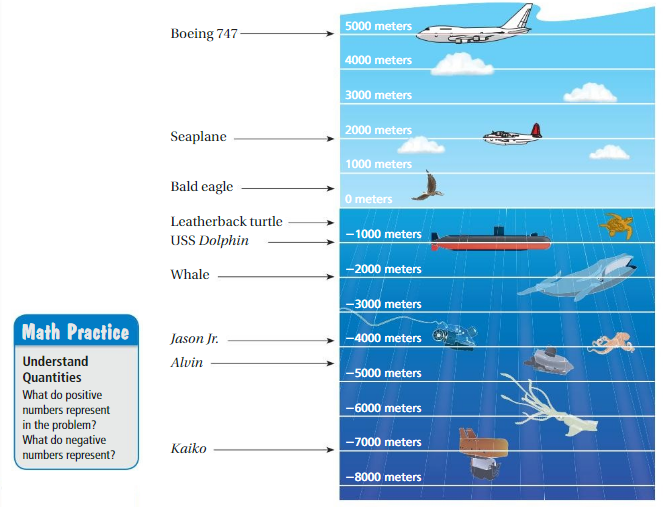
a. What integer represents sea level? How can you compare the positions of objects relative to sea level?
Answer:
An integer represents sea level = 0
You can compare the positions of objects relative to sea levels by number of meters above and below as given in the above figure.
b. Which pairs of objects are the same distance from sea level? How do you know?
Answer:
Whale and sea plane
Explanation:
Whale and sea plane are at -1000 and 1000 meters below and above respectively from sea level.
Both are at equidistant from the sea level.
c. The vesselsKaiko, Alvin, and Jason Jr.move to be the same distance from sea level as the Boeing 747. About how many meters did each vessel travel?
Answer:
Distance of Boeing 747 from sea level = 5000 metres.
Distance of Kaiko below sea level = – 7000 metres
Distance of Alvin below sea level = -4500 metres
Distance of Janson Jr.below sea level = 4000 metres
Explanation:
To travel same distance as Boeing 747 the Kaiko should travel + 2000 metres towards the sea level so that it comes at 5000 metres below sea level.
To travel same distance as Boeing 747 the Alvin should travel – 500 metres below the sea level so that it comes at 5000 metres below sea level.
To travel same distance as Boeing 747 the Janson Jr should travel -1000 metres below the sea level so that it comes at 5000 metres below sealevel.

Try It
Find the absolute value.
Question 1.
|8|
Answer:
|8| = 8
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Question 2.
|-6|
Answer:
|-6| = 6
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Question 3.
|0|
Answer:
|0| = 0
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Question 4.
\(\left| \frac { 1 }{ 4 } \right| \)
Answer:
\(\left| \frac { 1 }{ 4 } \right| \) = 0.25
|0.25| = 0.25
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Question 5.
\(\left|-7 \frac{1}{3}\right|\)
Answer:
\(\left|-7 \frac{1}{3}\right|\) = – 7.33
|-7.33|=7.33
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Question 6.
|- 12.9|
Answer:
|- 12.9| = 12.9
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Copy and complete the statement using <, >, or =.
Question 7.
![]()
Answer:
|-4|=4
4 > -2
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 8.
![]()
Answer:
|5| = 5
-5 < 5
Explanation:
All positive integers are greater than negative integers
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 9.
![]()
Answer:
|9|=9
9 < 10
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 10.
![]()
Answer:
|-3.9| = 3.9
3.9 = 3.9
Explanation:
Both the integers are same so equal.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
COMPARING VALUES Copy and complete the statement using <, >, or =.
Question 11.
![]()
Answer:
|-6| = 6
6 > 3
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 12.
![]()
Answer:
|-3.5| = 3.5
3.5 < 4
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 13.
![]()
Answer:
3\(\frac{1}{2}\) = \(\frac{5}{2}\)=2.5
-4\(\frac{3}{4}\)=-\(\frac{19}{4}\) = – 4.75
|-4.75|= 4.75
2.5 > 4.75
Explanation:
Convert the fraction form into decimals form . later write absolute values and compare the values. The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 14.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
What is the absolute value of – 3.
What integer is 3 units to the left of 0
Explanation:
Rest of the two statements describe the distance between -3 to 0.
Question 15.
Describe the position of an object in your classroom using a negative rational number. Then describe the position of a second object using a positive rational number. Which number has a greater absolute value? What does this mean?
Answer:
The position of my pen is -6 cms from my bench.
The position of my books is +3 cms from my bench.
The absolute value of -6 = 6
The absolute value of 3 = 3
6 > 3
Explanation:
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x . All absolute values are positive.
Question 16.
DIG DEEPER!
The table shows the elevations of several checkpoints along a hiking trail.
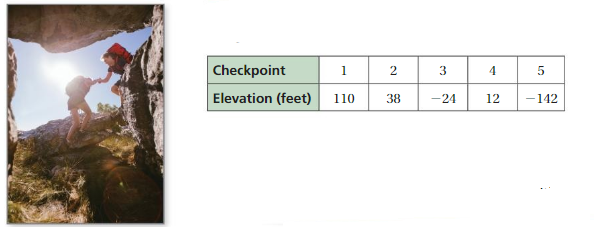
a. Which checkpoint is farthest from sea level?
b. Which checkpoint is closest to sea level?
c. Between which checkpoints do you reach sea level? Explain your reasoning.
Answer a :
The Farthest checkpoint from sea level = 5
Explanation:
It is -142 in elevation feet
Answer b :
The closest checkpoint from sea level = 4
Explanation:
It is 12 in elevation feet
Answer c :
No we cant .
Explanation:
Sea level = 0
We need to get 0 between two check points then the check points reach sea level.
Elevation feet between 1 and 2 check points = 110 – 38 = 72
Elevation feet between 2 and 3 check points = 38 – (-24) = 72
Elevation feet between 3 and 4 check points = – 24 -12 = -36
Elevation feet between 4 and 5 check points =12 – (-142) = 154
Absolute Value Homework & Practice 8.4
Review & Refresh
Order the numbers from least to greatest.
Question 1.
2.4, – 3.2, – 1.8, 0.6, – 1.3
Answer:
-3.2 < -1.8 < -1.3<0.6<2.4
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater. With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 2.
– 0.3, 0.7, – 1.5, 0, 2.2
Answer:
-1.5< -0.3<0<0.7<2.2
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 3.
\(\frac{3}{4}, \frac{1}{2}, \frac{2}{3}, 2, \frac{1}{4}\)
Answer:
0.75, 0.5, 0.6, 2,0.25
All the above fractions are represented in decimals now compare
0.25<0.5<0.6<0.75<2
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 4.
\(\frac{1}{5}, 1 \frac{2}{5},-2 \frac{3}{4}, \frac{4}{5},-2 \frac{1}{2}\)
Answer:
0.2, 1.4, -2.75, 0.8, -2.5
All the above fractions are represented in decimals now compare
-2.75<-2.5<0.2<0.8<1.4
Explanation:
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Represent the ratio relationship using a graph.
Question 5.
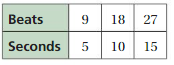
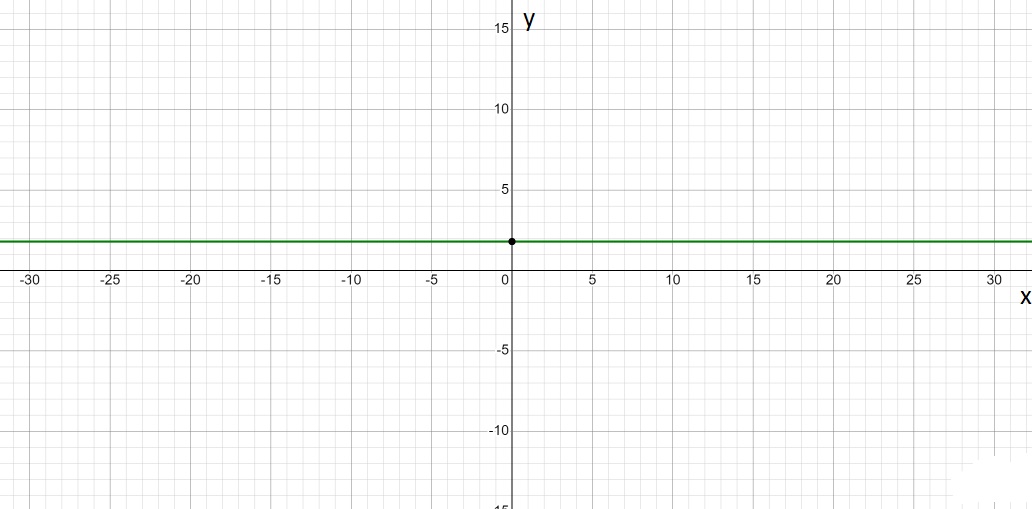
Answer:
Slope = 0
Y-intercept : (0 , 9/5)
Plot each graph on the same coordinate system.
9/5, 18/10 , 27/15.
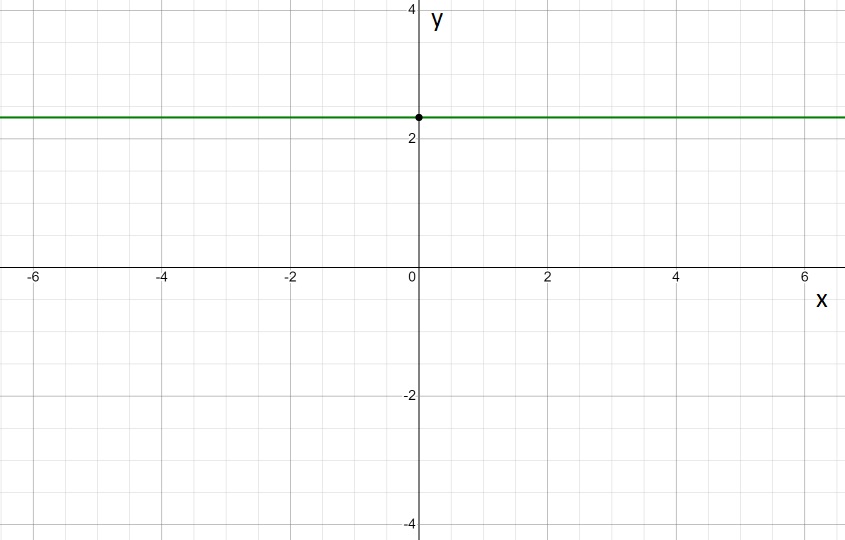
Question 6.
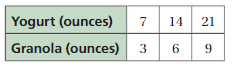
Answer:
Slope = 0
Y-intercept : (0 , 7/3)
Plot each graph on the same coordinate system.
7/3 , 14/6, 21/9 .
Evaluate the expression when a = 2, b = 5, and c = 8.
Question 7.
5 + c
Answer:
5 + c =
Take c = 8
5 + 8 = 13
Question 8.
b – 4
Answer:
take b=5
5 – 4 = 1
Question 9.
\(\frac{c}{a}\)
Answer:
take a =2 and c= 8
\(\frac{8}{2}\) = 4
Question 10.
b * c
Answer:
take b = 5 and c = 8
5 × 8 = 40
Concepts, Skills, &Problem Solving
COMPARING POSITIONS OF OBJECTS Tell which object is farther from sea level. Explain your reasoning. (See Exploration 1, p. 363.)
Question 11.
Scuba diver: −15 m
Dolphin: −22 m
Answer:
The Dolphin = – 22m is farther from sea level
Explanation:
Distance cant be negative so just consider the value and compare the distance which is greater.
15 < 22
Question 12.
Seagull: 12 m
School of fish: −4 m
Answer:
Seagull = 12m is farther from sea level
Explanation:
Distance cant be negative so just consider the value and compare the distance which is greater.
12 > 4
Question 13.
Shark:−40 m
Flag on a ship: 32 m
Answer:
Explanation:
Shark = – 40 m
Distance cant be negative so just consider the value and compare the distance which is greater.
40 > 32
FINDING ABSOLUTE VALUE Find the absolute value.
Question 14.
|- 2|
Answer:
|- 2| = 2
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 15.
|23|
Answer:
|23|=23
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 16.
|11|
Answer:
|11|=11
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 17.
|- 68|
Answer:
|-68|=68
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 18.
|- 8.35|
Answer:
|-8.35|=8.35
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 19.
\(\left|\frac{1}{6}\right|\)
Answer:
\(\left|\frac{1}{6}\right|\) = |0.16|=0.16
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 20.
|14.06|
Answer:
|14.06|=14.06
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 21.
\(\left|-\frac{5}{8}\right|\)
Answer:
\(\left|-\frac{5}{8}\right|\)= |-0.625| = 0.625
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 22.
\(\left|-3 \frac{2}{5}\right|\)
Answer:
\(\left|-3 \frac{2}{5}\right|\) = |-3.4|= 3.4
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 23.
|1.026|
Answer:
|1.026|=1.026
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 24.
\(\left|1 \frac{1}{3}\right|\)
Answer:
\(\left|1 \frac{1}{3}\right|\)= \(\left| \frac{4}{3}\right|\) =|1.3| = 1.3
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 25.
|- 6.308|
Answer:
|-6.308|=6.308
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 26.
REASONING
Write two integers that have an absolute value of 10.
Answer:
– 10 and 10
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 27.
YOU BE THE TEACHER
Your friend finds the absolute value of 14. Is your friend correct? Explain your reasoning.
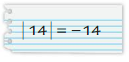
Answer:
Wrong
All absolute values are positive.
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
COMPARING VALUES Copy and complete the statement using <, >, or =.
Question 28.
![]()
Answer:
|-8| = 8
6 < 8
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 29.
![]()
Answer:
|-3|= 3
3 = 3
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 30.
![]()
Answer:
|-4.3| = 4.3
4.3 > 3.4
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 31.
![]()
Answer:
–\(\frac{2}{9}\)= -0.22
\(\frac{1}{5}\)= 0.2
|-0.22|=0.22
0.22>0.2
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 32.
![]()
Answer:
|-0.05|= 0.05
0.05 > 0
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 33.
![]()
Answer:
|-5.5|= 5.5
|-3.1| = 3.1
5.5 > 3.1
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 34.
![]()
Answer:
\(\frac{3}{4}\) = 0.75
–\(\frac{2}{5}\)= – 0.4
|-0.4| = 0.4
0.75 > 0.4
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 35.
![]()
Answer:
|-6.8|=6.8
|8.25|=8.25
6.8 < 8.25
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 36.
![]()
Answer:
|12| = 12
– 12 < 12
Explanation:
All positive integers are greater than negative integers
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 37.
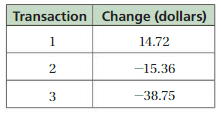
MODELING REAL LIFE
The table shows the change in the balance of a bank account after each of three transactions. Which transaction has the greatest effect on the balance of the account? Which transaction has the least effect on the balance of the account?
Answer:
Transaction has the greatest effect on the balance of the account = 3
Transaction which has the least effect on the balance of the account = 1
ORDERING VALUES Order the values from least to greatest.
Question 38.
5, 0, |- 1|, |4| , – 2
Answer:
|- 1| = 1
|4| = 4
-2<0<1<4<5
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 39.
|- 3|, |5| , – 3, – 4, |- 4|
Answer:
|- 3| = 3
|5| = 5
|- 4|=4
-4< -3< 3 < 4 < 5
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 40.
10, |- 6|, 9, |3|, -11, 0
Answer:
|- 6| = 6
|3| = 3
-11<0<3<6<9<10
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 41.
– 18, |30|, – 19, |- 22|, – 20, |- 18|
Answer:
|30| = 30
|- 22| = 22
|- 18|=18
-20 < -19< – 18 <18<22<30
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
The Negative Numbers which are near to the 0 are greater .Numbers to the right are greater .With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
SIMPLIFYING EXPRESSIONS Simplify the expression.
Question 42.
– |2|
Answer:
– |2| = – 2
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 43.
– |6|
Answer:
-|6| = -6
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive..
Question 44.
– |- 1|
Answer:
|1| = 1
-1
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 45.
REASONING
The coldest possible temperature is called absolute zero. It is represented by 0 K on the Kelvin temperature scale.
a. Which temperature is closer to 0 K: 32°F or − 50°C?
Answer:
As per the given we notice is 32°F
b. What do absolute values and temperatures on the Kelvin scale have in common?
Answer:
All the temperatures and absolute values are positive in kelvin scale.
CRITICAL THINKING
Tell whether the statement is always, sometimes, or never true. Explain.
Question 46.
The absolute value of a number is greater than the number.
Answer:
False
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 47.
The absolute value of a negative number is positive.
Answer:
True
Explanation:
All absolute values are positive.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x.
Question 48.
The absolute value of a positive number is its opposite.
Answer:
False
Explanation:
Opposite value of a positive number is negative. but all absolute values are positive so the given statement is wrong .
MATCHING Match the account balance with the debt that it represents. Explain your reasoning.
Question 49.
account balance = −$25
Answer: B. debt = $25
Question 50.
account balance < −$25
Answer: C. debt < $25
Question 51.
account balance > −$25
Answer: A. debt > $25
A. debt > $25
B. debt = $25
C. debt < $25
Question 52.
PATTERNS
A palindrome is a word or sentence that reads the same forward as it does backward.
a. Graph and label the following points on a number line: A =− 2, C =− 1, E = 0, R =− 3. Then, using the same letters as the original points, graph and label the absolute value of each point on the same number line.
b. What word do the letters spell? Is this a palindrome?
c. Assign letters to points on a number line to make up your own palindrome using the process in part(a).
Answer a :
Answer b :
Letters spell – RACE and ECAR Yes, it is a palindrome .
Answer c:
It is shown in the above diagram .
Question 53.
CRITICAL THINKING
Find values of x and y so that |x| < |y| and x > y.
Answer:
Lesson 8.5 The Coordinate Plane
Extending the Coordinate Plane
Work with a partner. Previously, you plotted points with positive coordinates in a coordinate plane like the one shown at the right.
a. You can also plot points in which one or both of the coordinates are negative numbers. Create ordered pairs with different combinations of positive and negative coordinates, as described below. Then plot the ordered pairs and explain how you extended the coordinate plane shown.
(positive, positive) (negative, positive)
(negative, negative) (positive, negative)
Answer:
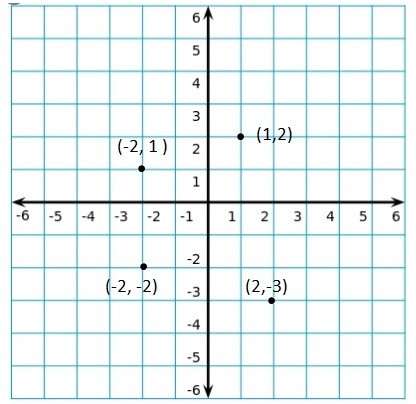
b. How many regions of the coordinate plane are created by the x-axis and y-axis? What do the points in each of these regions have in common?
Answer:
The four regions are covered with one point .
The numbers on a coordinate grid are used to locate points. Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
c. The photo shows the reflection, or mirror image, of a mountain in a lake. When you fold the photo on its axis, the mountain and its reflection align.

c. Actual A mountainoAxisAMath PracticeReflectionReof mountain Check ProgressHow can you check your progress to make sure you are reflecting your point correctly?
Plot a point and its reflection in one of the axes. Explain your reasoning. What do you notice about the coordinates of the points?
Answer:
As per the above image we notice that the axis is equal to the axis of the graph . the graph is divided into 4 Quadrants as shown in below graph.
A coordinate plane is a two-dimensional plane formed by the intersection of a vertical line called y-axis and a horizontal line called x-axis. These are perpendicular lines that intersect each other at zero, and this point is called the origin.
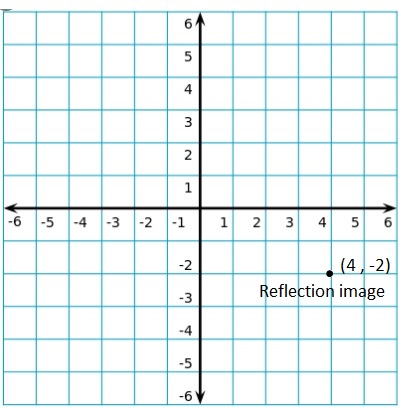
As the reflection is formed in fourth quadrant an example of reflection is marked in the above graph .

Try It
Use the graph in Example 1 to write an ordered pair corresponding to the point.
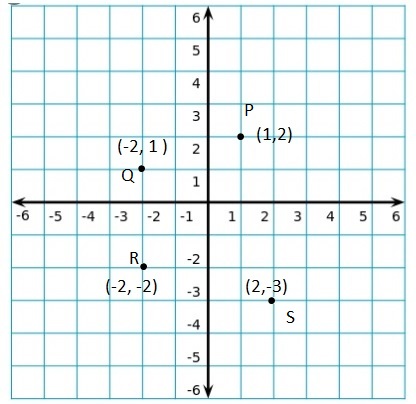
As shown in example one the points are mentioned below
Question 1.
Point P
Answer:
(1,2)
The point P is marked in the Quadrant I as shown in the above graph .
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 2.
Point Q
Answer:
(-2,1)
The point Q is marked in the Quadrant II as shown in the above graph .
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question3.
Point R
Answer:
(-2,2)
The point R is marked in the Quadrant III as shown in the above graph .
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 4.
Point S
Answer:
(2,-3)
The point S is marked in the Quadrant IV as shown in the above graph .
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 5.
(3, -1)
Answer:
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph.
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph. 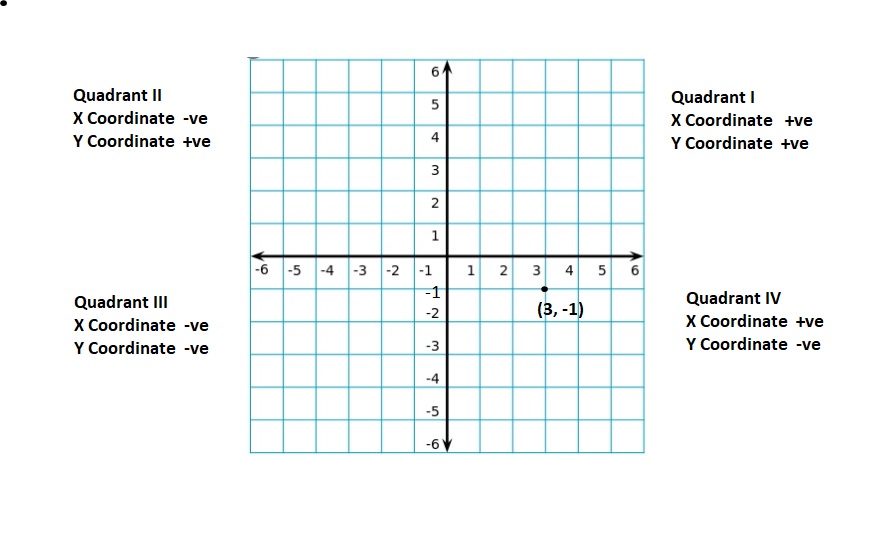
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 6.
(-5, 0)
Answer:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is positive as shown in the graph.
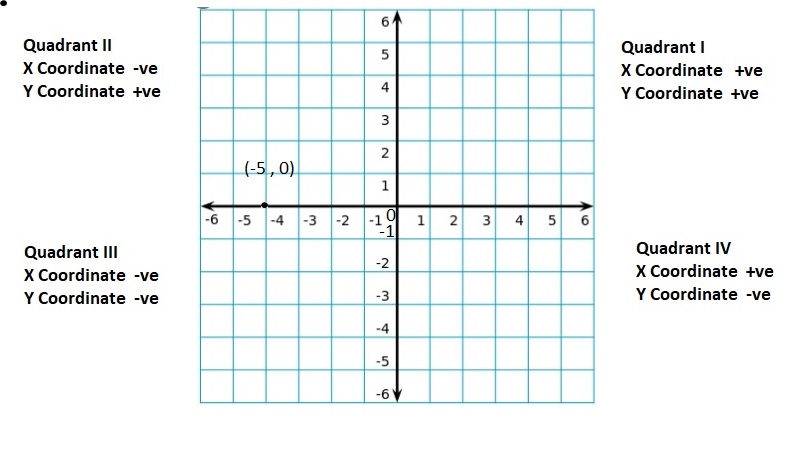
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 7.
(- 2.5, -1)
Answer:
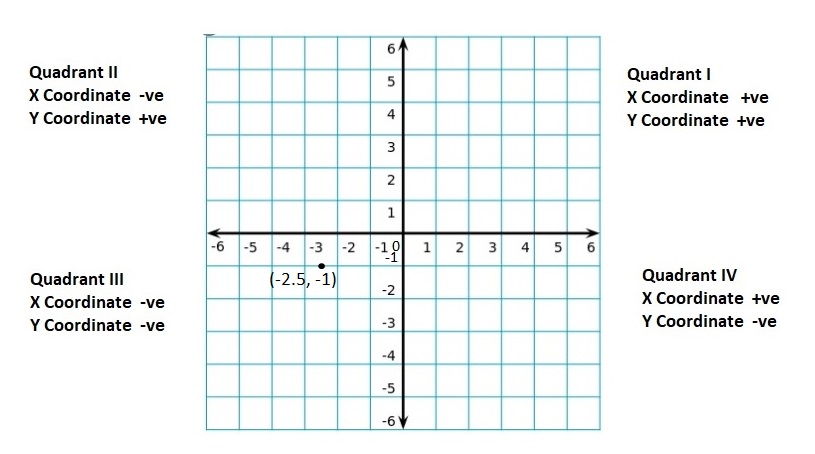
Explanation:
It is marked in the Quadrant III as X coordinate is Negative and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 8.
(-1\(\frac{1}{2}\), \(\frac{1}{2}\))
Answer:
-1\(\frac{1}{2}\) = –\(\frac{3}{2}\) = -1.5
\(\frac{1}{2}\) = 0.5
(-1.5, 0.5)
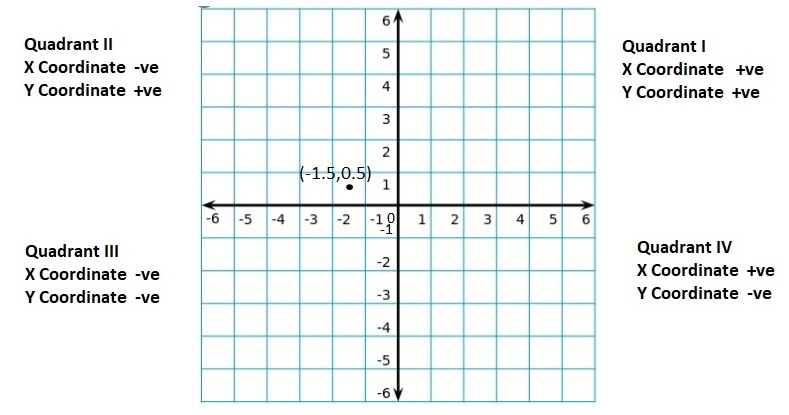
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Reflect the point in (a) the x-axis and (b) the y-axis.
Question 9.
(3, – 2)
Answer:
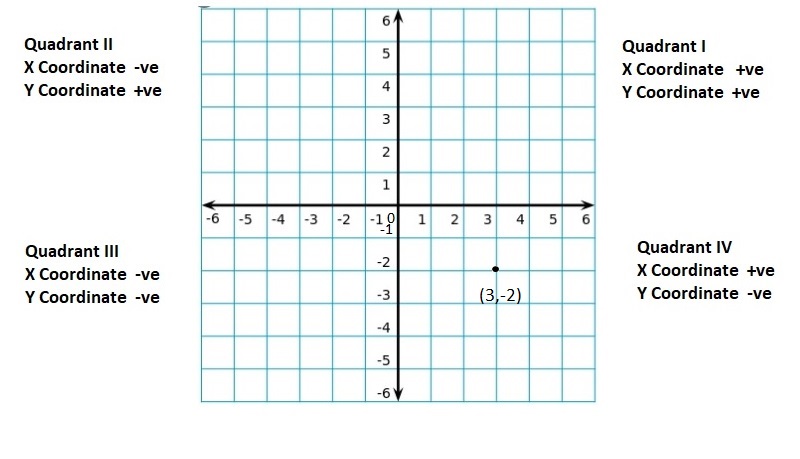
Explanation:
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 10.
(4, 0)
Answer:
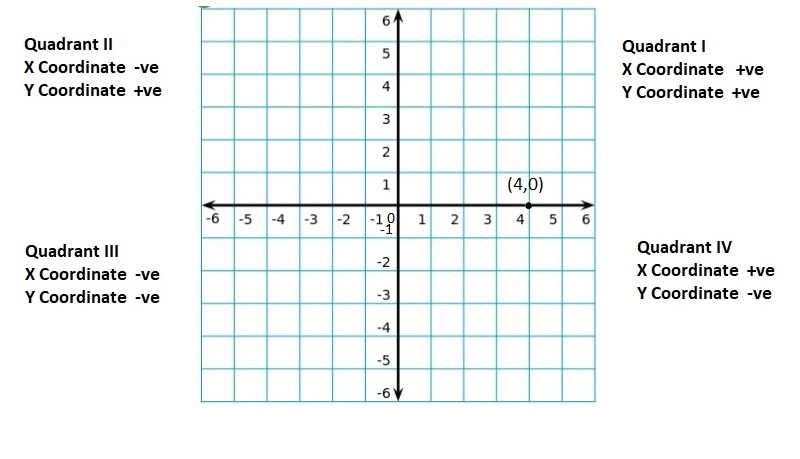
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 11.
(- 5, 1.5)
Answer:
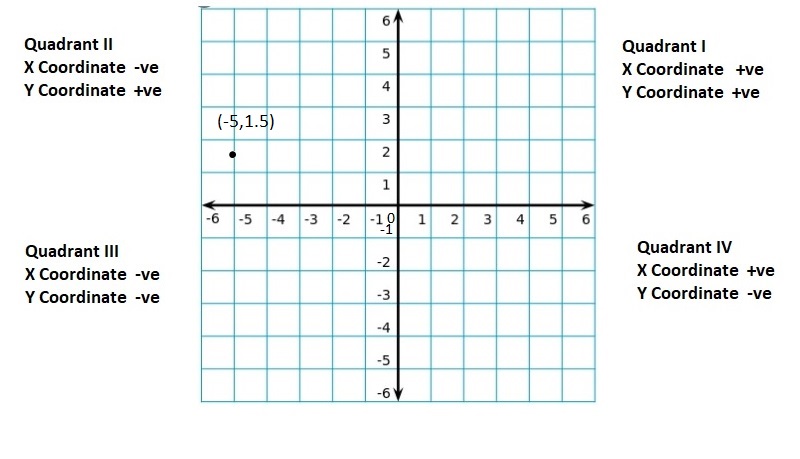
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Reflect the point in the x-axis followed by the y-axis.
Question 12.
(3, 2)
Answer:
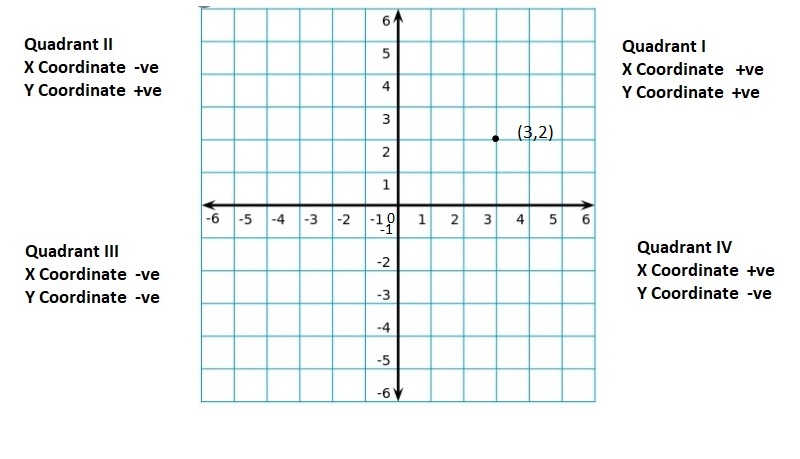 Explanation:
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 13.
(- 1, 2)
Answer:
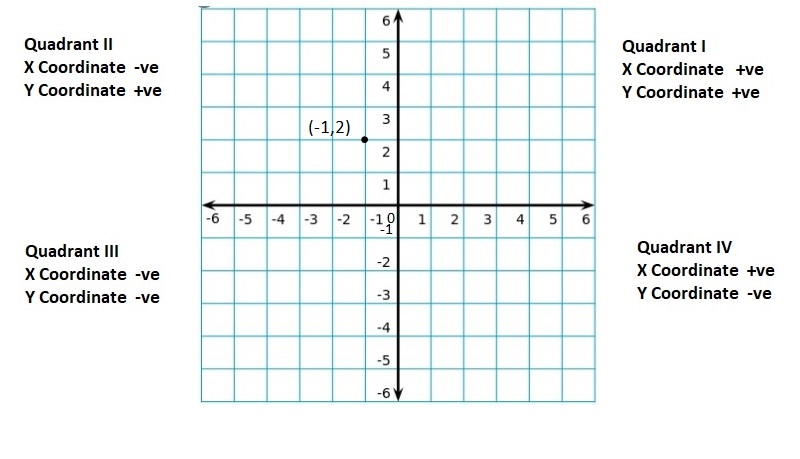
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 14.
(- 4, – 3)
Answer:
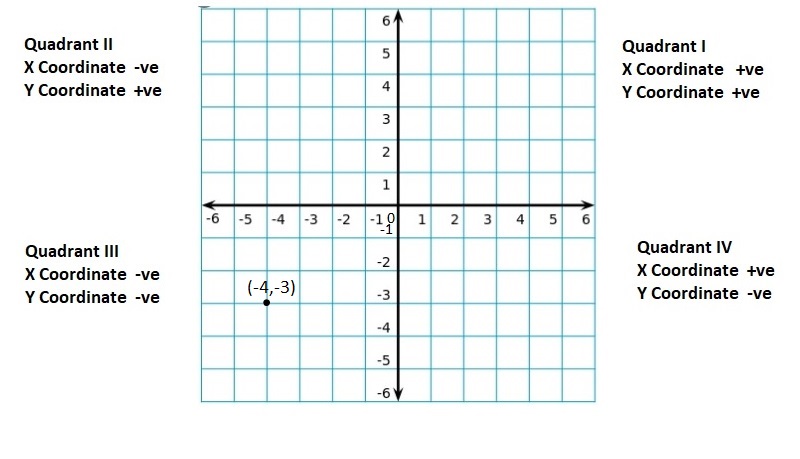
Explanation:
It is marked in the Quadrant III as X coordinate is Negative and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 15.
(5, – 2.5)
Answer:
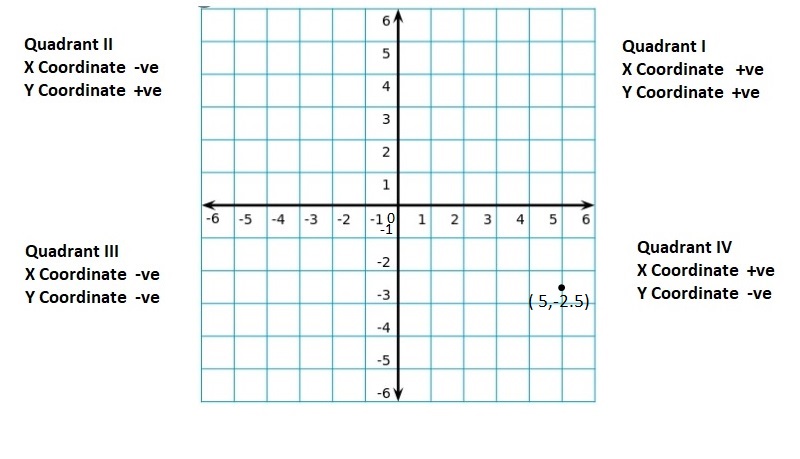
Explanation:
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING ORDERED PAIRS Write an ordered pair corresponding to the point shown in the coordinate plane.
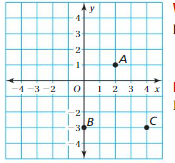
Question 16.
Point A
Answer:
X coordinate is 2
Y coordinate is 1
(2,1)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 17.
Point B
Answer:
X coordinate is 0
Y coordinate is -3
Explanation:
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 18.
Point C
Answer:
X coordinate is 4
Y coordinate is -3
Explanation:
It is marked in the Quadrant IV as X coordinate is positive and Y coordinate is negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
PLOTTING ORDERED PAIRS Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 19.
J(2, 5)
Answer:
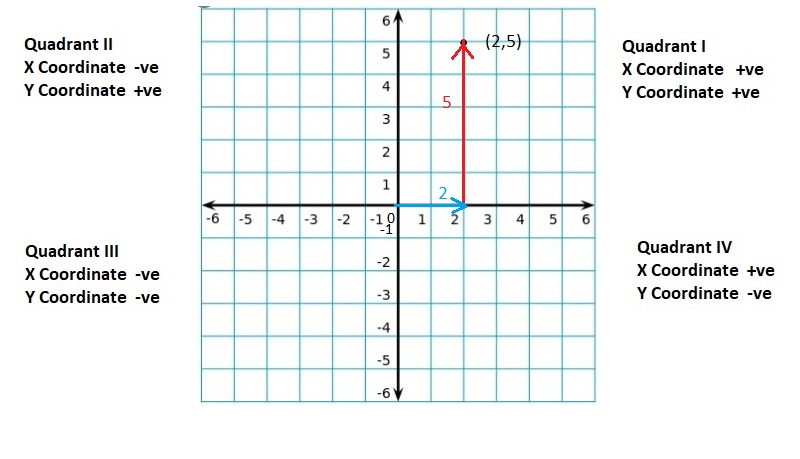
Explanation:
Start at the origin move 2 units right and 5 units up. Then plot the point
The Point is in Quadrant I
Question 20.
K (4, – 6)
Answer:
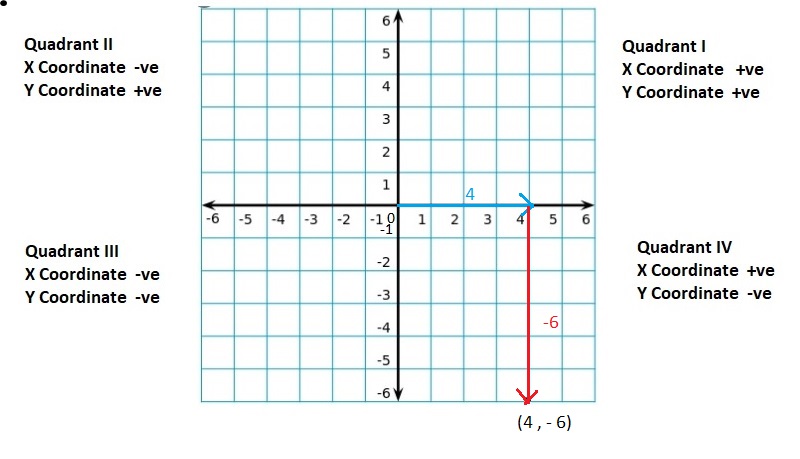
Explanation:
Start at the origin move 4 units right and 6 units down. Then plot the point
The Point is in Quadrant IV
Question 21.
L (- 3, – 2\(\frac{1}{2}\))
Answer:
– 2\(\frac{1}{2}\)=- \(\frac{5}{2}\))=-2.5
L (-3, -2.5)
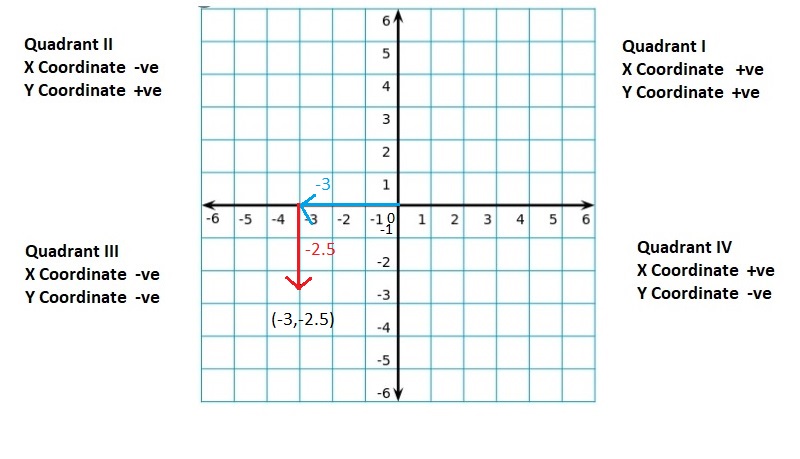
Explanation:
Start at the origin move 3 units left and 6 units down. Then plot the point
The Point is in Quadrant III
REFLECTING POINTS
Reflect the point in the given axis or axes.
Question 22.
(9, 8); x-axis
Answer:
Plot (9,8) and (9,-8)
Explanation:
To reflect (9,8) in the x axis, use the same x-coordinate, 9,the opposite of the y coordinate.The opposite of y coordinate 8 is -8
So the reflection of (9,8)in the x-axis is (9,-8)
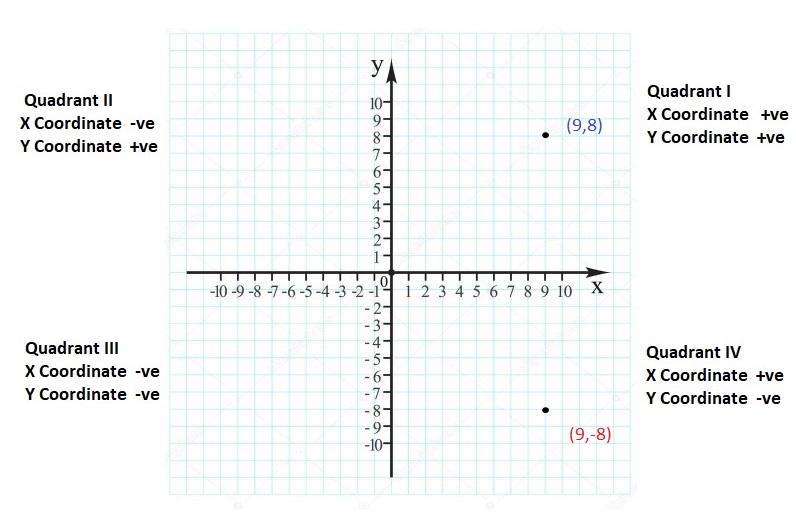
Question 23.
(−7, 3); y-axis
Answer:
Plot (-7,3) and (7,3)
Explanation:
To reflect (-7,3) in the y axis, use the same y-coordinate, 3,the opposite of the x coordinate.The opposite of x coordinate -7 is 7
So the reflection of (-7,3)in the x-axis is (7,3)
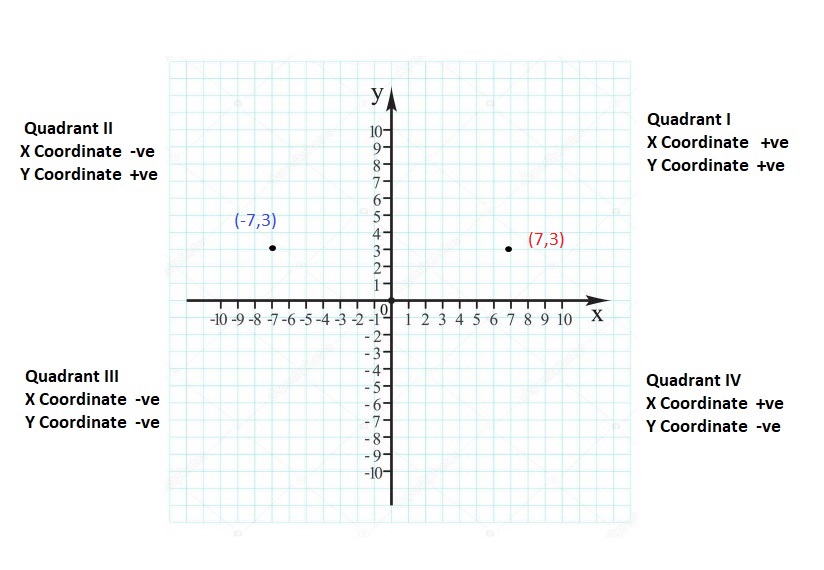
Question 24.
(6, −4); x-axis then y-axis
Answer:
Plot (6,-4), (6,4) and (-6,4)
Explanation:
To reflect (6,-4) in the x axis, use the same x-coordinate, 6,the opposite of the y coordinate.The opposite of y coordinate -4 is 4
To reflect (6,4) in the y axis, use the same y-coordinate, 4,the opposite of the x coordinate.The opposite of x coordinate 6 is -6
So the reflection of (6,-4)in the x-axis is (6,4)
So then reflection of (6,4)in the y-axis is (-6,4)
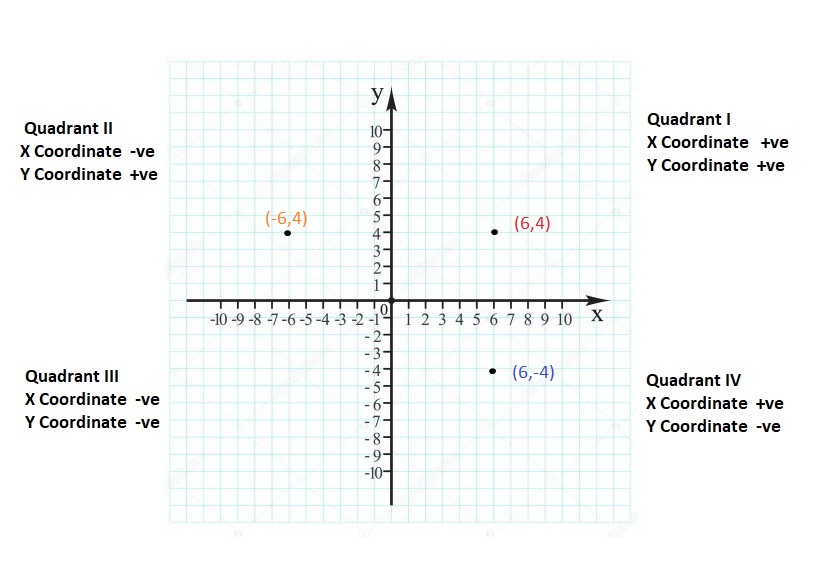
Question 25.
(2.5, −4); y-axis then x-axis
Answer:
Plot (2.5, -4) , (-2.5,-4) and (-2.5,4)
Explanation:
To reflect (2.5,-4) in the y axis, use the same y-coordinate, -4,the opposite of the x coordinate.The opposite of x coordinate 2.5 is -2.5
To reflect (-2.5,-4) in the x axis, use the same x-coordinate, -2.5,the opposite of the y coordinate.The opposite of y coordinate -4 is 4
So the reflection of (2.5,-4)in the y-axis is (-2.5,-4)
So then reflection of (-2.5,-4)in the x-axis is (-2.5,4)
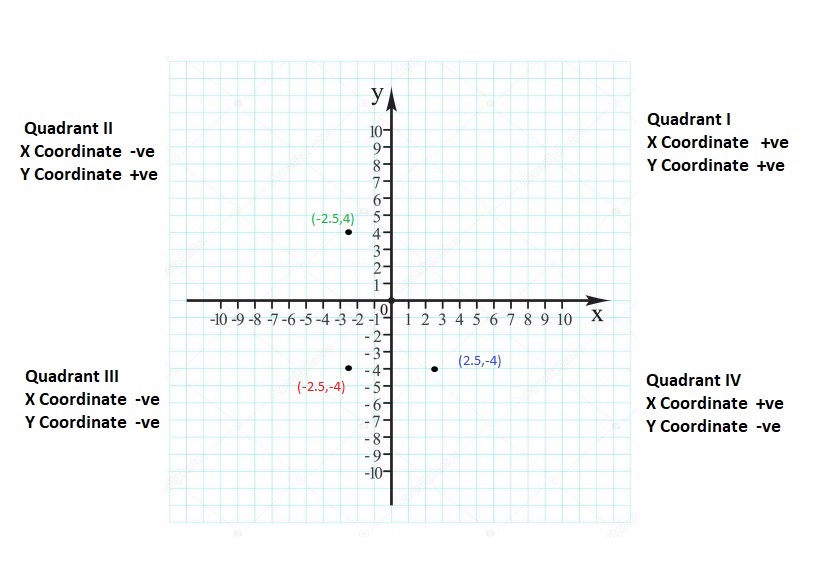
Question 26.
DIG DEEPER
At a park, the welcome center is located at (0, 0), the theater is located at(2, 4), and the restrooms are located at(−4.5, 6). The snack bar is exactly halfway between the welcome center and the theater. Graph each location in a coordinate plane.
Answer:
Welcome Centre is located at (0,0)
Theater is located at (2, 4)
Restrooms are located at (−4.5, 6)
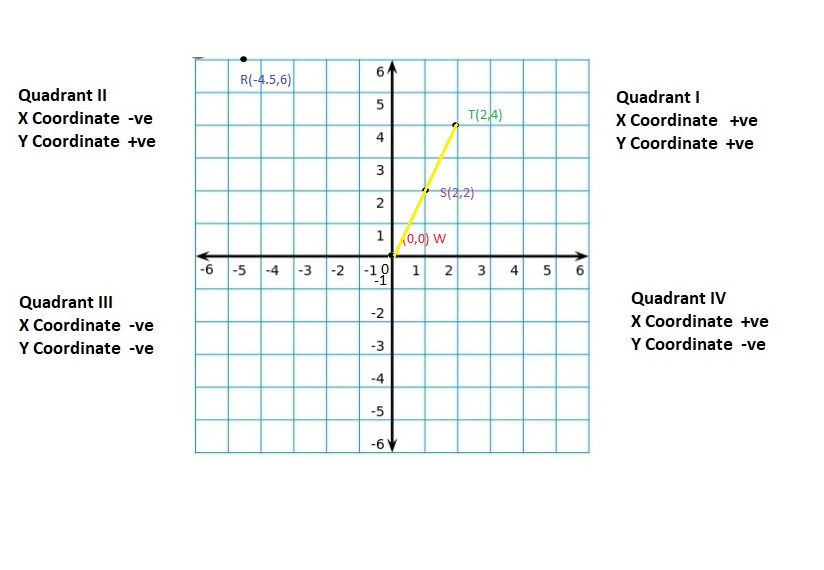
Explanation:
Halfway between the welcome center and the theater is known by joining both W and T points. we notice now that (2,2) is exactly half way between them so the Snack bar is at (2,2)
Question 27.
The table shows the elevations of a submarine each hour from noon to 5:00 P.M. Display the data in a line graph. Then describe the change in elevation over time.

Answer:
The ordered pairs are (0,-4.5), (1,-3), (2,-2.5), (3,-2), (4,-3.5) and (5,-4)
Plot the ordered pairs and then connect the points with line segments
The elevations of a submarine increases up to 3:00 P.M then later the elevations decreases up to 5:00 P.M
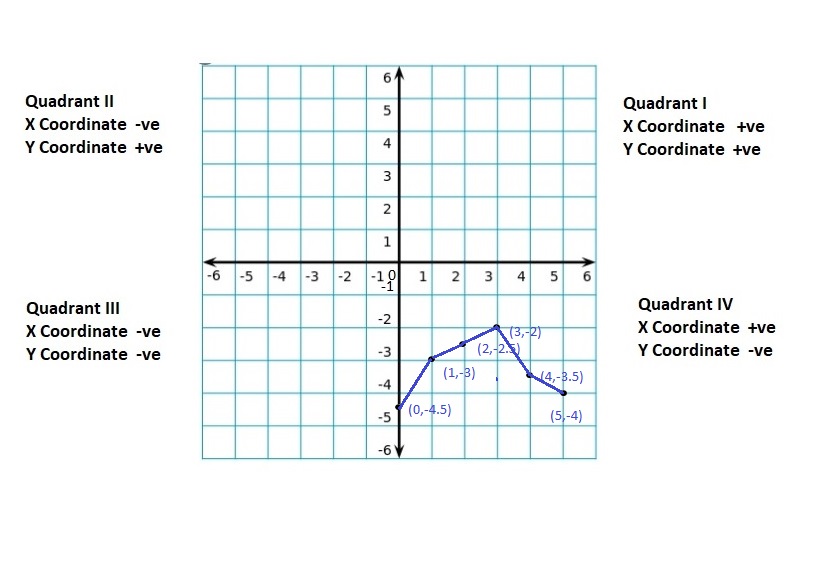
The Coordinate Plane Homework & Practice 8.5
Review & Refresh
Find the absolute value.
Question 1.
|35|
Answer:
|35| = 35
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Quest ion 2.
|- 18|
Answer:
|- 18| = 18
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 3.
|4.7|
Answer:
|4.7| = 4.7
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 4.
|- 6\(\frac{7}{12}\)|
Answer:
|- 6\(\frac{7}{12}\)|= |- \(\frac{79}{12}\)|= |-6.58| =6.58
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 5.
What is the ratio of ducks to swans?
A. 4 : 9
B. 4 : 5
C. 5 : 4
D. 5 : 9
Answer:
Total Number of Ducks = 5
Total Number of Swans = 4
Ratio = Total Number of Ducks ÷ Total Number of Swans = 5 ÷ 4 = \(\frac{5}{4}\)
Graph the equation.
Question 6.
y = 8x
Answer:
y-intercept:
x = 0
y = 0
and
x = 1
y= 8
Question 7.
y = 3x + 7
Answer:
y = 0
and
x = 0
y= 7
Question 8.
y = \(\frac{2}{5}\)x + 2
Answer:
y = \(\frac{2}{5}\)x + 2
y = 0.4x + 2
y = 0
and
x = 0
y= 2
Tell which property the statement illustrates.
Question 9.
(2 . P) . 3 = 2 . (p . 3)
Answer:
The Associative Property of Multiplication states that numbers in a multiplication expression can be regrouped using parentheses
Associative Property of Multiplication
For any real numbers a, b, and c, (a • b) • c = a • (b • c).
Question 10.
m + 0 = m
Answer:
The addition property of 0 states that for any number being added to zero, the sum is the same number.Zero is called the additive identity.
Question 11.
w . 1 = w
Answer:
The multiplication property of 1 states that for any number multiplied by one, that answer is that same number and one is called the multiplicative identity.
Question 12.
15 + k = k + 15
Answer:
Commutative property of addition: Changing the order of addends does not change the sum.
Concepts, Skills, &Problem Solving
DESCRIBING REFLECTIONS Describe the reflection shown in the image. (See Exploration 1, p. 369.)
Question 13.

Answer:
The image shows the reflection image or mirror image when folded on its y-axis . both the real image and reflection image gets aligned.
Question 14.

Answer:
The image shows the reflection image or mirror image of a arrow and shoes . when you fold the photo on its y-axis the arrow and shoes its reflection align.
Question 15.

Answer:
The image shows the reflection or mirror image of a den in water. when you fold the photo on its x-axis, the den in the water and its reflection align.
WRITING ORDERED PAIRS Write an ordered pair corresponding to the point.
Question 16.
Point A
Answer:
X coordinate is 3
Y coordinate is 1
(3,1)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 17.
Point B
Answer:
X coordinate is -3
Y coordinate is -2
(-3,-2)
Explanation:
It is marked in the Quadrant III as X coordinate is Negative and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 18.
Point C
Answer:
X coordinate is -2
Y coordinate is 4
(-2,4)
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 19.
Point D
Answer:
X coordinate is 1
Y coordinate is 2
(1,2)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 20.
Point E
Answer:
X coordinate is 2
Y coordinate is -2
(2,-2)
Explanation:
It is marked in the Quadrant IV as X coordinate is Positive and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 21.
Point F
Answer:
X coordinate is 0
Y coordinate is -4
(0,-4)
Explanation:
It is marked in the Quadrant IV as X coordinate is Positive and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 22.
Point G
Answer:
X coordinate is -4
Y coordinate is 2
(-4,2)
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 23.
Point H
Answer:
X coordinate is -4
Y coordinate is -4
(-4,-4)
Explanation:
It is marked in the Quadrant III as X coordinate is Negative and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 24.
Point I
Answer:
X coordinate is 4
Y coordinate is 0
(4,0)
Explanation:
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 25.
Point J
Answer:
X coordinate is 4
Y coordinate is -4
(4,-4)
Explanation:
It is marked in the Quadrant IV as X coordinate is Positive and Y coordinate is Negative as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
PLOTTING ORDERED PAIRS Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 26.
K (4, 3)
Answer: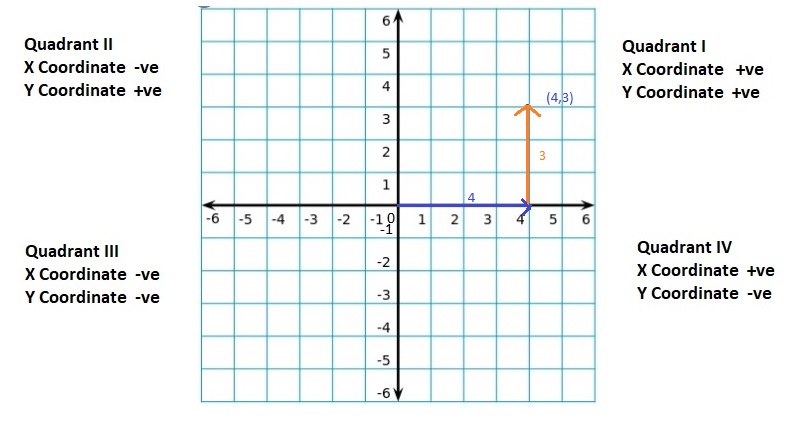
Explanation:
Start at the origin move 4 units Right and 3 units up. Then plot the point
The Point is in Quadrant I
Question 27.
L (1, 2)
Answer:
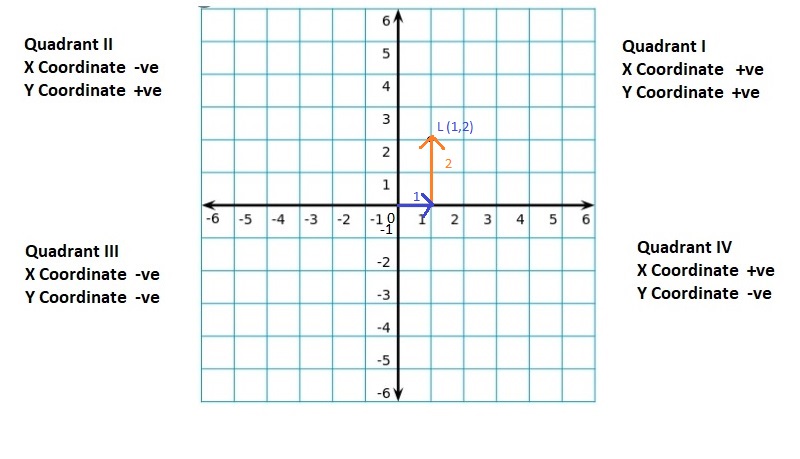
Explanation:
Start at the origin move 1 units Right and 2 units up. Then plot the point
The Point is in Quadrant I
Question 28.
M (0, 6)
Answer:
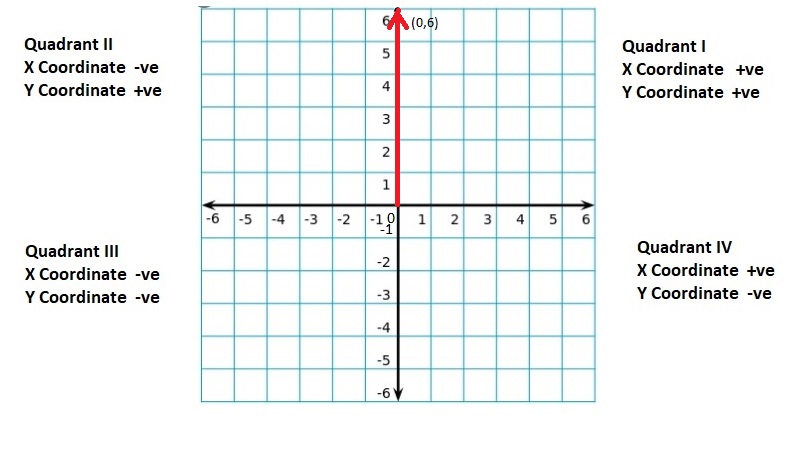
Explanation:
Start at the origin move 6 units up. Then plot the point
The Point is in Quadrant I
Question 29.
N (3, – 7)
Answer:
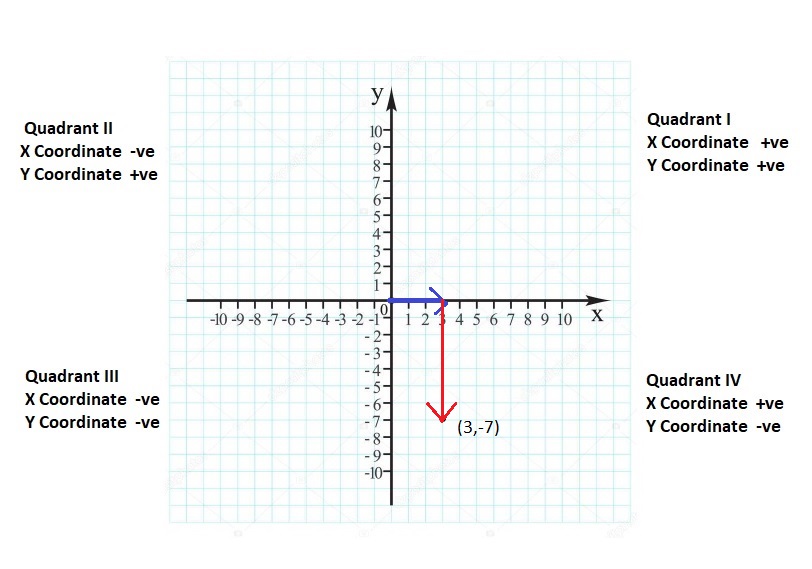
Explanation:
Start at the origin move 3 units Right and 7 units down. Then plot the point
The Point is in Quadrant IV
Question 30.
P (- 5, – 9)
Answer: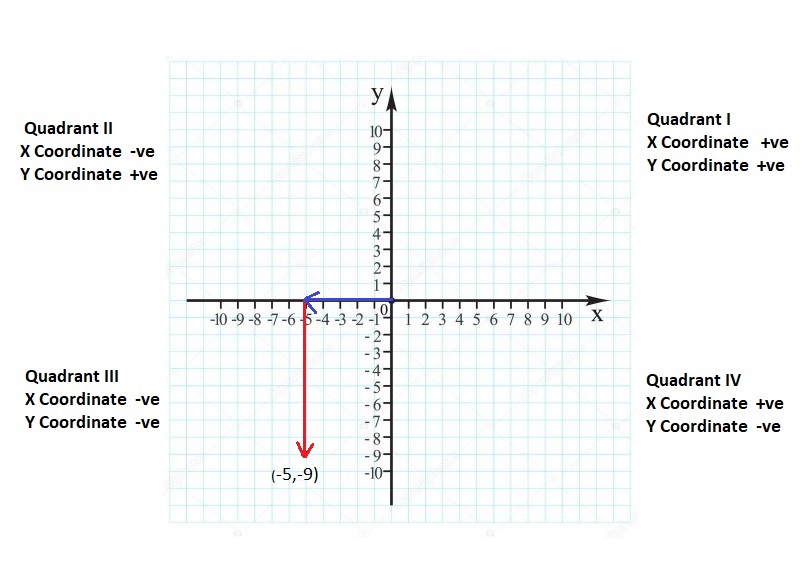
Explanation:
Start at the origin move 5 units left and 9 units down. Then plot the point
The Point is in Quadrant III
Question 31.
R (8, 0)
Answer: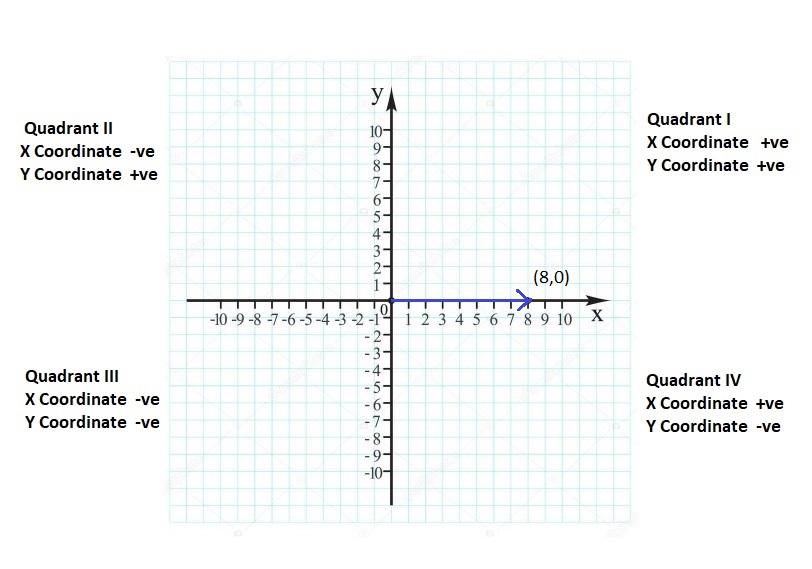
Explanation:
Start at the origin move 8 units Right and y is 0 remains at the same point. Then plot the point
The Point is in Quadrant I
Question 32.
S (- 1.5, 0)
Answer:
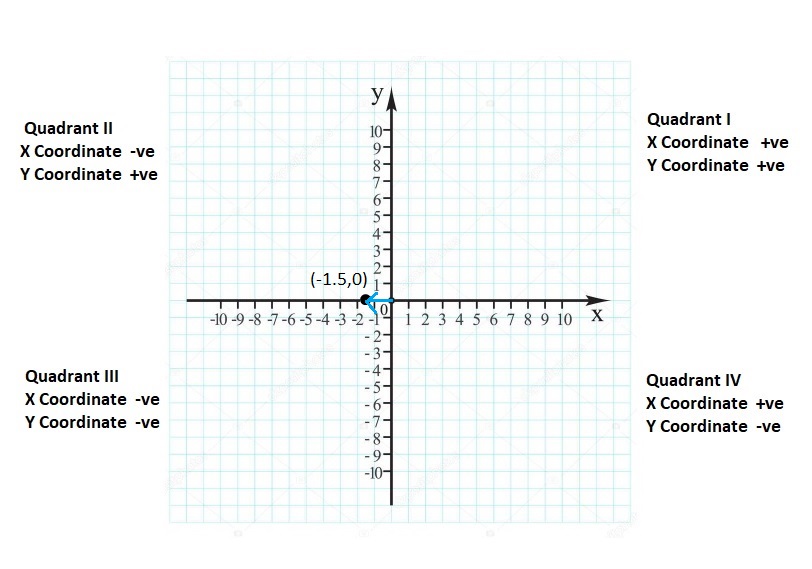
Explanation:
Start at the origin move 1.5 units left and y is 0 remains at the same point. Then plot the point
The Point is in Quadrant II
Question 33.
T (3.5, 1.5)
Answer: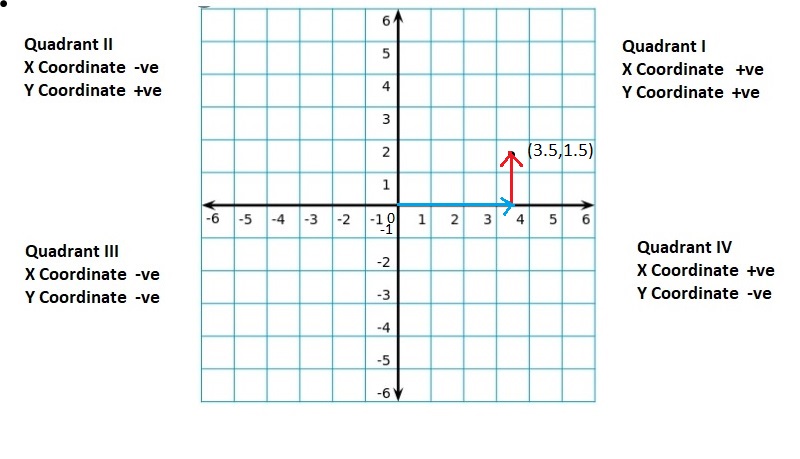
Explanation:
Start at the origin move 3.5 units Right and 1.5 units up Then plot the point
The Point is in Quadrant I
Question 34.
U (2, – 4)
Answer:
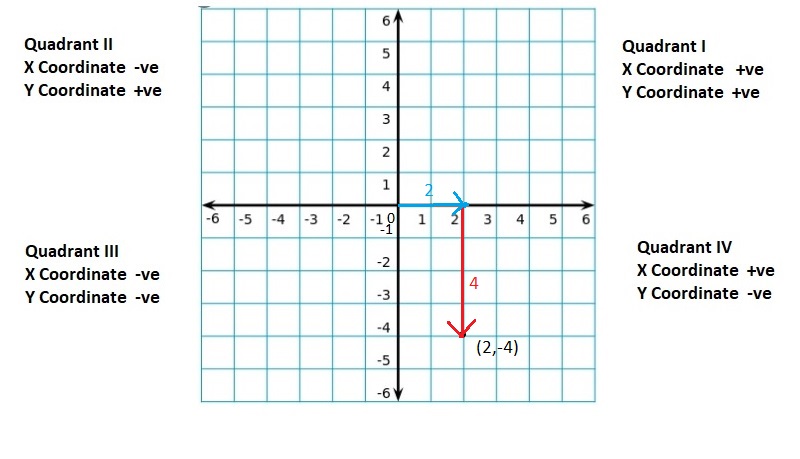
Explanation:
Start at the origin move 2 units left and 4 units down. Then plot the point
The Point is in Quadrant IV
Question 35.
V (- 4, 1)
Answer:
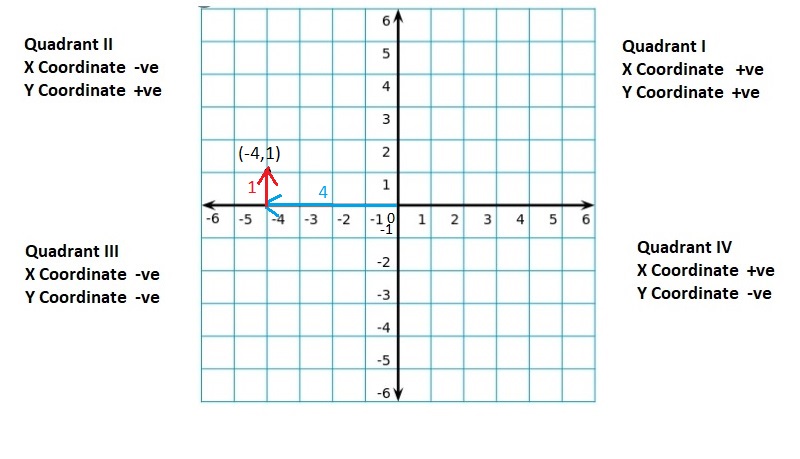
Explanation:
Start at the origin move 4 units left and 1 units up . Then plot the point
The Point is in Quadrant II
Question 36.
W (2\(\frac{1}{2}\), 0)
Answer:
2\(\frac{1}{2}\)=\(\frac{5}{2}\)=2.5
W(2.5,0)
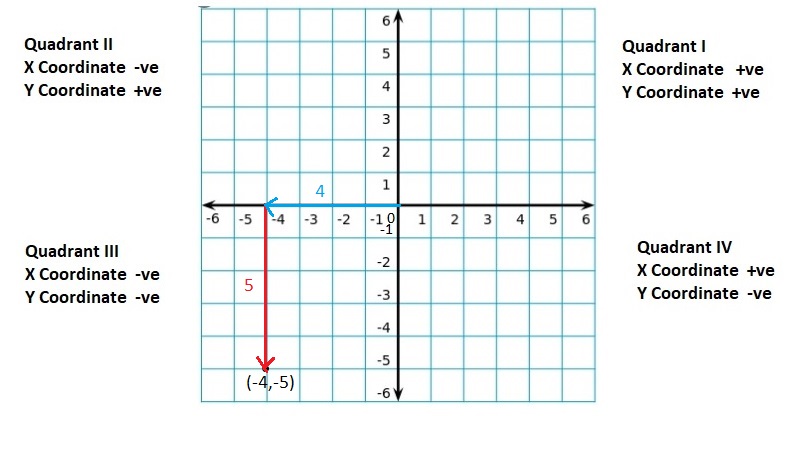
Explanation:
Start at the origin move 2.5 units Right and y is 0 so it remains on the same point . Then plot the point
The Point is in Quadrant I
Question 37.
Z (- 4, – 5)
Answer:
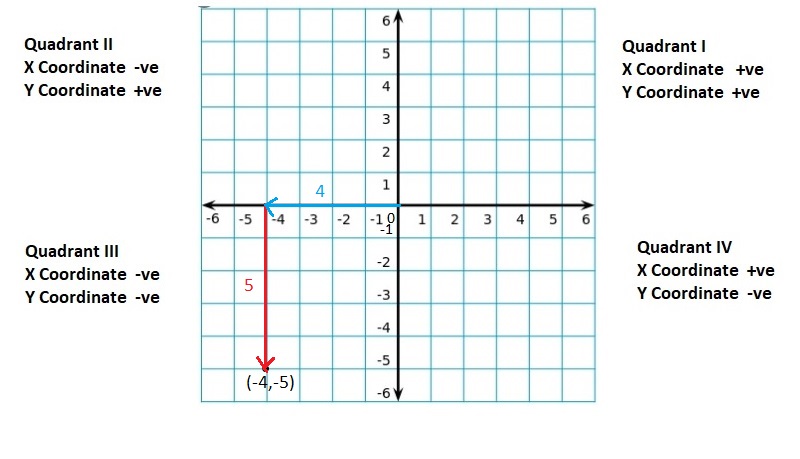
Explanation:
Start at the origin move 4 units left and 5 units down . Then plot the point
The Point is in Quadrant III
YOU BE THE TEACHER
Your friend describes how to plot the point. Is your friend correct? Explain your reasoning.
Question 38.

Answer:
No , he is wrong.
Explanation:
Start at the origin move 4 units Right and 5 units up . Then plot the point
The Point is in Quadrant I
Question 39.

Answer:
Yes he is right
The Point is in Quadrant II
MODELING REAL LIFE InExercises 40 – 44, use the map of the zoo.
Question 40.
Which exhibit is located at (2, 1)?
Answer:
Reptiles
Question 41.
Name an attraction on the positive y-axis.
Answer:
Flamingo cafe
Question 42.
Is parking available in Quadrant II? If not, name a quadrant in which you can park.
Answer:
No, You can Park in Quadrant III and Quadrant IV
Question 43.
Write two different ordered pairs that represent the location of the Rain Forest.
Answer:
(5,-2) and (5,-1)
Question 44.
Which exhibit is closest to (−8, −3)?
Answer:
Safari Africa
REFLECTING POINTS IN ONE AXIS
Reflect the point in (a) the x-axis and (b) the y-axis.
Question 45.
(3, 2)
Answer:
Plot (3, 2) , (3,-2) and (-3.-2)
Explanation:
To reflect (3,2) in the x axis, use the same x-coordinate, 3,the opposite of the y coordinate.The opposite of y coordinate 2 is -2
To reflect (3,2) in the y axis, use the same y-coordinate, 2,the opposite of the x coordinate.The opposite of x coordinate 3 is -3
So then reflection of (3,2)in the x-axis is (3,-2)
So the reflection of (3,2)in the y-axis is (-3,2)
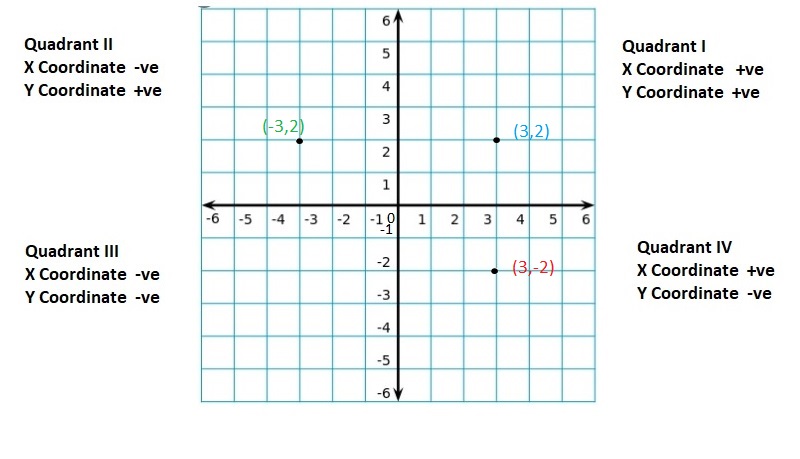
Question 46.
(- 4, 4)
Answer:
Plot (-4, 4) , (-4,-4) and (4,4)
Explanation:
To reflect (-4,4) in the x axis, use the same x-coordinate, -4,the opposite of the y coordinate.The opposite of y coordinate 4 is -4
To reflect (-4,4) in the y axis, use the same y-coordinate, 4,the opposite of the x coordinate.The opposite of x coordinate -4 is 4
So then reflection of (-4,4)in the x-axis is (-4,-4)
So the reflection of (-4,-4)in the y-axis is (4,4)
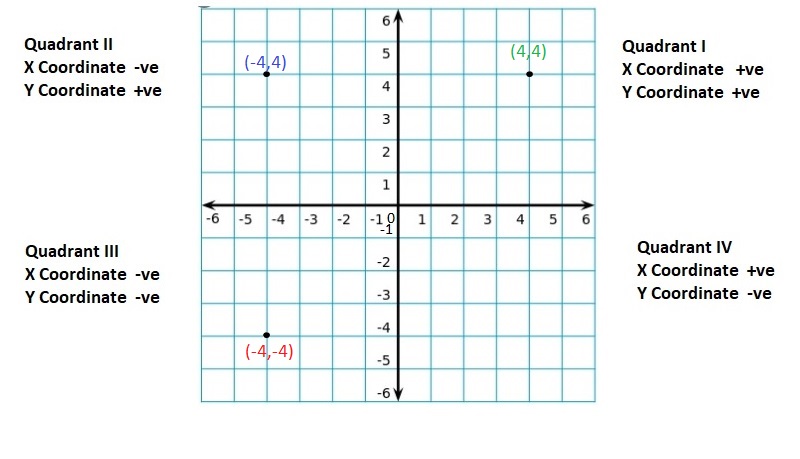
Question 47.
(- 5, – 6)
Answer:
Plot (-5, -6) , (-5,6) and (5,-6)
Explanation:
To reflect (-5,-6) in the x axis, use the same x-coordinate, -5,the opposite of the y coordinate.The opposite of y coordinate -6 is 6
To reflect (-5,-6) in the y axis, use the same y-coordinate, -6,the opposite of the x coordinate.The opposite of x coordinate -5 is 5
So then reflection of (-5,-6)in the x-axis is (-5,6)
So the reflection of (-5,-6)in the y-axis is (5,-6)
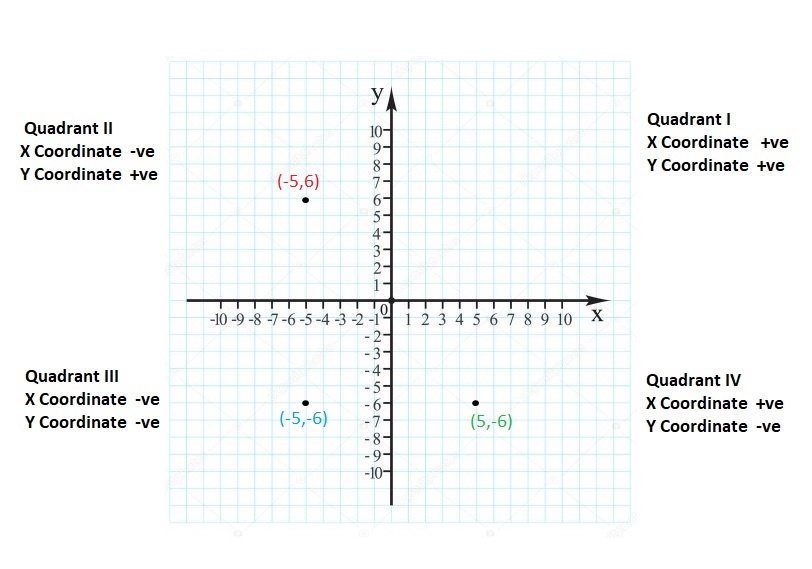
Question 48.
(4, – 7)
Answer:
Plot (4, -7) , (4,7) and (-4,-7)
Explanation:
To reflect (4,-7) in the x axis, use the same x-coordinate, 4,the opposite of the y coordinate.The opposite of y coordinate -7 is 7
To reflect (4,-7) in the y axis, use the same y-coordinate, -7,the opposite of the x coordinate.The opposite of x coordinate 4 is -4
So then reflection of (4,-7)in the x-axis is (4,7)
So the reflection of (4,-7)in the y-axis is (-4,-7)
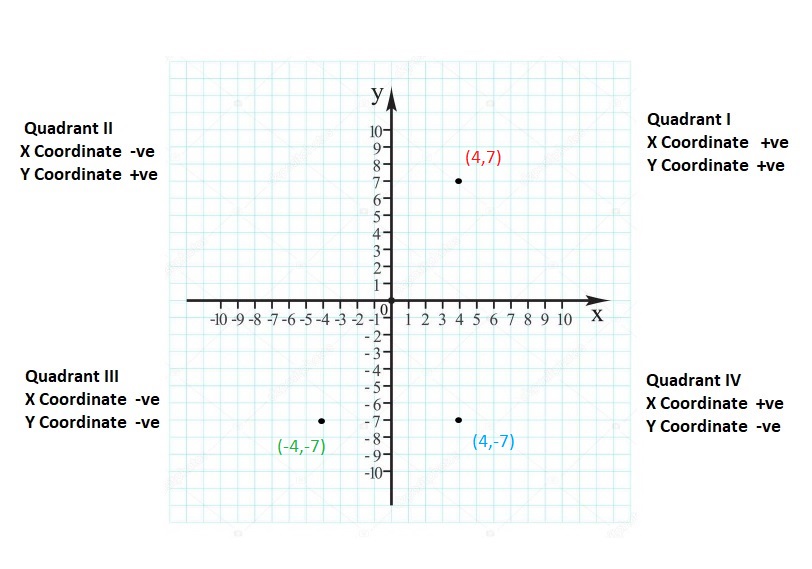
Question 49.
(- 9, 3)
Answer:
Plot (-9, 3) , (-9,-3) and (9,3)
Explanation:
To reflect (-9,3) in the x axis, use the same x-coordinate, -9,the opposite of the y coordinate.The opposite of y coordinate 3 is -3
To reflect (-9,3) in the y axis, use the same y-coordinate, 3,the opposite of the x coordinate.The opposite of x coordinate -9 is 9
So then reflection of (-9,3)in the x-axis is (-9,-3)
So the reflection of (-9,3)in the y-axis is (9,3)
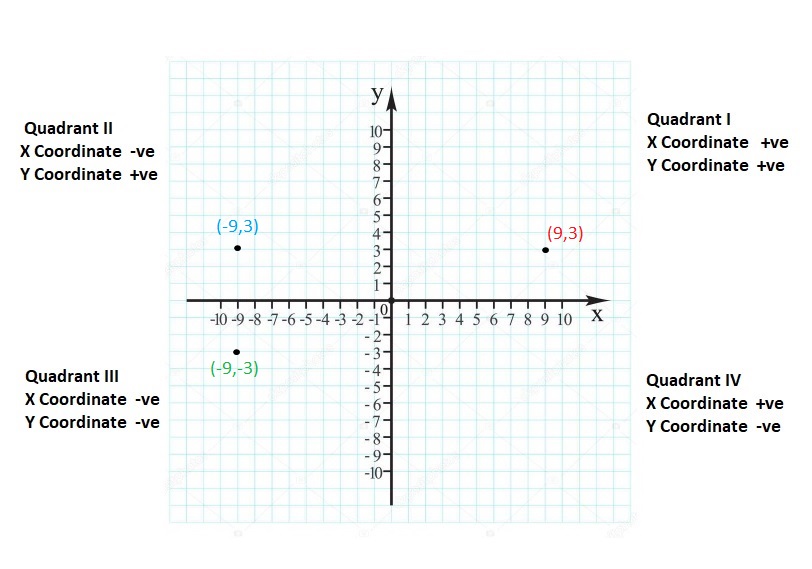
Question 50.
(6, – 2)
Answer:
Plot (6, -2) , (6,2) and (-6,-2)
Explanation:
To reflect (6, -2) in the x axis, use the same x-coordinate, 6,the opposite of the y coordinate.The opposite of y coordinate -2 is 2
To reflect (6, -2) in the y axis, use the same y-coordinate, -2,the opposite of the x coordinate.The opposite of x coordinate 6 is -6
So then reflection of (6, -2) in the x-axis is (6,2)
So the reflection of (6, -2) in the y-axis is (-6,-2)
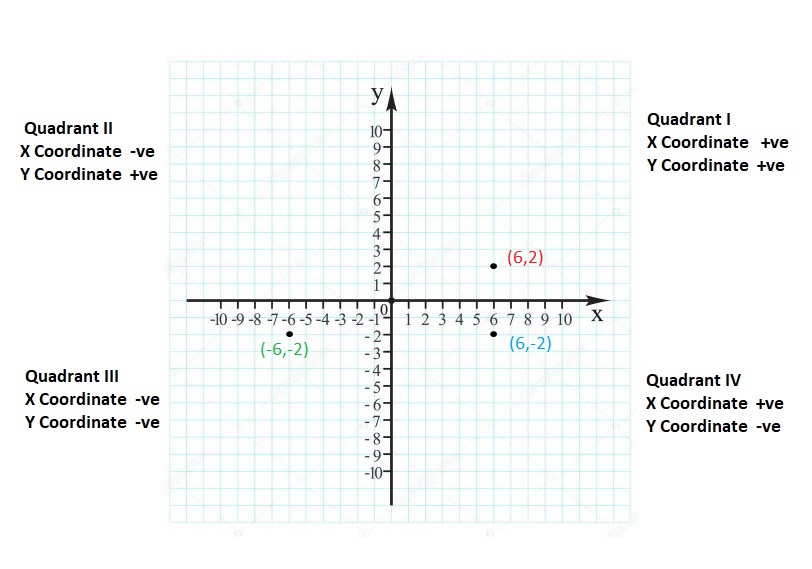
Question 51.
(0, – 1)
Answer:
Plot (0, – 1) , (0,1) and (0,-1)
Explanation:
To reflect (0, – 1) in the x axis, use the same x-coordinate, 0,the opposite of the y coordinate.The opposite of y coordinate -1 is 1
To reflect (0, – 1) in the y axis, use the same y-coordinate, -1,the opposite of the x coordinate.The opposite of x coordinate -1 is 1
So then reflection of (0, – 1) in the x-axis is (0,1)
So the reflection of ((0, – 1) in the y-axis is (0,-1)
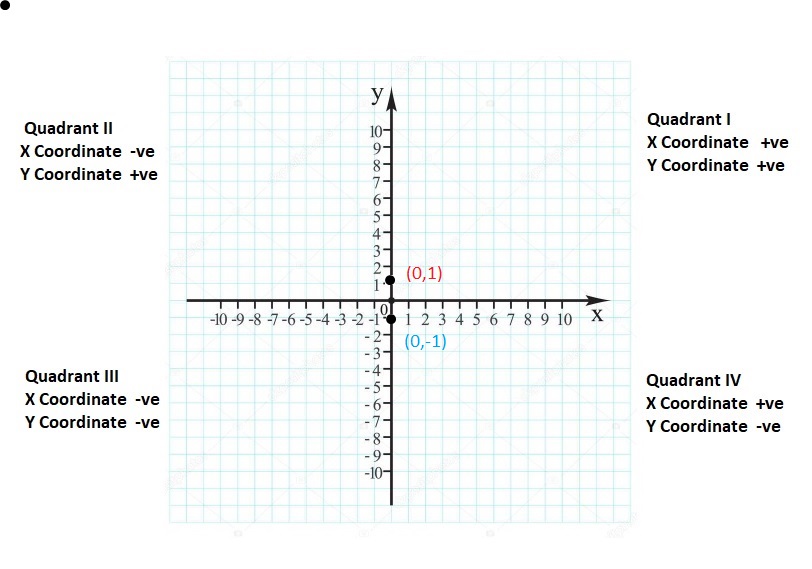
Question 52.
(- 8, 0)
Answer:
Plot (-8, 0) , (-8,0) and (8,0)
Explanation:
To reflect (-8, 0)in the x axis, use the same x-coordinate, -8,the opposite of the y coordinate.The opposite of y coordinate 0 is 0
To reflect (-8, 0) in the y axis, use the same y-coordinate, 0,the opposite of the x coordinate.The opposite of x coordinate -8 is 8
So then reflection of (-8, 0) in the x-axis is (-8,0)
So the reflection of (-8, 0) in the y-axis is (8,0)
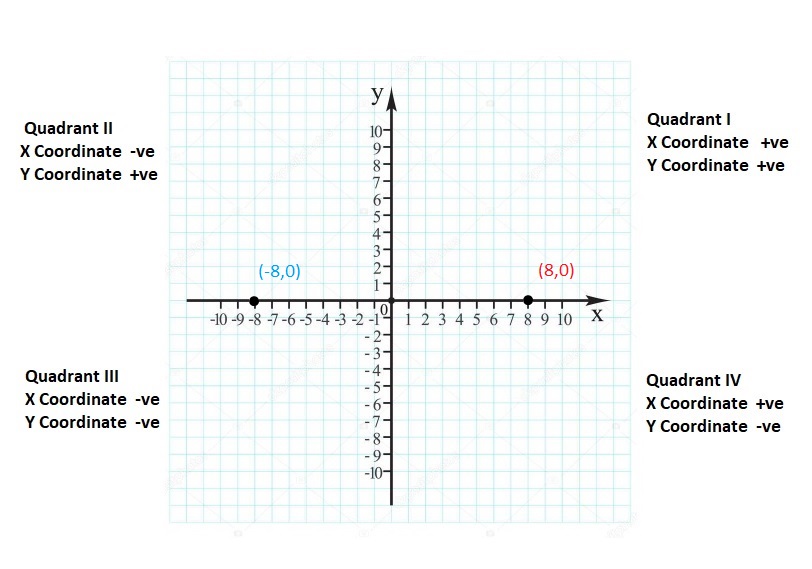
Question 53.
(- 3.5, 2)
Answer:
Plot (-3.5, 2) , (-3.5,-2) and (3.5,2)
Explanation:
To reflect (-3.5, 2) in the x axis, use the same x-coordinate, -3.5,the opposite of the y coordinate.The opposite of y coordinate 2 is -2
To reflect (-3.5, 2) in the y axis, use the same y-coordinate, 2,the opposite of the x coordinate.The opposite of x coordinate -3.5 is 3.5
So then reflection of (-3.5, 2) in the x-axis is (-3.5,-2)
So the reflection of (-3.5, 2) in the y-axis is (3.5,2)
Question 54.
(2.5, 4.5)
Answer:
Plot (2.5, 4.5) , (2.5,-4.5) and (-2.5,4.5)
Explanation:
To reflect (2.5, 4.5) in the x axis, use the same x-coordinate, 2.5 ,the opposite of the y coordinate.The opposite of y coordinate 4.5 is -4.5
To reflect (2.5, 4.5) in the y axis, use the same y-coordinate, 4.5,the opposite of the x coordinate.The opposite of x coordinate 2.5 is -2.5
So then reflection of (2.5, 4.5) in the x-axis is (2.5,-4.5)
So the reflection of (2.5, 4.5) in the y-axis is (-2.5,4.5)
Question 55.
(-5 \(\frac{1}{2}\), 3)
Answer:
-5 \(\frac{1}{2}\) = – \(\frac{11}{2}\) = -5.5
(-5.5, 3 )
Plot (-5.5, 3 ) , (-5.5,-3) and (5.5,3)
Explanation:
To reflect (-5.5, 3 ) in the x axis, use the same x-coordinate, -5.5,the opposite of the y coordinate.The opposite of y coordinate 3 is -3
To reflect (-5.5, 3 ) in the y axis, use the same y-coordinate, 3,the opposite of the x coordinate.The opposite of x coordinate -5.5 is 5.5
So then reflection of (-5.5, 3 ) in the x-axis is (-5.5,-3)
So the reflection of (-5.5, 3 ) in the y-axis is (5.5,3)
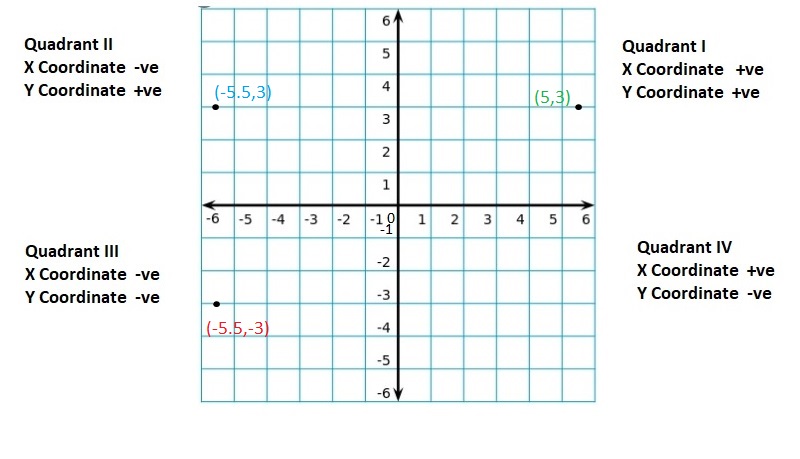
Question 56.
(\(\frac{1}{4}\), \(-\frac{7}{8}\))
Answer:
\(\frac{1}{4}\) = 0.25
\(-\frac{7}{8}\) = -0.8
(0.25,-0.8)
Plot (0.25,-0.8) , (0.25,0.8) and (-0.25,-0.8)
Explanation:
To reflect (0.25,-0.8) in the x axis, use the same x-coordinate, 0.25,the opposite of the y coordinate.The opposite of y coordinate -0.8 is 0.8
To reflect (0.25,-0.8)in the y axis, use the same y-coordinate, -0.8 ,the opposite of the x coordinate.The opposite of x coordinate 0.25 is -0.25
So then reflection of (0.25,-0.8) in the x-axis is (0.25,0.8)
So the reflection of (0.25,-0.8) in the y-axis is (-0.25,-0.8)
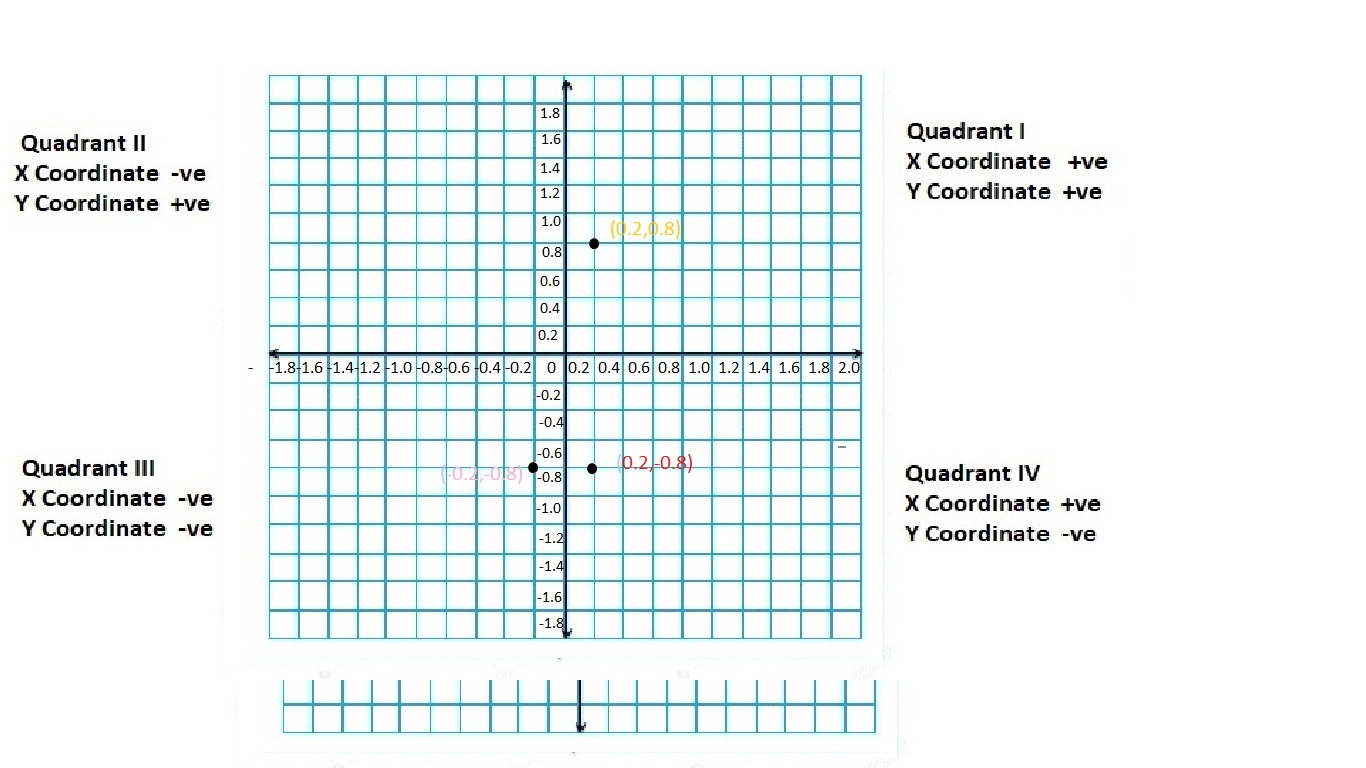
REFLECTING POINTS IN BOTH AXES
Reflect the point in the x-axis followed by the y-axis.
Question 57.
(4, 5)
Answer:
Plot (4, 5) , (4,-5) and (-4,-5)
Explanation:
To reflect(4, 5)in the x axis, use the same x-coordinate, 4,the opposite of the y coordinate.The opposite of y coordinate 5 is -5
To reflect (4, -5) in the y axis, use the same y-coordinate, -5,the opposite of the x coordinate.The opposite of x coordinate 4 is -4
So then reflection of (4, 5) in the x-axis is (4,-5)
So the reflection of (4,-5) in the y-axis is (-4,-5)
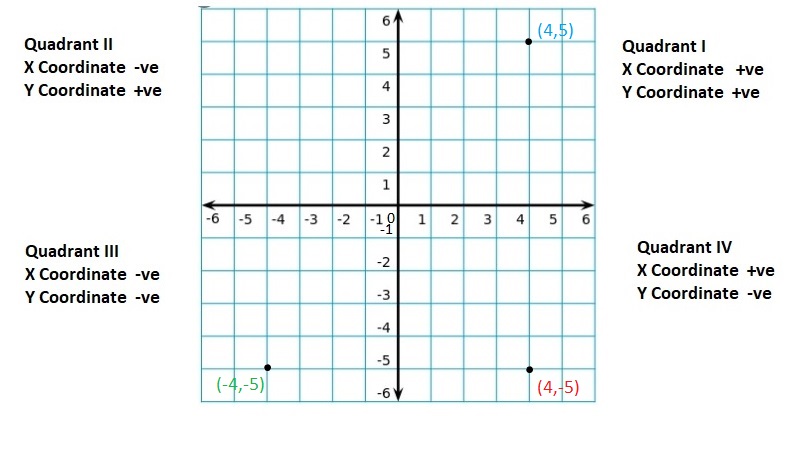
Question 58.
(- 1, 7)
Answer:
Plot (-1, 7) , (-1,-7) and (1,-7)
Explanation:
To reflect (-1, 7) in the x axis, use the same x-coordinate, -1,the opposite of the y coordinate.The opposite of y coordinate 7 is -7
To reflect (-1,-7) in the y axis, use the same y-coordinate, -7,the opposite of the x coordinate.The opposite of x coordinate -1 is 1
So then reflection of (-1, 7) in the x-axis is (-1,-7)
So the reflection of (-1,-7) in the y-axis is (1,-7)
Question 59.
(- 2, – 2)
Answer:
Plot (- 2, – 2) , (-2,2) and (2,2)
Explanation:
To reflect(- 2, – 2) in the x axis, use the same x-coordinate, -2,the opposite of the y coordinate.The opposite of y coordinate -2 is 2
To reflect (-2,2) in the y axis, use the same y-coordinate, 2,the opposite of the x coordinate.The opposite of x coordinate -2 is 2
So then reflection of (- 2, – 2) in the x-axis is (-2,2)
So the reflection of (-2,2) in the y-axis is (2,2)
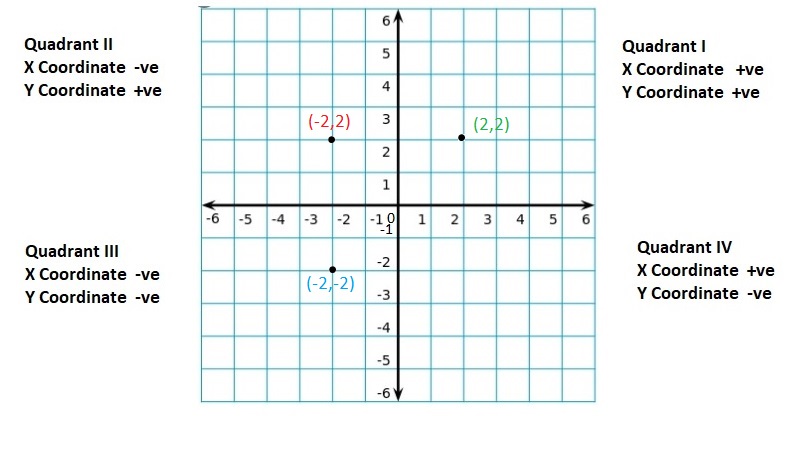
Question 60.
(6, – 7)
Answer:
Plot (6, – 7) , (6,7) and (-6,7)
Explanation:
To reflect (6, – 7) in the x axis, use the same x-coordinate, 6,the opposite of the y coordinate.The opposite of y coordinate -7 is 7
To reflect (6,7) in the y axis, use the same y-coordinate, 7,the opposite of the x coordinate.The opposite of x coordinate 6 is -6
So then reflection of (6, – 7) in the x-axis is (6,7)
So the reflection of (6,7) in the y-axis is (-6,7)
Question 61.
(- 8, – 8)
Answer:
Plot (- 8, – 8) , (-8,8) and (8,8)
Explanation:
To reflect (- 8, – 8) in the x axis, use the same x-coordinate, -8,the opposite of the y coordinate.The opposite of y coordinate -8 is 8
To reflect (-8,8) in the y axis, use the same y-coordinate, 8,the opposite of the x coordinate.The opposite of x coordinate 8 is -8
So then reflection of (- 8, – 8) in the x-axis is (-8,8)
So the reflection of (-8,8) in the y-axis is (8,8)
Question 62.
(5, 9)
Answer:
Plot (5, 9) , (5,-9) and (-5,-9)
Explanation:
To reflect (5, 9) in the x axis, use the same x-coordinate, 5,the opposite of the y coordinate.The opposite of y coordinate 9 is -9
To reflect (5,-9) in the y axis, use the same y-coordinate, -9,the opposite of the x coordinate.The opposite of x coordinate 5 is -5
So then reflection of (5, 9) in the x-axis is (5,-9)
So the reflection of (5,-9) in the y-axis is (-5,-9)
Question 63.
(0, – 2)
Answer:
Plot (0, – 2) , (0,2) and (0,2)
Explanation:
To reflect (0, – 2) in the x axis, use the same x-coordinate, 0,the opposite of the y coordinate.The opposite of y coordinate -2 is 2
To reflect (0,2) in the y axis, use the same y-coordinate, 0,the opposite of the x coordinate.The opposite of x coordinate 2 is -2
So then reflection of (0, – 2)in the x-axis is (0,2)
So the reflection of (0,2) in the y-axis is (0,2)
Question 64.
(- 9, 0)
Answer:
Plot (-9, 0) , (-9,0) and (9,0)
Explanation:
To reflect (-9, 0) in the x axis, use the same x-coordinate, -9,the opposite of the y coordinate.The opposite of y coordinate 0 is 0
To reflect (9,0) in the y axis, use the same y-coordinate, 0,the opposite of the x coordinate.The opposite of x coordinate 9 is -9
So then reflection of (-9, 0)in the x-axis is (-9,0)
So the reflection of (-9,0) in the y-axis is (9,0)
Question 65.
(6.5, – 10.5)
Answer:
Plot (6.5, -10.5) , (6.5,10.5) and (-6.5,10.5)
Explanation:
To reflect (6.5, -10.5) in the x axis, use the same x-coordinate, 6.5,the opposite of the y coordinate.The opposite of y coordinate -10.5 is 10.5
To reflect (6.5,10.5) in the y axis, use the same y-coordinate,10.5, the opposite of the x coordinate.The opposite of x coordinate 6.5 is -6.5
So then reflection of (6.5, -10.5) in the x-axis is (6.5,10.5)
So the reflection of (6.5,10.5) in the y-axis is (-6.5,10.5)
Question 66.
(- 0.4, 0.7)
Answer:
Plot (- 0.4, 0.7) , (-0.4,-0.7) and (0.4,-0.7)
Explanation:
To reflect (- 0.4, 0.7) in the x axis, use the same x-coordinate, -0.4,the opposite of the y coordinate.The opposite of y coordinate 0.7 is -0.7
To reflect (-0.4,-0.7) in the y axis, use the same y-coordinate, -0.7,the opposite of the x coordinate.The opposite of x coordinate -0.4 is 0.4
So then reflection of(- 0.4, 0.7) in the x-axis is (-0.4,-0.7)
So the reflection of (-0.4,-0.7) in the y-axis is (0.4,-0.7)
Question 67.
(\(\frac{1}{3}\), \(\frac{2}{3}\))
Answer:
\(\frac{1}{3}\)=0.3
\(\frac{2}{3}\)=0.6
Plot (0.3,0.6), (0.3,-0.6) and (-0.3,-0.6)
Explanation:
To reflect (0.3,0.6) in the x axis, use the same x-coordinate, 0.3,the opposite of the y coordinate.The opposite of y coordinate 0.6 is -0.6
To reflect (0.3,-0.6) in the y axis, use the same y-coordinate, -0.6,the opposite of the x coordinate.The opposite of x coordinate 0.3 is -0.3
So then reflection of (0.3,0.6) in the x-axis is (0.3,-0.6)
So the reflection of (0.3,-0.6) in the y-axis is (-0.3,-0.6)
Question 68.
(- 1\(\frac{2}{5}\), – 1\(\frac{4}{5}\))
Answer:
– 1\(\frac{2}{5}\) = –\(\frac{7}{5}\) = -1.4
– 1\(\frac{4}{5}\) = –\(\frac{9}{5}\) =-1.8
(-1.4,-1.8)
Plot (-1.4,-1.8) , (-1.4,1.8) and (1.4,-1.8)
Explanation:
To reflect (-1.4,-1.8) in the x axis, use the same x-coordinate, -1.4,the opposite of the y coordinate.The opposite of y coordinate -1.8 is 1.8
To reflect (-1.4,1.8) in the y axis, use the same y-coordinate, 1.8,the opposite of the x coordinate.The opposite of x coordinate -1.4 is 1.4
So then reflection of (-1.4,-1.8) in the x-axis is (-1.4,1.8)
So the reflection of (-1.4,1.8) in the y-axis is (1.4,-1.8)
Question 69.
STRUCTURE
Reflect a point in the x-axis followed by the y-axis. Then reflect the original point in the y-axis followed by the x-axis. Do you get the same results? Explain.
Answer:
REASONING Describe the possible location(s) of the point (x, y).
Question 70.
x > 0, y > 0
Answer:
For point (x,y) if x>0 then you would be going in the positive direction on the x axis. This eliminates quadrants II and III because the x axis is negative there. Now you’re down to either quadrant I or quadrant IV. Given that y>0, the y values on the y axis are more than 0 so they are becoming positive. This means that (x, y) must be in quadrant I.
Question 71.
x < 0, y < 0
Answer:
For Point (x,y) if x < 0 then you would be going in negative direction on the x axis , This elimates quadrants I and IV because the axis is positive there.Now you’re down to either Quadrant II or Quadrant III. Given that y< 0,the values on the y axis are less than 0 so they are becoming negative. This means that (x,y) must be in Quadrant III.
Question 72. x > 0, y < 0
Answer:
For point (x,y) if x>0 then you would be going in the positive direction on the x axis. This eliminates quadrants II and III because the x axis is negative there. Now you’re down to either quadrant I or quadrant IV. Given that y<0, the y values on the y axis are less than 0 so they are becoming negative. This means that (x, y) must be in quadrant IV
Question 73. x > 0
Answer:
For point (x,y) if x>0 then you would be going in the positive direction on the x axis. This eliminates quadrants II and III because the x axis is negative there. Now you’re down to either quadrant I or quadrant IV.
Question 74.
y < 0
Answer:
Given that y<0, the y values on the y axis are less than 0 so they are becoming negative. It can be in Quadrant III and Quadrant IV.
Question 75.
x = 0, y = 0
Answer:
Either x or y or both are on the x or y axis
CRITICAL THINKING
Tell whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 76.
The x-coordinate of a point on the x-axis is zero.
Answer:
True
Explanation:
Since every point on the x – axis has no distance (zero distance) from the x – axis, therefore, the y – coordinate of every point lying on the x – axis is always zero. Thus, the coordinates of any point on the x – axis are of the form (x, 0), where x is the distance of the point from the y – axis
Question 77.
The y-coordinates of points in Quadrant III are positive.
Answer:
No. Never True
Explanation:
In the III Quadrant all X- coordinates are negative.
In the III Quadrant all Y- coordinates are negative.
Question 78.
The x-coordinate of a point in Quadrant II has the same sign as the y-coordinate of a point in Quadrant IV.
Answer:
True.
Explanation:
In Quadrant II x-coordinate of a point is negative
In Quadrant IV y-coordinate of a point is negative.
Both the signs are negative and same.
Question 79.
MODELING REAL LIFE
The table shows the number of people who participate in a blood drive each year for 9 years. Display the data in a line graph. Then describe the change in the number of participants over time.

Answer:
Write the ordered pair
(1,140)
(2,136)
(3,134)
(4,132)
(5,131)
(6,135)
(7,136)
(8,142)
(9,145)
Plot and label the ordered pairs,then connect the ordered pairs with line segments.
The number of participants are decreased from year 1 to year 5. then later there is a increase in the participants from year 6 to year 9.
Question 80.
MODELING REAL LIFE
The table shows the amount of carbon dioxide emissions of a country, relative to an environmental standard, each year for 7 years. Display the data in a line graph. Then describe the change in carbon dioxide emissions over time.

Answer:
Question 81.
PATTERNS
The table shows the total miles run through each of 18 weeks for a marathon training program.
a. Create a table for the distance run during each week of training.
b. Display the data from part(a) in a line graph.
c. Explain the pattern shown in the graph. (a, b)
Answer:
Question 82.
LOGIC
Two points are plotted in the coordinate plane. Plot each of the following ordered pairs in the same coordinate plane.
a. P (a, – b)
b. Q (- a, b)
c. R (c, – d)
d. S (- c, – d)
e. T (c, – a)
f. U (- d, – b)
Answer:
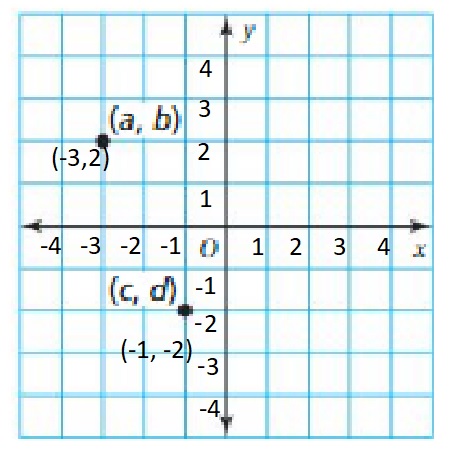
Explanation:
From the above Graph we know a , b c and d numbers
a = -3 ; b =2 ; c=-1 and d = -2
then now plot the given points.
a. P (a, – b) = (-3, -2)
b. Q (- a, b) = (3 , 2)
c. R (c, – d) = ( -1, 2)
d. S (- c, – d) = ( 1, 2)
e. T (c, – a) =( -1, 3)
f. U (- d, – b) = (2 , -2)

Lesson 8.6 Polygons in the Coordinate Plane
EXPLORATION 1
Drawing Polygons in the Coordinate Plane
Work with a partner.
a. Write three ordered pairs that meet the following requirements. Then plot the ordered pairs in a coordinate plane, like the one shown.
• Two of the ordered pairs have the same x-coordinates.
• Two of the ordered pairs have the same y-coordinates.
• Two of the points are in the same quadrant. The other point is in a different quadrant.
Answer:
The ordered pairs which follow above conditions are these points (1,2) (1,3)(-1,2)
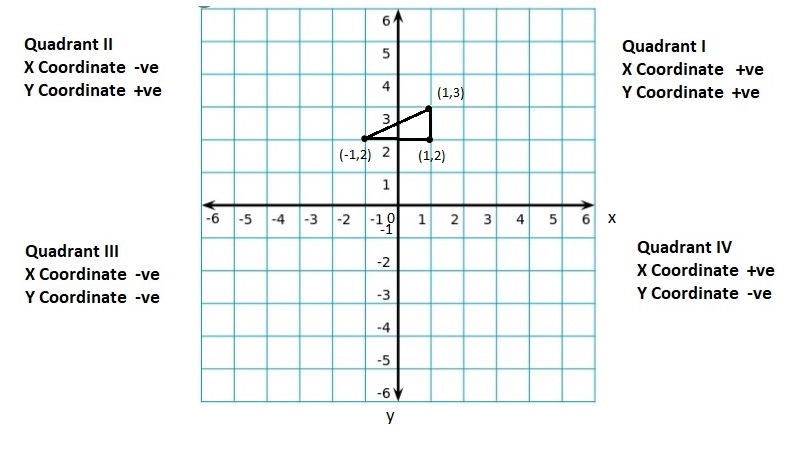
b. The points represent the vertices of a polygon. What conclusions can you make about the polygon?
Answer:
The points are joined with line segments. it forms a right angled triangle as shown in above graph.
c. Can you plot another point to form a rectangle? a trapezoid? If so, what measures of the quadrilateral can you calculate?
Answer:
From the below graph by marking point D(-1,3) it forms a Rectangle.
By marking another point you cant make trapezoid it is not possible.
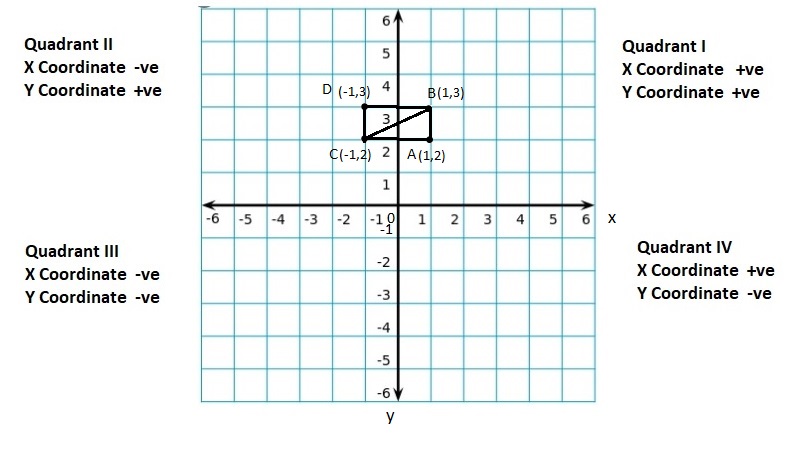
You can use ordered pairs to represent vertices of polygons. To draw a polygon in a coordinate plane, plot and connect the vertices.
Try It
Draw the polygon with the given vertices in a coordinate plane.
Question 1.
A (0, 0), B (5, 7), C (4, 3)
Answer:
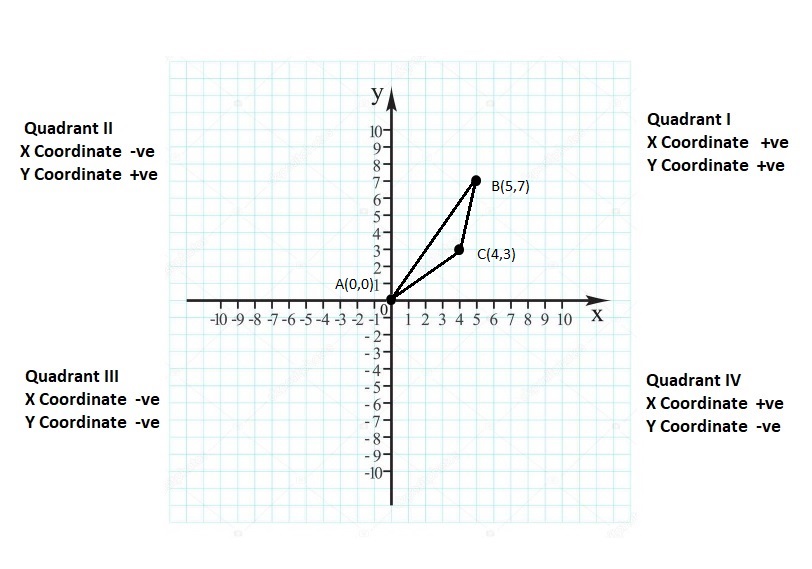
Question 2.
W (4, 4), X (7, 4), Y (2 \(\frac{1}{2}\), – 2), Z (-\(\frac{1}{2}\), – 2)
Answer:
Y (2 \(\frac{1}{2}\), – 2) = Y ( \(\frac{5}{2}\), – 2) = Y(2.5,-2)
Z (-\(\frac{1}{2}\), – 2) = Z (-0.5 , -2)
W (4, 4), X (7, 4), Y(2.5,-2) , Z (-0.5 , -2)
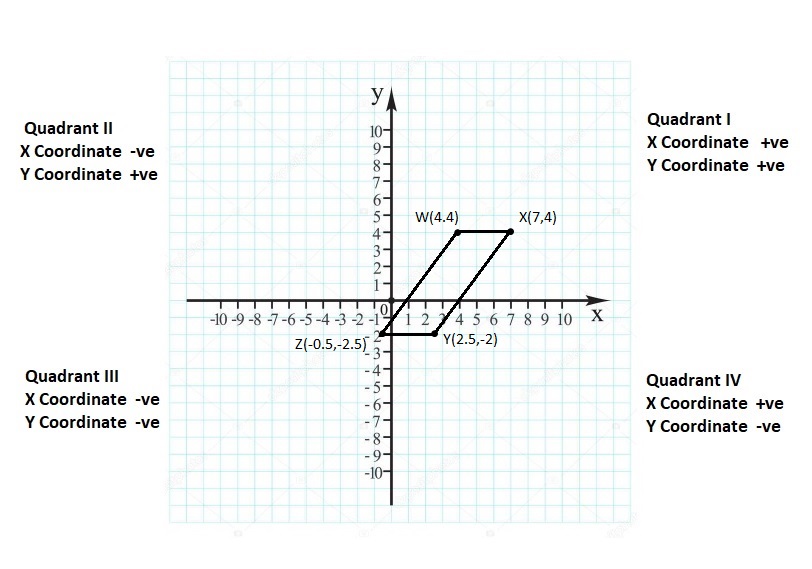
Find the distance between the points.
Question 3.
(6, 6.5), (2, 6.5)
Answer:
d=√((x_2-x_1)²+(y_2-y_1)²)
d=√((6-2)²+(6.5-6.5)²)
d=√((4)²+(0)²)
d=√((4)²) = 4
Question 4.
(- 4, 2), (- 4, – 5)
Answer:
d=√((x_2-x_1)²+(y_2-y_1)²)
d=√((-4-(-4))²+(-5-2)²)
d=√((0)²+(-7)²)
d=√((-7)²) = √(49) = 7
Distance cant be negative
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
DRAWING A POLYGON
Draw the polygon with the given vertices in a coordinate plane.
Question 5.
A (- 5, – 7), B (- 2, 4), C (5, -1)
Answer: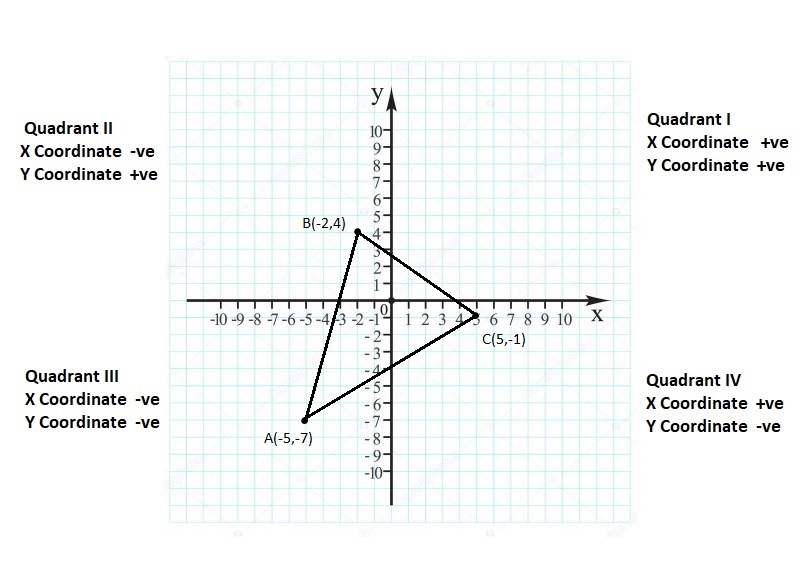
Question 6.
D (-\(\frac{1}{2}\), 6), E (3, 1), F (0, – 4\(\frac{1}{2}\))
Answer:
D (-\(\frac{1}{2}\), 6) = D(-0.5, 6)
F (0, – 4\(\frac{1}{2}\))= F (0, – \(\frac{9}{2}\)) = F( 0 , 4.5)
D(-0.5, 6),E (3, 1), F( 0 , 4.5)

FINDING DISTANCES Find the distance between the points.
Question 7.
(2, 7), (2, 9)
Answer:
Plot the points.
The points are in same Quadrants and have same x-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the y coordinate.
|9| – |7| = 2
So the distance between the points (2, 7), (2, 9) is 2
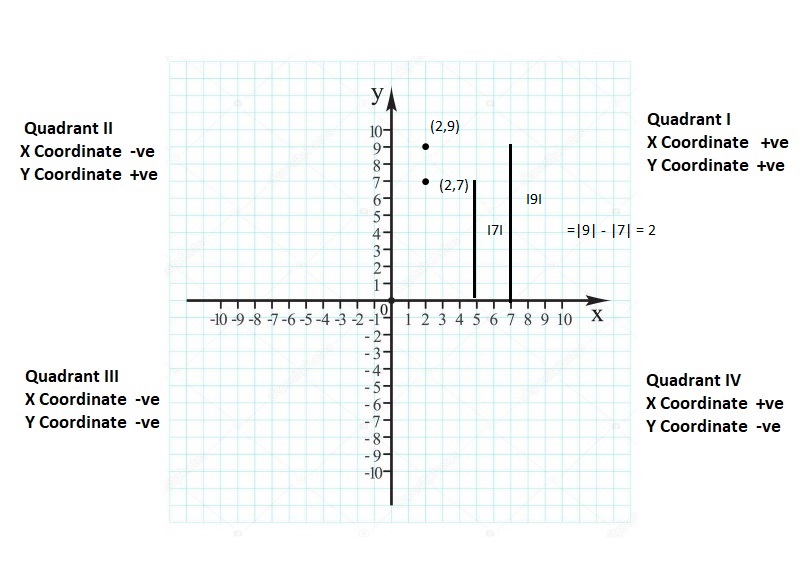
Question 8.
(- 3, – 8), (6, – 8)
Answer:
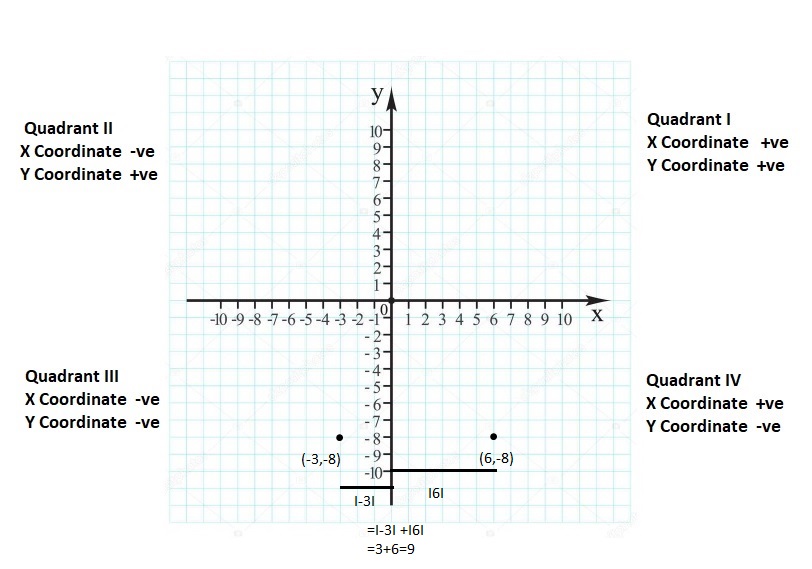
Explanation:
Plot the points.
The points are in different Quadrants and have same y-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|-3| + |6| = 9
So the distance between the points (- 3, – 8), (6, – 8) is 9
Question 9.
WHICH ONE DOESN’T BELONG?
Which pair of points does not belong with the other three? Explain your reasoning.
Answer:
(6,-3) and (6,3) is different from other 3 points.
Question 10.
A digital map of your hometown is shown in a coordinate plane in which the coordinates are measured in miles. The map shows your house at (−2, −7), your school at(5, −7), and your friend’s house at (−2, 1). How far is your house from your school? How far is your house from your friend’s house?

Answer:
Plot the points (−2, −7), (5, −7) and (−2, 1)
House is located at (-2,-7)
Friends house is located at ( – 2,1)
Plot the points.
The points are in different Quadrants and have same x-coordinates. The distance between the points is the sum of the absolute values of the y coordinate.
|-7| + |1| = 7 + 1 = 8
So the distance between the points (-2,-7) (-2,1) is 8
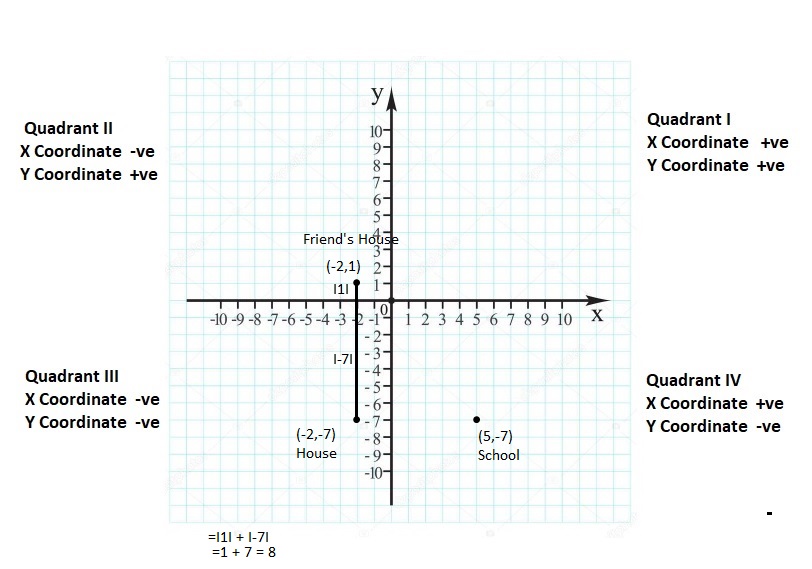
Question 11.
You design a tree house using a coordinate plane in which the coordinates are measured in feet. The vertices of the floor are (−2, −3), (−2, 4), (5, 4), and (5, −3). Find the perimeter (in yards) and the area (in square yards) of the floor.
Answer:
Plots the points (−2, −3), (−2, 4), (5, 4), and (5, −3)
The points are in different Quadrants and have same x-coordinates. The distance between the points is the sum of the absolute values of the y coordinate.
|4| + |-3| = 4 + 3 = 7
So the distance between the points (−2, −3), (−2, 4), is 7
The points are in different Quadrants and have same y-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|5| + |-2| = 5 + 2 = 7
So the distance between the points (5, 4), and (−2, 4), is 7
The image formed is a Square as its length and breadth are equal
Area of square = s × s = 7 × 7 = 49
Perimeter of square = 4s = 4 × 7 = 28
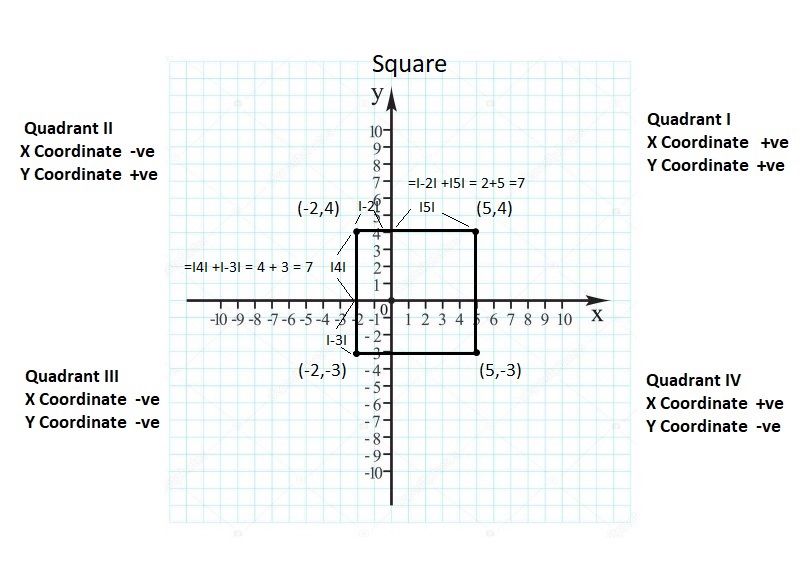
Polygons in the Coordinate Plane Homework & Practice 8.6
Review & Refresh
Write an ordered pair corresponding to the point.
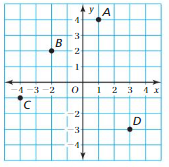
Question 1.
Point A
Answer:
(1,4)
Explanation:
x coordinate is 1
y coordinate is 4
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 2.
Point B
Answer:
X coordinate is -2
Y coordinate is 2
(-2,2)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 3.
Point C
Answer:
X coordinate is -4
Y coordinate is 1
(-4,1)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 4.
Point D
Answer:
X coordinate is 3
Y coordinate is -3
(3,-3)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Write the percent as a decimal.
Question 5.
62%
Answer:
62 ÷ 100 = 0.62
Question 6.
7%
Answer:
7 ÷ 100 = 0.07
Question 7.
133%
Answer:
133 ÷ 100 = 1.33
Question 8.
0.45%
Answer:
0.45 ÷ 100 = 0.0045
Question 9.
The tape diagram represents the ratio of the time you spend online to the time your friend spends online. You are online for 6 hours. How many hours does your friend spend online?
Answer:
Number of hours i was online = 6
Ratio of time spend online by me and my friend = \(\frac{3}{4}\)
Time spend by my friend in online = \(\frac{2}{3}\) = \(\frac{6}{x}\)
6 × 3 = x × 2
x = 18 ÷ 2
x=9
Time spend by my friend in online = 9 Hours.
Concepts, Skills, &Problem Solving
STRUCTURE Plot the ordered pairs in a coordinate plane. Then plot another point to form a rectangle. (See Exploration 1, p. 377.)
Question 10.
(3, 2), (3, 6), (- 5, 2)
Answer:
Plot the points (3, 2), (3, 6), (- 5, 2)
In order to form a rectangle we need to mark (-5,6) as shown in the above graph .
Question 11.
(- 4, 7), (- 1, 7), (- 4, – 2)
Answer:
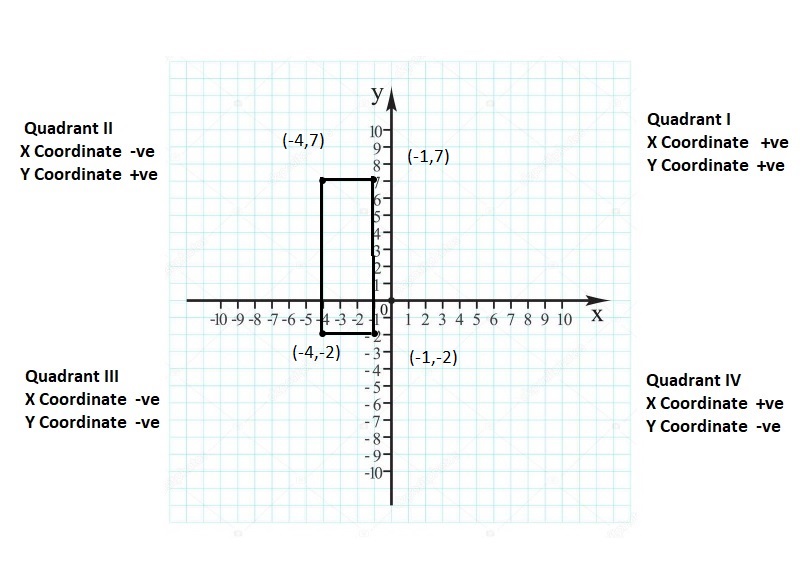
Explanation:
Plot the points (- 4, 7), (- 1, 7), (- 4, – 2)
In order to form a rectangle we need to mark (-1,-2) as shown in the above graph .
DRAWING A POLYGON Draw the polygon with the given vertices in a coordinate plane.
Question 12.
A (4, 7), B (6, 2), C(0, 0)
Answer:
Plot the points A (4, 7), B (6, 2), C(0, 0)
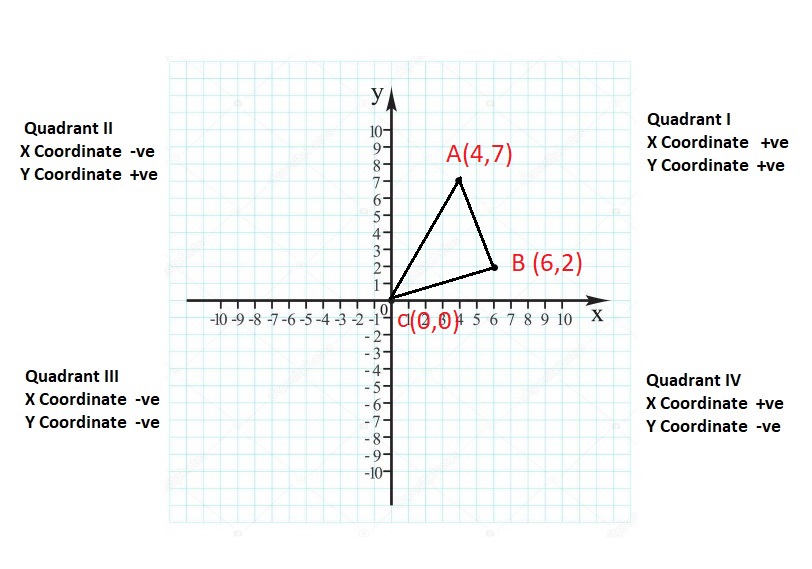
Question 13.
D (\(\frac{1}{2}\), 2), E (- 5, 5), F (- 4, 1)
Answer:
D (\(\frac{1}{2}\), 2) = D (0.5 , 2)
Plot the points D (0.5 , 2), E (- 5, 5), F (- 4, 1)
Question 14.
G (1\(\frac{1}{2}\), 4), H(1\(\frac{1}{2}\), – 8), J (5, – 8), K (5, 4)
Answer:
G (1\(\frac{1}{2}\), 4)= G (\(\frac{3}{2}\), 4) = G ( 1.5 , 4)
H(1\(\frac{1}{2}\), -8)= H(\(\frac{3}{2}\), -8) = H ( 1.5 , -8)
Plot the points G ( 1.5 , 4), H ( 1.5 , -8), J (5, – 8), K (5, 4)
Question 15.
L (- 3, 2), M (- 3, 5), N (2, 2), P (2, – 1)
Answer:
L (- 3, 2), M (- 3, 5), N (2, 2), P (2, – 1)
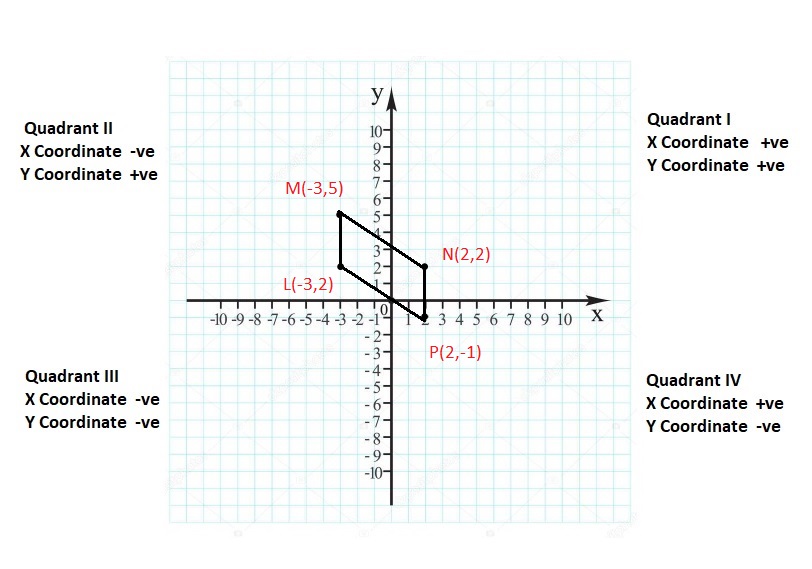
Question 16.
Q (0, 4), R (- 3, 8), S (- 7, 4), T (- 1, – 2), U (7, – 2)
Answer:
Plot the points Q (0, 4), R (- 3, 8), S (- 7, 4), T (- 1, – 2), U (7, – 2)
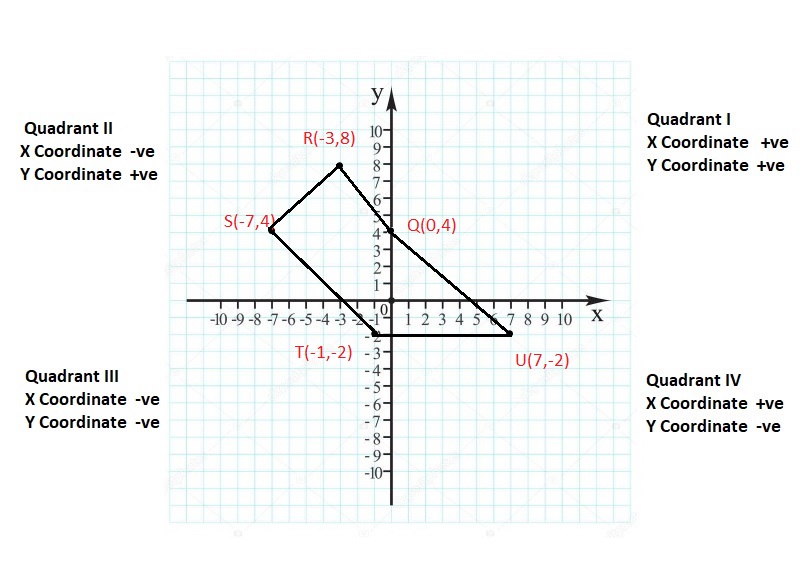
Question 17.
V(- 4, – 2), W(- 3, 3\(\frac{1}{2}\)), X (2, 3\(\frac{1}{2}\)), Y (4, 0), Z (1, – 4)
Answer:
W(- 3, 3\(\frac{1}{2}\))= W(- 3, \(\frac{7}{2}\)) = W(-3, 3.5)
X (2, 3\(\frac{1}{2}\))= X (2, \(\frac{7}{2}\)) = X(2, 3.5)
Plot the points V(- 4, – 2),W(-3, 3.5), X(2, 3.5), Y (4, 0), Z (1, – 4)
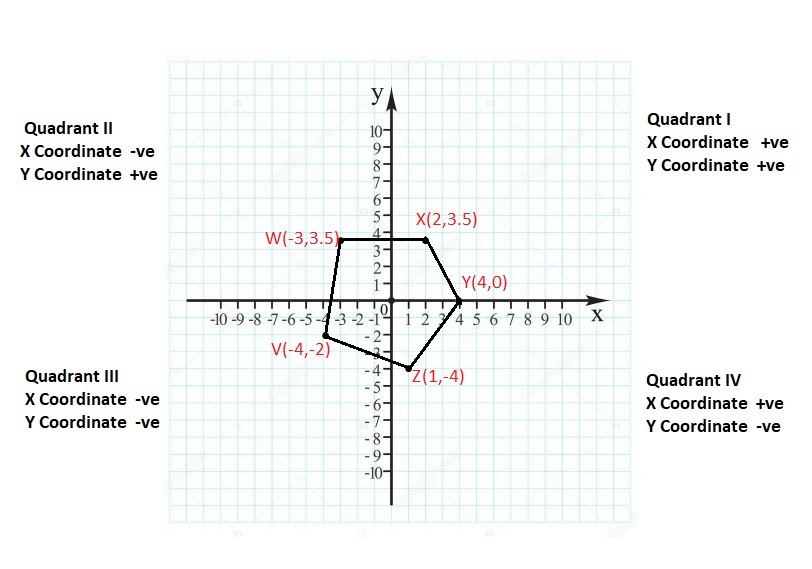
Question 18.
YOU BE THE TEACHER
Your friend draws a triangle with vertices A(3, −1), B (4, 3), and C (−1, 2). Is your friend correct? Explain your reasoning.
Answer:
No
Explanation:
As per the above graph the point A drawn as (3,1) not (3,-1).The Point A is drawn in Quadrant I, Here the x-coordinate is positive and y-coordinate is also positive.
The point (3,-1) will be represented in Quadrant IV, Here the x-coordinate is positive and y-coordinate is also negative.
FINDING DISTANCES Find the distance between the points.
Question 19.
(4, 6), (9, 6)
Answer:
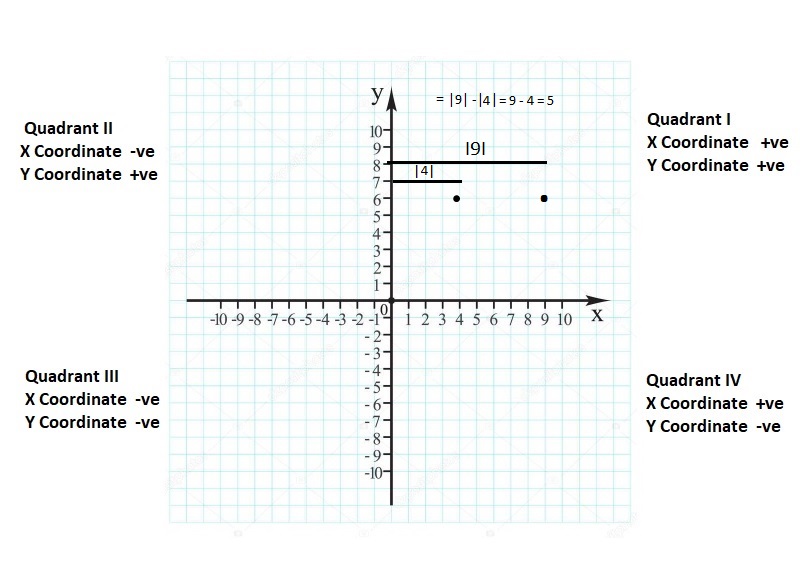
Answer:
Plot the points.
The points are in same Quadrants and have same y-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the x coordinate.
|9| – |4| = 9-4=5
So the distance between the points (4, 6), (9, 6) is 5
Question 20.
(5, 10), (5, 4)
Answer:
Plot the points.
The points are in same Quadrants and have same x-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the y coordinate.
|10| – |4| = 2
So the distance between the points (5, 10), (5, 4) is 6
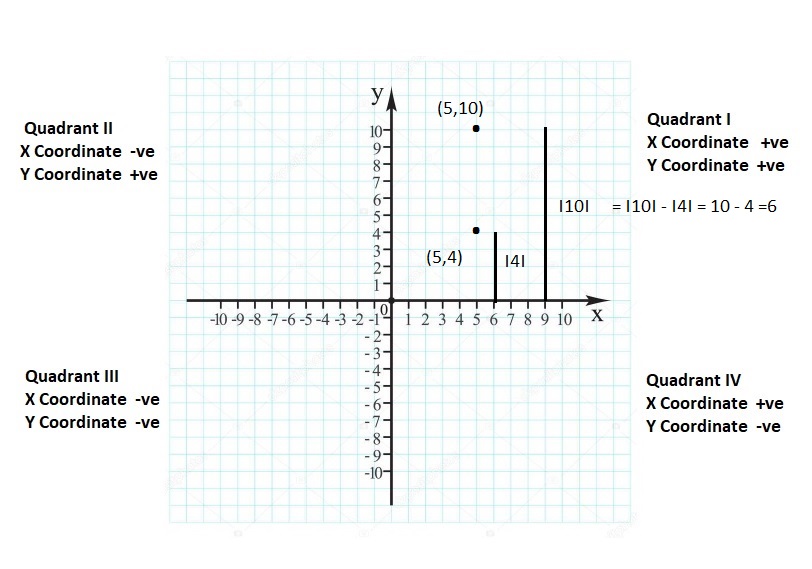
Question 21.
(3, 0), (3, – 2)
Answer:
Plot the points.
The points are in same Quadrants and have same x-coordinates. The distance between the points is the Sum of the absolute values of the y coordinate.
|0| + |-2| = 2
So the distance between the points (3, 0), (3, – 2) is 2
Question 22.
(5, – 2), (- 6, – 2)
Answer:
Explanation:
Plot the points.
The points are in different Quadrants and have same y-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|5| + |-6| = 5 + 6=11
So the distance between the points (5, – 2), (- 6, – 2) is 11
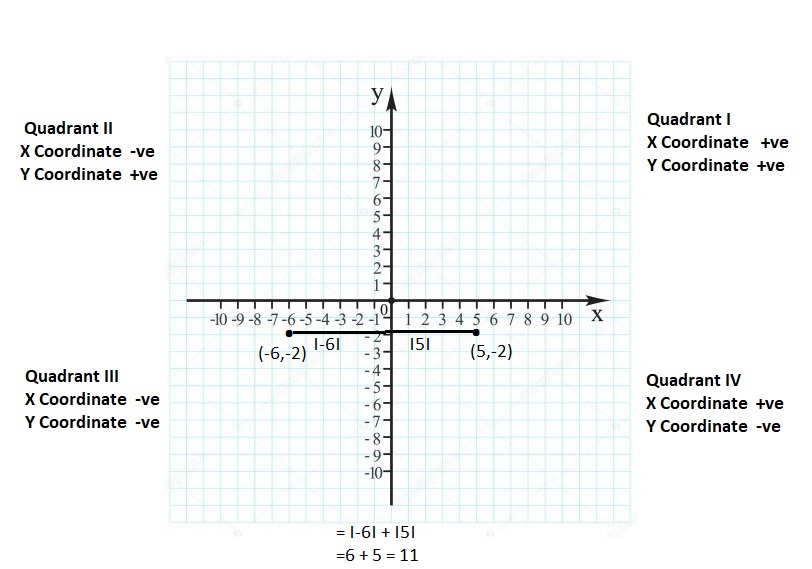
Question 23.
(- 1, 12), (- 1, – 3)
Answer:
Plot the points.
The points are in different Quadrants and have same x-coordinates. The distance between the points is the Sum of the absolute values of the y coordinate.
|12| + |-3| = 12 + 3 =15
So the distance between the points (- 1, 12), (- 1, – 3) is 15
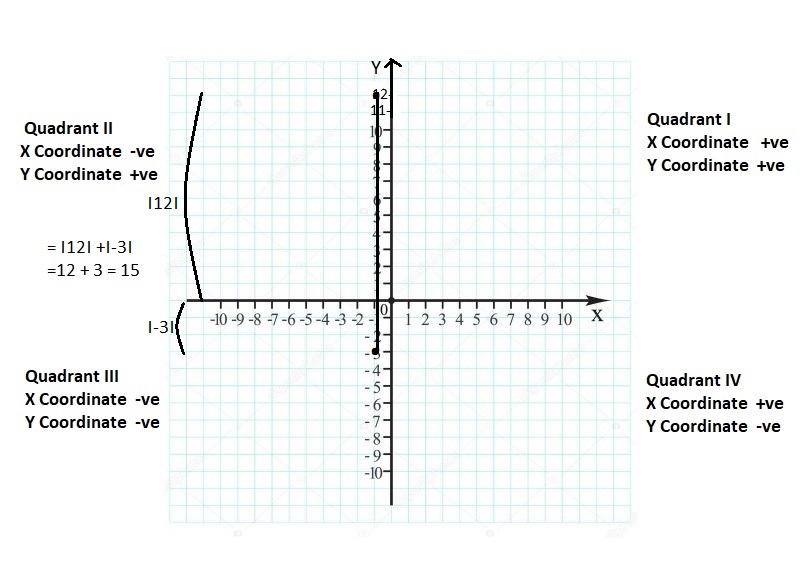
Question 24.
(- 7, 8), (7, 8)
Answer:
Plot the points.
The points are in different Quadrants and have same y-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|-7| + |7| = 7 + 7 = 14
So the distance between the points (- 7, 8), (7, 8) is 14
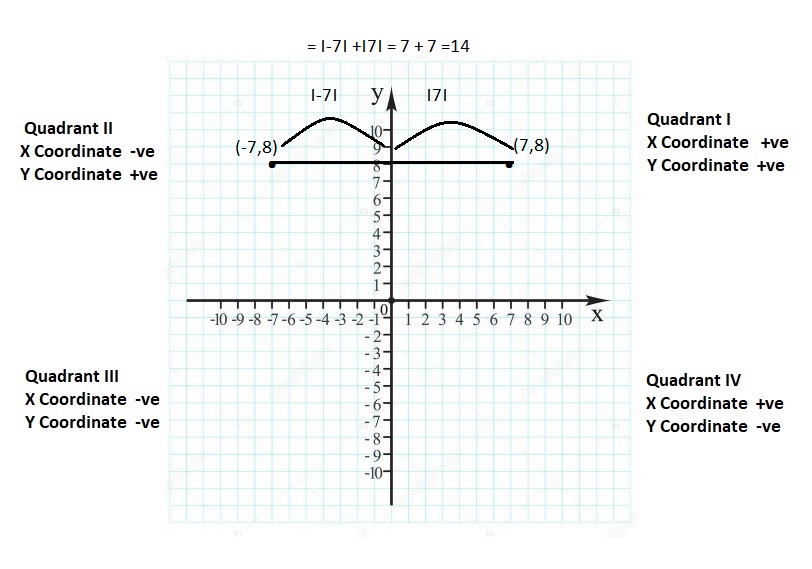
Question 25.
(- 6, 5), (- 6, – 3.5)
Answer:
Plot the points.
The points are in different Quadrants and have same x-coordinates. The distance between the points is the Sum of the absolute values of the y coordinate.
|5| + |-3.5| = 5 + 3.5 = 8.5
So the distance between the points (- 6, 5), (- 6, – 3.5) is 8.5
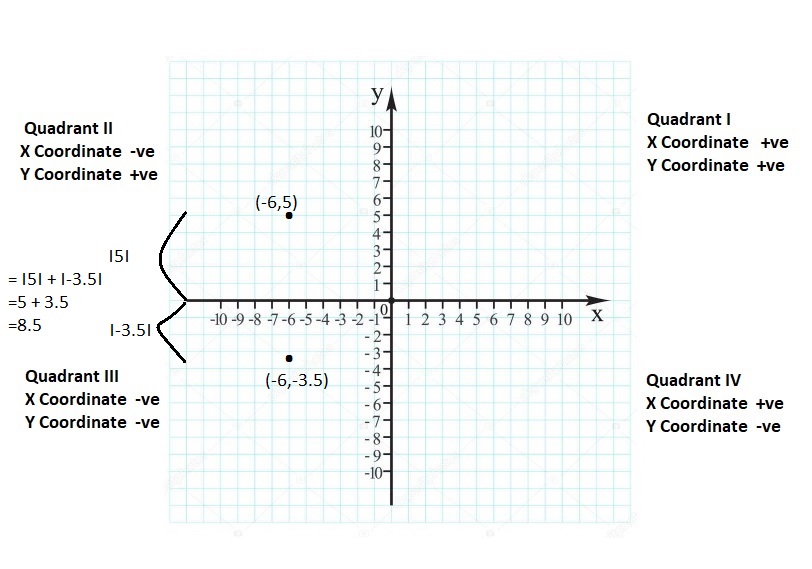
Question 26.
(- 2.5, 3), (5, 3)
Answer:
Plot the points.
The points are in different Quadrants and have same y-coordinates. The distance between the points is sum of the absolute values of the x coordinate.
|-2.5| + |5| = 2.5 + 5 = 7.5
So the distance between the points (- 2.5, 3), (5, 3) is 7.5
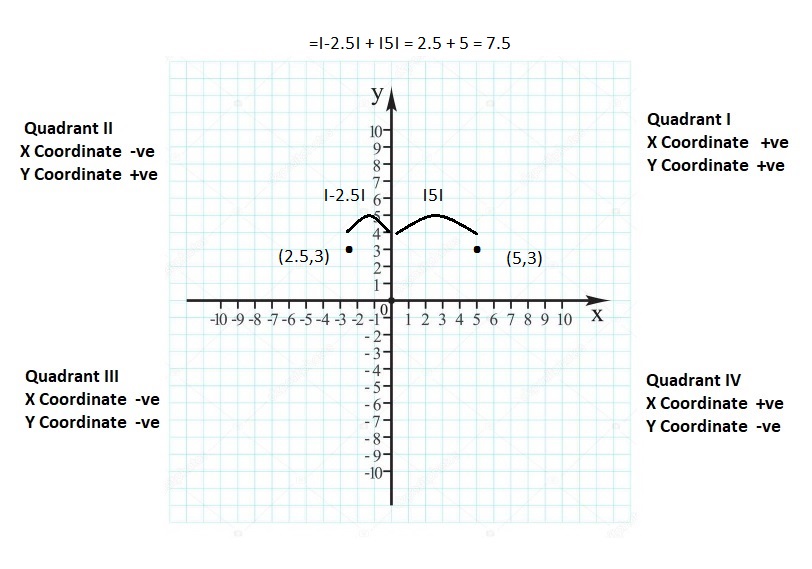
Question 27.
(4.5, – 1.5), (4.5, 7.25)
Answer:
Plot the points.
The points are in different Quadrants and have same x-coordinates. The distance between the points is the sum of the absolute values of the y coordinate.
|-1.5| + |7.25| = 1.5 + 7.25 = 8.75
So the distance between the points (4.5, – 1.5), (4.5, 7.25) is 8.75
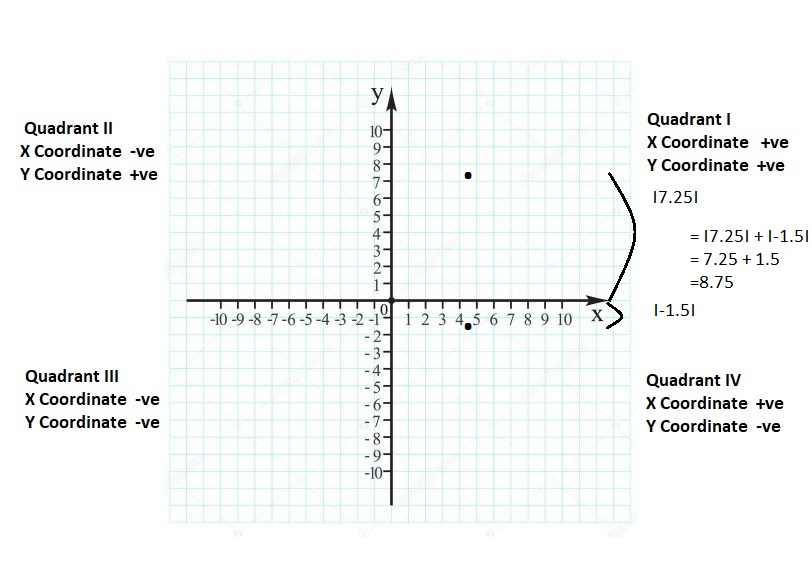
GEOMETRY Find the perimeter and the area of the polygon with the given vertices.
Question 28.
C (1, 1), D (1, 4), E (4, 4), F (4, 1)
Answer:
The polygon formed is square .
The area of the square = s × s = 3 × 3 = 9
The perimeter of the square = 4 s = 4 × 3 = 12
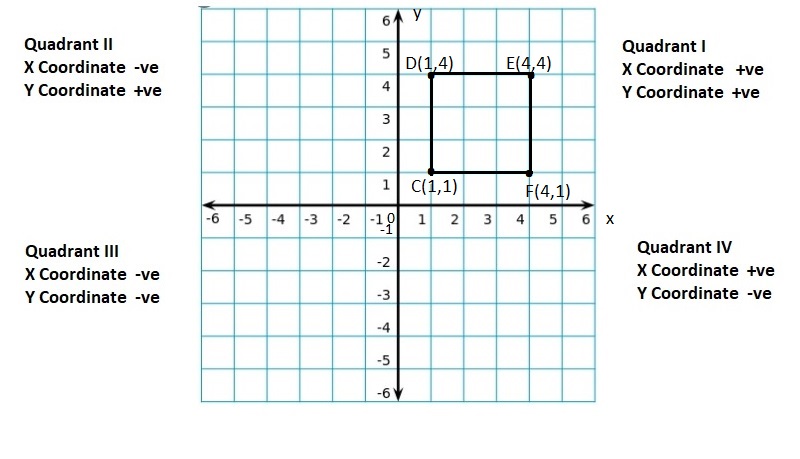
Question 29.
J (- 1, – 2), K(- 6, – 2), L (- 6, – 8), M (- 1, – 8)
Answer:
After plotting the points the polygon formed is Rectangle
Area of Rectangle = length × breadth = 6 × 5 = 30
Perimeter of Rectangle = 2 (length + breadth) = 2 ( 6 + 5) = 22
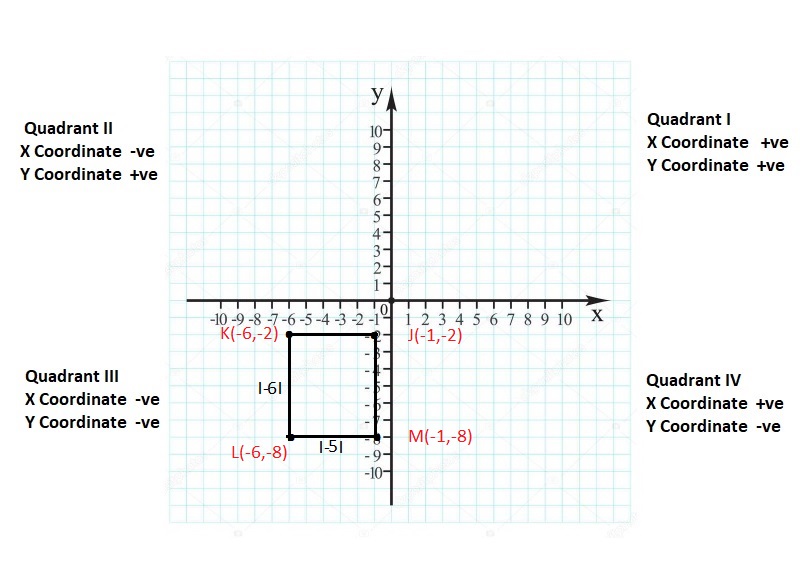
Question 30.
N (- 4, 2), P (5, 2), Q (5, 5), R (- 4, 5)
Answer:
After plotting the points the polygon formed is Rectangle
Area of Rectangle = length × breadth = 9 × 3 = 27
Perimeter of Rectangle = 2 (length + breadth) = 2 ( 9 + 3) = 24
Question 31.
S (- 11, – 8), T (- 11, 0), U (0, 0), V (0, – 8)
Answer:
After plotting the points the polygon formed is Rectangle
Area of Rectangle = length × breadth = 11 × 8 = 88
Perimeter of Rectangle = 2 (length + breadth) = 2 ( 11 + 8) = 38
Question 32.
MODELING REAL LIFE
The coordinates of several stars drawn in a coordinate plane are (8, 0), (7, −3), (3, −2.5), (3.5, 0.5), (−1, 3), (−3, 5), and (−7, 6). Plot the locations of the stars. Draw a constellation by connecting the points.

Answer:
Plot the given points (8, 0), (7, −3), (3, −2.5), (3.5, 0.5), (−1, 3), (−3, 5), and (−7, 6).
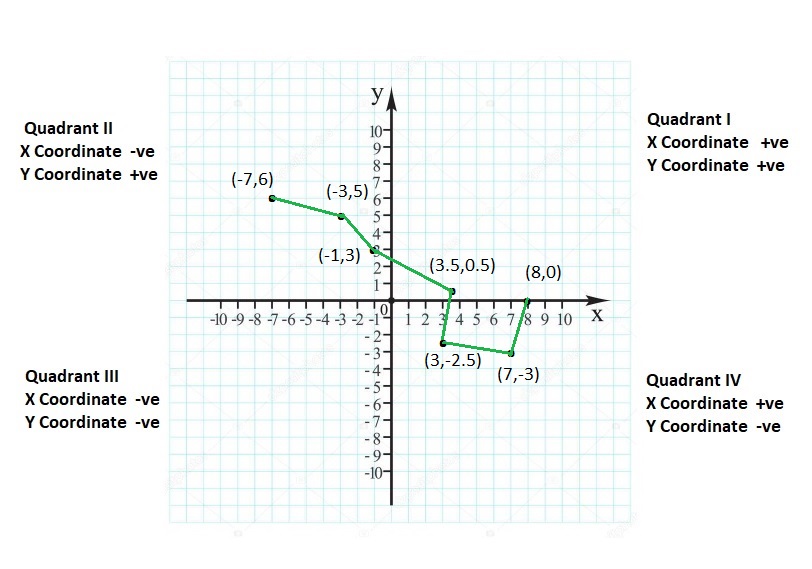
Question 33.
STRUCTURE
The coordinate plane shows three vertices of a parallelogram. Find two possible points that could represent the fourth vertex.
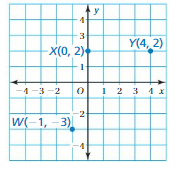
Answer:
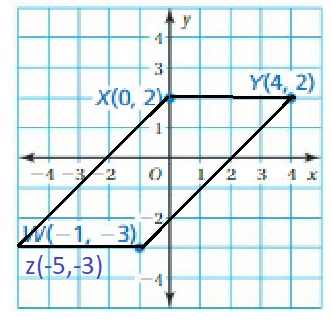
The fourth vertex is Z(-5,-3) as shown in the above graph.
Question 34.
PROBLEM SOLVING
Polygon JKLMNP represents a bus route. Each grid square represents 9 square miles. What is the shortest distance, in miles, from Station P to Station L using the bus route? Explain.
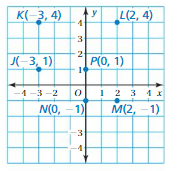
Answer:
Shortest distance between L to P is from PNML = 9 × 9 = 81 square miles
(Total grids from PNML = 9)
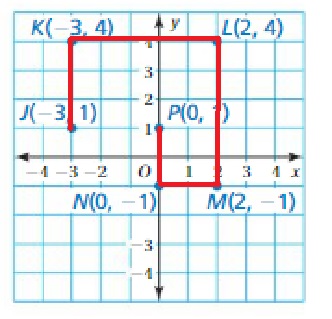
Question 35.
MODELING REAL LIFE
In a topographical map of a city, the vertices of the city limits are A(−7, 3), B (1, 3), C (1, −4), D (−3, −1.5), and E (−7, −1.5). The coordinates are measured in miles. What is the area of the city?
Answer:
Plot the given points A(−7, 3), B (1, 3), C (1, −4), D (−3, −1.5), and E (−7, −1.5)
Area of city = area of rectangle ABEF + area of triangle CDF
Area of Rectangle ABEF = length × breadth = 8 × 4.5 = 36
Area of triangle CDF = (Height × base) ÷ 2 =(4 × 2.5) ÷ 2 = 5
Question 36.
DIG DEEPER!
A map shows that the vertices of a backyard are W (−100, −70), X (−100, 0), Y (0, 0), and Z (−60, −70). The coordinates are measured in feet. The line segment XZseparates the backyard into a lawn and a garden. How many times larger is the lawn than the garden?
Answer:
Plot the given points W (−100, −70), X (−100, 0), Y (0, 0), and Z (−60, −70).
From the graph we can say that the 2 times larger the lawn than a garden.
OPEN-ENDED Draw a polygon with the given conditions in a coordinate plane where the vertices are not all in the same quadrant.
Question 37.
a square with a perimeter of 20 units
Answer:
Question 38.
a rectangle with a perimeter of 18 units
Answer:
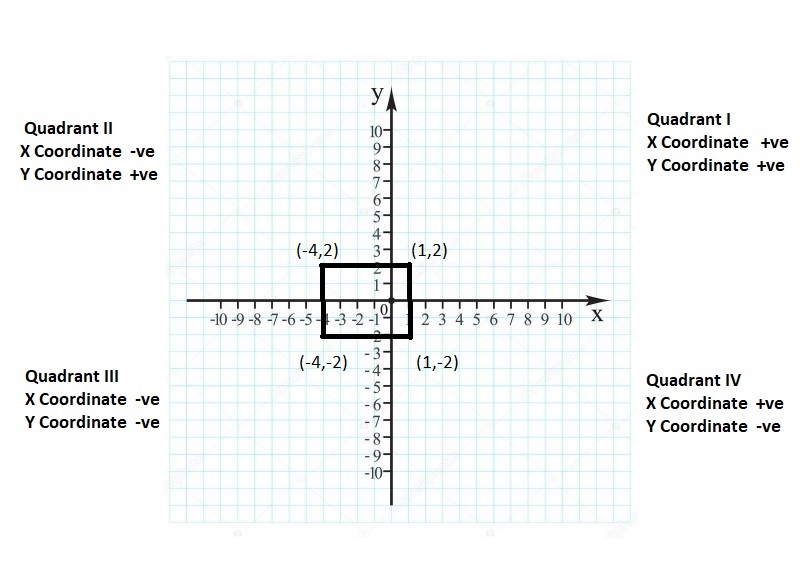
Question 39.
a rectangle with an area of 24 units2
Answer:
After plotting the points the polygon formed is Rectangle
Area of Rectangle = length × breadth = 6 × 4 = 24 units2
Question 40.
a triangle with an area of 15 units2
Answer:
After plotting the points in the graph
Area of triangle = (Height × base) ÷ 2 =(6 × 5) ÷ 2 = 15 units2
Question 41.
PRECISION
The vertices of a rectangle are (1, 0), (1, a), (5, a), and (5, 0). The vertices of a parallelogram are (1, 0), (2, b), (6, b), and (5, 0). The values of a and b are both positive and a > b. Which polygon has a greater area? Explain.
Answer:
The vertices of a rectangle are A(1, 0), B(1, a), C(5, a), and D(5, 0).
After plotting the above points in the graph we consider a = 3 to form a rectangle.
The vertices of a parallelogram are A(1, 0), E(2, b), F(6, b), and D(5, 0).
After plotting the above points in the graph we consider b = 2 to form a parallelogram
The area of the rectangle is greater than area of the parallelogram which can be easily noticed from the graph .
Lesson 8.7 Writing and Graphing Inequalities
EXPLORATION 1
Understanding Inequality Statements
Work with a partner. Create a number line on the floor with both positive and negative integers.
a. For each statement, stand at a number on your number line that makes the statement true. On what other numbers can you stand?
•Class starts more than 3 minutes late.

Answer:
c > 3
Explanation:

above 3 all points are solutions for above inequality statement.
• You need at least 3 peaches for a recipe.

Answer:
n ≥ 3.
Explanation:

Here the mark starts at 3 the point is closed circle which means here 3 is also included .
3 and above will be the solutions for the inequality equations.
• The temperature is at most 3 degrees Celsius.
Answer:
t ≤ 3
Explanation:
Here in the number line we observe that a circle is marked at point 3 it means it is not included and less than 3 are the solutions of the inequality equations

• After playing a video game for 5 minutes, you have fewer than 3 points.

Answer:
x+5 < 3
b. How can you represent the solutions of each statement in part(a) on a number line?
Answer:
An Inequality is a mathematical sentence that compares expressions. It contains symbols like < , > ,≤, ≥.
based on the phrases the symbol is used and expressions are written .

An inequality is a mathematical sentence that compares expressions. It contains the symbols <, >, ≤, or ≥. To write a word sentence as an inequality, look for the following phrases to determine where to place the inequality symbol.
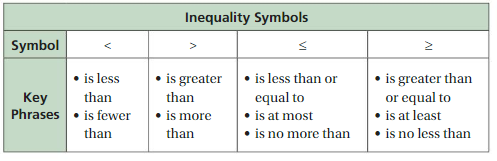
Try It
Write the word sentence as an inequality.
Question 1.
A number n is greater than 1.
Answer:
A number n is greater than 1
n > 1
An inequality is n>1
Question 2.
Twice a number p is fewer than 7.
Answer:
Twice a number p is fewer than 7.
2p < 7
An inequality equation is 2p>7
Question 3.
A number w minus 3 is less than or equal to 10.
Answer:
An inequality equation is w-3 ≤ 10
Question 4.
A number z divided by 2 is at least −6.
Answer:
An inequality equation is z ÷ 2 ≥ -6
Tell whether 3 is a solution of the inequality.
Question 5.
b + 4 < 6
Answer:
b + 4 < 6
b < 6 – 4
b < 2
No as b is less than 2
Question 6.
9 – n ≥ 6
Answer:
9 – n ≥ 6
9 + 6 ≥ n
15 ≥ n
Question 7.
10 ≤ 18 ÷ x
Answer:
10 ≤ 18 ÷ x = x ≤ 18 ÷ 10
x ≤ 1.8
Graph the inequality on a number line.
Question 8.
a < 4
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 9. f ≤ 7
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 10. n > 0
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 11.
– 3 ≤ p
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” inequalities.
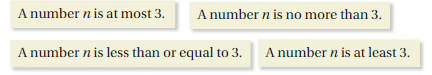
Answer:
Statement I – n ≤ 3
Statement II -n ≤ 3
Statement III -n ≤ 3
Statement IV-n ≥ 3 ≤
CHECKING SOLUTIONS Tell whether the given value is a solution of the inequality.
Question 13.
p + 5 ≤ 12; p = 6
Answer:
p + 5 ≤ 12
put p = 6
6 + 5 = 11
11 ≤ 12 is true
so the given value is the solution of the inequality .
Question 14.
w – 12 < 4; w = 16
Answer:
w – 12 < 4
put w = 16
16 – 12 =4
4 < 4 is not true
so the given value is not a solution for the inequality .
GRAPHING AN INEQUALITY Graph the inequality on a number line.
Question 15.
n > 8
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 16.
q ≤ – 4
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 17.
5 < s
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 18.
To obtain a babysitting license, you still need to train for at least 6 hours and 45 minutes. Describe the amounts of time that you can train and still not obtain a license.
Answer:
Time required to train for babysitting license ≤ 6 hours 45 minutes.
Question 19.
DIG DEEPER!
The farthest away a drone can fly is 200 meters. A building is 380 meters tall. You control the drone from a floor that is halfway to the top of the building. Can the drone reach the top of the building? Explain your reasoning.

Answer:
Distance a drone can fly = 200 metres
Height of a building = 380 metres tall
floor height = half of the building = 380 ÷ 2 = 190 metres.
Distance a drone can travel from floor = 190 metres + 200 = 390 metres.
390 > Distance of a building .
390 > 380
It means that drone can reach the top of the building .
Question 20.
Each visit to a water park costs $19.95. An annual pass to the park costs $89.95. Write an inequality that represents the numbers of times you would need to visit the park for the pass to be a better deal.

Answer:
Cost of water park for 1 visit= $19.95
Cost of Annual pass to water park = $89.95.
Number of visits in Annual pass = $89.95 ÷ $19.95 = 4.5
Number of visits = n
n ≥ 4.5
Writing and Graphing Inequalities Homework & Practice 8.7
Review & Refresh
Find the distance between the points.
Question 1.
(2, 8), (6, 8)
Answer:
Explanation:
Plot the points.
The points are in same Quadrants and have same y-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the x coordinate.
|6| – |2| = 6 – 2 = 4
So the distance between the points (2, 8), (6, 8) is 4
Question 2.
(5, 9), (7, 9)
Answer:
Explanation:
Plot the points.
The points are in same Quadrants and have same y-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the x coordinate.
|7| – |5| = 7- 5 = 2
So the distance between the points (5, 9), (7, 9) is 2
Question 3.
(- 3, 6), (- 3, – 2)
Answer:
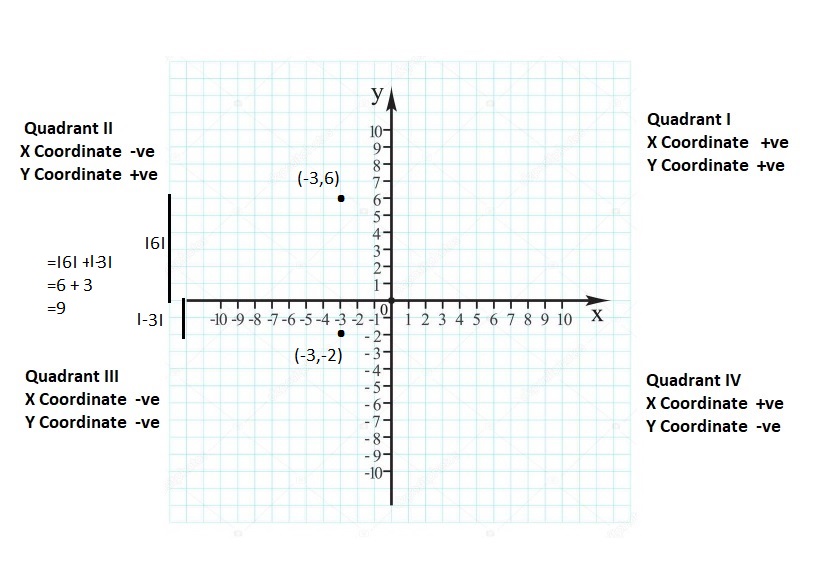
Explanation:
Plot the points.
The points are in different Quadrants and have same X-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|6| + |-3| = 6 + 3 = 9
So the distance between the points (- 3, 6), (- 3, – 2) is 9
Solve the equation. Check your solution
Question 4.
x + 3 = 12
Answer:
x + 3 = 12
x = 12 – 3
x = 9
solution is 9
Question 5.
x – 6 = 8
Answer:
x – 6 = 8
x = 8 + 6
x = 14
solution is 14
Question 6.
\(\frac{t}{12}\) = 4
Answer:
\(\frac{t}{12}\) = 4
t = 4 × 12
t = 48
Question 7.
8x = 72
Answer:
8x = 72
x = 72 ÷ 8
x = 9
Question 8.
A stack of boards is 24 inches high. e thickness of each board is \(\frac{3}{8}\) inch. How many boards are in the stack?
A. \(\frac{1}{9}\)
B. \(\frac{1}{6}\)
C. 9
D. 64
Answer:
Height of boards = 24 inches
Thickness of each board = \(\frac{3}{8}\) = 0.375 inch
Number of boards in stack = 24 ÷ 0.375 = 64 boards
Option D is the answer.
Find the area of the parallelogram.
Question 9.
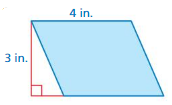
Answer:
Height of the Parallelogram = 3 inches
Base of the Parallelogram = 4 inches.
Area of the Parallelogram = base × height = 3 × 4 =12 inches.
Question 10.
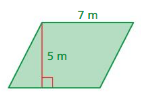
Answer:
Height of the Parallelogram = 5 m
Base of the Parallelogram = 7 m
Area of the Parallelogram = base × height = 7 × 5 = 35 metres
Question 11.
Answer:
Height of the Parallelogram = 15 m
Base of the Parallelogram = 8.5 m
Area of the Parallelogram = base × height = 15 × 8.5 = 127.5 sq metres
Concepts, Skills, & Problem Solving
UNDERSTANDING INEQUALITY STATEMENTS Choose a number that makes the statement true. What other numbers make the statement true? (See Exploration 1, p. 383.)
Question 12.
You are less than 3 miles from home.
Answer:
Y < 3.

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 13.
You need at least $5 for lunch.
Answer:
Y ≥ 5

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 14.
You buy more than 2 movie tickets.
Answer:
Y > 2

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 15.
A game lasts no more than 10 minutes.
Answer:
G ≤ 10

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
WRITING INEQUALITIES Write the word sentence as an inequality.
Question 16.
A number k is less than 10.
Answer:
k < 10
Question 17.
A number a is more than 6.
Answer:
n > 6
Question 18.
A number z is fewer than \(\frac{3}{4}\).
Answer:
z < \(\frac{3}{4}\)
Question 19.
A number b is at least −3.
Answer:
b ≥ -3
Question 20.
One plus a number y is no more than −13.
Answer:
1 + Y ≤ – 13
Question 21.
A number x divided by 3 is at most 5.
Answer:
x ÷ 3 ≤ 5
CHECKING SOLUTIONS Tell whether the given value is a solution of the inequality.
Question 22.
x – 1 ≤ 7; x = 6
Answer:
x – 1 ≤ 7
put x =6
6 – 1 = 5
5 ≤ 7
above statement is True
Yes, the given value is a solution of the inequality.
Question 23.
y + 5 < 13; y = 17
Answer:
y + 5 < 13
put = 17
17 + 5 = 22
22 < 13
above statement is wrong
So, the given value is not a solution of the inequality.
Question 24. 3z > 6; z = 3
Answer:
3z > 6
put z = 3
3 × 3 = 9
9 > 6
above statement is True
So, the given value is not a solution of the inequality.
Question 25.
6 ≤ \(\frac{b}{2}\); b = 10
Answer:
6 ≤ \(\frac{b}{2}\)
6 ≤ \(\frac{10}{2}\)
6 ≤ 5
The above statement is wrong .
So, the given value is not a solution of the inequality.
Question 26.
c + 2.5 < 4.3; c = 1.8
Answer:
c + 2.5 < 4.3
Put c = 1.8
1.8 + 2.5 = 4.3
4.3 < 4.3
above statement is wrong
So, the given value is not a solution of the inequality.
Question 27.
a ≤ 0; a = -5
Answer:
a ≤ 0
put a = -5
– 5 ≤ 0
above statement is True
So, the given value is not a solution of the inequality.
MATCHING Match the inequality with its graph.
Question 28.
x ≥ – 2
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 29.
x < – 2
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 30.
x > – 2
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 31.
x ≤ – 2
Answer:

Option C is correct.
Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
GRAPHING AN INEQUALITY Graph the inequality on a number line.
Question 32.
a > 4
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 33.
n ≥ 8
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 34.
3 ≥ x
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 35.
y < \(\frac{1}{2}\)
Answer:
y < \(\frac{1}{2}\) = y < 0.5

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 36.
x < \(\frac{2}{9}\)
Answer:
x < \(\frac{2}{9}\)
x < 0.2

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 37. -3 ≥ c
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 38. m > – 5
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 39.
0 ≤ b
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 40.
1.5 > f
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 41.
t ≥ – \(\frac{1}{2}\)
Answer:
t ≥ – \(\frac{1}{2}\) = t ≥ – 0.5

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 42.
t ≥ – 1.6
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 43.
\(\frac{7}{3}\) ≥ z
Answer:
\(\frac{7}{3}\) ≥ z
2.3 ≥ z

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
OPEN-ENDED Write an inequality and a word sentence that represent the graph.
Question 44.
![]()
Answer:
n < 1
Here in the number line the 1 is not selected and all the numbers are less than 1 so the inequality equation is
n < 1
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 45.
![]()
Answer:
Here in the number line the 1 is selected and all the numbers are less than 1 so the inequality equation is
n ≤ 1
Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 46.
![]()
Answer:
Here in the number line the 1 is selected and all the numbers are greater than -4 so the inequality equation is
-4 ≤ n
Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 47.
![]()
Answer:
Here in the number line the 5 is not selected and all the numbers are greater than 0 so the inequality equation is
0 < n
Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
YOU BE THE TEACHER
Your friend graphs the inequality. Is your friend correct? Explain your reasoning.
Question 48.

Answer:
Yes, my friend is true .
Here in the number line the 1 is not selected and all the numbers are greater than 1 so the inequality equation is
x > 1
Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 49.

Answer:
Here in the number line the -1 is not selected and all the numbers are less than -1 so the inequality equation is
-1 > x
Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
Question 50.
MODELING REAL LIFE
The world record for the farthest flight by hoverboard is 2252.4 meters. Write and graph an inequality that represents the distances that would set a new world record.
Answer:
Distance of the farthest flight by hoverboard = 2252.4
For new record the distance should be more than this distance.
Therefore the inequality of a new world record is w > 2252.4
Question 51.
MODELING REAL LIFE
You are fishing and are allowed to keep at most 3 striped bass. Each striped bass must be no less than 18 inches long.
a. Write and graph an inequality that represents the numbers of striped bass you are allowed to keep.
b. Write and graph an inequality that represents the lengths of striped bass you are allowed to keep.

Answer:
Number of striped bass allowed = n ≤ 3
Length of stripped bass = l ≥ 18
Answer a :

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Answer b:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 52.
REASONING
You have $33. You want to buy a necklace and one other item from the list.

a. Write an inequality that represents the situation.
b.Can the other item be a T-shirt? Explain.
c. Can the other item be a book? Explain.
Answer a :
Total Amount = t ≤ $33
Answer b:
Yes
Explanation:
Total Amount = $33
Amount for necklace = $16
Amount for T-Shirt = $15
Total Amount for necklace and T-Shirt = 16 + 15 = 31.
Therefore the required amount is 31 which is less than 33.
So it is possible to buy both .
Answer c :
No
Total Amount = $33
Amount for necklace = $16
Amount for Book = $20
Total Amount for necklace and Book = 16 + 20 = 36.
Therefore the required amount is 36 which is greater than 33.
So it is not possible to buy both .
Question 53.
LOGIC
For a food to be labeled low sodium, there must be no more than 140 milligrams of sodium per serving.

a. Write and graph an inequality that represents the amount of sodium in a low-sodium serving.
Answer:
Amount of sodium in a low-sodium serving = S ≤ 140

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
b.Write and graph an inequality that represents the amount of sodium in a serving that does not qualify as low sodium.
Answer:
Amount of sodium in a low-sodium serving which doesnot qualify = S > 140
Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions
c. Does the food represented by the nutrition facts label qualify as a low-sodium food? Explain.
Answer:
As per the above picture
Total sodium = 300 grams.
Sodium used for nutrition facts label qualify = 13 % of 300 grams = (13 × 300) ÷ 100 = 3 × 13 = 39 grams.
Amount of sodium in a low-sodium serving =140 milligrams = 0.149 grams
So the food represented by the nutrition facts label doesnot qualify as a low-sodium food.
CRITICAL THINKING Determine whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 54.
A number that is a solution of the inequality x > 5 is also a solution of the inequality x ≥ 5.
Answer:
Sometimes
Explanation:
Only when 5 is not a solution . above 5 all will be the solutions for the equations.
Question 55.
A number that is a solution of the inequality 5 ≤ x is also a solution of the inequality x > 5.
Answer:
Sometimes.
Explanation:
Only when 5 is not a solution . above 5 all will be the solutions for the equations.
5Question 6.
PROBLEM SOLVING
A subway ride costs $1.50. A 30-day subway pass costs $36. Write an inequality that represents the numbers of subway rides you would need to take for the pass to be a better deal.
Answer:
Cost of one ride of subway = $1.50
cost of 30-day subway = $36.
Number of rides in 30-day subway = $36 ÷ $1.50 = 24 rides.
Yes it is a fair deal because you pay only for 24 rides out of 30 rides.
r ≤ 24 .
Question 57.
PROBLEM SOLVING
Fifty people are seated in a movie theater. The maximum capacity of the theater is 425 people. Write an inequality that represents the numbers of additional people who can be seated.
Answer:
Number of people in theater = 50
Maximum Capacity = 425
The Numbers of additional people who can be seated = 50 + x < 425 .
Question 58.
CRITICAL THINKING
The map shows the elevations above sea level for an area of land.
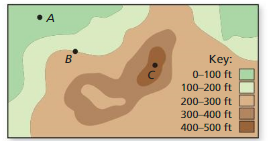
a Graph the possible elevations of A. Write the set of elevations as two inequalities.
Answer:
Point A = 0 – 100 ft
possible elevations of A ≤ 100.
b. Graph the possible elevations of C. How can you write this set of elevations as a single inequality? Explain.
Answer:
Point C = 400 – 500
possible elevations of 400 < C ≤ 500.
c. What is the elevation of B? Explain.
Answer:
Point C = 200 – 300
possible elevations of 200 < B ≤ 300.
Lesson 8.8 Solving Inequalities
EXPLORATION 1
Using Tape Diagrams
Work with a partner. In Section 6.2 Exploration 1, the tape diagram below was used to model the equation x + 4 = 12.
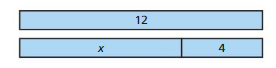
a. Suppose that x +4 is greater than 12. How can you change the equation to represent the new relationship between x + 4 and 12?
Answer:
x + 4 ≥ 12
To Change the equation to represent the new relationship
x + 4 ≥ 12 subtract 4 from both sides of the equation we get ,
x ≥ 8
b. A student finds the possible values of x using the tape diagrams below. What is the solution? How can you find the solution algebraically?
Answer:
None of the above diagrams help us to know the solutions.
c. Describe the relationship between 4x and 20 as shown by the tape diagram below. What can you conclude about x?

Answer:
4x + y = 20
Explanation:
Total 4x is not equal to 20 something if we add to 4x then only the sum becomes 20 .
Try It
Solve the inequality. Graph the solution.
Question 1.
x – 2 < 3
Answer:
x – 2 < 3
add 2 on both sides
x -2 + 2 < 3 + 2
x < 5

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 2.
10 ≥ z – 1
Answer:
10 ≥ z – 1 ( add by 1)
11 ≥ z

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 3.
y + 2 ≥ 17
Answer:
y + 2 ≥ 17
y ≥ 17 – 2 ( subtract by 2)
y ≥ 15

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Solve the inequality. Graph the solution.
Question 4.
p ÷ 3 ≥ 2
Answer:
p ÷ 3 ≥ 2
p ≥ 2 × 3 ( multiply by 3 )
p ≥ 6

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 5.
1 < \(\frac{s}{7}\)
Answer:
1 < \(\frac{s}{7}\)
7 < s (multiply by 7)

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 6. 11k ≤ 33
Answer:
11k ≤ 33
k ≤ 3 (divided by 11 )

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Solve the inequality. Graph the solution.
Question 7. \(\frac{3}{2}\)m > 1
Answer:
\(\frac{3}{2}\)m > 1
1.5m > 1 divide by 1.5
m > 0.6

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 8.
\(\frac{3}{5}\)q ≤ 6
Answer:
\(\frac{3}{5}\)q ≤ 6
0.6q ≤ 6
divide by 0.6
q ≤ (6 ÷ 0.6 )
q ≤ 10

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 9.
5 > \(\frac{5t}{6}\)
Answer:
5 > \(\frac{5t}{6}\)
multiply by 6
5 × 6 > 5t
30 > 5t
divide by 5
6 > t

Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING INEQUALITIES Solve the inequality. Graph the solution.
Question 10.
n + 6 < 10
Answer:
n + 6 < 10
subtract 6 on both sides
n < 4

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions.Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 11.
h – 13 ≥ 7
Answer:
h – 13 ≥ 7
add 13 on both sides
h ≥ 20

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 12.
5g > 45
Answer:
5g > 45
divide by 9 on both sides
g > 9

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 13.
\(\frac{3}{4}\)k ≤ 6
Answer:
\(\frac{3}{4}\)k ≤ 6
divide by \(\frac{4}{3}\)
k ≤ 8

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
OPEN-ENDED
Write an inequality that the graph represents. Then use the Addition Property of Inequality to write another inequality that the graph represents.

Answer:
x > 2
Then add 2 on both sides
x + 2 > 4.
Question 15.
REASONING
How is the graph of the solution of 2x ≥ 10 different from the graph of the solution of 2x = 10?
Answer:
2x ≥ 10
divide by 2
x ≥ 5

Here including 5 and above all are the solutions of the given inequality equation .
Question 16
OPEN-ENDED
Write two inequalities that have the same solution set: one that you can solve using division and one that you can solve using subtraction.
Answer:
Question 17.
A small pizza costs $4.50, and a salad costs $3.75. You plan to buy two small pizzas and four salads. Write and solve an inequality to find the additional amounts you can spend to get free delivery.

Answer:
Cost of pizza = $4.50
Cost of Salads = $3.75.
Free delivery on more than or equal to $40
d ≥ 40
Cost of 2 pizza = $4.50 × 2 = $9
Cost of 4 Salads = $3.75. × 4 = $15
Total Amount = $9 +$ 15 = $ 26.
Therefore , It is less than 40$ so free delivery is not possible .
Question 18.
DIG DEEPER!
Students at a playground are divided into 5 groups with at least 6 students in each group.
a. Find the possible numbers of students at the playground.
b. Suppose the students are divided into 5 equal groups. How does this change your answer in part(a)?
Answer a :
Number of Groups = 5
Number of students in each group = 6
Total students at play ground = 5 × 6 = 30
Answer b :
It doesnot change the answer because earlier there are 5 groups and even now we have 5 groups .
Solving Inequalities Homework & Practice 8.8
Review & Refresh
Tell whether the given value is a solution of the inequality.
Question 1.
n + 4 > 15; n = 9
Answer:
n + 4 > 15;
Put n = 9 in LHS
9 + 4 = 13
13 > 15 The statement is wrong
So it is not a solution for the given inequality .
Question 2.
s – 12 ≤ 8; s = 20
Answer:
s – 12 ≤ 8
Put s = 20 in LHS
20 – 12
8 ≤ 8 The statement is wrong as it is equal to 8 but not greater than 8 .
So it is not a solution for the given inequality .
Question 3.
\(\frac{z}{4}\) ≥ 7; z = 32
Answer:
latex]\frac{z}{4}[/latex] ≥ 7 (mutlipy by 4)
z ≥ 7 × 4
z ≥ 28
Put z = 32
32 ≥ 28 is true
as 32 is greater than 28.
so the given number is the solution for the inequality equation.
Question 4.
6g < 48; g = 8
Answer:
6g < 48
Put g = 8 in LHS
6 × 8 = 48
48 < 48 is wrong as both are equal .
so the given number is not a solution for the inequality equation .
Find the area of the triangle.
Question 5.
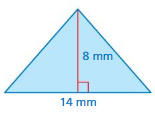
Answer:
Height of the triangle = 8mm
Base of the triangle = 14mm
Area of the Triangle = base × height = 14 × 8 =112 sq.mm
Question 6.
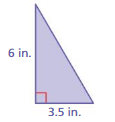
Answer:
Height of the triangle = 6 inches
Base of the triangle = 3.5 inches
Area of the Triangle = base × height = 6 × 3.5 = 21 sq.inches
Question 7.
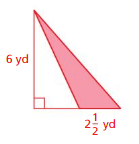
Answer:
Height of the triangle = 6 yd
Base of the triangle = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) = 2.5 yd
Area of the Triangle = base × height = 6 × 2.5 = 15 sq.yds
Write the product as a power.
Question 8.
7 × 7
Answer:
72
As we have 2 7 ‘s so the power is 2
Explanation:
The exponent is the amount of times the number will be multiplied by itself.
Question 9.
12 × 12 × 12 × 12
Answer:
124
As we have 4,12 ‘s so the power is 4
Explanation:
The exponent is the amount of times the number will be multiplied by itself.
Question 10.
1.4 × 1.4 × 1.4
Answer:
1.43
As we have 3, 1.4 ‘s so the power is 3
Explanation:
The exponent is the amount of times the number will be multiplied by itself.
Concepts, Skills, & Problem Solving
USING TOOLS Describe the relationship shown by the tape diagram. What can you conclude about x? (See Exploration 1, p. 391.)
Question 11.
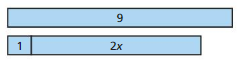
Answer:
1 + 2x < 9
Explanation:
1 + 2x is some part of 9 but not equal to 9 as 9 is greater than 1 + 2x. so the inequality equation is 1 + 2x < 9
Question 12.
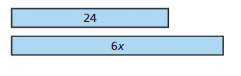
Answer:
6x > 24
Explanation:
24 is some part of 6x . an 6x is greater than 24. So the inequality equation is 6x > 24
SOLVING INEQUALITIES Solve the inequality. Graph the solution.
Question 13.
x – 4 < 5
Answer:
x – 4 < 5 (add 4)
x < 9

Question 14. 5 + h > 7
Answer:
14. 5 + h > 7
14.5 move towards RHS we get
h > 7 -14.5
h > – 7.5

Question 15.
3 ≥ y – 2
Answer:
3 ≥ y – 2
add 2 on both sides
5 ≥ y

Question 16.
y – 21 < 85
Answer:
y – 21 < 85
add 21 on both sides
y < 106

Question 17. 18 > 12 + x
Answer:
18 > 12 + x
subtract 12 on both sides we get ,
6 > x

Question 18.
\(\frac{m}{8}\) < 4
Answer:
\(\frac{m}{8}\) < 4
Multiply by 8 on both sides we get,
m < 8 × 4
m < 32

Question 19. n ÷ 6 > 2
Answer:
n ÷ 6 > 2
multiply by 6 on both sides we get,
n > 12

Question 20.
12x < 96
Answer:
12x < 96
divide by 12 on both sides we get,
x< 8

Question 21.
\(\frac{1}{11}\)c ≥ 9
Answer:
\(\frac{1}{11}\)c ≥ 9
multiply by 11 on both sides we get,
c ≥ 9 × 11
c ≥ 99

Question 22.
8w ≤ 72
Answer:
8w ≤ 72
divide by 8 on both sides we get,
w ≤ 9

Question 23.
7.2 < x + 4.2
Answer:
7.2 < x + 4.2
subtract 4.2 on both sides we get,
3 < x

Question 24.
12.7 ≥ s – 5.3
Answer:
12.7 ≥ s – 5.3
add 5.3 on both sides we get,
12.7 + 5.3 ≥ s
18 ≥ s

Question 25.
\(\frac{3}{4}\) ≤ \(\frac{1}{2}\) + n
Answer:
\(\frac{3}{4}\) ≤ \(\frac{1}{2}\) + n
0.75 ≤ 0.5 + n
subtract 0.5 on both sides we get,
0.25 ≤ n

Question 26.
7.5 p ≤ 45
Answer:
7.5 p ≤ 45
divide by 7.5 we get,
p ≤ 6

Question 27.
\(\frac{5}{9}\)v ≤ 45
Answer:
\(\frac{5}{9}\)v ≤ 45
multiply by \(\frac{9}{5}\) on both sides we get,
v ≤ 81

Question 28.
\(\frac{5x}{8}\) ≥ 30
Answer:
\(\frac{5x}{8}\) ≥ 30
Multiply by \(\frac{8}{5}\) on both sides we get,
x ≥ 48
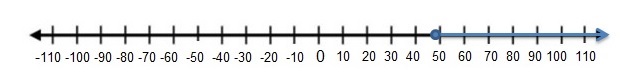
YOU BE THE TEACHER
Your friend solves the inequality. Is your friend correct? Explain your reasoning.
Question 29.

Answer:
No ,
Explanation:
we subtracted 19 on both sides we get
28 – 9 = 19
t – 9 – 9 = t – 18
so the inequality equation after change is
19 ≥ t – 18.
Question 30
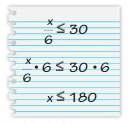
Answer:
Yes it is right.
WRITING INEQUALITIES Write the word sentence as an inequality. Then solve the inequality.
Question 31.
Five more than a number p is less than 17.
Answer:
5 + p < 17
Question 32.
Three less than a number b is more than 15.
Answer:
3 – b > 15
Question 33.
Eight times a number n is less than 72.
Answer:
8n < 72
Question 34.
A number t divided by 32 is at most 4.25.
Answer:
t ÷ 32 ≤ 4.25
Question 35.
225 is no less than \(\frac{3}{4}\) times a number w.
Answer:
225 ≥ \(\frac{3}{4}\)w
Question 36.
MODELING REAL LIFE
Your carry-on bag can weigh at most 40 pounds. Write and solve an inequality that represents how much more weight you can add to the bag and still meet the requirement.

Answer:
Weight of a bag ≤ 40
weight of the bag as per above image = 22
how much weight can be added = 40 – 22 = 18
22 + 18 ≤ 40
Question 37.
MODELING REAL LIFE
It costs $x for a round-trip bus ticket to the mall. You have $24. Write and solve an inequality that represents how much money you can spend for the bus ticket and still have enough to buy a hat that costs $18.99.
Answer:
Cost of bus ticket = $x
Total Amount with me = $24
Cost of Hat = $18.99
Amount can spend for bus ticket = $24 – $18.99 = $5.01
So Cost of bus ticket can be $5.01 ≥ x
Question 38.
GEOMETRY
The length of a rectangle is 8 feet, and its area is less than 168 square feet. Write and solve an inequality that represents the possible widths of the rectangle.
Answer:
Length of a rectangle = 8 feet.
Area of Rectangle < 168
Width of rectangle < Area ÷ length = 168 ÷ 8 = 21
width of rectangle can be < 21
Question 39.
MODELING REAL LIFE
A ticket to a dinosaur exhibit costs $7.50. A one-year pass to the exhibit costs $30. When is the one-year pass a better deal? Explain.

Answer:
Cost of ticket = $7.50
Cost of 1 year pass =$30
Number of times can go in one year = 30 ÷7.50 =4
The deal is fair because you pay only for 4 times to go and rest of the year it will be free.
So the one year pass is more beneficial.
Question 40.
REASONING
A thrill ride at an amusement park holds a maximum of 12 people per ride.

a. Find the possible numbers of rides needed for 15,000 people.
Answer:
Number of people for 1 ride = 12
Number of rides for 15,000 people = 15000 ÷ 12 = 1250 rides.
b. Is it reasonable for 15,000 people to ride the thrill ride in one day? Explain.
Answer:
The park opens from 10:00 a.m to 10:00 p.m
we cannot say the 15,000 people can ride in 1 day or not because we dont know for how much time will one ride takes.
Question 41.
OPEN-ENDED
Give an example of a real-life situation in which you can list all the solutions of an inequality. Give an example of a real-life situation in which you cannot list all the solutions of an inequality.
Answer:
Real-life situation of Inequalities.
| Speed limit | Legal speed on the highway ≤ 65 miles per hour |
| Credit card | Monthly payment ≥ 10% of your balance in that billing cycle |
| Text messaging | Allowable number of text messages per month ≤ 250 |
| Travel time | Time needed to walk from home to school ≥ 18 minutes |
real-life situation in which you cannot list all the solutions of an inequality are Money . money should be given exactly not greater or lesser.
Question 42.
LOGIC
Describe the solution of 7x < 7x. Explain your reasoning.
Answer:
7x < 7x
No solution.
Explanation:
this equation is wrong as both are equal . no solution can be possible if the inequality equation is wrong.
Question 43.
NUMBER SENSE
The possible values of x are given by x− 3 ≥ 2. What is the least possible value of 5x?
Answer:
x− 3 ≥ 2
add 3 on both sides we get,
x ≥ 5
Multiply by 5 on both sides we get,
5x ≥ 5 × 5
5x ≥ 25
SOLVING INEQUALITIES Solve the inequality. Graph the solution.
Question 44.
x + 9 – 3 ≤ 14
Answer:
x + 9 – 3 ≤ 14
x + 6 ≤ 14
subtract 6 on both sides we get ,
x≤ 8

Question 45.
44 > 7 + s + 26
Answer:
44 > 7 + s + 26
44 > 33 + s
subtract 33 on both sides we get,
11 > s

Question 46.
6.1 – 0.3 ≥ c + 1
Answer:
6.1 – 0.3 ≥ c + 1
5.8 ≥ c + 1
Subtract 1 on both sides we get,
4.8 ≥ c

Question 47.
2n < 4.6 × 12
Answer:
2n < 4.6 × 12
2n < 55.2
Divide by 2 on both sides we get,
n < 27.6

Question 48.
32 ≥ 2h + 6h
Answer:
32 ≥ 2h + 6h
32 ≥ 8h
Divide by 8 on both sides we get,
4 ≥ h

Question 49.
2\(\frac{2}{5}\)b – 1\(\frac{3}{10}\)b ≤ 6\(\frac{3}{5}\)
Answer:
\(\frac{12}{5}\)b – \(\frac{13}{10}\)b ≤ \(\frac{33}{5}\)
2.4b – 1.3b ≤ 6.6
1.1b ≤ 6.6
Divide by 1.1 on both sides we get,
b ≤ 6

Question 50.
PROBLEM SOLVING
The high score for a video game is 36,480. Your current score is 34,280. Each dragonfly you catch is worth 1 point. You also get a 1000-point bonus for reaching 35,000 points. Find the possible numbers of dragonflies you can catch to earn a new high score.

Answer:
High score of video game = 36,480
Current score =34,280
Score required to get 35,000 points = 35000 – 34280 = 720
You need to catch 720 dragon flies to get 35000 score after that 1000 bonus will be added so pesent score will be
34280 + 720 +1000 =36000
For new record how many dragon flies we should catch = 36480 – 36000 = 480
More than 480 then new record will be formed.
so possible number of dragon flies should we catch for new record = 720 + 480 = 1200
more than 1200 .
Question 51.
REASONING
A winning football team more than doubled the offensive yards gained by its opponent. The opponent gained 272 offensive yards. The winning team had 80 offensive plays. Find the possible numbers of yards per play for the winning team. Justify your answer.
Answer:
Opponent offensive yards = 272
Winning team offensive yards = double he offensive yards gained by its opponent =20 × 272 = 5440
Winning Team offensive plays = 80
possible numbers of yards per play for the winning team = 5440 yards.
Question 52.
DIG DEEPER!
You complete two events of a triathlon. Your goal is to finish with an overall time of less than 100 minutes.
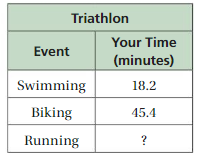
a. Find the possible numbers of minutes you can take to finish the running event and still meet your goal.
b. The running event is 3.1 miles long. Estimate how many minutes it would take you to run 3.1 miles. Would this time allow you to reach your goal? Explain your reasoning.
Answer a :
Total Time is less than 100 minutes.
Time for swimming = 18.2
Time for Biking = 45..4
Time for Running = 100 – 18.2 – 45.4 =36.4
Time for running should be lesser or equal to 36.4 to reach the goal time.
Answer b:
Time for running should be lesser or equal to 36.4 to reach the goal time.
Goal length =3.1 miles.
To reach goal he should travel 3.1 miles in less than or equal to 36.4 minutes.
SOLVING INEQUALITIES Graph the numbers that are solutions of both inequalities.
Question 53.
x + 7 > 9 and 8x ≤ 64
Answer:
x + 7 > 9
subtract 7 on both sides we get,
x >2
8x ≤ 64
Divide by 8 on both sides we get,
x ≤ 8
Question 54.
z – 3 ≤ 8 and 6z < 72
Answer:
z – 3 ≤ 8
add 3 on both sides we get,
z ≤ 11
6z < 72
Divide by 6 on both sides we get,
z < 12

Question 55. w + 5 ≥ 8 and 4w > 20
Answer:
w + 5 ≥ 8
subtract 5 on both sides we get,
w ≥ 3
4w > 20
Divide 4 on both sides we get,
w > 5

Question 56.
g – 6 ≤ 1 and 3g ≥ 21
Answer:
g – 6 ≤ 1
Add 6 on both sides we get,
g ≤ 7
3g ≥ 21
Divide by 3 on both sides we get,
g ≥ 7

Question 57.
2.7 + k ≥ 5.3 and 0.8k ≤ 3.36
Answer:
2.7 + k ≥ 5.3
Subtract 2.7 on both sides we get,
k ≥ 2.6
0.8k ≤ 3.36
Divide by 0.8 on both sides we get,
k ≤ 4.2

Question 58.
p + \(\frac{3}{4}\) < 3 and \(\frac{1}{4}\)p > \(\frac{3}{8}\)
Answer:
p + \(\frac{3}{4}\) < 3
p + 0.75 < 3
Subtract 0.75 on both sides we get,
p < 2.25
\(\frac{1}{4}\)p > \(\frac{3}{8}\)
0.25p > 0.375
Divide by 0.25 on both sides we get,
p > 1.5

Question 59.
PROBLEM SOLVING
You are selling items from a catalog for a school fundraiser. Find the range of sales that will earn you at least $40 and at most $50.

Answer:
Earn $5 for every $50 in sales + take one catalog.
$50 > 1 + $5
If you sell at most $50 that is $50 ≤ if it equal to 50 only you get $5 and 1 catalog.
If you sellat least $40 that is 40 ≥ if it is greater or equal to 40 only you get $5 and 1 catalog .
CRITICAL THINKING Let a > b> 0 and x > y> 0. Tell whether the statement is always true. Explain your reasoning.
Question 60.
a + x > b + y
Answer:
It is true
Explanation:
a > b> 0 and x > y> 0. in this both a and x are greater numbers. and if both numbers are added then the resultant will always be greater.
Question 61.
a – x > b – y
Answer:
Cant say as it depends on the values.
Explanation:
take a example take a=2 b=1 x=3 y= 2
2-3 = -2
1-2 = -1
-2 < -1
It is not true
Question 62.
ax > by
Answer:
It is true
Explanation:
a > b> 0 and x > y> 0. in this both a and x are greater numbers. and if both numbers are multipied then the resultant will always be greater.
Question 63.
\(\frac{a}{x}\) > \(\frac{y}{b}\)
Answer:
Cant say as it depends on the values.
Integers, Number Lines, and the Coordinate Plane Connecting Concepts
Using the Problem-Solving Plan
Question 1.
You use a coordinate plane to design a kite for a competition. The vertices of the design are A(0, 0), B(13.5, 9), C(27, 0), and D(13.5, −36). The coordinates are measured in inches. Find the least number of square yards of fabric you need to make the kite.
Understand the problem.
You know the vertices of your kite design in a coordinate plane, where the coordinates are measured in inches. You are asked to find the least number of square yards of fabric needed to make the kite.
Make a plan.
First, draw a diagram of the design in a coordinate plane. Then decompose the figure into two triangles to find the area of the kite in square inches. Finally, convert the area from square inches to square yards.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Question 2.
You have $240 in a savings account. You deposit $60 per month. The tape diagram represents the ratio of money deposited to money withdrawn each month. Find the monthly change in your account balance. How long will it take for the account to have a balance of $0? Justify your answer.

Answer:
Question 3.
A cord made of synthetic fiber can support 630 pounds, which is at least 450% of the weight that can be supported by a cord made of steel. Graph the possible weights that can be supported by the steel cord.
Answer:
Synthentic fibre = 630 pounds
Performance Task
Launching a CubeSat
At the beginning of this chapter, you watched a STEAM Video called “Designing a CubeSat.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Integers, Number Lines, and the Coordinate Plane Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use a Summary Triangle to explain a concept. Here is an example of a Summary Triangle for integers.
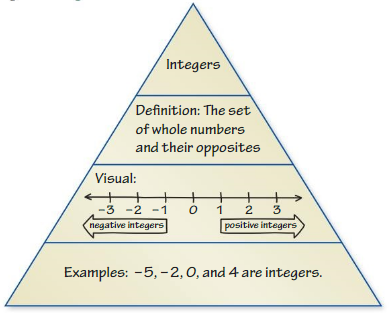
Choose and complete a graphic organizer to help you study the concept.
1. opposites
2. rational number
3. absolute value
4. coordinate plane
5. inequalities
6. solving inequalities using addition or subtraction
7. solving inequalities using multiplication or division

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

8.1 Integers (pp. 345–350)
Learning Target: Understand the concept of negative numbers and that they are used along with positive numbers to describe quantities.
Write a positive or negative integer that represents the situation.
Question 1.
An elevator goes down 8 floors.
Answer:
Down indicates negative number
-8
Question 2.
You earn $12.
Answer:
Earn indicates + number
so , +$12
Graph the integer and its opposite
Question 3.
-16
Answer:
The opposite of -16 is 16
Question 4.
13
Answer:
The opposite of 13 is -13
Question 5.
4
Answer:
The opposite of 4 is -4
Question 6.
– 100
Answer:
The opposite of -100 is 100
Identify the integer represented by the point on the number line.
Question 7.
A
Answer:
The point A represents 1
Explanation:
As it is exactly marked between 0 and 2
Question 8.
B
Answer:
The point B represents 10
Explanation:
It is marked on point 10
Question 9.
C
Answer:
The point C represents 7
Explanation:
As it is marked exactly in between 6 and 8.
Question 10.
D
Answer:
The point D represents -6
Explanation:
It is marked on point -6

8.2 Comparing and Ordering Integers (pp. 351–356)
Learning Target: Compare and order integers.
Copy and complete the statement using < or >.
Question 11.
![]()
Answer:
4 > -7
Explanation:
All positive numbers are greater than negative numbers.
Question 12.
![]()
Answer:
-1 < 0
Explanation:
All positive numbers are greater than negative numbers.
Question 13.
![]()
Answer:
-5 > -8
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Order the integers from least to greatest.
Question 14.
– 5, 4, 2, – 3, – 1
Answer:
-5, -3, -1, 2, 4
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 15.
5, – 20, – 10, 10, 15
Answer:
-20, -10, 5, 10, 15
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 16.
– 7, – 12, 9, 2, – 8
Answer:
-12, -8, -7, 2, 9
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 17.
Order the temperatures − 3°C, 8°C, − 12°C, − 7°C, and 0°C from coldest to warmest.
Answer:
− 12°C, − 7°C, − 3°C, 0°C, 8°C
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 18.
Your teacher writes five different integers on a note card that are between −10 and 14. When the integers are ordered from least to greatest, the middle number is 1. How many of the integers are positive? negative? Explain.
Answer:
8.3 Rational Numbers (pp. 357–362)
Learning Target: Compare and order rational numbers.
Graph the number and its opposite.
Question 19.
–\(\frac{2}{5}\)
Answer:
–\(\frac{2}{5}\) = -0.4
The opposite of -0.4 is 0.4
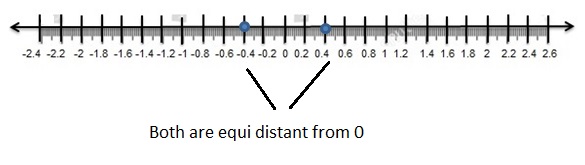
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 20.
1\(\frac{3}{4}\)
Answer:
1\(\frac{3}{4}\)=\(\frac{7}{4}\) = 1.75
The opposite of 1.75 is -1.75
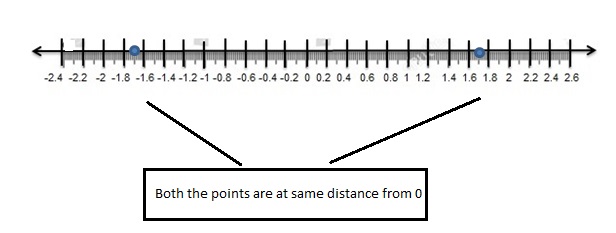
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 21.
– 1.2
Answer:
The opposite of -1.2 is 1.2
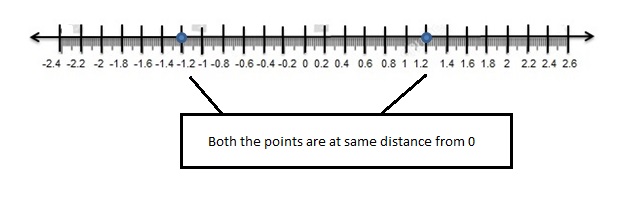
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Question 22.
2.75
Answer:
The opposite of 2.75 is -2.75
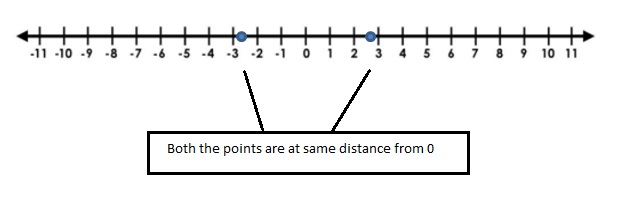
Explanation :
For any given integer ‘a’, the opposite integer is found at the same distance from 0 on the number line, but on the other side.
So, the opposite integer of integer ‘a’, is ‘-a’ on the number line, but on the other side of 0.
Copy and complete the statement using < or >.
Question 23.
![]()
Answer:
-2\(\frac{1}{6}\) = – = -2.1
-2\(\frac{5}{6}\) = –\(\frac{17}{6}[/late[latex]\frac{13}{6}\)x] =-2.8
-2.1 > -2.8
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 24.
![]()
Answer:
–\(\frac{1}{3}\)= -0.3
–\(\frac{1}{8}\) = – 0.125
-0.3 < -0.125
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 25.
![]()
Answer:
-3.27 < -2.68
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Order the numbers from least to greatest.
Question 26.
– 2.04, – 3, – 2.4, – 2.19, – 5.8
Answer:
-5.8 < -3 < 2.4 < -2.19 < -2.04
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 27.
– 3\(\frac{7}{8}\), 4, – 3\(\frac{3}{4}\), \(\frac{1}{2}\), \(\frac{1}{6}\)
Answer:
– 3\(\frac{7}{8}\) = – \(\frac{31}{8}\) = -3.8
– 3\(\frac{3}{4}\) = –\(\frac{15}{4}\) = – 3.75
\(\frac{1}{2}\) = 0.5
\(\frac{1}{6}\) = 0.16
-3.8, 4, -3.75, 0.5, 0.16
-3.8<-3.75<0.16<0.5<4
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 28.
Write a number that is greater than −7.81 and less than −7.
Answer:
-7>x>-7.81
it can be -7.1, -7.2 , ……
Question 29.
A dog buries a small bone −1\(\frac{5}{6}\) inches into the dirt. The dog buries a larger bone −1\(\frac{3}{4}\) inches into the dirt. Which bone is buried deeper?
Answer:
Small bone buried at −1\(\frac{5}{6}\) = −\(\frac{11}{6}\) = -1.83
Larger bone buried at −1\(\frac{3}{4}\) = −1\(\frac{7}{4}\) = – 1.75
Distance cant be in negative just compare the values and say which bone is buried deepest.
Small bone is buried deeper .
8.4 Absolute Value (pp. 363–368)
Learning Target: Understand the concept of absolute value.
Find the absolute value.
Question 30.
|- 8|
Answer:
The Absolute value of |- 8| = 8
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 31.
|13|
Answer:
The Absolute value of |13| = 13
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 32.
|3 \(\frac{6}{7}\)|
Answer:
|3 \(\frac{6}{7}\)|=|\(\frac{27}{7}\)|=|3.8|
The Absolute value of |3.8| = 8
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 33.
|- 1.34|
Answer:
The Absolute value of|- 1.34|= 1.34
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Copy and complete the statement using <, > , or =.
Question 34.
![]()
Answer:
The Absolute value of|-2|= 2
2 = 2
Question 35.
![]()
Answer:
The Absolute value of |4.4|= 4.4
The Absolute value of |- 2.8 |= 2.8
Question 36.

Answer:
The Absolute value of |\(\frac{1}{6}\)|= \(\frac{1}{6}\) = 0.16
The Absolute value of |-\(\frac{2}{9}\)| = \(\frac{2}{9}\) = 0.22
0.16 < 0.22
Order the values from least to greatest.
Question 37.
– 15, |- 21|, |19|, – 20, 25
Answer:
The Absolute value of |-21|= 21
The Absolute value of |19|= 19
– 15, 21, 19, – 20, 25
-20<-15<19<21<25
Question 38.
0, |- 1|, – 2, |2|, – 3
Answer:
The Absolute value of |-1|= 1
The Absolute value of |2|= 2
0, 1, – 2, 2, – 3
-3< -2 < 0 < 1 < 2
Question 39.
Simplify −|− 35 |.
Answer:
The Absolute value of |-35|= 35
−|− 35 |= -35
Question 40.
The latitude of Erie, Pennsylvania, is 42.129. The latitude of Sydney, Australia, is −33.865. Positive values of latitude are north of the equator, negative values of latitude are south of the equator, and the latitude of the equator is 0. Which city is closest to the equator?
Answer:
latitude of Erie, Pennsylvania = 42.129.
latitude of Sydney, Australia = −33.865.
42.129>0>-33.865
latitude of Sydney, Australia is closest to the Equator
8.5 The Coordinate Plane (pp. 369–376)
Learning Target: Plot and reflect ordered pairs in all four quadrants of a coordinate plane.
Write an ordered pair corresponding to the point.
Question 41.
Point J
Answer:
The Point J is located at (-2,0)
Explanation:
The x- coordinate is-2
The y- coordinate is 0
Question 42.
Point K
Answer:
The Point K is located at (-2,-4)
Explanation:
The x- coordinate is -2
The y- coordinate is -4
Question 43.
Point L
Answer:
The Point L is located at (5,2)
Explanation:
The x- coordinate is 5
The y- coordinate is 2
Question 44.
Point M
Answer:
The Point M is located at (-1,3)
Explanation:
The x- coordinate is -1
The y- coordinate is 3
Question 45.
Point N
Answer:
The Point N is located at (3,-4)
Explanation:
The x- coordinate is 3
The y- coordinate is -4
Question 46.
Point P
Answer:
The Point J is located at (1,0)
Explanation:
The x- coordinate is 1
The y- coordinate is 0
Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 47.
A (1, 3)
Answer:
X coordinate is 1
Y coordinate is 3
(1,3)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 48.
B (0, 3)
Answer:
X coordinate is 0
Y coordinate is 3
(0,3)
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 49.
C (4, 2)
Answer:
X coordinate is 4
Y coordinate is 2
C (4, 2)
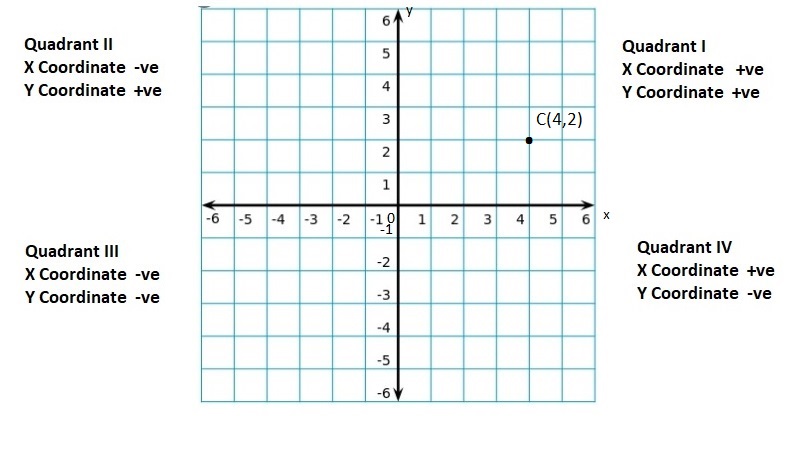
Explanation:
It is marked in the Quadrant I as X coordinate is Positive and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Question 50.
D (- 3, 1)
Answer:
X coordinate is -3
Y coordinate is 1
(-3,1)
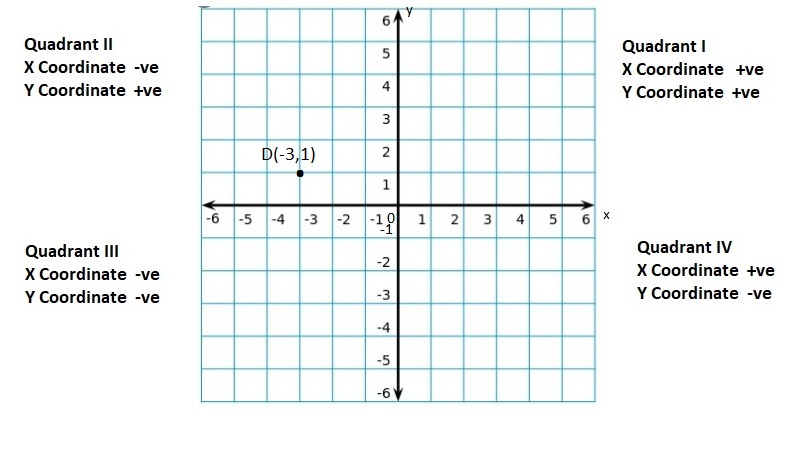
Explanation:
It is marked in the Quadrant II as X coordinate is Negative and Y coordinate is Positive as shown in the graph.
Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate).
Reflect the point in (a) the x-axis and (b) the y-axis.
Question 51.
(4, 1)
Answer:
Plot (4,1) , (4,-1) and (-4,1)
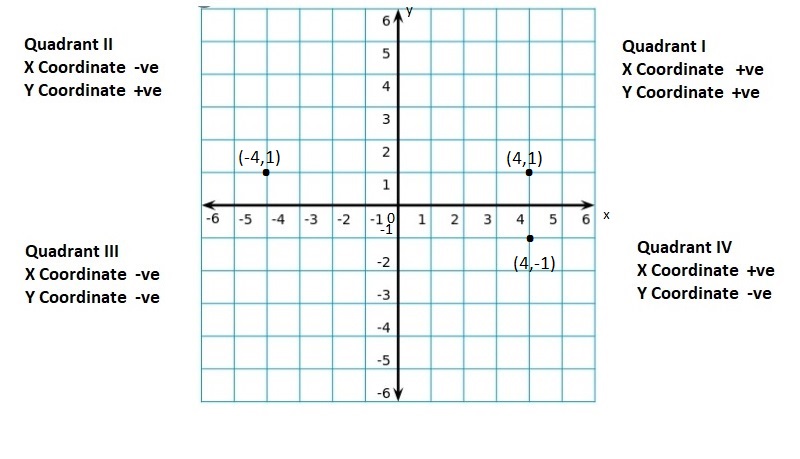
Explanation:
To reflect (4,1) in the x axis, use the same x-coordinate, 4,the opposite of the y coordinate.The opposite of y coordinate 1 is -1
To reflect (4,1) in the y axis, use the same y-coordinate, 1,the opposite of the x coordinate.The opposite of x coordinate 4 is -4
So the reflection of (4,1)in the x-axis is (4,-1)
So the reflection of (4,1)in the y-axis is(-4,1)
Question 52.
(- 2, 3)
Answer:
Plot (- 2, 3) , (-2,-3) and (2,3)
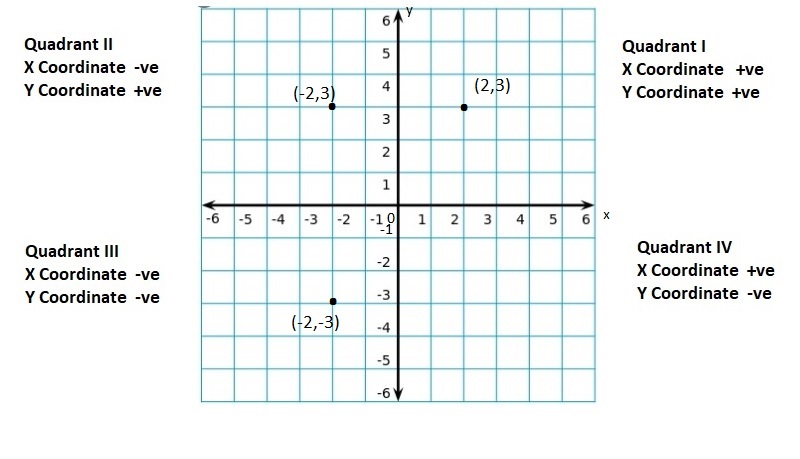
Explanation:
To reflect (- 2, 3) in the x axis, use the same x-coordinate, -2,the opposite of the y coordinate.The opposite of y coordinate 3 is -3
To reflect (- 2, 3) in the y axis, use the same y-coordinate, 3,the opposite of the x coordinate.The opposite of x coordinate -2 is 2
So the reflection of (- 2, 3) in the x-axis is (-2,-3)
So the reflection of(- 2, 3) in the y-axis is (2,3)
Question 53.
(2, – 5)
Answer:
Plot (2, – 5) , (2, 5) and (-2,-5)
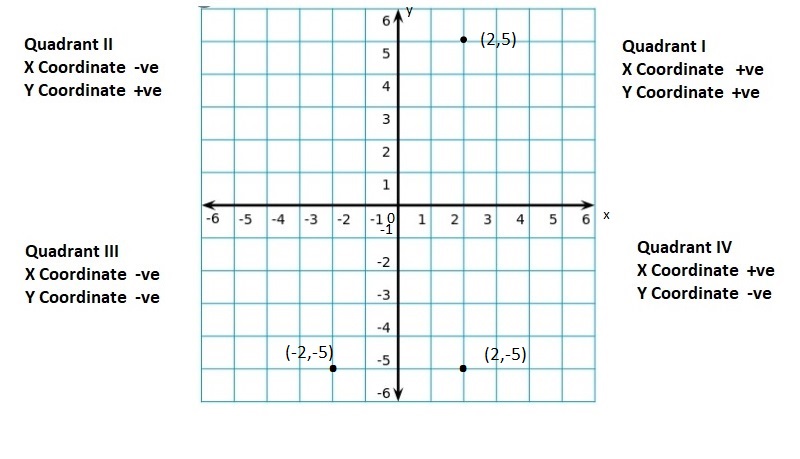
Explanation:
To reflect (2, – 5) in the x axis, use the same x-coordinate, 2,the opposite of the y coordinate.The opposite of y coordinate -5 is 5
To reflect(2, – 5)in the y axis, use the same y-coordinate, -5,the opposite of the x coordinate.The opposite of x coordinate 2 is -2
So the reflection of(2, – 5) in the x-axis is (2, 5)
So the reflection of (2, – 5) in the y-axis is(-2,-5)
Question 54.
(- 3.5, – 2.5)
Answer:
Plot (- 3.5, – 2.5), (- 3.5, 2.5) and (3.5, – 2.5)
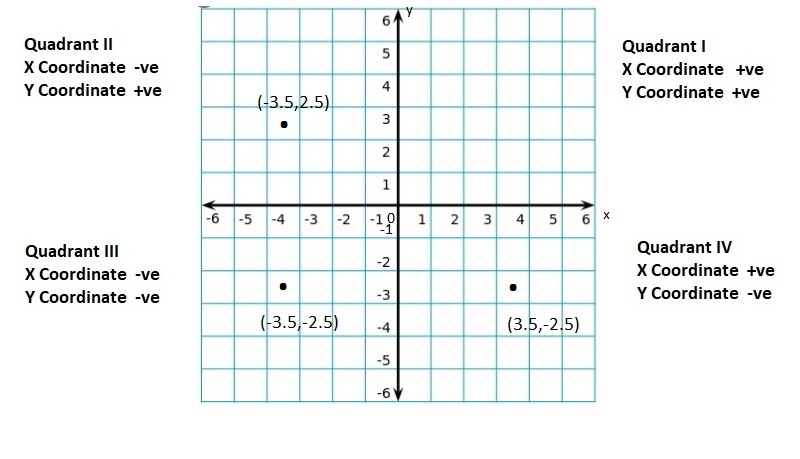
Explanation:
To reflect (- 3.5, – 2.5) in the x axis, use the same x-coordinate, -3.5,the opposite of the y coordinate.The opposite of y coordinate -2.5 is 2.5
To reflect (- 3.5, – 2.5) in the y axis, use the same y-coordinate, -2.5,the opposite of the x coordinate.The opposite of x coordinate -3.5 is 3.5
So the reflection of (- 3.5, – 2.5) in the x-axis is (- 3.5, 2.5)
So the reflection of (- 3.5, – 2.5) in the y-axis is (3.5, -2.5)
Reflect the point in the x-axis followed by the y-axis.
Question 55.
(1, 2)
Answer:
Plot (1,2) , (1,-2) and (-1,-2)
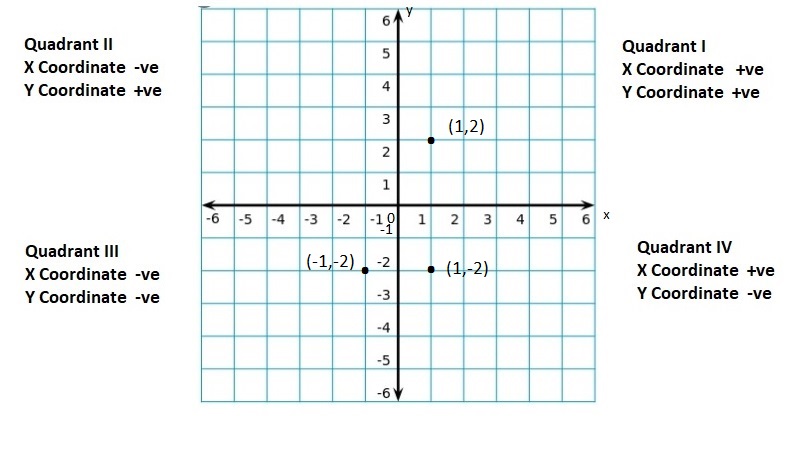
Explanation:
To reflect (1,2) in the x axis, use the same x-coordinate, 1,the opposite of the y coordinate.The opposite of y coordinate 2 is -2
To reflect (1,-2) in the y axis, use the same y-coordinate, -2,the opposite of the x coordinate.The opposite of x coordinate 1 is -1
So the reflection of (1,2) in the x-axis is (1,-2)
So the reflection of (1,-2) in the y-axis is(-1,-2)
Question 56.
(- 4, 6)
Answer:
Plot (- 4, 6) , (-4,-6) and (4, -6)
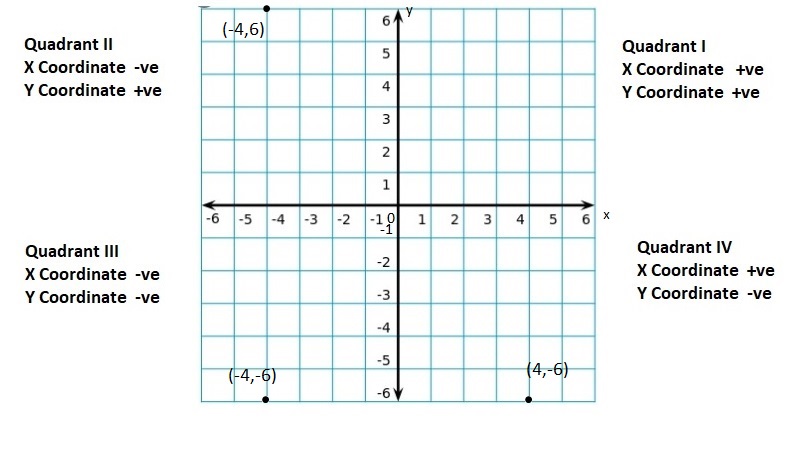
Explanation:
To reflect (- 4, 6) in the x axis, use the same x-coordinate, -4,the opposite of the y coordinate.The opposite of y coordinate 6 is -6
To reflect (- 4, -6) in the y axis, use the same y-coordinate, -6,the opposite of the x coordinate.The opposite of x coordinate -4 is 4
So the reflection of (- 4, 6) in the x-axis is (-4,-6)
So the reflection of (-4,-6) in the y-axis is (4, -6)
Question 57.
(3, – 4)
Answer:
Plot (3, – 4) , (3, 4) and (-3, 4)
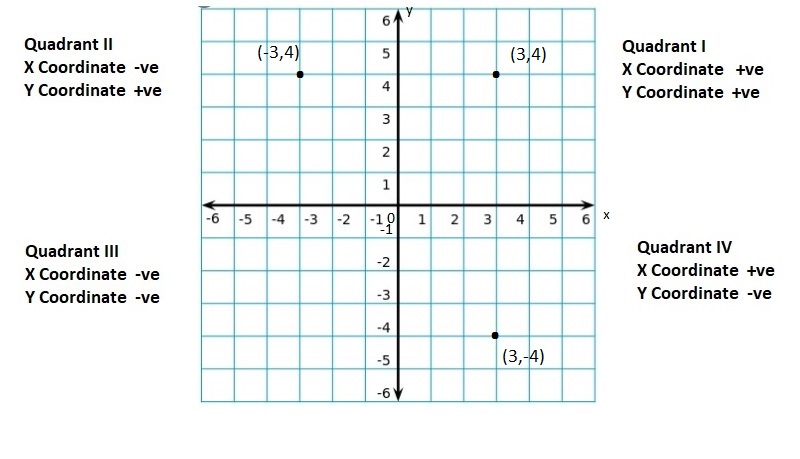
Explanation:
To reflect (3, – 4)in the x axis, use the same x-coordinate, 3,the opposite of the y coordinate.The opposite of y coordinate -4 is 4
To reflect (3, 4) in the y axis, use the same y-coordinate, 4,the opposite of the x coordinate.The opposite of x coordinate 3 is -3
So the reflection of (3, – 4) in the x-axis is (3, 4)
So the reflection of (3, 4) in the y-axis is (-3, 4)
Question 58.
(- 3, – 3)
Answer:
Plot (- 3, – 3) , (-3, 3) and (3, 3)
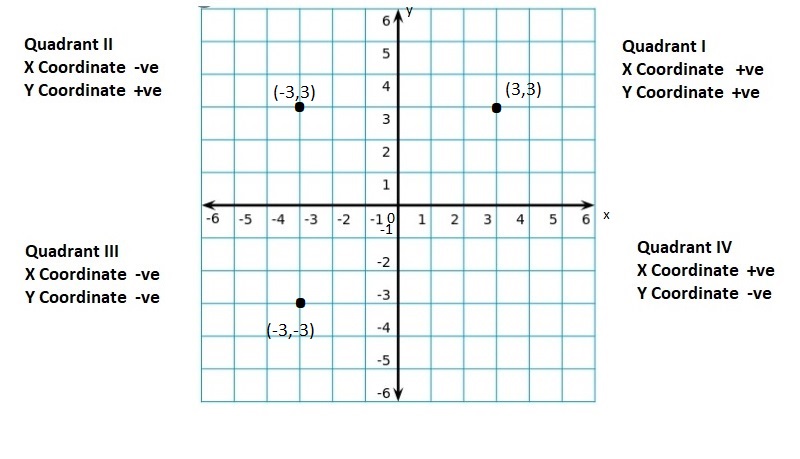
Explanation:
To reflect (- 3, – 3)in the x axis, use the same x-coordinate, -3,the opposite of the y coordinate.The opposite of y coordinate -3 is 3
To reflect (-3, 3) in the y axis, use the same y-coordinate, 3,the opposite of the x coordinate.The opposite of x coordinate -3 is 3
So the reflection of (- 3, – 3) in the x-axis is (-3, 3)
So the reflection of(-3, 3) in the y-axis is (3, 3)
Question 59.
Use the map of the town.
a. Which building is located at(−1, 1)?
b. Name a building on the positive x-axis.
c. In which quadrant is the bank located?
d. Write two different ordered pairs that represent the location of the train station.
e. You can find the original location of the movie theater by reflecting its location in the y-axis. What building is now in that location?
Answer a :
The Building which is located at (−1, 1) is Drug store
Answer b :
The building on the positive x-axis. is Hospital.
Answer c :
The bank located is located in Quadrant II.
Answer d :
The two different ordered pairs that represent the location of the train station are (-1,-3), (-2,-3)
Question 60.
Name the ordered pair that is 5 units right and 2 units down from (−3, 4).
Answer:
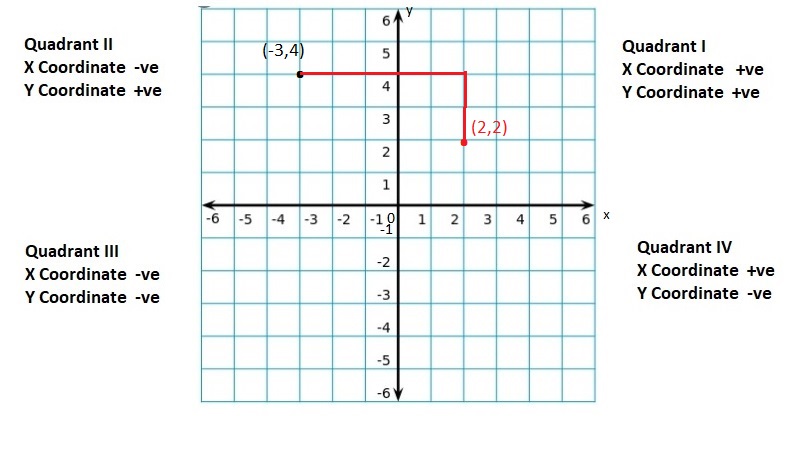
Explanation:
The ordered pair is located at (-3,4) it is then moved to 5 units right and the 2 units down then the new point is located at ( 2, 2)
Question 61.
A point is reflected in the x-axis. The reflected point is (3, −9). What is the original point?
Answer:
The reflected point is (3, −9)
The point is (3 , 9)
Explanation:
The reflected point in the x axis is (3, -9) It means x-axis reflection means it has same x coordinate and the y coordinate will be the opposite of the y-coordinate. when opposite is -9 then the y coordinate will be 9 .
8.6 Polygons in the Coordinate Plane (pp. 377–382)
Learning Target: Draw polygons in the coordinate plane and find distances between points in the coordinate plane.
Draw the polygon with the given vertices in a coordinate plane.
Question 62.
A (3, 2), B (4, 7), C (6, 0)
Answer:
Plot the given points .
The polygon formed after plotting given points is triangle.
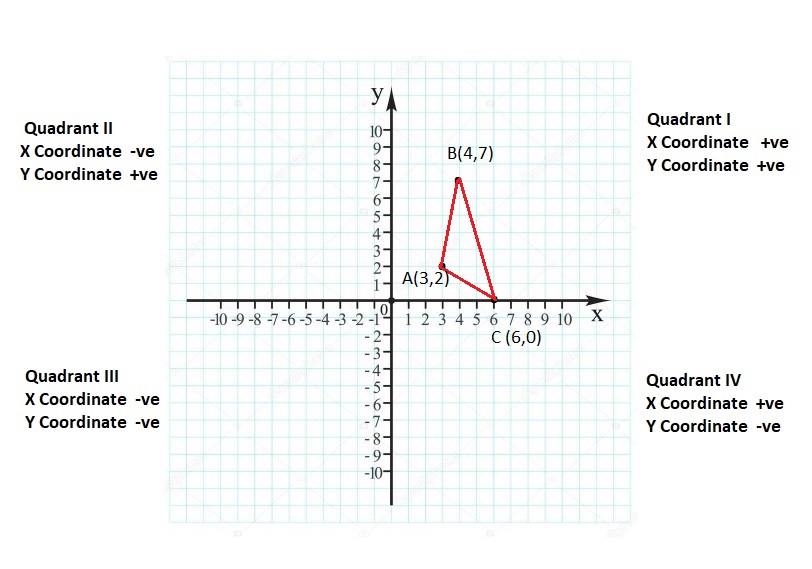
Question 63.
A (1, 2), B (1, – 7), C (5, – 7), D (8, 2)
Answer:
Plot the given points A (1, 2), B (1, – 7), C (5, – 7), D (8, 2)
The polygon formed is Trapezoid
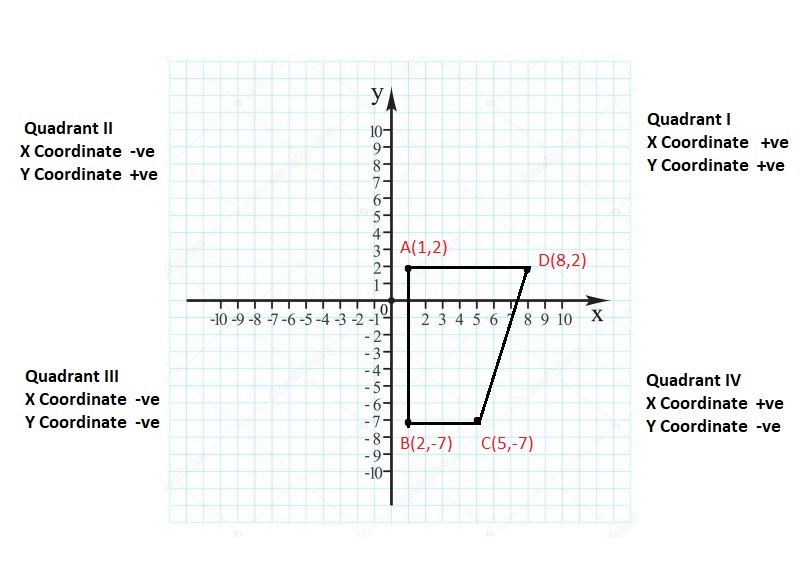
Question 64.
E (−1, 3\(\frac{1}{2}\)), F(1, 0), G(-2, 0), H(-4, -3\(\frac{1}{2}\))
Answer:
E (−1, 3\(\frac{1}{2}\)) = E (−1, \(\frac{7}{2}\)) = E ( -1, 3.5)
H(-4, -3\(\frac{1}{2}\)) = H(-4, –\(\frac{7}{2}\)) = H ( -4, – 3.5)
Plot the points E ( -1, 3.5), F(1, 0), G(-2, 0), H ( -4, – 3.5).
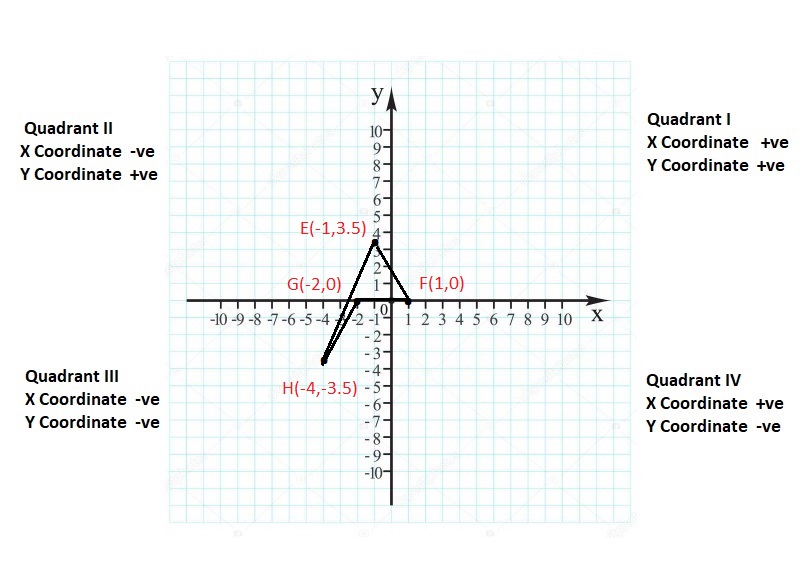
Find the distance between the points.
Question 65.
(4, – 2), (4, – 5)
Answer:
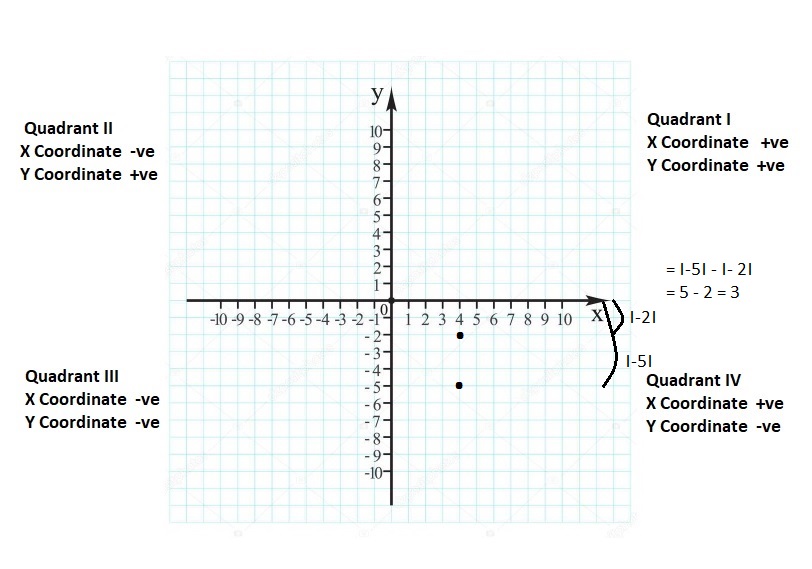
Answer:
Plot the points.
The points are in same Quadrants and have same x-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the y coordinate.
|-5| – |-2| = 3
So the distance between the points (4, – 2), (4, – 5) is 3
Question 66.
(7, 2), (- 4, 2)
Answer:
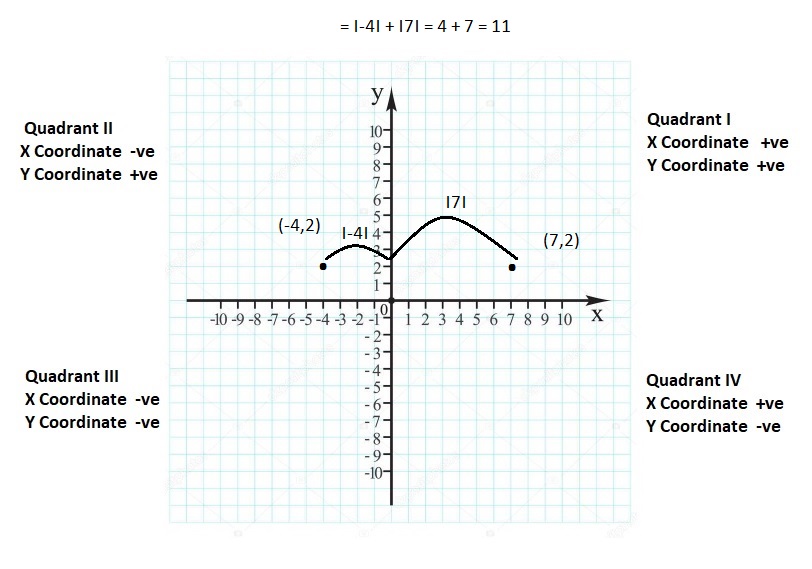
Explanation:
Plot the points.
The points are in different Quadrants and have same y-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|-4| + |7| = 4 + 7 = 11
So the distance between the points (7, 2), (- 4, 2) is 11
Question 67.
(- 1, 6), (- 1, – 3)
Answer:
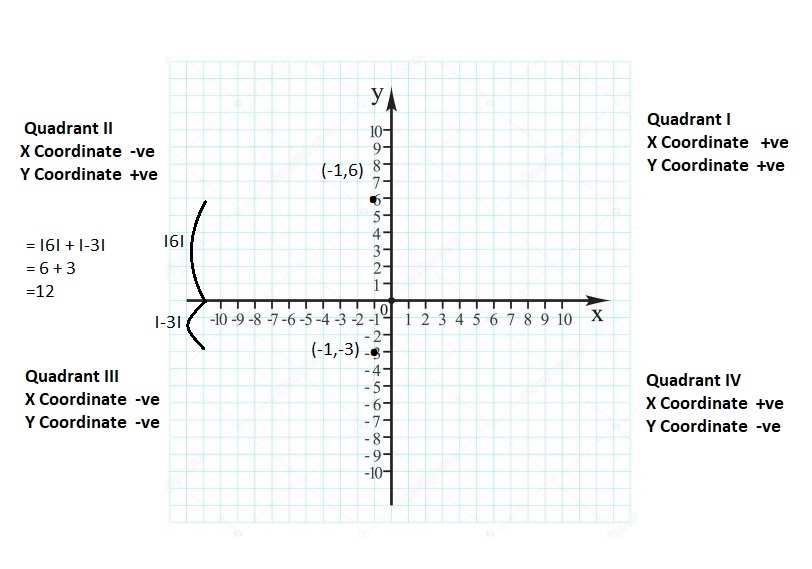
Explanation:
Plot the points.
The points are in different Quadrants and have same X-coordinates. The distance between the points is the sum of the absolute values of the x coordinate.
|6| + |-3| = 6 + 3 = 9
So the distance between the points (- 1, 6), (- 1, – 3) is 9
Question 68.
(- 5, – 8) , (- 9, – 8)
Answer:
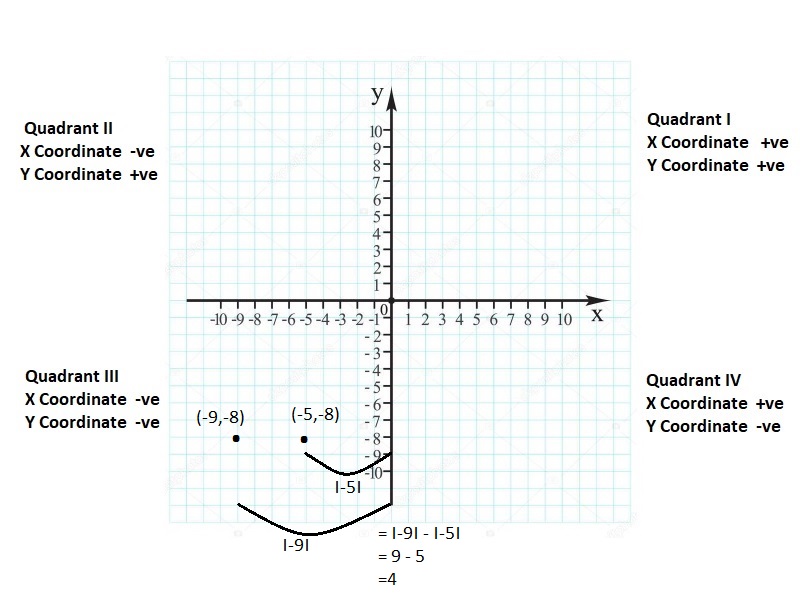
Explanation:
Plot the points.
The points are in same Quadrants and have same y-coordinates. The distance between the points is the difference between the points is the difference of the absolute values of the x coordinate.
|-9| – |-5| = 9 – 5 = 4
So the distance between the points (- 5, – 8) , (- 9, – 8) is 4
Find the perimeter and the area of the polygon with the given vertices.
Question 69.
T (2, 7), U (2, 9), V (5, 9), W(5, 7)
Answer:
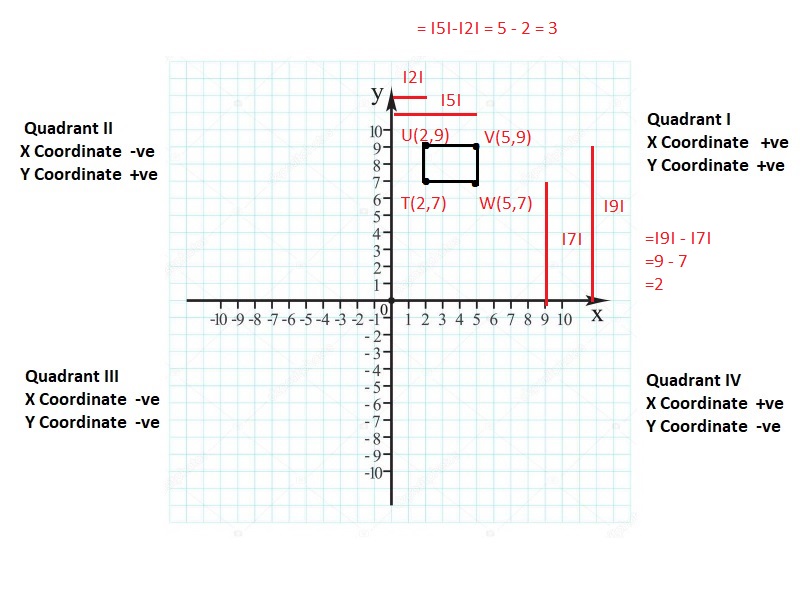
Explanation:
Plot the given points
The polygon formed is rectangle.
The length of the rectangle = 3 units
The breadth of the rectangle = 2 units
Area of the Rectangle = length × Breadth = 3 × 2 = 6 sq.units
Question 70.
P (4, – 3), Q (4, 2), R (9, 2), S (9, -3)
Answer:
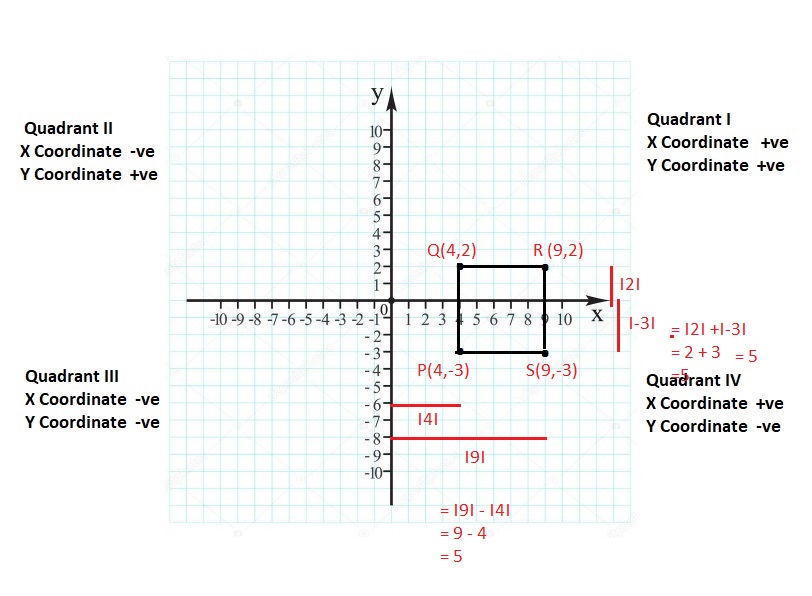
Explanation:
Plot the given points
The polygon formed is Square.
Side of the square = 5
Area of the Square = side × side = 5 × 5 = 25 sq.units
Question 71.
W (- 12, – 2), X (- 12, 13), Y (5, 13), Z (5, – 2)
Answer:
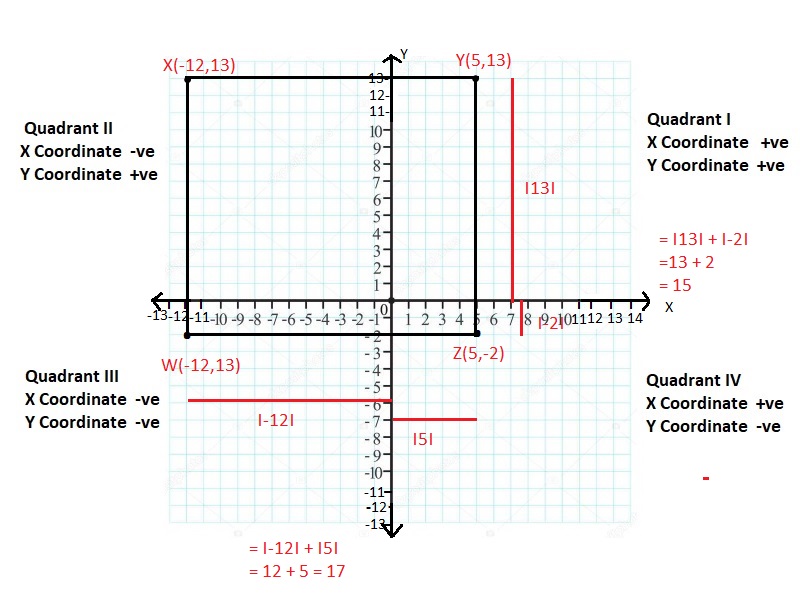
Explanation:
Plot the given points
The polygon formed is rectangle.
The length of the rectangle = 17 units
The breadth of the rectangle = 15 units
Area of the Rectangle = length × Breadth = 17 × 15 = 255 sq.units
Question 72.
You design the quilt shown using a coordinate plane in which the coordinates are measured in inches. The vertices of the quilt are (−3, 5), (−3, −7), (9, 5), and (9, −7).

a. Find the perimeter and the area of the quilt.
b. The quilt is made of identical-sized square pieces. What is the area of one of the square pieces?
Answer a :
The polygon formed is Square
Side of the square = 12
Perimeter of the square = 4 × side = 4 × 12 = 48 units
Area of the square = side × side = 12 × 12 = 144 sq units
Answer b :
Here the polygon is square
As per given figure we can see that 12 small squares are formed inside the square.
Total Side of the square = 12
The side is having 4 squares. to find the side of small square we should divide side of big square by 4
Side of small square = 12 ÷ 4 = 3
Side of small square = 3
Area of small square = side × side = 3 × 3 = 9 sq units
Question 73.
Draw a rectangle with a perimeter of 14 units in a coordinate plane where the vertices are in two quadrants.
Answer:
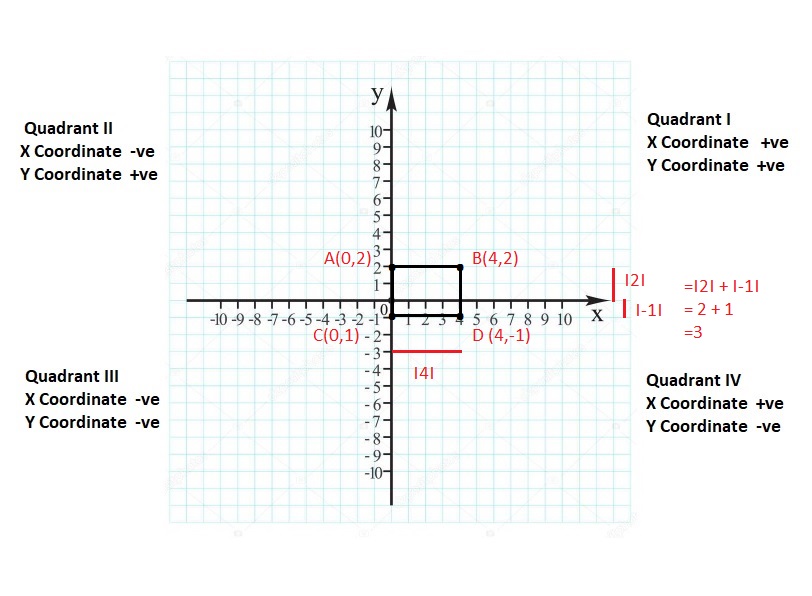
The length of the rectangle = 4 units
The breadth of the rectangle = 3 units
Question 74.
Draw a triangle with an area of 21 square units in a coordinate plane where the vertices are not all in the same quadrant.
Answer:
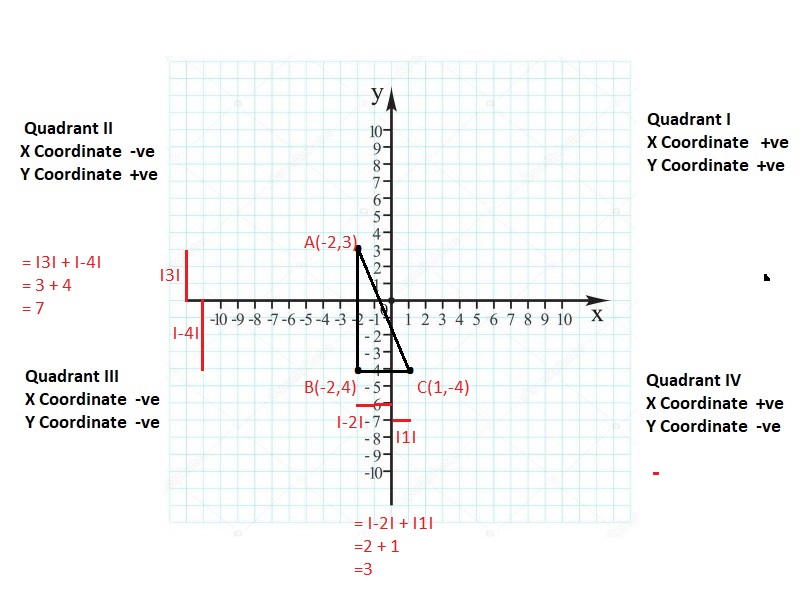
8.7 Writing and Graphing Inequalities (pp. 383 – 390)
Learning Target: Write inequalities and represent solutions of inequalities on a number line.
Write the word sentence as an inequality.
Question 75.
A number m is less than 5.
Answer:
m < 5
Question 76.
Three times a number h is at least − 12.
Answer:
3h ≥ – 12
Tell whether x = 8 is a solution of the inequality.
Question 77.
\(\frac{x}{2}\) ≥ 3
Answer:
\(\frac{x}{2}\) ≥ 3
Multiply by 2 on both sides we get,
x ≥ 6
Put x = 8 then
8 ≥ 6 is true.
So the given number is a solution for the inequality equation.
Question 78.
13 – x > 5
Answer:
13 – x > 5
subtract 13 on both sides we get
– x > -8
Mutlipy by – on both sides we get,
x > 8
Put x= 8 we get,
8 > 8 is wrong.
8 cant be the solution for the inequality equation .
Question 79.
19 > 2x
Answer:
19 > 2x
Divide by 2 on both sides we get,
9.5 > x
put x = 8 we get,
9.5 > 8 is true.
So the 8 is the solution for the inequality equation .
Graph the inequality on a number line.
Question 80.
x < 0
Answer:

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 81.
a ≥ 3
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 82.
n ≤ – 1
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 83.
The speed limit on a road is 35 miles per hour. Write and graph an inequality that represents the legal speeds on the road.
Answer:
Speed limit = S = 35 miles per hour
S ≤ 35
Speed should be 35 or less but not greater than 35 .
Below graph shows the speed limit

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 84.
Write an inequality and a word sentence that represent the graph.

Answer:
x < 3
You lose 3$ in a match .
Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
8.8 Solving Inequalities (pp. 391–398)
Learning Target: Write and solve inequalities.
Solve the inequality. Graph the solution.
Question 85.
x + 1 > 3
Answer:
x + 1 > 3
subtract 1 on both sides we get,
x > 2

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 86.
y + 8 ≥ 9
Answer:
y + 8 ≥ 9
subtract 8 on both sides we get,
y ≥ 1

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 87.
k – 7 ≤ 0
Answer:
k – 7 ≤ 0
Add 7 on both side we get,
k ≤ 7

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 88.
9n ≥ 63
Answer:
9n ≥ 63
Divide 9 on both sides we get,
n ≥ 7

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 89.
24 < 11 + x
Answer:
24 < 11 + x
subtract 11 on both sides we get,
13 < x

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 90.
x ÷ 2 < 4
Answer:
x ÷ 2 < 4
Multiply by 2 on both sides we get,
x < 8

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 91. 4 ≤ n – 4
Answer:
4 ≤ n – 4
Add 4 on both sides we get,
8 ≤ n

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 92.
10p > 40
Answer:
10p > 40
Divide 10 on both sides we get,
p > 4

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 93
s – 1.5 < 2.5
Answer:
s – 1.5 < 2.5
Add 1.5 on both sides we get,
s < 4

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 94.
\(\frac{5}{3}\)x ≤ 10
Answer:
\(\frac{5}{3}\)x ≤ 10
Multiply by \(\frac{3}{5}\) on both sides we get,
x ≤ 6

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 95.
\(\frac{1}{4}\) + m ≤ \(\frac{1}{2}\)
Answer:
\(\frac{1}{4}\) + m ≤ \(\frac{1}{2}\)
0.25 + m ≤ 0.5
Subtract 0.25 on both sides we get,
m ≤ 0.25

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 96.
\(\frac{3}{11}\)k < 15
Answer:
\(\frac{3}{11}\)k < 15
multiply by \(\frac{11}{3}\) on both sides we get,
k < 55

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 97.
Write two inequalities that have the same solution set and can be solved using different operations.
Answer:
s – 15 < 25
4s < 160
These are two equations which have same set of solutions that is s < 40.
Question 98.
You have $15 to spend on a ticket to a movie and snacks. Find the possible amounts you can spend on snacks.

Answer:
Total Amount with me = $15
Cost of movie theater = $ 6
Cost of snacks = $15 – $6 =$ 9
Possible amount can spend on snacks can be lesser than or equal to $9.
Question 99.
You want to use a square section of your yard for a chicken pen. You have at most 52 feet of fencing to form the pen. Find the possible lengths of each side of the chicken pen.
Answer:
fencing area of the pen = 52 feet.
Fencing is around the square borders which means it is the perimeter of the square
Perimeter of the square = 4 × side = 52
side = 52 ÷ 4 =13
Possible lengths of each side of the chicken pen = 13 feet.
Integers, Number Lines, and the Coordinate Plane Practice Test
Order the values from least to greatest.
Question 1.
0, – 2, 3, 1, – 4
Answer:
0, – 2, 3, 1, – 4
-4<-2<0<1<3
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 2.
– 8, |- 3|, |5|, 4, – 5
Answer:
Absolute values of |- 3| = 3 and |5|= 5
– 8, 3, 5, 4, – 5
-8<-5<3<4<5
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 3.
– 2.46, – 2.5, – 2, 1, – 2.293
Answer:
– 2.46, – 2.5, – 2, 1, – 2.293
-2.5<-2.46<-2.293<-2.1
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Graph the number and its opposite.
Question 14.
23
Answer:
The opposite of 23 is – 23.
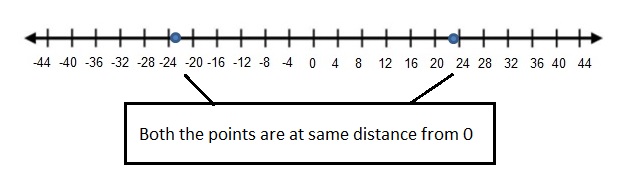
Question 15.
– 1 \(\frac{1}{3}\)
Answer:
– 1 \(\frac{1}{3}\) = – \(\frac{4}{3}\) = – 1.3
The opposite of -1.3 is 1.3.

Find the absolute value.
Question 16.
|7|
Answer:
The absolute value of |7| = 7
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x . All absolute values are positive.
Question 17.
|- 11|
Answer:
The Absolute value of |- 11| = 11
Explanation:
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x . All absolute values are positive.
Copy and complete the statement using <, >, or =.
Question 18.
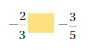
Answer:
–\(\frac{2}{3}\) = -0.66
–\(\frac{3}{5}\) = – 0.6
– 0.66 < – 0.6
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 19.
![]()
Answer:
Absolute value of |2.5| is 2.5
2.5 = 2.5
Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 20.
J (4, 0)
Answer:
Question 21.
L (1.5, – 3.5)
Answer:
Question 22.
M (- 2, – 3)
Answer:
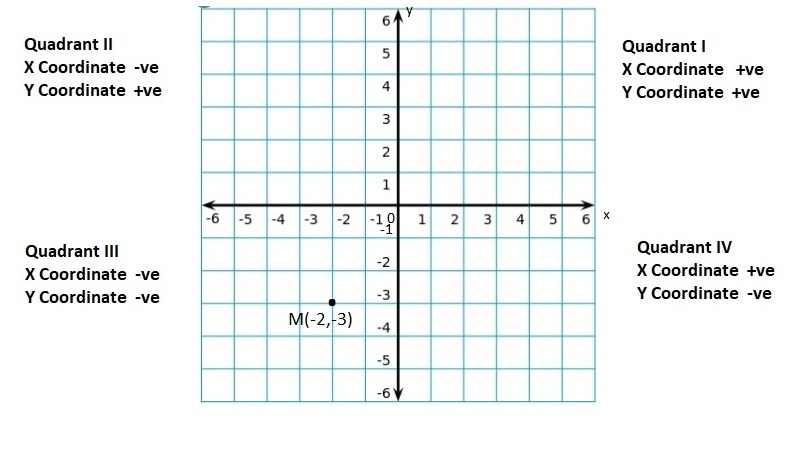
Question 23.
Reflect (- 5, 1) in (a) the x-axis, (b) the y -axis, and (c) the y -axis followed by the -axis.
Plot the points (- 5, 1) , (-5, -1), (5, 1) and (5, -1)
Answer a :
(- 5, 1)
Explanation:
To reflect(- 5, 1) in the x axis, use the same x-coordinate, -5,the opposite of the y coordinate.The opposite of y coordinate 1 is -1
So the reflection of (- 5, 1) in the x-axis is (-5, -1)
Answer b :
Explanation:
To reflect (- 5, 1) in the y axis, use the same y-coordinate, 1,the opposite of the x coordinate.The opposite of x coordinate -5 is 5
So the reflection of (- 5, 1) in the x-axis is (5, 1)
Answer c :
To reflect(- 5, 1) in the x axis, use the same x-coordinate, -5,the opposite of the y coordinate.The opposite of y coordinate 1 is -1
To reflect (- 5, -1) in the y axis, use the same y-coordinate, -1,the opposite of the x coordinate.The opposite of x coordinate -5 is 5
So the reflection of (- 5, 1) in the x-axis is (-5, -1)
So the reflection of (- 5, -1) in the y-axis is (5, -1)
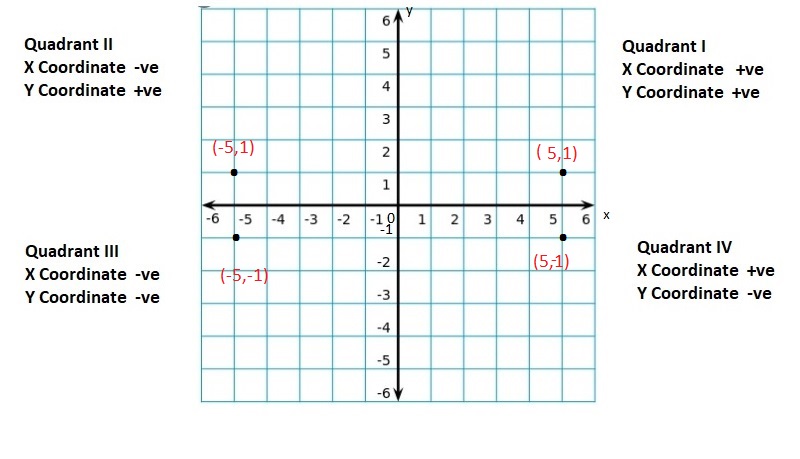
Graph the inequality on a number line.
Question 24.
x ≥ 5
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 25.
m ≤ – 2
Answer:

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Solve the inequality. Graph the solution.
Question 26.
x – 3 < 7
Answer:
x – 3 < 7
Add 3 on both sides we get,
x < 10

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 27.
12 ≥ n + 6
Answer:
12 ≥ n + 6
Subtract 6 on both sides we get,
6 ≥ n

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 28.
\(\frac{4}{3}\)b ≤ 12
Answer:
\(\frac{4}{3}\)b ≤ 12
Multiply \(\frac{3}{4}\) on both sides we get,
b ≤ 9

Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 29.
72 < 12p
Answer:
72 < 12p
Divide by 12 on both sides we get,
6 < p

Explanation:
Use a open circle that is not a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 30.
A hurricane has wind speeds that are greater than or equal to 74 miles per hour. Write an inequality that represents the possible wind speeds during a hurricane.

Answer:
Wind speed is greater than or equal to 74 miles per hour .
w ≥ 74
Question 31.
Two vertices of a triangle are F (1, – 4) and G(6, – 4). Find two possible points that represent the third vertex so that the triangle has an area of 20 square units.
Answer:
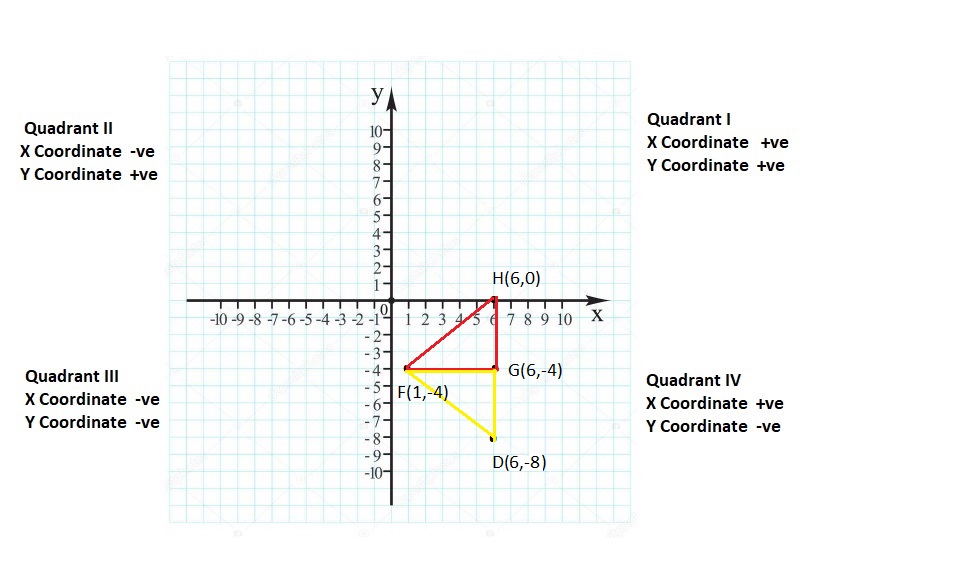
Explanation:
The possible two vertices are H(6,0) and D(6,-8).
Area of triangle = 20 ( Base × Height)
When base is 5 units from graph after plotting the given points it will be known
we have to mark H and D so that the height of triangle should have 4 units ( 20 ÷ 5) .
Question 32.
The table shows the melting points (in degrees Celsius) of several elements. Compare the melting point of mercury to the melting point of each of the other elements.

Answer:
Mercury > Randon
-38.83 > -71
Mercury < Bromine
-38.38 < -7.2
Mercury < Cesium
-38.38 < 28.5
Mercury <Francium
-38.38 < 27
Integers, Number Lines, and the Coordinate Plane Cumulative Practice

Question 1.
What is the value of the expression when a = 6, b = 5, and c = 4?
8a – 3c + 5b
A. 11
B. 53
C. 61
D. 107
Answer:
8a – 3c + 5b
Take a = 6, b = 5, and c = 4
8×6 -3×4 + 5×5
= 48 – 12 + 25
=48 +13
=61
Option C is correct
Question 2.
Point p is plotted in the coordinate plane.
What are the coordinates of point?
F. (- 5, – 3)
G. (- 5, 3)
H. (- 3, – 5)
I. (3, – 5)
Answer:
P(-5,3)
The x- coordinate is -5
The y coordinate is 3
Question 3.
What is the value of that makes the equation true?
a + 6 = 18
Answer:
a + 6 = 18
a = 18 – 6
a = 12
When a = 12 then the equation becomes true.
Question 4.
Which list of values is in order from least to greatest?
A. 2, |- 3|, |4|, – 6
B. – 6, |4| , 2, |- 3|
C. – 6, |- 3| , 2, |4|
D. – 6, 2, |- 3|, |4|
Answer:
Option D
-6, 2, |- 3|, |4|
Absolute values of |- 3|is 3 and |4| is 4
so we get the order as.
-6, 2, 3, 4
Question 5.
What is the height of the parallelogram?
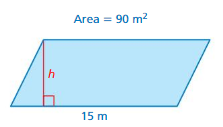
F. 6 meters
G. 12 meters
H. 75 meters
I. 1350 meters
Answer:
Area of the parallelogram = 90sq mtrs.
Base of the parallelogram = 15m
Area of the parallelogram = Base × Height
Height of the parallelogram = 90 ÷ 15 = 6 metres.
Question 6.
Which property is illustrated by the statement?
4 + (6 + n) = (4 + 6) + n
A. Associative Property of Addition
B. Commutative Property of Addition
C. Associative Property of Multiplication
D. Distributive Property
Answer:
Associative property of addition: Changing the grouping of addends does not change the sum.
Question 7.
Which number line shows the graph of x ≥ 5?
Answer:
Number line F shows x ≥ 5.
Explanation:
Use a closed circle that is a solution . shade the number line where you found the solutions. Every number on the shaded arrow is solutions of the inequality. so there are infinitely many solutions.
Question 8.
Which number is the greatest?
A. \(\frac{7}{8}\)
B. 0.86
C. \(\frac{22}{25}\)
D. 85%
Answer:
A. \(\frac{7}{8}\) = 0.875
B. 0.86
C. \(\frac{22}{25}\) =0.88
D. 85% = 0.85
Option is the greatest number 0.88
Question 9.
What is the area of the shaded region?
F. 23 units2
G. 40 units2
H. 48 units2
I. 60 units2
Answer:
Area of the Rectangle = Length × Breadth = 7 × 8 =56 units2
Area of the triangle = base × Height = 4 × 4 =16 units2
Area of the shaded region = Area of the rectangle – Area of the Triangle = 56 – 16 = 40 units2
Question 10.
Write 23.5% as a decimal.

Answer:
23.5% when % is removed we should divide the number by 100
23.5 ÷ 100 = 0.235 .
The decimal point is moved two points to the left .
Question 11.
Use grid paper to complete the following.

Part A Draw an x-axis and a y-axis of a coordinate plane. Then plot and label the point (2, 3).
Part B Plot and label four points that are 3 units away from (2, – 3).
Answer:
Question 12.
What is the perimeter of the rectangle with the vertices shown below?
A (- 4, – 1), B (- 4, 7), C (1, 7), D (1, – 1)
A. 8 units
B. 13 units
C. 26 units
D. 40 units
Answer:
Option C = 26 units
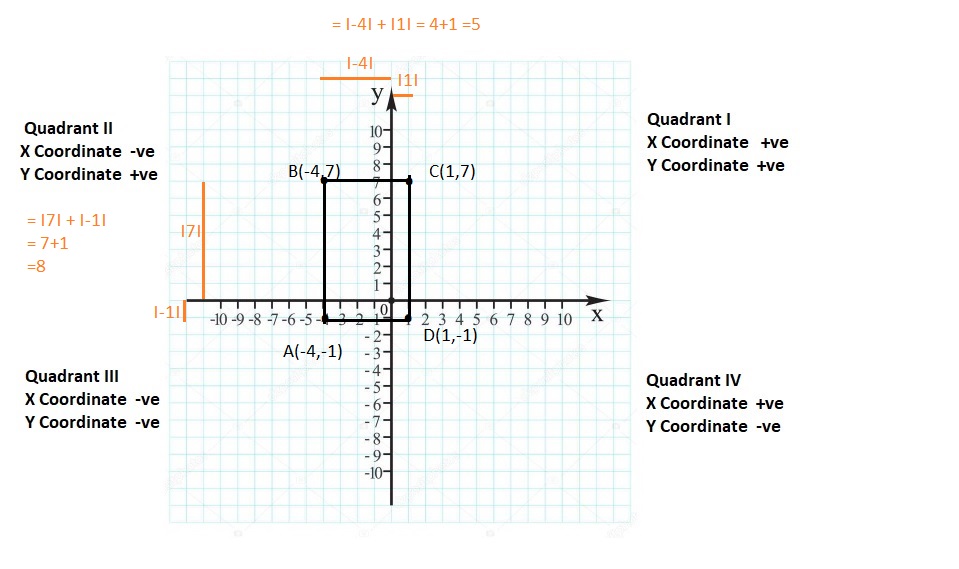
Explanation:
From the graph we know
length of the rectangle = 8
Breadth of the rectangle =5
Perimeter of the rectangle = 2 ( length + breadth) = 2 ( 8 + 5) = 2 ( 13) = 26 units
Question 13.
Which net does not form a cube?
Answer:
2, 3, 5, 10, 11 and 16 cannot make a cube and they are non-nets.
Option G does not form a cube.
Question 14.
Which value of makes the equation true?
\(\frac{3}{4}\)y = 12
A. 9
B. 11\(\frac{1}{4}\)
C. 12\(\frac{3}{4}\)
D. 16
Answer:
Option A is correct
Explanation:
\(\frac{3}{4}\)y = 12
Divide by \(\frac{4}{3}\) on both sides we get,
y = 9
Hope you are happy with the information given above. Get the Big Ideas Math Answer Grade 6 Integers, Number Lines, and the Coordinate Plane pdf’s for free of cost. You can get the various information of all math concepts at our site. Therefore, save our site to your favourites and also share it with your friends and peers to make your preparation success. Click on the subscribe button to get the instant updates of all the math concepts and preparation materials.