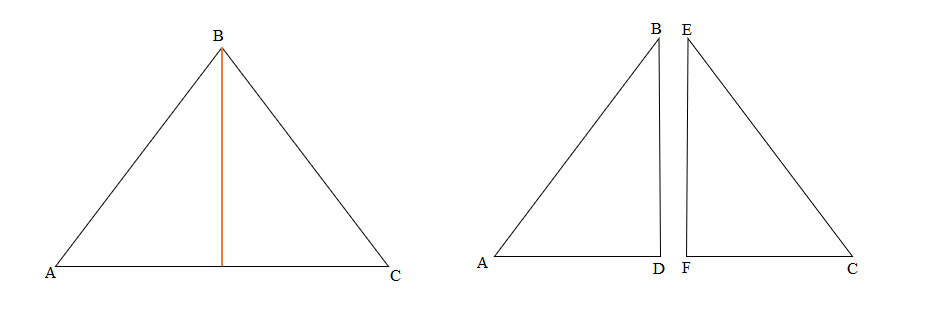Sudheer Venna

Engage NY Eureka Math 3rd Grade Module 7 Lesson 15 Answer Key

Eureka Math Grade 3 Module 7 Lesson 15 Pattern Sheet Answer Key

Multiply.

multiply by 9 (1–5)
Answer:

Explanation:
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45.

Eureka Math Grade 3 Module 7 Lesson 15 Problem Set Answer Key

Question 1.
Mrs. Kozlow put a border around a 5-foot by 6-foot rectangular bulletin board. How many feet of border did Mrs. Kozlow use?
Answer:
Mrs. Kozlow used 22ft of border.

Explanation:

Length of the side of the rectangular bulletin board = 6ft
Width of the side of the rectangular bulletin board = 5ft
Perimeter of the rectangular bulletin board = 2 (Length + Width)
= 2 ( 6ft + 5ft )
= 2 × 11ft
= 22ft.

Question 2.
Jason built a model of the Pentagon for a social studies project. He made each outside wall 33 centimeters long. What is the perimeter of Jason’s model pentagon?
Answer:
Perimeter of the Jason’s model Pentagon = 165 centimeters.

Explanation:

Length of the Side of the Jason’s model Pentagon = 33 centimeters
Perimeter of the Jason’s model Pentagon = 5 × Side
= 5 × 33 centimeters
= 165 centimeters.

Question 3.
The Holmes family plants a rectangular 8-yard by 9-yard vegetable garden. How many yards of fencing do they need to put a fence around the garden?
Answer:
Perimeter of the rectangular vegetable garden = 34-yard.

Explanation:

Length of the rectangular vegetable garden=  9-yard
Width of the rectangular vegetable garden = 8-yard
Perimeter of the rectangular vegetable garden = 2 ( Length + Width )
= 2 (9-yard + 8-yard)
= 2 × 17-yard
= 34-yard.

Question 4.
Marion paints a 5-pointed star on her bedroom wall. Each side of the star is 18 inches long. What is the perimeter of the star?

Answer:
Perimeter of the Star = 180 inches.

Explanation:

Length of the side of the Star = 18 inches
Number of sides of Star = 10
Perimeter of the Star = 10 × Side
= 10 ×18 inches
=180 inches.

Question 5.
The soccer team jogs around the outside of the soccer field twice to warm up. The rectangular field measures 60 yards by 100 yards. What is the total number of yards the team jogs?
Answer:
The total number of yards the team jogs = 640 yards.

Explanation:

Length of the rectangular soccer field = 100 yards
Width of the rectangular soccer field = 60 yards
Perimeter of the rectangular soccer field = 2 ( Length + Width )
= 2 ( 100 yards + 60 yards )
= 2 × 160 yards
= 320 yards.
Number of rounds the soccer team jogs around the outside of the soccer field to warm up = twice
The total number of yards the team jogs = 320 yards × 2
= 640 yards.

Question 6.
Troop 516 makes 3 triangular flags to carry at a parade. They sew ribbon around the outside edges of the flags. The flags’ side lengths each measure 24 inches. How many inches of ribbon does the troop use?
Answer:
The troop used  216inches  of ribbon.

Explanation:

Number of triangular flags Troop 516 makes = 3 or Three
Length of the triangular flags Troop 516 makes = 24inches
Perimeter of the triangular flags Troop 516 makes =  3 × Side
= 3 × 24inches
= 72inches.
Perimeter of the 3 triangular flags Troop 516 makes = 3 × 72inches
= 216inches.

Eureka Math Grade 3 Module 7 Lesson 15 Exit Ticket Answer Key

Marlene ropes off a square section of her yard where she plants grass. One side length of the square measures 9 yards. What is the total length of rope Marlene uses?
Answer:
The total length of rope Marlene uses = 36 yards.

Explanation:

Length of the side of the square = 9 yards.
Perimeter of the square = 4 × Side
= 4 × 9 yards
= 36 yards.

Eureka Math Grade 3 Module 7 Lesson 15 Homework Answer Key

Question 1.
Miguel glues a ribbon border around the edges of a 5-inch by 8-inch picture to create a frame. What is the total length of ribbon Miguel uses?
Answer:
The total length of ribbon Miguel uses = 26-inch.

Explanation:

Length of the rectangular picture = 8-inch
Width of the rectangular picture = 5-inch
Perimeter of the rectangular picture = 2 ( Length + Width )
= 2 ( 8-inch + 5-inch )
= 2 × 13-inch
= 26-inch.

Question 2.
A building at Elmira College has a room shaped like a regular octagon. The length of each side of the room is 5 feet. What is the perimeter of this room?
Answer:
The perimeter of this room = 40 feet.

Explanation:

length of each side of the regular octagon room = 5 feet
Perimeter of the regular octagon room = 8 × Side
= 8 × 5 feet
= 40 feet.

Question 3.
Manny fences in a rectangular area for his dog to play in the backyard. The area measures 35 yards by 45 yards. What is the total length of fence that Manny uses?
Answer:
The total length of fence that Manny uses = 160 yards.

Explanation:

Length of the rectangular fence  = 45 yards
Width of the rectangular fence  = 35 yards
Perimeter of rectangular fence  = 2 ( Length + Width )
= 2 (45 yards + 35 yards )
= 2 × 80 yards
= 160 yards.

Question 4.
Tyler uses 6 craft sticks to make a hexagon. Each craft stick is 6 inches long. What is the perimeter of Tyler’s hexagon?
Answer:
Perimeter of the Tyler’s hexagon = 36 inches.

Explanation:

Length of the side of the Tyler’s hexagon = 6 inches
Perimeter of the Tyler’s hexagon = 6 × Side
= 6 × 6 inches
= 36 inches.

Question 5.
Francis made a rectangular path from her driveway to the porch. The width of the path is 2 feet. The length is 28 feet longer than the width. What is the perimeter of the path?
Answer:
Perimeter of the rectangular path = 60 feet.

Explanation:

Length of the rectangular path = 28 feet
Width of the rectangular path = 2 feet
Perimeter of the rectangular path = 2 ( Length  + Width )
= 2 ( 28 feet + 2 feet )
= 2 × 30 feet
= 60 feet.

Question 6.
The gym teacher uses tape to mark a 4-square court on the gym floor as shown. The outer square has side lengths of 16 feet. What is the total length of tape the teacher uses to mark Square A?

Answer:
Perimeter of the Square court = 64 ft.
The total length of tape the teacher uses to mark Square A = 16 ft.

Explanation:

Length of the Square court = 16 ft
Perimeter of the Square court =  4 × Side
= 4 × 16 ft
= 64 ft.
The total length of tape the teacher uses to mark Square A = Perimeter of the Square court ÷ 4
= 64 ft ÷ 4
= 16 ft.

Must Read:

PETRONET Pivot Point Calculator

Engage NY Eureka Math 3rd Grade Module 7 Lesson 6 Answer Key

Eureka Math Grade 3 Module 7 Answer Key

Eureka Math Grade 3 Module 7 Lesson 6 Problem Set Answer Key

Use a ruler and a right angle tool to help you draw the figures with the attributes given below.
Question 1.
Draw a triangle with 1 right angle.
Answer:

Explanation:
ABC is an right angled triangle.

Question 2.
Draw a quadrilateral with 4 right angles and sides that are all 2 inches long.
Answer:

Explanation:
ABCD is a quadrilateral with 4 right angles and sides that are all 2 cm long.

Question 3.
Draw a quadrilateral with at least 1 set of parallel sides. Trace the parallel sides green.
Answer:

Explanation:
ABCD is a quadrilateral of having AD and BC Parallel sides.

Question 4.
Draw a pentagon with at least 2 equal sides. Label the 2 equal side lengths of your shape.
Answer:

Explanation:
Pentagon is an polygon having five sides.
ABCDE is having same length of sides of ED and BC of 2cm.

Question 5.
Draw a hexagon with at least 2 equal sides. Label the 2 equal side lengths of your shape.
Answer:

Explanation:
Hexagon is an polygon having six sides.
AB and ED are having the sides of same length of 3cm each.

Question 6.
Sam says that he drew a polygon with 2 sides and 2 angles. Can Sam be correct? Use pictures to help you explain your answer.
Answer:
Sam cannot be correct because we cannot draw a polygon with 2 sides and 2 angles. We need at least three lines to draw a polygon with three angles.

Explanation:

Eureka Math Grade 3 Module 7 Lesson 6 Exit Ticket Answer Key

Use a ruler and a right angle tool to help you draw a shape that matches the attributes of Jeanette’s shape. Label your drawing to explain your thinking.

Jeanette says her shape has 4 right angles and 2 sets of parallel sides. It is not a regular quadrilateral.
Answer:

Explanation:
ABCD is a Quadrilateral, where AB and DC are two parallel sides and  A and D are two right angles.

Eureka Math Grade 3 Module 7 Lesson 6 Homework Answer Key

Use a ruler and a right angle tool to help you draw the figures with the given attributes below.

Question 1.
Draw a triangle that has no right angles.
Answer:

Explanation:
Triangle ABC is an acute triangle.

Question 2.
Draw a quadrilateral that has at least 2 right angles.
Answer:

Explanation:
ABCD is an quadrilateral having at least 2 right angles.

Question 3.
Draw a quadrilateral with 2 equal sides. Label the 2 equal side lengths of your shape.
Answer:

Explanation:
ABCD is an quadrilateral of four sides, where AD and BC having same length of 2cms each.

Question 4.
Draw a hexagon with at least 2 equal sides. Label the 2 equal side lengths of your shape.
Answer:

Explanation:
Hexagon polygon has six sides in it.
ABCDEF is a Hexagon having six sides where AB and DE are having same length of 2cms each.

Question 5.
Draw a pentagon with at least 2 equal sides. Label the 2 equal side lengths of your shape.
Answer:

Explanation:
Pentagon is a figure having 5 sides in it.
ABCDE is an pentagon having five sides, where AB and BC sides of same length of 2cms each.

Question 6.
Cristina describes her shape. She says it has 3 equal sides that are each 4 centimeters in length. It has no right angles. Do your best to draw Cristina’s shape, and label the side lengths.
Answer:

Explanation:
Cristina figure described as below:
ABC is an equilateral Triangle of equal lengths sides of 4cm each which does not have any right angles in it.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 7 Answer Key

Eureka Math Grade 3 Module 7 Lesson 7 Pattern Sheet Answer Key

Multiply.

multiply by 5 (6–10)
Answer:

Explanation:
5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 5 = 25
5 × 6 = 30
5 × 7 = 35
5 × 8 = 40
5 × 9 = 45
5 × 10 = 50.

Eureka Math Grade 3 Module 7 Lesson 7 Problem Set Answer Key

Question 1.
Use tetrominoes to create at least two different rectangles. Then, color the grid below to show how you created your rectangles. You may use the same tetromino more than once.

Answer:

Explanation:
The rectangles in the given cubes chart are two different shapes with same number of cubes.
They are in two different colors.

Question 2.
Use tetrominoes to create at least two squares, each with an area of 36 square units. Then, color the grid below to show how you created your squares. You may use the same tetromino more than once.

Answer:

Explanation:
Two different colored Squares of same length of cubes = 6 units.

a. Write an equation to show the area of a square above as the sum of the areas of the tetrominoes you used to make the square.
Answer:
Side of the Square = 6 units.
Area of Square = Side × Side

Explanation:

b. Write an equation to show the area of a square above as the product of its side lengths.
Answer:
Area of Square = 36 square units.

Explanation:
Side of the Square = 6 units.
Area of Square = Side × Side
= 6 × 6
=  36 square units.

Question 3.
a. Use tetrominoes to create at least two different rectangles, each with an area of 12 square units. Then, color the grid below to show how you created the rectangles. You may use the same tetromino more than once.

Answer:

Explanation:
Two different rectangles are drawn with the same area of 12 square units.

b. Explain how you know the area of each rectangle is 12 square units.
Answer:
Area of the rectangle = 12 square units.

Explanation:
Area of the rectangle = Length × width
—> First Yellow color rectangle:
Length = 4 units
Width = 3 units
Area of the rectangle = Length × width
= 4 × 3
= 12 square units.
—>Second  Orange color rectangle:
Length = 6 units
Width = 2 units
Area of the rectangle = Length × width
= 6 × 2
= 12 square units.

Question 4.
Marco created a rectangle with tetrominoes and traced its outline in the space below. Use tetrominoes to re-create it. Estimate to draw lines inside the rectangle below to show how you re-created Marco’s rectangle.

Answer:

Explanation:
Marco created a rectangle with tetrominoes and traced its outline is re-created and shown above.

Eureka Math Grade 3 Module 7 Lesson 7 Exit Ticket Answer Key

Use your tetrominoes to make a rectangle that has an area of 20 square units. Then, color the grid to show how you made your rectangle. You may use the same tetromino more than once.

Answer:
Area of the rectangle = 20 square units.

Explanation:
Length of the rectangle drawn = 5 units
Width of the rectangle drawn = 4 units
Area of the rectangle = Length × Width
= 5 × 4
= 20 square units.

Eureka Math Grade 3 Module 7 Lesson 7 Homework Answer Key

Question 1.
Color tetrominoes on the grid to create three different rectangles. You may use the same tetromino more than once.

Answer:

Explanation:
There are three different shaped rectangle drawn above.

Question 2.
Color tetrominoes on the grid below to:
a. Create a square with an area of 16 square units.
Answer:
Area of Square = 16 Square units.

Explanation:
Side of the Square = 4 units
Area of Square = side × side
= 4 × 4
= 16 Square units.

b. Create at least two different rectangles, each with an area of 24 square units.
You may use the same tetromino more than once.

Answer:

Explanation:
Two different rectangles are drawn with the same area of 24 square units.

Question 3.
Explain how you know the rectangles you created in Problem 2(b) have the correct area.
Answer:
Area of the rectangles = 24 square units.

Explanation:
—> First rectangle:
Length of the First rectangle = 8 units
Width of the First rectangle = 3 units
Area of the First rectangle = Length × Width
= 8 × 3
= 24 square units.
—> Second rectangle:
Length of the Second rectangle = 8 units
Width of the Second rectangle = 3 units
Area of the Second rectangle = Length × Width
= 6 × 4
= 24 square units.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 14 Answer Key

Eureka Math Grade 3 Module 7 Lesson 14 Pattern Sheet Answer Key

Multiply.

multiply by 8 (6–10)
Answer:

Explanation:
8 × 5 = 40
8 × 6 = 48
8 × 7 = 56
8 × 8 = 64
8 × 9 = 72
8 × 10 = 80.

Eureka Math Grade 3 Module 7 Lesson 14 Problem Set Answer Key

Question 1.
Label the unknown side lengths of the regular shapes below. Then, find the perimeter of each shape.
a.

Perimeter = _______ in
Answer:
Length of the side of the ABCDEFG Octogen = 64in.

Explanation:

Length of the side of the ABCDEFG Octogen = 8in
Perimeter of the ABCDEFG Octogen = 8 × side
= 8 × 8in
= 64in.

b.

Perimeter = _______ ft
Answer:
Perimeter of the ABC Triangle = 21ft.

Explanation:

Length of the side of the ABC Triangle = 7ft
Perimeter of the ABC Triangle = 3 × Side
= 3 × 7ft
= 21ft.

c.

Perimeter = _______ m
Answer:
Perimeter of the ABCD Square = 36m.

Explanation:

Length of the Side of the ABCD Square = 9m
Perimeter of the ABCD Square = 4 × Side
= 4 × 9m
= 36m.

d.

Perimeter = _______ in
Answer:
Perimeter of the ABCDE Pentagon = 36in.

Explanation:

Length of the side of the ABCDE Pentagon = 6in
Perimeter of the ABCDE Pentagon = 6 × Side
= 6 × 6in
= 36in.

Question 2.
Label the unknown side lengths of the rectangle below. Then, find the perimeter of the rectangle.

Perimeter = _______ cm
Answer:
Perimeter of the side of the ABCD Rectangle = 18cm.

Explanation:

Length of the side of the ABCD Rectangle = 7cm
Width of the side of the ABCD Rectangle = 2cm
Perimeter of the side of the ABCD Rectangle = 2 (Length + Width)
= 2 ( 7cm + 2cm )
= 2 × 9cm
= 18cm.

Question 3.
David draws a regular octagon and labels a side length as shown below. Find the perimeter of David’s octagon.

Answer:
Perimeter of the ABCDEFGH Octogen = 36cm.

Explanation:

Length of the side of the ABCDEFGH Octogen = 6cm
Perimeter of the ABCDEFGH Octogen = 6 × Side
= 6 × 6cm
= 36cm.

Question 4.
Paige paints an 8-inch by 9-inch picture for her mom’s birthday. What is the total length of wood that Paige needs to make a frame for the picture?
Answer:
Perimeter of the Paige’s paints = 34inch.

Explanation:
Length of the Paige’s paints = 9inch
Width of the Paige’s paints = 8inch
Perimeter of the Paige’s paints = 2 (Length + Width )
= 2 (9inch + 8inch)
= 2 × 17inch
= 34inch.

Question 5.
Mr. Spooner draws a regular hexagon on the board. One of the sides measures 4 centimeters. Giles and Xander find the perimeter. Their work is shown below. Whose work is correct? Explain your answer.
Giles’s Work
Perimeter = 4 cm + 4 cm + 4 cm + 4 cm + 4 cm + 4 cm
Perimeter = 24 cm

Xander’s Work
Perimeter = 6 × 4 cm
Perimeter = 24 cm
Answer:
Perimeter of the Hexagon = 24 centimeters.
Both Giles and Xander’s work is correct because they got the calculation value correct even though the methodology was different of each.

Explanation:
Length of the side of the Hexagon = 4 centimeters
Perimeter of the Hexagon = 6 × Side
= 6 × 4 centimeters
= 24 centimeters.
Both are correct.

Eureka Math Grade 3 Module 7 Lesson 14 Exit Ticket Answer Key

Travis traces a regular pentagon on his paper. Each side measures 7 centimeters. He also traces a regular hexagon on his paper. Each side of the hexagon measures 5 centimeters. Which shape has a greater perimeter? Show your work.
Answer:
Perimeter of the Pentagon is greater than the Perimeter of the regular hexagon because the measurement value of the Pentagon is more than the measurement value of the regular hexagon.

Explanation:

Length of the side of the Pentagon = 7 centimeters
Perimeter of the Pentagon = 5 × Side
= 5 × 7 centimeters
= 35 centimeters.
Length of the side of the regular hexagon = 5 centimeters
Perimeter of the regular hexagon = 6 × Side
= 6 × 5 centimeters
= 30 centimeters.

Eureka Math Grade 3 Module 7 Lesson 14 Homework Answer Key

Question 1.
Label the unknown side lengths of the regular shapes below. Then, find the perimeter of each shape.
a.

Perimeter = _______ in
Answer:
Perimeter of the ABC Triangle = 16in.

Explanation:

Length of the Side of the ABC Triangle = 4in
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 4in + 4in + 4in
= 12in + 4in
=16in.

b.

Perimeter = _______ cm

Answer:
Perimeter of the square = 32cm.

Explanation:

Length of the Side of the square = 8cm
Perimeter of the square = 4 × Side
= 4 × 8cm
= 32cm.

c.

Perimeter = _______ m
Answer:
Perimeter of the Octagon = 72m.

Explanation:

Length of the side of the Octagon = 9m
Perimeter of the Octagon = 8 × Side
= 8 × 9m
= 72m.

d.

Perimeter = _______ in
Answer:
Perimeter of the Hexagon = 36in.

Explanation:

Length of the side of the Hexagon = 6in
Perimeter of the Hexagon = 6 × Side
= 6 × 6in
= 36in.

Question 2.
Label the unknown side lengths of the rectangle below. Then, find the perimeter of the rectangle.

Perimeter = _______ cm
Answer:
Perimeter of the rectangle =  2 ( Length + Width )
= 2 ( 9cm + 4cm )
= 2 × 13cm
= 26cm.

Explanation:
Length of the rectangle = 9cm
Width of the rectangle = 4cm
Perimeter of the rectangle =  2 ( Length + Width )
= 2 ( 9cm + 4cm )
= 2 × 13cm
= 26cm.

Question 3.
Roxanne draws a regular pentagon and labels a side length as shown below. Find the perimeter of Roxanne’s pentagon.

Answer:
Perimeter of the Roxanne’s pentagon = 5 × Side
= 5 × 7cm
= 35cm.

Explanation:
Length of the side of the Roxanne’s pentagon = 7cm
Perimeter of the Roxanne’s pentagon = 5 × Side
= 5 × 7cm
= 35cm.

Question 4.
Each side of a square field measures 24 meters. What is the perimeter of the field?
Answer:
Perimeter of the Square field = 4 × Side
= 4 × 24meters
= 96meters.

Explanation:
Length of the side of the Square field = 24 meters
Perimeter of the Square field = 4 × Side
= 4 × 24meters
= 96meters.

Question 5.
What is the perimeter of a rectangular sheet of paper that measures 8 inches by 11 inches?
Answer:
Perimeter of the rectangular sheet of paper = 2 ( Length  + Width )
= 2 (11inches + 8inches)
= 38inches.

Explanation:
Length of the rectangular sheet of paper = 11inches
Width of the rectangular sheet of paper = 8inches
Perimeter of the rectangular sheet of paper = 2 ( Length  + Width )
= 2 (11inches + 8inches)
= 2 × 19inches
= 38inches.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 13 Answer Key

Eureka Math Grade 3 Module 7 Lesson 13 Pattern Sheet Answer Key

Multiply.

multiply by 8 (1–5)
Answer:

Explanation:
8 × 1 = 8
8 × 2 = 16
8 × 3 = 24
8 × 4 = 32
8 × 5 = 40.

Eureka Math Grade 3 Module 7 Lesson 13 Problem Set Answer Key

Question 1.
Find the perimeter of the following shapes.
a.

P = 3 in + 8 in + 3 in + 8 in
= _________ in
Answer:
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC +CD + DA
= 8in + 3in + 8in + 3in
= 22in.

Explanation:

Length of the AB side of the Rectangle = 8in
Length of the BC side of the Rectangle = 3in
Length of the CA side of the Rectangle = 8in
Length of the DA side of the Rectangle = 3in
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC +CD + DA
= 8in + 3in + 8in + 3in
= 11in + 8in + 3in
= 19in + 3in
= 22in.

b.

P = ____ cm + ____ cm + ____ cm + ____ cm
= _________ cm
Answer:
Perimeter of the ABCD Square = Side + Side + Side + Side
= AB + BC +CD + DA
= 4cm + 4cm + 4cm + 4cm
= 16cm.

Explanation:

Length of the AB side of the ABCD Square = 4cm
Length of the BC side of the ABCD Square = 4cm
Length of the CD side of the ABCD Square = 4cm
Length of the DA side of the ABCD Square = 4cm
Perimeter of the ABCD Square = Side + Side + Side + Side
= AB + BC +CD + DA
= 4cm + 4cm + 4cm + 4cm
= 8cm + 4cm + 4cm
= 12cm + 4cm
= 16cm.

c.

P = ____ cm + ____ cm + ____ cm
= _________ cm
Answer:
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 9cm + 11cm + 6cm
= 26cm.

Explanation:

Length of the AB side of the ABC Triangle =  9cm
Length of the BC side of the ABC Triangle = 11cm
Length of the CA side of the ABC Triangle = 6cm
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 9cm + 11cm + 6cm
= 20cm + 6cm
= 26cm.

d.

P = ____ m + ____ m + ____ m + ____ m
= _________ m
Answer:
Perimeter of the ABCD Trapezium = Side + Side + Side + Side
= AB + BC + CD + DA
= 15m + 9m + 5m + 7m
= 36m.

Explanation:

Length of the AB side of the ABCD Trapezium = 15cm
Length of the BC side of the ABCD Trapezium = 9cm
Length of the CD side of the ABCD Trapezium = 5cm
Length of the DA side of the ABCD Trapezium = 7cm
Perimeter of the ABCD Trapezium = Side + Side + Side + Side
= AB + BC + CD + DA
= 15m + 9m + 5m + 7m
= 24m + 5m + 7m
= 29m + 7m
= 36m.

e.

P = ____ in + ____ in + ____ in + ____ in + ____ in
= _________ in
Answer:
Perimeter of the ABCDE Pentagon = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 2in + 2in + 9in + 3in
= 25in.

Explanation:

Length of the AB side of the ABCDE Pentagon = 9in
Length of the BC side of the ABCDE Pentagon = 2in
Length of the CD side of the ABCDE Pentagon = 2in
Length of the DE side of the ABCDE Pentagon = 9in
Length of the EA side of the ABCDE Pentagon = 3in
Perimeter of the ABCDE Pentagon = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 2in + 2in + 9in + 3in
= 11in + 2in + 9in + 3in
= 13in + 9in + 3in
= 22in + 3in
= 25in.

Question 2.
Alan’s rectangular swimming pool is 10 meters long and 16 meters wide. What is the perimeter?

Answer:
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 16m + 10m + 16m + 10m
= 52m.

Explanation:

Length of the AB side of the ABCD Rectangle = 16m
Length of the BC side of the ABCD Rectangle = 10m
Length of the CA side of the ABCD Rectangle = 16m
Length of the DA side of the ABCD Rectangle = 10m
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 16m + 10m + 16m + 10m
= 26m + 16m + 10m
= 42m + 10m
= 52m.

Question 3.
Lila measures each side of the shape below.

a. What is the perimeter of the shape?
b. Lila says the shape is a pentagon. Is she correct? Explain why or why not.
Answer:
a. The perimeter of the ABCDE shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 6in + 3in + 2in + 4in
= 24in.

b. Lila is correct because Pentagon is a figure which has five sides in it and her figure is a five sided shape.

Explanation:

a. The perimeter of the ABCDE shape = ???
Length of the AB side of the ABCDE shape = 9in
Length of the BC side of the ABCDE shape = 6in
Length of the CD side of the ABCDE shape = 3in
Length of the DE side of the ABCDE shape = 2in
Length of the EA side of the ABCDE shape = 4in
The perimeter of the ABCDE shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 9in + 6in + 3in + 2in + 4in
= 15in + 3in + 2in + 4in
= 18in + 2in + 4in
= 20in + 4in
= 24in.

b. Pentagon is a figure which has  five side in it. Lila is correct.

Eureka Math Grade 3 Module 7 Lesson 13 Exit Ticket Answer Key

Which shape below has the greater perimeter? Explain your answer.

Answer:
Perimeter of shape A = 14in
Perimeter of shape B = 15in
Perimeter of shape B is greater than the Perimeter of shape A because the measurement value of Perimeter of shape B is more than the the measurement value of Perimeter of shape A.

Explanation:

Perimeter of shape A = Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GA
= 2in + 2in + 2in + 2in + 2in + 2in + 2in
= 4in + 2in + 2in + 2in + 2in + 2in
= 6in + 2in + 2in + 2in + 2in
= 8in + 2in + 2in + 2in
= 10in + 2in + 2in
= 12in + 2in
= 14in.
Perimeter of shape B = Side + Side + Side + Side + Side
= HI + IJ + JK + KL +LH
= 4in + 2in + 2in + 4in + 3in
= 6in + 2in + 4in + 3in
= 8in +  4in + 3in
= 12in + 3in
= 15in.

Eureka Math Grade 3 Module 7 Lesson 13 Homework Answer Key

Question 1.
Find the perimeters of the shapes below. Include the units in your equations. Match the letter inside each shape to its perimeter to solve the riddle. The first one has been done for you.

What kind of meals do math teachers eat?

Answer:
Perimeter of q Triangle shape = 21in.
Perimeter of r Pentagon shape = 36ft.
Perimeter of s Parallelogram shape = 24cm.
Perimeter of a Trapezium shape = 28yd.
Perimeter of m rhombus shape = 16in.
Perimeter of e Rectangular shape = 26cm.
Perimeter of u quadrilateral shape = 20m.
Perimeter of l Pentagon shape = 15m.

Square meals kind of meals  math teachers eats.

Explanation:

Perimeter of q Triangle shape = Side + Side + Side
= 7in + 7in + 7in
= 14in + 7in
= 21in.

Perimeter of r Pentagon shape = Side + Side + Side + Side + Side
= 6ft + 9ft + 6ft + 6ft + 9ft
= 15ft + 6ft + 6ft + 9ft
= 21ft + 6ft + 9ft
= 27ft + 9ft
= 36ft.

Perimeter of s Parallelogram shape = Side + Side + Side + Side
= 7cm + 5cm + 7cm + 5cm
= 12cm + 7cm + 5cm
= 19cm + 5cm
= 24cm.

Perimeter of a Trapezium shape = Side + Side + Side + Side
= 9yd + 7yd + 5yd + 7yd
= 16yd + 5yd + 7yd
= 21yd +  7yd
= 28yd.

Perimeter of m rhombus shape = Side + Side + Side + Side
= 4in + 4in + 4in + 4in
= 8in  + 4in + 4in
= 12in + 4in
= 16in.

Perimeter of e Rectangular shape = Side + Side + Side + Side
= 8cm + 5cm + 8cm + 5cm
= 13cm + 8cm + 5cm
= 21cm + 5cm
= 26cm.

Perimeter of u quadrilateral shape = Side + Side + Side + Side
= 6m + 4m + 7m + 3m
= 10m + 7m + 3m
= 17m + 3m
= 20m.

Perimeter of l Pentagon shape= Side + Side + Side + Side + Side
= 4m + 2m + 2m + 4m + 3m
= 6m + 2m + 4m + 3m
= 8m + 4m + 3m
= 12m + 3m
= 15m.

Question 2.
Alicia’s rectangular garden is 33 feet long and 47 feet wide. What is the perimeter of Alicia’s garden?

Answer:
Perimeter of Alicia’s rectangular garden = 160ft.

Explanation:

Length of the ABCD Alicia’s rectangular garden = 33ft
Width of the ABCD Alicia’s rectangular garden = 47ft
Perimeter of ABCD Alicia’s rectangular garden = 2 (Length + Width)
= 2 ( 33ft + 47ft )
= 2 × 80ft
= 160ft.

Question 3.
Jaque’s measured the side lengths of the shape below.

a. Find the perimeter of Jaques’s shape.
b. Jaques says his shape is an octagon. Is he right? Why or why not?
Answer:
a. Perimeter of Jaques’s shape =  Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH +HA
= 7 in + 3 in + 4 in+ 5 in + 4 in + 3 in + 2 in +5 in
= 33in.

Explanation:
a.

Perimeter of Jaques’s shape =  Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH +HA
= 7 in + 3 in + 4 in+ 5 in + 4 in + 3 in + 2 in +5 in
= 10 in + 4 in + 5 in + 4 in + 3 in + 2 in +5 in
= 14 in + 5 in + 4 in + 3 in + 2 in +5 in
= 19 in + 4 in + 3 in + 2 in +5 in
= 23 in + 3 in + 2 in +5 in
= 26 in + 2 in+5 in
= 28 in + 5 in
= 33 in.

b.  Yes, he is correct. Jaques says his shape is an octagon because in geometry , an octagon is an eight-sided  polygon or 8-gon. His shape has eight sides.

Explanation:

His shape has eight sides. In geometry , an octagon is an eight-sided  polygon or 8-gon.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 12 Answer Key

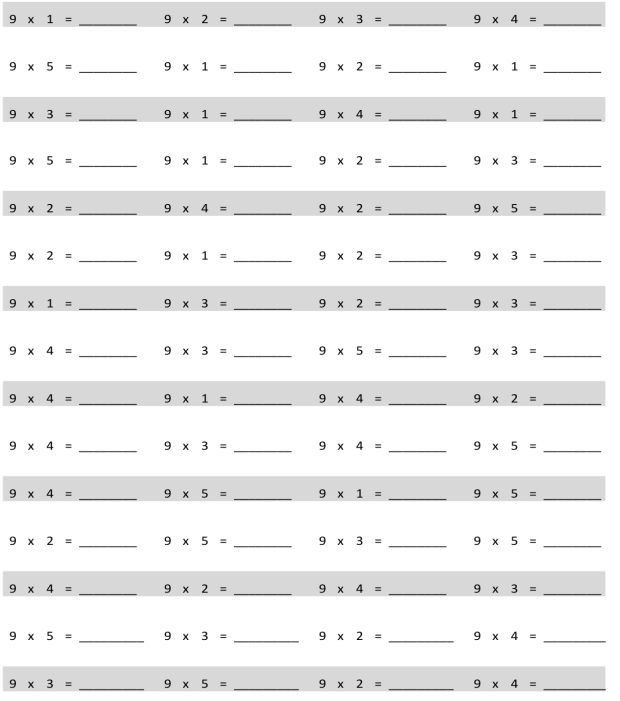
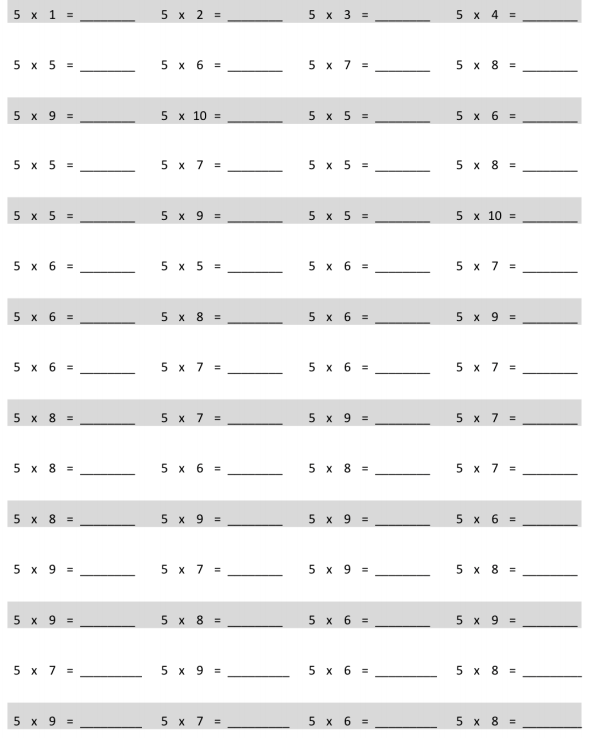
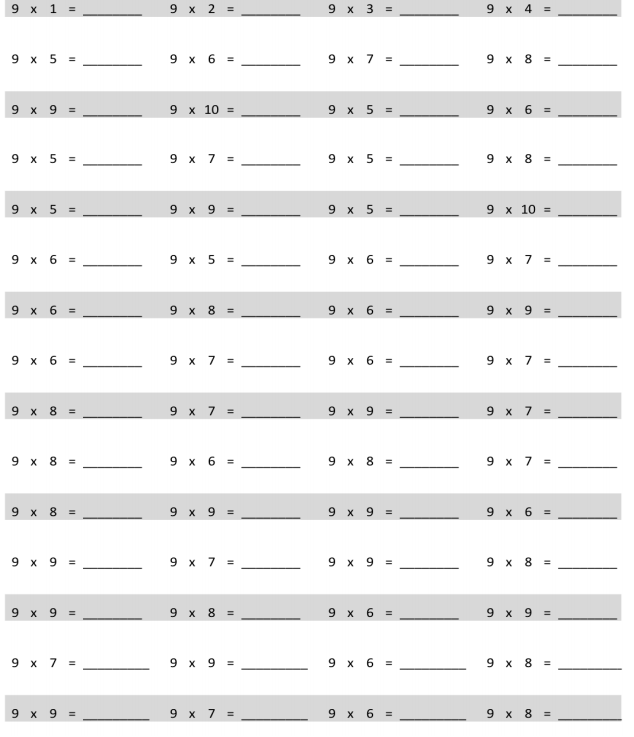
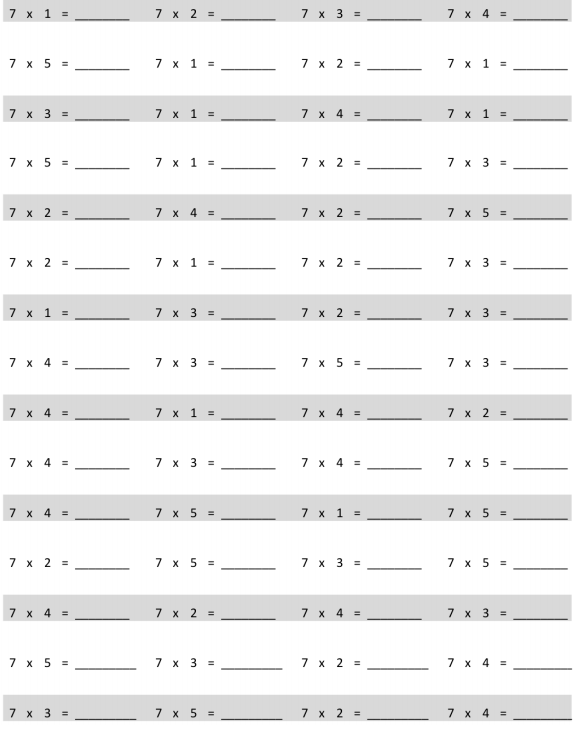
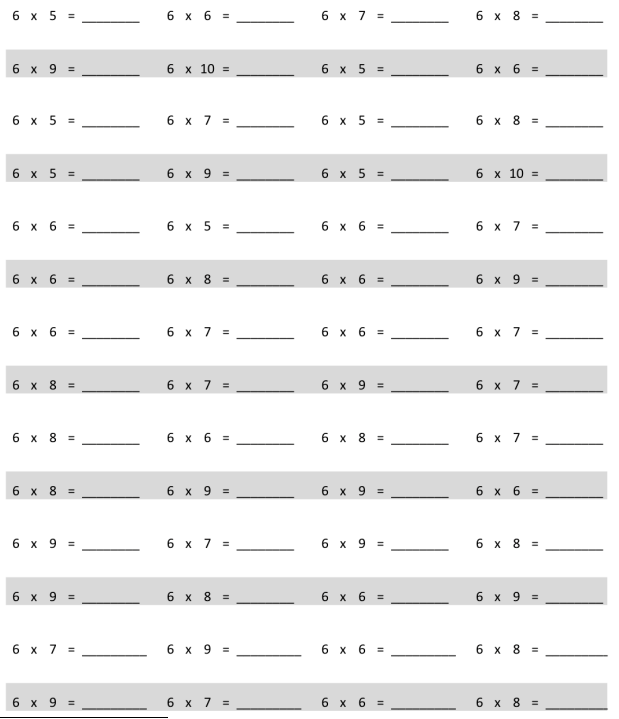
Eureka Math Grade 3 Module 7 Lesson 12 Pattern Sheet Answer Key

Multiply.

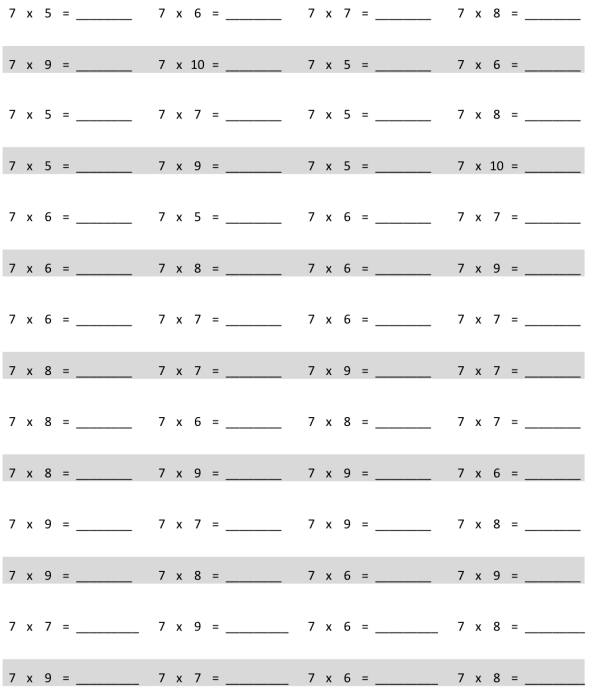
multiply by 7 (6–10)
Answer:

Explanation:
7 × 6 = 42
7 × 7 = 49
7 × 8 = 56
7 × 9 = 63
7 × 10 = 70.

Eureka Math Grade 3 Module 7 Lesson 12 Problem Set Answer Key

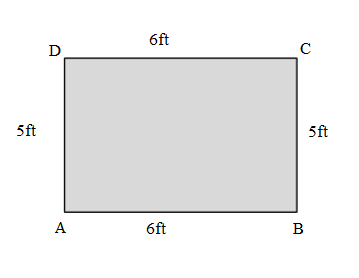
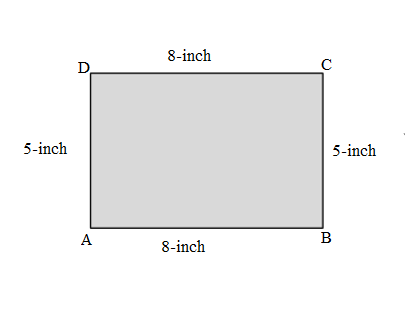
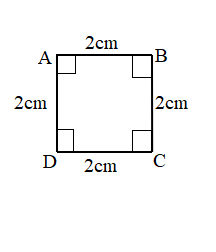
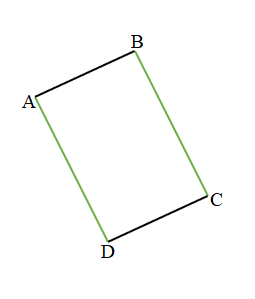
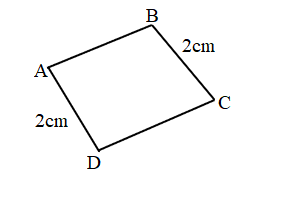
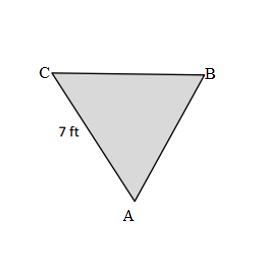
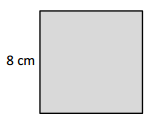
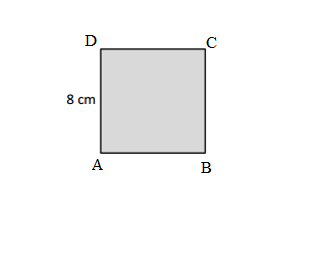
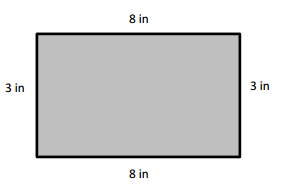
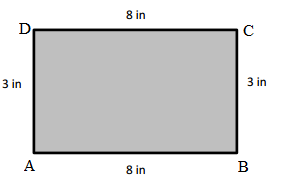
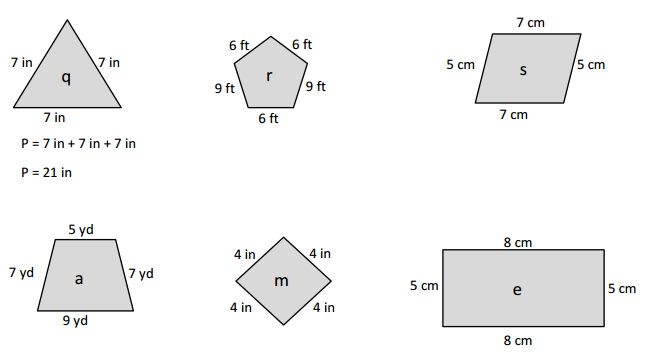
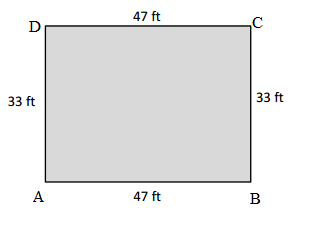
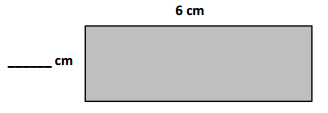
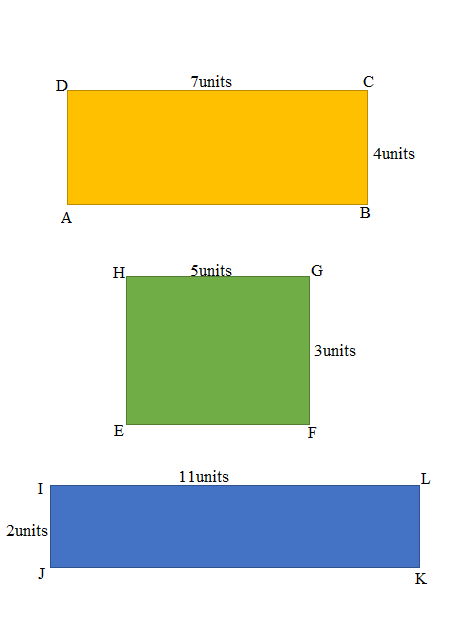
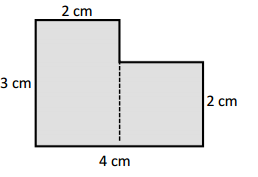
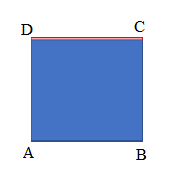
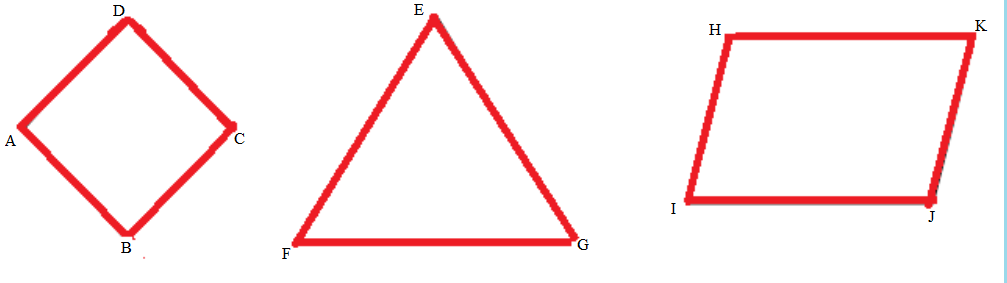
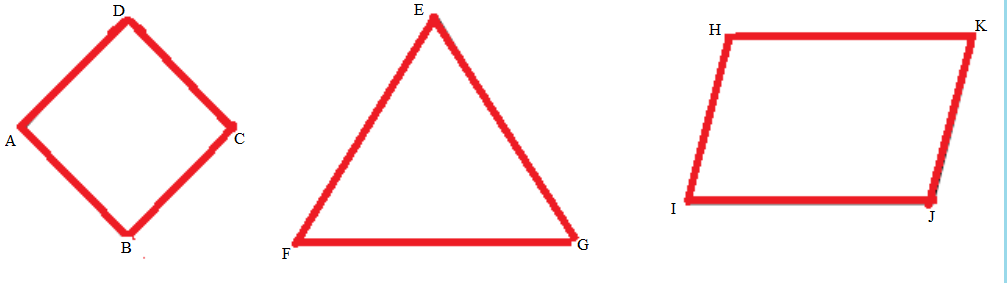
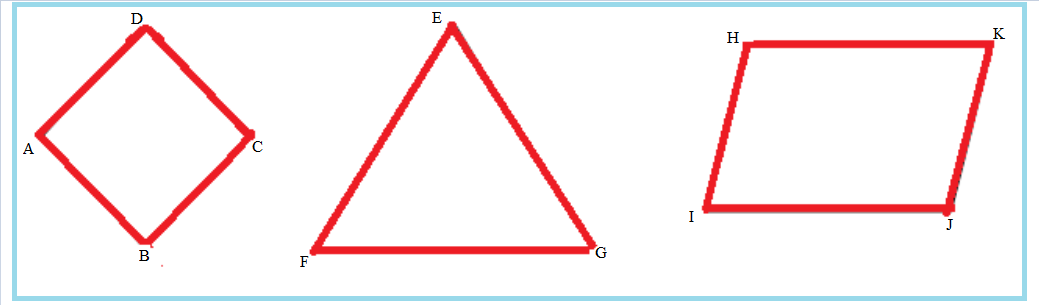
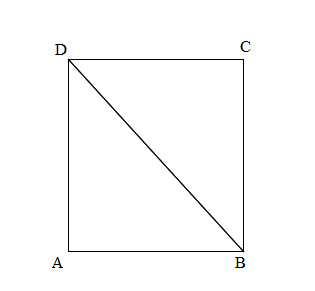
Question 1.
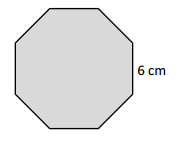
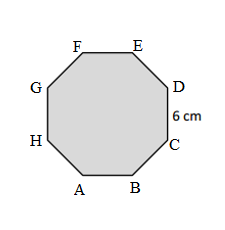
Measure and label the side lengths of the shapes below in centimeters. Then, find the perimeter of each shape.
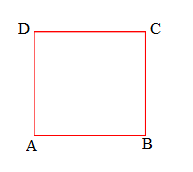
a.

Perimeter = _____cm +_____cm +_____cm +_____cm
= _______ cm
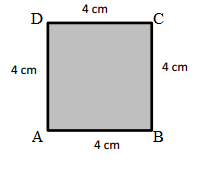
Answer:
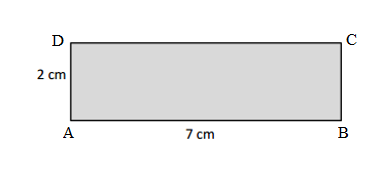
Perimeter of the ABCD given shape = Side + Side + Side + Side
= 2cm + 2cm + 2cm + 2cm
= 8cm.

Explanation:

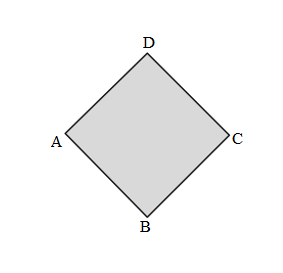
Length of the AB side of the ABCD shape = 2cm
Length of the BC side of the ABCD shape = 2cm
Length of the CD side of the ABCD shape = 2cm
Length of the DA side of the ABCD shape = 2cm
Perimeter of the given ABCD shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
= 4cm + 2cm + 2cm
= 6cm + 2cm
= 8cm.

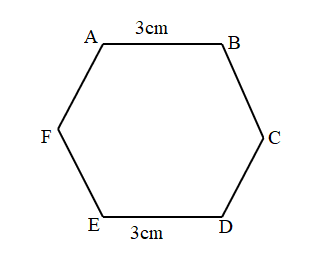
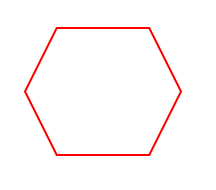
b.

Perimeter = _____________________
= _______ cm
Answer:
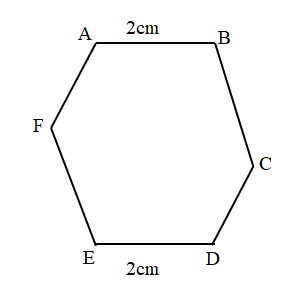
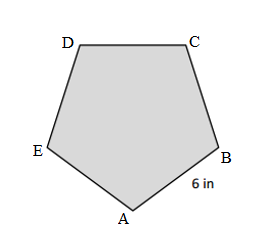
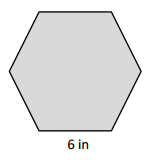
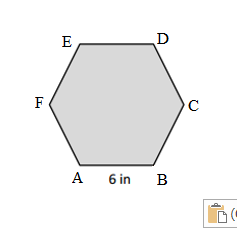
Perimeter of the given ABCDEF Hexagon shape = Side + Side + Side + Side + Side + Side
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 18cm.

Explanation:

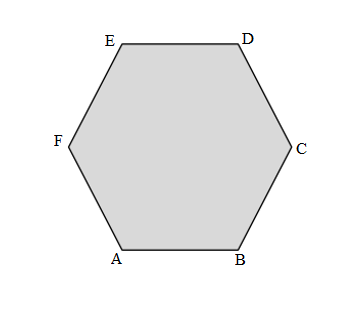
Length of the AB side of the given ABCDEF Hexagon shape = 3cm.
Length of the BC side of the given ABCDEF Hexagon shape = 3cm.
Length of the CD side of the given ABCDEF Hexagon shape = 3cm.
Length of the DE side of the given ABCDEF Hexagon shape = 3cm.
Length of the EF side of the given ABCDEF Hexagon shape = 3cm.
Length of the FA side of the given ABCDEF Hexagon shape = 3cm.
Perimeter of the given ABCDEF Hexagon shape = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm +3cm + 3cm + 3cm + 3cm
= 9cm +3cm + 3cm + 3cm
= 12cm +3cm + 3cm
= 15cm + 3cm
= 18cm.

c.

Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the given ABCD Parallelogram shape = Side + Side + Side + Side
= 4cm + 4cm + 4cm + 4cm
= 16cm.

Explanation:

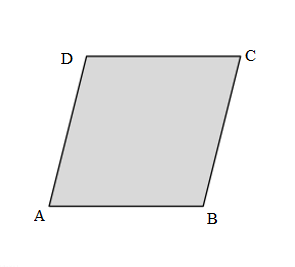
Length of the AB side of the given ABCD Parallelogram shape = 4cm
Length of the BC side of the given ABCD Parallelogram shape = 4cm
Length of the CD  side of the given ABCD Parallelogram shape = 4cm
Length of the DA side of the given ABCD Parallelogram shape = 4cm
Perimeter of the given ABCD Parallelogram shape = Side + Side + Side + Side
=AB + BC + CD +DA
= 4cm + 4cm + 4cm + 4cm
= 8cm + 4cm + 4cm
= 12cm + 4cm
=16cm.

d.

Perimeter = _____________________
= _______ cm
Answer:
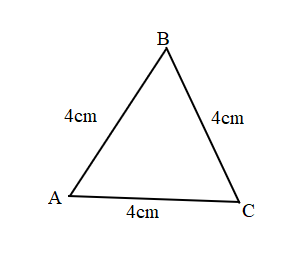
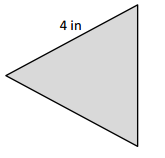
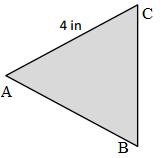
Perimeter of the ABC Triangle = Side + Side + Side
= 5cm + 5cm + 5cm
= 15cm.

Explanation:

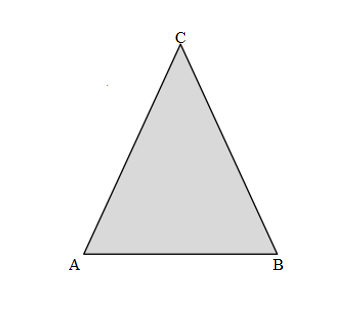
Length of the AB side of the ABC Triangle = 5cm
Length of the BC side of the ABC Triangle = 5cm
Length of the CA side of the ABC Triangle = 5cm
Perimeter of the ABC Triangle = Side + Side + Side
= AB + BC + CA
= 5cm + 5cm + 5cm
= 10cm + 5cm
= 15cm.

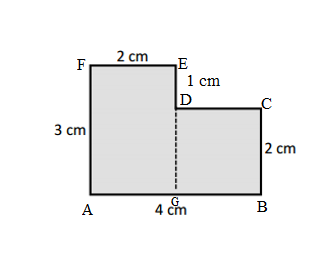
e.

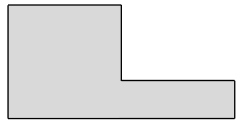
Perimeter = _____________________
= _______ cm
Answer:
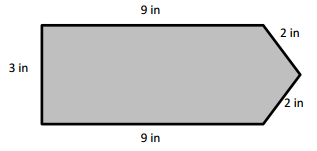
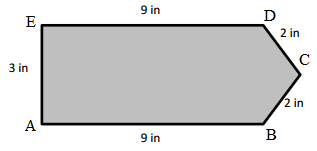
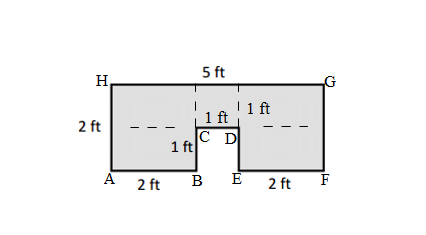
Perimeter of the given ABCDEF figure = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE+ EF + FA
= 5.5cm+ 1cm + 3cm + 2cm + 3cm + 3cm
= 17.5cm

Explanation:

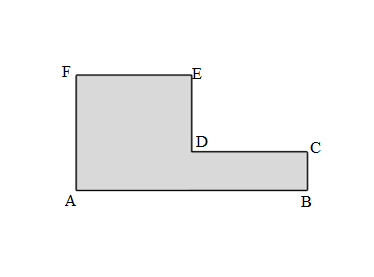
Length of AB side if the given ABCDEF figure = 5.5cm
Length of BC side if the given ABCDEF figure = 1cm
Length of CD side if the given ABCDEF figure = 3cm
Length of DE side if the given ABCDEF figure = 2cm
Length of EF side if the given ABCDEF figure = 3cm
Length of FA side if the given ABCDEF figure = 3cm
Perimeter of the given ABCDEF figure = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE+ EF + FA
= 5.5cm+ 1cm + 3cm + 2cm + 3cm + 3cm
= 6.5cm + 3cm + 2cm + 3cm + 3cm
= 9.5cm + 2cm + 3cm + 3cm
= 11.5cm + 3cm + 3cm
= 14.5cm + 3cm
= 17.5cm

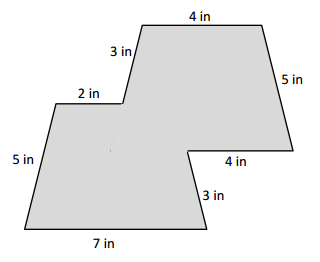
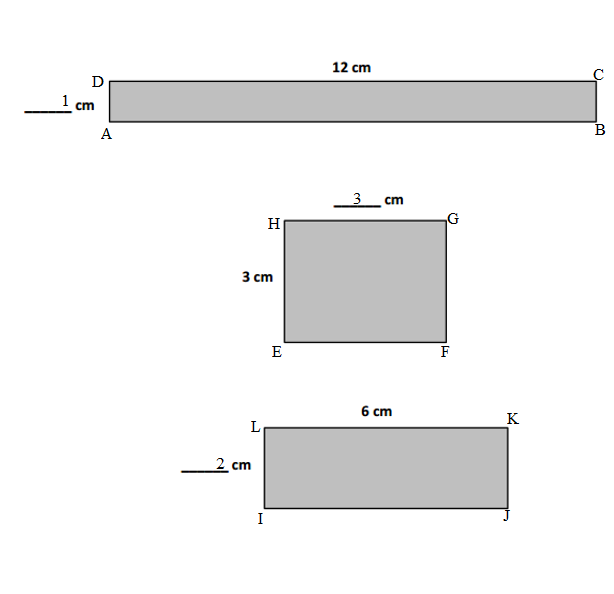
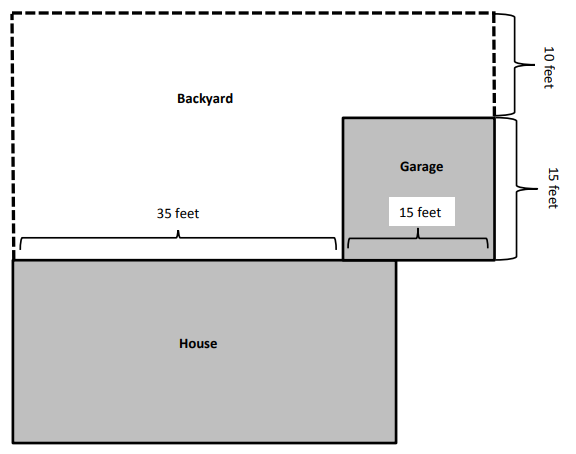
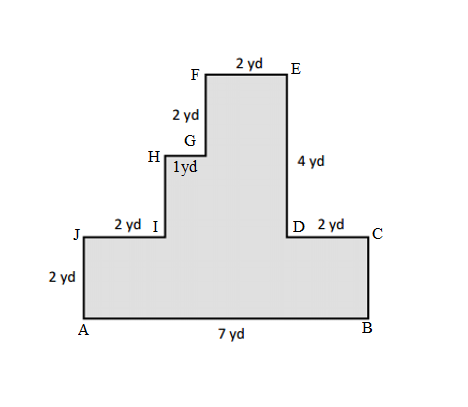
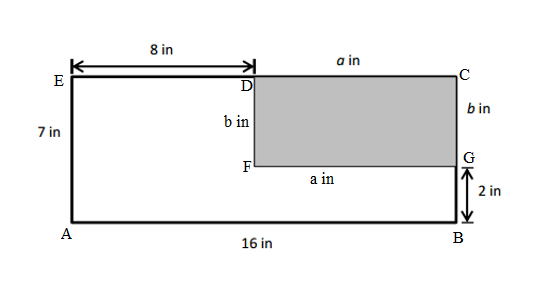
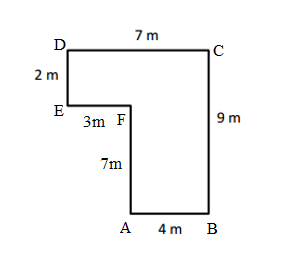
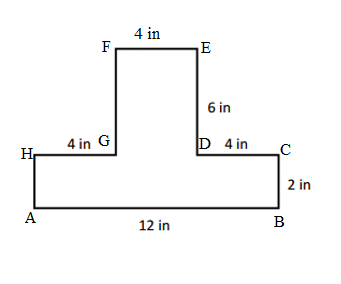
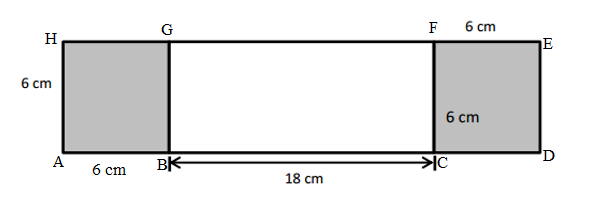
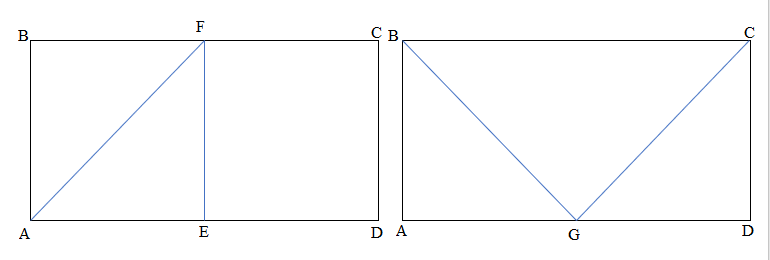
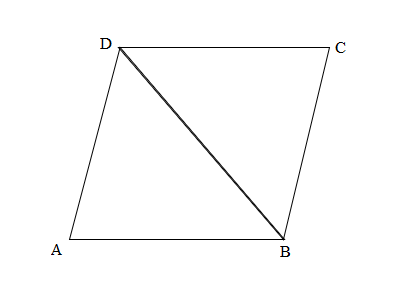
Question 2.
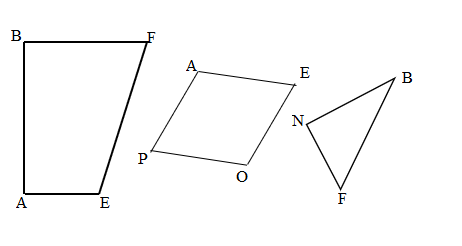
Carson draws two triangles to create the new shape shown below. Use a ruler to find the side lengths of Carson’s shape in centimeters. Then, find the perimeter.

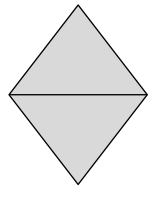
Answer:
Perimeter of ABCD Carson’s shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
=8cm.

Explanation:

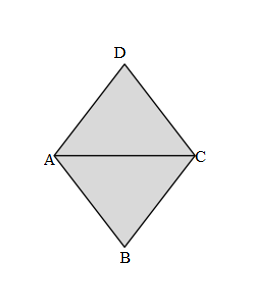
Length of AB side of ABCD Carson’s shape = 2cm
Length of BC side of ABCD Carson’s shape = 2cm
Length of CD side of ABCD Carson’s shape = 2cm
Length of DA side of ABCD Carson’s shape = 2cm
Perimeter of ABCD Carson’s shape = Side + Side + Side + Side
= AB + BC + CD+ DA
= 2cm + 2cm + 2cm + 2cm
=4cm + 2cm + 2cm
= 6cm + 2cm
=8cm.

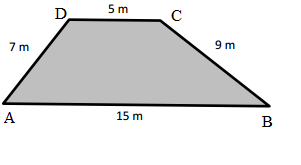
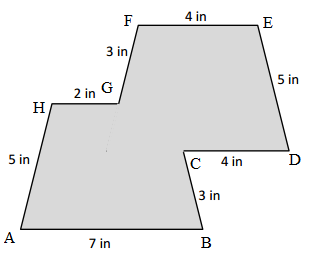
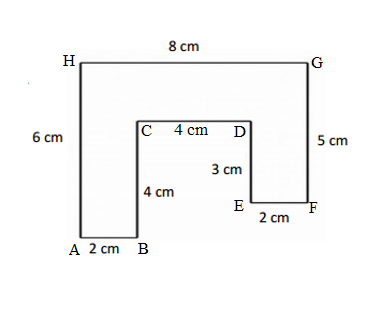
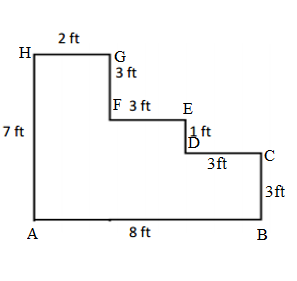
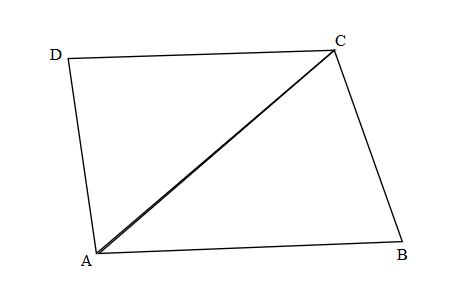
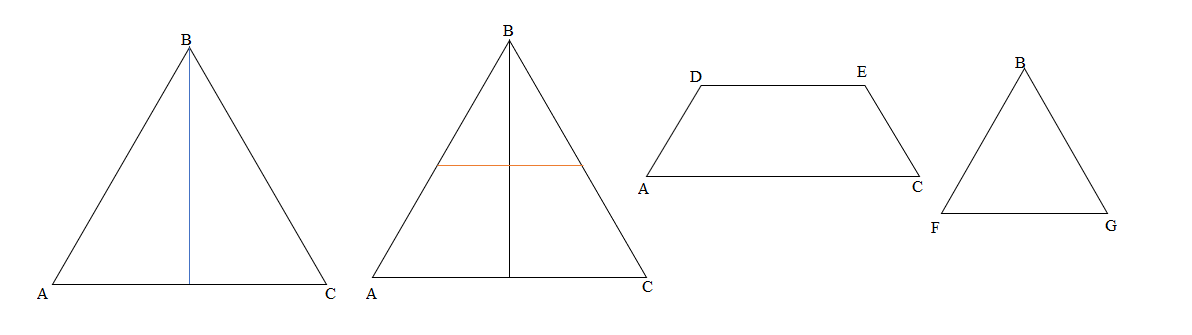
Question 3.
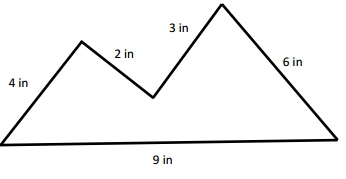
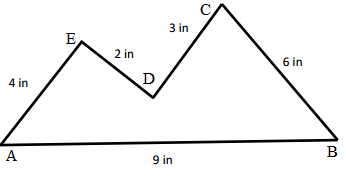
Hugh and Daisy draw the shapes shown below. Measure and label the side lengths in centimeters. Whose shape has a greater perimeter? How do you know?

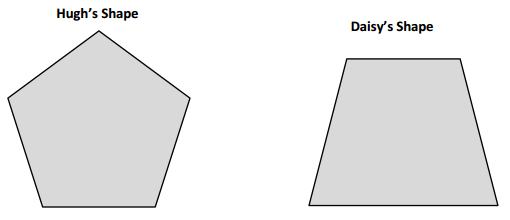
Answer:
Perimeter of ABCDE Hugh’s shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 3cm + 3cm + 3cm + 3cm + 3cm
= 15cm.
Perimeter of FGHI Daisy’s shape =  Side + Side + Side + Side
= FG+ GH+ HI+ IF
=  4cm + 5cm + 4cm + 3cm
= 16cm.
Perimeter of FGHI Daisy’s shape is greater than the Perimeter of ABCDE Hugh’s shape because the  measurement value is greater than the other one’s shape.

Explanation:

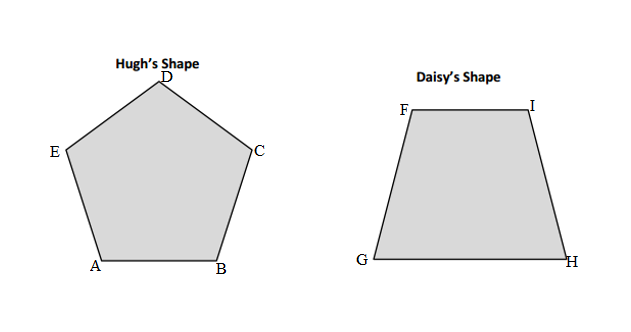
Length of the AB side of ABCDE Hugh’s shape = 3cm
Length of the BC side of ABCDE Hugh’s shape = 3cm
Length of the CD side of ABCDE Hugh’s shape = 3cm
Length of the DE side of ABCDE Hugh’s shape = 3cm
Length of the EA side of ABCDE Hugh’s shape = 3cm
Perimeter of ABCDE Hugh’s shape = Side + Side + Side + Side + Side
= AB + BC + CD + DE + EA
= 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm + 3cm
= 9cm + 3cm + 3cm
= 12cm + 3cm
= 15cm.

Length of the FG side of FGHI Daisy’s shape = 4cm
Length of the GH side of FGHI Daisy’s shape = 5cm
Length of the HI side of FGHI Daisy’s shape = 4cm
Length of the IF side of FGHI Daisy’s shape = 3cm
Perimeter of FGHI Daisy’s shape =  Side + Side + Side + Side
= FG+ GH+ HI+ IF
=  4cm + 5cm + 4cm + 3cm
= 9cm + 4cm +3cm
= 13cm + 3cm
= 16cm.

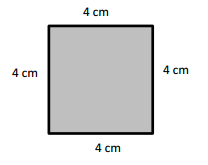
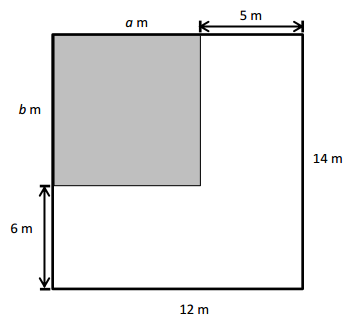
Question 4.
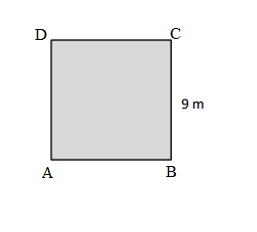
Andrea measures one side length of the square below and says she can find the perimeter with that measurement. Explain Andrea’s thinking. Then, find the perimeter in centimeters.

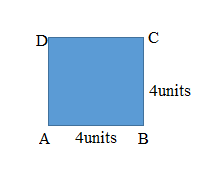
Answer:
Andrea’s figure is a Square. So, her figure’s  all sides are going to be equal. Yes, she is correct in her thinking.
Perimeter of ABCD Andrea’s Square = Side + Side + Side + Side
= 4cm + 4cm + 4cm+ 4cm
= 16cm.

Explanation:

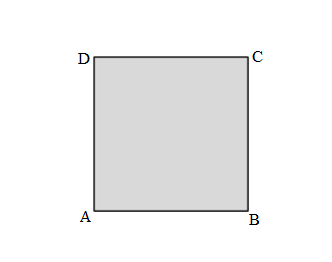
Andrea’s figure is a Square. So, her figure’s  all sides are going to be equal. Yes, she is correct in her thinking, ” measuring one side length of the square below, she can find the perimeter with that measurement.”
Length of AB side of Andrea’s Square = 4cm
Perimeter of ABCD Andrea’s Square = Side + Side + Side + Side
= 4cm + 4cm + 4cm+ 4cm
= 8cm + 4cm + 4cm
=12cm + 4cm
= 16cm.

Eureka Math Grade 3 Module 7 Lesson 12 Exit Ticket Answer Key

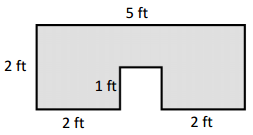
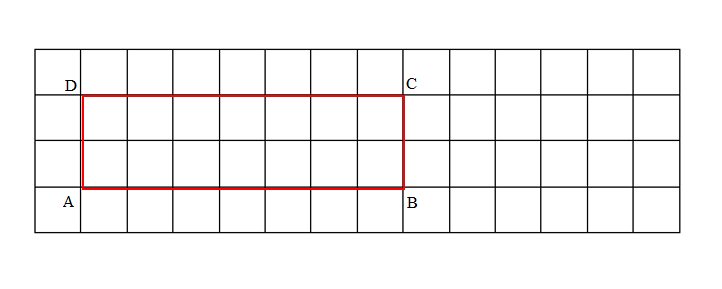
Measure and label the side lengths of the shape below in centimeters. Then, find the perimeter.

Perimeter = __________________________________________
= _______ cm
Answer:
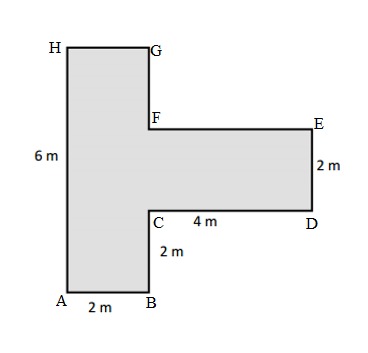
Perimeter of the given ABCDEFGHIJK Shape =  Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC+ CD + DE + EF + FG + GH + HI + IJ + JK +KL + LA
= 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 32cm.

Explanation:

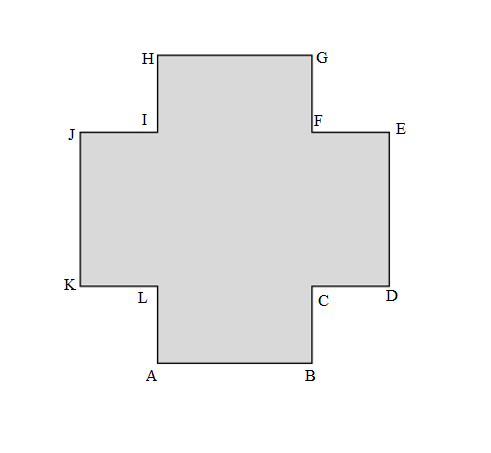
Length of the AB side of the given ABCDEFGHIJK Shape = 4cm
Length of the BC side of the given ABCDEFGHIJK Shape = 2cm
Length of the CD side of the given ABCDEFGHIJK Shape = 2cm
Length of the DE side of the given ABCDEFGHIJK Shape = 4cm
Length of the EF side of the given ABCDEFGHIJK Shape = 2cm
Length of the FG side of the given ABCDEFGHIJK Shape = 2cm
Length of the GH side of the given ABCDEFGHIJK Shape = 4cm
Length of the HI side of the given ABCDEFGHIJK Shape = 2cm
Length of the IJ side of the given ABCDEFGHIJK Shape =  2cm
Length of the JK side of the given ABCDEFGHIJK Shape = 4cm
Length of the KL side of the given ABCDEFGHIJK Shape = 2cm
Length of the LA side of the given ABCDEFGHIJK Shape = 2cm
Perimeter of the given ABCDEFGHIJK Shape =  Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC+ CD + DE + EF + FG + GH + HI + IJ + JK +KL + LA
= 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 6cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 8cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 12cm + 2cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 14cm + 2cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 16cm + 4cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 20 cm + 2cm + 2cm + 4cm + 2cm + 2cm
= 22cm + 2cm + 4cm + 2cm + 2cm
= 24cm + 4cm + 2cm + 2cm
= 28cm + 2cm + 2cm
= 30cm + 2cm
= 32cm.

Eureka Math Grade 3 Module 7 Lesson 12 Homework Answer Key

Question 1.
Measure and label the side lengths of the shapes below in centimeters. Then, find the perimeter of each shape.
a.

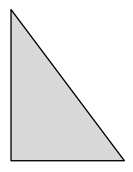
Perimeter = _____cm +_____cm +_____cm
= _______ cm
Answer:
Perimeter of ABC triangle = Side + Side + Side
= AB + BC + CA
= 3cm + 5cm + 4cm
= 12cm.

Explanation:

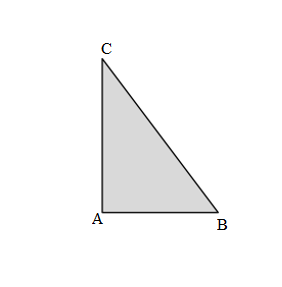
Length of the AB side of ABC triangle = 3cm
Length of the BC side of ABC triangle = 5cm
Length of the CA side of ABC triangle = 4cm
Perimeter of ABC triangle = Side + Side + Side
= AB + BC + CA
= 3cm + 5cm + 4cm
= 8cm + 4cm
= 12cm.

b.

Perimeter = _____________________
= _______ cm
Answer:
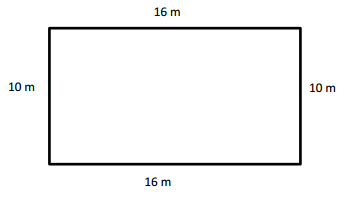
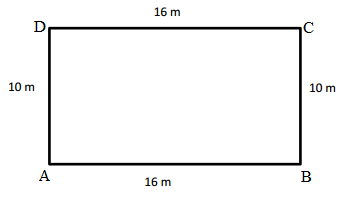
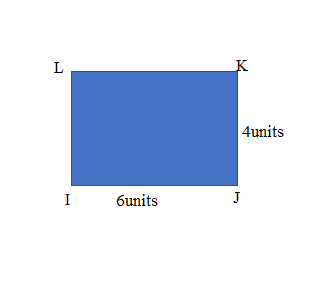
Perimeter of ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 6cm + 4cm + 6cm + 4cm
= 20cm.

Explanation:

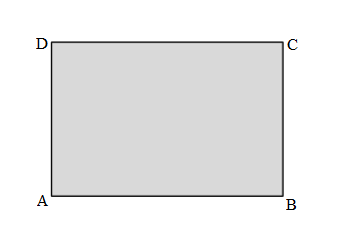
Length of the AB side of ABCD rectangle = 6cm
Length of the BC side of ABCD rectangle = 4cm
Length of the CD side of ABCD rectangle = 6cm
Length of the DA side of ABCD rectangle = 4cm
Perimeter of ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 6cm + 4cm + 6cm + 4cm
= 10cm + 6cm + 4cm
= 16cm + 4cm
= 20cm.

c.

Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the ABCD Quadrilateral = Side + Side + Side + Side
= AB + BC + CD + DA
= 3cm + 4cm + 5cm + 4cm
= 16cm.

Explanation:

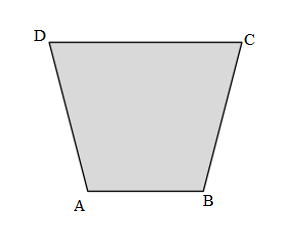
Length of the AB side in the ABCD Quadrilateral = 3cm
Length of the BC side in the ABCD Quadrilateral = 4cm
Length of the CD side in the ABCD Quadrilateral = 5cm
Length of the DA side in the ABCD Quadrilateral = 4cm
Perimeter of the ABCD Quadrilateral = Side + Side + Side + Side
= AB + BC + CD + DA
= 3cm + 4cm + 5cm + 4cm
= 7cm + 5cm + 4cm
= 12cm + 4cm
= 16cm.

d.

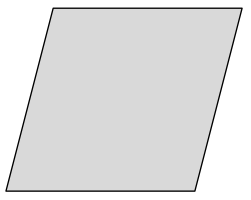
Perimeter = _____________________
= _______ cm
Answer:
Perimeter of the ABCD Parallelogram = Side + Side + Side + Side
= AB + BC + CD + DA
= 5cm + 5cm + 5cm + 5cm
= 20cm.

Explanation:

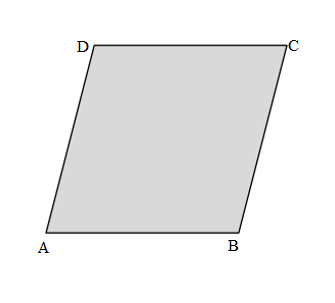
Length of the AB side of the ABCD parallelogram = 5cm
Length of the BC side of the ABCD parallelogram = 5cm
Length of the CD side of the ABCD parallelogram = 5cm
Length of the DA side of the ABCD parallelogram = 5cm
Perimeter of the ABCD Parallelogram = Side + Side + Side + Side
= AB + BC + CD + DA
= 5cm + 5cm + 5cm + 5cm
= 10cm + 5cm + 5cm
= 15cm + 5cm
= 20cm.

e.

Perimeter = _____________________
= _______ cm
Answer:
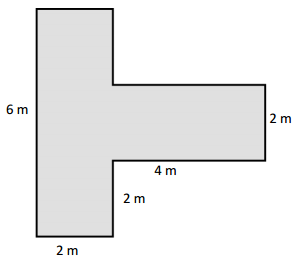
Perimeter of the given ABCDEFGH figure = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH + HA
= 2cm + 2cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 24cm.

Explanation:

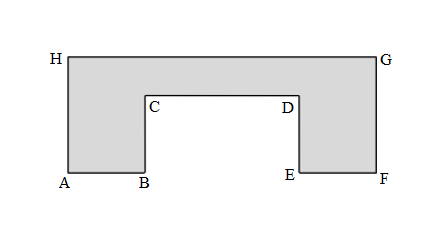
Length of AB side of the given ABCDEFGH figure = 2cm
Length of BC side of the given ABCDEFGH figure = 2cm
Length of CD side of the given ABCDEFGH figure = 3.5cm
Length of DE side of the given ABCDEFGH figure = 2cm
Length of EF side of the given ABCDEFGH figure = 2cm
Length of FG side of the given ABCDEFGH figure = 2.5cm
Length of GH side of the given ABCDEFGH figure = 7.5cm
Length of HA side of the given ABCDEFGH figure = 2.5cm
Perimeter of the given ABCDEFGH figure = Side + Side + Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF + FG + GH + HA
= 2cm + 2cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 4cm + 3.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 7.5cm + 2cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 9.5cm + 2cm + 2.5cm + 7.5cm + 2.5cm
= 11.5cm + 2.5cm + 7.5cm + 2.5cm
= 14cm + 7.5cm + 2.5cm
= 21.5cm + 2.5cm
= 24cm.

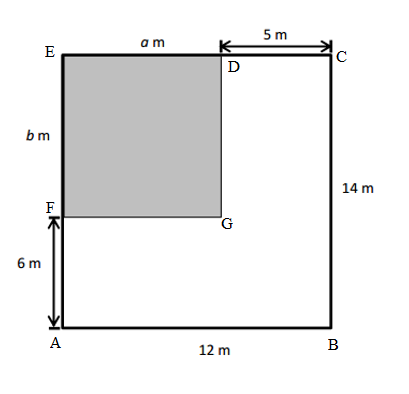
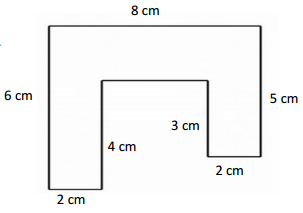
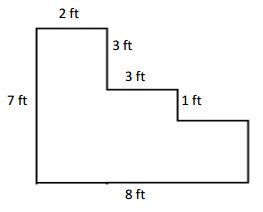
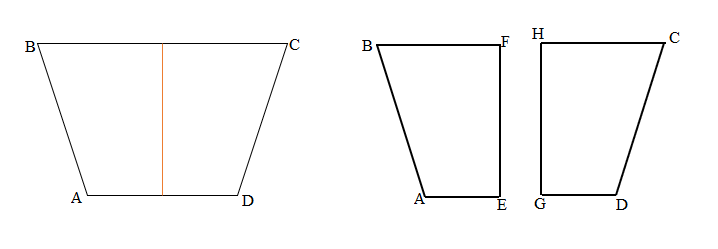
Question 2.
Melinda draws two trapezoids to create the hexagon shown below. Use a ruler to find the side lengths of Melinda’s hexagon in centimeters. Then, find the perimeter.

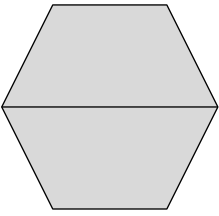
Answer:
Perimeter of ABCDEF Melinda’s hexagon = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF +FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 18cm.

Explanation:

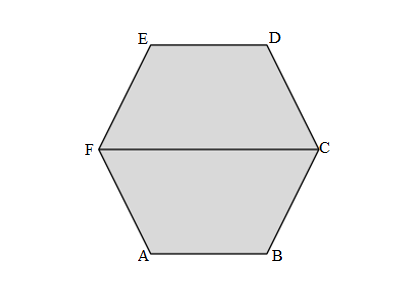
Length of the AB side of ABCDEF Melinda’s hexagon = 3cm
Length of the BC side of ABCDEF Melinda’s hexagon = 3cm
Length of the CD side of ABCDEF Melinda’s hexagon = 3cm
Length of the DE side of ABCDEF Melinda’s hexagon = 3cm
Length of the EF side of ABCDEF Melinda’s hexagon = 3cm
Length of the FA side of ABCDEF Melinda’s hexagon = 3cm
Perimeter of the ABCDEF Melinda’s hexagon = Side + Side + Side + Side + Side + Side
= AB + BC + CD + DE + EF +FA
= 3cm + 3cm + 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm + 3cm + 3cm
= 9cm + 3cm + 3cm + 3cm
= 12cm + 3cm + 3cm
= 15cm + 3cm
= 18cm.

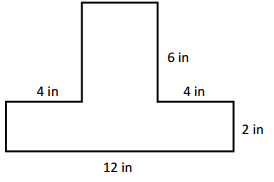
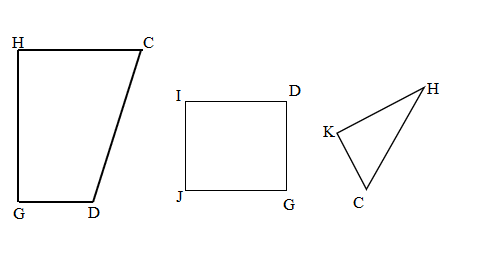
Question 3.
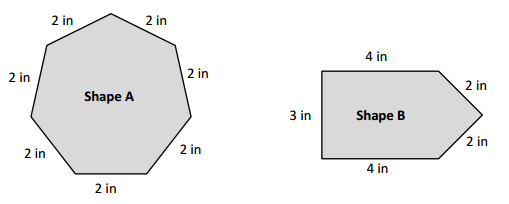
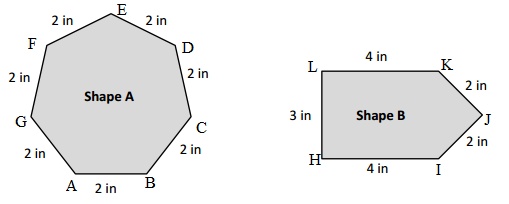
Victoria and Eric draw the shapes shown below. Eric says his shape has a greater perimeter because it has more sides than Victoria’s shape. Is Eric right? Explain your answer.

Answer:
Yes, Eric is correct because DEFG Square has more sides than the ABC Victoria’s triangle shape.
Perimeter of DEFG Eric’s Square shape is greater than the Perimeter of ABC Victoria’s triangle shape.
Perimeter of ABC Victoria’s triangle shape = 12cm

Explanation:

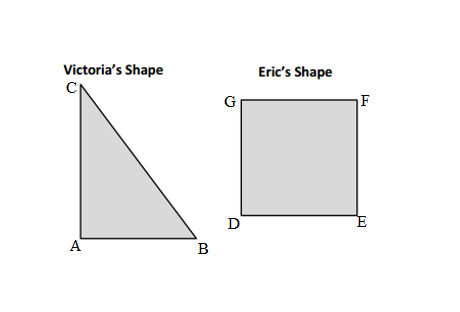
Length of AB Victoria’s triangle shape = 3cm
Length of BC Victoria’s triangle shape = 5cm
Length of CA Victoria’s triangle shape =4cm
Perimeter of ABC Victoria’s triangle shape = Side + Side + Side
= 3cm +  4cm + 5cm
= 7cm + 5cm
= 12cm.

Length of DEFG Eric’s Square shape = 4cm
Perimeter of DEFG Eric’s Square shape = Side × Side
= 4cm × 4cm
= 16cm.
Perimeter of Eric’s Square shape is greater than the Perimeter of Victoria’s triangle shape.

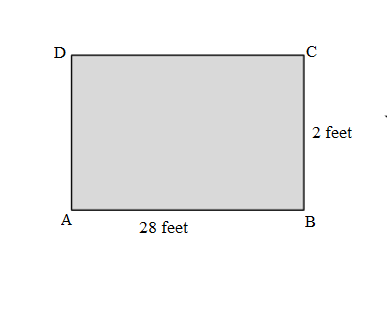
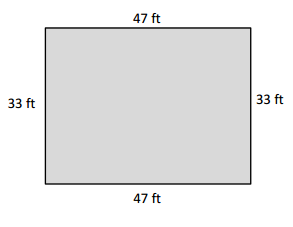
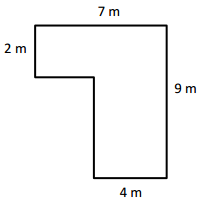
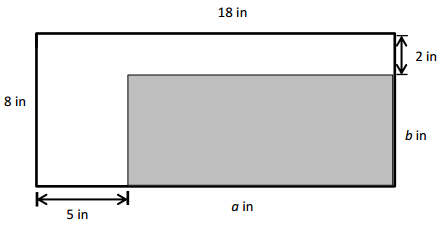
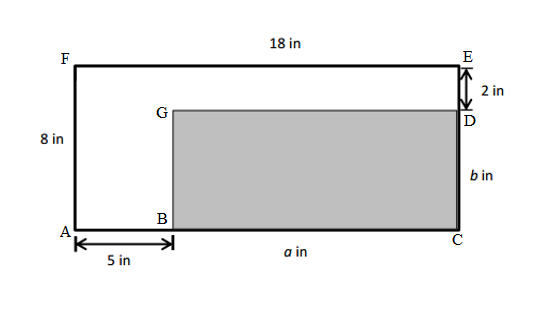
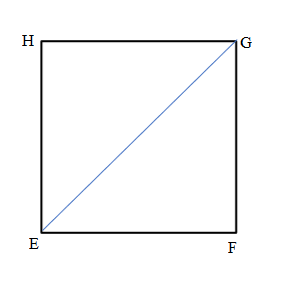
Question 4.
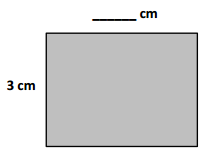
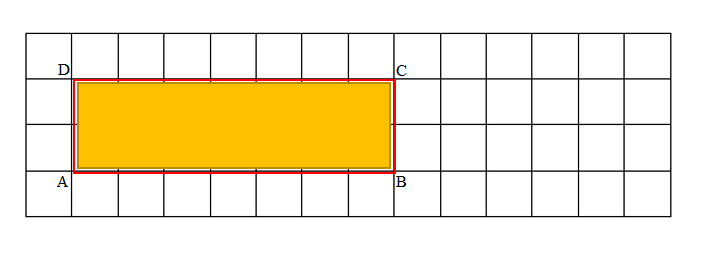
Jamal uses his ruler and a right angle tool to draw the rectangle shown below. He says the perimeter of his rectangle is 32 centimeters. Do you agree with Jamal? Why or why not?

Answer:
NO, I disagree with Jamal. Jamal answer is incorrect because actual Perimeter of his ABCD rectangle is 30cm not 32cm.

Explanation:

Length of the ABCD Rectangle Jamal drawn = 7.5cm
Width of the ABCD Rectangle Jamal drawn = 4cm
Perimeter of ABCD Rectangle Jamal drawn = Length × Width
= 7.5 × 4
= 30 cm.
Jamal answer is incorrect because actual Perimeter of his ABCD rectangle is 30cm not 32cm.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 11 Answer Key

Eureka Math Grade 3 Module 7 Lesson 11 Problem Set Answer Key

Question 1.
Follow the directions below using the shape you created yesterday.
a. Tessellate your shape on a blank piece of paper.
b. Color your tessellation to create a pattern.
c. Outline the perimeter of your tessellation with a highlighter.
d. Use a string to measure the perimeter of your tessellation.
Answer:
a.

b.

c.

d. A string is used to measure the perimeter of the figure.

Explanation:
The figure asked to draw has been drawn considering all the given points to follow while drawing it.

Question 2.
Compare the perimeter of your tessellation to a partner’s. Whose tessellation has a greater perimeter? How do you know?
Answer:
My tessellation has the greater perimeter than my friend’s tessellation perimeter.

Explanation:
My tessellation has the greater perimeter than my friend’s tessellation perimeter because I have compared both the tessellation perimeter with the string. My tessellation string was down that compared to my friend’s tessellation.

Question 3.
How could you increase the perimeter of your tessellation?
Answer:
I could increase the perimeter of my tessellation by tessellating it by adding some more rows to my shape.

Explanation:
I could increase the perimeter of my tessellation by tessellating  more shapes. If I wish to tessellating my figure   I would tesselate by adding some more rows to my shape.

Question 4.
How would overlapping your shape when you tessellated change the perimeter of your tessellation?
Answer:
If I overlap my figure, it wouldn’t  fit together I think. If I overlap my figure, I think the perimeter will decrease of the figure.

Explanation:
Overlapping any figure means covering the figure with same sized figure or different sized figure. If I overlap my figure, I think the perimeter will decrease of my figure that of the overlapped figure.

Eureka Math Grade 3 Module 7 Lesson 11 Exit Ticket Answer Key

Estimate to draw at least four copies of the given regular hexagon to make a new shape, without gaps or overlaps. Outline the perimeter of your new shape with a highlighter. Shade in the area with a colored pencil.

Answer:

Explanation:
The area of the new shape is shaded with Yellow color.
The perimeter of the new shape is highlighted with Red color.

Eureka Math Grade 3 Module 7 Lesson 11 Homework Answer Key

Question 1.
Samson tessellates regular hexagons to make the shape below.

a. Outline the perimeter of Samson’s new shape with a highlighter.
Answer:

Explanation:
Perimeter is the distance around the outside of a shape. Perimeter of the given figure is highlighted in red highlighter.

b. Explain how Samson could use a string to measure the perimeter of his new shape.
Answer:
Samson could use a string to measure the perimeter of his new shape by placing it all-around the outer layer of the new shape.

Explanation:

Perimeter is the distance around the outside of a shape.

c. How many sides does his new shape have?
Answer:
The new shape has 18 or eighteen sides in it.

Explanation:

The sides of the new shape are counted one by one.

d. Shade in the area of his new shape with a colored pencil.
Answer:

Explanation:
The new shape area has be shaded with light blue colored pencil in it.

Question 2.
Estimate to draw at least four copies of the given triangle to make a new shape, without gaps or overlaps. Outline the perimeter of your new shape with a highlighter. Shade in the area with a colored pencil.

Answer:

Explanation:
The Area of the new shape is shaded with light grey colored pencil in it.
The Perimeter of the new shape is highlighted with red color.

Question 3.
The marks on the strings below show the perimeters of Shyla’s and Frank’s shapes. Whose shape has a greater perimeter? How do you know?

Answer:
The perimeter of Frank’s shape is having greater perimeter than Shyla’s shape because the  string measurement of Frank’s shape is lower than the Shyla’s shape string measurement.

Explanation:

The string measurement of Frank’s shape has further crossed  the string measurement of Shyla’s shape.

Question 4.
India and Theo use the same shape to create the tessellations shown below.

a. Estimate to draw the shape India and Theo used to make their tessellations.
Answer:

Explanation:
The shape India and Theo used to make their tessellations is been draw in the figure highlighted in the yellow color.

b. Theo says both tessellations have the same perimeter. Do you think Theo is right? Why or why not?
Answer:
Yes, Theo says correct because the shape used to draw the tessellation of both India and Theo’s are the same.  The number of shapes used by both are the same in their respective own  tessellation yet the position differs one is in vertical presentation and horizontal presentation .

Explanation:

The number of shapes used by both are the same in their respective own  tessellation yet the position differs one is in vertical presentation and horizontal presentation .

Engage NY Eureka Math 3rd Grade Module 7 Lesson 18 Answer Key

Eureka Math Grade 3 Module 7 Lesson 18 Problem Set Answer Key

Question 1.
Use unit squares to build as many rectangles as you can with an area of 24 square units. Shade in squares on your grid paper to represent each rectangle that you made with an area of 24 square units.
a. Estimate to draw and label the side lengths of each rectangle you built in Problem 1. Then, find the perimeter of each rectangle. One rectangle is done for you.

P = 24 units + 1 unit + 24 units + 1 unit = 50 units
b. The areas of the rectangles in part (a) above are all the same. What do you notice about the perimeters?
Answer:
a. Perimeter of ABCD rectangle = 22units.
Perimeter of EFGH rectangle = 28units.
Perimeter of IJKL rectangle = 20units.

b. All rectangles drawn in the above1.a are not the same sided figures. They are not having same perimeters because their lengths are different compared to one another.

Explanation:
a.



Perimeter of ABCD rectangle =  Side + Side + Side + Side
= AB + BC + CD + DA
= 8units + 3units + 8units + 3units
= 11units + 8units + 3units
= 19units + 3units
= 22units.
Perimeter of EFGH rectangle = Side + Side + Side + Side
= EF + FG + GH + HE
= 12units + 2units + 12units + 2units
= 14units + 12units + 2units
= 26units + 2units
= 28units.
Perimeter of IJKL rectangle = Side + Side + Side + Side
= IJ + JK + KL + KI
= 6units + 4 units + 6units + 4 units
= 10units + 6units + 4units
= 16units + 4units
= 20units.

b. All rectangles drawn in the above1a are not the same figures. They are not having same perimeters.

Question 2.
Use unit square tiles to build as many rectangles as you can with an area of 16 square units. Estimate to draw each rectangle below. Label the side lengths.
a. Find the perimeters of the rectangles you built.
b. What is the perimeter of the square? Explain how you found your answer.
Answer:
a. Perimeter of OPQR Rectangle = 14units.
Perimeter of EFGH Rectangle = 34units.

b. Perimeter of ABCD Square= 16units. As, the sides in a square are equal, we can multiple the number of sides into the side value to get the Perimeter of square instead of adding them separately.

Explanation:
a.


Perimeter of OPQR Rectangle = Side + Side + Side + Side
= OP + PQ + QR + RO
= 5units + 2units + 5units + 2units
= 7units + 5units + 2units
= 12units + 2units
= 14units.
Perimeter of EFGH Rectangle = Side + Side + Side + Side
= EF + FG+ GH + HE
= 16units + 1unit + 16units + 1unit
= 17units + 16units + 1unit
= 33units + 1unit
= 34unit.

b.

Perimeter of ABCD Square= 4 × Side
= 4 × 4units
= 16units.

Question 3.
Doug uses square unit tiles to build rectangles with an area of 15 square units. He draws the rectangles as shown below but forgets to label the side lengths. Doug says that Rectangle A has a greater perimeter than Rectangle B. Do you agree? Why or why not?

Answer:
Yes, Doug is correct, the perimeter of rectangle A is greater than the perimeter of the rectangle B because in the appearance itself we notice that rectangle A is bigger in size than that of rectangle B.

Explanation:

Well, comparing the rectangles drawn by Doug its easy to say rectangle A is going to have the greater perimeter that compared to the perimeter of the rectangle B because the size of the rectangle A is bigger than that of rectangle B.

Eureka Math Grade 3 Module 7 Lesson 18 Exit Ticket Answer Key

Tessa uses square-centimeter tiles to build rectangles with an area of 12 square centimeters. She draws the rectangles as shown below. Label the unknown side lengths of each rectangle. Then, find the perimeter of each rectangle.

P = _____

P = _____

P = _____
Answer:
Perimeter of the ABCD Rectangle = 26cm.
Perimeter of the EFGH Rectangle = 12cm.
Perimeter of the IJKL Rectangle = 16cm.

Explanation:

The unknown side are measured by using a ruler by me.
Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 12cm + 1cm + 12cm + 1cm
= 13cm + 12cm + 1cm
= 25cm + 1cm
= 26cm.
Perimeter of the EFGH Rectangle = Side + Side + Side + Side
= EF + FG + GH+ HE
= 3cm + 3cm + 3cm + 3cm
= 6cm + 3cm + 3cm
= 9cm + 3cm
= 12cm.
Perimeter of the IJKL Rectangle = Side + Side + Side + Side
IJ + JK + KL + KI
= 6cm + 2cm + 6cm + 2cm
= 8cm + 6cm + 2cm
= 14cm + 2cm
= 16cm.

Eureka Math Grade 3 Module 7 Lesson 18 Homework Answer Key

Question 1.
Shade in squares on the grid below to create as many rectangles as you can with an area of 18 square centimeters.

Answer:
ABCD rectangle
EFGH rectangle
IJKL rectangle.

Explanation:

Question 2.
Find the perimeter of each rectangle in Problem 1 above.
Answer:
Perimeter of the ABCD rectangle = 20units.
Perimeter of the EFGH rectangle = 12units.
Perimeter of the IJKL rectangle = 18units.

Explanation:

Perimeter of the ABCD rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 8units + 2units + 8units + 2units
= 10units + 8units + 2units
= 18units + 2units
= 20units.
Perimeter of the EFGH rectangle = Side + Side + Side + Side
= EF + FG + GH+ HE
= 4units + 2units + 4units + 2units
= 6units + 4units + 2units
= 10units + 2units
= 12units.
Perimeter of the IJKL rectangle = Side + Side + Side + Side
= IJ + JK + KL + LI
=  5units + 4units + 5units + 4units
= 9units + 5units + 4units
= 14units + 4units
= 18units.

Question 3.
Estimate to draw as many rectangles as you can with an area of 20 square centimeters. Label the side lengths of each rectangle.
a. Which rectangle above has the greatest perimeter? How do you know just by looking at its shape?
b. Which rectangle above has the smallest perimeter? How do you know just by looking at its shape?
Answer:
a. Among all the three rectangles drawn, through looks  IJKL Rectangles is having greater perimeter compared to other rectangles. We can say that by seeing the length of the rectangles, which length is high that going to have greater perimeter.

b. Among all the three rectangles drawn, through looks  EFGH Rectangles is having smallest perimeter compared to other rectangles. We can say that by seeing the length of the rectangles.

Explanation:
a.

Perimeter of the ABCD Rectangle = Side + Side + Side + Side
= AB + BC + CD + DA
= 7units + 4units + 7units + 4units
= 11units + 7units + 4units
= 18units + 4units
= 22units.
Perimeter of the EFGH Rectangle = Side + Side + Side + Side
= EF + FG + GH + HE
= 5units + 3units + 5units + 3units
= 8units + 5units + 3units
= 13units + 3units
= 16units.
Perimeter of the IJKL Rectangle = Side + Side + Side + Side
= IJ + JK + KL + LI
= 11units + 2units + 11units + 2units
= 13units + 11units + 2units
= 24units + 2units
= 26 units.

b. Among all the three rectangles drawn, through looks  EFGH Rectangles is having smallest perimeter compared to other rectangles. We can say that by seeing the length of the rectangles, which length is small that going to have smallest perimeter.

Engage NY Eureka Math 3rd Grade Module 7 Mid Module Assessment Answer Key

Eureka Math Grade 3 Module 7 Mid Module Assessment Task Answer Key

Question 1.
Three shapes are shown below.
a. Circle the shape(s) with only one pair of parallel sides.
b. Cross out the shape(s) with two pairs of parallel sides.

c. Which of the three shapes are quadrilaterals? Explain how you know.
Answer:

Question 2.
Use your ruler and right angle tool to draw the following shapes.
a. Draw and name a shape with four right angles.
b. Draw a four-sided shape with no right angles and no equal sides. Label the side lengths.
c. Draw triangles to create a rhombus. Label the side lengths.
Answer:

Question 3.
Mr. Cooper builds a fence to make a rectangular horse stall. The stall is 5 meters long and 7 meters wide. How many meters of fence does Mr. Cooper use? Draw a picture and write an equation to show your thinking.
Answer:

Question 4.
Jamal wants to put wood trim around his rectangular bedroom and square closet. His bedroom is 10 feet wide and 8 feet long. His closet is 3 feet wide and 3 feet long.

a. Wood trim is sold by the foot. How many feet of wood trim does Jamal need to go around his bedroom and closet? Show your work.
b. How much more wood trim does Jamal need for his bedroom than his closet? Write and solve an equation. Use a letter to represent the unknown.
Answer:

Question 5.
The figure below is composed of rectangles. Use the picture and the descriptions to find the perimeter of the shape. Show your work.
Each side labeled with A is 6 inches.
Each side labeled with B is 3 inches.
Each side labeled with C is 8 inches.

Answer:

Question 6.
Mrs. Gomez builds a fence around her backyard. Her plan shows the fence as a dotted line below.

Together, the garage and backyard make a rectangle. The fence goes only where there is a dotted line. How many feet of fence does Mrs. Gomez need to build? Show your work.
Answer:

Engage NY Eureka Math 3rd Grade Module 7 Lesson 17 Answer Key

Eureka Math Grade 3 Module 7 Lesson 17 Problem Set Answer Key

Question 1.
The shapes below are made up of rectangles. Label the unknown side lengths. Then, write and solve an equation to find the perimeter of each shape.
a.

P =
Answer:
Perimeter of the given figure = 16 cm.

Explanation:

Length of the side AB in the given figure = 4 cm
Length of the side BC in the given figure = 2 cm
Length of the side CD in the given figure = 2 cm
Length of the side ED in the given figure = 1 cm
Length of the side EF in the given figure = 2 cm
Length of the side FA in the given figure = 3 cm
Length of the side GD in the given figure = 2 cm
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side ED + Length of the side EF + Length of the side FA + Length of the side GD
= 4 cm + 2 cm + 2 cm + 1 cm + 2 cm + 3 cm + 2cm
= 6 cm + 2 cm + 1 cm + 2 cm + 3 cm + 2cm
= 8 cm + 1 cm + 2 cm + 3 cm + 2cm
= 9 cm + 2 cm + 3 cm + 2cm
= 11 cm + 3 cm + 2cm
= 14 cm + 2 cm
= 16 cm.

b.

P =
Answer:
Perimeter of the given figure = 16ft.

Explanation:

Length of the side AB in the given figure = 2ft
Length of the side BC in the given figure = 1ft
Length of the side CD in the given figure = 1ft
Length of the side DE in the given figure = 1ft
Length of the side EF in the given figure = 2ft
Length of the side GF in the given figure = 2ft
Length of the side GH in the given figure = 5ft
Length of the side HA in the given figure = 2ft
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side GF + Length of the side GH + Length of the side HA
= 2ft + 1ft + 1ft + 1ft  + 2ft + 2ft+ 5ft + 2ft
= 3ft + 1ft + 1ft  + 2ft + 2ft+ 5ft + 2ft
= 4ft + 1ft  + 2ft + 2ft+ 5ft + 2ft
= 5ft + 2ft + 2ft+ 5ft + 2ft
= 7ft + 2ft + 5ft + 2ft
= 9ft + 5ft + 2ft
= 14ft + 2ft
= 16ft.

c.

P =
Answer:
Perimeter of the given figure = 24m.

Explanation:

Length of the side AB in the given figure = 2m
Length of the side BC in the given figure = 2m
Length of the side CD in the given figure = 4m
Length of the side DE in the given figure = 2m
Length of the side EF in the given figure = 4m
Length of the side GF in the given figure = 2m
Length of the side GH in the given figure = 2m
Length of the side HA in the given figure = 6m
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side GF + Length of the side GH + Length of the side HA
= 2m + 2m + 4m + 2m + 4m + 2m + 2m + 6m
= 4m + 4m + 2m + 4m + 2m + 2m + 6m
= 8m + 2m + 4m + 2m + 2m + 6m
= 10m + 4m + 2m + 2m + 6m
= 14m + 2m + 2m + 6m
= 16m + 2m + 6m
= 18m + 6m
= 24m.

d.

P =
Answer:
Perimeter of the given figure = 26yd.

Explanation:

Length of the side AB in the given figure = 7yd
Length of the side BC in the given figure = 2yd
Length of the side CD in the given figure = 2yd
Length of the side DE in the given figure = 4yd
Length of the side EF in the given figure = 2yd
Length of the side FG in the given figure = 2yd
Length of the side GH in the given figure = 1yd
Length of the side HI in the given figure = 2yd
Length of the side IJ in the given figure = 2yd
Length of the side JA in the given figure = 2yd
Perimeter of the given figure = Length of the side AB + Length of the side BC + Length of the side CD + Length of the side DE + Length of the side EF + Length of the side FG + Length of the side GH + Length of the side HI + Length of the side IJ + Length of the side JA
= 7yd + 2yd + 2yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 9yd + 2yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 11yd + 4yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 15yd + 2yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 17yd + 2yd + 1yd + 2yd + 2yd + 2yd
= 19yd + 1yd + 2yd + 2yd + 2yd
= 20yd + 2yd + 2yd + 2yd
= 22yd + 2yd + 2yd
= 24yd + 2yd
= 26yd.

Question 2.
Nathan draws and labels the square and rectangle below. Find the perimeter of the new shape.

Answer:
Perimeter of the  ACDF  new shape = 48cm.

Explanation:

Length of the side of AB in the given figure = 6cm
Length of the side of BC in the given figure = 12cm
Length of the side of CD in the given figure = 6cm
Length of the side of DE in the given figure = 12cm
Length of the side of EF in the given figure = 6cm
Length of the side of FA in the given figure = 6cm
Perimeter of the ACDF new shape = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FA
= 6cm + 12cm + 6cm + 12cm + 6cm + 6cm
= 18cm + 6cm + 12cm + 6cm + 6cm
= 24cm + 12cm + 6cm + 6cm
= 36cm + 6cm + 6cm
= 42cm + 6cm
= 48cm.

Question 3.
Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.

Answer:
Perimeter of the DFGC shaded rectangle = 26in.

Explanation:

Shaded rectangle = DFGC
Length of the side of AB of the given figure  = 16in
Length of the side of BG of the given figure = 2in
Length of the side of GC of the given figure = EA – BG = 7in – 2in = 5in.
Length of the side of CD of the given figure= AB – DE = 16in – 8in = 8in.
Length of the side of DE of the given figure= 8in
Length of the side of EA of the given figure= 7in
Length of the side of DF of the given figure= 5in
Length of the side of FG of the given figure= 8in
Perimeter of the DFGC shaded rectangle = Length of the side of FG + Length of the side of GC + Length of the side of CD + Length of the side of DF
= 8in + 5in + 8in + 5in
= 13in + 8in + 5in
= 21in + 5in
= 26in.

Eureka Math 3rd Grade Module 7 Lesson 17 Exit Ticket Answer Key

Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.

Answer:
Perimeter of the FGDE shaded rectangle = 30m.

Explanation:

Shaded rectangle = FGDE
Length of the side AB in the given figure = 12m
Length of the side BC in the given figure = 14m
Length of the side CD in the given figure = 5m
Length of the side DE in the given figure = AB – CD = 12m – 5m = 7m.
Length of the side EF in the given figure = BC – FA = 14m – 6m = 8m.
Length of the side FA in the given figure = 6m
Length of the side FG in the given figure = 7m
Length of the side GD in the given figure = 8m
Perimeter of the FGDE shaded rectangle = Length of the side FG  + Length of the side GD + Length of the side DE + Length of the side EF
= 7m + 8m + 7m + 8m
= 15m + 7m + 8m
= 22m + 8m
= 30m.

Eureka Math Grade 3 Module 7 Lesson 17 Homework Answer Key

Question 1.
The shapes below are made up of rectangles. Label the unknown side lengths. Then, write and solve an equation to find the perimeter of each shape.
a.

P =
Answer:
Perimeter of the given figure = 32m.

Explanation:

Length of the side of AB in the given figure = 4m
Length of the side of BC in the given figure = 9m
Length of the side of CD in the given figure = 7m
Length of the side of DE in the given figure = 2m
Length of the side of EF in the given figure = 3m
Length of the side of FA in the given figure = 7m
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FA
= 4m + 9m + 7m + 2m + 3m + 7m
= 13m + 7m + 2m + 3m + 7m
= 20m + 2m + 3m + 7m
= 22m + 3m + 7m
= 25m + 7m
= 32m.

b.

P =
Answer:
Perimeter of the given figure = 34 cm.

Explanation:

Length of the side of AB in the given figure = 2 cm
Length of the side of BC in the given figure = 4 cm
Length of the side of CD in the given figure = 4 cm
Length of the side of DE in the given figure = 3 cm
Length of the side of EF in the given figure = 2 cm
Length of the side of FG in the given figure = 5 cm
Length of the side of GH in the given figure = 8 cm
Length of the side of HA in the given figure = 6 cm
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 2 cm + 4 cm + 4 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 6 cm + 4 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 10 cm + 3 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 13 cm + 2 cm + 5 cm + 8 cm + 6 cm
= 15 cm + 5 cm + 8 cm + 6 cm
= 20 cm + 8 cm + 6 cm
= 28 cm + 6 cm
= 34 cm.

c.

P =
Answer:
Perimeter of the given figure = 40in.

Explanation:

Length of the side of AB in the given figure = 12in
Length of the side of BC in the given figure = 2in
Length of the side of CD in the given figure = 4in
Length of the side of DE in the given figure = 6in
Length of the side of EF in the given figure = 4in
Length of the side of FG in the given figure = 6in
Length of the side of GH in the given figure = 4in
Length of the side of HA in the given figure = 2in
Perimeter of the given figure = Length of the side of AB  + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 12in + 2in + 4in + 6in + 4in + 6in + 4in + 2in
= 14in + 4in + 6in + 4in + 6in + 4in + 2in
= 18in + 6in + 4in + 6in + 4in + 2in
= 24in + 4in + 6in + 4in + 2in
= 28in + 6in + 4in + 2in
= 34in + 4in + 2in
= 38in + 2in
= 40in.

d.

P =
Answer:
Perimeter of the given figure = 30ft.

Explanation:

Length of the side of AB in the given figure = 8ft
Length of the side of BC in the given figure = 3ft
Length of the side of CD in the given figure = 3ft
Length of the side of DE in the given figure = 1ft
Length of the side of EF in the given figure = 3ft
Length of the side of FG in the given figure = 3ft
Length of the side of GH in the given figure = 2ft
Length of the side of HA in the given figure = 7ft
Perimeter of the given figure = Length of the side of AB + Length of the side of BC + Length of the side of CD  + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 8ft + 3ft + 3ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 11ft + 3ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 14ft + 1ft + 3ft + 3ft + 2ft + 7ft
= 15ft + 3ft + 3ft + 2ft + 7ft
= 18ft + 3ft + 2ft + 7ft
= 21ft + 2ft + 7ft
= 23ft + 7ft
= 30ft.

Question 2.
Sari draws and labels the squares and rectangle below. Find the perimeter of the new shape.

Answer:
Perimeter of the new shape = 72cm.

Explanation:

Length of the side of AB in the given figure = 6cm
Length of the side of BC in the given figure = 18cm
Length of the side of CD in the given figure = 6cm
Length of the side of DE in the given figure = 6cm
Length of the side of EF in the given figure = 6cm
Length of the side of FG in the given figure = 18cm
Length of the side of GH in the given figure = 6cm
Length of the side of HA in the given figure = 6cm
Perimeter of the new shape = Length of the side of AB + Length of the side of BC + Length of the side of CD + Length of the side of DE + Length of the side of EF + Length of the side of FG + Length of the side of GH + Length of the side of HA
= 6cm + 18cm + 6cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 24cm + 6cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 30cm + 6cm + 6cm + 18cm + 6cm + 6cm
= 36cm + 6cm + 18cm + 6cm + 6cm
= 42cm + 18cm + 6cm + 6cm
= 60cm + 6cm + 6cm
= 66cm + 6cm
= 72cm.

Question 3.
Label the unknown side lengths. Then, find the perimeter of the shaded rectangle.

Answer:
Perimeter of the shaded rectangle = 37in.

Explanation:

Shaded rectangle =  BCDG
Length of the side of AB in the given figure = 5in
Length of the side of BC in the given figure =  EF – AB = 18in – 5in = 13in
Length of the side of CD in the given figure = FA – DE = 8in – 2in = 6in
Length of the side of DE in the given figure = 2in
Length of the side of EF in the given figure = 18in
Length of the side of FA in the given figure = 8in
Length of the side of GB in the given figure = 6in
Length of the side of GD in the given figure = 13in
Perimeter of the shaded rectangle = Length of the side of BC+ Length of the side of CD + Length of the side of GD + Length of the side of GB
= 13in + 6in + 13in + 6in
= 19in + 13in + 6in
= 31in + 6in
= 37in.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 16 Answer Key

Eureka Math Grade 3 Module 7 Lesson 16 Pattern Sheet Answer Key

Multiply.

multiply by 9 (6–10)
Answer:

Explanation:
9 × 5 = 45
9 × 6 = 54
9 × 7 = 63
9 × 8 = 72
9 × 9 = 81
9 × 10 = 90.

Eureka Math Grade 3 Module 7 Lesson 16 Problem Set Answer Key

Question 1.
Find the perimeter of 10 circular objects to the nearest quarter inch using string. Record the name and perimeter of each object in the chart below.

a. Explain the steps you used to find the perimeter of the circular objects in the chart above.

Answer:
Step 1: Took a string and wrapped around the object.
Step 2: Marked the string met.
Step 3: Measured the length of the string.

Explanation:
First I rolled the String around the object. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string.

b. Could the same process be used to find the perimeter of the shape below? Why or why not?

Answer: Yes, the same steps would be followed to find the perimeter of the given shape because I use the string to find the perimeter.

Explanation:
The same steps would be followed to find the perimeter of the given shape because I use the string to find the perimeter. First I rolled the String around the object. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string.

Question 2.
Can you find the perimeter of the shape below using just your ruler? Explain your answer.

Answer:
No, I cant find the perimeter of this given shape because it got curve line in it as which a ruler cant measure it.

Explanation:
A tool used to rule straight lines and measure distances is called as ruler.
No, I cant find the perimeter of this given shape because it got curve line in it as a ruler measures only straight lines.

Question 3.
Molly says the perimeter of the shape below is 6 \(\frac{1}{4}\) inches. Use your string to check her work. Do you agree with her? Why or why not?

Answer:
No, she is not correct has I have used my string and found the perimeter of the shape as 5 \(\frac{3}{4}\) inches.

Explanation:
Molly says the perimeter of the shape below is 6 \(\frac{1}{4}\) inches.
No, she is not correct has I have used my string and found the perimeter of the shape as 5 \(\frac{3}{4}\) inches.

Question 4.
Is the process you used to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle? Why or why not?
Answer:
No, I don’t think this process to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle, because I can just use a ruler to measure length of the straight lines.

Explanation:
No, I don’t think this process to find the perimeter of a circular object an efficient method to find the perimeter of a rectangle. A ruler is used to find the lengths of the straight lines which help in finding the perimeter of the shape.

Eureka Math Grade 3 Module 7 Lesson 16 Exit Ticket Answer Key

Use your string to the find the perimeter of the shape below to the nearest quarter inch.

Answer:
The perimeter of this circular shape is 26 3/4 inches.

Explanation:
I used my string to measure this circular shape. The perimeter of this circular shape is 26 3/4 inches.

Eureka Math Grade 3 Module 7 Lesson 16 Homework Answer Key

Question 1.
a. Find the perimeter of 5 circular objects from home to the nearest quarter inch using string. Record the name and perimeter of each object in the chart below.

b. Explain the steps you used to find the perimeter of the circular objects in the chart above.
Answer:
Well, as previously discussed I have used a string to measure the perimeter of the circular shapes. I wrapped string around the circular bodies and  noted the values where they met. Later I have used a ruler to measured the values.

Explanation:
Used string to measure the perimeter of the circular shapes. I wrapped string around the circular bodies and  noted the values where they met. Later I have used a ruler to measured the values.

Question 2.
Use your string and ruler to find the perimeter of the two shapes below to the nearest quarter inch.

a. Which shape has a greater perimeter?
b. Find the difference between the two perimeters.

Answer:
a. The perimeter of the given shape B is greater by 3inches than The perimeter of the given shape A.
b. The perimeter of the shape B given using string – The perimeter of the shape A given using string
= 17 1/4 inches – 14 1/4 inches
= 3 inches

Explanation:
a. The perimeter of the given shape A using string = 14 1/4 inches.
The perimeter of the given shape B using string = 17 1/4 inches.

b. Difference:
The perimeter of the shape  B given using string – The perimeter of the shape  A given using string
= 17 1/4 inches – 14 1/4 inches
= 3 inches.

Question 3.
Describe the steps you took to find the perimeter of the objects in Problem 2. Would you use this method to find the perimeter of a square? Explain why or why not.
Answer:
Step 1: Took a string and wrapped around the given shape A.
Step 2: Marked the string met.
Step 3: Measured the length of the string using ruler.
Step 4: Took a string and wrapped around the given shape B.
Step 5: Marked the string met.
Step 6: Measured the length of the string using ruler.

No, I cant use this process of finding perimeter for Square because Square’s perimeter can be found easily using ruler directly. For finding the perimeter of circular shapes we use string n later the ruler.

Explanation:
First I rolled the String around the given shape A. Later, I marked the string met. Afterwards, I took a ruler to measure the length of the string. same I did with the given  shape B.

For finding the perimeter of circular shapes we use string n later the ruler, to know their measurement value.  Square is a straight line shape, we can use ruler directly to find its perimeter no need of string.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 10 Answer Key

Eureka Math Grade 3 Module 7 Lesson 10 Pattern Sheet Answer Key

Multiply

multiply by 7 (1–5)
Answer:

Explanation:
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35.

Eureka Math Grade 3 Module 7 Lesson 10 Problem Set Answer Key

Question 1.
Use a 2-inch square to answer the questions below.
a. Trace the square in the space below with a red crayon.

Answer:

Explanation:
ABCD is a Square of having side as 2cm each.

b. Trace the new shape you made with the square in the space below with a red crayon.
Answer:

Explanation:
ABCD is a square transformed into a new shape with red crayon.

c. Which shape has a greater perimeter? How do you know?
Answer:
My new shape has a greater perimeter than the square because when I used my string to mark the both perimeters of the shapes, new shape was down the string.

Explanation:
My new shape has a greater perimeter than the square because when I used my string to mark the both perimeters of the shapes, new shape was down the string. So, new shape perimeter is greater than the square.

d. Color the inside of the shapes in Problem 1 (a) and (b) with a blue crayon.
Answer:

Explanation:
First, shape is square.
Second, shape is the new shape.

e. Which color represents the perimeters of the shapes? How do you know?
Answer:
Red color represents the Perimeter of the square.

Explanation:
The perimeter of a square is the length that its boundary covers. The perimeter of a square is obtained by adding all the sides together.

f. What does the other color represent? How do you know?
Answer:
Blue color represents the Area of the square.
Red color represents the Perimeter of the square.

Explanation:
The area is defined as the region occupied inside the boundary of a flat object or 2d figure.
Area of the square = Side × Side.
The perimeter of a square is the length that its boundary covers. The perimeter of a square is obtained by adding all the sides together.
Perimeter of the square = 4 × side.

g. Which shape has a greater area? How do you know?
Answer:
Neither, shape has greater area because the look of the shape of the square has been changed not the area.

Explanation:
Neither shapes have the greater area among themselves. the look of the square has just changed yet not the area.

Question 2.
a. Outline the perimeter of the shapes below with a red crayon.

Answer:

Explanation:
Rhombus ABCD, Triangle EFG, Parallelogram HIJK shapes are outlined the perimeter with red crayon.

b. Explain how you know you outlined the perimeters of the shapes above.
Answer:
The perimeter of any figure is the length that its boundary covers.

Explanation:

Question 3.
Outline the perimeter of this piece of paper with a highlighter.
Answer:

Explanation:
The Perimeter of this all figures is highlighted with a light blue crayon.

Eureka Math Grade 3 Module 7 Lesson 10 Exit Ticket Answer Key

Jason paints the outside edges of a rectangle purple. Celeste paints the inside of the rectangle yellow.
Question 1.
Use your crayons to color the rectangle that Jason and Celeste painted.

Answer:

Explanation:
ABCD is a rectangle.
Jason paints the outside edges of a rectangle purple. Celeste paints the inside of the rectangle yellow.

Question 2.
Which color represents the perimeter of the rectangle? How do you know?
Answer:
Purple Color represents the perimeter of the rectangle because it is the boundary color of the rectangle.

Explanation:

The perimeter of any figure is the length that its boundary covers.

Eureka Math Grade 3 Module 7 Lesson 10 Homework Answer Key

Question 1.
Trace the perimeter of the shapes below.

a. Explain how you know you traced the perimeters of the shapes above.

Answer:
The perimeter of any figure is the length that its boundary covers. The color used to trace the perimeter of the figures is Red color.

Explanation:

b. Explain how you could use a string to figure out which shape above has the greatest perimeter.
Answer:
Perimeter of any figure is calculated by adding its all sides. Place the string on all the sides of each figure and later add all sides of each figure to calculate the Perimeter of the figures to know which above figure as the greatest perimeter among all.

Explanation:
The perimeter of any figure is the length that its boundary covers.
Perimeter of any figure is calculated by adding its all sides.

Question 2.
Draw a rectangle on the grid below.

a. Trace the perimeter of the rectangle.

Answer:

Explanation:
ABCD is the rectangle drawn in the grid.
The perimeter of any figure is the length that its boundary covers.

b. Shade the area of the rectangle.

Answer:

Explanation:
The area is defined as the region occupied inside the boundary of a flat object or 2d figure.
Area of the rectangle is the inside part, which is shaded with yellow color.

c. How is the perimeter of the rectangle different from the area of the rectangle?
Answer:
The perimeter and the Area of the rectangle are two different topics.
They have different units for perimeter and area. The perimeter has the same units as its the length of the sides whereas the area’s unit are squared.

Explanation:
The perimeter is the length of the outline of a shape. To find the perimeter of a rectangle, you have to add the lengths of all the four sides.
Perimeter of the rectangle = 2(Length + Width) = 2(L + W)

The area is measurement of the surface of a shape. To find the area of a rectangle  you need to multiply the length and the width of a rectangle.
Area of the rectangle = Length × Width = L × W.

Question 3.
Maya draws the shape shown below. Noah colors the inside of Maya’s shape as shown. Noah says he colored the perimeter of Maya’s shape. Maya says Noah colored the area of her shape. Who is right? Explain your answer.

Answer:
Maya is  correct not Noah because she colored inside part of the figure, which is area not perimeter.

Explanation:
The area is defined as the region occupied inside the boundary of a flat object or 2d figure.
Area of the figure is the inside color, which Noah colored.
The perimeter of a figure is the length that its boundary covers.
Perimeter of the figure is the boundaries.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 9 Answer Key

Eureka Math Grade 3 Module 7 Lesson 9 Pattern Sheet Answer Key

Multiply.

multiply by 6 (6─10)
Answer:

Explanation:
6 × 5 = 30
6 × 6 = 36
6 × 7 = 42
6 × 8 = 48
6 × 9 = 54
6 × 10 = 60

Eureka Math Grade 3 Module 7 Lesson 9 Problem Set Answer Key

Question 1.
Use at least two tangram pieces to make and draw two of each of the following shapes. Draw lines to show where the tangram pieces meet.
a. A rectangle that does not have all equal sides.
Answer:

Explanation:
ABCD is an rectangle of different length size sides, folded half pointing EF.
After folding, they meet at BGC.

b. A triangle.
Answer:

Explanation:
ABC is a triangle, folded half pointing D.
After the folding EF is where they meet.

c. A parallelogram.
Answer:

Explanation:
ABCD is a parallelogram, half folded.
After folding, at BE and FD they meet.

d. A trapezoid.
Answer:

Explanation:
ABCD is a trapezium, folded at CE.
After the folding, they meet at BF and CG.

Question 2.
Use your two smallest triangles to create a square, a parallelogram, and a triangle. Show how you created them below.
Answer:

Explanation:
ABCD  is a square formed by joining two small triangles.
EFGH is a parallelogram formed by joining two small triangles.
IJK is a triangle formed by joining two small triangles.

Question 3.
Create your own shape on a separate sheet of paper using all seven pieces. Describe its attributes below.
Answer:

Explanation:
The figure which I have drawn using the seven pieces is having six sides known as a Hexagon. It has a pair of parallel sides. My figure does not have any right angles in it. It is not a regular hexagon because it does not have any equal sides in it.

Question 4.
Trade your outline with a partner to see if you can re-create her shape using your tangram pieces. Reflect on your experience below. What was easy? What was challenging?
Answer:

Explanation:
My partner has recreated the figure of mine into a trapezium. I have found it to be easy in identifying the figure by its outer size. It was challenging for me to identify how the pieces are kept to figure out the trapezium.

Eureka Math Grade 3 Module 7 Lesson 9 Exit Ticket Answer Key

Nancy uses her tangram pieces to make a trapezoid without using the square piece. Below, sketch how she might have created her trapezoid.
Answer:

Explanation:
Nancy uses her tangram pieces to make a trapezoid without using the square piece. She uses her five triangles to make a shape that has four sides with different size of sides, named as trapezium ADEG.

Eureka Math Grade 3 Module 7 Lesson 9 Homework Answer Key

Question 1.
Use at least two tangram pieces to make and draw each of the following shapes. Draw lines to show where the tangram pieces meet.
a. A triangle.
Answer:

Explanation:
ABC is a triangle formed by joining two triangle and they meet at CD.

b. A square.
Answer:

Explanation:
ABCD is a square, formed by joining two triangles joining at BD.

c. A parallelogram.
Answer:

Explanation:
ABCD is a parallelogram, formed by joining two triangles meeting at BD.

d. A trapezoid.
Answer:

Explanation:
ABCD is a trapezium formed by joining two triangles meeting at AC.

Question 2.
Use your tangram pieces to create the cat below. Draw lines to show where the tangram pieces meet.

Answer:

Explanation:
ABGE and  FQDC are two rectangles joined together to form the shape of the cat, they meet at B.
CHIP  Trapezium and PGKL  rectangle and RJK triangle are used to form the shape of the body, meeting at P.
NMOL is a combination of two triangle used together to form the shape of the cat’s tail meeting at OM.

Question 3.
Use the five smallest tangram pieces to make a square. Sketch your square below, and draw lines to show where the tangram pieces meet.
Answer:

Explanation:
ABCD is a square formed by combining five different sizes of triangles, meeting at A,B,C,D.

Engage NY Eureka Math 3rd Grade Module 7 Lesson 8 Answer Key

Eureka Math Grade 3 Module 7 Lesson 8 Pattern Sheet Answer Key

Multiply.

multiply by 6 (1─5)
Answer:

Explanation:
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 30.

Eureka Math Grade 3 Module 7 Lesson 8 Problem Set Answer Key

Question 1.
Fold and cut the square on the diagonal. Draw and label your 2 new shapes below.
Answer:

Explanation:
ABCD is a Square.
ABC is the half part of the square when folded and cut.
DEF  is the other half part of the square when folded and cut.

Question 2.
Fold and cut one of the triangles in half. Draw and label your 2 new shapes below.
Answer:

Explanation:
ABC is an Triangle.
ABD is the half part of of the Triangle when folded and cut.
CEF is the other half part of of the Triangle when folded and cut.

Question 3.
Fold twice, and cut your large triangle. Draw and label your 2 new shapes below.
Answer:

Explanation:
ABC Triangle is twice folded and cut into two halves.
ADEC is first half part of twice folded Triangle.
CFG is the second half part of twice folded Triangle.

Question 4.
Fold and cut your trapezoid in half. Draw and label your 2 new shapes below.
Answer:

Explanation:
ABCD is a Trapezium, folded and cut.
ABFE and CDHG are two parts of them formed.
We can call ABFE and CDHG  as Quadrilaterals.

Question 5.
Fold and cut one of your trapezoids. Draw and label your 2 new shapes below.
Answer:

Explanation:
GDCH is a half part of Trapezium.
When folded the Trapezium, we get a  GDIJ Square and a CHK Triangle  are formed.

Question 6.
Fold and cut your second trapezoid. Draw and label your 2 new shapes below.
Answer:

Explanation:
AEFB is the second Trapezium.
When the AEFB Trapezium is folded and cut, we get a AEOP Parallelogram  and a BFN Triangle .

Question 7.
Reconstruct the original square using the seven shapes.
a. Draw lines inside the square below to show how the shapes go together to form the square. The first one has been done for you.

Answer:

Explanation:
ABCD is the Square.
AC is the first line used to divide the Square.
EB is the second line drawn, AEB and BEC Triangles are formed.
GF is the third line drawn, GFC Triangle is formed.
GI is the fourth line drawn, DGI Triangle is formed.
IJ is the fifth line drawn, IJA Triangle is formed.
HE is the sixth line drawn, IJEH Rectangle  and HEFG Rectangle are formed.
We can reconstruct this seven shapes together to form the original square.

b. Describe the process of forming the square. What was easy, and what was challenging?
Answer:
I first put the two big triangles to form the Square, which was quiet easy. Later one by one shape I joined to put on the square, this process was challenging .

Explanation:
Firstly, dividing the square into two Triangle was the easy one. Later on forming other shapes which are smaller in size than the first step, was quiet difficult one because while reconstructing it back to original shape was little messy and challenging. Overall, it made me to go back to my problem and check the shapes in the list one by one, which finally gave me my original shape of square to rejoin with all seven different shapes.

Eureka Math Grade 3 Module 7 Lesson 8 Exit Ticket Answer Key

Choose three shapes from your tangram puzzle. Trace them below. Label the name of each shape, and describe at least one attribute that they have in common.
Answer:

Explanation:
ABJ, BJC, CIF, FED, KHG are the triangles in the ABCD square.
AEKG is a Parallelogram in the ABCD square.
KFIH is the Rectangle in the ABCD square.
They all are having one right angle in common in KHG, KFIH and AEKG shapes.

Eureka Math Grade 3 Module 7 Lesson 8 Homework Answer Key

Question 1.
Draw a line to divide the square below into 2 equal triangles.

Answer:

Explanation:
EFGH is a square.
EG is the line drawn in the square, making EFG and GHE two triangles into equal halves.

Question 2.
Draw a line to divide the triangle below into 2 equal, smaller triangles.

Answer:

Explanation:
ABC is the Triangle.
CD is the line drawn, which divides the triangle into two equal triangle ADC and BDC triangles.

Question 3.
Draw a line to divide the trapezoid below into 2 equal trapezoids.

Answer:

Explanation:
ABCD is the trapezoids
EF is the line drawn, dividing the trapezoids into two equal trapezoids AEFD and BEFC. trapezoids.

Question 4.
Draw 2 lines to divide the quadrilateral below into 4 equal triangles.

Answer:

Explanation:
EFGH is the quadrilateral.
Lines are drawn in the quadrilateral joining EG and HF center O, making EOF, FOG, GOH and HOE four equal triangles.

Question 5.
Draw 4 lines to divide the square below into 8 equal triangles.

Answer:

Explanation:
ABCD is a Square.
AC and BD are joined by drawing two lines.
EF and GH are another two lines drawn making center O.
AOH, HOB, BOF, FOC, COG, GOD, DOE, EOA  equal triangles are formed.

Question 6.
Describe the steps you took to divide the square in Problem 5 into 8 equal triangles.
Answer:
I have drawn two lines dividing the square into two equal triangles.
I  have later drawn two lines in between the two triangles formed.

Explanation:
I have drawn two lines dividing the square into two equal triangles.
ABC, ABD, BCD, CDA  Triangles are formed.
I  have later drawn two lines in between the two triangles formed.
AOH, HOB, BOF, FOC, COG, GOD, DOE, EOA eight equal triangles are formed having Center O.