Worried about Adding and Subtracting Rational Numbers? Stop your worry now! We are providing the complete material of Big Ideas Math Book 7th Grade Answer Key Chapter 1 Adding and Subtracting Rational Numbers pdf here. You can make your learning as fun with the help of various tricks mentioned here. Check the answer key provided here which helps you to know the step by step procedure of every problem.
Big Ideas Math Answers Grade 7 Chapter 1 Adding and Subtracting Rational Numbers helps you to build self confidence and grip on the subject. Download BIM Grade 7 Chapter 1 Pdf and complete your preparation. In the below sections, we are providing the complete guide to various topics of chapter 1 i.e., Adding Integers, Adding Rational Numbers, Subtracting Integers, Subtracting Rational Numbers, Adding and Subtracting Rational Number and so on.
Big Ideas Math Book 7th Grade Answer Key Chapter 1 Adding and Subtracting Rational Numbers
Check Big Ideas Math Answers Grade 7 Chapter 1 Adding and Subtracting Rational Numbers here. With the help of this material, you can attend the mock tests and know the areas in which you are weak. Attending mock tests is the most important aspect of clearing the exams. If you know the weak areas, then you can easily work on them and become perfect in that concept.
Big Ideas Math 7th Grade Solution Key Chapter 1 pdf is available here. You can get it for free of cost where the questions and step by step solutions are provided. Tap on the below given links and get access to each concept. Refer to important questions, concepts and prepare timetable according to the topics present in each chapter.
Performance
- Adding and Subtracting Rational Numbers STEAM VIDEO/Performance
- Adding and Subtracting Rational Numbers Getting Ready for Chapter 1
Lesson: 1 Rational Numbers
Lesson: 2 Adding Integers
Lesson: 3 Adding Rational Numbers
Lesson: 4 Subtracting Integers
Lesson: 5 Subtracting Rational Numbers
Chapter: 1 – Adding and Subtracting Rational Numbers
- Adding and Subtracting Rational Numbers Connecting Concepts
- Adding and Subtracting Rational Numbers Chapter Review
- Adding and Subtracting Rational Numbers Practice Test
- Adding and Subtracting Rational Numbers Cumulative Practice
Adding and Subtracting Rational Numbers STEAM VIDEO/Performance
STEAM Video
Freezing Solid
The Celsius temperature scale is defined using the freezing point,0°C, and the boiling point,100°C, of water. Why do you think the scale is defined using these two points?
Watch the STEAM Video “Freezing Solid.” Then answer the following questions.
1. In the video, Tony says that the freezing point of wax is 53°C and the boiling point of wax is 343°C.
a. Describe the temperature of wax that has just changed from liquid form to solid form. Explain your reasoning.
b. After Tony blows out the candle, he demonstrates that there is still gas in the smoke. What do you know about the temperature of the gas that is in the smoke?

c. In what form is wax when the temperature is at 100°C, the boiling point of water? Consider wax in solid, liquid, and gaseous forms. Which is hottest? coldest?
Performance Task
Melting Matters
After completing this chapter, you will be able to use the STEAM concepts you learned to answer the questions in the Video Performance Task. You will answer questions using the melting points of the substances below.


You will graph the melting points of the substances on a number line to make comparisons. How is the freezing point of a substance related to its melting point? What is meant when someone says it is below freezing outside? Explain.
Adding and Subtracting Rational Numbers Getting Ready for Chapter 1
Getting Ready for Chapter
Chapter Exploration
Question 1.
Work with a partner. Plot and connect the points to make a picture.

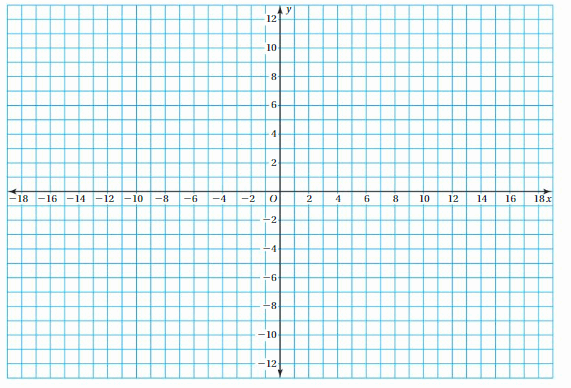
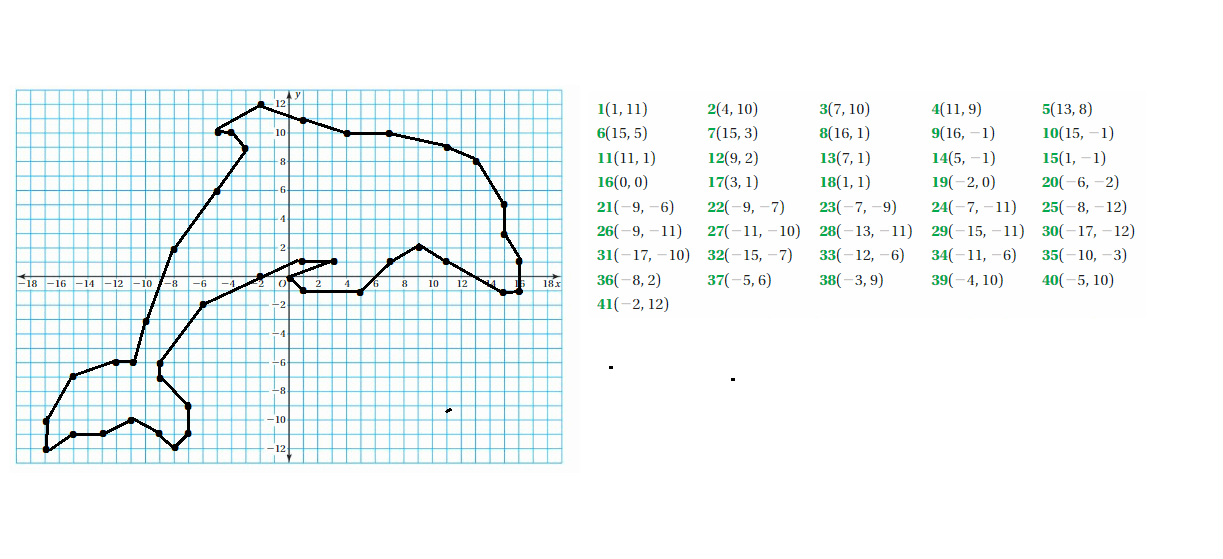
Question 2.
Create your own “dot-to-dot” picture. Use atleast 20 points.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
![]()
Lesson 1.1 Rational Numbers
Recall that integers are the set of whole numbers and their opposites. A rational number is a number that can be written as \(\frac{a}{b}\), where a and b are integers and b ≠ 0.
EXPLORATION 1
Using a Number Line
Work with a partner. Make a number line on the floor. Include both negative numbers and positive numbers.
a. Stand on an integer. Then have your partner stand on the opposite of the integer. How far are each of you from 0? What do you call the distance between a number and 0 on a number line?
Answer :
I stood on 4 and my friend stood on -4
The distance between 0 and 4 is 4 units
The distance between 0 and -4 is 4 units.
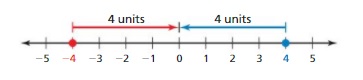
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
b. Stand on a rational number that is not an integer. Then have your partner stand on any other number. Which number is greater? How do you know?

Answer:
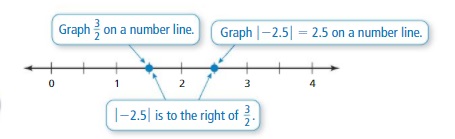
I stand on 3/2 and my friend stands on 2.5
2.5 > 3/2
Explanation:
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
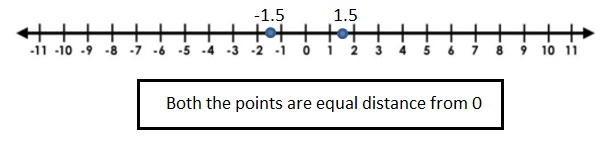
c. Stand on any number other than 0 on the number line. Can your partner stand on a number that is:

- greater than your number and farther from 0?
- greater than your number and closer to 0?
- less than your number and the same distance from 0?
- less than your number and farther from 0?
Answer 1 :
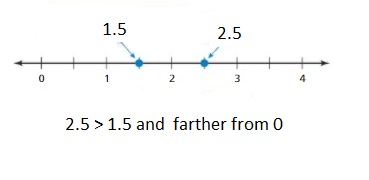
Answer 2 :
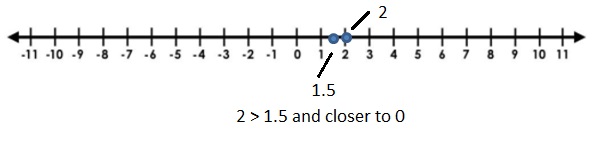
Answer 3 :
less than your number and the same distance from 0 will be only the opposite of the number .
The opposite of 1.5 is – 1.5 .
Answer 4 :
less than your number and farther from 0
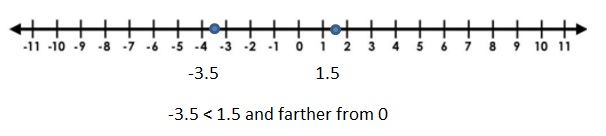
For each case in which it was not possible to stand on a number as directed, explain why it is not possible. In each of the other cases, how can you decide where your partner can stand?
1.1 Lesson
Try It
Find the absolute value.
Question 1.
| 7 |
Answer:
The Absolute value of 7 is 7
The distance between 0 and 7 is 7
| 7 | = 7
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .

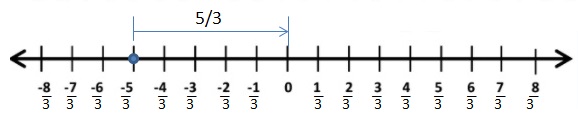
Question 2.
![]()
Answer:
The Absolute value of -5/3 is 5/3
The distance between 0 and -5/3 is 5/3
![]() = 5/3
= 5/3
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
Question 3.
| -2.6 |
Answer:
The Absolute value of -2.6 is 2.6
The distance between 0 and -2.6 is 2.6
| -2.6 | = 2.6
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .

Try It
Copy and complete the statement using <, >, or =.
Question 4.
![]()
Answer:
| 9 | = 9
| -9| = 9
both the values are same | 9 | = | -9 |

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 5.
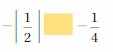
Answer:
|\(\frac{1}{2}\)| =\(\frac{1}{2}\)
–\(\frac{1}{2}\) < –\(\frac{1}{4}\)
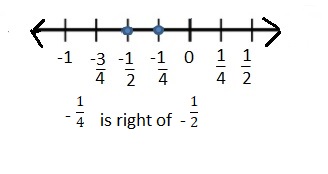
so –\(\frac{1}{2}\) < –\(\frac{1}{4}\)
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 6.
![]()
Answer:
|-4.5| =|4.5|
7 > -4.5

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
VOCABULARY
Which of the following numbers are integers?
![]()
Answer:
9,-1, 15 are integers
Explanation:
-3, -2, -1, 0, 1, 2, 3, ……) So, every natural number is an integer, every whole number is an integer, and every negative number is an integer. … The set of integers does not include fractions i.e p/q form or numbers which are in decimals eg: 2.4, 3.2 etc.
Question 8.
VOCABULARY
What is the absolute value of a number?
Answer:
The absolute value of a number means the distance from 0.
Example :-
5 is 5 units away from 0.
So the absolute value of that -5 is 5.
You cannot have negative distance, so it has to be positive.
The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
COMPARING RATIONAL NUMBERS
Copy and complete the statement using <, >, or =. Use a number line to justify your answer.
Question 9.

Answer:
|-\(\frac{7}{2}\)|=\(\frac{7}{2}\) = 3.5
3.5 = |-3.5|
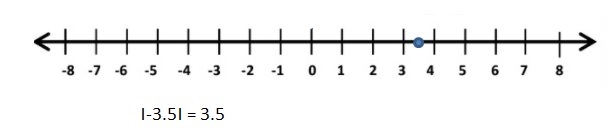
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 10.

Answer :
|\(\frac{11}{4}\)| = 2.75
|-2.8| = 2.8
2.75 < 2.8
2.75 and 2.8 . Graph both the points on number line .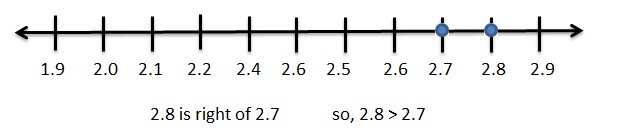
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 11.
WRITING
You compare two numbers, a and b. Explain how a > b and | a | < | b | can both be true statements.
Answer:
Take
a = 2
b = -4
Compare we get
a > b , 2 > -4
| a | = | 2 | = 2
| b | = | -4 | = 4
Compare we get
| a | < | b | , 2 < 4
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 12.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer :
Third number -6 is different
Explanation:
| 6 | = 6
| -6 | = – 6
Arrange the numbers in order
6 , 6 , – 6 , 6
The 3rd number that is -6 is a negative all other numbers are positive numbers so -6 is different from others.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
An airplane is at an elevation of 5.5 miles. A submarine is at an elevation of 10.9 kilometers. Which is closer to sea level? Explain.
Answer:
Airplane is closer to sea level as it is only 8.85 kilometres away from sea level
Explanation:
airplane is at an elevation of 5.5 miles = 5.5
1 mile = 1.6 kilometres
5.5 miles = 8.85 kilometres.
submarine is at an elevation of 10.9 kilometres. = 10.9 kms
Airplane is closer to sea level as it is only 8.85 kilometres away from sea level
8.85 < 10.9
Question 14.
The image shows the corrective powers (in diopters) of contact lenses for eight people. The farther the number of diopters is from 0, the farsightedness greater the power of the lens. Positive diopters correct nearsightedness and negative diopters correct nearsightedness. Who is the most nearsighted? the most farsighted? Who has the best eyesight?
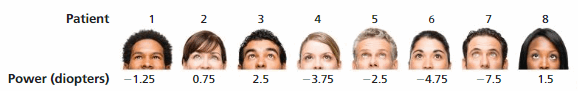
Answers:
The people with nearsightedness are with Positive diopters = 0.75 , 2.5, 1.5
0.75>1.5>2.5
the most nearsighted is 0.75 that is patient 2
The people with are farsightedness are with Negative diopters = -1.25, -3.75, -2.5, -4.75,-7.5
-7.5<-4.75<-3.75<-2.5<-1.25
the most farsighted is -7.5 that is patient 7
The best eyesight is for patient who has sight of 0 , after that patient 2 as best sight.
Rational Numbers Homework & Practice 1.1
Review & Refresh
Write the ratio.
- deer to bears
- bears to deer
- bears to animals
- animals to deer

Answer:
Number of Animals = 10
Number of Deer = 6
Number of Bears = 4
1. Ratio = \(\frac{Number of Deer}{Number of Bears}\) = \(\frac{6}{4}\)=\(\frac{3}{2}\)
2. Ratio = \(\frac{Number of Bears}{Number of Deer}\) = \(\frac{4}{6}\)=\(\frac{2}{3}\)
3. Ratio = \(\frac{Number of Bears}{Number of Animals}\) = \(\frac{4}{10}\)=\(\frac{2}{5}\)
4. Ratio = \(\frac{Number of Animals}{Number of Deer}\) = \(\frac{10}{6}\)= \(\frac{5}{3}\)
Find the GCF of the numbers.
Question 5.
8, 20
Answer:
Factors of 8 = 2 × 2 × 2
Factors of 20 = 2 × 2 × 5
The common in both numbers = 2 × 2 = 4
4 is the gcf
Explanation:
the GCF of two numbers: List the prime factors of each number. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.
Question 6.
12, 30
Answer:
Factors of 12 = 2 × 2 × 3
Factors of 30 = 2 × 3× 5
The common in both numbers = 2 × 3 = 6
6 is the gcf
Explanation:
the GCF of two numbers: List the prime factors of each number. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.
Question 7.
7, 28
Factors of 7 = 7
Factors of 28 = 2 × 2 × 7
The common in both numbers = 7
7 is the gcf
Explanation:
the GCF of two numbers: List the prime factors of each number. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.
Question 8.
48, 72
Factors of 48 = 2 × 2 × 2 ×2 × 3
Factors of 72 = 2 × 2 × 2 × 3 × 3
The common in both numbers = 2 × 2 × 2 × 3= 24
24 is the gcf
Explanation:
the GCF of two numbers: List the prime factors of each number. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.
Concepts, Skills, & Problem Solving
NUMBER SENSE
Determine which number is greater and which number is farther from 0. Explain your reasoning. (See Exploration 1, p. 3.)
Question 9.
4, -6
Answer:
4 > -6
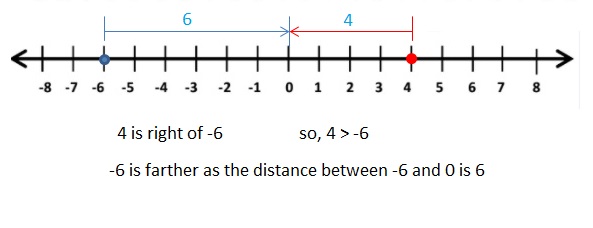
Explanation:
As distance cant be negative. so the -6 is farther from 0.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 10.
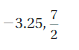
Answer:
\(\frac{7}{2}\) = 3.5
– 3.25 < 3.5
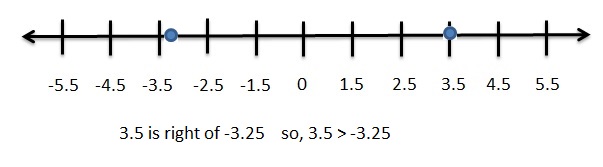
Explanation:
All negative numbers are lesser than positive numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 11.
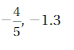
Answer:
–\(\frac{4}{5}\) = – 0.8
– 0.8 > -1.3

Explanation:
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
FINDING ABSOLUTE VALUES
Find the absolute value.
Question 12.
| 8 |
Answer :
The Absolute value of 8 is 8
The distance between 0 and 8 is 8
| 8 | = 8

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 13.
| -2 |
Answer:
The Absolute value of -2 is 2
The distance between 0 and -2 is 2
| -2 | = 2

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative.
Question 14.
| -10 |
Answer:
The Absolute value of -10 is 10
The distance between 0 and -10 is 10
| -10 | = 10
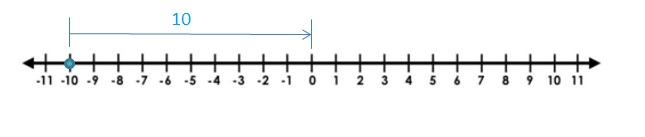
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative.
Question 15.
| 10 |
Answer:
The Absolute value of 10 is 10
The distance between 0 and 10 is 10
| 10 | = 10
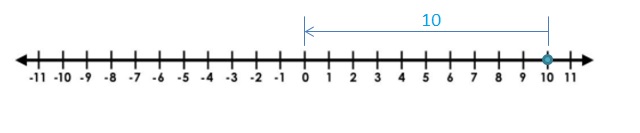
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 16.
| 0 |
Answer:
The Absolute value of 0 is 0
The distance between 0 and 0 is 0
| 0 | = 0

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 17.
![]()
Answer:
The Absolute value of \(\frac{1}{3}\) is \(\frac{1}{3}\)
The distance between 0 and \(\frac{1}{3}\) is \(\frac{1}{3}\)
| \(\frac{1}{3}\) | = \(\frac{1}{3}\)
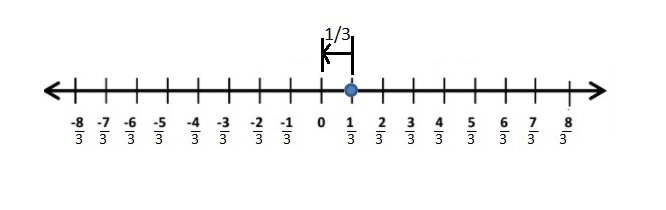
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 18.
![]()
Answer:
The Absolute value of \(\frac{7}{8}\) is \(\frac{7}{8}\)
The distance between 0 and \(\frac{7}{8}\) is \(\frac{7}{8}\)
| \(\frac{7}{8}\) | = \(\frac{7}{8}\)
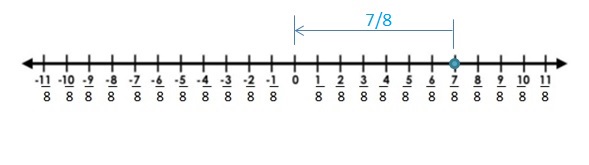
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 19.
![]()
Answer:
The Absolute value of –\(\frac{5}{9}\) is \(\frac{5}{9}\)
The distance between 0 and \(\frac{5}{9}\) is \(\frac{5}{9}\)
| –\(\frac{5}{9}\) | = \(\frac{5}{9}\)
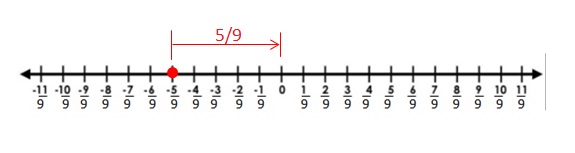
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative
Question 20.
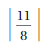
Answer:
The Absolute value of \(\frac{11}{8}\) is \(\frac{11}{8}\)
The distance between 0 and \(\frac{11}{8}\) is \(\frac{11}{8}\)
| \(\frac{11}{8}\) | = \(\frac{11}{8}\)
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 21.
| 3.8 |
Answer:
The Absolute value of 3.8 is 3.8
The distance between 0 and 3.8 is 3.8
| 3.8 | = 3.8

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 22.
| -5.3 |
Answer:
The Absolute value of -5.3 is 5.3
The distance between 0 and -5.3 is 5.3
| -5.3 | = 5.3
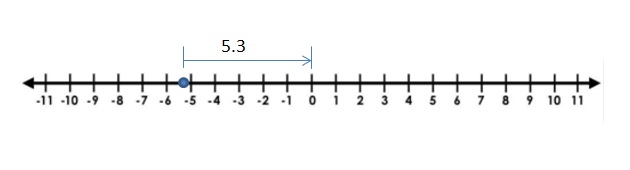
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative
Question 23.
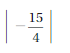
Answer:
The Absolute value of –\(\frac{15}{4}\) is \(\frac{15}{4}\)
The distance between 0 and –\(\frac{15}{4}\) is \(\frac{15}{4}\)
| –\(\frac{15}{4}\)| = \(\frac{15}{4}\) = 3.75
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative
Question 24.
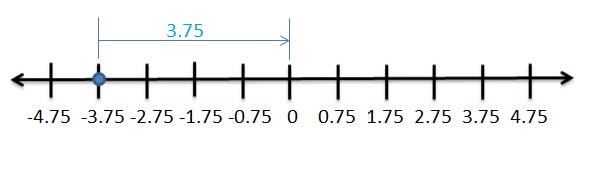
| 7.64 |
Answer:
The Absolute value of 7.64 is 7 .64
The distance between 0 and 7.64 is 7.64
| 7.64 | = 7.64
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
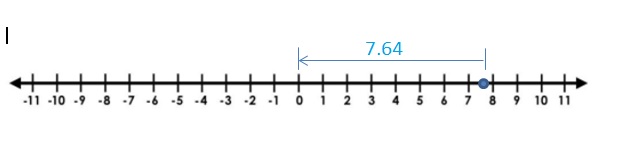
Question 25.
| -18.26 |
Answer:
The Absolute value of 18.26 is 18.26
The distance between 0 and -18.26 is 18.26
| -18.26 | = 18.26
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative
Question 26.
![]()
Answer:
4\(\frac{2}{5}\)=\(\frac{22}{5}\) = 4.4
The Absolute value of 4\(\frac{2}{5}\) is 4.4
The distance between 0 and 4.4 is 4.4
| 4.4 | = 4.4
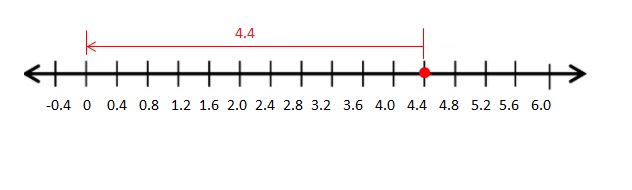
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Question 27.
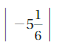
Answer:
-5\(\frac{1}{6}\) = –\(\frac{31}{6}\) =-5.1
The Absolute value of -5.1 is 5.1
The distance between 0 and -5.1 is 5.1
| -5.1 | = 5.1
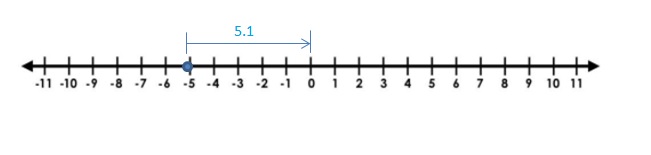
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive.
Distance cant be negative
COMPARING RATIONAL NUMBERS
Copy and complete the statement using <, >, or =.
Question 28.
![]()
Answer:
|-5| = 5
Graph 2 and 5
2 < 5
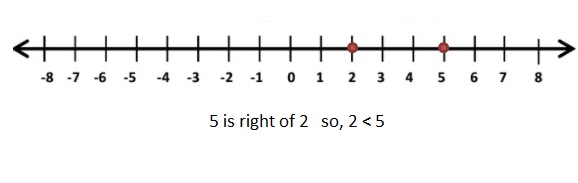
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 29.
![]()
Answer:
|-1| = 1
|-8| = 8
Graph 1 and 8
1 < 8
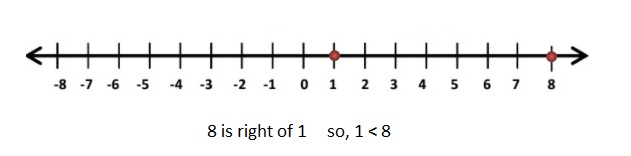
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 30.
![]()
Answer:
|5| = 5
|-5| = 5
Both are equal
|5| = |-5|

Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 31.
![]()
Answer:
|-2| = 2
Graph 2 and 0
|-2| > 0
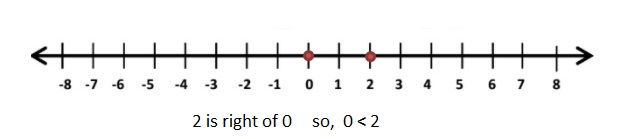
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 32.
![]()
Answer:
|-\(\frac{7}{8}\)| = I-0.875I = 0.875
Graph 0.4 and 0.8
0.4 < 0.875
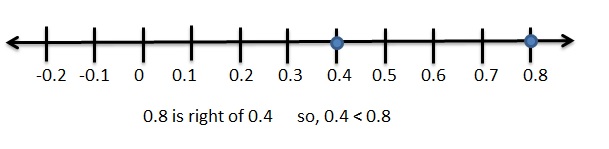
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 33.
![]()
Answer:
|4.9| = 4.9
|-5.3| = 5.3
Graph 4.9 and 5.3
|4.9| < |-5.3|
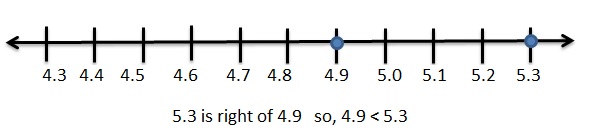
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 34.
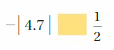
Answer:
|4.7| =4.7
1/2 = 0.5
– 4.7 < 0.5
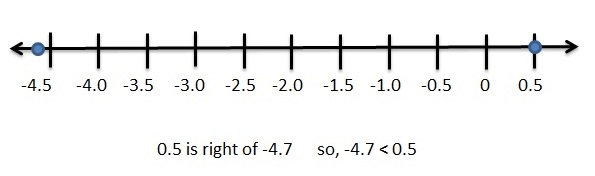
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 35.

Answer:
|-\(\frac{3}{4}\)| =\(\frac{3}{4}\)
|-\(\frac{3}{4}\)| > -|\(\frac{3}{4}\)|
Graph \(\frac{3}{4}\) and –\(\frac{3}{4}\)
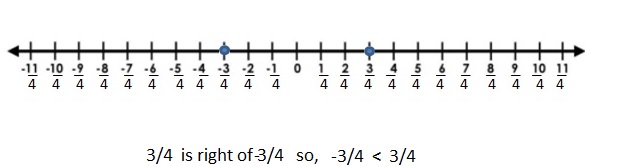
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 36.

Answer:
-|1\(\frac{1}{4}\)| = –\(\frac{5}{4}\) = -1.25
-|-1\(\frac{3}{8}\)| = –\(\frac{11}{8}\) = -1.375
Graph -1.25 and – 1.375
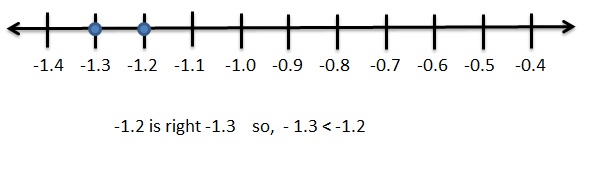
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
YOU BE THE TEACHER
Your friend compares two rational numbers. Is your friend correct? Explain your reasoning.
Question 37.
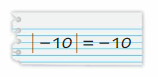
Answer:
No,
Explanation:
Absolute value of |-10| is 10
10 > -10
All Negative numbers are lesser than positive numbers.
Question 38.

Answer:
Yes,
Explanation:
|-\(\frac{4}{5}\)| = \(\frac{4}{5}\) = 0.8
-|\(\frac{1}{2}\)| = –\(\frac{1}{2}\) = – 0.5
0.8 > – 0.5
All Negative numbers are lesser than positive numbers.
Question 39.
OPEN-ENDED
Write a negative number whose absolute value is greater than 3
Answer:
Negative number -4
|-4| = 4
|-4| > 3
Question 40.
MODELING REAL LIFE
The summit elevation of a volcano is the elevation of the top of the volcano relative to sea level. The summit elevation of Kilauea, a volcano in Hawaii, is 1277 meters. The summit elevation of Loihi, an underwater volcano in Hawaii, is -969 meters. Which summit is higher? Which summit is closer to sea level?

Answer:
Summit elevation of Kilauea, a volcano in Hawaii = 1277 meters.
Summit elevation of Loihi, an underwater volcano in Hawaii, = -969 meters.
1277 > -969
The lesser summit is closer to the sea level
The summit is higher is elevation of Kilauea,a volcano in Hawaii
Question 41.
MODELING REAL LIFE
The freezing point of a liquid is the temperature at which the liquid becomes a solid.
a. Which liquid in the table has the lowest freezing point?
b. Is the freezing point of mercury or butter closer to the freezing point of water, 0°C?
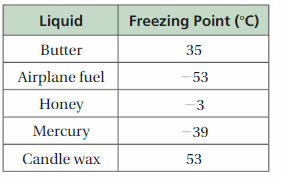
Answer:
a. The liquid which has low freezing point is Airplane Fuel that is -53 °C.
b. The Freezing point of mercury = -39 °C
The Freezing point of butter = 35 °C
The Freezing point of water = 0 °C
-39 > 0 > 35 °C
The Freezing point of butter is closer to freezing point of water .
ORDERING RATIONAL NUMBERS
Order the values from least to greatest.
Question 42.
8, | 3 |, -5, |-2|, -2
Answer:
| 3 | = 3
|-2| = 2
8, 3, -5, 2, -2
-5 < -2 < 2 < 3 <8
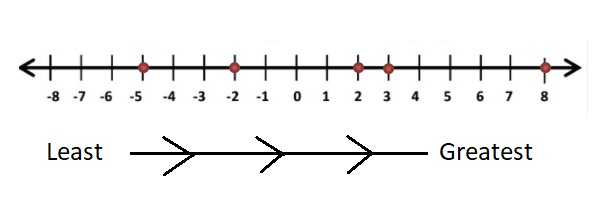
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 43.
| -6.3 |, -7.2, 8, | 5 |, -6.3
Answer:
| -6.3 | = 6.3
| 5 | = 5
6.3 , -7.2, 8, 5 , -6.3
-7.2 < -6.3 < 5 < 6.3 < 8
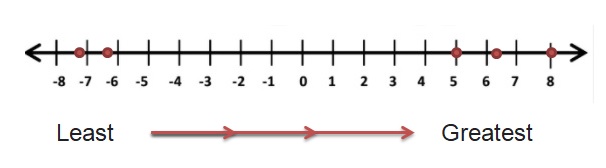
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 44.
![]()
Answer :
| 3.5 | = 3.5
| -1.8 | = 1.8
| 2.7 | = 2.7
3\(\frac{2}{5}\) = \(\frac{17}{5}\) = 3.4
3.5, 1.8, 4.6, 3.4, 2.7
1.8 < 2.7 < 3.4 < 3.5 < 4.6
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
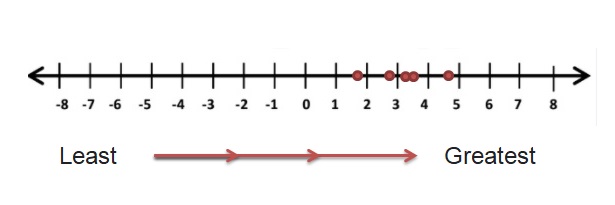
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 45.
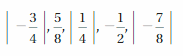
Answer:
|-\(\frac{3}{4}\)|=\(\frac{3}{4}\)
|\(\frac{5}{8}\)| = \(\frac{5}{8}\)
|\(\frac{1}{4}\)| = \(\frac{1}{4}\)
|-\(\frac{1}{2}\)|= \(\frac{1}{2}\)
|-\(\frac{7}{8}\)|= \(\frac{7}{8}\)
\(\frac{1}{4}\) < \(\frac{1}{2}\) < \(\frac{5}{8}\) <\(\frac{3}{4}\) < \(\frac{7}{8}\)
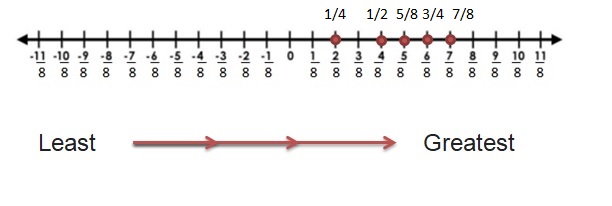
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 46.
PROBLEM SOLVING
The table shows golf scores, relative to par.
a. The player with the lowest score wins. Which player wins?
b. Which player is closest to par?
c. Which player is farthest from par?
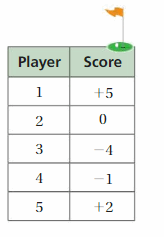
Answer a :
Player 3 < Player 4 < Player 2 < Player 5 < Player 1
-4 < -1 < 0 < 2 < 5
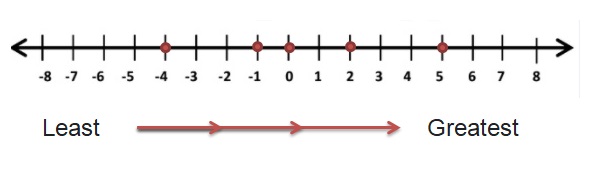
The Lowest score is -4 of player 3
Answer b :
The player closest to par is player 2 (0)
Answer c :
The player is farthest from par is player 1 (5)
Question 47.
DIG DEEPER!
You use the table below to record the temperature at the same location each hour for several hours. At what time is the temperature coldest? At what time is the temperature closest to the freezing point of water, 0°C?

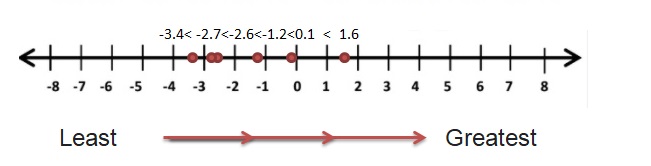
Answer :
3:00 p.m < 11:00 am <10:00 am < 2:00 p.m < 12:00 p.m < 1:00 p.m
-3.4 < – 2.7 < -2.6 < -1.25 < -0.15 < 1.6
The Temperature which is coldest is – 3.4 °C at 3:00 p.m
Time is the temperature closest to the freezing point of water, 0°C is – 1.25 at 2:00 p.m
Reasoning
Determine whether n ≥ 0 or n ≤ 0
Question 48.
n + | -n | = 2n
Answer:
| -n | = n
n + n = 2n
Above statement is true.
Question 49.
n + | -n | = 0
Answer:
| -n | = n
n + n = 2n not equal to 0
So, above equation is not equal to 0 .
TRUE OR FALSE?
Determine whether the statement is true or false. Explain your reasoning.
Question 50.
If x < 0, then | x | = −x
Answer:
False
| x | = x
Whatever the value may be | x | of all numbers is positive .
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
Question 51.
The absolute value of every rational number is positive.
Answer:
True.
Explanation:
The distance between a number and 0 on a number line is called as Absolute values. The absolute value is written as |x| , Namely, |x| = x and |-x| = x. All absolute values are positive .
Lesson 1.2 Adding Integers
EXPLORATION 1
Using Integer Counters to Find Sums
Work with a partner. You can use the integer counters shown at the left to find sums of integers.
a. How can you use integer counters to model a sum? a sum that equals 0?
Answer:
+1 + ( – 1 ) = 0
b. What expression is being modeled below? What is the value of the sum?

Answer :
– 3 + (+2) = -1
The Value of the sum = -1.
c. INDUCTIVE REASONING
Use integer counters to complete the table.
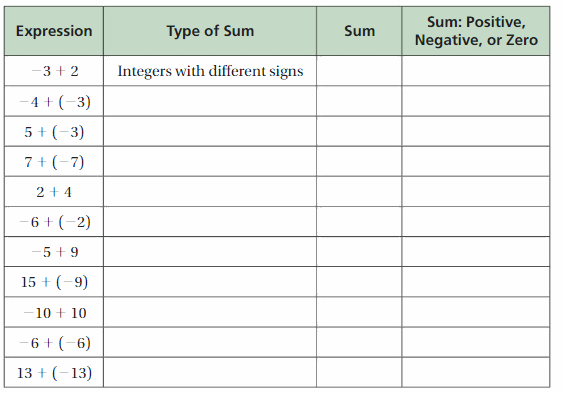
Answer:
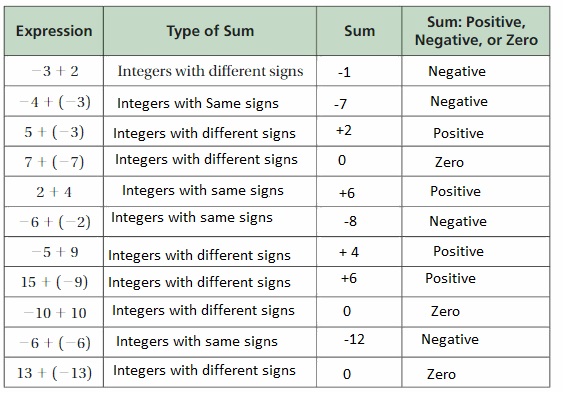
d. How can you tell whether the sum of two integers is positive, negative, or zero ?
Answer:
Adding two positive integers always yields a positive sum
Adding two negative integers always yields a negative sum.
e. Write rules for adding
- two integers with the same sign,
- two integers with different signs, and
- two opposite integers.

Answer e :
1.
There are two cases to consider when adding integers. When the signs are the same, you add the absolute values of the addends and use the same sign.
2.
When the signs are different, you find the difference of the absolute values and use the same sign as the addend with the greater absolute value.
3.
Rule: The sum of any integer and its opposite is equal to zero.
Summary: Adding two positive integers always yields a positive sum; adding two negative integers always yields a negative sum.
1.2 Lesson
Try It
Use a number line to find the sum.
Question 1.
-2 + 2
Answer:
2 + 2 =0
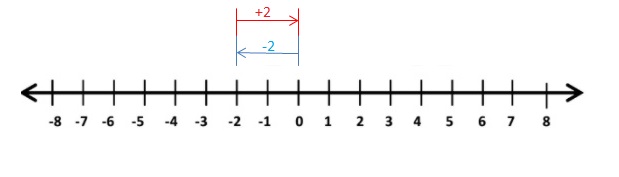
Explanation:
Draw an arrow from 0 to -2 to represent -2. Then draw an arrow 2 units to the right representing adding +2.
So, -2 + 2 =0
Question 2.
4 + (-5)
Answer:
4 + (-5) = -1.
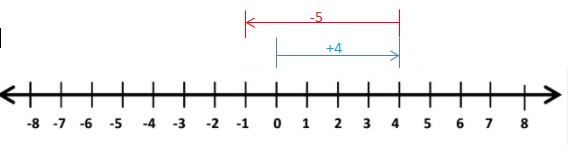
Explanation:
Draw an arrow from 0 to 4 to represent 4. Then draw an arrow 5 units to the left representing adding -5.
So, 4 + (-5) = -1
Question 3.
-3 + (-3)
Answer:
-3 + (-3) = -6
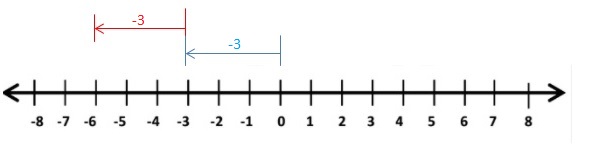
Explanation:
Draw an arrow from 0 to -3 to represent -3. Then draw an arrow 3 units to the left representing adding -3.
So, -3 + (-3) = -6
Try It
Find the sum.
Question 4.
7 + 13
Answer:
Words: Add absolute values of the integers. Then use the common sign.
Numbers : 7 + 13 = 20
Question 5.
– 8 + (-5)
Answer:
Words: Add absolute values of the integers. Then use the common sign.
Numbers : – 8 + (-5) = -13
Question 6.
– 2 + (-15)
Answer:
Words: Add absolute values of the integers. Then use the common sign.
Numbers : – 2 + (-15) = -17
Try It
Find the sum.
Question 7.
-2 + 11
Answer:
Words : Subtract lesser absolute value from the greater absolute value .Then use the sign of the integer with the greater absolute value .
Numbers : -2 + 11 = 9
Question 8.
9 + (-10)
Answer:
Words : Subtract lesser absolute value from the greater absolute value .Then use the sign of the integer with the greater absolute value .
Numbers : 9 + (-10) = -1
Question 9.
-31 + 31
Answer:
Words : Subtract lesser absolute value from the greater absolute value .Then use the sign of the integer with the greater absolute value .
Numbers : -31 + 31 = 0
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
WRITING
Explain how to use a number line to find the sum of two integers.
Answer:
To add two Positive integers using a number line:
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is positive, move that many units to the right from the location of the first integer. …
- Your answer will be the point you end on.
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is Negative, move that many units to the Left from the location of the first integer. …
- Your answer will be the point you end on.
ADDING INTEGERS
Find the sum. Use a number line to justify your answer.
Question 11.
– 8 + 20
Answer:
– 8 + 20 = 12
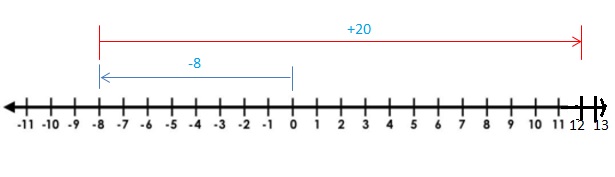
Explanation:
Draw an arrow from 0 to -8 to represent -8. Then draw an arrow 20 units to the right representing adding 20.
So, -8 + 20 = 12
Question 12.
30 + (-30)
Answer:
30 + (-30) = 0
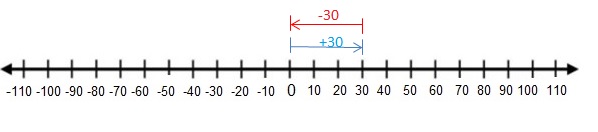
Explanation:
Draw an arrow from 0 to 30 to represent 30. Then draw an arrow 30 units to the left representing adding -30.
So,30 + (-30) = 0
Question 13.
– 10 + (-18)
Answer:
– 10 + (-18) = -28
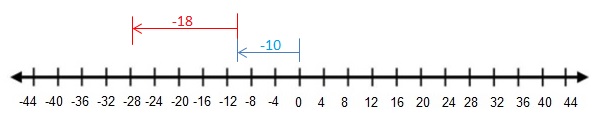
Explanation:
Draw an arrow from 0 to -10 to represent -10. Then draw an arrow -18 units to the left representing adding -18.
So,- 10 + (-18) = -28
Question 14.
NUMBER SENSE
Is 3 + (-4) the same as -4 + 3? Explain.
Answer:
3 + (-4) = – 1
-4 + 3 = -1
Explanation:
If the order of the addends changes, the sum stays the same. If the grouping of addends changes, the sum stays the same.
Subtract lesser absolute value from the greater absolute value .Then use the sign of the integer with the greater absolute value .
LOGIC
Tell whether the statement is true or false. Explain your reasoning.
Question 15.
The sum of two negative integers is always negative.
Answer:
True .
Explanation:
– 2 + (- 3) = – 5
-4 + ( – 5 ) = – 9
Then Use the sign of the integer with the greater absolute value.
Question 16.
The sum of an integer and its absolute value is always 0.
Answer:
Sometimes, if the integer is negative then the statement is true.
Example:
Sum of a negative integer and its absolute value is always 0
-4 and | -4| = | 4|
-4 + 4 = 0
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
At 12:00 P.M., the water pressure on a submarine is 435 pounds per square inch. From 12:00 P.M. to 12:30 P.M., the water pressure increases 58 pounds per square inch. From 12:30 P.M. to 1:00 P.M., the water pressure decreases 116 pounds per square inch. What is the water pressure at 1:00 P.M.?
Answer:
At 12:00 P.M. The water presure on a submarine = 435 pounds per square inch.
From 12:00 P.M. to 12:30 P.M., the water pressure increases 58 pounds per square inch.
From 12:00 P.M. to 12:30 P.M., the water pressure on a submarine = 435 + 58 = 493 pounds per square inch.
From 12:30 P.M. to 1:00 P.M., the water pressure decreases 116 pounds per square inch.
From 12:30 P.M. to 1:00 P.M., the water pressure on a submarine = 493 + 58 = 551 pounds per square inch.
Therefore the water pressure at 1:00 P.M. = 551 pounds per square inch.
Question 18.
DIG DEEPER!
The diagram shows the elevation changes between checkpoints on a trail. The trail begins atan elevation of 8136 feet. What is the elevation at the end of the trail?
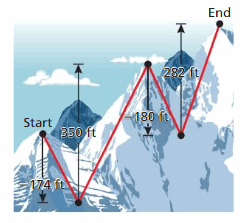
Answer:
The elevation at the start of the trail = 8136 Feet
The elevation gets decreases by 174 ft .
now the elevation is at = 8136 – 174 = 7962
From 7962 feet the elevation increased by 250 feet
Now The elevation is at = 7962 + 250 = 8212
8212 feet the elevation decreases by 182 feet
Now The elevation is at = 8212 – 182 = 8030
Now the elevation is increased by 282 feet .
Now The elevation at the end = 8030 + 282 = 8312 feets.
1.2 Practice
Review & Refresh
Copy and complete the statement using <, >, or =.
Question 1.
![]()
Answer:
| -7| = 7
5 < 7
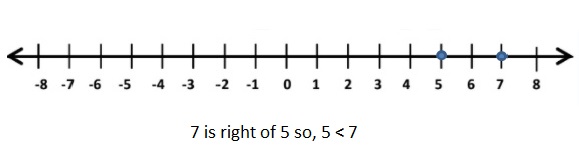
Explanation:
All negative numbers are lesser than positive numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 2.
![]()
Answer:
| -2.6| = 2.6
| -2.06| = 2.06
2.6 > 2.06
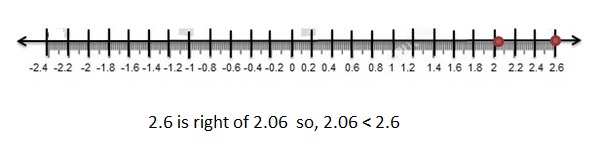
Explanation:
All negative numbers are lesser than positive numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Question 3.
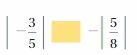
Answer:
|-\(\frac{3}{5}\)| = 0.6
|\(\frac{5}{8}\)| = 0.625
0.6 > – 0.625

Explanation:
All negative numbers are lesser than positive numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left.
Add.
Question 4.
8.43 + 5.21
Answer:
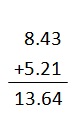
Explanation:
Write down the numbers, one under the other, with the decimal points lined up. Put in zeros so the numbers have the same length . Then add, using column addition, remembering to put the decimal point in the answer.
Question 5.
2.316 + 4.09
Answer:
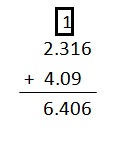
Explanation:
Write down the numbers, one under the other, with the decimal points lined up. Put in zeros so the numbers have the same length . Then add, using column addition, remembering to put the decimal point in the answer.
Question 6.
![]()
Answer:
\(\frac{5}{9}\) + \(\frac{3}{9}\) = \(\frac{5 + 3 }{9}\) =\(\frac{8}{9}\)
Explanation:
Step 1: Make sure the bottom numbers (the denominators) are the same.
Step 2: Add the top numbers (the numerators), put that answer over the denominator.
Step 3: Simplify the fraction (if needed)
Question 7.
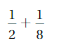
Answer:
\(\frac{1}{2}\) + \(\frac{1}{8}\)
Lcm of 2 , 8 is 8 Multiply 1/2 with 4 in numerator and denominator we get,
\(\frac{4}{8}\) + \(\frac{1}{8}\)
= \(\frac{5}{8}\)
Explanation:
Step 1: Make sure the bottom numbers (the denominators) are the same.
Step 2: Add the top numbers (the numerators), put that answer over the denominator.
Step 3: Simplify the fraction (if needed)
Question 8.
The regular price of a photograph printed on a canvas is $18. You have a coupon for 15% off. How much is the discount?
A. $2.70
B. $3
C. $15
D. $15.30
Answer:
Price of a photograph = $18
Discount = 15% off
Discount price = 15% of $18 = \(\frac{15}{100}\) × 18 = \(\frac{27}{10}\) = 2.7
Discount Price = 2.7$
Question 9.
Represent the ratio relationship using a graph.
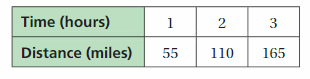
Answer:
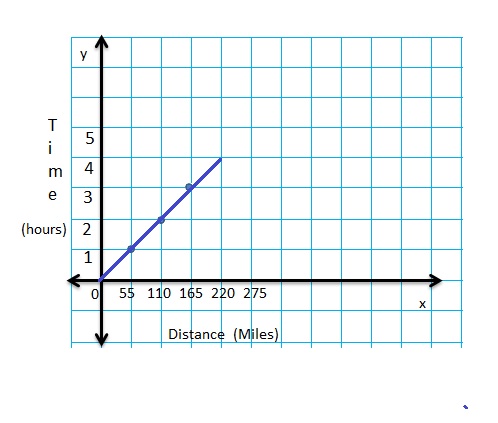
Concepts, Skills, & Problem Solving
USING INTEGER COUNTERS
Use integer counters to complete the table. (See Exploration 1, p. 9.)

Answer:

USING NUMBER LINES
Write an addition expression represented by the number line. Then find the sum.
Question 12.
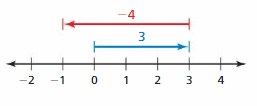
Answer:
3 + ( – 4) = -1
Explanation:
The arrow from 0 to 3 represent first integer that is 3 and from 3 the arrow moves to left representing adding -4 to the first integer and ends at -1 which is the sum.
Question 13.
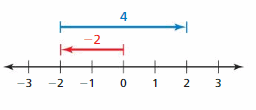
Answer:
-2 + 4 = 2
Explanation:
The arrow from 0 to -2 represent first integer that is -2 and from -2 the arrow moves to right representing adding 4 to the first integer and ends at 2 which is the sum.
Question 14.
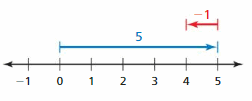
Answer:
5 + ( -1) = 4
Explanation:
The arrow from 0 to 5 represent first integer that is 5 and from 5 the arrow moves to left representing adding -1 to the first integer and ends at 4 which is the sum.
Question 15.
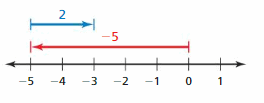
Answer:
-5 + 2 = -3
Explanation:
The arrow from 0 to -5 represent first integer that is -5 and from -5 the arrow moves to right representing adding 2 to the first integer and ends at -3 which is the sum.
ADDING INTEGERS
Find the sum. Use integer counters or a number line to verify your answer.
Question 16.
6 + 4
Answer:
6 + 4 = 10

Explanation:
Draw an arrow from 0 to 6 to represent 6. Then draw an arrow 4 units to the right representing adding 4. The arrow ends at 10 showing the sum.
So, 6 + 4 = 10
Question 17.
– 4 + (-6)
Answer:
– 4 + (-6) = -10
Explanation:
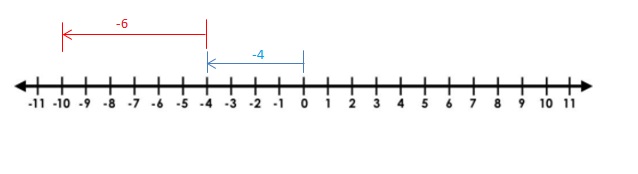
Draw an arrow from 0 to -4 to represent -4. Then draw an arrow 6 units to the left representing adding -6. The arrow ends at -10 showing the sum.
So,- 4 + (-6) = -10
Question 18.
-2 + (-3)
Answer:
-2 + (-3) = -5
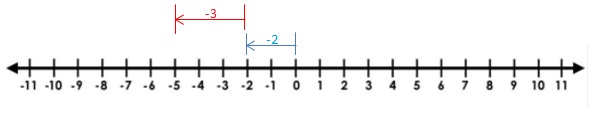
Explanation:
Draw an arrow from 0 to -2 to represent -2. Then draw an arrow 3 units to the left representing adding -3. The arrow ends at -5 showing the sum.
So, -2 + (-3) = -5
Question 19.
-5 + 12
Answer:
-5 + 12 = 7
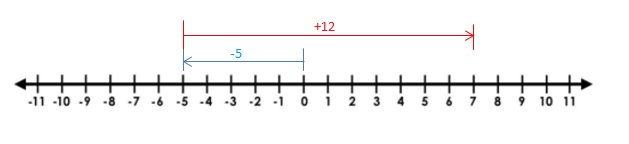
Explanation:
Draw an arrow from 0 to -5 to represent -5. Then draw an arrow 12 units to the right representing adding 12. The arrow ends at 7 showing the sum.
So, -5 + 12 = 7
Question 20.
5 + (-7)
Answer:
5 + (-7) = -2

Explanation:
Draw an arrow from 0 to 5 to represent 5. Then draw an arrow 7 units to the left representing adding -7. The arrow ends at -2 showing the sum.
So, 5 + (-7) = -2
Question 21.
8 + (-8)
Answer:
8 + (-8) = 0

Explanation:
Draw an arrow from 0 to 8 to represent 8. Then draw an arrow 8 units to the left representing adding -8. The arrow ends at 0 showing the sum.
So, 8 + (-8) = 0
Question 22.
9 + (-11)
Answer:
9 + (-11) = -2
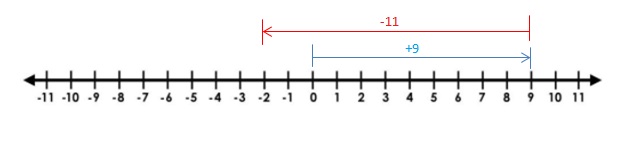
Explanation:
Draw an arrow from 0 to 9 to represent 9. Then draw an arrow 11 units to the left representing adding -11. The arrow ends at -2 showing the sum.
So, 9 + (-11) = -2
Question 23.
-3 + 13
Answer:
-3 + 13 = 10
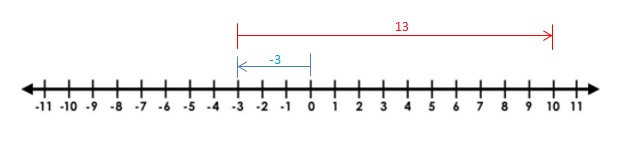
Explanation:
Draw an arrow from 0 to -3 to represent -3. Then draw an arrow 13 units to the right representing adding 13. The arrow ends at 10 showing the sum.
So, -3 + 13 = 10
Question 24.
-4 + (-16)
Answer:
-4 + (-16) = -20
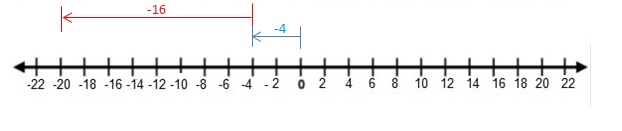
Explanation:
Draw an arrow from 0 to -4 to represent -4. Then draw an arrow 16 units to the left representing adding -16. The arrow ends at -20 showing the sum.
So, -4 + (-16) = -20
Question 25.
-3 + (-1)
Answer :
-3 + (-1) = -4
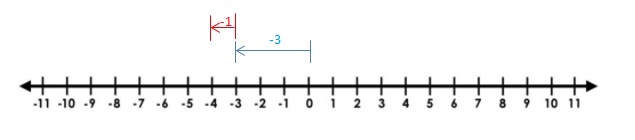
Explanation:
Draw an arrow from 0 to 6 to represent 6. Then draw an arrow 4 units to the right representing adding 4. The arrow ends at 10 showing the sum.
So, -3 + (-1) = -4
Question 26.
14 + (-5)
Answer:
14 + (-5) = 9
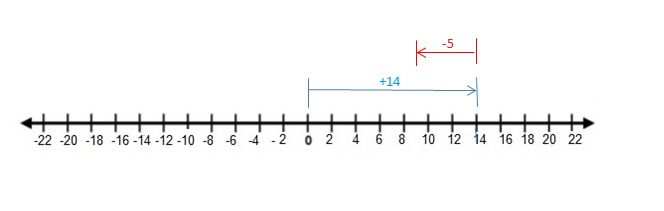
Explanation:
Draw an arrow from 0 to 14 to represent 14. Then draw an arrow 5 units to the left representing adding -5. The arrow ends at 9 showing the sum.
So, 14 + (-5) = 9
Question 27.
0 + (-11)
Answer:
0 + (-11) = -11
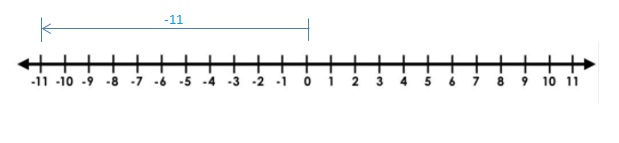
Explanation:
Draw an arrow from 0 to -11 to represent -11. The arrow ends at -11 showing the sum.
So, 0 + (-11) = -11
Question 28.
-10 + (-15)
Answer :
-10 + (-15) = – 25

Explanation:
Draw an arrow from 0 to -10 to represent -10. Then draw an arrow 15 units to the left representing adding -15. The arrow ends at -25 showing the sum.
So, -10 + (-15) – 25
Question 29.
-13 + 9
Answer :
-13 + 9 = -4
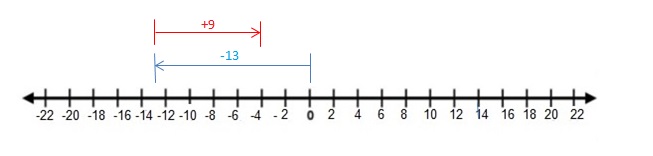
Explanation:
Draw an arrow from 0 to -13 to represent -13. Then draw an arrow 9 units to the right representing adding 9. The arrow ends at -4 showing the sum.
So, -13 + 9 = -4
Question 30.
-18 + 18
Answer:
-18 + 18 = 0
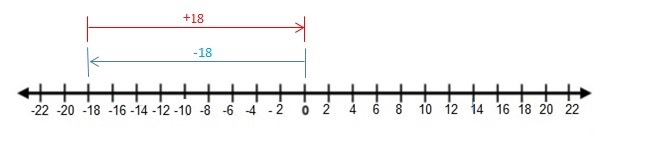
Explanation:
Draw an arrow from 0 to -18 to represent -18. Then draw an arrow 18 units to the right representing adding 18. The arrow ends at 0 showing the sum.
So, -18 + 18 = 0
Question 31.
-25 + (-9)
Answer :
-25 + (-9) = -36
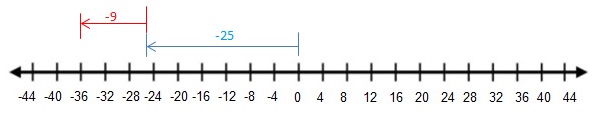
Explanation:
Draw an arrow from 0 to -25 to represent -25. Then draw an arrow 9 units to the left representing adding -9. The arrow ends at -36 showing the sum.
So, -25 + (-9) = -36
YOU BE THE TEACHER
Your friend finds the sum. Is your friend correct? Explain your reasoning.
Question 32.
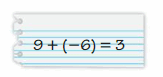
Answer :
9 + ( -6 ) = 3
Yes it is right.
Explanation:
|9| > |-6| so subtract |-6| from |9| we get 3.
Use the sign of greater number that is +
Question 33.
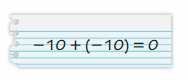
Answer :
No , it is wrong.
Explanation:
|-10| = |10| so add |10| to |10| we get 20
Use the sign of greater number that is –
Question 34.
MODELING REAL LIFE
The temperature is 3°F at 7:00 A.M. During the next 4 hours, the temperature increases 21°F. What is the temperature at 11:00 A.M.?
Answer :
The temperature at 7:00 A.M = 3°F
After 4 hours temperature increases to 21°F
The temperature at 11:00 A.M. = 3°F + 21°F = 24°F
Question 35.
MODELING REAL LIFE
Your bank account has a balance of -$12. You deposit $60. What is your new balance?
Answer :
Current bank balance =-$12
Money deposited = $60
New balance = -12 +60 = 48 $.
Question 36.
PROBLEM SOLVING
A lithium atom has positively charged protons and negatively charged electrons. The sum of the charges represents the charge of the lithium atom. Find the charge of the atom.
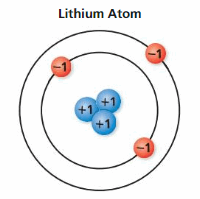
Answer :
Number of positively charged protons = 3
Number of negatively charged electrons = -3
Sum of the charges = 3 + (-3) = 0
Question 37.
OPEN-ENDED
Write two integers with different signs that have a sum of 25. Write two integers with the same sign that have a sum of -25.
Answer:
Two integers with different signs have sum of 25 are 36, -11
Two integers with same signs have sum of -25 are -16 , -9
USING PROPERTIES
Tell how the Commutative and Associative Properties of Addition can help you find the sum using mental math. Then find the sum.
Question 38.
9 + 6 + (-6)
Answer :
9 + 6 + ( -6) = 9 + ( 6 + ( -6)) = 9 + 0 = 9
We have one is positive and another 6 which is negative . so sum of a positive integer and its opposite gives the sum 0
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
We have one is positive and another 6 which is negative . so sum of a positive integer and its opposite gives the sum 0
Question 39.
-8 + 13 + (-13)
Answer:
-8 + 13 + (-13) = -8 + (13 + (-13) ) = -8
13 + ( -13) = 0
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
We have one 13 is positive and another 13 which is negative . so sum of a positive integer and its opposite gives the sum 0
Question 40.
9 + (-17) + (-9)
Answer:
9 + (-17) + (-9) = (-17) + ( 9 + (-9) ) = – 17
9 + (-9) = 0
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
We have one 9 is positive and another 9 which is negative . so sum of a positive integer and its opposite gives the sum 0
Question 41.
7 + (-12) + (-7)
Answer:
7 + (-12) + (-7) = (-12) + ( 7 + (-7)) = -12
7 + (-7) = 0
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
We have one 7 is positive and another 7 which is negative . so sum of a positive integer and its opposite gives the sum 0
Question 42.
-12 + 25 + (-15)
Answer:
-12 + 25 + (-15) = 25 + ( -12 + (-15) ) = 25 – 25 = 0
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
We have one 25 is positive and another 25 which is negative . so sum of a positive integer and its opposite gives the sum 0
Question 43.
6 + (-9) + 14
Answer :
6 + (-9) + 14 = (6 + 14 ) + ( – 9 ) = 20 +( -9) = 11
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
The commutative property of addition says that changing the order of addends does not change the sum.
ADDING INTEGERS
Find the sum.
Question 44.
13 + (-21) + 16
Answer :
13 + (-21) + 16
= (13 + 16) + ( -21)
= 29 + ( -21)
= 8
Question 45.
22 + (-14) + (-12)
Answer :
22 + (-14) + (-12)
= 22 + ((-14) + (-12))
= 22 + (-26)
= -4
Question 46.
-13 + 27 + (-18)
Answer:
-13 + 27 + (-18)
= 27 + (-13 + (-18))
= 27 + (-31)
= -4
Question 47.
-19 + 26 + 14
Answer:
-19 + (26 + 14)
=- 19 + 40
= – 21
Question 48.
-32 + (-17) + 42
Answer:
-32 + (-17) + 42
=(-32 + (-17) ) + 42
=-49 + 42
= -7
Question 49.
-41 + (15) + (-29)
Answer:
-41 + (15) + (-29)
=(-41 + (-29)) + 15
= -70 + 15
= – 55
DESCRIBING A SUM
Describe the location of the sum, relative to p, on a number line.
Question 50.
p + 3
Answer:
p + 3 = 0
Moving 3 to other side it becomes -3
p = – 3

Question 51.
p + (-7)
Answer :
p + (-7) = 0
Moving – 7 to other side it becomes +7
p = 7

Question 52.
p + 0
Answer :
p + 0 = 0
p = 0

Question 53.
p + q
Answer :
p + q = 0
p = – q
As q value is not mentioned so cannot estimate p value.
ALGEBRA
Evaluate the expression when a = 4, b = -5, and c = -8.
Question 54.
a + b
Answer:
a + b
Take a = 4, b = -5, we get
4 + ( -5) = -1
Question 55.
-b + c
Answer:
-b + c
Take c = -8, b = -5, we get
-(-5) + (-8) = 5 + (-8) = -3
Question 56.
| a + b + c |
Answer:
| a + b + c |
Take a = 4, b = -5, and c = -8, we get
| 4 + (-5) + (-8) | =| -9| = 9
Question 57.
MODELING REAL LIFE
The table shows the income and expenses for a school carnival. The school’s goal was to raise $1100. Did the school reach its goal? Explain.

Answer:
Income of games = $650
Income on concessions =$530
Income on Donations = $52
Total Income = $650 + $530 + $52 = $1232
Expenses on Flyers = -$28
Expenses on Decorations = -$75
Total Expenses = -($28 + $75) =-$103
School Amount = Total Income + Total Expenses = $1232 +(-$103) = 1129$
Yes the school reaches its goal as the school amount = $1129.
OPEN-ENDED
Write a real-life story using the given topic that involves the sum of an integer and its additive inverse.
Question 58.
income and expenses
Question 59.
the amount of water in a bottle
Question 60.
the elevation of a blimp
MENTAL MATH
Use mental math to solve the equation.
Question 61.
d + 12 = 2
Answer:
d + 12 = 2
d = 2 – 12
d = – 10
Question 62.
b + (-2) = 0
Answer:
b + (-2) = 0
b = 2
Question 63.
-8 + m = -15
Answer:
-8 + m = -15
m = -15 + 8
m = – 7
Question 64.
DIG DEEPER!
Starting at point A, the path of a dolphin jumping out of the water is shown.
a. Is the dolphin deeper at point C or point E? Explain your reasoning.
b. Is the dolphin higher at point B or point D? Explain your reasoning.
c. What is the change in elevation of the dolphin from point A to point E?
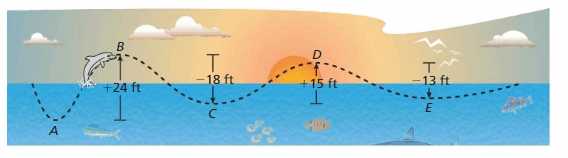
Answer:
From A the dolphin gets started
At B the dolphin is +24 feet
At C the dolphin is (+24 – 18)feet = 6 feet
At D the dolphin is (6 + 15 ) = 21 feet.
At E the dolphin is (21 – 13 ) = 8 feet.
Answer a :
The dolphin is deeper at Point E
Point E > Point D
8 > 6
Answer b :
The Dolphin is higher at Point B
Point B > Point D
24 > 21 feet.
Answer c :
The change in elevation of the dolphin from point A to point E is 8 feets.
Question 65.
NUMBER SENSE
Consider the integers p and q. Describe all of the possible values of p and q for each circumstance. Justify your answers.
a. p + q = 0
b. p + q < 0
c. p + q > 0
Answer a :
The values of the integers p and q are
p = 3
q = – 3
p + q = 3 + (-3) = 0
Answer b :
The values of the integers p and q are
p = 3
q = -4
p + q = 3 + (-4) = -1
p + q < 0
-1 <0
Answer c:
The values of the integers p and q are
p = 3
q = 4
p + q = 3 + (4) = 7
p + q > 0
7 <0
Question 66.
PUZZLE
According to a legend, the Chinese Emperor Yu-Huang saw a magic square on the back of a turtle. In magic square, the numbers in each row and in each column have the same sum. This sum is called the magic sum.
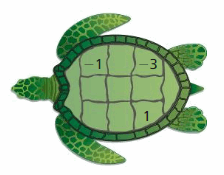
Copy and complete the magic square so that each row and each column has a magic sum of 0. Use each integer from 4 to 4 exactly once.
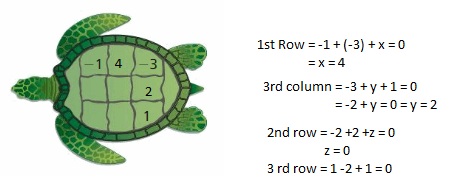
Answer:
Lesson 1.3 Adding Rational Numbers
EXPLORATION 1
Adding Rational Numbers
Work with a partner.
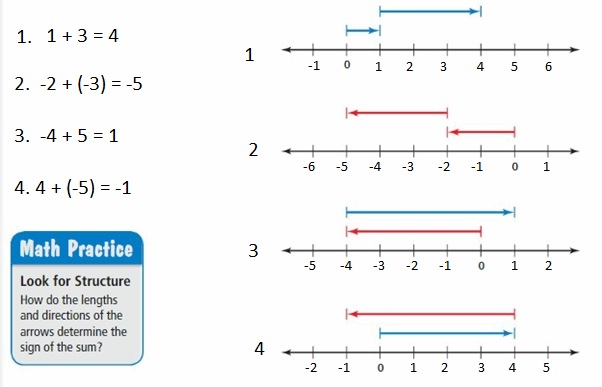
a. Choose a unit fraction to represent the space between the tick marks on each number line. What addition expressions are being modeled? What are the sums?
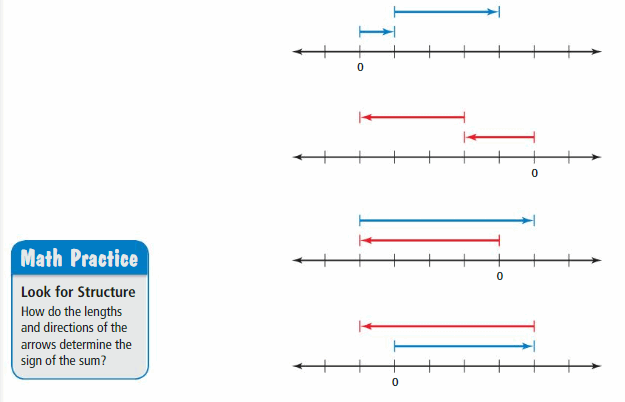
Answer :
b. Do the rules for adding integers apply to all rational numbers? Explain your reasoning.
Answer :
Yes
Explanation:
The rules for adding integers apply to other real numbers, including rational numbers. Add their absolute values. Give the sum the same sign. Find the difference of their absolute values.
If the two rational expressions that you want to add or subtract have the same denominator you just add/subtract the numerators which each other. When the denominators are not the same in all expressions that you want to add or subtract as in the example below you have to find a common denominator.
c. You have used the following properties to add integers. Do these properties apply to all rational numbers? Explain your reasoning.
- Commutative Property of Addition
- Associative Property of Addition
- Additive Inverse Property
Answer c :
Yes, Commutative property of addition and associative Property of addition are applied to all rational numbers.
Explanation:
Associative Property
Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Distributive Property
Distributive property states that for any three numbers x, y and z we have
x × ( y + z ) = (x × y) +( x × z)
1.3 Lesson
Try It
Find the sum. Write your answer in simplest form.
Question 1.
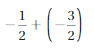
Answer:
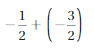
Because the signs are same
=|-\(\frac{1}{2}\)| + |-\(\frac{3}{2}\)|
= |\(\frac{4}{2}\)| = 2
Both the signs are negative so, use a negative sign in the sum .
Question 2.
![]()
Answer :
![]() = –\(\frac{5}{8}\)
= –\(\frac{5}{8}\)
= -1\(\frac{3}{8}\) + \(\frac{3}{4}\)
= –\(\frac{11}{8}\) + \(\frac{3}{4}\)
Lcm of 8 , 4 are 8
= –\(\frac{11}{8}\) + \(\frac{6}{8}\)
Both the signs are different
=|\(\frac{6}{8}\)| – |-\(\frac{11}{8}\)|
=\(\frac{6}{8}\) – \(\frac{11}{8}\)
=-\(\frac{5}{8}\)
|\(\frac{6}{8}\)| < |–\(\frac{11}{8}\)|
So use negative sign.
Question 3.
![]()
Answer:
![]()
Both the numbers have different signs.
write 4 as \(\frac{8}{2}\)
=|\(\frac{8}{2}\)| – |-\(\frac{7}{2}\)|
= \(\frac{8}{2}\) – \(\frac{7}{2}\)
=\(\frac{1}{2}\)
So use positive sign as \(\frac{8}{2}\) > \(\frac{7}{2}\)
Try It
Find the sum.
Question 4.
-3.3 + (-2.7)
Answer:
-3.3 + (-2.7)
=|-3.3| + |-2.7|
=3.3 +2.7
=6.0
Use negative sign as both numbers are negative. so, sum = -6.0
Question 5.
-5.35 + 4
Answer:
-5.35 + 4
=|-5.35| – |4|
= 5.35 – 4
=-1.35
Use negative sign as |-5.35| > |4| so, sum = -1.35
Question 6.
1.65 + (-0.9)
Answer:
=1.65 + (-0.9)
=|1.65| – |-0.9|
= 1.65 – 0.9
= 0.75
|1.65| > |-0.9| so use positive sign so sum = 0.75
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
Explain how to use a number line to find the sum of two rational numbers.
Answer:
Step 1 : first make the denominators of the numbers equal
Step 2 : Second, draw a number line.
Step 3 : Mark the first Rational number from 0 on the number line.
Step 4 :Next, if the second Rational Number is positive, move that many units to the right from the location of the first Rational Number … or Next, if the second Rational Number is Negative, move that many units to the left from the location of the first Rational Number
Step 5 :Your answer will be the point you end on.
ADDING RATIONAL NUMBERS
Find the sum.
Question 8.
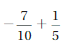
Answer:
= –\(\frac{7}{10}\) + \(\frac{1}{5}\)
Both the signs are different write \(\frac{1}{5}\) as \(\frac{2}{10}\)
=|\(\frac{2}{10}\)| – |-\(\frac{7}{10}\)|
=\(\frac{2}{10}\) – \(\frac{7}{10}\)
=-\(\frac{5}{10}\)
|\(\frac{2}{10}\)| < |–\(\frac{7}{10}\)|
So use negative sign. so sum is –\(\frac{5}{10}\)
Question 9.
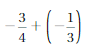
Answer:
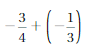
Because the signs are same
LCM of the denominators = 3 × 4 = 12
So –\(\frac{3}{4}\) should be multiplied with 3 to Numerator and Denominator
and –\(\frac{1}{3}\) should be multiplied with 4 to Numerator and Denominator we get,
=|-\(\frac{9}{12}\)| + |-\(\frac{4}{12}\)|
= –\(\frac{13}{12}\)
Both the signs are negative so, use a negative sign in the sum .
So sum is –\(\frac{13}{12}\)
Question 10.
-2.6 + 4.3
Answer:
=4.3 + (-2.6)
=|4.3| – |-2.6|
= 4.3 – 2.6
= 1.7
|4.3| > |-2.6| so use positive sign so sum = 1.7
Question 11.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer :
Add -4.5 and 3.5
Find the sum of -4.5 and 3.5
The above two statements means the same which sum of the numbers.
Where as , What is the distance between -4.5 and 3.5 and what is -4.5 increased by 3.5 ? these two statements are different from the above statements.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
A bottle contains 10.5 cups of orange juice. You drink 1.2 cups of the juice each morning and 0.9 cup of the juice each afternoon. How much total juice do you drink each day? When will you run out of juice?
Answer:
Volume of orange juice = 10.5 cups
Volume of juice drank in morning = 1.2 cups
Volume of juice drank in afternoon = 0.9 cups
Total Volume of juice drank in one day = 1.2 + 0.9 cups = 2.1 cups
Number of days juice gets completed = 10.5 ÷ 2.1 = 5 days.
You will run out of juice on 5 th day .
Question 13.
DIG DEEPER!
The table shows the changes in elevation of a hiker each day for three days. How many miles of elevation must the hiker gain on the fourth day to gain mile of elevation over \(\frac{1}{4}\) mile of elevation over the four days?
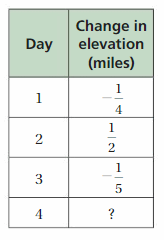
Answer:
Change in Elevation on first day = –\(\frac{1}{4}\)
Change in elevation on Second day = \(\frac{1}{2}\)
Change in elevation on third day = –\(\frac{1}{5}\)
Total change in elevation for 3 days = –\(\frac{1}{4}\) + \(\frac{1}{2}\) + (-\(\frac{1}{5}\) )
Lcm of 2,4 and 5 is 20
= –\(\frac{5}{20}\) + \(\frac{10}{20}\) + (-\(\frac{4}{20}\) )
= \(\frac{1}{20}\)
Gain in elevation = \(\frac{1}{4}\)
Change in elevation on fourth day = C
C + \(\frac{1}{20}\) = \(\frac{1}{4}\)
C = \(\frac{1}{4}\) – \(\frac{1}{20}\) ( \(\frac{1}{4}\) = \(\frac{5}{20}\) )
= \(\frac{5}{20}\) – \(\frac{1}{20}\) = \(\frac{4}{20}\) =\(\frac{1}{5}\)
Change in elevation on fourth day = \(\frac{1}{5}\)
Adding Rational Numbers Homework & Practice 1.3
Review & Refresh
Find the sum. Use a number line to verify your answer.
Question 1.
3 + 12
Answer:
3 + 12 = 15
|3| + |12| = 15
Both the signs are same so use positive sign to the sum .
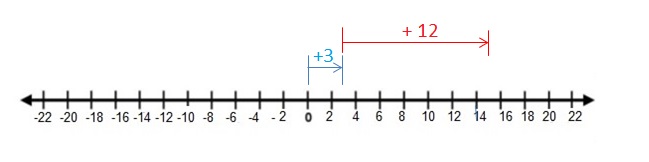
Explanation:
Draw an arrow from 0 to 3 to represent 3. Then draw an arrow 12 units to the right representing adding +12.The arrows end at showing the sum
So, 3 + 12 = 15
Question 2.
5 + (-7)
Answer:
5 + (-7)
|5| – |-7|
= 5 – 7
= -2
|5| < |-7| so use negative sign.
so , sum is – 2
Explanation:
Draw an arrow from 0 to 5 to represent 5. Then draw an arrow 7 units to the left representing adding -7.The arrows end at showing the sum
So, 5 + (-7) = -2
Question 3.
-4 + (-1)
Answer :
-4 + (-1)
|-4| + |-1|
= 4 + 1
= -5
Both have the same signs
so , sum is – 5
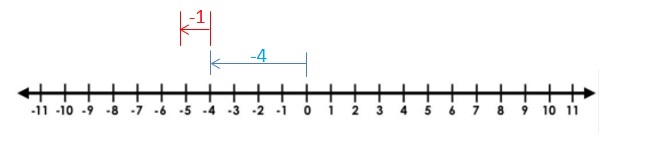
Explanation:
Draw an arrow from 0 to -4 to represent -4. Then draw an arrow 1 units to the left representing adding -1.The arrows end at showing the sum
So,-4 + (-1) -5
Question 4.
-6 + 6
Answer:
-6 + 6
|-6| – |6|
= 6 – 6
= 0
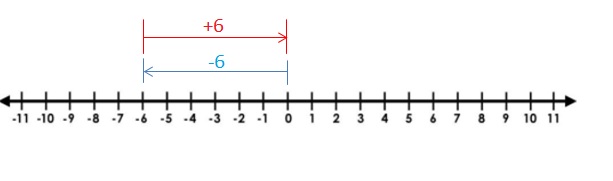
Explanation:
Draw an arrow from 0 to -6 to represent -6. Then draw an arrow 6 units to the right representing adding +6.The arrows end at showing the sum
So,-6 + 6 = 0
Subtract.
Question 5.
69 – 38
Answer :
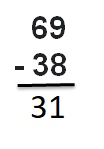
Question 6.
82 – 74
Answer:
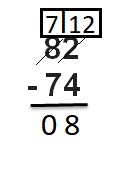
Question 7.
177 – 63
Answer :
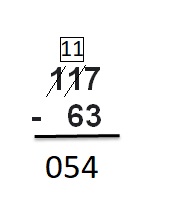
Question 8.
451 – 268
Answer:
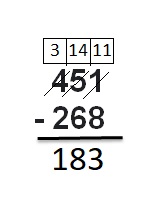
Question 9.
What is the range of the numbers below?
12, 8, 17, 12, 15, 18, 30
Answer :
8, 12 , 12 , 15 , 17, 18, 30
Smallest number = 8
Largest number = 30
Range = largest number – smallest number = 30 – 8 = 22
Explanation:
The range is the difference between the largest and smallest numbers. The midrange is the average of the largest and smallest number.
Concepts, Skills, & Problem Solving
USING TOOLS
Choose a unit fraction to represent the space between the tick marks on the number line. Write the addition expression being modeled. Then find the sum. (See Exploration 1, p. 17.)
Question 10.
Answer :
-2 + ( 5) = 3
-2 + 5
|-2| – |5|
= 2 – 5
= 3
|-2| < |5| so use positive sign so, sum is 5
Explanation:
An arrow is drawn from 0 to -2 represent -2 . Then another arrow is drawn from -2 to 3 represent adding of -5. then the arrow ends at 3 showing the sum .
Question 11.
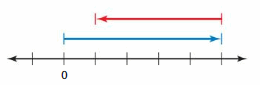
Answer :
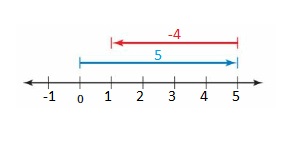
5 + (-4)
|5| – |-4|
= 5 – 4
= 1
|5| > |-4| so use positive sign so, sum is 1
Explanation:
An arrow is drawn from 0 to 5 represent 5 . Then another arrow is drawn from 5 to 1 represent adding of -4 then the arrow ends at 1 showing the sum .
ADDING RATIONAL NUMBERS
Find the sum. Write fractions in simplest form.
Question 12.
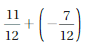
Answer :
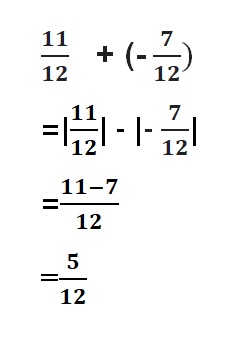
Question 13.
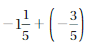
Answer :
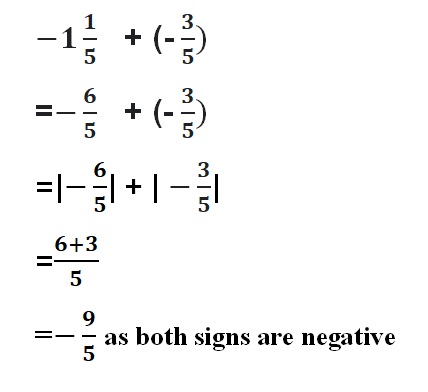
Question 14.
-4.2 + 3.3
Answer :
-4.2+ 3.3
|-4.2| – |3.3|
= 4.2 – 3.3
= 0.9
|-4.2| > |3.3|
so , sum is – 0.9
Question 15.
![]()
Question 16.
12.48 + (-10.636)
Answer :
12.48 + (-10.636)
|12.48| – |-10.636|
= 12.48 – 10.636
= 1.844
|12.48| > |-10.636|
so , sum is 1.844
Question 17.
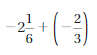
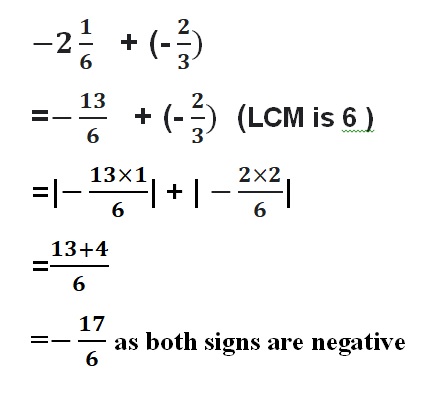
Question 18.
-20.25 + 15.711
Answer :
-20.25 + 15.711
|-20.25| – |15.711|
= 20.25 – 15.711
= – 4.539
|20.25| > |15.711|
so , sum is – 4.539
Question 19.
-32.306 + (-24.884)
Answer :
-32.306 + (-24.884)
|-32.306| + |-24.884|
= 32.306 + 24.884
= – 7.422
Both the signs are same
so , sum is – 7.422
Question 20.
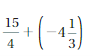
Answer :
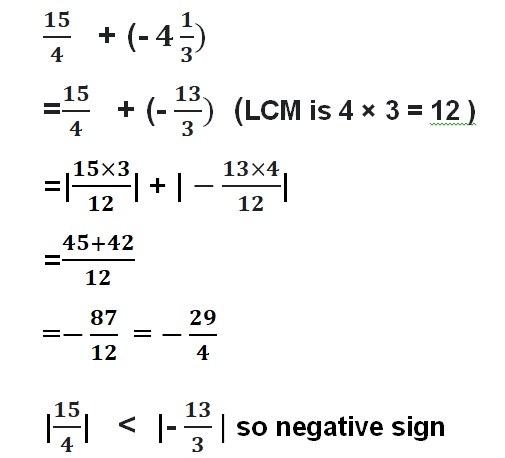
Question 21.
YOU BE THE TEACHER
Your friend finds the sum. Is your friend correct? Explain your reasoning.
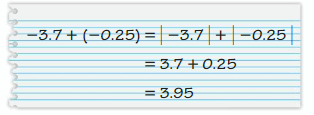
Answer :
No, the sum is -3.95
Explanation :
The procedure to solve above sum is right but in the last after adding the numbers he should put negative symbol to the sum as both the addends are negative.
The sum of negative numbers will always be negative .
OPEN-ENDED
Describe a real-life situation that can be represented by the addition expression modeled on the number line.
Question 22.
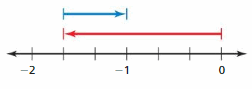
Answer :
Explanation:
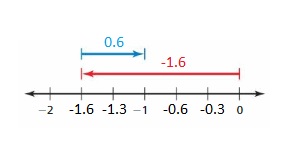
The coin is buried under ground of 1.6 metres. then again it is removed from ground and buried with increase of 0.6 length from previous buried length . Now where is the coin located.
Question 23.
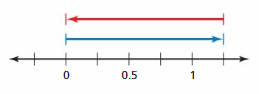
Answer :
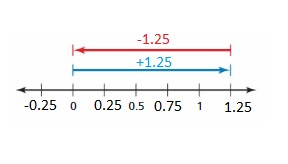
Explanation:
Rahul gained 1.25$ on his birthday and spent 1.25$ on video game . how much money is left over with rahul .
Question 24.
MODELING REAL LIFE
You eat \(\frac{3}{10}\) of a coconut. Your friend eats \(\frac{1}{5}\) of the coconut. What fraction of the coconut do you and your friend eat?

Answer :
Coconut part eaten by me = \(\frac{3}{10}\)
Coconut part eaten by friend = \(\frac{1}{5}\)
Total Coconut eaten by me and my friend = \(\frac{3}{10}\) + \(\frac{1}{5}\)
\(\frac{1}{5}\) is written as \(\frac{2}{10}\)
= \(\frac{3}{10}\) + \(\frac{2}{10}\)
= \(\frac{5}{10}\)
= \(\frac{1}{2}\)
Total Coconut eaten by me and my friend = \(\frac{1}{2}\)
Question 25.
MODELING REAL LIFE
Your bank account balance is $20.85. You deposit $15.50. What is your new balance?
Answer :
My Account Balance = $20.85
Deposited Money = $15.50
New Balance = $20.85 + $15.50 = .635
Question 26.
NUMBER SENSE
When is the sum of two negative mixed numbers an integer?
Answer :
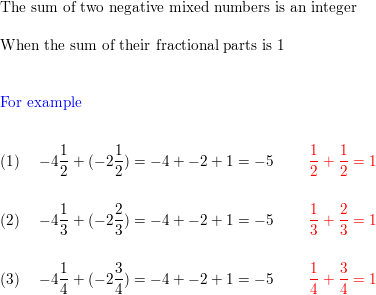
Question 27.
WRITING
You are adding two rational numbers with different signs. How can you tell if the sum will positive, negative, or zero?
Answer :
The sign of the sum will always be the sign of the absolute value of the greater number.
Explanation :

Question 28.
DIG DEEPER!
The table at the left shows the water level (in inches) of a reservoir for three months compared to the yearly average. Is the water level for the three-month period greater than or less than the yearly average? Explain.

Answer :
Water level in june month = -2\(\frac{1}{8}\) = –\(\frac{17}{8}\)
Water level in July month = 1\(\frac{1}{4}\) = \(\frac{5}{4}\)
Water level in August month = –\(\frac{7}{8}\)
Average of Yearly = Water level in (June + July + August ) ÷ 3
= (-\(\frac{17}{8}\) + \(\frac{5}{4}\) + (-\(\frac{7}{8}\) )) ÷ 3
Take \(\frac{5}{4}\) = \(\frac{10}{8}\) as it is multiplied by 2 with numerator and denominator
= (-\(\frac{17}{8}\) + \(\frac{10}{8}\) + (-\(\frac{7}{8}\) )) ÷ 3
= –\(\frac{14}{8}\) ÷ 3
= –\(\frac{7}{4}\) ÷ 3
= –\(\frac{7}{12}\)
Average of Yearly = –\(\frac{7}{12}\)
3 months water level = –\(\frac{7}{4}\)
–\(\frac{7}{4}\) > –\(\frac{7}{12}\)
3 months water level is greater than average of yearly .
USING PROPERTIES
Tell how the Commutative and Associative Properties of Addition can help you find the sum using mental math. Then find the sum.
Question 29.
4.5 + (-6.21) + (-4.5)
Answer :
4.5 + (-6.21) + (-4.5)
we know 4.5 – 4.5 = 0, we get
4.5 – 4.5 – 6.21 = -6.21
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 30.
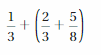
Answer :
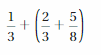
= 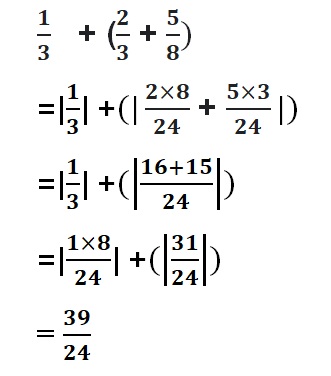
Question 31.
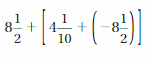
Answer :
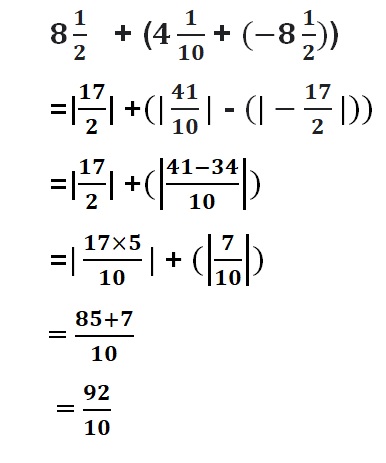
ADDING RATIONAL NUMBERS
Find the sum. Explain each step.
Question 32.
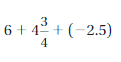
Answer :
Converting the fraction form into decimal form
4\(\frac{3}{4}\) = \(\frac{19}{4}\) = 4.75
= 6 + 4.75 + (-2.5)
add | 6|+ | 4.75 |we get,
= | 10.75 | – | -2.5 |
= | 8.55|
6 is greater number so we get positive sign for the sum.
Therefore sum = 8.55
Question 33.
![]()
Answer :
Convert the fraction form into decimal form we get ,
\(\frac{4}{5}\) = 0.8
= -4.3 + 0.8 + 12
absolute values of the numbers
= | -4.3 | + | 0.8 | + | 12 |
add | 0.8 | + | 12 | = | 12.8 |
= | -4.3 | + | 12.8 |
= 12.8 – 4.3
= 8.5
12 is greater number so sum sign is positive
Therefore sum = 8.5
Question 34.
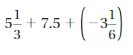
Answer :
Convert the fraction forms into decimal forms we get,
5\(\frac{1}{3}\) = \(\frac{16}{3}\) = 5.33
-3\(\frac{1}{6}\) = –\(\frac{19}{6}\) = -3.16
we get equation as ,
5.33 + 7.5 + (-3.16)
=| 5.33 | + | 7.5 | – | -3.16 |
= 5.33 + 7.5 – 3.16
= 12.53 – 3.16
= 9.37
as 7.5 is greater than all numbers so sum sign will be positive.
Therefore sum = 9.37
Question 35.
PROBLEM SOLVING
The table at the right shows the annual profits (in thousands of dollars) of a county fair from 2013 to 2016. What must the 2017 profit be (in hundreds of dollars) to break even over the five-year period?
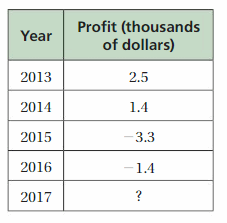
Answer :
Profit in 2013 = 2.5
Profit in 2014 = 1.4
Profit in 2015 = -3.3
Profit in 2016 = -1.4
Total Profit from 2013 to 2016 = 2.5 + 1.4 + ( -3.3 ) + (-1.4) = | 2.5 | + | 1.4 | – | -3.3 | – | -1.4 | = 2.5 + 1.4 -3.3 -1.4=2.5 – 3.3 = -0.8
– 3.3 is greater than all numbers so sum sign is negative.
The 2017 profit should be to break even over the five-year period is greater than -0.8 .
Question 36.
REASONING
Is | a + b | = | a | + | b | true for all rational numbers a and b? Explain.
Answer :
Sometimes based on the values of a and b
Explanation:

Question 37.
REPEATED REASONING
Evaluate the expression.
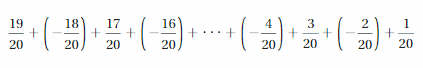
Answer :
\(\frac{1}{2}\)
Explanation:

Lesson 1.4 Subtracting Integers
EXPLORATION 1
Using Integer Counters to Find Differences
Work with a partner.
a. Use integer counters to find the following sum and difference. What do you notice?
![]()
Answer :
4 + (-2) = 2 and 4 – 2 = 2
Explanation:
When -2 is added to 4 or when2 is subtracted from 4 we get the same sum and difference.
b. In part (a), you removed zero pairs to find the sums. How can you use integer counters and zero pairs to find -3 – 1?
c. INDUCTIVE REASONING
Use integer counters to complete the table.
Answer :
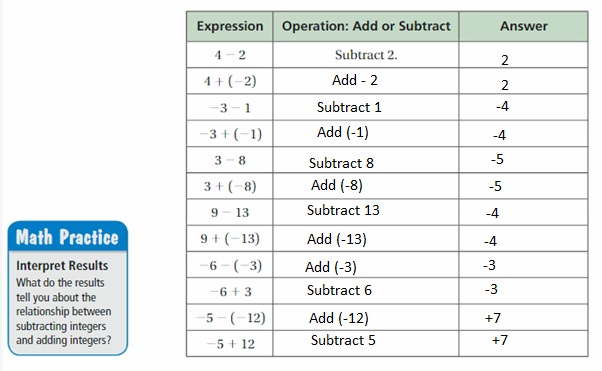
d. Write a general rule for subtracting integers.
Answer :
To subtract integers, change the sign on the integer that is to be subtracted. If both signs are positive, the answer will be positive. If both signs are negative, the answer will be negative. If the signs are different subtract the smaller absolute value from the larger absolute value.
1.4 Lesson
Try It
Use a number line to find the difference.
Question 1.
1 – 4
Answer :
1 – 4 = – 3
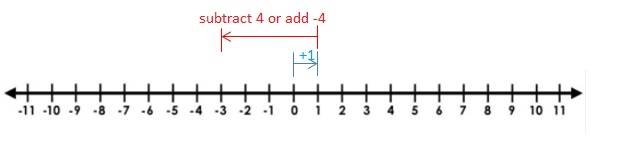
Explanation :
Draw a arrow from 0 to 1 represent 1 . Then , Draw an arrow 4 units to the left to represent subtracting 4, or adding -4.
So, 1 – 4 = – 3
Question 2.
-5 – 2
Answer :
-5 – 2 = -7
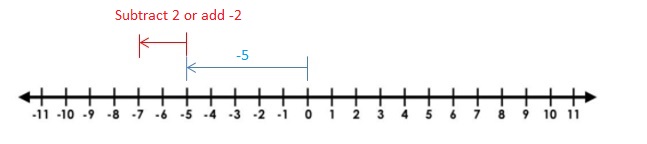
Explanation :
Draw a arrow from 0 to -5 represent -5 . Then , Draw an arrow 2 units to the left to represent subtracting 2, or adding -2.
So, -5 – 2 = -7
Question 3.
6 – (-5)
Answer :
6 – (-5) = 11
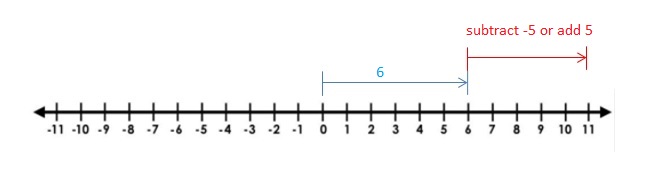
Explanation :
Draw a arrow from 0 to 6 represent 6 . Then, Draw an arrow 5 units to the right to represent subtracting -5, or adding 5.
So, 16 – (-5) = 11
Try It
Question 4.
8 – 3
Answer :
=8 – 3
=8 + ( – 3) Add opposite of 3
=5 Add
The difference is 5
Question 5.
9 – 17
Answer :
= 9 – 17
= 9 + ( – 17) Add opposite of 17
= -8 Add
The difference is -8
Question 6.
-3 – 3
Answer :
= -3 – 3
= -3 + ( – 3) Add opposite of 3
= -6 Add
The difference is -6
Question 7.
-14 – 9
Answer :
= -14 – 9
= -14 + ( – 9) Add opposite of 9
= -25 Add
The difference is -25
Question 8.
10 – (-8)
Answer :
= 10 – ( -8 )
= 10+ ( 8) Add opposite of -8
= 18 Add
The difference is 18
Question 9.
-12 – (-12)
Answer :
= -12 – ( -12 )
= -12 + ( 12) Add opposite of -12
= -24 Add
The difference is -24
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
WRITING
Explain how to use a number line to find the difference of two integers.
Answers :
To Subtract two Positive integers using a number line:
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is positive, move that many units to the right from the location of the first integer. …
- Your answer will be the point you end on.
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is Negative, move that many units to the Left from the location of the first integer. …
- Your answer will be the point you end on.
MATCHING
Match the subtraction expression with the corresponding addition expression. Explain your reasoning.
Question 11.
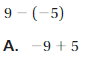
Question 12.
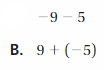
Question 13.
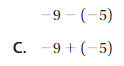
Question 14.
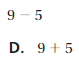
SUBTRACTING INTEGERS
Find the difference. Use a number line to justify your answer.
Question 15.
10 – 12
Answer :
10 – 12 = -2
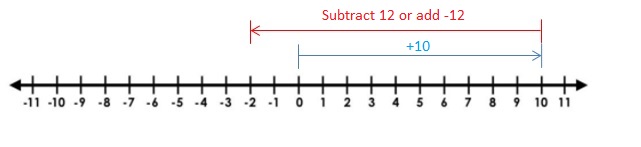
Explanation :
Draw a arrow from 0 to 10 represent 10 . Then, Draw an arrow 12 units to the left to represent subtracting 12, or adding -12.
So, 10 – 12 = -2
Question 16.
6 – (-8)
Answer :
6 – (-8) = 14
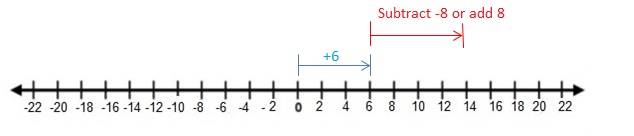
Explanation :
Draw a arrow from 0 to 6 represent 6 . Then, Draw an arrow 8 units to the right to represent subtracting -8, or adding 8.
So, 6 – (-8) = 14
Question 17.
-7 – (-4)
Answer :
-7 – (-4) = -3
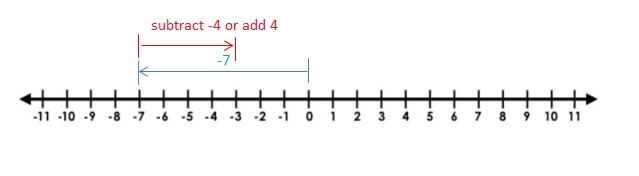
Explanation :
Draw a arrow from 0 to -7 represent -7 . Then, Draw an arrow 4 units to the left to represent subtracting -4, or adding 4.
So, -7 – (-4) = -3
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
A polar vortex causes the temperature to decrease from 3°C at 3:00 P.M. to -2°C at 4:00 P.M. The temperature continues to change by the same amount each hour until 8:00 P.M. Find the total change in temperature from 3:00 P.M. to 8:00 P.M.
Answer :
Temperature decrease from 3°C at 3:00 P.M. to -2°C at 4:00 P.M
Temperature decrease from 3:00 P.M. to 4:00 P.M = 3°C – (-2°C) = 5 °C
For one hour it decreases 5 °C
From to 3:00 P.M. to 8:00 P.M. = 5 hours
Temperature decrease from 3:00 P.M. to 8:00 P.M. = 5 hours × 5 °C = 25 °C
Question 19.
DIG DEEPER!
While on vacation, you map several locations using a coordinate plane in which each unit represents 1 mile. A cove is at(3, 7), an island is at(5, 4), and you are currently at (3, 4). Are you closer to the cove or the island? Justify your answer.

Answer :
Island is close to the cove
Subtracting Integers Homework & Practice 1.4
Review & Refresh
Find the sum. Write fractions in simplest form.
Question 1.
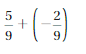
Answer :
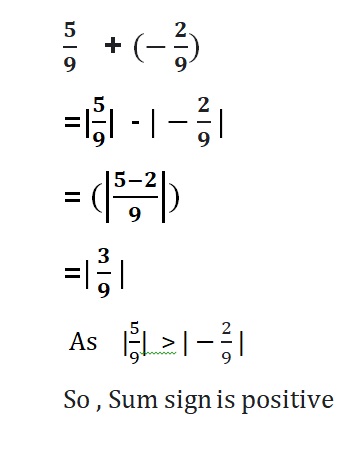
Question 2.
-8.75 + 2.43
Answer :
=2.43 – 8.75
=2.43 + (-8.75) Add opposite of 8.75
= -6.32
The difference is – 6.32
Question 3.
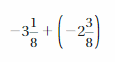
Answer :
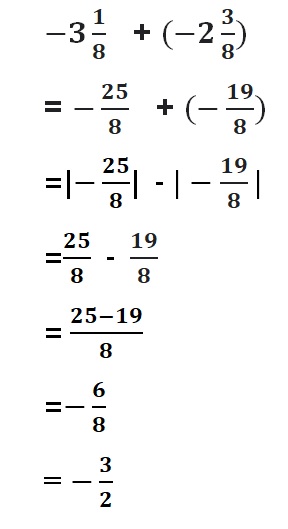
As both the numbers are negative so, sum is negative.
Add.
Question 4.
2.48 + 6.711
Answer :
Question 5.
12.807 + 7.116
Answer :
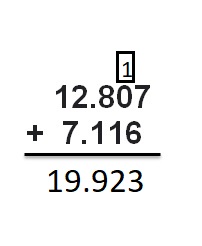
Question 6.
18.7126 + 14.033
Answer :

Write an addition expression represented by the number line. Then find the sum.
Question 7.
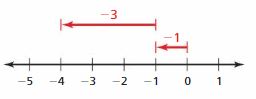
Answer :
– 1 + (-3) Add opposite of 3
= -4 Add
Explanation :
An arrow is drawn from 0 to -1 represent -1 and then an arrow from -1 drawn towards right represent – 3 units . so the sum is -4. the arrows end showing the sum at -4.
– 1 + (-3) = -4
Question 8.
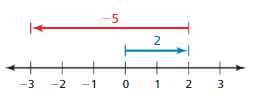
Answer :
2 + ( – 5 ) add opposite of 5
= -3
Explanation :
An arrow is drawn from 0 to 2 represent 2 and then an arrow from 2 drawn towards left represent – 5 units . so the sum is -3. the arrows end showing the sum at -3.
Concepts, Skills, & Problem Solving
USING INTEGER COUNTERS
Use integer counters to find the difference. (See Exploration 1, p. 23.)
Question 9.
5 – 3
Answer :
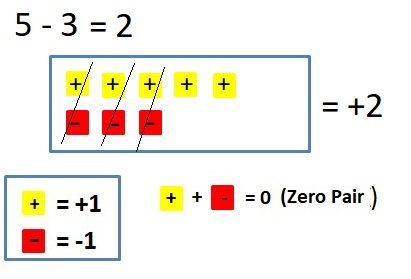
Explanation:
A Positive counter and negative counter form zero pair .
Take 5 positive counters and 3 negative counters then 3 zero pairs will be canceled and only 2 positive counters are left, the sum is +2
Question 10.
1 – 4
Answer :
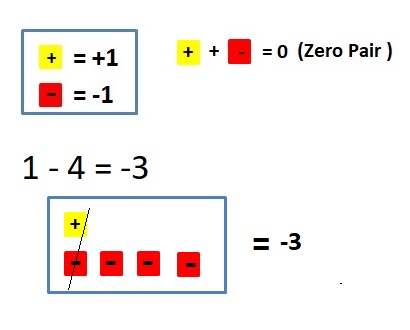
Explanation:
A Positive counter and negative counter form zero pair .
Take 1 positive counters and 4 negative counters then 1 zero pair will be canceled and only 3 negative counters are left, the sum is -3
Question 11.
-2 – (-6)
Answer :
Convert the equation in addition form
-2 – (-6) = -2 + 6
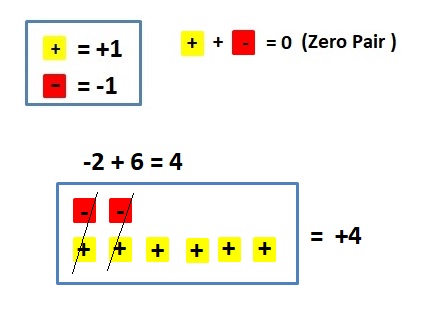
Explanation:
A Positive counter and negative counter form zero pair .
Take 6 positive counters and 2 negative counters then 2 zero pair will be canceled and only 4 positive counters are left, the sum is +4
USING NUMBER LINES
Write an addition expression and write a subtraction expression represented by the number line. Then evaluate the expressions.
Question 12.
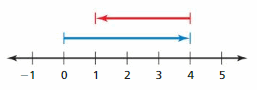
Answer :
4 – 3 = 1
Explanation :
An arrow is drawn from 0 to 4 represent 4 and then an arrow from 4 drawn towards left represent 3 units . so the sum is 1. the arrows end showing the sum at 1.
Question 13.
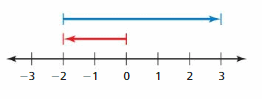
Answer :
-2 + 5 = 3
Explanation :
An arrow is drawn from 0 to -2 represent -2 and then an arrow from -2 drawn towards right represent 5 units . so the sum is 3. the arrows end showing the sum at +3.
SUBTRACTING INTEGERS
Find the difference. Use a number line to verify your answer.
Question 14.
4 – 7
Answer :
Words : To subtract an integer add its opposite .
Numbers : 4 – 7 = 4 + (-7) = -3
Model : 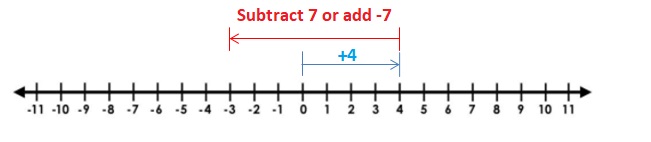
Explanation:
Draw a arrow from 0 to 4 represent 4 . Then, Draw an arrow 47units to the left to represent subtracting 7, or adding -7. The arrow ends at – 3 showing the difference.
So, 4 – 7 = -3
Question 15.
8 – (-5)
Answer :
8 – (-5) = 13
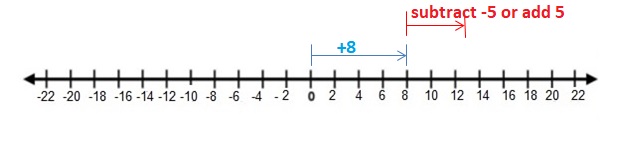
Explanation:
Draw a arrow from 0 to 8 represent 8 . Then, Draw an arrow 5 units to the right to represent subtracting -5, or adding 5. The arrow ends at 13 showing the difference.
So, 8 – (-5) = 13
Question 16.
– 6 – (-7)
Answer :
– 6 – (-7) = 1
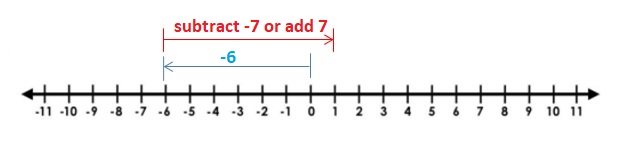
Explanation:
Draw a arrow from 0 to -6 represent -6 . Then, Draw an arrow 7 units to the left to represent subtracting -7, or adding 7. The arrow ends at 1 showing the difference.
So, – 6 – (-7) = 1
Question 17.
– 2 – 3
Answer :
– 2 – 3 = -5
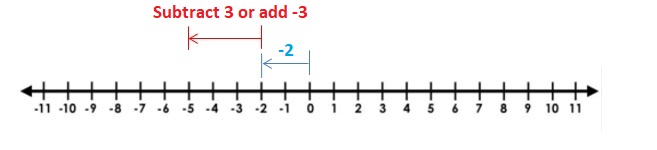
Explanation:
Draw a arrow from 0 to -2 represent -2 . Then, Draw an arrow 3 units to the left to represent subtracting 3, or adding -3. The arrow ends at – 5 showing the difference.
So, – 2 – 3 = -5
Question 18.
5 – 8
Answer :
5 – 8 = – 3
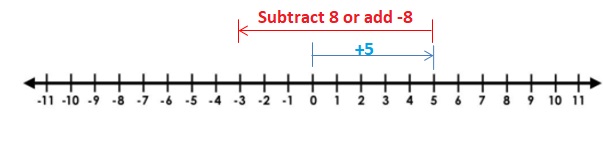
Explanation:
Draw a arrow from 0 to 5 represent 5 . Then, Draw an arrow 8 units to the left to represent subtracting 8, or adding -8. The arrow ends at – 3 showing the difference.
So, 5 – 8 = – 3
Question 19.
-4 – 6
Answer :
-4 – 6 = – 10
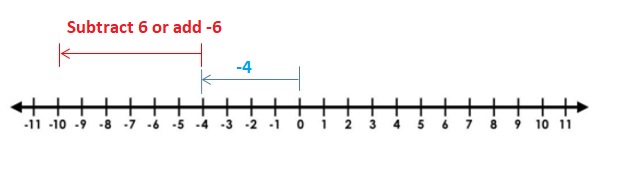
Explanation:
Draw a arrow from 0 to 4 represent -4 . Then, Draw an arrow 6 units to the left to represent subtracting 6, or adding -6. The arrow ends at – 10 showing the difference.
So, -4 – 6 = – 10
Question 20.
-8 – (-3)
Answer:
-8 – (-3) = -5
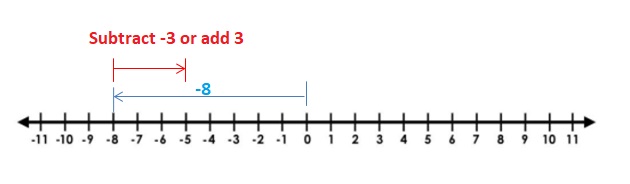
Explanation:
Draw a arrow from 0 to -8 represent -8 . Then, Draw an arrow 3 units to the Right to represent subtracting -3, or adding 3. The arrow ends at – 5 showing the difference.
So, -8 – (-3) = -5
Question 21.
10 – 7
Answer :
10 – 7 = 3
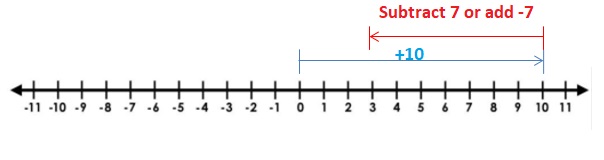
Explanation:
Draw a arrow from 0 to 10 represent 10 . Then, Draw an arrow 7 units to the left to represent subtracting 7, or adding -7. The arrow ends at 3 showing the difference.
So, 10 – 7 = 3
Question 22.
– 8 – 13
Answer :
– 8 – 13 = -21
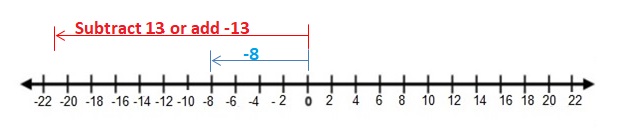
Explanation:
Draw a arrow from 0 to -8 represent -8 . Then, Draw an arrow 13 units to the left to represent subtracting 13, or adding -13. The arrow ends at – 21 showing the difference.
So, – 8 – 13 = – 21
Question 23.
15 – (-2)
Answer :
15 – (-2) = 17
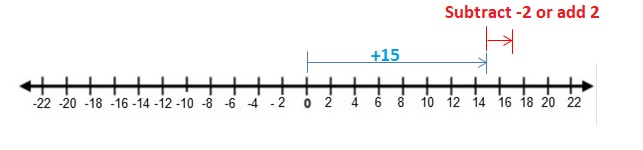
Explanation:
Draw a arrow from 0 to 15 represent 15 . Then, Draw an arrow 2 units to the Right to represent subtracting -2 or adding 2. The arrow ends at 17 showing the difference.
So, 15 – (-2) = 17
Question 24.
-9 – (-13)
Answer :
-9 – (-13) = 4
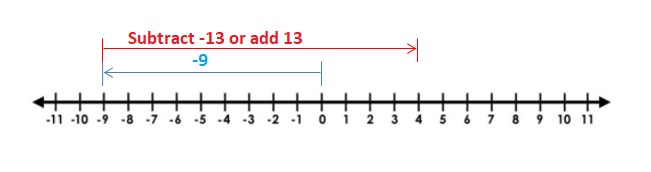
Explanation:
Draw a arrow from 0 to -9 represent -9 . Then, Draw an arrow 13 units to the Right to represent subtracting -13, or adding 13. The arrow ends at 4 showing the difference.
So, -9 – (-13) = 4
Question 25.
-7 – (-8)
Answer:
-7 – (-8) = 1
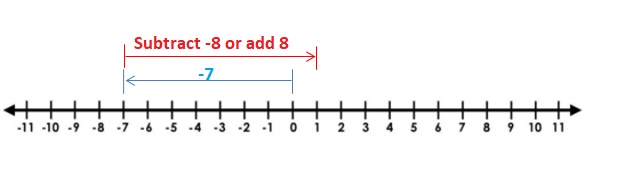
Explanation:
Draw a arrow from 0 to 4 represent 4 . Then, Draw an arrow 47units to the left to represent subtracting 7, or adding -7. The arrow ends at – 3 showing the difference.
So, -7 – (-8) = 1
Question 26.
– 6 – (-6)
Answer :
– 6 – (-6) = 0
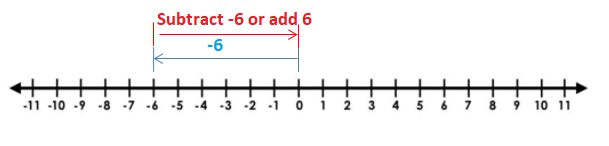
Explanation:
Draw a arrow from 0 to -6 represent -6 . Then, Draw an arrow 6 units to the left to represent subtracting -6, or adding 6. The arrow ends at 0 showing the difference.
So, – 6 – (-6) = 0
Question 27.
-10 – 12
Answer :
-10 – 12 = -22
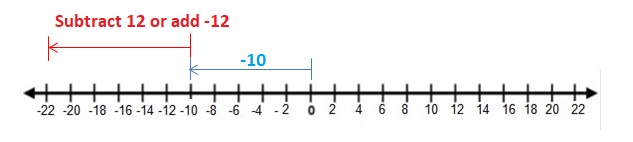
Explanation:
Draw a arrow from 0 to -10 represent -10 . Then, Draw an arrow 12 units to the left to represent subtracting 12, or adding -12. The arrow ends at – 22 showing the difference.
So, -10 – 12 = -22
Question 28.
32 – (-6)
Answer :
32 – (-6) = 38
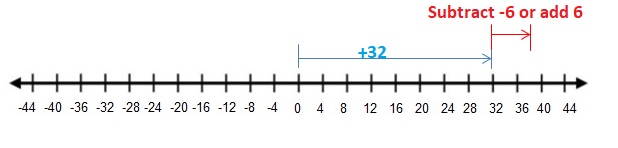
Explanation:
Draw a arrow from 0 to 32 represent 32. Then, Draw an arrow 6 units to the Right to represent subtracting -6, or adding 6 The arrow ends at 38 showing the difference.
So, 32 – (-6) = 38
Question 29.
0 – (-20)
Answer :
0 – (-20) = 20

Explanation:
Draw an arrow from 0 to 20 which represent 20 .
So, 0 – (-20) = 20
Question 30.
YOU BE THE TEACHER
Your friend finds the difference. Is your friend correct? Explain your reasoning.
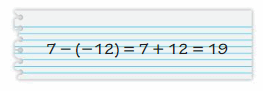
Answer :
Yes
Explanation :
7 – (- 12 )
= 7 + 12 Add opposite of -12
= 19 Add
Question 31.
A scientist records the water temperature and the air temperature in Antarctica. The water temperature is -2°C. The air is 9°C colder than the water. Which expression can be used to find the air temperature? Explain your reasoning.
Answer :
-2 – 9 is the correct option
Explanation :
Temperature of water = -2°C.
The air is 9°C colder than the water It means
Temperature of Air = -2 – 9 °C. = – 11 °C
Question 32.
MODELING REAL LIFE
A shark is 80 feet below the surface of the water. It swims up and jumps out of the water to a height of 15 feet above the surface. Find the vertical distance the shark travels. Justify your answer.
Answer :
The shark is located at = – 80 feet
The height of shark when jumps = + 15 feet .
The vertical Distance traveled by shark = 80 + 15 feet = 95 feet (As distance cant be negative )
Explanation :
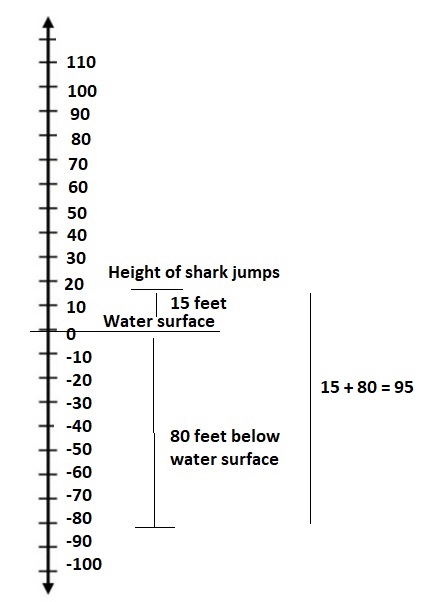
Question 33.
MODELING REAL LIFE
The figure shows a diver diving from a platform. The diver reaches a depth of 4 meters. What is the change in elevation of the diver?
Answer :
The diver reaches a depth of 4 meters.
Height of diver diving from a platform = 10 metres
The change in elevation of the driver =10 – (-4) = 10 + 4 = 14 metres.
Question 34.
OPEN-ENDED
Write two different pairs of negative integers, x and y, that make the statement x – y = 1 true.
Answer :
Let x = 1 and y = 2
x – y
= 1 – 2
= -1
Let x = 2 and y = 3
x – y
= 2 – 3
= – 1
From Above values of x and y the statement x – y = -1 is explained
USING PROPERTIES
Tell how the Commutative and Associative Properties of Addition can help you evaluate the expression using mental math. Then evaluate the expression.
Question 35.
2 – 7 + (-2)
Answer :
2 + (-2) is zero pair
=2 – 7 + (-2) (order of addends changed but sum remains the same )
= 2 – 2 – 7
= – 7
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 36.
– 6 – 8 + 6
Answer :
6 + (-6) is zero pair
=-6 – 8 + 6 (order of addends changed but sum remains the same )
= -6 + 6- 8
= – 8
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 37.
8 + (-8 – 5)
Answer :
8 – 8 = 0 zero pair
8 + (-8 – 5)
= (8 – 8)- 5 (order of addends changed but sum remains the same )
= -5
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 38.
-39 + 46 – (-39)
Answer :
39 + (-39) is zero pair
=-39 + 46 – (-39) (order of addends changed but sum remains the same )
= -39 + 39+ 46
= 46
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 39.
[13 + (-28)] – 13
Answer :
13 + (-13) is zero pair
=[13 + (-28)] – 13 (order of addends changed but sum remains the same )
= [13 + (-13)] – 28
= – 28
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 40.
-2 + (-47 – 8)
Answer :
– 2 + (-47 – 8)
= -2 – 8 +(-47) add -2 – 8
= – 10 + (-47 )
= – 57
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
ALGEBRA
Evaluate the expression when k = -3, m = -6, and n = 9.
Question 41.
4 – n
Answer :
4 – n
Take n = 9 we get,
4 – 9 = – 5
Question 42.
m – (-8)
Answer :
m – (-8)
Take m = ( -6)
= (-6) – ( -8)
= -6 + 8
= -2
Question 43.
-5 + k – n
Answer :
-5 + k – n
Take k =-3 and n = 9
– 5 + (-3) – 9
= -5 – 3 – 9
= -8 – 9
= – 17
Question 44.
| m – k |
Answer :
| m – k |
Take m = (-6) and k = (-3)
| (-6) – (-3) |
= | -6 + 3 |
= | – 3 |
= 3
Question 45.
MODELING REAL LIFE
The table shows the record monthly high and low temperatures for a city in Alaska.

a. Which month has the greatest range of temperatures?
Answer :
Range in Jan = 56 – (-35) = 91
Range in Feb = 57 – ( -38) = 95
Range in Mar = 56 – (-24 ) = 80
Range in Apr =72 – (-15) = 87
Range in May = 82 – 1 = 81
Range in Jun = 92 – 29 = 63
Range in Jul = 84 – 34 = 50
Range in Aug = 85 -31 = 54
Range in Sep = 73 – 19 = 54
Range in Oct = 64 – (-6) = 70
Range in Nov = 62 – (-21 ) = 83
Range in Dec = 53 – (-36) = 89
The Greatest Range of temperature is in February = 95
b. What is the range of temperatures for the year?
Answer :
Range of Year = (Jan + Feb + March +April +May +June +July +Aug +Sep +Oct +Nov +Dec ) ÷ 12
= (91 + 95 + 80 +87 + 81 + 63 + 50 + 54 + 54 + 70 + 83 + 89 ) ÷ 12
= 897 ÷ 12 = 74.75
REASONING
Tell whether the difference of the two integers is always, sometimes, or never positive. Explain your reasoning.
Question 46.
two positive integers
Answer :
True
Explanation :
Example :
2 integers are 2 , 4
4 – 2 = 2
Question 47.
a positive integer and a negative integer
Answer :
True
Explanation
Take X = 5 and Y = -6
X – Y = 5 – (-6) = 5 + 6 = 11
Question 48.
two negative integers
Answer :
Sometimes based on the values of integers
Explanation :
Take x = – 2 , y = – 4
x – y = (-2) – (-4) = -2 + 4 = 2
Here the difference is positive.
Take x = – 6 , y = – 2
x – y = -6 – (-2) = -6 + 2 = – 4
Here the difference is negative.
Question 49.
a negative integer and a positive integer
Answer :
Sometimes
Take X = -8 and Y = 3
X-Y = -8 – 3 = -8 + 3 = -5
Here we got negative differences
NUMBER SENSE
For what values of a and b is the statement true?
Question 50.
| a – b | = | b – a |
Answer :
True
Explanation:
Take a = -3 and b = 2
| a – b | = | (-3) – 2 | = | -3 – 2 | = | -5 | = 5
| b – a | = | 2 – (-3) | = | 2 + 3 | = | 5 | = 5
| a – b | = | b – a |
Question 51.
| a – b | = | a | – | b |
Answer :
False
Explanation :
| a – b | = | a | – | b |
Take a = -3 and b = 2
| a – b | = | (-3) – 2 | = | -3 – 2 | = | -5 | = 5
| -3 | – | 2 | = 3 – 2 = 1
| a – b | is not equal to | a | – | b |
Lesson 1.5 Subtracting Rational Numbers
EXPLORATION 1
Subtracting Rational Numbers
Work with a partner.
a. Choose a unit fraction to represent the space between the tick marks on each number line. What expressions involving subtraction are being modeled? What are the differences?
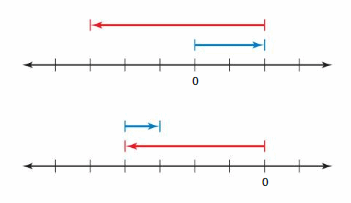
Answer :
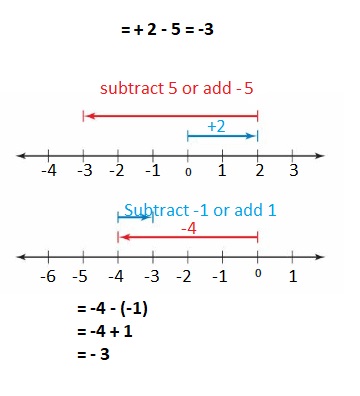
b. Do the rules for subtracting integers apply to all rational numbers? Explain your reasoning.
Answer :
- KEEP the sign of the first number the same.
- CHANGE subtraction to addition.
- CHANGE the sign of the second number to the opposite, positive becomes negative, negative becomes positive
c. You have used the commutative and associative properties to add integers. Do these properties apply in expressions involving subtraction? Explain your reasoning.
Answer :
No properties are followed
Explanation:
Properties of subtraction:
- Subtracting a number from itself.
- Subtracting 0 from a number.
- Order property.
- Subtraction of 1
EXPLORATION 2
Finding Distances on a Number Line
Work with a partner.
a. Find the distance between 3 and 2 on a number line.
Answer :
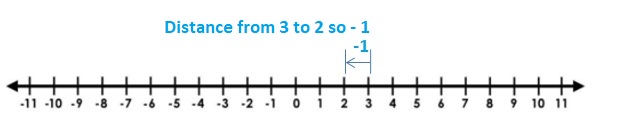
b. The distance between 3 and 0 is the absolute value of 3, because |3 – 0 | = 3. How can you use absolute values
to find the distance between 3 and 2? Justify your answer.

Answer b :
The distance between 3 and 0 is the absolute value of 3, because |3 – 0 | = 3.
The Distance between 3 and 2 is |3 – 2 | = 1
Explanation :
Absolute values of all numbers are positive
1.5 Lesson
Try It
Find the difference. Write your answer in simplest form.
Question 1.
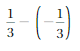
Answer :
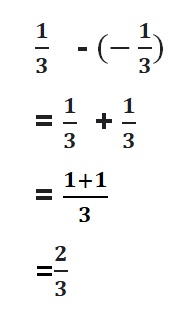
Question 2.
![]()
Answer :
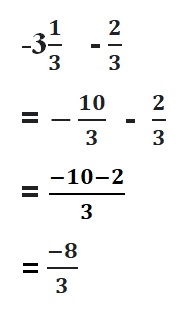
Question 3.
![]()
Answer :
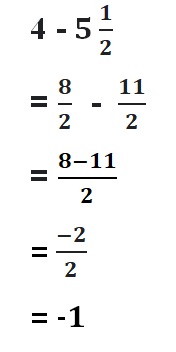
Try It
Find the difference.
Question 4.
-2.1 – 3.9
Answer :
– 2.1 – 3.9 = – 6.0
both have negative signs so, difference also have negative sign .
Question 5.
-8.8 – (-8.8)
Answer :
0
Explanation :
Rewrite the differences as a sum by adding the opposite.
= – 8.8 + 8.8
= 8.8 + ( -8.8 )
Because the signs are different and |8.8 | = |- 8. 8 |
we get ,
= 0 ( zero pair )
Question 6.
0.45 – (-0.05)
Answer :
0.45 – (-0.05)
= 0.45 + 0.05
= 0. 50
Try It
Evaluate the expression. Write fractions in simplest form.
Question 7.
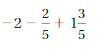
Answer :
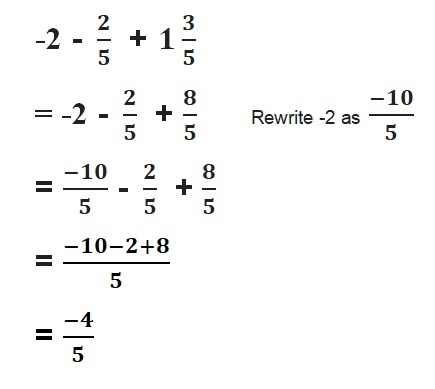
Question 8.
7.8 – 3.3 – (-1.2) + 4.3
Answer :
7.8 – 3.3 – (-1.2) + 4.3
= 7.8 – 3.3 + 1.2 + 4.3
Add all the positive numbers
= 7.8 + 1.2 + 4.3 – 3.3
=9.0 + 4.3 – 3.3
= 13.3 – 3.3
= 10.0
Try It
Find the distance between the two numbers on a number line.
Question 9.
– 3 and 9
Answer :
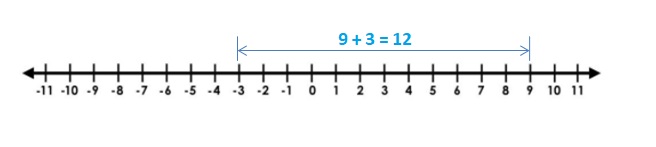
The distance between -3 and 9 is 12 units
Question 10.
-7.5 and -15.3
Answer :

Explanation :
The distance between -7.5 and -15.3 = 15.3 – 7.5 = -7.8
Question 11.
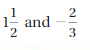
Answer :
1\(\frac{1}{2}\) = \(\frac{3}{2}\) = 1.5
–\(\frac{2}{3}\) = –\(\frac{2}{3}\) = – 0.6
Distance between 1.5 and -0.6
Explanation :
Distance between 1.5 and -0.6 = 1.5 + 0.6 = 2.1
Self-Assessmentfor Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
WRITING
Explain how to use a number line to find the difference of two rational numbers.
Answer :
Difference of two rational numbers using a number line:
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is positive, move that many units to the right from the location of the first integer. …
- Your answer will be the point you end on.
- First, draw a number line.
- Then, find the location of the first integer on the number line.
- Next, if the second integer is Negative, move that many units to the Left from the location of the first integer. …
- Your answer will be the point you end on.
SUBTRACTING RATIONAL NUMBERS
Find the difference. Use a number line to justify your answer.
Question 13.
4.9 – 1.6
Answer :
4.9 – 1.6 = 3.3
Explanation :
Draw a arrow from 0 to 4.9 represent 4.9 . Then, Draw an arrow 1.6 units to the left to represent subtracting 1.6, or adding -1.6. The arrow ends at 3.3 showing the difference.
So, 4.9 – 1.6 = 3.3
Question 14.
![]()
Answer :
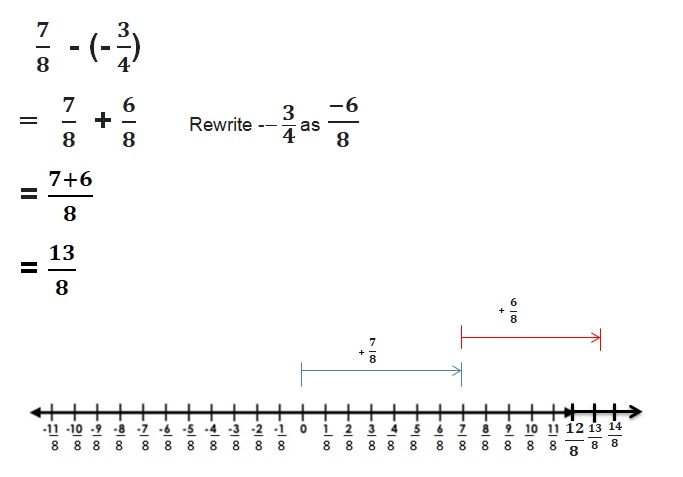
Explanation :
Draw a arrow from 0 to 7/8 represent 7/8 . Then, Draw an arrow 6/8 units to the right to represent subtracting -6/7, or adding 6/8. The arrow ends at 13/8 showing the difference.
So, ![]() = \(\frac{13}{8}\)
= \(\frac{13}{8}\)
Question 15.
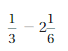
Answer :
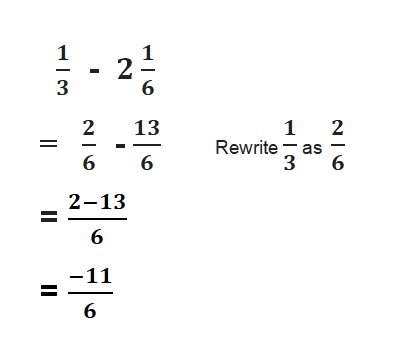
Self-Assessmentfor Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
A parasail is \(\frac{3}{100}\) mile above the water. After 5 minutes, the parasail is \(\frac{1}{50}\) mile above the water. Find and interpret the change in height of the parasail.
Answer :
Height of parasail above water = \(\frac{3}{100}\)
After 5 mins Height of parasil above water \(\frac{1}{50}\)
change in height of the parasail = \(\frac{3}{100}\) – \(\frac{1}{50}\)
Rewrite \(\frac{1}{50}\) as \(\frac{2}{100}\)
change in height of the parasail = \(\frac{3}{100}\) – \(\frac{2}{100}\) = \(\frac{1}{100}\)
Question 17.
DIG DEEPER!
You withdraw $55 from a bank account to purchase a game. Then you make a deposit. The number line shows the balances of the account after each transaction.
a. Find and interpret the distance between the points.
b. How much money was in your account before buying the game?
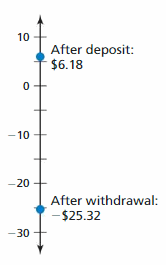
Answer :
a : Distance between the points. = $6.18 + $25.32 = $ 31.50
b : Withdrawal amount = $55
Balance after withdrawal = -$25.32
Money before buying the game = $55 +(-25.32$) = $29.68
Subtracting Rational Numbers Homework & Practice 1.5
Review & Refresh
Find the difference. Use a number line to verify your answer.
Question 1.
9 – 5
Answer :
9 – 5
= 9 + (- 5) Add opposite of 5
= 4 Add
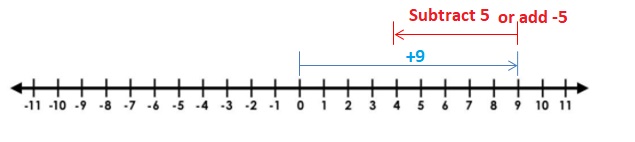
Explanation:
Draw a arrow from 0 to 9 represent 9 . Then, Draw an arrow 5 units to the left to represent subtracting 5, or adding -5. The arrow ends at 4 showing the difference.
So, 9 + (- 5) = 4
Question 2.
– 8 – (-8)
Answer :
– 8 – (-8)
8 – 8 = 0
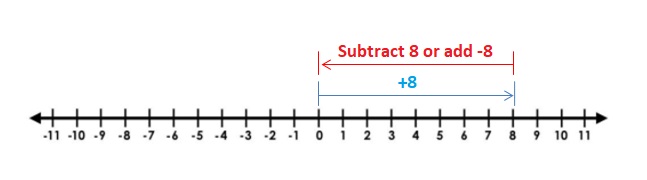
Explanation:
Draw a arrow from 0 to 8 represent 9 . Then, Draw an arrow 8 units to the left to represent subtracting 8, or adding -8. The arrow ends at 0 showing the difference.
So, 8 – 8 = 0
Question 3.
– 12 – 7
Answer :
– 12 – 7 = – 19
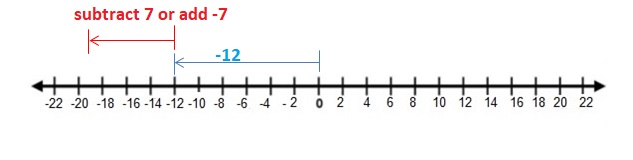
Explanation:
Draw a arrow from 0 to -12 represent -12 . Then, Draw an arrow 7 units to the left to represent subtracting 7, or adding -7. The arrow ends at -19 showing the difference.
So, – 12 – 7 = – 19
Question 4.
12 – (-3)
Answer :
12 – (-3)
= 12 + 3
=15

Explanation:
Draw a arrow from 0 to 12 represent 12 . Then, Draw an arrow 3 units to the right to represent subtracting -3, or adding 3. The arrow ends at 15 showing the difference.
So, 12 – (-3) = 15
Find the volume of the prism.
Question 5.
Answer :
Edge of a cube = 4 ft
Volume of cube = a × a × a = 4 × 4 × 4 = 12ft^3
Question 6.
Answer :
Width of cuboid = 3m
Height of cuboid = 3m
Length of cuboid = 5m
Volume of cuboid = length × width × height = 5 × 3 × 3 = 45 m^3
Order the values from least to greatest.
Question 7.
6, | 3 |, | -4 |, 1, -2
Answer :
The absolute values are | 3 | = 3 and | -4 | = 4
6, 3, 4, 1, – 2
-2, 1, 3, 4, 6 order from least to greatest
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 8.
| 4.5 |, -3.6, 2, | -1.8 |, 1.2
Answer :
| 4.5 | = 4.5 and | -1.8 | = 1.8
4.5 , -3.6, 2, 1.8, 1.2
-3.6 < 1.2< 1.8 < 2 < 4.5 order from least to greatest
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Concepts, Skills, & Problem Solving
USING TOOLS
Choosea unit fraction to represent the space between the tick marks on the number line. Write an expression involving subtraction that is being modeled. Then find the difference. (See Exploration 1, p. 29.)
Question 9.
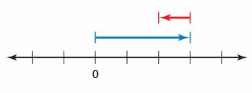
Answer :
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{1}{2}\)
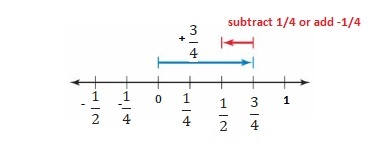
Explanation:
Draw a arrow from 0 to \(\frac{3}{4}\) represent \(\frac{3}{4}\). Then, Draw an arrow \(\frac{1}{4}\) units to the left to represent subtracting –\(\frac{1}{4}\), or adding –\(\frac{1}{4}\). The arrow ends at \(\frac{1}{2}\) showing the difference.
So, \(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{1}{2}\)
Question 10.
Answer :
-1 – (-\(\frac{3}{4}\)) = \(\frac{1}{4}\)
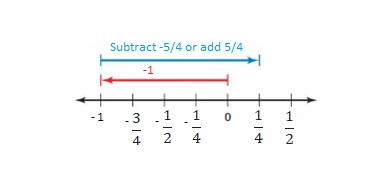
Explanation :
Draw a arrow from 0 to -1 represent -1. Then, Draw an arrow -1 units to the right to represent subtracting –\(\frac{5}{4}\), or adding \(\frac{5}{4}\). The arrow ends at \(\frac{1}{4}\) showing the difference.
So, -1 – (-\(\frac{3}{4}\)) = \(\frac{1}{4}\)
SUBTRACTING RATIONAL NUMBERS
Find the difference. Write fractions in simplest form.
Question 11.
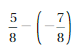
Answer :
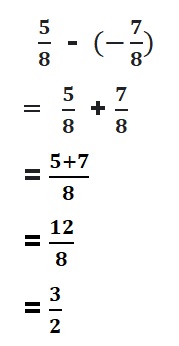
Question 12.
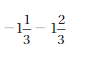
Answer :
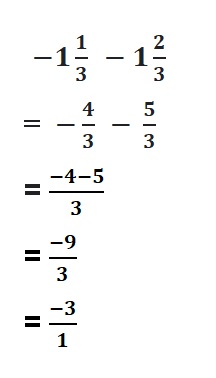
Question 13.
-1 – 2.5
Answer :
– 1 + (- 2.5) add opposite of 2.5
= – 3.5 add
Question 14.
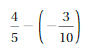
Answer :
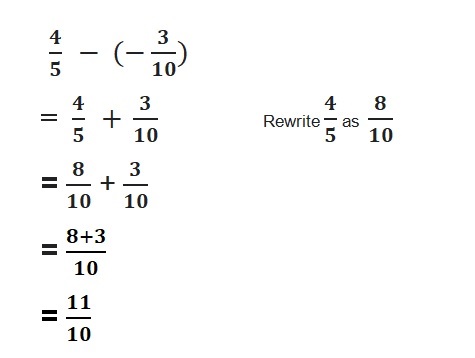
Question 15.
5.5 – 8.1
Answer :
5.5 – 8.1 = 5.5 + (-8.1 ) Add opposite of 8.1
= – 2.6 Add
Question 16.
![]()
Answer :

Question 17.
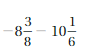
Answer :
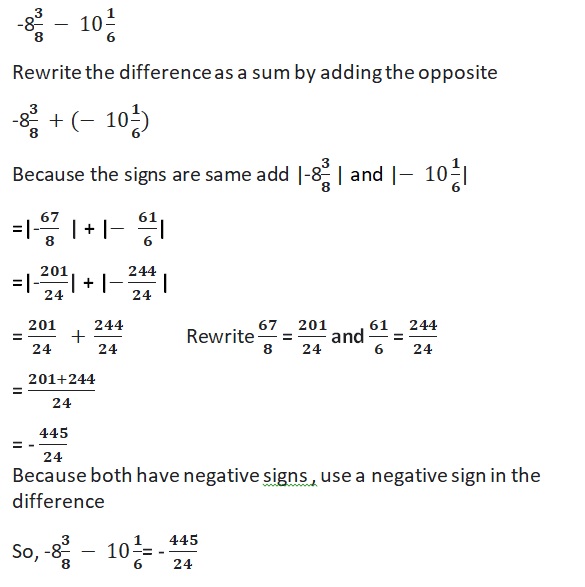
Question 18.
-4.62 – 3.51
Answer :
-4.62 – 3.51
= -4.62 + (-3.51) Add opposite of 3.51
= |-4.62 | + |-3.51 |
=4.62 + 3.51
= -8.13
Both the values are negative so use negative sign in the difference
So, -4.62 – 3.51 = -8.13
Question 19.
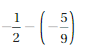
Answer :
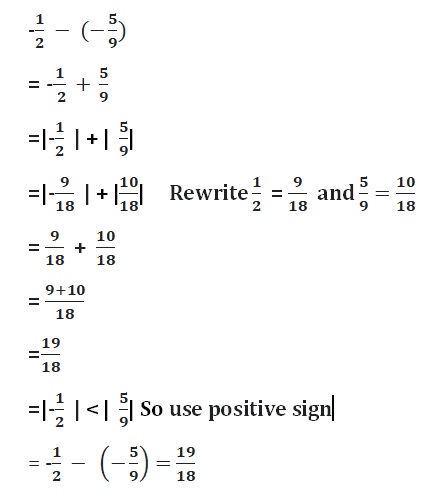
Question 20.
-7.34 – (-5.51)
Answer :
Answer :
-7.34 – (-5.51)
= -7.34 + 5.51
= | 7.34| – |5.51 |
=7.34 – 5.51
= – 1.83
| -7.34| > |5.51 | use negative sign to the difference
So, -7.34 – (-5.51) = – 1.83
Question 21.
6.673 – (-8.29)
Answer :
6.673 – (-8.29)
= 6.673 + 8.29
=14.963
Question 22.
![]()
Answer :
 Question 23.
Question 23.
YOU BE THE TEACHER
Question 23.
Your friend finds the difference. Is your friend correct? Explain your reasoning.

Answer :
No
Explanation :
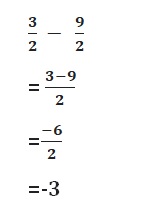
OPEN-ENDED
Describe a real-life situation that can be represented by the subtraction expression modeled on the number line.
Question 24.
Answer :
4.5 – 6 = -1.5
Explanation:
Draw a arrow from 0 to 4.5 represent 4.5 . Then, Draw an arrow 6 units to the left to represent subtracting 6, or adding -6. The arrow ends at -1.5 showing the difference.
So, 9 + (- 5) = 4
Question 25.
Answer :

Explanation:
Draw a arrow from 0 to –\(\frac{5}{8}\) represent –\(\frac{5}{8}\). Then, Draw an arrow \(\frac{5}{8}\)units to the left to represent subtracting –\(\frac{5}{8}\), or adding \(\frac{5}{8}\). The arrow ends at 0 showing the difference.
So, –\(\frac{5}{8}\) – ( –\(\frac{5}{8}\) ) = 0
Question 26.
MODELING REAL LIFE
Your water bottle is \(\frac{5}{6}\) full. After tennis practice, the bottle is \(\frac{3}{8}\) full. How much of the water did you drink?
Answer :
Amount of water in the bottle = \(\frac{5}{6}\)
Amount of water in the bottle after drinking = \(\frac{3}{8}\)
Amount of water drank = \(\frac{5}{6}\) – \(\frac{3}{8}\)
Rewrite \(\frac{5}{6}\) = \(\frac{20}{24}\) and \(\frac{3}{8}\) = \(\frac{9}{24}\)
Amount of water drank = \(\frac{20}{24}\) – \(\frac{9}{24}\) = \(\frac{11}{24}\)
Therefore, Amount of water drank = \(\frac{11}{24}\)
Question 27.
MODELING REAL LIFE
You have 2\(\frac{2}{3}\) ounces of sodium chloride. You want to replicate an experiment that uses 2\(\frac{3}{4}\) ounces of sodium chloride. Do you have enough sodium chloride? If not, how much more do you need?

Answer :
Amount of sodium chloride with me = 2\(\frac{2}{3}\) = \(\frac{8}{3}\)
Amount of sodium chloride required for experiment = 2\(\frac{3}{4}\) =\(\frac{11}{4}\)
Amount of sodium chloride more required for experiment = \(\frac{11}{4}\) – \(\frac{8}{3}\)
Rewrite \(\frac{11}{4}\) = \(\frac{33}{12}\) and \(\frac{8}{3}\) =\(\frac{24}{12}\)
Amount of sodium chloride more required for experiment = \(\frac{33}{12}\) – \(\frac{24}{12}\)
= \(\frac{9}{12}\)
Question 28.
REASONING
When is the difference of two decimals an integer? Explain.
Answer :
The difference between 2 decimals is an integer when the portion of each decimal to the right of the decimal point is the same,
Explanation:
example:
8.25 – 7.25 = 1
The decimal position of two numbers is same that is 0.25
USING PROPERTIES
Tell how the Commutative and Associative Properties of Addition can help you evaluate the expression. Then evaluate the expression.
Question 29.
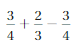
Answer :
\(\frac{3}{4}\) + \(\frac{2}{3}\) – \(\frac{3}{4}\)
= \(\frac{3}{4}\) – \(\frac{3}{4}\) + \(\frac{2}{3}\)
= \(\frac{2}{3}\) ( as \(\frac{3}{4}\) – \(\frac{3}{4}\) =0, zero pair)
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 30.
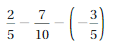
Answer :
\(\frac{2}{5}\) – \(\frac{7}{10}\) – ( – \(\frac{3}{5}\) )
= \(\frac{2}{5}\) – \(\frac{7}{10}\) + \(\frac{3}{5}\)
Add \(\frac{2}{5}\) and \(\frac{3}{5}\) we get,
= \(\frac{5}{5}\) – \(\frac{7}{10}\)
Rewrite \(\frac{5}{5}\) = \(\frac{10}{10}\)
= \(\frac{10}{10}\) – \(\frac{7}{10}\)
= \(\frac{3}{10}\)
Therefore \(\frac{2}{5}\) – \(\frac{7}{10}\) – ( – \(\frac{3}{5}\) ) = \(\frac{3}{10}\)
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 31.
8.5 + 3.4 – 6.5 – (-1.6)
Answer :
8.5 + 3.4 – 6.5 – (-1.6)
= 8.5 + 3.4 – 6.5 + 1.6
= 8.5 + 3.4 + 1.6 – 6.5
= 8.5 + 5.0 – 6.5 { as (3.4 + 1.6 = 5.0)}
= 13.5 – 6.5 { as 8.5 + 5.0 =13.5)}
= 7.0
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 32.
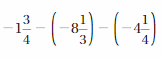
Answer :
-1\(\frac{3}{4}\) – (-8\(\frac{1}{3}\)) – ( -4\(\frac{1}{4}\))
= –\(\frac{7}{4}\) + \(\frac{25}{3}\) + \(\frac{17}{4}\)
=\(\frac{17}{4}\) –\(\frac{7}{4}\) + \(\frac{25}{3}\)
= \(\frac{10}{4}\) + \(\frac{25}{3}\)
= \(\frac{5}{2}\) + \(\frac{25}{3}\)
Rewrite \(\frac{5}{2}\) = \(\frac{15}{6}\) and \(\frac{25}{3}\) = \(\frac{50}{6}\)
= \(\frac{15}{6}\) + \(\frac{50}{6}\)
= \(\frac{65}{6}\)
-1\(\frac{3}{4}\) – (-8\(\frac{1}{3}\)) – ( -4\(\frac{1}{4}\)) = \(\frac{65}{6}\)
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 33.
2.1 + (5.8 – 4.1)
Answer :
2.1 + (5.8 – 4.1)
= 2.1 + 1.7
= 3.8
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 34.
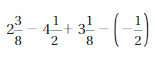
Answer :
2\(\frac{3}{8}\) – 4\(\frac{1}{2}\) + 3\(\frac{1}{8}\) – (-\(\frac{1}{2}\) )
= \(\frac{19}{8}\) – \(\frac{9}{2}\) + \(\frac{25}{8}\) + \(\frac{1}{2}\)
= \(\frac{19}{8}\) +\(\frac{25}{8}\) + \(\frac{1}{2}\) – \(\frac{9}{2}\)
= \(\frac{44}{8}\) – \(\frac{8}{2}\)
= \(\frac{11}{2}\) – \(\frac{8}{2}\)
= \(\frac{3}{2}\)
2\(\frac{3}{8}\) – 4\(\frac{1}{2}\) + 3\(\frac{1}{8}\) – (-\(\frac{1}{2}\) ) = \(\frac{3}{2}\)
Explanation:
Commutative Property : For any two rational numbers a and b, a + b = b+ a. We see that the two rational numbers can be added in any order. So addition is commutative for rational numbers.
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
FINDING DISTANCE ON A NUMBER LINE
Find the distance between the two numbers on a number line.
Question 35.
2.7 and 5.9
Answer :
The distance between 2.7 and 5.9 on a number line = | 2.7 – 5.9| = |-3.2 | = 3.2
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 36.
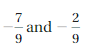
Answer :
The distance between –\(\frac{7}{9}\) and –\(\frac{2}{9}\) on a number line = | –\(\frac{7}{9}\) – (-\(\frac{2}{9}\) )| = | –\(\frac{7}{9}\) + \(\frac{2}{9}\) | =| –\(\frac{5}{9}\) |= \(\frac{5}{9}\)
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 37.
-2.2 and 8.4
Answer :
The distance between -2.2 and 8.4 on a number line = | -2.2 – 8.4| = | -10.6 | = 10.6
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 38.
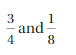
Answer :
The distance between \(\frac{3}{4}\)and \(\frac{1}{8}\) on a number line = | \(\frac{3}{4}\) – \(\frac{1}{8}\) |
Rewrite \(\frac{3}{4}\) = \(\frac{3}{8}\)
= | \(\frac{3}{8}\) +\(\frac{1}{8}\) | =| \(\frac{4}{8}\) |= 2
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 39.
-1.85 and 7.36
Answer :
The distance between -1.85 and 7.36 on a number line = | – 1.85 – 7.36| = | – 9.21 |= 9.21
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 40.
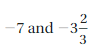
Answer :
-3\(\frac{2}{3}\)= – \(\frac{11}{3}\) =-3.6
-7 and -3.6
The distance between -7 and -3.6 on a number line = | -7 – (-3.6)| = | -7 + 3.6 | =| -3.4 |= 3.4
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 41.
2.491 and -3.065
Answer :
The distance between 2.491 and -3.065 on a number line = | 2.491 – (-3.065)| = | 2.491 + 3.065 | =|5.556 |= 5.556
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 42.
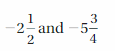
Answer :
-2\(\frac{1}{2}\) =-\(\frac{5}{2}\) = – \(\frac{10}{4}\)
-5\(\frac{3}{4}\) = –\(\frac{23}{4}\)
The distance between – \(\frac{10}{4}\) and –\(\frac{23}{4}\) a number line = | – \(\frac{10}{4}\) – (-\(\frac{23}{4}\) )| = | – \(\frac{10}{4}\) + \(\frac{23}{4}\) | = | – \(\frac{13}{4}\) |= \(\frac{13}{4}\)
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 43.
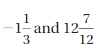
Answer :
-1\(\frac{1}{3}\) = –\(\frac{4}{3}\) = –\(\frac{16}{12}\)
12\(\frac{7}{12}\) = \(\frac{151}{12}\)
The distance between –\(\frac{16}{12}\) and \(\frac{151}{12}\) on a number line = | –\(\frac{16}{12}\) – \(\frac{151}{12}\) |=| –\(\frac{167}{12}\) |= \(\frac{167}{12}\)=13.91
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 44.
MODELING REAL LIFE
The number line shows the temperatures at 2:00 A.M. and 2:00 P.M. in the Gobi Desert. Find and interpret the distance between the points.
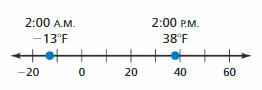
Answer :
Temperature at 2 A.M inthe Gobi Desert= -13 °F
Temperature at 2 P.M in the Gobi Desert = 38 °F
Distance between the two points as per above figure = -13 °F – (-38 °F) = |-13 + 38 | = |25| = 25
Explanation
The Distance between two numbers is the absolute values of the difference of the numbers .
Question 45.
PROBLEM SOLVING
A new road that connects Uniontown to Springville is 4\(\frac{1}{3}\) miles long. What is the change in distance when using the new road instead of the dirt roads?
Answer :
Distance between Springville to union town using L-shaped road = 2\(\frac{3}{8}\) + 3\(\frac{5}{6}\)
= \(\frac{19}{8}\) + \(\frac{23}{6}\)
Rewrite \(\frac{19}{8}\) = \(\frac{57}{24}\) and \(\frac{23}{6}\) = \(\frac{92}{24}\)
= \(\frac{57}{24}\) + \(\frac{92}{24}\)
= \(\frac{149}{24}\)
Change in distance from old to new road = \(\frac{149}{24}\) – 4\(\frac{1}{3}\)
= \(\frac{149}{24}\) – \(\frac{13}{3}\)
Rewrite \(\frac{13}{3}\) = \(\frac{104}{24}\)
= \(\frac{149}{24}\) – \(\frac{104}{24}\)
= \(\frac{45}{24}\)
= \(\frac{15}{8}\)
Change in distance from old to new road = \(\frac{15}{8}\).
FINDING DISTANCE IN A COORDINATE PLANE
Find the distance between the points in a coordinate plane.
Question 46.
(-4, 7.8), (-4, -3.5)
Answer :
d=√(x2−x1)2+(y2−y1)2
d=√(-4−(-4))2+(-3.5−7.8)2
d=√(-4+4)-2+(-11.3)2
d=√(-11.3)2
d = 11.3
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 47.
(-2.63, 7), (1.85, 7)
Answer :
d=√(1.85−(-2.63))2+(7−7)2
d=√(1.85+2.63)2+(0)2
d=√(4.48)2
d=4.48
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 48.
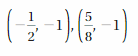
Answer :
–\(\frac{1}{2}\) = -0.5
\(\frac{5}{8}\) = 0.625
d=√(0.625−(-0.5))2+(-1−(-1))2
d=√(0.625+0.5)2+(-1+1)2
d=√(1.125)2+(0)2
d=1.125
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 49.
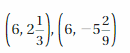
Answer :
2\(\frac{1}{3}\) = \(\frac{7}{3}\) = 2.3
-5\(\frac{2}{9}\) = –\(\frac{47}{9}\) = -5.2
d=√(6−6)2 + (-5.2−2.3)2
d=√(0)2 + (-7.5)2
d=7.5
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 50.
(-6.2, 1.4), (8.9, 1.4)
Answer :
d=√(8.9−(-6.2))2+(1.4−1.4)2
d=√(8.9+6.2)2+(0)2
d=√(15.1)2
d=15.1
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 51.
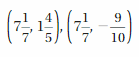
Answer :
7\(\frac{1}{7}\) = \(\frac{50}{7}\)
1\(\frac{4}{5}\) = \(\frac{9}{5}\)=\(\frac{18}{10}\)
–\(\frac{9}{10}\)
d=√(\(\frac{50}{7}\)−\(\frac{50}{7}\))2+(-\(\frac{9}{10}\)−\(\frac{18}{10}\))2
d=√(0)2+(-\(\frac{27}{10}\))2
d = \(\frac{27}{10}\)
Explanation:
Given endpoints (x1,y1)(x1,y1) and (x2,y2)(x2,y2), the distance between two points is given by
d=√(x2−x1)2+(y2−y1)2
Question 52.
DIG DEEPER!
The figure shows the elevations of a submarine.
a. Find the vertical distance traveled by the submarine.
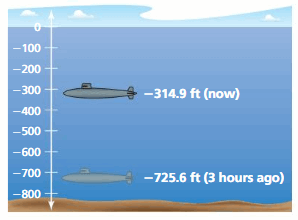
b. Find the mean hourly vertical distance traveled by the submarine.
Answer a :
Elevation of submarine 3 hours ago = -725.6 ft
Elevation of submarine now = -314.9 ft
Vertical Distance traveled by submarine = |-725.6 – (-314.9) | = |-725.6 + 314.9 |=|-410.7 | = 410.7
Answer b :
Vertical distance traveled in 3 hours = 410.7
Hourly vertical distance traveled by the submarine = 410.7 ÷ 3 = 136.9 feets
Question 53.
LOGIC
The bar graph shows how each month’s rainfall compares to the historical average.
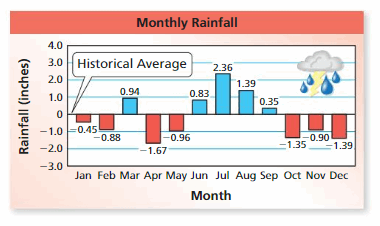
a. What is the difference in rainfall of the wettest month and the driest month?
Answer :
Rainfall of the wettest month = july = 2.36
Rainfall of the driest month =April = -1.67
The difference in rainfall of the wettest month and the driest month = 2.36 – (-1.67) = 2.36 +1.67 = 4.03
b. What do you know about the total amount of rainfall for the year?
Answer :
Rainfall in the Jan month = -0.45
Rainfall in the Feb month = -0.88
Rainfall in the Mar month = 0.94
Rainfall in the Apr month =-1.67
Rainfall in the May month =-0.96
Rainfall in the Jun month = 0.83
Rainfall in the Jul month = 2.36
Rainfall in the Aug month = 1.39
Rainfall in the Sep month = 0.35
Rainfall in the Oct month = -1.35
Rainfall in the Nov month = -0.90
Rainfall in the Dec month = -1.39
The total amount of rainfall for the year = Rainfall in the (Jan + Feb +mar + APR + may +jun +Jul +Aug +Sep +Oct +Nov +DEC ) months
= -0.45 + (-0.88) +0.94 + (-1.67) + (0.96) + 0.83 + 2.36 + 1.39 +0.35 +(-1.35)+ (-0.9) + (-1.39)
= 4.22
Question 54.
OPEN-ENDED
Write two different pairs of negative decimals, x and y that make the statement x – y = 0.6 true.
Answer :
Take x = -1 and y = -1.6
Explanation:
Take x = -1 and y = -1.6
x – y = -1 – (-1.6) = -1 +1.6 = 0.6
Then the above statement is proved .
REASONING
Tell whether the difference of the two numbers is always, sometimes, or never positive. Explain your reasoning.
Question 55.
two negative fractions
Answer :
Sometimes
Explanation :
Take x =- \(\frac{1}{3}\) and y =- \(\frac{2}{3}\)
x – y = – \(\frac{1}{3}\) – ( – \(\frac{2}{3}\)) = – \(\frac{1}{3}\) + \(\frac{2}{3}\)
– \(\frac{1}{3}\) – ( – \(\frac{2}{3}\)) = \(\frac{1}{3}\)
Question 56.
a positive decimal and a negative decimals
Answer :
Always
Because the operation – (-) becomes positive so adding of two numbers take place so difference will be the positive number .
Answer :
Take x = 5.6 and y = – 2.4
x – y =5.6 – ( -2.4) = 5.6 + 2.4 =8.0
Question 57.
STRUCTURE
Fill in the blanks to complete the decimals.

Answer :
5.54 – 9.51 = -3.61
Adding and Subtracting Rational Numbers Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A land surveyor uses a coordinate plane to draw a map of a park, where each unit represents 1 mile. The park is in the shape of a parallelogram with vertices (-2.5, 1.5), (-1.5, -2.25), (2.75, -2.25), and (1.75, 1.5). Find the area of the park.
Understand the problem.
You know the vertices of the parallelogram-shaped parkand that each unit represents 1 mile. You are asked to find the area of the park.
Make a plan.
Use a coordinate plane to draw a map of the park. Then find the height and base length of the park. Find the area by using the formula for the area of a parallelogram.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer :
Base of the parallelogram = 4.25
Height of the parallelogram = 3.75
Area of the parallelogram = base × height = 4.25 × 3.75 = 15.9375 sq.units
Question 2.
The diagram shows the height requirement for driving a go-cart. You are 5\(\frac{1}{4}\) feet tall. Write and solve an inequality to represent how much taller you must be to drive a go-cart.
Answer :
My Height = 5\(\frac{1}{4}\)
Height Required for driving a go-cart = 5\(\frac{1}{3}\)
Height more required for me for driving = 5\(\frac{1}{3}\) – 5\(\frac{1}{4}\)
= \(\frac{16}{3}\) – \(\frac{21}{4}\)
Rewrite \(\frac{16}{3}\) =\(\frac{64}{12}\) and \(\frac{21}{4}\) = \(\frac{63}{12}\)
= \(\frac{64}{12}\) – \(\frac{63}{12}\)
= \(\frac{1}{12}\)
Height more required for me for driving == \(\frac{1}{12}\)
H ≥ \(\frac{1}{12}\)
Performance Task
Melting Matters
At the beginning of this chapter, you watched a STEAM Video called “Freezing Solid.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Adding and Subtracting Rational Numbers Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Definition and Example Chart to organize information about a concept. Here is an example of a Definition and Example Chart for the vocabulary term absolute value.
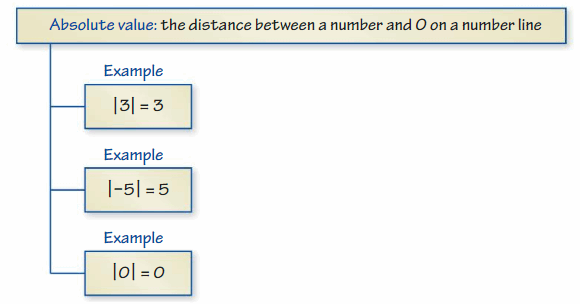
Choose and complete a graphic organizer to help you study the concept.
- integers
- rational numbers
- adding integers
- Additive Inverse Property
- adding rational numbers
- subtracting integers
- subtracting rational numbers

Answer :







Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

1.1 Rational Numbers (pp. 3-8)
Find the absolute value.
Question 1.
| 3 |
Answer :
Absolute value of 3 is 3
| 3 | = 3
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 2.
| -9 |
Answer :
Absolute value of -9 is 9
| -9 | = 9
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 3.
![]()
Answer :
Absolute value of ![]() is \(\frac{3}{4}\)
is \(\frac{3}{4}\)
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 4.
| -5.2 |
Answer :
| -5.2 | = 5.2
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 5.
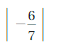
Answer :
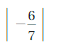 = \(\frac{6}{7}\)
= \(\frac{6}{7}\)
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 6.
| 4.15 |
Answer :
| 4.15 | = 4.15
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Copy and complete the statement using <, >, or =.
Question 7.

Answer :
|-2| = 2
2 > -2
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 8.

Answer :
|-\(\frac{1}{3}\)| = \(\frac{1}{3}\) = 0.33
|-\(\frac{5}{6}\)| =\(\frac{5}{6}\) = 0.3
0.33 > 0.3
|-\(\frac{1}{3}\)| > |-\(\frac{5}{6}\)|
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 9.

Answer :
|1.7| = 1.7
-1.7 = -1.7
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 10.
Order ![]() and −2 from least to greatest.
and −2 from least to greatest.
Answer :
|2.25| = 2.25
|-1.5| = 1.5
|2\(\frac{1}{2}\)| = |\(\frac{5}{2}\)| =\(\frac{5}{2}\) = 2.5
1\(\frac{1}{4}\)=\(\frac{5}{4}\) = 1.25
2.25, 1.5, 1.25, 2.5 and – 2
-2 < 1.25 < 1.5 < 2.25 < 2.5
Explanation:
All positive integers are greater than negative integers.
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 11.
Your friend is in Death Valley, California, at an elevation of −282 feet. You are near the Mississippi River in Illinois at an elevation of 279 feet. Who is closer to sea level?
Answer :
My friend is at Death Valley, California, at an elevation = −282 feet. = | -282 | =282 feet
I am at the Mississippi River in Illinois at an elevation = 279 feet. = | 279 |= 279 feet
Who is closer to sea level = 0 is 279 feet that means 279 > 282 feet
I am closer to sea level .
Question 12.
Give values for a and b so that a < b and | a | > | b |.
Answer :
Take a = -5 and b = 2
– 5 < 2
| a | = | -5 | = 5 and | b | = | 2 | = 2
| 5 | > | 2 |
Hence proved a < b and | a | > | b |
Question 13.
The map shows the longitudes (in degrees) for Salvador, Brazil, and Nairobi, Kenya.Which city is closer to the Prime Meridian?
Answer :
Longitudes of Salvador = -38.5108 (in degrees)
Distance of Longitudes of Salvador from prime meridian = | -38.5108| = 38.5108
Longitudes of Nairobi = 36.8167 (in degrees) = 36.8167
Distance of Longitudes of Nairobi from prime meridian = | 36.8167 | = 36.8167
Which is closer to prime meridian = | -38.5108| > | 36.8167 |
So, Longitudes of Nairobi from prime meridian is closer to prime meridian .
1.2 Adding Integers (pp. 9-16)
Question 14.
Write an addition expression represented by the number line. Then find the sum.
Find the sum. Use a number line to verify your answer.
Answer :
– 3 + 4 = 1
Explanation :
Draw an arrow from 0 to -3 to represent -3. Then draw an arrow 4 units to the right representing adding +2.The arrow ends at 1, showing the sum.
So,- 3 + 4 = 1
Question 15.
-16 + (-11)
Answer :
-16 + (-11)
=|-16 | +| -11 |
= 16 + 11
= -27
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 16.
-15 + 5
Answer :
-15 + 5
= |-15 | – |5 |
= 15 – 5
= -10 as |-15 | > |5 | so use negative sign.
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 17.
100 + (-75)
Answer :
100 – 75
= |100 | – |-75 |
= 100 – 75
= 25 as |100 | > |-75 | so use positive sign.
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 18.
-32 + (-2)
Answer :
-32 + (-2)
=|-32 | +| -2 |
= 32 + 2
= -34 (both the numbers are negative so use negative symbol in the sum)
Explanation:
Add Absolute values and then use the common sign in the sum .
Answer :
-16 + (-11)
=|-16 | +| -11 |
= 16 + 11
= -27
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 19.
-2 + (-7) + 15
Answer :
-2 + (-7) + 15
=|-2 | +| -7 | + 15
= -9 + 15
= 6
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 20.
9 + (-14) + 3
= 9 + 3 +(-14)
=12 +(-14)
= |12 | – |-14 |
= 12 – 14
= 2 as |-14 | > |12 | so use negative sign.
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 21.
During the first play of a football game, you lose 3 yards. You gain 7 yards during the second play. What is your total gain of yards for these two plays?
Answer :
First play of a foot ball game i lose 3 yards = -3 yards
Second play of a foot ball i gain 7 yards = + 7 yards
Total gain of yards for these two plays = -3 + 7 = 4
Question 22.
Write an addition expression using integers that equals -2. Use a number line to justify your answer.
Answer :
Take x = 3 and y = – 5
x + y
=3 +(-5)
= |3 | – |-5 |
= 3 – 5
= -2 as |-5 | > |3 | so use negative sign.

Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Draw an arrow from 0 to 3 to represent +3. Then draw an arrow 5 units to the left representing adding -5.
Question 23.
Describe a real-life situation that uses the sum of the integers -8 and 12.
Answer :
During the first play of a basketball game, you lose 8 yards. You gain 12 yards during the second play. What is your total loss of yards for these two plays.
First play of a Basketball ball game i lose 8 yards = -8 yards
Second play of a basket ball i gain 12 yards = + 12 yards
Total loss of yards for these two plays = 8 + ( -12 ) = -4
1.3 Adding Rational Numbers (pp. 17–22)
Find the sum. Write fractions in simplest form.
Question 24.
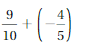
Answer :
\(\frac{9}{10}\) +(-\(\frac{4}{5}\))
Rewrite –\(\frac{4}{5}\) = –\(\frac{8}{10}\)
= |\(\frac{9}{10}\) | – |-\(\frac{8}{10}\) |
= \(\frac{9}{10}\) – \(\frac{8}{10}\)
= 1 as |\(\frac{9}{10}\) | > |-\(\frac{4}{5}\) | so use positive sign.
\(\frac{9}{10}\) +(-\(\frac{4}{5}\)) = 1
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 25.
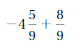
Answer :
-4\(\frac{5}{9}\) = –\(\frac{41}{9}\)
=-\(\frac{41}{9}\)+\(\frac{8}{9}\)
=|-\(\frac{41}{9}\) | – |\(\frac{8}{9}\)|
=\(\frac{41}{9}\) –\(\frac{8}{9}\)
= – \(\frac{33}{9}\)
–\(\frac{41}{9}\)+\(\frac{8}{9}\)= = – \(\frac{33}{9}\)
|-\(\frac{41}{9}\) | > |\(\frac{8}{9}\)| so, use negative sign
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 26.
-1.6 + (-2.4)
Answer :
-1.6 + (-2.4)
=|-1.6 | +| -2.4 |
= 1.6 + 2.4
= -4.0
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 27.
Find the sum of ![]() . Explain each step.
. Explain each step.
Answer :
– 4 + 6 \(\frac{2}{5}\) + (-2.7)
Convert the fraction form into decimal form
6 \(\frac{2}{5}\)= \(\frac{32}{5}\) =6.4
– 4 + 6.4 + (-2.7)
add negative numbers , we get,
-4 – 2.7 + 6.4
= -6.7 +6.4
= |-6.7 | – |6.4 |
= 6.7 – 6.4
= -0.3 as |-6.7 | > |6.4 | so use negative sign.
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 28.
You open a new bank account. The table shows the activity of your account for the first month. Positive numbers represent deposits and negative numbers represent withdrawals. What is your balance (in dollars) in the account at the end of the first month?
Answer :
Deposit on 3/5 = 100
Withdrawal on 3/12 = 12.25
Deposit on 3/16 = 25.82
Deposit on 3/21 = 14 .95
Withdrawal on 3/ 29 = 18.56
Total Balance in the end of the month = Total deposits – Total withdrawals = ( 100 + 25.82 + 14.95 ) -( 12.25 + 18.56 ) = 140.77 – 30.81 = 109.96
1.4 Subtracting Integers (pp. 23–28)
Find the difference. Use a number line to verify your answer.
Question 29.
8 – 18
Answer :
8 – 18 = -10
Explanation :
Draw an arrow from 0 to 8 to represent 8. Then draw an arrow 18 units to the left representing subtract 18 or adding -18.
So, 8 – 18 = -10
Question 30.
-16 – (-5)
Answer :
-16 – (-5) = -16 +5 = -11
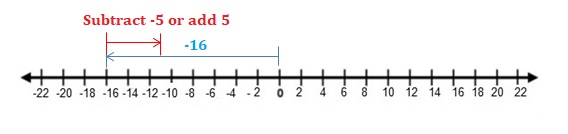
Explanation :
Draw an arrow from 0 to -16 to represent -16. Then draw an arrow 5 units to the right representing subtract -5 or adding +5.
So, -16 – (-5) = -11
Question 31.
-18 – 7
Answer :
-18 – 7 = -25
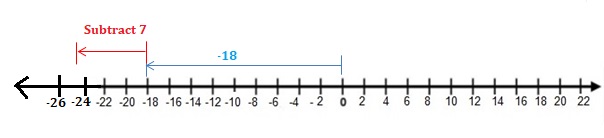
Explanation:
Draw an arrow from 0 to -18 to represent -18. Then draw an arrow 7 units to the left representing subtracting 7 or,adding -7.
The arrow ends at -25 showing the difference.
So,-18 – 7 = – 25
Question 32.
-12 – (-27)
Answer :
-12 – (-27) =-12 + 27 = 15
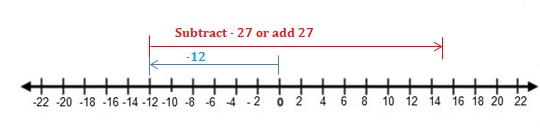
Explanation:
Draw an arrow from 0 to -12 to represent -12. Then draw an arrow 27 units to the right representing subtracting -27 or,adding 27.
The arrow ends at 15 showing the difference.
So, -12 – (-27) = 15
Question 33.
Your score on a game show is -300. You answer the final question incorrectly, so you lose 400 points. What is your final score?
Answer :
My score on game show = -300
Final question score = -400
Total score = – 300 + (-400 ) = -300 – 400 = -700
Question 34.
Oxygen has a boiling point of -183°C and a melting point of -219°C. What is the temperature difference of the melting point and the boiling point?
Answer :
Boiling point = -183°C
Melting point = -219°C
Temperature difference of the melting point and the boiling point = – 183 – (-219) = – 183 + 219 = 36 °C
Question 35.
In one month, you earn $16 for mowing the lawn, $15 for baby sitting, and $20 for allowance. You spend $12 at the movie theater. How much more money do you need to buy a $45 video game?
Answer :
Money earned in mowing the lawn =$16
Money earned for baby sitting = $15
Money earned for allowance = $20
Money spend on Movie Theater = $12
Total Money = Total Money earned – Money spend = (16+15+20) – (12 ) = 51 – 12 = 39
Cost price of video game = $45
More money required to buy video game = cost price of video game – Total Money with me = 45 – 39 = 6$
Question 36.
Write a subtraction expression using integers that equals -6.
Answer :
x – y = -6
Take x = -3 and y =3
x – y =-3 – 3 = -6
Question 37.
Write two negative integers whose difference is positive.
Answer :
Take x= -5 and y = -10
x – y = – 5 – (-10) = – 5 + 10 = 5
difference is positive
1.5 Subtracting Rational Numbers (pp. 29–36)
Find the difference. Write fractions in simplest form.
Question 38.
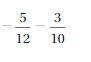
Answer :
–\(\frac{5}{12}\) – \(\frac{3}{10}\)
Rewrite \(\frac{5}{12}\) = \(\frac{25}{60}\) and \(\frac{3}{10}\)= \(\frac{18}{60}\)
= –\(\frac{25}{60}\) – \(\frac{18}{60}\)
= –\(\frac{43}{60}\) (as both have same signs)
Question 39.
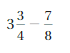
Answer :
3\(\frac{3}{4}\) – \(\frac{7}{8}\)
= \(\frac{15}{4}\) – \(\frac{7}{8}\)
Rewrite \(\frac{15}{4}\) = \(\frac{30}{8}\)
= \(\frac{30}{8}\) – \(\frac{7}{8}\)
Add opposite of – \(\frac{30}{8}\)
= \(\frac{30}{8}\) + (- \(\frac{7}{8}\))
Add
= \(\frac{23}{8}\)
3\(\frac{3}{4}\) – \(\frac{7}{8}\) = \(\frac{23}{8}\) .
Question 40.
3.8 – (-7.45)
Answer :
3.8 – (-7.45)
Add opposite of -7.45
3.8 + 7.45 = 11.25
Question 41.
Find the distance between -3.71 and -2.59 on a number line.
Answer :
The distance between -3.71 and -2.59 on a number line = | – 3.71 – (-2.59)| = | – 3.71 + 2.59 | =| -1.12 |= 1.12
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 42.
A turtle is 20\(\frac{5}{6}\) a pond. It dives to a depth of 32\(\frac{1}{4}\) inches. What is the change in the turtle’s position?

Answer :
The turtle is at = 20\(\frac{5}{6}\)
Turtle drives to a depth = 32\(\frac{1}{4}\)
Change in the turtle’s position = 20\(\frac{5}{6}\) – 32\(\frac{1}{4}\)
= \(\frac{125}{6}\) – \(\frac{129}{4}\)
Rewrite \(\frac{125}{6}\) = \(\frac{250}{12}\) and \(\frac{129}{4}\) =\(\frac{387}{12}\)
= \(\frac{250}{12}\) – \(\frac{387}{12}\)
= –\(\frac{137}{12}\)
Change in the turtle’s position = –\(\frac{137}{12}\)
Question 43.
The lowest temperature ever recorded on Earth was -89.2°C at Soviet Vostok Station in Antarctica. The highest temperature ever recorded was 56.7°C at Greenland Ranch in California. What is the difference between the highest and lowest recorded temperatures?
Answer :
The lowest temperature ever recorded on Earth = -89.2°C
The highest temperature ever recorded = 56.7°C
The difference between the highest and lowest recorded temperatures = 56.7 – ( -89.2 ) = 56.7 + 89.2 = 145.9°C
Adding and Subtracting Rational Numbers Practice Test
Practice Test
Find the absolute value.
Question 1.
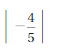
Answer :
|-\(\frac{4}{5}\)| = \(\frac{4}{5}\)
Explanation :
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 2.
| 6.43 |
Answer :
| 6.43 | = 6.43
Explanation :
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Question 3.
| – 22 |
Answer :
| – 22 | = 22
Explanation :
The absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x and |-x| = x .
Copy and complete the statement using <, >, or =.
Question 4.
![]()
Answer :
| – 8 | = 8
4 < 8
Explanation :
Explanation:
The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
So write the numbers which are bigger with negative symbol are smaller arrange all the negative numbers in this order and then follows 0 and positive numbers from least to greatest .
Question 5.
![]()
Answer :
| – 7 | = 7
7 > -12
Explanation :
All negative numbers are lesser than positive numbers. The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Question 6.
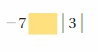
Answer :
| 3 | = 3
-7 < 3
Explanation:
All negative numbers are lesser than positive numbers. The Negative Numbers which are near to the 0 are greater.With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller.
Add or subtract. Write fractions in simplest form.
Question 7.
-6 + (-11)
Answer :
-6 + (-11)
=|-6 | +| -11 |
= 6 + 11
= -7
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 8.
2 – (-9)
Answer :
2 – (-9)
= 2 + 9 add opposite of -9
= 11 add
2 – (-9) = 11
Question 9.
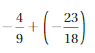
Answer :
–\(\frac{4}{9}\)+ (- \(\frac{23}{18}\))
Rewrite –\(\frac{4}{9}\) = –\(\frac{8}{18}\)
= |-\(\frac{8}{18}\) | + |- \(\frac{23}{18}\) |
= \(\frac{8}{18}\) + \(\frac{23}{18}\)
= –\(\frac{31}{18}\) as both signs are negative so use negative sign in the difference
–\(\frac{4}{9}\)+ (- \(\frac{23}{18}\)) = –\(\frac{31}{18}\)
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 10.
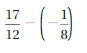
Answer :
\(\frac{17}{12}\) – (- \(\frac{1}{8}\) )
Rewrite –\(\frac{17}{12}\) = –\(\frac{34}{24}\) and –\(\frac{1}{8}\) =- \(\frac{3}{24}\)
= \(\frac{34}{24}\) + \(\frac{3}{24}\)
= \(\frac{31}{24}\) as | \(\frac{17}{12}\) | > | \(\frac{1}{8}\) | so use positive sign.
Explanation :
Subtract lesser absolute value from the greater absolute value . Then use the sign of the greater absolute value .
Question 11.
9.2 + (-2.8)
Answer :
9.2 + (-2.8) add opposite of 2.8
= 9.2 – 2.8
= 6.4
Question 12.
2.86 – 12.1
Answer :
2.86 + (-12.1) add opposite of 12.1
= 9.24
Question 13.
Write an addition expression and write a subtraction expression represented by the number line. Then evaluate the expressions.
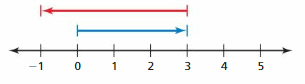
Answer :
3 + (-4) = -1
Explanation :
Explanation:
Draw an arrow from 0 to 3 to represent 3. Then draw an arrow 4 units to the left representing adding -4.
So, 3 + (-4) = -1
Question 14.
The table shows your scores, relative to par, for nine holes of golf. What is your total score for the nine holes?

Answer :
Total score of nine holes = score of ( 1st +2nd +3rd + 4th + 5th + 6th + 7th + 8th + 9 th ) holes
= 1 + (-2) + (-1) + 0 + (-1) + 3 + (-1) + (-3) + 1 = -3
Question 15.
The elevation of a fish is 27 feet. The fish descends 32 feet, and then rises 14 feet. What is its new elevation?
Answer :
Elevation of a fish = 27 feet
Fish descends = -32 feet
Fish Rises = 14 feet.
New elevation = 27 – 32 + 14 = 41 – 32 = 9 feet
Question 16.
The table shows the rainfall (in inches) for three months compared to the yearly average. Is the total rainfall for the three-month period greater than or less than the yearly average? Explain.

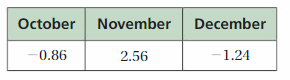
Answer :
Rainfall in October = -0.86
Rainfall in November = 2.56
Rainfall in December = -1.24
Total rainfall for the three-month period = rainfall in October +rainfall in November + rainfall in December = -0.86+2.56+ (-1.24) = 0.86+2.56-1.24 = 2.18
Average Rainfall of Yearly = Total rainfall for the three-month period ÷ 3 months = 2.18 ÷ 3 = 0.726
2.18 >0.726
The total rainfall for the three-month period greater than the yearly average .
Question 17.
Bank Account A has $750.92, and Bank Account B has $675.44. Account A changes by –$216.38, and Account B changes by – $168.49. Which account has the greater balance? Explain.
Answer :
Final balance of A > Final balance of B = $534.54 > $534.54
Explanation :
Bank Account of A = $750.92
Account A changes = -$216.83
Final balance of A= $750.92 – $216.83 = $534.54
Bank Account of B = $675.44
Account A changes = -$168.49
Final balance of B = $675.44 – $168.49 = $506.45
Therefore Final balance of A > Final balance of B = $534.54 > $534.54
Question 18.
On January 1, you recorded the lowest temperature as 23°F and the highest temperature as 6°C. A formula for converting from degrees Fahrenheit F to degrees Celsius C is ![]() What is the temperature range (in degrees Celsius) for January 1?
What is the temperature range (in degrees Celsius) for January 1?
Answer :
Lowest temperature = 23°F
Highest temperature = 6°C.
Converting lowest temperature into Celsius C = \(\frac{5}{9}\) 23°F – \(\frac{160}{9}\)
= \(\frac{115}{9}\) °F – \(\frac{160}{9}\)
= – \(\frac{45}{9}\) = -5
Lowest temperature = 23°F = -5°C
Adding and Subtracting Rational Numbers Cumulative Practice
Question 1.
A football team gains 2 yards on the first play, loses 5 yards on the second play, loses 3 yards on the third play, and gains 4 yards on the fourth play. What is the team’s total gain or loss?
A. a gain of 14 yards
B. a gain of 2 yards
C. a loss of 2 yards
D. a loss of 14 yards

Answer :
Option c – a loss of 2 yards
Explanation :
Gain on First play = 2 yards
Loss on Second play = -5 yards
Loss on third play = -3 yards
Gain on fourth play = 4
Total Gain = 2 + 4 = 6
Total Loss = -5 + (-3) = – 8
Total loss > total gain
|-8| > |6|
So overall there is a loss
Team Loss = 6 + (- 8 ) = – 2 loss
Question 2.
Which expression is not equal to 0?
F. 5 – 5
G. -7 + 7
H. 6 – (-6)
I. -8 – (-8)
Answer :
Option F = 5 – 5 = 0
Option G= -7 + 7 = 0
Option H = -6 – (-6) = 6 + 6 = 12
Option I = -8 – (-8) = -8 + 8 = 0
Explanation :
The sum of a number and its addictive inverse , or opposite , is 0 .
Example a + (-a) = 0
Question 3.
What is the value of the expression?
![]()
A. -4.5
B. -0.5
C. 0.5
D. 4.5
Answer :
Option C
Explanation :
|-2 – (-2.5 )| = |-2 + 2.5|= |0.5| = 0.5
Question 4.
What is the value of the expression?

17 – (-8)
Answer :
17 – (-8) = 17 + 8 = 25
Question 5.
What is the distance between the two numbers on the number line?
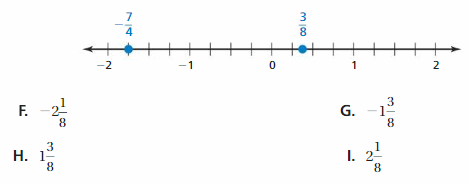
Answer :
Option H = 1\(\frac{3}{8}\)
Rewrite –\(\frac{7}{4}\) =-\(\frac{14}{8}\)
The distance between –\(\frac{7}{4}\) and \(\frac{3}{8}\) on a number line = | –\(\frac{14}{8}\) – \(\frac{3}{8}\) | =| –\(\frac{11}{8}\) |= 1\(\frac{3}{8}\)
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 6.
What is the value of the expression when a = 8, b = 3, and c = 6?
![]()
A. -65
B. -17
C. 17
D. 65
Answer :
Option C
Explanation :
Take a = 8, b = 3, and c = 6
![]() = | 8×8 – 2(8)(6) + 5(3) | = | 64 – 96 + 15| =| 79 – 96 | = | -17 | = 17
= | 8×8 – 2(8)(6) + 5(3) | = | 64 – 96 + 15| =| 79 – 96 | = | -17 | = 17
Question 7.
What is the value of the expression?

Answer :
-9.74 + (- 2.23)
=|-9.74 | +| -2.23 |
= 9.74 + 2.23
= -11.97 (both the numbers are negative so use negative symbol in the sum)
Explanation:
Add Absolute values and then use the common sign in the sum .
Question 8.
Four friends are playing a game using the spinner shown. Each friend starts with a score of 0 and then spins four times. When you spin blue, you add the number to your score. When you spin red, you subtract the number from your score. The highest score after four spins wins. Each friend’s spins are shown. Which spins belong to the winner?
F. 6, 7, 7, 6
G. -4, -4, 7, -5
H. 6, -5, -4, 7
I. -5, 6, -5, 6
Answer :
F. 6+7-7-6 = 0
G. -4+(-4)+ 7-(-5) = 8-7+5 = 4
H. 6+(-5)- (-4) +7= 6 -5+4+7 =12
I. -5-6+ (-5)- 6 = -22
Question 9.
What number belongs in the box to make the equation true?
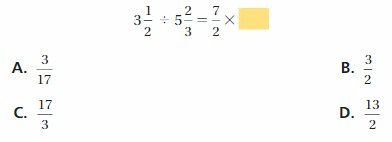
Answer :
Option A = \(\frac{3}{17}\)
Explanation :
3\(\frac{1}{2}\) ÷ 5\(\frac{2}{3}\) = \(\frac{7}{2}\) ÷ \(\frac{17}{3}\)
= \(\frac{7}{2}\) × \(\frac{3}{17}\)
The missing term is \(\frac{3}{17}\)
Question 10.
What is the value of the expression?
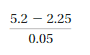
F. -346
G. 0.59
H. 5.9
I. 59
Answer :
Option I
Explanation :
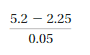 = 2.95 ÷ 0.05 = 295 ÷ 5 = 59
= 2.95 ÷ 0.05 = 295 ÷ 5 = 59
Question 11.
You leave school and walk 1.237 miles west. Your friend leaves school and walks 0.56 mile east. How far apart are you and your friend?
A. 0.677 mile
B. 0.69272 mile
C. 1.293 miles
D. 1.797 miles
Answer :
Distance between me and my friend = | 1.237 – 0.56 | = 0.677
Explanation:
The distance between any two numbers on a number line is the absolute value of the difference of the number .
| p – q | = | q – p |
Question 12.
Which property does the equation represent?
![]()
F. Commutative Property of Addition
G. Associative Property of Addition
H. Additive Inverse Property
I. Addition Property of Zero
Answer :
Option G. -Associative Property of Addition
Explanation:
Associative Property : Take any three rational numbers a, b and c. Firstly add a and b and then add c to the sum. (a + b) + c. Now again add b and c and then a to the sum, a + (b + c). Is (a + b) + c and a + (b + c) same? Yes and this is how associative property works. It states that you can add or multiply numbers regardless of how they are grouped.
Question 13.
The values of which two points have the greatest sum?

A. R and S
B. R and U
C. S and T
D. T and U
Answer :
Option B. – R and U is having greatest sum
R = -2.9
S = -0.3
T = 0.6
U =1.1
A. R and S = -2.9 + (-0.3) = -3.2
B. R and U = -2.9 + 1.1 = 4.0
C. S and T = -0.3 +0.6 = 0.3
D. T and U = 0.6 + 1.1 = 1.7
Question 14.
Consider the number line shown.
Part A
Use the number line to explain how to add -2 and -3.
Answer :
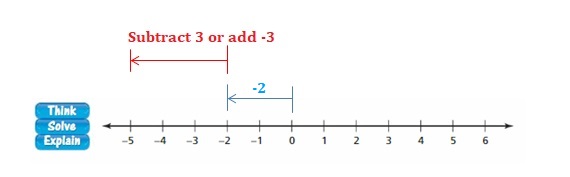
-2 + (-3) = -2 – 3 = -5
Explanation:
Draw an arrow from 0 to -3 to represent -3. Then draw an arrow 3 units to the left representing subtract 3 or adding -3.The arrows end at -5 showing the sum .
So, -2 + (-3) = -5
Part B
Use the number line to explain how to subtract 5 from 2.
Answer :
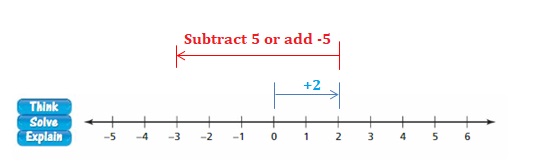
2 – 5 = -3
Explanation:
Draw an arrow from 0 to 2 to represent 2. Then draw an arrow 5 units to the left representing subtract 5 or adding -5. The arrow ending at-3 showing the difference .
So, 2 – 5 = -3
Question 15.
Which expression represents a negative value?
F. 2 – | -7 + 3 |
G. | -12 + 9 |
H. | 5 | + | 11 |
I. | 8 – 14 |
Answer :
Option F = -2
Explanation:
F. 2 – | -7 + 3 | = 2 – 4 = – 2
G. | -12 + 9 | = | -3| = 3
H. | 5 | + | 11 | = 5 + 11 = 16
I. | 8 – 14 | = | -6 | = 6
Final Verdict:
Big Ideas Math Answers Grade 7 Chapter 1 Adding and Subtracting Rational Numbers helps you in preparing the time table. With the help of the above given material you can know your mistakes and resolve your mistakes. Stay tuned to bigideasmathanswers.com to get the problems and solutions. We wish all the candidates best of luck for their preparation. Stay tuned to our site and get all the updates.
