Surface Area and Volume is an important concept to learn and score good marks. Big Ideas Math Answers Grade 7 Chapter 10 Surface Area and Volume pdf is here. Follow the detailed explanation of BIM Grade 7 Chapter 10 Surface Area and Volume and maximize your score. Get the detailed and explanatory concept and preparatory material from the upcoming sections.
There are various topics covered in surface area and volume. You can find a surface area and volume for a solid and an opaque object too. There are different objects for which you can find surface area and volume. If you want to imagine the 3-dimensional view of an object then surface area and volume play a major role.
Big Ideas Math Book 7th Grade Answer Key Chapter 10 Surface Area and Volume
You can get the guided notes for Surface Area and Volume Chapter 10 here. We help to provide you with the best resources that benefit you in understanding the topics in a better way by which you can improve your math skills. The topics in this Chapter include Surface Areas of Prisms, Cylinders, Pyramids, Volume of Prism, Pyramids, Cross Sections of Three-Dimensional Figures.
We make sure that you understand these topics by the end of this Chapter. We provide examples and different practice sums that help you to solve the problems on your own. You can practice different sums by taking different examples. For any further doubts refer to this site and you can get clarity on your doubts with a clearcut understanding. You can get line-to-line clarity by referring to our site which helps you to improve your basic skills.
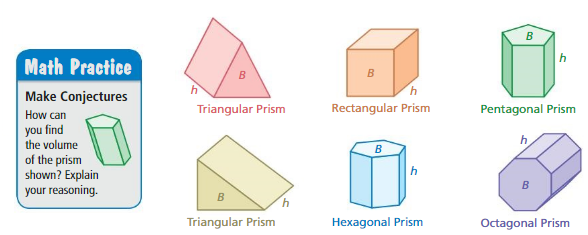
Performance Task
- Surface Area and Volume STEAM Video/Performance Task
- Surface Area and Volume Getting Ready for Chapter 10
Lesson: 1 Surface Areas of Prisms
Lesson: 2 Surface Areas of Cylinders
Lesson: 3 Surface Areas of Pyramids
Lesson: 4 Volumes of Prisms
Lesson: 5 Volumes of Pyramids
Lesson: 6 Cross-Sections of Three-Dimensional Figures
- Lesson 10.6 Cross Sections of Three-Dimensional Figures
- Cross Sections of Three-Dimensional Figures Homework & Practice 10.6
Chapter 10 – Surface Area and Volume
- Surface Area and Volume Connecting Concepts
- Surface Area and Volume Chapter Review
- Surface Area and Volume Practice Test
- Surface Area and Volume Cumulative Practice
Surface Area and Volume STEAM Video/Performance Task
STEAM Video
Paper Measurements
The thickness of a single piece of paper cannot be precisely measured using a ruler. What other method can you use to measure the thickness of a piece of paper?

Watch the STEAM Video “Paper Measurements.” Then answer the following questions.
1. A stack of 500 pieces of paper is 2 inches tall. How tall is a stack of 250 pieces? 100 pieces? 10 pieces? How thick is a single piece of paper?

2. You have a circular notepad. How can you find the volume of one piece of paper in the notepad?
Answer:
1. for 250 pieces = 46750 cubic inches
2. volume = 187 cubic inches
Explanation:
1. for 250 pieces = l w x h
250 pieces = 250 x 17 x 11
pieces = 46750
100 pieces = 100 x 17 x 11
pieces = 18,700
10 pieces = 10 x 17 x 11
pieces = 1870
piece = 1 x 17 x 11
piece = 187
2. volume = l x w x h
volume = 8.5 x 11 x 2
volume = 187
Performance Task
Volumes and Surface Areas of Small Objects
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the dimensions of a shipping box and the number of bouncy balls that fit in the box.

You will be asked to use the box to estimate the volume of each bouncy ball. Why might it be helpful to use the volume of a container of objects to estimate the volume of one of the objects?
Answer:
The volume of the object =11,809.8 cubic centimeters
Explanation:
The volume of rectangular prism = l x w x h
where l = length, w = width, h = height
rectangular prism = 27 x 27 x 16.2
volume = 11,809.8 cubic centimeters
Surface Area and Volume Getting Ready for Chapter 10
Chapter Exploration
Question 1.
Work with a partner. Perform each step for each of the given dimensions.
• Use 24 one-inch cubes to form a rectangular prism that has the given dimensions.
• Make a sketch of the prism.
• Find the surface area of the prism.
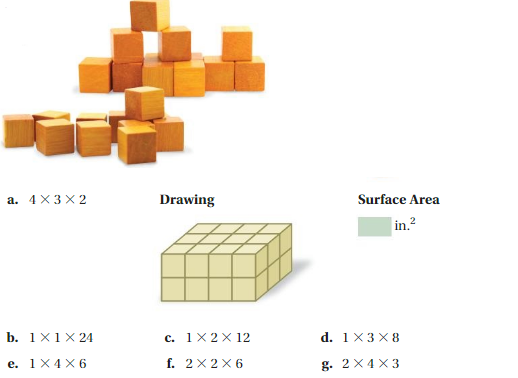
Answer:
a . 52 inches
b . 98 inches
c . 76 inches
d . 70 inches
e . 68 inches
f . 64 inches
g . 52 inches
prism :
The surface area of the square prism = 2lw + 2lh + 2wh
The surface area of the rectangle prism = 2(lw + lh + wh)
Explanation:
a . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 4 w = 3 h = 2
rectangular prism =2(4 x 3) +(2 x 3) +(4 x 2)
prism = 2(12) + (6) +(8)
surface area =2( 26)
surface area = 52
b . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 1 w = 1 h = 24
rectangular prism =2(1 x 1) +(1 x 24) +(1 x 24)
prism = 2(1) + (24) +(24)
surface area =2( 49)
surface area = 98
c . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 1 w = 2 h = 12
rectangular prism =2(1 x 2) +(2 x 12)+(1 x 12)
prism = 2(2) + (24) +(12)
surface area =2( 38)
surface area = 76
d. The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 1 w = 3 h = 8
rectangular prism =2(1 x 3) +(3 x 8)+(1 x 8)
prism = 2(3) + (24) +(8)
surface area =2( 35)
surface area = 70
e . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 1 w = 4 h = 6
rectangular prism =2(1 x 4) +(4 x 6)+(1 x 6)
prism = 2(4) + (24) +(6)
surface area =2( 34)
surface area = 68
f . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 2 w = 2 h = 6
rectangular prism =2(2 x 2) +(2 x 6)+(1 x 6)
prism = 2(4) + (12) +(6)
surface area =2( 32)
surface area = 64
g . The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 2 w = 4 h = 3
rectangular prism =2(2 x 4) +(4 x 3)+(2 x 3)
prism = 2(8) + (12) +(6)
surface area =2( 26)
surface area = 52
Question 2.
REASONING
Work with a partner. If two blocks of ice have the same volume, the block with the greater surface area will melt faster. The blocks below have equal volumes. Which block will melt faster? Explain your reasoning.

Answer:
The first block will melt faster.
Explanation:
The surface area of the square prism = 2lw + 2lh + 2wh
where l = 1ft w = 1ft h = 1 ft
surface area = 2(1 x 1)+2(1 x 1) + 2(1 x 1)
surface area = 2(1)+2(1) + 2(1)
surface area = 2+2+2
surface area = 6
The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 2 w = 1 h = 0.5
rectangular prism =2(2 x 1) +(2 x 0.5) +(1 x 0.5)
prism = 2(2) + (1) +(0.5)
surface area = 4 + 1 + 0.5
surface area = 5.5
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
lateral surface area
the slant height of a pyramid
regular pyramid
cross-section
Answer:
Lateral Surface Area = The lateral surface of an object is all of the sides of the object, excluding its base and top.
Slant Height of a Pyramid = The slant height of an object is the distance measured along a lateral face from the base to the apex along the center of the face.
Regular Pyramid = In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle.
Cross Section = a surface or shape exposed by making a straight cut through something, especially at the right angles to an axis. ( The cross-section of an octahedron is a square.)
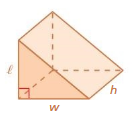
Lesson 10.1 Surface Areas of Prisms
EXPLORATION 1
Writing a Formula for Surface Area
Work with a partner.
a. Use the diagrams to write a formula for the surface area of a rectangular prism. Explain your reasoning.
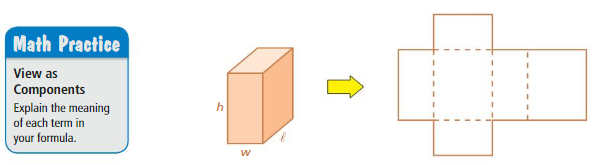
b. Choose dimensions for a rectangular prism. Then draw the prism and use your formula in part(a) to find the surface area.
Answer:
a :
b : The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height.
EXPLORATION 2
Surface Areas of Prisms
Work with a partner.
a. Identify the solid represented by the net. Then find the surface area of the solid.
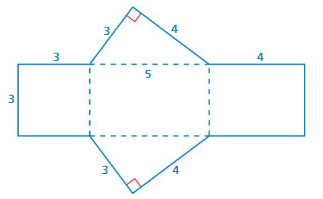
b. Describe a method for finding the surface area of any prism.
Answer:
a : The surface area of the solid = 94
b : The surface area of the solid = 2(lw + lh + wh)
Explanation:
a :

b :
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height.

Try It
Find the surface area of the prism.
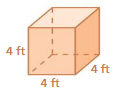
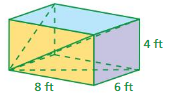
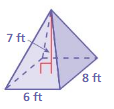
Question 1.
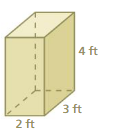
Answer:
The surface area of the prism = 52 ft
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(2 x 3) + 2(3 x 4) +2(2×4)
surface area = 2(6) + 2(12) + 2(8)
surface area = 12 + 24 + 16
surface area = 52 ft
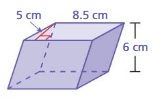
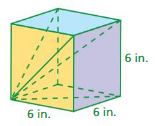
Question 2.
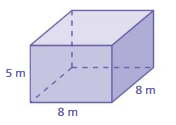
Answer:
The surface area of the prism = 288 sq. m
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(5 x 8) + 2(8 x 8) +2(5×8) where l = 8m,w = 8m, h= 8m
surface area = 2(40) + 2(64) + 2(40)
surface area = 80 + 128 + 80
surface area = 288 sq. m
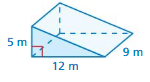
Question 3.
Find the surface area of the prism at the left.
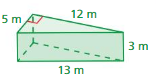
Answer:
The surface area of the prism at the left = 288 sq. m
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(5 x 12) + 2(12 x 13) +2(5×13) where l = 13m,w = 5m, h= 12m
surface area = 2(60) + 2(156) + 2(65)
surface area = 120 + 312 + 130
surface area = 562 sq. m
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
WRITING
Explain the meaning of each term in the formula for the surface area of a rectangular prism.
Answer:
The surface area of the rectangular prism = 2(lw + lh + wh)
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
Question 5.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
The surface area of the triangular prism = 26 sq. cm
The surface area of the bases of the prism = 26 sq. cm
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 3) + 4 (5)
surface area = 6 + 20
surface area = 26 sq. cm
The surface area of the bases of the prism = ph + 2B
surface area = 4(5) + 2(3)
surface area = 26 sq. cm
The area of the net of the prism = The sum of the areas of the bases and the lateral faces of the prism.
Question 6.
You want to stain the lateral faces of the wooden chest shown. Find the area that you want to stain in square inches.
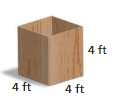
Answer:
The area that you want to stain in square inches = 3456 square inches.
Explanation:
The surface area of the lateral faces of the prism = ph + 2B
surface area = 4(4) + 2(4)
surface area = 24 ft
1 feet = 144 square inches
144 x 24 = 3456 square inches.
Question 7.
One can of frosting covers about 280 square inches. Is one can of frosting enough to frost the cake? Explain.
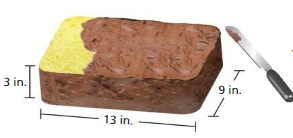
Answer:
no one can of frosting is not enough to frost the cake.
Explanation:
The cake piece is in the shape of a rectangle
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(39 + 117 + 27)
183 sq. inches.
Question 8.
DIG DEEPER!
Find the surface area of the bench shown. Justify your answer.

Answer:
The surface area of the bench = 16 sq. ft
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(1 x 1.5) +(1.5 x 2) +(2 x 5)
surace area = 2(1.5) + 3 + 10
surface area = 16 sq. ft
Surface Areas of Prisms Homework & Practice 10.1
Review & Refresh
Classify the pair of angles. Then find the value of x.
Question 1.
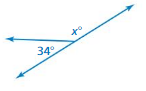
Answer:
The value of x = 146
Explanation:
The above-shown angle = obtuse angle
given that 34 degrees
180 – 34 = 146
Question 2.
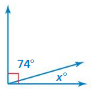
Answer:
The value of x = 106
Explanation:
The above-shown angle = right angle
given that 74 degrees
180 – 74 = 106Question 3.
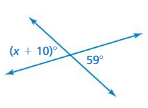
Answer:
The value of x = 121
Explanation:
The above-shown angle = acute angles.
given that 59 degrees
x + 10 = 59
x = 49
180 – 49 = 121
Question 3.
Find the area of a circle with the indicated dimensions. Use 3.14 or \(\frac{22}{7}\) for π.
Question 4.
radius: 21 in.
Answer:
The area of the circle = 1,384.74 sq. in
Explanation:
The area of the circle = πr2
area = 3.14 x 21 x 21 where π = 3.14 radius = 21 in
area = 1,384.74 sq. in
Question 5.
diameter: 36mm
Answer:
The area of the circle = 530.66 sq. mm
Explanation:
The area of the circle = πr2
area = 3.14 x 13 x 13 where π = 3.14 radius = 13 mm
area = 530.66 sq. mm
Question 6.
radius: 8.5 m
Answer:
The area of the circle = 226.865 sq. m
Explanation:
The area of the circle = πr2
area = 3.14 x 8.5 x 8.5 where π = 3.14 radius = 8.5 m
area = 226.865 sq. m
Concepts, Skills, & Problem Solving
SURFACE AREA OF A PRISM Identify the solid represented by the net. Then find the surface area of the solid. (See Explorations 1 & 2, p. 409.)
Question 7.
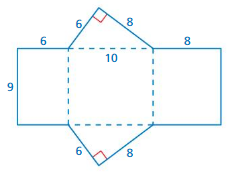
Answer:
The surface area of the prism = 182
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(6 x 8) +(9 x 6) +(10 x 8)
surace area = 2(48) + 54 + 80
surface area = 182
Question 8.
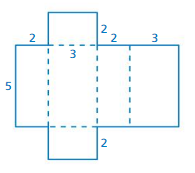
Answer:
The surface area of the prism = 44
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(5 x 2) +(2 x 3) +(3 x 2)
surace area = 2(10) + 6+ 6
surface area = 44 sq. units
FINDING THE SURFACE AREA OF A PRISM Find the surface area of the prism.
Question 9.
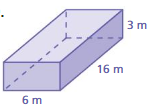
Answer:
The surface area of the prism = 324 sq. m
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(6 x 16) +(16 x 3) +(3 x 6)
surace area = 2(96) + 48+ 18
surface area = 324 sq. m
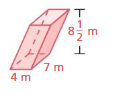
Question 10.
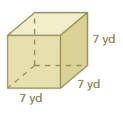
Answer:
The surface area of the prism = 294 sq. yd
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(7 x 7)+ 2(7 x 7) +2(7×7)
surface area = 2(49) + 2(49) + 2(49)
surface area = 98 + 98 + 98
surface area = 294 sq. yd
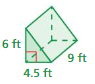
Question 11.
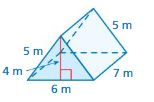
Answer:
The surface area of the triangular prism = 32 sq. m
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 6) + 4 (5)
surface area = 12 + 20
surface area = 32 sq. m
Question 12.
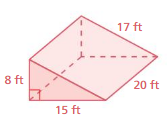
Answer:
The surface area of the triangular prism = 166 sq. ft
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 15) + 17 (8)
surface area = 30 + 136
surface area = 166 sq. ft
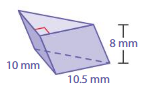
Question 13.
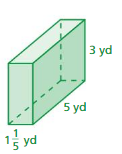
Answer:
The surface area of the prism = 46.4 yds
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(1.2 x 5) +(5 x 3) +(1.2 x 6)
surace area = 2(1) + 15+ 7.2
surface area = 23.2 x 2
surface area = 46.4 sq. yds
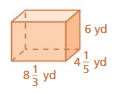
Question 14.
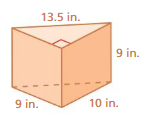
Answer:
The surface area of the prism = 693 sq. in
Explanation:
The surface area of the paralleloram prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(9 x 10) +(9 x 13.5) +(13.5 x 10)
surace area = 2(90) +121.5 + 135
surface area = 346.5 x 2
surface area = 693 sq. inches
Question 15.
YOU BE THE TEACHER
Your friend finds the surface area of the prism. Is your friend correct? Explain your reasoning.

Answer:
yes my friend is correct.
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(5 x 3)+ 2(3 x 4) +2(5×3)
surface area = 2(15) + 2(12) + 2(15)
surface area = 30+ 24 + 30
surface area = 84 sq. cm
Question 16.
MODELING REAL LIFE
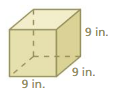
A cube-shaped satellite has side lengths of 10 centimeters. What is the least amount of aluminum needed to cover the satellite?
Answer:
The least amount of aluminum needed to cover the satellite = 90 centimeters.
Explanation:
Given that cube has the side lengths of 10 and 10 centimeters
10 x 10 = 100
100 -10 = 90
so the least amount of aluminum needed to cover = 90 centimeters.
FINDING SURFACE AREA Find the surface area of the prism.
Question 17.
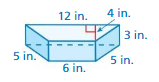
Answer:
The surface area of the triangular prism = 80 in
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 16) + 4 (12)
surface area = 32 + 48
surface area = 80 sq. in
Question 18.
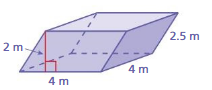
Answer:
The surface area of the prism = 58 sq. m
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(4 x 4) +(4 x 2) +(2.5 x 2)
surace area = 2(16) + 8+ 5
surface area = 29 x 2
surface area = 58 sq. m
Question 19.
OPEN-ENDED
Draw and label a rectangular prism that has a surface area of 158 square yards.
Answer:
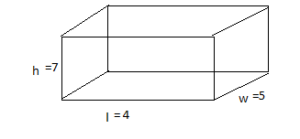
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(4 x 5) +(5x 6) +(4 x 7)
surace area = 2(20) + 30+ 29
surface area = 79 x 2
surface area = 158 square yards
Question 20.
DIG DEEPER!
A label that wraps around a box of golf balls covers 75% of its lateral surface area. What is the value of x?
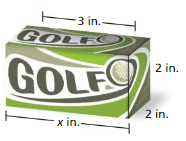
Answer:
The value of x = 25%
Explanation:
Given that the label that wraps around a box of golf covers 75%
That means for 100%
100 – 75 = 25%
Question 21.
STRUCTURE
You are painting the prize pedestals shown(including the bottoms). You need 0.5 pint of paint to paint the red pedestal.

a. The edge lengths of the green pedestal are one-half the edge lengths of the red pedestal. How much paint do you t do you need to paint the green pedestal?
b. The edge lengths of the blue pedestal are triple the edge lengths of the green pedestal. How much paint do you need to paint the blue pedestal?
c. Compare the ratio of paint volumes to the ratio of edge lengths for the green and red pedestals. Repeat for the green and blue pedestals. What do you notice?
Answer:
a. The paint you need to paint the green pedestal =1024 in
b. The paint you need to paint the blue pedestal = 5798464 in
c. 1 : 2 for green and red , 1 : 3 for green and blue.
b. Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
where l = length , w= width , h = height
surface area = 2(16 x 16) +(16x 24) +(16 x 24)
surace area = 2(256) + 384+ 384
surface area = 1024 x 2
surface area = 2048 sq. in
Question 22.
NUMBER SENSE
A key chain-sized puzzle cube is made up of small cubes. Each small cube has a surface area of 1.5 square inches.
a. What is the edge length of each small cube?
b. What is the surface area of the entire puzzle cube?

Answer:
The edge length of each small cube = 1
The surface area of the entire puzzle cube = 81
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(0 x 0)+ 2(0 x 0) +1.5(1x 1)
surface area = 2(0) +2(0) +1.5(1)
surface area = 0 + 0 + 1.5
surface area = 1.5
The surface area of the each small cube = 81
Lesson 10.2 Surface Areas of Cylinders
A is a solid that has two parallel, identical circular bases.
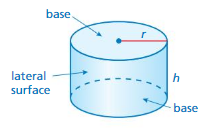
EXPLORATION 1
Finding the Surface Area of a Cylinder
Work with a partner.
a. Make a net for the can. Name each shape in the net.
b. How are the dimensions of the paper related to the dimensions of the can?

c. Write a formula that represents the surface area of a cylinder with h a height of and bases with a radius of r.
d. Estimate the dimensions of each can. Then use your formula in part(c) to estimate the surface area of each can.

Answer:
a. 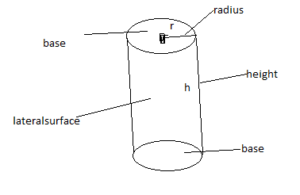
b. The dimensions of the paper = the dimensions of the can
c .

d. The surface area of the cylinder = 2πr (h + r)
Try It
Find the surface area of the cylinder. Round your answer to the nearest tenth if necessary.
Question 1.
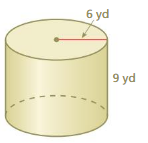
Answer:
The surface area of the cylinder = 34138.08 sq. yd
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where r = radius, h = height
2 x 3.14 x 36 + 2 x 3.14 x 6 x 9
226.08 + 33912
34138.08
Question 2.
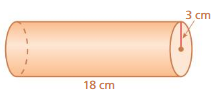
Answer:
The surface area of the cylinder = 395.64 sq. cm
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where r = radius, h = height
2 x 3.14 x 9+ 2 x 3.14 x 3 x 18
56.52 + 339.12
395.64 sq. cms
Find the lateral surface area of the cylinder. Round your answer to the nearest tenth.
Question 3.
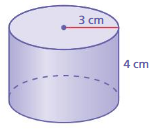
Answer:
The lateral surface of the cylinder = 75.36 sq. cms
Explanation:
The lateral surface area of the cylinder = 2πrh
area = 2 x 3.14 x 3 x 4
area = 75.36 sq. cms
Question 4.
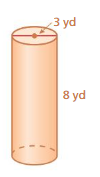
Answer:
The lateral surface of the cylinder = 150.72 sq. yds
Explanation:
The lateral surface area of the cylinder = 2πrh
area = 2 x 3.14 x 3 x 8
area = 150.72 sq. yds
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
WRITING
Which part of the formula S = 2πr2 + 2πrh represents the lateral surface area of a cylinder? the areas of the bases?
Answer:
The area of the bases of the cylinder.
Explanation:
The area of the bases of the cylinder = 2πr2 + 2πrh
where r = radius , h = height
Question 6.
CRITICAL THINKING
You are given the height of a cylinder and the circumference of its base. Describe how to find the surface area of the cylinder.
Answer:
The surface area of the cylinder = 2πr2 + 2πrh
Explanation:
The area of the bases of the cylinder =2πr2 + 2πrh
where r = radius, h = height
Question 7.
FINDING A SURFACE AREA
Find the surface area of the cylinder at the left. Round your answer to the nearest tenth.
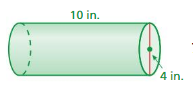
Answer:
The lateral surface of the cylinder = 351.68 sq. in
Explanation:
The lateral surface area of the cylinder = 2πrh
area = 2 x 3.14 x 16 + 2 x 3.14x 4 x 10
area = 100.48 + 251.2
area = 351.68 sq. in
Question 8.
FINDING A LATERAL SURFACE AREA
Find the lateral surface area of the cylinder at the right. Round your answer to the nearest tenth.
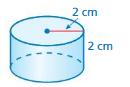
Answer:
The lateral surface of the cylinder = 351 sq. in
Explanation:
The lateral surface area of the cylinder = 2πrh
area = 2 x 3.14 x 16 + 2 x 3.14x 4 x 10
area = 100.48 + 251.2
area = 351.68 sq. in
IN the question given that round to the nearest tenth
area = 351 sq. in
Question 9.
You remove the lid of the can. What is the percent of change in the surface area of the can?

Answer:
The percent of the change in the surface area of the can = 22,019.25 mm
Explanation:
The surface area of the can = 2π rx r+ 2πrh
2 x 3.14 x 1806.25 + 2 x 3.14 x 42.5 x 40
22,019.25 mm
The surface area of the triangular prism = 166 sq. ft
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 15) + 17 (8)
surface area = 30 + 136
surface area = 166 sq. ft
Question 10.
After burning half of a cylindrical candle, the surface area is 176 square inches. The radius of the candle is 2 inches. What was the original height of the candle?
Answer:
The original height of the
Question 11.
DIG DEEPER!
The area of the sheet of wrapping paper is equal to the lateral surface area of a cylindrical tube. The tube is 14 inches tall. What is the surface area of the tube, including the bases? Explain your reasoning.
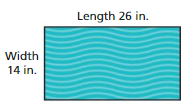
Answer:
The surface area of the tube including the bases = 42.96 inches
Explanation:
The lateral surface area of the cylinder = 2 x 3.14 x r x h
surface area = 2 x 3.14 x 13 x 14
surface area = 1142.96 inchs
Surface Areas of Cylinders Homework & Practice 10.2
Review & Refresh
Find the surface area of the prism.
Question 1.
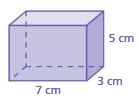
Answer:
The surface area of the prism = 142 sq. cms
Explanation:
The surface area of the prism = 2lw + 2lh + 2wh
surface area = 2(7 x 3)+ 2(3 x 5) +2(5×7)
surface area = 2(21) + 2(15) + 2(35)
surface area = 42+ 30 + 70
surface area = 142 sq. cm
Question 2.
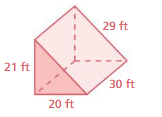
Answer:
The surface area of the triangular prism = 649 sq. ft
Explanation:
The surface area of the triangular prism = 2B + ph
where B = area of the base, p = perimeter of the base, h = height
surface area = 2( 20) + 29 (21)
surface area = 40+ 609
surface area = 649 sq. ft
Question 3.
Which of the following is equivalent to 0.625?
A. \(\frac{5}{8}\)
B. \(\frac{625}{100}\)
C. 0.625%
D. 6.25%
Answer:
A is the correct answer
Explanation:
(5/8) = 0.625
Concepts, Skills, & Problem Solving
FINDING SURFACE AREA Find the surface area of the cylinder. (See Exploration 1, p. 415.)
Question 4.
a can with a radius of 60 millimeters and a height of 160 millimeters
Answer:
The surface area of the cylinder = 82,896 millimeters
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 60 millimeters , height = 160 given
surface area = 2 x 3.14 x 60 x 60 + 2 x 3.14 x 60 x 160
surface area = 22608 + 60,288
surface area = 82,896 sq. millimeters
Question 5.
a hay bale with a diameter of 30 inches and a height of 72 inches
Answer:
The surface area of the cylinder = 8195.4 inches
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 15 inches , height = 72 inches given
surface area = 2 x 3.14 x 15 x 15 + 2 x 3.14 x 15 x 72
surface area = 1413 + 6,782.4
surface area = 8195.4 sq. inches
FINDING SURFACE AREA Find the surface area of the cylinder. Round your answer to the nearest tenth if necessary.
Question 6.
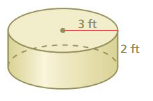
Answer:
The surface area of the cylinder = 94.2 ft
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 3 ft , height = 2 ft given
surface area = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 3 x 2
surface area = 56.52 + 37.68
surface area = 94.2 sq. ft
Question 7.
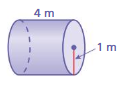
Answer:
The surface area of the cylinder = 31.4 sq. m
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 1 m , height = 4 m given
surface area = 2 x 3.14 x 1 x 1 + 2 x 3.14 x 1 x 4
surface area = 6.28+ 25.12
surface area = 31.4 sq. m
Question 8.
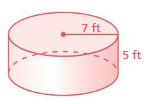
Answer:
The surface area of the cylinder = 527.52 sq. ft
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 7 ft , height = 5 ft given
surface area = 2 x 3.14 x 7 x 7 + 2 x 3.14 x 7 x 5
surface area = 307.72+ 219.8
surface area = 527.52 sq. ft
Question 9.
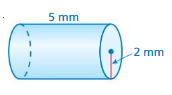
Answer:
The surface area of the cylinder = 87.92 sq. mm
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 2mm , height = 5 mm given
surface area = 2 x 3.14 x 2 x 2 + 2 x 3.14 x 2 x 5
surface area = 25.12+ 62.8
surface area = 87.92 sq. mm
Question 10.
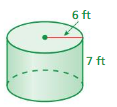
Answer:
The surface area of the cylinder = 489.84 sq. ft
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 6 ft , height = 7 ft given
surface area = 2 x 3.14 x 6 x 6 + 2 x 3.14 x 6 x 7
surface area = 226.08+ 263.76
surface area = 489.84 sq. ft
Question 11.
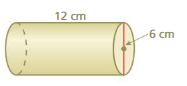
Answer:
The surface area of the cylinder = 678.24 sq. cm
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 6 cm , height = 12 cm given
surface area = 2 x 3.14 x 6 x 6 + 2 x 3.14 x 6 x 12
surface area = 226.08+ 452.16
surface area = 678.24 sq. cm
FINDING LATERAL SURFACE AREA Find the lateral surface area of the cylinder. Round your answer to the nearest tenth if necessary.
Question 12.
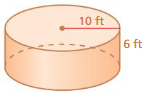
Answer:
The lateral surface area of the cylinder = 376.8 sq. ft
Explanation:
The surface area of the cylinder = 2πrh
where radius = 10 ft , height = 6 ft given
surface area = 2 x 3.14 x 10 x 6
surface area = 376.8 sq. ft
Question 13.
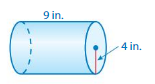
Answer:
The lateral surface area of the cylinder = 226.08 sq. in
Explanation:
The surface area of the cylinder = 2πrh
where radius = 4 in , height = 9 in given
surface area = 2 x 3.14 x 4 x 9
surface area = 226.08 sq. in
Question 14.
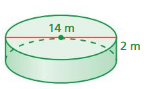
Answer:
The lateral surface area of the cylinder = 87.92 sq. m
Explanation:
The surface area of the cylinder = 2πrh
where radius = 7 m , height = 2 m given
surface area = 2 x 3.14 x 7 x 2
surface area = 87.92 sq. m
Question 15.
YOU BE THE TEACHER
Your friend finds the surface area of the cylinder. Is your friend correct? Explain your reasoning.

Answer:
No my friend is not correct.
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
surface area = 2 x 3.14 x 5 x 5 + 2 x 3.14 x 5 x 10.6
surface area = 157 + 332.84
surface area = 489.84 sq. yds
Question 16.
MODELING REAL LIFE
The tank of a tanker truck is a stainless steel cylinder. Find the surface area of the tank.
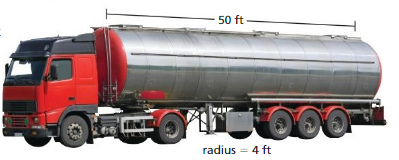
Answer:
The surface area of the tank = 1356.48 sq. ft
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
surface area = 2 x 3.14 x 4 x 4 + 2 x 3.14 x 4 x 50
surface area = 100.48+ 1256
surface area = 1,356.48 sq. ft
Question 17.
MODELING REAL LIFE
The Petri dish shown has no lid. What is the surface area of the outside of the Petri dish?
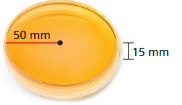
Answer:
The surface area of the outside of the petri dish= 20,410 sq. mm
Explanation:
The surface area of the outside of the petri dish = 2πr2 + 2πrh
surface area = 2 x 3.14 x 50 x 50 + 2 x 3.14 x 50x 15
surface area = 15700+ 4710
surface area = 20410 sq. mm
Question 18.
REASONING
You have two 8.5-by-11-inch pieces of paper. You form the lateral surfaces of two different cylinders by taping together a pair of opposite sides on each piece of paper so that one cylinder has a height of 8.5 inches and the other has a height of 11 inches. Without calculating, compare the surface areas of the cylinders (including the bases). Explain.
Answer:
The surface area of the cylinder 1= 44.826012 sq. inches
The surface area of the cylinder 2= 56.915012 sq. inches
Explanation:
The surface area of the cylinder 1 = 2πr2 + 2πrh
surface area = 2 x 3.14 x 0.77 x 0.77 + 2 x 3.14 x 0.77x 8.5
surface area = 3.723412+ 41.1026
surface area = 44.826012 inches
The surface area of the cylinder 1 = 2πr2 + 2πrh
surface area = 2 x 3.14 x 0.77 x 0.77 + 2 x 3.14 x 0.77x 11
surface area = 3.723412+ 53.1916
surface area = 56.915012 inches
Question 19.
DIG DEEPER!
A ganza is a percussion instrument used in samba music.

a. Find the surface area of each of the two labeled ganzas.
b. The smaller ganza weighs 1.1 pounds. Assume that the surface area is proportional to the weight. What is the weight of the larger ganza?
Answer:
a. The surface area of the smaller ganza= 296.73 sq. cm
The surface area of the larger ganza= 1036.2 sq. cm
Explanation:
The surface area of the smaller ganza = 2πr2 + 2πrh
surface area = 2 x 3.14 x 3.5 x 3.5 + 2 x 3.14 x 3.5x 10
surface area = 76.93+ 219.8
surface area = 296.73 sq. cm
The surface area of the larger ganza = 2πr2 + 2πrh
surface area = 2 x 3.14 x 5.5 x 5.5 + 2 x 3.14 x 5.5x 24.5
surface area = 189.97+846.23
surface area = 1036.2 sq. cm
Question 20.
PROBLEM SOLVING
The wedge is one-eighth of the wheel of cheese.

a. Find the surface area of the cheese before it is cut.
b. Find the surface area of the remaining cheese after the wedge is removed. Did the surface area increase, decrease, or remain the same?
Answer:
a. The surface area of the cheese before it is cut= 75.36 sq. in
b. The surface area of the cheese after the wedge is removed = 58.875 sq. in
The surface area decreases.
Explanation:
The surface area of the cheese after the wedge is removed = 2πr2 + 2πrh
surface area = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 3 x 1
surface area = 56.52+ 18.84 in
surface area = 75.36 sq. in
The surface area of the cheese after the wedge is removed = 2πr2 + 2πrh
surface area = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 3 x (1/8) (1/8) = 0.125
surface area = 56.52+ 2.355
surface area = 58.875 in
The surface area decreases
Question 21.
REPEATED REASONING
A cylinder has radius r and height h.
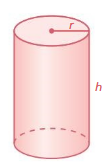
a. How many times greater is the surface area of a cylinder when both dimensions are multiplied by2? 3? 5? 10?
b. Describe the pattern in part(a). Write an expression for the surface area of the cylinder when both dimensions are multiplied by a number.
Answer:
a. 2 times greater, 3 times greater, 5 times greater,10 times greater.
b. The expression for the surface area of the cylinder when both dimensions are multiplied 2 = 2r + 2h,3r + 3h,5r + 5h, 10r + 10 h
Lesson 10.3 Surface Areas of Pyramids
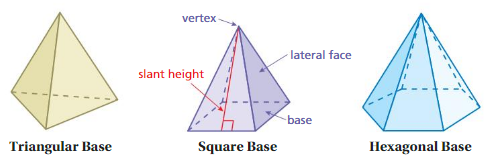
Many well-known pyramids have square bases, however, the base of a pyramid can be any polygon.
EXPLORATION 1
Making a Scale Model
Work with a partner. Each pyramid below has a square base.

a. Draw a net for a scale model of one of the pyramids. Describe the scale factor.
b. Find the lateral surface area of the real-life pyramid that you chose in part(a). Explain how you found your answer.
c. Draw a net for a pyramid with a non-rectangular base and find its lateral surface area. Explain how you found your answer.
Answer:
a. 
b. The lateral surface of the real life pyramid = A + (1/2 ) ps
where A = area of base ,p= perimeter of base , s = slant height.
c. 
The lateral surface area of the rectangular pyramid = A + (1/2)ps
where A = area of base ,p= perimeter of base , s = slant height.
A regular pyramid is a pyramid whose base is a regular polygon. The slant height lateral faces are triangles. The height of each triangle is the of the pyramid.

Try It
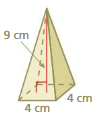
Question 1.
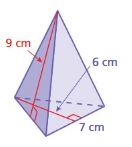
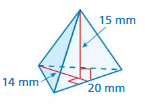
What is the surface area of a square pyramid with a base side length of 9 centimeters and a slant height of 7 centimeters?
Answer:
The surface area of the square pyramid = 94.5 sq. centimeters
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 63 +(1/2) 9 x 7
surface area = 63 + 0.5 x 63
surface area = 31.5 + 63
94.5 sq. centimeters.
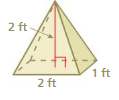
Question 2.
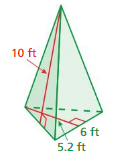
Find the surface area of the regular pyramid at the left.
Answer:
The surface area of the triangle pyramid = 86 sq. ft
Explanation:
The surface area of the triangle pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 60 +(1/2) 5.2 x 10
surface area = 60 + 2.6 x 10
surface area = 60+ 26
surface area = 86 sq. ft
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
VOCABULARY
Can a pyramid have rectangles as lateral faces? Explain.
Answer:
Yes, pyramids have rectangles as lateral faces.
Explanation:
In the pyramid diagram, the rectangles included the lateral surfaces.
FINDING THE SURFACE AREA OF A PYRAMID Find the surface area of the regular pyramid.
Question 4.
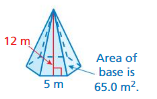
Answer:
The surface area of the triangle pyramid = 95 sq. m
Explanation:
The surface area of the triangle pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 65+(1/2) 5 x 12
surface area = 65 + 2.5 x 12
surface area = 65 + 30
surface area = 95 sq. m
Question 5.
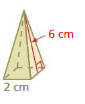
Answer:
The surface area of the triangle pyramid = 24 sq. cm
Explanation:
The surface area of the triangle pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 12+(1/2) 2 x 6
surface area = 12 + 1 x 12
surface area = 12 + 12
surface area = 24 sq. cm
Question 6.
WHICH ONE DOESN’T BELONG?
Which description of the solid does not belong with the other three? Explain your reasoning.

Answer:
regular pyramid does not belong with the other three;
Explanation:
the remaining are square pyramid, rectangular pyramid, triangular pyramid are the three pyramids with different shapes.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
A building in the shape of a square pyramid is covered with solar panels. The building has a slant height of 12 feet and a base with side lengths of 15 feet. The solar panels cost $70 per square foot to install. How much does it cost to install enough solar panels to cover the entire surface of the building?

Answer:
$ 270 is enough for solar planets to cover the entire surface of the building.
Explanation:
The building is in the shape of square pyramid.
surface area = A + (1/2) ps
area = 180 + (1/2) x 180
area = 180 + 90
area = 270 $
Question 8.
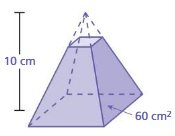
You use the glass pyramid shown to display rainbows on the walls of a room. The pyramid is regular and has a surface area of 105.35 square centimeters. Find the height of each triangular face. Justify your answer.
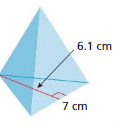
Answer:
Surface Areas of Pyramids Homework & Practice 10.3
Review & Refresh
Find the surface area of the cylinder. Round your answer to the nearest tenth.
Question 1.
Answer:
The surface area of the cylinder = 182.12 sq. ft
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 3 ft , height = 10 ft given
surface area = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 2 x 10
surface area = 56.52+ 125.6
surface area = 182.12 sq. ft
Question 2.
Answer:
The surface area of the cylinder = 345.4 sq. m
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 5 m , height = 6 m given
surface area = 2 x 3.14 x 5 x 5 + 2 x 3.14 x 5 x 6
surface area = 157+ 188.4
surface area = 345.4 sq. m
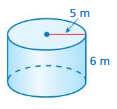
Question 3.
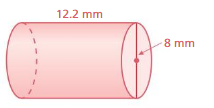
Answer:
The surface area of the cylinder = 406.944 sq. mm
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 4mm , height = 12.2mm given
surface area = 2 x 3.14 x 4 x 4+ 2 x 3.14 x 4 x 12.2
surface area = 100.48+ 306.464
surface area = 406.944 sq. mm
Question 4.
The ratio of the distance between bases on a professional baseball field to the distance between bases on a youth baseball field is 3 : 2. Bases on a professional baseball field are 90 feet apart. What is the distance between bases on a youth baseball field?
A. 30 ft
B. 45 ft
C. 60 ft
D. 135 ft
Answer:
The distance between bases on a youth baseball = 60 ft
Explanation:
The ratios between professional base and youth baseball = 3 : 2 already given
90 given
so 60 ft is the distance between bases on a youth baseball field.
Concepts, Skills, & Problem Solving
USING A NET Use the net to find the surface area of the regular pyramid. (See Exploration 1, p. 421.)
Question 5.
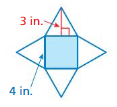
Answer:
The surface area of the square pyramid = 18 sq. in
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 12+(1/2) 4 x 3
surface area = 12 + 0.5x 12
surface area = 12 + 6
surface area = 18 sq. in
Question 6.
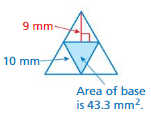
Answer:
The surface area of the square pyramid = 88.3 sq. mm
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of th base, s = slant height
surface area = 43.3+(1/2) 10 x 9
surface area = 43.3 + 0.5x 90
surface area = 43.3 + 45
surface area = 88.3 sq. mm
Question 7.
Answer:
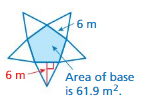
The surface area of the square pyramid = 79.9 sq. m
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 61.9 +(1/2) 6 x 6
surface area = 61.9 + 0.5x 36
surface area = 61.9 + 18
surface area = 79.9 sq. m
FINDING THE SURFACE AREA OF A PYRAMID Find the surface area of the regular pyramid.
Question 8.
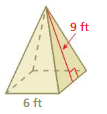
Answer:
The surface area of the triangular pyramid = 81 sq. ft
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 54 +(1/2) 6 x 9
surface area = 54 + 0.5x 54
surface area = 54 + 27
surface area = 81 sq. ft
Question 9.
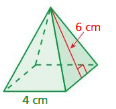
Answer:
The surface area of the triangular pyramid = 36 sq. cm
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 24 +(1/2) 6 x 4
surface area = 24 + 0.5x 24
surface area = 24 + 12
surface area = 36 sq. cm
Question 10.
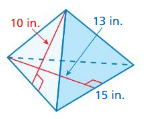
Answer:
The surface area of the triangular pyramid = 36 sq. in
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 13 +(1/2) 15 x 10
surface area = 13 + 0.5x 150
surface area = 13 + 75
surface area = 88 sq. in
Question 11.
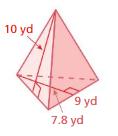
Answer:
The surface area of the triangular pyramid = 126 sq. yd
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 7.8 +(1/2) 10 x 9
surface area = 7.8 + 0.5x 90
surface area = 7.8 + 48
surface area = 126 sq. yd
Question 12.
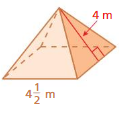
Answer:
The surface area of the triangular pyramid = 13.5 sq. m
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 4.5 +(1/2) 4 x 4.5
surface area = 4.5 + 0.5x 18
surface area = 4.5 + 9
surface area = 13.5 sq. m
Question 13.
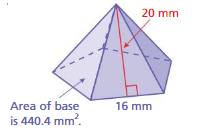
Answer:
The surface area of the triangular pyramid = 600.4 sq. mm
Explanation:
The surface area of the triangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 440.4 +(1/2) 16 x 20
surface area = 440.4+ 0.5x 320
surface area = 440.4+ 160
surface area = 600.4 sq. mm
Question 14.
MODELING REAL LIFE
The base of the lampshade is a regular hexagon with side lengths of 8 inches. Estimate the amount of glass needed to make the lampshade.

Answer:
The amount of glass needed to make the lampshade = 26.6666667 in
Explanation:
hexagon = 1/3 x b x h
where base = 8 inches , height = 10 in given
hexagon = (80/3)
hexagon = 26.6666667 in
Question 15.
GEOMETRY
The surface area of a square pyramid is 85 square meters. The side length of the base is 5 meters. What is the slant height?
Answer:
The slant height = 6 meters
Explanation:
The area of the base = side x side = 5 x 5 = 25 m
area of the lateral face = (1/2)bh= (1/2)5h= 2.5 h m
There are 4 identical lateral faces.
area of lateral faces = 4(2.5h) = 10 hm
surface area of regular pyramid = area of base + area of lateral faces
85 = 25 + 10 h
85-25 = 10 h
60 = 10 h
h = (60/10)
h = 6 meters
FINDING SURFACE AREA Find the surface area of the solid.
Question 16.
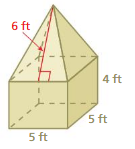
Answer:
The surface area of the square pyramid = 20 sq. ft
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 5 +(1/2) 5 x 6
surface area = 5 + 0.5x 30
surface area = 5 + 15
surface area = 20 sq. ft
Question 17.
Answer:
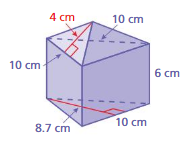
The surface area of the square pyramid = 22 sq. cm
Explanation:
The surface area of the square pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 10 +(1/2) 4 x 6
surface area = 10 + 0.5x 24
surface area = 10 + 12
surface area = 22 sq. cm
Question 18.
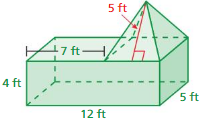
Answer:
The surface area of the rectangular pyramid = 22 sq. ft
Explanation:
The surface area of the rectangular pyramid = A + (1/2) ps
where A = area of the base ,p = perimeter of the base, s = slant height
surface area = 12 +(1/2) 4 x 5
surface area = 12 + 0.5x 20
surface area = 12 + 10
surface area = 22 sq. ft
Question 19.
GEOMETRY
A tetrahedron is a triangular pyramid with four faces that are identical equilateral triangles. The total lateral surface area of a tetrahedron is 93 square centimeters. Find the surface area of the tetrahedron.
Answer:
The surface area of the tetrahedron = 124 square cm
Explanation:
Area of lateral face (equilateral triangle) = 93/3 = 31
The tetrahedron has four identical equilateral triangles = 4 X 31 =124 cm
Question 20.
PROBLEM SOLVING
You are making an umbrella that is shaped like a regular octagonal pyramid.
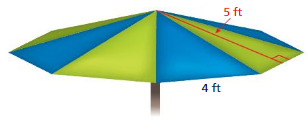
a. Estimate the amount of fabric that you need to make the umbrella.
b. The fabric comes in rolls that are 60 inches wide. Draw a diagram of how you can cut the fabric from rolls that are 10 feet long.
c. How much fabric is wasted?
Answer:
Question 21.
REASONING
The height of a pyramid is the perpendicular distance between the base and the top of the pyramid. Which is greater, the height of a pyramid or the slant height? Explain your reasoning.
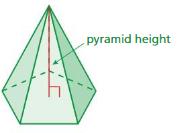
Answer:
The height of the pyramid is greater .
Explanation:
In the above shown figure the slant height is less than the height of the pyramid.
Question 22.
DIG DEEPER!
Both pyramids at the right have regular bases.
a. Without calculating, determine which pyramid has the greater surface area. Explain.
b. Verify your answer to part(a) by finding the surface area of each pyramid.
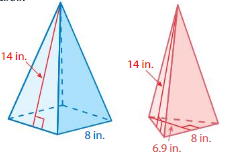
Answer:
The first figure has the greatest surface area.
Explanation:
The surface area of 1st pyramid = A + (1/2) ps
surface area = 112 + (1/2) 8 x 14
surface area = 112 +(112/2)
surface area = 56 +112
surface area = 168 in
The surface area of 2nd pyramid = A + (1/2) ps
surface area = 6.9 + (1/2) 8 x 14
surface area = 6.9 +(112/2)
surface area = 56 +6.9
surface area = 62.9 sq. in
Question 23.
REASONING
Is the total area of the lateral faces of a pyramid greater than, less than or equal to the area of the base? Explain.
Answer:
The lateral surface area of a regular pyramid is the sum of the area of its lateral faces.
The total surface area of a regular pyramid is the sum of the areas of its lateral faces and its base.
Lesson 10.4 Volumes of Prisms
EXPLORATION 1
Finding a Formula for Volume
Work with a partner.
a. In the figures shown, each cube has a volume of 1 cubic unit. Compare the volume V (in cubic units) of each rectangular prism to the area B(in square units) of its base. What do you notice?
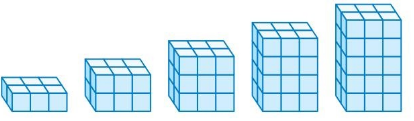
b. Repeat part(a) using the prisms below.
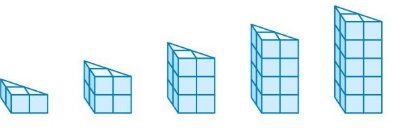
c. Use what you learned in parts (a) and (b) to write a formula that gives the volume of any prism.
Answer:
a. The 1st cube has a volume of 1 cubic unit. and it is increased by one horizontal in each cube.
b. The 1st prism has a volume of 1 cubic unit and it is increased by one horizontal in each cube.
c. Triangular prism = 2B + ph
where b = base ,h = height, l = length, p = perimeter of base, B = area of base
Rectangular prism = 2(lw +lh + wh)
where l = length, w = width, h = height
pentagonal prism = (1/2)(5s x a)h
Hexagonal prism = v = bh
octagonal prism = 2(1 +square root )a square
The volume of a three-dimensional figure is a measure of the amount of space that it occupies. Volume is measured in cubic units.
Try It
Find the volume of the prism.
Question 1.
Answer:
The volume of the prism = 16 cu. ft
Explanation:
The volume of the prism = bh
where b = 4 ft , h = 4 ft given
volume of the prism = 16 cu. ft
Question 2.
Answer:
The volume of the prism = 51 cu. cm
Explanation:
The volume of the prism = bh
where b = 8.5 cm , h = 6 cm given
volume of the prism = 8.5 x 6 = 51 cu. cm
Find the volume of the prism.
Question 3.
Answer:
The volume of prism = 162 cu. m
Explanation:
The volume of triangular prism = a x b x c x h
where a = b = c = base side , h = height
prism = 12 x 9 x 12 x 5
volume = 60 + 102
volume = 162 cu. m
Question 4.
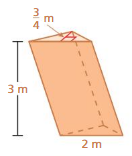
Answer:
The volume of prism = 9 cu. m
Explanation:
The volume of triangular prism = a x b x c x h
where a = b = c = base side , h = height
prism = 0.75x 2 x 2 x 3
volume = 0.75 x12
volume = 9 cu. m
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING THE VOLUME OF A PRISM Find the volume of the prism.
Question 5.
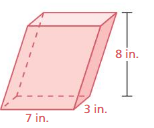
Answer:
The volume of the prism = 56 cu. in
Explanation:
volume v = B h
v = 7 x 8
v = 56 cu. in
Question 6.
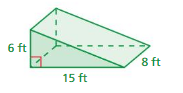
Answer:
The volume of the prism = 75 cu. ft
Explanation:
volume v = B h
v = 15 x 5
v = 75 cu. ft
Question 7.
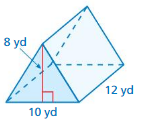
Answer:
The volume of the prism = 96 cu. yd
Explanation:
volume v = B h
v = 12 x 8
v = 96 cu. yd
Question 8.
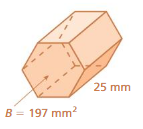
Answer:
The volume of the prism = 4925 cu. mm
Explanation:
volume v = B h
v = 197 x 25
v = 4925 cu. mm
Question 9.
OPEN-ENDED
Draw and label a prism with a volume of 144 cubic inches. Justify your answer.
Answer:
v = b x h
144 = 12 x 12
so base = 7 and height = 7 inches.
Explanation:
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
DIG DEEPER!
You visit an aquarium. One of the tanks at the aquarium holds 450 gallons of water. Draw a diagram to show one possible set of dimensions of the tank. Justify your answer. (1 gal = 231 in.3)

Answer:
Question 11.
A stack of paper contains 400 sheets. The volume of the stack is 140.25 cubic inches. Each sheet of paper is identical, with a length of 11 inches and a width of 8.5 inches. Find the height of each sheet of paper. Justify your answer.
Answer:
Each sheet of paper = 0.0075 inches.
Volumes of Prisms Homework & Practice 10.4
Review & Refresh
Find the surface area of the regular pyramid.
Question 1.
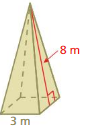
Answer:
Surface area of the regular pyramid = 15 sq. m
Explanation:
Surface area of the regular pyramid = A + (1/2) ps
area = 3 +(1/2) 3 x 8
surface area = 3 + 12
surface area = 15 sq. m
Question 2.
Answer:
Surface area of the regular pyramid =550 sq. mm
Explanation:
Surface area of the regular pyramid = A + (1/2) ps
area = 30 +(1/2) 20 x 26
surface area = 30 + 520
surface area = 550 sq. mm
Question 3.
Answer:
Surface area of the regular pyramid =61 sq. cm
Explanation:
Surface area of the regular pyramid = A + (1/2) ps
area = 7 +(1/2) 6 x 9
surface area = 7 + 54
surface area = 61 sq. cm
Find the selling price.
Question 4.
Cost to store: $75
Markup: 20%
Answer:
Selling price = 1665 $
Explanation:
Selling price = cost to store x markup + cost to store
selling price = $75 x 20% + $75
selling price = $75x 0.20 + $75
s p = 1665 $
Question 5.
Cost to store: $90
Markup: 60%
Answer:
Selling price = 5490$
Explanation:
Selling price = cost to store x markup + cost to store
selling price = $90 x 60% + $90
selling price = $90x 0.60+ $90
s p = 5490 $
Question 6.
Cost to store: $130
Markup: 85%
Answer:
Selling price =10,530 $
Explanation:
Selling price = cost to store x markup + cost to store
selling price = $130 x 85% + $130
selling price = $130 x 0.80+ $130
s p = 10,530$
Concepts, Skills, & Problem Solving
USING TOOLS In the figure, each cube has a volume of 1 cubic unit. Find the volume of the figure and the area of its base. (See Exploration 1, p. 427.)
Question 7.

Answer:
The volume of the cube = length + breadth + height
1 x 3 = 3
Explanation:
The volume of the cube = length + breadth + height
where length = l, width = w ,height = h
Question 8.

Answer:
The volume of the cube = length + breadth + height
1 x 4 = 4
Explanation:
The volume of the cube = length + breadth + height
where length = l, width = w ,height = h
Question 9.
Answer:
The volume of the cube = length + breadth + height
1 x 2 = 2
Explanation:
The volume of the cube = length + breadth + height
where length = l, width = w ,height = h
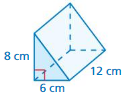
FINDING THE VOLUME OF A PRISM Find the volume of the prism.
Question 10.
Answer:
The volume of the prism = 81 cu. in
Explanation:
volume v = B h
v = 9 x 9
v = 81 cu.in
Question 11.
Answer:
The volume of the prism = 48 cu. cm
Explanation:
volume v = B h
v = 6 x 8
v = 48 cu. cm
Question 12.
Answer:
The volume of the prism = 48 cu. m
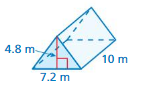
Explanation:
volume v = B h
v = 7 x 8.5
v = 59.5 cu. m
Question 13.
Answer:
The volume of the prism = 48 cu. yd
Explanation:
volume v = B h
v = 8.33 x 6
v = 50 cu. yd
Question 14.
Answer:
The volume of the prism = 54 cu.ft
Explanation:
volume v = B h
v = 9 x 6
v = 54 cu.ft
Question 15.
Answer:
The volume of the prism = 84 cu.mm
Explanation:
volume v = B h
v = 10.5 x 8
v = 84 cu.mm
Question 16.
Answer:
The volume of the prism = 48 cu.m
Explanation:
volume v = B h
v = 10 x 4.8
v = 48 cu.m
Question 17.
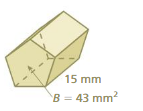
Answer:
The volume of the prism = 645 cu. mm
Explanation:
volume v = B h
v = 15 x 43
v = 645 cu. mm
Question 18.
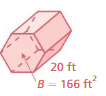
Answer:
The volume of the prism =3320 cu. feet
Explanation:
volume v = B h
v = 166 x 20
v = 3320 cu. ft
Question 19.
YOU BE THE TEACHER
Your friend finds the volume of the triangular prism. Is your friend correct? Explain your reasoning.
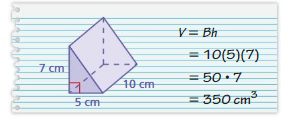
Answer:
Yes my friend is correct.
Explanation:
Volume of triangular prism = B h
volume = 10 x (5 x 7)
volume = 10 x (35)
volume = 350 cubic centimeters
Question 20.
MODELING REAL LIFE
A battery for an underwater drone is in the shape of a square prism. It is designed to draw in seawater that is then used to produce energy. The base of the battery has side lengths of 15 centimeters and the height of the battery is 10 centimeters. Find the volume of the battery.
Answer:
The volume of the battery = 2250 cu. centimeters.
Explanation:
Volume of a square prism = a square h
given that a = 15 cm, h = 10 cm
volume = 15 x 15x 10
volume = 2250 cu. centimeters.
Question 21.
MODELING REAL LIFE
A cereal box has a volume of 225 cubic inches. The length of the base is 9 inches and the width of the base is 2.5 inches. What is the height of the box? Justify your answer.
Answer:
The heightt of the box = 10 inches.
Explanation:
v = length x width x height
v = 225 cubic inches, l = 9 inches,w = 2.5 in
225 = 9 x 2.5 x h
225 = 22.5 h
h = 225/22.5
h = 10 inches
Question 22.
REASONING
Each locker is shaped like a rectangular prism. Which has more storage space? Explain.
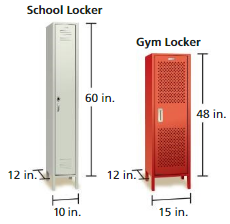
Answer:
The school locker has the more storage space.
Explanation:
2. The surface area of the rectangular prism = 2(lw + lh + wh)
area = 2(10 x 12) +(15 x 48) +(12 x 48) where l= 15 in,w = 12 in,h= 48 in
area = 2(120) +(720) +(576)
area = 2(1416)
area = 2832 sq. in
1. The surface area of the rectangular prism = 2(lw + lh + wh)
area = 2(15 x 12) +(10 x 60) +(12 x 60) where l= 10 in,w = 12 in,h= 60 in
area = 2(120) +(600) +(720)
area = 2(1440)
area = 2880 sq. in
Question 23.
USING TOOLS
How many cubic inches are in 1 cubic foot? Use a sketch to explain your reasoning.
Answer:
1 cubic foot = 1728 cubic inches.
Explanation:
Question 24.
PROBLEM SOLVING
A concrete construction block has the measurements shown. How much concrete is used to make the block? Justify your answer.
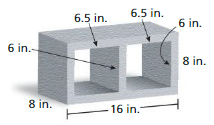
Answer:
The concrete used to make the block = 544 sq. in
Explanation:
The surface area of the rectangular prism = 2(lw + lh + wh)
area = 2(16 x 8) +(16 x 6) +(8 x 6) where l= 16in,w = 8 in,h= 6 in
area = 2(128) +(96) +(48)
area = 2(272)
area = 544 sq. in
Question 25.
RESEARCH
The gas tank is 20% full. Use the current price of regular gasoline in your community to find the cost to fill the tank. (1 gal = 231 in.3)
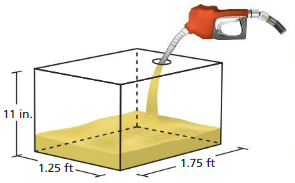
Answer:
Question 26.
DIG DEEPER!
Two liters of water are poured into an empty vase shaped like an octagonal prism. The base area is 100 square centimeters. What is the height of the water? (1 L = 1000 cm3)
Answer:
The height of the water = 20 centimeters
Explanation:
1 liter = 1000 cubic centimeters.
area of the base = 100 square cm
height = h
the volume of water in the vase = 2 liters = 2000 cubic centimeters
the volume of water in the vase = area of base x-height of the prism
2000 = 100 h
h = 20 cm
Question 27.
LOGIC
Two prisms have the same volume. Do they always, sometimes never, or have the same surface area? Justify your answer.
Answer:
If the volume is the same, they do not have the surface area.
Explanation:
if we take two prisms at random that have the same volume, it’s very likely that they don’t have the same surface area.
Question 28.
CRITICAL THINKING
How many times greater is the volume of a triangular prism when one of its dimensions is doubled? when all three dimensions are doubled?
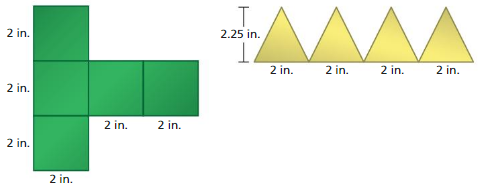
Answer:
The volume is 8 times greater when we double all 3 dimensions.
Explanation:
we are doubling only one dimension means that you are multiplying by 2 only 1 time.
Lesson 10.5 Volumes of Pyramids
EXPLORATION 1
Finding a Formula for the Volume of a Pyramid
Work with a partner. Draw the two nets on cardboard and cut them out. Fold and tape the nets to form an open cube and an open square pyramid. Both figures should have the same size square base and the same height.
a. Compare the volumes of the figures. What do you notice?
b. Use your observations in part(a) to write a formula for the volume of a pyramid.
c. The rectangular prism below can be cut to form three pyramids. Use your formula in part(b) to show that the sum of the volumes of the three pyramids is equal to the volume of the prism.
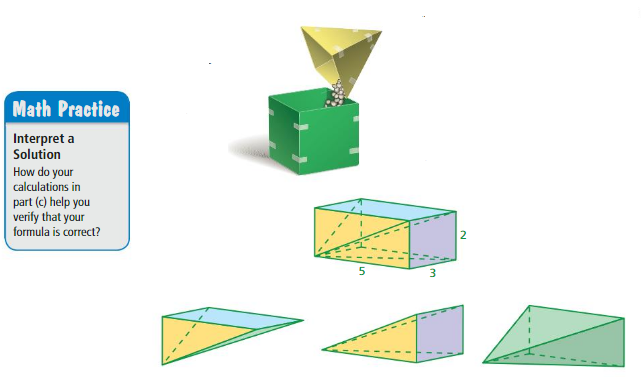
Answer:
The volume of the pyramid = (1/3) Bh
Explanation:
a. the volume of the pyramid =(1/3) B h
1. v = (1/3) x 2 x2
v = (1/3) x 4
v = 1.33 in
the volume of the pyramid =(1/3) B h
1. v = (1/3) x 2 x2.5
v = (1/3) x 5
v = 1.66 in
b. the second figure has a greater volume than the 1st figure
c. the volume of the pyramid = (1/3) B h
the volume of the prism = Bh
The volume of the 3 pyramids is equal to the volume of the prism.
Try It
Find the volume of the pyramid.
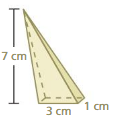
Question 1.
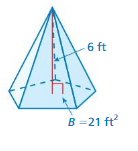
Answer:
The volume of the pyramid = 42 cubic feet
Explanation:
The volume of the pyramid = (1/3) B h
B = 21 square feet h= 6 ft
volume = (1/3) x 21×6
volume = (126/3)
volume = 42 cu. ft
Question 2.
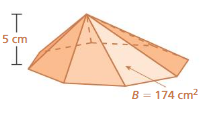
Answer:
The volume of the pyramid = 290 cubic centimeter
Explanation:
The volume of the pyramid = (1/3) B h
B =174 square cm h= 5 cm
volume = (1/3) x 174 x 5
volume = (870/3)
volume = 290 cubic centimeter
Find the volume of the pyramid.
Question 3.
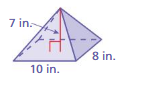
Answer:
The volume of the pyramid = 290 cubic centimeter
Explanation:
The volume of the pyramid = (1/3) B h
B =18 in h= 7 in
volume = (1/3) x 18x 7
volume = (126/3)
volume = 42 inches
Question 4.
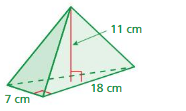
Answer:
The volume of the pyramid = 91.66 square centimeter
Explanation:
The volume of the pyramid = (1/3) B h
B =25 cm h= 11 cm
volume = (1/3) x 25x 11
volume = (275/3)
volume = 91.66 cm
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
WRITING
How is the formula for the volume of a pyramid different from the formula for the volume of a prism?
Answer:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid h = height
the volume of the prism = B h
where B = base of the prism h= height
Explanation:
The volume of the pyramid is 3 times greater the volume of the prism.
Question 6.
PROBLEM SOLVING
How many different pyramids can you draw with the same height and volume? Explain.
Answer:
We can draw the 2 or 3 pyramids with the same height and volume
Explanation:
We can draw the 2 or 3 pyramids with the same height and volume .
it is our wish to draw as many as possible
FINDING THE VOLUME OF A PYRAMID Find the volume of the pyramid.
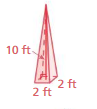
Question 7.
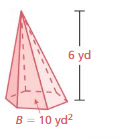
Answer:
The volume of the pyramid = cubic yard
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 10 and h= 6
v = (1/3) x 10 x 6
v = (60/3)
v = 20 cubic yds
Question 8.
Answer:
The volume of the pyramid = 12 cubic centimeters
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 4 and h= 9
v = (1/3) x 4 x 9
v = (36/3)
v = 12 cu. cm
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
A resort features a square pyramid with a water slide. The length of the water slide is 90% of the height of the pyramid. The base of the pyramid has side lengths of 60 feet. The volume of the pyramid is 60,000 cubic feet. What is the length of the water slide?

Answer:
The length of the water slide = 50 cubic feet
Question 10.
DIG DEEPER!
To make a candle, you use a mold to create the wax pyramid shown. You cut off the top 3 centimeters of the pyramid to make space for a wick. If the base area of the removed portion is 5.4 square centimeters, what percentage of the wax did you remove?
Answer:
The percentage of the wax we remove = 140 cubic centimeters.
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) x 60 x 7
volume =( 420/3)
volume = 140 cubic centimeters.
Volumes of Pyramids Homework & Practice 10.5
Review & Refresh
Find the volume of the prism.
Question 1.
Answer:
The volume of the prism = 189 cubic feets
Explanation:
The volume of the rectangular prism = l x w x h
v = 9 x 7 x 3
v = 189 cubic feets
Question 2.
Answer:
The volume of the prism = 189 cubic centimeters
Explanation:
The volume of the triangular prism = (b x h x l)/ 2
v = (5 x 3 x 8)/2
v = 60 cubic centimeters
Solve the inequality. Graph the solution.
Question 3.
r + 0.5 < – 0.4
Answer:
r = – 0.9
Explanation:
r = -0.4 -0.5
r = -0.9
Question 4.
z – 2.4 ≥ – 0.6
Answer:
z = 1.8
Explanation:
z = -0.6 (+ 2.4)
z = 1.8
Question 5.
h – 5 ≤ – 3.7
Answer:
h = -1.3
Explanation:
h = -3.7 +5
h = -1.3
Concepts, Skills, & Problem Solving
VOLUMES OF PYRAMIDS The rectangular prism is cut to form three pyramids. Show that the sum of the volumes of the three pyramids is equal to the volume of the prism. (See Exploration 1, p. 433.)
Question 6.
Answer:
The volume of the 3 pyramids is equal to the volume of the prism.
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 6 and h= 4
v = (1/3) x 6 x 4
v = (24/3)
v = 8 cubic feet
the volume of the pyramid is 3 times greater than volume of the prism.
The volume of the prism = B h
where B = base of the prism, h = height
v = B xh where B = 6 and h= 4
v = 6 x 4
v = 24
8 x 3 = 24
Question 7.
Answer:
The volume of the 3 pyramids is equal to the volume of the prism.
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 6 and h= 6
v = (1/3) x 6 x 6
v = (36/3)
v = 12 inches
the volume of the pyramid is 3 times greater than volume of the prism.
The volume of the prism= B h
where B = base of the prism, h = height
v = B xh where B = 6 and h= 6
v = 6 x 6
v = 36 in
12 x 3 = 36
FINDING THE VOLUME OF A PYRAMID Find the volume of the pyramid.
Question 8.
Answer:
The volume of the pyramid = 0.66 cubic feet
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 1 and h= 2
v = (1/3) x 1 x 2
v = (2/3)
v = 0.66 cubic feet
Question 9.
Answer:
The volume of the pyramid = 6.66 cubic feet
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 2 and h= 10
v = (1/3) x 10 x 2
v = (20/3)
v = 6.66 cubic feet
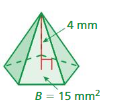
Question 10.
Answer:
The volume of the pyramid = 16 cubic feet
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 8 and h= 7
v = (1/3) x 8 x 7
v = (48/3)
v = 16 cubic feet
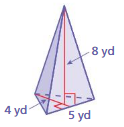
Question 11.
Answer:
The volume of the pyramid = 20 cubic millimeters
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 15 mm and h= 4
v = (1/3) x 15 x 4
v = (60/3)
v = 20 cubic mm
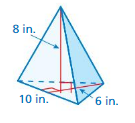
Question 12.
Answer:
The volume of the pyramid = 10.666 cu. yds
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 4 and h= 8
v = (1/3) x 4 x 8
v = (32/3)
v = 10.666 cu. yd
Question 13.
Answer:
The volume of the pyramid = 36 cu. in
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 6 and h= 8
v = (1/3) x 6 x 8
v = (48/3)
v = 36 cu. in
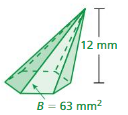
Question 14.
Answer:
The volume of the pyramid = 70 cu. mm
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 14 and h = 15 mm
v = (1/3) x 14x 15
v = (210/3)
v = 70 cu. mm
Question 15.
Answer:
The volume of the pyramid = 2.333 cubic centimeters
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 1 and h = 7 cm
v = (1/3) x 1 x 7
v = (7/3)
v = 2.333 cubic centimeters
Question 16.
Answer:
The volume of the pyramid = 252 cubic millimeters
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 63 and h = 12 mm
v = (1/3) x 63 x 12
v = (756/3)
v = 252 cubic millimeters
Question 17.
YOU BE THE TEACHER
Your friend finds the volume of the pyramid. Is your friend correct? Explain your reasoning.

Answer:
No my friend is not correct.
Explanation:
The volume of the pyramid = (1/3) x B x h
volume = (8 x 4 x 7)/3
volume = (224/3)
volume = 74.666 cu. in
Question 18.
MODELING REAL LIFE
A researcher develops a cage for a living cell in the shape of a square-based pyramid. A scale model of the cage is shown. What is the volume of the model?
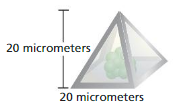
Answer:
The volume of the model = 133.33 cu. millimeters
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B = 20 and h = 20 mm
v = (1/3) x 20 x 20
v = (400/3)
v = 133.33 cu. millimeters
Question 19.
FINDING VOLUME
Find the volume of the composite solid. Justify your answer.
Answer:
The volume of the compositte solid =48 cu. feet
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =36 and h = 4 ft
v = (1/3) x 36 x 4
v = (144/3)
v = 48 cu. feet
Question 20.
MODELING REAL LIFE
In 1483, Leonardo da Vinci designed a parachute. It is believed that this was the first parachute ever designed. In a notebook, he wrote, “If a man is provided with a length of gummed linen cloth with a length of 12 yards on each side and 12 yards high, he can jump from any great height whatsoever without injury.” Find the volume of air inside Leonardo’s parachute.
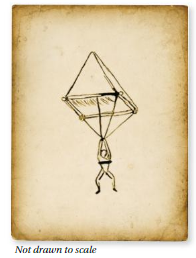
Answer:
The volume of the air inside parachute =48 cu. yd
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =12 and h = 12
v = (1/3) x 12 x 12
v = (144/3)
v = 48 cu. yds
Question 21.
MODELING REAL LIFE
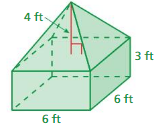
Which sandcastle spire has a greater volume? How much more sand do you need to make the spire with the greater volume?
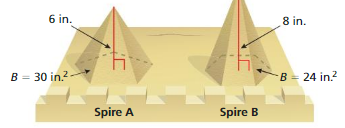
Answer:
spire B has greater volume
4 % of sand is needed to make the spire
Explanation:
The volume of the spire A = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =30 and h = 6
v = (1/3) x 30 x 6
v = (180/3)
v = 60 in
The volume of the spire B = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =24 and h = 8
v = (1/3) x 24 x 8
v = (192/3)
v = 64 cu. in
Question 22.
PROBLEM SOLVING
Use the photo of the tepee.

a. What is the shape of the base? How can you tell?
b. The tepee’s height is about 10 feet. Estimate the volume of the tepee.
Answer:
a. The shape of the base is a triangular pyramid .
b . The volume of the triangular pyramid = 3.33
Explanation:
b . The volume of the triangular pyramid = (1/3) B h
volume = (1/3) B 10
volume = (10 b /3)
10 B = 3
B = (10/3)
B = 3.33
Question 23.
OPEN-ENDED
A rectangular pyramid has a volume of 40 cubic feet and a height of 6 feet. Find one possible set of dimensions of the base.
Answer:
The dimensions of the base = 20 feet
Explanation:
The volume of the rectangular pyramid = (1/3) xB x h
volume = (1/3) x B x 6 where h = 6 ,v= 40 given
40 = (1/3) x 6 B
2 B = 40
B = 20 feet
Question 24.
REASONING
Do the two solids have the same volume? Explain.
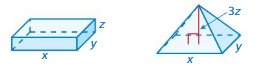
Answer:
No, the two solids did not have the same volume.
Explanation:
The volume of rectangular prism = l wh
volume = xyz
The volume of the triangular prism = b hl/2
volume = (xy3z/2)
Lesson 10.6 Cross Sections of Three-Dimensional Figures
EXPLORATION 1
Describing Cross Sections
Work with a partner. A baker is thinking of different ways to slice zucchini bread that is in the shape of a rectangular prism. The shape that is formed by the cut is called a cross section.

a. What is the shape of the cross section when the baker slices the bread vertically, as shown above?
b. What is the shape of the cross section when the baker slices the bread horizontally?

c. What is the shape of the cross section when the baker slices off a corner of the bread?

d. Is it possible to obtain a cross section that is a trapezoid? Explain.
e. Name at least 3 cross sections that are possible to obtain from a rectangular pyramid. Explain your reasoning.
Answer:
Consider a plane “slicing” through a solid. The intersection of the plane and the solid is a two-dimensional shape called a cross section. For example, the diagram shows that the intersection of the plane and the rectangular prism is a rectangle.
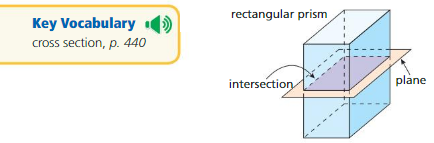
Try It
Describe the intersection of the plane and the solid.
Question 1.
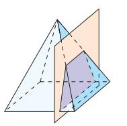
Answer:
The intersection of the plane of the solid = one dimensional
Question 2.
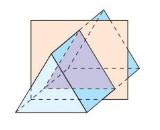
Answer:
The intersection of the plane of the solid = two dimensional
Describe the intersection of the plane and the solid.
Question 3.
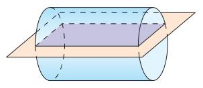
Answer:
The intersection of the plane of the cylinder = two dimensional
Question 4.
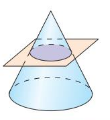
Answer:
The intersection of the plane of the cone = two dimensional
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
VOCABULARY
What is a cross section?
Answer:
The intersection of the plane of the solid is a two-dimensional is called crosssection.
Question 6.
DESCRIBING CROSS SECTIONS
Describe the intersection of the plane and the solid at the left.
Answer:
The intersection of the plane and the solid at the left is a two dimensional.
Question 7.
REASONING
Name all possible cross sections of a cylinder.
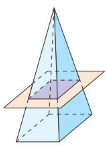
Answer:
The cross-section of the sphere is a circle. The vertical cross-section of a cone is a triangle, and the horizontal cross- section is a circle.
Question 8.
WHICH ONE DOESN’T BELONG?
You slice a square prism. Which cross section does not belong with the other three? Explain your reasoning.
![]()
Answer:
circle crosssection does not belong with the other three.
Explanation:
square, triangle, the rectangle does not belong with the three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
A steel beam that is 12 meters long is cut into four equal parts. The cross sections are rectangles with side lengths of 1 meter and 2 meters.
a. What is the perimeter of each cross section?
b. What is the area of each cross section?
c. What is the volume of the original beam?
Answer:
a. The perimeter of each cross-section = 3 meters
b. The area of each cross-section = 2 meters
c. The volume of the original beam = 12 meters.
Question 10.
DIG DEEPER!
A lumberjack saws a cylindrical tree trunk at an angle. Is the cross-section a circle? Explain your reasoning.
Answer:
Yes, the cross-section is a circle.
Explanation:
The cross-section of the sphere is a circle
Cross Sections of Three-Dimensional Figures Homework & Practice 10.6
Review & Refresh
Find the volume of the pyramid.
Question 1.
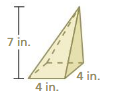
Answer:
The volume of the pyramid = 37.33 cu. in
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =16 and h = 7 in
v = (1/3) x16 x 7
v = (112/3)
v = 37.33 cu. in
Question 2.
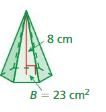
Answer:
The volume of the pyramid = 2.875 cubic centimeters.
Explanation:
The volume of the pyramid = (1/3) B h
where B = base of the pyramid, h = height
v = (1/3) x B xh where B =23 and h = 8
v = (1/3) x23 x 8
v = (112/3)
v = 2.875 cubic centimeters.
Find the sum.
Question 3.
(w – 7) + (- 6w – 5)
Answer:
w = -2
Explanation:
w = -11w+7
w=-4w
2w = -4
w= -2
Question 4.
(8 – b) + (5b + 6)
Answer:
b = 2.33
Explanation:
-b = 5b-2
5b + 6b = 2
b = 2.33
Concepts, Skills, & Problem Solving
DESCRIBING CROSS SECTIONS Determine whether it is possible to obtain the cross section from a cube. (See Exploration 2, p. 439.)
Question 5.
circle
Answer:
No it is not possible to obtain the crosssection from a cube.
Question 6.
square
Answer:
No it is not possible to obtain the crosssection from a cube.
Question 7.
equilateral triangle
Answer:
No it is not possible to obtain the crosssection from a cube.
Explanation:
equilateral triangle is not possible to obtain the crosssection from a cube.
Question 8.
pentagon
Answer:
No it is not possible to obtain the crosssection from a cube.
Explanation:
pentagon is not possible to obtain the crosssection from a cube.
Question 9.
non-rectangular parallelogram
Answer:
No it is not possible to obtain the crosssection from a cube.
Explanation:
non rectangular parallelogram is not possible to obtain the crosssection from a cube.
Question 10.
octagon
Answer:
No it is not possible to obtain the crosssection from a cube.
Explanation:
octagon is not possible to obtain the crosssection from a cube.
DESCRIBING CROSS SECTIONS OF PRISMS AND PYRAMIDS Describe the intersection of the plane and the solid.
Question 11.
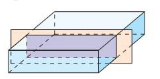
Answer:
The intersection of the prism and the solid is a two dimensional.
Question 12.
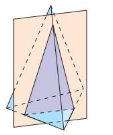
Answer:
The intersection of the pyramid and the solid is a one dimensional.
Question 13.
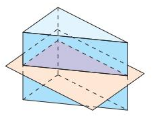
Answer:
The intersection of the pyramid and the solid is a two dimensional.
Question 14.
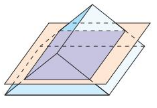
Answer:
The intersection of the pyramid and the solid is a three dimensional.
DESCRIBING CROSS SECTIONS OF CYLINDERS AND CONES Describe the intersection of the plane and the solid.
Question 15.
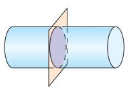
Answer:
The intersection of the plane and the solid is a circle
Explanation:
The cross section of the cylinder is a circle.
Question 16.
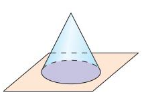
Answer:
The intersection of the plane and the solid is a circle
Explanation:
The cross section of the cone is a circle.
DESCRIBING CROSS SECTIONS Describe the shape that is formed by the cut in the food.
Question 17.

Answer:
The shape that is formed is circle.
Explanation:
The cross section when it is cut it is formed a circle.
Question 18.

Answer:
The shape that is formed is semi-circle.
Explanation:
The cross section when it is cut it is formed a semi circle.
Question 19.

Answer:
The shape that is formed is circle.
Explanation:
The cross section when it is cut it is formed circle.
Question 20.
DESCRIBING CROSS SECTIONS
Describe the intersection of the plane and the cylinder.
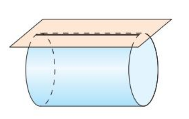
Answer:
The intersection of a plane and a cylinder is a rectangle.
REASONING Determine whether the given intersection is possible. If so, draw the solid and the cross section.
Question 21.
The intersection of a plane and a cone is a rectangle.
Answer:
No the intersection of a plane and a cone is a circle.
Explanation:

Question 22.
The intersection of a plane and a square pyramid is a triangle.
Answer:
Yes the intersection of a plane and a square pyramid is a triangle.
Explanation:

Question 23.
REASONING
A plane that intersects a prism is parallel to the bases of the prism. Describe the intersection of the plane and the prism.
Answer:
when a plane intersects a prism and is parallel to the bases of the prism , the intersection is the same shape as the base.
Question 24.
REASONING
Explain how a plane can be parallel to the base of a cone and intersect the cone at exactly one point.
Answer:
A plane will be parallel to the base and intersecting the cone at only one point is only possible when the plana will pass through
Question 25.
DIG DEEPER!
An artist plans to paint bricks.

a. Find the surface area of the brick.
b. The artist cuts along the length of the brick to form two bricks, each with a width of 2 inches. What is the percent of increase in the surface area? Justify your answer.
Answer:
a. The surface area of the brick = 164 in
b. The surface area of the percent increase = 2 %
Explanation:
b.The surface area of the rectangular prism = 2(lw +lh +wh)
surface area = 2(12 x 6 +12 x5 +6 x 5)
surface area = 2(72 + 60+30)
surface area = 2(162)
surface area = 81 in
a. The surface area of the rectangular prism = 2(lw +lh +wh)
surface area = 2(10 x 4 +10 x3 +4 x 3)
surface area = 2(40 + 30 +12)
surface area = 2(82)
surface area = 164 in
Question 26.
MODELING REAL LIFE
A cross section of an artery is shown.

a. Describe the cross section of the artery.
b. The radius of the artery is 0.22 millimeter. What is the circumference of the artery?
Answer:
a. The cross section of the artery is a circle.
b. The circumference of the artery = 1.3816 millimeters
Explanation:
The circumference of the circle = 2πr
where r= 0.22 mm given π = 3.14
circumference = 2 x 3.14 x 0.22
circumference= 1.3816 millimeters
Question 27.
REASONING
Three identical square pyramids each with a height of meters and a base area of 100 square meters are shown. For each pyramid, a cross section parallel to the base is shown. Describe the relationship between the area of the base and the area of any cross section parallel to the base.
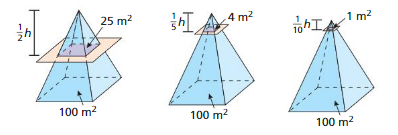
Answer:
The relationship between the area of the base and the area of any cross section parallel to the base for 1st figure = 1: 2 %
The relationship between the area of the base and the area of any cross section parallel to the base for 2nd figure = 1: 5%
The relationship between the area of the base and the area of any cross section parallel to the base for 3rd figure = 1: 10%
Explanation:
In the above 3 figures the base area is same for all the 3 figures = 100 square meters
Surface Area and Volume Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A store pays $2 per pound for popcorn kernels. One cubic foot of kernels weighs about 45 pounds. Wha tis the selling price of the container shown when the markup is 30%?

Understand the problem.
You are given the dimensions of a container of popcorn kernels and the price that a store pays for the kernels. You also know the weight of one cubic foot of popcorn kernels. You are asked to find the selling price of the container when the markup is 30%.
Make a plan.
Use the volume of the container to find the weight of the kernels. Then use the weight of the kernels to find the cost to the store. Finally, use the percent markup to find the selling price of the container.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Selling price = 525 $
Explanation:
Selling price = cost to store x markup + cost to store
selling price = $2 x 30% + $45
selling price = $2x 0.30 + $45
selling price = $525
Question 2.
The pyramid shown has a square base. What is the height of the pyramid? Justify your answer.
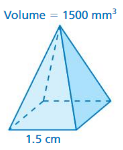
Answer:
The height of the pyramid = 3000 cm
Explanation:
The volume of the triangular pyramid = (1/3) x B h
1500 = (1/3) x 1.5 h
1500 = 0.5 h
h = (1500/3)
h = 3000 cm
Question 3.
A cylindrical can of soup has a height of 7 centimeters and a lateral surface area of 63π square centimeters. The can is redesigned to have a lateral surface area of 45π square centimeters without changing the radius of the can. What is the height of the new design? Justify your answer.
Answer:
The height of the new design can = 5 centimeters.
Explanation:
The can when it is redesigned to have a lateral surface area of 45π = 5 x 9 = 45
The height of the can when it is redesigned = 5 centimeters.
Performance Task
Volumes and Surface Areas of Small Objects
At the beginning of this chapter, you watched a STEAM Video called “Paper Measurements.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Surface Area and Volume Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
Information Frame You can use an to help organize and remember a concept. Here is an example of an Information Frame for Surface Areas of Rectangular Prisms.
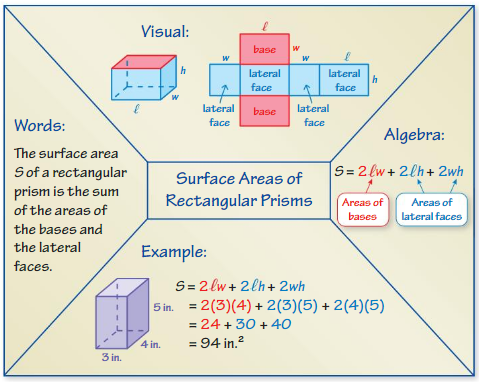
Choose and complete a graphic organizer to help you study the concept.

1. surface areas of prisms
2. surface areas of cylinders
3. surface areas of pyramids
4. volumes of prisms
5. volumes of pyramids
6. cross sections of three-dimensional figures
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

10.1 Surface Areas of Prisms (pp. 409–414)
Learning Target: Find the surface area of a prism.
Find the surface area of the prism.
Question 1.
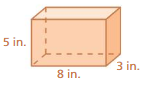
Answer:
The surface area of the Rectangular prism = 158 sq. in
Explanation:
The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 8 w = 3 h = 5
rectangular prism =2(8 x 3) +(8 x 5) +(3 x 5)
prism = 2(24) + (40) +(15)
surface area =2(79)
surface area = 158 sq. in
Question 2.
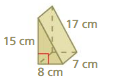
Answer:
The surface area of the triangular prism = 562 sq. cm
Explanation:
The surface area of the triangular prism = 2lw + 2lh + 2wh
surface area = 2(7 x 8) + 2(8 x 15) +2(15×7) where l = 8m,w = 8m, h= 8m
surface area = 2(56) + 2(120)+ 2(105)
surface area =112 + 240 + 210
surface area = 562 sq. cm
Question 3.
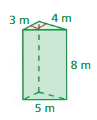
Answer:
The surface area of the triangular prism = 262 sq. m
Explanation:
The surface area of the triangular prism = 2lw + 2lh + 2wh
surface area = 2(5 x 7) + 2(5x 8) +2(8×7) where l = 5m,w = 7m, h= 8m
surface area = 2(35) + 2(40)+ 2(56)
surface area =70 + 80 + 112
surface area = 262 sq. m
Question 4.
You want to wrap the box using a piece of wrapping paper that is 76 centimeters long by56 centimeters wide. Do you have enough wrapping paper to wrap the box? Explain.
Answer:
The enough wrapping paper to wrap the box = 4180 cm
Explanation:
The surface area of the Rectangular prism = 2(lw + lh +wh)
where l = 35 w = 50 h = 4
rectangular prism =2(35 x 50) +(50 x 4) +(35 x 4)
prism = 2(1750) + (200) +(140)
surface area =2(2090)
surface area = 4180 sq. cm
Question 5.
To finish a project, you need to paint the lateral surfaces of a cube with side length 2.5 inches. Find the area that you need to paint.
Answer:
10.2 Surface Areas of Cylinders (pp. 415–420)
Learning Target: Find the surface area of a cylinder.
Find the surface area and lateral surface area of the cylinder. Round your answers to the nearest tenth.
Question 6.
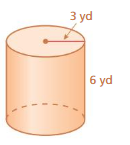
Answer:
The surface area of the cylinder = 169.56 square yards
The lateral surface area of the cylinder = 113.04 square yards
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 3 , height = 6 given
surface area = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 3 x 6
surface area = 56.52+ 113.04
surface area = 169.56
The lateral surface area of the cylinder = 2πrh
where radius = 3 , height = 6 given
surface area = 2 x 3.14 x 3 x 6
surface area = 113.04 sq. yards
Question 7.

Answer:
The surface area of the cylinder = 34.196 square centimeters
The lateral surface area of the cylinder =30.144 square centimeters
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 0.8 , height = 6 given
surface area = 2 x 3.14 x 0.8 x 0.8 + 2 x 3.14 x 0.8 x 6
surface area = 4.0192+ 30.144
surface area = 34.196 square centimeters
The lateral surface area of the cylinder = 2πrh
where radius = 0.8 , height = 6 given
surface area = 2 x 3.14 x 0.8 x 6
surface area = 30.144 square centimeters
Question 8.
The label covers the entire lateral surface area of the can. How much of the can is not covered by the label?

Answer:
The can that is not covered =276.32 square centimeters
Explanation:
The lateral surface area of the cylinder = 2πrh
where radius = 4 , height = 11 given
surface area = 2 x 3.14 x 4 x11
surface area = 276.32 square centimeters
10.3 Surface Areas of Pyramids (pp. 421–426)
Learning Target: Find the surface area of a pyramid.
Find the surface area of the regular pyramid.
Question 9.
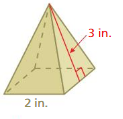
Answer:
The surface area of the pyramid = 5 square inches.
Explanation:
The surface area of the pyramid = A + (1/2) ps
surface area = 2 +(1/2) x 3 x 2
surface area= 2 +3
surface area= 5 sq. in
Question 10.
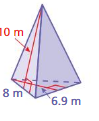
Answer:
The surface area of the pyramid = 42.5 sq. meters
Explanation:
The surface area of the pyramid = A + (1/2) ps
surface area = 8 +(1/2) x 10 x 6.9
surface area= 8 +34.5
surface area= 42.5 sq. m
Question 11.
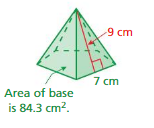
Answer:
The surface area of the pyramid = 115.8 sq. cm
Explanation:
The surface area of the pyramid = A + (1/2) ps
surface area = 84.3+(1/2) x 9 x 7
surface area= 84.3 +31.5
surface area= 115.8 sq. cm
Question 12.
The tent is shaped like a square pyramid. There is no fabric covering the ground.

a. Estimate the amount of fabric needed to make the tent.
b. Fabric costs $5.25 per square yard. How much will it cost to make the tent?
Answer:
a. The amount of fabric needed to make the tent = 12 ft
b. The cost to make the tent =
Explanation:
The surface area of the pyramid = A + (1/2) ps
surface area = 3+(1/2) x 3 x 6
surface area= 3 +9
surface area= 12 sq. ft
10.4 Volumes of Prisms (pp. 427–432)
Learning Target: Find the volume of a prism.
Find the volume of the prism.
Question 13.
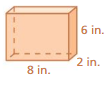
Answer:
The volume of prism = 96 cu. in
Explanation:
The volume of prism = lwh
where l = 8,w=2,h = 6
volume = 8 x 2 x 6
volume = 96 cu. in
Question 14.
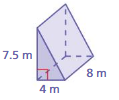
Answer:
The volume of prism = 240 cu. m
Explanation:
The volume of prism =( lbh/2)
where l = 4,w=8,h = 7.5
volume = 8 x 4 x 7.5
volume = 240 cu. m
Question 15.
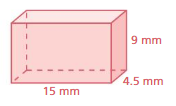
Answer:
The volume of prism =607.5 cu. mm
Explanation:
The volume of prism = lwh
where l = 15,w=4.5,h = 9
volume = 15 x 4.5 x 9
volume = 607.5 cu. mm
Question 16.
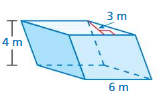
Answer:
The volume of prism =96 cu. m
Explanation:
The volume of prism = lwh
where l = 6,w=3,h = 4
volume = 6 x 3 x 4
volume = 96 cu. m
Question 17.
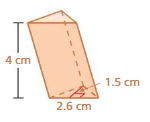
Answer:
The volume of prism = 15.6 cu. cm
Explanation:
The volume of prism = lwh
where l = 2.6 ,w=1.5 ,h = 4
volume = 2.6 x1.5 x 4
volume = 15.6 cu. cm
Question 18.
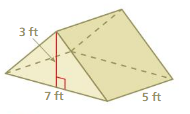
Answer:
The volume of prism = 105 cubic feet
Explanation:
The volume of prism =( lbh/2)
where l = 7 ,w=5 ,h = 3
volume = 7 x 5 x 3
volume = 105 cu. feet
Question 19.
Two cereal boxes each hold exactly 192 cubic inches of cereal. Which box should a manufacturer choose to minimize the amount of cardboard needed to make the cereal boxes?

Answer:
The first cereal box is used to minimize
10.5 Volumes of Pyramids (pp.433-438)
Learning Target: Find the volume of a pyramid.
Find the volume of the pyramid.
Question 20.
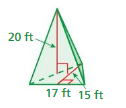
Answer:
The volume of the pyramid = 133.33 cu. ft
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 17 20
volume = (340/3)
volume = 113.33 cu. ft
Question 21.
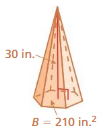
Answer:
The volume of the pyramid = 2100 cubic in
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 210 x 30
volume = (6300/3)
volume = 2100 cubic in
Question 22.
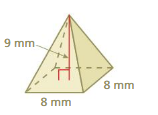
Answer:
The volume of the pyramid = 48 cu. mm
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 16 x 9
volume = (144/3)
volume =48 cu. mm
Question 23.
A pyramid-shaped hip roof is a good choice for a house in an area with many hurricanes.
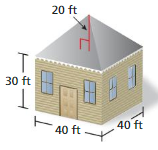
a. What is the volume of the roof to the nearest tenth of a foot?
b. What is the volume of the entire house, including the roof?
Answer:
a. The volume of the pyramid = 800 cu. ft
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 80 x 30
volume = (2400/3)
volume =800 cu. ft
b.
The volume of the pyramid = 400 cu. ft
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 40 x 30
volume = (1200/3)
volume =400 cu. ft
Question 24.
A laboratory creates calcite crystals for use in the study of light. The crystal is made up of two pieces of calcite that form a square pyramid. The base length of the top piece is 2 inches.
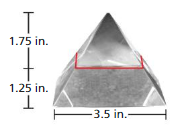
a. Find the volume of the entire pyramid.
b. Find the volume of each piece of the pyramid.
Answer:
a. The volume of the entire pyramid = 1.58 cu. in
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 3.5 x 3
volume = (4.75/3)
volume =1.58 cu. in
b.The volume of the pyramid = 1.458 cu. in
Explanation:
The volume of the pyramid = (1/3) B h
volume = (1/3) 3.5 x 1.25
volume = (4.375/3)
volume =1.458 cu. in
10.6 Cross Sections of Three-Dimensional Figures (pp. 439–444)
Learning Target: Describe the cross sections of a solid.
Describe the intersection of the plane and the solid.
Question 25.
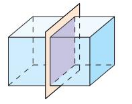
Answer:
The intersection of the plane of the solid = two dimensional
The cross section of a solid = rectangular prism
Question 26.
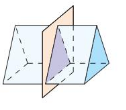
Answer:
The intersection of the plane of the solid = two dimensional
The cross section of a solid = triangular prism
Sketch how a plane can intersect with a cylinder to form a cross section of the given shape.
Question 27.
rectangle
Answer:
Question 28.
circle
Answer:
Question 29.
line segment
Answer:
Surface Area and Volume Practice Test
Find the surface area of the prism or regular pyramid.
Question 1.
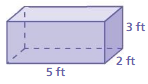
Answer:
The surface area of the pyramid = 7 ft
Explanation:
The surface area of the pyramid = (1/3) x B h
surface area = (1/3) X 7 x 3
surface area = (21/3)
surface area = 7 sq. ft
Question 2.
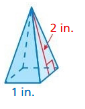
Answer:
The surface area of the pyramid = 0.66 sq. in
Explanation:
The surface area of the pyramid = (1/3) x B h
surface area = (1/3) X 1 x 2
surface area = (2/3)
surface area = 0.66 sq. in
Question 3.
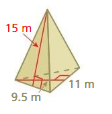
Answer:
The surface area of the pyramid = 47.5 sq. m
Explanation:
The surface area of the pyramid = (1/3) x B h
surface area = (1/3) X 9.5 x 15
surface area = (142.5/3)
surface area = 47.5 sq. m
Find the surface area and lateral surface area of the cylinder. Round your answers to the nearest tenth.
Question 4.
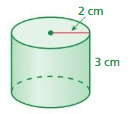
Answer:
The surface area of the cylinder = 62.8 sq. cm
The lateral surface area of the cylinder = 37.68 sq. cm
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 2 , height = 3 given
surface area = 2 x 3.14 x 2 x 2 + 2 x 3.14 x 2 x 3
surface area = 25.12+ 37.68
surface area = 62.8 sq. cm
The lateral surface area of the cylinder = 2πrh
where radius = 2 , height = 3 given
surface area = 2 x 3.14 x 2 x 3
surface area = 37.68 sq. cm
Question 5.
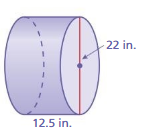
Answer:
The surface area of the cylinder = 1623.38 sq. in
The lateral surface area of the cylinder = 863.5 sq. in
Explanation:
The surface area of the cylinder = 2πr2 + 2πrh
where radius = 11 , height = 12.5 given
surface area = 2 x 3.14 x 11 x 11 + 2 x 3.14 x 11 x 12.5
surface area = 759.88+ 863.5
surface area = 1623.38 sq. in
The lateral surface area of the cylinder = 2πrh
where radius = 11 , height = 12.5 given
surface area = 2 x 3.14 x 11 x 12.5
surface area = 863.5 sq. in
Find the volume of the solid.
Question 6.
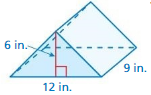
Answer:
Volume of the prism = 324 cu. in
Explanation:
Volume of the prism =( bhl/2)
volume = (9 x `12 x 6/2)
volume =(648 /2)
volume = 324 cu. in
Question 7.
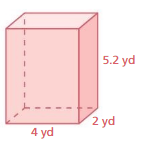
Answer:
Volume of the prism = 41.6 cu. yd
Explanation
Volume of the prism =lwh
volume = (4 x `2 x 5.2)
volume =(41.6)
Question 8.
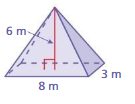
Answer:
Volume of the prism = 72 cu. m
Explanation:
Volume of the prism =( bhl/2)
volume = (3 x `8 x 6/2)
volume =(144/2)
volume = 72 cu. m
Question 9.
A quart of paint covers 80 square feet. How many quarts should you buy to paint the ramp with two coats? (Assume you will not paint the bottom of the ramp.)
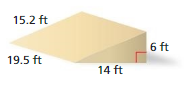
Answer:
Volume of the prism = 2914.8 cu. ft
Explanation:
Volume of the prism =lwh
volume = (14x 34.7 x 6)
volume =2914.8 cu. ft
Question 10.
A manufacturer wants to double the volume of the graham cracker box. The manufacturer will either double the height or double the width.

a. What is the volume of the new graham cracker box?
b. Which option uses less cardboard? Justify your answer.
c. A graham cracker takes up about 1.5 cubic inches of space. Write an inequality that represents the numbers of graham crackers that can fit in the new box.
Answer:
a. the volume of the new graham cracker box = 108 cu. in
Explanation:
Volume of the prism =lwh
volume = (9 x 2 x 6)
volume = 108 cu. in
Question 11.
The label on the can of soup covers about 354.2 square centimeters. What is the height of the can? Round your answer to the nearest whole number.

Answer:
The height of the can = 10,454.5672 cm
Explanation:
The lateral surface area of the cylinder = 2πrh
where radius = 4.7 , height = 354.2 given
surface area = 2 x 3.14 x 4.7 x 354.2
surface area = 10,454.5672 cm
Question 12.
A lumberjack splits the cylindrical log from top to bottom with an ax, dividing it in half. Describe the shape that is formed by the cut.
![]()
Answer:
cylinder.
Explanation:
The shape that formed by the cut = cylinder
Surface Area and Volume Cumulative Practice

Question 1.
A gift box and its dimensions are shown.

What is the least amount of wrapping paper that you need to wrap the box?
A. 20 in.2
B. 56 in.2
C. 64 in.2
D. 112 in.2
Answer:
option C is correct.
Explanation:
The least amount of wrapping paper that need to wrap the box = l x w x h
8 x 4 x 2
64
Question 2.
James is getting ready for wrestling season. As part of his preparation, he plans to lose 5% of his body weight. James currently weighs 160 pounds. How much will he weigh, in pounds, after he loses 5% of his weight?

Answer:
he weigh after he loses 5 % = 128
Question 3.
How far will the tip of the hour hand of the clock travel in 2 hours? (Use \(\frac{22}{7}\) for π.)
F. 44 mm
G. 88 mm
H. 264 mm
I. 528 mm
Answer:
option G is correct
Explanation:
The circumference of circle = 2 π r h
Question 4.
Which value of x makes the equation true?
5x – 3 = 11
A. 1.6
B. 2.8
C. 40
D. 70
Answer:
option B is correct
Explanation:
5x – 3 = 11
5x = 11 + 3
5x = 14
x = (14/3)
x = 2.8
Question 5.
A hockey rink contains 5 face-off circles. Each of these circles has a radius of 15 feet. What is the total area of all the face-off circles? (Use 3.14 for π.)
F. 706.5 ft 2
G. 2826 ft2
H. 3532.5 ft2
I. 14,130 ft2
Answer:
Option G is correct
Explanation:
The surface area of circle = 2rhπ
circle = 2 x 15 x 5 x 3.14
Question 6.
How much material is needed to make the popcorn container?

A. 76π in.2
B. 84π in.2
C. 92π in.2
D. 108π in.2
Answer:
The material needed to make the popcorn container = 76π in.2
Explanation:
The lateral surface area = 2πrh
surface area = 2 x 9.5 x 4 π
surface area = 76π in.2
Question 7.
What is the surface area of the square pyramid?
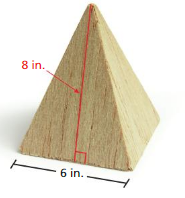
F. 24 in.2
G. 96 in.2
H. 132 in.2
I. 228 in.2
Answer:
Option g is correct
Explanation:
surface area = 2 x l x h
surface area = 2 x 8 x 6
surface area = 96 square inches
Question 8.
A rectangular prism and its dimensions are shown.
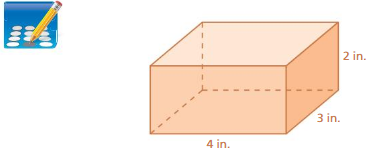
What is the volume, in cubic inches, of a rectangular prism whose dimensions are three times greater?
Answer:
The volume of rectangular prism = 24 cu. in
Explanation:
The volume of rectangular prism l w h
volume = 4 x 3 x 2
volume = 24 cu. in
Question 9.
What is the value of x?
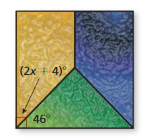
A. 20
B. 43
C. 44
D. 65
Answer:
option A is correct
Explanation:
(2x + 4) = 46
2x = (46 – 4)
2x = 42
x = 21
Question 10.
Which of the following are possible angle measures of a triangle?
F. 60°, 50°, 20°
G. 40°, 80°, 90°
H. 30°, 60°, 90°
I. 0°, 90°, 90°
Answer:
option H is the correct
Explanation:
The angles of a triangle = 30°, 60°, 90°
Question 11.
The table shows the costs of buying matinee movie tickets.

Part A Graph the data.
Part B Find and interpret the constant of proportionality for the graph of the line.
Part C How much does it cost to buy 8 matinee movie tickets?
Answer:
Big Ideas Math Answers Grade 7 Chapter 10 Surface Area and Volume
Here you are at the end of the page. You have learned about formula solving and many other things that have helped you to solve the problems at the next level. If you come across some problems of a higher level then this site helps you to attempt those topics and even solve some. If in the future you want to refer by starting from trash, take a look at this site and clear all your doubts. Bookmark the site for future use and reach us whenever needed.
