Get Big Ideas Math Grade 7 Chapter 2 Multiplying and Dividing Rational Numbers Answer Key PDF here. If you are seeking help in learning math problems and various concepts, then refer to this page. The professionals and experts suggested several ways to learn Multiplying and Dividing Rational Numbers questions.
Find the best solutions and methods to solve various problems. Practice the questions of Big Ideas Math Answers Grade 7 Chapter 2 Multiplying and Dividing Rational Numbers to score better marks in the exam. Refer to the next sections to get the complete idea of various topics involved in Multiplying and Dividing Rational Numbers. Practice as many questions as from the material and get perfect in all ways.
Big Ideas Math Book 7th Grade Answer Key Chapter 2 Multiplying and Dividing Rational Numbers
Big Ideas Math Answers Grade 7 Chapter 2 involves various topics like dividing integers, multiplying rational numbers, dividing rational numbers, multiplying integers, dividing integers, conversion between fractions and decimals. We are providing the various Cumulative Practice material, Chapter Review material, multiplying rational numbers, dividing rational numbers, etc.
Practice all these topics and get a clear idea of what is important and what is not. Follow all the important tips and tricks to get perfection in multiplying and dividing rational numbers. Get a final conclusion on advantages, formulae, and important concepts of rational numbers. Attend many mock tests and know how to manage your time to answer all the questions in the exam.
Performance
- Multiplying and Dividing Rational Numbers STEAM Video/Performance
- Multiplying and Dividing Rational Numbers Getting Ready for Chapter 2
Lesson: 1 Multiplying Integers
Lesson: 2 Dividing Integers
Lesson: 3 Converting Between Fractions and Decimals
- Lesson 2.3 Converting Between Fractions and Decimals
- Converting Between Fractions and Decimals Homework & Practice 2.3
Lesson: 4 Multiplying Rational Numbers
Lesson: 5 Dividing Rational Numbers
Chapter: 2 – Multiplying and Dividing Rational Numbers
- Multiplying and Dividing Rational Numbers Connecting Concepts
- Multiplying and Dividing Rational Numbers Chapter Review
- Multiplying and Dividing Rational Numbers Practice Test
- Multiplying and Dividing Rational Numbers Cumulative Practice
Multiplying and Dividing Rational Numbers STEAM Video/Performance
STEAM Video
Carpenter or Joiner
Carpenters and joiners must be precise with their measurements when building structures. In what other real-life situations must measurements be precise?

Watch the STEAM Video “Carpenter or Joiner.” Then answer the following questions.
Question 1.
Robert says that changes in water content cause wood to shrink or expand across the grain more than along the grain. What does this mean?
Answer:
Robert says that changes in water content cause wood to expand across the grain. So, the carpenter has to make the measurements 1/16 inches.
Question 2.
Describe how you can cut a log so that the pieces shrink in different ways as they dry out.

Answer:
While cutting the log, you need to take the correct measurement to avoid the pieces shrink in different ways as they dry out.
Performance Task
Precisely Perfect
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the Video Performance Task. You will be given the accuracies of seven telescopes. For example:


You will be asked to compare the accuracies of the telescopes. Why do different telescopes have different accuracies?
Multiplying and Dividing Rational Numbers Getting Ready for Chapter 2
Chapter Exploration
Question 1.
Work with a partner. Use integer counters to find each product. 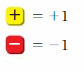

Work with a partner. Use integer counters to find the product.
Answer:
Explanation:
a. (+3) x (-2) = -6
The integers have different signs, so the product is a negative value.
b. (-2) x (-2) = 4
The integers have the same sign, so the product is a positive value.
c. (-2) x (+3) = -6
Question 2.
(+3) × (+2)
Answer:
(+3) x (+2) = +6
Explanation:
The given expression is (+3) x (+2)
The integers have the same sign. So the product is a positive value.
(+3) x (+2) = +6
Question 3.
(+3) × (-1)
Answer:
(+3) × (-1) = -3
Explanation:
The given expression is (+3) × (-1)
The integers have different signs. So the product is a negative value.
(+3) × (-1) = -3
Question 4.
(+2) × (-4)
Answer:
(+2) × (-4) = -8
Explanation:
The given expression is (+2) × (-4)
The integers have different signs. So the product is a negative value.
(+2) × (-4) =-8
Question 5.
(-3) × (+2)
Answer:
(-3) × (+2) = -6
Explanation:
The given expression is
The integers have different signs. So the product is a negative value.
(-3) × (+2) = -6
Question 6.
(-2) × (-3)
Answer:
(-2) × (-3) = +6
Explanation:
The given expression is (-2) × (-3)
The integers have the same sign. So the product is a positive value.
(-2) × (-3) = +6
Question 7.
(-1) × (-4)
Answer:
(-1) × (-4) = +4
Explanation:
The given expression is (-1) × (-4)
The integers have the same sign. So the product is a positive value.
(-1) × (-4) = +4
Question 8.
(-1) × (-2)
Answer:
(-1) × (-2) = +2
Explanation:
The given expression is (-1) × (-2)
The integers have the same sign. So the product is a positive value.
(-1) × (-2) = +2
Question 9.
(+3) × (+1)
Answer:
(+3) × (+1) = 3
Explanation:
The given expression is (+3) × (+1) = 3
The integers have the same sign. So the product is a positive value.
(+3) × (+1) = 3
Question 10.
(-3) × (-2)
Answer:
(-3) × (-2) = +6
Explanation:
The given expression is (-3) × (-2)
The integers have the same sign. So the product is a positive value.
(-3) × (-2) = +6
Question 11.
(-2) × (+2)
Answer:
(-2) × (+2) = -4
Explanation:
The given expression is (-2) × (+2)
The integers have different signs. So the product is a negative value.
(-2) × (+2) = -4
Question 12.
(-2) × (+4)
Answer:
(-2) × (+4) = -8
Explanation:
The given expression is (-2) × (+4)
The integers have different signs. So the product is a negative value.
(-2) × (+4) = -8
Question 13.
(-4) × (-2)
Answer:
(-4) × (-2) = +8
Explanation:
The given expression is (-4) × (-2)
The integers have the same sign. So the product is a positive value.
(-4) × (-2) = +8
Question 14.
MAKE A CONJECTURE
Use your results in Exercises 1–13 to determine the sign of each product.
a. negative integer and a positive integer
b. two negative integers
c. two positive integers
Answer:
a. When you multiply a negative integer and a positive integer, the product is a negative integer.
b. When you multiply two negative integers, then the product is a positive integer.
c. If you multiply two positive integers, then the product is a positive integer.
Explanation:
a. negative integer and a positive integer
When you multiply a negative integer and a positive integer, the product is a negative integer.
b. two negative integers
When you multiply two negative integers, then the product is a positive integer.
c. two positive integers
If you multiply two positive integers, then the product is a positive integer.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
![]()
Lesson 2.1 Multiplying Integers
EXPLORATION 1
Understanding Products Involving Negative Integers
Work with a partner.
a. The number line and integer counters model the product 3 • 2. How can you find 3 • (-2)? Explain.
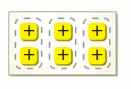
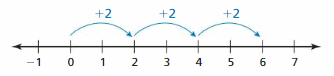
b. Use the tables to find -3 • 2 and -3 • (-2). Explain your reasoning.
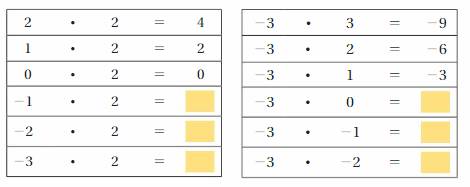
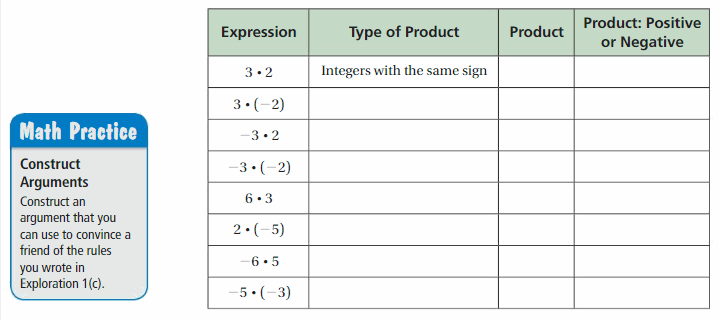
c.
INDUCTIVE REASONING
Complete the table. Then write general rules for multiplying
- two integers with the same sign and
- two integers with different signs.
Answer:
a. 3 . 2 = 6
3 . (-2) = -6
b. 
c. 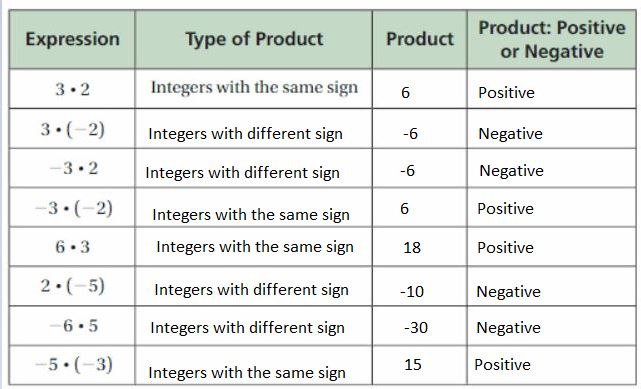
Explanation:
a. The product of 3 and 2 is 6
Both the integers are positive. So, the product is also positive.
3 . (-2) = -6
The reason is one integer is positive and another integer is negative. So, the result is negative.
b. The product of two positive or negative integers is a positive integer. The product of one positive and second negative integers is a negative integer.
c. In any expression, integers are having the same sign, which means the product is positive. If the integers are having a different sign, then the product is negative.
2.1 Lesson
Try It
Find the product.
Question 1.
5 • 5
Answer:
5 . 5 = 25
Explanation:
The given expression is 5 . 5
The given integers have the same sign. So the product is a positive integer.
5 . 5 = 25
Question 2.
-1(-9)
Answer:
-1(-9) = +9
Explanation:
The given expression is -1(-9)
The given integers have the same sign. So the product is a positive integer.
-1(-9) = +9
Question 3.
-7 • (-8)
Answer:
-7 • (-8) = 56
Explanation:
The given expression is -7 • (-8)
The given integers have the same sign. So the product is a positive integer.
-7 • (-8) = 56
Question 4.
12 • (-2)
Answer:
12 • (-2) = -24
Explanation:
The given integers are 12, -2
Integers have different signs. So, the product is a negative integer.
12 • (-2) = -24
Question 5.
4(-6)
Answer:
4(-6) = -24
Explanation:
The given integers are 4, -6
Integers have different signs. So, the product is a negative integer.
4(-6) = -24
Question 6.
-25(0)
Answer:
-25(0) = 0
Explanation:
The given integers are -25, 0
Integers have different signs. So, the product is a negative integer.
-25(0) = 0
When you multiply any number with zero, the product is also zero.
Try It
Evaluate the expression.
Question 7.
8 • (-15) • 0
Answer:
8 • (-15) • 0 = 0
Explanation:
The given expression is 8 • (-15) • 0
Use the commutative property of the multiplication
= -120 . 0
= 0
Question 8.
24 – 33
Answer:
24 – 3³ = -3
Explanation:
The given expression is 24 – 3³
Write 3³ as a repeated multiplication
= 24 – (3 . 3 . 3)
= 24 – 27
= -3
Question 9.
10 – 7(3 – 5)
Answer:
10 – 7(3 – 5) = 24
Explanation:
The given expression is 10 – 7(3 – 5)
Perform the operations in the parenthesis
= 10 – 7(-2)
= 10 + 14
= 24
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
WRITING
What can you conclude about two integers whose product is (a) positive and (b) negative?
Answer:
If the product of two integers is positive, then those integers are with the same sign. If the product of two integers is negative, then those integers are having different signs.
Explanation:
The two integers product is a positive integer means those integers are with two positive signs or two negative signs.
For example 4 . 2 = 8, (-4) . (-2) = 8
The two integers is a negative integer means those are having one positive integer and negative integer irrespective of the order.
Examples are -4 . 2 = -8, 4 . -2 = -8
EVALUATING AN EXPRESSION
Evaluate the expression.
Question 11.
4(-8)
Answer:
4(-8) = -32
Explanation:
The given expression is 4(-8)
Here integers are having different signs. So the product is a negative integer.
4(-8) = -32
Question 12.
-5(-7)
Answer:
-5(-7) = 35
Explanation:
The given expression is -5(-7)
The product of two integers with the same sign is positive.
-5(-7) = 35
Question 13.
12 – 32 • (-2)
Answer:
12 – 3² • (-2) = 30
Explanation:
The given expression is 12 – 3² • (-2)
Write 3² as a repeated multiplication
= 12 – (3 . 3) . (-2)
= 12 – 9 . (-2)
The product of two integers with the same sign is positive.
= 12 + 18
= 30
REASONING
Tell whether the statement is true or false. Explain your reasoning.
Question 14.
The product of three positive integers is positive.
Answer:
True
Explanation:
The product of three positive integers is positive The reason is the product of two positive integers is positive. Again perform the product of an obtained positive integer with the third positive integer to get a positive integer.
Question 15.
The product of three negative integers is positive.
Answer:
False
Explanation:
The product of three negative integers is always a negative integer. Because the product of two negative integers is a positive integer. The product of obtained positive integer and remaining negative integer is a negative integer. So, the product of three integers is not positive.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
On a mountain, the temperature decreases by 18°F for each 5000-foot increase in elevation. At 7000 feet, the temperature is 41°F. What is the temperature at 22,000 feet? Justify your answer.
Answer:
The temperature at 22,000 feet is 95°F
Explanation:
Change in temperature over 5000 feet = 18°F
The temperature at 7000 feet = 41°F
The temperature at 22000 feet = 7000 + 5000x
22000 – 7000 = 5000x
15000 = 5000x
x = 15000/5000
x = 3
So, the temperature at 22000 feet is 41 + 3(18)
= 41 + 54 = 95°F
Question 17.
Players in a racing game earn 3 points for each coin they collect. Each player loses 5 points for each second that he or she finishes after the first-place finisher. The table shows the results of a race. List the players in order from greatest to least number of points.

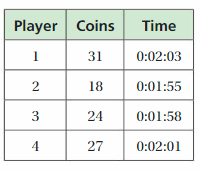
Answer:
Player 3, Player 2, Player 1, Player 4.
Explanation:
Players in a racing game earn 3 points for each coin they collect.
The number of coins earned by the players are listed here.
Player 2 = 18 x 3 = 54 points
Player 3 takes 3 seconds more than player 2 to finish the game.
So, player 3 number of points = (24 . 3) – (5 . 3) = 72 – 15 = 57
Player 4 takes 6 seconds more than player 2 to finish the game.
So, the number of points earned by player 4 = (27 . 3) – (5 . 6)
= 81 – 30 = 51
Player 1 takes 8 seconds more than player 2 to finish the game.
So, the number of points earned by player 1 = (31 . 3) – (5 . 8)
= 93 – 40 = 53
Hence, the number of coins earned by the players are Player 3 = 57, Player 2 = 53, Player 1 = 53, Player 4 = 51
Multiplying Integers Homework & Practice 2.1
Review & Refresh
Find the distance between the two numbers on a number line.
Question 1.
-4.3 and 0.8
Answer:
5.1
Explanation:
The distance between -4.3 and 0.8 = | 0.8 – (-4.3) |
= | 0.8 + 4.3 | = | 5.1 |
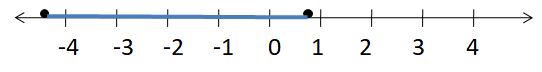
Question 2.
-7.7 and -6.4
Answer:
1.3
Explanation:
The distance between -7.7 and -6.4 = | -6.4 – (-7.7) |
= | -6.4 + 7.7 | = | 1.3 |
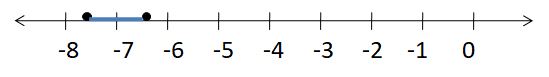
Question 3.
-2\(\frac{3}{5}\) and -1
Answer:
3.6
Explanation:
The distance between -2(3/5) or -13/5 and 1 = | 1 – (-13/5) |
= | 1 + 13/5 | = | (5 + 13)/5 |
= | 18/5 | = | 3.6 |
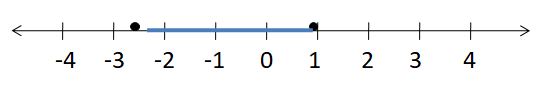
Divide.
Question 4.
27 ÷ 9
Answer:
27 ÷ 9 = 3
Explanation:
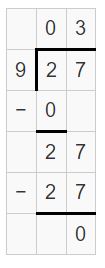
Question 5.
48 ÷ 6
Answer:
48 ÷ 6 = 8
Explanation:
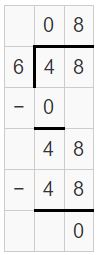
Question 6.
56 ÷ 4
Answer:
56 ÷ 4 = 14
Explanation:
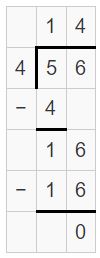
Question 7.
153 ÷ 8
Answer:
153 ÷ 8 = 19 R 1
Explanation:

Question 8.
What is the prime factorization of 84?
A. 22 × 32
B. 23 × 7
C. 33 × 7
D. 22 × 3 × 7
Answer:
D. 2² x 3 x 7
Explanation:
Divide 84 by 2
84/2 = 42
Divide 42 by 2
42/2 = 21
divide 21 by 3
21/3 = 7
Divide 7 by 7
7/7 = 1
So, the prime factorization of 84 is 2 x 2 x 3 x 7 = 2² x 3 x 7
Concepts, Skills, & Problem Solving
CHOOSE TOOLS
Use a number line or integer counters to find the product. (See Exploration 1, p. 49.)
Question 9.
2(-4)
Answer:
2(-4) = -8
Explanation:
2 . -4
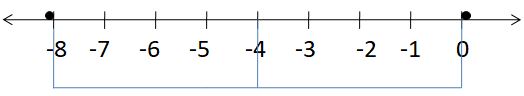
Question 10.
-6(3) = -18
Answer:
-6(3)
Explanation:
-6. 3

Question 11.
4(-5)
Answer:
4(-5) = -20
Explanation:
4(-5)

So, 4(-5) = -20
MULTIPLYING INTEGERS
Find the product.
Question 12.
6 • 4
Answer:
6 • 4 = 24
Explanation:
The product of two integers with the same sign is positive.
6 • 4 = 24
Question 13.
7(-3)
Answer:
7(-3) = -21
Explanation:
The product of two integers with the different sign is negative.
7(-3) = -21
Question 14.
-2(8)
Answer:
-2(8) = -16
Explanation:
The product of two integers with different sign is negative.
-2(8) = -16
Question 15.
-3(-4)
Answer:
-3(-4) = 12
Explanation:
The product of two integers with the same sign is positive.
-3(-4)= 12
Question 16.
-6 • 7
Answer:
-6 • 7= -42
Explanation:
The product of two integers with different sign is negative.
-6 • 7 = -42
Question 17.
3 • 9
Answer:
3 • 9 = 27
Explanation:
The product of two integers with the same sign is positive.
3 • 9 = 27
Question 18.
8 • (-5)
Answer:
8 • (-5) = -40
Explanation:
The product of two integers with different sign is negative.
8 • (-5) = -40
Question 19.
-1 • (-12)
Answer:
-1 • (-12) = 12
Explanation:
The product of two integers with the same sign is positive.
-1 • (-12) = 12
Question 20.
-5(10)
Answer:
-5(10) = -50
Explanation:
The product of two integers with different sign is negative.
-5(10) = -50
Question 21.
-13(0)
Answer:
-13(0) = 0
Explanation:
The product of two integers with different sign is negative.
-13(0) = -0 = 0
Question 22.
-9 • 9
Answer:
-9 • 9 = -81
Explanation:
The product of two integers with different sign is negative.
-9 • 9 = -81
Question 23.
15(-2)
Answer:
15(-2) = -30
Explanation:
The product of two integers with different sign is negative.
15(-2) = -30
Question 24.
-10 • 11
Answer:
-10 • 11 = -110
Explanation:
The product of two integers with different sign is negative.
-10 • 11 = -110
Question 25.
-6 • (-13)
Answer:
-6 • (-13) = 78
Explanation:
The product of two integers with the same sign is positive.
-6 • (-13) = 78
Question 26.
7(-14)
Answer:
7(-14) = -98
Explanation:
The product of two integers with different sign is negative.
7(-14) = -98
Question 27.
-11 • (-11)
Answer:
-11 • (-11) = 121
Explanation:
The product of two integers with the same sign is positive.
-11 • (-11) = 121
Question 28.
MODELING REAL LIFE
You burn 10 calories each minute you jog. What integer represents the change in your calories after you jog for 20 minutes?
Answer:
The change in your calories after you jog for 20 minutes is 200.
Explanation:
The number of calories you burn per minute = 10
The change in your calories after you jog for 20 minutes = 20 x 10 = 200
Question 29.
MODELING REAL LIFE
In a four-year period, about 80,000 acres of coastal wetlands in the United States are lost each year. What integer represents the total change in coastal wetlands?

Answer:
The total change in coastal wetlands is 20000 acres.
Explanation:
In A 4 year period, About 80,000 acres of coastal wetlands in United States are lost each year.
so, total area =80000 acres
total time = 4 years
now, we can use formula
total change in wetlands = ( total area)/(total time)
now, we can put values
total change in wetlands = 80000/4 = 20000
EVALUATING EXPRESSIONS
Evaluate the expression.
Question 30.
(-4)2
Answer:
(-4)² = 16
Explanation:
(-4)² = -4 . -4 = 16
Question 31.
-62
Answer:
-6² = -36
Explanation:
-6² = -6. 6 = -36
Question 32.
-5 • 3 • (-2)
Answer:
-5 • 3 • (-2) = 30
Explanation:
-5 • 3 • (-2) = -15 . (-2)
= 30
Question 33.
3 • (-12) • 0
Answer:
3 • (-12) • 0 = 0
Explanation:
3 • (-12) • 0 = -36 . 0 = 0
Question 34.
-5(-7)(-20)
Answer:
-5(-7)(-20) = -700
Explanation:
-5(-7)(-20) = -5 . -7 (-20) = 35 . -20 = -700
Question 35.
5 – 82
Answer:
5 – 8² = -59
Explanation:
5 – 8² = 5 – (8 . 8)
= 5 – 64 = -59
Question 36.
-52 • 4
Answer:
-5² . 4 = -100
Explanation:
-5² . 4 = -5 . 5 . 4
= -25 . 4 = -100
Question 37.
-2 • (-3)3
Answer:
-2 • (-3)³ = 54
Explanation:
-2 • (-3)³ = -2 . (-3 . -3 . -3)
= -2 . (-3 . 9)
= -2 . -27 = 54
Question 38.
2 + 1 • (-7 + 5)
Answer:
2 + 1 • (-7 + 5) = 0
Explanation:
2 + 1 • (-7 + 5) = 2 + 1 . (-2)
= 2 – 2 = 0
Question 39.
4 – (-2)3
Answer:
4 – (-2)³ = 12
Explanation:
4 – (-2)³ = 4 – (-2 . -2 . -2)
= 4 – (-2 . 4) = 4 – (-8)
= 4 + 8 = 12
Question 40.
4 • (25 • 32)
Answer:
4 • (25 • 3²) = 900
Explanation:
4 • (25 • 3²) = 4 . (25 . 3 . 3)
= 4 . (25 . 9) = 4 . 225
= 900
Question 41.
-4(32 – 8) + 1
Answer:
-4(3² – 8) + 1 = -3
Explanation:
-4(3² – 8) + 1 = -4(3 . 3 – 8) + 1
= -4(9 – 8) + 1
= -4(1) + 1 = -4 + 1 = -3
YOU BE THE TEACHER
Your friend evaluates the expression. Is your friend correct? Explain your reasoning.
Question 42.

Answer:
Wrong
Explanation:
The product of two integers with the same sign is positive.
So, -2(-7) = 14
Question 43.
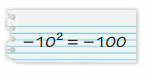
Answer:
Correct
Explanation:
The product of two integers with different sign is negative.
-10² = -10 . 10 = -100
PATTERNS
Find the next two numbers in the pattern.
Question 44.
-12, 60, -300, 1500, ….
Answer:
The next two numbers in the pattern are -7500, 37500
Explanation:
Multiply each integer by -5
-12 x -5 = 60
60 x -5 = -300
-300 x -5 = 1500
1500 x -5 = -7500
-7500 x -5 = 37500
Question 45.
7, -28, 112, -448,…..
Answer:
The next two numbers in the pattern are 1792, -7168
Explanation:
Multiply each integer by -4
7 x -4 = -28
-28 x -4 = 112
112 x -4 = -448
-448 x -4 = 1792
1792 x -4 = -7168
Question 46.
PROBLEM SOLVING
In a scavenger hunt, each team earns 25 points for each item that they find. Each team loses 15 points for every minute after 4:00 P.M. that they report to the city park. The table shows the number of items found by each team and the time that each team reported to the park. Which team wins the scavenger hunt? Justify your answer.
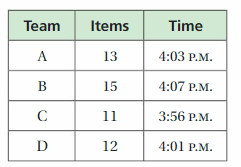
Answer:
Team D wins the scavenger hunt.
Explanation:
Each team earns 25 points for each item that they find. Each team loses 15 points for every minute after 4:00 P.M
The points earned by Team A = (13 x 25) – (15 x 3) = 325 – 45 = 280
The points earned by Team B = (15 x 25) – (15 x 7) = 375 – 105 = 270
The points earned by Team C = (11 x 25) = 275
The points earned by Team D = (12 x 25) – (1 x 15) = 300 – 15 = 285
Finally, Team D scores the highest points.
Hence, Team D wins the scavenger hunt.
Question 47.
REASONING
The height of an airplane during a landing is given by 22,000 + (-480t), where t is the time in minutes. Estimate how many minutes it takes the plane to land. Explain your reasoning.
Answer:
It takes 45 minutes for the plane to land.
Explanation:
The height of an airplane during a landing = 22,000 + (-480t)
= 22,000 – 480t
After landing, the height of the airplane = 0
So, 22,000 – 480t = 0
22000 = 0 + 480t
480t = 22000
t = 22000/480
t = 2200/48
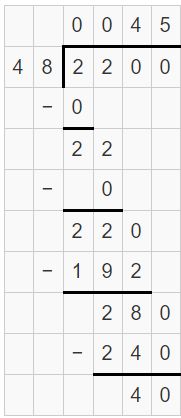
So, it takes 45 minutes for the plane to land.
Question 48.
PROBLEM SOLVING
The table shows the price of a bluetooth speaker each month for 4 months.
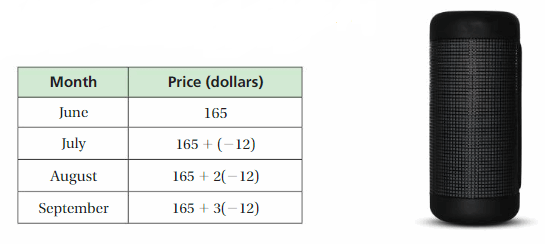
a. Describe the change in the price of the speaker.
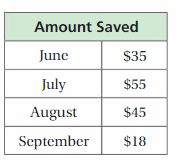
b. The table at the right shows the amount of money you save each month. When do you have enough money saved to buy the speaker? Explain your reasoning.
Answer:
a. The Bluetooth speaker price decreased by 12 dollars every month.
b. You can buy the speaker in the month of September.
Explanation:
a. The table shows that the change in the price of the Bluetooth speaker per every month is -12. So, the Bluetooth speaker price decreased by 12 dollars per every month.
b.
The amount of money you saved in June is $35, the price of the speaker is $165.
The amount of money you saved in July is 35 + 55 = $90, the price of the speaker is 165 – 12 = $153
The amount of money you saved in august is 90 + 45 = $135, the price of the speaker is 165 – 24 = $141
The amount of money you saved in September is 135 + 18 = $153, the price of the speaker is 165 – 36 = 129
So, you can buy the speaker in the month of September.
Question 49.
DIG DEEPER!
Two integers, a and b, have a product of 24. What is the least possible sum of a and b?
Answer:
The least possible sum of a and b is -25.
Explanation:
The product of a and b = 24
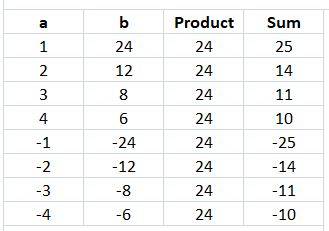
The least possible sum of a and b is -25.
Question 50.
NUMBER SENSE
Consider two integers p and q. Explain why p × (-q) = (-p) × q = -pq
Answer:
We know that,
the product of two integers with the different sign is negative.
p × (-q)
Here p is a positive integer, q is a negative integer
(-p) × q
Here p is a negative integer and q is a positive integer.
So, the product is negative
Lesson 2.2 Dividing Integers
EXPLORATION 1
Understanding Quotients Involving Negative Integers
Work with a partner.
a. Discuss the relationship between multiplication and division with your partner.
b. INDUCTIVE REASONING
Complete the table. Then write general rules for dividing
- two integers with the same sign and
- two integers with different signs.
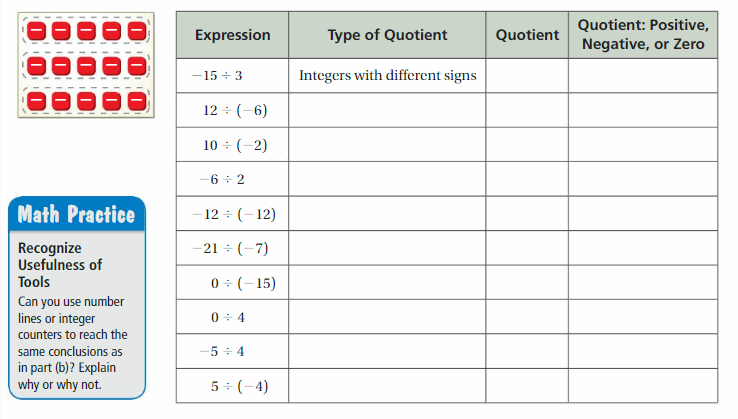
c. Find the values of 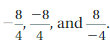 What do you notice? Is this true for
What do you notice? Is this true for ![]() when a and b are integers? Explain.
when a and b are integers? Explain.
d. Is every quotient of integers a rational number? Explain your reasoning.
Answer:
a. Multiplication and division are two opposite operations.
b. 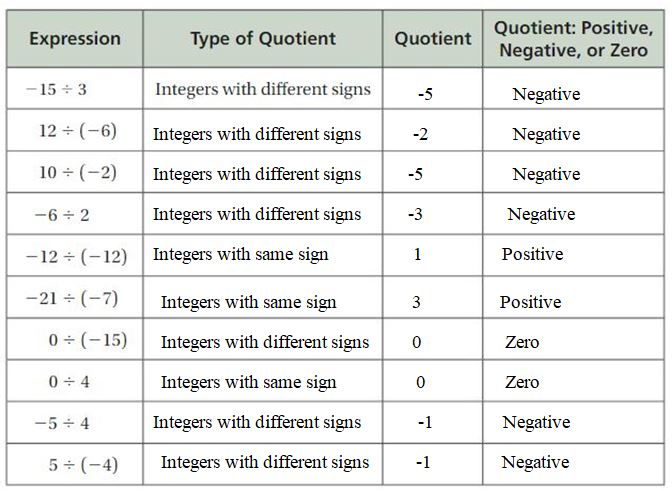
c. True
d. Yes
Explanation:
a. Multiplication and division are the reverse operations. When you multiply two numbers, you will get the product. Divide the product by any one of the multiplicand to get another multiplicand.
b. When two integers have the same sign then the quotient is positive. If two integers have different signs then the quotient is negative. When any one of the integers is zero, then the quotient is zero.
c. -(8/4) = -(2) = -2
-8/4 = -2
8/-4 = -2
Yes, -(8/4), 8/-4, -8/4 are true.
d. Every quotient of integers a rational number.
2.2 Lesson
Try It
Find the quotient.
Question 1.
14 ÷ 2
Answer:
14 ÷ 2 = 7
Explanation:
The quotient of two integers with the same sign is positive.
14 ÷ 2 = 7
Question 2.
-32 ÷ (-4)
Answer:
-32 ÷ (-4) = 8
Explanation:
The quotient of two integers with the same sign is positive.
-32 ÷ (-4) = 8
Question 3.
-40 ÷ (-8)
Answer:
-40 ÷ (-8) = 5
Explanation:
The quotient of two integers with the same sign is positive.
-40 ÷ (-8) = 5
Try It
Find the quotient.
Question 4.
0 ÷ (-6)
Answer:
0 ÷ (-6) = 0
Explanation:
The quotient of two integers with the different signs is negative.
0 ÷ (-6) = 0
Question 5.
\(\frac{-49}{7}\)
Answer:
-49 ÷ 7 = -7
Explanation:
The quotient of two integers with the different signs is negative.
-49 ÷ 7 = -7
Question 6.
\(\frac{21}{-3}\)
Answer:
21 ÷ -3 = -7
Explanation:
The quotient of two integers with the different signs is negative.
21 ÷ -3 = -7
Try It
Evaluate the expression when a = 18 and b = -6.
Question 7.
a ÷ b
Answer:
18 ÷ -6 = -3
Explanation:
a ÷ b
Put a = 18, b = -6
18 ÷ -6 = -3
The quotient of two integers with the different signs is negative.
Question 8.
![]()
Answer:
8
Explanation:
The given expression is (a + 6)/3
Put a = 18
= (18 + 6)/3 = 24/3
The quotient of two integers with the same sign is positive.
24/3 = 8
Question 9.
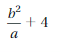
Answer:
-50
Explanation:
The given expression is b²/a + 4
Put a = 18, b = -6
= 18²/-6 + 4
= 324/-6 + 4
The quotient of two integers with the different signs is negative.
= -54 + 4 = -50
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
WRITING
What can you conclude about two integers whose quotient is (a) positive, (b) negative, or (c) zero?
Answer:
If the quotient of two integers is positive then the integers are having the same sign.
The quotient of two integers is negative when the integers are having different signs.
The quotient of two integers is zero when any one of the integers is zero.
DIVIDING INTEGERS
Find the quotient.
Question 11.
-12 ÷ 4
Answer:
-12 ÷ 4 = -3
Explanation:
The quotient of two integers with the different signs is negative.
-12 ÷ 4 = -3
Question 12.
\(\frac{-6}{-2}\)
Answer:
-6 ÷ -2 = 3
Explanation:
The quotient of two integers with the same sign is positive.
-6 ÷ -2 = 3
Question 13.
15 ÷ (-3)
Answer:
15 ÷ (-3) = -5
Explanation:
The quotient of two integers with the different signs is negative.
15 ÷ (-3) = -5
Question 14.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer:
-10/-5
Explanation:
Out of all expressions, -10/-5 is different. Because in all remaining expressions, the negative sign is applicable to either numerator or denominator. But in -10/-5 the negative sign is applicable to both numerator and denominator.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 15.
A female grizzly bear weighs 500 pounds. After hibernating for 6 months, she weighs only 350 pounds. What is the mean monthly change in weight?

Answer:
The mean change in weight per month is 50 pounds.
Explanation:
A female grizzly bear weighs 500 pounds
After hibernating for 6 months, she weighs only 200 pounds
Mean change in weight = 500 – 200 = 300
6 months = 300 pounds
Divide both sides by 6
6 months/6 = 300/6
1 month = 50 pounds
The mean change in weight per month is 50 pounds.
Question 16.
The table shows the change in the number of crimes committed in a city each year for 4 years. What is the mean yearly change in the number of crimes?
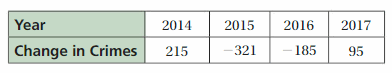
Answer:
The mean yearly change in the number of crimes are -49.
Explanation:
Mean = (sum of observations)/ number of observations
= (215 – 321 – 185 + 95)/4
= -196/4 = -49
The mean yearly change in the number of crimes are -49.
Question 17.
DIG DEEPER!
At a restaurant, when a customer buys 4 pretzels, the fifth pretzel is free. Soft pretzels cost $3.90 each. You order 12 soft pretzels. What is your mean cost per pretzel?
Answer:
The mean cost per pretzel is $2.925.
Explanation:
At a restaurant, when a customer buys 4 pretzels, the fifth pretzel is free.
The cost of soft pretzels is $3.90
You order 12 soft pretzels
So, you need to pay for (4 + 4 + 4) – 3 = 12 – 3 = 9
The cost for 9 soft pretzels = 9 x 3.90 =35.1
The mean cost per pretzel = (35.1)/12 = $2.925
Dividing Integers Homework & Practice 2.2
Review & Refresh
Find the product.
Question 1.
8 • 10
Answer:
8 • 10 = 80
Explanation:
The product of two integers with the same sign is positive.
8 • 10 = 80
Question 2.
-6(9)
Answer:
-6(9) = -54
Explanation:
The product of two integers with different signs is negative.
-6(9) = -54
Question 3.
4(7)
Answer:
4(7) = 28
Explanation:
The product of two integers with the same sign is positive.
4(7) = 28
Question 4.
-9(-8)
Answer:
-9(-8) = 72
Explanation:
The product of two integers with the same sign is positive.
-9(-8) = 72
Order the numbers from least to greatest.
Question 5.
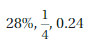
Answer:
0.24, 1/4, 28%
Explanation:
28% = 28/100 = 0.28
1/4 = 0.25
0.24
The order of numbers from the least to greatest is 0.24, 0.25, 0.28
Question 6.
![]()
Answer:
2/5, 42%, 0.45
Explanation:
42% = 42/100 = 0.42
0.45
2/5 = 0.4
The order of numbers from the least to greatest is 0.4, 0.42, 0.45
Question 7.
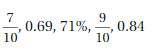
Answer:
0.69, 7/10, 71%, 0.84, 9/10
Explanation:
7/10 = 0.7
0.69
71% = 71/100 = 0.71
9/10 = 0.9
0.84
The order of numbers from the least to greatest is 0.69, 0.7, 0.71, 0.84, 0.9
Write an addition expression and write a subtraction expression represented by the number line. Then evaluate the expressions.
Question 8.
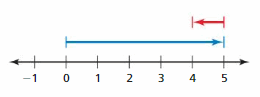
Answer:
Addition expression is 0 + 5 = 5
Subtraction expression is 5 – 1 = 4
Explanation:
The red line on the number line represents
5 – 1 = 4
The blue line on the number line represents
0 + 5 = 5
Question 9.
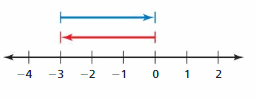
Answer:
The addition expression is -3 + 3 = 0
The subtraction expression is 0 – 3 = -3
Explanation:
The red line on the number line represents
0 – 3 = -3
The blue line on the number line represents
-3 + 3 = 0
Concepts, Skills, & Problem Solving
CHOOSE TOOLS
Complete the table. (See Exploration 1, p. 55.)
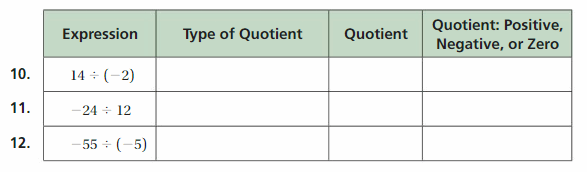
Answer:
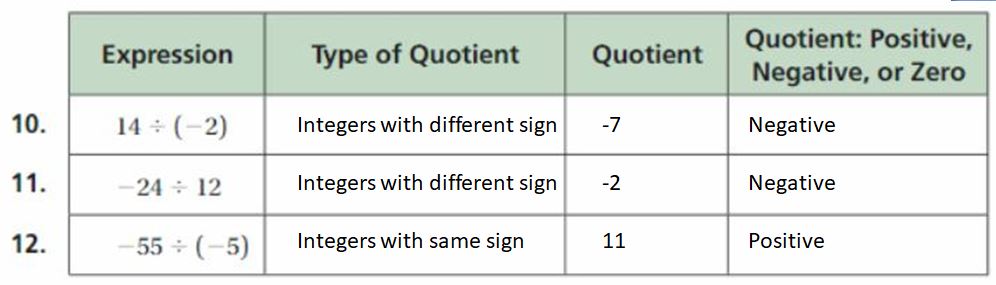
Explanation:
10. 14 ÷ (-2) = -7
11. -24 ÷ 12 = -2
12. -55 ÷ (-5) = 11
DIVIDING INTEGERS
Find the quotient, if possible.
Question 13.
4 ÷ (-2)
Answer:
4 ÷ (-2) = -2
Explanation:
The quotient of two integers with the different signs is negative.
4 ÷ (-2) = -2
Question 14.
21 ÷ (-7)
Answer:
21 ÷ (-7) = -3
Explanation:
The quotient of two integers with the different signs is negative.
21 ÷ (-7) = -3
Question 15.
-20 ÷ 4
Answer:
-20 ÷ 4 = -5
Explanation:
The quotient of two integers with the different signs is negative.
-20 ÷ 4 = -5
Question 16.
-18 ÷ (-3)
Answer:
-18 ÷ (-3) = 6
Explanation:
The quotient of two integers with the same sign is positive.
-18 ÷ (-3) = 6
Question 17.
\(\frac{-14}{2}\)
Answer:
-14 ÷ 2 = -7
Explanation:
The quotient of two integers with the different signs is negative.
-14 ÷ 2 = -7
Question 18.
\(\frac{0}{6}\)
Answer:
0 ÷ 6 = 0
Explanation:
If any of the integers is zero in the division expression, then the quotient is zero.
0 ÷ 6 = 0
Question 19.
\(\frac{-15}{-5}\)
Answer:
-15 ÷ -5 = 3
Explanation:
The quotient of two integers with the same sign is positive.
-15 ÷ -5 = 3
Question 20.
\(\frac{54}{-9}\)
Answer:
54 ÷ -9 = -6
Explanation:
The quotient of two integers with the different signs is negative.
54 ÷ -9 = -6
Question 21.
\(-\frac{33}{11}\)
Answer:
-33 ÷ 11 = -3
Explanation:
The quotient of two integers with the different signs is negative.
-33 ÷ 11 = -3
Question 22.
-49 ÷ (-7)
Answer:
-49 ÷ (-7) = 7
Explanation:
The quotient of two integers with the same sign is positive.
-49 ÷ (-7) = 7
Question 23.
0 ÷ (-2)
Answer:
0 ÷ (-2) = 0
Explanation:
If any of the integers is zero in the division expression, then the quotient is zero.
0 ÷ (-2) = 0
Question 24.
\(\frac{60}{-6}\)
Answer:
60 ÷ -6 = -10
Explanation:
The quotient of two integers with the different signs is negative.
60 ÷ -6 = -10
Question 25.
\(\frac{-56}{14}\)
Answer:
-56 ÷ 14 = -4
Explanation:
The quotient of two integers with the different signs is negative.
-56 ÷ 14 = -4
Question 26.
\(\frac{18}{0}\)
Answer:
18 ÷ 0 = 0
Explanation:
If any of the integers is zero in the division expression, then the quotient is zero.
18 ÷ 0 = 0
Question 27.
\(-\frac{65}{5}\)
Answer:
-65 ÷ 5 = -13
Explanation:
The quotient of two integers with the different signs is negative.
-65 ÷ 5 = -13
Question 28.
\(\frac{-84}{-7}\)
Answer:
-84 ÷ -7 = 12
Explanation:
The quotient of two integers with the same sign is positive.
-84 ÷ -7 = 12
YOU BE THE TEACHER
Your friend finds the quotient. Is your friend correct? Explain your reasoning.
Question 29.
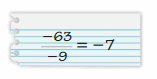
Answer:
Wrong
Explanation:
The quotient of two integers with the same sign is positive.
-63 ÷ -9 = 7
Question 30.
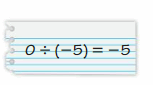
Answer:
0 ÷ (-5) = 0
Explanation:
If any of the integers is zero in the division expression, then the quotient is zero.
0 ÷ (-5) = 0
Question 31.
MODELING REAL LIFE
You read 105 pages of a novel over 7 days. What is the mean number of pages you read each day?

Answer:
The mean is 15 pages a day.
Explanation:
To find the mean of the pages we read each day we will evaluate the quotient of the division of the number of pages we read over these days (105 days) by the number of days (7 days).
105 / 7 = 15
The mean is 15 pages a day.
USING ORDER OF OPERATIONS
Evaluate the expression.
Question 32.
-8 – 14 ÷ 2 + 5
Answer:
-8 – 14 ÷ 2 + 5 = -10
Explanation:
The given expression is -8 – 14 ÷ 2 + 5
-8 – (14 / 2) + 5
= -8 – 7 + 5
= -15 + 5 = -10
Question 33.
24 ÷ (-4) + (-2) • (-5)
Answer:
24 ÷ (-4) + (-2) • (-5) = 4
Explanation:
The given expression is 24 ÷ (-4) + (-2) • (-5)
= -6 + (-2) . (-5)
= -6 + 10
= 4
EVALUATING EXPRESSIONS
Evaluate the expression when x = 10, y = -2, and z = -5.
Question 34.
x ÷ y
Answer:
-5
Explanation:
The given expression is x ÷ y
Put x = 10, y = -2
= 10 ÷ -2
The quotient of two integers with the different signs is negative.
= -5
Question 35.
12 ÷ 3y
Answer:
-2
Explanation:
The given expression is 12 ÷ 3y
Put y = -2
= 12 ÷ 3(-2)
= 12 ÷ -6
The quotient of two integers with the different signs is negative.
= -2
Question 36.
\(\frac{2 z}{y}\)
Answer:
5
Explanation:
The given expression is 2z/y
Put y = -2, and z = -5.
= 2(-5)/(-2)
= -10/-2
The quotient of two integers with the same sign is positive.
= 5
Question 37.
![]()
Answer:
-2
Explanation:
The given expression is (-x + y)/6
Put x = 10, y = -2
= (-10 + (-2))/6
= (-10 – 2)/6
= -12/6
The quotient of two integers with the different signs is negative.
= -2
Question 38.
100 ÷ (-z2)
Answer:
4
Explanation:
The given expression is 100 ÷ (-z2)
Put z = -5
= 100 ÷(-(-5)²)
= 100 ÷ (25)
The quotient of two integers with the same sign is positive.
= 4
Question 39.
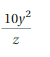
Answer:
-8
Explanation:
The given expression is (10y²)/z
Put y = -2, and z = -5
= (10(-2)²)/-5
= 10(4)/-5
= 40/-5
The quotient of two integers with the different signs is negative.
= -8
Question 40.
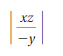
Answer:
25
Explanation:
The given expression is | (xz)/-y |
Put x = 10, y = -2, and z = -5
= | (10 . -5)/-(-2) |
= | -50/2 |
= 50/2
= 25
Question 41.
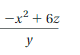
Answer:
65
Explanation:
The given expression is (-x² + 6z)/y
Put x = 10, y = -2, and z = -5
= (-(10)² + 6(-5))/-2
= (-100 – 30)/-2
= -130/-2
= 65
Question 42.
PATTERNS
Find the next two numbers in the pattern -128, 64, -32, 16, . . .. Explain your reasoning.
Answer:
The next two numbers in the pattern are -8, 4.
Explanation:
Divide each integer by -2
-128/-2 = 64
64/-2 = -32
-32/-2 = 16
16/-2 = -8
-8/-2 = 4
So, the next two numbers in the pattern are -8, 4.
Question 43.
MODELING REAL LIFE
The Detroit-Windsor Tunnel is an underwater highway that connects the cities of Detroit, Michigan, and Windsor, Ontario. How many times deeper is the roadway than the bottom of the ship?
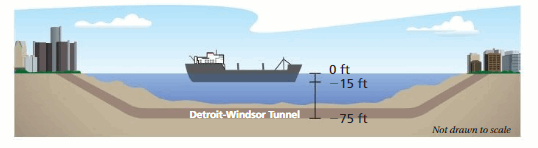
Answer:
5 times deeper is the roadway than the bottom of the ship.
Explanation:
The deep of the bottom of the ship = -15 ft
The deep of the roadway = -75 ft
To find out how many times deeper is the roadway than the bottom of the ship, divide the deep of the roadway by the deep of the bottom of the ship
-75 / -15 = 5 times
So, 5 times deeper is the roadway than the bottom of the ship
Question 44.
MODELING REAL LIFE
A snowboarder descends from an elevation of 2253 feet to an elevation of 1011 feet in 3 minutes. What is the mean change in elevation per minute?
Answer:
The mean change in elevation per minute is 414 ft.
Explanation:
A snowboarder descends from an elevation of 2253 feet to an elevation of 1011 feet in 3 minutes
So, the mean change in elevation per minute = (2253 – 1011)/3
= 1242/3 = 414 ft
Question 45.
REASONING
The table shows a golfer’s scores relative to par for three out of four rounds of a tournament.
a. What was the golfer’s mean score per round for the first 3 rounds?
b. The golfer’s goal for the tournament is to have a mean score no greater than -3. Describe how the golfer can achieve this goal.
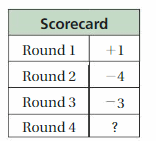

Answer:
a. The golfer’s mean score per round for the first 3 rounds is -2
b. The score in round 4 should be less than -6.
Explanation:
a. The golfer’s mean score per round for the first 3 rounds = (1 + (-4) + (-3))/3
= (1 – 4 – 3)/3 = (1 – 7)/3
= -6/3 = -2
b. The golfer’s goal for the tournament is to have a mean score no greater than -3.
(1 + (-4) + (-3) + x)/4 < -3
(1 – 4 – 3 + x)/4 <-3
(1 – 7 + x)/4 <-3
(-6 + x)/4 < -3
(-6 + x) < -3 . 4
(-6 + x) < -12
x < -12 + 6
x < -6
The score at the round 4 should be less than -6.
Question 46.
PROBLEM SOLVING
The regular admission price for an amusement park is $72. For a group of 15 or more, the admission price is reduced by $25 per person. How many people need to be in a group to save $500?
Answer:
20 people needed in the group to save $500.
Explanation:
Let the number of people is x
The price of the person reduced by $25
The total price we want to save is $500
x = 500/25 = 20
So, the number of people x needs to be in the group to save $500 is 20 people.
Question 47.
DIG DEEPER!
Write a set of five different integers that has a mean of -10. Explain how you found your answer.
Answer:
The set of five different integers whose mean is -10 are (-12, -11, -10, -9 -8).
Explanation:
Let us take the 5 integers as x, x + 1, x + 2, x + 3, x + 4
The mean of these integers is -10
(x + x + 1 + x + 2 + x + 3 + x + 4)/5 = -10
(5x + 10)/5 = -10
5x + 10 = -10 . 5
5x + 10 = -50
5x = -50 – 10
5x = -60
x = -60/5
x = -12
So, the set of 5 integers are -12, -12 + 1 = -11, -12 + 2 = -10, -12 +3 = -9, -12 + 4 = -8
Lesson 2.3 Converting Between Fractions and Decimals
EXPLORATION 1
Analyzing Denominators of Decimal Fractions
Work with a partner.
a. Write each decimal as a fraction or mixed number.

b. What do the factors of the denominators of the fractions you wrote have in common? Is this always true for decimal fractions?

EXPLORATION 2
Exploring Decimal Representations
Work with a partner.
a. A fraction \(\frac{a}{b}\) can be interpreted as a ÷ b. Use a calculator to convert each unit fraction to a decimal. Do some of the decimals look different than the others? Explain.
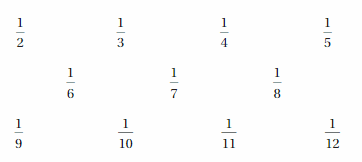
b. Compare and contrast the fractions in part(a) with the fractions you wrote in Exploration 1. What conclusions can you make?

c. Does every fraction have a decimal form that either terminates or repeats? Explain your reasoning.
2.3 Lesson
Try It
Write the fraction or mixed number as a decimal.
Question 1.
\(-\frac{6}{5}\)
Answer:
-6/5 = -1.2
Explanation:
Question 2.
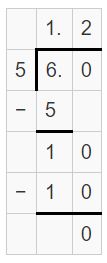
-7\(\frac{3}{8}\)
Answer:
-7(3/8) = -7.375
Explanation:
-7(3/8) = -59/8
Use long division to divide 59 by 8
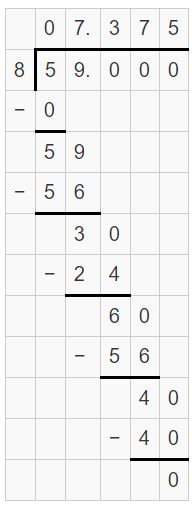
Question 3.
\(-\frac{3}{11}\)
Answer:
-3/11 = 0.2727
Explanation:
The remainder repeats. So, it is a repeating decimal.
Question 4.
1\(\frac{5}{27}\)
Answer:
1(5/27) =1.185
Explanation:
1(5/27) =32/27

Try It
Write the decimal as a fraction or mixed number in simplest form.
Question 5.
-0.3
Answer:
-0.3 = -3/10
Explanation:
-0.3 = -3/10
Question 6.
0.125
Answer:
0.125 = 1/8
Explanation:
0.125 = 125/1000
= (5 . 25)/(5 . 200)
= (5 . 5)/(5 . 40)
= 5/(8 . 5)
= 1/8
Question 7.
-3.1
Answer:
-3.1 = -31/10
Explanation:
-3.1 = -31/10
Question 8.
-10.25
Answer:
-10.25 = -41/4
Explanation:
-10.25 = -1025/100
= -(5 . 205)/(20 . 5)
= -(5 . 41)/(5 . 4)
= -41/4
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
WRITING
Compare and contrast terminating decimals and repeating decimals.
Answer:
A rational number can be expressed as either a terminating decimal or a repeating decimal. Divide numerator by the denominator you will get a remainder of 0, then you have a terminating decimal. The remainders will begin to repeat after some point, and you have a repeating decimal.
The example for terminating decimal is 5/8 = 0.625
The example for repeating decimal is 7/12 = 0.58333.
WRITING A FRACTION OR MIXED NUMBER AS A DECIMAL
Write the fraction or mixed number as a decimal.
Question 10.
\(\frac{3}{16}\)
Answer:
3/16 = 0.1875
Explanation:
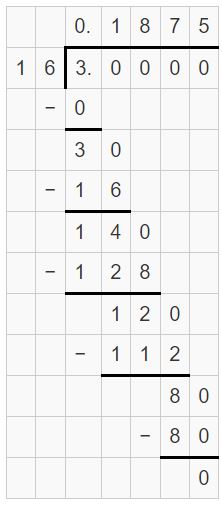
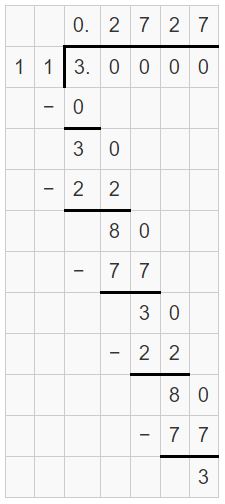
Question 11.
–\(\frac{7}{15}\)
Answer:
-7/15 = -0.4666
Explanation:
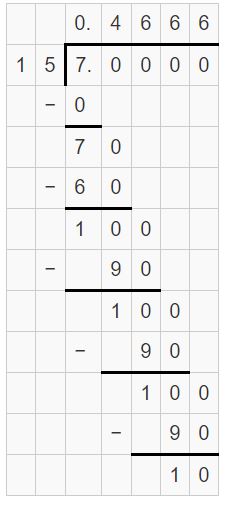
Question 12.
6\(\frac{17}{20}\)
Answer:
6(17/20) = 6.85
Explanation:
6(17/20) = 137/20
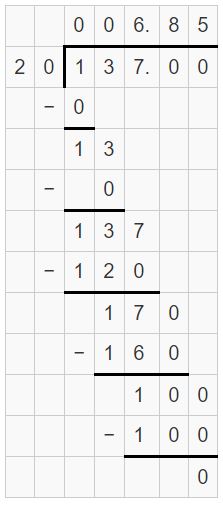
WRITING A DECIMAL AS A FRACTION OR MIXED NUMBER
Write the decimal as a fraction or mixed number in simplest form.
Question 13.
0.6
Answer:
0.6 = 3/5
Explanation:
0.6 = 6/10
= 3/5
Question 14.
-12.48
Answer:
-12.48 = -312/25
Explanation:
-12.48 = -1248/100
= -(4 . 312)/(4 . 25)
= -312/25
Question 15.
0.408
Answer:
0.408 = 51/125
Explanation:
0.408 = 408/1000
= (51 . 8)/(125 . 8)
= 51/125
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
A box turtle hibernates in sand at an elevation of 1.625 feet. A spotted turtle hibernates at an elevation of -1\(\frac{7}{12}\) feet. Which turtle hibernates deeper in the sand? How much deeper?

Answer:
Box turtle hibernates deeper in the sand.
Explanation:
A box turtle hibernates in sand at an elevation of 1.625 feet.
A spotted turtle hibernates at an elevation of -1(7/12) feet
= -19/12 = -1.58333
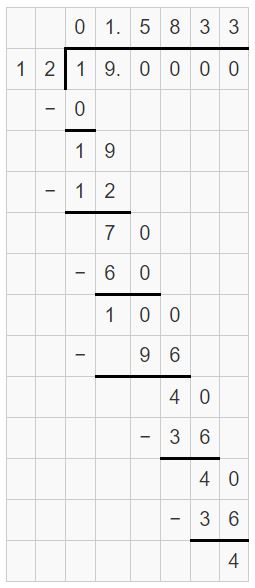
1.625 is greater than -1.5833.
So, box turtle hibernates deeper in the sand.
Question 17.
A red sprite is an electrical flash that occurs in Earth’s upper atmosphere. The table shows the elevations of four red sprites. What is the range of the elevations?
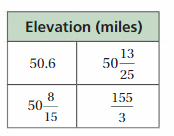
Answer:
The range of elevations are 51.66 miles, 50.6 miles, 50.53 miles, 50.52 miles.
Explanation:
First, write each fraction or mixed fraction as a decimal.
50.6
50(8/15) = 758/15 = 50.533
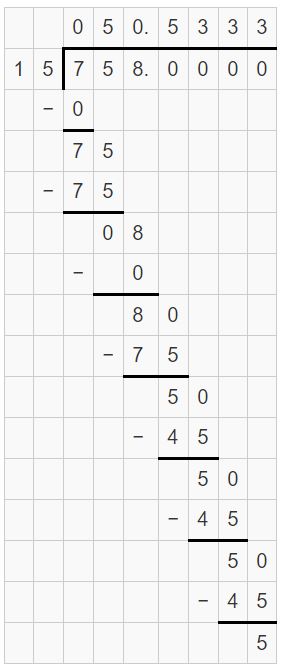
50(13/25) = 1263/25 = 50.52
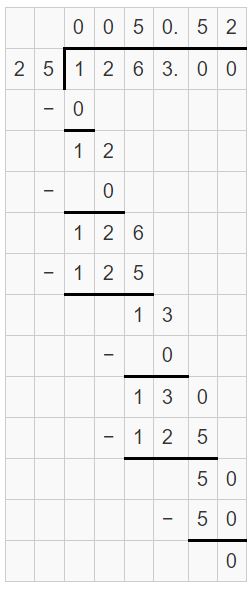
155/3 = 51.66
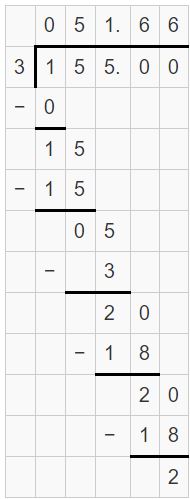
So, the range of elevations are 51.66, 50.6, 50.53, 50.52
Converting Between Fractions and Decimals Homework & Practice 2.3
Review & Refresh
Find the quotient.
Question 1.
12 ÷ (-6)
Answer:
12 ÷ (-6) = -2
Explanation:
The quotient of two integers with the different signs is negative.
12 ÷ (-6) = -2
Question 2.
-48 ÷ 8
Answer:
-48 ÷ 8 = -6
Explanation:
The quotient of two integers with the different signs is negative.
-48 ÷ 8 = -6
Question 3.
-42 ÷ (-7)
Answer:
-42 ÷ (-7) = 6
Explanation:
The quotient of two integers with the same sign is positive.
-42 ÷ (-7) = 6
Question 4.
-33 ÷ (-3)
Answer:
-33 ÷ (-3) = 11
Explanation:
The quotient of two integers with the same sign is positive.
-33 ÷ (-3) = 11
Find the product.
Question 5.
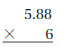
Answer:
35.28
Explanation:

Question 6.
2.0035 • 4
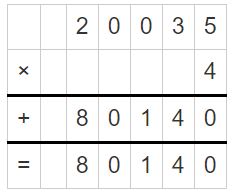
Answer:
2.0035 • 4 = 8.0140
Explanation:
Question 7.
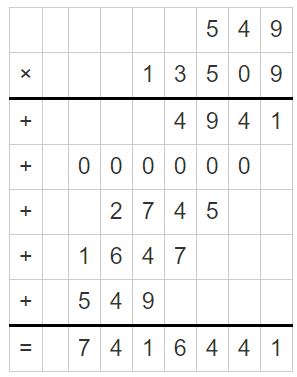
5.49 × 13.509
Answer:
5.49 × 13.509 = 74.16441
Explanation:
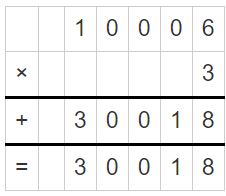
Question 8.
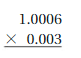
Answer:
0.0030018
Explanation:
Question 9.
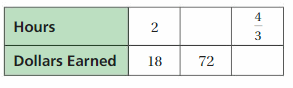
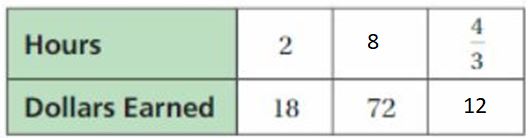
Find the missing values in the ratio table. Then write the equivalent ratios.
Answer:
Explanation:
72/18 = 4. So, x/2 = 4
x = 4 . 2
x = 8
2 . 2/3 = 4/3
So, 18 . 2/3 = 36/3 = 12
Concepts, Skills, & Problem Solving
STRUCTURE
Without dividing, determine whether the decimal form of the terminates or repeats. Explain. (See Explorations 1 & 2, p. 61.)
Question 10.
\(\frac{3}{8}\)
Answer:
3/8 is a terminating decimal.
Explanation:
3, 8 have no common factors.
The denominator 8 is in the form of 2m x 5n
Hence, 3/8 is a terminating decimal.
3/8 = 0.375
Question 11.
\(\frac{5}{7}\)
Answer:
5/7 is a repeating decimal.
Explanation:
5, 7 have no common factors
The denominator 7 is not in the form of 2m x 5n
Hence, 5/7 is a repeating decimal.
Question 12.
\(\frac{11}{40}\)
Answer:
11/40 is a terminating decimal.
Explanation:
11, 40 have no common factors
The denominator 40 is in the form of 2³ x 5¹
Hence, 11/40 is a terminating decimal.
Question 13.
\(\frac{5}{24}\)
Answer:
5/24 is a repeating decimal.
Explanation:
5, 24 have no common factors
The denominator 24 is not in the form of 2m x 5n
Hence, 5/24 is a repeating decimal.
WRITING A FRACTION OR MIXED NUMBER AS A DECIMAL
Write the fraction or mixed number as a decimal.
Question 14.
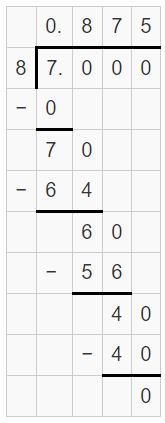
\(\frac{7}{8}\)
Answer:
7/8 = 0.875
Explanation:
Question 15.
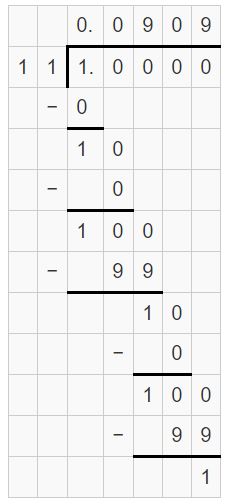
\(\frac{1}{11}\)
Answer:
1/11 = 0.9090
Explanation:
Question 16.
-3\(\frac{1}{2}\)
Answer:
-3(1/2) = -3.5
Explanation:
-3(1/2) = -7/2
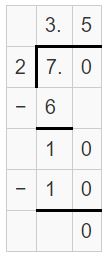
Question 17.
–\(\frac{7}{9}\)
Answer:
-7/9 = -0.77
Explanation:
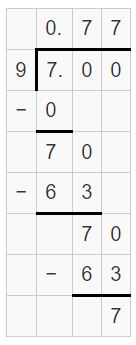
Question 18.
–\(\frac{17}{40}\)
Answer:
-17/40 = -0.425
Explanation:
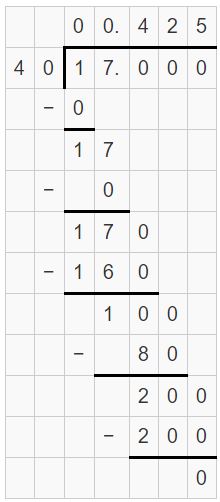
Question 19.
1\(\frac{5}{6}\)
Answer:
1(5/6) = 1.83333
Explanation:
1(5/6) = 11/6
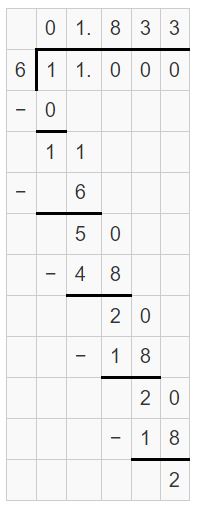
Question 20.
4\(\frac{2}{15}\)
Answer:
4(2/15) = 4.133
Explanation:
4(2/15) = 62/15
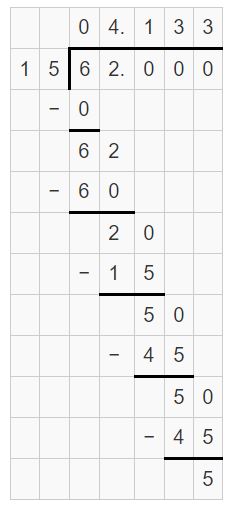
Question 21.
\(\frac{25}{24}\)
Answer:
25/24 = 1.04166
Explanation:
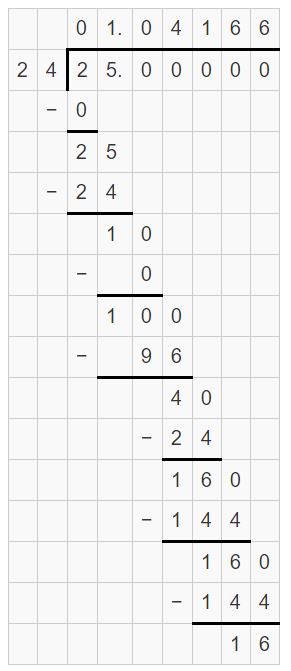
Question 22.
–\(\frac{13}{11}\)
Answer:
-13 / 11 = -1.1818
Explanation:
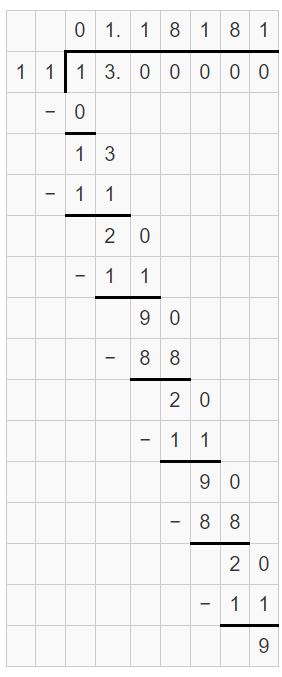
Question 23.
-2\(\frac{17}{18}\)
Answer:
-2(17/18) = -2.944
Explanation:
-2(17/18) = -53/18
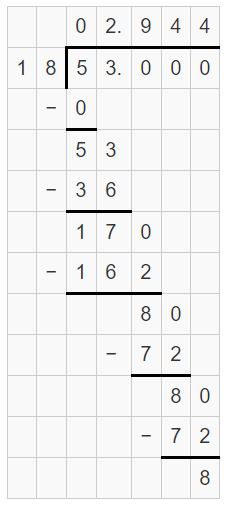
Question 24.
-5\(\frac{7}{12}\)
Answer:
-5(7/12) = -5.5833
Explanation:
-5(7/12) = -67/12

Question 25.
8\(\frac{15}{22}\)
Answer:
8(15/22) = 8.681818
Explanation:
8(15/22) = 191/22
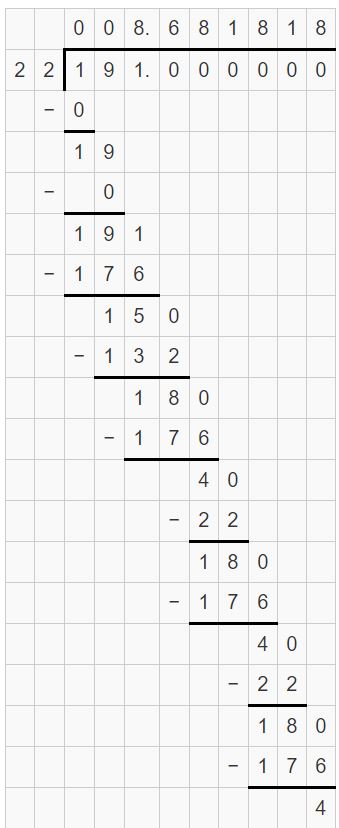
Question 26.
YOU BE THE TEACHER
Your friend writes –\(\frac{7}{11}\) as a decimal. Is your friend correct? Explain your reasoning.
Answer:
Correct
Explanation:
-7/11 = -0.636363

WRITING A DECIMAL AS A FRACTION OR MIXED NUMBER
Write the decimal as a fraction or mixed number in simplest form.
Question 27.
-0.9
Answer:
-0.9 = -9/10
Explanation:
-0.9 = -9/10
Question 28.
0.45
Answer:
0.45 = 9/20
Explanation:
0.45 = 45/100
= (9 . 5)/(20 . 5)
= 9/20
Question 29.
-0.258
Answer:
-0.258 = -129/500
Explanation:
-0.258 = -258/1000
= -(129 . 2)/(500 . 2)
= -129/500
Question 30.
-0.312
Answer:
-0.312 = 39/125
Explanation:
-0.312 = -312/1000
= (39 . 8) / (125 . 8)
= 39/125
Question 31.
-2.32
Answer:
-2.32 = -58/25
Explanation:
-2.32 = -232/100
= -(58 . 4)/(25 . 4)
= -58/25
Question 32.
-1.64
Answer:
-1.64 = -41/25
Explanation:
-1.64 = -164/100
= -(41 . 4)/(25 . 4)
= -41/25
Question 33.
6.012
Answer:
6.012 = 1503/250
Explanation:
6.012 = 6012/1000
= (1503 . 4)/(250 . 4)
= 1503/250
Question 34.
-12.405
Answer:
-12.405 = -2481/200
Explanation:
-12.405 = -12405/1000
= -(2481 . 5)/(200 . 5)
= -2481/200
Question 35.
MODELING REAL LIFE
You find one quarter, two dimes, and two nickels.
a. Write the dollar amount as a decimal.
b. Write the dollar amount as a fraction or mixed number in simplest form.

Answer:
a. $0.55
b. 11/20
Explanation:
You find one quarter, two dimes, and two nickels.
a. Convert each one into dollars
1 quarter is equal to 0.25 dollars
1 dime is equal to 0.1 dollars.
1 nickels is equal to 0.05 dollars.
$0.25 + 2(0.1) + 2(0.05)
= 0.25 + 0.2 + 0.1
= $0.55
b. $0.55 = 55/100
= (5 . 11)/(5. 20)
= 11/20
COMPARING RATIONAL NUMBERS
Copy and complete the statement using < or >.
Question 36.
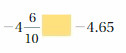
Answer:
-4(6/10) > -4.65
Explanation:
-4(6/10) = -46/10 = -4.6
-4.65 < -4.6
So, -4(6/10) > -4.65
Question 37.
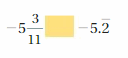
Answer:
![]()
Explanation:
-5(3/11) = -58/11 = -5.2727
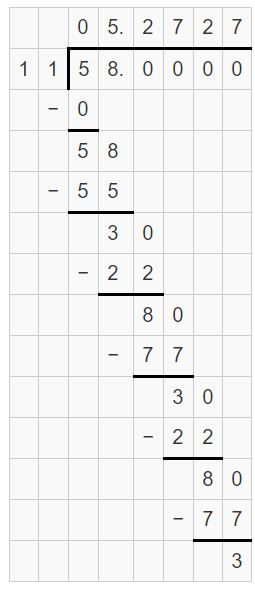
-5.2727 < -5.222
Question 38.
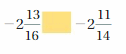
Answer:
-2(13/16) < -2(11/14)
Explanation:
-2(13/16) = -45/16 = -2.8125
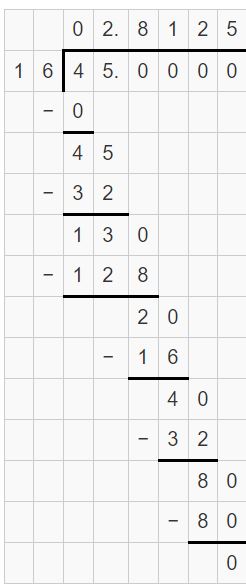
-2(11/14) = -39/14 = -2.7857
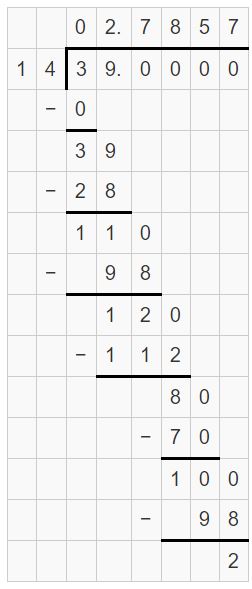
-2(13/16) < -2(11/14)
Question 39.
MODELING REAL LIFE
Is the half pipe deeper than the skating bowl? Explain.
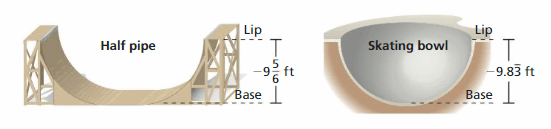
Answer:
No. They have the same depth.
Explanation:
As a decimal, 5/6 = 0.833333
9(5/6) = 59/6 = 9.838383
This means that half-pipe and the skating bowl have the same depth.
No. They have the same depth.
Question 40.
MODELING REAL LIFE
In softball, a batting average is the number of hits divided by the number of times at bat. Does Player 1 or Player 2 have the greater batting average?
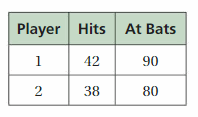
Answer:
Player 2 has the greater batting average.
Explanation:
Batting average = Number of hits / number of times at bat
Player 1 average = 42 / 90 = 0.466
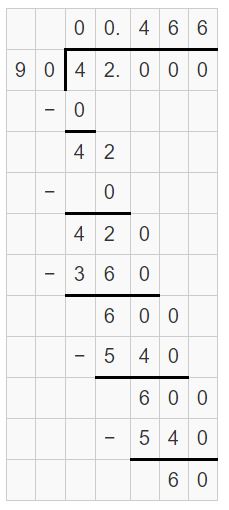
Player 2 average = 38/80 = 0.475
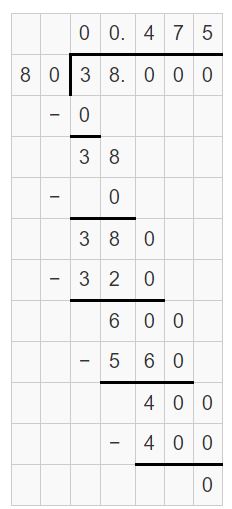
Player 2 has the greater batting average
ORDERING RATIONAL NUMBERS
Order the numbers from least to greatest.
Question 41.
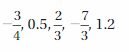
Answer:
The order from least to greatest -7/3, -3/4, 0.5, 2/3, 1.2
Explanation:
Express each term as a decimal
-3/4 = -0.75
2/3 = 0.666
-7/3 = -2.333
The order from least to greatest -7/3, -3/4, 0.5, 2/3, 1.2
Question 42.
![]()
Answer:
The order from least to greatest is -2.5, -1.1, -4/5, 0.8, 9/5
Explanation:
Express each term as a decimal
9/5 = 1.8
-4/5 = -0.8
The order from least to greatest is -2.5, -1.1, -4/5, 0.8, 9/5
Question 43.
![]()
Answer:
The order from least to greatest is -8/5, -1.4, -0.9, 1/4, 0.6
Explanation:
Express each term as a decimal
-8/5 = -1.6
1/4 = 0.25
The order from least to greatest is -1.6 < -1.4 < -0.9 < 0.25 < 0.6
Question 44.
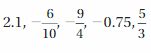
Answer:
The order from least to greatest is -9/4, -0.75, -6/10, 5/3, 2.1
Explanation:
Express each term as a decimal
-6/10 = -0.6
-9/4 = -2.25
5/3 = 1.666
The order from least to greatest is -2.25 < -0.75 < -0.6 < 1.666 < 2.1
Question 45.
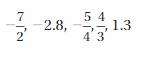
Answer:
The order from least to greatest is -7/2, -2.8, -5/4, 1.3, 4/3
Explanation:
Express each term as a decimal
-7/2 = -3.5
-5/4 = -1.25
4/3 = 1.333
The order from least to greatest is -3.5 < -2.8 < -1.25 < 1.3 < 1.333
Question 46.
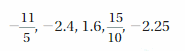
Answer:
The order from least to greatest is -2.4 -2.25, -11/5, 15/10, 1.6
Explanation:
Express each term as a decimal
-11/5 = -2.2
15/10 = 1.5
The order from least to greatest is -2.4 < -2.25 < -2.2 < 1.5 < 1.6
Question 47.
MODELING REAL LIFE
The table shows the changes in the water level of a pond over several weeks. Order the numbers from least to greatest.
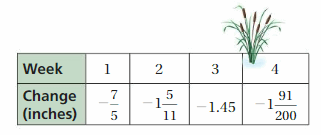
Answer:
The order from the least to greatest is Week 4, Week 2, Week 3, Week 1.
Explanation:
Week 1 = -7/5 = -1.4
Week 2 = -1(5/11) = -1.4545
Week 3 = -1.45
Week 4 = -1(91/200) = -1.455
The order from the least to greatest is Week 4 < Week 2 < Week 3 < Week 1
Question 48.
OPEN-ENDED
Find one terminating decimal and one repeating decimal between \(-\frac{1}{2}\) and \(-\frac{1}{3}\).
Answer:
-23/60 = -0.383333 is a repeating decimal
-24/60 = -0.4 is a terminating decimal.
Explanation:
To find one terminating decimal and one repeating decimal between -1/2 and -1/3 multiply each fraction by the denominator of the other fraction
-1/2 . 3/3 = -3/6 and -1/3 . 2/2 = -2/6
Multiply the resulting fractions by 10
-3/6 . 10/10 = -30/60 and -2/6 . 10/10 = -20/60
Find two numbers between -20 and -30
-23/60 = -0.383333 is a repeating decimal
-24/60 = -0.4 is a terminating decimal.
Question 49.
PROBLEM SOLVING
You miss 3 out of 10 questions on a science quiz and 4 out of 15 questions on a math quiz. On which quiz did you have a greater percentage of correct answers?
Answer:
You have a higher percent of correct answers on a math quiz.
Explanation:
You miss 3 out of 10 questions on a science quiz
So, the coorect answers = 10 – 3 = 7
The percent of correct answers on a science quiz = 7/10 . 100 = 70%
You miss 4 out of 15 questions on a math quiz
So, the correct answers = 15 – 4 = 11
The percent of correct answers on a math quiz = 11/15 . 100 = 73.3%
Thus, you have a higher percent of correct answers on a math quiz.
Question 50.
CRITICAL THINKING
A hackberry tree has roots that reach a depth of 6\(\frac{5}{12}\) meters. The top of the tree is \(18.2 \overline{8}\) meters above the ground. Find the total height from the bottom of the roots to the top of the tree.

Answer:
The total height from the bottom of the roots to the top of the tree is 23.70544 meters.
Explanation:
The depth of the tree = 6(5/12) = 65/12 meters
The top of the tree = 18.288 meters
The total height from the bottom of the roots to the top of the tree = 65/12 + 18.288
= 5.41666 + 18.2888
= 23.70544 meters
So, the total height from the bottom of the roots to the top of the tree is 23.70544 meters.
Question 51.
DIG DEEPER!
Let a and b be integers.
a. When can –\(\frac{1}{a}\) be written as a positive, repeating decimal?
b. When can \(\frac{1}{ab}\) be written as a positive, terminating decimal?
Answer:
a. a = -7
b. b = -2
Explanation:
a. Let us take a = -7
Then -1/a = -1/-7 = 0.142857142
b. 1/ab = 1/(-7)(-2) = 1/14 = 0.7142
Lesson 2.4 Multiplying Rational Numbers
EXPLORATION 1
Finding Products of Rational Numbers
Work with a partner.
a. Write a multiplication expression represented by each area model. Then find the product.
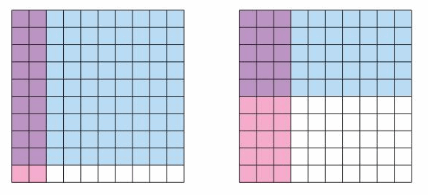
b. Complete the table.

c. Do the rules for multiplying integers apply to all rational numbers? Explain your reasoning.
Answer:
a. 9 x 10 = 90
5 x 10 = 50
b. 
c. The rules for multiplying integers apply to all rational numbers.
2.4 Lesson
Try It
Find the product. Write fractions in simplest form.
Question 1.
-5.1 × 1.8
Answer:
-5.1 × 1.8 = -9.18
Explanation:
Question 2.
-6.3(-0.6) = 3.78
Answer:
-6.3(-0.6)
Explanation:

Question 3.
Answer:
-4/5(-2/3) = 8/15
Explanation:
-4/5(-2/3) = (-4 . -2)/(5 . 3)
= 8/15
Question 4.
Answer:
4(1/2) . (-2(1/3)) = -21/2
Explanation:
4(1/2) . (-2(1/3)) = 9/2 . (-7/3)
= (9 . -7)/(2 . 3)
= (-7 . 3)/2 = -21/2
Try It
Find the product. Write fractions in simplest form.
Question 5.
![]()
Answer:
-2/3 . 7(7/8) . 3/2 = -63/8
Explanation:
-2/3 . 7(7/8) . 3/2 = -2/3 . 63/8 . 3/2
= (-2 . 63 . 3)/(3 . 8 . 2)
= -63/8
Question 6.
-7.02(0.1)(100)(-10)
Answer:
-7.02(0.1)(100)(-10) = 702
Explanation:
-7.02(0.1)(100)(-10) = (-7.02 . 0.1)(100 . -10)
= (-0.702)(-1000)
= 702
Self-Assessmentfor Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
Explain how to determine whether a product of two rational numbers is positive or negative.
Answer:
The product of two rational numbers is positive when they have the same sign.
The product of two rational numbers is negative when they have different signs.
MULTIPLYING RATIONAL NUMBERS
Find the product. Write fractions in simplest form.
Question 8.
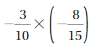
Answer:
-3/10 x (-8/15) = 4/25
Explanation:
-3/10 x (-8/15) = (-3 x -8)/(10 x 15)
= 24/150 = 4/25
Question 9.
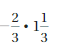
Answer:
-2/3 . 1(1/3) = -8/9
Explanation:
-2/3 . 1(1/3) = -2/3 . 4/3
= (-2 . 4)/(3 . 3) = -8/9
Question 10.
-2.8(-1.7)
Answer:
-2.8(-1.7) = 4.76
Explanation:
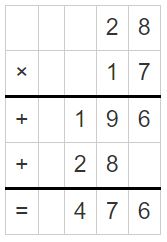
Question 11.
![]()
Answer:
1(3/5) . (-3(3/4)) = -10
Explanation:
1(3/5) . (-3(3/4)) = 8/3 . -15/4
= (8 . -15)/(3 . 4)
= (2 . -5) = -10
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
A swimmer’s best time in an event is 53.87 seconds. On average, his best time decreases by 0.28 second each of the next five times he swims the event. Does he accomplish his goal of swimming the event in less than 52.5 seconds?

Answer:
Yes. This is because his fifth attempt was 52.47 seconds
Explanation:
From the question, we are informed that Swimmers best time in an event is 53.87 seconds and that on average, his best time decreases by 0.28 seconds each of the next five times he swims the event.
The time for the fifth time he swims will be = 53.87 – 5(0.28)
= 53.87 – 1.4
= 52.47 seconds
This means that he accomplishes his goal of swimming the event in less than 52.5 seconds.
Question 13.
DIG DEEPER!
Terminal velocity is the fastest speed that an object can fall through the air. A skydiver reaches a terminal velocity of 120 miles per hour. What is the change in elevation of the skydiver after falling at terminal velocity for 15 seconds? Justify your answer.
Answer:
The change in elevation of the skydiver after falling at terminal velocity for 15 seconds is 30 miles.
Explanation:
A skydiver reaches a terminal velocity of 120 miles per hour = 120/60 = 2 miles per seconds
The change in elevation of the skydiver after falling at terminal velocity for 15 seconds is 2 x 15 = 30 miles
Multiplying Rational Numbers Homework & Practice 2.4
Review & Refresh
Write the fraction or mixed number as a decimal.
Question 1.
\(\frac{5}{16}\)
Answer:
5/16 = 0.3125
Explanation:
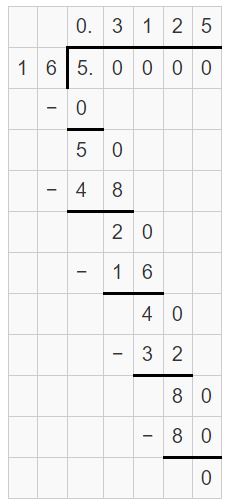
Question 2.
–\(\frac{9}{22}\)
Answer:
-9/22 = -0.4090909
Explanation:
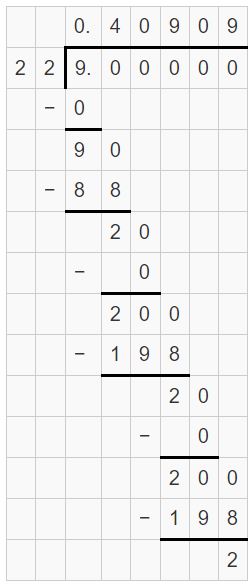
Question 3.
6\(\frac{8}{11}\)
Answer:
6(8/11) = 6.727272
Explanation:
6(8/11) = 74/11
Question 4.
–\(\frac{26}{24}\)
Answer:
-26/24 = -1.08333
Explanation:

Find the area of the figure.
Question 5.
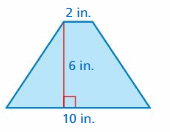
Answer:
Area is 36 sq inches
Explanation:
Given that,
a = 2 in, b = 10 in, h = 6 in
Area of the trapezoid = 1/2 (a + b) . h
= 1/2 (2 + 10) . 6
= (12) . 3
= 36 sq inches
Question 6.
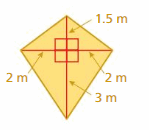
Answer:
Area is 9 m².
Explanation:
p = 1.5 + 3 = 4.5 m
q = 2 + 2 = 4 m
Area of rhombus = (pq)/2
= (4.5 . 4)/2
= 18/2 = 9 m²
Question 7.
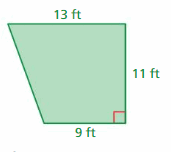
Answer:
The area is 121 ft².
Explanation:
The area of the rectangle formed by extending the base line and the top line is l x b
= 13 x 11 = 143 ft²
The area of the formed triangle is 1/2 x b x h
base = 13 – 9 = 4 ft
height = 11 ft
Triangle area = 1/2 x 4 x 11
= 2 x 11 = 22 ft²
Area of the given shape = Area of the rectangle – area of the triangle
= 143 – 22 = 121 ft²
Concepts, Skills, &Problem Solving
FINDING PRODUCTS OF RATIONAL NUMBERS
Write a multiplication expression represented by the area model. Then find the product. (See Exploration 1, p. 67.)
Question 8.
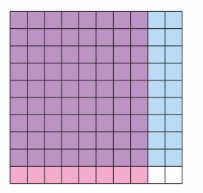
Answer:
The area is 90 sq units.
Explanation:
The number of shaded rows = 9
The number of shaded columns = 10
Area model = rows x columns
= 9 . 10 = 90
Question 9.
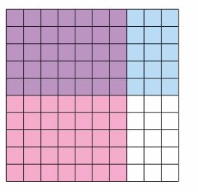
Answer:
The area is 50 sq units.
Explanation:
The number of shaded rows = 5
The number of shaded columns = 10
Area model = rows x columns
= 5 . 10 = 50
REASONING
Without multiplying, tell whether the value of the expression is positive or negative. Explain your reasoning.
Question 10.
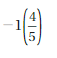
Answer:
The expression is negative.
Explanation:
When you multiply a positive fraction by a negative integer, you will get a negative fraction.
Question 11.
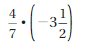
Answer:
The expression is negative.
Explanation:
The product of two fractions with different signs is negative.
Question 12.
-0.25(-3.659)
Answer:
The expression is positive.
Explanation:
The product of two fractions with different signs is positive.
MULTIPLYING RATIONAL NUMBERS
Find the product. Write fractions in simplest form.
Question 13.
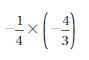
Answer:
-1/4 x (-4/3) = 1/3
Explanation:
-1/4 x (-4/3) = (-1 . -4)/(4 . 3)
= 1/3
Question 14.
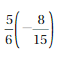
Answer:
5/6(-8/15) = -4/9
Explanation:
5/6(-8/15) = (5 . -8) / (6 . 15)
= (5 . -2 . 4) / (3 . 2 . 5 . 3)
= -4/9
Question 15.
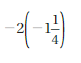
Answer:
-2(-1(1/4)) = 5/2
Explanation:
-2(-1(1/4)) = -2(-5/4)
= -2(-5/2 . 2) = 5/2
Question 16.
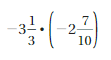
Answer:
-3(1/3) . (-2(7/10)) = 9
Explanation:
-3(1/3) . (-2(7/10)) = -10/3 . -27/10
= (-10 . -27)/(3 . 10)
= (9 . 3)/3 = 9
Question 17.
0.4 × (-0.03)
Answer:
0.4 × (-0.03) = -3/250
Explanation:
0.4 × (-0.03) = 4/10 . (-3/100)
= (4 . -3)/(10 . 100)
= (2 . 2 . -3)/(5 . 2 . 50 . 2)
= -3/250
Question 18.
-0.05 × (-0.5)
Answer:
-0.05 × (-0.5) = 1/40
Explanation:
-0.05 × (-0.5) = -5/100 x -5/10
= (-5 x -5)/(100 x 10)
= (-5 x -5)/(5 x 20 x 5 x 2)
= 1/40
Question 19.
-8(0.09)(-0.5)
Answer:
-8(0.09)(-0.5) = 9/25
Explanation:
-8(0.09)(-0.5) = -8(9/100)(-5/10)
= (-8 . 9 . -5)/(100 . 10)
= 9/25
Question 20.
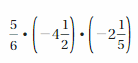
Answer:
5/6 . (-4(1/2)) . (-2(1/5)) = 33/4
Explanation:
5/6 . (-4(1/2)) . (-2(1/5)) = 5/6 . -9/2 . -11/5
= (5 . -9 . -11)/(6 . 2 . 5) = 33/4
Question 21.
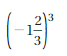
Answer:
(-1(2/3))³ = -125/27
Explanation:
(-1(2/3))³ = (-5/3)³
= (-5 . -5 . -5)/(3 . 3 . 3)
= -125/27
YOU BE THE TEACHER
Your friend evaluates the expression. Is your friend correct? Explain your reasoning.
Question 22.

Answer:
Correct
Explanation:
-14 x 3/2 = (-1 . 3)/(4 . 2)
= -3/8
Question 23.
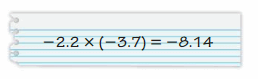
Answer:
Wrong
Explanation:
-2.2 x (-3.7) = 8.14
Question 24.
MODELING REAL LIFE
The hour hand of a clock moves 30° every hour. How many degrees does it move in 2\(\frac{1}{5}\) hours?

Answer:
In 2(1/5) hours, the hour hand of a clock moves -66 degrees.
Explanation:
2(1/5) = 11/5 = 2.2You can here use the rule of three as an easier way, and let x be the degrees it moves in 2(1/5) hours.
1 hour –> -30
2.2 hour –>x
x = 2.2 * -30
x = -66
So, in 2(1/5) hours, the hour hand of a clock moves -66 degrees.
Question 25.
MODELING REAL LIFE
A 14.5-gallon gasoline tank is \(\frac{3}{4}\) full. How many gallons will it take to fill the tank?
Answer:
We need 3.625 gallons to fill the tank.
Explanation:
3/4 of the tank is full so, 1/4 of the tank is empty
The number of gallons will it take to fill the tank = 1/4 * 14.5
= 0.25 * 14.5 = 3.625
We need 3.625 gallons to fill the tank.
Question 26.
OPEN-ENDED
Write two fractions whose product is –\(\frac{3}{5}\).
Answer:
The two fractions are -2/3 and 9/10
Explanation:
= -2/3 . 9/10
= (-2 . 9)/(3 . 10)
= -3/5
USING PROPERTIES
Find the product. Write fractions in simplest form.
Question 27.
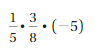
Answer:
1/5 . 3/8 . (-5) = -3/8
Explanation:
1/5 . 3/8 . (-5) = (1 . 3 . -5)/(5 . 8)
= -3/8
Question 28.
0.01(4.6)(-200)
Answer:
0.01(4.6)(-200) = -46/5
Explanation:
0.01(4.6)(-200) = 1/100 . 46/10 . -200
= (1 . 46 . -200)/(100 . 10)
= -46/5
Question 29.
(-17.2 × 2.5) × 4
Answer:
(-17.2 × 2.5) × 4 = -172
Explanation:
(-17.2 × 2.5) × 4 = (-172/10 x 25/10) x 4
= (-172 x 25)/(10 x 10) x 4
= (-172 / 2 x 2) x 4
= -172
Question 30.
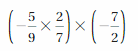
Answer:
(-5/9 x 2/7) x (-7/2) = 5/9
Explanation:
(-5/9 x 2/7) x (-7/2) = (-5 x 2)/(9 x 7) x (-7/2)
= (-10/63) (-7/2)
= (-10 x -7)/(63 x 2)
= 5/9
Question 31.
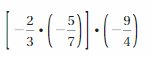
Answer:
[-2/3 . (-5/7)] . (-9/4) = -15/14
Explanation:
[-2/3 . (-5/7)] . (-9/4) = (-2 . -5)/(3 . 7) . (-9/4)
= 10/21 . (-9/4)
= (10 . -9)/(21 . 4)
= (5 . -3)/(7 . 2)
= -15/14
Question 32.
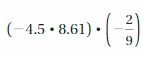
Answer:
(-4.5 . 8.61) . (-2/9) = 861/100
Explanation:
(-4.5 . 8.61) . (-2/9) = (-45/10 . 861/100) . (-2/9)
= (-45 . 861)/(10 . 100) . (-2/9)
= 861/100
Question 33.
PROBLEM SOLVING
Fencing costs $25.80 per yard. How much does it cost to enclose two adjacent rectangular pastures as shown? Justify your answer.
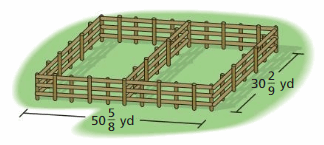
Answer:
The cost of fencing is $3558.249312.
Explanation:
Fencing costs $25.80 per yard.
Length = 30(2/9) = 272/9 yd
Width = 50(5/8) = 405/8 yd
The rectangular pastures perimeter = 2(length + width) + length
= 2(272/9 + 405/8) + 272/9
= 2(30.222 + 50.625) + 30.2222
= 2(53.8472) + 30.2222
= 107.6944 + 30.2222
= 137.91664 yards
Multiply the perimeter by $25.80 to get the cost
= 137.91664 x 25.80 = $3558.249312
So, the cost of fencing is $3558.249312.
ALGEBRA
Evaluate the expression when x = -2, y = 3, and z = –\(\frac{1}{5}\).
Question 34.
x • z
Answer:
2/5
Explanation:
The given expression is x • z
Put x = -2, z = -1/5
= -2 . (-1/5)
= 2/5
Question 35.
xyz
Answer:
6/5
Explanation:
The given expression is xyz
x = -2, y = 3, and z = –\(\frac{1}{5}\)
= -2 . 3 . (-1/5)
= -6 . (-1/5)
= 6/5
Question 36.
\(\frac{1}{3}\) + x • z
Answer:
11/15
Explanation:
The given expression is 1/3 + x . z
Put x = -2, z = -1/5
= 1/3 + (-2) . (-1/5)
= 1/3 + 2/5
= (5 + 6)/15
= 11/15
Question 37.
\(\frac{1}{2}\)z – \(\frac{2}{3}\)y
Answer:
-21/10
Explanation:
The given expression is 1/2 z – 2/3 y
Put y = 3 , z = -1/5
= 1/2 . (-1/5) – 2/3 . 3
= -1/10 – 2
= (-1 – 20)/10
= -21/10
EVALUATING AN EXPRESSION
Evaluate the expression. Write fractions in simplest form.
Question 38.
-4.2 + 8.1 × (-1.9)
Answer:
-4.2 + 8.1 × (-1.9) = -19.59
Explanation:
-4.2 + 8.1 × (-1.9) = -4.2 + (8.1 x -1.9)
= -4.2 – 15.39
= -19.59
Question 39.
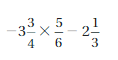
Answer:
-3(3/4) x 5/6 – 2(1/3) = -131/24
Explanation:
-3(3/4) x 5/6 – 2(1/3) = (-15/4) x 5/6 – 7/3
= (-15 . 5)/(4 . 6) – 7/3
= -25/8 – 7/3
= (-75 – 56)/24
= -131/24
Question 40.
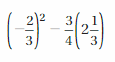
Answer:
(-2/3)² – 3/4 (2(1/3)) = -47/36
Explanation:
(-2/3)² – 3/4 (2(1/3)) = (-2/3).(-2/3) – 3/4 (7/3)
= 4/9 – 7/4
= (16 – 63)/36
= -47/36
Question 41.
DIG DEEPER!
Use positive or negative integers to fill in the blanks so that the product is \(\frac{1}{4}\). Justify your answer.
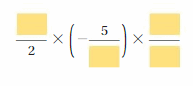
Answer:
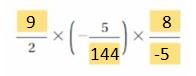 = 1/4
= 1/4
Explanation:
One of the possibilities of arranging numbers in the fill in the blanks are as follows:
9/2 x (-5/144) x (8/-5) = (9 x -5 x 8)/(2 x x -5)
= 1/4
Lesson 2.5 Dividing Rational Numbers
EXPLORATION 1
Work with a partner
a. Write two division expressions represented by the area model. Then find the quotients.
b. Complete the table.
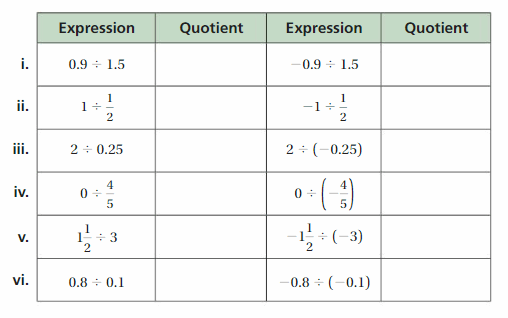

c. Do the rules for dividing integers apply to all rational numbers? Explain your reasoning.
d. Write a real-life story involving the quotient 0.75 ÷ 3. Interpret the quotient in the context of the story.
Answer:
a. 100 ÷ 60 = 1.666, 200 ÷ 120 = 1.666
b. 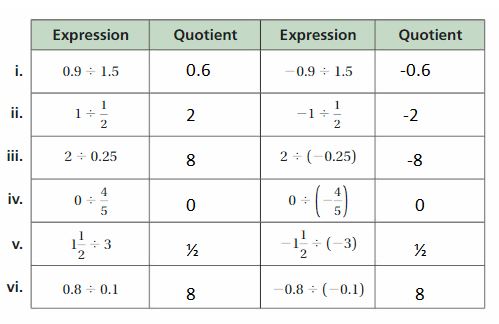
c. Yes
d. 0.75 ÷ 3 = 0.25
2.5 Lesson
Try It
Find the quotient. Write fractions in simplest form.
Question 1.
-2.4 ÷ 3.2
Answer:
-2.4 ÷ 3.2 = -0.75
Explanation:
-2.4 ÷ 3.2
Write the division expression as a fraction.
= -24/32 = -0.75
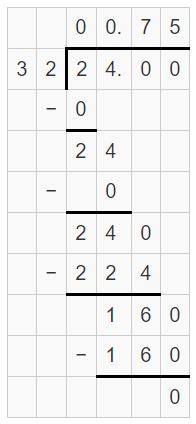
Question 2.
-6 ÷ (-1.1)
Answer:
-6 ÷ (-1.1) = 5.454545
Explanation:
-6 ÷ (-1.1)
= 60/11
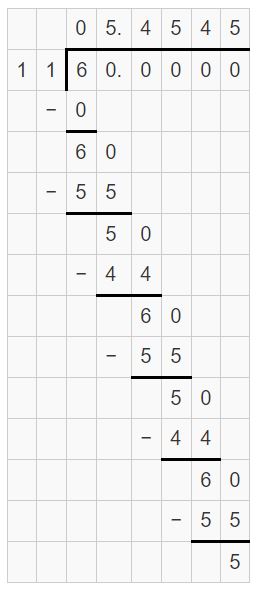
Question 3.
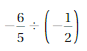
Answer:
-6/5 ÷ (-1/2) = 12/5
Explanation:
-6/5 ÷ (-1/2)
= 6/5 ÷ 1/2
= 6/5 . (2/1)
= (6 . 2)/(5 . 1)
= 12/5
Question 4.
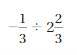
Answer:
-1/3 ÷ 2(2/3) = -1/8
Explanation:
-1/3 ÷ 2(2/3)
= -1/3 ÷ 8/3
= -1/3 . (3/8)
= (-1 . 3)/(3 . 8)
= -1/8
Try It
Evaluate the expression. Write fractions in simplest form.
Question 5.
![]()
Answer:
-1/2 / 6 = -1/12
Explanation:
-1/2 / 6 = (-1/2) . (1/6)
= (-1 . 1)/(2 . 6)
= -1/12
Question 6.
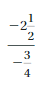
Answer:
-2(1/2) / -3/4 = 10/3
Explanation:
-2(1/2) / -3/4 = -5/2 / -3/4
= (-5/2) . (4/-3)
= (-5 . 4)/(2 . -3)
= 10/3
Question 7.
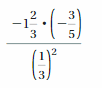
Answer:
[-1(2/3) . (-3/5)] / (1/3)² = 9
Explanation:
[-1(2/3) . (-3/5)] / (1/3)² = [(-5/3) . (-3/5)] / (1/9)
= [(-5 . -3)/(3 . 5)]/(1/9)
= (1/1) / (1/9)
= (1/1) . (9/1)
= 9
Self-Assessmentfor Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
WRITING
Explain how to determine whether a quotient of two rational numbers is positive or negative.
Answer:
The simple and easy strategy to find whether the quotient of two rational numbers is positive or negative is mentioned here.
The quotient of two rational numbers is positive when those numbers have the same sign.
The quotient of two rational numbers is negative when they have different signs.
EVALUATING AN EXPRESSION
Evaluate the expression. Write fractions in simplest form.
Question 9.
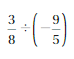
Answer:
3/8 ÷ (-9/5) = -5/24
Explanation:
3/8 ÷ (-9/5) = 3/8 . (-5/9)
= (3 . -5)/(8 . 9)
= -5/(8 . 3)
= -5/24
Question 10.
-6.8 ÷ (-3.6)
Answer:
-6.8 ÷ (-3.6) = 17/9
Explanation:
-6.8 ÷ (-3.6) = -68/10 ÷ (-36/10)
= -68/10 . (-10/36)
= (-68 . -10)/(10 . 36)
= 68/36
= 17/9
Question 11.
![]()
Answer:
(-2/9)/(2(2/5)) = -5/54
Explanation:
(-2/9)/(2(2/5)) = (-2/9)/(12/5)
= -2/9 . 5/12
= (-2 . 5)/(9 . 12)
= (-5)/(9 . 6)
= -5/54
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
DIG DEEPER!
Soil is composed of several layers. A geologist measures the depths of the subsoil and the bedrock, as shown. Find and interpret two quotients involving the depths of the subsoil and the bedrock.
Answer:
The depths of the subsoil and the bedrock is 2.244 ft
Explanation:
The depth of the subsoil = -22.5 ft
The depth of the bedrock = -50.5 ft
The distance between subsoil and bedrock =50.5 – 22.5
= 28 ft
The depths of the subsoil and the bedrock = -50.5/-22.5
= 2.244
Question 13.
The restaurant in Example 3 receives additional scores of 0.75, 1.5, 1.25, 4.75, 0.25, 0.5, 5, and 0.5 for the lasagna. Given the additional data, should the restaurant consider changing the recipe? Explain.
Answer:
The restaurant should not change the recipe.
Explanation:
The restaurant received scores are 2.25, -3.5, 0, -4.5, 1.75, -1, 3.5, -2.5, -0.75, -1.5, -1.25, 4.75, -0.25, -0.5, 5 and -0.5
The mean of scores = sum of scores / number of scores
= (2.25 + (-3.5) + 0 + (-4.5) + 1.75 + (-1) + 3.5 + (-2.5) + (-0.75) + (-1.5) + (-1.25) + 4.75 + (-0.25) + (-0.5) + 5 + (-0.5))/16
= (2.25 – 3.5 – 4.5 + 1.75 – 1 + 3.5 – 2.5 – 0.75 – 1.5 – 1.25 + 4.75 – 0.25 – 0.5 + 5 – 0.5)/16
= 1/16 = 0.0625
The mean score is above 0.
So, the restaurant should not change the recipe.
Dividing Rational Numbers Homework & Practice 2.5
Review & Refresh
Find the product. Write fractions in simplest form.
Question 1.
-0.5(1.31)
Answer:
-0.5(1.31) = -131/200
Explanation:
-0.5(1.31) = -5/10 (131/100)
= (-5 . 131) / (10 . 100)
= -131/(2 . 100)
= -131/200
Question 2.
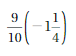
Answer:
9/10 (-1(1/4)) = -9/8
Explanation:
9/10 (-1(1/4)) = 9/10 (-5/4)
= (9 . -5)/(10 . 4)
= -9/(2 . 4)
= -9/8
Question 3.
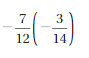
Answer:
-7/12 (-3/14) = 1/8
Explanation:
-7/12 (-3/14) = (-7 . -3) / (12 . 14)
= (-1 . -1)/(4 . 2)
= 1/8
Identify the terms, coefficients, and constants in the expression.
Question 4.
3b + 12
Answer:
The coefficients are 3, the constant is 12, terms are 3b, 12
Explanation:
The coefficients are 3, the constant is 12, terms are 3b, 12
Question 5.
14 + z + 6f
Answer:
The terms are 14, z, 6f, coefficients are 6, 1 and constant is 14 in 14 + z + 6f
Explanation:
The terms are 14, z, 6f, coefficients are 6, 1 and constant is 14 in 14 + z + 6f
Question 6.
8g + 14 + 5c + 7
Answer:
The terms are 8g, 14, 5c, 7 and coefficients are 8, 5, and constants are 14, 7
Explanation:
The terms are 8g, 14, 5c, 7 and coefficients are 8, 5, and constants are 14, 7
Question 7.
42m + 18 + 12c2
Answer:
The terms are 42m, 18, 12c², coefficients are 42, 12 and constants are 18.
Explanation:
The terms are 42m, 18, 12c², coefficients are 42, 12 and constants are 18.
Concepts, Skills, &Problem Solving
USING TOOLS
Write two division expressions represented by the area model. Then find the quotients. (See Exploration 1, p. 73.)
Question 8.
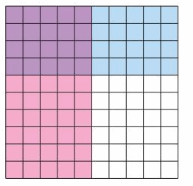
Answer:
20/50, 40/100
Explanation:
The first division expression is 20/50 = 0.4
The second division expression is 40/100 = 0.4
Question 9.
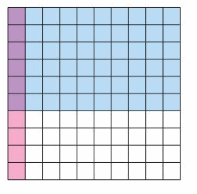
Answer:
6/10, 54/100
Explanation:
The first division expression is 6/10 = 0.6
The second division expression is 54/100 = 0.54
DIVIDING RATIONAL NUMBERS
Find the quotient. Write fractions in simplest form.
Question 10.
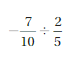
Answer:
-7/5 ÷ 2/5 = -3.5
Explanation:
-7/5 ÷ 2/5 = -7/5 . 5/2
= (-7 . 5)/(5 . 2)
= -7/2
= -3.5
Question 11.
-0.18 ÷ 0.03
Answer:
-0.18 ÷ 0.03 = -6
Explanation:
-0.18 ÷ 0.03 = -18/100 ÷ 3/100
= -18/100 . 100/3
= (-18 . 100) / (100 . 3)
= -6
Question 12.
-3.45 ÷ (-15)
Answer:
-3.45 ÷ (-15) = 0.03
Explanation:
-3.45 ÷ (-15) = -45/100 ÷ -15/1
= -45/100 . -1/15
= (-45 . -1)/(100 . 15)
= 3/100
= 0.03
Question 13.
-8 ÷ (-2.2)
Answer:
-8 ÷ (-2.2) = 3.636363
Explanation:
-8 ÷ (-2.2) = -8 ÷ -22/10
= -8/1 . -10/22
= (-8 . -10) / (1 . 22)
= (-4 . -10) / 11
= 40/11 = 3.636363

Question 14.
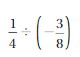
Answer:
1/4 ÷ (-3/8) = -0.6666
Explanation:
1/4 ÷ (-3/8) = 1/4 . (-8/3)
= (1 . -8) / (4 . 3)
= -2/3
= -0.66666
Question 15.
8.722 ÷ (-3.56)
Answer:
8.722 ÷ (-3.56) = -2.45
Explanation:
8.722 ÷ (-3.56) = 8722/1000 ÷ (-356/100)
= 8722/1000 . (100/-356)
= (8722 . 100)/(1000 . -356)
= (8722) / (10 . -356)
= -8722/3560 = -2.45
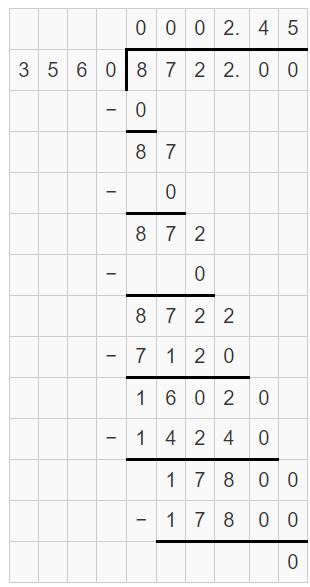
Question 16.
12.42 ÷ (-4.8)
Answer:
12.42 ÷ (-4.8) = -2.5875
Explanation:
12.42 ÷ (-4.8) = 1242/100 ÷ (-48/10)
= 1242/100 . (-10/48)
= (1242 . -10)/(100 . 48)
= (-1242) / (480)
= -2.5875
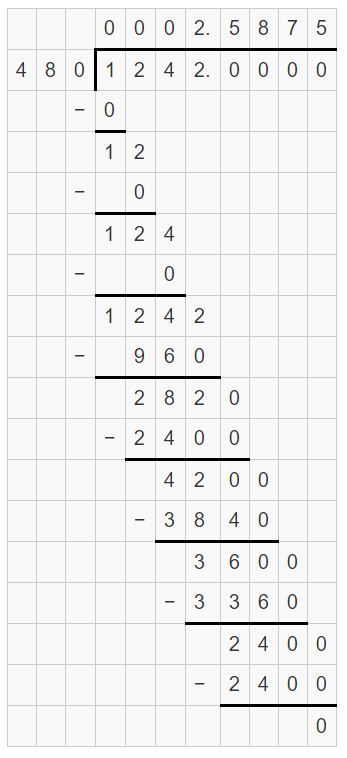
Question 17.
![]()
Answer:
-2(4/5) ÷ (-7) = 0.4
Explanation:
-2(4/5) ÷ (-7) = -14/5 ÷ (-7)
= -14/5 . -1/7
= (-14 . -1) / (7 . 5)
= 2/5
= 0.4
Question 18.
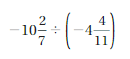
Answer:
-10(2/7) ÷ (-4(4/11)) = 2.3571
Explanation:
-10(2/7) ÷ (-4(4/11)) = -72/7 ÷ -48/11
= -72/7 . (-11/48)
= (-72 . -11) / (7 . 48)
= 99/42 = 2.3571
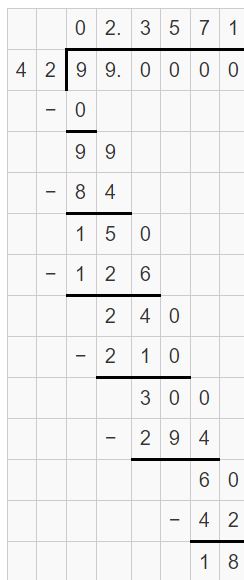
YOU BE THE TEACHER
Your friend evaluates the expression. Is your friend correct? Explain your reasoning.
Question 19.

Answer:
wrong
Explanation:
-2/3 ÷ 4/5 = -2/3 . 5/4
= (-2 . 5)/(3 . 4)
= -5/6
Question 20.
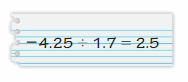
Answer:
Wrong
Explanation:
-4.25 ÷ 1.7 = -2.5

Question 21.
MODELING REAL LIFE
How many 0.75-pound packages can you make with 4.5 pounds of sunflower seeds?
Answer:
6 0.75-pound packages are required to make 4.5 pounds of sunflower seeds.
Explanation:
Divide 4.5 by 0.75 to get the solution.
= 4.5 ÷ 0.75 = 45/10 ÷ 75/100
= 45/10 . 100/75
= (45 . 100)/ (10 . 75)
= 6
So, 6 0.75-pound packages are required to make 4.5 pounds of sunflower seeds.
EVALUATING AN EXPRESSION
Evaluate the expression. Write fractions in simplest form.
Question 22.
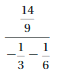
Answer:
(14/9) / (-1/3-1/6) = -28/9
Explanation:
(14/9) / (-1/3-1/6) = (14/9) / ((-2 – 1)/6)
= 14/9 / -3/6
= 14/9 . (-6/3)
= (14 . -6) / (3 . 9)
= -28/9
Question 23.
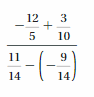
Answer:
(-125 + 3/10) / (11/4 – (-9/14)) = -77/100
Explanation:
(-125 + 3/10) / (11/4 – (-9/14)) = (-24 + 13)/10 / (11/14 + 9/14)
= -11/10 / (20/14)
= -11/10 . 14/20
= (-11 . 14) / (10 . 20)
= (-11 . 7) / (5 . 20)
= -77/100
Question 24.
-0.42 ÷ 0.8 + 0.2
Answer:
-0.42 ÷ 0.8 + 0.2 = -13/40
Explanation:
-0.42 ÷ 0.8 + 0.2 = -4.2 ÷ 8 + 0.2
= -0.525 + 0.2
= -0.325 = -325/1000
= -13/40
Question 25.
2.85 ÷ 6.2 ÷ 22
Answer:
2.85 ÷ 6.2 ÷ 2² = 28.25/248
Explanation:
2.85 ÷ 6.2 ÷ 2² = 2.85 ÷ 6.2 ÷ 4
= (2.825 ÷ 6.2) ÷ 4
= 2.825/6.2 . 1/4
= (2.825 . 1) / (6.2 . 4)
= 2.825/24.8
= 28.25/248
Question 26.
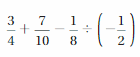
Answer:
3/4 + 7/10 – 1/8 ÷ (-1/2) = 17/10
Explanation:
3/4 + 7/10 – 1/8 ÷ (-1/2) = 3/4 + 7/10 + (1/8 ÷ 1/2)
= 3/4 + 7/10 + (1/8 . 2)
= 3/4 + 7/10 + 1/4
= 1 + 7/10
= 17/10
Question 27.
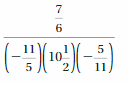
Answer:
7/6 / [(-11/5)(10(1/2))(-5/11)] = 1/9
Explanation:
7/6 / [(-11/5)(10(1/2))(-5/11)] = 7/6 / [(-11/5)(21/2)(-5/11)]
= 7/6 / [(-11 . 21 . -5) / (5 . 2 . 11)]
= 7/6 / [21/2]
= 7/6 . 2/21
= (7 . 2) / (6 . 21)
= 1/9
Question 28.
PROBLEM SOLVING
The section of the boardwalk shown is made using boards that are each 9\(\frac{1}{4}\)inches wide. The spacing between each board is equal. What is the width of the spacing between each board?
Answer:
The width of the spacing between each section is 5.25 inches
Explanation:
15 boards each board is 9(1/4) inches wide
The total width of 15 boards = 9(1/4) . 15
= 37/4 . 15
= 555/4 = 138.75
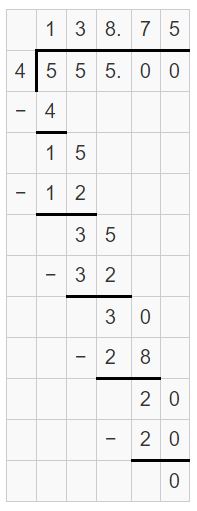
The total width of 15 boards = 138.75 inches
The total width of the section = 144 inches
The width of the spacing between each section = 144 – 138.75 = 5.25 inches
Question 29.
REASONING
The table shows the daily changes in the barometric pressure(in inches of mercury) for four days.
a. What is the mean change?
b. The mean change for Monday through Friday is -0.01 inch. What is the change in the barometric pressure on Friday? Explain.
Answer:
a. Mean change is -0.02
b. The change in the barometric pressure on Friday is 0.03
Explanation:
a. Mean change = sum of observations / total number of observations
= (-0.05 + 0.09 – 0.04 – 0.08)/4
= -0.08/4
= -0.02
b. The mean change for Monday through Friday is -0.01 inch
Mean change = sum of observations / total number of observations
-0.01 = (-0.05 + 0.09 – 0.04 – 0.08 + x)/5
-0.01 = (-0.08 + x)/5
5 * -0.01 = -0.08 + x
-0.05 = -0.08 + x
-0.05 + 0.08 = x
0.03 = x
So, the change in the barometric pressure on Friday is 0.03
Question 30.
LOGIC
In an online survey, gym members react to the statement shown by adjusting the position of the needle. The responses have values of -4.2, 1.6, 0.4, 0, 2.1, -5.0, -4.7, 0.6, 1.1, 0.8, 0.4, and 2.1. Explain how two people can use the results of the survey to reach different conclusions about whether the gym should adjust its membership prices.
Answer:
The gym should adjust its membership prices.
Explanation:
Use mean to determine whether adjust the gym membership prices or not.
Mean = sum of observations / total number of observations
= (-4.2 + 1.6 + 0.4 + 0 + 2.1 – 5.0 – 4.7 + 0.6 + 1.1 + 0.8 + 0.4 + 2.1)/12
= -4.8/12
= -0.4
The mean score is below 0.
So, the gym should adjust its membership prices.
Question 31.
CRITICAL THINKING
Determine whether the statement is sometimes, always, or never true. Explain your reasoning.
a. The product of two terminating decimals is a terminating decimal.
b. The quotient of two terminating decimals is a terminating decimal.
Answer:
a. The product of two terminating decimals is always a terminating decimal
b. The quotient of two terminating decimals is always a terminating decimal.
Explanation:
a. The product of two terminating decimals is always a terminating decimal
The example to check the product of terminating decimals is a terminating decimal
4.5 x 6.27 = 28.215
b. The quotient of two terminating decimals is a terminating decimal.
The example is 36.257 / 24.85
= 1.459034205
Multiplying and Dividing Rational Numbers Connecting Concepts
Using the Problem-Solving Plan
Question 1.
You feed several adult hamsters equal amounts of a new food recipe over a period of 1 month. You record the changes in the weights of the hamsters in the table. Use the data to answer the question “What is the typical weight change of a hamster that is fed the new recipe?

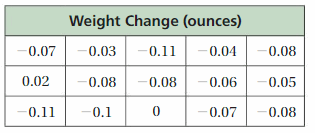
Understand the problem.
You know the weight changes of 15 hamsters. You want to use this information to find the typical weight change.
Make a plan.
Display the data in a dot plot to see the distribution of the data. Then use the distribution to determine the most appropriate measure of center.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
The typical weight change of a hamster that is fed the new recipe is -0.06266 ounces.
Explanation:
The typical weight change is measured by calculating the mean change.
Mean = (-0.07 – 0.03 – 0.11 – 0.04 – 0.08 + 0.02 – 0.08 – 0.08 – 0.06 – 0.05 – 0.11 – 0.1 + 0 – 0.07 – 0.08)/15
= -0.94/15
= -0.06266
So, typical weight change of a hamster that is fed the new recipe is -0.06266 ounces
Question 2.
Evaluate the expression shown at the right. Write your answer in simplest form.
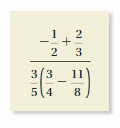
Answer:
-4/9
Explanation:
(-1/2 + 2/3) / [3/5(3/4 – 11/8)] = [(-3 + 4)/6] / [3/5((6 – 11)/8)]
= 1/6 / [3/5(-5/8)
= 1/6 / -3/8
= 1/6 . -8/3
= (1 . -8) / (3 . 6)
= -4/9
Question 3.
You drop a racquetball from a height of 60 inches. On each bounce, the racquetball bounces to a height that is 70% of its previous height. What is the change in the height of the racquetball after 3 bounces?
Answer:
The change in height of the racquetball after 3 bounces is 20.58 inches
Explanation:
You drop a racquetball from a height of 60 inches. On each bounce, the racquetball bounces to a height that is 70% of its previous height.
The change in height of the racquetball after 1 bounce = (60 x 70)/100
= 4200 / 100 = 42 inches
The change in height of the racquetball after 2 bounces = (42 x 70)/100
= 29.4
The change in height of the racquetball after 3 bounces = (29.4 x 70)/100
= 2058/100 = 20.58 inches
Performance Task
Precisely Perfect
At the beginning of this chapter, you watched a STEAM Video called “Carpenter or Joiner.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Multiplying and Dividing Rational Numbers Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
![]()
Graphic Organizers
You can use an Information Frame to help organize and remember a concept. Here is an example of an Information Frame for multiplying integers.
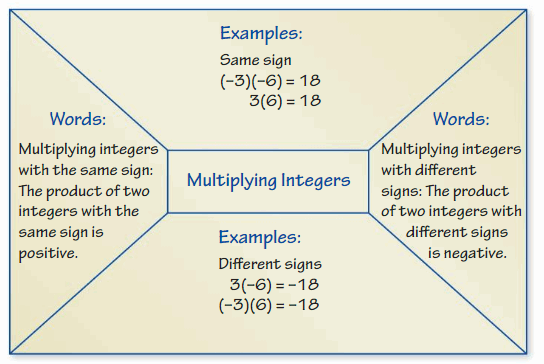
Choose and complete a graphic organizer to help you study the concept.
- dividing integers
- writing fractions or mixed numbers as decimals
- writing decimals as fractions or mixed numbers
- multiplying rational numbers
- dividing rational numbers

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

2.1 Multiplying Integers (pp. 49–54)
Find the product.
Question 1.
-8 • 6
Answer:
-8 • 6 = -48
Explanation:
The product of two integers with different signs is negative.
-8 • 6 = -48
Question 2.
10(-7)
Answer:
10(-7) = -70
Explanation:
The product of two integers with different signs is negative.
10(-7) = -70
Question 3.
-3 • (-6)
Answer:
-3 • (-6) = 18
Explanation:
-3 • (-6) = 18
The product of two integers with the same sign is positive.
Question 4.
You and a group of friends participate in a game where you must use clues to escape from a room. You have a limited amount of time to escape and are allowed 3 free clues. Additional clues may be requested, but each removes 5 minutes from your remaining time. What integer represents the total change in the time when you use 5 clues?
Answer:
The total change in time when you use 5 clues is -10 minutes
Explanation:
You are allowed 3 clues for free
The amount of time removes for each clue is 5 minutes
If you want to take 2 clues, then 5 x 2 = 10 minutes are removed
So, the total change in time when you use 5 clues is -10 minutes
Evaluate the expression.
Question 5.
(-3)3
Answer:
(-3)³ = -27
Explanation:
(-3)³ = -3 • -3 • -3
= 9 • -3
= -27
Question 6.
(-3)(-4)(10)
Answer:
(-3)(-4)(10) = 120
Explanation:
(-3)(-4)(10) = 12(10)
= 120
Question 7.
24 – 3(2 – 42)
Answer:
24 – 3(2 – 4²) = 66
Explanation:
24 – 3(2 – 4²) = 24 – 3(2 – 16)
= 24 – 3(-14)
= 24 + 42
= 66
Question 8.
Write three integers whose product is negative.
Answer:
-5, -2, 6
Explanation:
If three integers product is negative, then all integers would have negative signs or only one integer should have a negative sign.
(-5)(-2)6 = 10(6)
= 60
Question 9.
You are playing laser tag. The table shows how many points you gain or lose when you tag or are tagged by another player in different locations. You are tagged three times on the back, twice on the shoulder, and twice on the laser. You tag two players on the front, four players on the back, and one player on the laser. What is your score?
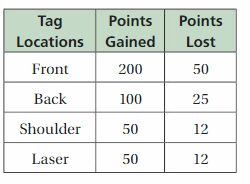
Answer:
Score = 727 points
Explanation:
You are tagged three times on the back, twice on the shoulder, and twice on the laser.
You have tagged means points lost.
= 3(25) + 2(12) + 2(12)
= 123
You tag two players on the front, four players on the back, and one player on the laser.
you tagged others means points gained
= 2(200) + 4(100) + 1(50)
= 850
Score = points gained – points lost
= 850 – 123 = 727
Question 10.
The product of three integers is positive. How many of the integers can be negative? Explain.
Answer:
If the product of three integers is positive, then only 2 integers can be negative.
Explanation:
If the product of three integers is positive, then only 2 integers can be negative.
We know the product of two negative integers is positive.
Find the product of an obtained positive integer with the third integer.
Question 11.
Two integers, c and d, have a product of -6. What is the greatest possible sum of c and d?
Answer:
The greatest possible sum of c and d are {-1, 6}
Explanation:
Two integers, c and d, have a product of -6
cd = -6
The possibilities of c, d are {-1, 6}, {1, -6}, {6, -1}, {-6, 1}, {-2, 3}, {3, -2}, {2, -3}, {-3, 2}
Find sum of c and d = 5, -5, 5, -5, 1, 1, -1, -1
The greatest possible sum of c and d are {-1, 6}
Dividing Integers (pp. 55–60)
Find the quotient.
Question 12.
-18 ÷ 9
Answer:
-18 ÷ 9 = -2
Explanation:
-18 ÷ 9 = -2
The quotient of two integers with the different signs is negative.
Question 13.
\(\frac{-42}{-6}\)
Answer:
-42/-6 = 7
Explanation:
The quotient of two integers with the same sign is positive.
-42/-6 = 7
Question 14.
\(\frac{-30}{6}\)
Answer:
-30/6 = -5
Explanation:
The quotient of two integers with the different signs is negative.
-30/6 = -5
Question 15.
84 ÷ (-7)
Answer:
84 ÷ (-7) = -12
Explanation:
The quotient of two integers with the different signs is negative.
84 ÷ (-7) = -12
Evaluate the expression when x = 3, y = -4, and z = -6.
Question 16.
z ÷ x
Answer:
z ÷ x = -2
Explanation:
The given expression is z ÷ x
Put x = 3, z = -6
-6 ÷ 3 = -2
Question 17.
\(\frac{xy}{z}\)
Answer:
xy/z = 2
Explanation:
The given expression is xy/z
Put x = 3, y = -4, and z = -6
= (3 . -4)/-6
= -4/-2
= 2
Question 18.
\(\frac{z – 2x}{y}\)
Answer:
(z – 2x)/y = 3
Explanation:
The given expression is (z – 2x)/y
Put x = 3, y = -4, and z = -6
= (-6 – 2(3))/-4
= (-6 – 6)/-4
= -12/-4
= 3
Find the mean of the integers.
Question 19.
-3, -8, 12, -15, 9
Answer:
Mean = -1
Explanation:
Mean = sum of integers / total number of integers
= (-3 – 8 + 12 – 15 + 9)/5
= -5/5
= -1
Question 20.
-54, -32, -70, -25, -65, -42
Answer:
Mean = -48
Explanation:
Mean = (-54 – 32 – 70 – 25 – 65 – 42)/6
= -288/6
= -48
Question 21.
The table shows the weekly profits of a fruit vendor. What is the mean profit for these weeks?
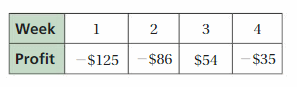

Answer:
The mean profit for 4 weeks is -$48
Explanation:
The mean profit = (sum of the profits) / number of weeks
= (-125 – 86 + 54 – 35)/4
= -192/4
= -48
The mean profit for 4 weeks is -$48.
2.3 Converting Between Fractions and Decimals (pp. 61–66)
Write the fraction or mixed number as a decimal.
Question 22.
– \(\frac{8}{15}\)
Answer:
-8/15 = -0.533333
Explanation:
-8/15 = -0.533333
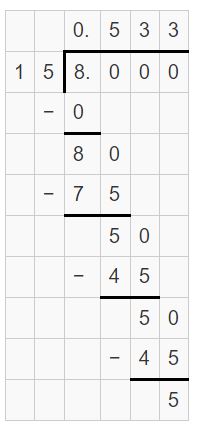
Question 23.
\(\frac{5}{8}\)
Answer:
5/8 = 0.625
Explanation:
5/8 = 0.625
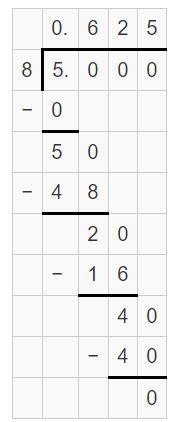
Question 24.
–\(\frac{13}{6}\)
Answer:
-13/6 = -2.16666
Explanation:
-13/6 = -2.16666
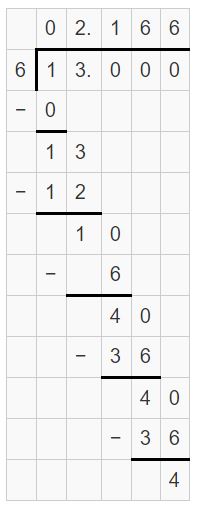
Question 25.
1\(\frac{7}{16}\)
Answer:
1\(\frac{7}{16}\) = 1.4375
Explanation:
1(7/16) = 23/16

Write the decimal as a fraction or mixed number in simplest form.
Question 26.
-0.6
Answer:
-0.6 = -3/5
Explanation:
-0.6 = -6/10
= -3/5
Question 27.
-0.35
Answer:
-0.35 = -7/20
Explanation:
-0.35 = -35/100
= -7/20
Question 28.
-5.8
Answer:
-5.8 = -29/5
Explanation:
-5.8 = -58/10
= -29/5
Question 29.
24.23
Answer:
24.23 = 2423/100
Explanation:
24.23 = 2423/100
Question 30.
The table shows the changes in the average yearly precipitation (in inches) in a city for several months. Order the numbers from least to greatest.
Answer:
The order of numbers from least to greatest is -1(7/9), -1.75, 3/11, 0.3
Explanation:
Order the numbers -1.75, 3/11, 0.3, -1(7/9) from least to greatest
Express each number as a decimal
3/11 = 0.272727
-1(7/9) = -16/9 = -1.77777
-1.7777 < -1.75 < 0.272727 < 0.3
The order of numbers from least to greatest is -1(7/9), -1.75, 3/11, 0.3
2.4 Multiplying Rational Numbers (pp. 67–72)
Find the product. Write fractions in simplest form.
Question 31.
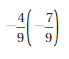
Answer:
-4/9(-7/9) = 28/81
Explanation:
-4/9(-7/9) = (-4 . -7)/(9 . 9)
= 28/81
Question 32.
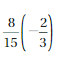
Answer:
8/15(-2/3) = -16/45
Explanation:
8/15(-2/3) = (8 . -2)/(15 . 3)
= -16/45
Question 33.
-5.9(-9.7)
Answer:
-5.9(-9.7) = 5723/100
Explanation:
-5.9(-9.7) = -59/10 (-97/10)
= (-59 . -97)/100
= 5723/100
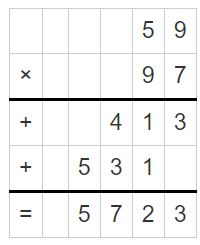
Question 34.
4.5(-5.26)
Answer:
4.5(-5.26) = 2367/100
Explanation:
4.5(-5.26) = 45/10 (-526/100)
= (45 . -526) / (10 . 100)
= (9 . 263) / 100
= 2367/100

Question 35.
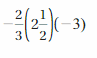
Answer:
-2/3 (2(1/2))(-3) = -5
Explanation:
-2/3 (2(1/2))(-3) = -2/3 (5/2) (-3)
= (-2 . 5 . -3) / (2 . 3)
= -5
Question 36.
-1.6(0.5)(-20)
Answer:
-1.6(0.5)(-20) = 16
Explanation:
-1.6(0.5)(-20) = -16/10(5/10)(-20)
= (-16 . 5 . -20)/(10 . 10)
= 16
Question 37.
The elevation of a sunken ship is -120 feet. You are in a submarine at an elevation that is \(\frac{5}{8}\) of the ship’s elevation. What is your elevation?

Answer:
Your elevation is -300 feet.
Explanation:
You are in a submarine at an elevation that is 5/8 of the ship’s elevation
Ship elevation = -120 feet
Your elevation = 5/8 (-120)
= 15(-20) = -300
Question 38.
Write two fractions whose product \(\frac{1}{5}\) and \(\frac{1}{2}\), and whose sum is negative.
Answer:
Two fractions are-1/2 and -1/2
Explanation:
The product of two fractions is between 1/5 and 1/2 and sum is negative.
Let us say the product of fractions is 1/4.
Then two fractions are -1/2 and -1/2
the sum is -1/2 – 1/2 = -2/2 = -1
2.5 Dividing Rational Numbers (pp. 73–78)
Find the quotient. Write fractions in simplest form.
Question 39.
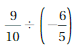
Answer:
-3/4
Explanation:
9/10 ÷ (-6/5) = 9/10 • (-5/6)
= (9 • -5)/ (10 . 6)
= -3/4
Question 40.
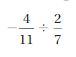
Answer:
-14/11
Explanation:
-4/11 ÷ 2/7 = -4/11 • 7/2
= (-4 • 7) / (2 • 11)
= -14/11
Question 41.
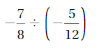
Answer:
21/10
Explanation:
-7/8 ÷ (-5/12) = -7/8 • (-12/5)
= (-7 • -12) / (8 • 5)
= 21/10
Question 42.
6.4 ÷ (-3.2)
Answer:
-512/25
Explanation:
6.4 ÷ (-3.2) = 64/10 ÷ (-32/10)
= (64 • -32) / (10 • 10)
= -512/25
Question 43.
-15.4 ÷ (-2.5)
Answer:
77/2
Explanation:
-15.4 ÷ (-2.5) = -154/10 ÷(-25/10)
= (-154 • -25)/(10 • 10)
= 77/2
Question 44.
-23.8 ÷ 5.6
Answer:
-3332/25
Explanation:
-23.8 ÷ 5.6 = -238/10 ÷ 56/10
= (-238 • 56) / (10 • 10)
= -3332/25
Question 45.
You use a debit card to purchase several shirts. Your account balance after buying the shirts changes by -$30.60. For each shirt you purchased, the change in your account balance was -$6.12. How many shirts did you buy?
Answer:
The number of T-shirts bought was 5
Explanation:
After using a debit card, to purchase several t-shirts. Your account balance after buying the t-shirts changes by -$30.60. The negative sign means there was a total debit of $30.6 after your transactions.
For each t-shirt you purchased, the changes in your account balance were -6.12. If you purchased n T-shirts, the changes would be n × -6.12 = -6.12n. This means a total debit of 6.12n for all the T-shirts you bought.
Therefore, 6.12n = 30.6
n = 30.6/6.12 = 5
So the number of T-shirts bought was 5
Question 46.
Evaluate 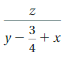 when x = 4, y = -3, and \(-\frac{1}{8}\).
when x = 4, y = -3, and \(-\frac{1}{8}\).
Answer:
-1/2
Explanation:
The given expression is z / (y – 3/4 + x)
Put x = 4, y = -3 and z = -1/8
= -1/8 / (-3 – 3/4 + 4)
= -1/8 / ((-12 – 3 + 16)/4)
= -1/8 / (1/4)
= -1/8 • 4/1
= -1/2
Multiplying and Dividing Rational Numbers Practice Test
Evaluate the expression. Write fractions in simplest form.
Question 1.
-9 • 2
Answer:
-9 • 2 = -18
Explanation:
-9 • 2 = -18
The product of two integers with different signs is negative.
Question 2.
-72 ÷ (-3)
Answer:
-72 ÷ (-3) = 24
Explanation:
-72 ÷ (-3) = 24
The quotient of two integers with the same sign is positive.
Question 3.
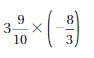
Answer:
-52/5
Explanation:
3(9/10) x (-8/3) = 39/10 x (-8/3)
= (39 . -8) / (10 . 3)
= (13 . -4)/5
= -52/5
Question 4.
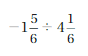
Answer:
-11/25
Explanation:
-1(5/6) ÷ 4(1/6) = -11/6 ÷ 25/6
= -11/6 • 6/25
= (-11 • 6) / (6 • 25)
= -11/25
Question 5.
-4.4 × (-6.02)
Answer:
-4.4 × (-6.02) = 6622/25
Explanation:
-4.4 × (-6.02) = -44/10 x -602/10
= (-44 x -602) / (10 x 10)
= (-11 x -602)/25
= 6622/25
Question 6.
-5 ÷ 1.5
Answer:
-5 ÷ 1.5 = -10/3
Explanation:
-5 ÷ 1.5 = -5 ÷ 15/10
= -5 • 10/15
=(-5 • 10) / 15
= -10/3
Write the fraction or mixed number as a decimal.
Question 7.
\(\frac{7}{40}\)
Answer:
\(\frac{7}{40}\) = 0.175
Explanation:
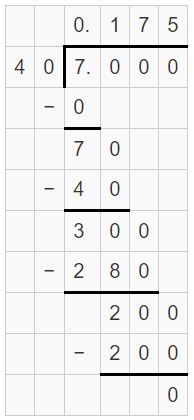
Question 8.
\(-\frac{1}{9}\)
Answer:
\(-\frac{1}{9}\) = -0.11111
Explanation:
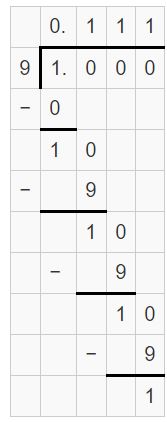
Question 9.
-1\(\frac{5}{16}\)
Answer:
-1\(\frac{5}{16}\) = -1.3125
Explanation:
-1\(\frac{5}{16}\) = -21/16

Write the decimal as a fraction or mixed number in simplest form.
Question 10.
-0.122
Answer:
-0.122 = -61/500
Explanation:
-0.122 = -122/1000
= (-2 x 61) / (2 x 500)
= -61/500
Question 11.
0.33
Answer:
0.33 = 33/100
Explanation:
0.33 = 33/100
Question 12.
-7.09
Answer:
-7.09 = -709/100
Explanation:
-7.09 = -709/100
Evaluate the expression when x = 5, y = -3, and z = -2.
Question 13.
![]()
Answer:
-6/5
Explanation:
The given expression is (y + z)/x
Put x = 5, y = -3, and z = -2
= (-3 + (-2)) / 5
= (-3 – 2)/5
= -6/5
Question 14.
![]()
Answer:
-5
Explanation:
The given expression is (x – 5z)/y
Put x = 5, y = -3, and z = -2
= (5 – 5(-2))/-3
= (5 + 10)/-3
= 15/-3 = -5
Question 15.
![]()
Answer:
10/9
Explanation:
The given expression is 1/3 x / y/z
Put x = 5, y = -3, and z = -2
= [1/3 (5)]/[-3/-2]
= 5/3 / 3/2
= 5/3 . 2/3
= 10/9
Question 16.
Find the mean of 11, -7, -14, 10, and -5.
Answer:
Mean = -1
Explanation:
Mean = (11 – 7 – 14 + 10 – 5)/5
= -5/5
= -1
Question 17.
A driver receives -25 points for each rule violation. What integer represents the change in points after 4 rule violations?

Answer:
The change in points after 4 rule violations is -100 points
Explanation:
A driver receives -25 points for each rule violation.
The change in points after 4 rule violations = 4(-25)
= -100
Question 18.
How many 2.25-pound containers can you fill with 24.75 pounds of almonds?
Answer:
The number of containers = 11
Explanation:
The number of containers = 24.75 / 2.25
= 2475/225 = (495 . 5)/(45 . 5)
= (99 . 5) / (9 . 5)
= 11
Question 19.
In a recent 10-year period, the change in the number of visitors to U.S.national parks was about 11,150,000 visitors.
a. What was the mean yearly change in the number of visitors?
b. During the seventh year, the change in the number of visitors was about 10,800,000. Explain how the change for the 10-year period can be negative.

Answer:
a. Mean yearly change in the number of visitors = 1,15,000
b. The change is -35000
Explanation:
a. Mean yearly change in the number of visitors = 11,150,000/10
= 1,15,000
b. During the seventh year, the change in the number of visitors was about 10,800,000
The change in the number of visitors to U.S.national parks was about 11,150,000 visitors
(10,800,000 – 11,150,000)/10 = -350000/10 = -35000
Question 20.
You have a $50 gift card to go shopping for school supplies. You buy 2 packs of pencils, 5 notebooks, 6 folders, 1 pack of pens, 3 packs of paper, 1 pack of highlighters, and 2 binders.

a. What number represents the change in the value of the gift card after buying your school supplies?
b. What percentage of the value remains on your gift card?
Answer:
a. The change in the value of the gift card after buying your school supplies = $12.06
b. The percentage of the value that remains on your gift card = 24.12%
Explanation:
You buy 2 packs of pencils, 5 notebooks, 6 folders, 1 pack of pens, 3 packs of paper, 1 pack of highlighters, and 2 binders.
a. The change in the value of the gift card after buying your school supplies = 50 – [2(1.98) + 5(2.95) + 6(0.75) + 1(1.57) + 3(0.89) + 1(3.45) + 2(3.55)]
= 50 – [3.9 + 14.75 + 4.5 + 1.57 + 2.67 + 3.45 + 7.1]
= 50 – 37.94
= 12.06
b. The amount remains on the gift card = $12.06
The percentage of the value that remains on your gift card = (100 x 12.06)/50
= 2 x 12.06 = 24.12%
Multiplying and Dividing Rational Numbers Cumulative Practice
Question 1.
When José and Sean were each 5 years old, José was 1\(\frac{1}{2}\) inches taller than Sean. Then José grew at an average rate of 2\(\frac{3}{4}\) inches per year until he was 13 years old. José was 63 inches tall when he was 13 years old. How tall was Sean when he was 5 years old?


Answer:
A. 39(1/2)
Explanation:
José grew at an average rate of 2\(\frac{3}{4}\) inches per year until he was 13 years old.
2.75 * (13 – 5) = 2.75 (8) = 22
José was 63 inches
= 63 – 22 = 41
41 – 1.5 = 39.5 = 39(1/2)
sean was only 39.5 inches tall when he was 5.
Question 2.
Whatis the value of -5 + (-7) ?
F. -12
G. -2
H. 2
I. 12
Answer:
F. -12
Explanation:
-5 + (-7) = -5 – 7
= -12
Question 3.
What is the value of the expression?
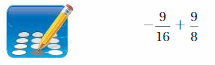
Answer:
9/16
Explanation:
-9/16 + 9/8 = (-9 + 18)/16
= 9/16
Question 4.
What is the value of ![]() when a = -2, b = 3, and c = -5?
when a = -2, b = 3, and c = -5?
A. -9
B. -1
C. 1
D. 9
Answer:
C. 1
Explanation:
| a² – 2ac + 5b |
Put a = -2, b = 3, and c = -5
= | (-2)² – 2(-2)(-5) + 5(3) |
= | 4 – 20 + 15 |
= | -1 |
= 1
Question 5.
Your friend evaluated the expression.
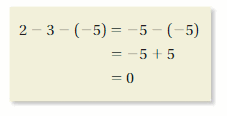
What should your friend do to correct the error that he made?
F. Subtract 5 from -5 instead of adding.
G. Rewrite 2 – 3 as -1.
H. Subtract -5 from 3 before subtracting 3 from 2.
I. Rewrite -5 + 5 as -10
Answer:
H. Subtract -5 from 3 before subtracting 3 from 2.
Explanation:
2 – 3 – (-5) = 2 – 3 + 5
= -1 + 5
= 4
Question 6.
What is the value of 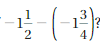 ?
?

Answer:
B. 1/4
Explanation:
-1(1/2) – (-1(3/4)) = -3/2 + 7/4
= (-6 + 7)/4
= 1/4
Question 7.
What is the value of the expression when q = -2, r = -12, and s = 8?
![]()
F. -2
G. -1
H. 1
I. 2
Answer:
H. 1
Explanation:
The given expression is (-q² – r)/s
Put q = -2, r = -12, and s = 8
= (-(-2)² – (-12))/8
= (-4 + 12)/8
= 8/8 = 1
Question 8.
You are stacking wooden blocks with the dimensions shown. How many blocks do you need to stack vertically to build a block tower that is 7\(\frac{1}{2}\) inches tall?
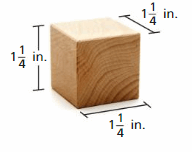

Answer:
We need 6 blocks to stack vertically to build a block tower.
Explanation:
The length of block tower = 7(1/2) = 15/2 inches
The length of each block = 1(1/4) = 5/4 inches
So, 5/4 x = 15/2
x = 15/2 . 4/5
x = 6
Therefore, we need 6 blocks to stack vertically to build a block tower.
Question 9.
Your friend evaluated an expression.

What should your friend do to correct the error that she made?
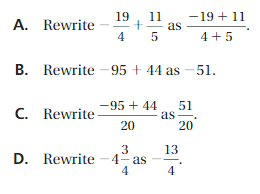
Answer:
C.
Explanation:
-4(3/4) + 2(1/5) = -19/4 + 11/5
= (-95 + 44)/20
= -51/20
Question 10.
Which expression has the greatest value when x = 2 and y = -3?
F. -xy
G. xy
H. x – y
I. -x – y
Answer:
F. -xy
Explanation:
Put x = 2 and y = -3
F. -xy
= -2(-3) = 6
G. xy = 2(-3) = -6
H. x – y = 2 – (-3) = 2 + 3 = 5
I. -x – y = -2 – (-3) = -2 + 3 = 1
Question 11.
Four points are graphed on the number line.

Part A
Choose the two points whose values have the greatest sum. Approximate this sum. Explain your reasoning.
Part B
Choose the two points whose values have the greatest difference. Approximate this difference. Explain your reasoning.
Part C
Choose the two points whose values have the greatest product. Approximate this product. Explain your reasoning.
Part D
Choose the two points whose values have the greatest quotient. Approximate this quotient. Explain your reasoning.
Answer:
A. T + U
B. R – S
C. R . S
D. U/T
Explanation:
Values of the points are R = -2.75, S = -1.25, T = 0.4, U = 2.1
A. T + U = 0.4 + 2.1 = 2.5
B. R – S = -2.75 – (-1.25) = -2.75 + 1.25 = -1.5
S – T = -1.25 – 0.4 = -1.65
T – U = 0.4 – 2.1 = -1.7
S – U = -1.25 – 2.1 = -3.35
R – T = -2.75 – 0.4 = -3.15
R – U = -2.75 – 2.1 = -4.85
Out of all R – S has the greatest difference.
C. R . S = -2.75 . -1.25 = 3.4375
T. U = 0.4 . 2.1 = 0.84
D. R/s = -2.75/1.25 = 2.2
T/U = 0.4/2.1 = 0.19
U/T = 2.1/0.4 = 5.25
Question 12.
What number belongs in the box to make the equation true?
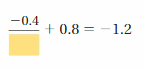
A. -1
B. -0.2
C. 0.2
D. 1
Answer:
A. -1
Explanation:
-0.4/-1 + 0.8 = 0.4 + 0.8 = 1.2
-0.4/1 + 0.8 = -0.4 + 0.8 = 0.4
-0.4/0.2 + 0.8 = -2
Question 13.
Which expression has a negative value when x = -4 and y = 2?
F. -x + y
G. y – x
H. x – y
I. -x – y
Answer:
H. x – y
Explanation:
Put x = -4 and y = 2
F. -x + y = -(-4) + 2 = 4 + 2 = 6
G. y – x = 2 – (-4) = 6
H. x – y = -4 – 2 = -6
I. -x – y = -(-4) – 2 = 4 – 2 = 2
Question 14.
What is the area of a triangle with a base of 2\(\frac{1}{2}\) inches and a height of 2 inches?

Answer:
B
Explanation:
Area of triangle = 1/2 . base . height
= 1/2 . 2(1/2) . 2
= 2(1/2)
Question 15.
Which decimal is equivalent to \(\frac{2}{9}\)?
F. 0.2
G. \(0 . \overline{2}\)
H. 0.29
I. 4.5
Answer:
F. 0.2
Explanation:
2/9 = 0.222
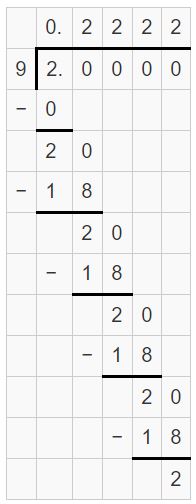
Conclusion:
The final verdict of Multiplying and Dividing Rational Numbers is that you get various problems and solutions that helps you in your preparation. With the help of the pdfs given above, you can practice even in the offline mode. Check out all the topics and concepts and feel free to clarify your doubts by adding them in the comments box. Hope you are satisfied with the information given in the article. We wish all the luck to all the candidates for the exam preparation.
