Looking across the web for a friendly site that caters to all your needs regarding the Big Ideas Math Geometry Concepts? Don’t worry we are with you in this and we will provide you the Complete Big Ideas Math Geometry Answers Chapter 1 Basics of Geometry. All the Solutions covered in the BIM Geometry Ch 1 Basics of Geometry Answer Key are as per the latest Common Core State Standards guidelines. Practice using the BigIdeas Math Chapter 1 Solutions via quick links available and clear the exams with flying colors.
Big Ideas Math Book Geometry Answer Key Chapter 1 Basics of Geometry
Access the Big Ideas Math Geometry Ch 1 Answers for all the topics and prepare accordingly. Find complete assistance on Geometry Chapter 1 including questions from Lessons 1.1-1.6, Performance Tests, Review Tests, Cumulative Practice, Assessment Tests, etc. All you have to do is simply tap on the quick links available and clear your ambiguities in no time. To make it easy for you we have compiled the BIM Geometry Chapter 1 Basics of Geometry Textbook Solutions aligned as per the BIM Textbooks.
- Basics of Geometry Maintaining Mathematical Proficiency – Page 1
- Basics of Geometry Mathematical Practices – Page 2
- 1.1 Points, Lines, and Planes – Page(3-10)
- Lesson 1.1 Points, Lines, and Planes – Page(4-7)
- Exercise 1.1 Points, Lines, and Planes – Page(8-10)
- 1.2 Measuring and Constructing Segments – Page(11-18)
- Lesson 1.2 Measuring and Constructing Segments – Page(12-15)
- Exercise 1.2 Measuring and Constructing Segments – Page(16-18)
- 1.3 Using Midpoint and Distance Formulas – Page(19-26)
- Lesson 1.3 Using Midpoint and Distance Formulas – Page(20-23)
- Exercise 1.3 Using Midpoint and Distance Formulas -Page(24-26)
- Study Skills: Keeping Your Mind Focused – Page 27
- 1.1 – 1.3 Quiz – Page 28
- 1.4 Perimeter and Area in the Coordinate Plane – Page(28-36)
- Lesson 1.4 Perimeter and Area in the Coordinate Plane – Page(30-33)
- Exercise 1.4 Perimeter and Area in the Coordinate Plane – Pae(34-36)
- 1.5 Measuring and Constructing Angles – Page(37-46)
- Lesson 1.5 Measuring and Constructing Angles – Page(38-43)
- Exercise 1.5 Measuring and Constructing Angles – Page(43-46)
- 1.6 Describing Pairs of Angles – Page(47-54)
- Lesson 1.6 Describing Pairs of Angles – Page(48-51)
- Exercise 1.6 Describing Pairs of Angles – Page(52-54)
- 1.4 – 1.6 Performance Task: Comfortable Horse Stalls – Page 55
- Basics of Geometry Chapter Review – Page(56-58)
- Basics of Geometry Chapter Test – Page 59
- Basics of Geometry Cumulative Assessment – Page(60-61)
Basics of Geometry Maintaining Mathematical Proficiency
Simplify the expression.
Question 1.
|8 – 12|
Answer:
The given absolute value expression is:
| 8 – 12|
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 8 – 12 |= | -4| = 4
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 4
Question 2.
|- 6 – 5|
Answer:
The given absolute value expression is:
| -6 – 5|
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| -6 – 5| = | -11 | = 11
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 11
Question 3.
|4 + (-9)|
Answer:
The given absolute value expression is:
| 4 + (-9) |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 4 + (-9) | = | 4 – 9 |
= | -5 | = 5
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 5
Question 4.
|13 + (-4)|
Answer:
The given absolute value expression is:
| 13 + (-4) |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 13 + (-4) | = | 13 – 4 |
= | 9 | = 9
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 9
Question 5.
|6 – (- 2)|
Answer:
The given absolute value expression is:
| 6 – (-2) |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 6 – (-2) | = | 6 + 2 |
= | 8 | = 8
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 8
Question 6.
|5 – (- 1)|
Answer:
The given absolute value expression is:
| 5 – (-1) |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 5 – (-1) | = | 5 + 1 |
= | 6 | = 6
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 6
Question 7.
|- 8 – (- 7)|
Answer:
The given absolute value expression is:
| -8 – (-7) |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| -8 – (-7) | = | -8 + 7 |
= | -1 | = 1
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 1
Question 8.
|8 – 13|
Answer:
The given absolute value expression is:
| 8 – 13 |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 8 – 13 | = | -5 | = 5
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 5
Question 9.
|- 14 – 3|
Answer:
The given absolute value expression is:
| -14 – 3 |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| -14 – 3 | = | -17 | = 17
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 17
Find the area of the triangle.
Question 10.
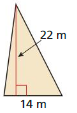
Answer:
The given figure is:

We know that,
The area of the triangle (A) is given as:
A = 1/2 ×Base × Height
So,
The area of the given triangle is:
A = 1/2 × 14m × 22m
= 11 × 14
= 154 m²
Hence, from the above,
We can conclude that the area of the given triangle is: 154 m²
Question 11.
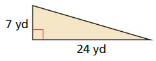
Answer:
The given figure is:

We know that,
The area of the triangle (A) is given as:
A = \(\frac{1}{2}\) ×Base × Height
So,
The area of the given triangle is:
A = \(\frac{1}{2}\) × 7yd × 24yd
= \(\frac{1}{2}\) × \(\frac{24}{1}\) × 7
= 12 × 7
= 84 yd²
Hence, from the above,
We can conclude that the area of the given triangle is: 84 yd²
Question 12.
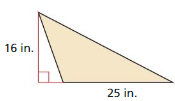
Answer:
The given figure is:

We know that,
The area of the triangle (A) is given as:
A = \(\frac{1}{2}\) ×Base × Height
So,
The area of the given triangle is:
A = \(\frac{1}{2}\) × 16 in × 25 in
= \(\frac{1}{2}\) × \(\frac{16}{1}\) × 25
= 8 × 25
= 200 in²
Hence, from the above,
We can conclude that the area of the given triangle is: 200 in²
Question 13.
ABSTRACT REASONING
Describe the possible values for x and y when |x – y| > 0. What does it mean when |x – y| = 0 ? Can |x – y| < 0? Explain your reasoning.
Answer:
We know that,
The value of the absolute expression must be greater than or equal to 0 but not less than 0
So,
The values for | x – y | do not exist
Now,
The possible values of | x – y | > 0 should be greater than 0 and maybe x > y and x < y
The possible values of | x – y | = 0 should be only one value i.e., 0 as x and y must be equal to make the difference value 0
Basics of Geometry Mathematical Practices
Monitoring Progress
Question 1.
Find the area of the polygon using the specified units. Round your answer to the nearest hundredth.
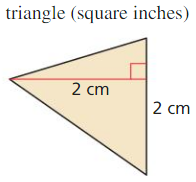
Answer:
The given figure is:

We know that,
Area of the triangle = \(\frac{1}{2}\) × Base × Height
So,
From the figure,
The value of the Base is: 2 cm
The value of Height is: 2 cm
We know that,
1 cm = \(\frac{25}{64}\) inch = 0.3937 inch
So,
2cm = \(\frac{25}{32}\) inch = 0.7874 inch
So,
The area of the given triangle = \(\frac{1}{2}\) × \(\frac{25}{32}\) × \(\frac{25}{32}\)
= \(\frac{1}{2}\) × \(\frac{625}{1024}\)
= \(\frac{625}{2,048}\) inch²
= 0.3051 inch²
Hence, from the above,
We can conclude that the area of the given triangle in square inches is: 0.3051 inch²
Question 2.
parallelogram (square centimeters)
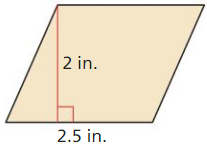
Answer:
The given figure is:

WE know hat,
The area of the parallelogram = Base × Height
So,
From the given figure,
The base of the parallelogram is: 2.5 in
The height of the parallelogram = 2 in
We know that,
1 inch = 2.54 cm
So,
2 inch = 2.08 cm
2.5 inch = 6.35 cm
So,
The area of the given parallelogram = 2.08 × 6.35
= 13.208 cm²
Hence, from the above,
We can conclude that the area of the given parallelogram in square cm is: 13.208 cm²
Question 3.
The distance between the two cities is 120 miles. What is the distance in kilometers? Round your answer to the nearest whole number.
Answer:
It is given that the distance between the two cities is 120 miles.
Now,
We know that,
1 mile = 1.609 kilometer
So,
The distance between the two cities in kilometers = 120 × 1.609
= 193 kilometers
Hence, from the above,
We can conclude that the distance between the two cities in kilometers is: 193 kilometers
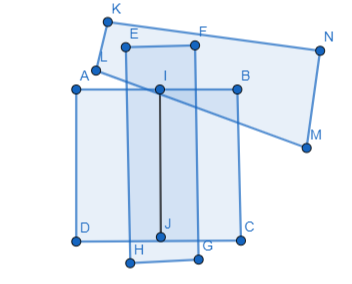
1.1 Points, Lines, and Planes
Exploration 1
Using Dynamic Geometry Software
Work with a partner: Use dynamic geometry software to draw several points. Also draw some lines, line segments, and rays. What is the difference between a line, a line segment, and a ray?
Sample
Answer:
From the above,
The differences between a line, a ray, and a line segment are:
A Ray has no starting and ending points
A line has a starting point but no ending point
A line segment has both starting point and an ending point
Exploration 2
Intersections of Lines and Planes
Work with a partner:
a. Describe and sketch the ways in which two lines can intersect or not intersect. Give examples of each using the lines formed by the walls. floor. and ceiling in your classroom.
Answer:
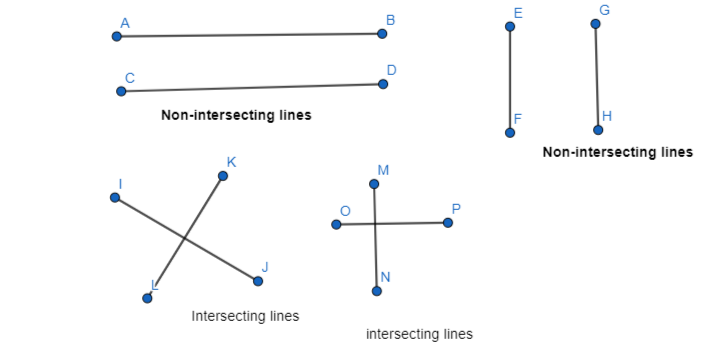
Examples of non-intersecting lines are: Floor and ceiling
Examples of intersecting lines are: Walls and floor
b. Describe and sketch the ways in which a line and a plane can intersect or not intersect. Give examples of each using the walls. floor, and ceiling in your classroom.
Answer:
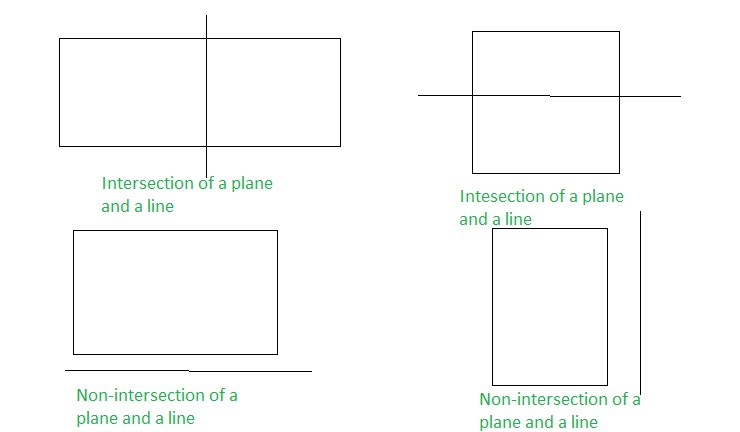
Examples of the intersection of a plane and a line are: Walls and ceiling
Examples of the non-intersection of a plane and a line are: Floor and a blackboard
c. Describe and sketch the ways in which two planes can intersect or not intersect. Give examples of each using the walls. floor, and ceiling in your classroom.
Answer:
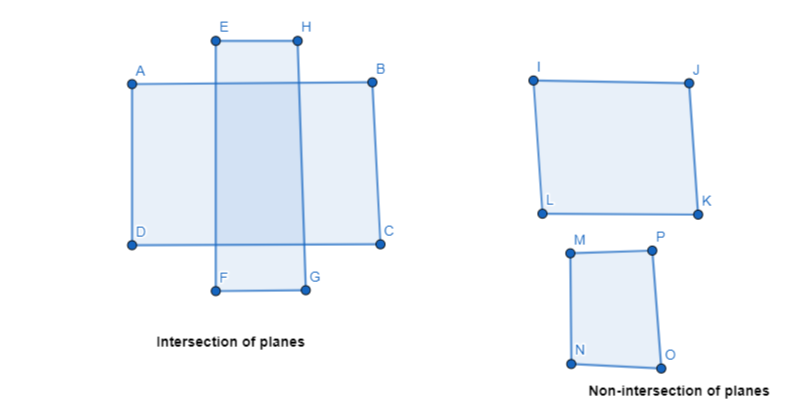
Examples of the intersection of planes are: Floor and benches
Examples of the non-intersection of planes are: Floor and ceiling
Exploration 3
Exploring Dynamic Geometry Software
UNDERSTANDING MATHEMATICAL TERMS
To be proficient in math, you need to understand definitions and previously established results. An appropriate tool, such as a software package, can sometimes help.
Work with a partner. Use dynamic geometry software to explore geometry. Use the software to find a term or concept that is unfamiliar to you. Then use the capabilities of the software to determine the meaning of the term or concept.
Answer:
The dynamic geometry software used is “GeoGebra”
The URL for “GeoGebra – Geometry” is:
https://www.geogebra.org/calculator
So,
Using the above URL,
Check the term that you are unfamiliar to you and find the meaning of that term using the above URL
Communicate Your Answer
Question 4.
How can you use dynamic geometry software to visualize geometric concepts?
Answer:
Some of the uses dynamic geometry software to visualize geometric concepts are:
a. Request dispatching for cheap energy prices in cloud data centers
b. Springerlink training kit
c. Luminosity measurements at Hadron colliders
d. From word embeddings to document distances
Lesson 1.1 Points, Lines, and Planes
Monitoring Progress
Question 1.
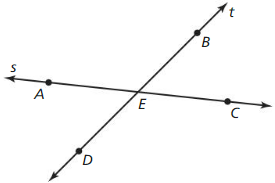
Use the diagram in Example 1. Give two other names for ![]() . Name a point that is not coplanar with points Q. S, and T.
. Name a point that is not coplanar with points Q. S, and T.
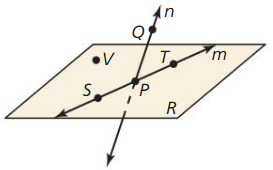
Answer:
The given plane is:

The definition of a ray is:
A ray has no starting and ending points
So,
The other names for \(\overline{S T}\) are: Line m and \(\overline{T S}\)
We know that,
“Co-planar points” are the points if all of them lie in the same plane
Hence, among the points Q, S, and T,
S and T are co-planar since they lie in the same plane and Q is not co-planar
Question 2.
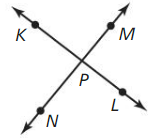
Give another name for \(\overline{K L}\).
Answer:
The given figure is:

So,
The other name of \(\overline{K L}\) is: \(\overline{L K}\)
Question 3.
Are \(\vec{K}\)P and \(\vec{P}\)K the same ray? Are \(\vec{N}\)P and \(\vec{N}\)M the same ray? Explain.

Answer:
The given figure is:

So,
From the above figure,
We can observe that
\(\vec{K}\)P and \(\vec{P}\)K are not the same ray
Reason:
\(\overline{K L}\) is the ray and KP is the line segment
Now,
We can also observe that
\(\vec{N}\)P and \(\vec{N}\)M are in the same ray
Reason:
Since the points N, P, and M are collinear, the ray \(\vec{N}\)M and \(\vec{N}\)P are in the same plane
Question 4.
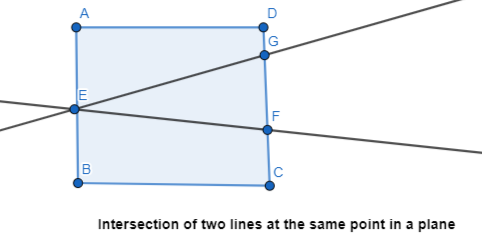
Sketch two different lines that intersect a plane at the same point.
Answer:
The representation of the two different lines that intersect a plane at the same point is:
Question 5.
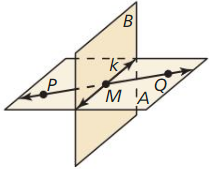
Name the intersection of ![]() and line k.
and line k.
Answer:
The given figure is:

From the above figure,
We can observe that the intersection of \(\overline{P Q}\) and line k is: M
Question 6.
Name the intersection of plane A and plane B.

Answer:
The given figure is:

From the above figure,
We can observe that the intersection of plane A and plane B is: Line k
Question 7.
Name the intersection of line k and plane A.

Answer:
The given figure is:

From the given figure,
We can observe that the intersection of line k and plane A is: Line k
Monitoring Progress
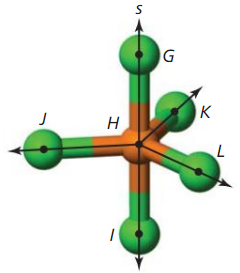
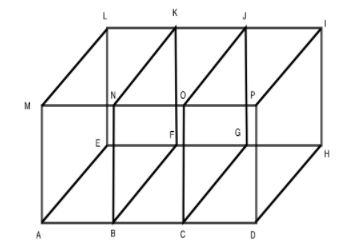
Use the diagram that shows a molecule of phosphorus pentachloride.
Question 8.
Name two different planes that contain line s.
Answer:
The given figure is:

We know that,
A ‘Plane” can be formed by using any three non-collinear points on the same plane
Now,
From the given figure,
We can observe that
The different planes that contain line s are: JHG and KLI
Question 9.
Name three different planes that contain point K.
Answer:
The given figure is:

From the above figure,
The three different planes that contain pint K are: HGK, HKL, and KLI
Question 10.
Name two different planes that contain \(\vec{H}\)J.
Answer:
The given figure is:

From the above figure,
We can say that
The 2 different planes that contain \(\vec{H}\)J are: HJI and HJL
Exercise 1.1 Points, Lines, and Planes
Vocabulary and Core Concept Check
Question 1.
WRITING
Compare collinear points and coplanar points.
Answer:
Question 2.
WHICH ONE DOES DOESN’T BELONG?
Which term does not belong with the other three? Explain your reasoning.

Answer:
The given expressions are:
a. \(\overline{A B}\)
b. plane CDE
c. \(\vec{FG}\)
d. \(\vec{H}\)I
So,
From the above four expressions,
We can observe that the three expressions are 2-dimensional geometrical expressions whereas 1 figure is a 3-dimensional geometrical expression
The 2-dimensional geometrical expressions from the given expressions are: a), c), and d)
Hence, from the above,
We can conclude that expression c. does not belong with the other three
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, use the diagram.
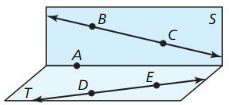
Question 3.
Name four points.
Answer:
![]()
Question 4.
Name two lines.
Answer:
The given figure is:

Hence,
From the above figure,
We can conclude that the two lines are: \(\vec{B}\)C and \(\vec{D}\)E
Question 5.
Name the plane that contains points A, B, and C.
Answer:
![]()
Question 6.
Name the plane that contains points A, D, and E.
Answer:
The given figure is:

From the given figure,
We can observe that there are 2 planes. They are:
a. plane S b. plane T
Hence,
From the above figure,
We can conclude that points A, D, and E lie in Plane T
In Exercises 7 – 10. use the diagram. (See Example 1.)
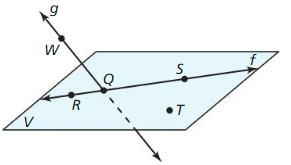
Question 7.
Give two other names for ![]() .
.
Answer:
![]()
Question 8.
Give another name or plane V.
Answer:
The given figure is:

We know that,
A plane is also named by a group of 3 or more co-planar points
Hence, from the above,
We can conclude that another name for plane V is: plane QRT
Question 9.
Name three points that are collinear. Then name a fourth point that is not collinear with these three points.
Answer:
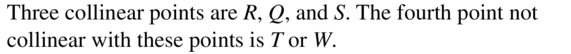
Question 10.
Name a point that is not coplanar with R, S, and T.
Answer:
The given figure is:

We know that,
The points that are present in the same plane are called “Co-planar points”
Hence, from the above,
We can conclude that the point that is co-planar with R, S, and T is: W
In Exercises 11 – 16, use the diagram.
Question 11.
What is another name for \(\overline{B D}\)?
Answer:
![]()
Question 12.
What is another name for \(\overline{A C}\)?
Answer:
The given figure is:

We know that,
The line segment is the same from both sides if we can consider any point starting or ending point
Ex: \(\overline{A B}\) is the same as \(\overline{B A}\)
because we can consider here either starting point A or starting point B, then the ending points will be either B or A
Hence, from the above,
We can conclude that the other name for \(\overline{A C}\) is: \(\overline{C A}\)
Question 13.
What is another name for ray \(\vec{A}\)E?
Answer:
![]()
Question 14.
Name all rays with endpoint E.
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that the rays with endpoint E are: s and t
Question 15.
Name two pairs of opposite rays.
Answer:
![]()
Question 16.
Name one pair of rays that are not opposite rays.
Answer:
The given figure is:

We know that “opposite” means “Opposite direction”
Hence, from the above,
We can conclude that the pair of rays that are not opposite rays are:
\(\vec{E}\)B and\(\vec{E}\)C
In Exercises 17 – 24, sketch the figure described.
Question 17.
plane P and line l intersecting at one point
Answer:
Question 18.
plane K and line m intersecting at all points on line m
Answer:
The given statement is:
plane K and line m intersecting at all points on line m
Hence,
The representation of the given statement is:
Question 19.
![]()
Answer:
Question 20.
\(\vec{M}\)N and \(\vec{N}\)X
Answer:
The given vectors are:
\(\vec{M}\)N and \(\vec{N}\)X
Hence,
The representation of vectors along with their direction is:
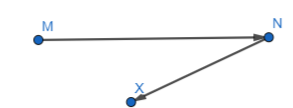
Question 21.
plane M and \(\vec{N}\)B intersecting at B
Answer:
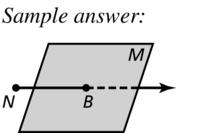
Question 22.
plane M and \(\vec{N}\)B intersecting at A
Answer:
The given statement is:
plane M and \(\vec{N}\)B intersecting at A
Hence,
The representation of the given statement is:
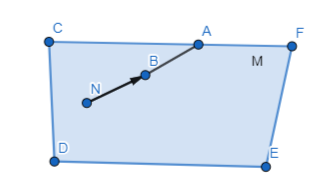
Question 23.
plane A and plane B not intersecting
Answer:
Question 24.
plane C and plane D intersecting at ![]()
Answer:
The given statement is:
plane C and plane D intersecting at ![]()
Hence,
The representation of the given statement is:
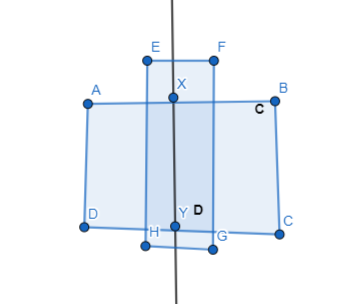
ERROR ANALYSIS
In Exercises 25 and 26, describe and correct the error in naming opposite rays in the diagram.

Question 25.
Answer:

Question 26.

Answer:
The given figure is:

From the above,
We can observe that \(\vec{Y}\)C and \(\vec{Y}\)E are the opposite rays because Y, C, and E are the collinear points and Y is in between C and E
In Exercises 27 – 34. use the diagram.
Question 27.
Name a point that is collinear with points E and H.
Answer:
![]()
Question 28.
Name a point that is collinear with points B and I
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that C is collinear with B and I
Question 29.
Name a p0int that is not collinear with points E and H.
Answer:
![]()
Question 30.
Name a point that is not collinear with points B and I.
Answer:
The given figure is:

We know that,
The points that are in the same line are called “Collinear points”
Hence, from the above figure,
We can conclude that A, D, E, F, G, H, J are not collinear with points B and I
Question 31.
Name a point that is coplanar with points D, A, and B.
Answer:
![]()
Question 32.
Name a point that is coplanar with points C, G, and F.
Answer:
The given figure is;

We know that,
The points that are in the same plane are called “Co-planar points”
From the above figure,
We can observe that CGFB is a plane
Hence, from the above figure,
We can conclude that B and I are co-planar with points C, G, and F
Question 33.
Name the intersection of plane AEH and plane FBE.
Answer:
![]()
Question 34.
Name the intersection of plane BGF and plane HDG.
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that the intersection of plane BGF and plane HDG is: \(\overline{C G}\)
In Exercises 35 – 38, name the geometric term modeled by the object.
Question 35.

Answer:
![]()
Question 36.

Answer:
The given object is:

Hence, from the above,
We can conclude that the geometric term modeled by the object is: Plane
Question 37.

Answer:
![]()
Question 38.

Answer:
The given figure is:

Hence, from the above figure,
We can conclude that the geometric term modeled from the given object is: Line
In Exercises 39 – 44. use the diagram to name all the points that are not coplanar with the given points.
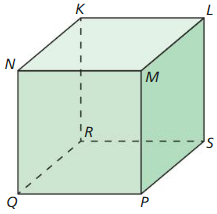
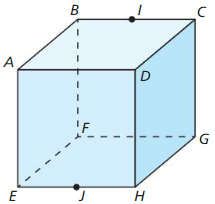
Question 39.
N, K, and L
Answer:
![]()
Question 40.
P, Q, and N
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that R, S, L, and K are not co-planar with P, Q, and N
Question 41.
P, Q, and R
Answer:
![]()
Question 42.
R, K, and N
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that P, S, L, and M are not co-planar with R, K, and N
Question 43.
P, S, and K
Answer:
![]()
Question 44.
Q, K, and L
Answer:
The given figure is:

Hence, from the above figure,
We can conclude that R, M, P, and S are not co-planar with Q, K, and L
Question 45.
CRITICAL THINKING
Given two points on a line and a third point not on the line. is it possible to draw
a plane that includes the line and the third point? Explain your reasoning.
Answer:

Question 46.
CRITICAL THINKING
Is it possible for one point to be in two different planes? Explain your reasoning.
Answer:
Yes, it is possible for one point to be in two different planes. This can be explained in the following way:
The Intersection of two planes is a line.
Hence,
yes, one point or an Infinite number of points can be common between two different planes.
Question 47.
REASONING
Explain why a four-legged chair may rock from side to side even if the floor is level. Would a three-legged chair on the same level floor rock from side to side? Why or why not?
Answer:

Question 48.
THOUGHT-PROVOKING
You are designing the living room of an apartment. Counting the floor, walls, and ceiling, you want the design to contain at least eight different planes. Draw a diagram of your design. Label each plane in your design.
Answer:
It is given that you are designing the living room of an apartment and you want the design to contain at least eight different planes which include the floor, walls, and ceiling
Hence,
The representation of the design that contain floor, walls, and ceiling is:
Question 49.
LOOKING FOR STRUCTURE
Two coplanar intersecting lines will always intersect at one point. What is the greatest number of intersection points that exist if you draw tour coplanar lines? Explain.
Answer:

Question 50.
HOW DO YOU SEE IT?
You and your friend walk in opposite directions, forming opposite rays. You were originally on the comer of Apple Avenue and Cherry Court.
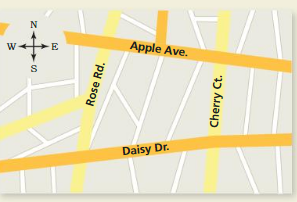
a. Name two possibilities of the road and direction you and your friend may have traveled.
Answer:
It is given that you are at the corner of Apple Avenue and Cherry court
Hence, from the above,
The 2 possibilities that you and your friend travel in the opposite directions are:
i)
If you traveled from the corner of Apple Avenue and Cherry court i.e., towards the east, then your friend will travel from the corner of Apple Avenue and Rose Rd. i.e., towards the west
ii).
If you traveled from the corner of Apple Avenue and Cherry court i.e., towards the west, then your friend will travel from the corner of Apple Avenue and Rose Rd. i.e., towards the east
b. Your friend claims he went north on Cherry Court. and you went east on Apple Avenue. Make an argument as to why you know this could not have happened.
Answer:
It is given that your friend claims he went north on Cherry Court. and you went east on Apple Avenue
But, from the above,
It is given that you and your friend have to travel in the opposite directions
But, according to the given statement,
You and your friend travels in the perpendicular directions
Hence,
We can conclude that the claim of your friend is not possible
MATHEMATICAL CONNECTIONS
In Exercises 51 – 54. graph the inequality on a number line. Tell whether the graph is a segment a ray or rays. a point, or a line.
Question 51.
x ≤ 3
Answer:
![]()
Question 52.
– 7 ≤ x ≤ 4
Answer:
The given inequality is:
-7 ≤ x ≤ 4
Hence,
The representation of the given inequality in the number line is:
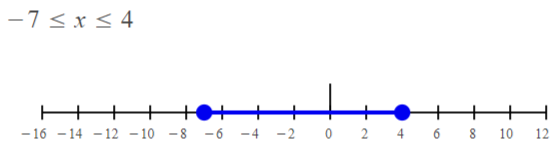
Hence, from the above number line,
We can conclude that the given inequality represents a line segment in the number line
Question 53.
x ≥ 5 or x ≤ – 2
Answer:
![]()
Question 54.
|x| ≤ 0
Answer:
The given inequality is:
| x | ≤ 0
Hence,
The representation of the given inequality in the number line is:
Hence, from the above number line,
We can conclude that the given inequality represents the plane in the number line
Question 55.
MODELING WITH MATHEMATICS
Use the diagram.
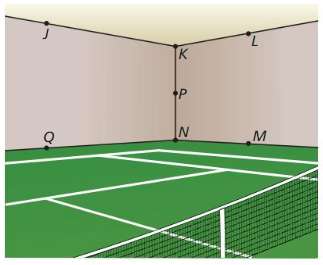
a. Name two points that arc collinear with P.
b. Name two planes that contain J.
c. Name all the points that are in more than One plane.
Answer:

CRITICAL THINKING
In Exercises 56 – 63. complete the
statement with always, sometimes, or never. Explain your reasoning.
Question 56.
A line ________________ has endpoints.
Answer:
The given statement is:
A line ________________ has endpoints.
Hence,
The completed statement is:
A line never has endpoints.
Question 57.
A line and a point _________________ intersect
Answer:
![]()
Question 58.
A plane and a point ________________ intersect.
Answer:
The given statement is:
A plane and a point ________________ intersect.
Hence,
The completed statement is:
A plane and a point sometimes intersect.
Question 59.
Two planes _________________ intersect in a line.
Answer:
![]()
Question 60.
Two points ____________________ determine a line.
Answer:
The given statement is:
Two points ____________________ determine a line.
Hence,
The completed statement is:
Two points always determine a line.
Question 61.
Any three points ____________________ determine a plane.
Answer:

Question 62.
Any three points not on the same line ____________________ determine a plane.
Answer:
The given statement is:
Any three points not on the same line ____________________ determine a plane.
Hence,
The completed statement is:
Any three points not on the same line always determine a plane.
Question 63.
Two lines that are not parallel _________________ intersect.
Answer:
Question 64.
ABSTRACT REASONING
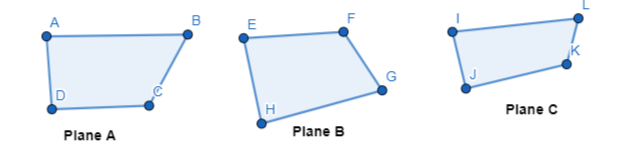
Is it possible for three planes to never intersect? intersect in one line? intersect in one point? Sketch the possible situations.
Answer:
case (1):
It is not possible for three planes to intersect when the three planes are parallel
So,
The representation of this case is:
case (2):
To intersect in 1 line, the two planes must be perpendicular and the third plane should pass through that line
So,
The representation of this case is:
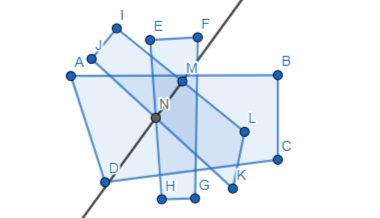
case (3):
To intersect in 1 point, the two planes must be intersected with a line and the third plane passes through a point of that line
So,
The representation of this case is:
Maintaining Mathematical Proficiency
Find the absolute value.
Question 65.
|6 + 2|
Answer:
![]()
Question 66.
|3 – 9|
Answer:
The given absolute value expression is:
| 3 – 9 |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 3 – 9 | = | -6 | = 6
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 6
Question 67.
|- 8 – 2|
Answer:
![]()
Question 68.
|7 – 11|
Answer:
The given absolute value expression is:
| 7 – 11 |
We know that,
| x | = x for x > 0
| -x | = x for x > 0
So,
| 7 – 11 | = | -4 | = 4
Hence, from the above,
We can conclude that the value of the given absolute value expression is: 4
Solve the equation
Question 69.
18 + x = 43
Answer:
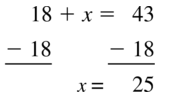
Question 70.
36 + x = 20
Answer:
The given equation is:
36 + x = 20
So,
x = 20 – 36
x = -16
Hence, from the above,
We can conclude that the value of x is: -16
Question 71.
x – 15 = 7
Answer:
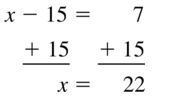
Question 72.
x – 23 = 19
Answer:
The given equation is:
x – 23 = 19
So,
x = 19 + 23
x = 42
Hence, from the above,
We can conclude that the value of x is: 42
1.2 Measuring and Constructing Segments
Essential Question
How can you measure and construct a line segment?
Answer:
The steps used to measure a line segment are:
a. Pick up a scale to measure the length of a line segment.
b. Identify the line segment you want to measure
c. Place the tip of the ruler at the starting of the line segment
The steps used to construct a line segment are:
a. Place the compass at one end of the line
b. Adjust the compass to slightly longer than half of the line’s length
c. Draw arcs above and below the line
d. Keeping the same compass width, draw arcs from the other end of the line
e. Place ruler where the arcs cross and draw the line segment
Exploration 1
Measuring Line Segments Using Nonstandard Units
Work with a partner.
a. Draw a line segment that has a length of 6 inches.
Answer:
We will use a ruler to draw a line segment and the ruler we use generally is the “Centimeter ruler”
But,
It is given that we have to draw a line segment that has a length of 6 inches
But, it is not possible
So,
Convert inches into centimeters
We know that,
1 inch = 2.54 centimeters
So,
6 inches = 15.24 cm
Hence,
The representation of the line segment that has the length of 6 inches in terms of cm is:

b. Use a standard-sized paper clip to measure the length of the line segment. Explain how you measured the line segment in “paper clips.”

![]()
Answer:
Take a standard-sized paper clip and measure the length of the paper clip using a ruler
So,
Using a standard-sized paper clip, the length of the line segment is: 3.4925 cm or 3.5 cm
Hence,
The representation of the length of the line segment that is measured in the paper clip is:

c. Write conversion factors from paper clips to inches and vice versa.
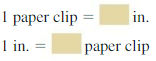
Answer:
From part (b),
We know that
The length of a paper clip is: 3.5 cm
We know that,
1 cm = 0.393 inches
So,
3.5 cm = 1.377 inches
Hence,
1 paper clip = 1.377 in
Now,
We know that,
1 inch = 2.54 cm
Hence,
1 inch = 2.54 paperclip
Hence, from the above,
We can conclude that the conversion of paper clips into inches and vice-versa is:
1 paperclip = 1.377 inch
1 inch = 2.54 paperclip
d. A straightedge is a tool that you can use to draw a straight line. An example of a straightedge is a ruler. Use only a pencil, straightedge, paper clip, and paper to draw another line segment that is 6 inches long. Explain your process.
Answer:
The process using a pencil, a straightedge, paperclip, and paper to draw a line segment of 6 inches is:
Step 1:
Attach a paper to the paperclip and verify that the paper sets correctly in the paperclip
Step 2:
Now, use a straightedge tool like a ruler to draw a line segment on the paper
Step 3:
The line segment must start from the starting of the ruler i.e, 0. Mark the point at 0 as A
Step 4:
Continue the line segment from 0 to 6 on the ruler and make the endpoint at 6 and label it as B
Hence, from the above steps,
We draw the lines segment AB of length 6 inches
But,
We know that,
A ruler consists of the only cm.
So, convert inches into cm
So,
1 inch = 2.54cm
So,
6 inches = 15.24 cm
Hence,
The representation of the line segment AB of 6 inches long is:

Exploration 2
Measuring Line Segments Using Nonstandard Units
Work with a partner.
a. Fold a 3-inch by 5-inch index card on one of its diagonals.
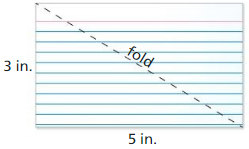
Answer:
The given index card is:

When we fold the given index card,
We can only see the right-angled triangle
Hence,
The representation of the folded index card at its diagonal is:
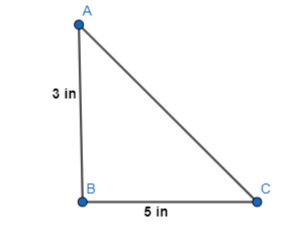
b. Use the Pythagoras Theorem to algebraically determine the length of the diagonal in inches. Use a ruler to check your answer.
Answer:
From part (a),
The index card folded at its diagonal is:

We know that,
According to Pythagoras theorem,
Hypotenuse² = Side² + Side²
Where,
The hypotenuse is the longest side in a right-angled triangle
So,
In the given triangle,
AB and BC are the sides
AC is the hypotenuse
So,
AC² = 3² + 5²
AC² = 9 + 25
AC² = 34
AC = √34 ≅ 6 in
Hence, from the above,
We can conclude that the length of the diagonal is approximately equal to 6 inches
c. Measure the length and width of the index card in paper clips.
Answer:
We know that,
The length of the index card in paper clips is: 4 cm (Approximately )
The width of the index card in the paper clips is: 1 cm
d. Use the Pythagoras Theorem to algebraically determine the length of the diagonal in paper clips. Then check your answer by measuring the length of the diagonal in paper clips. Does the Pythagorean Theorem work for any unit of measure? Justify your answer.
Answer:
The representation of the length and width of the paper clips is:
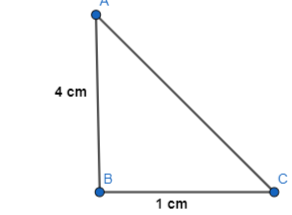
We know that,
According to Pythagoras theorem,
Hypotenuse² = Side² + Side²
Where,
The hypotenuse is the longest side in a right-angled triangle
So,
In the given triangle,
AB and BC are the sides
AC is the hypotenuse
So,
AC² = 4² + 1²
AC² = 16 + 1
AC² = 17
AC = √17 ≅ 4 cm
Hence, from the above,
We can conclude that the length of the diagonal in paper clips is: 4 cm
Yes, the Pythagoras work for any unit of measure but it is applicable only for the right-angled triangles
Exploration 3
Measuring Heights Using Nonstandard Units
Work with a partner.
Consider a unit of length that is equal to the length of the diagonal you found in Exploration 2. Call this length “1 diag.” How tall are you in diags? Explain how you obtained your answer.
Answer:
From Exploration 2,
The length of the diagonal we have found is approximately equal to 6 inches
So,
According to the given problem,
1 diag = 6 inches
We know that,
The height can be measured in the foot
So,
1 inch = 0.08 feet
So,
63.6 inch = 5.3 feet
So,
In terms of diags,
63.6inches = 60 + 3.6 inches
= 10 (6 inches) + 6 (0.6 inches)
= 10 diags + 0.6 diags
= 10.6 diags
Hence, from the above,
We can conclude that you are 10.6 diags tall
Communicate Your Answer:
Question 4.
How can you measure and construct a line segment?
Answer:
The steps used to measure a line segment are:
a. Pick up a scale to measure the length of a line segment.
b. Identify the line segment you want to measure
c. Place the tip of the ruler at the starting of the line segment
The steps used to construct a line segment are:
a. Place the compass at one end of line
b. Adjust the compass to slightly longer than half of the line’s length
c. Draw arcs above and below the line
d. Keeping the same compass width, draw arcs from the other end of line
e. Place ruler where the arcs cross and draw the line segment
Lesson 1.2 Measuring and Constructing Segments
Monitoring Progress
Use a ruler to measure the length of the segment.
Question 1.
![]()
Answer:
The length of the given segment in cm is:
![]()
Question 2.
![]()
Answer:
The length of the given line segment in cm is:
![]()
Question 3.
![]()
Answer:
The length of the given line segment in cm is:
![]()
Question 4.
![]()
Answer:
The length of the given line segment in cm is:
![]()
Question 5.
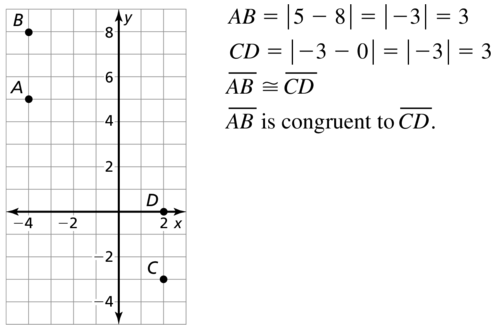
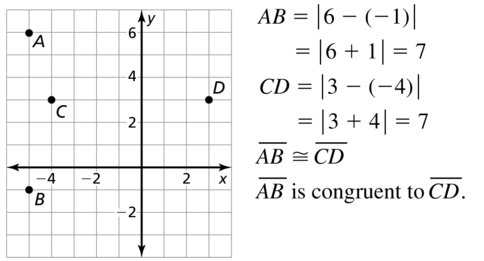
Plot A(- 2, 4), B(3, 4), C(0, 2), and D(0, – 2) in a coordinate plane. Then
determine whether \(\overline{A B}\) and \(\overline{C D}\) are congruent.
Answer:
The given points are:
A (-2, 4), B (3, 4), C (0, 2), and D (0, -2)
We know that,
The distance between 2 points is:
d = √(x2 – x1)² + (y2 – y1)²
Now,
The representation of the given points in the coordinate plane is:
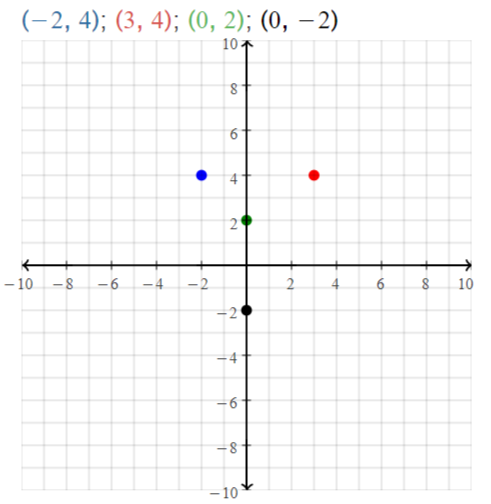
Now,
The distance between AB = √(4 – 4)² + (3 + 2)²
= √0 + 5²
= √5² = 5
The distance between CD = √(0 – 0)² + (-2 – 2)²
= √0 + 4²
= √4² = 4
Since the distance between \(\overline{A B}\) and \(\overline{C D}\) are not same,
\(\overline{A B}\) is not congruent to \(\overline{C D}\)
Hence,
\(\overline{A B}\) ≠ \(\overline{C D}\)
Question 6.
Use the Segment Addition Postulate to find XZ.
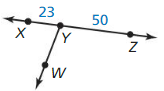
Answer:
The given figure is:

We know that,
“The Segment Addition Postulate” states that given 2 points A and C, a third point B lies on the line segment AC if and only if the distances between the points satisfy the equation
AB + BC = AC
So,
From the above figure,
XZ = XY + YZ
XZ = 23 + 50
XZ = 73
Hence, from the above,
We can conclude that the value of XZ is: 73
Question 7.
In the diagram. WY = 30. Can you use the Segment Addition Postulate to find the distance between points W and Z? Explain your reasoning.

Answer:
The given figure is:

We know that,
“The Segment Addition Postulate” states that given 2 points A and C, a third point B lies on the line segment AC if and only if the distances between the points satisfy the equation
AB + BC = AC
It is also given that
WY = 30
Now,
To find the distance between the points W and Z, we have to use the “Segment Addition Postulate”
So,
WZ = WY + YZ
WZ = 30 + 50
WZ = 80
Hence, from the above,
We can conclude that the distance between points W and Z is: 80
Question 8.
Use the diagram at the left to find KL.

Answer:
The given figure is:

We know that,
By using the Segment Addition Postulate,
If we have three points A, B, and C and we know the distance AB and AC, then the value of AC is given as:
The total distance (AC) = Segment distance 1 (AB) + Segment distance 2 (BC)
So,
JL = JK + KL
144 = 37 + KL
KL = 144 – 37
KL = 107
Hence, from the above,
WE can conclude that the value of KL is: 107
Question 9.
The cities shown on the map lie approximately in a straight line. Find the distance from Albuquerque. New Mexico. to Provo. Utah.
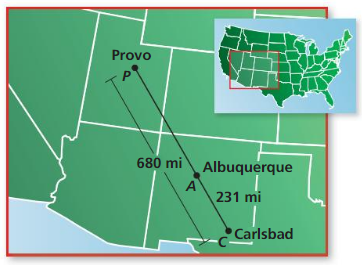
Answer:
From the given map,
It is given that
The distance between Albuquerque and Carlsbad is: 231mi
The distance between Carlsbad and Provo is: 680mi
Now,
Let the distance between Albuquerque and Provo be x
So,
Now,
By using the “Segment Addition Postulate”,
The distance between Carlsbad and Provo = (The distance between Albuquerque and Carlsbad) + (The distance between Albuquerque and Provo)
680 = 231 + x
x = 680 – 231
x = 449
Hence, from the above,
We can conclude that the distance between Albuquerque and Provo is: 449 mi
Exercise 1.2 Measuring and Constructing Segments
Question 1.
WRITING
Explain how \(\overline{X Y}\) and XY arc different.
Answer:
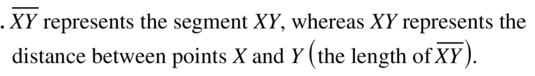
Question 2.
DIFFERENT WORDS. SAME QUESTION
Which is different? Find “both” answers.
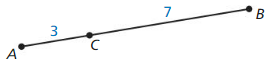
Find AC + CB
Find BC – AC
Find AB
Find CA + BC.
Answer:
The given line segment is:

From the given line segment,
AC = 3 and CB = 7
Now,
a.
AC + CB =3 + 7 = 10
b.
BC – AC = 7 – 3 = 4
c.
AB = AC + CB (By using the Segment Addition Postulate)
So,
AB = 3 + 7 = 10
d.
CA + BC = 3 + 7 = 10
Hence, from the above,
We can conclude that the expressions a, c, and d are the same
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, use a ruler to measure the length of the segment to the nearest tenth of a centimeter.
Question 3.
![]()
Answer:
![]()
Question 4.
![]()
Answer:
The length of the given line segment in cm is:
![]()
Question 5.
![]()
Answer:
![]()
Question 6.
![]()
Answer:
The length of the given line segment is:
![]()
CONSTRUCTION
In Exercises 7 and 8. use a compass and straightedge to construct a copy of the segment.
Question 7.
Copy the segment in Exercise 3.
Answer:

Question 8.
Copy the segment in Exercise 4.
Answer:
Using a straightedge, draw a ray where the left endpoint will be the beginning of the segment.
With a compass, measure the segment in Exercise 4 by placing the point of the compass on the segment endpoint on the left and the pencil point on the segment endpoint on the right
Without changing the compass setting, place the point of the compass on the endpoint on the left of the ray you drew and mark the ray with an arc
Where the arc and ray intersect is the right endpoint of the segment in Exercise 4.
Hence,
The segment in Exercise 4 is:
![]()
In Exercises 9 – 14, plot the points in a coordinate plane. Then determine whether \(\overline{A B}\) and \(\overline{C D}\) are congruent.
Question 9.
A(- 4, 5), B(- 4, 8), C(2, – 3), D(2, 0)
Answer:
Question 10.
A(6, – 1), B(1, – 1), C(2, – 3), D(4, – 3)
Answer:
The given points are:
A (6, -1), B (1, -1), C (2, -3), and D (4, -3)
Let the points be represented as:
A (x1, y1), B (x2, y2), C (x3, y3), and D (x4, y4)
We know that,
The distance between points A and B is:
D = √(x2 – x1)² + (y2 – y1)²
So,
\(\overline{A B}\) = √(1 – 6)² + (-1 + 1)²
= √(-5)²
= 5
The distance between points C and D is:
\(\overline{C D}\) = √(x4 – x3)² + (y4 – y3)²
= √(4 – 2)² + (-3 + 3)²
= √2²
= 2
Hence, from the above,
We can conclude that \(\overline{A B}\) is not congruent with \(\overline{C D}\)
The representation of the given points in the coordinate plane is:
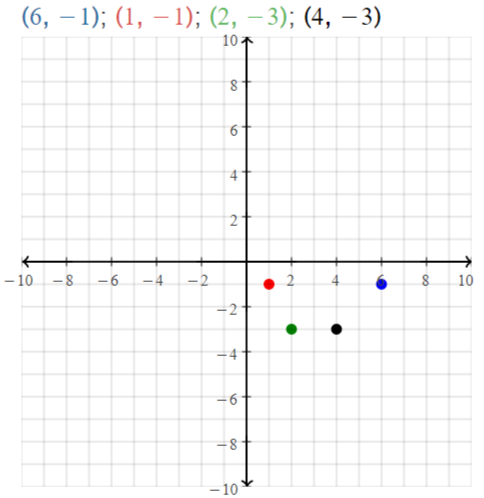
Question 11.
A(8, 3), B(- 1, 3), C(5, 10), D(5, 3)
Answer:
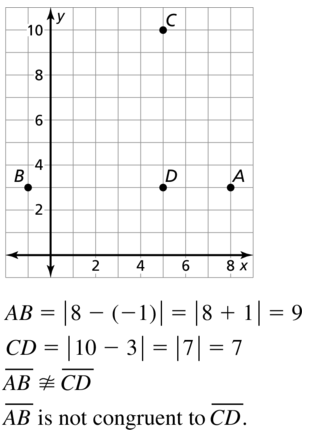
Question 12.
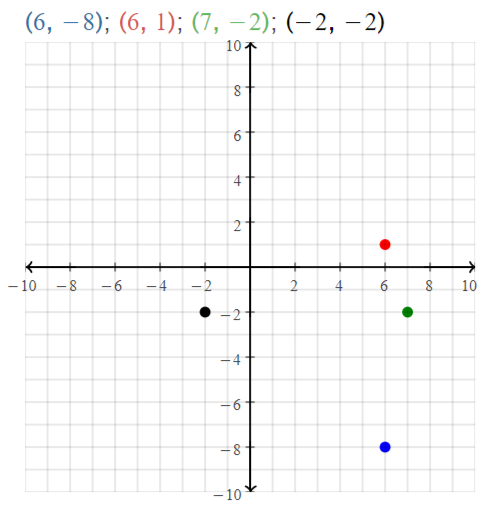
A(6, – 8), B(6, 1), C(7, – 2), D(- 2, – 2)
Answer:
The given points are:
A (6, -8), B (6, 1), C (7, -2), and D (-2, -2)
Let the points be represented as:
A (x1, y1), B (x2, y2), C (x3, y3), and D (x4, y4)
We know that,
The distance between points A and B is:
D = √(x2 – x1)² + (y2 – y1)²
So,
\(\overline{A B}\) = √(6 – 6)² + (8 + 1)²
= √(9)²
= 9
The distance between points C and D is:
\(\overline{C D}\) = √(x4 – x3)² + (y4 – y3)²
= √(-7 – 2)² + (-2 + 2)²
= √(-9)²
= 9
Hence, from the above,
We can conclude that \(\overline{A B}\) is congruent with \(\overline{C D}\)
The representation of the given points in the coordinate plane is:
Question 13.
A(- 5, 6), B(- 5, – 1), C(- 4, 3), D(3, 3)
Answer:
Question 14.
A(10, – 4), B(3, – 4), C(- 1, 2), D(- 1, 5)
Answer:
The given points are:
A (10, -4), B (3, -4), C (-1, 2), and D (-1, 5)
Let the points be represented as:
A (x1, y1), B (x2, y2), C (x3, y3), and D (x4, y4)
We know that,
The distance between points A and B is:
D = √(x2 – x1)² + (y2 – y1)²
So,
\(\overline{A B}\) = √(3 – 10)² + (-4 + 4)²
= √(-7)²
= 7
The distance between points C and D is:
\(\overline{C D}\) = √(x4 – x3)² + (y4 – y3)²
= √(1 – 1)² + (-2 + 5)²
= √3²
= 3
Hence, from the above,
We can conclude that \(\overline{A B}\) is not congruent with \(\overline{C D}\)
The representation of the given points in the coordinate plane is:

In Exercises 15 – 22. find FH.
Question 15.
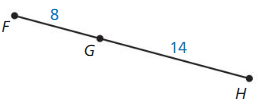
Answer:
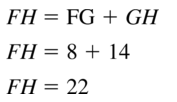
Question 16.
Answer:
The given line segment is:

By using the Segment Addition Postulate,
FH = FG + GH
FH = 19 + 7
FH = 26
Hence, from the above,
We can conclude that the value of FH is: 26
Question 17.
Answer:
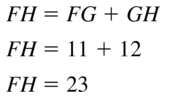
Question 18.
Answer:
The given line segment is:

By using the Segment Addition Postulate,
FH = FG + GH
FH = 4 + 15
FH = 19
Hence, from the above,
We can conclude that the value of FH is: 19
Question 19.
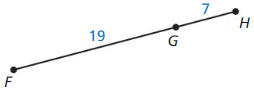
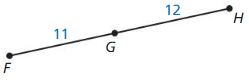
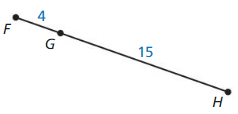
Answer:
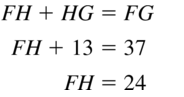
Question 20.
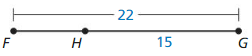
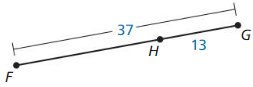
Answer:
The given line segment is:
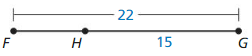
By using the Segment Addition Postulate,
FG = FH + HG
FG = FH + 15
22 = FH + 15
FH = 22 – 15
FH = 7
Hence, from the above,
We can conclude that the value of FH is: 7
Question 21.
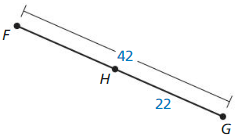
Answer:
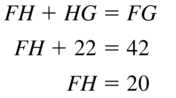
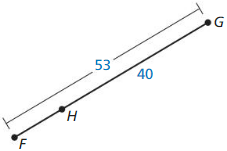
Question 22.
Answer:
Answer:
The given line segment is:

By using the Segment Addition Postulate,
FG = FH + HG
53 = FH + 40
FH = 53 – 40
FH = 13
Hence, from the above,
We can conclude that the value of FH is: 13
ERROR ANALYSIS
In Exercises 23 and 24, describe and correct the error in finding the length of \(\overline{A B}\).
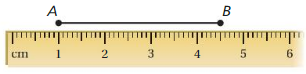
Question 23.

Answer:
Question 24.
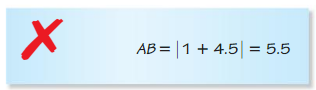
Answer:
We know that,
| x | = x for x > 0
| x | = -x for x < 0
| -x | = x for x > 0
So,
The distance between points A and B is:
| AB| = | 1 – 4.5| or | 4.5 – 1|
Hence,
| AB | = 3.5
Hence, from the above,
We can conclude that the distance between the points A and B is: 3.5
Question 25.
ATTENDING TO PRECISION
The diagram shows an insect called a walking stick. Use the ruler to estimate the length of the abdomen and the length of the thorax to the nearest \(\frac{1}{4}\) inch. How much longer is the walking stick’s abdomen than its thorax? How many times longer is its abdomen than its thorax?
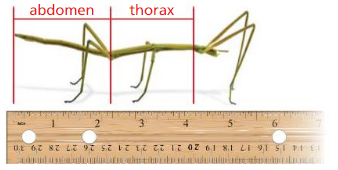
Answer:

Question 26.
MODELING WITH MATHEMATICS
In 2003, a remote-controlled model airplane became the first-ever to fly nonstop across the Atlantic Ocean. The map shows the airplane’s position at three different points during its flight. Point A represents Cape Spear. New foundland. point B represents the approximate position after 1 day, and point C represents Mannin Bay’ Ireland. The airplane left Cape Spear and landed in Mannin Bay.
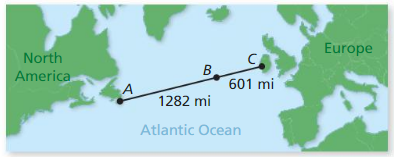
a. Find the total distance the model airplane flew.
Answer:
It is given that a remote-controlled airplane flies from Cape Spear to Mannin Bay that is located across the Atlantic Ocean
Now,
The total distance traveled by the model airplane is represented as the total distance from A to C on the map
Now,
From the map,
AC represents the total distance traveled by the model airplane
AB represents the distance traveled by model airplane from Cape Spear and it is in flight mode after 1 day and it represents as B
BC represents the distance traveled from the middle of the flight to Mannin Bay
So,
Now,
By using the Segment Addition Postulate,
AC = AB + BC
So,
AC = 1281 miles + 601 miles
AC = 1881 miles
Hence, from the above,
We can conclude that the total distance traveled by the model airplane is: 1881 miles
b. The model airplane’s flight lasted nearly 38 hours. Estimate the airplane’s average speed in miles per hour.
Answer:
From part (a),
We observed that,
The total distance traveled by the model airplane is: 1881 miles
It is given that
The model airplane’s flight lasted nearly 38 hours
We know that,
Average speed = \(\frac{Total distance}{Total time}\)
So,
Average speed = \(\frac{1881}{38}\)
= 49.5 miles per hour
Hence, from the above,
We can conclude that the average speed of the airplane is: 49.5 miles per hour
Question 27.
USING STRUCTURE
Determine whether the statements are true or False. Explain your reasoning.
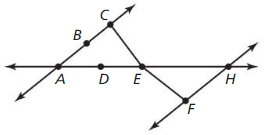
a. B is between A and C.
b. C is between B and E.
c. D is between A and H.
d. E is between C and F.
Answer:
Question 28.
MATHEMATICAL CONNECTIONS
Write an expression for the length of the segment.
a. \(\overline{A C}\)
![]()
Answer:
The given line segment is:
![]()
So,
By using the Segment Addition Postulate,
\(\overline{A C}\) = \(\overline{A B}\) + \(\overline{B C}\)
\(\overline{A C}\) = (x + 2) + (7x – 3)
\(\overline{A C}\) = 8x – 1
Hence, from the above,
We can conclude that the expression of the given line segment is: (8x – 1)
b. \(\overline{Q R}\)
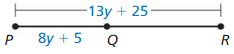
Answer:
The given line segment is:
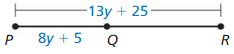
So,
By using the Segment Addition Postulate,
\(\overline{P R}\) = \(\overline{P Q}\) + \(\overline{Q R}\)
13y + 25 = (8y + 5) + \(\overline{Q R}\)
\(\overline{Q R}\) = 13y + 25 – 8y – 5
\(\overline{Q R}\) = 5y + 20
Hence, from the above,
We can conclude that the expression of the given line segment is: (5y + 20)
Question 29.
MATHEMATICAL CONNECTIONS
Point S is between points R and T on \(\overline{R T}\). Use the information to write an equation in term of x. Then Solve the equation and find RS, ST, and RT.
a. RS = 2x + 10
ST = x – 4
RT = 21
b. RS = 3x – 16
ST = 4x – 8
RT = 60
c. RS = 4x – 9
ST=11
RTx+IO
d. RS = 4x – 9
ST = 19
RT = 8x – 14
Answer:


Question 30.
THOUGHT-PROVOKING
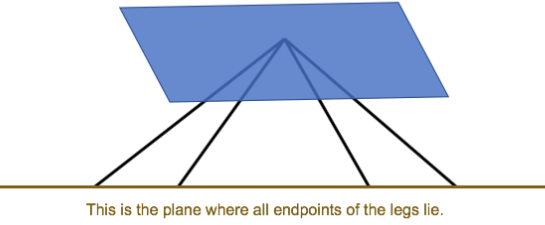
Is it possible to design a table where no two legs have the same length? Assume that the endpoints of the legs must all lie in the same plane. Include a diagram as part o! your answer.
Answer:
It is possible to design a table where no two legs have the same length and that the endpoints of the legs all lie in the same plane. They just have to be attached to the table at different angles as seen in the below figure:
Question 31.
MODELING WITH MATHEMATICS
You have w walk from Room 103 to Room 117.
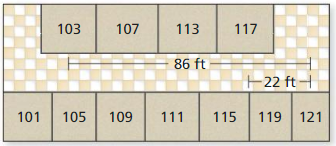
a. How many feet do you travel from Room 103 to Room 117?
b. You can walk 4.4 feet per second. How many minutes will it take you to get to Room 117?
c. Why might it take you longer than the time in Part (b)?
Answer:

Question 32.
MAKING AN ARGUMENT
Your friend and your Cousin discuss measuring with a ruler. Your friend says that you must always line up objects at the zero on a ruler. Your cousin says it does not matter. Decide who is correct and explain your reasoning.
Answer:
Your cousin is correct
Explanation:
It is given that,
Your friend said that you must always line up objects at the zero on a ruler and your cousin said that it does not matter
Now,
We just have to deduce the endpoint length from the start point length on the ruler
Example:
If you measure a segment that is 5 cm long, it is the same if you put zero on the start point or 5 on the start point, then 10 is on the endpoint
Remember that the starting point will be any number on the ruler and the ending point will be n units away from that number
So,
5 – 0 = 5 is same as 10 – 5 = 5
Question 33.
REASONING
You travel twin City X to City Y. You know that the round-trip distance is 647 miles. City Z, a city you pass on the way, is 27 miles from City X. Find the distance from City Z to City Y. Justify your answer.
Answer:

Question 34.
HOW DO YOU SEE IT?
The bar graph shows the win-loss record for a lacrosse team over a period of three years. Explain how you can apply the Ruler Postulate (Post. 1.1) and the Segment Addition Postulate (Post. 1.2) when interpreting a stacked bar graph like the one shown.

Answer:
We know that,
Ruler Postulate:
The points on a line can be put into a one-to-one correspondence (paired) with the real numbers. The distance between any two points is represented by the absolute value of the difference between the numbers.
Segment Addition Postulate:
The Segment Addition Postulate states that given 2 points A and C, a third point B lies on the line segment AC if and only if the distances between the points satisfy the equation
AB + BC = AC
Hence,
By using the ruler and Segment Addition Postulates,
We can conclude that the number of games is equal to the number of wins and the number of losses
Question 35.
ABSTRACT REASONING
The points (a,b) and (c, b) from a segment, and the points (d, e) and (d, f ) from a segment. Create an equation assuming the segments are congruent. Are there any letters not used in the equation? Explain.
Answer:

Question 36.
MATHEMATICAL CONNECTIONS
In the diagram, \(\overline{A B}\) ≅ \(\overline{B C}\), \(\overline{A C}\) ≅ \(\overline{C D}\), and AD = 12. Find the lengths of all segments in the diagram. Suppose you choose one of the segments at random. What is the probability that the measure of the segment is greater than 3? Explain your reasoning.
Answer:
The given figure is:

It is given that,
\(\overline{A B}\) ≅ \(\overline{B C}\)
\(\overline{A C}\) ≅ \(\overline{C D}\)
\(\overline{A D}\) = 12
Now,
By using the Segment Addition Postulate,
AD = AB + BC + CD
12 = AB + BC + CD
Now,
AD = AC + CD
AD = 2CD
CD = \(\frac{12}{2}\)
CD = 6
So,
AC = 6
Now,
Fro the given line segment,
AC = AB + BC
AC = 2BC
BC = \(\frac{6}{2}\)
BC = 3
Henc,
AB = 3
Now,
We know that,
Probability = \(\frac{The number of favorable cases}{The total number of cases}\)
So,
The probability of getting the segment that the length is greater than 3 is:
P = \(\frac{The number of segments that the length is greater than 3}{The number of total segments}\)
P = 3 / 6
P = 0.5
Hence, from the above,
We can conclude that the probability of getting the length of the line segments greater than 3 is: 0.5
Question 37.
CRITICAL THINKING
Is it possible to use the Segment Addition Postulate (Post. 1.2) to show FB > CB or that AC > DB? Explain your reasoning.
![]()
Answer:

Maintaining Mathematical Proficiency
Simplify.
Question 38.
\(\frac{-4+6}{2}\)
Answer:
The given expression is: \(\frac{-6 + 4}{2}\)
So,
\(\frac{-4+6}{2}\) = \(\frac{2}{2}\)
= \(\frac{1}{1}\)
= 1
Hence, from the above,
We can conclude that the value of the given expression is: 1
Question 39.
\(\sqrt{20+5}\)
Answer:
![]()
Question 40.
\(\sqrt{25+9}\)
Answer:
The given expression is: \(\sqrt{25 + 9}\)
So,
\(\sqrt{25+9}\) = \(\sqrt{34}\)
Hence, from the above,
We can conclude that the value of the given expression is: \(\sqrt{34}\)
Question 41.
\(\frac{7+6}{2}\)
Answer:
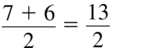
Solve the equation.
Question 42.
5x + 7 = 9x – 17
Answer:
The given equation is:
5x + 7 = 9x – 17
So,
5x – 9x = -17 – 7
-4x = -24
4x = 24
x = \(\frac{24}{4}[/larex]
x = 6
Hence, from the above,
We can conclude that the value of x for the given equation is: 6
Question 43.
[latex]\frac{3+y}{2}=6\) = 6
Answer:
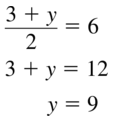
Question 44.
\(\frac{-5+x}{2}\) = – 9
Answer:
The given equation is:
\(\frac{-5+x}{2}\) = – 9
So,
-5 + x = -9 (2)
-5 + x = -18
x = -18 + 5
x = -13
Hence, from the above,
We can conclude that the value of x for the given equation is: -13
Question 45.
– 6x – 13 = – x = 23
Answer:

1.3 Using Midpoint and Distance Formulas
EssentiaI Question
How can you find the midpoint and length of a line segment in a coordinate plane?
Answer:
Let the line segment is formed by the points A (x1, y1), B (x2, y2)
So,
The coordinates of the midpoint of the line segment are given as:
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
The length of the line segment in a coordinate plane is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
Exploration 1
Finding the Midpoint of a Line Segment
Work with a partner.
Use centimeter graph paper.
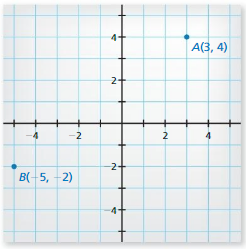
a. Graph \(\overline{A B}\), where the points A and B are as shown.
Answer:
From the given graph,
The given points are:
A (3, 4), B (-5, -2)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points A and B is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(-5 – 3)² + (-2 – 4)²}\)
D = \(\sqrt{(-8)² + (-6)²}\)
D = \(\sqrt{64 + 36}\)
D = \(\sqrt{100}\)
D = 10 cm
Hence, from the above,
We can conclude that the length of \(\overline{A B}\) is: 10cm
The representation of \(\overline{A B}\) is:

b. Explain how to bisect \(\overline{A B}\), that is, to divide AB into two congruent line segments. Then
bisects \(\overline{A B}\) and use the result to find the midpoint M of \(\overline{A B}\).
Answer:
The steps to find the bisector of \(\overline{A B}\) is:
a. Place the compass at one end of the line segment
b. Adjust the compass to slightly longer than half of the line segment length
c. Draw arcs above and below the line
d. Keeping the same compass width, draw arcs from the other end of line
e. Place ruler where the arcs cross and draw the line segment
Now,
From part (a),
The representation of \(\overline{A B}\) is:

Now,
The representation of the perpendicular bisector and the midpoint M of \(\overline{A B}\) is:
Hence, from the above figure,
The midpoint of \(\overline{A B}\) is: 5 cm
c. What are the coordinates of the midpoint M?
Answer:
We know that,
The coordinates of the midpoint of the line segment are given as:
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{3 – 5}{2}\),\(\frac{4 – 2}{2}\))
M = (\(\frac{-2}{2}\),\(\frac{2}{2}\))
M = (-1, 1)
Hence,
The coordinates of the midpoint M is: (-1, 1)
d. Compare the x-coordinates of A, B, and M. Compare the y-coordinates of A, B, and M. How arc the coordinates of the 4 midpoints M related to the coordinates of A and B?
Answer:
The coordinates of A, B, and M are:
A (3, 4), B (-5, -2), and M (-1, 1)
Compare the given coordinates with
A (x1, y1), B (x2, y2), C (x3, y3)
Hence,
The x-coordinates and y-coordinates of M are related to the coordinates of A and B are:
M= (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}[/latex}
Exploration 2
Finding the Length of a Line Segment work with a partner. Use centimeter graph paper.
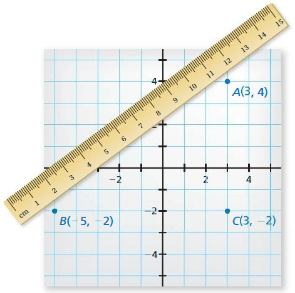
a. Add point C to your graph as shown.
Answer:
From the graph,
The given points are:
A (3, 4), B (-5, -2), and C (3, 2)
Compare the given points with
A (x1, y1), B (x2, y2), and C (x3, y3)
So,
The coordinates of the length between points A and B is:
D = ( |x2 + x1|, |y2 + y1| )
So,
D = ( |-5 + 3|, |-2 + 4| )
D = ( |-2|, |2| )
D = (-2, 2)
Now,
The length between AB and C is:
D = ( |x2 + x1|, |y2 + y1| )
So,
D = ( |-2 + 3|, |2 + 3| )
D = ( |1|, |5| )
D = ( 1, 5)
Hence, frm the above,
We can conclude that the coordinates of the total length by adding point C is: (1, 5)
b. Use the Pythagorean Theorem to find the length of AB.
Answer:
The given points are:
A (3, 4), B (-5, -2), and C (3, 2)
Compare the given points with
A (x1, y1), B (x2, y2), and C (x3, y3)
We know that,
The length of a segment is:
D = [latex]\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
\(\overline{B C}\) = \(\sqrt{(-5 + 3)² + (-2 + 2)²}\)
= \(\sqrt{(-2)² + (0)²}\)
= \(\sqrt{4 + 0}\)
=\(\sqrt{4}\) = 2
\(\overline{A C}\) = \(\sqrt{(-3 + 3)² + (-2 + 4)²}\)
= \(\sqrt{0² + 2²}\)
= \(\sqrt{2²}\) = 2
Now,
According to Pythagoras theorem,
Hypotenuse² = Side² + Side²
So,
From the graph,
AB represents the hypotenuse
AC represents the side
BC represents the side
So,
AB² = AC² + BC²
AB² = 2² + 2²
AB² = 4 + 4
AB² = 8
AB = \(\sqrt{8}\)
Hence, from the above,
We can conclude that the length of AB is: \(\sqrt{8}\)
c. Use a centimeter ruler to verify the length you found in part (b).
MAKING SENSE OF PROBLEMS
To be proficient in math, you need to check your answers and continually ask yourself, “Does this make sense?’
Answer:
From part (b),
We found the length of \(\overline{A B}\) as: \(\sqrt{8}\)
Now,
To verify the length of \(\overline{A B}\), use the “Distance formula”
We know that,
The distance beween 2 points of a line segment is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
\(\overline{A B}\) = \(\sqrt{(-5 + 3)² + (-2 + 4)²}\)
= \(\sqrt{(-2)² + (2)²}\)
= \(\sqrt{4 + 4}\)
=\(\sqrt{8}\)
d. Use the Pythagorean Theorem and point M from Exploration 1 to find the lengths of \(\overline{A M}\) and \(\overline{M B}\). What can you conclude?
Answer:
Communicate Your Answer
Question 3.
How can you find the midpoint and length ola line segment in a coordinate plane?
Answer:
Let the line segment is formed by the points A (x1, y1), B (x2, y2)
So,
The coordinates of the midpoint of the line segment are given as:
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
The length of the line segment in a coordinate plane is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
Question 4.
Find the coordinates of the midpoint M and the length of the line segment whose endpoints are given.
a. D(- 10, – 4), E(14, 6)
Answer:
The given points are:
D (-10, -4), E (14, 6)
We know that,
The coordinates of the midpoint of the line segment are given as:
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
M = (\(\frac{14 – 10}{2}\), \(\frac{6 – 4}{2}\))
M = (\(\frac{4}{2}\), \(\frac{2}{2}\))
M = (2, 1)
Hence, from the above,
We can conclude that the coordinates of the midpoint of the given points are: (2, 1)
b. F(- 4, 8), G(9, 0)
Answer:
The given points are:
F (-4, 8), G (9, 0)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{9 – 4}{2}\), \(\frac{8 + 0}{2}\))
M = (\(\frac{5}{2}\), \(\frac{8}{2}\))
M = (\(\frac{5}{2}\), 4)
Hence, from the above,
We can conclude that the coordinates of the midpoint of the given points are: (\(\frac{5}{2}\), 4)
Lesson 1.3 Using Midpoint and Distance Formulas
Monitoring Progress
Identify the segment, bisector of \(\overline{P Q}\). Then find PQ.
Question 1.
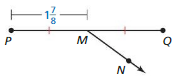
Answer:
The given line segment is:

We know that,
A segment has a starting point and an ending point
So,
From the above figure,
We can observe that
\(\overline{P Q}\) is a “Segment”
We know that,
A “Bisector” is a line that divides a line segment into two congruent (or) equal parts
So,
From the above figure,
We can observe that
The bisector of \(\overline{P Q}\) is: MN
Now,
From the above figure,
The bisector divided the given line segment into 2 equal parts and given the length of 1 part
So,
It is given that,
\(\overline{P M}\) = 1\(\frac{7}{8}\)
Hence,
The length of \(\overline{P Q}\) = \(\overline{P M}\) + \(\overline{M Q}\)
= 2 × 1\(\frac{7}{8}\)
= 2 × \(\frac{15}{8}\)
= \(\frac{2}{1}\) × \(\frac{15}{8}\)
= \(\frac{15}{4}\)
Hence, from the above,
We can conclude that the length of \(\overline{p Q} \) is: \(\frac{15}{4}\)
Question 2.
![]()
Answer:
The given line segment is:
![]()
We know that,
A segment has a starting point and an ending point
So,
From the above figure,
We can observe that
\(\overline{P Q}\) is a “Segment”
We know that,
A “Bisector” is a line that divides a line segment into two congruent (or) equal parts
So,
From the above figure,
We can observe that
The bisector of \(\overline{P Q}\) is: M
Now,
From the above figure,
The bisector divided the given line segment into 2 equal parts and given the length of 1 part
So,
It is given that,
\(\overline{M Q}\) = 2\(\frac{2}{7}\)
Hence,
The length of \(\overline{P Q}\) = \(\overline{P M}\) + \(\overline{M Q}\)
= 2 × 2\(\frac{2}{7}\)
= 2 × \(\frac{16}{7}\)
= \(\frac{2}{1}\) × \(\frac{16}{7}\)
= \(\frac{32}{7}\)
Hence, from the above,
We can conclude that the length of \(\overline{P Q} \) is: \(\frac{32}{7}\)
Question 3.
Identify the segment bisector of \(\overline{P Q}\). Then find MQ.
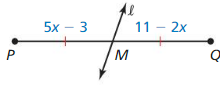
Answer:
The given figure is:

We know that,
A “Bisector” is a line that divides a line segment into 2 congruent (or) equal parts
So,
The bisector of \(\overline{P Q}\) is: line l
We know that,
Due to a Bisector,
In \(\overline{P Q}\),
\(\overline{P M}\) = \(\overline{M Q}\)
So,
5x – 3 = 11 – 2x
5x + 2x = 11 + 3
7x = 14
x = \(\frac{14}{7}\)
x = 2
So,
MQ = 11 – 2x
MQ = 11 – 2 (2)
MQ = 11 – 4
MQ = 7
Hence, from theabove,
We can conclude that the value of MQ is:7
Question 4.
Identify the segment bisector or \(\overline{R S}\). Then find RS.
Answer:
Question 5.
The endpoints of \(\overline{A B}\) are A (1, 2) and B(7, 8). Find the coordinates of the midpoint M.
Answer:
The given endpoints of \(\overline{A B}\) are:
A (1, 2), B (7, 8)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{1 + 7}{2}\), \(\frac{8 + 2}{2}\))
M = (\(\frac{8}{2}\), \(\frac{10}{2}\))
M = (4, 5)
Hence, from the above,
We can conclude that the coordinates of the midpoint of \(\overline{A B}\) are: (4, 5)
Question 6.
The endpoints of \(\overline{C D}\) are C( – 4, 3) and D(6, 5). Find the coordinates of the midpoint M.
Answer:
The given endpoints of \(\overline{C D}\) are:
C (-4, 3), D (6, 5)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{6 – 4}{2}\), \(\frac{5 + 3}{2}\))
M = (\(\frac{2}{2}\), \(\frac{8}{2}\))
M = (1, 4)
Hence, from the above,
We can conclude that the coordinates of the midpoint of \(\overline{C D}\) are: (1, 4)
Question 7.
The midpoint of \(\overline{T U}\) is M(2, 4). One endpoint is T(1, 1). Find the coordinates of endpoint U.
Answer:
The given points of \(\overline{T U}\) are:
M (2, 4), T (1, 1)
Let the one endpoint be T
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(2, 4) = (\(\frac{x1 + 1}{2}\), \(\frac{y1 + 1}{2}\))
So,
\(\frac{x1 + 1}{2}\) = 2 \(\frac{y1 + 1}{2}\) = 4
x1 + 1 = 2 (2) y1 + 1 = 4 (2)
x1 = 4 – 1 y1 = 8 – 1
x1 = 3 y1 = 7
Hence, from the above,
We can conclude that the other endpoint of \(\overline{T U}\) is: (3, 7)
Question 8.
The midpoint of \(\overline{V W}\) is M (- 1, – 2). One endpoint is W(4, 4). Find the coordinates of endpoint V.
Answer:
The given points of \(\overline{V W}\) are:
M (-1, -2), W (4, 4)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(-1, -2) = (\(\frac{x1 + 4}{2}\), \(\frac{y1 + 4}{2}\))
So,
\(\frac{x1 + 4}{2}\) = -1 \(\frac{y1 + 4}{2}\) = -2
x1 + 4 = -1 (2) y1 + 4 = -2 (2)
x1 = -2 – 4 y1 = -4 – 4
x1 = -6 y1 = -8
Hence, from the above,
We can conclude that the other endpoint V is: (-6, -8)
Question 9.
In Example 4, a park is 3 miles east and 4 miles south of your apartment. Find the distance between the park and your school.
Answer:
Exercise 1.3 Using Midpoint and Distance Formulas
Question 1.
VOCABULARY
If a point ray, line, line segment, or plane intersects a segment at its midpoint, then what does it do to the segment?
Answer:
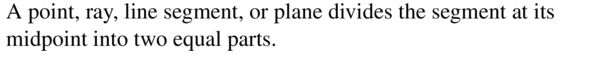
Question 2.
COMPLETE THE SENTENCE
To find the length of \(\overline{A B}\), with endpoints A(- 7, 5) and B(4, – 6). you can use the _________ .
Answer:
We know that,
To find the length with two endpoints, we use the “Distance formula”
The distance between the 2 endpoints is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
Hence, from the above,
We can conclude that
To find the length of \(\overline{A B}\), with endpoints A(- 7, 5) and B(4, – 6). you can use the ” Distance formula ”
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6. identify the segment bisector of \(\overline{R S}\). Then find RS.
Question 3.
Answer:
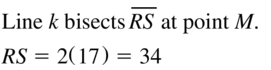
Question 4.
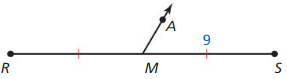
Answer:
The given line segment is:

We know that,
A “Bisector” is a line that divides a line segment into 2 equal parts
So,
The bisector of \(\overline{R S}\) is: line A
From the given figure,
It is given that
\(\overline{M S}\) = 9
Hence,
\(\overline{R S}\) = 9 (2)
\(\overline{R S}\) = 18
Hence, from the above,
We can conclude that the length of \(\overline{R S}\) is: 18
Question 5.

Answer:
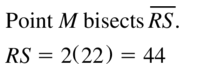
Question 6.
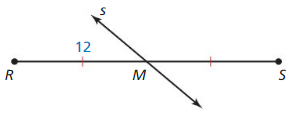
Answer:
The given line segment is:

We know that,
A “Bisector” is a line that divides a line segment into 2 equal parts
So,
The bisector of \(\overline{R S}\) is: line s
From the given figure,
It is given that
\(\overline{R M}\) = 12
Hence,
\(\overline{R S}\) = 12 (2)
\(\overline{R S}\) = 24
Hence, from the above,
We can conclude that the length of \(\overline{R S}\) is: 24
In Exercises 7 and 8, identify the segment bisector of \(\overline{J K}\). Then find JM.
Question 7.
![]()
Answer:

Question 8.
Answer:
The given line segment is:

From the above figure,
A “Bisector” is a line that divides a line segment into 2 equal parts
So,
The bisector of \(\overline{J K}\) is: line l
Since the 2 parts are equal,
\(\overline{J M}\) = \(\overline{M K}\)
So,
3x + 15 = 8x + 25
3x – 8x = 25 – 15
-5x = 10
x = \(\frac{10}{-5}\)
x = -2
So,
JM = 3x + 15
JM = 3 (-2) + 15
JM = -6 + 15
JM = 9
Hence, from he above,
We can conclude that the length of JM is: 9
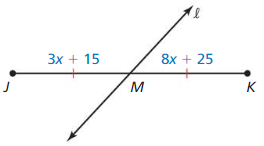
In Exercises 9 and 10. identify the segment bisector of \(\overline{X Y}\). Then find XY.
Question 9.
Answer:
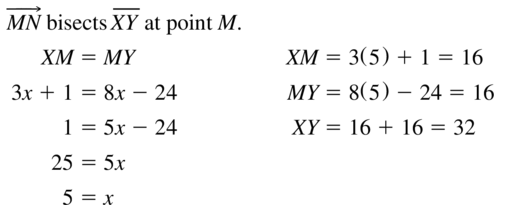
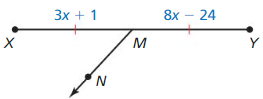
Question 10.
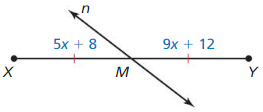
Answer:
The given line segment is:

From the above figure,
A “Bisector” is a line that divides a line segment into 2 equal parts
So,
The bisector of \(\overline{X Y}\) is: line n
Since the 2 parts are equal,
\(\overline{X M}\) = \(\overline{M Y}\)
So,
5x + 8 = 9x + 12
5x – 9x = 12 – 8
-4x = 4
x = \(\frac{-4}{4}\)
x = -1
So,
XY = XM + MY
XY = 5x + 8 + 9x + 12
XY = 14x + 20
XY = 14 (-1) + 20
XY = 20 – 14
XY = 6
Hence, from the above,
We can conclude that the length of XY is: 6
CONSTRUCTION
In Exercises 11 – 14, copy the segment and construct a segment bisector by paper folding. Then label the midpoint M.
Question 11.
![]()
Answer:

Question 12.
![]()
Answer:
The given line segment is:
![]()
We know that,
A “Bisector” is a line or point that divides a line segment into 2 equal parts
Hence,
The representation of the bisector along with midpoint M of the given segment is:

Question 13.

Answer:

Question 14.
Answer:
The given line segment is:

We know that,
A “Bisector” is a line or point that divides a line segment into 2 equal parts
Hence,
The representation of the bisector along with midpoint M of the given segment is:
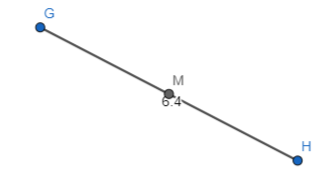
In Exercises 15 – 18, the endpoints of \(\overline{C D}\) are given. Find the coordinates of the midpoint M.
Question 15.
C (3, – 5) and D (7, 9)
Answer:
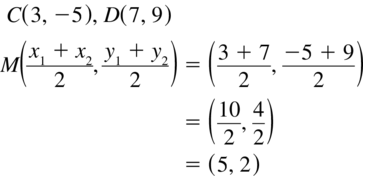
Question 16.
C (4, 7) and D (0, – 3)
Answer:
The given endpoints of \(\overline{C D}\) are:
C (4, 7), D (0, -3)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{4 + 0}{2}\), \(\frac{7 – 3}{2}\))
M = (\(\frac{4}{2}\), \(\frac{4}{2}\))
M = (2, 2)
Hence, from the above,
We can conclude that the coordinates of the midpoint of \(\overline{C D}\) are: (2, 2)
Question 17.
C (- 2, 0) and D (4, 9)
Answer:
Question 18.
C (- 8, – 6) and D (- 4, 10)
Answer:
The given endpoints of \(\overline{C D}\) are:
C (-8, -6), D (-4, 10)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{-8 – 4}{2}\), \(\frac{10 – 6}{2}\))
M = (\(\frac{-12}{2}\), \(\frac{4}{2}\))
M = (-6, 2)
Hence, from the above,
We can conclude that the coordinates of the midpoint of \(\overline{C D}\) are: (-6, 2)
In Exercises 19 – 22. the midpoint M and one endpoint of \(\overline{G H}\) are given. Find the coordinates of the other endpoint.
Question 19.
G (5, – 6) and M (4, 3)
Answer:
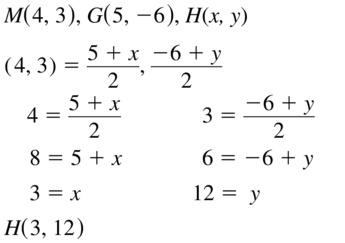
Question 20.
H (- 3, 7) and M (- 2, 5)
Answer:
The given points of \(\overline{G H}\) are:
M (-2, 5), H (-3, 7)
Let the point G be: (x1, y1)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(-2, 5) = (\(\frac{x1 -3}{2}\), \(\frac{y1 + 7}{2}\))
So,
\(\frac{x1 – 3}{2}\) = -2 \(\frac{y1 + 7}{2}\) = 5
x1 – 3 = -2 (2) y1 + 7 = 5 (2)
x1 = -4 – 3 y1 = 10 – 7
x1 = -7 y1 = 3
Hence, from the above,
We can conclude that the other endpoint G is: (-7, 3)
Question 21.
H ( – 2, 9) and M(8, 0)
Answer:
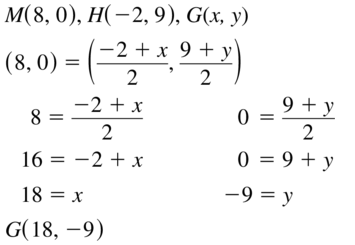
Question 22.
G (- 4, 1) and M (- \(\frac{13}{2}\), – 6)
Answer:
The given points of \(\overline{G H}\) are:
M (- \(\frac{13}{2}\), – 6), G (-4, 1)
Let the other endpoint be H (x2, y2)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(- \(\frac{13}{2}\), – 6) = (\(\frac{x2 – 4}{2}\), \(\frac{y2 + 1}{2}\))
So,
\(\frac{x2 – 4}{2}\) = – \(\frac{13}{2}\) \(\frac{y2 + 1}{2}\) = -6
x2 – 4 = – \(\frac{13}{2}\) (2) y2 + 1 = -6 (2)
x1 = -13 + 4 y2 = -12 – 1
x1 = -9 y1 = -13
Hence, from the above,
We can conclude that the other endpoint H is: (-9, -13)
In Exercises 23 – 30, find the distance between the two points.
Question 23.
A (13, 2) and B (7, 10)
Answer:
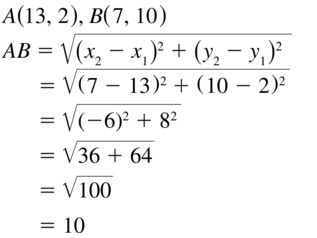
Question 24.
C (- 6, 5) and D (- 3, 1)
Answer:
The given points are:
C (-6, 5), D (-3, 1)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points C and D is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(6 – 3)² + (1 – 5)²}\)
D = \(\sqrt{(3)² + (-4)²}\)
D = \(\sqrt{9 + 16}\)
D = \(\sqrt{25}\)
D = 5
Hence, from the above,
We can conclude that the distance between 2 given points is: 5
Question 25.
E (3, 7) and F (6, 5)
Answer:
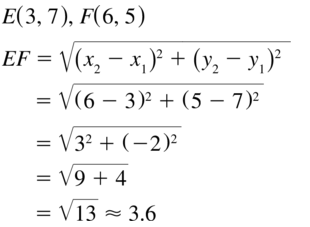
Question 26.
G (- 5, 4) and H (2, 6)
Answer:
The given points are:
G (-5, 4), H (2, 6)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points A and B is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(2 + 5)² + (6 – 4)²}\)
D = \(\sqrt{(7)² + (2)²}\)
D = \(\sqrt{49 + 4}\)
D = \(\sqrt{53}\)
Hence, from the above,
We can conclude that the distance between 2 given points is: \(\sqrt{53}\)
Question 27.
J (- 8, 0) and K (1, 4)
Answer:
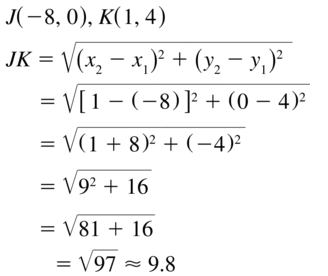
Question 28.
L (7, – 1) and M (- 2, 4)
Answer:
The given points are:
L (7, -1), M (-2, 4)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points A and B is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(-2 – 7)² + (4 + 1)²}\)
D = \(\sqrt{(-9)² + (5)²}\)
D = \(\sqrt{81 + 25}\)
D = \(\sqrt{106}\)
Hence, from the above,
We can conclude that the distance between 2 given points is: \(\sqrt{106}\)
Question 29.
R (0, 1) and S (6, 3.5)
Answer:
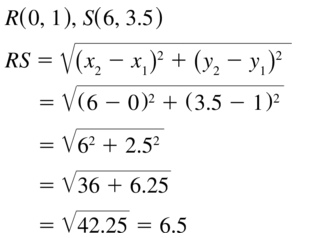
Question 30.
T (13, 1.6) and V (5.4, 3.7)
Answer:
The given points are:
T (13, 1.6), V (5.4, 3.7)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points A and B is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(13 – 5.4)² + (1.6 – 3.7)²}\)
D = \(\sqrt{(7.6)² + (2.1)²}\)
D = \(\sqrt{57.76 + 4.41}\)
D = \(\sqrt{62.17}\)
D = 7.884
Hence, from the above,
We can conclude that the distance between 2 given points is: 7.884
ERROR ANALYSIS
In Exercises 31 and 32, describe and correct the error in finding the distance between A(6, 2) and 8(1, – 4).
Question 31.
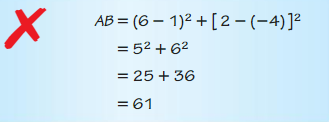
Answer:

Question 32.
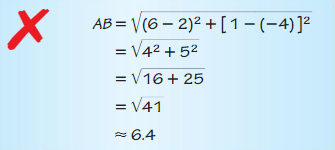
Answer:
In the above figure,
The distance between A and B is given by using the formula:
D = \(\sqrt{(x1 – y1)² + (x2 – y2)²}\)
But,
The used formula is wrong
Now,
The given points are:
A (6, 2), B (1, -4)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points A and B is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(6 – 1)² + (2 + 4)²}\)
D = \(\sqrt{(5)² + (6)²}\)
D = \(\sqrt{25 + 36}\)
D = \(\sqrt{61}\)
D = 7.8
Hence, from the above,
We can conclude that the distance between A and B is: 7.8
COMPARING SEGMENTS
In Exercises 33 and 34, the endpoints of two segments are given. Find each segment length. Tell whether the segments are congruent. If they are not congruent, a state which segment length is greater.
Question 33.
\(\overline{A B}\): A(0, 2), B(- 3, 8) and \(\overline{C D}\): C(- 2, 2), D(0, – 4)
Answer:

Question 34.
\(\overline{E F}\): E(1, 4),F(5, 1) and \(\overline{G H}\): G(-3, 1), H(1, 6)
Answer:
The given points of \(\overline{E F}\) are:
E (1, 4), F (5, 1)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points E and F is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(5 – 1)² + (1 – 4)²}\)
D = \(\sqrt{(4)² + (-3)²}\)
D = \(\sqrt{16 + 9}\)
D = \(\sqrt{25}\)
D = 5
Now,
The given points are:
G (-3, 1), H (1, 6)
Compare the given points with
A (x1, y1), B (x2, y2)
So,
The distance between points G and H is given as:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
D = \(\sqrt{(-1 – 3)² + (1 – 6)²}\)
D = \(\sqrt{(-4)² + (-5)²}\)
D = \(\sqrt{16 + 25}\)
D = \(\sqrt{41}\)
D = 6.4
Hence, from the above,
We can conclude that
The lengths of \(\overline{E F}\) and \(\overline{G H}\) are not congruent
The comparison of the lengths is:
\(\overline{E F}\) < \(\overline{G H}\)
Question 35.
WRITING
Your friend is having trouble understanding the Midpoint Formula.
a. Explain how to find the midpoint when given the two endpoints in your own words.
b. Explain how to tind the other endpoint when given one endpoint and the midpoint in your own words.
Answer:

Question 36.
PROBLEM-SOLVING
In baseball, the strike zone is the region a baseball needs to pass through for the umpire to declare it a strike when the butler does not swing. The top of the strike zone is a horizontal plane passing through the midpoint in the top of the batter’s shoulders and the top of the uniform pants when the player is in a batting stance. Find the height of T. (Note: All heights are in inches.)

Answer:
It is given that the strike zone is the region a baseball needs to pass through for the umpire to declare it a strike when the butler does not swing. The top of the strike zone is a horizontal plane passing through the midpoint in the top of the batter’s shoulders and the top of the uniform pants when the player is in a batting stance.
So,
From the figure,
we can observe that the height of T lies between 60 and 42
So,
When we find the mid value of 60 and 42, we will get the height of T
So,
T = \(\frac{60 + 42}{2}\)
T = \(\frac{102}{2}\)
T = 51
Hence, from he above,
We can conclude that the height of T is: 51 inches
Question 37.
MODELING WITH MATHEMATICS
The figure shows the position of three players during part of a water polo match. Player A throws the ball to Player B. who then throws the ball to Player C.
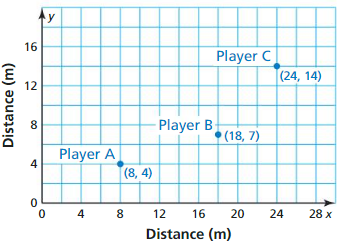
a. Ho far did Player A throw the hail? Player B?
b. How far would Player A have to throw the ball to throw it directly to Player C?
Answer:

Question 38.
MODELING WITH MATHEMATICS
Your school is 20 blocks east and 12 blocks south of your house. The mall is 10 blocks north and 7 blocks west of our house. You plan on going to the mall right after school. Find the distance between your school and the mall assuming there is a road directly connecting the school and the mall. One block is 0.1 mile.
Answer:
The representation of the coordinates of school and Mall in the coordinate plane is:
From the above graph,
The coordinates of the school and Mall are:
S (20, -12), M (-7, 10)
Compare the given points with
A (x1, y), B (x2, y2)
So,
The distance between the schoola and Mall is given as:
SM = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
SM = \(\sqrt{(-7 – 20)² + (10 + 12)²}\)
SM = \(\sqrt{(-27)² +(22)²}\)
SM = \(\sqrt{1213}\)
SM = 34.8 miles
Hence, from the above,
We can conclude that the distance between the school and the Mall is: 34.8 miles
Question 39.
PROBLEM-SOLVING
A path goes around a triangular park, as shown.
a. Find the distance around the park to the nearest yard.
b. A new path and a bridge are constructed from point Q to the midpoint M of \(\overline{P R}\). Find QM to the nearest yard.
c. A man jogs from P to Q to M Lo R to Q and back to P at an average speed of 150 yards per minute. About how many minutes does it take? Explain your reasoning.
Answer:


Question 40.
MAKING AN ARGUMENT
Your friend claims there is an easier way to find the length of a segment than the Distance Formula when the x-coordinates of the endpoints are equal. He claims all you have to do is subtract the y-coordinates. Do you agree with his statement? Explain your reasoning.
Answer:
Yes, your friend is correct
Explanation:
We know that,
Distance between 2 points = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
It is given that the x-coordinates are equal
So,
x1 = x2 = 0
So,
Distance between 2 points = y2 – y1
Hence, from the above,
We can conclude that your friend is correct
Question 41.
MATHEMATICAL CONNECTIONS
Two points are located at (a, c) and (b, c). Find the midpoint and the distance between the two points.
Answer:
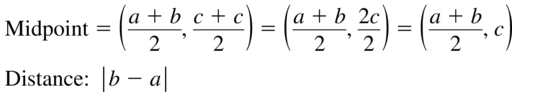
Question 42.
HOW DO YOU SEE IT?
\(\overline{A B}\) contains midpoint M and points C and D. as shown. Compare the lengths. If you cannot draw a conclusion. write impossible to tell. Explain your reasoning.
a. AM and MB
b. AC and MB
c. MC and MD
d. MB and DB
Answer:
Question 43.
ABSTRACT REASONING
Use the diagram in Exercise 42. The points on \(\overline{A B}\) represent locations you pass on your commute to work. You travel from your home at location A to location M before realizing that your left your lunch at home. You could turn around to get your lunch and then continue to work at location B. Or you could go to work and go to location D for lunch today. You want to choose the option that involves the least distance you must travel. which option should you choose? Explain your reasoning.
Answer:

Question 44.
THOUGHT-PROVOKING
Describe three ways to divide a rectangle into two congruent regions. Do the regions have to he triangles? Use a diagram to support your answer.
Answer:
The division of triangles into 2 congruent regions don’t have to be a triangle
Now,
case (i):
In the above case,
The 2 regions are rectangles
case (ii):
In the above case,
The 2 regions are triangles
case (iii):

In the above case,
The 2 regions are squares
Question 45.
ANALYZING RELATIONSHIPS
The length of \(\overline{X Y}\) is 24 centimeters. The midpoint of \(\overline{X Y}\) is M. and C is on \(\overline{X M}\) so that XC is \(\frac{2}{3}\) of XM. Point D is on \(\overline{M Y}\) so that MD is \(\frac{3}{4}\) of MY. What is the length of \(\overline{C D}\)?
Answer:
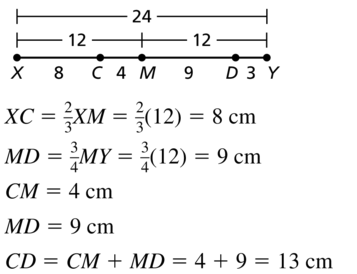
Maintaining Mathematical Proficiency
Find the perimeter and area of the figure.
Question 46.
Answer:
The given figure is:

The above figure is: Square
So,
We know that,
The perimeter of a square = 4 × Side
The area of a square = Side²
From the above figure,
The length of the side = 5 cm
So,
The perimeter of a square = 4 (5) = 20 cm
The area of a square = 5² = 25 cm²
Hence, from the above,
We can conclude that
The perimeter of a square is: 20 cm
The area of a square is: 25 cm²
Question 47.
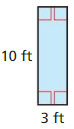
Answer:
Question 48.
Answer:
The given figure is:

From the above,
The given figure is: Triangle
We know that,
The perimeter of triangle = The sum of all the sides of the given triangle
The area of triangle = \(\frac{1}{2}\) × Base × Height
So,
The perimeter of triangle = 3 + 4 + 5 = 12 m
The area of triangle = \(\frac{1}{2}\) × 3 × 4
= \(\frac{1}{2}\) × \(\frac{4}{1}\) × 3
= 6 m²
Hence, from the above,
We can conclude that
The perimeter of triangle is: 12 m
The area oftriangle is: 6 m²
Question 49.
Answer:
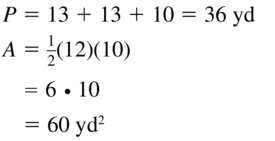
Solve the inequality. Graph the solution.
Question 50.
a + 18 < 7
Answer:
The given inequality is:
a + 18 < 7
So,
a < 7 – 18
a < -11
Hence, from the above,
We can conclude that the solution to the given inequality is: a < -11
The representation of the solution of the given inequality in the graph is:
![]()
Question 51.
y – 5 ≥ 8
Answer:

Question 52.
– 3x > 24
Answer:
The given inequality is:
-3x > 24
x < –\(\frac{24}{3}\)
x < -8
Hence, from the above,
We can conclude that the solution to the given inequality is: x < -8
The representation of the solution of the given inequality in the graph is:

Question 53.
\(\frac{z}{4}\) ≤ 12
Answer:

Study Skills: Keeping Your Mind Focused
1.1 – 1.3 What did you learn
Mathematical Practices
Question 1.
Sketch an example of the situation described in Exercise 49 on page 10. Label your figure.
Answer:
The representation of the example of the situation described in Exercise 49 on page 10 is:
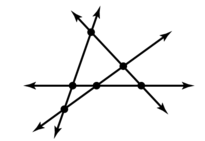
Question 2.
Explain how you arrived at your answer for Exercise 35 on page 18.
Answer:
we arrived at the answer for Exercise 35 on page 18 by using the distance formula between 2 points.
We know that,
The distance between the 2 points = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
Question 3.
What assumptions did you make when solving Exercise 43 0n page 26?
Answer:
The assumptions we make when solving Exercise 43 on page 26 is:
All the lengths between the 2 points in the segment are equal
1.1 – 1.3 Quiz
Use the diagram
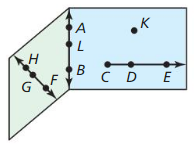
Question 1.
Name four points.
Answer:
From the above figure,
The four points are: A, L, B, and K
Question 2.
Name three collinear points.
Answer:
We know that,
The points that lie in the same line are called “Collinear points”
Hence, from the above figure,
The three collinear points are: A, L, and B
Question 3.
Name two lines.
Answer:
We know that,
A line has a starting point but no ending point
From the above figure,
The lines are GHF, ALB
Question 4.
Name three coplanar points.
Answer:
We know that,
The points that are present in the same plane are called “Co-planar points”
Hence, from the above figure,
The coplanar points are: G, H, and F
Question 5.
Name the plane that is shaded green.
Answer:
From the above figure,
The plane that is shaded green is named as Plane GHF
Question 6.
Give two names for the plane that is shaded blue.
Answer:
From the figure,
The two names for the plane that is shaded blue are: Plane AKL, Plane BCD
Question 7.
Name three line segments.
Answer:
From the figure,
The 3 line segments are: CD, HG, DE
Question 8.
Name three rays.
Answer:
From the figure,
The names of the 3 rays are: Ray GHF, ray CDE, Ray ALB
Sketch the figure described.
Question 9.
\(\vec{Q}\)R and ![]()
Answer:
The representation of \(\vec{Q}\)R and QS is:
Question 10.
plane P intersecting ![]() at Z
at Z
Answer:
The representation of plane P intersecting YZ at z is:
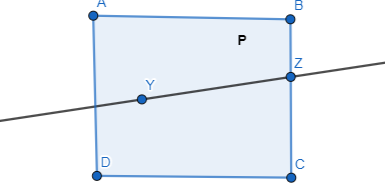
Plot the points in a coordinate plane. Then determine whether \(\overline{A B}\) and \(\overline{C D}\) are congruent.
Question 11.
A(- 3, 3), B( 1, 3), C(3, 2), D(3, – 2)
Answer:
The given points are:
A (-3, 3), B (1, 3), C (3, 2), D (3, -2)
Compare any 2 points with (x1, y1), (x2, y2)
We know that,
The distance can be calculated by using:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
\(\overline{A B}\) = \(\sqrt{(1 + 3)² + (3 – 3)²}\)
= \(\sqrt{(4)²}\) = 4
\(\overline{C D}\) = \(\sqrt{(3 – 3)² + (2 + 2)²}\)
= \(\sqrt{(4)²}\) = 4
So, from the above,
\(\overline{A B}\) is congruent to \(\overline{C D}\) since both the lengths are the same
Hence, from the above,
The representation of the given points in the coordinate plane is:
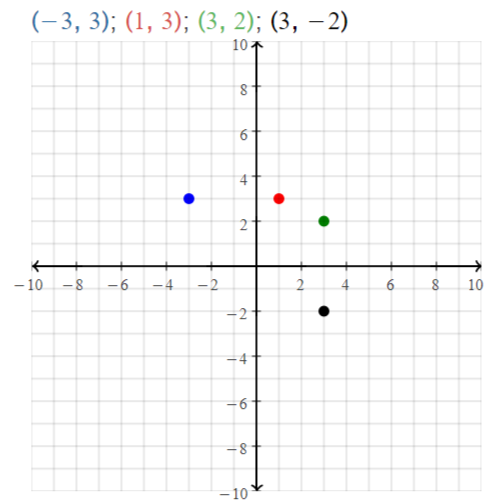
\(\overline{A B}\) is congruent to \(\overline{C D}\)
Question 12.
A(- 8, 7), B(1, 7), C(- 3, – 6), D(5, – 6)
Answer:
The given points are:
A (-8, 7), B (1, 7), C (-3, -6), D (5, -6)
Compare any 2 points with (x1, y1), (x2, y2)
We know that,
The distance can be calculated by using:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
\(\overline{A B}\) = \(\sqrt{(1 + 8)² + (7 – 7)²}\)
= \(\sqrt{(9)²}\) = 9
\(\overline{C D}\) = \(\sqrt{(5 + 3)² + (6 – 6)²}\)
= \(\sqrt{(8)²}\) = 8
So, from the above,
\(\overline{A B}\) is not congruent to \(\overline{C D}\) since both the lengths are not the same
Hence, from the above,
The representation of the given points in the coordinate plane is:
\(\overline{A B}\) is not congruent to \(\overline{C D}\)
Find AC. (Section 1.2)
Question 13.
![]()
Answer:
The given line segment is:
![]()
So,
From the Segment Addition Postulate,
\(\overline{A C}\) = \(\overline{A B}\) + \(\overline{B C}\)
\(\overline{A C}\) = 13 + 26
\(\overline{A C}\) = 39
Hence, from the above,
We can conclude that the length of \(\overline{A C}\) is: 39
Question 14.

Answer:
The given line segment is:

So,
From the Segment Addition Postulate,
\(\overline{A B}\) = \(\overline{A C}\) + \(\overline{B C}\)
62 = \(\overline{A C}\) + 11
\(\overline{A C}\) = 62 – 11
\(\overline{A C}\) = 51
Hence, from the above,
We can conclude that the length of \(\overline{A C}\) is: 51
Find the coordinates of the midpoint M and the distance between the two points.
Question 15.
J(4, 3) and K(2, – 3)
Answer:
The given points are:
J (4, 3), K (2, -3)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{4 + 2}{2}\), \(\frac{3 – 3}{2}\))
M = (\(\frac{6}{2}\), \(\frac{0}{2}\))
M = (3, 0)
Hence, from the above,
We can conclude that the coordinates of the midpoint are: (3, 0)
Question 16.
L(- 4, 5) and N(5, – 3)
Answer:
The given points are:
L (-4, 5), N (5, -3)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{-4 + 5}{2}\), \(\frac{5 – 3}{2}\))
M = (\(\frac{1}{2}\), \(\frac{2}{2}\))
M = (\(\frac{1}{2}\), 1)
Hence, from the above,
We can conclude that the coordinates of the midpoint are: (\(\frac{1}{2}\), 1)
Question 17.
P(- 6, – 1) and Q(1, 2)
Answer:
The given points are:
P (-6, -1), Q (1, 2)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
M = (\(\frac{-6 + 1}{2}\), \(\frac{2 – 1}{2}\))
M = (\(\frac{-5}{2}\), \(\frac{1}{2}\))
M = (-\(\frac{5}{2}\), \(\frac{1}{2}\))
Hence, from the above,
We can conclude that the coordinates of the midpoint are: (-\(\frac{5}{2}\), \(\frac{1}{2}\))
Question 18.
Identify the segment bisector of \(\overline{R S}\). Then find RS.

Answer:
The given line segment is:

We know that,
A bisector is a point or a line that divides a line segment into 2 congruent parts
So,
From the above figure,
M is the bisector of \(\overline{R S}\)
So,
6x – 2 = 3x + 7
6x – 3x = 7 + 2
3x = 9
x = \(\frac{9}{3}\)
x = 3
So,
\(\overline{R S}\) = 6x – 2 + 3x + 7
= 9x + 5
= 9 (3) + 5
= 27 + 5
= 32
Hence, from the above,
We can conclude that the length of [altex]\overline{R S}[/latex] is: 32
Question 19.
The midpoint of \(\overline{J K}\) is M(0, 1). One endpoint is J(- 6, 3). Find the coordinates of endpoint K.
Answer:
The given points of \(\overline{J K}\) are:
M (0, 1), H (-6, 3)
Let the point G be: (x1, y1)
We know that,
M = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(0, 1) = (\(\frac{x1 -6}{2}\), \(\frac{y1 + 3}{2}\))
So,
\(\frac{x1 – 6}{2}\) = 0 \(\frac{y1 + 3}{2}\) = 1
x1 – 12 = 0 (2) y1 + 7 = 1 (2)
x1 = 0 + 12 y1 = 2 – 7
x1 = 12 y1 = -5
Hence, from the above,
We can conclude that the other endpoint G is: (12, -5)
Question 20.
Your mom asks you to run some errands on your way home from school. She wants you to Stop at the post office and the grocery store, which is both on the same straight road between your school and your house. The distance from your school to the post office is 376 yards. the distance from the post office to your house is 929 yards. and the distance from the grocery store to your house is 513 yards.
a. Where should you stop first?
Answer:
It is given that your mom asks you to run some errands on your way home from school. She wants you to stop at the post office and the grocery store, which is both on the same straight road between your school and your house.
Hence, from the above,
We can conclude that you should first stop at the post office
b. What is the distance from the post office to the grocery store?
Answer:
It is given that the distance from your school to the post office is 376 yards. the distance from the post office to your house is 929 yards. and the distance from the grocery store to your house is 513 yards.
So,
The distance from the post office to the grocery store = (The distance from the post office to your house) + (The distance from the grocery store to your house)
= 929 + 513
= 1442 yards
Hence, from the above,
We can conclude that the distance from the post office to the grocery store is: 1442 yards
c. What is the distance from your school to your house?
Answer:
It is given that the distance from your school to the post office is 376 yards. the distance from the post office to your house is 929 yards. and the distance from the grocery store to your house is 513 yards.
So,
The distance from your school to your house = (The distance from your school to the post office) + (The distance from the post office to the grocery store)
= 376 + 1442
= 1818 yards
Hence, from the above,
We can conclude that the distance from your school to your house is: 1818 yards
d. you walk at a speed of 75 yards per minute. How long does it take you to walk straight home from school? Explain your answer.
Answer:
We know that,
Time = \(\frac{Distance}{Speed}\)
From part (c),
The total distance is: 1818 yards
The given speed is: 75 yards per minute
So,
Time = \(\frac{1818}{75}\)
Time = 24.24 minutes
Hence, from the above,
We can conclude that the time taken for you to walk straight home from school is: 24.24 minutes
Question 21.
The figure shows a coordinate plane on a baseball held. The distance from home plate to first base is 90 feet. The pitching mound is the midpoint between home plate and second base. Find the distance from home plate to second base. Find the distance between the home plate and the pitching mound. Explain how you found our answers.
Answer:
From the figure,
The coordinates to the home plate are: (0, 0), and (0, 6)
The coordinates to the second plate are: (6, 6), and (6, 0)
The coordinate of the pitching mound is: (3, 3)
Now,
The length of the home plate is:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 – 0)² + (6 – 6)²}\)
= (0, 6)
The length of the second plate is:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(6 – 6)² + (6 – 0)²}\)
= (0, 6)
Now,
The distance from the home plate to the second base is:
D = (0, 6) – (0, 6)
D = (0, 0)
The distance between the home plate and the pitching mound is:
D = (3, 3) – (0, 0)
D = (3, 3)
Hence, from the above,
We can conclude that
The distance from the home plate to the second base is: (0, 0)
The distance from the home plate to the pitching mound is: (3, 3)
1.4 Perimeter and Area in the Coordinate Plane
Essential Question
How can you find the perimeter and area of a polygon in a coordinate plane?
Answer:
When two-dimensional figures are shown on the coordinate plane, a mix of counting and the Pythagorean Theorem can be used to determine the lengths of each side. Then add up the lengths to determine the perimeter or use the basic area formulas for triangles and rectangles to determine the area of the figure.
Exploration 1
Finding the Perimeter and Area of a Quadrilateral
Work with a partner
a. On a piece of centimeter graph paper. draw quadrilateral ABCD in a coordinate plane. Label the points A(1, 4), B(- 3, 1) C(0, – 3), and D(4, 0).
Answer:
The given points are:
A (1, 4), B (-3, 1), C (0, -3), and D (4, 0)
Hence,
The representation of the given points in the coordinate plane are:
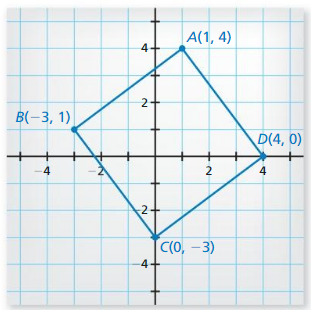
b. Find the perimeter of quadrilateral ABCD.
Answer:
The given points are:
A (1, 4), B (-3, 1), C (0, -3), and D (4, 0)
We know that,
The perimeter is defined as the sum of all the sides of a polygon
So,
In a coordinate plane, the perimeter of the polygon can be found by finding the lengths of the given sides
We know that,
The length of the side of a polygon in a coordinate plane is:
D = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
So,
AB = \(\sqrt{(1 + 3)² + (4 – 1)²}\)
= \(\sqrt{(4)² + (3)²}\)
= \(\sqrt{16 + 9}\)
= \(\sqrt{25}\)
= 5 cm
BC = \(\sqrt{(0 + 3)² + (1 + 3)²}\)
= \(\sqrt{(3)² + (4)²}\)
=\(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
= 5 cm
CD = \(\sqrt{(4 – 0)² + (0 + 3)²}\)
= \(\sqrt{(4)² + (3)²}\)
= \(\sqrt{(16 + 9}\)
= \(\sqrt{25}\)
= 5 cm
DA = \(\sqrt{(4 – 1)² + (4 – 0)²}\)
= \(\sqrt{(3)² + (4)²}\)
= \(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
= 5 cm
Hence,
The perimeter of the Quadrilateral ABCD = AB + BC + CD + DA
= 5 + 5 + 5 + 5
= 20 cm
c. Are adjacent sides of quadrilateral ABCD perpendicular to each other? How can you tell?
Answer:
From part (a),
The lengths of all the sides of a quadrilateral are: 5 cm
We know that,
For a square, the lengths of all the sides are equal and the angle between all the sides of the square is 90°
Hence, from the above,
We can conclude that the adjacent sides of quadrilateral ABCD are perpendicular to each other
d. What is the definition of a square? Is quadrilateral ABCD a square? Justify your answer. Find the area of quadrilateral ABCD.
Answer:
Definition of the square:
A “Square” is a quadrilateral that has the length of all the sides equal and all the angles 90°
From part (b),
We found out the lengths of all the sides are equal and all the angles are 90°
So,
Quadrilateral ABCD is a square
So,
Area of a square = Side²
= 5²
= 25 cm²
Exploration 2
Finding the Area of a Polygon Work with a partner.
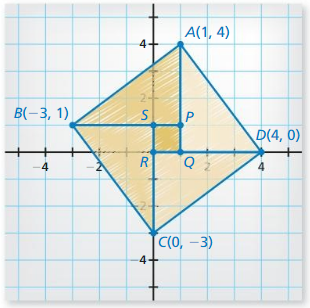
a. Partition quadrilateral ABCD into four right triangles and one square, as shown. Find the coordinates of the vertices for the five smaller polygons.
Answer:
From the figure,
The five smaller polygons are:
ΔAQD, ΔBPA, ΔDRC, ΔCSB, and square PQRS
Now,
The coordinates for the given vertices polygons are:
The coordinates of ΔAQD are:
A (1, 4), Q (1, 0), and D (4, 0)
The coordinates of ΔBPA are:
B (-3, 1), P (1, 1), and A (1, 4)
The coordinates of ΔDRC are:
D (4, 0), R (0, 0), and C (0, -3)
The coordinates of ΔCSB are:
C (0, -3), S (0, 1), and B (-3, 1)
The coordinates of square PQRS are:
P (1, 1), Q (1, 0), R (0, 0), and S (0, 1)
b. Find the areas of the five smaller polygons.

Answer:
From part (a),
The coordinates of ΔAQD are:
A (1, 4), Q (1, 0), and D (4, 0)
The coordinates of ΔBPA are:
B (-3, 1), P (1, 1), and A (1, 4)
The coordinates of ΔDRC are:
D (4, 0), R (0, 0), and C (0, -3)
The coordinates of ΔCSB are:
C (0, -3), S (0, 1), and B (-3, 1)
The coordinates of square PQRS are:
P (1, 1), Q (1, 0), R (0, 0), and S (0, 1)
Now,
The area of Δ AQD:
The length of AQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (4 – 0)²}\)
= 4
The length of QD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 1)² + (0 – 0)²}\)
= 3
The length of DA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 1)² + (4 – 0)²}\)
= 5
So,
The area of ΔAQD = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) (4) (3)
= 6
The area of Δ BPA:
The length of BP = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (1 – 1)²}\)
= 4
The length of PA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (4 – 1)²}\)
= 3
The length of BA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 1)² + (1 + 3)²}\)
= 5
So,
The area of ΔBPA = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) (4) (3)
= 6
The area of Δ DRC:
The length of DR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 – 0)² + (4 – 0)²}\)
= 4
The length of RC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 0)² + (0 – 0)²}\)
= 3
The length of CD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 3)² + (4 – 0)²}\)
= 5
So,
The area of ΔDRC = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) (4) (3)
= 6
The area of Δ CSB:
The length of CS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 – 0)² + (1 + 3)²}\)
= 4
The length of SB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (0 + 3)²}\)
= 3
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (0+ 3)²}\)
= 5
So,
The area of ΔCSB = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) (4) (3)
= 6
The area of square PQRS:
The length of PQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (1 – 0)²}\)
= 1
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 0)² + (0 – 0)²}\)
= 1
The length of RS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 0)² + (0 – 0)²}\)
= 1
The length of PS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 – 0)² + (1 – 1)²}\)
= 1
So,
The area of square PQRS = Side²
= 1
c. Is the sum of the areas of the five smaller polygons equal to the area of quadrilateral ABCD? Justify your answer.
Answer:
From the given figure,
The coordinates of the quadrilateral ABCD are:
A (1, 4), B(-3, 1), C (0, -3), and D (4, 0)
Now,
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 + 3)² + (4 – 1)²}\)
= 5
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(0 + 3)² + (1 + 3)²}\)
= 5
The length of CD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 – 0)² + (0 + 3)²}\)
= 5
The length of DA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 – 0)² + (4 – 1)²}\)
= 5
So, from the above
We can observe that all the lengths of the sides are equal and the product of the slopes of the perpendicular sides is -1
Hence,
The area of quadrilateral ABCD = Side²
= 5² = 25
Now,
The sum of the areas of the five smaller polygons = 6 + 6 + 6 + 6 + 1
= 25
Hence, from the above,
We can conclude that the sum of the areas of the five smaller polygons equal to the area of quadrilateral ABCD
Communicate Your Answer
Question 3.
How can you find the perimeter and area of a polygon in a coordinate plane?
Answer:
When two-dimensional figures are shown on the coordinate plane, a mix of counting and the Pythagorean Theorem can be used to determine the lengths of each side. Then add up the lengths to determine the perimeter or use the basic area formulas for triangles and rectangles to determine the area of the figure.
Question 4.
Repeat Exploration 1 for quadrilateral EFGH. where the coordinates of the vertices are E(- 3, 6), F(- 7, 3), G(- 1, – 5), and H(3, – 2).
Answer:
The coordinates of the vertices of quadrilateral EFGH are:
E (-3, 6), F (-7, 3), G (-1, -5), and H (3, -2)
Now,
The length of EF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(7 – 3)² + (6 – 3)²}\)
= 5
The length of FG = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(7 – 1)² + (3 + 5)²}\)
= 10
The length of GH = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 1)² + (5 – 2)²}\)
= 5
The length of HE = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 3)² + (6 + 2)²}\)
= 10
Hence,
The perimeter of quadrilateral EFGH = EF + FG + GH + HE
= 5 + 5 + 10 + 10
= 30
From the lengths of the sides,
We can observe that the opposite sides have the same lengths and the product of the slopes of the perpendicular sides is -1
So,
The figure is: Rectangle
We know that,
The area of a rectangle = Length × Width
So,
The area of quadrilateral EFGH = 5 × 10 = 50
Hence, from the above,
We can conclude that
The perimeter of quadrilateral EFGH is: 30
The area of quadrilateral EFGH is: 50
Lesson 1.4 Perimeter and Area in the Coordinate Plane
Monitoring Progress
Classify the polygon the number of sides. Tell whether it is convex or concave.
Question 1.

Answer:
The given polygon is:

From the given polygon,
The number of sides is: 5
So,
The given polygon is “Pentagon”
We know that,
The figure is concave if all the interior angles are greater than 180°
The figure is convex if all the interior angles are less than 180°
Hence, from the above,
We can conclude that the given polygon is “Pentagon” and it is convex
Question 2.
Answer:
The given polygon is:

From the above polygon,
We can observe that
The number of sides is: 6
So,
The given polygon is: Hexagon
We know that,
The figure is concave if all the interior angles are greater than 180°
The figure is convex if all the interior angles are less than 180°
Hence, from the above,
We can conclude that the given polygon is “Hexagon” and it is convex
Find the perimeter of the polygon with the given vertices.
Question 3.
D(- 3, 2), E(4, 2), F(4, – 3)
Answer:
The given vertices are:
D (-3, 2), E (4, 2), F (4, -3)
Now,
The length of DE = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 + 3)² + (2 – 2)²}\)
= 7
The length of EF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 – 4)² + (3 + 2)²}\)
= 5
The length of FD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 + 3)² + (2 + 3)²}\)
= 8.60
So,
The perimeter of the given vertices = 7 + 5 + 8.60
= 20.60
Hence, from the above,
We can conclude that the perimeter of the given vertices is: 20.60
Question 4.
G(- 3, 2), H(2, 2), J(- 1, – 3)
Answer:
The given vertices are:
G (-3, 2), H (2, 2), I (-1, -3)
Now,
The length of GH = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 3)² + (2 – 2)²}\)
= 5
The length of HI = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 1)² + (3 + 2)²}\)
= 5.8
The length of IG = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 – 1)² + (2 + 3)²}\)
= 5.3
So,
The perimeter of the given vertices = 5 + 5.8 + 5.3
= 16.1
Hence, from the above,
We can conclude that the perimeter of the given vertices is: 16.1
Question 5.
K( – 1, 1), L(4, 1), M(2, – 2), N(- 3, – 2)
Answer:
The given vertices are:
K (-1, 1), L (4, 1), M (2, -2), N (-3, -2)
Now,
The length of KL = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 + 1)² + (1 – 1)²}\)
= 5
The length of LM = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 – 2)² + (1 + 2)²}\)
= 3.6
The length of MN = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 3)² + (2 – 2)²}\)
= 5
The length of NK = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3- 1)² + (1 + 2)²}\)
= 3.6
So,
The perimeter of the given vertices = 5 + 5 + 3.6 + 3.6
= 17.2
Hence, from the above,
We can conclude that the perimeter of the given vertices is: 17.2
Question 6.
Q(- 4, – 1), R(1, 4), S(4, 1), T(- 1, – 4)
Answer:
The given vertices are;
Q (-4, -1), R (1, 4), S (4, 1), T (-1, -4)
Now,
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 + 1)² + (4 + 1)²}\)
= 7.07
The length of RS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 – 1)² + (4 – 1)²}\)
= 4.2
The length of ST = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(4 + 1)² + (1 + 4)²}\)
= 7.07
The length of TQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4- 1)² + (4 – 1)²}\)
= 4.2
So,
The perimeter of the given vertices = 7.07 + 7.07 + 4.2 + 4.2
= 22.54
Hence, from the above,
We can conclude that the perimeter of the given vertices is: 22.54
Find the area of the polygon with the given vertices.
Question 7.
G(2, 2), H(3, – 1), J(- 2, – 1)
Answer:
The given vertices are:
G (2, 2), H (3, -1), I (-2, -1)
Now,
The length of GH = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 3)² + (2 + 1)²}\)
= 3.16
The length of HI = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 – 1)² + (3 + 2)²}\)
= 5
The length of IG = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 2)² + (2 + 1)²}\)
= 5
So,
The area of the given vertices = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × 5 × 5
= 12.5
Hence, from the above,
We can conclude that the area of the given vertices is: 12.5
Question 8.
N(- 1, 1), P(2, 1), Q(2, – 2), R(- 1, – 2)
Answer:
The given vertices are:
N (-1, 1), P (2, 1), Q (2, -2), R (-1, -2)
Now,
The length of NP = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 1)² + (1 – 1)²}\)
= 3
The length of PQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 2)² + (1 + 2)²}\)
= 3
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 1)² + (2 – 2)²}\)
= 3
The length of RN = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1- 1)² + (1 + 2)²}\)
= 3
So,
From the lengths of all of the sides,
We can say that the vertices belong to a square
So,
The area of a square = Side²
= 3² = 9
Hence, from the above,
We can conclude that the area of the given vertices is: 9
Question 9.
F(- 2, 3), G(1, 3), H(1, – 1), J(- 2, – 1)
Answer:
The given vertices are:
F (-2, 3), G (1, 3), H (1, -1), J (-2, -1)
Now,
The length of FG = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 1)² + (3 – 3)²}\)
= 3
The length of GH = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 – 1)² + (1 + 3)²}\)
= 4
The length of HJ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 + 1)² + (1 – 1)²}\)
= 3
The length of JF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2- 2)² + (1 + 3)²}\)
= 4
So,
From the lengths of all of the sides,
We can say that the vertices belong to a rectangle since the lengths of the opposite sides are the same
So,
The area of a rectangle = Length × Width
= 3 × 4 = 12
Hence, from the above,
We can conclude that the area of the given vertices is: 12
Question 10.
K(- 3, 3), L(3, 3), M(3, – 1), N(- 3, – 1)
Answer:
The given vertices are:
K (-3, 3), L (3, 3), M (3, -1), N (-3, -1)
Now,
The length of KL = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 3)² + (3 – 3)²}\)
= 6
The length of LM = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 – 3)² + (1 + 3)²}\)
= 4
The length of MN = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 3)² + (1 – 1)²}\)
= 6
The length of NK = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3- 3)² + (1 + 3)²}\)
= 4
So,
From the lengths of all of the sides,
We can say that the vertices belong to a rectangle
So,
The area of a rectangle = Length × Width
= 6 × 4 = 24
Hence, from the above,
We can conclude that the area of the given vertices is: 24
Question 11.
You are building a patio in your school’s courtyard. In the diagram at the left, the coordinates represent the four vertices of the patio. Each unit in the coordinate plane represents 1 foot. Find the area of the patio.
Answer:
From the given graph,
The coordinates of a patio is:
M (2, 2), N (6, 2), P (6, -3), R (2, -3)
Now,
The length of MN = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(6 – 2)² + (2 – 2)²}\)
= 4
The length of NP = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(6 – 6)² + (3 + 2)²}\)
= 5
The length of PR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(6 – 2)² + (3 – 3)²}\)
= 4
The length of RM = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2- 2)² + (3 + 2)²}\)
= 5
So,
From the lengths of all of the sides,
We can say that the vertices belong to a rectangle
So,
The area of a rectangle = Length × Width
= 5 × 4 = 20
Hence, from the above,
We can conclude that the area of the patio is: 20
Exercise 1.4 Perimeter and Area in the Coordinate Plane
Question 1.
COMPLETE THE SENTENCE
The perimeter of a square with side length s is P = _________ .
Answer:
![]()
Question 2.
WRITING
What formulas can you use to find the area of a triangle in a coordinate plane?
Answer:
We know that,
The formula you can use to find the area of a triangle in a coordinate plane is:
Area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, classify the polygon by the number of sides. Tell whether it is convex or concave.
Question 3.
Answer:
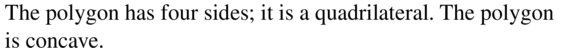
Question 4.
Answer:
The given polygon is:

From the given polygon,
We can observe that
The number of sides is: 3
We know that,
The figure is concave if all the interior angles are greater than 180°
The figure is convex if all the interior angles are less than 180°
Hence, from the above,
We can conclude that the given polygon is a triangle and it is a concave polygon as it has interior angles greater than 180°
Question 5.
Answer:
Question 6.
Answer:
The given polygon is:

From the given polygon,
We can observe that
The number of sides is: 6
We know that,
The figure is concave if all the interior angles are greater than 180°
The figure is convex if all the interior angles are less than 180°
Hence, from the above,
We can conclude that the given polygon is a hexagon and it is a concave polygon as it has interior angles greater than 180°
In Exercises 7 – 12. find the perimeter of the polygon with the given vertices.
Question 7.
G(2, 4), H(2, – 3), J(- 2, – 3), K(- 2, 4)
Answer:
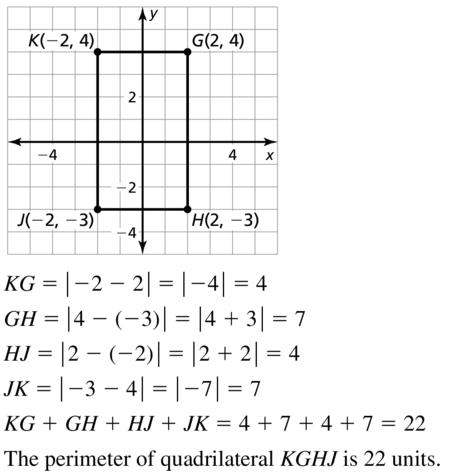
Question 8.
Q(- 3, 2), R(1, 2), s(1, – 2), T(- 3, – 2)
Answer:
The given vertices of a polygon are:
Q (-3, 2), R (1, 2), S (1, -2), T (-3, -2)
Now,
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 + 3)² + (2 – 2)²}\)
= 4
The length of RS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 – 1)² + (2 + 2)²}\)
= 4
The length of ST = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 2)² + (1 + 3)²}\)
= 4
The length of TQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3- 3)² + (2 + 2)²}\)
= 4
So,
From the lengths of all of the sides,
We can say that the vertices belong to a square
So,
The perimeter of a square = 4 × Side
= 4 × 4
= 16
Hence, from the above,
We can conclude that the perimeter of the given polygon is: 16
Question 9.
U(- 2, 4), V(3, 4), W(3, – 4)
Answer:
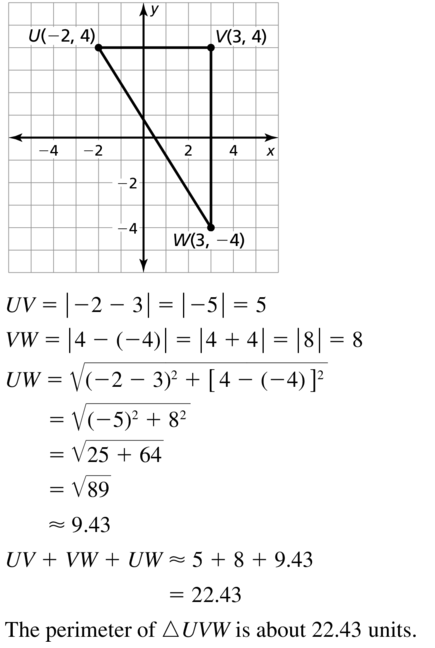
Question 10.
X(- 1, 3), Y(3, 0), Z(- 1, – 2)
Answer:
The given vertices of a polygon are:
X (-1, 3), Y (3, 0), Z (-1, -2)
Now,
The length of XY = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 1)² + (3 – 0)²}\)
= 5
The length of YZ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(3 + 1)² + (0 + 2)²}\)
= 4.47
The length of ZX = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(1 – 1)² + (3 + 2)²}\)
= 5
So,
The perimeter of the given polygon = 5 + 5 + 4.7
= 14.47
Hence, from the above,
WE can conclude that the perimeter of the given polygon is: 14.47
Question 11.
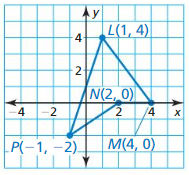
Answer:
Question 12.
Answer:
From the given coordinate plane,
The given vertices of the hexagon are:
A (0, 4), B (2, 0), C (2, -2), D (0, -2), E (-2, 2), F (-2, 4)
Now,
Now,
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 0)² + (4 – 0)²}\)
= 4.47
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 2)² + (0 + 2)²}\)
= 2
The length of CD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
=\(\sqrt{(2 – 0)² + (2 – 2)²}\)
= 2
The length of DE = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 2)² + (2 + 2)²}\)
= 4.47
The length of EF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2 – 2)² + (4 – 2)²}\)
= 2
The length of FA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 2)² + (4 – 4)²}\)
= 2
So,
The perimeter of the hexagon = AB + BC + CD + DE + EF + FA
= 4.47 + 2 + 2 + 4.47 + 2 + 2
= 16.94
Hence, from the above,
We can conclude that the perimeter of the given hexagon is: 16.94
In Exercises 13 – 16. find the area of the polygon with the given vertices.
Question 13.
E(3, 1), F(3, – 2), G(- 2, – 2)
Answer:

Question 14.
J(- 3, 4), K(4, 4), L(3, – 3)
Answer:
The given vertices are:
J (-3, 4), K (4, 4), L (3, -3)
Now,
The length of JK = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 + 3)² + (4 – 4)²}\)
= 7
The length of KL = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 3)² + (4 + 3)²}\)
= 7.07
The length of LJ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 3)² + (3 + 4)²}\)
= 9.21
So,
The area of the given vertices = \(\frac{1}{2}]/latex] × JK ×KL
= [latex/]frac{1}{2}\) × 7 × 7.07
= 24.74
Hence, from the above,
We can conclude that the area of the given vertices is: 24.74
Question 15.
W(0, 0), X(0, 3), Y(- 3, 3), Z(- 3, 0)
Answer:

Question 16.
N(- 2, 1), P(3, 1), Q(3, – 1), R(- 2, 1)
Answer:
The given vertices are:
N (-2, 1), P (3, 1), Q (3, -1), R (-2, 1)
Now,
The length of NP = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 2)² + (1 – 1)²}\)
= 5
The length of PQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 – 3)² + (1 + 1)²}\)
= 2
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 2)² + (1 + 1)²}\)
= 5.38
The length of RN = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2 – 2)² + (1 – 1)²}\)
= 0
So,
The area of the given vertices = 5 × 2 × 5.38
= 28.97
Hence, from the above,
We can conclude that the area of the given vertices is: 28.97
In Exercises 17 – 24, use the diagram.
Question 17.
Find the perimeter of △CDE.
Answer:

Question 18.
Find the perimeter of the rectangle BCEF.
Answer:
From the given figure,
The coordinates of the rectangle BCEF are:
B (0, 3) C (4, -1), E (2, -3), F (-2, 1)
Now,
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 0)² + (3 + 1)²}\)
= 5.65
The length of CE = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 2)² + (3 – 1)²}\)
= 2.82
The length of EF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (2 + 2)²}\)
= 5.65
The length of FB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 2)² + (3 – 1)²}\)
= 2.82
So,
The perimeter of the rectangle BCEF = BC + CE + EF + FB
= 5.65 + 2.82 + 5.65 + 2.82
= 16.94
Hence, from the above,
We can conclude that the perimeter of the rectangle BCEF is: 16.94
Question 19.
Find the perimeter of △ABF.
Answer:
Question 20.
Find the perimeter of quadrilateral ABCD.
Answer:
From the given figure,
The given vertices of the quadrilateral ABCD are:
A (-5, 4), B (0, 3), C (4, -1), D (4, -5)
Now,
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 5)² + (4 – 3)²}\)
= 5.09
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 0)² + (1 + 3)²}\)
= 5.65
The length of CD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 4)² + (5 – 1)²}\)
= 4
The length of DA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 + 5)² + (4 + 5)²}\)
= 12.72
So,
The perimeter of quadrilateral ABCD = AB + BC + CD + DA
= 5.09 + 5.65 + 4 + 12.72
= 31.37
Hence, from the above,
We can conclude that the perimeter of quadrilateral ABCD is: 31.37
Question 21.
Find the area of △CDE.
Answer:

Question 22.
Find the area of rectangle BCEF
Answer:
From the given figure,
The coordinates of the rectangle BCEF are:
B (0, 3) C (4, -1), E (2, -3), F (-2, 1)
Now,
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 0)² + (3 + 1)²}\)
= 5.65
The length of CE = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 2)² + (3 – 1)²}\)
= 2.82
The length of EF = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (2 + 2)²}\)
= 5.65
The length of FB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 2)² + (3 – 1)²}\)
= 2.82
So,
The area of the rectangle BCEF = Length × Width
= 2.82 × 5.65
= 15.93
Hence, from the above,
We can conclude that the area of the rectangle BCEF is: 15.93
Question 23.
Find the area of △ABF
Answer:

Question 24.
Find the area of quadrilateral ABCD.
Answer:
The given vertices of the quadrilateral ABCD are:
A (-5, 4), B (0, 3), C (4, -1), D (4, -5)
Now,
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(0 + 5)² + (4 – 3)²}\)
= 5.09
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 0)² + (1 + 3)²}\)
= 5.65
The length of CD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 4)² + (5 – 1)²}\)
= 4
The length of DA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 + 5)² + (4 + 5)²}\)
= 12.72
The length of AC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 + 5)² + (4 + 1)²}\)
= 10.29
The length of BD = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 0)² + (3 + 5)²}\)
= 8.94
So,
The area of the quadrilateral ABCD = \(\frac{1}{2}\) ×AC × BD
= \(\frac{1}{2}\) × 10.29 × 8.94
= 45.99
Hence, from the above,
We can conclude that the area f the quadrilateral ABCD is: 45.99
ERROR ANALYSIS
In Exercises 25 and 26, describe and correct the error in finding the perimeter or area of the polygon.
Question 25.

Answer:
Question 26.

Answer:
From the given figure,
The coordinates of the vertices of ΔABC are:
A (4, 3), B (5, 1), C (1, 1)
Now,
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 4)² + (3 – 1)²}\)
= 2.23
The length of BC = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 1)² + (1 – 1)²}\)
= 4
The length of CA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 1)² + (3 – 1)²}\)
= 3.60
So,
The area of ΔABC = \(\frac{1}{2}\) ×AB × BC
= \(\frac{1}{2}\) × 2.23 × 4
= 4.46
Hence, from the above,
We can conclude that the area of ΔABC is: 4.46 sq. units
In Exercises 27 and 28, use the diagram.
Question 27.
Determine which point is the remaining vertex of a triangle with an area of 4 square units.
A. R(2, 0)
B. S(- 2, – 1)
C. T(- 1, 0)
D. U(2, – 2)
Answer:

Question 28.
Determine which points are the remaining vertices of a rectangle with a perimeter of 14 units.
A. A(2, – 2) and B(2, – 1)
B. C(- 2, – 2) and D(- 2, 2)
C. E(- 2, – 2) and F(2, – 2)
D. G(2, 0) and H(2, 0)
Answer:
From the given figure,
The given vertices are:
P (-2, 1), Q (2, 1)
We know that,
The perimeter is defined as the sum of all the sides of a given polygon
Now,
Let,
A (x, y), and B(p, q) are the remaining 2 points of a rectangle
Now,
The length of PQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{2 + 2)² + (1 – 1)²}\)
= 4
The length of QA = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(x – 2)² + (y – 1)²}\)
The length of AB = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(x – p)² + (y – q)²}\)
The length of BP = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(p + 2)² + (q – 1)²}\)
So,
The perimeter of the rectangle = PQ + QA + AB + BP
= 4 + \(\sqrt{(x – 2)² + (y – 1)²}\) + \(\sqrt{(x – p)² + (y – q)²}\) + \(\sqrt{(p + 2)² + (q – 1)²}\)
It is given that,
The perimeter of the rectangle = 14
So,
4 + \(\sqrt{(x – 2)² + (y – 1)²}\) + \(\sqrt{(x – p)² + (y – q)²}\) + \(\sqrt{(p + 2)² + (q – 1)²}\) = 14
\(\sqrt{(x – 2)² + (y – 1)²}\) + \(\sqrt{(x – p)² + (y – q)²}\) + \(\sqrt{(p + 2)² + (q – 1)²}\) = 14 – 4
\(\sqrt{(x – 2)² + (y – 1)²}\) + \(\sqrt{(x – p)² + (y – q)²}\) + \(\sqrt{(p + 2)² + (q – 1)²}\) = 10
Now, from the given options,
a.
The given remaining vertices are:
A (2, -2), B (2, -1)
Compare the above vertices with
A (x, y), and B (p, q)
So,
\(\sqrt{(2- 2)² + (-2 – 1)²}\) + \(\sqrt{(2 – 2)² + (-2 + 1)²}\) + \(\sqrt{(2 + 2)² + (-1 – 1)²}\) = 10
3 + 1 + 4.47 = 10
8.47 ≠ 10
b.
The given remaining vertices are:
C (-2, -2), and D (-2, 2)
Compare the above vertices with
A (x, y), and B (p, q)
So,
\(\sqrt{(-2 – 2)² + (-2 – 1)²}\) + \(\sqrt{(2 – 2)² + (-2 – 2)²}\) + \(\sqrt{(-2 + 2)² + (2 – 1)²}\) = 10
5 + 4 +1 = 10
10 = 10
Hence, from the above,
We can conclude that the remaining two vertices which gives the perimeter of 14 units are:
C (-2, -2), and D (-2, 2)
Question 29.
USING STRUCTURE
Use the diagram.
a. Find the areas of square EFGH and square EJKL. What happens to the area when the perimeter of square EFGH is doubled?
b. Is this true for every square? Explain.
Answer:

Question 30.
MODELING WITH MATHEMATICS
You are growing zucchini plants in your garden. In the figure. the entire garden is rectangle QRST. Each unit in the coordinate plane represents 1 foot.
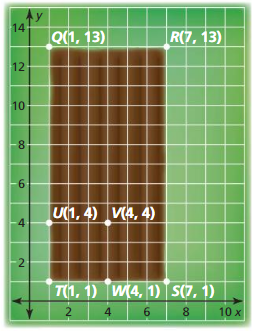
a. Find the area of the garden.
Answer:
It is given that the rectangle QRST represents the garden
So,
From the figure,
The coordinates of the garden are:
Q (1, 13), R (7, 13), S (7, 1), and T (1, 1)
Now,
The length of QR = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{13 – 13)² + (7 – 1)²}\)
= 6
The length of RS = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{13 – 1)² + (7 – 7)²}\)
= 12
The length of ST = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{1 – 1)² + (7 – 1)²}\)
= 6
The length of TQ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{13 – 1)² + (1 – 1)²}\)
= 12
So,
The area of the garden = (Length of the garden) × (Width of the garden)
= 12 × 6
= 72 square feet
Hence, from the above,
We can conclude that the area of the garden is: 72 square feet
b. Zucchini plants require 9 square feet around each plant. How many zucchini plants can you plant?
Answer:
From part (a),
The area of the entire garden is: 72 square feet
It is given that zucchini plants require 9 square feet around each plant
So,
The number of zucchini plants you can plant = \(\frac{The area of the entire garden}{The area required for each zucchini plant}\)
= \(\frac{72}{9}\)
= 8
Hence, from the above,
We can conclude that the number of zucchini plants you can plant is: 8 plants
c. You decide to use square TUVW to grow lettuce. you can plant lour heads of lettuce per square loot. How many of each vegetable can you plant? Explain.
Answer:
From the figure,
The coordinates of the vertices of the rectangle TUVW are:
T (1, 1), U (1, 4), V (4, 4), W (4, 1)
Now,
The length of TU = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{1 – 1)² + (4 – 1)²}\)
= 3
The length of UV = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{4 – 4)² + (4 – 1)²}\)
= 3
The length of VW = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{4 – 4)² + (4 – 1)²}\)
= 3
The length of WT = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{4 – 1)² + (1 – 1)²}\)
= 3
So,
The area of square TUVW = Side²
= 3² = 9 square feet
It is given that,
1 square foot = 4 heads of lettuce
So,
9 square feet = 9 × 4 = 36 heads of lettuce
Hence, from the above,
We can conclude that you can plant 36 vegetables of each type
Question 31.
MODELING WITH MATHEMATICS
You are going for a hike in the woods. You hike to a waterfall that is 4 miles east of where you left your car. You then hike to a lookout point that is 2 miles north of your car. From the lookout point. you return to our ear.
a. Map out your route in a coordinate plane with our car at the origin. Let each unit in the coordinate plane represent 1 mile. Assume you travel along straight paths.
b. How far do you travel during the entire hike?
c. When you leave the waterfall, you decide to hike to an old wishing well before going to the lookout point. The wishing well is 3 miles north and 2 miles west of the lookout point. How far do you travel during the entire hike?
Answer:

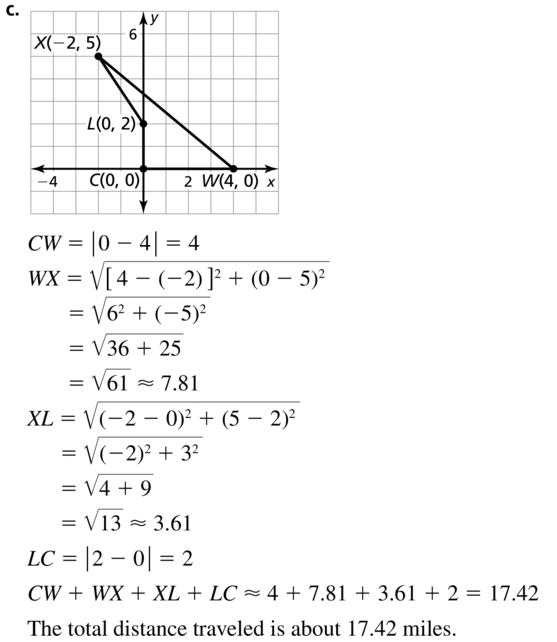
Question 32.
HOW DO YOU SEE IT?
Without performing any calculations, determine whether the triangle or the rectangle has a greater area. Which one has a greater perimeter? Explain your reasoning.
Answer:
From the given graph,
We can observe that the size of the rectangle is greater than the size of the triangle
So,
We can say that
The area of the rectangle is greater than the area of the triangle
The perimeter of the rectangle is greater than the perimeter of the triangle
Hence, from the above,
We can conclude that
The area and the perimeter of the rectangle is greater than the area and the perimeter of the triangle
Question 33.
MATHEMATICAL CONNECTIONS
The lines y1 = 2x – 6, y2 = – 3x + 4, and y3 = – \(\frac{1}{2}\) + 4 are the sides of a right triangle.
a. Use slopes to determine which sides are perpendicular.
b. Find the vertices of the triangle.
c. Find the perimeter and area of the triangle.
Answer:


Question 34.
THOUGHT-PROVOKING
Your bedroom has an area of 350 square feet. You are remodeling to include an attached bathroom that has an area of 150 square feet. Draw a diagram of the remodeled bedroom and bathroom in a coordinate plane.
Answer:
It is given that your bedroom has an area of 350 square feet. You are remodeling to include an attached bathroom that has an area of 150 square feet.
So,
The dimensions of the bedroom that has an area of 350 square feet are:
Length: 20 feet and Width: 17.5 feet (Remember that any of the factor products of 350 will be the dimensions of the bedroom)
So,
The dimensions of the bedroom that has an area of 350 square feet in the coordinate plane are:
(0, 0), (0, 17.5), (20, 17.5), and (20, 0)
Now,
The dimensions of an attached bathroom that has an area of 150 square feet are:
Length: 10 feet and Width: 15 feet (Remember that any of the factor products of 350 will be the dimensions of the bedroom)
So,
The dimensions of the attached bathroom that has an area of 150 square feet in the coordinate plane are:
(0, 0), (0, 5), (10, 15), (5, 0)
Hence,
The representation of the attached bedroom and the bathroom in a coordinate plane is:
Question 35.
PROBLEM-SOLVING
Use the diagram
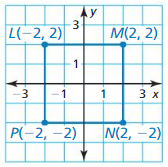
a. Find the perimeter and area of the square.
b. Connect the midpoints of the sides of the given square to make a quadrilateral. Is this quadrilateral a square? Explain our reasoning.
c. Find the perimeter and area of the quadrilateral you made in part (b). Compare this area to the area you found in part (a).
Answer:

Question 36.
MAKING AN ARGUMENT
Your friend claims that a rectangle with the same perimeter as △QRS will have the same area as the triangle. Is your friend correct? Explain your reasoning.
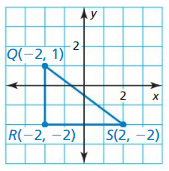
Answer:
No, your friend is not correct
Explanation:
It is given that your friend claims that a rectangle with the same perimeter as △QRS will have the same area as the triangle.
But,
We know that,
The size of the rectangle is greater than the size of the triangle
So,
The area of the rectangle will be greater than the area of the triangle even though the perimeter of the rectangle and the triangle are the same
Hence, from the above,
We can conclude that your friend is not correct
Question 37.
REASONING
Triangle ABC has a perimeter of 12 units. The vertices of the triangle are A(x, 2), B(2, – 2), and C(- 1, 2). Find the value of x.
Answer:

Maintaining Mathematical Proficiency
Solve the equation.
Question 38.
3x – 7 = 2
Answer:
The given equatio is:
3x – 7 = 2
So,
3x = 2 + 7
3x = 9
x = \(\frac{9}{3}\)
x = 3
Hence, from the above,
We can conclude that the value of x to the given equation is: 3
Question 39.
5x + 9 = 4
Answer:
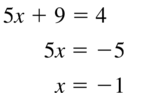
Question 40.
x + 4 = x – 12
Answer:
The given equation is:
x + 4 = x – 12
x – x + 4 = -12
4 = -12
Hence, from the above,
We can conclude that the given equation has no solution
Question 41.
4x- 9 = 3x + 5
Answer:
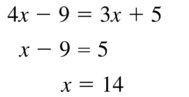
Question 42.
11 – 2x = 5x – 3
Answer:
The given equation is:
11 – 2x = 5x – 3
11 + 3 = 5x + 2x
7x = 14
x = \(\frac{14}{7}\)
x = 2
Hence, from the above,
We can conclude that the value of x to the given equation is: 2
Question 43.
\(\frac{x+1}{2}\) = 4x – 3
Answer:
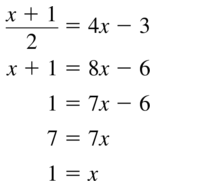
Question 44.
Use a compass and straightedge to construct a copy of the line segment.
![]()
Answer:
The steps used to construct a line segment are:
Step 1:
You are given line segment AB to copy.
Step 2:
Draw a line segment that is longer than line segment AB. Label one of its endpoints C.
Step 3:
Open your compass so that the anchor is on one endpoint of line segment AB and the pencil point is on the other endpoint.
1.5 Measuring and Constructing Angles
Essential Question
How can you measure and classify an angle?
Answer:
An angle is formed when two rays have the same endpoint or vertex.
An “Angle” will be measured by using a protractor
Classification of angles:
An angle can be classified according to the size of the
opening between its rays.
An acute angle measures greater than 0° and less
than 90°.
A right-angle forms a square corner and measures 90°.
An obtuse angle measures greater than 90° and less than 180°
Exploration 1
Measuring and Classifying Angles
Work with a partner: Find the degree measure of each of the following angles. Classify each angle as acute, right, or obtuse.
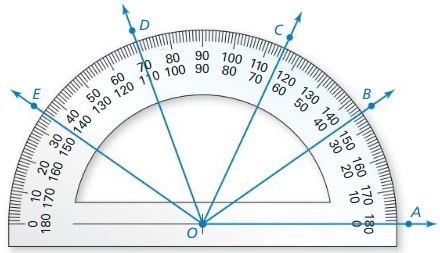
a. ∠AOB
b. ∠AOC
c. ∠BOC
d. ∠BOE
e. ∠COE
f. ∠COD
g. ∠BOD
h. ∠AOE
Answer:
The given figure is:

a. ∠AOB
From the above figure,
∠AOB = 35°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠AOB is an acute angle
b. ∠AOC
From the above figure,
∠AOC = 65°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠AOC is an acute angle
c. ∠BOC
From the above figure,
∠BOC = |65° – 35°| = 30°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠BOC is an acute angle
d. ∠BOE
From the above figure,
∠BOE = |145° – 35°| = 110°
We know that,
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
Hence,
∠BOE is an acute angle
e. ∠COE
From the above figure,
∠COE = |145° – 65°| = 80°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠COE is an acute angle
f. ∠COD
From the above figure,
∠COD =|70° – 65°| = 5°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠COD is an acute angle
g. ∠BOD
From the above figure,
∠BOD = |70° – 35°| = 35°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠BOD is an acute angle
h. ∠AOE
From the above figure,
∠AOE = 145°
We know that,
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
Hence,
∠AOE is an obtuse angle
Exploration 2
Drawing a Regular Polygon
Work with a partner.
a. Use a ruler and protractor to draw the triangular pattern shown at the right.
Answer:
The representation of the triangular pattern by using a ruler and a protractor is:
b. Cut out the pattern and use it to draw three regular hexagons
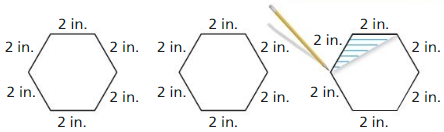
C. The sum of the angle measures of a polygon with n sides is equal to 180(n – 2)°. Do the angle measures at your hexagons agree with this rule? Explain.
ATTENDING TO PRECISION
To be proficient in math, you need to calculate and measure accurately and efficiently.
Answer:
It is given that the sum of the angle measures of a polygon with n sides is equal to 180 (n – 2)°
This rule will be applicable for all the angle measures of all polygons
Hence,
We can conclude that the above rule will be applicable for the angle measures of the hexagon
d. Partition your hexagons into smaller polygons. as shown below. For each hexagon. find the sum of the angle measures of the smaller polygons Does each sum equal the sum of the angle measures of a hexagon? Explain.
Answer:
We know that,
If a polygon is divided into n partitions, then the angle measures of that polygon will also be divided into n partitions
So,
The sum of the angle measures of hexagon = 180(n – 2)°
= 180 ( 6 – 2 )°
= 720°
So,
In the first figure, the polygon is divided into 2 partitions
So,
The sum of the angle measures of each partition = 720 / 2
= 360°
In the second figure, the polygon is divided into 3 partitions
So,
The sum of the angle measures of each partition = 720 / 3
= 240°
In the third figure, the polygon is divided into 6 partitions
So,
The sum of the angle measures of each partition = 720 / 6
= 120°
Communicate Your Answer
Question 3.
How can you measure and classify an angle?
Answer:
An angle is formed when two rays have the same endpoint or vertex.
An “Angle” will be measured by using a protractor
Classification of angles:
An angle can be classified according to the size of the
opening between its rays.
An acute angle measures greater than 0° and less
than 90°.
A right-angle forms a square corner and measures 90°.
An obtuse angle measures greater than 90° and less than 180°
Lesson 1.5 Measuring and Constructing Angles
Monitoring Progress
Write three names for the angle.
Question 1.
Answer:
An “Angle” is formed when two rays have the same endpoint or vertex.
So,
Here, the angle is Q
Hence,
The three names for the given angle are: ∠Q, ∠PQR, and ∠RQP
Question 2.
Answer:
An “Angle” is formed when two rays have the same endpoint or vertex.
So,
Here, the angle is Y
Hence,
The three names for the given angle are: ∠1, ∠XYZ, and ∠ZYX
Question 3.
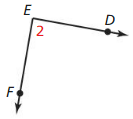
Answer:
An “Angle” is formed when two rays have the same endpoint or vertex.
So,
Here, the angle is E
Hence,
The three names for the given angle are: ∠2, ∠FED, and ∠DEF
Use the diagram in Example 2 to find the angle measure. Then classify the angle.
Question 4.
∠JHM
Answer:
From the above figure,
∠JHM =|145° – 0°| = 145°
We know that,
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
Hence,
∠JHM is an obtuse angle
Question 5.
∠MHK
Answer:
From the above figure,
∠MHK =|145° – 55°| = 110°
We know that,
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
Hence,
∠MHK is an obtuse angle
Question 6.
∠MHL
Answer:
From the above figure,
∠MHL =|145° – 90°| = 55°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠MHL is an acute angle
Question 7.
Without measuring, is ∠DAB ≅ ∠FEH in Example 3? Explain your reasoning. Use a protractor to verify your answer.
Answer:
From the given figure,
We can observe that,
∠DAB ≅ 90°
∠FEH > 90°
Hence, from the above,
We can conclude that ∠DAB is not congruent to ∠FEH
Find the indicated angle measures.
Question 8.
Given that ∠KLM is a straight angle. find in ∠KLN and, m∠NLM.
Answer:
Angle Addition Postulate:
If point B lies in the interior of angle AOC, then. the postulate describes that putting two angles side by side with their vertices together creates a new angle whose measure equals the sum of the measures of the two original angles
It is given that ∠KLM is a straight angle
So,
∠KLM = 180°
So,
180° = (10x – 5)° + (4x + 3)°
180° = (14x -2)°
180 + 2 = 14x
14x = 182
x = \(\frac{182}{14}\)
x = 13°
So,
∠KLN = (10x – 5)°
= 10 (13) – 5
= 130 – 5
= 125°
∠NLM = (4x + 3)°
= 4 (13) + 3
= 52 + 3
= 55°
Hence, from the above,
We can conclude that
∠KLN and ∠NLM are 125° and 55° respectively
Question 9.
Given that ∠EFG is a right angle. find, m∠EFH and m∠HFG.
Answer:
Angle Addition Postulate:
If point B lies in the interior of angle AOC, then. the postulate describes that putting two angles side by side with their vertices together creates a new angle whose measure equals the sum of the measures of the two original angles
It is given that ∠EFG is a right angle
So,
∠EFG = 90°
So,
90° = (2x + 2)° + (x + 1)°
90° = (3x + 3)°
90 – 3 = 3x
3x = 87
x = \(\frac{87}{3}\)
x = 29°
So,
∠EFH = (2x + 2)°
= 2 (29) + 2
= 58 + 2
= 60°
∠HFG = (x + 1)°
= 29 + 1
= 30°
Hence, from the above,
We can conclude that
∠EFH and ∠HFG are 60° and 30° respectively
Question 10.
Angle MNP is a straight angle, and \(\vec{N}\)Q bisects ∠MNP. Draw ∠MNP and \(\vec{N}\)Q. Use arcs to mark the congruent angles in your diagram. Find the angle measures of these congruent angles.
Answer:
It is given that angle MNP is a straight angle, and \(\vec{N}\)Q bisects ∠MNP. Draw ∠MNP and \(\vec{N}\)Q.
So,
The representation of the above statement is:
Hence, from the above,
We can conclude that the angle measure of each congruent angle is: 55.3°
Exercise 1.5 Measuring and Constructing Angles
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Two angles are __________ angles when they have the same measure.
Answer:
Question 2.
WHICH ONE DOES DOESN’T BELONG?
Which angle name does not belong with the other three? Explain your reasoning.
∠BCA
∠BAC
∠1
∠CAB
Answer:
We know that,
An angle can be defined as the figure formed by two rays meeting at a common endpoint
So,
From the given figure,
A, B, and C are the given angles
So,
In ∠BCA, C is the angle
In ∠BAC, A is the angle
In ∠1, A is the angle
In ∠CAB, A is the angle
Hence, from the above,
We can conclude that ∠BCA doesn’t belong with the other three
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6. write three names for the angle.
Question 3.
Answer:
![]()
Question 4.
Answer:
We know that,
An angle can be defined as the figure formed by two rays meeting at a common endpoint
Hence,
The names for the given angle are: ∠G, ∠FGH, and ∠HGF
Question 5.
Answer:
![]()
Question 6.
Answer:
We know that,
An angle can be defined as the figure formed by two rays meeting at a common endpoint
Hence,
The names for the given angle are: ∠8, ∠R, ∠QRS, and ∠SRQ
In Exercises 7 and 8, name three different angles in the diagram.
Question 7.
Answer:
![]()
Question 8.
Answer:
We know that,
An angle can be defined as the figure formed by two rays meeting at a common endpoint
Hence,
The three different angles are: ∠GJF, ∠CJF, and ∠CJG
In Exercises 9 – 12 find the angle measure. Then classify the angle.
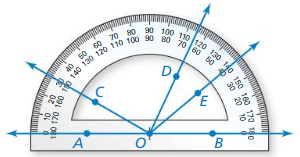
Question 9.
m∠AOC
Answer:

Question 10.
m∠BOD
Answer:
From the above figure,
∠BOD = |0° – 65°| = 65°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠BOD is an acute angle
Question 11.
m∠COD
Answer:

Question 12.
m∠EOD
Answer:
From the above figure,
∠EOD = |40° – 65°| = 25°
We know that,
The angle that is greater than 0° and less than 90° is an “Acute angle”
Hence,
∠EOD is an acute angle
ERROR ANALYSIS
In Exercises 13 and 14. describe and correct the error in finding the angle measure. Use the diagram from Exercises 9 – 12.
Question 13.

Answer:

Question 14.

Answer:
From the given figure,
We can observe that
∠D is at 40° and ∠E is at 65°
So,
∠DOE = |40° – 65°| = 25°
Hence,
∠DOE = 25°
CONSTRUCTION
In Exercises 15 and 16. use a compass and straightedge to copy the angle.
Question 15.
Answer:

Question 16.
Answer:
The steps to copy the angle are:
Step 1:
Label the vertex of the original angle as A. Draw a segment and label a point D on the segment.
Step 2:
Draw an arc with the center at A. Label the two intersecting points as B and C.
Step 3:
Using the same radius, draw an arc with center D. Label the intersecting point as E.
Step 4:
Draw an arc with radius BC and center E. Label the intersection F.
Step 5:
Draw \(\overline{D F}\)
In Exercises 17 – 20, in m∠AED = 34° and m∠EAD = 112°.
Question 17.
Identify the angles congruent to ∠IED.
Answer:
Question 18.
Identify the angles congruent to ∠EAD.
Answer:
From the given figure,
The angles congruent to ∠EAD are:
∠DBC, ∠ADB, and ∠DAE
Question 19.
Find m∠BDC.
Answer:
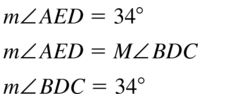
Question 20.
Find m∠ADB.
Answer:
From the given figure,
∠EAD = 112°
Hence,
By the property of Congruence,
∠EAD ≡ ∠ADB
Hence, from the above,
We can conclude that
∠ADB = 112°
In Exercises 21 – 24, find the indicated angle measure.
Question 21.
Find m∠ABC.
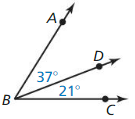
Answer:
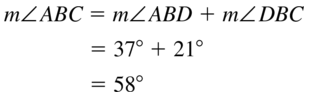
Question 22.
Find m∠LMN.
Answer:
By using the Angle Addition postulate,
∠LMN = ∠LMP + ∠PMN
∠LMN = 85° + 23°
∠LMN = 108°
Question 23.
m∠RST = 114°. Find m∠RSV.
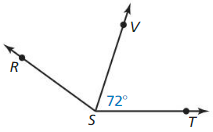
Answer:
Question 24.
∠GHK is a straight angle. Find m∠LHK.
Answer:
By using the Angle Addition Postulate,
∠GHK = ∠GHL + ∠LHK
It is given that ∠GHK is a straight line
So,
∠GHK = 180°
So,
180° = 79° + ∠LHK
∠LHK = 180° – 79°
∠LHK = 101°
Hence, from the above,
We can conclude that
∠LHK = 101°
In Exercises 25 – 30. find the indicated angle measures.
Question 25.
m∠ABC = 95°. Find m∠ABD and m∠DBC.
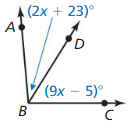
Answer:
Question 26.
m∠XYZ = 117°. Find m∠XYW and m∠WYZ
Answer:
By using the Angle Addition Postulate,
∠XYZ = ∠XYW + ∠WYZ
It is given that ∠XYZ = 117°
So,
117° = (6x + 44)° + (-10x + 65)°
117° = (-4x + 109)°
-4x = 117 – 109
-4x = 8
x = \(\frac{-8}{4}\)
x = -2
Hence,
∠XYW = (6x + 44)°
= 6 (-2) + 44
= 44 – 12
= 32°
∠WYZ = (-10x + 65)°
= -10 (-2) + 65
= 20 + 65
= 85°
Hence, from the above,
We can conclude that
∠XYW = 32° and ∠WYZ = 85°
Question 27.
∠LMN is a straight angle. Find m∠LMP and m∠NMP
Answer:
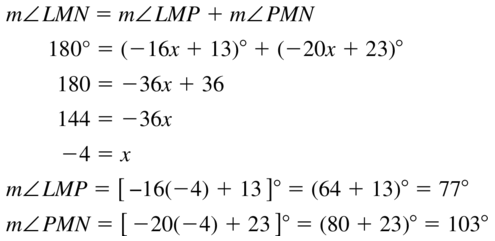
Question 28.
∠ABC is a straight angle. Find m∠ABX and m∠CBX.
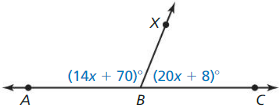
Answer:
From the Angle Addition Postulate,
∠ABC = ∠ABX + ∠CBX
It is given that ∠ABC is a straight angle
So,
∠ABC = 180°
So,
180° = (14x + 70)° + (20x + 8)°
180° = 34x + 78
180 – 78 = 34x
34x = 102°
x = \(\frac{102}{34}\)
x = 3°
So,
∠ABX = (14x + 70)°
= 14 (3) + 70
= 42 + 70
= 112°
∠CBX = (20x + 8)°
= 20 (3) + 8
= 60 + 8
= 68°
Hence, from the above,
We can conclude that
∠ABX = 112° and ∠CBX = 68°
Question 29.
Find m∠RSQ and M∠TSQ.
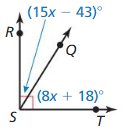
Answer:
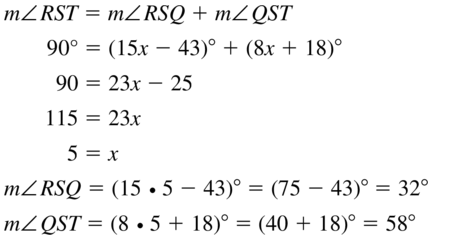
Question 30.
Find m∠DEH and m∠FEH.
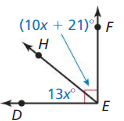
Answer:
From the Angle Addition Postulate,
∠DEF = ∠DEH + ∠FEH
From the figure,
We can observe that ∠DEF is a right angle
So,
∠DEF = 90°
So,
90° = 13x° + (10x + 21)°
90° = 23x + 21
90 – 21 = 23x
23x = 69°
x = \(\frac{69}{23}\)
x = 3°
So,
∠DEH = 13x°
= 13 (3)
= 39°
∠FEH = (10x + 21)°
= 10 (3) + 21
= 30 + 21
= 51°
Hence, from the above,
We can conclude that
∠DEH = 39° and ∠FEH = 51°
CONSTRUCTION
In Exercises 31 and 32. copy the angle. Then construct the angle bisector with a compass and straightedge.
Question 31.
Answer:

Question 32.
Answer:
The steps for the construction of the angle bisector and copying of the angle is:
Step 1:
Label the vertex of the angle as A. Place the compass at A.
Step 2:
Draw an arc that intersects both sides of the angle. Label the intersections B and C.
Step 3:
Place the compass at C and draw an arc, then place the compass point at B. Using the same radius, draw another arc. Label the intersection D.
Step 4:
Use a straightedge to draw a ray through A and D.
Step 5:
\(\overline{A D}\) bisects ∠A
In Exercises 33 – 36, \(\vec{Q}\)S bisects ∠PQR. Use the diagram and the given angle measure to find the indicated angle measures.
Question 33.
m∠PQS = 63°. Find m∠RQS and m∠PQR.
Answer:
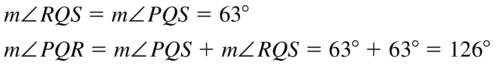
Question 34.
m∠RQS = 71°. Find m∠PQS and m∠PQR.
Answer:
We know that,
An “Angle Bisector” makes the two angles congruent i.e., equal
So,
From the above figure,
We can say that,
∠PQS = ∠RQS
Now,
By using the Angle Addition Postulate,
∠PQR = ∠PQS + ∠RQS
It is given that,
∠RQS = 71°
So,
∠PQS = 71°
So,
∠PQR = 71 + 71 = 142°
Hence, from the above,
We can conclude that
∠PQS = 71° and ∠PQR = 142°
Question 35.
m∠PQR = 124°. Find m∠PQS and m∠RQS.
Answer:
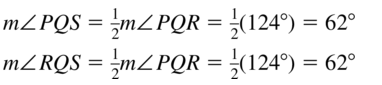
Question 36.
m∠PQR = 119°. Find m∠PQS and m∠RQS.
Answer:
We know that,
An “Angle Bisector” makes the two angles congruent i.e., equal
So,
From the above figure,
We can say that,
∠PQS = ∠RQS
Now,
By using the Angle Addition Postulate,
∠PQR = ∠PQS + ∠RQS
It is given that,
∠PQR = 119°
So,
119° = 2 (∠PQS)
∠PQS = 59.5°
Hence, from the above,
We can conclude that
∠PQS = 59.5° and ∠RQS = 59.5°
In Exercises 37 – 40, \(\overrightarrow{B D}\) bisects ∠ABC. Find m∠ABD, m∠CBD, and m∠ABC.
Question 37.
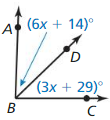
Answer:
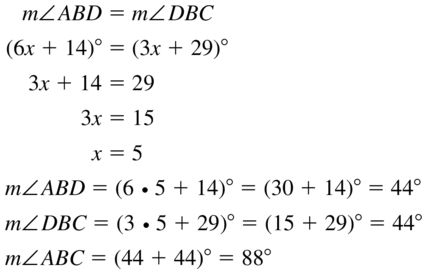
Question 38.
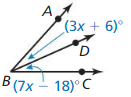
Answer:
It is given that \(\overrightarrow{B D}\) bisects ∠ABC
So,
By using the bisector property,
∠ABD = ∠DBC
So,
(3x + 6)° = (7x – 18)°
3x – 7x = -18 – 6
-4x = -24
4x = 24
x = \(\frac{24}{4}\)
x = 6°
So,
∠ABD = (3x + 6)°
= 3 (6) + 6
= 18 + 6
= 24°
∠DBC = (7x – 18)°
= 7 (6) – 18
= 42 – 18
= 24°
∠ABC = ∠ABD + ∠DBC
= 24 + 24 = 48°
Hence, from the above,
We can conclude that
∠ABC = 48°, ∠ABD = 24°, and ∠CBD = 24°
Question 39.
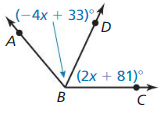
Answer:
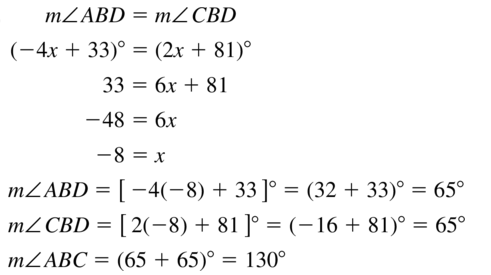
Question 4o.
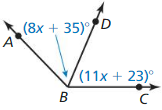
Answer:
It is given that \(\overrightarrow{B D}\) bisects ∠ABC
So,
By using the bisector property,
∠ABD = ∠DBC
So,
(8x + 35)° = (11x + 23)°
8x – 11x = 23 35
-3x = -12
3x = 12
x = \(\frac{12}{3}\)
x = 4°
So,
∠ABD = (8x + 35)°
= 8 (4) + 35
= 32 + 35
= 67°
∠DBC = (11x + 23)°
= 11 (4) + 23
= 44 + 23
= 67°
∠ABC = ∠ABD + ∠DBC
= 67 + 67 = 134°
Hence, from the above,
We can conclude that
∠ABC = 134°, ∠ABD = 67°, and ∠CBD = 67°
Question 41.
WRITING
Explain how to find m∠ABD when you are given m∠ABC and m∠CBD.
Answer:

Question 42.
ANALYZING RELATIONSHIPS
The map shows the intersections of three roads. Malcolm Way intersects Sydney Street at an angle of 162°. Park Road intersects Sydney Street at an anÌe of 87°. Find the angle at which Malcom Way intersects Park Road.
Answer:
It is given that Malcolm Way intersects Sydney Street at an angle of 162°. Park Road intersects Sydney Street at an anÌe of 87°.
From the figure,
We can observe that
The angle between Malcolm Way and Sydney street = The angle between Sydney street and Park Road + The angle between Malcolm way and Park road
So,
162° = 87° + The angle between Malcolm way and Park Road
The angle between Malcolm Way and Park Road = 162 – 87
The angle between Malcolm Way and Park Road = 75°
Hence, from the above,
We can conclude that the angle at which Malcolm Way intersects Park Road is: 75°
Question 43.
ANALYZING RELATIONSHIPS
In the sculpture shown in the photograph. the measure of ∠LMN is 76° and the measure of ∠PMN is 36°. What is the measure of ∠LMP?

Answer:
USING STRUCTURE
In Exercise 44 – 46. use the diagram of the roof truss.
Question 44.
In the roof truss, \(\vec{B}\)G bisects ∠ABC and ∠DEF. m∠ABC = 112°. and ∠ABC ≅ ∠DEF Find the measure of each angle.
a. m∠DEF
Answer:
It is given that
\(\vec{B}\)G bisects ∠ABC and ∠DEF
It is also given that
∠ABC = ∠DEF
∠ABC = 112°
Hence,
∠DEF = 112°
b. m∠ABG
Answer:
It is given that \(\vec{B}\)G bisects ∠ABC and ∠DEF
So,
For ∠ABC,
By congruence property,
∠ABG = ∠CBG
Hence,
∠ABG = ∠ABC / 2
= 112 / 2
= 56°
c. m∠CBG
Answer:
It is given that \(\vec{B}\)G bisects ∠ABC and ∠DEF
So,
For ∠ABC,
By congruence property,
∠ABG = ∠CBG
Hence,
∠CBG = ∠ABC / 2
= 112 / 2
= 56°
d. m∠DEG
Answer:
It is given that \(\vec{B}\)G bisects ∠ABC and ∠DEF
So,
For ∠DEF,
By congruence property,
∠DEG = ∠EGF
Hence,
∠DEG = ∠DEF / 2
= 112 / 2
= 56°
Question 45.
In the roof truss, ∠DGF is a straight angle, and \(\vec{G}\)B bisects ∠DGF Find m∠DGE and m∠FGE.
Answer:
Question 46.
Name an example of each of the four types of angles according to their measures in the diagram.
Answer:
There are 4 types of angles. They are:
a. Acute angle:
The angle that is greater than 0° and less than 90° is an “Acute angle”
b. Obtuse angle:
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
c. Straight angle:
The angle 180° is called a “Straight angle”
d. Right angle:
The angle 90° is called a “Right angle”
MATHEMATICAL CONNECTIONS
47. In ∠ABC. \(\vec{B}\)X is in the interior 0f the angle. m∠ABX is 12 more than 4 times m∠CBX. and in m∠ABC = 92°.
a. Draw a diagram to represent the situation.
b. Write and solve an equation to find m∠ABX and, m∠CBX.
Answer:
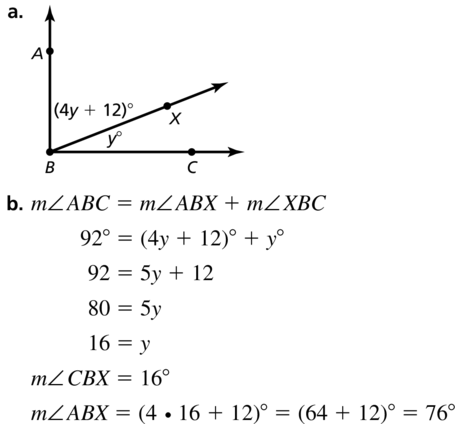
Question 48.
THOUGHT-PROVOKING
The angle between the minute hand and the hour hand of a clock is 90° What time is it? Justify your answer.
Answer:
From the clock,
We can observe that the angle between the minute hand and the hour hand of a clock is 90° when the time will be 3:00 and 9:00
Question 49.
ABSTRACT REASONING
Classify the angles that result from bisecting each type of angle.
a. acute angle
b. right angle
c. obtuse angle
d. straight angle
Answer:

Question 50.
ABSTRACT REASONING
Classify the angles that result from drawing a ray in the interior of each type of angle. Include all possibilities and explain your reasoning.
a. acute angle
b. right angle
c. obtuse angle
d. straight angle
Answer:
The classification of angles that result from drawing a ray in the interior of each type of angle is:
a. Acute angle:
The angle that is greater than 0° and less than 90° is an “Acute angle”
b. Obtuse angle:
The angle that is greater than 90° and less than 180° is an “Obtuse angle”
c. Straight angle:
The angle 180° is called a “Straight angle”
d. Right angle:
The angle 90° is called a “Right angle”
Question 51.
CRITICAL THINKING
The ray from the origin through (4, 0) forms one side of an angle. Use the numbers below as x- and y-coordinates to create each type of angle in a coordinate plane.
– 2 – 1 0 1 2
a. acute angle
b. right angle
c. obtuse angle
d. straight angle
Answer:

Question 52.
MAKING AN ARGUMENT
Your friend claims it is possible for a straight angle to Consist of two obtuse angles. Is your friend correct? Explain your reasoning.
Answer:
No, your friend is not correct
We know that,
A straight angle consists of 2 Right angles or a Right angle and an obtuse angle
So,
The claim of your friend which is a straight angle consists of two obtuse angles is not correct
Hence, from the above,
We can conclude that the claim of your friend is not correct
Question 53.
CRITICAL THINKING
Two acute angles are added together. What type(s) of angle(s) do they form? Explain your reasoning.
Answer:
Question 54.
HOW DO YOU SEE IT?
Use the diagram
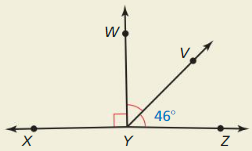
a. Is it possible for ∠XYZ to be a straight angle? Explain your reasoning.
Answer:
From the figure,
∠XYZ is a flat line i.e., there is no angle
So,
∠XYZ = 0° or 180°
We know that,
The line that has an angle of 0° or 180° is called a “Straight line”
Hence, from the above,
We can conclude that
∠XYZ is a straight angle
b. What can you change in the diagram so that ∠XYZ is a straight angle?
Answer:
From the given figure,
∠XYZ is already a straight angle
So,
There is no change to make ∠XYZ a straight line
Question 55.
WRITING
Explain the process of bisecting an angle in your own words. Compare it to bisecting a segment.
Answer:

Question 56.
ANALYZING RELATIONSHIPS
\(\vec{S}\)Q bisects ∠RST, \(\vec{S}\)P bisects ∠RSQ. and \(\vec{S}\)V bisects ∠RSP. The measure of ∠VSP is 17°. Find in m∠TSQ. Explain.
Answer:
Question 57.
ABSTRACT REASONING
A bubble level is a tool used
to determine whether a surface is horizontal. like the top of a picture frame. If the bubble is not exactly in the middle when the level is placed on the surface. then the surface is not horizontal. What is the most realistic type of angle Formed by the level and a horizontal line when the bubble is not in the middle? Explain your reasoning.

Answer:

Maintaining Mathematical Proficiency
Solve the equation.
Question 58.
x + 67 = 180
Answer:
The given equation is:
x + 67 = 180
So,
x = 180 – 67
x = 113
Hence, from the above,
We can conclude that the value of x is: 113
Question 59.
x + 58 = 90
Answer:
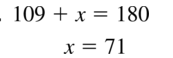
Question 60.
16 + x = 90
Answer:
The given equation is:
16 + x = 90
So,
x = 90 – 16
x = 74
Hence, from the above,
We can conclude that the value of x is: 74
Question 61.
109 + x = 180
Answer:
The given equation is:
109 + x = 180
So,
x = 180 – 109
x = 71
Hence, from the above,
We can conclude that the value of x is: 71
Question 62.
(6x + 7) + (13x + 21) = 180
Answer:
The given equation is:
(6x + 7) + (13x + 21) = 180
So,
19x + 28 = 180
19x = 180 – 28
19x = 152
x = \(\frac{152}{9}\)
x = 8
Hence, from the above,
We can conclude that the value of x is: 8
Question 63.
(3x + 15) + (4x – 9) = 90
Answer:
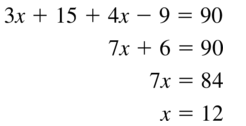
Question 64.
(11x – 25) + (24x + 10) = 90
Answer:
The given equation is:
(11x – 25) + (24x + 10) = 90
So,
35x – 15 = 90
35x = 90 + 15
35x = 105
x = \(\frac{105}{35}\)
x = 3
Hence, from the above,
We can conclude that the value of x is: 3
Question 65.
(14x – 18) + (5x + 8) = 180
Answer:
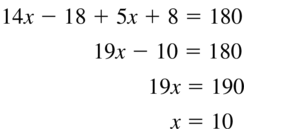
1.6 Describing Pairs of Angles
Essential Question
How can you describe angle pair relationships and use these descriptions to find angle measures?
Answer:
Two adjacent angles are a linear pair when their non-common sides are opposite rays. The angles in a linear pair are supplementary angles. common side L1+22=180°. Two angles are vertical angles when their sides form two pairs of opposite rays
Exploration 1
Work with a partner: The five-pointed star has a regular pentagon at its center.
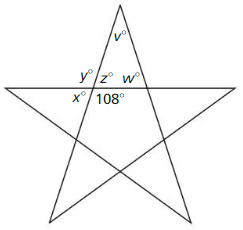
a. What do you notice about the following angle pairs?
x° and y°
Answer:
From the given figure,
x and y share a common line
We know that,
The angles that share a common side are called “Adjacent angles”
Hence,
x° and y° are called “Adjacent angles”
y° and z°
Answer:
From the given figure,
y and z share a common line
We know that,
The angles that share a common side are called “Adjacent angles”
Hence,
y° and z° are called “Adjacent angles”
x° and z°
Answer:
From the given figure,
x and z share a common vertex
We know that,
The angles that share a common vertex are called “Vertical angles”
Hence,
x° and z° are called “Vertical angles”
b. Find the values of the indicated variables. Do not use a protractor to measure the angles.
Explain how you obtained each answer.
Answer:
we know that,
Adjacent angles will always be 180° or 90°
Vertical angles are equal
So,
From the figure,
We can observe that
x + 108° = 180°
x° = 180° – 108°
x° = 72°
Now,
From the figure,
We can observe that x and y are the vertical angles
So,
y° = 72°
Now,
From the figure,
We can observe that y and z are the adjacent angles
So,
y° + z° = 180°
z° = 180° – 72°
z° = 108°
Now,
We know that,
The vertically opposite angles are equal
So,
y = v
So,
v° = 72°
Now,
We know that,
The vertically opposite angles are equal
So,
w = v
So,
w° = 72°
Hence, from the above,
We can conclude that the angle measures are:
x° = 72°, y° = 72°, z° = 108°, v° = 72° and w° = 72°
Exploration 2
Finding Angle Measures
Work with a partner: A square is divided by its diagonals into four triangles.
a. What do you notice about the following angle pairs?
a° and b°
Answer:
From the above figure,
We can observe that a° and b° are adjacent angles
So,
We can say that
a° + b° = 90°
c° and d°
Answer:
From the above figure,
We can observe that c° and d° are adjacent angles
So,
We can say that
c° + d° = 90°
c° and e°
Answer:
From the above figure,
We can observe that c and e are the opposite angles
So,
We can say that,
c° = e°
b. Find the values of the indicated variables. Do not use a protractor to measure the angles.
Explain how you obtained each answer.
Answer:
The given figure is: Square
So,
We know that,
All the angles in the square are: 90°
Hence, from the above,
We can conclude that
c° = 90°, d° = 90°, and e° = 90°
Communicate Your Answer
Question 3.
How can you describe angle pair relationships and use these descriptions to find angle measures?
Answer:
Two adjacent angles are a linear pair when their non-common sides are opposite rays. The angles in a linear pair are supplementary angles. common side L1+22=180°. Two angles are vertical angles when their sides form two pairs of opposite rays
Question 4.
What do you notice about the angle measures of complementary angles, supplementary angles, and vertical angles?
ATTENDING TO PRECISION
To be proficient in math, you need to communicate precisely with others.
Answer:
The “Complementary angles” are the angles that the measure of angles is 90°
The “Supplementary angles” are the angles that the measure of angles is 180°
The opposite angles are the angles that have a common side and opposite to each other
Lesson 1.6 Describing Pairs of Angles
Monitoring Progress
In Exercises 1 and 2. use the figure.
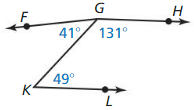
Question 1.
Name a pair of complementary angles, a pair of supplementary angles, and a pair of adjacent angles.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 90° is called “Complementary angles”
The pair of angles that the sum of the angle measures is 180° is called “Supplementary angles”
The angle that is the same in more than 1 angle-pair is called “Adjacent Angle”
So,
From the given figure,
The pair of complementary angles is: ∠FGK and ∠LKG
The pair of supplementary angles is: ∠HGK and ∠GKL
The pair of adjacent angles is: ∠FGK and ∠HGK
Question 2.
Are ∠KGH and ∠LKG adjacent angles? Are ∠FGK and ∠FGH adjacent angles? Explain.
Answer:
We know that,
The angle that is the same in more than 1 angle-pair is called “Adjacent Angle”
But,
In ∠KGH and ∠LKG, the angle is not the same
So,
∠KGH and ∠LKG are not the adjacent angles
In ∠FGK and ∠FGH, the angle is the same
So,
∠FGK and ∠FGH are adjacent angles
Question 3.
∠1 is a complement of ∠2. arid m∠2 = 5°. Find m∠1.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 90° is called “Complementary angles”
It is given that
∠1 is a complement of ∠2
So,
∠1 + ∠2 = 90°
It is also given that
∠2 = 5°
So,
∠1 = 90° – ∠2
∠1 = 90° – 5°
∠1 = 85°
Hence, from the above,
We can conclude that
∠1 = 85°
Question 4.
∠3 is a supplement of ∠4. and m∠3 = 148°. Find m∠4.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 180° is called “Supplementary angles”
It is given that
∠3 is a supplement of ∠4
So,
∠3 + ∠4 = 180°
It is also given that
∠3 = 148°
So,
∠4 = 180° – ∠3
∠4 = 180° – 148°
∠4 = 32°
Hence, from the above,
We can conclude that
∠4 = 32°
Question 5.
∠LMN and ∠PQR are complementary angles. Find the measures of the angles when in m∠LMN = (4x – 2)° and m∠PQR = (9x + 1)°.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 90° is called “Complementary angles”
It is given that
∠LMN and ∠PQR are complementary angles
So,
∠LMN + ∠PQR = 90°
It is also given that
∠LMN = (4x – 2)° and ∠PQR = (9x + 1)°
So,
(4x – 2)° + (9x + 1)° = 90°
13x – 1 = 90°
13x = 90 + 1
x = \(\frac{91}{13}\)
x = 7°
So,
∠LMN = (4x – 2)°
= 4 (7) – 2
= 28 – 2
= 26°
∠PQR = (9x + 1)°
= 9 (7) + 1
= 63 + 1
= 64°
Hence, from the above,
We can conclude that
∠LMN = 26° and ∠PQR = 64°
Question 6.
Do any of the numbered angles in the figure form a linear pair? Which angles are vertical angles? Explain your reasoning.
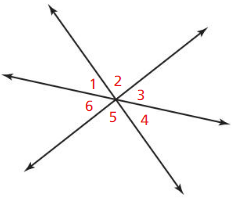
Answer:
From the above figure,
We can observe that 1, 2, 3, 4, 5, and 6 are the angles
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
Hence,
The linear pair of angles in the given figure are: ∠1 and ∠2; ∠3 and ∠4; ∠5 and ∠6
The vertical angles from the given figure are: ∠1 and ∠2; ∠2 and ∠5; ∠3 and ∠6
Question 7.
The measure of an angle is twice the measure of its complement. Find the measure of each angle.

Answer:
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
So,
∠1 and ∠2 (or) ∠3 and ∠4 (or) ∠5 and ∠6 are the complementary angles
It is given that,
The measure of an angle is twice the measure of its component
Let the angle be x°
So,
x + 2x = 90°
3x = 90°
x = \(\frac{90}{3}\)
x = 30°
Hence, from the above,
We can conclude that
∠1 = ∠3 = ∠5 = 30°
∠2 = ∠4 = ∠6 = 60°
Question 8.
Two angles form a linear pair. The measure of one angle is 1\(\frac{1}{2}\) times the measure of the other angle. Find the measure of each angle.

Answer:
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
So,
∠1 and ∠2 (or) ∠3 and ∠4 (or) ∠5 and ∠6 are the supplementary angles
It is given that,
The measure of one angle is 1\(\frac{1}{2}\) times the measure of the other angle
Let the angle be x°
So,
x + 1\(\frac{1}{2}\)x = 180°
x + \(\frac{3}{2}\)x = 180°
\(\frac{5x}{2}\) = 180°
5x = 180° (2)
5x = 360°
x = \(\frac{360}{5}\)
x = 72°
Hence, from the above,
We can conclude that
∠1 = ∠3 = ∠5 = 72°
∠2 = ∠4 = ∠6 = 108°
Exercise 1.6 Describing Pairs of Angles
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain what is different between adjacent angles and vertical angles.
Answer:
Question 2.
WHICH ONE DID DOESN’T BELONG?
Which one does hot belong with the other three? Explain your reasoning.

Answer:
The angle that is the same in more than 1 angle-pair and has a common side is called “Adjacent Angle”
So,
From the above figure,
We can observe that only the first figure has an adjacent angle whereas all the three figures don’t have any adjacent angles
Hence, from the above,
We can conclude that the first figure does not belong with the other three
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, use the figure.
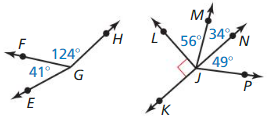
Question 3.
Name a pair of adjacent complementary angles.
Answer:
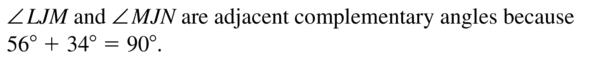
Question 4.
Name a pair of adjacent supplementary angles.
Answer:
We know that,
The angles that have the sum of the angle measures 180° are called “Supplementary angles
Hence, from the figure,
A pair of adjacent supplementary angles are: ∠LJN + ∠LJK
Question 5.
Name a pair of nonadjacent complementary angles.
Answer:
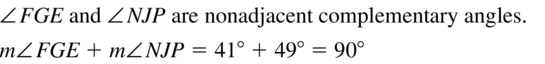
Question 6.
Name a pair of nonadjacent supplementary angles.
Answer:
We know that,
The angles that have the sum of the angle measures 180° are called “Supplementary angles
Hence, from the figure,
A pair of adjacent supplementary angles are: ∠LJN + ∠LJK and ∠NGP + ∠HGF
In Exercises 7 – 10. find the angle measure.
Question 7.
∠1 is a complement of ∠2, and m∠1 = 23°. Find, m∠2.
Answer:
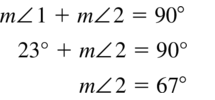
Question 8.
∠3 is a complement of ∠4. and m∠3 = 46°. Find, m∠4.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 90° is called “Complementary angles”
It is given that
∠3 is a complement of ∠4
So,
∠3 + ∠4 = 90°
It is also given that
∠3 = 46°
So,
∠4 = 90° – ∠3
∠4 = 90° – 46°
∠4 = 44°
Hence, from the above,
We can conclude that
∠4 = 44°
Question 9.
∠5 is a supplement of ∠6. and m∠5 = 78°. Find m∠6.
Answer:
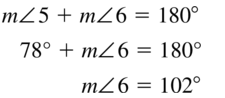
Question 10.
∠7 is a supplement of ∠8. and m∠7 = 109°. Find m∠8.
Answer:
We know that,
The pair of angles that the sum of the angle measures is 180° is called “Supplementary angles”
It is given that
∠7 is a supplement of ∠8
So,
∠7 + ∠8 = 180°
It is also given that
∠7 = 109°
So,
∠8 = 180° – ∠7
∠8 = 180° – 109°
∠8 = 71°
Hence, from the above,
We can conclude that
∠8 = 71°
In Exercises 11 – 14. find the measure of each angle.
Question 11.
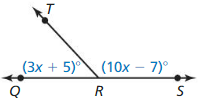
Answer:

Question 12.
Answer:
We know that,
By using the Angle Addition Postulate,
∠BAD = ∠CAB + ∠CAD
From the given figure,
We can observe that
∠BAD = 90°
So,
(15x – 2)° + (7x + 4)° = 90°
22x + 2 = 90°
22x = 88°
x = \(\frac{88}{22}\)
x = 4°
So,
∠CAB = (15x – 2)°
= 15 (4) – 2
= 60 – 2
= 58°
∠CAD = (7x + 4)°
= 7 (4) + 4
= 28 + 4
= 32°
Hence, from the above,
We can conclude that
∠CAB = 58° and ∠CAD = 32°
Question 13.
∠UVW and ∠XYZ arc complementary angles, m∠UVW = (x – 10)°. and m∠XYZ = (4x – 10)°.
Answer:
Question 14.
∠EFG and ∠LMN are supplementary angles. m∠EFG = (3x + 17)°, and m∠LMN = (\(\frac{1}{2} x\) – 5)°
Answer:
We know that,
The pair of angles that the sum of the angle measures is 180° is called “Supplementary angles”
It is given that
∠EFG and ∠LMN are supplementary angles
So,
∠LMN + ∠EFG = 180°
It is also given that
∠LMN = (\(\frac{1}{2} x\) – 5)° and ∠EFG = (3x + 17)°
So,
(\(\frac{1}{2} x\) – 5)° + (3x + 17)° = 180°
\(\frac{7}{2} x\) + 12 = 180°
\(\frac{7}{2} x\) = 180 – 12
\(\frac{7}{2} x\) = 168°
7x = 168 (2)
7x = 336
x = \(\frac{336}{7}\)
x = 48°
So,
∠LMN = (\(\frac{1}{2} x\) – 5)°
= \(\frac{1}{2} \) × 48 – 5
= 24 – 5
= 19°
∠EFG = (3x + 17)°
= 3 (48) + 17
= 144 + 17
= 161°
Hence, from the above,
We can conclude that
∠LMN = 19° and ∠EFG = 161°
In Exercises 15 – 18. use the figure.
Question 15.
Identify the linear pair(s) that include ∠1.
Answer:
![]()
Question 16.
Identify the linear pair(s) that include ∠7.
Answer:
We know that,
The angle that is the same in more than 1 angle-pair is called “Adjacent Angle”
Hence, from the figure,
We can conclude that
The linear pairs that include ∠7 are: ∠6 and ∠7 and ∠7 and ∠8
Question 17.
Are ∠6 and ∠8 vertical angles? Explain your reasoning.
Answer:
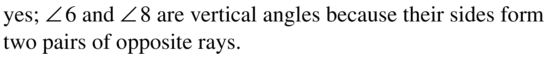
Question 18.
Are ∠2 and ∠5 vertical angles? Explain your reasoning.
Answer:
We know that,
The angles that have the same vertex are called “Vertical angles”
Hence, from the figure,
We can conclude that ∠2 and ∠5 are vertical angles
In Exercises 19 – 22, find the measure of each angle.
Question 19.
Two angles form a linear pair. The measure of one angle is twice the measure of the other angle.
Answer:
Question 20.
Two angles form a linear pair. The measure of one angle is \(\frac{1}{3}\) the measure of the other angle.
Answer:
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
So,
The given angles are the supplementary angles
It is given that,
The measure of one angle is \(\frac{1}{3}\) times the measure of the other angle
Let the angle be x°
So,
x + \(\frac{1}{3}\)x = 180°
\(\frac{4}{3}\)x = 180°
4x = 180° (3)
4x = 540°
x = \(\frac{540}{4}\)
x = 135°
Hence, from the above,
We can conclude that
The measure of one angle is 135° and the measure of the other angle is 270°
Question 21.
The measure of an angle is nine times the measure of its complement.
Answer:
Question 22.
The measure of an angle is \(\frac{1}{4}\) the measure of its complement.
Answer:
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
So,
The given angles are the complementary angles
It is given that,
The measure of one angle is \(\frac{1}{4}\) times the measure of the other angle
Let the angle be x°
So,
x + \(\frac{1}{4}\)x = 90°
\(\frac{5}{4}\)x = 90°
5x = 90° (4)
5x = 360°
x = \(\frac{360}{5}\)
x = 72°
Hence, from the above,
We can conclude that
The measure of one angle is 72° and the measure of the other angle is 144°
ERROR ANALYSIS
In Exercises 23 and 24, describe and correct the error in identifying pairs of angles in the figure.
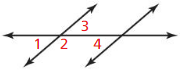
Question 23.

Answer:
Question 24.

Answer:
We know that,
A linear pair of angles are formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines
Hence, from the figure,
We can conclude that ∠1 and ∠3 do not form a linear pair
In Exercises 25 and 26. the picture shows the Alamillo Bridge in Seville, Spain. In the picture, m∠1 = 58° and m∠2 = 24°.

Question 25.
Find the measure of the supplement of ∠1
Answer:
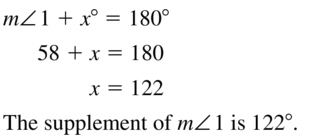
Question 26.
Find the measure of the supplement of ∠2.
Answer:
Let the other angle with ∠2 be x°
We know that,
The sum of the angle measures of supplementary angles is: 180°
So,
∠2 + x° = 180°
Fro the above,
It is given that
∠2 = 24°
So,
24° + x° = 180°
x° = 180° – 24°
x° = 156°
Hence, from the above,
We can conclude that the supplement of ∠2 is: 156°
Question 27.
PROBLEM-SOLVING
The arm of a crossing gate moves 42° from a vertical position. How many more degrees does the arm have to move so that it is horizontal?

A. 42°
B. 138°
C. 48°
D. 90°
Answer:

Question 28.
REASONING
The foul lines of a baseball field intersect at home plate to form a right angle. A batter hits a fair ball such that the path of the baseball forms an angle of 27° with the third base foul line. What is the measure of the angle between the first base foul line and the path of the baseball?
Answer:
It is given that the foul lines of a baseball field intersect at home plate to form a right angle. A batter hits a fair ball such that the path of the baseball forms an angle of 27° with the third base foul line.
So,
We can say that
The angle between the path of the baseball and the third base foul line is complementary i.e., 90° with the angle between the path of the baseball and the base of the first foul line
So,
The angle between the first base foul line and the path of the baseball = 90° – (The angle between the path of the baseball and the third base foul line)
=90° – 27°
= 63°
Hence, from the above,
We can conclude that the angle between the first base foul line and the path of the baseball is: 63°
Question 29.
CONSTRUCTION
Construct a linear pair where one angle measure is 115°.
Answer:
Question 30.
CONSTRUCTION
Construct a pair of adjacent angles that have angle measures of 45° and 97°.
Answer:
The representation of the pair of adjacent angles that has the angle measures of 45° and 97° is:
Question 31.
PROBLEM-SOLVING
m∠U = 2x°, and m∠V = 4m∠U. Which value of x makes ∠U and ∠V complements of each other?
A. 25
B. 9
C. 36
D. 18
Answer:
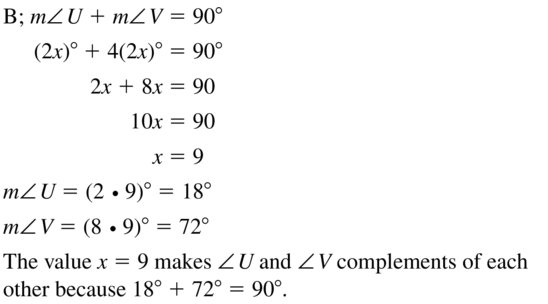
MATHEMATICAL CONNECTIONS
In Exercises 32 – 35, write and solve an algebraic equation to find the measure of each angle based on the given description.
Question 32.
The measure of an angle is 6° less than the measure of its complement.
Answer:
It is given that the measure of an angle is 6° less than the measure of its complement
Let the angle be x°
S0,
The complement of the angle is: (90 – x)°
So,
(90 – x)° = x – 6°
90 + 6 = x + x
2x = 96°
x = \(\frac{96}{2}\)
x = 48°
So,
The measures of the two angles are: 48°, 90° – 48° = 42°
Hence, from the above,
We can conclude that the measures of the angles are: 48°, 42°
Question 33.
The measure of an angle is 12° more than twice the measure of its complement.
Answer:
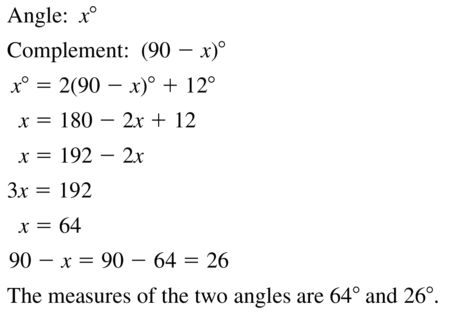
Question 34.
The measure of one angle is 3° more than \(\frac{2}{3}\) the measure of its supplement.
Answer:
It is given that the measure of an angle is 3° more than \(\frac{2}{3}\) the measure of its supplement
Now,
Let the measure of an angle be x°
So,
The measure of the other angle is (180 – x)°
So,
x° = 3° + \(\frac{2}{3}\) (180 – x)°
3x° = 9° + 360° – 2x°
5x° = 369°
x = \(\frac{369}{5}\)
x° = 73.4°
So,
The measures of the angles are: 73.4° and 180° – 73.4° = 106.6°
Hence, from the above,
We can conclude that the measures of the angles are: 73.4v and 106.6°
Question 35.
Two angles form a linear pair. The measure of one angle is 15° less than \(\frac{2}{3}\) the measure of the other angle.
Answer:
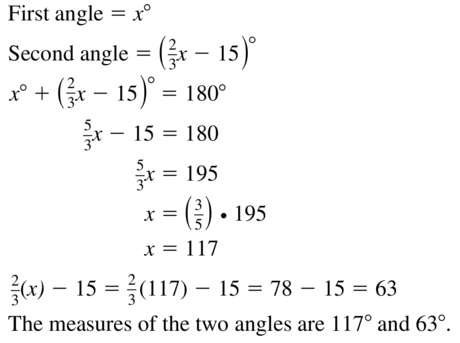
CRITICAL THINKING
In Exercises 36 – 41. tell whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 36.
Complementary angles are adjacent.
Answer:
The given statement is “Complementary angles are adjacent”
We know that,
The complementary angles sometimes will be vertical angles or sometimes adjacent angles or sometimes non-adjacent angles
Hence, from the above,
We can conclude that the given statement is sometimes true
Question 37.
Angles in a linear pair are supplements of each other.
Answer:
![]()
Question 38.
Vertical angles are adjacent.
Answer:
The given statement is “Vertical angles are adjacent”
We know that,
The vertical angles are the angles formed by the intersection of two lines whereas adjacent angles share a common side and a common vertex
Hence, from the above,
We can conclude that vertical angles are never adjacent
Question 39.
Vertical angles are supplements of each other.
Answer:
![]()
Question 40.
If an angle is acute. then its complement is greater than its supplement.
Answer:
The given statement is “If an angle is acute, then its complement is greater than its supplement”
we know that,
The sum of complementary angles is 90° i.e., the measures of the angles are always acute
The sum of the supplementary angles is 180° i.e., the measure of 1 angle is acute and the measure of the other angle is obtuse
Hence, from the above,
We can conclude that if an angle is acute, then its complement will never be greater than its supplement
Question 41.
If two complementary angles are congruent, then the measure of each angle is 45°,
Answer:
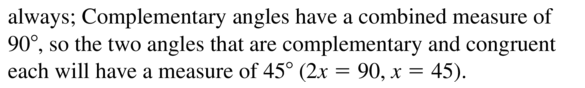
Question 42.
WRITING
Explain why the supplement of an acute angle must be obtuse.
Answer:
We know that,
The sum of the measures of the supplementary angles is: 180°
So,
If one angle is acute i.e., the angle less than 90°, then the other angle must be obtuse to make the sum 180°
Hence,
The supplement of an acute angle must be obtuse
Question 43.
WRITING
Explain why an obtuse angle does not have a complement.
Answer:

Question 44.
THOUGHT-PROVOKING
Sketch an intersection of roads. Identify any supplementary, complementary, or vertical angles.
Answer:
The representation of the intersection of roads is:
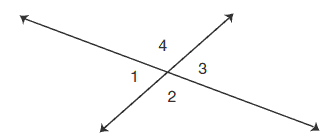
We know that,
The angles that have the sum of the angle measures 90° are “Complementary angles”
The angles that have the sum of the angle measures 180° are “Supplementary angles”
The angles that form with the intersection of 2 lines are “Vertical angles”
So,
From the figure,
The supplementary angles are:
∠1 and ∠2; ∠2 and ∠3; ∠3 and ∠4; ∠4 and ∠1
There are no complementary angles
The vertical angles are:
∠1 and ∠3; ∠2 and ∠4
Question 45.
ATTENDING TO PRECISION
Use the figure.
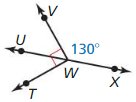
a. Find m∠UWV, m∠TWU, and m∠TWX.
b. YOU write the measures of ∠TWU, ∠TWX, ∠UWV and ∠VWX on separate pieces of paper and place the pieces of paper in a box. Then you pick two pieces of paper out of the box at random. What is the probability that the angle measures you choose are supplementary? Explain your reasoning.
Answer:

Question 46.
HOW DO YOU SEE IT?
Tell whether you can conclude that each statement is true based on the figure. Explain your reasoning.
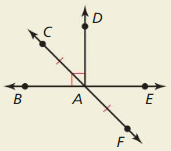
a. \(\overline{C A}\) ≅ \(\overline{A F}\)
Answer:
From the given figure,
We can observe that \(\overline{C A}\) has the same length as \(\overline{A F}\)
Hence, from the above,
We can conclude that
\(\overline{C A}\) ≅ \(\overline{A F}\)
b. Points C, A, and F are collinear
Answer:
We know that,
The points that are present on the same line are called “Collinear points”
From the figure,
We can observe that C, A, and F lie on the same line
Hence, from the above,
We can conclude that C, A, and F are collinear points
c. ∠CAD ≅ ∠EAF.
Answer:
From the figure,
We can observe that point A is the angle bisector of C and D
Hence, from the above,
We can conclude that
∠CAD ≅ ∠EAF
d. \(\overline{B A}\) ≅ \(\overline{A E}\)
Answer:
We know that,
C is the Bisector”
A “Bisector” divides anything into 2 congruent parts
Hence, from the above,
We can conclude that
\(\overline{B A}\) ≅ \(\overline{A E}\)
e. ![]()
Answer:
From the figure,
We can observe that there are 3 lines intersect at point A
Hence, from the above,
We can conclude that
\(\overline{C F}\), \(\overline{B E}\), and \(\overline{A D}\) intersect at point A
f. ∠BAC and ∠CAD are complementary angles.
Answer:
From the figure,
We can observe that ∠A has a complementary angle
Hence, from the above,
We can conclude that ∠BAC and ∠CAD are complementary angles
g. ∠DAE is a right angle.
Answer:
From the figure,
We can observe that,
D is perpendicular to E and A has a complementary angle
Hence, from the above,
We can conclude that ∠DAE is a right angle
Question 47.
REASONING
∠KJL and ∠LJM arc complements, and ∠MJN and ∠LJM are complements. Can you show that ∠KJL ≅ ∠MJN? Explain your reasoning.
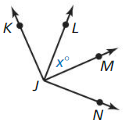
Answer:
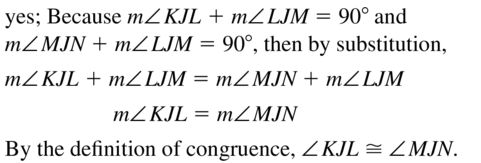
Question 48.
MAKING AN ARGUMENT
Light from a flashlight strikes a mirror and is reflected so that the angle of reflection is congruent to the angle of incidence. Your classmate claims that ∠QPR is congruent to ∠TPU regardless of the measure of ∠RPS. Is your classmate correct? Explain your reasoning.
Answer:
Yes, your classmate is correct
Explanation:
It is given that the light from a flashlight strikes a mirror and is reflected so that the angle of reflection is congruent to the angle of incidence. Your classmate claims that ∠QPR is congruent to ∠TPU regardless of the measure of ∠RPS.
We know that,
The vertical angle is the intersection of two lines and \(\overline{S P}\) is the angle bisector
So,
∠QPR is congruent to ∠TPU regardless of the measure of ∠RPS.
Hence, from the above,
We can conclude that the claim of your friend is correct
Question 49.
DRAWING CONCLUSIONS
Use the figure.
a. Write expressions for the measures of ∠BAE, ∠DAE, and ∠CAB.
b. What do you notice about the measures of vertical angles? Explain your reasoning.
Answer:

Question 50.
MATHEMATICAL CONNECTIONS
Let m∠1 = x°, m∠2 = y1°, and m∠3 = y2° ∠2 is the complement of ∠1, and ∠3 is the supplement of ∠1.
a. Write equations for y1 as a function of x and for y2 as a function of x. What is the domain of each function? Explain.
Answer:
It is given that
m∠1 = x°, m∠2 = y1°, and m∠3 = y2°
∠2 is the complement of ∠1, and ∠3 is the supplement of ∠1
So,
∠1 + ∠2 = 90° and ∠3 + ∠1 = 180°
x° + y1° = 90° and y2° + x° = 180°
So,
y1° = 90° – x° and y2° = 180° – x°
Hence, from the above,
The domain of y1 can be given as: 0° ≤ x ≤ 90°
The domain of y2 can be given as: 0° ≤ x ≤ 180°
b. Graph each function and describe its range.
Answer:
From part (a),
The 2 functions are:
y1° = 90° – x° and y2° = 180° – x°
Hence,
The representations of the 2 functions in the coordinate plane are:
Hence, from the above graph,
The range of y1 is: 90 ≤ y ≤ 200
The range of y2 is: 0 ≤ y ≤ 200
Question 51.
MATHEMATICAL CONNECTIONS
The sum of the measures of two complementary angles is 74° greater than the difference of their measures. Find the measure of each angle. Explain how you found the angle measures.
Answer:

Maintaining MathematicaI Proficiency
Determine whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 52.
An integer is a whole number.
Answer:
The given statement is “An integer is a whole number”
We know that,
All whole numbers must be integers but all integers are not whole numbers
Example:
–6 is an integer but not a whole number
3 is a whole number and also an integer
Hence, from the above,
We can conclude that an integer is sometimes a whole number
Question 53.
An integer is an irrational number.
Answer:
Question 54.
An irrational number is a real number.
Answer:
The given statement is “An irrational number is a real number”
We know that,
“Real numbers” are the numbers that can be written in the form of \(\frac{p}{q}\) whereas “Irrational numbers” can’t be written in the form of \(\frac{p}{q}\)
Hence, from the above,
We can conclude that an irrational number is never a real number
Question 55.
A whole number is negative.
Answer:
![]()
Question 56.
A rational number is an integer.
Answer:
The given statement is “A rational number is an integer”
We know that,
Rational numbers are the numbers that can be written in the form of \(\frac{p}{q}\)
Hence, from the above,
We can conclude that a rational number is sometimes an integer
Question 57.
A natural number is an integer.
Answer:
Question 58.
A whole number is a rational number.
Answer:
The given statement is “A whole number is a rational number”
We know that,
A whole number can be written in the form of \(\frac{p}{q}\)
Hence, from the above,
We can conclude that a whole number is always a rational number
Question 59.
An irrational number is negative.
Answer:
![]()
1.4 – 1.6 Performance Task: Comfortable Horse Stalls
Mathematical Practices
Question 1.
How could you explain your answers to Exercise 33 on page 36 to a friend who is unable to hear’?
Answer:
In Exercise 33 on page 36,
The given vertices of the triangle are in the form of the standard linear equation
So,
Compare the given vertices with the standard linear equation and find the slopes and x and y-intercepts for the coordinates of the vertices of the triangle
Question 2.
What tool(s) could you use to verify your answers to Exercises 25 – 30 on page 44?
Answer:
To verify the answers to Exercise 25 – 30 on page 44,
We can use “Angle Addition Postulate”
Question 3.
Your friend says that the angles in Exercise 28 on page 53 are supplementary angles. Explain why you agree or disagree.
Answer:
In Exercise 28 on page 53,
It is given that a right-angled triangle is formed
We know that,
The sum of the complementary angles is: 90°
Hence, from the above,
We can conclude that you disagree with your friend about supplementary angle
Basics of Geometry Chapter Review
1.1 Points, Lines, and Planes
Use the diagram.
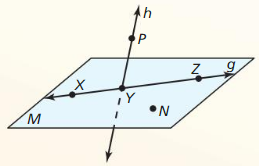
Question 1.
Give another name for plane M.
Answer:
From the given figure,
We can conclude that
Another name for plane M is: Plane XNZ or plane g
Question 2.
Name a line in the plane.
Answer:
From the given figure,
We can conclude that
The names of lines in the pane are: Line PY or Line XZ
Question 3.
Name a line intersecting the plane.
Answer:
From the above figure,
We can conclude that
The line intersecting the plane is: Line PY
Question 4.
Name two rays.
Answer:
From the above figure,
We can conclude that
The two rays are: Ray g and Ray h
Question 5.
Name a pair of opposite rays.
Answer:
From the above figure,
We can conclude that
The opposite rays are: Rays g and h
Question 6.
Name a point, not in plane M.
Answer:
From the above figure,
We can conclude that
The point that is not in plane M is: point p
1.2 Measuring and Constructing Segments
Find XZ.
Question 7.
![]()
Answer:
From the given figure,
By using the Segment Addition Postulate,
XZ = XY + YZ
XZ = 17 + 24
XZ = 41
Hence, from the above,
We can conclude that the value of XZ is: 41
Question 8.
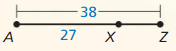
Answer:
From the given figure,
By using the Segment Addition Postulate,
AZ = AX + XZ
38 = 27 + XZ
XZ = 38 – 27
XZ = 11
Hence, from the above,
We can conclude that the value of XZ is: 11
Question 9.
Plot A(8, – 4), B(3, – 4), C(7, 1), and D(7, – 3) in a coordinate plane.
Then determine whether \(\overline{A B}\) and \(\overline{C D}\) are congruent.
Answer:
The given points are:
A (8, -4), B (3, -4), C (7, 1), and D (7, -3)
Compare the given points with
A (x1, y1), B (x2, y2), C (x3, y3), and D (x4, y4)
Now,
\(\overline{A B}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(8 – 3)² + (4 – 4)²}\)
= 5
\(\overline{C D}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(7 – 7)² + (1 + 3)²}\)
= 4
Hence,
The representation of the given points in the coordinate plane is:
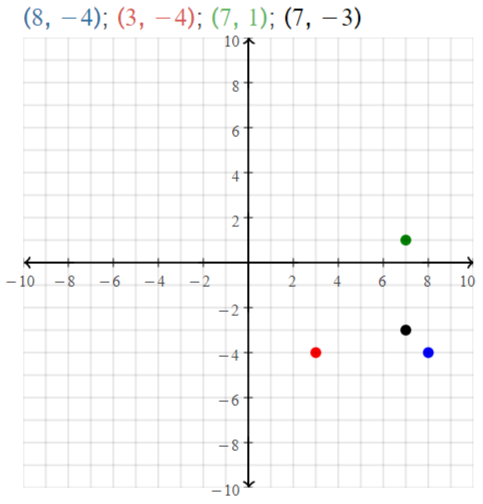
\(\overline{A B}\) is not congruent to \(\overline{C D}\)
1.3 Using Midpoint and Distance Formulas
Find the coordinates of the midpoint M. Then find the distance between points S and T.
Question 10.
S(- 2, 4) and T(3, 9)
Answer:
The given points are:
S (-2, 4) and T (3, 9)
We know that,
The coordinates of the Midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
The coordinates of the Midpoint = (\(\frac{3 – 2}{2}\), \(\frac{9 + 4}{2}\))
The coordinates of the Midpoint = (\(\frac{1}{2}\), \(\frac{13}{2}\) )
Hence, from the above,
We can conclude that the coordinates of the Midpoint are: (\(\frac{1}{2}\), \(\frac{13}{2}\))
Question 11.
S(6, – 3) and T(7, – 2)
Answer:
The given points are:
S (6, -3) and T (7, -2)
We know that,
The coordinates of the Midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
The coordinates of the Midpoint = (\(\frac{7 + 6}{2}\), \(\frac{-2 – 3}{2}\))
The coordinates of the Midpoint = (\(\frac{13}{2}\), \(\frac{-5}{2}\))
Hence, from the above,
We can conclude that the coordinates of the Midpoint are: (\(\frac{13}{2}\), \(\frac{-5}{2}\))
Question 12.
The midpoint of \(\overline{J K}\) is M(6, 3). One endpoint is J(14, 9). Find the coordinates of endpoint K.
Answer:
The given points of \(\overline{J K}\) are:
M (6, 3) and J (14, 9)
Let H be (x. y)
We know that,
The coordinates of the Midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(6, 3) = (\(\frac{x + 14}{2}\), \(\frac{y + 9}{2}\))
\(\frac{x + 14}{2}\) = 6 \(\frac{y + 9}{2}\) = 3
x + 14 = 6 (2) y + 9 = 3 (2)
x = 12 – 14 y = 6 – 9
x = -2 y = -3
Hence, from the above,
We can conclude that the coordinates of H are: (-2, -3)
Question 13.
Point M is the midpoint of \(\overline{A B}\) here AM = 3x + 8 and MB = 6x – 4. Find AB.
Answer:
It is given that Point M is the midpoint of \(\overline{A B}\) here AM = 3x + 8 and MB = 6x – 4.
Now,
By using the Segment Addition Postulate,
AB = AM + MB
AB = (3x + 8) + (6x – 4)
AB = 9x – 4
1.4 Perimeter and Area in the Coordinate Plane
Find the perimeter and area of the polygon with the given vertices.
Question 14.
W(5, – 1), X(5, 6), Y(2, 1) Z(2, 6)
Answer:
The given points are:
W (5, -1), X (5, 6), Y (2, 1), Z (2, 6)
Now,
\(\overline{W X}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 5)² + (1 + 6)²}\)
= 7
\(\overline{X Y}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 2)² + (6 – 1)²}\)
= 5.8
\(\overline{Y Z}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2 – 2)² + (6 – 1)²}\)
= 5
\(\overline{Z W}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 2)² + (6 + 1)²}\)
= 7.6
\(\overline{W Y}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 2)² + (1 + 1)²}\)
= 3.6
\(\overline{X Z}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 – 2)² + (6 – 6)²}\)
= 3
Hence,
The perimeter of the given polygon = WX + XY + YZ + ZW
= 7 + 5.8 + 5 + 7.6
= 25.4
Since all the lengths of the sides are different,
The area of the given polygon = \(\frac{1}{2}\) (d1) (d2)
Where,
d1 and d2 are the diagonals
So,
The area of the polygon = \(\frac{1}{2}\) (WY) (XZ)
= \(\frac{1}{2}\) (3) (3.6)
= 5.4
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 25.4
The area of the given polygon is: 5.4
Question 15.
E(6, – 2) , F(6, 5), G(- 1, 5)
Answer:
The given points are:
E (6, -2), F (6, 5), G (-1, 5)
Now,
\(\overline{E F}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(6 – 6)² + (2 + 5)²}\)
= 7
\(\overline{F G}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(6 + 1)² + (5 – 5)²}\)
= 7
\(\overline{G E}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(6 + 1)² + (5 + 2)²}\)
= 9.8
Hence,
The perimeter of the given polygon = EF + FG + GE
= 7 + 7 + 9.8
= 23.8
Now,
The area of the given polygon = \(\frac{1}{2}\) (Base) (Height)
So,
The area of the polygon = \(\frac{1}{2}\) (EF) (FG)
= \(\frac{1}{2}\) (7) (7)
= 24.5
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 23.8
The area of the given polygon is: 24.5
1.5 Measuring and Constructing Angles
Find m∠ABD and m∠CBD.
Question 16.
m∠ABC = 77°
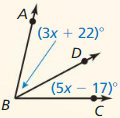
Answer:
From the above figure,
By using the Angle Addition Postulate,
∠ABC = ∠ABD + ∠DBC
It is given that
∠ABC = 77°
So,
77° = (3x + 22)° + (5x – 17)°
8x + 5 = 77°
8x = 77° – 5°
8x = 72°
x = \(\frac{72}{8}\)
x = 9°
So,
∠ABD = (3x + 22)°
= 3 (9) + 22
= 27 + 22
= 49°
∠CBD = (5x – 17)°
= 5 (9) – 17
= 45 – 17
= 28°
Hence, from the above,
We can conclude that
∠ABD = 49° and ∠CBD = 28°
Question 17.
m∠ABC = 111°
Answer:
From the above figure,
By using the Angle Addition Postulate,
∠ABC = ∠ABD + ∠DBC
It is given that
∠ABC = 111°
So,
111° = (-10x + 58)° + (6x + 41)°
-4x + 99 = 111°
-4x = 111° – 99°
-4x = 12°
x = \(\frac{-12}{4}\)
x = -3°
So,
∠ABD = (-10x + 58)°
= -10 (-3) + 58
= 30 + 58
= 88°
∠CBD = (6x + 41)°
= 6 (-3) + 41
= 41 – 18
= 23°
Hence, from the above,
We can conclude that
∠ABD = 88° and ∠CBD = 23°
Question 18.
Find the measure of the angle using a protractor.
Answer:
The measure of the angle of the given figure using a protractor is:
Hence, from the above,
We can conclude that the angle is: 127.3°
1.6 Describing Pairs of Angles
∠1 and ∠2 are complementary angles. Given m∠1, find m∠2.
Question 19.
m∠1 = 12°
Answer:
It is given that ∠1 and ∠2 are the complementary angles
∠1 = 12°
So,
∠1 + ∠2 = 90°
So,
∠2 = 90° – 12°
∠2 = 78°
Hence, from the above,
We can conclude that
∠2 = 78°
Question 20.
m∠1 = 83°
Answer:
It is given that ∠1 and ∠2 are the complementary angles
∠1 = 83°
So,
∠1 + ∠2 = 90°
So,
∠2 = 90° – 83°
∠2 = 7°
Hence, from the above,
We can conclude that
∠2 = 7°
∠3 and ∠4 are supplementary angles. Given m∠3, find m∠4.
Question 21.
m∠3 = 116°
Answer:
It is given that ∠3 and ∠4 are the supplementary angles
∠3 = 116°
So,
∠3 + ∠4 = 180°
So,
∠4 = 180° – 116°
∠4 = 64°
Hence, from the above,
We can conclude that
∠4 = 64°
Question 22.
m∠3 = 56°
Answer:
It is given that ∠3 and ∠4 are the supplementary angles
∠3 = 56°
So,
∠3 + ∠4 = 180°
So,
∠4 = 180° – 56°
∠4 = 124°
Hence, from the above,
We can conclude that
∠4 = 124°
Basics of Geometry Chapter Test
Find the length of \(\overline{Q S}\). Explain how you found your answer.
Question 1.
![]()
Answer:
From the given figure,
By using the Segment Addition Postulate,
\(\overline{Q S}\) = \(\overline{Q R}\) + \(\overline{R S}\)
= 12 + 19
= 31
Hence, from the above,
We can conclude that the length of \(\overline{Q S}\) is: 31
Question 2.

Answer:
From the given figure,
By using the Segment Addition Postulate,
\(\overline{Q R}\) = \(\overline{Q S}\) + \(\overline{S R}\)
59 = \(\overline{Q S}\) + 47
\(\overline{Q S}\) = 59 – 47
\(\overline{Q S}\) = 12
Hence, from the above,
We can conclude that the length of \(\overline{Q S}\) is: 12
Find the coordinates of tile midpoint M. Then find the distance between the two points.
Question 3.
A(- 4, – 8) and B(- 1, 4)
Answer:
The given points are:
A (-4, -8), and B (-1, 4)
We know that,
The coordinates of the midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
The coordinates of the midpoint = (\(\frac{-1 – 4}{2}\), \(\frac{-8 + 4}{2}\))
The coordinates of the midpoint = (\(\frac{-5}{2}\), \(\frac{-4}{2}\))
The coordinates of the midpoint = (\(\frac{-5}{2}\), \(\frac{-2}\))
Hence, from the above,
We can conclude that the coordinates of the midpoint are: (\(\frac{-5}{2}\), -2)
Question 4.
C(- 1, 7) and D(- 8, – 3)
Answer:
The given points are:
C (-1, 7), and D (-8, -3)
We know that,
The coordinates of the midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
The coordinates of the midpoint = (\(\frac{-1 – 8}{2}\), \(\frac{-3 + 7}{2}\))
The coordinates of the midpoint = (\(\frac{-9}{2}\), \(\frac{4}{2}\))
The coordinates of the midpoint = (\(\frac{-9}{2}\), 2)
Hence, from the above,
We can conclude that the coordinates of the midpoint are: (\(\frac{-9}{2}\), 2)
Question 5.
The midpoint of \(\overline{E F}\) is M(1, – 1). One endpoint is E(- 3, 2). Find the coordinates of
endpoint F.
Answer:
The given points of \(\overline{E F}\) are:
M (1, -1), and E (-3, 2)
Let the other endpoint be F (x, y)
We know that,
The coordinates of the midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
So,
(1, -1) = (\(\frac{x – 3}{2}\), \(\frac{y + 2}{2}\))
\(\frac{x – 3}{2}\) = 1 \(\frac{y + 2}{2}\) = -1
x – 3 = 2 y + 2 = -2
x = 5 y = -4
Hence, from the above,
We can conclude that the coordinates of the other endpoint are: (5, -4)
Use the diagram to decide whether the statement is true or false.
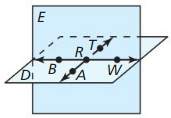
Question 6.
Points A, R, and B are collinear.
Answer:
We know that,
The points that lie in the same line are called “Collinear points”
From the figure,
We can observe that A, R, and B are in the same plane but not in the same line
Hence, from the above,
We can conclude that A, R, and B are not collinear
Question 7.
![]()
Answer:
From the given figure,
We can observe there are two lines in the plane
Hence, from the above,
We can conclude that BW and AT are lines
Question 8.
![]()
Answer:
From the given figure,
We can observe that BR and RT are perpendicular lines
Hence, from the above,
We can conclude that BR and RT are opposite rays
Question 9.
Plane D could also be named plane ART.
Answer:
We know that,
The points that are coplanar in the given plane can also be named for the name of the plane
Hence, from the above,
We can conclude that plane D can also be named plane ART
Find the perimeter and area of the polygon with the given vertices. Explain how you found your answer.
Question 10.
P(- 3, 4), Q(1, 4), R(- 3, – 2), S(3, – 2)
Answer:
The given points are:
P(- 3, 4), Q(1, 4), R(- 3, – 2), S(3, – 2)
Now,
\(\overline{P Q}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (4 – 4)²}\)
= 4
\(\overline{Q R}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 3)² + (4 + 2)²}\)
= 7.2
\(\overline{R S}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2 – 2)² + (3 + 3)²}\)
= 6
\(\overline{S P}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 3)² + (4 + 2)²}\)
= 7.2
Hence,
The perimeter of the given polygon = PQ + QR + RS + SP
= 4 + 6 + 7.2 + 7.2
= 24.4
The area of the given polygon = \(\frac{1}{2}\) (a + b) (h)
Where,
a and b are the sides that are not equal
So,
The area of the polygon = \(\frac{1}{2}\) (4 + 6) (7.2)
= \(\frac{1}{2}\) (10) (7.2)
= 36
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 24.4
The area of the given polygon is: 36
Question 11.
J(- 1, 3), K(5, 3), L(2, – 2)
Answer:
The given points are:
J(- 1, 3), K(5, 3), L(2, – 2)
Now,
\(\overline{J K}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 – 3)² + (1 + 5)²}\)
= 6
\(\overline{K L}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 2)² + (5 – 2)²}\)
= 5.8
\(\overline{L J}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(2 + 1)² + (3 + 2)²}\)
= 5.8
Hence,
The perimeter of the given polygon = JK + KL + LJ
= 6 + 5.8 + 5.8
= 17.8
Now,
The area of the given polygon = \(\frac{1}{2}\) (Base) (Height)
So,
The area of the polygon = \(\frac{1}{2}\) (JK) (KL)
= \(\frac{1}{2}\) (6) (5.8)
= 17.4
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 17.8
The area of the given polygon is: 17.4
Question 12.
In the diagram. ∠AFE is a straight angle and ∠CFE is a right angle. Identify all supplementary and complementary angles. Explain. Then find, m∠DFE, m∠BFC, and m∠BFE.
Answer:
Question 13.
Use the clock at the left.

a. What is the measure of the acute angle created when the clock is at 10:00?
Answer:
We know that,
12 sectors = 360°
From the above clock,
We can observe that there are 2 sectors at 10:00
So,
The angle created when the clock is at 10:00 = 2 (30)
= 60°
Hence, from the above,
We can conclude that the measure of the acute angle created when the clock is at 10:00 is: 60°
b. What is the measure of the obtuse angle created when the clock is at 5:00?
Answer:
From the figure,
We can observe that there are 4 sectors between 12 and at 5:00
So,
The acute angle created when the clock is at 5:00 = 4 (30)
= 120°
So,
The obtuse angle created when the clock is at 5:00 = 360 – 120
= 240°
Hence, from the above,
We can conclude that the obtuse angle created when the clock is at 5:00 is: 240°
c. Find a time where the hour and minute hands create a straight angle.
Answer:
we know that,
A straight angle is an angle that is 180°
Now,
From the figure,
We can observe that the hour and minute hands create a straight angle is: 6:00, 2:45
Hence, from the above,
We can conclude that the time where the hour and minute hands create a straight angle is: 6:00 and 2:45
Question 14.
Sketch a figure that contains a plane and two lines that intersect the plane at one point.
Answer:
The representation of a plane and two planes intersection at a point is:

Question 15.
Your parents decide they would like to install a rectangular swimming pool in the backyard. There is a 15-foot by the 20-foot rectangular area available. Your parents request a 3-foot edge around each side of the pool. Draw a diagram of this situation in a coordinate plane. What is the perimeter and area of the largest swimming pool that will fit?
Answer:
It is given that your parents decide they would like to install a rectangular swimming pool in the backyard. There is a 15-foot by the 20-foot rectangular area available. Your parents request a 3-foot edge around each side of the pool.
Since the 3 ft edge is on both sides of the pool, each dimension of the pool is 6 ft shorter than the corresponding dimension of the space.
So,
The pool will be
15 ft -6 ft = 9 ft in one direction and 20 ft -6 ft = 14 ft in the other direction.
We know that,
The perimeter of the pool is the sum of its side lengths:
So,
P = 9 ft + 14 ft + 9 ft + 14 ft = 2(9 ft +14 ft)
= 2(23 ft)
= 46 ft
Now,
The area of the pool = 14 (9)
= 126 ft²
Hence, from the above,
We can conclude that
The perimeter of the pool is: 46 ft
The area of the pool is 126 ft²
The representation of the pool in the coordinate plane is:
Question 16.
The picture shows the arrangement of balls in a game of boccie. The object of the game is to throw your ball closest to the small. while ball, which is called the Pallino. The green ball is the midpoint between the red ball and the Pallino. The distance between the green hail and the red ball is 10 inches. The distance between the yellow ball and the Pallino is 8 inches. Which bail is closer to the Pallino. the green ball or the yellow ball? Explain.

Answer:
It is given that the picture shows the arrangement of balls in a game of boccie. The object of the game is to throw your ball closest to the small. while ball, which is called the Pallino. The green ball is the midpoint between the red ball and the Pallino. The distance between the green hail and the red ball is 10 inches. The distance between the yellow ball and the Pallino is 8 inches.
Now,
When we compare the distances between the Pallino and the green ball and between the yellow ball and the Pallino,
We can observe that the distance between the yellow ball and Pallino is less
Hence, from the above,
We can conclude that the yellow ball is closer to the Pallino
Basics of Geometry Cumulative Assessment
Question 1.
Use the diagram to determine which segments, if any, are congruent. List all congruent segments.
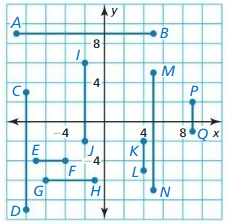
Answer:
We know that,
The “Congruency” means having the same size and the same length
But, from the above coordinate plane,
We can observe that there are no congruent lines
Hence, from the above,
We can conclude that there are no congruent line segments in the coordinate plane
Question 2.
Order the terms so that each consecutive term builds off the previous term.
plane segment line point ray
Answer:
The given terms are:
a. Plane b. Segment c. Line d. Point e. Ray
Hence,
The order of the given terms are:
Point, Line, Ray, Segment, and Plane
Question 3.
The endpoints of a line segment are (- 6, 13) and (11, 5). Which choice shows the correct midpoint and distance between these two points?
(A) \(\left(\frac{5}{2}, 4\right)\); 18.8 units
(B) \(\left(\frac{5}{2}, 9\right)\); 18.8 units
(C) \(\left(\frac{5}{2}, 4\right)\); 9.4 units
(D) \(\left(\frac{5}{2}, 9\right)\); 9.4 units
Answer:
The given endpoints of a line segment are: (-6, 13) and (11, 5)
We know that,
The coordinates of the midpoint = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
= (\(\frac{11 – 6}{2}\), \(\frac{13 + 5}{2}\))
= (\(\frac{5}{2}\), \(\frac{18}{2}\))
= (\(\frac{5}{2}\), 9)
We know that,
The distance between the coordinates = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(11 + 6)² + (13 – 5)²}\)
= 18.78 ≈ 18.8
Hence, from the above,
We can conclude that option (B) shows the correct midpoint and distance
Question 4.
Find the perimeter and area of the figure shown
Answer:
From the coordinate plane,
The points are:
Q (-4, 3), R (2, 3), S (3, 3), and T (-3, 3)
Now,
\(\overline{Q R}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 – 3)² + (4 + 2)²}\)
= 6
\(\overline{R S}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 – 2)² + (3 – 3)²}\)
= 1
\(\overline{S T}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 + 3)² + (3 – 3)²}\)
= 6
\(\overline{T Q}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 3)² + (3 – 3)²}\)
= 1
Hence,
The perimeter of the given polygon = QR + RS + ST + TQ
= 6 + 1 + 6 + 1
= 14
The area of the given polygon = Length × Width
So,
The area of the polygon = 6 (1)
= 6
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 14
The area of the given polygon is: 6
Question 5.
Plot the points W(- 1, 1), X(5, 1), Y(5, – 2), and Z(- 1, – 2) in a coordinate plane. What type of polygon do the points form? Your friend claims that you could use this figure to represent a basketball court with an area of 4050 square feet and a perimeter of 270 feet. Do you support your friend’s claim? Explain.
Answer:
The given points are:
W (-1, 1), X (5, 1), Y (5, -2), and Z (-1, -2)
Now,
\(\overline{W X}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (5 + 1)²}\)
= 6
\(\overline{X Y}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 + 2)² + (5 – 5)²}\)
= 3
\(\overline{Y Z}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(5 + 1)² + (2 – 2)²}\)
= 6
\(\overline{Z W}\) = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(1 – 1)² + (2 + 1)²}\)
= 3
Hence,
The perimeter of the given polygon = WX + XY + YZ + ZW
= 6 + 3 + 6 + 3
= 18
But,
It is given that the actual perimeter is: 270 ft
So,
The scale = 270 / 18 = 15
Now,
The area of the given polygon = Length × Width
So,
The area of the polygon = 6 (3)
= 18
The area of the basketball = 15 (15) (18)
= 4050 ft²
Hence, from the above,
We can conclude that the claim of your friend is correct
Question 6.
Use the steps in the construction to explain how you know that \(\vec{A}\)G is the angle bisector
of ∠CAB.
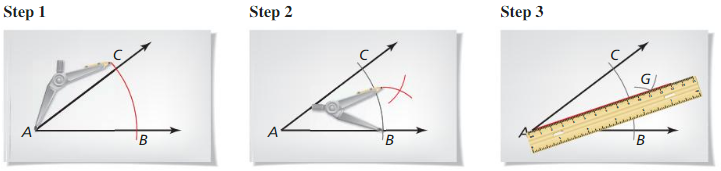
Answer:
Step 1:
Draw an angle ∠CAB. Measure the length of AC and draw an arc by using the compass by taking the length more than half of the length of AC
Step 2:
From the arc, by using a compass, draw 2 arcs by taking more than half of the length of the arc on both sides of the arc
Step 3:
Use a straightedge to measure the length from the arcs to angle A and that line is called “Angle Bisector”
Question 7.
The picture shows an aerial view of a city. Use the streets highlighted in red to identify all congruent angles. Assume all streets are straight angles.
Answer:
We know that,
The “Congruent angles” are the angles that have the same angle measure
Hence, from the above figure,
The congruent angles are: ∠E and ∠M; ∠O and ∠R
Question 8.
Three roads come to an intersection point that the People in your town call Five Corners. as shown in the figure.
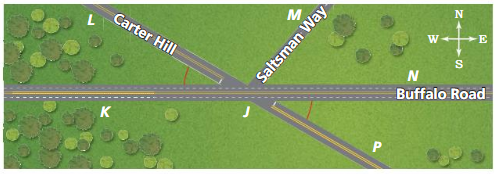
a. Identify all vertical angÌes.
Answer:
From the given figure,
The vertical angles are ∠LJK, ∠MJP, ∠MJN
b. Identify all linear pairs.
Answer:
From the given figure,
The linear pairs are: ∠LJK, ∠MJP, ∠MJN
C. you are traveling east on Buffalo Road and decide to turn left onto Carter Hill.
Name the angle of the turn you made.
∠KJL ∠KJM ∠KJN ∠KJP ∠LJM
∠LJN ∠LJP ∠MJN ∠MJP ∠NJP
Answer:
From the above figure,
The angle made by you when you are traveling east n BuffaloRoad and decide to turn left onto Carter hill is: ∠KJL
