Big Ideas Math Geometry Answers Chapter 2 Reasoning and Proofs

Reasoning and Proofs Chapter Answers provided are aligned as per the Big Ideas Math Geometry Textbooks. Have an overview of the concepts you need to learn in BIM Geometry Ch 2 Reasoning and Proofs and test your understanding. Master the topics of BIM Geometry Chapter 2 Reasoning and Proofs by practicing from the quick links available below. Identify the knowledge gap and concentrate on the areas you are lagging and improvise on them accordingly. You will find the Big Ideas Math Geometry Answers and attempt the exam with utmost confidence.

Big Ideas Math Book Geometry Answer Key Chapter 2 Reasoning and Proofs

Become proficient in the concepts of BIM Geometry Chapter 2 Reasoning and Proofs by referring to the quick links available. Solve the Questions available in BIM Book Geometry Chapter 2 Reasoning and Proofs Answer Key on a frequent basis and get a good hold of the concepts. Geometry Big Ideas Math Chapter 2 Reasoning and Proofs Answers here include questions from Lessons, Review Tests, Cumulative Practice, Assessment Tests, Practice Tests, etc. aligned as per the Textbooks. Download the Big Ideas Math Book Geometry Ch 2 Reasoning and Proofs Solution Key for free of cost and ace your preparation.

• • Reasoning and Proofs Maintaining Mathematical Proficiency – Page 63
  • Reasoning and Proofs Mathematical Practices – Page 64
  • 2.1 Conditional Statements – Page(65-74)
  • Lesson 2.1 Conditional Statements – Page(66-70)
  • Exercise 2.1 Conditional Statements – Page(71-74)
  • 2.2 Inductive and Deductive Reasoning – Page(75-82)
  • Lesson 2.2 Inductive and Deductive Reasoning – Page(76-79)
  • Exercise 2.2 Inductive and Deductive Reasoning – Page(80-82)
  • 2.3 Postulates and Diagrams – Page(83-88)
  • Lesson 2.3 Postulates and Diagrams – Page(84-86)
  • Exercise 2.3 Postulates and Diagrams – Page(87-88)
  • 2.1 – 2.3 Study Skills: Using the Features of Your Textbook to Prepare for Quizzes and Tests – Page 89
  • 2.1 – 2.3 Quiz – Page 90
  • 2.4 Algebraic Reasoning – Page(91-98)
  • Lesson 2.4 Algebraic Reasoning – Page(92-95)
  • Exercise 2.4 Algebraic Reasoning – Page(96-98)
  • 2.5 Proving Statements about Segments and Angles – Page(99-104)
  • Lesson 2.5 Proving Statements about Segments and Angles – Page(100-102)
  • Exercise 2.5 Proving Statements about Segments and Angles – Page(103-104)
  • 2.6 Proving Geometric Relationships – Page 105
  • Lesson 2.6 Proving Geometric Relationships – Page(106-114)
  • Exercise 2.6 Proving Geometric Relationships – Page(111-114)
  • 2.4 – 2.6 Performance Task: Induction and the Next Dimension – Page 115
  • Reasoning and Proofs Chapter Review – Page(116-118)
  • Reasoning and Proofs Test – Page 119
  • Reasoning and Proofs Cumulative Assessment – Page(120-121)

Reasoning and Proofs Maintaining Mathematical Proficiency

Write an equation for the nth term of the arithmetic sequence. Then find a₅₀.

Question 1.
3, 9, 15, 21, ……..
Answer:

Question 2.
– 29, – 12, 5, 22, ……..
Answer:

Question 3.
2.8, 3.4, 4.0, 4.6, ………
Answer:

Question 4.
\(\frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{5}{6}\), ………
Answer:

Question 5.
26, 22, 18, 14, ………
Answer:

Question 6.
8, 2, – 4, – 10, ………
Answer:

Solve the literal equation for x.

Question 7.
2y – 2x = 10
Answer:

Question 8.
20y + 5x = 15
Answer:

Question 9.
4y – 5 = 4x + 7
Answer:

Question 10.
y = 8x – x
Answer:

Question 11.
y = 4x + zx + 6
Answer:

Question 12.
z = 2x + 6xy
Answer:

Question 13.
ABSTRACT REASONING
Can you use the equation for an arithmetic sequence to write an equation for the sequence 3, 9, 27, 81. . . . ? Explain our reasoning.
Answer:

Reasoning and Proofs Mathematical Practices

Monitoring Progress

Decide whether the syllogism represents correct or flawed reasoning, If flawed, explain why the conclusion Is not valid.

Question 1.
All triangles are polygons.
Figure ABC is a triangle.
Therefore, figure ABC is a polygon.
Answer:

Question 2.
No trapezoids are rectangles.
Some rectangles are not squares.
Therefore, some squares are not trapezoids.
Answer:

Question 3.
If polygon ABCD is a square. then ills a rectangle.
Polygon ABCD is a rectangle.
Therefore, polygon ABCD is a square.
Answer:

Question 4.
If polygon ABCD is a square, then it is a rectangle.
Polygon ABCD is not a square.
Therefore, polygon ABCD is not a rectangle.
Answer:

2.1 Conditional Statements

Exploration 1

Determining Whether a Statement is True or False

Work with a partner: A hypothesis can either be true or false. The same is true of a conclusion. For a conditional statement to be true, the hypothesis and conclusion do not necessarily both have to be true. Determine whether each conditional statement is true or false. Justify your answer.

a. If yesterday was Wednesday, then today is Thursday.
Answer:

b. If an angle is acute. then it has a measure of 30°.
Answer:

c. If a month has 30 days. then it is June.
Answer:

d. If an even number is not divisible by 2. then 9 is a perfect cube.
Answer:

Exploration 2

Determining Whether a Statement is True or False

Work with a partner: Use the points in the coordinate plane to determine whether each statement is true or false. Justify your answer.

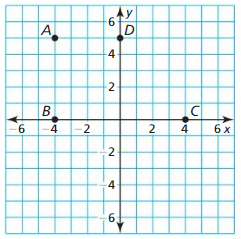
a. ∆ABC is a right triangle.
Answer:

b. ∆BDC is an equilateral triangle.
Answer:

c. ∆BDC is an isosceles triangle.
Answer:

d. Quadrilateral ABCD is a trapezoid.
Answer:

e. Quadrilateral ABCD is a parallelogram.
Answer:

Exploration 3

Determining Whether a Statement is True or False

Work with a partner: Determine whether each conditional statement is true or false. Justify your answer.

CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to distinguish correct logic or reasoning from that which is flawed.

a. If ∆ ADC is a right triangle, then the Pythagorean Theorem is valid for ∆ADC.
Answer:

b. If ∠A and ∠B are complementary, then the sum of their measures is 180°.
Answer:

c. If figure ABCD is a quadrilateral, then the sum of its angle measures is 180°.
Answer:

d. If points A, B, and C are collinear, then the lie on the same line.
Answer:

e. It and intersect at a point, then they form two pairs of vertical angles.
Answer:

Communicate Your Answer

Question 4.
When is a conditional statement true or false?
Answer:

Question 5.
Write one true conditional statement and one false conditional statement that are different from those given in Exploration 3. Justify your answer.
Answer:

Lesson 2.1 Conditional Statements

Monitoring Progress

Use red to identify the hypothesis and blue to identify the conclusion. Then
rewrite the conditional statement in if-then form.

Question 1.
All 30° angles are acute angles.
Answer:

Question 2.
2x + 7 = 1. because x = – 3.
Answer:

In Exercises 3 and 4, write the negation of the statement.

Question 3.
The shirt is green.
Answer:

Question 4.
The Shoes are not red.
Answer:

Question 5.
Repeat Example 3. Let p be “the stars are visible” and let q be “it is night.”
Answer:

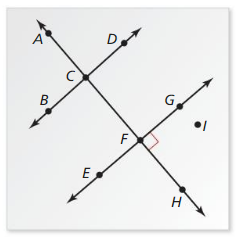
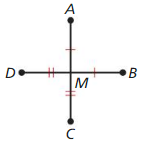
Use the diagram. Decide whether the statement is true. Explain your answer using the definitions you have learned.

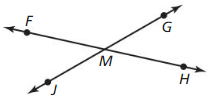
Question 6.
∠JMF and ∠FMG are supplementary.
Answer:

Question 7.
Point M is the midpoint of \(\overline{F H}\).
Answer:

Question 8.
∠JMF and ∠HMG arc vertical angles.
Answer:

Question 9.

Answer:

Question 10.
Rewrite the definition of a right angle as a single biconditional statement.
Definition: If an angle is a right angle. then its measure is 90°.
Answer:

Question 11.
Rewrite the definition of congruent segments as a single biconditional statement.
Definition: If two line segments have the same length. then they are congruent segments.
Answer:

Question 12.
Rewrite the statements as a single biconditional statement.
If Mary is in theater class, then she will be in the fall play. If Mary is in the fall play. then she must be taking theater class.
Answer:

Question 13.
Rewrite the statements as a single biconditional statement.
If you can run for President. then you are at least 35 years old. If you are at least 35 years old. then you can run for President.
Answer:

Question 14.
Make a truth table for the conditional statement p → ~ q.
Answer:

Question 15.
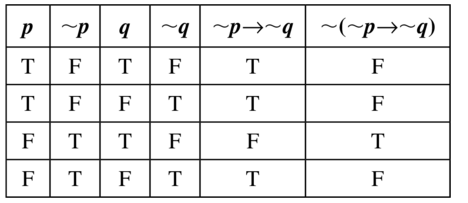
Make a truth table for the conditional statement ~(p → q).
Answer:

Exercise 2.1 Conditional Statements

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
What type of statements are either both true or both false?
Answer:

Question 2.
WHICH ONE DOESN’T BELONG?
Which statement does not belong with the other three? Explain your reasoning.
If today is Tuesday, then tomorrow is Wednesday
If it is Independence Day, then it is July.
If an angle is acute. then its measure is less than 90°.
If you are an athlete, then you play soccer.
Answer:

In Exercises 3 – 6. copy the conditional statement. Underline the hypothesis and circle the conclusion.

Question 3.
If a polygon is a pentagon, then it has five sides.
Answer:

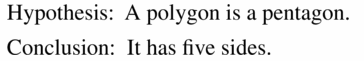
Question 4.
If two lines form vertical angles, then they intersect.
Answer:

Question 5.
If you run, then you are fast.
Answer:

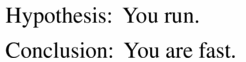
Question 6.
If you like math. then you like science.
Answer:

In Exercises 7 – 12. rewrite the conditional statement in if-then form.

Question 7.
9x + 5 = 23, because x = 2.
Answer:

Question 8.
Today is Friday, and tomorrow is the weekend.
Answer:

Question 9.
You are in a hand. and you play the drums.
Answer:

Question 10.
Two right angles are supplementary angles.
Answer:

Question 11.
Only people who are registered are allowed to vote.
Answer:

Question 12.
The measures complementary angles sum to 90°
Answer:

In Exercises 13 – 16. write the negation of the statement.

Question 13.
The sky is blue.
Answer:

Question 14.
The lake is cold.
Answer:

Question 15.
The ball is not pink.
Answer:

Question 16.
The dog is not a Lab.
Answer:

In Exercises 17 – 24. write the conditional statement p → q. the converse q → p, the inverse ~ p → ~ q, and the contrapositive ~ q → ~ p in words. Then decide whether each statement is true or false.

Question 17.
Let p be “two angles are supplementary” and let q be “the measures of the angles sum to 180°
Answer:

Question 18.
Let p be “you are in math class” and let q be “you are in Geometry:”
Answer:

Question 19.
Let p be “you do your math homework” and let q be “you will do well on the test.”
Answer:

Question 20.
Let p be “you are not an only child” and let q be “you have a sibling.
Answer:

Question 21.
Let p be “it does not snow” and let q be I will run outside.”
Answer:

Question 22.
Let p be “the Sun is out” and let q be “it is day time”
Answer:

Question 23.
Let p be “3x – 7 = 20” and let q be “x = 9.”
Answer:

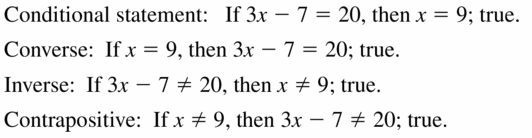
Question 24.
Let p be “it is Valentine’s Day” and let q be “it is February.
Answer:

In Exercises 25 – 28, decide whether the statement about the diagram is true. Explain your answer using the definitions you have learned.

Question 25.
m∠ABC = 90°

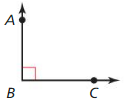
Answer:

Question 26.


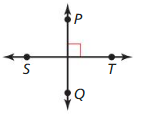
Answer:

Question 27.
m∠2 + m∠3 = 180°

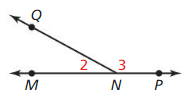
Answer:

Question 28.
M is the midpoint of \(\overline{A B}\).

Answer:

In Exercises 29 – 32. rewrite the definition of the term as a biconditional statement.

Question 29.
The midpoint of a segment is the point that divides the segment into two congruent segments.
Answer:

Question 30.
Two angles are vertical angles when their sides form two pairs of opposite rays.
Answer:

Question 31.
Adjacent angles are two angles that share a common vertex and side but have no common interior points.
Answer:

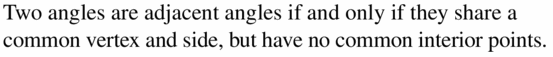
Question 32.
Two angles are supplementary angles when the sum of their measures 180°.
Answer:

In Exercises 33 – 36. rewrite the statements as a single biconditional statement.

Question 33.
If a polygon has three sides. then it is a triangle.
If a polygon is a triangle, then it has three sides.
Answer:

Question 34.
If a polygon has four sides, then it is a quadrilateral.
If a polygon is a quadrilateral, then it has four sides.
Answer:

Question 35.
If an angle is a right angle. then it measures 90°.
If an angle measures 90°. then it is a right angle.
Answer:

Question 36.
If an angle is obtuse, then ii has a measure between 90° and 180°.
If an angle has a measure between 90° and 180°. then it is obtuse.
Answer:

Question 37.
ERROR ANALYSIS
Describe and correct the error in rewriting the conditional statement in if – then form.

Answer:

Question 38.
ERROR ANALYSIS
Describe and correct the error in writing the converse of the conditional statement.

Answer:

In Exercises 39 – 44. create a truth table for the logical statement.
Question 39.
~ p → q
Answer:

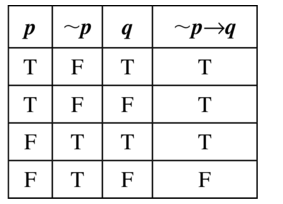
Question 40.
~ q → p
Answer:

Question 41.
~(~ p → ~ q)
Answer:

Question 42.
~ (p → ~ q)
Answer:

Question 43.
q → ~ p
Answer:

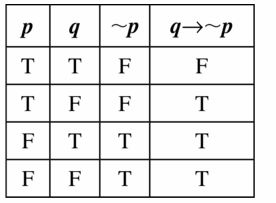
Question 44.
~ (q → p)
Answer:

Question 45.
USING STRUCTURE
The statements below describe three ways that rocks are formed.

Igneous rock is formed from the cooling of Molten rock.

Sedimentary rock is formed from pieces of other rocks.

Metamorphic rock is formed by changing, temperature, pressure, or chemistry.

a. Write each sLaternenl in if-then form.
b. Write the converse of each of the statements in part (a). Is the converse of each statement true? Explain your reasoning.
c. Write a true if-then statement about rocks that is different from the ones in parts (a) and (b). Is the converse of our statement true or false? Explain your reasoning
Answer:

Question 46.
MAKING AN ARGUMENT
Your friend claims the statement “If I bought a shirt, then I went to the mall’ can he written as a true biconditional statement. Your sister says you cannot write it as a biconditional. Who is correct? Explain your reasoning.
Answer:

Question 47.
REASONING
You are told that the contrapositive of a statement is true. Will that help you determine whether the statement can be written as a true biconditional statement’? Explain your reasoning.
Answer:

Question 48.
PROBLEM SOLVING
Use the conditional statement to identify the if-then statement as the converse. inverse. or contrapositive of the conditional statement. Then use the symbols to represent both statements.
Conditional statement: It I rode my bike to school, then I did not walk to school.
If-then statement: If did not ride my bike to school, then I walked to school.
p      q     ~    →    ↔
Answer:

USING STRUCTURE
In Exercises 49 – 52. rewrite the conditional statement in if-then form. Then underline the hypothesis and circle the conclusion.
Question 49.

Answer:

Question 50.

Answer:

Question 51.

Answer:

Question 52.

Answer:

Question 53.
MATHEMATICAL CONNECTIONS
Can the statement “If x² – 10 = x + 2. then x = 4″ be combined with its converse to form a true biconditional statement?
Answer:

Question 54.
CRITICAL THINKING
The largest natural arch in the United States is Landscape Arch. located in Thompson, Utah. h spans 290 feet.

a. Use the information to write at least two true conditional statements.
Answer:

b. Which type of related conditional statement must also be true? Write the related conditional statements.
Answer:

C. What are the other two types of related conditional statements? Write the related conditional statements. Then determine their truth values. Explain your reasoning.
Answer:

Question 55.
REASONING
Which statement has the same meaning as the given statement?
Given statement:
You can watch a movie after you do your homework.
(A) If you do your homework, then you can watch a movie afterward.
(B) If you do not do your homework, then you can watch a movie afterward.
(C) If you cannot watch a movie afterward. then do your homework.
(D) If you can watch a movie afterward, then do not do your homework.
Answer:

Question 56.
THOUGHT PROVOKING
Write three conditional statements. where one is always true, one is always false, and one depends on the person interpreting the statement.
Answer:

Question 57.
CRITICAL THINKING
One example of a conditional statement involving dates is “If today is August 31, then tomorrow is September 1 Write a conditional statement using dates from two different months so that the truth value depends on when the statement is read.
Answer:

Question 58.
HOW DO YOU SEE IT?
The Venn diagram represents all the musicians at a high school. Write three conditional statements in if-then form describing the relationships between the various groups of musicians.

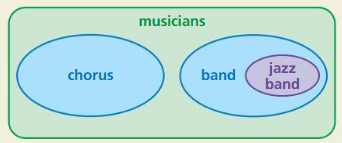
Answer:

Question 59.
MULTIPLE REPRESENTATIONS
Create a Venn diagram representing each conditional statement. Write the converse of each conditional statement. Then determine whether each conditional statement and its converse are true or false. Explain your reasoning.
a. If you go to the zoo to see a lion, then you will see a Cat.
b. If you play a sport. then you wear a helmet.
c. If this month has 31 days. then it is not February.
Answer:

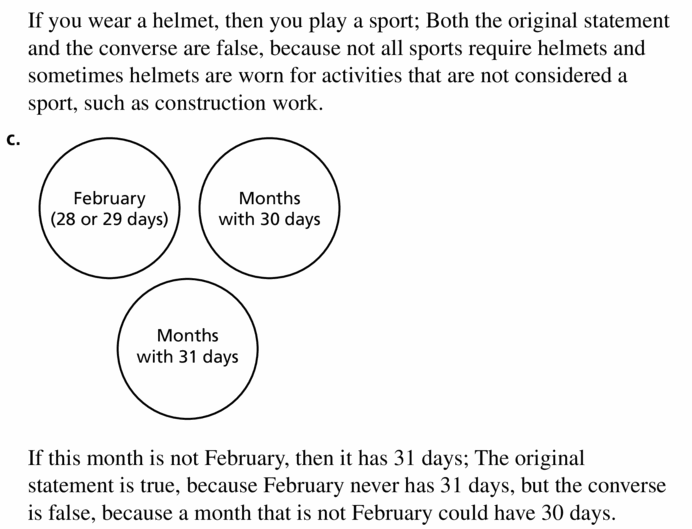
Question 60.
DRAWING CONCLUSIONS
You measure the heights of your classmates to gel a data set.
a. Tell whether this statement is true: If s and y are the least and greatest values in your data set, then the mean of the data is between x and y.
Answer:

b. Write the converse of the statement in part (a). Is the converse true? Explain your reasoning.
Answer:

c. Copy and complete the statement below using mean, median, or mode to make a conditional statement that is true for an data set. Explain your reasoning.
If a data set has a mean. median, and a mode. then the _____________ of the data set will always be a data value.
Answer:

Question 61.
WRITING
Write a conditional statement that is true, but its converse is false.
Answer:

Question 62.
CRITICAL THINKING
write a series of if-then statements that allow you to find the measure of each angle, given that m∠1 = 90° Use the definition of linear pairs.

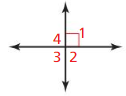
Answer:

Question 63.
WRITING
Advertising slogans such as “Buy these shoes! They will make you a better athlete!” often imply conditional statements. Find an advertisement or write your own slogan. Then write it as a conditional statement.
Answer:

Maintaining Mathematical Proficiency

Find the pattern. Then draw the next two figures in the sequence.

Question 64.

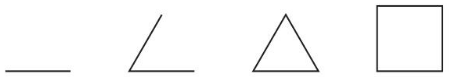
Answer:

Question 65.

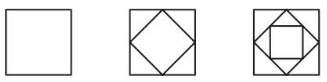
Answer:

Find the pattern. Then write the next two numbers.

Question 66.
1, 3, 5, 7 ……..
Answer:

Question 67.
12, 23, 34, 45 ……..
Answer:

Question 68.
2, \(\frac{4}{3}, \frac{8}{9}, \frac{16}{27}\), ……..
Answer:

Question 69.
1, 4, 9, 16, ……..
Answer:

2.2 Inductive and Deductive Reasoning

Exploration 1

Writing a Conjecture

Work with a partner: Write a conjecture about the pattern. Then use your conjecture to draw the 10th object in the pattern.
a.

Answer:

b.

Answer:

c.

Answer:

Exploration 2

Using a Venn Diagram

Work with a partner: Use the Venn diagram to determine whether the statement is true or false. Justify your answer. Assume that no region of the Venn diagram is empty.

CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to justify your conclusions and communicate them to others.

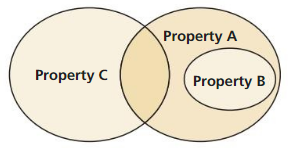
a. If an item has Property B. then it has Property A.
Answer:

b. If an item has Property A. then it has Property B.
Answer:

c. If an item has Property A, then it has Property C.
Answer:

d. Some items that have Property A do not have Property B.
Answer:

e. If an item has Property C. then it does not have Property B.
Answer:

f. Sonic items have both Properties A and C.
Answer:

g. Some items have both Properties B and C.
Answer:

Exploration 3

Reasoning and Venn Diagrams

Work with a partner: Draw a Venn diagram that shows the relationship between different types of quadrilateral: squares. rectangles. parallelograms. trapezoids. rhombuses, and kites. Then write several conditional statements that are shown in your diagram. such as “If a quadrilateral is a square. then it is a rectangle.”
Answer:

Communicate Your Answer

Question 4.
How can you use reasoning to solve problems?
Answer:

Question 5.
Give an example of how you used reasoning to solve a real-life problem.
Answer:

Lesson 2.2 Inductive and Deductive Reasoning

Monitoring Progress

Question 1.
Sketch the fifth figure in the pattern in Example 1.
Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.
Make and test a conjecture about the sign o1 the product of any three negative integers.
Answer:

Question 5.
Make and test a conjecture about the sum of any five consecutive integers.
Answer:

Find a counterexample to show that the conjecture is false.

Question 6.
The value of x² is always greater than the value of x.
Answer:

Question 7.
The sum of two numbers is always greater than their difference.
Answer:

Question 8.
If 90° ∠ m ∠ R ∠ 180°, then ∠R is obtuse. The measure of ∠R is 155°. Using the Law of Detachment. what statement can you make?
Answer:

Question 9.
Use the Law of Syllogism to write a new conditional statement that follows from the pair of true statements.
If you get an A on your math test. then you can go to the movies.
If you go to the movies, then you can watch your favorite actor.
Answer:

Question 10.
Use inductive reasoning to make a conjecture about the sum of a number and itself. Then use deductive reasoning to show that the conjecture is true.
Answer:

Question 11.
Decide whether inductive reasoning or deductive reasoning is used to reach the
conclusion. Explain your reasoning.
All multiples of 8 are divisible by 4.
64 is a multiple of 8.
So, 64 is divisible by 4.
Answer:

Exercise 2.2 Inductive and Deductive Reasoning

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
How does the prefix “counter” help you understand the term counterexample?
Answer:

Question 2.
WRITING
Explain the difference between inductive reasoning and deductive reasoning.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 8, describe the pattern. Then write or draw the next two numbers, letters, or figures.

Question 3.
1, – 2, 3, – 4, 5, ……..
Answer:

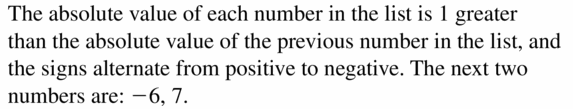
Question 4.
0, 2, 6, 12, 20, ……..
Answer:

Question 5.
Z, Y, X, W, V, ……..
Answer:

Question 6.
J, F, M, A, M, ……..
Answer:

Question 7.

Answer:

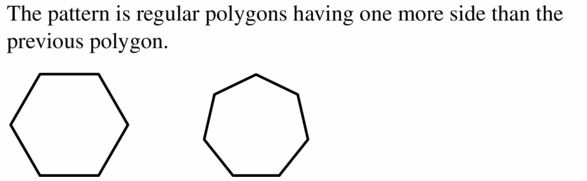
Question 8.

Answer:

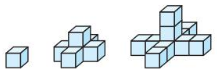
In Exercises 9 – 12. make and test a conjecture about the given quantity.

Question 9.
the product of any two even integers
Answer:

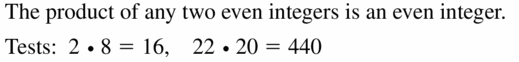
Question 10.
the sum of an even integer and an odd integer
Answer:

Question 11.
the quotient of a number and its reciprocal
Answer:

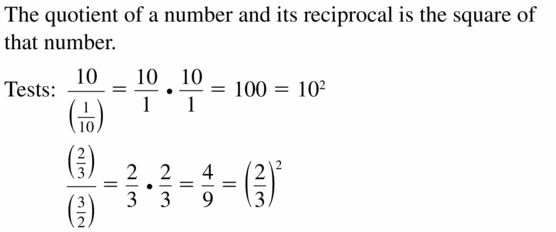
Question 12.
the quotient of two negative integers
Answer:

In Exercises 13 – 16, find a counter example to show that the conjecture is false.

Question 13.
The product of two positive numbers is always greater than either number,
Answer:

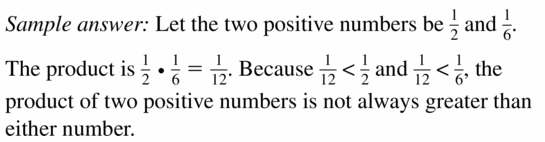
Question 14.
If n is a nonzero integer, then \(\frac{n+1}{n}\) is always greater than 1.
Answer:

Question 15.
If two angles are supplements of each other. then one of the angles must be acute.
Answer:

Question 16.
A line s divides \(\overline{M N}\) into two line segments. So, the lines is a segment bisector of \(\overline{M N}\)
Answer:

In Exercises 17 – 20. use the Law of Detachment to determine what you can conclude from the given information, if possible.

Question 17.
If you pass the final, then you pass the class. You passed the final.
Answer:

Question 18.
If your parents let you borrow the ear, then you will go to the movies with your friend. you will go to the movies with your friend.
Answer:

Question 19.
If a quadrilateral is a square. then it has four right angles. Quadrilateral QRST has four right angles.
Answer:

Question 20.
If a point divides a line segment into two congruent line segments. then the point is a midpoint. Point P divides \(\overline{L H}\) into two congruent line segments.
Answer:

In Exercises 21 – 24, use the Law of Syllogism to write a new conditional statement that follows from the pair of true statements, if possible.

Question 21.
If x < – 2, then |x| > 2. If x > 2. then |x| > 2.
Answer:

Question 22.
If a = 3. then 5a = 15. If \(\frac{1}{2}\)a = 1\(\frac{1}{2}\), then a = 3.
Answer:

Question 23.
If a figure is a rhombus then the figure is a parallelogram. If a figure is a parallelogram, then the figure has two pairs of opposite sides that are parallel.
Answer:

Question 24.
If a figure is a square, then the figure has four congruent sides. If a figure is a square, then the figure has tour right angles.
Answer:

In Exercises 25 – 28. state the law of logic that is illustrated.

Question 25.
If you do your homework, then you can watch TV If you watch TV, then you can watch your favorite show.
If you do your homework. then you can watch your favorite show.
Answer:

Question 26.
If you miss practice the day before a game. then you will not be a starting player in the game.
You miss practice on Tuesday. You will not start the game Wednesday.
Answer:

Question 27.
If x > 12, then x + 9 > 20. The value of x is 14. So, x + 9 > 20.
Answer:

Question 28.
If ∠1 and ∠2 are vertical angles. then ∠1 ≅∠2.
If ∠1 ≅∠2 then m∠1 ≅ m∠2.
If ∠1 and ∠2 are vertical angles. then m∠1 = m∠2.
Answer:

In Exercises 29 and 30, use inductive reasoning to make a conjecture about the given quantity. Then use deductive reasoning to show that the conjecture is true.

Question 29.
the sum of two odd integers
Answer:

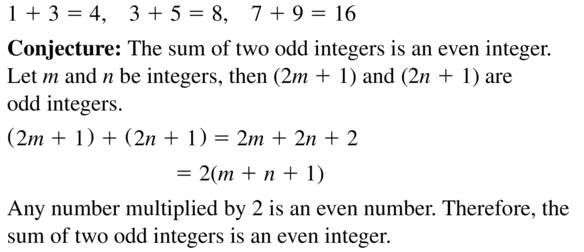
Question 30.
the product of two odd integers
Answer:

In Exercises 31 – 34. decide whether inductive reasoning or deductive reasoning is used to reach the conclusion. Explain your reasoning.

Question 31.
Each time your mom goes to the store. she buy s milk. So. the next time your mom goes to the store. she will buy milk.
Answer:

Question 32.
Rational numbers can be written as fractions. Irrational numbers cannot be written as tractions. So. \(\frac{1}{2}\) is a rational number
Answer:

Question 33.
All men are mortal. Mozart is a man. so Mozart is mortal.
Answer:

Question 34.
Each time you clean your room. you are allowed to go out with your friends. So, the next time you clean your room. you will be allowed to go out with your friends.
Answer:

ERROR ANALYSIS
In Exercises 35 and 36, describe and correct the error in interpreting the statement.

Question 35.
If a figure is a rectangle. then the figure has four sides.
A trapezoid has four sides.

Answer:

Question 36.
Each day, you get to school before your friend.

Answer:

Question 37.
REASONING
The table Shows the average weights of several subspecies of tigers. What conjecture can you make about the relation between the weights of female tigers and the weights of male tigers? Explain our reasoning.

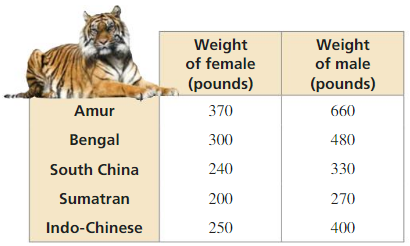
Answer:

Question 38.
HOW DO YOU SEE IT?
Determine whether you can make each conjecture from the graph. Explain your reasoning.

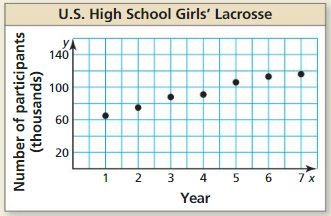
a. More girls will participate in high school lacrosse in Year 8 than those who participated in Year 7.
Answer:

b. The number of girls participating in high school lacrosse will exceed the number of boys participating in high school lacrosse in Year 9.
Answer:

Question 39.
MATHEMATICAL CONNECTIONS
Use inductive reasoning to write a formula for the sum of the first n positive even integers.
Answer:

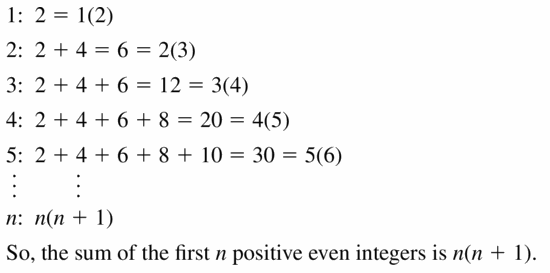
Question 40.
FINDING A PATTERN
The following are the first nine Fibonacci numbers.
1, 1, 2, 3, 5, 8, 13, 21, 34, …….
a. Make a conjecture about each of the Fibonacci numbers after the first two.
Answer:

b. Write the next three numbers in the pattern.
Answer:

c. Research to find a real-world example of this pattern.
Answer:

Question 41.
MAKING AN ARGUMENT
Which argument is correct? Explain your reasoning.
Argument 1: If two angles measure 30° and 60° then the angles are complementary. ∠1 and ∠2 are complementary. So. m∠1 = 30° and m∠2 = 60°

Argument 2: If two angles measure 30° and 60°. then the angles are complementary. The measure of ∠1 is 30° and the measure of ∠2 is 60°. So, ∠1 and ∠2 are complementary.
Answer:

Question 42.
THOUGHT PROVOKING
The first two terms of a sequence are \(\frac{1}{4}\) and \(\frac{1}{2}\) Describe three different possible Patterns for the sequence. List the first five terms for each sequence.
Answer:

Question 43.
MATHEMATICAL CONNECTIONS
Use the table to make a conjecture about the relationship between x and y. Then write an equation for y in terms of x. Use the equation to test your conjecture for other values of x.

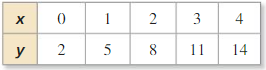
Answer:

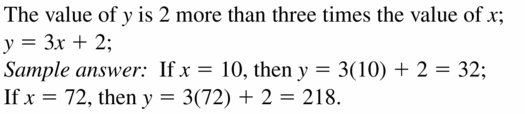
Question 44.
REASONING
Use the pattern below. Each figure is made of squares that are 1 unit by 1 unit.

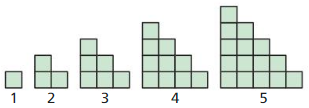
a. Find the perimeter of each figure. Describe the pattern of the perimeters.
Answer:

b. Predict the perimeter of the 20th figure.
Answer:

Question 45.
DRAWING CONCLUSIONS
Decide whether each conclusion is valid. Explain your reasoning.

• Yellowstone is a national park in Wyoming.
• You and your Friend went camping at Yellowstone National Park.
• When you go camping. you go canoeing.
• If you go on a hike, your Friend goes with you.
• You go on a hike.
• There is a 3-mile-long trail near your campsite.

a. You went camping in Wyoming.
b. Your Friend went canoeing.
c. Your friend went on a hike.
d. You and your Friend went on a hike on a 3-mile-long trail.
Answer:

Question 46.
CRITICAL THINKING
Geologists use the Mohs’ scale to determine a mineral’s hardness. Using the scale. a mineral with a higher rating will leave a scratch on a mineral with a lower rating. Testing a mineral’s hardness can help identify the mineral.

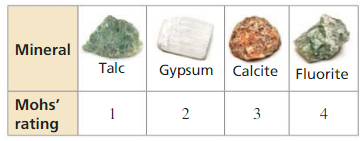
a. The four minerals are randomly labeled A, B, C, and D. Mineral A is scratched by Mineral B. Mineral C is scratched by all three of the other minerals. What can you conclude? Explain your reasoning.
Answer:

b. What additional test(s) can you use to identify all the minerals in part (a)?
Answer:

Maintaining Mathematical Proficiency

Determine which postulate is illustrated by the statement.

Question 47.
AB + BC = AC
Answer:

Question 48.
m∠DAC = m∠DAE + m∠EAB
Answer:

Question 49.
AD is the absolute value of the difference of the coordinates of A and D.
Answer:

Question 50.
m∠DAC is equal to the absolute value of the difference between the real numbers matched with \(\vec{A}\)D and \(\vec{A}\)C on a protractor.
Answer:

2.3 Postulates and Diagrams

Exploration 1

Looking at a Diagram

Work with a partner. On a piece of paper. draw two perpendicular lines. Label them and . Look at the diagram from different angles. Do the lines appear perpendicular regardless of the angle at which you look at them? Describe all the angles at which you can l00k at the lines and have them appear perpendicular.

Answer:

Exploration 2

Interpreting a Diagram

Work with a partner: When you draw a diagram, you are communicating with others. It is important that you include sufficient information in the diagram. Use the diagram to determine which of the following statements you can assume to be true. Explain your reasoning.

ATTENDING TO PRECISION
To be proficient in math, you need to state the meanings of the symbols you choose.



Answer:

Communicate Your Answer

Question 3.
In a diagram, what can be assumed and what needs to be labeled?
Answer:

Question 4.
Use the diagram in Exploration 2 to write two statements you can assume to be true and two statements you cannot assume to be true. Your statements should be different from those given in Exploration 2. Explain our reasoning.
Answer:

Lesson 2.3 Postulates and Diagrams

Monitoring progress

Question 1.
Use the diagram in Example 2. Which postulate allows you to say that the intersection of plane P and plane Q is a line?
Answer:

Question 2.
Use the diagram in Example 2 to write an example of the postulate.
a. Two Point Postulate
Answer:

b. Line-Point Postulate
Answer:

c. Line Intersection Postulate
Answer:

Refer back to Example 3.

Question 3.
If the given information states that \(\overline{P W}\) and \(\overline{Q W}\) arc congruent. how can you indicate that in the diagram?
Answer:

Question 4.
Name a pair of supplementary angles in the diagram. Explain.
Answer:

Use the diagram in Example 4.

Question 5.
Can you assume that plane S intersects plane T at ?
Answer:

Question 6.
Explain how you know
Answer:

Exercise 2.3 Postulates and Diagrams

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
Through any ___________ non collinear points. there exists exactly one plane.
Answer:

Question 2.
WRITING
Explain why you need at least three noncollinear points to determine a plane.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4. state the postulate illustrated by the diagram.

Question 3.

Answer:

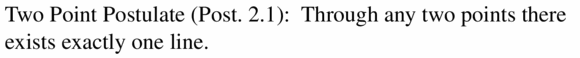
Question 4.

Answer:

In Exercises 5 – 8, use the diagram to write an example of the postulate.

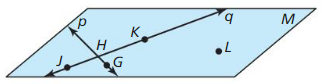
Question 5.
Line-Point Postulate (Postulate 2.2)
Answer:

Question 6.
Line Intersection Postulate (Postulate 2.3)
Answer:

Question 7.
Three Point Postulate (Postulate 2.4)
Answer:

Question 8.
Plane-Line Postulate (Postulate 2.6)
Answer:

In Exercises 9 – 12. sketch a diagram of the description.

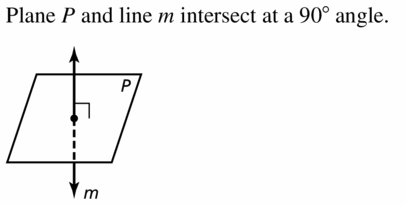
Question 9.
plane P and line m intersection plane P at a 90° angle
Answer:

Question 10.
\(\overline{X Y}\) in plane P, \(\overline{X Y}\) bisected by point A. and point C not
on \(\overline{X Y}\)
Answer:

Question 11.
\(\overline{X Y}\) intersecting \(\overline{W V}\) at point A. so that XA = VA
Answer:

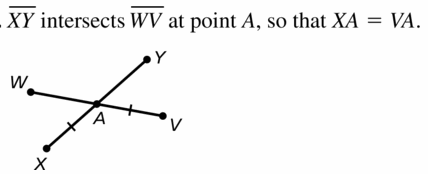
Question 12.
\(\overline{A B}\), \(\overline{C D}\), and \(\overline{E F}\) are all in plane P. and point x is the midpoint of all three segments.
Answer:

In Exercises 13 – 20, use the diagram to determine whether you can assume the statement.

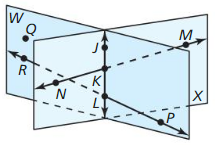
Question 13.
Planes Wand X intersect at .
Answer:

Question 14.
Points K, L, M, and N are coplanar.
Answer:

Question 15.
Points Q, J, and M are collinear.
Answer:

Question 16.

Answer:

Question 17.
lies in plane X.
Answer:

Question 18.
∠PLK is a right angle.
Answer:

Question 19.
∠NKL and ∠JKM are vertical angles.
Answer:

Question 20.
∠NKI and ∠JKM are supplementary angles.
Answer:

ERROR ANALYSIS
In Exercises 21 and 22. describe and correct the error in the statement made about the diagram.

Question 21.

Answer:

Question 22.

Answer:

Question 23.
ATTENDING TO PRECISION
Select all the statements about the diagram that you cannot conclude.

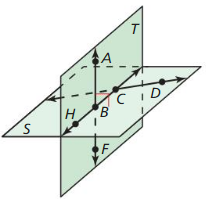
(A) A, B, and C are coplanar.
(B) Plane T intersects plane S in .
(C) intersects .
(D) H, F, and D are coplanar.
(E) Plane T ⊥ plane S.
(F) Point B bisects \(\overline{H C}\).
(G) ∠ABH and ∠HBF are a linear pair.
(H)
Answer:

Question 24.
HOW DO YOU SEE IT?
Use the diagram of line m and point C. Make a conjecture about how many planes can be drawn so that line m and point C lie in the same plane. Use postulates too justify your conjecture.

Answer:

Question 25.
MATHEMATICAL CONNECTIONS
One way to graph a linear equation is to plot two points whose coordinates satisfy the equation and then connect them with a line. Which postulate guarantees this process works for any linear equation?
Answer:

Question 26.
MATHEMATICAL CONNECTIONS
A way to solve a system of two linear equations that intersect is to graph the lines and find the coordinates of their intersection. Which postulate guarantees this process works for an two linear equations?
Answer:

In Exercises 27 and 28, (a) rewrite the postulate in if-then form. Then (b) write the converse, inverse, and contrapositive and state which ones are true.

Question 27.
Two Point Postulate (Postulate 2.1)
Answer:

Question 28.
Plane-Point Postulate (Postulate 2.5)
Answer:

Question 29.
REASONING
Choose the correct symbol to go between the statements.
65
<         ≤         =        ≥          >
Answer:

Question 30.
CRITICAL THINKING
If two lines intersect, then they intersect in exactly one point by the Line Intersection Postulate (Postulate 2.3). Do the two lines have to be in the same plane ? Draw a picture to support your answer. Then explain your reasoning.
Answer:

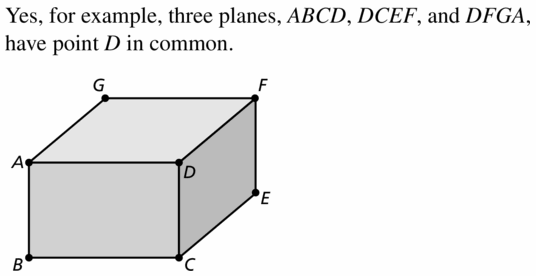
Question 31.
MAKING AN ARGUMENT
Your friend claims that even though two planes intersect in a line, it is possible for three planes to intersect in a point. Is your friend correct? Explain your reasoning.
Answer:

Question 32.
MAKING AN ARGUMENT
Your friend claims that by the Plane Intersection Postulate (Post. 2.7), any two planes intersect in a line. Is your friend’s interpretation 0f the Plane Intersection Postulate (Post. 2.7) correct? Explain your reasoning.
Answer:

Question 33.
ABSTRACT REASONING
Points E, F, and G all lie in plane P and in plane Q. What must be true about points E, F. and G so that planes P and Q are different planes? What must be true about points E, F, and G to force planes P and Q to be the same plane? Make sketches to support your answers.
Answer:

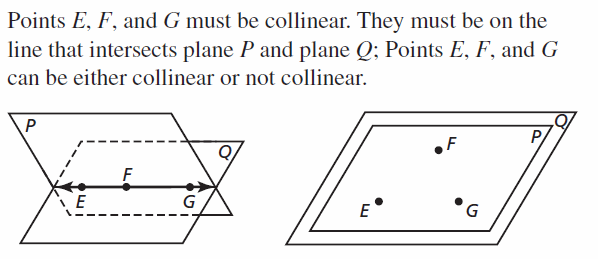
Question 34.
THOUGHT PROVOKING
The postulates in this book represent Euclidean geometry. In spherical geometry. all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. A plane is the surface of the sphere. Find a postulate on page 84 that is not true in spherical geometry. Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency

Solve the equation. Tell which algebraic property of equality you used.

Question 35.
t – 6 = – 4
Answer:

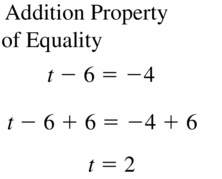
Question 36.
3x = 21
Answer:

Question 37.
9 + x = 13
Answer:

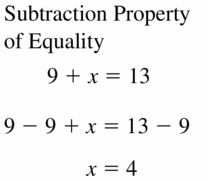
Question 38.
\(\frac{x}{7}\) = 5
Answer:

2.1 – 2.3 Study Skills: Using the Features of Your Textbook to Prepare for Quizzes and Tests

Mathematical Practices

Question 1.
Provide a counter example for each false conditional statement in Exercises 17 – 24 on page 71.
(You do not need to consider the converse. inverse, and contrapositive statements.)

Question 2.
Create a truth table for each of your answers to Exercise 59 on page 74.
Answer:

Question 3.
For Exercise 32 on page 88. write a question you would ask your friend about his or her interpretation.
Answer:

2.1 – 2.3 Quiz

Rewrite the conditional statement in if-then form. Then write the converse, inverse, and contrapositive of the conditional statement. Decide whether each statement is true or false.

Question 1.
An angle measure of 167° is an obtuse angle.
Answer:

Question 2.
You are in a physics class, so you always have homework.
Answer:

Question 3.
I will take my driving test, So I will get my driver’s license.
Answer:

Find a countereample to show that the conjecture is false.

Question 4.
The sum of a positive number and a negative number is always positive.
Answer:

Question 5.
If a figure has four sides, then it is a rectangle.
Answer:

Use inductive reasoning to make a conjecture about the given quantity. Then use deductive reasoning to show that the conjecture is true.

Question 6.
the sum of two negative integers
Answer:

Question 7.
the difference of two even integers
Answer:

Use the diagram to determine whether you can assume the statement.

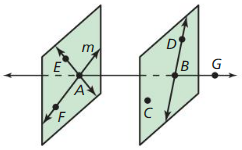
Question 8.
Points D, B, and C are coplanar.
Answer:

Question 9.
Plane EAF is parallel to plane DBC.
Answer:

Question 10.
Line m intersects line at point it.
Answer:

Question 11.
Line lies in plane DBC.
Answer:

Question 12.
m∠DBG = 90°
Answer:

Question 13.
You and your friend are bowling. Your friend claims that the statement “If I got a strike, then I used thegreen ball” can be written as a true biconditional statement. Is your friend correct? Explain your reasoning. (Section 2.1)
Answer:

Question 14.
The table shows the 1 – mile running times of the members of a high school track team.

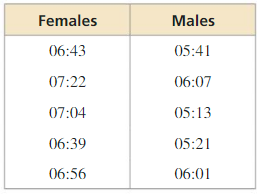
a. What conjecture can you make about the running times of females and males?
Answer:

b. What type of reasoning did you use? Explain.
Answer:

Question 15.
List five of the seven Point, Line, and Plane Postulates on page 84 that the diagram of the house demonstrates. Explain how the postulate is demonstrated in the diagram.

Answer:

2.4 Algebraic Reasoning

Exploration 1

Justifying steps in a solution

Work with a partner: In previous courses. you studied diíIrcnt properties. such as the properties of equality and the Distributive, Commutative, and Associative Properties. Write the property that justifies each of the following solution steps.

Answer:

Exploration 2

Stating Algebraic Properties

Work with a partner: The symbols and represent addition and multiplication (not necessarily in that order). Determine which symbol represents which operation. Justify your answer. Then state each algebraic property being illustrated.

LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.

Answer:

Communicate Your Answer

Question 3.
How can algebraic properties help you solve an equation?
Answer:

Question 4.
Solve 3(x + 1) – 1 = – 13. Justify each step.
Answer:

Lesson 2.4 Algebraic Reasoning

Monitoring Progress

Solve the equation. Justify each step.

Question 1.
6x – 11 = – 35
Answer:

Question 2.
– 2p – 9 = 10p – 17
Answer:

Question 3.
39 – 5z = -1 + 5z
Answer:

Question 4.
3(3x + 14) = – 3
Answer:

Question 5.
4 = – 10b + 6(2 – b)
Answer:

Question 6.
Solve the formula A = \(\frac{1}{2}\)bh for b. Justify each step. Then find the base of a
triangle whose area is 952 square feet and whose height is 56 feet.
Answer:

Name the property of equality that the statement illustrates.

Question 7.
If m∠6 = m∠7, then m∠7 = m∠6.
Answer:

Question 8.
34° = 34°
Answer:

Question 9.
m∠1 = m∠2 and m∠2 = m∠5. So, m∠1 = m∠5.
Answer:

Question 10.
If JK = KL and KL = 16, then JK = 16.
Answer:

Question 11.
PQ = ST, so ST = PQ.
Answer:

Question 12.
ZY = ZY
Answer:

Question 13.
In Example 5. a hot dog stand is located halfway between the shoe store and the pizza shop. at point H. Show that PH = HM.
Answer:

Exercise 2.4 Algebraic Reasoning

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
The statement “The measure of an angle is equal to itself” is true because of what property?
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find both answers.
What property justifies the following statement?
If c = d, then d = c.
If JK = LW. then LM = JK.
If e = f and f = g, then e = g.
If m∠R = m∠S, then m∠S = m∠R.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4, write the property that justifies each step.

Question 3.
3x – 12 = 7x + 8             Given
– 4x – 12 = 8                   ___________
– 4x = 20                        ___________
x = – 5                            ___________
Answer:

Question 4.
5(x – 1) = 4x + 13                Given
5x – 5 = 4x + 13                  ___________
x – 5 = 13                            ___________
x = 18                                 ___________
Answer:

In Exercises 5 – 14. solve the equation. Justify each step.

Question 5.
5x – 10 = – 40
Answer:

Question 6.
6x + 17 = – 7
Answer:

Question 7.
2x – 8 = 6x – 20
Answer:

Question 8.
4x + 9 = 16 – 3x
Answer:

Question 9.
5(3x – 20) = – 10
Answer:

Question 10.
3(2x + 11) = 9
Answer:

Question 11.
2(- x – 5) = 12
Answer:

Question 12.
44 – 2(3x + 4) = – 18x
Answer:

Question 13.
4(5x – 9) = – 2(x + 7)
Answer:

Question 14.
3(4x + 7) = 5(3x + 3)
Answer:

In Exercises 15 – 20, solve the equation for y. Justify each step.

Question 15.
5x + y = 18
Answer:

Question 16.
– 4x + 2y = 8
Answer:

Question 17.
2y – 0.5x = 16
Answer:

Question 18.
\(\frac{1}{2} x-\frac{3}{4} y\) = – 2
Answer:

Question 19.
12 – 3y = 30x + 6
Answer:

Question 20.
3x + 7 = – 7 + 9y
Answer:

In Exercises 21 – 24. solve the equation for the given variable. Justify each step

Question 21.
C = 2πr; r
Answer:

Question 22.
I = Prt;P
Answer:

Question 23.
S = 180(n – 2); n
Answer:

Question 24.
5 = 2πr² + 2πrh; h
Answer:

In Exercises 25 – 32, name the property of equality that the statement illustrates.

Question 25.
If x = y, then 3x = 3y.
Answer:

Question 26.
If AM = MB. then AM + 5 = MB + 5.
Answer:

Question 27.
x = x
Answer:

Question 28.
If x = y, then y = x.
Answer:

Question 29.
m∠Z = m∠Z
Answer:

Question 30.
If m∠Z = 29° and m∠B = 29°, then m∠A = m∠B
Answer:

Question 31.
If AB = LM, then LM = AB.
Answer:

Question 32.
If BC = XY and XY = 8, then BC = 8.
Answer:

In Exercises 33 – 40. use the property to copy and complete the statement.

Question 33.
Substitution Property of Equality:
If AB = 20. then AB + CD = ________ .
Answer:

Question 34.
Symmetric Property oÌ Equality:
If m∠1 = m∠2. then ________ .
Answer:

Question 35.
Addition Property of Equality:
If AB = CD. then AB + EF = ________ .
Answer:

Question 36.
Multiplication Property of Equality:
If AB = CD, then 5 • AB = ________ .
Answer:

Question 37.
Subtraction Property of Equality:
If LM = XY, then LM – GH = ________ .
Answer:

Question 38.
Distributive Property:
If 5(x + 8) = 2, then ___ + ___ = 2.
Answer:

Question 39.
Transitive Property of Equality:
If m∠1 = m∠2 and m∠2 = m∠3, then ________ .
Answer:

Question 40.
Reflexive Properly of Equality:
m∠ABC = ________ .
Answer:

ERROR ANALYSIS
In Exercises 41 and 42, describe and correct the error in solving the equation.

Question 41.

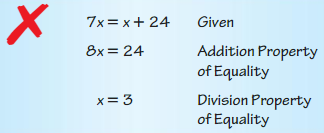
Answer:

Question 42.

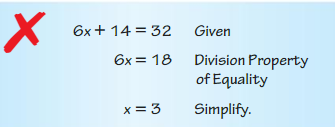
Answer:

Question 43.
REWRITING A FORMULA
The formula for the perimeter P of a rectangle is P = 2l + 2w, where l is the length and w is the width. Solve the formula for l. Justify each step. Then find the length of a rectangular lawn with a perimeter of 32 meters and a width of 5 meters.
Answer:

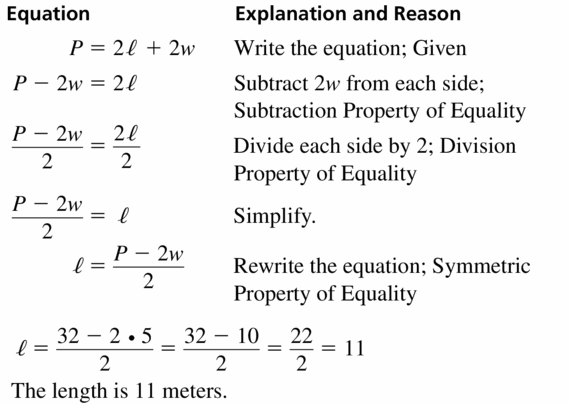
Question 44.
REWRITING A FORMULA
The formula for the area
A of a trapezoid is A = \(\frac{1}{2}\)h (b₁ + b₂), where h is the
height and b₁ and b₂ are the lengths of the two bases. Solve the formula for b₁. Justify each step. Then find the length of one of the bases of the trapezoid when the area of the trapezoid is 91 square meters. the height is 7 meters. and the length of the other base is 20 meters.
Answer:

Question 45.
ANALYZING RELATIONSHIPS
In the diagram,
m∠ABD = m∠CBE. Show that m∠1 = m∠3.

Answer:

Question 46.
ANALYZING RELATIONSHIPS
In the diagram,
AC = BD. Show that AB = CD.

Answer:

Question 47.
ANALYZING RELATIONSHIPS
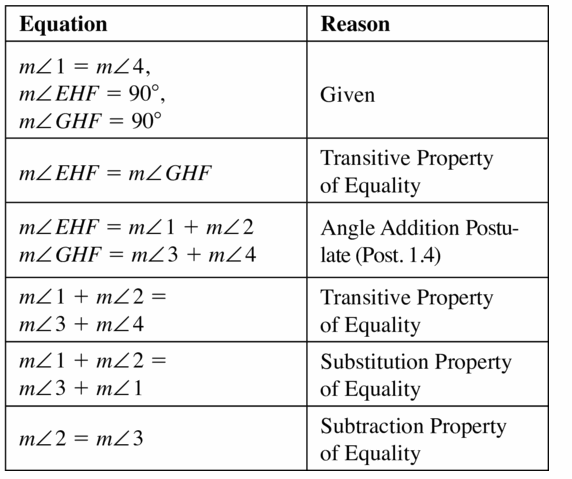
Copy and complete the table to show that m∠2 = m∠3.

Equation	Reason
m∠1 = m∠4, m∠EFH = 90°, m∠GHF = 90°	Given
m∠EHF = m∠GHF
m∠EHF = m∠1 + m∠2 m∠GHF = m∠3 + m∠4
m∠1 + m∠2 = m∠3 + m∠4
	Substitution Property of Equality
m∠2 = m∠3

Answer:

Question 48.
WRITING
Compare the Reflexive Property of Equality with the Symmetric Property of Equality. How are the properties similar? How are they different?
Answer:

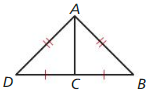
REASONING
In Exercises 49 and 50. show that the perimeter of ∆ABC is equal to the perimeter of ∆ADC.

Question 49.

Answer:

Question 50.

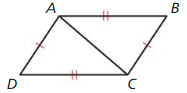
Answer:

Question 51.
MATHEMATICAL CONNECTIONS
In the figure, \(\overline{Z Y}\) ≅ \(\overline{X W}\), ZX = 5x + 17, YW = 10 – 2x, and YX = 3. Find ZY and XW

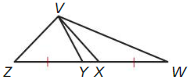
Answer:

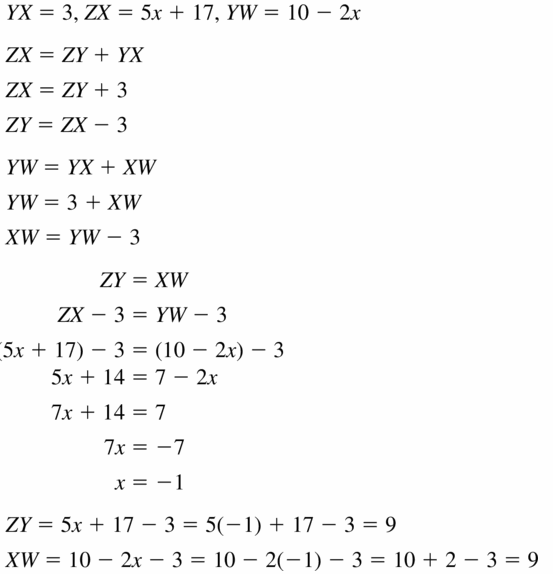
Question 52.
HOW DO YOU SEE IT?
The bar graph shows the number of hours each employee works at a grocery store. Give an example of the Reflexive, Symmetric, and Transitive Properties of Equality.

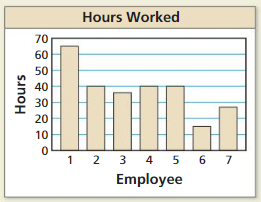
Answer:

Question 53.
ATTENDING TO PRECISION
Which of the following statements illustrate the Symmetric Property of Equality? Select all that apply.
(A) If AC = RS, then RS = AC.
(B) If x = 9 then 9 = x.
(C) If AD = BC, then DA = CB.
(D) AB = BA
(E) If AB = LW and LM = RT, then AB = RT.
(F) If XY = EF, then FE = XY.
Answer:

Question 54.
THOUGHT PROVOKING
Write examples from your everyday life lo help you remember the Reflexive, Symmetric, and Transitive Properties of Equality. Justify your answers.
Answer:

Question 55.
MULTIPLE REPRESENTATIONS
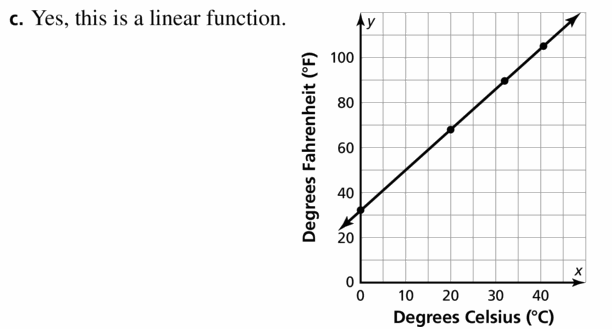
The formula to convert
a temperature in degrees Fahrenheit (°F) to degrees
Celsius (°C) is C = \(\frac{5}{9}\)(F – 32).
a. Solve the formula for F. Justify each step.
b. Make a table that shows the conversion to Fahrenheit for each temperature: 0°C. 20°C, 32°C. and 41°C.
c. Use your table to graph the temperature in degrees Fahrenheit as a function of the temperature in degrees Celsius. Is this a linear function?

Answer:

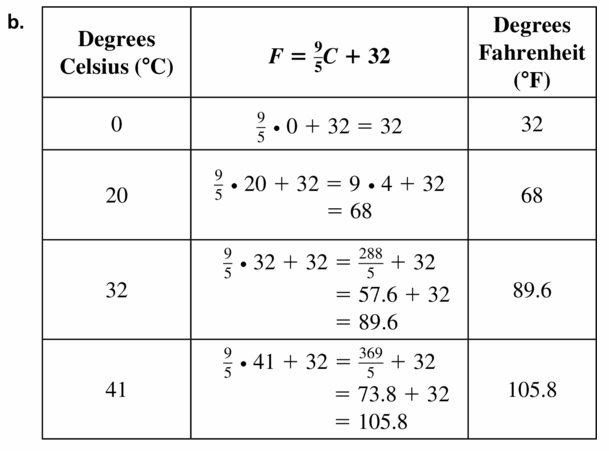
Question 56.
REASONING
Select all the properties that would also apply to inequalities. Explain your reasoning.
(A) Addition Property
Answer:

(B) Subtraction Properly
Answer:

(C) Substitution Property
Answer:

(D) Reflexive Property
Answer:

(E) Symmetric Property
Answer:

(F) Transitive Property
Answer:

Maintaining Mathematical Proficiency

Name the definition property, or postulate that is represented by each diagram.

Question 57.

XY + YZ = XZ
Answer:

Question 58.

Answer:

Question 59.

Answer:

Question 60.

m∠ABD + m∠DBC = m∠ABC
Answer:

2.5 Proving Statements about Segments and Angles

Exploration 1

Writing Reasons in a proof

Work with a partner: Four steps of a proof are shown. Write the reasons for each statement
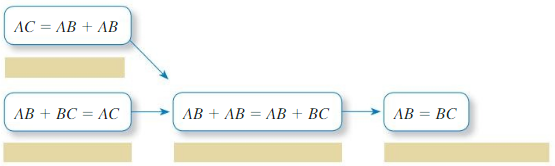
Given AC = AB + AB
Prove AB = BC

REASONING ABSTRACTLY
To be proficient in math, you need to know and be able to use algebraic properties.

Statements	Reasons
1. AC = AB + AB	1. Given
2. AB = BC  = AC	2. ______________________
3. AB + AB = AB + BC	3. ______________________
4. AB = BC	4. ______________________

Answer:

Exploration 2

Writing Steps in a Proof

Work with a partner: Six steps of a proof are shown. Complete the statements that correspond to each reason.
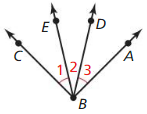
Given m∠1 = m∠3
Prove m∠EBA = m∠CBD

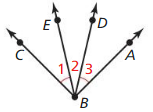
Statements	Reasons
1. ___________________________	1. Given
2. m∠EBA = m∠2 + m∠3	2. Angle Addition Postulate (Post.1.4)
3. m∠EBA = m∠2 + m∠1	3. Substitution Property of Equality
4. m∠EBA = ___________________________	4. Commutative Property of Addition
5. m∠1 + m∠2 = ______________________	5. Angle Addition Postulate (Post. 1.4)
6. ________________________________________	6. Transitive Property of Equality

Answer:

Communicate Your Answer

Question 3.
How can you prove a mathematical statement?
Answer:

Question 4.
Use the given information and the figure to write a proof for the statement.
Given B is the midpoint of \(\overline{A C}\).
C is the midpoint of \(\overline{B D}\).
Prove AB = CD

Answer:

Lesson 2.5 Proving Statements about Segments and Angles

Monitoring Progress

Question 1.
Six Steps of a two-column proof are shown. Copy and complete the proof.

Given T is the midpoint of \(\overline{S U}\).
Prove x = 5

Statement	Reason
1. T is the midpoint of \(\overline{S U}\).	1. ________________________________________
2. \( \overline{S T} \cong \overline{T U} \)	2. Definition of midpoint
3. ST = TU	3. Definition of congruent segments
4. 7x = 3x + 20	4. ________________________________________
5. ________________________________________	5. Subtraction Property of Equality
6. x = 5	6. ________________________________________

Answer:

Exercise 2.5 Proving Statements about Segments and Angles

Vocabulary and Core Concept Check

Question 1.
WRITING
How is a theorem different from a postulate?
Answer:

Question 2.
COMPLETE THE SENTENCE
In a two-column proof, each __________ is on the left and each __________ is on the right.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4. copy and complete the proof.

Question 3.
Given PQ = RS
Prove PR = QS

Statements	Reasons
1. PQ = RS	1. ________________________________________
2. PQ + QR = RS + QR	2. ________________________________________
3. ________________________________________	3. Segment Addition Postulate (Post. 1.2)
4. RS + QR = QS	4. Segment Addition Postulate (Post. 1.2)
5. PR = QS	5. ________________________________________

Answer:

Question 4.
Given ∠1 is a complement of ∠2.
∠2 ≅ ∠3
Prove ∠1 is a complement of ∠3.

Statements	Reasons
1. ∠1 is a complement of ∠2.	1. Given
2. ∠2 ≅ ∠3	2. _____________________________
3. m∠1 + m∠2 = 90°	3. _____________________________
4. m∠2 = m∠3	4.  Definition of congruent angles
5. _____________________________	5. Substitution Property Of Equality
6. ∠1 is a complement of ∠3.	6. _____________________________

Answer:

In Exercises 5-10, name the property that the statement illustrates.

Question 5.
If \(\overline{P Q} \cong \overline{S T}\) and \(\overline{S T} \cong \overline{U V}\), then \(\overline{P Q} \cong \overline{U V}\).\
Answer:

Question 6.
∠F ≅ ∠F
Answer:

Question 7.
If ∠G ≅∠H. then ∠H ≅ ∠G.
Answer:

Question 8.
\(\overline{D E} \cong \overline{D E}\)
Answer:

Question 9.
If \(\overline{X Y} \cong \overline{U V}\), then \(\overline{U V} \cong \overline{X Y}\).
Answer:

Question 10.
If ∠L ≅∠M and ∠M ≅∠N, then ∠L ≅∠N.
Answer:

PROOF
In Exercises 11 and 12, write a two-column proof for the property.

Question 11.
Reflexive Property of Segment Congruence (Thm. 2.1)
Answer:

Question 12.
Transitive Property of Angle Congruence (Thm. 2.2)
Answer:

PROOF
Exercises 13 and 14. write a two-column proof.

Question 13.
Given ∠GFH ≅ ∠GHF
Prove ∠EFG and ∠GHF are supplementary

Answer:

Question 14.


Answer:

Question 15.
ERROR ANALYSIS
In the diagram \(\overline{M N} \cong \overline{L Q}\) and \(\overrightarrow{L Q} \cong \overrightarrow{P N}\). Describe and correct the error in the reasoning.

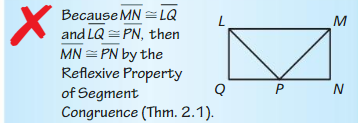
Answer:

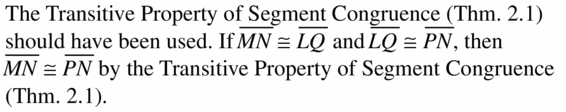
Question 16.
MODELING WITH MATHEMATICS
The distance fr the restaurant to the shoe store is the same as the distance from the cafe to the florist. The distance from the shoe store to the movie theater is the same as the distance from the movie theater to the cafe, and from the florist to the dry cleaners.

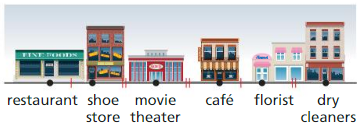
Use the steps below to prove that the distance from the restaurant to the movie theater is the same as the distance from the cafe to the dry cleaners.
a. State what is given and what is to be proven for the situation.
Answer:

b. Write a two-column proof.
Answer:

Question 17.
REASONING
In the sculpture shown, \(\angle 1 \cong \angle 2\) and \(\angle 2 \cong \angle 3\) classify the triangle and justify your answer.

Answer:

Question 18.
MAKING AN ARGUMENT
In the figure, \(\overline{S R} \cong \overline{C B}\) and \(\overline{A C} \cong \overline{Q R}\) Your friend claims that, because of this. \( \overline{C B} \cong \overline{A C}\) by the Transitive Property of Segment Congruence (Thin. 2. 1). Is your friend correct? Explain your reasoning.

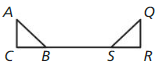
Answer:

Question 19.
WRITING
Explain why you do not use inductive reasoning when writing a proof.
Answer:

Question 20.
HOW DO YOU SEE IT?
Use the figure to write Given and Prove statements for each conclusion.

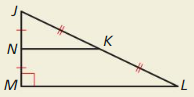
a. The acute angles of a right triangle are complementary.
b. A segment connecting the midpoints of two sides of a triangle is half as long as the third side.
Answer:

Question 21.
REASONING
Fold two corners of a piece of paper So their edges match. as shown.

a. What do you notice about the angle formed at the top of the page by the folds?
b. Write a two-column proof to show that the angle measure is always the same no matter how you make the folds.
Answer:

Question 22.
THOUGHT PROVOKING
The distance from Springfield
to Lakewood City is equal to the distance from Springfield Lo BettsilIe. Janisburg is 50 miles farther from Springfield titan Bettsville. Moon Valley is 50 miles Farther from Springfield than Lakewood City is. Use line segments to draw a diagram that represents this situation.
Answer:

Question 23.
MATHEMATICAL CONNECTIONS
Solve for x using the given information. Justify each step.
Given \(\overline{Q R} \cong \overline{P Q}, \overline{R S} \cong \overline{P Q}\)

Answer:

Maintaining Mathematical Proficiency

Use the figure

Question 24.
∠ 1 is a complement of ∠4. and m∠1 33°. Find in m∠4.
Answer:

Question 25.
∠3 is a supplement of ∠2, and m∠2 = 147°. Find m∠3.
Answer:

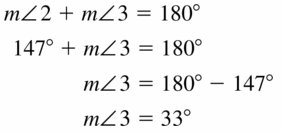
Question 26.
Name a pair of vertical angles.

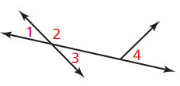
Answer:

2.6 Proving Geometric Relationships

Exploration 1

Matching Reasons in a Flowchart Proof

work with a partner: Match each reason with the correct step in the flowchart.

Given AC = AB + AB
Prove AB = BC

MODELING WITH MATHEMATICS
To be proficient in math, you need to map relationships using such tools as diagrams, two-way tables, graphs, flowcharts, and formulas.

A. Segment Addition Postulate (Post. 1.2)
Answer:

B. Given
Answer:

C. Transitive Property of Equality
Answer:

D. Subtraction Property of Equality
Answer:

Exploration 2

Matching Reasons in a Flowchart Proof

Work with a partner. Match each reason with the Correct step in the flowchart.

Given m∠1 = m∠3
Prove m∠EBA = m∠CBD

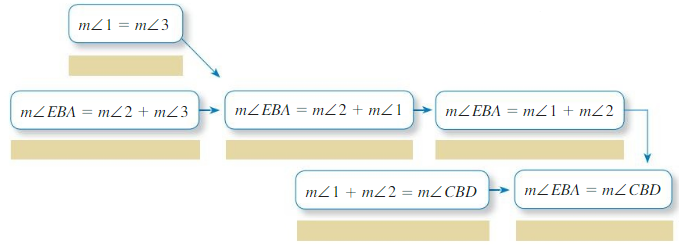
A. Angle Addition Postulate (Post. 1.4)
Answer:

B. Transitive Property of Equality
Answer:

C. Substitution Property of Equality
Answer:

D. Angle Addition Postulate (Post. 1.4)
Answer:

E. Given
Answer:

F. Commutative Property of Addition
Answer:

Communicate Your Answer

Question 3.
How can you use a flowchart to prove a mathematical statement?
Answer:

Question 4.
Compare the flowchart proofs above with the two-column proofs in the Section 2.5 Explorations. Explain the advantages and disadvantages of each.
Answer:

Lessson 2.6 Proving Geometric Relationships

Monitoring Progress

Question 1.
Copy and complete the flowchart proof. Then write a two-column proof.

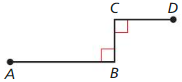
Given \(\overline{A B}\) ⊥ \(\overline{B C}\), \(\overline{D C}\) ⊥ \(\overline{B C}\)
Prove ∠B ≅∠C

Answer:

Question 2.
Copy and complete the two-column proof. Then write a flowchart proof.

Given AB = DE, BC = CD
Prove \(\overline{A C} \cong \overline{C E}\)

Statements	Reasons
1. AB = DE, BC = CD	1. Given
2. AB + BC = BC + DE	2. Addition Property of Equality
3. _____________________________	3. Substitution Property of Equality
4. AB + BC = AC, CD + DE = CE	4. _____________________________
5. _____________________________	5. Substitution Property of Equality
6. \( \overline{A C} \cong \overline{C E} \)	6. _____________________________

Answer:

Question 3.
Rewrite the two-column proof in Example 3 without using the Congruent Supplements Theorem. How many steps do you save by using the theorem?
Answer:

Use the diagram and the given angle measure to find the other three angle measures.

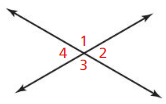
Question 4.
m∠1 = 117°
Answer:

Question 5.
m∠2 = 59°
Answer:

Question 6.
m∠4 = 88°
Answer:

Question 7.
Find the value of w.

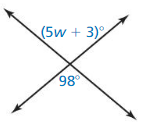
Answer:

Question 8.
write a paragraph proof.

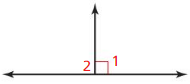
Given ∠1 is a right angle.
Prove ∠2 is a right angle.
Answer:

Exercise 2.6 Proving Geometric Relationships

Vocabulary and Core Concept Check

Question 1.
WRITING
Explain why all right angles are congruent.
Answer:

Question 2.
VOCABULARY
What are the two types of angles that are formed by intersecting lines?
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3-6. identify the pairs) of congruent angles in the figures. Explain how you know they are congruent.

Question 3.

Answer:

Question 4.

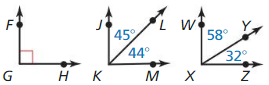
Answer:

Question 5.

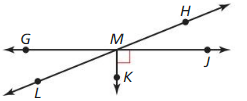
Answer:

Question 6.
∠ABC is supplementary to ∠CBD
∠CBD is supplementary to ∠DEF

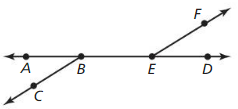
Answer:

In Exercises 7 – 10. use the diagram and the given angle measure to find the other three measures.

Question 7.
m∠1 = 143°
Answer:

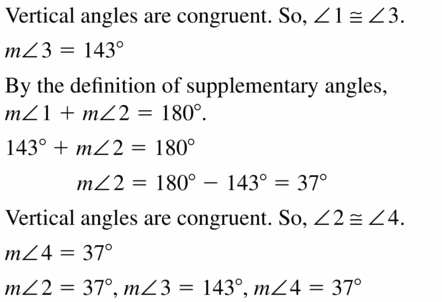
Question 8.
m∠3 = 159°
Answer:

Question 9.
m∠2 = 34°
Answer:

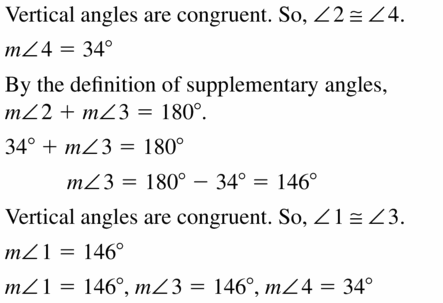
Question 10.
m∠4 = 29°
Answer:

In Exercises 11 – 14, find the values of x and y.

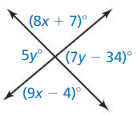
Question 11.

Answer:

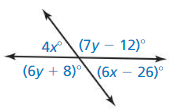
Question 12.

Answer:

Question 13.

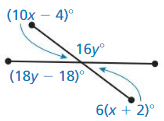
Answer:

Question 14.

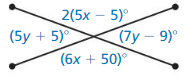
Answer:

ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in using the diagram to find the value of x.

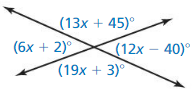
Question 15.

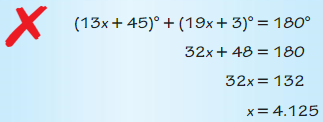
Answer:

Question 16.

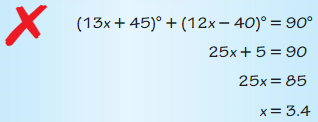
Answer:

Question 17.
PROOF
Copy and complete the flowchart proof. Then write a two-column proof.

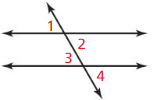
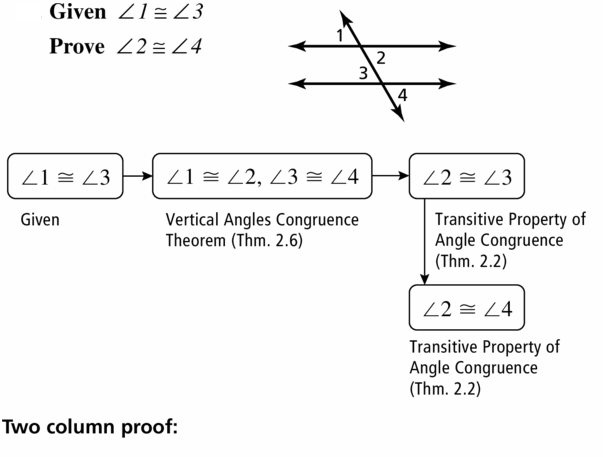
Given ∠1 ≅ ∠3
Prove ∠2 ≅ ∠4

Answer:

Question 18.
PROOF
Copy and complete the two-column proof. Then write a flowchart proof.

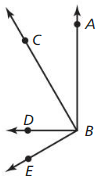
Given ∠ABD is a right angle
∠CBE is a right angle
Prove ∠ABC ≅ ∠DBE

Statements	Reasons
1. ∠ABD is a right angle. ∠CBE is a right angle.	1. _____________________________
2. ∠ABC and ∠CBD are complementary.	2. Definition of complementary
3. ∠DBE and ∠CBD are complementary	3. _____________________________
4. ∠ABE ≅ ∠DBE	4. _____________________________

Question 19.
PROVING A THEOREM
Copy and complete the paragraph proof be the Congruent Complements Theorem (Theorem 2.5). Then write a two-column proof.

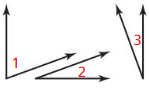
Given ∠1 and ∠2 are complementary
∠1 and ∠3 are complementary
Prove ∠2 ≅ ∠3
∠1 and ∠2 are complementary, and ∠1 and ∠3 are complementary. By the definition
of ____________ angles. m∠1 + m∠2 = 90° and ____________ = 90°. By the ____________ m∠1 + m∠2 = m∠1 + m∠3. By the Subtraction ____________
Property of Equality, ____________ . So. ∠2 ≅∠3 by the definition of ____________ .
Answer:

Question 20.
PROVING A THEOREM
Copy and complete the two – column proof for the Congruent Supplement Theorem (Theorem 2.4). Then write a paragraph proof. (See Example 5.)

Given ∠1 and ∠2 are supplementary
∠3 and ∠4 are supplementary
∠1 and ∠4
Prove ∠2 ≅∠3

Statements	Reasons
1. ∠1 and ∠2 are supplementary ∠3 and ∠4 are supplementary ∠1 ≅ ∠4	1. Given
2. m∠1 + m∠2 = 180 m∠3 + m∠4 = 180	2. _____________________________
3. ______________ = m∠3 + m∠4	3. Transitive Property of Equality
4. m∠1 = m∠4	4. Definition of Congruent angles
5. m∠1 + m∠2 = ___________________	5. Substitution property of Equality
6. m∠2 = m∠3	6. _____________________________
7. __________________________	7. _____________________________

Answer:

PROOF
In Exercises 21 – 24. write a proof using any format.

Question 21.
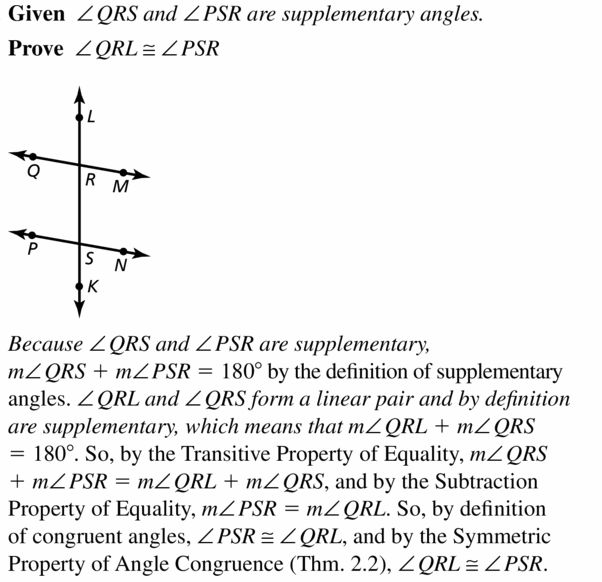
Given ∠QRS and ∠PSR are supplementary
Prove ∠QRL ≅ ∠PSR

Answer:

Question 22.
Given ∠1 and ∠3 are complementary.
∠2 and ∠4 are complementary.
Prove ∠1 ≅ ∠4

Answer:

Question 23.
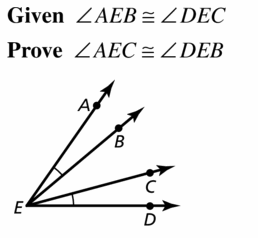
Given ∠AEB ≅ ∠DEC
Prove ∠AEC ≅ ∠DEB

Answer:

Question 24.


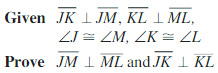
Answer:

Question 25.
MAKING AN ARGUMENT
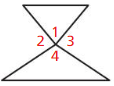
You overhear your friend discussing the diagram shown with a classmate. Your classmate claims ∠1 ≅∠4 because they are vertical angles Your friend claims they are not congruent because he can tell by looking at the diagram. Who is correct? Support your answer with definitions or theorems.

Answer:

Question 26.
THOUGHT PROVOKING
Draw three lines all intersecting at the same point. Explain how you can give two of the angle measures so that you can find the remaining four angle measures.
Answer:

Question 27.
CRITICAL THINKING
Is the converse of the Linear Pair Postulate (Postulate 2.8) true? If so, write a biconditional statement. Explain your reasoning.
Answer:

Question 28.
WRITING
How can you save time writing proofs?
Answer:

Question 29.
MATHEMATICAL CONNECTIONS
Find the measure of each angle in the diagram.

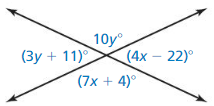
Answer:

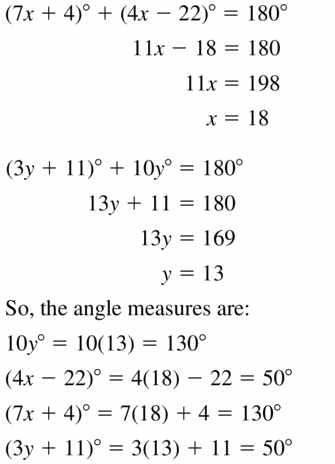
Question 30.
HOW DO YOU SEE IT?
Use the student’s two-column proof.
Given ∠1 ≅ ∠2
∠1 and ∠2 are supplementary.
Prove ___________

Statements	Reasons
1. ∠1 ≅ ∠2 ∠1 and ∠2 are supplementary	1. Given
2. m∠1 = m∠2	2. Definitions of congruent angles
3. m∠1 + m∠2 = 180°	3. Definition of supplementary angles
4. m∠1 + m∠1 = 180°	4. substitution property of Equality
5. 2m∠1 = 180°	5. Simplify
6. m∠1 = 90°	6. Division Property of Equality
7. m∠2 = 90°	7. Transitive Property of Equality
8. __________________________	8. ________________________________________

a What is the student trying to prove?
Answer:

b. Your friend claims that the last line of the proof should be ∠1 ≅ ∠2. because the measures of the angles are both 90°. Is your friend correct? Explain.
Answer:

Maintaining Mathematical Proficiency

Use the cube

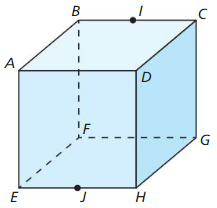
Question 31.
Name three collinear points.
Answer:

Question 32.
Name the intersection of plane ABF and plane EHG.
Answer:

Question 33.
Name two planes containing \(\overline{B C}\).
Answer:

Question 34.
Name three planes containing point D.
Answer:

Question 35.
Name three points that are not collinear,
Answer:

Question 36.
Name two planes containing point J.
Answer:

2.4 – 2.6 Performance Task: Induction and the Next Dimension

Mathematical Practices

Question 1.
Explain the purpose of justifying each step in Exercises 5-14 on page 96.
Answer:

Question 2.
Create a diagram to model each statement in Exercises 5-10 on page 103.
Answer:

Question 3.
Explain why you would not be able to prove the statement in Exercise 21 on page 113 if you were provided with the given information or able to use an postulates or theorems.
Answer:

Reasoning and Proofs Chapter Review

2.1 Conditional Statements

Write the if-then form, the converse, the inverse, the contrapositive. and the biconditional of the conditional statement.

Question 1.
Two lines intersect in a Point.

Question 2.
4x + 9 = 21 because x = 3.
Answer:

Question 3.
Supplementary angles sum to 180°.
Answer:

Question 4.
Right angles are 90°.
Answer:

2.2 Inductive and Deductive Reasoning

Question 5
conclusion can you make about the difference of any two odd integers?
Answer:

Question 6.
What conclusion can you make about the product of an even and an odd integer?
Answer:

Question 7.
Use the Law of Detachment to make a valid conclusion.
If an angle is a right angle, then the angle measures 90°. ∠B is a right angle.
Answer:

Question 8.
Use the Law of Syllogism to write a new conditional statement that follows from the pair of true statements: If x = 3, then 2x = 6. If 4x = 12. then x = 3.
Answer:

2.3 Postulates and Diagrams

Use the diagram at the right to determine whether you can assume the statement.

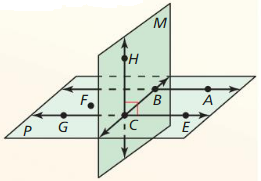
Question 9.
Points A, B, C, and E are coplanar.
Answer:

Question 10.

Answer:

Question 11.
Points F, B, and G are collinear.
Answer:

Question 12.

Answer:

sketch a diagram of the description.

Question 13.
∠ABC, an acute angle, is bisected by .
Answer:

Question 14.
∠CDE, a straight angle, is bisected by .
Answer:

Question 15.
Plane P and plane R intersect perpendicularly in . \(\overline{Z W}\) lies in plane P
Answer:

2.4 Algebraic Reasoning

Solve the equation. Justify each step.

Question 16.
– 9x – 21 = – 20x – 87
Answer:

Question 17.
15x + 22 = 7x + 62
Answer:

Question 18.
3(2x + 9) = 30
Answer:

Question 19.
5x + 2(2x – 23) = – 154
Answer:

Name the property of equality that the statement illustrates.

Question 20.
If LM = RS and RS = 25, then LM = 25.
Answer:

Question 21.
AM = AM
Answer:

2.5 Proving Statements about Segments and Angles

Name the property that the statement illustrates.

Question 22.
If ∠DEF ≅∠JKL, then ∠JKL ≅ ∠DEF
Answer:

Question 23.
∠C ≅ ∠C
Answer:

Question 24.
If MN = PQ and PQ = RS. then MN = RS.
Answer:

Question 25.
Write a two-column proof be the Reflexive Property of Angle Congruence (Thm. 2.2).
Answer:

2.6 Proving Geometric Relationships

Question 26.
Write a proof using any format
Given ∠3 and ∠2 are complementary.
m∠1 + m∠2 = 90°
Prove ∠3 ≅∠1
Answer:

Reasoning and Proofs Test

Use the diagram to determine whether you can assume the statement.
Explain your reasoning.

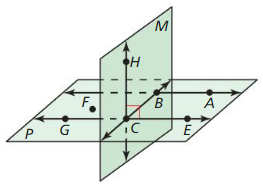
Question 1.
⊥ plane M
Answer:

Question 2.
Points F, G, and A are coplanar.
Answer:

Question 3.
Points E, C, and G are collinear.
Answer:

Question 4.
Planes M and P intersect at .
Answer:

Question 5.
lies in plane P.
Answer:

Question 6.

Answer:

Solve the equation. Justify each step.

Question 7.
9x + 31 = – 23 + 3x
Answer:

Question 8.
26 + 2(3x + 11) = – 18
Answer:

Question 9.
3(7x – 9) – 19x – 15
Answer:

Write the if-then form, the converse, the inverse, the contrapositive. and the biconditional of the conditional statement.

Question 10.
Two planes intersect at a line.
Answer:

Question 11.
A relation that pairs each input with exactly one output is a function.
Answer:

Use inductive reasoning to make a conjecture about the given quantity. Then use deductive reasoning to sIm that the conjecture is true.

Question 12.
the sum of three odd integers
Answer:

Question 13.
the product of three even integers
Answer:

Question 14.
Give an example of two statements for which the Law of Detachment does not apply.
Answer:

Question 15.
The formula for the area A of a triangle is A = \(\frac{1}{2}\)bh, where b is the base and h is the height. Solve the formula for h and justify each step. Then find the height of a standard yield sign when the area is 558 square inches and each side is 36 inches.

Answer:

Question 16.
You visit the zoo and notice the following

• The elephants, giraffes, lions, tigers, and zebras are located along a straight walkway.
• The giraffes are halfway between the elephants and the lions.
• The tigers are halfway between the lions and the zebras.
• The lions are hallway between the giraffes and the tigers.

Draw and label a diagram that represents this information. Then prove that the distance between the elephants and the giraffes is equal to the distance between the tigers and the zebras. Use any proof format.
Answer:

Question 17.
Write a proof using an format.
Given ∠2 ≅∠3
\(\vec{T}\)V bisects ∠UTW.
Prove ∠1 ≅ ∠3

Answer:

Reasoning and Proofs Cumulative Assessment

Question 1.
Use the diagram to write an example of each postulate.

a. Two Point Postulate (Postulate 2.1): Through any two points, there exists exactly one line.
Answer:

b. Line Intersection Postulate (Postulate 2.3): If two lines intersect, then their intersection is exactly one point.
Answer:

c. Three Point Postulate (Postulate 2.4): Through any three noncollinear points, there exists exactly one plane.
Answer:

d. Plane-Line Postulate (Postulate 2.6): If two points lie in a plane, then the line containing them lies in the plane.
Answer:

e. Plane Intersection Postulate (Postulate 2.7): If two planes intersect, then their intersection is a line
Answer:

Question 2.
Enter the reasons in the correct positions to complete the two-column proof.

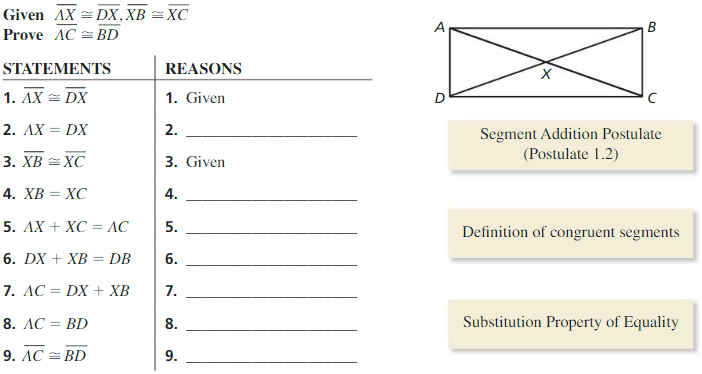
Answer:

Question 3.
Classify each related conditional statement. based on the conditional statement
“If I study, then I will pass the final exam.”
a. I will pass the final exam if and only if I study.
Answer:

b. If I do not study, then I will not pass the final exam.
Answer:

c. If I pass the final exam, then I studied.
Answer:

d. If I do not pass the final exam, then I did not study.
Answer:

Question 4.
List all segment bisectors given x = 3.

Answer:

Question 5.
You are given m∠FHE = m∠BHG = m∠AHF = 90°. Choose the symbol that makes each statement true. State which theorem or postulate. if any, supports your answer.

=       ≅         ≠
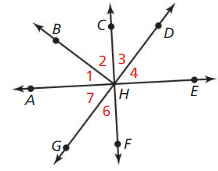
a. ∠3 _____ ∠6
Answer:

b. m∠4 ______ m∠7
Answer:

c. m∠FHE _______ m∠AHG
Answer:

d. m∠AHG + m∠GHE _______180°
Answer:

Question 6.
Find the distance between each pair of points. Then order each line
segment from longest to shortest.
a. A(- 6, 1), B(- 1, 6)
Answer:

b. C(- 5, 8), D(5, 8)
Answer:

c. E(2, 7), F(4, – 2)
Answer:

d. G(7, 3), H(7, – 1)
Answer:

e. J(- 4, – 2), K(1, – 5)
Answer:

f. L(3, – 8), M(7, – 5)
Answer:

Question 7.
The proof shows that ∠MRL is congruent to ∠NSR. Select all other angles that are also congruent to ∠NSR.
Given ∠MRS and ∠NSR are supplementary.
Prove ∠MRL ≅ ∠VSR

Statements	Reasons
1. ∠MRS and ∠NSR are supplementary	1. Given
2. ∠MRL and ∠MRS are a linear pair.	2. Definition of linear pair, as shown in the diagram
3. ∠MRL and ∠MRS are supplementary.	3. Linear Pair Postulate (Postulate 2.8)
4. ∠MRL ≅ ∠NSR	4. Congruent Supplements Theorem (Theorem 2.4)

∠PSK         ∠KSN        ∠PSR       ∠QRS          ∠QRL
Answer:

Question 8.
Your teacher assigns your class a homework problem that asks you to prove the Vertical Angles Congruence Theorem (Theorem 2.6) using the picture and information given at the right. Your friend claims that this can be proved without using the Linear Pair Postulate (Postulate 2.8). Is our friend correct? Explain your reasoning.
Given ∠1 and ∠3 arc vertical angles.
Prove ∠1 ≅ ∠3

Answer: