HMH Go Math

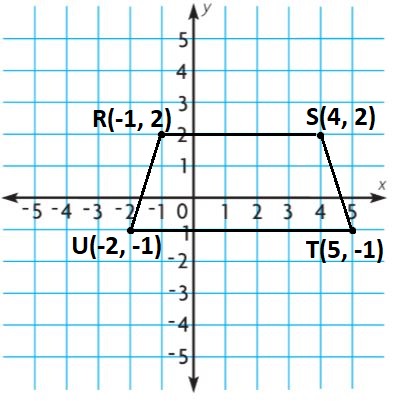
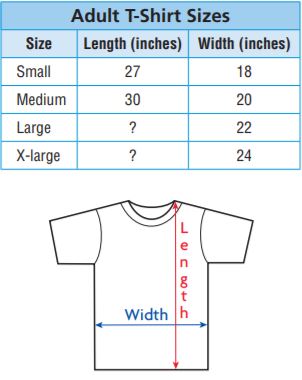
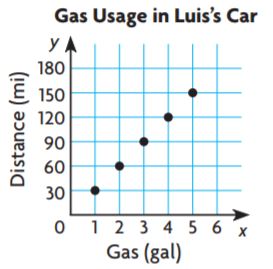
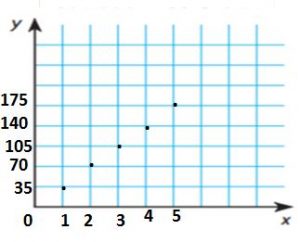
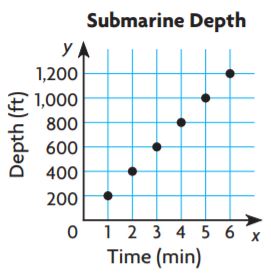
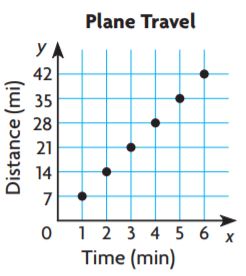
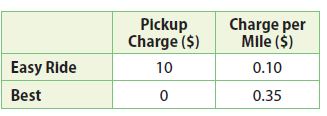
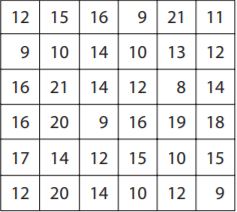
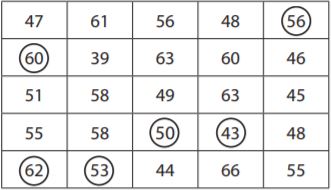
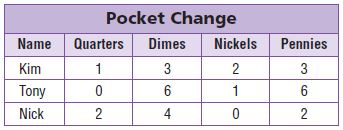
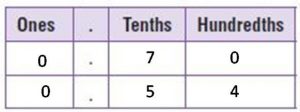
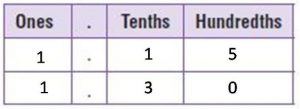
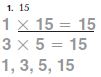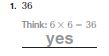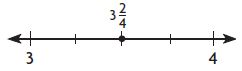Go Math Grade 5 Answer Key Chapter 6 Add and Subtract Fractions with Unlike Denominators can be downloaded free of cost from here. HMH Go Math Grade 5 Answer Key includes topics such as Addition and Subtraction with unlike denominators, Estimate fraction sums and differences, Least Common Denominators, etc. Begin your preparation from Go Math Grade 5 Chapter 6 Solution Key Add and Subtract Fractions with Unlike Denominators and score better grades in your exams.

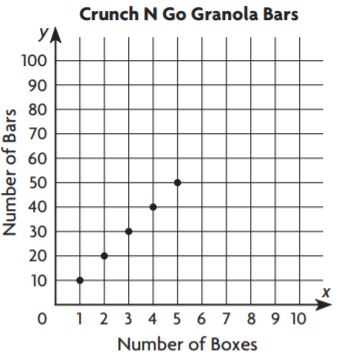
Go Math Grade 5 Answer Key Chapter 6 Add and Subtract Fractions with Unlike Denominators

The Go Math Grade 5 Answer Key Add and Subtract Fractions with Unlike Denominators covers all the Questions in Chapter Tests, Practice Tests, etc., and has detailed solutions for all of them. Try to solve as many problems as possible from the  Go Math Answer Key for Grade 5 Chapter 6 Add and Subtract Fractions with Unlike Denominators and know the concepts behind them easily. Access the Topics in 5th Grade Go Math Ch 6 Add and Subtract Fractions with Unlike Denominators via quick links available in the forthcoming modules.

Lesson 1: Investigate • Addition with Unlike Denominators

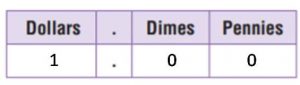
• Share and Show – Page No. 244
• Investigate • Addition with Unlike Denominators Page No. 245
• Problem Solving – Page No. 246

Lesson 2: Investigate • Subtraction with Unlike Denominators

• Share and Show – Page No. 248
• Investigate • Subtraction with Unlike Denominators Page No. 249
• UNLOCK the Problem – Page No. 250

Lesson 3: Estimate Fraction Sums and Differences

• Share and Show – Page No. 253
• Problem Solving – Page No. 254

Lesson 4: Common Denominators and Equivalent Fractions

• Share and Show – Page No. 256
• Common Denominators and Equivalent Fractions Page No. 257
• UNLOCK the Problem – Page No. 258

Lesson 5: Add and Subtract Fractions

• Share and Show – Page No. 260
• On Your Own – Page No. 261
• Problem Solving – Page No. 262

Mid-Chapter Checkpoint

• Mid-Chapter Checkpoint – Vocabulary – Page No. 263
• Mid-Chapter Checkpoint – Page No. 264

Lesson 6: Add and Subtract Mixed Numbers

• Share and Show – Page No. 266
• Page No. 267
• Problem Solving – Page No. 268

Lesson 7: Subtraction with Renaming

• Share and Show – Page No. 270
• Subtraction with Renaming Page No. 271
• Subtraction with Renaming Page No. 272

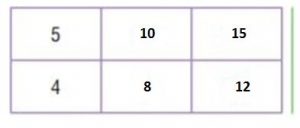
Lesson 8: Algebra • Patterns with Fractions

• Share and Show – Page No. 275
• Problem Solving – Page No. 276

Lesson 9: Problem Solving • Practice Addition and Subtraction

• Share and Show – Page No. 279
• On Your Own – Page No. 280

Lesson 10: Algebra • Use Properties of Addition

• Share and Show – Page No. 283
• Problem Solving – Page No. 284

Chapter 6 Review/Test

• Chapter Review/Test – Vocabulary – Page No. 285
• Chapter Review/Test – Page No. 286
• Chapter Review/Test – Page No. 287
• Chapter Review/Test – Page No. 288

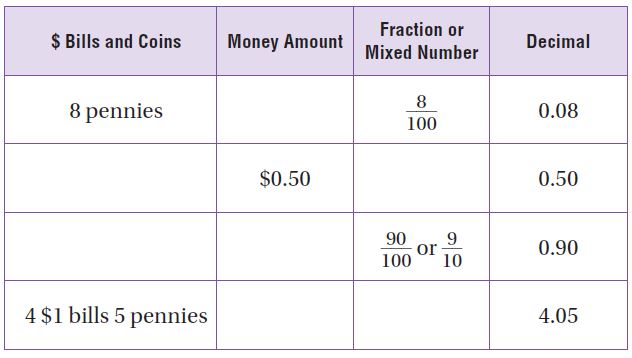
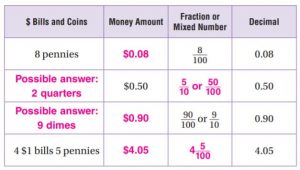
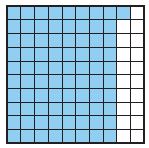
Share and Show – Page No. 244

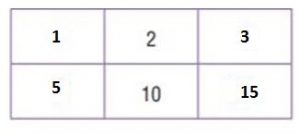
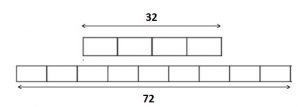
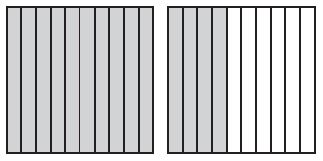
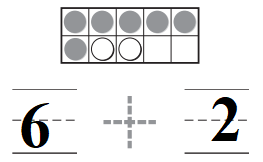
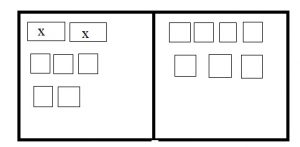
Use fraction strips to find the sum. Write your answer in simplest form.

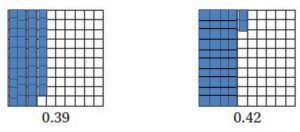
Question 1.

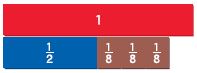
\(\frac{1}{2}+\frac{3}{8}=\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{8}\)
Explanation:
Step 1:
Place three \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{8}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{3}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{4}{4}\) = \(\frac{4}{8}\)
\(\frac{3}{8}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)

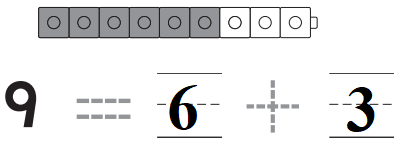
Question 2.

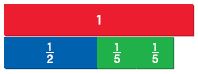
\(\frac{1}{2}+\frac{2}{5}=\)
\(\frac{□}{□}\)

Answer: \(\frac{9}{10}\)
Explanation:
Step 1:
Place two \(\frac{1}{5}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the two \(\frac{1}{5}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{2}{5}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{5}{5}\) = \(\frac{5}{10}\)
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{2}{2}\) = \(\frac{4}{10}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{5}{10}\) + \(\frac{4}{10}\) = \(\frac{9}{10}\)
Thus, \(\frac{1}{2}\) + \(\frac{2}{5}\) = \(\frac{9}{10}\)

Page No. 245

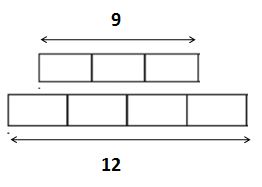
Use fraction strips to find the sum. Write your answer in simplest form.

Question 3.

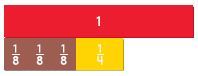
\(\frac{3}{8}+\frac{1}{4}=\)
\(\frac{□}{□}\)

Answer: \(\frac{5}{8}\)
Explanation:
Step 1:
Place three \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the three \(\frac{1}{8}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{4}\) and \(\frac{3}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{4}\) × \(\frac{2}{2}\) = \(\frac{2}{8}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{5}{8}\)

Question 4.

\(\frac{3}{4}+\frac{1}{3}=\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{12}\)
Explanation:
Step 1:
Place three \(\frac{3}{4}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{3}\) fraction strip beside the three \(\frac{1}{4}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{3}\) and \(\frac{3}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{3}\) × \(\frac{4}{4}\) = \(\frac{4}{12}\)
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{4}{12}\) + \(\frac{9}{12}\) = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\)

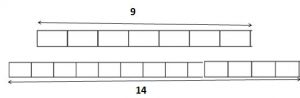
Use fraction strips to find the sum. Write your answer in simplest form.

Question 5.
\(\frac{2}{5}+\frac{3}{10}=\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{10}\)
Explanation:
Step 1:
Place three \(\frac{1}{10}\) fractions strips under the 1 whole strip on your Mathboard. Then place a two \(\frac{2}{5}\) fraction strip beside the three \(\frac{1}{10}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{2}{5}\) and \(\frac{3}{10}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{2}{5}\) • \(\frac{2}{2}\) = \(\frac{4}{10}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{4}{10}\) + \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 6.
\(\frac{1}{4}+\frac{1}{12}=\)
\(\frac{□}{□}\)

Answer: \(\frac{4}{12}\)
Explanation:
Step 1:
Place \(\frac{1}{12}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the \(\frac{1}{12}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{12}\) and \(\frac{1}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{4}\) • \(\frac{3}{3}\) = \(\frac{3}{12}\)
\(\frac{1}{12}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{3}{12}\) + \(\frac{1}{12}\) = \(\frac{4}{12}\)

Question 7.
\(\frac{1}{2}+\frac{3}{10}=\)
\(\frac{□}{□}\)

Answer: \(\frac{8}{10}\)
Explanation:
Step 1:
Place three \(\frac{1}{10}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{10}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{3}{10}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{2}\) • \(\frac{5}{5}\) = \(\frac{5}{10}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{5}{10}\) + \(\frac{3}{10}\) = \(\frac{8}{10}\)

Question 8.
\(\frac{2}{3}+\frac{1}{6}=\)
\(\frac{□}{□}\)

Answer: \(\frac{5}{6}\)
Explanation:
Step 1:
Place two \(\frac{1}{3}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{6}\) fraction strip beside the two \(\frac{1}{3}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{6}\) and \(\frac{2}{3}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{2}{3}\) = \(\frac{2}{3}\) • \(\frac{2}{2}\) = \(\frac{4}{6}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\)

Question 9.
\(\frac{5}{8}+\frac{1}{4}=\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{8}\)
Explanation:
Step 1:
Place five \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the five \(\frac{1}{8}\) strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{4}\) and \(\frac{5}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{4}\) • \(\frac{2}{2}\) = \(\frac{2}{8}\)
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{2}{8}\) + \(\frac{5}{8}\) = \(\frac{7}{8}\)

Question 10.
\(\frac{1}{2}+\frac{1}{5}=\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{10}\)
Explanation:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{5}\) and \(\frac{1}{2}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{5}\) • \(\frac{2}{2}\) = \(\frac{2}{10}\)
\(\frac{1}{2}\) • \(\frac{5}{5}\) = \(\frac{5}{10}\)
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)

Question 11.
\(\frac{3}{4}+\frac{1}{6}=\)
\(\frac{□}{□}\)

Answer: \(\frac{11}{12}\)
Explanation:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{3}{4}\) and \(\frac{1}{6}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{3}{4}\) • \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{1}{6}\) • \(\frac{2}{2}\)  = \(\frac{2}{12}\)
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\)

Question 12.
\(\frac{1}{2}+\frac{2}{3}=\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{6}\)
Explanation:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{2}{3}\) and \(\frac{1}{2}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{2}{3}\) • \(\frac{2}{2}\) = \(\frac{4}{6}\)
\(\frac{1}{2}\) • \(\frac{3}{3}\) = \(\frac{3}{6}\)
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{4}{6}\) + \(\frac{3}{6}\) = \(\frac{7}{6}\)
\(\frac{7}{6}\) is greater than 1.
Convert the fraction into the mixed fraction
\(\frac{7}{6}\) = 1 \(\frac{1}{6}\)

Question 13.
\(\frac{7}{8}+\frac{1}{4}=\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{8}\)
Explanation:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{7}{8}\) and \(\frac{1}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{1}{4}\) • \(\frac{2}{2}\) = \(\frac{2}{8}\)
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
\(\frac{7}{8}\) + \(\frac{2}{8}\) = \(\frac{9}{8}\)
Convert \(\frac{9}{8}\) into the mixed fraction.
\(\frac{9}{8}\) = 1 \(\frac{1}{8}\)

Question 14.
Explain how using fraction strips with like denominators makes it possible to add fractions with unlike denominators.
Type below:
_________

Answer: The strips for both fractions need to be the same size. Finding like denominators is done by trying smaller strips so they can all be the same size.

Problem Solving – Page No. 246

Question 15.
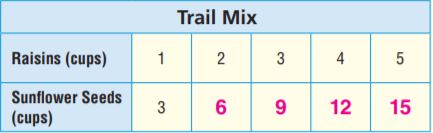
Maya makes trail mix by combining \(\frac{1}{3}\) cup of mixed nuts and \(\frac{1}{4}\) cup of dried fruit. What is the total amount of ingredients in her trail mix?
\(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)
Maya uses \(\frac{1}{12}\) cup of ingredients.
Write a new problem using different amounts for each ingredient. Each amount should be a fraction with a denominator of 2, 3, or 4. Then use fraction strips to solve your problem.
Pose a problem                          Solve your problem. Draw a picture of the
fraction strips you use to solve the problem.
Explain why you chose the amounts you did for your problem.
Type below:
_________

Answer:
\(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)
Maya uses \(\frac{1}{12}\) cup of ingredients.
Maya makes trail mix by combining \(\frac{1}{2}\) cup of mixed nuts and \(\frac{1}{3}\) cup of dried fruit and \(\frac{1}{4}\) cup of chocolate morsels. What is the total amount of ingredients in her trail mix?
\(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) = x
2 • \(\frac{1}{2}\) +  2 • \(\frac{1}{3}\) +  2 • \(\frac{1}{4}\) =  2 • x
1 + \(\frac{2}{3}\) + \(\frac{1}{2}\) = 2x
Now multiply with 3 on both sides
3 • 1 + 3 • \(\frac{2}{3}\) + 3 • \(\frac{1}{2}\) = 3 • 2x
3 + 2 + \(\frac{3}{2}\) = 6x
6 + 4 + 1 = 12 x
11 = 12x
x = \(\frac{11}{12}\)
\(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) = \(\frac{11}{12}\)

Share and Show – Page No. 248

Use fraction strips to find the difference. Write your answer in simplest form.

Question 1.

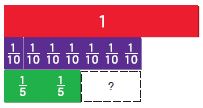
\(\frac{7}{10}-\frac{2}{5}=\)
\(\frac{□}{□}\)

Answer:
\(\frac{7}{10}\) – \(\frac{2}{5}\)
\(\frac{7}{10}\) – \(\frac{2}{5}\) • \(\frac{2}{2}\)
\(\frac{7}{10}\) – \(\frac{4}{10}\) = \(\frac{3}{10}\)

Question 2.

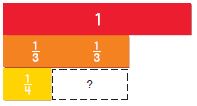
\(\frac{2}{3}-\frac{1}{4}=\)
\(\frac{□}{□}\)

Answer:
\(\frac{2}{3}\) – \(\frac{1}{4}\)
Now we have to make the fractions like denominators
\(\frac{2}{3}\) • \(\frac{4}{4}\) – \(\frac{1}{4}\) • \(\frac{3}{3}\)
\(\frac{8}{12}\) – \(\frac{3}{12}\) = \(\frac{5}{12}\)

Page No. 249

Use fraction strips to find the difference. Write your answer in simplest form.

Question 3.

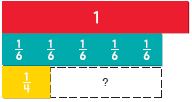
\(\frac{5}{6}-\frac{1}{4}=\)
\(\frac{□}{□}\)

Answer:
Step 1:
Find fraction strips, all with the same denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\)
Step 2:
Find another set of fraction strips, all with the same the denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\)
Step 3:
Find other fraction strips, all with the same denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\)
\(\frac{5}{6}\) • \(\frac{4}{4}\) – \(\frac{1}{4}\) • \(\frac{6}{6}\)
\(\frac{20}{24}\) – \(\frac{6}{24}\) = \(\frac{14}{24}\) = \(\frac{7}{12}\)
Thus, \(\frac{5}{6}-\frac{1}{4}\) = \(\frac{7}{12}\)

Question 4.

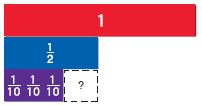
\(\frac{1}{2}-\frac{3}{10}=\)
\(\frac{□}{□}\)

Answer:
\(\frac{1}{2}-\frac{3}{10}\)
\(\frac{1}{2}\) • \(\frac{5}{5}\) – \(\frac{3}{10}\)
\(\frac{5}{10}\) – \(\frac{3}{10}\) = \(\frac{2}{10}\)

Question 5.

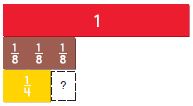
\(\frac{3}{8}-\frac{1}{4}=\)
\(\frac{□}{□}\)

Answer:
\(\frac{3}{8}-\frac{1}{4}\)
\(\frac{3}{8}\) – \(\frac{1}{4}\) • \(\frac{2}{2}\)
= \(\frac{3}{8}\) – \(\frac{2}{8}\) = \(\frac{1}{8}\)

Question 6.

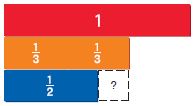
\(\frac{2}{3}-\frac{1}{2}=\)
\(\frac{□}{□}\)

Answer:
\(\frac{2}{3}-\frac{1}{2}\)
\(\frac{2}{3}\) • \(\frac{2}{2}\) – \(\frac{1}{2}\) • \(\frac{3}{3}\)
\(\frac{4}{6}-\frac{3}{6}\) = \(\frac{1}{6}\)

Use fraction strips to find the difference. Write your answer in simplest form.

Question 7.
\(\frac{3}{5}-\frac{3}{10}=\) \(\frac{□}{□}\)

Answer:
\(\frac{3}{5}-\frac{3}{10}\)
\(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{3}{10}\)
= \(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\)

Question 8.
\(\frac{5}{12}-\frac{1}{3}=\) \(\frac{□}{□}\)

Answer:
\(\frac{5}{12}-\frac{1}{3}\)
Make the denominators equal and then subtract the subtract the fraction with lide denominators.
\(\frac{5}{12}\) – \(\frac{1}{3}\) • \(\frac{4}{4}\)
\(\frac{5}{12}\) – \(\frac{4}{12}\) = \(\frac{1}{12}\)

Question 9.
\(\frac{1}{2}-\frac{1}{10}=\) \(\frac{□}{□}\)

Answer:
\(\frac{1}{2}-\frac{1}{10}\)
Make the denominators equal and then subtract the subtract the fraction with lide denominators.
\(\frac{1}{2}\) • \(\frac{5}{5}\) – \(\frac{1}{10}\)
\(\frac{5}{10}\) – \(\frac{1}{10}\) = \(\frac{4}{10}\)

Question 10.
\(\frac{3}{5}-\frac{1}{2}=\) \(\frac{□}{□}\)

Answer:
\(\frac{3}{5}-\frac{1}{2}\)
Make the denominators equal and then subtract the subtract the fraction with lide denominators.
\(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{1}{2}\) • \(\frac{5}{5}\)
\(\frac{6}{10}-\frac{5}{10}\) = \(\frac{1}{10}\)

Question 11.
\(\frac{7}{8}-\frac{1}{4}=\) \(\frac{□}{□}\)

Answer:
\(\frac{7}{8}-\frac{1}{4}\)
Make the denominators equal and then subtract the subtract the fraction with lide denominators.
\(\frac{7}{8}\) – \(\frac{1}{4}\) • \(\frac{2}{2}\)
\(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\)

Question 12.
\(\frac{5}{6}-\frac{2}{3}=\) \(\frac{□}{□}\)

Answer:
\(\frac{5}{6}-\frac{2}{3}\)
Make the denominators equal and then subtract the subtract the fraction with lide denominators.
\(\frac{5}{6}\) – \(\frac{2}{3}\) • \(\frac{2}{2}\)
\(\frac{5}{6}\) – \(\frac{4}{6}\)
\(\frac{1}{6}\)

Question 13.
\(\frac{3}{4}-\frac{1}{3}=\) \(\frac{□}{□}\)

Answer:
\(\frac{3}{4}-\frac{1}{3}\)
\(\frac{3}{4}\) • \(\frac{3}{3}\) – \(\frac{1}{3}\) • \(\frac{4}{4}\)
\(\frac{9}{12}\) – \(\frac{4}{12}\) = \(\frac{5}{12}\)

Question 14.
\(\frac{5}{6}-\frac{1}{2}=\) \(\frac{□}{□}\)

Answer:
\(\frac{5}{6}-\frac{1}{2}\)
\(\frac{5}{6}\) – \(\frac{1}{2}\) • \(\frac{3}{3}\)
\(\frac{5}{6}\) – \(\frac{3}{6}\) = \(\frac{2}{6}\)
\(\frac{5}{6}-\frac{1}{2}=\) \(\frac{2}{6}\)

Question 15.
\(\frac{3}{4}-\frac{7}{12}=\) \(\frac{□}{□}\)

Answer:
\(\frac{3}{4}-\frac{7}{12}\)
\(\frac{3}{4}\) • \(\frac{3}{3}\) – \(\frac{7}{12}\)
\(\frac{9}{12}\) – \(\frac{7}{12}\) = \(\frac{2}{12}\)
\(\frac{3}{4}-\frac{7}{12}=\) \(\frac{2}{12}\)

Question 16.
Explain how your model for \(\frac{3}{5}-\frac{1}{2}\) is different from your model for \(\frac{3}{5}-\frac{3}{10}\).
Type below:
_________

Answer:
\(\frac{3}{5}-\frac{3}{10}\)
\(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{3}{10}\)
\(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\)

UNLOCK the Problem – Page No. 250

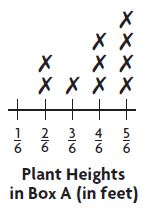
Question 17.
The picture at the right shows how much pizza was left over from lunch. Jason eats \(\frac{1}{4}\) of the whole pizza for dinner. Which subtraction sentence represents the amount of pizza that is remaining after dinner?

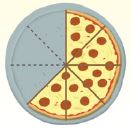
a. What problem are you being asked to solve?
Type below:
_________

Answer: I am asked to solve which subtraction sentence represents the amount of pizza that is remaining after dinner.

Question 17.
b. How will you use the diagram to solve the problem?
Type below:
_________

Answer: I will use number of slices left in the pizza to solve the problem.

Question 17.
c. Jason eats \(\frac{1}{4}\) of the whole pizza. How many slices does he eat?
______ slices

Answer: 2 slices

Explanation:
Given that, Jason eats \(\frac{1}{4}\) of the whole pizza.
The pizza is cut into 8 slices.
So, 8 × \(\frac{1}{4}\) = 2 slices.
Thus Jason ate 2 slices.

Question 17.
d. Redraw the diagram of the pizza. Shade the sections of pizza that are remaining after Jason eats his dinner.
Type below:
_________

Question 17.
e. Write a fraction to represent the amount of pizza that is remaining.
\(\frac{□}{□}\) of a pizza

Answer: \(\frac{3}{8}\) of a pizza

Explanation:
The fraction of pizzz Jason ate = \(\frac{1}{4}\)
Number of slices left = \(\frac{5}{8}\)
Now subtract \(\frac{5}{8}\) – \(\frac{1}{4}\)
= \(\frac{3}{8}\)
Thus the fraction to represent the amount of pizza that is remaining is \(\frac{3}{8}\)

Question 17.
f. Fill in the bubble for the correct answer choice above.
Options:
a. 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
b. \(\frac{5}{8}\) – \(\frac{1}{4}\) = \(\frac{3}{8}\)
c. \(\frac{3}{8}\) – \(\frac{1}{4}\) = \(\frac{2}{8}\)
d. 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)

Answer: B
The fraction of pizzz Jason ate = \(\frac{1}{4}\)
Number of slices left = \(\frac{5}{8}\)
Now subtract \(\frac{5}{8}\) – \(\frac{1}{4}\) = \(\frac{3}{8}\)
Thus the correct answer is option B.

Question 18.
The diagram shows what Tina had left from a yard of fabric. She now uses \(\frac{2}{3}\) yard of fabric for a project. How much of the original yard of fabric does Tina have left after the project?

Options:
a. \(\frac{2}{3}\) yard
b. \(\frac{1}{2}\) yard
c. \(\frac{1}{3}\) yard
d. \(\frac{1}{6}\) yard

Answer: \(\frac{1}{3}\) yard

Explanation:
The original yard of fabric is 6
Tina uses \(\frac{2}{3}\) yard of fabric for a project.
\(\frac{1}{1}\) – \(\frac{2}{3}\)
\(\frac{3}{3}\) – \(\frac{2}{3}\) = \(\frac{1}{3}\) yard

Share and Show – Page No. 253

Estimate the sum or difference.

Question 1.
\(\frac{5}{6}+\frac{3}{8}\)
a. Round \(\frac{5}{6}\) to its closest benchmark. ____
b. Round \(\frac{3}{8}\) to its closest benchmark. ____
c. Add to find the estimate. ____ + ____ = ____
_____ \(\frac{□}{□}\)

Answer:
a. Round \(\frac{5}{6}\) to its closest benchmark. \(\frac{6}{6}\) or 1.
b. Round \(\frac{3}{8}\) to its closest benchmark. \(\frac{4}{8}\) or \(\frac{1}{2}\)
c. Add to find the estimate. ____ + ____ = ____
1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)

Question 2.
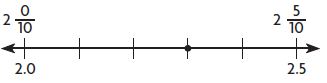
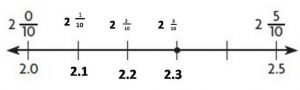
\(\frac{5}{9}-\frac{3}{8}\)
_____

Answer: 0

Explanation:
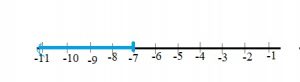
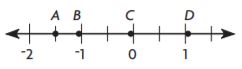
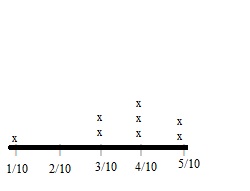
Step 1: Place a point at \(\frac{5}{9}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
The fraction rounded to \(\frac{5}{9}\) is \(\frac{1}{2}\)
Step 2: Place a point at \(\frac{3}{8}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
The fraction rounded to \(\frac{3}{8}\) is \(\frac{1}{2}\).
\(\frac{1}{2}\) – \(\frac{1}{2}\) = 0

Question 3.
\(\frac{6}{7}+2 \frac{4}{5}\)
_____

Answer: 4

Explanation:
Step 1: Place a point at \(\frac{6}{7}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{4}{5}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
1 + 3 = 4

Question 4.
\(\frac{5}{6}+\frac{2}{5}\)
_____ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{5}{6}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{2}{5}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)

Question 5.
\(3 \frac{9}{10}-1 \frac{2}{9}\)
_____

Answer: 3

Explanation:

Step 1: Place a point at \(\frac{9}{10}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{2}{9}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
3 × 1 – 1 × 0 = 3 – 0 = 3
\(3 \frac{9}{10}-1 \frac{2}{9}\) = 3

Question 6.
\(\frac{4}{6}+\frac{1}{9}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:

Step 1: Place a point at \(\frac{4}{6}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{1}{9}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
So, \(\frac{1}{2}\) + 0 = \(\frac{1}{2}\)
\(\frac{4}{6}+\frac{1}{9}\) = \(\frac{1}{2}\)

Question 7.
\(\frac{9}{10}-\frac{1}{9}\)
_____

Answer: 1

Explanation:
Step 1: Place a point at \(\frac{9}{10}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{1}{9}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
1 – 0 = 1
\(\frac{9}{10}-\frac{1}{9}\) = 1

On Your Own

Estimate the sum or difference.

Question 8.
\(\frac{5}{8}-\frac{1}{5}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{5}{8}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{1}{5}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 9.
\(\frac{1}{6}+\frac{3}{8}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{1}{6}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
Step 2: Place a point at \(\frac{3}{8}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 10.
\(\frac{6}{7}-\frac{1}{5}\)
_____

Answer: 1

Explanation:
Step 1: Place a point at \(\frac{6}{7}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{1}{5}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
1 – 0 = 1
\(\frac{6}{7}-\frac{1}{5}\) = 1

Question 11.
\(\frac{11}{12}+\frac{6}{10}\)
_____ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{11}{12}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1
Step 2: Place a point at \(\frac{6}{10}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1
1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)
\(\frac{11}{12}+\frac{6}{10}\) = 1 \(\frac{1}{2}\)

Question 12.
\(\frac{9}{10}-\frac{1}{2}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{9}{10}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{1}{2}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
\(\frac{9}{10}-\frac{1}{2}\) = \(\frac{1}{2}\)

Question 13.
\(\frac{3}{6}+\frac{4}{5}\)
_____ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{3}{6}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
Step 2: Place a point at \(\frac{4}{5}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1
\(\frac{1}{2}\) + 1 = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)
\(\frac{3}{6}+\frac{4}{5}\) = 1 \(\frac{1}{2}\)

Question 14.
\(\frac{5}{6}-\frac{3}{8}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{5}{6}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place a point at \(\frac{3}{8}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
\(\frac{5}{6}-\frac{3}{8}\) = \(\frac{1}{2}\)

Question 15.
\(\frac{1}{7}+\frac{8}{9}\)
_____

Answer: 1

Explanation:
Step 1: Place a point at \(\frac{1}{7}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
Step 2: Place a point at \(\frac{8}{9}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
0 + 1 = 1
\(\frac{1}{7}+\frac{8}{9}\) = 1

Question 16.
\(3 \frac{5}{12}-3 \frac{1}{10}\)
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Step 1: Place a point at \(\frac{5}{12}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
Step 2: Place a point at \(\frac{1}{10}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\)
\(\frac{1}{2}\) – 0 = \(\frac{1}{2}\)
\(3 \frac{5}{12}-3 \frac{1}{10}\) = \(\frac{1}{2}\)

Problem Solving – Page No. 254

Question 17.
Lisa and Valerie are picnicking in Trough Creek State Park in Pennsylvania. Lisa has brought a salad that she made with \(\frac{3}{4}\) cup of strawberries, \(\frac{7}{8}\) cup of peaches, and \(\frac{1}{6}\) cup of blueberries. About how many total cups of fruit are in the salad?
_____ cups

Answer: 2 cups

Explanation:
Lisa and Valerie are picnicking in Trough Creek State Park in Pennsylvania.
Lisa has brought a salad that she made with \(\frac{3}{4}\) cup of strawberries, \(\frac{7}{8}\) cup of peaches, and \(\frac{1}{6}\) cup of blueberries.
Step 1: Place \(\frac{3}{4}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 2: Place \(\frac{7}{8}\) on the number line.
The fraction is between \(\frac{1}{2}\) and 1.
Step 3: Place \(\frac{1}{6}\) on the number line.
The fraction is between 0 and \(\frac{1}{2}\).
1 + 1 + 0 = 2
Thus 2 cups of fruit are in the salad.

Question 18.
At Trace State Park in Mississippi, there is a 25-mile mountain bike trail. If Tommy rode \(\frac{1}{2}\) of the trail on Saturday and \(\frac{1}{5}\) of the trail on Sunday, about what fraction of the trail did he ride?
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
At Trace State Park in Mississippi, there is a 25-mile mountain bike trail.
If Tommy rode \(\frac{1}{2}\) of the trail on Saturday and \(\frac{1}{5}\) of the trail on Sunday
Step 1: Place \(\frac{1}{2}\) on the number line.
\(\frac{1}{2}\) lies between 0 and \(\frac{1}{2}\)
Step 2: Place \(\frac{1}{5}\) on the number line.
\(\frac{1}{5}\) 0 and \(\frac{1}{2}\)
The number closer to \(\frac{1}{5}\) is 0
\(\frac{1}{2}\) – 0 = \(\frac{1}{2}\)
The estimated fraction of the trail he ride is \(\frac{1}{2}\)

Question 19.
Explain how you know that \(\frac{5}{8}+\frac{6}{10}\) is greater than 1.
Type below:
__________

Answer:
Step 1: Place \(\frac{5}{8}\) on the number line.
\(\frac{5}{8}\) is closer to \(\frac{1}{2}\)
Step 2: Place \(\frac{6}{10}\) on the number line.
\(\frac{6}{10}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{6}{10}\) is closer to \(\frac{1}{2}\)
\(\frac{1}{2}\) + \(\frac{1}{2}\) = 1

Question 20.
Nick estimated that \(\frac{5}{8}+\frac{4}{7}\) is about 2.
Explain how you know his estimate is not reasonable.
Type below:
__________

Answer:
Step 1: Place \(\frac{5}{8}\) on the number line.
\(\frac{5}{8}\) is closer to \(\frac{1}{2}\)
Step 2: Place \(\frac{4}{7}\) on the number line.
\(\frac{4}{7}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
By this, we can say that Nick’s estimation was wrong.

Question 21.
Test Prep Jake added \(\frac{1}{8}\) cup of sunflower seeds and \(\frac{4}{5}\) cup of banana chips to his sundae. Which is the best estimate of the total amount of toppings Jake added to his sundae?
Options:
a. about \(\frac{1}{2}\) cup
b. about 1 cup
c. about 1 \(\frac{1}{2}\) cups
d. about 2 cups

Answer: about 1 cup

Explanation:
Given, Test Prep Jake added \(\frac{1}{8}\) cup of sunflower seeds and \(\frac{4}{5}\) cup of banana chips to his sundae
Step 1: Place \(\frac{1}{8}\) on the number line.
\(\frac{1}{8}\) lies between 0 and \(\frac{1}{2}\)
Step 2: Place \(\frac{4}{5}\) on the number line.
\(\frac{4}{5}\) lies between \(\frac{1}{2}\) and 1.
0 + 1 = 1
The best estimate of the total amount of toppings Jake added to his sundae is about 1 cup.

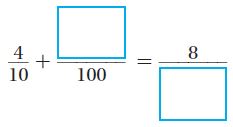
Share and Show – Page No. 256

Question 1.
Find a common denominator of \(\frac{1}{6}\) and \(\frac{1}{9}\) . Rewrite the pair of fractions using the common denominator.
• Multiply the denominators.
A common denominator of \(\frac{1}{6}\) and \(\frac{1}{9}\) is ____.
• Rewrite the pair of fractions using the common denominator.
Type below:
_________

Answer:
Common denominator is 18.
\(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\)
\(\frac{1}{9}\) × \(\frac{2}{2}\) = \(\frac{2}{18}\)
The pair of fractions using the common denominator is \(\frac{3}{18}\), \(\frac{2}{18}\)

Use a common denominator to write an equivalent fraction for each fraction.

Question 2.
\(\frac{1}{3}, \frac{1}{5}\)
common denominator: _________
Type below:
_________

Answer: 15

Explanation:
Multiply the denominators of the fraction.
\(\frac{1}{3}\) × \(\frac{1}{5}\) = \(\frac{1}{15}\)
Thus the common denominator is 15.

Question 3.
\(\frac{2}{3}, \frac{5}{9}\)
common denominator: _________
Type below:
_________

Answer: 27

Explanation:
Multiply the denominators
\(\frac{2}{3}\) × \(\frac{5}{9}\)
= 3 × 9 = 27
Thus the common denominator of \(\frac{2}{3}, \frac{5}{9}\) is 27.

Question 4.
\(\frac{2}{9}, \frac{1}{15}\)
common denominator: _________
Type below:
_________

Answer: 45

Explanation:
Multiply the denominators
\(\frac{2}{9}\) × \(\frac{1}{15}\)
The least common denominator of 15 and 9 is 45.
So, the common denominator of \(\frac{2}{9}, \frac{1}{15}\) is 45.

Page No. 257

Use the least common denominator to write an equivalent fraction for each fraction.

Question 5.
\(\frac{1}{4}, \frac{3}{8}\)
least common denominator: ______
Type below:
_________

Answer: 8

Explanation:

First multiply the denominators of the fractions \(\frac{1}{4}, \frac{3}{8}\)
4 × 8 = 32
The least common denominator is 8
The equivalent fractions with LCD
\(\frac{1}{4}\) = \(\frac{2}{8}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\)

Question 6.
\(\frac{11}{12}, \frac{5}{8}\)
least common denominator: ______
Type below:
_________

Answer: 24

Explanation:
First, multiply the denominators of the fractions.
12 × 8 = 96
The least common denominator of 12 and 8 is 24.
The equivalent fractions with LCD
\(\frac{11}{12}\) × \(\frac{2}{2}\)= \(\frac{22}{24}\)
\(\frac{5}{8}\) × \(\frac{3}{3}\) = \(\frac{15}{24}\)

Question 7.
\(\frac{4}{5}, \frac{1}{6}\)
least common denominator: ______
Type below:
_________

Answer: 30

Explanation:
First, multiply the denominators of the fractions.
5 × 6 = 30
The least common denominator (LCD) = 30
\(\frac{4}{5}\) × \(\frac{6}{6}\)= \(\frac{24}{30}\)
\(\frac{1}{6}\) × \(\frac{5}{5}\) = \(\frac{5}{30}\)

On Your Own

Use a common denominator to write an equivalent fraction for each fraction.

Question 8.
\(\frac{3}{5}, \frac{1}{4}\)
common denominator: ______
Type below:
_________

Answer: 20

Explanation:
Multiply the denominators of the fractions to find the common denominator.
5 × 4 = 20
So, the common denominator of \(\frac{3}{5}, \frac{1}{4}\) is 20.

Question 9.
\(\frac{5}{8}, \frac{1}{5}\)
common denominator: ______
Type below:
_________

Answer: 40

Explanation:
Multiply the denominators of the fractions to find the common denominator.
8 × 5 = 40
So, the common denominator of \(\frac{5}{8}, \frac{1}{5}\) is 40.

Question 10.
\(\frac{1}{12}, \frac{1}{2}\)
common denominator: ______
Type below:
_________

Answer: 24

Explanation:
Multiply the denominators of the fractions to find the common denominator.
12 × 2 = 24
The common denominator of \(\frac{1}{12}, \frac{1}{2}\) is 24.

Practice: Copy and Solve Use the least common denominator to write an equivalent fraction for each fraction.

Question 11.
\(\frac{1}{6}, \frac{4}{9}\)
Type below:
_________

Answer: \(\frac{3}{18}, \frac{8}{18}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 18
Now rewrite the fractions
\(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\)
\(\frac{4}{9}\) × \(\frac{2}{2}\) = \(\frac{8}{18}\)

Question 12.
\(\frac{7}{9}, \frac{8}{27}\)
Type below:
_________

Answer: \(\frac{21}{27}, \frac{8}{27}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 27
Now rewrite the fractions
\(\frac{7}{9}\) × \(\frac{3}{3}\) = \(\frac{21}{27}\)
\(\frac{8}{27}\) × \(\frac{1}{1}\) = \(\frac{8}{27}\)

Question 13.
\(\frac{7}{10}, \frac{3}{8}\)
Type below:
_________

Answer: \(\frac{28}{40}, \frac{15}{40}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 40
Now rewrite the fractions
\(\frac{7}{10}\) × \(\frac{4}{4}\) = \(\frac{28}{40}\)
\(\frac{3}{8}\) × \(\frac{5}{5}\) = \(\frac{15}{40}\)

Question 14.
\(\frac{1}{3}, \frac{5}{11}\)
Type below:
_________

Answer: \(\frac{11}{33}, \frac{15}{33}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 33
Now rewrite the fractions
\(\frac{1}{3}\) × \(\frac{11}{11}\) = \(\frac{11}{33}\)
\(\frac{5}{11}\) × \(\frac{3}{3}\) = \(\frac{15}{33}\)

Question 15.
\(\frac{5}{9}, \frac{4}{15}\)
Type below:
_________

Answer: \(\frac{25}{45}, \frac{12}{45}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator of \(\frac{5}{9}, \frac{4}{15}\)= 45
Now rewrite the input fractions
\(\frac{5}{9}\) × \(\frac{5}{5}\) = \(\frac{25}{45}\)
\(\frac{4}{15}\) × \(\frac{3}{3}\) = \(\frac{12}{45}\)

Question 16.
\(\frac{1}{6}, \frac{4}{21}\)
Type below:
_________

Answer: \(\frac{7}{42}, \frac{8}{42}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 42
Now rewrite the fractions
\(\frac{1}{6}\) × \(\frac{7}{7}\) = \(\frac{7}{42}\)
\(\frac{4}{21}\) × \(\frac{2}{2}\) = \(\frac{8}{42}\)

Question 17.
\(\frac{5}{14}, \frac{8}{42}\)
Type below:
_________

Answer: \(\frac{15}{42}, \frac{8}{42}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 42
Now rewrite the fractions
\(\frac{5}{14}\) × \(\frac{3}{3}\) = \(\frac{15}{42}\)
\(\frac{8}{42}\) × \(\frac{1}{1}\) = \(\frac{8}{42}\)

Question 18.
\(\frac{7}{12}, \frac{5}{18}\)
Type below:
_________

Answer: \(\frac{21}{36}, \frac{10}{36}\)

Explanation:
Multiply the denominators of the fractions.
The Least Common Denominator = 36
Now rewrite the fractions
\(\frac{7}{12}\) × \(\frac{3}{3}\) = \(\frac{21}{36}\)
\(\frac{5}{18}\) × \(\frac{2}{2}\) = \(\frac{10}{36}\)

Algebra Write the unknown number for each ■.

Question 19.
\(\frac{1}{5}, \frac{1}{8}\)
least common denominator: ■
■ = ______

Answer: 40

Explanation:
Multiply the denominators of the fractions.
5 × 8 = 40
Therefore, ■ = 40

Question 20.
\(\frac{2}{5}, \frac{1}{■}\)
least common denominator: 15
■ = ______

Answer: 3

Explanation:
Multiply the denominators of the fractions.
5 × ■ = 15
■ = 15/5 = 3
Thus ■ = 3

Question 21.
\(\frac{3}{■}, \frac{5}{6}\)
least common denominator: 42
■ = ______

Answer: 7

Explanation:
\(\frac{3}{■}, \frac{5}{6}\)
■ × 6 = 42
■ = 42/6
■ = 7

UNLOCK the Problem – Page No. 258

Question 22.
Katie made two pies for the bake sale. One was cut into three equal slices and the other into 5 equal slices. She will continue to cut the pies so each one has the same number of equal-sized slices. What is the least number of equal-sized slices each pie could have?
a. What information are you given?
Type below:
_________

Answer: I have the information about the two pies for the bake sale. One was cut into three equal slices and the other into 5 equal slices. She will continue to cut the pies so each one has the same number of equal-sized slices.

Question 22.
b. What problem are you being asked to solve?
Type below:
_________

Answer: I am asked to solve the least number of equal-sized slices each pie could have.

Question 22.
c. When Katie cuts the pies more, can she cut each pie the same number of times and have all the slices the same size? Explain.
Type below:
_________

Answer: Yes she can cut into more equal pieces. Katie can cut the pie into 6 equal pieces and 10 equal pieces. But the least number of equal-sized slices each pie could have is 3 and 5.

Question 22.
d. Use the diagram to show the steps you use to solve the problem.

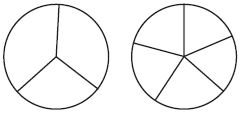
Type below:
_________

Answer:
There are 2 pies. One pie is cut into 3 equal pieces and the second pie is cut into 5 equal pieces.
So, there are 15 pieces of pies.

Question 22.
e. Complete the sentences.
The least common denominator of \(\frac{1}{3}\) and \(\frac{1}{5}\) is ____.
Katie can cut each piece of the first pie into ____ and each piece of the second pie into ____ .
That means that Katie can cut each pie into pieces that are ____ of the whole pie.
Type below:
_________

Answer:
The least common denominator of \(\frac{1}{3}\) and \(\frac{1}{5}\) is 15
5 × 3 = 15
Katie can cut each piece of the first pie into three and each piece of the second pie into five.
That means that Katie can cut each pie into pieces that are 15 of the whole pie.

Question 23.
A cookie recipe calls for \(\frac{1}{3}\) cup of brown sugar and \(\frac{1}{8}\) cup of walnuts. Find the least common denominator of the fractions used in the recipe.
____

Answer: 24

Explanation:

A cookie recipe calls for \(\frac{1}{3}\) cup of brown sugar and \(\frac{1}{8}\) cup of walnuts.
We can calculate the LCD by multiplying the denominators of the fraction.
3 × 8 = 24.

Question 24.
Test Prep Which fractions use the least common denominator and are equivalent to \(\frac{5}{8}\) and \(\frac{7}{10}\) ?
Options:
a. \(\frac{10}{40} \text { and } \frac{14}{40}\)
b. \(\frac{25}{40} \text { and } \frac{28}{40}\)
c. \(\frac{25}{80} \text { and } \frac{21}{80}\)
d. \(\frac{50}{80} \text { and } \frac{56}{80}\)

Answer: \(\frac{50}{80} \text { and } \frac{56}{80}\)

Explanation:
The least common denominator of \(\frac{5}{8}\) and \(\frac{7}{10}\) is 80.
\(\frac{5}{8}\) × \(\frac{10}{10}\) and \(\frac{7}{10}\) × \(\frac{8}{8}\)
= \(\frac{50}{80} \text { and } \frac{56}{80}\)
Thus the correct answer is option D.

Share and Show – Page No. 260

Find the sum or difference. Write your answer in simplest form.

Question 1.
\(\frac{5}{12}+\frac{1}{3}\)
\(\frac{□}{□}\)

Answer:
Find a common denominator by multiplying the denominators.
\(\frac{5}{12}+\frac{1}{3}\)
\(\frac{5}{12}\) + \(\frac{1}{3}\) × \(\frac{4}{4}\)
\(\frac{5}{12}\) + \(\frac{4}{12}\)
\(\frac{9}{12}\)

Question 2.
\(\frac{2}{5}+\frac{3}{7}\)
\(\frac{□}{□}\)

Answer:
Find a common denominator by multiplying the denominators.
Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form.
\(\frac{2}{5}+\frac{3}{7}\)
\(\frac{2}{5}\) × \(\frac{7}{7}\) + \(\frac{3}{7}\) × \(\frac{5}{5}\)
\(\frac{14}{35}+\frac{15}{35}\)
= \(\frac{29}{35}\)
\(\frac{2}{5}+\frac{3}{7}\) = \(\frac{29}{35}\)

Question 3.
\(\frac{1}{6}+\frac{3}{4}\)
\(\frac{□}{□}\)

Answer:
Find a common denominator by multiplying the denominators.
Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form.
\(\frac{1}{6}\) × \(\frac{2}{2}\) + \(\frac{3}{4}\) × \(\frac{3}{3}\)
\(\frac{2}{12}+\frac{9}{12}\) = \(\frac{11}{12}\)
So, \(\frac{1}{6}+\frac{3}{4}\) = \(\frac{11}{12}\)

Question 4.
\(\frac{3}{4}-\frac{1}{8}\)
\(\frac{□}{□}\)

Answer:
First, find a common denominator by multiplying the denominators.
Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form.
\(\frac{3}{4}-\frac{1}{8}\)
\(\frac{3}{4}\) × \(\frac{2}{2}\) – \(\frac{1}{8}\)
\(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\)
Thus \(\frac{3}{4}-\frac{1}{8}\) = \(\frac{5}{8}\)

Question 5.
\(\frac{1}{4}-\frac{1}{7}\)
\(\frac{□}{□}\)

Answer:
First, find a common denominator by multiplying the denominators.
Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form.
\(\frac{1}{4}-\frac{1}{7}\)
\(\frac{1}{4}\) × \(\frac{7}{7}\) – \(\frac{1}{7}\) × \(\frac{4}{4}\)
\(\frac{7}{28}\) – \(\frac{4}{28}\) = \(\frac{3}{28}\)
\(\frac{1}{4}-\frac{1}{7}\) = \(\frac{3}{28}\)

Question 6.
\(\frac{9}{10}-\frac{1}{4}\)
\(\frac{□}{□}\)

Answer:
First, find a common denominator by multiplying the denominators.
Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form.
\(\frac{9}{10}-\frac{1}{4}\)
\(\frac{9}{10}\) × \(\frac{4}{4}\) – \(\frac{1}{4}\) × \(\frac{10}{10}\)
\(\frac{36}{40}\) – \(\frac{10}{40}\) = \(\frac{26}{40}\)
\(\frac{9}{10}-\frac{1}{4}\) = \(\frac{26}{40}\)

On Your Own – Page No. 261

Find the sum or difference. Write your answer in simplest form.

Question 7.
\(\frac{3}{8}+\frac{1}{4}\)
\(\frac{□}{□}\)

Answer: \(\frac{5}{8}\)

Explanation:
\(\frac{3}{8}+\frac{1}{4}\) = \(\frac{3}{8}\) + \(\frac{1}{4}\)
LCD = 8
\(\frac{3}{8}\) + \(\frac{1}{4}\) × \(\frac{2}{2}\)
\(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\)
Thus \(\frac{3}{8}+\frac{1}{4}\) = \(\frac{5}{8}\)

Question 8.
\(\frac{7}{8}+\frac{1}{10}\)
\(\frac{□}{□}\)

Answer:
\(\frac{7}{8}+\frac{1}{10}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 40
\(\frac{7}{8}\) × \(\frac{5}{5}\) + \(\frac{1}{10}\) × \(\frac{4}{4}\)
\(\frac{35}{40}\) + \(\frac{4}{40}\) = \(\frac{39}{40}\)
\(\frac{7}{8}+\frac{1}{10}\) = \(\frac{39}{40}\)

Question 9.
\(\frac{2}{7}+\frac{3}{10}\)
\(\frac{□}{□}\)

Answer:
\(\frac{2}{7}+\frac{3}{10}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 70
\(\frac{2}{7}\) × \(\frac{10}{10}\) + \(\frac{3}{10}\) × \(\frac{7}{7}\)
\(\frac{20}{70}\) + \(\frac{21}{70}\) = \(\frac{41}{70}\)
\(\frac{2}{7}+\frac{3}{10}\) = \(\frac{41}{70}\)

Question 10.
\(\frac{5}{6}+\frac{1}{8}\)
\(\frac{□}{□}\)

Answer:
\(\frac{5}{6}+\frac{1}{8}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
\(\frac{5}{6}\) + \(\frac{1}{8}\)
LCD = 24
\(\frac{5}{6}\) × \(\frac{4}{4}\) + \(\frac{1}{8}\) × \(\frac{3}{3}\)
\(\frac{20}{24}\) + \(\frac{3}{24}\) = \(\frac{23}{24}\)
\(\frac{5}{6}+\frac{1}{8}\) = \(\frac{23}{24}\)

Question 11.
\(\frac{5}{12}+\frac{5}{18}\)
\(\frac{□}{□}\)

Answer:
\(\frac{5}{12}+\frac{5}{18}\) = \(\frac{5}{12}\) + \(\frac{5}{18}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 36
\(\frac{5}{12}\) × \(\frac{3}{3}\) + \(\frac{5}{18}\) × \(\frac{2}{2}\)
\(\frac{15}{36}\) + \(\frac{10}{36}\) = \(\frac{25}{36}\)
\(\frac{5}{12}+\frac{5}{18}\) = \(\frac{25}{36}\)

Question 12.
\(\frac{7}{16}+\frac{1}{4}\)
\(\frac{□}{□}\)

Answer:
\(\frac{7}{16}+\frac{1}{4}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 16
\(\frac{7}{16}\) + \(\frac{1}{4}\) = \(\frac{7}{16}\) + \(\frac{1}{4}\) × \(\frac{4}{4}\)
\(\frac{7}{16}\) + \(\frac{4}{16}\) = \(\frac{11}{16}\)

Question 13.
\(\frac{5}{6}+\frac{3}{8}\)
\(\frac{□}{□}\)

Answer:
\(\frac{5}{6}+\frac{3}{8}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
\(\frac{5}{6}\) + \(\frac{3}{8}\)
LCD = 24
\(\frac{5}{6}\) × \(\frac{4}{4}\) + \(\frac{3}{8}\) × \(\frac{3}{3}\)
= \(\frac{20}{24}\) + \(\frac{9}{24}\) = \(\frac{29}{24}\)
\(\frac{5}{6}+\frac{3}{8}\) = \(\frac{29}{24}\)

Question 14.
\(\frac{3}{4}+\frac{1}{2}\)
\(\frac{□}{□}\)

Answer:
\(\frac{3}{4}+\frac{1}{2}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
\(\frac{3}{4}\) + \(\frac{1}{2}\)
LCD = 4
\(\frac{3}{4}\) + \(\frac{1}{2}\) × \(\frac{2}{2}\)
= \(\frac{3}{4}\) + \(\frac{2}{4}\) = \(\frac{5}{4}\)
The miced fractiion of \(\frac{5}{4}\) is 1 \(\frac{1}{4}\)

Question 15.
\(\frac{5}{12}+\frac{1}{4}\)
\(\frac{□}{□}\)

Answer:
\(\frac{5}{12}+\frac{1}{4}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
\(\frac{5}{12}\) + \(\frac{1}{4}\)
LCD = 12
\(\frac{5}{12}\) + \(\frac{1}{4}\) × \(\frac{3}{3}\)
\(\frac{5}{12}\) + \(\frac{3}{12}\) = \(\frac{8}{12}\) = \(\frac{2}{3}\)

Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.

Question 16.
\(\frac{1}{3}+\frac{4}{18}\)
\(\frac{□}{□}\)

Answer:
\(\frac{1}{3}+\frac{4}{18}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 18
\(\frac{1}{3}\) + \(\frac{4}{18}\)
\(\frac{1}{3}\) × \(\frac{6}{6}\) + \(\frac{4}{18}\)
\(\frac{6}{18}\) + \(\frac{4}{18}\) = \(\frac{10}{18}\) = \(\frac{5}{9}\)
\(\frac{1}{3}+\frac{4}{18}\) = \(\frac{5}{9}\)

Question 17.
\(\frac{3}{5}+\frac{1}{3}\)
\(\frac{□}{□}\)

Answer:
\(\frac{3}{5}+\frac{1}{3}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 15
\(\frac{3}{5}\) + \(\frac{1}{3}\)
\(\frac{3}{5}\) × \(\frac{3}{3}\) + \(\frac{1}{3}\) × \(\frac{5}{5}\)
\(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\)
\(\frac{3}{5}+\frac{1}{3}\) = \(\frac{14}{15}\)

Question 18.
\(\frac{3}{10}+\frac{1}{6}\)
\(\frac{□}{□}\)

Answer:
\(\frac{3}{10}+\frac{1}{6}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 30
\(\frac{3}{10}\) + \(\frac{1}{6}\)
\(\frac{3}{10}\) × \(\frac{3}{3}\) + \(\frac{1}{6}\) × \(\frac{5}{5}\)
\(\frac{9}{30}\) + \(\frac{5}{30}\) = \(\frac{14}{30}\)
\(\frac{3}{10}+\frac{1}{6}\) = \(\frac{14}{30}\)

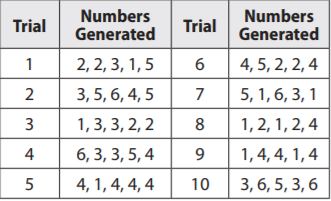
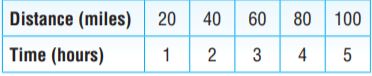
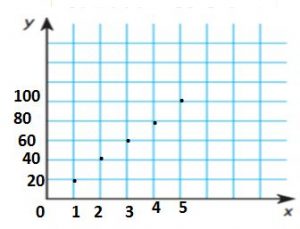
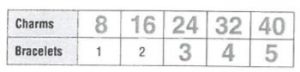
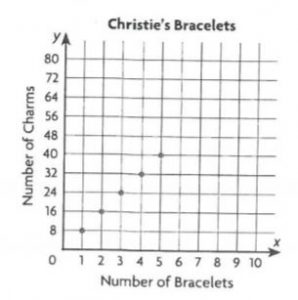
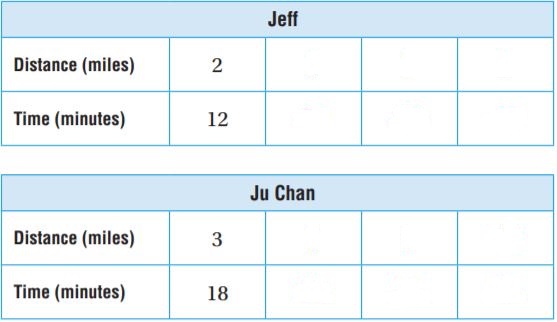
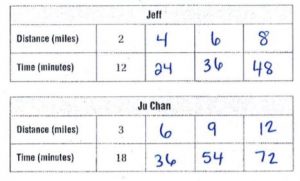
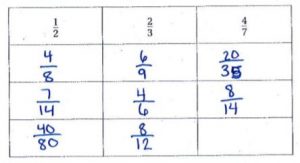
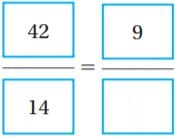
Question 19.
\(\frac{1}{2}+\frac{4}{9}\)
\(\frac{□}{□}\)

Answer:
\(\frac{1}{2}+\frac{4}{9}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 18
\(\frac{1}{2}\) + \(\frac{4}{9}\)
\(\frac{1}{2}\) × \(\frac{9}{9}\) + \(\frac{4}{9}\) × \(\frac{2}{2}\)
= \(\frac{9}{18}\) + \(\frac{8}{18}\) = \(\frac{17}{18}\)
\(\frac{1}{2}+\frac{4}{9}\) = \(\frac{17}{18}\)

Question 20.
\(\frac{1}{2}-\frac{3}{8}\)
\(\frac{□}{□}\)

Answer:
\(\frac{1}{2}-\frac{3}{8}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 8
\(\frac{1}{2}\) – \(\frac{3}{8}\)
\(\frac{1}{2}\) × \(\frac{4}{4}\) – \(\frac{3}{8}\)
\(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)
\(\frac{1}{2}-\frac{3}{8}\) = \(\frac{1}{8}\)

Question 21.
\(\frac{5}{7}-\frac{2}{3}\)
\(\frac{□}{□}\)

Answer:
\(\frac{5}{7}-\frac{2}{3}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 21
\(\frac{5}{7}\) – \(\frac{2}{3}\)
\(\frac{5}{7}\) × \(\frac{3}{3}\) – \(\frac{2}{3}\) × \(\frac{7}{7}\)
\(\frac{15}{21}\) – \(\frac{14}{21}\) = \(\frac{1}{21}\)
\(\frac{5}{7}-\frac{2}{3}\) = \(\frac{1}{21}\)

Question 22.
\(\frac{4}{9}-\frac{1}{6}\)
\(\frac{□}{□}\)

Answer:
\(\frac{4}{9}-\frac{1}{6}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 18
\(\frac{4}{9}\) – \(\frac{1}{6}\)
\(\frac{4}{9}\) × \(\frac{2}{2}\) – \(\frac{1}{6}\) × \(\frac{3}{3}\)
\(\frac{8}{18}\) – \(\frac{3}{18}\) = \(\frac{5}{18}\)
\(\frac{4}{9}-\frac{1}{6}\) = \(\frac{5}{18}\)

Question 23.
\(\frac{11}{12}-\frac{7}{15}\)
\(\frac{□}{□}\)

Answer:
\(\frac{11}{12}-\frac{7}{15}\)
First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD = 60
\(\frac{11}{12}\) – \(\frac{7}{15}\)
\(\frac{11}{12}\) × \(\frac{5}{5}\) – \(\frac{7}{15}\) × \(\frac{4}{4}\)
\(\frac{55}{60}\) – \(\frac{28}{60}\) = \(\frac{27}{60}\)
\(\frac{11}{12}-\frac{7}{15}\) = \(\frac{27}{60}\) = \(\frac{9}{20}\)

Algebra Find the unknown number.

Question 24.
\(\frac{9}{10}\) − ■ = \(\frac{1}{5}\)
■ = \(\frac{□}{□}\)

Answer:
\(\frac{9}{10}\) – \(\frac{1}{5}\) = ■
■ = \(\frac{9}{10}\) – \(\frac{1}{5}\)
■ = \(\frac{9}{10}\) – \(\frac{2}{10}\) = \(\frac{7}{10}\)
■ = \(\frac{7}{10}\)

Question 25.
\(\frac{5}{12}\) + ■ = \(\frac{1}{2}\)
■ = \(\frac{□}{□}\)

Answer:
\(\frac{5}{12}\) + ■ = \(\frac{1}{2}\)
\(\frac{5}{12}\) − \(\frac{1}{2}\) = – ■
– ■ = \(\frac{5}{12}\) − \(\frac{1}{2}\)
– ■ = \(\frac{5}{12}\) − \(\frac{1}{2}\) × \(\frac{6}{6}\)
– ■ = \(\frac{5}{12}\) − \(\frac{6}{12}\) = – \(\frac{1}{12}\)
■ = \(\frac{1}{12}\)

Problem Solving – Page No. 262

Use the picture for 26–27.

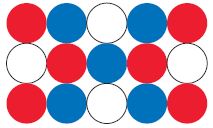
Question 26.
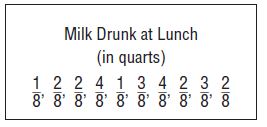
Sara is making a key chain using the bead design shown. What fraction of the beads in her design are either blue or red?
\(\frac{□}{□}\)

Answer: \(\frac{11}{15}\)

Explanation:
Total number of red beads = 6
Total number of blue beads = 5
Total number of beads = 6 + 5 = 11
The fraction of beads = \(\frac{11}{15}\)

Question 27.
In making the key chain, Sara uses the pattern of beads 3 times. After the key chain is complete, what fraction of the beads in the key chain are either white or blue?
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{4}{5}\)

Explanation:
In making the key chain, Sara uses the pattern of beads 3 times.
Given that Sara uses the pattern of beads 3 times.
Total number of blue beads = 5
5 × 3 = 15
Number of white beads = 4
4 × 3 = 12
15 + 12 = 27
Actual number of beads = 15
So, the fraction is \(\frac{27}{15}\) = \(\frac{9}{5}\)
The mixed fraction of \(\frac{9}{5}\) is 1 \(\frac{4}{5}\)

Question 28.
Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine left over. Explain how you know whether Jamie’s claim is reasonable.
Type below:
_________

Answer: Jamie’s claim is reasonable

Explanation:
Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine left over.
To know whether his estimation is reasonable or not we have to subtract the total spool of twine from used spool of twine.
\(\frac{4}{5}\) – \(\frac{1}{2}\)
LCD = 10
\(\frac{4}{5}\) × \(\frac{2}{2}\)  – \(\frac{1}{2}\) × \(\frac{5}{5}\)
\(\frac{8}{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\)
By this is can that Jamie’s claim is reasonable.

Question 29.
Test Prep Which equation represents the fraction of beads that are green or yellow?

Options:
a. \(\frac{1}{4}+\frac{1}{8}=\frac{3}{8}\)
b. [atex]\frac{1}{2}+\frac{1}{4}=\frac{3}{4}[/latex]
c. \(\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\)
d. \(\frac{3}{4}+\frac{2}{8}=1\)

Answer: [atex]\frac{1}{2}+\frac{1}{4}=\frac{3}{4}[/latex]

Explanation:
Number of green beads = 4 = [atex]\frac{1}{2}[/latex]
Number of blue beads = 3 = [atex]\frac{3}{4}[/latex]
Number of yellow beads = 1 [atex]\frac{1}{4}[/latex]
The fraction of beads that are green or yellow is [atex]\frac{1}{2}+\frac{1}{4}=\frac{3}{4}[/latex]
The correct answer is option B.

Mid-Chapter Checkpoint – Vocabulary – Page No. 263

Choose the best term from the box.

Question 1.
A ________ is a number that is a multiple of two or more numbers.
________

Answer: Common Multiple
A Common Multiple is a number that is a multiple of two or more numbers.

Question 2.
A ________ is a common multiple of two or more denominators.
________

Answer: Common denominator
A Common denominator is a common multiple of two or more denominators.

Concepts and Skills

Estimate the sum or difference.

Question 3.
\(\frac{8}{9}+\frac{4}{7}\)
about ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{2}\)

Place \(\frac{8}{9}\) on the number line.
\(\frac{8}{9}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{8}{9}\) is closer to 1.
Place \(\frac{4}{7}\) on the number line.
\(\frac{4}{7}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{4}{7}\) is closer to \(\frac{1}{2}\).
1 + \(\frac{1}{2}\) = 1 \(\frac{1}{2}\)

Question 4.
\(3 \frac{2}{5}-\frac{5}{8}\)
about ______

Answer: 3

Explanation:
Place \(\frac{2}{5}\) on the number line.
\(\frac{2}{5}\) lies between 0 and \(\frac{1}{2}\)
\(\frac{2}{5}\) is closer to \(\frac{1}{2}\)
Place \(\frac{5}{8}\) on the number line.
\(\frac{5}{8}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{5}{8}\) is closer to \(\frac{1}{2}\)
3 + \(\frac{1}{2}\) – \(\frac{1}{2}\) = 3
\(3 \frac{2}{5}-\frac{5}{8}\) = 3

Question 5.
\(1 \frac{5}{6}+2 \frac{2}{11}\)
about ______

Answer: 4

Explanation:
Place \(\frac{5}{6}\) on the number line.
\(\frac{5}{6}\) lies between \(\frac{1}{2}\) and 1.
\(\frac{5}{6}\) is closer to 1.
Place \(\frac{2}{11}\) on the number line.
\(\frac{2}{11}\) lies between \(\frac{1}{2}\) and 0.
\(\frac{2}{11}\) is closer to 0
1 + 1 + 2 + 0 = 4
\(1 \frac{5}{6}+2 \frac{2}{11}\) = 4

Use a common denominator to write an equivalent fraction for each fraction.

Question 6.
\(\frac{1}{6}, \frac{1}{9}\)
common denominator:
Type below:
__________

Answer: 54
Multiply the denominators
6 × 9 = 54
Thus the common denominator of \(\frac{1}{6}, \frac{1}{9}\) is 54

Question 7.
\(\frac{3}{8}, \frac{3}{10}\)
common denominator:
Type below:
__________

Answer: 80
Multiply the denominators
8 × 10 = 80
The common denominator of \(\frac{3}{8}, \frac{3}{10}\) is 80

Question 8.
\(\frac{1}{9}, \frac{5}{12}\)
common denominator:
Type below:
__________

Answer: 36
Multiply the denominators
9 × 12 = 108
The common denominator of \(\frac{1}{9}, \frac{5}{12}\) is 108

Use the least common denominator to write an equivalent fraction for each fraction.

Question 9.
\(\frac{2}{5}, \frac{1}{10}\)
least common denominator: ______
Explain:
__________

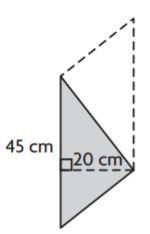
Answer: 10

Explanation:
Multiply the denominators
5 × 10 = 50
The least common denominators of \(\frac{2}{5}, \frac{1}{10}\) is 10.

Question 10.
\(\frac{5}{6}, \frac{3}{8}\)
least common denominator: ______
Explain:
__________

Answer: 24

Explanation:
Multiply the denominators
The least common denominator of 6 and 8 is 24
Thus the LCD of \(\frac{5}{6}, \frac{3}{8}\) is 24

Question 11.
\(\frac{1}{3}, \frac{2}{7}\)
least common denominator: ______
Explain:
__________

Answer: 21

Explanation:
Multiply the denominators
The least common denominator of 3 and 7 is 21.
Thus the LCD of \(\frac{1}{3}, \frac{2}{7}\) is 21.

Find the sum or difference. Write your answer in simplest form.

Question 12.
\(\frac{11}{18}-\frac{1}{6}\)
\(\frac{□}{□}\)

Answer: \(\frac{8}{18}\)

Explanation:
Make the fractions like denominators.
\(\frac{11}{18}\) – \(\frac{1}{6}\)
\(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\)
\(\frac{11}{18}\) – \(\frac{3}{18}\) = \(\frac{8}{18}\)

Question 13.
\(\frac{2}{7}+\frac{2}{5}\)
\(\frac{□}{□}\)

Answer: \(\frac{24}{35}\)

Explanation:
Make the fractions like denominators.
\(\frac{2}{7}\) × \(\frac{5}{5}\) = \(\frac{10}{35}\)
\(\frac{2}{5}\) × \(\frac{7}{7}\) = \(\frac{14}{35}\)
\(\frac{10}{35}\) + \(\frac{14}{35}\) = \(\frac{24}{35}\)
Thus \(\frac{2}{7}+\frac{2}{5}\) = \(\frac{24}{35}\)

Question 14.
\(\frac{3}{4}-\frac{3}{10}\)
\(\frac{□}{□}\)

Answer: \(\frac{18}{40}\)

Explanation:
Make the fractions like denominators.
\(\frac{3}{4}\) × \(\frac{10}{10}\) = \(\frac{30}{40}\)
\(\frac{3}{10}\) × \(\frac{4}{4}\) = \(\frac{12}{40}\)
\(\frac{30}{40}\) – \(\frac{12}{40}\) = \(\frac{18}{40}\)

Mid-Chapter Checkpoint – Page No. 264

Question 15.
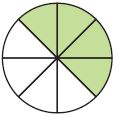
Mrs. Vargas bakes a pie for her book club meeting. The shaded part of the diagram below shows the amount of pie left after the meeting. That evening, Mr. Vargas eats \(\frac{1}{4}\) of the whole pie. What fraction represents the amount of pie remaining?

\(\frac{□}{□}\)

Answer: \(\frac{1}{4}\)

Explanation:
Mrs. Vargas bakes a pie for her book club meeting. The shaded part of the diagram below shows the amount of pie left after the meeting.
So, the fraction of the pie is \(\frac{1}{2}\)
That evening, Mr. Vargas eats \(\frac{1}{4}\) of the whole pie.
\(\frac{1}{2}\) – \(\frac{1}{4}\) = \(\frac{1}{4}\)
Thus the fraction represents the amount of pie remaining is \(\frac{1}{4}\)

Question 16.
Keisha makes a large sandwich for a family picnic. She takes \(\frac{1}{2}\) of the sandwich to the picnic. At the picnic, her family eats \(\frac{3}{8}\) of the whole sandwich. What fraction of the whole sandwich does Keisha bring back from the picnic?
\(\frac{□}{□}\)

Answer: \(\frac{1}{8}\)

Explanation:
Keisha makes a large sandwich for a family picnic. She takes \(\frac{1}{2}\) of the sandwich to the picnic.
At the picnic, her family eats \(\frac{3}{8}\) of the whole sandwich.
\(\frac{1}{2}\) – \(\frac{3}{8}\)
\(\frac{1}{2}\) × \(\frac{4}{4}\) – \(\frac{3}{8}\)
\(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)
Thus Keisha brought \(\frac{1}{8}\) of the sandwich from the picnic.

Question 17.
Mike is mixing paint for his walls. He mixes \(\frac{1}{6}\) gallon blue paint and \(\frac{5}{8}\) gallon green paint in a large container. What fraction represents the total amount of paint Mike mixes?
\(\frac{□}{□}\)

Answer: \(\frac{19}{24}\)

Explanation:
Mike is mixing paint for his walls. He mixes \(\frac{1}{6}\) gallon blue paint and \(\frac{5}{8}\) gallon green paint in a large container.
\(\frac{1}{6}\) + \(\frac{5}{8}\)
\(\frac{1}{6}\) × \(\frac{8}{8}\)  + \(\frac{5}{8}\) × \(\frac{6}{6}\)
\(\frac{8}{48}\)  + \(\frac{30}{48}\)
\(\frac{38}{48}\) = \(\frac{19}{24}\)
Therefore the total amount of paint Mike mixes is \(\frac{19}{24}\)

Share and Show – Page No. 266

Question 1.
Use a common denominator to write equivalent fractions with like denominators and then find the sum. Write your answer in simplest form.
7 \(\frac{2}{5}\) = ■
+ 4 \(\frac{3}{4}\) = + ■
—————————
■
_____ \(\frac{□}{□}\)

Answer: 12 \(\frac{3}{20}\)

Explanation:
First convert the mixed fraction to proper fraction.
7 \(\frac{2}{5}\) = \(\frac{37}{5}\)
4 \(\frac{3}{4}\) = \(\frac{19}{4}\)
\(\frac{37}{5}\) + \(\frac{19}{4}\)
= \(\frac{37}{5}\) × \(\frac{4}{4}\) = \(\frac{148}{20}\)
\(\frac{19}{4}\) × \(\frac{5}{5}\) = \(\frac{95}{20}\)
\(\frac{148}{20}\) + \(\frac{95}{20}\) = \(\frac{243}{20}\)
Now convert it into mixed fraction = 12 \(\frac{3}{20}\)

Find the sum. Write your answer in simplest form.

Question 2.
\(2 \frac{3}{4}+3 \frac{3}{10}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{1}{20}\)

Explanation:
First convert the mixed fraction to proper fraction.
\(2 \frac{3}{4}\) = \(\frac{11}{4}\)
3 \(\frac{3}{10}\) = \(\frac{33}{10}\)
Now make the common denominators of the above fractions.
\(\frac{11}{4}\) × \(\frac{10}{10}\) = \(\frac{110}{40}\)
\(\frac{33}{10}\) × \(\frac{4}{4}\) = \(\frac{132}{40}\) = \(\frac{121}{20}\)
Now convert the fraction into mixed fraction.
\(\frac{121}{20}\) = 6 \(\frac{1}{20}\)

Question 3.
\(5 \frac{3}{4}+1 \frac{1}{3}\)
_____ \(\frac{□}{□}\)

Answer: 7 \(\frac{1}{12}\)

Explanation:
First convert the mixed fraction to proper fraction.
5 \(\frac{3}{4}\) = \(\frac{23}{4}\)
1 \(\frac{1}{3}\) = \(\frac{4}{3}\)
\(\frac{23}{4}\) + \(\frac{4}{3}\)
\(\frac{23}{4}\) × \(\frac{3}{3}\) = \(\frac{69}{12}\)
\(\frac{4}{3}\) × \(\frac{4}{4}\) = \(\frac{16}{12}\)
\(\frac{69}{12}\) + \(\frac{16}{12}\) = \(\frac{85}{12}\)
The mixed fraction of \(\frac{85}{12}\) = 7 \(\frac{1}{12}\)

Question 4.
\(3 \frac{4}{5}+2 \frac{3}{10}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{1}{10}\)

Explanation:
First convert the mixed fraction to proper fraction.
3 \(\frac{4}{5}\) = \(\frac{19}{5}\)
2 \(\frac{3}{10}\) = \(\frac{23}{10}\)
\(\frac{19}{5}\) + \(\frac{23}{10}\)
Now make the common denominators of the above fractions.
\(\frac{19}{5}\) × \(\frac{2}{2}\) = \(\frac{38}{10}\)
\(\frac{38}{10}\) + \(\frac{23}{10}\) = \(\frac{61}{10}\)
The mixed fraction of \(\frac{61}{10}\) = 6 \(\frac{1}{10}\)

Page No. 267

Find the difference. Write your answer in simplest form.

Question 5.
\(9 \frac{5}{6}-2 \frac{1}{3}\)
_____ \(\frac{□}{□}\)

Answer: 7 \(\frac{1}{2}\)

Explanation:
\(9 \frac{5}{6}-2 \frac{1}{3}\) = \(\frac{59}{6}\) – \(\frac{14}{6}\)
= \(\frac{45}{6}\) = \(\frac{15}{2}\) = 7 \(\frac{1}{2}\)

Question 6.
\(10 \frac{5}{9}-9 \frac{1}{6}\)
_____ \(\frac{□}{□}\)

Answer: 1 \(\frac{7}{18}\)

Explanation:
\(10 \frac{5}{9}-9 \frac{1}{6}\) = \(\frac{95}{9}\) – \(\frac{55}{6}\)
= \(\frac{190}{18}\) – \(\frac{165}{18}\) = \(\frac{25}{18}\)
= 1 \(\frac{7}{18}\)
\(10 \frac{5}{9}-9 \frac{1}{6}\) = 1 \(\frac{7}{18}\)

Question 7.
\(7 \frac{2}{3}-3 \frac{1}{6}\)
_____ \(\frac{□}{□}\)

Answer: 4 \(\frac{1}{2}\)

Explanation:
\(7 \frac{2}{3}-3 \frac{1}{6}\)
\(\frac{23}{3}\) – \(\frac{19}{6}\) = \(\frac{46}{6}\) – \(\frac{19}{6}\)
= \(\frac{27}{6}\) = 4 \(\frac{1}{2}\)
\(7 \frac{2}{3}-3 \frac{1}{6}\) = 4 \(\frac{1}{2}\)

On Your Own

Find the sum or difference. Write your answer in simplest form.

Question 8.
\(1 \frac{3}{10}+2 \frac{2}{5}\)
_____ \(\frac{□}{□}\)

Answer: 3 \(\frac{7}{10}\)

Explanation:
\(1 \frac{3}{10}+2 \frac{2}{5}\)
\(\frac{13}{10}\) + \(\frac{12}{5}\) = \(\frac{13}{10}\) + \(\frac{24}{10}\)
= \(\frac{37}{10}\) = 3 \(\frac{7}{10}\)
Thus \(1 \frac{3}{10}+2 \frac{2}{5}\) = 3 \(\frac{7}{10}\)

Question 9.
\(3 \frac{4}{9}+3 \frac{1}{2}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{17}{18}\)

Explanation:
\(3 \frac{4}{9}+3 \frac{1}{2}\)
\(\frac{31}{9}\) + \(\frac{7}{2}\) = \(\frac{62}{18}\) + \(\frac{63}{18}\)
\(\frac{125}{18}\) = 6 \(\frac{17}{18}\)
\(3 \frac{4}{9}+3 \frac{1}{2}\) = 6 \(\frac{17}{18}\)

Question 10.
\(2 \frac{1}{2}+2 \frac{1}{3}\)
_____ \(\frac{□}{□}\)

Answer: 4 \(\frac{5}{6}\)

Explanation:
\(2 \frac{1}{2}+2 \frac{1}{3}\) = \(\frac{5}{2}\) + \(\frac{7}{3}\)
\(\frac{15}{6}\) + \(\frac{14}{6}\)= \(\frac{29}{6}\)
The mixed fraction of \(\frac{29}{6}\) is 4 \(\frac{5}{6}\)

Question 11.
\(5 \frac{1}{4}+9 \frac{1}{3}\)
_____ \(\frac{□}{□}\)

Answer: 14 \(\frac{7}{12}\)

Explanation:
\(5 \frac{1}{4}+9 \frac{1}{3}\) = \(\frac{21}{4}\) + \(\frac{28}{3}\)
\(\frac{63}{12}\) + \(\frac{112}{12}\) = \(\frac{175}{12}\)
The mixed fraction of \(\frac{175}{12}\) is 14 \(\frac{7}{12}\)

Question 12.
\(8 \frac{1}{6}+7 \frac{3}{8}\)
_____ \(\frac{□}{□}\)

Answer: 15 \(\frac{13}{24}\)

Explanation:
\(8 \frac{1}{6}+7 \frac{3}{8}\) = \(\frac{49}{6}\) + \(\frac{59}{8}\)
\(\frac{196}{24}\) + \(\frac{177}{24}\) = \(\frac{373}{24}\)
The mixed fraction of \(\frac{373}{24}\) is 15 \(\frac{13}{24}\)

Question 13.
\(14 \frac{7}{12}-5 \frac{1}{4}\)
_____ \(\frac{□}{□}\)

Answer: 9 \(\frac{1}{3}\)

Explanation:
\(14 \frac{7}{12}-5 \frac{1}{4}\) = \(\frac{175}{12}\) – \(\frac{21}{4}\)
\(\frac{175}{12}\) – \(\frac{63}{12}\) = \(\frac{112}{12}\)
The mixed fraction of \(\frac{112}{12}\) is 9 \(\frac{1}{3}\)

Question 14.
\(12 \frac{3}{4}-6 \frac{1}{6}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{7}{12}\)

Explanation:
\(12 \frac{3}{4}-6 \frac{1}{6}\) = \(\frac{51}{4}\) – \(\frac{37}{6}\)
\(\frac{153}{12}\) – \(\frac{74}{12}\) = \(\frac{79}{12}\)
The mixed fraction of \(\frac{79}{12}\) is 6 \(\frac{7}{12}\)

Question 15.
\(2 \frac{5}{8}-1 \frac{1}{4}\)
_____ \(\frac{□}{□}\)

Answer: 1 \(\frac{3}{8}\)

Explanation:
\(2 \frac{5}{8}-1 \frac{1}{4}\)
\(\frac{21}{8}\) – \(\frac{5}{4}\) = \(\frac{21}{8}\) – \(\frac{10}{8}\)
= \(\frac{11}{8}\)
The mixed fraction of \(\frac{11}{8}\) is 1 \(\frac{3}{8}\)

Question 16.
\(10 \frac{1}{2}-2 \frac{1}{5}\)
_____ \(\frac{□}{□}\)

Answer: 8 \(\frac{3}{10}\)

Explanation:
\(10 \frac{1}{2}-2 \frac{1}{5}\) = \(\frac{21}{2}\) – \(\frac{11}{5}\)
\(\frac{105}{10}\) – \(\frac{22}{10}\) = \(\frac{83}{10}\)
The mixed fraction of \(\frac{83}{10}\) is 8 \(\frac{3}{10}\)

Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.

Question 17.
\(1 \frac{5}{12}+4 \frac{1}{6}\)
_____ \(\frac{□}{□}\)

Answer: 5 \(\frac{7}{12}\)

Explanation:
\(1 \frac{5}{12}+4 \frac{1}{6}\) = \(\frac{17}{12}\) + \(\frac{25}{6}\)
\(\frac{17}{12}\) + \(\frac{50}{12}\) = \(\frac{67}{12}\)
The mixed fraction of \(\frac{67}{12}\) is 5 \(\frac{7}{12}\)

Question 18.
\(8 \frac{1}{2}+6 \frac{3}{5}\)
_____ \(\frac{□}{□}\)

Answer: 15 \(\frac{1}{10}\)

Explanation:
\(8 \frac{1}{2}+6 \frac{3}{5}\) = \(\frac{17}{2}\) + \(\frac{33}{5}\)
\(\frac{85}{10}\) + \(\frac{66}{10}\) = \(\frac{151}{10}\)
The mixed fraction of \(\frac{151}{10}\) is 15 \(\frac{1}{10}\)
\(8 \frac{1}{2}+6 \frac{3}{5}\) = 15 \(\frac{1}{10}\)

Question 19.
\(2 \frac{1}{6}+4 \frac{5}{9}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{13}{18}\)

Explanation:
\(2 \frac{1}{6}+4 \frac{5}{9}\) = \(\frac{13}{6}\) + \(\frac{41}{9}\)
\(\frac{39}{18}\) + \(\frac{82}{18}\) = \(\frac{121}{18}\)
The mixed fraction of \(\frac{121}{18}\) is 6 \(\frac{13}{18}\)
\(2 \frac{1}{6}+4 \frac{5}{9}\) = 6 \(\frac{13}{18}\)

Question 20.
\(20 \frac{5}{8}+\frac{5}{12}\)
_____ \(\frac{□}{□}\)

Answer: 21 \(\frac{1}{24}\)

Explanation:
\(20 \frac{5}{8}+\frac{5}{12}\) = \(\frac{165}{8}\) + \(\frac{5}{12}\)
\(\frac{495}{24}\) + \(\frac{10}{24}\) = \(\frac{505}{24}\)
The mixed fraction of \(\frac{505}{24}\) is 21 \(\frac{1}{24}\)
\(20 \frac{5}{8}+\frac{5}{12}\) = 21 \(\frac{1}{24}\)

Question 21.
\(3 \frac{2}{3}-1 \frac{1}{6}\)
_____ \(\frac{□}{□}\)

Answer: 2 \(\frac{1}{2}\)

Explanation:
\(3 \frac{2}{3}-1 \frac{1}{6}\) = \(\frac{11}{3}\) – \(\frac{7}{6}\)
\(\frac{22}{6}\) – \(\frac{7}{6}\) = \(\frac{15}{6}\) = \(\frac{5}{2}\)
The mixed fraction of \(\frac{5}{2}\) is 2 \(\frac{1}{2}\)
\(3 \frac{2}{3}-1 \frac{1}{6}\) = 2 \(\frac{1}{2}\)

Question 22.
\(5 \frac{6}{7}-1 \frac{2}{3}\)
_____ \(\frac{□}{□}\)

Answer: 4 \(\frac{4}{21}\)

Explanation:
\(5 \frac{6}{7}-1 \frac{2}{3}\) = \(\frac{41}{7}\) – \(\frac{5}{3}\)
\(\frac{123}{21}\) – \(\frac{35}{21}\) = \(\frac{88}{21}\)
The mixed fraction of \(\frac{88}{21}\) is 4 \(\frac{4}{21}\)

Question 23.
\(2 \frac{7}{8}-\frac{1}{2}\)
_____ \(\frac{□}{□}\)

Answer: 2 \(\frac{3}{8}\)

Explanation:
\(2 \frac{7}{8}-\frac{1}{2}\) = \(\frac{23}{8}\) – \(\frac{1}{2}\)
= \(\frac{23}{8}\) – \(\frac{4}{8}\) = \(\frac{19}{8}\)
The mixed fraction of \(\frac{19}{8}\) is 2 \(\frac{3}{8}\)
So, \(2 \frac{7}{8}-\frac{1}{2}\) = 2 \(\frac{3}{8}\)

Question 24.
\(4 \frac{7}{12}-1 \frac{2}{9}\)
_____ \(\frac{□}{□}\)

Answer: 3 \(\frac{13}{36}\)

Explanation:
\(4 \frac{7}{12}-1 \frac{2}{9}\) = \(\frac{55}{12}\) – \(\frac{11}{9}\)
\(\frac{165}{36}\) – \(\frac{44}{36}\) = \(\frac{121}{36}\)
The mixed fraction of \(\frac{121}{36}\) is 3 \(\frac{13}{36}\)

Problem Solving – Page No. 268

Use the table to solve 25–28.

Question 25.
Gavin is mixing a batch of Sunrise Orange paint for an art project. How much paint does Gavin mix?
_____ \(\frac{□}{□}\) ounces

Answer: 5 \(\frac{7}{8}\) ounces

Explanation:
Gavin is mixing a batch of Sunrise Orange paint for an art project.
2 \(\frac{5}{8}\) + 3 \(\frac{1}{4}\)
Solving the whole numbers
2 + 3 = 5
Add the fraction parts
\(\frac{5}{8}\) + \(\frac{1}{4}\)
LCD = 8
\(\frac{5}{8}\) + \(\frac{2}{8}\) = \(\frac{7}{8}\)
5 + \(\frac{7}{8}\) = 5 \(\frac{7}{8}\) ounces

Question 26.
Gavin plans to mix a batch of Tangerine paint. He expects to have a total of 5 \(\frac{3}{10}\) ounces of paint after he mixes the amounts of red and yellow. Explain how you can tell if Gavin’s expectation is reasonable.
Type below:
_________

Answer:
Gavin plans to mix a batch of Tangerine paint. He expects to have a total of 5 \(\frac{3}{10}\) ounces of paint after he mixes the amounts of red and yellow.
To mix a batch of Tangerine paint he need 3 \(\frac{9}{10}\) red and 2 \(\frac{3}{8}\) yellow paint.
Add the fractions
3 + \(\frac{9}{10}\) + 2 + \(\frac{3}{8}\)
Solving the whole numbers
3 + 2 = 5
\(\frac{9}{10}\) + \(\frac{3}{8}\)
LCD = 40
\(\frac{9}{10}\) + \(\frac{3}{8}\) = \(\frac{36}{40}\) + \(\frac{15}{40}\) = \(\frac{51}{40}\) = 1 \(\frac{11}{40}\)
5 + 1 \(\frac{11}{40}\) = 6 \(\frac{11}{40}\)

Question 27.
For a special project, Gavin mixes the amount of red from one shade of paint with the amount of yellow from a different shade. He mixes the batch so he will have the greatest possible amount of paint. What amounts of red and yellow from which shades are used in the mixture for the special project? Explain your answer.
Type below:
_________

Answer:
Gavin used red paint from mango and yellow paint from Sunrise Orange.
5 \(\frac{5}{6}\) + 3 \(\frac{1}{4}\)
Solving the whole numbers parts
5 + 3 = 8
Solving the fraction part
\(\frac{5}{6}\) + \(\frac{1}{4}\)
LCD = 12
\(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\)
\(\frac{13}{12}\) = 1 \(\frac{1}{12}\)

Question 28.
Gavin needs to make 2 batches of Mango paint. Explain how you could find the total amount of paint Gavin mixed.
Type below:
_________

Answer:
Gavin used Red paint and Yellow Paint to make Mango shade.
For one batch he need to add 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\)
Foe 2 batches
5 \(\frac{5}{6}\)+ 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\)
Solving the whole numbers
5 + 5 + 5 + 5 = 20
Solving the fractions part
\(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) = \(\frac{20}{6}\)
= \(\frac{10}{3}\)
Gavin mixed \(\frac{10}{3}\) of paint to make 2 batches of Mango Paint.

Question 29.
Test Prep Yolanda walked 3 \(\frac{6}{10}\) miles. Then she walked 4 \(\frac{1}{2}\) more miles. How many miles did Yolanda walk?
Options:
a. 7 \(\frac{1}{10}\) miles
b. 7 \(\frac{7}{10}\) miles
c. 8 \(\frac{1}{10}\) miles
d. 8 \(\frac{7}{10}\) miles

Answer: 8 \(\frac{1}{10}\) miles

Explanation:
Test Prep Yolanda walked 3 \(\frac{6}{10}\) miles.
Then she walked 4 \(\frac{1}{2}\) more miles.
3 \(\frac{6}{10}\) + 4 \(\frac{1}{2}\) = 3 + \(\frac{6}{10}\) + 4 + \(\frac{1}{2}\)
Add whole numbers
3 + 4 = 7
Add the fractions
\(\frac{6}{10}\) + \(\frac{1}{2}\)
LCD = 10
\(\frac{6}{10}\) + \(\frac{5}{10}\) = \(\frac{11}{10}\)
\(\frac{11}{10}\) = 8 \(\frac{1}{10}\) miles
Thus the correct answer is option C.

Share and Show – Page No. 270

Estimate. Then find the difference and write it in simplest form.

Question 1.
Estimate: ______
1 \(\frac{3}{4}-\frac{7}{8}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 1
Difference: \(\frac{7}{8}\)

Explanation:
Estimation: 1 + \(\frac{3}{4}\) – \(\frac{7}{8}\)
\(\frac{7}{8}\) is close to 1.
\(\frac{3}{4}\) is close to 1.
1 + 1 – 1 = 1
Difference: 1 \(\frac{3}{4}-\frac{7}{8}\)
1 + \(\frac{3}{4}\) – \(\frac{7}{8}\)
\(\frac{3}{4}\) – \(\frac{7}{8}\)
\(\frac{3}{4}\) × \(\frac{8}{8}\) – \(\frac{7}{8}\) × \(\frac{4}{4}\)
\(\frac{24}{32}\) – \(\frac{28}{32}\) = – \(\frac{1}{8}\)
1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 2.
Estimate: ______
\(12 \frac{1}{9}-7 \frac{1}{3}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 5
Difference: 4 \(\frac{7}{9}\)

Explanation:
Estimate: 12 + 0 – 7 – 0 = 5
Difference:
12 + \(\frac{1}{9}\) – 7 – \(\frac{1}{3}\)
12 – 7 = 5
\(\frac{1}{9}\) – \(\frac{1}{3}\) = \(\frac{1}{9}\) – \(\frac{3}{9}\) = – \(\frac{2}{9}\)
5 – \(\frac{2}{9}\) = 4 \(\frac{7}{9}\)

Page No. 271

Estimate. Then find the difference and write it in simplest form.

Question 3.
Estimate: ________
\(4 \frac{1}{2}-3 \frac{4}{5}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: \(\frac{1}{2}\)
Difference: \(\frac{7}{10}\)

Explanation:
\(4 \frac{1}{2}-3 \frac{4}{5}\)
4 – \(\frac{1}{2}\) – 3 – 1
= \(\frac{1}{2}\)
Difference:
\(4 \frac{1}{2}-3 \frac{4}{5}\)
4 \(\frac{1}{2}\) – 3 \(\frac{4}{5}\)
Solving the whole number parts
4 – 3 = 1
Solving the fraction parts
\(\frac{1}{2}\) – \(\frac{4}{5}\)
LCD = 10
\(\frac{5}{10}\) – \(\frac{8}{10}\) = – \(\frac{3}{10}\)
1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 4.
Estimate: ________
\(9 \frac{1}{6}-2 \frac{3}{4}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 6
Difference: 6 \(\frac{5}{12}\)

Explanation:
\(9 \frac{1}{6}-2 \frac{3}{4}\)
9 + 0 – 2 – 1 = 6
Difference:
\(9 \frac{1}{6}-2 \frac{3}{4}\)
9 + \(\frac{1}{6}\) – 2 – \(\frac{3}{4}\)
9 – 2 = 7
\(\frac{1}{6}\) – \(\frac{3}{4}\)
LCD = 12
\(\frac{2}{12}\) – \(\frac{9}{12}\) = – \(\frac{7}{12}\)
7 – \(\frac{7}{12}\) = 6 \(\frac{5}{12}\)
\(9 \frac{1}{6}-2 \frac{3}{4}\) = 6 \(\frac{5}{12}\)

On Your Own

Estimate. Then find the difference and write it in simplest form.

Question 5.
Estimate: ________
\(3 \frac{2}{3}-1 \frac{11}{12}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 2
Difference: 1 \(\frac{3}{4}\)

Explanation:
Estimate:
\(3 \frac{2}{3}-1 \frac{11}{12}\)
\(\frac{2}{3}\) is close to 1.
\(\frac{11}{12}\) is close to 1.
3 + 1 – 1 – 1 = 2
Difference:
\(3 \frac{2}{3}-1 \frac{11}{12}\)
3 + \(\frac{2}{3}\) – 1 – \(\frac{11}{12}\)
3 – 1 = 2
Solving the fractions part
\(\frac{2}{3}\) – \(\frac{11}{12}\)
LCD = 12
\(\frac{8}{12}\) – \(\frac{11}{12}\) = – \(\frac{3}{12}\) = – \(\frac{1}{4}\)
3 – \(\frac{1}{4}\) = 1 \(\frac{3}{4}\)
\(3 \frac{2}{3}-1 \frac{11}{12}\) = 1 \(\frac{3}{4}\)

Question 6.
Estimate: ________
\(4 \frac{1}{4}-2 \frac{1}{3}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 2
Difference: 1 \(\frac{11}{12}\)

Explanation:
\(4 \frac{1}{4}-2 \frac{1}{3}\)
\(\frac{1}{4}\) is close to 0.
\(\frac{1}{3}\) is close to 0.
4 – 2 = 2
Solving the fractions part
\(\frac{1}{4}\) – \(\frac{1}{3}\)
LCD = 12
\(\frac{1}{4}\) × \(\frac{3}{3}\) – \(\frac{1}{3}\) × \(\frac{4}{4}\)
\(\frac{3}{12}\) – \(\frac{4}{12}\) = – \(\frac{1}{12}\)
2 – \(\frac{1}{12}\) = 1 \(\frac{11}{12}\)

Question 7.
Estimate: ________
\(5 \frac{2}{5}-1 \frac{1}{2}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 4
Difference: 3 \(\frac{9}{10}\)

Explanation:
Estimate:
\(5 \frac{2}{5}-1 \frac{1}{2}\)
5 + \(\frac{1}{2}\) – 1 – \(\frac{1}{2}\)
5 – 1 = 4
Solving the fractions part
\(5 \frac{2}{5}-1 \frac{1}{2}\)
LCD = 10
\(\frac{4}{10}\) – \(\frac{5}{10}\) = – \(\frac{1}{10}\)
4 – \(\frac{1}{10}\) = 3 \(\frac{9}{10}\)

Question 8.
\(7 \frac{5}{9}-2 \frac{5}{6}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 4 \(\frac{1}{2}\)
Difference: 4 \(\frac{13}{18}\)

Explanation:
Estimate:
\(7 \frac{5}{9}-2 \frac{5}{6}\)
\(\frac{5}{9}\) is close to \(\frac{1}{2}\)
\(\frac{5}{6}\) is close to 1.
7 + \(\frac{1}{2}\) – 2 – 1
4 \(\frac{1}{2}\)
Difference:
\(7 \frac{5}{9}-2 \frac{5}{6}\)
7 + \(\frac{5}{9}\) – 2 – \(\frac{5}{6}\)
Solving the whole numbers
7 – 2 = 5
Solving the fraction part
\(\frac{5}{9}\) – \(\frac{5}{6}\)
LCD = 18
\(\frac{10}{18}\) – \(\frac{15}{18}\) = – \(\frac{5}{18}\)
5 – \(\frac{5}{18}\) = 4 \(\frac{13}{18}\)

Question 9.
Estimate: ________
\(7-5 \frac{2}{3}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 1
Difference: 1 \(\frac{1}{3}\)

Explanation:
Estimate:
\(7-5 \frac{2}{3}\)
7 – 5 – \(\frac{2}{3}\)
7 – 5 – 1 = 1
Difference:
\(7-5 \frac{2}{3}\)
7 – 5 = 2
2 – \(\frac{2}{3}\) = 1 \(\frac{1}{3}\)
Thus \(7-5 \frac{2}{3}\) = 1 \(\frac{1}{3}\)

Question 10.
Estimate: ________
\(2 \frac{1}{5}-1 \frac{9}{10}\)
Estimate: _____ \(\frac{□}{□}\)
Difference: _____ \(\frac{□}{□}\)

Answer:
Estimate: 0
Difference: \(\frac{3}{10}\)

Explanation:
Estimate:
\(2 \frac{1}{5}-1 \frac{9}{10}\)
2 + 0 – 1 – 1 = 0
Difference:
\(2 \frac{1}{5}-1 \frac{9}{10}\)
2 \(\frac{1}{5}\) – 1 \(\frac{9}{10}\)
2 + \(\frac{1}{5}\) – 1 – \(\frac{9}{10}\)
Solving the whole number parts
2 – 1 = 1
\(\frac{1}{5}\) – \(\frac{9}{10}\)
LCD = 10
\(\frac{2}{10}\) – \(\frac{9}{10}\) = – \(\frac{7}{10}\)
1 – \(\frac{7}{10}\) = \(\frac{3}{10}\)

Practice: Copy and Solve Find the difference and write it in simplest form.

Question 11.
\(11 \frac{1}{9}-3 \frac{2}{3}\)
_____ \(\frac{□}{□}\)

Answer: 7 \(\frac{4}{9}\)

Explanation:
Rewriting our equation with parts separated
11 + \(\frac{1}{9}\) – 3 – \(\frac{2}{3}\)
Solving the whole number parts
11 – 3 = 8
Solving the fraction parts
LCD = 9
\(\frac{1}{9}\) – \(\frac{2}{3}\)
\(\frac{1}{9}\) – \(\frac{6}{9}\) = – \(\frac{5}{9}\)
8 – \(\frac{5}{9}\) = 7 \(\frac{4}{9}\)

Question 12.
\(6-3 \frac{1}{2}\)
_____ \(\frac{□}{□}\)

Answer: 2 \(\frac{1}{2}\)

Explanation:
Rewriting our equation with parts separated
6 – 3 – \(\frac{1}{2}\)
3 – \(\frac{1}{2}\) = 2 \(\frac{1}{2}\)

Question 13.
\(4 \frac{3}{8}-3 \frac{1}{2}\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{8}\)

Explanation:
Rewriting our equation with parts separated
4 + \(\frac{3}{8}\) – 3 – \(\frac{1}{2}\)
Solving the whole number parts
4 – 3 = 1
Solving the fraction parts
\(\frac{3}{8}\) – \(\frac{1}{2}\) = \(\frac{3}{8}\) – \(\frac{4}{8}\)
= – \(\frac{1}{8}\)
1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 14.
\(9 \frac{1}{6}-3 \frac{5}{8}\)
_____ \(\frac{□}{□}\)

Answer: 5 \(\frac{13}{24}\)

Explanation:
Rewriting our equation with parts separated
9 + \(\frac{1}{6}\) – 3 – \(\frac{5}{8}\)
Solving the whole number parts
9 – 3 = 6
Solving the fraction parts
\(\frac{1}{6}\) – \(\frac{5}{8}\)
\(\frac{4}{24}\) – \(\frac{15}{24}\) = – \(\frac{11}{24}\)
6 – \(\frac{11}{24}\) = 5 \(\frac{13}{24}\)

Question 15.
\(1 \frac{1}{5}-\frac{1}{2}\)
\(\frac{□}{□}\)

Answer: \(\frac{7}{10}\)

Explanation:
Rewriting our equation with parts separated
1 + \(\frac{1}{5}\) – \(\frac{1}{2}\)
Solving the whole number parts
1 + 0 = 1
Solving the fraction parts
\(\frac{1}{5}\) – \(\frac{1}{2}\)
LCD = 10
\(\frac{2}{10}\) – \(\frac{5}{10}\) = – \(\frac{3}{10}\)
1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 16.
\(13 \frac{1}{6}-3 \frac{4}{5}\)
_____ \(\frac{□}{□}\)

Answer: 9 \(\frac{11}{30}\)

Explanation:
Rewriting our equation with parts separated
13 + \(\frac{1}{6}\) – 3 – \(\frac{4}{5}\)
Solving the whole number parts
13 – 3 = 10
Solving the fraction parts
\(\frac{1}{6}\) – \(\frac{4}{5}\)
LCD = 30
\(\frac{5}{30}\) – \(\frac{24}{30}\) = – \(\frac{19}{30}\)
10 – \(\frac{19}{30}\) = 9 \(\frac{11}{30}\)

Question 17.
\(12 \frac{2}{5}-5 \frac{3}{4}\)
_____ \(\frac{□}{□}\)

Answer: 6 \(\frac{13}{20}\)

Explanation:
Rewriting our equation with parts separated
12 + \(\frac{2}{5}\) – 5 – \(\frac{3}{4}\)
Solving the whole number parts
12 – 5 = 7
Solving the fraction parts
\(\frac{2}{5}\) – \(\frac{3}{4}\)
LCD = 20
\(\frac{8}{20}\) – \(\frac{15}{20}\) = – \(\frac{7}{20}\)
7 – \(\frac{7}{20}\) = 6 \(\frac{13}{20}\)

Question 18.
\(7 \frac{3}{8}-2 \frac{7}{9}\)
_____ \(\frac{□}{□}\)

Answer: 4 \(\frac{43}{72}\)

Explanation:
7 + \(\frac{3}{8}\) – 2 – \(\frac{7}{9}\)
7 – 2 = 5
\(\frac{3}{8}\) – \(\frac{7}{9}\) = \(\frac{27}{72}\) – \(\frac{56}{72}\)
– \(\frac{29}{72}\)
5 – \(\frac{29}{72}\) = 4 \(\frac{43}{72}\)

Page No. 272

Connect to Reading

Summarize
An amusement park in Sandusky, Ohio, offers 17 amazing roller coasters for visitors to ride. One of the roller coasters runs at 60 miles per hour and has 3,900 feet of twisting track. This coaster also has 3 trains with 8 rows per train. Riders stand in rows of 4, for a total of 32 riders per train.

The operators of the coaster recorded the number of riders on each train during a run. On the first train, the operators reported that 7 \(\frac{1}{4}\) rows were filled. On the second train, all 8 rows were filled, and on the third train, 5 \(\frac{1}{2}\) rows were filled. How many more rows were filled on the first train than on the third train?

When you summarize, you restate the most important information in a shortened form to more easily understand what you have read.
Summarize the information given.
______________________
Use the summary to solve.

Question 19.
Solve the problem above.
Type below:
_________

Answer:
On the first train, the operators reported that 7 \(\frac{1}{4}\) rows were filled.
On the third train, 5 \(\frac{1}{2}\) rows were filled.
7 \(\frac{1}{4}\) – 5 \(\frac{1}{2}\)
Solving the whole numbers
7 – 5 = 2
Solving the fractions
\(\frac{1}{4}\) – \(\frac{1}{2}\) = – \(\frac{1}{4}\)
2 – \(\frac{1}{4}\) = 1 \(\frac{3}{4}\)
1 \(\frac{3}{4}\) more rows were filled on the first train than on the third train.

Question 20.
How many rows were empty on the third train? How many additional riders would it take to fill the empty rows? Explain your answer.
Type below:
_________

Answer:
The coaster also has 3 trains with 8 rows per train.
The third train has 8 rows.
On the third train, 5 \(\frac{1}{2}\) rows were filled.
8 – 5 \(\frac{1}{2}\)
8 – 5 – \(\frac{1}{2}\) = 2 \(\frac{1}{2}\)
2 \(\frac{1}{2}\) rows are empty.
So, it takes 10 additional riders to fill the empty rows on the third train.

Share and Show – Page No. 275

Write a rule for the sequence.

Question 1.
\(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}, \cdots\)
Think: Is the sequence increasing or decreasing?
Rule: _________
Type below:
_________

Answer: The sequence is increasing order with difference \(\frac{1}{4}\)

Question 2.
\(\frac{1}{9}, \frac{1}{3}, \frac{5}{9}, \ldots\)
Type below:
_________

Answer: The sequence is increasing order with difference 2 in numerataor.

Write a rule for the sequence. Then, find the unknown term.

Question 3.
\(\frac{3}{10}, \frac{2}{5}\), \(\frac{□}{□}\) , \(\frac{3}{5}, \frac{7}{10}\)

Answer: The sequence is increasing order with difference \(\frac{1}{2}\)
LCD = 10
Add \(\frac{1}{2}\) to each term
Let the unknown fraction be x
\(\frac{3}{10}\), \(\frac{4}{10}\), x, \(\frac{6}{10}\), \(\frac{7}{10}\)
x = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 4.
\(10 \frac{2}{3}, 9 \frac{11}{18}, 8 \frac{5}{9}\), ______ \(\frac{□}{□}\) , \(6 \frac{4}{9}\)

Answer: 7 \(\frac{1}{2}\)

Explanation:
\(\frac{32}{3}\), \(\frac{173}{18}\), \(\frac{77}{9}\), x, \(\frac{58}{9}\)
LCD = 54
\(\frac{576}{54}\), \(\frac{519}{54}\), \(\frac{462}{54}\), x, \(\frac{348}{54}\)
According to the series x = \(\frac{405}{54}\) = \(\frac{15}{2}\)
The mixed fraction of \(\frac{15}{2}\) is 7 \(\frac{1}{2}\)

Question 5.
\(1 \frac{1}{6}\), ______ \(\frac{□}{□}\) , \(1, \frac{11}{12}, \frac{5}{6}\)

Answer: 1 \(\frac{1}{12}\)

Explanation:
\(1 \frac{1}{6}\), ______ \(\frac{□}{□}\) , \(1, \frac{11}{12}, \frac{5}{6}\)
The LCD of the above fractons is 12
Convert them into improper fractions
\(\frac{14}{12}\), x, \(\frac{12}{12}\), \(\frac{11}{12}\), \(\frac{10}{12}\)
According to the series x = \(\frac{13}{12}\)
The mixed fraction of \(\frac{13}{12}\) is 1 \(\frac{1}{12}\)

Question 6.
\(2 \frac{3}{4}, 4,5 \frac{1}{4}, 6 \frac{1}{2}\), ______ \(\frac{□}{□}\)

Answer: 7 \(\frac{3}{4}\)

Explanation:
\(2 \frac{3}{4}, 4,5 \frac{1}{4}, 6 \frac{1}{2}\), ______ \(\frac{□}{□}\)
Convert the mixed fractions into improper fractions
\(\frac{11}{4}\), \(\frac{4}{1}\), \(\frac{21}{4}\), \(\frac{13}{2}\), x
\(\frac{11}{4}\), \(\frac{16}{4}\), \(\frac{21}{4}\), \(\frac{26}{4}\), x
According to the series x = \(\frac{31}{4}\)
The mixed fraction of \(\frac{31}{4}\) is 7 \(\frac{3}{4}\)

On Your Own

Write a rule for the sequence. Then, find the unknown term.

Question 7.
\(\frac{1}{8}, \frac{1}{2}\), \(\frac{□}{□}\) , \(1 \frac{1}{4}, 1 \frac{5}{8}\)

Answer: \(\frac{7}{8}\)

Explanation:
\(\frac{1}{8}, \frac{1}{2}\), \(1 \frac{1}{4}, 1 \frac{5}{8}\), x
LCD = 8
\(\frac{1}{8}, \frac{4}{8}\), \(\frac{10}{8}, \frac{26}{8}\), x
\(\frac{1}{8}\), \(\frac{4}{8}\), x, \(\frac{10}{8}\), \(\frac{26}{8}\)
The difference between the series is 3 in numerator.
x = \(\frac{7}{8}\)

Question 8.
\(1 \frac{2}{3}, 1 \frac{3}{4}, 1 \frac{5}{6}, 1 \frac{11}{12}\), ______

Answer: 2

Explanation:
1 \(\frac{2}{3}\), 1 \(\frac{3}{4}\), 1 \(\frac{5}{6}\), 1 \(\frac{11}{12}\)
Convert the mixed fractions into improper fractions
\(\frac{5}{3}\), \(\frac{7}{4}\), \(\frac{11}{6}\), \(\frac{23}{12}\), x
The LCD is 12
\(\frac{20}{12}\), \(\frac{21}{12}\), \(\frac{22}{12}\), \(\frac{23}{12}\), x
x = \(\frac{24}{12}\) = 2

Question 9.
\(12 \frac{7}{8}, 10 \frac{3}{4}\), ______ \(\frac{□}{□}\) , \(6 \frac{1}{2}, 4 \frac{3}{8}\)

Answer: 8 \(\frac{5}{8}\)

Explanation:
\(12 \frac{7}{8}, 10 \frac{3}{4}\), x , \(6 \frac{1}{2}, 4 \frac{3}{8}\)
Convert the mixed fractions into improper fractions
\(\frac{103}{8}\), \(\frac{43}{4}\), x, \(\frac{13}{2}\), \(\frac{35}{8}\)
The LCD is 8
\(\frac{103}{8}\), \(\frac{86}{8}\), x, \(\frac{52}{8}\), \(\frac{35}{8}\)
x = \(\frac{69}{8}\)
The mixed fraction of \(\frac{69}{8}\) is 8 \(\frac{5}{8}\)

Question 10.
\(9 \frac{1}{3}\), ______ \(\frac{□}{□}\) , \(6 \frac{8}{9}, 5 \frac{2}{3}, 4 \frac{4}{9}\)

Answer: 8 \(\frac{1}{9}\)

Explanation:
\(9 \frac{1}{3}\), x , \(6 \frac{8}{9}, 5 \frac{2}{3}, 4 \frac{4}{9}\)
Convert the mixed fractions into improper fractions
\(\frac{28}{3}\), x, \(\frac{62}{9}\), \(\frac{17}{3}\), \(\frac{40}{9}\)
LCD = 9
\(\frac{84}{9}\), x, \(\frac{62}{9}\), \(\frac{51}{9}\), \(\frac{40}{9}\)
According to the series x =  \(\frac{73}{9}\) = 8 \(\frac{1}{9}\)

Write the first four terms of the sequence.

Question 11.
Rule: start at 5 \(\frac{3}{4}\), subtract \(\frac{5}{8}\)
First term: ______ \(\frac{□}{□}\)
Second term: ______ \(\frac{□}{□}\)
Third term: ______ \(\frac{□}{□}\)
Fourth term: ______ \(\frac{□}{□}\)

Answer:
Let the first term be 5 \(\frac{3}{4}\)
Second term = 5 \(\frac{3}{4}\) – \(\frac{5}{8}\) = \(\frac{41}{8}\) = 5 \(\frac{1}{8}\)
Third term = 5 \(\frac{1}{8}\) – \(\frac{5}{8}\) = \(\frac{36}{8}\) = 4 \(\frac{1}{2}\)
Fourth term = \(\frac{36}{8}\) – \(\frac{5}{8}\) = \(\frac{31}{8}\) = 3 \(\frac{7}{8}\)

Question 12.
Rule: start at \(\frac{3}{8}\), add \(\frac{3}{16}\)
Type below:
_________

Answer:
Let the first term be \(\frac{3}{8}\)
Second term = \(\frac{3}{8}\) + \(\frac{3}{16}\) = \(\frac{9}{16}\)
Third term = \(\frac{9}{16}\) + \(\frac{3}{16}\) = \(\frac{12}{16}\)
Fourth term = \(\frac{12}{16}\) + \(\frac{3}{16}\) = \(\frac{15}{16}\)

Question 13.
Rule: start at 2 \(\frac{1}{3}\), add 2 \(\frac{1}{4}\)
First term: ______ \(\frac{□}{□}\)
Second term: ______ \(\frac{□}{□}\)
Third term: ______ \(\frac{□}{□}\)
Fourth term: ______ \(\frac{□}{□}\)

Answer:
Let the first term be 2 \(\frac{1}{3}\)
Second term = 2 \(\frac{1}{3}\) + 2 \(\frac{1}{4}\) = \(\frac{7}{3}\) + \(\frac{9}{4}\)
= \(\frac{55}{12}\) = 4 \(\frac{7}{12}\)
Third term = 4 \(\frac{7}{12}\) + 2 \(\frac{1}{4}\) = 6 \(\frac{5}{6}\)
Fourth term = 6 \(\frac{5}{6}\) + 2 \(\frac{1}{4}\) = 9 \(\frac{1}{12}\)

Question 14.
Rule: start at \(\frac{8}{9}\), subtract \(\frac{1}{18}\)
Type below:
_________

Answer:
Let the first term be \(\frac{8}{9}\)
Second term = \(\frac{8}{9}\) – \(\frac{1}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)
Third term = \(\frac{15}{18}\) – \(\frac{1}{18}\) = \(\frac{14}{18}\) = \(\frac{7}{9}\)
Fourth term = \(\frac{14}{18}\) – \(\frac{1}{18}\) = \(\frac{13}{18}\)

Problem Solving – Page No. 276

Question 15.
When Bill bought a marigold plant, it was \(\frac{1}{4}\) inch tall. After the first week, it measured 1 \(\frac{1}{12}\) inches tall. After the second week, it was 1 \(\frac{11}{12}\) inches. After week 3, it was 2 \(\frac{3}{4}\) inches tall. Assuming the growth of the plant was constant, what was the height of the plant at the end of week 4?
______ \(\frac{□}{□}\) inches

Answer: 3 \(\frac{7}{12}\) inches

The sequence is the increasing where the first term is \(\frac{1}{4}\)
LCD = 12
First week is \(\frac{3}{12}\)
Second week = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\)
Third week = 1 \(\frac{11}{12}\) = \(\frac{23}{12}\)
Fourth week = \(\frac{33}{12}\) = 2 \(\frac{3}{4}\)
At the end of fourth week = \(\frac{43}{12}\) = 3 \(\frac{7}{12}\) inches
The height of the plant at the end of the week is 3 \(\frac{7}{12}\) inches.

Question 16.
What if Bill’s plant grew at the same rate but was 1 \(\frac{1}{2}\) inches when he bought it? How tall would the plant be after 3 weeks?
______ inches

Answer: 4 inches

Explanation:
The sequence is increasing.
First week 1 \(\frac{1}{2}\)
Let the first term is \(\frac{6}{12}\)
Second term is 1 \(\frac{16}{12}\)
Third term is 1 \(\frac{26}{12}\)
Fourth week is 1 \(\frac{36}{12}\)
1 \(\frac{36}{12}\) = 1 \(\frac{3}{1}\) = 1 + 3 = 4
After 4 weeks the plant grew 4 inches.

Question 17.
Vicki wanted to start jogging. The first time she ran, she ran \(\frac{3}{16}\) mile. The second time, she ran \(\frac{3}{8}\) mile, and the third time, she ran \(\frac{9}{16}\) mile. If she continued this pattern, when was the first time she ran more than 1 mile? Explain.
Type below:
_________

Answer: Sixth time

Explanation:
Vicki wanted to start jogging. The first time she ran, she ran \(\frac{3}{16}\) mile. The second time, she ran \(\frac{3}{8}\) mile, and the third time, she ran \(\frac{9}{16}\) mile.
The difference is \(\frac{3}{16}\)
First time = \(\frac{3}{16}\) mile
Second time = \(\frac{3}{16}\) + \(\frac{3}{16}\) = \(\frac{3}{8}\) mile
Third time = \(\frac{3}{8}\) + \(\frac{3}{16}\) = \(\frac{9}{16}\) mile
Fourth time = \(\frac{9}{16}\) + \(\frac{3}{16}\) = \(\frac{12}{16}\) mile
Fifth time = \(\frac{12}{16}\) + \(\frac{3}{16}\) = \(\frac{15}{16}\) mile
Sixth time = \(\frac{15}{16}\) + \(\frac{3}{16}\) = \(\frac{18}{16}\) mile
\(\frac{18}{16}\) = 1 \(\frac{2}{16}\) = 1 \(\frac{1}{8}\)

Question 18.
Mr. Conners drove 78 \(\frac{1}{3}\) miles on Monday, 77 \(\frac{1}{12}\) miles on Tuesday, and 75 \(\frac{5}{6}\) miles on Wednesday. If he continues this pattern on Thursday and Friday, how many miles will he drive on Friday?
______ \(\frac{□}{□}\) miles

Answer:
Given that,
Mr. Conners drove 78 \(\frac{1}{3}\) miles on Monday, 77 \(\frac{1}{12}\) miles on Tuesday, and 75 \(\frac{5}{6}\) miles on Wednesday.
The sequence is the decreasing where the first term is 78 \(\frac{4}{12}\)
78 \(\frac{4}{12}\) – 77 \(\frac{1}{12}\) = 1 \(\frac{3}{12}\)
The difference between the term is 1 \(\frac{3}{12}\)
On thursday, 75 \(\frac{5}{6}\) – 1 \(\frac{3}{12}\) = 74 \(\frac{7}{12}\)
On friday, 74 \(\frac{7}{12}\) – 1 \(\frac{3}{12}\) = 73 \(\frac{4}{12}\) = 73 \(\frac{1}{3}\)

Question 19.
Test Prep Zack watered his garden with 1 \(\frac{3}{8}\) gallons of water the first week he planted it. He watered it with 1 \(\frac{3}{4}\) gallons the second week, and 2 \(\frac{1}{8}\) gallons the third week. If he continued watering in this pattern, how much water did he use on the fifth week?
Options:
a. 2 \(\frac{1}{2}\) gallons
b. 2 \(\frac{7}{8}\) gallons
c. 3 \(\frac{1}{4}\) gallons
d. 6 \(\frac{7}{8}\) gallons

Answer: 2 \(\frac{7}{8}\) gallons

Explanation:
First term = 1 \(\frac{3}{8}\)
The difference is \(\frac{3}{4}\) – \(\frac{3}{8}\) = \(\frac{3}{8}\)
Second term is 1 \(\frac{3}{8}\) + \(\frac{3}{8}\) = 1 \(\frac{3}{4}\)
Third term = 1 \(\frac{3}{4}\) + \(\frac{3}{8}\) = 1 + 1 \(\frac{1}{8}\) = 2 \(\frac{1}{8}\)
Fourth term = 2 \(\frac{1}{8}\) + \(\frac{3}{8}\) = 2 \(\frac{1}{2}\)
Fifth term = 2 \(\frac{1}{2}\) + \(\frac{3}{8}\) = 2 \(\frac{7}{8}\) gallons
Thus the correct answer is option B.

Share and Show – Page No. 279

Question 1.
Caitlin has 4 \(\frac{3}{4}\) pounds of clay. She uses 1 \(\frac{1}{10}\) pounds to make a cup, and another 2 pounds to make a jar. How many pounds are left?
First, write an equation to model the problem.
Type below:
_________

Answer: 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Explanation:
Subtract the total pound of clay from used clay.
So, the equation of the clay leftover is 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Question 1.
Next, work backwards and rewrite the equation to find x.
Type below:
_________

Answer: 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 = x

Explanation:
Let the leftover clay be x
4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 = x
x = 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Question 1.
Solve.
_____________________
So, ________ pounds of clay remain.
Type below:
_________

Answer: 1 \(\frac{13}{20}\) pounds

Explanation:
4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2
4 + \(\frac{3}{4}\) – 1 – \(\frac{1}{10}\) – 2
4 – 3 = 1
\(\frac{3}{4}\) – \(\frac{1}{10}\) = \(\frac{13}{20}\)
1 + \(\frac{13}{20}\) = 1 \(\frac{13}{20}\) pounds

Question 2.
What if Caitlin had used more than 2 pounds of clay to make a jar? Would the amount remaining have been more or less than your answer to Exercise 1?
Type below:
_________

Answer:
Let us assume that Catlin used 2 \(\frac{1}{4}\) pounds of clay to make a jar and 1 \(\frac{1}{10}\) pounds to make a cup.
4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 \(\frac{1}{4}\) = 2 \(\frac{1}{20}\)

Question 3.
A pet store donated 50 pounds of food for adult dogs, puppies, and cats to an animal shelter. 19 \(\frac{3}{4}\) pounds was adult dog food and 18 \(\frac{7}{8}\) pounds was puppy food. How many pounds of cat food did the pet store donate?
______ \(\frac{□}{□}\) pounds of cat food

Answer: 11 \(\frac{3}{8}\) pounds of cat food

Explanation:
A pet store donated 50 pounds of food for adult dogs, puppies, and cats to an animal shelter.
19 \(\frac{3}{4}\) pounds was adult dog food and 18 \(\frac{7}{8}\) pounds was puppy food.
19 \(\frac{3}{4}\) + 18 \(\frac{7}{8}\) = 38 \(\frac{5}{8}\)
50 – 38 \(\frac{5}{8}\) = 11 \(\frac{3}{8}\) pounds of cat food
Thus the pet store donate 11 \(\frac{3}{8}\) pounds of cat food

Question 4.
Thelma spent \(\frac{1}{6}\) of her weekly allowance on dog toys, \(\frac{1}{4}\) on a dog collar, and \(\frac{1}{3}\) on dog food. What fraction of her weekly allowance is left?
\(\frac{□}{□}\) of her weekly allowance

Answer: \(\frac{1}{4}\)

Explanation:
Given that, Thelma spent \(\frac{1}{6}\) of her weekly allowance on dog toys, \(\frac{1}{4}\) on a dog collar, and \(\frac{1}{3}\) on dog food.
\(\frac{1}{6}\) + \(\frac{1}{4}\) + \(\frac{1}{3}\)  = \(\frac{3}{4}\)
1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
\(\frac{1}{4}\) of her weekly allowance.

On Your Own – Page No. 280

Question 5.
Martin is making a model of a Native American canoe. He has 5 \(\frac{1}{2}\) feet of wood. He uses 2 \(\frac{3}{4}\) feet for the hull and 1 \(\frac{1}{4}\) feet for the paddles and struts. How much wood does he have left?
______ \(\frac{□}{□}\) feet

Answer: 1 \(\frac{1}{2}\) feet

Explanation:
Martin is making a model of a Native American canoe.
He has 5 \(\frac{1}{2}\) feet of wood.
He uses 2 \(\frac{3}{4}\) feet for the hull and 1 \(\frac{1}{4}\) feet for the paddles and struts.
2 \(\frac{3}{4}\) + 1 \(\frac{1}{4}\)
2 + \(\frac{3}{4}\) + 1 + \(\frac{1}{4}\)
2 + 1 = 3
\(\frac{3}{4}\) + \(\frac{1}{4}\) = 1
3 + 1 = 4
5 \(\frac{1}{2}\) – 4 = 1 \(\frac{1}{2}\)

Question 6.
What if Martin makes a hull and two sets of paddles and struts? How much wood does he have left?

Answer: 1 \(\frac{1}{4}\)

Explanation:
He has 5 \(\frac{1}{2}\) feet of wood.
If Martin makes a hull and two sets of paddles and struts
1 \(\frac{1}{4}\) + 1 \(\frac{1}{4}\) = 2 \(\frac{1}{2}\)
2 \(\frac{1}{2}\) + 2 \(\frac{3}{4}\) = 4 \(\frac{1}{4}\)
5 \(\frac{1}{2}\) – 4 \(\frac{1}{4}\)
5 + \(\frac{1}{2}\) – 4 – \(\frac{1}{4}\)
1 + \(\frac{1}{4}\) = 1 \(\frac{1}{4}\)

Question 7.
Beth’s summer vacation lasted 87 days. At the beginning of her vacation, she spent 3 weeks at soccer camp, 5 days at her grandmother’s house, and 13 days visiting Glacier National Park with her parents. How many vacation days remained?
______ days

Answer: 48 days

Explanation:
Given,
Beth’s summer vacation lasted 87 days.
At the beginning of her vacation, she spent 3 weeks at soccer camp, 5 days at her grandmother’s house, and 13 days visiting Glacier National Park with her parents.
87 – 21 – 5 – 13 = 48 days
The remaining vacation days are 48.

Question 8.
You can buy 2 DVDs for the same price you would pay for 3 CDs selling for $13.20 apiece. Explain how you could find the price of 1 DVD.
$ ______

Answer: $19.8

Explanation:
To find what is the price of 1 DVD we will find what is the price of 3 DVDs and then because 2 DVDs price is the same than 3 CDs we can easily find the price of 1 DVD.
$13.20 × 3 = $39.6
We will divide $39.6 by 2.
$39.6 ÷ 2 = $19.8
The price of 1 DVD is $19.8

Question 9.
Test Prep During the 9 hours between 8 A.M. and 5 P.M., Bret spent 5 \(\frac{3}{4}\) hours in class and 1 \(\frac{1}{2}\) hours at band practice. How much time did he spend on other activities?
Options:
a. \(\frac{3}{4}\) hour
b. 1 \(\frac{1}{4}\) hour
c. 1 \(\frac{1}{2}\) hour
d. 1 \(\frac{3}{4}\) hour

Answer: 1 \(\frac{3}{4}\) hour

Explanation:
Test Prep During the 9 hours between 8 A.M. and 5 P.M., Bret spent 5 \(\frac{3}{4}\) hours in class and 1 \(\frac{1}{2}\) hours at band practice.
5 \(\frac{3}{4}\) + 1 \(\frac{1}{2}\) = 7 \(\frac{1}{4}\) hour
9 – 7 \(\frac{1}{4}\) hour
8 + 1 – 7 – \(\frac{1}{4}\)
1 \(\frac{3}{4}\) hour
The correct answer is option D.

Share and Show – Page No. 283

Use the properties and mental math to solve. Write your answer in simplest form.

Question 1.
\(\left(2 \frac{5}{8}+\frac{5}{6}\right)+1 \frac{1}{8}\)
______ \(\frac{□}{□}\)

Answer:
\(\left(2 \frac{5}{8}+\frac{5}{6}\right)+1 \frac{1}{8}\)
2 \(\frac{5}{8}\) + \(\frac{5}{6}\)
2 + \(\frac{5}{8}\) + \(\frac{5}{6}\)
LCD = 24
\(\frac{15}{24}\) + \(\frac{20}{24}\) = \(\frac{35}{24}\)
\(\frac{35}{24}\) = 1 \(\frac{11}{24}\)
2 + 1 \(\frac{11}{24}\) = 3 \(\frac{11}{24}\)
3 \(\frac{11}{24}\) + 1 \(\frac{1}{8}\) = 4 \(\frac{7}{12}\)

Question 2.
\(\frac{5}{12}+\left(\frac{5}{12}+\frac{3}{4}\right)\)
______ \(\frac{□}{□}\)

Answer:
\(\frac{5}{12}+\left(\frac{5}{12}+\frac{3}{4}\right)\)
\(\frac{5}{12}\) + \(\frac{3}{4}\)
LCD = 12
\(\frac{5}{12}\) + \(\frac{3}{4}\) × \(\frac{3}{3}\)
\(\frac{5}{12}\) + \(\frac{9}{12}\) = \(\frac{14}{12}\)
\(\frac{5}{12}\) + \(\frac{14}{12}\) = \(\frac{19}{12}\)
\(\frac{19}{12}\) = 1 \(\frac{7}{12}\)

Question 3.
\(\left(3 \frac{1}{4}+2 \frac{5}{6}\right)+1 \frac{3}{4}\)
______ \(\frac{□}{□}\)

Answer:

\(\left(3 \frac{1}{4}+2 \frac{5}{6}\right)\)
2 + \(\frac{5}{6}\) + 3 + \(\frac{1}{4}\)
2 + 3 = 5
\(\frac{5}{6}\) + \(\frac{1}{4}\)
LCD = 12
\(\frac{5}{6}\) × \(\frac{2}{2}\) + \(\frac{1}{4}\) × \(\frac{3}{3}\)
\(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\)
5 + 1 \(\frac{1}{12}\) = 6 \(\frac{1}{12}\)
6 \(\frac{1}{12}\) + 1 \(\frac{3}{4}\)
6 + \(\frac{1}{12}\) + 1 + \(\frac{3}{4}\)
6 + 1 = 7
\(\frac{1}{12}\) + \(\frac{3}{4}\)
\(\frac{1}{12}\) + \(\frac{9}{12}\) = \(\frac{10}{12}\) = \(\frac{5}{6}\)
7 + \(\frac{5}{6}\) = 7 \(\frac{5}{6}\)

On Your Own

Use the properties and mental math to solve. Write your answer in simplest form.

Question 4.
\(\left(\frac{2}{7}+\frac{1}{3}\right)+\frac{2}{3}\)
______ \(\frac{□}{□}\)

Answer:
\(\left(\frac{2}{7}+\frac{1}{3}\right)+\frac{2}{3}\)
\(\left(\frac{2}{7}+\frac{1}{3}\right)\)
LCD = 21
\(\left(\frac{6}{21}+\frac{7}{21}\right)\) = \(\frac{13}{21}\)
\(\frac{13}{21}\) + \(\frac{2}{3}\)
LCD = 21
\(\frac{13}{21}\) + \(\frac{14}{21}\)
\(\frac{27}{21}\) = \(\frac{9}{7}\)
= 1 \(\frac{2}{7}\)

Question 5.
\(\left(\frac{1}{5}+\frac{1}{2}\right)+\frac{2}{5}\)
______ \(\frac{□}{□}\)

Answer:
\(\left(\frac{1}{5}+\frac{1}{2}\right)\)
\(\frac{1}{5}\) + \(\frac{1}{2}\)
LCD = 10
\(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)
\(\frac{7}{10}\) + \(\frac{2}{5}\)
\(\frac{7}{10}\) + \(\frac{4}{10}\) = \(\frac{11}{10}\)
\(\frac{11}{10}\) = 1 \(\frac{1}{10}\)

Question 6.
\(\left(\frac{1}{6}+\frac{3}{7}\right)+\frac{2}{7}\)
\(\frac{□}{□}\)

Answer:
\(\left(\frac{1}{6}+\frac{3}{7}\right)\)
LCD = 42
\(\left(\frac{7}{42}+\frac{18}{42}\right)\) = \(\frac{25}{42}\)
\(\frac{25}{42}\) + \(\frac{2}{7}\)
LCD = 42
\(\frac{25}{42}\) + \(\frac{12}{42}\) = \(\frac{37}{42}\)
\(\left(\frac{1}{6}+\frac{3}{7}\right)+\frac{2}{7}\) = \(\frac{37}{42}\)

Question 7.
\(\left(2 \frac{5}{12}+4 \frac{1}{4}\right)+\frac{1}{4}\)
______ \(\frac{□}{□}\)

Answer:
\(\left(2 \frac{5}{12}+4 \frac{1}{4}\right)\)
2 \(\frac{5}{12}\) + 4 \(\frac{1}{4}\)
2 + \(\frac{5}{12}\) + 4 + \(\frac{1}{4}\)
2 + 4 = 6
\(\frac{5}{12}\) + \(\frac{1}{4}\) = \(\frac{8}{12}\)
6 \(\frac{8}{12}\) = 6 \(\frac{2}{3}\)
6 \(\frac{2}{3}\) + \(\frac{1}{4}\) = 6 \(\frac{11}{12}\)

Question 8.
\(1 \frac{1}{8}+\left(5 \frac{1}{2}+2 \frac{3}{8}\right)\)
______

Answer:
5 \(\frac{1}{2}\) + 2 \(\frac{3}{8}\)
5 + 2 = 7
\(\frac{1}{2}\) + \(\frac{3}{8}\)
LCD = 8
\(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)
= 7 \(\frac{7}{8}\)
1 \(\frac{1}{8}\) + 7 \(\frac{7}{8}\) = 9

Question 9.
\(\frac{5}{9}+\left(\frac{1}{9}+\frac{4}{5}\right)\)
______ \(\frac{□}{□}\)

Answer:
\(\frac{1}{9}\) + \(\frac{4}{5}\)
LCD = 45
\(\frac{5}{45}\) + \(\frac{36}{45}\) = \(\frac{41}{45}\)
\(\frac{41}{45}\) + \(\frac{5}{9}\)
LCD = 45
\(\frac{41}{45}\) + \(\frac{25}{45}\) = \(\frac{66}{45}\)
\(\frac{66}{45}\) = 1 \(\frac{7}{15}\)

Problem Solving – Page No. 284

Use the map to solve 10–12.

Question 10.
In the morning, Julie rides her bike from the sports complex to the school. In the afternoon, she rides from the school to the mall, and then to Kyle’s house. How far does Julie ride her bike?
______ \(\frac{□}{□}\) miles

Answer: 1 \(\frac{13}{15}\) miles

Explanation:
Julie rides her bike from the sports complex to the school = \(\frac{2}{3}\) mile
In the afternoon, she rides from the school to the mall, and then to Kyle’s house. = \(\frac{2}{5}\) + \(\frac{4}{5}\) = \(\frac{6}{5}\) = 1 \(\frac{1}{5}\)
1 \(\frac{1}{5}\) + \(\frac{2}{3}\) mile = 1 \(\frac{13}{15}\) miles

Question 11.
On one afternoon, Mario walks from his house to the library. That evening, Mario walks from the library to the mall, and then to Kyle’s house. Describe how you can use the properties to find how far Mario walks.
______ \(\frac{□}{□}\) miles

Answer:
Mario walks from his house to the library = 1 \(\frac{3}{5}\) miles
Mario walks from the library to the mall, and then to Kyle’s house = 1 \(\frac{1}{3}\) and \(\frac{4}{5}\)
1 \(\frac{3}{5}\) + (1 \(\frac{1}{3}\) + \(\frac{4}{5}\))
1 \(\frac{3}{5}\) + 2 \(\frac{2}{15}\) = 3 \(\frac{11}{15}\) miles

Question 12.
Pose a Problem Write and solve a new problem that uses the distances between four locations.
Type below:
_________

Answer:
In the evening Kyle rides his bike from the sports complex to school. Then he rides from School to the mall and then to his house. How far does Kyle ride his bike?
The distance from Sports complex to School is \(\frac{2}{3}\) mile
The distance from School to the mall is \(\frac{2}{5}\)
The distance from the mall to Kyle house is \(\frac{4}{5}\)
\(\frac{2}{3}\) + (\(\frac{2}{5}\) + \(\frac{4}{5}\))
\(\frac{2}{3}\) + \(\frac{6}{5}\) = 1 \(\frac{13}{15}\) miles

Question 13.
Test Prep Which property or properties does the problem below use?
\(\frac{1}{9}+\left(\frac{4}{9}+\frac{1}{6}\right)=\left(\frac{1}{9}+\frac{4}{9}\right)+\frac{1}{6}\)
Options:
a. Commutative Property
b. Associative Property
c. Commutative Property and Associative Property
d. Distributive Property

Answer: Associative Property
The associative property states that you can add or multiply regardless of how the numbers are grouped. By ‘grouped’ we mean ‘how you use parenthesis’. In other words, if you are adding or multiplying it does not matter where you put the parenthesis.

Chapter Review/Test – Vocabulary – Page No. 285

Choose the best term from the box.

Question 1.
A _________ is a number that is a common multiple of two or more denominators.
_________

Answer: Common Denominator

Concepts and Skills

Use a common denominator to write an equivalent fraction for each fraction.

Question 2.
\(\frac{2}{5}, \frac{1}{8}\)
common denominator: ______
Explain:
_________

Answer: 40
Multiply the denominators of the fractions
5 × 8 = 40

Question 3.
\(\frac{3}{4}, \frac{1}{2}\)
common denominator: ______
Explain:
_________

Answer: 8
Multiply the denominators of the fractions
4 × 2 = 8

Question 4.
\(\frac{2}{3}, \frac{1}{6}\)
common denominator: ______
Explain:
_________

Answer: 18
Multiply the denominators of the fractions
3 × 6 = 18

Find the sum or difference. Write your answer in simplest form

Question 5.
\(\frac{5}{6}+\frac{7}{8}\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{17}{24}\)

Explanation:
\(\frac{5}{6}+\frac{7}{8}\) = \(\frac{20}{24}\) + \(\frac{21}{24}\)
= \(\frac{41}{24}\) = 1 \(\frac{17}{24}\)

Question 6.
\(2 \frac{2}{3}-1 \frac{2}{5}\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{4}{15}\)

Question 7.
\(7 \frac{3}{4}+3 \frac{7}{20}\)
______ \(\frac{□}{□}\)

Answer: 11 \(\frac{1}{10 }\)

Estimate. Then find the difference and write it in simplest form.

Question 8.
\(1 \frac{2}{5}-\frac{2}{3}\)
Type below:
________

Answer:
Estimate: \(\frac{1}{2}\)
Difference:
Rewriting our equation with parts separated
1 + \(\frac{2}{5}\) – \(\frac{2}{3}\)
\(\frac{7}{5}\) – \(\frac{2}{3}\)
\(\frac{7}{5}\) × \(\frac{3}{3}\) – \(\frac{2}{3}\) × \(\frac{5}{5}\)
= \(\frac{21}{15}\) – \(\frac{10}{15}\)
= \(\frac{11}{15}\)

Question 9.
\(7-\frac{3}{7}\)
Type below:
________

Answer: 6 \(\frac{4}{7}\)

Explanation:
\(7-\frac{3}{7}\) = \(\frac{49}{7}\) – \(\frac{3}{7}\)
\(\frac{46}{7}\) = 6 \(\frac{4}{7}\)
\(7-\frac{3}{7}\) = 6 \(\frac{4}{7}\)

Question 10.
\(5 \frac{1}{9}-3 \frac{5}{6}\)
Type below:
________

Answer: 1 \(\frac{5}{18}\)

Explanation:
\(5 \frac{1}{9}-3 \frac{5}{6}\) = 5 + \(\frac{1}{9}\) – 3 – \(\frac{5}{6}\)
5 – 3 = 2
\(\frac{1}{9}\) – \(\frac{5}{6}\) = \(\frac{2}{18}\) – \(\frac{15}{18}\) = – \(\frac{13}{18}\)
2 – \(\frac{13}{18}\) = 1 \(\frac{5}{18}\)

Use the properties and mental math to solve. Write your answer in simplest form.

Question 11.
\(\left(\frac{3}{8}+\frac{2}{3}\right)+\frac{1}{3}\)
______ \(\frac{□}{□}\)

Answer: 1 \(\frac{3}{8}\)

Explanation:
\(\frac{3}{8}\) + \(\frac{2}{3}\) = \(\frac{9}{24}\) + \(\frac{16}{24}\) = \(\frac{25}{24}\)
\(\frac{25}{24}\) + \(\frac{1}{3}\)
= \(\frac{25}{24}\) + \(\frac{8}{24}\) = \(\frac{33}{24}\) = \(\frac{11}{8}\)
The mixed fraction of \(\frac{11}{8}\) is 1 \(\frac{3}{8}\).

Question 12.
\(1 \frac{4}{5}+\left(2 \frac{3}{20}+\frac{3}{5}\right)\)
______ \(\frac{□}{□}\)

Answer: 4 \(\frac{11}{20}\)

Explanation:
Rewriting our equation with parts separated
2 \(\frac{3}{20}\) + \(\frac{3}{5}\) = \(\frac{43}{20}\) + \(\frac{3}{5}\)
\(\frac{43}{20}\) + \(\frac{3}{5}\) = \(\frac{215}{100}\) + \(\frac{60}{100}\)
= \(\frac{275}{100}\) = 2 \(\frac{3}{4}\)
2 \(\frac{3}{4}\) + 1 \(\frac{4}{5}\) = 2 + \(\frac{3}{4}\) + 1 + \(\frac{4}{5}\)
2 + 1 = 3
\(\frac{3}{4}\) + \(\frac{4}{5}\) = \(\frac{15}{20}\) + \(\frac{16}{20}\) = \(\frac{31}{20}\)
\(\frac{31}{20}\) = 4 \(\frac{11}{20}\)

Question 13.
\(3 \frac{5}{9}+\left(1 \frac{7}{9}+2 \frac{5}{12}\right)\)
______ \(\frac{□}{□}\)

Answer: 7 \(\frac{3}{4}\)

Explanation:
1 \(\frac{7}{9}\) + 2 \(\frac{5}{12}\)
1 + 2 = 3
\(\frac{7}{9}\) + \(\frac{5}{12}\)
LCD is 36
\(\frac{28}{36}\) + \(\frac{15}{36}\) = \(\frac{43}{36}\)
\(\frac{43}{36}\) = 1 \(\frac{7}{36}\)
3 + 1 + \(\frac{7}{36}\) = 4 \(\frac{7}{36}\)
4 \(\frac{7}{36}\) + 3 \(\frac{5}{9}\)
4 + \(\frac{7}{36}\) + 3 + \(\frac{5}{9}\)
4 + 3 = 7
\(\frac{7}{36}\) + \(\frac{5}{9}\)
= \(\frac{7}{36}\) + \(\frac{20}{36}\) = \(\frac{27}{36}\) = \(\frac{3}{4}\)
7 + \(\frac{3}{4}\) = 7 \(\frac{3}{4}\)

Chapter Review/Test – Page No. 286

Question 14.
Ursula mixed 3 \(\frac{1}{8}\) cups of dry ingredients with 1 \(\frac{2}{5}\) cups of liquid ingredients. Which answer represents the best estimate of the total amount of ingredients Ursula mixed?
Options:
a. about 4 cups
b. about 4 \(\frac{1}{2}\) cups
c. about 5 cups
d. about 5 \(\frac{1}{2}\) cups

Answer: about 4 \(\frac{1}{2}\) cups

Explanation:
Ursula mixed 3 \(\frac{1}{8}\) cups of dry ingredients with 1 \(\frac{2}{5}\) cups of liquid ingredients.
3 + 1 = 4
\(\frac{1}{8}\) is closer to 0.
\(\frac{2}{5}\) is closer to \(\frac{1}{2}\)
4 + \(\frac{1}{2}\) = 4 \(\frac{1}{2}\)
Thus the correct answer is option B.

Question 15.
Samuel walks in the Labor Day parade. He walks 3 \(\frac{1}{4}\) miles along the parade route and 2 \(\frac{5}{6}\) miles home. How many miles does Samuel walk?
Options:
a. \(\frac{5}{10}\) mile
b. 5 \(\frac{1}{12}\) miles
c. 5 \(\frac{11}{12}\) miles
d. 6 \(\frac{1}{12}\) miles

Answer: 6 \(\frac{1}{12}\) miles

Explanation:
Samuel walks in the Labor Day parade.
He walks 3 \(\frac{1}{4}\) miles along the parade route and 2 \(\frac{5}{6}\) miles home.
3 + \(\frac{1}{4}\) + 2 + \(\frac{5}{6}\)
3 + 2 =5
\(\frac{5}{6}\) + \(\frac{1}{4}\) = \(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\)
\(\frac{13}{12}\) = 6 \(\frac{1}{12}\) miles
Thus the correct answer is option D.

Question 16.
A gardener has a container with 6 \(\frac{1}{5}\) ounces of liquid plant fertilizer. On Sunday, the gardener uses 2 \(\frac{1}{2}\) ounces on a flower garden. How many ounces of liquid plant fertilizer are left?
Options:
a. 3 \(\frac{7}{10}\) ounces
b. 5 \(\frac{7}{10}\) ounces
c. 6 \(\frac{7}{10}\) ounces
d. 9 \(\frac{7}{10}\) ounces

Answer: 9 \(\frac{7}{10}\) ounces

Explanation:
A gardener has a container with 6 \(\frac{1}{5}\) ounces of liquid plant fertilizer.
On Sunday, the gardener uses 2 \(\frac{1}{2}\) ounces on a flower garden.
6 + \(\frac{1}{5}\) + 2 + \(\frac{1}{2}\)
6 + 2 = 8
\(\frac{1}{5}\) + \(\frac{1}{2}\)
LCD = 10
\(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)
8 \(\frac{7}{10}\)

Question 17.
Aaron is practicing for a triathlon. On Sunday, he bikes 12 \(\frac{5}{8}\) miles and swims 5 \(\frac{2}{3}\) miles. On Monday, he runs 6 \(\frac{3}{8}\) miles. How many total miles does Aaron cover on the two days?
Options:
a. 23 \(\frac{1}{6}\) miles
b. 24 \(\frac{7}{12}\) miles
c. 24 \(\frac{2}{3}\) miles
d. 25 \(\frac{7}{12}\) miles

Answer: 24 \(\frac{2}{3}\) miles

Explanation:
Aaron is practicing for a triathlon.
On Sunday, he bikes 12 \(\frac{5}{8}\) miles and swims 5 \(\frac{2}{3}\) miles.
On Monday, he runs 6 \(\frac{3}{8}\) miles.
5 \(\frac{2}{3}\) + 6 \(\frac{3}{8}\) = 12 \(\frac{1}{24}\)
12 \(\frac{1}{24}\) + 12 \(\frac{5}{8}\) miles
12 + \(\frac{1}{24}\) + 12 + \(\frac{5}{8}\)
12 + 12 = 24
\(\frac{1}{24}\) + \(\frac{5}{8}\) = \(\frac{1}{24}\) + \(\frac{15}{24}\) = \(\frac{16}{24}\) = \(\frac{2}{3}\)
24 + \(\frac{2}{3}\) = 24 \(\frac{2}{3}\) mile
The correct answer is option D.

Chapter Review/Test – Page No. 287

Fill in the bubble completely to show your answer.

Question 18.
Mrs. Friedmon baked a walnut cake for her class. The pictures below show how much cake she brought to school and how much she had left at the end of the day.

Which fraction represents the difference between the amounts of cake Mrs. Friedmon had before school and after school?
Options:
a. \(\frac{5}{8}\)
b. 1 \(\frac{1}{2}\)
c. 1 \(\frac{5}{8}\)
d. 2 \(\frac{1}{2}\)

Answer: 1 \(\frac{5}{8}\)

Explanation:
The fraction for the above figure is 1 \(\frac{7}{8}\)
The fraction for the second figure is \(\frac{1}{4}\)
1 + \(\frac{7}{8}\) – \(\frac{1}{4}\)
\(\frac{7}{8}\) – \(\frac{1}{4}\) = \(\frac{7}{8}\) – \(\frac{2}{8}\)
\(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\)
1 + \(\frac{5}{8}\) = 1 \(\frac{5}{8}\)
The correct answer is option C.

Question 19.
Cody is designing a pattern for a wood floor. The length of the pieces of wood are 1 \(\frac{1}{2}\) inches, 1 \(\frac{13}{16}\) inches, and 2 \(\frac{1}{8}\) inches. What is the length of the 5th piece of wood if the pattern continues?
Options:
a. 2 \(\frac{7}{6}\) inches
b. 2 \(\frac{3}{4}\) inches
c. 3 \(\frac{1}{2}\) inches
d. 4 inches

Answer: 2 \(\frac{3}{4}\) inches

Explanation:
The length of the pieces of wood are 1 \(\frac{1}{2}\) inches, 1 \(\frac{13}{16}\) inches, and 2 \(\frac{1}{8}\) inches
1 \(\frac{1}{2}\) = \(\frac{3}{2}\)
1 \(\frac{13}{16}\) inches = \(\frac{29}{16}\)
\(\frac{29}{16}\) – \(\frac{3}{2}\) = latex]\frac{5}{16}[/latex]
5th piece = \(\frac{3}{2}\) + latex]\frac{5}{16}[/latex] (5 – 1)
= \(\frac{3}{2}\) + latex]\frac{5}{16}[/latex] 4
= \(\frac{3}{2}\) + latex]\frac{20}{16}[/latex]
= \(\frac{3}{2}\) × latex]\frac{8}{8}[/latex] + latex]\frac{20}{16}[/latex]
= latex]\frac{44}{16}[/latex] = 2 latex]\frac{3}{4}[/latex]
Thus the correct answer is option B.

Question 20.
Julie spends \(\frac{3}{4}\) hour studying on Monday and \(\frac{1}{6}\) hour studying on Tuesday. How many hours does Julie study on those two days?
Options:
a. \(\frac{1}{3}\) hour
b. \(\frac{2}{5}\) hour
c. \(\frac{5}{6}\) hour
d. \(\frac{11}{12}\) hour

Answer: \(\frac{11}{12}\) hour

Explanation:
Julie spends \(\frac{3}{4}\) hour studying on Monday and \(\frac{1}{6}\) hour studying on Tuesday.
\(\frac{3}{4}\) + \(\frac{1}{6}\)
LCD = 12
\(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\) hour
So, the correct answer is option D.

Chapter Review/Test – Page No. 288

Constructed Response

Question 21.
A class uses 8 \(\frac{5}{6}\) sheets of white paper and 3 \(\frac{1}{12}\) sheets of red paper for a project. How much more white paper is used than red paper? Show your work using words, pictures, or numbers. Explain how you know your answer is reasonable.
______ \(\frac{□}{□}\) sheet of white paper

Answer: 5 \(\frac{3}{4}\) sheet of white paper

Explanation:
A class uses 8 \(\frac{5}{6}\) sheets of white paper and 3 \(\frac{1}{12}\) sheets of red paper for a project.
8 \(\frac{5}{6}\) – 3 \(\frac{1}{12}\)
8 + \(\frac{5}{6}\) – 3 – \(\frac{1}{12}\)
8 – 3 = 5
\(\frac{5}{6}\) – \(\frac{1}{12}\)
\(\frac{10}{12}\) – \(\frac{1}{12}\) = \(\frac{9}{12}\)
\(\frac{9}{12}\) = \(\frac{3}{4}\)
5 + \(\frac{3}{4}\) = 5 \(\frac{3}{4}\)

Performance Task

Question 22.
For a family gathering, Marcos uses the recipe below to make a lemon-lime punch.

A). How would you decide the size of a container you need for one batch of the Lemon-Lime Punch?
Type below:
________

Answer: He may use \(\frac{1}{4}\) gallon lime juice for one batch of the lemon-lime punch.

Question 22.
B). If Marcos needs to make two batches of the recipe, how much of each ingredient will he need? How many gallons of punch will he have? Show your math solution and explain your thinking when you solve both questions.
Type below:
________

Answer: \(\frac{2}{3}\) gallon lime juice

Question 22.
C). Marcos had 1 \(\frac{1}{3}\) gallons of punch left over. He poured all of it into several containers for family members to take home. Use fractional parts of a gallon to suggest a way he could have shared the punch in three different-sized containers.
Type below:
________

Answer: 1 \(\frac{1}{12}\)

Conclusion

Answering the concepts in Go Math Grade 5 Chapter 6 Solution Key helps students to attempt the exam with confidence and prepare accordingly. Once you get to know the concept better you can solve any kind of question framed on Addition and Subtraction of Fractions with Unlike Denominators. Check your knowledge by taking an Assessment Test on Chapter 6 available.

Are you browsing for Go Math Grade 8 Answer Key for Chapter 11 Angle Relationships in Parallel Lines and Triangles on the various websites? Don’t worry discover all the questions, answers, and explanations on Go Math Grade 8 Solution Key Ch 11 Angle Relationships in Parallel Lines and Triangles here. Get free access to Download Go Math Grade 8 Chapter 11 Angle Relationships in Parallel Lines and Triangles Solution Key PDF from this page. Finish your homework in time with the help of Go Math Grade 8 Answer Key.

Download Go Math Grade 8 Chapter 11 Angle Relationships in Parallel Lines and Triangles Answer Key PDF

Enhance your skills by using the Go Math Grade 8 Answer Key Chapter 11 Angle Relationships in Parallel Lines and Triangles. Download Go Math Grade 8 Chapter 11 Answer Key and go through Questions and Answers on our website. Follow the below given Go Math Grade 8 Chapter 11 Angle Relationships in Parallel Lines and Triangles Answer Key topic wise links and start your preparation. Make use of the links and secure a good percentage in the exam.

Lesson 1: Parallel Lines Cut by a Transversal

• Parallel Lines Cut by a Transversal – Page No. 350
• Parallel Lines Cut by a Transversal – Page No. 351
• Parallel Lines Cut by a Transversal Lesson Check – Page No. 352

Lesson 2: Angle Theorems for Triangles

• Angle Theorems for Triangles – Page No. 358
• Angle Theorems for Triangles – Page No. 359
• Angle Theorems for Triangles Lesson Check – Page No. 360

Lesson 3: Angle-Angle Similarity

• Angle-Angle Similarity – Page No. 366
• Angle-Angle Similarity – Page No. 367
• Angle-Angle Similarity Lesson Check – Page No. 368

Model Quiz

• • Model Quiz – Page No. 369

Review

• • Mixed Review – Page No. 370

Guided Practice – Parallel Lines Cut by a Transversal – Page No. 350

Use the figure for Exercises 1–4.

Question 1.
∠UVY and ____ are a pair of corresponding angles.
∠ _________

Answer:
∠ VWZ

Explanation:
∠UVY and ∠ VWZ are a pair of corresponding angles.
When two lines are crossed by Transversal the angles in matching corners are called corresponding angles.

Question 2.
∠WVY and ∠VWT are _________ angles.
____________

Answer:
∠WVY and ∠VWT are alternate interior angles.
Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.

Explanation:
∠WVY and ∠VWT are alternate interior angles.
Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.

Question 3.
Find m∠SVW.
_________ °

Answer:
80º

Explanation:
∠SVW and ∠VWT are same sider interior angles. Therefore,
m∠SVW + m∠VWT = 180º
4xº +5xº = 180º
9x = 180º
x = 180/9
x = 20
m∠SVW = 4xº = (4.20)º = 80º

Question 4.
Find m∠VWT.
_________ °

Answer:
100º

Explanation:
∠SVW and ∠VWT are same sider interior angles. Therefore,
m∠SVW + m∠VWT = 180º
4xº +5xº = 180º
9x = 180º
x = 180/9
x = 20
m∠VWT = 5xº = (5.20)º = 100º

Question 5.
Vocabulary When two parallel lines are cut by a transversal, _______________ angles are supplementary.
____________

Answer:
If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent. If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.

ESSENTIAL QUESTION CHECK-IN

Question 6.
What can you conclude about the interior angles formed when two parallel lines are cut by a transversal?
Type below:
____________

Answer:
Alternate interior angles are congruent; same-side interior angles are supplementary.

Explanation:
When two parallel lines are cut by a transversal, the interior angles will be the angles between the two parallel lines. Alternate interior angles will be on opposite sides of the transversal; the measures of these angles are the same.
Same-side interior angles will be on the same side of the transversal; the measures of these angles will be supplementary, adding up to 180 degrees.

11.1 Independent Practice – Parallel Lines Cut by a Transversal – Page No. 351

Vocabulary Use the figure for Exercises 7–10.

Question 7.
Name all pairs of corresponding angles.
Type below:
____________

Answer:
∠1 and ∠5
∠3 and ∠7
∠2 and ∠6
∠4 and ∠8

Explanation:
Corresponding angles are
∠1 and ∠5
∠3 and ∠7
∠2 and ∠6
∠4 and ∠8

Question 8.
Name both pairs of alternate exterior angles.
Type below:
____________

Answer:
∠1 and ∠8
∠2 and ∠7

Explanation:
Alternate exterior angles
∠1 and ∠8
∠2 and ∠7

Question 9.
Name the relationship between ∠ 3 and ∠6.
Type below:
____________

Answer:
alternate interior angles

Explanation:
∠3 and ∠6 are alternate interior angles.
Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.

Question 10.
Name the relationship between ∠4 and ∠6.
Type below:
____________

Answer:
same-side interior angles

Explanation:
∠4 and ∠6 are same-side interior angles.

Find each angle measure.

Question 11.
m∠AGE when m∠FHD = 30°
_________ °

Answer:
m∠AGE = 30°

Explanation:
∠AGE and ∠FHD are alternate exterior angles.
Therefore, m∠AGE = m∠FHD = 30°
m∠AGE = 30°

Question 12.
m∠AGH when m∠CHF = 150°
_________ °

Answer:
150°

Explanation:
∠AGH and ∠CHF are corresponding angles.
Therefore, m∠AGH = m∠CHF = 150°
m∠AGH = 150°

Question 13.
m∠CHF when m∠BGE = 110°
_________ °

Answer:
110°

Explanation:
∠CHF and ∠BGE are alternate exterior angles.
Therefore, m∠CHF = m∠BGE = 110°
m∠CHF = 110°

Question 14.
m∠CHG when m∠HGA = 120°
_________ °

Answer:
m∠CHG = 60º

Explanation:
∠CHF and ∠HGA are same-side interior angles.
m∠CHG + m∠HGA = 180°
m∠CHG + 120° = 180°
m∠CHG = 180 – 120 = 60
m∠CHG = 60º

Question 15.
m∠BGH
_________ °

Answer:
78º

Explanation:
∠BGH and ∠GHD are same-side interior angles.
So, ∠BGH + ∠GHD = 180º
3x + (2x + 50)º = 180º
5x = 180º – 50º = 130º
x = 130/5 = 26º
∠BGH = 3xº = 3 × 26º = 78º
∠GHD = (2x + 50) += (2 × 26 + 50) = 102º

Question 16.
m∠GHD
_________ °

Answer:
102º

Explanation:
∠BGH and ∠GHD are same-side interior angles.
So, ∠BGH + ∠GHD = 180º
3x + (2x + 50)º = 180º
5x = 180º – 50º = 130º
x = 130/5 = 26º
∠BGH = 3xº = 3 × 26º = 78º
∠GHD = (2x + 50) += (2 × 26 + 50) = 102º

Question 17.
The Cross Country Bike Trail follows a straight line where it crosses 350th and 360th Streets. The two streets are parallel to each other. What is the measure of the larger angle formed at the intersection of the bike trail and 360th Street? Explain.

_________ °

Answer:
The larger angle formed at the intersection of the bike trail and 360th Street is 132º

Explanation:

The larger angle formed at the intersection of the bike trail and 360th Street is the angle 5 in our schema. ∠5 and ∠3 are same-side interior angles. Therefore, m∠5 + m∠3 = 180º
m∠5 + 48º = 180º
m∠5 = 180º – 48º
m∠5 = 132º

Question 18.
Critical Thinking How many different angles would be formed by a transversal intersecting three parallel lines? How many different angle measures would there be?
_________ different angles
_________ different angle measures

Answer:
12 different angles
2 different angle measures

Explanation:
There are 12 different angles formed by a transversal intersecting three parallel lines.
There are 2 different angle measures:
m∠1 = m∠4 = m∠5 = m∠8 = m∠9 = m∠12
m∠2 = m∠3 = m∠6 = m∠7 = m∠10 = m∠11

Parallel Lines Cut by a Transversal – Page No. 352

Question 19.
Communicate Mathematical Ideas In the diagram at the right, suppose m∠6 = 125°. Explain how to find the measures of each of the other seven numbered angles.

Type below:
____________

Answer:
m∠2 = m∠6 = 125º because ∠2 and ∠6 are corresponding angles.
m∠3 = m∠2 = 125º because ∠3 and ∠2 are vertical angles.
m∠7 = m∠3 = 125º because ∠7 and ∠3 are corresponding angles.
∠4 and ∠6 are same-side interior angles.
Therefore, m∠4 + m∠6 = 180º
m∠4 + 125º = 180º
m∠4 = 180º – 125º
m∠4 = 55º
m∠8 = m∠4 = 55º because ∠8 and ∠4 are corresponding angles.
m∠1 = m∠4 = 55º because ∠1 and ∠4 are vertical angles.
m∠5 = m∠1 = 55º because ∠5 and ∠1 are corresponding angles.

FOCUS ON HIGHER ORDER THINKING

Question 20.
Draw Conclusions In a diagram showing two parallel lines cut by a transversal, the measures of two same-side interior angles are both given as 3x°. Without writing and solving an equation, can you determine the measures of both angles? Explain. Then write and solve an equation to find the measures.

Answer:
m∠1 and m∠2 are same-side interior angles is 180º
Therefore, m∠1 + m∠2 = 180º
3x + 3x = 180º
6x = 180º
x = 180/6 = 30
m∠1 = m∠2 = 3x = 3(30) = 90º

Question 21.
Make a Conjecture Draw two parallel lines and a transversal. Choose one of the eight angles that are formed. How many of the other seven angles are congruent to the angle you selected? How many of the other seven angles are supplementary to your angle? Will your answer change if you select a different angle?
Type below:
____________

Answer:

We have to select ∠a form of eight angles that are formed. There are two other angles that are congruent to the angle ∠a. Two other angles are ∠e and ∠g.
There are no supplementary to ∠a.
If we select a different angle then the answer will also change.

Question 22.
Critique Reasoning In the diagram at the right, ∠2, ∠3, ∠5, and∠8 are all congruent, and∠1, ∠4, ∠6, and ∠7 are all congruent. Aiden says that this is enough information to conclude that the diagram shows two parallel lines cut by a transversal. Is he correct? Justify your answer.

____________

Answer:
This is not enough information to conclude that the diagram shows two parallel lines cut by a transversal. Because ∠2 and ∠3 are same-side interior angles. But ∠5 and ∠8 are not congruent with each other. And ∠6 and ∠7 are same-side interior angles. But ∠1 and ∠4 are not congruent with each other.

Guided Practice – Angle Theorems for Triangles – Page No. 358

Find each missing angle measure.

Question 1.

m∠M = _________ °

Answer:
m∠M = 71º

Explanation:
From the Triangle Sum Theorem,
m∠L + m∠N + m∠M = 180º
78º + 31º + m∠M = 180º
109º + m∠M = 180º
m∠M = 180º – 109º
m∠M = 71º

Question 2.

m∠Q = _________ °

Answer:
m∠Q = 30º

Explanation:
From the Triangle Sum Theorem,
m∠Q + m∠S + m∠R = 180º
m∠Q + 24º + 126º = 180º
m∠Q + 150º = 180º
m∠Q = 180º – 150º
m∠Q = 30º

Use the Triangle Sum Theorem to find the measure of each angle in degrees.

Question 3.

m∠T = _________ °
m∠V = _________ °
m∠U = _________ °

Answer:
m∠T = 88°
m∠V = 63°
m∠U = 29°

Explanation:
From the Triangle Sum Theorem,
m∠U + m∠T + m∠V = 180º
(2x + 5)º + (7x + 4)º + (5x + 3)º = 180º
2xº + 5º + 7xº + 4º + 5xº + 3º = 180º
14xº + 12º = 180º
14xº = 168º
x = 168/14 = 12
Substitute x value to find the angles
m∠U = (2x + 5)º = ((2 . 12) + 5)º = 29º
m∠U = 29º
m∠T = (7x + 4)º = ((7 . 12) + 4)º = 88º
m∠T = 88º
m∠V = (5x + 3)º = ((5 . 12) + 3)º = 63º
m∠V = 63º

Question 4.

m∠X = _________ °
m∠Y = _________ °
m∠Z = _________ °

Answer:
m∠X = 90°
m∠Y = 45 °
m∠Z = 45°

Explanation:
From the Triangle Sum Theorem,
m∠X + m∠Y + m∠Z = 180º
nº + (1/2 . n)º + (1/2 . n)º = 180º
2nº = 180º
n = 90
Substitute n values to find the angles
m∠X = nº = 90º
m∠X = 90º
m∠Y = (1/2 . n)º = (1/2 . 90)º = 45º
m∠Y = 45º
m∠Z = (1/2 . n)º = (1/2 . 90)º = 45º
m∠Z = 45º

Use the Exterior Angle Theorem to find the measure of each angle in degrees.

Question 5.

m∠C = _________ °
m∠D = _________ °

Answer:
m∠C = 40°
m∠D = 76°

Explanation:
Given m∠C = 4y°, m∠D = (7y + 6)°, m∠E = 116°
By using exterior angle theorem,
∠DEC + ∠DEF = 180°

∠DEC + 116° = 180°
∠E = ∠DEC = 180° – 116° = 64°
The sum of the angles of a traingle = 180°
∠C +∠D + ∠E = 180°
4y° + (7y + 6)°+ 64° = 180°
11y° + 70° = 180°
11y° = 180° – 70° = 110°
y = 10
∠C = 4y° = 4. 10 = 40°
∠D = (7y + 6)° = ((7 . 10)  + 6)° = (70 + 6)° = 76°

Question 6.

m∠L = _________ °
m∠M = _________ °

Answer:
m∠L = 129°
m∠M = 32°

Explanation:
Given that m∠M = (5z – 3)°, m∠L = (18z + 3)°, m∠JKM = 161°
From the Exterior Angle Theorem,
m∠M + m∠L = m∠JKM
(5z – 3)° + (18z + 3)° = 161°
5z° – 3° + 18z° + 3° = 161°
23z° = 161°
z = 161/23 = 7
Substitute z values to find the angles
m∠M = (5z – 3)° = ((5 . 7) – 3)° = 32°
m∠L = (18z + 3)° = ((18 . 7) + 3)° = 129°
From the Triangle Sum Theorem,
m∠M + m∠L + m∠LKM = 180º
32º + 129º + m∠LKM = 180º
161º + m∠LKM = 180º
m∠LKM = 19º

ESSENTIAL QUESTION CHECK-IN

Question 7.
Describe the relationships among the measures of the angles of a triangle.
Type below:
______________

Answer:
The sum of all measures of the interior angles of a triangle is 180°. The measure of an exterior angle of a triangle is equal to the sum of its remote interior angles.

11.2 Independent Practice – Angle Theorems for Triangles – Page No. 359

Find the measure of each angle.

Question 8.

m∠E = _________ °
m∠F = _________ °

Answer:
m∠E = 41°
m∠F = 41°

Explanation:
m∠E = x°, m∠F = x°,  m∠D = 98°
From the Triangle Sum Theorem, sum of the angles of the traingle is 180°
m∠E + m∠D + m∠F = 180°
x + 98 + x = 180°
2x + 98 = 180°
2x = 82°
x = 41°
So, m∠E = 41°
m∠F = 41°

Question 9.

m∠T = _________ °
m∠V = _________ °

Answer:
m∠T = 60°
m∠V = 30°

Explanation:
m∠W = 90°, m∠T = 2x°,  m∠V = x°
From the Triangle Sum Theorem, sum of the angles of the traingle is 180°
m∠T + m∠V + m∠W = 180°
2x + x + 90 = 180°
3x = 90°
x = 30°
So, m∠T = 2x° = 2 . 30° = 60°
m∠V = x° = 30°

Question 10.

m∠G = _________ °
m∠H = _________ °
m∠J = _________ °

Answer:
m∠G = 75°
m∠H = 60°
m∠J = 45°

Explanation:
m∠G = 5x°, m∠H = 4x°,  m∠J = 3x°
From the Triangle Sum Theorem, sum of the angles of the traingle is 180°
m∠G + m∠H + m∠J = 180°
5x + 4x + 3x = 180°
12x = 90°
x = 15°
So, m∠G = 5x° = 5 . 15° = 75°
m∠H = 4x° = 4. 15° = 60°
m∠J = 3x° = 3. 15° = 45°

Question 11.

m∠Q = _________ °
m∠P = _________ °
m∠QRP = _________ °

Answer:
m∠Q = 98°
m∠P = 55°
m∠QRP = 27°

Explanation:
Given that m∠Q = (3y + 5)°, m∠P = (2y – 7)°, m∠QRS = 153°
From the exterior angle Theorem,
∠QRS + ∠QRP = 180°
153° + ∠QRP = 180°

m∠R = m∠QRP = 180° – 153° = 27°
From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°
m∠P + m∠Q + m∠R = 180°
(3y + 5)° + (2y – 7)°+ 27° = 180°
5y° + 25 = 180°
5y° = 155°
y = 31°
m∠Q = (3y + 5)° = ((3 . 31°) + 5)° = 98°
m∠P = (2y – 7)° = ((2. 31° – 7)° = 55°
m∠QRP = 27°

Question 12.

m∠ACB = _________ °
m∠DCE = _________ °
m∠BCD = _________ °

Answer:
m∠ACB = 44°
m∠DCE = 35°
m∠BCD = 101°

Explanation:
In traingle ABC, m∠A = 78°, m∠B = 58°, m∠ACB = ?°
From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°
m∠A + m∠B + m∠ACB = 180°
78° + 58° + m∠ACB = 180°
m∠ACB = 180° – 136°
m∠ACB = 44°
In traingle CDE, m∠D = 85°, m∠E = 60°, m∠CDE = ?°
From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°
m∠D + m∠E + m∠CDE = 180°
85° + 60° + m∠CDE = 180°
m∠CDE = 180° – 145°
m∠CDE = 35°
From the Exterior Angle Theorem,
m∠ACB + m∠CDE + m∠BCD = 180°
44° + 35° + m∠BCD = 180°
m∠BCD = 180° – 79°
m∠BCD = 101°

Question 13.

m∠K = _________ °
m∠L = _________ °
m∠KML = _________ °
m∠LMN = _________ °

Answer:

Explanation:
m∠K = 2x°, m∠L = 3x°, m∠KML = x°
So, From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°.
m∠K + m∠L + m∠KML = 180°
2x° + 3x° + x° = 180°
6x° = 180°
x= 30°
∠KML = x = 30°
∠L = 3x = 3 . 30° = 90°
∠K = 2x = 2 . 30° = 60°
From the Exterior Angle Theorem,
∠KML + ∠LMN = 180°
∠LMN = 180° – 30° = 150°

Question 14.
Multistep The second angle in a triangle is five times as large as the first. The third angle is two-thirds as large as the first. Find the angle measures.
The measure of the first angle: _________ °
The measure of the second angle: _________ °
The measure of the third angle: _________ °

Answer:
The measure of the first angle: 27°
The measure of the second angle: 135°
The measure of the third angle: 18°

Explanation:
Let us name the angles of a triangle as ∠1, ∠2, ∠3.
Consider ∠1 as x.
∠2 is 5 times as large as the first.
∠2 = 5x
Also, ∠3 = 2/3 . x
So, From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°.
x+ 5x + (2/3 . x) = 180°
20x = 540°
x = 27°
So, ∠1 = x = 27°
∠2 = 5x = 5 . 27° = 135°
∠3 = 2/3 . x = 2/3 . 27° = 18°
The measure of the first angle: 27°
The measure of the second angle: 135°
The measure of the third angle: 18°

Angle Theorems for Triangles – Page No. 360

Question 15.
Analyze Relationships Can a triangle have two obtuse angles? Explain.
___________

Answer:
No; a triangle can NOT have two obtuse angles

Explanation:
The measure of an obtuse angle is greater than 90°. Two obtuse angles and the third angle would have a sum greater than 180°

FOCUS ON HIGHER ORDER THINKING

Question 16.
Critical Thinking Explain how you can use the Triangle Sum Theorem to find the measures of the angles of an equilateral triangle.
Type below:
___________

Answer:
All angles have the same measure in an equilateral triangle

Explanation:
Using the Triangle Sum Theorem,
∠x + ∠x + ∠x = 180°
3∠x = 180°
∠x = 60°
All angles have the same measure in an equilateral triangle

Question 17.
a. Draw Conclusions Find the sum of the measures of the angles in quadrilateral ABCD. (Hint: Draw diagonal \(\overline { AC } \). How can you use the figures you have formed to find the sum?)

Sum: _________ °

Answer:
Sum: 360°

Question 17.
b. Make a Conjecture Write a “Quadrilateral Sum Theorem.” Explain why you think it is true.
Type below:
___________

Answer:
The sum of the angle measures of a quadrilateral is 360°
Any quadrilateral can be divided into two triangles (180 + 180 = 360)

Question 18.
Communicate Mathematical Ideas Describe two ways that an exterior angle of a triangle is related to one or more of the interior angles.
Type below:
___________

Answer:
An exterior angle and it’s an adjacent interior angle equal 180°
An exterior angle equals the sum of the two remote interior angles.

Guided Practice – Angle-Angle Similarity – Page No. 366

Question 1.
Explain whether the triangles are similar. Label the angle measures in the figure.

Type below:
___________
△ABC has angle measures _______and △DEF has angle measures______. Because _______in one triangle are congruent to ______in the other triangle, the triangles are_____.

Answer:
△ABC has angle measures 40°, 30°, and 109° and △DEF has angle measures 41°, 109°, and 30°. Because 2∠s in one triangle are congruent to in the other triangle, the triangles similar.

Question 2.
A flagpole casts a shadow 23.5 feet long. At the same time of day, Mrs. Gilbert, who is 5.5 feet tall, casts a shadow that is 7.5 feet long. How tall in feet is the flagpole? Round your answer to the nearest tenth.

_________ ft

Answer:
17.2 ft

Explanation:
In similar triangles, corresponding side lengths are proportional.
5.5/7.5 = h/23.5
h (7.5) = 129.25
h = 129.25/7.5
h = 17.23
Rounding to the nearest tenth
h = 17.2 feet

Question 3.
Two transversals intersect two parallel lines as shown. Explain whether △ABC and △DEC are similar.

∠BAC and∠EDC are ___________ since they are ___________.
∠ABC and∠DEC are ___________ since they are ___________.
By ________, △ABC and△DEC are ___________.
Type below:
___________

Answer:
∠BAC and∠EDC are congruent since they are alt. interior ∠s
∠ABC and∠DEC are congruent since they are alt. interior ∠s.
By AA similarity, △ABC and△DEC are similar.

ESSENTIAL QUESTION CHECK-IN

Question 4.
How can you determine when two triangles are similar?
Type below:
___________

Answer:
If 2 angles of one triangle are congruent to 2 angles of another triangle, the triangles are similar by the Angle-Angle Similarity Postulate

11.3 Independent Practice – Angle-Angle Similarity – Page No. 367

Use the diagrams for Exercises 5–7.

Question 5.
Find the missing angle measures in the triangles.
Type below:
___________

Answer:
m∠B = 42°
m∠F = 69°
m∠H = 64°
m∠K = 53°

Explanation:
Using the Triangle Sum Theorem,
m∠A + m∠B + m∠C = 180°
85° + m∠B + 53° = 180°
138° + m∠B = 180°
m∠B = 180° – 138°
m∠B = 42°
Using the Triangle Sum Theorem,
m∠D + m∠E + m∠F = 180°
We substitute the given angle measures and we solve for m∠F
64° + 47° + m∠F = 180°
111° + m∠F = 180°
m∠F = 180° – 111°
m∠F = 69°
Using the Triangle Sum Theorem,
m∠G + m∠H + m∠J = 180°
We substitute the given angle measures and we solve for m∠H
47° + m∠H + 69° = 180°
116° + m∠H = 180°
m∠H = 180° – 116°
m∠H = 64°
Using the Triangle Sum Theorem,
m∠J + m∠K + m∠L = 180°
We substitute the given angle measures and we solve for m∠K
85° + m∠K + 42° = 180°
127° + m∠K = 180°
m∠K = 180° – 127°
m∠K = 53°

Question 6.
Which triangles are similar?
Type below:
___________

Answer:
△ABC and △JKL are similar because their corresponding angles are congruent. Also, △DEF and △GHJ are similar because their corresponding is congruent.

Question 7.
Analyze Relationships Determine which angles are congruent to the angles in △ABC.
∠A ≅ ∠ ________
∠B ≅ ∠ ________
∠C ≅ ∠ ________

Answer:
△JKL ≅ △ABC

Explanation:
△JKL has angle measures that are the same as those is △ABC
∠A ≅ ∠ J
∠B ≅ ∠ L
∠C ≅ ∠ K
Therefore, they are congruent.

Question 8.
Multistep A tree casts a shadow that is 20 feet long. Frank is 6 feet tall,and while standing next to the tree he casts a shadow that is 4 feet long.

a. How tall is the tree?
h = ________ ft

Answer:
h = 30 ft

Explanation:
In similar triangles, corresponding side lengths are proportional.
20/4 = h/6
5 = h/6
h = 30
The tree is 30 feet tall.

Question 8.
b. How much taller is the tree than Frank?
________ ft

Answer:
24 ft

Explanation:
30 – 6 = 24
The tree is 24 feet taller than Frank.

Question 9.
Represent Real-World Problems Sheila is climbing on a ladder that is attached against the side of a jungle gym wall. She is 5 feet off the ground and 3 feet from the base of the ladder, which is 15 feet from the wall. Draw a diagram to help you solve the problem. How high up the wall is the top of the ladder?
________ ft

Answer:
25 ft

Explanation:

3/15 = 5/h
15 ×3 = 3h
75 = 3h
h = 75/3 = 25

Question 10.
Justify Reasoning Are two equilateral triangles always similar? Explain.
______________

Answer:
yes; two equilateral triangles are always similar.
Each angle of an equilateral triangle is 60°. Since both triangles are equilateral then they are similar.

Angle-Angle Similarity – Page No. 368

Question 11.
Critique Reasoning Ryan calculated the missing measure in the diagram shown. What was his mistake?

\(\frac{3.4}{6.5}=\frac{h}{19.5}\)
19.5 × \(\frac{3.4}{6.5}=\frac{h}{19.5}\) × 19.5
\(\frac{66.3}{6.5}\) = h
10.2cm = h
Type below:
___________

Answer:
In the first line, Ryan did not take the sum of 6.5 and 19.5 to get the denominator on the right.
The denominator on the right should be 26 instead of 19.5
the correct value for h
3.4/6.5 = h/26
h = (3.4/6.5) × 26
h = 13.6cm

FOCUS ON HIGHER ORDER THINKING

Question 12.
Communicate Mathematical Ideas For a pair of triangular earrings, how can you tell if they are similar? How can you tell if they are congruent?
Type below:
___________

Answer:
The earrings are similar if two angle measures of one are equal to two angle measures of the other.
The earrings are congruent if they are similar and if the side lengths of one are equal to the side lengths of the other.

Question 13.
Critical Thinking When does it make sense to use similar triangles to measure the height and length of objects in real life?
Type below:
___________

Answer:
If the item is too tall or the distance is too long to measure directly, similar triangles can help with measuring.

Question 14.
Justify Reasoning Two right triangles on a coordinate plane are similar but not congruent. Each of the legs of both triangles are extended by 1 unit, creating two new right triangles. Are the resulting triangles similar? Explain using an example.
___________

Answer:
Two triangles are similar if their corresponding angles are congruent and the lengths of their corresponding sides are proportional. If each of the legs of both triangles is extended by 1 unit, the ratio between proportional sides does not change. Therefore, the resulting triangles are similar.

Ready to Go On? – Model Quiz – Page No. 369

11.1 Parallel Lines Cut by a Transversal

In the figure, line p || line q. Find the measure of each angle if m∠8 = 115°.

Question 1.
m∠7 = _________ °

Answer:
m∠7 = 65°

Explanation:
According to the exterior angle theorem,
m∠7 + m∠8 = 180°
m∠7 + 115° = 180°
m∠7 = 180° – 115°
m∠7 = 65°

Question 2.
m∠6 = _________ °

Answer:
m∠6 = 115°

Explanation:
From the given figure, Line P is parallel to line Q. So, the angles given in line P is equal to the angles in line Q. They are corresponding angles.
So, m∠8 is parallel is m∠6 or m∠8 = m∠6 = 115°

Question 3.
m∠1 = _________ °

Answer:
m∠1 = 115°

Explanation:
∠1 and ∠6 are alternative exterior angles.
So, m∠1 = m∠6 = 115°

11.2 Angle Theorems for Triangles

Find the measure of each angle.

Question 4.
m∠A = _________ °

Answer:
m∠A = 48°

Explanation:
m∠A + m∠B + m∠C = 180°
4y° + (3y + 22)° + 74° = 180°
7y = 180 – 96 = 84
y = 12°
m∠A = 4y° = 4 (12°) = 48°
m∠B = (3y + 22)° = (3(12°) + 22)° = 58°

Question 5.
m∠B = _________ °

Answer:
m∠B = 58°

Explanation:
m∠A + m∠B + m∠C = 180°
4y° + (3y + 22)° + 74° = 180°
7y = 180 – 96 = 84
y = 12°
m∠A = 4y° = 4 (12°) = 48°
m∠B = (3y + 22)° = (3(12°) + 22)° = 58°

Question 6.
m∠BCA = _________ °

Answer:
m∠BCA = 74°

Explanation:
m∠BCD + m∠BCA = 180°
106° + m∠BCA = 180°
m∠BCA = 180° – 106°
m∠BCA = 74°
So, m∠BCA = 74°

11.3 Angle-Angle Similarity

Triangle FEG is similar to triangle IHJ. Find the missing values.

Question 7.
x = _________

Answer:
x = 16

Explanation:
In similar triangles, corresponding side lengths are proportional.
HJ/EG = IJ/FG
(x + 12)/42 = 40/60
(x + 12)/42 = 4/6
6x = 96
x = 16

Question 8.
y = _________

Answer:
y = 9

Explanation:
In similar triangles, corresponding side lengths are congruent.
m∠HJI = m∠EGF
(5y + 7)° = 52°
5y° + 7° = 52°
5y° = 45°
y = 9

Question 9.
m∠H = _________°

Answer:
m∠H = 92°

Explanation:
Using the Triangle Sum Theorem,
m∠E + m∠F + m∠G = 180°
We substitute the given angle measures and we solve for m∠E
m∠E + 36° + 52° = 180°
m∠E + 88° = 180°
m∠E = 92°
In similar angles, corresponding side lengths are congruent
m∠H = m∠E
m∠H = 92°

ESSENTIAL QUESTION

Question 10.
How can you use similar triangles to solve real-world problems?
Type below:
____________

Answer:
we know that if two triangles are similar, then their corresponding angles are congruent and the lengths of their corresponding sides are proportional. We can use this to determine values that we cannot measure directly. For example, we can calculate the length of the tree if we measure its shadow and our shadow on a sunny day.

Selected Response – Mixed Review – Page No. 370

Use the figure for Exercises 1 and 2.

Question 1.
Which angle pair is a pair of alternate exterior angles?
Options:
A. ∠5 and ∠6
B. ∠6 and∠7
C. ∠5 and ∠4
D. ∠5 and ∠2

Answer:
C. ∠5 and ∠4

Explanation:
∠5 and ∠4 are alternate exterior angles

Question 2.
Which of the following angles is not congruent to ∠3?
Options:
A. ∠1
B. ∠2
C. ∠6
D. ∠8

Answer:
B. ∠2

Explanation:
∠2 and ∠3 are same-side interior angles. They are not congruent instead their sum is equal to 180°

Question 3.
The measures, in degrees, of the three angles of a triangle are given by 2x + 1, 3x – 3, and 9x. What is the measure of the smallest angle?
Options:
A. 13°
B. 27°
C. 36°
D. 117°

Answer:
B. 27°

Explanation:
From the Triangle Sum Theorem, the sum of the angles of the triangle is 180°
m∠1 + m∠2 + m∠3 = 180°
(2x + 1)° + (3x – 3)° + (9x)° = 180°
2x° + 1° + 3x° – 3° + 9x° = 180°
14x° – 2° = 180°
14x° = 178°
x = 13
Substitute the value of x to find the m∠1, m∠2, and m∠3
m∠1 = (2x + 1)° = (2(13) + 1)° = 27°
m∠2 = (3x – 3)° = (3(13) – 3)° = 36°
m∠3 = (9x)° = (9(13))° = 117°
The smallest angle is 27°

Question 4.
Which is a possible measure of ∠DCA in the triangle below?

Options:
A. 36°
B. 38°
C. 40°
D 70°

Answer:
D 70°

Explanation:
Using the Exterior Angle Theorem
m∠A + m∠B = m∠DCA
m∠A + 40° = m∠DCA
m∠DCA will be greater than 40°. The only suitable option is D, 70°.

Question 5.
Kaylee wrote in her dinosaur report that the Jurassic period was 1.75 × 10⁸ years ago. What is this number written in standard form?
Options:
A. 1,750,000
B. 17,500,000
C. 175,000,000
D. 17,500,000,000

Answer:
C. 175,000,000

Explanation:
1.75 × 10⁸ standard form
Move the decimal point to 8 right places.
175,000,000

Question 6.
Given that y is proportional to x, what linear equation can you write if y is 16 when x is 20?
Options:
A. y = 20x
B. y = \(\frac{5}{4}\) x
C. y = \(\frac{4}{5}\)x
D. y = 0.6x

Answer:
C. y = \(\frac{4}{5}\)x

Explanation:
Y=4/5x
16=4/5(20)
4/5×20/1=80/5
80/5=16

Mini-Task

Question 7.
Two transversals intersect two parallel lines as shown.

a. What is the value of x?
x = ________

Answer:
x = 4

Explanation:
m∠JKL = m∠LNM
6x + 1 = 25
6x = 24
x = 4

Question 7.
b. What is the measure of ∠LMN?
_________°

Answer:
23°

Explanation:
m∠LMN = 3x + 11 = 3(4) + 11 = 12 + 11 = 23

Question 7.
c. What is the measure of ∠KLM?
∠KLM = _________°

Answer:
∠KLM = 48°

Explanation:
∠KLM exterior angle of the triangle LMN
m∠KLM = m∠LNM + m∠LMN
= 25 + 23 = 48

Question 7.
d. Which two triangles are similar? How do you know?
Type below:
_____________

Answer:
triangle JKL = triangle LNM
triangle KJL = triangle LMN

Explanation:
triangle JLK and triangle LNM are similar.
triangle JKL = triangle LNM
triangle KJL = triangle LMN

Summary:

The solutions provided in the Go Math Grade 8 Answer Key Chapter 11 Angle Relationships in Parallel Lines and Triangles are made by the professionals. Practice all the math questions available on the 8th Grade Text Book and learn how to solve the questions in a simple way. Hope the information provided in this article is beneficial for all the students of grade 8. Keep in touch with our website to get the pdfs of all the Go Math Grade 8 Answer Key Chapterwise.

Theoretical Probability is the most interesting topic in grade 7 math. Students can get the best solutions for each and every question in Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations. The Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability & Simulations consists of questions on experimental and theoretical probability. So, Download Go Math Grade 7 Chapter 13 Theoretical Probability and Simulations pdf and schedule your practice.

Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations

Theoretical Probability tells us how likely something is to happen in the long run. We can calculate the problems on probability by looking at the outcomes of the experiment or by reasoning about the possible outcomes. It is very easy if you understand the concept of theoretical probability. Enhance your math skills by following HMH Go Math Grade 7 Theoretical Probability and Simulations Answer Key pdf.

Chapter 13 Theoretical Probability and Simulations – Lesson: 1

• Guided Practice – Page No. 402
• Independent Practice – Page No. 403
• H.O.T. – Page No. 404

Chapter 13 Theoretical Probability and Simulati+ons – Lesson: 2

• Guided Practice – Page No. 408
• Independent Practice – Page No. 409
• Page No. 410

Chapter 13 Theoretical Probability and Simulations – Lesson: 3

• Guided Practice – Page No. 414
• Independent Practice – Page No. 415
• Page No. 416

Chapter 13 Theoretical Probability and Simulations – Lesson: 4

• Guided Practice – Page No. 420
• Independent Practice – Page No. 421
• Page No. 422

Chapter 13 Theoretical Probability and Simulations – Lesson: 5

• 13.1, 13.2 Theoretical Probability of Simple and Compound Events – Page No. 423
• Selected Response – Page No. 424

Chapter 13 Theoretical Probability and Simulations – Lesson: 6

• EXERCISES – Page No. 425
• Page No. 426

Chapter 13 Theoretical Probability and Simulations – Lesson: 7

• EXERCISES – Page No. 427
• Page No. 428

Chapter 13 Theoretical Probability and Simulations – Lesson: 8

• Selected Response – Page No. 429
• Page No. 430

Guided Practice – Page No. 402

At a school fair, you have a choice of randomly picking a ball from Basket A or Basket B. Basket A has 5 green balls, 3 red balls, and 8 yellow balls. Basket B has 7 green balls, 4 red balls, and 9 yellow balls. You can win a digital book reader if you pick a red ball.

Question 1.
Complete the chart. Write each answer in simplest form.
Type below:
______________

Answer:
We complete the table:

Question 2.
Which basket should you choose if you want the better chance of winning?
______

Answer: Basket B

Explanation:
In Exercise 1 we determined the probabilities Pa, Pb to pick a red ball from basket A, B
Pa = \(\frac{3}{16}\)
Pb = \(\frac{1}{5}\)
We compare the two probabilities
Pa = \(\frac{3}{16}\) . \(\frac{5}{5}\) = \(\frac{15}{80}\)
Pb = \(\frac{1}{5}\) . \(\frac{5}{5}\) = \(\frac{16}{80}\)
\(\frac{16}{80}\) > \(\frac{15}{80}\)
Pb > Pa
Since Pb > Pa, the better chance to win is in choosing Basket B.

A spinner has 11 equal-sized sections marked 1 through 11. Find each probability.

Question 3.
You spin once and land on an odd number.
\(\frac{□}{□}\)

Answer: \(\frac{6}{11}\)

Explanation:
We are given an 11 equal sized sections marked 1-11:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
We compute the probability that spinning once we would land on an odd number (1, 3, 5, 7, 9, 11):
P(odd) = number of odd sections/total number of sections = \(\frac{6}{11}\)

Question 4.
You spin once and land on an even number.
\(\frac{□}{□}\)

Answer: \(\frac{5}{11}\)

Explanation:
We are given an 11 equal sized sections marked 1-11:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
P(even) = number of even sections/total number of sections = \(\frac{5}{11}\)
We compute the probability that spinning once we would land on an even number (2, 4, 6, 8, 10)

You roll a number cube once.

Question 5.
What is the theoretical probability that you roll a 3 or 4?
\(\frac{□}{□}\)

Answer: \(\frac{1}{3}\)

Explanation:
P(3 or 4) = number of 3 or 4/total number of numbers on the number cube
\(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 6.
Suppose you rolled the number cube 199 more times. Would you expect the experimental probability of rolling a 3 or 4 to be the same as your answer to Exercise 5?
Type below:
______________

Answer:
When rolling a number cube a large number of times, we expect the experimental probability not to be the same, but to get closer and closer to the theoretical probability.
Since 199 is not such a big number, we should not expect the experimental probability to be extremely close \(\frac{1}{3}\), but close enough.

Essential Question Check-In

Question 7.
How can you find the probability of a simple event if the total number of equally likely outcomes is 20?
Type below:
______________

Answer:
P(Simple event) = 1/total number of equally likely events
= \(\frac{1}{20}\)

Independent Practice – Page No. 403

Find the probability of each event. Write each answer as a fraction in simplest form, as a decimal to the nearest hundredth, and as a percent to the nearest whole number.

Question 8.
You spin the spinner shown. The spinner lands on yellow.

Type below:
______________

Answer: \(\frac{2}{6}\)

Explanation:
There are 2 yellow and 4 blue and we landed on yellow what is the probability of landing on yellow.
The probability is \(\frac{2}{6}\) because there are 2 yellow and the rest is blue.

Question 9.
You spin the spinner shown. The spinner lands on blue or green.

Type below:
______________

Answer: 67%

Explanation:
The yellow area, the blue area, and the green area have 3 sections each from the whole area.
We determine the probability that the spinner lands on a blue or green sections:
P(spinner lands on blue or green) = (the number of blue sections + the number of green sections)/the total number f sections
= (4 + 4)/12 = \(\frac{8}{12}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) ≈ 0.67 = 67%

Question 10.
A jar contains 4 cherry cough drops and 10 honey cough drops. You choose one cough drop without looking. The cough drop is cherry.
Type below:
______________

Answer: 28%

Explanation:
We are given the data:
A jar contains 4 cherry cough drops and 10 honey cough drops.
P(to pick a cherry drop) = (the number of cherry drops)/the total number of drops
4/(4 + 10) = \(\frac{4}{14}\) = \(\frac{2}{7}\)
\(\frac{2}{3}\) ≈ 0.28 = 28%

Question 11.
You pick one card at random from a standard deck of 52 playing cards. You pick a black card.
Type below:
______________

Answer: 50%

Explanation:
We are given the data
You pick one card at random from a standard deck of 52 playing cards.
26 red cards
26 black cards
P(to pick a black card) = the number of black cards/the total number of cards

Question 12.
There are 12 pieces of fruit in a bowl. Five are lemons and the rest are limes. You choose a piece of fruit without looking. The piece of fruit is a lime.
Type below:
______________

Answer: 58%

Explanation:
There are 12 pieces of fruit in a bowl. Five are lemons and the rest are limes.
12 fruits:
5 lemons
7 limes
P(to pick a lime) =the number of lines/the total number of fruits
W determine the probability that we pick a lime:
\(\frac{7}{12}\) ≈ 0.58 = 58%

Question 13.
You choose a movie CD at random from a case containing 8 comedy CDs, 5 science fiction CDs, and 7 adventure CDs. The CD is not a comedy.
Type below:
______________

Answer: 60%

Explanation:
We are given the data:
8 comedy CDs
5 science fiction CDs
7 adventure CDs
P(to pick a CD which is not a comedy) = (the number of Sf CDs + the number of adventure CDs)/ the total number of CDs
= (5 + 7)/(8 + 5 + 7) = \(\frac{12}{20}\) = \(\frac{3}{5}\) = 0.60 = 60%

Question 14.
You roll a number cube. You roll a number that is greater than 2 and less than 5.
Type below:
______________

Answer: 33%

Explanation:
Rolling a number greater than 2 and less than 5 means to roll one of the numbers:
3, 4
P(to roll 3 or 4) = the number of 3 or 4 numbers/the total number of numbers
= (1 + 1)/6 = \(\frac{2}{6}\) = \(\frac{1}{3}\) = 0.33 = 33%

Question 15.
Communicate Mathematical Ideas
The theoretical probability of a given event is \(\frac{9}{13}\). Explain what each number represents.
Type below:
______________

Answer:
The theoretical probability is the ratio between the number of favorable outcomes and the number of possible outcomes. The numerator 9 describes the number of desired events, while the denominator 13 describes the total number of events.
\(\frac{9}{13}\)

Question 16.
Leona has 4 nickels, 6 pennies, 4 dimes, and 2 quarters in a change purse. Leona lets her little sister Daisy pick a coin at random. If Daisy is equally likely to pick each type of coin, what is the probability that her coin is worth more than five cents? Explain.
\(\frac{□}{□}\)

Answer: \(\frac{3}{8}\)

Explanation:
Leona has 4 nickels, 6 pennies, 4 dimes, and 2 quarters in a change purse. Leona lets her little sister Daisy pick a coin at random.
1 penny = 1 cent
1 nickel = 5 cents
1 dime = 10 cents
1 quarter = 25 cents
We determine the probability that she picks a coin which is worth more than 5 cents is:
P(to pick a coin worth more than 5 cents) = the number of dimes+the number of quarters/the total number of coins
= (4 + 2)/(4 + 6 + 4 + 2) = \(\frac{6}{16}\) = \(\frac{3}{8}\) = 0.375 = 37.5%

H.O.T. – Page No. 404

Focus on Higher Order Thinking

Question 17.
Critique Reasoning
A bowl of flower seeds contains 5 petunia seeds and 15 begonia seeds. Riley calculated the probability that a randomly selected seed is a petunia seed as \(\frac{1}{3}\). Describe and correct Riley’s error.
Type below:
______________

Answer:
We are given the data
5 petunia seeds
15 begonia seeds
P(to pick a petunia seed) = the number of petunia seeds/the total number of seeds
We determine the probability that a randomly selected seed is the petunia seed
5/(5 + 15) = 5/20 = 1/4
Wrong:
Riley made the mistake in dividing the number of petunia seeds by the number of begonia seeds instead of dividing the number of petunia seeds to the total number of seeds:
P(to pick a petunia seed) = the number of petunia seeds/the total number of begonia seeds
= 5/15 = 1/3

Question 18.
There are 20 seventh graders and 15 eighth graders in a club. A club president will be chosen at random.
a. Analyze Relationships
Compare the probabilities of choosing a seventh grader or an eighth grader.
Type below:
______________

Answer:
We are given the data:
20 seventh graders
15 eighth graders
P(to pick a seventh-grader) = the number of seventh-graders/the total number of members
= 20/(20 + 15) = 20/35 = 4/7
We determine the probability of choosing a seventh-grader:
P(to pick an eighth-grader) = the number of eighth-graders/the total number of members
= 15/(20 + 15) = 15/35 = 3/7
Since 4/7 > 3/7, the probability of choosing a seventh-grader is higher than the probability of choosing an eighth-grader.

Question 18.
b. Critical Thinking
If a student from one grade is more likely to be chosen than a student from the other, is the method unfair? Explain.
Type below:
______________

Answer:
The method is not unfair because the number of seventh graders is greater than the number of eighth members (20 > 15), thus the seventh graders should be represented at a higher degree than the eighth graders.

A jar contains 8 red marbles, 10 blue ones, and 2 yellow ones. One marble is chosen at random. The color is recorded in the table, and then it is returned to the jar. This is repeated 40 times.

Question 19.
Communicate Mathematical Ideas
Use proportional reasoning to explain how you know that for each color, the theoretical and experimental probabilities are not the same.
Type below:
______________

Answer:
We are given the data
8 red marbles
10 blue marbles
2 yellow marbles
We determine the theoretical probability Pt of choosing each type of marble:
Pt(to pick a red marble) = the number of red marbles/the total number of marbles
= 8/(8 + 10 + 2) = 8/20 = 4/10
Pt(to pick a blue marble) = the number of blue marbles/the total number of marbles
= 10/(8 + 10 + 2) = 10/20 = 5/10
Pt(to pick a yellow marble) = the number of yellow marbles/the total number of marbles
= 2/(8 + 10 + 2) = 2/20 = 1/10
We determine the theoretical probability Pe of choosing each type of marble
Pe(to pick a red marble) = the number of red marbles/the total number of marbles
14/14+16+10 = 14/40 = 7/20
Pe(to pick a blue marble) = the number of blue marbles/the total number of marbles
16/14+16+10 = 16/40 = 8/20
Pe(to pick a yellow marble) = the number of yellow marbles/the total number of marbles
10/14+16+10 = 10/40 = 5/20
We notice that the number of red marbles is 4 times the number of yellow marbles, thus the theoretical probability to choose a red marble is 4 times greater than the one of choosing a yellow marble, while the experimental case shows that the probability of choosing a red marble is less than 1.5 times greater than the one of choosing a yellow one.
In the same way, we notice that the number of blue marbles is 5 times the number of yellow marbles, thus the theoretical probability to choose a blue marble is 5 times greater than the one of choosing a yellow marble, while the experimental case shows that the probability of choosing a blue marble is less than 2 times greater than the one of choosing a yellow one.
The exact probabilities are computed above.

Question 20.
Persevere in Problem Solving
For which color marble is the experimental probability closest to the theoretical probability? Explain.
______________

Answer:
We are given the data
8 red marbles
10 blue marbles
2 yellow marbles
Pt(to pick a red marble) = 8/20 = 4/10
Pt(to pick a blue marble) = 10/20 = 5/10
Pt(to pick a yellow marble) = 2/20 = 1/10
Pe(to pick a red marble) = 14/40 = 7/20
Pe(to pick a blue marble) = 16/40 = 8/20
Pe(to pick a yellow marble) = 10/40 = 5/20
|\(\frac{7}{20}\) – \(\frac{8}{20}\)| = \(\frac{1}{20}\)
|\(\frac{8}{20}\) – \(\frac{10}{20}\)| = \(\frac{2}{20}\)
|\(\frac{5}{20}\) – \(\frac{2}{20}\)| = \(\frac{3}{20}\)
\(\frac{1}{20}\) < \(\frac{2}{20}\) < \(\frac{3}{20}\)
Thus the answer is red.

Guided Practice – Page No. 408

Drake rolls two fair number cubes.

Question 1.
Complete the table to find the sample space for rolling a particular product on two number cubes.

Type below:
______________

Answer:
We complete the table to find the sample space for rolling a particular product on two number cubes:

Question 2.
What is the probability that the product of the two numbers Drake rolls is a multiple of 4?
\(\frac{□}{□}\)

Answer: \(\frac{5}{12}\)

Explanation:

We find the products which are multiplies of 4:
4, 4, 8, 12, 12, 4, 8, 12, 14, 20, 24, 20, 12, 24, 36.
The number of multiples of 4 is 15.
The total number of products is
6 × 6 = 36
We determine the probability that the product is multiple of 4:
\(\frac{15}{36}\) = \(\frac{5}{12}\)

Question 3.
What is the probability that the product of the two numbers Drake rolls is less than 13?
\(\frac{□}{□}\)

Answer: \(\frac{23}{36}\)

Explanation:

We find products which are less than 13:
1, 2, 3, 4, 5, 6, 2, 4, 6, 8, 10, 12, 3, 6, 9, 12, 4, 8, 12, 5, 10, 6, 12
The number of products of less than 13 is 6 × 6 = 36.
The total number of products is
23/36

You flip three coins and want to explore probabilities of certain events.

Question 4.
Complete the tree diagram and make a list to find the sample space.

Type below:
______________

Answer:
We complete the given tree diagram placing one H and one T under each H and each T:

Question 5.
How many outcomes are in the sample space?
_______

Answer: 8 outcomes

Explanation:

Since each coin can land in two possible ways, the total possible number of outcomes is
2³ = 8
Thus there are 8 outcomes in the sample space.

Question 6.
List all the ways to get three tails.
Type below:
______________

Answer:
We are given the tree diagram we determined in Exercise 4:

The list of the 8 possible outcoes is
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
We list the outcomes containing 3 tails is TTT.

Question 7.
Complete the expression to find the probability of getting three tails.
\(\frac{□}{□}\)

Answer: \(\frac{1}{8}\)

Explanation:
P = number of outcomes with 3T/ total number of possible outcomes
The probability of getting three tails when three coins are flipped is \(\frac{1}{8}\)

Question 8.
What is the probability of getting exactly two heads?
\(\frac{□}{□}\)

Answer: \(\frac{3}{8}\)

Explanation:
The list of the 8 possible outcomes is:
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
We list the outcomes of 2H
HHT, HTH, THH
There are 3 ways to obtain exactly two heads is HHT, HTH, THH
P = number of outcomes with 3H/ total number of possible outcomes
P = \(\frac{3}{8}\)

Essential Question Check-In

Question 9.
There are 6 ways a given compound event can occur. What else do you need to know to find the theoretical probability of the event?
Type below:
______________

Answer:
We know that there are 6 ways in which a given compound event can occur and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(event) = favorable outcomes/possible outcomes
Since we know the number of favorable outcomes, we also require the number of possible outcomes in order to determine the probability.

Independent Practice – Page No. 409

In Exercises 10–12, use the following information. Mattias gets dressed in the dark one morning and chooses his clothes at random. He chooses a shirt (green, red, or yellow), a pair of pants (black or blue), and a pair of shoes (checkered or red).

Question 10.
Use the space below to make a tree diagram to find the sample space.
Type below:
______________

Answer:
The sample space is:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
yellow Black Red
Yellow Black Checkered

Question 11.
What is the probability that Mattias picks an outfit at random that includes red shoes?
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
Shirt Pants Shoes:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
Yellow Black Red
Yellow Black Checkered
P = the number of outfits with red shoes/the total number of outfits
P = \(\frac{6}{12}\)
P = \(\frac{1}{2}\)

Question 12.
What is the probability that no part of Mattias’s outfit is red?
\(\frac{□}{□}\)

Answer: \(\frac{1}{3}\)

Explanation:
Shirt Pants Shoes:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
Yellow Black Red
Yellow Black Checkered
P = the number of outfits with no red shoes/the total number of outfits
P = \(\frac{4}{12}\)
P = \(\frac{1}{3}\)

Question 13.
Rhee and Pamela are two of the five members of a band. Every week, the band picks two members at random to play on their own for five minutes. What is the probability that Rhee and Pamela are chosen this week?
\(\frac{□}{□}\)

Answer: \(\frac{1}{10}\)

Explanation:
Let’s note the 5 members of the band:
R = Rhee
P = Pamela
A, B, C = the other 3 members
The list of the possible outcomes is:
RP, RA, RB, RC, PR, PA, PB, AP, AR, AB, AC, BP, BR, BA, BC, CP, CR, CA, CB.
P = the number of outcomes containing P and R/the total number of outcomes
P = \(\frac{2}{20}\)
P = \(\frac{1}{10}\)

Question 14.
Ben rolls two number cubes. What is the probability that the sum of the numbers he rolls is less than 6?
\(\frac{□}{□}\)

Answer: \(\frac{5}{18}\)

The sums less than 6 are:
2, 3, 4, 5, 3, 4, 5, 4, 5, 5
P = the number of sums less than 6/the total number of sums
P = \(\frac{10}{36}\)
P = \(\frac{5}{18}\)

Question 15.
Nhan is getting dressed. He considers two different shirts, three pairs of pants, and three pairs of shoes. He chooses one of each of the articles at random. What is the probability that he will wear his jeans but not his sneakers?

\(\frac{□}{□}\)

Answer: \(\frac{2}{9}\)

Explanation:
We are given the data
Shirt: collared/T-shirt
Pants: Khakis/jeans/shorts
Shoes: sneakers/flip-flops/sandals
We determine the outcomes including jeans and not sneakers
P = the outcome including jeans and not sneakers/all possible outcomes
P = \(\frac{4}{18}\) = \(\frac{2}{9}\)

Question 16.
Communicate Mathematical Ideas
A ski resort has 3 chair lifts, each with access to 6 ski trails. Explain how you can find the number of possible outcomes when choosing a chair lift and a ski trail without making a list, a tree diagram, or table.
Type below:
______________

Answer: 18

Explanation:
We are given the data:
Chair lifts: Chair lift 1/chair lift 2/chair lift 3
Ski trails: ski trail 1/ski trail 2/ski trail 3/ski trail 4/ski trail 5/ski trail 6
The sample space for choosing one of each is the product between the number of chair lifts and the number of ski lifts:
3 × 6 = 18

Question 17.
Explain the Error
For breakfast, Sarah can choose eggs, granola or oatmeal as a main course, and orange juice or milk for a drink. Sarah says that the sample space for choosing one of each contains 3² = 9 outcomes. What is her error? Explain.
Type below:
______________

Answer:
We are given the data:
Main course: eggs/granola/oatmeal
Drink: orange juice/milk
The sample space for choosing one of each is:
3 × 2 = 6
eggs-orange juice
eggs-milk
granola-orange juice
granola-milk
oatmeal-orange juice
oatmeal-milk
The error made by Sarah is that she considered only the number of main courses and forgetting the number of drinks.

Page No. 410

Question 18.
Represent Real-World Problems
A new shoe comes in two colors, black or red, and in sizes from 5 to 12, including half sizes. If a pair of the shoes is chosen at random for a store display, what is the probability it will be red and size 9 or larger?
\(\frac{□}{□}\)

Answer: \(\frac{7}{30}\)

Explanation:
We are given the data
Colors: black/red
Sizes: 5/5.5/6/6.5/7/7.5/8/8.5/9/9.5/10/10.5/11/11.5/12
The possible outcomes of red shoes with size greater or equal 9 are
red 9
red 9.5
red 10
red 10.5
red 11
red 11.5
red 12
P = the number of red shoes with size greater or equal 9/the total number of outcomes
P = 7/(2 × 15) = \(\frac{7}{30}\)

H.O.T.

Focus on Higher Order Thinking

Question 19.
Analyze Relationships
At a diner, Sondra tells the server, “Give me one item from each column.” Gretchen says, “Give me one main dish and a vegetable.” Who has a greater probability of getting a meal that includes salmon? Explain.

______________

Answer:
We are given the data:
Main Dish: Pasta/salmon/beef/pork
Vegetable: carrots/peas/asparagus/sweet potato
Side: tomato soup/tossed salad
Psondra = (1 . 4 . 2)/(4 . 4 . 2) = \(\frac{8}{32}\) = \(\frac{1}{4}\)
Pgretchen = 4/16 = \(\frac{1}{4}\)

Question 20.
The digits 1 through 5 are used for a set of locker codes.
a. Look for a Pattern
Suppose the digits cannot repeat. Find the number of possible two-digit codes and three-digit codes. Describe any pattern and use it to predict the number of possible five-digit codes.
Type below:
______________

Answer: 20, 60, 120

Explanation:
We are given the data
Digits: 1, 2, 3, 4, 5
We find the two digits codes when digits do not repeat
12, 13, 14, 15
21, 23, 24, 25
31, 32, 34, 35
41, 42, 43, 45
51, 52, 53, 54
There are 5 × 4 = 20 possible codes.
We find the three digits codes when digits do not repeat:
123, 124, 125
132, 134, 135
142, 143, 145
152, 153, 154
213, 214, 215
231, 124, 135
…
….
512, 513, 514
521, 523, 524
531, 532, 534
541, 542, 543
There are 5 × 4 × 3 = 60 possible outcomes
If we use 5 digits and none can repeat, the first digit can be one of the numbers 1 2 3 4 5, the second digit can be one of the 4 remaining numbers, the third digit is one of the 3 remaining numbers, the fourth digit is one of the two remaining numbers, thus the number of possible outcomes is:
5 × 4 × 3 × 2 = 120

Question 20.
b. Look for a Pattern
Repeat part a, but allow digits to repeat.
Type below:
______________

Answer:
We find the two digits codes when digits can repeat:
11, 12, 13, 14, 15,
21, 22, 23, 24, 25
31, 32, 33, 34, 35
41, 42, 43, 44, 45
51, 52, 53, 54, 55
There are 5 . 5 = 25 possible codes.
There are 5 × 5 × 5 = 125 possible codes.
If we use 5 digits and they can repeat, the first digit can be one of the numbers 1 2 3 4 5, the second digit can be one of the same numbers 1 2 3 4 5, the third digit is one of the 5 numbers, the fourth digit is one of the 5 numbers, the fifth digit is one of the 5 numbers, thus the number of possible outcomes is
5 × 5 × 5 × 5 × 5 = 3125

Question 20.
c. Justify Reasoning
Suppose that a gym plans to issue numbered locker codes by choosing the digits at random. Should the gym use codes in which the digits can repeat or not? Justify your reasoning.
Type below:
______________

Answer:
The probability P1 to get a 2 digits code when digits do not repeat and the probability P2 to get a 2 digits code when digits can repeat:
P1 = 1/20
P2 = 1/25
The probability P1 to get a 3 digits code when digits do not repeat and the probability P2 to get a 3 digits code when digits can repeat:
P1 = 1/60
P2 = 1/125
The probability P1 to get a 5 digits code when digits do not repeat and the probability P2 to get a 5 digits code when digits can repeat:
P1 = 1/120
P2 = 1/3125
Thus the gym should use codes in which digits can repeat because the probability to be guessed is much smaller.

Guided Practice – Page No. 414

Question 1.
Bob works at a construction company. He has an equally likely chance to be assigned to work different crews every day. He can be assigned to work on crews building apartments, condominiums, or houses. If he works 18 days a month, about how many times should he expect to be assigned to the house crew?
_______ times

Answer:
Step 1:
Apartment: \(\frac{1}{3}\) Condo: \(\frac{1}{3}\) House: \(\frac{1}{3}\)
Probability of being assigned to the house crew: \(\frac{1}{3}\)
Step 2:
\(\frac{1}{3}\) = \(\frac{x}{18}\)
x = 6
6 times out of 18.

Question 2.
During a raffle drawing, half of the ticket holders will receive a prize. The winners are equally likely to win one of three prizes: a book, a gift certificate to a restaurant, or a movie ticket. If there are 300 ticket holders, predict the number of people who will win a movie ticket.
_______ people

Answer: 50 people

Explanation:
If 300 people buy tickets and half of them will receive a prize then 300 × 1/2 = 150 ticket holders will receive a prize. If they are equally likely to win one of the three prizes, then the probability of winning a movie ticket is 1/3. The number of people who will win a movie ticket is then 1/3 × 150 = 50 people.

Question 3.
In Mr. Jawarani’s first period math class, there are 9 students with hazel eyes, 10 students with brown eyes, 7 students with blue eyes, and 2 students with green eyes. Mr. Jawarani picks a student at random. Which color eyes is the student most likely to have? Explain.
______________

Answer: Brown

Explanation:
There are more students with brown eyes then any other colored eyes so if he picks a student at random, they will most likely have brown eyes.

Essential Question Check-In

Question 4.
How do you make predictions using theoretical probability?
Type below:
______________

Answer:
To make a prediction using theoretical probability, you can multiply the theoretical probability by the number of events to get a prediction. You can find the prediction by setting the theoretical probability equal to the ratio of x/number of events and then solving for x, where x is the prediction.

Independent Practice – Page No. 415

Question 5.
A bag contains 6 red marbles, 2 white marbles, and 1 gray marble. You randomly pick out a marble, record its color, and put it back in the bag. You repeat this process 45 times. How many white or gray marbles do you expect to get?
_______ marbles

Answer: 15

Explanation:
Given that there are 6 red marbles, 2 white marbles, and 1 gray marble, which are thus 6 + 2 + 1 = 9 marbles in total.
possible outcomes = 9
2 + 1 = 3 of the marbles are either white or gray and thus there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(white or gray) = favorable outcomes/possible outcomes = \(\frac{3}{9}\)
= \(\frac{1}{3}\)
The predicted number of white or gray marbles is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P (white or gray)
= 45 × \(\frac{1}{3}\)
= 15
Thus we predict that we obtain a white or gray marble about 15 times.

Question 6.
Using the blank circle below, draw a spinner with 8 equal sections and 3 colors—red, green, and yellow. The spinner should be such that you are equally likely to land on green or yellow, but more likely to land on red than either on green or yellow.

Type below:
______________

Answer:
A possible spinner would be to have 4 red sections, 2 green sections, and 2 yellow sections. That way there is an equal chance of landing on yellow and green and there is a more likely chance of landing on yellow and green and there is a more likely chance of landing on red than landing on green or landing on yellow.
A second possible spinner could be to have 6 red sections, 1 yellow section, and 1 green section. This would still give an equal chance to land on green or yellow and a higher chance to land on red than to land on green or land on yellow.

Use the following for Exercises 7–9. In a standard 52-card deck, half of the cards are red and half are black. The 52 cards are divided evenly into 4 suits: spades, hearts, diamonds, and clubs. Each suit has three face cards (jack, queen, king), and an ace. Each suit also has 9 cards numbered from 2 to 10.

Question 7.
Dawn draws 1 card, replaces it, and draws another card. Is it more likely that she draws 2 red cards or 2 face cards?
______________

Answer: 2 red cards

Explanation:
There are 26 red cards in the deck and 12 face cards in the deck so it is more likely to draw two red cards than it is to draw two face cards.

Question 8.
Luis draws 1 card from a deck, 39 times. Predict how many times he draws an ace.
_______ times

Answer: About 3 times

Explanation:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs), and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q, and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
4 of the 52 cards in a standard deck of cards area aces and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(white or gray) = favorable outcomes/possible outcomes = \(\frac{4}{52}\)
= \(\frac{1}{13}\)
The predicted number of aces is then obtained by multiplying the number of draws by the probability.
Prediction = Number of draws × P(Ace)
= 39 × \(\frac{1}{3}\)
Thus we predict that 3 of the drawn cards will be aces.

Question 9.
Suppose a solitaire player has played 1,000 games. Predict how many times the player turned over a red card as the first card.
_______ times

Answer: 500 times

Explanation:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs) and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
26 of the 52 cards in a standard deck of cards are red. This then implies that there are 26 favorable outcomes.
favorable outcomes = 26
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{26}{52}\) = 1/2
The predicted number of aces is then obtained by multiplying the number of draws by the probability.
Prediction = Number of draws × P(Red)
= 1000 × \(\frac{1}{2}\)
= 500
Thus we predict that 500 of the drawn cards will be red.

Question 10.
John and O’Neal are playing a board game in which they roll two number cubes. John needs to get a sum of 8 on the number cubes to win. O’Neal needs a sum of 11. If they take turns rolling the number cube, who is more likely to win? Explain.
______________

Answer: John

Explanation:
To get a sum of 8, John can roll the following numbers:
2, 6
3, 5
4, 4
5, 3
6, 2
To get a sum of 11, O’Neal can roll the following numbers:
5, 6
6, 5
Since there are more ways to roll a sum of 8 than there are to roll a sum of 11, John is more likely to win.

Question 11.
Every day, Navya’s teacher randomly picks a number from 1 to 20 to be the number of the day. The number of the day can be repeated. There are 180 days in the school year. Predict how many days the number of the day will be greater than 15.
_______ days

Answer: 45 days

Explanation:
There are 20 numbers from 1 to 20 and thus there are 20 possible outcomes.
possible outcomes = 20
5 of the 20 numbers from 1 to 20 are greater than 15 (16, 17, 18, 19, 20) and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(greater than 15) = favorable outcomes/possible outcomes = \(\frac{5}{20}\) = \(\frac{1}{4}\)
The predicted is the number of favorable outcomes divided by the number of possible outcomes/
Prediction = Number of days × P(Greater than 15)
180 × \(\frac{1}{4}\)
= 45
Thus we predict that 45 of the days have a number greater than 15.

Question 12.
Eben rolls two standard number cubes 36 times. Predict how many times he will roll a sum of 4.
_______ times

Answer: 3 times

Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6.
There are then 6 × 6 = 36 possible outcomes when rolling 2 dice.
possible outcomes = 6 . 6 = 36
3 of the outcomes in the image below result in a sum of 4 ((1, 3), (2, 2), (3, 1)) and thus there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(sum is 4) = favorable outcomes/possible outcomes = \(\frac{3}{36}\) = 1/12
The predicted is the number of rolls that result in a sum of 4 is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(sum is 4)
= 36 × 1/12
= 3
Thus we predict that 3 of the rolls result in a sum of 4.

Question 13.
Communicate Mathematical Ideas
Can you always show that a prediction based on theoretical probability is true by performing the event often enough? If so, explain why. If not, describe a situation that justifies your response.
Type below:
______________

Answer:
You cannot show that a prediction based on theoretical probability is true by performing the event often enough. The prediction value will get closer to the actual value as more events are performed but will not always equal the actual value.

Page No. 416

Question 14.
Represent Real-World Problems
Give a real-world example of an experiment in which all of the outcomes are not equally likely. Can you make a prediction for this experiment, using theoretical probability?
Type below:
______________

Answer:
A real work example of an experiment in which all of the outcomes are not equally likely could be spinning a spinner that has 1 red section, 2 orange sections, and 3 blue sections, and the sections are of the same size. Since there are not the same number of sections for each other, the outcomes of red, orange, and blue do not have the same probabilities. A prediction can still be made because the theoretical probabilities of landing on each color can be found. If you wanted to predict the number of times you would land on blue in 100 spins, you would first need to find the theoretical probability of landing on blue. Since there are 3 blue sections and a total of 6 sections, the theoretical probability is \(\frac{3}{6}\) = \(\frac{1}{2}\). The prediction would then be \(\frac{1}{2}\) × 100 = 50 times.

H.O.T.

Focus on Higher Order Thinking

Question 15.
Critical Thinking
Pierre asks Sherry a question involving the theoretical probability of a compound event in which you flip a coin and draw a marble from a bag of marbles. The bag of marbles contains 3 white marbles, 8 green marbles, and 9 black marbles. Sherry’s answer, which is correct, is \(\frac{12}{40}\). What was Pierre’s question?
Type below:
______________

Answer: What is the probability of drawing a white or black marble and flipping heads?

Question 16.
Make a Prediction
Horace is going to roll a standard number cube and flip a coin. He wonders if it is more likely that he rolls a 5 and the coin lands on heads, or that he rolls a 5 or the coin lands on heads. Which event do you think is more likely to happen? Find the probability of both events to justify or reject your initial prediction.
Type below:
______________

Answer:
It is more likely that he rolls a 5 or flips heads than it is to roll a 5 and flip heads. This is because the probability of two events occurring at the same time is always less than the probability of one or another event occurring. The probability of rolling a 5 is 1/6 and the probability of flipping heads is 1/2 so the probability of both occurring is 1/6 × 1/2 = 1/12.
There are 12 possible outcomes to rolling a number cube and flipping a coin since there are 6 outcomes for the cube and 2 outcomes for the coin and 6 × 2 = 12.
Of those 12 outcomes, 7 of them are rolling a 5 or flipping heads (1H, 2H, 3H, 4H, 5H, 6H, 5T). The probability of rolling a 5 or flipping heads is then 7/12 which is greater than 1/12.

Question 17.
Communicate Mathematical Ideas
Cecil solved a theoretical prediction problem and got this answer: “The spinner will land on the red section 4.5 times.” Is it possible to have a prediction that is not a whole number? If so, give an example.
Type below:
______________

Answer: Yes
It is possible if what is being predicted does not have to be a whole number, like time. A possible example could be, the theoretical probability that there will be 50 people in a line at a store during a one-hour interval is 1/12. What is the predicted number of hours that there will be 50 people in line if the store is open for 9 hours? The prediction would then be 1/12 × 9 = 0.75 hours.

Guided Practice – Page No. 420

There is a 30% chance that T’Shana’s county will have a drought during any given year. She performs a simulation to find the experimental probability of a drought in at least 1 of the next 4 years.

Question 1.
T’Shana’s model involves the whole numbers from 1 to 10. Complete the description of her model.
Type below:
______________

Answer:
Since the chance of drought is 30%, let the numbers 1 to 3 represent a drought year and the numbers 4 to 10 represent a year without a drought. Since you are concerned with the number of droughts in the next 4 years, generate 4 random numbers in each trial.

Question 2.
Suppose T’Shana used the model described in Exercise 1 and got the results shown in the table. Complete the table.

Type below:
______________

Answer:
The number of drought years is the number of times 1 to 3 was generated in each trial so count the number of times in each trial that the number 1 to 3 occurred:

Question 3.
According to the simulation, what is the experimental probability that there will be a drought in the county in at least 1 of the next 4 years?
\(\frac{□}{□}\)

Answer: \(\frac{4}{5}\)

Explanation:
There are 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
In the previous exercise, we obtained at least 1 drought year in 8 of the 10 trials and thus there are 8 favorable outcomes.
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(At least 1 drought year) = favorable outcomes/possible outcomes = \(\frac{8}{10}\)
= \(\frac{4}{5}\) = 0.8 = 80%

Essential Question Check-In

Question 4.
You want to generate random numbers to simulate an event with a 75% chance of occurring. Describe a model you could use.
Type below:
______________

Answer:
75% in fraction form is \(\frac{3}{4}\) so you can randomly generate numbers from 1 to 4. The numbers 1 to 3 would mean success and 4 would mean unsuccessful.

Independent Practice – Page No. 421

Every contestant on a game show has a 40% chance of winning. In the simulation below, the numbers 1–4 represent a winner, and the numbers 5–10 represent a nonwinner. Numbers were generated until one that represented a winner was produced.

Question 5.
In how many of the trials did it take exactly 4 contestants to get a winner?
_____ trial(s)

Answer: 1

Explanation:
Only trial 6 took 4 contestants to get a winner so 1 trial.

Question 6.
Based on the simulation, what is the experimental probability that it will take exactly 4 contestants to get a winner?
\(\frac{□}{□}\)

Answer: \(\frac{1}{10}\)

Explanation:
We have data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
1 of the 10 trials required exactly 4 numbers to get a winner and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(exactly 4 contestants) = favorable outcomes/possible outcomes = \(\frac{1}{10}\) = 0.1 = 10%

Over a 100-year period, the probability that a hurricane struck Rob’s city in any given year was 20%. Rob performed a simulation to find an experimental probability that a hurricane would strike the city in at least 4 of the next 10 years. In Rob’s simulation, 1 represents a year with a hurricane.

Question 7.
According to Rob’s simulation, what was the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years?
\(\frac{□}{□}\)

Answer: \(\frac{1}{5}\)

Explanation:
We have been given data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
A 1 represents a hurricane. We then note that trial 2 and trial 7 both have at least 4 ones and thus there are 4 trials that result in at least 4 hurricanes.
Thus there are 2 favorable outcomes.
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(At least 4) = favorable outcomes/possible outcomes = \(\frac{2}{10}\) = \(\frac{1}{5}\)
= 0.2 = 20%

Question 8.
Analyze Relationships
Suppose that over the 10 years following Rob’s simulation, there was actually 1 year in which a hurricane struck. How did this compare to the results of Rob’s simulation?
Type below:
______________

Answer:
If a hurricane struck in 1 year the next 10 years following the simulation, it would match with the results of his simulation. In 3 of his trials, exactly 1 year had a hurricane which means the experimental probability that there will be 1 hurricane in 10 years is \(\frac{3}{10}\).
In all of the trials, there was at least 1 year with a hurricane which means the experimental probability is 100% that a hurricane will occur the next 10 years.

Page No. 422

Question 9.
Communicate Mathematical Ideas
You generate three random whole numbers from 1 to 10. Do you think that it is unlikely or even impossible that all of the numbers could be 10? Explain?
Type below:
______________

Answer:
It is unlikely that all three numbers would be 10. The theoretical probability that a random whole number from 1 to 10 is 10 is 1/10.
The theoretical probability that three random whole numbers from 1 to 10 are all 10s is then \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) = \(\frac{1}{1000}\).
This is a very small probability so it is unlikely.

Question 10.
Erika collects baseball cards, and 60% of the packs contain a player from her favorite team. Use a simulation to find an experimental probability that she has to buy exactly 2 packs before she gets a player from her favorite team
Type below:
______________

Answer:
Generate random numbers from 1 to 10 using 10 trials. Since 60% of the packs contain a player from her favorite team, let the numbers 1 to 6 represent a pack with a player from her favorite team and the numbers 7 to 10 represent packs without a player from her favorite team.
Out of 10 trials she had to buy exactly 10 packs before getting a player from her favorite team only in 2 trials so the experimental probability is \(\frac{2}{10}\) = \(\frac{1}{5}\).

H.O.T.

Focus on Higher Order Thinking

Question 11.
Represent Real-World Problems
When Kate plays basketball, she usually makes 37.5% of her shots. Design and conduct a simulation to find the experimental probability that she makes at least 3 of her next 10 shots. Justify the model for your simulation.
Type below:
______________

Answer: \(\frac{7}{10}\)

Explanation:
Since 37.5% = 3/8 perform simulation by randomly generating 10 members from 1 to 8 where the numbers 1 to 3 are when she makes the shot and 4 to 8 are when she doesn’t make the shot. Perform 10 trials.
She made at least 3  shots in 7 of the 10 trials so the experimental probability is \(\frac{7}{10}\)

Question 12.
Justify Reasoning
George and Susannah used a simulation to simulate the flipping of 8 coins 50 times. In all of the trials, at least 5 heads came up. What can you say about their simulation? Explain.
Type below:
______________

Answer:
If at least 5 heads came up in every trial, then the simulation they used does not accurately model flipping a coin 8 times. Since each coin has a theoretical probability of 1/2 and \(\frac{1}{2}\) × 8 = 4, there should be around 4 heads in each trial. Getting at least 5 heads in every trial means that the coin is more likely to land on heads than to land on tails.

13.1, 13.2 Theoretical Probability of Simple and Compound Events – Page No. 423

Find the probability of each event. Write your answer as a fraction, as a decimal, and as a percent.

Question 1.
You choose a marble at random from a bag containing 12 red, 12 blue, 15 green, 9 yellow, and 12 black marbles. The marble is red.
Type below:
______________

Answer:
The bag contains 12 red, 12 blue, 15 green, 9 yellow, and 12 black marbles, which are thus 12 + 12 + 15 + 9 + 12 = 60 marbles in total and thus there are 60 possible outcomes.
possible outcomes = 60
12 of the 60 marbles are red and thus there are 12 favorable outcomes.
favorable outcomes = 12
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{12}{60}\) = 1/5 = 0.2 = 20%

Question 2.
You draw a card at random from a shuffled deck of 52 cards. The deck has four 13-card suits (diamonds, hearts, clubs, spades). The card is a diamond or a spade.
Type below:
______________

Answer:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs) and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
13 of the cards are diamonds and 13 of the cards are spades, thus there are 13 + 13 = 26 cards that are diamonds or spades. This then implies that there are 26 favorable outcomes.
favorable outcomes = 26
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{26}{52}\) = 1/2 = 50%

13.3 Making Predictions with Theoretical Probability

Question 3.
A bag contains 23 red marbles, 25 green marbles, and 18 blue marbles. You choose a marble at random from the bag. What color marble will you most likely choose?
______________

Answer: Green

Explanation:
There are more green marbles than any other color so you are more likely to choose a green marble.

13.4 Using Technology to Conduct a Simulation

Question 4.
Bay City has a 25% chance of having a flood in any given decade. The table shows the results of a simulation using random numbers to find the experimental probability that there will be a flood in Bay City in at least 1 of the next 5 decades. In the table, the number 1 represents a decade with a flood. The numbers 2 through 5 represent a decade without a flood.

According to the simulation, what is the experimental probability of a flood in Bay City in at least 1 of the next 5 decades?
\(\frac{□}{□}\)

Answer: \(\frac{2}{5}\)

Explanation:
We have been given information about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a decade with a flood. We then note that 4 of the 10 trials contained at least one 1 and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(Flood) = favorable outcomes/possible outcomes = 4/10 = \(\frac{2}{5}\)

Essential Question

Question 5.
How can you use theoretical probability to make predictions in real-world situations?
Type below:
______________

Answer:
You can use theoretical probabilities to make predictions by multiplying the theoretical probability times the number of events.
An example would be flipping a coin 50 times and wanting to predict the number of heads.
Since the theoretical probability of landing on heads is 1/2, a prediction is
50 × 1/2 = 25 heads.

Selected Response – Page No. 424

Question 1.
What is the probability of flipping two fair coins and having both show tails?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{3}\)
d. \(\frac{1}{2}\)

Answer: \(\frac{1}{4}\)

Explanation:
Each coin has 2 possible outcomes: Heads H and tails T
We then note that there are 4 possible outcomes for the 2 coins: HH, HT, TH, TT
Possible outcomes = 4
1 of the 4 possible outcomes results in two tails TT and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(two tails) = favorable outcomes/possible outcomes = \(\frac{1}{4}\)
Thus the correct answer is option B.

Question 2.
A bag contains 8 white marbles and 2 black marbles. You pick out a marble, record its color, and put the marble back in the bag. If you repeat this process 45 times, how many times would you expect to remove a white marble from the bag?
Options:
a. 9
b. 32
c. 36
d. 40

Answer: 36

Explanation:
The bag contains 8 white marbles and 2 black marbles, which are thus 8 + 2 = 10 marbles in total and thus there are 10 possible outcomes.
possible outcomes = 10
We note that 8 of the marbles in the bag are white and thus there are 8 favorable outcomes.
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(white) = favorable outcomes/possible outcomes = \(\frac{8}{10}\) = \(\frac{4}{5}\)
The predicted number of times we select a white marble is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × \(\frac{4}{5}\)
= 45 × \(\frac{4}{5}\)
= 9 × 4 = 36
Thus we predict that we will get a white marble about 36 times.
Thus the correct answer is option C.

Question 3.
Philip rolls a standard number cube 24 times. Which is the best prediction for the number of times he will roll a number that is even and less than 4?
Options:
a. 2
b. 3
c. 4
d. 6

Answer: 4

Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6.
possible outcomes = 6
1 of the 6 possible outcomes results in an even number less than 4, that is the outcome 2.
favorable outcome = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(even and less than 4) = favorable outcomes/possible outcomes = 1/6
The predicted number of times we select an even number less than 4 is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(even and less than 4)
= 24 × 1/6
= 4
Thus we predict that we roll an even number less than 4 about 4 times.
Thus the correct answer is option C.

Question 4.
A set of cards includes 24 yellow cards, 18 green cards, and 18 blue cards. What is the probability that a card chosen at random is not green?
Options:
a. \(\frac{3}{10}\)
b. \(\frac{4}{10}\)
c. \(\frac{3}{5}\)
d. \(\frac{7}{10}\)

Answer: \(\frac{7}{10}\)

Explanation:
The set of cards includes 24 yellow, 18 green and 18 blue cards, which are thus 24 + 18 + 18 = 60 cards in total and thus there are 60 possible outcomes.
possible outcomes = 60
18 of the 60 cards are green and thus 60 – 18 = 42 of the 60 cards are not green. This then implies that there are 42 favorable outcomes.
favorable outcomes = 42
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(not green) = favorable outcomes/possible outcomes = 42/60 = \(\frac{7}{10}\)
Thus the correct answer is option D.

Question 5.
A rectangle made of square tiles measures 10 tiles long and 8 tiles wide. What is the width of a similar rectangle whose length is 15 tiles?
Options:
a. 3 tiles
b. 12 tiles
c. 13 tiles
d. 18.75 tiles

Answer: 12 tiles

Explanation:
Write the proportion relating to the lengths and widths of each rectangle.
length/width = 10/8 = 15/w
10w = 120
w = 12
Thus the correct answer is option B.

Question 6.
The Fernandez family drove 273 miles in 5.25 hours. How far would they have driven at that rate in 4 hours?
Options:
a. 208 miles
b. 220 miles
c. 280 miles
d. 358 miles

Answer: 208 miles

Explanation:
Write the proportion relating the number of miles and hours.
miles/hours = 273/5.25 = m/4
5.25m = 1092
m = 208 miles
Thus the correct answer is option A.

Question 7.
There are 20 tennis balls in a bag. Five are orange, 7 are white, 2 are yellow, and 6 are green. You choose one at random. Which color ball are you least likely to choose?
Options:
a. green
b. orange
c. white
d. yellow

Answer: yellow

Explanation:
The color with the fewest number of balls is yellow so you are least likely to choose yellow.
Thus the correct answer is option D.

Mini-Task

Question 8.
Center County has had a 1 in 6 (or about 16.7%) chance of a tornado in any given decade. In a simulation to consider the probability of tornadoes in the next 5 decades, Ava rolled a number cube. She let a 1 represent a decade with a tornado, and 2–6 represent decades without tornadoes. What experimental probability did Ava find for each event?

a. That Center County has a tornado in at least one of the next five decades.
\(\frac{□}{□}\)

Answer: \(\frac{3}{5}\)

Explanation:
We have been given the data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a tornado. We then note that 6 of the 10 trials contain at least one 1 and thus 6 of the 10 trials resulting in at least one tornado. This then implies that there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(at least one tornado) = favorable outcomes/possible outcomes = 6/10 = \(\frac{3}{5}\)

Question 8.
b. That Center County has a tornado in exactly one of the next five decades
\(\frac{□}{□}\)

Answer: \(\frac{3}{10}\)

Explanation:
We have been given data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a tornado. We then note that 3 of the 10 trials contain at least one 1 and thus 3 of the 10 trials resulting in exactly one tornado. This then implies that there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(exactly one tornado) = favorable outcomes/possible outcomes = 3/10 = 0.3

EXERCISES – Page No. 425

Find the probability of each event.

Question 1.
Rolling a 5 on a fair number cube.
\(\frac{□}{□}\)

Answer: \(\frac{1}{6}\)

Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
possible outcomes = 6
We note that 1 of the 6 possible outcomes results in a 5 and thus there is a favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(5) = favorable outcomes/possible outcomes
\(\frac{1}{6}\) ≈ 0.1667 = 16.67%

Question 2.
Picking a 7 from a standard deck of 52 cards. A standard deck includes 4 cards of each number from 2 to 10.
\(\frac{□}{□}\)

Answer: \(\frac{1}{13}\)

Explanation:
There are 52 cards in the standard deck of cards and thus there are 52 possible outcomes.
possible outcomes = 52
We note that 4 of the 52 cards are 7’s and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(7) = favorable outcomes/possible outcomes
4/52 = \(\frac{1}{13}\) ≈ 0.0769 = 7.69%

Question 3.
Picking a blue marble from a bag of 4 red marbles, 6 blue marbles, and 1 white marble.
\(\frac{□}{□}\)

Answer: \(\frac{6}{11}\)

Explanation:
The bag contains 4 red, 6 blue, and 1 white marble, thus the bag contains 4 + 6 + 1 = 11 marbles in total and thus there are 11 possible outcomes.
possible outcomes = 11
We note that 6 of the 11 marbles in the bag are blue and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(blue) = favorable outcomes/possible outcomes = \(\frac{6}{11}\) ≈ 0.5455 = 54.55%

Question 4.
Rolling a number greater than 7 on a 12-sided number cube.
\(\frac{□}{□}\)

Answer: \(\frac{5}{12}\)

Explanation:
A 12 side number cube has 12 possible outcomes: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
possible outcomes = 12
We note that 5 of the 12 possible outcomes result in a number greater than 7 (that is 8, 9, 10, 11, 12) and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Greater than 7) = favorable outcomes/possible outcomes = \(\frac{5}{12}\) ≈ 0.4167 = 41.67%

Page No. 426

Question 5.
Christopher picked coins randomly from his piggy bank and got the numbers of coins shown in the table. Find each experimental probability.

a. The next coin that Christopher picks is a quarter.
\(\frac{□}{□}\)

Answer: \(\frac{6}{23}\)

Explanation:
The table contains 7 pennies, 2 nickels, 8 dimes and 6 quarters, which are 7 + 2 + 8 + 6 = 23 coins in total and thus there are 23 possible outcomes.
possible outcomes = 23
We note that 6 of the 23 coins are quarters and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Quarter) = favorable outcomes/possible outcomes = \(\frac{6}{23}\) ≈ 0.2609 = 26.09%

Question 5.
b. The next coin that Christopher picks is not a quarter.
\(\frac{□}{□}\)

Answer: \(\frac{17}{23}\)

Explanation:
The sum of the probabilities of an event and its complement is always equal to 1.
P(not a Quarter) + P(Quarter) = 1
Let us then determine the probability of picking the marble that is not marked with the number 5.
P(not a Quarter) + P(Quarter) = 1
P(not a Quarter) = 1 – P(Quarter)
1 – \(\frac{6}{23}\)
= \(\frac{17}{23}\) ≈ 0.7391 = 73..91%

Question 5.
c. The next coin that Christopher picks is a penny or a nickel.
\(\frac{□}{□}\)

Answer: \(\frac{9}{23}\)

Explanation:
The table contains 7 pennies, 2 nickels, 8 dimes and 6 quarters, which are 7 + 2 + 8 + 6 = 23 coins in total and thus there are 23 possible outcomes.
possible outcomes = 23
There are 7 pennies and 2 nickels, thus 7 + 2 = 9 of the coins are pennies or nickels and thus there are 9 favorable outcomes.
favorable outcomes = 9
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Penny or nickel) = favorable outcomes/possible outcomes = \(\frac{9}{23}\) ≈ 0.3913 = 39.13%

Question 6.
A grocery store manager found that 54% of customers usually bring their own bags. In one afternoon, 82 out of 124 customers brought their own grocery bags. Did a greater or lesser number of people than usual bring their own bags?
_____________

Answer: Greater

Explanation:
54% of 124 is 0.54 × 124 ≈ 67 so more customers than usual brought their own bag.

EXERCISES – Page No. 427

Find the probability of each event.

Question 1.
Graciela picks a white mouse at random from a bin of 8 white mice, 2 gray mice, and 2 brown mice.
\(\frac{□}{□}\)

Answer: \(\frac{2}{3}\)

Explanation:
There are 8 white, 2 gray, and 2 brown mice, thus there are 8 + 2 + 2 = 12 mice in total and thus there are 12 possible outcomes.
possible outcomes = 12
8 of the mice are white and thus there are 8 favorable outcomes
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(white) = favorable outcomes/possible outcomes = \(\frac{8}{12}\) ≈ 0.6667 = 66.67%

Question 2.
Theo spins a spinner that has 12 equal sections marked 1 through 12. It does not land on 1.
\(\frac{□}{□}\)

Answer: \(\frac{11}{12}\)

Explanation:
There are 12 numbers from 1 to 12 and thus there are 12 possible outcomes.
possible outcomes = 12
11 of the 12 numbers from 1 to 12 are not 1 and thus there are 11 favorable outcomes
favorable outcomes = 11
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(not 1) = favorable outcomes/possible outcomes = \(\frac{11}{12}\) ≈ 0.9167 = 91.67%

Question 3.
Tania flips a coin three times. The coin lands on heads twice and on tails once, not necessarily in that order.
\(\frac{□}{□}\)

Answer: \(\frac{3}{8}\)

Explanation:
A fair coin has 2 possible outcomes: Heads and Tails T.
There are then 8 possible outcomes when tossing 3 coins: HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
possible outcomes = 8
We note that 3 of the possible outcomes result in two heads and one tail HHT, HTH, TTH and thus there are 3 favorable outcomes
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(two heads and one tail) = favorable outcomes/possible outcomes = \(\frac{3}{8}\)

Question 4.
Students are randomly assigned two-digit codes. Each digit is either 1, 2, 3, or 4. Guy is given the number 11.
\(\frac{□}{□}\)

Answer: \(\frac{1}{16}\)

Explanation:
Each digit has 4 possible outcomes so there are 4 × 4 = 16 possible two-digit numbers with digits of 1, 2, 3 or 4. There is only one way to 11 as the two-digit number so the probability is \(\frac{1}{16}\)

Question 5.
Patty tosses a coin and rolls a number cube.
a. Find the probability that the coin lands on heads and the cube lands on an even number.
\(\frac{□}{□}\)

Answer:
A coin has 2 possible outcomes: heads H and tails T.
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
We then note that there are 2 . 6 = 12 possible outcomes for the coin and the number cube: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6
possible outcomes = 12
We then note that 3 of the 12 possible outcomes result in heads and an even number: H2, H4, H6.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(heads and even) = favorable outcomes/possible outcomes = \(\frac{3}{12}\) = \(\frac{1}{4}\)

Question 5.
b. Patty tosses the coin and rolls the number cube 60 times. Predict how many times the coin will land on heads and the cube will land on an even number.
______ times

Answer:
The predicted number of repetitions resulting in heads and an even number is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P
= 60 × \(\frac{1}{4}\)
= 15
Thus we predict taht we obtain heads with an even number about 15 times.

Question 6.
Rajan’s school is having a raffle. The school sold raffle tickets with 3-digit numbers. Each digit is either 1, 2, or 3. The school also sold 2 tickets with the number 000. Which number is more likely to be picked, 123 or 000?
____________

Answer: 000

Explanation:
There is only 1 ticket that has the number 123 and 2 tickets that have 000 so it is more likely that 000 will be picked.

Page No. 428

Question 7.
Suppose you know that over the last 10 years, the probability that your town would have at least one major storm was 40%. Describe a simulation that you could use to find the experimental probability that your town will have at least one major storm in at least 3 of the next 5 years.
Type below:
____________

Answer:
Since the probability is 40% = 4/10 = 2/5, randomly generate numbers from 1 to 5 where 1 and 2 is a year with a major storm and 3 to 5 is a year without a major storm.

Unit 6 Performance Tasks

Question 8.
Meteorologist
A meteorologist predicts a 20% chance of rain for the next two nights and a 75% chance of rain on the third night.
a. On which night is it most likely to rain? On that night, is it likely to rain or unlikely to rain?
Type below:
____________

Answer: 3rd night

Explanation:
The third night it is most likely to rain since the probability of rain is higher that night. Since the probability of 75% is greater than 50%, it is likely that it will rain.

Question 8.
b. Tara would like to go camping for the next 3 nights, but will not go if it is likely to rain on all 3 nights. Should she go? Use probability to justify your answer.
Type below:
____________

Answer:
The probability that it will rain all three nights is 0.2 × 0.2 × 0.75 = 0.03 = 3%. It is unlikely that it will rain all 3 nights since the probability is 3% so she should go.

Question 9.
Sinead tossed 4 coins at the same time. She did this 50 times, and 6 of those times, all 4 coins showed the same result (heads or tails).
a. Find the experimental probability that all 4 coins show the same result when tossed.
\(\frac{□}{□}\)

Answer: \(\frac{3}{25}\)

Explanation:
The 4 coins were tossed 50 times and thus there are 50 possible outcomes.
possible outcomes = 50
The result showed that all 4 coins have the same result on 6 of the 50 tosses.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Same result) = favorable outcomes/possible outcomes = \(\frac{6}{50}\) = \(\frac{3}{25}\)

Question 9.
b. Can you determine the experimental probability that no coin shows heads? Explain.
Type below:
____________

Answer:
The 4 coins were tossed 50 times and thus there are 50 possible outcomes.
possible outcomes = 50
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(No heads) = favorable outcomes/possible outcomes
Since we know the number of possible outcomes, we require the knowledge of the number of favorable outcomes to determine the probability.
That is, we require the knowledge of how many of the tosses resulted in no heads. Since this has not been given, we cannot determine the experimental probability that no coin show heads.

Question 9.
c. Suppose Sinead tosses the coins 125 more times. Use experimental probability to predict the number of times that all 4 coins will show heads or tails. Show your work.
_______ times

Answer:
The predicted number of times that all 4 coins will show heads or tails is then obtained by multiplying the number of times by the probability.
Since the coins were tossed 50 times initially and now were tossed 125 more times, the coins were tossed 50 + 125 = 175 times in total.
Prediction = Number of times × P
= 175 × \(\frac{3}{25}\)
= 7 × 3 = 21
Thus we predict that we obtain that all 4 coins will show heads or tails about 21 times.

Selected Response – Page No. 429

Question 1.
A pizza parlor offers thin, thick, and traditional style pizza crusts. You can get pepperoni, beef, mushrooms, olives, or peppers for toppings. You order a one-topping pizza. How many outcomes are in the sample space?
Options:
a. 3
b. 5
c. 8
d. 15

Answer: 15

Explanation:
The Fundamental Counting Principle (also called the counting rule) is a way to figure out the number of outcomes in a probability problem. Basically, you multiply the events together to get the total number of outcomes.
Crust: 3 ways (thin, thick, traditional)
Topping: 5 ways (pepperoni, beef, mushrooms, olives, peppers)
Use the Fundamental Counting Principle:
3 × 5 = 15
Thus there are 15 possible outcomes in the sample space.
Thus the correct answer is option D.

Question 2.
A bag contains 9 purple marbles, 2 blue marbles, and 4 pink marbles. The probability of randomly drawing a blue marble is \(\frac{2}{15}\). What is the probability of not drawing a blue marble?
Options:
a. \(\frac{2}{15}\)
b. \(\frac{4}{15}\)
c. \(\frac{11}{15}\)
d. \(\frac{13}{15}\)

Answer: \(\frac{13}{15}\)

Explanation:
Given,
P(blue) = \(\frac{2}{15}\)
The sum of the probabilities of an event and its complement is always equal to 1.
P(not blue) + P(blue) = 1
Let us determine the probability of picking the marble that is not marked with the number 5.
P(not blue) = 1 – P(blue)
= 1 – \(\frac{2}{15}\)
= \(\frac{15}{15}\) – \(\frac{2}{15}\)
= \(\frac{13}{15}\)
Thus the correct answer is option D.

Question 3.
During the month of April, Dora kept track of the bugs she saw in her garden. She saw a ladybug on 23 days of the month. What is the experimental probability that she will see a ladybug on May 1?
Options:
a. \(\frac{1}{23}\)
b. \(\frac{7}{30}\)
c. \(\frac{1}{2}\)
d. \(\frac{23}{30}\)

Answer: \(\frac{23}{30}\)

Explanation:
There are 30 days in the month of April and thus there are 30 possible outcomes.
possible outcomes = 30
A ladybug was seen on 23 of the 30 days and thus there are 23 favorable outcomes.
favorable outcomes = 23
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(see ladybug) = favorable outcomes/possible outcomes = \(\frac{23}{30}\)
Thus the correct answer is option D.

Question 4.
Ryan flips a coin 8 times and gets tails all 8 times. What is the experimental probability that Ryan will get heads the next time he flips the coin?
Options:
a. 1
b. \(\frac{1}{2}\)
c. \(\frac{1}{8}\)
d. 0

Answer: 0

Explanation:
The coin was flipped 8 times and thus there are 8 possible outcomes.
possible outcomes = 5
All 8 flips resulted in tails and thus heads occurred on 0 of the flips, which implies that there are 0 favorable outcomes.
favorable outcomes = 0
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(heads) = favorable outcomes/possible outcomes = \(\frac{0}{8}\) = 0
Thus the correct answer is option D.

Question 5.
A used guitar is on sale for $280. Derek offers the seller \(\frac{3}{4}\) of the advertised price. How much does Derek offer for the guitar?
Options:
a. $180
b. $210
c. $240
d. $270

Answer: $210

Explanation:
Since 280(3/4) = 210, he offered $210 for the guitar.
Thus the correct answer is option B.

Question 6.
Jay tossed two coins several times and then recorded the results in the table below

What is the experimental probability that the coins will land on different sides on his next toss?
Options:
a. \(\frac{1}{5}\)
b. \(\frac{2}{5}\)
c. \(\frac{3}{5}\)
d. \(\frac{4}{5}\)

Answer: \(\frac{3}{5}\)

Explanation:
We have the coin toss results of 5 tosses and thus there are 5 possible outcomes.
possible outcomes = 5
Wwe note that 3 of the 5 tosses resulted in two different sides (H, T or T, H) and thus there are 3 favorable outcomes.
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(different sides) = favorable outcomes/possible outcomes = \(\frac{3}{5}\)
Thus the correct answer is option C.

Question 7.
What is the probability of tossing two fair coins and having exactly one land tails side up?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{3}\)
d. \(\frac{1}{2}\)

Answer: \(\frac{1}{2}\)

Explanation:
Each coin has 2 possible outcomes: Heads H and Tails T.
When tossing 2 fair coins, then there are 4 possible outcomes: HH, HT, TH, TT.
possible outcomes = 4
We note that 2 of the 4 possible outcomes result in exactly one tail (TH or HT) and thus there are 2 favorable outcomes.
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(exacly one tail) = favorable outcomes/possible outcomes = \(\frac{2}{4}\) = \(\frac{1}{2}\)
Thus the correct answer is option D.

Question 8.
Find the percent change from 60 to 96.
Options:
a. 37.5% decrease
b. 37.5% increase
c. 60% decrease
d. 60% increase

Answer: 60% increase

Explanation:
Percent change = (amount of change)/(original amount).
The amount of change is 96 – 60 = 36 and the original amount is 60.
The percent change is then 36/60 = 0.6 = 60%.
Since the amounts got larger, it is an increase.
Thus the correct answer is option D.

Question 9.
A bag contains 6 white beads and 4 black beads. You pick out a bead, record its color, and put the bead back in the bag. You repeat this process 35 times. Which is the best prediction of how many times you would expect to remove a white bead from the bag?
Options:
a. 6
b. 10
c. 18
d. 21

Answer: 21

Explanation:
The bag contains 6 white and 4 black beads, which are thus 6 + 4 = 10 beads in total and thus there are 10 favorable outcomes.
possible outcomes = 10
6 of the 10 beads are white and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(white) = favorable outcomes/possible outcomes = 6/10 = 3/5 = 0.6 = 60%
The predicted number of selected white beads is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P(white)
35 × 6/10
= 210/10
= 21
Thus we predict that we removed 21 white beads from the bag.
Thus the correct answer is option D.

Question 10.
A set of cards includes 20 yellow cards, 16 green cards, and 24 blue cards. What is the probability that a blue card is chosen at random?
Options:
a. 0.04
b. 0.24
c. 0.4
d. 0.66

Answer: 0.4

Explanation:
There are 20 yellow, 16 green and 24 blue cards, which are thus 20 + 16 + 21 = 60 cards and thus there are 60 possible outcomes.
possible outcomes = 60
24 of the 60 cards are blue and thus there are 24 favorable outcomes.
favorable outcomes = 24
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(blue) = favorable outcomes/possible outcomes = \(\frac{24}{60}\) = \(\frac{2}{5}\)
Thus the correct answer is option C.

Page No. 430

Question 11.
Jason, Erik, and Jamie are friends in art class. The teacher randomly chooses 2 of the 21 students in the class to work together on a project. What is the probability that two of these three friends will be chosen?
Options:
a. \(\frac{1}{105}\)
b. \(\frac{1}{70}\)
c. \(\frac{34}{140}\)
d. \(\frac{4}{50}\)

Answer: \(\frac{1}{70}\)

Explanation:
The probability that one of the friends is chosen as the first student is 3/21 = 1/7 since there are 3 friends and 21 total students.
The probability that a second friend is chosen is then 2/20 = 1/10 since there are 2 remaining friends and a total of 20 remaining students.
The probability that two friends is chosen is then (1/7)(1/10) = \(\frac{1}{70}\)
Thus the correct answer is option B.

Question 12.
Philip rolls a number cube 12 times. Which is the best prediction for the number of times that he will roll a number that is odd and less than 5?
Options:
a. 2
b. 3
c. 4
d. 6

Answer: 4

Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
possible outcomes = 6
2 of the 6 possible outcomes are odd and less than 5
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(odd and less than 5) = favorable outcomes/possible outcomes = \(\frac{2}{6}\) = \(\frac{1}{3}\)
The predicted number of odd numbers less than 5 that is rolled is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(odd and less than 5)
= 12 × \(\frac{1}{3}\)
= 4
Thus 4 of the trolls are expected to result in an odd number less than 5.
Thus the correct answer is option C.

Question 13.
A survey reveals that one airline’s flights have a 92% probability of being on time. Based on this, out of 4000 flights in a year, how many flights would you predict will arrive on time?
Options:
a. 368
b. 386
c. 3680
d. 3860

Answer: 3680

Explanation:
Given,
P(on time) = 92% = 0.92
The predicted number of flights that arrive on time is then obtained by multiplying the number of flights by the probability.
Prediction = Number of flights × P(on time)
= 4000 × 0.92
= 3680
Thus we predict that about 3680 of the flights are on time.
Thus the correct answer is option C.

Question 14.
Matt’s house number is a two-digit number. Neither of the digits is 0 and the house number is even. What is the probability that Matt’s house number is 18?
Options:
a. \(\frac{1}{45}\)
b. \(\frac{1}{36}\)
c. \(\frac{1}{18}\)
d. \(\frac{1}{16}\)

Answer: \(\frac{1}{36}\)

Explanation:
The Fundamental Counting Principle (also called the counting rule) is a way to figure out the number of outcomes in a probability problem. Basically, you multiply the events together to get the total number of outcomes.
There are 9 digits excluding 0 (1, 2, 3, 4, 5, 6, 7, 8, 9) and there are 4 even digits excluding 0 (2, 4, 6, 8). By the fundamental counting principle, there are then 9 . 4 =36 two digit numbers that do not contain a 0 and that are even. Thus there are 36 possible outcomes.
possible outcomes = 36
18 is 1 of the 36 possible outcomes and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(blue) = favorable outcomes/possible outcomes = \(\frac{1}{36}\)
Thus the correct answer is option B.

Mini-Tasks

Question 15.
Laura picked a crayon randomly from a box, recorded the color, and then placed it back in the box. She repeated the process and recorded the results in the table.

Find each experimental probability. Write your answers in simplest form.
a. The next crayon Laura picks is red.
\(\frac{□}{□}\)

Answer:
There are 5 red, 6 blue, 7 yellow and 2 green crayons, which are thus 5 + 6 + 7 + 2 = 20 crayons in total and thus there are 20 possible outcomes.
possible outcomes = 20
5 of the 20 crayons are red and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(red) = favorable outcomes/possible outcomes = \(\frac{5}{20}\) = \(\frac{1}{4}\)

Question 15.
b. The next crayon Laura picks is not red.
\(\frac{□}{□}\)

Answer:
The sum of the probabilities of an event and its complement is always equal to 1.
P(not red) + P(red) = 1
Let us then determine the probability of picking the marble that is not marked with the number 5.
P(not red) = 1 – P(red)
= 1 – 1/4
= 3/4

Question 16.
For breakfast, Trevor has a choice of 3 types of bagels (plain, sesame, or multigrain), 2 types of eggs (scrambled or poached), and 2 juices (orange or apple).
a. Use the space below to make a tree diagram to find the sample space.
Type below:
_____________

Answer:
There are 3 types of bagels and thus we draw a root with 3 possible children labeled plain, sesame, and multigrain.
There are 2 types of eggs, thus we draw 2 children for each of the 3 previous children and label these two children as scrambled and poached.
There are 2 juices, thus we draw 2 children for each of the 2 previous children and label these two children as orange or apple.

Question 16.
b. If he chooses at random, what is the probability that Trevor eats a breakfast that has orange juice?
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:
The bottom row of the tree diagram of part (a) contains 12 elements and thus there are 12 possible outcomes.
possible outcomes = 12
6 of the labels in the bottom row are “orange” and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(orange juice) = favorable outcomes/possible outcomes = \(\frac{6}{12}\) = \(\frac{1}{2}\)

Conclusion:

I hope this Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations helped you to understand the logic in theoretical probability. Bookmark our site to get the latest info on Go Math Answer Key for all the chapters of grade 7. For any doubts the 7th grade students can post their comments in the below mentioned comment box.

Get Chapter 10 Area of Parallelograms Go Math Grade 6 Answer Key from this page. Here you can know the formulas of the area of a parallelogram. In order to solve the problems first, you have to know what is parallelogram and how to calculate the area of a parallelogram. Download HMH Go Math Grade 6 Solution Key Area of Parallelograms pdf here.

Go Math Grade 6 Answer Key Chapter 10 Area of Parallelograms

Check out the topics covered in Chapter 10 Area of Parallelograms before you start practicing the problems. Area of Parallelograms includes topics like the area of triangles, Area of Trapezoids, Area of Regular Polygons, Composite Figures, etc. Practice the problems a number of times and enhance your math skills. After that solve the questions given in the mid-chapter checkpoint and review test. We have also provided the solutions of mid-chapter and review test here.

Lesson 1: Algebra • Area of Parallelograms

• Share and Show – Page No. 535
• Problem Solving + Applications – Page No. 536
• Area of Parallelograms – Page No. 537
• Lesson Check – Page No. 538

Lesson 2: Investigate • Explore Area of Triangles

• Share and Show – Page No. 541
• Sense or Nonsense? – Page No. 542
• Explore Area of Triangles – Page No. 543
• Lesson Check – Page No. 544

Lesson 3: Algebra • Area of Triangles

• Share and Show – Page No. 547
• Unlock the Problem – Page No. 548
• Area of Triangles – Page No. 549
• Lesson Check – Page No. 550

Lesson 4: Investigate • Explore Area of Trapezoids

• Share and Show – Page No. 553
• What’s the Error? – Page No. 554
• Explore Area of Trapezoids – Page No. 555
• Lesson Check – Page No. 556

Lesson 5: Algebra • Area of Trapezoids

• Share and Show – Page No. 559
• Problem Solving + Applications – Page No. 560
• Area of Trapezoids – Page No. 561
• Lesson Check – Page No. 562

Mid-Chapter Checkpoint

• Mid-Chapter Checkpoint – Vocabulary – Page No. 563
• Mid-Chapter Checkpoint – Page No. 564

Lesson 6: Area of Regular Polygons

• Share and Show – Page No. 567
• Page No. 568
• Area of Regular Polygons – Page No. 569
• Lesson Check – Page No. 570

Lesson 7: Composite Figures

• Share and Show – Page No. 573
• Unlock the Problem – Page No. 574
• Composite Figures – Page No. 575
• Lesson Check – Page No. 576

Lesson 8: Problem Solving • Changing Dimensions

• Share and Show – Page No. 579
• On Your Own – Page No. 580
• Problem Solving Changing Dimensions – Page No. 581
• Lesson Check – Page No. 582

Lesson 9: Figures on the Coordinate Plane

• Share and Show – Page No. 585
• Problem Solving + Applications – Page No. 586
• Figures on the Coordinate Plane – Page No. 587
• Lesson Check – Page No. 588

Chapter 10 Review/Test

• Chapter 10 Review/Test – Page No. 589
• Chapter 10 Review/Test – Page No. 590
• Chapter 10 Review/Test – Page No. 591
• Chapter 10 Review/Test – Page No. 592
• Chapter 10 Review/Test – Page No. 593
• Chapter 10 Review/Test – Page No. 594

Share and Show – Page No. 535

Find the area of the parallelogram or square.

Question 1.

_______ m²

Answer: 9.96

Explanation:
Given that
Base = 8.3 m
Height = 1.2 m
We know that the area of the parallelogram is base × height
A = bh
A = 8.3 m × 1.2 m
A = 9.96 square meters
Thus the area of the parallelogram for the above figure is 9.96 m²

Question 2.

_______ ft²

Answer: 90

Explanation:
Given,
Base = 15 ft
Height = 6 ft
Area = ?
We know that,
Area of the parallelogram = bh
A = 15 ft × 6 ft
A = 90 square feet
Thus the area of the parallelogram for the above figure is 90 ft²

Question 3.

_______ mm²

Answer: 6.25

Explanation:
The above figure is a square
The side of the square is a × a
A = 2.5 mm × 2.5 mm
A = 6.25 square mm
Thus the area of the square is 6.25 mm²

Question 4.

\(\frac{□}{□}\) ft²

Answer: 1/2

Explanation:
Given
Base = 3/4 ft
Height = 2/3 ft
Area of the parallelogram is base × height
A = bh
A = 3/4 × 2/3
A = 1/2
Thus the area of the above parallelogram is 1/2 ft²

Find the unknown measurement for the parallelogram.

Question 5.
Area = 11 yd²

_______ yd

Answer: 2

Explanation:
Given,
A = 11 yd²
B = 5 1/2 yd
We know that
A = bh
11 = 5 1/2 × h
11 = 11/2 × h
22 = 11 × h
H = 2 yd
Thus the height of the above figure is 2 yards.

Question 6.
Area = 32 yd²

_______ yd

Answer: 8 yd

Explanation:
Given
Area = 32 yd²
Base = 4 yd
Height = ?
We know that
A = b × h
32 = 4 yd × h
H = 32/4
H = 8 yd
Therefore the height of the above figure is 8 yards.

On Your Own

Find the area of the parallelogram.

Question 7.

_______ m²

Answer: 58.24

Explanation:
Given
Base = 9.1 m
Height = 6.4 m
A = b × h
A = 9.1 m × 6.4 m
A = 58.24 square meters
Thus the area of the parallelogram for the above figure is 58.24 m²

Question 8.

_______ ft²

Answer: 168

Explanation:
Given
Base = 21 ft
Height = 8ft
We know that the area of the parallelogram is  base × height
A = 21 ft × 8ft
A = 168 square feet
Therefore the area of the above figure is 168 ft²

Find the unknown measurement for the figure.

Question 9.
square
A = ?
s = 15 ft
A = _______ ft

Answer: 225

Explanation:
Given,
S = 15 ft
The area of the square is s × s
A = 15 ft × 15 ft
A = 225 ft²
Thus the area of the square is 225 square feet.

Question 10.
parallelogram
A = 32 m²
b = ?
h = 8 m
b = _______ m

Answer: 4

Explanation:
Given
A = 32 m²
H = 8m
B = ?
To find the base we have to use the area of parallelogram formula
A = bh
32 m² = b × 8 m
B = 32/8
B = 4 m
Thus the base is 4 meters

Question 11.
parallelogram
A = 51 \(\frac{1}{4}\) in.²
b = 8 \(\frac{1}{5}\) in.
h = ?
________ \(\frac{□}{□}\) in.

Answer: 6 \(\frac{1}{4}\) in.

Explanation:
Given,
A = 51 \(\frac{1}{4}\) in.²
b = 8 \(\frac{1}{5}\) in.
H = ?
We know that the area of the parallelogram is  base × height
A = bh
51 \(\frac{1}{4}\) = h × 8 \(\frac{1}{5}\) in.
h = 51 \(\frac{1}{4}\) ÷ 8 \(\frac{1}{5}\) in.
h = 205/4 ÷ 41/5
h = 1025/164
h = 6 \(\frac{1}{4}\) in.
Thus the height of the parallelogram is 6 \(\frac{1}{4}\) in.

Question 12.
parallelogram
A = 121 mm²
b = 11 mm
h = ?
________ mm

Answer: 11 mm

Explanation:
Given
A = 121 mm²
B = 11 mm
H = ?
We know that
A = b × h
121 mm² = 11 mm × h
H = 121/11
H = 11 mm
Thus the height is 11 mm.

Question 13.
The height of a parallelogram is four times the base. The base measures 3 \(\frac{1}{2}\) ft. Find the area of the parallelogram.
________ ft²

Answer: 49

Explanation:
Given
B= 3 \(\frac{1}{2}\)
H = 4b
H = 4 × 3 \(\frac{1}{2}\)
H = 4 × 7/2
H = 14
A = bh
A = 7/2 × 14
A = 7 × 7 = 49
Thus the area of the parallelogram is 49 ft²

Problem Solving + Applications – Page No. 536

Question 14.
Jane’s backyard is shaped like a parallelogram. The base of the parallelogram is 90 feet, and the height is 25 feet. What is the area of Jane’s backyard?

________ ft²

Answer: 2250

Explanation:
Jane’s backyard is shaped like a parallelogram.
The base of the parallelogram is 90 feet, and the height is 25 feet.
A = bh
A = 90 ft × 25 ft
A = 2250 square feet
Therefore the area of the parallelogram for the above figure is 2250 ft²

Question 15.
Jack made a parallelogram by putting together two congruent triangles and a square, like the figures shown at the right. The triangles have the same height as the square. What is the area of Jack’s parallelogram?

________ cm²

Answer: 104

Explanation:
Jack made a parallelogram by putting together two congruent triangles and a square, like the figures shown at the right.
The triangles have the same height as the square.
Base = 8 cm + 5 cm = 13 cm
Height = 8 cm
Area = bh
A = 13 cm × 5 cm
A = 104 square cm
Thus the area of the parallelogram is 104 cm²

Question 16.
The base of a parallelogram is 2 times the parallelogram’s height. If the base is 12 inches, what is the area?
________ ft²

Answer: 72

Explanation:
The base of a parallelogram is 2 times the parallelogram’s height.
Base = 12 ft
Height = 12/2 = 6 ft
Area of parallelogram is  base × height
A = bh
A = 12 ft × 6 ft
A = 72 ft²
Thus the area of the parallelogram is 72 ft²

Question 17.
Verify the Reasoning of Others Li Ping says that a square with 3-inch sides has a greater area than a parallelogram that is not a square but has sides that have the same length. Does Li Ping’s statement make sense? Explain.

Type below:
_______________

Answer: 9

Explanation:
Base = 3 in
Height = 3 in
A = bh
A = 3 in × 3 in
A = 9 square inches
Therefore the area of the above figure is 9 in²

Question 18.
Find the area of the parallelogram.

________ in.²

Answer: 60

Explanation:
Base = 12 in
H = 5 in
A = bh
A = 12 in × 5 in
A = 60 square inches
A = 60 in²

Area of Parallelograms – Page No. 537

Find the area of the figure.

Question 1.

________ ft²

Answer: 126

Explanation:
The base of the figure is 18 ft
Height = 7 ft
The area of the parallelogram is bh
A = 18 ft × 7 ft
A = 126 square feet
Thus the area of the parallelogram is 126 ft²

Question 2.

________ cm²

Answer: 35

Explanation:
Base = 7 cm
Height = 5 cm
A = bh
A = 7 cm × 5 cm
A = 35 square cm
A = 35 cm²

Find the unknown measurement for the figure.

Question 3.
parallelogram
A = 9.18 m²
b = 2.7 m
h = ?
h = ________ m

Answer: 3.4

Explanation:
A = 9.18 m²
b = 2.7 m
h = ?
A = bh
9.18 m² = 2.7 m × h
h = 9.18/2.7
A = 3.4 m

Question 4.
parallelogram
A = ?
b = 4 \(\frac{3}{10}\) m
h = 2 \(\frac{1}{10}\) m
A = ________ \(\frac{□}{□}\) m²

Explanation:
b = 4 \(\frac{3}{10}\) m
h = 2 \(\frac{1}{10}\) m
A = ?
A = bh
A = 4 \(\frac{3}{10}\) m × 2 \(\frac{1}{10}\) m
A = \(\frac{43}{10}\) m × \(\frac{21}{10}\) m
A = \(\frac{903}{100}\) m²
A = 9 \(\frac{3}{100}\) m²

Question 5.
square
A = ?
s = 35 cm
A = ________ cm²

Answer: 1225

Explanation:
s = 35 cm
A = s × s
A = 35 cm × 35 cm
A = 1225 cm²
Area of the parallelogram is 1225 cm²

Question 6.
parallelogram
A = 6.3 mm²
b = ?
h = 0.9 mm
b = ________ mm

Answer: 7

Explanation:
A = 6.3 mm²
b = ?
h = 0.9 mm
A = bh
6.3 mm² = b × 0.9 mm
b = 6.3/0.9
b = 7 mm
Thus the base of the parallelogram is 7 mm.

Problem Solving

Question 7.
Ronna has a sticker in the shape of a parallelogram. The sticker has a base of 6.5 cm and a height of 10.1 cm. What is the area of the sticker?
________ cm²

Answer: 65.65

Explanation:
Ronna has a sticker in the shape of a parallelogram.
The sticker has a base of 6.5 cm and a height of 10.1 cm.
A = bh
A = 6.5 cm × 10.1 cm
A = 65.65 cm²

Question 8.
A parallelogram-shaped tile has an area of 48 in.². The base of the tile measures 12 in. What is the measure of its height?
________ in.

Answer: 4

Explanation:
A parallelogram-shaped tile has an area of 48 in.²
The base of the tile measures 12 in.
A = bh
48 = 12 × h
h = 48/12 = 4 in
Therefore the height of the parallelogram is 4 inches

Question 9.
Copy the two triangles and the square in Exercise 15 on page 536. Show how you found the area of each piece. Draw the parallelogram formed when the three figures are put together. Calculate its area using the formula for the area of a parallelogram.
Type below:
_______________

Answer:

First, we need to add the base of the triangle and square
So, base = 8 cm + 5 cm
base = 13 cm
The height of the triangle and square are the same.
So, h = 8 cm
Area of the parallelogram is base × height
A = bh
A = 13 cm × 5 cm
A = 104 square cm
Thus the area of the parallelogram is 104 cm²

Lesson Check – Page No. 538

Question 1.
Cougar Park is shaped like a parallelogram and has an area of \(\frac{1}{16}\) square mile. Its base is \(\frac{3}{8}\) mile. What is its height?
\(\frac{□}{□}\) mile

Answer: \(\frac{1}{6}\) mile

Explanation:
Cougar Park is shaped like a parallelogram and has an area of \(\frac{1}{16}\) square mile.
Its base is \(\frac{3}{8}\) mile.
A = bh
\(\frac{1}{16}\) = \(\frac{3}{8}\) × h
\(\frac{1}{16}\) × \(\frac{8}{3}\) = h
h =  \(\frac{1}{6}\) mile

Question 2.
Square County is a square-shaped county divided into 16 equal-sized square districts. If the side length of each district is 4 miles, what is the area of Square County?
________ square miles

Answer: 256 square miles

Explanation:
Square County is a square-shaped county divided into 16 equal-sized square districts.
If the side length of each district is 4 miles
4 × 4 = 16
A = 16 × 16 = 256 square miles

Spiral Review

Question 3.
Which of the following values of y make the inequality y < ^–4 true?
y = ^–4     y = ^–6      y = 0    y = ^–8    y = 2
Type below:
_______________

Answer: y = -6

Question 4.
On a winter’s day, 9°F is the highest temperature recorded. Write an inequality that represents the temperature t in degrees Fahrenheit at any time on this day.
Type below:
_______________

Answer: t ≤ 9

Explanation:
On a winter’s day, 9°F is the highest temperature recorded.
t will be less than or equal to 9.
The inequality is t ≤ 9

Question 5.
In 2 seconds, an elevator travels 40 feet. In 3 seconds, the elevator travels 60 feet. In 4 seconds, the elevator travels 80 feet. Write an equation that gives the relationship between the number of seconds x and the distance y the elevator travels.
Type below:
_______________

Answer: y = 20x

Explanation:
x represents the number of seconds
y represents the distance the elevator travels.
The elevator travels 20 feet per second.
Thus the equation is y = 20x

Question 6.
The linear equation y = 4x represents the number of bracelets y that Jolene can make in x hours. Which ordered pair lies on the graph of the equation?
Type below:
_______________

Answer: (4, 16)

Explanation:
y = 4x
If x = 4
Then y = 4(4)
y = 16
Thus the ordered pairs are (4, 16)

Share and Show – Page No. 541

Question 1.
Trace the parallelogram, and cut it into two congruent triangles. Find the areas of the parallelogram and one triangle, using square units.

Type below:
_______________

Answer:
Base = 9 units
Height = 4 units
Area of the parallelogram = base × height
A = 9 × 4
A = 36 sq. units
Area of the triangle = ab/2
A = (9 × 4)/2
A = 18 sq. units
Area of another triangle = ab/2
A = (9 × 4)/2
A = 18 sq. units

Find the area of each triangle.

Question 2.

_______ in.²

Answer: 40

Explanation:
The area of the right triangle is bh/2
A = (8 × 10)/2
A = 80/2
A = 40 in.²
Thus the area of the triangle for the above figure is 40 in.²

Question 3.

_______ ft²

Answer: 180

Explanation:
The area of the right triangle is bh/2
A = (18 × 20)/2
A = 360/2
A = 180 ft²

Question 4.

_______ yd²

Answer: 22

Explanation:
The area of the right triangle is bh/2
A = (4 × 11)/2
A = 44/2
A = 22
A = 22 yd²
Thus the area of the triangle is 22 yd²

Question 5.

_______ mm²

Answer: 495

Explanation:
The area of the right triangle is bh/2
A = (30 × 33)/2
A = 990/2
A = 495 mm²
Thus the area of the triangle is 495 mm²

Question 6.

_______ in.²

Answer: 190

Explanation:
The area of the right triangle is bh/2
A = (19 × 20)/2
A = 380/2
A = 190 in.²
Thus the area of the triangle is 190 in.²

Question 7.

_______ cm²

Answer: 96

Explanation:
The area of the right triangle is bh/2
A = (16 × 12)/2
A = 192/2
A = 96 Sq. cm
Thus the area of the triangle is 96 Sq. cm

Problem Solving + Applications

Question 8.
Communicate Describe how you can use two triangles of the same shape and size to form a parallelogram.
Type below:
_______________

Answer: Put them together like a puzzle. if the sides are parallel then it would be a parallelogram.

Question 9.
A school flag is in the shape of a right triangle. The height of the flag is 36 inches and the base is \(\frac{3}{4}\) of the height. What is the area of the flag?
_______ in.²

Answer: 486 in.²

Explanation:
A school flag is in the shape of a right triangle.
The height of the flag is 36 inches and the base is \(\frac{3}{4}\) of the height.
B = 36 × \(\frac{3}{4}\)
B = 27
Area of the triangle = bh/2
A = (36 × 27)/2
A = 486 sq. in
Thus the area of the triangle is 486 in.²

Sense or Nonsense? – Page No. 542

Question 10.
Cyndi and Tyson drew the models below. Each said his or her drawing represents a triangle with an area of 600 square inches. Whose statement makes sense? Whose statement is nonsense? Explain your reasoning.
Tyson’s Model:

Cyndi’s Model:

Type below:
_______________

Answer: Tyson’s Model makes sense.
The base of the figure is 30 in.
The height of the figure is 40 in
Area of the triangle = bh/2
A = (30 × 40)/2
A = 1200/2 = 600 sq. in
Cyndi’s Model doesn’t make sense because there is no base for the triangle.

Question 11.
A flag is separated into two different colors. Find the area of the white region. Show your work.

_______ ft.²

Answer: 7.5 ft.²

Explanation:
A flag is separated into two different colors.
B = 5 ft
H = 3 ft
Area of the triangle = bh/2
A = (3 × 5)/2
A = 15/2
A = 7.5 sq. ft

Explore Area of Triangles – Page No. 543

Find the area of each triangle.

Question 1.

_______ ft²

Answer: 30

Explanation:
Given,
Base = 6 ft
Height = 10 ft
Area of the triangle = bh/2
A = (6 ft × 10 ft)/2
A = 60 sq. ft/2
A = 30 ft²
Thus the area of the triangle for the above figure is 0 ft²

Question 2.

_______ cm²

Answer: 925

Explanation:
Given,
Base = 50 cm
Height = 37 cm
Area of the triangle = bh/2
A = (50 × 37)/2
A = 1850/2
A = 925 sq. cm
Therefore the area of the above figure is 925 cm²

Question 3.

_______ mm²

Answer: 400

Explanation:
Given,
Base = 40 mm
Height = 20 mm
Area of the triangle = bh/2
A = (40 × 20)/2
A = 800/2
A = 400 mm²
Therefore the area of the above figure is 400 mm²

Question 4.

_______ in.²

Answer: 180

Explanation:
Given,
Base = 12 in.
Height = 30 in.
Area of the triangle = bh/2
A = (12 × 30)/2
A = 360/2
A = 180 in.²
Therefore the area of the above figure is 180 in.²

Question 5.

_______ cm²

Answer: 225

Explanation:
Given,
Base = 15 cm
Height = 30 cm
Area of the triangle = bh/2
A = (15 × 30)/2
A = 450/2
A = 225 cm²
Therefore the area of the above figure is 225 cm²

Question 6.

_______ cm²

Answer: 450

Explanation:
Given,
Base = 20 cm
Height = 45 cm
Area of the triangle = bh/2
A = (20 × 45)/2
A = 900/2
A = 450 cm²
Therefore the area of the above figure is 450 cm²

Problem Solving

Question 7.
Fabian is decorating a triangular pennant for a football game. The pennant has a base of 10 inches and a height of 24 inches. What is the total area of the pennant?
_______ in.²

Answer: 120

Explanation:
Fabian is decorating a triangular pennant for a football game.
The pennant has a base of 10 inches and a height of 24 inches.
Area of the triangle = bh/2
A = (10 × 24)/2
A = 240/2
A = 120 in.²
Therefore the area of the above figure is 120 in.²

Question 8.
Ryan is buying a triangular tract of land. The triangle has a base of 100 yards and a height of 300 yards. What is the area of the tract of land?
_______ yd²

Answer: 15000

Explanation:
Given,
Base = 100 yards
Height = 300 yards
Area of the triangle = bh/2
A = (100 × 300)/2
A = 30000/2
A = 15000 yd²
Therefore the area of the above figure is 15000 yd²

Question 9.
Draw 3 triangles on grid paper. Draw appropriate parallelograms to support the formula for the area of the triangle. Tape your drawings to this page.
Type below:
_______________

Lesson Check – Page No. 544

Question 1.
What is the area of a triangle with a height of 14 feet and a base of 10 feet?
_______ ft²

Answer: 70

Explanation:
Given,
Base = 10 feet
Height = 14 feet
Area of the triangle = bh/2
A = (14 × 10)/2
A = 140/2
A = 70 ft²
Therefore the area of the triangle is 70 ft²

Question 2.
What is the area of a triangle with a height of 40 millimeters and a base of 380 millimeters?
_______ mm²

Answer: 7600

Explanation:
Given,
Base = 380 millimeters
Height = 40 millimeters
Area of the triangle = bh/2
A = (380 × 40)/2
A = 15200/2
A = 7600 mm²

Spiral Review

Question 3.
Jack bought 3 protein bars for a total of $4.26. Which equation could be used to find the cost c in dollars of each protein bar?
Type below:
_______________

Answer: 3c = 4.26

Explanation:
Jack bought 3 protein bars for a total of $4.26.
c represents the cost of each protein bar
3c = 4.26

Question 4.
Coach Herrera is buying tennis balls for his team. He can solve the equation 4c = 92 to find how many cans c of balls he needs. How many cans does he need?
_______ cans

Answer: 23

Explanation:
Coach Herrera is buying tennis balls for his team.
4c = 92
c = 92/4
c = 23
Therefore he need 23 cans.

Question 5.
Sketch the graph of y ≤ ^–7 on a number line.
Type below:
_______________

Answer:

Question 6.
A square photograph has a perimeter of 20 inches. What is the area of the photograph?
_______ in.²

Answer: 25

Explanation:
A square photograph has a perimeter of 20 inches.
p = 4s
20 = 4s
s = 20/4
s = 5 in.
Area of the square is s × s
A = 5 × 5 = 25
Thus the area of square photograph = 25 in.²

Share and Show – Page No. 547

Question 1.
Find the area of the triangle.

A = _______ cm²

Answer: 56

Explanation:
B = 14 cm
H = 8 cm
Area of the triangle = bh/2
A = (14 × 8)/2
A = 14 × 4
A = 56 sq. cm
Thus the area of the above figure is 56 cm²

Question 2.
The area of the triangle is 132 in.². Find the height of the triangle

h = _______ in.

Answer: 12

Explanation:
B = 22 in.
H = ?
A = 132 in.²
Area of the triangle = bh/2
132 sq. in  = 22 in × h
h = 132 sq. in/22 in
h = 12 in
Thus the height of the above figure is 12 in.

Find the area of the triangle.

Question 3.

A = _______ mm²

Answer: 540

Explanation:
B = 27 mm
H = 40 mm
Area of the triangle = bh/2
A = (27 × 40)/2
A = 27 × 20 = 540
A = 540 mm²
Therefore the area of the above figure is 540 mm²

Question 4.

A = _______ mm²

Answer: 11

Explanation:
B = 5.5 mm
H = 4 mm
Area of the triangle = bh/2
A = (5.5 mm × 4 mm)/2
A = 5.5 mm × 2 mm
A = 11 mm²
Therefore the area of the above figure is 11 mm²

On Your Own

Find the unknown measurement for the figure.

Question 5.

h = _______ in.

Answer: 21

Explanation:
B = 5 in
H =?
A = 52.5 sq. in
Area of the triangle = bh/2
52.5 sq. in = (5 × h)/2
52.5 sq. in × 2 = 5h
h = 21 in
Thus the height of the above figure is 21 in

Question 6.

h = _______ cm

Answer: 4.3

Explanation:
B = 80 mm = 8 cm
H = ?
A = 17.2 sq. cm
Area of the triangle = bh/2
17.2 sq. cm = (8 cm × h)/2
17.2 × 2 = 8 × h
h = 4.3 cm
Thus the height of the above figure is 4.3 cm

Question 7.
Verify the Reasoning of Others The height of a triangle is twice the base. The area of the triangle is 625 in.². Carson says the base of the triangle is at least 50 in. Is Carson’s estimate reasonable? Explain.
Type below:
_______________

Answer:
A = 625 in.²
B = 50 in
H = 2b
H = 2 × 50 in
H = 100 in
Area of the triangle = bh/2
625 in.² = (50 × 100)/2
625 in.² = 2500
No Carson’s estimation is not reasonable.

Unlock the Problem – Page No. 548

Question 8.
Alani is building a set of 4 shelves. Each shelf will have 2 supports in the shape of right isosceles triangles. Each shelf is 14 inches deep. How many square inches of wood will she need to make all of the supports?

a. What are the base and height of each triangle?
Base: ___________ in.
Height: ___________ in.

Answer:
Base: 14 in
Height: 14 in

Explanation:
Given that,
Each shelf is 14 inches deep.
Height = 14 inches
By seeing the above figure we can say that the base of the shelves is 14 inches
Base = 14 inches

Question 8.
b. What formula can you use to find the area of a triangle?
Type below:
_______________

Answer: The formula to find the Area of the triangle = bh/2

Question 8.
c. Explain how you can find the area of one triangular support.
Type below:
_______________

Answer:
We can find the area of one triangle support by substituting the base and height in the formula.
A = (14 × 14)/2
A = 98 sq. in

Question 8.
d. How many triangular supports are needed to build 4 shelves?
_______ supports

Answer: 8
By seeing the above figure we can say that 8 triangular supports are needed to build 4 shelves.

Question 8.
e. How many square inches of wood will Alani need to make all the supports?
_______ in.²

Answer: 784

Explanation:
The depth of each shelf made by Alamo is 14 inches.
So the base of the right isosceles triangular supporter is 14 inches.
So one equal side is 14 cm. Now by using the Pythagoras theorem we can calculate the other side of the supporter = = 19.8 inches.
The area of the right isosceles triangle is given by × base ×height. Here the base and height are equal to 14 inches.
Therefore the area of each right isosceles triangular supporter is
A = (14 × 14)/2
A = 98 sq. in
Each shelf would require two such supporters and there are 4 such shelves. Thus the total number of supporters required is 8.
Square inches of wood necessary for 8 right isosceles triangular supporters = 98 × 8 = 784 square inches.

Question 9.
The area of a triangle is 97.5 cm². The height of the triangle is 13 cm. Find the base of the triangle. Explain your work.
b = _______ cm

Answer: 15 cm

Explanation:
Given,
The area of a triangle is 97.5 cm².
The height of the triangle is 13 cm.
Area of the triangle = bh/2
97.5 cm² = (b × 13 cm)/2
b = 2 × 97.5cm²/13 cm
b = 15 cm
Therefore the base of the triangle is 15 cm

Question 10.
The area of a triangle is 30 ft².
For numbers 10a–10d, select Yes or No to tell if the dimensions given could be the height and base of the triangle.
10a. h = 3, b = 10
10b. h = 3, b = 20
10c. h = 5, b = 12
10d. h = 5, b = 24
10a. ___________
10b. ___________
10c. ___________
10d. ___________

Answer:
10a. No
10b. yes
10c. Yes
10d. No

Explanation:
The area of a triangle is 30 ft².
10a. h = 3, b = 10
Area of the triangle = bh/2
A = (3 × 10)/2
A = 15 ft².
Thus the answer is no.
10b. h = 3, b = 20
Area of the triangle = bh/2
A = (3 × 20)/2
A = 30 ft².
Thus the answer is yes.
10c. h = 5, b = 12
Area of the triangle = bh/2
A = (5 × 12)/2
A = 30 ft².
Thus the answer is yes.
10d. h = 5, b = 24
Area of the triangle = bh/2
A = (5 × 24)/2
A = 60 ft².
Thus the answer is no.

Area of Triangles – Page No. 549

Find the area.

Question 1.

_______ in.²

Answer: 45

Explanation:
Given,
Base = 15 in.
Height = 6 in.
Area of the triangle = bh/2
A = (15 × 6)/2
A = 90/2
A = 45 in.²

Question 2.

_______ m²

Answer: 0.36

Explanation:
Given,
Base = 1.2 m
Height = 0.6 m
Area of the triangle = bh/2
A = (1.2 × 0.6)/2
A = 0.72/2
A = 0.36 m²

Question 3.

_______ ft²

Answer: 6

Explanation:
Given,
Base = 4 1/2 ft
Height = 2 2/3 ft
Area of the triangle = bh/2
A = (4 1/2 × 2 2/3)/2
A = 12/2
A = 6 ft²

Find the unknown measurement for the triangle.

Question 4.
A = 0.225 mi²
b = 0.6 mi
h = ?
h = _______ mi

Answer: 0.75

Explanation:
Given,
A = 0.225 mi²
b = 0.6 mi
h = ?
Area of the triangle = bh/2
0.225 = (0.6 × h)/2
0.450 = 0.6 × h
h = 0.450/0.6
h = 0.75 mi

Question 5.
A = 4.86 yd²
b = ?
h = 1.8 yd
b = _______ yd

Answer: 5.4 yd

Explanation:
Given,
A = 4.86 yd²
b = ?
h = 1.8 yd
Area of the triangle = bh/2
4.86 yd² = (b × 1.8 yd)/2
4.86 × 2 = b × 1.8
9.72 = b × 1.8
b = 9.72/1.8
b = 5.4 yd

Question 6.
A = 63 m²
b = ?
h = 12 m
b = _______ m

Answer: 10.5

Explanation:
Given,
A = 63 m²
b = ?
h = 12 m
Area of the triangle = bh/2
63 = (b × 12)/2
63 = b × 6
b = 63/6
b = 10.5 m

Question 7.
A = 2.5 km²
b = 5 km
h = ?
h = _______ km

Answer: 1

Explanation:
Given,
A = 2.5 km²
b = 5 km
h = ?
Area of the triangle = bh/2
2.5 = (5 km × h)/2
2.5 km² = 2.5 km × h
h = 2.5/2.5
h = 1 km

Problem Solving

Question 8.
Bayla draws a triangle with a base of 15 cm and a height of 8.5 cm. If she colors the space inside the triangle, what area does she color?
_______ cm²

Answer: 63.75 cm²

Explanation:
Bayla draws a triangle with a base of 15 cm and a height of 8.5 cm.
B = 15 cm
h = 8.5 cm
Area of the triangle = bh/2
A = (15 cm × 8.5 cm)/2
A = 7.5 cm × 8.5 cm
A = 63.75 cm²

Question 9.
Alicia is making a triangular sign for the school play. The area of the sign is 558 in.². The base of the triangle is 36 in. What is the height of the triangle?
_______ in.

Answer: 31

Explanation:
Given,
Alicia is making a triangular sign for the school play.
The area of the sign is 558 in.²
The base of the triangle is 36 in.
Area of the triangle = bh/2
558 = (36 × h)/2
558 = 18 × h
h = 558/18
h = 31 inches

Question 10.
Describe how you would find how much grass seed is needed to cover a triangular plot of land.
Type below:
_______________

Answer:

You will need to find the area
A=height multiplied by the base divided by 2
Area of the triangle = bh/2

Lesson Check – Page No. 550

Question 1.
A triangular flag has an area of 187.5 square inches. The base of the flag measures 25 inches. How tall is the triangular flag?
_______ in.

Answer: 15 in.

Explanation:
A triangular flag has an area of 187.5 square inches.
The base of the flag measures 25 inches.
Area of the triangle = bh/2
187.5 square inches = (25 inches × h)/2
187.5 sq. in × 2 = 25h
375 sq. in = 25h
h = 375 sq. in/25
h = 15 inches

Question 2.
A piece of stained glass in the shape of a right triangle has sides measuring 8 centimeters, 15 centimeters, and 17 centimeters. What is the area of the piece?
_______ cm²

Answer: 60

Explanation:
A piece of stained glass in the shape of a right triangle has sides measuring 8 centimeters, 15 centimeters, and 17 centimeters.
b = 8 cm
h = 15 cm
Area of the triangle = bh/2
A = (8 × 15)/2
A = 4 cm × 15 cm
A = 60 sq. cm

Spiral Review

Question 3.
Tina bought a t-shirt and sandals. The total cost was $41.50. The t-shirt cost $8.95. The equation 8.95 + c = 41.50 can be used to find the cost c in dollars of the sandals. How much did the sandals cost?
$ _______

Answer: $32.55

Explanation:
Tina bought a t-shirt and sandals.
The total cost was $41.50.
The t-shirt cost $8.95.
8.95 + c = 41.50
c = 41.50 – 8.95
c = $32.55

Question 4.
There are 37 paper clips in a box. Carmen places more paper clips in the box. Write an equation to show the total number of paper clips p in the box after Carmen places n more paper clips in the box.
Type below:
_______________

Answer: 37 + n = p

Explanation:
There are 37 paper clips in a box. Carmen places more paper clips in the box.
n represents number of paper clips in the box
The equation is 37 + n = p

Question 5.
Name another ordered pair that is on the graph of the equation represented by the table.

Type below:
_______________

Answer: The ordered pairs are (1, 6), (2, 12), (3, 18), (4, 16)

Question 6.
Find the area of the triangle that divides the parallelogram in half.

_______ cm²

Answer: 58.5

Explanation:
Given,
b = 13 cm
h = 9 cm
Area of the triangle = bh/2
A = (13 × 9)/2
A = 117/2
A = 58.5 cm²

Share and Show – Page No. 553

Question 1.
Trace and cut out two copies of the trapezoid. Arrange the trapezoids to form a parallelogram. Find the areas of the parallelogram and one trapezoid using square units

Type below:
_______________

Answer:
Figure 1:
Base 1 = 3 units
Base 2= 7 units
Height = 4 units
Area of the trapezium = (b1 + b2)h/2
A = (3 + 7)4/2
A = 10 × 2
A = 20 sq. units
Figure 2:
Base 1 = 7 units
Base 2= 3 units
Height = 4 units
Area of the trapezium = (b1 + b2)h/2
A = (7 + 3)4/2
A = 10 × 2
A = 20 sq. units

Find the area of the trapezoid.

Question 2.

_______ cm²

Answer: 40

Explanation:
Base 1 = 6 cm
Base 2 = 10 cm
Height = 5 cm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (6 cm + 10 cm)5 /2
A = (16 × 5)/2
A = 40 sq. cm

Question 3.

_______ in.²

Answer: 48

Explanation:
b1 = 3 in
b2 = 9 in.
h = 8 in.
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (3 + 9)8/2
A = 12 × 4
A = 48 sq. in

Question 4.

_______ ft²

Answer: 64

Explanation:
b1 = 11 ft
b2 = 5 ft
h = 8 ft
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (11 + 5)8/2
A = 16 × 4
A = 64 sq. ft

Question 5.

_______ cm²

Answer: 266

Explanation:
b1 = 16 cm
b2 = 22 cm
h = 14 cm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (16 + 22)14/2
A = 38 × 7
A = 266 sq. cm

Question 6.

_______ mm²

Answer: 71.5

Explanation:
b1 = 8 mm
b2 = 14 mm
h = 6.5 mm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (8 + 14)6.5/2
A = 11 × 6.5
A = 71.5 sq. mm

Question 7.

_______ in.²

Answer: 31.5

Explanation:
b1 = 3 1/2 in.
b2 = 8 1/2 in.
h = 5 1/4 in.
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
b = 3 1/2 + 8 1/2
b = 12
A = 5 1/4 × 12/2
A = 5 1/4 × 6
A = 31.5 sq. in

Problem Solving + Applications

Question 8.
Describe a Method Explain one way to find the height of a trapezoid if you know the area of the trapezoid and the length of both bases.
Type below:
_______________

Answer:
1) Add the length of both bases: [Total Length = Length 1 + Length 2]
2) Divide the length that you found by 2. [Average Length = Total Length ÷ 2]
3) Divide the Area with the length found [Height = Area ÷ average length]

Question 9.
A patio is in the shape of a trapezoid. The length of the longer base is 18 feet. The length of the shorter base is two feet less than half the longer base. The height is 8 feet. What is the area of the patio?
_______ ft²

Answer: 100

Explanation:
trapezoid area = ((sum of the bases) ÷ 2) × height
long base = 18
short base = 7
height = 8
trapezoid area = [(18 + 7) / 2] × 8
trapezoid area = [(12.5)] × 8
trapezoid area = 100 square feet

What’s the Error? – Page No. 554

Question 10.
Except for a small region near its southeast corner, the state of Nevada is shaped like a trapezoid. The map at the right shows the approximate dimensions of the trapezoid. Sabrina used the map to estimate the area of Nevada.
Look at how Sabrina solved the problem. Find her error.
Two copies of the trapezoid can be put together to form a rectangle.
length of rectangle: 200 + 480 = 680 mi
width of rectangle: 300 mi
A = lw
A = 680 × 300
A = 204,000
The area of Nevada is about 204,000 square miles.
Describe the error. Find the area of the trapezoid to estimate the area of Nevada.
Type below:
_______________

Answer:
The area of Nevada is she didn’t divide by 2.
Area of the trapezium = (b1 + b2)h/2
A = (200 + 480)300/2
A = 680 × 150
A = 102000 sq. miles

Question 11.
A photo was cut in half at an angle. What is the area of one of the cut pieces?

_______ in.²

Answer: 30

Explanation:
b1= 3 in
b2 = 7 in
h = 6 in.
Area of the trapezium = (b1 + b2)h/2
A = (3 + 7)6/2
A = 10 × 3
A = 30 sq. in
Thus the area of the trapezium is 30 in.²

Explore Area of Trapezoids – Page No. 555

Question 1.
Trace and cut out two copies of the trapezoid. Arrange the trapezoids to form a parallelogram. Find the areas of the parallelogram and the trapezoids using square units.

Type below:
_______________

Answer:
Figure 1:
b1 = 2 units
b2 = 6 units
h = 3 units
Area of the trapezium = (b1 + b2)h/2
A = (2 + 6)3/2
A = (8)(3)/2
A = 24/2 = 12
A = 12 sq. units
Figure 2:
b1 = 6 units
b2 = 2 units
h = 3 units
Area of the trapezium = (b1 + b2)h/2
A = (6 + 2)3/2
A = (8)(3)/2
A = 24/2 = 12
The area of figure 2 is 12 sq. units

Find the area of the trapezoid.

Question 2.

_______ in.²

Answer: 38.5

Explanation:
Given,
b1 = 9 in
b2 = 2 in
h = 7 in
Area of the trapezium = (b1 + b2)h/2
A = (9 + 2)7/2
A = (11 × 7)/2
A = 77/2 = 38.5 in.²

Question 3.

_______ yd²

Answer: 3600

Explanation:
Given,
b1 = 24 yd
b2 = 48 yd
h = 100 yd
Area of the trapezium = (b1 + b2)h/2
A = (24 + 48)100/2
A = 72 × 50
A = 3600 yd²

Question 4.

_______ ft²

Answer: 64

Explanation:
Given,
b1 = 4.5 ft
b2 = 11.5 ft
h = 8 ft
Area of the trapezium = (b1 + b2)h/2
A = (4.5 + 11.5)8/2
A = 16 × 4
A = 64 sq. ft

Problem Solving

Question 5.
A cake is made out of two identical trapezoids. Each trapezoid has a height of 11 inches and bases of 9 inches and 14 inches. What is the area of one of the trapezoid pieces?
_______ in.²

Answer: 126.5

Explanation:
Given,
A cake is made out of two identical trapezoids.
Each trapezoid has a height of 11 inches and bases of 9 inches and 14 inches.
Area of the trapezium = (b1 + b2)h/2
A = (9 + 14)11/2
A = 23 × 11/2
A = 126.5 in.²

Question 6.
A sticker is in the shape of a trapezoid. The height is 3 centimeters, and the bases are 2.5 centimeters and 5.5 centimeters. What is the area of the sticker?
_______ cm²

Answer: 12

Explanation:
Given,
A sticker is in the shape of a trapezoid.
The height is 3 centimeters, and the bases are 2.5 centimeters and 5.5 centimeters.
Area of the trapezium = (b1 + b2)h/2
A = (2.5 + 5.5)3/2
A = 8 × 3/2
A = 4 × 3
A = 12 sq. cm

Question 7.
Find the area of a trapezoid that has bases that are 15 inches and 20 inches and a height of 9 inches.
_______ in.²

Answer: 157.5

Explanation:
b1 = 15 inches
b2 = 20 inches
h = 9 inches
Area of the trapezium = (b1 + b2)h/2
A = (15 + 20)9/2
A = (35 × 9)/2
A = 157.5 sq. in

Lesson Check – Page No. 556

Question 8.

_______ yd²

Answer: 84

Explanation:
b1 = 9 yd
b2 = 15 yd
h = 7 yd
Area of the trapezium = (b1 + b2)h/2
A = (9 + 15)7/2
A = 24 × 3.5
A = 84 sq. yd

Question 2.
Maggie colors a figure in the shape of a trapezoid. The trapezoid is 6 inches tall. The bases are 4.5 inches and 8 inches. What is the area of the figure that Maggie colored?
_______ in.²

Answer: 37.5

Explanation:
Maggie colors a figure in the shape of a trapezoid.
The trapezoid is 6 inches tall.
The bases are 4.5 inches and 8 inches.
b1 = 4.5 in
b2 = 8 in
h = 6 in
Area of the trapezium = (b1 + b2)h/2
A = (4.5 in + 8 in)6/2
A = 12.5 in × 3
A = 37.5 sq. in

Spiral Review

Question 3.
Cassandra wants to solve the equation 30 = \(\frac{2}{5}\)p. What operation should she perform to isolate the variable?
Type below:
_______________

Answer: Divide two sides by \(\frac{2}{5}\)

Explanation:
In order to make p independent
We have to divide \(\frac{2}{5}\) on both sides.
30 = \(\frac{2}{5}\)p
30 ÷ \(\frac{2}{5}\) p ÷ \(\frac{2}{5}\)
p = 75

Question 4.
Ginger makes pies and sells them for $14 each. Write an equation that represents the situation, if y represents the money that Ginger earns and x represents the number of pies sold.
Type below:
_______________

Answer: y = 14x

Explanation:
Ginger makes pies and sells them for $14 each.
y represents the money that Ginger earns
x represents the number of pies sold
The equation is y = 14x

Question 5.
What is the equation for the graph shown below?

Type below:
_______________

Answer: y = 2x
By seeing the graph we can say that y = 2x

Question 6.
Cesar made a rectangular banner that is 4 feet by 3 feet. He wants to make a triangular banner that has the same area as the other banner. The triangular banner will have a base of 4 feet. What should its height be?
_______ feet

Answer: 6

Explanation:
6 Because 4×3=12 and (4× 6)/2=12

Share and Show – Page No. 559

Question 1.
Find the area of the trapezoid.

A = _______ cm²

Answer: 18

Explanation:
Given,
b1 = 6 cm
b2 = 3 cm
h = 4 cm
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (6 cm + 3 cm)4 cm/2
A = 9 cm × 2 cm
A = 18 sq. cm
Therefore the area of the trapezoid is 18 cm²

Question 2.
The area of the trapezoid is 45 ft². Find the height of the trapezoid.

h = _______ ft

Answer: 5

Explanation:
b1 = 10 ft
b2 = 8 ft
The area of the trapezoid is 45 ft²
We know that,
Area of the trapezium = (b1 + b2)h/2
45 ft² = (10 ft + 8 ft)h/2
90 = 18 × h
h = 90/18
h = 5 ft
Thus the height of the above figure is 5 ft.

Question 3.
Find the area of the trapezoid.

_______ mm²

Answer: 540

Explanation:
b1 = 17 mm
b2 = 43 mm
h = 18 mm
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (17 + 43)18/2
A = 60 mm × 9 mm
A = 540 sq. mm
Thus the area of the trapezoid is 540 mm²

On Your Own

Find the area of the trapezoid.

Question 4.

A = _______ in.²

Answer: 266

Explanation:
Given,
b1 = 17 in
b2 = 21 in
h = 14 in
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (17 in + 21 in)14/2
A = 38 in × 7 in
A = 266 sq. in
Therefore Area of the trapezium is 266 in.²

Question 5.

A = _______ m²

Answer: 25.2 m²

Explanation:
Given,
b1 = 9.2 m
b2 = 2.8 m
h = 4.2 m
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (9.2 + 2.8)4.2/2
A = 12 × 2.1
A = 25.2 sq. m
Therefore the area of the trapezium is 25.2 m²

Find the height of the trapezoid.

Question 6.

h = _______ in.

Answer: 25

Explanation:
Given,
b1 = 27.5 in
b2 = 12.5 in
h = ?
A = 500 sq. in
We know that,
Area of the trapezium = (b1 + b2)h/2
500 sq. in = (27.5 in + 12.5 in)h/2
500 sq. in = 40 × h/2
500 sq. in = 20h
h = 500/20
h = 25 inches
Thus the height of the above figure is 25 inches.

Question 7.

h = _______ cm

Answer: 15

Explanation:
A = 99 sq. cm
b1 = 3.2 cm
b2 = 10 cm
h = ?
We know that,
Area of the trapezium = (b1 + b2)h/2
99 sq. cm = (3.2 cm+ 10 cm)h/2
99 sq. cm = (13.2 cm)h/2
99 sq. cm = 6.6 × h
h = 99 sq. cm/6.6 cm
h = 15 cm

Problem Solving + Applications – Page No. 560

Use the diagram for 8–9.

Question 8.
A baseball home plate can be divided into two trapezoids with the dimensions shown in the drawing. Find the area of home plate.
_______ in.²

Answer: 21.75

Explanation:
The bases of the trapezoid area 8.5 in and 17 in and the height is 8.5 in.
We know that,
Area of the trapezium = (b1 + b2)h/2
A = 1/2 (8.5 + 17)8.5
A = (25.5)(8.5)/2
A = 1/2 × 216.75
The area of the home plate is double the area of a trapezoid.
So, the area of the home plate is 216.75 sq. in.