Are you searching for Go Math Grade 8 Answer Key Chapter 7 Solving Linear Equations? If your answer is yes, then you are on the right page. Students of 8th standard can get the Download link of HMH Go Math Grade 8 Solution Key Chapter 7 Solving Linear Equations for free. Get the best maths tactics and ways of solving the problems for all the questions with the help of the Go Math Grade 8 Chapter 7 Solving Linear Equations Answer Key. You can practice all the questions to have a perfect grip on the Grade 8 maths subject. Go Math Grade 8 Answer Key is the best resource to improve math skills.
Go Math Grade 8 Chapter 7 Solving Linear Equations Answer Key
Improve your performance in exams with the help of Go Math Grade 8 Answer Key Chapter 7 Solving Linear Equations. You can find the review questions at the end of the chapter to test your knowledge. The topics covered in this Solving Linear Equations chapter are equations with the variable on both sides, equations with rational numbers, equations with the distributive property, equations with many solutions or no solution, etc. Just go through the online pdf and start practicing now. By looking into the questions and answers available on Go Math Grade 8 Answer Key Chapter 7 Solving Linear Equations.
Lesson 1: Equations with the Variable on Both Sides
- · Equations with the Variable on Both Sides – Page No. 200
- · Equations with the Variable on Both Sides – Page No. 201
- · Equations with the Variable on Both Sides Lesson Check – Page No. 202
Lesson 2: Equations with Rational Numbers
- · Equations with Rational Numbers – Page No. 206
- · Equations with Rational Numbers – Page No. 207
- · Equations with Rational Numbers Lesson Check – Page No. 208
Lesson 3: Equations with the Distributive Property
- · Equations with the Distributive Property – Page No. 212
- · Equations with the Distributive Property – Page No. 213
- · Equations with the Distributive Property Lesson Check – Page No. 214
Lesson 4: Equations with Many Solutions or No Solution
- · Equations with Many Solutions or No Solution – Page No. 218
- · Equations with Many Solutions or No Solution – Page No. 219
- · Equations with Many Solutions or No Solution Lesson Check – Page No. 220
Lesson 5: Equations with the Variable on Both Sides
Reviews
Guided Practice – Equations with the Variable on Both Sides – Page No. 200
Use algebra tiles to model and solve each equation.
Question 1.
x + 4 = -x – 4
x = ________
Answer:
x = -4
Explanation:
Model x + 4 on the left side of the mat and -x -4 on the right side.
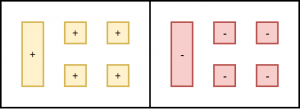
Add one c-tile to both sides. This represents adding x to both sides of the equation. Remove zero pairs.
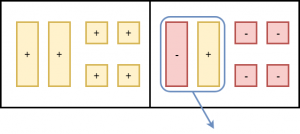
Place four -1-tiles on both sides. This represents subtracting -4 from both sides of the equation. Remove zero pairs.
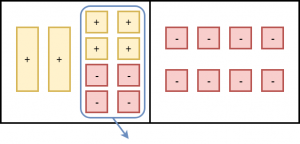
Separate each side into 2 equal groups. One x-tile is equivalent to four -1-tiles.
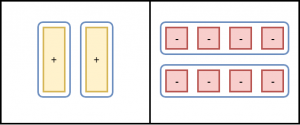
x = -4
Question 2.
2 – 3x = -x – 8
x = ________
Answer:
Explanation:
Given 2 – 3x = -x – 8
Model 2-3x on the left side of the mat and -x-8 on the right side.
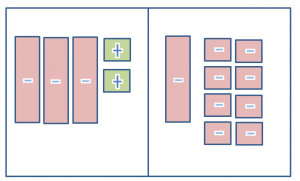
Place one x tile to both sides. This represents subtracting from both sides of the equation.
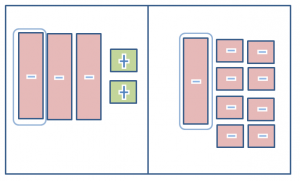
Remove 2 1 tiles from sides. This represents subtracting from both sides of the equation.
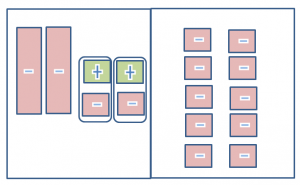
Separate each side into 2 equal groups. One -x tile is equivalent to 5 – 1 tile.
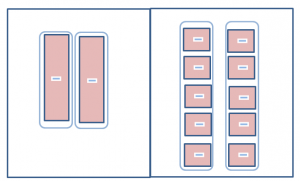
The solution is -x = -5 or x = 5
Question 3.
At Silver Gym, membership is $25 per month, and personal training sessions are $30 each. At Fit Factor, membership is $65 per month, and personal training sessions are $20 each. In one month, how many personal training sessions would Sarah have to buy to make the total cost at the two gyms equal?
________ sessions
Answer:
4 sessions
Explanation:
At Silver Gym, membership is $25 per month, and personal training sessions are $30 each.
Membership + Personal training session = 25 + 30x
At Fit Factor, membership is $65 per month, and personal training sessions are $20 each.
Membership + Personal training session = 65 + 20x
Membership at Silver Gym = Membership at Fit Factor
25 + 30x = 65 + 20x
30x – 20x = 65 – 25
10x = 40
x = 4
Sarah would have to buy 4 sessions for the total cost at the two gyms to be equal.
Question 4.
Write a real-world situation that could be modeled by the equation 120 + 25x = 45x.
Type below:
_______________
Answer:
120 + 25x = 45x
Sarah offers a plan to tutor a student at $25 per her plus a one-time registration fee of $ 120.
Surah offers an alternative plan to tutor a student at $45 per hour and no registration fee.
120 + 25x = 45x
Question 5.
Write a real-world situation that could be modeled by the equation 100 – 6x = 160 – 10x.
Type below:
_______________
Answer:
100 – 6x = 160 – 10x
The initial water in Tank A is 100 gallons and leaks at 6 gallons per week.
The initial water in Tank B is 160 gallon and leaks at 10 gallons per week
100 – 6x = 160 – 10x
Essential Question Check-In
Question 6.
How can you solve an equation with the variable on both sides?
Type below:
_______________
Answer:
Isolate the variable on one side. Add/subtract the variable with a lower coefficient from both sides. Add/subtract the constant (with the variable) from both sides. Divide both sides by coefficient of isolated variable.
Independent Practice – Equations with the Variable on Both Sides – Page No. 201
Question 7.
Derrick’s Dog Sitting and Darlene’s Dog Sitting are competing for new business. The companies ran the ads shown.

a. Write and solve an equation to find the number of hours for which the total cost will be the same for the two services.
________ hours
Answer:
3 hours
Explanation:
Hourly rate + One time fee = 5x + 12
Hourly rate + One time fee = 3x + 18
5x + 12 = 3x + 18
5x – 3x = 18 – 12
2x = 6
x = 3
the cost of the two dog sitting would be same for 3 hrs.
Question 7.
b. Analyze Relationships
Which dog sitting service is more economical to use if you need 5 hours of service? Explain.
____________
Answer:
Darlene’s Dog Sitting would be cheaper
Explanation:
Let y be the cost of dog sitting after x hours for both companies
y = 5x +12
y = 3x +18
Substitute x = 5
y = 5(5) + 12 = 37
y = 3 (5) + 18 = 33
compare the cost for both companies for x = 5hr.
$37 > $33
Darlene’s Dog Sitting would be cheaper
Question 8.
Country Carpets charges $22 per square yard for carpeting, and an additional installation fee of $100. City Carpets charges $25 per square yard for the same carpeting, and an additional installation fee of $70.
a. Write and solve an equation to find the number of square yards of carpeting for which the total cost charged by the two companies will be the same.
_______ square yards
Answer:
10 square yards
Explanation:
Unit square rate + One time installation fee = 22x + 100
Unit square rate + One time installation fee = 25x + 70
22x + 100 = 25x + 70
25x – 22x = 100 – 70
3x = 30
x = 10
the total cost charged by the two companies will be the same for 10 square yards of carpeting.
Question 8.
b. Justify Reasoning
Mr. Shu wants to hire one of the two carpet companies to install carpeting in his basement. Is he more likely to hire Country Carpets or City Carpets? Explain your reasoning.
___________
Answer:
City Carpets are cheaper when x < 10
y = 25(9) + 70 = 295
y = 22(9) + 100 = 298
Country Carpets are cheaper when x > 10
y = 25(11) + 70 = 345
y = 25(11) + 100 = 342
If Mr.Shu needs the carpenting done for less than 10square yards, he will hire City Carpets and if he needs carpenting for more than 10 square yard, he will hire Country Carpets.
Write an equation to represent each relationship. Then solve the equation.
Question 9.
Two less than 3 times a number is the same as the number plus 10.
________
Answer:
3x – 2 = x + 10
x = 6
Explanation:
Two less than 3 times a number is the same as the number plus 10.
Two less than 3 times x is the same as the x plus 10.
Two less than 3x is the same as the x + 10
3x – 2 is the same as x + 10
3x – 2 = x + 10
3x – x = 10 + 2
2x = 12
x = 6
Question 10.
A number increased by 4 is the same as 19 minus 2 times the number.
______
Answer:
x + 4 = 19 – 2x
x = 5
Explanation:
A number increased by 4 is the same as 19 minus 2 times the number.
x increased by 4 is the same as 19 minus 2x.
x + 4 is the same as 19 – 2x
x + 4 = 19 – 2x
x + 2x = 19 – 4
3x = 15
x = 15/3
x = 5
Question 11.
Twenty less than 8 times a number is the same as 15 more than the number.
Type below:
____________
Answer:
8x – 20 = x + 15
x = 5
Explanation:
Twenty less than 8 times a number is the same as 15 more than the number.
Twenty less than 8 times x is the same as 15 more than the x.
Twenty less than 8x is the same as 15 more than the x
8x – 20 is the same as x + 15
8x – 20 = x + 15
8x – x = 15 + 20
7x = 35
x = 35/7 = 5
x = 5
Equations with the Variable on Both Sides – Page No. 202
Question 12.
The charges for an international call made using the calling card for two phone companies are shown in the table.
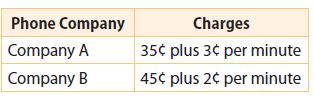
a. What is the length of a phone call that would cost the same no matter which company is used?
_______ minutes
Answer:
10 minutes
Explanation:
Cost of minutes + One time fee = 3x + 35
Cost of minutes + One time fee = 2x + 45
3x + 35 = 2x + 45
3x – 2x = 45 – 35
x = 10
The cost would be same for 10 minutes.
Question 12.
b. Analyze Relationships
When is it better to use the card from Company B?
Type below:
____________
Answer:
y = 3x + 35
y = 3(11) + 35 = $68
y = 2x + 45
y = 2(11) + 45 = $67
Since when x > 10, Company B is cheaper so it should be better to use when the length of the call is greater than 10 minutes.
H.O.T.
Focus on Higher Order Thinking
Question 13.
Draw Conclusions
Liam is setting up folding chairs for a meeting. If he arranges the chairs in 9 rows of the same length, he has 3 chairs left over. If he arranges the chairs in 7 rows of that same length, he has 19 left over. How many chairs does Liam have?
______ chairs
Answer:
75 chairs
Explanation:
Number of chairs in 9 row + left over chairs = 9x + 3
Number of chairs in 7 row + left over chairs = 7x + 19
9x + 3 = 7x + 19
9x – 7x = 19 – 3
2x = 16
x = 16/2
x = 8
Total number of chairs = 9(8) + 3 = 75
Question 14.
Explain the Error
Rent-A-Tent rents party tents for a flat fee of $365 plus $125 a day. Capital Rentals rents party tents for a flat fee of $250 plus $175 a day. Delia wrote the following equation to find the number of days for which the total cost charged by the two companies would be the same:
365x + 125 = 250x + 175
Find and explain the error in Delia’s work. Then write the correct equation.
Type below:
____________
Answer:
Delia’s equation
365x + 125 = 250x + 175
The error is that she attached the variable with the flat fee (which is constant) and put the daily rent as a constant (which is variable).
Correct equation
125x + 365 = 175x + 250
Question 15.
Persevere in Problem Solving
Lilliana is training for a marathon. She runs the same distance every day for a week. On Monday, Wednesday, and Friday, she runs 3 laps on a running trail and then runs 6 more miles.On Tuesday and Sunday, she runs 5 laps on the trail and then runs 2 more miles. On Saturday, she just runs laps. How many laps does Lilliana run on Saturday?
________ laps
Answer:
2 laps
Explanation:
Miles covered by lap + Addition number of miles = 3x + 6
Miles covered by lap + Addition number of miles = 5x + 2
3x + 6 = 5x + 2
5x – 3x = 6 – 2
2x = 4
x = 4/2
x = 2
Guided Practice – Equations with Rational Numbers – Page No. 206
Question 1.
Sandy is upgrading her Internet service. Fast Internet charges $60 for installation and $50.45 per month. Quick Internet has free installation but charges $57.95 per month.
a. Write an equation that can be used to find the number of months at which the Internet service would cost the same.
Type below:
____________
Answer:
50.45x + 60 = 57.95x
Explanation:
Write an equation for Fast Internet, where x is the number of months.
Charge per Month × Number of Month + Installation Fee
50.45x + 60
Write an equation for Quick Internet, where x is the number of months.
Charge per Month × Number of Month + Installation Fee
57.95x
50.45x + 60 = 57.95x
Question 1.
b. Solve the equation.
_______ hours
Answer:
8
Explanation:
50.45x + 60 = 57.95x
57.95x – 50.45x = 60
7.5x = 60
x = 60/7.5
x = 8
The total cost will be the same for 8 months.
Solve.
Question 2.
\(\frac{3}{4}\) n – 18 = \(\frac{1}{4}\) n – 4
______
Answer:
n = 28
Explanation:
3/4 . n – 18 = 1/4 . n – 4
Determine the least common multiple of the denominators
LCM is 4
Multiply both sides of the equation by the LCM
4(3/4 . n – 18) = 4(1/4 . n – 4)
3n – 72 = n – 16
3n – n = -16 + 72
2n = 56
n = 56/2
n = 28
Question 3.
6 + \(\frac{4}{5}\) b = \(\frac{9}{10}\) b
_______
Answer:
b = 60
Explanation:
6 + \(\frac{4}{5}\) b = \(\frac{9}{10}\) b
LCM is 10
10(6 + \(\frac{4}{5}\) b) = 10(\(\frac{9}{10}\) b)
60 + 8b = 9b
9b – 8b = 60
b = 60
Question 4.
\(\frac{2}{11}\) m + 16 = 4 + \(\frac{6}{11}\) m
_______
Answer:
m = 33
Explanation:
\(\frac{2}{11}\) m + 16 = 4 + \(\frac{6}{11}\) m
The LCM is 11
11(\(\frac{2}{11}\) m + 16) = 11(4 + \(\frac{6}{11}\) m)
2m + 176 = 44 + 6m
6m – 2m = 176 – 44
4m = 132
m = 132/4
m = 33
Question 5.
2.25t + 5 = 13.5t + 14
_______
Answer:
t = -0.8
Explanation:
2.25t + 5 = 13.5t + 14
13.5t – 2.25t = 5 – 14
11.25t = -9
t = -9/11.25
t = -0.8
Question 6.
3.6w = 1.6w + 24
_______
Answer:
w = 12
Explanation:
3.6w = 1.6w + 24
3.6w – 1.6w = 24
2w = 24
w = 24/2
w = 12
Question 7.
-0.75p – 2 = 0.25p
_______
Answer:
p = -2
Explanation:
-0.75p – 2 = 0.25p
-2 = 0.25p + 0.75p
-2 = p
p = -2
Question 8.
Write a real-world problem that can be modeled by the equation 1.25x = 0.75x + 50.
Type below:
______________
Answer:
1.25x = 0.75x + 50.
Cell offer Plan A for no base fee and $1.25 per minute.
Cell offer Plan B for a $50 base fee and $0.75 per minute.
The equation shows when the total cost of the plan would be equal.
Essential Question Check-In
Question 9.
How does the method for solving equations with fractional or decimal coefficients and constants compare with the method for solving equations with integer coefficients and constants?
Type below:
______________
Answer:
When solving equations with fractional or decimal coefficients, the equations need to be multiplied by the multiple of denominator such that the equations have integer coefficients and constants.
Independent Practice – Equations with Rational Numbers – Page No. 207
Question 10.
Members of the Wide Waters Club pay $105 per summer season, plus $9.50 each time they rent a boat. Nonmembers must pay $14.75 each time they rent a boat. How many times would a member and a non-member have to rent a boat in order to pay the same amount?
_______ times
Answer:
20 times
Explanation:
Members of the Wide Waters Club pay $105 per summer season, plus $9.50 each time they rent a boat.
9.5x + $105
Nonmembers must pay $14.75 each time they rent a boat.
9.5x + $105 = 14.75x
9.5x – 14.75x = $105
5.25x = 105
x = 105/5.25
x = 20
The cost for members and non-members will be the same for 8 visits.
Question 11.
Margo can purchase tile at a store for $0.79 per tile and rent a tile saw for $24. At another store she can borrow the tile saw for free if she buys tiles there for $1.19 per tile. How many tiles must she buy for the cost to be the same at both stores?
_______ tiles
Answer:
60 tiles
Explanation:
Margo can purchase tile at a store for $0.79 per tile and rent a tile saw for $24.
0.79x + 24
At another store she can borrow the tile saw for free if she buys tiles there for $1.19 per tile.
1.19x
0.79x + 24 = 1.19x
1.19x – 0.79x = 24
0.4x = 24
x = 24/0.4
x = 60
Margo should buy 60 tiles for the cost to be the same at both stores.
Question 12.
The charges for two shuttle services are shown in the table. Find the number of miles for which the cost of both shuttles is the same.
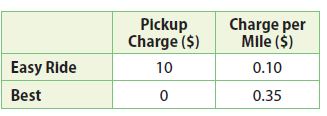
_______ miles
Answer:
40 miles
Explanation:
0.1x + 10
0.35x
0.1x + 10 = 0.35x
0.35x – 0.1x = 10
0.25x = 10
x = 10/0.25
x = 40
The cost of shuttles would be the same for 40 miles.
Question 13.
Multistep
Rapid Rental Car charges a $40 rental fee, $15 for gas, and $0.25 per mile driven. For the same car, Capital Cars charges $45 for rental and gas and $0.35 per mile.
a. For how many miles is the rental cost at both companies the same?
_______ miles
Answer:
100 miles
Explanation:
0.25x + 40 + 15 = 0.35x + 45
0.35x – 0.25x = 55 – 45
0.1x = 10
x = 10/0.1
x = 100
The cost of car rentals would be the same for 100 miles.
Question 13.
b. What is that cost?
$ _______
Answer:
$80
Explanation:
Let y be the total cost. Substitute 100 miles in any one of the two equations
y = 0.35x + 45
y = 0.35(100) + 45 = $80
Total cost would be $80.
Question 14.
Write an equation with the solution x = 20. The equation should have the variable on both sides, a fractional coefficient on the left side, and a fraction anywhere on the right side.
Type below:
______________
Answer:
4/3x + 10 = 50/3 + x
Explanation:
Write an equation with the solution x = 20. The equation should have the variable on both sides, a fractional coefficient on the left side, and a fraction anywhere on the right side.
1/3 . x = 1/3 . 20
1/3 . x + x = 1/3 . 20 + x
4/3x = 20/3 + x
4/3x + 10 = 20/3 + x + 10
4/3x + 10 = 50/3 + x
Question 15.
Write an equation with the solution x = 25. The equation should have the variable on both sides, a decimal coefficient on the left side, and a decimal anywhere on the right side. One of the decimals should be written in tenths, the other in hundredths.
Type below:
______________
Answer:
x=25
divide both sides by 25
x/25 = 1
convert 1/25 to decimal form 0.04
0.04x = 1
add x on both sides
1.04x = 1 + x
add 0.1 on both sides
1.04x + 0.1 = x + 1.1
Question 16.
Geometry
The perimeters of the rectangles shown are equal. What is the perimeter of each rectangle?
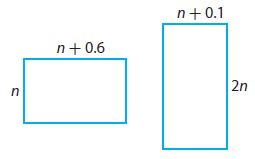
Perimeter = _______
Answer:
Perimeter = 3.2
Explanation:
Perimeter of the first rectangle
P = 2(n + n + 0.6) = 2(2n + 0.6) = 4n + 1.2
Perimeter of the second rectangle
P = 2(n + 0.1 + 2n) = 2(3n + 0.1) = 6n + 0.2
the perimeter is equal
4n + 1.2 = 6n + 0.2
6n – 4n = 1.2 – 0.2
2n = 1
n = 1/2
n = 0.5
P = 4n + 1.2 = 4(0.5) + 1.2 = 3.2
Question 17.
Analyze Relationships
The formula F = 1.8C + 32 gives the temperature in degrees Fahrenheit (F) for a given temperature in degrees Celsius (C). There is one temperature for which the number of degrees Fahrenheit is equal to the number of degrees Celsius. Write an equation you can solve to find that temperature and then use it to find the temperature
Type below:
______________
Answer:
x = 1.8x + 32
Explanation:
F = 1.8C +32
let x be the temperature such that it is same in both celsius and in fahrenheit
Then the required equation is
x = 1.8x + 32
subtract 1.8x from both sides
-0.8x = 32
divide by -0.8 on both sides
x = -40
So -40 degree celsius
Equations with Rational Numbers – Page No. 208
Question 18.
Explain the Error
Agustin solved an equation as shown. What error did Agustin make? What is the correct answer?
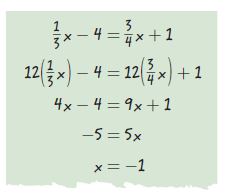
x = _______
Answer:
x = -12
Explanation:
Agustin did not multiply by 12 on both sides in step 2. He only partially multiplied the variable and left the constants as such, which doesn’t make any sense.
The correct solution is
12(x/3 – 4) = 12(3x/4 + 1)
4x – 48 = 9x + 12
subtract 12 on both sides
4x – 60 = 9x
subtract 4x on both sides
-60 = 5x
x = -12
H.O.T.
Focus on Higher Order Thinking
Question 19.
Draw Conclusions
Solve the equation \(\frac{1}{2} x-5+\frac{2}{3} x=\frac{7}{6} x+4\). Explain your results.
Type below:
_____________
Answer:
\(\frac{1}{2} x-5+\frac{2}{3} x=\frac{7}{6} x+4\)
The least common multiple of the denominators: LCM(2, 3, 6) = 6
6(\(\frac{1}{2} x-5+\frac{2}{3} x=\frac{7}{6} x+4\))
6.1/2x – 6.5 + 6.2/3x = 6.7/6x +6.4
3x – 30 + 4x = 7x + 24
7x – 30 = 7x + 24
-30 = 24
This is not true. The equation has no solution.
Question 20.
Look for a Pattern
Describe the pattern in the equation. Then solve the equation.
0.3x + 0.03x + 0.003x + 0.0003x + .. = 3
x = ______
Answer:
x = 9
Explanation:
0.3x + 0.03x + 0.003x + 0.0003x + .. = 3
0.3x = 3
0.9x = 9
x = 9
Question 21.
Critique Reasoning
Jared wanted to find three consecutive even integers whose sum was 4 times the first of those integers. He let k represent the first integer, then wrote and solved this equation : k + (k + 1) + (k + 2) = 4k. Did he get the correct answer? Explain.
__________
Answer:
No, it is wrong on two accounts.
First, he has not specified if k is even or not. An easy way of doing so would assume x to be any integer and k=2a
This ensures that k is an even integer.
Nest the question asks for 3 consecutive even integers, Jared just took 3 consecutive integers, and thus at least 1 of them is odd.
So correct representation would be
k + (k+2) + (k + 4) = 4k
which upon solving yields k=6
Guided Practice – Equations with the Distributive Property – Page No. 212
Solve each equation.
Question 1.
4(x + 8) – 4 = 34 – 2x
________
Answer:
x = 1
Explanation:
4(x + 8) – 4 = 34 – 2x
4x + 32 – 4 = 34 – 2x
4x + 2x = 34 – 28
6x = 6
x = 6/6
x = 1
Question 2.
\(\frac{2}{3}\)(9 + x) = -5(4 – x)
________
Answer:
x = 6
Explanation:
\(\frac{2}{3}\)(9 + x) = -5(4 – x)
2/3(9 + x) = -5(4 – x)
3 (2/3(9 + x)) = 3(-5(4 – x))
2(9 + x ) = -15 (4 – x)
18 + 2x = -60 + 15x
15x – 2x = 18 + 60
13x = 78
x = 78/13
x = 6
Question 3.
-3(x + 4) + 15 = 6 – 4x
________
Answer:
x = 3
Explanation:
-3(x + 4) + 15 = 6 – 4x
-3x – 12 + 15 = 6 – 4x
-3x + 3 = 6 – 4x
-3x + 4x = 6 – 3
x = 3
Question 4.
10 + 4x = 5(x – 6) + 33
________
Answer:
x = 7
Explanation:
10 + 4x = 5(x – 6) + 33
10 + 4x = 5x – 30 + 33
10 + 4x = 5x + 3
5x – 4x = 10 – 3
x = 7
Question 5.
x – 9 = 8(2x + 3) – 18
________
Answer:
x = -1
Explanation:
x – 9 = 8(2x + 3) – 18
x – 9 = 16x + 24 – 18
x – 9 = 16x + 6
16x – x = -9 – 6
15x = – 15
x = -15/15
x = -1
Question 6.
-6(x – 1) – 7 = -7x + 2
________
Answer:
x = 3
Explanation:
-6(x – 1) – 7 = -7x + 2
-6x + 6 – 7 = -7x + 2
-6x – 1 = -7x + 2
-7x + 6x = -1 -2
-x = -3
x = 3
Question 7.
\(\frac{1}{10}\)(x + 11) = -2(8 – x)
________
Answer:
x = 9
Explanation:
\(\frac{1}{10}\)(x + 11) = -2(8 – x)
10(\(\frac{1}{10}\)(x + 11)) = 10 (-2(8 – x))
x + 11 = -20(8 – x)
x + 11 = -160 + 20x
20x – x = 11 + 160
19x = 171
x = 171/19 = 9
Question 8.
-(4 – x) = \(\frac{3}{4}\)(x – 6)
________
Answer:
x = -2
Explanation:
-(4 – x) = \(\frac{3}{4}\)(x – 6)
4(-(4 – x)) = 4 (3/4(x – 6))
-16 + 4x = 3x – 18
4x – 3x = -18 + 16
x = -2
Question 9.
-8(8 – x) = \(\frac{4}{5}\)(x + 10)
________
Answer:
x = 10
Explanation:
-8(8 – x) = \(\frac{4}{5}\)(x + 10)
5(-8(8 – x)) = 5(\(\frac{4}{5}\)(x + 10))
-40(8 – x) = 4(x + 10)
-320 + 40x = 4x + 40
40x – 4x = 40 + 320
36x = 360
x = 360/36
x = 10
Question 10.
\(\frac{1}{2}\)(16 – x) = -12(x + 7)
________
Answer:
x = 8
Explanation:
\(\frac{1}{2}\)(16 – x) = -12(x + 7)
2 (\(\frac{1}{2}\)(16 – x)) = 2 (-12(x + 7))
16 – x = -24 (x + 7)
16 – x = -24x – 168
24x – x = -168 – 16
23x = 184
x = 184/23
x = 8
Question 11.
Sandra saves 12% of her salary for retirement. This year her salary was $3,000 more than in the previous year, and she saved $4,200.What was her salary in the previous year?
Write an equation _____
Sandra’s salary in the previous year was _____
Salary = $ _____
Answer:
Write an equation 0.12x + 360 = 4200
Sandra’s salary in the previous year was $32000
Salary = $3000
Explanation:
0.12(x + 3000) = 4200
0.12x + 360 = 4200
0.12x = 4200 – 360
0.12x = 3840
x = 3840/0.12
x = 32000
Sandra’s salary in the previous year was $32000
Essential Question Check-In
Question 12.
When solving an equation using the Distributive Property, if the numbers being distributed are fractions, what is your first step? Why?
Type below:
___________
Answer:
Multiply both sides by the denominator of the fraction
Independent Practice – Equations with the Distributive Property – Page No. 213
Question 13.
Multistep
Martina is currently 14 years older than her cousin Joey. In 5 years she will be 3 times as old as Joey. Use this information to answer the following questions.
a. If you let x represent Joey’s current age, what expression can you use to represent Martina’s current age?
Type below:
___________
Answer:
y = x + 14
Explanation:
y = x + 14
where x is Joey’s current age and t is Martna’s current age.
Question 13.
b. Based on your answer to part a, what expression represents Joey’s age in 5 years? What expression represents Martina’s age in 5 years?
Type below:
___________
Answer:
Ages in 5 years
Joey’s age = x + 5
Martina’s age = x + 14 + 5 = x + 19
Question 13.
c. What equation can you write based on the information given?
Type below:
___________
Answer:
3(x + 5) = x + 19
Explanation:
In 5 years, Martina will be three times as old as Joey
3(x + 5) = x + 19
Question 13.
d. What is Joey’s current age? What is Martina’s current age?
Joey’s current age ___________
Martina’s current age ___________
Answer:
Joey’s current age 2
Martina’s current age 16
Explanation:
3(x + 5) = x + 19
3x + 15 = x + 19
3x – x = 19 – 15
2x = 4
x = 2
Question 14.
As part of a school contest, Sarah and Luis are playing a math game. Sarah must pick a number between 1 and 50 and give Luis clues so he can write an equation to find her number. Sarah says, “If I subtract 5 from my number, multiply that quantity by 4, and then add 7 to the result, I get 35.” What equation can Luis write based on Sarah’s clues and what is Sarah’s number?
Type below:
___________
Answer:
x = 12
Explanation:
As part of a school contest, Sarah and Luis are playing a math game. Sarah must pick a number between 1 and 50 and give Luis clues so he can write an equation to find her number. Sarah says, “If I subtract 5 from my number, multiply that quantity by 4, and then add 7 to the result, I get 35.”
4 (x – 5) + 7 = 35
4x – 20 + 7 = 35
4x – 13 = 35
4x = 35 + 13
4x = 48
x = 48/4
x = 12
Question 15.
Critical Thinking
When solving an equation using the Distributive Property that involves distributing fractions, usually the first step is to multiply by the LCD to eliminate the fractions in order to simplify computation. Is it necessary to do this to solve \(\frac{1}{2}\)(4x + 6) = 13(9x – 24)? Why or why not?
___________
Answer:
It is not necessary. In this case, distributing the fractions directly results in whole-number coefficients and constants, however, if the results are not in whole-number coefficients and constants it is harder to solve fractions.
Question 16.
Solve the equation given in Exercise 15 with and without using the LCD of the fractions. Are your answers the same?
___________
Answer:
x = 11
Explanation:
\(\frac{1}{2}\)(4x + 6) = 13(9x – 24)
6(\(\frac{1}{2}\)(4x + 6)) = 6(13(9x – 24))
3(4x + 6) = 2(9x – 24)
12x + 18 = 18x – 48
18x – 12x = 18 + 48
6x = 66
x = 66/6
x = 11
Equations with the Distributive Property – Page No. 214
Question 17.
Represent Real-World Problems
A chemist mixed x milliliters of 25% acid solution with some 15% acid solution to produce 100 milliliters of a 19% acid solution. Use this information to fill in the missing information in the table and answer the questions that follow.
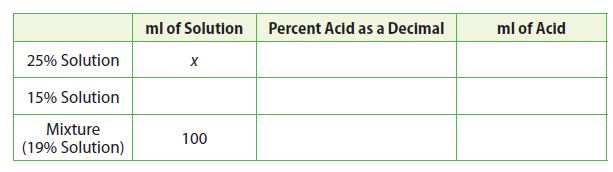
a. What is the relationship between the milliliters of acid in the 25% solution, the milliliters of acid in the 15% solution, and the milliliters of acid in the mixture?
Type below:
_____________
Answer:
The milliliters of acid in the 25% solution plus the milliliters of acid in the 15% solution equals the milliliters of acid in the mixture
Explanation:
![]()
Question 17.
b. What equation can you use to solve for x based on your answer to part a?
Type below:
_____________
Answer:
0.25x + 0.15(100 – x) = 19
Question 17.
c. How many milliliters of the 25% solution and the 15% solution did the chemist use in the mixture?

Type below:
_____________
Answer:
0.25x + 0.15(100 – x) = 19
0.25x + 15 – 0.15x = 19
0.1x + 15 = 19
0.1x = 4
x = 4/0.1
x = 40
The chemist used 40ml of the 25% solution and 100 – 40 = 60ml of the 15% solution.
H.O.T.
Focus on Higher Order Thinking
Question 18.
Explain the Error
Anne solved 5(2x) – 3 = 20x + 15 for x by first distributing 5 on the left side of the equation. She got the answer x = -3. However, when she substituted -3 into the original equation for x, she saw that her answer was wrong. What did Anne do wrong, and what is the correct answer?
x = ________
Answer:
x = -1.8
Explanation:
Dado que 5 solo se multiplica por 2x, no tiene sentido usar la distribución aquí. Básicamente, distribuir 5 fue el problema
Solución correcta:
5 (2x) – 3 = 20x + 15
10x -3 = 20x + 15
restar 15 en ambos lados
10x – 18 = 20x
restar 10x de ambos lados
-18 = 10x
x = -1.8
Question 19.
Communicate Mathematical Ideas
Explain a procedure that can be used to solve 5[3(x + 4) – 2(1 – x)] – x – 15 = 14x + 45. Then solve the equation.
x = ________
Answer:
x = 1
Explanation:
5[3(x + 4) – 2(1 – x)] – x – 15 = 14x + 45
5[3x + 12 – 2 + 2x] – x – 15 = 14x + 45
5[5x + 10] – x – 15 = 14x + 45
25x + 50 – x – 15 = 14x + 45
24x + 35 = 14x + 45
24x – 14x = 45 – 35
10x = 10
x = 1
Guided Practice – Equations with Many Solutions or No Solution – Page No. 218
Use the properties of equality to simplify each equation. Tell whether the final equation is a true statement.
Question 1.
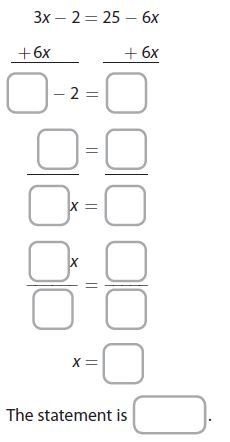
The statement is: _______
Answer:
The statement is: true
Explanation:
3x – 2 = 25 – 6x
3x + 6x -2 = 25 -6x + 6x
9x – 2 = 25
9x -2 + 2 = 25 + 2
9x = 27
x = 27/9
x = 3
The statement is true.
Question 2.
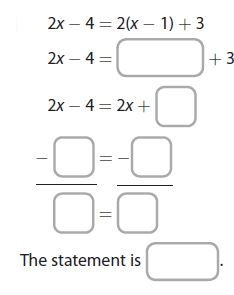
____________
Answer:
The statement is false.
Explanation:
2x – 4 = 2(x – 1) + 3
2x – 4 = 2x – 2 + 3
2x – 4 = 2x + 1
2x – 4 – 2x = 2x + 1 – 2x
-4 not equal to 1
The statement is false.
Question 3.
How many solutions are there to the equation in Exercise 2?
____________
Answer:
There is no solution to exercise 2.
Question 4.
After simplifying an equation, Juana gets 6 = 6. Explain what this means.
____________
Answer:
When 6 = 6, there are infinite solutions.
Write a linear equation in one variable that has infinitely many solutions.
Question 5.
Start with a _____ statement.
Add the _____ to both sides.
Add the _____ to both sides.
Combine _____ terms.
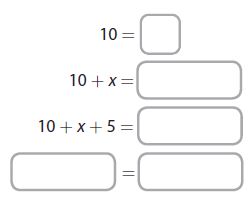
Type below:
____________
Answer:
Start with a “true” statement
Add the “same variable” to both sides
Add the “same constant” to both sides
Combine “like” terms
Explanation:
Start with a “true” statement
10 = 10
Add the “same variable” to both sides
10 + x = 10 + x
Add the “same constant” to both sides
10 + x + 5 = 10 + x + 5
Combine “like” terms
15 + x = 15 + x
Essential Question Check-In
Question 6.
Give an example of an equation with an infinite number of solutions. Then make one change to the equation so that it has no solution.
Type below:
____________
Answer:
An equation with infinitely many solutions
x – 2x + 3 = 3 – x
-x + 3 = 3 – x
+x/3 = +x/3
An equation for no solution
x – 2x + 3 = 3 – x + 4
-x + 3 = 7 – x
-x/3 = -x/7
Independent Practice – Equations with Many Solutions or No Solution – Page No. 219
Tell whether each equation has one, zero, or infinitely many solutions.
Question 7.
-(2x + 2) – 1 = -x – (x + 3)
____________
Answer:
The statement is true
Explanation:
-(2x + 2) – 1 = -x – (x + 3)
-2x – 2 – 1 = -x – x + 3
-2x – 3 = -2x + 3
-3 = -3
The statement is true
Question 8.
-2(z + 3) – z = -z – 4(z + 2)
____________
Answer:
The statement is false.
Explanation:
-2(z + 3) – z = -z – 4(z + 2)
-3z – 6 = -3z -8
-3z -6 + 3z = -3z – 8 + 3z
-6 not equal to -8
The statement is false.
Create an equation with the indicated number of solutions.
Question 9.
No solution:
3(x – \(\frac{4}{3}\)) = 3x + _____
Type below:
______________
Answer:
3(x – \(\frac{4}{3}\)) = 3x + ?
3x – 4 = 3x + ?
3x – 4 = 3x + 2
When there is no solution, the statement should be false. Any number except -4 would make the equation have no solutions.
Question 10.
Infinitely many solutions:
2(x – 1) + 6x = 4( _____ – 1) + 2
Type below:
______________
Answer:
2(x – 1) + 6x = 4( _____ – 1) + 2
2(x – 1) + 6x = 4( ? – 1) + 2
2x – 2 + 6x = 4(? – 1) + 2
8x – 2 = 4(? – 1) + 2
8x – 2 = 4(2x – 1) + 2
8x – 2 = 8x – 4 + 2
8x – 2 = 8x – 2
When there are infinitely many solutions, the statement should be true
Question 11.
One solution of x = -1:
5x – (x – 2) = 2x – ( _____ )
Type below:
______________
Answer:
Put x = -1 in the equation
-5 – (-1 – 2) = -2 – blank
simplifying
-2 = -2 – blank
add 2 on both sides
0 = blank
Question 12.
Infinitely many solutions:
-(x – 8) + 4x = 2( _____ ) + x
Type below:
______________
Answer:
-(x – 8) + 4x = 2( ?) + x
-x + 8 + 4x = 2(?) + x
3x + 8 = 2(?) + x
3x + 8 = 2 (x + 4) + x
3x + 8 = 2x + 8x + x
3x + 8 = 3x + 8
When there are infinitely many solutions, the statement should be true.
Question 13.
Persevere in Problem Solving
The Dig It Project is designing two gardens that have the same perimeter. One garden is a trapezoid whose nonparallel sides are equal. The other is a quadrilateral. Two possible designs are shown at the right.
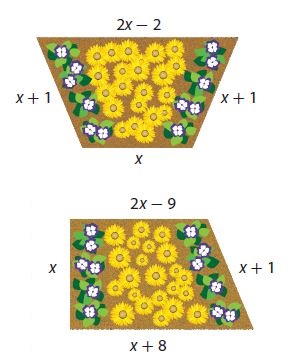
a. Based on these designs, is there more than one value for x? Explain how you know this.
______________
Answer:
There are more than one value of x
Explanation:
Perimeter of the trapezoid
P = 2x – 2 + x + 1 + x + x + 1 = 5x
Perimeter of the quadrilateral
P = 2x – 9 + x + x + 8 + x + 1 = 5x
5x = 5x
There are more than one value of x
Question 13.
b. Why does your answer to part a make sense in this context?
Type below:
______________
Answer:
The condition was that the two perimeters are to be equal. However, a specific number was not given, so there are an infinite number of possible perimeters
Explanation:
Interpretation of part a in this context
The condition was that the two perimeters are to be equal. However, a specific number was not given, so there are an infinite number of possible perimeters
Question 13.
c. Suppose the Dig It Project wants the perimeter of each garden to be 60 meters. What is the value of x in this case? How did you find this?
______ meters
Answer:
12 meters
Explanation:
2x – 2 + x + 1 + x + x + 1 = 60
5x = 60
x = 60/5
x = 12
Equations with Many Solutions or No Solution – Page No. 220
Question 14.
Critique Reasoning
Lisa says that the indicated angles cannot have the same measure. Marita disagrees and says she can prove that they can have the same measure. Who do you agree with? Justify your answer.
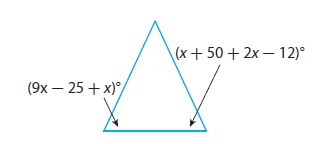
I agree with: ______________
Answer:
I agree with: Marita
Explanation:
9x – 25 + x = x + 50 + 2x – 12
10x – 25 = 3x + 38
10x – 3x = 38 + 25
7x = 63
x = 63/7
x = 9
When x = 9 the angles will be same and for any other value of x, the angles will not be the same.
Question 15.
Represent Real-World Problems
Adele opens an account with $100 and deposits $35 a month. Kent opens an account with $50 and also deposits $35 a month. Will they have the same amount in their accounts at any point? If so, in how many months and how much will be in each account? Explain.
______________
Answer:
Adele’s amount after x months
A = 100 + 35x
Kent’s amount after x months
A = 50 + 35x
100 + 35x = 50 + 35x
100 is not equal to 50
The statement is false, the amounts in two accounts would never be equal.
H.O.T.
Focus on Higher Order Thinking
Question 16.
Communicate Mathematical Ideas
Frank solved an equation and got the result x = x. Sarah solved the same equation and got 12 = 12. Frank says that one of them is incorrect because you cannot get different results for the same equation. What would you say to Frank? If both results are indeed correct, explain how this happened.
Frank is: ____________
Answer:
Both of them can be correct as both equations give the same result i.e. there are infinitely many solutions. Frank eliminated the constant from both sides while Sarah eliminated the variable from both sides.
Question 17.
Critique Reasoning
Matt said 2x – 7 = 2(x – 7) has infinitely many solutions. Is he correct? Justify Matt’s answer or show how he is incorrect.
Matt is: ____________
Answer:
Explanation:
2x – 7 = 2(x – 7)
2x – 7 = 2x – 14
-7 not equal to -14
The statement is false, there is no solution. Matt is incorrect.
7.1 Equations with the Variable on Both Sides – Model Quiz – Page No. 221
Solve.
Question 1.
4a – 4 = 8 + a
_______
Answer:
a = 4
Explanation:
4a – 4 = 8 + a
4a – a = 8 + 4
3a = 12
a = 12/3
a = 4
Question 2.
4x + 5 = x + 8
_______
Answer:
x = 1
Explanation:
4x + 5 = x + 8
4x – x = 8 – 5
3x = 3
x = 3/3
x = 1
Question 3.
Hue is arranging chairs. She can form 6 rows of a given length with 3 chairs left over, or 8 rows of that same length if she gets 11 more chairs. Write and solve an equation to find how many chairs are in that row length.
_______ chairs
Answer:
7 chairs
Explanation:
Hue is arranging chairs. She can form 6 rows of a given length with 3 chairs left over, or 8 rows of that same length if she gets 11 more chairs.
6x + 3 = 8x – 11
8x – 6x = 3 + 11
2x = 14
x = 14/2
x = 7
There are 7 chairs in each row.
7.2 Equations with Rational Numbers
Solve.
Question 4.
\(\frac{2}{3} n-\frac{2}{3}=\frac{n}{6}+\frac{4}{3}\)
_______
Answer:
n = 4
Explanation:
\(\frac{2}{3} n-\frac{2}{3}=\frac{n}{6}+\frac{4}{3}\)
The LCM is 6.
6(2/3n – 2/3) = 6(n/6 + 4/3)
6(2/3n) -6(2/3) = 6(n/6) + 6(4/3)
4n – 4 = n + 8
4n – n = 8 + 4
3n = 12
n = 12/3
n = 4
Question 5.
1.5d + 3.25 = 1 + 2.25d
_______
Answer:
d = 3
Explanation:
1.5d + 3.25 = 1 + 2.25d
2.25d – 1.5d = 3.25 – 1
0.75d = 2.25
d = 2.25/0.75
d = 3
Question 6.
Happy Paws charges $19.00 plus $1.50 per hour to keep a dog during the day. Woof Watchers charges $14.00 plus $2.75 per hour. Write and solve an equation to find for how many hours the total cost of the services is equal.
_______ hours
Answer:
3.2 hours
Explanation:
Happy Paws charges $19.00 plus $1.50 per hour to keep a dog during the day.
1.5x + 19
Woof Watchers charges $14.00 plus $2.75 per hour.
2.75x + 15
1.5x + 19 = 2.75x + 15
2.75x – 1.5x = 19 – 15
1.25x = 4
x = 4/1.25
x = 3.2
The total cost of the services is equal after 3.2 hrs.
7.3 Equations with the Distributive Property
Solve.
Question 7.
14 + 5x = 3(-x + 3) – 11
_______
Answer:
x = -2
Explanation:
14 + 5x = 3(-x + 3) – 11
14 + 5x = -3x + 9 – 11
14 + 5x = -3x – 2
5x + 3x = -2 – 14
8x = – 16
x = -16/8
x = -2
Question 8.
\(\frac{1}{4}\)(x – 7) = 1 + 3x
_______
Answer:
x = -1
Explanation:
\(\frac{1}{4}\)(x – 7) = 1 + 3x
4(\(\frac{1}{4}\)(x – 7)) = 4(1 + 3x)
(x – 7) = 4 + 12x
12x – x = -7 – 4
11x = -11
x = -11/11
x = -1
Question 9.
-5(2x – 9) = 2(x – 8) – 11
_______
Answer:
x = 6
Explanation:
-5(2x – 9) = 2(x – 8) – 11
-10x + 45 = 2x – 16 – 11
-10x + 45 = 2x – 27
2x + 10x = 45 + 27
12x = 72
x = 72/12
x = 6
Question 10.
3(x + 5) = 2(3x + 12)
_______
Answer:
x = -3
Explanation:
3(x + 5) = 2(3x + 12)
3x + 15 = 6x + 24
6x – 3x = 15 – 24
3x = -9
x = -9/3
x = -3
7.4 Equations with Many Solutions or No Solution
Tell whether each equation has one, zero, or infinitely many solutions.
Question 11.
5(x – 3) + 6 = 5x – 9
____________
Answer:
There are infinitely many solutions
Explanation:
5(x – 3) + 6 = 5x – 9
5x – 15 + 6 = 5x – 9
5x – 9 = 5x – 9
The statement is true. There are infinitely many solutions.
Question 12.
5(x – 3) + 6 = 5x – 10
____________
Answer:
There are no solutions
Explanation:
5(x – 3) + 6 = 5x – 10
5x – 15 + 6 = 5x – 10
5x – 9 = 5x – 10
-9 not equal to -10
The statement is false. There are no solutions.
Question 13.
5(x – 3) + 6 = 4x + 3
____________
Answer:
There is one solution
Explanation:
5(x – 3) + 6 = 4x + 3
5x – 15 + 6 = 4x + 3
5x – 9 = 4x + 3
5x – 4x = 3 + 9
x = 12
There is one solution
Selected Response – Mixed Review – Page No. 222
Question 1.
Two cars are traveling in the same direction. The first car is going 40 mi/h, and the second car is going 55 mi/h. The first car left 3 hours before the second car. Which equation could you solve to find how many hours it will take for the second car to catch up to the first car?
Options:
a. 55t + 3 = 40t
b. 55t + 165 = 40t
c. 40t + 3 = 55t
d. 40t + 120 = 55t
Answer:
d. 40t + 120 = 55t
Explanation:
Two cars are traveling in the same direction. The first car is going 40 mi/h, and the second car is going 55 mi/h. The first car left 3 hours before the second car.
3 × 40 + 40t = 120 + 40t
55t
40t + 120 = 55t
Question 2.
Which linear equation is represented by the table?
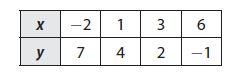
Options:
a. y = -x + 5
b. y = 2x – 1
c. y = x + 3
d. y = -3x + 11
Answer:
a. y = -x + 5
Explanation:
Find the slope using
m = (y2 – y1)/(x2 – x1)
where (x1, y1) = (3, 2), (x2, y2) = (1, 4)
Slope = (4 – 2)/(1 – 3) = -2/2 = -1
Question 3.
Shawn’s Rentals charges $27.50 per hour to rent a surfboard and a wetsuit. Darla’s Surf Shop charges $23.25 per hour to rent a surfboard plus $17 extra for a wetsuit. For what total number of hours are the charges for Shawn’s Rentals the same as the charges for Darla’s Surf Shop?
Options:
a. 3
b. 4
c. 5
d. 6
Answer:
b. 4
Explanation:
Shawn’s Rentals charges $27.50 per hour to rent a surfboard and a wetsuit.
27.5x
Darla’s Surf Shop charges $23.25 per hour to rent a surfboard plus $17 extra for a wetsuit.
23.25x + 17
23.25x + 17 = 27.5x
27.5x – 23.25x = 17
4.25x = 17
x = 17/4.25
x = 4
The charge would be equal after 4 hrs
Question 4.
Which of the following is irrational?
Options:
a. -8
b. 4.63
c. \(\sqrt { x } \)
d. \(\frac{1}{3}\)
Answer:
c. \(\sqrt { x } \)
Explanation:
\(\sqrt { x } \) is irrational
Question 5.
Greg and Jane left a 15% tip after dinner. The amount of the tip was $9. Greg’s dinner cost $24. Which equation can you use to find x, the cost of Jane’s dinner?
Options:
a. 0.15x + 24 = 9
b. 0.15(x + 24) = 9
c. 15(x + 24) = 9
d. 0.15x = 24 + 9
Answer:
b. 0.15(x + 24) = 9
Explanation:
Let x be the cost of Jane’s dinner. The amount of tip is the 15% of the total cost of dinner.
0.15(x + 24) = 9
Question 6.
For the equation 3(2x − 5) = 6x + k, which value of k will create an equation with infinitely many solutions?
Options:
a. 15
b. -5
c. 5
d. -15
Answer:
d. -15
Explanation:
3(2x – 5) = 6x + k
6x – 15 = 6x + k
6x – 15 = 6x – 15
The statement is true. k = -15
Question 7.
Which of the following is equivalent to 2−4?
Options:
a. \(\frac{1}{16}\)
b. \(\frac{1}{8}\)
c. -2
d. -16
Answer:
a. \(\frac{1}{16}\)
Explanation:
2−4
1/24
1/16
Mini-Task
Question 8.
Use the figures below for parts a and b.
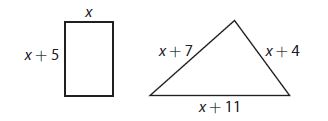
a. Both figures have the same perimeter. Solve for x.
_______
Answer:
x=12
Explanation:
4x+10=3x+22
4x – 3x = 22 – 10
x = 12
Answer: x=12
Question 8.
b. What is the perimeter of each figure?
_______
Answer:
Both are 58
Explanation:
x + x + 5 + x + x + 5
12 + 12 + 5 + 12 + 12 + 5
58
x + 7 + x + 4 + x + 11
12 + 7 + 12 + 4 + 12 + 11
58
Conclusion:
Go Math Grade 8 Answer Key is the best source to enhance your math skills. Learn all the solutions from Go Math Grade 8 Answer Key Chapter 7 Solving Linear Equations and complete your homework. Hope the information provided in Go Math Grade 8 Chapter 7 Solving Linear Equations Answer Key is satisfactory for all the 8th standard students. Stay with our CCSS Math Answers website to get the solutions of all grade 8 chapters.
