Practice with the help of enVision Math Common Core Grade 3 Answer Key Topic 12 Understand Fractions as Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 12 Understand Fractions as Numbers
Essential Question:
What are different interpretations of a fraction?
Answer:
There are five different interpretations of fractions.
Explanation:
Fractions as parts of wholes or parts of sets.
Fractions as the result of dividing two numbers.
Fractions as the ratio of two quantities.
Fractions as operators.
Fractions as measures.

EnVision STEM Project: Fossils and Environment
Do Research Use the Internet or other sources to find out more about what fossils tell us about past environments. Research and make a booklet of fossils found in your state. Find at least 5 fossils and use one page for each fossil. Include where each fossil was found and what type of environment each location is now.
Write a Report: Journal Include what you found. Also in your report:
- List the types of food each of the 5 creatures ate when they were alive.
- Explain whether each of the 5 creatures on your list could live in today’s environment.
- Find the lengths of different fossils to the nearest half inch. Record the lengths in a line plot.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- halves
- thirds
- inch
- yard
Question 1.
If a shape is divided into 2 equal parts, the parts can be called _________.
Answer:
Halves
Question 2.
The width of an adult’s thumb is about 1 _________.
Answer:
Inch
Question 3.
If a shape is divided into 3 equal parts, the parts can be called _________.
Answer:
Thirds
Skip Counting on the Number Line
Skip count on the number line. Write the missing numbers.
Question 4.

Answer:
125, 130, 135, 140, 145, 150, 155
Explanation:
Add 5 to each number present on number line.
110 + 5 = 115
115 + 5 = 120
120 + 5 = 125
125 + 5 = 130
130 + 5 = 135
135 + 5 = 140
140 + 5 = 145
145 + 5 = 150
150 + 5 = 155
Question 5.

Answer:
240, 260
Explanation:
Add 20 to each number present on number line
180 + 20 = 200
200 + 20 = 220
220 + 20 = 240
240 + 20 = 260
Equal Parts
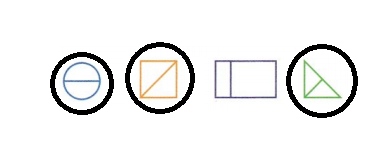
Question 6.
Circle the shapes that show halves.

Answer:
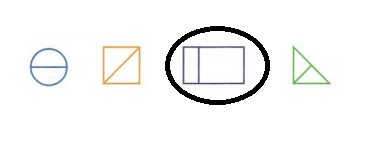
Question 7.
Circle the shapes that show fourths.
Answer:
Measurement
Question 8.
How long is the nail to the nearest inch? Explain how you know.
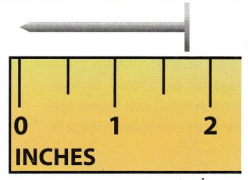
Answer :
2 inches
Explanation :
The nail is in between the 1.5 marks and 2 inch mark
so the nearest inch the nail is 2 inches
Pick a Project
PROJECT 12A
How long would it take to drive across the Florida Keys?
Project: Make a Map

Answer:
The Florida Keys Overseas Highway is 113 miles in length, joining the mainland of Florida (starting in Florida City, just south of Homestead) to Key West. If you drove directly from Key Largo to Key West, it would take you roughly 2.5 hours, traveling distance of 100 miles.
PROJECT 12B
Why are there so many different floors in a building?
Project: Create a flooring design

Answer:
A floor is the bottom surface of a room or vehicle. Floors vary from simple dirt in a cave to many-layered surfaces made with modern technology. Floors may be stone, wood, bamboo, metal or any other material that can support the expected load. The levels of a building are often referred to as floors, although a more proper term is storey.
- Choose an area. Determine the area to be drawn.
- Take measurements. If the building exists, measure the walls, doors, and pertinent furniture so that the floor plan will be accurate.
- Draw walls.
- Add architectural features.
- Add furniture
PROJECT 12C
What is the most common hat size?
Project: Collect Hat Size Data and Create a Line Plot

Answer:
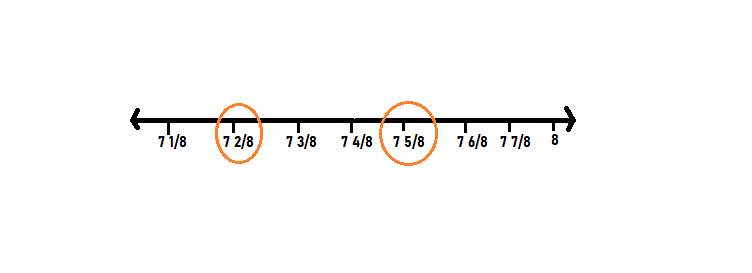
Head sizes and shapes differ from region to region. The most common male size is 7-5/8 and the average hat size for females 7-2/8
PROJECT 12D
What are the most popular fruits and vegetables?
Project: Draw a Garden Plot

Answer:
The most popular fruits and vegetables are,
Fruits like Mango ,Banana ,Apple, Grapes, Water melon.. so on
Vegetables like Carrot, Potato, Tomato, Brinjal … So on

Lesson 12.1 Partition Regions into Equal Parts
Solve & Share
Show two different ways to divide a 2 x 6 region into 6 equal parts. How do you know the parts are equal?
I can … read and write a unit fraction.

Look Back! How are the parts of the regions alike? How are they different?
Essential Question
How Can You Name the Equal Parts of a Whole?
Answer:
Each equal part of a whole is called one-half.
Explanation:
One half is expressed as 1/2 and read as one over two or one upon two.
Visual Learning Bridge
You can divide a whole into equal parts. What fraction can you write to represent one of these equal parts?
A fraction is a part of a whole.
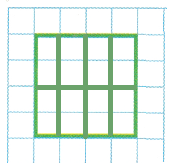
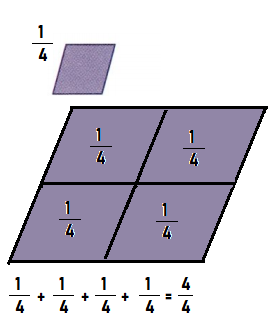
Divide each green whole into four equal parts.
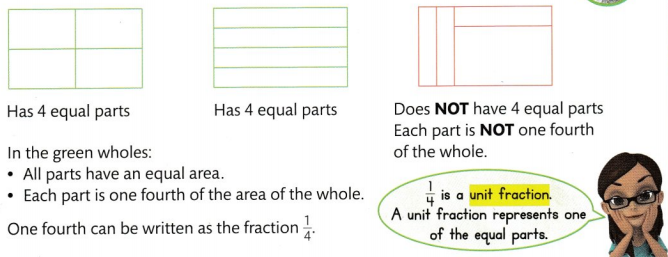
Divide each green whole into six equal parts.

In the green wholes:
- All parts have an equal area.
- Each part is one sixth of the area of the whole.
- One sixth can be written as the fraction \(\frac{1}{6}\).
Convince Me! Critique Reasoning Kim says that the figure at the right is divided into fourths because there are 4 equal parts. Carrie says it is not divided into fourths because the parts are not the same shape. Who is correct? Explain.

Answer:
Carrie is correct.
Explanation:
In the given figure it is not divided into fourths because the parts are not of the same shape.
Guided Practice
Do You Understand?
Question 1.
In the examples in Box A on the previous page, explain how you know the 4 parts are equal.
Answer:
All parts are equal.
Explanation:
All parts have an equal area.
Each part is one-fourth or a quarter of the whole sheet.
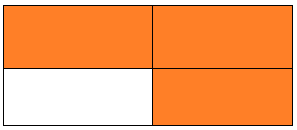
In 2 and 3, tell if each shape shows equal or unequal parts. If the parts are equal, label 1 of the parts using a unit fraction.
Question 2.

Answer:
Equal parts
Explanation:
The area and size of each part of the figure are equal so the figure is divided into equal parts.
Question 3.

Answer:
Unequal parts
Explanation:
The area and size of each part of the figure are not equal so the figure is divided into unequal parts.
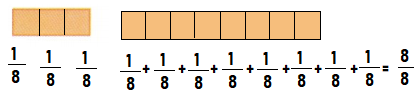
Do You Know How?
Question 4.
Draw lines to divide the shape into 8 equal parts. Then write the fraction that represents 1 part.
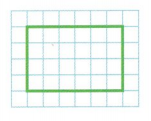
Answer:
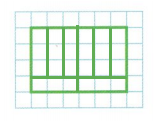
1/8 unit fraction
Explanation:
The area and size of each part of the figure must be equal .
Then the figure is divided into equal parts
The total area of the figure is 24
So we need 8 parts
24 ÷ 8 = 3
Independent Practice
In 5-7, tell if each shape shows equal or unequal parts. If the parts are equal, label 1 of the parts using a unit fraction.
Question 5.
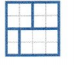
Answer:
Unequal parts
Explanation:
The given square has unequal parts, so it is difficult to denote in fraction
Question 6.

Answer:
Equal parts
Explanation:
The area and size of each part of the figure must be equal.
Then the figure is divided into equal parts.
Question 7.
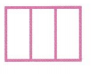
Answer:
Equal parts
Explanation:
The area and size of each part of the figure must be equal.
Then the figure is divided into equal parts.
In 8-10, draw lines to divide the shape into the given number of equal parts. Then write the fraction that represents one part.
Question 8.
6 equal parts
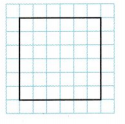
Answer:
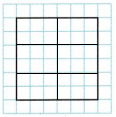
Question 9.
3 equal parts
Answer:
Question 10.
4 equal parts
Answer:
Problem Solving
In 11-14, use the table of flags to answer the questions.

Question 11.
What fraction represents the white part of Nigeria’s flag?
Answer:
one third[1/3]
Question 12.
Which nation’s flag is \(\frac{1}{2}\) red?
Answer:
Poland
Question 13.
Higher Order Thinking The flag of this nation has more than 3 equal parts. Which nation is it, and what fraction represents 1 part of its flag?
Answer:
Mauritius has more than 3 equal parts.
One fourth fraction represents 1 part of its flag.
Question 14.
Which nation’s flag is NOT divided into equal parts?
Answer:
Seychelles
Question 15.
Maryann buys 24 cans of soda. The soda comes in packs of 6 cans. How many packs does she purchase? Write a multiplication equation and a division equation to show your answer.
Answer:
4 packs of can soda
Explanation:
Maryann buys 24 cans of soda
1 pack of soda cans consist of 6 cans
so :
24 ÷ 6 = 4
Maryann buys 4 packs of soda cans
6 x 4 = 24
Question 16.
Make Sense and Persevere Jim has stickers in an array of 8 rows and 4 columns. He also has a packet of 14 stickers. How many stickers does Jim have in all?
Answer:
46 stickers
Explanation:
Jim has stickers in an array of 8 rows and 4 columns.
No of stickers in array are:
8 x 4 = 32 stickers
He also has a packet of 14 stickers.
total no of stickers Jim has are:
32 + 14 = 46 stickers
Assessment Practice
Question 17.
Draw lines to show how to divide this square into 8 equal pieces. Then select the fraction that represents 1 of the pieces.
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{4}\)
D. \(\frac{1}{8}\)
Answer:
option D
1/8 unit fracttion
Lesson 12.2 Fractions and Regions
Solve & Share
Pat made a garden in the shape of a rectangle and divided it into 4 equal parts. She planted flowers in 3 of the parts. Draw a picture of what Pat’s garden might look like.
Answer:
Pat’s garden might look like this.
I can… use a fraction to represent multiple copies of a unit fraction.

Look Back! How many parts of Pat’s garden do NOT have flowers? Explain.
Answer:
1/4 part of Pat’s garden do NOT have flowers.
Explanation:
As she planted only 3/4 of his garden with flowers.
Essential Question
How Can You Show and Name Parts of a Region?
Answer:
Fractions name parts of a whole region.
Explanation:
When an object is divided into a number of equal parts then each part is called a faction.
There are 2 parts that make up a faction:
Numerator: Which is the number that goes on top of the fraction, tells how many parts of the whole.
Denominator: Which is the number that goes on the bottom of the fraction, tells how many equal parts in all.
Visual Learning Bridge
Mr. Peters served part of a pan of enchiladas to a friend. What does each part of the whole pan represent? What part was served? What part is left?

Answer:
Each part of the whole represent fraction.
2/6 part is served.
4/6 part is left.
Convince Me! Be Precise Below is a picture of a pie pan. Draw lines and use shading to show that five \(\frac{1}{8}\)-pieces are still in the pan, and that three \(\frac{1}{8}\)-pieces were eaten. Use a fraction to label the part of the pie that is in the pan.

Answer:
3/8 pie in the pan is eaten.
5/8 pie in the pan is left over.
Guided Practice
Do You Understand?
Question 1.
In the problem in Box A on the previous page, what fraction names all of the pieces in the pan?
Answer:
The whole pan is divided into 6 equal parts. Each part is 1/6 of the whole
Explanation:
6 copies of 1/6 is 6/6.
So the whole is 6/6.
The unit fraction is 1/6.
Question 2.
Mrs. Patel made a cake. What fraction of the whole cake does each piece represent?
Answer:
1/8 fraction of the whole cake represents each piece
Question 3.
In the picture in Exercise 2, how many \(\frac{1}{8}\)-pieces were eaten? What fraction of the whole cake was eaten?
Answer:
2 pieces were eaten.
2/8 pieces were eaten.
Explanation:
In the given picture cake is divided into 8 equal parts.
Out of which 2 pieces were eaten.
Do You Know How?
In 4-6, use the figure below.

Question 4.
How many \(\frac{1}{3}\)-parts are blue?
Answer:
Two
Explanation:
Out of 3 parts in a given picture 2 parts are blue and 1 part is yellow.
Question 5.
What fraction of the whole is blue?
Answer:
Two third
Explanation:
In the given picture 2/3 of the whole is colored with blue
Question 6.
What fraction names all of the parts in the whole?
Answer:
1/3 one thirds
Independent Practice
In 7-10, write the unit fraction that represents each part of the whole. Then write the number of blue parts and the fraction of the whole that is blue.
Question 7.

Answer:
One part is blue
The fraction of whole is 1/2
Explanation:
The given triangle is equally divided into two,
one half colored with blue and the the other with yellow.
So the fraction of whole is 1/2.
Question 8.

Answer:
3 parts are blue
The fraction of whole is 3/6
Explanation:
Given hexagon is equally divided into six equal parts,
out of six, three are colored with blue and three with yellow
So the fraction of hexagon is written as 3/6.
Question 9.
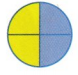
Answer:
2 parts are blue
The fraction of whole is 2/4
Explanation:
Given circle is equally divided into 4 parts,
out of which 2 are colored with blue and 2 with yellow.
So the fraction of circle is written as 2/4.
Question 10.

Answer:
6 parts are blue
The fraction of whole is 6/8
Explanation:
Given picture is equally divided into 8 parts,
Out of which 6 are colored with blue and 2 with yellow.
So the fraction of given picture is written as 6/8.
Question 11.
Draw a rectangle that shows 6 equal parts. Write the unit fraction that represents each part. Then shade \(\frac{2}{6}\) of the rectangle. Explain how you know you shaded \(\frac{2}{6}\) of the rectangle.
Answer:
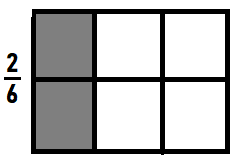
The unit fraction that represents the part of the rectangle is 116
Problem Solving
Question 12.
Vocabulary Fill in the blanks.
In the fraction \(\frac{4}{7}\), 4 is the ______ and 7 is the ________.
Answer:
4 is the numerator and 7 is denominator
Question 13.
Generalize Divide the grid below into fourths. Shade 3 of the parts. Write a fraction that represents the shaded area. Write a fraction that represents the unshaded area. What can you generalize about your fractions?

Answer:
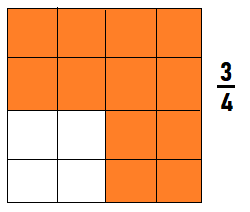
Question 14.
Christine has 6 red scarves and 3 blue scarves. Each scarf has 2 stripes. How many stripes does Christine have on her scarves? Write equations to represent and solve the problem.
Answer:
Christine has 18 stripes in total on her scarves.
Explanation:
No of red scarves = 6
No of stripes on red scarves = 6 x 2 = 12
No of blue scarves + 3
No of stripes on blue scarves = 3 x 2 = 6
Total no of stripes = 12 + 6 = 18
Question 15.
Higher Order Thinking Draw a circle that shows 6 equal parts. Shade more than \(\frac{3}{6}\) of the circle, but less than \(\frac{5}{6}\) of the circle. What fraction have you shaded?
Answer:
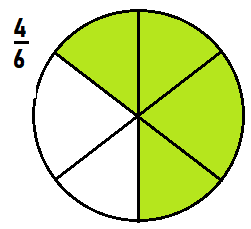
Explanation:
A fraction more than 3/6 is 4/6 and a fraction less than 5/6 is 4/6
so we have to shade 4/6 of the circle
Question 16.
Number Sense What is the area of the baseball card? Show your work.

Answer:
The area of baseball card is 70 cm.
Explanation:
Baseball card is in the shape of rectangle.
So the area of rectangle is length X breadth ( l x b )
Length = 10 cm
Breadth = 7 cm
Area = length x breadth
= 10 x 7
= 70 cm.
Assessment Practice
Question 17.
Select numbers from the box to write fractions to show 3 parts of each of these vegetable trays.

Answer:
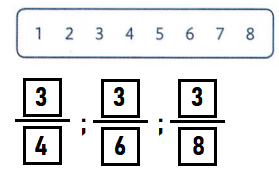
Explanation:
The first plate is divided into 4 parts out of which three parts are removed
The second plate is divided into 6 parts out of which three parts are removed
The third plate is divided into 8 parts out of which three parts are removed
Lesson 12.3 Understand the Whole
Solve & Shar
Mrs. Garcia’s third-grade class is planting a flower garden and a vegetable garden.
Draw a picture of the whole flower garden and the whole vegetable garden based on the parts shown. How did you decide what the whole of each garden looked like?
I can … identify the whole by seeing a part.

Look Back! What do the fractions and tell you about the number of equal parts in the whole?
Answer:
A basic way to interpret a fraction is by dividing a whole object into several equal parts.
The denominator tells how many equal parts the whole is subdivided into.
The numerator tells the number of those parts that are under consideration.
Essential Question
How Can You Use a Fractional Part to Find the Whole?
Answer:
For finding a fraction of a whole number, we multiply the numerator of the fraction by the given number and then divide the product by the denominator of the fraction.
Visual Learning Bridge
Anya and Novi are running in different races. The diagrams below show how much of their races each runner has completed.
Draw a picture of the whole of each track. Write a fraction to represent the whole.
You can look at the fraction to find how many parts will make up the whole.
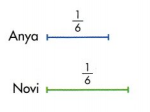
You know Anya and Novi have each completed \(\frac{1}{6}\) of their races.
Six lengths of \(\frac{1}{6}\) make \(\frac{6}{6}\), or 1 whole.
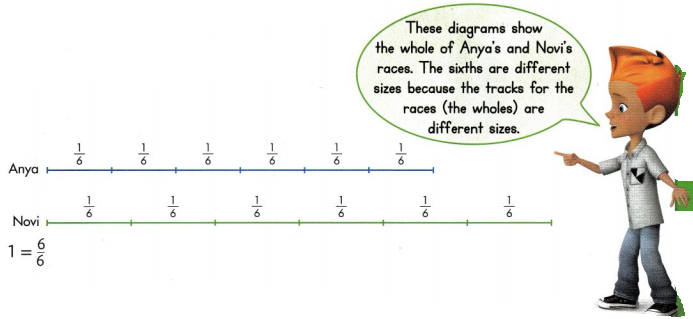
Convince Me! Reasoning Why is Novi’s track longer than Anya’s track?
Answer:
Novi’s track is longer than Anya’s track because 1/6th of the track were of different size.
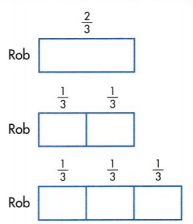
Another Example! The part of a race Rob completed is shown at the right. You can use fractional parts like this to identify the whole.
\(\frac{2}{3}\) is 2 copies of \(\frac{1}{3}\). Divide Rob’s track into 2 equal parts.
Three copies of \(\frac{1}{3}\) make \(\frac{3}{3}\), or 1 whole. Draw one more third.
1 = \(\frac{3}{3}\).
Guided Practice
Do You Understand?
Question 1.
If the distance Anya ran was of the length of the track, what fraction would you use to represent the whole track?
Answer:
The fraction of whole track = 6/6
Explanation:
Six lengths of 1/6 make 6/6 or whole.
Question 2.
What is true about the numerator and denominator of each fraction that represents one whole?
Answer:
A fraction represents a part of a whole.
Explanation:
The numerator represents how many parts of that whole are being considered,
while the denominator represents the total number of parts created from the whole.
Do You Know How?
3. Draw a picture of the whole and write a fraction to represent the whole.
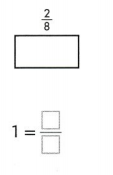
Answer:
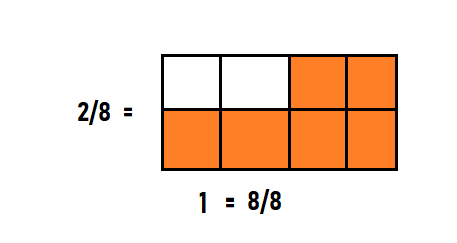
Independent Practice
In 4-7, draw a picture of the whole and write a fraction to represent the whole.
Question 4.
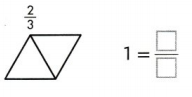
Answer:

1 = 3/3
Question 5.
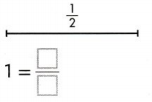
Answer:
![]()
1 = 2/2
Question 6.
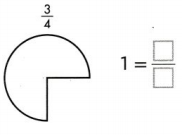
Answer:
 1 = 4/4
1 = 4/4
Question 7.
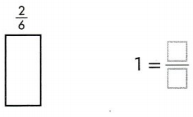
Answer:
1 = 6/6
Problem Solving
Question 8.
Ronnie and Gina were shown \(\frac{1}{2}\) of a table. They each drew a picture of the whole table. Whose drawing could be correct? Explain.
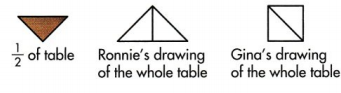
Answer:
Gina’s drawing of the whole table is correct
Explanation:
Both Ronnie and Gina were correct.
but tables are generally square , rectangle or circle in shape so Gina’s table is correct
Question 9.
Higher Order Thinking If the part shown in Exercise 8 is \(\frac{1}{4}\) of a table, what could the whole table look like? Draw a picture and write a fraction to represent the whole.
Answer:
One whole
Question 10.
The Florida panther is endangered. In 1970, the population was estimated at 20 panthers. In 2017, the population was estimated at 230 panthers. About how many more panthers were there in 2017 than in 1970?

Answer:
About 210 more panthers were there in 2017 than in 1970.
Explanation:
In 1970, the population was 20 panthers.
In 2017, the population was estimated at 230 panthers.
So 230 – 20 = 210.
Question 11.
Construct Arguments Jenna and Jamal are making rugs. They have finished the parts shown. Draw pictures to show each whole rug. Whose rug will be longer when it is finished? Explain.
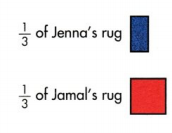
Answer:
Jenna: I have finished 1/3 of my rug.
Jamal: I have finished 1/3 of my rug.
Jamal: My rug is bigger than you.
Jenna: How is your rug bigger than mine. Explain?
Jamal: My 1/3 of the rug is bigger than your 1/3 of the rug
Explanation:
Jamal’s 1/3 rd of the rug is bigger than Jenna’s 1/3 of the rug
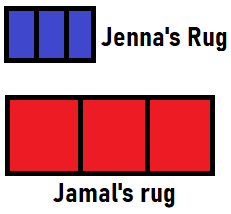
So Jamal’s rug is longer than Jenna.
Assessment Practice
Question 12.
The picture shows \(\frac{2}{3}\) of a granola bar. Which shows the whole granola bar?

Answer:
Option B
Question 13.
Each part below is \(\frac{1}{2}\) of a different whole. Which is part of the largest whole?
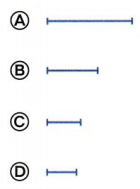
Answer:
Option A
Lesson 12.4 Number Line: Fractions Less Than 1
Solve & Share
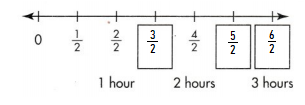
At a state park, there is a 1-mile hiking path between the park entrance and the beach. Scenic lookouts are located at points and of the distance from the park entrance to the beach. Show about where the lookout points are located on the line below.
I can… represent fractions on a number line.
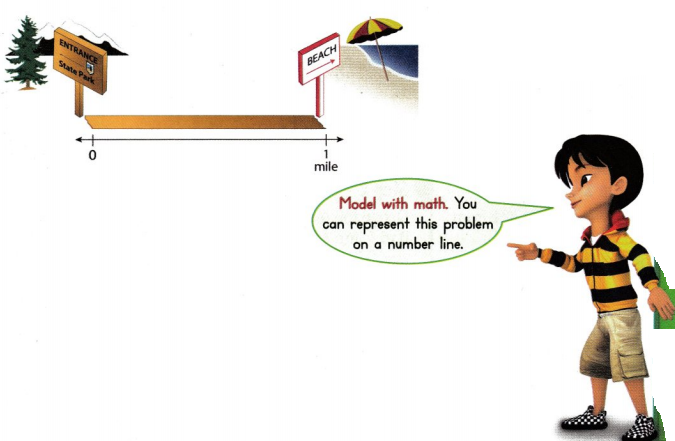
Look Back! If you know about where the point for \(\frac{1}{3}\) is located, how can you find about where the point for \(\frac{2}{3}\) is located?
Answer:
The line is divided into 3 parts,
We know 1/3 location on number line.
The point next to 1/3is 2/3, so we know where 2/3 point is located.
Essential Question
How Can You Record Fractions on a Number Line?
Answer:
Fractions expand our number system beyond whole numbers and integers.
Explanation:
Fractions help us to denote any decimal number with higher precision.
Representation of Fractions on the number line is important to understand how fractions represent part of a whole.
Visual Learning Bridge
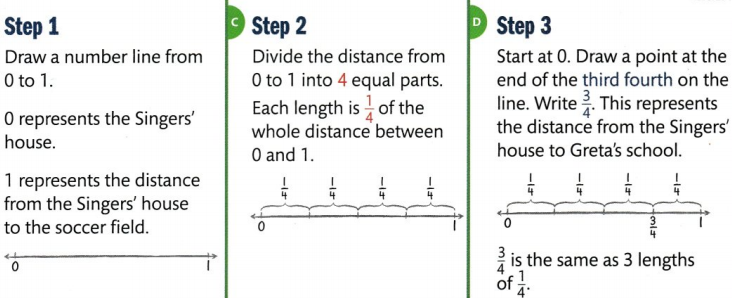
Mr. Singer is picking up his daughter, Greta, from school to go to soccer practice. Greta’s school is located at \(\frac{3}{4}\) of the distance from the Singers’ house to the soccer field. How can you represent \(\frac{3}{4}\) on a number line?
Every number on a number line represents a distance from 0.

Convince Me! Critique Reasoning Jenna and Benito each marked \(\frac{1}{4}\) on a number line. The length of the part from 0 to \(\frac{1}{4}\) on Jenna’s number line is shorter than on Benito at Benito’s. Did someone make a mistake? Explain your thinking.
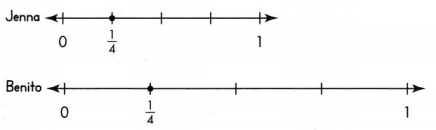
Jenna did a mistake by marking unit fraction on a small number line, compared with Benito number line.
Guided Practice
Do You Understand?
Question 1.
Maliya divides a number line from 0 to 1 into 6 equal lengths. What unit fraction represents each equal length? What should Maliya label the tick mark just to the left of 1? Explain.
Answer:
5/6 unit fraction
Explanation:
0 to 1 is divided in to 6 fractions
Each 1/6 unit fraction
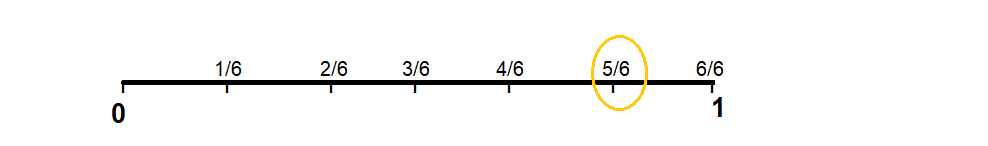
Question 2.
Josh divides a number line from 0 to 1 into 8 equal lengths. What should he label the first tick mark just to the right of 0? Explain.
Answer:
1/8 unit fraction.
Explanation:

Do You Know How?
In 3 and 4, divide the number line into the given number of equal lengths. Then mark and label the given fraction on the number line.
Question 3.
2 equal lengths; \(\frac{1}{2}\)

Answer:
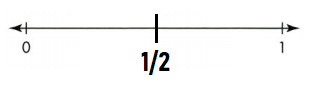
Question 4.
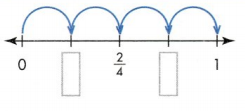
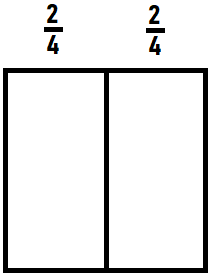
4 equal lengths; \(\frac{2}{4}\)

Answer:
Explanation :
Draw a line and make 3 equal parts on number line and then mark 1/4, 2/4 and 3/4unit fraction.
Leveled Practice In 5 and 6, divide the number line into the given number of equal lengths. Then mark and label the given fraction on the number line.
Question 5.
3 equal lengths; \(\frac{2}{3}\)

Answer:
2/3 unit fraction.
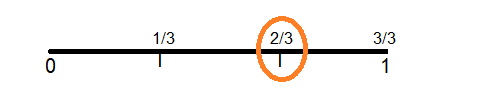
Explanation : Draw a line and make 3 equal parts on number line and then mark 1/3, 2/3 and 3/3 units
Question 6.
6 equal lengths; \(\frac{2}{6}\)

Answer: 2/6
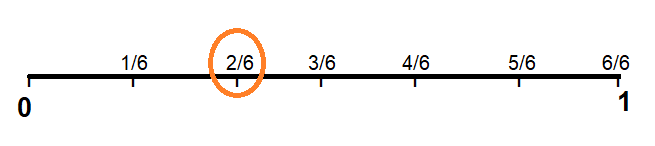
Explanation :
Draw a line and make 6 equal parts on number line and then mark 1/6, 2/6,3/6,4/6,5/6 and 6/6units
In 7 and 8, draw a number line from 0 to 1. Divide the number line into equal lengths for the given fraction. Then mark and label the given fraction on the number line.
Question 7.
\(\frac{4}{6}\)
Answer: 4/6
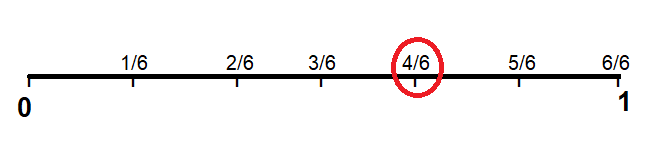
Explanation :
Draw a line and make 6 equal parts on number line and then mark 1/6, 2/6,3/6,4/6,5/6 and 6/6units
Question 8.
\(\frac{5}{8}\)
Answer: 5/8

Explanation :
Draw a line and make 8 equal parts on number line and then mark 1/8 , 2/8 , 3/8 , 4/8 , 5/8 , 6/8 , 7/8 and 8/8units
Problem Solving
Question 9.
Construct Arguments Terrance and Dana each drew a number line and marked \(\frac{3}{4}\). Did each person represent \(\frac{3}{4}\) in the correct place on his or her line? Explain.
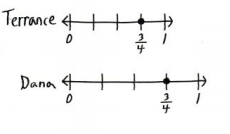
Answer:
yes
Explanation:
Terrance number line is a bit smaller that Dana’s but both the number lines are divided into equal parts.
Question 10.
A gymnast starts at the left end of the balance beam and does some handsprings. When she is finished, she is at the point shown on the diagram. What fraction represents how far she went on the balance beam?

Answer:
6/8 unit fraction.
Explanation :
The balance beam is divided in to 8 equal parts of same unit lengths
the point is market at 6/8 on the balance beam.
Question 11.
Mark draws a number line and labels the points for 0 and 1. He divides the distance from 0 to 1 into 2 equal lengths and labels the fraction \(\frac{1}{2}\). If Mark divides each half into 2 equal lengths, what fractions can Mark label on his number line?
Answer:
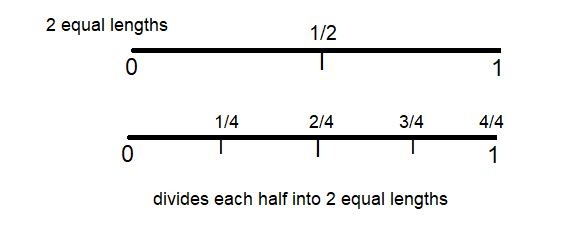
Explanation:
Mark draws a number line and labels the points for 0 and 1 of two equal lengths and labels the fraction and label 0 , 1/2 and 1.
Mark divides each half into 2 equal lengths, each fractions is marked labels on his number line as 1/4, 2/4, 3/4 and 4/4
as shown in the above figure.
Question 12.
Higher Order Thinking Show 3 ways you can represent three eighths.
Answer:
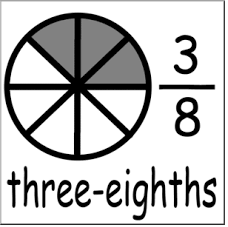
The number ABOVE the line tells HOW MANY PARTS
we have (the colored parts).The number BELOW the line tells how many EQUAL parts
the whole is divided into. To find 3/8 of a number, we multiply the numerator 3 by the given whole number and then divide the product by the denominator 8.
Assessment Practice
Question 13.
What fraction does the red point on this number line represent?
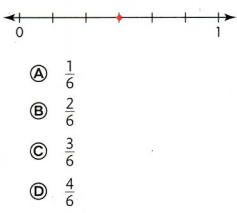
Answer:
Option C
Explanation:
The above line is of 6 equal parts of each label 1/6, 2/6, 3/6, 4/6, 5/6 and 6/6
Question 14.
Which number line has a red point at \(\frac{1}{3}\)?
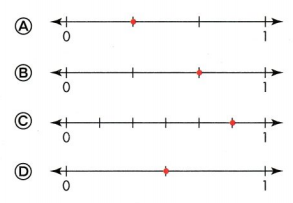
Answer:
Option A
Explanation :
In the number line has a red point at \(\frac{1}{3}\)
Lesson 12.5 Number Line: Fractions Greater Than 1
Solve & Share
The length of one strip of paper is 1 whole unit. Fold two strips of paper in half. Open the two strips and place them end to end.
How many halves do you have? Use fractions to name each fold line. Tell how you decided. Draw a picture to show your work.
Answer:
2 halves
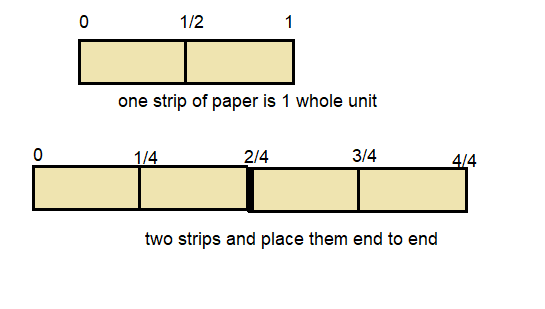
strip of paper is 1 whole unit. Fold two strips of paper in half,
two halves for two strips of papers , if it unfolded and kept end to end open
I can … represent fractions equal to or greater than 1 on a number line

Look Back! If you added a third strip of paper folded in half, how could you use halves to name the fold lines? Explain.
Answer:
If you add a third strip of paper folded in half, as 5/4 and 6/4.
Explanation:
One can represent fractions equal to or greater than 1 on a number line.
Essential Question
How Can You Use a Number Line to Represent Fractions Greater Than 1?
Answer:
Fractions greater than 1 have numerators larger than their denominators, those that are less than 1 have numerators smaller than their denominators; the rest are equal to 1.
Visual Learning Bridge
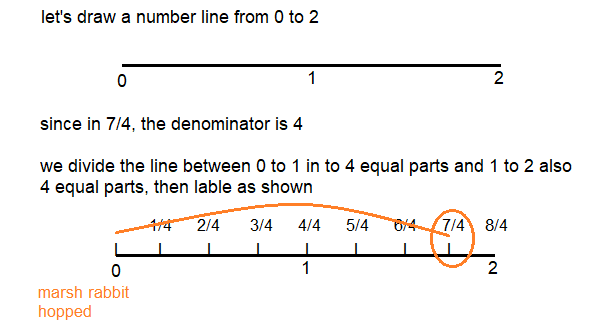
A marsh rabbit hopped \(\frac{7}{4}\) the length of a rabbit trail. How can you show this on a number line?
Number lines can represent fractions that are greater than 1 whole \(\frac{7}{4}\). 5 is greater than 1 whole, but less than 2 wholes. The whole is the distance between 0 and 1.
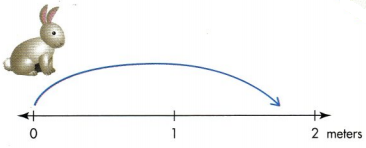
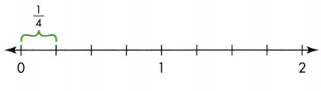
Divide each whole into 4 equal lengths.
Each length is \(\frac{1}{4}\) of the whole.
\(\frac{4}{4}\) is the same as 1 whole.
The marsh rabbit hopped 7 lengths of the unit fraction \(\frac{1}{4}\).
The point showing 7 lengths of \(\frac{1}{4}\) can be labeled as \(\frac{7}{4}\)

Answer: 7/4
Explanation:
Marsh rabbit hopped shown in the number line.
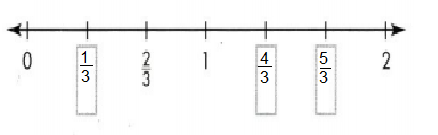
Convince Me! Be Precise One tick mark on the number line below has been named with the fraction \(\frac{2}{3}\). On the number line the lengths marked are equal. Write fractions for the other tick marks shown.
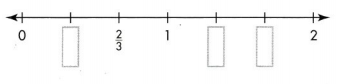
Answer:
Explanation:
Divided a number line from 0 to 1 into 3 equal lengths. Each unit fraction represents 1/3 of equal length.
Guided Practice
Do You Understand?
Question 1.
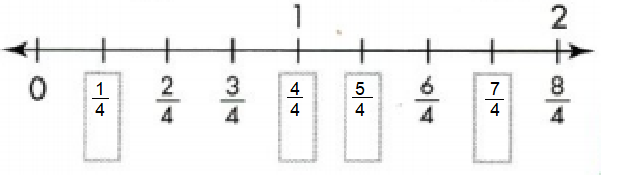
Name a fraction that is to the right of the tick mark for 2 on a number line.
Answer: 7/3
Explanation :
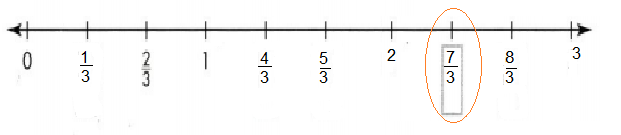
Question 2.
Quinn says that \(\frac{10}{8}\) comes to the right of \(\frac{9}{8}\) on a number line. Do you agree? Why or why not?
Answer: YES
Explanation:

Do You Know How?
In 3 and 4, each number line has equal lengths marked. Write the missing fractions.
Question 3.
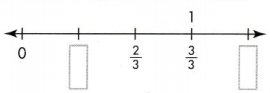
Answer:
1/3 and 4/3 of unit fraction.
Explanation:
Marked on number line.
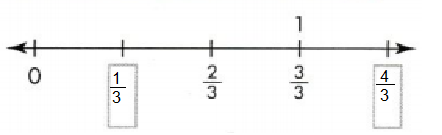
Question 4.
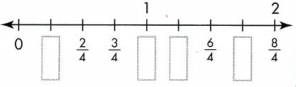
Answer:
1/4, 4/4, 5/4 and 7/4 are marked on number line.
Explanation:
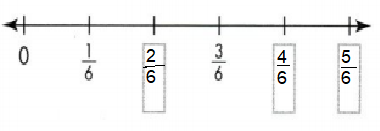
Independent Practice
Leveled Practice In 5-7, each number line has equal lengths marked. Write the missing fractions.
Question 5.
Answer:
1/2 and 3/2 are missing marked on number line.
Explanation:
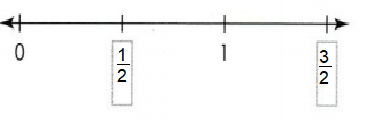
Question 6.
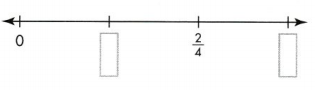
Answer:
1/4 and 4/4 or 1 are marked on number line.
Explanation:
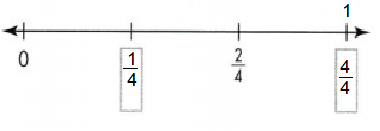
Question 7.
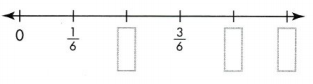
Answer:
2/6, 4/6 and 5/6 are missing marked on number line.
Explanation:
In 8 and 9, divide the number lines into equal lengths. Write the missing fractions.

Question 8.

Answer:
1/3, 4/3, 5/3 7/3 and 8/3 are marked on number line.
Explanation:
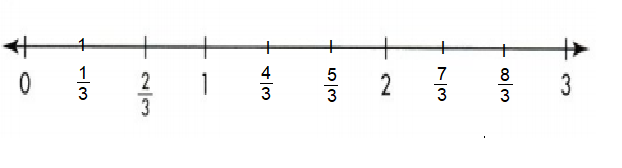
Question 9.

Answer:
2/8, 3/8, 5/8 and 6/8 are missing numbers marked on number line.
Explanation:
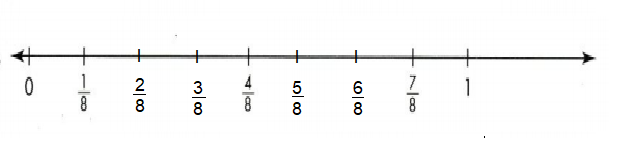
Problem Solving
In 10 and 11, use the number line below.
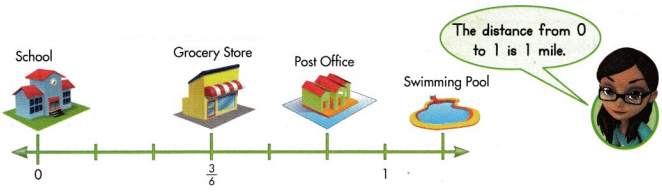
Question 10.
What fraction tells how far the swimming pool is from the school? Explain how you know.
Answer:
1⅓ mile from school.
Explanation :
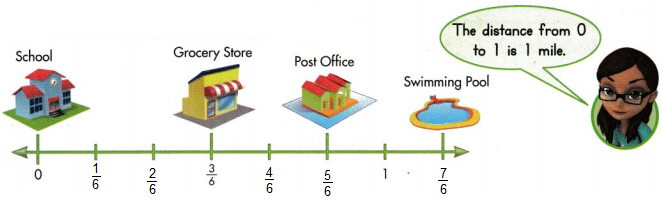
Question 11.
Higher Order Thinking The hospital is halfway between the grocery store and the post office. What fraction tells how far the hospital is from the school? Explain.
Answer:
4/6 unit fraction.
Explanation :
The hospital is 4/6 mile distance from the school, it is located at 4/6 on number line.
Question 12.
Tim has 78 board games. He has 10 boxes. Each box holds 9 games. If Tim puts all the games he has into the boxes, how many more games can he fit? Complete the bar diagram and solve the problem.
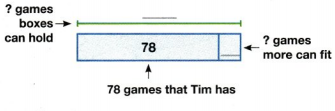
Answer:
12 more games.
Explanation:

Tim has 10 Boxes, each box holds 9 games.
Total boxes can hold 90 games, but the Tim has 78 games.
Required games = 90-78 = 12 games.
Question 13.
Critique Reasoning Rachel says that she can find (7 × 5) × 2 by calculating (7 × 2) + (5 × 2) = 14 + 10. Then add to get 24. Does Rachel’s reasoning make sense? Use properties of operations to explain.
Answer:
Rachel’s reasoning doesn’t make any sense.
Explanation:
Commutative Property x + y = y+ x
Associative Property x + (y + z) = (x + y) + z
According to the above two properties (7×5)x2=70 and
(7 × 2) + (5 × 2) = 14 + 10 =24.
Assessment Practice
Question 14.
What fraction is represented by the total length marked on the number line? Select the correct fraction from the box.

Answer:
4/3 fraction on number length.
Explanation:
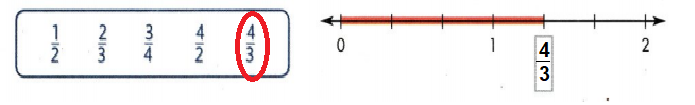
Lesson 12.6 Line Plots and Length
Solve & Share
Jamie measured the lengths of 6 beetles. She measured each beetle’s length to the nearest inch and to the nearest half inch. She recorded the lengths in the two line plots below. Measure the length of each beetle below to the nearest inch and to the nearest half inch. Record your measurements in Jamie’s line plots.
I can … measure to the nearest half inch and show the data on a line plot.
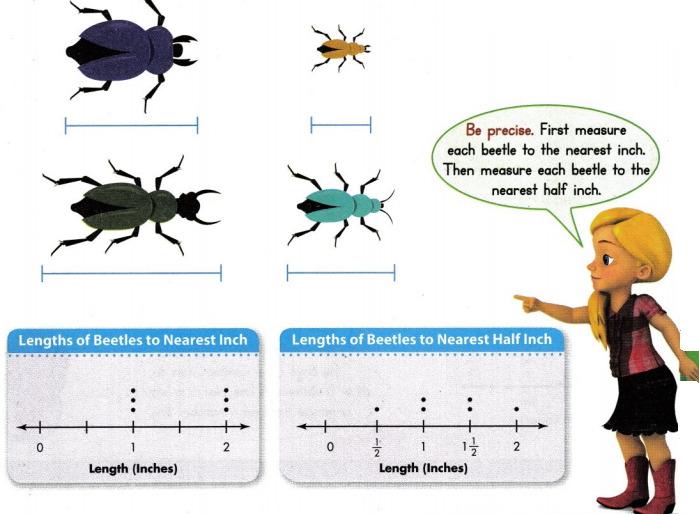
Look Back! What tool did you use to measure the length of each beetle? How did you use this tool?
Answer :
I used a scale to measure the beetle.
We have to place the beetle beside the scale and then we have to mark the length of the beetle on a piece of paper.
Essential Question
How Can You Measure Lengths and Use Line Plots to Show the Data?
Answer:
Line plots, are particularly useful for showing measurement data.
Explanation:
If a class of students all measured the length of their pencils, a line plot would highlight the range and frequency of the measurements.
Visual Learning Bridge
Julio is measuring some lengths of yarn in inches. How can he use a ruler to measure to the nearest half inch?
Line up one end of the object with 0.
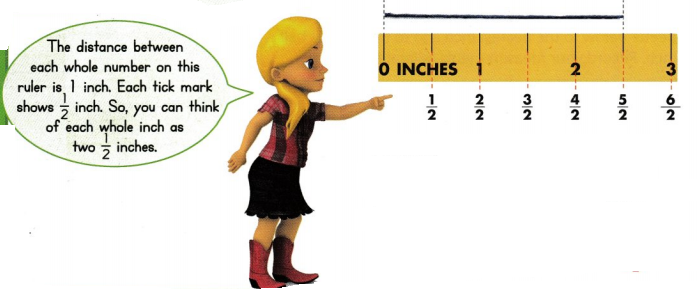
The fifth \(\frac{1}{2}\)-inch tick mark is closest to the end of the length of yarn.
So, to the nearest half inch, the yarn measures \(\frac{5}{2}\) inches.
This length is two whole inches and one \(\frac{1}{2}\) inch. You can write this length as 2\(\frac{1}{2}\) inches.
Answer:
Julio measured 9 other lengths of yarn in inches:
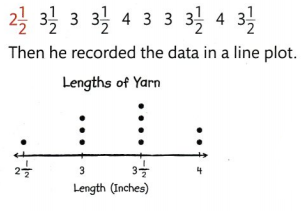
Explanation:
One can use number lines to show fractions.
A line plot is a way to organize data on a number line.
Steps to Make a Line Plot
- Draw a number line. Show a scale based on the data.
- Write a title for the line plot.
- Mark a dot for each data value.
Answer:
Convince Me! Reasoning Suppose you measured a length of yarn that was about 4\(\frac{1}{2}\) inches. How would you need to change the line plot above to record this length?
Answer:
It has to extend up to 9/2.
Explanation:
The line is extended to right side and the values are increases as shown in the above line plot,
values on line is extended up to 9/2 for 4½.
Guided Practice
Do You Understand?
Question 1.
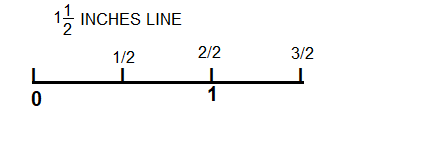
Draw a line that is 1½ inches long.
Answer:
Question 2.
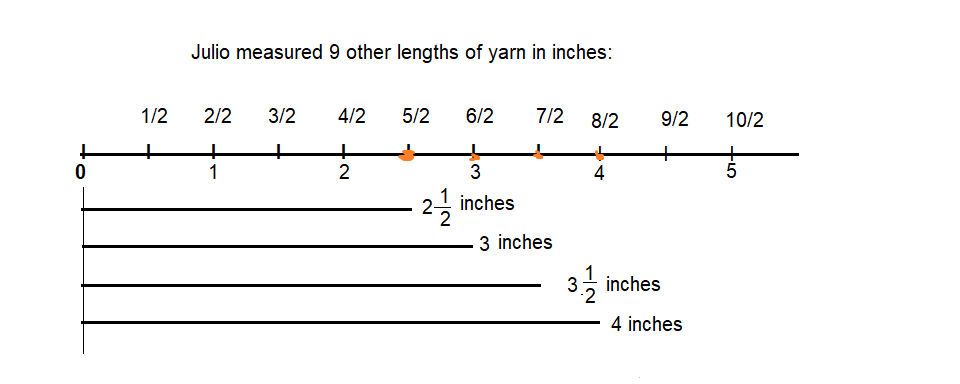
If a line measures halfway between 3 and 3\(\frac{1}{2}\) inches and you need to measure to the nearest \(\frac{1}{2}\) inch, what length will you record? Why?
Answer:
3 inches is the nearest inch.
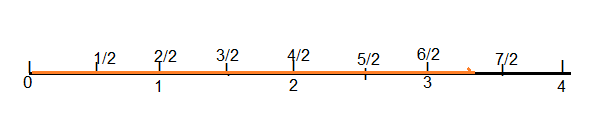
Explanation:
The line is nearer to 3 inch mark.
Do You Know How?
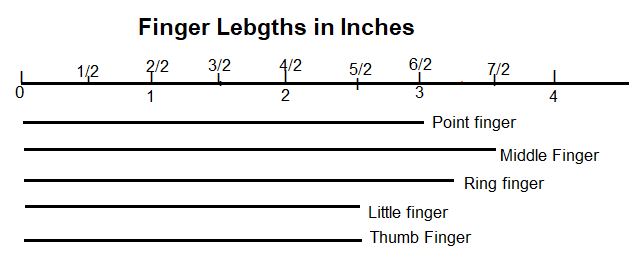
Question 3.
Measure the length of each of your fingers. List the measurements to the nearest half inch.
Answer:
1 Index or Point Finger of Length 3 inches
2 Middle Finger of Length 3½ inches
3 Ring Finger of Length 3 inches
4 Little Finger of Length 2½ inches
5 Thumb Finger of Length 2½ inches
Explanation:
Answers may vary from hand to hand.
Question 4.
Make a line plot to show the measurements of your fingers.
Answer:
Inches of fingers may vary from person to person.
Explanation:
Question 5.
Measure the lengths of the pieces of yarn at the right to the nearest half inch. Write the length for each piece.

Answer:
First – 3 inches
Second – 2½ inches
Third – 3 inches
Forth – 2 inches
Fifth – 2 inches
Explanation:
Length of yarn may vary.
Question 6.
Draw a line to represent another length of yarn. Measure your line to the nearest half inch.
Answer:
3½ inches length yarn.
Question 7.
Make a line plot to show the measurements of the yarn.

Answer:
3½ inches length yarn.
Problem Solving
Question 8.
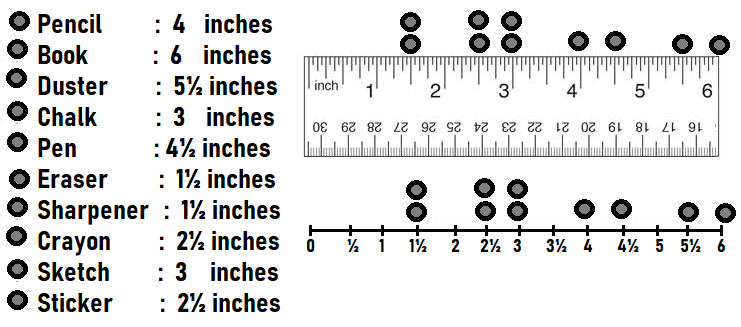
Measure the lengths of 10 classroom objects to the nearest half inch. Choose objects that are between 1 and 6 inches long. Record your measurements.
Answer:

Question 9.
On grid paper, draw a line plot to show your data from Exercise 8.
Answer:
Question 10.
Make Sense and Persevere Raymond weighed his three dogs. The oldest dog weighs 74 pounds. The other two dogs each weigh 34 pounds. How many more pounds does the oldest dog weigh than the other two dogs combined?
Answer:
The oldest dog weighs 6 more ponds than the other two dogs.
Explanation:
Weight of oldest dog is 74
Weight of other two dogs (34+34) is 68
So the oldest dog weighs 6 ponds more
74 – 68 = 6
Question 11.
Draw a number line from 0 to 2. Label the wholes. Divide each whole into thirds. Label each fraction.
Answer:
In 12 and 13, use the table at the right.

Question 12.
How many more of the shortest paper chains does Rico have than the longest paper chains? Explain.
Answer:
Shortest paper chain length 6½
Rico has 3 shortest paper chains each of length 6½
Explanation :
In the table the shortest length of the paper chain is 6½
There are 3 shortest 6½
Question 13.
Higher Order Thinking Look at Rico’s measurements. Can you tell if he measured the paper chains to the nearest half inch or to the nearest inch? Explain.
Answer:
Rico’s measurements are to the nearest half inch
Explanation:
If we look at Rico’s measurements all of the measurements are in inches and nearest half inches,
there are no one fourth inches.
So Rico’s measurements are in nearest half inches.
Assessment Practice
Question 14.
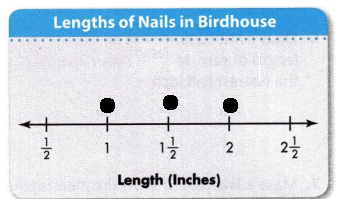
Jessica used 4 of Nail A, 2 of Nail B, and 3 of Nail C to build a birdhouse. Measure each nail to the nearest half inch. Then complete the line plot.
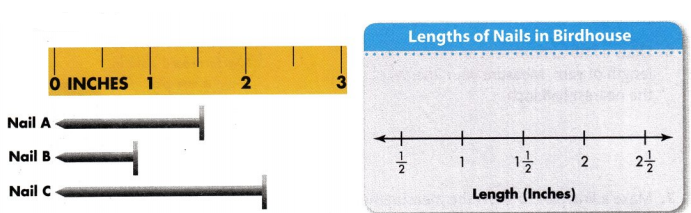
Answer:
Lesson 12.7 More Line Plots and Length
Solve & Share
Monica and her friends measured the lengths of their shoes. Show this data by marking a dot for each length on the line plot below.
Measure the length of three classmates’ shoes. Add a dot to represent each length on the line plot. What length was the most common?
I can … measure to the nearest fourth inch and show the data on a line plot.

Look Back! Are there different ways to record the results of a data collection? Explain.
Answer:
Yes, there are different ways to record the results of a data collection.
Explanation:
We can use a scale, measuring tape, and so on to measure the data.
Essentials Question
How Can You Make and Use Line Plots?
Answer:
A line plot is a graph that shows frequency of data along a number line. It is best to use a line plot when comparing fewer than 25 numbers. It is a quick, simple way to organize data.
Visual Learning Bridge
Anna is measuring the length of her crayons. How can she use a ruler to measure to the nearest fourth inch?
Line up one end of the object with 0.

The tenth \(\frac{1}{4}\)-inch tick mark is closest to the end of the length of the crayon.
So, to the nearest fourth inch, the crayon measures \(\frac{10}{4}\) inches.
This length is two whole inches and two \(\frac{1}{4}\) inches. You can write this length as 2\(\frac{2}{4}\) inches.
Anna measured her other crayons.
She then recorded the data in a line plot.
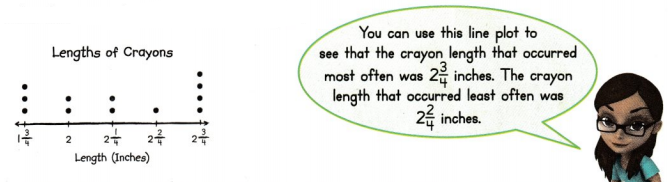
Convince Me! Make Sense and Persevere Nathan also made a line plot to show the lengths of his crayons. Tell three things you know about the lengths of Nathan’s crayons.
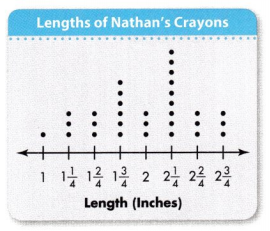
Answer:
Nathan’s measured his crayons nearest ¼th
Most of Nathan’s crayons are 2¼ inches
The smallest crayon Nathan’s has 1 inch.
Guided Practice
Do You Understand?
Question 1.
Measure the length of this line to the nearest fourth inch.
![]()
Answer:
Length = 3¾ inches
Explanation:
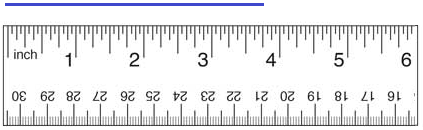
Question 2.
Describe how you would show this measurement on a line plot.
Answer:
Do You Know How?
Question 3.
Draw a line plot to show the data.

Answer:
Question 4.
Measure your pencil to the nearest fourth inch. Show the length on your line plot.
Answer:
length of pencil : 3 \(\frac{3}{4}\)
Independent Practice
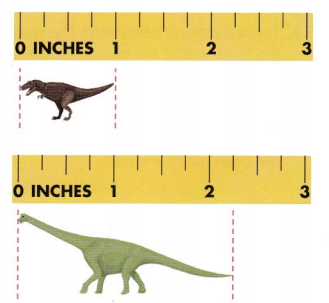
Question 5.
Daisy measured the lengths of her toy dinosaurs to the nearest fourth inch. She listed the lengths. Make a line plot to show the data.
1\(\frac{2}{4}\) in., 2\(\frac{1}{4}\) in., 1 in., 1\(\frac{2}{4}\) in., 1\(\frac{3}{4}\) in.
Answer:
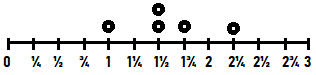
Question 6.
Measure the lengths of the toy dinosaurs at the right to the nearest fourth inch. Write the length for each toy. Show the lengths on your line plot.
Answer:
length of toy 1 : 1\(\frac{2}{4}\) in.
length of toy 2 : 2\(\frac{1}{4}\) in.
length of toy 3 : 1 in.
length of toy 4 : 1\(\frac{2}{4}\) in.
length of toy 5 : 1\(\frac{3}{4}\) in.
Problem Solving
In 7 and 8, use the line plot at the right.
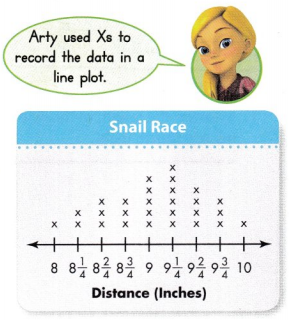
Question 7.
Arty made a line plot to show the number of inches that different snails crawled in a 5-minute race. What was the most common distance that the snails crawled?
Answer:
the most common distance that the snails crawled is 9 \(\frac{1}{4}\) inches
Question 8.
Higher Order Thinking How many more snails crawled a length more than 8\(\frac{3}{4}\) inches than a length less than 8\(\frac{3}{4}\) inches?
Answer:
snails that crawled length less than 8\(\frac{3}{4}\) inches are : 6
snails that crawled length more than 8\(\frac{3}{4}\) inches are : 19
difference : 19 – 6 = 13 snails
13 more snails crawled a length more than 8\(\frac{3}{4}\) inches than a length less than 8\(\frac{3}{4}\) inches
Question 9.
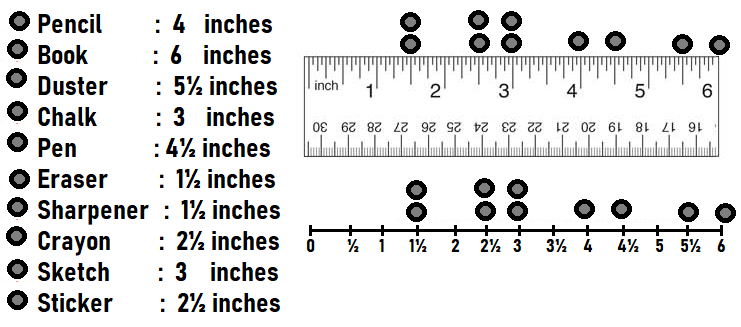
Measure the lengths of 10 classroom objects to the nearest fourth inch. Choose objects that are between 1 and 5 inches long. Record your measurements.
Answer:

Question 10.
On grid paper, draw a line plot to show your data from Exercise 9.
Answer:
Question 11.
Jackson bought 5 books that cost $7 each. How much change did he get from $40?
Answer:
Jackson got $5 change.
Explanation:
Cost of each book = $7
Cost of 5 books = 5×7
Total cost of 5 books =$35
Total amount paid = $40
Total change he received = 40-35
= $5.
Question 12.
Use Structure Use the digits 2, 6, and 8 to make as many 3-digit numbers as you can. Use place value to arrange the numbers in order from least to greatest.
Answer:
H T U
2 6 8
2 8 6
6 2 8
6 8 2
8 2 6
8 6 2
Assessment Practice
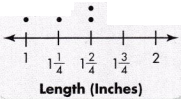
Question 13.
Tonya is making headbands. She recorded the lengths of all the blue bows she purchased for the headbands. Tonya also purchased 4 red bows with lengths of 1 inch, 1\(\frac{1}{4}\) inches, 1\(\frac{2}{4}\) inches, and 1\(\frac{2}{4}\) inches. Record the lengths of Tonya’s red bows in the line plot.

Answer:
Red bows are : 1 inch , 1\(\frac{1}{4}\) inches, 1\(\frac{2}{4}\) inches, and 1\(\frac{2}{4}\) inches.
so there are 4 red bows.
Lesson 12.8 Problem Solving
Make Sense and Persevere
Solve & Share
Marcus, Mariah, and Tony painted a mural. They divided it into equal parts. Marcus painted 2 parts, Mariah painted 3 parts, and Tony painted the rest. What fraction of the mural did each student paint?
This problem may have missing or extra information. If information you need is missing, make up some reasonable information and then solve the problem.
I can … make sense of problems and keep working if I get stuck.
Thinking Habits
Be a good thinker! These questions can help you.
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?

Look Back! Make Sense and Persevere What information was not given in the problem? How did you still solve the problem?
Answer:
The number of parts the mural is divided into was not given
Additional information:
Marcus, Mariah, and Tony painted a mural. They divided it into 8 equal parts. Marcus painted 2 parts, Mariah painted 3 parts, and Tony painted the rest. What fraction of the mural did each student paint?
Answer:
Marcus painted 2 parts
Mariah painted 3 parts
and Tony painted the rest
= 8 – ( 2 + 3 )
= 8 – 5
= 3 parts
Tony painted 3 parts
Marcus painted : \(\frac{2}{8}\)
Mariah painted : \(\frac{3}{8}\)
Tony painted : \(\frac{3}{8}\)
Essential Question
How Can You Make Sense of a Problem and Persevere in Solving It?
Answer:
The meaning of a problem and looking for entry points to its solution. Helps to analyze givens, constraints, relationships, and goals.
Suki divides her garden into 6 equal parts. She plants daisies, roses, and violets. It takes Suki 1 hour to plant the flowers. She plants daisies in 1 part, roses in 2 parts, and violets in the rest of the garden.
In what fraction of the garden does Suki plant violets?

What is a good plan for solving the problem?
I need to make sense of the given information. I need to think about what I can use to help me solve the problem.
How can I make sense of and solve this problem?
Answer:
I can…..
- identify the quantities given.
- understand which quantities are needed to solve the problem.
- choose and implement an appropriate strategy.
- check to be sure my work and answer make sense.
Explanation:
The information about 1 hour to plant the flowers is not needed to solve the problem.
I can use a picture to help make sense.
1 equal part for daisies is \(\frac{1}{6}\) of the whole.
2 equal parts for roses is \(\frac{2}{6}\) of the whole.
There are 3 equal parts left for violets.
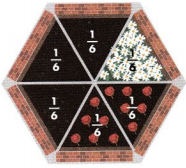
3 copies of \(\frac{1}{6}\) is \(\frac{3}{6}\).
So, Suki plants violets in \(\frac{3}{6}\) of the garden.
Convince Me! Make Sense and Persevere How can you check to make sure the work and answer given above make sense?
Answer:
Total number of parts garden is divided into is: 6 parts
Daisies are planted in 1 part [ 1/6 fraction]
Roses are planted in 2 parts [ 2/6 fraction]
So Suki plants violets in 3 parts as :
1 + 2 = 3
6 – 3 = 3 parts
3/6 unit fraction.
Guided Practice
Make Sense and Persevere Keira and Matt cut a sandwich into 4 equal parts. They each ate 1 part. Keira is 9 years old. Matt is the same age as Keira. What fraction of the sandwich is not eaten?

Question 1.
Is there any missing or extra information? Explain.
Answer:
Missing information : none
Extra information : the ages of Keira and Matt are given [we don’t need their ages to determine the parts of the sandwich left]
Question 2.
What do you need to find before you can determine how much of the sandwich is left?
Answer:
We don’t need to find the any other information as all the needed information is given in the question
Question 3.
Solve the problem. If information you need is missing, make up some reasonable information for the problem.
Answer:
The sandwich is divided into 4 equal parts
Keira and Matt each ate one part so total parts eaten : 2 parts
number of parts left is : 4- 2 = 2 parts
Independent Practice
Make Sense and Persevere Marni planted a vegetable garden. She put lettuce in 1 part, carrots in 4 parts, and broccoli in the rest of her garden. In what fraction of the garden did Marni plant broccoli?
Question 4.
Is there any missing or extra information?
Answer:
Missing information : the question did not specify the number of the parts Marni’s garden is divided into
Extra information : none
Question 5.
Solve the problem. If information you need is missing, make up some reasonable information for the problem.
Answer:
Additional information : Marni’s garden is divided into 8 parts. She put lettuce in 1 part, carrots in 4 parts, and broccoli in the rest of her garden. In what fraction of the garden did Marni plant broccoli?
Answer:
fraction in which broccoli is planted : 3/8
Explanation:
Total number of parts Marni’s garden is divided into is 8 parts
lettuce : 1 part
carrots : 4 parts
broccoli : 8 – (1 + 4)
. : 8 – 5 = 3
fraction in which broccoli is planted : 3/8
Question 6.
Can you use a different number of parts and still solve the problem? Explain.
Answer:
yes
Explanation :
If Total number of parts Marni’s garden is divided into is 6 parts
lettuce : 1 part
carrots : 4 parts
broccoli : 6 – (1 + 4)
. : 6 – 5 = 1
fraction in which broccoli is planted : 1/8
Problem Solving
Performance Task
Sports Day
Green School divides its school gym into 8 equal parts for a sports day. Basketball is in 2 parts, soccer is in 1 part, and volleyball and tennis are in the rest.

Question 7.
Make Sense and Persevere The gym teacher wants to know what fraction of the gym is used for tennis. What missing information do you need to solve the problem?
Answer:
School gym is divides into 8 equal parts.
Tennis and Volleyball not clearly mentioned, these two are missing information do you need to solve the problem.
In 8 and 9, draw a picture to represent the number of parts in each plan.
Question 8.
Reasoning What fraction of the gym would be used for tennis if 2 parts were for volleyball?

Answer: 3 parts

Explanation:
if 2 parts were used for volleyball , three parts used for tennis
Question 9.
Reasoning What fraction of the gym would be used for tennis if 3 parts were used for volleyball?
Answer: 2 PARTS
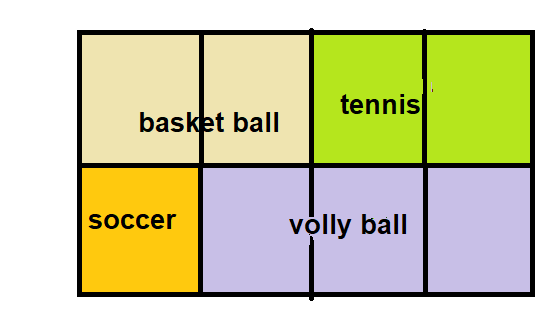
Explanation : if 3 parts were used for volleyball , two parts used for tennis as shown in that above picture
Question 10.
Construct Arguments To have the same fraction for tennis as for basketball, which plan, Exercise 8 or 9, should be used? Justify your answer.
Answer:
plan 9 should be used
Explanation:
for tennis and basket ball to be equal we need to have equal number of parts for tennis and basket ball
in question 9 plan tennis and basket ball both are takin a space of 2 parts
whereas in question 8 plan tennis is taking up more space than that of basket ball
so,
for tennis and basket ball to be equal we need to have equal number of parts for tennis and basket ball
Topic 12 Fluency Practice Activity
Follow the path
Shade a path from START to FINISH. Follow the sums and differences where the digit in the hundreds place is greater than the digit in the tens place. You can only move up, down, right, or left.
I can … add and subtract within 1,000.
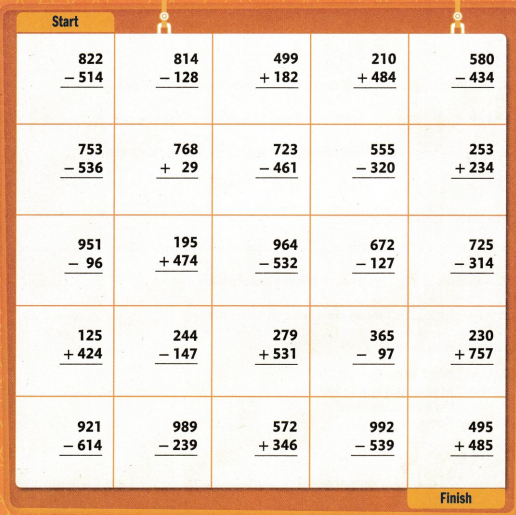
Answer :
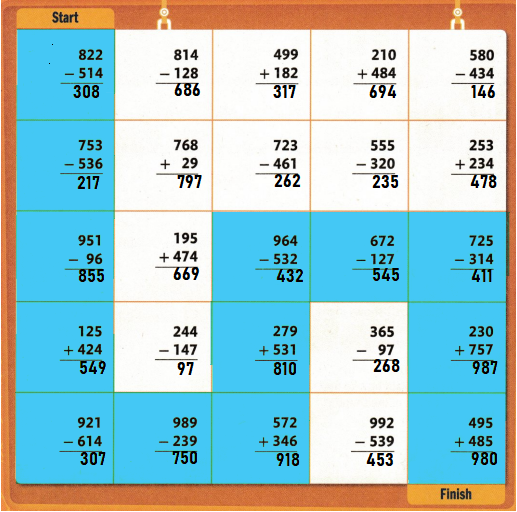
Topic 12 Vocabulary Review
Understand Vocabulary
Word List
- denominator
- fraction
- line plot
- nearest fourth inch
- nearest half inch
- numerator
- unit fraction
Question 1.
Circle each unit fraction.
\(\frac{1}{4}\)
\(\frac{3}{8}\)
\(\frac{1}{6}\)
\(\frac{1}{8}\)
\(\frac{2}{3}\)
Answer:
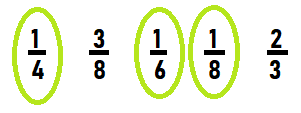
Question 2.
Circle each fraction where 6 is the denominator.
\(\frac{3}{6}\)
\(\frac{6}{8}\)
\(\frac{1}{6}\)
\(\frac{5}{6}\)
\(\frac{4}{8}\)
Answer:
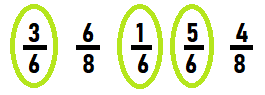
Question 3.
Circle each fraction where 4 is the numerator.
\(\frac{2}{4}\)
\(\frac{4}{8}\)
\(\frac{1}{4}\)
\(\frac{3}{4}\)
\(\frac{4}{6}\)
Answer:
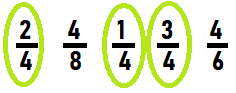
Question 4.
Circle the lengths that could be measurements to the nearest half inch.
2\(\frac{1}{2}\) in.
4 in.
3\(\frac{3}{4}\) in.
7\(\frac{1}{4}\) in.
6 in.
Answer:
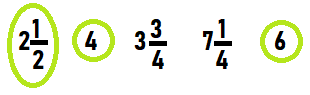
Question 5.
Circle the lengths that could be measurements to the nearest fourth inch.
8\(\frac{3}{4}\) in.
1\(\frac{1}{4}\) in.
11 in.
7\(\frac{1}{4}\) in.
6 in.
Answer:

Write always, sometimes, or never.
Question 6.
The numerator in a fraction is _?_ greater than the denominator. _________
Answer:
Some times
Explanation:
In a proper fraction, the numerator is sometimes more than the denominator.
Question 7.
A fraction ? _ has a numerator and denominator. __________
Answer:
Always
Explanation:
A fraction represents a part of a whole or any number of equal parts.
For example, one-half, eight-fifths, three-quarters.
Question 8
A line plot_?_ shows measurements of lengths. _________
Answer:
Never
Explanation:
A Line plot can be defined as a graph that displays data as points or check marks above a number line, showing the frequency of each value.
Question 9.
Use at least 2 terms from the Word List to explain how to find the unit fraction of the shape shown below.
Answer:
1/6
Explanation:
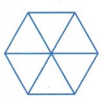
A unit fraction is any fraction with 1 as its numerator (top number), and a whole number for the denominator (bottom number).
If we divide the hexagon into 6 equal parts
then each part will be one part of the six parts
that is 1/6
Topic 12 Reteaching
Set A pages 437-440
This is one way to divide a whole into fourths.
Because each of the 4 parts has the same area, each part is one fourth of the whole.
You can write this fraction as \(\frac{1}{4}\)
A unit fraction represents one of the equal parts \(\frac{1}{4}\) is a unit fraction.
Remember that fractions can name equal parts of a whole.
In 1 and 2, draw lines to divide the shape into the given number of equal parts. Then write the fraction that represents 1 part.
Question 1.
6 equal parts
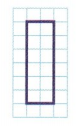
Answer:
Explanation:
total area of the figure : 12
12 divided into 6 parts is 12 ÷ 6 = 2
Question 2.
2 equal parts

Answer:
Explanation:
total area of the figure : 12
12 divided into 2 parts is 12 ÷ 2 = 6
Question 3.
Martin divides a shape into 3 equal parts. What unit fraction can he write to represent 1 part?
Answer:
Set B pages 441-444
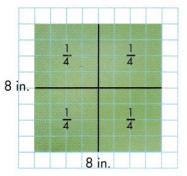
What fraction of this rectangle is shaded?

The rectangle is divided into 8 equal parts. So, the unit fraction of the rectangle is \(\frac{1}{8}\).
In the whole rectangle, there are 8 parts of \(\frac{1}{8}\).
8 copies of \(\frac{1}{8}\) is \(\frac{8}{8}\)
For the shaded part there are 6 parts of \(\frac{1}{8}\).

6 copies of \(\frac{1}{8}\) is \(\frac{6}{8}\)
So, \(\frac{6}{8}\) of the rectangle is shaded.
Remember that you need to think about how many parts there are in all and how many parts are shaded.
In 1-4, write the unit fraction that represents each part of the whole. Next, write the number of shaded parts. Last, write the fraction of the whole that is shaded.
Question 1.

Answer:
Unit fraction = 1/3
Number of shaded part is one.
Fraction of whole that is shaded = 1/3
Question 2.
Answer:
Unit fraction = 5/6
Number of shaded parts are 5
Fraction of whole that is shaded = 5/6
Question 3.

Answer:
Unit fraction = 3/4
Number of shaded parts are 3
Fraction of whole that is shaded = 3/4
Question 4.

Answer:
Unit fraction = 2/4
Number of shaded parts are 2
Fraction of whole that is shaded = 2/4
Set C pages 445-448
This shape is \(\frac{2}{4}\) of a piece of fabric Tina used in a quilt. You can draw a picture and write a fraction to represent the whole piece of fabric.
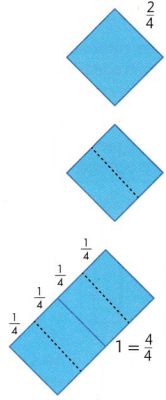
\(\frac{2}{4}\) is 2 copies of \(\frac{1}{4}\)
Divide the piece of fabric into 2 equal parts.
4 copies of \(\frac{1}{4}\) makes \(\frac{4}{4}\). or 1 whole.
Remember that the denominator shows the total number of equal parts in a whole.
In 1 and 2, draw a picture and write a fraction to represent the whole.
Question 1.
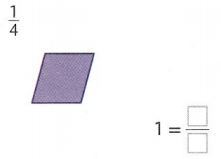
Answer:
1 = 4/4
Question 2.

Answer:
1 = 8/8
Set D pages 449-452
You can show fractions on a number line.
The fraction \(\frac{5}{6}\) is labeled. What are the missing fractions?
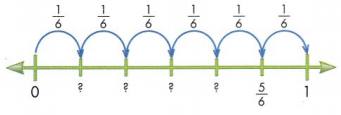
First, find the unit fraction. The line is divided into six equal lengths. So, the number line shows sixths.
Each jump represents \(\frac{1}{6}\). So, the first tick mark is labeled \(\frac{1}{6}\). The second tick mark is labeled \(\frac{2}{6}\), and so on.
The missing fractions on the number line are \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}\), and \(\frac{4}{6}\)
Remember to first decide what unit fraction is shown on each number line.
In 1 and 2, write the missing fractions on each number line.
Question 1.
Answer:
1/4 and 3/4
Question 2.
Answer:
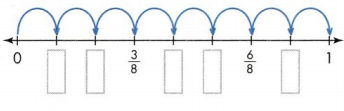
1/8 , 2/8 , 4/8 , 5/8 , 7/8
Question 3.
Divide the number line below into 3 equal parts and mark \(\frac{2}{3}\) on the line.

Answer:

Set E pages 453-456
Number lines can have fractions greater than 1.
The number line below is divided into thirds.
The denominator is 3 because the unit fraction is \(\frac{1}{3}\). The numerator shows how many copies of the unit fraction each point represents.
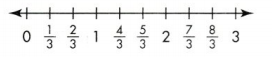
Remember that the numerator increases by 1 because each part of the number line is 1 more copy of the unit fraction.
Question 1.
The number line has equal lengths marked. Write the missing fractions.
Answer:
1/6 , 4/6 , 5/6 , 7/6 , 8/6
Question 2.
Divide the number line into fourths. Label each point.

Answer:
![]()
Set F pages 457-460
You can use a line plot to show data, such as lengths measured to the nearest half inch.
Steps to make a line plot:
- Draw a number line and choose a scale.
- The scale should show data values from the least to the greatest.
- Write a title for the line plot.
- Mark a dot for each value.
Remember to mark a dot for each length. Check your completed line plot against the data in the chart.
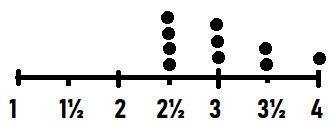
Question 1.
Draw a line plot to show the data.
Answer:
Question 2.
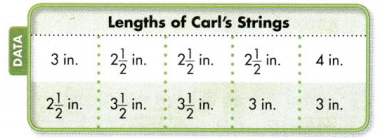
How many strings does Carl have in all?
Answer:
10 strings
Explanation:
2½ inch strings – 04
3 inch strings – 03
3½ inch strings – 02
4 inch strings – 01
Question 3.
Draw a line that is the same length as the most common string length.
Answer:
Most common string is 2½ inch
Set G pages 461-464
You can measure to different lengths, such as to the nearest fourth inch.
The closest fourth-inch mark to the end of the length of the rectangle is the 2\(\frac{1}{4}\)-inch mark.
The lengths can be shown on a line plot.
Remember to think about the scale of the line plot. It needs to include the least and greatest values.
Question 1.
Measure and record the lengths of 5 classroom objects to the nearest fourth inch. Use objects that are between 1 and 3 inches long.
Answer:
Eraser : 1.5 inches
Pencil : 2.7 inches
Pen Cap : 2.3 inches
Chalk : 2.3 inches
Sticker : 1 inch
Question 2.
Draw a line plot to show your data.
Answer:
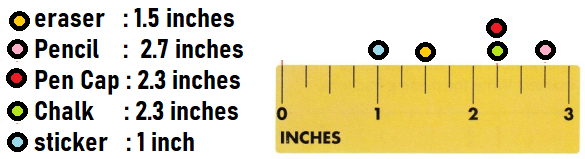
Set H pages 465-468
Think about these questions to help you make sense and persevere in solving problems.
Thinking Habits
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?

Remember to make sense of the problem by identifying the quantities. Then use what you know to solve.
Gavin divided his notebook into 8 equal parts. He plans to use 3 parts to take notes for math and 2 parts for reading. He has school from 8:30 A.M. to 3:30 P.M. What fraction of his notebook does he have left?
Question 1.
Is there any missing or extra information? Explain.
Answer:
Gavin divided his book into 8 equal parts
3 parts are used for math 3/8
2 parts are used for reading 2/8
The fraction of notebook he has left is :
3 + 2 = 5
8 – 5 = 3
The fraction of notebook he has left is 3/5
Question 2.
Solve the problem. If information you need is missing, make up some reasonable information for the problem. You can draw a picture to help.
Answer:
The missing information is:
3/8 part of the book was used for science
Topic 12 Assessment Practice
Question 1.
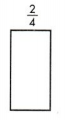
What fraction of the whole is colored green? What fraction of the whole is colored yellow?
![]()
Answer:
3/6 fraction of the whole is colored green.
3/6 fraction of the whole is colored yellow.
Question 2.
Write a fraction to name the equal parts of the whole pizza. How many parts would you need to make two whole pizzas? Explain.

Answer:
Fraction name : 1/8
we need 16 parts to make 2 whole pizzas
Explanation:
1 pizza needs 8 parts to make 1 whole so we need 16 parts [8 + 8 = 16] to make 2 wholes
Question 3.
This line segment represents \(\frac{1}{3}\) of the distance from Mal’s house to the library. Which represents the whole distance and has an accurate explanation?
![]()
A. ![]() The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 3 times as long.
The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 3 times as long.
B. ![]() The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 2 times as long.
The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 2 times as long.
C. ![]() The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 4 times as long.
The line segment represents \(\frac{1}{3}\) the distance from Mal’s house to the library. So, the whole distance is 4 times as long.
D. ![]() The line segment represents the distance from Mal’s house to the library. So, the whole distance is the identical line segment.
The line segment represents the distance from Mal’s house to the library. So, the whole distance is the identical line segment.
Answer:
Option A
Explanation:
The line segment represents 1/3 the distance from Mal’s house to the library. So, the whole distance is 3 times as long.
Question 4.
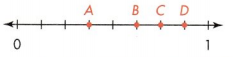
Which point is at \(\frac{3}{6}\) on the number line?
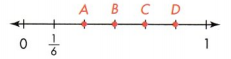
A. Point A
B. Point B
C. Point C
D. Point D
Answer:
Point B
Question 5.
Which of the fractions would be to the right of 1 on a number line? Select all that apply.

Answer:
5/4
Question 6.
A. Draw a picture to show \(\frac{2}{4}\).
Answer:
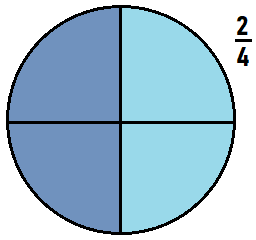
B. Explain how you knew you had shaded the correct amount of your picture.
Answer:
Divide the circle into fourths and then shade 2 of the 4 parts blue
Question 7.
Jeremy put pepperoni on \(\frac{1}{2}\) of a pizza. He put olives on \(\frac{1}{3}\) of the pizza. What fraction of the pizza did NOT have pepperoni? What fraction of the pizza did NOT have olives?
Answer:
1/2 of the fraction did not have pepperoni.
2/3 of the fraction did not have olives.
Question 8.
One point on the number line below has been named with the fraction \(\frac{2}{4}\). Write a fraction for each of the other points shown.
Answer:
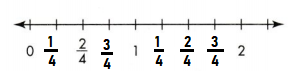
Question 9.
Explain how you know \(\frac{3}{3}\) represents a whole.
Answer:
Fraction 3/3 means 3 parts of 3 parts
Dividing 3 with 3 we get 1
So the fraction 3/3 is a whole 1
Question 10.
Jared folded a piece of paper 9 inches by 12 inches into sections as shown below. What fraction of the total area is in each section? Explain.

Answer:
Fraction of total Area is 36
Explanation:
Area of total paper = 9 x 12 = 108 sq.inches
The paper is divided into 3 equal part
Area of each part = 108 ÷ 3 = 36 sq.inches
Question 11.
How many \(\frac{2}{8}\)s do you need to get \(\frac{8}{8}\)?
Answer:
Four
Explanation:
we need four 2/8 fractions to get 8/8
2/8 + 2/8 + 2/8 + 2/8 = 8/8
Question 12.
Lane’s class is painting a mural with 6 equal parts. They spent 45 minutes painting on each of 2 days. On the first day, the class painted \(\frac{1}{6}\) of the mural. The next day, the class painted another \(\frac{1}{6}\) of the mural. How many \(\frac{1}{6}\) parts did the class paint in the two days?
A. 1
B. 2
C. 3
D. 4
Answer:
Option B
Explanation:
The class paints 1/6 part each day in d days the class paints 2/6 parts
1/6 – day 1
1/6 – day 2
By day 2 no of parts painted are 1/6 + 1/6 = 2/6
Question 13.
How many \(\frac{1}{8}\) s do you need to get \(\frac{5}{8}\)? Use the number line below for help.
A. 1
B. 3
C. 5
D. 8

Answer:
Option C
Explanation:
You need 5 yards to make 1/8 as 5/8
Question 14.
Which point represents 6 lengths of \(\frac{1}{8}\) on the number line? Explain.
Answer:
Point D
Question 15.
Divide the circle into 8 equal parts. What fraction does each part represent?

Answer:
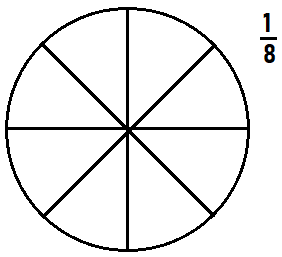
Each part represent1/8 fraction.
Question 16.
Seth drew \(\frac{2}{4}\) of a shape below. Draw a picture to show the whole shape and write a fraction to represent the whole.
Answer:
Explanation:
One whole is 4/4 that means to get 4/4 we need to have 2 parts of 2/4
As 2/4 + 2/4 = 4/4
Question 17.
Mara believes the point marked on the number line is \(\frac{2}{3}\). Is she correct? Explain.
![]()
Answer:
Mara is wrong
Explanation:
the markings of the fractions on the number line are not correct
[the markings are not even there is a lot of gap between 1/3 and 3/3]
Question 18.
Select all the sentences that describe this shape.

Answer:

Question 19.
Divide the number line into equal lengths. Then mark and label the given fraction.
6 equal lengths; \(\frac{5}{6}\)
![]()
Answer:
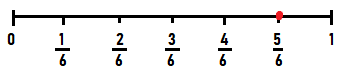
Explanation:
First divide the number line into 6 equal parts like in the picture below
Then mark the 5/6th point
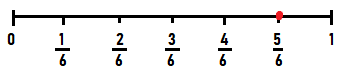
Question 20.
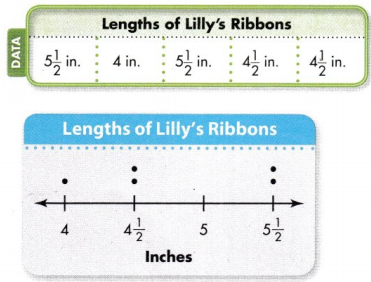
Tony collects colored strings. The table shows the lengths of some of his strings.

A. Measure the lengths of Tony’s red and brown strings shown below to the nearest fourth inch.

Answer:
Red string : 3 inches
Brown string : 2¾ inches
B. Draw a line plot to show the lengths of Tony’s 7 strings to the nearest fourth inch.
Answer:

Topic 12 Performance Task
Art Display
Three students, Zach, Allie, and Paige, are making an art display.
Use the Paint Colors list and the design at the right to answer Questions 1-4.
Question 1.
The display will be divided into 8 equal parts. Paint Colors Draw lines to show one way to do this. Then write the fraction that describes the the total shape that is represented by 1 equal part.
Paint Colors
- Allie is painting the blue parts.
- Paige is painting the red parts.
- Zach is painting the yellow parts.
- Each student will paint at least 2 parts.

Answer:
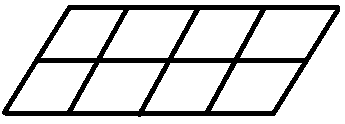
1/8 part
Question 2.
Shade the parts blue, yellow, or red to show how many parts each student could paint. Write fractions to show how much of the total display Allie and Paige painted.
Answer:
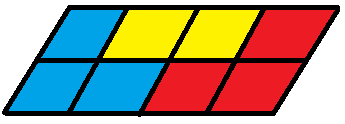
- Allie is painting the 3 blue parts. 3/8
- Paige is painting the 3 red parts. 3/8
- Zach is painting the 2 yellow parts.
Question 3.
Divide the number line into the number of equal parts of the display. Then mark a dot to show the fraction of the display that Zach painted on the number line.

Answer:

Question 4.
Which fraction represents the whole display? Explain. Then mark a dot to show where this fraction is located on the number line above.
Answer:
8/8 is the whole fraction

Use the Ribbon Lengths diagram on the right and the Number of Ribbons table below to answer Question 5.

Question 5.
The students will use the ribbon lengths at the right in their display
Part A
Measure and record the lengths of each of these ribbons to the nearest fourth inch.
Answer:
RED Ribbon : 3¾
BLUE Ribbon : 3 2/4 [3½]
GREEN Ribbon : 3¼
Part B
The Number of Ribbons table shows how many of each color ribbon will be used. Draw a line plot to show this data.

Answer:
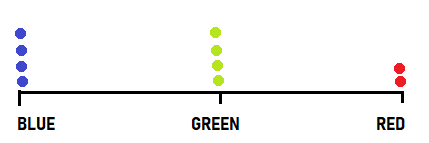
Question 6.
In order to complete the display, the students recorded the number of half-hour sessions they spent working together. The number line below is divided into equal parts. Each part represents half an hour. Write the missing fractions on the number line.
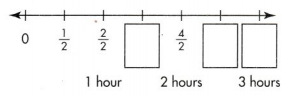
Answer: