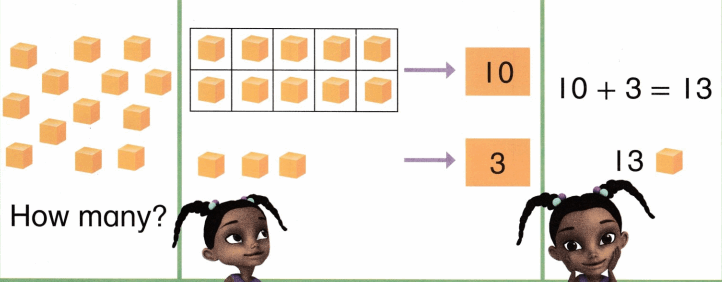
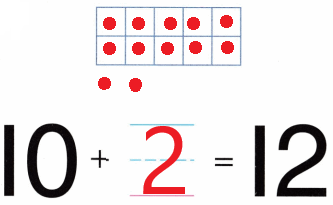
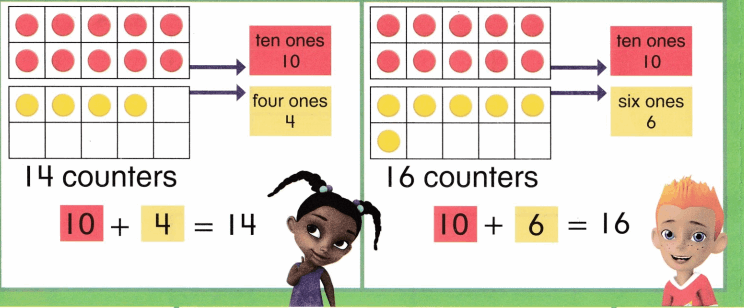
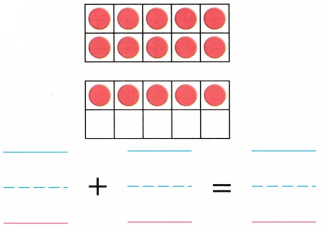
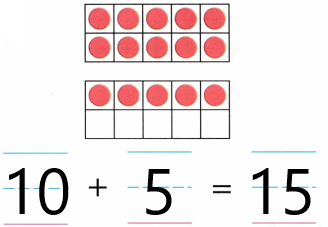
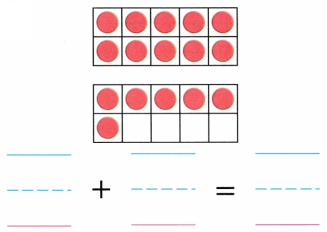
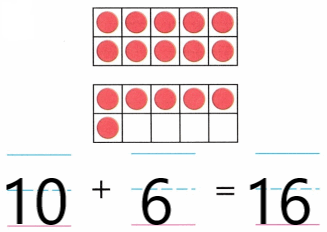
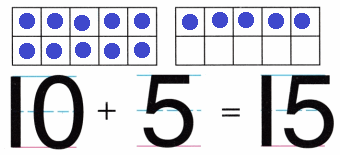
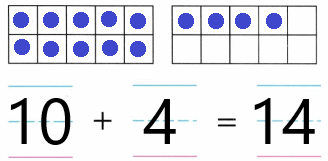
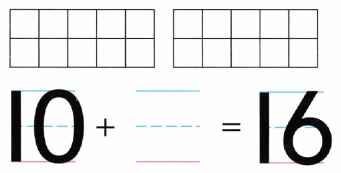
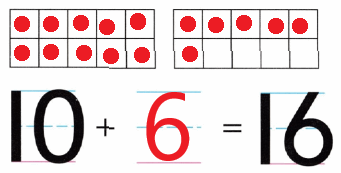
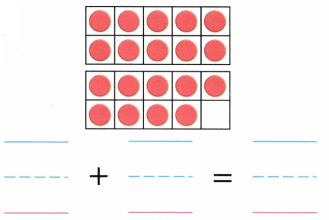
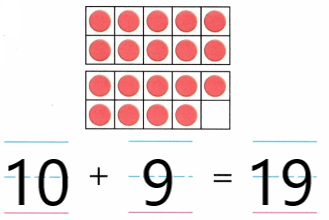
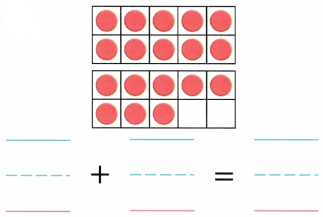
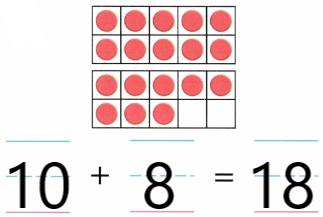
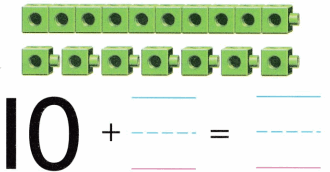
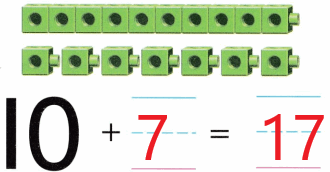
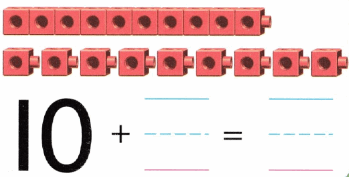
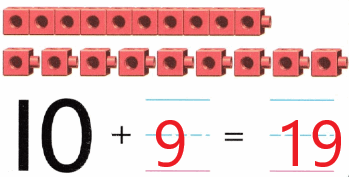
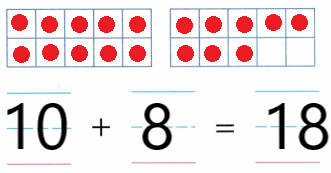
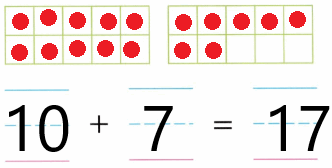
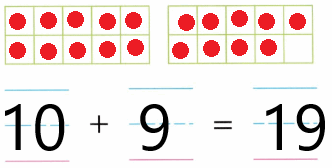
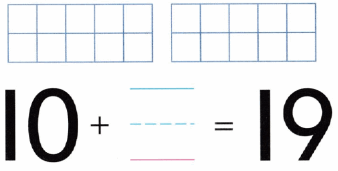
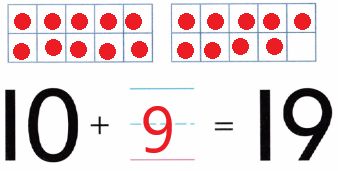
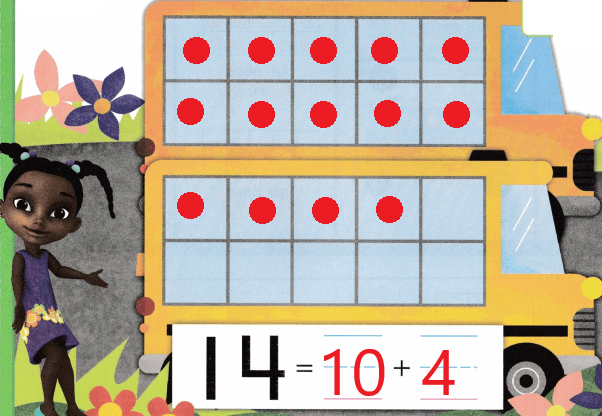
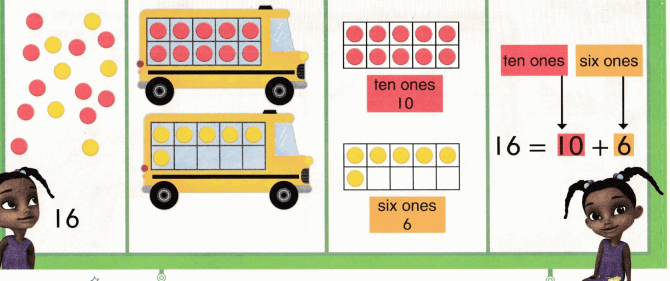
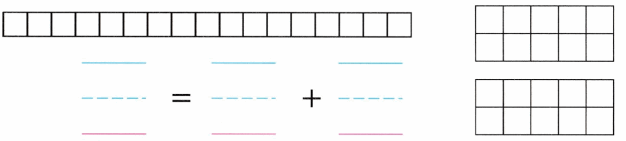
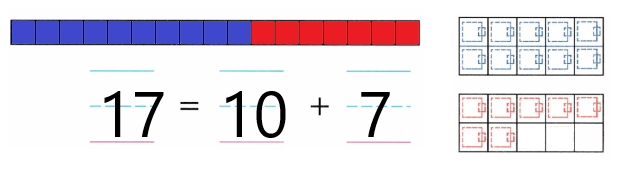
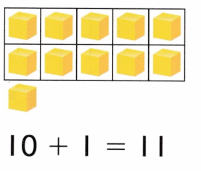
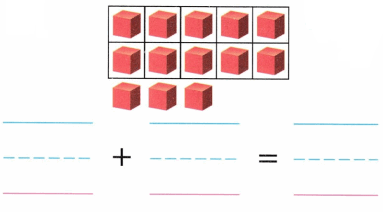
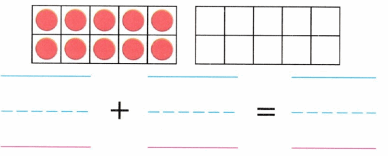
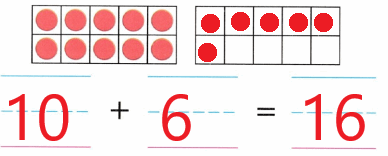
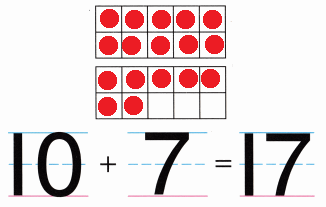
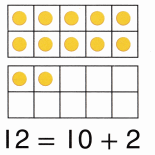
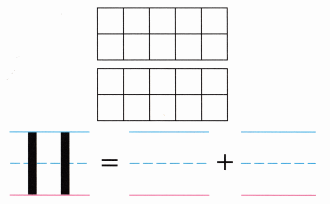
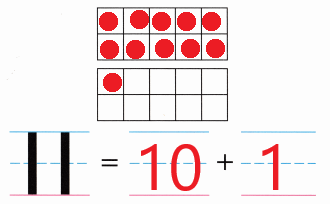
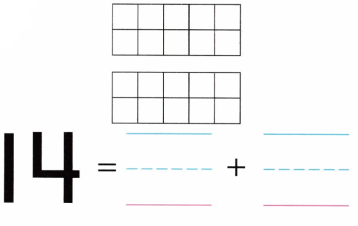
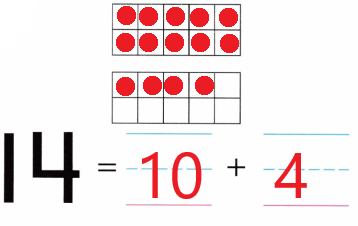
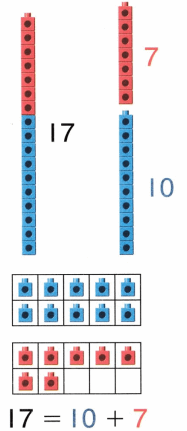
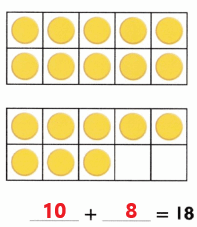
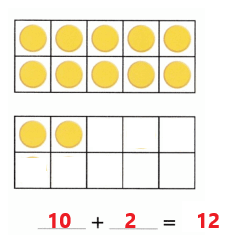
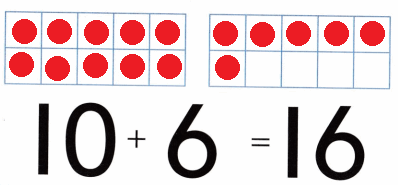
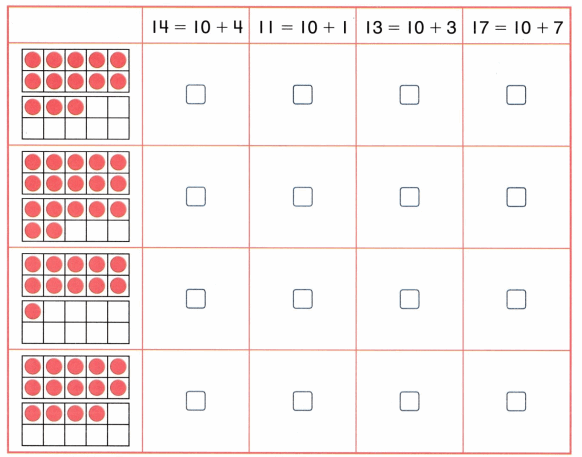
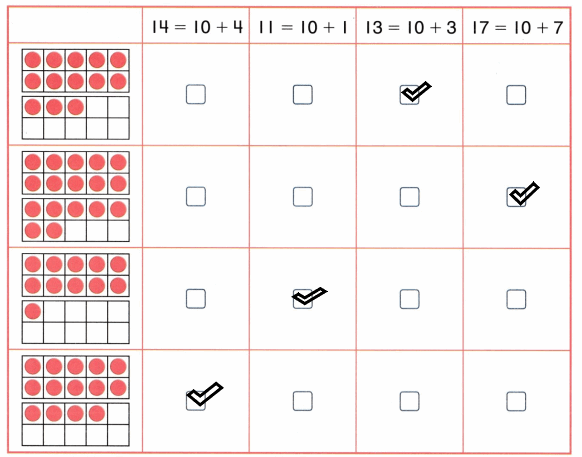
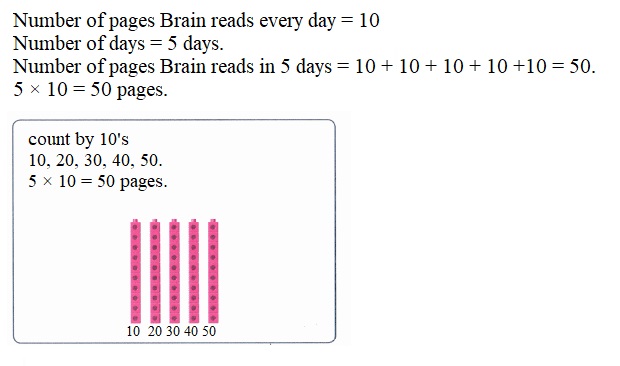
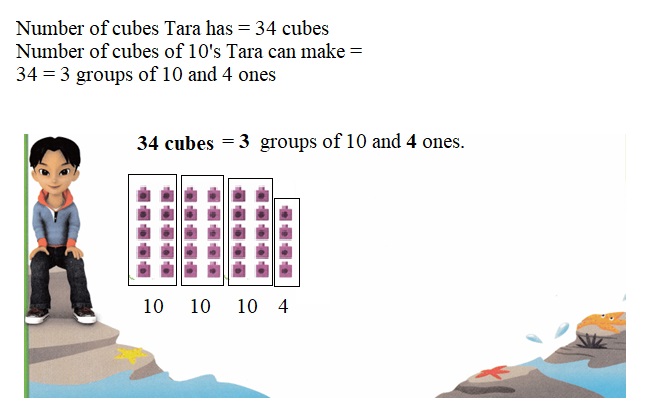
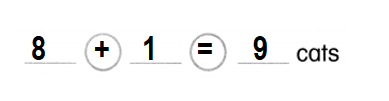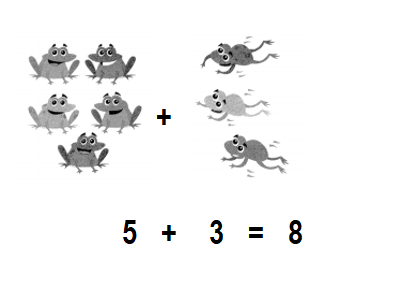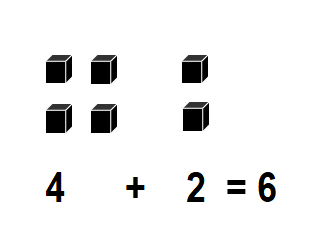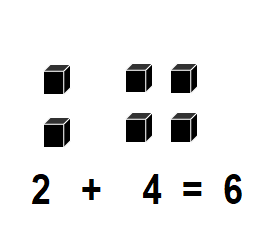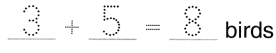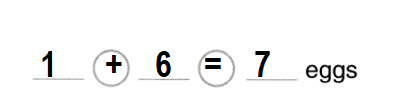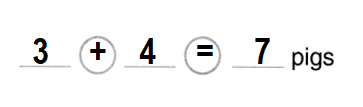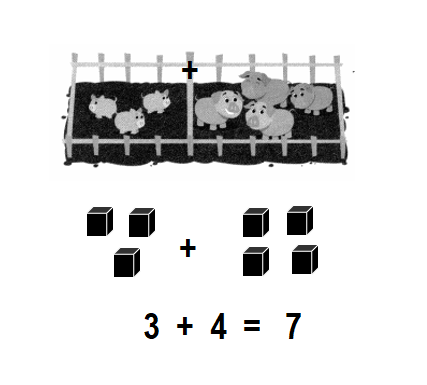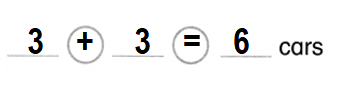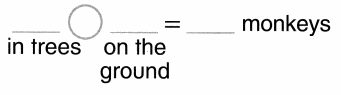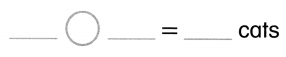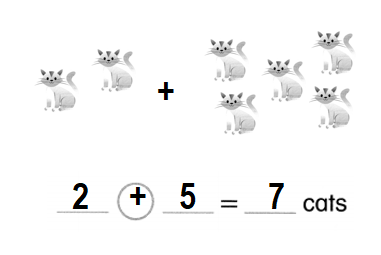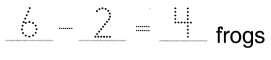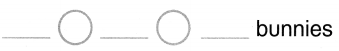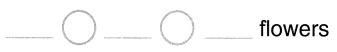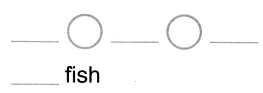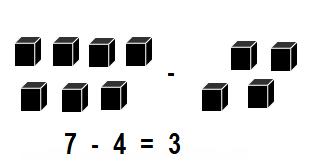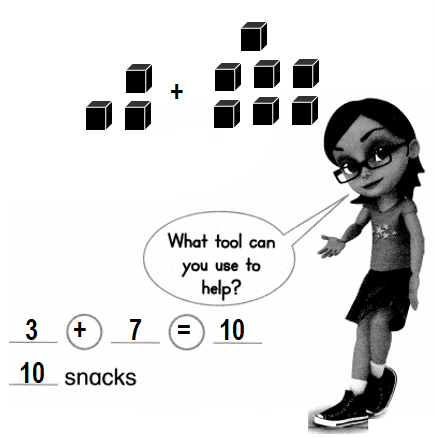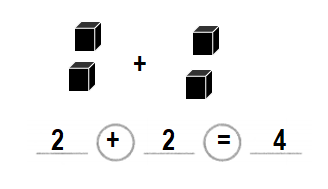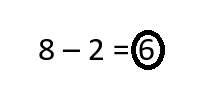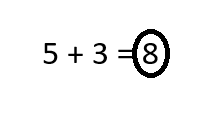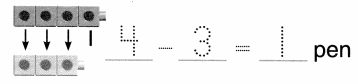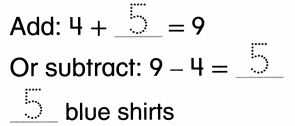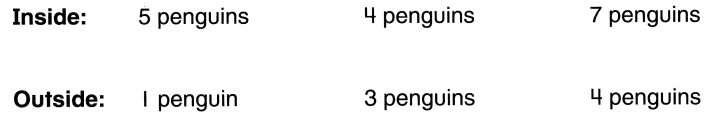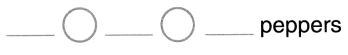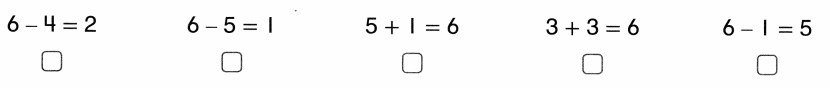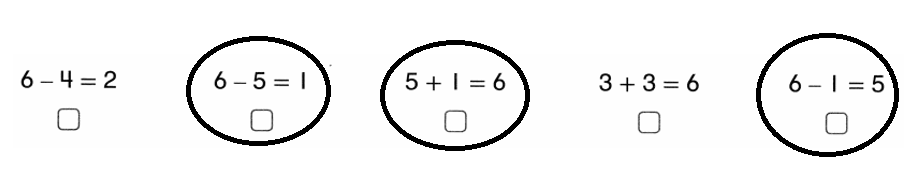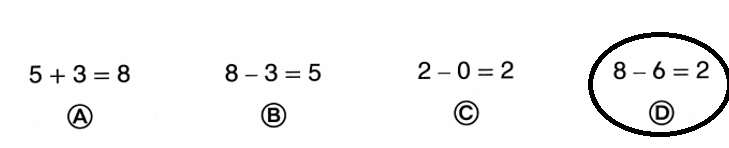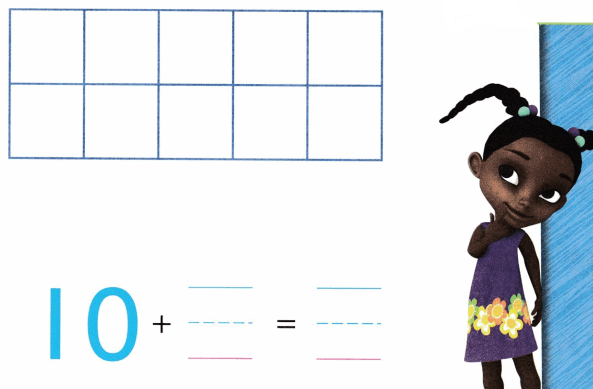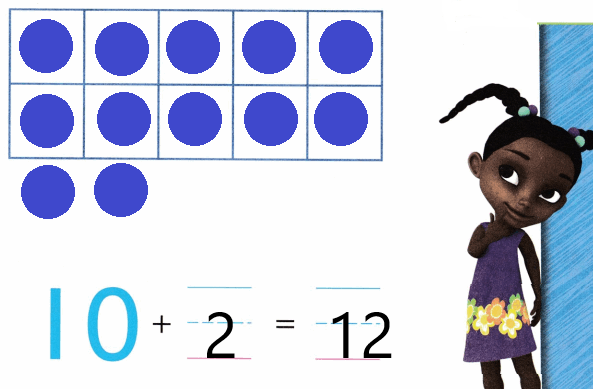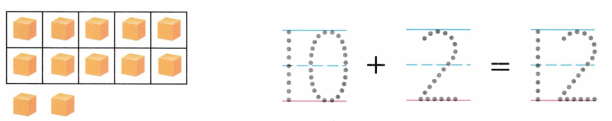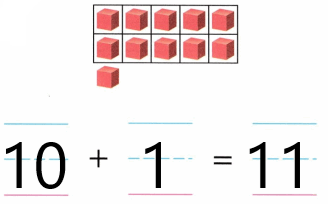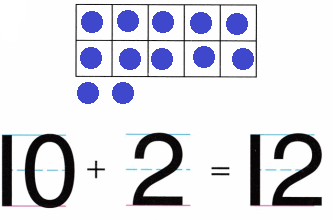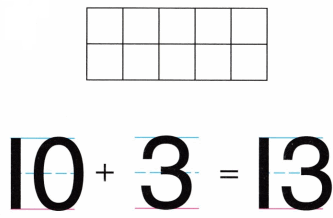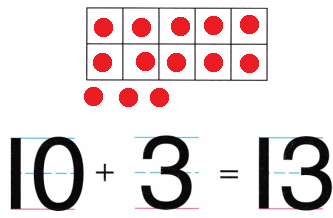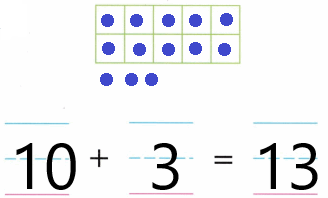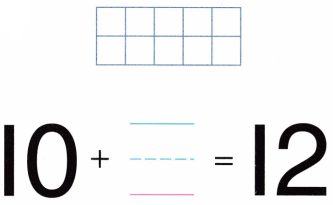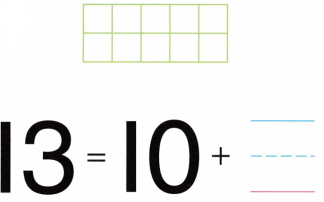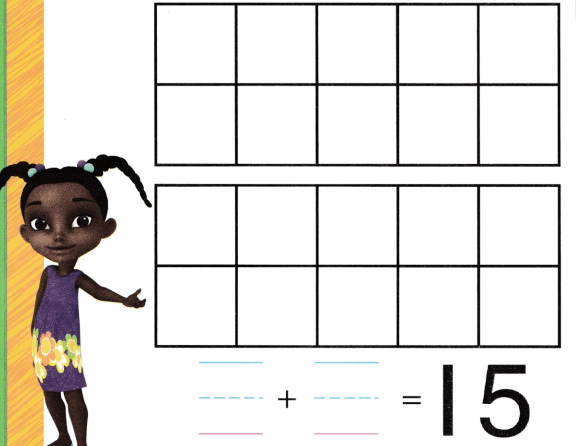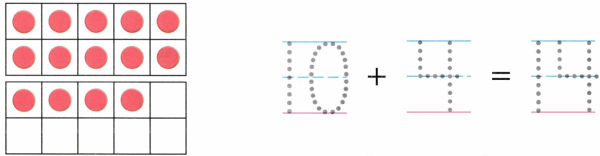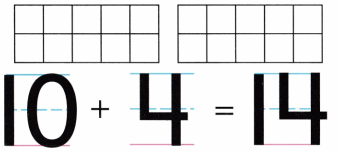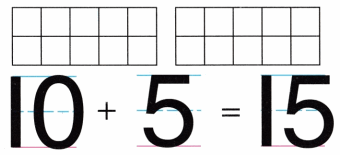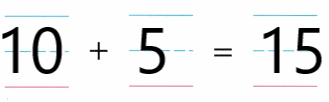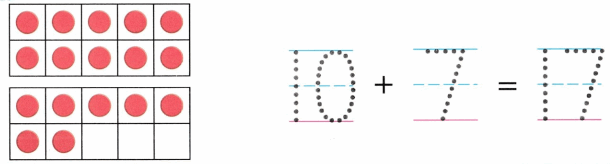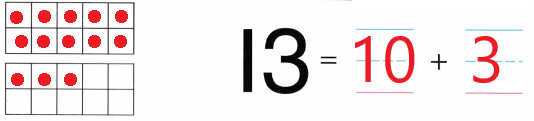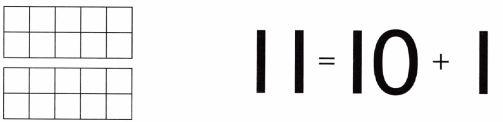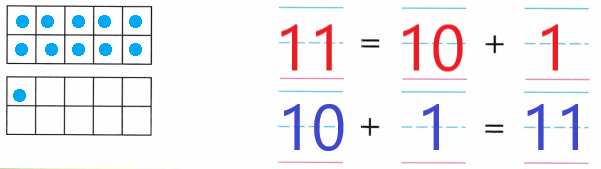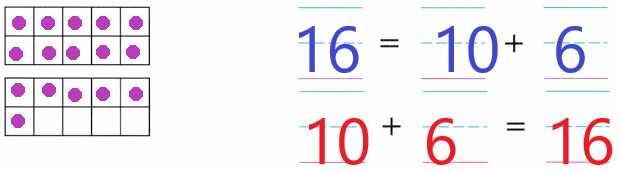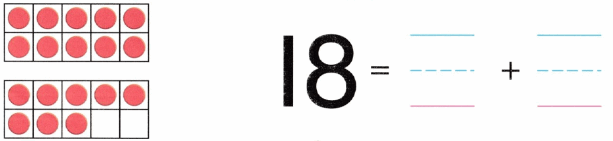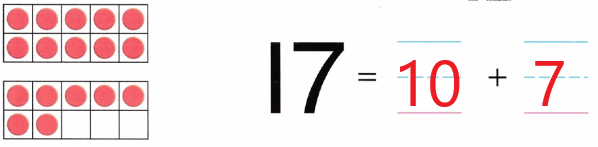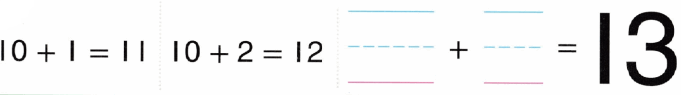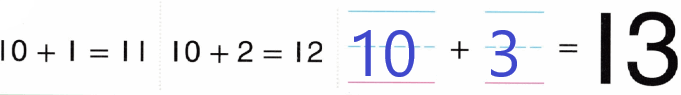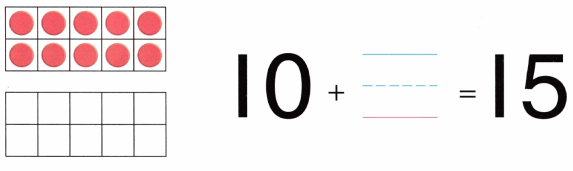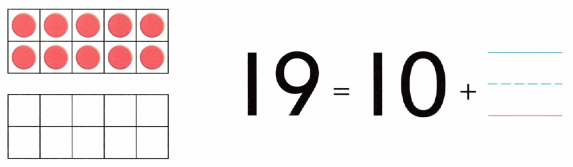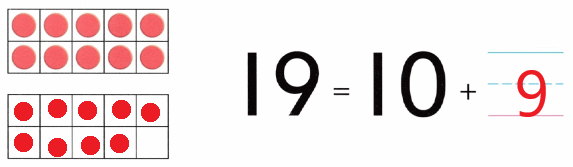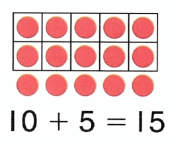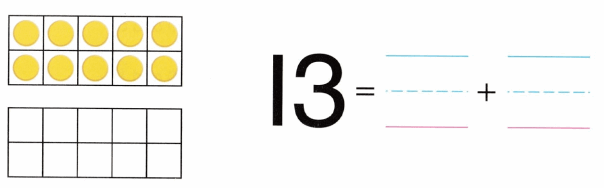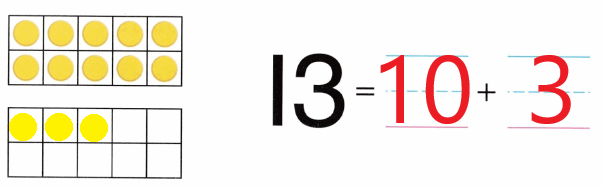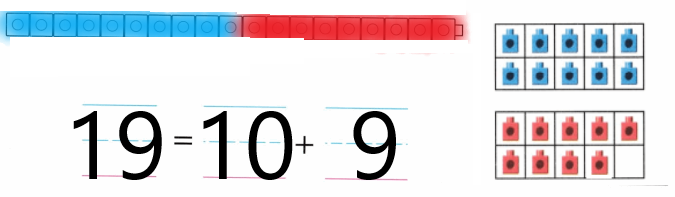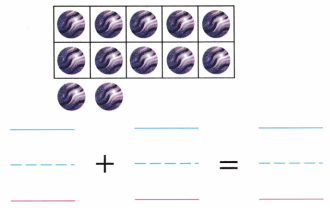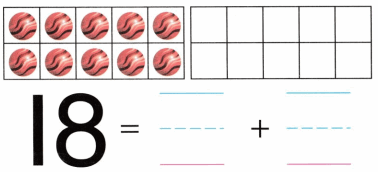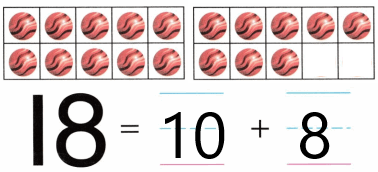Practice with the help of enVision Math Common Core Grade 1 Answer Key Topic 1 Understand Addition and Subtraction regularly and improve your accuracy in solving questions.
enVision Math Common Core 1st Grade Answers Key Topic 1 Understand Addition and Subtraction
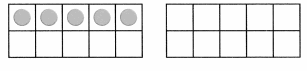
Essential Question:
What are ways to think about addition and subtraction?
Look at the adult and baby giraffes.
How are they the same? How are they different?

Wow! Let’s do this project and learn more.
envision STEM Project: Parents and Babies
Find Out Talk to friends and relatives about different animals and their babies.
Ask them how the parents and babies are the same and how they are different.
Journal: Make a Book Show what you found.
In your book, also:
- Draw some animals, including the parents and babies.
- Create and solve addition and subtraction stories about some animals and their babies.
Review What You Know
Vocabulary
Question 1.
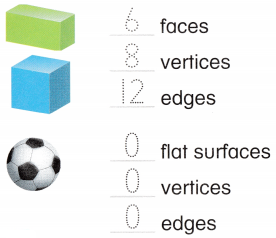
Count the fish. Write the number that tells how many.

Answer:
Number of fishes given in the picture = 5 or Five.

Explanation:
Number of fishes given in the picture = 5 or Five.
Question 2.
Join the two groups and write how many.

Answer:
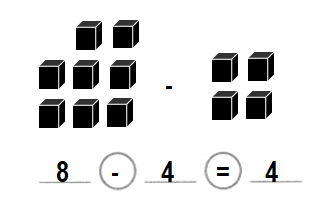
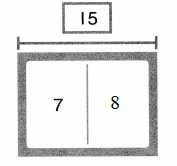
Total number of apples in the figure = 4 or Four.
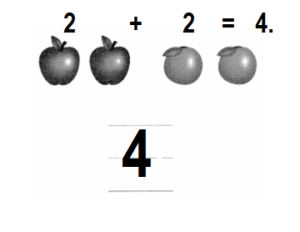
Explanation:
Number of black apples in the figure = 2 or Two.
Number of grey apples in the figure = 2 or Two.
Total number of apples in the figure = Number of black apples in the figure + Number of grey apples in the figure
= 2 + 2
= 4 or Four.
Question 3.
Write how many soccer balls there are in all.

Answer:
Total number of balls in the figure = 4 or Four.

Explanation:
Number of foot balls in the figure = 3 or Three.
Number of tennis balls in the figure =1 or One.
Total number of balls in the figure = Number of foot balls in the figure + Number of tennis balls in the figure
= 3 + 1
= 4 or Four.
Counting
Question 4.
Tammy has 4 balloons. Draw a picture of her balloons.
Answer:
Number of balloons Tammy has = 4 or Four.

Explanation:
Number of balloons Tammy has = 4 or Four.
Question 5.
Write the number that tells how many cats.
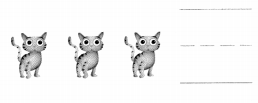
Answer:
Number of cats in the given picture = 3 or Three.

Explanation:
Number of cats in the given picture = 3 or Three.
Sums
Question 6.
Circle the number that shows how many crabs you see.
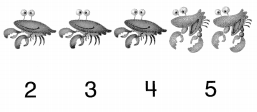
Answer:
Number of crabs in the given picture = 3 or Three.
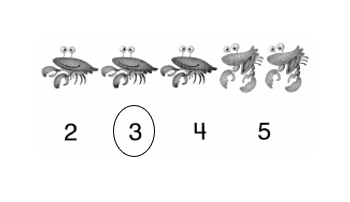
Explanation:
Number of crabs in the given picture = 3 or Three.
Number of scorpions in the given picture = 2 or Two.
Pick a Project
Project 1A
Where do birds lay their eggs?
Project: Draw a bird Clutch

Answer:
Birds lay their Eggs in their nests.
Explanation:

Project 1B
What is the most popular fruit juice in the world?
Project: Find Fruit Facts

Answer:
The most popular fruit juice in the world is orange juice.
Explanation:
The most popular fruit juice in the world is orange juice.

Project 1C
What are different homes made of?
Project: Build a model

Answer:
Many houses are now made with steel frames put together with rivets and bolts.
Explanation:
Generally houses are made of steel , iron, mud ,clay ,stones , cement.
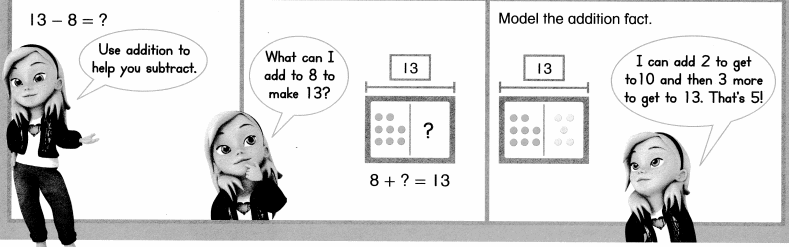
Lesson 1.1 Add To
Solve and Share
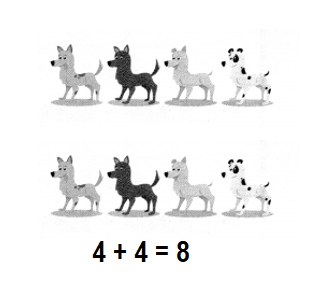
4 dogs
Some dogs join.
How many dogs now?
Show how you solve.

_______ dogs now
Answer:
Total number of dogs = 8 or Eight.
___8____ dogs now.
Explanation:
Number of dogs given in the picture = 4 or Four.
Number of dogs joined more = 4 or Four.
Total number of dogs = Number of dogs given in the picture + Number of dogs joined more
= 4 + 4
= 8 or Eight.
Visual Learning Bridge
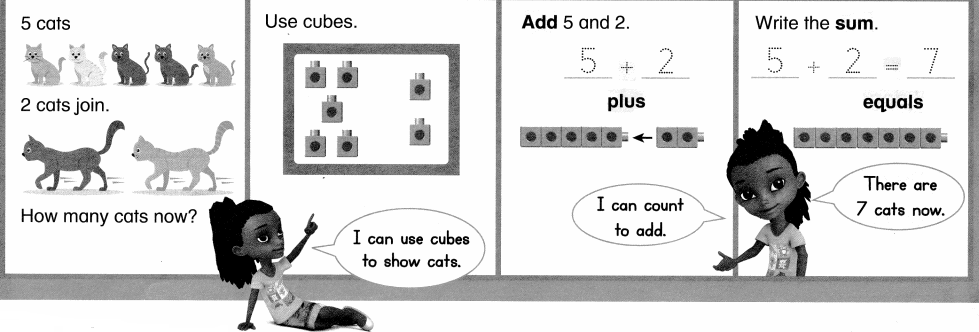
Convince Me!
How do cubes help you solve the problem?
Answer:
Cubes helps to solve the problem easier in counting.
Explanation:
Cubes helps to solve the problem easier in counting without any confusion.

Guided Practice
Solve. Use cubes to help.
Question 1.
3 cows

3 cows join.

How many cows now?

Answer:
Total number of cows now = 6 or Six.

Explanation:
Number of cows in the given picture = 3 or Three.
Number of cows more joined = 3 or Three.
Total number of cows now = Number of cows in the given picture + Number of cows more joined
= 3 + 3
= 6 or Six.


Question 2.
2 birds
6 birds join.

How many birds now?

Answer:
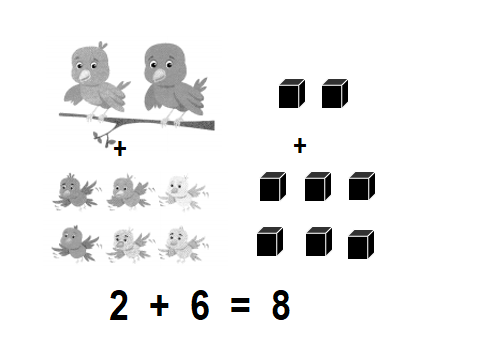
Total number of birds now = 8 or Eight.
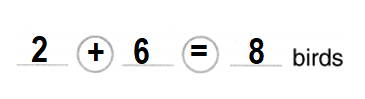
Explanation:
Number of birds in the given picture = 2 or Two.
Number of birds more joined = 6 or Six.
Total number of birds now = Number of birds in the given picture + Number of birds more joined
= 2 + 6
= 8 or Eight.
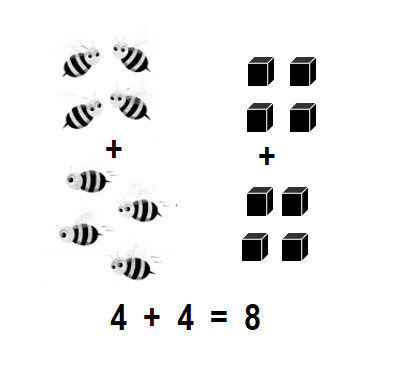
Question 3.
4 bees

4 bees join

How many bees now?

Answer:
Total number of bees now = 8 or Eight.

Explanation:
Number of bees in the given picture = 4 or Four.
Number of bees more joined = 4 or Four.
Total number of bees now = Number of bees in the given picture + Number of bees more joined
= 4 + 4
= 8 or Eight.
Question 4.
3 bugs

6 bugs join.

How many bugs now?

Answer:
Total number of bugs now = 9 or Nine.

Explanation:
Number of bugs in the given picture = 3 or Three.
Number of bugs more joined = 6 or Six.
Total number of bugs now = Number of bugs in the given picture + Number of bugs more joined
= 3 + 6
= 9 or Nine.
Solve the problem.
Draw a picture to help.
Question 5.
Higher Order Thinking
6 ducks
4 chickens
2 ducks join.
How many ducks in all?
_____ ducks in all.
Answer:
Total number of ducks now in all = 8 or Eight.
__8___ ducks in all.
Explanation:
Number of ducks given = 6 or Six.
Number of chickens given = 4 or Four.
Number of ducks more joined = 2 or Two.
Total number of ducks now in all = Number of ducks given + Number of ducks more joined
= 6 + 2
= 8 or Eight.
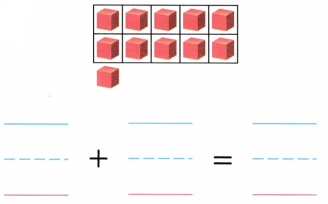
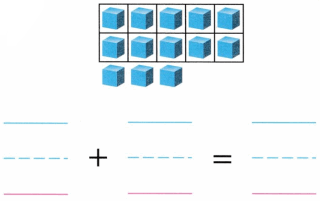
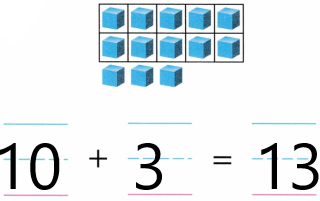
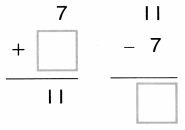
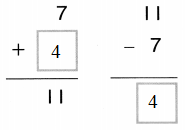
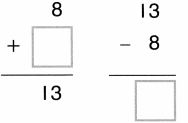
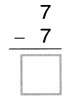
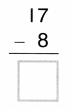
 1
1

Problem Solving
Solve each problem.
Question 6.
Vocabulary
3 dogs
4 dogs join.
Add to find the sum.

Answer:
Total number of dogs now in all = 7 or Seven.
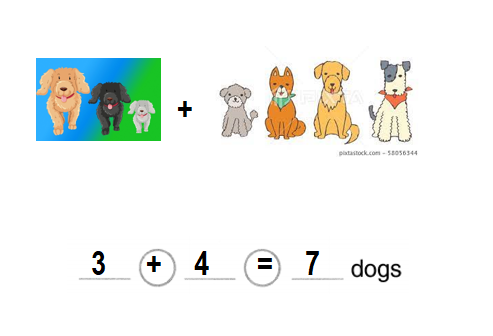
Explanation:
Number of dogs given = 3 or Three.
Number of dogs more joined = 4 or Four.
Total number of dogs now in all = Number of dogs given + Number of dogs more joined
= 3 + 4
= 7 or Seven.
Question 7.
Model
8 cats
1 cat joins.
How many cats now?

Answer:
Total number of cats now in all = 9 or Nine.
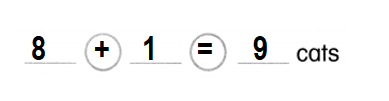
Explanation:
Number of cats given in the picture = 8 or Eight.
Number of cats more joined = 1 or One.
Total number of cats now in all = Number of cats given in the picture + Number of cats more joined
= 8 + 1
= 9 or Nine.

Question 8.
Higher Order Thinking
Make up an addition story about the birds.

Answer:
There are 3 birds on a tree sitting. Later 1 bird joined them. How many birds are in all.
Total number of birds in all now = 4 or Four.

Explanation:
Number of birds sitting on tree = 3 or Three.
Number of birds joined later = 1 or One.
Total number of birds in all now = Number of birds sitting on tree + Number of birds joined later
= 3 + 1
= 4 or Four.
Question 9.
Assessment Practice
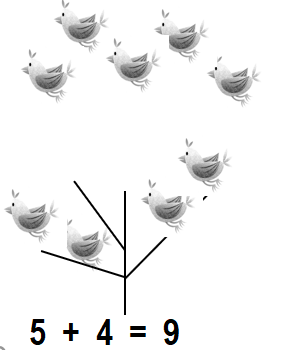
5 frogs

3 frogs join

How many frogs now?
A. 5 + 1 = 6 frogs
B. 5 + 2 = 7 frogs
C. 5 + 3 = 8 frogs
D. 5 + 4 = 9 frogs
Answer:
Total number of frogs now in all = 8 or Eight.
C. 5 + 3 = 8 frogs.
Explanation:
Number of frogs given = 5 or Five.
Number of frogs more joined = 3 or Three.
Total number of frogs now in all = Number of frogs given + Number of frogs more joined
= 5 + 3
= 8 or Eight.
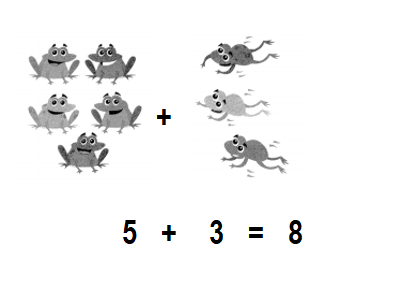
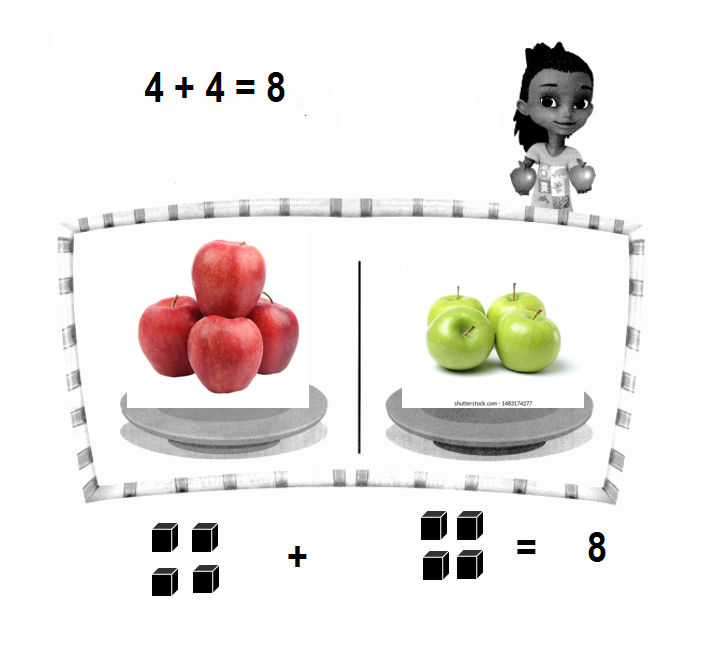
Lesson 1.2 Put Together
4 red apples and 4 green apples How many apples in all?
Show how you solve.
Use cubes to help.

___ apples in all
Answer:
Total number of apples now in all = 8 or Eight.
_8__ apples in all.
Explanation:
Number of red apples = 4 or Four.
Number of green apples = 4 or Four.
Total number of apples now in all = Number of red apples + Number of green apples
= 4 + 4
= 8 or Eight.
Visual Learning Bridge
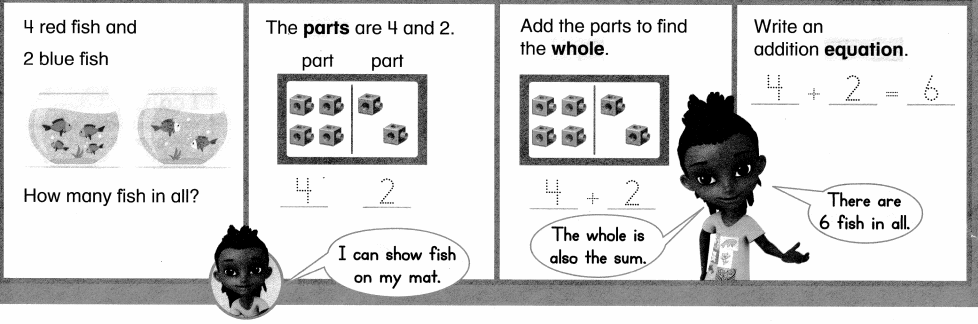
Convince Me!
Use cubes.
show 4 + 2.
Then show 2 + 4.
What do you notice?
Answer:
Sum of 4 + 2 = ??
4 + 2 = 6 or Six.
Sum of 2 + 4 = ??
2 + 4 = 6 or Six.
It is noticed the sum of (4 + 2) is same as (2 + 4) = 6 or Six.
Explanation:
Sum of 4 + 2 = ??
4 + 2 = 6 or Six.
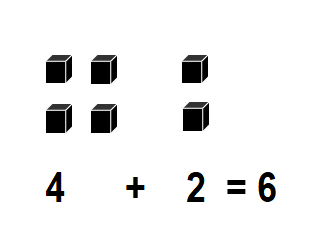
Sum of 2 + 4 = ??
2 + 4 = 6 or Six.
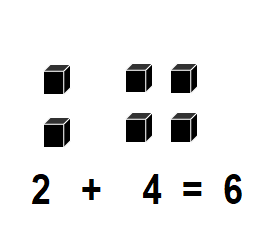
Guided Practice
Solve. Use cubes to help. Write an addition equation.
Question 1.
3 yellow birds and 5 blue birds

How many birds in all?
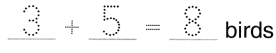
Answer:
Total number of birds in all = 8 or Eight.
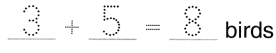
Explanation:
Number of yellow birds = 3 or Three.
Number of blue birds = 5 or Five.
Total number of birds in all = Number of yellow birds + Number of blue birds
= 3 + 5
= 8 or Eight.
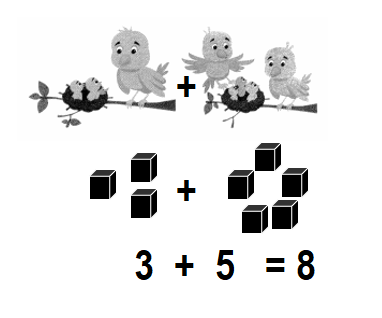
Question 2.
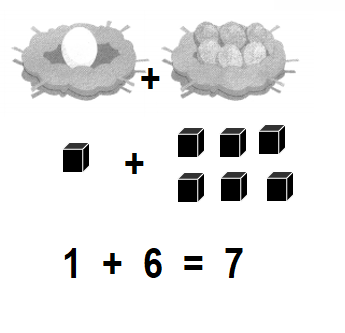
1 white egg and 6 blue eggs

How many eggs in all?

Answer:
Total number of eggs in all = 7 or Seven.
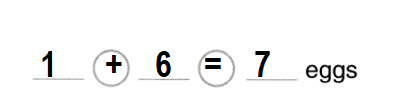
Explanation:
Number of white eggs = 1 or One.
Number of blue eggs = 6 or Six.
Total number of eggs in all = Number of white eggs + Number of blue eggs
= 1 + 6
= 7 or Seven.
Independent Practice
Solve. Use cubes or draw a picture. Write an addition equation.
Question 3.
3 little pigs and 4 big pigs

How many pigs in all?

Answer:
Total number of pigs in all = 7 or Seven.
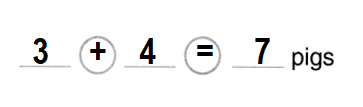
Explanation:
Number of little pigs = 3 or Three.
Number of big pigs = 4 or Four.
Total number of pigs in all = Number of little pigs + Number of big pigs
= 3 + 4
= 7 or Seven.
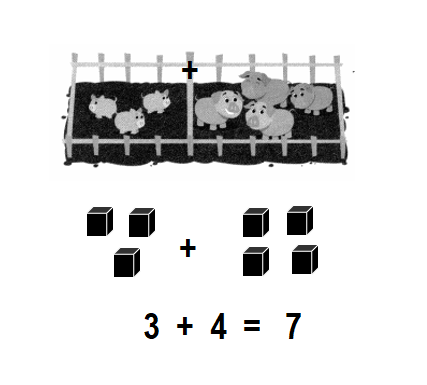
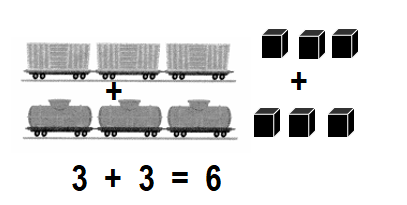
Question 4.
3 box cars and 3 tank cars
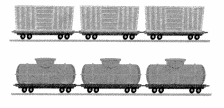
How many cars in all?
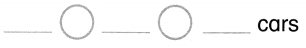
Answer:
Total number of cars in all = 6 or Six.
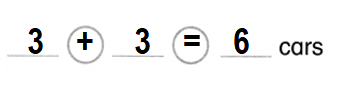
Explanation:
Number of box cars = 3 or Three.
Number of tank cars = 3 or Three.
Total number of cars in all = Number of box cars + Number of tank cars
= 3 + 3
= 6 or Six.
Question 5.
Higher Order Thinking
2 red hats
3 shoes
7 blue hats
How many hats in all?
Draw a picture.
Write an addition equation.
Answer:
Total number of hats in all = 9 or Nine.
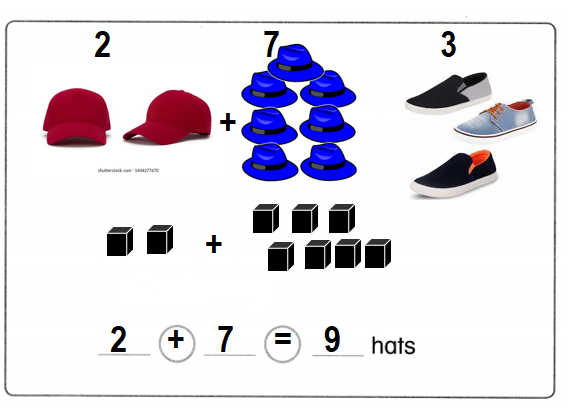
Explanation:
Number of red hats = 2 or Two.
Number of shoes = 3 or Three.
Number of blue hats = 7 or Seven.
Total number of hats in all = Number of red hats + Number of blue hats
= 2 + 7
= 9 or Nine.

Problem Solving
Solve each problem.
Question 6.
Make Sense
Jen has 2 red flowers and 5 blue flowers. How many flowers in all? Write an equation.
Answer:
Total number of flowers Jen has in all = 7 or Seven.

Explanation:
Number of red flowers Jen has = 2 or Two.
Number of blue flowers Jen has = 5 or Five.
Total number of flowers Jen has in all = Number of red flowers Jen has + Number of blue flowers Jen has
= 2 + 5
= 7 or Seven.
Question 7.
Higher Order Thinking
Write a picture story. Show blue fish and green fish. Write an addition equation. Tell how many fish in all.
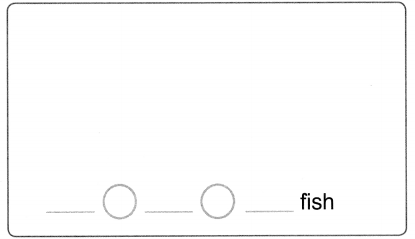
Answer:
There are 2 blue fishes in a tank. 2 green fishes were added into the tank. How many fishes are all in the tank.
Total number of fishes all in the tank = 4 or Four.
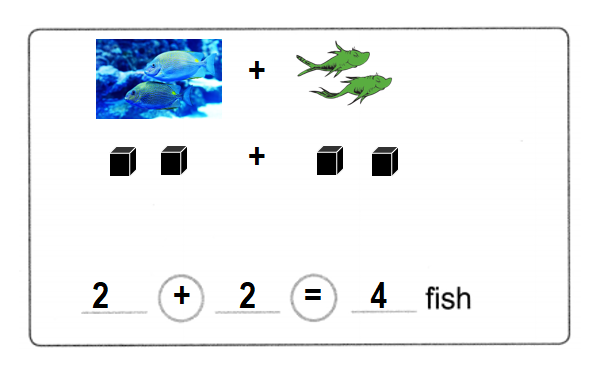
Explanation:
There are 2 blue fishes in a tank. 2 green fishes were added into the tank. How many fishes are all in the tank.
Number of blue fishes in the tank = 2 or Two.
Number of green fishes in the tank = 2 or Two.
Total number of fishes all in the tank = Number of blue fishes in the tank + Number of green fishes in the tank
= 2 + 2
= 4 or Four.
Question 8.
Assessment Practice
4 red apples and 5 green apples

How many apples in all?

Answer:
Total number of apples in all = 9 or Nine.
B. 4 + 5 = 9 apples.
Explanation:
Number of red apples = 4 or Four.
Number of green apples = 5 or Five.
Total number of apples in all = Number of red apples + Number of green apples
= 4 + 5
= 9 or Nine.

Lesson 1.3 Both Addends Unknown
Sarah has 5 pencils.
She puts some in the green cup.
She puts some in the red cup.
How many pencils could be in each cup?

Answer:
Number of pencils Sarah puts in green cup = 3 or Three.
Number of pencils Sarah puts in red cup = 2 or Two.
Number of pencils Sarah’s partner puts in green cup = 2 or Two.
Number of pencils Sarah’s partner puts in red cup = 3 or Three.
Answers of both are different.
Explanation:
Total number of pencils Sarah has = 5 or Five.
IF
Number of pencils Sarah puts in green cup = 3 or Three.
Number of pencils Sarah puts in red cup = Total number of pencils Sarah has – Number of pencils Sarah puts in green cup
= 5 – 3
= 2 or Two.
Total number of pencils Sarah has = 5 or Five.
IF
Number of pencils Sarah’s partner puts in green cup = 2 or Two.
Number of pencils Sarah’s partner puts in red cup = Total number of pencils Sarah’s partner has – Number of pencils Sarah’s partner puts in green cup
= 5 – 2
= 3 or Three.
Visual Learning Bridge
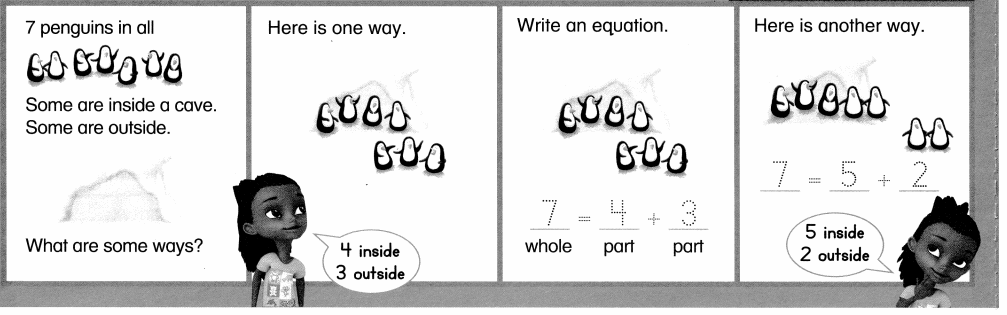
Convince Me!
With 7 penguins, could 4 be inside the cave, and 4 be outside the cave? Why or why not?
Answer:
With 7 penguins, could 4 be inside the cave, and 4 be outside the cave cannot happen because the total number of penguins count does not match, it shows more (4 + 4 = 8 not 7).
Explanation:
It cannot happen because the total number of penguins count does not match, it shows more (4 + 4 = 8 not 7).
Guided Practice
How many penguins are inside and outside? Use cubes or draw a picture. Write an equation.
Answer:
Case:1:
Number of penguins inside the cave = 4 or Four.
Number of penguins outside the cave = 3 or Three.
Case:2:
Number of penguins outside the cave = 4 or Four.
Number of penguins inside the cave = 3 or Three.
Explanation:
Case:1:
Number of penguins inside the cave = 4 or Four.
Number of penguins outside the cave = 3 or Three.
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 4 + 3
= 7 or Seven.

Case:2:
Number of penguins outside the cave = 4 or Four.
Number of penguins inside the cave = 3 or Three.
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 3 + 4
= 7 or Seven.
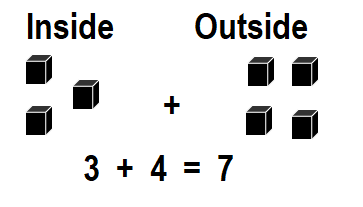
Question 1.
5 penguins in all

Answer:
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 3 + 2
= 5 or Five.
Explanation:
Number of penguins inside the cave = 3 or Three.
Number of penguins outside the cave = 2 or Two.
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 3 + 2
= 5 or Five.

Question 2.
8 penguins in all

Answer:
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 4 + 4
= 8 or Eight.
Explanation:
Number of penguins inside the cave = 4 or Four.
Number of penguins outside the cave = 4 or Four.
Total number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 4 + 4
= 8 or Eight.

Independent Practice
How many bats are inside and outside? Use cubes or draw a picture. Write an equation.
Question 3.
9 bats in all
Answer:
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 5 + 4
= 9 or Nine.
Explanation:
Number of bats inside the cave = 5 or Five.
Number of bats outside the cave = 4 or Four.
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 5 + 4
= 9 or Nine.
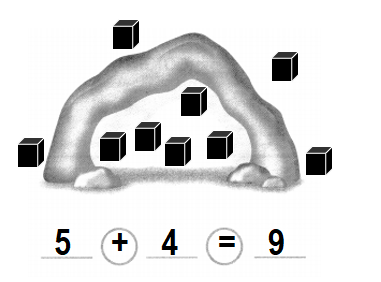
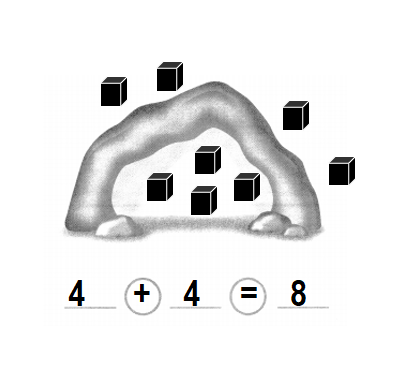
Question 4.
8 bats in all
Answer:
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 4 + 4
= 8 or Eight.
Explanation:
Number of bats inside the cave = 4 or Four.
Number of bats outside the cave = 4 or Four.
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 4 + 4
= 8 or Eight.
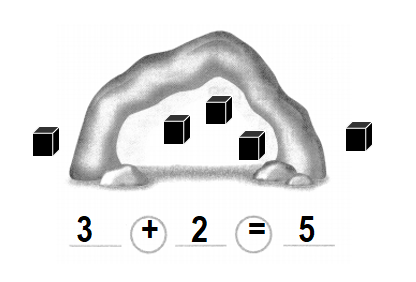
Question 5.
5 bats in all

Answer:
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 3 + 2
= 5 or Five.
Explanation:
Number of bats inside the cave = 3 or Three.
Number of bats outside the cave = 2 or Two.
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 3 + 2
= 5 or Five.
Question 6.
4 bats in all
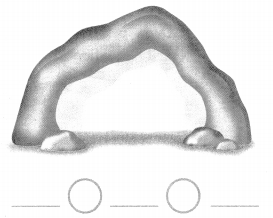
Answer:
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 2 + 2
= 4 or Four.
Explanation:
Number of bats inside the cave = 2 or Two.
Number of bats outside the cave = 2 or Two.
Total number of bats in all = Number of bats inside the cave + Number of bats outside the cave
= 2 + 2
= 4 or Four.
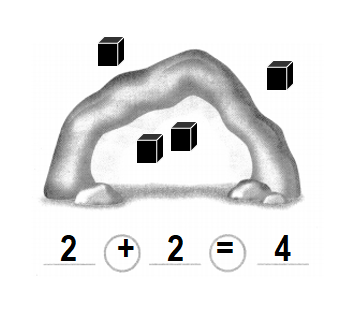
Problem Solving
Solve each problem.
Question 7.
envision® STEM
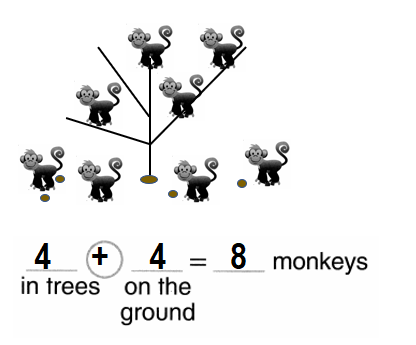
8 monkeys in all. Some live in trees. Some live on the ground. Show one way.

Answer:
Total number of monkeys in all = Number of monkeys live in trees + Number of monkeys live on the ground
= 4 + 4
= 8 or Eight.
Explanation:
Number of monkeys live in trees = 4 or Four.
Number of monkeys live on the ground =4 or Four.
Total number of monkeys in all = Number of monkeys live in trees + Number of monkeys live on the ground
= 4 + 4
= 8 or Eight.
Question 8.
Reasoning
Anna draws 2 cats. She draws 5 more cats. How many cats in all? Write an equation.

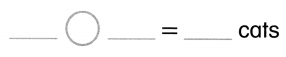
Answer:
Total number of cats Anna draws in all = 7 or Seven.
Explanation:
Number of cats Anna draws = 2 or Two.
Number of cats Anna draws more = 5 or Five.
Total number of cats Anna draws in all = Number of cats Anna draws + Number of cats Anna draws more
= 2 + 5
= 7 or Seven.
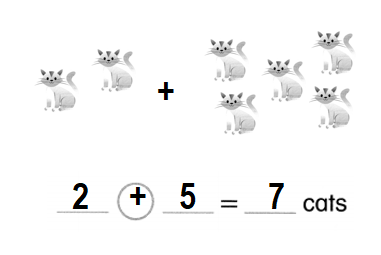
Question 9.
Higher Order Thinking
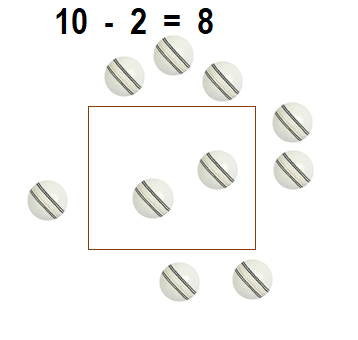
Andy has 10 balls. 1 or 2 balls are inside the toy box. How many balls are outside the toy box? Tell how you know.

Answer:
Total number of outside the toy box = 8 or Eight.
Explanation:
Number of balls Andy has = 10 or Ten.
Number of balls inside the toy box = 2 or Two.
Total number of outside the toy box = Number of balls Andy has + Number of balls inside the toy box
= 10 – 2
= 8 or Eight.
Question 10.
Assessment Practice
9 birds in all. Some birds are flying. Some birds are in a tree.

Which shows one way?
A. 4 flying, 3 in a tree
B. 5 flying, 4 in a tree
C. 1 flying, 7 in a tree
D. 8 flying, 2 in a tree
Answer:
Total number of birds in all = Number of birds flying + Number of birds in a tree
= 5 + 4
= 9 or Nine.
B. 5 flying, 4 in a tree shows one way.
Explanation:
Number of birds flying = 5 or Five.
Number of birds in a tree = 4 or Four.
Total number of birds in all = Number of birds flying + Number of birds in a tree
= 5 + 4
= 9 or Nine.
Lesson 1.4 Take from
Solve and Share
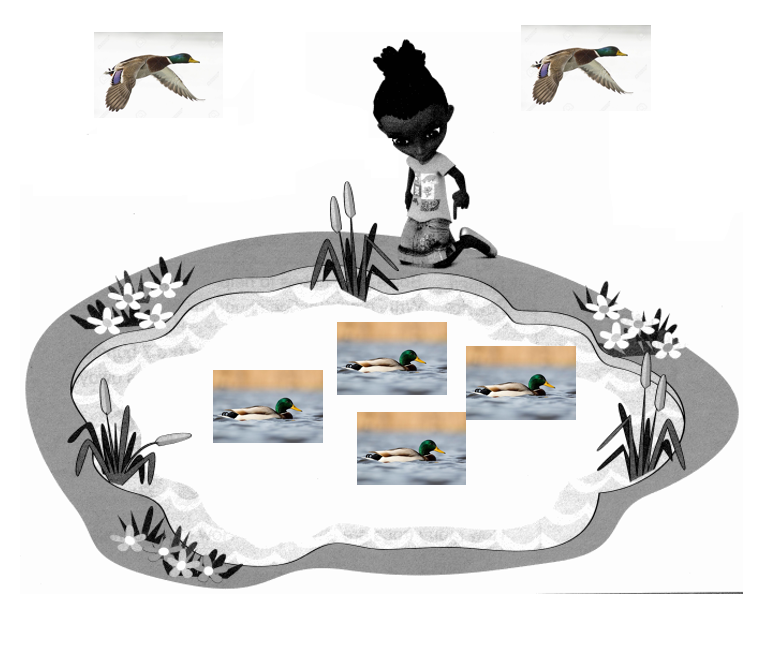
There are 6 ducks. Some fly away. How many ducks are left?

Answer:
Number of ducks left = 4 or Four.
Explanation:
Total number of ducks = 6 or Six.
Number of ducks flying away = 2 or Two.
Number of ducks left = Total number of ducks – Number of ducks flying away
= 6 – 2
= 4 or Four.
Visual Learning Bridge

Convince Me!
How do cubes help you solve the problem?
Answer:
The cubes strategy is a simple tool that helps in step-by-step calculation of addition or subtraction and to solve the problem asked.
Explanation:
The cubes strategy is a simple tool that helps in step-by-step calculation of addition or subtraction and to solve the problem asked. It helps in easy calculation and to understand the problem and solve it.
Guided Practice
Solve. Use cubes to help. Write a subtraction equation.
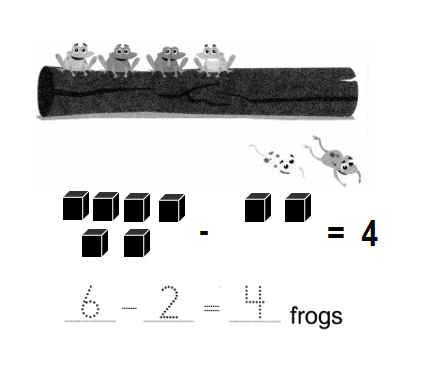
Question 1.
There are 6 frogs. 2 frogs jump off.

How many frogs are left?
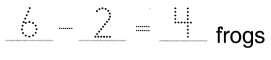
Answer:
Number of frogs are left = 4 or Four.
Explanation:
Total number of frogs in all = 6 or Six.
Number of frogs jump off = 2 Or Two.
Number of frogs are left = Total number of frogs in all – Number of frogs jump off
= 6 – 2
= 4 or Four.
Question 2.
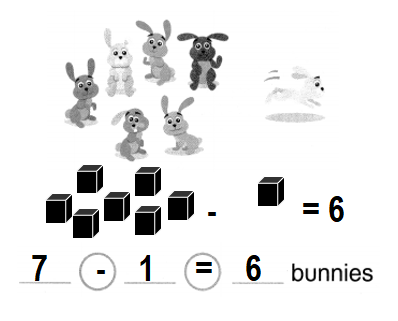
There are 7 bunnies. 1 bunny hops away.
How many bunnies are left?
Answer:
Number of bunnies are left = 6 or Six.
Explanation:
Total number of bunnies in all = 7 or Seven.
Number of bunnies hops away = 1 or One.
Number of bunnies are left = Total number of bunnies in all – Number of bunnies hops away
= 7 – 1
= 6 or Six.
Independent Practice
Solve. Use cubes or draw a picture. Write a subtraction equation.
Question 3.
There are 8 bugs. 4 bugs fly away.

How many bugs are left?

Answer:
Number of bugs are left = 4 or Four.
Explanation:
Total number of bugs in all = 8 or Eight.
Number of bugs fly away = 4 or Four.
Number of bugs are left = Total number of bugs in all – Number of bugs fly away
= 8 – 4
= 4 or Four.

Question 4.
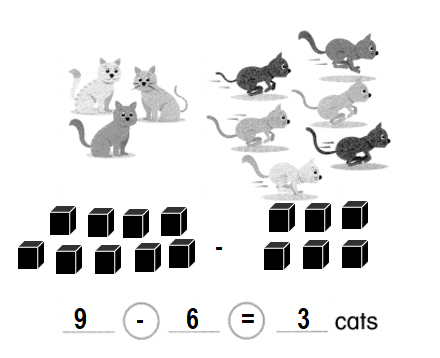
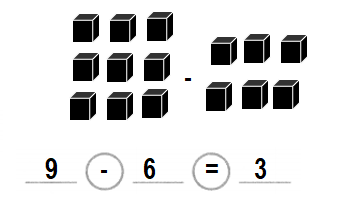
There are 9 cats. 6 cats run away.

How many cats are left?

Answer:
Number of cats are left = 3 or Three.
Explanation:
Total number of cats in all = 9 or Nine.
Number of cats run away = 6 or Six.
Number of cats are left = Total number of cats in all – Number of cats run away
= 9 – 6
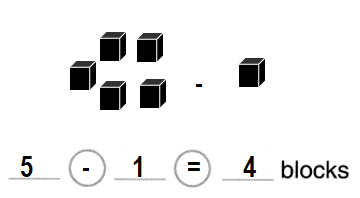
= 3 or Three.
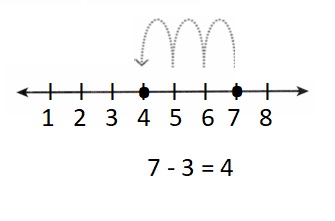
Question 5.
Higher Order thinking
There are 7 dogs. Some run away. 3 dogs are left. How many dogs ran away.

____ dogs
Answer:
Number of dogs run away = 4 or Four.
Explanation:
Total number of dogs in all = 7 or Seven.
Number of dogs left = 3 or Three.
Number of dogs run away = Total number of dogs in all – Number of dogs left
= 7 – 3
= 4 or Four.

Problem Solving
Solve each problem.
Question 6.
Reasoning
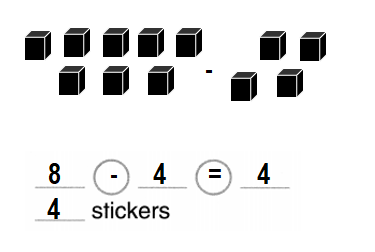
Lin has 9 stamps. She gives away 4 stamps. How many stamps are left?

Answer:
Number of stamps left with Lin = 5 or Five.
Explanation:
Total number of stamps Lin has in all = 9 or Nine.
Number of stamps Lin gives away = 4 or Four.
Number of stamps left with Lin = Total number of stamps Lin has in all – Number of stamps Lin gives away
= 9 – 4
= 5 or Five.
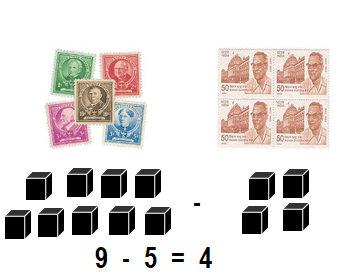
Question 7.
Reasoning
Gloria has 8 flowers. She gives away 5 flowers. How many flowers are left?
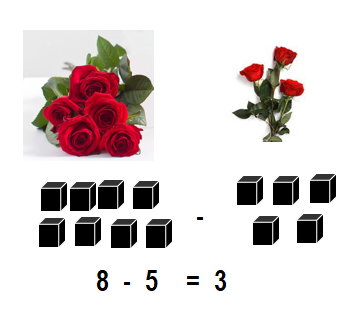
Answer:
Number of flowers left with Gloria = 3 or Three.
Explanation:
Total number of flowers Gloria has in all = 8 or Eight.
Number of flowers Gloria gives away = 5 or Five.
Number of flowers left with Gloria = Total number of flowers Gloria has in all – Number of flowers Gloria gives away
= 8 – 5
= 3 or Three.
Question 8.
Higher Order Thinking
Find the missing number. Write a subtraction story for the equation.
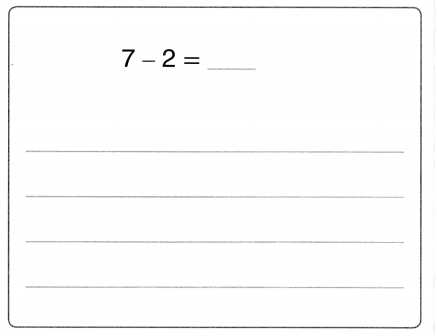
Answer:
Mrs. Shas has 7 balloons. She gives away 2 balloons. How many balloons are left?
Number of balloons left with Mrs. Shas = 5 or Five.
Explanation:
Mrs. Shas has 7 balloons. She gives away 2 balloons. How many balloons are left?
Total number of balloons Mrs. Shas has in all = 7 or Seven.
Number of balloons Mrs. Shas gives away = 2 or Two.
Number of balloons left with Mrs. Shas = Total number of balloons Mrs. Shas has in all – Number of balloons Mrs. Shas gives away
= 7 – 2
= 5 or Five.

Question 9.
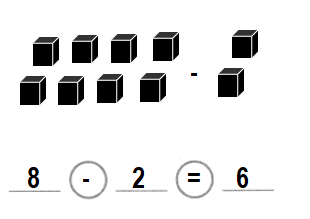
Assessment Practice
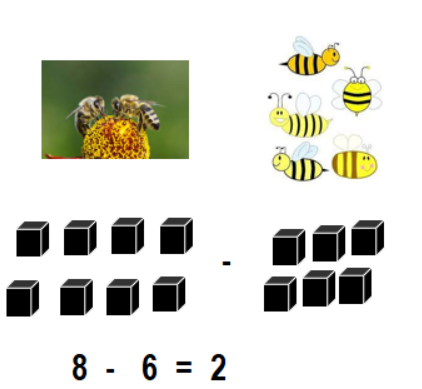
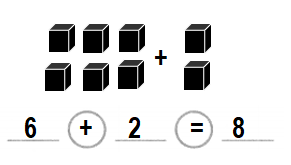
There are 8 bees. 6 bees fly away. How many bees are left?

A. 8 – 2 = 6 bees
B. 8 – 7 = 1 bees
C. 7 – 2 = 5 bees
D. 8 – 6 = 2 bees
Answer:
Number of bees are left = 2 or Two.
D. 8 – 6 = 2 bees
Explanation:
Total number of bees in all = 8 or Eight.
Number of bees fly away = 6 or Six.
Number of bees are left = Total number of bees in all – Number of bees fly away
= 8 – 6
= 2 or Two.
Lesson 1.5 Compare Situations
There are 5 red cars and 3 blue cars. Are there more red cars or blue cars? How many more? Show how you know.

Answer:
There are 2 red cars more than the blue cars.

Explanation:
Number of red cars = 5 or Five.
Number of blue cars = 3 or Three.
Difference = Number of red cars – Number of blue cars
= 5 – 3
= 2 or Two.

Convince Mel
Can you also add to solve the problem above? Explain.
Answer:
No, you can not add to solve the problem because you need to find the difference between the blue hats and orange hats to know how many more.
Explanation:
You need to find the difference between the blue hats and orange hats to know how many more.
Guided Practice
Use cubes to help. Write an equation. Then solve.
Question 1.
6 yellow frogs 3 green frogs
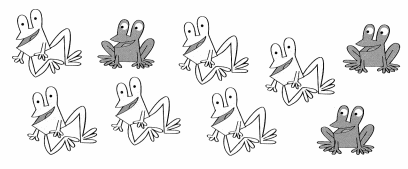
How many more yellow frogs than green frogs are there? more yellow frogs

Answer:
There are 3 yellow frogs more than the green frogs.
Explanation:
Number of yellow frogs = 6 or Six.
Number of green frogs = 3 or Three.
Difference = Number of yellow frogs – Number of green frogs
= 6 – 3
= 3 or Three.
Independent Practice
Use cubes or draw a picture. Write an equation. Then solve.
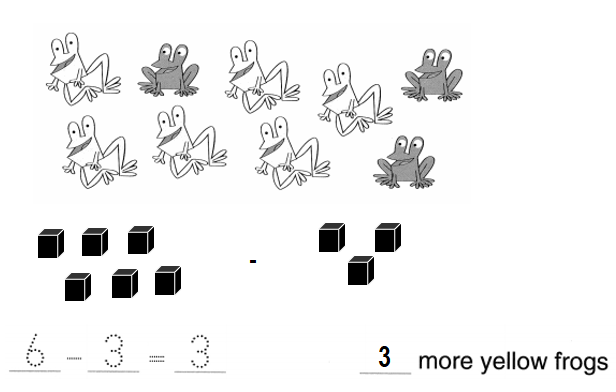
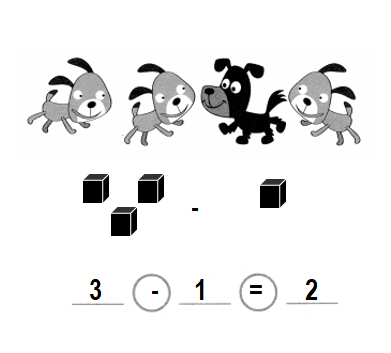
Question 2.
3 brown dogs I black dog

How many more brown dogs than black dogs are there?

____ more brown dogs
Answer:
There are 2 brown dogs more than the black dogs.
_2__ more brown dogs.
Explanation:
Number of brown dogs = 3 or Three.
Number of black dogs = 1 or One.
Difference = Number of brown dogs – Number of black dogs
= 3 – 1
= 2 or Two.
Question 3.
7 red beads 4 green beads

How many more red beads than green beads are there?

___ more red beads
Answer:
There are 3 red beads more than the green beads.
Explanation:
Number of red beads= 7 or Seven.
Number of green beads = 4 or Four.
Difference = Number of red beads – Number of green beads
= 7 – 4
= 3 or Three.
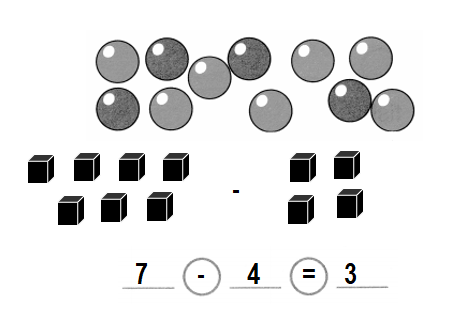
Higher Order Thinking
There are more blue birds than yellow birds. Write 2 equations to show. Then solve.

Question 4.
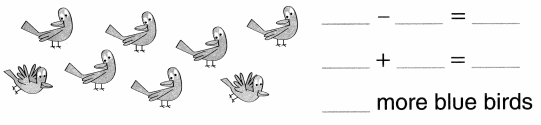
Answer:
Equation:1:
Difference = Number of blue birds – Number of yellow birds
= 5 – 3
= 2 or Two.
Equation:2:
Number of blue birds = Number of birds flu away + Number of yellow birds
= 2 + 3
= 5 or Five.
Explanation:
Equation:1:
Number of blue birds = 5 or Five.
Number of yellow birds = 3 or Three.
Difference = Number of blue birds – Number of yellow birds
= 5 – 3
= 2 or Two.
Equation:2:
Number of birds flu away = 2 or Two.
Number of yellow birds = 3 or Three.
Number of blue birds = Number of birds flu away + Number of yellow birds
= 2 + 3
= 5 or Five.

Problem Solving
Solve each problem. Use cubes or draw a picture.
Question 5.
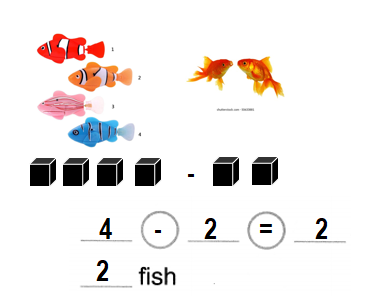
Number Sense 4 fish are in a tank. 2 fish are sold. How many fish are left?
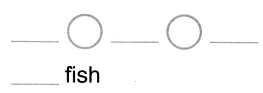
Answer:
Number of fishes left in the tank = 2 or Two.
Explanation:
Number of fishes in a tank = 4 or Four.
Number of fishes sold = 2 or Two.
Number of fishes left in the tank = Number of fishes in a tank – Number of fishes sold
= 4 – 2
= 2 or Two.
Question 6.
Model
Luis sees 5 green frogs. He sees I blue frog. How many more green frogs than blue frogs does Luis see?

___ more green frogs
Answer:
There are 4 green frogs seen by Luis more than the blue frogs seen by her.
_4__ more green frogs.
Explanation:
Number of green frogs Luis sees = 5 or Five.
Number of blue frogs Luis sees = 1 or One.
Difference = Number of green frogs Luis sees – Number of blue frogs Luis sees
= 5 – 1
= 4 or Four.
Question 7.
Higher Order Thinking
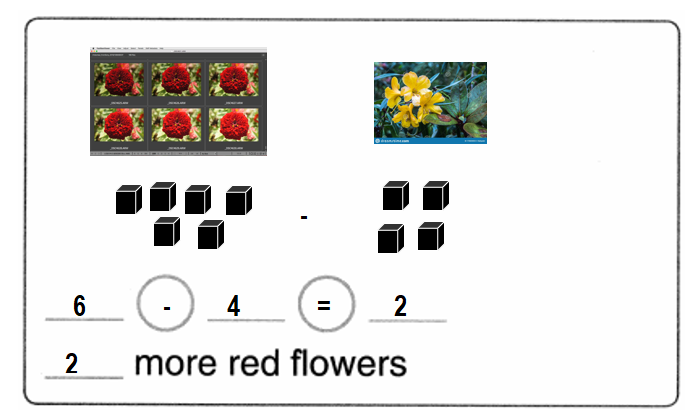
Draw some yellow flowers. Draw more red flowers than yellow flowers. How many more red flowers than yellow flowers are there?
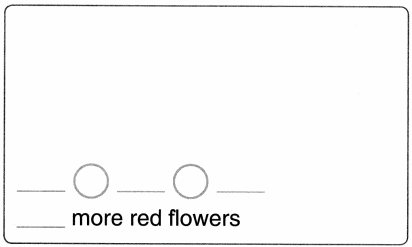
Answer:
There are 2 red flowers more than the yellow flowers.
Explanation:
Number of red flowers = 6 or Six.
Number of yellow flowers = 4 or Four.
Difference = Number of red flowers – Number of yellow flowers
= 6 – 4
= 2 or Two.
Question 8.
Assessment Practice
6 gray cats
4 white cats
How many more gray cats than white cats are there?
A. 2 more gray cats
B. 4 more gray cats
C. 6 more gray cats
D. 10 more gray cats

Answer:
There are 2 gray cats more than the white cats.
A. 2 more gray cats
Explanation:
Number of gray cats = 6 or Six.
Number of white cats = 4 or Four.
Difference = Number of gray cats – Number of white cats
= 6 – 4
= 2 or Two.

Lesson 1.6 More Compare Situations

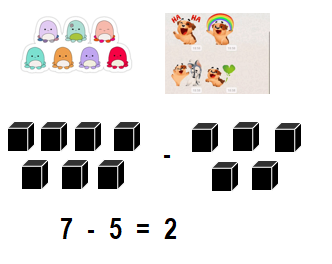
Amy has 7 stickers. Tim has 5 stickers. Who has fewer stickers? How many fewer? Show how you know.
Answer:
Tim has 2 stickers fewer than Amy.
Explanation:
Number of stickers Amy has = 7 or Seven.
Number of stickers Tim has = 5 or Five.
Difference = Number of stickers Amy has – Number of stickers Tim has
= 7 – 5
= 2 or Two.
Visual Learning Bridge

Convince Me!
How is finding how many fewer like finding how many more?
Answer:
Finding how many fewer is same like finding how many more because the process is to find how much and how many.
Explanation:
Finding how many fewer is same like finding how many more because the process is to find how much and how many. They are just in difference of calculation terms one is adding and other is subtracting.
Guided Practice
Use cubes to help. Write an equation. Then solve.
Question 1.
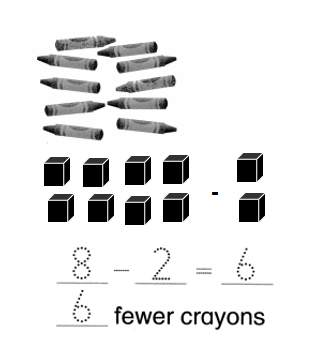
Juan has 8 red crayons. Sue has 2 blue crayons.

How many fewer crayons does Sue have than Juan?

Answer:
6 fewer crayons Sue has than Juan has.
Explanation:
Number of red crayons Juan has = 8 or Eight.
Number of blue crayons Sue has = 2 or Two,.
Difference = Number of red crayons Juan has – Number of blue crayons Sue has
= 8 – 2
= 6 or Six.
Question 2.
Ann has 4 purple grapes. Sam has 7 green grapes.

How many fewer grapes does Ann have than Sam?
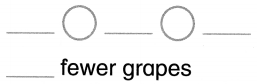
Answer:
3 fewer grapes Ann have than Sam.
Explanation:
Number of purple grapes Ann has = 4 or Four.
Number of green grapes Sam has = 7 or Seven,.
Difference = Number of green grapes Sam has – Number of purple grapes Ann has
= 7 – 4
= 3 or Three.

Independent Practice
Use cubes or draw a picture. Write an equation. Then solve.
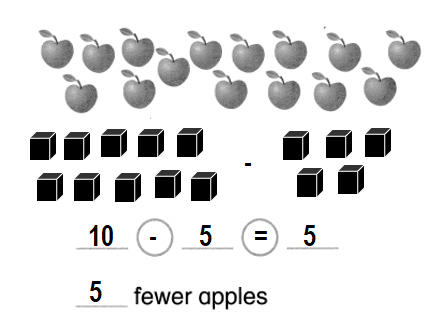
Question 3.
Emma buys 10 red apples. She buys 5 green apples.

How many fewer green apples than red apples does Emma buy?

Answer:
5 fewer green apples than red apples Emma buys.
Explanation:
Number of red apples Emma buys = 10 or Ten.
Number of green apples Emma buys = 5 or Five.
Difference = Number of red apples Emma buys – Number of green apples Emma buys
= 10 – 5
= 5 or Five.
Question 4.
Beth writes on 3 cards. Joe writes on 9 cards.

How many fewer cards does Beth write on than Joe?

Answer:
6 fewer cards Beth writes on than Joe.
Explanation:
Number of cards Beth writes = 3 or Three.
Number of cards Joe writes = 9 or Nine.
Difference = Number of cards Joe writes – Number of cards Beth writes
= 9 – 3
= 6 or Six.

Question 5.
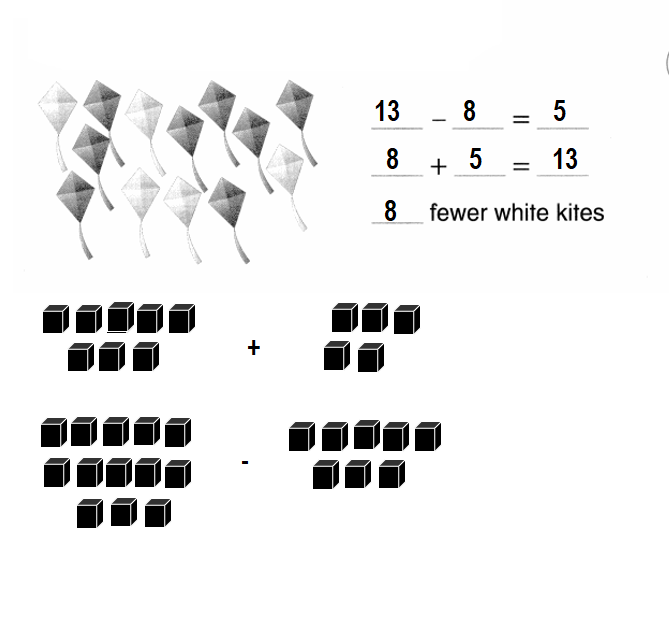
Higher Order Thinking
There are fewer white kites than blue kites. Write 2 equations to show. Then solve.
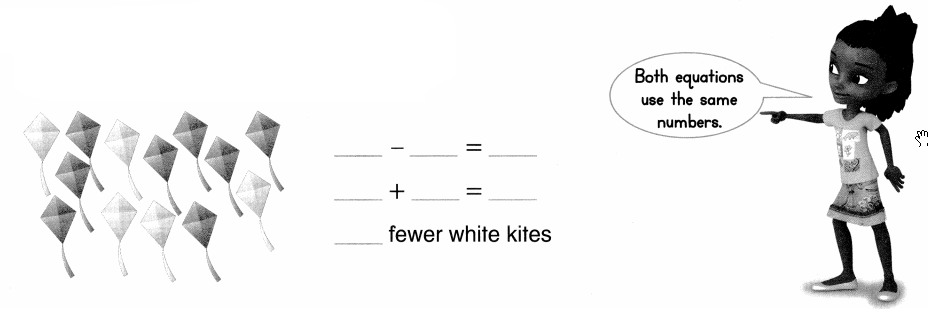
Answer:
Equation:1:
Difference = Number of blue kites – Number of white kites
= 13 – 8
= 5 or Five.
Equation:2:
Number of white kites = Number of blue kites + Difference between the white and blue kites
= 8 + 5
= 13 or Thirteen.
Explanation:
Equation:1:
Number of white kites = 8 or Eight.
Number of blue kites = 13 or Thirteen.
Difference = Number of blue kites – Number of white kites
= 13 – 8
= 5 or Five.
Equation:2:
Number of white kites = ??
Number of blue kites = 13 or Thirteen.
Difference between the white and blue kites = 5 or Five.
Number of white kites = Number of blue kites + Difference between the white and blue kites
= 8 + 5
= 13 or Thirteen.
Problem Solving
Question 6.
Reasoning
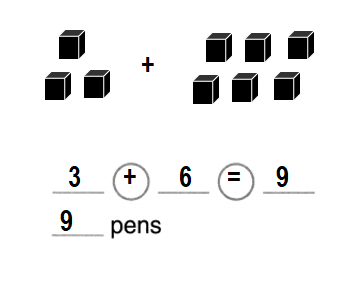
Leah has 3 pens. Scott has 6 pens. How many pens do they have in all?
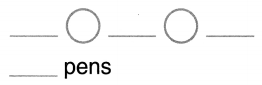
Answer:
Total number of pens they have in all = 9 or Nine.
Explanation:
Number of pens Leah has = 3 or Three.
Number of pens Scott has = 6 or Six.
Total number of pens they have in all = Number of pens Leah has + Number of pens Scott has
= 3 + 6
= 9 or Nine.
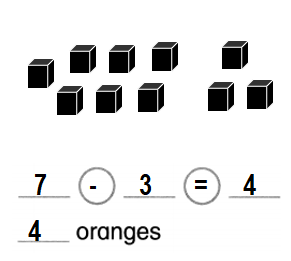
Question 7.
Reasoning
There are 7 oranges on a branch. 3 oranges fall off.

How many oranges are left?
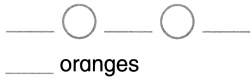
Answer:
Number of oranges left = 4 or Four.
Explanation:
Number of oranges on a branch = 7 or Seven
Number of oranges fell off = 3 or Three.
Number of oranges left = Number of oranges on a branch – Number of oranges fell off
= 7 – 3
= 4 or Four.
Question 8.
Higher Order Thinking
Draw some blue balloons. Draw fewer yellow balloons. How many fewer yellow balloons than blue balloons are there?

Answer:
There are 2 fewer yellow balloons than blue balloons.
Explanation:
Number of blue balloons = 5 or Five.
Number of yellow balloons = 3 or Three.
Difference = Number of blue balloons – Number of yellow balloons
= 5 – 3
= 2 or Two.
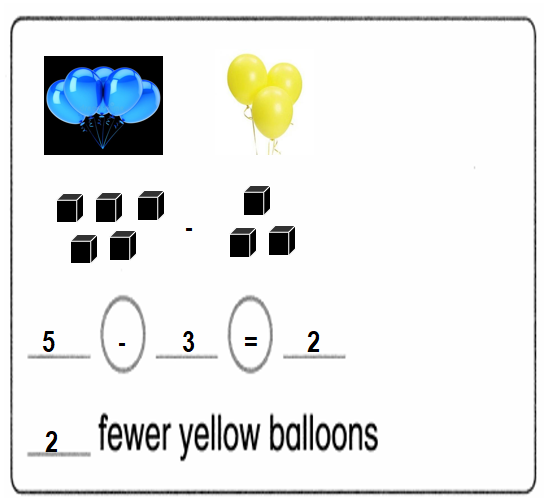
Question 9.
Assessment Practice
8 apple trees
6 pear trees
How many fewer pear trees than apple trees are there?
A. 2 fewer pear trees
B. 3 fewer pear trees
C. 6 fewer pear trees
D. 8 fewer pear trees
Answer:
There are 2 fewer pear trees than apple trees.
A. 2 fewer pear trees
Explanation:
Number of apple trees = 8 or eight.
Number of pear trees = 6 or Six.
Difference = Number of apple trees – Number of pear trees
= 8 – 6
= 2 or Two.
Lesson 1.7 Change Unknown
Solve and Share
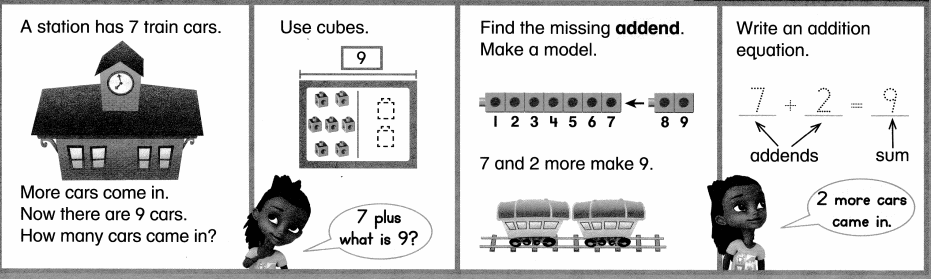
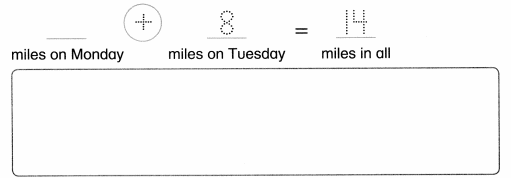
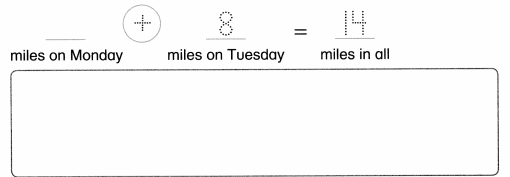
There are 5 train cars. More train cars join. Now there are 9 train cars. How many train cars joined?

__ trains cars joined.
Answer:
Number of trains cars joined = 4 or Four.
__4__ trains cars joined.
Explanation:
Number of train cars = 5 or Five.
Number of train cars now = 9 or nine.
Number of trains cars joined = Number of train cars now – Number of train cars
= 9 – 5
= 4 or Four.

Visual Learning Bridge
Convince Me!
Can you also subtract to solve the problem above? Explain.
Answer:
Yes, you can subtract to solve the problem above.
Number of cars = 5 or Five
Number of cars now = 9 or Nine.
Number of cars came more = Number of cars now – Number of cars
= 9 – 5
= 4 or Four.
Explanation:
Number of cars = 5 or Five
Number of cars now = 9 or Nine.
Difference:
Number of cars came more = Number of cars now – Number of cars
= 9 – 5
= 4 or Four.
Guided Practice
Use cubes to help. Write an equation. Then solve.
Question 1.
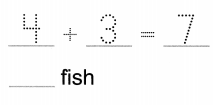
Bobby has 4 fish.

He buys more fish. Now he has 7 fish. How many fish did Bobby buy?
Answer:
Number of fishes Bobby buys = 3 or Three.
Explanation:
Number of fishes Bobby has = 4 or Four.
Number of fishes Bobby has now = 7 or seven.
Number of fishes Bobby buys = Number of fishes Bobby has now – Number of fishes Bobby has
= 7 – 4
= 3 or Three.
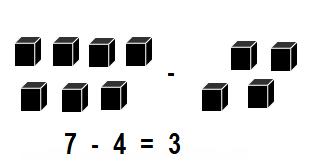
Independent Practice
Use cubes or draw a picture. Write an equation. Then solve.
Question 2.
Mary has 4 stickers.

Pat gives her more stickers. Now Mary has 8 stickers. How many stickers did Pat give Mary?

Answer:
Number of stickers Pat gives her more = 4 or Four.
Explanation:
Number of stickers Mary has = 4 or Four.
Number of stickers Mary has now = 8 or Eight.
Number of stickers Pat gives her more = Number of stickers Mary has now – Number of stickers Mary has
= 8 – 4
= 4 or Four.
Question 3.
Billy draws 4 red cars.
Then he draws some blue cars. Now there are 10 cars. How many blue cars did Billy draw?

Answer:
Number of blue cars Billy draws = 6 or Six.
Explanation:
Number of red cars Billy draws = 4 or Four.
Number of cars Billy has now = 10 or Ten.
Number of blue cars Billy draws = Number of cars Billy has now – Number of red cars Billy draws
= 10 – 4
= 6 or Six.
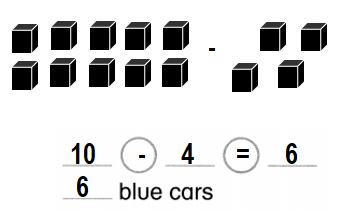
Question 4.
Higher Order Thinking
Some girls are on the bus. 2 boys get on the bus. Now there are 7 children on the bus. How many girls are on the bus? Write 2 equations to show. Then solve.
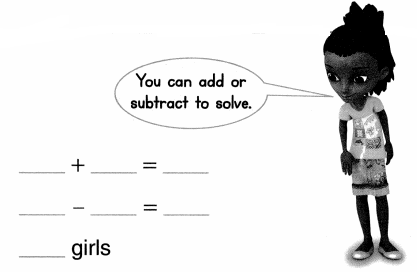
Answer:
Equation:1:
Number of girls are on the bus = Number of children on the bus now – Number of boys get on the bus
= 7 – 2
= 5 or Five.
Equation:2:
Number of children on the bus now = Number of boys get on the bus + Number of girls are on the bus
=> 7 = 2 + Number of girls are on the bus
=> 7 – 2 = Number of girls are on the bus
=> 5 or Five = Number of girls are on the bus.
Explanation:
Equation:1:
Number of boys get on the bus = 2 or Two.
Number of children on the bus now =7 or Seven.
Number of girls are on the bus = Number of children on the bus now – Number of boys get on the bus
= 7 – 2
= 5 or Five.
Equation:2:
Number of children on the bus now =7 or Seven.
Number of boys get on the bus = 2 or Two.
Number of girls are on the bus = ??
Number of children on the bus now = Number of boys get on the bus + Number of girls are on the bus
=> 7 = 2 + Number of girls are on the bus
=> 7 – 2 = Number of girls are on the bus
=> 5 = Number of girls are on the bus.
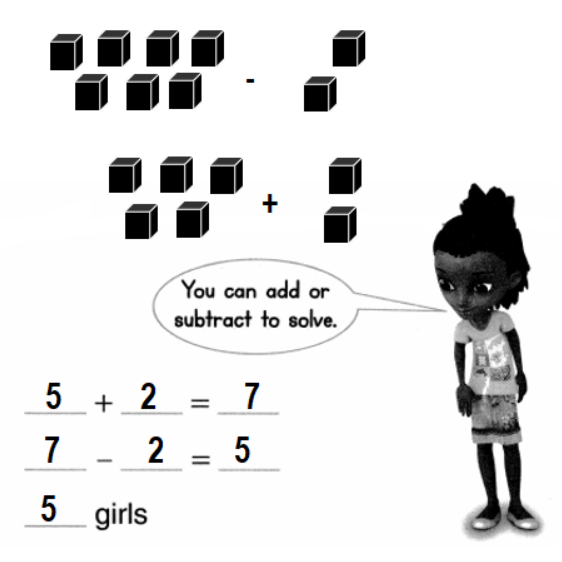
Problem Solving
Solve each problem.
Question 5.
6 pencils are on the desk.
Bob adds more pencils. Now there are 9 pencils. How many pencils did Bob add?
Answer:
Number of pencils Bob added more = 3 or Three.
Explanation:
Number of pencils are on the desk = 6 or Six.
Number of pencils now = 9 or Nine.
Number of pencils Bob added more = Number of pencils now – Number of pencils are on the desk
= 9 – 6
= 3 or Three.

Question 6.
Use Tools
Nora has 3 pretzels and 7 crackers. How many snacks does she have in all?

Answer:
Number of snacks Nora has in all = 10 or Ten.
Explanation:
Number of pretzels Nora has = 3 or Three.
Number of crackers Nora has = 7 or Seven.
Number of snacks Nora has in all = Number of pretzels Nora has + Number of crackers Nora has
= 3 + 7
= 10 or Ten.
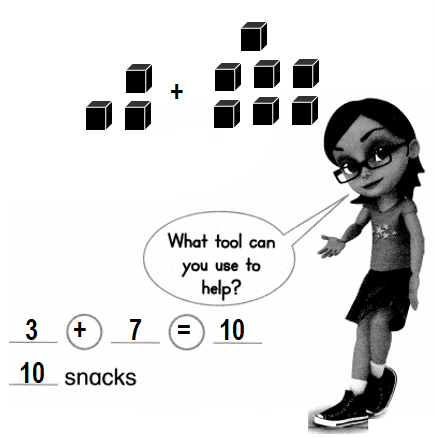
Question 7.
Higher Order Thinking
Some yellow birds are in a tree. Some blue birds join them. Now there are 5 birds in the tree. How many yellow birds and blue birds could there be?

___ yellow birds and _____ blue birds
Answer:
Case:1: _2__ yellow birds and _3____ blue birds
Total number of birds in a tree = Number of yellow birds in a tree + Number of blue birds joined them
= 2 + 3
= 5 or Five.
Case:2: __3__ yellow birds and __2___ blue birds
Total number of birds in a tree = Number of yellow birds in a tree + Number of blue birds joined them
= 3 + 2
= 5 or Five.
Explanation:
Case:1:
Number of yellow birds in a tree = 2 or Two.
Number of blue birds joined them = 3 or Three.
Total number of birds in a tree = Number of yellow birds in a tree + Number of blue birds joined them
= 2 + 3
= 5 or Five.
Case:2:
Number of yellow birds in a tree= 3 or Three.
Number of blue birds joined them = 2 or Two.
Total number of birds in a tree = Number of yellow birds in a tree + Number of blue birds joined them
= 3 + 2
= 5 or Five.
Question 8.
Assessment Practice
4 puppies play. More puppies join them. Now there are 7 puppies. How many puppies joined?
A. 5 puppies
B. 4 puppies
C. 3 puppies
D. 2 puppies
Answer:
Total number of puppies joined = 3 or Three.
C. 3 puppies
Explanation:
Number of puppies play = 4 or Four.
Number of puppies now = 7 or Seven.
Total number of puppies joined = Number of puppies now + Number of puppies play
= 7 – 4
= 3 or Three.
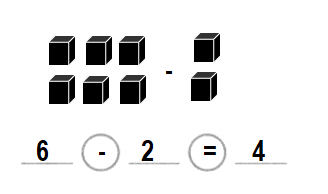
Lesson 1.8 Practice Adding and Subtracting
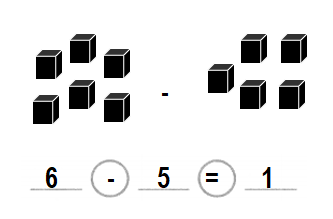
Solve & Share
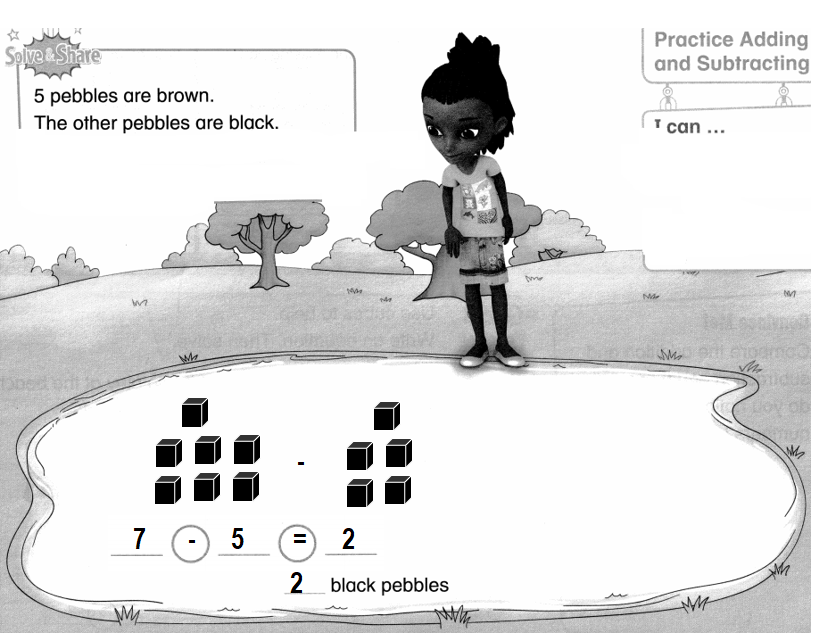
5 pebbles are brown. The other pebbles are black. There are 7 pebbles in all. How many black pebbles are there?

Answer:
Number of black pebbles = 2 or Two.
Explanation:
Number of brown pebbles = 5 or Five.
Number of pebbles in all = 7 or Seven.
Number of black pebbles = Number of pebbles in all – Number of brown pebbles
= 7 – 5
= 2 or Two.
Visual Learning Bridge

Convince Me!
Compare the addition and subtraction equations. What do you notice about the numbers?
Answer:
Its noticed that both the addition equation and subtraction equation results of finding the girls strength are same.
Explanation:
Addition equation:
Number of boys in the class = 5 or Five.
Total number of students in the class = 8 or Eight.
Number of girls in the class + Number of boys in the class = Total number of students in the class
=> ?? + 5 = 8.
=> 3 + 5 = 8
Subtraction equation:
Number of boys in the class = 5 or Five.
Total number of students in the class = 8 or Eight.
Number of girls in the class = Total number of students in the class – Number of boys in the class
= 8 – 5
= 3 or Three.
Guided Practice
Use cubes to help.
Write an equation. Then solve.
Question 1.
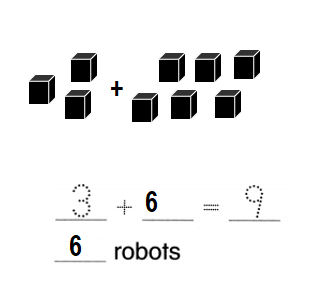
Nick has 9 robots. 3 of the robots can talk.

How many robots cannot talk?

Answer:
Number of robots cannot walk = 6 or Six.
Explanation:
Number of robots Nick has = 9 or Nine.
Number of robots can walk = 3 or Three.
Number of robots Nick has = Number of robots can walk + Number of robots cannot walk
=> 9 = 3 + ??
=> 9 = 3 + 6
Question 2.
6 children play at the beach. 2 children are girls.
How many are boys?
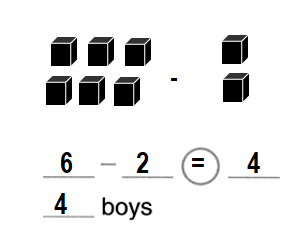
Answer:
Number of boys playing at the beach = 4 or Four.
Explanation:
Number of girls playing at the beach = 2 or Two.
Total number of children playing at the beach = 6 or Six.
Number of boys playing at the beach = Total number of children playing at the beach – Number of girls playing at the beach
= 6 – 2
= 4 or Four.
Independent Practice
Use cubes or draw a picture. Write an equation. Then solve.
Question 3.
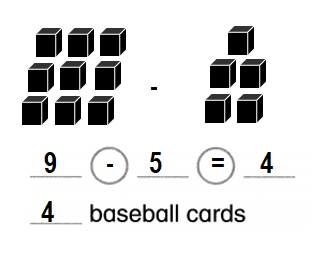
Jill has 9 cards. 5 cards are soccer cards.

The rest are baseball cards. How many baseball cards are there?

___ baseball cards
Answer:
Number of baseball cards = 4 or Four.
__4__ baseball cards.
Explanation:
Total number of cards Jill has = 9 or Nine.
Number of soccer cards = 5 or Five.
Number of baseball cards = Total number of cards Jill has – Number of soccer cards
= 9 – 5
= 4 or Four.
Question 4.
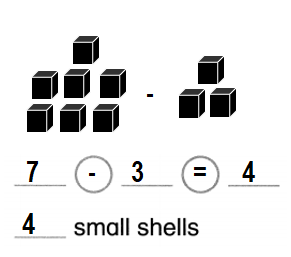
Rita has 7 Shells.

3 shells are big. The rest are small. How many small shells does Rita have?

__ small shells
Answer:
Number of shells are small = 4 or Four.
_4_ small shells.
Explanation:
Number of shells are big = 3 or Three.
Total number of shells Rita has = 7 or Seven.
Number of shells are small = Total number of shells Rita has – Number of shells are big
= 7 – 3
= 4 or Four.
Question 5.
Higher Order Thinking
Henry has 6 candles on his cake. I candle is green. The rest are blue. How many blue candles are there? Write 2 equations to show. Then solve.

Answer:
Equation:1:
Number of blue candles = Total number of candles on Henry cake – Number of green candles
= 6 – 1
= 5 or five.
Equation:2:
Number of green candles + Number of blue candles = Total number of candles on Henry cake
=> 1 + ?? = 6
=> 1 + 5 = 6.
Number of blue candles = 5 or five.
Explanation:
Equation:1:
Number of green candles = 1 or One.
Total number of candles on Henry cake = 6 or Six.
Number of blue candles = Total number of candles on Henry cake – Number of green candles
= 6 – 1
= 5 or five.
Equation:2:
Number of green candles = 1 or One.
Total number of candles on Henry cake = 6 or Six.
Number of green candles + Number of blue candles = Total number of candles on Henry cake
=> 1 + ?? = 6
=> 1 + 5 = 6.

Problem Solving
Solve each problem.
Question 6.
Make Sense
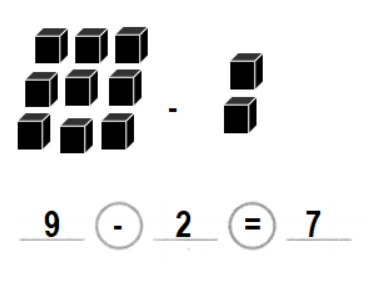
Joe buys 2 red fish. He buys some blue fish. He buys 9 fish in all. How many blue fish does Joe buy?

____ blue fish
Answer:
Number of blue fishes Joe buys = 7 or Seven.
__7__ blue fish.
Explanation:
Number of red fishes Joe buys = 2 or Two.
Total number of fishes Joe buys in all = 9 or Nine.
Number of blue fishes Joe buys = Total number of fishes Joe buys in all – Number of red fishes Joe buys
= 9 – 2
= 7 or Seven.
Question 7.
Make Sense
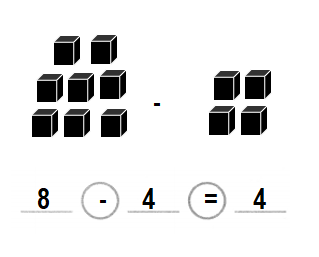
Rachel has 8 nickels. She gives away 4 nickels. How many nickels are left?

__ nickels
Answer:
Number of nickels left = 4 or Four.
__4__ nickels.
Explanation:
Number of nickels Rachel gives away = 4 or Four.
Total number of nickels Rachel has in all = 8 or Eight.
Number of nickels left = Total number of nickels Rachel has in all – Number of nickels Rachel gives away
= 8 – 4
= 4 or Four.
Question 8.
Higher Order Thinking
Nina has 8 stuffed animals. Some are bears. Some are tigers. How many of each animal could Nina have?

__ bears and __ tigers
Answer:
Nina can have 4 bears and 4 tigers each.
_4_ bears and _4_ tigers.
Explanation:
Total number of stuffed animals Nina has = 8 or Eight.
Number of bears + Number of tigers = Total number of stuffed animals Nina has
=> ?? + ?? = 8
=> 4 + 4 = 8.
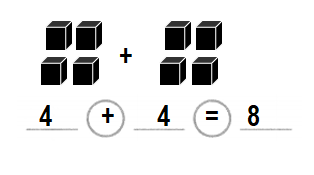
Question 9.
Assessment Practice
Liz and Mary have 7 fish in all. Liz has 2 fish. How many fish does Mary have? Which equation matches the story?
A. 9 – 2 = 7 fish
B. 7 – 1 = 6 fish
C. 7 – 2 = 5 fish
D. 8 – 7 = 1 fish

Answer:
Number of fishes Mary has = 5 or Five.
C. 7 – 2 = 5 fish
Explanation:
Number of fishes Liz has = 2 or Two.
Number of fishes Liz and Mary have in all = 7 or Seven.
Number of fishes Mary has = Number of fishes Liz and Mary have in all – Number of fishes Liz has
= 7 – 2
= 5 or Five.
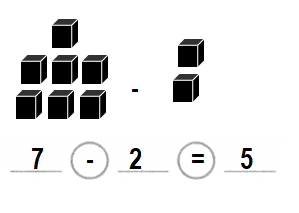
Lesson 1.9 Construct Arguments
Do you add or subtract to solve the problem? Tell why. Show how to solve. Use pictures, numbers, or words

Answer:
Number of more rabbits than turtles = 4 or Four.
Explanation:
Number of rabbits = 7 or Seven.
Number of turtles = 3 or Three.
Number of more rabbits than turtles = Number of rabbits – Number of turtles
= 7 – 3
= 4 or Four.

Thinking Habits
How can I use math to explain my work?
Is my explanation clear?

Answer:
I can use math to explain my work by taking the support of pictures ,diagrams to explain to solve the problem in a simple and easy way.
Yes, my is explanation clear.
Explanation:
I can use math to explain my work by taking the support of pictures ,diagrams to explain to solve the problem in a simple and easy way.
Yes, my is explanation clear because it is simple and easy to understand.
Visual Learning Bridge

Convince Me!
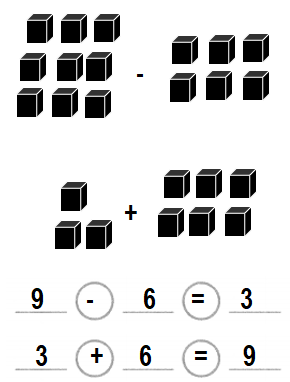
Look at the two ways to find the number of red crayons. How are the ways alike? How are the ways different?
Answer:
The two ways to find the number of red crayons are alike because the process is done to find the count how many are red crayons. The ways are different because the process differs as one is addition and other is subtraction.
Explanation:
Way:1:
Number of blue crayons = 6 or Six.
Total number of crayons in all = 9 or Nine.
Number of red crayons = Total number of crayons in all – Number of blue crayons
= 9 – 6
= 3 or Three.
Way:2:
Number of blue crayons = 6 or Six.
Total number of crayons in all = 9 or Nine.
Number of red crayons + Number of blue crayons = Total number of crayons in all
=> ?? + 6 = 9
=> 3 + 6 = 9.
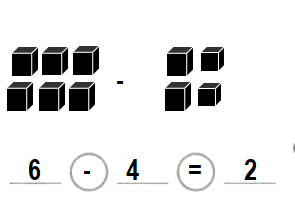
Guided Practice
Solve. Use pictures, numbers, or words to explain.
Question 1.
Manny draws 6 tiles. 4 tiles are red. The others are green. How many green tiles does Manny draw?

Answer:
Number of green tiles Manny draws = 2 or Two.
Explanation:
Number of tiles Manny draws = 6 or Six.
Number of red tiles Manny draws = 4 or Four.
Number of green tiles Manny draws = Number of tiles Manny draws – Number of red tiles
= 6 – 4
= 2 or Two.
Independent Practice
Solve. Use pictures, numbers, or words to explain.
Question 2.
Jan has 8 pennies. She spends 5 pennies. How many pennies does Jan have left?
Answer:
Number of pennies left = 3 or Three.
Explanation:
Number of pennies Jan has = 8 or Eight.
Number of pennies Jan spends = 5 or Five.
Number of pennies left = Number of pennies Jan has – Number of pennies Jan spends
= 8 – 5
= 3 or Three.
Question 3.
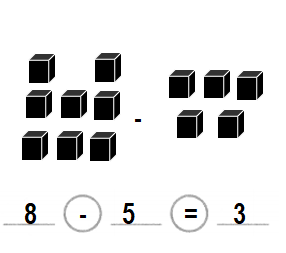
Lidia has 7 pencils. Jon has 2 pencils. Who has fewer pencils? How many fewer?
Answer:
Jon has fewer pencils by 5 or five.
Explanation:
Number of pencils Lidia has = 7 or Seven
Number of pencils Jon has = 2 or Two.
Difference =Number of pencils Lidia has – Number of pencils Jon has
= 7 – 2
= 5 or Five.
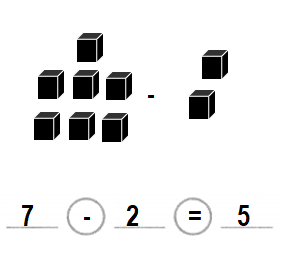
Question 4.
Higher Order Thinking
Max has 3 apples. He buys 2 more apples. He gives away 4 apples. How many apples does Max have left? Explain.
Answer:
Number of apples left = 1 or One.
Explanation:
Number of apples Max has = 3 or Three.
Number of more apples Max buys = 2 or Two.
Total number of apples Max has = Number of apples Max has + Number of more apples Max buys
= 3 + 2
= 5 or Five.
Number of apples Max gives away = 4 or Four.
Number of apples left = Total number of apples Max has – Number of apples Max gives away
= 5 – 4
= 1 or One.
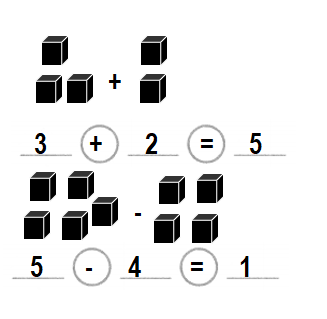
Problem Solving
Performance Task
Lemonade Stand
Some friends sell lemonade. Solve each problem. Use pictures, numbers, or words to explain.

Question 5.
Explain
Alex sells 3 cups. Mark sells 5 cups. How many cups do they sell in all? Here is Alex’s work.
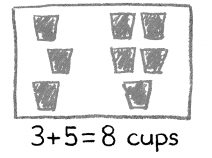
Is his work correct? Tell why.
Answer:
Total number of cups sold in all = 8 or Eight.
His work is correct has the answer is correct.
Explanation:
Number of cups Alex sells = 3 or Three.
Number of cups Mark sells = 5 or Five.
Total number of cups sold in all = Number of cups Alex sells + Number of cups Mark sells
= 3 + 5
= 8 or Eight.
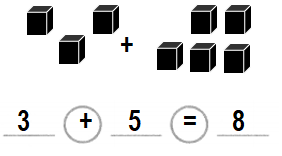
Question 6.
Be Precise
Mia sells 2 cups.
Gina sells 6 cups.
How many more cups does Gina sell than Mia?
Answer:
4 more cups Gina sells than Mia.
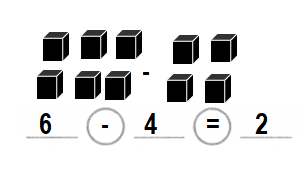
Explanation:
Number of cups Mia sells = 2 or Two.
Number of cups Gina sells = 6 or Six.
Difference = Number of cups Gina sells – Number of cups Mia sells
= 6 – 2
= 4 or Four.
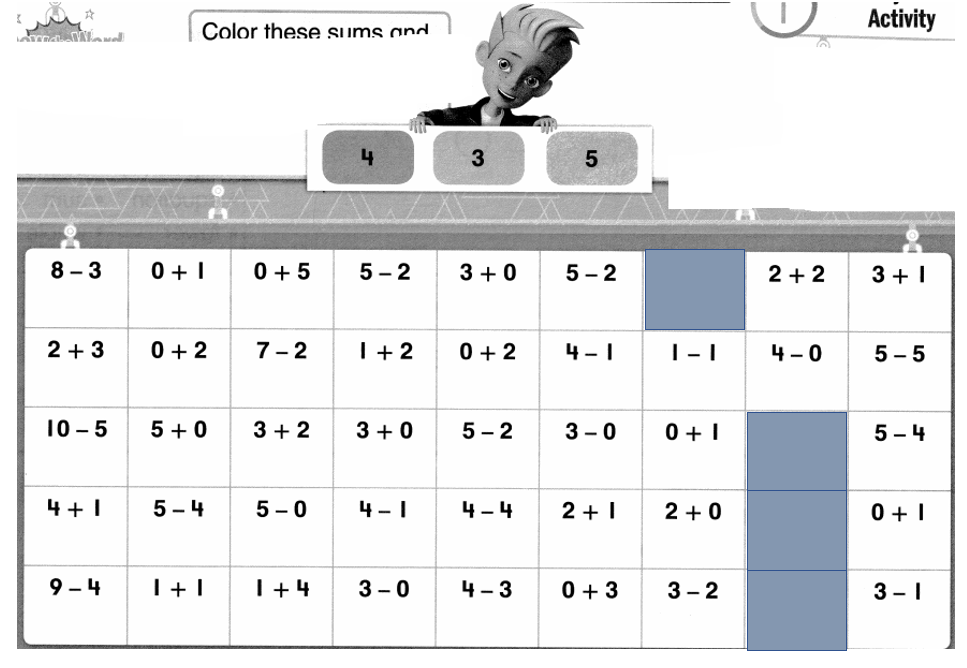
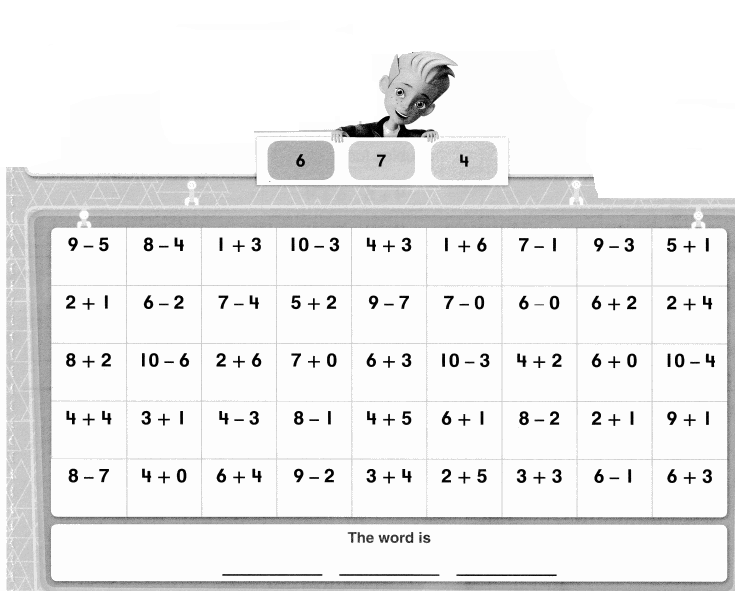
Fluency Review Activity
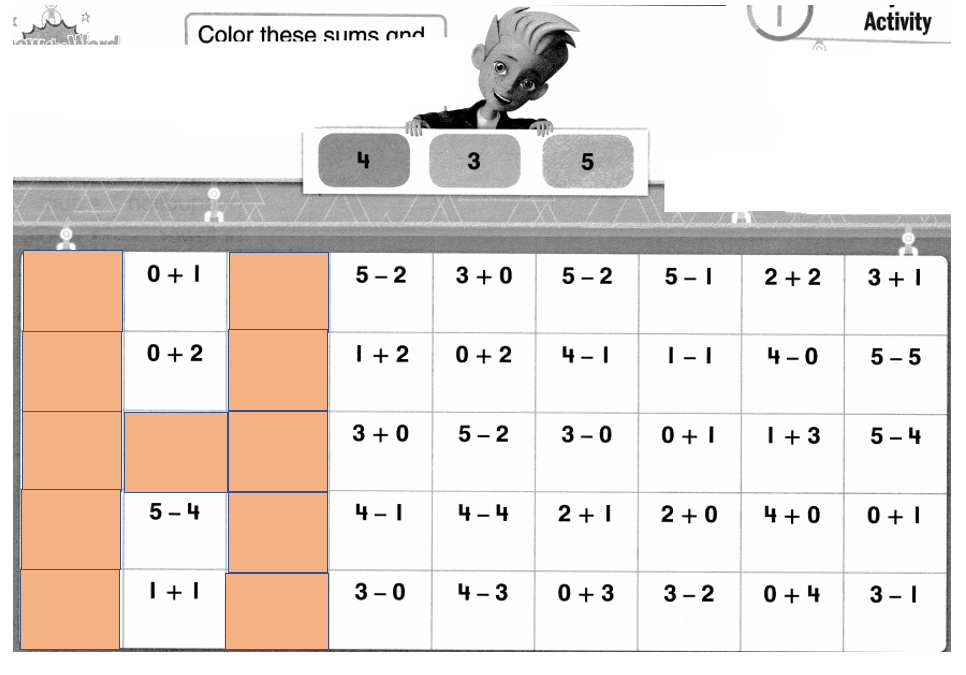
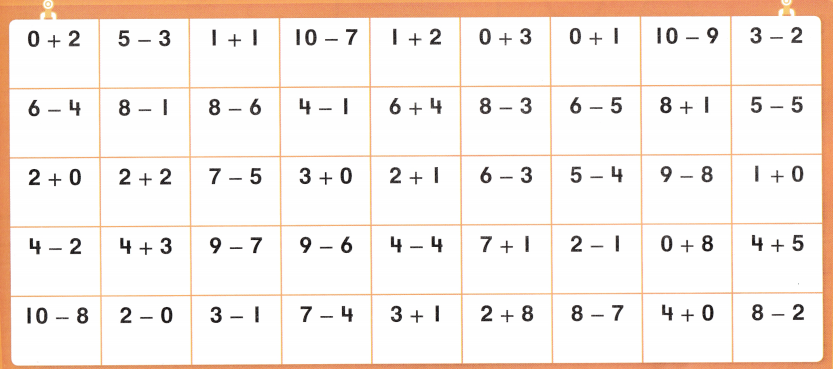
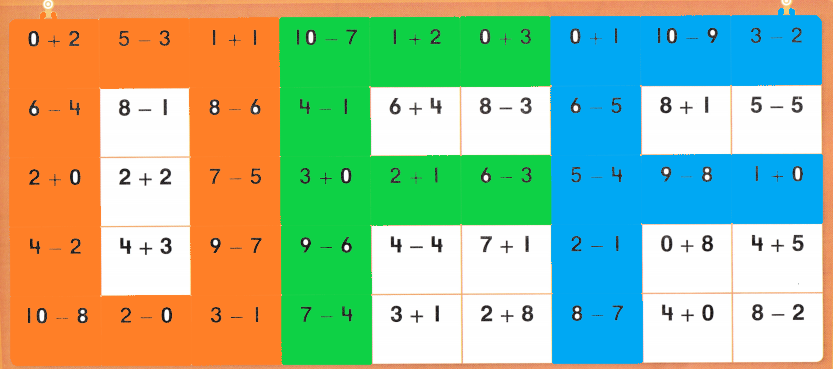
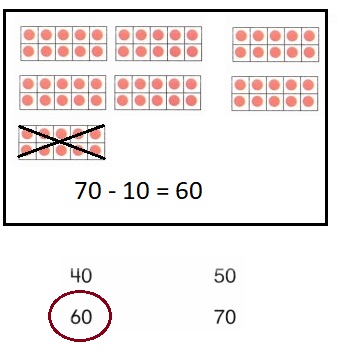
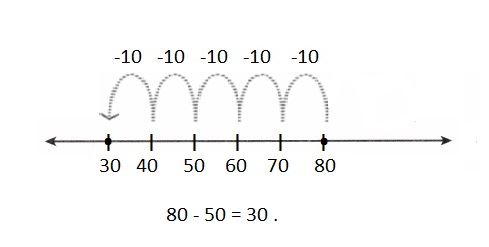
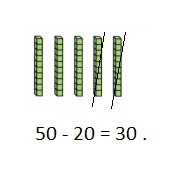
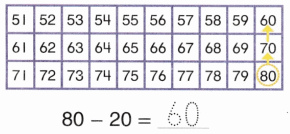
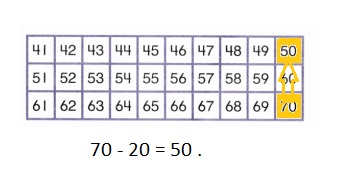
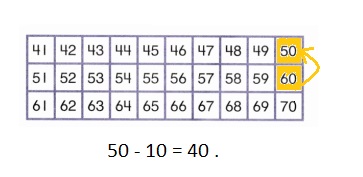
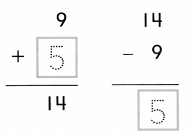
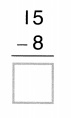
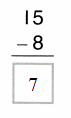
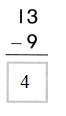
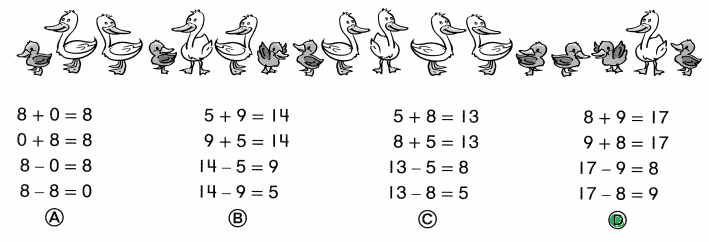
Color these sums and differences. Leave the rest white.
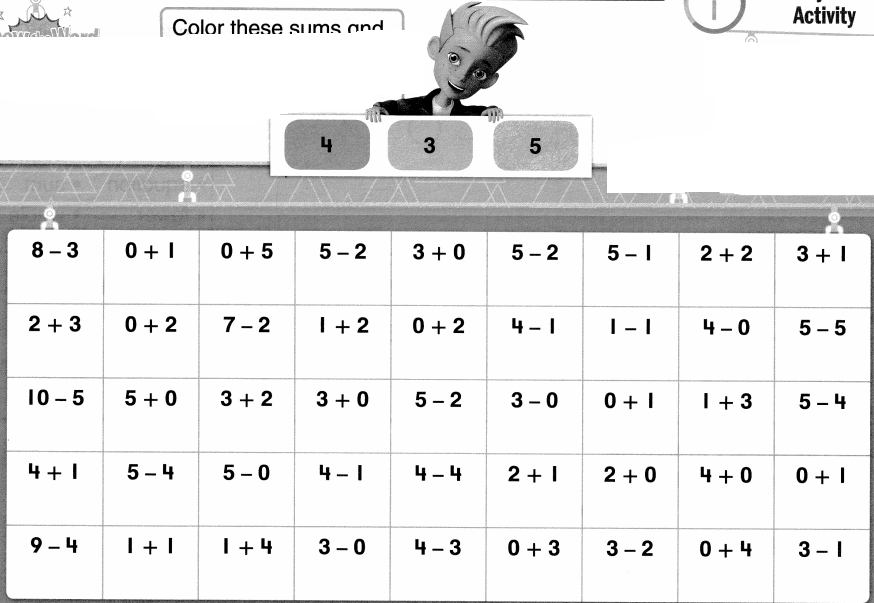
Answer:

Vocabulary Review
Understand Vocabulary
Question 1.
Write an addition equation

Answer:
Addition equation:
2 + 2 = 4.
Explanation:
Addition equation:
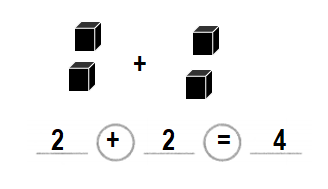
Question 2.
Write a subtraction equation.

Answer:
Subtraction equation:
8 – 3 = 5.
Explanation:
Subtraction equation:

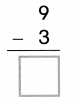
Question 3.
Circle the difference
8 – 2 = 6
Answer:
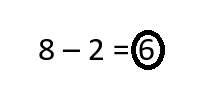
Explanation:
Difference:
8 – 2 = 6.
Question 4.
Circle one part.
5 + 3 = 8
Answer:
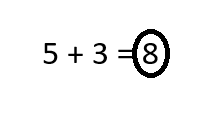
Explanation:
Addition Equation:
5 + 3 = 8.
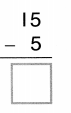
Question 5.
Circle the plus sign.
3 + 4 = 7
Answer:

Explanation:
Addition Equation:
3 + 4 = 7.
Use Vocabulary in Writing
Question 6.
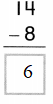
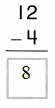
Tell how to find 8-4. Use at least one word from the Word List.
Answer:
Eight – Four = Four.
Explanation:
Eight – Four = Four.
8- 4 = 4 or Four.
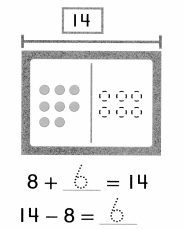
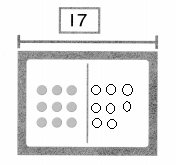
Set A
You can solve problems about adding to.
3 turtles
1 more joins.
How many turtles now?
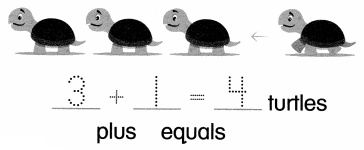
Answer:
Number of turtles now = 4 or Four.
Explanation:
Number of turtles = 3 or Three.
Number of turtles more joined = 1 or One.
Number of turtles now = Number of turtles + Number of turtles more joined
= 3 + 1
= 4 or Four.

Solve. Use cubes or draw a picture.
Question 1.
5 flowers
2 more flowers
How many flowers now?
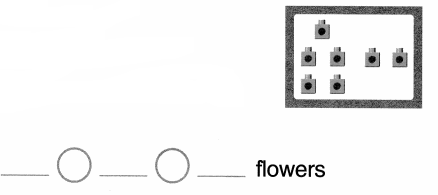
Answer:
Number of flowers now = 7 or Seven.
Explanation:
Number of flowers = 5 or Five.
Number of more flowers = 2 or Two.
Number of flowers now = Number of flowers + Number of more flowers
= 5 + 2
= 7 or Seven.
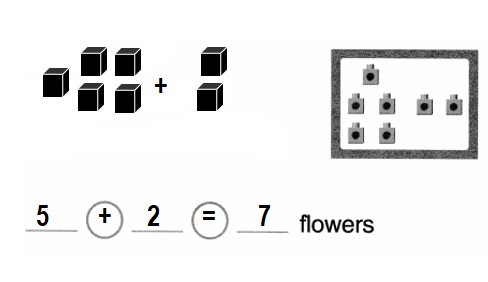
Set B
You can solve problems about putting together.
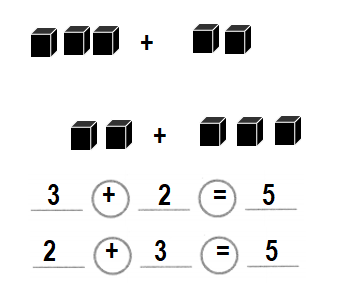
3 red markers and 2 blue markers How many markers in all?
Answer:
Number of markers in all = 5 or Five.
Explanation:
Number of red markers = 3 or Three.
Number of blue markers = 2 or Two.
Number of markers in all = Number of red markers + Number of blue markers
= 3 + 2
= 5 or Five.
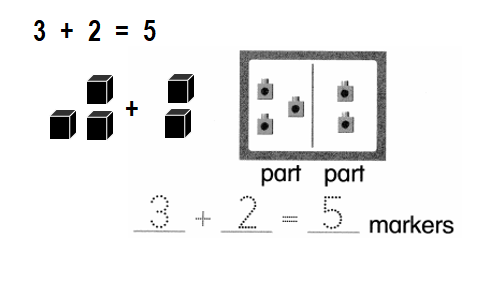
Solve. Use cubes or draw a picture.
Question 2.
4 red cars and 2 blue cars
How many cars in all?

Answer:
Number of cars in all = 6 or Six.
Explanation:
Number of red cars = 4 or Four.
Number of blue cars = 2 or Two.
Number of cars in all = Number of red cars + Number of blue cars
= 4 + 2
= 6 or Six.

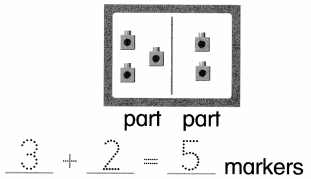
Set C
You can solve problems with both addends unknown.
7 penguins in all . Some are inside a cave. Some are outside. Here is one way.
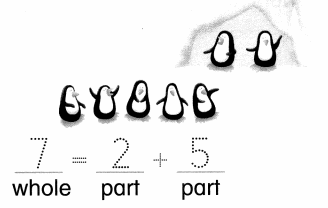
Use cubes or draw a picture. Write an equation to solve.
Answer:
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 5 + 2
= 7 or Seven.
Explanation:
Number of penguins inside the cave = 2 or Two.
Number of penguins outside the cave = 5 or Five.
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 2 + 5
= 7 or Seven.

Question 3.
6 penguins in all Some are inside. Some are outside. Show one way.

Answer:
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 2 + 4
= 6 or Six.
Explanation:
Number of penguins inside the cave = 2 or Two.
Number of penguins outside the cave = 4 or Four.
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
= 2 + 4
= 6 or Six.
Question 4.
9 penguins in all Some are inside. Some are outside. Show one way.
Answer:
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
=> 9 = 4 + 5
Number of penguins inside the cave = 4 or Four.
Number of penguins outside the cave = 5 or Five.
Explanation:
Number of penguins in all = 9 or Nine.
Number of penguins inside the cave = 4 or Four.
Number of penguins outside the cave = 5 or Five.
Number of penguins in all = Number of penguins inside the cave + Number of penguins outside the cave
=> 9 = 4 + 5

Set D
You can solve problems about taking from.
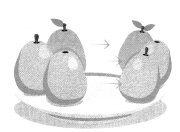
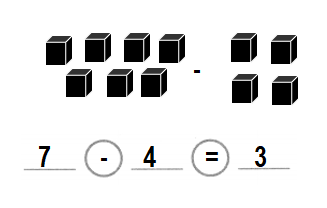
There are 6 pears. Mia takes 3 pears away. How many pears are left?

Answer:
Number of pears are left = 3 or Three.
Explanation:
Number of pears in all = 6 or Six.
Number of pears Mia takes away = 3 or Three.
Number of pears are left = Number of pears in all – Number of pears Mia takes away
= 6 – 3
= 3 or Three.

Use cubes or draw a picture. Write an equation and solve.
Question 5.
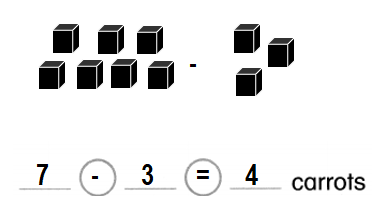
There are 7 carrots.
3 carrots are picked.
How many carrots are left?

Answer:
Number of carrots are left = 4 or Four.
Explanation:
Number of carrots in all = 7 or Seven.
Number of carrots picked away = 3 or Three.
Number of carrots are left = Number of carrots in all – Number of carrots picked away
= 7 – 3
= 4 or Four.
Set E
You can solve problems about comparing.
4 blue pens
3 yellow pens
How many more blue pens than yellow pens are there?
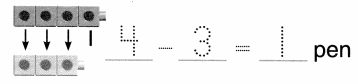
Answer:
There are 1 more blue pens than yellow pens.
Explanation:
Number of yellow pens = 3 or Three.
Number of blue pens = 4 or Four.
Difference = Number of blue pens – Number of yellow pens
= 4 – 3
= 1 or One.
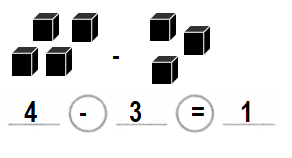
Use cubes or draw a picture. Write an equation and solve.
Question 6.
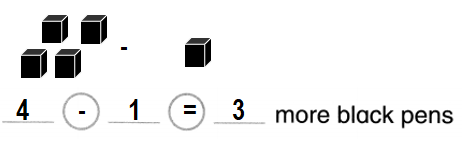
4 black pens and I red pen
How many more black pens than red pens?

Answer:
There are 3 more black pens than red pens.
Explanation:
Number of black pens = 4 or Four.
Number of red pens = 1 or One.
Difference = Number of black pens – Number of red pens
= 4 – 1
= 3 or Three.
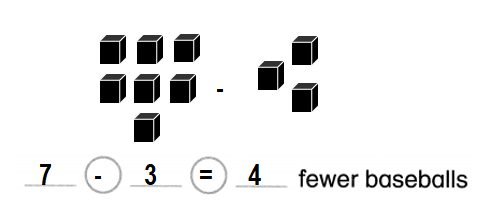
Question 7.
3 baseballs and 7 soccer balls
How many fewer baseballs than soccer balls?
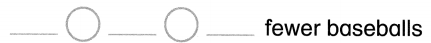
Answer:
4 fewer baseballs than soccer balls.
Explanation:
Number of baseballs = 3 or Three.
Number of soccer balls = 7 or Seven.
Difference = Number of soccer balls – Number of baseballs
= 7 – 3
= 4 or Four.
Set F
You can find a missing addend to solve problems.
Ty has 4 grapes.
He takes some more grapes.
Now he has 9 grapes
How many grapes did Ty take?
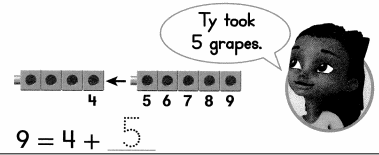
Use cubes or draw a picture. Write an equation and solve.
Answer:
Number of grapes ty takes more = 5 or Five.
Explanation:
Number of grapes ty has = 4 or Four.
Total number of grapes ty has = 9 or Nine.
Number of grapes ty takes more = Total number of grapes ty has – Number of grapes ty has
= 9 – 4
= 5 or Five.

Question 8.
Ivy has 2 fish in a bowl. She adds some more fish. Now Ivy has 5 fish. How many fish did she add?

Answer:
Number of fishes Ivy has added = 3 or Three.
Explanation:
Number of fishes Ivy has in a bowl = 2 or Two.
Total number of fishes Ivy has in a bowl = 5 or Five.
Number of fishes Ivy has added = Total number of fishes Ivy has in a bowl – Number of fishes Ivy has in a bowl
= 5 – 2
= 3 or Three.
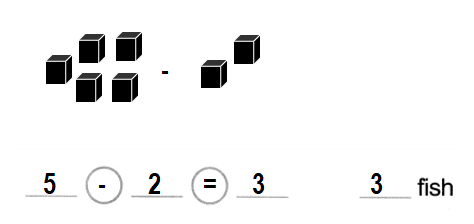
Set G
You can add or subtract to find a missing part.
Tom has 9 shirts.
He has 4 red shirts.
The rest are blue.
How many blue shirts does Tom have?
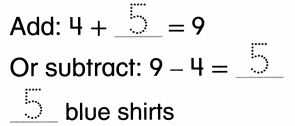
Use cubes or draw a picture. Write an equation and solve.
Answer:
Number of blue shirts Tom has = Total number of shirts Tom has -Number of red shirts Tom has
= 9 – 4
= 5 or Five.
Explanation:
Total number of shirts Tom has = 9 or Nine.
Number of red shirts Tom has = 4 or Four.
Number of blue shirts Tom has = Total number of shirts Tom has -Number of red shirts Tom has
= 9 – 4
= 5 or Five.
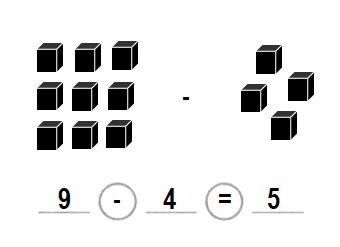
Question 9.
Gigi has 8 pairs of shoes. 4 pairs are tennis shoes. The rest are sandals. How many pairs are sandals?

Answer:
Number of pair of sandals Gigi has = 4 or Four.
Explanation:
Total number of pairs of shoes Gigi has = 8 or Eight.
Number of pairs of tennis shoes Gigi has = 4 or Four.
Number of pair of sandals Gigi has = Total number of pairs of shoes Gigi has – Number of pairs of tennis shoes Gigi has
= 8 – 4
= 4 or Four.
Set H
Thinking Habits
Construct Arguments
How can I use math to explain my work?
Is my explanation clear?

Answer:
You can use math in easy and simplify the calculations of the problem to explain your work.
Yes, your explanation is clear and easy.
Explanation:
Using math helps in making easy calculations and understand to solve the problem in an easy way.
Solve. Use pictures, numbers, or words to explain.
Question 10.
Luc has 8 fish.
He gives away 4 fish.
How many fish does Luc have left?
Answer:
Number of fishes Luc has left = 4 or Four.
Explanation:
Total number of fishes Luc has = 8 or Eight.
Number of fishes Luc gives away = 4 or Four.
Number of fishes Luc has left = Total number of fishes Luc has – Number of fishes Luc gives away
= 8 – 4
= 4 or Four.
Topic 1 Assessment Practice
Question 1.
There are 8 penguins.
Some go inside the cave.
Some stay outside.
Match the number of penguins inside the cave with the number of penguins outside.

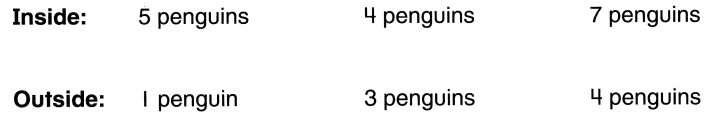
Answer:
Number of penguins inside the cave = 4 or Four.
Number of penguins inside the cave = 5 or Five.
Explanation:
Total number of penguins = 8 or Eight.
Total number of penguins = Number of penguins inside the cave + Number of penguins outside the cave
=> 8 = ?? + ??
=> 8 = 4 + 5

Question 2.
Sage had 10 peppers. She cooks 3 of them. How many peppers are left?
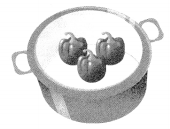
Write a subtraction equation to solve.
Answer:
Number of peppers left = 7 or Seven.
Explanation:
Number of peppers Sage had = 10 or Ten.
Number of peppers Sage had cooked = 3 or Three.
Number of peppers left = Number of peppers Sage had – Number of peppers Sage had cooked
= 10 – 3
= 7 or Seven.
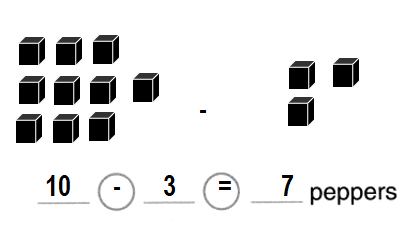
Question 3.
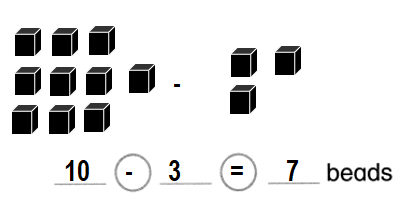
Sara has 5 green beads and 3 red beads. How many beads does she have in all?

Write an addition equation to solve.

Answer:
Total number of beads Sara has in all = 7 or Seven.
Explanation:
Number of beads Sara has = 10 or Ten.
Number of beads Sara has = 3 or Three.
Total number of beads Sara has in all = Number of beads Sara has – Number of beads Sara has
= 10 – 3
= 7 or Seven.
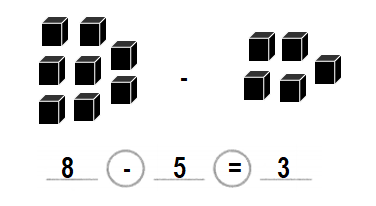
Question 4.
Trina has 8 markers. Then she gives 5 markers to David.

Which equation shows how many markers Trina has left?
A. 7 – 2 = 5
B. 7 – 3 = 4
C. 8 – 5 = 3
D. 9 – 3 = 6
Answer:
Number of markers Trina has left = 3 or Three.
C. 8 – 5 = 3
Explanation:
Total number of markers Trina has = 8 or Eight.
Number of markers given to David = 5 or Five.
Number of markers Trina has left =Total number of markers Trina has – Number of markers given to David
= 8 – 5
= 3 or Three.
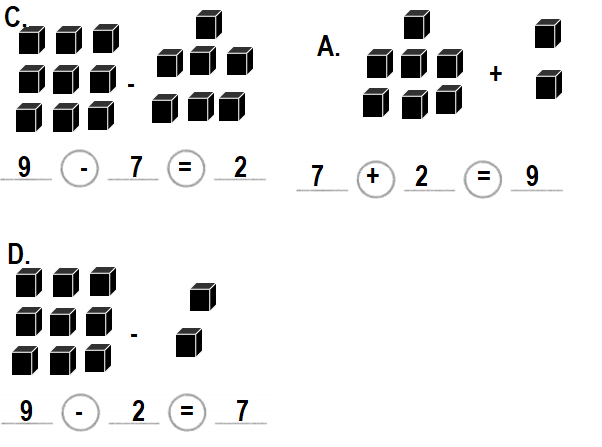
Question 5.
George had 7 postcards. Then he gets some more. Now he has 9 postcards.

Which equation does NOT describe the story?
A. 7 + 2 = 9
B. 6 + 3 = 9
C. 9 – 7 = 2
D. 9 – 2 = 7
Answer:
B. 6 + 3 = 9 does NOT describe the story.
Explanation:
Number of postcards George had = 7 or Seven.
Total number of postcards now he has = 9 or Nine.
Equation: A:
Number of postcards George had + Number of postcards George gets more = Total number of postcards now he has
=> 7 + 2
= 9 or Nine.
Equation: C:
Number of postcards George gets more = Total number of postcards now he has – Number of postcards George had
= 9 – 7
= 2 or Two.
Equation: D:
Total number of postcards now he has – Number of postcards George gets more = Number of postcards George had
= 9 – 2
= 7 or Seven.
Question 6.
Dante has 5 books. He wants to have 7 books. How many more books does Dante need to have 7 in all?
Answer:
Number of books he needs more to have 7 in all = 2 or Two.

Explanation:
Number of books Dante has = 5 or Five.
Number of books he want to have = 7 or Seven.
Number of books he needs more to have 7 in all = Number of books he want to have – Number of books Dante has
= 7 – 5
= 2 or Two.
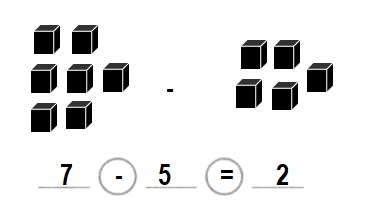
Question 7.
Lucy and Ellie have 6 cubes in all.
Ellie has 5 cubes.

How many cubes does Lucy have?
Choose three equations that show the story.
Answer:
Number of cubes Lucy has = 1 or one.
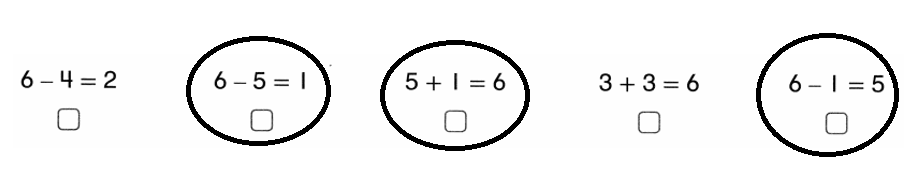
Explanation:
Equation:1:
Number of cubes Lucy and Ellie have in all = 6 or Six.
Number of cubes Ellie has = 5 or Five.
Number of cubes Lucy has = Number of cubes Lucy and Ellie have in all – Number of cubes Ellie has
= 6 – 5
= 1 or one.
Equation:2:
Number of cubes Lucy and Ellie have in all + Number of cubes Lucy has = Number of cubes Lucy and Ellie have in all
= 5 + 1
= 6 or Six.
Equation:3:
Number of cubes Lucy and Ellie have in all – Number of cubes Ellie has = Number of cubes Lucy has
= 6-1
= 5 or Five.
Question 8.
Trina has 6 ribbons. Julie has 2 ribbons. What could happen for them to have the same number of ribbons?
A. Julie gives I of her ribbons to Trina.
B. Trina gives I of her ribbons to Julie.
C. Trina gives 2 of her ribbons to Julie.
D. Trina gives 4 of her ribbons to Julie.

Answer:
Number of ribbons them to have the same number = 4 or Four.
D. Trina gives 4 of her ribbons to Julie.
Explanation:
Number of ribbons Trina has = 6 or Six.
Number of ribbons Julie has = 2 or Two.
Number of ribbons them to have the same number = Number of ribbons Trina has – Number of ribbons Julie has
= 6 – 2
= 4 or Four.
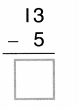
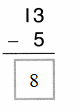
Question 9.
Draw the missing cubes on the mat.
Then write a subtraction equation that shows the story.
Owen has 5 blocks. He gives I to Jordan.
How many blocks does Owen have left?
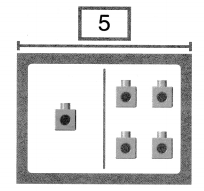
Answer:
Number of blocks Owen have left = 4 or Four.
Explanation:
Number of blocks Owen has = 5 or Five.
Number of blocks Own gives to Jordan = 1 or One.
Number of blocks Owen have left = Number of blocks Owen has – Number of blocks Own gives to Jordan
= 5 – 1
= 4 or Four.
Question 10.
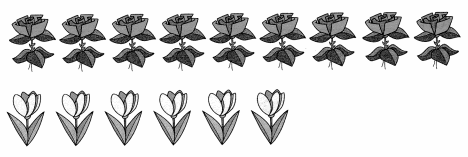
Hannah has 9 flowers. Carrie has 6 flowers. Which equation shows how many fewer flowers Carrie has than Hannah?

Answer:
Number of fewer flowers Carrie has than Hannah = 3 or Three.

Explanation:
Number of flowers Hannah has = 9 or Nine.
Number of flowers Carrie has = 6 or Six.
Number of fewer flowers Carrie has than Hannah = Number of flowers Hannah has – Number of flowers Carrie has
= 9 – 6
= 3 or Three.
Question 11.
Laura has 7 pears.
She wants to keep 2 pears for herself and give one to each of 6 friends.
Will Laura have enough pears?
Use pictures and words to explain.
Answer:
Laura is not having enough pears to give to her friends.
Number of pears left with her are five, which are less to give to her 6 friends each.
Explanation:
Total number of pears Laura has = 7 or Seven.
Number of pears She wants to keep for herself = 2 or Two.
Number of pears left = Total number of pears Laura has – Number of pears She wants to keep for herself
= 7 or 2
= 5 or Five.
Number of pears She give one to each of 6 friends.
=> Number of pears required to be with her to give to her friends = 1 × 6
=> 6 or Six.
Number of pears left with her are 5, which are less to give to her friends.
Therefore, Laura does not have enough pears to give to her friends.

Question 12.
Nikki has 8 tennis balls. Thomas has 6 tennis balls. Which equation shows how many more tennis Nikki has than Thomas?

Answer:
Number of more tennis balls Nikki has than Thomas = 2 or Two.
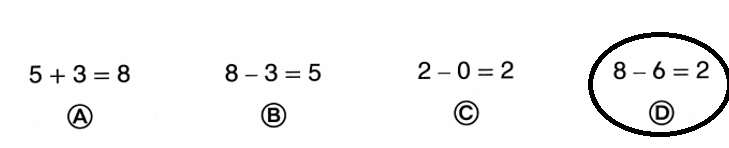
Explanation:
Number of tennis balls Nikki has = 8 or Eight
Number of tennis balls Thomas has = 6 or Six.
Number of more tennis balls Nikki has than Thomas = Number of tennis balls Nikki has – Number of tennis balls Thomas has
= 8 – 6
= 2 or Two.

Topic 1 Assessment Practice
Skating Ribbons
Marta is an ice skater.
She wins ribbons for her skating.

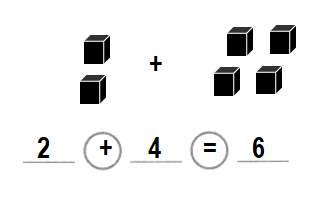
Question 1.
Marta wins 2 blue ribbons. She wins 4 red ribbons.
How many ribbons does she win in all?
____ ribbons
Answer:
Number of ribbons Marta wins in all = 6 or Six.
_6__ ribbons.
Explanation:
Number of blue ribbons Marta wins = 2 or Two.
Number of red ribbons Marta wins = 4 or Four.
Number of ribbons Marta wins in all = Number of blue ribbons Marta wins + Number of red ribbons Marta wins
= 2 + 4
= 6 or Six.
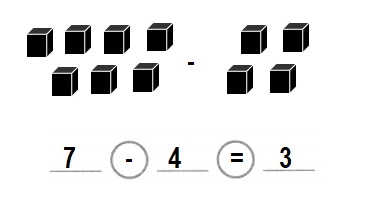
Question 2.
Marta has 4 red ribbons.
She wins some more red ribbons.
Now she has 7 red ribbons.
How many more red ribbons did Marta win? ___ more red ribbons
Write an equation to show why your answer is correct.
Answer:
3 more red ribbons Marta wins.
_3__ more red ribbons.
Explanation:
Number of red ribbons Marta has = 4 or Four.
Total number of red ribbons Marta has now = 7 or Seven.
Number of red ribbons Marta wins more = Total number of red ribbons Marta has now – Number of red ribbons Marta has
= 7 – 4
= 3 or Three.
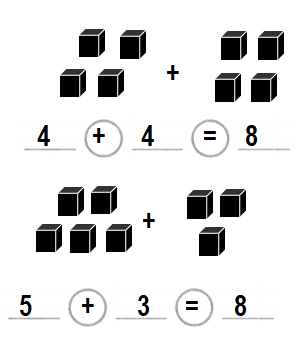
Question 3.
Marta has 8 yellow ribbons. She put some on her door. She puts the rest on her wall.

Write two different addition equations to show two ways she can put the ribbons on her door or on her wall.
Answer:
Equation:1:
Number of yellow ribbons She puts on her door = 4 or Four.
Number of yellow ribbons She puts on her wall = 4 or Four.
Equation:2:
Number of yellow ribbons She puts on her door = 5 or Five.
Number of yellow ribbons She puts on her wall = 3 or Three.
Explanation:
Equation:1:
Number of yellow ribbons Marta has = 8 or Eight.
Number of yellow ribbons Marta has = Number of yellow ribbons She puts on her door + Number of yellow ribbons She puts on her wall
= 4+ 4
= 8 or Eight.
Equation:2:
Number of yellow ribbons Marta has = 8 or Eight.
Number of yellow ribbons Marta has = Number of yellow ribbons She puts on her door + Number of yellow ribbons She puts on her wall
= 5 + 3
= 8 or Eight.
Question 4.
Marta has 8 yellow ribbons.
She has 2 blue ribbons.
How many more yellow ribbons than blue ribbons does Marta have?
___ more yellow ribbons
Answer:
6 more yellow ribbons than blue ribbons Marta has.
_6__ more yellow ribbons.
Explanation:
Number of yellow ribbons Marta has = 8 or Eight.
Number of blue ribbons Marta has = 2 or Two.
Difference = Number of yellow ribbons Marta has – Number of blue ribbons Marta has
= 8 – 2
= 6 or Six.
Question 5.
Explain why your answer to item 4 is correct. Use numbers, pictures, or words.
Answer:
My answer is correct to item 4 because:
Difference of more yellow ribbons than blue ribbons Marta has + Number of blue ribbons Marta has
=> 6 + 2
=> 8 = Number of yellow ribbons Marta has.
Explanation:
My answer is correct to item 4 because:
Difference of more yellow ribbons than blue ribbons Marta has + Number of blue ribbons Marta has
=> 6 + 2
=> 8 = Number of yellow ribbons Marta has.





































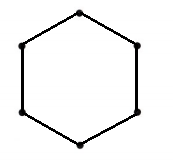
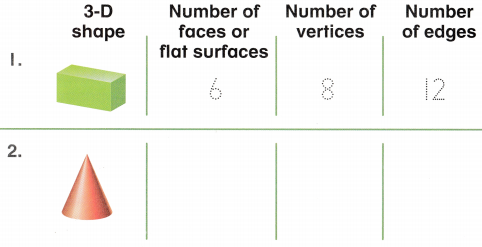
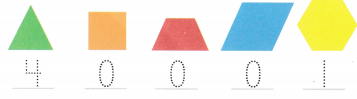
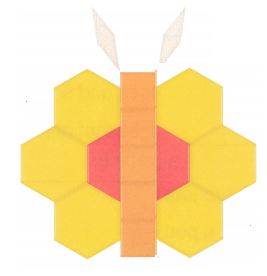
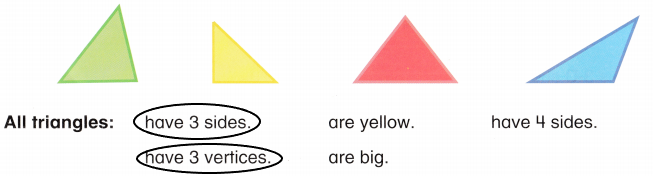
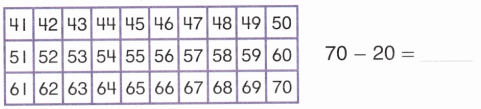
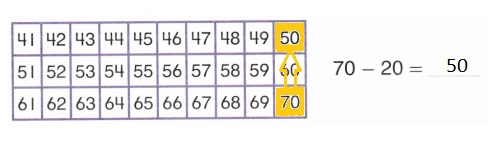
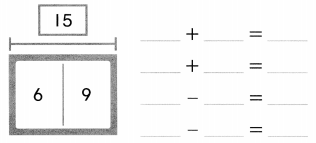
 . Write how many of each shape you use. Then add the three numbers to find how many pieces in all. See if you can make the hexagon with less than 15 pieces in all!
. Write how many of each shape you use. Then add the three numbers to find how many pieces in all. See if you can make the hexagon with less than 15 pieces in all!



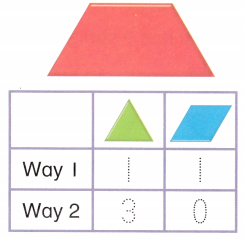
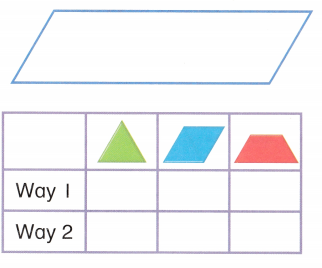
 to make a
to make a  . Draw the
. Draw the  ?
? ?
?

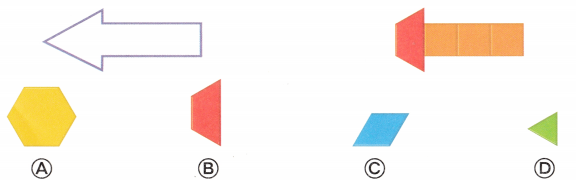
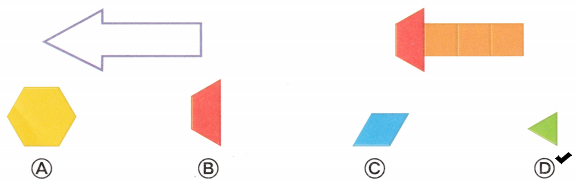
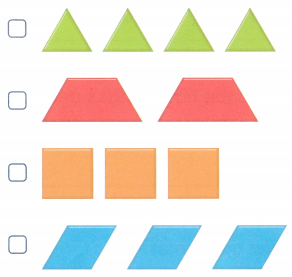
 Which set of other shapes could she use to complete the
Which set of other shapes could she use to complete the 


















































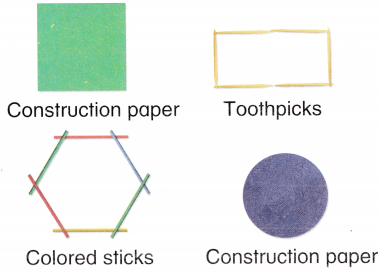











 .
.










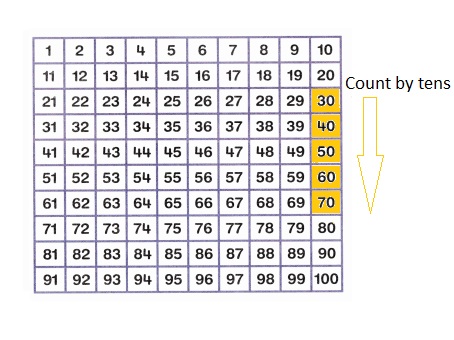







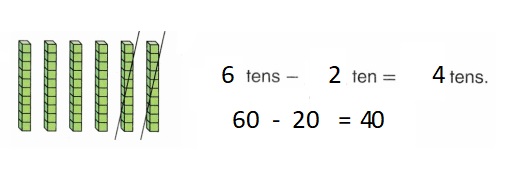
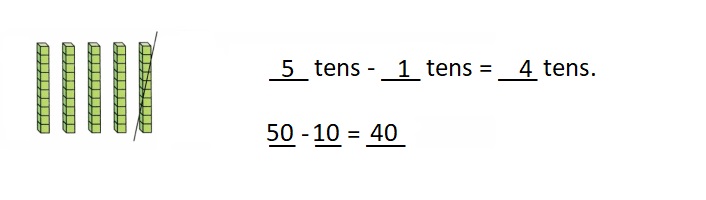



























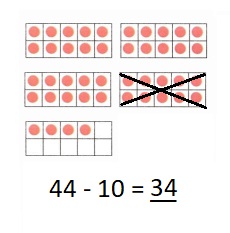
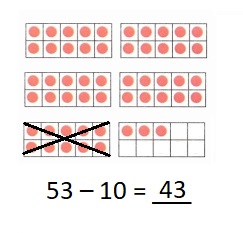

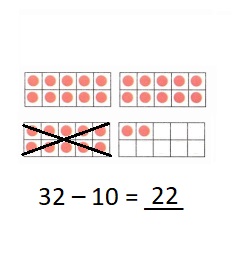
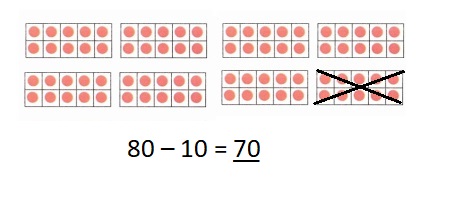

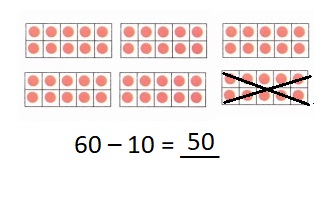
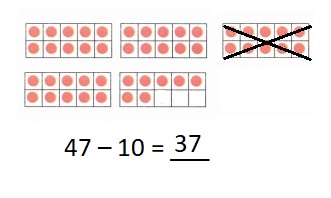
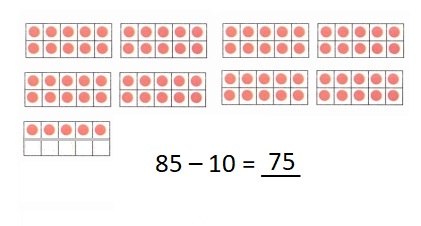
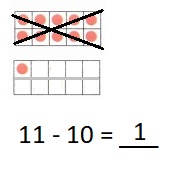
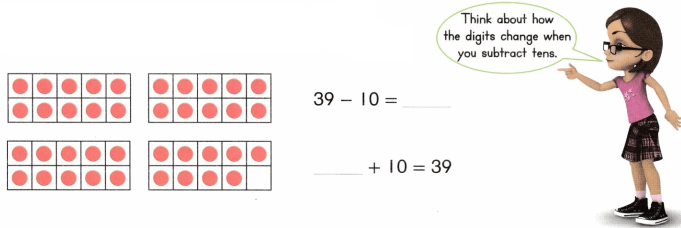
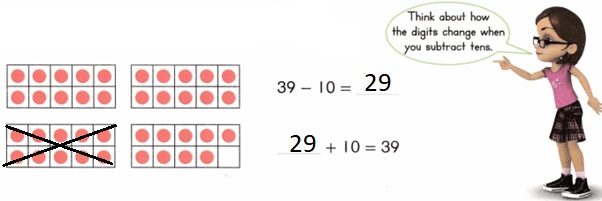

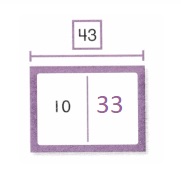


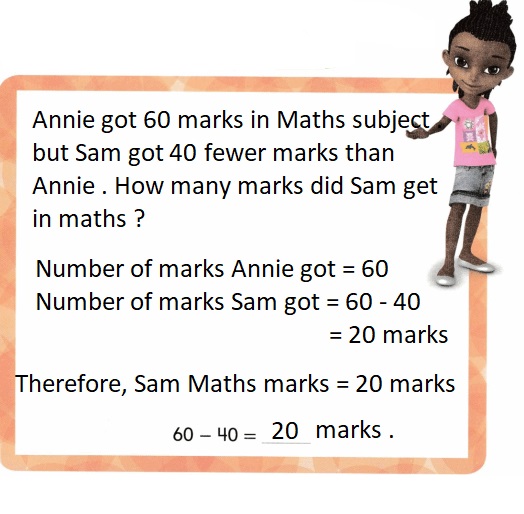
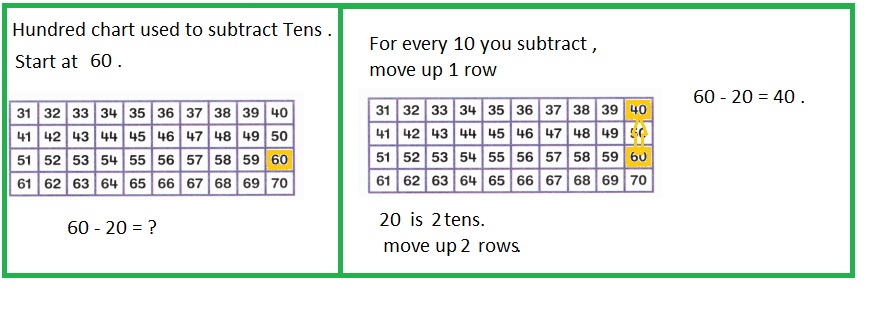
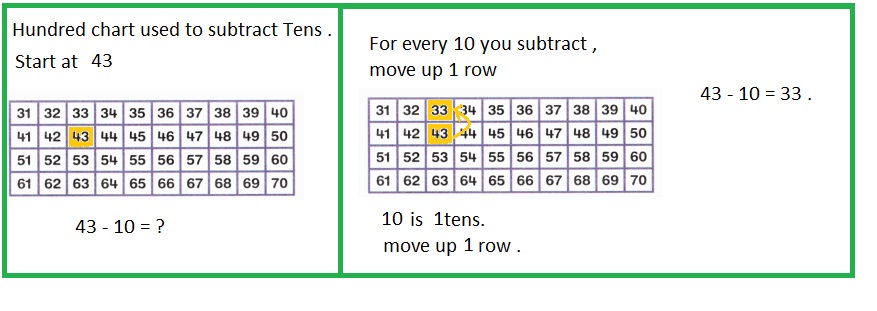
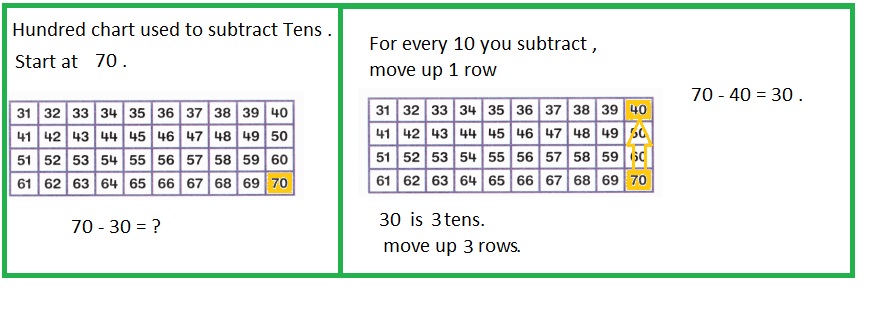
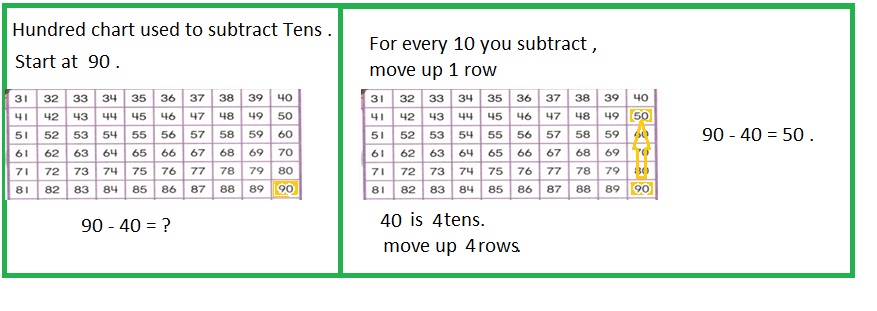





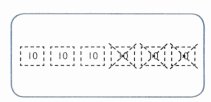
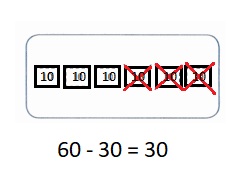

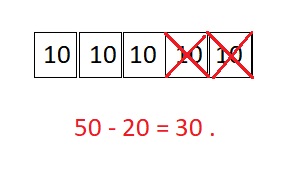



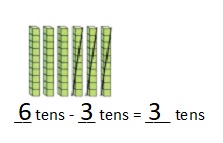

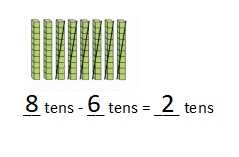

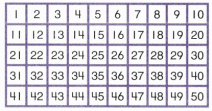
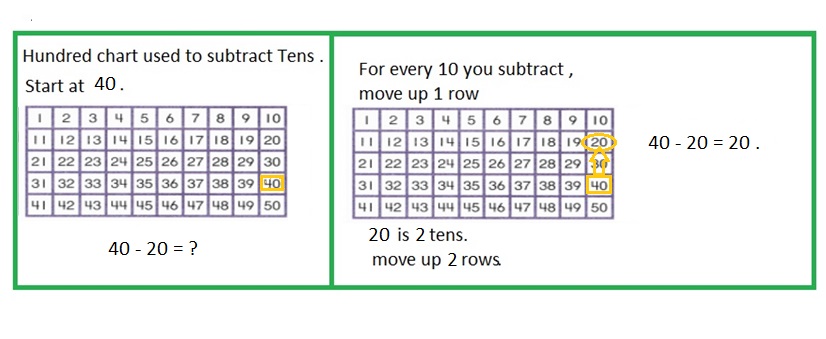



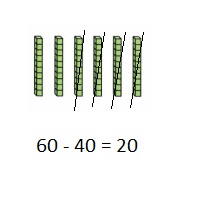



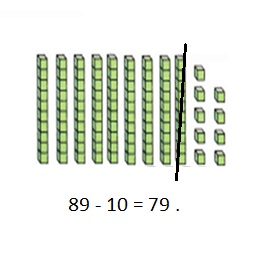




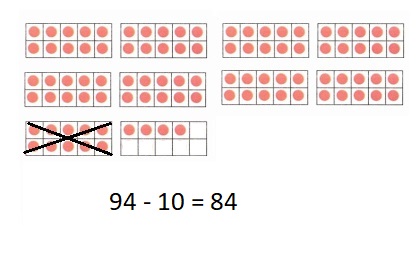
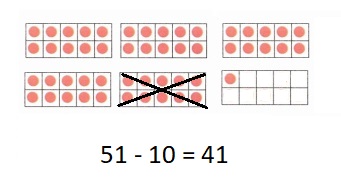
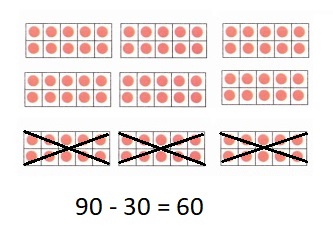















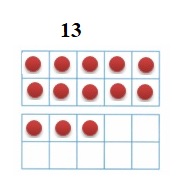
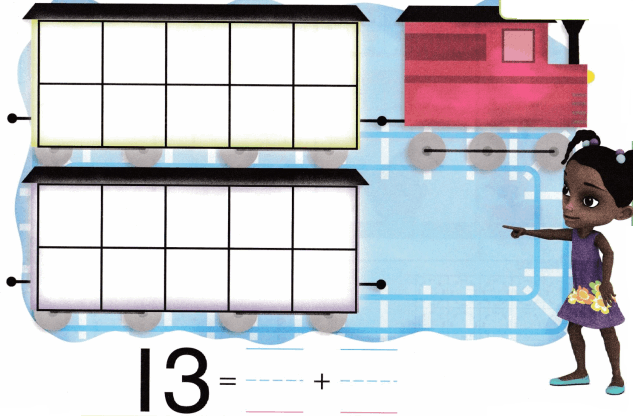
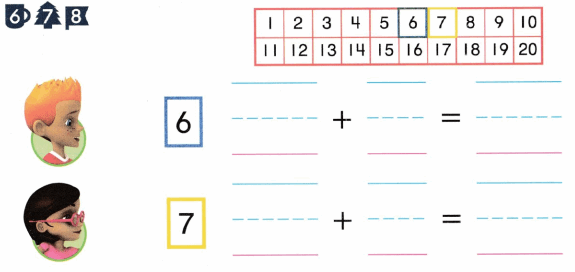
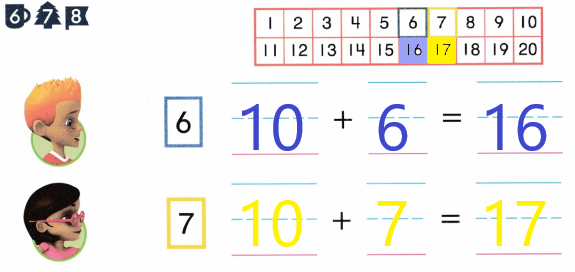
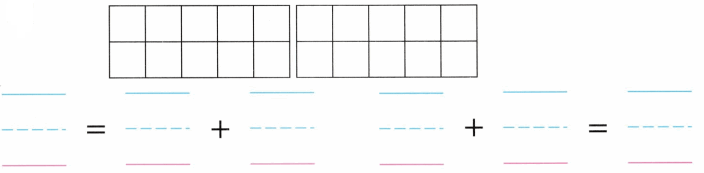
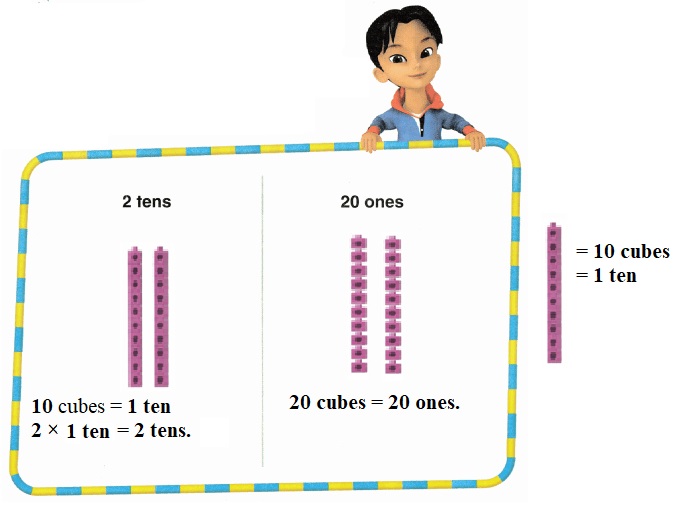
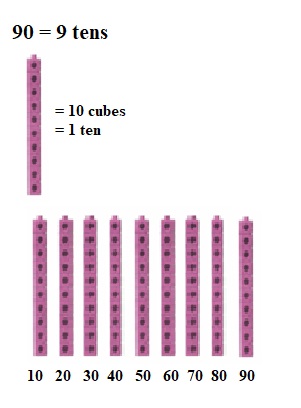
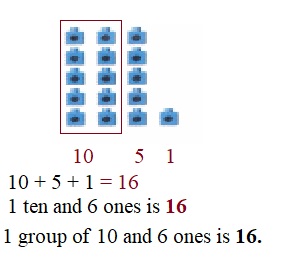
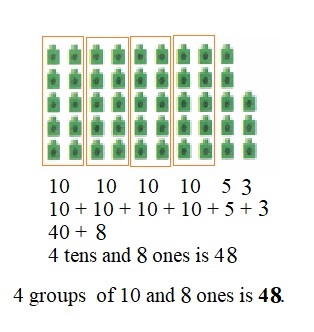
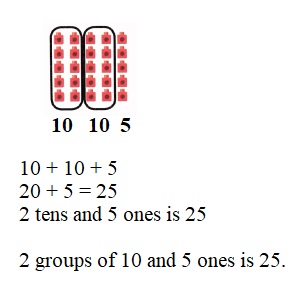
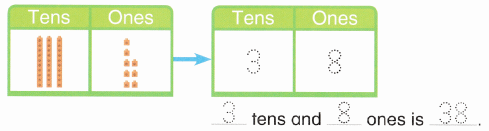
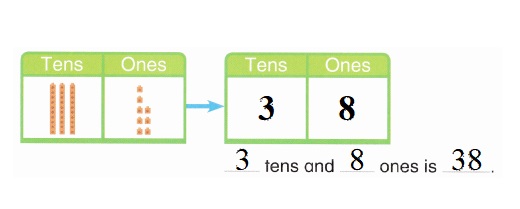
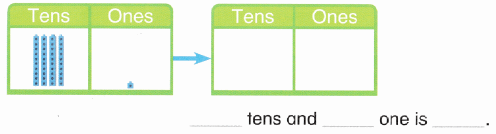
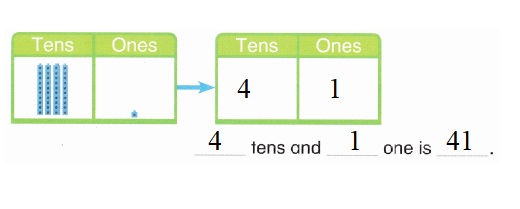
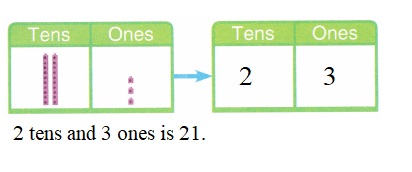
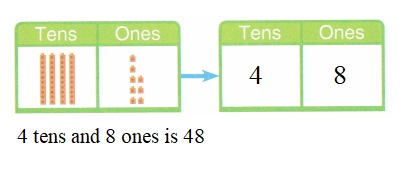
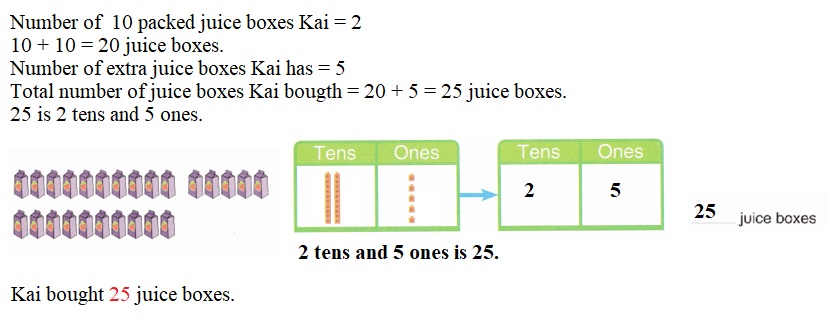
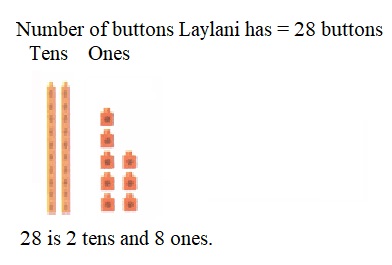
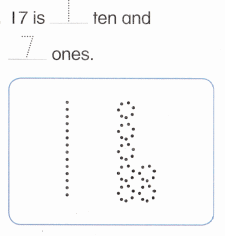
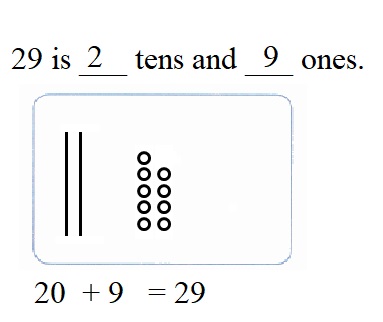
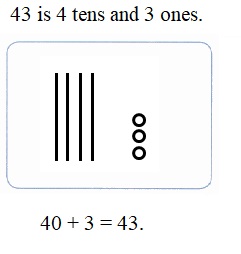
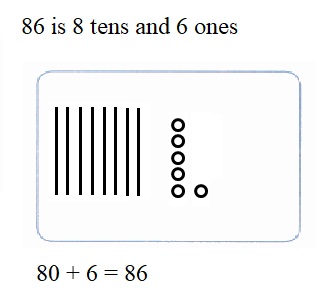
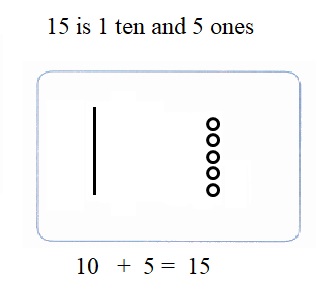
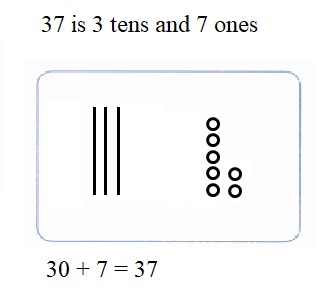
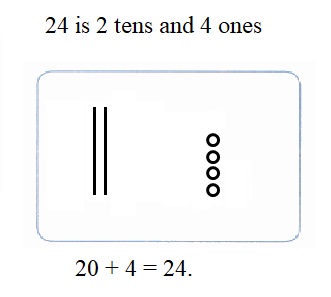
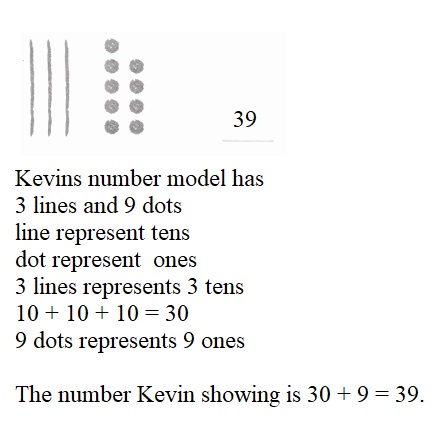
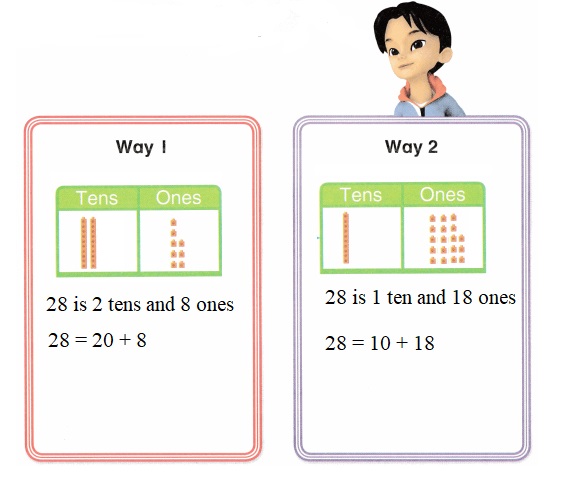
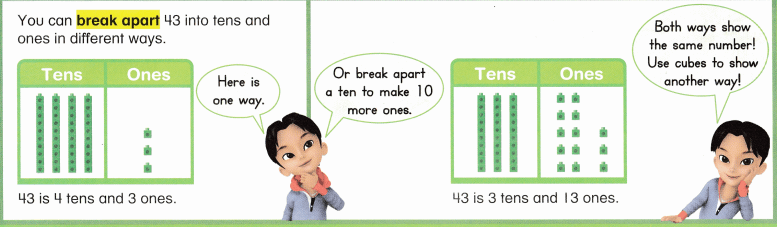
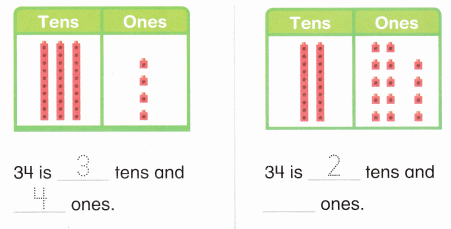
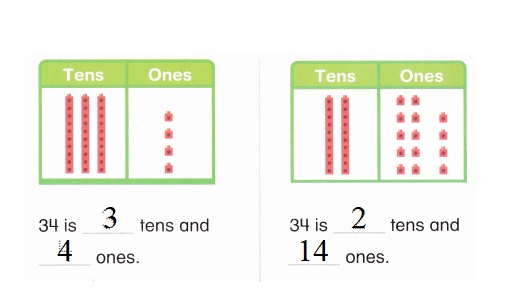
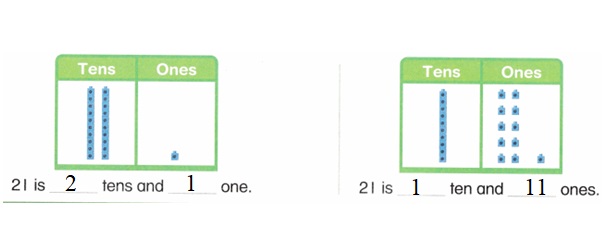
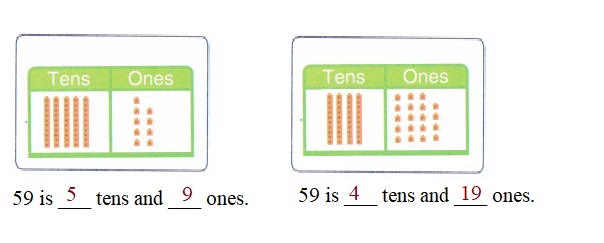
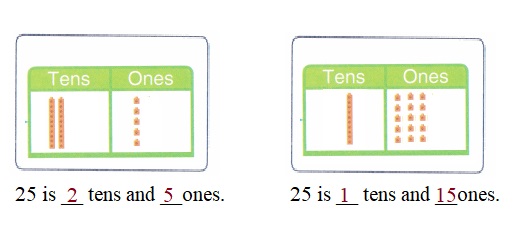
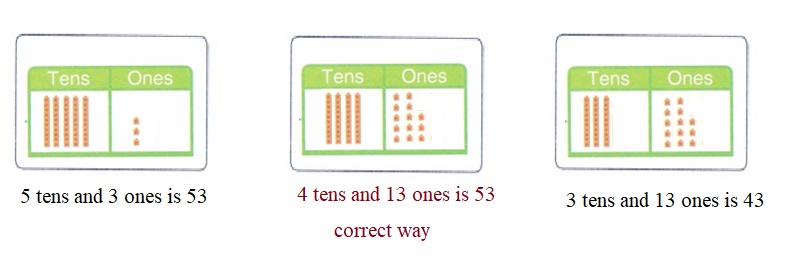
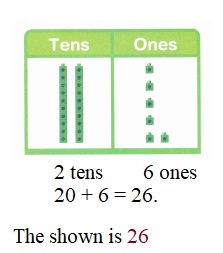
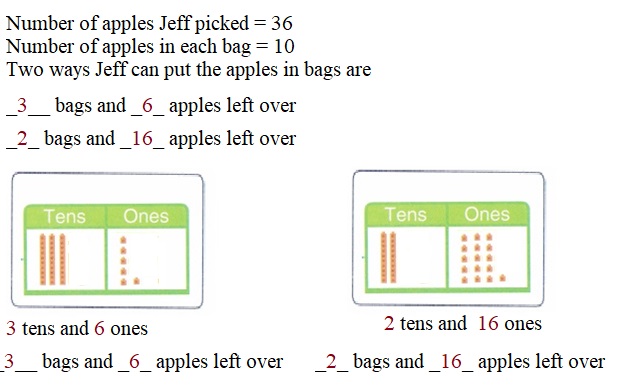
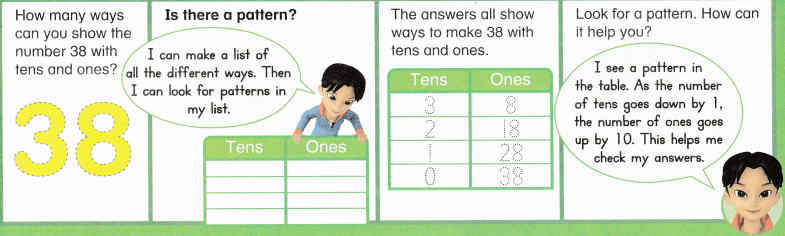
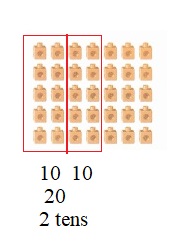
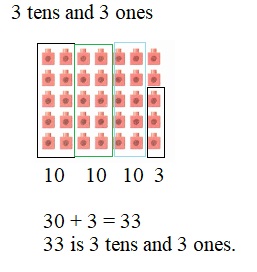
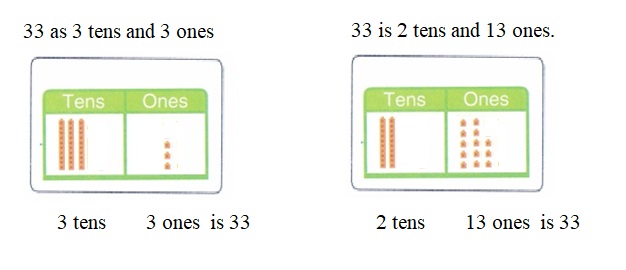
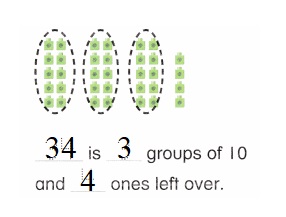
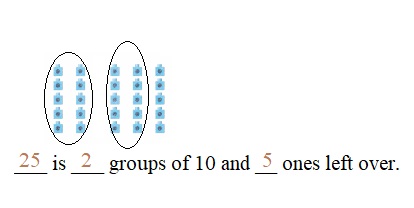
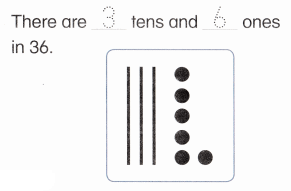
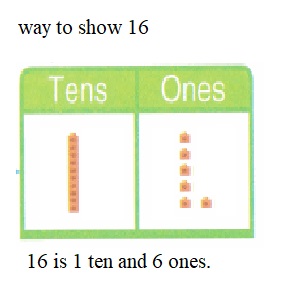
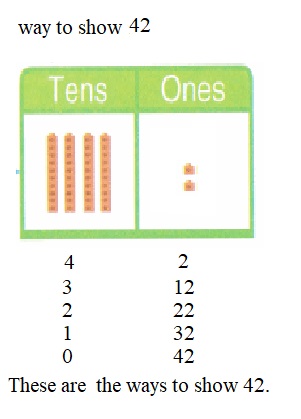
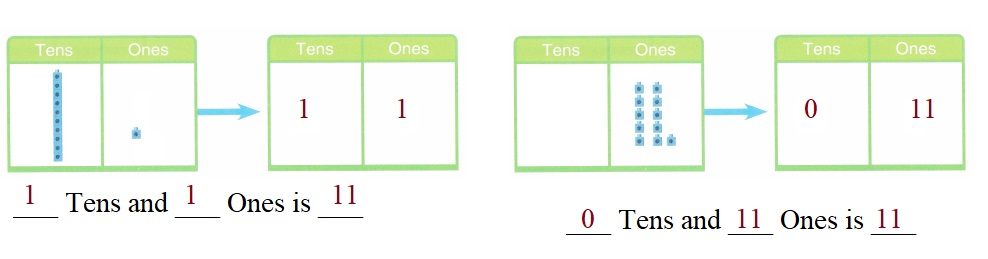
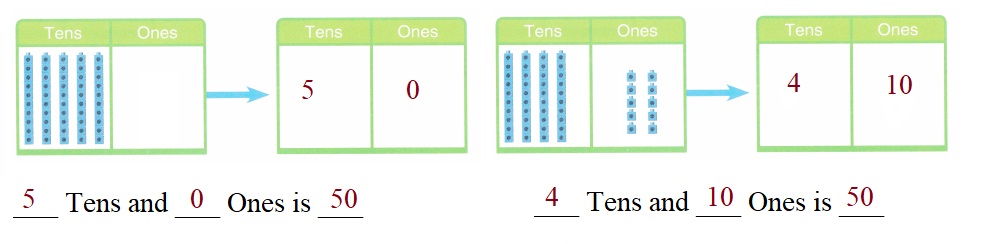
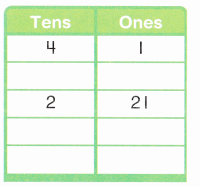
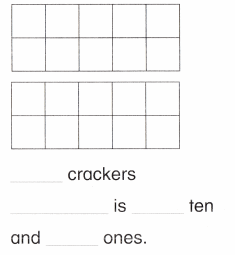
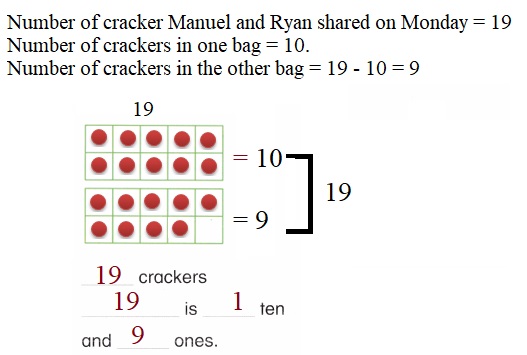
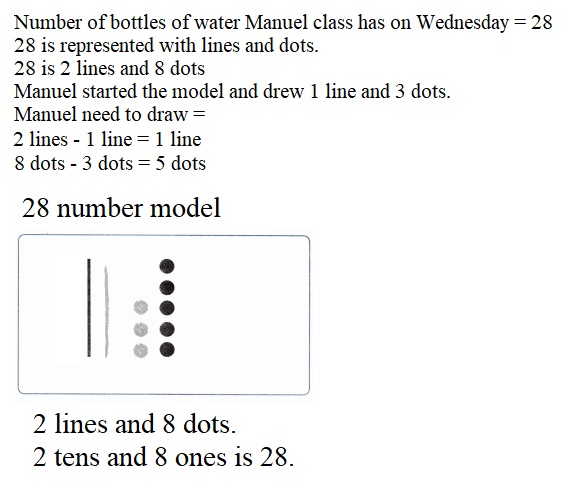
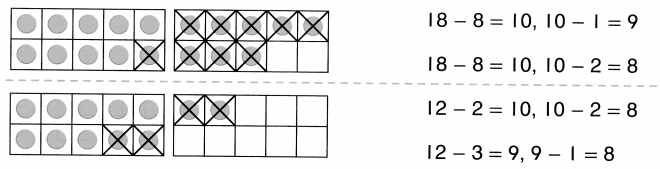
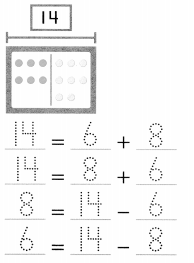
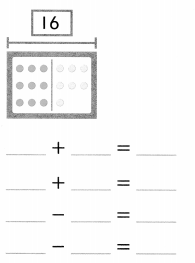
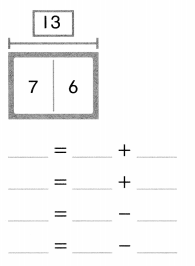
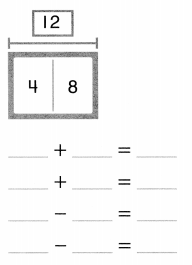
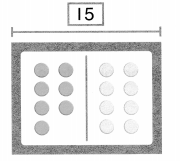
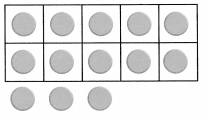
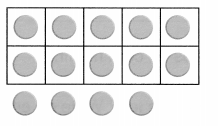
 is 1 ten and
is 1 ten and 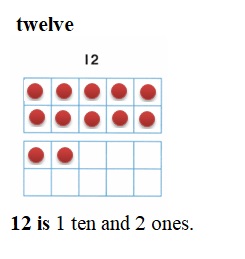
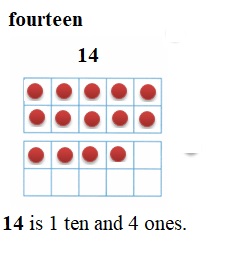
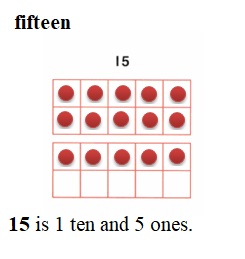
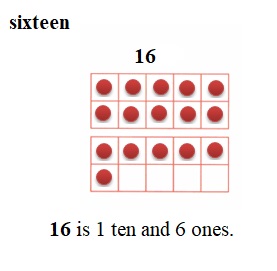
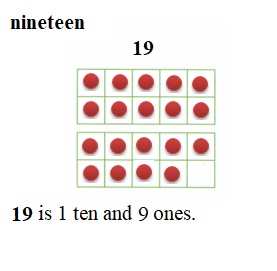
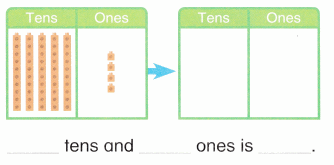
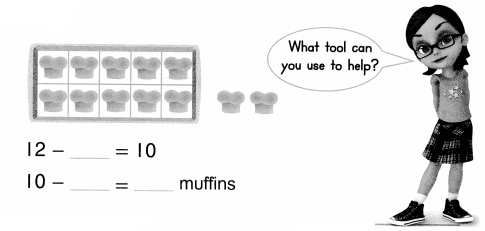
 is 1 ten and __ ones.
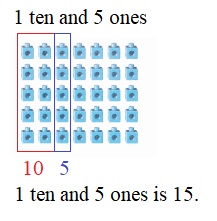
is 1 ten and __ ones.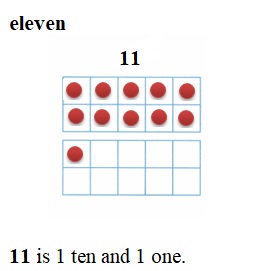
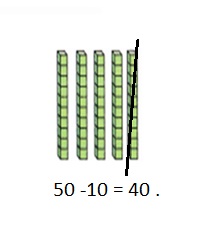
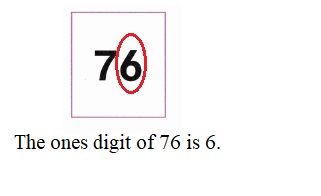
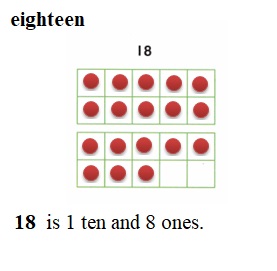
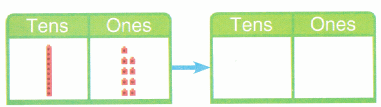
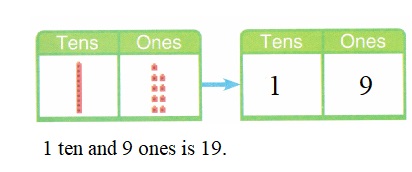
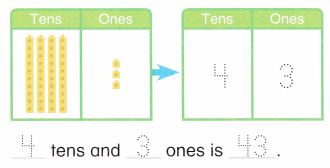
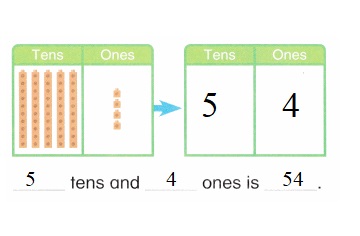
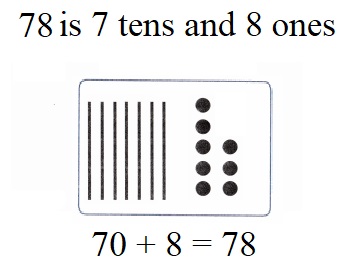
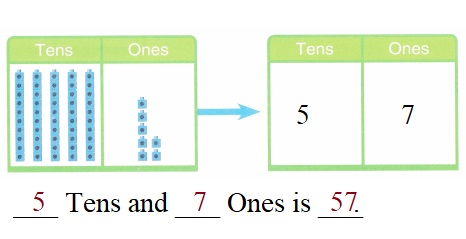
 is 1 and 7 ones.
is 1 and 7 ones.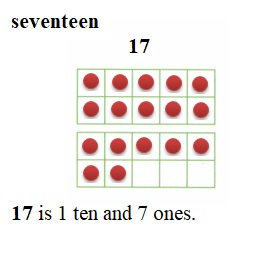



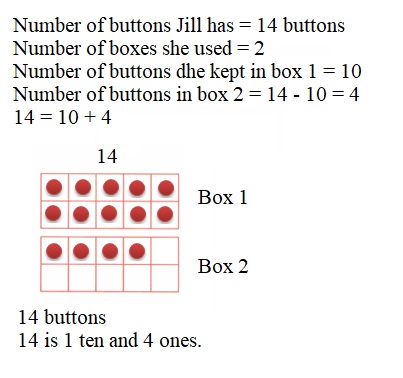



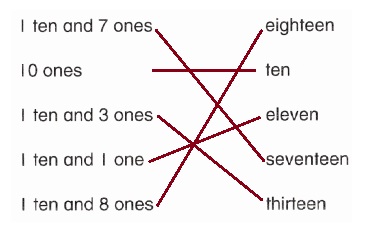

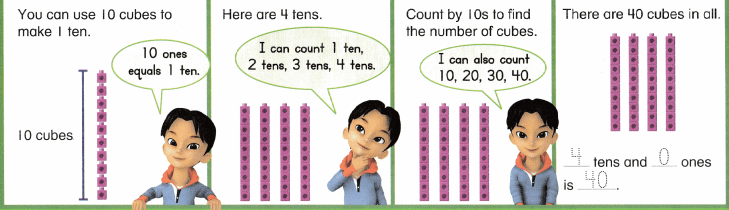



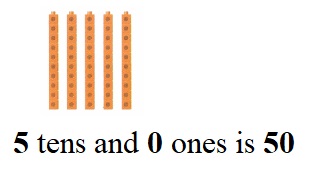










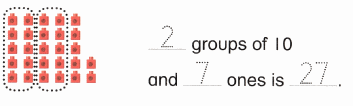
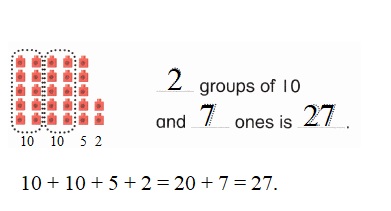
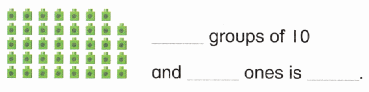
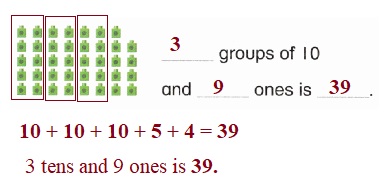

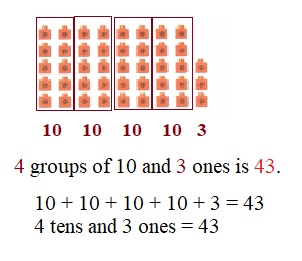

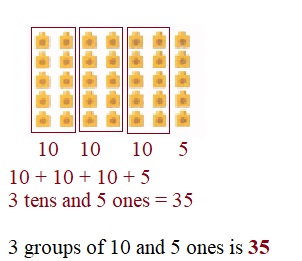





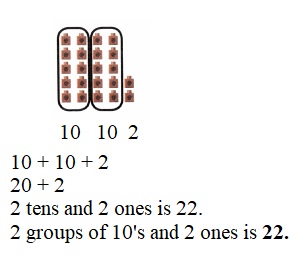























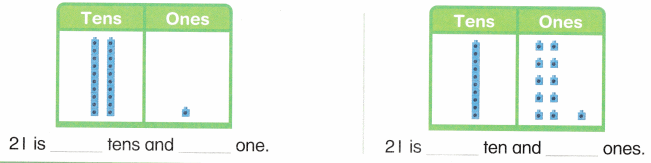

























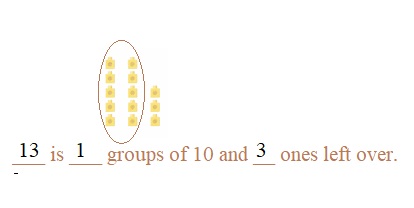






























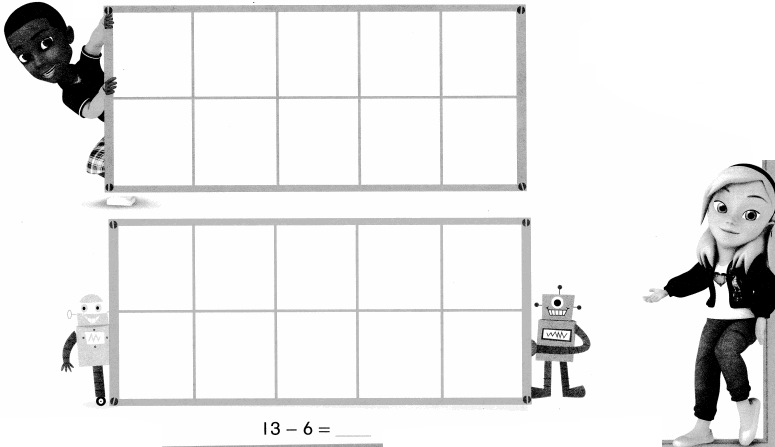

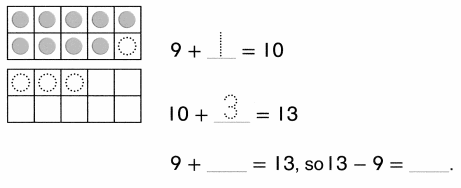
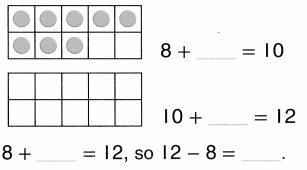
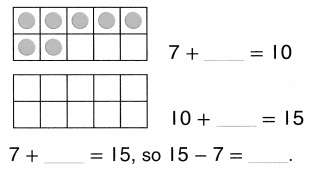

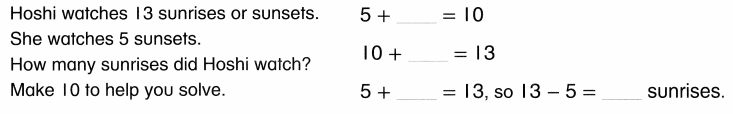














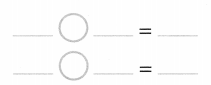



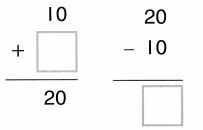
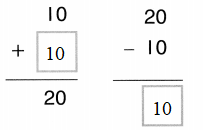
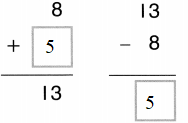




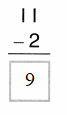

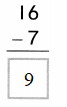


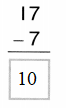









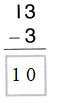


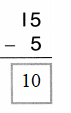
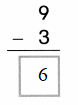

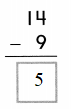
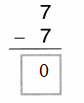



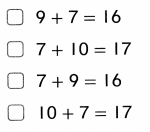



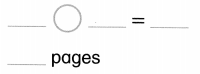


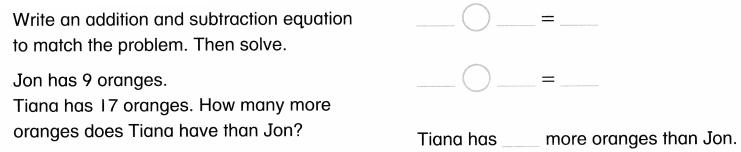






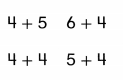







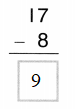











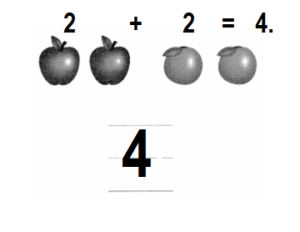



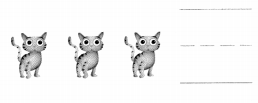


















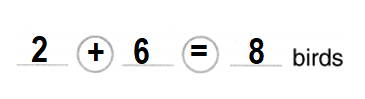










 1
1