Practice with the help of enVision Math Common Core Grade 3 Answer Key Topic 3 Apply Properties: Multiplication Facts for 3, 4, 6, 7, 8 regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 3 Apply Properties: Multiplication Facts for 3, 4, 6, 7, 8
Essential Question:
How can you use known multiplication facts to solve unknown facts?

enVision STEM Project: Inherited Traits
Do Research Some characteristics of organisms are inherited. The traits are passed from generation to generation. In flowers, one of the inherited traits is color. Use the Internet or other sources to make a list of other traits that flowers inherit from their parent plants.
Journal: Write a Report Include what you found. Also in your report:
- Compare your list of traits with lists of traits other students have made. If there is a trait you do not have, add it to your list.
- Draw flowers or animals with similar traits in an array. Show how to break apart the array and use multiplication facts to find the total number.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- skip counting
- The Commutative (Order) Property of Multiplication
- The Identity (One) Property of Multiplication
- The Zero Property of Multiplication
Question 1.
________ says that the product of any number and zero is zero.
Answer:
The zero property of multiplication says that the product of any number and zero is zero.
Explanation:
The multiplication property states that the product of any number and zero is zero. It doesn’t matter what the number is, when you multiply it to zero, you get zero as the answer.
Question 2.
________ says that 1 times any number is that number.
Answer:
The Identity (One) Property of Multiplication says that 1 times any number is that number.
Explanation:
The identity property of 1 says that any number multiplied by 1 keeps its identity. The reason the number stays the same is because multiplying by 1 means we have 1 copy of the number.
Question 3.
_________ says that you can multiply factors in any order, and the product stays the same.
Answer:
The Commutative (Order) Property of Multiplication says that you can multiply factors in any order, and the product stays the same.
Explanation:
The math rule that says the order in which we multiply the factors does not change the product is the commutative property.
Multiplying Use multiplication to solve.
Question 4.
10 × 1 = ________
Answer:
10 × 1 = 10.
Question 5.
2 × 10 = _______
Answer:
2 × 10 = 20.
Question 6.
0 × 5 = _______
Answer:
0 × 5 = 0.
Question 7.
9 × 5 = _______
Answer:
9 × 5 = 45.
Question 8.
2 × 7 = _________
Answer:
2 × 7 = 14.
Question 9.
1 × 8 = _______
Answer:
1 × 8 = 8.
Question 10.
5 × 7 = ?
A. 7 + 5
B. 5 + 7
C. 7 × 5
D. 7 ÷ 5
Answer:
5 × 7 = 35.
Explanation:
5 × 7 = ?
=> 5 × 7 = 35.
Adding 2-Digit Numbers
Find the sum.
Question 11.
16 + 12 = _______
Answer:
16 + 12 = 28.
Explanation:
16 + 12 = ??
Ten’s place: 2+1=3.
Ones place: 6+2=8.
Question 12.
21 + 14 = _______
Answer:
21 + 14 = 35.
Explanation:
21 + 14 = ??
Ten’s place: 2+1=3.
Ones place: 1+4=5.
Question 13.
24 + 12 = _______
Answer:
24 + 12 = 36.
Explanation:
24 + 12 = ??
Ten’s place: 2+1=3.
Ones place: 4+2=6.
Arrays
Question 14.
How can you represent 3 × 6 using an array? Draw an array, and explain how to use it to find the product.
Answer:
3 × 6 = 18 or Eighteen.
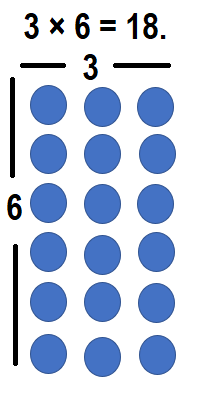
Explanation:
Number of rows = 3
Number of columns = 6
Multiplication:
Number of rows × Number of columns
= 3 × 6
= 18 or Eighteen.
Pick a Project
PROJECT ЗА
How many points can you score?
Project: Make a Basketball Data Display

Answer:
It is calculated by taking the difference in the score when the player enters the game and subtracting it from the score when the player exits the game. These differences are added up over the entire game to give the score.
Explanation:
It is calculated by taking the difference in the score when the player enters the game and subtracting it from the score when the player exits the game.

PROJECT 3B
Do you like collecting seashells?
Project: Draw a Shell Array

Answer:
Yes, I like collecting seashells.

Explanation:
Number of rows of shells = 3
Number of columns of the shells = 2
Multiplication:
Number of rows of shells × Number of columns of the shells
= 3 × 2
= 6.
PROJECT 3C
Would you like to run for president?
Project: Write a Presidential Report

Answer:
Yes, I would like to run for president.
Explanation:
Writing a Report on a US President.
Getting Started:
First, read about the President you will be writing the report on. Read as much information about the President
as you can find. Try the Internet and the library; try Whitehouse.gov, presidentsusa.net, .ipl.org/div/potus/, an
encyclopedia, books, or even videos.
As you’re finding out about your President, take notes on key information, such as important dates, critical
events in the President’s life, people who influenced his life, major world events during his life, etc.
3-ACT MATH PREVIEW
Math Modeling
Thirsty Students
I can .. model with math to solve a problem that involves using multiplication facts and computing
Lesson 3.1 The Distributive Property
Solve & Share
Find two ways to break the array below into two smaller arrays. What multiplication equation can you write for each array? What is the total? Tell how you decided.
I can … break apart unknown facts into known facts and solve multiplication problems.

Look Back! Find the total number of items in both of the smaller arrays. Compare their combined total to the total number of items in the one large array. Why are the totals the same even though the arrays are different?
Answer:
The totals are the same even though the arrays are different because Distributive law, in mathematics, the law relating the operations of multiplication and addition, stated symbolically, a(b + c) = ab + ac; that is, the monomial factor a is distributed, or separately applied, to each term of the binomial factor b + c, resulting in the product ab + ac.
Explanation:
Array:1:
Number of Rows = 4 or Four.
Number of columns = 5 or Five.
Number of items = Number of Rows × Number of columns
= 4 × 5
= 20 or Twenty.
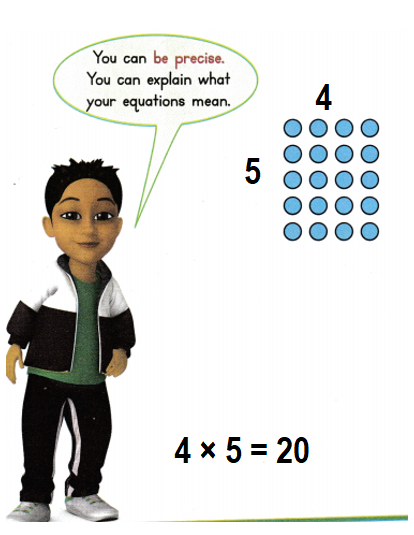
Array:2:
Number of Rows = 5 or Five.
Number of columns = 4 or Four.
Number of items = Number of Rows × Number of columns
= 5 × 4
= 20 or Twenty.

Essential Question
How Can You Break Up a Multiplication Fact?
Answer:
You can Break Up a Multiplication Fact using distributive property for multiplication.
Explanation:
To “distribute” means to divide something or give a share or part of something. According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
Visual Learning Bridge
Maria wants to set up 7 rows of 4 chairs for a meeting. She wants to know how many chairs she needs but does not know the product of 7 4.

What You Think
Maria thinks of 7 rows of 4 chairs as 5 rows of 4 chairs and another 2 rows of 4 chairs.
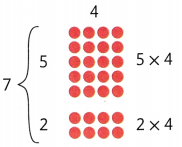
What You Write
The Distributive Property says that a multiplication fact can be broken apart into the sum of two other multiplication facts.
Maria knows the two new facts.
7 × 4 = (5 × 4) + (2 × 4)
7 × 4 = 20 + 8
7 × 4 = 28
So, 7 × 4 = 28.
Maria needs 28 chairs.
Convince Me! Use Structure What are two ways that Maria could break up the array for 7 × 4? Draw a picture of the two new arrays and write the new facts.
Answer:
The new facts are :
Way:1:
7 × 4 = (4 × 4) + (3 × 4)
7 × 4 = 16 + 12
7 × 4 = 28
So, 7 × 4 = 28.
Way:2:
7 × 4 = (6 × 4) + (1 × 4)
7 × 4 = 24 + 4
7 × 4 = 28
So, 7 × 4 = 28.
Explanation:
Way:1:
7 × 4 = (4 × 4) + (3 × 4)
7 × 4 = 16 + 12
7 × 4 = 28
So, 7 × 4 = 28.
Maria needs 28 chairs.
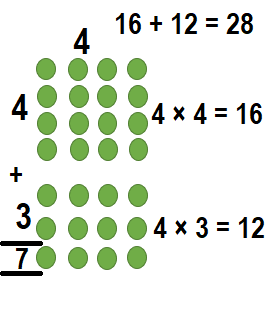
Way:2:
7 × 4 = (6 × 4) + (1 × 4)
7 × 4 = 24 + 4
7 × 4 = 28
So, 7 × 4 = 28.
Maria needs 28 chairs.
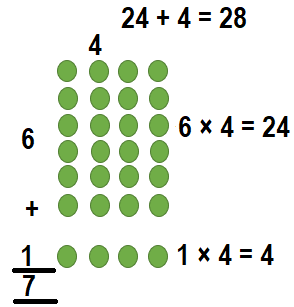
Guided Practice
Do You Understand?
Question 1.
Rafael broke up an array for 6×3 into two new arrays. Both of his new arrays are the same. What were the two arrays?
Answer:
The two arrays are :
Way:1:
6 × 3 = (5 × 3) + (1 × 3)
6 × 3 = 15 + 3
6 × 3 = 18
So, 6 × 3 = 18.
Way:2:
6 × 3 = (4 × 3) + (2 × 3)
6 × 3 = 12 + 6
6 × 3 = 18
So, 6 × 3 = 18.
Explanation:
The two arrays are :
Way:1:
6 × 3 = (5 × 3) + (1 × 3)
6 × 3 = 15 + 3
6 × 3 = 18
So, 6 × 3 = 18.
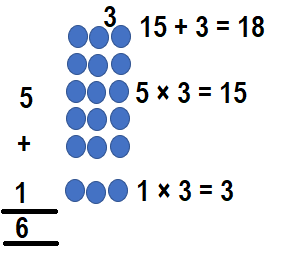
Way:2:
6 × 3 = (4 × 3) + (2 × 3)
6 × 3 = 12 + 6
6 × 3 = 18
So, 6 × 3 = 18.
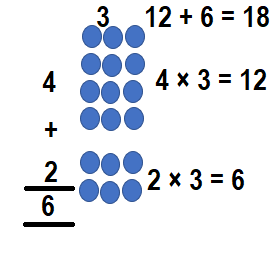
Question 2.
Ann broke up a large array into two smaller arrays. The two smaller arrays show 1 × 8 and 4 × 8. What was the large array that Ann started with?
Answer:
The large array that Ann started with :
5 × 8 = 40
So, 5 × 8 = 40..
Explanation:
The large array that Ann started with :
5 × 8 = (5 × 8)
5 × 8 = 40.
So, 5 × 8 = 40.
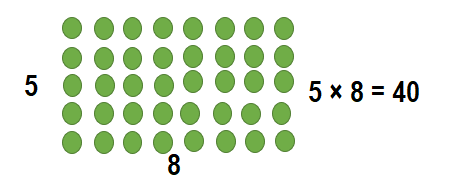
Do You Know How?
In 3 and 4, use the smaller arrays and the Distributive Property to find each missing factor. You may use counters to help
Question 3.
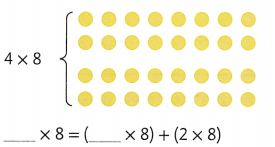
Answer:
__4__ × 8 = (__2__ × 8) + (2 × 8)
4 × 8 = 16 + 16
4 × 8 = 32.
Explanation:
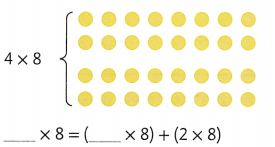
4 × 8 = (2 × 8) + (2 × 8)
4 × 8 = 16 + 16
4 × 8 = 32.
So, 4 × 8 = 32.
Question 4.
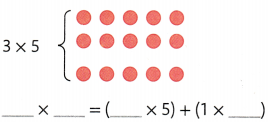
Answer:
__3__ × __5__ = (__2__ × 5) + (1 × __5__)
3 × 5 = 10 + 5
3 × 5 = 15.
Explanation:
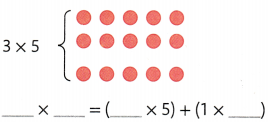
3 × 5 = (2 × 5) + (1 × 5)
3 × 5 = 10 + 5
3 × 5 = 15.
So, 3 × 5 = 15.
Independent Practice
In 5 and 6, separate the rows in the large array into two smaller arrays. Write the new facts.
Question 5.
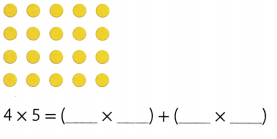
Answer:
4 × 5 = ( __2__ × __5__) + ( __2__ × __5__)
4 × 5 = 10 + 10
4 × 5 = 20.
Explanation:
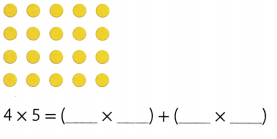
4 × 5 = ( 2 × 5) + ( 2 × 5)
4 × 5 = 10 + 10
4 × 5 = 20.
So, 4 × 5 = 20.
Question 6.
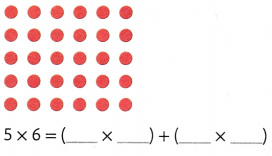
Answer:
5 × 6 = (__3__ × __6__) + ( __2__ × __6__)
5 × 6 = 18 + 12
5 × 6 = 30.
Explanation:
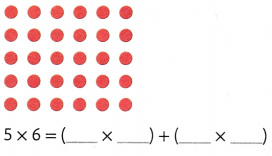
5 × 6 = (3 × 6) + ( 2 × 6)
5 × 6 = 18 + 12
5 × 6 = 30.
So, 5 × 6 = 30.
In 7-10, use the Distributive Property to find each missing factor. Use counters and arrays to help.
Question 7.
6 × 8 = (4 × _____) +(2 × 8)
Answer:
6 × 8 = (4 × ___8____) +(2 × 8)
6 × 8 = 32 + 16
6 × 8 = 48.
Explanation:
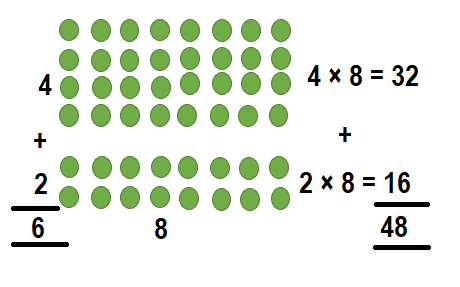
6 × 8 = (4 × 8) + (2 × 8)
6 × 8 = 32 + 16
6 × 8 = 48.
So, 6 × 8 = 48.
Question 8.
10 × 3= (____ × 3) + (2 × 3)
Answer:
10 × 3= (__8__ × 3) + (2 × 3)
10 × 3 = 24 + 6
10 × 3 = 30.
Explanation:
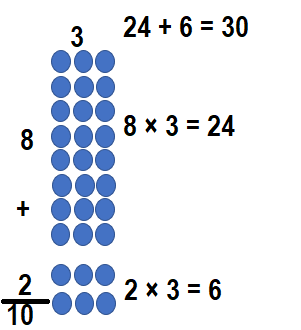
10 × 3 = (__8__ × 3) + (2 × 3)
10 × 3 = 24 + 6
10 × 3 = 30.
So, 10 × 3 = 30.
Question 9.
(_____ × 7) = (3 × 7) + (2 × _____)
Answer:
(___5__ × 7) = (3 × 7) + (2 × __7___)
5 × 7 = 21 + 14
5 × 7 = 35.
Explanation:
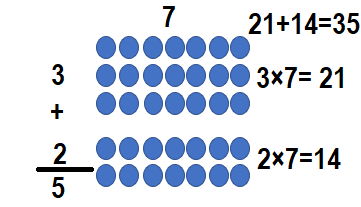
5 × 7 = (3 × 7) + (2 × 7)
5 × 7 = 21 + 14
5 × 7 = 35.
So, 5 × 7 = 35.
Question 10.
(8 × _____) = (_____ × 8) + (4 × 8)
Answer:
(8 × __8___) = (___4__ × 8) + (4 × 8)
(8 × 8 ) = 32 + 32
(8 × 8 ) = 64.
Explanation:
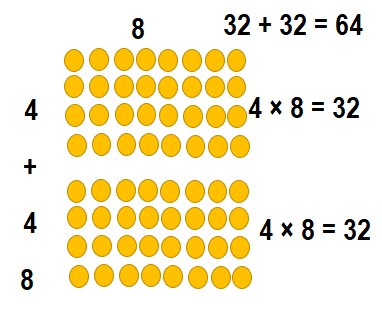
(8 × 8 ) = (4 × 8) + (4 × 8)
(8 × 8 ) = 32 + 32
(8 × 8 ) = 64.
So, (8 × 8 ) = 64.
Problem Solving
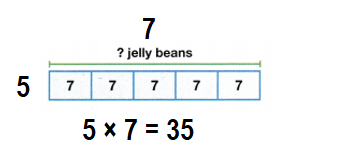
Question 11.
Paige bakes 5 cupcakes. She puts 7 jelly beans on each cupcake. How many jelly beans does Paige need? Use the bar diagram to help write an equation.

Answer:
Total number of jelly beans she needs = 35 or Thirty Five.
Explanation:
Number of cupcakes Paige bakes = 5 or Five.
Number of jelly beans on each cupcake she puts = 7 or Seven.
Total number of jelly beans she needs = Number of cupcakes Paige bakes × Number of jelly beans on each cupcake she puts
= 5 × 7
= 35 or Thirty Five.
Question 12.
Critique Reasoning
Fred wants to separate the rows of the array below into a 2 × 4 array and a 3 × 4 array. Can Fred do this? Explain.

Answer:
No, Fred cannot separate the rows of the array below into a 2 × 4 array and a 3 × 4 array because number of rows are four yet number of columns are 4 not five.
Explanation:

No, Fred cannot separate the rows of the array below into a 2 × 4 array and a 3 × 4 array because number of rows are four yet number of columns are 4 not five. He can separate into 2 × 4 array and 2 × 4 array yet not 2 × 4 array and 3 × 4 array .
Question 13.
Lane uses counters to make a 4 × 7 array and a 1 × 7 array. What size array can he make using all of these counters?
Answer:
The two arrays given = 4 × 7 and 1 × 7.
=> (4+1) × 7
=> 5 × 7.
The size array he make using all of these counters = 5 × 7.
Explanation:
The two arrays given = 4 × 7 and 1 × 7.
=> (4+1) × 7
=> 5 × 7.
The size array he make using all of these counters = 5 × 7.
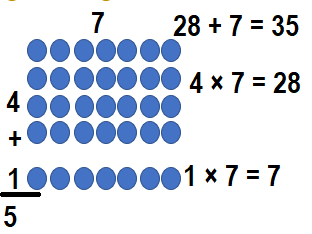
Question 14.
Gavin had $75 on Monday. On Tuesday, he spent $23. Then he spent $14 on Wednesday. How much money does Gavin have left?
Answer:
Amount Gavin has left = $38.
Explanation:
Total amount Gavin has on Monday = $75.
Amount Gavin spent on Tuesday = $23.
Amount Gavin spent on Wednesday = $14
Amount Gavin has left = Total amount Gavin has on Monday – ( Amount Gavin spent on Tuesday + Amount Gavin spent on Wednesday )
= $75 – ($23 + $14)
= $75 – $37
= $38.
Question 15.
Vocabulary
Explain how you can use the Distributive Property to solve 9 × 6.
Answer:
9 × 6 = (5 × 6) + (4 × 6).
To “distribute” means to divide something or give a share or part of something. According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
Explanation:
To “distribute” means to divide something or give a share or part of something. According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
9 × 6 = (5 × 6) + (4 × 6).
Question 16.
Higher Order Thinking
How can you use 3 × 5 = 15 to help find 6 × 5?
Answer:
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30.
So, 6 × 5 = 30.
Explanation:
We can use 3 × 5 = 15 to help find 6 × 5 by distributive property.
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30.
So, 6 × 5 = 30.
Assessment Practice
Question 17.
Using the Distributive Property, which of the following expressions are equivalent to 7 × 7? Select all that apply.
☐ (7 × 7) + (7 × 7)
☐ (5 × 7) + (2 × 7)
☐ (2 × 7) + (5 × 7)
☐ (7 × 7) + (1 × 7)
☐ (7 × 7) + (2 × 7)
Answer:
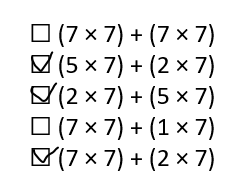
Explanation:
Expressions equivalent to 7 × 7 are as below:
7 × 7 = (4 × 7)+ (3 × 7)
7 × 7 = (2 × 7)+ (5 × 7)
7 × 7 = (6 × 7)+ (1 × 7)
7 × 7 = (5 × 7)+ (2 × 7)
7 × 7 = (3 × 7)+ (4 × 7)
7 × 7 = (1 × 7)+ (6 × 7)
Question 18.
An equation is shown. Select all the ways you can use the Distributive Property to find the missing factors. 7 × 3 = ( × 3) + ( × 3)
☐ 7 × 3 = (5 × 3) + (2 × 3)
☐ 7 × 3 = (2 × 3) + (5 × 3)
☐ × 3 = (7 × 3) + (1 × 3)
☐ × 3 = (1 × 3) + (6 × 3)
☐ × 3 = (6 × 3) + (1 × 3)
Answer:
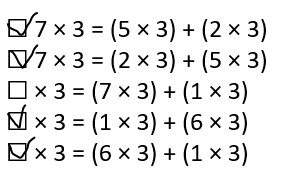
Explanation:
All the ways you can use the Distributive Property to find the missing factors:
7 × 3 = ( 5 × 3) + ( 2 × 3)
7 × 3 = ( 2 × 3) + ( 5 × 3)
7 × 3 = ( 1 × 3) + ( 6 × 3)
7 × 3 = ( 6 × 3) + ( 1 × 3)
7 × 3 = ( 4 × 3) + ( 3 × 3)
7 × 3 = ( 3 × 3) + ( 4 × 3)
Lesson 3.2 Apply Properties: 3 and 4 as Factors
Solve & Share
There are 3 rows of pictures on a wall. Each row has 7 pictures. How many pictures are on the wall?
I can … use tools and properties strategically to solve problems when I multiply by 3 or 4.

Look Back! How can you use what you know about multiplication facts for 1s facts and 2s facts to solve multiplication facts for 3s facts?
Answer:
Number of rows of Pictures = 3 or Three.
Number of Pictures in each row = 7 or Seven.
Number of pictures are on the wall = Number of rows of Pictures × Number of Pictures in each row
= 3 × 7
= 21.
Explanation:
Number of rows of Pictures = 3 or Three.
Number of Pictures in each row = 7 or Seven.
Number of pictures are on the wall = Number of rows of Pictures × Number of Pictures in each row
= 3 × 7
= 21.
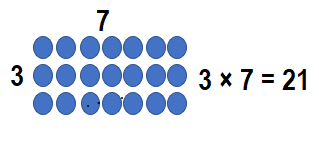
Essential Question
How Can You Break Apart Arrays to Multiply with 3?
Answer:
You can break Arrays to Multiply with 3 are:
3 = 1 + 2
3 = 2 + 1
Explanation: You can break Arrays to Multiply with 3 are:
3 = 1 + 2
3 = 2 + 1
Visual Learning Bridge
The Park District has canoes stored in 3 rows. There are 6 canoes in each row. What is the total number of canoes stored?

What You Show
Find 3 × 6.

What You Think
3 × 6 is 3 rows of 6. That is 2 sixes plus 1 more six.
2 sixes are 12. 1 six is 6.
12 + 6 = 18
3 × 6 = 18
There are 18 canoes.
Convince Me! Use Structure Suppose there were 7 canoes in each of 3 rows. How can 2 × 7 = 14 help you find the total number of canoes?
Answer:
The total number of canoes = Number of rows of canons + Number of canons in each row
= 3 × 7
= (2 × 7) + (1 × 7)
= 14 + 7
= 21.
Explanation:
Number of rows of canons = 3 or Three.
Number of canons in each row = 7 or Seven.
The total number of canoes = Number of rows of canons + Number of canons in each row
= 3 × 7
= (2 × 7) + (1 × 7)
= 14 + 7
= 21.
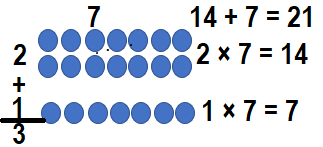
Another Example !
Find 4 × 7.

What You Think
4 × 7 is 4 rows of 7.
That is 2 sevens plus 2 sevens. 2 sevens are 14.
14 + 14 = 28
So, 4 × 7 = 28
Guided Practice
Do You Understand?
Question 1.
Besides using a 2s fact and doubling it, what is another way to break apart 4 × 7 using facts you already know?
Answer:
Another ways to break 4 × 7 using facts known by me:
4 × 7 = (1 × 7) + (3 × 7)
4 × 7 = (3 × 7) + (1 × 7 )
Explanation:
Another ways to break 4 × 7 using facts known by me:
4 × 7 = (1 × 7) + (3 × 7)
4 × 7 = (3 × 7) + (1 × 7 )
Question 2.
Selena arranged 3 rows of plants in her garden. She put 9 plants in each row. How many plants did Selena arrange?
Answer:
Number of plants Selena arrange = 27 or Twenty Seven.
Explanation:
Number of Rows of plants = 3 or Three.
Number of plants in each row = 9 or Nine.
Number of plants Selena arrange = Number of Rows of plants × Number of plants in each row
= 3 × 9
= 27 or Twenty Seven.
Do You Know How?
In 3-8, multiply. You may use counters or pictures to help.
Question 3.
3 × 10 = ______
Answer:
3 × 10 = __30__.
Explanation:
3 × 10 = 30.

Question 4.
______ = 5 × 4
Answer:
___20___ = 5 × 4.
Explanation:
5 × 4 = 20.
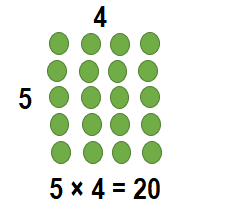
Question 5.
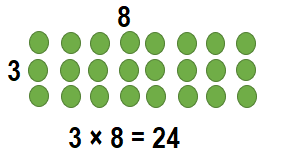
______ = 3 × 8
Answer:
__24____ = 3 × 8.
Explanation:
3 × 8 = 24.
Question 6.
1 × 4 = ______
Answer:
1 × 4 = __4___.
Explanation:
1 × 4 = ______.
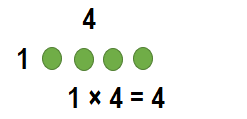
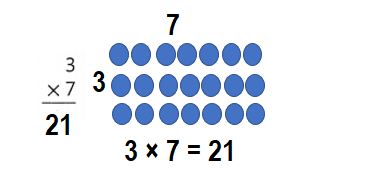
Question 7.
![]()
Answer:
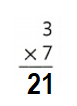
Explanation:
3 × 7 = 21.
Question 8.
![]()
Answer:
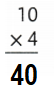
Explanation:
10 × 4 = 40.
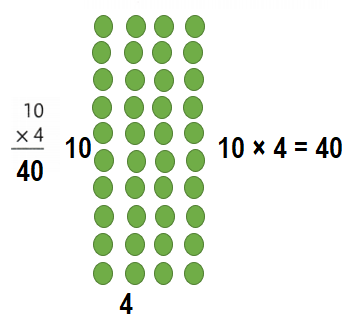
Independent Practice
Leveled Practice In 9-13, multiply. You may use counters or pictures to help.
Question 9.
Find 3 × 4.
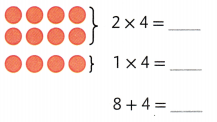
So, 3 × 4 = _______
Answer:
So, 3 × 4 = ___12____.
Explanation:
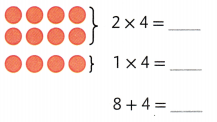
3 × 4 = (2 × 4) + (1 × 4)
3 × 4 = 8 + 4
3 × 4 = 12.
So, 3 × 4 = 12.
Question 10.
Find 4 × 9.
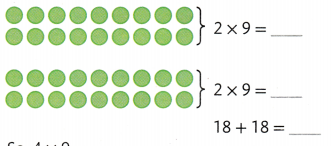
So, 4 × 9 = ________
Answer:
So, 4 × 9 = ____36____.
Explanation:
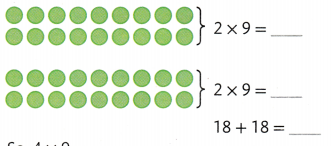
4 × 9 = (2 × 9) + (2 × 9)
4 × 9 = 18 + 18
4 × 9 = 36.
So, 4 × 9 = 36.
Question 11.
7 × 3 = _______
Answer:
7 × 3 = ____21___.
Explanation:
7 × 3 = 21.
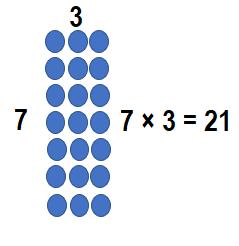
Question 12.
_____ = 4 × 3
Answer:
__12___ = 4 × 3.
Explanation:
__12___ = 4 × 3.
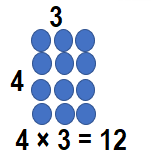
Question 13.
10 × 3 = ______
Answer:
10 × 3 = __30___.
Explanation:
10 × 3 = __30____.
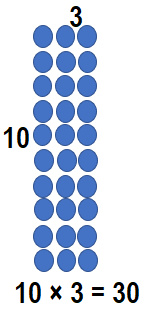
Problem Solving
Question 14.
Make Sense and Persevere James needs to buy supplies for his trail walk. What is the total number of cereal bars James needs to buy? Explain how you used the table to find the answer.

Answer:
Number of Cereal bars James needed = 4 or Four.
The tables is used in knowing the number of packages needed James needed for trial walk supplies.
Explanation:
Number of Cereal bars James needed = 4 or Four.
The tables is used in collecting data of cereal bars. It helps in knowing the number of packages needed James needed for trial walk supplies.
Question 15.
How many more apples than juice drinks does James need? Show how you found the answer.
Answer:
Number of more apples than juice drinks does James need = 5 or Five.
Explanation:
Number of Apples James needed = 8 or Eight.
Number of juice drinks James needed =3 or Three.
Number of more apples than juice drinks does James need = Number of juice drinks James needed – Number of Apples James needed
= 8 – 3
= 5 or Five.
Question 16.
Allison bought 10 packages of energy bars. Each package contains 6 bars. Allison says she has a total of 65 energy bars. Is her answer reasonable? Why or why not?
Answer:
Her answer is not reasonable because the total number of energy bars Allison bought = 60 or Sixty not 65.
Explanation:
Number of packages of energy bars Allison bought = 10 or Ten.
Number of bars each package contains = 6 or Six.
Total number of energy bars = Number of packages of energy bars Allison bought × Number of bars each package contains
= 10 × 6
= 60 or Sixty.
Question 17.
Higher Order Thinking What two multiplication facts can help you find 3 × 9? How could you use 3 × 9 to find 9 × 3?
Answer:
First multiplication fact:
3 × 9 = (2 × 9) + (1 × 9)
3 × 9 = 18 + 9
3 × 9 = 27.
Second multiplication fact:
3 × 9 = (1 × 9) + (2 × 9)
3 × 9 = 9 + 18
3 × 9 = 27.
You cannot use 3 × 9 for finding 9 × 3 because number of rows and number of items it , does not match.
Explanation:
First multiplication fact:
3 × 9 = (2 × 9) + (1 × 9)
3 × 9 = 18 + 9
3 × 9 = 27.
So, 3 × 9 = 27.
Second multiplication fact:
3 × 9 = (1 × 9) + (2 × 9)
3 × 9 = 9 + 18
3 × 9 = 27.
So, 3 × 9 = 27.
Assessment Practice
Question 18.
Bess has 6 boxes of candles. There are 4 candles in each box. Which equation can be used to find the number of candles Bess has?

A. (3 × 4) + (3 × 4) = ?
B. (6 × 2) + (6 × 6) = ?
C. (6 × 2) + (3 × 2) = ?
D. (2 × 2) + (6 × 6) = ?
Answer:
Total number of candles Bess has = 24 or Twenty Four.
A. (3 × 4) + (3 × 4) = 12 + 12 = 24 can be used to find the number of candles Bess has.
Explanation:
Number of boxes of candles Bess has = 6 or Six.
Number of candles each box has = 4 or Four.
Total number of candles Bess has = Number of boxes of candles Bess has × Number of candles each box has
= 6 × 4
= (3 × 4) + (3 × 4)
= 12 + 12
= 24 or Twenty Four.
Question 19.
Which of the following shows one way to use the Distributive Property to find 9 × 3?
A. (3 × 2) + (3 × 1)
B. (9 × 2) + (9 × 1)
C. (9 × 2) + (3 × 2)
D. (9 + 2) × (9 + 1)
Answer:
B. (9 × 2) + (9 × 1) shows one way to use the Distributive Property to find 9 × 3.
Explanation:
9 × 3 = ??
9 × 3 = (9 × 2) + (9 × 1)
9 × 3 = 18 + 9
9 × 3 = 27.
So, 9 × 3 = 27.
Lesson 3.3 Apply Properties: 6 and 7 as Factors
Solve & Share
Students set up 6 rows of seats for a music concert. They put 6 seats in each row. What is the total number of seats?
I can … make and use models to solve multiplication problems that have 6 and 7 as factors.

Answer:
Total number of seats = 36 or Thirty Six.
Explanation:
Number of rows of seats Students set up for a music concert = 6 or Six.
Number of seats in each row Students set up for a music concert = 6 or Six.
Total number of seats = Number of rows of seats Students set up for a music concert × Number of seats in each row Students set up for a music concert
= 6 × 6
= 36 or Thirty Six.
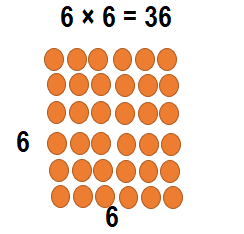
Essential Question
How Can You Break Apart Arrays to Multiply?
Answer:
You can break apart Arrays to multiply by using the Distributive Property.
Explanation:
Yes, you can Break Apart Arrays to Multiply. It says that you can break apart a multiplication fact into the sum of two other multiplication facts.
Visual Learning Bridge
The members of the band march in 6 equal rows. There are 8 band members in each row. How many are in the band?
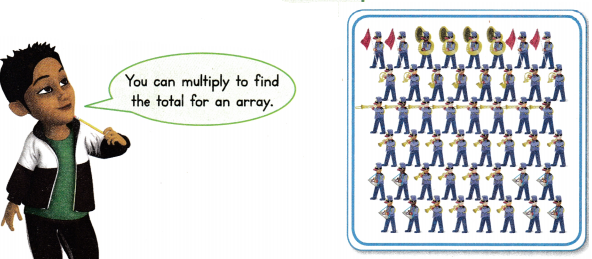
What You Show
Find 6 × 8.
Use 5s facts and 1s facts.
Make an array for each multiplication sentence.
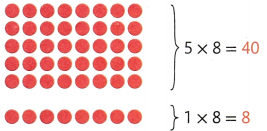
What You Think
6 × 8 is 6 rows of 8. That is 5 eights plus 1 more eight.
5 eights are 40.
8 more is 48.
40 + 8 = 48
So, 6 × 8 = 48.
The band has 48 members.
Convince Me! Use Structure Use a 5s fact and a 1s fact to find 6 x 9. Draw two arrays. Explain your drawings.
Another Example !
Find 7 × 8.
Use 5s facts and 2s facts to help multiply by 7.
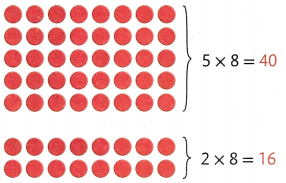
7 × 8 equals 7 rows of 8.
That is 5 eights plus 2 eights.
5 eights are 40.
2 eights are 16.
40+ 16 = 56
So, 7 × 8 = 56.
Guided Practice
Do You Understand?
Question 1.
The students who are graduating are standing in 7 equal rows. There are 9 students in each row. How many students are graduating? Use a 5s fact and a 2s fact.
Answer:
Total number of students are graduating = 63 or Sixty Three.
Explanation:
Number of rows students who are graduating are standing in = 7 or Seven.
Number of students in each row = 9 or nine.
Total number of students are graduating = Number of rows students who are graduating are standing in × Number of students in each row
= 7 × 9
= (5 × 9) + ( 2 × 9)
= 45 + 18
= 63 or Sixty Three.

Question 2.
Chrissy bakes 3 cherry pies. She cuts each pie into 6 slices. How many slices does Chrissy have?
Answer:
Number of slices Chrissy has = 18 or Eighteen.
Explanation:
Number of cherry pies Chrissy bakes = 3 or Three.
Number of slices she cuts each pie = 6 or Six.
Number of slices Chrissy has = Number of cherry pies Chrissy bakes × Number of slices she cuts each pie
= 3 × 6
= (2 × 6) + (1 × 6)
= 12 + 6
= 18 or Eighteen.

Do You Know How?
In 3-8, multiply. You may draw pictures or use counters to help.
Question 3.
6 × 10 = ________
Answer:
6 × 10 = ___60_____.
Explanation:
6 × 10 = ( 3 ×10) + ( 3 ×10)
6 × 10 = 30 + 30
6 × 10 = 60.

Question 4.
7 × 6 = ________
Answer:
7 × 6 = ___42_____.
Explanation:
7 × 6 = (6 × 6) + (1 × 6)
7 × 6 = 36 + 6
7 × 6 = 42.
So, 7 × 6 = 42.

Question 5.
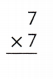
Answer:

Explanation:
7 × 7 = (3 ×7) + (4 ×7)
7 × 7 = 21 + 28
7 × 7 = 49.
So, 7 × 7 = 49.

Question 6.
![]()
Answer:

Explanation:
9 × 7 = (5 × 7) + (4 × 7)
9 × 7 = 35 + 28
9 × 7 = 63.
So, 9 × 7 = 63.

Question 7.
Find 4 times 7. ______
Answer:
4 × 7 = 28.
Explanation:
4 × 7 = 28.
4 × 7 = ( 2 × 7) + ( 2 × 7)
4 × 7 =14 + 14
4 × 7 = 28.
So, 4 × 7 = 28.

Question 8.
Multiply 6 times 5. ________
Answer:
Multiply 6 times 5.
=> 6 × 5 = 30.
Explanation:
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30.
So, 6 × 5 = 30.

Independent Practice
In 9-16, find the product. You may draw pictures to help.
Question 9.
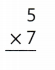
Answer:

Explanation:
5 × 7 = (3 × 7) + (2 × 7)
5 × 7 = 21 + 14
5 × 7 = 35.
So, 5 × 7 = 35.

Question 10.
![]()
Answer:

Explanation:
3 × 6 = (2 × 6) + (1 × 6)
3 × 6 = 12 + 6
3 × 6 = 18.
So, 3 × 6 = 18.

Question 11.
![]()
Answer:

Explanation:
7 × 8 = (4 × 8) + (3 × 8)
7 × 8 = 32+ 24
7 × 8 = 56.
So, 7 × 8= 56.

Question 12.
![]()
Answer:

Explanation:
1 × 7 = 7.
So, 1 × 7 = 7.

Question 13.
![]()
Answer:

Explanation:
10 × 6 = (5 × 6) + (5 × 6)
10 × 6 = 30+ 30
10 × 6 = 60.
So, 10 × 6 = 60.

Question 14.
![]()
Answer:

Explanation:4
4 × 7 = (2 × 7) + (2 × 7)
4 × 7 = 14+ 14
4 × 7 = 28.
So, 4 × 7 = 28.

Question 15.
![]()
Answer:

Explanation:
7 × 3 = (4 × 3) + (3 × 3)
7 × 3 = 12 + 9
7 × 3 = 21.
So, 7 × 3 = 21.

Question 16.
![]()
Answer:

Explanation:
8 × 6 = (4 × 6) + (4 × 6)
8 × 6 = 24+ 24
8 × 6 = 48.
So, 8 × 6 = 48.

Problem Solving
Question 17.
The National Toy Train Museum has 5 exhibits for trains. In one of the exhibits, the trains are on 5 tracks. How many trains are on display at that exhibit? Write an equation to solve the problem.

Answer:
Number of trains are on display at that exhibit = 25 or Twenty five.
Explanation:
Number of trains exhibits the National Toy Train Museum has = 5 or Five.
Number of trains each exhibits track the National Toy Train Museum has = 5 or Five.
Number of trains are on display at that exhibit = Number of trains exhibits the National Toy Train Museum has × Number of trains each exhibits track the National Toy Train Museum has
= 5 × 5
= (3 × 5) + (2 × 5)
= 15 + 10
= 25 or Twenty five.
Question 18.
Tracy used the flat surface of a cube to draw a plane shape. What plane shape did Tracy draw? How do you know?
Answer:
A cube is comprised of 6 congruent squares. Therefore, the only shape Tracy could have drawn is a square
Explanation:
In geometry a cube is a three- dimensional solid object bounded by six square faces. So, Tracy could have drawn is a square.
Question 19.
The dance team lines up in 4 rows of 6 dancers each. How many dancers are on the dance team?
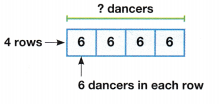
Answer:
Number of dancers are on the dance team = 24 or Twenty Four.
Explanation:
Number of rows the dance team lines up = 4 or Four.
Number of dancers in each row = 6 or Six.
Number of dancers are on the dance team = Number of rows the dance team lines up × Number of dancers in each row
= 4 × 6
= (2 × 6) + (2 × 6)
= 12 + 12
= 24 or Twenty Four.
Question 20.
Higher Order Thinking
Marge says 7 × 0 is equal to 7 + 0. Is Marge correct? Why or why not?
Answer:
No, Marge is not correct because 7 × 0 = 0 where as 7 + 0 = 7.
Explanation:
Marge says 7 × 0 is equal to 7 + 0.
7 × 0 = 0.
7 + 0 = 7.
Question 21.
Use Structure : There are 7 rows of 10 seats. How can you use the Distributive Property to find the total number of seats?
Answer:
Total number of seats = Number of rows × Number of seats in each row
= 7 × 10
= (3 × 10) + (4 × 10)
= 30 + 40
= 70 or Seventy.
Explanation:
The distributive property tells us how to solve expressions in the form of a(b + c). The distributive property is sometimes called the distributive law of multiplication and division.
Number of rows = 7 or Seven.
Number of seats in each row = 10 or Ten.
Total number of seats = Number of rows × Number of seats in each row
= 7 × 10
= (3 × 10) + (4 × 10)
= 30 + 40
= 70 or Seventy.
Assessment Practice
Question 22.
Select numbers to create a different expression that is equal to 7 × 8.

Answer:
Different expression that is equal to 7 × 8.
8 × 7 = (5 × 7) + (3 × 7)
8 × 7 = 35 + 21
8 × 7 = 56 or Fifty Six.
So, 8 × 7 = 56 or Fifty Six.
Explanation:
7 × 8 = (4 × 8) + (3 × 8)
7 × 8 = 32 + 24
7 × 8 = 56.
So, 7 × 8 = 56 or Fifty Six.
Different expression that is equal to 7 × 8.
8 × 7 = (5 × 7) + (3 × 7)
8 × 7 = 35 + 21
8 × 7 = 56 or Fifty Six.
So, 8 × 7 = 56 or Fifty Six.
Question 23.
Select numbers to create a different expression that is equal to 8 × 6.

Answer:
Different expression that is equal to 8 × 6.
6 × 8 = (5 × 8) + (1 × 8)
6 × 8 = 40 + 8
6 × 8 = 48.
So, 6 × 8 = 48 or Forty Eight.
Explanation:
8 × 6 = (4 × 6) + (4 × 6)
8 × 6 = 24 + 24
8 × 6 = 48 or Forty Eight.
So, 8 × 6 = 48 or Forty Eight.
Different expression that is equal to 8 × 6.
6 × 8 = (5 × 8) + (1 × 8)
6 × 8 = 40 + 8
6 × 8 = 48.
So, 6 × 8 = 48 or Forty Eight.
Lesson 3.4 Apply Properties: 8 as a Factor
Solve & Share
There are 8 rows of prizes. There are 6 prizes in each row. How many prizes are there?
I can … use known facts and properties to multiply by 8.

Look Back! Tell how you can use 2s, 3s, or 4s facts to solve the problem.
Essential Question
How Can You Use Doubles on to Multiply with 8?
Answer:
Doubles on to Multiply with 8:
8 = ( 2 × 2 × 2)
Explanation:
Doubles multiplication on 8:
8 = 4 × 2 = 2 × 2 × 2.
Visual Learning Bridge
At a school fun fair, students try to toss a table tennis ball into a bowl. There are 8 rows of bowls. There are 8 bowls in each row. How many bowls are there?

One Way
Use 2s facts to find 8 × 8.
8 × 8 equals 4 groups of 2 eights.

16 + 16 + 16 + 16 = 64
So, 8 × 8 = 64.
Another Way
Double a 4s fact to find 8 × 8.
8 × 8 equals 4 eights plus 4 eights.
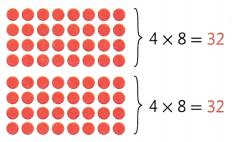
32 + 32 = 64
So, 8 × 8 = 64.
Convince Me! Use Structure How does knowing 5 × 8 = 40 help you find 8 × 8?
Guided Practice
Do You Understand?
Question 1.
Multiply 8 times 3. Write and solve a multiplication equation.
Answer:
Multiply 8 times 3.
=> 8 × 3 = (5 × 3) + (3 × 3)
=> 8 × 3 = 15 + 9
=> 8 × 3 = 24 or Twenty Four.
Explanation:
Multiply 8 times 3.
=> 8 × 3 = (5 × 3) + (3 × 3)
=> 8 × 3 = 15 + 9
=> 8 × 3 = 24 or Twenty Four.
So, 8 × 3 = 24 or Twenty Four.
Question 2.
Multiply 5 times 8. Write and solve a multiplication equation.
Answer:
Multiply 5 times 8.
=> 5 × 8 = (3 × 8) + (2 × 8)
=> 5 × 8 = 24 + 16
=> 5 × 8 = 40 or Forty.
Explanation:
Multiply 5 times 8.
=> 5 × 8 = (3 × 8) + (2 × 8)
=> 5 × 8 = 24 + 16
=> 5 × 8 = 40 or Forty.
So, 5 × 8 = 40 or Forty.
Question 3.
Multiply 8 times 1. Write and solve a multiplication equation.
Answer:
Multiply 8 times 1.
=> 8 × 1 = (4 × 1) + (4 × 1)
=> 8 × 1= 4 + 4
=> 8 × 1 = 8 or Eight.
Explanation:
Multiply 8 times 1.
=> 8 × 1 = (4 × 1) + (4 × 1)
=> 8 × 1= 4 + 4
=> 8 × 1 = 8 or Eight.
So, 8 × 1 = 8 or Eight.
Do You Know How?
In 4-9, multiply. You may draw pictures or use counters to help.
Question 4.
8 × 7 = ______
Answer:
8 × 7 = __56____.
Explanation:
8 × 7 = ( 4 × 7) + ( 4 × 7)
8 × 7 = 28 + 28
8 × 7 = 56 or Fifty Six.
So, 8 × 7 = 56 or Fifty Six.
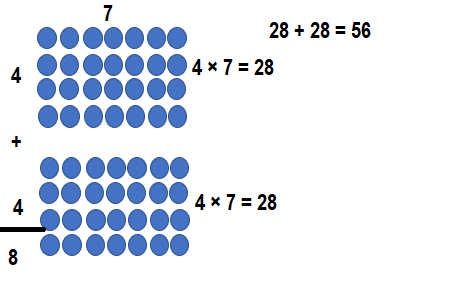
Question 5.
______ = 8 × 4
Answer:
__32____ = 8 × 4.
Explanation:
8 × 4 = (4 × 4) + (4 × 4)
8 × 4 = 16 + 16
8 × 4 = 32 or Thirty Two.
So, 8 × 4 = 32 or Thirty Two.
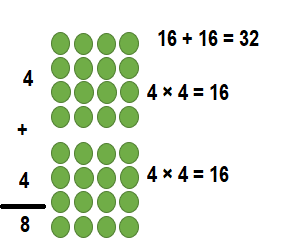
Question 6.
6 × 8 = ________
Answer:
6 × 8 = ___48_____.
Explanation:
6 × 8 = (3 × 8) + (3 × 8)
6 × 8 = 24 + 24
6 × 8 = 48 or Forty Eight.
So, 6 × 8 = 48 or Forty Eight.
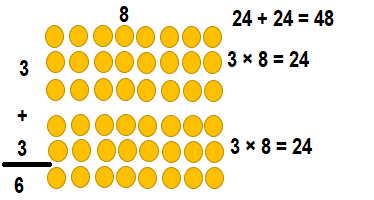
Question 7.
______ = 10 × 8
Answer:
__80____ = 10 × 8.
Explanation:
10 × 8 = (5× 8) + (5 × 8)
10 × 8 = 40 + 40
10 × 8 = 80.
So, 10 × 8 = 80 or Eighty.
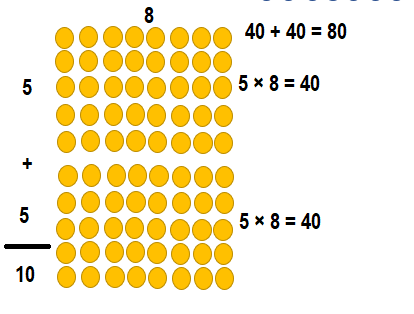
Question 8.
![]()
Answer:
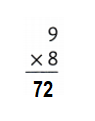
Explanation:
9 × 8 = (5 × 8) + (4 × 8)
9 × 8 = 40 + 32
9 × 8 = 72.
So, 9 × 8 = 72 or Seventy Two.
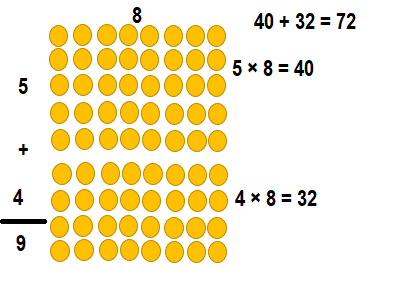
Question 9.
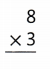
Answer:
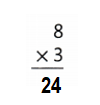
Explanation:
8 × 3 = (5 × 3) + (3 × 3)
8 × 3 = 15+ 9
8 × 3 = 24.
So, 8 × 3 = 24 or Twenty Four.
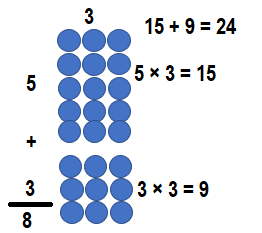
Independent Practice
In 10-23, find the product. You may draw pictures to help.
Question 10.
8 × 4 = ________
Answer:
8 × 4 = ___32_____.
Explanation:
8 × 4 = (4 × 4) + (4 × 4)
8 × 4 = 16+ 16
8 × 4 = 32.
So, 8 × 4 = 32 or Thirty Two.
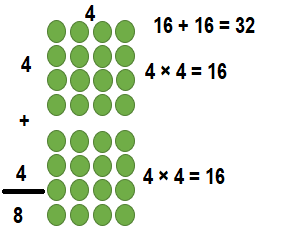
Question 11.
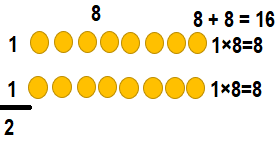
1 × 8 = _______
Answer:
1 × 8 = ___8____.
Explanation:
1 × 8 = 8.

Question 12.
_____ = 2 × 8
Answer:
__16___ = 2 × 8.
Explanation:
2 × 8 = (1 × 8) + (1 × 8)
2 × 8 = 8 + 8
2 × 8 = 16.
So, 2 × 8 = 16 or Sixteen.
Question 13.
___ = 5 × 8
Answer:
__40__ = 5 × 8.
Explanation:
5 × 8 = (3 × 8) + (2 × 8)
5 × 8 = 24 + 16
5 × 8 = 40.
So, 5 × 8 = 40 or Forty.
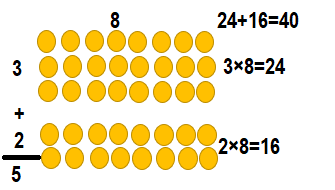
Question 14.
8 × 2 = ________
Answer:
8 × 2 = ___16_____.
Explanation:
8 × 2 = (4 × 2) + (4 × 2)
8 × 2 = 8 + 8
8 × 2 = 16.
So, 8 × 2 = 16 or Sixteen.
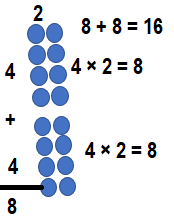
Question 15.
8 × 6 = _______
Answer:
8 × 6 = __48_____.
Explanation:
8 × 6 = (4 × 6) + (4 × 6 )
8 × 6 = 24 + 24
8 × 6 = 48.
So, 8 × 6 = 48 or Forty Eight.
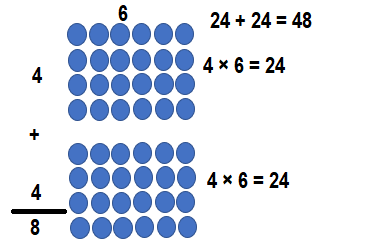
Question 16.
![]()
Answer:
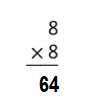
Explanation:
8 ×8 = (4 × 8) + (4 × 8)
8 ×8 = 32 + 32
8 ×8 = 64.
So, 8 ×8 = 64 or Sixty Four.
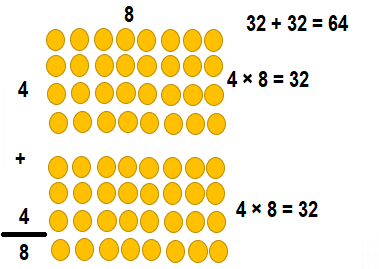
Question 17.
![]()
Answer:
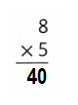
Explanation:
8 × 5 = (5 × 5) + (3 × 5)
8 × 5 = 25 + 15
8 × 5 = 40.
So, 8 × 5 = 40 or Forty.
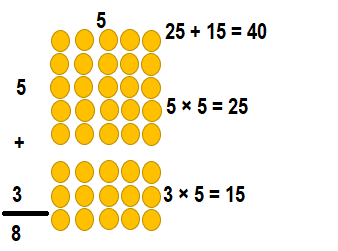
Question 18.
![]()
Answer:
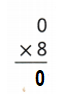
Explanation:
0 × 8 = 0 or Zero.
Question 19.
![]()
Answer:
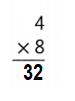
Explanation:
4 × 8 = (2 × 8) + (2 × 8)
4 × 8 = 16 + 16
4 × 8 = 32.
So, 8 × 5 = 32 or Thirty Two..
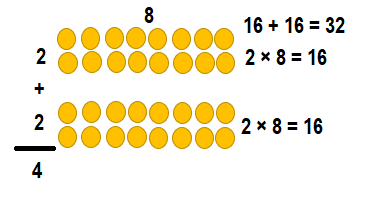
Question 20.
![]()
Answer:
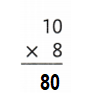
Explanation:
10 × 8 = (5 × 8) + (5 × 8)
10 × 8= 40+ 40
10 × 8 = 80.
So, 10 × 8 = 80 or Eighty.
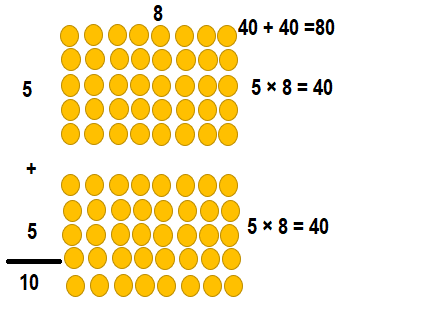
Question 21.
![]()
Answer:
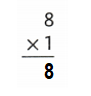
Explanation:
8 × 1 = (5 × 1) + (3 × 1)
8 × 1 = 5 + 3
8 × 1 = 8.
So, 8 × 1 = 8 or Eight.
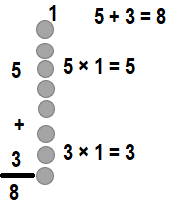
Question 22.
![]()
Answer:
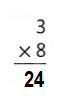
Explanation:
3 × 8 = (2 × 8) + (1 × 8)
3 × 8 = 16+ 8
3 × 8 = 24.
So, 3 × 8 = 24 or Twenty Four.
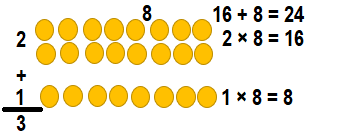
Question 23.
![]()
Answer:
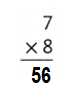
Explanation:
7 × 8 = (2 × 8) + (5 × 8)
7 × 8 = 16+ 40
7 × 8 = 56.
So, 7 × 8 = 56 or Fifty Six.

Problem Solving

Question 24.
Use Structure Ming bought 8 belts for gifts. How much money did Ming spend? Show how you can use a 4s fact to find the answer.
Answer:
Amount spent by Ming in buying belts = $72.
Explanation:
Number of belts bought by Ming for gifts = 8 or Eight.
Cost of each belt bought by Ming for gifts = $9
Amount spent by Ming in buying belts = Number of belts bought by Ming for gifts × Cost of each belt bought by Ming for gifts
= 8 × $9
= (4 × $9) + (4 × $9) { use a 4s fact }
= $36 + $36
= $72.
Question 25.
Willa bought a shirt and a sweater. She had $14 left. How much money did Willa start with? How do you know?
Answer:
Amount of money Willa stated with = $75.
Explanation:
Cost of the shirt = $23
Cost of a sweater = $38
Cost of the money left with her = $14
Amount of money Willa stated with = Cost of the shirt + Cost of a sweater + Cost of the money left with her
= $23 + $38 + $14
= $61 + $14
= $75.
Question 26.
Mr. Garner spends $52 on groceries and $24 on gas. How much does Mr. Garner spend? Write an equation and solve.

Answer:
Total amount spent by Mr. Garner = $76.
Explanation:
Amount spent on groceries by Mr. Garner = $52
Amount spent on gas by Mr. Garner = $24
Total amount spent by Mr. Garner = Amount spent on groceries by Mr. Garner + Amount spent on gas by Mr. Garner
= $52 + $24
= $76.
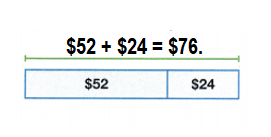
Question 27.
Algebra Mischa bought 7 boxes of orange tiles. There are 8 tiles in each box. How many tiles did Mischa buy? Write an equation and solve. Use ? to represent the unknown quantity of tiles.
Answer:
Number of tiles Mischa buys = 56 or Fifty Six.
Explanation:
Number of tiles Mischa buys = ??
Amount of orange tiles boxes Algebra Mischa bought = 7 or Seven.
Number of orange tiles in each box = 8 or Eight.
Number of tiles Mischa buys = Amount of orange tiles boxes Algebra Mischa bought × Number of orange tiles in each box
= 7 × 8
= 56 or Fifty Six.
Question 28.
Aaron bought 6 packs of sports cards. There are 7 cards in each pack. How many sports cards did Aaron buy in all? Use properties to solve the problem.
Answer:
Number of sports cards did Aaron buy in all = 42 or Forty Two.
Explanation:
Number of packs of sports cards Aaron bought = 6 or Six.
Number of cards in each pack = 7 or Seven.
Number of sports cards did Aaron buy in all = Number of packs of sports cards Aaron bought × Number of cards in each pack
= 6 × 7
= (3 × 7) + (3 × 7)
= 21 + 21
= 42 or Forty Two.
Question 29.
Higher Order Thinking
Sophie says, “To find 8 × 8, I can find 8 × (4 + 4).” Do you agree? Explain.
Answer:
Yes, agree with what Sophie says “To find 8 × 8, I can find 8 × (4 + 4).” Because both are the same.
Explanation:
Sophie says, “To find 8 × 8, I can find 8 × (4 + 4).”
8 × 8 = 64
8 × (4 + 4)
=> 8 × 8 = 64.
Assessment Practice
Question 30.
Ms. Vero has 8 boxes of crayons. Each box has 8 crayons. Select all the correct equations that could show how many crayons Ms. Vero has.
☐ 8 × 8 = 64
☐ 4 × 8 = 32
☐ 2 × 8 = 15
☐ 3 × 8 = 24
☐ 6 × 8 = 84
Answer:
Total number of crayons Ms. Vero has = 8 × 8 = 64 or Sixty Four.
☐ 8 × 8 = 64 is the expression that can be used to find 8 × 7.
Explanation:
Number of crayons boxes Ms. Vero has = 8 or Eight.
Number of crayons in each box = 8 or Eight.
Total number of crayons Ms. Vero has = Number of crayons boxes Ms. Vero has × Number of crayons in each box
= 8 × 8
= 64 or Sixty Four.
Question 31.
Select all the expressions that can be used to find 8 × 7.
☐ (4 × 7) + (4 × 7)
☐ (4 × 6) + (4 × 1)
☐ (4 × 5) + (4 × 2)
☐ (8 × 5) + (8 × 2)
☐ (2 × 7) + (2 × 7) + (2 × 7) + (2 × 7)
Answer:
8 × 7 = (4 × 7) + (4 × 7)
8 × 7 = (2 × 7) + (2 × 7) + (2 × 7) + (2 × 7) are the expressions that can be used to find 8 × 7.
So, 8 × 7 = 56 or Fifty Six.
Explanation:
8 × 7 = (4 × 7) + (4 × 7)
8 × 7 = 28 + 28
8 × 7 = 56 or Fifty Six.
8 × 7 = (2 × 7) + (2 × 7) + (2 × 7) + (2 × 7)
8 × 7 = 14 + 14 + 14 + 14
8 × 7 = 28 + 14 + 14
8 × 7 = 42 + 14
8 × 7 = 56 or Fifty Six.
Lesson 3.5 Practice Multiplication Facts
Solve & Share
Jermaine has 7 coolers. Each cooler contains 8 bottles of sports drink. How many bottles of sports drink does Jermaine have in all?
I can … use strategies and tools to represent and solve multiplication facts.

Look Back! Jermaine now has 8 coolers with 7 bottles of sports drink in each cooler. Does that change the total number of bottles of sports drink that Jermaine has? Explain why or why not.
Answer:
Equation:1:
Number of coolers Jermaine has = 7 or Seven.
Number of bottles of sports drink in each cooler = 8 or Eight.
Total number of bottles she has = Number of coolers Jermaine has × Number of bottles of sports drink in each cooler
= 7 × 8
= 56 or Fifty Six.
Equation:2:
Number of coolers Jermaine has = 8 or Eight.
Number of bottles of sports drink in each cooler = 7 or Seven.
Total number of bottles she has = Number of coolers Jermaine has × Number of bottles of sports drink in each cooler
= 8 × 7
= 56 or Fifty Six.
Essentials Question
How Do You Use Strategies on to Multiply?
Answer:
We use Strategies on to Multiply accordingly to the process which it is required to get the correct solution.
Explanation:
We use Strategies on to Multiply accordingly to the process which it is required to get the correct solution. It is an important foundational strategy that leads to more efficient strategies (and helps with conceptual understanding).
Visual Learning Bridge
Justin and Dolores made a dragon float for a parade. They connected 9 equal sections to make the dragon’s body. What is the total length of the dragon’s body in feet?
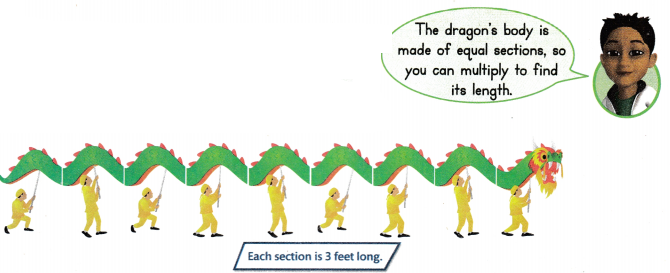
One Way
Draw a picture to find 9 × 3.
9 × 3 means 9 groups of 3. Combine the groups to find the product.
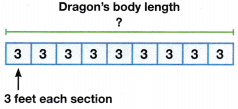
9 × 3 = 27
The dragon’s body is 27 feet long.
Another Way
Use known facts to find 9 × 3.
Use 4s facts and 5s facts to help.
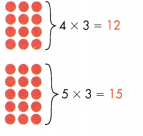
12 + 15 = 27
The dragon’s body is 27 feet long.
Convince Me! Make Sense and Persevere What two other facts can you use to find 9 × 3? Explain.
Answer:
The two other facts can you use to find 9 × 3 are:
First way:
9 × 3 = (6 × 3) + (3 × 3)
9 × 3 = 18 + 9
9 × 3 = 27 or Twenty Seven.
Second way:
9 × 3 = (8 × 3) + (1 × 3)
9 × 3 = 24 + 3
9 × 3 = 27 or Twenty Seven.
Explanation:
Two other facts can you use to find 9 × 3 are:
First way:
9 × 3 = (6 × 3) + (3 × 3)
9 × 3 = 18 + 9
9 × 3 = 27 or Twenty Seven.
Second way:
9 × 3 = (8 × 3) + (1 × 3)
9 × 3 = 24 + 3
9 × 3 = 27 or Twenty Seven.
Guided Practice
Do You Understand?
Question 1.
What known facts can you use to find 7 × 5?
Answer:
Known facts which can be used to find 7 × 5 are 3s, 5s, 2s, 4s.
Explanation:
7 × 5 = (5 × 5) + ( 2 × 5)
7 × 5 = 25 + 10
7 × 5 = 35 or Thirty Five.
7 × 5 = (4 × 5) + ( 3 × 5)
7 × 5 = 20 + 15
7 × 5 = 35 or Thirty Five.
Question 2.
To find 8 × 6, how does knowing 6 × 6 = 36 help you?
Answer:
8 × 6 = ( 6 × 6) + ( 2 × 6) = 36 + 12 = 48 or Forty Eight.
Explanation:
8 × 6 = ( 6 × 6) + ( 2 × 6)
8 × 6 = 36 + 12
8 × 6 = 48 or Forty Eight.
Do You Know How?
In 3-8, multiply.
Question 3.
3 × 7 = _______
Answer:
3 × 7 = __21___.
Explanation:
3 × 7 = (1 × 7) + (2 × 7)
3 × 7 = 7 + 14
3 × 7 = 21 or Twenty One.
Question 4.
______ = 6 × 5
Answer:
__30____ = 6 × 5
Explanation:
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30 or Thirty.
Question 5.
9 × 4 = _______
Answer:
9 × 4 = ___36____.
Explanation:
9 × 4 = (5 × 4) + (4 × 4)
9 × 4 = 20 + 16
9 × 4 = 36 or Thirty Six.
Question 6.
____= 3 × 0
Answer:
__0__= 3 × 0.
Explanation:
3 × 0 = 0 or Zero.
Question 7.
![]()
Answer:
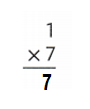
Explanation:
1 × 7 = 7 or Seven.
Question 8.
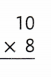
Answer:
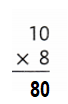
Explanation:
10 × 8 = (5× 8) + (5× 8)
10 × 8 = 40 + 40
10 × 8 = 80 or Eighty.
Independent Practice
In 9-25, use known facts and strategies to find the product.
Question 9.
7 × 7 = _______
Answer:
7 × 7 = ___49____.
Explanation:
7 × 7 = (4 × 7) + (3 × 7)
7 × 7 = 28 + 21
7 × 7 = 49 or Forty Nine.
Question 10.
8 × 2 = _______
Answer:
8 × 2 = __16_____.
Explanation:
8 × 2 = (6 × 2) + (2 × 2)
8 × 2 = 12 + 4
8 × 2 = 16 or Sixteen.
Question 11.
3 × 10 = ______
Answer:
3 × 10 = __30____.
Explanation:
3 × 10 = (2 × 10 ) + (1 × 10 )
3 × 10 = 20 + 10
3 × 10 = 30 or Thirty.
Question 12.
_____ = 8 × 9
Answer:
__72___ = 8 × 9.
Explanation:
8 × 9 = (6 × 9) + (2 × 9)
8 × 9 = 54 + 18
8 × 9 = 72 or Seventy Two.
Question 13.
_____ = 4 × 6
Answer:
__24___ = 4 × 6.
Explanation:
4 × 6 = (2 × 6) + (2 × 6)
4 × 6 = 12 + 12
4 × 6 = 24 or Twenty Four.
Question 14.
_____ = 4 × 4
Answer:
__16___ = 4 × 4.
Explanation:
4 × 4 = (2 × 4) + (2 × 4)
4 × 4 = 8 + 8
4 × 4 = 16 or sixteen.
Question 15.
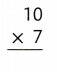
Answer:
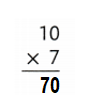
Explanation:
10 × 7 = (6× 7) + (4× 7)
10 × 7 = 42 + 28
10 × 7 = 70 or Seventy.
Question 16.
![]()
Answer:
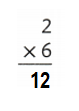
Explanation:
2 × 6 = (1 × 6) + (1 × 6)
2 × 6 = 6 + 6
2 × 6 = 12 or Twelve.
Question 17.
![]()
Answer:
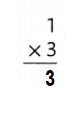
Explanation:
1 × 3 = 3 or Three.
Question 18.
![]()
Answer:
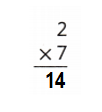
Explanation:
2 × 7 = (1 × 7) + (1 × 7)
2 × 7 = 7 + 7
2 × 7 = 14 or Fourteen.
Question 19.
![]()
Answer:
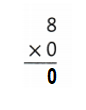
Explanation:
8 × 0 = 0 or zero.
Question 20.
![]()
Answer:
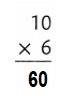
Explanation:
10 × 6 = (5 × 6) + (5 × 6)
10 × 6 = 30 + 30
10 × 6 = 60 or Sixty.
Question 21.
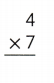
Answer:
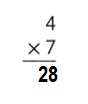
Explanation:
4 × 7 = (2 × 7) + (2 × 7)
4 × 7 = 14 + 14
4 × 7 = 28 or Twenty Eight.
Question 22.
![]()
Answer:
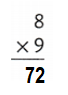
Explanation:
8 × 9 = (3 × 9) + (5 × 9)
8 × 9 = 27 + 45
8 × 9 = 72 or Seventy Two.
Question 23.
What is 6 × 9?
Answer:
6 × 9 = 54 or Fifty Four.
Explanation:
6 × 9 = (3 × 9) + (3 × 9)
6 × 9 = 27 + 27
6 × 9 = 54 or Fifty Four.
Question 24.
What is 7 × 2?
Answer:
7 × 2 = 14 or Fourteen.
Explanation:
7 × 2 = (4 × 2) + (3 × 2)
7 × 2 = 8 + 6
7 × 2 = 14 or Fourteen.
Question 25.
What is 8 × 1?
Answer:
8 × 1 = 8 or Eight.
Explanation:
8 × 1 = (4 × 1) + (4 × 1)
8 × 1 = 4 + 4
8 × 1 = 8 or Eight.
Problem Solving
Question 26.
Reasoning Mr. Ling walks 5 miles each day. How many total miles does he walk in one week? Explain.
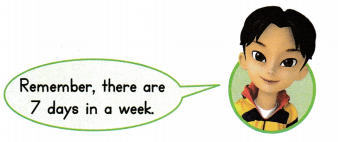
Answer:
Total number of miles he walks in one week = 35 or Thirty Five.
Explanation:
Number of miles each day Mr. Ling walks = 5 or Five.
Number of days in a week = 7 or Seven.
Total number of miles he walks in one week = Number of miles each day Mr. Ling walks × Number of days in a week
= 5 × 7
= (3 × 7) + (2 × 7)
= 21 + 14
= 35 or Thirty Five.
Question 27.
David wants to buy new shoes and a jersey. The shoes cost $56. The jersey costs $42. How much money does David need to buy both items?
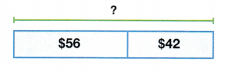
Answer:
Amount of money David needs to buy both items = $98.
Explanation:
Cost of shoes David buys = $56
Cost of jersey David buys = $42
Amount of money David needs to buy both items = Cost of shoes David buys + Cost of jersey David buys
= $56 + $42
= $98.

Question 28.
Ms. Wilson drank three 8-ounce glasses of tea before lunch. Then she drank three 8-ounce glasses of water before dinner. How many ounces of liquid did she drink in all? Write an equation to help solve.
Answer:
Number of 8-ounces of liquid did she drink in all = Number of 8-ounce glasses of tea before lunch Ms. Wilson drank + Number of 8-ounce glasses of water before dinner Ms. Wilson drank
= 3 + 3 = 6 or Six.
Explanation:
Number of 8-ounce glasses of tea before lunch Ms. Wilson drank = 3 or Three.
Number of 8-ounce glasses of water before dinner Ms. Wilson drank = 3 or Three.
Number of 8-ounces of liquid did she drink in all = Number of 8-ounce glasses of tea before lunch Ms. Wilson drank + Number of 8-ounce glasses of water before dinner Ms. Wilson drank
= 3 + 3
= 6 or Six.
Question 29.
Higher Order Thinking
Show how you can use known facts to find 4 × 11. Explain how you chose the known facts.
Answer:
In this problem, 4 × 11 represents multiplication, or finding the product of the two numbers. In this case, this problem represents four multiplied eleven times, or adding the number four eleven times. So the number four added to the number four a total of eleven times is Forty-four.
Explanation:
4 × 11 = (2 × 11) + (2 × 11)
4 × 11 = 22 + 22
4 × 11 = 44 or Forty Four.
So, 4 × 11 = 44.
Question 30.
Mr. Evans needs to assign 32 students into 8 equal groups. He says, “I can use repeated subtraction. Because I subtract 3 times, each group has 3 students.” Do you agree with Mr. Evans? Explain why or why not.
32 – 16 = 16
16 – 8 = 8
8 – 8 = 0
Answer:
No, I does not agree with Mr. Evans because dividing 32 students equally into 8 groups means in each group four students will be.
Number of members in each group = 32 ÷ 8 = 4 or Four.
Explanation:
Number of students needs to assign = 32.
Number of equal groups to be assigned = 8.
Number of members in each group = Number of students needs to assign ÷ Number of equal groups to be assigned
= 32 ÷ 8
= 4 or Four.
Assessment Practice
Question 31.
Select the possible ways to display 20 counters in equal groups.
☐ 2 groups of 10
☐ 4 groups of 5
☐ 5 groups of 4
☐ 4 groups of 6
☐ 10 groups of 2
Answer:
The possible ways to display 20 counters in equal groups.
☐ 2 groups of 10.
☐ 4 groups of 5.
☐ 5 groups of 4.
☐ 10 groups of 2.
Explanation:
The possible ways to display 20 counters in equal groups.
☐ 2 groups of 10 = 2 × 10 = 20.
☐ 4 groups of 5 = 4 × 5 = 20.
☐ 5 groups of 4 = 5 × 4 = 20.
☐ 10 groups of 2 = 10 × 2 = 20.
Question 32.
Select the possible ways to display 24 counters in an array.
☐ 8 rows of 4
☐ 3 rows of 6
☐ 6 rows of 4
☐ 3 rows of 8
☐ 2 rows of 9
Answer:
The possible ways to display 24 counters in an array:
☐ 3 rows of 6
☐ 6 rows of 4
☐ 3 rows of 8
Explanation:
The possible ways to display 24 counters in an array:
☐ 3 rows of 6 = 3 × 6 = 24.
☐ 6 rows of 4 = 6 × 4 = 24.
☐ 3 rows of 8 = 3 × 8 = 24.
Lesson 3.6 The Associative Property: Multiply with 3 Factors
Solve & Share
Gina has 2 quilts. Each quilt has 5 rows with 3 squares in each row. How many squares are in both quilts? Solve this problem any way you choose. Then find another way to solve the problem.
I can … multiply 3 factors in any order to find a product.

You can make sense and persevere in solving problems. You can solve this problem in more than one way.
Look Back! Did you get a different answer when you solved the problem a different way? Explain why or why not.
Answer:
Number of squares in both quilts = 30 or Thirty.
Explanation:
Number of quilts Gina has = 2 or Two.
Number of rows each quilt has = 5 or Five.
Number of squares in each row = 3 or Three.
Number of squares in both quilts = Number of quilts Gina has × ( Number of rows each quilt has × Number of squares in each row )
= 2 × ( 5 × 3)
= 2 × 15
= 30 or Thirty.
Essential Question
How Can You Multiply 3 Numbers?
Answer:
Multiply the first number by the second number.
Multiply the product of the first multiplication by the third number.
Explanation:
How to multiply three numbers:
Multiply the first number by the second number.
Multiply the product of the first multiplication by the third number.
Visual Learning Bridge
Drew is joining 3 sections of a quilt. Each section has 2 rows with 4 squares in each row. How many squares are in these 3 sections? Find 3 × 2 × 4.
You can multiply to find the total for an array

One Way
Find 3 × 2 first.
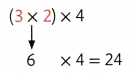
6 rows, 4 squares in each row
There are 24 squares in all.
Another Way
Find 2 × 4 first.

3 sections, 8 squares in each section
There are 24 squares in Drew’s quilt.
Convince Me! Generalize Use the Associative Property of Multiplication to show two different ways to find c Did you get the same answer both ways? What can you generalize?
Answer:
First Way:
5 × 2 × 3 = 5 × (2 × 3) = 5 × 6 = 30 or Thirty..
Second Way:
5 × 2 × 3 = (5 × 2) × 3 = 10 × 3 = 30 or Thirty.
It is generalize that the result for both ways, the answers are same.
Explanation:
First Way:
5 × 2 × 3 = 5 × (2 × 3)
5 × 2 × 3 = 5 × 6
5 × 2 × 3 = 30 or Thirty..
Second Way:
5 × 2 × 3 = (5 × 2) × 3
5 × 2 × 3 = 10 × 3
5 × 2 × 3 = 30 or Thirty.
Guided Practice
Do You Understand?
Question 1.
Sarah has 4 pages of stickers in an album. Each page has 3 rows with 2 stickers in each row. How many stickers are in Sarah’s album? You may use objects to help.
Answer:
Number of stickers are in Sarah’s album = 24 or Twenty Four.
Explanation:
Number of pages of stickers in an album Sarah has = 4 or Four.
Number of rows each page has = 3 or Three.
Number of stickers in each row = 2 or Two.
Number of stickers are in Sarah’s album = Number of pages of stickers in an album Sarah has × Number of rows each page has × Number of stickers in each row
= (4 × 3)× 2
= 12 × 2
= 24 or Twenty Four.
Question 2.
Billy concludes the product of (2 × 3) × 5 is not equal to the product of 2 × (3 × 5). Is Billy correct? Explain.
Answer:
Well, Billy concludes the product of (2 × 3) × 5 is not equal to the product of 2 × (3 × 5) is not correct because both the answers are same.
Explanation:
(2 × 3) × 5 = 6 × 5 = 30 or Thirty.
2 × (3 × 5) = 2 × 15 = 30 or Thirty.
Do You Know How?
In 3-6, use the Associative Property of Multiplication to find the missing number. You may use objects or draw a picture to help.
Question 3.
2 × (4 × 2) = (2 × 4) × ______
Answer:
2 × (4 × 2) = (2 × 4) × ______
2 × (4 × 2) = (2 × 4) × __2____
2 × 8 = 8 × 2
16.
Explanation:
2 × (4 × 2) = (2 × 4) × ?
2 × (4 × 2) = (2 × 4) × 2
2 × 8 = 8 × 2
16 = 16 or Sixteen.
Question 4.
(3 × 4) × 3 = 3 × (_____ × 3)
Answer:
(3 × 4) × 3 = 3 × (_____ × 3)
(3 × 4) × 3 = 3 × (__4___ × 3)
12× 3 = 3 × 12
36 or Thirty Six.
Explanation:
(3 × 4) × 3 = 3 × (?× 3)
(3 × 4) × 3 = 3 × (4× 3)
12× 3 = 3 × 12
36= 36 or Thirty Six.
Question 5.
2 × (2 × 3) = (2 × 2) × _______
Answer:
2 × (2 × 3) = (2 × 2) × ?
2 × (2 × 3) = (2 × 2) × ___3____
2 × 6 = 4 × 3
12 or Twelve.
Explanation:
2 × (2 × 3) = (2 × 2) × _______.
2 × (2 × 3) = (2 × 2) × ?.
2 × (2 × 3) = (2 × 2) × 3.
2 × 6 = 4 × 3
12 = 12 or Twelve.
Question 6.
(3 × 2) × 4 = ______ × (2 × 4)
Answer:
(3 × 2) × 4 = ______ × (2 × 4)
(3 × 2) × 4 = __3____ × (2 × 4)
6 × 4 = 3 × 8
24 or Twenty Four.
Explanation:
(3 × 2) × 4 = ______ × (2 × 4)
(3 × 2) × 4 = ? × (2 × 4)
(3 × 2) × 4 = 3 × (2 × 4)
6 × 4 = 3 × 8
24 = 24 or Twenty Four.
Independent Practice
In 7-12, use the Associative Property of Multiplication to find the missing number. You may use objects or draw a picture to help.
Question 7.
8 × (3 × 6) = (8 × 3) × ______
Answer:
8 × (3 × 6) = (8 × 3) × ______
8 × (3 × 6) = (8 × 3) × __6____.
8 × 18 = 24 × 6
144 or One hundred and Forty Four.
Explanation:
8 × (3 × 6) = (8 × 3) × ______.
8 × (3 × 6) = (8 × 3) × ?
8 × (3 × 6) = (8 × 3) × 6
8 × 18 = 24 × 6
144 = 144 or One hundred and Forty Four.
Question 8.
5 × (6 × 9) = (5 × 6) × _______
Answer:
5 × (6 × 9) = (5 × 6) × _______
5 × (6 × 9) = (5 × 6) × ?
5 × 54 = 30 × 9
270 = 270 or Two hundred and seventy.
Explanation:
5 × (6 × 9) = (5 × 6) × _______.
5 × (6 × 9) = (5 × 6) × ?
5 × (6 × 9) = (5 × 6) × 9
5 × 54 = 30 × 9
270 = 270 or Two hundred and seventy.
Question 9.
5 × (7 × 2) = (5 × 7) × _______
Answer:
5 × (7 × 2) = (5 × 7) × _______
5 × (7 × 2) = (5 × 7) × ?
5 × 14 = 35 × 2
70 or 70 or Seventy.
Explanation:
5 × (7 × 2) = (5 × 7) × _______.
5 × (7 × 2) = (5 × 7) × ?
5 × (7 × 2) = (5 × 7) × 2
5 × 14 = 35 × 2
70 or 70 or Seventy.
Question 10.
5 × (2 × 9) = (5 × _____) × 9
Answer:
5 × (2 × 9) = (5 × _____) × 9
5 × (2 × 9) = (5 × ?) × 9
5 × (2 × 9) = (5 × 2) × 9
5 × 18 = 10 × 9
90 = 90 or Ninety.
Explanation:
5 × (2 × 9) = (5 × _____) × 9
5 × (2 × 9) = (5 × ?) × 9
5 × (2 × 9) = (5 × 2) × 9
5 × 18 = 10 × 9
90 = 90 or Ninety.
Question 11.
3 × (2 × 5) = (3 × 2) × ______
Answer:
3 × (2 × 5) = (3 × 2) × ?
3 × (2 × 5) = (3 × 2) × 5
3 × 10 = 6 × 5
30 = 30 or Thirty.
Explanation:
3 × (2 × 5) = (3 × 2) × ______
3 × (2 × 5) = (3 × 2) × ?
3 × (2 × 5) = (3 × 2) × 5
3 × 10 = 6 × 5
30 = 30 or Thirty.
Question 12.
4 × (2 × 2) = (4 × _____) × 2
Answer:
4 × (2 × 2) = (4 × _____) × 2
4 × (2 × 2) = (4 × ?) × 2
4 × (2 × 2) = (4 × 2) × 2
4 × 4 = 8 × 2
16 = 16 or Sixteen.
Explanation:
4 × (2 × 2) = (4 × _____) × 2
4 × (2 × 2) = (4 × ?) × 2
4 × (2 × 2) = (4 × 2) × 2
4 × 4 = 8 × 2
16 = 16 or Sixteen.
In 13-18, use the Associative Property of Multiplication to find the product. You may use objects or draw a picture to help.
Question 13.
2 × 3 × 2 = ______
Answer:
2 × 3 × 2 = __12 or Twelve____.
Explanation:
2 × 3 × 2 = ??
= (2 × 3) × 2
= 6 × 2
= 12 or Twelve.
Question 14.
3 × 6 × 2 = ______
Answer:
3 × 6 × 2 = ______
Explanation:
3 × 6 × 2 = ??
3 × 6 × 2
= (3 × 6) × 2
= 18 × 2
= 36 or Thirty Six.
Question 15.
2 × 6 × 2 = ______
Answer:
2 × 6 × 2 = __24 or Twenty Four____.
Explanation:
2 × 6 × 2 = ??
(2 × 6) × 2
= 12 × 2
= 24 or Twenty Four.
Question 16.
5 × 2 × 4 = _______
Answer:
5 × 2 × 4 = __ 40 or Forty_____.
Explanation:
5 × 2 × 4 = ??
(5 × 2) × 4
= 10 × 4
= 40 or Forty.
Question 17.
5 × 2 × 2 = ________
Answer:
5 × 2 × 2 = __20 or Twenty.______.
Explanation:
5 × 2 × 2 = ??
(5 × 2) × 2
= 10 × 2
= 20 or Twenty.
Question 18.
3 × 3 × 2 = _______
Answer:
3 × 3 × 2 = __18 or Eighteen.____.
Explanation:
3 × 3 × 2 = ??
(3 × 3) × 2
= 9 × 2
= 18 or Eighteen.
Problem Solving
Question 19.
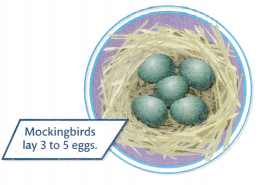
Reasoning There are 7 mockingbird nests at a park with eggs in them. What is the greatest number of eggs there could be at this park? What is the least number of eggs there could be?
Answer:
The greatest number of eggs there could be at this park = 35 or Thirty Five.
The least number of eggs there could be at this park = 21 or Twenty One.
Explanation:
Case:1: If mockingbird lays 3 eggs in the nests at a park.
Number of mockingbird nests at a park = 7 or Seven.
Number of mockingbird nests at a park with eggs = 3 or Three.
Number of eggs there could be at this park = Number of mockingbird nests at a park × Number of mockingbird nests at a park with eggs
= 7 × 3
= 21 or Twenty One.
Case:2: If mockingbird lays 3 eggs in the nests at a park.
Number of mockingbird nests at a park = 7 or Seven.
Number of mockingbird nests at a park with eggs = 4 or Four.
Number of eggs there could be at this park = Number of mockingbird nests at a park × Number of mockingbird nests at a park with eggs
= 7 × 4
= 28 or Twenty Eight.
Case:3: If mockingbird lays 5 eggs in the nests at a park.
Number of mockingbird nests at a park = 7 or Seven.
Number of mockingbird nests at a park with eggs = 5 or Five.
Number of eggs there could be at this park = Number of mockingbird nests at a park × Number of mockingbird nests at a park with eggs
= 7 × 5
= 35 or Thirty Five.
Question 20.
At another park, there are 3 mockingbird nests with 4 eggs in each nest and 1 more nest with 3 eggs. How many eggs are there at this park?
Answer:
Total number of eggs at this park = 15 or Fifteen.
Explanation:
Number of mockingbird nests at a park = 3 or Three.
Number of mockingbird nests at a park with eggs = 4 or Four.
Number of mockingbird nests at a park extra = 1 or One.
Number of mockingbird nests at a park with eggs extra = 3 or Three.
Total number of eggs at this park = (Number of mockingbird nests at a park × Number of mockingbird nests at a park with eggs ) + (Number of mockingbird nests at a park extra × Number of mockingbird nests at a park with eggs extra)
= (3 × 4) + (1 × 3)
= 12 + 3
= 15 or Fifteen.
Question 21.
Maria says she can find the product for 2 × 3 × 4 by solving 3 × 2 × 4. Is Maria correct? Explain.
Answer:
Yes, Maria is correct because both the equations are same.
Explanation:
2 × 3 × 4
= (2 × 3) × 4
= 6 × 4
= 24 or Twenty Four.
3 × 2 × 4
= (3 × 2) × 4
= 6 × 4
= 24 or Twenty Four.
Question 22.
Anita has 2 arrays. Each array has 3 rows of 3 counters. Explain why Anita can use the Associative Property to find the total number of counters in two different ways.
Answer:
Way:1:
Total number of counters = Number of Arrays Anita has × Number of rows in each Array × Number of counters in each Array
= 2 × 3 × 3
= 6 × 3
= 18 or Eighteen.
Way:2:
Total number of counters = Number of counters in each Array × Number of rows in each Array × Number of Arrays Anita has
= 3 × 3 × 2
= 9 × 2
= 18 or Eighteen.
Explanation:
Way:1:
Number of Arrays Anita has = 2 or Two.
Number of rows in each Array = 3 or Three.
Number of counters in each Array = 3 or Three.
Total number of counters = Number of Arrays Anita has × Number of rows in each Array × Number of counters in each Array
= 2 × 3 × 3
= (2 × 3) × 3
= 6 × 3
= 18 or Eighteen.
Way:2:
Number of counters in each Array = 3 or Three.
Number of rows in each Array = 3 or Three.
Number of Arrays Anita has = 2 or Two.
Total number of counters = Number of counters in each Array × Number of rows in each Array × Number of Arrays Anita has
= 3 × 3 × 2
= (3 × 3) × 2
= 9 × 2
= 18 or Eighteen.
Question 23.
Algebra Which number makes both equations true?
4 × (3 × 2) = (4 × ?) × 2
3 × (5 × 2) = (? × 5) × 2
Answer:
3 or Three number makes both equations true.
Explanation:
4 × (3 × 2) = (4 × ?) × 2
= 4 × (3 × 2) = (4 × 3) × 2
= 4 × 6 = 12 ×2
= 24 = 24.
3 × (5 × 2) = (? × 5) × 2
= 3 × (5 × 2) = (3 × 5) × 2
= 3 × 10 = 15 × 2
= 30 = 30.
Question 24.
Higher Order Thinking
How do you know that 4 × 2 × 2 is the same as 4 × 4? Explain.
Answer:
4 × 2 × 2 is the same as 4 × 4 because their product value is same.
Explanation:
4 × 2 × 2
= (4 × 2) × 2
= 8 × 2
= 16 or Sixteen.
4 × 4
= 16 or Sixteen.
Assessment Practice
Question 25.
Use properties of operations to select all the expressions that could be used to find 7 × 1 × 3.
☐ (7 × 1) × 3
☐ 7 × (1 × 3)
☐ (1 × 7) × 3
☐ 7 × 1 × 1
☐ 7 × (3 × 1)
Answer:
Expressions that could be used to find 7 × 1 × 3:
☐ (7 × 1) × 3
☐ 7 × (1 × 3)
☐ (1 × 7) × 3
☐ 7 × (3 × 1)
Explanation:
Expressions that could be used to find 7 × 1 × 3:
(7 × 1) × 3
7 × (1 × 3)
(7 × 3) × 1
7 × (3 × 1)
(1 × 7) × 3
1 × (7 × 3)
Question 26.
An expression is shown. Select all the equivalent expressions.
4 × 2 × 3
You can use properties to solve problems in different ways.
☐ 4 × (2 × 3)
☐ (4 × 2) × 3
☐ (2 × 4) × 3
☐ (4 × 2) × 4
☐ (3 × 2) × 2.
Answer:
Expressions that could be used to find 4 × 2 × 3:
☐ 4 × (2 × 3)
☐ (4 × 2) × 3
☐ (2 × 4) × 3
Explanation:
Expressions that could be used to find 4 × 2 × 3:
(4 × 2) × 3
4 × (2 × 3)
(4 × 3) × 2
4 × (3 × 2)
(2 × 4) × 3:
2 × (4 × 3)
Lesson 3.7 Problem Solving
Repeated Reasoning
Solve
You have learned that you can use known facts to find unknown facts. For each of the 4 multiplication facts below, list two multiplication facts from the box that can be added to find the given product. The first solution is completed for you.
What do you notice about the facts you used to find the products when 6 or 7 is a factor?
I can.. use reasoning to look for and describe general strategies for finding products.
Thinking Habits
Be a good thinker! These questions can help you.
- Are any calculations repeated?
- Can I generalize from examples?
- What shortcuts do I notice?

Look Back! Generalize Use your observations from your work above to complete these facts.
(______ × 6) + (_____ × 6) = 36
(______ × 7) + (_____ × 7) = 49
Answer:
(______ × 6) + (_____ × 6)
= (___5___ × 6) + (__1___ × 6)
= 30 + 6
= 36.
(______ × 7) + (_____ × 7)
= (___6___ × 7) + (__1___ × 7)
= 42 + 7
= 49.
Explanation:
(______ × 6) + (_____ × 6) = 36.
(___5___ × 6) + (__1___ × 6) = 36.
30 + 6= 36.
(______ × 7) + (_____ × 7) = 49.
(___6___ × 7) + (__1___ × 7) = 49.
42 + 7= 49.
Essential Question
How Can You Use Repeated Reasoning When Multiplying?
Answer:
“Repeated reasoning” means, why looking for and expressing regularity in it is such a valuable mathematical habit of mind, and how that differs from analyzing structure (MP 7) and from finding patterns in numerical results.
Explanation:
To make sense of the Common Core State Standards mathematical practice (MP) 8, this article illustrates what “repeated reasoning” means, why looking for and expressing regularity in it is such a valuable mathematical habit of mind, and how that differs from analyzing structure (MP 7) and from finding patterns in numerical results.
Visual Learning Bridge
Ellie wrote the equations below to find the total number of squares in each of these rectangles. Look at the equations. Known facts with which factors are used repeatedly to find the products?
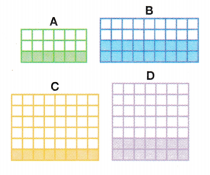
A. 3 × 6 = (2 × 6) + (1 × 6) = 12 + 6 = 18
B. 4 × 9 = (2 × 9) + (2 × 9) = 18 + 18 = 36
C. 6 × 8 = (5 × 8) + (1 × 8) = 40 + 8 = 48
D. 7 × 7 = (5 × 7) + (2 × 7) = 35 + 14 = 49
What do I need to do to complete the task?
I need to see if there are known facts that can be used repeatedly to find other facts.
How can I make a generalization from repeated reasoning?
I can
- look for repeated calculations.
- make generalizations about the repeated calculations.
- test whether my generalizations work for other numbers.
Here’s my thinking…
I see that the factors
1, 2, and 5 are used repeatedly.
I see two generalizations.
I can break facts with 3 or 4 into 2s and 1s facts.
3 × 6 = (2 × 6) + (1× 6)
4 × 9 = (2 × 9) + (2 × 9)
I can break facts with 6 or 7 into 5s, 25, and 1s facts.
6 × 8 = (5 × 8) + (1 × 8)
7 × 7 = (5 × 7) + (2 × 7)
I can test this with other facts.
3 × 5 = (2 × 5) + (1 × 5)
6 × 7 = (5 × 7) + (1 × 7)
Convince Me! Generalize Use the generalizations above to complete each of the following. Tell how you decided.
7 × 5 = (____) + (______)
7 × 6 = (____) + (______)
Answer:
7 × 5 = (____) + (______)
7 × 5 = (4 × 5) + (3 × 5) = 35 or Thirty Five.
7 × 6 = (____) + (______)
7 × 6 = (2 × 6) + (5 × 6) = 42 or Forty Two.
Explanation:
7 × 5 = (4 × 5) + (3 × 5)
7 × 5 = 20 + 15
7 × 5 = 35 or Thirty Five.
7 × 6 = (____) + (______)
7 × 6 = (2 × 6) + (5 × 6)
7 × 6 = 12 + 30
7 × 6 = 42 or Forty Two.
Guided Practice
Generalize Ricardo wrote the equations below.

Question 1.
Which factors did Ricardo use repeatedly to find the products? Make a generalization.
3 × 8 = (2 × 8) + (1 × 8) = 24
3 × 7 = (2 × 7) + (1 × 7) = 21
6 × 3 = (6 × 1) + (6 × 2) = 18
Answer:
3 × 8 = (2 × 8) + (1 × 8) = 24 True.
3 × 7 = (2 × 7) + (1 × 7) = 21 True.
6 × 3 = (6 × 1) + (6 × 2) = 18 False.
Explanation:
Factors which Ricardo used repeatedly to find the products:
3 × 8 = (2 × 8) + (1 × 8) = 24 True.
3 × 7 = (2 × 7) + (1 × 7) = 21 True.
6 × 3 = (6 × 1) + (6 × 2) = 18False.
Question 2.
Complete this equation to test whether your generalization is true for other facts. Explain.
3 × 9 = (__ × ____) + (____ × ____) = _____
Answer:
3 × 9 = (_2__ × __9__) + (__1__ × __9__) = __ 27 or Twenty Seven___.
Explanation:
3 × 9 = (2 × 9 ) + (1 × 9)
3 × 9 = 18 + 9
3 × 9 = 27 or Twenty Seven.
Independent Practice
Generalize
Mary wrote the equations at the right.
Question 3.
Which factors did Mary use repeatedly to find the products? Make a generalization.
8 × 7 = (5 × 7) + (3 × 7) = 56
6 × 8 = (6 × 5) + (6 × 3) = 48
8 × 9 = (3 × 9) + (5 × 9) = 72
Answer:
8 × 7 = (5 × 7) + (3 × 7) = 56. True.
6 × 8 = (6 × 5) + (6 × 3) = 48. False.
8 × 9 = (3 × 9) + (5 × 9) = 72. True.
Explanation:
8 × 7 = (5 × 7) + (3 × 7) = 35 + 21 = 56. True.
6 × 8 = (6 × 5) + (6 × 3) = 30 + 18 = 48. False.
8 × 9 = (3 × 9) + (5 × 9) = 27 + 45 = 72. True.
Question 4.
Complete this equation to test whether your generalization is true for other facts. Explain.
8 × 3 = (____ × _____) + (____ × _____) = ______
Answer:
8 × 3 = (__5__ × __3___) + (__3__ × _3____) = __24 or Twenty Four____.
Explanation:
8 × 3 = (5 × 3) + (3 × 3)
8 × 3 = 15 + 9
8 × 3 = 24 or Twenty Four.
Question 5.
What is another way you can use known facts to solve 8 × 3? What generalization can you make from this way?
Answer:
Another way:
8 × 3 = (2 ×3) + (2 ×3) + (2 ×3) + (2 ×3)
= 6 + 6 + 6 + 6
= 12 + 6 + 6
= 18 + 6 = 24 or Twenty Four.
Explanation:
Another way:
8 × 3 = (2 ×3) + (2 ×3) + (2 ×3) + (2 ×3)
8 × 3 = 6 + 6 + 6 + 6
8 × 3 = 12 + 6 + 6
8 × 3 = 18 + 6
8 × 3 = 24 or Twenty Four.
Problem Solving
Performance Task
Baking Pizzas
Adam is baking 4 pizzas. Each pizza is a rectangle. It takes Adam 35 minutes to bake the pizzas. He divides each pizza into the equal-size square slices shown.
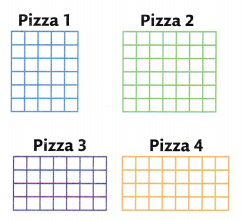
Question 6.
Make Sense and Persevere Adam multiplies to find the total number of square slices for each pizza. For each pizza, tell the factors Adam multiplies.
Answer:
Number of square slices in pizza 1 = 6 × 5 = 30 or Thirty.
Number of square slices in pizza 2 = 6 × 7 = 42 or Forty Two.
Number of square slices in pizza 3 = 4 × 7 = 28 or Twenty Eight.
Number of square slices in pizza 4 = 4 × 8 = 32 or Thirty Two.
Explanation:
Number of pizzas Adam bakes = 4 or Four.
Number of square slices in pizza 1 = 6 × 5 = (3 × 5) + (3 × 5) = 15 + 15 = 30 or Thirty.
Number of square slices in pizza 2 = 6 × 7 = (3 × 7) + (3 × 7) = 21+ 21= 42 or Forty Two.
Number of square slices in pizza 3 = 4 × 7 = (2 × 7) + (2 × 7) = 14 + 14 = 28 or Twenty Eight.
Number of square slices in pizza 4 = 4 × 8 = (2 × 8) + (2 × 8) = 16 + 16 = 32 or Thirty Two.
Question 7.
Use Structure Look at the facts you wrote in Exercise 6. Break apart these facts into 1s, 2s, or 5s facts to find the total number of slices for each pizza.
Pizza 1
(____ × _____) = (____ × _____) + (_____ × ______) = ______
Pizza 2
(____ × _____) = (____ × _____) + (_____ × ______) = ______
Pizza 3
(____ × _____) = (____ × _____) + (_____ × ______) = ______
Pizza 4
(____ × _____) = (____ × _____) + (_____ × ______) = ______
Answer:
Pizza 1
(__6__ × __5___) = (__3__ × __5___) + (___3__ × ___5___) = __30____.
Pizza 2
(__6__ × _7____) = (__3__ × __7___) + (__3___ × ___7___) = __42____.
Pizza 3
(__4__ × __7___) = (__2__ × ___7__) + (__2___ × __7____) = __28____.
Pizza 4
(__4__ × __8___) = (__2__ × __8___) + (__2___ × ___8___) = ___32___.
Explanation:
Pizza 1
6 × 5 = (3 × 5) + (3 × 5) = 15 + 15 = 30 or Thirty.
Pizza 2
(3 × 7) + (3 × 7) = 21+ 21 = 42 or Forty Two.
Pizza 3
4 × 7 = (2 × 7) + (2 × 7) = 14 + 14 = 28 or Twenty Eight.
Pizza 4
4 × 8 = (2 × 8) + (2 × 8) = 16 + 16 = 32 or Thirty Two.
Question 8.
Generalize Look at how you used the 1s, 2s, and 5s facts above. What generalizations can you make? Test your generalizations with another fact.

Answer:
The generalizations we can make is that using1s,2s,3s,4s and 5s , we can multiply the numbers and get the correct answer asked in the problem.
Explanation:
By using 1s,2s,3s,4s,5s,6s we can get the correct solution for the problem using multiplication.
Question 9.
Critique Reasoning
Look at the model for Pizza 3. Adam says he can use 2s facts to solve 4 × 7 or 7 × 4. Is he correct? Explain.
Answer:
He is correct, we can use 2s facts to solve 4 × 7 or 7 × 4.
Explanation:
4 × 7 = (2 × 7) + (2 × 7)
4 × 7 = 14 + 14
4 × 7 = 28 or Twenty Eight.
7 × 4 = (2 × 4) + (2 × 4) + (3 × 4)
7 × 4 = 8+ 8+ 12
7 × 4 = 16+ 12
7 × 4 = 28 or Twenty Eight.
Topic 3 Fluency Review Activity
Follow the path
Shade a path from START to FINISH. Follow the differences that are correct. You can only move up, down, right, or left.
I can … subtract within 100.

Answer:
Explanation:
Correct Subtraction equations which are shaded:
Start: 75 – 13 = 62.
99 – 36 = 63.
59 – 37 = 22.
46 – 27 = 19.
65 – 59 = 6.
81 – 29 = 52.
67 – 19 = 48.
78 – 35 = 43. Finish
Other equations are wrongly subtracted.
Topic 3 Vocabulary Review
Understand Vocabulary
Word List
- Associative (Grouping) Property of Multiplication
- Commutative (Order) Property of Multiplication
- Distributive Property
- factor
- Identity (One) Property of Multiplication
- multiple
- product
- Zero Property of Multiplication
Match the example to the term.

Answer:
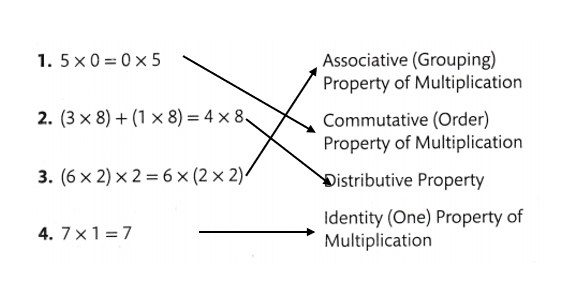
Explanation:
The Associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Commutative property states that the change in the order of numbers in an addition or multiplication operation does not change the sum or the product. The Commutative property of addition is written as: A + B = B + A.
The distributive property tells us how to solve expressions in the form of a(b + c). The distributive property is sometimes called the distributive law of multiplication.
The identity property of 1 says that any number multiplied by 1 keeps its identity . In other words, any number multiplied by 1 stays the same. The reason the number stays the same is because multiplying by 1 means we have 1 copy of the number
Write T for true or F for false.
Question 5.
______ 3 and 8 are multiples of 24.
Answer:
___T___ 3 and 8 are multiples of 24.
Explanation:
3 × 8 = 24.
Question 6.
________ You can multiply factors in any order.
Answer:
___T_____ You can multiply factors in any order.
Explanation:
True you can multiply factors in any order.
Example:
3 × 8 = 24.
8 × 3 = 24.
Question 7.
________ The product of zero and any number is that number.
Answer:
___F_____ The product of zero and any number is that number.
Explanation:
0 × 2 = infinity.
2 × 0 = 0 or Zero.
Question 8.
________ There are 3 factors in the equation 5 × 3 × 2 = 30.
Answer:
____T____ There are 3 factors in the equation 5 × 3 × 2 = 30.
Explanation:
2 × 15 = 30.
3 × 10 = 30.
5 × 6 = 30.
Use Vocabulary in Writing
Question 9.
Explain how to use 8 × 5 = 40 to find 8 × 6. Use at least 2 terms from the Word List in your explanation.
Answer:
8 × 5 = 40.
8 × 6 = (8 × 5 ) + (8 × 1 ) = 48 or Forty Eight.
Explanation:
8 × 5 = 40.
8 × 6 = (8 × 5 ) + (8 × 1 )
8 × 6 = 40 + 8
8 × 6 = 48 or Forty Eight.
Topic 3 Reteaching
Set A pages 77-80
You can break an array into 2 smaller arrays.

You can write an unknown fact as the sum of 2 known facts.
4 × 8 = (3 × 8) + (1 × 8)
Remember that the Distributive Property says that a multiplication fact can be broken apart into the sum of two other multiplication facts.
In 1 and 2, find the missing value.
Question 1.
_____ × 4 = (2 × 4) + (2 × 4)
Answer:
__4___ × 4 = (2 × 4) + (2 × 4).
Explanation:
_____ × 4 = (2 × 4) + (2 × 4).
? × 4 = (2 × 4) + (2 × 4)
4 × 4 = (2 × 4) + (2 × 4)
4 × 4 = 8 + 8
4 × 4 = 16 or Sixteen.
Question 2.
6 × 5 = (4 × 5) + (______ × 5)
Answer:
6 × 5 = (4 × 5) + (__2____ × 5)
Explanation:
6 × 5 = (4 × 5) + (? × 5)
6 × 5 = (4 × 5) + (2 × 5)
6 × 5 = 20 + 10
6 × 5 = 30 or Thirty.
Set B pages 81-84
Find 3 × 4.
You can use a 2s fact to help multiply by 3.
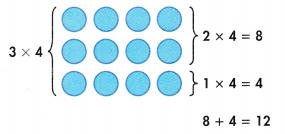
You can also find 4s facts.
3 × 4 = (3 × 2) + (3 × 2) = 6 + 6 = 12
Remember that to find a 3s fact, add a 2s fact and a 1s fact. To find a 4s fact, double the product of a 2s fact.
Question 1.
3 × 7 = _______
Answer:
3 × 7 = __(3 × 2) + (3 × 2) + (3 × 3)_= 6 + 6 + 9_= 21 or Twenty One__.
Explanation:
3 × 7 = (3 × 2) + (3 × 2) + (3 × 3)
3 × 7 = 6 + 6 + 9
3 × 7 = 12 + 9
3 × 7 = 21 or Twenty One.
Question 2.
4 × 9 = _______
Answer:
4 × 9 = _ (4 × 5) + (4 × 2) + (4 × 2)__= 20 + 8 + 8__= 36 or Thirty Six__.
Explanation:
4 × 9 = (4 × 5) + (4 × 2) + (4 × 2)
4 × 9 = 20 + 8 + 8
4 × 9 = 28 + 8
4 × 9 = 36 or Thirty Six.
Question 3.
4 × 10 = _______
Answer:
4 × 10 = _(4 × 2) + (4 × 2) + (4 × 2) + (4 × 2) + (4 × 2)_= 8 + 8 + 8 + 8 + 8_= 40 or Forty____.
Explanation:
4 × 10 = (4 × 2) + (4 × 2) + (4 × 2) + (4 × 2) + (4 × 2)
4 × 10 = 8 + 8 + 8 + 8 + 8
4 × 10 = 16 + 8 + 8 + 8
4 × 10 = 24 + 8 + 8
4 × 10 = 32 + 8
4 × 10 = 40 or Forty.
Question 4.
3 × 10 = ______
Answer:
3 × 10 = _(3 × 2) + (3 × 2) + (3 × 2) + (3 × 2) + (3 × 2)_= 6 + 6 + 6 + 6 + 6_= 30 or Thirty____.
Explanation:
3 × 10 = (3 × 2) + (3 × 2) + (3 × 2) + (3 × 2) + (3 × 2)
3 × 10 = 6 + 6 + 6 + 6 + 6
3 × 10 = 12 + 6 + 6 + 6
3 × 10 = 18 + 6 + 6
3 × 10 = 24 + 6
3 × 10 = 30 or Thirty.
Question 5.
3 × 8 = ______
Answer:
3 × 8 = __ (3 × 2)+ (3 × 2) + (3 × 2) + (3 × 2)_= 6 + 6 + 6 + 6 =_ 24 or Twenty Eight___
Explanation:
3 × 8 = (3 × 2)+ (3 × 2) + (3 × 2) + (3 × 2)
3 × 8 = 6 + 6 + 6 + 6
3 × 8 = 12 + 6 + 6
3 × 8 = 18 + 6
3 × 8 = 24 or Twenty Eight.
Question 6.
8 × 4 = ______
Answer:
8 × 4 = _ (8 × 2) + (8 × 2) _= 16 + 16_= 32 or Thirty Two___.
Explanation:
8 × 4 = (8 × 2) + (8 × 2)
8 × 4 = 16 + 16
8 × 4 = 32 or Thirty Two.
Question 7.
9 × 3 = _______
Answer:
9 × 3 = __(9 × 2) + (9 × 1)_= 18 + 9_= 27 or Twenty Seven___.
Explanation:
9 × 3 = (9 × 2) + (9 × 1)
9 × 3 = 18 + 9
9 × 3 = 27 or Twenty Seven.
Question 8.
10 × 4 = ______
Answer:
10 × 4 = _ (10 × 2) + (10 × 2)_= 20 + 20_= 40 or Forty.___.
Explanation:
10 × 4 = (10 × 2) + (10 × 2)
10 × 4 = 20 + 20
10 × 4 = 40 or Forty.
Set C pages 85-88
You can use known facts to help multiply. Find 6 × 9.
6 × 9 = (5 × 9) + (1 × 9)
6 × 9 = 45 + 9
6 × 9 = 54
Find 7 × 4.
7 × 4 = (5 × 4) + (2 × 4)
7 × 4 = 20 + 8
7 × 4 = 28
Remember that you can break a multiplication problem into two smaller problems.
Question 1.
6 × 6 = _____
Answer:
6 × 6 = _(3 ×6) + (3 ×6)_= 18 + 18_= 36 or Thirty Six.__.
Explanation:
6 × 6 = (3 ×6) + (3 ×6)
6 × 6 = 18 + 18
6 × 6 = 36 or Thirty Six.
Question 2.
7 × 9 = _____
Answer:
7 × 9 = _(2×9) + (2×9) + (3×9) = 18 + 18 + 27 = 63 or Sixty Three___.
Explanation:
7 × 9 = (2×9) + (2×9) + (3×9)
7 × 9 = 18 + 18 + 27
7 × 9 = 36 + 27
7 × 9 = 63 or Sixty Three.
Question 3.
7 × 7 = _____
Answer:
7 × 7 = (2×7) + (2×7) + (3×7)_= 14 + 14 + 21_= 49 or Forty Nine___.
Explanation:
7 × 7 = (2×7) + (2×7) + (3×7)
7 × 7 = 14 + 14 + 21
7 × 7 = 28 + 21
7 × 7 = 49 or Forty Nine.
Question 4.
6 × 8 = _______
Answer:
6 × 8 = _(3×8) + (2×8) + (1×8)_= 24 + 16 + 8__= 48 or Forty Eight___.
Explanation:
6 × 8 = (3×8) + (2×8) + (1×8)
6 × 8 = 24 + 16 + 8
6 × 8 = 40 + 8
6 × 8 = 48 or Forty Eight.
Question 5.
![]()
Answer:
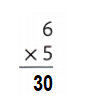
Explanation:
6 × 5 = (3×5) + (3×5)
6 × 5 = 15 + 15
6 × 5 = 30 or Thirty.
Question 6.
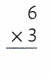
Answer:
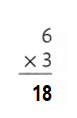
Explanation:
6 × 3 = (2×3) + (2×3) + (2×3)
6 × 3 = 6 + 6 + 6
6 × 3 = 12 + 6
6 × 3 = 18 or Eighteen.
Question 7.
![]()
Answer:
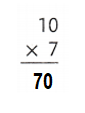
Explanation:
10 × 7 = (5×7) + (3×7) + (2×7)
10 × 7 = 35 + 21 + 14
10 × 7 = 56 + 14
10 × 7 = 70 or Seventy.
Set D pages 89-96
Find 8 × 9.
You can use 2s facts.
8 × 9 = (2 × 9) + (2 × 9) + (2 × 9) + (2 × 9)
8 × 9 = 18 + 18 + 18 + 18
8 × 9 = 72
You can use skip counting.
8, 16, 24, 32, 40, 48, 56, 64, 72
Remember to use patterns, known facts, or skip counting to find products.
Question 1.
8 × 6 = _______
Answer:
8 × 6 = _ (2 × 6) + (2 × 6) + (2 × 6) + (2 × 6)_= 12 + 12 + 12 + 12_= 48 or Forty Eight____.
Explanation:
8 × 6 = (2 × 6) + (2 × 6) + (2 × 6) + (2 × 6)
8 × 6 = 12 + 12 + 12 + 12
8 × 6 = 24 + 12 + 12
8 × 6 = 36 + 12
8 × 6 = 48 or Forty Eight.
Skip counting:
8, 16, 24, 32, 40, 48.
Question 2.
8 × 8 = ______
Answer:
8 × 8 = _(2 × 8) + (2 × 8) + (2 × 8) + (2 × 8)_= 16 + 16 + 16 + 16_= 64 or Sixty Four___.
Explanation:
8 × 8 = (2 × 8) + (2 × 8) + (2 × 8) + (2 × 8)
8 × 8 = 16 + 16 + 16 + 16
8 × 8 = 32 + 16 + 16
8 × 8 = 48 + 16
8 × 8 = 64 or Sixty Four.
Skip counting:
8, 16, 24, 32, 40, 48, 56, 64.
Question 3.
8 × 7 = _____
Answer:
8 × 7 = (2 × 7) + (2 × 7) + (2 × 7) + (2 × 7)_= 14 + 14 + 14 + 14_= 56 or Fifty Six___.
Explanation:
8 × 7 = (2 × 7) + (2 × 7) + (2 × 7) + (2 × 7)
8 × 7 = 14 + 14 + 14 + 14
8 × 7 = 28 + 14 + 14
8 × 7 = 42 + 14
8 × 7 = 56 or Fifty Six.
Skip counting:
8, 16, 24, 32, 40, 48, 56.
Question 4.
8 × 10 = ______
Answer:
8 × 10 = _(2 × 10) + (2 × 10) + (2 × 10) + (2 × 10)_= 20 + 20 + 20 + 20 _= 80 or Eighty___.
Explanation:
8 × 10 = (2 × 10) + (2 × 10) + (2 × 10) + (2 × 10)
8 × 10 = 20 + 20 + 20 + 20
8 × 10 = 40 + 20 + 20
8 × 10 = 60 + 20
8 × 10 = 80 or Eighty.
Skip counting:
8, 16, 24, 32, 40, 48, 56 , 64 , 72 , 80.
Question 5.
1 × 8 = _______
Answer:
1 × 8 = __8 or Eight_____.
Explanation:
1 × 8 = 8 or Eight.
Skip counting:
8.
Question 6.
0 × 8 = ______
Answer:
0 × 8 = __infinity____.
Explanation:
0 × 8 = infinity.
Question 7.
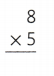
Answer:
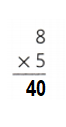
Explanation:
8 × 5 = (2×5) + (2×5) + (2×5) + (2×5)
8 × 5 = 10 + 10 + 10 + 10
8 × 5 = 20 + 10 + 10
8 × 5 = 30+ 10
8 × 5 = 40 or Forty.
Skip counting:
8, 16, 24, 32, 40.
Question 8.
![]()
Answer:
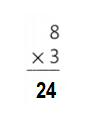
Explanation:
8 × 3 = (2×3) + (2×3) + (2×3) + (2×3)
8 × 3 = 6 + 6 + 6 + 6
8 × 3 = 12 + 6 + 6
8 × 3 = 18 + 6
8 × 3 = 24 or Twenty Four.
Skip counting:
8, 16, 24.
Question 9.
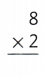
Answer:
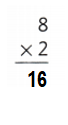
Explanation:
8 × 2 = (2×2) + (2×2) + (2×2) + (2×2)
8 × 2 = 4 + 4 + 4 + 4
8 × 2 = 8 + 4 + 4
8 × 2 = 12 + 4
8 × 2 = 16 or Sixteen.
Skip counting:
8, 16.
Set E pages 97-100
You can use the Associative Property to group the factors. The product does not change.
Find 4 × 2 × 2.
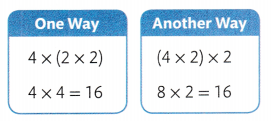
Remember that you can use properties to write unknown facts as known facts.
In 1-3, find the product. Show how you grouped the factors.
Question 1.
4 × 2 × 5 = _____ × ______ = _______
Answer:
4 × 2 × 5 = (4 × 2) × 5 = __8___ × ___5___ = __40 or Forty_____.
Explanation:
4 × 2 × 5 = (4 × 2) × 5 = 8 × 5 = 40 or Forty.
Question 2.
3 × 3 × 7 = _____ × ______ = _______
Answer:
3 × 3 × 7 = __3___ × ___21___ = __63 or Sixty Three_____.
Explanation:
3 × 3 × 7 = 3 × (3 × 7) =__3___ × __21____ = ___63 or Sixty Three____.
Question 3.
5 × 5 × 2 = _____ × ______ = _______
Answer:
5 × 5 × 2 = (5 × 5) × 2 = __25___ × __2____ = __50 or Fifty_____.
Explanation:
5 × 5 × 2 = (5 × 5) × 2 =__25___ × ___2___ = ___50 or Fifty____.
Set F pages 101-104
Think about these questions to help you use repeated reasoning.
Thinking Habits
- Are any calculations repeated?
- Can I generalize from examples?
- What shortcuts do I notice?

Remember that patterns can help you make a generalization.
Question 1.
What is repeated in these equations? Use what you see to make a generalization.
6 × 6 = (6 × 3) + (6 × 3) = 18 + 18 = 36
7 × 6 = (7 × 3) + (7 × 3) = 21 + 21 = 42
8 × 6 = (8 × 3) + (8 × 3) = 24 + 24 = 48
Answer:
In these equations, 6 number is repeated.
Explanation:
6 × 6 = (6 × 3) + (6 × 3) = 18 + 18 = 36.
7 × 6 = (7 × 3) + (7 × 3) = 21 + 21 = 42.
8 × 6 = (8 × 3) + (8 × 3) = 24 + 24 = 48.
6 number is repeated in all the equations.
Question 2.
Solve this equation to test whether your generalization is true.
10 × 6 = ?
______ × _______ = (_____ × ______) + (______ × ______)
= ______ + ______ = ______
Answer:
10 × 6 = ?
__10____ × ___6____ = (___10__ × ___3___) + (___10___ × ___3___)
= __30____ + __30____ = __Sixty____.
Explanation:
10 × 6 = ?
10 × 6 = (10 × 3) + (10 × 3)
10 × 6 = 30 + 30
10 × 6 = 60 or Sixty.
Topic 3 Assessment Practice
Question 1.
Krista arranged her buttons in an array. Which two expressions can be used to find the total number of buttons?

A. 6 × 7 and 6 × 1
B. 4 × 7 and 2 × 7
C. 4 × 4 and 2 × 3
D. 3 × 7 and 4 × 7
Answer:
B. 4 × 7 and 2 × 7 is the expression used to find the total buttons.
Explanation:
Number of rows of buttons Krista arranged = 7 or Seven.
Number of columns of buttons Krista arranged = 6 or Six.
Total number of buttons = Number of columns of buttons Krista arranged × Number of rows of buttons Krista arranged
= 6 × 7
= (4 × 7) + (2 × 7)
= 28 + 14
= 42 or Forty Two.
Question 2.
Choose Yes or No to tell if the Distributive Property is being used.
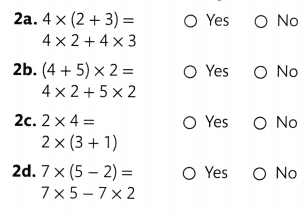
Answer:
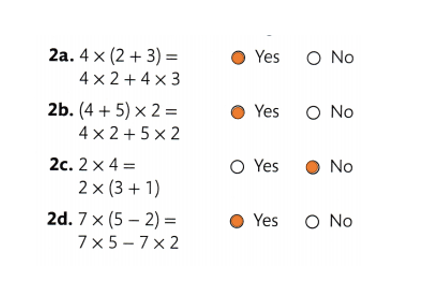
Explanation:
2a. 4 × (2 + 3) = (4 × 2) + (4 ×3) = 8 + 12 = 20. True.
2b. (4 + 5) × 2 = (4 × 2) + (5 ×2) = 8 + 10 = 18. True.
2c. 2 × 4 = 2 × (3 + 1) False.
2d. 7 × (5 – 2) = (7 × 5) – (7 × 2) = 35 – 14 = 21. True.
Question 3.
Jeff makes the generalization that a 10s fact can be broken into two 5s facts. Write an equation to test his generalization.
Answer:
10 × 2 = (5 × 2) + (5 × 2) = 20 or Twenty.
Explanation:
10 × 2 = (5 × 2) + (5 × 2)
10 × 2 = 10 + 10
10 × 2 = 20 or Twenty.
Question 4.
June broke up a large array into a 3 × 4 array and a 5 × 4 array. What was the large array? Show your work.
Answer:
Larger array = (First smaller array) + (Second smaller array)
Larger array = (3 × 4) + (5 × 4 )
Larger array = (8 × 4)
Explanation:
First smaller array = 3 × 4
Second smaller array = 5 × 4
Larger array = (First smaller array) + (Second smaller array)
Larger array = (3 × 4) + (5 × 4 )
Larger array = (8 × 4)
Question 5.
Which facts can you use to find 4 x 8? Select all that apply.
☐ 2 × 8 and 2 × 9
☐ 2 × 8 and 2 × 8
☐ 2 × 4 and 1 × 8
☐ 4 × 5 and 4 × 3
☐ 3 × 8 and 1 × 8
Answer:
The facts used to apply to find 4 x 8 are:
☐ 2 × 8 and 2 × 8
☐ 4 × 5 and 4 × 3
☐ 3 × 8 and 1 × 8
Explanation:
4 × 8 = (2 × 8) + (2 × 8) = 16 + 16 = 32 or Thirty Two.
4 × 8 = (4 × 5) + (4 × 3) = 20 + 12 = 32 or Thirty Two.
4 × 8 = (3 ×8) + (1 × 8) = 24 + 8 = 32 or Thirty Two.
Question 6.
A bakery uses 3 cups of flour for each loaf of bread. There are 3 loaves of bread on a tray. There are 6 trays on a cart. How many cups of flour are used to make the bread on the cart? Show your work.
Answer:
Number of cups of flour are used to make the bread on the cart = 54 or Fifty Four.
Explanation:
Number of cups of flour for each loaf of bread a bakery uses = 3 or Three.
Number of loaves of bread on a tray = 3 or Three.
Number of trays on a cart = 6 or Six.
Number of cups of flour are used to make the bread on the cart = (Number of cups of flour for each loaf of bread a bakery uses) × Number of loaves of bread on a tray × Number of trays on a cart
= (3 × 3) × 6
= 9 × 6
= (5 × 6) + (4 × 6)
= 30 + 24
= 54 or Fifty Four.
Question 7.
Find the number that makes the equation correct. Explain your reasoning.
(3 × 4) + (3 × 4) = ______
Answer:
(3 × 4) + (3 × 4) = ____(6 × 4)___= 24 or Twenty Four.___.
Explanation:
(3 × 4) + (3 × 4) = (6 × 4) = 24 or Twenty Four.
Two small arrays combined together to make a large array.
Question 8.
Casey has 3 bags of baseballs. Each bag has 6 baseballs. How many baseballs does he have? Show your work.
☐ baseballs
Answer:
Total number of baseballs Casey has = 18 or Eighteen.
Explanation:
Number of bags of baseballs Casey has = 3 or Three.
Number of each bag has baseballs = 6 or Six.
Total number of baseballs Casey has = Number of bags of baseballs Casey has × Number of each bag has baseballs
= 3 × 6
= (1 × 6) + (2 × 6)
= 6 + 12
= 18 or Eighteen.
Question 9.
Jonathan organizes his pictures into a 6 × 4 array. Kim organizes her pictures into a 7 × 5 array. How can Kim and Jonathan break apart their arrays? Write each pair of facts in the correct space.
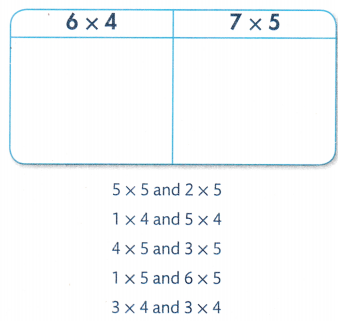
Answer:

Explanation:
Jonathan pictures array = 6 × 4.
6 × 4 = (5 × 4) + (1 × 4) = 20 + 4 = 24 or Twenty Four.
6 × 4 = (3 × 4) + (3 × 4) = 12 + 12 = 24 or Twenty Four.
6 × 4 = (1 × 4) + (5 × 4) = 4 + 20 = 24 or Twenty Four.
Kim pictures array = 7 × 5.
7 × 5 = (4 × 5) + (3 × 5) = 20 + 15 = 35 or Thirty Five.
7 × 5 = (5 × 5) + (2 × 5) = 25 + 10 = 35 or Thirty Five.
Question 10.
A farm stand has cherries on 2 shelves. Each shelf has 4 boxes. Each box has 8 ounces of cherries. How many ounces of cherries are displayed in all? Write an expression that represents the amount.
☐ ounces
Answer:
Total number of ounces of cherries are displayed in all = 64 or Sixty Four.
Explanation:
Number of cherries on shelves on a farm stand has = 2 or Two.
Number of boxes on each shelves = 4 or Four.
Number of ounces of cherries on each box = 8 or Eight.
Total number of ounces of cherries are displayed in all = Number of cherries on shelves on a farm stand has × (Number of boxes on each shelves × Number of ounces of cherries on each box)
= 2 × (4 × 8)
= 2 × 32
= 64 or Sixty Four.
Question 11.
Amy arranged her counters into this array.

A. What two facts could Amy use to write an equation for the array?
Answer:
3 × 9 = (1 × 9) + (2 × 9) = 9 + 18 = 27 or Twenty Seven.
Explanation:
Two facts could Amy use to write an equation for the array:
3 × 9 = (1 × 9) + (2 × 9)
3 × 9 = 9 + 18
3 × 9 = 27 or Twenty Seven.
B. If Amy adds one more row of 9 counters to her array, can she still use the facts you wrote in Part A to find the total number? Explain why or why not.
Answer:
She can use the two facts which are wrote in Part A to find the total number.
Explanation:
Number of rows added = 1 or One.
Total number of array = (4 × 9)
(4 × 9) = (1 × 9)+ (3 × 9) = 9 + 27 = 36 or Thirty six.
(4 × 9) = (2 × 9) + (2 × 9) = 18 + 18 = 36 or Thirty six.
Question 12.
Tim’s family rented a canoe for 6 hours on Monday and 2 hours on Tuesday. How much did they spend? Show any equations you used.

Answer:
Total cost they spent = $56 or $Fifty Six.
Explanation:
Number of hours Tim’s family rented a canoe on Monday = 6 or Six.
Number of hours Tim’s family rented a canoe on Tuesday = 2 or Two.
Cost of the canoe Tim’s family rented on Monday for each hour = $7
Total cost they spent = (Number of hours Tim’s family rented a canoe on Monday × Cost of the canoe Tim’s family rented on Monday for each hour ) + (Number of hours Tim’s family rented a canoe on Tuesday + Cost of the canoe Tim’s family rented on Monday for each hour )
= (6 ×$7) + (2 ×$7)
= (2 ×$7) + (2 ×$7)+ (2 ×$7)+ (2 ×$7)
= $14 + $14 + $14 + $14
= $28 + $14 + $14
= $42 + $14
= $56 or $Fifty Six.
Topic 3 Performance Task
School Fair
Kay and Ben are helping to organize the School Fair. Kay is organizing the school band. Ben is organizing the bake sale.
The 3 × 7 array at the right shows how chairs have been set up for the school band. Use the array to answer Exercises 1 and 2.
Question 1.
Kay wants to have chairs in a 6 × 7 array. Add to the array to show how the new array will look.
Answer:
The new array will look 6 × 7 = (3 × 7) + (3 × 7).
Explanation:
Kay wants to have chairs in a 6 × 7 array.
The new array:
=> 6 × 7 = (3 × 7) + (3 × 7).
Question 2.
Kay needs a path between two of the rows, so she separates the chairs into two smaller arrays.
Part A
Draw a line to show one way Kay can separate the chairs into two smaller arrays.

Answer:
3 × 7 = (2 × 7) + (1 ×7)

Explanation:
Chairs array:
3 × 7 = (2 × 7) + (1 ×7)
Part B
Kay wants to know the number of chairs in each new array. Write a multiplication fact for each of the new arrays to show how she can find this.
Answer:
Number of chairs in each array = 21 or Twenty One.
Explanation:
The new array:
=> 6 × 7 = (3 × 7) + (3 × 7)
=> 6 × 7 = 21 + 21
Part C
Kay wants to find the total number of chairs that are being used. Show how to use the facts in Part B to find the total number of chairs.
Answer:
The total number of chairs = 6 × 7 = (3 × 7) + (3 × 7) = 42 or Forty Two.
Explanation:
The total number of chairs = 6 × 7 .
=> 6 × 7 = (3 × 7) + (3 × 7)
=> 6 × 7 = 21 + 21
=> 6 × 7 = 42 or Forty Two.
The Bake Sale table shows the baked goods Ben has for sale at the School Fair. Use the Bake Sale table to answer Exercises 3-5.
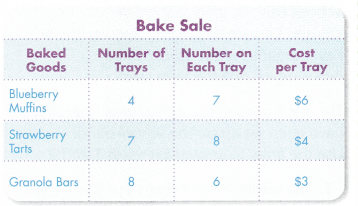
Question 3.
Ben sells 4 trays of granola bars in the morning and 4 trays of granola bars in the afternoon. How much money does this raise? Show your work.
Answer:
Amount of money this raise = $24 or $Twenty Four.
Explanation:
Number of trays of granola bars in the morning Ben sells = 4 or Four.
Number of trays of granola bars in the afternoon Ben sells = 4 or Four.
Cost the each trays of granola bars Ben sells = $3.
Amount of money this raise = (Number of trays of granola bars in the morning Ben sells × Cost the each trays of granola bars Ben sells ) + (Number of trays of granola bars in the afternoon Ben sells × Cost the each trays of granola bars Ben sells )
= (4 × $3) + (4 × $3)
= $12 + $12
= $24 or $Twenty Four.
Question 4.
Ben organizes the blueberry muffins into a 4 × 7 array
Part A
Ben breaks up the array of blueberry muffins into 2 arrays that look the same. At the right, draw the 2 arrays of blueberry muffins.
Answer:

Explanation:
Ben organizes the blueberry muffins into a 4 × 7 array.
=> 4 × 7 = ( 2 × 7) + ( 2 × 7).
Part B
Ben wants to check the total number of blueberry muffins. He knows 2 × 7 = 14. How can he use this to find the total number of blueberry muffins?
Answer:
Total number of blueberry muffins = 4 × 7 = (2 × 7) + (2 × 7) = 14 + 14 = 28 or Twenty Eight.
Explanation:
Ben organizes the blueberry muffins into a 4 × 7 array.
Total number of blueberry muffins = 4 × 7
4 × 7 = (2 × 7) + (2 × 7)
4 × 7 = 14 + 14
4 × 7 = 28 or Twenty Eight.
Question 5.
Two friends each bought 3 trays of strawberry tarts. Ben says they spent more than $20 in total. Do you agree? Explain.
Answer:
Yes, I agree with what Ben says “Ben says they spent more than $20 in total” because they spent $24 in total.
Explanation:
Cost of each trays of strawberry tarts = $4
Number of trays of strawberry tarts two friends each bought = 3 or Three.
Cost of trays of strawberry tarts Two friends each bought = (Cost of each trays of strawberry tarts × ( 2 × Number of trays of strawberry tarts two friends each bought)
= $4 × (2 × 3)
= $4 × 6
= $24 or $Twenty Four.