Practice with the help of enVision Math Common Core Grade 4 Answer Key Topic 16 Lines, Angles, and Shapes regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 16 Lines, Angles, and Shapes
Essential Questions:
How can you classify triangles and quadrilaterals? What is line symmetry?

enVision STEM Project: Senses and Symmetry
Do Research The location of an animal’s eyes helps it to survive in the wild. Use the Internet or other sources to find why some animals have eyes on the sides of their head and others have eyes on the front.
Journal: Write a Report Include what you found. Also in your report:
Most animals are the same on both sides of their body. Use a line of symmetry to help make a simple drawing of your favorite animal’s face. Draw both sides of the animal’s face the same. Explain how you know that both sides of your drawing are the same.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- angle
- polygon
- quadrilateral
- triangle
Question 1.
A ___________ is a closed figure made up of straight-line segments.
Answer:
A polygon is a closed figure made up of straight-line segments
Question 2.
A polygon with three sides is a(n) _________.
Answer:
A polygon with three sides is a(n) Triangle
Question 3.
A(n) _________ is formed by two rays with the same endpoint.
Answer:
A(n) Angle is formed by two rays with the same endpoint.
Shapes
Choose the best term to describe each shape. Use each term once.
Rectangle
Rhombus
Trapezoid
Question 4.

Answer:
Rhombus
Explanation :
2 pairs of parallel sides
4 equal sides
Question 5.

Answer:
Trapezoid – only 1 pair of parallel sides
Question 6.

Answer:
Rectangle
Explanation :
2 pairs of parallel sides
4 right angles
Lines
Use geometric terms to describe what is shown.
Question 7.

Answer:
It is said as line AB and represented a \(\overleftrightarrow{\mathrm{AB}}\)
Explanation :
A line is a straight path of points that goes without end in both directions .
Question 8.

Answer:
It is called as Ray \(\overrightarrow{C D}\). The symbol of a ray is →
Explanation :
A ray is a part of line that has one end point and goes on without end in one direction .
Question 9.

Answer:
Line segment – It is represented as \(\overline{E F}\)
Explanation :
It is a line segment EF. Line segments are represented by a single overbar with no arrowheads over the letters representing the two endpoints.
Problem Solving
Question 10.
Generalize Which generalization about these figures is NOT true?

A. Each figure is a quadrilateral.
B. Each figure has two pairs of parallel sides.
C. Each figure has at least two sides of equal length.
D. Each figure has 4 angles.
Answer:
Option B is not true
Explanation :
Figure 2 that is trapezoid EFGH has only one pair of parallel lines .
Pick a Project
PROJECT 16A
How are dictionaries useful?
Project: Create a Picture Dictionary

PROJECT 16B
How can shapes be used in art at the Dali Museum?
Project: Create Cubist Art

PROJECT 16C
Do snowflakes have lines of symmetry?
Project: Make Snowflakes

PROJECT 16D
Can animals have symmetry?
Project: Draw a Line-Symmetric Animal

Lesson 16-1 Lines
Solve & Share
The number line below is an example of a line. A line goes on forever in a straight path in two directions. Draw the following pairs of lines: two lines that will never cross, two lines that cross at one point, two lines that cross at two points. If you cannot draw the lines, tell why.
I can … draw and identify perpendicular, parallel, and intersecting lines.

Look Back! Terry said, “The lines shown intersect at three points.” Is Terry correct? Explain.
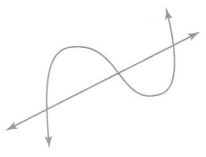
Answer :
No Terry is not correct .
Explanation :
A line can be defined as a straight one- dimensional figure that has no thickness and extends endlessly in both directions. It is often described as the shortest distance between any two points.
Essential Question
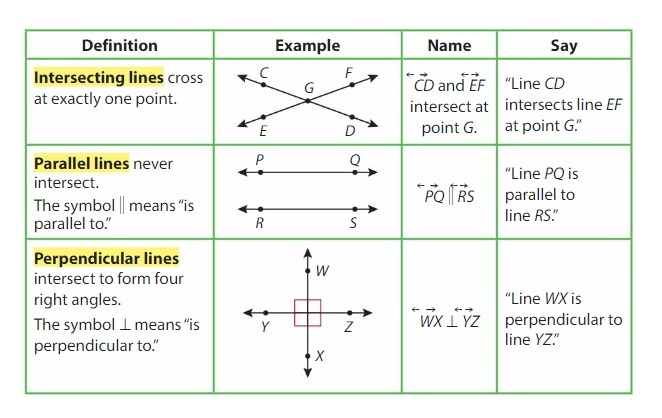
How Can You Describe Pairs of Lines?
Answer :
A pair of lines, line segments or rays are intersecting if they have a common point. This common point is their point of intersection.
For example, two adjacent sides of a sheet of paper, a ruler, a door, a window and letters.
Visual Learning Bridge
A line is a straight path of points that goes on and on in opposite directions. A pair of lines can be described as parallel, perpendicular, or intersecting.

Pairs of lines are given special names depending on their relationship.
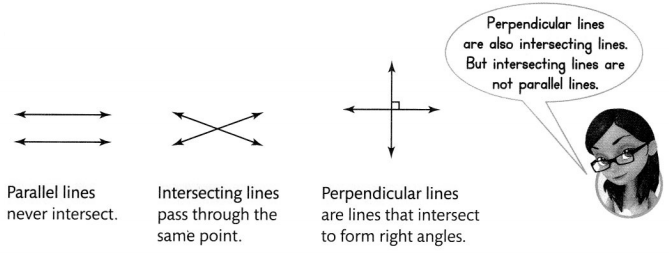
Convince Me!
Be Precise Find examples in your classroom where you can identify parallel lines, intersecting lines, and perpendicular lines. Explain.
Answer :
(i) Intersecting lines – Edges of my Textbook and Notebook through any corner .
(ii) Parallel lines – Opposite Edges of my textbook and notebook
(iii) Perpendicular lines – Adjacent edges of my textbook and black board in my classroom.
Guided Practice
Do You Understand?
Question 1.
What geometric term could you use to describe the top and bottom edges of a book? Why?
Answer:
The top and bottom edges of a book are parallel lines.
Explanation :
Both the lines are equidistant from each other and they never intersect each other lines .
Question 2.
The blades of an open pair of scissors look like what pair of lines? Why?
Answer:
perpendicular lines .
Explanation :
When the scissor is open it look like perpendicular lines intersecting at right angle .
Do You Know How?
For 3-6, use the diagram.
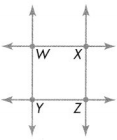
Question 3.
Name four points.
Answer:
The Four points are W, X, Y and Z .
Explanation :
A point is a location represented by a dot. A point does not have any length, width, shape or size, it only has a position.
When two distinct points are connected they form a line.
Question 4.
Name four lines.
Answer:
The four lines are WX, XZ, ZY and YW .
Question 5.
Name two pairs of parallel lines.
Answer:
The two pairs of parallel lines are WX ll YZ .
Question 6.
Name two pairs of perpendicular lines.
Answer:
The two pairs of perpendicular lines are WY ⊥ YZ and ZX ⊥ WX .
Independent Practice
For 7-12, use geometric terms to describe what is shown. Be as specific as possible.
Question 7.
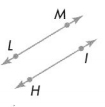
Answer:
LM ll to HI .
Explanation :
Both the lines are equidistant and doesn’t intersect so the given lines are parallel lines .
Question 8.
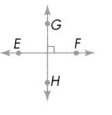
Answer:
GH ⊥ EF
Explanation :
Both the lines are intersecting at a point forming Right angle so, the lines are perpendicular lines .
Question 9.
![]()
Answer:
It is a point A .
Explanation :
A point is a location represented by a dot. A point does not have any length, width, shape or size, it only has a position.
When two distinct points are connected they form a line.
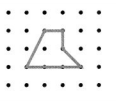
Question 10.

Answer:
Perpendicular paths
Explanation :
Perpendicular lines are lines that intersect at a right (90 degrees) angle.
Both the Road paths are intersecting at a point forming Right angle so, the Road paths are perpendicular to each other .
Question 11.

Answer:
Parallel paths .
Explanation :
The two straight lines in a plane that do not intersect at any point are said to be parallel.
Question 12.

Answer:
Intersecting Lines
Explanation :
A pair of lines, line segments or rays are intersecting if they have a common point. This common point is their point of intersection .
For 13-15, draw what is described by the geometric terms.
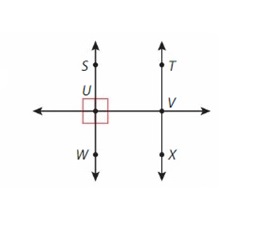
Question 13.
Perpendicular lines
Answer:
Perpendicular lines – SW ⊥ UV and TX ⊥ UV .
Question 14.
Intersecting lines
Answer:
Intersecting lines – Line SW is interescted at point U and Line TX is interescted at V .
Question 15.
Parallel lines
Answer:
Parallel lines – SW ll TX .
Problem Solving
Question 16.
Critique Reasoning
Bella names this line \(\overleftrightarrow{\mathrm{LM}}\). Miguel names the line \(\overleftrightarrow{L N}\). Who is correct? Explain.

Answer:
Both are correct
Explanation :
These three points L, M and N all lie on the same line.
This line could be called ‘Line LM’, ‘Line MN’, ‘Line LN’, ‘Line NL’, ‘Line NM’, or ‘Line ML’
Question 17.
Construct Arguments if all perpendicular lines are also intersecting lines, are all intersecting lines also perpendicular lines? Explain.
Answer:
Perpendicular lines always intersect each other, however, all intersecting lines are not always perpendicular to each other.
The two main properties of perpendicular lines are: Perpendicular lines always meet or intersect each other.
The angle between any two perpendicular lines is always equal to 90.
Perpendicular lines intersect at a right angle. and do not intersect in this image, but if you imagine extending both lines, they will intersect soon. So, they are neither parallel nor perpendicular.
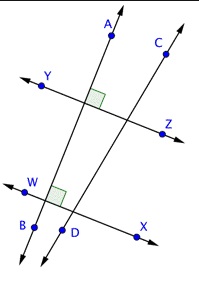
Question 18.
Draw three lines so two of the lines are perpendicular and the third line intersects the perpendicular lines at exactly one point. Label the lines with points.
Answer:
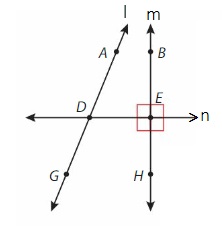
Explanation :
line m and n are perpendicular lines and line l intersects the perpendicular line at D point as shown in above figure .
Question 19.
Higher Order Thinking \(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C D}\), and \(\overleftrightarrow{C D}\) is perpendicular to \(\overleftrightarrow{E F}\). If a line through B and D is perpendicular to \(\overleftrightarrow{A B}\), what is the relationship between \(\overleftrightarrow{B D}\) and \(\overleftrightarrow{E F}\)?
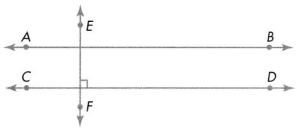
Answer:
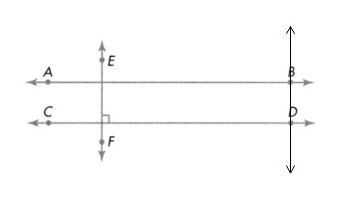
Explanation :
\(\overleftrightarrow{A B}\) ll \(\overleftrightarrow{C D}\) .
\(\overleftrightarrow{C D}\) ⊥ \(\overleftrightarrow{E F}\)
if \(\overleftrightarrow{A B}\) ⊥ \(\overleftrightarrow{B D}\) then ,
\(\overleftrightarrow{B D}\) and \(\overleftrightarrow{E F}\) are parallel lines asshown in above figure .
Assessment Practice
Question 20.
Which geometric term would you use to describe the power cables shown at the right?

A. Perpendicular lines
B. Parallel lines
C. Intersecting lines
D. Points
Answer:
Option B – Parallel lines .
Explanation :
Both the power cables are parallel to each other as there are equidistant from each other .
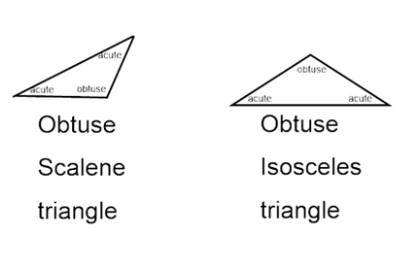
Lesson 16.2 Classify Triangles
Solve & Share
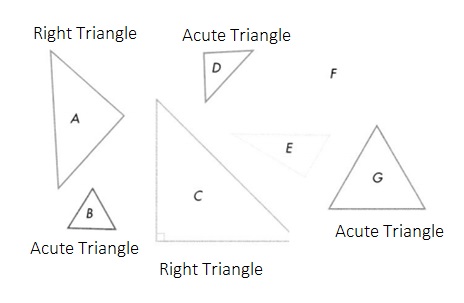
Sort the triangles shown below into two or more groups. Explain how you sorted them. Solve this problem any way you choose.
I can … reason about line segments and angles to classify triangles.

Look Back! Generalize What is true about all 7 triangles you sorted?
Answer :
Essential Question
How Can You Classify Triangles?
Visual Learning Bridge
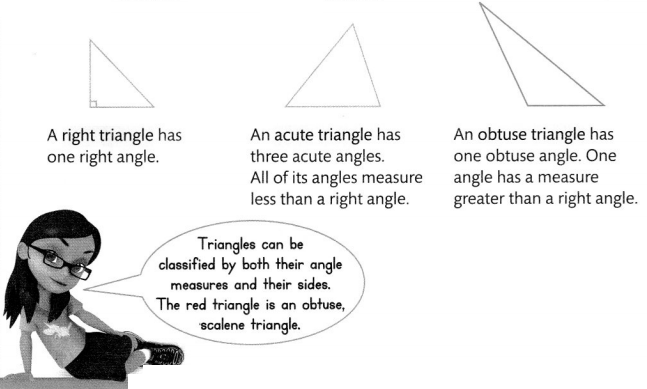
Triangles can be classified by the line segments that make their sides.

Triangles can be classified by their angle measures.
Convince Me!
Be Precise Can a triangle have more than one obtuse angle? Explain.
Answer :
No
Explanation :
Because sum of angles in the triangle = 180 degree .
if one angle is obtuse angle that is 120 degrees .
then , other two angles will be 180 – 120 = 60 degrees .
that means a triangle can have only one obtuse angle .
Another Example!
The pattern follows the rule: right triangle, acute triangle, right triangle, acute triangle…. It also follows the rule: isosceles, scalene, scalene, isosceles, scalene…. Draw a triangle that could be next in the pattern and explain.
For the first rule, the next triangle is acute. For the second rule, it is scalene. So, the next triangle is an acute, scalene triangle. It can be the same as the second triangle in the pattern or it can be a different acute, scalene triangle.
Guided Practice
Do You Understand?
Question 1.
Is it possible to have an obtuse acute triangle? Explain.
Answer:
No, it is not possible
Explanation :
Because sum of angles in the triangle = 180 degree .
if one angle is obtuse angle that is 120 degrees .
then , other two angles will be 180 – 120 = 60 degrees .
that means a triangle can have only one obtuse angle .
Question 2.
Can a triangle have more than one right angle? If so, draw an example.
Answer:
No a triangle cannot have more than one right angle
Explanation :
As if there are 2 right angles the their sum will be 180° and the third angle will exceed the sum. … As the sum of all three angles is , the third angle would have to be zero resulting in a degenerate shape which is a line rather than a triangle.
Do You Know How?
For 3-4, classify each triangle by its sides, and then by its angles.
Question 3.
![]()
Answer:
Isosceles triangle
Acute Triangle
Explanation :
An Isosceles triangle has at least 2 sides of same length .
An Acute triangle has three acute angles. all angles measure less than a right angle .
Question 4.

Answer:
Equilateral Triangle
Acute Triangle
Explanation :
An Equilateral Triangle has 3 sides equal .
An Acute triangle has three acute angles. all angles measure less than a right angle .
Independent Practice
For 5-10, classify each triangle by its sides, and then by its angles.
Question 5.

Answer:
Scalene Triangle
Right angle Triangle
Explanation :
Scalene Triangle has no sides of same length .
A Right Triangle has one Right Triangle .
Question 6.

Answer:
Obtuse Triangle
Scalene Triangle
Explanation :
An Obtuse Triangle has one obtuse angle . One angle has a measure greater than a right angle .
Scalene Triangle has no sides of same length .
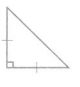
Question 7.
Answer:
Isosceles Triangle
Right Triangle
Explanation :
A Right Triangle has one Right Triangle .
An Isosceles triangle has at least 2 sides of same length .
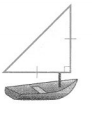
Question 8.
Answer:
Isosceles Triangle
Right Triangle
Explanation :
A Right Triangle has one Right Triangle .
An Isosceles triangle has at least 2 sides of same length .
Question 9.
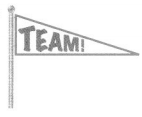
Answer:
Scalene Triangle
Obtuse Triangle
Explanation :
An Obtuse Triangle has one obtuse angle . One angle has a measure greater than a right angle .
Scalene Triangle has no sides of same length .
Question 10.

Answer:
Isosceles Triangle
Acute triangle
Explanation :
An Acute triangle has three acute angles. all angles measure less than a right angle .
An Isosceles triangle has at least 2 sides of same length .
Problem Solving
Question 11.
Reasoning The backyard shown at the right is an equilateral triangle. What do you know about the lengths of the other two sides that are not labeled? Explain.
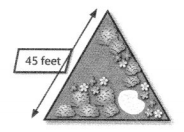
Answer:
the length of one side = 45 feet .
The lengths of the other two sides = 45 feet
Explanation :
An Equilateral Triangle has 3 sides equal .
Question 12.
en Vision® STEM
A rabbit’s field of vision is so wide that it can see predators that approach from behind. The diagram shows the field of vision of one rabbit and the field where the rabbit cannot see. Classify the triangle by its sides and its angles.
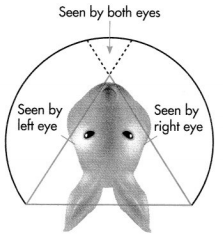
Answer:
The Triangle formed is a Isosceles Triangle and Acute Triangle .
Explanation :
An Acute triangle has three acute angles. all angles measure less than a right angle .
An Isosceles triangle has at least 2 sides of same length .
Question 13.
A pattern follows the rule: obtuse triangle, obtuse triangle, right triangle, obtuse triangle…. It also follows the rule: isosceles, scalene, isosceles, scalene… Draw a triangle that could be the fifth shape in the pattern and explain.
Answer:
Obtuse triangle , Isosceles Triangle is the fifth shape
Question 14.
Higher Order Thinking Mitch draws a triangle with one obtuse angle. What are all the possible ways to classify the triangle by its angle measures and side lengths? Explain.
Answer:
Explanation :
Obtuse angle angle is formed with all different sides and with two sides equal .
Assessment Practice
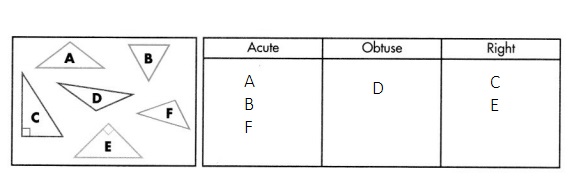
Question 15.
Draw each triangle in its correct angle classification.

Answer:
Lesson 16.3 Classify Quadrilaterals
Solve & Share
Draw three different four-sided shapes that have opposite sides parallel. Explain how your shapes are alike and how they are different. Solve this problem any way you choose.
I can … reason about line segments and angles to classify quadrilaterals.

Look Back! What attributes do your shapes have in common?
Answer :
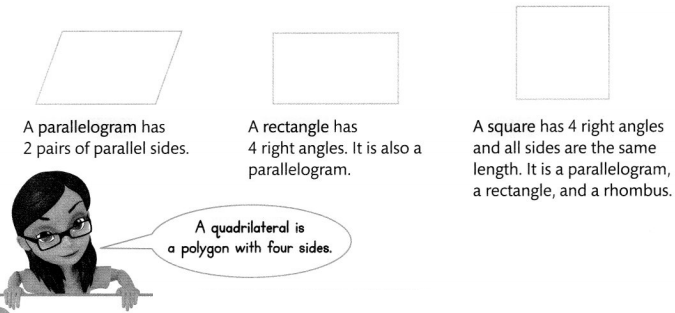
A Parallelogram is a quadrilateral in which both pairs of opposite sides are parallel .

A Rectangle is a parallelogram with four right angles, so all rectangles are also parallelograms and quadrilaterals. On the other hand, not all quadrilaterals and parallelograms are rectangles.

A Trapezoid is a quadrilateral with exactly one pair of parallel sides.

Essential Question
How Can You Classify Quadrilaterals?
Visual Learning Bridge
Quadrilaterals can be classified by their angles or the line segments that make their sides. Which of the quadrilaterals shown have only one pair of parallel sides? Which have two pairs of parallel sides?
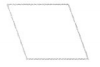
A rhombus is a quadrilateral that has opposite sides that are parallel and all of its sides are the same length. It is also a parallelogram.

A trapezoid is a quadrilateral with only one pair of parallel sides.
Trapezoids have only one pair of parallel sides.
Parallelograms, rectangles, squares, and rhombuses all have two pairs of parallel sides.
Convince Me! Use Structure How are a parallelogram and a rectangle the same? How are they different?
Another Example!
Perpendicular sides form right angles. Can a trapezoid have perpendicular sides?
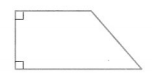
A trapezoid can have two right angles that form perpendicular sides. A trapezoid with two right angles is called a right trapezoid.
Guided Practice
Do You Understand?
Question 1.
What is true about all quadrilaterals?
Answer:
All Quadrilaterals have four sides, are coplanar, have two diagonals, and the sum of their four interior angles equals 360 degrees.
Question 2.
What is the difference between a square and a rhombus?
Answer:
The sides of a square are perpendicular to each other and its diagonals are of equal length.
A rhombus is a quadrilateral in which the opposite sides are parallel and the opposite angles are equal.
Question 3.
Shane drew a quadrilateral with at least 2 right angles and at least 1 pair of parallel sides. Name three quadrilaterals Shane could have drawn.
Answer:
The Three Quadrilaterals with at least 2 right angles and at least 1 pair of parallel sides are Trapezoid , Rectangle and Square .
Explanation :
A trapezoid can have two right angles that form perpendicular sides. A trapezoid with two right angles is called a right trapezoid.

A Rectangle is a parallelogram with four right angles, so all rectangles are also parallelograms and quadrilaterals. On the other hand, not all quadrilaterals and parallelograms are rectangles.

A Square can be defined as a rhombus which is also a rectangle – in other words, a parallelogram with four congruent sides and four right angles.
Do You Know How?
For 4-7, write all the names possible for each quadrilateral.
Question 4.
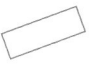
Answer:
Rectangle
Explanation :
Opposite sides are equal and parallel
Four Right Angles .
Question 5.

Answer:
Rhombus
Explanation :
All Four sides are equal and parallel
Question 6.

Answer:
Square
Explanation :
All four sides are equal and parallel
Four Right Angles .
Question 7.

Answer:
Scalene Quadrilateral
Explanation :
A scalene quadrilateral is a four-sided polygon that has no congruent sides.
Independent Practice
For 8-11, write all the names possible for each quadrilateral.
Question 8.
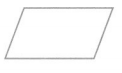
Answer:
Parallelogram
Explanation :
A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel
Question 9.

Answer:
Rhombus
Explanation :
A Rhombus is a parallelogram with four equal sides.
Question 10.

Answer:
Square
Explanation :
All four sides are equal and parallel
Four Right Angles .
Question 11.
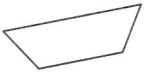
Answer:
Rectangle
Explanation :
A Rectangle is a parallelogram with four right angles .
Problem Solving
Question 12.
The pattern follows the rule: quadrilateral with no parallel sides, quadrilateral with two pairs of parallel sides, quadrilateral with two pairs of parallel sides, quadrilateral with no parallel sides, quadrilateral with two pairs of parallel sides…. Draw quadrilaterals that could be the next three in the pattern.

Answer:

Question 13.
Critique Reasoning Tia says every square is a rectangle, and every square is a rhombus, so every rectangle must be a rhombus. Do you agree? Explain.
Answer:
No, Every Rectangle is not a Rhombus .
Explanation :
A square is a quadrilateral with all 4 angles right angles and all 4 sides of same length.
So a square is a special kind of rectangle, it is one where all the sides have the same length. Thus every square is a rectangle because it is a quadrilateral with all 4 angles right angles.
Yes, a rhombus is a quadrilateral with 4 equal sides.
Every square has 4 equal length sides, so every square is a rhombus.
No, every rectangle is not a rhombus because Rectangle have only opposite sides , whereas in Rhombus all four sides are equal .
Question 14.
Number Sense What number comes next in the pattern? The rule is “Multiply the position number by itself.” Describe a feature of the pattern.
1, 4, 9, 16, ☐
Answer:
1, 4, 9, 16, 25 .
Explanation :
Multiply the position to itself means squaring the position of the number

Question 15.
Higher Order Thinking
Could you use the formula for finding the perimeter of a square to find the perimeter of another quadrilateral? Explain.
The formula for the perimeter of a square is P = 4 × s.
Answer:
Assessment Practice
Question 16.
Select all the possible names for the shape below.
☐ Quadrilateral
☐ Rhombus
☐ Trapezoid
☐ Parallelogram
☐ Rectangle
Answer:
Quadrilateral and Trapezoid
Question 17.
Which shape has only 1 pair of parallel sides?
A. Rhombus
B. Square
C. Right trapezoid
D. Parallelogram
Answer:
Right Trapezoid
Lesson 16.4 Line Symmetry
Solve & Share
Question :
How many ways can you fold the square so one half fits exactly on top of the other half? How many ways can you fold the letter so one half fits exactly on top of the other half? Solve this problem any way you choose.
I can …recognize and draw lines of symmetry and identify line-symmetric figures.

Look Back! Reasoning What figures can you form when you fold a square in half? How are the different figures related to symmetry?
Answer :
The G have zero lines of symmetry.
The rest of the letters, A, B, C, D, and E all have only 1 line of symmetry. Notice that the A has a vertical line of symmetry, while the B, C, D, and E have a horizontal line of symmetry.
Essential Question
What is Line Symmetry
Visual Learning Bridge
A figure is line symmetric if it can be folded on a line to form two matching parts that fit exactly on top of each other. The fold line is called a line of symmetry. There is one line of symmetry drawn on the picture of the truck. How many lines of symmetry do the figures below have?
Count the lines of symmetry drawn on each figure below.
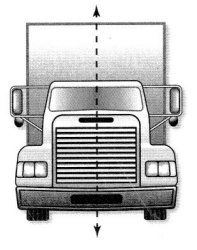
A figure can have more than one line of symmetry.

This figure is line symmetric. It has 2 lines of symmetry. It can be folded on each line of symmetry into matching parts.
A figure can have many lines of symmetry.
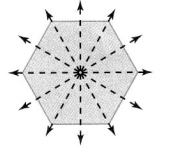
This figure is line symmetric. It has 6 lines of symmetry. It can be folded on each line of symmetry into matching parts.
A figure can have no lines of symmetry.

This figure is NOT line symmetric. It has O lines of symmetry. It cannot be folded to have matching parts.
Convince Me! Look for Relationships Find two capital letters that have exactly one line of symmetry. Find two capital letters that have exactly two lines of symmetry.
Guided Practices
Do You Understand?
Question 1.
How many lines of symmetry does the letter R have?
Answer:
Letter R have Zero lines of symmetry as it cannot be divided into two identical shapes .
Question 2.
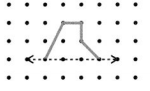
How many lines of symmetry does the figure below have?

Answer:
The given figure have One line of symmetry .
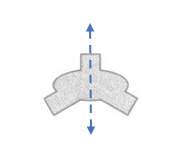
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
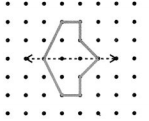
Question 3.
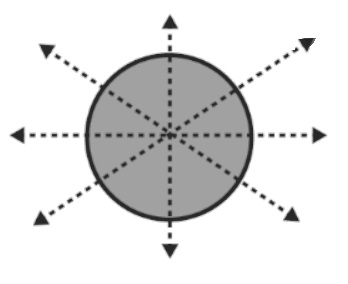
How many lines of symmetry can you find for a circle? Do you think you can count them?
Answer:
A circle has infinite lines of symmetry. A circle is symmetric about all its diagonals.
Do You Know How?
For 4-5, tell if each line is a line of symmetry.
Question 4.
![]()
Answer:
Line of symmetry
Question 5.
Answer:
Yes , it is a line of symmetry as two identical shapes are formed .
For 6-7, tell how many lines of symmetry each figure has.
Question 6.
![]()
Answer:
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 7.

Answer:
This figure is NOT line symmetric. It has O lines of symmetry. It cannot be folded to have matching parts.
Independent Practice
For 8-11, tell if each line is a line of symmetry.
Question 8.
Answer:
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 9.
Answer:
No
Explanation :
This figure is NOT line symmetric. It has O lines of symmetry. It cannot be folded to have matching parts.
Question 10.
![]()
Answer:
Question 11.
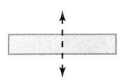
Answer:
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
For 12-19, decide if each figure is line symmetric. Draw and tell how many lines of symmetry each figure has.
Question 12.

Answer:
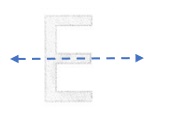
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 13.

Answer:
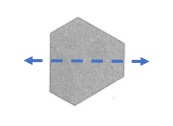
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 14.

Answer:
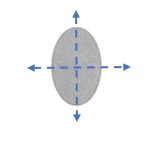
Explanation :
A line of symmetry is defined as the line that a figure can be divided into half, with the end result of the two halves matching up exactly.
Question 15.

Answer:
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 16.

Answer:

Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 17.

Answer:
Explanation :
This figure is line symmetric. It has 3 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 18.

Answer:
zero .
Explanation :
This figure is NOT line symmetric. It has O lines of symmetry. It cannot be folded to have matching parts.
Question 19.

Answer:
Explanation :
This figure is line symmetric. It has 4 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Problem Solving
Question 20.
The Thomas Jefferson Memorial is located in Washington, D.C. Use the picture of the memorial at the right to decide whether the building is line symmetric. If so, describe where the line of symmetry is.

Answer:

Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 21.
Name the type of triangle outlined in green on the picture of the memorial.
Answer:
Acute Triangle .
Question 22.
Construct Arguments
How can you tell when a line is NOT a line of symmetry?
Answer:
Folding Test : You can find if a shape has a Line of Symmetry by folding it. When the folded part sits perfectly on top (all edges matching), then the fold line is a Line of Symmetry.
It cannot be folded to have matching parts. then it have zero lines of symmetry .
Question 23.
Higher Order Thinking How many lines of symmetry can a parallelogram have? Explain.
Answer:
zero
Explanation :
- A parallelogram has no lines of symmetry.
- It has rotational symmetry of order two.
Assessment Practice
Question 24.
Which figure has six lines of symmetry? Draw lines as needed.

Answer:
Option C – has 6 lines of symmetry .
Explanation :
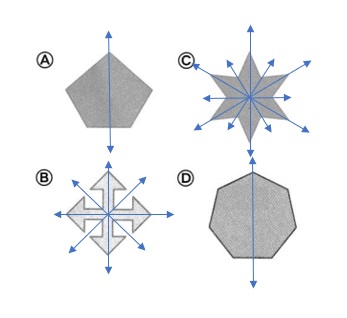
Question 25.
Which figure is NOT line symmetric?

Answer:
Option A .
Lesson 16.5 Draw Shapes with Line Symmetry
Solve & Share
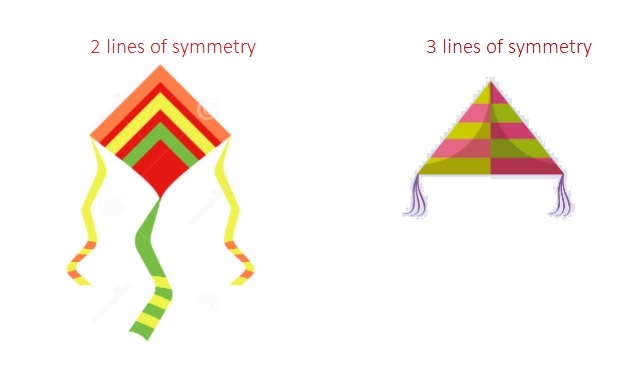
Craig and Julia are designing kites. A kite will fly well if the kite has line symmetry. Does Craig’s or Julia’s kite have line symmetry? Explain. Then, design your own kites. Design one kite with 2 lines of symmetry and another kite with 3 lines of symmetry. Solve this problem any way you choose.
I can…draw a figure that has line symmetry.

Question :
Look Back! Can both Craig’s and Julia’s kites be folded into matching parts? If one of the kites is not line symmetric, can it be changed so that it is? Explain.
Answer :
Essential Question
How Can You Draw Figures one with Line Symmetry?
Visual Learning Bridge
Sarah wants to design a line-symmetric tabletop. She sketched half of the tabletop. What are two ways Sarah can complete her design?
The tabletop is line symmetric if the design can be folded along a line of symmetry, into matching parts.
One Way
Draw a line of symmetry.
Complete Sarah’s design on the opposite side of the line of symmetry.
The design for the tabletop is now line symmetric.
Another Way
Draw a different line of symmetry.
Complete Sarah’s design on the opposite side of the line of symmetry.
The design for the tabletop is now line symmetric.
Convince Me!
Question :
Model with Math Sarah sketched different designs for a smaller tabletop. Use the lines of symmetry to draw ways Sarah can complete each design.
Answer :

Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Guided Practice
Do You Understand?
Question 1.
Chandler tried to complete Sarah’s design from the previous page. Describe the error Chandler made.
Answer:
the image formed is not the exact reflection .
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 2.
How can folding a piece of paper help to determine if a line in a figure is a line of symmetry?
Answer:
If the figure can be folded along a straight line so that one half of the figure exactly matches the other half, the figure has line symmetry. The crease is the line of symmetry.
Do You Know How?
For 3-4, use the line of symmetry to draw a line-symmetric figure.
Question 3.
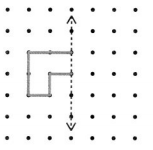
Answer:
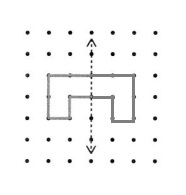
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 4.
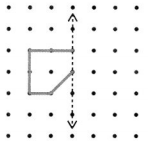
Answer:
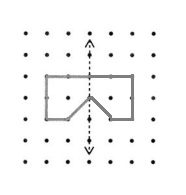
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Independent Practice
For 5-10, use the line of symmetry to draw a line-symmetric figure.
Question 5.

Answer:
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 6.
Answer:
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 7.

Answer:

Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 8.
Answer:
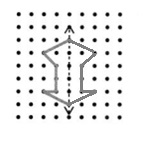
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 9.
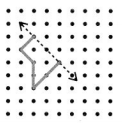
Answer:
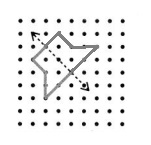
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 10.
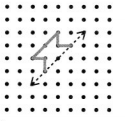
Answer:

Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Problem Solving
Question 11.
Draw a figure that has no lines of symmetry.
Answer:
A scalene triangle, have no lines of symmetry – it is not possible to fold the shape about a line so that the two halves fit exactly on top of one another.
Question 12.
Vanessa drew a figure that has an infinite number of lines of symmetry. What figure could Vanessa have drawn?
Answer:
Circle have infinite number of lines of symmetry .
Question 13.
enVision® STEM
Dogs can smell odors that humans cannot. Dogs can be trained to alert their owners when they smell odors associated with illness. If a dog trains 2 hours every day for 1 year, how many hours has the dog trained?

Answer:
Number of hours dog train for a day = 2 hours
Number of hours dog train for 1 year = 2 hours × 365 days = 730 hours .
Question 14.
Make Sense and Persevere
Clare trained for a long-distance marathon. She ran a total of 225 miles in 3 months. The first month she ran 50 miles. If she ran 25 more miles each month, how many miles did she run in her third month of training?
Answer:
Total Distance ran = 225 miles
Distance covered in First month = 50 miles .
Distance covered in Second month = 50 + 25 = 75 miles .
Distance covered in third month = 75 + 25 = 100 miles .
Question 15.
Higher Order Thinking Can you draw a line that divides a figure in half but is NOT a line of symmetry? Use the figures below to explain.

Answer:
No, because the given line drawn are lines of symmetry it divides the figure into identical halves .
Assessment Practice
Question 16.
Which of the following figures is line symmetric about the dashed line?

Answer:
Option B – as two identical halves are formed by line of symmetry .
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Lesson 16.6 Problem Solving
Critique Reasoning
Solve & Share
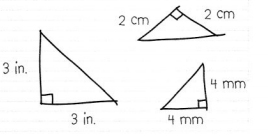
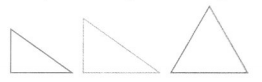
Nathan gave the answer shown to the following question. True or False? All right triangles have two sides the same length. How do you respond to Nathan’s reasoning?
I can … critique the reasoning of others by using what I know about two-dimensional shapes.
Nathan
That’s true. Here are three different sizes of right triangles. In each, two sides are the same length.
Thinking Habits
Be a good thinker! These questions can help you.
- What questions can I ask to understand other people’s thinking?
- Are there mistakes in other people’s thinking?
- Can I improve other people’s thinking?
Look Back! Critique Reasoning Nathan answered another question. True or false: A triangle can have two right angles. Nathan says this is not possible. Do you agree or disagree? Explain.
Answer :
Because of the fact that the sum of the three interior angles of a triangle must be 180 degrees, a triangle could not have two right angles
Essential Question
How Can You Critique the Reasoning of Others?
Visual Learning Bridge
Abby gave the answer shown to the following question.
True or False? Every quadrilateral has at least one right angle.
Abby
True. Here are different quadrilaterals. They all have four sides and four right angles.
What is Abby’s reasoning to support her statement?
Abby drew quadrilaterals that have right angles.

How can I critique the reasoning of others?
I can
- ask questions about Abby’s reasoning
- look for flaws in her reasoning.
- decide whether all cases have been considered.
Here’s my thinking.
Abby’s reasoning has flaws.
She used only special kinds of quadrilaterals in her argument. For these special cases, the statement is true.
Here is a quadrilateral that has no right angles. It shows the statement is not true about every quadrilateral.

The statement is false.
Convince Me! Be Precise Would Abby’s reasoning be correct if the question was changed to: True or False? Some quadrilaterals have at least one right angle. Explain.
Guided Practice
Critique Reasoning
Anthony said all multiples of 4 end in 2, 4, or 8. He gave 4, 8, 12, 24, and 28 as examples.
Question 1.
What is Anthony’s argument? How does he support it?
Answer:
No – Anthony is wrong .
Explanation :
all multiples of 4 end in 0, 2, 4, 6 and 8 .
Examples –
4 × 4 = 16
4 × 5 = 20 and e t c .
Question 2.
Describe at least one thing you could do to critique Anthony’s reasoning.
Answer:
Look flaws in the statement and checking for all numbers .
Question 3.
Does Anthony’s reasoning make sense? Explain.
Answer:
Yes – As he is calculated the values of 4 of squares of 2 and their respective square numbers .
Independent Practice
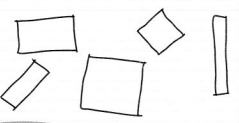
Critique Reasoning Marista said the polygons shown all have the same number of angles as they have sides.

Question 4.
Describe at least one thing you could do to critique Marista’s reasoning.
Answer:
Number of interior angles of a polygon is equal number of Number of sides irrespective of exterior angles .
Question 5.
Does Marista’s reasoning make sense? Explain.

Answer:
Question 6.
Can you think of any examples that prove all polygons don’t have the same number of sides as angles? Explain.
Answer:
No,
A polygon has the same number of sides and angles.
Problem Solving
Performance Task
Dog Pen
Caleb is designing a dog pen for the animal shelter. He has 16 feet of fence, including the gate. His designs and explanation are shown. Critique Caleb’s reasoning.
Dog pens usually have right angles, so I just used rectangles.
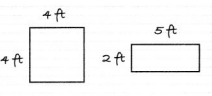
Both my pens used 16 feet of fence. I think the square one is better, because it has more area.
Question 7.
Reasoning What quantities are given in the problem and what do the numbers mean?
Answer:
The Quantities given are the length and Breadth of the Rectangle pen and the side of the square .
the numbers help in calculating the Area .
Question 8.
Critique Reasoning What can you do to critique Caleb’s thinking?
Answer:
The two shapes are given Rectangle and Square with their respective Quantities .
The Area of Rectangle is smaller than the Rectangle of the Square .
The area of the Square is preferred because it has more area than Rectangle .
Question 9.
Be Precise Did Caleb correctly calculate the perimeter of each fence? Explain.

Answer:
No,
Explanation :
Length of Rectangle = 5 feet
Breadth of Rectangle = 2 feet
Perimeter of Rectangle = 2 ( Length + Breadth ) = 2 ( 5 + 2 ) = 2 ( 7 ) = 14 feets .
Side of Square = 4 feet .
Perimeter of Square = 4 ( Side ) = 4 ( 4 ) = 16 feets .
Question 10.
Critique Reasoning Does Caleb’s reasoning make sense? Explain.
Answer:
No,
Explanation :
As, perimeter and area are not calculated correctly .
Length of Rectangle = 5 feet
Breadth of Rectangle = 2 feet
Perimeter of Rectangle = 2 ( Length + Breadth ) = 2 ( 5 + 2 ) = 2 ( 7 ) = 14 feet .
Side of Square = 4 feet .
Perimeter of Square = 4 ( Side ) = 4 ( 4 ) = 16 feet .
Question 11.
Be Precise Explain how you know what units to use in your explanation.
Answer:
Perimeter measured in feet .
Area measured in square feet .
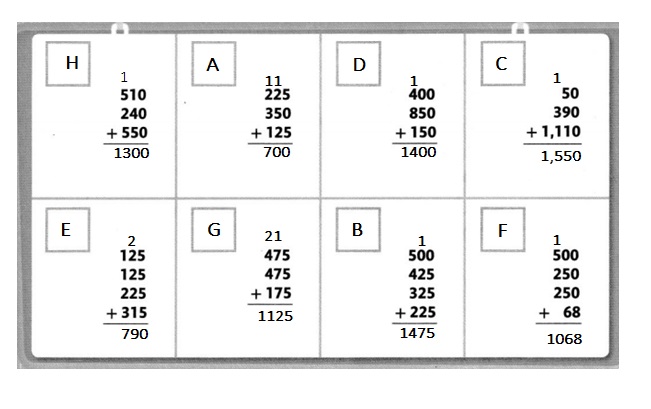
Topic 16 Fluency Practice Activity
Find a Match
Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box next to the match. Find a match for every clue.
I can … add multi-digit whole numbers.
Clues
A. The sum is between 650 and 750.
B. The sum is between 1,470 and 1,480.
C. The sum is exactly 1,550.
D. The sum is between 1,350 and 1,450.
E. The sum is exactly 790.
F. The sum is exactly 1,068.
G. The sum is between 1,100 and 1,225.
H. The sum is exactly 1,300.

Answer :
Topic 16 Vocabulary Review
Understand Vocabulary
Word List
- acute triangle
- equilateral triangle
- intersecting lines
- isosceles triangle
- line of symmetry
- line symmetric
- obtuse triangle
- parallel lines
- parallelogram
- perpendicular lines
- rectangle
- rhombus
- right triangle
- scalene triangle
- square
- trapezoid
Write T for true and F for false.
Question 1.
________ An acute triangle is a triangle with one acute angle.
Answer:
True
Question 2.
_________ An isosceles triangle has at least two equal sides.
Answer:
True
Question 3.
______ A figure is line symmetric if it has at least one line of symmetry
Answer:
True
Question 4.
__________ Perpendicular lines form obtuse angles where they intersect.
Answer:
False
Question 6.
__________ A trapezoid has two pairs of parallel sides.
Answer:
False
Write always, sometimes, or never.
Question 6.
An equilateral triangle __________ has three equal sides.
Answer:
An equilateral triangle always has three equal sides.
Question 7.
Parallel lines _________ intersect.
Answer:
Parallel lines Never intersect.
Question 8.
A scalene triangle __________ has equal sides.
Answer:
A scalene triangle never has equal sides.
Question 9.
A rectangle is _________ a square.
Answer:
A rectangle is sometimes a square.
Question 10.
A rhombus __________ has opposite sides that are parallel.
Answer:
A rhombus always has opposite sides that are parallel.
Use Vocabulary in Writing
Question 11.
Rebecca drew a figure. Describe Rebecca’s figure. Use at least 3 terms from the Word List in your description.

Answer:
Quadrilateral
Parallelogram
Topic 16 Reteaching
Set A pages 585-588
Pairs of lines are given special names: parallel, intersecting, or perpendicular.

\(\overleftrightarrow{D E}\) and \(\overleftrightarrow{F G}\) are parallel lines.
Remember to use geometric terms when describing what is shown.
Question 1.
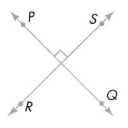
Answer:
\(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{R S}\) are perpendicular lines.
Question 2.
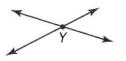
Answer:
Both lines are perpendicular intersect at point Y .
Set B pages 589-592
Triangles can be classified by their sides and angles.
Two sides are the same length, and each angle measures less than a right angle. It is an isosceles, acute triangle.
Remember to classify each triangle by its sides and then by its angles.
Question 1.
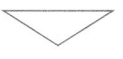
Answer:
Two sides are the same length – Isosceles
All angles are less than 90 degrees
so, isosceles acute triangle .
Question 2.
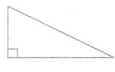
Answer:
all sides are different
Right angle
so, Scalene right triangle
Set C pages 593-596
Name the quadrilateral.

Opposite sides are parallel. There are no right angles. All sides are not the same length. It is a parallelogram, but not a rectangle, rhombus, or square.
Remember that a quadrilateral can be a rectangle, square, trapezoid, parallelogram, or rhombus.
Write all the names possible for each quadrilateral.
Question 1.

Answer:
Trapezoid – only 1 pair of parallel sides
Question 2.
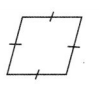
Answer:
Rhombus
Explanation :
2 pairs of parallel sides
4 equal sides
Set D pages 597-600
How many lines of symmetry does the figure have?
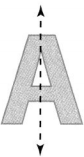
Fold the figure along the dashed line. The two halves are equal and fit one on top of the other. The figure is line symmetric.
It cannot be folded on another line, so it has 1 line of symmetry.
Remember that figures can have many lines of symmetry.
Draw and tell how many lines of symmetry for each figure.
Question 1.

Answer:
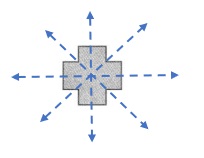
Explanation :
This figure is line symmetric. It has 4 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Question 2.

Answer:
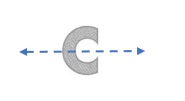
Explanation :
This figure is line symmetric. It has 1 lines of symmetry. It can be folded on each line of symmetry into matching parts.
Set E pages 601-604
Complete a design with line symmetry.
Draw a line of symmetry for the shape.
Complete the design on the opposite side of the line of symmetry.
Remember, for a figure to be line symmetric, it must have a line of symmetry.
Complete the designs.
Question 1.

Answer:
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Question 2.
Answer:
Explanation :
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created. The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Set F pages 605-608
Think about these questions to help you critique the reasoning of others.
Thinking Habits
Be a good thinker! These questions can help you.
- What questions can I ask to understand other people’s thinking?
- Are there mistakes in other people’s thinking?
- Can I improve other people’s thinking?

Remember that it only takes one counterexample to show the statement is false.
Derek says, “All triangles have 1 right angle.”
Question 1.
Use the figures above to critique Derek’s statement.
Answer:
The First two triangles ( from left to Right )in the figure are Right triangle but the third triangle is a Equilateral Triangle .
Question 2.
What kinds of triangles NEVER have right angles?
Answer:
Since a right-angled triangle has one right angle, the other two angles are acute. Therefore, an obtuse-angled triangle can never have a right angle; and vice versa. The side opposite the obtuse angle in the triangle is the longest.
Any triangle that is not a right triangle is an oblique triangle. Solving an oblique triangle means finding the measurements of all three angles and all three sides.
Topic 16 Assessment Practice
Question 1.
Of a parallelogram, rectangle, rhombus, and trapezoid, which cannot describe a square? Explain.
Answer:
A square can be a rhombus, parallelogram, a rectangle do not have to be a Trapezoid .
Explanation:
A rhombus is a quadrilateral with all four sides being of equal length.
A parallelogram is a quadrilateral with two pairs of parallel sides.
A rectangle is a quadrilateral with four right angles and 2 parallel sides .
A square is a quadrilateral with four right angles and equal side lengths.
Where as a A trapezoid is a quadrilateral with at least one pair of parallel sides.
it sides are not of different lengths .
Looking at the definitions, a square is already guaranteed to be a rhombus. Here are examples of each of the other shapes which are not rhombuses.
Question 2.
How many acute angles are there in an equilateral triangle?
Answer:
An equilateral triangle has three acute angles .
Question 3.
Gavin drew different-colored lines. Draw a line that is parallel to \(\overleftrightarrow{S R}\).
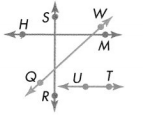
Answer:
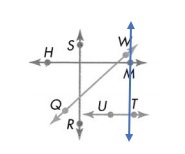
Explanation :
A line is drawn from M which is parallel to \(\overleftrightarrow{S R}\) .
Question 4.
Marci described the light from the sun as a line that starts at the sun and continues on forever. Which geometric term best describes Marci’s description of the sun’s light?
Answer:
It is a Ray
Explanation :
A ray can be defined as a part of a line that has a fixed starting point but no end point. It can extend infinitely in one direction.

Question 5.
Four of Mrs. Cromwell’s students decorated a bulletin board with the shapes shown below. Order the students’ shapes in order from fewest lines of symmetry to most lines of symmetry.

Answer:
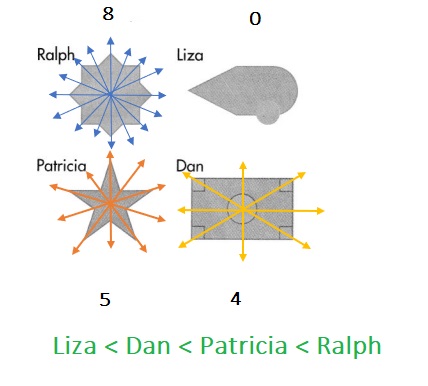
Question 6.
Are all intersecting lines perpendicular? Draw a picture to help explain your answer.
Answer:
Perpendicular lines are a particular case of intersecting lines when an angle between them is 90o.
Explanation:
Perpendicular lines always intersect each other, however, all intersecting lines are not always perpendicular to each other. The two main properties of perpendicular lines are: Perpendicular lines always meet or intersect each other. The angle between any two perpendicular lines is always equal to 90.

Question 7.
A four-sided figure with two pairs of parallel sides cannot be what type of quadrilateral? Explain.
Answer:
Trapezoids have only one pair of parallel sides; parallelograms have two pairs of parallel sides. A trapezoid can never be a parallelogram.
The correct answer is that all trapezoids are quadrilaterals. . Trapezoids are four-sided polygons, so they are all quadrilaterals.

Question 8.
Equilateral triangle ABC has one side with a length of 4 inches. What are the lengths of each of the other two sides of the triangle? Explain.
Answer:
An equilateral triangle is a triangle with all three sides of equal length , corresponding to what could also be known as a “regular” triangle .
if one side is 4 inches then other two ides will also be 4 inches .
Question 9.
Which set of angles could form a triangle?
A. Two right angles, one acute angle
B. One obtuse angle, one right angle, one acute angle
C. Two obtuse angles, one acute angle
D. One right angle, two acute angles
Answer:
Option D .
Question 10.
A figure has one angle formed from a pair of perpendicular lines, one pair of parallel sides, and no sides with equal lengths. What geometric term can be used to name this figure?
Answer:
Question 11.
Dina’s teacher asks her to describe the top and bottom edges of her ruler using a geometric term. What term could Dina use?
Answer:
The top and bottom edge of the ruler is like a straight line .
Question 12.
Shapes are divided into two groups. These are the shapes in the first group.
The following shapes do not belong in the group above. These are the shapes in the second group.

What generalization can be made about the shapes in the first group?
Answer:

In the above group we have shapes like Parallelogram , Trapezoid and Equilateral Triangle

In the above group, We have shapes like Trapezoid , right Triangle and Square .
Generalization made is square can be a parallelogram in few statements .
Question 13.
Complete the drawing so the figure is line symmetric.
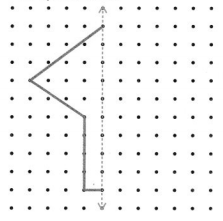
Answer:
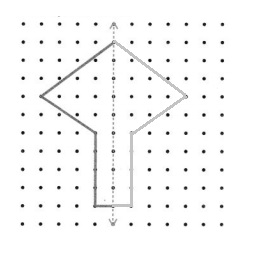
Explanation :
Fold the figure along the dashed line. The two halves are equal and fit one on top of the other. The figure is line symmetric.
It cannot be folded on another line, so it has 1 line of symmetry.
Topic 16 Performance Task
Ottoman Art
The Ottoman Empire lasted from 1299 until 1922. Much of the art from this period contained geometric shapes.
Question 1.
Use the Ottoman Empire figure to answer the following.
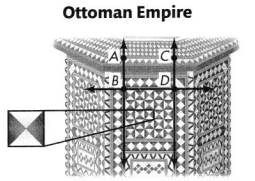
Part A – Question
Name a pair of parallel lines and explain why the lines are parallel.
Answer:
AB ll CD .
Explanation :
Because the points A and B are equi distant from points C and D . and they don’t intersect each other
Part B – Question
The enlarged part of the figure shows 4 triangles that are all the same type. Classify these triangles by their sides and by their angles. Explain.
Answer:
all the sides are equal then it is Equilateral Triangle .
all angles will be 60 degrees .
Part C
Olivia said the 4 triangles were inside a square. When asked other possible names for the square, she said it was a quadrilateral, a parallelogram, and a rectangle. Critique Olivia’s reasoning.
Answer:
A parallelogram is a quadrilateral in which each pair of opposite sides is parallel.
A quadrilateral is a polygon having only four sides.
A rectangle is a parallelogram in which one angle is of 90 degrees .
Yes, a square is a special type of rectangle because it possesses all the properties of a rectangle. Similar to a rectangle, a square has: interior angles which measure 90∘ each. opposite sides that are parallel and equal.
Question 2
The basic shape used in the Ottoman Scarf is a quadrilateral. Answer the following about this shape.

Part A – Question
What are all the names you can use for this quadrilateral? Explain.
Answer:
Rhombus and parallelogram
A parallelogram is a quadrilateral in which each pair of opposite sides is parallel.
A rhombus is a parallelogram in which adjacent sides are equal.
Part B – Question
Corbin drew a triangle by connecting the points W, X, and Y. He said the triangle is acute because it has acute angles. Critique Corbin’s reasoning.
Answer:
Yes the Triangle formed is WXY . The triangle is acute Triangle because the triangles have acute angles .
Part C – Question
Draw all lines of symmetry on the Decorative Plate. How many lines of symmetry does the plate have? Explain.

Answer:
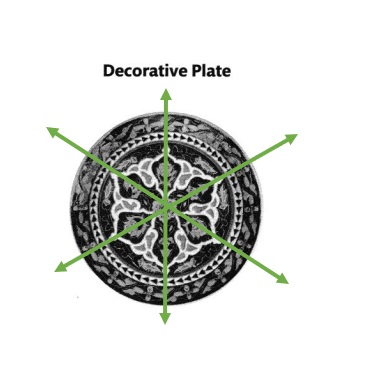
Explanation :
Fold the figure along the dashed line. The two halves are equal and fit one on top of the other. The figure is line symmetric.
It cannot be folded on another line, so it has 1 line of symmetry.