enVision Math Common Core Grade 4 Answer Key Topic 5 Use Strategies and Properties to Divide by 1-Digit Numbers

Practice with the help of enVision Math Common Core Grade 4 Answer Key Topic 5 Use Strategies and Properties to Divide by 1-Digit Numbers regularly and improve your accuracy in solving questions.

enVision Math Common Core 4th Grade Answers Key Topic 5 Use Strategies and Properties to Divide by 1-Digit Numbers

Essential Questions:
How can mental math be used to divide? How can quotients be estimated? How can the steps for dividing be explained?

enVision STEM Project: Music and Division
Do Research: Use the Internet or other resources to find an example of a woodwind instrument, a brass instrument, a stringed instrument, and a percussion instrument.
Journal: Write a Report Include what you found. Also in your report:

• Explain how each instrument you researched uses energy to make sounds. Include information about how the sounds are produced.
• An octave spans 8 white keys on a piano. The last key of an octave begins the next octave. Explain why you can divide by 7 to find the number of octaves on a piano with 52 white keys.

Review What You Know

Vocabulary

Choose the best term from the box. Write it on the blank.

• compatible numbers
• equation
• divisible
• round
• division
• variable

Question 1.
A(n) __________ uses the equal sign (=) to show two expressions have the same value.
Answer:
An equation uses the equal sign (=) to show two expressions have the same value.

Question 2.
One way to estimate a product is to _________ each factor.
Answer:
One way to estimate a product is to round each factor.

Question 3.
You use ________ when you find the number of equal groups.
Answer:
You use division when you find the number of equal groups.

Question 4.
Numbers that are easy to compute mentally are called __________
Answer:
Numbers that are easy to compute mentally are called Compatible numbers.

Division Facts

Find each quotient.
Question 5.
27 ÷ 9
Answer:
The quotient of 27 ÷ 9 is 3.

Explanation:
Given that 27 ÷ 9, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 27 ÷ 9 is 3.

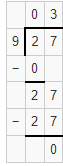
Question 6.
30 ÷ 5
Answer:
The quotient of 30 ÷ 5 is 6.

Explanation:
Given that 30 ÷ 5, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 30 ÷ 5 is 6.

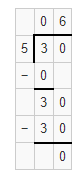
Question 7.
32 ÷ 4
Answer:
The quotient of 32 ÷ 4 is 8.

Explanation:
Given that 32 ÷ 4, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 32 ÷ 4 is 8.

Question 8.
54 ÷ 9
Answer:
The quotient of 54 ÷ 9 is 6.

Explanation:
Given that 54 ÷ 9, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 54 ÷ 9 is 6.

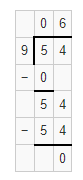
Question 9.
28 ÷ 7
Answer:
The quotient of 28 ÷ 7 is 4.

Explanation:
Given that 28 ÷ 7, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 28 ÷ 7 is 4.

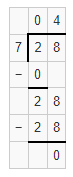
Question 10.
72 ÷ 9
Answer:
The quotient of 72 ÷ 9 is 8.

Explanation:
Given that 72 ÷ 9, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 72 ÷ 9 is 8.

Question 11.
56 ÷ 8
Answer:
The quotient of 56 ÷ 8 is 7.

Explanation:
Given that 56 ÷ 8, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 56 ÷ 8 is 7.

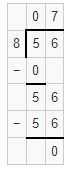
Question 12.
18 ÷ 3
Answer:
The quotient of 18 ÷ 3 is 6.

Explanation:
Given that 18 ÷ 3, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 18 ÷ 3 is 6.

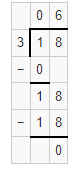
Question 13.
15 ÷ 5
Answer:
The quotient of 15 ÷ 5 is 3.

Explanation:
Given that 15 ÷ 5, here we need to find the quotient. The quotient is the number obtained by dividing one number by another diving number. So the quotient of 15 ÷ 5 is 3.

Rounding

Round each number to the nearest hundred.

Question 14.
864
Answer:
900.

Explanation:
The rounding to the nearest 864 is 900.

Question 15.
651
Answer:
700.

Explanation:
The rounding to the nearest 651 is 700.

Question 16.
348
Answer:
400.

Explanation:
The rounding to the nearest 348 is 400.

Question 17.
985
Answer:
1000.

Explanation:
The rounding to the nearest 985 is 1000.

Question 18.
451
Answer:
500.

Explanation:
The rounding to the nearest 451 is 500.

Question 19.
749
Answer:
800.

Explanation:
The rounding to the nearest 749 is 800.

Division as Sharing

Question 20.
Make Sense and Persevere Julio has 47 marbles. He keeps his two favorite marbles, then equally shares the remaining marbles between 5 friends. How many marbles does each friend receive? Explain.
Answer:
The number of marbles does each friend receive is 9 marbles.

Explanation:
Given that Julio has 47 marbles and he keeps his two favorite marbles, so Julio has 47 – 2 =45 marbles. And then equally shares the remaining marbles between 5 friends. So the number of marbles does each friend receive is 45 ÷ 5 which is 9 marbles.

Pick a Project

PROJECT 5A
How many passengers did trains like those in the Gold Coast Railroad Museum carry? Project: Make a Model of a Train

PROJECT 5B
How far do sailfish migrate?
Project: Make a Migration Map

PROJECT 5C
How much food do Portuguese Water Dogs need?
Project: Create a Brochure on Portuguese Water Dogs

3-ACT MATH PREVIEW

Math Modeling
Snack Attack

I can … model with math to solve a problem that involves rounding, estimating and computing with whole numbers.

Lesson 5.1 Mental Math: Find Quotients

Solve & Share
José has 270 hockey cards to arrange equally in 9 boxes. Each box can hold the same number of cards. How many cards should José place in each box? Solve this problem using any strategy you choose.
I can … make sense of quantities and use mental math and place-value strategies to divide.

Look Back! Reasoning What multiplication equation could help you find the number of cards José should place in each box?

Answer:
Jose should place 30 cards in each box.

Explanation:
Given that Jose has 270 hockey cards to arrange equally in 9 boxes. As each box can hold the same number of cards. So the number of cards in each box will be 270 ÷ 9 which will be 30 cards.

Essential Question
How Can You Divide Mentally?

Visual Learning Bridge
Mr. Díaz ordered a supply of 1,800 pastels. He wants to divide them equally among his class and 5 other art classes. How many pastels does each class receive?
If Mr. Diaz stores the pastels so each class will receive new pastels 5 times a year, how many pastels are handed out each of the 5 times?

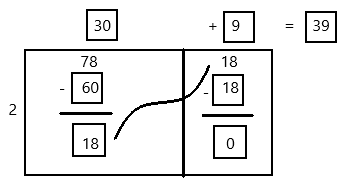
Find 1,800 ÷ 6.

The basic division fact is 18 ÷ 6 = 3.
18 hundreds ÷ 6= 3 hundreds or 300.
1,800 ÷ 6 = 300
Each class will receive 300 pastels.

Find 300 ÷ 5.

The basic division fact is 30 ÷ 5= 6.
30 tens ÷ 5 = 6 tens or 60.
300 ÷ 5 = 60
Each class will receive 60 pastels 5 times a year.

Convince Me! Use Structure Write the missing dividends for each of the following equations. How did you determine each dividend?
_______ ÷ 7 = 70
______ ÷ 8 = 50
______ ÷ 4 = 800

Answer:
The missing digits will be 490, 400, 3200.

Explanation:
To find the missing dividend, we will perform multiplication. So the missing digit will be
70 × 7 which is 490. So the missing digit will be 490 ÷ 7 = 70.
50 × 8 which is 400. So the missing digit will be 400 ÷ 8 = 50.
800 × 4 which is 3200. So the missing digit will be 3200 ÷ 4 = 800.

Guided Practice

Do You Understand?
Question 1.
Explain how 32 ÷ 4 can help you solve 320 ÷ 4.
Answer:
32 ÷ 4 = 8.
320 ÷ 4 = 80.

Explanation:
Since 320 is 10 times 32. The answer for 320 divided by 4 is going to be 10 times the answer for 32 divided by 4.
32 ÷ 4 = 8.
320 ÷ 4 = 80.

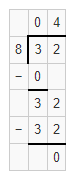
Question 2.
Mrs. Gall orders 240 folders and divides them equally among 3 classes. How many folders does each class receive? What basic fact did you use?
Answer:
The number of folders does each class receive is 80 folders.

Explanation:
Given that Mrs. Gall orders 240 folders and divides them equally among 3 classes. So the number of folders does each class receive is 240 ÷ 3 which is 80 folders. The basic fact that we have used is 24 ÷ 3 = 8.

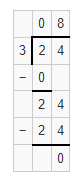
Do You Know How?
For 3-4, use basic facts and place value to find each quotient.
Question 3.
28 ÷ 7 = ______
280 ÷ 7 = _______
2,800 ÷ 7 = ________
Answer:
28 ÷ 7 = 4.
280 ÷ 7 = 40.
2,800 ÷ 7 = 400.
The basic fact that we have used is 28 ÷ 7 = 4.

Explanation:
Given that 28 ÷ 7 and we need to find the quotient of the given equation. So the quotient of 28 ÷ 7 is 4.
The quotient of 280 ÷ 7 is 40.
The quotient of 2,800 ÷ 7 is 400. The basic fact that we have used is 28 ÷ 7 = 4.

Question 4.
______ = 64 ÷ 8
______ = 640 ÷ 8
______ = 6,400 ÷ 8
Answer:
8 = 64 ÷ 8
80 = 640 ÷ 8
800 = 6,400 ÷ 8
The basic fact that we have used is 64 ÷ 8 = 8.

Explanation:
Given that 64 ÷ 8 and we need to find the quotient of the given equation. So the quotient of 64 ÷ 8 is 8.
The quotient of 640 ÷ 8 is 80.
The quotient of 6,400 ÷ 8 is 800. The basic fact that we have used is 64 ÷ 8 = 8.

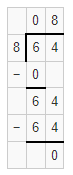
Independent Practice

Leveled Practice For 5-24, use basic facts and place value to divide.
Question 5.
36 ÷ 9 = _______
360 ÷ 9 = _______
3,600 ÷ 9 = _______
Answer:
36 ÷ 9 = 4.
360 ÷ 9 = 40.
3,600 ÷ 9 = 400.
The basic fact that we have used is 36 ÷ 9 = 4.

Explanation:
Given that 36 ÷ 9 and we need to find the quotient of the given equation. So the quotient of 36 ÷ 9 is 4.
The quotient of 360 ÷ 9 is 40.
The quotient of 3,600 ÷ 9 is 400. The basic fact that we have used is 36 ÷ 9 = 4.

Question 6.
______ = 10 ÷ 2
______ = 100 ÷ 2
______ = 1,000 ÷ 2
Answer:
5 = 10 ÷ 2
50 = 100 ÷ 2
500 = 1,000 ÷ 2
The basic fact that we have used is 10 ÷ 2 = 5.

Explanation:
Given that 10 ÷ 2 and we need to find the quotient of the given equation. So the quotient of 10 ÷ 2 is 5.
The quotient of 100 ÷ 2 is 50.
The quotient of 1,000 ÷ 2 is 500. The basic fact that we have used is 10 ÷ 2 = 5.

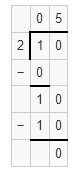
Question 7.
45 ÷ 5 = _______
450 ÷ 5 = ________
4,500 ÷ 5 = _________
Answer:
45 ÷ 5 = 9.
450 ÷ 5 = 90.
4,500 ÷ 5 =900.
The basic fact that we have used is 45 ÷ 5 = 9.

Explanation:
Given that 45 ÷ 5 and we need to find the quotient of the given equation. So the quotient of 45 ÷ 5 is 9.
The quotient of 450 ÷ 5 is 90.
The quotient of 4,500 ÷ 5 is 900. The basic fact that we have used is 45 ÷ 5 = 9.

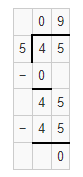
Question 8.
_______ = 24 ÷ 8
_______ = 240 ÷ 8
_______ = 2,400 ÷ 8
Answer:
3 = 24 ÷ 8
30 = 240 ÷ 8
300 = 2,400 ÷ 8
The basic fact that we have used is 24 ÷ 8 = 3.

Explanation:
Given that 24 ÷ 8 and we need to find the quotient of the given equation. So the quotient of 24 ÷ 8 is 3.
The quotient of 240 ÷ 8 is 30.
The quotient of 2,400 ÷ 8 is 300. The basic fact that we have used is 24 ÷ 8 = 3.

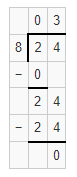
Question 9.
2,000 ÷ 5
Answer:
The quotient is 400.

Explanation:
Given that 2,000 ÷ 5 and we need to find the quotient of the given equation. So the quotient of 2,000 ÷ 5 is 400.

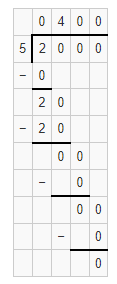
Question 10.
360 ÷ 4
Answer:
The quotient is 90.

Explanation:
Given that 360 ÷ 4 and we need to find the quotient of the given equation. So the quotient of 360 ÷ 4 is 900.

Question 11.
540 ÷ 9
Answer:
The quotient is 60.

Explanation:
Given that 540 ÷ 9 and we need to find the quotient of the given equation. So the quotient of 540 ÷ 9 is 60.

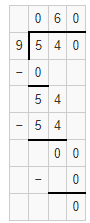
Question 12.
160 ÷ 4
Answer:
The quotient is 40.

Explanation:
Given that 160 ÷ 4 and we need to find the quotient of the given equation. So the quotient of 160 ÷ 4 is 40.

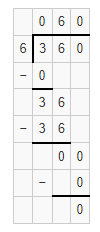
Question 13.
900 ÷ 3
Answer:
The quotient is 300.

Explanation:
Given that 900 ÷ 3 and we need to find the quotient of the given equation. So the quotient of 900 ÷ 3 is 300.

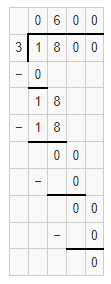
Question 14.
3,200 ÷ 8
Answer:
The quotient is 400.

Explanation:
Given that 3,200 ÷ 8 and we need to find the quotient of the given equation. So the quotient of 3,200 ÷ 8 is 400.

Question 15.
360 ÷ 6
Answer:
The quotient is 60.

Explanation:
Given that 360 ÷ 6 and we need to find the quotient of the given equation. So the quotient of 360 ÷ 6 is 60.

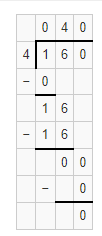
Question 16.
1,800 ÷ 3
Answer:
The quotient is 600.

Explanation:
Given that 1,800 ÷ 3 and we need to find the quotient of the given equation. So the quotient of 1,800 ÷ 3 is 600.

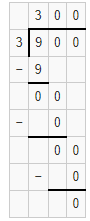
Question 17.
7,200 ÷ 8
Answer:
The quotient is 900.

Explanation:
Given that 7,200 ÷ 8 and we need to find the quotient of the given equation. So the quotient of 7,200 ÷ 8 is 900.

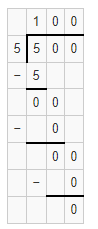
Question 18.
500 ÷ 5
Answer:
The quotient is 100.

Explanation:
Given that 500 ÷ 5 and we need to find the quotient of the given equation. So the quotient of 500 ÷ 5 is 100.

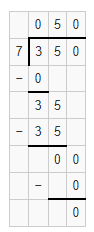
Question 19.
350 ÷ 7
Answer:
The quotient is 50.

Explanation:
Given that 350 ÷ 7 and we need to find the quotient of the given equation. So the quotient of 350 ÷ 7 is 50.

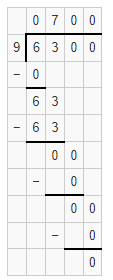
Question 20.
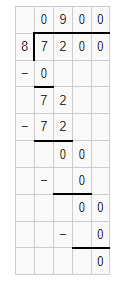
6,300 ÷ 9
Answer:
The quotient is 700.

Explanation:
Given that 6,300 ÷ 9 and we need to find the quotient of the given equation. So the quotient of 6,300 ÷ 9 is 700.

Question 21.
1,600 ÷ 2
Answer:
The quotient is 800.

Explanation:
Given that 1,600 ÷ 2 and we need to find the quotient of the given equation. So the quotient of 1,600 ÷ 2 is 800.

Question 22.
210 ÷ 7
Answer:
The quotient is 30.

Explanation:
Given that 210 ÷ 7 and we need to find the quotient of the given equation. So the quotient of 210 ÷ 7 is 30.

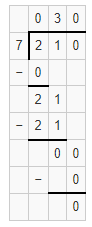
Question 23.
4,800 ÷ 6
Answer:
The quotient is 800.

Explanation:
Given that 4,800 ÷ 6 and we need to find the quotient of the given equation. So the quotient of 4,800 ÷ 6 is 800.

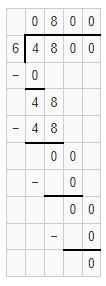
Question 24.
600 ÷ 6
Answer:
The quotient is 100.

Explanation:
Given that 600 ÷ 6 and we need to find the quotient of the given equation. So the quotient of 600 ÷ 6 is 100.

Problem Solving

Question 25.
If you know 20 ÷ 5 = 4, how does that help you calculate 200 ÷ 5?
Answer:
200 ÷ 5 = 40.

Explanation:
Here, 20 ÷ 5 = 4 is a basic fact. So the value of 200 ÷ 5 = 40

Question 26.
A bakery produced two batches of bread with 80 loaves in each batch. It sold 30 loaves each hour. How many loaves of bread were sold in 4 hours? How many loaves of bread were left to sell?
Answer:
The number of loaves of bread that were sold in 4 hours is loaves is 120 loaves.

Explanation:
Given that the bakery produced two batches of bread with 80 loaves in each batch and it was sold 30 loaves each hour. So the number of loaves of bread that were sold in 4 hours is loaves.30 × 4 = 120 loaves.

Question 27.
An engineer designed and built a solar race car. If there are 810 solar cells arranged in 9 rows, how many solar cells are in each row?

Answer:
The number of solar cells is in each row is 90rows.

Explanation:
Given that if there are 810 solar cells arranged in 9 rows. So the number of solar cells are in each row is 810 ÷ 9 which is 90 rows.

Question 28.
Model with Math On Saturday afternoon, 350 people attended a play. The seating was arranged in 7 equal rows. Draw a bar diagram and solve an equation to find p, how many people sat in each row.
Answer:
The number of people sat in each row is 50 people.

Explanation:
Given that 350 people attended a play and seating was arranged in 7 equal rows. So the number of people sat in each row is 350 ÷ 7 which is 50 people.

Question 29.
Higher Order Thinking Molly and five friends picked a total of 300 oranges. If they each picked the same number of oranges, how many oranges did Molly pick? Explain.
Answer:
The number of oranges did Molly picked is 60 oranges.

Explanation:
Given that Molly and five friends picked a total of 300 oranges, so the number of oranges did Molly picked is 300 ÷ 5 which is 60 oranges.

Assessment Practice

Question 30.
Find 240 ÷ 8.
A. 3
B. 10
C. 30
D. 80
Answer:
30.

Explanation:
Given that 240 ÷ 8 will be 30.

Question 31.
What basic fact helps to solve 180 ÷ 6? What is 180 ÷ 6?
A. 18 ÷ 3; 60
B. 18 ÷ 3; 30
C. 18 ÷ 6; 60
D. 18 ÷ 6; 30
Answer:
Option D.

Explanation:
Given that to solve 180 ÷ 6 with the basic fact. So the basic fact will be 18 ÷ 6 which is 3.

Lesson 5.2 Mental Math: Estimate Quotients

Solve & Share
Three friends at a video arcade win a total of 248 tickets. They decide to share the tickets equally. About how many tickets will each friend receive? Solve this problem using any strategy you choose.
I can … use compatible numbers to estimate quotients when dividing with 3-digit dividends.

Look Back! is an exact answer or an estimate needed for the problem above? Explain.

Answer:
Each friend will receive 82.67 tickets.

Explanation:
Given that there are three friends at a video arcade who win a total of 248 tickets and they decide to share the tickets equally. Let the number of tickets each friend would receive be X. So
238 = 3 × X
X = 248 ÷ 3
On solving we will get 82.67 tickets.

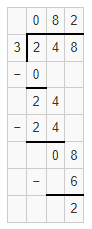
Essential Question
How Can You Estimate Quotients to Solve Problems?

Visual Learning Bridge
Max wants to make 9 rubber band balls using about the same number of rubber bands for each ball. He bought a jar of 700 rubber bands. Estimate to find about how many rubber bands Max can use for each ball.

Use Compatible Numbers
Estimate 700 ÷ 9.
What number close to 700 is easily divided by 9?
Try multiples of ten near 700.
710 is not easily divided by 9.
720 is 72 tens and can be divided by 9.
720 ÷ 9= 80
Max can use about 80 rubber bands for each ball.

Use Multiplication
Estimate 700 ÷ 9.
9 times what number is about 700?
9 × 8 = 72, so 9 × 80 = 720.
700 ÷ 9 is about 80.
Max can use about 80 rubber bands for each ball.

Convince Me! Construct Arguments What compatible numbers can you use to estimate 132 ÷ 6? Why is rounding not a good way to estimate 132 ÷ 6?

Guided Practice

Do You Understand?
Question 1.
Max wants to make 9 rubber band balls using 80 bands each from his package of 700. Will Max be able to make more or fewer balls than he wanted?
Answer:

Question 2.
Max decides to use 700 rubber bands to make 8 balls. Is it reasonable to say he would use about 90 rubber bands to make each ball? Explain.
Answer:

Do You Know How?
For 3-10, estimate each quotient. Use multiplication or compatible numbers. Show your work.
Question 3.
48 ÷ 5
Answer:
The estimated quotient will be 10.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 48 ÷ 5 will be 50 ÷ 5 which is 10. So the estimated quotient will be 10.

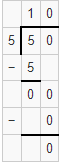
Question 4.
235 ÷ 8
Answer:
The estimated quotient will be 30.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 235 ÷ 8 will be 240 ÷ 8 which is 30. So the estimated quotient will be 30.

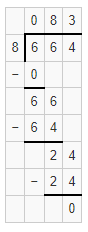
Question 5.
547 ÷ 6
Answer:
The estimated quotient will be 90.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 547 ÷ 6 will be 540 ÷ 6 which is 90. So the estimated quotient will be 90.

Question 6.
192 ÷ 5
Answer:
The estimated quotient will be 38.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 192 ÷ 5 will be 190 ÷ 5 which is 38. So the estimated quotient will be 38.

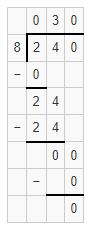
Question 7.
662 ÷ 8
Answer:
The estimated quotient will be 83.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 662 ÷ 8 will be 664 ÷ 8 which is 83. So the estimated quotient will be 83.

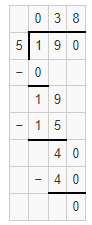
Question 8.
362 ÷ 3
Answer:
The estimated quotient will be 120.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 362 ÷ 3 will be 360 ÷ 3 which is 120. So the estimated quotient will be 120.

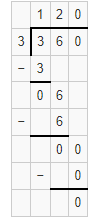
Question 9.
41 ÷ 2
Answer:
The estimated quotient will be 20.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 41 ÷ 2 will be 40 ÷ 2 which is 20. So the estimated quotient will be 20.

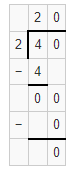
Question 10.
211 ÷ 4
Answer:
The estimated quotient will be 55.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 211 ÷ 4 will be 220 ÷ 4 which is 55. So the estimated quotient will be 55.

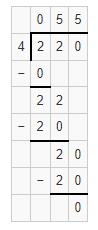
Independent Practice

For 11-26, estimate each quotient.

Question 11.
430 ÷ 9
Answer:
The estimated quotient will be 50.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 430 ÷ 9 will be 450 ÷ 9 which is 50. So the estimated quotient will be 50.

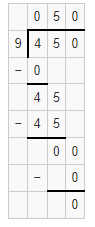
Question 12.
620 ÷ 7
Answer:
The estimated quotient will be 90.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 620 ÷ 7 will be 630 ÷ 7 which is 90. So the estimated quotient will be 90.

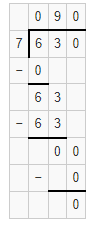
Question 13.
138 ÷ 5
Answer:
The estimated quotient will be 28.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 138 ÷ 5 will be 140 ÷ 5 which is 28. So the estimated quotient will be 28.

Question 14.
232 ÷ 6
Answer:
The estimated quotient will be 40.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 232 ÷ 6 will be 240 ÷ 6 which is 40. So the estimated quotient will be 40.

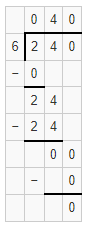
Question 15.
342 ÷ 8
Answer:
The estimated quotient will be 45.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 342 ÷ 8 will be 360 ÷ 8 which is 45. So the estimated quotient will be 45.

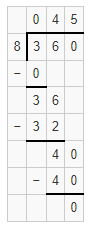
Question 16.
652 ÷ 6
Answer:
The estimated quotient will be 110.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 652 ÷ 6 will be 660 ÷ 6 which is 110. So the estimated quotient will be 110.

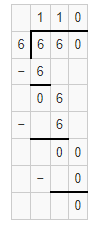
Question 17.
59 ÷ 9
Answer:
The estimated quotient will be 7.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 59 ÷ 6 will be 63 ÷ 9 which is 7. So the estimated quotient will be 7.

Question 18.
813 ÷ 8
Answer:
The estimated quotient will be 100.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 813 ÷ 8 will be 800 ÷ 8 which is 100. So the estimated quotient will be 100.

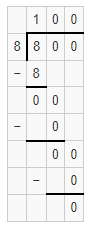
Question 19.
637 ÷ 6
Answer:
The estimated quotient will be 105.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 637 ÷ 6 will be 630 ÷ 6 which is 105. So the estimated quotient will be 105.

Question 20.
481 ÷ 4
Answer:
The estimated quotient will be 120.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 481 ÷ 4 will be 480 ÷ 4 which is 120. So the estimated quotient will be 120.

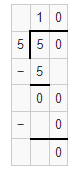
Question 21.
747 ÷ 8
Answer:
The estimated quotient will be 95.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 747 ÷ 8 will be 760 ÷ 8 which is 95. So the estimated quotient will be 95.

Question 22.
232 ÷ 9
Answer:
The estimated quotient will be 25.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 232 ÷ 9 will be 225 ÷ 9 which is 25. So the estimated quotient will be 25.

Question 23.
552 ÷ 7
Answer:
The estimated quotient will be 80.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 552 ÷ 7 will be 560 ÷ 7 which is 80. So the estimated quotient will be 80.

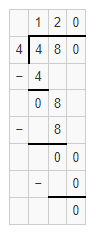
Question 24.
52 ÷ 5
Answer:
The estimated quotient will be 10.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 52 ÷ 5 will be 50 ÷ 5 which is 10. So the estimated quotient will be 10.

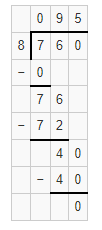
Question 25.
392 ÷ 2
Answer:
The quotient will be 196.

Explanation:
Here, the quotient of 392 ÷2 is 196.

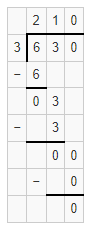
Question 26.
625 ÷ 3
Answer:
The estimated quotient will be 210.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 625 ÷ 3 will be 630 ÷ 3 which is 210. So the estimated quotient will be 210.

Problem Solving

For 27-28, use the table at the right.

Question 27.
Ada sold her mugs in 3 weeks. About how many mugs did Ada sell each week?
Answer:
The number of mugs Ada sells each week will be 80 mugs.

Explanation:
Given that Ada sold her mugs in 3 weeks and there are five mugs and each mug is equal to 50 mugs. So there will be 5 × 50 which is 250 mugs. So the number of mugs Ada sells each week will be 250 ÷ 3, so the estimated quotient will be 240 ÷ 3 which will be 80 mugs.

Question 28.
Ben sold his mugs in 6 weeks. About how many mugs did Ben sell each week?
Answer:
The number of mugs Ben sells each week will be 30 mugs.

Explanation:
Given that Ada sold her mugs in 6 weeks and there are five mugs and each mug is equal to 50 mugs. So there will be 4 × 50 which is 200 mugs. So the number of mugs Ada sells each week will be 200 ÷ 6, so the estimated quotient will be 180 ÷ 6 which will be 30 mugs.

Question 29.
enVision® STEM The International Space Station takes 644 minutes to orbit Earth 7 times. About how long does each orbit take?

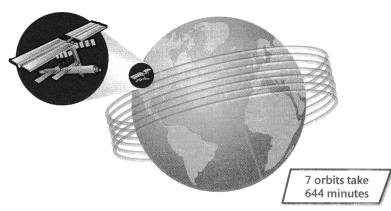
Answer:
The number of minutes does each orbit takes is 92 minutes.

Explanation:
Given that the International Space Station takes 644 minutes to orbit Earth 7 times, so the number of minutes does each orbit takes is 644 ÷ 7 which is 92 minutes.

Question 30.
There are 60 minutes in 1 hour and 24 hours in 1 day. About how many times does the International Space Station orbit Earth each day?
Answer:

Question 31.
Construct Arguments Complete by writing > or < in the . Without dividing, explain how you know which quotient is greater.
930 ÷ 4 762 ÷ 4
Answer:
930 ÷ 4 > 762 ÷ 4.

Explanation:
Given that to find out which quotient is greater without dividing. Here, we can say that by seeing the dividend, 930 is greater than 762. So 930 ÷ 4 quotient is greater than 762 ÷ 4.

Question 32.
Higher Order Thinking Explain how to find a better estimate for 260 ÷ 5 than the one shown below.
Round 260 to 300, and then estimate 300 ÷ 5.
300 ÷ 5 = 60, so 260 ÷ 5 is about 60.
Answer:

Assessment Practice

Question 33.
Kaylee wanted to divide 133 pieces of candy equally into 7 boxes. She decides to put 19 pieces in each box. Use estimation to determine if this answer seems reasonable.
Answer:
Kaylee is correct.

Explanation:
Given that Kaylee wanted to divide 133 pieces of candy equally into 7 boxes and she decides to put 19 pieces in each box. So the estimated answer will be 140 ÷ 7 which will be 20 pieces. So Kaylee is correct.

Lesson 5.3 Mental Math: Estimate Quotients for Greater Dividends

Solve & Share
Jimi has 3,000 tickets to sell at the school carnival. Jimi separated the tickets into groups of 8 tickets. About how many groups did Jimi make? Solve this problem using any strategy you choose.
I can … estimate quotients for 4-digit dividends.

Look Back! Reasoning What basic fact did you use to solve the problem above? How does this help you?

Essential Question
How Can You Estimate Quotients Using Patterns and Place Value?

Visual Learning Bridge
On “Clean Up Your Town Day,” 1,320 people volunteered to clean up the Springville parks. The volunteers were divided equally into teams to work in each of the town’s parks. About how many people were on each team?

Use Multiplication Patterns
Estimate 1,320 ÷ 6.
6 times what number is about 1,320?
You know 6 × 2 = 12, and
6 × 20 = 120, so
6 × 200 = 1,200.
1,200 is close to 1,320.
There are about 200 people on each team.

Use Division Facts and Place-Value Patterns
Find compatible numbers to estimate 1,320 ÷ 6.
You know 12 ÷ 6 = 2, and
120 ÷ 6 = 20, So
1,200 ÷ 6 = 200.
1,320 ÷ 6 is about 200.
There are about 200 people on each team.

Convince Me! Construct Arguments Complete the calculations at the right. Explain how you can use the calculations to estimate 1,296 ÷ 4.
4 × 100 = __________
4 × 200 = __________
4 × 300 = __________
4 × 400 = __________

Another Example!
You can use rounding to estimate quotients.
Estimate 357 ÷ 8 by rounding the dividend.
Round: 400 ÷ 8
4008 ÷ 50
So, 357 ÷ 8 is about 50.

Estimate 5,582 ÷ 7 by rounding the dividend.
Round: 5,600 ÷ 7
5,600 ÷ 7 = 800
So, 5,582 ÷ 7 = is about 800.

Guided Practice

Do You Understand?
Question 1.
When estimating 1,320 ÷ 6, why is rounding not a good strategy?
Answer:
1,320 ÷ 6 is 220.

Explanation:
Given that the equation is 1,320 ÷ 6 which is 220. As the dividend is divisible by 6. So rounding is not a good strategy.

Question 2.
When dividing a 4-digit number by a 1-digit number, how many digits can the quotient have?
Answer:
Here, the quotient can still have 4 digits depending on the 1 digit.

Do You Know How?
For 3-8, estimate each quotient.
Question 3.
3,340 ÷ 8
Answer:
The estimated quotient will be 417.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 3,340 ÷ 8 will be 3,336 ÷ 8 which is 417. So the estimated quotient will be 417.

Question 4.
2,943 ÷ 7
Answer:
The estimated quotient will be 420.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 2,943 ÷ 7 will be 2,940 ÷ 7 which is 420. So the estimated quotient will be 420.

Question 5.
552 ÷ 9
Answer:
The estimated quotient will be 60.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 552 ÷ 9 will be 540 ÷ 9 which is 60. So the estimated quotient will be 60.

Question 6.
776 ÷ 4
Answer:
The quotient will be 194.

Explanation:
Here, the quotient of 776 ÷ 4 is 194.

Question 7.
2,013 ÷ 5
Answer:
The estimated quotient will be 400.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 2,013 ÷ 5 will be 2,000 ÷ 5 which is 400. So the estimated quotient will be 400.

Question 8.
281 ÷ 3
Answer:
The estimated quotient will be 90.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 281 ÷ 3 will be 270 ÷ 3 which is 90. So the estimated quotient will be 90.

Independent Practice

For 9-20, estimate each quotient.
Question 9.
61 ÷ 2
Answer:
The estimated quotient will be 30.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 61 ÷ 2 will be 60 ÷ 2 which is 30. So the estimated quotient will be 30.

Question 10.
7,779 ÷ 7
Answer:
The estimated quotient will be 1,100.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 7,779 ÷ 7 will be 7,770 ÷ 7 which is 1,100. So the estimated quotient will be 1,100.

Question 11.
3,688 ÷ 6
Answer:
The estimated quotient will be 600.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 3,688 ÷ 6 will be 3,600 ÷ 6 which is 600. So the estimated quotient will be 600.

Question 12.
497 ÷ 8
Answer:
The estimated quotient will be 60.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 497 ÷ 8 will be 480 ÷ 8 which is 60. So the estimated quotient will be 60.

Question 13.
5,684 ÷ 9
Answer:
The estimated quotient will be 600.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 5,684 ÷ 9 will be 5,400 ÷ 9 which is 600. So the estimated quotient will be 600.

Question 14.
5,346 ÷ 6
Answer:
The estimated quotient will be 900.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 5,346 ÷ 6 will be 5,400 ÷ 6 which is 900. So the estimated quotient will be 900.

Question 15.
508 ÷ 7
Answer:
The estimated quotient will be 70.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 508 ÷ 7 will be 490 ÷ 7 which is 70. So the estimated quotient will be 70.

Question 16.
92 ÷ 3
Answer:
The estimated quotient will be 30.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 92 ÷ 3 will be 90 ÷ 3 which is 30. So the estimated quotient will be 30.

Question 17.
647 ÷ 3
Answer:
The estimated quotient will be 200.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 647 ÷ 3 will be 600 ÷ 3 which is 200. So the estimated quotient will be 200.

Question 18.
3,958 ÷ 8
Answer:
The estimated quotient will be 500.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 3,958 ÷ 8 will be 4,000 ÷ 8 which is 500. So the estimated quotient will be 500.

Question 19.
224 ÷ 3
Answer:
The estimated quotient will be 70.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 224 ÷ 3 will be 210 ÷ 3 which is 70. So the estimated quotient will be 70.

Question 20.
2,438 ÷ 5
Answer:
The estimated quotient will be 500.

Explanation:
Here, Compatible numbers are numbers that are easy to compute with mental math. We can also use compatible to find two estimates that the quotient is between. So 2,438 ÷ 5 will be 2,500 ÷ 5 which is 500. So the estimated quotient will be 500.

Problem Solving

Question 21.
Laura’s dog eats 1 bag of dog food every 6 days. About how many bags will her dog eat in 1 year? About how many bags will Laura’s dog eat in 10 years? Explain.
Answer:
The number of bags will Laura’s dog eat in 10 years is 600 bags.

Explanation:
Given that Laura’s dog eats 1 bag of dog food every 6 days, as there are 365 days for 1 year. So for 1 year, it will be 365 ÷ 6 which will be approx 360 ÷ 6 = 60 bags. So the number of bags will Laura’s dog eat in 10 years is 60 × 10 which will be 600 bags.

Question 22.
Model with Math During the school year, a bus driver made 7 trips to the museum. The distance from the school to the museum is 36 miles. Write and solve equations to find how many miles the bus driver drove for the 7 trips.
Answer:
The number of miles the bus driver drives for 7 trips is approx 280 miles.

Explanation:
Given that a bus driver made 7 trips to the museum. The distance from the school to the museum is 36 miles. So the equation for 7 trips will be 36 × 7 which will be 252 miles, which will be approx 40 × 7 = 280 miles.

Question 23.
Vocabulary Use a vocabulary word to complete the statement.
Multiplication and division are _________ operations because they undo each other.
Answer:
Multiplication and division are inverse operations because they undo each other.

Question 24.
Ramón’s sister wants to buy a car that costs $7,993. She earns $9 for every hour she works. About how many hours must Ramón’s sister work to earn enough money to buy the car?
Answer:
The number of hours must Ramón’s sister work to earn enough money to buy a car is 900 hours.

Explanation:
Given that Ramón’s sister wants to buy a car that costs $7,993 and she earns $9 for every hour she works. So the number of hours must Ramón’s sister work to earn enough money to buy a car is 7,993 ÷ 9 which will be 8,100 ÷ 9 which is 900 hours.

Question 25.
Number Sense Eight students can sit at one cafeteria table. About how many tables are needed for 231 students? Explain.
Answer:
The number of tables required for 231 students is approx 30 tables.

Explanation:
Given that eight students can sit at one cafeteria table. So the number of tables required for 231 students is 231 ÷ 8 which will be 240 ÷ 8 which is 30 tables.

Question 26.
Higher Order Thinking At Camp Summer Fun, 4 campers share a tent. The camp is expecting 331 campers. About how many tents will they need? Will the actual number of tents needed be more or less than your estimate? Explain.
Answer:
The number of tents will they need is 80 tents.

Explanation:
Given that 4 campers share a tent and the camp is expecting 331 campers. So the number of tents will they need is 320 ÷ 4 which is 80 tents. Here, we need more tents for the extra 11 students.

Assessment Practice

Question 27.
Nadine has 1,424 pictures to put in 7 folders on her computer. She wants the same number in each folder. Which is the best estimate of the number of pictures she should put in each folder?
A. About 200
B. About 300
C. About 2,000
D. About 3,000
Answer:
The number of pictures she should put in each folder is about 200.

Explanation:
Given that Nadine has 1,424 pictures to put in 7 folders on her computer and she wants the same number in each folder. So the number of pictures she should put in each folder is 1424 ÷ 7 which will be 1400 ÷ 7 which is about 200.

Question 28.
Sven needs to save $239 to buy a bike. Which is the best estimate of the amount he needs to save each month to have enough in 3 months?
A. About $60
B. About $70
C. About $80
D. About $90
Answer:
The best estimate of the amount he needs to save each month to have enough in 3 months is about $80.

Explanation:
Given that Sven needs to save $239 to buy a bike, so the best estimate of the amount he needs to save each month to have enough in 3 months is 239 ÷ 3 which is 240 ÷ 3 which is about $80.

Lesson 5.4 Interpret Remainders

Solve & Share
There are 47 students taking a field trip. The students are being driven in cars to a play by adult volunteers. Each driver can take at most 4 students. How many cars are needed for the field trip? Will each car have four students? Use counters or draw pictures to solve this problem. Explain how you found your answer.
I can… apply what I know about dividing items into equal groups to solve problems.

Look Back! Suppose there were only 46 students. Would the number of cars needed for the field trip change? Explain.

Essential Question
After Dividing, What Do You Do Question her with the Remainder?

Visual Learning Bridge
When you divide with whole numbers, any whole number that remains after the division is complete is called the remainder.

Ned has 27 soccer cards in an album. He put 6 cards on each page. He knows 27 ÷ 6 = 4 with 3 left over, because 6 × 4 = 24 and 24 + 3 = 27.
Use an R to represent the remainder: 27 ÷ 6 = 4 R3
How do you use the remainder to answer questions about division?

How many pages did Ned fill?
To answer this question, find how many groups of 6 there are. The remainder can be ignored.
27 ÷ 6 = 4 R3
Ned filled 4 pages.

How many pages did Ned work on?
To answer this question, find how many groups of 6 are filled or started. Because there is a remainder, add 1 to the quotient.
27 ÷ 6 = 4 R3
Ned worked on 5 pages.

How many cards did Ned put on the fifth page?
The answer to this question is the remainder.
27 ÷ 6= 4 R3
Ned put 3 cards on the fifth page.

Convince Me! Critique Reasoning The calculation to the right is incorrect. What error was made? What is the correct answer?
45 ÷6 = 6 R9

Another Example!
There are 20 apples to arrange in gift baskets, with 6 apples in each basket. How many baskets can be filled? Explain the meaning of the remainder.

3 equal groups of 6 with 2 left over
20 ÷ 3 = 6 R2, because
3 × 6 = 18 and 18 + 2 = 20.
The remainder, 2, represents the number of apples not placed into gift baskets.

Guided Practice

Do You Understand?
Question 1.
When a divisor is 3, can the remainder be 5? Explain.
Answer:
No, the remainder cannot be 5.

Explanation:
No, the remainder cannot be 5. Because in the division the remainder will always be less than the divisor.

Question 2.
Dave is packing 23 sweaters into boxes. Each box will hold 3 sweaters. How many boxes will he need? Explain how the remainder affects your answer.
Answer:
The number of boxes required is about 8 boxes.

Explanation:
Given that Dave is packing 23 sweaters into boxes and each box will hold 3 sweaters. So the number of boxes required is 23 ÷ 3 which is 7.6 approx 8 boxes. Here the remainder will be rounded off.

Do You Know How?
For 3-6, find the number of groups and the number left over. Draw an array if needed.
Question 3.
47 ÷ 3 = ________ with _________ left over
Answer:
47 ÷ 3 = 15 with 2 left over.

Explanation:
Given that 47 ÷ 3, so the remainder will be 15, and the leftover will be 2.

Question 4.
29 ÷ 2 = ________ with _________ left over
Answer:
29 ÷ 2 = 14 with 1 left over.

Explanation:
Given that 29 ÷ 2, so the remainder will be 14 and the leftover will be 1.

Question 5.
62 ÷ 5 = ________ with _________ left over
Answer:
62 ÷ 5 = 12 with 2 left over.

Explanation:
Given that 62 ÷ 5, so the remainder will be 12 and the leftover will be 2.

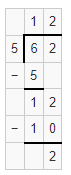
Question 6.
86 ÷ 6 = ________ with _________ left over
Answer:
86 ÷ 6 = 14 with 2 left over.

Explanation:
Given that 86 ÷ 6, so the remainder will be 14 and the leftover will be 2.

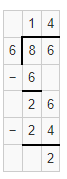
Independent Practice

For 7-10, find the number of groups and the number left over.
Question 7.
18 ÷ 4 = ______ with ______ left over
Answer:
18 ÷ 4 = 4 with 2 left over.

Explanation:
Given that 18 ÷ 4, so the remainder will be 4 and the leftover will be 2.

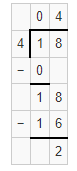
Question 8.
22 ÷ 6 = _______ with ________ left over
Answer:
22 ÷ 6 = 3 with 4 left over.

Explanation:
Given that 22 ÷ 6, so the remainder will be 3 and the leftover will be 4.

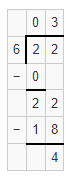
Question 9.
31 ÷ 8 = ________ with _________ left over
Answer:
31 ÷ 8 = 3 with 7 left over.

Explanation:
Given that 31 ÷ 8, so the remainder will be 3 and the leftover will be 7.

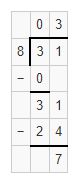
Question 10.
32 ÷ 9 = _______ with _________ left over
Answer:
32 ÷ 9 = 3 with 5 left over.

Explanation:
Given that 32 ÷ 9, so the remainder will be 3 and the leftover will be 5.

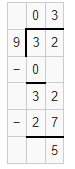
For 11-13, interpret each remainder.
Question 11.
59 football cards 3 cards on each page. How many pages can Alex complete?
Answer:
The number of pages can Alex complete is 19 pages.

Explanation:
Given that 59 football cards and 3 cards on each page, so the number of pages can Alex complete is 59 ÷ 3 which is about 19 pages.

Question 12.
55 baseball cards 4 cards on each page. How many cards are on the last page?
Answer:
The number of cards is on the last page is about 13 pages.

Explanation:
Given that 55 baseball cards and 4 cards on each page, so the number of cards is on the last page is about 13 pages.

Question 13.
84 stickers 5 stickers on each page. How many pages will have some stickers on them?
Answer:
The number of pages that will have stickers on them is 17 pages.

Explanation:
Given that 84 stickers and 5 stickers on each page, so the number of pages that will have stickers on them are 84 ÷ 5 which is about 17 pages.

Problem Solving

For 14-15, use the table at the right.

Question 14.
Samuel has 85 prize tickets. How many marbles can he get?
Answer:
The number of marbles can he get is about 12 marbles.

Explanation:
Given that Samuel has 85 prize tickets, so the number of marbles can he get is 85 ÷ 7 which is about 12 marbles.

Question 15.
Inez chose 8 rings and 12 stickers. How many tickets did she use?
Answer:
The total number of tickets is 120 tickets.

Explanation:
Given that Inez chose 8 rings which is 8 × 9 = 72 and 12 stickers which is 12 × 4 = 48. So the total number of tickets is 72 + 48 which is 120 tickets.

Question 16.
Keiko makes necklaces like the one in the picture at the right. She has 19 blue beads and 13 red beads. How many necklaces can Keiko make? How many of each color bead will be left over?

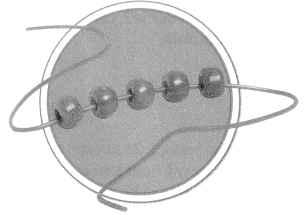
Answer:
Keiko makes 6 necklaces and 1 bead of each color.

Explanation:
Given that Keiko has 19 blue beads and 13 red beads, as she places one blue bead and one red bead. So she can make 6 necklaces and one red bead, the blue bead will be leftover.

Question 17.
Critique Reasoning Amanda calculated 34 ÷ 8= 3 R10. Is Amanda’s answer correct? If not, what is the correct answer? Explain.
Answer:
No, Amanda is not correct.

Explanation:
No, Amanda is not correct. Here, we can see the remainder is greater than the divisor, as remainder should not be greater than the divisor.

Question 18.
Higher Order Thinking Write a problem that requires adding 1 to the quotient when interpreting the remainder.
Answer:
Each table can seat 4 students. How many tables will be needed to seat 26 students?

Assessment Practice

Question 19.
There are 39 children at a park. They want to make teams with 9 children on each team. Two of the children go home. How many complete teams can they make? Explain.

Answer:
The number of complete teams can they make is 4 teams.

Explanation:
Given that there are 39 children at a park and they want to make teams with 9 children on each team and two of the children go home, so there will be 39 – 2 = 37 students. So the number of complete teams can they make is 37 ÷ 9 is about 4 teams.

Lesson 5.5 Use Partial Quotients to Divide

Solve & Share
Sally’s bird feeder holds 6 cups of bird feed. How many times can Sally’s bird feeder be filled using a 72-cup bag of bird feed? Use counters or draw pictures to solve this problem. Explain how you found your answer.
I can … divide by thinking about multiplication, estimation, properties, and place value.

Look Back! Reasoning How can you use multiplication to check your answer?

Essential Question
How Can You Use Partial Quotients to Solve Division Problems?

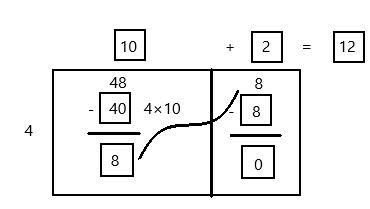
Visual Learning Bridge
There are 3 seats in each row of an airplane for passengers. If there are 63 people boarding the airplane, how many rows of seats are needed for the passengers?

One Way

There are 21 groups of 3 in 63.
21 rows of seats are needed.

Another Way
Sometimes you can use a different first estimate.

There are 21 groups of 3 in 63.
21 rows of seats are needed.

Convince Me! Use Structure How can you use the relationships between multiplication and division to check your answer?

Another Example!
Break apart 69 using place value. Use the Distributive Property to show 69 ÷ 3.

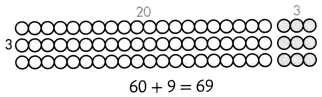
69 ÷ 3 = (60 + 9) ÷ 3
= (60 ÷ 3) + (9 ÷ 3)
= 20 + 3
= 23

Guided Practice

Do You Understand?
Question 1.
Harry used the model below to find 84 ÷ 4. Use the Distributive Property to show why Harry’s strategy works.

Answer:
84 ÷ 4 is 21.

Explanation:
Given that Harry used the model to find 84 ÷ 4, so the Distributive Property shows why Harry’s strategy works is
= (80 ÷ 4) + (4 ÷ 4)
= 20 + 1
= 21.

Do You Know How?
For 2-3, use partial quotients to divide. Use counters or draw pictures as needed.
Question 2.
How many groups of 4 are in 48?

Answer:
There are 12 groups of 4 in 48.

Explanation:
There are 12 groups of 4 in 48.

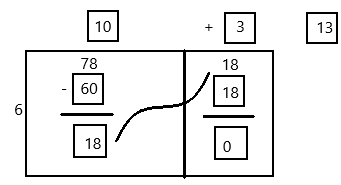
Question 3.
How many groups of 6 are in 78?

Answer:
There are 13 groups of 6 in 78.

Explanation:

Independent Practice

For 4-9, use partial quotients to divide. You may use counters or draw pictures to help.
Question 4.
How many groups of 6 are in 90?
90 ÷ 6
Answer:
There are 15 groups of 6 in 90.

Explanation:
There are 15 groups of 6 in 90.

Question 5.
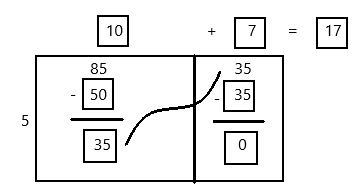
How many groups of 5 are in 85?
85 ÷ 5
Answer:
There are 17 groups of 5 in 85.

Explanation:
There are 17 groups of 5 in 85.

Question 6.

Answer:
There are 39 groups of 2 in 78.

Explanation:
There are 39 groups of 2 in 78.

Question 7.

Answer:

Question 8.

Answer:
There are 42 groups of 2 in 84.

Explanation:
There are 42 groups of 2 in 84.

Question 9.

Answer:
There are 19 groups of 3 in 57.

Explanation:
There are 19 groups of 3 in 57.

Problem Solving

Question 10.
Model with Math A collection of 64 stickers is placed into 4 equal piles. How many stickers are placed in each pile? Use the bar diagram to write and solve an equation.

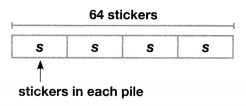
Answer:
The number of stickers is placed in each pile is 16 piles.

Explanation:
Given that 64 stickers are placed into 4 equal piles, so the number of stickers are placed in each pile is

Question 11.
A chef is baking cookies for 3 parties. For each party, the chef uses the same number of eggs. She has 2 dozen eggs. What is the greatest number of eggs the chef can use for each party?
Answer:
The greatest number of eggs the chef can use for each party is 8 eggs.

Explanation:
Given that A chef is baking cookies for 3 parties and for each party, the chef uses the same number of eggs and she has 2 dozen eggs which are 2 × 12 = 24 eggs. So the greatest number of eggs the chef can use for each party is 24 ÷ 3 which is 8 eggs.

Question 12.
Show how to use the Distributive Property to divide 54 by 2 by breaking 54 into 40 + 14.
Answer:

Question 13.
Higher Order Thinking Amanda wants to put some of her books on 4 shelves with 6 books on each shelf and the rest on 6 shelves with 3 books on each shelf. Can Amanda arrange her books this way? Explain.

Answer:
Amanda can arrange books 4 by 6 and 3 by 6.

Explanation:
Given that Amanda put some of her books on 4 shelves with 6 books, so there will be 4 × 6 which is 24. As the total number of books is 42, so the remaining books will be 42 – 24 = 18. And the rest are on 6 shelves with 3 books on each shelf, these can be arranged as 18 ÷ 6 which is 3.

Assessment Practice

Question 14.
Select all correct combinations of partial quotients that can be used to find 96 ÷ 3.
☐ 30, 2
☐ 30,10,2
☐ 10, 10, 10, 2
☐ 10, 10, 10, 6
☐ 20, 10, 2
Answer:
The correct combination of partial quotients is options A, C, and E.

Explanation:
The correct combination of partial quotients that can be used to find 96 ÷ 3 is 30,2 and 10, 10, 10, 2 and 20, 10, 2.

Question 15.
Use the Distributive Property to find 84 ÷ 7. Which is the missing number?
84 ÷ 7 = (70 + _______) = 7
= (70 ÷ 7) + (_____ ÷ 7)
= 10 + 2
= 12
A. 4
B. 14
C. 24
D. 34
Answer:
The missing number is 14.

Explanation:
Here, we are using Distributive Property to find 84 ÷ 7 which is
84 ÷ 7 = (70 + 14) = 7
= (70 ÷ 7) + (14 ÷ 7)
= 10 + 2
= 12.

Lesson 5.6 Use Partial Quotients to Divide: Greater Dividends

Solve & Share
The new reading room in the library is 9 feet long. It is divided into a reading area and a help desk area. It has a total area of 153 square feet. What is the total width of the new reading room? Use the model to help solve this problem. Solve this problem using any strategy you choose.
I can … divide by thinking about multiplication, estimation, and place value.

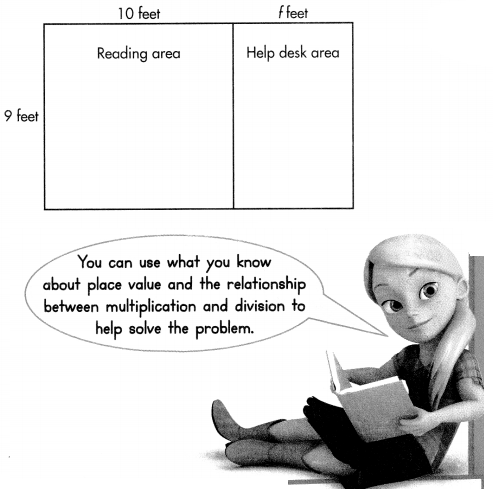
Look Back! Reasoning If the area of the reading room was 216 square feet and the length was still 9 feet, would the width be more or less than 20? Explain.

Essential Question
How Can You Use Partial Quotients to Divide Greater Dividends?

Visual Learning Bridge
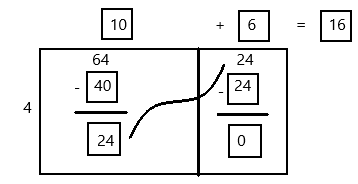
A total of 277 people signed up to audition for a talent show. Five people at a time were brought in for a group interview. How many group interviews were needed to audition all 277 people?

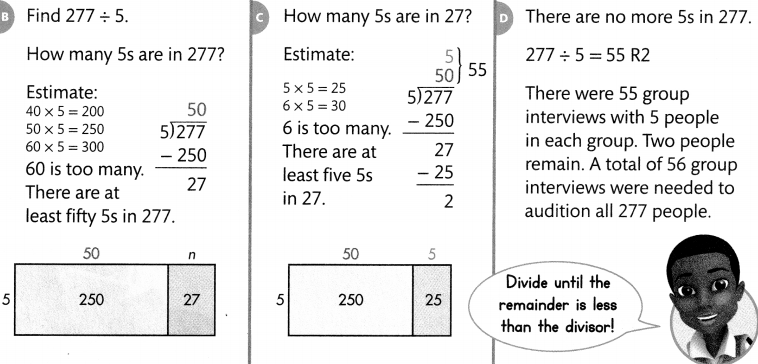
Convince Me! Use Structure How can you use multiplication and addition to check the answer above?

Another Example!

Guided Practice

Do You Understand?
Question 1.
Hilary has 254 tokens to use for games at Pizza Mania. She would like to use an equal number of tokens for each of 3 visits she has planned. Will Hilary be able to use the same amount of tokens for each visit?
Answer:
She can use 84 tokens with 2 visits.

Explanation:
Given that Hilary has 254 tokens to use for games at Pizza Mania and she would like to use an equal number of tokens for each of the 3 visits she has planned. So, Hilary can use 254 ÷ 3 which is 84 with 2 leftovers. So she can use 84 tokens with 2 visits.

Do You Know How?
For 2-3, use partial quotients to divide.
Question 2.
How many 4s are in 6,787?
6,787 ÷ 4
Answer:
The number of 4’s in 6,787 is 1696 with the remainder 3.

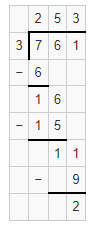
Explanation:
Given that 6,787 ÷ 4, so the number of 4’s in 6,787 is 1696 with the remainder 3.

Question 3.
How many 5s are in 6,209?
6,209 ÷ 5
Answer:
The number of 5’s in 6,209 is 1241 with the remainder 4.

Explanation:
Given that 6,209 ÷ 5, so the number of 5’s in 6,209 is 1241 with the remainder 4.

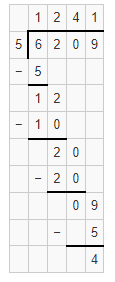
Independent Practice

For 4-11, use partial quotients to divide.
Question 4.

Answer:
The partial quotient is 17.

Explanation:
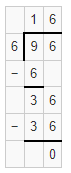
Given that 153 ÷ 9, the partial quotient is 17.

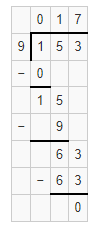
Question 5.

Answer:
The partial quotient is 56 with 2 leftovers.

Explanation:
Given that 450 ÷ 8, the partial quotient is 56 with 2 leftovers.

Question 6.

Answer:
The partial quotient is 942.

Explanation:
Given that 2,826 ÷ 3, the partial quotient is 942.

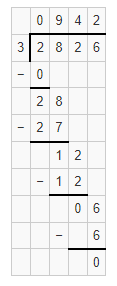
Question 7.

Answer:
The partial quotient is 1346 with 6 leftovers.

Explanation:
Given that 9,428 ÷ 7, the partial quotient is 1346 with 6 leftovers.

Question 8.

Answer:
The partial quotient is 616 with 6 leftovers.

Explanation:
Given that 4,318 ÷ 7, the partial quotient is 616 with 6 leftovers.

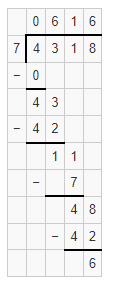
Question 9.

Answer:
The partial quotient is 2,114 with 1 leftover.

Explanation:
Given that 8,457 ÷ 4, the partial quotient is 2,114 with 1 leftover.

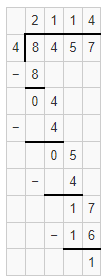
Question 10.

Answer:
The partial quotient is 712 with 3 leftovers.

Explanation:
Given that 5,699 ÷ 8, the partial quotient is 712 with 3 leftovers.

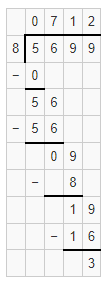
Question 11.

Answer:
The partial quotient is 1,522 with 1 leftover.

Explanation:
Given that 4,567 ÷ 3, the partial quotient is 1,522 with 1 leftover.

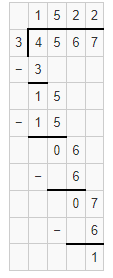
Problem Solving

Question 12.
After a state fair, three 4th-grade classes volunteered to clean up the trash from the fairgrounds. In total, they collected 1,281 pounds of trash. If each class collected the same amount, how many pounds of trash did each class collect?
Answer:
The number of pounds of trash did each class collects is 427 pounds.

Explanation:
Given that after a state fair, three 4th-grade classes volunteered to clean up the trash from the fairgrounds. In total, they collected 1,281 pounds of trash. If each class collected the same amount, the number of pounds of trash did each class collects is 1281 ÷ 3 which is 427 pounds.

Question 13.
enVision® STEM An electric car can travel 4 miles on one-kilowatt hour of electricity. How many kilowatt hours of electricity would it take for Shawn to drive his electric car to his grandmother’s house and back? Shawn lives 56 miles from his grandmother.
Answer:
The number of kilowatt-hours is 28 kilowatt-hours.

Explanation:
Given that an electric car can travel 4 miles on the one-kilowatt hour of electricity and Shawn to drive his electric car to his grandmother’s house and back, so 56 × 2 which is 112 miles Shawn needs to drive. So the number of kilowatt-hours of electricity would it take for Shawn to drive his electric car to his grandmother’s house and back is 112 ÷ 4 which is 28 miles.

For 14-15, use the table at the right.

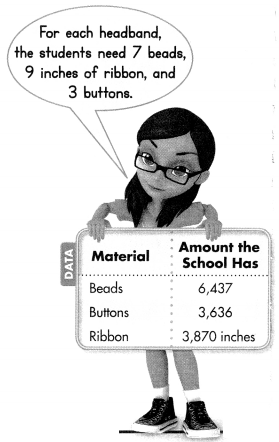
Question 14.
Number Sense Use estimation to find which material allows the students to make the least number of headbands.
Answer:
Given that the beads are 6,437 ÷ 7 which is around 900, buttons are 3,636 ÷ 3 which is around 1000 and ribbons are 3,870 ÷ 9 which is around 450. So the ribbon allows students to make the least number of headbands.

Question 15.
Higher Order Thinking How many headbands can the students make? Explain.
Answer:

Assessment Practice

Question 16.
Select all correct combinations of partial quotients and a remainder that can be used to find 4,567 ÷ 7.
☐ 600; 50; 2.
☐ 500; 10; 50; R3
☐ 500; 100; 50; 2; R3
☐ 600; 50; R17
☐ 600; 50; 2; R3
Answer:
600; 50; 2; R3.

Explanation:
The correct combinations of partial quotients and a remainder that can be used to find 4,567 ÷ 7 is 600; 50; 2; R3.

Question 17.
Which is the quotient? 3,858 ÷ 8
A. 4,082 R2
B. 472 R2
C. 482 R2
D. 481 R8
Answer:
482 with 2 leftovers.

Explanation:
The quotient of 3,858 ÷ 8 is 482 with 2 leftovers.

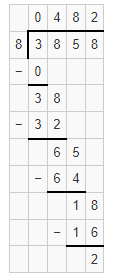
Lesson 5.7 Use Sharing to Divide

Solve & Share
A class collected $238 to be distributed equally to two charities. How much money will each charity receive? Use objects or draw pictures to help solve this problem. Explain how you found your answer.
I can … sort objects into equal-sized groups to divide.

Look Back! When might you need to divide something into equal groups in everyday life?
Answer:
The money will each charity receive is $119.

Explanation:
Given that a class collected $238 to be distributed equally to two charities. So the money will each charity receive is $238 ÷ 2 which is $119.

Essential Question
How Can Place Value don Help You Divide?

Visual Learning Bridge
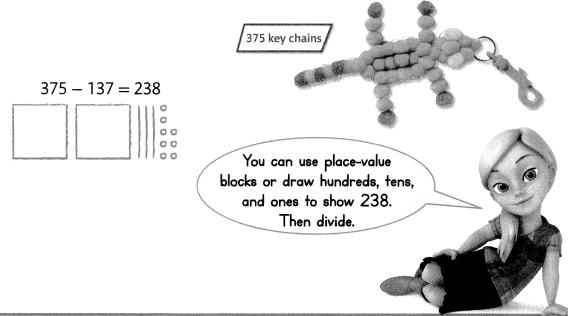
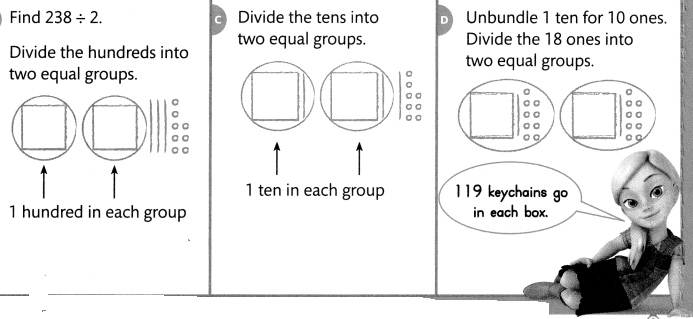
The craft club made 375 key chains. They sold 137 of the key chains at the school fair. The rest need to be packed into 2 boxes with the same number of key chains in each box. How many key chains will go in each box?
First, subtract to find how many key chains need to be packed.

Convince Me! Use Appropriate Tools Tell how you would evenly divide the money shown among 4 people using only $10 bills and $1 bills.

Another Example!
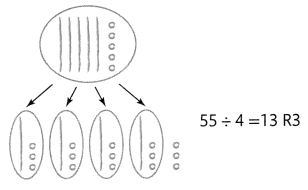
Find 55 ÷ 4.
Divide the tens equally into 4 groups. Regroup 1 ten as 10 ones and then divide the ones equally into 4 groups. There are 3 ones left over.

Guided Practice

Do You Understand?
Question 1.
Draw a picture to explain why 423 ÷ 3 = 141.
Answer:

Question 2.
The art teacher displayed 48 paintings on 3 walls. If each wall had the same number of paintings, how many paintings were on each wall?
Answer:
The number of paintings was on each wall is 16 paintings.

Explanation:
Given that the art teacher displayed 48 paintings on 3 walls and if each wall had the same number of paintings, so the number of paintings were on each wall is 48 ÷ 3 which is 16 paintings.

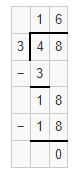
Do You Know How?

For 3-4, tell how many are in each group and how many are left over. Use placevalue blocks or draw pictures as needed.
Question 3.
176 magazines divided equally into 5 boxes
Answer:
35 with 1 leftover.

Explanation:
Given that 176 magazines were divided equally into 5 boxes which is 176 ÷ 5 = 35 with 1 leftover.

Question 4.
56 marbles divided equally into 3 bags
Answer:
18 with 2 leftovers.

Explanation:
Given that 56 marbles were divided equally into 3 bags which is 56 ÷ 3 = 18 with 2 leftovers.

Independent Practice

For 5-8, use place-value blocks or a drawing to divide. Record remainders.
Question 5.
71 ÷ _____ = ______ R2

Answer:
The equation will be 71 ÷ 3 = 23 with 2 leftovers.

Explanation:
In the above image, we can see that there are three circles with 23 in each circle and 2 ones that are leftover. So the equation will be 71 ÷ 3 = 23 with 2 leftovers.

Question 6.
_____ = 176 ÷ ______

Answer:
The equation will be 176 ÷ 4 = 44.

Explanation:
In the above image, we can see that there are three circles with 23 in each circle and 2 ones that are leftover. So the equation will be 176 ÷ 4 = 44.

Question 7.
46 ÷ 3
Answer:
The equation will be 46 ÷ 3 = 15 with 1 leftover.

Explanation:
On solving the equation we will get 46 ÷ 3 = 15 with 1 leftover.

Question 8.
65 ÷ 4
Answer:
The equation will be 65 ÷ 4 = 16 with 1 leftover.

Explanation:
On solving the equation we will get 65 ÷ 4 = 16 with 1 leftover.

Problem Solving

Question 9.
Model with Math A company with 65 employees is moving to a new location. All of the employees are divided into groups of 5 for the move. Write an equation and find g, the number of groups used for the move.

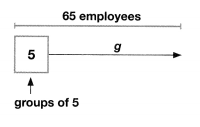
Answer:
The equation will be 65 ÷ 5 = 13.

Explanation:
Given that a company with 65 employees is moving to a new location and all of the employees are divided into groups of 5 for the move. So the equation will be 65 ÷ 5 = g, and the value of g is 13.

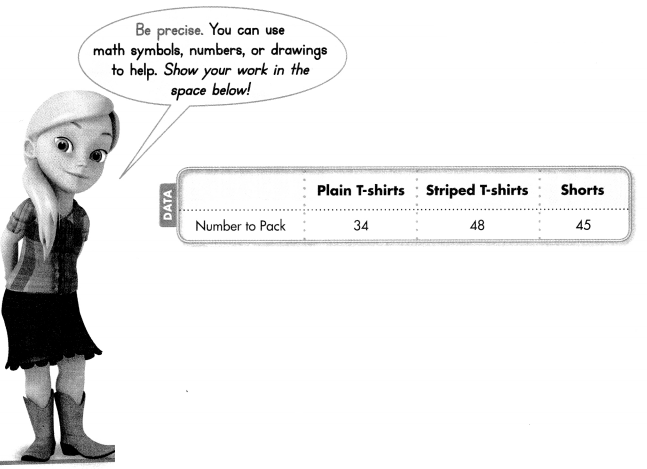
Question 10.
Maya used a drawing to divide 86. She made groups of 17 with 1 left over. Draw a picture to determine how many groups Maya made.
Answer:
Given that Maya used a drawing to divide 86 she made groups of 17 with 1 leftover, so the picture will be

Question 11.
Number Sense A science museum has 2,400 gemstones displayed equally in 3 cases. How many gemstones are in each case? What basic fact did you use to determine the quotient?
Answer:

Explanation:
Given that a science museum has 2,400 gemstones displayed equally in 3 cases, so the number of gemstones is in each case is 2400 ÷ 3 which can also be written as 24 ÷ 3 = 8. So the number of gemstones is in each case is 8 gemstones.

Question 12.
Mr. Harold has 268 books on 4 shelves in the classroom library. He has the same number of books on each shelf. To find the number of books on each shelf, he divided 268 by 4. How many books are on each shelf?
Answer:
The number of books on each shelf is 67 books.

Explanation:
Given that Mr. Harnold has 268 books on 4 shelves in the classroom library and he has the same number of books on each shelf, so the number of books on each shelf is 268 ÷ 4 which is 67 books are on each shelf.

Question 13.
Higher Order Thinking Five fourth grade classes from an elementary school took a trip to the United States Capitol. There were 25 students in each class. At the Capitol, a maximum of 40 students were allowed on a tour at one time. What is the least number of tours needed so all the students were able to take a tour?
Answer:
The least number of tours was needed so all the students were able to take a tour is 3 with 1 leftover.

Explanation:
Given that five fourth grade classes from an elementary school took a trip to the United States Capitol and there were 25 students in each class and at the Capitol, so the number of students will be 25 × 5 which is 25 students. And a maximum of 40 students was allowed on a tour at one time, so the least number of tours was needed so all the students were able to take a tour is 125 ÷ 40 which is 3 with 1 leftover.

Assessment Practice

Question 14.
Which division equation is represented by the drawing below?

A. 72 ÷ 6 = 12
B. 62 ÷ 3 = 24
C. 64 ÷ 3 = 24
D. 72 ÷ 3 = 24
Answer:
72 ÷ 3 = 24.

Explanation:
In the above image, we can see that three circles with 24 in each circle. So the equation will be 72 ÷ 3 = 24.

Question 15.
What is the missing divisor? 2,244 ÷ n = 374
A. 3
B. 4
C. 6
D. 7
Answer:
The missing divisor is 6.

Explanation:
The missing divisor for the equation 2,244 ÷ n =374 is 2,244 ÷ 374 which is 6.

Lesson 5.8 Continue Sharing to Divide

Solve & Share
Sara volunteers at a clothing recycling center. She packs T-shirts into bins for display. She packs the same number of T-shirts into 3 bins. How many T-shirts does Sara pack in each bin? She packs shorts into 2 bins with the same number in each bin. How many pairs of shorts does Sara pack in each bin?
I can … use place value and sharing to divide.

Look Back! Explain how you can estimate answers to the problems above.

Essential Question
How Can You Record Division With a 1-Digit Divisor?

Visual Learning Bridge
Helen has 55 postcards. As an art project, she plans to glue the same number of postcards onto 4 poster boards. How many postcards can Helen put on each poster board?
You can use place-value blocks to solve the problem.

Divide the tens.
Estimate: 55 ÷ 4 is close to 60 ÷ 4 = 15.

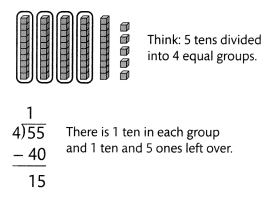
Divide the ones.

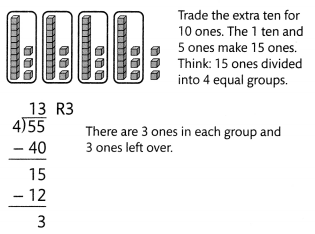
Helen can put 13 postcards on each of the poster boards. This quotient is reasonable since it is close to the estimate of 15.

Convince Me! Reasoning What does the remainder mean in the problem above?

Another Example!

Guided Practice

Do You Understand?
Question 1.
Explain how place-value blocks can help you with division.
Answer:
Here, place-value allows us to take the complication addition, subtraction, multiplication, and division problems and reduce and reduce them to a simpler problem.

Do You Know How?
For 2-3, estimate, and then find the quotient. Use place-value blocks or draw pictures as needed.
Question 2.

Answer:
16 with 2 leftovers.

Explanation:
The quotient of 82 ÷ 5 is 16 with 2 leftovers.

Question 3.

Answer:
94 with 1 leftover.

Explanation:
The quotient of 659 ÷ 7 is 94 with 1 leftover.

Independent Practice

For 4-11, find each quotient. Use place-value blocks or draw pictures as needed.
Question 4.

Answer:
26.

Explanation:
The quotient of 78 ÷ 3 is 26.

Question 5.

Answer:
28 with 2 leftovers.

Explanation:
The quotient of 86 ÷ 3 is 28 with 2 leftovers.

Question 6.

Answer:
52 with 1 leftover.

Explanation:
The quotient of 417 ÷ 8 is 52 with 1 leftover.

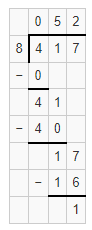
Question 7.

Answer:
23 with 1 leftover.

Explanation:
The quotient of 93 ÷ 4 is 23 with 1 leftover.

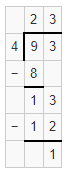
Question 8.

Answer:
65 with 6 leftovers.

Explanation:
The quotient of 526 ÷ 8 is 65 with 6 leftovers.

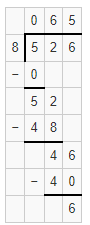
Question 9.

Answer:
12 with 4 leftovers.

Explanation:
The quotient of 88 ÷ 7 is 12 with 4 leftovers.

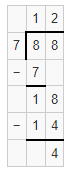
Question 10.

Answer:
253 with 2 leftovers.

Explanation:
The quotient of 761 ÷ 3 is 253 with 2 leftovers.

Question 11.

Answer:
16.

Explanation:
The quotient of 96 ÷ 6 is 16.

Problem Solving

Question 12.
Some of the tallest selenite crystals in a cave in Chihuahua, Mexico are 40 feet tall. Nathan is 4 feet tall. About how many times as tall as Nathan are the tallest crystals?

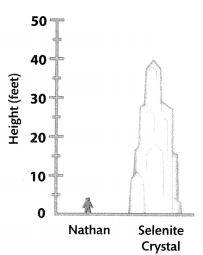
Answer:

Question 13.
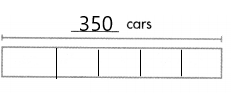
Model with Math The Galveston-Port Bolivar Ferry takes cars across Galveston Bay. One day, the ferry transported a total of 350 cars over a 5-hour period. The ferry took the same number of cars each hour. How many cars did it take each hour? Complete the bar diagram to help.

Answer:
The number of cars did it take each hour is 70 cars.

Explanation:
Given that the Galveston-Port Bolivar Ferry takes cars across Galveston Bay. One day, the ferry transported a total of 350 cars over a 5-hour period. So the number of cars did it take each hour is 350 ÷ 5 which is 70 cars.

Question 14.
Zelda has a piece of fabric that is 74 inches long. She wants to divide it into 2 equal pieces. What is the length of each piece?
Answer:
The length of each piece is 37 inches long.

Explanation:
Given that Zelda has a piece of fabric that is 74 inches long and she wants to divide it into 2 equal pieces. So the length of each piece is 74 ÷ 2 which is 37 inches long.

Question 15.
Higher Order Thinking Maggie is making trail mix. She makes 4 batches of the recipe shown. She divides it into 3 equal-sized bags. How many ounces are in each bag?

Answer:
There will be 24 ounces in each bag.

Explanation:
Given that Maggie is making trail mix. So the total weight of trail mix is 8 + 5 + 2 + 3 which is 18 oz. As she makes 4 batches it will be 18 × 4 which is 72 and she divides it into 3 equal-sized bags, so 72 ÷ 3 which is 24 ounces in each bag.

Assessment Practice

Question 16.
Find the quotient.

A. 112
B. 114
C. 121
D. 122
Answer:
112.

Explanation:
The quotient of 784 ÷ 7 is 112.

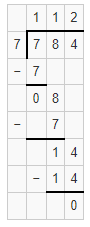
Question 17.
Find the quotient. 60 ÷ 5
A. 10
B. 12
C. 25
D. 55
Answer:
12.

Explanation:
The quotient of 60 ÷ 5 is 12.

Lesson 5.9 Choose a Strategy to Divide

Solve & Share
Choose a strategy to solve each problem. Explain your solutions. Problem 1 There are 135 fourth-grade students. Each lunch table seats 6 students. How many tables are needed to seat all of the fourth graders? Problem 2 A high school football stadium has 5 sections. Each section seats the same number of people. A total of 1,950 people can be seated in the stadium. How many people can sit in each section?
I can … follow a series of steps that breaks the division into simpler calculations.

Look Back! Look for Relationships Are either of the problems above easily solved using mental math? Explain.

Essential Question
How Do You Choose a Strategy to Divide?

Visual Learning Bridge
What strategy should I use to solve the problems below?

How many packages of hot dogs were used on Saturday?
Think: I can use partia! quotients.

There were 105 packages of hot dogs used on Saturday.

On Sunday, the 3 food stands each sold the same number of hot dogs. How many hot dogs were sold at each stand?
Think: I can break 216 apart and divide with mental math.
216 ÷ 3 = (210 + 6) ÷ 3
= (210 ÷ 3) + (6 ÷ 3)
= 70 + 2
= 72
72 hot dogs were sold at each stand.
You can use the Distributive Property.

Convince Me! Reasoning How do you decide which is the best method to use?

Another Example!
Only 75 cookies were sold on Monday, Tuesday, and Thursday. The same number of cookies were sold each day. How many cookies were sold each day? 75 ÷ 3 = c

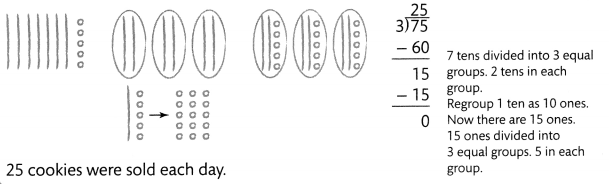
Guided Practice

Do You Understand?
Question 1.
Vickie’s estimated quotient was 80. The actual quotient she calculated was 48. Is her actual quotient reasonable? Explain.
Answer:

Do You Know How?
For 2 and 3, divide.
Question 2.

Answer:
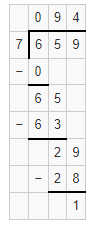
The quotient is 319.

Explanation:
Given that 2,871 ÷ 9 which we will get 319 as quotient.

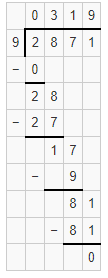
Question 3.

Answer:
The quotient is 117.

Explanation:
Given that 468 ÷ 4 which we will get 117 as quotient.

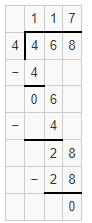
Independent Practice

For 4-11, divide.
You can use different strategies to divide.
Question 4.

Answer:
The quotient is 411.

Explanation:
Given that 3,288 ÷ 8 which we will get 411 as quotient.

Question 5.

Answer:
The quotient is 49 with 2 leftovers.

Explanation:
Given that 247 ÷ 5 which we will get 49 as a quotient with 2 leftovers.

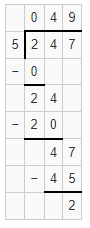
Question 6.

Answer:
The quotient is 230.

Explanation:
Given that 1,380 ÷ 6 which we will get 230 as a quotient.

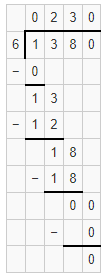
Question 7.

Answer:
The quotient is 796.

Explanation:
Given that 3,980 ÷ 5 which we will get 796 as a quotient.

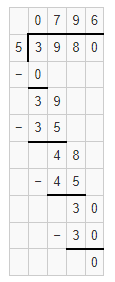
Question 8.

Answer:
The quotient is 61 as a quotient with 1 leftover.

Explanation:
Given that 367 ÷ 6 which we will get 61 as a quotient with 1 leftover.

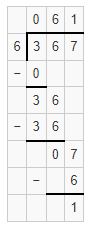
Question 9.

Answer:
The quotient is 1194 as a quotient.

Explanation:
Given that 3,582 ÷ 3 which we will get 1194 as a quotient.

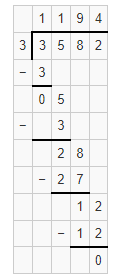
Question 10.

Answer:
The quotient is 189 as a quotient.

Explanation:
Given that 756 ÷ 4 which we will get 189 as a quotient.

Question 11.

Answer:
The quotient is 166 as a quotient with 3 leftovers.

Explanation:
Given that 999 ÷ 6 which we will get 166 as a quotient with 3 leftovers.

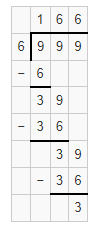
Problem Solving

Question 12.
A family of four drove from San Francisco to New York. They drove the same number of miles each day for 6 days. How many miles did they drive each day? How can you interpret the remainder?

Answer:
The number of miles did they drive each day is about 484 miles and extra 2 miles.

Explanation:
Given that a family of four drove from San Francisco to New York and then they drove the same number of miles each day for 6 days. So the number of miles did they drive each day is 2906 ÷ 6 which is about 484 miles and on 1 day they drove an extra 2 miles.

Question 13.
Without dividing, how can you tell if the quotient for 5,873 ÷ 8 is greater than 700? Explain whether the quotient is less than 800.
Answer:
Yes, the quotient is less than 800.

Explanation:
The quotient for 5,873 ÷ 8 is 734, and here the quotient is less than 800.

Question 14.
Reasoning A square dance set is made up of 4 couples (8 dancers). There are 150 people at a square dance. What is the greatest number of sets possible at the dance? Describe the steps you would take to solve this problem.
Answer:
The greatest number of sets possible at the dance is 18 with 6 leftovers.

Explanation:
Given that a square dance set is made up of 4 couples (8 dancers) and there are 150 people at a square dance. So the greatest number of sets possible at the dance is 150 ÷ 8 which is 18 with 6 leftovers.

Question 15.
Higher Order Thinking Is rounding or using compatible numbers a more useful method when finding quotients in division problems? Explain.
Answer:
Compatible number is better because they always give me groups that we can divide by. For example, if we take 151 ÷ 3 we will round off 151 to 150 and then we will perform division.

Question 16.
Ron’s Tires has 1,767 tires for heavy-duty trucks. Each heavy-duty truck needs 6 tires. How many heavy-duty trucks can get all new tires at Ron’s?
Answer:
The number of heavy-duty trucks can get all new tires at Ron is 294 new tries.

Explanation:
Given that Ron’s Tires has 1,767 tires for heavy-duty trucks and each heavy-duty truck needs 6 tires. So the number of heavy-duty trucks can get all new tires at Ron is 1,767 ÷ 6 which is 294 new tires.

Assessment Practice

Question 17.
Select all correct equations.
☐ 5658 ÷ 70 R5
☐ 3,613 ÷ 6 = 600 R13
☐ 3,288 ÷ 4 = 822
☐ 218 ÷ 3 = 72 R2
☐ 6,379 ÷ 7 = 911
Answer:
The correct equations are 3,288 ÷ 4 = 822 and 218 ÷ 3 = 72 R2.

Question 18.
Find 6,357 ÷ 8.
A. 814 R1
B. 794 R5
C. 794 R1
D. 784
Answer:
794 R5

Explanation:
The quotient of 6,357 ÷ 8 is 794 with 5 as remainder.

Lesson 5.10 Problem Solving

Model with Math
Solve & Share
Allen set a goal to do at least 120 minutes of outdoor activities a day, Monday through Friday. He made a list of each activity and the amount of time he spends doing it every week. The same amount of time is spent every day doing the activities. Is Allen spending enough time each day on outdoor activities to meet his goal? What math can you use to solve this problem?
I can … use a drawing, diagram, or table to model a problem.

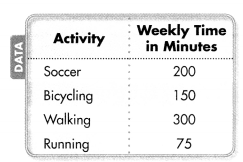
Thinking Habits
Be a good thinker! These questions can help you.

• How can I use math I know to help solve this problem?
• Can I use pictures, objects, or an equation to represent this problem?
• How can I use numbers, words, and symbols to solve the problem?

Look Back! Model with Math What hidden question do you have to answer before you can determine if Allen met his goal? What math can you use to find the answer to this hidden question and the original question?

Essential Question
How Can You Apply Math You Know to Solve Problems?

Visual Learning Bridge
A class is making decorations using same-size straws. They use the straws to make triangles, squares, pentagons, and hexagons. One package of straws is used for each group of polygons with the same number of sides. How many decorations can the class make?

What math can you use to solve the problem? I need to divide to find how many decorations can be made from one box of straws.

How can I model with math?
I can

• use previously learned concepts and skills. find and answer any hidden questions.
• decide if my results make sense.

Here’s my thinking.

Each polygon has a different number of sides.
I will divide 1,500 straws by the number of sides for each polygon:
1,500 ÷ 3 = 500 triangles
1,500 ÷ 4 = 375 squares
1,500 ÷ 5 = 300 pentagons
1,500 ÷ 6 = 250 hexagons
I will add all the decorations together:
500 + 375 + 300 + 250 = 1,425
The class can make 1,425 decorations.

Convince Me! Reasoning Another class made 200 octagon-shaped decorations. How many straws did they use?

Guided Practice

Model with Math Miguel is going camping with 3 friends. He packed sandwiches for everyone to share equally. How many sandwiches did Miguel pack for each camper?

Question 1.
What hidden question do you need to solve first? Write and solve an equation to find the answer. Tell what your variable represents.
Answer:

Question 2.
Complete the bar diagram. Write and solve an equation to find the number of sandwiches, s, for each camper.
You can use a bar diagram and write an equation to model with math.
Answer:

Independent Practice

Model with Math
Jodi delivers 54 newspapers on Saturday and 78 newspapers on Sunday. She makes bundles of 6 newspapers. How many bundles does Jodi make on Saturday and Sunday combined?
Question 3.
Explain how you could use a picture to represent the problem and show the relationships. Define variables.
Answer:

Question 4.
Write and solve equations to represent the problem. Explain how you can check that your solution is reasonable.
Answer:

Problem Solving

Assessment Practice
Dog Grooming
Patricia and Antonio own a dog grooming business. To attract new customers, they offered free dog baths with the purchase of a grooming service. During the first 6 days of the promotion, they bathed 26 beagles, 12 boxers, 17 pugs, and 5 golden retrievers. Patricia and Antonio each bathed the same number of dogs each day.

Question 5.
Reasoning What are the quantities given in the problem?
Answer:

Question 6.
Make Sense and Persevere What do you need to know to determine how many dogs Patricia bathed each day?
Answer:

Question 7.
Model with Math Draw a bar diagram. Write and solve an equation to find d, how many dogs were bathed in all.
You model with math when you use a picture or equation to represent the problem.
Answer:

Question 8.
Make Sense and Persevere Find how many dogs Patricia bathed each day. Explain how you were able to find the solution.
Answer:

Topic 5 Fluency Practice Activity

Follow the path
Shade a path from START to FINISH. Follow the sums and differences that are between 1,000 and 1,200. You can only move up, down, right, or left.
I can … add and subtract whole numbers with regrouping.

Topic 5 Vocabulary Review

Understand Vocabulary
Choose the best term from the box. Write it on the blank.
Word List

• dividend
• division
• divisor
• equation
• partial quotients
• quotient
• remainder

Question 1.
The answer to a division problem is called the ________
Answer:
The answer to a division problem is called the quotients.

Question 2.
The number to be divided in a division problem is called the ___________
Answer:
The number to be divided in a division problem is called the dividend.

Question 3.
A way to divide that finds quotients in parts until only a remainder, if any, is left is using __________
Answer:
A way to divide that finds quotients in parts until only a remainder, if any, is left is using

Question 4.
The number by which another number is divided is called the ___________
Answer:

Question 5.
The operation that tells how many equal groups there are or how many are in each group is called __________
Answer:

For each of these terms, give an example and a non-example.

Answer:

Use Vocabulary in Writing
Question 8.
Megan made 21 loom bracelets to share equally among her 7 friends. How many bracelets will each friend receive? Write and solve an equation. Use at least 3 terms from the Word List to describe your equation.
Answer:

Topic 5 Reteaching

Set A pages 169-172

A school district shares 2,700 chairs equally among 3 school buildings. How many chairs will each school building have?

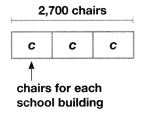
Find 2,700 ÷ 3 = c.
The basic fact is 27 ÷ 3 = 9.
27 hundreds = 3 = 9 hundreds, or 900.
2,700 ÷ 3 = 900
Each school building will have 900 chairs.

Remember you can use basic division facts and place value to divide mentally.

Question 1.
250 ÷ 5
Answer:

Question 2.
810 ÷ 9
Answer:

Question 3.
3,200 ÷ 4
Answer:

Question 4.
4,200 ÷ 7
Answer:

Question 5.
1,000 ÷ 2
Answer:

Question 6.
240 ÷ 4.
Answer:

Question 7.
450 ÷ 5
Answer:

Question 8.
720 ÷ 9
Answer:

Question 9.
3,600 ÷ 4
Answer:

Question 10.
4,900 ÷ 7
Answer:

Question 11.
2,000 ÷ 2
Answer:

Question 12.
280 ÷ 4
Answer:

Question 13.
2,100 ÷ 7
Answer:

Question 14.
560 ÷ 8
Answer:

Set B pages 173-180

Use multiplication to estimate 420 ÷ 8.
8 times what number is about 420?
8 × 5 = 40,
So, 8 × 50 = 400.
So, 420 ÷ 8 is about 50.
Use compatible numbers to estimate 1,519 ÷ 7.
What number close to 1,519 is easily divided by 7?
Try division facts to help find compatible numbers for 1,519
1,519 is close to 1,400.
14 ÷ 7 = 2,
so 1,400 ÷ 7 = 200.
So, 1,519 ÷ 7 is about 200.

Remember basic facts can help you find a number that is easily divided by the divisor.

Estimate each quotient.

Question 1.
718 ÷ 8
Answer:

Question 2.
156 ÷ 4
Answer:

Question 3.
482 ÷ 8
Answer:

Question 4.
174 ÷ 3
Answer:

Question 5.
843 ÷ 7
Answer:

Question 6.
321 ÷ 2
Answer:

Question 7.
428 ÷ 6
Answer:

Question 8.
811 ÷ 9
Answer:

Question 9.
5,616 ÷ 8
Answer:

Question 10.
7,224 ÷ 8
Answer:

Question 11.
6,324 ÷ 9
Answer:

Question 12.
3,627 ÷ 9
Answer:

Question 13.
331 ÷ 4
Answer:

Question 14.
1,222 ÷ 6
Answer:

Question 15.
2,511 ÷ 5
Answer:

Question 16.
362 ÷ 6
Answer:

Question 17.
4,940 ÷ 7
Answer:

Question 18.
9,312 ÷ 3
Answer:

Set C pages 181-184

Tom is putting 14 apples into bags. Each bag holds 4 apples. How many bags can Tom fill? Will any apples be left over?

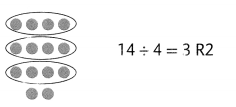
Use a model to represent 14 ÷ 4.
Tom can fill 3 bags. There will be 2 apples left over.

Remember to make sure the remainder is less than the divisor.
Question 1.
22 pickles
3 pickles on each plate
22 ÷ 3 = _____ with ______ left over
How many plates have 3 pickles?
Answer:

Question 2.
19 stamps
2 stamps on each envelope
19 ÷ 2 = _____ with _____ left over
How many stamps are not on an envelope?
Answer:

Set D pages 185-192

Find 357 ÷ 7.
Use a model. Divide by finding partial quotients.

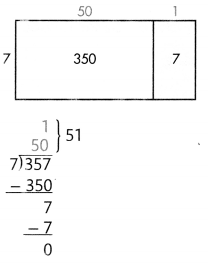
Divide. Use the Distributive Property.
357 ÷ 7 = (350 + 7) ÷ 7
= (350 ÷ 7) + (7 ÷ 7)
= 50 + 1
= 51

Remember to add the partial quotients to find the actual quotient.

Use partial quotients to solve.
Question 1.
There are 81 chairs in 3 equal groups. How many chairs are in each group?
Answer:

Question 2.
There are 174 games scheduled for 6 different leagues. Each league has the same number of games scheduled. How many games does each league have scheduled?
Answer:

Question 3.
There were 1,278 people at the last basketball game. The stands were divided into 6 sections. The same number of people sat in each section. How many people sat in each section?
Answer:

Set E pages 193–196

Margaret packed 68 books equally into 2 boxes. How many books did Margaret pack in each box?
Find 68 ÷ 2.

Divide the tens into two equal groups. Then divide the ones into two equal groups.

68 ÷ 2 = 34, because 2 × 34 = 68.
Margaret packed 34 books in each box.

Remember to check if your answer is reasonable.

Tell how many are in each group and how many are left over.
Question 1.
138 books; 5 stacks
Answer:

Question 2.
55 shells; 3 jars
Answer:

Question 3.
217 pens; 7 cases
Answer:

Question 4.
154 shoes; 4 boxes
Answer:

Question 5.
195 seeds; 6 planters
Answer:

Set F pages 197-200

Find 147 ÷ 6.
Estimate 120 ÷ 6 = 20.

147 ÷ 6 = 24 R3 is close to 20, so the answer is reasonable.

Remember to estimate the quotient to check if your answer is reasonable.

Question 1.
710 ÷ 9
Answer:

Question 2.
657 ÷ 5
Answer:

Question 3.
398 ÷ 8
Answer:

Question 4.
429 ÷ 2
Answer:

Question 5.
470 ÷ 6
Answer:

Question 6.
255 ÷ 4
Answer:

Set G pages 201-204

Find 8,951 ÷ 8.
Estimate: 8,800 ÷ 8 = 1,100.
One strategy is partial quotients.

Remember you can use your estimate to check if your answer is reasonable.

Choose a strategy to divide.
Question 1.
4,649 ÷ 4
Answer:

Question 2.
2,843 ÷ 3
Answer:

Question 3.
8,478 ÷ 6
Answer:

Question 4.
6,399 ÷ 9
Answer:

Question 5.
379 ÷ 2
Answer:

Question 6.
3,812 ÷ 5
Answer:

Question 7.
4,793 ÷ 5
Answer:

Question 8.
5,957 ÷ 7
Answer:

Set H pages 205-208

Think about these questions to help you model with math.
Thinking Habits

• How can I use math I know to help solve this problem?
• Can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?
  

Remember a bar diagram can help you write an equation.

A paint supplier delivered 1,345 cans of paint to 5 different hardware stores. Each store got the same number of paint cans. How many cans of paint were delivered to each store?
Question 1.
How can you use pictures, a bar diagram, and an equation to find the number of paint cans delivered to each store?
Answer:

Question 2.
How can you decide if your answer makes sense?
Answer:

Topic 5 Assessment Practice

Question 1.
Select all the equations that are reasonable estimates for the quotient 184 ÷ 8.
☐ 160 ÷ 8 = 20
☐ 200 ÷ 5 = 40
☐ 180 ÷ 9 = 20
☐ 150 ÷ 5 = 30
☐ 180 ÷ 6 = 30
Answer:

Question 2.
Draw a bar diagram for the equation, and then solve. 2,400 ÷ 6 = m
Answer:

Question 3.
Mrs. Bollis has two pieces of fabric to make costumes. One piece is 11 yards long and the other is 15 yards long. Each costume requires 3 yards of fabric. How many costumes can Mrs. Bollis make? How do the remainders affect the number of costumes she can make?
Answer:

Question 4.
A. Write an equation to show how to divide 453 into 3 equal groups.
Answer:

B. Complete the model to solve the equation in A.

Answer:

Question 5.
What is the best estimate for 3,350 ÷ 8?
A. 600
B. 200
C. 400
D. 800
Answer:

Question 6.
Draw an array and solve the equation. 48 ÷ 9 = ?
Answer:

Question 7.
Use compatible numbers to estimate the quotient 530 ÷ 9. Then find the exact answer.
Answer:

Question 8.
Find 4,800 ÷ 6 using a place-value strategy. What basic fact did you use?
Answer:

Question 9.
Select all the equations in which the remainder is 5.
☐ 59 ÷ 9 = 6 R?
☐ 352 ÷ 6 = 58 R?
☐ 788 ÷ 9 = 87 R?
☐ 1,486 ÷ 7 = 212 R?
☐ 2,957 ÷ 8 = 369 R?
Answer:

Question 10.
Which of the following expressions does NOT have a remainder of 3?
A. 52 ÷ 7
B. 123 ÷ 7
C. 451 ÷ 7
D. 794 ÷ 7
Answer:

Question 11.
Which of the following is NOT equivalent to 63 ÷ 3?
A. (60 + 3) ÷ 3
B. (33 + 30) ÷ 3
C. (60 ÷ 3) + 3
D. (60 ÷ 3) + (3 ÷ 3)
Answer:

Question 12.
Select all the quotients that are reasonable estimates for 472 ÷ 6.
☐ 450 ÷ 5
☐ 480 ÷ 6
☐ 500 ÷ 5
☐ 450 ÷ 3
☐ 1,200 ÷ 6 = 200
Answer:

Question 13.
Use partial quotients to find the quotient. Choose numbers from the box to complete the calculations. Use each number once.

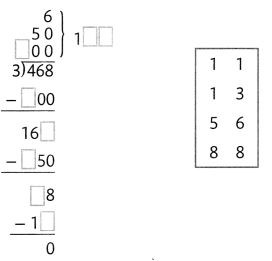
Answer:

Question 14.
Find 1,600 ÷ 8. What basic fact did you use?
Answer:

Question 15.
The fourth graders are going to the science museum.

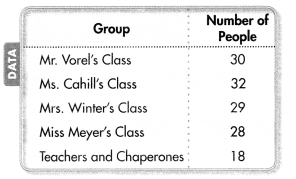
Groups of 8 students can see a special exhibit on space travel. How many groups will be needed so everyone can see the exhibit?
Answer:

Question 16.
A. Divide.
432 ÷ 8 = _________
Answer:

B. How can you use the answer from Part A to find 4,320 ÷ 8?
Answer:

Question 17.
The Pizza Stand gives patrons a free pizza when they collect 8 coupons. How many free pizzas can Mrs. Fowler get if she has 78 coupons? How does the remainder affect the number of free pizza’s she gets? How many more coupons does she need for the next free pizza? Explain.
Answer:

Question 18.
Estimate 257 ÷ 5. Explain how you can use multiplication to estimate the quotient.
Answer:

Question 19.
Use an equation to show how to separate 128 into 4 equal groups. Explain how to check the answer using multiplication.
Answer:

Question 20.
Write and solve an equation that shows one way to estimate 1,792 ÷ 6.
Answer:

Question 21.
Draw a picture to explain why 675 ÷ 5 = 131 R2.
Answer:

Question 22.
For each equation, mark a check to show the correct missing number.

Answer:

Question 23.
Holly uses 7 sheets of tissue paper to make one flower. If she bought a package with 500 sheets of tissue paper, about how many flowers will Holly be able to make? Use compatible numbers to estimate the number of flowers.
Answer:

Topic 5 Performance Task

Saving What You Earn
Trista’s older brother Ryan got a job. Ryan would like to buy the items shown with his earnings. Ryan earns $8 for each hour he works.
Question 1.
Ryan is curious and wants to know the amount of time it will take him to earn enough money to buy the items shown.
Part A
How many hours does Ryan need to work to earn enough money to buy the computer? Explain how to use place value and mental math to solve.

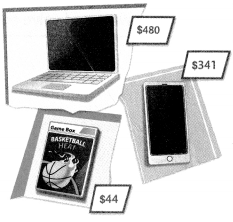
Answer:

Part B
How many hours does Ryan need to work to buy the video game? Use a model to show how to find the quotient. Explain how to interpret the remainder.
Answer:

Part C
How many hours will Ryan need to work to earn enough money to buy the smart phone? Use partial quotients to divide.
Answer:

Question 2.
Ryan gets a raise. He now earns $9 an hour. Ryan decides to start saving for a car. He works 9 hours a week.

Part A
How many hours does Ryan need to work to earn enough money to buy the car, as well as pay for the taxes, title, and plates as shown? Draw bar diagrams to help write and solve equations.
Answer:
Ryan has to work 5,887hrs and 55 min.

Explanation:
Ryan earns $9 an hr. He works 9hrs a week, or 1hr 17 min a day. $11.52 per day. The car costs $52,753, + $235(taxes, titles, and plates)= $52,988. 52,988/9=5,887:55

Part B
About how many weeks will Ryan need to work to buy the car and pay for the taxes, title, and plates? Explain.
Answer:
3,504 weeks

Explanation:
One week= 168 hrs.
5,887:55/168=3,504 weeks

Part C
How many actual weeks does Ryan need to work to buy the car and pay for the taxes, title, and plates? Show your work. Explain why your solution is reasonable.
Answer: