Practice with the help of enVision Math Common Core Grade 4 Answer Key Topic 6 Use Operations with Whole Numbers to Solve Problems regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 6 Use Operations with Whole Numbers to Solve Problems
Essential Questions:
How is comparing with multiplication different from comparing with addition? How can you use equations to solve multi-step problems?
Answer:
In an additive comparison, we find the relation between two amounts by asking or telling how much more is one compared to the other. In multiplicative comparison, there are two different sets being compared. The first set contains a certain number of items. The second set contains multiple copies of the first set
Example:
Additive Comparison:
2 + 2 + 5 + 3 + … n
Multiplicative Comparison:
3 × 4 × 5 × … n

enVision STEM Project: Energy and Multiplication
Do Research
Use the Internet or other sources to find and describe 3 examples of renewable energy?
Answer:
The examples of renewable energy are:
a. Solar energy
b. Wind energy
c. Tidal energy
d. Geothermal energy
Journal: Write a Report that Includes what you found. Also in your report:
A)
Solar panels are made up of smaller modules or sections called cells. Find a picture of a solar panel. How many cells are in 6 solar panels? How many cells are in 9 solar panels? How many more cells are in the 9 solar panels than the 6 solar panels?
Answer:
It is given that
Solar panels are made up of smaller modules or sections called cells
Now,
We know that,
A solar power panel is made of photovoltaic cells arranged in a configuration that can contain 32, 36, 48, 60, 72, and 96 cells
Now,
Let a solar panel contains 32 cells
So,
The number of cells that present in 6 solar panels = (The number of solar panels) × (The number of cells present in a solar panel)
= 6 × 32
= 6 × (30 + 2)
= (6 × 30) + (6 × 2)
= 180 + 12
= 192 cells
So,
The number of cells that present in 9 solar panels = (The number of solar panels) × (The number of cells present in a solar panel)
= 9 × 32
= 9 × (30 + 2)
= (9 × 30) + (9 × 2)
= 270 + 18
= 288 cells
So,
The difference between the two solar panels = 288 – 192
= 96 cells
Now,
The picture of a solar panel is:

Hence, from the above,
We can conclude that
The difference of the cells between 9 solar panels and 6 solar panels is: 96 cells
B)
Find examples of other items that use solar power?
Answer:
Some of the items that use solar power are:
A) Solar charger.
B) Solar cell phone charger. Strawberry Tree.
C) Solar chimney.
D) Solar-powered waste compacting bin.
E) Solar cooker.
F) Solar dryer.
G) Solar-powered fan.
H) Solar furnace.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- Associative Property of Multiplication
- Commutative Property of Multiplication
- Compatible numbers
- Distributive Property
Question 1.
The __________ says that factors can be multiplied in any order and the product remains the same.
Answer:
We know that,
The “Commutative Property of Multiplication” says that factors can be multiplied in any order and the product remains the same.
Hence, from the above,
We can conclude that the best term that is suitable for the given definition is: Cumulative Property of Multiplication
Question 2.
Breaking apart a multiplication problem into the sum or difference of two simpler multiplication problems is an example of using the __________
Answer:
We know that,
Breaking apart a multiplication problem into the sum or difference of two simpler multiplication problems is an example of using the “Distributive Property”
Hence, from the above,
We can conclude that the best term that is suitable for the given definition is: Distributive Property
Question 3.
According to the ________, factors can be regrouped and the product remains the same.
Answer:
We know that,
According to the “Associative property of Multiplication”, factors can be regrouped and the product remains the same.
Hence, from the above,
We can conclude that the best term that is suitable for the given definition is: Associative Property of Multiplication
Dividing by 1-Digit Numbers
Estimate each quotient.
Question 4.
16 ÷ 3
Answer:
The given expression is: 16 ÷ 3
Now,
By using the Long Division method,

Hence, from the above,
We can conclude that the quotient value for the given expression is: 5
Question 5.
25 ÷ 4
Answer:
The given expression is: 25 ÷ 4
Now,
By using the Long Division method,
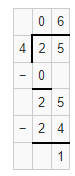
Hence, from the above,
We can conclude that the quotient value for the given expression is: 6
Question 6.
155 ÷ 4
Answer:
The given expression is: 155 ÷ 4
Now,
By using the Long Division method,
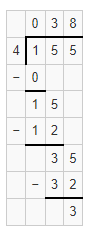
Hence, from the above,
We can conclude that the quotient value for the given expression is: 38
Question 7.
304 ÷ 3
Answer:
The given expression is: 304 ÷ 3
Now,
By using the Long Division method,
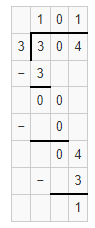
Hence, from the above,
We can conclude that the quotient value for the given expression is: 101
Question 8.
1,283 ÷ 6
Answer:
The given expression is: 1,283 ÷ 6
Now,
By using the Long Division method,
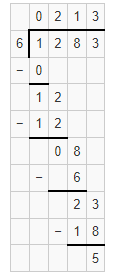
Hence, from the above,
We can conclude that the quotient value for the given expression is: 213
Question 9.
1,999 ÷ 4
Answer:
The given expression is: 1,999 ÷ 4
Now,
By using the Long Division method,
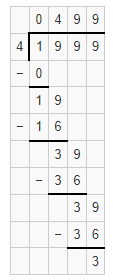
Hence, from the above,
We can conclude that the quotient value for the given expression is: 499
Multiplying by 1-Digit Numbers
Find each product.
Question 10.
53 × 9
Answer:
The given expression is: 53 × 9
Now,
By using the partial Products method,
53 × 9
= (50 + 3) × 9
= (50 × 9) + (3 × 9)
= 450 + 27
= 477
Hence, from the above,
We can conclude that the product value for the given expression is: 477
Question 11.
1,127 × 7
Answer:
The given expression is: 1,127 × 7
Now,
By using the partial Products method,
1,127 × 7
= (1,000 + 100 + 27) × 7
= (1,000 × 7) + (100 × 7) + (27 × 7)
= 7,000 + 700 + 189
= 7,889
Hence, from the above,
We can conclude that the product value for the given expression is: 7,889
Question 12.
2,769 × 5
Answer:
The given expression is: 2,769 × 5
Now,
By using the partial Products method,
2,769 × 5
= (2,000 + 700 + 60 + 9) × 5
= (2,000 × 5) + (700 × 5) + (60 × 5) + (9 × 5)
= 10,000 + 3,500 + 300 + 45
= 13,845
Hence, from the above,
We can conclude that the product value for the given expression is: 13,845
Question 13.
3 × 215
Answer:
The given expression is: 3 × 215
Now,
By using the partial Products method,
3 × 215
= 3 × (200 + 15)
= (3 × 200) + (3 × 15)
= 600 + 45
= 645
Hence, from the above,
We can conclude that the product value for the given expression is: 645
Question 14.
914 × 5
Answer:
The given expression is: 914 × 5
Now,
By using the partial Products method,
914 × 5
= (900 + 14) × 5
= (900 × 5) + (14 × 5)
= 4,500 + 70
= 4,570
Hence, from the above,
We can conclude that the product value for the given expression is: 4,570
Question 15.
1,238 × 5
Answer:
The given expression is: 1,238 × 5
Now,
By using the partial Products method,
1,238 × 5
= (1,000 + 200 + 30 + 8) × 5
= (1,000 × 5) + (200 × 5) + (30 × 5) + (8 × 5)
= 5,000 + 1,000 + 150 + 40
= 6,190
Hence, from the above,
We can conclude that the product value for the given expression is: 6,190
Problem Solving
Question 16.
Construct Arguments Explain why the array represents 3 × 21
Answer:
The given array is:

Now,
We know that,
An “Array” is a collection of rows and columns
Now,
From the given figure,
We can observe that
The number of rows is: 21
The number of columns is: 3
So,
To find the number of cells in a given array,
We have to multiply the rows and columns
Hence, from the above,
We can conclude that the given array represents 21 × 3 since it represents the number of rows and number of columns
Question 17.
James multiplies 38 by 55. He finds three of the four partial products: 40, 150, and 400. Which partial product is James missing? What is the solution?
Answer:
It is given that
James multiplies 38 by 55. He finds three of the four partial products: 40, 150, and 400.
Now,
The given expression is: 38 × 55
Now,
By using the partial Products method,
38 × 55
= (30 + 8) × (50 + 5)
= (30 × 50) + (30 × 5) + (8 × 50) + (8 × 5)
= 1,500 + 150 +400 + 40
= 2,090
Hence, from the above,
We can conclude that
The Partial product James is missing is: 1,500
The solution for the given expression is: 2,090
Pick a Project
PROJECT 6A
How tall is tall?
Project: Model the Height of a Redwood Tree

PROJECT 6B
What are some interesting number facts about a manatee?
Project: Make a Presentation with Manatee Number Facts

PROJECT 6C
How does temperature affect an alligator egg?
Project: Create a Bar Diagram

PROJECT 6D
How many eggs does the loggerhead turtle lay?
Project: Model a Turtle’s Egg

Lesson 6.1 Solve Comparison Problems
Solve & Share
Sarah is making a square pillow with edges that each measure 18 inches long. She needs a strip of fabric 4 times as long as one edge of the pillow to make a border around the pillow. How long does the strip of fabric need to be? Solve this problem any way you choose.
I can … use multiplication or addition to compare one quantity to another.

Answer:
It is given that
Sarah is making a square pillow with edges that each measure 18 inches long. She needs a strip of fabric 4 times as long as one edge of the pillow to make a border around the pillow
Now,
Let the length of the strip of fabric be x
So,
According to the given data,
The length of the strip (x) = 4 × (The length of the pillow at the edges)
= 4 × 18
= 72 inches
Hence, from the above,
We can conclude that
The length of the fabric needed is: 72 inches
Look Back!
Model with Math
How could a bar diagram help you write and solve an equation for the problem?
Answer:
It is given that
Sarah is making a square pillow with edges that each measure 18 inches long. She needs a strip of fabric 4 times as long as one edge of the pillow to make a border around the pillow
Now,
The representation of the given situation in the form of a bar diagram is:
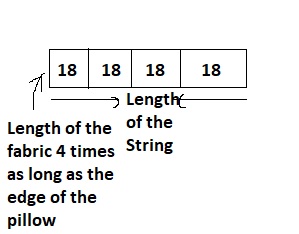
So,
From the above bar diagram,
We can observe that
The length of the string = 4 × (The length of the edge of the pillow)
= 4 × 18
= 72 inches
Hence, from the above,
We can conclude that
By using the bar diagram, the length of the string is: 72 inches
Essential Question
How Is Comparing with Multiplication Different from Comparing with Addition?
Answer:
In an additive comparison, we find the relation between two amounts by asking or telling how much more is one compared to the other. In multiplicative comparison, there are two different sets being compared. The first set contains a certain number of items. The second set contains multiple copies of the first set
Example:
Additive Comparison:
2 + 2 + 5 + 3 + … n
Multiplicative Comparison:
3 × 4 × 5 × … n
Visual Learning Bridge
Max said the Rangers scored 3 times as many runs as the Stars. Jody said the Rangers scored 8 more runs than the Stars. Could both Max and Jody be correct?

Compare with Multiplication
Find 3 times as many as 4 runs.
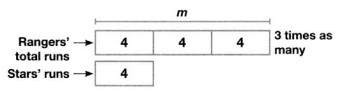
m = 3 × 4
m = 12 runs
According to Max, the Rangers scored 12 runs.
Compare with Addition
Find 8 more than 4 runs.
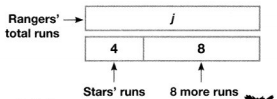
j = 4 + 8
j = 12 runs
According to Jody, the Rangers scored 12 runs.
Max and Jody are both correct.
Convince Me!
Construct Arguments Describe when you would use multiplication and when you would use addition to make a comparison?
Answer:
When distinguishing multiplicative comparison from additive comparison,
We should note that “Additive comparisons” focus on the difference between two quantities whereas “Multiplicative comparisons” focus on the difference between two qualities
Guided Practice
Do You Understand?
Question 1.
Use the information from the previous page. If the Rangers scored 5 times as many runs as the Stars, how many runs would the Rangers have scored?
a. Compare using multiplication. Write and solve an equation.
Answer:
It is given that
Rangers scored 5 times as many runs as the Stars
Now,
The given figure is:

Now,
The representation of the given situation in the form of a bar diagram is:
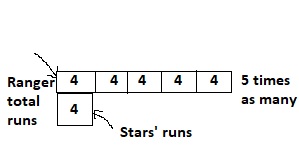
So,
The total number of runs rangers scored = 5 × (The number of runs Stars scored)
= 5 × 4
= 20 runs
Hence, from the above,
We can conclude that the number of runs scored by Rangers is: 20
b. How could you use addition to compare the runs for the two teams?
Answer:
It is given that
Rangers scored 5 times as many runs as the Stars
Now,
The given figure is:

Now,
The representation of the given situation in the form of a bar diagram is:

So,
The total number of runs rangers scored = (The number of runs Stars scored) + (The number of runs Stars scored) + (The number of runs Stars scored) + (The number of runs Stars scored) + (The number of runs Stars scored)
= 5 + 5 + 5 + 5 +5
= 20 runs
Hence, from the above,
We can conclude that the number of runs scored by Rangers is: 20
Do You Know How?
For 2-3, complete the comparison sentence. Find the value of the variable that makes the sentence true.
Question 2.
Sam’s baseball team has 4 times as many helmets as Ed’s team. Ed’s team has 21 helmets. Let h = the number of helmets Sam’s team has.
h is ___________ times as many as ________.
h = _________
Answer:
It is given that
Sam’s baseball team has 4 times as many helmets as Ed’s team. Ed’s team has 21 helmets.
So,
The number of helmets Sam’s team has (h) = 4 × (The number of helmets Ed’s team has)
= 4 × 21
= 4 × (20 + 1)
= (4 × 20) + (4 × 1)
= 80 + 4
= 84 helmets
Hence, from the above,
We can conclude that
h is 4 times as many as the number of helmets Ed’s team has
The number of helmets Sam’s team has is: 84 helmets
Question 3.
There are 128 more trees in the park than at Ty’s house. There are 3 trees at Ty’s house. Let t = the number of trees in the park.
_______ more than _____ is t.
t = __________
Answer:
It is given that
There are 128 more trees in the park than at Ty’s house. There are 3 trees at Ty’s house.
So,
The number of trees in the park (t) = (The number of trees at Ty’s house) + (The number of more trees in the park)
= 3 + 128
= 131 trees
Hence, from the above,
We can conclude that
128 trees more than 3 trees is t
The total number of trees in the park is: 131 trees
Independent Practice
Use times as many as or more than to compare the amounts.
For 4-9, write a comparison sentence. For 4-7, find the value of the variable that makes the sentence true.

Question 4.
Katy has 6 times as many nickels as Shaun. Shaun has 18 nickels. Let n = the number of nickels Katy has.
n is _____________
n = ___________.
Answer:
It is given that
Katy has 6 times as many nickels as Shaun. Shaun has 18 nickels.
So,
The number of nickels Katy has (n) = 6 × (The number of nickels Shaun has)
= 6 × 18
= 6 × (10 + 8)
= (6 × 10) + (6 × 8)
= 60 + 48
= 108 nickels
Hence, from the above,
We can conclude that
n is 6 times as many as the number of nickels Shaun has
The number of nickels Katy has: 108 nickels
Question 5.
Kyle has watched 238 movies. Jason has watched 49 more movies than Kyle. Let m = the number of movies Jason has watched.
m is _____________
m = _____________
Answer:
It is given that
Kyle has watched 238 movies. Jason has watched 49 more movies than Kyle
So,
The number of movies Jason has watched (m) = The number of movies Kyle watched + 49
= 238 + 49
= 287 movies
Hence, from the above,
We can conclude that
m is 49 mere than the number of movies Kyle has watched
The number of movies Jason has watched is: 287 movies
Question 6.
Amber tied 89 knots to make a macrame wall hanging. Hunter tied 3 times as many knots as Amber. Let k= the number of knots Hunter tied. k is _____________
k = _____________
Answer:
It is given that
Amber tied 89 knots to make a macrame wall hanging. Hunter tied 3 times as many knots as Amber
So,
The number of knots Hunter tied (k) = 3 × (The number of knots Amber tied)
= 3 × 89
= 3 × (80 + 9)
= (3 × 80) + (3 × 9)
= 240 + 27
= 267
Hence, from the above,
We can conclude that
k is 3 times as many knots as Amber
The number of knots Hunter tied is: 267 knots
Question 7.
Tia sells 292 newspapers. Tess sells 117 more newspapers than Tia. Let n = the number of newspapers Tess sells.
n is _____________
n = _____________
Answer:
It is given that
Tia sells 292 newspapers. Tess sells 117 more newspapers than Tia
So,
The number of newspapers Tess sells (n) = 117 + (The number of newspapers tia sells)
= 117 + 292
= 409 newspapers
Hence, from the above,
We can conclude that
n is 117 more than Tia’s newspapers
The number of newspapers Tess sells is: 409 newspapers
Question 8.
Trent has 48 markers. Sharon has 8 markers.
Answer:
Question 9.
Lucy has 317 bottles. Craig has 82 bottles.
Answer:
Problem Solving
Question 10.
Model with Math
Roger swam 19 laps in the pool. Anna Maria swam 4 times as many laps as Roger. How many laps did Anna Maria swim? Draw a bar diagram and write an equation to solve the problem.
Answer:
It is given that
Roger swam 19 laps in the pool. Anna Maria swam 4 times as many laps as Roger
So,
The representation of the given situation in the form of a bar diagram is:
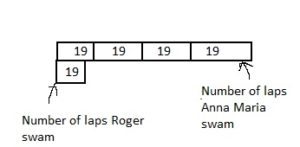
So,
The number of laps did Anna maria swam = 4 × (The number of laps did Roger swam)
= 4 × 19
= 4 × (10 + 9)
= (4 × 10) + (4 × 9)
= 40 + 36
= 76 laps
Hence, from the above,
We can conclude that the number of laps did Anna swam is: 76 laps
Question 11.
Critique Reasoning Nina says the equation 600 = 12 × 50 means 600 is 12 times as many as 50. Julio says the equation means 600 is 50 times as many as 12. Who is correct? Explain.
Answer:
It is given that
Nina says the equation 600 = 12 × 50 means 600 is 12 times as many as 50. Julio says the equation means 600 is 50 times as many as 12
Now,
We know that,
According to Commutative Property of Multiplication,
a × b = b × a
So,
12 × 50 is the same as 50 × 12
“12 times as many as 50” is the same as “50 times as many as 12”
Hence, from the above,
We can conclude that
Both Nina and Julio are correct
Question 12.
Vocabulary The amount that is left after dividing a number into equal parts is called the _________.
13 ÷ 4 = ________
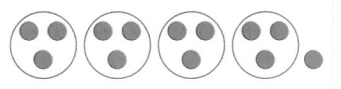
Answer:
We know that,
The amount that is left after dividing a number into equal parts is called the “Remainder”
Now,
The given expression is: 13 ÷ 4
Now,
By using the Long division method,
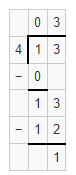
Hence, from the above,
We can conclude that the remainder for the given expression is: 1
Question 13.
Higher-Order Thinking A shirt is on sale for d dollars. The regular price is 4 times as much. Todd has enough money to buy 2 shirts at the regular price. How many shirts can Todd buy at the sale price? Explain.
Answer:
It is given that
A shirt is on sale for d dollars. The regular price is 4 times as much. Todd has enough money to buy 2 shirts at the regular price
So,
The regular price of a shirt = 4 × (The sale price of a shirt)
= 4 × d
= 4d
Now,
According to the given information,
The sale price of the shirts that Todd can buy = (Regular price of a shirt) × (The number of shirts Todd can buy)
= 4d × 2
= 8d
So,
The number of shirts Todd can buy = \(\frac{The sale price of the shirts Todd can buy}{The sale price of a shirt}\)
= \(\frac{8d}{d}\)
= 8
Hence, from the above,
We can conclude that Todd can buy 8 shirts at the sale price
Assessment Practice
Question 14.
Select all the sentences that involve a comparison using multiplication.
☐ k is 26 times as many as 7.
☐ u is 18 more than 314.
☐ Tom ran 4 miles. Cindy ran 2 more miles than Tom. How many miles did Cindy run?
☐ Yuan has 2 dogs and Jon has 3 times as many dogs. How many dogs does Jon have?
☐ Kris has 4 times as many pairs of shoes as her brother. Her brother has 8 pairs of shoes.
Answer:
The sentences that involve a comparison using multiplication are:

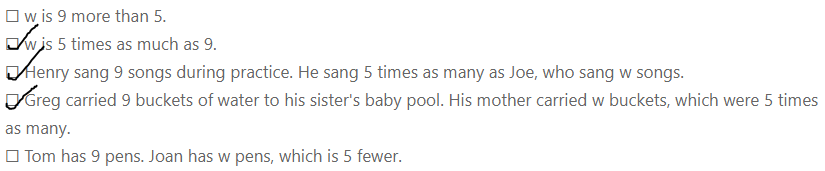
Question 15.
Select all the statements that can be represented by the equation 5 × 9 = w.
☐ w is 9 more than 5.
☐ w is 5 times as much as 9.
☐ Henry sang 9 songs during practice. He sang 5 times as many as Joe, who sang w songs.
☐ Greg carried 9 buckets of water to his sister’s baby pool. His mother carried w buckets, which were 5 times as many.
☐ Tom has 9 pens. Joan has w pens, which is 5 fewer.
Answer:
The sentences that can be represented by the equation 5 × 9 = w are:
Lesson 6.2 Continue to solve Comparison Problems
Solve & Share
The students in Ms. Chang’s fourth-grade class plant a tree every year. One tree they planted is now 288 inches tall. This height is 6 times as great as when the tree was first planted. How tall was the tree when it was first planted? Solve this problem any way you choose. Show your work.
I can … use multiplication or division to compare one quantity to another.

Answer:
It is given that
The students in Ms. Chang’s fourth-grade class plant a tree every year. One tree they planted is now 288 inches tall. This height is 6 times as great as when the tree was first planted
Now,
Let the height of the tree when first planted be x
Now,
According to the given information,
6 × x = 288
x = \(\frac{288}{6}\)
x = 48 inches
Hence, from the above,
We can conclude that
The height of the tree when it was first planted is: 48 inches
Look Back! Compare the heights of the 2 trees using addition.
Answer:
From part (a),
We can observe that
The height of the tree when it was first planted is: 48 inches
The current height of the tree is: 288 inches
So,
The difference between the heights of the two trees = (The current height of the tree) – (The height of the tree when it was first planted)
= 288 – 48
= 240 inches
Hence, from the above,
We can conclude that the current height of the tree is 240 inches more than the height of the tree when it was first planted
Essential Question
How Can You Solve a Problem Involving Multiplication as Comparison?
Answer:
Interpret a multiplication equation as a comparison
Example:
Interpret 35 = 5 × 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5.
Visual Learning Bridge
Carla and Calvin are twins that attend different colleges. Carla’s college is four times as far from home as Calvin’s college. How far does Calvin travel to college?
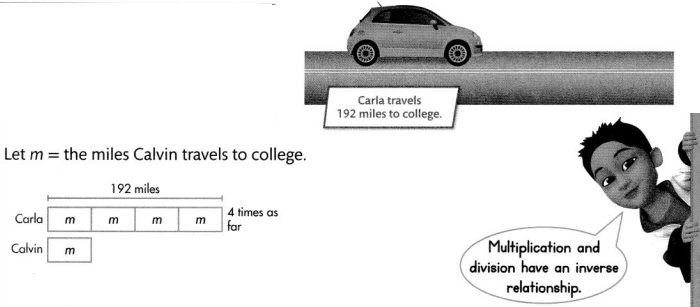
The number of miles Carla travels, or 192 miles, is 4 times as far as Calvin travels.
Write a multiplication equation to find the number of miles Calvin travels to college.
192 = 4 × m
m = 48 miles
What number times 4 equals 192?
If 192 = 4 × m, them m = 192 ÷ 4.
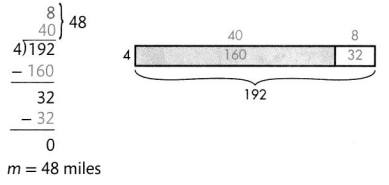
Calvin travels 48 miles to college.
Convince Me!
Use Structure When do you use division to make a comparison?
Answer:
A ratio is a comparison of two numbers by division. The value of a ratio is the quotient that results from dividing the two numbers.
Example:
The value of the ratio 35: 7 is 5, which you find by computing 35 ÷ 7 = 5.
Guided Practice
Do You Understand?
Question 1.
Carla travels 3 times as far to college as her friend Mandy travels to college. Write and solve a related multiplication and division equation to find how far Mandy travels to college.
Answer:
It is given that
Carla travels 3 times as far to college as her friend Mandy travels to college
Now,
From the example on the previous page,
We can observe that
Carla travels 192 miles to college
Now,
Let x be how far Mandy travels to college
So,
From the given information,
192 = 3 × x
x = \(\frac{192}{3}\)
x = 64 miles
Hence, from the above,
We can conclude that Mandy travels 64 miles to the college
Do You Know How?
Question 2.
Complete the comparison sentence. Find the value of the variable that makes the sentence true.
If 3 × m = 48, then m = 48 ÷ 3.
3 times as many as m is 48.
m = 16
Answer:
The given expression is:
3 × m = 48
m = \(\frac{48}{3}\)
m = 16
Hence, from the above,
We can conclude that
3 times as many as m is 48
The value of m is: 16
Independent Practice
For 3-8, write a comparison sentence and an equation. Find the value of the variable that makes the sentence true.
Question 3.
Connor has 77 magazines. That is 7 times as many magazines Kristen has. How many magazines, n, does Kristen have?
Answer:
It is given that
Connor has 77 magazines. That is 7 times as many magazines Kristen has
Now,
Let n be the number of magazines Kristen has
So,
According to the given information,
7 × n = 77
n = \(\frac{77}{7}\)
n = 11
Hence, from the above,
We can conclude that
The number of magazines that Kristen has: 11
Question 4.
Eric completed 75 math problems. That is 5 times as many math problems as Katie completed. How many math problems, m, did Katie complete?
Answer:
It is given that
Eric completed 75 math problems. That is 5 times as many math problems as Katie completed
Now,
Let m be the math problems Katie completed
So,
According to the given information,
5 × m = 75
m = \(\frac{75}{5}\)
m = 15
Hence, from the above,
We can conclude that
The number of math problems Katie completed is: 15
Question 5.
Clare counted 117 different colors at the paint store. That is 9 times as many as the number James counted. How many different colors, c, did James count?
Answer:
It is given that
Clare counted 117 different colors at the paint store. That is 9 times as many as the number James counted.
Now,
Let c be the number of colors James counted
So,
According to the given information,
9 × c = 117
c = \(\frac{117}{9}\)
c = 13
Hence, from the above,
We can conclude that
The number of different colors James counted is: 13
Question 6.
Alisa has 153 dominoes. That is 3 times as many dominoes as Stan has. How many dominoes, d, does Stan have?
Answer:
It is given that
Alisa has 153 dominoes. That is 3 times as many dominoes as Stan has
Now,
Let d be the number of dominoes does Stan have
So,
According to the given information,
3 × d = 153
d = \(\frac{153}{3}\)
d = 51
Hence, from the above,
We can conclude that
The number of dominoes does Stan have is: 51
Question 7.
Justin practiced piano for h hours. His sister practiced for 12 hours, which was 3 times as many hours as Justin practiced. Write and solve an equation to find how many hours Justin practiced piano.
Answer:
It is given that
Justin practiced piano for h hours. His sister practiced for 12 hours, which was 3 times as many hours as Justin practiced
Now,
Let h be the number of hours Justin practiced piano
So,
According to the given information,
h × 3 = 12
h = \(\frac{12}{3}\)
h = 4
Hence, from the above,
We can conclude that
The number of hours that Justin practiced piano is: 4 hours
Question 8.
Mary practiced violin for 2 hours and her brother practiced trombone t times as long or 8 hours. Write and solve an equation to find how many times as long Mary’s brother practiced trombone.
Answer:
It is given that
Mary practiced violin for 2 hours and her brother practiced trombone t times as long or 8 hours
Now,
Let t be the number of hours Mary’s brother practiced trombone
So,
According to the given information,
2 × t = 8
t = \(\frac{8}{2}\)
t = 4
Hence, from the above,
We can conclude that
The number of hours mary’s brother practiced trombone is: 4 hours
Problem Solving
Question 9.
Model with Math
Dave is making soup that includes 12 cups of water and 3 cups of broth. How many times as much water as the broth will be in the soup? Draw a bar diagram and write and solve an equation.
Answer:
It is given that
Dave is making soup that includes 12 cups of water and 3 cups of broth.
Now,
Let x be the number of cups of water present in the broth
So,
According to the given information,
3 × x = 12
x = \(\frac{12}{3}\)
x = 4
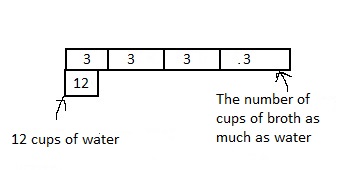
Hence, from the above,
We can conclude that
The number of cups of water present in the broth is: 4
Question 10.
Trevor wants to buy three light fixtures that cost $168 each. He has $500. Does he have enough money to buy the three light fixtures? Use a comparison sentence to explain your reasoning.
Answer:
It is given that
Trevor wants to buy three light fixtures that cost $168 each. He has $500.
So,
The cost of three light fixtures that Trevor wants to buy = 3 × (The cost of each light fixture)
= 3 × 168
= 3 × (100 + 68)
= (3 × 100) + (3 × 68)
= 300 + 204
= $504
So,
From the given information,
$500 < $504
Hence, from the above,
We can conclude that
The cost of the three light fixtures that Trevor wants to buy is $4 more than the amount of money Trevor has
He does not have enough money to buy the three light fixtures
Question 11.
Miranda has 4 times as many leaves in her collection as Joy Joy has 13 more leaves than Armani. Armani has 10 leaves in his collection. How many leaves does Miranda have in her collection? Explain.
Answer:
It is given that
Miranda has 4 times as many leaves in her collection as Joy Joy has 13 more leaves than Armani. Armani has 10 leaves in his collection
Now,
Let the number of leaves Miranda has in her collection be x
Let the number of leaves Joy has be j
Let the number of leaves Armani has be a
So,
According to the given information,
a = 10
j = a + 13
4 × j = x
Now,
j = 10 + 13
j = 23
So,
4 × 23 = x
x = 4 × (20 + 3)
x = (4 × 20) + (4 × 3)
x = 80 + 12
x = 92 leaves
Hence, from the above,
We can conclude that the number of leaves Miranda has in her collection is: 92
Question 12.
Higher-Order Thinking Jordan needs $9,240 for her first year of college tuition. Each of her two grandfathers said they would match what she saves. She has 8 years before she goes to college. How much does Jordan need to save on her own each year to have enough for her first year with the help from her two grandfathers?

Answer:
It is given that
Jordan needs $9,240 for her first year of college tuition. Each of her two grandfathers said they would match what she saves. She has 8 years before she goes to college
So,
The amount of money that will be saved by Jordan and her 2 grandfathers = \(\frac{$9,240}{3}\)
= $3,080
So,
The amount of money Jordan has to save each year so that she would have enough money for her first year = \(\frac{$3,080}{8}\)
= $385
Hence, from the above,
We can conclude that
Jordan needs to save on her own each year to have enough for her first year with the help from her two grandfathers will be: $385
Assessment Practice
Question 13.
Tina walked 20 miles for a fundraiser. Lia walked m miles. Tina walked 4 times as far as Lia. Which equation can be used to find m, the number of miles Lia walked?
A. m = 4 × 20
B. 20 = 4 × m
C. 20 = m ÷ 4
D. m = 20 + 4
Answer:
It is given that
Tina walked 20 miles for a fundraiser. Lia walked m miles. Tina walked 4 times as far as Lia
So,
According to the given information,
4 × m = 20
Hence, from the above,
We can conclude that the number of miles Lia walked is:
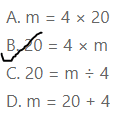
Question 14.
Jason and Raul kept a reading log for the year. Jason read 7 books and Raul read 105. How many times as many books as Jason did Raul read?
A. 13 times
B. 14 times
C. 15 times
D. 16 times
Answer:
It is given that
Jason and Raul kept a reading log for the year. Jason read 7 books and Raul read 105
Now,
Let the number of times Jason read as many as Raul did be x
So,
(The number of books Jason read) × (The number of times Jason read as many as Raul did) = The number of books Raul did
7 × x = 105
x = \(\frac{105}{7}\)
x = 15
Hence,from the above,
We can conclude that the number of times Raul read as many books as Jason is:
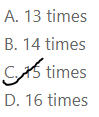
Lesson 6.3 Model Multi-Step Problems
Solve & Share
Last year, 18 people went on a family camping trip. This year, three times as many people went. How many more people went this year than last year? Complete the bar diagram and show how you solve it?
I can … find hidden questions and use bar diagrams and equations to model and solve multi-step problems.

Answer:
It is given that
Last year, 18 people went on a family camping trip. This year, three times as many people went
So,
The number of people that went on a family camping trip this year = 3 × (The number of people that went on a family camping trip last year)
= 3 × 18
= 3 × (10 + 8)
= (3 × 10) + (3 × 8)
= 30 + 24
= 54 people
So,
The representation of the number of people that went on a camping trip in the form of a bar diagram is:
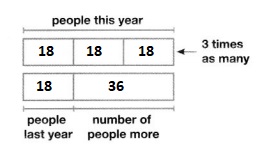
Hence, from the above,
We can conclude that the number of people that went on a camping trip this year is: 54
Look Back!
How can you use estimation to decide if your answer is reasonable?
Answer:
From the above problem,
We can observe that
The expression we used to find the number of people that went on a camping trip this year is:
3 × 18
Now,
Estimate:
3 × 18
= 3 × 20
= 3 × 2 ×10
= (3 × 2) × 10
= 6 × 10
= 60
So,
The difference between the number of people we obtained in the previous problem and in this problem is not large
Hence, from the above,
We can conclude that your estimation for the answer is reasonable
Essential Question
How Can You Use Diagrams and Equations to Solve Multi-Step Problems?
Answer:
The process we can use to solve Multi-step problems is:
Step 1:
Circle and underline. Circle only the necessary information and underline what ultimately needs to be figured out.
Step 2:
Figure out the first step/problem in the paragraph and solve it.
Step 3:
Find the answer by using the information from Steps 1 and 2
Visual Learning Bridge
A school uses 8 buses to transport the fourth-grade students and 6 vans to transport the third-grade students on a field trip. How many fewer third-grade students than fourth-grade students are on the field trip?

Step 1
Find and answer the hidden questions.
Hidden Question: How many fourth-grade students are on the field trip?

F = 8 × 24
= 192 fourth-grade students
Hidden Question: How many third-grade students are on the field trip?
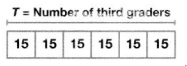
T= 6 × 15
= 90 third-grade students
Step 2
Use the answers to the hidden questions to answer the original question.
Original Question: How many fewer third-grade students than fourth-grade students are on the field trip?
S = the number fewer third-grade students than fourth-grade students

S = 192 – 90
= 102
102 fewer third-grade students than fourth-grade students are on the field trip.
Convince Me!
Construct Arguments Amanda says she can solve the problem using the equation below. Do you agree? Explain.
S = (8 × 24) – (6 × 15)
Answer:
It is given that
Amanda says she can solve the problem using the equation below.
S = (8 × 24) – (6 × 15)
Now,
From the example on the previous page,
We have to find out the number of fewer third-grade students than the fourth-grade students
So,
We can find the difference between the third-grade and the fourth-grade students by finding the total number of third-grade and the fourth-grade students
So,
The total number of fourth-grade students = (The number of buses) × (The number of students in each bus)
= 8 × 24
The total number of third-grade students = (The number of vans) × (The number of students in each van)
= 6 × 15
So,
The difference between the fourth-grade and the third-grade students = (8 × 24) – (6 × 15)
Hence, from the above,
We can conclude that we can agree with Amanda
Another Example!
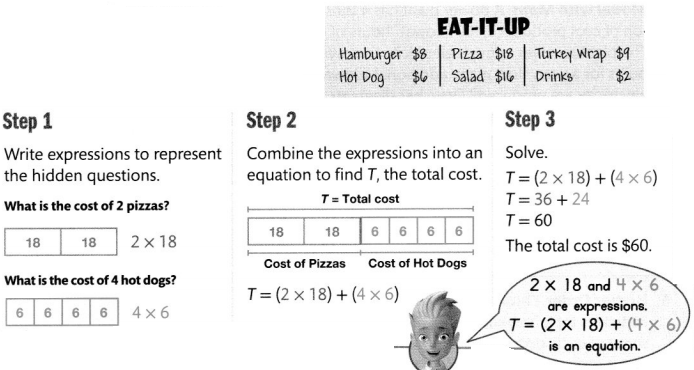
The Lopez family gets 2 pizzas and 4 hot dogs at Eat-It-Up. What is the total cost?
Guided Practice
Do You Understand?
Question 1.
Doug says he can use the equation T = 18 + 18 + 6 + 6 + 6 + 6 to solve the problem above. Is Doug correct? Explain.
Answer:
It is given that
Doug says he can use the equation T = 18 + 18 + 6 + 6 + 6 + 6 to solve the problem above.
Now,
From the example on the previous page,
We can observe that
The cost of each pizza is $18 and there are 2 pizzas
The cost of each hot-dog is $6 and there are 4 hot-dogs
So,
The total cost = (The total cost of pizzas) + (The total cost of hot-dogs)
= [(The cost of each pizza) × (The total number of pizzas)] + [(The cost of each hot-dog) × (The total number of hot-dogs)]
= [18 × 2] + [6 × 4]
= [18 + 18] + [6 + 6 + 6 + 6]
Hence, from the above,
We can conclude that Doug is correct
Question 2.
Write one or more equations you could use to find the total cost C, of 2 turkey wraps, 2 hamburgers, and 4 drinks.

Answer:
It is given that
There are 2 turkey wraps, 2 hamburgers, and 4 drinks
Now,
The given table is:

So,
The total cost of the three items (C) = [(The cost of each turkey wrap) × (The number of turkey wraps)] + [(The cost of each hamburger) × (The number of hamburgers)] + [(The cost of each drink) × (The number of drinks)]
= (2 × $4) + (2 × $8) + (4 × $2) ———-> 1 way of writing the equation to find the total cost
= ($4 + $4) + ($8 + $8) + ($2 + $2 + $2 + $2) —– > Other way of writing the equation to find the total cost
= $8 + $16 + $8
= $32
Hence, from the above,
We can conclude that
The total cost of all the given items is: $32
Do You Know How?
Question 3.
In the problem on the previous page, suppose the school fills 11 buses and lets the remaining students ride in vans. How many students ride in vans? Use one or more bar diagrams and equations to show how you solve.
Answer:
It is given that
In the problem on the previous page, the school fills 11 buses and the remaining students ride in vans.
Now,
From the example on the previous page,
The total number of students = (The number of fourth-grade students that travel in buses) + (The number of third-grade students that travel in vans)
= 192 + 90
= 282 students
Now,
We know that,
The number of students each bus carries is: 24
So,
The total number of students present in 11 buses = (The number of students present in each bus) × (The number of buses)
= 24 × 11
= 24 × (10 + 1)
= (24 × 10) + (24 × 1)
= 240 + 24
= 264 students
So,
The number of remaining students who travel in vans = (The total number of students) – (The number of students who travel in 11 buses)
= 282 – 264
= 18 students
Now,
The representation of the given problem in the form of bar diagrams is:

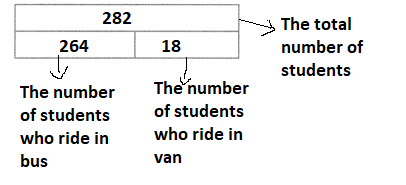
Hence, from the above,
We can conclude that the number of students that ride in vans is: 18
Independent Practice
Draw a bar diagram, and write an equation to solve the problem. Use a variable to represent an unknown quantity and tell what the variable represents.
Question 4.
Four boys and five girls went to the movies together. Between them, they had $120 to spend. Tickets cost $8 each. How much money did they have to buy refreshments?
Answer:
It is given that
Four boys and five girls went to the movies together. Between them, they had $120 to spend. Tickets cost $8 each
So,
The total number of people that went to the movies = 4 + 5
= 9
Now,
We know that,
The total money spent by 9 people = (The amount of money spent on Tickets) + (The amount of money spent to buy refreshments)
$120 = [(The total number of people) × (The cost of each ticket)] + (The amount of money spent to buy refreshments)
$120 = (9 × $8) + (The amount of money spent to buy refreshments)
The amount of money spent to buy refreshments = $120 – $72
= $48
Now,
The representation of the given information in the form of a bar diagram is:

Hence, from the above,
We can conclude that the amount of money spent on refreshments is: $48
Problem Solving
Question 5.
Model with Math
A power plant has 4 tons of coal. A ton of coal produces 2,460 kilowatt-hours of electricity. The plant reserves enough electricity to power 9 light bulbs for a year. How many additional kilowatt-hours of electricity is produced? Draw the bar diagrams and write one or more equations to show how you solve them. Tell what your variables represent.

Answer:
It is given that
A power plant has 4 tons of coal. A ton of coal produces 2,460 kilowatt-hours of electricity. The plant reserves enough electricity to power 9 light bulbs for a year
Now,
The energy produced by 4 tons of coal = (The energy produced by a ton of coal) × (The number of tons of coal)
= 2,460 × 4
(2,000 + 400 + 60) × 4
= (2,000 × 4) + (400 × 4) + (60 × 4)
= 8,000 + 1,600 + 240
= 9,280 Kilowatt-hours
Now,
The energy produced by 9 light bulbs for a year = (The energy produced by a light bulb for a year) × (The number of light bulbs)
= 876 × 9
= (800 + 70 + 6) × 9
= (800 × 9) + (70 × 9) + (6 × 9)
= 7,200 + 630 + 54
= 7,884 Kilowatt-hours
So,
The number of additional Kilowatt-hours produced = (The energy produced by 4 tons of coal) – (The energy produced by 9 light bulbs for a year)
= 9,280 – 7,884
= 1,396 Kilowatt-hours
Now,
The representation of the given information in the form of a bar diagram is:

Hence, from the above,
We can conclude that the amount of additional Kilowatt-hours produced is: 1,39 Kilowatt-hours
Question 6.
Higher-Order Thinking You have $360 to buy 26 tickets for a baseball game. You need to buy some of each kind of seat. You want to spend most of the money. How many of each type of ticket can you buy? Find two different solutions to the problem. Use an equation to show each solution.

Answer:
It is given that
You have $360 to buy 26 tickets for a baseball game. You need to buy some of each kind of seat. You want to spend most of the money.
Now,
The given cost for each type of seat is:

Now,
Let the number of tickets for Box seats be b
Let the number of tickets for Upper deck be u
So,
In terms of total number of tickets,
b + u = 26 —- (1)
So,
In terms of cost of the tickets,
Total cost =[ (The cost of each ticket of box seat) × (The number of tickets of box seats)] + [(The cost of each ticket of Upper deck) × (The number of tickets of Upper deck)]
18b + 12u = 360 —- (2)
So,
b = 26 – u —- (3)
Now,
By using the method of substitution,
18 (26 – u) + 12u = 350
(18 × 26) – 18u + 12u = 350
[18 × (20 + 6)] – 6u = 350
[(18 × 20) + (18 × 6)] – 6u = 350
[360 + 108] – 6u = 350
468 – 6u = 350
6u = 468 – 360
6u = 108
u = \(\frac{108}{6}\)
u = 18 tickets
So,
b = 26 -u
= 26 -18
= 8 tickets
Hence, from the above,
We can conclude that
The number of tickets of box seat is: 8
The number of tickets of Upper desk is: 18
Assessment Practice
Question 7.
The gym teacher has $250 to spend on volleyball equipment. She buys 4 volleyball nets for $28 each volleyball costs $7 each. How many volleyballs can she buy? Explain how you solve. Use one or more equations and bar diagrams in your explanation. Tell what your variables represent.
Answer:
It is given that
The gym teacher has $250 to spend on volleyball equipment. She buys 4 volleyball nets for $28 each volleyball costs $7 each.
Now,
Let the number of volleyballs be x
So,
The total cost of volleyball equipment = (The total cost of volleyball nets) + (The total cost of volleyballs)
$250 = [(The cost of each volleyball net) × (The number of volleyballs)] + [(The number of volleyballs) × (The cost of each volleyball)]
$250 = (4 × $28) + (x × $7)
$250 = 4 × (20 + 8) + x × 7
$250 = (4 × 20) + (4 × 8) + x× 7
$250 = 80 + 32 + 7x
$250 = 112 + 7x
7x = 250 – 112
7x = 138
x = \(\frac{138}{7}\)
x = 19.7
x ≈ 20
Now,
The representation of the given information in the form of a bar diagram is:
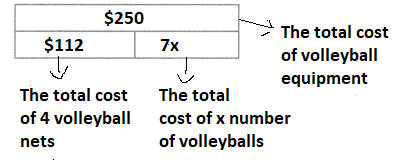
Hence, from the above,
We can conclude that the number of volleyballs is: 20
Lesson 6.4 More Model MultiStep Problems
Solve & Share
Three eight-year-old children, one adult, and one senior had $125 saved to go to the Happy Days amusement park. After buying tickets, how much money did they have left to buy refreshments? Complete the bar diagram, and use it to write one or more equations to solve the problem. Tell what your variables represent.
I can … Solve multi-step problems by drawing bar diagrams and writing expressions and equations.

Answer:
It is given that
Three eight-year-old children, one adult, and one senior had $125 saved to go to the Happy Days amusement park
Now,
The given table is:

Now,
From the given table,
The ticket cost of 1 8-year old child is: $12
The ticket cost of 1 adult is: $25
The ticket cost of 1 senior is: $18
So,
The total amount of money saved by the given people = (The total ticket cost of the people) + (The total cost of buying refreshments for the people)
= $125 = [(3 × The ticket cost of each 8-year old child) + (The ticket cost of 1 adult) + (The ticket cost of 1 senior)] + (The total cost of buying refreshments for the people)
$125 = [(3 × $12) + $25 + $18] + (The total cost of buying refreshments for the people)
$125 = ($36 + $25 + $18) + (The total cost of buying refreshments for the people)
The total cost of buying refreshments for the people = $125 – $79
The total cost of buying refreshments for the people = $46
Now,
The representation of the given information in the form of a bar diagram is:

Hence, from the above,
We can conclude that
The total cost spent on refreshments by the given people is: $46
Look Back! What expressions and equations did you use to solve this problem? What hidden questions did you need to answer?
Answer:
The equation used to solve the above problem is:
The total amount of money saved by the given people = (The total ticket cost of the people) + (The total cost of buying refreshments for the people)
Now,
The hidden question we have to answer for the above problem is:
What is the total cost of the tickets for 3 8-year old children, 1 adult, and 1 senior?
Essential Question
How Can You Model and Solve Multi-Step Problems?
Answer:
The steps to solve Multi-steps Problems are:
Step 1:
Circle and underline. Circle only the necessary information and underline what ultimately needs to be figured out.
Step 2:
Figure out the first step/problem in the paragraph and solve it.
Step 3:
Find the answer by using the information from Steps 1 and 2
Visual Learning Bridge
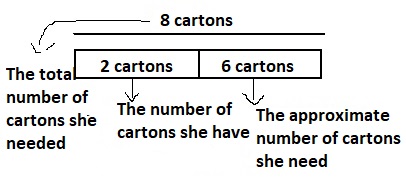
Chef Angela needs 8 cartons of eggs to make the cakes that are ordered. She has 2 cartons of eggs and 4 single eggs in the refrigerator. How many more eggs does she need to make all of the cakes?

One Way
How many eggs does the chef have?
(2 × 12) + 4 = 24 + 4
= 28 eggs
How many more eggs does the chef need?
N = number of additional eggs needed
N = (8 × 12) – 28
= 96 – 28 = 68
The expression 8 × 12 is how many eggs the chef needs in all.
The chef needs 68 more eggs.
Since 68 is close to 72, the answer is reasonable.
Another Way
How many full cartons should the chef buy?
8 – 2 = 6 full cartons
How many more eggs does the chef need?
N = number of additional eggs needed
N =(6 × 12) – 4
= 72 – 4 = 68
The expression 6 × 12 is the number of eggs in 6 cartons.
The chef needs 68 more eggs.
Since 68 is close to 72, the answer is reasonable.
Convince Me!
A model with Math
Draw the bar diagrams to represent a solution to the problem above.
Answer:
The representations of the bar diagrams for the above problem are:

Guided Practice
Do You Understand?
Question 1.
Explain the meaning of the expression (2 × 12) + 4 in the problem on the previous page.
Answer:
In the problem on the previous page,
The meaning of the expression (2 × 12) + 4 is:
2 × 12:
The number of single eggs present in the 2 cartons
4:
The number of single eggs that are present separately
Hence, from the above,
We can conclude that
(2 × 12) + 4:
The total number of single eggs present for chef Angela to make a cake
Question 2.
In the problem on the previous page, how many eggs will the chef have leftover? Explain.
Answer:
In the problem on the previous page,
It is given that
The total number of cartons the chef needed is: 8 cartons
The number of cartons the chef have: 2 cartons
So,
The remaining number of cartons the chef needed = (The total number of cartons the chef needed) – (The number of cartons the chef have)
= 8 – 2
= 6 cartons
Now,
We know that,
A single carton has 12 eggs
So,
The number of eggs present in 6 cartons = 12 × 6
= 72 eggs
But,
It is given that the 4 single eggs are present
So,
From 72 eggs, only 8 single eggs are needed along with 2 cartons
Hence, from the above,
We can conclude that
The number of eggs will the chef have leftover is: 4 eggs
Do You Know How?
Question 3.
Carrie’s stamp book has 20 pages and each page can hold 15 stamps. She has 45 international stamps. She has 4 times as many U.S. stamps. Can all her stamps fit in her book? Use the bar diagram below to help solve this problem. Draw other bar diagrams as needed. Show the equations used to solve this problem.
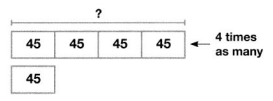
Answer:
It is given that
Carrie’s stamp book has 20 pages and each page can hold 15 stamps. She has 45 international stamps. She has 4 times as many U.S. stamps
So,
The total number of stamps present in Carrie’s stamp book = (The number of pages present in Carrie’s stamp book) × (The number of stamps that each stamp can hold)
= 20 × 15
= 20 × (10 + 5)
= (20 × 10) + (20 × 5)
= 200 + 100
= 300 stamps
Now,
According to the given information,
The number of U.S stamps Carrie have = 4 × (The number of International stamps)
= 4 × 45
= 4 × (40 + 5)
= (4 × 40) + (4 × 5)
= 160 +20
= 180 U.S stamps
So,
300 > 180
Now,
The representation of the given information in the form of a bar diagram is:
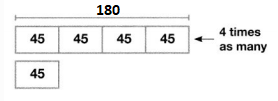
Hence, from the above,
We can conclude that all of Carrie’s stamps fit in her book since the number of stamps Carrie’s book can accommodate is greater than the number of stamps Carrie have
Independent Practice
For 4-5, draw the bar diagrams, and write equations to solve each problem. Use variables to represent unknown quantities and tell what each variable represents.
Question 4.
Five toymakers each carved 28 blocks and 17 airplanes. Three other toymakers each carved the same number of airplanes and twice as many blocks. How many toys did the eight carve in all?
Answer:
It is given that
Five toymakers each carved 28 blocks and 17 airplanes. Three other toymakers each carved the same number of airplanes and twice as many blocks.
So,
The total number of toys the eight people carved = (The number of toys 5 toymakers carved) + (The number of toys the remaining 3 toymakers carved)
= ([The number of blocks] + [The number of airplanes]) + ([The number of airplanes as the same as 5 toymakers made] + [The number of blocks as the same as 5 toymakers made] × 2)
= (28 + 17) + (17 + [28 × 2])
= 45 + (17 + 56)
= 45 + 73
= 118 toys
Now,
The representation of the given information in the form of a bar diagram is:

Hence, from the above,
We can conclude that
The total number of toys that the eight toymakers carved are: 118 toys
Question 5.
Kendra is using 27 blue patches and some white patches to make a quilt. The quilt has a total area of 540 square inches. Each patch has an area of 9 square inches. How much of the area of the quilt is white?
Answer:
It is given that
Kendra is using 27 blue patches and some white patches to make a quilt. The quilt has a total area of 540 square inches. Each patch has an area of 9 square inches.
Now,
Let the area of the white patch be x
Now,
The total number of patches = (The number of blue patches) + (The number of white patches)
= (27 + x)
Now,
The total area of the patches (or) The total area of the quilt = (The total number of patches) × (The area of each patch)
= (27 + x) × 9 square inches
Now,
According to the given information,
(27 + x) × 9 = 540
27 + x = \(\frac{540}{9}\)
27 + x = 60
x = 60 – 27
x = 33 square inches
Now,
The representation of the given information in the form of a bar diagram is:
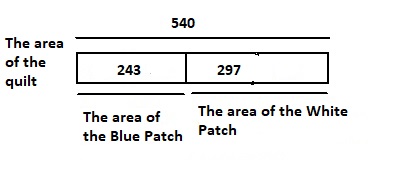
Hence, from the above,
We can conclude that
The area of the white patch is: 33 square inches
Problem Solving
Question 6.
Make Sense and Persevere A ticket to a movie for a student is $7. The cost for an adult is $2 more than for a student. How much would it cost 5 adults and 29 students for tickets to the movie?
Answer:
It is given that
A ticket to a movie for a student is $7. The cost for an adult is $2 more than for a student
Now,
The cost of a ticket for an adult = $2 + (The cost of a ticket for a student)
= $2 + $7
= $9
So,
The cost of the tickets for 5 adults = 5 × (The cost of a ticket for an adult)
= 5 × $9
= $45
So,
The cost of the tickets for 29 students = 29 × (The cost of a ticket for a student)
= 29 × $7
= (20 + 9) × $7
= (20 × $7) + (9 × $7)
= 140 + 63
= $203
So,
The total cost of the tickets for 5 adults and 29 students = $45 + $203
= $248
Hence, from the above,
We can conclude that the total cost of the tickets for 5 adults and 29 students to a movie is: $248
Question 7.
Vocabulary Give an example of an expression. Then give an example of an equation.
Answer:
An example of an expression is:
25 × 3
An example of an equation is:
20 × 3 + a × 3 = 250
Where,
‘a’ is an unknown variable
Question 8.
Higher-Order Thinking Cody and Max both solve the problem below correctly. Explain how each solves.
Emma has $79 to spend at the toy store. She wants to buy a building set, a board game, and 2 action figures from her favorite movie. What else can she buy?

Answer:
It is given that
Emma has $79 to spend at the toy store. She wants to buy a building set, a board game, and 2 action figures from her favorite movie
Now,
The given table is:

Now,
According to Max:
Let the money Emma has after she bought the mentioned items be x
So,
The amount of money Emma has left = (The total amount of money Emma has) – (The total amount of money spent on buying the items)
= $79 – ($32 + $19 + 2 ($8))
= $79 – ($32 + $19 + $16)
= $79 – 67
= $12
So,
From the given table,
We can observe that
For $12, we can buy a doll or an action figure
Now,
According to Cody:
The amount of money Emma have after she bought a building set = (The total amount of money Emma have) – (The amount of money spent by Emma on buying a building set)
= $79 – $32
= $47
The amount of money Emma have after she bought a board game = (The remaining amount of money Emma have after she bought a building set) – (The amount of money spent by Emma on buying a board game)
= $47 – $19
= $28
The amount of money Emma have after she bought 2 action figures = (The remaining amount of money Emma have after she bought a board game) – (The amount of money spent by Emma on buying 2 action figures)
= $28 – 2 ($8)
= $28 – $16
= $12
Hence, from the above,
We can conclude that Emma can buy a doll or an action figure
Assessment Practice
Question 9.
A company has 2 geothermal plants which can power a total of 2,034 homes. After they build 3 additional, more powerful, geothermal plants, they can power a total of 5,799 homes. How many homes does each of the new plants’ power? Explain how you solve. Use one or more equations and bar diagrams in your explanation. Tell what your variables represent.
Answer:
It is given that
A company has 2 geothermal plants which can power a total of 2,034 homes. After they build 3 additional, more powerful, geothermal plants, they can power a total of 5,799 homes
So,
The total number of geothermal plants = 2 + 3
= 5 geothermal plants
The number of homes that can be powered by all the geothermal plants =(The number of homes powered by 2 geothermal plants) + (The number of homes powered by 3 geothermal plants)
= 2,034 + 5,799
= 7,833 homes
So,
The number of homes powered by each geothermal plant = \(\frac{The number of homes powered by all the geothermal plants}{5}\)
= \(\frac{7,833}{5}\)
= 1,766.5
≅ 1,777 homes
Now,
The representation of the given information in the form of a bar diagram is:

Hence, from the above,
We can conclude that the number of homes provided by each geothermal plant is: 1,777 homes
Lesson 6.5 Solve Multi-Step Problems
Solve & Share
A farmer needs $3,500 to buy a previously owned truck. If she sells 45 maple trees and 27 pine trees, will she earn enough to buy the truck? If not, how much more money does she need? Solve this problem any way you choose.
I can … solve multi-step problems by finding and solving hidden questions and by writing expressions and equations.

Answer:
It is given that
A farmer needs $3,500 to buy a previously owned truck and she sells 45 maple trees and 27 pine trees
Now,
The given table is:

Now,
The amount earned by selling 45 maple trees = (The number of maple trees) × (The cost of each maple tree)
= 45 × $56
= (40 + 5) × (50 + 6)
= (40 × 50) + (40 × 6) + (5 × 50) + (5 × 6)
= 2,000 + 240 + 250 + 30
= $2,520
Now,
The amount earned by selling 27 pine trees = (The number of pine trees) × (The cost of each pine tree)
= 27 × $33
= (20 + 7) × (30 + 3)
= (20 × 30) + (20 × 3) + (7 × 30) + (7 × 3)
= 600 + 60 + 210 + 21
= $891
So,
The total amount of money earned by selling 45 maple trees and 27 pine trees = $2,520 + $891
= $3,411
But,
A farmer needs $3,500
Hence, from the above,
We can conclude that she will not earn enough money to buy the truck
Look Back! In the question above, how many more of each tree could the farmer sell to get enough money to buy the truck? Explain.
Answer:
From the above problem,
We can observe that
The total amount of money earned by selling 45 maple trees and 27 pine trees is: $3,411
She will need $3,500
Now,
The extra money she have = $3,500 – $3,411
= $189
Hence, from the above,
We can conclude that
With the remaining money,
She can buy
The number of maple trees she can buy are: 2
The number of pine trees she can buy are: 2
Essential Question
How Can You Use Equations to Solve Multi-Step Problems?
Answer:
The steps to solve Multi-Step problems using equations are:
a. Multiply to clear any fractions or decimals.
b. Simplify each side by clearing parentheses and combining like terms.
c. Add or subtract to isolate the variable term—you may have to move a term with the variable.
d. Multiply or divide to isolate the variable.
e. Check the solution.
Visual Learning Bridge
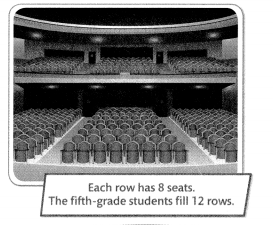
The students in the fourth and fifth grades are going to a concert. There are 178 students. How many rows are needed for the fourth graders?

Step 1
Find and solve the first hidden question.
Hidden Question: How many fifth graders are there?
12 × 8 = s
S = 96
There are 96 fifth graders.
Step 2
Find and solve the second hidden question.
Hidden Question: How many fourth graders are there?
178 – 96 = f
f = 82
There are 82 fourth graders.
Step 3
Answer the original question.
Original Question: How many rows are needed for the fourth graders?
82 ÷ 8 = r
r = 10 R2
Ten rows will be filled with 2 fourth graders left over. So, 11 rows will be needed.
Convince Me!
Construct Arguments Does the answer of 11 rows makes sense for the problem above? Explain.
Answer:
From the above problem,
We can observe that
The number of rows needed for the fourth graders is: 10 R 2
Now,
The meaning of 10 R 2 in the given situation is:
10 rows with the remainder 2 seats and we have to arrange that remainder in the next row
So,
The total number of rows is: 11
Hence, from the above,
We can conclude that the answer of 11 rows makes sense for the above problem
Guided Practice
Do You Understand?
Question 1.
On the previous page, suppose there were only 11 rows of fifth-graders, but the same total number of students. Do you need to solve the whole problem again to find how many rows are needed for the fourth graders? Explain.
Answer:
It is given that
On the previous page, there were only 11 rows of fifth-graders, but the same total number of students
Now,
In the example on the previous page,
It is given that
There are 8 students in each row and the total number of students are 178
So,
The number of rows needed for the fourth-grade students = [(The total number of students) – (The number of rows needed for the fifth-graders) × (The number of students in each row)] ÷ 8
Hence, from the above,
We can conclude that
We need to solve the whole problem again to find the number of rows needed for the fourth-graders
Do You Know How?
Question 2.
Show another way to solve the problem on the previous page.
Answer:
The given figure is:
Now,
In the previous example on the previous page,
It is given that
There are a total of 178 students
Now,
The number of students in the fifth-grade = (The number of rows filled by the fifth-graders) × (The number of students in each row)
= 12 × 8
= (10 + 2) × 8
= (10 × 8) + (2 × 8)
= 80 + 16
= 96 students
So,
The number of students in the fourth-grade = (The total number of students) – (The number of students in the fifth grade)
= 178 – 96
= 82 students
So,
The number of rows filled by the fourth-graders = \(\frac{The number of students in the fourth-grade}{8}\)
= \(\frac{82}{8}\)
= 10 R 2
Hence,from the above,
We can conclude that the number of rows filled by the fourth-grade students is: 11
Independent Practice
For 3-4, solve each multi-step problem. Write equations to show how you solve. Draw the bar diagrams to help if needed. Use estimation to decide if your answer is reasonable.

Question 3.
Vanya bought 5 medium packages of buttons and 3 small packages of buttons. What was the total number of buttons Vanya bought?
Answer:
The given data is:

So,
The total number of buttons Vanya bought = (The number of buttons present in 5 medium packages of buttons) + (The number of buttons present in 3 small packages of buttons)
= (5 × The number of buttons present in a medium package of buttons) + (3 × The number of buttons present in a small package of buttons)
= (5 × 38) + (3 × 18)
= 5 × (30 + 8) + 3 × (10 + 8)
= (5 × 30) + (5 × 8) + (3 × 10) + (3 × 8)
= 150 + 40 + 30 + 24
= 244 buttons
Hence, from the above,
We can conclude that
The total number of buttons Vanya bought is: 244 buttons
Question 4.
Vance bought 2 packages of large beads, 1 package of medium beads, 2 packages of large buttons, and 2 packages of medium buttons. How many more beads than buttons did Vance buy?
Answer:
The given data is:

So,
The total number of beads Vance bought = (The total number of beads present in 2 packages of large beads) + (The total number of beads present in 1 package of medium beads)
= (2 × 96) + (1 × 64)
= 2 × (90 + 6) + 64
= (2 × 90) + (2 × 6) + 64
= 180 + 12 + 64
= 256 beads
So,
The total number of buttons Vance bought = (The total number of buttons present in 2 packages of large buttons) + (The total numbr of buttons present in 2 packages of medium buttons)
= (2 × 56) + (2 × 38)
= 2 × (50 + 6) + 2 × (30 + 8)
= (2 × 50) + (2 × 6) + (2 × 30) + (2 × 8)
= 100 + 12 + 600 + 16
= 728 buttons
So,
The difference between the number of buttons and beads = 728 – 256
= 472 beads
Hence, from the above,
We can conclude that there are 472 more buttons than beads that Vance bought
Problem Solving
Question 5.
en Vision® STEM How much more does it cost to generate 9 megawatt-hours of electricity with conventional coal than with wind energy? Write one or more equations to show how you solve. Tell what your variables represent.

Answer:
The given figure is:

Now,
The cost to generate 9 megawatt hours of electricity with wind energy = 9 × (The cost to generate 1 megawatt hours of electricity with wind energy)
= 9 × $87
= 9 × (80 + 7)
= (9 × 80) + (9 × 7)
= 720 + 63
= $783
Now,
The cost to generate 9 megawatt hours of electricity with conventional coal = 9 × (The cost to generate 1 megawatt hours of electricity with conventional coal)
= 9 × $105
= 9 × (100 + 5)
= (9 × 100) + (9 × 5)
= 900 + 45
= $945
So,
The difference between the energy produced with conventional coal and the wind energy = $945 – $783
= $162
Hence, from the above,
We can conclude that
It takes $162 more to generate 9 megawatt-hours of electricity with conventional coal than the wind energy
Question 6.
A model with Math Anna earns $8 an hour babysitting and $6 an hour working in the garden. Last month, she worked 15 hours babysitting and 8 hours in the garden. How much more money does she need to buy a robot which costs $199? Explain how you solve. Use one or more equations in your explanation. Tell what your variables represent.
Answer:
It is given that
Anna earns $8 an hour babysitting and $6 an hour working in the garden. Last month, she worked 15 hours babysitting and 8 hours in the garden.
So,
The amount of money earned by Anna for babysitting = (The number of hours Anna did babysitting) × (The amount of money earned by Anna for 1 hour of babysitting)
= 15 × $8
= (10 + 5) × $8
= (10 × 8) + (5 × 8)
= 80 + 40
= $120
So,
The amount of money earned by Anna for working in the garden = (The number of hours Anna did work in the garden) × (The amount of money earned by Anna for 1 hour working in the garden)
= 8 × $6
= $48
So,
The total amount of money earned by Anna = $120 + $48
= $168
But,
She needed to buy a robot which costs $199
So,
The amount of more money she needed to buy a robot = $199 – $168
= $31
Hence, from the above,
We can conclude that
She needs $31 more to buy a robot which costs $199
Question 7.
Higher-Order Thinking Show two different ways to find the answer to the problem below.
Dog and cat food are sold in 20-pound bags. There are 14 bags of dog food and 12 bags of cat food on the store shelves. How many pounds of dog and cat food is on the shelves?
Answer:
It is given that
Dog and cat food are sold in 20-pound bags. There are 14 bags of dog food and 12 bags of cat food on the store shelves
So,
The number of pounds of dog food = (The number of bags of dog food) × (The number of pounds each bag contains)
= 14 × 20
= (10 + 4) × 20
= (10 × 20) + (4 × 20)
= 200 + 80
= 280 pounds
The number of pounds of cat food = (The number of bags of cat food) × (The number of pounds each bag consists)
= 12 × 20
= (10 + 2) × 20
= (10 × 20) + (2 × 20)
= 200 + 40
= 240 pounds
Hence, from the above,
We can conclude that
The number of pounds of dog food present on the shelves is: 280 pounds
The number of pounds of cat food present on the shelves is: 240 pounds
Assessment Practice
Question 8.
Chris needs $858 to buy a computer. She has already saved $575. She gets $15 an hour for babysitting and will babysit 12 hours in the next month. She can save $8 a week from her allowance. How many weeks of allowance will it take Chris to save enough to buy the computer? Explain how you solve. Use one or more equations in your explanation. Tell what your variables represent.
Answer:
It is given that
Chris needs $858 to buy a computer. She has already saved $575. She gets $15 an hour for babysitting and will babysit 12 hours in the next month. She can save $8 a week from her allowance
So,
The amount of money she required to buy a computer = (The amount of money Chris needs to buy a computer) – (The amount of money she already saved)
= $858 – $575
= $283
Now,
The amount of money she will earn for babysitting = (The number of hours she did babysitting) × (The amount of money she gets for babysitting for an hour)
= 12 × $15
= (10 + 2) × $15
= (10 × 15) + (2 × 15)
= 150 + 30
= $180
So,
The remaining money she will need to buy a computer = $283 – $180
= $103
Now,
The amount of money she earned from allowance = (The number of weeks) × (The amount of money she will earn for a week as an allowance)
$103 = x × $8
x = \(\frac{103}{8}\)
x = 12.8
x ≈ 13 weeks
Hence, from the above,
We can conclude that
About 13 weeks of allowance will it take Chris to save enough to buy the computer
Lesson 6.6 Problem Solving
Make Sense and Persevere
Solve & Share
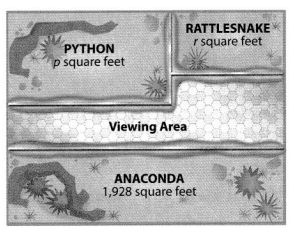
Ms. Valenzuela had her students design a snake house for the zoo. In the design shown, the anaconda has 538 more square feet than the python. The python has twice as many square feet as the rattlesnake. How much of the house’s area does each snake have? Solve this problem any way you choose.
I can … make sense of problems and keep working if I get stuck.
Thinking Habits
Be a good thinker! These questions can help you.
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?
Answer:
It is given that
Ms. Valenzuela had her students design a snake house for the zoo. In the design shown, the anaconda has 538 more square feet than the python. The python has twice as many square feet as the rattlesnake
Now,
The given figure is:

Now,
Let the area of the rattlesnake be r square feet
Let the area of the python be p square feet
So,
The area of the python = 2 × (The area of the rattlesnake)
= 2r square feet
Now,
According to the given information,
(The area of the anaconda) – (The area of the python) = 538
So,
1,928 – p = 538
p = 1,928 – 538
p = 1,390 square feet
So,
The area of the rattlesnake = \(\frac{The area of the python (p)}{2}\)
= \(\frac{1,390}{2}\)
= 695 square feet
Hence, from the above,
We can conclude that
The area of an anaconda is: 1,928 square feet
The area of python is: 1,390 square feet
The area of the rattlesnake is: 695 square feet
Look Back!
Make Sense and Persevere How can you check that your solution makes sense?
Answer:
To check whether the given solution makes sense or not,
Estimate the solution
Now,
By the process of Estimation,
The area of the anaconda is: 1,900 square feet
So,
(The area of the anaconda) – (The area of python) = 540
The area of python = 1,900 – 540
= 1,360 square feet
So,
The area of rattlesnake = \(\frac{The area of python}{2}\)
= \(\frac{1,360}{2}\)
= 685 square feet
So,
The area of the anaconda is: 1,900 square feet
The area of python is: 1,360 square feet
The area of the rattlesnake is: 685 square feet
Now,
By observing the answers in the above problem and the answers for this problem,
We can say that your answer is reasonable
Hence, from the above,
We can conclude that your solution makes sense
Essential Question
How Do You Make Sense of a Multi-Step Problem and Persevere in Solving It?
Answer:
The steps to make sense of a Multi-Step Problem and Persevere in Solving it are:
a. Identify the Problem. Begin by determining the scenario the problem wants you to solve.
b. Gather Information.
c. Create an Equation.
d. Solve the Problem.
e. Verify the Answer.
Visual Learning Bridge
Bryan and Alex have to buy their own instruments for the band. Alex made $1,025 from a fundraiser. He has a part-time job that pays $8 an hour. How many hours does Alex need to work to have enough money to buy his instrument?
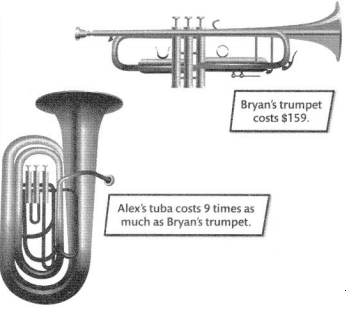
What do you need to do to solve this problem?
I need to determine how much Alex’s tuba costs and how much Alex needs to earn to buy the tuba.
How can I make sense of and solve this problem?
I can
- identify the quantities given.
- understand how the quantities are related.
- choose and implement an appropriate strategy.
- check to be sure my work and answer make sense.
Here’s my thinking
Use the cost of the trumpet to find the cost of the tuba.
$159 x 9 = $1,431 Alex’s tuba costs $1,431.
Find how much more money Alex needs to earn.
$1,431 – $1,025 = $406 Alex needs to earn $406.
Find how many hours Alex needs to work.
$406 ÷ 8 = 50 R6
Alex will not have enough money by working 50 hours, so he needs to work 51 hours.
Convince Me!
Make Sense and Persevere How can you check to make sure the work and answer given above make sense?
Answer:
To check whether the given answer is reasonable or not,
Estimate the answer by using Estimation methods
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The cost of Bryan’s trumpet is about $160
So,
The cost of Alex’s tuba = 9 × (The cost of Bryan’s trumpet)
= 9 × $160
= 9 × (100 + 60)
= (9 × 100) + (9 × 60)
= 900 + 540
= $1,440
Now,
The more money Alex must have to buy his instrument = (The cost of Alex’s tuba) – (The money raised by fundraiser)
= $1,440 – $1,025
= $415
Now,
The number of hours needed for Alex to earn more money = \(\frac{The more money Alex must have to buy his instrument}{8}\)
= \(\frac{$415}{8}\)
= 51 R 7
Hence, from the above,
We can conclude that Alex needs about 7 hours for Alex to earn more money
Your solution is reasonable since the difference between the number of hours in the above example and this problem is not large
Guided Practice
Make Sense and Persevere In the problem on the previous page, suppose Alex wanted to know how many weeks it would take him to work
Think about 51 hours. Alex works 3 hours a day and 4 days a week. this question to help you

Question 1.
What are you asked to find and what is the hidden question What’s a good plan for solving question?
Answer:
The hidden question to answer is:
How many weeks it would take him to work?
Now,
A good plan for solving the given question is:
a. The number of hours in a day that Alex works
b. The number of days in a week that Alex works
c. The number of weeks Alex will take to complete the work
Question 2.
Write and solve equations to solve the problem. Be sure to tell what each variable represents.
Answer:
It is given that
Alex works 3 hours a day and 4 days a week
So,
The number of hours in a week that Alex will work = (The number of hours a day) × (The number of days in a week that Alex will work)
= 3 × 4
= 12 hours a week
So,
The number of weeks Alex will need to complete the work = \(\frac{The total number of hore Alex completed the week}{The number of hours in a week that Alex will work}\)
= \(\frac{51}{12}\)
= 4 R 3
Hence, from the above,
We can conclude that Alex will need about 4 weeks to complete the work
Question 3.
Does your answer make sense? Explain.
Answer:
To make whether your answer makes sense or not,
Estimate the solution using the Estimation methods
Now,
The number of hours in a week that Alex will work = (The number of hours a day) × (The number of days in a week that Alex will work)
= 3 × 4
= 12 hours a week
So,
The number of hours in a week that Alex will work is about 10 hours
So,
The number of weeks Alex will need to complete the work = \(\frac{The total number of hore Alex completed the week}{The number of hours in a week that Alex will work}\)
= \(\frac{51}{10}\)
= 5 R 1
So,
We can conclude that Alex will need about 5 weeks to complete the work
Hence, from the above,
We can conclude that your answer is reasonable since the difference between the actual answer and the estimated answer is not large
Independent Practice
Make Sense and Persevere The high school tennis team is selling tennis balls to raise $500 for new equipment. They sell the balls for $2 each. Will they make enough money if they sell 4 cases?

Question 4.
What are the hidden questions? Write equations to solve each.
Answer:
It is given that
The high school tennis team is selling tennis balls to raise $500 for new equipment. They sell the balls for $2 each
So,
The hidden question for the given problem is:
What is the cost of each case?
Now,
The cost of each case = (The number of packages in each case) × (The number of tennis balls in each package) × (The cost of each tennis ball)
= 24 × 3 × $2
= 24 × $6
= (20 + 4) × 6
= (20 × 6) + (6 × 4)
= 120 + 24
= $144
So,
The cost of 4 cases = 4 × (The cost of each case)
= 4 × $144
= 4 × (100 + 40 + 4)
= (4 × 100) + (4 × 40) + (4 × 4)
= 400 + 160 + 16
= $576
But,
It is given that the high school tennis team is selling tennis balls to raise $500 for new equipment
Hence, from the above,
We can conclude that they will not make enough money if they sell 4 cases
Question 5.
Will the team makes enough money? Explain.
Answer:
From the above problem,
We can observe that
The high school tennis team is selling tennis balls to raise $500 for new equipment
The cost of tennis balls present in 4 cases is: $576
So,
$500 < $576
Hence, from the above,
We can conclude that the team will not make enough money
Problem Solving
Performance Task
Designing a Flag Rainey’s group designed the flag shown for a class project. They used 234 square inches of green fabric. After making one flag, Rainey’s group has 35 square inches of yellow fabric left. How can Rainey’s group determine the total area of the flag?

Question 6.
Make Sense and Persevere What hidden question(s) do you need to answer first?
Answer:
It is given that
Rainey’s group designed the flag shown for a class project. They used 234 square inches of green fabric. After making one flag, Rainey’s group has 35 square inches of yellow fabric left
Now,
The hidden questions you need to answer first are:
a. Find the remaining colors present in the flag?
b. What is the area of the remaining colors in the flag?
c. What is the total area of the flag?
Question 7.
Appropriate Tools Draw diagrams and write equations to represent the hidden question(s). Be sure to tell what each variable represents.

Answer:
The given figure is:

Now,
It is given that
They used 234 square inches of green fabric
So,
The area of the orange fabric = 2 × (The area of the green fabric)
= 2 × 234
= 2 × (200 + 30 + 4)
= (2 × 200) + (2 × 30) + (2 × 4)
= 400 + 60 + 8
= 468 square inches
So,
The area of the yellow fabric = 3 × (The arae of the green fabric)
= 3 × 234
= (2 × 234) + (1 × 234)
= 468 + 234
= 702 square inches
But,
It is given that Rainey’s group has 35 square inches of yellow fabric left
So,
The area of the yellow fabric = 702 – 35
= 667 square inches
So,
The total area of the flag = (The area of the green flag) + (The area of the orange flag) + (The area of the yellow flag)
= 234 + 702 + 667
= 1,603 square inches
Hence, from the above,
We can conclude that
The total area of the flag is: 1,603 square inches
Question 8.
Be Precise Use your drawings and equations to find the total area of the flag. Explain carefully, using the correct units.
Answer:
From the above problem,
We can observe that
The total area of the flag can be found out by adding the areas of the three colors
So,
The total area of the flag = (The area of the green flag) + (The area of the orange flag) + (The area of the yellow flag)
= 234 + 702 + 667
= 1,603 square inches
Hence, from the above,
We can conclude that
The total area of the flag is: 1,603 square inches
Question 9.
Make Sense and Persevere What information was not needed to solve the problem?
Answer:
There is not any unnecessary information present that is not used to solve the given problem
Topic 6 Fluency Practice Activity
Find a Match
Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box next to the match. Find a match for every clue.
I can … subtract multi-digit whole numbers.
Clues
A. The difference is exactly 528.
B. The difference is between 550 and 560.
C. The difference is between 800 and 900.
D. The difference is exactly 614.
E. The difference is between 100 and 105.
F. The difference is between 470 and 480.
G. The difference is exactly 392.
H. The difference is between 70 and 80.

Answer:

Topic 6 Vocabulary Review
Understand Vocabulary
Word List
- addition comparison
- Associative Property of Multiplication
- Commutative Property of Multiplication
- Distributive Property of Multiplication
- equation
- multiplication comparison
- product
- variable
Write T for true and F for false.
Question 1.
__________ Addition comparison is used when you can multiply to find how one quantity is related to another.
Answer:
We know that,
Additive comparisons focus on the difference between two quantities
Hence, from the above,
We can conclude that the given statement is: False
Question 2.
___________ Multiplication comparison is used when one quantity is x times more than another quantity.
Answer:
We know that,
In multiplicative comparison, there are two different sets being compared. The first set contains a certain number of items. The second set contains multiple copies of the first set.
Hence, from the above,
We can conclude that the given statement is: False
Question 3.
__________ A number sentence that uses an equal sign to show that two expressions have the same value is called an equation.
Answer:
We know that,
A number sentence that uses an equal sign to show that two expressions have the same value is called an “Equation”
Hence, from the above,
We can conclude that the given statement is: True
Question 4.
___________ The answer to a subtraction problem is called the product.
Answer:
We know that,
The answer to a multiplication problem is called the “Product”
Hence, from the above,
We can conclude that the given statement is: True
Question 5.
_________ A symbol or letter that stands for a number is called a variable.
Answer:
We know that,
A “Variable” is a symbol that works as a placeholder for expression or quantities that may vary or change
Hence, from the above,
We can conclude that the given statement is: True
Label each example with a term from the Word List.
Question 6.
(3 × 4) × 5 = 3 (4 × 5) _______________
Answer:
We know that,
According to Associative Property of Multiplication,
a × (b × c) = (a × b) × c
So,
we can observe that
The given expression is also in the same form
Hence, from the above,
We can conclude that the term that is suitable for the given problem is: Associative Property of Multiplication
Question 7.
3 × (4 + 5) = (3 × 4) + (3 × 5) _______________
Answer:
We know that,
According to the Distributive Property of Multiplication,
a × (b + c) = (a × b) + (a × c)
So,
we can observe that
The given expression is also in the same form
Hence, from the above,
We can conclude that the term that is suitable for the given problem is: Distributive Property of Multiplication
Question 8.
3 × 4 × 5 = 4 × 3 × 5 _______________
Answer:
We know that,
According to the Commutative Property of Multiplication,
a × b = b × a
So,
We can observe that
The given expression is also in the same form
Hence, from the above,
We can conclude that the term that is suitable for the given problem is: Commutative Property of Multiplication
Use Vocabulary in Writing
Question 9.
Seth wrote and solved the following comparison:
Find 6 times as many as 5.
6 × 5 = n
n = 30
Use at least 3 terms from the Word List to describe Seth’s comparison.
Answer:
It is given that
Find 6 times as many as 5 ———-> Multiplication comparison
So,
The given sentence can be written as:
6 × 5 = n ——-> Equation
n = 30 ——-> Product
Where,
n ——> variable
Topic 6 Reteaching
Set A pages 225-232
Write an equation for each comparison. Find the value of the variable that makes the equation true.
k is 9 times as many as 3.
k = 9 × 3
k = 27
m is 6 more than 21.
m = 6 + 21
m = 27
There are 30 apples and 6 bananas in a basket. How many times as many apples as bananas are in the basket?
Let t = the number of times as many apples as bananas.
t times as many as 6 is 30.
t × 6 = 30
Since 5 × 6 = 30, there are 5 times as many apples as bananas in the basket.
Remember to use addition or subtraction when you know how much more, and multiplication or division when you know how many times as many.
Write and solve an equation to match each comparison.
Question 1.
x is 21 more than 21.
Answer:
It is given that
x is 21 more than 21
So,
According to the Property of Addition comparison,
x = 21 + 21
x = 42
Hence, from the above,
We can conclude that the value of x is: 42
Question 2.
Macon has 32 rocks in his collection. He has 4 times as many rocks as his brother. How many rocks, r, does Macon’s brother have?
Answer:
It is given that
Macon has 32 rocks in his collection. He has 4 times as many rocks as his brother
Now,
Let the number of rocks Macon’s brother has to be: r
So,
According to the given information,
r × 4 = 32
r = \(\frac{32}{4}\)
r = 8 rocks
Hence from the above,
We can conclude that Macon’s brother has 8 rocks
Question 3.
Pam has 24 pencils and 6 erasers. How many times, t, as many pencils as erasers does Pam have?
Answer:
It is given that
Pam has 24 pencils and 6 erasers
Now,
Let the number of erasers be: x
So,
According to the given information,
x × 6 = 24
x = \(\frac{24}{6}\)
x = 4 erasers
Hence, from the above,
We can conclude that
Pam has the number of pencils 4 times as many as erasers
Set B pages 233-240
At a restaurant, a children’s meal costs $5, and an adult meal costs $9. Four children and 2 adults order meals. The family has a $25 gift certificate to use. How much will their total be before tax?
Remember to first find and answer any hidden questions.
Question 1.
There are 64 singers in the choir. The tenors and sopranos are in separate rows. There are 8 singers in each row. There are 4 rows of tenors. How many rows of sopranos are there?
Answer:
It is given that
There are 64 singers in the choir. The tenors and sopranos are in separate rows. There are 8 singers in each row. There are 4 rows of tenors.
Now,
Let the number of rows of sopranos be x
So,
The total number of rows = (The number of rows of sopranos) + (The number of rows of tenors)
= (x + 4)
Now,
According to the given information,
The total number of rows = \(\frac{The total number of singers}{The number of singers in each row}\)
= \(\frac{64}{8}\)
= 8
So,
x + 4 = 8
x = 8 – 4
x = 4 rows
Now,
The representation of the given information in the form of a bar diagram is:
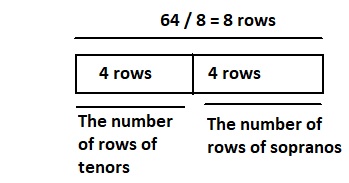
Hence, from the above,
We can conclude that
The total number of rows of sopranos is: 4 rows
Question 2.
Samantha has $600 saved for a trip. She buys an airline ticket for $120 and reserves a hotel room for $55 each night for 4 nights. If Samantha’s trip lasts for 5 days and she spends the same amount each day, how much can Samantha spend each day?
Answer:
It is given that
Samantha has $600 saved for a trip. She buys an airline ticket for $120 and reserves a hotel room for $55 each night for 4 nights and Samantha’s trip lasts for 5 days and she spends the same amount each day
Now,
The amount of money Spent by Samantha = (The amount of money spent to buy an airline ticket) + (The amount of money spent to reserve a hotel room for 4 nights)
= $120 + ($55 × 4)
= $120 + (50 + 5) × 4
= 120 + (50 × 4) + (5 × 4)
= 120 + 200 + 20
= $120 + $220
= $340
So,
The amount of money spent by Samantha for 5 days = $340 × 5
= (300 + 40) × 5
= (300 × 5) + (40 × 5)
= 1,500 + 200
= $1,700
But,
Samantha can buy the airline ticket only once
So,
The amount of money Samantha spent for 5 days = $1,700 – $120
= $580
So,
The amount of money spent by Samantha each day = \(\frac{$580}{5}[latex]
= $116
Hence, from the above,
We can conclude that the amount of money spent by Samantha each day is: $116
Set C pages 241-244
There are 13 girls and 14 boys signed up to join volleyball. Each team needs 6 players. How many teams can be formed, and how many more players are needed to form one more team?
Find the total number of players signed up.
13 + 14 = p
27 = p
Divide to find the number of teams that can be formed.
27 ÷ 6 = t
4 R 3 = t
There are 3 students left not on a team. Subtract to find the number of players still needed to make a team.
6 – 3 = p
3 = p
4 teams can be formed. 3 more players are needed to make one more team.
Remember to draw the bar diagrams to help if needed.
Solve each multi-step problem. Write equations to show how you solve.
Question 1.
Kevin made $96 in necklace sales and half that amount in bracelet sales. How much money did Kevin make in necklace and bracelet sales?
Answer:
It is given that
Kevin made $96 in necklace sales and half that amount in bracelet sales
So,
The amount made by Kevin in bracelet sales = (The amount made by Kevin in necklace sales) ÷ 2
= [latex]\frac{96}{2}\)
= $48
So,
The amount of money made by Kevin in necklace and bracelet sales = (The amount of money made by Kevin in necklace sales) + (The amount of money made by Kevin in bracelet sales)
= $96 + $48
= $144
Hence, from the above,
We can conclude that
The amount made by Kevin in necklace and bracelet sales is: $144
Question 2.
A dog and cat rescue use 40 pounds of dog food and 15 pounds of cat food to feed its animals each day. How many pounds of dog and cat food do they use in seven days?
Answer:
It is given that
A dog and cat rescue use 40 pounds of dog food and 15 pounds of cat food to feed its animals each day
So,
The number of pounds of dog and cat food they use each day = (The number of pounds of dog food) + (The number of pounds of cat food)
= 40 + 15
= 55 pounds
So,
The number of pounds of dog and cat food they use in 7 days = 7 × (The number of pounds of dog and cat food they use each day)
= 7 × 55
= 7 × (50 + 5)
= (7 × 50) + (7 × 5)
= 350 + 35
= 385 pounds
Hence, from the above,
We can conclude that
The number of pounds of dog and cat food they use in 7 days is: 385 pounds
Set D pages 245-248
Think about these questions to help you make sense of the problem.
Thinking Habits
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?

Remember to make sense of the problem before starting to solve it.
At a local shelter, each large dog can be adopted for $10 and each small dog for $5. There are 17 large dogs up for adoption. If all the dogs are adopted, the shelter will make $215. How many small dogs were at the shelter?
Question 1.
Find the hidden questions. Write equations to solve each.
Answer:
It is given that
At a local shelter, each large dog can be adopted for $10 and each small dog for $5. There are 17 large dogs up for adoption. If all the dogs are adopted, the shelter will make $215.
So,
The hidden questions for the given problem are:
a. What is the cost for the adoption of 17 large dogs?
b. What is the cost for the adoption of the small dogs?
Question 2.
How many small dogs are at the shelter?
Answer:
It is given that
At a local shelter, each large dog can be adopted for $10 and each small dog for $5. There are 17 large dogs up for adoption. If all the dogs are adopted, the shelter will make $215.
Now,
Let the number of small dogs be x
So,
The total cost for the adoption of all dogs = (The total cost for the adoption of large dogs) + (The total cost for the adoption of small dogs)
$215 = [(The number of large dogs) × (The cost for the adoption of each large dog)] + [(The number of small dogs) × (The cost for the adoption of each small dog)]
$215 = (17 × $10) + (x × $5)
$215 = (17 × 1 × 10) + (x × $5)
$215 = $170 + (x × $5)
x × $5 = $215 – $170
x × $5 = $45
x = \(\frac{45}{5}\)
x = 9
Hence, from the above,
We can conclude that the total number of small dogs is: 9 small dogs
Topic 6 Assessment Practice
Question 1.
Jason and his 3 brothers want to buy a gift for their mother. They have $314 saved. Each of them will save $17 a week until they have at least $515 for her gift. How much money will they save after 3 weeks? Will they have enough money to buy the gift?
A. What are the hidden questions?
Answer:
It is given that
Jason and his 3 brothers want to buy a gift for their mother. They have $314 saved. Each of them will save $17 a week until they have at least $515 for her gift
Hence,
The hidden questions for the given problem are:
a. How much money Jason and his 3 brothers will save each week?
b. How much amount of money do Jason and his brothers need to save?
B. Write an equation that can be used to answer each hidden question. Then solve.
Answer:
It is given that
Jason and his 3 brothers want to buy a gift for their mother. They have $314 saved. Each of them will save $17 a week until they have at least $515 for her gift
Now,
The amount of money jason and his 3 brothers will save each week = 4 × $17
= 4 × (10 + 7)
= (4 × 10) + (4 × 7)
= 40 + 28
= $68
Now,
The amount of enough money Jason and his 3 brothers will have to save = $515 – $314
= $201
Hence, from the above,
We can conclude that
The amount of money Jason and his 3 brothers will save each week is: $68
The amount of enough money Jason and his 3 brothers will have to save is: $201
C. Write and solve an equation to find how much money they will save after 3 weeks. Will they have enough to buy the gift? Explain.
Answer:
From part (a),
We can observe that
The amount of money Jason and his 3 brothers will save each week is: $68
So,
The amount of money Jason and his 3 brothers will save in 3 weeks = 3 × $68
= 3 × (60 + 8)
= (3 × 60) + (3 × 8)
= 180 + 24
= $204
So,
The amount of money Jason and his 3 brothers will save after 3 weeks = $204 – $201
= $3
So,
The amount of money Jason and his 3 brothers will have = $515 + $3
= $518
Hence, from the above,
We can conclude that Jason and his 3 brothers will have enough money to buy the gift
Question 2.
Marco ordered 2 reclining chairs for $230 each and a coffee table for $350. The shipping cost is $100. Marco is going to pay off his bill in 5 equal payments. How much is each of Marco’s payments?
Answer:
It is given that
Marco ordered 2 reclining chairs for $230 each and a coffee table for $350. The shipping cost is $100. Marco is going to pay off his bill in 5 equal payments
So,
The total payment made by Marco = (The payment made by Marco for 2 reclining chairs) + (The payment made by Marco for a coffee table) + (The shipping cost)
= (2 × 230) + 350 + 100
= [(2 × 23) × 10] + 450
= 460 + 450
= $910
Now,
The payment made by Marco in each equal installment = \(\frac{$910}{5}\)
= $182
Hence, from the above,
We can conclude that each of Marco’s payments is: $182
Question 3.
Mitchell wants to beat the record for the most points scored in a season. This season, he has scored 51 points. If he scores 27 points at each of the next 7 games, he will break the record by 1 point. How many total points will break the record by 1 point?
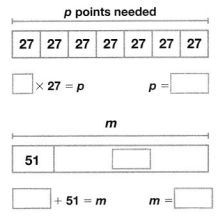
Mitchell will break the record by 1 point if he scores a total of ________ points.
Answer:
It is given that
Mitchell wants to beat the record for the most points scored in a season. This season, he has scored 51 points. and if he scores 27 points at each of the next 7 games, he will break the record by 1 point.
Now,
The number of points scored by Mitchell in the next 7 games = 27 × 7
= (20 + 7) × 7
= (20 × 7) + (7 × 7)
= 140 + 49
= 189 points
So,
The total number of points scored by Mitchell in this season = 189 + 51
= 240 points
So,
The representation of the given situation in the form of a bar diagram is:

Hence, from the above,
We can conclude that
Mitchell will break the record by 1 point if he scores a total of 240 points.
Question 4.
Select all the sentences that describe a comparison using multiplication.
☐ 9 is 3 times as many as p.
☐ 27 more than r is 41.
☐ A bus can travel 3 times as fast as a boat.
☐ It costs d dollars for 9 packages.
☐ There are 4 times as many girls as boys.
Answer:
The sentences that describe a comparison using multiplication are:

Question 5.
Choose the correct word from the box to complete each statement.
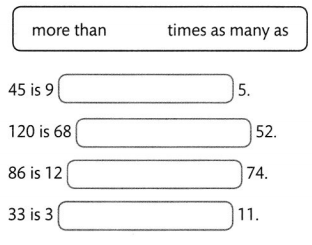
Answer:
The completed statements with the suitable word from the given box are:
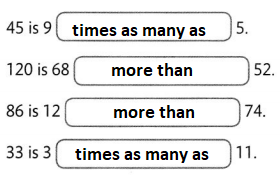
Question 6.
Dee has $120 to spend. She went to the grocery store and spent $55. She then bought 3 potted flowers for $18 each at the nursery. How much money did Dee have left? Select each correct equation or set of equations that could be used to solve the question.
☐ $120 – $55 = M; M – (3 × $18)
☐ $120 – $55 – (3 × $18) = M
☐ (3 × $18) – $55 – $120 = M
☐ ($120 – $55) – (3 × $18) = M
☐ $120 + $55 – (3 × $18) = M.
Answer:
It is given that
Dee has $120 to spend. She went to the grocery store and spent $55. She then bought 3 potted flowers for $18 each at the nursery.
Now,
The cost of the 3 potted flowers = 3 × $18
= 3 × (10 + 8)
= (3 × 10) + (3 × 8)
= 30 + 24
= $54
So,
The amount of money spent by Dee = $55 + $54
= $109
So,
The amount of money Dee left = (The amount of money Dee has to spend) – (The amount of money Dee has spent)
= $120 – $109
= $11
Hence, from the above,
We can conclude that
Each correct equation or set of equations that could be used to solve the given question is:

Question 7.
Darcy ordered 18 boxes of red balloons and 12 boxes of blue balloons for a party. She ordered a total of 240 balloons. How many balloons are in each box?
A. 6
B. 8
C. 7
D. 9
Answer:
It is given that
Darcy ordered 18 boxes of red balloons and 12 boxes of blue balloons for a party. She ordered a total of 240 balloons
So,
The total number of balloons present in 2 boxes = (The number of red balloons) + (The number of blue balloons)
= 18 + 12
= 30 balloons
So,
The number of balloons present in each box = \(\frac{The total number of balloons}{The total number of balloons present i 2 boxes}\)
= \(\frac{240}{30}\)
= 8 balloons
Hence, from the above,
We can conclude that
The number of balloons present in each box is:
![]()
Question 8.
Select all of the sentences that are true for the number 9.
☐ 18 × _____ = 162
☐ 20 more than _____ = 180
☐ _____ times as many as 16 is 145.
☐ 315 is _____ times as many as 35.
☐ 16 × _______ = 128
Answer:
The sentences that are true for the number 9 are:
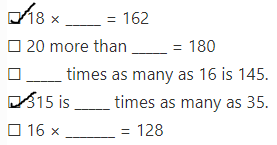
Question 9.
Select all the expressions that are equal to the product of 14 and 9.
☐ (2 × 7) + 9
☐ 9 times as many as 14
☐ 14 × 9
☐ 14 more than 9
☐ 9 less than 14
Answer:
We know that,
According to the Commutative Property of Multiplication,
a × b = b × a
So,
14 × 9 = 14 × 9
Hence, from the above,
We can conclude that
All the expressions that are equal to the product of 14 and 9 are:
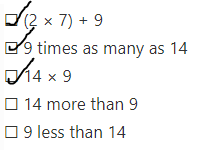
Question 10.
Maggie collected 63 pounds of paper for recycling. Carl collected 9 pounds. How many times as many pounds did Maggie collect as Carl?
A. 3 times
B. 5 times
C. 7 times
D. 8 times
Answer:
It is given that
Maggie collected 63 pounds of paper for recycling. Carl collected 9 pounds
Now,
Let the number of pounds as many times collected be x
So,
According to the given information,
9 × x = 63
x = \(\frac{63}{9}\)
x = 7
Hence, from the above,
We can conclude that
The number of times as many pounds did Maggie collect as Carl are:
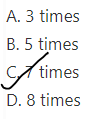
Topic 6 Performance Task
Ski Jumping
Jackie and her older brother Robert went skiing. The Ski Jumping table shows their best jumps, including the distance they jumped and the total length of their run.

Question 1.
Jackie wants to find how much farther Robert’s run was than her run.
Part A
What is the total length of Robert’s run? Draw a bar diagram and write and solve an equation to represent the problem. Does this situation use addition or multiplication to compare?
Answer:
The given table is:

Now,
From the given table,
We can observe that
The total length of Robert’s run = 3 × (The jump distance of Robert)
= 3 × 297
= 3 × (200 + 90 + 7)
= (3 × 200) + (3 × 90) + (3 × 7)
= 600 + 270 + 21
= 891 feet
Now,
The representation of the given information about Robert in the form of a bar diagram is:

So,
The given situation uses multiplication to compare
Hence, from the above,
We can conclude that the total length of Robert’s run is: 891 feet
Part B
How much farther was Robert’s run than Jackie’s run? Write equations to represent each step of the problem. Tell what your variables represent.
Answer:
The given table is:

Now,
From the given table,
The total length of Jackie’s run = 3 × (The jump distance of Jackie)
= 3 × 189
= 3 × (100 + 80 + 9)
= (3 × 100) + (3 × 80) + (3 × 9)
= 300 + 240 + 27
= 567 feet
Now,
From part (A),
The total length of Robert’s run is: 891 feet
So,
The difference between Robert and Jackie’s length = 891 – 567
= 324 feet
Hence, from the above,
We can conclude that Robert’s run was 324 feet farther than Jackie’s run
Question 2.
Jackie’s run was the same on two different jumps. In the first, she jumped 145 feet and went an additional 167 feet after the jump. In the second, she jumped 135 feet. How many feet, f, did she go after the jump?
Answer:
It is given that
Jackie’s run was the same on two different jumps. In the first, she jumped 145 feet and went an additional 167 feet after the jump. In the second, she jumped 135 feet
So,
The total run of Jackie in the first jump = (The total run of Jackie before she jumped) + (The additional run of Jackie after she jumped)
= 145 + 167
= 312 feet
Now,
Let the additional run of Jackie after the second jump be x
So,
According to the given information,
312 = 135 + x
x = 312 – 135
x = 177 feet
Hence, from the above,
We can conclude that Jackie had gone 177 feet after her second jump
Question 3.
Use the Beginner Jump information to find how much longer the total length of the ski jump hill for an advanced jump is than a beginner jump. The advanced jump distance is 408 feet.

Part A
What are the hidden questions you need to answer to solve the problem? Name a variable for each question.
Answer:
It is given that
The advanced jump distance is 408 feet.
Now,
The given information is:

Hence, from the above,
We can conclude that
The hidden questions you need to answer to solve the given problem are:
a. What is the jump distance of the beginner jump distance?
b What is the total length of a beginner jump?
Part B
How much longer is d, the total length of an advanced jump hill, then a beginner jump hill? Write equations and explain how to solve the hidden questions and the original question.
Answer:
It is given that
The advanced jump distance is 408 feet.
Now,
The given table is:

Now,
Let the advanced jump distance is x times as the beginner jump distance
So,
According to the given information,
x × 8 = 408
x = \(\frac{408}{8}\)
x = 51 feet
So,
The beginner jump distance is: 51 feet
Now,
According to the given information,
x × 3 = 51
x = \(\frac{51}{3}\)
x = 17 feet
So,
The toatl length of a beginner jump is: 17 feet
So,
The length of an advanced jump hill, greater than a beginner jump hill = 51 – 17
= 34 feet
Hence, from the above,
We can conclude that
The length of an advanced jump hill is 34 feet longer than a beginner jump hill