Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 16 Geometric Measurement: Classify Two-Dimensional Figures regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 16 Geometric Measurement: Classify Two-Dimensional Figures

enVision STEM Project: Ecosystems
Do Research Use the Internet or other sources to learn more about ecosystems. Look for examples of changes that living organisms might cause. List three different ecosystems and describe any changes that humans might have made to each one.
Journal: Write a Report Include what you found. Also in your report:
• Compare two ecosystems. List 10 living things and 5 non-living things you might find in each one.
• Think about changes that can occur in an ecosystem. Are the changes positive or negative? Why?
• Use two-dimensional shapes to make a map or diagram of an ecosystem.
Review What You Know
A-Z Vocabulary
Choose the best term from the box. Write it on the blank.
• degree
• polygon
• line segment
• quadrilateral
• parallel
• vertex
• perimeter
Question 1.
A ___ is a polygon with four sides.
Answer:
A quadrilateral is a polygon with four sides.
Explanation:
In the above-given question,
given that,
A quadrilateral is a polygon with four sides.
for example:
square is a quadrilateral.
square has four sides of equal length.
square has four internal right angles.
so a quadrilateral is a polygon with four sides.
Question 2.
The point where two sides of a polygon intersect is a ___
Answer:
The point where two sides of a polygon intersect is a vertex.
Explanation:
In the above-given question,
given that,
the point where two sides of a polygon intersect is a vertex.
for example:
triangle is a polygon.
a polygon with three sides is a triangle.
we name a triangle by its three vertices.
so the point where two sides of a polygon intersect is a vertex.
Question 3.
The distance between ____ sides of a polygon is always the same.
Answer:
The distance between parallel sides of a polygon is always the same.
Explanation:
In the above-given question,
given that,
the distance between the number of sides of a polygon is always the same.
for example:
the rectangle is a polygon.
the rectangle has opposite sides that are equal.
so the distance between parallel sides of a polygon is always the same.
Question 4.
The ____ is a unit of measure for angles.
Answer:
A degree is a unit of measure for angles.
Explanation:
In the above-given question,
given that,
a degree is a unit of measure for angles.
for example:
a circle is divided into 360 equal degrees.
so that a right angle is 90 degrees.
so the degree is a unit of measure for angles.
Decimals
Find each answer.
Question 5.
2.75 + 9.08
Answer:
2.75 + 9.08 = 11.83.
Explanation:
In the above-given question,
given that,
addition of two numbers.
the numbers are 2.75 and 9.08.
2.75 + 9.08.
11.83.
Question 6.
17.6 – 3.08
Answer:
17.6 – 3.08 = 14.52.
Explanation:
In the above-given question,
given that,
subtraction of two numbers.
the numbers are 17.6 and 3.08.
17.6 – 3.08.
14.52.
Question 7.
83.2 × 0.1
Answer:
83.2 x 0.1 = 8.32.
Explanation:
In the above-given question,
given that,
multiplication of two numbers.
the numbers are 83.2 and 0.1.
83.2 x 0.1.
8.32.
Question 8.
24.27 × 103
Answer:
24.27 x 1000 = 24270.
Explanation:
In the above-given question,
given that,
multiplication of two numbers.
the numbers are 24.27 and 10 x 10 x 10.
10 x 10 x 10 = 1000.
24.27 x 1000 = 24270.
Fractions
Find each answer.
Question 9.
3\(\frac{2}{3}\) + 6\(\frac{9}{10}\)
Answer:
3(2/3) + 6(9/10) = 7.2.
Explanation:
In the above-given question,
given that,
addition of two numbers.
the numbers are 3(2/3) and 6(9/10).
2/3 = 0.6.
9/10 = 0.9.
3(0.6) + 6(0.9).
1.8 + 5.4 = 7.2.
3(2/3) + 6(9/10) = 7.2.
Question 10.
8\(\frac{1}{2}\) – 4\(\frac{4}{5}\)
Answer:
8(1/2) – 4(4/5) = 0.8.
Explanation:
In the above-given question,
given that,
subtraction of two numbers.
the numbers are 8(1/2) and 4(4/5).
1/2 = 0.5.
4/5 = 0.8.
8(0.5) – 4(0.8).
4 – 3.2 = 0.8.
8(1/2) – 4(4/5) = 0.8.
Question 11.
8 ÷ \(\frac{1}{2}\)
Answer:
8 ÷ \(\frac{1}{2}\) = 16.
Explanation:
In the above-given question,
given that,
division of two numbers.
the numbers are 8 and 1/2.
8 / 0.5.
16.
8 ÷ \(\frac{1}{2}\) = 16.
Question 12.
\(\frac{1}{3}\) ÷ 6
Answer:
\(\frac{1}{3}\) ÷ 6 = 0.05.
Explanation:
In the above-given question,
given that,
division of two numbers.
the numbers are 6 and 1/3.
1/3 = 0.3.
0.3 / 6 = 0.05.
\(\frac{1}{3}\) ÷ 6 = 0.05.
Write an Equation
Question 13.
Louisa drew a polygon with six sides of equal length. If the perimeter of Louisa’s polygon is 95.4 centimeters, how long is each side? Use an equation to solve.
Answer:
The length of each side = 15.9 cm.
Explanation:
In the above-given question,
given that,
If the perimeter of Louisa’s polygon is 95.4 centimeters.
a polygon with 6 sides is called a hexagon.
perimeter of hexagon = 6a.
where a = side.
p = 6 a.
95.4 = 6 a.
a = 95.4 / 6.
a = 15.9 cm.
so the length of each side = 15.9 cm.
Question 14.
The area of a rectangle is 112 square inches. If the length of the rectangle is 16 inches, what is the width of the rectangle? Use an equation to solve.
Answer:
The width of the rectangle is = 7 in.
Explanation:
In the above-given question,
given that,
The area of a rectangle is 112 square inches.
If the length of the rectangle is 16 inches.
area of the rectangle = l x w.
where l = length and w = width.
112 = 16 x w.
112 /16 = w.
w = 7.
so the width of the rectangle = 7 in.
Pick a Project
PROJECT 16A
Where can you find a pyramid?
Project: Build a Pyramid

PROJECT 16B
How do blueprints use different shapes?
Project: Draw a Blueprint

PROJECT 16C
What shapes make up a map?
Project: Hunt for Shapes in a Map
PROJECT 16D
What does the Florida flag look like?
Project: Design a Flag

Answer:
The Florida flag looks like a cross mark.
Explanation:
In the above-given question,
given that,
in the flag, has the cross mark.
the cross mark is inside the flag.
so the Florida flag looks like a cross mark.
cross mark indicates it is not correct.
Lesson 16.1 Classify Triangles
Solve & Share
One triangle is shown below. Draw five more triangles with different properties. Next to each triangle, list its properties such as 2 equal sides, 1 right angle, 3 acute angles, and so on. Work with a partner to solve this problem.
In a triangle, angles will be either acute, right, or obtuse.

Look Back! Reasoning What are some different ways you can put triangles into categories? Explain.
Answer:
They are acute, obtuse, equilateral, right triangles.
Explanation:
In the above-given question,
given that,
the equilateral triangle has all the sides equal length.
an acute triangle is a trigon with three sides and three angles each less than 90 degrees.
an obtuse triangle will have one and only one obtuse angle.
the other two angles are acute angles.
a right triangle is a triangle in which one angle is a right angle.
an isosceles triangle has at least two sides of the same length.
so the triangles are acute, obtuse, equilateral, right triangles.
Visual Learning Bridge
Essential Question How Can You Classify Triangles?
A.
Triangles can be classified by the lengths of their sides.

Equilateral triangle All sides are the same length.

Isosceles triangle At least two sides are the same length.
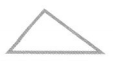
Scalene triangle No sides are the same length
Can you tell if the sides of a triangle are the same length without measuring them?

The total measure of all the angles in a triangle is 180°.

B.
Triangles can also be classified by the measures of their angles.
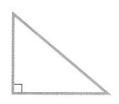
Right triangle One angle is a right angle.
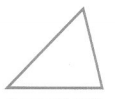
Acute triangle All three angles are acute angles.
Obtuse triangle One angle is an obtuse angle.
Convince Me! Construct Arguments Can you draw an equilateral right triangle? Explain using precise mathematical language.
To justify a mathematical argument, you must use precise mathematical language and ideas to explain your thinking

Answer:
Yes, we can draw an equilateral right triangle.
Explanation:
In the above-given question,
given that,
we can draw an equilateral triangle with 90 degrees.
right angle means it has 90 degrees.
an equilateral triangle has all the sides are equal.
so we can draw an equilateral right triangle.
Guided Practices
Do You Understand?
Question 1.
Can a right triangle have an obtuse angle? Why or why not?
Answer:
No, the right triangle has an obtuse angle.
Explanation:
In the above-given question,
given that,
the right triangle cannot be an obtuse angle.
since a right-angled triangle has one right angle, the other two angles are acute.
therefore, an obtuse-angled triangle can never have a right angle.
the side opposite the obtuse angle in a triangle is the longest.
so the right triangle is not an obtuse angle.
Question 2.
Can an equilateral triangle have only two sides of equal length? Why or why not?
Answer:
No, an equilateral triangle has only two sides of equal length.
Explanation:
In the above-given question,
given that,
an equilateral triangle has all three sides are equal.
if only two sides are equal in length, then it is an isosceles triangle.
so the equilateral triangle does not have only two sides of equal length.
Do You Know How?
In 3 and 4, classify each triangle by its sides and then by its angles.
Question 3.
Answer:
The triangle is an equilateral triangle.
Explanation:
In the above-given question,
given that,
the three angles are equal.
the three sides are equal sides.
an equilateral triangle has all the sides are equal.
so the triangle is an equilateral triangle.
Question 4.

Answer:
The triangle is an isosceles triangle.
Explanation:
In the above-given question,
given that,
the two sides have an equal length.
they are 7 inches.
the other side is 9.9 in.
an isosceles triangle has only two sides are equal.
so the above triangle is an isosceles triangle.
Independent Practice
In 5-10, classify each triangle by its sides and then by its angles.
Question 5.
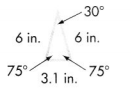
Answer:
The above triangle is an acute-angle triangle.
Explanation:
In the above-given question,
given that,
the two sides and the two sides have the same length.
they are 75 degrees and 6 in.
the other side has a different side length.
acute angle triangle has two equal lengths.
so the above triangle is an acute-angled triangle.
Question 6.
Answer:
The triangle is a scalene triangle.
Explanation:
In the above-given question,
given that,
the triangle has three sides.
the three sides have three different lengths.
a scalene triangle has different lengths.
so the above-given triangle is a scalene triangle.
Think about what you need to compare to classify the triangle correctly.

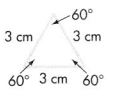
Question 7.

Answer:
The triangle is an equilateral triangle.
Explanation:
In the above-given question,
given that,
the triangle has the 3 equal sides and three equal angles.
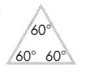
60 + 60 + 60 = 180.
an equilateral triangle has all three sides equal in length.
so the above triangle is an equilateral triangle.
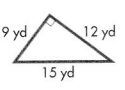
Question 8.
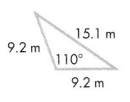
Answer:
The triangle is an obtuse-angled triangle.
Explanation:
In the above-given question,
given that,
the triangle has 2 equal sides.
obtuse-angled triangle has only two equal side lengths.
so the triangle is an obtuse-angled triangle.
Question 9.

Answer:
The triangle is a scalene triangle.
Explanation:
In the above-given question,
given that,
the triangle has three different side lengths.
the side lengths are 6m, 10m, and 8m.
a scalene triangle has three different side lengths.
so the triangle is a scalene triangle.
Question 10.
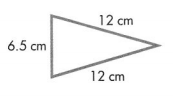
Answer:
The triangle is an isosceles triangle.
Explanation:
In the above-given question,
given that,
the triangle has two different side lengths.
they are 12 cm and 6.5 cm.
an isosceles triangle has the two sides equal.
so the triangle is an isosceles triangle.
Problem Solving
Question 11.
The Louvre Pyramid serves as an entrance to the Louvre Museum in Paris. The base of the pyramid is 35 meters long and the sides are 32 meters long. Classify the triangle on the front of the Louvre Pyramid by the lengths of its sides and the measures of its angles.
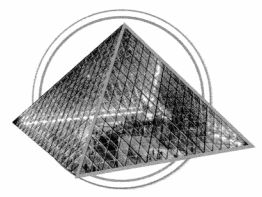
Answer:
The Louvre triangle is in the shape of an isosceles triangle.
Explanation:
In the above-given question,
given that,
The Louvre Pyramid serves as an entrance to the Louvre Museum in Paris.
The base of the pyramid is 35 meters long and the sides are 32 meters long.
an isosceles triangle has two equal side lengths.
the other side is a difference in length.
so the Louvre triangle is in the shape of an isosceles triangle.
Question 12.
A pizza is divided into twelve equal slices. Glenn and Ben each ate \(\frac{1}{6}\) of the pizza on Monday. The next day Ben ate \(\frac{1}{2}\) of the pizza that was left over. How many slices of the original pizza remain? Explain your reasoning.
Answer:
The number of slices of the original pizza remains = 2 pieces.
Explanation:
In the above-given question,
given that,
A pizza is divided into twelve equal slices.
Glenn and Ben each ate \(\frac{1}{6}\) of the pizza on Monday.
The next day Ben ate \(\frac{1}{2}\) of the pizza that was leftover.
1/6 + 1/2.
1/6 = 0.16.
1/2 = 0.5.
0.16 + 0.5 = 0.66.
so the number of slices of the original pizza remains = 2 pieces.
Question 13.
During a sale at the bookstore, books sold for $3 and magazines sold for $2.50. Jan spent $16 and bought a total of 6 books and magazines. How many of each did she buy?
Answer:
The number of each did she buy = $17.
Explanation:
In the above-given question,
given that,
During a sale at the bookstore, books sold for $3, and magazines sold for $2.50.
Jan spent $16 and bought a total of 6 books and magazines.
6 x 3 = $18.
6 x $2.50 = $15.
$18 + $15 = 33.
$33 – $16 = $17.
so the number of each did she buy = $17.
Question 14.
Higher Order Thinking The measures of two angles of a triangle are 23° and 67°. Is the triangle acute, right, or obtuse? Use geometric terms in your explanation.
Answer:
The triangle is an acute-angled triangle.
Explanation:
In the above-given question,
given that,
The measures of two angles of a triangle are 23° and 67°.
the triangles have two different angles.
they are 23° and 67°.
so the triangle is an acute-angled triangle.
Question 15.
Make Sense and Persevere An animal shelter houses dogs, cats, and rabbits. There are 126 animals at the shelter. Of the animals, \(\frac{1}{3}\) are cats. Three fourths of the remaining animals are dogs. How many of the animals are rabbits? Show your work.
Answer:
The number of animals is rabbits = 21.
Explanation:
In the above-given question,
given that,
An animal shelter houses dogs, cats, and rabbits.
There are 126 animals at the shelter.
Of the animals, \(\frac{1}{3}\) are cats.
Three-fourths of the remaining animals are dogs.
1/3 = 0.3.
3/4 = 0.75.
0.3 + 0.75 = 1.05.
so the number of animals is rabbits = 21.
Assessment Practice
Question 16.
Two sides of a triangle measure 5 inches and 6 inches. Jason says the triangle must be scalene. Is Jason correct? Explain.
Answer:
No, Jason is not correct.
Explanation:
In the above-given question,
given that,
Two sides of a triangle measure 5 inches and 6 inches.
a scalene triangle has all three sides have different lengths.
an isosceles triangle has the two sides are equal.
so Jason is not correct.
Lesson 16.2 Classify Quadrilaterals
Solve & Share
Draw any length line segment that will fit in the space below. The line segment can go in any direction, but it must be straight. Draw another line segment of any length that is parallel to the first one. Connect the ends of each line segment with line segments to make a closed four-sided figure. What does your shape look like? Can you classify it? Discuss your ideas with a partner.
Answer:
The shape looks like is a rectangle.
Explanation:
In the above-given question,
given that,
the line segment has 5 cm in length.
the other line segment has the same 2 cm in length.
so the lines joined is formed a rectangle.
the rectangle has two opposite sides that are equal.
the rectangle has the area = length x width.
so the shape looks like a rectangle.
You can use reasoning to find the differences and similarities between shapes when classifying quadrilaterals. Show your work!

Look Back! Reasoning How can you draw a quadrilateral different from the one above? Describe what you can change and why it changes the quadrilateral.
Answer:
The quadrilateral formed is square.
Explanation:
In the above-given question,
given that,
the line segment is increased by 3 cm.
5 – 2 = 3.
so it has 4 equal side lengths.
area of the square = 4 s.
where S = sides.
so the quadrilateral formed is square.
Visual Learning Bridge
Essential Question What Are Some Properties of Quadrilaterals?
A.
Categories of quadrilaterals are classified by their properties.
• How many pairs of opposite sides are parallel?
• Which sides have equal lengths?
• How many right angles are there?
Think about the questions below when you are classifying quadrilaterals.

B.
A trapezoid has one pair of parallel sides.
A parallelogram has two pairs of opposite sides parallel and equal in length.
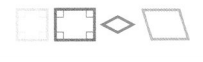
C.
A rectangle has four right angles.

A rhombus has all sides the same length.

D.
A square has all sides the same length.

A square has four right angles.
Convince Me! Generalize How is a parallelogram different from a rhombus? How are they similar?
Guided Practice
Do You Understand?
Question 1.
A-Z Vocabulary How are a square and a rhombus alike?
Answer:
Yes, a square and a rhombus have four equal sides.
Explanation:
In the above-given question,
given that,
the square has four sides of the same length.
square has four right angles.
rhombus has all sides the same length.
so the square and a rhombus have four equal sides.
Question 2.
Vocabulary How is a trapezoid different from a parallelogram?
Answer:
Yes, both of them are different.
Explanation:
In the above-given question,
given that,
a trapezoid has one pair of parallel sides.
a parallelogram has two pairs of opposite sides and is equal in length.
so both of them are different.
Do You Know How?
In 3-6, use as many names as possible to identify each polygon. Tell which name is most specific.
Use the questions at the top of page 626 to help you classify the quadrilaterals.

Question 3.

Answer:
The quadrilateral is a square.
Explanation:
In the above-given question,
given that,
the quadrilateral has 4 equal sides.
four right angles.
so the square has 4 equal sides.
so the quadrilateral is a square.
Question 4.

Answer:
The quadrilateral is a rectangle.
Explanation:
In the above-given question,
given that,
the quadrilateral has opposite equal sides.
four right angles.
so the rectangle has opposite equal sides.
so the quadrilateral is a rectangle.
Question 5.

Answer:
The quadrilateral is a rhombus.
Explanation:
In the above-given question,
given that,
the quadrilateral has 4 equal sides.
so the rhombus has 4 equal sides.
so the quadrilateral is a rhombus.
Question 6.

Answer:
The quadrilateral is a parallelogram.
Explanation:
In the above-given question,
given that,
the quadrilateral has opposite sides are equal.
four right angles.
so the rectangle has opposite equal sides.
so the quadrilateral is a parallelogram.
Independent Practice
Question 7.
Identify the polygon using as many names as possible.

Answer:
The polygon is a square and rhombus.
Explanation:
In the above-given question,
given that,
the polygon has 4 equal sides.
the polygon has 4 equal angles.
so the polygon is a square and rhombus.
Question 8.
Identify the polygon using as many names as possible.
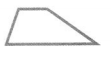
Answer:
The polygon is a quadrilateral and trapezoid.
Explanation:
In the above-given question,
given that,
the polygon has 4 different sides.
the polygon has one right angle.
so the polygon is a quadrilateral and trapezoid.
Question 9.
Why is a square also a rectangle?
Answer:
Yes, a square is also a rectangle.
Explanation:
In the above-given question,
given that,
the square has 4 equal right angles.
the rectangle has 4 equal right angles.
so square and rectangle are the same.
so the square is also a rectangle.
Question 10.
Which special quadrilateral is both a rectangle and a rhombus? Explain how you know.
Answer:
The special quadrilateral is a square.
Explanation:
In the above-given question,
given that,
the square is a rectangle.
square has 4 equal right angles.
rectangle also has 4 equal right angles.
rhombus also has 4 equal right angles.
so the special quadrilateral is a square.
Problem Solving
Question 11.
Each time Sophie makes a cut to a polygon, she can make a new type of polygon. What kind of polygon is left if Sophie cuts off the top of the isosceles triangle shown?

Answer:
The polygon formed is a trapezoid.
Explanation:
In the above-given question,
given that,
Each time Sophie makes a cut to a polygon, she can make a new type of polygon.
the polygon is an isosceles triangle.
after Sophie makes a cut to a polygon.
so the polygon formed is a trapezoid.
Question 12.
Number Sense Donald’s car gets about 30 miles per gallon. About how many miles can Donald drive on 9.2 gallons of gas? At $3.15 a gallon, about how much would that amount of gas cost?
Answer:
The amount of gas cost = $869.4 miles.
Explanation:
In the above-given question,
given that,
Donald’s car gets about 30 miles per gallon.
9.2 x 30 = 276 miles.
276 x $3.15 = $869.4 miles.
so the amount of gas cost = $869.4 miles.
Question 13.
Is it possible to draw a quadrilateral that is not a rectangle but has at least one right angle? Explain.
Answer:
Yes, it is possible to draw a quadrilateral that is not a rectangle.
Explanation:
In the above-given question,
given that,
the square is also a quadrilateral.
square has 4 equal right angles.
square has 4 equal side lengths.
so it is possible to draw a quadrilateral that is not a rectangle.
Question 14.
The area of a quadrilateral is 8.4 square feet. Find two decimals that give a product close to 8.4.
Answer:
The two decimals are 2.1 and 4.0.
Explanation:
In the above-given question,
given that,
the area of a quadrilateral is 8.4 square feet.
area = l x w.
where l = 2.1 and w = 4.0.
area = 2.1 x 4.0.
area = 8.4.
so the two decimals are 2.1 and 4.0.
Question 15.
Be Precise Suppose you cut a square into two identical triangles. What type of triangles will you make?
Answer:
The triangle I make is the isosceles triangle.
Explanation:
In the above-given question,
given that,
Suppose you cut a square into two identical triangles.
an isosceles triangle has the two sides equal.
the triangle formed is the isosceles triangle.
so the triangle I can make is an isosceles triangle.
Question 16.
Higher Order Thinking A parallelogram has four sides that are the same length. Is it a square? Explain how you know.
What do you know about the sides of a parallelogram?

Assessment Practice
Question 17.
Which quadrilateral could have side lengths 1 m, 5 m, 1 m, 5 m?
A. square
B. rectangle
C. trapezoid
D. rhombus
Answer:
Option B is the correct answer.
Explanation:
In the above-given question,
given that,
the quadrilateral could have side lengths 1 m, 5 m, 1 m, and 5 m.
the rectangle has the opposite sides equal.
so option B is the correct answer.
Question 18.
Which of the following statements is NOT true?
A. A rectangle is also a parallelogram.
B. A trapezoid is also a quadrilateral.
C. A rhombus is also a rectangle.
D. A square is also a rectangle.
Answer:
Option C is the correct answer.
Explanation:
In the above-given question,
given that,
a rectangle is also a parallelogram.
a trapezoid is also a quadrilateral.
a square is also a rectangle.
a rhombus is not a rectangle.
rhombus has all four equal sides.
so option C is the correct answer.
Lesson 16.3 Continue to Classify Quadrilaterals
Solve & Share
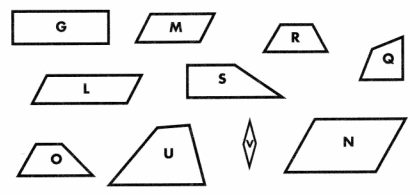
Look at the quadrilaterals below. In the table, write the letters for all the figures that are trapezoids. Then do the same with each of the other quadrilaterals. Work with a partner to solve this problem.
You can classify quadrilaterals that have more than one property. Show your work!

List the letter of each figure in each group.

Answer:
The number of trapezoids is Q, R, S, U, and O.
parallelograms are L, M, and N.
the rectangle is G.
the rhombus is V.
Explanation:
In the above-given question,
given that,
the number of trapezoids is Q, R, S, U, and O.
parallelograms are L, M, and N.
the rectangle is G.
the rhombus is V.
Look Back! Construct Arguments which quadrilateral had the most figures listed? Explain why this group had the most.
Visual Learning Bridge
Essential Question
How Are Special Quadrilaterals Related to Each Other?
A.
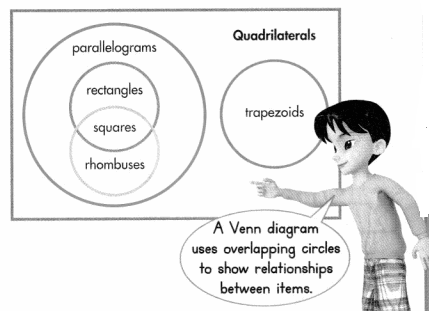
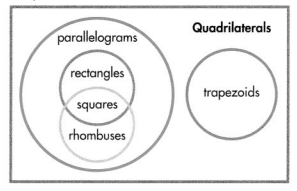
This Venn diagram shows how special quadrilaterals are related to each other.
How can you use the Venn diagram to describe other ways to classify a square? What does the diagram show about how a trapezoid relates to other special quadrilaterals?
B.
Each circle in the Venn diagram shows a category of quadrilateral.
Items in overlapping sections of the Venn diagram belong to more than one group.
“Square” is in more than one circle in the Venn diagram.

A square is also a rectangle, rhombus, parallelogram, and quadrilateral.
C.
In the diagram, the circle for trapezoids does not intersect with any other circles. This shows that a trapezoid is also a quadrilateral, but never a parallelogram, rectangle, rhombus, or square.
Convince Me! Construct Arguments When can a rectangle be a rhombus? Can a rhombus be a rectangle? Explain using examples.
Guided Practice
Do You Understand?
Question 1.
Explain how the Venn diagram on page 630 shows that every rectangle is a parallelogram.
Answer:
Yes, every rectangle is a parallelogram.
Explanation:
In the above-given question,
given that,
square is a rectangle, parallelogram, rhombus, and quadrilateral.
square is also a rectangle.
square has 4 equal right angles.
a rectangle has 4 equal right angles.
so every rectangle is a parallelogram.
Question 2.
How are a rectangle and a rhombus alike?
Answer:
The rectangle and rhombus are alike when they have 4 equal right angles.
Explanation:
In the above-given question,
given that,
square is a rectangle, parallelogram, rhombus, and quadrilateral.
square is also a rectangle.
square has 4 equal right angles.
a rectangle has 4 equal right angles.
so every rectangle is a parallelogram.
rhombus also have 4 equal right angles.
so the rectangle and rhombus are alike.
Do You Know How?
In 3-6, tell whether each statement is true or false. If false, explain.
Question 3.
All rectangles are squares.
Answer:
Yes, all rectangles are squares.
Explanation:
In the above-given question,
given that,
the square is a rectangle.
square has 4 equal right angles.
rectangles have 4 equal right angles.
so all rectangles are squares.
Question 4.
Every rhombus is a parallelogram.
Answer:
Yes, the rhombus is a parallelogram.
Explanation:
In the above-given question,
given that,
a rhombus has 4 equal sides lengths.
rhombus has 4 equal right angles.
a parallelogram has opposite sides equal.
so the rhombus is a parallelogram.
Question 5.
Parallelograms are special rectangles.
Answer:
Parallelograms are special rectangles.
Explanation:
In the above-given question,
given that,
rectangles have two opposite side lengths.
the parallelogram has two opposite side lengths.
so parallelograms are special rectangles.
Question 6.
A trapezoid can be a square.
Answer:
No, the trapezoid cannot be a square.
Explanation:
In the above-given question,
given that,
the square has 4 sides.
trapezoid also has 4 sides.
square has all sides equal.
a trapezoid has all sides not equal.
so trapezoid is not a square.
Independent Practice
In 7-10, write whether each statement is true or false. If false, explain why.
Question 7.
All rhombuses are rectangles.
Answer:
False.
Explanation:
In the above-given question,
given that,
a rhombus has 4 equal side lengths.
rectangles have 2 opposite side lengths.
so the statement is not correct.
Question 8.
Every trapezoid is a quadrilateral.
Answer:
Yes, the trapezoid is a quadrilateral.
Explanation:
In the above-given question,
given that,
the trapezoid is also a quadrilateral but never a parallelogram, rectangle, rhombus, or square.
so the trapezoid is a quadrilateral.
Question 9.
Rhombuses are special parallelograms.
Answer:
Yes, the rhombus is a special parallelogram.
Explanation:
In the above-given question,
given that,
a rhombus has 4 equal sides.
parallelograms have 4 sides.
so rhombus is a special parallelogram.
Question 10.
All rectangles are quadrilaterals.
Answer:
The statement is not correct.
Explanation:
In the above-given question,
given that,
rectangles have two opposite side lengths.
the quadrilateral has two opposite side lengths.
so the statement is not correct.
Question 11.
What properties does the shape have? Why is it not a parallelogram?

Answer:
The shape formed is a rhombus.
Explanation:
In the above-given question,
given that,
the shape formed is a rhombus.
rhombus has 4 equal side lengths.
rhombus has 4 equal right angles.
so the shape formed is a rhombus.
Question 12.
Why is a square also a rhombus?
Answer:
Yes, a square is also a rhombus.
Explanation:
In the above-given question,
given that,
a square has 4 equal sides.
square has 4 equal right angles.
rhombus has 4 equal sides.
rhombus has 4 equal right angles.
so the square is also a rhombus.
Problem Solving
Question 13.
Construct Arguments Draw a quadrilateral with one pair of parallel sides and two right angles. Explain why this figure is a trapezoid.
Answer:
Yes, it is a trapezoid.
Explanation:
In the above-given question,
given that,
a trapezoid has one pair of parallel sides and two right angles.
a quadrilateral with one pair of parallel sides and two right angles.
so the figure formed is a trapezoid.
Question 14.
A reflecting pool is shaped like a rhombus with a side length of 6 meters. What is the perimeter of the pool? Explain how you found your answer.
Think about the properties of a rhombus to help you solve.

Answer:
The perimeter of the pool is
Explanation:
In the above-given question,
given that,
A reflecting pool is shaped like a rhombus with a side length of 6 meters.
the perimeter of rhombus = 6 a.
where a = sides.
perimeter = 6 x 6.
perimeter = 36 sq m.
so the perimeter of the pool is 36 sq m.
Question 15.
A bakery sold 31 bagels in the first hour of business and 42 bagels in the second hour. If the bakery had 246 bagels to start with, how many bagels were left after the second hour?
img 42.7
Answer:
The number of bagels was left after the second hour = 3.36 bagels.
Explanation:
In the above-given question,
given that,
A bakery sold 31 bagels in the first hour of business and 42 bagels in the second hour.
If the bakery had 246 bagels to start with.
42 + 31 = 73.
246/73 = 3.36.
so the number of bagels were left after the second hour = 3.36 bagels.
Question 16.
Higher Order Thinking Ann says the figure below is a square. Pablo says that it is a parallelogram. Felix says that it is a rectangle. Can they all be right? Explain.

Answer:
Ann was correct.
Explanation:
In the above-given question,
given that,
the figure has 4 equal sides.
the figures have 4 equal angles.
the above figure is a square.
so Ann was correct.
Assessment Practice
Question 17.
Below is the Venn diagram of quadrilaterals.
Part A
Are rhombuses also rectangles? Explain.
Part B
What are all of the names that describe a rhombus?
Answer:
Squares and rectangles describe a rhombus.
Explanation:
In the above-given question,
given that,
rhombuses, squares, and rectangles are over-linked with each other.
square has 4 equal side lengths.
square has 4 equal right angles.
rectangles have 2 opposite equal sides.
rhombus has 4 equal side lengths.
so squares and rectangles describe a rhombus.
Lesson 16.4 Construct Arguments
Activity
Problem Solving
Solve & Share
Alfie thinks that if he cuts a parallelogram along a diagonal, he will get two triangles that have the same shape and size. Is he correct? Solve this problem any way you choose. Construct a math argument to justify your answer.

Answer:
The two triangles are Scalene triangles.
Explanation:
In the above-given question,
given that,
Alfie thinks that if he cuts a parallelogram along a diagonal.
he will get two triangles that have the same shape and size.
the triangles formed are scalene triangles.
a scalene triangle has 3 different side lengths.
Thinking Habits
Be a good thinker! These questions can help you.
• How can I use numbers, objects, drawings, or actions to justify my argument?
• Am I using numbers and symbols correctly?
• Is my explanation clear and complete?
• Can I use a counterexample in my argument?
Look Back! Construct Arguments Suppose you cut along a diagonal of a rhombus, a rectangle, or a square. Would you get two triangles that have the same shape and size? Construct an argument to justify your answer.
Visual Learning Bridge
Essential Question How Can You Construct Arguments?
A.
Anika says, “If I draw a diagonal in a parallelogram, I will always form two right triangles.” Is she correct? Construct a math argument to justify your answer.

You can construct an argument using what you know about triangles and quadrilaterals.

What do I need to do to solve the problem?
I need to examine several cases, including special parallelograms. Then I need to state my conclusion and write a good argument to justify it.
Here’s my thinking..

B.
How can I construct an argument?
I can
• use math to explain my reasoning
• use the correct words and symbols.
• give a complete explanation.
• use a counterexample in my argument.
C.
Anika is incorrect. The triangles are right triangles only when the parallelogram is a rectangle or square. Rectangles and squares have four right angles. So, each triangle formed by drawing a diagonal will have a right angle and be a right triangle. But if the parallelogram does not have right angles, each triangle will not have a right angle.
Convince Me! Construct Arguments How can counterexamples be helpful in constructing an argument?
Guided Practice
Jamal says, “Two equilateral triangles that are the same size can be joined to make a rhombus.”
Question 1.
What is the definition of an equilateral triangle? What is the definition of a rhombus?

Answer:
Yes, two equilateral triangles that are the same size can be joined to make a rhombus.
Explanation:
In the above-given question,
given that,
an equilateral triangle has all three sides has an equal length.
rhombus has all 4 sides are equal.
rhombus has all 4 equal right angles.
so the two equilateral triangles that are the same size can be joined to make a rhombus.
Question 2.
How could knowing these definitions help in constructing your argument?
Answer:
Question 3.
Is Jamal correct? Construct an argument to justify your answer.
Answer:
Yes, Jamal was correct.
Explanation:
In the above-given question,
given that,
an equilateral triangle has all three sides has an equal length.
rhombus has all 4 sides are equal.
rhombus has all 4 equal right angles.
so the two equilateral triangles that are the same size can be joined to make a rhombus.
Independent Practice
Construct Arguments
Lauren says, “If I draw a diagonal in a trapezoid, neither of the triangles formed will have a right angle.”
Stuck? Answering this question might help. Have I interpreted all word meanings correctly?

A diagram can help you construct arguments.
Question 4.
What is the definition of a trapezoid?
Answer:
The trapezoid is a quadrilateral with one pair of parallel sides.
Explanation:
In the above-given question,
given that,
the trapezoid is a quadrilateral with one pair of parallel sides.
area of trapezoid = 1/2(a + b) h.
where a and b are the bases.
h is the height.
Question 5.
Draw examples of a diagonal in a trapezoid.
Answer:
The shape formed is a triangle.
Explanation:
In the above-given question,
given that,
if the trapezoid is divided into two equal halves.
we can get the two triangles.
so the shape formed is a triangle.
Question 6.
How can you use a drawing to construct an argument?
Answer:
Question 7.
Is Lauren correct? Construct a math argument to justify your answer.
Answer:
Problem Solving
Performance Task
Flag Making
Mr. Herrera’s class is studying quadrilaterals. The class worked in groups, and each group made a “quadrilateral flag.”

Question 8.
Construct Arguments Which flags show parallelograms? Construct a math argument to justify your answer.
Answer:
Flag 1 shows a parallelogram.
Explanation:
In the above-given question,
given that,
Mr. Herrera’s class is studying quadrilaterals.
The class worked in groups, and each group made a “quadrilateral flag.
in 1st flag there are parallelograms.
so flag 1 shows a parallelogram.
Question 9.
Reasoning Explain how you would classify the quadrilaterals on the green flag and the blue flag.
Answer:
The definitions of the different quadrilaterals will help you construct arguments.

Question 10.
Critique Reasoning Marcia’s group made the red flag. Bev’s group made the orange flag. Both girls say their flag shows all rectangles. Critique the reasoning of both girls and explain who is correct.
Answer:
Question 11.
Make Sense and Persevere Does it make sense for this quadrilateral to be on any of the flags?
Answer:
Topic 16 Fluency Practice
Activity
Point & Tally
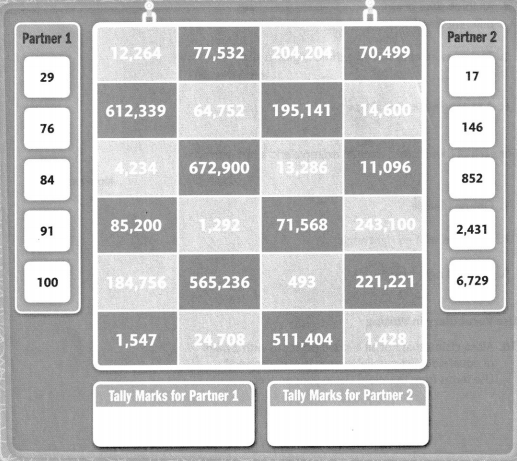
Find a partner. Get paper and a pencil. Each partner chooses light blue or dark blue.
At the same time, Partner 1 and Partner 2 each point to one of their black numbers. Both partners find the product of the two numbers.
The partner who chose the color where the product appears gets a tally mark. Work until one partner has seven tally marks.
Topic 16 Vocabulary Review
Understand Vocabulary
Word List
• acute triangle
• equilateral triangle
• isosceles triangle
• obtuse triangle
• parallelogram
• rectangle
• rhombus
• right triangle
• scalene triangle
• square
• trapezoid
Choose the best term from the Word List. Write it on the blank.
Question 1.
A 3-sided polygon with at least two sides the same length is a(n) _____
Answer:
A 3-sided polygon with at least two sides of the same length is a(n) is an equilateral triangle.
Explanation:
In the above-given question,
given that,
a 3-sided polygon with at least two sides of the same length is a(n) is an equilateral triangle.
for example:
an equilateral triangle has three sides that are all the same length and three angles that all measure 60 degrees.
Question 2.
A polygon with one pair of parallel sides is a(n) ____
Answer:
A polygon with one pair of parallel sides is a(n) is a trapezium.
Explanation:
In the above-given question,
given that,
a polygon with one pair of parallel sides is a(n) is a trapezium.
for example:
if the polygon has one pair of parallel sides is a trapezoid.
Question 3.
A(n) ____ has four right angles and all four sides the same length.
Answer:
A(n) rhombus has four right angles and all four sides the same length.
Explanation:
In the above-given question,
given that,
a(n) rhombus has four right angles and all four sides the same length.
for example:
a rhombus is a parallelogram with 4 sides of equal length.
area of rhombus = 6 a.
where a = sides.
Question 4.
All three sides of a(n) ____ are different lengths.
Answer:
All three sides of a(n) are scalene triangle are different lengths.
Explanation:
In the above-given question,
given that,
All three sides of a(n) are scalene triangle are different lengths.
for example:
a scalene triangle is a triangle in which all three sides have different lengths.
Question 5.
The measure of each of the three angles in a(n) ____ is less than 90°
Answer:
The measure of each of the three angles in a(n) acute angle triangle is less than 90°.
Explanation:
In the above-given question,
given that,
the measure of each of the three angles in a(n) acute angle triangle is less than 90°.
for example:
an acute angle triangle has three angles that each measure less than 90 degrees.
Question 6.
A rectangle is a special type of ____
Answer:
A rectangle is a special type of parallelogram.
Explanation:
In the above-given question,
given that,
a rectangle is a special type of parallelogram.
for example:
a rectangle is a special case of a parallelogram in which each pair of adjacent sides is perpendicular.
For each of these terms, draw an example and a non-example.

Answer:
An obtuse triangle is an isosceles triangle.
Rhombus with no right angle is a quadrilateral.
An isosceles right triangle is two equal sides.
Explanation:
In the above-given question,
given that,
An obtuse triangle is an isosceles triangle.
Rhombus with no right angle is a quadrilateral.
An isosceles right triangle is two equal sides.
Use Vocabulary in Writing
Question 10.
Alana claims that not all 4-sided polygons with 2 pairs of equal sides are parallelograms. Is Alana correct? Use terms from the Word List in your answer.
Answer:
No, she is not correct.
Explanation:
In the above-given question,
given that,
Alana claims that not all 4-sided polygons with 2 pairs of equal sides are parallelograms.
2 pairs of equal sides are not parallelograms.
so she was not correct.
Topic 16 Reteaching
Set A
pages 621-624
Classify the triangle by the measures of its angles and the lengths of its sides.
Since one of the angles is right, this is a right triangle. Since two of the sides are the same length, this is an isosceles triangle.
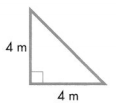
It is a right, isosceles triangle.
Remember that right, obtuse, and acute describe the angles of a triangle. Equilateral, scalene, and isosceles describe the sides of a triangle.
Classify each triangle by the measures of its angles and the lengths of its sides.
Question 1.
Answer:
The triangle is an equilateral triangle.
Explanation:
In the above-given question,
given that,
the triangles have 3 equal sides and three equal angles.
so the triangle is an equilateral triangle.
Question 2.

Answer:
The triangle is a scalene triangle.
Explanation:
In the above-given question,
given that,
the triangle has 3 different sides.
they are 3 in, 5 in, and 4 in.
the three side lengths are different.
so the triangle is a scalene triangle.
Question 3.
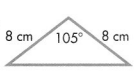
Answer:
The triangle is an isosceles triangle.
Explanation:
In the above-given question,
given that,
the triangle has 2 sides of equal length.
they are 8cm and 8 cm.
so the triangle is an isosceles triangle.
Question 4.
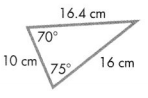
Answer:
The triangle is a scalene triangle.
Explanation:
In the above-given question,
given that,
the triangle has 3 different sides.
they are 16.4 cm, 16 cm, and 10 cm.
so the triangle is a scalene triangle.
Set B
pages 625-628
Quadrilaterals are classified by their properties.
A trapezoid has one pair of parallel sides.
![]()
A parallelogram has two pairs of equal parallel sides.

A rectangle is a parallelogram with 4 right angles.

A rhombus is a parallelogram with 4 equal sides.

A square is a parallelogram with 4 right angles and 4 equal sides.

Remember that some quadrilaterals can be identified by more than one name.
Identify each quadrilateral. Describe each quadrilateral by as many names as possible.
Question 1.
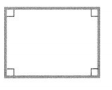
Answer:
The quadrilateral is a rectangle.
Explanation:
In the above-given question,
given that,
the polygon has 4 right angles.
the polygon with 4 right angles is a rectangle.
so the quadrilateral is a rectangle.
Question 2.

Answer:
The quadrilateral is a rhombus.
Explanation:
In the above-given question,
given that,
the polygon has 4 equal sides.
rhombus is a parallelogram with 4 equal sides.
so the quadrilateral is a rhombus.
Question 3.
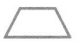
Answer:
The polygon is a trapezoid.
Explanation:
In the above-given question,
given that,
the quadrilateral has 4 sides.
a trapezoid has one pair of parallel sides.
so the polygon is a trapezoid.
Question 4.

Answer:
The polygon is a square.
Explanation:
In the above-given question,
given that,
the quadrilateral has 4 equal sides and 4 equal angles.
a square is a parallelogram with 4 right angles and 4 equal sides.
so the polygon is a square.
Set C
pages 629-632
This Venn diagram shows how special quadrilaterals are related to each other.

Remember that each circle of the Venn diagram shows a subgroup of quadrilaterals.
Tell whether each statement is true or false.
Question 1.
All squares are rectangles.
Answer:
True.
Explanation:
In the above-given question,
given that,
all squares are rectangles.
square is a rectangle.
area of the square = 4s.
Question 2.
Every parallelogram is a rectangle.
Answer:
False.
Explanation:
In the above-given question,
given that,
a rectangle is a parallelogram.
but every parallelogram is a rectangle.
so the statement is false.
Question 3.
Rhombuses are special parallelograms.
Answer:
True.
Explanation:
In the above-given question,
given that,
rhombuses are special parallelograms.
rhombus is a special parallelogram.
area of the rhombus = 4 a.
Question 4.
All trapezoids are quadrilaterals.
Answer:
False.
Explanation:
In the above-given question,
given that,
a trapezoid is not a quadrilateral.
so the above statement is false.
Set D
pages 633-636
Think about these questions to help you construct arguments.
Thinking Habits
• How can I use numbers, objects, drawings, or actions to justify my argument?
• Am I using numbers and symbols correctly?
• Is my explanation clear and complete?
• Can I use a counterexample in my argument?
Remember that using definitions of geometric figures can help you construct arguments. Malcolm says, “The sum of the angle measures in any rectangle is 180°.”
Question 1.
What is the definition of a rectangle?
Answer:
A rectangle is a parallelogram with 4 right angles.
Explanation:
In the above-given question,
given that,
a rectangle is a parallelogram with 4 right angles.
area of the rectangles = length x width.
Question 2.
Draw a picture of a rectangle and label its angles.
Answer:
A rectangle is a parallelogram with 4 right angles.
Explanation:
In the above-given question,
given that,
a rectangle is a parallelogram with 4 right angles.
area of the rectangles = length x width.
Question 3.
Is Malcolm correct? Construct a math argument to justify your answer.
Answer:
Topic 16 Assessment Practice
Question 1.
Which of the following correctly describes the triangles? Select all that apply.

![]() Both triangles have a right angle.
Both triangles have a right angle.
![]() Only one triangle is a right triangle.
Only one triangle is a right triangle.
![]() Only one triangle has an acute angle.
Only one triangle has an acute angle.
![]() Both triangles have an obtuse angle.
Both triangles have an obtuse angle.
![]() Both triangles have at least two acute angles.
Both triangles have at least two acute angles.
Answer:
Only one triangle is a right triangle.
only one triangle has an acute angle.
Explanation:
In the above-given question,
given that,
there are two triangles.
they have only one triangle is a right triangle.
only one triangle has an acute angle.
Question 2.
Which statement is true?
A. Trapezoids are parallelograms.
B. A square is always a rectangle.
C. A rectangle is always a square.
D. A rhombus is a trapezoid.
Answer:
Option B is correct.
Explanation:
In the above-given question,
given that,
a square is always a rectangle.
square has 4 equal right angles.
the rectangle has 4 equal right angles.
Question 3.
Select all the shapes that are parallelograms.

Answer:
Option 4 is correct.
Explanation:
In the above-given question,
given that,
the shapes are hexagon, rectangle, trapezoid, and parallelogram.
so option 4 is correct.
Question 4.
The necklace charm shown has one pair of m parallel sides. What type of quadrilateral is the charm? Explain.
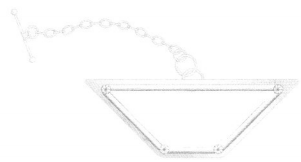
Answer:
The charm is in the shape of a trapezoid.
Explanation:
In the above-given question,
given that,
The necklace charm shown has one pair of m parallel sides.
a trapezoid has one pair of parallel sides.
the above charm has one pair of parallel sides.
so the charm is in the shape of a trapezoid.
Question 5.
Identify the figure below using as many names as possible.

Answer:
The figure is a rhombus.
Explanation:
In the above-given question,
given that,
the square has 4 equal sides and 4 equal angles.
rhombus has 4 equal sides.
so the figure is a rhombus.
Question 6.
Claim 1: A square is a rectangle because it has 4 right angles.
Claim 2: A square is a rhombus because it has 4 equal sides.
Which claim is correct? Explain.
Answer:
Yes, both of them are correct.
Explanation:
In the above-given question,
given that,
a square is a rectangle because it has 4 right angles.
a square is a rhombus because it has 4 equal sides.
so both of them are correct.
Assessment Practice
Question 7.
Look at the rhombus and square below.
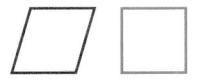
A. How are the two figures the same?
B. How are the two figures different?
Answer:
They are the same when they have 4 equal sides.
They are different when they have 4 equal right angles.
Explanation:
In the above-given question,
given that,
a square is a rectangle because it has 4 right angles.
a square is a rhombus because it has 4 equal sides.
they are the same when they have 4 equal sides.
they are different when they have 4 equal right angles.
Question 8.
Identify the figure below using as many names as possible.
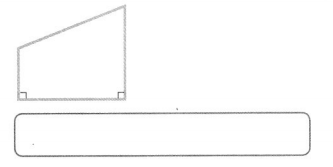
Answer:
The polygon is a trapezoid.
Explanation:
In the above-given question,
given that,
the figure has 4 different sides.
so the polygon is a trapezoid.
Question 9.
Identify the figure below using as many names as possible.
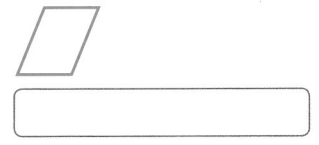
Answer:
The polygon is a parallelogram.
Explanation:
In the above-given question,
given that,
the figure has opposite sides equal lengths.
parallelogram also has the opposite sides equal lengths.
so the polygon is a parallelogram.
Question 10.
What shape has two pairs of opposite sides that are parallel and has all sides of equal length but does NOT have four right angles?
A. Square
B. Rectangle
C. Rhombus
D. Trapezoid
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
rhombus has two pairs of opposite sides that are parallel.
all sides of equal length but do not have 4 right angles.
so option C is correct.
Question 11.
Use the Venn diagram. Are rhombuses always, sometimes, or never also parallelograms? Explain.
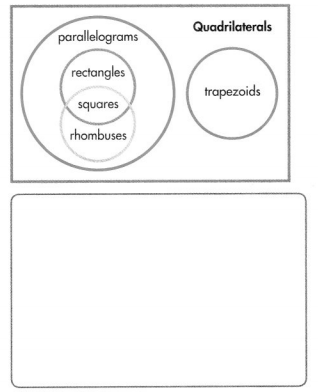
Answer:
Rhombuses are always a parallelogram.
Explanation:
In the above-given question,
given that,
rhombuses are parallelograms.
rhombus is a parallelogram with 4 equal sides.
area of the rhombus = 4 a.
where a = side.
so rhombuses are always a parallelogram.
Question 12.
Describe triangle HJK in terms of its sides and angles.
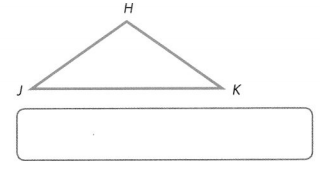
Answer:
The triangle is an isosceles triangle.
Explanation:
In the above-given question,
given that,
triangle HJK is an isosceles triangle.
an isosceles triangle has 2 sides equal.
so the triangle HJK is an isosceles triangle.
Topic 16 Performance Task
Geometry in Art
Artists often use triangles and quadrilaterals in their pictures.
Question 1.
Use the Poster to answer the following questions.
Part A
Classify Triangle 1 in the Poster by its angles and by its sides.

Answer:
The triangle is a scalene triangle.
Explanation:
In the above-given question,
given that,
triangle 1 is a scalene triangle.
a scalene triangle has three different sides.
Part B
What are all of the names you can use to describe Shape 2 in the Poster?
Answer:
Shape 2 is a parallelogram.
Explanation:
In the above-given question,
given that,
shape 2 is a parallelogram.
a parallelogram has two pairs of equal parallel sides.
shape 2 is a parallelogram.
Part C
Triangles 3 and 4 are identical. They are joined in the Poster to form a square. Construct a math argument to show why Triangles 3 and 4 are isosceles right triangles.
Part D
If Triangle 3 is joined with another triangle that is the same size and shape, do the two triangles always form a square? Construct a math argument to explain your reasoning.
Part E
What are the measures of the angles of Triangle 3? Note that two angles in an isosceles triangle always have the same measure. Explain.
Answer:
Triangle 3 is a rhombus.
Explanation:
In the above-given question,
given that,
triangle 3 is a rhombus.
in the rhombus, there are 2 equilateral triangles.
triangles 3 and 4 are equilateral triangles.
so triangle 3 is a rhombus.
Question 2.
Classify the triangles and quadrilaterals in the Houses drawing to answer the following questions.
Part A
Are all the triangles shown in the design isosceles? Are they all equilateral? Construct a math argument, using properties, to explain why or why not.

Answer:
Yes, the triangles are equilateral and isosceles triangle.
Explanation:
In the above-given question,
given that,
there are equilateral and isosceles triangles.
an equilateral triangle has all the 3 sides are equal.
an isosceles triangle has only two sides that are equal.
so the triangles are both equilateral and isosceles triangle.
Part B
All of the quadrilaterals in the Houses drawing are rectangles. Does that mean all of the quadrilaterals are parallelograms? Does that mean all are squares? Construct a math argument, using properties, to explain your reasoning.
Answer:
Yes, all of the quadrilaterals in the house drawing are rectangles.
Explanation:
In the above-given question,
given that,
all of the quadrilaterals in the house drawing are rectangles.
all the quadrilaterals are parallelograms.
all squares are rectangles.
so all of the quadrilaterals in the house drawing are rectangles.