Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 7 Use Equivalent Fractions to Add and Subtract Fractions regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 7 Use Equivalent Fractions to Add and Subtract Fractions
Use Equivalent Fractions to Add and Subtract Fractions
Essential Questions: How can sums and differences of fractions and mixed numbers be estimated? What are common procedures for adding and subtracting fractions and mixed numbers?

enVision STEM Project: Fossils Tell Story
Do Research Use the Internet or other sources to find out more about fossils. What are fossils? How and where do we find them? What do they tell us about the past? What can they tell us about the future? Pay particular attention to fossils from the Eocene epoch.
Journal: Write a Report Include what you found. Also in your report:
• Describe a fossil that you have seen or would like to find.
• Tell if there are any fossils where you live.
• Make up and solve addition and subtraction problems about fossils. Use fractions and mixed numbers in your problems.
Review What You Know
Choose the best term from the box. Write it on the blank.
Vocabulary
• denominator
• numerator
• unit fraction
• fraction
• mixed number
Question 1.
A ___ has a whole number part and a fraction part.
Answer:
A Mixed Number has a whole number part and a fraction part.
Question 2.
A ___ represents the number of equal parts in one whole.
Answer:
A Denominator represents the number of equal parts in one whole
Question 3.
A ___ has a numerator of 1.
Answer:
A Unit Fraction has a numerator of 1.
Question 4.
A symbol used to name one or more parts of a whole or a set, or a location on the number line, is a ____.
Answer:
A symbol used to name one or more parts of a whole or a set, or a location on the number line, is a Fraction.
Compare Fractions
Compare. Write >, <, or = for each ![]() .
.
Question 5.
\(\frac{1}{5}\) ![]() \(\frac{1}{15}\)
\(\frac{1}{15}\)
Answer:
\(\frac{1}{5}\) ![]() \(\frac{1}{15}\)
\(\frac{1}{15}\)
Question 6.
\(\frac{17}{10}\) ![]() \(\frac{17}{5}\)
\(\frac{17}{5}\)
Answer:
\(\frac{17}{10}\) ![]() \(\frac{17}{5}\)
\(\frac{17}{5}\)
Question 7.
\(\frac{5}{25}\) ![]() \(\frac{2}{5}\)
\(\frac{2}{5}\)
Answer:
\(\frac{5}{25}\) ![]() \(\frac{2}{5}\)
\(\frac{2}{5}\)
Question 8.
\(\frac{12}{27}\) ![]() \(\frac{6}{9}\)
\(\frac{6}{9}\)
Answer:
\(\frac{12}{27}\) ![]() \(\frac{6}{9}\)
\(\frac{6}{9}\)
Question 9.
\(\frac{11}{16}\) ![]() \(\frac{2}{8}\)
\(\frac{2}{8}\)
Answer:
\(\frac{11}{16}\) ![]() \(\frac{2}{8}\)
\(\frac{2}{8}\)
Question 10.
\(\frac{2}{7}\) ![]() \(\frac{1}{5}\)
\(\frac{1}{5}\)
Answer:
\(\frac{2}{7}\) ![]() \(\frac{1}{5}\)
\(\frac{1}{5}\)
Question 11.
Liam bought \(\frac{5}{8}\) pound of cherries. Harrison bought more cherries than Liam. Which could be the amount of cherries that Harrison bought?
A. \(\frac{1}{2}\) pound
B. \(\frac{2}{5}\) pound
C. \(\frac{2}{3}\) pound
D. \(\frac{3}{5}\) pound
Answer:
D. \(\frac{3}{5}\) pound
Question 12.
Jamie has read \(\frac{1}{4}\) of a book. Raul has read of the same book. Who is closer to reading the whole book? Explain.
Answer: Jamie and Raul are in the same position to complete the book because Jamie has read \(\frac{1}{4}\) of a book and also Raul has read \(\frac{1}{4}\) of a book. They both completed the same book with same amount. Both are equal.
Equivalent Fractions
Write a fraction equivalent to each fraction.
Question 13.
\(\frac{6}{18}\)
Answer:
\(\frac{6}{18}\) x 2 = \(\frac{12}{32}\)
Question 14.
\(\frac{12}{22}\)
Answer:
\(\frac{12}{22}\) x 2 = \(\frac{24}{44}\)
Question 15.
\(\frac{15}{25}\)
Answer:
\(\frac{15}{25}\) x 2 = \(\frac{30}{50}\)
Question 16.
\(\frac{8}{26}\)
Answer:
\(\frac{8}{26}\) x 2 = \(\frac{16}{52}\)
Question 17.
\(\frac{14}{35}\)
Answer:
\(\frac{14}{35}\) x 2 = \(\frac{28}{70}\)
Question 18.
\(\frac{4}{18}\)
Answer:
\(\frac{4}{18}\) x 2 = \(\frac{8}{36}\)
Question 19.
\(\frac{1}{7}\)
Answer:
\(\frac{1}{7}\) x 2 = \(\frac{1}{14}\)
Question 20.
\(\frac{4}{11}\)
Answer:
\(\frac{4}{11}\) x 2 = \(\frac{8}{22}\)
Pick a Project
PROJECT 7A
What’s in your gumbo?
Project: Record a Cooking Show

PROJECT 7B
Does this story sound fishy?
Project: Write a Tall Tale about Fishing Friends

PROJECT 7C
How many cups of juice can you get from 5 oranges?
Project: Get the Juice from Oranges

3-ACT MATH PREVIEW
Math Modeling
The Gif Recipe
Before watching the video, think: Some recipes are easier to follow than others. I’ve never made this one before. Maybe I should read the entire recipe before starting to cook.

Lesson 7.1 Estimate Sums and Differences of Fractions
Activity
Solve&Share
Jack needs about 1\(\frac{1}{2}\) yards of string. He has three pieces of string that are different lengths. Without finding the exact amount, which two pieces should he choose to get closest to 1\(\frac{1}{2}\) yards of string? Solve this problem any way you choose.
Reasoning You can use number sense to estimate the answer. Show your work!
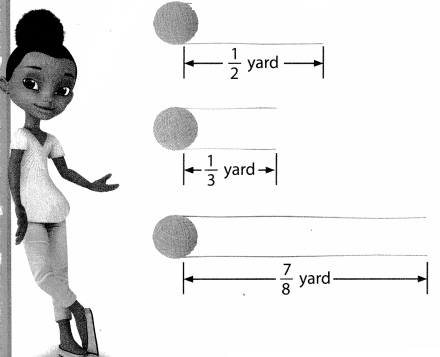
Answer:

Look Back! How can a number line help you estimate?
Answer: It helps me to estimate the appropriate answer. It makes easy to add the yards and easy to find the yards which are closet to the given yard. It is somewhat in a elaborate way.
Visual Learning Bridge
Essential Question How Can You Estimate the Sum of Two Fractions?
A.
Mr. Fish is welding together two copper pipes to repair a leak. He will use the pipes shown. Is the new pipe closer to \(\frac{1}{2}\) foot or 1 foot long? Explain.

B.
Step 1
Replace each fraction with the nearest half or whole. A number line can make it easy to decide if each fraction is closest to 0, \(\frac{1}{2}\), or 1.
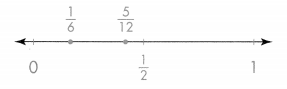
\(\frac{1}{6}\) is between 0 and 2, but is closer to 0.
\(\frac{5}{12}\) is also between 0 and 2, but is closer to the benchmark fraction \(\frac{1}{2}\).
C.
Step 2
Add to find the estimate.
A good estimate of \(\frac{1}{6}\) + \(\frac{5}{12}\) is 0 + \(\frac{1}{2}\), or \(\frac{1}{2}\). So, the welded pipes will be closer to 2 foot than 1 foot long
Since each addend is less than 5, it is reasonable that their sum is less than 1.

Convince Me! Critique Reasoning Nolini says that if the denominator is more than twice the numerator, the fraction can always be replaced with 0. Is she correct? Give an example in your explanation.
Answer: Yes,
It depends on how accurate you want your answer to be, but basically yes, imagine we set our numerator to be x, and our denominator to be 2x, if we built our fraction we will get that: If the denominator of a fraction is exactly twice the numerator, then the fraction will be simplified to 1/2 or 0.5.Now, the greater the denominator is, the closer the fraction will get to zero.
Take for example I had an fraction like this:
which approximates to 0. If we made the denominator bigger, let’s say 7, we would get:
notice the answer is closer to 0 this time, so it’s valid to round it to zero. If we made the denominator greater, let’s say 25, we would get: and so on. So it is true that if the denominator of a fraction is greater than twice the numerator, we can always replace the fraction with a 0
(depending on how accurate you want your answer to be).
Guided Practice
Do You Understand?
Question 1.
In the problem at the top of page 270, would you get the same estimate if Mr. Fish’s pipes measured foot and \(\frac{7}{12}\) foot?
Answer:
Yes, The estimation would be the same because Mr. Fish’s pipes measured foot is \(\frac{1}{6}\) + \(\frac{5}{12}\) = 0.5 and the \(\frac{7}{12}\) = 0.5
Question 2.
Number Sense If a fraction has a 1 in the numerator and a number greater than 2 in the denominator, will the fraction be closer to 0, \(\frac{1}{2}\), or 1? Explain.
Answer:
If a fraction has a 1 in the numerator and a number greater than 2 in the denominator, will the fraction be closer to \(\frac{1}{2}\) because the numerator is 1 and the denominator is 2 that means \(\frac{1}{2}\) = 0.5
Do You Know How?
In 3 and 4, use a number line to tell if each fraction is closest to 0, \(\frac{1}{2}\), or 1. Then estimate the sum or difference.
Question 3.
a. \(\frac{11}{12}\) Closest to: ___
b. \(\frac{1}{6}\) Closest to: _____
Estimate the sum \(\frac{11}{12}\) + \(\frac{1}{6}\)
c. 1 + __ = __
Answer:
a. \(\frac{11}{12}\) Closest to: 1
b. \(\frac{1}{6}\) Closest to: \(\frac{1}{2}\)
Estimate the sum \(\frac{11}{12}\) + \(\frac{1}{6}\)
c. 1 +\(\frac{1}{2}\) = 1.5
Question 4.
![]()
a. \(\frac{14}{16}\) Closest to: ___
b. \(\frac{5}{8}\) Closest to: ___
Estimate the difference \(\frac{14}{16}\) – \(\frac{5}{8}\).
c. ___ – ___ = ___
Answer:
a. \(\frac{14}{16}\) Closest to: 1
b. \(\frac{5}{8}\) Closest to: \(\frac{1}{2}\)
Estimate the difference \(\frac{14}{16}\) – \(\frac{5}{8}\).
c. 1 – \(\frac{1}{2}\) = 0.5
Independent Practice
Leveled Practice In 5, use a number line to tell if each fraction is closest to 0, \(\frac{1}{2}\), or 1
In 6-11, estimate the sum or difference by replacing each fraction with 0, \(\frac{1}{2}\), or 1.
Question 5.
![]()
a. \(\frac{7}{8}\) Closest to: ____
b. \(\frac{5}{12}\) Closest to: ___
Estimate the difference \(\frac{7}{8}\) – \(\frac{5}{12}\)
c. ___ – ___ = ___
Answer:
a. \(\frac{7}{8}\) Closest to: 1
b. \(\frac{5}{12}\) Closest to: \(\frac{1}{2}\)
Estimate the difference \(\frac{7}{8}\) – \(\frac{5}{12}\)
c. 1 – 0.5 = 0.5
Question 6.
\(\frac{9}{10}\) + \(\frac{5}{6}\)
Answer:
\(\frac{9}{10}\) + \(\frac{5}{6}\) = 1.7
Question 7.
\(\frac{11}{18}\) – \(\frac{2}{9}\)
Answer:
\(\frac{11}{18}\) – \(\frac{2}{9}\) = 0.2
Question 8.
\(\frac{1}{16}\) + \(\frac{2}{15}\)
Answer:
\(\frac{1}{16}\) + \(\frac{2}{15}\) = 0.16
Question 9.
\(\frac{24}{25}\) – \(\frac{1}{9}\)
Answer:
\(\frac{24}{25}\) – \(\frac{1}{9}\) = 0.86
Question 10.
\(\frac{3}{36}\) + \(\frac{1}{10}\)
Answer:
\(\frac{3}{36}\) + \(\frac{1}{10}\) = 0.18
Question 11.
\(\frac{37}{40}\) – \(\frac{26}{50}\)
Answer:
\(\frac{37}{40}\) – \(\frac{26}{50}\) = 0.4
Problem Solving
Question 12.
Number Sense Name two fractions that are closer to 1 than to \(\frac{1}{2}\). Then, name two fractions that are closer to \(\frac{1}{2}\) than to 0 or 1 and two other fractions that are closer to 0 than to \(\frac{1}{2}\). Find two of your fractions that have a sum of about 1\(\frac{1}{2}\).

Answer:
a(1). \(\frac{25}{30}\) = 0.8 which is closet to 1.
(2). \(\frac{9}{10}\) = 0.9 which is closet to 1.
b(1). \(\frac{5}{12}\) = 0.4 which is closet to \(\frac{1}{2}\).
(2). \(\frac{3}{6}\) = 0.5 which is closet to \(\frac{1}{2}\).
c(1).\(\frac{1}{16}\) = 0.06 which is closet to 0
(2).\(\frac{2}{30}\) = 0.06 which is closet to 0
The two fractions that have a sum of about 1\(\frac{1}{2}\) = \(\frac{25}{30}\) + \(\frac{3}{6}\) = 1.4
Question 13.
Higher Order Thinking How would you estimate whether \(\frac{27}{50}\) is closer to c or 1 without using a number line? Explain.
Answer: \(\frac{27}{50}\) is closer to \(\frac{1}{2}\).
Because I find it by dividing them \(\frac{27}{50}\) = 0.5 and \(\frac{1}{2}\) = 0.5
Question 14.
Katie made a bag of trail mix with \(\frac{1}{2}\) cup of raisins, \(\frac{3}{5}\) cup of banana chips, and \(\frac{3}{8}\) cup of peanuts. About how much trail mix did Katie make?
Answer: \(\frac{1}{2}\) + \(\frac{3}{5}\) + \(\frac{3}{8}\) = 1\(\frac{1}{2}\)
Question 15.
Reasoning The Annual Mug Race is the longest river sailboat race in the world. The event is run along the St. Johns River, which is 310 miles long. About how many times as long as the race is the river?
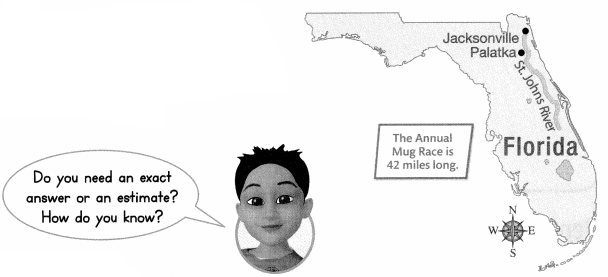
Answer: The Annual Mug Race is 42 miles and the St. Johns River, which is 310 miles long. So to find out the answer for this we need to divide the River by race so then we can find the times as answer.
310/42 = 7.4 times the river is long as the race
Assessment Practice
Question 16.
Part A
Steve is making breakfast. The recipes call for a cup of milk for grits and cup for biscuits. He only has 2 cups of milk. Does he have enough to make his breakfast? Explain.
Answer: Yes! He has enough cups of milk to make breakfast that means he has 2 cups of milk and one cup is for grits and another cup is for biscuits. So, Total 2 cups of milk.
Part B
If he has enough milk, about how much milk will he have left? If he doesn’t have enough milk, about how much will he need?
Answer: He has enough cups of milk to make breakfast that means he has 2 cups of milk and one cup is for grits and another cup is for biscuits. So, Total 2 cups of milk. He has enough cups of milk he will be left nothing at the end. If he has only one cup of milk means he need other cup of milk for biscuits.
Lesson 7.2 Find Common Denominators
Solve&Share
Sue wants \(\frac{1}{2}\) of a rectangular pan of cornbread. Dena wants of the same pan of cornbread. How should you cut the cornbread so that each girl gets the size portion she wants? Solve this problem any way you choose.
You can draw a picture to represent the pan as 1 whole. Then solve. Show your work!

Answer:-

Look Back! Construct Arguments Is there more than one way to divide the pan of cornbread into equal-sized parts? Explain how you know.
Answer: Sue wants half of the cornbread and Dena wants same amount. Here, we have 1 whole pan from this we gonna share into two for that we divided the whole pan into two. i.e., \(\frac{1}{2}\) = 0.5 and we have shared it to Sue and Dena.
Visual Learning Bridge
Essential Question
How Can You Find Common Denominators?
A.
Tyrone partitioned a rectangle into thirds. Sally partitioned a rectangle of the same size into fourths. How could you partition a rectangle of the same size so that you see both thirds and fourths?
You can partition a rectangle to show thirds or fourths.

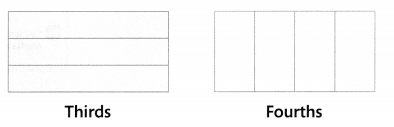
B.
This rectangle is partitioned into thirds and fourths.

The rectangle is partitioned into 12 equal parts. Each part is \(\frac{1}{12}\)
C.
The fractions \(\frac{1}{3}\) and \(\frac{1}{4}\) can be renamed with equivalent fractions.
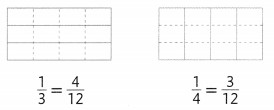
Fractions that have the same denominators, such as \(\frac{4}{12}\) and \(\frac{3}{12}\), are said to have common denominators.
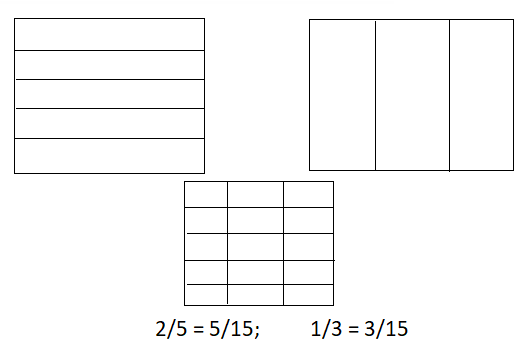
Convince Me! Use Appropriate Tools Draw rectangles such as the ones above to find fractions equivalent to \(\frac{2}{5}\) and \(\frac{1}{3}\) that have the same denominator.
Answer:
Another Example
Find a common denominator for \(\frac{2}{3}\) and \(\frac{5}{6}\). Then rename each fraction with an equivalent fraction.

One Way
Multiply the denominators to find a common denominator: 3 × 6 = 18.
Write equivalent fractions with denominators of 18.
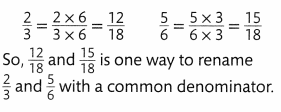
Another Way
Use the fact that one denominator is a multiple of the other.
You know that 6 is a multiple of 3.
![]()
So, \(\frac{4}{6}\) and \(\frac{5}{6}\) is one way to rename \(\frac{2}{3}\) and \(\frac{5}{6}\) with a common denominator.
Guided Practice
Do You Understand?
Question 1.
In the example on the previous page, how many twelfths are in \(\frac{1}{3}\) each section of Tyrone’s rectangle? How many twelfths are in each \(\frac{1}{4}\) section of Sally’s rectangle?
Answer:
In Tyrone’s rectangle there are \(\frac{4}{12}\) twelfths in \(\frac{1}{3}\) and there are \(\frac{3}{12}\) are there in \(\frac{1}{4}\)
Do You Know How?
In 2 and 3, find a common denominator for each pair of fractions.
Question 2.
\(\frac{3}{8}\) and \(\frac{2}{3}\)
Answer:

Question 3.
\(\frac{1}{6}\) and \(\frac{4}{3}\)
Answer:
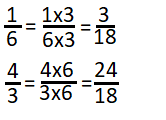
Independent Practice
In 4-11, find a common denominator for each pair of fractions. Then write equivalent fractions with the common denominator.
Question 4.
\(\frac{2}{5}\) and \(\frac{1}{6}\)
Answer:
\(\frac{2}{5}\) = \(\frac{2}{5}\) x \(\frac{6}{6}\) = \(\frac{12}{30}\)
\(\frac{1}{6}\) = \(\frac{1}{6}\) x \(\frac{5}{5}\) = \(\frac{5}{30}\)
Question 5.
\(\frac{1}{3}\) and \(\frac{4}{5}\)
Answer:
\(\frac{1}{3}\) = \(\frac{1}{3}\) x \(\frac{5}{5}\) = \(\frac{5}{5}\)
\(\frac{4}{5}\) = \(\frac{4}{5}\) x \(\frac{3}{3}\) = \(\frac{12}{15}\)
Question 6.
\(\frac{5}{8}\) and \(\frac{3}{4}\)
Answer:
\(\frac{5}{8}\)v = \(\frac{5}{8}\) x \(\frac{4}{4}\) = \(\frac{20}{32}\)
\(\frac{3}{4}\) = \(\frac{3}{4}\) x \(\frac{8}{8}\) = \(\frac{24}{32}\)
Question 7.
\(\frac{3}{10}\) and \(\frac{9}{8}\)
Answer:
\(\frac{3}{10}\) = \(\frac{3}{10}\) x \(\frac{8}{8}\) = \(\frac{24}{80}\)
\(\frac{9}{8}\) = \(\frac{9}{8}\) x \(\frac{10}{10}\) = \(\frac{90}{80}\)
Question 8.
\(\frac{3}{7}\) and \(\frac{1}{2}\)
Answer:
\(\frac{3}{7}\) = \(\frac{3}{7}\) x \(\frac{2}{2}\) = \(\frac{6}{14}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) x \(\frac{7}{7}\) = \(\frac{7}{14}\)
Question 9.
\(\frac{5}{12}\) and \(\frac{3}{5}\)
Answer:
\(\frac{5}{12}\) = \(\frac{5}{12}\) x \(\frac{5}{5}\) = \(\frac{25}{60}\)
\(\frac{3}{5}\) = \(\frac{3}{5}\) x \(\frac{12}{12}\) = \(\frac{36}{60}\)
Question 10.
\(\frac{7}{9}\) and \(\frac{2}{3}\)
Answer:
\(\frac{7}{9}\) = \(\frac{7}{9}\) x \(\frac{3}{3}\) = \(\frac{21}{27}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) x \(\frac{9}{9}\) = \(\frac{18}{27}\)
Question 11.
\(\frac{3}{8}\) and \(\frac{9}{20}\)
Answer:
\(\frac{3}{8}\) = \(\frac{3}{8}\) x \(\frac{20}{20}\) = \(\frac{60}{160}\)
\(\frac{9}{20}\) = \(\frac{9}{20}\) x \(\frac{8}{8}\) = \(\frac{72}{160}\)
Problem Solving
Question 12.
Critique Reasoning Explain any mistakes in the renaming of the fractions below. Show the correct renaming.
\(\frac{3}{4}\) = \(\frac{9}{12}\) \(\frac{2}{3}\) = \(\frac{6}{12}\)
Answer:
\(\frac{3}{4}\) = \(\frac{9}{12}\)
\(\frac{2}{3}\) = \(\frac{8}{12}\)
Question 13.
Higher Order Thinking For keeping business records, every three months of a year is called a quarter. How many months are equal to three-quarters of a year? Explain how you found your answer.
Answer: One quarter = \(\frac{3}{12}\) So, 3 quarters = \(\frac{9}{12}\)
Here, 12 = 12 months and 3 months = 1 quarter. Therefore, 3 + 3 + 3 = 9 months
Question 14.
Nelda baked two kinds of pasta in pans. Each pan was the same size. She sliced one pan of pasta into 6 equal pieces. She sliced the other pan into 8 equal pieces. How can the pans of pasta now be sliced so that both pans have the same-sized pieces? Draw on the pictures to show your work. If Nelda has served 6 pieces from one pan so far, what fraction of one pan has she served?

Answer:
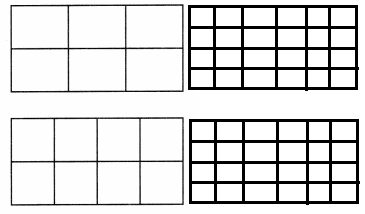
To reach her goal that both pans should have same sized pieces. So,
\(\frac{1}{6}\) x 4 pieces = \(\frac{1}{24}\). Therefore to set goal for the other pan also she needs to multiply with 3 pieces \(\frac{1}{8}\) x 3 = \(\frac{1}{24}\). So, Finally she sets her goal.
If Nelda has served 6 pieces from one pan so far, then there will be \(\frac{1}{24}\) – \(\frac{1}{6}\) = \(\frac{1}{18}\) will be left.
Question 15.
Number Sense What is the price of premium gasoline rounded to the nearest dollar? rounded to the nearest dime? rounded to the nearest penny?

Answer:
$4.409 to the nearest dime: $4.40
to the nearest penny: $4.41
to the nearest dollar: $4.00
Assessment Practice
Question 16.
Choose all the numbers that could be common denominators for and
![]() 8
8
![]() 12
12
![]() 16
16
![]() 36
36
![]() 48
48
Answer:
Question 17.
Choose all the numbers that could be common denominators for \(\frac{11}{12}\) and \(\frac{4}{5}\)
![]() 12
12
![]() 17
17
![]() 30
30
![]() 60
60
![]() 125
125
Answer:
![]()
Lesson 7.3 Add Fractions with Unlike Denominators
Activity
Solve & Share
Over the weekend, Eleni ate \(\frac{1}{4}\) box of cereal, and Freddie ate \(\frac{3}{8}\) of the same box. What portion of the box of cereal did they eat in all? Solve this problem any way you choose.

You can use fraction strips to represent adding fractions. Show your work!

Answer:
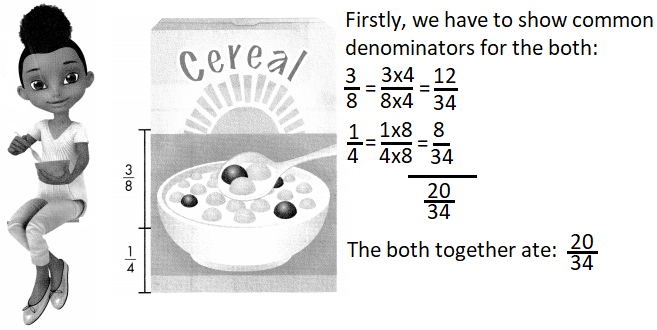
Look Back! Make Sense and Persevere What steps did you take to solve this problem?
Answer: Step 1: Finding their common fractions for common denominator
Step2: Multiply with the factor to get common denominator.
Step3: Adding the fractions after getting the common denominator.
Visual Learning Bridge
Essential Question
How Can You Add Fractions with Unlike Denominators?
A.
Alex rode his scooter from his house to the park. Later, he rode from the park to baseball practice. How far did Alex ride?
You can add to find the total distance that Alex rode his scooter.
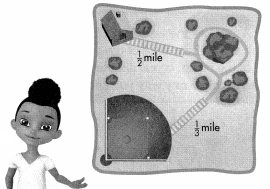
B.
Step 1
Change the fractions to equivalent fractions with a common, or like, denominator
The number 6 is a common multiple of 2 and 3, so \(\frac{1}{2}\) and \(\frac{1}{3}\) can both be rewritten with a common denominator of 6.
Step 2
Write equivalent fractions with a common denominator.
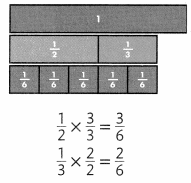
Step 3
Add the fractions to find the total number of sixths.
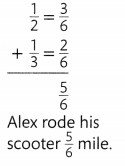
Convince Me! Construct Arguments in the example above, would you get the same sum if you used 12 as the common denominator? Explain.
Answer:
Step 1:
Place 112 fractions strips under the 1 whole strip on your Matboard. Then place a 14 fraction strip beside the 112 strips.
Step 2:
Find fraction strips, all with the same denominator, that are equivalent to 112 and 14. Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
14 x 33 = 312
112
Step 3:
Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form.
312 + 112 = 412
Another Example
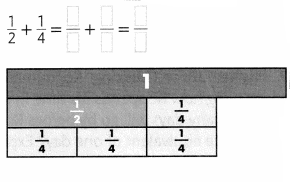
Find \(\frac{5}{12}\) + \(\frac{1}{4}\).
\(\frac{5}{12}\) + \(\frac{1}{4}\) = \(\frac{5}{12}\) + \(\frac{3}{12}\) Write equivalent fractions with common denominators.
= \(\frac{5+3}{12}\) = \(\frac{8}{12}\) or \(\frac{2}{3}\) Find the total number of twelfths by adding the numerators.
Guided Practice
Do You Understand?
Question 1.
In the example at the top of page 278, if the park was \(\frac{1}{8}\) mile from baseball practice instead of \(\frac{1}{3}\) mile, how far would Alex ride his scooter in all?
Answer:
\(\frac{1}{8}\) mile from baseball and \(\frac{1}{2}\) park to home then:
\(\frac{1}{8}\) = \(\frac{1}{8}\) x \(\frac{2}{2}\) = \(\frac{2}{16}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) x \(\frac{8}{8}\) = \(\frac{8}{16}\)
So, \(\frac{2}{16}\) + \(\frac{8}{16}\) = \(\frac{10}{16}\) or \(\frac{5}{8}\)
Question 2.
Vocabulary Rico and Nita solved the same problem. Rico got \(\frac{6}{8}\) for an answer, and Nita got \(\frac{3}{4}\). Which answer is correct? Use the term equivalent fraction in your explanation.
Answer:
No, They both were wrong. Rico and Nita got wrong answer. The answer is \(\frac{5}{8}\).
\(\frac{1}{8}\) mile from baseball and \(\frac{1}{2}\) park to home then:
\(\frac{1}{8}\) = \(\frac{1}{8}\) x \(\frac{2}{2}\) = \(\frac{2}{16}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) x \(\frac{8}{8}\) = \(\frac{8}{16}\)
So, \(\frac{2}{16}\) + \(\frac{8}{16}\) = \(\frac{10}{16}\) or \(\frac{5}{8}\)
Do You Know How?
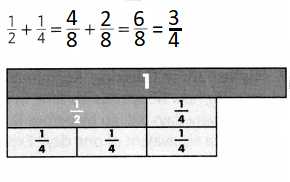
Find the sum. Use fraction strips to help.
Question 3.
Answer:
Independent Practice
In 4 and 5, find each sum. Use fraction strips to help.
Remember that you can use multiples to find a common denominator.

Question 4.
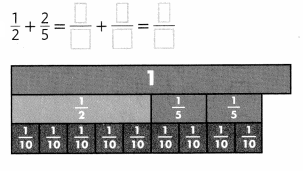
Answer:
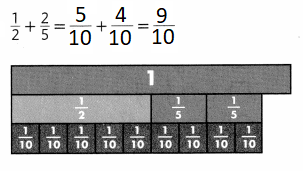
Question 5.
Answer:
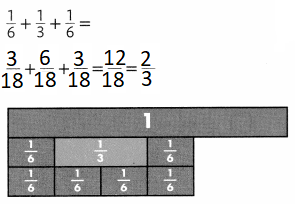
Problem Solving
Question 6.
Explain why the denominator 6 in \(\frac{3}{6}\) is not changed when adding the fractions.
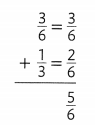
Answer:
A denominator indicates how many equal pieces make one unit. If you add the denominators when adding fractions, the new denominator will not show how many equal pieces are in one unit.
Question 7.
Model with Math About \(\frac{1}{10}\) of the bones in your body are in your skull. Your hands have about \(\frac{1}{4}\) of the bones in your body. Write and solve an equation to find the fraction of the bones in your body that are in your hands or skull.
Answer:
\(\frac{1}{10}\) = \(\frac{1}{10}\) x \(\frac{4}{4}\) = \(\frac{4}{40}\)
\(\frac{1}{4}\) = \(\frac{1}{4}\) x \(\frac{10}{10}\) = \(\frac{10}{40}\)
the fraction of the bones in your body that are in your hands or skull are: \(\frac{4}{40}\) + \(\frac{10}{40}\) = \(\frac{14}{40}\)
Question 8.
enVision® STEM Of 36 chemical elements, 2 are named for women scientists and 25 are named for places. What fraction of these 36 elements are named for women or places? Show your work.
Answer:

Question 9.
Higher Order Thinking Roger made a table showing how he spends his time in one day. How many days will go by before Roger has slept the equivalent of one day? Explain how you found your answer.

Answer:
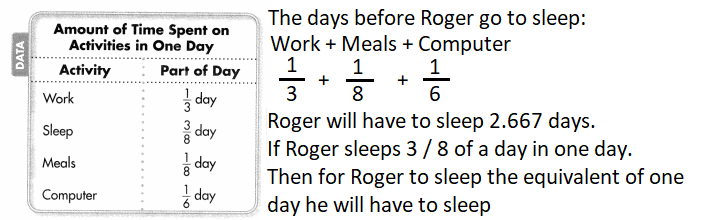
Assessment Practice
Question 10.
Which equations are true when is \(\frac{1}{2}\) is placed in the box?

Answer:
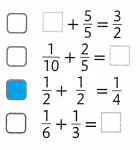
Question 11.
Which equations are true when \(\frac{4}{7}\) placed in the box?
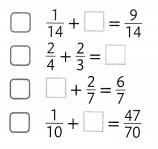
Answer:

Lesson 7.4 Subtract Fractions with Unlike Denominators
Activity
Solve & Share
Rose bought the length of copper pipe shown below. She used 5 yard to repair a water line in her house. How much pipe does she have left? Solve this problem any way you choose.
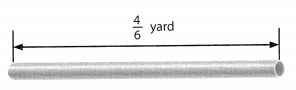
You can use mental math to find equivalent fractions so that \(\frac{1}{2}\) and \(\frac{4}{6}\) will have like denominators. Show your work!

Answer:-
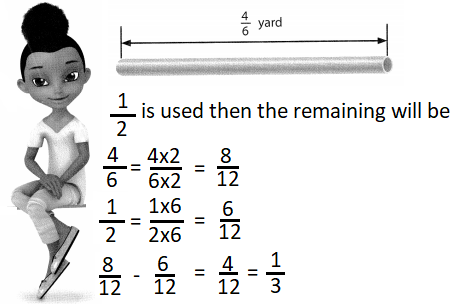
Look Back! Generalize How is subtracting fractions with unlike denominators similar to adding fractions with unlike denominators?
Answer:- Subtracting fractions with unlike denominators similar to adding fractions with unlike denominators because in addition firstly we do to set denominators alike and then we add them. Same here also of unlike denominators are there we do them alike and then we subtract. Adding and subtracting is the only difference remaining all the steps are same.
Visual Learning Bridge
Essential Question How Can You Subtract Fractions with Unlike Denominators?
A.
Linda used \(\frac{1}{4}\) yard of the fabric she bought for a sewing project. How much fabric did she have left?

You can use subtraction to find how much fabric was left.

B.
Step 1
Find a common multiple of the denominators.
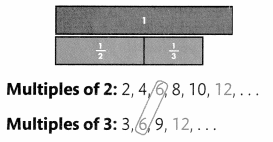
Multiples of 3: 3,6,9,12,…
Multiples of 4: 4, 8, 12,…
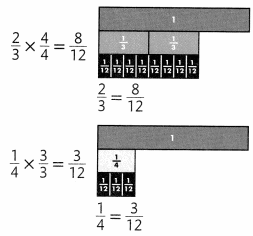
The number 12 is a multiple of 3 and 4. Write equivalent fractions with a denominator of 12 for \(\frac{2}{3}\) and \(\frac{1}{4}\).
C.
Step 2
Use the Identity Property to rename the fractions with a common denominator.
C.
Step 3
Subtract the numerators.
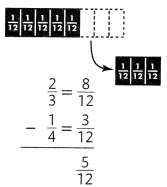
Linda has \(\frac{5}{12}\) yard of fabric left.
Convince Me! Critique Reasoning Suppose Linda had \(\frac{2}{3}\) of a yard of fabric and told Sandra that she used of a yard. Šandra says this is not possible. Do you agree? Explain your answer.
Answer:- No, That is not possible because Linda had \(\frac{2}{3}\) of a yard that is 0.6 yard then how can she use 1 yard of fabric that is why Sandra says this is not possible. So, here Sandra is correct in her way and Linda cannot use the 1 yard of fabric.
Guided Practice
Do You Understand?
Question 1.
In the example on page 282, is it possible to use a common denominator greater than 12 and get the correct answer? Why or why not?
Answer: We use the common denominator by figuring common multiply factors in the fraction if in the above example if we got common factor which is greater than 12 then it is always possible to get denominator which is greater than 12.
In the above example if we got common factor as 20 then it is easy to get denominator which is actually greater than 12 and if not we have to go with the common factor either 12 or below 12.
Question 2.
In the example on page 282, if Linda had started with one yard of fabric and used \(\frac{5}{8}\) of a yard, how much fabric would be left?
Answer: Linda had one yard of fabric and she used \(\frac{5}{8}\) of a yard, The she left with 1 – \(\frac{5}{8}\) = 0.4
Do You Know How?
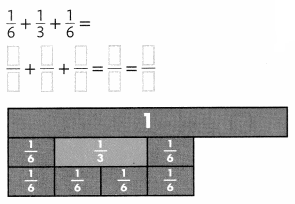
For 3-6, find each difference.
Question 3.
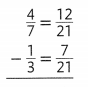
Answer:
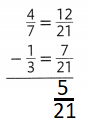
Question 4.
![]()
Answer:
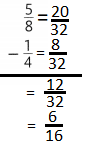
Question 5.
![]()
Answer:
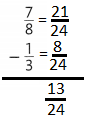
Question 6.
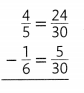
Answer:
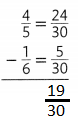
Independent Practice
Leveled Practice In 7-16, find each difference.
Question 7.
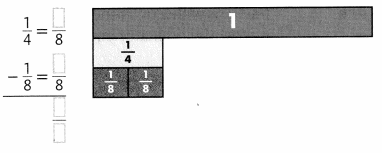
Answer:
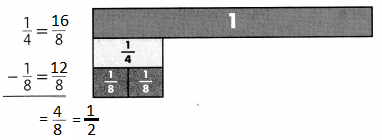
Question 8.

Answer:
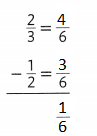
Question 9.
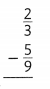
Answer:
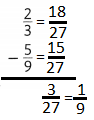
Question 10.
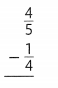
Answer:
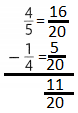
Question 11.
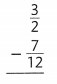
Answer:
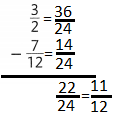
Question 12.
![]()
Answer:
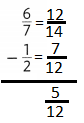
Question 13.
\(\frac{7}{10}\) – \(\frac{2}{5}\)
Answer:
\(\frac{7}{10}\) = \(\frac{7}{10}\) x \(\frac{5}{5}\) = \(\frac{21}{50}\)
\(\frac{2}{5}\) = \(\frac{2}{5}\) x \(\frac{10}{10}\) = \(\frac{20}{50}\)
\(\frac{21}{50}\) – \(\frac{20}{50}\) = \(\frac{1}{50}\)
Question 14.
\(\frac{13}{16}\) – \(\frac{1}{4}\)
Answer:
\(\frac{13}{16}\) = \(\frac{13}{16}\) x \(\frac{4}{4}\) = \(\frac{52}{64}\)
\(\frac{1}{4}\) = \(\frac{1}{4}\) x \(\frac{16}{16}\) = \(\frac{16}{64}\)
\(\frac{52}{64}\) – \(\frac{16}{64}\) = \(\frac{36}{64}\)
Question 15.
\(\frac{2}{9}\) – \(\frac{1}{6}\)
Answer:
\(\frac{2}{9}\) = \(\frac{2}{9}\) x \(\frac{6}{6}\) = \(\frac{12}{54}\)
\(\frac{1}{6}\) = \(\frac{1}{6}\) x \(\frac{9}{9}\) = \(\frac{9}{54}\)
\(\frac{12}{54}\) – \(\frac{9}{54}\) = \(\frac{3}{54}\)
Question 1
\(\frac{6}{5}\) – \(\frac{3}{8}\)
Answer:
\(\frac{6}{5}\) = \(\frac{6}{5}\) x \(\frac{8}{8}\) = \(\frac{48}{40}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\) x \(\frac{5}{5}\) = \(\frac{15}{40}\)
\(\frac{48}{40}\) – \(\frac{15}{40}\) = \(\frac{33}{40}\)
Problem Solving
Question 17.
Model with Math Write and solve an equation to find the difference between the location of Point A and Point B on the ruler.

Answer:
Point A: \(\frac{1}{4}\)
Point B: \(\frac{2}{5}\)
Point A: \(\frac{1}{4}\) x \(\frac{5}{5}\) = \(\frac{5}{20}\)
Point B: \(\frac{2}{5}\) x \(\frac{4}{4}\) = \(\frac{8}{20}\)
Point A – Point B = \(\frac{5}{20}\) – \(\frac{8}{20}\) = \(\frac{3}{20}\)
Question 18.
Algebra Write an addition and a subtraction equation for the diagram. Then, find the missing value.
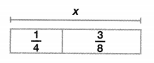
Answer:

Question 19.
Why do fractions need to have a common denominator before you add or subtract them?
Answer:
In order to add fractions, the fractions must have a common denominator. We need the pieces of each fraction to be the same size to combine them together. Since the pieces are all the same size, we can add these two fractions together.
Question 20.
Number Sense Without using paper and pencil, how would you find the sum of 9.8 and 2.6?
Answer: The sum of 9.8 and 2.6 is 9.8 + 2.6 = 12.4
Question 21.
Higher Order Thinking Find two fractions with a difference of \(\frac{1}{5}\) but with neither denominator equal to 5.
Answer:
There an infinite family of solutions. Any two fractions of the form:
(a+ b)/5a and b/5a
will work. Thus,
(a+b)/5a – b/5a = (a+b-b)/5a = a/5a = 1/5
of course, you can multiply each of the above fraction by 1, written as c/c, so you have c(a+b)/5ac if you wish to further obfuscate things. Similarly, you can also multiply the second fraction by 1 to get bd/5bd.
I’m sure there are other general answers as well, if an infinity of solutions is insufficient. You may wish to be sure that the product ac is even, so 5 won’t appear at all in the fraction as the last digit.
Assessment Practice
Question 22.
Choose the correct numbers from the box below to complete the subtraction sentence that follows.
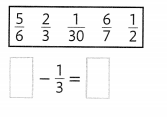
Answer:

Question 23.
Choose the correct numbers from the box below to complete the subtraction sentence that follows.

Answer:
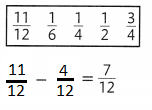
Lesson 7.5 Add and Subtract Fractions
Activity
Solver & Share
Tyler and Dean ordered pizza. Tyler ate \(\frac{1}{2}\) of the pizza and Dean ate \(\frac{1}{3}\) of the pizza. How much of the pizza was eaten, and how much is left? Solve this problem any way you choose.
Reasoning You can use number sense to help you solve this problem. Show your work!

Answer:

Look Back! How can you check that your answer makes sense?
Answer: It is easy to identify the answer because if we want how much pizza did they eat we can directly add the amount which they have ate and if we want to know how much pizza left we easily get by subtracting both.
Visual Learning Bridge
Essential Question
How Can Adding and Subtracting Fractions Help You Solve Problems?
A.
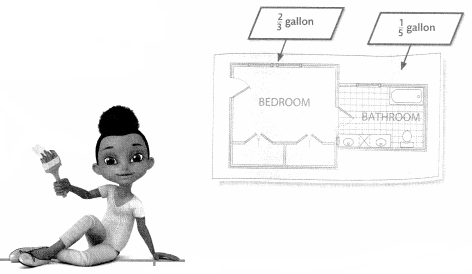
Kayla had \(\frac{9}{10}\) gallon of paint. She painted the ceilings in her bedroom and bathroom. How much paint does she have left after painting the two ceilings?
You can use both addition and subtraction to find how much paint she has left.
B.
Step 1
Add to find out how much paint Kayla used for the two ceilings.

Kayla used \(\frac{13}{15}\) gallon of paint
C.
Step 2
Subtract the amount of paint Kayla used from the amount she started with.

Kayla used \(\frac{1}{30}\) gallon of paint left.
Convince Me! Make Sense and Persevere For the problem above, how would you use estimation to check that the answer is reasonable?
Add to find out how much paint Kayla used for the two ceilings.

Kayla used \(\frac{13}{15}\) gallon of paint.
Subtract the amount of paint Kayla used from the amount she started with.

Kayla used \(\frac{1}{30}\) gallon of paint left.
Guided Practice
Do You Understand?
Question 1.
In the example on page 286, how much more paint did Kayla use to paint the bedroom ceiling than the bathroom ceiling?
Answer:
Add to find out how much paint Kayla used for the two ceilings.

Question 2.
Number Sense Kevin estimated the difference of \(\frac{9}{10}\) – \(\frac{4}{8}\) to be 0. Is his estimate reasonable? Explain.
Answer:
\(\frac{9}{10}\) = \(\frac{9}{10}\) x \(\frac{8}{8}\) = \(\frac{72}{80}\)
\(\frac{4}{8}\) = \(\frac{4}{8}\) x \(\frac{10}{10}\) = \(\frac{40}{80}\)
\(\frac{72}{80}\) – \(\frac{40}{80}\) = \(\frac{32}{80}\) = 0.4
Kevin estimated the difference of \(\frac{9}{10}\) – \(\frac{4}{8}\) to be 0 and his estimation was wrong because 0.4 is closest to \(\frac{1}{2}\) not closest to 0
Do You Know How?
For 3-6, find the sum or difference.
Question 3.

Answer:
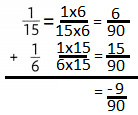
Question 4.
Answer:

Question 5.
\(\frac{7}{8}\) – \(\frac{3}{6}\)
Answer:
\(\frac{7}{8}\) = \(\frac{7}{8}\) x \(\frac{6}{6}\) = \(\frac{42}{48}\)
\(\frac{3}{6}\) = \(\frac{3}{6}\) x \(\frac{8}{8}\) = \(\frac{24}{48}\)
\(\frac{42}{48}\) – \(\frac{24}{48}\) = \(\frac{18}{48}\)
Question 6.
\(\frac{7}{8}\) + (\(\frac{4}{8}\) – \(\frac{2}{4}\))
Answer:
\(\frac{4}{8}\) = \(\frac{4}{8}\) x \(\frac{4}{4}\) = \(\frac{16}{32}\)
\(\frac{2}{4}\) = \(\frac{2}{4}\) x \(\frac{8}{8}\) = \(\frac{16}{32}\)
\(\frac{16}{32}\) – \(\frac{16}{32}\) = \(\frac{16}{32}\) = 0
\(\frac{7}{8}\) + (0) = \(\frac{7}{8}\)
Independent Practice
In 7-22, find the sum or difference.
Question 7.
![]()
Answer:
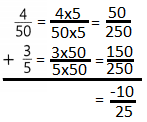
Question 8.
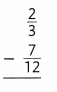
Answer:

Question 9.
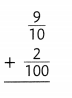
Answer:
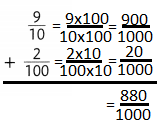
Question 10.

Answer:
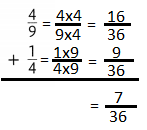
Question 11.
\(\frac{17}{15}\) – \(\frac{1}{3}\)
Answer:
\(\frac{17}{15}\) = \(\frac{17}{15}\) x \(\frac{3}{3}\) = \(\frac{51}{45}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) x \(\frac{15}{15}\) = \(\frac{15}{45}\)
\(\frac{51}{45}\) – \(\frac{15}{45}\) = \(\frac{36}{45}\)
Question 12.
\(\frac{7}{16}\) + \(\frac{3}{8}\)
Answer:
\(\frac{7}{16}\) = \(\frac{7}{16}\) x \(\frac{8}{8}\) = \(\frac{56}{128}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\) x \(\frac{16}{16}\) = \(\frac{48}{128}\)
\(\frac{56}{128}\) + \(\frac{48}{128}\) = \(\frac{8}{128}\)
Question 13.
\(\frac{2}{5}\) + \(\frac{1}{4}\)
Answer:
\(\frac{8}{20}\) + \(\frac{5}{20}\) = \(\frac{13}{20}\)
Question 14.
\(\frac{1}{7}\) + \(\frac{1}{2}\)
Answer:
\(\frac{2}{14}\) + \(\frac{7}{14}\) = \(\frac{9}{14}\)
Question 15.
\(\frac{1}{2}\) – \(\frac{3}{16}\)
Answer:
\(\frac{16}{32}\) – \(\frac{6}{32}\) = \(\frac{10}{32}\)
Question 16.
\(\frac{7}{8}\) – \(\frac{2}{3}\)
Answer:
\(\frac{14}{24}\) – \(\frac{16}{24}\) = – \(\frac{2}{24}\)
Question 17.
\(\frac{11}{12}\) – \(\frac{4}{6}\)
Answer:
\(\frac{66}{72}\) – \(\frac{48}{72}\) = \(\frac{18}{72}\)
Question 18.
\(\frac{7}{18}\) + \(\frac{5}{9}\)
Answer:
\(\frac{63}{162}\) + \(\frac{90}{162}\) = \(\frac{153}{162}\)
Question 19.
(\(\frac{7}{8}\) + \(\frac{1}{12}\)) – \(\frac{1}{2}\)
Answer:
\(\frac{84}{108}\) + \(\frac{8}{108}\) = \(\frac{92}{108}\)
\(\frac{184}{216}\) – \(\frac{92}{216}\) = \(\frac{92}{216}\)
Question 20.
(\(\frac{11}{18}\) – \(\frac{4}{9}\)) + \(\frac{1}{6}\)
Answer:
\(\frac{99}{162}\) – \(\frac{72}{162}\) = \(\frac{29}{162}\)
\(\frac{174}{648}\) + \(\frac{162}{648}\) = \(\frac{12}{648}\)
Question 21.
\(\frac{13}{14}\) – (\(\frac{1}{2}\) + \(\frac{2}{7}\))
Answer:
\(\frac{7}{14}\) + \(\frac{4}{14}\) = \(\frac{11}{14}\)
\(\frac{13}{14}\) – \(\frac{11}{14}\) = \(\frac{2}{14}\)
Question 22.
\(\frac{1}{6}\) + (\(\frac{15}{15}\) – \(\frac{7}{10}\))
Answer:
\(\frac{150}{150}\) – \(\frac{105}{150}\) = \(\frac{45}{150}\)
\(\frac{150}{900}\) + \(\frac{270}{900}\) = \(\frac{420}{900}\)
Problem Solving
Question 23.
The table shows the amounts of ingredients needed to make a pizza. How much more cheese do you need than pepperoni and mushrooms combined? Show how you solved the problem.

Answer:
Question 24.
Charlie’s goal is to use less than 50 gallons of water per day. His water bill for the month showed that he used 1,524 gallons of water in 30 days. Did Charlie meet his goal this month? Explain how you decided.
Answer:
Question 25.
Construct Arguments Jereen spent \(\frac{1}{4}\) hour on homework before school, another \(\frac{1}{2}\) hour after she got home, and a final \(\frac{1}{3}\) hour after dinner. Did she spend more or less than 1 hour on homework in all? Explain.
Answer:
Question 26.
Carl has three lengths of cable, \(\frac{5}{6}\) yard long, \(\frac{1}{4}\) yard long, and \(\frac{2}{3}\) yard long. If he uses 1 yard of cable, how much cable is left? Explain your work.
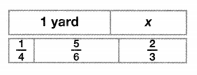
Answer:
Question 27.
Higher Order Thinking Find two fractions with a sum of \(\frac{2}{3}\) but with neither denominator equal to 3.
Answer:
Assessment Practice
Question 28.
What fraction is missing from the following equation?
![]()
A. \(\frac{4}{12}\)
B. \(\frac{3}{8}\)
C. \(\frac{5}{12}\)
D. \(\frac{8}{8}\)
Answer:
Question 29.
What is the value of the expression?
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{3}{8}\)
A. \(\frac{5}{8}\)
B. \(\frac{7}{8}\)
C. \(\frac{7}{16}\)
D. \(\frac{7}{32}\)
Answer:
Lesson 7.6 Estimate Sums and Differences of Mixed Numbers
Activity
Solve&Share
Alex has five cups of strawberries. He wants to use 1\(\frac{3}{4}\) cups of strawberries for a fruit salad and 3\(\frac{1}{2}\) cups for jam. Does Alex have enough strawberries to make both recipes? Solve this problem any way you choose.
Generalize You can estimate because you just need to know if Alex has enough. Show your work!

Look Back! Does it make sense to use 1 cup and 3 cups to estimate if Alex has enough strawberries? Explain.
Visual Learning Bridge
Essential Question What Are Some Ways to Estimate?
A.
Jamila’s mom wants to make a size 10 dress and jacket. About how many yards of fabric does she need?

B.
One Way
Use a number line to round fractions and mixed numbers to the nearest whole number
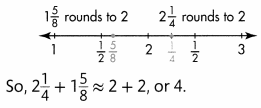
Jamila’s mom needs about 4 yards of fabric.
C.
Another Way
Use \(\frac{1}{2}\) as a benchmark fraction.
Replace each fraction with the nearest \(\frac{1}{2}\) unit.
1\(\frac{5}{8}\) is close to 1\(\frac{1}{2}\).
2\(\frac{1}{4}\) is halfway between 2 and 2\(\frac{1}{2}\)
You can replace 2\(\frac{1}{4}\) with 2\(\frac{1}{2}\).

So, 2\(\frac{1}{4}\) + 1\(\frac{5}{8}\) is about 2\(\frac{1}{2}\) + 1\(\frac{1}{2}\) = 4.
Convince Me! Critique Reasoning In Box C above, why does it make sense to replace 2\(\frac{1}{4}\) with 2\(\frac{1}{2}\) rather than 2?
Guided Practice
Do You Understand?
Question 1.
To estimate with mixed numbers, when should you round to the next greater whole number?
Answer:
Question 2.
When should you estimate a sum or difference?
Answer:
Do You Know How?
In 3-5, round to the nearest whole number.
Question 3.
2\(\frac{3}{4}\)
Answer:
Question 4.
1\(\frac{5}{7}\)
Answer:
Question 5.
2\(\frac{3}{10}\)
Answer:
In 6 and 7, estimate each sum or difference using benchmark fractions.
Question 6.
2\(\frac{5}{9}\) – 1\(\frac{1}{3}\)
Answer:
Question 7.
2\(\frac{4}{10}\) + 3\(\frac{5}{8}\)
Answer:
Independent Practice
Leveled Practice In 8-11, use the number line to round the mixed numbers to the nearest whole numbers.
Question 8.
11\(\frac{4}{6}\)
Answer:
Question 9.
11\(\frac{2}{8}\)
Answer:
Question 10.
11\(\frac{8}{12}\)
Answer:
Question 11.
11\(\frac{4}{10}\)
Answer:
In 12-20, estimate each sum or difference.
Question 12.
2\(\frac{1}{8}\) – \(\frac{5}{7}\)
Answer:
Question 13.
12\(\frac{1}{3}\) + 2\(\frac{1}{4}\)
Answer:
Question 14.
2\(\frac{2}{3}\) + \(\frac{7}{8}\) + 6\(\frac{7}{12}\)
Answer:
Question 15.
1\(\frac{10}{15}\) – \(\frac{8}{9}\)
Answer:
Question 16.
10\(\frac{5}{6}\) – 2\(\frac{3}{8}\)
Answer:
Question 17.
12\(\frac{8}{25}\) + 13\(\frac{5}{9}\)
Answer:
Question 18.
48\(\frac{1}{10}\) – 2\(\frac{7}{9}\)
Answer:
Question 19.
33\(\frac{14}{15}\) + 23\(\frac{9}{25}\)
Answer:
Question 20.
14\(\frac{4}{9}\) + 25\(\frac{1}{6}\) + 7\(\frac{11}{18}\)
Answer:
Problem Solving
Question 21.
Use the recipes to answer the questions.
a. Estimate how many cups of Fruit Trail Mix the recipe can make.

b Estimate how many cups of Traditional Trail Mix the recipe can make.
c Estimate how much trail mix you would have if you made both recipes.
Answer:
Question 22.
Kim is 3\(\frac{5}{8}\) inches taller than Colleen. If Kim is 60 inches tall, what is the best estimate of Colleen’s height?
Answer:
Question 23.
Higher Order Thinking Last week Jason walked 3\(\frac{1}{4}\) miles each day for 3 days and 4\(\frac{5}{8}\). miles each day for 4 days. About how many miles did Jason walk last week?
Answer:
Question 24.
Make Sense and Persevere Cal has $12.50 to spend. He wants to ride the roller coaster twice and the Ferris wheel once. Does Cal have enough money? Explain. What are 3 possible combinations of rides Cal can take using the money he has?
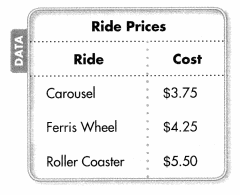
Answer:
Assessment Practice
Question 25.
Liam used 2\(\frac{2}{9}\) cups of milk for a pancake recipe and drank another 93 cups of milk. About how much milk did he use in all?
A. 8 cups
B. 10 cups
C. 12 cups
D. 13 cups
Answer:
Question 26.
Annie has 13\(\frac{1}{2}\) yards of string. She uses 1\(\frac{9}{10}\) yards to fix her backpack. About how much string does she have left?
A. 11 yards
B. 12 yards
C. 14 yards
D. 15 yards
Answer:
Lesson 7.7 Use Models to Add Mixed Numbers
Solve&Share
Martina is baking bread. She mixes 1\(\frac{3}{4}\) cups of flour with other ingredients. Then she adds 4\(\frac{1}{2}\) cups of flour to the mixture. How many cups of flour does she need? Solve this problem any way you choose.
Use Appropriate Tools You can use fraction strips to help add mixed numbers. Show your work!

Look Back! Explain how you can estimate the sum above.
Visual Learning Bridge
Essential Question How Can You Model Addition master of Mixed Numbers?
A.
Bill has 2 boards he will use to make picture frames. What is the total length of the boards Bill has to make picture frames?
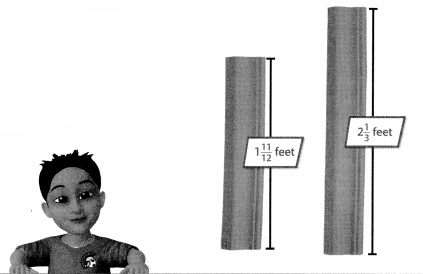
You can find a common denominator to add the fractions.
B.
Step 1
Rename the fractional parts as equivalent fractions with a like denominator. Add the fractions.
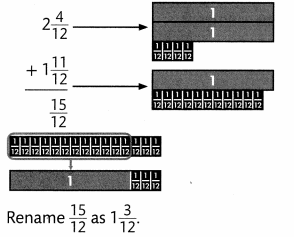
C.
Step 2
Add the whole number parts.

Then add the sum of the fractional parts.
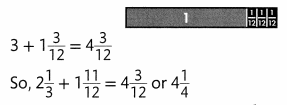
The total length of the boards is 4\(\frac{1}{4}\) feet.
Convince Me! Critique Reasoning Tom has 2 boards that are the same length as Bill’s. He says that he found the total length of the boards by adding 28 twelfths and 23 twelfths. Does his method work? Explain.
Guided Practice
Do You Understand?
Question 1.
When adding two mixed numbers, does it ever make sense to rename the fractional sum? Explain.
Answer:
Do You Know How?
In 2-5, use fraction strips to find each sum.
Question 2.
1\(\frac{1}{10}\) + 2\(\frac{4}{5}\)
Answer:
Question 3.
1\(\frac{1}{2}\) + 2\(\frac{3}{4}\)
Answer:
Question 4.
3\(\frac{2}{3}\) + 1\(\frac{4}{6}\)
Answer:
Question 5.
3\(\frac{1}{6}\) + 2\(\frac{2}{3}\)
Answer:
Independent Practice
Leveled Practice In 6 and 7, use each model to find the sum.
Question 6.
Charles used 1\(\frac{2}{3}\) cups of walnuts and 2\(\frac{1}{6}\) cups of cranberries to make breakfast bread. How many cups of walnuts and cranberries did he use in all?
Answer:
Question 7.
Mary worked 2\(\frac{3}{4}\) hours on Monday and 1\(\frac{1}{2}\) hours on Tuesday. How many hours did she work in all on Monday and Tuesday?
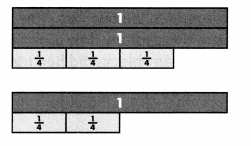
Answer:
In 8-16, use fraction strips to find each sum.
Question 8.
2\(\frac{6}{10}\) + 1\(\frac{3}{5}\)
Answer:
Question 9.
4\(\frac{5}{6}\) + 1\(\frac{7}{12}\)
Answer:
Question 10.
4\(\frac{2}{5}\) + 3\(\frac{7}{10}\)
Answer:
Question 11.
3\(\frac{1}{2}\) +1\(\frac{3}{4}\)
Answer:
Question 12.
1\(\frac{7}{8}\) + 5\(\frac{1}{4}\)
Answer:
Question 13.
2\(\frac{6}{12}\) + 1\(\frac{1}{2}\)
Answer:
Question 14.
3\(\frac{2}{5}\) + 1\(\frac{9}{10}\)
Answer:
Question 15.
2\(\frac{7}{12}\) + 1\(\frac{3}{4}\)
Answer:
Question 16.
2\(\frac{7}{8}\) + 5\(\frac{1}{2}\)
Answer:
Problem Solving
Question 17.
Lindsey used 1\(\frac{1}{4}\) gallons of tan paint for the ceiling and 4\(\frac{3}{8}\). gallons of green paint for the walls of her kitchen. How much paint did Lindsey use in all? Use fraction strips to help
Answer:
Question 18.
Paul said, “I walked 2\(\frac{1}{2}\) miles on Saturday and 2\(\frac{3}{4}\) miles on Sunday.” How many miles is that in all?
Answer:
Question 19.
Higher Order Thinking Tori is making muffins. The recipe calls for 2\(\frac{5}{6}\) cups of brown sugar for the muffins and 1\(\frac{1}{3}\) cups of brown sugar for the topping. Tori has 4 cups of brown sugar. Does she have enough brown sugar to make the muffins and the topping? Explain.
You can use fraction strips or a number line to compare amounts.

In 20 and 21, use the map. Each unit represents one block.
Question 20.
Ben left the museum and walked 4 blocks to his next destination. What was Ben’s destination?
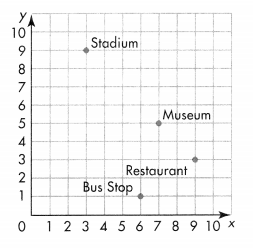
Answer:
Question 21.
Make Sense and Persevere Ben walked from the restaurant to the bus stop. Then, he took the bus to the stadium. If he took the shortest route, how many blocks did Ben travel? Note that Ben can only travel along the grid lines.
Answer:
Assessment Practice
Question 22.
Marta used 2\(\frac{3}{4}\) cups of milk and 15 cups of cheese in a recipe. How many cups of cheese and milk did Marta use?
A. 3 cups
B. 3\(\frac{4}{6}\) cups
C. 4\(\frac{1}{4}\) cups
D. 4\(\frac{3}{4}\) cups
Answer:
Question 23.
Garrett ran 21\(\frac{1}{2}\) miles last week. He ran 17\(\frac{7}{8}\) miles this week. How many miles did he run in all?
A. 38 miles
B. 38\(\frac{1}{2}\) miles
C. 39\(\frac{3}{8}\) miles
D. 39\(\frac{7}{8}\) miles
Answer:
Lesson 7.8 Add Mixed Numbers
Solve & Share
Joaquin used two types of flour in a muffin recipe. How much flour did he use in all? Solve any way you choose.
Use Structure Use what you know about adding fractions. Show your work!


Look Back! How is adding mixed numbers with unlike denominators the same as adding fractions with unlike denominators? How is it different?
Visual Learning Bridge
Essential Question How Can You Add Mixed Numbers?
You can use addition to find the total amount of soil.

A.
Rhoda mixes 1\(\frac{1}{2}\) cups of sand with 2\(\frac{2}{3}\) cups of potting mixture to prepare soil for her cactus plants. After mixing them together, how many cups of soil does Rhoda have?

B.
Step 1
Find 2\(\frac{2}{3}\) + 1\(\frac{1}{2}\).
Write equivalent fractions with a common denominator.
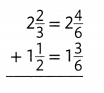
C.
Step 2
Add the fractions.
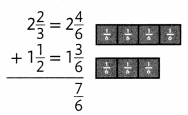
C.
Step 3
Add the whole numbers.
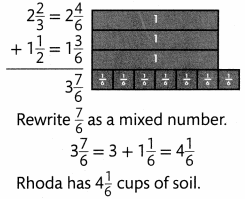
Convince Me! Critique Reasoning Kyle used 9 as an estimate for 3\(\frac{1}{6}\) + 5\(\frac{7}{8}\). He got 9\(\frac{1}{24}\) for the exact sum. Is his calculated answer reasonable? Explain.
Guided Practice
Do You Understand?
Question 1.
How is adding mixed numbers like adding fractions and whole numbers?
Answer:
Question 2.
Look at the example on page 298. Why is the denominator 6 used in the equivalent fractions?
Answer:
Do You Know How?
In 3-6, estimate and then find each sum.
Question 3.
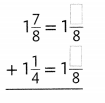
Answer:
Question 4.
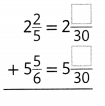
Answer:
Question 5.
4\(\frac{1}{9}\) + 1\(\frac{1}{3}\)
Answer:
Question 6.
6\(\frac{5}{12}\) + 4\(\frac{5}{8}\)
Answer:
Independent Practice
Leveled Practice In 7-18, estimate and then find each sum.
Remember, fractions must have a common, or like, denominator before they can be added.

Question 7.
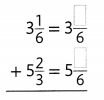
Answer:
Question 8.

Answer:
Question 9.
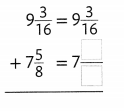
Answer:
Question 10.

Answer:
Question 11.
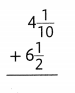
Answer:
Question 12.
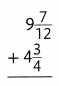
Answer:
Question 13.
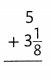
Answer:
Question 14.

Answer:
Question 15.
2\(\frac{3}{4}\) + 7\(\frac{3}{5}\)
Answer:
Question 16.
3\(\frac{8}{9}\) + 8\(\frac{1}{2}\)
Answer:
Question 17.
1\(\frac{7}{12}\) + 2\(\frac{3}{8}\)
Answer:
Question 18.
3\(\frac{11}{12}\) + 9\(\frac{1}{16}\)
Answer:
Problem Solving
Question 19.
Use the map to find the answer.

a What is the distance from the start to the end of the trail?
b Louise walked from the start of the trail to the bird lookout and back. Did she walk a longer or shorter distance than if she had walked from the start of the trail to the end? Explain.
c Another day, Louise walked from the start of the trail to the end. At the end, she realized she forgot her binoculars at the bird lookout. She walked from the end of the trail to the bird lookout and back. What is the total distance she walked?
Answer:
Question 20.
Higher Order Thinking Twice a day Cameron’s cat eats 4 ounces of dry cat food and 2 ounces of wet cat food. Dry food comes in 5-pound bags. Wet food comes in 6-ounce cans.
a How many cans of wet food should he buy to feed his cat for a week?
b How many ounces of wet cat food will be left over at the end of the week?
c How many days can he feed his cat from a 5-pound bag of dry food?
Remember: There are 16 ounces in a pound.

Question 21.
Julia bought 12 bags of cucumber seeds. Each bag contains 42 seeds. If she plants one half of the seeds, how many seeds does she have left?
Answer:
Question 22.
Critique Reasoning John added 2\(\frac{7}{12}\) and 5\(\frac{2}{3}\) and got 7\(\frac{1}{4}\) as the sum. Is John’s answer reasonable? Explain.
Answer:
Assessment Practice
Question 23.
What is the missing number in the following equation?

Answer:
Question 24.
Arnie skated 1\(\frac{3}{4}\) miles from home to the lake. He skated 1\(\frac{1}{3}\) miles around the lake, and then skated back home. Write an addition sentence to show how many miles Arnie skated in all.
Answer:
Lesson 7.9 Use Models to Subtract Mixed Numbers
Solve & Share
Clara and Erin volunteered at an animal shelter a total of 9\(\frac{5}{6}\) hours. Clara worked for 4\(\frac{1}{3}\) hours. How many hours did Erin work? You can use fraction strips to solve this problem.
Generalize How can you use what you know about adding mixed numbers to help you subtract mixed numbers? Show your work!

Look Back! How can you estimate the difference for the problem above? Explain your thinking.
Visual Learning Bridge
Essential Question How Can You Model Subtraction question of Mixed Numbers?
A.
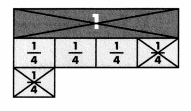
James needs 1\(\frac{11}{12}\) inches of pipe to repair a small part of a bicycle frame. He has a pipe that is 2\(\frac{1}{2}\) inches long. Does he have enough pipe left over to fix a \(\frac{3}{4}\)-inch piece of frame on another bike?
Rename 2\(\frac{1}{2}\) as 2\(\frac{6}{12}\) that the fractions have a common denominator.
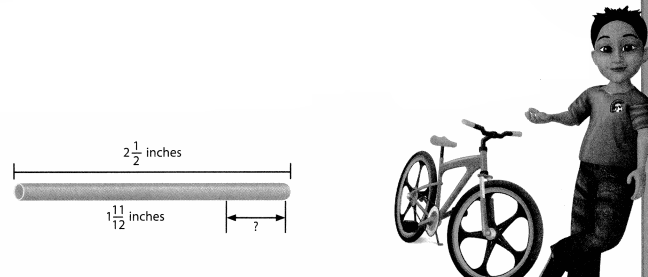
B.
Step 1
Model the number you are subtracting from, 2\(\frac{6}{12}\)
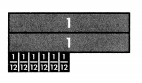
If the fraction you will be subtracting is greater than the fraction part of the number you model, rename 1 whole.
Since \(\frac{11}{12}\) > \(\frac{6}{12}\), rename 1 whole as \(\frac{12}{12}\).

Step 2
Use your renamed model to cross out the number that you are subtracting, 1\(\frac{11}{12}\)
There are \(\frac{7}{12}\) left.
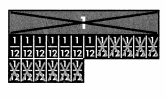
So, 2\(\frac{1}{2}\) – 1\(\frac{11}{12}\) = \(\frac{7}{12}\)
James will have \(\frac{7}{12}\) inch of pipe left. He does not have enough for the other bike.
Convince Me! Use Appropriate Tools Use fraction strips to find 5\(\frac{1}{2}\) – 2\(\frac{3}{4}\).
Guided Practice
Do You Understand?
Question 1.
When subtracting two mixed numbers, is it always necessary to rename one of the wholes? Explain.
Do You Know How?
In 2-5, use fraction strips to find each difference.
Question 2.
4\(\frac{5}{6}\) – 2\(\frac{1}{3}\)
Answer:
Question 3.
4\(\frac{1}{8}\) – 3\(\frac{3}{4}\)
Answer:
Question 4.
5\(\frac{1}{2}\) – 2\(\frac{5}{6}\)
Answer:
Question 5.
5\(\frac{4}{10}\) – 3\(\frac{4}{5}\)
Answer:
Independent Practice
In 6 and 7, use each model to find the difference.
Question 6.
Terrell lives 2\(\frac{5}{6}\) blocks away from his best friend. His school is 4\(\frac{1}{3}\) blocks away in the same direction. If he stops at his best friend’s house first, how much farther do they have to walk to school?
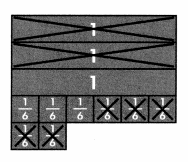
Answer:
Question 7.
Tina bought 3\(\frac{1}{2}\) pounds of turkey and 2\(\frac{1}{4}\) pounds of cheese. She used 1\(\frac{1}{2}\) pounds of cheese to make macaroni and cheese. How much cheese does she have left?
Answer:
In 8-15, use fraction strips to find each difference.
Question 8.
12\(\frac{3}{4}\) – 9\(\frac{5}{8}\)
Answer:
Question 9.
8\(\frac{1}{6}\) – 7\(\frac{2}{3}\)
Answer:
Question 10.
13\(\frac{7}{9}\) – 10\(\frac{2}{3}\)
Answer:
Question 11.
3\(\frac{1}{12}\) – 2\(\frac{3}{4}\)
Answer:
Question 12.
6\(\frac{3}{4}\) – 3\(\frac{11}{12}\)
Answer:
Question 13.
4\(\frac{3}{5}\) – 1\(\frac{1}{10}\)
Answer:
Question 14.
6\(\frac{1}{2}\) – 3\(\frac{7}{10}\)
Answer:
Question 15.
6\(\frac{2}{3}\) – 4\(\frac{2}{9}\)
Answer:
Problem Solving
For 16 and 17, use the table at the right.
Question 16.
How much longer is a Red Oak leaf than a Sugar Maple leaf? Write an equation to model your work.
Answer:

Question 17.
How much longer is a Red Oak leaf than a Paper Birch leaf? Write an equation to model your work.
Question 18.
Higher Order Thinking Lemmy walked 3\(\frac{1}{2}\) miles on Saturday and 4\(\frac{3}{4}\) miles on Sunday. Ronnie walked 5\(\frac{3}{8}\) miles on Saturday. Who walked farther? How much farther?
Answer:
Question 19.
Model with Math Jamal is buying lunch for his family. He buys 4 drinks that each cost $1.75 and 4 sandwiches that each cost $7.50. If the prices include tax and he also leaves a $7 tip, how much does he spend in all? Write equations to show your work.
Answer:
Assessment Practice
Question 20.
What is the missing number in the following equation?
![]()
Answer:
Question 21.
What is the missing number in the following equation?
![]()
Answer:
Lesson 7.10 Subtract Mixed Numbers
Solve&Share
Evan walks 2-miles to his aunt’s house. He has already walked mile. How much farther does he have to go? Solve this problem any way you choose.
Use Structure Use what you know about subtracting fractions. Show your work!

Look Back! Jon said, “Changing \(\frac{3}{4}\) to \(\frac{6}{8}\) makes this problem easier.” What do you think Jon meant?
Visual Learning Bridge
Essential Question How Can You Subtract Mixed Numbers?
A.
A golf ball measures about 1\(\frac{2}{3}\) inches across the center. What is the difference between the distance across the center of the hole and the golf ball?

You can use subtraction to find the difference.

B.
Step 1
Write equivalent fractions with a common denominator.

C.
Step 2
Rename 4\(\frac{3}{12}\) to show more twelfths.
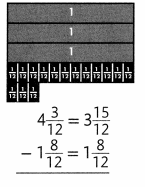
D.
Step 3
Subtract the fractions. Then subtract the whole numbers.

The hole is 2\(\frac{7}{12}\) inches wider.
Convince Me! Critique Reasoning Estimate 8\(\frac{1}{3}\) – 3\(\frac{3}{4}\). Tell how you got your estimate. Susi subtracted and found the actual difference to be 5\(\frac{7}{12}\). Is her answer reasonable? Explain.
Another Example
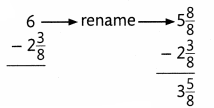
Sometimes you may have to rename a whole number to subtract. Find the difference of 6 – 2\(\frac{3}{8}\).
Guided Practice
Do You Understand?
Question 1.
In the example above, why do you need to rename the 6?
Answer:
Question 2.
In the example on page 306, could two golf balls fall into the hole at the same time? Explain your reasoning.
Answer:
In 3-6, estimate and then find each difference.
Question 3.
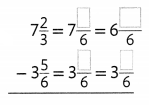
Answer:
Question 4.
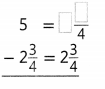
Answer:
Question 5.
6\(\frac{3}{10}\) – 1\(\frac{4}{5}\)
Answer:
Question 6.
9\(\frac{1}{3}\) – 4\(\frac{3}{4}\)
Answer:
Independent Practice
In 7-18, estimate and then find each difference.
Remember to check that your answer makes sense by comparing it to the estimate.

Question 7.
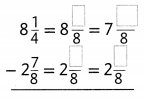
Answer:
Question 8.
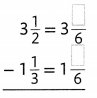
Answer:
Question 9.

Answer:
Question 10.
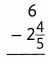
Answer:
Question 11.
6\(\frac{1}{3}\) – 5\(\frac{2}{3}\)
Answer:
Question 12.
9\(\frac{1}{2}\) – 6\(\frac{3}{4}\)
Answer:
Question 13.
8\(\frac{3}{16}\) – 3\(\frac{5}{8}\)
Answer:
Question 14.
7\(\frac{1}{2}\) – \(\frac{7}{10}\)
Answer:
Question 15.
15\(\frac{1}{6}\) – 4\(\frac{3}{8}\)
Answer:
Question 16.
13\(\frac{1}{12}\) – 8\(\frac{1}{4}\)
Answer:
Question 17.
6\(\frac{1}{3}\) – 2\(\frac{3}{5}\)
Answer:
Question 18.
10\(\frac{5}{12}\) – 4\(\frac{7}{8}\)
Answer:
Problem Solving
Question 19.
The average weight of a basketball is 21\(\frac{1}{10}\) ounces. The average weight of a baseball is 5\(\frac{1}{4}\) ounces. How many more ounces does the basketball weigh? Write the missing numbers in the diagram.
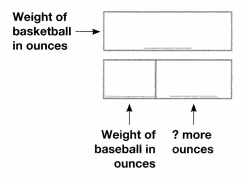
Answer:
Question 20.
enVision® STEM The smallest mammals on Earth are the bumblebee bat and the Etruscan pygmy shrew. The length of a certain bumblebee bat is 1\(\frac{9}{50}\) inches. The length of a certain Etruscan pygmy shrew is 1\(\frac{21}{50}\) inches. How much smaller is the bat than the shrew?
Answer:
Question 21.
Be Precise How are the purple quadrilateral and the green quadrilateral alike? How are they different?
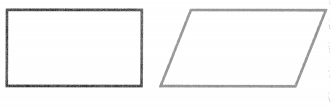
Answer:
Question 22.
Higher Order Thinking Sam used the model to find 2\(\frac{5}{12}\) – 1\(\frac{7}{12}\). Did Sam model the problem correctly? Explain. If not, show how the problem should have been modeled and find the difference.
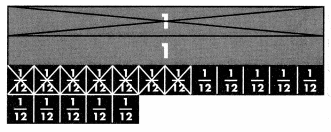
Answer:
Assessment Practice
Question 23.
Choose the correct number from the box below to complete the subtraction sentence that follows.

Answer:
Question 24.
Choose the correct number from the box below to complete the subtraction sentence that follows.
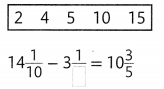
Answer:
Lesson 7.11 Add and Subtract Mixed Numbers
Activity
Solve&Share
Tim has 15 feet of wrapping paper. He uses 4\(\frac{1}{3}\) feet for his daughter’s present and 5\(\frac{3}{8}\) feet for his niece’s present. How much wrapping paper does Tim have left? Solve this problem any way you choose.
Reasoning What steps are needed to solve the problem? Show your work!
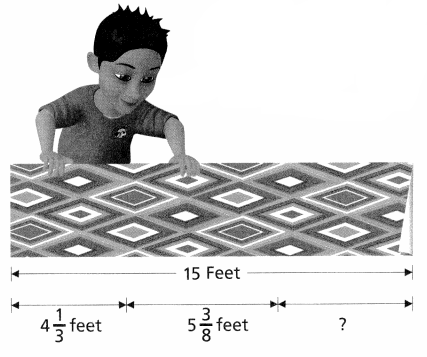
Look Back! In the problem above, how could you have estimated the amount of wrapping paper that is left?
Visual Learning Bridge
Essential Question
How Can Adding and Subtracting Mixed Numbers Help You Solve Problems?
A.
Clarisse has two lengths of fabric to make covers for a sofa and chair. The covers require 9\(\frac{2}{3}\) yards of fabric. How much fabric will Clarisse have left?
Find a common denominator when adding and subtracting fractions.

B.
Step 1
Add to find out how much fabric Clarisse has in all.
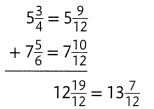
Clarisse has 13\(\frac{7}{12}\) yards of fabric in all.
C.
Step 2
Subtract the amount she will use from the total length of fabric.

Clarisse will have 3\(\frac{11}{12}\) yards of fabric left.
Convince Me! Make Sense and Persevere Clarisse has 14\(\frac{3}{4}\) yards of fabric to cover another sofa and chair. The new sofa needs 9\(\frac{1}{6}\) yards of fabric and the new chair needs 4\(\frac{1}{3}\) yards of fabric. Estimate to decide if Clarisse has enough fabric. If so, how much fabric will she have left?
Guided Practices
Do You Understand?
Question 1.
In the example on page 310, why do you add before you subtract?
Answer:
Question 2.
In the example on page 310, does Clarisse have enough fabric left over to make two cushions that each use 2\(\frac{7}{12}\) yards of fabric? Explain.
Answer:
Do You Know How?
In 3-5, find the sum or difference.
Question 3.
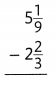
Answer:
Question 4.
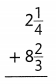
Answer:
Question 5.
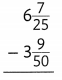
Answer:
In 6-9, solve. Do the addition in the parentheses first.
Question 6.
4\(\frac{3}{5}\) + 11\(\frac{2}{15}\)
Answer:
Question 7.
8\(\frac{2}{3}\) – 3\(\frac{3}{4}\)
Answer:
Question 8.
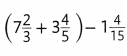
Answer:
Question 9.
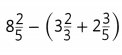
Answer:
Independent Practice
In 10-14, find each sum or difference.
Question 10.
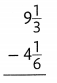
Answer:
Question 11.
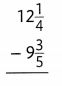
Answer:
Question 12.
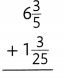
Answer:
Question 13.
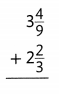
Answer:
Question 14.
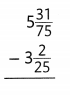
Answer:
In 15-20, solve. Do the operation in the parentheses first.
Question 15.

Answer:
Question 16.
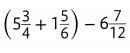
Answer:
Question 17.
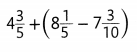
Answer:
Question 18.
![]()
Answer:
Question 19.

Answer:
Question 20.
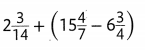
Answer:
Problem Solving
In 21-23, use the table below.
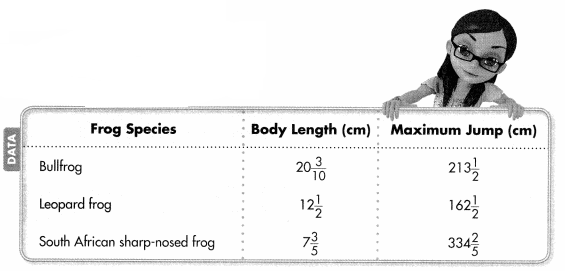
Question 21.
Be Precise How much longer is the maximum jump of a South African sharp-nosed frog than the maximum jump of a leopard frog?
Answer:
Question 22.
How many centimeters long is a bullfrog? Round to the nearest whole number.
Answer:
Question 23.
Higher Order Thinking Which frog jumps about 10 times its body length? Explain how you found your answer.
Answer:
Question 24.
A-Z Vocabulary Write three numbers that are common denominators of \(\frac{7}{15}\) and \(\frac{3}{5}\).
Answer:
Question 25.
Marie plants 12 packages of vegetable seeds in a community garden. Each package costs $1.97 with tax. What is the total cost of the seeds?
Answer:
Assessment Practice
Question 26.
Which equations are true when 5\(\frac{3}{8}\) is placed in the box?
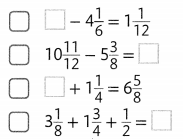
Answer:
Question 27.
Which equations are true when 3\(\frac{1}{3}\) is placed in the box?
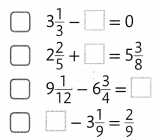
Answer:
Lesson 7.12 Model with Math
Problem Solving
Solve & Share
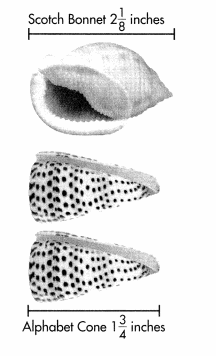
Annie found three seashells at the beach. How much shorter is the Scotch Bonnet seashell than the combined lengths of the two Alphabet Cone seashells? Solve this problem any way you choose. Use a diagram to help.
Thinking Habits
Be a good thinker! These questions can help you.
• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• Can I write an equation to show the problem?

Look Back! Model with Mathematics What is another way to represent this problem?
Visual Learning Bridge
Essential Question How Can You Represent a Problem Question with a Bar Diagram?
A.
The first step of a recipe is to mix the flour, white sugar, and brown sugar. Will a bowl that holds 4 cups be large enough?
Use a model to represent the problem.

What do I need to do to solve the problem?
I need to find the total amount of the first three ingredients and compare that amount to 4 cups.
Here’s my thinking.

B.
How can I model with math?
I can
• use math I know to help solve this problem.
• use a diagram to represent and solve this problem.
• write an equation involving fractions or mixed numbers.
• decide if my results make sense.
C.
I will use a bar diagram and an equation to represent the situation.
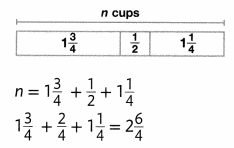
I can write this answer as a mixed number. 2\(\frac{6}{4}\) = 3\(\frac{2}{4}\) or 3\(\frac{1}{2}\)
There are 3\(\frac{1}{2}\) cups of ingredients, and 3. is less than 4. So, the 4-cup bowl is large enough.
Convince Me! Model with Mathematics How many more cups of ingredients could still fit in the bowl? Use a bar diagram and an equation to represent the problem.
Guided Practice
Phillip wants to run a total of 3 miles each day. Monday morning, he ran 1\(\frac{7}{8}\) miles. How many more miles does he still need to run?
Question 1.
Draw a diagram to represent the problem.
Answer:
Bar diagrams show how the quantities in a problem are related.

Question 2.
Write and solve an equation for this problem. How did you find the solution?
Answer:
Question 3.
How many more miles does Phillip still need to run?
Answer:
Independent Practice
Model with Math
A landscaper used 2\(\frac{1}{2}\) tons of sunburst pebbles, 3\(\frac{1}{4}\) tons of black polished pebbles, and a ton of river pebbles. What was the total weight of the pebbles?
Question 4.
Draw a diagram and write an equation to represent the problem.
Answer:
Question 5.
Solve the equation. What fraction computations did you do?
Answer:
Question 6.
How many tons of pebbles did the landscaper use?
Answer:
Problem Solving
Performance Task
Camp Activities
During the 6-hour session at day camp, Roland participated in boating, hiking, and lunch. The rest of the session was free time. How much time did Roland spend on the three activities? How much free time did he have?

Question 7.
Make Sense and Persevere What do you know and what do you need to find?
Answer:
When you model with math, you use the math you know to solve new problems.

Question 8.
Reasoning Describe the quantities and operations you will use to find how much time Roland spent on the planned activities. Which quantities and operations will you use to find how much free time Roland had?
Answer:
Question 9.
Model with Math Draw a diagram and use an equation to help you find how much time Roland spent on the activities. Then, draw a diagram and use an equation to help you find how much free time Roland had.
Answer:
Topic 7 Fluency Practice
Activity
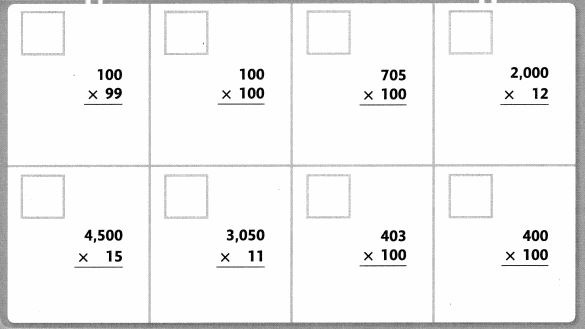
Find a Match
Work with a partner. Point to a clue.
Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
Clues

Topic 7 Vocabulary Review
Word List
Glossary
Understand Vocabulary
Write always, sometimes, or never.
• benchmark fractions
• common denominator
• equivalent fractions
• mixed number
Question 1.
A fraction can ____ be renamed as a mixed number.
Answer:
Question 2.
The sum of a mixed number and a whole number is ____ a mixed number
Answer:
Question 3.
\(\frac{1}{5}\) is__ used as a benchmark fraction.
Answer:
Question 4.
Equivalent fractions ___ have the same value.
Answer:
For each of these terms, give an example and a non-example.

Draw a line from each number in Column A to the same value in Column B.

Use Vocabulary in Writing
Question 12.
How can you write a fraction equivalent to \(\frac{60}{80}\) with a denominator that is less than 80?
Answer:
Topic 7 Reteaching
Set A
pages 269-272
Estimate the sum or difference by replacing each fraction with 0, \(\frac{1}{2}\), or 1.
Estimate \(\frac{4}{5}\) + \(\frac{5}{8}\)
Step 1
\(\frac{4}{5}\) is close to 1.
Step 2
\(\frac{5}{8}\) is close to \(\frac{4}{8}\) or \(\frac{1}{2}\)
Step 3
1 + \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
Step 1
\(\frac{7}{12}\) is closes to \(\frac{6}{12}\) or \(\frac{1}{2}\).
Step 2
\(\frac{1}{8}\) is close to 0.
Step 3
\(\frac{1}{2}\) – 0 = \(\frac{1}{2}\)
So, \(\frac{7}{12}\) – \(\frac{1}{8}\) is about \(\frac{1}{2}\).
Remember that you can use as number line to decide if a fraction is closest to 0, \(\frac{1}{2}\), or 1.
Estimate each sum or difference.
Question 1.
\(\frac{2}{3}\) + \(\frac{5}{6}\)
Answer:
Question 2.
\(\frac{7}{8}\) – \(\frac{5}{12}\)
Answer:
Question 3.
\(\frac{1}{8}\) + \(\frac{1}{16}\)
Answer:
Question 4.
\(\frac{5}{8}\) – \(\frac{1}{6}\)
Answer:
Question 5.
\(\frac{1}{5}\) + \(\frac{1}{3}\)
Answer:
Question 6.
\(\frac{11}{12}\) – \(\frac{1}{10}\)
Answer:
Question 7.
\(\frac{9}{10}\) + \(\frac{1}{5}\)
Answer:
Question 8.
\(\frac{3}{5}\) – \(\frac{1}{12}\)
Answer:
Set B
pages 273-276
Find a common denominator for \(\frac{4}{9}\) and \(\frac{1}{3}\). Then rename each fraction as an equivalent fraction with the common denominator.
Step 1
Multiply the denominators:
9 × 3 = 27, so 27 is a common denominator.
Step 2
Rename the fractions:
\(\frac{4}{9}\) = \(\frac{4}{9}\) × \(\frac{3}{3}\) = \(\frac{4}{9}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{9}{9}\) = \(\frac{9}{27}\)
So, \(\frac{4}{9}\) = \(\frac{12}{27}\) and \(\frac{1}{3}\) = \(\frac{9}{27}\).
Remember you can check to see if one denominator is a multiple of the other. Since 9 is a multiple of 3, another common denominator for the fractions and is 9. Find a common denominator. Then rename each fraction as an equivalent fraction with the common denominator.
Question 1.
\(\frac{3}{5}\) and \(\frac{7}{10}\)
Answer:
Question 2.
\(\frac{5}{6}\) and \(\frac{7}{18}\)
Answer:
Question 3.
\(\frac{3}{7}\) and \(\frac{1}{4}\)
Answer:
Set C
pages 277-280, 281-284, 285-288
Find \(\frac{5}{6}\) – \(\frac{3}{4}\)
Step 1
Find a common denominator by listing multiples of 6 and 4.
6:6, 12, 18, 24, 30, 36, 42
4:4, 8, 12, 16, 20, 24, 28, 32
12 is a common multiple of 6 and 4, so use 12 as the common denominator.
Step 2
Use the Identity Property to write equivalent fractions.
\(\frac{5}{6}\) = \(\frac{5 \times 2}{6 \times 2}\) = \(\frac{10}{12}\)
\(\frac{3}{4}\) = \(\frac{3 \times 3}{4 \times 3}\) = \(\frac{9}{12}\)
Step 3
Subtract.
\(\frac{10}{12}\) – \(\frac{9}{12}\) = \(\frac{1}{12}\)
Remember to multiply the numerator and denominator by the same number when writing an equivalent fraction.
Question 1.
\(\frac{2}{5}\) + \(\frac{3}{10}\)
Answer:
Question 2.
\(\frac{1}{9}\) + \(\frac{5}{6}\)
Answer:
Question 3.
\(\frac{3}{4}\) – \(\frac{5}{12}\)
Answer:
Question 4.
\(\frac{7}{8}\) – \(\frac{2}{3}\)
Answer:
Question 5.
\(\frac{1}{12}\) + \(\frac{3}{8}\)
Answer:
Question 6.
\(\frac{4}{5}\) – \(\frac{2}{15}\)
Answer:
Question 7.
Teresa spends \(\frac{1}{3}\) of her day at school. She spends \(\frac{1}{12}\) of her day eating meals. What fraction of the day does Teresa spend at school or eating meals?
Answer:
Set D
pages 289-292
Estimate 5\(\frac{1}{3}\) + 9\(\frac{9}{11}\)
To round a mixed number to the nearest whole number, compare the fraction part of the mixed number to \(\frac{1}{2}\).
If the fraction part is less than \(\frac{1}{2}\), round to the nearest lesser whole number.
5\(\frac{1}{3}\) rounds to 5.
If the fraction part is greater than or equal to \(\frac{1}{2}\), round to the nearest greater whole number.
9\(\frac{9}{11}\) rounds to 10.
So, 5\(\frac{1}{3}\) + 9\(\frac{9}{11}\) ≈ 5 + 10 = 15.
Remember that means ≈ is approximately equal to.”

Remember that you can also use benchmark fractions such as \(\frac{1}{4}\), \(\frac{1}{3}\), \(\frac{1}{2}\), and \(\frac{3}{4}\) to help you estimate.
Estimate each sum or difference.
Question 1.
3\(\frac{1}{4}\) – 1\(\frac{1}{2}\)
Answer:
Question 2.
5\(\frac{2}{9}\) + 4\(\frac{11}{13}\)
Answer:
Question 3.
2\(\frac{3}{8}\) + 5\(\frac{3}{5}\).
Answer:
Question 4.
9\(\frac{3}{7}\) – 6\(\frac{2}{5}\)
Answer:
Question 5.
8\(\frac{5}{6}\) – 2\(\frac{1}{2}\)
Answer:
Question 6.
7\(\frac{3}{4}\) + 5\(\frac{1}{8}\)
Answer:
Question 7.
11\(\frac{5}{12}\) + \(\frac{7}{8}\)
Answer:
Question 8.
13\(\frac{4}{5}\) – 8\(\frac{1}{6}\)
Answer:
Question 9.
A mark on the side of a pier shows the water is 4\(\frac{7}{8}\) feet deep. At high tide, the water level rises 2\(\frac{1}{4}\) feet. About how deep is the water at high tide?
Answer:
Set E
pages 293-296
Find 1\(\frac{1}{4}\) + 1\(\frac{7}{8}\)
Step 1
Rename the fractions with a common denominator. Model the addends and add the fractional parts.
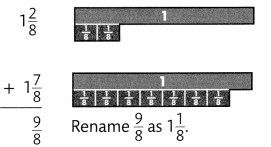
Step 2
Add the whole numbers to the regrouped fractions.

So, 1\(\frac{1}{4}\) + 1\(\frac{7}{8}\) = 3\(\frac{1}{8}\)
Remember that you may need to rename a fraction as a mixed number.
Use a model to find each sum.
Question 1.
2\(\frac{5}{6}\) + 1\(\frac{5}{6}\)
Answer:
Question 2.
1\(\frac{1}{2}\) + 3\(\frac{3}{4}\)
Answer:
Question 3.
2\(\frac{3}{10}\) + 2\(\frac{4}{5}\)
Answer:
Question 4.
2\(\frac{1}{4}\) + 5\(\frac{11}{12}\)
Answer:
Question 5.
6\(\frac{2}{3}\) + 5\(\frac{5}{6}\)
Answer:
Question 6.
7\(\frac{1}{3}\) + 8\(\frac{7}{9}\)
Answer:
Question 7.
8\(\frac{4}{10}\) + 2\(\frac{3}{5}\)
Answer:
Question 8.
3\(\frac{1}{3}\) + 9\(\frac{11}{12}\)
Answer:
Set F
pages 301-304
Find 2\(\frac{1}{3}\) – 1\(\frac{5}{6}\). Rename 2\(\frac{1}{3}\) as 2\(\frac{2}{6}\)
Step 1
Model the number you are subtracting from, 2\(\frac{1}{3}\) or 2\(\frac{2}{6}\)
Since \(\frac{5}{6}\) > \(\frac{2}{6}\), rename 1 whole as \(\frac{6}{6}\)
Step 2
Cross out the number you are subtracting, 1\(\frac{5}{6}\).
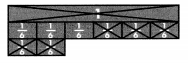
The answer is the amount that is left.
So, 2\(\frac{1}{3}\) – 1\(\frac{5}{6}\) = \(\frac{3}{6}\) or \(\frac{1}{2}\)
Remember that the difference is the part of the model that is not crossed out. Use a model to find each difference.
Question 1.
15\(\frac{6}{10}\) – 3\(\frac{4}{5}\)
Answer:
Question 2.
6\(\frac{3}{4}\) – 5\(\frac{1}{2}\)
Answer:
Question 3.
4\(\frac{1}{6}\) – 1\(\frac{2}{3}\)
Answer:
Question 4.
12\(\frac{1}{4}\) – 7\(\frac{1}{2}\)
Answer:
Question 5.
9\(\frac{7}{10}\) – 3\(\frac{4}{5}\)
Answer:
Question 6.
5\(\frac{5}{8}\) – 3\(\frac{1}{4}\)
Answer:
Set G
pages 297-300, 305-308, 309-312
Gil had two lengths of wallpaper, 2\(\frac{3}{4}\) yards and 1\(\frac{7}{8}\) yards long. He used some and now has 1\(\frac{5}{6}\) yards left. How many yards of wallpaper did Gil use?
Step 1
Add to find the total amount of wallpaper Gil had.
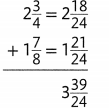
Step 2
Subtract to find the amount of wallpaper Gil used.
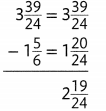
Gil used 2\(\frac{19}{24}\) yards of wallpaper.
Remember when you add or subtract mixed numbers, rename the fractional parts to have a common denominator.
Solve. Do the operation in the parentheses first.
Question 1.
5\(\frac{1}{2}\) + 2\(\frac{1}{8}\)
Answer:
Question 2.
7\(\frac{5}{6}\) – 3\(\frac{2}{3}\)
Answer:
Question 3.
3\(\frac{1}{4}\) + 1\(\frac{5}{6}\)
Answer:
Question 4.
9 – 3\(\frac{3}{8}\)
Answer:
Question 5.
![]()
Answer:
Question 6.
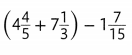
Answer:
Set H
pages 313-316
Think about these questions to help you model with math.
Thinking Habits
• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?

Remember that a bar diagram can help you write an addition or a subtraction equation. Draw a bar diagram and write an equation to solve.
Question 1.
Justin jogs 3\(\frac{2}{5}\) miles every morning. He jogs 4\(\frac{6}{10}\) miles every evening. How many miles does he jog every day?
Answer:
Question 2.
Last year Mia planted a tree that was 5\(\frac{11}{12}\) feet tall. This year the tree is 7\(\frac{2}{3}\) feet tall. How many feet did the tree grow?
Answer:
Topic 7 Assessment Practice
Question 1.
Estimate the sum of \(\frac{3}{4}\) and \(\frac{1}{5}\). Write an equation.
Answer:
Question 2.
Select all the expressions that are equal to \(\frac{2}{3}\). Explain.
![]() \(\frac{1}{6}\) + \(\frac{1}{2}\); I found a common denominator and then added the
\(\frac{1}{6}\) + \(\frac{1}{2}\); I found a common denominator and then added the
numerators to get \(\frac{2}{3}\)
![]() \(\frac{2}{9}\) + \(\frac{7}{18}\); I added the numerators and denominators to get \(\frac{2}{3}\)
\(\frac{2}{9}\) + \(\frac{7}{18}\); I added the numerators and denominators to get \(\frac{2}{3}\)
![]() \(\frac{5}{12}\) + \(\frac{1}{4}\); I added the numerators and denominators to get \(\frac{2}{3}\)
\(\frac{5}{12}\) + \(\frac{1}{4}\); I added the numerators and denominators to get \(\frac{2}{3}\)
![]() 1\(\frac{1}{6}\) – \(\frac{1}{3}\); I found a common denominator and then subtracted the numerators to get \(\frac{2}{3}\)
1\(\frac{1}{6}\) – \(\frac{1}{3}\); I found a common denominator and then subtracted the numerators to get \(\frac{2}{3}\)
![]() 2 – 1\(\frac{1}{3}\) found a common denominator and then subtracted the numerators to get \(\frac{2}{3}\)
2 – 1\(\frac{1}{3}\) found a common denominator and then subtracted the numerators to get \(\frac{2}{3}\)
Answer:
Question 3.
Tim has \(\frac{5}{12}\) of a jar of blackberry jam and \(\frac{3}{8}\) of a jar of strawberry jam. Write \(\frac{5}{12}\) and \(\frac{3}{8}\) using a common denominator. What fraction represents the total amount of jam Tim has?
Answer:
Question 4.
Sandra drove for \(\frac{1}{3}\) hour to get to the store. Then she drove \(\frac{1}{5}\) hour to get to the library. What fraction of an hour did Sandra drive in all? Explain.
Answer:
Question 5.
The bar diagram below shows the fractional parts of a pizza eaten by Pablo and Jamie.

A. Rename each fraction using a common denominator.
B. Use the renamed fractions to write and solve an equation to find the total amount of pizza eaten.
Answer:
Question 6.
Choose the correct sum for each expression.

Answer:
Question 7.
Benjamin and his sister shared a large sandwich. Benjamin ate of the sandwich and his sister ate of the sandwich.
A. Estimate how much more Benjamin ate than his sister. Explain how you found your estimate.
B. How much more did Benjamin eat than his sister? Find the exact amount.
Answer:
Question 8.
Alicia had 3\(\frac{1}{8}\) feet of wood. She used 1\(\frac{3}{4}\) feet of wood. Estimate the amount of wood Alicia has left.
A. 2 feet
B. 1 foot
C. 0 feet
D. 3 feet
Answer:
Question 9.
Explain why you must rename 2\(\frac{7}{12}\) in order to find 2\(\frac{7}{12}\) – \(\frac{5}{6}\)
Answer:
Question 10.
Mona bought 3\(\frac{3}{8}\) pounds of cheddar cheese. She used 2\(\frac{3}{4}\) pounds to make sandwiches. Write and solve an expression to find how much cheese is left.
Answer:
Question 11.
Marie needs 2\(\frac{1}{4}\) yards of fabric. She already has 1\(\frac{3}{8}\) yards. Which equation shows how many more yards of fabric Marie has to buy?
A. 2\(\frac{1}{4}\) + 1\(\frac{3}{8}\) = 1\(\frac{1}{8}\)
B. \(\frac{1}{4}\) + \(\frac{3}{8}\) = \(\frac{3}{4}\)
C. 2\(\frac{1}{4}\) – 1\(\frac{3}{8}\) = \(\frac{7}{8}\)
D. \(\frac{3}{8}\) – \(\frac{1}{4}\) = \(\frac{1}{8}\)
Answer:
Question 12.
During a trip, Martha drove \(\frac{1}{6}\) of the time, Chris drove \(\frac{1}{4}\) a of the time, and Juan drove the rest of the time. What fraction of the time did Juan drive?
Answer:
Question 13.
Gilberto worked 3\(\frac{1}{4}\) hours on Thursday, 4\(\frac{2}{5}\) hours on Friday, and 6\(\frac{1}{2}\) hours on Saturday. How many hours did he work in all during the three days?
A. 13\(\frac{1}{10}\) hours
B. 13\(\frac{3}{20}\) hours
C. 14\(\frac{1}{10}\) hours
D. 14\(\frac{3}{20}\) hours
Answer:
Question 14.
The model below can be used to find the sum of two mixed numbers. What is the sum? What is the difference? Show your work.
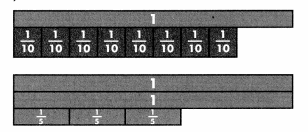
Answer:
Question 15.
Estimate the sum of 1\(\frac{1}{3}\) and 2\(\frac{3}{4}\). Explain how you found your estimate.
Answer:
Question 16.
Find 4\(\frac{1}{5}\) – \(\frac{7}{10}\)
A. Explain why 4\(\frac{1}{5}\) must be renamed in order to do the subtraction.
B. Explain how to rename 4\(\frac{1}{5}\) in order to do the subtraction.
Answer:
Question 17.
Mark is making a small frame in the shape of an equilateral triangle with the dimensions shown below. What is the perimeter of the frame?
A. 6\(\frac{1}{2}\) cm
B. 9\(\frac{1}{2}\) cm
C. 9\(\frac{1}{6}\) cm
D. 10\(\frac{1}{2}\) cm
Answer:
Question 18.
A baker uses food coloring to color cake batter. He needs 4\(\frac{1}{8}\) ounces of green food coloring. The baker only has 2\(\frac{1}{3}\) ounces. How much more green food coloring does he need? If the baker only finds 1 ounce of food coloring at the store, how many more ounces does the baker need?
Answer:
Question 19.
Models for two mixed numbers are shown below. What is the sum of the numbers? What is the difference? Show your work.
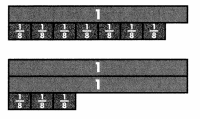
Answer:
Question 20.
Dawson says that the expression ![]() is equal to a whole number. Do you agree? Explain.
is equal to a whole number. Do you agree? Explain.
Answer:
Topic 7 Performance Task
Tying Knots
Liam and Pam each have a length of thick rope. Liam has tied an overhand knot in his rope. The overhand knot is a basic knot often used as a basis for other types of knots.
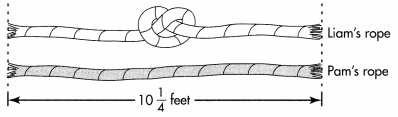
Question 1.
Liam untied the overhand knot. The full length of the rope is shown below. How much rope did the knot use?
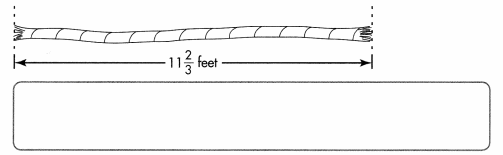
Answer:
Question 2.
Liam laid his untied rope end-to-end with Pam’s rope.
Part A
About how long would the two ropes be? Explain how you got your estimate.
Part B
Explain whether the actual length would be greater or less than your estimate.
Answer:
Question 3.
Liam and Pam tied their two ropes together with a square knot. The knot used 15 feet of rope. How long is their rope? Explain.
Answer:
Question 4.
Marco has a rope that is 16 feet long. He ties his rope to Liam and Pam’s rope with a square knot that uses 1\(\frac{1}{8}\) feet of rope.
Part A
How long are the three ropes tied together? Write an equation to model the problem. Then solve the equation.
Part B
Liam, Pam, and Marco decide to shorten the tied ropes by cutting off \(\frac{2}{5}\) foot from one end and \(\frac{1}{6}\) foot from the other end. About how much rope is cut off in all? Explain.
Part C
How long are the tied ropes now? Show your work.
Answer: