Practice with the help of enVision Math Common Core Grade 7 Answer Key Topic 5 Solve Problems Using Equations and Inequalities regularly and improve your accuracy in solving questions.
enVision Math Common Core 7th Grade Answers Key Topic 5 Solve Problems Using Equations and Inequalities
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
Question 1.
A statement that contains the symbols
<, >, ≤, or ≥ is called a(n)
Answer:
Inequality,
Explanation:
An open sentence that contains the symbol
< , ≤ , > , or ≥ is called an inequality.
Inequalities can be solved the same way as equations.
Question 2.
Properties that state that performing the same
operation on both sides of an equation will keep
the equation true are called
Answer:
Properties of equation,
Explanation:
The first four properties of equality–those that
deal with operations–allow us to add, subtract,
multiply and divide variables.
They also formally express the idea that when we
perform the same operations on both sides of an equation,
the two sides are still equivalent.
In other words, that we can perform the same
operation on both sides without changing
the values of the variables these are called as
properties of equation.
Question 3.
Addition and subtraction have a(n) ___
because they can “undo” each other.
Answer:
Inverse relationship,
Explanation:
An inverse operation are two operations that undo each other,
e.g. addition and subtraction or multiplication and division.
Can perform the same inverse operation on each side of
an equivalent equation without changing the equality.
Question 4.
Terms that have the same variable are called ___
Answer:
Liketerms,
Explanation:
Terms that have the same variable are called like terms as
like terms are terms that have the same variables and
powers example ax + bx here there are two terms ax, bx
both have x a same variable x and power also same.
Properties of Equality
Use properties to solve each equation for x.
Question 5.
x + 9.8 = 14.2
Answer:
x = 4.4,
Explanation:
Given x + 9.8 = 14.2,
after subtracting 9.8 both sides we get
x + 9.8 – 9.8 = 14.2 – 9.8,
x + 0 = 4.4, therefore x = 4.4.
Question 6.
14x = 91
Answer:
x = 6 remainder 7,
Explanation:
Given 14x = 91,
dividing both sides by 14 we get
14x ÷14 = 91 ÷ 14,
x = 91 ÷14,
6
14)91(
84
7
therefore x = 6 with remainder 7.
Question 7.
\(\frac{1}{3}\)x = 24
Answer:
x = 72,
Explanation:
Given \(\frac{1}{3}\)x = 24,
multiplying both sides by 3 we get
\(\frac{1}{3}\)x X 3 = 24 X 3,
therefore x= 24 X 3= 72.
Like Terms
Combine like terms in each expression.
Question 8.
\(\frac{1}{4}\)k + \(\frac{1}{4}\)m –
\(\frac{2}{3}\)k + \(\frac{5}{9}\)m
Answer:
\(\frac{1}{4}\)k + \(\frac{1}{4}\)m –
\(\frac{2}{3}\)k + \(\frac{5}{9}\)m =
– \(\frac{5}{12}\)k + \(\frac{29}{36}\)m,
Explanation:
Given \(\frac{1}{4}\)k + \(\frac{1}{4}\)m –
\(\frac{2}{3}\)k + \(\frac{5}{9}\)m,
we combine like terms in expression as
(\(\frac{1}{4}\)k – latex]\frac{2}{3}[/latex]k) +
(\(\frac{1}{4}\)m + \(\frac{5}{9}\)m) =
(\(\frac{1}{4}\) – \(\frac{2}{3}\))k +
(\(\frac{1}{4}\) + \(\frac{5}{9}\))m,
before subtracting or adding we make common
denominators for the both terms so
\(\frac{1 X 3 – 2 X 4}{12}\)k +
\(\frac{1 X 9 + 5 X 4}{36}\)m =
\(\frac{3 – 8}{12}\)k + \(\frac{ 9+ 20}{36}\)m = \(\frac{- 5}{12}\)k + \(\frac{29}{36}\)m =
–\(\frac{5}{12}\)k + \(\frac{29}{36}\)m.
Question 9.
-4b + 2w +(-4b) + 8w
Answer:
-8b + 10w,
Explanation:
Given -4b + 2w +(-4b) + 8w we combine like terms as
– 4b + (-4b) and 2 w + 8w =
– 4b + (-4b) + 2w + 8w =
– 8b + 10w, therefore -4b + 2w +(-4b) + 8w = -8b + 10w.
Question 10.
6 – 5z + 8 – 4z + 1
Answer:
-9z + 15 or 15 – 9z,
Explanation:
Given 6 – 5z + 8 – 4z + 1 we combine like terms as
(6 + 8 + 1) and (-5z – 4z) as
6 + 8 + 1 – 5z – 4z = 15 – 9z,
therefore 6 – 5z + 8 – 4z + 1 = 15 – 9z or -9z + 15.
Inequalities
Question 11.
Write an inequality that represents the situation:
A large box of golf balls has more than 12 balls.
Describe how your inequality represents the situation.
Answer:
12 > x is Inequality,
Explanation:
Given a large box of golf balls has more than 12 balls means
12 > x is inequality, where x = the number of golf balls,
inequality states that the number of golf balls is over 12.
Language Development
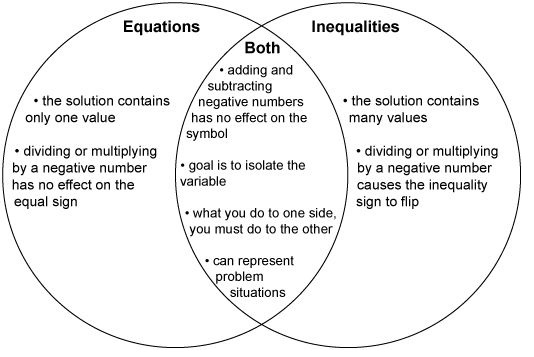
Fill in the Venn diagram to compare and contrast equations and inequalities.
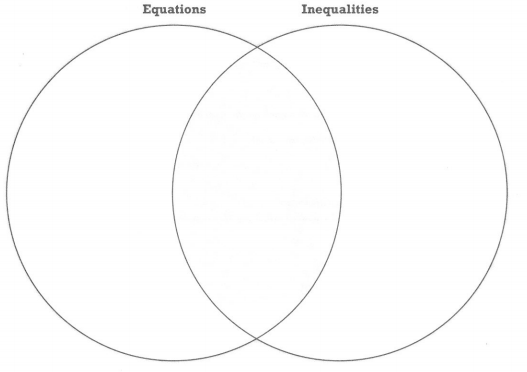
In the box below, draw pictures to represent the
terms and phrases in the overlap section of your diagram.
Answer:
PICK A PROJECT
PROJECT 5A
How many different ways could you sort a basket of vegetables?
PROJECT: COMPARING WITH A VENN DIAGRAM


Explanation:
Ways of sorting a basket of vegetables as per
1. A part of a plant used as a food (spinach),
2. Do not contain seeds (potatoes),
3. Distinct in taste – can be sweet (sweet potato), salty,
sore or bitter (bitter gourd),
4. Mostly green in color (cucumber),
5. Supply fiber, vitamins, minerals and trace elements,
6. Involved in vegetative reproduction.
PROJECT 5B
Which character would you be from your favorite play? Why?
PROJECT: WRITE A PLAY

Answer:
Character I would be from my favorite plays is Cinderella,
Always Be Kind No Matter What –
A little kindness goes a long way, and no doubt
Cinderella is a kind soul. Her kindness can make
her seem like a pushover (especially when her evil
stepmother and stepsisters are overloading her with housework!).
Explanation:
Play:
- Cinderella is a princess.
- She was born to 2 lovely parents.
- Her mother dies early, and her father remarries.
- But the stepmother and Cinderella’s two
stepsisters treated her like a servant. - Cinderella meets the Prince once in the forest.
- She goes to the royal ball ceremony with the
fairy godmother’s help and dances with the prince. - The carriage, driver, horse, dress, etc.,
were all magical and would have returned
to normal just after the clock struck midnight. - In a hurry to leave the palace before midnight,
Cinderella forgets her slippers. - The prince traces her back by those slippers and marries her.
- They live happily ever after.
At the end Cinderella kind heart wins,
so it’s my favorite play.
PROJECT 5C
If you could live in another country, where would you live, and why?
PROJECT: EXCHANGE SOUVENIRS

Answer:
I would live in Canada,
Many people have the dream of living in another country for at least some time during their life. And with good reason. Their are so many benefits.
Moving overseas can dramatically changes my life for the better.
In fact, there are a whole host of reasons why I decided to move to another country.
Living overseas can offer new opportunities, new lifestyles,
new careers and a new direction, financially better prospects.
Explanation:
I would prefer living in canada because
It’s an absolutely stunning place,
Great job opportunities,
People are family friendly,
The best of modern metropolitan living,
Familiar culture and language,
Free health care,
The Canadian sense of humor,
Canadian crime rates are incredibly low,
Canada is an ‘education superpower’ country,
World leaders in quantum computing,
medical research and space science,
Canada has a wonderfully varied climate,
Canadians breathe some of the cleanest air on this planet,
Great food, Niagara Falls, Cheap living costs,
A country you can be proud of living.
PROJECT 5D
How would you prepare for being on a game show?
PROJECT: SOLVE RANDOMIZED EQUATIONS AND INEQUALITIES

Preparing for being on a game show
1. Studying the format of the show,
2.Taking it seriously and practice,
3. Don’t be guilt – No matter how much I am
losing by keep myself cool and dignity,
4. Stay positive,
5. Enjoy it.
Lesson 5.1 Write Two-Step Equations
Marley collects golf balls. His neighbor Tucker
collects 3 more than twice as many golf balls as Marley.

A. How can you use a table to represent the number of golf balls in Marley’s collection, m, and the number of golf balls in Tucker’s collection?
B. How can you use an algebraic expression to represent
the number of golf balls in Tucker’s collection?
a.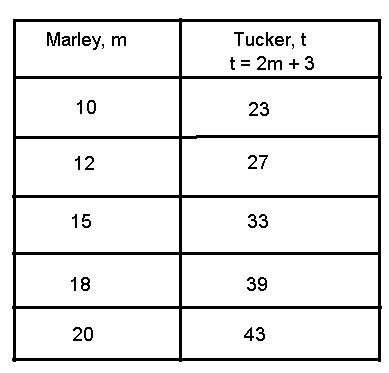
b. Algebraic expression is t = 2m + 3,
Explanation:
Given Marley collects golf balls. His neighbor Tucker
collects 3 more than twice as many golf balls as Marley so
a. The table to represent the number of golf balls in
Marley’s collection m and the number of golf balls
in Tucker’s collection are if Marley’s has 10 golf balls
then Tucker will have 2 X 10 + 3 = 20 + 3 = 23,
if Marley’s has 12 golf balls then Tucker will have
2 X 12 + 3 = 24 + 3 = 27, if Marley’s has 15 golf balls
then Tucker will have 2 X 15 + 3 = 30 + 3 = 33,
if Marley’s has 18 golf balls
then Tucker will have 2 X 18 + 3 = 36 + 3 = 39 and
if Marley’s has 20 golf balls
then Tucker will have 2 X 20 + 3 = 40 + 3 = 43 golf balls
as shown above in the table.
b. As Marley collects golf balls, His neighbor Tucker
collects 3 more than twice as many golf balls as Marley so
the algebraic expression to represent
the number of golf balls in Tucker’s collection is
t = 2m + 3 here t is to represent Tucker and m
is to represent Marley.
Focus on math practices
Look for Relationships How do the terms of the
expression you wrote in Part B relate to the values in the table?
Answer:
Yes, the terms of the expression I wrote in Part B
relate to the values in the table,
Explanation:
As the values in the table of Marley’s collection of
golf balls and Tucker’s collection of golf balls are related
with the terms of expression as Tucker’s collection
of golf balls are dependent on collection of
Marley’s golf balls as twice plus 3 more so values
of table are m = m and t = 2m + 3,
therefore the terms of expression I wrote in Part B
relate to the values in the table.
Essential Question
How does an equation show the relationship between variables and
other quantities in a situation?
Answer:
Yes, an equation show the relationship between
variables and other quantities in a situation with
equality and inequalities signs,
Explanation:
An equation is distinct because it has an equals sign and
that in itself creates a relationship.
Usually, it’s relating the left side to the right side in
terms of that fact that they’re equal to each other and
unlike inequalities which form more of a relation between two quantities that can be greater than or less than.
Try It!
Cole buys a new laptop for $335. He makes a down
payment of $50 and pays the rest in 6 equal monthly payments, p.
What equation represents the relationship between the cost of the laptop and Cole’s payments?
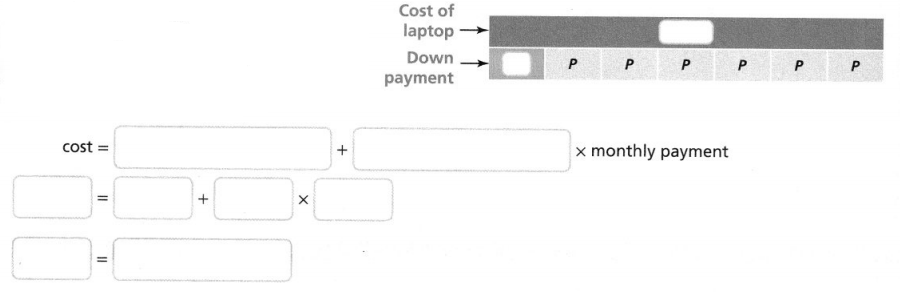 Answer:
Answer:
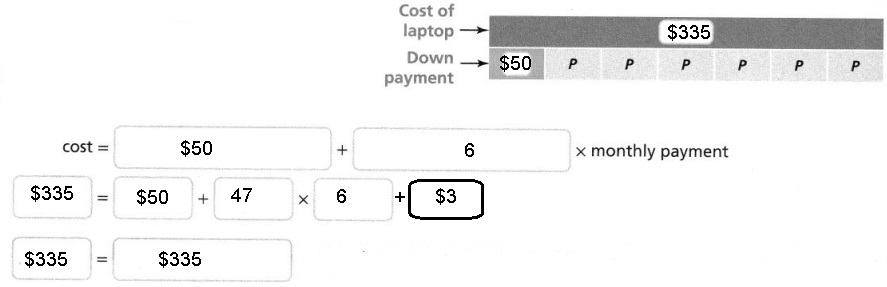
Explanation:
Given Cole buys a new laptop for $335. He makes a down
payment of $50 and pays the rest in 6 equal monthly payments, p.
The equation cost = $50 + 6 X p represents
the relationship between the cost of the laptop and
Cole’s payments as shown above.
Convince Me!
Why are both multiplication and addition used in the equation that
represents Cole’s monthly payments?
Answer:
Cole’s makes a down payment of $50 first and pays
the rest in 6 equal monthly payments, p not all at same time,
So, both multiplication and addition are used in the equation,
Explanation:
As given Cole buys a new laptop for $335.
He makes a down payment of $50 first and
pays the rest in 6 equal monthly payments, p.
So first we write multiplication as 6 X p then we add
initial down payment $50 in the equation.
Try It!
Marcia and Tamara are running a race. Marcia has run 4 kilometers.
Tamara has completed of the race and is 2.5 kilometers ahead of Marcia.
Write an equation that represents the relationship between the distances each girl has run.
Let k represent the total length of the race in kilometers.
Answer:
Marica = m = 4km,
k = Tamara = t = 2. 5km + m = 2.5km + 4km = 6.5km,
Explanation:
Given Marcia and Tamara are running a race. Marcia has run 4 kilometers.
Tamara has completed of the race and is 2.5 kilometers ahead of Marcia.
Let k represent the total length of the race in kilometers, m for Marica and t for Tamara and
Marica m = 4 km and Tamara and total length of the race
is t or k = 2.5km + 4km = 6.5km,
Equation that represents the relationship between
the distances each girl has run is k = t = 2.5 km + m.
Try It!
At the mall, Claire buys a hat that is 60% off and socks that are reduced to $5.49.
She spends a total of $9.49. Let x represent the cost of the hat. Which of the following
equations correctly represents Claire’s shopping trip?
![]()
Answer:
Equation correctly representing Claire’s shopping trip is
0.4x + 5.49 = 9.49,
Explanation:
Given at the mall, Claire buys a hat that is 60% off and socks that are reduced to $5.49.
She spends a total of $9.49.
Let x represent the cost of the hat means and 60% off
so 40%x = 0.4x,
Socks = $5.49 and total = $9.49,
So the following equation correctly represents
Claire’s shopping trip is 0.4x + 5.49 = 9.49.
KEY CONCEPT
You can write an equation with more than
one operation to represent a situation.
 Do You Understand?
Do You Understand?
Question 1.
Essential Question How does an equation show the
relationship between variables and other quantities in a situation?
Answer:
Yes, an equation show the relationship between
variables and other quantities in a situation with
equality and inequalities signs,
Explanation:
An equation is distinct because it has an equals sign and
that in itself creates a relationship.
Usually, it’s relating the left side to the right side in
terms of that fact that they’re equal to each other and
unlike inequalities which form more of a relation between two quantities that
can be greater than or less than.
Question 2.
Use Structure
Do the equations \(\frac{1}{5}\)x + 2 = 6 and
\(\frac{1}{5}\)(x + 2) represent the same situation? Explain.
Answer:
Equations \(\frac{1}{5}\)x + 2 = 6 and
\(\frac{1}{5}\)(x + 2) do not represent the same situation,
Explanation:
Given equations are
1. \(\frac{1}{5}\)x + 2 = 6 and
2. \(\frac{1}{5}\)(x + 2),
1. If we solve \(\frac{1}{5}\)x + 2 = 6 we get
\(\frac{1}{5}\)x = 6 -2,
\(\frac{1}{5}\)x = 4,
x = 4 X 5 = 20 and
2. If we solve \(\frac{1}{5}\)(x + 2) we get
\(\frac{1}{5}\) X x + \(\frac{1}{5}\) X 2 =
\(\frac{1}{5}\) X x = \(\frac{5}{2}\),
x = \(\frac{5}{2}\) X 5,
therefore x = \(\frac{25}{2}\) as
20 ≠ \(\frac{25}{2}\),
So equations \(\frac{1}{5}\)x + 2 = 6 and
\(\frac{1}{5}\)(x + 2) do not represent the same situation.
Question 3.
How do you decide which operations to use when writing an equation?
Answer:
The order of operations is a rule that tells the
correct sequence of steps for evaluating a math expression.
We can remember the order using PEMDAS:
Parentheses, Exponents, Multiplication and
Division (from left to right), Addition and
Subtraction (from left to right).
Explanation:
The order of operations define the priority in which complex equations are solved.
The top priority is your parenthesis, then exponents,
followed by multiplication and division, and
finally addition and subtraction (PEMDAS).
Do You Know How?
Question 4.
Rita started the day with r apps. Then she deleted 5 apps and still had
twice as many apps as Cora has. Write an equation that represents the
number of apps each girl has.

Answer:
Equation : r – 5 = 2c,
Cora = 36 apps,
Rita =77 apps,
Explanation:
Given Rita started the day with r apps.
Then she deleted 5 apps and still had
twice as many apps as Cora has.
Let us take Cora as c = 36 apps and
Rita has twice as Cora after deleting 5 apps
means the equation is 2c = r – 5,
and Rita has r = 2c + 5 = 2 X 36 + 5 = 72 + 5 = 77 apps,
therefore, Equation : r – 5 = 2c,
Cora = 36 apps,
Rita =77 apps respectively.
Question 5.
Write a problem that could be represented by the equation 5n – 6 = 19.
Answer:
Jim’s age is 6 years less than 5 times
his younger brother’s age,
Explanation:
Given to write a problem that could be represented
by the equation 5n – 6 = 19, So, lets take Jim’s age at
present is 19 years which is 6 years less than 5 times
his younger brother’s age.
Question 6.
Kayleigh babysat for 11 hours this week. That was 5 fewer than \(\frac{2}{3}\) as
many hours as she babysat last week, h.
Write an equation to represent the number of hours she babysat each week.
Answer:
Equation to represent the number of hours she
babysat each week is \(\frac{2}{3}\)h – 5 = 11,
Explanation:
Given Kayleigh babysat for 11 hours this week.
That was 5 fewer than \(\frac{2}{3}\)
as many hours as she babysat last week, h.
The equation to represent the number of hours she
babysat each week is \(\frac{2}{3}\)h – 5 = 11.
Practice & Problem Solving
Question 7.
A farmer ships oranges in wooden crates. Suppose each orange weighs the same amount.
The total weight of a crate filled with g oranges is 24.5 pounds. Write an equation that
represents the relationship between the weight of the crate and the number of oranges it contains.

Answer:
Equation that represents the relationship between
the weight of the crate and the number of
oranges it contains is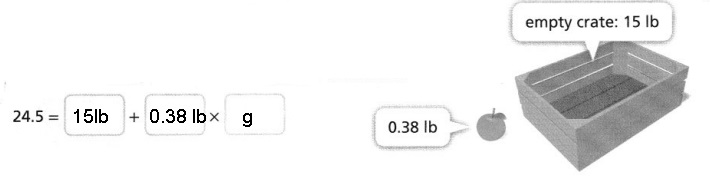
Explanation:
Given a farmer ships oranges in wooden crates.
Suppose each orange weighs the same amount as 0.38lb.
The total weight of a crate filled with g oranges is 24.5 pounds.
So an equation that represents the relationship between
the weight of the crate and the number of oranges
it contains is 24.5 = 15lb + (0.38lb X g) and 1 pound = 1 lb.
Question 8.
Jordan wrote the following description:
Three fewer than one fourth of x is 12.
Write an equation to represent the description.
Answer:
Equation: \(\frac{1}{4}\)x – 3 = 12,
Explanation:
Given Jordan wrote the following description:
Three fewer than one fourth of x is 12.
So the equation to represent the description is
\(\frac{1}{4}\)x – 3 = 12.
Question 9.
At a graduation dinner, an equal number of guests were seated at each of 3 large tables, and
7 late-arriving guests were seated at a smaller table. There were 37 guests in all
. If n represents the number of people seated at each of the large tables,
what equation represents the situation?
Answer:
The number of people seated at each of the large tables,
represented by an equation is \(\frac{1}{3}\)n + 7 = 37,
Explanation:
Given at a graduation dinner, an equal number of
guests were seated at each of 3 large tables and
7 late-arriving guests were seated at a smaller table.
There were 37 guests in all. If n represents the
number of people seated at each of the large tables,
The equation representing the situation is
\(\frac{1}{3}\)n + 7 = 37.
Question 10.
Last night, 4 friends went out to dinner at a restaurant.
They split the bill evenly. Each friend paid $12.75 for
his or her meal and each left the same amount for a tip, t.
The total dinner bill including the tip was $61.
What equation could you use to describe the situation?
Answer:
Equation: 4 X $12.75 + 4t = $61,
Explanation:
Given last night, 4 friends went out to dinner at a restaurant.
They split the bill evenly. Each friend paid $12.75 for
his or her meal and each left the same amount for a tip, t.
The total dinner bill including the tip was $61.
Therefore, equation to describe the situation is
4 X $12.75 + 4t = $61.
Question 11.
Mia buys 4\(\frac{1}{5}\) pounds of plums.
The total cost after using a coupon for 55¢ off her entire
purchase was $3.23. If c represents the cost of the plums
in dollars per pound, what equation could represent the situation?
Answer:
Equation: $3.23 = 4\(\frac{1}{5}\) – .55,
Explanation:
Given Mia buys 4\(\frac{1}{5}\) pounds of plums.
The total cost after using a coupon for 55¢ off her entire
purchase was $3.23. If c represents the cost of the plums
in dollars per pound, the equation representing
the situation is $3.23 = 4\(\frac{1}{5}\) – .55,
as 1 dollar = 100 cents.
For 12 and 13, use the equation shown at the right.
Question 12.
Describe a situation that the equation could represent.
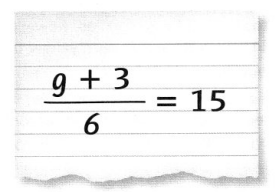
Answer:
There are 6 groups of children each group there are 15 students
and out of which 3 students are absent, so number of students
present are g represented by equation g + 3 ÷ 6 = 15,
Explanation:
Given equation as g + 3 ÷ 6 = 15, let us take the situation as
there are 6 groups of children each group there are 15 students
and out of which 3 students are absent,
so number of students present are g, so that g + 3 = 15 X 6,
therefore g + 3 ÷ 6 = 15.
Given the Question 13.
Reasoning Would the situation you wrote for Problem 12
work if the denominator in the equation were doubled?
Explain why or why not.
Answer:
Yes,
Explanation:
Reasoning is that if the situation I wrote for Problem 12
will work if the denominator in the equation were doubled
because the value of number of students present
will change or increase.
Question 14.
You want to buy a pet iguana. You already have $12 and
plan to save $9 per week.

a. Model with Math If w represents the number of weeks until
you have enough money to buy the iguana, what equation
represents your plan to afford the iguana?
b. Explain how you could set up an equation to
find the amount of money you should save each week to
buy the iguana in 6 weeks.
Answer:
a. Equation : $48 = $12 + $9w,
b. Equation to find the amount(a) of money I should save
each week to buy the iguana in 6 weeks is $48 = $12 + 6a or $60 by 6,
Explanation:
Given I want to buy a pet iguana. I already have $12 and
plan to save $9 per week and iguana costs $48,
a. If w represents the number of weeks until
I have enough money to buy the iguana, the equation
representing my plan to afford the iguana is $48 = $12 + $9w,
b. If the amount(a) of money I should save each week to
buy the iguana in 6 weeks is $48 = $12 + 6a or a = $60 by 6.
Question 15.
In a certain country, the life expectancy of a
woman born in 1995 was 80.2 years.
Between 1995 and 2005, the life expectancy
increased 0.4 year every 5 years.
a. If L represents the life expectancy of a woman born in 2005,
what equation could you use to represent the situation?
b. Reasoning Could two differences equations be used to
find the value of L? Explain.
Answer:
a. L = 80.2 + 80.2 X 2(0.4),
b. Yes, Equation 1: L = 80.2 + 80.2 X 2(0.4) and
Equation 2: L – 80.2 = 2 X 0.4 X 80.2,
Explanation:
Given in a certain country, the life expectancy of a
woman born in 1995 was 80.2 years.
Between 1995 and 2005, the life expectancy
increased 0.4 year every 5 years.
a. If L represents the life expectancy of a woman born in 2005,
The equation that could be used to represent the situation is
L = 80.2 + 80.2 X 2(0.4), we multiply 80.2 with 2 of 0.4 as
every 5 years it is increased by 0.4 and it means from
1995 and 2005 it will increases twice of 0.4,
b. Yes two equations can be used to find the value of L as
First we calculate L by Equation 1: L = 80.2 + 80.2 X 2(0.4) and
Second we calculate L by Equation 2: L – 80.2 = 2 X 0.4 X 80.2.
Question 16.
Higher Order Thinking Use the equation 5x – 13 = 12
a. Write a description that represents the equation.
b. Of the numbers 1, 2, 3, 4, and 5, which are solutions to the equation?
Answer:
a. Description:
There are few sets of books as x in the library and
each set contains 5 books in that 13 books children
took to home and rest are 12 books in the libray,
So find out how many number of books x were there in the library,
b. Solution to the equation is 5,
Explanation:
Given the equation 5x – 13 = 12,
a. Wrote the description that represents the equation as
there are few sets of books as x in the library and
each set contains 5 books in that 13 books children
took to home and rest are 12 books in the libray,
So find out how many number of books x were there in the library,
b. Of the numbers 1, 2, 3, 4, and 5, the solution to the equation
5x – 13 = 12 is 5x = 12 + 13,
5x = 25, therefore x = 25 by 5 = 5, therefore solution to
the equation 5x – 13 = 12 is 5.
Assessment Practice
Question 17.
A garden contains 135 flowers, each of which is either red or yellow.
There are 3 beds of yellow flowers and 3 beds of red flowers.
There are 30 yellow flowers in each yellow flower bed.
PART A
If r represents the number of red flowers in each red flower bed,
what equation could you use to represent the number of red and yellow flowers?
PART B
Write another real-world situation that your equation from Part A could represent.
Answer:
Part A:
Equation to represent the number of red and
yellow flowers is 135 = 3 X 30 + 3r,
Part B:
Real World situation :
There are 135 number of mangoes with fruit seller out of
which 3 baskets mangoes are green in color and 3 baskets of
mangoes are yellow in color and there are total 30 yellow mangoes
in each yellow basket, write an equation to represent the number of
green and yellow mangoes?,
Explanation:
Given a garden contains 135 flowers, each of which is either red or yellow.
There are 3 beds of yellow flowers and 3 beds of red flowers.
There are 30 yellow flowers in each yellow flower bed.
PART A
If r represents the number of red flowers in each red flower bed,
the equation I could use to represent the number of red and
yellow flowers is 135 = 3 X 30 + 3r and
PART B
Wrote another real-world situation that my equation
from Part A could represent as Real World situation :
There are 135 number of mangoes with fruit seller out of
which 3 baskets mangoes are green in color and 3 baskets of
mangoes are yellow in color and there are total 30 yellow mangoes
in each yellow basket, write an equation to represent the number of
green and yellow mangoes? respectively.
Lesson 5.2 Solve Two-Step Equations
Elizabeth wrote the following clues. What is the relationship between the shapes?
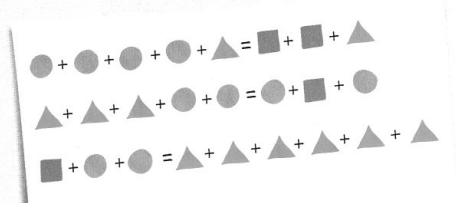
Answer:
1. 4c + t = 2s + t, 2 circles = square
2. 3t + 2c = 2c + s, 3 triangles = square
3. s + 2c = 6t, square = 6 triangles – 2 circles,
Explanation:
Elizabeth wrote the clues as
1. 4 circles + 1 triangle = 2 squares and 1 triangle which means
4 circles = 2 squares, so 1 square is equal to 2 circles.
2. 3 triangles + 2 circles = 2 circles + 1 square,
so 1 square is equal to 3 triangles,
3. 1 square + 2 circles = 6 triangles,
so, 1 square = 6 triangles – 2 circles.
Use Structure
How can you use properties of equality to reason about these equations?
Answer:
1. Addition Property,
2. Addition property,
3. Substitution property,
Explanation:
As we know
1. 4c + t = 2s + t,
Addition Property says for all real numbers x, y, and z ,
if x=y , then x + z = y + z, So 4c + t = 2s + t means 4c = 2s,
2. 3t + 2c = 2c + s means as per Addition Property
3t = s,
3. 1 square + 2 circles = 6 triangles we use
substitution property for circles and triangles as
1 square = 2 circles and 1 square = 3 triangles,
So 1 square + 1 square = 2 X 3 triangles = 2 squares,
2 squares = 2 squares.
Focus on math practices
Look for Relationships Complete the equation with only triangles
using the relationships from the clues shown above.

Answer:
Equation : 4c + 1t = 7t,
Explanation:
As we know 4c = 2s and 1s = 3t means 1s = 2c,
so 3t = 2c therefore 4c = 6t as given 4c +1t = 6t + 1t = 7t
therefore the equation with only triangles
using the relationships from the clues shown above is 4c + 1t = 7t.
Essential Question
How is solving a two-step equation similar to solving a one-step equation?
Answer:
Yes, solving a two-step equation is similar to solving a one-step equation,
Explanation:
Solving a one-step or two-step equation:
In solving an equation is to have only variables on
one side of the equal sign and numbers on the
other side of the equal sign.
The other alike is to have the number in front of the variable
equal to one the variable does not always have to be x.
These equations can use any letter as a variable.
Try It!
Andrew rents bowling shoes for $4. He bowls 2 games.
Andrew spent a total of $22. How much was the cost of each game, b?
Complete the bar diagrams, and then solve the problem.
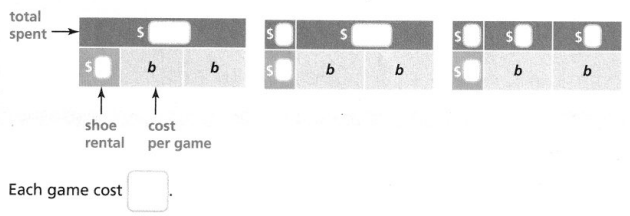
Answer:
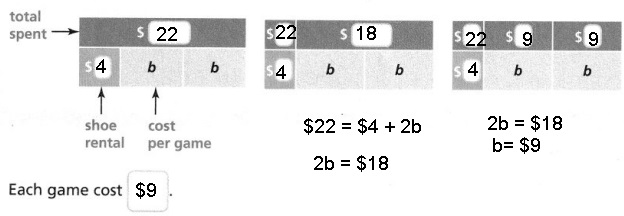
Explanation:
Given Andrew rents bowling shoes for $4. He bowls 2 games.
Andrew spent a total of $22. How much was the cost of each game, b,
Completed the bar diagrams as shown above,
Total spent = shoe rental + 2 X cost of each game,
$22 = $4 + 2 X b,
$22 – $4 = $4 + 2b – $4,
$18 = 2b,
Now each game cost is
$18 by 2 = 2b by 2
b = $9, therefore cost of each game is $9.
Convince Me!
What were the two steps you used to solve this equation?
Answer:
Two step equations can be solved in two steps using two different
properties of equality, I used subtraction property and Division property,
Explanation:
Total spent = shoe rental + 2 X cost of each game is given
$22 = $4 + 2 X b,
First we use the subtraction property of equality to
isolate the term containing the variable,
$22 – $4 = $4 + 2b – $4,
$18 = 2b,
Secondly we use the division property of equality to
isolate the variable or get the variable by itself on
one side of the equation as
$18 by 2 = 2b by 2
b = $9, therefore cost of each game is $9.
Try It!
Kirsty ran 24 laps in a charity run and then walked
0.2 kilometer to the presentation table.
The total distance Kirsty traveled was 29.6 kilometers.
What was the distance of each lap? Explain how you solved the problem.
Answer:
1.225km is equal to each laps,
Explanation:
Given Kristy total distance traveled = 29.6km
and Kristy ran 24 laps and later walk 0.2km.
It simply implies that
Total distance traveled = distance covered running + distance covered walking,
Since we know that Total distance traveled = 29.6km,
distance covered running = 24 laps,
distance covered walking = 0.2km,
Distance covered running in km = total distance traveled – distance covered walking,
Distance covered running in km = 29.6km – 0.2km = 29.4km.
To now find the distance for each lap.
Since we have: Distance covered running in km = 29.4km.
Distance covered running in lap = 24 laps i.e 24 laps = 29.4km,
1 lap = x Use cross-multiple 24 laps X x =
29.4km × 1 lap x = 29.4km / 24 x = 1.225km,
Therefore 1.225km is equal to each laps.
KEY CONCEPT
The properties of equality can be applied the same way when
solving two-step equations as when solving one-step equations.

Answer:
Yes, The properties of equality can be applied the same way when
solving two-step equations as when solving one-step equations.
Two step equations can be solved in two steps using two different
properties of equality, We used subtraction property and division property,
Explanation:
We have 5x + 27 = 122,
First we use the subtraction property of equality to
isolate the term containing the variable,
5x + 27 – 27 = 122 – 27,
5x = 95,
Secondly we use the division property of equality to
isolate the variable or get the variable by itself on
one side of the equation as 5x by 5 = 95 by 5
x = 19, therefore the properties of equality can be applied
the same way when solving two-step equations as
when solving one-step equations.
Do You Understand?
Question 1.
Essential Question How is solving a two step equation similar to
solving a one-step equation?
Answer:
Yes, solving a two-step equation is similar to solving a one-step equation,
Explanation:
Solving a one-step or two-step equation:
In solving an equation is to have only variables on
one side of the equal sign and numbers on the
other side of the equal sign.
The other alike is to have the number in front of the variable
equal to one the variable does not always have to be x.
These equations can use any letter as a variable.
Question 2.
Use Structure Preston uses the bar diagram below to represent 4x – 3 = 13.
How would you use the bar diagram to solve for x?
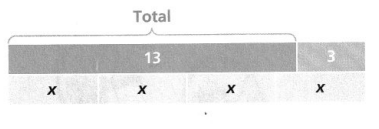
Answer:
By using bar diagram we solve x = 4,
Explanation:
A helpful way to solve problem is to use a bar diagram.
A bar is used to represent the whole. So we label it
with the amount of the whole. Finally, we indicate the required
number of parts with a question mark and determine the value,
By seeing bar diagram we have the total + 3 is divided into
4 parts of x now we solve x as 4x – 3 = 13 by adding 3 both sides,
4x – 3 + 3 = 13 + 3,
4x = 16, Now dividing both sides by 4 we get
4x ÷ 4 = 16 ÷ 4,
x = 4.
Question 3.
Clara has solved the problem 6p – 12 = 72 and says that p = 14.
How can you check to see if Clara is correct?
Answer:
By solving using two-step equation we get p = 14,
we check Clara is correct,
Explanation:
Given Clara equation as 6p – 12 = 72 we solve
First by the addition property of equality to
isolate the term containing the variable,
6p – 12 + 12 = 72 + 12,
6p = 84,
Secondly use the division property of equality to
isolate the variable or get the variable by itself on
one side of the equation as
6p by 6 = 84 by 6, we get p = 14, so checked Clara is correct.
Do You Know How?
Question 4.
Clyde is baking, and the recipe requires 1\(\frac{1}{3}\) cups of flour.
Clyde has 2 cups of flour, but he is doubling the recipe to make twice as much.
How much more flour does Clyde need?

a. Write an equation to represent the problem.
Let c represent the amount of flour Clyde needs.
b. Solve the equation.
Answer:
a. Equation: c = 2 X 1\(\frac{1}{3}\) – 2,
b. Clyde needs \(\frac{2}{3}\) cup more,
Explanation:
Given Clyde is baking, and the recipe requires 1\(\frac{1}{3}\) cups of flour.
Clyde has 2 cups of flour, but he is doubling the recipe to make twice as much.
If c represent the amount of flour Clyde needs the equation is
c = 2 X 1\(\frac{1}{3}\) – 2,
b. Now solving c = 2 X \(\frac{1 X 3 + 1}{3}\) – 2,
c = 2 X \(\frac{4}{3}\) – 2,
c = \(\frac{2 X 4}{3}\) – 2,
c = \(\frac{8}{3}\) – 2,
c = \(\frac{8 – 6}{3}\),
c = \(\frac{2}{3}\) .
Question 5.
Four times a number, n, added to 3 is 47.
a. Write an equation that you can use to find the number.
b. What is the number represented by n?
Answer:
a. Equation: 4n + 3 = 47,
b. The number represented by n is 11,
Explanation:
Given four times a number n added to 3 is 47 means
a. 4 X n + 3 is equal to 47,
therefore the equation is 4n + 3 = 47,
b. Upon solving 4n + 3 = 47 we get value of n, So
first we subtract 3 both sides as
4n + 3 – 3 = 47 – 3,
4n = 44, now we divide both sides by 4 we get
4n ÷ 4 = 44 ÷ 4, so n = 11, therefore the number
represented by n is 11.
Practice & Problem Solving
Question 6.
Use the bar diagram to help you solve the equation 4x – 12 = 16.

Answer:
By using bar diagram we solve x = 7,
Explanation:
A helpful way to solve problem is to use a bar diagram.
A bar is used to represent the whole. So we label it
with the amount of the whole. Finally, we indicate the required
number of parts with a question mark and determine the value,
By seeing bar diagram we have the total + 12 is divided into
4 parts of x now we solve x as 4x – 12 = 16 by adding 12 both sides,
4x – 12 + 12 = 16 + 12,
4x = 28, Now dividing both sides by 4 we get
4x ÷ 4 = 28 ÷ 4,
x = 7.
Question 7.
Complete the steps to solve the equation.
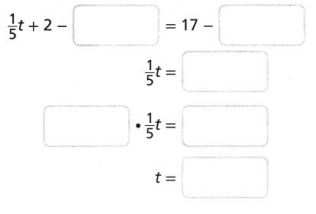
Answer:
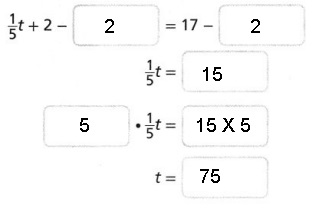
Explanation:
Completed the steps to solve the equation as shown above
first we subtract 2 both sides as
1/5t + 2 – 2 = 17 – 2,
1/5t = 15, now we multiply both sides by 5 we get
1/5t = 15 X 5, we get t = 75.
Question 8.
Use the bar diagram to write an equation. Then solve for x.
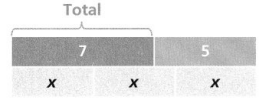
Answer:
Equation is 3x – 5 = 7 and x = 4,
Explanation:
Using the bar diagram we have 3 times x and subtracting 5
we are getting total as 7, so the equation will be
3x – 5 = 7, now solving to get x first we add 5 both sides as
3x – 5 + 5 = 7 + 5,
3x = 12, now we divide both sides by 3,
3x ÷ 3 = 12 ÷ 3, we get x = 4.
Question 9.
While shopping for clothes, Tracy spent $38 less than 3 times what Daniel spent.
Write and solve an equation to find how much Daniel spent.
Let x represent how much Daniel spent.

Answer:
Equation for Daniel spent is : 3x – 38 = 10,
Daniel spent is $16,
Explanation:
Given while shopping for clothes, Tracy spent $38
less than 3 times what Daniel spent.
Let x represent how much Daniel spent.
So an equation to find how much Daniel spent is
3x – 38 = 10, now we solve by adding 38 both sides as
3x – 38 + 38 = 10 + 38,
3x = 48, now we divide both sides by 3,
3x ÷ 3 = 48 ÷ 3, we get x = 16,
therefore, Daniel spent is $16.
Question 10.
Solve the equation 0.5p – 3.45 = -1.2.
Answer:
p = 4.5,
Explanation:
Given to solve the equation 0.5p – 3.45 = -1.2, first
we add +3.45 both side as
0.5p – 3.45 + 3.45 = -1.2 + 3.45,
0.5p = 2.25, now we divide both sides by 0.5 as
0.5p ÷ 0.5 = 2.25 ÷ 0.5, we get p = 4.5.
Question 11.
Solve the equation \(\frac{n}{10}\) + 7 = 10.
Answer:
n = 30,
Explanation:
Given to solve the equation \(\frac{n}{10}\) + 7 = 10,
first we subtract 7 both sides as
\(\frac{n}{10}\) + 7 – 7 = 10 – 7,
\(\frac{n}{10}\) = 3, now we multiply both sides by 10 as
\(\frac{n}{10}\) X 10 = 3 X 10,
we get n = 30.
Question 12.
A group of 4 friends went to the movies. In addition to their tickets,
they bought a large bag of popcorn to share for $6.25. The total was $44.25.
a. Write and solve an equation to find the cost of one movie ticket, m.
b. Draw a model to represent the equation.
Answer:
a. 4m + 6.25 = 44.25,
The cost of one movie ticket m is $9.5,
b.

Explanation:
Given a group of 4 friends went to the movies.
In addition to their tickets, they bought a large bag
of popcorn to share for $6.25. The total was $44.25.
a. Wrote and solved an equation to find the cost of
one movie ticket, m as 4m + 6.25 = 44.25, first we subtract
6.25 both sides as 4m + 6.25 – 6.25 = 44.25 – 6.25,
4m = 38, now we divide both sides by 4 as
4m ÷ 4 = 38 ÷ 4, we get m = $9.5.
b. Drawn a bar diagram model to represent the equation
as shown above.
Question 13.
Oliver incorrectly solved the equation 2x + 4 = 10.
He says the solution is x = 7.
a. What is the correct solution?
b. What mistake might Oliver have made?
Answer:
a. The correct solution is x = 3,
b. Instead of subtracting 4 both sides Oliver added
4 both sides,
Explanation:
Given Oliver incorrectly solved the equation 2x + 4 = 10 as
he says the solution is x = 7,
a. The correct solution is first subtract 4 both sides as
2x + 4 – 4 = 10 – 4,
2x = 6 now divide both sides by 2 as
2x ÷ 2 = 6 ÷ 2, we get x = 3,
b. Mistake Oliver had made is if he says
solution is x = 7 and after solving we are getting
x as 3 means he added more 4 both sides.
Question 14.
Use the equation 4.9x – 1.9 = 27.5.
a. Make Sense and Persevere What two properties of equality
do you need to use to solve the equation?
b. The solution is x = ![]() .
.
Answer:
a. We need two properties of equality as
1. Addition property of equality and
2. Division property of equality,
b. The solution is x = 6,
Explanation:
Given the equation 4.9x – 1.9 = 27.5,
two properties of equality we need to use to solve the equation is
first addition property of equality by adding 1.9 both sides as
4.9x – 1.9 + 1.9 = 27.5 + 1.9,
4.9x = 29.4 now we use division property of equality by
dividing 4.9 both sides as
4.9x ÷ 4.9 =29.4 ÷ 4.9, we get x = 6,
b. As solved in bit a. we get the solution for x as 6.
Question 15.
Higher Order Thinking
At a party, the number of people who ate meatballs was
11 fewer than \(\frac{1}{3}\) of the total number of people.
Five people ate meatballs

a. Write and solve an equation to find the number of people at the party.
Let x represent the number of people at the party.
b. Write a one-step equation that has the same solution.
Answer:
a. Equation: 5 = \(\frac{1}{3}\) x – 11,
The number of people at the party are x = 48,
b. One-step equation that has the same solution is
\(\frac{1}{3}\) x = 16,
Explanation:
At a party, the number of people who ate meatballs was
11 fewer than \(\frac{1}{3}\) of the total number of people.
Five people ate meatballs, So equation to find the number of
people at the party.
a. Let x represent the number of people at the party. Therefore
Equation is \(\frac{1}{3}\) x – 11 = 5,
b. As we have 5 people ate meatballs and 11 are fewer than \(\frac{1}{3}\)
of the total number of people. Total number of people a are equal to 16,
therefore one-step equation that has the same solution is
\(\frac{1}{3}\) x = 16.
Assessment Practice
Question 16.
In a week, Tracy earns $12.45 less than twice the amount Kayla earns.
Tracy earns $102.45. How much does Kayla earn?
Answer:
Kayla earns = $57.45,
Explanation:
Given in a week, Tracy earns $12.45 less than twice the amount Kayla earns.
Let Kayla earns x and Tracy earns Earns in week= $102.45,
Tracy = 2x – 12.45,
102.45 = 2x – 12.45,
2x = 102.45 + 12.45,
2x = 114.90,
x= 114.90/2,
x = $57.45, therefore Kayla earns 57.45 dollars.
Question 17.
Solve the equation 2x + 4\(\frac{1}{5}\) = 9.
Explain the steps and properties you used.
Answer:
x = \(\frac{12}{5}\),
Properties used are 1. Subtraction property of equation and
2. Division property of equation,
Explanation:
Given the equation as 2x + 4\(\frac{1}{5}\) = 9,
2x + \(\frac{4 X 5 + 1}{5}\) = 9,
2x + \(\frac{21}{5}\) = 9, Now we use subtraction property of equation
both sides we subtract \(\frac{21}{5}\) as
2x + \(\frac{21}{5}\) – \(\frac{21}{5}\) = 9 – \(\frac{21}{5}\),
2x = \(\frac{45 – 21}{5}\),
2x = \(\frac{24}{5}\), Now we use division property of equation so we
divide both sides by 2 as 2x/2 = \(\frac{24}{5}\)/2, we get
x = \(\frac{12}{5}\).
Lesson 5.3 Solve Equations Using the Distributive Property
Explain It!
Six friends go jet skiing. The total cost for the adventure is $683.88,
including a $12 fee per person to rent flotation vests.
Marcella says they can use the equation 6r + 12 = 683.88
to find the jet ski rental cost, r, per person.
Julia says they need to use the equation 6(r + 12) = 683.88.

A. Construct Arguments Whose equation accurately represents the situation?
Construct an argument to support your response.
B. What error in thinking might explain the inaccurate equation?
Answer:
A. Argument : Julia is right the equation 6(r +12) = 683.33 is true,
B. Error in thinking may be instead of 6 persons X $12 fee
per person to rent flotation vests, Marcella says they
can use the equation 6r + 12 = 683.88 not 6r + 6 X 12 = 683.88,
Explanation: Given Six friends go jet skiing. The total cost
for the adventure is $683.88,
including a $12 fee per person to rent flotation vests.
Marcella says they can use the equation 6r + 12 = 683.88
to find the jet ski rental cost, r, per person.
Julia says they need to use the equation 6(r + 12) = 683.88.
A. Argument : Julia is right the equation 6(r +12) = 683.33 is true,
because the total cost for the adventure is $683.88,
including a $12 fee per person to rent flotation vests
means 6 multiply by r in addition to 6 multiply by $12 is
equal to total cost, but not Marcella as she says they
can use the equation 6r + 12 = 683.88,
B. Error in thinking may be instead of 6 persons X $12 fee per
person to rent flotation vests, Marcella says they can use
the equation 6r + 12 = 683.88 means she is not considering 6
persons rent flotation vests only for one person she is considering,
i.e Marcella is saying in the equation for 1 person rent flotation vests
instead of for six persons which makes inaccurate equation.
Focus on math practices
Use Structure How can you use the correct equation to
determine the jet ski rental cost per person?
Answer:
The correct equation is 6(r + $12) = $683.88 and
the jet ski rental cost per person is $101.98,
Explanation:
Given six friends go jet skiing. The total cost for the adventure is $683.88,
including a $12 fee per person to rent flotation vests.
We have correct equation as 6(r + $12) = $683.88,
r + 12 = 683.88 ÷ 6,
r = (683.88 ÷ 6) – 12,
So the correct equation to determine the jet ski rental cost per person is
r = $113.98 – $12 = $101.98, therefore The correct equation is 6(r + $12) = $683.88 and
the jet ski rental cost per person is $101.98.
Essential Question
How does the Distributive Property help you solve equations?
Answer:
Distributive property helps in simplifying the problems by
breaking the expressions into addition or subtraction.
The distributive property states that when a factor is multiplied
by the sum or subtract of two numbers, we can multiply each of the two numbers
by that factor and then add or subtract them.
Explanation:
Distributive property is defined as the algebraic property used
to multiply two or more numbers within the parenthesis.
We can say that the distributive property helps in simplifying
the problems by breaking the expressions into addition or subtraction.
It multiplies the number outside parentheses which is equal
to the addition or subtraction of product.
Apart from distributive property, there are two types of properties
known as Commutative and Associative.
This property of multiplication is basically used in addition or subtraction.
To solve equation of distributive property, we need to expand the equation,
find the products and add or subtract.
Try It!
A collector has a box of 32 figurines. The value of each figurine
increased by $2.32 over the past year. The box of figurines is now
worth $114.24. What was the original cost, x, of one figurine?
The original cost of one figurine was ![]() .
.
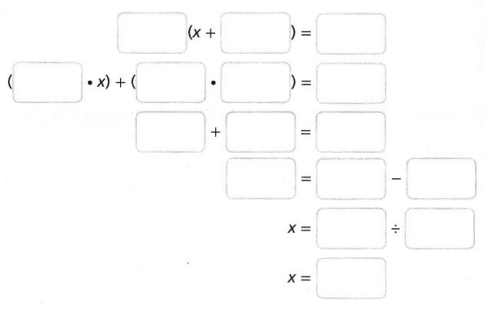
Answer:
The original cost of one figurine was $1.25

Explanation:
Given a collector has a box of 32 figurines.
The value of each figurine increased by $2.32 over the past year.
The box of figurines is now worth $114.24.
The original cost of one figurine was
32(x + 2.32) = 114.24, Applying distributive property as
32 X x + 32 X 2.32 = 114.24,
32x + 74.24 = 114.24,
32x = 114.24 – 74.24,
32x = 40,
x = 40 ÷ 32,
x= 1.25.
Convince Me!
Can the equation 32x + 2.32 = 114.24 be used to
find the original cost of each figurine in the problem above? Explain.
Answer:
No, the equation 32x + 2.32 = 114.24 cannot be used to
find the original cost of each figurine in the problem above,
Explanation:
As the given equation is 32x + 2.32 = 114.24 cannot be used to
find the original cost of each figurine in the problem above
because here in the equation it is not using the value of
each figurine increased by $2.32 over the past year,
instead of using for 32 figurines it is using only for 1 figurine
it has to use as 32(x + 2.32) = 114.24 not 32x + 2.32 = 114.24,
therefor, the equation 32x + 2.32 = 114.24 cannot be used to
find the original cost of each figurine in the problem above.
Try It!
Use the Distributive Property to solve each equation.
a. –\(\frac{1}{2}\)(b – 6) = 5,
Answer:
b = -2,
Explanation:
Given equation as –\(\frac{1}{2}\)(b – 6) = 5 using
distributive property as –\(\frac{1}{2}\) X b + (-\(\frac{1}{2}\)) X (-6) = 5,
–\(\frac{b}{2}\) + \(\frac{6}{2}\) = 5,
–\(\frac{b}{2}\) + 3 = 5,
–\(\frac{b}{2}\) = 5 – 3,
–\(\frac{b}{2}\) = 2,
-b = 2 X 2,
– b = 4, therefore b = -4.
b. 0.4(x – 0.45) = 9.2,
Answer:
x = 23.45,
Explanation:
Given equation as 0.4(x-0.45) = 9.2 using distributive property as
0.4 X x – 0.4 X 0.45 = 9.2,
0.4x – 0.18 = 9.2,
0.4x = 9.38,
x = 9.38 ÷ 0.4,
x = 23.45.
c. -4(p – 212) = 44,
Answer:
p = 201,
Explanation:
Given equation as -4(p-212) = 44 using distributive property as
-4 X p – 4 X -212 = 44,
-4p + 848 = 44,
-4p = 44 – 848,
p = -804 ÷ -4,
p = 201.
KEY CONCEPT
When solving equations written in the form p(x + 9) = r,
you can use the Distributive Property to multiply the
two terms in the parentheses by the term outside the parentheses.

Do You Understand?
Question 1.
Essential Question How does the Distributive Property help you solve equations?
Answer:
Distributive property helps in simplifying the problems by
breaking the expressions into addition or subtraction.
The distributive property states that when a factor is multiplied
by the sum or subtract of two numbers,
we can multiply each of the two numbers
by that factor and then add or subtract them,
for equation 6(x + 8.5) = 123 we use distributive property
we get x = 12,
Explanation:
Distributive property is defined as the algebraic property used
to multiply two or more numbers within the parenthesis.
We can say that the distributive property helps in simplifying
the problems by breaking the expressions into addition or subtraction.
It multiplies the number outside parentheses which is equal
to the addition or subtraction of product.
Apart from distributive property, there are two types of properties
known as Commutative and Associative.
This property of multiplication is basically used in addition or subtraction.
To solve equation of distributive property, we need to expand the equation,
find the products and add or subtract for equation 6(x + 8.5) = 123
we use distributive property as 6x + 6 X 8.5 = 123,
6x + 51 = 123,
6x = 123 -51,
6x = 72,
x = 72 ÷ 6 = 12.
Question 2.
Make Sense and Persevere How are the terms in parentheses
affected when multiplied by a negative coefficient when the
Distributive Property is applied?
Answer:
If a number outside the parentheses has a negative sign then
the first and simplest way is to change each positive or negative sign
of the terms that were inside the parentheses.
Negative or minus signs become positive or plus signs.
Similarly, positive or plus signs become negative or minus signs,
Explanation:
The terms in parentheses affected when multiplied by a
negative coefficient when the distributive property is applied is the first and
simplest way is to change each positive or negative sign
of the terms that were inside the parentheses.
Negative or minus signs become positive or plus signs.
Similarly, positive or plus signs become negative or minus signs,
Example : If equation is -6(x – 4) if we apply distributive property
-6 X x -6 X -4,
-6x + 24, means positive x becomes negative 6x and negative 4
has become positive 24 when multiplied by -6.
Question 3.
Reasoning How can an area model help you set up an equation
for a problem situation?
Answer:
Area of a shape is the space occupied by the shape.
The area of the given shape is the shaded part which means
we can set up an equation for a problem situation given,
Explanation:
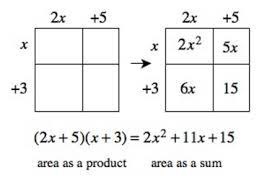
As shown above the area model for the equation is
(2x + 5)(x+3) as shown.
Do You Know How?
Question 4.
A family of 7 bought tickets to the circus. Each family member also
bought a souvenir that cost $6. The total amount they spent was $147.
How much did one ticket cost?
Answer:
Equation : 7(t + 6) = $147,
The cost of one ticket is $15,
Explanation:
Given a family of 7 bought tickets to the circus. Each family member also
bought a souvenir that cost $6. The total amount they spent was $147.
So the equation is 7(t + 6) = 147 on solving we get cost of one ticket as
7t + 42 = 147,
7t = 147 – 42,
7t = 105,
t = 105/7 = 15,
therefore cost of one ticket is $15.
Question 5.
David reads the problem:
Ally bought a T-shirt and a pair of shorts on sale,
which reduced prices by \(\frac{1}{4}\).
The total savings on the two garments was $10.25.
Find the original price for the pair of shorts.

David says that the original price of the shorts was $41.
Does his answer seem reasonable?
Defend your answer by writing and solving an
equation that represents the situation.
Answer:
No, David answer is not reasonable,
the correct equation is \(\frac{1}{4}\) (18 + s) = 10.25,
where s is price of the shorts,
Explanation:
Given David reads the problem:
Ally bought a T-shirt and a pair of shorts on sale,
which reduced prices by \(\frac{1}{4}\).
The total savings on the two garments was $10.25.
Find the original price for the pair of shorts.
David says that the original price of the shorts was $41.
Now we will check let us take s for price of the shorts, and
price of T-shirt is $18,
So the equation is \(\frac{1}{4}\) (18 + s) = 10.25,
\(\frac{1}{4}\) X 18 + \(\frac{1}{4}\) X s = 10.25,
18 + s = 10.25 X 4,
18 + s = 41,
therefore s = 41 – 18 = 23,
So No, David answer is not reasonable the price of shorts is $23 not $41.
Question 6.
Which of the following shows the correct use of the
Distributive Property when solving (33 – x) = 135.2?
A. (33 – x) = 1_-3 • 135.2
B. \(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = \(\frac{1}{3}\) • 135.2
C. \(\frac{1}{3}\) • 33 + \(\frac{1}{3}\)x = 135.2
D. \(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = 135.2
Answer:
B. \(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = \(\frac{1}{3}\) • 135.2,
Explanation:
Given to show the correct use of the
Distributive Property when solving (33 – x) = 135.2? as
the correct answer is B. \(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = \(\frac{1}{3}\) • 135.2, if we multiply both sides with \(\frac{1}{3}\)
we get the correct equation as (33 – x) = 135.2 because
\(\frac{1}{3}\)(33 – x) = \(\frac{1}{3}\) X135.2 means,
\(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = \(\frac{1}{3}\) • 135.2,
therefore the correct answer is B. \(\frac{1}{3}\) • 33 – \(\frac{1}{3}\)x = \(\frac{1}{3}\) • 135.2.
Practice & Problem Solving
Leveled Practice For 7-10, use the Distributive Property to solve the equations.
Question 7.
-2(x + 5) = 4
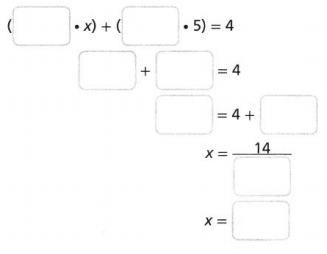
Answer:
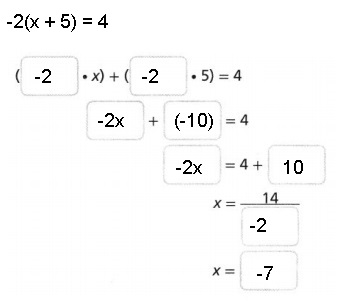
Explanation:
Given equation as -2(x + 5) = 4, using Distributive Property
we get -2 X x + (-2 X 5) = 4,
-2x – 10 = 4,
-2x = 14, So x = -14/2 = -7,
therefore x = -7.
Question 8.
3.2 = \(\frac{4}{5}\)(b – 5)
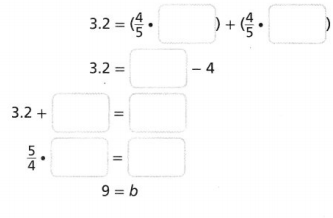
Answer:

Explanation:
Given equation as 3.2 = \(\frac{4}{5}\)(b – 5) using Distributive Property,
we get 3.2 = \(\frac{4}{5}\) X b + \(\frac{4}{5}\)(-5),
3.2 = \(\frac{4}{5}\)b – 4,
3.2 + 4 = \(\frac{4}{5}\)b,
7.2 = \(\frac{4}{5}\)b,
b = \(\frac{5}{4}\) X 7.2,
b = 5 X 1.8,
therefore b = 9.
Question 9.
\(\frac{1}{8}\)(p + 24) = 9
Answer:

Explanation:
Given equation as \(\frac{1}{8}\)(p + 24) = 9 using Distributive Property,
\(\frac{1}{8}\) X p + \(\frac{1}{8}\) X 24 = 9,
\(\frac{1}{8}\)p + 3 = 9,
\(\frac{1}{8}\) p = 9 – 3,
\(\frac{1}{8}\)p = 6,
p = 6 X 8 = 48 or we can solve \(\frac{1}{8}\)(p + 24) = 9 as
p + 24 = 9 X 8,
p + 24 =72,
p = 72 – 24 = 48.
Question 10.
\(\frac{2}{3}\)(6a + 9) = 20.4

Answer:
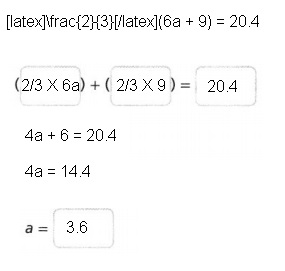
Explanation:
Given equation as \(\frac{2}{3}\)(6a + 9) = 20.4 using Distributive Property,
\(\frac{2}{3}\) X 6a + \(\frac{2}{3}\) X 9 = 20.4 9,
4a + 6 = 20.4,
4a = 20.4 – 6,
4a = 14.4,
a = 14.4/4,
a = 3.6.
Question 11.
Use the equation at the right.
a. Make Sense and Persevere If you apply the Distributive Property first to solve the equation,
what operation will you need to use last?
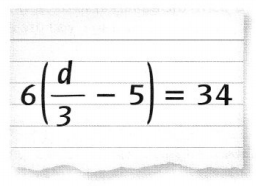
b. If instead you divide first to solve the equation,
what operation would you need to use last?
Answer:
a. We use division operation last, If we apply
the Distributive Property first to solve the equation,
b. We use multiplication last If instead we divide first to solve the equation,
Explanation:
Given equation as 6(\(\frac{d}{3}\) – 5) = 34,
a. If we apply the Distributive Property first to solve the equation,
operation I will need to use last is division as we know
1.. Multiply the term outside of the parentheses by each term
in the parentheses,
2. We combine like terms,
3. we divide to find the final solution,
so 6 X \(\frac{d}{3}\) – 6 X 5 = 34,
2d – 30 = 34,
2d = 34 + 30,
2d = 64,
d = 64/2 = 32,
b. Now If instead I divide first to solve the equation,
operation I would need to use last is
6 X \(\frac{d}{3}\) – 6 X 5 = 34,
\(\frac{d}{3}\) – 5 = 34/6,
\(\frac{d}{3}\) = 5.66 + 5,
\(\frac{d}{3}\) = 10.66
d= 10.66 X 3 = 31.98 ≈ 32, we use multiplication.
Question 12.
A family buys 4 airline tickets online. The family buys travel
insurance that costs $19 per ticket. The total cost is $752.
Let x represent the price of one ticket.
a. Write an equation to represent this situation.
b. What is the price of one ticket?
Answer:
a. Equation: 4(x + 19) = 752,
b. The price of one ticket is $169,
Explanation:
Given a family buys 4 airline tickets online. The family buys travel
insurance that costs $19 per ticket. The total cost is $752.
Let x represent the price of one ticket.
a. As 4 tickets multiplied by each ticket and 4 tickets multiplied
by travel insurance of $19 is equal to $752,
So, the equation is 4(x + 19) = 752,
b. Now solving the equation 4(x + 19) = 752,
4x + 76 = 752,
4x = 752 – 76,
4x = 676,
x = 676/4 = 169, therefore the price of one ticket is $169.
Question 13.
A local charity receives \(\frac{1}{3}\) of funds
raised during a craft fair and a bake sale.
The total amount given to charity was $137.45.
How much did the bake sale raise?

Answer:
The Bake Sale raised funds of $159.75,
Explanation:
Given a local charity receives \(\frac{1}{3}\) of funds
raised during a craft fair and a bake sale.
The total amount given to charity was $137.45 and
Craft Fair raised $252.60, lets take Bake sale raised funds of b,
So \(\frac{1}{3}\)(252.60 + b) = 137.45,
252.60 + b = 137.45 X 3,
252.60 + b = 412.35,
b= 412.35 – 252.60,
b = 159.75,
therefore the Bake Sale raised funds of $159.75.
Question 14.
The solution shown for the equation is incorrect.
a. What is the correct solution?
b. What was the likely error?

Answer:
a. The correct solution is r = 8,
b. Instead of +8 it is showing -8,
Explanation:
a. The given equation is -3(6 – r) = 6,
-3 X 6 -3 X -r = 6,
-18 + 3r = 6,
3r = 6 + 18,
3r = 24,
r = 24/3 = 8,
b. The likely error while solving is -3 X -r it is
+3r, but instead of 3r it is taken as -3r so it is showing
r = -8 but the correct solution is r =8.
Question 15.
Vita wants to center a towel bar on her door that is
27\(\frac{1}{2}\) inches wide.
She determines that the distance from each end of
the towel bar to the end of the door is 9 inches.
Write and solve an equation to find the length of the towel bar.
Answer:
Equation: x + 18 = 27\(\frac{1}{2}\),
The length of the towel bar is 9\(\frac{1}{2}\) inches,
Explanation:
Let x inches be the length of the towel bar,
The width of the door is 9 inches on the each side of the
towel bar so the width of the door is 9 + x + 9 = x + 18 inches.
It is given that the width of the door is 27\(\frac{1}{2}\) inches,
S0 27\(\frac{1}{2}\) inches = x +18,
x = 27\(\frac{1}{2}\) – 18,
x = \(\frac{55}{2}\) – 18,
x = \(\frac{55 – 36}{2}\),
x = \(\frac{19}{2}\) as numerator is greater than denominator,
we write mixed fraction as x = 9\(\frac{1}{2}\) inches.
therefore, the length of the towel bar is 9\(\frac{1}{2}\) inches.
Question 16.
Higher Order Thinking A cell phone plan is shown at the right.
The rates, which include an unlimited data plan, are the same
each month for 7 months. The total cost for all 7 months is $180.39.
Let m represent the average number of minutes that exceeds
700 minutes each month.
a. Write an equation to represent the given situation.

b. Solve the equation to determine how many additional minutes,
on average, you use each month.
Answer:
a. Equation : 7(19.70 + 1.97 + m X 0.05) = 180.39,
b. 82 additional minutes, on average, can be used each month,
Explanation:
Given a cell phone plan is shown at the right.
The rates, which include an unlimited data plan, are the same
each month for 7 months. The total cost for all 7 months is $180.39.
Let m represent the average number of minutes that exceeds
700 minutes each month.
a. Equation is 7(19.70 + 1.97 + m X 0.05) = 180.39,
b. Solving 7(19.70 + 1.97 + m X 0.05) = 180.39,
21.67 + 0.05m = 180.39/ 7,
0.05m = 25.77 – 21.67,
0.05m = 4.1,
m = 4.1/0.05 = 82,
therefore, 82 additional minutes, on average, can be used each month.
Assessment Practice
Question 17.
Fidel earns a fixed amount, m, for each television he sells, and
an additional $15 if the buyer gets an extended warranty.
Fidel sells 12 televisions with extended warranties, earning $900.
Write an equation to represent the situation.
Then solve the equation to find the amount earned for each television sold.
Answer:
Equation: 12(m +15) = 900,
The amount earned for each television sold is $60,
Explanation:
Given, Amount earned by Fidel for each TV is m,
Additional amount for extended warranty is $15,
Televisions sold are 12,
Amount of televisions sold is $900,
Amount earned by each TV * Number of TV’s +
Additional amount * Number of TV’s = Total amount,
So the equation is 12(m + 15) = 900,
Dividing both sides by 12, we get m + 15 = 900/12,
m +15 = 75, m =75 – 15 = 60,
therefore, Fidel earns $60 for each television sold.
TOPIC 5 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary Explain how to isolate the variable in the equation
–\(\frac{2}{3}\)n + 7 = 15. Lesson 5-2
Answer:
n = -12,
Explanation:
To isolate a variable is to perform the following steps:
1. Eliminate any fractions present by multiplying both sides
by any denominators present.
2. Get all terms with the variable on the left side of the
equation and all terms without the variable on the other side.
3. Combine the terms on the left side, if possible.
4. Factor out the variable on the left side, if necessary.
5. Divide both sides by the coefficient of the variable,
leaving the variable isolated. Now the equation given is
–\(\frac{2}{3}\)n + 7 = 15, solving
–\(\frac{2}{3}\)n = 15 – 7,
n = – \(\frac{3{2}\) X 8,
n = -12.
Question 2.
Jake paid $13.50 for admission to the county fair and
bought 9 tickets to play games.
If he spent a total of $36, what is the cost, c, of one ticket?
Write and solve an equation. Lessons 5-1 and 5-2
Answer:
Equation: 9c + 13.50 = 36,
The cost of one ticket is $2.5,
Explanation:
Given Jake paid $13.50 for admission to the county fair and
bought 9 tickets to play games.
If he spent a total of $36 and the cost c of one ticket is
Equation 9c + 13.5 = 36,
9c + $13.50 = $36, subtracting 13.5 both sides
9c + 13.50 – 13.5 = 36 -13.5,
9c = 22.5, dividing both sides by 9 we get
9c/9 = 22.5/9,
c = 2.5, therefore cost of one ticket is $2.5.
Question 3.
Select all the equations that are equivalent to \(\frac{1}{2}\)(4 + 8x) = 17.
Lesson 5-3
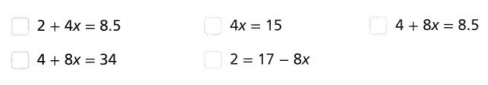
Answer:
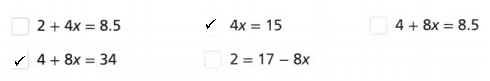
The equations that are equivalent to \(\frac{1}{2}\)(4 + 8x) = 17 are
4x = 15 and 4 + 8x = 34,
Explanation:
Given equation is \(\frac{1}{2}\)(4 + 8x) = 17,
multiplying both side by 2 we get 4 + 8x = 34 and now dividing
both sides by 2 we get 2 + 4x = 17, 4x = 15,
so the equations that are equivalent to \(\frac{1}{2}\)(4 + 8x) = 17 are
4x = 15 and 4 + 8x = 34.
Question 4.
Clara has 9 pounds of apples. She needs 1\(\frac{1}{4}\) pounds
to make one apple pie. If she sets aside 1.5 pounds of
apples to make applesauce, how many pies, p, can she make?
Write and solve an equation. Lessons 5-1 and 5-2
Answer:
Equation: 1\(\frac{1}{4}\)p + 1.5 = 9,
Number of apple pies Clara can make are 6,
Explanation:
Given Clara has 9 pounds of apples.
She needs 1\(\frac{1}{4}\) pounds to make one apple pie.
If she sets aside 1.5 pounds of apples to make applesauce,
Number of pie’s p she can make are
equation is 1\(\frac{1}{4}\)p + 1.5 = 9,
\(\frac{4 X 1 + 1}{4}\)p + 1.5 = 9,
\(\frac{5}{4}\)p + 1.5 = 9,
\(\frac{5}{4}\)p = 9 – 1.5,
\(\frac{5}{4}\)p = 7.5,
5p = 7.5 X 4,
5p = 30,
p = 30/5 = 6, therefore number of apple pies Clara can make are 6.
Question 5.
Solve the equation -4(1.75 + x) = 18. Show your work. Lesson 5-3
Answer:
Solving the equation -4(1.75 + x) = 18 we get x = -6.25,
Explanation:
Given equation is -4(1.75 + x) = 18, dividing both side by -4,
-4(1.75 + x)/-4 = 18/-4,
1.75 + x = – 4.5,
x = – 4.5 -1.75,
x = – 6.25.
Question 6.
Four friends attend a school play and pay $6.75 per ticket.
Each also buys a Healthy Snack Bag sold by the Theater Club.
If the friends spent a total of $37.00, how much did each Healthy
Snack Bag cost, b? Write and solve an equation. Lessons 5-1, 5-2,5-3
Answer:
Equation:4(6.75 + b) = 37,
Each Healthy Snack Bag cost is $2.5,
Explanation:
Given four friends attend a school play and pay $6.75 per ticket.
Each also buys a Healthy Snack Bag sold by the Theater Club.
If the friends spent a total of $37.00, Now if each Healthy
Snack Bag cost, b then the is equation 4(6.75 + b) = 37,
dividing both sides by 4 we get 6.75 + b = 37/4,
6.75 + b = 9.25,
b = 9.25 – 6.75,
b = 2.5, therefore each Healthy Snack Bag cost is $2.5.
How well did you do on the mid-topic checkpoint? Fill in the stars. 
![]()
TOPIC 5 MID-TOPIC PERFORMANCE TASK
Marven and three friends are renting a car for a trip.
Rental prices are shown in the table.

PART A
Marven has a coupon that discounts the rental of a full-size car by $25.
They decide to buy insurance for each day. If the cost is $465,
how many days, d, will they rent the car? Write and solve an equation.
Answer:
Equation : 49d + 21d – 25 = 465,
Number of days they will rent the car is 7 days,
Explanation:
Given Marven has a coupon that discounts the rental of a full-size car by $25.
They decide to buy insurance for each day. If the cost is $465,
So number of many days, d, will they rent the car is
49d + 21d – 25 = 465,
70d = 465 + 25,
70d = 490,
d = 490/70,
d= 7, therefore number of days they will rent the car is 7 days.
PART B
If they still use the coupon, how many days could they rent the small car
with insurance if they have $465 to spend?
Answer:
If they still use the coupon, how many days could they rent the small car
with insurance if they have $465 to spend is 8 days,
Explanation:
If they still use the coupon, Number of days could they rent the small car
with insurance if they have $465 to spend is
39d + 21d – 25 = 465,
60d = 465 + 25,
60d = 490,
d = 8.166, minimum 8 days.
PART C
They rent a car with insurance for 5 days but lost their coupon.
If Marven and the three friends spend $75 each, which car did they rent?
Write and solve an equation to justify your answer.
Answer:
Equation:
5(p + 21) = 4 X 75,
They rent the small car,
Explanation:
If they rent a car with insurance for 5 days but lost their coupon.
If Marven and the three friends spend $75 each means 4 X 75,
Let price be p for the rent of the car,
5(p + 21) = 4 X 75,
5p + 105 = 300,
5p = 300 – 105,
5p = 195,
p = 195/5,
p = 39, So car did they rent is small car.
Lesson 5.4 Solve Inequalities Using Addition or Subtraction
Explain It!
Selena and Martin are waiting at the bus stop. The number lines show the
possible wait times in minutes, t, for Selena and Martin.
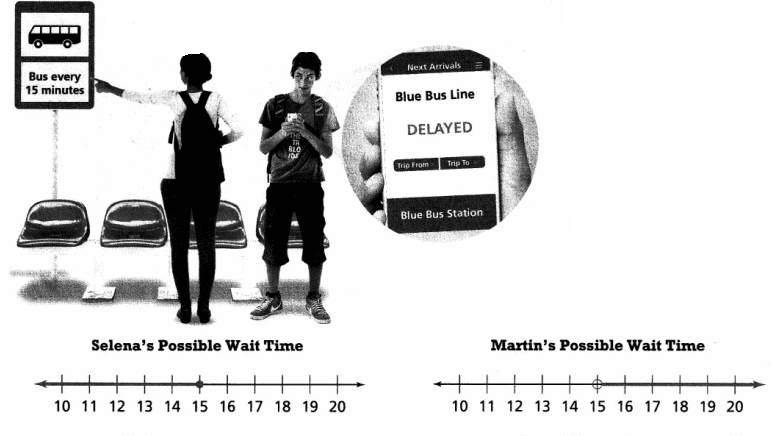
A. Construct Arguments Who anticipates a longer wait?
Justify your response with a mathematical explanation.
Answer:
Martin anticipated longer,
Explanation:
Based on inequalities, Martin anticipated a longer waiting time.
This is because he thinks that the bus will arrive greater than 15 minutes.
B. If Selena and Martin both wait 10 minutes for the bus,
whose possible wait time was closer to his or her actual wait time? Explain.
Answer:
Selena is closer,
Explanation:
If both Selena and Martin waited 10 minutes for the bus. Selena is closer to the actual wait time because she anticipated the waiting time for the bus less than 15 minutes before it arrives.
Focus on math practices
Be Precise If Selena and Martin both wait exactly 15 minutes for the bus,
whose possible wait time was closer to his or her actual wait time? Explain.
Answer:
Selena is closer to actual wait time,
Explanation:
If Selena and Martin both wait exactly 15 minutes for the bus.
Selena is closer to the actual wait time.
This is because her possible wait time included 15 minutes.
Her anticipation for the waiting time is exactly the same as the actual waiting time.
Unlike Martin that he anticipated waiting time is greater than 15 mins,
which does not include 15 minutes.
Essential Question
How is solving inequalities with addition and subtraction similar to and
different from solving equations with addition and subtraction?
Answer:
Similarity: Both uses properties of equality or inequality,
Different: An equation has one solution while an inequality has more than one solution,
Explanation:
There is a similarity when solving inequalities with addition and subtraction
from solving equations with addition and subtraction because
both uses properties of equality or inequality.
Inverse relationship between addition and subtraction to
isolate the variable in an equation or inequality. The difference
between the two is the solution for inequality and equation,
There is only one solution for an equation while in an inequality
there can be more than one solution.
Try It!
Kyoko has completed 26 hours of community service.
Her goal is to complete at least 90 hours this semester.
Write and solve an inequality to show how many more hours, h,
Kyoko needs to complete to meet her goal.
Use the number line to graph the solutions.
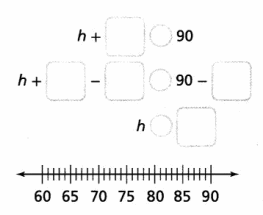
Answer:
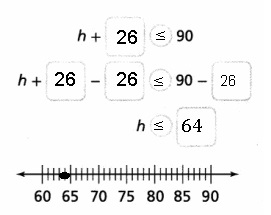
Explanation:
Given Kyoko has completed 26 hours of community service.
Her goal is to complete at least 90 hours this semester.
Wrote and solved an inequality to show how many more hours, h,
Kyoko needs to complete to meet her goal as h + 26 ≤ 90,
Used the number line to graph the solutions as shown above.
Convince Me!
Is there more than one solution to the problem about Kyoko?
Explain. Give one value that is a solution and one value that is not a solution.
Answer:
Yes , there more than one solution to the problem about Kyoko,
Explanation:
Yes , there more than one solution to the problem about Kyoko
because of the indicated range for time.
Kyoko must complete at least 64 hours more to achieve her
goal in the community service.
She cannot go beyond 64 hours because it will be more than
the required number of hours. 65 hours is not a solution to the problem.
The speed limit on a road drops down to 15 miles per hour around a curve.
Mr. Gerard slows down by 10 miles per hour as he drives around the curve.
He never drives above the speed limit.
At what speed was Mr. Gerard driving before the curve? Graph the solution.
Answer:
Mr. Gerard was driving less than or equal to 25 miles per hour before the curve,
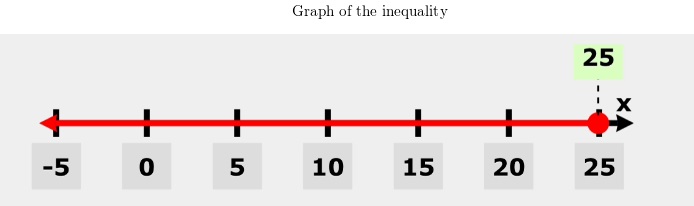
Explanation:
Given the speed limit on a road drops down to
15 miles per hour around a curve.
Mr. Gerard slows down by 10 miles per hour
as he drives around the curve.
He never drives above the speed limit.
The speed Mr. Gerard was driving before the curve is
x – 10 ≤ 15, inequality for the situation,
x – 10 + 10 ≤ 15 + 10, addition property of inequality,
x ≤ 25, his driving speed before the curve,
therefore, Mr. Gerard was driving less than or equal to
25 miles per hour before the curve.
Try It!
Solve the inequality n – 1\(\frac{3}{4}\) ≤ –\(\frac{5}{8}\) Then graph the solution.
Answer:
n ≤ 1\(\frac{1}{8}\) or n ≤ 1.125,
Explanation:
n – 1\(\frac{3}{4}\) ≤ –\(\frac{5}{8}\),
n – 1\(\frac{3}{4}\) + 1\(\frac{3}{4}\) ≤ –\(\frac{5}{8}\) + 1\(\frac{3}{4}\), addition property of inequality,
n ≤ –\(\frac{5}{8}\) + \(\frac{7}{4}\), simplifying
n ≤ \(\frac{-5 + 14}{8}\),
n ≤ \(\frac{9}{8}\), as numerator is greater we write in mixed fraction as
n ≤ 1\(\frac{1}{8}\) or n ≤ 1.125.
KEY CONCEPT
Solving inequalities with addition and subtraction is the same as solving equations with addition and subtraction.
Use the inverse relationship between addition and subtraction to isolate the variable.

Do You Understand?
Question 1.
Essential Question How is solving inequalities with addition and subtraction
similar to and different from solving equations with addition and subtraction?
Answer:
Similarity: Both uses properties of equality or inequality,
Different: An equation has one solution while an inequality has more than one solution,
Explanation:
There is a similarity when solving inequalities with addition and subtraction
from solving equations with addition and subtraction because
both uses properties of equality or inequality.
Inverse relationship between addition and subtraction to
isolate the variable in an equation or inequality. The difference
between the two is the solution for inequality and equation,
There is only one solution for an equation while in an inequality
there can be more than one solution.
Question 2.
Be Precise How do the solutions of the two inequalities differ?
Are any of the solutions the same? Explain.
a. x+ 5 < 8 and x + 5 > 8
b. x + 5 ≤ 8 and x + 5 ≥ 8
Answer:
a. The number 3 is not part of the solution for both inequalities,

b. The number 3 is one the solutions for both inequalities,

Explanation:
a. x + 5 – 5 < 8 – 5, (subtraction property of inequality)
x < 3, (solution to the equation) and
x + 5 – 5 > 8 – 5, (subtraction property of inequality)
x > 3, (solution to the equation),
Both solution uses subtraction property of equality,
However the value of the solutions are different,
One is less than 3 while the other is greater than 3.
b. x + 5 – 5 ≤ 8 – 5, (subtraction property of inequality)
x ≤ 3, (solution to the equation) and
x + 5 – 5 ≥ 8 – 5, (subtraction property of inequality)
x ≥ 3, (solution to the equation),
Both solution uses subtraction property of equality,
Both inequalities have 3 as part of the solution.
Question 3.
Reasoning Write two different inequalities in which one of the solutions is
the same as the solution to x – 23 = 191.
Answer:
The inequalities are x- 23 ≤ 191 and x – 23 < 191,
the first inequality has a similar solution to the indicated equation
because of the inequality symbol,
Explanation:
1. x -23 ≤ 191 (first inequality)
x -23 + 23 ≤ 191 + 23 (addition property)
x ≤ 214 (range of solution to the inequality),
x -23 < 191 (second inequality)
x -23 + 23 < 191 + 23 (addition property)
x < 214 (range of solution to the inequality),
2. The solution to the equation is
x – 23 + 23 = 191 + 23,(addition property of equality)
x = 214 (solution to the equation).
Do You Know How?
Question 4.
Solve each inequality. Then graph the solution.
a. x + 5 > 3

Answer:
x > -2,
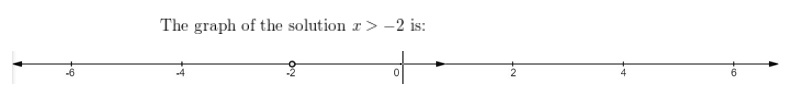
Explanation:
x + 5 > 3( inequality),
x + 5 – 5 > 3 – 5, subtract 5 from both sides,
x > -2,
The graph of the solution x > -2 is shown above.
b. x + 5 ≤ 3

Answer:
x ≤ -2,

Explanation:
x + 5 ≤ 3 (inequality),
x + 5 – 5 ≤ 3 – 5, subtract 5 from both sides,
x ≤ -2,
The graph of the solution x ≤ -2 is shown above.
c. x – \(\frac{3}{2}\) ≤ -3

Answer:
x ≤ –\(\frac{3}{2}\),
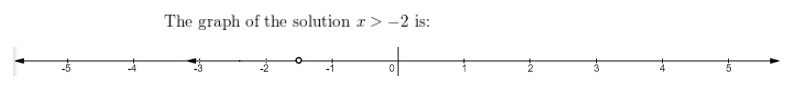
Explanation:
x – \(\frac{3}{2}\) ≤ -3 (inequality),
x – \(\frac{3}{2}\) + \(\frac{3}{2}\) ≤ -3 + \(\frac{3}{2}\)(adding \(\frac{3}{2}\) both sides),
x ≤ –\(\frac{3}{2}\),
The graph of the solution x > -2 is shown above.
Question 5.
Elanor is driving below the speed limit on a highway.
a. Write the inequality to show how much faster Elanor can drive without going over the speed limit.

b. Solve the inequality you wrote. By how much can Elanor increase her speed?
Answer:
a. x + 43.5 < 55,
b. Elanor increase her speed by x < 11.5,
Explanation:
a. Let x be the increase in the speed limit,
The inequality for the given situation where Elanor can
drive without going over the speed limit is x + 43.5 < 55,
b. Now we find the value of x in the given inequality is
x + 43.5 < 55, subtracting 43.5 both sides as
x + 43.5 – 43.5 < 55 – 43.5, we get
x< 11.5, So Elanor increase her speed by x < 11.5.
Practice & Problem Solving
Leveled Practice In 6 and 7, fill in the boxes to solve each inequality. Then graph the solutions.
Leveled Practice In 6 and 7, fill in the boxes to solve each inequality. Then graph the solutions.
Question 6.
x + 5 < 7

Answer:
x < 2,
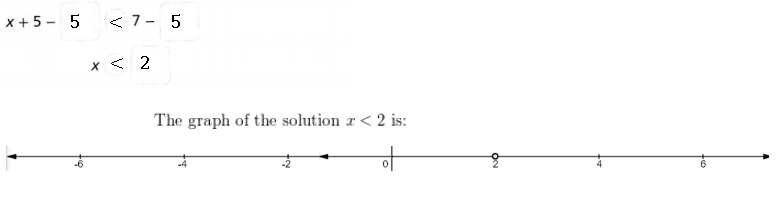
Explanation:
Given inequality as x + 5 < 7, now we subtract 5 from both sides,
x + 5 – 5 < 7 – 5, we get
x < 2.
Question 7.
x – 4 ≥ 12
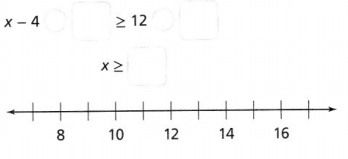
Answer:
x ≥ 16,
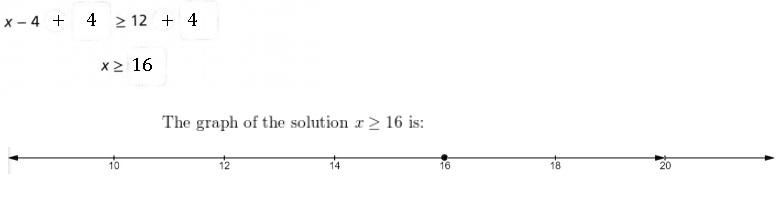
Explanation:
Given inequality as x – 4 ≥ 12, now we add 4 on both sides,
x – 4 + 4 ≥ 12 + 4, we get
x ≥ 16.
Question 8.
Solve x + 10 ≥ 14. Then graph the solution.

Answer:
x ≥ 4,
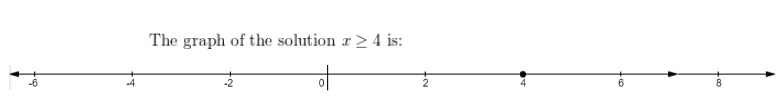
Explanation:
Given inequality as x + 10 ≥ 14, now we subtract 10 from both sides,
x + 10 – 10 ≥ 14 – 10, we get x ≥ 4.
Question 9.
Solve x – 20 ≤ -11. Then graph the solution.
![]()
Answer:
x ≤ 9,
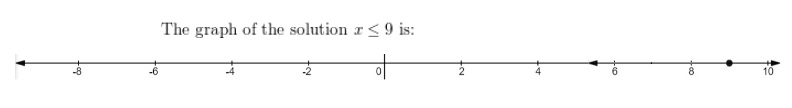
Explanation:
Given inequality as x – 20 ≤ – 11, now we add 20 on both sides,
x – 20 + 20 ≥ -11 + 20, we get
x ≤ 9.
Question 10.
The maximum number of students in a classroom is 26.
If there are 16 students signed up for the art class, how many more
students can join the class without exceeding the maximum?
Answer:
There are at most 10 students who can join the art class,
Explanation:
Let x be the number of students that can join the art class,
x + 16 ≤ 26,
x + 16 – 16 ≤ 26 – 16, subtract 16 from both sides,
x ≤ 10, Therefore there are at most 10 students who can join the art class.
Question 11.
Higher Order Thinking The inequality x + c > -2.55 has the
solution x > 4.85 What is the value of c? How do you know?
Answer:
c = -7.4,
Explanation:
x + c = -2.55,
4.85 + c = -2.55, Substitute the value of x,
4.85 + c – 4.85 = -2.55 – 4.85, subtract -4.85 from both sides,
c = -7.4,
The value of c = -7.4, substitute this to the original inequality,
so that it will make the inequality true,
x + c > -2.55,
x + (-7.4) > -2.55, substitute the value of c,
x + (-7.4) + 7.4 > -2.55 + 7.4, add 7.4 on both sides,
x > 4.85 which is true.
Question 12.
Rina is climbing a mountain. She has not yet reached base camp.
Write an inequality to show the remaining distance, d, in feet
she must climb to reach the peak.

Answer:
Inequality: d + 9,695 > 12,358,
Rina must climb d > 2,663 feet to reach the peak,
Explanation:
The inequality to determine the distance is
d + 9,695 > 12,358,
d + 9,695 – 9,695 > 12,358 – 9,695, subtract 9,695 from both sides,
d > 2,663, therefore, Rina must climb d > 2,663 feet to reach the peak.
Question 13.
On a math test, students must solve the inequality x – 5< 11 and then graph the solution. Mason said the solution is x < 6 and graphed the solution as shown below.
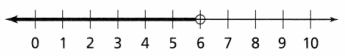
a. What error did Mason make?
b. Show the correct solution on the number line.
![]()
Answer:
a. Mason did not use the inverse operations to determine the solution,
b. 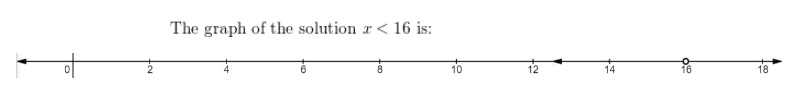
Explanation:
a. Mason did not use the inverse operations to determine the solution of x,
Mason subtracted 5 to the right side when it should have been added this
is the correct way of using inverse operation,
b. x – 5 < 11,
x – 5 + 5 < 11 + 6, adding 5 on both sides,
x < 16, the graph of solution is shown on number line above.
Question 14.
Model with Math Dani’s neighbors paid her to take care of their bird during their vacation.
Dani spent $4 of her earnings on an afternoon snack and $16 on a new book.
Afterward, she had at least $8 left. Write an inequality to represent how much Dani’s neighbors paid her.
Answer:
Inequality : x – (4 + 16) ≥ 8,
Dani’s neighbors paid her x ≥ 28,
Explanation:
Given Dani’s neighbors paid her to take care of their bird
during their vacation.
Dani spent $4 of her earnings on an afternoon snack and
$16 on a new book. Afterward, she had at least $8 left,
Let x be the amount Dani’s neighbors paid her, So the inequality is
x – (4 + 16) ≥ 8, now solving the inequality
x – 20 + 20 ≥ 8 + 20, adding 20 on both sides,
x ≥ 28, therefore, Dani’s neighbors paid her x ≥ 28.
Question 15.
Reasoning The temperature in a greenhouse should be 67°F or higher.
One morning, the heater stopped working.
The temperature dropped 4 degrees before someone fixed the heater.
The temperature was still at least 67°F when the heater started working again.
How can you best describe the temperature in the greenhouse before
the heater stopped working?

Answer:
The temperature in the greenhouse before
the heater stopped working is at least 71°F,
Explanation:
The temperature in a greenhouse should be 67°F or higher.
One morning, the heater stopped working.
The temperature dropped 4 degrees before someone fixed the heater.
The temperature was still at least 67°F when the heater started working again.
Let x be the initial temperature of the heater, so
x – 4 ≥ 67,
x + 4 + 4 ≥ 67 + 4, adding 4 on both sides,
x ≥ 71, therefore, the temperature in the greenhouse before
the heater stopped working is at least 71°F.
Assessment Practice
Question 16.
Ramiro has $21. He wants to buy a skateboard that costs $47.
How much more money does he need to have at least $47?
Write an inequality that represents the situation.
Solve the inequality and graph your solution.

Answer:
Inequality : 47 ≤ x + 21,
26 ≤ x or x ≥ 26,
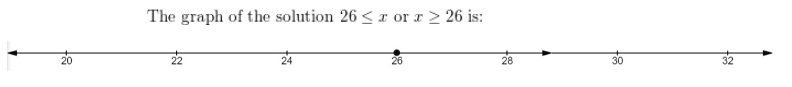
Explanation:
Given Ramiro has $21. He wants to buy a skateboard that costs $47.
Let x be more money does he need to have at least $47,
So the inequality is 47 ≤ x+21,
47 – 21≤ x + 21 – 21, subtract 21 from both sides,
26 ≤ x, The graph 26 ≤ x or x ≥ 26 is shown above.
Question 17.
Kendra has $7.35 in her purse. She needs at least $2.87 more to buy a special bead.
What is the total amount, x, she needs for the bead?
Which inequalities can be used to represent the situation?
Select all that apply.

Answer:
Inequalities that can be used to represent the
situation x = 10.22 are
1. x – 7.35 ≤ 2.87,
2. x + 7.35 ≥ 2.87,
3. x – 7.35 ≥ 2.87,
4. x ≥ 10.22,
5. x ≤ 10.22,
Explanation:
Given Kendra has $7.35 in her purse. She needs at least $2.87
more to buy a special bead.
The total amount, x, she needs for the bead is x = 7.35 + 2.87,
So x = 10.22, Given
1. x + 7.35 ≤ 2.87, on solving
x + 7.35 – 7.35 ≤ 2.87 – 7.35, subtracting 7.35 from both sides,
x ≤ 4.48 but we got x = 10.22, So
x + 7.35 ≤ 2.87 is incorrect as x is not equal to x = 10.22 and
also not less than 4.48.
2. x – 7.35 ≤ 2.87, on solving
x – 7.35 + 7.35 ≤ 2.87 + 7.35, adding 7.35 from both sides,
x ≤ 10.22 we got x = 10.22, So
x – 7.35 ≤ 2.87 is correct as x is equal to x = 10.22.
3. x + 7.35 ≥ 2.87,on solving
x + 7.35 – 7.35 ≥ 2.87 – 7.35, subtracting 7.35 from both sides,
x ≥ 4.48 but we got x = 10.22, So
x + 7.35 ≥ 2.87 is correct as x = 10.22 whose value is
greater than 4.48.
4. x – 7.35 ≥ 2.87,on solving
x – 7.35 + 7.35 ≥ 2.87 + 7.35, adding 7.35 from both sides,
x ≥ 10.22 but we got x = 10.22, So
x – 7.35 ≥ 2.87 is correct as x value is equal to 10.22.
5. x ≥ 10.22 is correct as x is equal to x = 10.22.
6. x ≤ 2.87 is incorrect as x is not equal to 10.22 and is not
also less than 2.87.
7. x ≤ 10.22 is correct as x is equal to 10.22.
8. x ≤ 4.48 is incorrect as x value is not equal to 10.22 and
also not less than 4.48.
Therefore,
Inequalities that can be used to represent the
situation x = 10.22 are
1. x – 7.35 ≤ 2.87,
2. x + 7.35 ≥ 2.87,
3. x – 7.35 ≥ 2.87,
4. x ≥ 10.22,
5. x ≤ 10.22,
Lesson 5.5 Solve Inequalities Using Multiplication or Division
Solve & Discuss It!
Alex and Hope were trying to solve -6x > 24.
Whose inequality shows the solution? Show your work.
Answer:
Hope’s work x < -4 shows the inequality to the solution,
Explanation:
Given Alex and Hope were trying to solve -6x > 24.
Hope shows the solution as x < -4 means x values are less than
-4 which will be -5,-6, -7 and so on, if we substitute x as -5,
we get -6(-5) = 30 which is greater than 24,
therefore, Hope’s work x < -4 shows the inequality to the solution,
Construct Arguments Why does more than one value of x
make the inequality true?
Answer:
Yes, because there may be more than one solutions to make
make the inequality true,
Explanation:
Most of the time, an inequality has more than one or even infinity solutions.
For example the inequality: x>3 . The solutions of this inequality are
“all numbers strictly greater than 3”, therefore more than one value of x
make the inequality true.
Focus on math practices
Be Precise What do you notice about the inequality symbols used
in the original inequality and in the correct solution?
Answer:
The inequality symbol in the solution changed,
Explanation:
The inequality symbol (>) changed in the solution,
The inequality symbol became <, This is because of the
negative integer divided to both sides of the inequality.
Essential Question
How is solving inequalities with multiplication and division similar to and
different from solving equations with multiplication and division?
Answer:
Solving inequalities is very similar to solving equations,
but sometimes we have to reverse the symbol.
we must reverse the inequality symbol when we multiply or
divide both sides of the equation by a negative number.
1) It must be multiplication or division (not addition or subtraction)
2) The number being multiplied or divided must be negative.
Explanation:
Solving inequalities is very similar to solving equations,
but sometimes we have to reverse the symbol.
For example:
Multiplication Properties of Inequality,
c is positive,
a<b, then ac<bc ← -2<3,
a>b, then ac>bc ←-2(4)<3(4),
c is negative,
a<b, then ac>bc ← -2<3,
a>b, then ac<bc ←-2(-4)>3(-4),
Division property of inequality,
c is positive,
a<b, then a/c<b/c ← 2<8,
a>b, than a/c>b/c ←2/4<8/4,
c is negative,
a<b, then a/c>b/c ←2<8,
a>b, then a/c<b/c ← 2/-4>8/-4, or
Solving Inequalities is very similar to solving Equations.
The same general technique applies.
That technique for solving equations is:
Whatever we do to one side of the equation,
we have to do to the other side to preserve the equality,
The technique for solving inequalities is:
Whatever we do to one side of the inequality,
we have to do to the other side to preserve the inequality
the techniques are the same.
The technique means:
If we multiply or divide one side of an equation or inequality
by the same number, we have to multiply or divide the other side
of the equation or inequality by the same number.
The difference between solving equations and solving inequalities is:
If you multiply or divide an inequality by a negative number,
then the inequality reverses.
The following examples will show this rule in action.
The first example will be multiplication.
The second example will be division.
The first example starts with:
7 is greater than 5.
Multiply both sides of that inequality by -5 and we get:
7*-5 = -35 on the left side of the inequality.
5*-5 = -25 on the right side of the inequality.
The result is -35 is smaller than -25.
The inequality started as greater than and
became smaller than because we were multiplying both sides
of the inequality by a negative number.
It’s clear to see that 7 really is greater than 5.
It is also clear to see that -35 is less than -25.
The second example is simply the reverse of the first example and starts with:
-35 is smaller than -25.
Divide both sides of this inequality by -5 and we get:
-35 / -5 = 7 on the left side of the inequality.
-25 / -5 = 5 on the right side of the inequality.
The result is 7 is greater than 5.
The inequality started as less than and became greater than
because you were dividing both sides of the inequality by a negative number.
We needed to do that to preserve the inequality.
It’s clear with these numbers that reversing the inequality is
essential when we are multiplying both sides of the inequality or
dividing both sides of the inequality by a negative number.
Try It!
Solve the inequality \(\frac{d}{7}\) > 15. Then graph the solution.
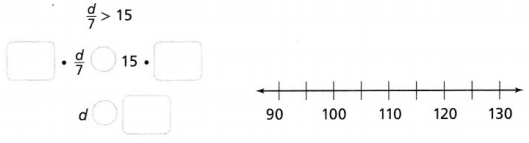
Answer:
d> 105,
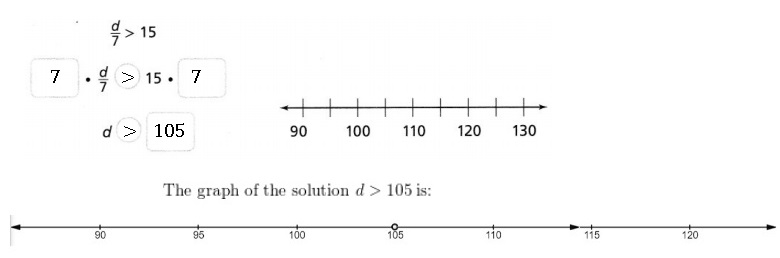
Explanation:
Solved the inequality \(\frac{d}{7}\) > 15 as
\(\frac{d}{7}\) > 15, multiplying both sides by 7,
we get d > 105, Shown the graph of the solution d > 105 above.
Convince Me!
Frances solved the inequality 5g ≥ 35. She says that 7 is
a solution to the inequality. Is Frances correct? Explain.
Answer:
Yes, Frances is correct,
Explanation:
Given Frances solved the inequality 5g ≥ 35.
She says that 7 is a solution to the inequality on solving
5g ≥ 35, dividing both sides by 5 we get
g ≥ 7, means g is greater than 7 and we get g is
equal to 7, therefore, Yes, Frances is correct.
Try It!
Solve each inequality. Then graph the solution.
a. 149.76 > -19.2x
Answer:
-7.8 < x or x > -7.8,
Explanation:
Given to solve inequality 149.76 > -19.2x,
149.76/- 19.2 > -19.2x/-19.2, dividing both sides by -19.2 and
reverse the inequality symbol,
-7.8 < x, shown the value of x as -7.8 < x or x > -7.8 on the graph above.
b. -3.25y < -61.75

Answer:
-3.25y < -61.75,

Explanation:
Given to solve inequality -3.25y < -61.75,
-3.25y/- 3.25 > -61.75/-3.25, dividing both sides by -3.25 and
reverse the inequality symbol,
y > 19, shown the value of y as y > 19 on the graph above.
Try It!
Solve each inequality. Then graph the solution.
a. \(\frac{k}{-0.5}\) < 12
![]()
Answer:
k> -6,

Explanation:
Given to solve \(\frac{k}{-0.5}\) < 12 inequality,
– 0.5\(\frac{k}{-0.5}\) > – 0.5(12), multiplying both sides by -0.5 and
reverse the inequality symbol,
k > -6, The graph of the solution k > -6 is as shown above.
b. –\(\frac{5}{4}\)h ≥ 25

Answer:
h ≤ -20,

Explanation:
Given to solve –\(\frac{5}{4}\)h ≥ 25 inequality,
-4 (-\(\frac{5}{4}\)h) ≤ -4(25) multiplying both sides by -4 and
reverse the inequality symbol,
5h ≤ -100,
5h/5 ≤ -100/5, divide both sides by 5,
5h ≤ -20,The graph of the solution 5h ≤ -20 is as shown above.
KEY CONCEPT
Solving inequalities with multiplication and division is the
same as solving equations with multiplication and division
when the values are positive. Use the inverse relationship
between multiplication and division to isolate the variable.

When multiplying or dividing by negative values, the inequality symbol is reversed.

Do You Understand?
Question 1.
Essential Question
How is solving inequalities with multiplication and division
similar to and different from solving equations with multiplication and division?
Answer:
Solving inequalities is very similar to solving equations,
but sometimes you have to reverse the symbol.
we must reverse the inequality symbol when we multiply or
divide both sides of the equation by a negative number.
1) It must be multiplication or division (not addition or subtraction)
2) The number being multiplied or divided must be negative.
Explanation:
Solving inequalities is very similar to solving equations,
but sometimes you have to reverse the symbol.
For example:
Multiplication Properties of Inequality,
c is positive,
a<b, then ac<bc ← -2<3,
a>b, then ac>bc ←-2(4)<3(4),
c is negative,
a<b, then ac>bc ← -2<3,
a>b, then ac<bc ←-2(-4)>3(-4),
Division property of inequality,
c is positive,
a<b, then a/c<b/c ← 2<8,
a>b, than a/c>b/c ←2/4<8/4,
c is negative,
a<b, then a/c>b/c ←2<8,
a>b, then a/c<b/c ← 2/-4>8/-4, or
Solving Inequalities is very similar to solving Equations.
The same general technique applies.
That technique for solving equations is:
Whatever we do to one side of the equation,
we have to do to the other side to preserve the equality,
The technique for solving inequalities is:
Whatever we do to one side of the inequality,
we have to do to the other side to preserve the inequality
the techniques are the same.
The technique means:
If you multiply or divide one side of an equation or inequality
by the same number, we have to multiply or divide the other side
of the equation or inequality by the same number.
The difference between solving equations and solving inequalities is:
If we multiply or divide an inequality by a negative number,
then the inequality reverses.
The following examples will show this rule in action.
The first example will be multiplication.
The second example will be division.
The first example starts with:
7 is greater than 5.
Multiply both sides of that inequality by -5 and we get:
7*-5 = -35 on the left side of the inequality.
5*-5 = -25 on the right side of the inequality.
The result is -35 is smaller than -25.
The inequality started as greater than and
became smaller than because we were multiplying both sides
of the inequality by a negative number.
It’s clear to see that 7 really is greater than 5.
It is also clear to see that -35 is less than -25.
The second example is simply the reverse of the first example and starts with:
-35 is smaller than -25.
Divide both sides of this inequality by -5 and we get:
-35 / -5 = 7 on the left side of the inequality.
-25 / -5 = 5 on the right side of the inequality.
The result is 7 is greater than 5.
The inequality started as less than and became greater than
because you were dividing both sides of the inequality by a negative number.
We needed to do that to preserve the inequality.
It’s clear with these numbers that reversing the inequality is
essential when we are multiplying both sides of the inequality or
dividing both sides of the inequality by a negative number.
or
The similarity is the method of solving it when the
values are positive. The difference is the method of
solving it when the values are negative.
Explanation:
The similarities of solving equation and solving inequalities
Both are used in determining the values of variable
Both can be solved either by one step or two steps
Both have same process when the values are positive
The difference between solving equation and solving inequalities
The properties used when solving equations and solving inequalities
The method of solving equation and inequalities differ
when the values are negative.
Question 2.
Construct Arguments Why is -x < 3 equivalent to x > -3?
Provide a convincing argument.
Answer:
The two inequalities are equivalent,
Explanation:
The variable cannot be negative, therefore it is need
to show the variable as positive.
-x < 3,
-1x/-1 > 3/-1, divide both sides by -1 and
reverse the inequality symbol,
x > -3,
The two inequalities are equivalent, this is because
the first inequality has negative variable.
it needs to be changed into a positive variable.
After solving the first inequality, the result is the same
with the second inequality.
Question 3.
If a, b, and care rational numbers and a > b,
is ac > bc always true? Justify your answer.
Answer:
The given inequality is not always true,
Explanation:
The inequality ac > bc is not always true,
This is because when c is a negative integer,
the inequality becomes false.
Example for this is a = 3, b = 2, c = -1,
Substituting to the inequality ac > bc =
3(-1) > 2(-1) = -3 < -2.
Do You Know How?
Question 4.
Solve each inequality. Then graph the solution.
a. 4x > 12
![]()
Answer:
x > 3,

Explanation:
Given to solve inequality 4x > 12,
4x/4 > 12/4, divide both sides by 4
x > 3, shown the value of x as x > 3 on the graph above.
b. \(\frac{x}{4}\) ≤ -12
![]()
Answer:
x ≤ -48,
Given to solve inequality \(\frac{x}{4}\) ≤ -12
4 X \(\frac{x}{4}\) ≤ 4 X -12, multiplying both sides by 4
x ≤ -48, shown the value of x as x ≤ -48 on the graph above.
c. -4x > 12
![]()
Answer:
x < -3,

Explanation:
Given to solve -4x > 12 inequality,
-4x/-4 < 12/-4 dividing both sides by -4 and
reverse the inequality symbol,
x < -3,
x < -3,The graph of the solution x <-3 is as shown above.
Question 5.
Vanna is saving for a trip. The hotel room will be $298.17 for 3 nights, and
there will be additional fees. What is her daily cost?

a. Write an inequality for the situation.
b. Solve the inequality. Then provide a statement that
represents the solution of the problem.
Answer:
a. 3x ≥ 298.17,
b. x≥ 99.39 , The stay of Vanna in the hotel plus additional cost fees
cost at least $99.39,
Explanation:
Given Vanna is saving for a trip. The hotel room will be $298.17 for 3 nights, and
there will be additional fees, Let x be the daily cost of the stay in the hotel room, So
a. The inequality for the situation is 3x ≥ 298.17,
b. Solving 3x ≥ 298.17 we get daily cost
3x/3 ≥ 298.17/3, dividing both sides by 3 we get
x ≥ 99.39, therefore the stay of Vanna in the hotel plus additional cost fees
cost at least $99.39.
Practice & Problem Solving
Leveled Practice In 6-9, fill in the boxes to solve the inequality.
Then graph the solution.
Question 6.
Answer:
m ≤ 7,
Explanation:
Given to fill the boxes and to solve the 8m ≤ 56 inequality,
8m/8 ≤ 56/8 dividing both sides by 8,
m ≤ 7,The graph of the solution m ≤ 7 is as shown above.
Question 7.
Answer:
x> 6,
Explanation:
Given to fill the boxes and to solve the –\(\frac{4}{3}\)x < -8 inequality,
-3 X \(\frac{4}{3}\) x > -3(-8), multiplying both sides by -3 and
reverse the inequality symbol,
4x > 24,
4x/4 > 24/4, dividing both sides by 4 we get
x > 6, so the graph of the solution x > 6 is as shown above.
Question 8.
Answer:
x < -8,
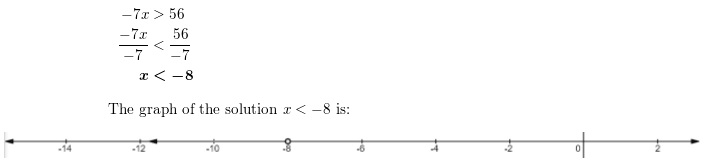
Explanation:
Given to fill the boxes and to solve the -7x > 56 inequality,
– 7x/(-7) < 56/(-8), dividing both sides by -7 and
reverse the inequality symbol,
x < -8, so the graph of the solution x < -8 is as shown above.
Question 9.
Answer:
m ≤ -10,
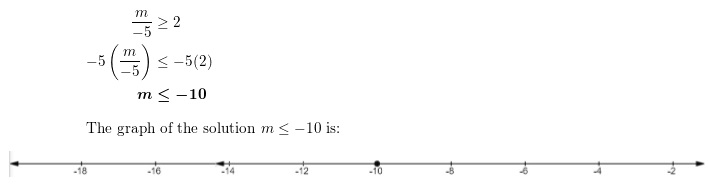
Explanation:
Given to fill the boxes and to solve the \(\frac{m}{-5}\) ≥ 2 inequality,
-5 X \(\frac{m}{-5}\) ≤ -5(2), multiplying both sides by -5 and
reverse the inequality symbol,
m ≤ -10, so the graph of the solution m ≤ -10 is as shown above.
Question 10.
Kyra and five friends shared a bag of fruit snacks.
Each person got no more than 3 fruit snacks.
The inequality x ÷ 6 ≤ 3 represents this situation.
Solve the inequality to find the possible numbers of fruit
snacks that were in the bag.
Answer:
There are at most 18 fruit snacks that were in the bag,
Explanation:
Given Kyra and five friends shared a bag of fruit snacks.
Each person got no more than 3 fruit snacks.
The inequality x ÷ 6 ≤ 3 represents this situation the
possible numbers of fruit snacks that were in the bag are
x ÷ 6 ≤ 3,
6 X (x ÷ 6) ≤ 6 X 3, multiplying both sides by 6,
x ≤ 18, therefore, there are at most 18 fruit snacks that were in the bag.
Question 11.
Over the next 17 months, Eli needs to read more than 102 e-books.
The inequality 17x > 102 represents the number of e-books he
needs to read per month.
Solve the inequality to find the number of e-books Eli needs to read per month.
Answer:
Eli needs to read at least 6 e -books per month,
Explanation:
Given over the next 17 months, Eli needs to read more than 102 e-books.
The inequality 17x > 102 represents the number of e-books he
needs to read per month. Now solving the inequality to
find the number of e-books Eli needs to read per month as
17x > 102,
17x ÷17 > 102 ÷17, dividing both sides by 17,
x > 6, therefore, Eli needs to read at least 6 e -books per month.
Question 12.
Brittney can spend no more than $15 for new fish in her aquarium.
a. Let f be the number of fish she can buy. What inequality represents the problem?

b. How many fish can Brittney buy?
Answer:
a. 3f ≤ 15,
b. Brittney can buy no more than 5 fishes,
Explanation:
Given Brittney can spend no more than $15 for new fish in her aquarium.
a. Let f be the number of fish she can buy.
So inequality that represents the problem is 3f ≤ 15,
b. Solving the inequality equation 3f ≤ 15,
3f ÷ 3 ≤ 15 ÷ 3, dividing both sides by 3 we get,
f ≤ 5, So Brittney can buy no more than 5 fishes.
Question 13.
Isaac has a bag of n peanuts. He shares the peanuts with 5 of his friends.
Each person gets at least 18 peanuts. The inequality 18 ≤ n ÷ 6
represents this situation. Graph the solution of this inequality.
Answer:
The number of peanuts Isaac has a bag of at least 108,
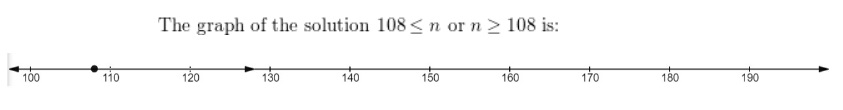
Explanation:
Given Isaac has a bag of n peanuts. He shares the peanuts with 5 of his friends.
Each person gets at least 18 peanuts. The inequality 18 ≤ n ÷ 6
represents this situation. So the number of peanuts Isaac have are
6 X 18 ≤ 6 X n ÷ 6, multiplying the inequality both sides by 6,
108 ≤ n or n ≥ 108, so the graph of the solution
108 ≤ n or n ≥ 108 is as shown above.
Question 14.
a. Solve the inequality – 3x < 12.
b. Reasoning
Describe how you know the direction of the inequality sign
without solving the inequality.
Answer:
a. x > -4,
b. The inequality sign changes because of the
negative integer in the variable,
Explanation:
a. Given to solve the inequality -3x < 12,
-3x ÷ -3< 12 ÷ -3, dividing both sides by -3 and
reverse the inequality symbol,
x > -4.
b. The inequality sign can be determined without solving
because there is negative integer in the variable.
With the negative integer, automatically the inequality sign
changes.
Question 15.
Higher Order Thinking Renata and her family go through an
average of more than 15 cans of sparkling water each day.
They buy cases of 24 cans at $3.50 a case.

a. Write an inequality for the number of cases they go through in 30 days.
b. Solve the inequality in part a. If they buy only full cases,
how much do they spend on sparkling water in 30 days?
Answer:
a. x ≥ 18.75 is the inequality for the number of cases
they go through in 30 days,
b. $66.50 they spend on sparkling water in 30 days,
Explanation:
Given Renata and her family go through an
average of more than 15 cans of sparkling water each day.
They buy cases of 24 cans at $3.50 a case.
a.
1 day = 15 cans and 24 cans = $3.50,
So let x be number of cases
30 multiply 15 ÷ 24 = 18.75 almost 19,
therefore x ≥ 18.75 is the inequality for the
number of cases they go through in 30 days,
b. 19 X 3.5 = $66.50 they spend on sparkling water in 30 days.
Question 16.
Solve the inequality. Graph the solution on the number line.
-6.25x > -38\(\frac{3}{4}\)

Answer:
x < 6.2,

Explanation:
Given to solve the inequality -6.25x > -38\(\frac{3}{4}\),
converting the mixed number to decimal before solving the inequality,
-38\(\frac{3}{4}\) = -38.75,
-6.25x > -38.75,
-6.25x ÷ -6.25 > -38.75 ÷ -6.25, dividing both sides by -6.25 and
reverse the inequality symbol,
x < 6.2, the graph of the solution x < 6.2 is shown above.
Assessment Practice
Question 17.
Cynthia plans to build a tree house that is \(\frac{1}{3}\) the
size of Andrew’s tree house. Cynthia plans to make the area of her
tree house at least 13 square feet.
PART A
Write and solve an inequality to find the area of Andrew’s tree house.
Let x be the area of Andrew’s tree house.
Answer:
\(\frac{1}{3}\)x ≥ 13,
Explanation:
Given Cynthia plans to build a tree house that is \(\frac{1}{3}\) the
size of Andrew’s tree house. Cynthia plans to make the area of her
tree house at least 13 square feet.
The inequality for the given situation is \(\frac{1}{3}\)x ≥ 13,
Now solving 3 X \(\frac{1}{3}\)x ≥ 3 X 13,
multiplying both sides by 3 we get
x ≥ 39 is the area of Andrew’s tree house.
PART B
Describe how you know which tree house is larger without solving the inequality.
Answer:
It is because of the factor that was multiplied to the
area of the Andrew’s tree house which is less than 1,
Explanation:
Since the factor that was multiplied to the
area of the Andrew’s tree house which is less than 1,
it can be easily be determined that Cynthia’s tree house is
smaller than Andrew’s tree house.
3-ACT Math

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Make a prediction to answer this Main Question. Explain your prediction.
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large. Too small


Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?

Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem?
Explain how you would use them strategically
Answer:
Question 8.
Model with Math Represent the situation using mathematics.
Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your initial prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?

Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:

ACT 3
Extension
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation.
How did the model help you answer the Main Question?
Answer:
Question 14.
Reasoning If all single tracks were on sale for 10% off, how would your model change?
How would the answer to the Main Question change?
Answer:
SEQUEL
Question 15.
Make Sense and Persevere Suppose you have a $50 gift card to the same site.
You want to buy an album with 16 tracks for $12.99 and then use the rest of the
gift card for single tracks. How many songs can you buy with the gift card?
Answer:
Lesson 5.6 Solve Two-Step Inequalities
Solve & Discuss It!
Rico and Halima are shopping for craft sticks, glue, and electrical tape for a science project.
Together, they have $30 to spend on supplies.
How should they spend their $30 if they need at least 1,000 craft sticks?

Focus on math practices
Make Sense and Persevere At the store, Rico and Halima find
boxes of 500 craft sticks for $7.50.
Which boxes of craft sticks should they buy?
Answer:
Rico and Halima should buy the box with 500 craft sticks,
Explanation:
Rico and Halima should buy the box with 500 craft sticks,
buying 2 boxes of 500 craft sticks will give them a total
of 1000 craft sticks at a lower price which will cost them $15,
instead of buying at least 4 boxes of 275 craft sticks.
Essential Question
How is solving a two-step inequality similar to and different from solving a two-step equation?
Answer:
Equations and Inequalities – Two-step equations and inequalities –
It takes two steps to solve an equation or inequality that has more than one operation:
Simplify using the inverse of addition or subtraction. Simplify further by using
the inverse of multiplication or division.
Explanation:
It takes two steps to solve an equation or inequality that has more than one operation:
Simplify using the inverse of addition or subtraction.
Simplify further by using the inverse of multiplication or division.
when you multiply or divide an inequality by a negative number,
we must reverse the inequality symbol.
Try It!
Erin has $52 to spend at the florist. She wants to buy a vase for $11.75 and
several roses for $3.50 each. What are the possible numbers of roses Erin can buy?
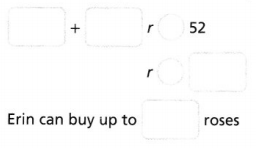
Answer:
Erwin can buy up to 11 roses,

Explanation:
Given Erin has $52 to spend at the florist. She wants to buy a vase for $11.75 and
several roses for $3.50 each. The possible numbers of roses Erin can buy are
11.75 + 3.50r ≤ 52,
11.75 + 3.50r – 11.75 ≤ 52 – 11.75, subtracting 11.75 from both sides,
3.50r ≤ 40.25,
3.50r ÷ 3.50 ≤ 40.25 ÷ 3.50, dividing both sides by 3.50 we get
r ≤ 11.50, therefore Erwin can buy up to 11 roses.
Convince Me!
What properties did you use to solve the inequality? 300 5-6 Solve Two-Step Inequalities.
Answer:
Subtraction property,
Division property.
Explanation:
Solving two-step inequalities,
Example:
x + 8 > 5,
Isolated the variable x by subtracting 8 from both sides of the inequality.
x + 8 – 8 > 5 – 8 => x > −3, Therefore, x > −3.
Try It!
The Jazz Band needs to raise at least $600 to travel to an upcoming competition.
The members of the band have already raised $350. If they sell calendars for $8 each,
how many calendars would they need to sell to exceed their goal?
Answer:
Jazz band needs to sell at least 32 calendars to exceed their goal,
Explanation:
Given the Jazz Band needs to raise at least $600 to travel to an upcoming competition.
The members of the band have already raised $350. If they sell calendars for $8 each,
number of calendars would they need to sell to exceed their goal if x is the
number of calendars,
350 + 8x ≥ 600,
350 + 8x – 350 ≥ 600 -350, subtracting 350 from both sides,
8x ≥ 250,
8x ÷ 8 ≥ 250 ÷ 8, dividing both sides by 8,
x ≥ 31.25, therefore, Jazz band needs to sell at least 32 calendars to exceed their goal.
Try It!
Solve the inequality 5 – \(\frac{1}{2}\)x > 30.
Answer:
x < -50,
Explanation:
Given the inequality 5 – \(\frac{1}{2}\)x > 30,
5 – \(\frac{1}{2}\)x -5 > 30 – 5, subtract 5 from both the sides,
–\(\frac{1}{2}\)x > 25,
-2 X – \(\frac{1}{2}\)x > -2 X 25, multiplying both sides by -2 and reverse
the inequality symbol as x < -50.
KEY CONCEPT
Like two-step equations, solving two-step inequalities involves carrying out
two different operations—addition or subtraction, and multiplication or division.
Unlike two-step equations, which have a single solution,
two-step inequalities have multiple solutions.
Do You Understand?
Question 1.
Essential Question How is solving a two-step inequality similar to and
different from solving a two-step equation?
Answer:
The similarity between the two is that they are carrying out two
different operations,
The difference is that the number of solutions they have,
Explanation:
The similarity between solving a two-step inequality and
two-step equation is that they are carrying out two
different operations,
The difference between solving a two-step inequality and
two-step equation is that two-step equation only have
single solution unlike two-step inequalities have multiple solutions.
Question 2.
Reasoning What is the difference between the number of solutions for
a two-step equation and for a two-step inequality?
Answer:
Two-step equations only have a single solution,
Two-step inequalities have multiple solutions,
Explanation:
Two-step equations there is only a single solution,
Two-step inequalities there are multiple solutions,
this is because of the inequality symbol, which makes
the inequality true for as long as the value of the variable
is within the given solution.
Question 3.
Why are inverse relationships between operations used to solve two-step inequalities?
Answer:
Inverse relationships between operations are used to isolate the variable on the one side
of the inequality,
Explanation:
Inverse relationships between operations are used to solve two-step inequalities
in order to isolate the variable on the one side of the inequality, removing the
values together with the variable means that the inverse operation should be used
on both sides.
Do You Know How?
Question 4.
Joe ran 3 miles yesterday and wants to run at least 12 miles this week.
Write an inequality that can be used to determine the additional number
of days Joe must run this week if each run is 3 miles. Then solve the inequality.

Answer:
The inequality for the given situation is 3 + 3x ≥ 12,
Joe need to run at least 3 days to meet his target,
Explanation:
Given Joe ran 3 miles yesterday and wants to run at least 12 miles this week.
Let x be number of days Joe must run this week if each run is 3 miles.
The inequality for the given situation is 3 + 3x ≥ 12,
3 + 3x -3 ≥ 12 -3, subtracting 3 both sides,
3x ≥ 9, dividing both sides by 3 we get
x ≥ 3, therefore, Joe need to run at least 3 days to meet his target.
Question 5.
Solve 4 + 6.5x < 36.5.
Answer:
Solving 4 + 6.5x < 36.5, we get x < 5,
Explanation;
Given the inequality 4 + 6.5x < 36.5,
4 + 6.5x -4 < 36.5 -4, subtracting 4 from both the sides,
6.5x < 32.5,
6.5x ÷ 6.5 < 32.5 ÷ 6.5, dividing both sides by 6.5,
x < 5.
Question 6.
Tomas has $1,000 to spend on a vacation. His plane ticket costs $348.25.
If he stays 5.5 days at his destination, how much can he spend each day?
Write an inequality and then solve.
Answer:
Inequality: 348.25 + 5.5x ≤ 1000,
Tomas can spend no more than $118.50 per day,
Explanation:
Given Tomas has $1,000 to spend on a vacation. His plane ticket costs $348.25.
If he stays 5.5 days at his destination let x be the amount,
the inequality for the given situation is 348.25 + 5.5x ≤ 1000,
348.25 + 5.5x – 348.25 ≤ 1000 – 348.25, subtracting 348.25 from both the sides,
5.5x ≤ 651.75,
5.5x ÷ 5.5 ≤ 651.75 ÷ 5.5, dividing both sides by 5.5,
x ≤ 118.50, therefore, Tomas can spend no more than $118.50 per day.
Question 7.
Solve 12 – \(\frac{3}{5}\)x > 39.
Answer:
Solving 12 – \(\frac{3}{5}\)x > 39, we get x < -45,
Explanation:
Given 12 – \(\frac{3}{5}\)x > 39,
12 – \(\frac{3}{5}\)x – 12 > 39 – 12, subtracting 12 from both sides,
– \(\frac{3}{5}\)x > 27,
– 5 X- \(\frac{3}{5}\)x < – 5 X 27, multiplying both sides by -5 and
reverse the inequality symbol,
3x < -135,
3x ÷ 3 < -135 ÷ 3, divide both sides by 3,
x < -45.
Practice & Problem Solving
Leveled Practice For 8 and 9, fill in the boxes to write and solve each inequality.
Question 8.
Eight less than the product of a number n and \(\frac{1}{5}\) is no more than 95.
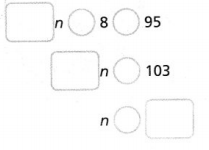
Answer:
n ≤ 515,
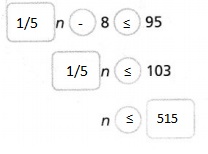
Explanation:
The inequality is \(\frac{1}{5}\) x – 8 ≤ 95,
\(\frac{1}{5}\) x – 8 + 8 ≤ 95 +8, adding 8 on both sides,
\(\frac{1}{5}\) x ≤ 103,
5 X \(\frac{1}{5}\) x ≤ 5 X 103, multiplying both sides by 5,
x ≤ 515.
Question 9.
Seven more than the quotient of a number b and 45 is greater than 5.
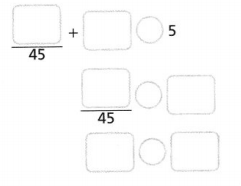
Answer:
b > -90,
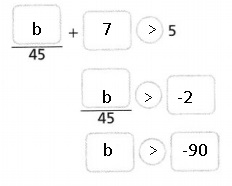
Explanation:
Given \(\frac{b}{45}\) + 7 > 5,
\(\frac{b}{45}\) + 7 – 7 > 5 – 7, subtracting 7 from both sides
\(\frac{b}{45}\) > -2,
45 X \(\frac{b}{45}\) > 45 X (-2), multiplying both sides by 45 we get,
b > -90.
Question 10.
Solve the inequalities and compare.
a. Solve 2x + 6 < 10.
b. Solve -2x + 22 < 18.
c. Which is the correct comparison of solutions for
2x + 6 < 10 and -2x + 22 < 18?
A. The inequalities have some common solutions.
B. The inequalities have one common solution.
C. The inequalities have no common solutions.
D. The inequalities have the same solutions.
Answer:
a. x < 2,
b. x > 2,
c. C. The inequalities have no common solutions,
Explanation:
a. Solving 2x + 6 < 10,
2x + 6 -6 < 10 -6, subtracting 6 from both sides,
2x < 4,
2x ÷ 2 < 4 ÷ 2, dividing both sides by 2,
so x < 2,
b. Solving -2x + 22 < 18,
-2x +22 -22 < 18 -22, subtracting 22 from both sides,
-2x < -4,
-2x ÷ -2 > -4 ÷ -2, dividing both sides by -2 and reverse the inequality symbol,
so x > 2,
c. The correct comparison of solutions for the two given
inequalities 2x + 6 < 10 and -2x + 22 < 18 are
the inequalities have no common solutions, the first inequality
has a solution that the value of x should be less than 2 to make the
inequality true, the second inequality has a solution that the value of
x should be greater than 2.
Question 11.
Make Sense and Persevere Talia has a daily budget of $94 for a car rental.
Write and solve an inequality to find the greatest distance Talia can drive
each day while staying within her budget.

Answer:
Tali can drive no more than 320 miles,
Explanation:
Let x be the distance per mile,
The inequality for the given situation is 30 + 0.20x ≤ 94,
solving 30 + 0.20x ≤ 94,
30 + 0.20x -30 ≤ 94 -30, subtracting 30 from both sides,
0.20 x ≤ 64,
0.20 x ÷0.20 ≤ 64 ÷ 0.20,dividing both sides by 0.20
x ≤ 320, therefore, Tali can drive no more than 320 miles.
Question 12.
Model with Math A manager needs to rope off a
rectangular section for a private party. The length of
the section must be 7.6 meters. The manager can use
no more than 28 meters of rope. What inequality could
you use to find the possible width, w, of the roped-off section?
Answer:
Inequality:
2(7.6) + 2(w) ≤ 28,
The width of the roped – off section should be no
more than 6.4 meters,
Explanation:
Given A manager needs to rope off a
rectangular section for a private party. The length of
the section must be 7.6 meters. The manager can use
no more than 28 meters of rope. The inequality to find
the possible width, w, of the roped-off section is 2(7.6) + 2(w) ≤ 28,
15.2 + 2w ≤ 28, multiplying the values,
15.2 + 2w – 15.2 ≤ 28 – 15.2, substracting 15.2 from both sides,
2w ≤ 12.8,
2w ÷ 2 ≤ 12.8 ÷ 2, dividing both sides by 2,
w ≤ 6.4 , therefore, the width of the roped – off section should be no
more than 6.4 meters.
Question 13.
Higher Order Thinking Andrea went to the store to buy a
sweater that was on sale for 40% off the original price.
It was then put on clearance at an additional 25% off the sale price.
She also used a coupon that saved her an additional $5.
Andrea did not spend more than $7.60 for the sweater.
What are the possible values for the original price of the sweater?

Answer:
The price of the sweater is no more than $28,
Explanation:
Given Andrea went to the store to buy a
sweater that was on sale for 40% off the original price.
It was then put on clearance at an additional 25% off the sale price.
She also used a coupon that saved her an additional $5.
Andrea did not spend more than $7.60 for the sweater.
Let x be the original price of the sweater so the inequality
is 0.75(0.6x) – 5 ≤ 7.6, multiplying the values
0.75(0.6x) – 5 ≤ 7.6, adding 5 both sides,
0.45 x – 5 + 5 ≤ 7.6 + 5,
0.45x ≤ 12.6,
0.45x ÷ 0.45 ≤ 12.6 ÷ 0.45, dividing both sides by 0.45,
x ≤ 28, the price of the sweater is no more than $28.
Question 14.
A pool can hold 850 gallons. It now has 598 gallons of
water and is being filled at the rate shown.
How many more minutes, m, can water continue to
flow into the pool before it overflows? Write and solve an inequality.

Answer:
Inequality :
598 + 15.75m ≤ 850,
The water can continue to flow into the pool before it overflows
no more 16 minutes,
Explanation:
Given A pool can hold 850 gallons. It now has 598 gallons of
water and is being filled at the rate shown. So more minutes, m,
can water continue to flow into the pool before it overflows is
solving the inequality 598 + 15.75m ≤ 850,
598 + 15.75m – 598 ≤ 850 – 598, subtracting 598 from both sides,
15.75m ≤ 252,
15.75m ÷15.75 ≤ 252 ÷ 15.75, dividing both sides by 15.75 we get
m ≤ 16, therefore the water can continue to flow into the pool
before it overflows no more 16 minutes.
Assessment Practice
Question 15.
Use the rectangle diagram at the right.
PART A
Write and solve an inequality to find the values of x for
which the perimeter of the rectangle is less than 120.
Answer:
Inequality:
2(x + 4) + 2x < 120,
x < 28,
Explanation:
Given length of rectangle x + 4 and breadth as x and
for which the perimeter of the rectangle is less than 120,
The inequality for the given situation is 2(x + 4) + 2x < 120,
2x + 8 +2x < 120, using distributive property,
4x + 8 < 120, combining like terms,
4x + 8 – 8 < 120 – 8, subtracting 8 from both sides,
4x < 112,
4x ÷ 4 < 112 ÷ 4, dividing both sides by 4 we get
x < 24.
PART B
Based on your answer to Part A, are there any values that
can be eliminated from the solution set? Explain.
Answer:
Yes, 28 can be eliminated from the solution set,
Explanation:
There is a value that can be eliminated in the solution set,
28 is not part of the solution set since the solution set is
less than 28, it means any value that is 27 or below.
Question 16.
Kari is building a rectangular garden bed. The length is 6 feet.
She has 20 feet of boards to make the sides.
Write and solve an inequality to find the possible width of her garden bed.
Answer:
2(6 + w) ≤ 20,
The width of Kari garden bed is less than 4,
Explanation:
Given Kari is building a rectangular garden bed. The length is 6 feet.
She has 20 feet of boards to make the sides.
Let w be the possible width of her garden bed.
The inequality is 2(6 + w) ≤ 20,solving for w,
2(6 + w) ≤ 20, multiplying the values,
12 + 2w ≤ 20, subtracting 12 both sides,
12 + 2w -12 ≤ 20 -12, subtracting 12 both sides,
2w ≤ 8,
2w ÷ 2 ≤ 8 ÷ 2, dividing both sides by 2,
w ≤ 4, therefore the width of Kari garden bed is less than 4.
Lesson 5.7 Solve Multi-Step Inequalities
Explore It
Charlene has 2 flash drives of the same size that
she uses to store pictures and videos. Each drive is
holding the same number of GB of data, d.
She wants to move everything to a memory card that can hold up to 8 GB.

A. Charlene is going to delete 1 GB of data from each flash drive.
How can the total amount of data left on the two flash drives be
represented as an expression?
B. How can the expression you wrote be used to
write an inequality that shows the maximum amount of
data each flash drive can have on it in order to have all
the data transfer to the 8 GB memory card?
Answer:
a. 2(d – 1),
b. 2(d – 1) ≤ 8,
Explanation:
Given Charlene has 2 flash drives of the same size that
she uses to store pictures and videos. Each drive is
holding the same number of GB of data, d.
She wants to move everything to a memory card that can hold up to 8 GB.
a. Charlene is going to delete 1 GB of data from each flash drive.
So the total amount of data left on the two flash drives be
represented as an expression as 2(d – 1).
b. The expression I wrote can be used
for the inequality that shows the maximum amount of
data each flash drive can have on it in order to have all
the data transfer to the 8 GB memory card is 2(d – 1) ≤ 8.
Focus on math practices
Reasoning If each flash drive has 5 GB of memory, can all of
the data be transferred to the memory card? Explain.
Answer:
A flash drive has 5 GB of memory, can have all of its
data be transferred to the memory card,
Explanation:
Using the inequality to determine If each flash drive
has 5 GB of memory can be transferred to the memory card so
2(d – 1) ≤ 8,
2d – 2 ≤ 8, applying distributive property,
2d – 2 + 2 ≤ 8 + 2, adding 2 on both sides,
2d ≤ 10,
2d ÷ 2 ≤ 10 ÷ 2, dividing both sides by 2,
d ≤ 5,
From the solution set, a flash drive can hold no more than
5 GB, therefore, a flash drive has 5 GB of memory,
can have all of its data be transferred to the memory card.
Essential Question
How is solving a multi-step inequality similar to and different
from solving a multi-step equation.
Answer:
Two are similar because of the methods used in solving,
The difference between the two is the number of solution,
Explanation:
Solving a multi-step inequality and solving a multi-step equation is similar
because of the methods used in solving like using the Distributive Property,
combining like terms and use inverse relationships and properties to solve them.
The difference between a multi-step inequality and solving a multi-step equation is
the number of solution. For multi-step equation there is one possible solution,
for multi-step inequality there are many possible solutions.
Try It!
Twice the difference of Felipe’s age, f, and 4 is at least 2.
What are possible values for Felipe’s age? Graph the solution.
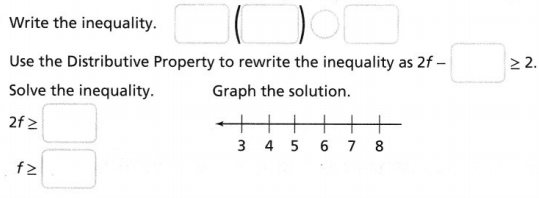
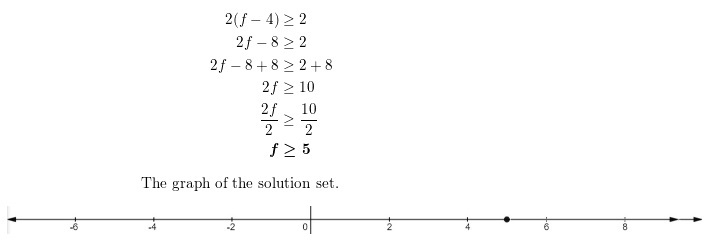
Explanation:
Given twice the difference of Felipe’s age, f, and 4 is at least 2,
the possible values for Felipe’s age are inequality 2(f-4) ≥ 2,
2f – 8 ≥ 2, used distributive property,
2f – 8 + 8 ≥ 2 + 8, adding 8 on both sides,
2f ÷ 2 ≥ 10 ÷ 2, dividing both sides by 2,
f ≥ 5, so the graph of the solution f ≥ 5 is as shown above.
Convince Me!
Describe the similarity between the process of solving an inequality with two steps and
solving an inequality with more than two steps.
Try It!
Solve the inequality – 1 – 6(6 + 2x) < 11. Then graph the solution.

Solve the inequality 3(4 – 6) + 2 ≥ 2(-t + 3) + 4. Then graph the solution.

Answer:
Explanation:
Solving the inequality – 1 – 6(6 + 2x) < 11,
-1 -36 -12x < 11, used distributive property,
-37 -12x < 11, combining like terms,
-37 -12x + 37 < 11 + 37, Adding 37 on both sides,
-12x > 48,
-12x ÷ 12 > 48 ÷ 12, dividing both sides by -12 and reverse inequality symbol,
x > 4, so the graph of the solution x > 4 is as shown above.
Solving the inequality 3(4 – 6) + 2 ≥ 2(-t + 3) + 4,
12 – 18 + 2 ≥ -2t + 6 + 4, used distributive property,
-4 ≥ -2t + 10, combining like terms,
-4 – 10 ≥ -2t + 10 – 10, subtracting 10 from both sides,
-14 ≥ -2t,
-14 ÷ -2 ≤ -2t ÷ -2, dividing both sides by -2 and reverse inequality symbol,
7 ≤ t, so the graph of the solution 7 ≤ t is as shown above.
KEY CONCEPT
Solving multi-step inequalities is similar to solving multi-step equations.
You may need to use the Distributive Property, combine like terms, and
use inverse relationships and properties to solve them.
4(y – 4) + 8 ≤ 20
4y – 16 + 8 ≤ 20
4y – 8 ≤ 20
4y – 8 + 8 ≤ 20 + 8
4y ≤ 28

Do You Understand?
Question 1.
Essential Question How is solving a multi step inequality similar to and
different from solving a multi-step equation?
Answer:
Two are similar because of the methods used in solving,
The difference between the two is the number of solution,
Explanation:
Solving a multi-step inequality and solving a multi-step equation is similar
because of the methods used in solving like using the Distributive Property,
combining like terms and use inverse relationships and properties to solve them.
The difference between a multi-step inequality and solving a multi-step equation is
the number of solution. For multi-step equation there is one possible solution,
for multi-step inequality there are many possible solutions.
Question 2.
Be Precise Explain how you would combine like terms and use properties of
operations to solve the inequality 5(2t + 3) – 3t < 16.
Answer:
t < 1/7,
Explanation:
Given to solve the inequality 5(2t + 3) – 3t < 16,
10t + 15 – 3t <16, used distributive property,
7t + 15 < 16, combining like terms,
7t + 15 -15 < 16 – 15, subtracting 15 from both sides of the inequality,
7t < 1,
7t ÷ 7 < 1 ÷7, dividing both sides by 7 we get,
t < 1/7.
Question 3.
Critique Reasoning Gloria’s solution to a multi-step inequality is r> 7.
She states that the graph will have an open dot at 7 and extend with
an arrow to the right indefinitely. Is she correct? Explain.
Answer:
Gloria’s describes the solution correctly,
Explanation:
Gloria is correct because it will open dot as the solution does not
include 7 as the part of the solution, the inequality symbol is greater
than which means that the arrow will extend to the right.
Do You Know How?
Question 4.
Solve the inequality 2(n + 3) – 4 < 6. Then graph the solution.

Answer:

Explanation:
Given 2(n + 3) – 4 < 6,
2n + 6 – 4 < 6, using distributive property,
2n + 2 < 6, combined like terms,
2n + 2 – 2 < 6 – 2, subtracting 2 from both sides,
2n < 4,
2n ÷ 2 < 4 ÷ 2, dividing both sides by 2,
n < 2, so the graph of the solution n < 2 is as shown above.
Question 5.
Solve the inequality -2(x + 3) + 2 ≥ 6. Then graph the solution.

Answer:

Explanation:
Given -2(x + 3) + 2 ≥ 6,
-2x – 6 + 2 ≥ 6, using distributive property,
-2x – 4 ≥ 6, combined like terms,
-2x – 4 + 4 ≥ 6 + 4, adding 4 on both sides,
-2x ≥ 10,
-2x ÷ -2 ≤ 10 ÷ -2, dividing both sides by -2 and reversing inequality symbol,
x ≤ 5, so the graph of the solution x ≤ 5 is as shown above.
Question 6.
Three times the difference of Federico’s age and 4, increased by 7, is greater than 37.
What are possible values of Federico’s age? Graph his possible ages on the number line.
![]()
Answer:

Explanation:
Given three times the difference of Federico’s age and 4, increased by 7
is greater than 37. The possible values of Federico’s age are
3(x – 4) + 7 > 37,
3x – 12 + 7 > 37, using distributive property,
3x – 5 > 37, combined like terms,
3x – 5 + 5 > 37 + 5, adding 5 on both sides,
3x > 42,
3x ÷ 3 > 42 ÷ 3, dividing both sides by 3,
x > 14, so there Federico’s age should be greater than 14,
The graph of the possible ages of Federico’s is as shown above.
Practice & Problem Solving
Question 7.
Use the inequality 18 < -3(4x – 2).
a. Solve the inequality for x.
b. Which graph shows the solution to the inequality?

Answer:

Explanation:
a. Given to solve the inequality 18 < -3(4x -2),
18 < -12x + 6, using distributive property,
18 – 6 < -12x + 6 – 6, subtracting 6 from both sides,
12 < -12x,
12 ÷ -12 > -12x ÷ -12, dividing both sides by -12 and reversing inequality symbol,
-1 > x,
b. Graph A shows the solution to the inequality 18 < -3(4x -2) as -1 > x which
is shown above.
Question 8.
Michelle says that the solution to the inequality 2(4y – 3) > -22 is y> -3.5.
Her work is shown.
2(4y – 3) > -22
8y > -28
y > -3.5
a. What was Michelle’s mistake?
b. What is the solution to the inequality?
Answer:
a. Michelle did not use the inverse relationship in order to isolate the variable,
b. The solution is y > -2,
Explanation:
a. After using distributive property, Michelle did not use the inverse relationship
in order to isolate the variable, she thought that subtracting 6 on the right side of inequality
will remove the 6 as well on left side of the inequality,
b. Solving the inequality 2(4y – 3) > -22,
8y – 6 > -22, using distributive property,
8y – 6 + 6 > -22 + 6, adding 6 on both sides,
8y > -16,
8y ÷ 8 > -16 ÷ 8, dividing both sides by 8 we get
y > -2.
Question 9.
Model with Math The length of a picture frame is 7 inches more than the width.
For what values of x is the perimeter of the picture frame greater than 154 inches?

Answer:
The width of the picture frame is greater than 35 inches,
Explanation:
Given the length of a picture frame is 7 inches more than the width.
So the values of x for which the perimeter of the picture frame will be
greater than 154 inches is
2(x + 7) + 2 (x) > 154,
2x + 14 + 2x > 154, using distributive property,
4x + 14 > 154, combined like terms,
4x + 14 – 14 > 154 – 14, subtracting 14 on both sides,
4x > 140,
4x ÷ 4 > 140 ÷ 4, dividing both sides by 4 we get
x > 35, therefore the width of the picture frame is greater than 35 inches.
Question 10.
Critique Reasoning Sierra says that she can simplify the left side of
the inequality 2(-3 + 5) + 2 ≥ -4(x – 2) – 3 by combining the terms
within the parentheses, but that she can’t do the same on the right side.
Is Sierra correct? Explain.
Answer:
Sierra is correct about combining the terms,
Explanation:
Sierra is correct as the terms inside the parentheses are both constant,
Performing the operation inside the parentheses can combine
the two constants. She is also correct that on the right side of inequality,
the term are not the same, therefore it cannot be combined.
Question 11.
a. Solve the inequality 30 ≥ 6(\(\frac{2}{3}\)z + \(\frac{1}{3}\)).
b. Solve the inequality 15.6 < 2.7(z – 1) – 0.6.
c. Are there any values of z that solve both inequalities?
Use a number line to support your answer.
Answer:
a. 7 ≥ z,
b. 7< z,
c. 
Explanation:
a. Solving the inequality 30 ≥ 6(\(\frac{2}{3}\)z + \(\frac{1}{3}\)),
30 ≥ 4z + 2, using distributive property,
30 – 2 ≥ 4z + 2 – 2, subtracting 2 on both sides,
28 ≥ 4z,
28 ÷ 4 ≥ 4z ÷ 4, dividing both sides by 4 we get 7 ≥ z.
b. Solving the inequality 15.6 < 2.7(z – 1) – 0.6,
15.6 < 2.7z – 2.7 – 0.6, using distributive property,
15.6 < 2.7z – 3.3, combined like terms,
15.6 + 3.3 < 2.7z – 3.3 + 3.3, adding 3.3 on both sides,
18.9 < 2.7z,
18.9 ÷ 2.7 < 2.7z ÷ 2.7, dividing both sides by 2.7,
we get 7 < z.
c. There are no values that could solve both inequalities,
This is because, the first inequality has the solution set of any
value no more than 7 while the second inequality has the solution
set of any value greater than 7. The solution of first inequality, includes
7 while the solution for the second inequality does not include 7.
Question 12.
Mr. Lin baked banana bread for a bake sale to raise money for the math team.
He said that he added a spoonful of walnuts for each of the students in
his three classes, and that he added more than 250 walnuts. He used the
inequality 16W + 24W + 10w > 250 to represent the situation, where w represents
the number of walnuts in each spoonful. How many walnuts could be in each spoonful?
Answer:
Each spoonful have greater than 5 walnuts,
Explanation:
Given Mr. Lin baked banana bread for a bake sale to raise money for the math team.
He said that he added a spoonful of walnuts for each of the students in
his three classes and that he added more than 250 walnuts. He used the
inequality 16W + 24W + 10w > 250 to represent the situation, where w represents
the number of walnuts in each spoonful. So number of many walnuts could be in
each spoonful is writing inequality 16W + 24W + 10w > 250 and solving as
50w > 250, combining like terms,
50w ÷ 50 > 250 ÷ 50, dividing both sides by 50,
we get w >5, therefore, each spoonful have greater than 5 walnuts.
Question 13.
Use both the Addition and Multiplication Properties of Inequality
to solve the inequality.
Graph the solutions on a number line. 2(3y – 5) < -16

Answer:

Explanation:
Solving the inequality 2(3y – 5) < -16,
6y – 10 < -16, using distributive property,
6y – 10 + 10 < -16 + 10, adding 10 on both sides,
6y < -6,
6y ÷ 6 < -6 ÷ 6, dividing both sides by 6,
we get y < -1.
Question 14.
Higher Order Thinking Solve each of the given inequalities for z.
Which of the inequalities has 5 as a solution?

Answer:
The inequality that has a solution of 5 is Inequality 1,
Explanation:
Given to solve the inequality 4(2.8z +1.75) > -26.6,
11.2z + 7 > -26.6, using distributive property,
11.2z + 7 – 7 > -26.6 – 7, subtracting 7 on both sides,
11.2z > -33.6,
11.2z ÷ 11.2 > -33.6 ÷ 11.2, dividing both sides by 11.2,
z > -3,
Given to solve the inequality 2(1.9z +1.5) ≤ 18.2,
3.8z + 3 ≤ 18.2, using distributive property,
3.8z + 3 – 3 ≤ 18.2 – 3 subtracting 7 on both sides,
3.8z ≤ 15.2,
3.8z ÷ 3.8 ≤ 15.2 ÷ 3.8, dividing both sides by 3.8,
z ≤ 4,
So the inequality that has a solution of 5 is Inequality 1.
Assessment Practice
Question 15.
The school band needs $500 to buy new hats. They already have $200.
They are selling bumper stickers for $1.50 each.
How many bumper stickers do they need to sell to have
at least $500? Write and solve an inequality that represents the situation.
Answer:
200 bumper stickers do they need to sell,
Inequality : 1.50b + 200 = 500,
Explanation:
Given the school band needs $500 to buy new hats. They already have $200.
They are selling bumper stickers for $1.50 each.
Let b be the number of bumper stickers do they need to sell to have
at least $500? The inequality that represents the situation is
1.50b + 200 ≤ 500, solving,
1.50b + 200 – 200 ≤ 500 – 200, subtracting 200 both sides,
1.50b ≤ 300,
1.50b ÷1.50 ≤ 300 ÷ 1.50, dividing both sides by 1.50,
b ≤ 200, therefore 200 bumper stickers do they need to sell and
Inequality : 1.50b + 200 = 500.
Topic 5 REVIEW
Topic Essential Question
How can you solve real-world and mathematical problems with numerical and
algebraic equations and inequalities?
Answer:
Through the use of equations and inequalities , we will be able to determine
the possible solutions to the problem,
Explanation:
Real world and mathematical problems can be solved through the use
of numerical and algebraic equations and inequalities.
In a certain problem there are unknown that needs to be solved.
Therefore, using equations and inequalities in order to determine
the unknown it will help to easily solve the problem.
Through the use of equations and inequalities we will be
able to determine the possible solutions to the problem.
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word used.

Question 1.
You ![]() when you divide both sides of the equation 3n = 12 by 3.
when you divide both sides of the equation 3n = 12 by 3.
Answer:
Isolate the variable,
When we divide both sides of the equation 3n = 12 by 3, we isolate
the variable,
Explanation:
3n = 12,
3n ÷ 3 = 12 ÷ 3, Dividing both sides by 3 we get n = 4.
Question 2.
A statement that contains >, <, ≥, ≤, or ≠ to compare two expressions is a(n)
Answer:
Inequality,
Explanation:
Inequality is a statement that contains >, <, ≥, ≤, or ≠ to compare two expressions.
Question 3.
You can use the ![]() to remove parentheses in
to remove parentheses in
the process of solving the equation – 10(x + 5) = 40.
Answer:
Distributive Property,
Explanation:
In the the process of solving the equation – 10(x + 5) = 40,
we use distributive property to remove parentheses as
-10x -50 = 40.
Use Vocabulary in Writing
Write an equation or inequality to represent the following situation:
17 is at least 5 more than 3 times x. Explain how you wrote your
equation or inequality. Use vocabulary from Topic 5 in your explanation.
Answer:
Equation or Inequality : 17 > 3x + 5,
Explanation:
Given the situation as 17 is at least 5 more than 3 times x,
So wrote the equation or inequality as 17 > 5 + 3x means
17 is greater than 5 and 3 times of x(3x), Vocabulary used is
equation or inequality.
Concepts and Skills Review
LESSONS 5-1 AND 5-2
Write Two-Step Equations | Solve Two-Step Equations
Quick Review
Equations can be used to represent situations. Two-step equations have two
different operations.
The properties of equality can be applied the same way when solving
two-step equations as when solving one-step equations.
Practice
Question 1.
The total number of students in the seventh grade is 9 more than 4 times
as many students as are in the art class. There are 101 students in the seventh grade.
Write and solve an equation to find the number of students in the art class.
Let x represent the number of students in the art class.
Answer:
Equation : 4x + 9 = 101,
There are 23 students in the art class,
Explanation:
Given the total number of students in the seventh grade is 9 more than 4 times
as many students as are in the art class. There are 101 students in the seventh grade.
Let x represent the number of students in the art class.
So the equation to find the number of students in the art class is 4x + 9 = 101, on solving
4x + 9 – 9 = 101 – 9, subtracting 9 from both sides,
4x ÷ 4 = 92 ÷ 4, Dividing both sides by 4 we get
x = 23, therefore there are 23 students in the art class,
Question 2.
List the steps to solve the following equation: 5x – 6 = 44.
Then solve for x.
Answer:
x = 10,
Explanation:
The steps to solve the following equation : 5x – 6 = 44 is
5x – 6 + 6 = 44 + 6, adding 6 on both sides,
5x = 50,
5x ÷ 5 = 50 ÷ 5, dividing both sides by 5 we get x = 10.
Question 3.
Solve for the given variable.
a. 4y + 3 = 19
b. \(\frac{1}{2}\)n – 3 = 5
Answer:
a. y = 4,
b. n = 16,
Explanation:
Solving:
a. 4y + 3 = 19,
4y + 3 – 3 = 19 – 3, subtracting 3 on both sides,
4y = 16,
4y ÷ 4 = 16 ÷ 4, dividing both sides by 4 we get y = 4.
b. \(\frac{1}{2}\)n – 3 = 5,
\(\frac{1}{2}\)n – 3 + 3 = 5 + 3, adding 3 on both sides,
\(\frac{1}{2}\)n = 8,
2 X \(\frac{1}{2}\)n = 2 X 8, multiplying both sides by 2 we get
n = 16.
LESSON 5.3 Solve Equations Using the Distributive Property
Quick Review
Use the Distributive Property to solve problems of the form p(x + q) = r.
Practice
Question 1.
There are 450 seats in the lower level of a concert hall with
b balcony seats in the upper level. So far, 170 tickets have been sold,
which is \(\frac{1}{5}\) of the total number of seats in the concert hall.
How many tickets sold are balcony seats?
Answer:
There are 400 balcony seats in the concert hall,
Explanation:
Given there are 450 seats in the lower level of a concert hall with
b balcony seats in the upper level. So far, 170 tickets have been sold,
which is \(\frac{1}{5}\) of the total number of seats in the concert hall.
Number of tickets sold which are balcony seats are
Equation: \(\frac{1}{5}\)(b + 450) = 170,
\(\frac{1}{5}\)b + 90 = 170, Using distributive property,
\(\frac{1}{5}\)b + 90 – 90 = 170 – 90, subtracting 90 from both sides,
\(\frac{1}{5}\)b = 80,
5 X \(\frac{1}{5}\)b = 5 X 80 , multiplying both sides by 5 we get
b = 400, therefore there are 400 balcony seats in the concert hall.
Question 2.
Solve the equation -4(8 + y) = 90.
Answer:
y = -30.5,
Explanation:
Given to solve -4(8 + y) = 90,
-32 – 4y = 90, Using distributive property,
-32 – 4y + 32 = 90 + 32, adding 32 on both sides,
-4y = 122,
-4y ÷ -4 = 122 ÷ -4, dividing both sides by -4 we get y = -30.5.
LESSON 5-4 Solve Inequalities Using Addition or Subtraction
Quick Review
When you add or subtract the same number on both sides of an inequality,
the relationship between the sides stays the same.
Solutions to inequalities can be graphed on number lines.
Practice
Question 1.
Carson’s wheelbarrow can hold 345 pounds. If he has 121 pounds
of rock in the wheelbarrow, what number of pounds, p, can he put in
the wheelbarrow without going over the weight limit?
Answer:
The weight that can put in the wheelbarrow is no more than 224 pounds,
Explanation:
Given Carson’s wheelbarrow can hold 345 pounds.
If he has 121 pounds of rock in the wheelbarrow,
So number of pounds p can he put in the wheelbarrow without
going over the weight limit is 121 + p ≤ 345,
121 + p – 121 ≤ 345 – 121, subtracting 121 from both sides we get
p ≤ 224, therefore the weight that can put in the wheelbarrow is
no more than 224 pounds.
Question 2.
Solve x – 19 < 81. Then graph the solution.
Answer:
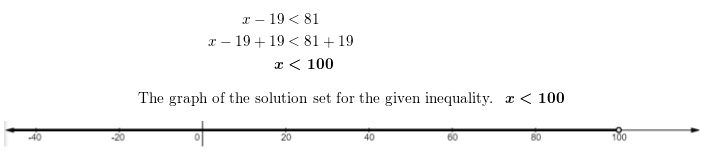
Explanation:
Solving x – 19 < 81 as
x – 19 + 19 < 81 + 19, adding 19 on both sides,
x < 100 and graph of the solution x < 100 is as shown above.
LESSON 5-5 Solve Inequalities Using Multiplication or Division
Quick Review
When you multiply or divide both sides of an inequality by the same positive number,
the inequality remains true. When you multiply or divide both sides of an inequality by
the same negative number, you need to reverse the inequality symbol,
but the inequality remains true.
Practice
Question 1.
Travis has 3 months to save money for a trip. An airplane ticket costs more than $300.
If he saves the same amount of money, a, each month, how much does he need to
save each month to pay for the ticket?
Answer:
Inequality : 3a > 300,
Travis should save more than $100 each month to pay for the ticket,
Explanation:
Given Travis has 3 months to save money for a trip.
An airplane ticket costs more than $300.
If he saves the same amount of money a each month,
So he need to save each month to pay for the ticket is 3a > 300,
Now on simplifying 3a ÷ 3 = 300 ÷ 3, Dividing both sides by 3 we get a >100,
therefore, Travis should save more than $100 each month to pay for the ticket.
Question 2.
Solve –\(\frac{1}{8}\)y ≤ 34. Then graph the solution.
Answer:
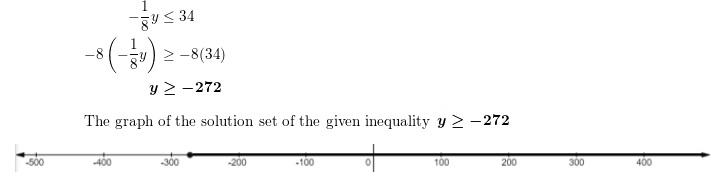
Explanation:
Solving –\(\frac{1}{8}\)y ≤ 34,
-8 X –\(\frac{1}{8}\)y ≤ -8 X 34, Multiplying both sides by -8 and
reverse the inequality symbol,
y ≥ -272 and graph of the solution y ≥ -272 is as shown above.
LESSON 5-6 Solve Two-Step Inequalities
Quick Review
Inverse relationships and properties can be used to isolate the variable and
solve two step inequalities in the form px + q < r or px + q > r in the same way
that they are used to solve two-step equations.
Practice
Question 1.
The school band gets $5 for each T-shirt they sell at a fundraiser.
They have a goal of raising $150. If $45 has been raised so far,
how many more T-shirts do they have to sell to reach or exceed the goal?
Answer:
The school band needs to sell at least 21 T-shirts,
Explanation:
Given the school band gets $5 for each T-shirt they sell at a fundraiser.
They have a goal of raising $150. If $45 has been raised so far,
more T-shirts they do have to sell to reach or exceed the goal are
45 + 5x ≥ 150,
45 + 5x – 45 ≥ 150 – 45, subtracting 45 from both sides,
5x ≥ 105,
5x ÷ 5 ≥ 105 ÷ 5, dividing both sides by 5 we get x ≥ 21,
therefore the school band needs to sell at least 21 T-shirts.
Question 2.
Solve the inequality –8 –\(\frac{1}{3}\)n ≤ -25.
Answer:
n ≥ 51,
Explanation:
Solving the inequality –8 –\(\frac{1}{3}\)n ≤ -25,
–8 –\(\frac{1}{3}\)n + 8 ≤ -25 + 8, adding 8 on both sides,
–\(\frac{1}{3}\)n ≤ -17,
-3 X –\(\frac{1}{3}\)n ≥ – 3 X -17, Multiplying both sides by -3 and
reverse the inequality symbol we get n ≥ 51.
LESSON 5-7 Solve Multi-Step Inequalities
Quick Review
Solving a multi-step inequality is similar to solving a multi-step equation.
All of the rules and properties for solving one- and
two step inequalities apply to solving multi-step inequalities.
Practice
Question 1.
Solve 1.9(2.3n + 6) + 10.45 > 43.7. Then graph the solution.
![]()
Answer:

Explanation:
Given to solve 1.9(2.3n + 6) + 10.45 > 43.7,
4.37n + 11.4 + 10.45 > 43.7, using distributive property,
4.37n + 21.85 > 43.7, combining like terms,
4.37n + 21.85 – 21.85 > 43.7 – 21.85, subtracting 21.85 from both sides,
4.37n > 21.85,
4.37n ÷ 4.37 > 21.85 ÷ 4.37, dividing both sides by 4.37 we get
n > 5 and graph of the solution n > 5 is as shown above.
Question 2.
Solve 4(-2n + 2.5) – 8 ≤ 50. Then graph the solution.
![]()
Answer:
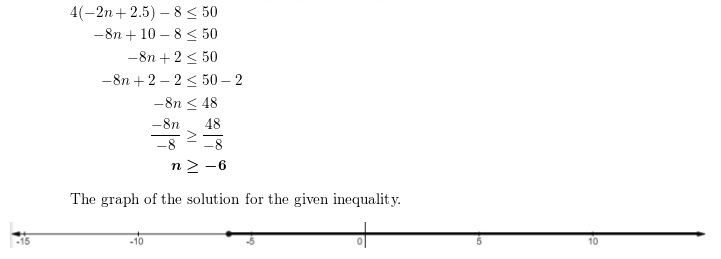
Explanation:
Given to solve 4(-2n + 2.5) – 8 ≤ 50,
-8n + 10 – 8 ≤ 50, using distributive property,
-8n + 2 ≤ 50, combining like terms,
-8n +2 -2 ≤ 50 – 2, subtracting -2 from both sides,
-8n ≤ 48,
-8n ÷ -8 ≥ 48 ÷ -8, dividing both sides by -8 and reverse
the inequality symbol we get n ≥ -6 and
graph of the solution n ≥ -6 is as shown above.
Topic 5 Fluency Practice
Crisscrossed
Solve each problem. Write your answers in the cross-number puzzle below.
Each digit, decimal point, dollar sign, and percent symbol of your answer goes in its own box.
Round money amounts to the nearest cent as needed.

ACROSS
A. Antonia buys 0.75 yard of fabric at $12.00 per yard.
If she pays 5% sales tax, what is the total cost of the fabric?
B. Five friends plan to split a restaurant bill evenly.
The total cost of the meal is $89.75, and they want to leave a 20% tip.
What amount should each friend pay?
E. Kaylie buys a sweater on sale for $40.11. If the discount is 20% off and
she pays $1.91 in sales tax, what is the original price of the sweater?
F. Randy buys a pair of shoes that were originally priced at $147.
He receives a 35% discount and pays 8.5% sales tax. How much does Randy pay?
G. A basketball player makes 8 of 22 shots in Game 1, 6 of 15 shots in
Game 2, and 10 of 23 shots in Game 3.
What percent of the shots did the player make in the three games?
Answer:

Across:
A. The total cost of the fabric is $9.45,
B. The amount should each friend pay is $21.54,
E. The original price of the sweater is $47.75,
F. Randy paid $103.67,
G. Percent of the shots did the player make in the three games is 40%,
Explanation:
Across:
A. Given Antonia buys 0.75 yard of fabric at $12.00 per yard.
If she pays 5% sales tax, so 0.75 X $12 = $9,
Now 5% on $9 is 5 X 9 ÷100 = $0.45,
therefore the total cost of the fabric is $9 + $0.45 = $9.45.
B. Given five friends plan to split a restaurant bill evenly.
The total cost of the meal is $89.75 and they want to leave a 20% tip.
So amount should each friend pay must be
89.75 X 20 ÷100 = $17.95 is the tip,
the total amount is $89.75 + $17.95 = $107.7 which is paid by
5 friends, therefore the amount each friend must pay is
$107.7 ÷ 5 = $21.54.
E. Given Kaylie buys a sweater on sale for $40.11.
If the discount is 20% off and she pays $1.91 in sales tax,
Let x be the original price of the sweater so
Original Price = (Paid Price – Tax) + 20% discount,
x = (40.11 -1.91) + 20% discount,
x = $38.20 +( (20 X x) ÷ 100),
x – (20x ÷ 100)= $38.20,
100x – 20x = $38.20 X 100,
80x = $3,820.
x = $3,820 ÷ 80,
x = $47.75.
F. Given Randy buys a pair of shoes that were originally priced at $147.
He receives a 35% discount and pays 8.5% sales tax.
Let Randy paid p,
Randy receives 35% discount means
($147 – ($147 X 35% discount)) = ($147 – $51.45) = $95.55,
on $95.55 Randy pays 8.5% sales tax so 95.55 X 8.5 ÷ 100 = $8.12175,
Therefore Randy paid p = $95.55 + $8.12175 = $103.67175 ≈ $103.67.
G. Given a basketball player makes 8 of 22 shots in Game 1,
6 of 15 shots in Game 2 and 10 of 23 shots in Game 3,
In Game 1 percent of the shots did the player make is 8 ÷ 22 = 0.36 = 36%,
In Game 2 percent of the shots did the player make is 6 ÷ 15 = 0.40 = 40%,
In Game 3 percent of the shots did the player make is 10 ÷ 23 = 0.43 = 43%,
Therefore percent of the shots did the player make in the three games is
(36% + 40% + 43%) ÷ 3 = 39.33% ≈ 40%.
DOWN
A. Jack buys a tablet that costs $99 and a memory card that costs $15.
He has a coupon for a 15% discount. What is the amount of the discount on the two items?
B. Tara buys two pairs of socks for $4.99 each and three T-shirts for $11.45 each.
If she pays 6% sales tax, what is the total amount of her purchase?
C. Sunil receives a 20% discount on a concert ticket that costs $75.
If Sunil pays $3.30 in sales tax on the discounted ticket, what is the sales tax rate?
D. Dylan works for 4 hours and is paid $17.50 per hour. He must pay 15% in income taxes.
What amount does he earn after taxes?
E. Miles earns a 6% commission on each vehicle he sells.
Today he sold a truck for $18,500 and a car for $9,600.
What is the total amount of his commission for these vehicles?
Answer:
A. The amount of the discount on the two items is $17.10,
B. The total amount of Tara’s purchase is $47.00,
C. The sales tax rate is 5.5%,
D. Dylan earn after taxes is $59.50,
E. The total amount of Miles commission for these vehicles is $1,686,
Explanation:
A. Given Jack buys a tablet that costs $99 and a memory card that costs $15.
He has a coupon for a 15% discount. So tablet costs $99 – ($99 X 15 ÷ 100) =
$99 – $14.85 = $84.15 and Memory card costs $15 – ($15 X 15 ÷ 100) =
$15 – $2.25 = $12. 75, Therefore the amount of the discount on the two items is
discount amount on tablet + discount amount on memory card = $ 14.85 + $ 2.25 = $17.10.
B. Given Tara buys two pairs of socks for $4.99 each and three T-shirts for $11.45 each.
If she pays 6% sales tax, To find the total amount of her purchase first we will calculate
cost for socks + cost for T-shirts and then add sales tax too, so
2($4.99) + 3(11.45) = $9.98 + $34.35 = $44.33,
Now sales tax = $44.33 X 6 ÷ 100 = $2.6598, therefore $44.33 + $2.6598 = $46.9898 ≈ $47.00.
C. Given Sunil receives a 20% discount on a concert ticket that costs $75.
If Sunil pays $3.30 in sales tax on the discounted ticket,
The discounted ticket price is ($75 – $75 X 20 ÷ 100) = $75 – $15 = $60,
let the sales rate tax is r, so $3.30 = r% of 60, therefore r = (3.30 ÷ 60) X 100= 0.55 X 100 = 5.5%.
D. Given Dylan works for 4 hours and is paid $17.50 per hour.
He must pay 15% in income taxes. So amount does he earn after taxes would be
first he gets $17.50 X 4 = $70, So amount paid to income tax will be $70 X 15 ÷ 100 = $10.5,
Therefore Dylan earn after taxes is $70 – $10.5 = $59.50.
E. Given Miles earns a 6% commission on each vehicle he sells.
Today he sold a truck for $18,500 and a car for $9,600.
So first commission on truck sold is $18,500 X 6 ÷ 100 = $1,110 and
commission on car sold is $9,600 X 6 ÷ 100 = $576,
therefore the total amount of his commission for these vehicles is
$1,110 + $576 = $1,686.