Practice with the help of enVision Math Common Core Grade 8 Answer Key Topic 8 Solve Problems Involving Surface Area and Volume regularly and improve your accuracy in solving questions.
enVision Math Common Core 8th Grade Answers Key Topic 8 Solve Problems Involving Surface Area And Volume
Topic 8 Essential Question
How can you find volumes and surface areas of three-dimensional figures?
Answer:
The “Surface area” is the sum of the areas of all faces (or surfaces) on a 3D shape.
Ex:
A cuboid has 6 rectangular faces. To find the surface area of a cuboid, add the areas of all 6 faces
We know that,
The volume of a three-dimensional figure = Cross-sectional area × length
3-ACT MATH

Measure Up
Have you ever heard of the terms griffin beaker, Erlenmeyer flask, or graduated cylinder? Maybe you’ve used them in your science class. Each piece of equipment in a chemistry lab has a specific purpose, so containers come in many shapes. It’s sometimes necessary to pour a solution from one container to another. Think about this during the 3-Act Mathematical Modeling lesson.
Topic 8 ënVision STEM Project
Did You Know?
The production of packaging is a huge industry employing over five million people with annual sales of more than 400 billion dollars.
Packaging materials protect and deliver food and products to consumers.

A plastic bottle takes 450–1,000 years to biodegrade.

Seabirds are dying of starvation with stomachs full of plastic and Styrofoam.

Polystyrene foam lasts forever!
Eco-friendly packaging materials are being made from mushrooms and bamboo.

There is even a drink bottle made from recyclable paper.

New technology results in packaging materials that are both affordable and biodegradable.
Environmentally friendly companies are producing sustainable packaging. In addition to using recyclable materials, they reduce the water, natural resources, and energy needed for production. They minimize waste when designing products.
Your Task: Wrap it Up!

Engineers consider several factors when designing product packaging. These factors include cost efficiency and eco-friendly design so that materials are disposable, recyclable, biodegradable, and not wasted. Suppose you are an engineer working for Liquid Assets, an environmentally friendly company that designs, builds, and packages water purifiers. You and your classmates will use your knowledge of volume and surface area to determine an environmentally sound way to package the purifiers.
Topic 8 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
base
diameter
radius
three-dimensional
two-dimensional
Question 1.
The __________ is the distance from the center to the edge of a circle.
Answer:
We know that,
The “Radius” is the distance from the center to the edge of a circle
Hence, from the above,
We can conclude that the best term to complete the given definition is: Radius
Question 2.
A shape that has length, width, and height is ___________.
Answer:
We know that,
A shape that has a length, width, and height is known as “Three-dimensional”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Three dimensional
Question 3.
Any side of a cube can be considered a __________.
Answer:
We know that,
Any side of a cube can be considered a “Base”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Base
Question 4.
A shape that has length and width, but not height, is ___________.
Answer:
We know that,
A shape that has length and width, but not height is known as “Two-dimensional”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Two-dimensional
Question 5.
The _____________ of a circle is a line segment that passes through its center and has endpoints on the circle.
Answer:
We know that,
The “Diameter” of a circle is a line segment that passed through its center and has endpoints on the circle
Hence, from the above,
We can conclude that the best term to complete the given definition is: Diameter
Multiplying with Decimals
Find the product.
Question 6.
14 ∙ 3.5 = _______
Answer:
The given expression is:
14 × 3.5
So,
14 × 3.5 = 49.0
Hence, from the above,
We can conclude that the value for the given expression is: 49
Question 7.
9 ∙ 3.14 = _________
Answer:
The given expression is:
9 × 3.14
So,
9 × 3.14 = 28.26
Hence, from the above,
We can conclude that the value for the given expression is: 28.26
Question 8.
4.2 ∙ 10.5 = _________
Answer:
The given expression is:
4.2 × 10.5
So,
4.2 × 10.5 = 44.1
Hence, from the above,
We can conclude that the value for the given expression is: 44.1
Areas of Circles
Find the area of each circle. Use 3.14 for π.
Question 9.
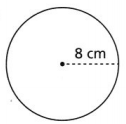
A = ________
Answer:
The given circle is:

From the given circle,
The radius is: 8 cm
Now,
We know that,
The area of the circle = πr²
So,
The area of the given circle = 3.14 × 8²
= 200.96 cm²
Hence, from the above,
We can conclude that the area for the given circle is: 200.96 cm²
Question 10.
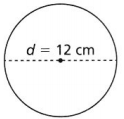
A = _________
Answer:
The given circle is:

From the given circle,
The diameter is: 12 cm
Now,
We know that,
Radius = \(\frac{Diameter}{2}\)
Radius = \(\frac{12}{2}\)
Radius = 6 cm
Now,
We know that,
The area of the circle = πr²
So,
The area of the given circle = 3.14 × 6²
= 113.04 cm²
Hence, from the above,
We can conclude that the area of the given circle is: 113.04 cm²
Use the Pythagorean Theorem
Find the missing side length of the triangle.
Question 11.
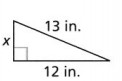
x = _________
Answer:
The given triangle is:

Now,
Fro the given figure,
We can observe that the triangle is a right triangle
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the side lengths
So,
13² = 12²+ x²
x²= 169 – 144
x² = 25
x = \(\sqrt{25}\)
x = 5 in.
Hence, from the above,
We can conclude that the missing side length of the given triangle is: 5 in.
Question 12.
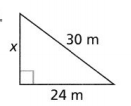
x = __________
Answer:
The given triangle is:

Now,
Fro the given figure,
We can observe that the triangle is a right triangle
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the side lengths
So,
30² = 24²+ x²
x²= 900 – 576
x² = 324
x = \(\sqrt{324}\)
x = 18 in.
Hence, from the above,
We can conclude that the missing side length of the given triangle is: 18 in.
Language Development
Complete the word web. Write keywords, ideas, examples, or illustrations that connect to each new vocabulary term.

Topic 8 Pick A Project
PROJECT 8A
What makes a concert rock?
PROJECT: DESIGN PROPS OR STAGE STRUCTURES

PROJECT 8B
What is the most interesting museum you have visited?
PROJECT: MAKE A MODEL OF A MUSEUM

PROJECT 8C
Where around the United States can you find quarries?
PROJECT: POUR AND MEASURE SAND

PROJECT 8D
If you were cast in a play, would it be a comedy or a drama? Why?
PROJECT: WRITE A SKIT

Lesson 8.1 Find Surface Area of Three-Dimensional Figures
Explore It!
Andrea is designing the packaging for a tube-shaped container.

I can… find the surface areas of cylinders, cones, and spheres.
A. Model with Math What two-dimensional shape represents the top and bottom of the container? What two-dimensional shape represents the tube? Draw a net of the tube-shaped container.
Answer:
It is given that Andrea is designing the packaging for a tube-shaped container.
Now,
The given arrangement for tube shaped container is:

Now,
From the given arrangement,
We can observe that
The two-dimensional shape that represents the top and bottom of the container is: Circle
The two-dimensional shape that represents the tube is: Rectangle
Hence,
The representation of the tube-shaped container is:
B. Look for Relationships The circular top and bottom fit perfectly on the ends of the container. How are the measures of the circles and the rectangle related?
Answer:
The representation of the tube-shaped container is:

Now,
From the given figure,
We can observe that the tube-shaped container is made up of 2 circles and 1 rectangle
So,
The total surface area of the tube-shaped container is the sum of the areas of 2 circles and 1 rectangle
Now,
We know that,
The area of a circle = πr²
The area of a rectangle = Height× Base
Where,
The base of the rectangle is a circle
So,
The circumference of the circle = 2πr
Hence,
The surface area of the tube-shaped container = 2πr² + 2πrh
Focus on math practices
Model with Math
How can you check whether the net that you drew accurately represents the tube-shaped container?
Answer:
The representation of the tube-shaped container is:

Now,
When the top and bottom of the container correctly fit the tube,
That is the representation that the net you drew accurately represents the tube-shaped container
Essential Question
How are the areas of polygons used to find the surface area formulas for three-dimensional figures?
Answer:
We know that,
A three-dimensional figure is a combination of some two-dimensional figures
Ex:
We can make a “Cuboid” from the combination of “Rectangles”
We can make a “Sphere” from the combination of ‘Circles”
So,
The total surface area of a three-dimensional figure can be given as the sum of all the areas of the two-dimensional figures that are used to make the three-dimensional figure
Try it
What is the surface area of a cylinder with a height of 9.5 inches and a radius of 2.5 inches?
The surface area of the cylinder is __________ square inches.
Answer:
It is given that
The height of a cylinder is: 9.5 inches
The radius of a cylinder is: 2.5 inches
Now,
We know that,
The surface area of the cylinder (S.A) = 2πr² + 2πrh
= 2 × 3.14 × (2.5)² + 2 × 3.14 × 9.5 × 2.5
= 39.25 + 149.15
= 188.4 square inches
Hence, from the above,
We can conclude that the surface area of the given cylinder is: 188.4 square inches
Convince Me! How can you find the surface area of a cylinder if you only know its height and the circumference of its base?
S.A. = 2(πr2) + (2πr)h
= 2π(________2) + 2π(_______)(________)
= _______π + _______π
= _______π
Answer:
It is given that
We know only the height of the cylinder and the circumference of its base
Now,
We know that,
The surface area of a cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2π (r²) + 2π (r) (h)
S.A = 2π + π
S.A = 3π
Hence, from the above,
We can conclude that the surface area of a cylinder with only its height and the circumference of its base is: 3π
Try It!
a. What is the surface area of a cone with a radius of 7 feet and a slant height of 9 feet? Use \(\frac{22}{7}\) for π.
Answer:
It is given that
The radius of the cone is (r): 7 feet
The slant height of the cone is (l): 9 feet
Now,
We know that,
The surface area of the cone (S.A) = πr² + πrl
So,
S.A = \(\frac{22}{7}\) × 7² + \(\frac{22}{7}\) × 7 × 9
= 154 + 198
= 352 square feet
Hence, from the above,
We can conclude that the surface area of the given cone is: 352 square feet
b. What is the surface area of a sphere with a diameter of 2.7 inches? Use 3.14 for π.
Answer:
It is given that,
The diameter of a sphere is: 2.7 inches
Now,
We know that,
Radius = \(\frac{Diameter}{2}\)
So,
Radius of the sphere = \(\frac{2.7}{2}\)
So,
The radius of the sphere (r) = 1.35 inches
Now,
We know that,
The surface area of the sphere (S.A) = 4πr²
So,
S.A = 4 × 3.14 × (1.35)²
= 22.89 square inches
Hence, from the above,
We can conclude that the surface area of the given sphere is: 22.89 square inches
KEY CONCEPT
Formulas for finding the area of polygons can be used to find the surface areas of cylinders, cones, and spheres.
Do You Understand?
Question 1.
Essential Question How are the areas of polygons used to find the surface area formulas for three-dimensional figures?
Answer:
We know that,
A three-dimensional figure is a combination of some two-dimensional figures
Ex:
We can make a “Cuboid” from the combination of “Rectangles”
We can make a “Sphere” from the combination of ‘Circles”
So,
The total surface area of a three-dimensional figure can be given as the sum of all the areas of the two-dimensional figures that are used to make the three-dimensional figure
Question 2.
Reasoning Why is the length of the base of the rectangle the same as the circumference of the circles in the net of a cylinder?
Answer:
The representation of the cylinder is:

Now,
If you look at the net, the curved surface of the cylinder is rectangular in shape. The length of the rectangle is the same as the circumference of the circle. Since the length of the rectangle wraps around the circle rim, it is the same length as the circumference of the circle.
Question 3.
Construct Arguments Aaron says that all cones with a base circumference of 8 inches will have the same surface area. Is Aaron correct? Explain.
Answer:
It is given that
Aaron says that all cones with a base circumference of 8 inches will have the same surface area
Now,
We know that,
The surface area of a cone = πr² + πrl
Now,
From the above formula,
We can conclude that the surface area of the cone does not depend only on the circumference of the base but also we need the side length of the cone part as well
So,
All cones with a base circumference of 8 inches will not have the same surface area.
Hence, from the above,
We can conclude that Aaron is not correct
Do You Know How?
Question 4.
What is the surface area of the cylinder? Use 3.14 for π, and round to the nearest tenth.
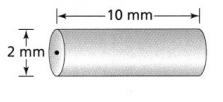
Answer:
The given figure is:

From the given figure,
The diameter of the cylinder is: 2 mm
The height of the cylinder is: 10 mm
So,
Radius of the cylinder = \(\frac{Diameter of the cylinder}{2}\)
= \(\frac{2}{2}\)
= 1 mm
Now,
We know that,
The surface area of the cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × 1² + 2 × 3.14 × 1 × 10
= 6.28 + 62.8
= 69.08 mm²
Hence, from the above,
We can conclude that the surface area of the given cylinder is: 69.08 mm²
Question 5.
What is the surface area of the cone to the nearest tenth? Use 3.14 for π.
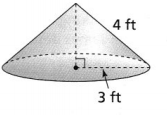
Answer:
The given figure is:

From the given figure,
The slant height of the cone is (l): 4 ft
The radius of the cone is: 3 ft
Now,
We know that,
The surface area of the cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 3² + 3.14 × 3 × 4
= 28.26 + 37.68
= 65.94 ft²
Hence, from the above,
We can conclude that the surface area of the given cone is: 65.94 ft²
Question 6.
What is the surface area of the sphere in terms of π?
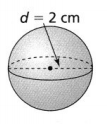
Answer:
The given figure is:

From the given figure,
The diameter of the sphere is: 2 cm
Now,
We know that,
The radius of the sphere (r) = \(\frac{Diameter of the sphere}{2}\)
= \(\frac{2}{2}\)
= 1 cm
Now,
We know that,
The surface area of the sphere (S.A) = 4πr²
So,
S.A = 4 × 3.14 × 1²
= 12.56 cm²
Hence, from the above,
We can conclude that the surface area of the given sphere is: 12.56 cm²
Practice & Problem Solving
Leveled Practice In 7-8, find the surface area.
Question 7.
What is the surface area of the cylinder? Use 3.14 for π, and round to the nearest tenth.
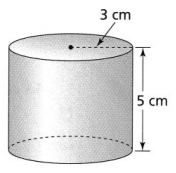
S.A. = 2(πr2) + (2πr)h
= 2π(________2) + 2 π(_______)(________)
= 2 π(________) + 2 π(_________)
= _______π + _______π
= _______π
≈ ________ cm2
Answer:
The given figure is:

From the given figure,
The radius of the cylinder is: 3 cm
The height of the cylinder is: 5 cm
Now,
We know that,
The surface area of the cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × 3² + 2 × 3.14 × 3 × 5
= 56.52 + 94.2
= 150.72 cm²
Hence, from the above,
We can conclude that the surface area of the given cylinder is: 150.72 cm²
Question 8.
What is the surface area of the cone? Use 3.14 for π.

S.A. = πr2 + πlr
= π(________2) + π(_______)(________)
= ________ π + _________π
= _______π
≈ ________ cm2
Answer:
The given figure is:

From the given figure,
The radius of the cone (r) is: 7 cm
The slant height of the cone (l) is: 13 cm
Now,
We know that,
The surface area of the cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 7² + 3.14 × 7 × 13
= 153.86 + 285.74
= 439.6 cm²
Hence, from the above,
We can conclude that the surface area of the given cone is: 439.6 cm²
Question 9.
Construct Arguments Sasha incorrectly claimed that the surface area of the cylinder is about 76.9 square inches. Explain her likely error and find the correct surface area of the cylinder.

Answer
The given figure is:
:
Now,
From the given figure,
The diameter of the cylinder is: 7 in.
The height of the cylinder is: 19 in.
Now,
We know that,
Radius = \(\frac{Diameter}{2}\)
So,
Radius of the circle = \(\frac{7}{2}\)
= 3.5 in.
Now,
We know that,
The surface area of the cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × (3.5)² + 2 × 3.14 × 3.5 × 19
= 76.93 + 417.62
= 494.55 in.²
Hence, from the above,
We can conclude that
The correct surface area of the given cylinder is: 494.55 in.²
The mistake made by Sasha is:
She adds only the area of the top and bottom but not the area of the rectangle and the area of the top and bottom of the cylinder
Question 10.
A theme park has a ride that is located in half a sphere. The ride goes around the widest part of the sphere, which has a circumference of 514.96 yards. What is the surface area of the sphere? Estimate to the nearest hundredth using 3.14 for π.

Answer:
It is given that
A theme park has a ride that is located in half a sphere. The ride goes around the widest part of the sphere, which has a circumference of 514.96 yards
Now,
The given sphere is:

Now,
We know that,
Circumference = 2πr
So,
Circumference of the theme park = 514.96 yd
2πr = 514.96
r = \(\frac{514.96}{2 × 3.14}\)
= 2.38 yd
Now,
We know that,
The surface area of the sphere (S.A) = 4πr²
So,
S.A = 4 × 3.14 × (2.38)²
= 71.14 yd²
Hence, from the above,
We can conclude that the surface area of the given sphere is: 71.14 yd²
Question 11.
Find the amount of wrapping paper you need to wrap a gift in the cylindrical box shown. You need to cover the top, the bottom, and all the way around the box. Use 3.14 for π, and round to the nearest tenth.
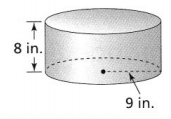
Answer:
The given figure is:

Now,
From the given figure,
The radius of the cylinder is 9 in.
The height of the cylinder is: 8 in
Now,
We know that,
The surface area of the cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × 9² + 2 × 3.14 × 9 × 8
= 508.68 + 452.16
= 960.84 in.²
Hence, from the above,
We can conclude that the amount of wrapping paper you need to wrap a gift in the cylindrical box is: 960.84 in.²
Question 12.
Donna paints ornaments for a school play. Each ornament is made up of two identical cones, as shown. How many bottles of paint does she need to paint 70 ornaments?
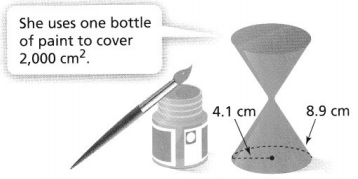
Answer:
It is given that
Donna paints ornaments for a school play. Each ornament is made up of two identical cones, as shown
Now,
From the given figure,
We can observe that
The radius of a cone is: 4.1 cm
The slant height of a cone is: 8.9 cm
Now,
We know that,
The surface area of a cone (S.A) = πr² + πrl
So,
S.A = 3.14 × (4.1)² + 3.14 × 4.1 × 8.9
= 52.78 + 114.57
= 167.35 cm²
So,
The surface area of the second cone (S.A) = 167.35 cm²
So,
The S.A of 70 ornaments = 70 × (167.35 × 2)
= 23,429 cm²
So,
The number of bottles of paint she needed to paint 70 ornaments = \(\frac{23,429}{2,000}\)
= 11.7
≅ 12 bottles
Hence, from the above,
We can conclude that she need 12 bottles of paint to paint 70 ornaments
Question 13.
Higher-Order Thinking
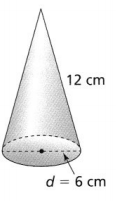
a. What is the surface area of the cone? Use 3.14 for π, and round to the nearest whole number.
Answer:
The given figure is:

Now,
From the given figure,
The diameter of the cone is: 6 cm
The slant height of the cone is: 12 cm
Now,
We know that,
Radius = \(\frac{Diameter}{2}\)
Radius = \(\frac{6}{2}\)
Radius = 3 cm
Now,
We know that,
The surface area of the cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 3² + 3.14 × 3 × 12
= 28.26 + 113.04
= 141.3 cm²
Hence, from the above,
We can conclude that the surface area of the given cone is: 141.3 cm²
b. Reasoning Suppose the diameter and the slant height of the cone are cut in half. How does this affect the surface area of the cone? Explain.
Answer:
It is given that the diameter and the slant height of the cone are cut in half
So,
S.A = π(\(\frac{d}{2}\))² + π (\(\frac{d}{2}\)) (\(\frac{l}{2}\))
= 3.14 × \(\frac{6²}{4}\) + 3.14 × 3 × 6
= 28.26 + 56.52
= 84.78 cm²
Now,
From part (a),
The S.A of the cone is: 141.3 cm²
So,
The ratio of S.A of the cones obtained from part (a) and part (b) respectively = \(\frac{141.3}{84.78}\)
= 1.666
Hence, from the above,
We can conclude that the S.A of the cone we obtained in part (b) is 1.666 times of the S.A of the cone we obtained in part (b)
Assessment Practice
Question 14.
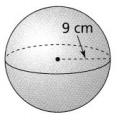
What is the surface area of the sphere? Use 3.14 for π, and round to the nearest tenth.
A 254.5 cm2
B. 56.55 cm2
C. 1,017.4 cm2
D. 4,071.5 cm2
Answer:
The given figure is:

From the given figure,
The radius of the sphere is: 9 cm
Now,
We know that,
The surface area of the sphere (S.A) = 4πr²
So,
S.A = 4 × 3.14 × 9²
= 1,017.36 cm²
≈ 1,017.4 cm²
Hence, from the above,
We can conclude that the S.A of the given sphere is: 1,017.4 cm²
Question 15.
What is the approximate surface area of the cone, in square inches? Use 3.14 for π, and round to the nearest whole number.

Answer:
The given figure is:

Now,
From the given figure,
The slant height of the cone (l) is 40 in.
The diameter of the cone (d) is 40 in.
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{40}{2}\)
r = 20 in.
Now,
We know that,
The surface area of the cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 20² + 3.14 × 20 × 40
= 1,256 + 2,512
= 3,768 in.²
Hence, from the above,
We can conclude that the surface area of the given cone is: 3,768 in²
Lesson 8.2 Find Volume of Cylinders
Explain It!
Jenna and Ricardo are buying a new fish tank for the growing population of zebrafish in their science lab. Jenna says the tanks hold the same amount of water because they have the same dimensions. Ricardo says that he can fill the bottom of the rectangular tank with more cubes, so it can hold more water.

I can… use what I know about finding volumes of rectangular prisms to find the volume of a cylinder.
A. Look for Relationships How are the shapes of the two fish tanks alike? How are they different?
Answer:
When we observe the fish tanks of Jenna and Ricardo,
We can observe that
a. The heights of the two fish tanks are the same
b. The number of cubes that can be filled at the bottom is different
c. The number of cubes filled in Jenna’s fish tank is less than that of the number of cubes filled in Ricardo’s fish tank
d. The amount of water that can hold in Jenna’s fish tank is less than the amount of water that can hold in Ricardo’s fish tank
B. Critique Arguments Who do you think is correct, Ricardo or Jenna? Explain.
Answer:
It is given that
Jenna and Ricardo are buying a new fish tank for the growing population of zebrafish in their science lab. Jenna says the tanks hold the same amount of water because they have the same dimensions. Ricardo says that he can fill the bottom of the rectangular tank with more cubes, so it can hold more water.
Now,
To find which fish tank holds more water, find the volume of the two fish tanks
Now,
For Jenna’s fish tank:
The fish tank is in the form of a cylinder
Now,
We know that,
The volume of the cylinder (V) = πr²h
= \(\frac{πd²h}{4}\)
So,
V = \(\frac{3.14 × 24 × 24 × 48}{4}\)
= \(\frac{86,814.72}{4}\)
= 21,073.68 in³
For Ricardo’s fish tank:
The fish tank is in the form of a rectangular prism
Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
So,
V = 24 × 24 × 48
= 27,648 in³
Hence, from the above,
We can conclude that Ricardo is correct on the basis of volumes of their fish tanks
Focus on math practices
Use Structure How can you use what you know about areas of two-dimensional figures and volumes of prisms to compare the volumes of the fish tanks?
Answer:
We know that,
Volume = Area × Length (or) Height (or) Depth
Where,
“Area” is the area of two-dimensional figures like rectangles, circles, etc.
Essential Question
How is the volume of a cylinder related to the volume of a rectangular prism?
Answer:
Rectangular prisms and cylinders are somewhat similar because they both have two bases and a height.
The formula for the volume of a rectangular solid is
V=Bh
can also be used to find the volume of a cylinder
Where,
“B” in the rectangular prism is the area of the rectangle
“B” in the cylinder is the area of the circle
Try It!
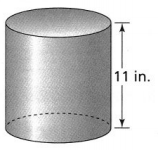
The area of the base of the cylinder is 78.5 in.2. What is the volume of the cylinder?
V = Bh
= _______ ∙ _______
= _______
The volume of the cylinder is ________ cubic inches.
Answer:
It is given that
The area of the base of the cylinder is 78.5 in.2
Now,
The given figure is:

Now,
We know that,
The volume of a cylinder (V) = Bh
Where,
“B” is defined as the area of the circle
So,
V = 78.5 × 11
= 863.5 in.³
Hence, from the above,
We can conclude that the volume of the given cylinder is: 863.5 cubic inches
Convince Me!
Why can you use the formula V = Bh to find the volume of a cylinder?
Answer:
The representation of the cylinder is:
Now,
From the given figure,
We know that,
The two circles that are in the top and bottom positions are congruent
So,
The area for both the circles is also the same
Now,
We know that,
Volume = Area × Height
Now,
We know that,
Area of the circle = πr²
Hence,
The volume of the cylinder (V) = πr²h
Try It!
Lin is building a cylindrical planter with a base diameter of 15 inches. She has 5,000 cubic inches of soil to fill her planter. What is the height of the largest planter Lin can build? Use 3.14 for π, and round to the nearest inch.
Answer:
It is given that
Lin is building a cylindrical planter with a base diameter of 15 inches. She has 5,000 cubic inches of soil to fill her planter.
So,
From the given information,
The volume of the cylindrical planter = 5,000 cubic inches
The diameter of the cylindrical planter = 15 inches
Now,
We know that,
The volume of a cylinder (V) = πr²h
= \(\frac{πd²h}{4}\)
So,
5,000 = \(\frac{3.14 × 15 × 15 × h}{4}\)
5,000 = 176.625h
h = \(\frac{5,000}{176.625}\)
h = 28.3 inches
Hence, from the above,
We can conclude that the height of the largest planter Lin can build is: 28.3 inches
KEY CONCEPT
The formula for the volume of a cylinder is the same as the formula for the volume of a prism. The formula for the volume of a cylinder is V= Bh, where B is the area of the circular base and h is the height of the cylinder.

Do You Understand?
Question 1.
Essential Question How is the volume of a cylinder related to the volume of a rectangular prism?
Answer:
Rectangular prisms and cylinders are somewhat similar because they both have two bases and a height.
The formula for the volume of a rectangular solid is
V=Bh
can also be used to find the volume of a cylinder
Where,
“B” in the rectangular prism is the area of the rectangle
“B” in the cylinder is the area of the circle
Question 2.
Use Structure What two measurements do you need to know to find the volume of a cylinder?
Answer:
We know that,
The volume of a cylinder (V) = πr²h
Now,
From the given formula,
We can observe that
π is a constant
Hence, from the above,
We can conclude that the two measurements that needed to be known are:
a. Radius of the cylinder
b. The height of the cylinder
Question 3.
Reasoning Cylinder A has a greater radius than Cylinder B. Does Cylinder A necessarily have a greater volume than Cylinder B? Explain.
Answer:
It is given that
Cylinder A has a greater radius than Cylinder B
Now,
We know that,
The volume of a cylinder (V) = πr²h
Now,
Fro the above,
We can observe that
Volume (V) ∝ Radius²
So,
When we increase the value of the radius, the value of the volume will automatically increase
Hence, from the above,
We can conclude that cylinder A has a greater volume than Cylinder B
Do You Know How?
Question 4.
What is the volume of the cylinder? Express your answer in terms of π.
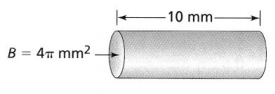
Answer:
The given figure is:

Now,
We know that,
The volume of a cylinder (V) = Bh
Where,
B = πr²
So,
V = 4π × 10
V = 40π mm³
Hence, from the above,
We can conclude that the volume of the given cylinder in terms of π is: 40π mm³
Question 5.
What is the approximate height of the cylinder? Use 3.14 for π, and if necessary, round to the nearest tenth.
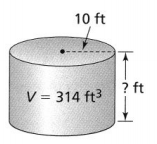
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The volume of a cylinder (V) = 314 ft³
The radius of a cylinder = 10 ft
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
314 = 3.14 × 10 × 10 × h
h = \(\frac{314}{3.14 × 10 × 10}\)
h = 1 ft
Hence, from the above,
We can conclude that the height of the given cylinder is: 1 ft
Question 6.
What is the volume of the cylinder? Use 3.14 for π, and if necessary, round to the nearest tenth.
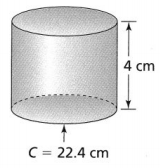
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The height of a cylinder = 4 cm
The circumference of a circle = 22.4 cm
Now,
We know that,
The circumference of a circle = 2πr
So,
2πr = 22.4
r = \(\frac{22.4}{2 × 3.14}\)
r = 3.56 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = 3.14 × 3.56 × 3.56 × 4
= 159.2 cm³
Hence, from the above,
We can conclude that the volume of the given cylinder is: 159.2 cm³
Practice & Problem Solving
Question 7.
Leveled Practice What is the volume of a cylinder with a radius of 5 centimeters and height of 2.5 centimeters? Use 3.14 for π.
V = π ________ 2 ∙ ________
= π ______ ∙ ________
= _______ π
The volume of the cylinder is about _______ cubic centimeters.
Answer:
It is given that
The radius of a cylinder (r) = 5 cm
The height of a cylinder (h) = 2.5 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = 3.14 × 5 × 5 × 2.5
= 196.25 cm
Hence, from the above,
We can conclude that the volume of the given cylinder is: 196.25 cm³ (or) 62.5π cm³
Question 8.
Find the volume of each cylinder in terms of. Which cylinder has the greater volume?
Cylinder A: Area of Base = 61 ft2, height = 10 ft
Cylinder B: Circumference = 6π ft, height = 6 ft
Answer:
The given data is:
Cylinder A: Area of Base = 61 ft2, height = 10 ft
Cylinder B: Circumference = 6π ft, height = 6 ft
Now,
We know that,
The volume of a cylinder (V) = Bh
Where,
B is the area of the circle
Now,
For Cylinder A:
V = 61 × 10
= 610 ft³
For Cylinder B:
We know that,
Circumference = 2πr
So,
2πr = 6π
r = \(\frac{6π}{2π}\)
= 3 ft
So,
V = 3.14 × 3 × 3 × 6
= 169.56 ft³
Hence, from the above,
We can conclude that Cylinder A has the greatest volume when we compare the volumes of Cylinder A and Cylinder B
Question 9.
The volume of a cylinder is 2251 cubic inches, and the height of the cylinder is 1 inch. What is the radius of the cylinder?
Answer:
It is given that
The volume of a cylinder is 2251 cubic inches, and the height of the cylinder is 1 inch
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
2251 = 3.14 × r² × 1
r² = \(\frac{2251}{3.14}\)
r² = 716.87 in²
r = 26.77 in
Hence, from the above,
We can conclude that the radius of the given cylinder is: 26.77 in.
Question 10.
A company is designing a new cylindrical water bottle. The volume of the bottle is 103 cubic centimeters. What is the radius of the water bottle? Estimate using 3.14 for π, and round to the nearest hundredth.

Answer:
It is given that
A company is designing a new cylindrical water bottle. The volume of the bottle is 103 cubic centimeters
Now,
The given figure is:

Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
103 = 3.14 × r² × 8.1
r² = \(\frac{103}{3.14 × 8.1}\)
r² = 4.05cm²
r = 2.01 cm
Hence, from the above,
We can conclude that the radius of the given cylinder is: 2.01 cm
Question 11.
Use the figure at the right.
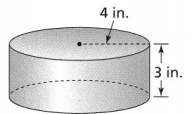
a. Find the volume of the cylinder in terms of π.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the cylinder (r) = 4 in.
The height of the cylinder (h) = 3 in
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = π × 4 × 4 × 3
V = 48π in.³
Hence, from the above,
We can conclude that the volume of the given cylinder in terms of π is: 48π in.³
b. Is the volume of a cylinder, which has the same radius but twice the height, greater or less than the original cylinder? Explain.
Answer:
From part (a),
The radius of the cylinder (r) = 4 in.
The height of the cylinder (h) = 3 in
So,
Now,
For part (b),
The radius of the cylinder (r) = 4 in.
The height of the cylinder (h) = 6 in.
So,
V = π × 4 × 4 × 6
= 96π in.³
Hence, from the above,
We can conclude that the volume of the cylinder we obtained in part (b) is greater than the volume of the cylinder we obtained in part (a)
Question 12.
Reasoning A rectangular piece of cardboard with dimensions 6 inches by 8 inches is used to make the curved side of a cylinder-shaped container. Using this cardboard, what is the greatest volume the cylinder can hold? Explain.
Answer:
It is given that
A rectangular piece of cardboard with dimensions 6 inches by 8 inches is used to make the curved side of a cylinder-shaped container.
Now,
Let the height of the cylinder be: 6 inches (or) 8 inches
Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
So,
For h = 6 inches:
V = 6 × 8 × 6
= 288 cubic inches
For h = 8 inches:
V = 6 × 8 × 8
= 384 cubic inches
Hence, from the above,
We can conclude that the greatest volume the given cylinder can hold is: 384 cubic inches
Question 13.
The cylinder shown has a volume of 885 cubic inches.
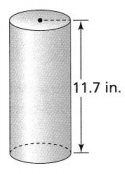
a. What is the radius of the cylinder? Use 3.14 for π.
Answer:
It is given that
The cylinder shown has a volume of 885 cubic inches.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The height of a cylinder (h) = 11.7 in.
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
885 = 3.14 × r² × 11.7
r² = \(\frac{885}{3.14 × 11.7}\)
r² = 24.08
r = 4.9 in.
Hence, from the above,
We can conclude that the radius of the given cylinder is: 4.9 in.
b. Reasoning If the height of the cylinder is changed, but the volume stays the same, then how will the radius change? Explain.
Answer:
We know that,
The volume of a cylinder (V) = πr²h
Now,
It is given that
Volume —–> Constant
Height —– > Changed
Now,
From the given formula,
If the volume is constant, then
h ∝ \(\frac{1}{r²}\)
Hence, from the above relation,
We can conclude that
If the value of height increases, then the value of radius decreases
If the value of height decreases, then the value of radius increases
Question 14.
Toy rubber balls are packaged in a cylinder that holds 3 balls. Find the volume of the cylinder. Use 3.14 for π, and round to the nearest tenth.

Answer:
It is given that
Toy rubber balls are packaged in a cylinder that holds 3 balls
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cylinder (h) = 20.7 cm
The diameter of the cylinder (d) = 6.9 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
= \(\frac{πd²h}{4}\)
So,
V = \(\frac{3.14 × 20.7 × 20.7 × 6.9}{4}\)
= 2,321 cm³
Hence, from the above,
We can conclude that the volume of the given cylinder is: 2,321 cm³
Question 15.
Higher-Order Thinking
An insulated collar is made to cover a pipe. Find the volume of the material used to make the collar. Let r = 3 inches, R= 5 inches, and h = 21 inches. Use 3.14 for π, and round to the nearest hundredth.
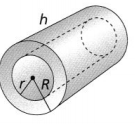
Answer:
It is given that
An insulated collar is made to cover a pipe.
Now,
The given data is:
r = 3 inches, R= 5 inches, and h = 21 inches
Now,
The radius of insulated collar = R – r
= 5 – 3
= 2 inches
Now,
The volume of a cylinder (V) = πr²h
So,
The volume of the material that is used to make the collar (V) = 3.14 × 2 × 2 × 21
= 263.76 cubic inches
Hence, from the above,
We can conclude that the volume of the material that is used to make the collar is: 263.76 cubic inches
Assessment Practice
Question 16.
The volume of a cylinder is 1,029π cubic centimeters. The height of the cylinder is 21 centimeters. What is the radius, to the nearest centimeter, of the cylinder?
Answer:
It is given that
The volume of a cylinder is 1,0291 cubic centimeters. The height of the cylinder is 21 centimeters.
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
1,029π = πr² × 21
r² = \(\frac{1,029}{21}\)
r² = 49
r = 7 cm
Hence, from the above,
We can conclude that the radius of the given cylinder is: 7 cm
Question 17.
The diameter of a cylinder is 7 yards. The height is 12 yards. What is the volume, in terms of π and to the nearest cubic yard, of the cylinder?
Answer:
It is given that
The diameter of a cylinder is 7 yards. The height is 12 yards
Now,
We know that,
The volume of a cylinder (V) = πr²h
= \(\frac{πd²h}{4}\)
So,
V = \(\frac{3.14 × 7 × 12 × 7}{4}\)
= 1,846.32 yards³ (or) 588π yards³
Hence, from the above,
We can conclude that the volume of the given cylinder is: 1,846.32 cubic yards (or) 588π cubic yards
Question 18.
A cylinder is shown. What statements about the cylinder are true?

☐ The radius of the cylinder is 2 ft.
☐ The diameter of the cylinder is 4 yd.
☐ The height of the cylinder is 8 in.
☐ The volume of the cylinder is 32 in.2.
☐ The volume of the cylinder is 32π in.3.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The diameter of the cylinder = 4 in.
The height of the cylinder = 8 in.
So,
The radius of the cylinder = \(\frac{Diameter}{2}\)
= 2 in.
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = 3.14 × 2 × 2 × 8
= 32π in.³
= 100.48 in.³
Hence, from the above,
We can conclude that the statements that are true about the given cylinder are:

Topic 8 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary Select all the statements that describe surface area and volume. Lessons 8-1 and 8-2
☐ Surface area is the sum of the areas of all the surfaces of a figure.
☐ Volume is the distance around a figure.
☐ The surface area is a three-dimensional measure.
☐ Volume is the amount of space a figure occupies.
☐ Volume is a three-dimensional measure.
Answer:
The above statements that describe the surface area and volume are:

In 2-4, use the figure at the right. Sallie packed a cone-shaped cup inside of a cylindrical package.
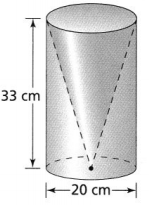
Question 2.
The cone-shaped cup is made out of paper. How much paper was used to make the cup, excluding the opening at the top of the cup? Use 3.14 for π, and round to the nearest tenth. Lesson 8-1
Answer:
It is given that
Sallie packed a cone-shaped cup inside of a cylindrical package and the cone-shaped cup is made out of paper
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The slant height of cone (l) is: 33 cm
The diameter of the cone (d) is: 20 cm
So,
The radius of cone (r) = \(\frac{Diameter}{2}\)
= 10 cm
Now,
We know that,
The surface area of a cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 10 × 10 + 3.14 × 10 × 33
= 314 + 1,036.2
= 1,350.2 cm²
Hence, from the above,
We can conclude that
We have to use 1,350.2 cm² of paper was used to make the cup, excluding the opening at the top of the cup
Question 3.
The cylindrical package is made out of cardboard. In terms of π, how much cardboard was used to make the package? Lesson 8-1
Answer:
It is given that the cylindrical package is made out of cardboard
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cylinder (h) is: 33 cm
The diameter of the cylinder (d) is: 20 cm
So,
Radius = \(\frac{Diameter}{2}\)
= \(\frac{20}{2}\)
= 10 cm
Now,
We know that,
The surface area of a cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2π × 10² + 2π × 10 × 33
= 200π + 660π
= 860π cm²
Hence, from the above,
We can conclude that 860π cm² of cardboard was used to make the package
Question 4.
How much space does the package occupy in terms of π? Lesson 8-1
Answer:
The given figure is:

Now,
From the above,
We can observe that the given figure is a cylinder
Now,
From the given figure,
We can observe that
The height of the cylinder (h) is: 33 cm
The diameter of the cylinder (d) is: 20 cm
So,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{20}{2}\)
r = 10 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = π × 10² × 33
= 3,300π cm³
Hence, from the above,
We can conclude that 3,300π cm³ of space does the package occupy in terms of π
Question 5.
What is the surface area of the sphere in terms of π? Lesson 8-1
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the sphere (r) is: 3 ft
Now,
We know that,
The surface area of a sphere (S.A) = 4πr²
So,
S.A = 4π × 3²
= 36π ft²
Hence, from the above,
We can conclude that the surface area of the given sphere is: 36π ft²
Question 6.
The volume of the cylinder is 400π cm3. What is the height of the cylinder? Lesson 8-2
A. 5 cm
B. 16 cm
C. 25 cm
D. 80 cm
Answer:
It is given that
The volume of the cylinder is 400π cm³
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The diameter of the cylinder (d) is: 10 cm
So,
Radius = \(\frac{Diameter}{2}\)
= \(\frac{10}{2}\)
= 5 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
400π = π × 5² × h
h = \(\frac{400}{25}\)
h = 16 cm
Hence, from the above,
We can conclude that the volume of the given cylinder is: 16 cm
Topic 8 MID-TOPIC PERFORMANCE TASK
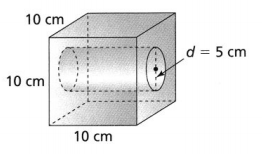
Melissa designed a sculpture in which a cylinder-shaped section was removed from a cube.
PART A
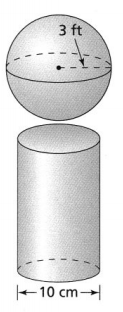
Before painting the surface of the sculpture, Melissa wants to sand the surface where the cylinder section was removed. What is the surface area of the section she will sand? Use 3.14 for π. Explain how you found the surface area.
Answer:
It is given that
Melissa designed a sculpture in which a cylinder-shaped section was removed from a cube.
Now,
The given figure is:
 Now,
Now,
From the given figure,
The diameter of the cylinder (d) is: 5 cm
The height of the cylinder (d) is: 10 cm
So,
The radius of the cylinder (r) = \(\frac{Diameter of the cylinder}{2}\)
r = 2.5 cm
Now,
We know that,
We know that,
The surface area of a cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × 2.5 × 2.5 + 2 × 3.14 × 2.5 × 10
= 39.25 + 157
= 196.25 cm²
Hence, from the above,
We can conclude that 196.25 cm² is the surface area of the section Melissa will sand
PART B
Melissa has a can of spray paint that covers about 6,500 square centimeters. Can Melissa apply two coats of paint to the entire sculpture? Explain. Use 3.14 for π.
Answer:
The given figure is:

Now,
From the above,
We can observe that
The scripture is the combination of the cube and the cylinder
Now,
We know that,
The surface area of a cube (S.A) = 6a²
Where,
a is the side of the cube
So,
S.A of the cube = 6 × 10²
= 600 cm²
Now,
From part (a),
The S.A of the cylinder = 196.25 cm²
So,
The S.A of the scripture = 600 + 196.25
= 796.25 cm²
So,
6,500 > 796.25 × 2
Hence, from the above,
We can conclude that Melissa can apply two coats of paint to the entire sculpture
PART C
What is the volume of the sculpture? Use 3.14 for π.
Answer:
The given figure is:

Now,
From the above,
We can observe that
The scripture is the combination of the cube and the cylinder
Now,
The diameter of the cylinder (d) is: 5 cm
The height of the cylinder (h) is: 10 cm
So,
The radius of the cylinder (r) is: 2.5 cm
Now,
We know that,
The volume of the cylinder (V) = πr²h
The volume of the cube (V) = a³
Where,
a is the side of the cube
So,
The volume of the scripture (V) = πr²h + a³
So,
V = 3.14 × 2.5 × 2.5 × 10 + 10³
= 196.25 + 1,000
= 1,196.25 cm³
Hence, from the above,
We can conclude that the volume of the scripture is: 1,196.25 cm³
Lesson 8.3 Find Volume of Cones
Solve & Discuss It!
A landscape architect uses molds for casting rectangular pyramids and rectangular prisms to make garden statues. He plans to place each finished pyramid on top of a prism. If one batch of concrete mix makes one prism or three pyramids, how does the volume of one pyramid compare to the volume of one prism? Explain.

I can… find the volume of cones.
Answer:
It is given that
A landscape architect uses molds for casting rectangular pyramids and rectangular prisms to make garden statues. He plans to place each finished pyramid on top of a prism and one batch of concrete mix makes one prism or three pyramids
Now,
We know that,
The prism is in the shape of the cylinder
The pyramid is in the shape of the cone
Now,
We know that,
The volume of a prism (V) = πr²h
The volume of a pyramid (V) = \(\frac{1}{3}\)πr²h
So,
The volume of a prism = 3 × The volume of a pyramid
Hence, from the above,
We can conclude that
The volume of a prism is 3 times the volume of a pyramid
Look for Relationships
What do you notice about the dimensions of the bases of the pyramid and prism? How are the heights of the two solids related?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
a. The dimensions of the bases of the prism and the pyramid are the same
b. The heights of the pyramid and the prism are the same
Focus on math practices
Make Sense and Persevere If the architect mixes 10 batches of concrete, how many sculptures combining 1 prism and 1 pyramid could he make? Explain.
Answer:
It is given that
one batch of concrete mix makes one prism or three pyramids
So,
The ratio of the mix of prism and pyramid in 1 batch is: 1 : 3
Hence,
For 10 batches of the mix of concrete,
We can make sculptures combining 1 prism and 1pyramid are: 10 prisms and 30 pyramids
Essential Question
How is the volume of a cone related to the volume of a cylinder?
Answer:
The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism is related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is 3 times as much as the volume of a cone
Try It!
Find the volume of the cone. Use 3.14 for π.
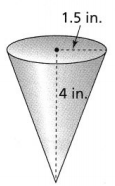
The volume of the cone is about ________ cubic inches.
V = ____ πr²h
≈ _______(3.14) (______)2 (4)
= ________ (3.14) (______)(4)
= _________
Answer:
The given figure is:

From the above figure,
We can observe that
The radius of the cone (r) is 1.5 in.
The height of the cone (h) is 4 in.
Now,
We know that,
The volume of the cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × (1.5)² × 4
= 9.42 in.³
Hence, from the above,
We can conclude that the volume of the given cone is: 9.42 in.³
Convince Me!
If you know the volume of a cone, how can you find the volume of a cylinder that has the same height and radius as the cone?
Answer:
We know that,
If the cylinder and the cone has the same height and radius, then
The volume of cone = \(\frac{1}{3}\) × The volume of cylinder
Try It!
Find the volume of each cone.
a. Use \(\frac{22}{7}\) for π. Express the answer as a fraction.
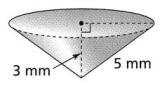
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The slant height (l) is: 5 mm
The height of the cone (h) is: 3 mm
Now,
We know that,
l² = r²+ h²
So,
5² = r² + 3²
r² = 25 – 9
r² = 16
r = 4 mm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 4² × 3
= \(\frac{1,056}{21}\) mm³
Hence, from the above,
We can conclude that the volume of the given cone in the fraction form is: \(\frac{1,056}{66}\) mm³
b. Express the volume in terms of π.
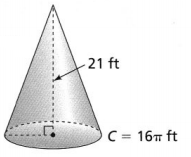
Answer:
The given figure is:

From the given figure,
We can observe that
The height of the cone (h) is: 21 ft
The circumference of the circle (C) is: 16π ft
Now,
We know that,
The circumference of the circle (C) = 2πr
So,
2πr = 16π
r = 8 ft
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × π × 8² × 21
= 448π ft³
Hence, from the above,
We can conclude that the volume of the given cone in terms of π is: 448π ft³
KEY CONCEPT
The volume of a cone is \(\frac{1}{3}\) the volume of a cylinder with the same base and height. The formula for the volume of a cone is V = \(\frac{1}{3}\)Bh, where B is the area of the base and his the height of the cone.

Do You Understand?
Question 1.
Essential Question How is the volume of a cone related to the volume of a cylinder?
Answer:
The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism is related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is 3 times as much as the volume of a cone
Question 2.
Use Structure What dimensions do you need to find the volume of a cone?
Answer:
To find the volume of a cone,
The dimensions we need are:
a. The radius of the cone
b. The height of the cone
Question 3.
Look for Relationships If you know a cone’s radius and slant height, what must you do before you can find its volume?
Answer:
If you know a cone’s radius (r) and slant height(l), then
The volume of a cone (V) is given as:
V = \(\frac{1}{3}\)πr² × \(\sqrt{l² – r²}\)
Do You Know How?
Question 4.
Wanda found a cone-shaped seashell on the beach. The shell has a height of 63 millimeters and a base radius of 8 millimeters. What is the volume of the seashell? Estimate 63 mm using \(\frac{22}{7}\) for π.
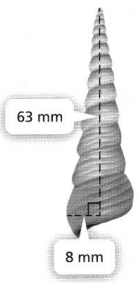
Answer:
It is given that
Wanda found a cone-shaped seashell on the beach. The shell has a height of 63 millimeters and a base radius of 8 millimeters
Now,
The given figure is:

Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 8² × 63
= 4,224 mm³
Hence, from the above,
We can conclude that the volume of the seashell is: 4,224 mm³
Question 5.
What is the volume of the cone? Estimate using 3.14 for π, and round to the nearest tenth.
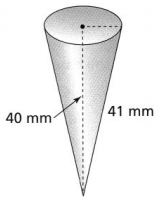
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cone (h) is: 40mm
The slant height of the cone (l) is: 41 mm
Now,
We know that,
l² = r² + h²
So,
41² = r²+ 40²
r² = 81
r = 9 mm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 9² × 40
= 3,391.2 mm³
Hence, from the above,
We can conclude that the volume of the given cone is: 3,391.2 mm³
Question 6.
What is the volume of the cone in terms of π if the circumference of the base is 1.4π feet?
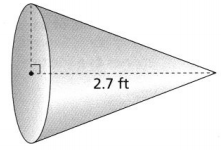
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cone (h) is: 2.7 ft
Now,
We know that,
Circumference (C) = 2πr
So,
2πr = 1.4π
r = 0.7 ft
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × π × (0.7)² × 2.7
= 0.441π ft³
Hence, from the above,
We can conclude that the volume of the given cone is: 0.441π ft³
Practice & Problem Solving
Multimedia Leveled Practice In 7 and 8, find the volumes of the cones.
Question 7.
What is the volume of the cone? Write your answer in terms of π.
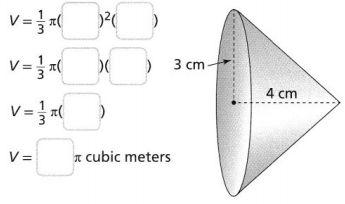
Answer:
From the given figure,
We can observe that
The radius of the cone (r) is: 3 cm
The height of the cone (h) is: 4 cm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × π × 3² × 4
= 12π cm³
Hence, from the above,
We can conclude that the volume of the given cone is: 12π cm³
Question 8.
What is the volume of the cone to the nearest hundredth? Use 3.14 for π.
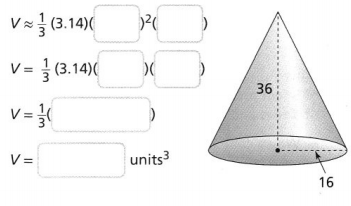
Answer:
From the given figure,
We can observe that
The radius of the cone (r) is: 16 units
The height of the cone (h) is: 36 units
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 16² × 36
= 9,646.08 units³
Hence, from the above,
We can conclude that the volume of the given cone is: 9,646.08 units³
Question 9.
If a cone-shaped hole is 3 feet deep and the circumference of the base of the hole is 44 feet, what is the volume of the hole? Use \(\frac{22}{7}\) for π.
Answer:
It is given that
A cone-shaped hole is 3 feet deep and the circumference of the base of the hole is 44 feet
Now,
We know that,
Circumference (C) = 2πr
So,
2πr = 44
r = \(\frac{44}{2π}\)
r = 7 feet
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 7² × 3
= 154 feet³
Hence, from the above,
We can conclude that the volume of the given cone-shaped hole is: 154 feet³
Question 10.
The volume of the cone is 462 cubic yards. What is the radius of the cone? Use \(\frac{22}{7}\) for π.
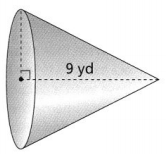
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cone (h) is: 9 yd
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
462 = \(\frac{1}{3}\) × \(\frac{22}{7}\) × r² × 9
r² = \(\frac{462}{9.428}\)
r = 7 yd
Hence, from the above,
We can conclude that the radius of the given cone is: 7 yd
Question 11.
A city engineer determines that 5,500 cubic meters of sand will be needed to combat erosion at the city’s beach. Does the city have enough sand to combat erosion? Use \(\frac{22}{7}\) for π. Explain.

Answer:
It is given that
A city engineer determines that 5,500 cubic meters of sand will be needed to combat erosion at the city’s beach.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The slant height of the cone(l) is: 37 m
The height of the cone (h) is: 35 m
Now,
We know that,
l² = r²+ h²
37² = r² + 35²
r² = 37² – 35²
r = 12 m
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 12² × 35
= 5,280 m³
So,
5,500 > 5,280
Hence, from the above,
We can conclude that the city has enough sand to combat erosion
Question 12.
A water tank is shaped like the cone shown.
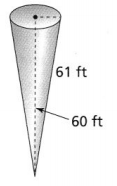
a. How much water can the tank hold? Use 3.14 for π, and round to the nearest tenth.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The slant height of the cone (l) is: 61 ft
The height of the cone (h) is: 60 ft
Now,
We know that,
l² = r²+ h²
61² = r² + 60²
r² = 61² – 60²
r = 11 ft
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 11² × 60
= 7,598.8 ft³
Hence, from the above,
We can conclude that the amount of water that the tank can hold is: 7,598.8 ft³
b. If water is drained from the tank to fill smaller tanks that each hold 500 cubic feet of water, how many smaller tanks can be filled?
Answer:
It is given that the water is drained from the tank to fill smaller tanks that each holds 500 cubic feet of water
Now,
From part (a),
We know that,
The amount of water that the tank can hold is: 7,598.8 ft³
Now,
The number of smaller tanks that can be filled = \(\frac{The amount of water that the tank can hold}{The amount of water that the smaller tank can hold}\)
= \(\frac{7,598.8}{500}\)
≅ 15
Hence, from the above,
We can conclude that the number of smaller tanks that can be filled is: 15
Question 13.
An ice cream cone is filled exactly level with the top of a cone. The cone has a 9-centimeter depth and a base with a circumference of 91 centimeters. How much ice cream is in the cone in terms of π?
Answer:
It is given that
An ice cream cone is filled exactly level with the top of a cone. The cone has a 9-centimeter depth and a base with a circumference of 91 centimeters
Now,
We know that,
Circumference (C) = 2πr
So,
2πr = 91
r = \(\frac{91}{2π}\)
r = 14.49 cm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × π × (14.49)² × 9
= 629.88π cm³
Hence, from the above,
We can conclude that the amount of ice cream that is in the cone in terms of π is: 629.88π cm³
Question 14.
In the scale model of a park, small green cones represent trees. What is the volume of one green cone? Use \(\frac{22}{7}\) for π.
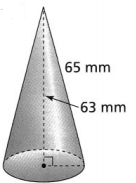
Answer:
The given green cone is:

Now,
From the given green cone,
We can observe that
The slant height of the cone (l) is: 65 mm
The height of the cone (h) is: 63 mm
Now,
We know that,
l² = r²+ h²
65² = r² + 603²
r² = 65² – 63²
r = 16 mm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 16² × 63
= 16,896 mm³
Hence, from the above,
We can conclude that the volume of one green cone is: 16,896 mm³
Question 15.
Reasoning Compare the volumes of two cones. One has a radius of 5 feet and a slant height of 13 feet. The other one has a height of 5 feet and a slant height of 13 feet.
a. Which cone has the greater volume?
Answer:
The given data is:
Cone 1: Radius: 5 feet Slant height: 13 feet
Cone 2: Height: 5 feet Slant height: 13 feet
Now,
We know that,
l² = r²+ h²
So,
For cone 1:
13² = h² + 5²
h² = 13² – 5²
h = 12 feet
For cone 2:
13² = r² + 5²
r² = 13² – 5²
r = 12 feet
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
For Cone 1:
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 5² × 12
= 314.28 feet³
For Cone 2:
V = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 12² × 5
= 754.28 feet³
Hence, from the above,
We can conclude that Cone 2 has the greater volume
b. What is the volume of the larger cone in terms of π?
Answer:
From part (a),
We can observe that,
Cone 2 has a greater volume
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × π × 12² × 5
= 240π feet³
Question 16.
An artist makes a cone-shaped sculpture for an art exhibit. If the sculpture is 7 feet tall and has a base with a circumference of 24.492 feet, what is the volume of the sculpture? Use 3.14 for π, and round to the nearest hundredth.
Answer:
It is given that
An artist makes a cone-shaped sculpture for an art exhibit and the sculpture is 7 feet tall and has a base with a circumference of 24.492 feet
Now,
We know that,
Circumference (C) = 2πr
So,
2πr = 24.492
r = \(\frac{24.492}{2π}\)
r = 3.9 feet
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 3.9² × 7
= 111.43 feet³
Hence, from the above,
We can conclude that the volume of the given cone-shaped sculpture is: 111.43 feet³
Question 17.
Higher-Order Thinking A cone has a radius of 3 and a height of 11.
a. Suppose the radius is increased by 4 times its original measure. How many times greater is the volume of the larger cone than the smaller cone?
Answer:
It is given that
A cone has a radius of 3 and a height of 11
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 3² × 11
= 103.62 units³
Now,
If the radius is increased by 4 times of its original measure, then
V = \(\frac{1}{3}\) × 3.14 × (3 × 4)² × 11
= 1,657.92 units³
Now,
The number of times the volume of the larger cone than the smaller cone = \(\frac{1,657.92}{103.62}\)
= 16
Hence, from the above,
We can conclude that the volume of the larger cone is 16 times greater than the volume of the smaller cone
b. How would the volume of the cone change if the radius were divided by four?
Answer:
From part (a),
We know that,
The volume of the cone with a radius of 3 and a height of 11 units is: 103.62 units³
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × (3 ÷ 4)² × 11
= 6.476 units³
Now,
The ratio of the volume of the changed cone to the volume of the original cone = \(\frac{6.476}{103.62}\)
= 0.06
Hence, from the above,
We can conclude that the volume of the cone will be 0.06 times of the original cone
Assessment Practice
Question 18.
List the cones described below in order from least volume to greatest volume.
• Cone 1: radius 6 cm and height 12 cm
• Cone 2: radius 12 cm and height 6 cm
• Cone 3: radius 9 cm and height 8 cm
A. Cone 2, Cone 3, Cone 1
B. Cone 1, Cone 3, Cone 2
C. Cone 2, Cone 1, Cone 3
D. Cone 1, Cone 2, Cone 3
Answer:
The given data is:
a. Cone 1: radius 6 cm and height 12 cm
b. Cone 2: radius 12 cm and height 6 cm
c. Cone 3: radius 9 cm and height 8 cm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
For Cone 1:
V = \(\frac{1}{3}\) × 3.14 × 6² × 12
= 452.16 cm³
For Cone 2:
V = \(\frac{1}{3}\) × 3.14 × 12² × 6
= 904.32 cm³
For Cone 3:
V = \(\frac{1}{3}\) × 3.14 × 9² × 8
= 678.24 cm³
Hence, from the above,
We can conclude that the order of the volumes from the least to the greatest is:
Cone 1 < Cone 3 < Cone 2
Question 19.
What is the volume, in cubic inches, of a cone that has a radius of 8 inches and a height of 12 inches? Use 3.14 for π, and round to the nearest hundredth.
Answer:
It is given that
A cone has a radius of 8 inches and a height of 12 inches
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 8² × 12
= 803.84 inches³
Hence, from the above,
We can conclude that the volume of the given cone is: 803.84 inches³
Lesson 8.4 Find Volume of Spheres
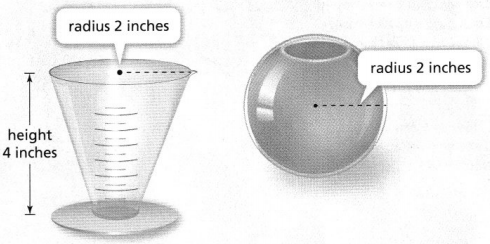
Explore It!
Marshall uses the beaker to fill the bowl with water.
I can… find the volume of a sphere and use it to solve problems.
A. Draw and label three-dimensional figures to represent the beaker and the bowl.
Answer:
The representation of the three-dimensional figures that represent the beaker and bowl are:
B. Marshall has to fill the beaker twice to completely fill the bowl with water. How can you use an equation to represent the volume of the bowl?
Answer:
The given figures are:

Now,
It is given that
Marshall has to fill the beaker twice to completely fill the bowl with water
Now,
From part (a),
We can observe that the beaker is in the form of a cone
Now,
We know that,
The volume of a cone = \(\frac{1}{3}\)πr²h
Now,
According to the given situation,
The volume of the bowl(V’) = 2 × The volume of the beaker(V)
V’ = 2 × \(\frac{1}{3}\)πr²h
Now,
From the given figures,
We can observe that
The height of a bowl is 2 times its radius
So,
V’ = \(\frac{2}{3}\)πr² (2r)
V’ = \(\frac{4}{3}\)πr³
Hence, from the above,
We can conclude that the volume of the bowl is: \(\frac{4}{3}\)πr³
Focus on math practices
Reasoning How is the volume of a sphere and the volume of a cone related? What must be true about the radius and height measurements for these relationships to be valid?
Answer:
We know that,
The relationship between the volume of the sphere and the volume of the cone is:
The volume of the sphere = 2 × The volume of the cone
Now,
For the above relationship to be valid,
a. The heights of the sphere and the cone must be the same
b. The radius of the sphere and the cone must be the same
Essential Question
How is the volume of a sphere related to the volume of a cone?
Answer:
The volume of a sphere is twice the volume of a cone that has the same circular base and height. i.e.,
The volume of the sphere = 2 × The volume of the cone
Try It!
What is the volume of a ball with a diameter of 6 centimeters? Use 3.14 for π.
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π _______3
≈ ________ ∙ ________
= __________
The volume of the ball is about _______ cm3
Answer:
It is given that
The diameter of a ball is: 6 cm
Now,
We know that,
The ball is in the form of a sphere
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{6}{2}\)
r = 3 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × 3³
= 113.04 cm³
Hence, from the above,
We can conclude that the volume of the given ball is about 113.04 cm³
Convince Me!
How is the volume of a sphere related to the volume of a cone that has the same circular base and height?
Answer:
The relationship between the volume of a cone and the volume of a sphere that has the same circular base and height is:
The volume of the sphere = 2 × The volume of the cone
Try It!
What is the volume of the composite figure shown? Use 3.14 for π.
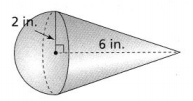
Answer:
The given composite figure is:

Now,
We know that,
A composite figure is made up of 2 or more two-dimensional figures
Now,
The given composite figure is made up of Hemisphere and Cone
Now,
We know that,
The volume of the given composite figure = The volume of the Hemisphere + The volume of the cone
Now,
From the given composite figure,
We can observe that
Radius (r) = 2 in.
Height (h) = 6 in.
Now,
We know that,
The volume of the Hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\) × 3.14 × 2³
= 16.74 in.³
Now,
We know that,
The volume of the cone (V’) = \(\frac{1}{3}\)πr²h
So,
V’ = \(\frac{1}{3}\) × 3.14 × 2² × 6
= 25.12 in.³
So,
The volume of the given composite figure = 16.74 + 25.12
= 41.84 in.³
Hence, from the above,
We can conclude that the volume of the given composite figure is: 41.84 in.³
KEY CONCEPT
The volume of a sphere is twice the volume of a cone that has the same circular base and height. The formula for the volume of a sphere with radius r is V = \(\frac{4}{3}\) πr3.
Do You Understand?
Question 1.
Essential Question How is the volume of a sphere related to the volume of a cone?
Answer:
The volume of a sphere is twice the volume of a cone that has the same circular base and height. i.e.,
The volume of the sphere = 2 × The volume of the cone
Question 2.
Critique Reasoning Kristy incorrectly says that the volume of the sphere below is 144π cubic units. What mistake might Kristy have made?

Answer:
The given sphere is:

Now,
It is given that
Kristy incorrectly says that the volume of the sphere below is 144π cubic units
Now,
From the given sphere,
We can observe that
Radius (r) = 6 units
Now,
We know that,
The volume of a spher (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × π × 6³
= 288π units³
Hence, from the above,
We can conclude that the mistake done by Kristy is:
Considering the sphere as the hemisphere and calculated the volume of the hemisphere instead of the sphere
Question 3.
Generalize Mehnaj has a set of blocks that are all the same height. The cone-shaped block has a volume of 125 cubic inches. The sphere-shaped block has a volume of 250 cubic inches. What do you know about the radius of the base of the cone-shaped block? Explain.
Answer:
It is given that
Mehnaj has a set of blocks that are all the same height. The cone-shaped block has a volume of 125 cubic inches. The sphere-shaped block has a volume of 250 cubic inches
So,
From the given situation,
We can observe that
a. The heights of the two cone-shaped blocks are the same
b. The volumes of the two cone-shaped blocks are different
Now,
We know that,
The volume of a cone = \(\frac{1}{3}\)πr²h
So,
V1 = \(\frac{1}{3}\)πr1²h1
V2 = \(\frac{1}{3}\)πr2²h2
So,
V1/V2 = r1²/ r2²
r1²/ r2² = \(\frac{125}{250}\)
r1² / r2² = 0.5
r1 / r2 = 0.707
Hence, from the above,
We can conclude that the radius of the first cone-based block is 0.707 times the radius of the second cone-shaped block
Do You Know How?
Question 4.
Clarissa has a decorative bulb in the shape of a sphere. If it has a radius of 3 inches, what is its volume? Use 3.14 for π.
Answer:
It is given that
Clarissa has a decorative bulb in the shape of a sphere and it has a radius of 3 inches
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × 3³
= 113.04 inches³
Hence, from the above,
We can conclude that the volume of the given decorative bulb is: 113.04 inches³
Question 5.
A sphere has a surface area of about 803.84 square centimeters. What is the volume of the sphere? Use 3.14 for π and round to the nearest whole number.
Answer:
It is given that
A sphere has a surface area of about 803.84 square centimeters
Now,
We know that,
The surface area of a sphere (S.A) = 4πr²
So,
4πr² = 803.84
r² = \(\frac{803.84}{4π}\)
r² = 64
r = 8 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × 8³
= 2,143.57 cm³
≈2,144 cm³
Hence, from the above,
We can conclude that the volume of the given sphere is about 2,144 cm³
Question 6.
A water pipe is a cylinder 30 inches long, with a radius of 1 inch. At one end of the cylinder, there is a hemisphere. What is the volume of the water pipe? Explain.
Answer:
It is given that
A water pipe is a cylinder 30 inches long, with a radius of 1 inch. At one end of the cylinder, there is a hemisphere.
So,
The volume of the water pipe = The volume of the cylinder + The volume of the hemisphere
Now,
From the given water pipe,
We can observe that
Radius (r) = 1 in.
Height (h) = 30 in.
Now,
We know that,
The volume of the Hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\) × 3.14 × 1³
= 2.09 in.³
Now,
We know that,
The volume of the cylinder (V’) = πr²h
So,
V’ = 3.14 × 1² × 30
= 94.2 in.³
So,
The volume of the given water pipe = 2.09 + 94.2
= 96.29 in.³
Hence, from the above,
We can conclude that the volume of the given water pipe is: 96.29 in.³
Practice & Problem Solving
Question 7.
Leveled Practice What is the amount of air, in cubic centimeters, needed to fill the stability ball? Use 3.14 for π, and round to the nearest whole number. Use the formula
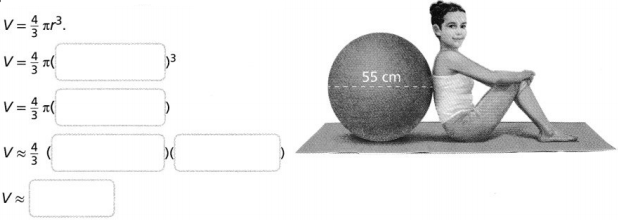
The volume of the stability ball is approximately __________ cubic centimeters.
Answer:
From the given figure,
We can observe that
The stability ball is in the form of a sphere
Now,
The diameter of the stability ball (d) is: 55 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{55}{2}\)
r = 27.5 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × (27.5)³
= 87,069.53 cm³
≈87,070 cm³
Hence, from the above,
We can conclude that the volume of the stability ball is approximately 87,070 cm³
Question 8.
The spherical balloon has a 22-inch. diameter when it is fully inflated. Half of the air is let out of the balloon. Assume that the balloon remains a sphere. Keep all answers in terms of π.
a. Find the volume of the fully-inflated balloon.
Answer:
It is given that
The spherical balloon has a 22-inch. diameter when it is fully inflated. Half of the air is let out of the balloon.
Now,
From the given situation,
The diameter of the fully inflated balloon (d) is: 22 inches
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{22}{2}\)
r = 11 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × π × 11³
= 1,774.6π cm³
Hence, from the above,
We can conclude that the volume of the fully inflated balloon is: 1,774.6π cm³
b. Find the volume of the half-inflated balloon.
Answer:
It is given that
The spherical balloon has a 22-inch. diameter when it is fully inflated. Half of the air is let out of the balloon.
So,
The diameter of half-inflated balloon (d) = \(\frac{The diameter of fully inflated balloon}{2}\)
d = \(\frac{22}{2}\)
d = 11 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{11}{2}\)
r = 5.5 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × π × (5.5)³
= 221.8π cm³
Hence, from the above,
We can conclude that the volume of the half-inflated balloon is: 221.8π cm³
c. What is the radius of the half-inflated balloon? Round to the nearest tenth.
Answer:
From part (b),
We can observe that
The diameter of half-inflated balloon (d) = \(\frac{The diameter of fully inflated balloon}{2}\)
d = \(\frac{22}{2}\)
d = 11 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{11}{2}\)
r = 5.5 cm
Hence, from the above,
We can conclude that the radius of the half-inflated balloon is: 5.5 cm
Question 9.
Find the volume of the figure. Use 3.14 for π, and round to the nearest whole number.
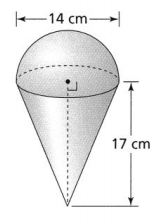
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The figure is a combination of a hemisphere and a cone
So,
From the given figure,
Diameter (d) =14 cm
Height (h) = 17 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{14}{2}\)
r = 7 cm
Now,
We know that,
The volume of the figure (V) = The volume of a hemisphere + The volume of a cone
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 7² × 17
= 871.87 cm³
Now,
We know that,
The volume of a hemisphere (V’) = \(\frac{2}{3}\)πr³
So,
V’ = \(\frac{2}{3}\) × 3.14 × 7³
= 718.01 cm³
So,
The volume of the given figure = 871.87 + 718.01
= 1,589.88 cm³
≈1,590 cm³
Hence, from the above,
We can conclude that the volume of the given figure is: 1,590 cm³
Question 10.
The surface area of a sphere is about 2,826 square millimeters. What is the volume of the sphere? Use 3.14 for π, and round to the nearest whole number.
Answer:
It is given that
The surface area of a sphere is about 2,826 square millimeters
Now,
We know that,
The surface area of a sphere (S.A) = 4πr²
So,
4πr² = 2,826
r² = \(\frac{2,826}{4π}\)
r² = 225
r = 15 mm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × 15³
= 14,130 mm³
Hence, from the above,
We can conclude that the volume of the given sphere is: 14,130 mm³
Question 11.
A sphere has a volume of 1,837.35 cubic centimeters. What is the radius of the sphere? Use 3.14 for π, and round to the nearest tenth.
Answer:
It is given that
A sphere has a volume of 1,837.35 cubic centimeters
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
1,837.35 = \(\frac{4}{3}\)πr³
πr³ = \(\frac{1,837.35 × 3}{4}\)
πr³ = 1,378.01
r³ = \(\frac{1,378.01}{π}\)
r³ = 438.85
r = 0.333 cm
Hence, from the above,
We can conclude that the radius of the given sphere is: 0.333 cm
Question 12.
Find the volume of the solid. Use 3.14 for π, and round to the nearest whole number.
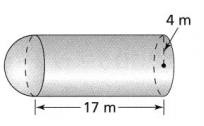
Answer:
The given figure is:

From the above,
We can observe that the given figure is a composite figure
Now,
From the given figure,
We can observe that
Radius (r) = 4 m
Height (h) = 17 m
Now,
We know that,
The volume of the given figure = The volume of a hemisphere + The volume of a cylinder
Now,
We know that,
The volume of the Hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\) × 3.14 × 4³
= 133.97 m³
Now,
We know that,
The volume of the cylinder (V’) = πr²h
So,
V’ = 3.14 × 4² × 17
= 854.08 m³
So,
The volume of the given figure = 133.9 + 854.08
= 987.98 m³
Hence, from the above,
We can conclude that the volume of the given figure is: 987.98 m³
Question 13.
Your friend says that the volume of a sphere with a diameter of 3.4 meters is 164.55 cubic meters. What mistake might your friend have made? Find the correct volume. Use 3.14 for π and round to the nearest hundredth.
Answer:
It is given that
Your friend says that the volume of a sphere with a diameter of 3.4 meters is 164.55 cubic meters
Now,
From the given information,
Diameter (d) = 3.4 m
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{3.4}{2}\)
r = 1.7 m
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × 3.14 × (1.7)³
= 20.56 m³
Hence, from the above,
We can conclude that
The mistake made by your friend is:
Consideration of diameter as radius and find the volume of the given sphere
Question 14.
A solid figure has a cone and hemisphere hollowed out of it. What is the volume of the remaining part of the solid? Use 3.14 for π, and round to the nearest whole number.
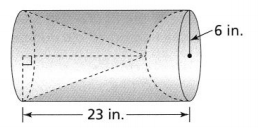
Answer:
It is given that
A solid figure has a cone and hemisphere hollowed out of it
So,
The volume of the remaining part of the solid = | The volume of a hemisphere – The volume of a cone |
Now,
From the given solid,
We can observe that
Radius (r) = 6 in.
Height = 23 in.
Now,
We know that,
The volume of a hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\)π × 6³
= 144π in.³
Now,
We know that,
The volume of a cone (V’) = \(\frac{1}{3}\)πr²h
So,
V’ = \(\frac{1}{3}\)π × 6² × 23
= 276π in.³
So,
The volume of the remaining part of the solid = |144π – 276π|
= 132π
= 132 × 3.14
= 414.48 in.³
≈415 in.³
Hence, from the above,
We can conclude that the volume of the remaining part of the given solid is about 415 in.³
Question 15.
Higher-Order Thinking A student was asked to find the volume of a solid where the inner cylinder is hollow. She incorrectly said the volume is 2,034.72 cubic inches.
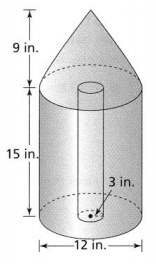
Answer:
It is given that
A student was asked to find the volume of a solid where the inner cylinder is hollow. She incorrectly said the volume is 2,034.72 cubic inches.
a. Find the volume of the solid. Use 3.14 for π. Round to the nearest whole number.
Answer:
The given solid is:

Now,
From the given solid,
We can observe that it is a combination of a cone and a cylinder
So,
The volume of the given solid = The volume of a cylinder + The volume of a cone
Now,
From the given solid,
We can observe that
The radius of the cylinder is 3 in.
The height of the cylinder is 15 in.
The diameter of the cone is 12 in.
The slant height of the cone is 9 in.
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = 3.14 × 3² × 15
= 423.9 in.³
Now,
The volume of a cone:
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{12}{2}\)
r = 6 in.
Now,
We know that,
l² = r² + h²
So,
9² = 6² + h²
h² = 9² – 6²
h² = 45
h = 6.70 in.
Now,
We know that,
The volume of a cone (V’) = \(\frac{1}{3}\)πr²h
So,
V’ = \(\frac{1}{3}\) × 3.14 × 6² × 6.70
= 252.45 in.³
So,
The volume of the given solid = 423.9 + 252.45
= 676.3 in.³
≈676 in.³
Hence, from the above,
We can conclude that the volume of the given solid is about 676 in.³
b. What mistake might the student have made?
Answer:
Assessment Practice
Question 16.
The spherical boulder is 20 feet in diameter and weighs almost 8 tons. Find its volume. Use 3.14 for π. Round to the nearest cubic foot.
Answer:
It is given that
The spherical boulder is 20 feet in diameter and weighs almost 8 tons.
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{20}{2}\)
r = 10 feet
So,
V = \(\frac{4}{3}\) × 3.14 × 10³
= 4,186.6 feet³
≈ 4,187 feet³
Hence, from the above,
We can conclude that the volume of the given spherical boulder is: 4,187 feet³
Question 17.
A bowl is in the shape of a hemisphere (half a sphere) with a diameter of 13 inches. Find the volume of the bowl. Use 3.14 for π, and round to the nearest cubic inch.
Answer:
It is given that
A bowl is in the shape of a hemisphere (half a sphere) with a diameter of 13 inches. Find the volume of the bowl
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{13}{2}\)
r = 6.5 inches
Now,
We know that,
The volume of a hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\) × 3.14 × (6.5)³
= 574.88 inches³
≈ 575 inches³
Hence, from the above,
We can conclude that the volume of the given bowl is about 575 inches³
3-ACT MATH
3-Act Mathematical Modeling:
Measure Up

ACT 1
1. After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.
Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math
Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.
Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
ACT 3 Extension
Reflect
Question 13.
Model with Math
Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Make Sense and Persevere When did you struggle most while solving the problem? How did you overcome that obstacle?
Answer:
SEQUEL
Question 15.
Generalize Suppose you have a graduated cylinder half the height of the one in the video. How wide does the cylinder need to be to hold the liquid in the flask?
Answer:
Topic 8 REVIEW
Topic Essential Question
How can you find volumes and surface areas of three-dimensional figures?
Answer:
The “Surface area” is the sum of the areas of all faces (or surfaces) on a 3D shape.
Ex:
A cuboid has 6 rectangular faces. To find the surface area of a cuboid, add the areas of all 6 faces
We know that,
The volume of a three-dimensional figure = Cross-sectional area × length
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Vocabulary
composite figure
cone
cylinder
sphere

Answer:
Use Vocabulary in Writing
Draw a composite figure that includes any two of the following: a cylinder, a cone, a sphere, and a hemisphere. Label each part of your drawing. Then describe each part of your composite figure. Use vocabulary terms in your description.
Concepts and Skills Review
Lesson 8.1 Find Surface Area of Three-Dimensional Figures
Quick Review
Surface area is the total area of the surfaces of a three-dimensional figure. The chart gives formulas for finding the surface area of a cylinder, a cone, and a sphere.
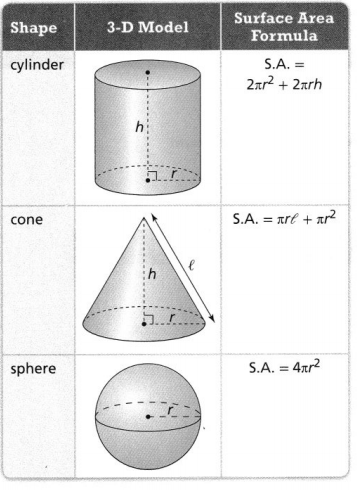
Example
What is the surface area of the cylinder? Use 3.14 for π.
Answer:
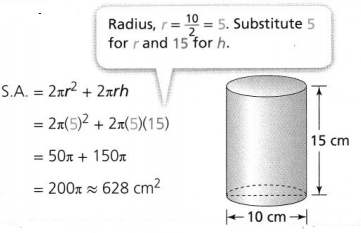
Practice
Question 1.
What is the surface area of the cone? Use 3.14 for π.
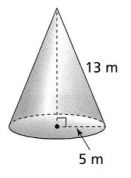
Answer:
The given figure is:

From the given figure,
We can observe that
The slant height of the cone (l) is: 13 m
The radius of the cone (r) is: 5 m
Now,
We know that,
The surface area of a cone (S.A) = πr² + πrl
So,
S.A = 3.14 × 5² + 3.14 × 5 × 13
= 78.5 + 204.1
= 282.6 m²
Hence, from the above,
We can conclude that the surface area of the given cone is: 282.6 m²
Question 2.
What is the surface area of the sphere in terms of π?

Answer:
The given figure is:

From the given figure,
We can observe that
The diameter of the sphere (d) is: 10 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{10}{2}\)
r = 5 cm
Now,
We know that,
The surface area of a sphere (S.A) = 4πr²
So,
S.A = 4 × 3.14 × 5²
= 314 cm²
Hence, from the above,
We can conclude that the surface area of the given sphere is: 314 cm²
Question 3.
What is the surface area of the cylinder in terms of π?
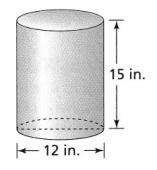
Answer:
The given figure is:

Now,
From the given figure,
We can observe that,
The diameter of the cylinder (d) is 12 in.
The height of the cylinder (h) is 15 in.
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{12}{2}\)
r = 6 in.
Now,
We know that,
The surface area of a cylinder (S.A) = 2πr² + 2πrh
So,
S.A = 2 × 3.14 × 6² + 2 × 3.14 × 6 × 15
= 226.08 + 565.2
= 791.28 in.³
Hence, from the above,
We can conclude that the surface area of the given cylinder is: 791.28 in.³
Lesson 8.2 Find Volume of Cylinders
Quick Review
The volume of a cylinder is equal to the area of its base times its height.
V = area of base · height, or V = πr²h
Example
What is the volume of the cylinder? Use 3.14 for π.
Answer:
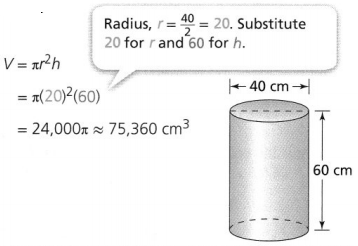
Practice
Question 1.
What is the volume of the cylinder in terms of π?
Answer:
The given figure is:

From the given figure,
We can observe that
The diameter of the cylinder (d) is: 2 m
The height of the cylinder (h) is: 6 m
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{2}{2}\)
r = 1 m
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
V = 3.14 × 1² × 6
= 18.84 m³
Hence, from the above,
We can conclude that the volume of the given cylinder is: 18.84 m³
Question 2.
The volume of the cylinder is 141.3 cubic centimeters. What is the radius of the cylinder? Use 3.14 for π.
Answer:
It is given that
The volume of the cylinder is 141.3 cubic centimeters
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The height of the cylinder (h) is: 5 cm
Now,
We know that,
The volume of a cylinder (V) = πr²h
So,
141.3 = 3.14 × r² × 5
r² = \(\frac{141.3}{3.14 × 5}\)
r²= 9
r = 3 cm
Hence, from the above,
We can conclude that the radius of the given cylinder is: 3 cm
Lesson 8.3 Find Volume of Cones
Quick Review
To find the volume of a cone, use the formula V = \(\frac{1}{3}\)πr2h.
Example
What is the volume of the cone? Use 3.14 for π.
Answer:
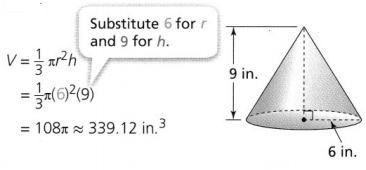
Practice
Question 1.
What is the volume of the cone in terms of π?
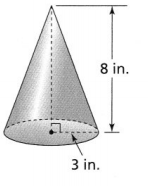
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the cone (r) is 3 in.
The height of the cone (h) is 8 in.
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 3² × 8
= 75.36 in.³
Hence, from the above,
We can conclude that the volume of the given cone is: 75.36 in.³
Question 2.
What is the volume of the cone? Use 3.14 for π.
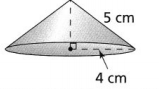
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the cone (r) is: 4 cm
The slant height of the cone (h) is: 5 cm
Now,
We know that,
l² = r² + h²
5² = 4² + h²
h² = 5² – 4²
h² = 9
h = 3 cm
Now,
We know that,
The volume of a cone (V) = \(\frac{1}{3}\)πr²h
So,
V = \(\frac{1}{3}\) × 3.14 × 4² × 3
= 50.24 cm³
Hence, from the above,
We can conclude that the volume of the given cone is: 50.24 cm³
Lesson 8.4 Find Volume of Spheres
Quick Review
To find the volume of a sphere, use the formula V = \(\frac{4}{3}\)πr3
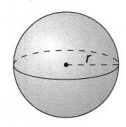
Example
Find the volume of the composite figure. Use 3.14 for π.
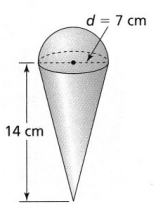
Answer:
First, find the volume of the sphere. Use 3.14 for π.
V = \(\frac{4}{3}\)πr3
= \(\frac{4}{3}\)π(3.5)3 → Substitute 3.5 for r.
= 57.17π ≈ 179.5 cm3
Divide by 2 to find the volume of the hemisphere: 179.5 ÷ 2 ≈ 89.75 cubic centimeters.
Then, find the volume of the cone. Use 3.14 for π.
V = \(\frac{1}{3}\)πr2 h
= \(\frac{1}{3}\)π(3.5)2(14) → Substitute 3.5 for r and 14 for h.
= 57.171 ≈ 179.5 cm3
The volume of the composite figure is approximately 89.75 + 179.5 ≈ 269.25 cubic centimeters.
Practice
Question 1.
What is the volume of the sphere? Use \(\frac{22}{7}\) for π.

Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the sphere (r) is: 14 cm
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 14³
= 11,498.6 cm³
Hence, from the above,
We can conclude that the volume of the given sphere is: 11,498.6 cm³
Question 2.
The surface area of a sphere is 1,017.36 square inches. What is the volume of the sphere? Use \(\frac{22}{7}\) for π.
Answer:
It is given that
The surface area of a sphere is 1,017.36 square inches.
Now,
We know that,
The surface area of a sphere (S.A) = 4πr²
So,
4πr² = 1,017.36
r² = \(\frac{1,017.36}{4π}\)
r² = 80.92
r = 8.99 inches
Now,
We know that,
The volume of a sphere (V) = \(\frac{4}{3}\)πr³
So,
V = \(\frac{4}{3}\) × \(\frac{22}{7}\) × (8.99)³
= 3,044.68 inches³
Hence, from the above,
We can conclude that the volume of the given sphere is: 3,044.68 inches³
Question 3.
What is the volume of the composite figure? Use \(\frac{22}{7}\) for π.
Answer:
The given figure is:

Now,
From the above,
We can observe that the given figure is a combination of a hemisphere and a cone
So,
The volume of the given figure = The volume of a hemisphere + The volume of a cone
Now,
From the given figure,
We can observe that
Diameter (d) = 4 cm
Height (h) = 10 cm
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{4}{2}\)
r = 2 cm
Now,
We know that,
The volume of a hemisphere (V) = \(\frac{2}{3}\)πr³
So,
V = \(\frac{2}{3}\) × \(\frac{22}{7}\) × 2³
= 16.76 cm³
Now,
We know that,
The volume of a cone (V’) = \(\frac{1}{3}\)πr²h
So,
V’ = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 2² × 10
= 41.90 cm³
So,
The volume of the given figure = 41.90 + 16.76
= 58.66 cm³
Hence, from the above,
We can conclude that the volume of the given figure is: 58.66 cm³
Topic 8 Fluency Practice
Hidden Clue
For each ordered pair, solve the equation to find the unknown coordinate. Then locate and label the corresponding point on the graph. Draw line segments to connect the points in alphabetical order. Use the completed picture to help answer the riddle below.

What do squares, triangles, pentagons, and octagons have in common?


Answer:
Step 1:
For each ordered pair, solve the equation to find the unknown coordinate.

Step 2:
Then locate and label the corresponding point on the graph.
Step 3:
Draw line segments to connect the points in alphabetical order.
Step 4:
Use the completed picture to help answer the riddle below.
All the squares, triangles, pentagons, and octagons have in common the sum of all the total angles i.e., 360°