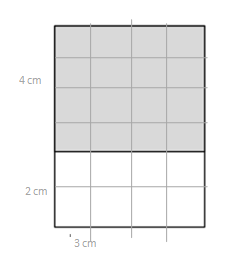
Eureka Math Answer Key for Grade 3 aids teachers to differentiate instruction, building, and reinforcing foundational mathematics skills that alter from the classroom to real life.
With the help of the Eureka Primary School Grade 3 Answer Key, You can think deeply regarding what you are learning, and you will really learn math easily just like that. So teachers and students can find this Eureka Answer Key for Grade 3 more helpful in raising students’ scores and supporting teachers to educate the students.
Engage NY Eureka Math 3rd Grade Module 4 Lesson 10 Answer Key
Students of Grade 3 can get a strong foundation on mathematics concepts by referring to the Eureka Math Book. It was developed by highly professional mathematics educators and the solutions prepared by them are in a concise manner for easy grasping. To achieve high scores in Grade 3, students need to solve all questions and exercises included in Eureka’s Math Grade 3 Book.
Eureka Math Grade 3 Module 4 Lesson 10 Problem Set Answer Key
Question 1.
Label the side lengths of the shaded and unshaded rectangles when needed. Then, find the total area of the large rectangle by adding the areas of the two smaller rectangles.
a.
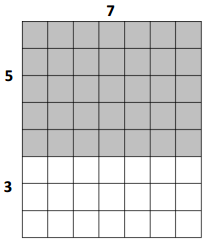
8 × 7 = (5 + 3) × 7
= (5 × 7) + (3 × 7)
= ___35___ + ___21___
= __56____
Area: ___56___ square units
Answer:
The area of the larger rectangle = 56 sq unit.
the area of the small rectangle A = 35 sq unit.
the area of the small rectangle B = 21 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 56 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 7.
area = 56.
the area of the rectangle A = 35 sq unit.
area = length x breadth.
area = l x b.
area = 5 x 7.
area = 35.
the area of the rectangle B = 21 sq unit.
area = length x breadth.
area = l x b.
area = 3 x 7.
area = 21.
b.

12 × 4 = (___10___ + 2) × 4
= (__10____ × 4) + (2 × 4)
= ___40___ + 8
= ___48___
Area: __48____ square units
Answer:
The area of the larger rectangle = 48 sq unit.
the area of the small rectangle A = 40 sq unit.
the area of the small rectangle B = 8 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 48 sq unit.
area = length x breadth.
area = l x b.
area = 12 x 4.
area = 48.
the area of the rectangle A = 40 sq unit.
area = length x breadth.
area = l x b.
area = 10 x 4.
area = 40.
the area of the rectangle B = 8 sq unit.
area = length x breadth.
area = l x b.
area = 2 x 4.
area = 8.
c.
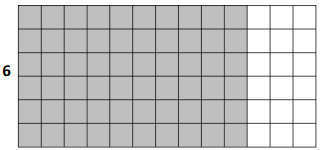
6 × 13 = 6 × (___10___ + 3)
= (6 ×___10___) + (6 × 3)
= __60____ + ___18___
= ___78___
Area: __78____ square units
Answer:
The area of the larger rectangle = 78 sq unit.
the area of the small rectangle A = 60 sq unit.
the area of the small rectangle B = 18 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 78 sq unit.
area = length x breadth.
area = l x b.
area = 6 x 13.
area = 78.
the area of the rectangle A = 60 sq unit.
area = length x breadth.
area = l x b.
area = 10 x 6.
area = 60.
the area of the rectangle B = 8 sq unit.
area = length x breadth.
area = l x b.
area = 6 x 3.
area = 18.
d.

8 × 12 = 8 × (___10___ + ___2___)
= (8 × __10____) + (8 × ___2___)
= ___80___ + __16____
= __96____
Area: __96____ square units
Answer:
The area of the larger rectangle = 96 sq unit.
the area of the small rectangle A = 80 sq unit.
the area of the small rectangle B = 16 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 96 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 12.
area = 96.
the area of the rectangle A = 80 sq unit.
area = length x breadth.
area = l x b.
area = 10 x 8.
area = 80.
the area of the rectangle B = 16 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 2.
Question 2.
Vince imagines 1 more row of eight to find the total area of a 9 × 8 rectangle. Explain how this could help him solve 9 × 8.
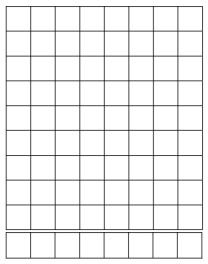
Answer:
The area of the rectangle = 72 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 9 x 8.
area = 72 sq cm.
so the area of the rectangle = 72 sq cm.
Question 3.
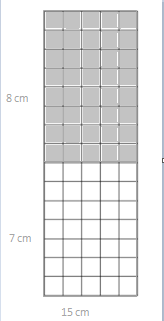
Break the 15 × 5 rectangle into 2 rectangles by shading one smaller rectangle within it. Then, find the sum of the areas of the 2 smaller rectangles and show how it relates to the total area. Explain your thinking.
Answer:
The area of the rectangle = 40 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 5 x 8.
area = 40 sq cm.
so the area of the rectangle = 40 sq cm.
Answer:
The area of the rectangle = 35 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 5 x 7.
area = 35 sq cm.
so the area of the rectangle = 35 sq cm.
Eureka Math Grade 3 Module 4 Lesson 10 Exit Ticket Answer Key
Label the side lengths of the shaded and unshaded rectangles. Then, find the total area of the large rectangle by adding the areas of the 2 smaller rectangles.
Question 1.
8 × 7 = 8 × (___5___ + __2____)
= (8 ×___5___) + (8 ×___2___)
= __40____ + __16____
= ___56___
Area: __56____ square units
Answer:
The area of the larger rectangle = 56 sq unit.
the area of the small rectangle A = 40 sq unit.
the area of the small rectangle B = 16 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 56 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 7.
area = 56.
the area of the rectangle A = 40 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 5.
area = 40.
the area of the rectangle B = 16 sq unit.
area = length x breadth.
area = l x b.
area = 8 x 2.
area = 16.
Question 2.

9 × 13 = 9 × (___10___+___3___)
= (___9___ × ___10___) + (__9____×___3___)
= __90____ + ___27___
= __117____
Area: ___117___ square units
Answer:
The area of the larger rectangle = 117 sq unit.
the area of the small rectangle A = 90 sq unit.
the area of the small rectangle B = 27 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 117 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 13.
area = 117.
the area of the rectangle A = 90 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 10.
area = 90.
the area of the rectangle B = 27 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 3.
area = 27.
Eureka Math Grade 3 Module 4 Lesson 10 Homework Answer Key
Question 1.
Label the side lengths of the shaded and unshaded rectangles. Then, find the total area of the large rectangle by adding the areas of the 2 smaller rectangles.
a.
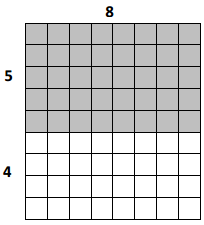
9 × 8 = (5 + 4) × 8
= (5 × 8) + (4 × 8)
= ___40___ + __32____
= __72____
Area: ___72___ square units
Answer:
The area of the larger rectangle = 72 sq unit.
the area of the small rectangle A = 40 sq unit.
the area of the small rectangle B = 32 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 78 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 8.
area = 72.
the area of the rectangle A = 40 sq unit.
area = length x breadth.
area = l x b.
area = 5 x 8.
area = 40.
the area of the rectangle B = 32 sq unit.
area = length x breadth.
area = l x b.
area = 4 x 8.
area = 32.
b.

12 × 5 = (__10____ + 2) × 5
= (___10___ × 5) + (2 × 5)
= ___50___ + 10
= ___60___
Area: __60____ square units
Answer:
The area of the larger rectangle = 60 sq unit.
the area of the small rectangle A = 50 sq unit.
the area of the small rectangle B = 10 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 60 sq unit.
area = length x breadth.
area = l x b.
area = 12 x 5.
area = 60.
the area of the rectangle A = 50 sq unit.
area = length x breadth.
area = l x b.
area = 10 x 5.
area = 50.
the area of the rectangle B = 10 sq unit.
area = length x breadth.
area = l x b.
area = 2 x 5.
area = 10.
c.

7 × 13 = 7 × (___10___+ 3)
= (7 × ___10___) + (7 × 3)
= __70____ + __21____
= __91____
Area: __91____ square units
Answer:
The area of the larger rectangle = 91 sq unit.
the area of the small rectangle A = 70 sq unit.
the area of the small rectangle B = 21 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 91 sq unit.
area = length x breadth.
area = l x b.
area = 7 x 13.
area = 91.
the area of the rectangle A = 70 sq unit.
area = length x breadth.
area = l x b.
area = 7 x 10.
area = 70.
the area of the rectangle B = 21 sq unit.
area = length x breadth.
area = l x b.
area = 7 x 3.
area = 21.
d.
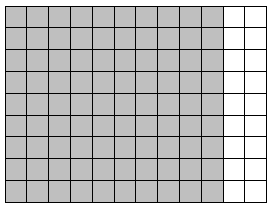
9 × 12 = 9 × (___10___ + __2____)
= (9 × ___10___) + (9 × __2____)
= __90____ + ___18___
= __108____
Area: __108____ square units
Answer:
The area of the larger rectangle = 108 sq unit.
the area of the small rectangle A = 90 sq unit.
the area of the small rectangle B = 18 sq unit.
Explanation:
In the above-given question,
given that,
the area of the larger rectangle = 108 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 12.
area = 108.
the area of the rectangle A = 90 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 10.
area = 90.
the area of the rectangle B = 18 sq unit.
area = length x breadth.
area = l x b.
area = 9 x 2.
area = 18.
Question 2.
Finn imagines 1 more row of nine to find the total area of 9 × 9 rectangle. Explain how this could help him solve 9 × 9.

Answer:
The area of the rectangle = 81 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 9 x 9.
area = 81 sq cm.
so the area of the rectangle = 81 sq cm.
Question 3.
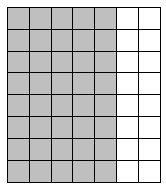
Shade an area to break the 16 × 4 rectangle into 2 smaller rectangles. Then, find the sum of the areas of the 2 smaller rectangles to find the total area. Explain your thinking.
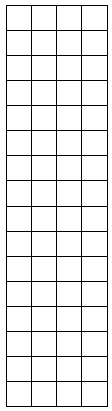
Answer:
The area of the rectangle = 40 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 10 x 4.
area = 40 sq cm.
so the area of the rectangle = 40 sq cm.
Answer:
The area of the rectangle = 24 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 6 x 4.
area = 24 sq cm.
so the area of the rectangle = 24 sq cm.
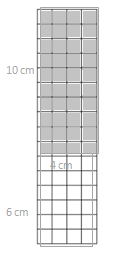
Eureka Math Grade 3 Module 4 Lesson 10 Template Answer Key

____24__sq__cm______
tiling
Answer:
The area of the rectangle = 16 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16 sq cm.
so the area of the rectangle = 16 sq cm.
Answer:
The area of the rectangle = 8 sq cm.
Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 2.
area = 8 sq cm.
so the area of the rectangle = 8 sq cm.