Engage NY Eureka Math 3rd Grade Module 7 Lesson 22 Answer Key
Eureka Math Grade 3 Module 7 Lesson 22 Sprint Answer Key
A
Multiply or Divide by 4

Answer:
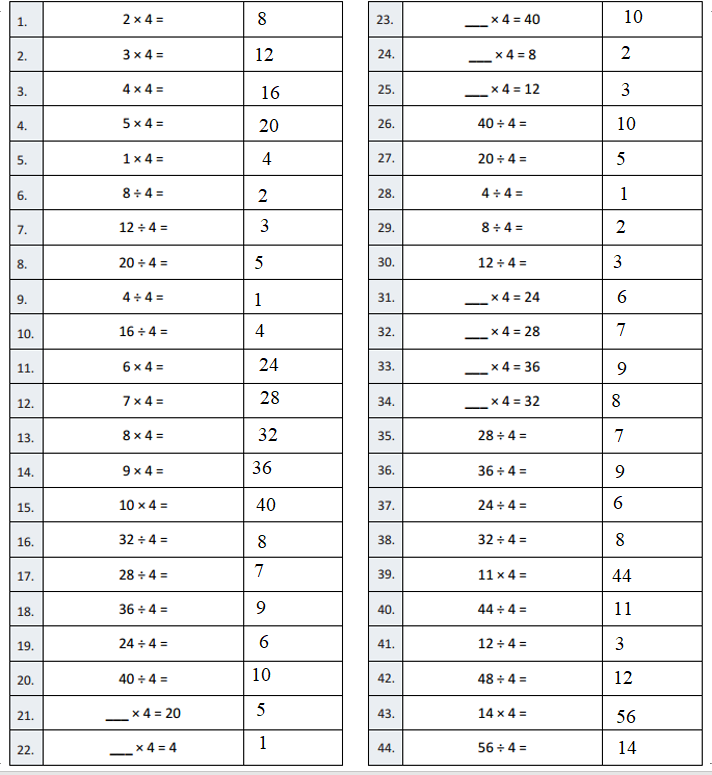
Question 1.
2 × 4 =
Answer:
2 × 4 = 8.
Question 2.
3 × 4 =
Answer:
3 × 4 = 12.
Question 3.
4 × 4 =
Answer:
4 × 4 = 16.
Question 4.
5 × 4 =
Answer:
5 × 4 = 20.
Question 5.
1 × 4 =
Answer:
1 × 4 = 4.
Question 6.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2.
Question 7.
12 ÷ 4 =
Answer:
12 ÷ 4 = 3.
Question 8.
20 ÷ 4 =
Answer:
20 ÷ 4 = 5.
Question 9.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1.
Question 10.
16 ÷ 4 =
Answer:
16 ÷ 4 = 4.
Question 11.
6 × 4 =
Answer:
6 × 4 = 24.
Question 12.
7 × 4 =
Answer:
7 × 4 = 28.
Question 13.
8 × 4 =
Answer:
8 × 4 = 32.
Question 14.
9 × 4 =
Answer:
9 × 4 = 36.
Question 15.
10 × 4 =
Answer:
10 × 4 = 40.
Question 16.
32 ÷ 4 =
Answer:
32 ÷ 4 = 8.
Question 17.
28 ÷ 4 =
Answer:
28 ÷ 4 = 7.
Question 18.
36 ÷ 4 =
Answer:
36 ÷ 4 = 9.
Question 19.
24 ÷ 4 =
Answer:
24 ÷ 4 = 6.
Question 20.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10.
Question 21.
___ × 4 = 20
Answer:
_5__ × 4 = 20.
Question 22.
___ × 4 = 4
Answer:
_1__ × 4 = 4.
Question 23.
___ × 4 = 40
Answer:
_10__ × 4 = 40.
Question 24.
___ × 4 = 8
Answer:
_2__ × 4 = 8.
Question 25.
___ × 4 = 12
Answer:
_3__ × 4 = 12.
Question 26.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10.
Question 27.
20 ÷ 4 =
Answer:
20 ÷ 4 = 5.
Question 28.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1.
Question 29.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2.
Question 30.
12 ÷ 4 =
Answer:
12 ÷ 4 = 3.
Question 31.
___ × 4 = 24
Answer:
_6__ × 4 = 24.
Question 32.
___ × 4 = 28
Answer:
_7__ × 4 = 28.
Question 33.
___ × 4 = 36
Answer:
_9__ × 4 = 36.
Question 34.
___ × 4 = 32
Answer:
_8__ × 4 = 32.
Question 35.
28 ÷ 4 =
Answer:
28 ÷ 4 = 7.
Question 36.
36 ÷ 4 =
Answer:
36 ÷ 4 = 9.
Question 37.
24 ÷ 4 =
Answer:
24 ÷ 4 = 6.
Question 38.
32 ÷ 4 =
Answer:
32 ÷ 4 = 8.
Question 39.
11 × 4 =
Answer:
11 × 4 = 44.
Question 40.
44 ÷ 4 =
Answer:
44 ÷ 4 = 11.
Question 41.
12 ÷ 4 =
Answer:
12 ÷ 4 = 3.
Question 42.
48 ÷ 4 =
Answer:
48 ÷ 4 = 12.
Question 43.
14 × 4 =
Answer:
14 × 4 = 56.
Question 44.
56 ÷ 4 =
Answer:
56 ÷ 4 = 14.
B
Multiply or Divide by 4
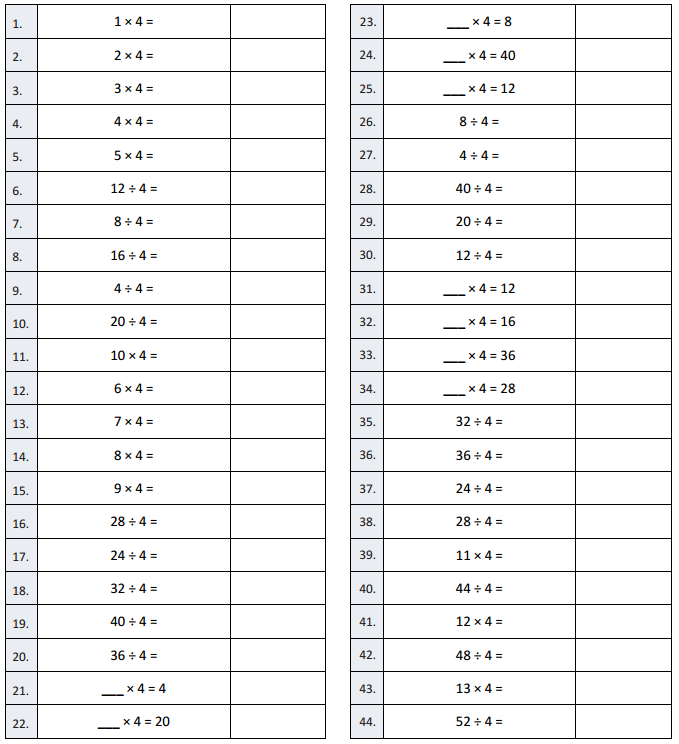
Answer:
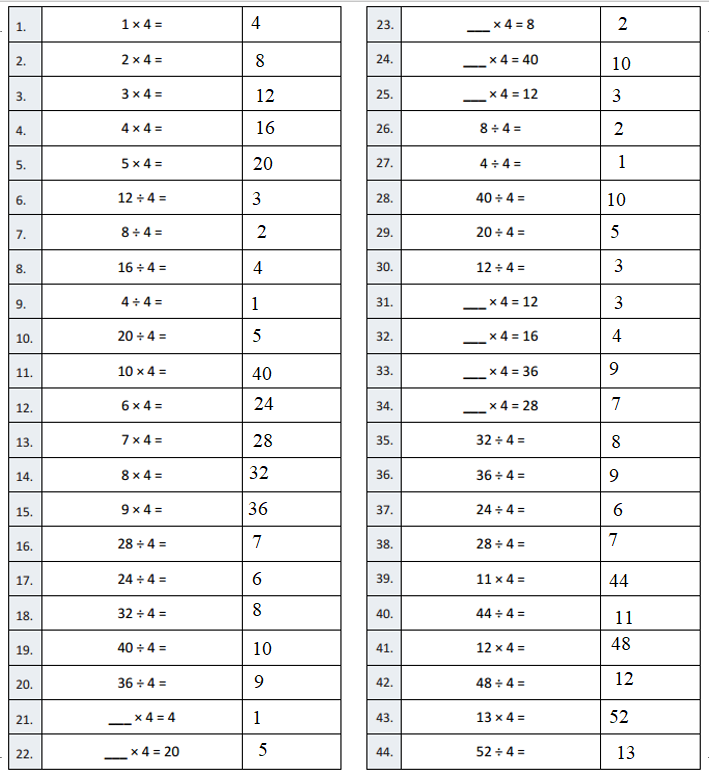
Question 1.
1 × 4 =
Answer:
1 × 4 = 4.
Question 2.
2 × 4 =
Answer:
2 × 4 = 8.
Question 3.
3 × 4 =
Answer:
3 × 4 = 12.
Question 4.
4 × 4 =
Answer:
4 × 4 = 16.
Question 5.
5 × 4 =
Answer:
5 × 4 = 20.
Question 6.
12 ÷ 4 =
Answer:
12 ÷ 4 = 3.
Question 7.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2.
Question 8.
16 ÷ 4 =
Answer:
16 ÷ 4 = 4.
Question 9.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1.
Question 10.
20 ÷ 4 =
Answer:
20 ÷ 4 = 5.
Question 11.
10 × 4 =
Answer:
10 × 4 = 40.
Question 12.
6 × 4 =
Answer:
6 × 4 = 24.
Question 13.
7 × 4 =
Answer:
7 × 4 = 28.
Question 14.
8 × 4 =
Answer:
8 × 4 = 32.
Question 15.
9 × 4 =
Answer:
9 × 4 = 36.
Question 16.
28 ÷ 4 =
Answer:
28 ÷ 4 = 7.
Question 17.
24 ÷ 4 =
Answer:
24 ÷ 4 = 6.
Question 18.
32 ÷ 4 =
Answer:
32 ÷ 4 = 8.
Question 19.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10.
Question 20.
36 ÷ 4 =
Answer:
36 ÷ 4 = 9.
Question 21.
___ × 4 = 4
Answer:
_1__ × 4 = 4.
Question 22.
___ × 4 = 20
Answer:
_5__ × 4 = 20.
Question 23.
___ × 4 = 8
Answer:
_2__ × 4 = 8.
Question 24.
___ × 4 = 40
Answer:
_10__ × 4 = 40.
Question 25.
___ × 4 = 12
Answer:
_3__ × 4 = 12.
Question 26.
8 ÷ 4 =
Answer:
8 ÷ 4 = 2.
Question 27.
4 ÷ 4 =
Answer:
4 ÷ 4 = 1.
Question 28.
40 ÷ 4 =
Answer:
40 ÷ 4 = 10.
Question 29.
20 ÷ 4 =
Answer:
20 ÷ 4 = 10.
Question 30.
12 ÷ 4 =
Answer:
12 ÷ 4 = 3.
Question 31.
___ × 4 = 12
Answer:
_3__ × 4 = 12.
Question 32.
___ × 4 = 16
Answer:
_4__ × 4 = 16.
Question 33.
___ × 4 = 36
Answer:
_9__ × 4 = 36.
Question 34.
___ × 4 = 28
Answer:
_7__ × 4 = 28.
Question 35.
32 ÷ 4 =
Answer:
32 ÷ 4 = 8.
Question 36.
36 ÷ 4 =
Answer:
36 ÷ 4 = 9.
Question 37.
24 ÷ 4 =
Answer:
24 ÷ 4 = 6.
Question 38.
28 ÷ 4 =
Answer:
28 ÷ 4 = 7.
Question 39.
11 × 4 =
Answer:
11 × 4 = 44.
Question 40.
44 ÷ 4 =
Answer:
44 ÷ 4 = 11.
Question 41.
12 × 4 =
Answer:
12 × 4 = 48.
Question 42.
48 ÷ 4 =
Answer:
48 ÷ 4 = 12.
Question 43.
13 × 4 =
Answer:
13 × 4 = 52.
Question 44.
52 ÷ 4 =
Answer:
52 ÷ 4 = 13.
Eureka Math Grade 3 Module 7 Lesson 22 Problem Set Answer Key
Question 1.
Use the data you gathered from your Problem Sets to create a line plot for the number of rectangles you created with each given perimeter.
Number of Rectangles Made with a Given Perimeter

Answer:
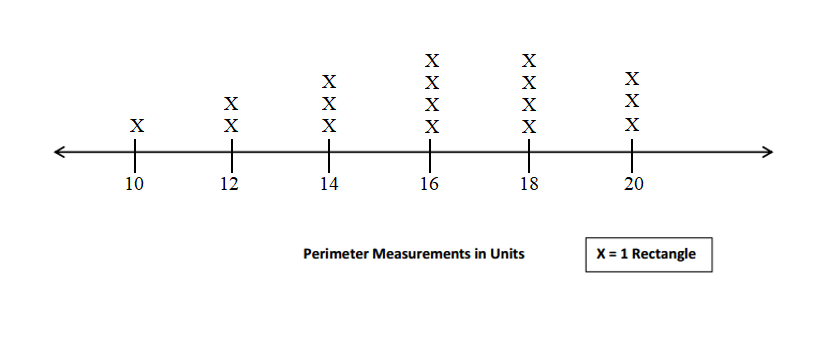
Explanation:
The data gathered from Problem Sets to create a line plot for the number of rectangles created with each given perimeter are : 10 units, 12 units, 14 units, 16 units,18 units, 20 units.
Question 2.
Why are all of the perimeter measurements even? Do all rectangles have an even perimeter?
Answer:
Well all perimeters of the rectangles are even because we have used the whole numbers and when we add them twice, we get the even numbers as the result.
Explanation:
Well all perimeters of the rectangles are even because we have used the whole numbers and when we add them twice, we get the even numbers as the result. Generally we used rulers to find the lengths of rectangles not the string. We have used string to show to get an odd perimeter.
Question 3.
Compare the two line plots we created. Is there any reason to think that knowing only the area of a rectangle would help you to figure out its perimeter or knowing only the perimeter of a rectangle would help you figure out its area?
Answer:
No, there is no reason to think that knowing only the area of a rectangle would help you to figure out its perimeter or knowing only the perimeter of a rectangle would help you figure out its area.
Explanation:
There is no connection between the area and perimeter of rectangle. Knowing one, doesnot help you to find the other.
Question 4.
Sumi uses unit square tiles to build 3 rectangles that have an area of 32 square units. Does knowing this help her find the number of rectangles she can build for a perimeter of 32 units? Why or why not?
Answer:
No, knowing the number of rectangles she built with the area of 32 square units does not help her to find the number of rectangles she can build for a perimeter of 32 units.
Explanation:
For example, if we do half 32 square units, we have the chance to make more than 3 pairs of number that add to 16. No, knowing the number of rectangles she built with the area of 32 square units does not help her to find the number of rectangles she can build for a perimeter of 32 units.
Question 5.
George draws 3 rectangles that have a perimeter of 14 centimeters. Alicia tells George that there are more than 3 rectangles that have a perimeter of 14 centimeters. Explain why Alicia is correct.
Answer:
Yes, I completely agree with Alicia because George probably drew the rectangles using the whole numbers side lengths. He could have drawn more rectangles using fraction values as lengths.
Explanation:
Yes, I completely agree with Alicia ” George that there are more than 3 rectangles that have a perimeter of 14 centimeters. ” because George probably drew the rectangles using the whole numbers side lengths. He could have drawn more rectangles using fraction values as lengths.
Eureka Math Grade 3 Module 7 Lesson 22 Exit Ticket Answer Key
Suppose you have a rectangle with a perimeter of 2 cm. What can you conclude about the side lengths? Can all 4 sides of the rectangle measure a whole number of centimeters?
Answer:
Well, if the rectangles perimeter is 2cm, I do not think the lengths are going to be whole numbers of centimeters. Because perimeter is the total distance covered by the rectangle around its outside.
Explanation:
Perimeter is the total distance covered by the rectangle around its outside. Well, if the rectangles perimeter is 2cm, I do not think the lengths are going to be whole numbers of centimeters.
Eureka Math Grade 3 Module 7 Lesson 22 Homework Answer Key
Question 1.
The following line plot shows the number of rectangles a student made using square unit tiles. Use the line plot to answer the questions below.

a. Why are all of the perimeter measurements even? Do all rectangles have even perimeters?
b. Explain the pattern in the line plot. What types of side lengths make this pattern possible?
c. How many X’s would you draw for a perimeter of 32? Explain how you know.
Answer:
a. Well all perimeters of the rectangles are even because the student has used the whole numbers and when they are added twice, we get the even numbers as the result. Yes, mostly all rectangles have even perimeters as we use whole numbers not fractions.
b. The pattern in the line plot is showing all rectangles Perimeters which are even in numbers. Whole numbers types of side lengths make this pattern possible.
c. Number of X’s would be drawn for a perimeter of 32 are six or 6: : (2,14) (3,13) (4,12) (5,11) (6,10) (7,9).
Explanation:
a. Well all perimeters of the rectangles are even because the student has used the whole numbers and when they are added twice, we get the even numbers as the result. Generally we used rulers to find the lengths of rectangles not the string. We have used string to show to get an odd perimeter.
b. The whole numbers are the part of the number system in which it includes all the positive integers from 0 to infinity. The pattern in the line plot is showing all rectangles Perimeters which are even in numbers.
c. Number of X’s would be drawn for a perimeter of 32 are six or 6 : (2,14) (3,13) (4,12) (5,11) (6,10) (7,9).
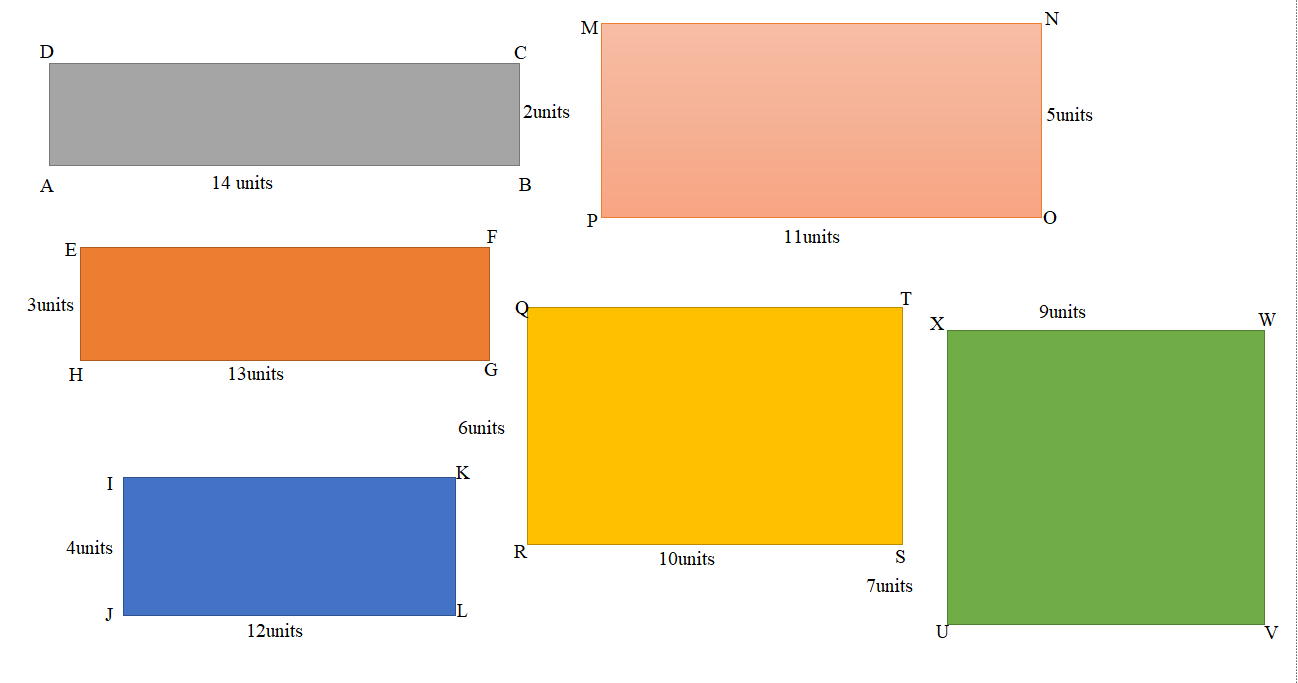
Question 2.
Luis uses square inch tiles to build a rectangle with a perimeter of 24 inches. Does knowing this help him find the number of rectangles he can build with an area of 24 square inches? Why or why not?
Answer:
Luis uses square inch tiles to build a rectangle with a perimeter of 24 inches.
No, knowing this cannot help him find the number of rectangles he can build with an area of 24 square inches because there is no connection between the area and perimeter to find the number of rectangles to be obtained.
Explanation:
No, knowing this cannot help him find the number of rectangles he can build with an area of 24 square inches because there is no connection between the area and perimeter to find the number of rectangles to be obtained.
Question 3.
Esperanza makes a rectangle with a piece of string. She says the perimeter of her rectangle is 33 centimeters. Explain how it’s possible for her rectangle to have an odd perimeter.
Answer:
Well, Esperanza is correct in what she says ” the perimeter of her rectangle is 33 centimeters.”
because she is using her string to find the lengths of her rectangle.
Explanation:
Well, Esperanza is correct in what she says ” the perimeter of her rectangle is 33 centimeters.”
because she is using her string to find the lengths of her rectangle. The measurements of rectangles forming an odd perimeter of Esperanza rectangles can be: (2,14.5) (4,12.5) (4.5,12) (5,11.5) (6, 10.5) ( 7, 9.5).