Engage NY Eureka Math 5th Grade Module 6 End of Module Assessment Answer Key
Eureka Math Grade 5 Module 6 End of Module Assessment Task Answer Key
Question 1.
Follow the directions.
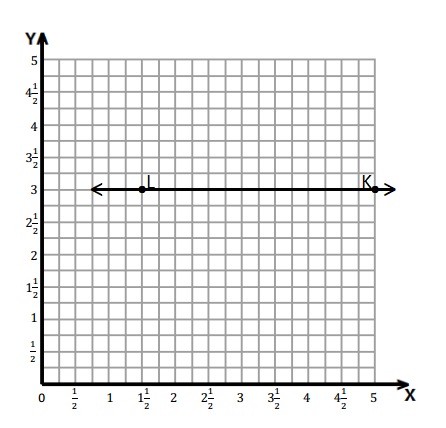
a. Draw a ray that starts at point L at (1\(\frac{1}{2}\), 3) and includes point K at (5, 3). Label points K and L.
b. Give the coordinates of three other points on the ray.
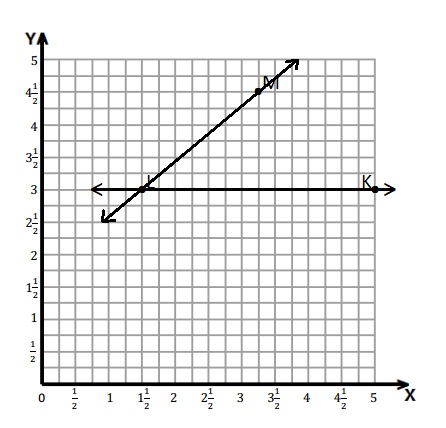
c. Draw a second ray with the same initial point and containing point M with coordinates (3\(\frac{1}{4}\), 4\(\frac{1}{2}\)). Label point M.
Answer:
a.
Explanation :
Point L and K are marked and a ray is drawn passing from these points .
b. The 3 points on the ray are ( 2, 3) , (4, 3) , (3\(\frac{1}{2}\), 3).
c. The initial point is L (1\(\frac{1}{2}\), 3) and M (3\(\frac{1}{4}\), 4\(\frac{1}{2}\)) are plotted and a ray is drawn through these points .
Question 2.
David draws a line segment from point Q (\(\frac{1}{4}\), \(\frac{7}{8}\)) to point R (\(\frac{5}{8}\), \(\frac{1}{2}\)). He then draws a line perpendicular to the first segment that intersects segment \(\overline{Q R}\) and includes point S (\(\frac{3}{4}\), 1).
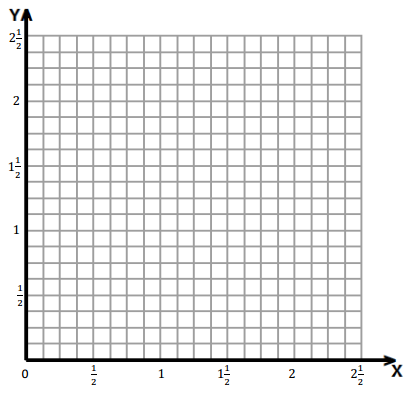
a. Draw \(\overline{Q R}\), and label the endpoints on the grid.
b. Draw the perpendicular line, and label point S.
c. Name another point that lies on the perpendicular line whose x-coordinate is between 1 and 1\(\frac{1}{2}\).
Answer:
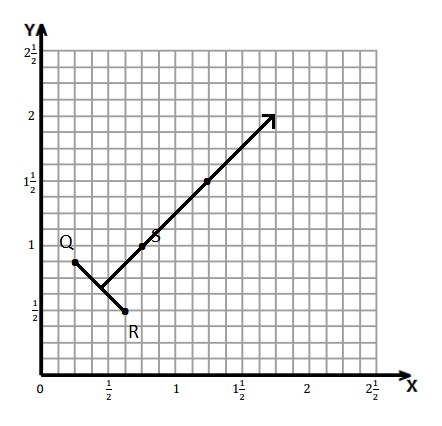
Explanation :
The Points Q and R are plotted then Point S ia marked then a straight line from point S is drawn and intersect the \(\overline{Q R}\) . Then Point between 1 and 1\(\frac{1}{2}\) is marked at (1\(\frac{1}{4}\), 1\(\frac{1}{2}\) ).
Question 3.
Complete the table for the rule multiply by 2 and then add 2 for the values of x from 0 to 4. Then, use the coordinate plane to answer the questions.
| x | y |
( x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
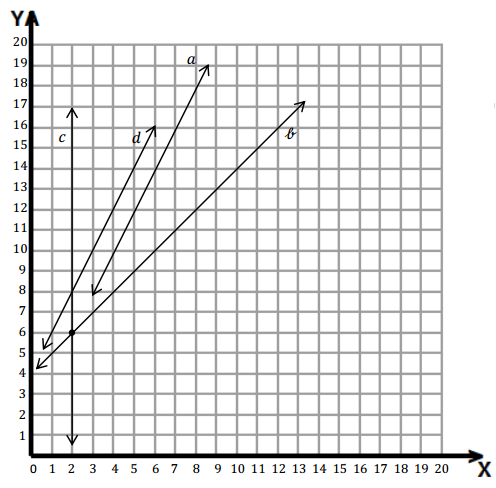
a. Which line shows the rule in the table?
b. Give the coordinates for the intersection of lines b and c.
c. Draw a line on the graph such that any point on the line has a y-coordinate of 2. Label your line as e.
d. Which coordinate is 2 for any point on line c?
e. Write a rule that tells how to find the y-coordinate when the x-coordinate is given for the points on line b.
f. Kim and Lacy want to draw a line on the coordinate plane that is parallel to line a. Kim uses the rule multiply by 4 and add 2 to generate her y-coordinates. Lacy uses the rule multiply by 2 and add 4 to generate her y-coordinates. Which girl’s line will be parallel to line a? Without graphing the lines, explain how you know.
Answer:
Rule : multiply by 2 and then add 2
y = 2x + 2
| x | y |
( x, y) |
| 0 | 0 | (0, 0) |
| 1 | 4 | (1, 4) |
| 2 | 6 | (2, 6) |
| 3 | 8 | (3, 8) |
| 4 | 10 | (4, 10) |
x= 0 ; y = 2(0) + 2 = 2
x= 1 ; y = 2(1) + 2 = 4
x=2 ; y = 2(2) + 2 = 6
x=3 ; y = 2(3) + 2 = 8
x= 4; y = 2(4) + 2 = 10
a. Line a follows the rule .
b. The coordinates for the intersection of lines b and c is (2, 6)
c. For all x-coordinates the y coordinate is 2 line is drawn and labeled as line e. 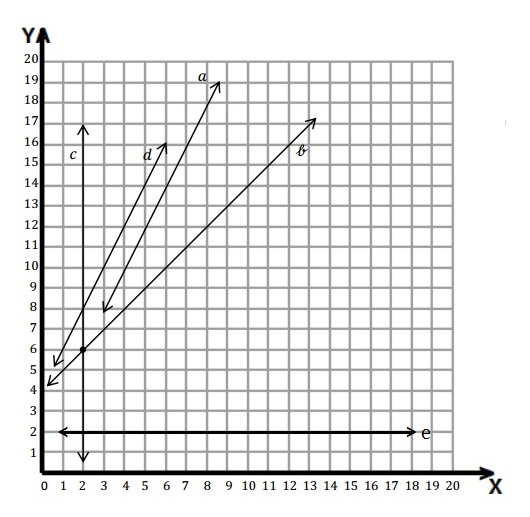
d. The x-coordinate is 2 for all y-coordinates on line c .
e.
The coordinates are (2, 6) , (3, 7) , ( 4, 8 )
The Rule for y-coordinate when the x-coordinate is given for the points on line b is x-coordinate and add 4 .
f. Lacy’s line rule will make a line parallel to line a .The rule for line 𝒶 is multiply 𝑥 by 2, and then add 2. The rule for Lacy’s line is multiply 𝑥- coordinate by 2, and then add 4. Lacy’s line is parallel because the steepness of the line is the same. (That is, the multiplication part of the rule is the same.) The adding part of the rule will make the 𝑦- coordinates two more than those in line 𝒶.)
Question 4.
An airplane is descending into an airport. When its altitude is 5 miles, it is 275 miles from the airport. When its altitude is 4 miles, it is 200 miles from the airport. At 3 miles, it is 125 miles from the airport.
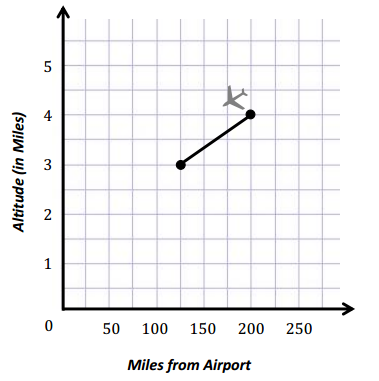
a. If the pilot follows the same pattern, what will the plane’s altitude be at 50 miles from the airport?
b. For the plane to land at the airport, the altitude will need to be 0, and the distance from the airport will need to be 0. Should the pilot continue this pattern? Why or why not?
Answer:
a. 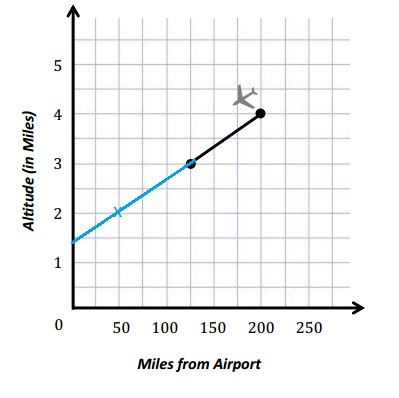
For 50miles the attitude will be 2 miles as we can notice from the above graph .
b. 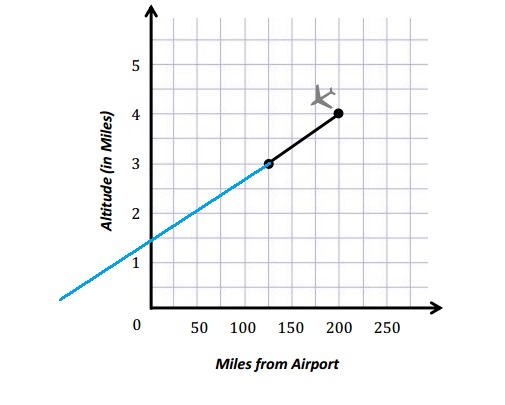
The pilot should not follow this pattern . He will be way past the airport when his altitude will be 0 .