Engage NY Eureka Math 5th Grade Module 6 Lesson 31 Answer Key
Eureka Math Grade 5 Module 6 Lesson 31 Problem Set Answer Key

Answer :
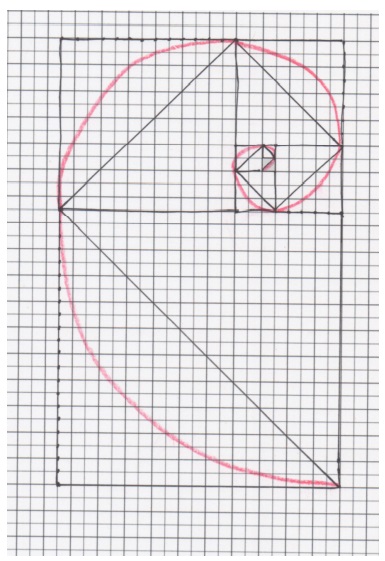
Eureka Math Grade 5 Module 6 Lesson 31 Reflection Answer Key
Today, when we saw a video on the Fibonacci sequence in the spiral and in nature, it may have felt a bit like “math magic.” Have you ever felt math magic in your elementary school years? If so, when did you experience it? If not, did you experience it today? Explain.
Answer:
Yes , It is math magic .
Explanation :
The Fibonacci sequence is a series of numbers where a number is the addition of the last two numbers, starting with 0, and 1. The Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
we look for patterns as
The brain looks for patterns and fills in the blanks. It uses patterns to understand the relationship between things—putting them in context. “The human brain is a pattern-recognition machine. … They are learning patterns and developing rules that guide their decision and make them faster and more accurate.”
Eureka Math Grade 5 Module 6 Lesson 31 Homework Answer Key
Question 1.
List the Fibonacci numbers up to 21, and create, on the graph below, a spiral of squares corresponding to each of the numbers you write.

Answer:
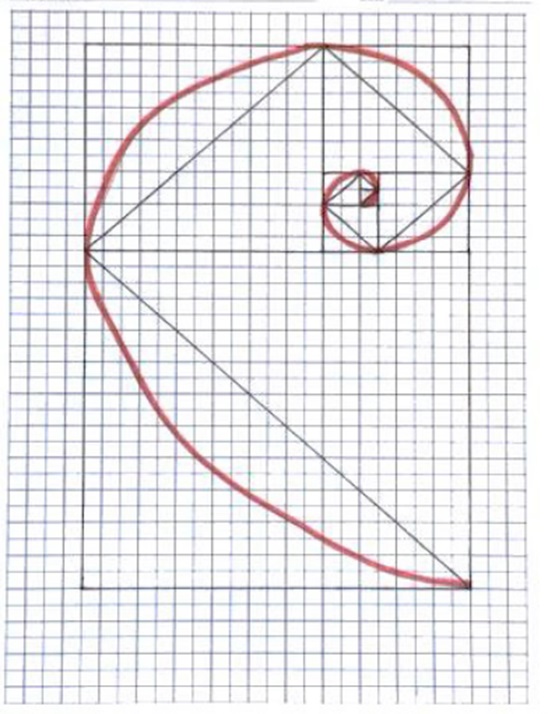
Explanation :
The Fibonacci Sequence can be written as a “Rule
The Rule is xn = xn−1 + xn−2
First, the terms are numbered from 0 onwards like this:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 392 |
So term number 6 is called x6 (which equals 8).
| Example: the 8th term is the 7th term plus the 6th term: x8 = x7 + x6 |
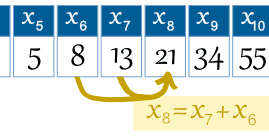 |
So we can write the rule:
The Rule is xn = xn−1 + xn−2
where:
xn is term number “n”
xn−1 is the previous term (n−1)
xn−2 is the term before that (n−2)
Question 2.
In the space below, write a rule that generates the Fibonacci sequence.
Answer:
The Fibonacci Sequence can be written as a “Rule
The Rule is xn = xn−1 + xn−2
Question 3.
Write at least the first 15 numbers of the Fibonacci sequence.
Answer:
The Fibonacci Sequence can be written as a “Rule
The Rule is xn = xn−1 + xn−2
The first 15 numbers of the Fibonacci sequence are :
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 392 |