Engage NY Eureka Math 5th Grade Module 6 Lesson 32 Answer Key
Eureka Math Grade 5 Module 6 Lesson 32 Problem Set Answer Key
Question 1.
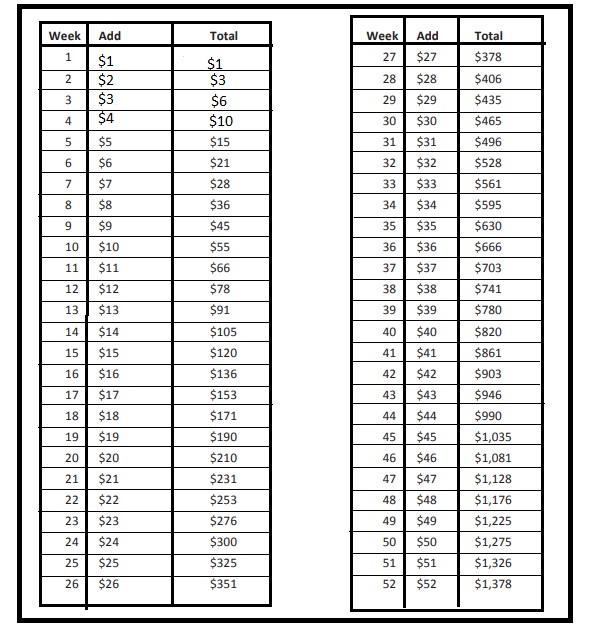
Ashley decides to save money, but she wants to build it up over a year. She starts with $1.00 and adds 1 more dollar each week. Complete the table to show how much she will have saved after a year.
Answer:
Explanation :
Amount with which ashley started = $1
Each week she adds $1 more that the previous week
So, Week she has $1 in her account
Week 2 she adds one more dollar than previous week so, that is $2 after adding her account balance is $2 +$1 = $3
Week 3 she adds one more than than previous week so, that is $3 after adding her account balance is $3 + $3 = $ 6 and so on …. till Week 52 the balance amount is calculated .
Question 2.
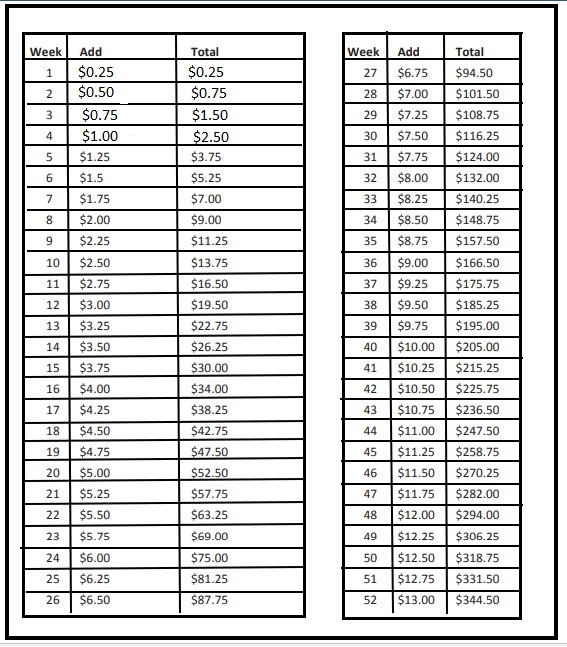
Carly wants to save money, too, but she has to start with the smaller denomination of quarters. Complete the second chart to show how much she will have saved by the end of the year if she adds a quarter more each week. Try it yourself, if you can and want to!
Answer:
Explanation :
Amount with which Carlie started = $0.25 (Quarters)
Each week she adds $0.25 more that the previous week
So, Week 1 she starts with $0.25 in her account
Week 2 she adds one more Quarter dollar than previous week so, that is $0.50 after adding her account balance is $0.25 +$0.50 = $0.75
Week 3 she adds one more Quarter dollar than previous week so, that is $0.75 after adding her account balance is $0.75 + $0.75 = $ 1.50 and so on …. till week 52 amount is calculated .
Question 3.
David decides he wants to save even more money than Ashley did. He does so by adding the next Fibonacci number instead of adding $1.00 each week. Use your calculator to fill in the chart and find out how much money he will have saved by the end of the year. Is this realistic for most people? Explain your answer.
Answer:
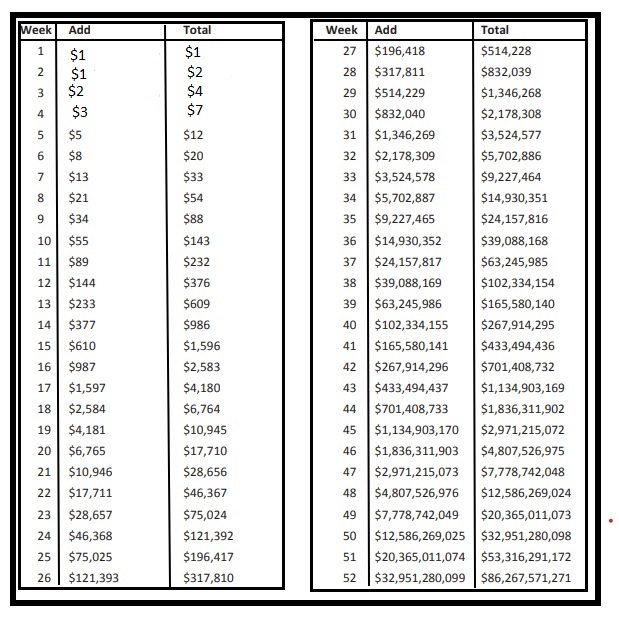
Explanation :
By end of the year he will save $86,267,571,271 .
It is not realistic because In Fibonacci number the rule is followed
So we can write the rule:
The Rule is xn = xn−1 + xn−2
where:
xn is term number “n”
xn−1 is the previous term (n−1)
xn−2 is the term before that (n−2)
In Fibonacci rule the previous term and the term before that is added to get next fibonacci number , That means the David should starts with $1 . for week he should add $1 for week1 later, he should add $1 the previous money and before that week in week 2 total is $2,
In week 3 he should add $2 that double of previous then amount becomes $4. and so on till week 52 for every week he should add nearly 2 weeks amount which will be difficulty to add. so this not realistic to follow this rule as Savings are done with smaller amounts not with huge amounts .
Eureka Math Grade 5 Module 6 Lesson 32 Reflection Answer Key
Today, we watched how savings can grow over time, but we did not discuss how the money saved was earned. Have you ever thought about how math skills might help you to earn money? If so, what are some jobs that might require strong math skills? If not, think about it now. How might you make a living using math skills?
Answer:
Money math involves many of the math skills you learn in school, such as addition, subtraction, multiplication, division, fractions, decimals, and percentages. … Handling money can help you learn how to count it. Making purchases in a store can help you become comfortable counting money.
Some jobs that might require strong math skills are in Auditor, Statistician, Actuary, Mathematician, Operations Research Analyst, Math Professor, Banking , Cashier ,
Managing money $$$
Balancing the checkbook.
Shopping for the best price.
Preparing food.
Figuring out distance, time and cost for travel.
Understanding loans for cars, trucks, homes, schooling or other purposes.
Eureka Math Grade 5 Module 6 Lesson 32 Homework Answer Key
Question 1.
Jonas played with the Fibonacci sequence he learned in class. Complete the table he started.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 5 | 8 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Answer:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
Explanation :
The Fibonacci Sequence can be written as a “Rule”
First, the terms are numbered from 0 onwards like this:
So we can write the rule:
The Rule is xn = xn−1 + xn−2
where:
xn is term number “n”
xn−1 is the previous term (n−1)
xn−2 is the term before that (n−2)
With this rule all the terms are calculated .
Question 2.
As he looked at the numbers, Jonas realized he could play with them. He took two consecutive numbers in the pattern and multiplied them by themselves and then added them together. He found they made another number in the pattern. For example, (3 × 3) + (2 × 2) = 13, another number in the pattern. Jonas said this was true for any two consecutive Fibonacci numbers. Was Jonas correct? Show your reasoning by giving at least two examples of why he was or was not correct.
Answer:
Yes he is write .
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
Explanation :
The Fibonacci number of 6 is 8
The Fibonacci number of 7 is 5
Taking two consecutive numbers and squaring and adding them we get,
( 3 × 3)+(5 × 5 ) = 9 + 25 = 34
34 is the Fibonacci number of 9 (4 + 5 = 9) It is true
The Fibonacci number of 6 is 8
The Fibonacci number of 7 is 13
Taking two consecutive numbers and squaring and adding them we get,
( 8 × 8 )+(13 × 13 ) = 64 + 169 = 233
233 is the Fibonacci number of 13 (6 + 7 = 13) It is true
Question 3.
Fibonacci numbers can be found in many places in nature, for example, the number of petals in a daisy, the number of spirals in a pine cone or a pineapple, and even the way branches grow on a tree. Find an example of something natural where you can see a Fibonacci number in action, and sketch it here.
Answer:
In the below figure we see two different pine cone patterns.
In figure 1 The Fibonacci spirals are shown clearly
In Figure 2 The Fibonacci spirals of another pine cone is shown
