Engage NY Eureka Math 6th Grade Module 2 Lesson 4 Answer Key
Eureka Math Grade 6 Module 2 Lesson 4 Example Answer Key
Example 1.
Molly has 1\(\frac{3}{8}\) cups of strawberries. She needs \(\frac{3}{8}\) cup of strawberries to make one batch of muffins. How many batches can Molly make?
Use a model to support your answer.
Answer:
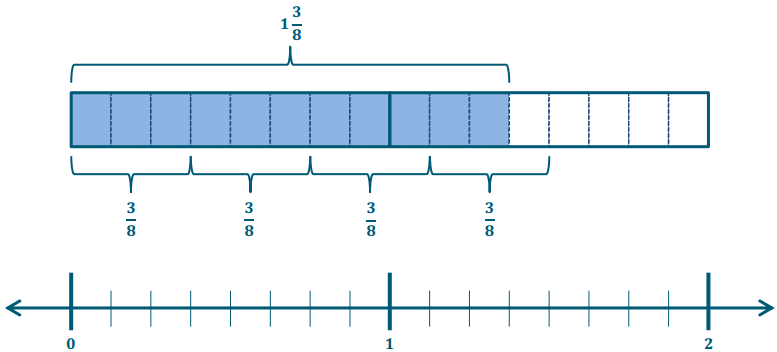
\(\frac{11}{8} \div \frac{3}{8}\) = 11 eighths ÷ 3 eighths = \(\frac{11}{3}\) = 3\(\frac{2}{3}\)
Molly can make 3\(\frac{2}{3}\) batches of muffins.
Example 2.
Molly’s friend, Xavier, also has \(\frac{11}{8}\) cups of strawberries. He needs \(\frac{3}{4}\) cup of strawberries to make a batch of tarts. How many batches can he make? Draw a model to support your solution.
Answer:
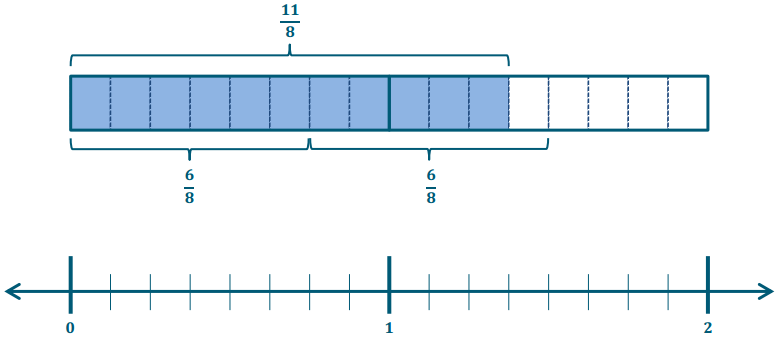
\(\frac{11}{8} \div \frac{6}{8}\) = 11 eighths ÷ 6 eighths = \(\frac{11}{6}\) = 1\(\frac{5}{6}\)
Xavier has enough to make 1 and \(\frac{5}{6}\) batches.
Example 3.
Find the quotient: \(\frac{6}{8} \div \frac{2}{8}\). Use a model to show your answer.
Answer:
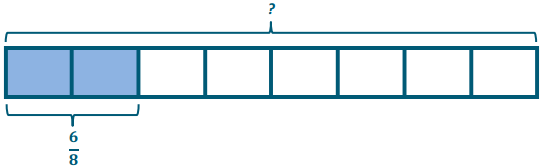
2 units = 6 eighths
1 unit = 6 eighths ÷ 2 = 3 eighths
8 units = 8 × 3 eIghths = 24 eighths = 3
Example 4.
Find the quotient: \(\frac{3}{4} \div \frac{2}{3}\). Use a model to show your answer.
Answer:
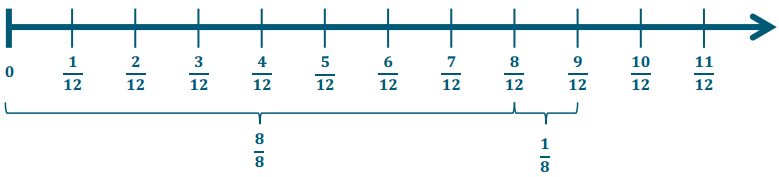
We could rewrite this problem to ask \(\frac{9}{12} \div \frac{8}{12}\) = 9 twelfths ÷ 8 twelfths = \(\frac{9}{8}\) = 1\(\frac{1}{8}\).
Eureka Math Grade 6 Module 2 Lesson 4 Exercise Answer Key
Find each quotient.
Exercise 1.
\(\frac{6}{2} \div \frac{3}{4}\)
Answer:
We could rewrite this expression and solve as \(\frac{12}{4} \div \frac{3}{4}=\frac{12}{3}\) = 4.
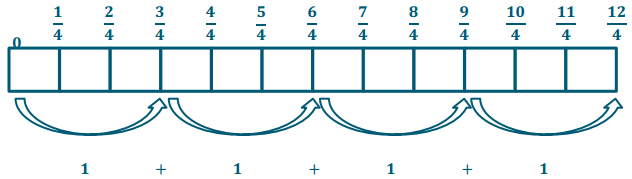
Exercise 2.
\(\frac{2}{3} \div \frac{2}{5}\)
Answer:
We could rewrite this expression and solve as \(\frac{10}{15} \div \frac{6}{15}=\frac{10}{6}=1 \frac{4}{6}\)
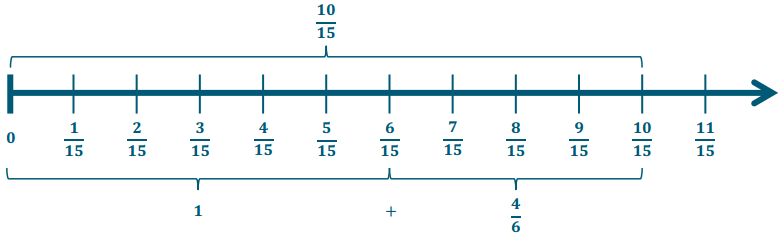
Exercise 3.
\(\frac{7}{8} \div \frac{1}{2}\)
Answer:
We could rewrite this as \(\frac{7}{8} \div \frac{4}{8}=\frac{7}{4}=1 \frac{3}{4}\)
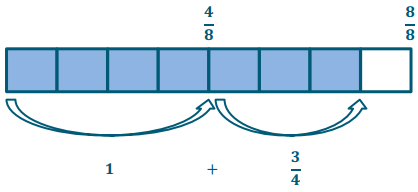
Exercise 4.
\(\frac{3}{5} \div \frac{1}{4}\)
Answer:
This can be rewritten as \(\frac{12}{20} \div \frac{5}{20}=\frac{12}{5}=2 \frac{2}{5}\)
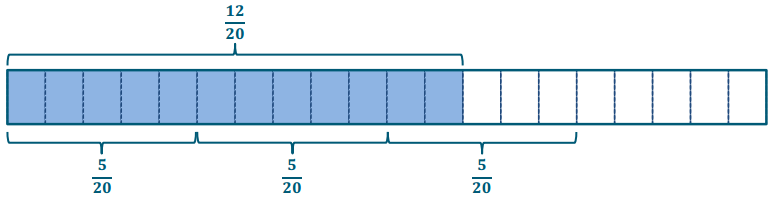
Exercise 5.
\(\frac{5}{4} \div \frac{1}{3}\)
Answer:
We can be written this as \(\frac{15}{12} \div \frac{4}{12}=\frac{15}{4}=3 \frac{3}{4}\)
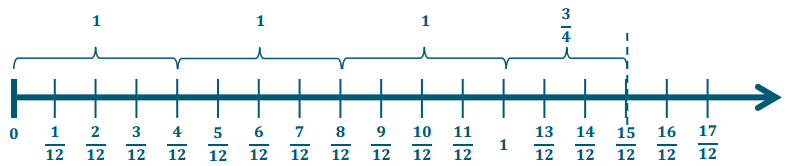
Eureka Math Grade 6 Module 2 Lesson 4 Problem Set Answer Key
Calculate the quotient. If needed, draw a model.
Question 1.
\(\frac{8}{9} \div \frac{4}{9}\)
Answer:
8 ninths ÷ 4 ninths = 2

Question 2.
\(\frac{9}{10} \div \frac{4}{10}\)
Answer:
9 tenths ÷ 4 tenths = 2\(\frac{1}{4}\)

Question 3.
\(\frac{3}{5} \div \frac{1}{3}\)
Answer:
\(\frac{9}{15} \div \frac{5}{15}\) = 9 fifteenths ÷ 5 fifteenths = \(\frac{9}{5}=1 \frac{4}{5}\)
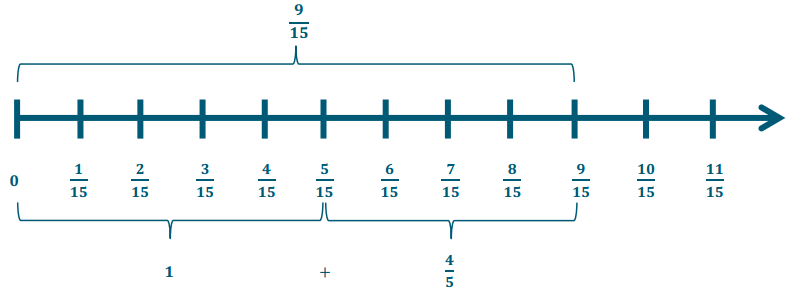
Question 4.
\(\frac{3}{4} \div \frac{1}{5}\)
Answer:
\(\frac{15}{20} \div \frac{4}{20}\) = 15 twentieths ÷ 4 twentieths = \(\frac{15}{4}\)
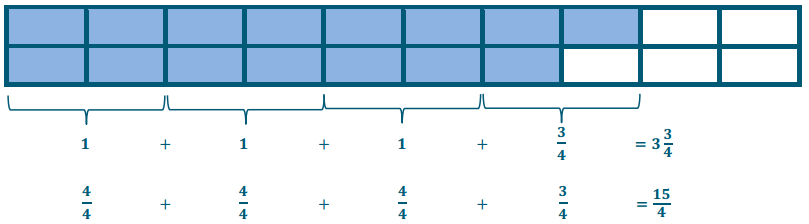
Eureka Math Grade 6 Module 2 Lesson 4 Exit Ticket Answer Key
Calculate each quotient. If needed, draw a model.
Question 1.
\(\frac{9}{4} \div \frac{3}{8}\)
Answer:
This can be rewritten as \(\frac{18}{8} \div \frac{3}{8}\) = 18 eighths divided by 3 eighths = \(\frac{18}{3}\) = 6.
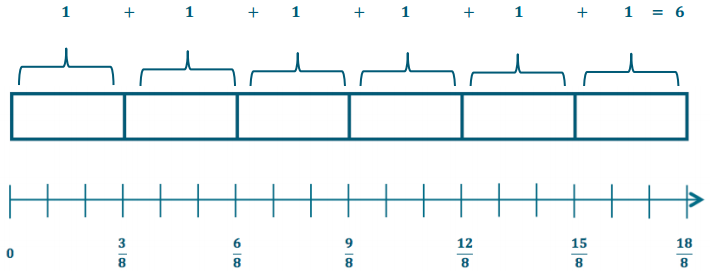
Question 2.
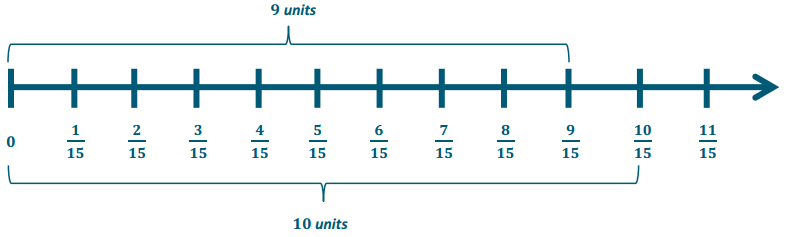
\(\frac{3}{5} \div \frac{2}{3}\)
Answer:
This can be rewritten as \(\frac{9}{15} \div \frac{10}{15}\) = 9fifteenths divided by 10 fifteenths, or 9 units ÷ 10 units. So, this is equal to \(\frac{9}{10}\).
Eureka Math Grade 6 Module 2 Lesson 4 Opening Exercise Answer Key
Write at least three equivalent fractions for each fraction below.
a. \(\frac{2}{3}\)
Answer:
Sample solution include \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}, \frac{12}{18}\)
b. \(\frac{10}{12}\)
Answer:
Sample solution include \(\frac{5}{6}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30^{\prime}} \frac{30}{36}\)