Engage NY Eureka Math Grade 6 Module 5 Lesson 1 Answer Key
Eureka Math Grade 6 Module 5 Lesson 1 Exercise Answer Key
Opening Exercise:
Question 1.
Name each shape.
a. 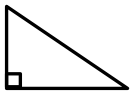
Answer:
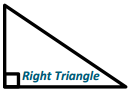
b. 
Answer:

c. 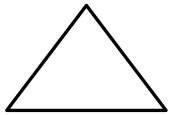
Answer:
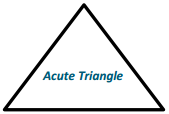
d. 
Answer:
e. 
Answer:

Exercises:
Question 1.
Find the area of each parallelogram below. Note that the figures are not drawn to scale.
a. 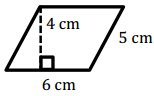
Answer:
A = bh
= (6 cm)(4 cm)
= 24 cm2
b. 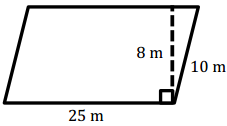
A = bh
= (25 m)(8 m)
= 200 m2
c. 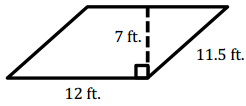
A = bh
= (12 ft.)(7 ft.)
84 ft2
Question 2.
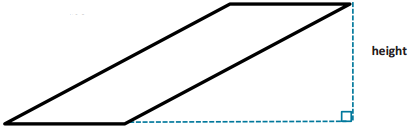
Draw and label the height of each parallelogram. Use the correct mathematical tool to measure (in inches) the base and height, and calculate the area of each parallelogram.
a. 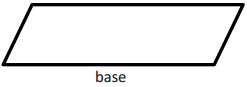
Answer:
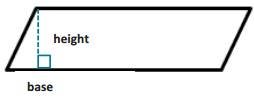
A = bh = (0.5 in.) (2 in.) = 1 in2
b. 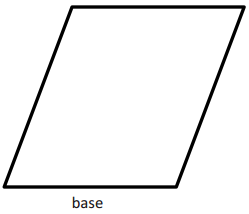
Answer:
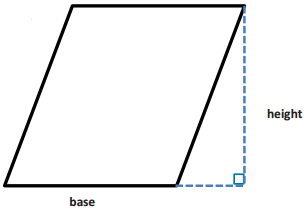
A = bh = (1.5 in.) (2 in.) = 3 in2
c. 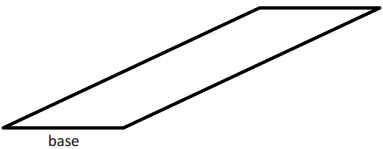
Answer:
A = bh = (1 in.) (1 in.) = 1 in2
Question 3.
If the area of a parallelogram is \(\frac{35}{42}\) cm<sup>2</sup> and the height is \(\frac{1}{7}\) cm, write an equation that relates the height, base, and area of the parallelogram. Solve the equation.
Answer:
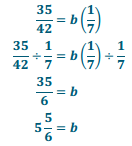
Therefore, the base is 5\(\frac{5}{6}\) cm.
Eureka Math Grade 6 Module 5 Lesson 1 Problem Set Answer Key
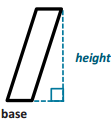
Draw and label the height of each parallelogram.
Question 1.
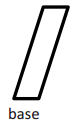
Answer:
Question 2.
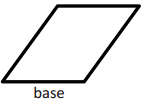
Answer:
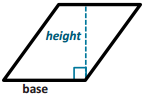
Calculate the area of each parallelogram. The figures are not drawn to scale.
Question 3.
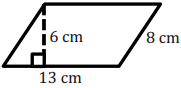
Answer:
A = bh
= (13 cm) (6 cm)
= 78 cm2
Question 4.
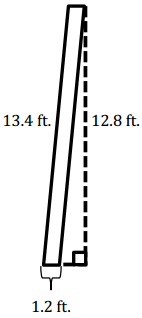
Answer:
A = bh
= (1.2 ft.) (12.8 ft)
= 15.36 ft2
Question 5.
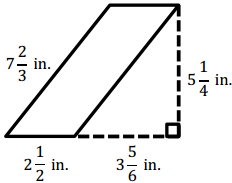
Answer:
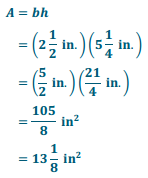
Question 6.
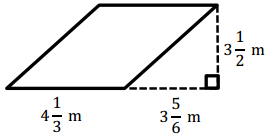
Answer:
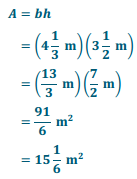
Question 7.
Brittany and Sid were both asked to draw the height of a parallelogram. Their answers are below.
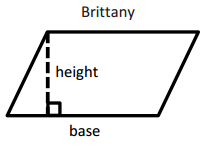
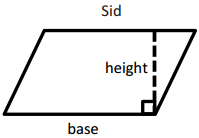
Are both Brittany and Sid correct? If not, who is correct? Explain your answer
Answer:
Both Brittany and Sid are correct because both of their heights represent a line segment that is perpendicular to the base and whose endpoint is on the opposite side of the parallelogram.
Question 8.
Do the rectangle and parallelogram below have the same area? Explain why or why not.
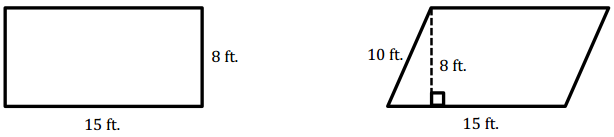
Answer:
Yes, the rectangle and parallelogram have the same area because if we cut off the right triangle on the left side of the parallelogram, we can move it over to the right side and make the parallelogram into a rectangle. After transforming the parallelogram into a rectangle, both rectangles would have the same dimensions; therefore, their areas would be the same.
Question 9.
A parallelogram has an area of 20.3 cm<sup>2</sup> and a base of 2. 5 cm. Write an equation that relates the area to the base and height, h. Solve the equation to determine the height of the parallelogram.
Answer:
20.3 = (2.5)(h)
20.3 ÷ 2.5 = (2. 5)(h) ÷ 2.5
8.12 = h
Therefore, the height of the parallelogram is 8. 12 cm.
Eureka Math Grade 6 Module 5 Lesson 1 Exit Ticket Answer Key
Calculate the area of each parallelogram. Note that the figures are not drawn to scale.
Question 1.
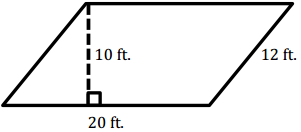
Answer:
A = bh = (20 ft.) (10 ft.) = 200 ft2
Question 2.
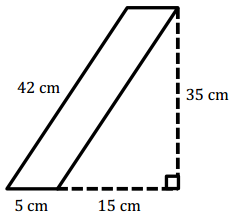
Answer:
A = bh = (5 cm) (35 cm) = 175 cm2
Question 3.
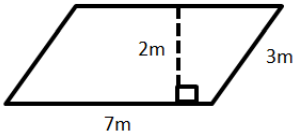
Answer:
A = bh = (7 m) (2 m) = 14 m2
Eureka Math Grade 6 Module 5 Lesson 1 Multiplication of Fractions Answer Key
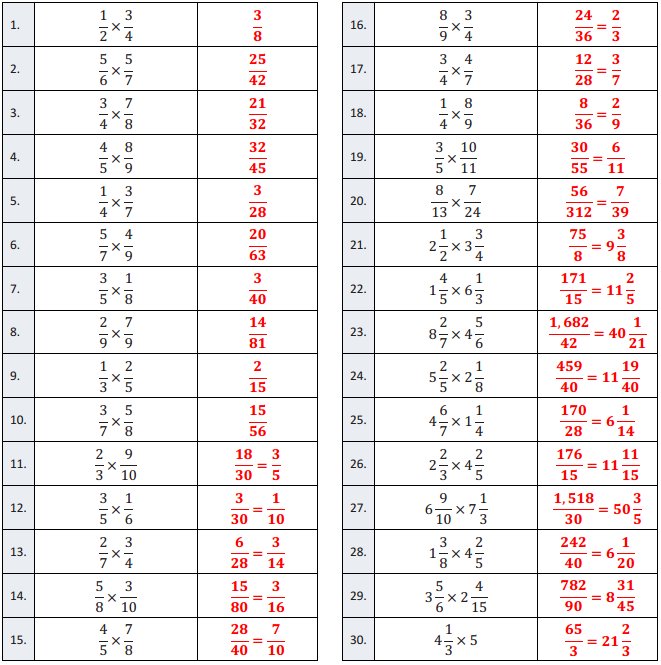
Multiplication of Fractions I – Round 1
Directions: Determine the product of the fractions and simplify.
Question 1.
\(\frac{1}{2}\) × \(\frac{3}{4}\)
Answer:
\(\frac{3}{8}\)
Question 2.
\(\frac{5}{6}\) × \(\frac{5}{7}\)
Answer:
\(\frac{25}{42}\)
Question 3.
\(\frac{3}{4}\) × \(\frac{7}{8}\)
Answer:
\(\frac{21}{32}\)
Question 4.
\(\frac{4}{5}\) × \(\frac{8}{9}\)
Answer:
\(\frac{32}{45}\)
Question 5.
\(\frac{1}{4}\) × \(\frac{3}{7}\)
Answer:
\(\frac{3}{28}\)
Question 6.
\(\frac{5}{7}\) × \(\frac{4}{9}\)
Answer:
\(\frac{20}{63}\)
Question 7.
\(\frac{3}{5}\) × \(\frac{1}{8}\)
Answer:
\(\frac{3}{40}\)
Question 8.
\(\frac{2}{9}\) × \(\frac{7}{9}\)
Answer:
\(\frac{14}{81}\)
Question 9.
\(\frac{1}{3}\) × \(\frac{2}{5}\)
Answer:
\(\frac{2}{15}\)
Question 10.
\(\frac{3}{7}\) × \(\frac{5}{8}\)
Answer:
\(\frac{15}{56}\)
Question 11.
\(\frac{2}{3}\) × \(\frac{9}{10}\)
Answer:
\(\frac{18}{30}\) = \(\frac{3}{5}\)
Question 12.
\(\frac{3}{5}\) × \(\frac{1}{6}\)
Answer:
\(\frac{3}{30}\) = \(\frac{1}{10}\)
Question 13.
\(\frac{2}{7}\) × \(\frac{3}{4}\)
Answer:
\(\frac{6}{28}\) = \(\frac{3}{14}\)
Question 14.
\(\frac{5}{8}\) × \(\frac{3}{10}\)
Answer:
\(\frac{15}{80}\)
= \(\frac{3}{16}\)
Question 15.
\(\frac{4}{5}\) × \(\frac{7}{8}\)
Answer:
\(\frac{28}{40}\) = \(\frac{7}{10}\)
Question 16.
\(\frac{8}{9}\) × \(\frac{3}{4}\)
Answer:
\(\frac{24}{36}\) = \(\frac{2}{3}\)
Question 17.
\(\frac{3}{4}\) × \(\frac{4}{7}\)
Answer:
\(\frac{12}{28}\) = \(\frac{3}{7}\)
Question 18.
\(\frac{1}{4}\) × \(\frac{8}{9}\)
Answer:
\(\frac{8}{36}\) = \(\frac{2}{9}\)
Question 19.
\(\frac{3}{5}\) × \(\frac{10}{11}\)
Answer:
\(\frac{30}{55}\) = \(\frac{6}{11}\)
Question 20.
\(\frac{8}{13}\) × \(\frac{7}{24}\)
Answer:
\(\frac{56}{312}\) = \(\frac{7}{39}\)
Question 21.
2\(\frac{1}{2}\) × 3\(\frac{3}{4}\)
Answer: \(\frac{75}{8}\) = 9\(\frac{3}{8}\)
Question 22.
1\(\frac{4}{5}\) × 6\(\frac{1}{3}\)
Answer:
\(\frac{171}{15}\) = 11\(\frac{2}{5}\)
Question 23.
8\(\frac{2}{7}\) × 4\(\frac{5}{6}\)
Answer:
\(\frac{1682}{42}\) = 40\(\frac{1}{21}\)
Question 24.
5\(\frac{2}{5}\) × 2\(\frac{1}{8}\)
Answer:
\(\frac{459}{40}\) = 11\(\frac{19}{40}\)
Question 25.
4\(\frac{6}{7}\) × 1\(\frac{1}{4}\)
Answer:
\(\frac{170}{28}\) = 6 \(\frac{1}{14}\)
Question 26.
2\(\frac{2}{3}\) × 4\(\frac{2}{5}\)
Answer:
\(\frac{176}{15}\) = 11 \(\frac{11}{15}\)
Question 27.
6\(\frac{9}{10}\) × 7\(\frac{1}{3}\)
Answer:
\(\frac{1518}{30}\) = 50 \(\frac{3}{5}\)
Question 28.
1\(\frac{3}{8}\) × 4\(\frac{2}{5}\)
Answer:
\(\frac{242}{40}\) = 6 \(\frac{1}{20}\)
Question 29.
3\(\frac{5}{6}\) × 2\(\frac{4}{15}\)
Answer:
\(\frac{782}{90}\) = 8 \(\frac{31}{45}\)
Question 30.
4\(\frac{1}{3}\) × 5
Answer:
\(\frac{65}{3}\) = 21 \(\frac{2}{3}\)
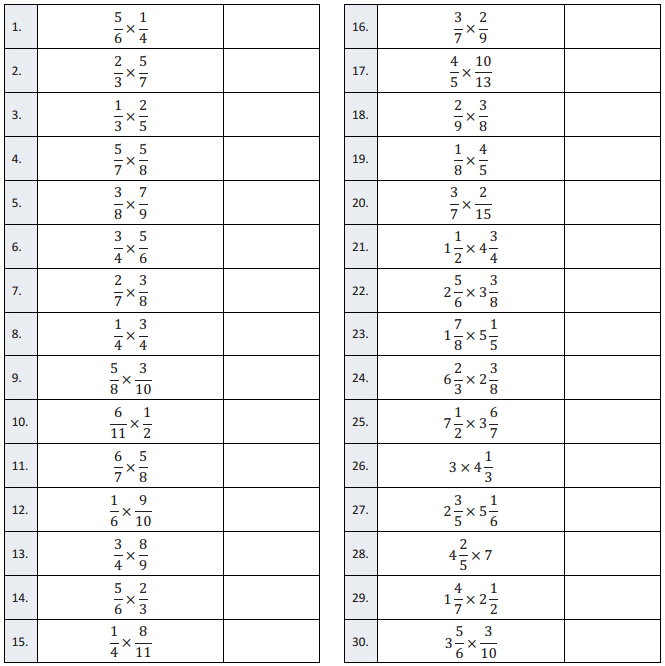
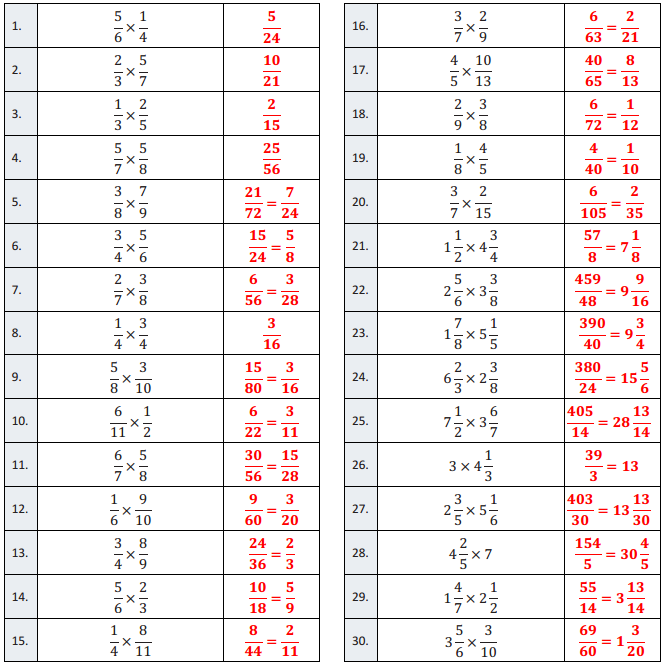
Multiplication of Fractions I – Round 2
Directions: Determine the product of the fractions and simplify.
Question 1.
\(\frac{5}{6}\) × \(\frac{1}{4}\)
Answer:
\(\frac{5}{24}\)
Question 2.
\(\frac{2}{3}\) × \(\frac{5}{7}\)
Answer:
\(\frac{10}{21}\)
Question 3.
\(\frac{1}{3}\) × \(\frac{2}{5}\)
Answer:
\(\frac{2}{15}\)
Question 4.
\(\frac{5}{7}\) × \(\frac{5}{8}\)
Answer:
\(\frac{25}{56}\)
Question 5.
\(\frac{3}{8}\) × \(\frac{7}{9}\)
Answer:
\(\frac{21}{72}\) = \(\frac{7}{24}\)
Question 6.
\(\frac{3}{4}\) × \(\frac{5}{6}\)
Answer:
\(\frac{15}{24}\) = \(\frac{5}{8}\)
Question 7.
\(\frac{2}{7}\) × \(\frac{3}{8}\)
Answer:
\(\frac{6}{56}\) = \(\frac{3}{28}\)
Question 8.
\(\frac{1}{4}\) × \(\frac{3}{4}\)
Answer:
\(\frac{3}{16}\)
Question 9.
\(\frac{5}{8}\) × \(\frac{3}{10}\)
Answer:
\(\frac{15}{80}\) = \(\frac{3}{16}\)
Question 10.
\(\frac{6}{11}\) × \(\frac{1}{2}\)
Answer:
\(\frac{6}{22}\) = \(\frac{3}{11}\)
Question 11.
\(\frac{6}{7}\) × \(\frac{5}{8}\)
Answer:
\(\frac{30}{56}\) = \(\frac{15}{28}\)
Question 12.
\(\frac{1}{6}\) × \(\frac{9}{10}\)
Answer:
\(\frac{9}{60}\) = \(\frac{3}{20}\)
Question 13.
\(\frac{3}{4}\) × \(\frac{8}{9}\)
Answer:
\(\frac{24}{36}\) = \(\frac{2}{3}\)
Question 14.
\(\frac{5}{6}\) × \(\frac{2}{3}\)
Answer:
\(\frac{10}{18}\) = \(\frac{5}{9}\)
Question 15.
\(\frac{1}{4}\) × \(\frac{8}{11}\)
Answer:
\(\frac{8}{44}\) = \(\frac{2}{11}\)
Question 16.
\(\frac{3}{7}\) × \(\frac{2}{9}\)
Answer:
\(\frac{6}{63}\) = \(\frac{2}{21}\)
Question 17.
\(\frac{4}{5}\) × \(\frac{10}{13}\)
Answer:
\(\frac{40}{65}\) = \(\frac{8}{13}\)
Question 18.
\(\frac{2}{9}\) × \(\frac{3}{8}\)
Answer:
\(\frac{6}{72}\) = \(\frac{1}{12}\)
Question 19.
\(\frac{1}{8}\) × \(\frac{4}{5}\)
Answer:
\(\frac{4}{40}\) = \(\frac{1}{10}\)
Question 20.
\(\frac{3}{7}\) × \(\frac{2}{15}\)
Answer:
\(\frac{6}{105}\) = \(\frac{2}{35}\)
Question 21.
1\(\frac{1}{2}\) × 4\(\frac{3}{4}\)
Answer:
\(\frac{57}{8}\) = 7\(\frac{1}{8}\)
Question 22.
2\(\frac{5}{6}\) × 3\(\frac{3}{8}\)
Answer:
\(\frac{459}{48}\) = 9\(\frac{9}{16}\)
Question 23.
1\(\frac{7}{8}\) × 5\(\frac{1}{5}\)
Answer:
\(\frac{390}{40}\) = 9\(\frac{3}{4}\)
Question 24.
6\(\frac{2}{3}\) × 2\(\frac{3}{8}\)
Answer:
\(\frac{380}{24}\) = 15\(\frac{5}{6}\)
Question 25.
7\(\frac{1}{2}\) × 3\(\frac{6}{7}\)
Answer:
\(\frac{405}{14}\) = 28\(\frac{13}{14}\)
Question 26.
3 × 4\(\frac{1}{3}\)
Answer:
\(\frac{39}{3}\) = 13
Question 27.
2\(\frac{3}{5}\) × 5\(\frac{1}{6}\)
Answer:
\(\frac{403}{30}\) = 13\(\frac{13}{30}\)
Question 28.
4\(\frac{2}{5}\) × 7
Answer:
\(\frac{154}{5}\) = 30\(\frac{4}{5}\)
Question 29.
1\(\frac{4}{7}\) × 2\(\frac{1}{2}\)
Answer:
\(\frac{55}{14}\) = 3\(\frac{13}{14}\)
Question 30.
3\(\frac{5}{6}\) × \(\frac{3}{10}\)
Answer:
\(\frac{69}{60}\) = 1\(\frac{3}{20}\)