Eureka Math Grade 6 Module 5 Lesson 5 Answer Key

Engage NY Eureka Math Grade 6 Module 5 Lesson 5 Answer Key

Eureka Math Grade 6 Module 5 Lesson 5 Exercise Answer Key

Opening Exercise:

Here is an aerial view of a woodlot.

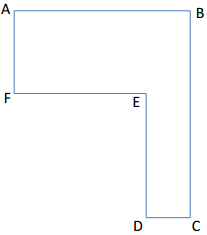
Question 1.
If AB = 10 units, FE = 8 units, AF = 6 units, and DE = 7 units, find the lengths of the other two sides.
DC =
BC =
Answer:
DC = 2 units
BC = 13 units

Question 2.
If DC = 10 units, FE = 30 units, AF = 28 units, and BC = 54 units, find the lengths of the other two sides.
AB =
DE =
Answer:
AB = 40 units
DE = 26 units

Eureka Math Grade 6 Module 5 Lesson 5 Example Answer Key

Example 1: Decomposing Polygons into Rectangles

The Intermediate School is producing a play that needs a special stage built. A diagram of the stage is shown below (not to scale).

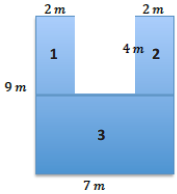
Question a.
On the first diagram, divide the stage into three rectangles using two horizontal lines. Find the dimensions of these rectangles, and calculate the area of each. Then, find the total area of the stage.
Answer:
Dimensions: 2 m by 4m, 2 m by 4 m, and 7 m by 5 m
Area: 2 m × 4m = 8 m², 2 m × 4 m = 8 m², 7 m × 5 m = 35 m²
Total: 8 m² + 8 m² + 35 m² = 51 m²

Question b.
On the second diagram, divide the stage into three rectangles using two vertical lines. Find the dimensions of these rectangles, and calculate the area of each. Then, find the total area of the stage.
Answer:
Dimensions: 2 m by 9 m, 2 m by 9 m, and 3 m by 5 m
Area: 2 m × 9 m = 18 m × 2 m × 9 m = 18 m², 3 m × 5m = 15 m²
Total: 51 m²

Question c.
On the third diagram, divide the stage into three rectangles using one horizontal line and one vertical line. Find the dimensions of these rectangles, and calculate the area of each. Then, find the total area of the stage.

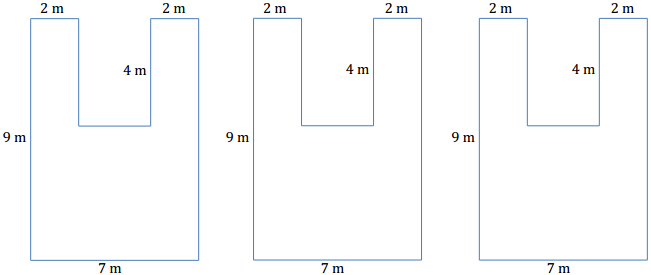
Answer:
Dimensions: 2 m by 9 m, 2 m by 4 m, and 5 m by 5 m
Area: 2 m × 9 m = 18 m², 2 m × 4 m = 8 m², 5 m × 5 m = 25 m²
Total: 51 m²

Question d.
Think of this as a large rectangle with a piece removed.

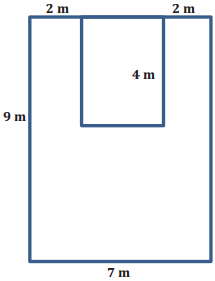
i. What are the dimensions of the large rectangle and the small rectangle?
Answer:
Dimensions: 9 m by 7 m and 3 m by 4 m

ii. What are the areas of the two rectangles?
Answer:
Area: 9 m × 7 m = 63 m², 3 m × 4 m = 12 m²

iii. What operation Is needed to find the area of the original figure?
Answer:
Subtraction

iv. What is the difference in area between the two rectangles?
Answer:
63 m² – 12 m² = 51 m²

v. What do you notice about your answers to (a), (b), (c), and (d)? 7 m
Answer:
The area is the same.

vi. Why do you think this is true?
Answer:
No matter how we decompose the figure, the total area is the sum of its ports. Even if we take the area around the figure and subtract the part that is not included, the area of the figure remains the same, 51 m².

Area of Rectangle 1: b . h
2m . 4m = 8m²
Area of Rectangle 2: b . h
2 m 4m = 8 m²
Area of Rectangle 3: b . h
7m 5m 35 m²
Area of Polygon: 8m² + 8m² + 35 m² = 51 m²

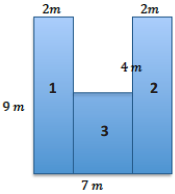
Area of Rectangle 1: b . h
9m . 2m = 18 m²
Area of Rectangle 2: b . h
9m . 2m =18 m²
Area of Rectangle 3: b . h
3m . 5m = 15 m²
Area of Polygon: 18 m² + 18 m² + 15 m² = 51 m²

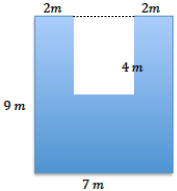
Area of Rectangle: b . h
9m . 7 m = 63 m²
Area of Missing Rectangle 2: b . h
3m . 4m = 12 m²
Area of Polygon: 63 m² – 12 m² = 51 m²

Example 2: Decomposing Polygons into Rectangles and Triangles

Parallelogram ABCD is part of a large solar power collector. The base measures 6 m and the height is 4 m.

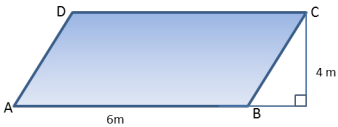
Question a.
Draw a diagonal from A to C. Find the area of both triangles ABC and ACD.
Answer:

Triangle ABC
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 m) (4 m)
A = 12 m².

Triangle ACD
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6m)(4m)
A = 12 m²

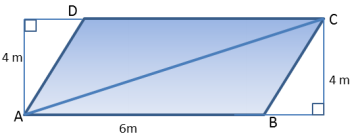
Question b.
Find the area of both triangles ABD and BCD. Then find the area of the trapezoid.
Answer:

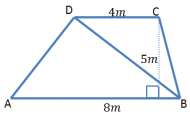
Triangle ABD
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8m)(5m)
A = 20 m²

Triangle BCD
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 m) (5 m)
A = 10 m²

A = 20 m² + 10 m² = 30 m²

Question c.
How else could we find this area?
Answer:
We could consider the rectangle that surrounds the trapezoid. Find the area of that rectangle, and then subtract the area of both right triangles.

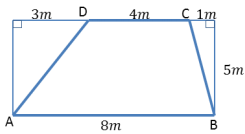
Area of Rectangle;
A = bh
A = (8 m) (5 m)
A = 40 m²

Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 m) (5 m)
A = 7.5 m²

Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1 m) (5 m)
A = 2.5 m²

A = 40 m² – 7.5 m² – 2.5 m² = 30 m² (or)

A = 40 m² – (7.5 m² + 2.5 m²) = 30 m²

Eureka Math Grade 6 Module 5 Lesson 5 Problem Set Answer Key

Question 1.
If AB = 20 units, FE = 12 units, AF = 9 units, and DE = 12 units, find the length of the other two sides. Then, find the area of the irregular polygon.

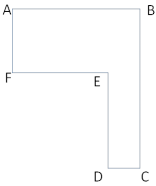
Answer:
CD = 8 units, BC = 21 units, Area = 276 square units.

Question 2.
If DC = 1.9 cm, FE = 5.6 cm, AF = 4.8 cm, and BC = 10.9 cm, find the length of the other two sides. Then, find the area of the irregular polygon.

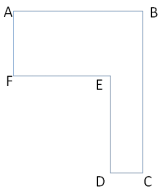
Answer:
AB = 7.5 cm, DE = 6.1 cm, Area = 47.59 cm²

Question 3.
Determine the area of the trapezoid below. The trapezoid is not drawn to scale.

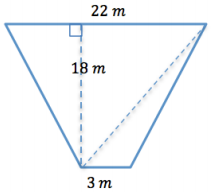
Answer:
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) × 22 m × 13 m
A = 198 m²

Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) × 3 m × 18 m
A = 27 m²

Area of Trapezoid = Area of Triangle 1 + Area of Triangle 2
Area = 198 m² + 27 m² = 225 m²

Question 4.
Determine the area of the shaded isosceles trapezoid below. The image is not drawn to scale.

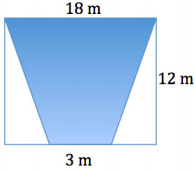
Answer:
Area of Rectangle
A = bh
A = 18 m × 12 m
A = 216 m²

Area of Triangles 1 and 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) × 7.5 m × 12 m
A = 45 m²

Area of Trapezoid = Area of Rectangle – Area of Triangle 1 – Area of Triangle 2
A = 216 m² – 45 m² – 45 m² = 126 m²

Question 5.
Here is a sketch of a wall that needs to be painted:

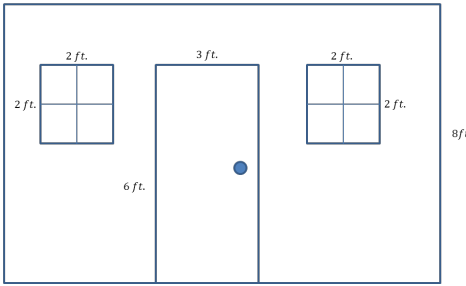
a. The windows and door will not be painted. Calculate the area of the wall that will be painted.
Answer:
Whole wall: 12 ft. × 8 ft. = 96 ft²
Window: 2 ft. × 2 ft. = 4 ft²
There are two identical windows, 4 ft² × 2 = 8 ft²
Door: 6 ft. × 3 ft. = 18 ft²
96 ft² – 8 ft² – 18 ft² = 70 ft²

b. If a quart of Extra-Thick Gooey Sparkle paint covers 30 ft². how many quarts must be purchased for the painting job?
Answer:
70 ÷ 30 = 2\(\frac{1}{3}\)
Therefore, 3 quarts must be purchased.

Question 6.
The figure below shows a floor plan of a new apartment. New carpeting has been ordered, which will cover the living room and bedroom but not the kitchen or bathroom. Determine the carpeted area by composing or decomposing in two different ways, and then explain why they are equivalent.

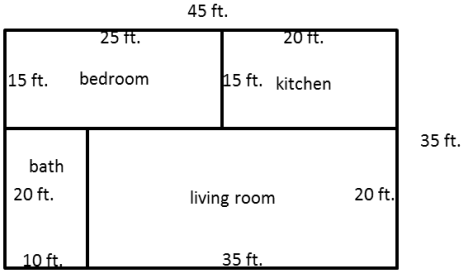
Answer:
Answers will vary. Sample student responses are shown.
Bedroom: 15 ft. × 25 ft. = 375 ft²
Living room: 35 ft. × 20 ft. = 700 ft²
Sum of bedroom and living room: 375 ft² + 700 ft² = 1,075 ft²

Alternatively, the whole apartment is 45 ft. × 35 ft. = 1,575 ft²
Subtracting the kitchen and bath (300 ft² and 200 ft²) still gives 1,075 ft².
The two areas are equivalent because they both represent the area of the living room and bedroom.

Eureka Math Grade 6 Module 5 Lesson 5 Exit Ticket Answer Key

Question 1.
Find the missing dimensions of the figure below, and then find the area. The figure is not drawn to scale.

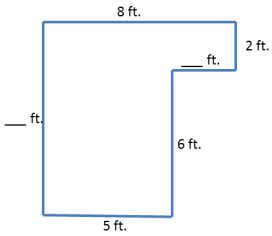
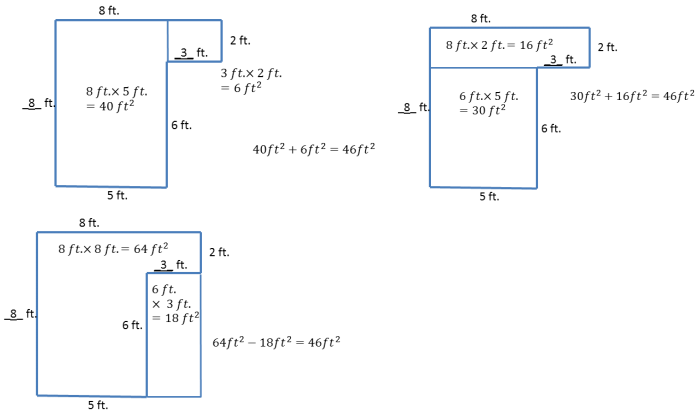
Answer:
The solution can be any of these below.

Question 2.
Find the area of the parallelogram below by decomposing it into two triangles. The figure is not drawn to scale.

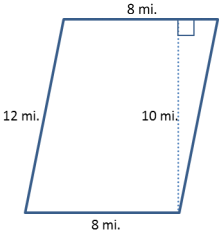
Answer:
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) × 8 mi.× 10 mi.
A = 40 mi²

Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) × 8 mi. × 10 mi.
A = 40 mi²

Area of Parallelogram = Area of Triangle 1 + Area of Triangle 2
A = 40 mi² + 40 mi² = 80 mi²
The area of the parallelogram is 80 mi².