Engage NY Eureka Math Grade 6 Module 6 Lesson 3 Answer Key
Eureka Math Grade 6 Module 6 Lesson 3 Example Answer Key
Robert, a sixth-grader at Roosevelt Middle School, usually goes to bed around 10:00 p.m. and gets up around 6:00 a.m. to get ready for school. That means he gets about 8 hours of sleep on a school night. He decided to investigate the statistical question: How many hours per night do sixth graders usually sleep when they have school the next day?
Robert took a survey of 29 sixth graders and collected the following data to answer the question.
7 8 5 9 9 9 7 7 10 10 11 9 8 8 8 12 6 11 10 8 8 9 9 9 8 10 9 9 8
Robert decided to make a dot plot of the data to help him answer his statistical question. Robert first drew a number line and labeled it from 5 to 12 to match the lowest and highest number of hours slept. Robert’s datum is not included.

He then placed a dot above 7 for the first value in the data set. He continued to place dots above the numbers until each number in the data set was represented by a dot.
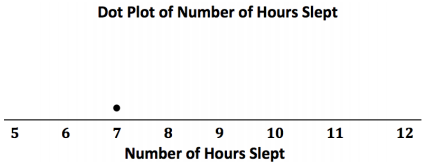
Exercises 1 – 9:
Exercise 1.
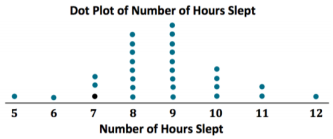
Complete Robert’s dot plot by placing a dot above the corresponding number on the number line for each value in the data set. If there is already a dot above a number, then add another dot above the dot already there. Robert’s datum is not included.
Answer:
Exercise 2.
What are the least and the most hours of sleep reported In the survey of sixth graders?
Answer:
The least number of hours students slept is 5, and the most number of hours slept is 12.
Exercise 3.
What number of hours slept occurred most often in the data set?
Answer:
9 is the most common number of hours that students slept.
Exercise 4.
What number of hours of sleep would you use to describe the center of the data?
Answer:
The center is around 8 or 9. (Answers may vary, but students’ responses should be around the center of the data
distribution.)
Exercise 5.
Think about how many hours of sleep you usually get on a school night. How does your number compare with the number of hours of sleep from the survey of sixth graders?
Answer:
Answers will vary. For example, a student might say that the number of hours she sleeps is similar to what these students reported, or she might say that she generally gets less (or more) sleep than the sixth graders who were
surveyed.
Here are the data for the number of hours the sixth graders usually sleep when they do not have school the next day.
7 8 10 11 5 6 12 13 13 7 9 8 10 12 11 12 8 9 10 11 10 12 11 11 11 12 11 11 10
Exercise 6.
Make a dot plot of the number of hours slept when there is no school the next day.
Answer:
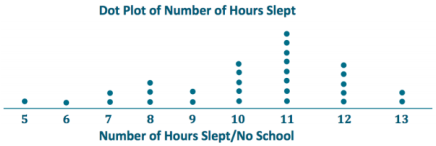
Exercise 7.
When there is no school the next day, what number of hours of sleep would you use to describe the center of the
data?
Answer:
The center of the data is around 11 hours. (Answers may vary, but student responses should be around the center of the data distribution.)
Exercise 8.
What are the least and most number of hours slept with no school the next day reported in the survey?
Answer:
The least number of hours students sleep is 5, and the most number of hours students sleep is 13.
Exercise 9.
Do students tend to sleep longer when they do not have school the next day than when they do have school the next day? Explain your answer using the data in both dot plots.
Answer:
Yes, because more of the data points are in the 10, 11, 12, and 13 categories in the no school dot plot than in the have school dot plot.
Example 2: Building and Interpreting a Frequency Table
A group of sixth-graders investigated the statistical question, “How many hours per week do sixth graders spend playing a sport or an outdoor game?”
Here are the data students collected from a sample of 26 sixth graders showing the number of hours per week spent playing a sport or a game outdoors.
3 2 0 6 3 3 3 1 1 2 2 8 12 4 4 4 3 3 1 1 0 0 6 2 3 2
To help organize the data, students summarized the data in a frequency table. A frequency table lists possible data values and how often each value occurs.
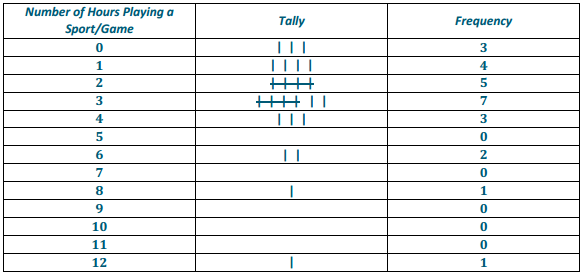
To build a frequency table, first make three columns. Label one column “Number of Hours Playing a Sport/Game,” label the second column “Tally,” and label the third column “Frequency.” Since the least number of hours was 0 and the most was 12, list the numbers from 0 to 12 in the “Number of Hours” column.
Exercises 10 – 15:
Exercise 10.
Complete the tally mark column in the table created in Example 2.
Answer:
Exercise 11.
For each number of hours, find the total number of tally marks, and place this in the frequency column in the table created in Example 2.
Answer:

Exercise 12.
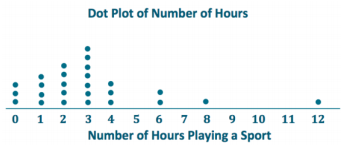
Make a dot plot of the number of hours playing a sport or playing outdoors.
Answer:
Exercise 13.
What number of hours describes the center of the data?
Answer:
The center of data is around 3. (Answers may vary, but student responses should be around the center of the data distribution.)
Exercise 14.
How many of the sixth graders reported that they spend eight or more hours a week playing a sport or playing
outdoors?
Answer:
Only 2 sixth graders reported they spent 8 or more hours a week playing a sport or playing outdoors.
Exercise 15.
The sixth graders wanted to answer the question, “How many hours do sixth graders spend per week playing a sport or playing an outdoor game?” Using the frequency table and the dot plot, how would you answer the sixth graders’ question?
Answer:
Most sixth graders spend about Z to 4 hours per week playing a sport or playing outdoors.
Eureka Math Grade 6 Module 6 Lesson 3 Problem Set Answer Key
Question 1.
The data below are the number of goals scored by a professional indoor soccer team over its last 23 games.
8 16 10 9 11 11 10 15 16 11 15 13 8 9 11 9 8 11 16 15 10 9 12
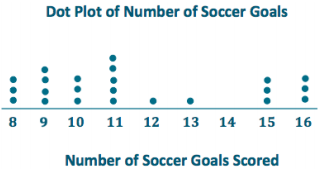
a. Make a dot plot of the number of goals scored.
Answer:
b. What number of goals describes the center of the data?
Answer:
The center of the data is around 11 or 12. (Answers may vary, but student responses should be around the center of the data distribution.)
c. What is the least and most number of goals scored by the team?
Answer:
The least number of goals scored is 8, and 16 is the most.
d. Over the 23 games played, the team lost 10 games. Circle the dots on the plot that you think represent the games that the team lost. Explain your answer.
Answer:
Students will most likely circle the lowest 10 scores, but answers may vary. Students need to supply on explanation in order to defend their answers.
Question 2.
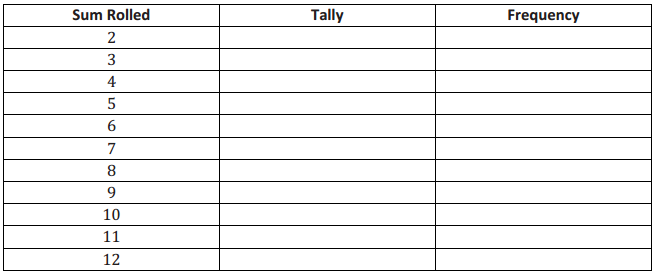
A sixth grader rolled two number cubes 21 times. The student found the sum of the two numbers that he rolled each time. The following are the sums for the 21 rolls of the two number cubes.
9 2 4 6 5 7 8 11 9 4 6 5 7 7 8 8 7 5 7 6 6
a. Complete the frequency table.
Answer:
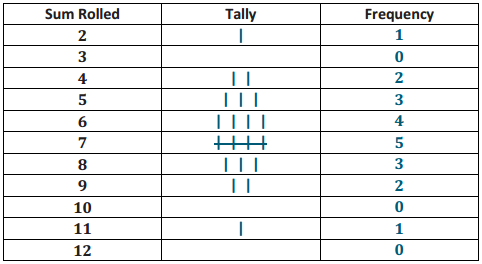
b. What sum describes the center of the data?
Answer:
7
c. What sum occurred most often for these 21 rolls of the number cubes?
Answer:
7
Question 3.
The dot plot below shows the number of raisins in 25 small boxes of raisins.
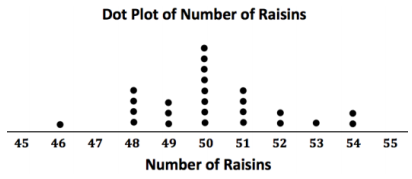
a. Complete the frequency table.
Answer:
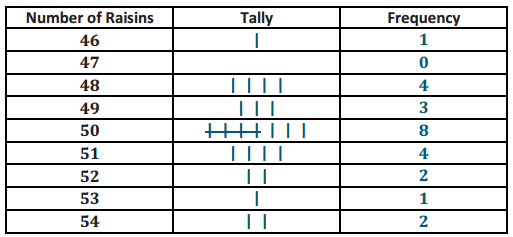
b. Another student opened up a box of raisins and reported that It had 63 raisins. Do you think that this student had the same size box of raisins? Why or why not?
Answer:
I think the student did not have the same size box because the 21 small boxes opened had at most 54 raisins, and 63 is too high.
Eureka Math Grade 6 Module 6 Lesson 3 Exit Ticket Answer Key
A biologist collected data to answer the question, “How many eggs do robins lay?”
The following is a frequency table of the data she collected:
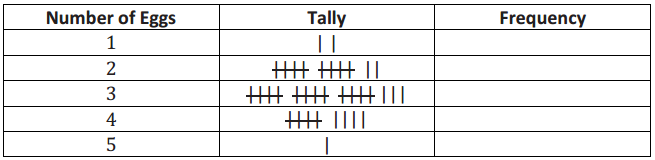
Question 1.
Complete the frequency column.
Answer:
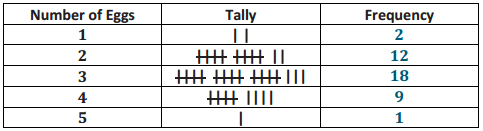
Question 2.
Draw a dot plot of the data on the number of eggs a robin lays.
Answer:
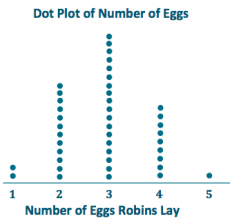
Question 3.
What number of eggs describe the center of the data?
Answer:
The center of the data is around 3. (Answer may vary, but student responses should be around the center of the data distribution.)