Engage NY Eureka Math 7th Grade Module 1 Lesson 19 Answer Key
Eureka Math Grade 7 Module 1 Lesson 19 Example Answer Key
Exploring Area Relationships
Use the diagrams below to find the scale factor and then find the area of each figure.
Example 1
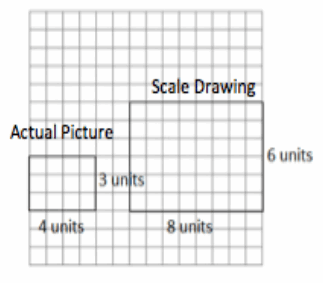
Scale factor: _________
Actual Area = ______________
Scale Drawing Area = ________________
Value of the Ratio of the Scale Drawing Area to the Actual Area: _________
Answer:
Scale factor: 2
Actual Area = 12 square units
Scale Drawing Area = 48 square units
Value of the Ratio of the Scale Drawing Area to the Actual Area:
\(\frac{48}{12}\) = 4
Example 2.
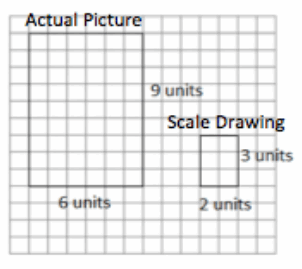
Scale factor: _________
Actual Area = ______________
Scale Drawing Area = ________________
Value of the Ratio of the Scale Drawing Area to the Actual Area: _________
Answer:
Scale factor: \(\frac{1}{3}\)
Actual Area = 54 square units
Scale Drawing Area = 6 square units
Value of the Ratio of Scale Drawing Area to Actual Area:
\(\frac{6}{54}\) = \(\frac{1}{9}\)
Example 3.
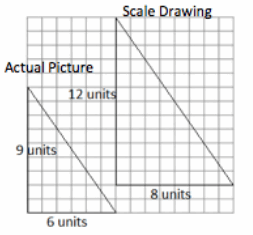
Scale factor: \(\frac{4}{3}\)
Actual Area = 27 square units
Scale Drawing Area = 48 square units
Value of the Ratio of Scale Drawing Area to Actual Area:
\(\frac{48}{27}\) = \(\frac{16}{9}\)
Guide students through completing the results statements on the student materials.
Results:
What do you notice about the ratio of the areas in Examples 1–3? Complete the statements below.
When the scale factor of the sides was 2, then the value of the ratio of the areas was __ .
Answer:
4
When the scale factor of the sides was \(\frac{1}{3}\), then the value of the ratio of the areas was __.
Answer:
\(\frac{1}{9}\)
When the scale factor of the sides was \(\frac{4}{3}\), then the value of the ratio of the areas was ___.
Answer:
\(\frac{16}{9}\)
Based on these observations, what conclusion can you draw about scale factor and area?
Answer:
The ratio of the areas is the scale factor multiplied by itself or squared.
If the scale factor is r, then the ratio of the areas is ___.
Answer:
r2 to 1.
→ Why do you think this is? Why do you think it is squared (opposed to cubed or something else)?
→ When you are comparing areas, you are dealing with two dimensions instead of comparing one linear measurement to another.
→ How might you use this information in working with scale drawings?
→ In working with scale drawings, you could take the scale factor, r, and calculate r2 to determine the relationship between the area of the scale drawing and the area of the actual picture. Given a blueprint for a room, the scale drawing dimensions could be used to find the scale drawing area and could then be applied to determine the actual area. The actual dimensions would not be needed.
→ Suppose a rectangle has an area of 12 square meters. If the rectangle is enlarged by a scale factor of three, what is the area of the enlarged rectangle based on Examples 1–3? Look and think carefully!
→ If the scale factor is 3, then the ratio of scale drawing area to actual area is 32 to 12, or 9 to 1. So, if its area is 12 square meters before it is enlarged to scale, then the enlarged rectangle will have an area of 12∙(\(\frac{9}{1}\)), or 12∙9, resulting in an area of 108 square meters.
Example 4:
They Said Yes!
The Student Government liked your half-court basketball plan. They have asked you to calculate the actual area of the court so that they can estimate the cost of the project.
Based on your drawing below, what will the area of the planned half-court be?
Scale Drawing: 1 inch on the drawing corresponds to 15 feet of actual length
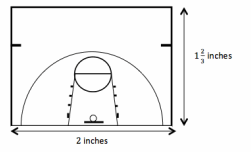
Does the actual area you found reflect the results we found from Examples 1–3? Explain how you know.
Answer:
Method 1: Use the measurements we found in yesterday’s lesson to calculate the area of the half-court.
Actual area = 25 feet × 30 feet =750 square feet
Method 2: Apply the newly discovered Ratio of Area relationship.
Note to teachers: This can be applied to the given scale with no unit conversions (shown on left) or to the scale factor (shown on right). Both options are included here as possible student work and would provide for a rich discussion of why they both work and what method is preferred. See guiding questions below.
Answer:
Using Scale:
The Value of the Ratio of Areas: (\(\frac{15}{1}\))2 = 225
Scale Drawing Area = 2 in.× 1\(\frac{2}{3}\) in.
= \(\frac{10}{3}\) square inches
Let x = scale drawing area, and let y = actual area.
y = kx
y = 225(\(\frac{10}{3}\))
y = \(\frac{225}{1}\).\(\frac{10}{3}\)
y = 750
The actual area using the given scale is 750 square feet.
Using Scale Factor:
The Value of the Ratio of Areas (\(\frac{180}{1}\))2 = 32400
Scale Drawing Area = 2 in.×1\(\frac{2}{3}\) in.
= \(\frac{10}{3}\) square inches
Let x = scale drawing area, and let y = actual area.
y = kx
y = 32400(\(\frac{10}{3}\))
y = \(\frac{324000}{3}\)
y = 108000
The actual area is 108,000 square inches, or
108000 square inches × \(\frac{1 square feet}{144 square feet}\) = 750 square feet.
Ask students to share how they found their answer. Use guiding questions to find all three options as noted above.
→ What method do you prefer?
→ Is there a time you would choose one method over the other?
→ If we do not already know the actual dimensions, it might be faster to use Method 1 (ratio of areas). If we are re-carpeting a room based upon a scale drawing, we could just take the dimensions from the scale drawing, calculate area, and then apply the ratio of areas to find the actual amount of carpet we need to buy.
Guide students to complete the follow-up question in their student materials.
Does the actual area you found reflect the results we found from Examples 1–3? Explain how you know.
Answer:
Yes, the scale of 1 inch to 15 feet has a scale factor of 180, so the ratio of area should be (180)2, or 32,400.
The drawing area is (2)(1\(\frac{2}{3}\)), or \(\frac{10}{3}\) square inches.
The actual area is 25 feet by 30 feet, or 750 square feet, or 108,000 square inches.
The value of the ratio of the areas is \(\frac{108,000}{\frac{10}{3}}\), or \(\frac{324,000}{10}\), or 32,400
It would be more efficient to apply this understanding to the scale, eliminating the need to convert units.
If we use the scale of \(\frac{15}{1}\), then the ratio of area is \(\frac{225}{1}\).
The drawing area is (2)(1\(\frac{2}{3}\)), or \(\frac{10}{3}\) square inches.
The actual area is 25 feet by 30 feet, or 750 square feet.
The ratio of area is \(\frac{750}{\frac{10}{3}}\), \(\frac{2250}{10}\), or \(\frac{225}{1}\).
Eureka Math Grade 7 Module 1 Lesson 19 Exercise Answer Key
Allow time for students to answer independently and then share results.
Question 1.
The triangle depicted by the drawing has an actual area of 36 square units. What is the scale of the drawing? (Note: Each square on the grid has a length of 1 unit.)
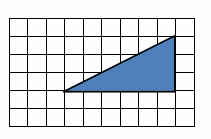
Answer:
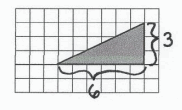
Scale Drawing Area: \(\frac{1}{2}\) ∙ 6∙ 3 = 9 square units. Ratio of Scale Drawing Area to Actual Area: \(\frac{9}{36}\) = r2
Therefore, r (scale factor) = \(\frac{3}{6}\) since \(\frac{3}{6}\) ∙ \(\frac{3}{6}\) = \(\frac{9}{36}\). The scale factor is \(\frac{1}{2}\) . The scale is 1 unit of drawing length represents 2 units of actual length.
For Exercise 2, allow students time to measure the drawings of the apartments using a ruler and then compare measurements with a partner. Students then continue to complete parts (a)–(f) with a partner. Allow students time to share responses. Sample answers to questions are given below.
Question 2.
Use the scale drawings of two different apartments to answer the questions. Use a ruler to measure.
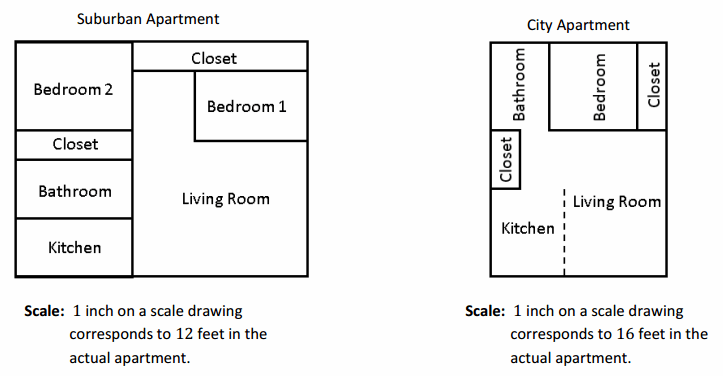
Answer:
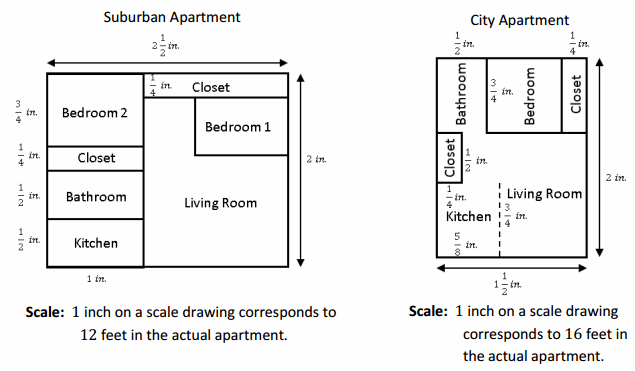
a. Find the scale drawing area for both apartments, and then use it to find the actual area of both apartments.
Answer:
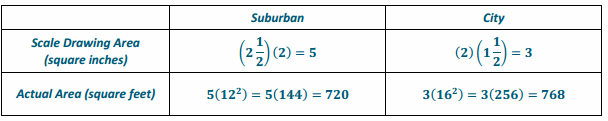
b. Which apartment has closets with more square footage? Justify your thinking.
Answer:
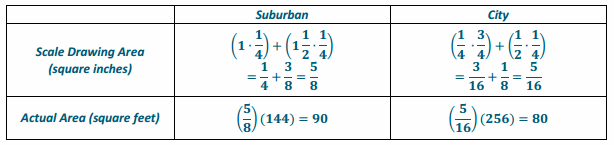
The suburban apartment has greater square footage in the closet floors.
c. Which apartment has the largest bathroom? Justify your thinking.
Answer:

The city apartment has the largest bathroom.
d. A one-year lease for the suburban apartment costs $750 per month. A one-year lease for the city apartment costs $925. Which apartment offers the greater value in terms of the cost per square foot?
Answer:
The suburban cost per square foot is \(\frac{750}{720}\), or approximately $1.04 per square foot. The city cost per square foot is \(\frac{925}{768}\), or approximately $1.20 per square foot. The suburban apartment offers a greater value (cheaper cost per square foot), $1.04 versus $1.20.
Eureka Math Grade 7 Module 1 Lesson 19 Exit Ticket Answer Key
A 1-inch length in the scale drawing below corresponds to a length of 12 feet in the actual room.
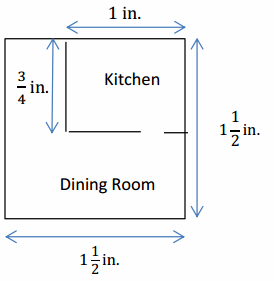
Question 1.
Describe how the scale or the scale factor can be used to determine the area of the actual dining room.
Answer:
The scale drawing will need to be enlarged to get the area or dimensions of the actual dining room. Calculate the area of the scale drawing, and then multiply by the square of the scale (or scale factor) to determine the actual area.
Question 2.
Find the actual area of the dining room.
Answer:
Scale drawing area of dining room: (1\(\frac{1}{2}\) in.×\(\frac{3}{4}\) in.) + (\(\frac{3}{4}\) in. × \(\frac{1}{2}\)in.) = \(\frac{12}{8}\) in2 or 1\(\frac{1}{2}\) in2
Actual area of the dining room: \(\frac{12}{8}\) ft.× 144 ft. = 216 ft2
Or similar work completing conversions and using scale factor
Question 3.
Can a rectangular table that is 7 ft. long and 4 ft. wide fit into the narrower section of the dining room? Explain your answer.
Answer:
The narrower section of the dining room measures \(\frac{3}{4}\) by \(\frac{1}{2}\) in the drawing, or 9 feet by 6 feet in the actual room. Yes, the table will fit; however, it will only allow for 1 additional foot around all sides of the table for movement or chairs.
